93 trang 2 lượt tải

08 đề ôn tập giữa học kỳ 1 Toán 11 năm 2025 – 2026 có lời giải chi tiết

3

Tài liệu gồm 93 trang, được biên soạn bởi Trung Tâm Bồi Dưỡng Văn Hóa Lam Sơn, tuyển tập 08 đề ôn tập kiểm tra giữa học kỳ 1 môn Toán 11 năm học 2025 – 2026, có đáp án và lời giải chi tiết. Các đề được biên soạn theo cấu trúc 30% trắc nghiệm nhiều phương án lựa chọn + 40% trắc nghiệm đúng sai + 30% trắc nghiệm trả lời ngắn, thời gian làm bài 90 phút.Mời các bạn tham khảo

Chủ đề: Đề giữa HK1 Toán 11 359 tài liệu

Môn: Toán 11 3.5 K tài liệu

Tác giả:

Profile

jang linh

4 giờ trước
Danh sách Quiz
/93
1
ĐỀ ÔN TẬP GIỮA HỌC KỲ I NĂM HỌC 2025
–
2026
MÔN: TOÁN 11
ĐỀ SỐ 01
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu
1
đến câu 12. Mỗi câu
hỏi thí sinh chỉ chọn một phương án.
Câu 1: Đổi số đo của góc
120

sang đơn vị radian ta được
A.
2
3
. B.
6
. C.
3
. D.
4
.
Câu 2: Cho
2
cos
5
với
3
2.
2

Tìm giá trị lượng giác
A.
21
25
. B.
21
5
. C.
21
5
. D.
21
25
.
Câu 3: Trong các đẳng thức sau, đẳng thức nào SAI?
A.
2
cos 2 1 2 sinaa
. B.
2
2 tan
tan 2
1 tan
a
a
a
.
C.
sin 2 2 sin cosa aa
. D.
22
cos 2 cos sina aa

.
Câu 4: Tập xác định của hàm số
cotyx
là:
A.
\,
2
D kk









. B.
\,
4
D kk









.
C.
\,
82
D kk










. D.
\,D kk

.
Câu 5: Tập nghiệm của phương trình
2 sin 2 1 0x 
là
A.
7
,,
12 12
S k kk










. B.
7
2, 2,
6 12
S k kk










.
C.
7
2, 2,
12 12
S k kk










. D.
7
,,
6 12
S k kk










.
Câu 6: Cho dãy số
n
u
thỏa mãn
1
2
n
n
u
. Tìm số hạng thứ
10
của dãy số đã cho.
A.
11
2
. B.
9
2
. C.
10
2
. D.
8
2
.
Câu 7: Cho cấp số cộng
n
u
có số hạng đầu
1
3u 
, công sai
2d
. Tìm số hạng thứ
5
của cấp số cộng
đó.
A.
5
5u 
. B.
5
1u 
. C.
5
1
u
. D.
5
5u
.
Câu 8: Cho cấp số nhân
n
u
có
35
18; 162uu
. Số
1458
là số hạng thứ bao nhiêu của cấp số nhân đó,
biết rằng cấp số nhân có công bội dương.
A. Số hạng thứ bảy. B. Số hạng thứ sáu. C. Số hạng thứ tám. D. Số hạng thứ chín.
Câu 9: Cho tứ diện
ABCD
. Gọi
G
là trọng tâm của tam giác
.BCD
Giao tuyến của mặt phẳng
ACD
và
GAB
là:
A.
(AM M
là trung điểm của
AB
). B.
(AN N
là trung điểm của
CD
).
C.
(AH H
là hình chiếu của
B
trên
D.
AK
(
K
là hình chiếu của
C
trên
BD
).
Câu 10: Cho hình chóp
.S ABCD
có đáy là
ABCD
hình thang
//AB CD
. Giao tuyến của hai mặt phẳng
SAB
và
SCD
là
2
A. Đường thẳng qua
S
và song song với
AB
và
CD
.
B. Đường thẳng qua
S
và song song với
AD
và
BC
.
C. Đường thẳng qua
S
và giao điểm của
AD
và
BC
.
D. Đường thẳng qua
S
và giao điểm của
AC
và
BD
.
Câu 11: Cho tứ diện
DABC
có
,MN
lần lượt là trung điểm của
,AB AC
. Mặt phẳng nào sau đây song
song với đường thẳng
MN
?
A.
()ACD
. B.
()ABD
. C.
()
ABC
. D.
()
BCD
.
Câu 12: Cho hai mặt phẳng song song
và
,
a
là đường thẳng bất kì. Tìm mệnh đề sai trong các
mệnh đề sau:
A. Nếu
a
cắt mp
thì
a
cắt mp
.
B. Nếu
a
thì
a
song song với mp
.
C. Nếu
a
thì
a
song song với mp
.
D. Nếu
a
song song với mp
thì
a
song song với mp
.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1: Cho góc lượng giác
25
6
và
5
sin
8
x 
với
;0
2
x



.
a)
6
0
25
75

.
b) Điểm biểu diễn trên đường tròn lượng giác của góc đã cho thuộc phần tư thứ IV.
c)
3 13 5
16
cos x

.
d)
2
6 tan 15 26
281
5 tan 4
x
P
x


.
Câu 2: Cho hàm số
3 tan 2
3
y fx x



.
a) Tập xác định của hàm số
D
.
b) Phương trình
3fx
có nghiệm
,
3 2
k
xk


.
c) Phương trình
3fx
có nghiệm âm lớn nhất bằng
3
.
d) Khi
2
43
x


thì phương trình
3fx
có hai nghiệm.
Câu 3: Cho dãy số
n
u
, biết
1
1
1
3
nn
u
uu


với
1n
.
a) Dãy số trên là một cấp số nhân.
b) Số hạng thứ năm của dãy là
13
.
c) 101 là số hạng thứ 35 của dãy số đã cho.
d) Tổng các số hạng từ số hạng thứ 10 đến số hạng thứ 20 của dãy số bằng
451
.
Câu 4: Cho hình hộp
ABCD A B C D

. Gọi
12
,GG
là trọng tâm của các tam giác
,A BD B D C

.
a) Đường thẳng
AB
cắt đường thẳng
CD
.
b)
A D CB

là hình bình hành
c)
//
A BD B D C

d)
12
2
3
G G AC
3
PHẦN III. Câu trắc nghiệm trả lời ngắn
Câu 1: Gọi
M
,
N
,
E
là các điểm trên đường tròn lượng giác sao cho số đo của các góc lượng giác
,
OA OM
,
,OA ON
,
,
OA OE
lần lượt bằng
2
;
;
6
. Khi đó, diện tích tam giác
MNE
làm
tròn đến hàng phần chục bằng bao nhiêu?
Câu 2: Tính
23
sin sin si
4
in
2
2023
2024 202 2
sn
24 240 0
S


.
Câu 3: Một chất điểm dao động điều hoà theo phương trình
2 cos 2 ,
2
xt



t
tính bằng giây và
x
tính bằng
.cm
Gọi
0
t
là thời điểm đầu tiên vật có li độ lớn nhất. Giá trị của
0
t
bằng bao nhiêu.
Câu 4: Cho dãy số
n
u
xác định bởi
1
1
5 ,1
nn
ua
u un

. Tìm
a
để
n
u
là cấp số cộng.
Câu 5: Cho hình tứ diện đều
DABC
có cạnh bằng
12
. Gọi
,MN
lần lượt là trung điểm của cạnh
AB
và
CD
. Gọi
P
là trung điểm đoạn thẳng
CM
. Giao điểm
I
của đường thẳng
DP
và mặt phẳng
ABN
cách điểm
D
một khoảng bằng bao nhiêu?
Câu 6: Cho hình chóp
.S ABCD
có đáy là hình bình hành
ABCD
,
O
là giao điểm của
AC
và
BD
. Tam
giác
là tam giác đều cạnh
2
. Mặt phẳng
P
đi qua
O
và song song với mặt phẳng
SCD
. Tính diện tích hình tạo bởi mặt phẳng
P
và các mặt của hình chóp
.S ABCD
.
--------HẾT--------
4
HƯỚNG DẪN GIẢI
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu
1
đến câu 12. Mỗi câu
hỏi thí sinh chỉ chọn một phương án.
Câu 1: Đổi số đo của góc
120 
sang đơn vị radian ta được
A.
2
3
. B.
6
. C.
3
. D.
4
.
Lời giải
Áp dụng công thức đổi từ độ sang radian ta có:
0
180
aa
ta có
2
120 120
180 3


.
Câu 2: Cho
2
cos
5
với
3
2.
2

Tìm giá trị lượng giác
A.
21
25
. B.
21
5
. C.
21
5
. D.
21
25
.
Lời giải
Vì
3
2
2

nên
sin 0
.
Ta có
22 2
21
sin cos 1 sin 1 cos
5


.
Câu 3: Trong các đẳng thức sau, đẳng thức nào SAI?
A.
2
cos 2 1 2 sinaa
. B.
2
2 tan
tan 2
1 tan
a
a
a
.
C.
sin 2 2 sin cosa aa
. D.
22
cos 2 cos sina aa
.
Lời giải
Ta có:
2
2 tan
tan 2
1 tan
a
a
a
nên B sai.
Câu 4: Tập xác định của hàm số
cot
yx
là:
A.
\,
2
D kk









. B.
\,
4
D kk









.
C.
\,
82
D kk










. D.
\,D kk

.
Lời giải
Hàm số
cos
cot
sin
x
yx
x

xác định khi và chỉ khi
sin 0 , x x kk
nên
\,D kk
.
Câu 5: Tập nghiệm của phương trình
2 sin 2 1 0x 
là
A.
7
,,
12 12
S k kk










. B.
7
2, 2,
6 12
S k kk










.
C.
7
2, 2,
12 12
S k kk










. D.
7
,,
6 12
S k kk










.
Lời giải
Ta có:
2 sin 2 1 0x 
1
sin 2
2
x 
sin 2 sin
6
x



22
6
,
7
22
6
xk
k
xk



12
,
7
12
xk
k
xk



.
5
Vậy tập nghiệm của phương trình là
7
,,
12 12
S k kk










.
Câu 6: Cho dãy số
n
u
thỏa mãn
1
2
n
n
u
. Tìm số hạng thứ
10
của dãy số đã cho.
A.
11
2
. B.
9
2
. C.
10
2
. D.
8
2
.
Lời giải
Ta có
10 1 9
10
22u

.
Câu 7: Cho cấp số cộng
n
u
có số hạng đầu
1
3u 
, công sai
2d
. Tìm số hạng thứ
5
của cấp số cộng
đó.
A.
5
5u 
. B.
5
1u 
. C.
5
1u
. D.
5
5u
.
Lời giải
Áp dụng công thức của số hạng tổng quát:
51
45uu d
.
Câu 8: Cho cấp số nhân
n
u
có
35
18; 162uu
. Số
1458
là số hạng thứ bao nhiêu của cấp số nhân đó,
biết rằng cấp số nhân có công bội dương.
A. Số hạng thứ bảy. B. Số hạng thứ sáu. C. Số hạng thứ tám. D. Số hạng thứ chín.
Lời giải
Áp dụng công thức của số hạng tổng quát:
1
1
.
n
n
u uq
.
Ta có:
2
31
22
53
4
51
.
. 162 18. 3
.
u uq
u uq q q
u uq

.
Khi đó
1
2u
. Nên
1
2.3
n
n
u
.
Giả sử
1
1458 2.3 1458 7
n
n
un
 
. Vậy
1458
là số hạng thứ bảy của cấp số nhân đó.
Câu 9: Cho tứ diện
ABCD
. Gọi
G
là trọng tâm của tam giác
.BCD
Giao tuyến của mặt phẳng
ACD
và
GAB
là:
A.
(AM M
là trung điểm của
AB
). B.
(
AN N
là trung điểm của
CD
).
C.
(
AH H
là hình chiếu của
B
trên
D.
AK
(
K
là hình chiếu của
C
trên
BD
).
Lời giải
A
là điểm chung thứ nhất của hai mặt phẳng
ACD
và
.GAB
Ta có
BG CD N
nên
N BG ABG N ABG
N
N CD ACD N ACD










là điểm chung thứ hai của
hai mặt phẳng
ACD
và
.GA B
Vậy
.ABG ACD AN
Câu 10: Cho hình chóp
.S ABCD
có đáy là
ABCD
hình thang
//AB CD
. Giao tuyến của hai mặt phẳng
SAB
và
SCD
là
A. Đường thẳng qua
S
và song song với
AB
và
CD
.
G
N
A
C
D
B
6
B. Đường thẳng qua
S
và song song với
AD
và
BC
.
C. Đường thẳng qua
S
và giao điểm của
AD
và
BC
.
D. Đường thẳng qua
S
và giao điểm của
AC
và
BD
.
Lời giải
Hai mặt phẳng
SAB
và
SCD
lần lượt đi qua hai đường thẳng
//AB CD
và có
S
là điểm
chung nên giao tuyến của chúng là đường thẳng đi qua
S
và song song với
AB
và
CD
.
Câu 11: Cho tứ diện
DABC
có
,
MN
lần lượt là trung điểm của
,AB AC
. Mặt phẳng nào sau đây song
song với đường thẳng
MN
?
A.
()ACD
. B.
()ABD
. C.
()ABC
. D.
()BCD
.
Lời giải
Vì
,MN
lần lượt là trung điểm của
,AB AC
nên
MN
là đường trung bình của tam giác
ABC
,
do đó
//
MN BC
, lại có
()MN BCD
và
()BC BCD
nên
//( )MN BCD
.
Vậy đáp án D đúng.
Câu 12: Cho hai mặt phẳng song song
và
,
a
là đường thẳng bất kì. Tìm mệnh đề sai trong các
mệnh đề sau:
A. Nếu
a
cắt mp
thì
a
cắt mp
.
B. Nếu
a
thì
a
song song với mp
.
C. Nếu
a
thì
a
song song với mp
.
D. Nếu
a
song song với mp
thì
a
song song với mp
.
Lời giải
Nếu
a
song song với mp
thì
a
song song với mp
hoặc
a
nằm trên mp
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1: Cho góc lượng giác
25
6
và
5
sin
8
x 
với
;0
2
x



.
a)
6
0
25
75

.
b) Điểm biểu diễn trên đường tròn lượng giác của góc đã cho thuộc phần tư thứ IV.
7
c)
3 13 5
16
cos
x

.
d)
2
6 tan 15 26
281
5 tan 4
x
P
x


.
Lời giải
a) Đúng | b) Sai | c) Sai | d) Đúng
a) Ta có:
25 25 180
. 750
66




. Suy ra mệnh đề Đúng.
b)
25
4
66

 
. Điểm biểu diễn trên đường tròn lượng giác của góc đã cho thuộc phần tư
thứ I. Suy ra mệnh đề Sai.
c) Vì
;0
2
x



nên
cos 0
x
2
2
5 39
cos 1 sin 1
88
xx

 

.
Ta có
25 1
sin sin sin 4 sin
6 6 62





,
25 3
cos cos cos 4 cos
6 6 62





.
Khi đó:
39 3 5 1 3 13 5
cos cos . cos sin .sin . .
8 2 8 2 16
x xx 



.
Suy ra mệnh đề Sai
d) Ta có
5
sin 5 39
8
tan
cos 39
39
8
x
x
x

.
Khi đó
22
5 39
6.
39
6 tan 15 26
281
5 tan 4
5 39
54
39
x
P
x







. Suy ra mệnh đề Đúng.
Câu 2: Cho hàm số
3 tan 2
3
y fx x



.
a) Tập xác định của hàm số
D
.
b) Phương trình
3fx
có nghiệm
,
3 2
k
xk


.
c) Phương trình
3
fx
có nghiệm âm lớn nhất bằng
3
.
d) Khi
2
43
x


thì phương trình
3
fx
có hai nghiệm.
Lời giải
a) Sai | b) Đúng| c) Sai| d) Đúng
a) Điều kiện
5
cos 2 0 2 ,
3 3 2 12 2
x x k x kk




. Suy ra mệnh đề Sai.
b) Phương trình tương đương với
tan 2 3 ,
3 32
k
x xk




. Suy ra mệnh đề
Đúng.
c)
2
00
32 3
k
xk

 
. Vậy nghiệm âm lớn nhất là
632
x


. Suy ra mệnh
đề Sai.
d) Vì
2 27 2
4 3 4 32 3 6 3
k
xk
 
 
.
8
Do
k
nên
{ 1; 0}k

.
Với
1k 
thì
6
x
.
Với
0
k
thì
3
x
.
Vậy
6
x
và
3
x
thỏa mãn yêu cầu bài toán. Suy ra mệnh đề Đúng.
Câu 3: Cho dãy số
n
u
, biết
1
1
1
3
nn
u
uu


với
1n
.
a) Dãy số trên là một cấp số nhân.
b) Số hạng thứ năm của dãy là
13
.
c) 101 là số hạng thứ 35 của dãy số đã cho.
d) Tổng các số hạng từ số hạng thứ 10 đến số hạng thứ 20 của dãy số bằng
451
.
Lời giải
a) Sai |b) Sai |c) Đúng |d) Đúng
a) Ta có:
1
3
nn
uu

suy ra dãy số
n
u
là cấp số cộng với công sai
3d
. Vậy a) sai.
b)
15
4 11
uu d
. Vậy b) sai.
c) Xét
101 3 4 101 35
n
un n

.
Vậy 101 là số hạng thứ 35 của dãy số đã cho.
d)
n
u
là cấp số cộng với số hạng đầu
1
1u 
và công sai
3d
.
Ta có:
1
9
92 8
2
ud
S
9 2. 1 8.3
99
2




.
1
20
20 2 19
2
ud
S
20 2. 1 19.3
550
2




.
Vậy
10 11 20 20 9
...uu u SS 
550 99 451 
.
Câu 4: Cho hình hộp
ABCD A B C D

. Gọi
12
,GG
là trọng tâm của các tam giác
,A BD B D C

.
a) Đường thẳng
AB
cắt đường thẳng
CD
.
b)
A D CB

là hình bình hành.
c)
//A BD B D C

.
d)
12
2
3
G G AC
.
Lời giải
a) Sai |b) Đúng |c) Đúng |d) Sai
a) Do
A BCD
nên đường thẳng
AB
và đường thẳng
CD
chéo nhau.
Vậy mệnh đề a) sai.
b)
Vì
.ABCD A B C D

là hình hộp nên
//A D BC
A D CB
A D BC



là hình bình hành.
Vậy mệnh đề b) đúng.
9
c)
Vì
A D CB

là hình bình hành.
Suy ra
// //AB CD AB BDC

.
Tương tự, ta có:
//A B CD
A B CD
A B CD



là hình bình hành.
Suy ra
// //AD BC AD BDC

.
Từ và
(2)
suy ra
//A BD B D C

.
Vậy mệnh đề c) đúng.
d)
Gọi
,,OO I
theo thứ tự là tâm của các hình bình hành
,
ABCD A B C D

,
ACC A

.
Vì
1
G
là trọng tâm tam giác
AB D
nên
1
2
3
AG
AO
1
G
là trọng tâm tam giác
A AC
, suy ra
1
G AI A O

.
Tương tự,
2
G
là trọng tâm tam giác
BDC

nên
2
2
3
CG
CO
2
G
là trọng tâm tam giác
ACC

, suy ra
2
G C I CO


.
Từ và suy ra
12
,
GG
cùng thuộc
AC
.
Chứng minh
1 12 2
1
3
AG G G G C AC


:
Ta có:
1 12 2
2 12 1
;
3 33 3
AG AG C G C G
AI AC C I AC

 

.
Do vậy
1 12 2
1
3
AG G G G C AC


.
Vậy
12
,GG
cùng thuộc
AC
, đồng thời chia
AC
thành ba phần bằng nhau.
PHẦN III. Câu trắc nghiệm trả lời ngắn
Câu 1: Gọi
M
,
N
,
E
là các điểm trên đường tròn lượng giác sao cho số đo của các góc lượng giác
,OA OM
,
,OA ON
,
,OA OE
lần lượt bằng
2
;
;
6
. Khi đó, diện tích tam giác
MNE
làm
tròn đến hàng phần chục bằng bao nhiêu?
Lời giải
Đáp án: 1,3
Trên đường tròn lượng giác đi theo chiều dương, từ vị trí điểm gốc
A
, thứ tự các điểm lần lượt là:
E
;
N
;
M
và
2
3
EON NOM MOE

.
10
Mà
1OE ON OM
nên
EN NM ME
do đó
MNE
đều cạnh
3MN
2
3 .3
33
1, 3
44
MNE
S 
.
Câu 2: Tính
23
sin sin si
4
in
2
2023
2024 202 2
sn
24 240
0
S


(làm tròn kết quả đến hàng đơn vị).
Lời giải
Đáp án: 1289
Xét bài toán tổng quát. Tính tổng
sin sin 2 si sin3 1nSxxx nx  
.
Nhân cả hai vế với
2 sin
2
x
ta có:
2 sin . 2 sin .sin 2 sin .sin 2 2 sin .sin 3 2 sin .sin 1
22 2 2 2
xx x x x
S x x x nx

c2 sin .
2
23
3 35 57
cos cos cos cos os co
21
cos cos
s
22 2 2 2
2
2
2
x
xx xx
S
x
n
x
x
n
x













 












21
2 sin . cos cos
22 2
x xn
Sx



1
2 sin . 2 sin .sin
2 22
nx
x nx
S

1
sin .sin
22
sin
2
nx
nx
S
x

Áp dụng với
2024
x
và
2024n
ta được:
2
2023
sin .sin sin
2.2024 2 2.2024
1289
sin sin
2.2024 2.202
2
4
20 3
S



.
Câu 3: Một chất điểm dao động điều hoà theo phương trình
2 cos 2 ,
2
xt



t
tính bằng giây và
x
tính bằng
.cm
Gọi
0
t
là thời điểm đầu tiên vật có li độ lớn nhất. Giá trị của
0
t
(viết kết quả dưới
dạng thập phân, nếu có) bằng bao nhiêu.
Lời giải
Đáp án: 0,75
Với mọi
0
t
ta có
1 cos 2 1 2 2 cos 2 2.
22
tt


 


 





 
Do đó li độ lớn nhất là
2
x cm
xảy ra khi
1
cos 2 1 2 2 , .
22 4
t t k tk k





Vì
11
00
44
tk k
Vì
,k
suy ra thời điểm đầu tiên thoả mãn ứng với
0
3
1 0, 75
4
kt
giây.
Câu 4: Cho dãy số
n
u
xác định bởi
1
1
5 ,1
nn
ua
u un

. Tìm
a
để
n
u
là cấp số cộng (Viết kết quả
dưới dạng thập phân, nếu có).
Lời giải
11
Đáp án: 2,5
Giả sử
n
u
là cấp số cộng. Khi đó, tồn tại một hằng số
d
sao cho
1
1, 1
nn
n u ud

.
Từ hệ thức xác định dãy số
n
u
ta suy ra
1
1, 5 2 2
nn n
nuu u

.
Từ
1
và
2
ta có
5
,1
2
n
d
un

.
n
u
là một dãy số không đổi.
21
5
55
2
u aa u aa  
.
Với
5
2
a
, ta cũng chứng minh được
5
2
n
u
.
Vậy
5
2
a
là giá trị cần tìm.
Câu 5: Cho hình tứ diện đều
ABCD
có cạnh bằng
12
. Gọi
,MN
lần lượt là trung điểm của cạnh
AB
và
CD
. Gọi
P
là trung điểm đoạn thẳng
CM
. Giao điểm
I
của đường thẳng
DP
và mặt phẳng
ABN
cách điểm D một khoảng bằng bao nhiêu?(làm tròn kết quả đến hàng phần
trăm)?
Lời giải
Đán án: 6,63
Trong mặt phẳng
DMC
, gọi
I
là giao điểm của
MN
và
DP
.
Khi đó
I MN ABN I A BN 
Vậy
I
là giao điểm của
DP
và
ABN
.
Tam giác
DMC
có
MN
và
DP
là hai đường trung tuyến nên giao điểm
I
là trọng tâm
DMC
Ta có tam giác
ABD
đều bằng 12 và có
DM
là đường cao nên
3
12. 6 3
2
DM 
.
Tương tự ta có
63CM
Do đó tam giác
DMC
cân tại
M
. Suy ra
MN
cũng là đường cao của tam giác
DMC
hay
MN CD
.
Ta có
1
6 3, 6
2
DM DN DC 
nên
22
62MN DM DN 
Khi đó
1
22
3
IN MN
.
Tam giác
vuông tại
N
nên
22
2 11DI DN IN 
Vậy
I
cách điểm D một khoảng bằng
2 11 6,63
12
Câu 6: Cho hình chóp
.
S ABCD
có đáy là hình bình hành
ABCD
,
O
là giao điểm của
AC
và
BD
. Tam
giác
là tam giác đều cạnh
2
. Mặt phẳng
P
đi qua
O
và song song với mặt phẳng
SCD
. Tính diện tích hình tạo bởi mặt phẳng
P
và các mặt của hình chóp
.S ABCD
.(làm tròn kết quả
đến hàng phần mười)
Lời giải
Đán án: 1,3
+ Do mặt phẳng
//P SCD
mà
ABCD SCD CD ABCD P MN 
đi qua
O
và
song song với
CD
.
Tương tự ta có:
//SAD P MF SD
;
//SBC P NE SC
.
Vậy hình tạo bởi mặt phẳng
P
và các mặt của hình chóp
.S ABCD
là tứ giác
MNEF
.
+ Ta có
MN
đi qua
O
và song song với
CD
nên
M
,
N
lần lượt là trung điểm của
AD
,
BC
.
Suy ra
E
,
F
lần lượt là trung điểm
SB
,
SA
.
Gọi
I
,
K
lần lượt là trung điểm
SC
,
SD
. Khi đó ta có
,;,; , ; ,IK EF IK EF IC EN IC EN KD F M KD FM MN CD MN CD

Vì thế ta có diện tích hình
NMEF
là
2
3 3 3 33
. . 2 1, 3
4 44 4
MNEF DCIK SCD
SS S 
.
-----------HẾT-----------
1
ĐỀ ÔN TẬP GIỮA HỌC KỲ I NĂM HỌC 2025
–
2026
MÔN: TOÁN 11
ĐỀ SỐ 02
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu
1
đến câu 12. Mỗi câu
hỏi thí sinh chỉ chọn một phương án.
Câu 1: Cho điểm
M
trên đường tròn lượng giác như hình vẽ:
Mệnh đề nào sau đây đúng?
A.
; 60 360 ,OA OM k k 
. B.
; 60 180 ,OA OM k k 
.
C.
; 60 180 ,OA OM k k 
. D.
; 60 360 ,OA OM k k 
.
Câu 2: Cho góc
;
2



thỏa mãn
2
sin
3
. Tính
cos
.
A.
1
cos
3
. B.
5
cos
3
. C.
1
cos
3

. D.
5
cos
3

.
Câu 3: Công thức nào dưới đây đúng?
A.
22
sin cos 2
. B.
cos cos 
.
C.
sin cos
2




. D.
tan cot
2




.
Câu 4: Chu kỳ tuần hoàn của hàm số
cosyx
là
A.
2
. B.
. C.
4
. D.
2
.
Câu 5: Phương trình
sin 2 1x 
có bao nhiêu nghiệm thuộc đoạn
;2




?
A.
3
. B.
1
. C.
4
. D.
2
.
Câu 6: Cho dãy số
n
u
, biết
1
1
1
4
nn
u
uu


với
1n
. Ba số hạng đầu tiên của dãy số đó lần lượt là
những số nào dưới đây?
A.
1; 4; 7.
B.
1; 3; 5.
C.
1; 4; 6
. D.
1; 3; 7.
Câu 7: Cho cấp số cộng
n
u
có:
1
0, 1; 0, 1ud
. Số hạng thứ 7 của cấp số cộng này là
A.
1, 6
. B.
6
. C.
0, 5
. D.
0, 6
.
Câu 8: Cho cấp số nhân
n
u
với
17
1
; u 32
2
u  
. Tìm q ?
A.
1
2
q 
. B.
2q 
. C.
4q 
. D.
1q 
.
Câu 9: Trong các khẳng định sau, khẳng định nào đúng?
A. Qua
2
điểm phân biệt có duy nhất một mặt phẳng
.
x
y
60
o
O
M
A
2
B. Qua
3
điểm phân biệt bất kì có duy nhất một mặt phẳng
.
C. Qua
3
điểm không thẳng hàng có duy nhất một mặt phẳng
.
D. Qua
4
điểm phân biệt bất kì có duy nhất một mặt phẳng
.
Câu 10: Cho hai đường thẳng phân biệt không có điểm chung cùng nằm trong một mặt phẳng thì hai
đường thẳng đó
A. song song. B. chéo nhau. C. cắt nhau. D. trùng nhau.
Câu 11: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành tâm
O
,
M
là trung điểm
SA
. Khẳng
định nào sau đây là đúng?
A.
// D
OM SC
. B.
// D
OM SB
. C.
//OM SAB
. D.
// D
OM SA
.
Câu 12: Có bao nhiêu mặt phẳng song song với cả hai đường thẳng chéo nhau?
A. Vô số. B.
3
. C.
2
. D.
1
.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1: Cho
tan 4x 
với
2
x

.
a) Giá trị của
cos x
là
1
4
.
b) Giá trị của
tan 2
x
là
8
15
.
c) Giá trị của
tan
4
x


là
3
5
.
d) Giá trị của biểu thức
2sin 5cos
3 cos sin
xx
A
xx
là 13.
Câu 2: Cho hàm số lượng giác
2 sin 2 2 1
3
y xm



.
a) Hàm số có tập xác định
D
.
b) Với
0m
hàm số có tập giá trị
3;1T




.
c) Với
2m
hàm số luôn có giao điểm với trục
Ox
.
d) Có
3
giá trị nguyên của tham số
m
để đường thẳng
3y
cắt đồ thị hàm số.
Câu 3: Một sinh viên sau khi ra trường và xin vào làm cho một trung tâm với mức lương khởi điểm là
120
triệu đồng một năm. Cứ sau mỗi năm, trung tâm trả thêm cho sinh viên
24
triệu đồng. Gọi
n
u
là số tiền lương mà sinh viên đó nhận được ở năm thứ
n
.
a) Số tiền lương sinh viên nhận được ở năm thứ hai là
144
triệu đồng.
b) Số tiền lương sinh viên nhận được ở năm thứ
10
là
330
triệu đồng.
c) Dãy số
n
u
là cấp số cộng có
1
120u
và công sai
20d
.
d) Giả sử, mỗi năm bạn sinh viên chi tiêu tiết kiệm hết 70 triệu đồng. Vậy sau ít nhất
10
năm
thì sinh viên đó mua được căn chung cư
2
tỉ đồng.
Câu 4: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành và
O
là giao điểm của hai đường chéo
của hình bình hành
ABCD
. Gọi
,MN
lần lượt là trung điểm của
SA
và
SD
. Khi đó:
a) Điểm
O
là điểm chung của
OMN
và
ABCD
.
b)
//MN BC
.
c)
//OM SBC
.
d) Giao tuyến của
OMN
và
SBC
là đường thẳng
d
song song với hai đường thẳng
MN
và
BC
.
3
PHẦN III. Câu trắc nghiệm trả lời ngắn
Câu 1: Biết
22
sin 4 cot cos 1 3 tan sin cosx x x x a xb x
.Tính
ab
?
Câu 2: Biết với mọi
x
thì
66
sin cos cos 4 ;x x a b x ab Q 
. Tính
ab
Câu 3: Phương trình
3
sin 2 sin
44
xx











có tổng các nghiệm thuộc khoảng
0;
bằng
.
a
. Tìm
a
?
Câu 4: Cho một cấp số cộng
n
u
có số hạng đầu
1
1
u
và tổng của
100
số hạng đầu bằng
24850
. Khi
đó
1 2 2 3 3 4 28 29 29 30
111 1 1
...
... . .
a
S
uu uu uu u u u u b

, trong đó
a
b
là phân số tối giản và
*
,ab
. Tính tổng
ab
.
Câu 5: Cho hình chóp
..S ABC
Gọi
,MN
lần lượt là trung điểm của
SA
và
BC
;
P
là điểm thuộc cạnh
AB
sao cho
2
3
AP
AB
. Đường thẳng
SC
cắt mặt phẳng
MNP
tại
Q
. Biết tỉ số
SQ a
SC b
, trong
đó
a
b
là phân số tối giản và
*
,ab
. Tổng
22
ab
bằng bao nhiêu?
Câu 6: Cho lăng trụ
.ABCD A B C D

có đáy
ABCD
là hình vuông,
1; 2AB AA

. Gọi
L
là trung
điểm
BD
, mặt phẳng
P
qua
L
và song song
AC
lần lượt cắt
;;AA CC DD

tại
;;EFK
. Đặt
DK
x
DD
. Khi
//
EFK MA C

thì
2025
1005
x
P
bằng bao nhiêu? (Làm tròn đến hàng phần
trăm).
--------HẾT--------
4
HƯỚNG DẪN GIẢI
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu
1
đến câu 12. Mỗi câu
hỏi thí sinh chỉ chọn một phương án.
Câu 1: Cho điểm
M
trên đường tròn lượng giác như hình vẽ:
Mệnh đề nào sau đây đúng?
A.
; 60 360 ,OA OM k k 
. B.
; 60 180 ,OA OM k k 
.
C.
; 60 180 ,OA OM k k 
. D.
; 60 360 ,OA OM k k 
.
Lời giải
Ta có
; 60 360 ,OA OM k k 
.
Câu 2: Cho góc
;
2



thỏa mãn
2
sin
3
. Tính
cos
.
A.
1
cos
3
. B.
5
cos
3
. C.
1
cos
3

. D.
5
cos
3

.
Lời giải
Ta có
22 2 2
45
sin cos 1 cos 1 sin 1
99
  
5
cos
3

.
Do
;
2



nên
5
cos 0 cos
3
 
.
Câu 3: Công thức nào dưới đây đúng?
A.
22
sin cos 2

. B.
cos cos 
.
C.
sin cos
2




. D.
tan cot
2




.
Lời giải
Ta có
sin cos
2




.
Câu 4: Chu kỳ tuần hoàn của hàm số
cosyx
là
A.
2
. B.
. C.
4
. D.
2
.
Lời giải
Chu kỳ tuần hoàn của hàm số
cosyx
là
2
.
Câu 5: Phương trình
sin 2 1x 
có bao nhiêu nghiệm thuộc đoạn
;2



?
A.
3
. B.
1
. C.
4
. D.
2
.
Lời giải
Ta có
sin 2 1x

22
2
xk

4
x kk

.
Xét trên đoạn
;2



:
2x
2
4
k
 
39
44
k

Mà
0; 1; 2kk 
.
x
y
60
o
O
M
A
5
Vậy phương trình có 3 nghiệm thuộc đoạn
;2




.
Câu 6: Cho dãy số
n
u
, biết
1
1
1
4
nn
u
uu


với
1n
. Ba số hạng đầu tiên của dãy số đó lần lượt là
những số nào dưới đây?
A.
1; 4; 7.
B.
1; 3; 5.
C.
1; 4; 6
. D.
1; 3; 7.
Lời giải
Ta có
1
1
u 
,
21
43
uu

,
32
47uu 
.
Vậy ba số hạng đầu tiên của dãy là:
1; 3; 7
.
Câu 7: Cho cấp số cộng
n
u
có:
1
0, 1; 0, 1ud
. Số hạng thứ 7 của cấp số cộng này là
A.
1, 6
. B.
6
. C.
0, 5
. D.
0, 6
.
Lời giải
Số hạng tổng quát của cấp số cộng
n
u
là:
17
1
1 .0, 1 0, 1 7 1 .0, 1
2
n
uu n u

.
Câu 8: Cho cấp số nhân
n
u
với
17
1
; u 32
2
u  
. Tìm q ?
A.
1
2
q 
. B.
2q 
. C.
4q 
. D.
1q 
.
Lời giải
Áp dụng công thức số hạng tổng quát cấp số nhân ta có
1 66
1 71
2
. 64
2
n
n
q
u uq u u q q
q


.
Câu 9: Trong các khẳng định sau, khẳng định nào đúng?
A. Qua
2
điểm phân biệt có duy nhất một mặt phẳng
.
B. Qua
3
điểm phân biệt bất kì có duy nhất một mặt phẳng
.
C. Qua
3
điểm không thẳng hàng có duy nhất một mặt phẳng
.
D. Qua
4
điểm phân biệt bất kì có duy nhất một mặt phẳng
.
Lời giải
Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng cho trước.
Câu 10: Cho hai đường thẳng phân biệt không có điểm chung cùng nằm trong một mặt phẳng thì hai
đường thẳng đó
A. song song. B. chéo nhau. C. cắt nhau. D. trùng nhau.
Lời giải
Câu 11: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành tâm
O
,
M
là trung điểm
SA
. Khẳng
định nào sau đây là đúng?
A.
//
OM SCD
. B.
//OM SBD
. C.
//
OM SAB
. D.
//OM SAD
.
Lời giải
Ta có:
M
là trung điểm
SA
;
O
là trung điểm
AC
OM
là đường trung bình
SAC
.
//OM SC
.
6
Mà
D
// D
SC SCD
OM SC
OM SC
Câu 12: Có bao nhiêu mặt phẳng song song với cả hai đường thẳng chéo nhau?
A. Vô số. B.
3
. C.
2
. D.
1
.
Lời giải
Gọi hai đường thẳng chéo nhau là
a
và
b
,
c
là đường thẳng song song với
a
và cắt
b
.
Gọi mặt phẳng
,bc
. Do
// //ac a
Giả sử mặt phẳng
//

mà
//bb
Mặt khác
// //aa
. Có vô số mặt phẳng
//

nên có vô số mặt phẳng song song với cả hai đường thẳng chéo nhau.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1: Cho
tan 4
x 
với
2
x

.
a) Giá trị của
cos
x
là
1
4
.
b) Giá trị của
tan 2x
là
8
15
.
c) Giá trị của
tan
4
x


là
3
5
.
d) Giá trị của biểu thức
2sin 5cos
3 cos sin
xx
A
xx
là 13.
Lời giải
a) Sai | b) Đúng| c) Sai| d) Đúng
a) Sai
Ta có
2
2
1 17
tan 1 17 cos
17
cos
xx
x

b) Đúng
Ta có
22
2. 4
2 tan 8
tan 2
15
1 tan
14
x
x
x


c) Sai
Ta có
tan tan
41 5
4
tan
4 1 1. 4 3
1 tan . tan
4
x
x
x





.
d) Đúng
Ta có:
sin cos
25
2. 4 5
2 sin 5 cos 2 tan 5
cos cos
13
3 cos sin cos sin 3 tan 3 4
3
cos cos
xx
xx x
xx
A
xx x x x
xx




.
7
Câu 2: Cho hàm số lượng giác
2 sin 2 2 1
3
y xm



.
a) Hàm số có tập xác định
D
.
b) Với
0m
hàm số có tập giá trị
3;1
T




.
c) Với
2m
hàm số luôn có giao điểm với trục
Ox
.
d) Có
3
giá trị nguyên của tham số
m
để đường thẳng
3y
cắt đồ thị hàm số.
Lời giải
a) Đúng | b) Đúng| c) Sai| d) Đúng
a) Đúng
Hàm số có tập xác định là
D
.
b) Đúng
Với
0m
hàm số trở thành
2 sin 2 1
3
yx



.
Ta có:
1 sin 2 1
3
x



2 2 sin 2 2
3
x



.
3 2 sin 2 1 1
3
x



.
Vậy tập giá trị của hàm số là
3;1T




.
c) Sai
Với
2m
hàm số trở thành
2 sin 2 3
3
yx



.
Số giao điểm với trục
Ox
là số nghiệm của phương trình hoành độ giao điểm của hai hàm số:
2 sin 2 3
3
0
yx
y



Khi đó ta có phương trình:
2 sin 2 3 0
3
x



3
sin 2
32
x



.
Vậy hàm số không có giao điểm với trục
Ox
.
d) Đúng
Đường thẳng
3y
cắt đồ thị hàm số
2 sin 2 2 1
3
y xm



khi phương trình hoành độ
giao điểm
2 sin 2 2 1
3
3
y xm
y



có nghiệm.
2 sin 2 2 1 3
3
xm



có nghiệm.
sin 2 2
3
xm



có nghiệm.
Phương trình trên có nghiệm khi
2 1 12 1 1 3m mm 
Suy ra
1; 2; 3m
.
Vậy có
3
giá trị nguyên của tham số
m
để đường thẳng
3y
cắt đồ thị hàm số.
8
Câu 3: Một sinh viên sau khi ra trường và xin vào làm cho một trung tâm với mức lương khởi điểm là
120
triệu đồng một năm. Cứ sau mỗi năm, trung tâm trả thêm cho sinh viên
24
triệu đồng. Gọi
n
u
là số tiền lương mà sinh viên đó nhận được ở năm thứ
n
.
a) Số tiền lương sinh viên nhận được ở năm thứ hai là
144
triệu đồng.
b) Số tiền lương sinh viên nhận được ở năm thứ
10
là
330
triệu đồng.
c) Dãy số
n
u
là cấp số cộng có
1
120u
và công sai
20
d
.
d) Giả sử, mỗi năm bạn sinh viên chi tiêu tiết kiệm hết 70 triệu đồng. Vậy sau ít nhất
10
năm
thì sinh viên đó mua được căn chung cư
2
tỉ đồng.
Lời giải
a) Đúng | b) Sai| c) Sai| d) Sai
a) Đúng.
Ta thấy, số tiền lương năm sau hơn năm trước
24
triệu đồng nên số tiền lương hằng năm
n
u
là cấp số cộng có
1
120
u
và công sai
24d
. Do đó:
1
1 120 1 .24 24 96
n
uu n d n n
 
Số tiền lương sinh viên nhận được ở năm thứ hai là
2
144
u
.
Vậy mệnh đề a) là Đúng.
b) Sai.
Số tiền lương sinh viên nhận được ở năm thứ 10 là
10
24.10 96 336u 
.
Vậy mệnh đề b) là Sai.
c) Sai.
Mệnh đề c) là sai vì
24d
.
d) Sai.
Tổng số tiền bạn sinh viên tiết kiệm được sau
n
năm là:
2
1
2 1 70 2.120 1 .24 70 12 38
22
nn
S un d n n n n n

 

.
Ta có:
2000S
2
11, 42
12 38 2000 0
14, 59
n
nn
n


.
Do đó sau ít nhất sau
12
năm thì sinh viên đó có thể mua được chung cư
2
tỉ đồng.
Vậy mệnh đề d) là Sai.
Câu 4: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành và
O
là giao điểm của hai đường chéo
của hình bình hành
ABCD
. Gọi
,MN
lần lượt là trung điểm của
SA
và
SD
. Khi đó:
a) Điểm
O
là điểm chung của
OMN
và
ABCD
.
b)
//MN BC
.
c)
//OM SBC
.
d) Giao tuyến của
OMN
và
SBC
là đường thẳng
d
song song với hai đường thẳng
MN
và
BC
.
Lời giải
a) Đúng | b) Đúng| c) Đúng| d) Sai

Tài liệu khác của Toán 11

Preview text:

ĐỀ ÔN TẬP GIỮA HỌC KỲ I NĂM HỌC 2025 – 2026 MÔN: TOÁN 11 ĐỀ SỐ 01
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu
hỏi thí sinh chỉ chọn một phương án.
Câu 1: Đổi số đo của góc  120 sang đơn vị radian ta được A. 2  .
B.  .
C.  . D.  . 3 6 3 4 Câu 2: Cho 2
cos với 3   2 .
Tìm giá trị lượng giác sin . 5 2 A. 21 . B. 21 . C. 21  . D. 21  . 25 5 5 25
Câu 3: Trong các đẳng thức sau, đẳng thức nào SAI? A. 2 tana 2
cos 2a  1  2 sin a . B. tan 2a  . 2 1  tan a
C. sin 2a  2 sina cosa . D. 2 2
cos 2a  cos a  sin a .
Câu 4: Tập xác định của hàm số y  cotx là:     A. D  \  k ,  k      . B. D  \  k ,  k      .   2     4      C. D  \  k ,k     .
D. D   \ k ,  k   .  8 2   
Câu 5: Tập nghiệm của phương trình 2 sin2x  1  0 là     A. 7 S  k , k ,  k        . B. 7 S  k2 , k2 ,  k        .   12 12     6 12        C. 7 S  k2 , k2 ,  k        . D. 7 S  k , k ,  k        .   12 12     6 12   
Câu 6: Cho dãy số u thỏa mãn 1 u 2n 
. Tìm số hạng thứ 10 của dãy số đã cho. n n A. 11 2 . B. 9 2 . C. 10 2 . D. 8 2 .
Câu 7: Cho cấp số cộng u có số hạng đầu u  3 , công sai d  2 . Tìm số hạng thứ 5 của cấp số cộng n  1 đó. A. u  5 . B. u  1. C. u  1. D. u  5 . 5 5 5 5
Câu 8: Cho cấp số nhân u có u  18; 162 u
. Số 1458 là số hạng thứ bao nhiêu của cấp số nhân đó, n  3 5
biết rằng cấp số nhân có công bội dương.
A. Số hạng thứ bảy.
B. Số hạng thứ sáu. C. Số hạng thứ tám. D. Số hạng thứ chín.
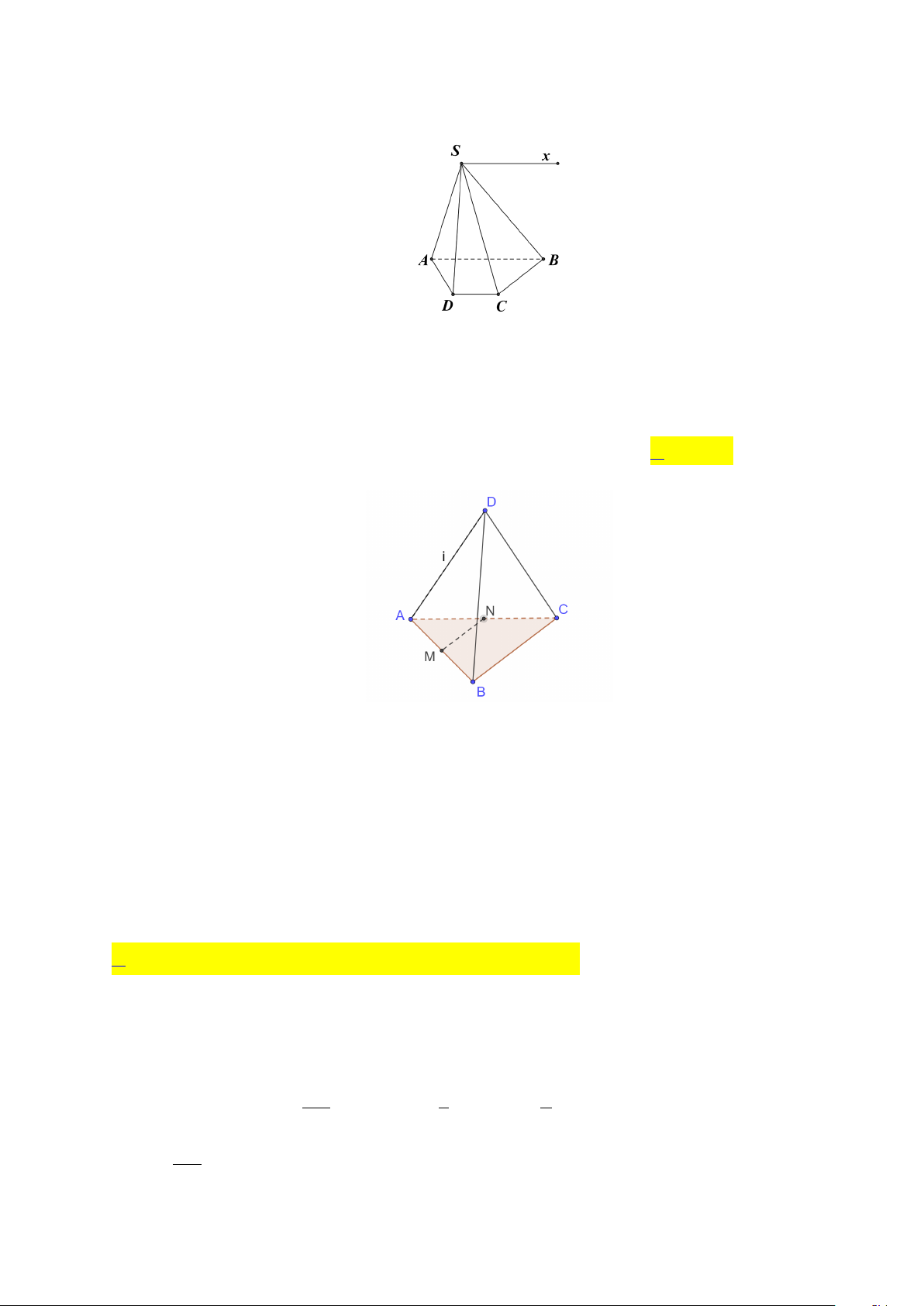
Câu 9: Cho tứ diện ABCD . Gọi G là trọng tâm của tam giácBCD. Giao tuyến của mặt phẳng ACD  và GAB  là:
A. AM (M là trung điểm của AB ).
B. AN (N là trung điểm của CD ).
C. AH (H là hình chiếu của B trên CD).
D. AK (K là hình chiếu của C trên BD ).
Câu 10: Cho hình chóp S.ABCD có đáy là ABCD hình thangAB//CD . Giao tuyến của hai mặt phẳng
SAB  và SCD  là 1
A. Đường thẳng qua S và song song với AB và CD .
B. Đường thẳng qua S và song song với AD và BC .
C. Đường thẳng qua S và giao điểm của AD và BC .
D. Đường thẳng qua S và giao điểm của AC và BD .
Câu 11: Cho tứ diện ABCD có M,N lần lượt là trung điểm của AB,AC . Mặt phẳng nào sau đây song
song với đường thẳng MN ? A. (ACD). B. (ABD). C. (ABC) . D. (BCD) .
Câu 12: Cho hai mặt phẳng song song  và , a là đường thẳng bất kì. Tìm mệnh đề sai trong các mệnh đề sau:
A. Nếu a cắt mp thì a cắt mp.
B. Nếu a   thì a song song với mp.
C. Nếu a   thì a song song với mp.
D. Nếu a song song với mp thì a song song với mp.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.  
Câu 1: Cho góc lượng giác 25  và 5
sin x   với x    ;0 . 6 8  2  a) 25   750 . 6
b) Điểm biểu diễn trên đường tròn lượng giác của góc đã cho thuộc phần tư thứ IV. c)
cosx  3 13 5  . 16 d) 6 tan x 15 26 P   . 2 5 tan x  4 281   Câu 2: Cho hàm số y f x  3 tan   2x   .  3 
a) Tập xác định của hàm số D   . b) Phương trình k
f x   3 có nghiệm x   ,k   . 3 2 c) Phương trình
f x   3 có nghiệm âm lớn nhất bằng  . 3 d) Khi  2x
thì phương trình f x   3 có hai nghiệm. 4 3 u  1
Câu 3: Cho dãy số u , biết  1  với n  1. n  uu  3  n1 n
a) Dãy số trên là một cấp số nhân.
b) Số hạng thứ năm của dãy là 13 .
c) 101 là số hạng thứ 35 của dãy số đã cho.
d) Tổng các số hạng từ số hạng thứ 10 đến số hạng thứ 20 của dãy số bằng 451 .
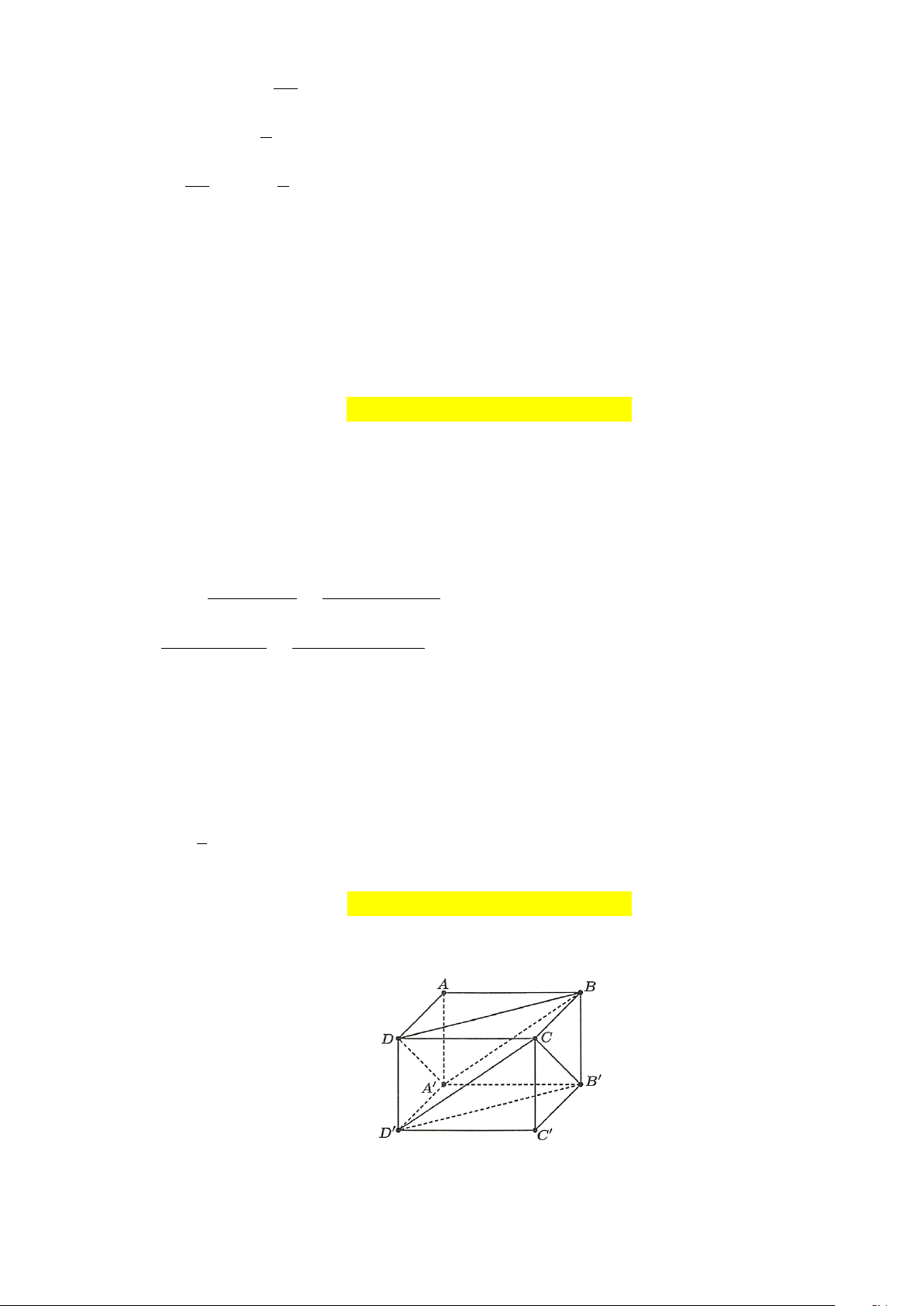
Câu 4: Cho hình hộp ABCD AB CD
  . Gọi G ,G là trọng tâm của các tam giác A , BD B DC  . 1 2
a) Đường thẳng AB cắt đường thẳng CD .
b) AD CB  là hình bình hành
c)ABD //B DC   d) 2 G G AC  1 2 3 2
PHẦN III. Câu trắc nghiệm trả lời ngắn
Câu 1: Gọi M , N , E là các điểm trên đường tròn lượng giác sao cho số đo của các góc lượng giác    , OA OM ,  , OA ON  ,  ,
OA OE  lần lượt bằng  ; 7 
; . Khi đó, diện tích tam giác MNE làm 2 6 6
tròn đến hàng phần chục bằng bao nhiêu? Câu 2: Tính 2 3 2023 S  sin  sin  sin    i s n . 2024 2024 2024 20 4 2  
Câu 3: Một chất điểm dao động điều hoà theo phương trình x 2 cos  2 t   , 
t tính bằng giây và x  2 
tính bằng cm. Gọi t là thời điểm đầu tiên vật có li độ lớn nhất. Giá trị của t bằng bao nhiêu. 0 0 u a
Câu 4: Cho dãy số u xác định bởi  1 
. Tìm a để u là cấp số cộng. n n  u
 5  u ,n  1  n1 n
Câu 5: Cho hình tứ diện đều ABCD có cạnh bằng 12 . Gọi M,N lần lượt là trung điểm của cạnh AB và
CD . Gọi P là trung điểm đoạn thẳng CM . Giao điểm I của đường thẳng DP và mặt phẳng
ABN  cách điểm D một khoảng bằng bao nhiêu?
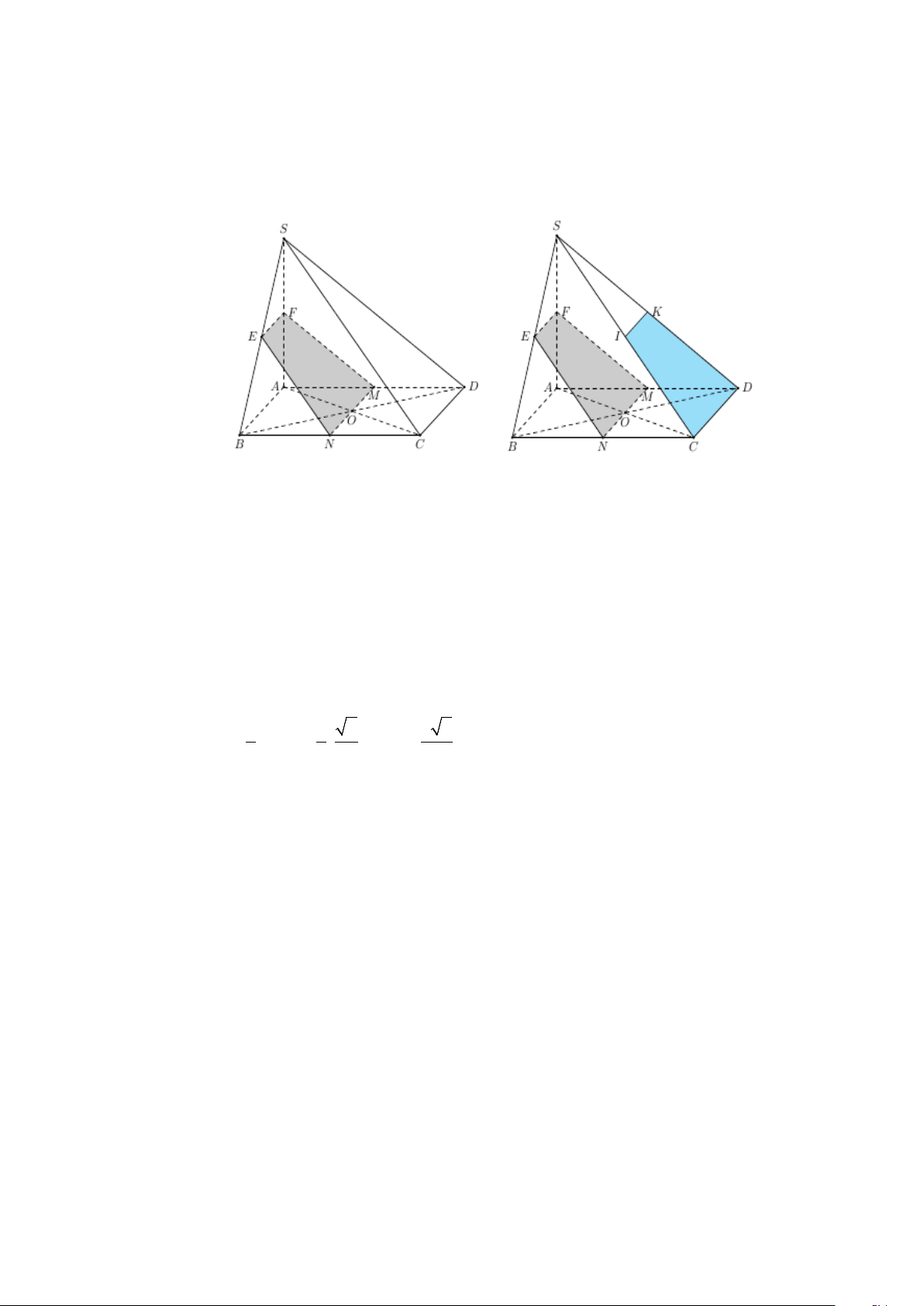
Câu 6: Cho hình chóp S.ABCD có đáy là hình bình hành ABCD , O là giao điểm của AC và BD . Tam
giác SCD là tam giác đều cạnh 2 . Mặt phẳng P  đi qua O và song song với mặt phẳng SCD
. Tính diện tích hình tạo bởi mặt phẳng P  và các mặt của hình chóp S.ABCD . --------HẾT-------- 3 HƯỚNG DẪN GIẢI
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu
hỏi thí sinh chỉ chọn một phương án.
Câu 1: Đổi số đo của góc  120 sang đơn vị radian ta được A. 2  .
B.  .
C.  . D.  . 3 6 3 4 Lời giải
Áp dụng công thức đổi từ độ sang radian ta có: 0 a a ta có 2  120  120  . 180 180 3 Câu 2: Cho 2
cos với 3   2 .
Tìm giá trị lượng giác sin . 5 2 A. 21 . B. 21 . C. 21  . D. 21  . 25 5 5 25 Lời giải
Vì 3 2 nên sin  0 . 2 Ta có  21 2 2 2
sin  cos  1  sin   1  cos  . 5
Câu 3: Trong các đẳng thức sau, đẳng thức nào SAI? A. 2 tana 2
cos 2a  1  2 sin a . B. tan 2a  . 2 1  tan a
C. sin 2a  2 sina cosa . D. 2 2
cos 2a  cos a  sin a . Lời giải Ta có: 2 tana tan 2a  nên B sai. 2 1  tan a
Câu 4: Tập xác định của hàm số y  cotx là:     A. D  \  k ,  k      . B. D  \  k ,  k      .   2     4      C. D  \  k ,k     .
D. D   \ k ,  k   .  8 2    Lời giải Hàm số cos x y  cotx
xác định khi và chỉ khi sin x  0  x k ,
k   nên sin x
D   \ k ,  k   .
Câu 5: Tập nghiệm của phương trình 2 sin2x  1  0 là     A. 7 S  k , k ,  k        . B. 7 S  k2 , k2 ,  k        .   12 12     6 12        C. 7 S  k2 , k2 ,  k        . D. 7 S  k , k ,  k        .   12 12     6 12    Lời giải  
2x    k2 Ta có: 1
2 sin 2x  1  0  sin 2x    sin 2x  sin     6   ,k 2  6   7 2x   k2  6  x    k  12   ,k .  7 x   k  12 4  
Vậy tập nghiệm của phương trình là 7S  k , k ,  k        .  12 12   
Câu 6: Cho dãy số u thỏa mãn 1 u 2n 
. Tìm số hạng thứ 10 của dãy số đã cho. n n A. 11 2 . B. 9 2 . C. 10 2 . D. 8 2 . Lời giải Ta có 10 1  9 u  2  2 . 10
Câu 7: Cho cấp số cộng u có số hạng đầu u  3 , công sai d  2 . Tìm số hạng thứ 5 của cấp số cộng n  1 đó. A. u  5 . B. u  1. C. u  1. D. u  5 . 5 5 5 5 Lời giải
Áp dụng công thức của số hạng tổng quát: u u  4d  5 . 5 1
Câu 8: Cho cấp số nhân u có u  18; 162 u
. Số 1458 là số hạng thứ bao nhiêu của cấp số nhân đó, n  3 5
biết rằng cấp số nhân có công bội dương.
A. Số hạng thứ bảy.
B. Số hạng thứ sáu. C. Số hạng thứ tám. D. Số hạng thứ chín. Lời giải
Áp dụng công thức của số hạng tổng quát: 1 u u . n q   . n 1 2
u u .q Ta có:  3 1 2 2 
u u .q  162  18.q q  3 . 4 5 3
u u .q  5 1 
Khi đó u  2 . Nên 1 u 2.3n  . 1 n Giả sử n 1 u 1458 2.3   
 1458  n  7 . Vậy 1458 là số hạng thứ bảy của cấp số nhân đó. n
Câu 9: Cho tứ diện ABCD . Gọi G là trọng tâm của tam giácBCD. Giao tuyến của mặt phẳng ACD  và GAB  là:
A. AM (M là trung điểm của AB ).
B. AN (N là trung điểm của CD ).
C. AH (H là hình chiếu của B trên CD).
D. AK (K là hình chiếu của C trên BD ). Lời giải A B D G N C
A là điểm chung thứ nhất của hai mặt phẳng ACD  và GAB .
N BG  ABG
N  ABG
 Ta có BG CD N nên   
là điểm chung thứ hai của               N N CD ACD N ACD
hai mặt phẳng ACD  và GAB .
Vậy ABG   ACD   AN.
Câu 10: Cho hình chóp S.ABCD có đáy là ABCD hình thang AB//CD . Giao tuyến của hai mặt phẳng
SAB  và SCD  là
A. Đường thẳng qua S và song song với AB và CD . 5
B. Đường thẳng qua S và song song với AD và BC .
C. Đường thẳng qua S và giao điểm của AD và BC .
D. Đường thẳng qua S và giao điểm của AC và BD . Lời giải
Hai mặt phẳng SAB  và SCD  lần lượt đi qua hai đường thẳng AB//CD và có S là điểm
chung nên giao tuyến của chúng là đường thẳng đi qua S và song song với AB và CD .
Câu 11: Cho tứ diện ABCD có M,N lần lượt là trung điểm của AB,AC . Mặt phẳng nào sau đây song
song với đường thẳng MN ? A. (ACD). B. (ABD). C. (ABC) . D. (BCD) . Lời giải
Vì M,N lần lượt là trung điểm của AB,AC nên MN là đường trung bình của tam giác ABC ,
do đó MN //BC , lại có MN  (BCD) và BC  (BCD) nên MN //(BCD) .
Vậy đáp án D đúng.
Câu 12: Cho hai mặt phẳng song song  và , a là đường thẳng bất kì. Tìm mệnh đề sai trong các mệnh đề sau:
A. Nếu a cắt mp thì a cắt mp.
B. Nếu a   thì a song song với mp.
C. Nếu a   thì a song song với mp.
D. Nếu a song song với mp thì a song song với mp. Lời giải
Nếu a song song với mp thì a song song với mphoặc a nằm trên mp
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.  
Câu 1: Cho góc lượng giác 25  và 5
sin x   với x    ;0 . 6 8  2  a) 25   750 . 6
b) Điểm biểu diễn trên đường tròn lượng giác của góc đã cho thuộc phần tư thứ IV. 6 c)
cosx  3 13 5  . 16 d) 6 tan x 15 26 P   . 2 5 tan x  4 281 Lời giải
a) Đúng | b) Sai | c) Sai | d) Đúng    a) Ta có: 25 25180     .
  750 . Suy ra mệnh đề Đúng. 6  6  b) 25  
 4. Điểm biểu diễn trên đường tròn lượng giác của góc đã cho thuộc phần tư 6 6
thứ I. Suy ra mệnh đề Sai.   2   c) Vì 5 39 x    ;0 nên 2   . 
cos x  0  cos x  1  sin x  1      2   8  8     Ta có 25 1 sin sin sin  
  4  sin  , 25 3 cos cos cos  
  4  cos  . 6  6  6 2 6  6  6 2   Khi đó:   x  39 3 5 1 3 13 5 cos
 cos x.cos  sin x.sin  .     .  . 8 2  8  2 16
Suy ra mệnh đề Sai 5  d) Ta có sin x 5 39 8 tan x     . cos x 39 39 8  5 39  6.      6 tan x  39  Khi đó  15 26 P   
. Suy ra mệnh đề Đúng. 2 2 5 tan x  4   281  5 39 5     4  39    Câu 2: Cho hàm số y f x  3 tan   2x   .  3 
a) Tập xác định của hàm số D   . b) Phương trình k
f x   3 có nghiệm x   ,k   . 3 2 c) Phương trình
f x   3 có nghiệm âm lớn nhất bằng  . 3 d) Khi  2x
thì phương trình f x   3 có hai nghiệm. 4 3 Lời giải
a) Sai | b) Đúng| c) Sai| d) Đúng   a) Điều kiện 5 cos2x
   0  2x  
k x   k ,k  
 . Suy ra mệnh đề Sai.  3  3 2 12 2  
b) Phương trình tương đương với k tan2x     3  x   ,k    . Suy ra mệnh đề  3  3 2 Đúng. c) k 2 x  0  
 0  k   . Vậy nghiệm âm lớn nhất là x     . Suy ra mệnh 3 2 3 3 2 6 đề Sai. d) Vì  2 k 2 7 2  x        k  . 4 3 4 3 2 3 6 3 7
Do k   nên k  {1;0} . Với
k  1 thì x  . 6 Với
k  0 thì x  . 3 Vậy x
và x  thỏa mãn yêu cầu bài toán. Suy ra mệnh đề Đúng. 6 3u  1
Câu 3: Cho dãy số u , biết  1  với n  1. n  uu  3  n1 n
a) Dãy số trên là một cấp số nhân.
b) Số hạng thứ năm của dãy là 13 .
c) 101 là số hạng thứ 35 của dãy số đã cho.
d) Tổng các số hạng từ số hạng thứ 10 đến số hạng thứ 20 của dãy số bằng 451 . Lời giải
a) Sai |b) Sai |c) Đúng |d) Đúng a) Ta có: u
u  3 suy ra dãy số u là cấp số cộng với công sai d  3 . Vậy a) sai. n n 1 n
b) u u  4d  11 . Vậy b) sai. 5 1
c) Xét u  101  3n  4  101  n  35 . n
Vậy 101 là số hạng thứ 35 của dãy số đã cho.
d)u là cấp số cộng với số hạng đầu u  1 và công sai d  3 . n  1 92u  8d 9 2.1  8.3 1  Ta có: S      99 . 9 2 2 202u  19d 20 2.1  19.3 1  S      550 . 20 2 2
Vậy u u  ...  u S S  550  99  451. 10 11 20 20 9
Câu 4: Cho hình hộp ABCD AB CD
  . Gọi G ,G là trọng tâm của các tam giác A , BD B DC  . 1 2
a) Đường thẳng AB cắt đường thẳng CD .
b) AD CB  là hình bình hành.
c)ABD //B DC   . d) 2
G G AC  . 1 2 3 Lời giải
a) Sai |b) Đúng |c) Đúng |d) Sai
a) Do A  BCD  nên đường thẳng AB và đường thẳng CD chéo nhau.
Vậy mệnh đề a) sai. b) AD //  BC
Vì ABCD.AB CD
  là hình hộp nên   AD CB  là hình bình hành.
AD  BC 
Vậy mệnh đề b) đúng. 8 c) Vì AD CB  là hình bình hành.
Suy ra AB//CD  AB//B DC  . AB //  CD Tương tự, ta có:   AB CD  là hình bình hành.
AB  CD 
Suy ra AD//B C
  AD//B DC   .
Từ và (2) suy ra ABD //B DC   .
Vậy mệnh đề c) đúng. d)
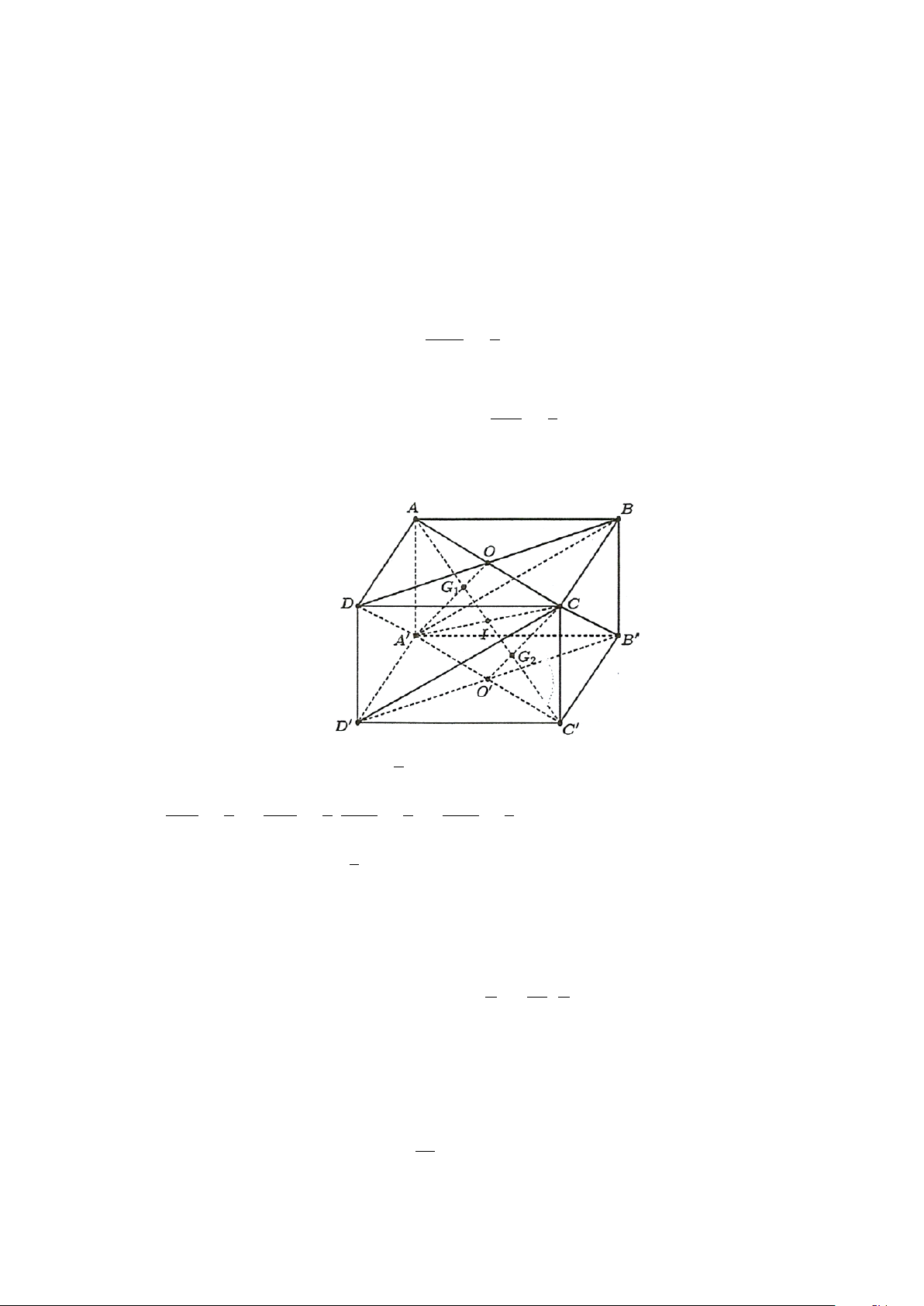
Gọi O,O ,I theo thứ tự là tâm của các hình bình hành ABC , D AB CD   , ACC A   .  Vì A G 2
G là trọng tâm tam giác AB D  nên
1   G là trọng tâm tam giác AAC , suy ra 1 AO 3 1
G AI AO . 1 Tương tự, CG 2
G là trọng tâm tam giác B DC  nên 2  2 CO 3
G là trọng tâm tam giác AC C
 , suy ra G C I  CO . 2 2
Từ và suy ra G ,G cùng thuộc AC  . 1 2 Chứng minh 1
AG G G G C   AC  : 1 1 2 2 3   Ta có: AG 2 AG 1 C G 2 C G 1 1 1 2 2    ;    . AI 3 AC  3 C I 3 AC  3 Do vậy 1
AG G G G C   AC  . 1 1 2 2 3
Vậy G ,G cùng thuộc AC  , đồng thời chia AC  thành ba phần bằng nhau. 1 2
PHẦN III. Câu trắc nghiệm trả lời ngắn
Câu 1: Gọi M , N , E là các điểm trên đường tròn lượng giác sao cho số đo của các góc lượng giác    , OA OM ,  , OA ON  ,  ,
OA OE  lần lượt bằng  ; 7 
; . Khi đó, diện tích tam giác MNE làm 2 6 6
tròn đến hàng phần chục bằng bao nhiêu? Lời giải Đáp án: 1,3
Trên đường tròn lượng giác đi theo chiều dương, từ vị trí điểm gốc A , thứ tự các điểm lần lượt là:
E ; N ; M và    2
EON NOM MOE  . 3 9
Mà OE ON OM  1 nên EN NM ME do đó MN
E đều cạnh MN  3  2 3 . 3 3 3  S    1, 3 . MNE 4 4 Câu 2: Tính 2 3 2023 S  sin  sin  sin    i s n
(làm tròn kết quả đến hàng đơn vị). 2024 2024 2024 20 4 2 Lời giải Đáp án: 1289
Xét bài toán tổng quát. Tính tổng S  sin x  sin 2x  sin 3x    sinn  1x . Nhân cả hai vế với x 2 sin ta có: 2 x x x x x
2 sin .S  2 sin .sin x  2 sin .sin 2x  2 sin .sin 3x    2 sin .sinn  1x 2 2 2 2 2 xx 3x   3x 5x   5x 7x   2 sin .S cos cos      cos cos           cos  cos    2  2 2   2 2     2 2    2n  3   2n  1    cos   x  cos      x   2     2     x x  2n  1
 2 sin .S  cos  cos   x 2 2  2  xn  1x nx  2 sin .S  2 sin .sin 2 2 2 n  1x nx sin .sin 2 2  S x sin 2 2023 2023 sin .sin sin Áp dụng với x
và n  2024 ta được: 2.2024 2 2.2024 S    1289 . 2024 2 sin sin 2.2024 2.2024  
Câu 3: Một chất điểm dao động điều hoà theo phương trình x 2 cos  2 t   , 
t tính bằng giây và x  2 
tính bằng cm. Gọi t là thời điểm đầu tiên vật có li độ lớn nhất. Giá trị của t (viết kết quả dưới 0 0
dạng thập phân, nếu có) bằng bao nhiêu. Lời giải Đáp án: 0,75     Với mọi t  0 ta có 1 cos2 t  1 2 2 cos          2 t     2.  2     2  Do đó li độ lớn nhất là x  2 cm xảy ra khi  1 cos2 t     1  2 t
k2t k  ,k  .    2  2 4 Vì 1 1
t  0  k   0  k  4 4 Vì 3 k  ,
 suy ra thời điểm đầu tiên thoả mãn ứng với k  1  t   0, 75 giây. 0 4 u a
Câu 4: Cho dãy số u xác định bởi  1 
. Tìm a để u là cấp số cộng (Viết kết quả n n  u
 5  u ,n  1  n1 n
dưới dạng thập phân, nếu có). Lời giải 10 Đáp án: 2,5
Giả sử u là cấp số cộng. Khi đó, tồn tại một hằng số d sao cho n  1, uu d 1 . n 1 n   n
Từ hệ thức xác định dãy số u ta suy ra n  1,u
u  5  2u 2 . n 1 n n   n  Từ   d 1 và 2 ta có 5 u  , n  1 . n 2
u là một dãy số không đổi. n  5
u a a  5  u  5  a a  . 2 1 2 Với 5
a  , ta cũng chứng minh được 5 u  . 2 n 2 Vậy 5
a  là giá trị cần tìm. 2
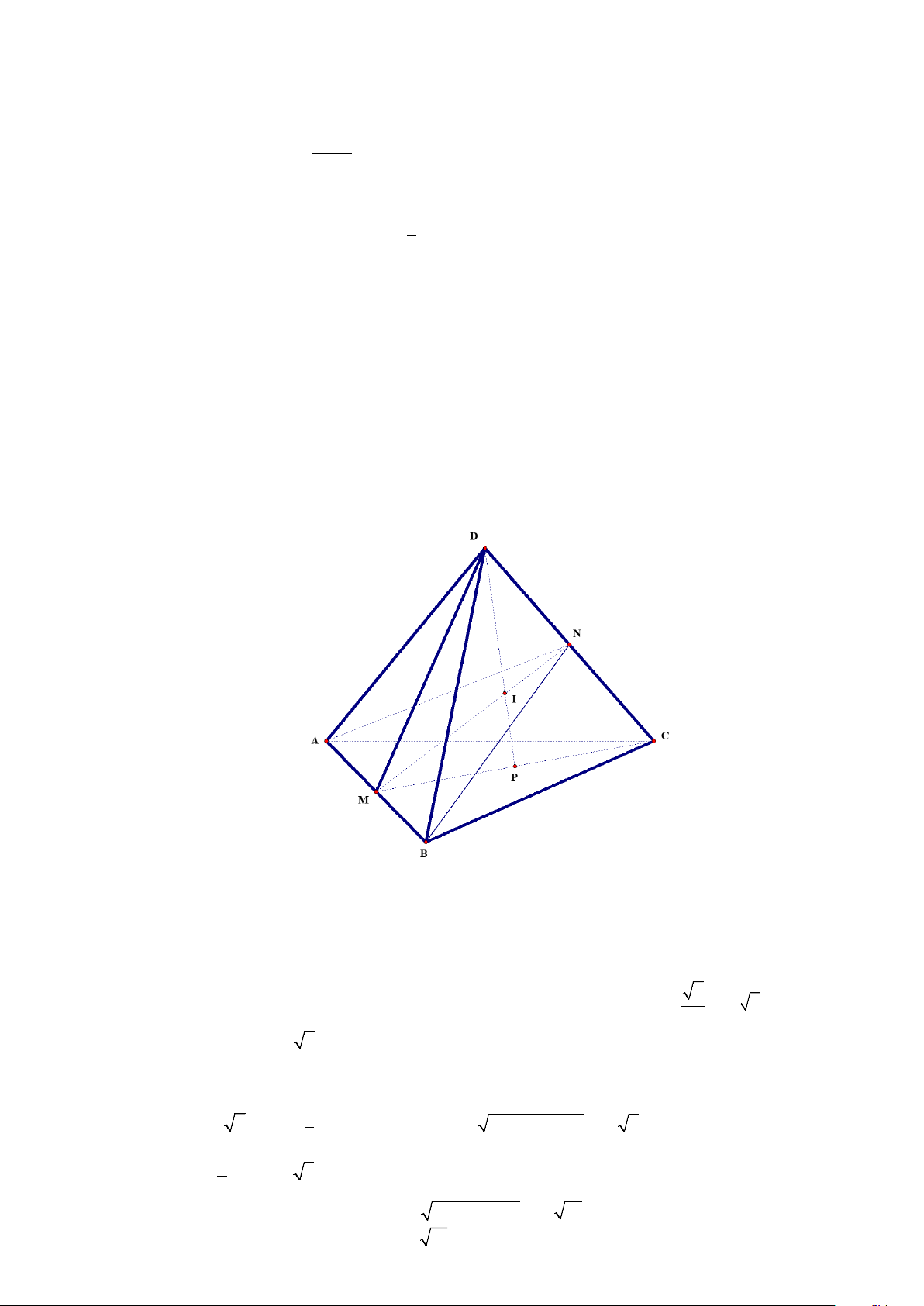
Câu 5: Cho hình tứ diện đều ABCD có cạnh bằng 12 . Gọi M,N lần lượt là trung điểm của cạnh AB và
CD . Gọi P là trung điểm đoạn thẳng CM . Giao điểm I của đường thẳng DP và mặt phẳng
ABN  cách điểm D một khoảng bằng bao nhiêu?(làm tròn kết quả đến hàng phần trăm)? Lời giải Đán án: 6,63
Trong mặt phẳng DMC , gọi I là giao điểm của MN và DP .
Khi đó I MN  ABN   I  ABN
Vậy I là giao điểm của DP và ABN  .
Tam giác DMC có MN và DP là hai đường trung tuyến nên giao điểm I là trọng tâm DMC
Ta có tam giác ABD đều bằng 12 và có DM là đường cao nên 3 DM  12.  6 3 . 2
Tương tự ta có CM  6 3
Do đó tam giác DMC cân tại M . Suy ra MN cũng là đường cao của tam giác DMC hay MN CD . Ta có 1
DM  6 3,DN DC  6 nên 2 2
MN DM DN  6 2 2 Khi đó 1
IN MN  2 2 . 3
Tam giác DNI vuông tại N nên 2 2
DI DN IN  2 11
Vậy I cách điểm D một khoảng bằng 2 11  6,63 11
Câu 6: Cho hình chóp S.ABCD có đáy là hình bình hành ABCD , O là giao điểm của AC và BD . Tam
giác SCD là tam giác đều cạnh 2 . Mặt phẳng P  đi qua O và song song với mặt phẳng SCD
. Tính diện tích hình tạo bởi mặt phẳng P và các mặt của hình chóp S.ABCD .(làm tròn kết quả
đến hàng phần mười) Lời giải Đán án: 1,3
+ Do mặt phẳng P //SCD  mà ABCD   SCD   CD  ABCD   P   MN đi qua O và song song với CD .
Tương tự ta có: SAD   P   MF//SD ; SBC   P   NE//SC .
Vậy hình tạo bởi mặt phẳng P và các mặt của hình chóp S.ABCD là tứ giác MNEF .
+ Ta có MN đi qua O và song song với CD nên M , N lần lượt là trung điểm của AD , BC .
Suy ra E , F lần lượt là trung điểm SB , SA.
Gọi I , K lần lượt là trung điểm SC , SD . Khi đó ta có
IK EF,IK EF;IC EN,IC EN;KD FM,KD FM;MN C , D MN CD
Vì thế ta có diện tích hình NMEF là 3 3 3 SSS    . MNEF DCIK SCD  2 3 3 . . 2 1, 3 4 4 4 4
-----------HẾT----------- 12
ĐỀ ÔN TẬP GIỮA HỌC KỲ I NĂM HỌC 2025 – 2026 MÔN: TOÁN 11 ĐỀ SỐ 02
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu
hỏi thí sinh chỉ chọn một phương án.
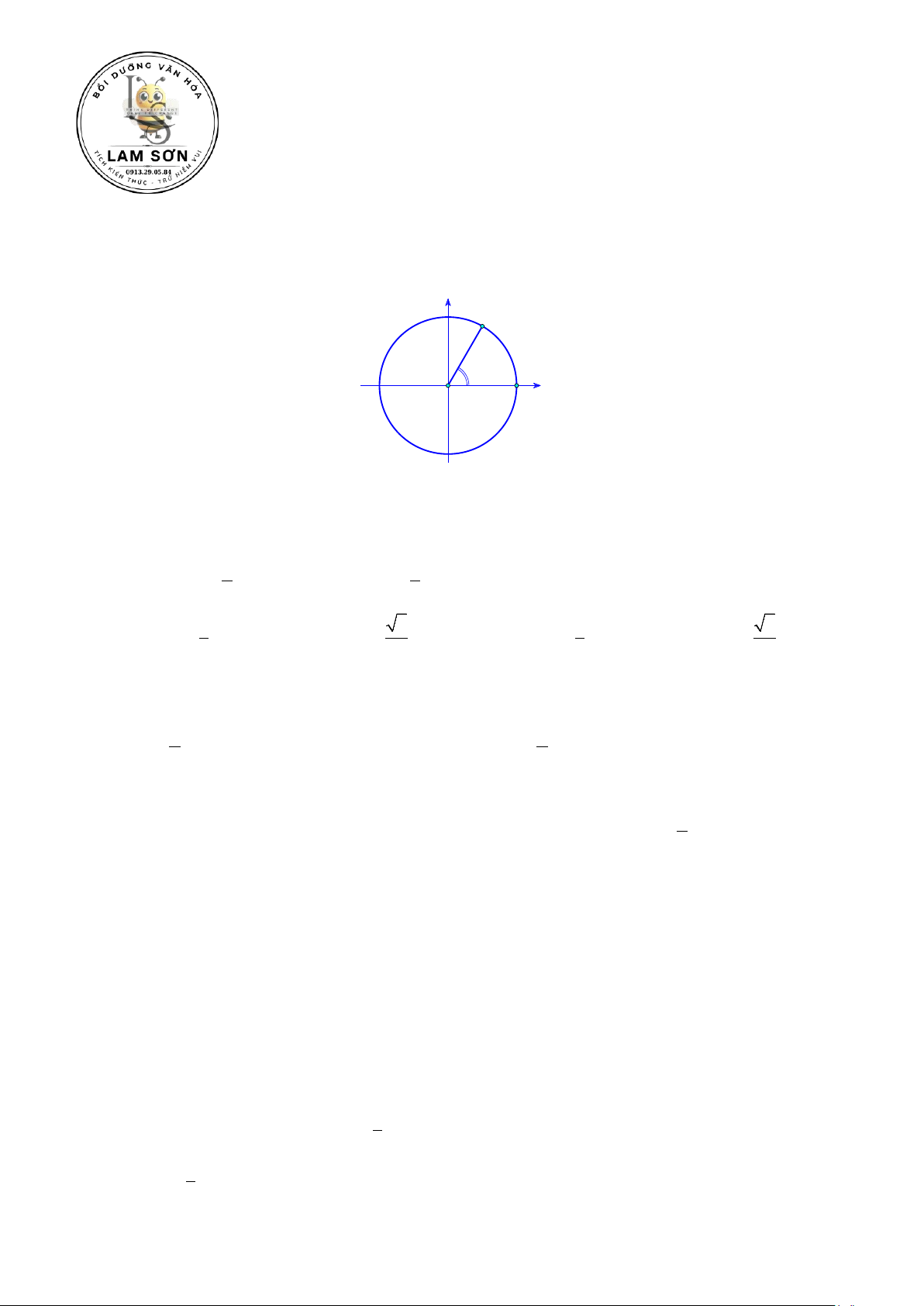
Câu 1: Cho điểm M trên đường tròn lượng giác như hình vẽ: y M 60o x O A
Mệnh đề nào sau đây đúng? A.  ;
OA OM   60  k360 , k   . B.  ;
OA OM   60  k180 , k   . C.  ;
OA OM   60  k180 , k   . D.  ;
OA OM   60  k360 , k   .   Câu 2: Cho góc
  ; thỏa mãn 2 
sin  . Tính cos .  2  3 A. 1 cos  . B. 5 cos  . C. 1
cos   . D. 5 cos   . 3 3 3 3
Câu 3: Công thức nào dưới đây đúng? A. 2 2
sin  cos  2 .
B. cos  cos.     C.
sin    cos . D.   .
tan    cot  2   2 
Câu 4: Chu kỳ tuần hoàn của hàm số y  cosx là A. 2. B. . C. 4. D. . 2
Câu 5: Phương trình sin2x  1 có bao nhiêu nghiệm thuộc đoạn  ; 2    ? A. 3 . B. 1 . C. 4 . D. 2 . u  1
Câu 6: Cho dãy số u , biết  1 
với n  1. Ba số hạng đầu tiên của dãy số đó lần lượt là n  uu  4  n1 n
những số nào dưới đây? A. 1;4;7. B. 1;3;5. C. 1;4;6 . D. 1;3;7.
Câu 7: Cho cấp số cộng u có: u  0,1; d  0,1. Số hạng thứ 7 của cấp số cộng này là n  1 A. 1,6 . B. 6 . C. 0,5 . D. 0,6 .
Câu 8: Cho cấp số nhân  1
u với u   ; u  32 . Tìm q ? n  1 7 2 A. 1 q   . B. q  2 . C. q  4 . D. q  1 . 2
Câu 9: Trong các khẳng định sau, khẳng định nào đúng?
A. Qua 2 điểm phân biệt có duy nhất một mặt phẳng. 1
B. Qua 3 điểm phân biệt bất kì có duy nhất một mặt phẳng.
C. Qua 3 điểm không thẳng hàng có duy nhất một mặt phẳng.
D. Qua 4 điểm phân biệt bất kì có duy nhất một mặt phẳng.
Câu 10: Cho hai đường thẳng phân biệt không có điểm chung cùng nằm trong một mặt phẳng thì hai đường thẳng đó A. song song. B. chéo nhau. C. cắt nhau. D. trùng nhau.
Câu 11: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O , M là trung điểm SA. Khẳng
định nào sau đây là đúng?
A. OM//SCD .
B. OM//S D B  .
C. OM//SAB .
D. OM//SAD.
Câu 12: Có bao nhiêu mặt phẳng song song với cả hai đường thẳng chéo nhau? A. Vô số. B. 3 . C. 2 . D. 1 .
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai. Câu 1: Cho tan x  4 với  x . 2 a) Giá trị của  cos x là 1 . 4
b) Giá trị của tan 2x là 8 . 15  
c) Giá trị của tanx    là 3 .  4  5
d) Giá trị của biểu thức
2 sin x  5 cos x A  là 13.
3 cos x  sin x  
Câu 2: Cho hàm số lượng giác y 2 sin  2x     2m  1.  3 
a) Hàm số có tập xác định D   .
b) Với m  0 hàm số có tập giá trị T  3;1     .
c) Với m  2 hàm số luôn có giao điểm với trục Ox .
d) Có 3 giá trị nguyên của tham số m để đường thẳng y  3 cắt đồ thị hàm số.
Câu 3: Một sinh viên sau khi ra trường và xin vào làm cho một trung tâm với mức lương khởi điểm là
120 triệu đồng một năm. Cứ sau mỗi năm, trung tâm trả thêm cho sinh viên 24 triệu đồng. Gọi
u là số tiền lương mà sinh viên đó nhận được ở năm thứ n . n
a) Số tiền lương sinh viên nhận được ở năm thứ hai là 144 triệu đồng.
b) Số tiền lương sinh viên nhận được ở năm thứ 10 là 330 triệu đồng.
c) Dãy số u là cấp số cộng có u  120 và công sai d  20. n  1
d) Giả sử, mỗi năm bạn sinh viên chi tiêu tiết kiệm hết 70 triệu đồng. Vậy sau ít nhất 10 năm
thì sinh viên đó mua được căn chung cư 2 tỉ đồng.
Câu 4: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và O là giao điểm của hai đường chéo
của hình bình hành ABCD . Gọi M,N lần lượt là trung điểm của SA và SD . Khi đó:
a) Điểm O là điểm chung của OMN  và ABCD  .
b) MN //BC .
c) OM //SBC  .
d) Giao tuyến của OMN  và SBC  là đường thẳng d song song với hai đường thẳng MN và BC . 2
PHẦN III. Câu trắc nghiệm trả lời ngắn Câu 1: Biết 2 x   x  2 sin 4 cot
 cos x 1  3 tan x   a sin x b cosx .Tính a b ?
Câu 2: Biết với mọi x thì 6 6
sin x  cos x a b cos 4x a;b Q  . Tính a b    
Câu 3: Phương trình 3 sin2x  sin  
có tổng các nghiệm thuộc khoảng bằng   x    0;a.. Tìm  4     4  a ?
Câu 4: Cho một cấp số cộng u có số hạng đầu u  1 và tổng của 100 số hạng đầu bằng 24850 . Khi n  1 đó 1 1 1 1 1 a S     ...  
 , trong đó a là phân số tối giản và * a,b   u .u u .u u .u u .u u .u b b 1 2 2 3 3 4 28 29 29 30
. Tính tổng a b .
Câu 5: Cho hình chóp S.ABC. Gọi M, N lần lượt là trung điểm của SA và BC ; P là điểm thuộc cạnh AP AB sao cho 2
 . Đường thẳng SC cắt mặt phẳng MNP  tại Q . Biết tỉ số SQ a  , trong AB 3 SC b
đó a là phân số tối giản và *
a,b   . Tổng 2 2
a b bằng bao nhiêu? b
Câu 6: Cho lăng trụ ABCD.AB CD
  có đáy ABCD là hình vuông, AB  1;AA  2 . Gọi L là trung điểm B D
 , mặt phẳng P  qua L và song song AC lần lượt cắt AA ;CC ;DD tại E;F;K . Đặt DK x
x . Khi EFK //MAC  thì 2025 P
bằng bao nhiêu? (Làm tròn đến hàng phần DD 1005 trăm). --------HẾT-------- 3 HƯỚNG DẪN GIẢI
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu
hỏi thí sinh chỉ chọn một phương án.
Câu 1: Cho điểm M trên đường tròn lượng giác như hình vẽ: y M 60o x O A
Mệnh đề nào sau đây đúng? A.  ;
OA OM   60  k360 , k   . B.  ;
OA OM   60  k180 , k   . C.  ;
OA OM   60  k180 , k   . D.  ;
OA OM   60  k360 , k   . Lời giải Ta có  ;
OA OM   60  k360 , k   .   Câu 2: Cho góc
  ; thỏa mãn 2 
sin  . Tính cos .  2  3 A. 1 cos  . B. 5 cos  . C. 1
cos   . D. 5 cos   . 3 3 3 3 Lời giải Ta có 4 5 2 2 2 2
sin  cos  1  cos  1  sin  1   5  cos   . 9 9 3   Do
  ; nên 5 
cos  0  cos   .  2  3
Câu 3: Công thức nào dưới đây đúng? A. 2 2
sin  cos  2 .
B. cos  cos.     C.
sin    cos . D.   .
tan    cot  2   2  Lời giải   Ta có
sin    cos .  2 
Câu 4: Chu kỳ tuần hoàn của hàm số y  cosx là A. 2. B. . C. 4. D. . 2 Lời giải
Chu kỳ tuần hoàn của hàm số y  cosx là 2.
Câu 5: Phương trình sin2x  1 có bao nhiêu nghiệm thuộc đoạn  ; 2    ? A. 3 . B. 1 . C. 4 . D. 2 . Lời giải Ta có
sin 2x  1  2x    k2x    k k  . 2 4 Xét trên đoạn  3 9 ; 2    :
  x  2
    k  2   k  4 4 4
Mà k    k  0;1;2. 4
Vậy phương trình có 3 nghiệm thuộc đoạn  ; 2    . u  1
Câu 6: Cho dãy số u , biết  1 
với n  1. Ba số hạng đầu tiên của dãy số đó lần lượt là n  uu  4  n1 n
những số nào dưới đây? A. 1;4;7. B. 1;3;5. C. 1;4;6 . D. 1;3;7. Lời giải
Ta có u  1 , u u  4  3, u u  4  7 . 1 2 1 3 2
Vậy ba số hạng đầu tiên của dãy là: 1;3;7 .
Câu 7: Cho cấp số cộng u có: u  0,1; d  0,1. Số hạng thứ 7 của cấp số cộng này là n  1 A. 1,6 . B. 6 . C. 0,5 . D. 0,6 . Lời giải
Số hạng tổng quát của cấp số cộng  1
u là: u u n  1 .0,1  u  0,1  7  1 .0,1  . n 1   7   n  2
Câu 8: Cho cấp số nhân  1
u với u   ; u  32 . Tìm q ? n  1 7 2 A. 1 q   . B. q  2 . C. q  4 . D. q  1 . 2 Lời giải
Áp dụng công thức số hạng tổng quát cấp số nhân ta có q  2 n 1  6 6 u u q u u .q q 64        . n 1 7 1 q  2 
Câu 9: Trong các khẳng định sau, khẳng định nào đúng?
A. Qua 2 điểm phân biệt có duy nhất một mặt phẳng.
B. Qua 3 điểm phân biệt bất kì có duy nhất một mặt phẳng.
C. Qua 3 điểm không thẳng hàng có duy nhất một mặt phẳng.
D. Qua 4 điểm phân biệt bất kì có duy nhất một mặt phẳng. Lời giải
Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng cho trước.
Câu 10: Cho hai đường thẳng phân biệt không có điểm chung cùng nằm trong một mặt phẳng thì hai đường thẳng đó A. song song. B. chéo nhau. C. cắt nhau. D. trùng nhau. Lời giải
Câu 11: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O , M là trung điểm SA. Khẳng
định nào sau đây là đúng?
A. OM//SCD  .
B. OM//SBD .
C. OM//SAB .
D. OM//SAD . Lời giải
Ta có: M là trung điểm SA ; O là trung điểm AC OM là đường trung bình SAC .  OM / /SC . 5 Mà
SC  SCD  OM    SCD 
OM //SCD
Câu 12: Có bao nhiêu mặt phẳng song song với cả hai đường thẳng chéo nhau? A. Vô số. B. 3 . C. 2 . D. 1 . Lời giải
Gọi hai đường thẳng chéo nhau là a và b , c là đường thẳng song song với a và cắt b .
Gọi mặt phẳng    ,bc. Do a//c a//
Giả sử mặt phẳng // mà b    b//
Mặt khác a//  a// . Có vô số mặt phẳng //
nên có vô số mặt phẳng song song với cả hai đường thẳng chéo nhau.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai. Câu 1: Cho tan x  4 với  x . 2 a) Giá trị của  cos x là 1 . 4
b) Giá trị của tan 2x là 8 . 15  
c) Giá trị của tanx    là 3 .  4  5
d) Giá trị của biểu thức
2 sin x  5 cos x A  là 13.
3 cos x  sin x Lời giải
a) Sai | b) Đúng| c) Sai| d) Đúng a) Sai Ta có 1  17 2
 tan x  1  17  cos x  2 cos x 17 b) Đúng 2 tan x 2.4 Ta có 8 tan 2x    2 1  tan x 1  42 15 c) Sai tan x  tan   Ta có 4  1 5   4 tanx      .  4  1  1.4 3 1  tan x. tan 4 d) Đúng sin x cos x 2  5
2 sin x  5 cos x 2 tan x  5 2.4  5 Ta có: cos x cos x A      . x x x xx    13 3 cos sin cos sin 3 tan 3 4 3  cos x cos x 6  
Câu 2: Cho hàm số lượng giác y 2 sin  2x     2m  1.  3 
a) Hàm số có tập xác định D   .
b) Với m  0 hàm số có tập giá trị T  3;1     .
c) Với m  2 hàm số luôn có giao điểm với trục Ox .
d) Có 3 giá trị nguyên của tham số m để đường thẳng y  3 cắt đồ thị hàm số. Lời giải
a) Đúng | b) Đúng| c) Sai| d) Đúng a) Đúng
Hàm số có tập xác định là D   . b) Đúng   Với
m  0 hàm số trở thành y 2 sin  2x     1.  3    Ta có: 1 sin   2x     1  3    2 2 sin    2x     2 .  3    3 2 sin    2x     1  1.  3 
Vậy tập giá trị của hàm số là T  3;1     . c) Sai   Với
m  2 hàm số trở thành y 2 sin  2x     3 .  3 
Số giao điểm với trục Ox là số nghiệm của phương trình hoành độ giao điểm của hai hàm số:  
y  2sin2x     3     3  y  0   
Khi đó ta có phương trình: 2 sin2x     3  0  3    3 sin  2x      .  3  2
Vậy hàm số không có giao điểm với trục Ox . d) Đúng   Đường thẳng
y  3 cắt đồ thị hàm sốy 2 sin  2x
   2m  1 khi phương trình hoành độ  3   
y  2sin2x     2m  1 giao điểm     3  có nghiệm. y  3    2 sin  2x
   2m  1  3 có nghiệm.  3    sin  2x
   2  m có nghiệm.  3 
Phương trình trên có nghiệm khi 2  m  1 1  2  m  1  1  m  3
Suy ra m  1;2;3.
Vậy có 3 giá trị nguyên của tham số m để đường thẳng y  3 cắt đồ thị hàm số. 7
Câu 3: Một sinh viên sau khi ra trường và xin vào làm cho một trung tâm với mức lương khởi điểm là
120 triệu đồng một năm. Cứ sau mỗi năm, trung tâm trả thêm cho sinh viên 24 triệu đồng. Gọi
u là số tiền lương mà sinh viên đó nhận được ở năm thứ n . n
a) Số tiền lương sinh viên nhận được ở năm thứ hai là 144 triệu đồng.
b) Số tiền lương sinh viên nhận được ở năm thứ 10 là 330 triệu đồng.
c) Dãy số u là cấp số cộng có u  120 và công sai d  20. n  1
d) Giả sử, mỗi năm bạn sinh viên chi tiêu tiết kiệm hết 70 triệu đồng. Vậy sau ít nhất 10 năm
thì sinh viên đó mua được căn chung cư 2 tỉ đồng. Lời giải
a) Đúng | b) Sai| c) Sai| d) Sai a) Đúng.
Ta thấy, số tiền lương năm sau hơn năm trước 24 triệu đồng nên số tiền lương hằng năm u n
là cấp số cộng có u  120 và công sai d  24 . Do đó: 1
u u n  1 d  120  n  1 .24  24n  96 n 1    
Số tiền lương sinh viên nhận được ở năm thứ hai là u  144 . 2
Vậy mệnh đề a) là Đúng. b) Sai.
Số tiền lương sinh viên nhận được ở năm thứ 10 là u  24.10  96  336 . 10
Vậy mệnh đề b) là Sai. c) Sai.
Mệnh đề c) là sai vì d  24 . d) Sai.
Tổng số tiền bạn sinh viên tiết kiệm được sau n năm là: n n S
2u  n  1d   70n  2.120  n  1 2
.24   70n  12n  38n  1 2  2   . n  11,42 Ta có: S  2000 2 12n 38n 2000 0        . n  14, 59 
Do đó sau ít nhất sau 12 năm thì sinh viên đó có thể mua được chung cư 2 tỉ đồng.
Vậy mệnh đề d) là Sai.
Câu 4: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và O là giao điểm của hai đường chéo
của hình bình hành ABCD . Gọi M,N lần lượt là trung điểm của SA và SD . Khi đó:
a) Điểm O là điểm chung của OMN  và ABCD  .
b) MN //BC .
c) OM //SBC  .
d) Giao tuyến của OMN  và SBC  là đường thẳng d song song với hai đường thẳng MN và BC . Lời giải
a) Đúng | b) Đúng| c) Đúng| d) Sai 8

Tài liệu liên quan: