10 Đề Kiểm Tra Giữa HK1 Toán 9 Cánh Diều Có Đáp Án Chi Tiết
Một người đi xe máy từ địa điểm A đến địa điểm B cách nhau 60km. Khi từ B trở về A, do trời mưa người đó giảm tốc độ 10km/h so với lúc đi nên thời gian về nhiều hơn thời gian đi là 30 phút. Tính tốc độ lúc về của người đó. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Chủ đề: Đề giữa HK1 Toán 9 294 tài liệu
Môn: Toán 9 2.6 K tài liệu
Sách: Cánh diều
Tác giả:
Preview text:
ĐỀ 1
ĐỀ KIỂM TRA GIỮA HỌC KỲ I MÔN: TOÁN 9 Thời gian: 90 phút
I. Trắc nghiệm (3,0 điểm)
Câu 1: Trong các phương trình sau phương trình nào không phải là phương trình bậc nhất hai ẩn?
A. 2x + 3y = 5
B. 0x + 2y = 4
C. 2x − 0y = 3
D. 0x + 0y = 6
Câu 2: Trong các hệ hai phương trình bậc nhất hai ẩn sau, hệ phương trình nào nhận cặp số (−1;−2) là nghiệm? 1
2x − 3y = 6 −
0,2x − 3y = 0,7 −x + y =1 x + 3y = 2 A. B. C. D. 5 − x = 5
−x − 0,8y = 2 3 x + y = 2 − 3 1x + 5y = 1 −
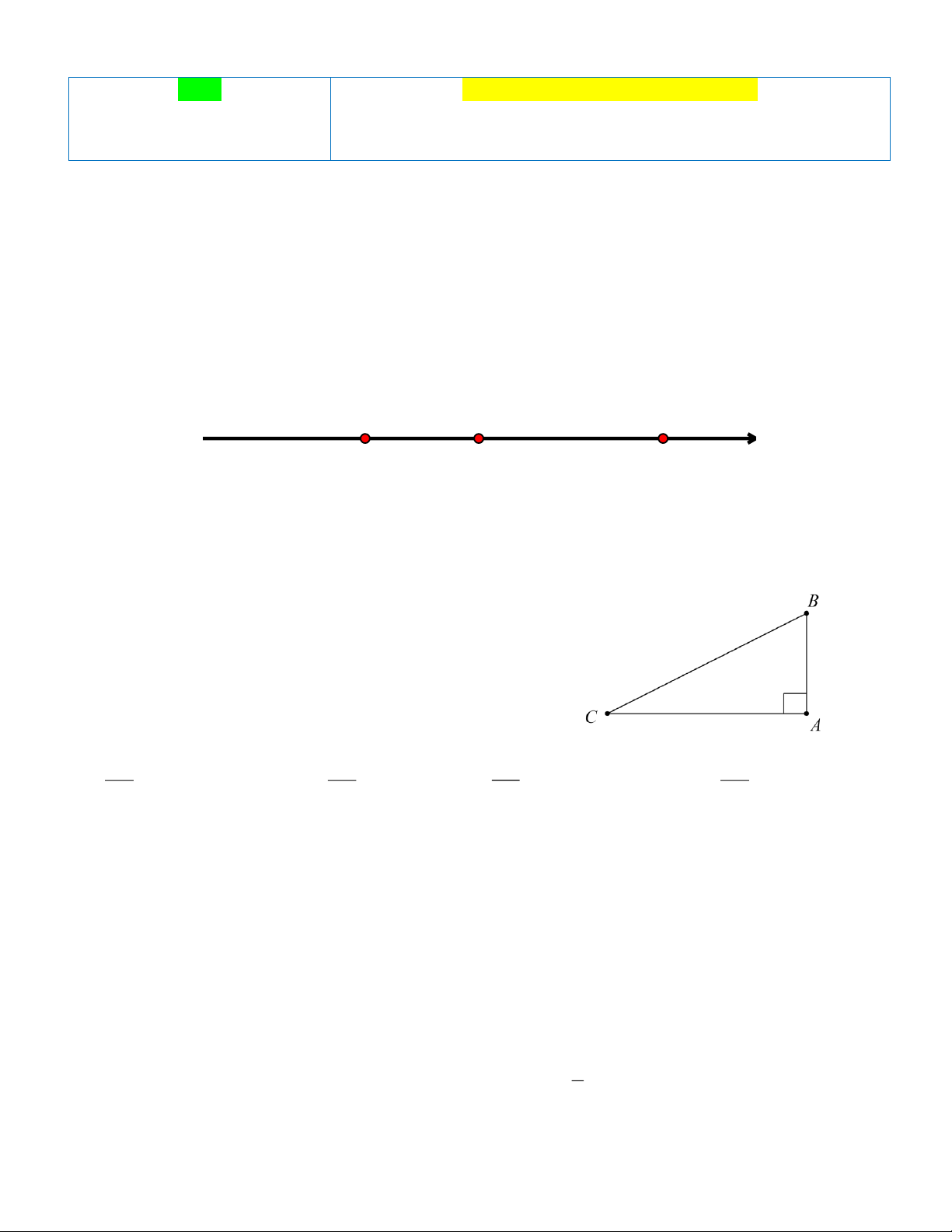
Câu 3: Cho hai số a, b được biểu diễn trên trục số như Hình 1 Phát biểu nào sau đây là đúng? a O b Hình 1
A. a b vµ b 0 . B. 0 b vµ b a . C. a 0 0 vµ b . D. 0 a a vµ b .
Câu 4: Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn? A. 2 2
− x + 5 0 .
B. 3x − y 0 .
C. −4x − 2 0 .
D. 5 + 0x −7 .
Câu 5: Cho tam giác A BC vuông tại A như Hình 2. Ta có sin B bằng Hình 2 A. AB . B. AC . C. AB . D. AC . AC AB BC BC
Câu 6: Khẳng định nào sau đây là đúng khi nói về trục đối xứng của đường tròn
A. Đường tròn không có trục đối xứng
B. Đường tròn có duy nhất một trục đối xứng là đường kính
C. Đường tròn có hai trục đối xứng là hai đường kính vuông góc với nhau
D. Đường tròn có vô số trục đối xứng là đường kính x − 3y = 2 −
Câu 7: Cho hệ phương trình 2x + 3y = 2
Sử dụng máy tính cầm tay Casio tìm nghiệm đúng của hệ phương trình đã cho trong các cặp số dưới đây 2 A. ( 1; ) 1 . B. (0; ) 1 . C. 0; . D. (4;5) . 3 Trang 5 x − 2y =1
Câu 8: Cho hệ phương trình 2x − 4y = 2
Nghiệm của hệ phương trình đã cho A. (0;− ) 1 . B. vô số nghiệm. C. (3;−5) . D. vô nghiệm.
Câu 9: Cho a là số dương, kết luận nào sau đây không đúng?
A. −4a 2a .
B. 3a 15a .
C. 24a 6a .
D. 5a 10a.
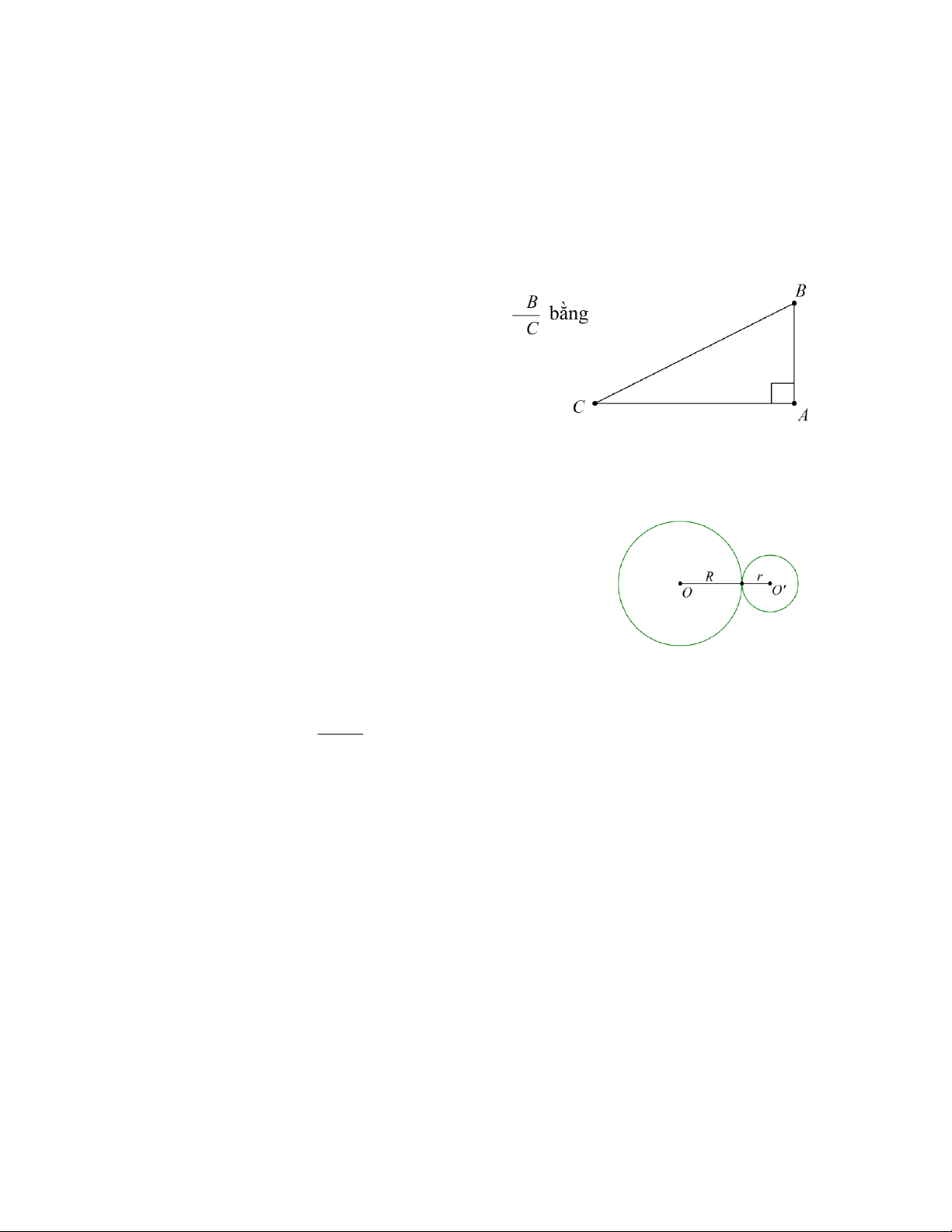
Câu 10: Cho ABC vuông tại A như Hình 3 Tỉ số AB bằng AC Hình 3 A. tan B . B. cotC . C. tan C . D. sin C .
Câu 11: Cho hai đường tròn (O R) vµ( ' ,
O , r ) như Hình 4
Hệ thức nào sau đây là đúng Hình 4
A. OO ' = R − r 0 .
B. OO ' R + r .
C. 0 OO ' R − r . D. OO ' = R + r . −
Câu 12: Cho phương trình 2x 5 = 3 (x 5 − ) x + 5
Trong các số dưới đây số nào là nghiệm của phương trình đã cho A. −5 B. 5 C. −20 D. 15
II. Tự luận (7 điểm)
Câu 13. (1,0 điểm). Viết bất đẳng thức để mô tả tình huống sau:
a) Bạn An ít nhất 18 tuổi mới được đi bầu cử đại biểu Quốc hội.
b) Một thang máy chở được tối đa 700kg.
c) Bạn phải mua hàng có tổng trị giá ít nhất 1 triệu đồng mới được giảm giá.
d) Bạn ném vào rổ ít nhất 5 quả bóng mới vào được đội tuyển bóng rổ.
Câu 14. (1,0 điểm). Cân bằng phương trình hóa học sau bằng phương pháp đại số: Trang 6
CO + C → CO 2
Câu 15. (2,0 điểm). Giải phương trình và bất phương trình sau: x − 3 1− 2x
a) (2 − 3x)(4x + 5) = 0 b) 6 − 5 5
Câu 16. (1,0 điểm).
a) Vì sao nói cặp số (2; 3) là nghiệm của phương trình 2x − 3y = −5 ? 3 x − 4y =1
b) Giải hệ phương trình sau: 4x − 3y = 8 −
Câu 17. (1,0 điểm).
a) Hãy giải thích tại sao 0 0 0 0
sin 35 = cos55 ; tan 35 = cot 55 .
b) Cho tam giác A BC vuông tại A có cạnh huyền bằng 20 cm, 0
B = 36 . Hãy giải thích vì sao
AB 16,18cm .
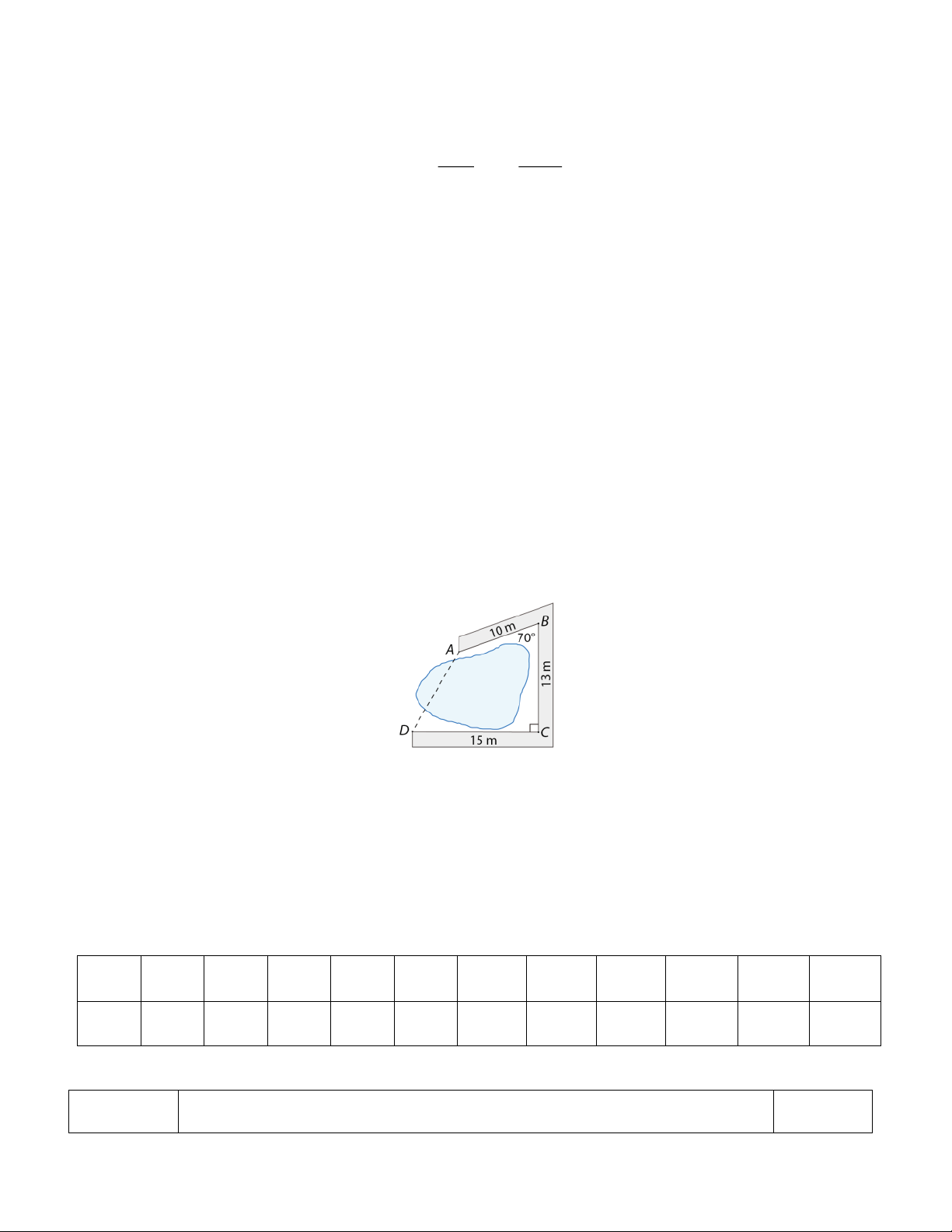
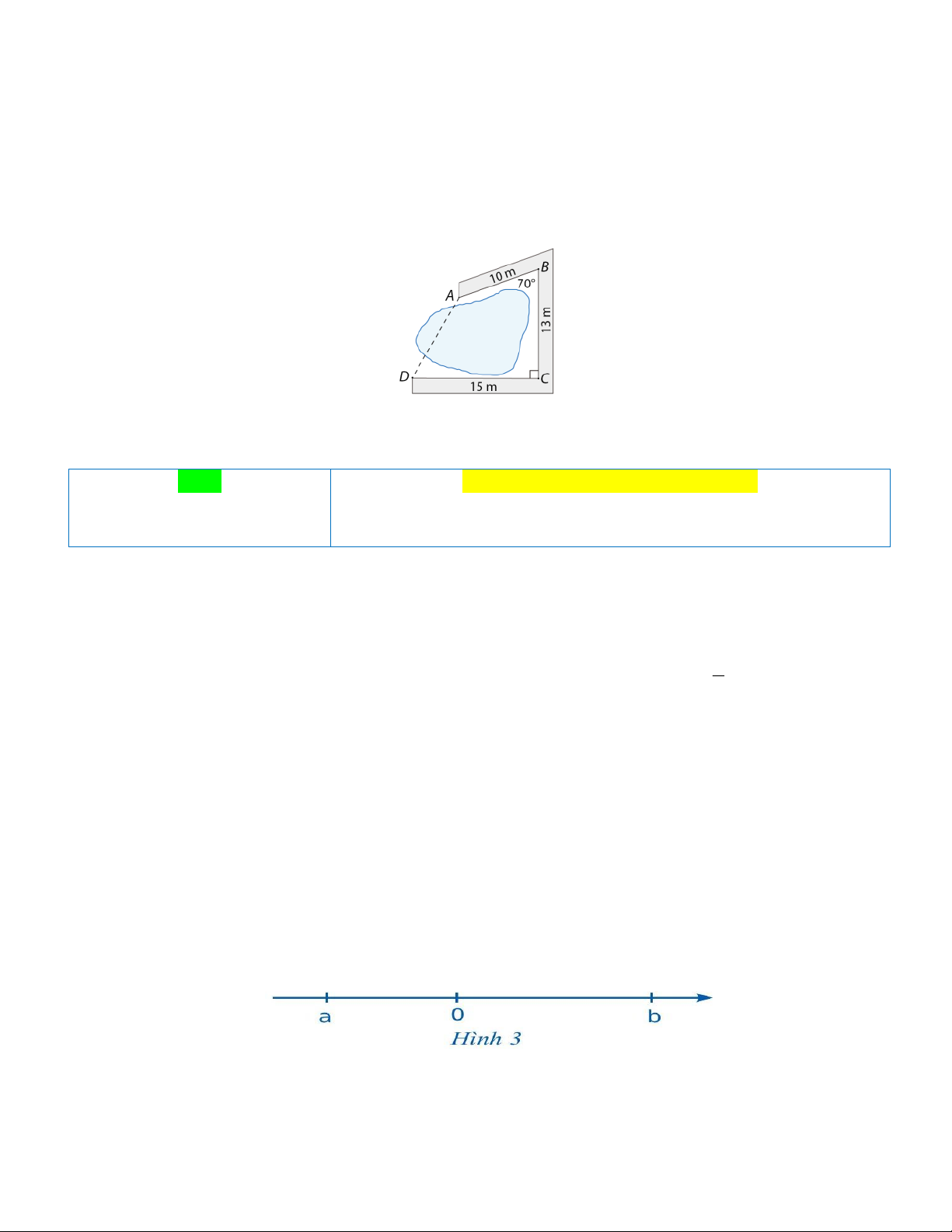
Câu 18. (1 điểm). Người ta làm một con đường gồm ba đoạn thẳng A B, BC ,CD bao quanh hồ
nước (Hình 5). Tính khoảng cách A D . (làm tròn kết quả đến chữ số thập phân thứ 2). Hình 5
-------- Hết --------
ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM
I. Trắc nghiệm (3,0 điểm)
Mỗi câu đúng 0,25 điểm 1 2 3 4 5 6 7 8 9 10 11 12 D A C C D D C B B C D C
II. Tự luận (7 điểm) Câu Nội dung Điểm Trang 7 Câu 13.
Viết bất đẳng thức để mô tả tình huống sau: (1,0 điểm)
a) Gọi số tuổi của bạn An là x (tuổi), * x N 0,25
Bất đẳng thức để mô tả bạn An ít nhất 18 tuổi mới được đi bầu cử đại
biểu Quốc hội là: x 18
b) Gọi khối lượng thang máy chở được là a (kg) , a 0
Bất đẳng thức để mô tả một thang máy chở được tối đa 700kg là: 0,25 0 a 700
c) Gọi số tiền mua hàng là x (triệu đồng), x 0
Bất đẳng thức để mô tả bạn phải mua hàng có tổng trị giá ít nhất 1 triệu 0,25
đồng mới được giảm giá là x 1
d) Gọi số quả bóng bạn ném vào rổ là x (quả bóng), * x N
Bất đẳng thức để mô tả bạn ném vào rổ ít nhất 5 quả bóng mới vào 0,25
được đội tuyển bóng rổ là: x 5 Câu 14.
Cân bằng phương trình hóa học sau bằng phương pháp đại số:
(1,0 điểm) CO +C → CO 2 Giải
Gọi x, y lần lượt là hệ số của CO và CO thỏa mãn cân bằng phương 2
trình hóa học xCO + C → yCO , điều kiện *
x, y N 0,25 2
Theo định luật bảo toàn nguyên tố đối với C vµ O , ta có: x +1 = y 2x = y 0,25 x − y = 1 − 2x − y = 0 −x = 1 − 2x − y = 0 x =1 2.1− y = 0 x =1 (tháa m·n) y = 2 (tháa m·n) 0,25
Vậy ta được phương trình hóa học cân bằng là CO + C → 2CO 2 0,25 Câu 15. Giải PT và BPT sau:
(2,0 điểm) a) (2 −3x)(4x + 5) = 0
* 2 − 3x = 0 * 4x + 5 = 0 0,25 Trang 8
2 = 3x 4x = −5 0,25 2 5 x = x = − 3 4 2 5 0,25 Vậy x = vµ x = − 3 4 x − 3 1− 2x b) 6 − 5 5
x − 3 65 1− 2x − 5 5 5 0,25
x − 3 30 −1+ 2x 0,25
x − 2x 30 −1+ 3 −x 42 0,25 x 42 0,25
Vậy nghiệm của bất phương trình đã cho là x 42 0,25 − = − Câu 16.
a) Vì sao nói cặp số (2; 3) là nghiệm của phương trình 2x 3y 5? (1,0 điểm) Giải Vì khi thay x = 2
vµ y = 3 vào phương trình 2x − 3y = 5 − ta được: 0,25 2 2 − 33 = −5
Vậy cặp số (2; 3) là nghiệm của phương trình đã cho 3 x − 4y =1 b) 4x − 3y = 8 − 1
2x −16y = 4 1 2x −9y = 2 − 4 0,25 3 x − 4y =1 7 − y = 28 3 x − 4( 4 − ) =1 y = 4 − 3 x +16 =1 y = 4 − 3 x = 1 − 5 y = 4 − x = 5 − 0,25 y = 4 −
Vậy hệ phương trình có nghiệm duy nhất là ( ; x y) = ( 5 − ; 4) − 0,25 Câu 17.
a) Hãy giải thích tại sao trong một tam giác vuông (1,0 điểm) 0 0 0 0
sin 35 = cos55 ; tan 35 = cot 55 Giải Trang 9 Vì 0 0 35 v µ 55 là hai góc phụ nhau 0,25 Nên: 0 0 0 0
sin 35 = cos55 ; tan 35 = cot 55 0,25
b) Cho tam giác A BC vuông tại A C
có cạnh huyền bằng 20 cm, 0 B = 36 .
Hãy giải thích vì sao AB 16,18 cm 20cm Giải
Trong tam giác A BC vuông tại A , ta có 0,25 0 0
AB = BC cos36 = 20cos36 16,18 cm 360 0,25 B A Câu 18.
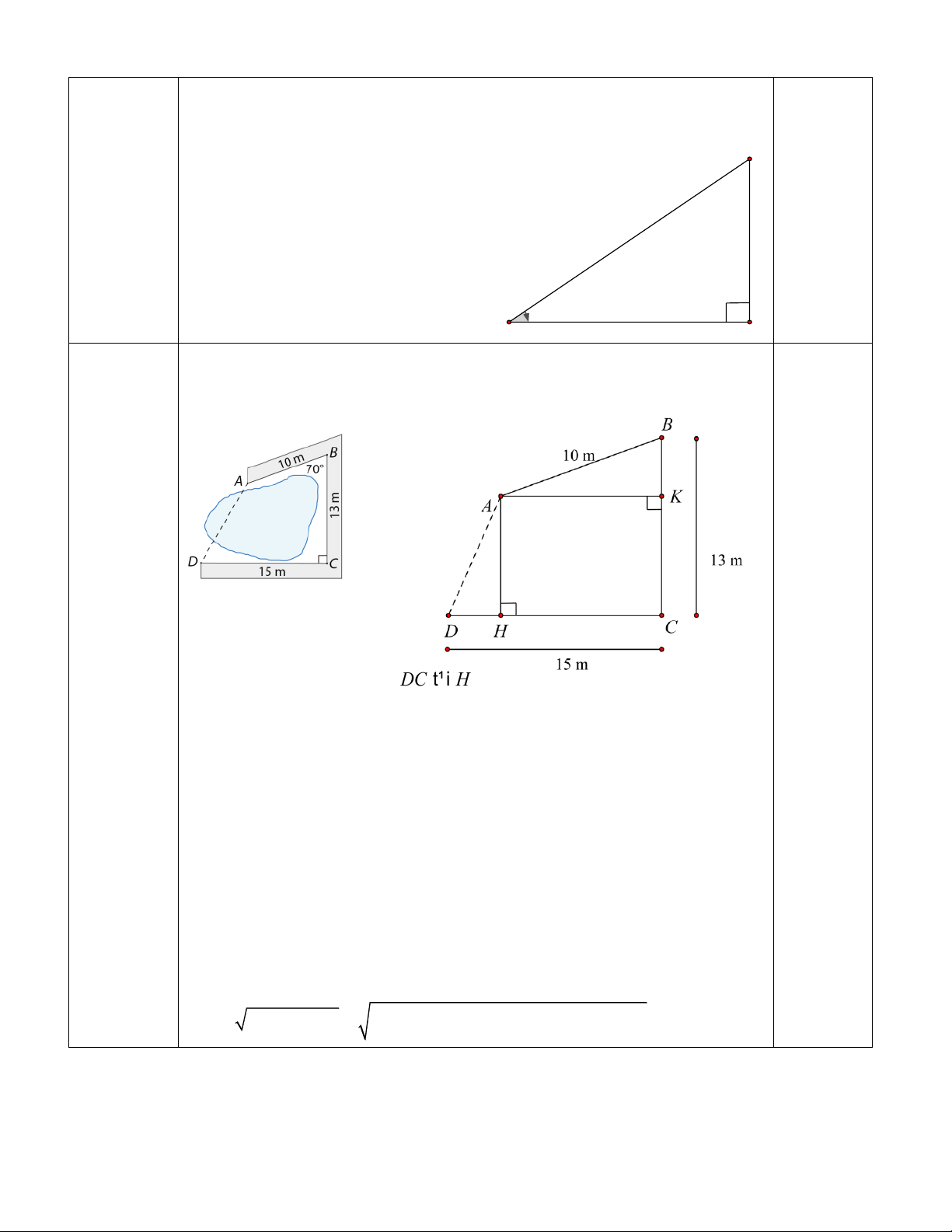
Người ta làm một con đường gồm ba đoạn thẳng A B, BC ,CD bao
(1,0 điểm) quanh hồ nước như hình vẽ sau. Tính khoảng cách A D . 700 Hình 5
Vẽ AK ⊥ BC t¹i K
, AH ⊥ DC t¹i H
Khi đó tứ giác AKCH là hình chữ nhật 0,25
Nên: AK = CH; AH = CK
Trong tam giác vuông AKB vuông tại K có AB = 10cm , · 0 A BK = 70 0 0
AK = AB sin 70 = 10 sin70 Suy ra 0
AK = CH = 10 sin70 Hay 0
DH = CD − HC = 15 −10 sin70 0 0
BK = AB cos70 = 10cos70 0,25 Suy ra 0
CK = CB − BK = 13 −10cos70 Hay 0
AH = CK = 13 −10cos70 0,25
Theo định lí Pytagore trong tam giác vuông ADH
AD = AH + DH = ( − cos )2 +( − sin )2 2 2 0 0 13 10 70 15 10 70 11,1 m 0,25
➢ HS làm cách khác có kết quả đúng vẫn được điểm tối đa. Trang 10 ĐỀ 2
ĐỀ KIỂM TRA GIỮA HỌC KỲ I MÔN: TOÁN 9 Thời gian: 90 phút
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất trong mỗi câu sau vào bài làm.
Câu 1. Phương trình (x − 2)(x + ) 3 = 0 có nghiệm là ? A. x = 2 B. x = −3
C. x = 2 hoặc x = −3
D. x = 2 và x = −3
Câu 2. Điều kiện xác định của phương trình x + 3 x − 2 + = 2 là ? x −1 x A. x ; 0 x 1 B. x = ; 0 x = 1 C. x 0 D. x 1
Câu 3. Các phương trình sau phương trình nào là phương trình bậc nhất hai ẩn x, y? A. 2 x + 3y = 4 B. 2x − y = 3 C. 0x + 0y = 3 D. x + 2 2 y = 0
Câu 4. Trong các cặp số sau cặp số nào là nghiệm phương trình 3x + 2y = 7 . A. (1;-2) B. (1;2) C. (-1;2) D. (2;1) x + 2y = 4
Câu 5. Hệ phương trình có nghiệm là? 3x − 2y = 4 A. ( ; x y) = ( ; 0 2) B. ( ; x y) = ( ; 4 4) C. ( ; x y) = ( ) 1 ; 2 D. ( ; x y) = ( ; 1 2)
Câu 6. Cho a b . Kết quả nào sau đậy là đúng?
A. a + 3 b + 5
B. a − 2 b − 2
C. − 2a − b 2 D. 2a b 3
Câu 7. Cho − 2a − b
2 . Kết quả nào sau đậy là đúng? A. a b
B. a − 2 b −1 C. a b D. 2a b 2
Câu 8. Trong các bất phương trình sau, bất phương trình nào không phải bất phương trình bậc nhất một ẩn? A. 5x + 3 0 B. − 2x + 7 0 C. 3x 0 D. 2 2 x − 5 0
Câu 9. Trong các số sau số nào là nghiệm của bất phương trình 2 − 3x 0 ? A. − 2 B. 2 C. 3 D. 2 2 3
Câu 10. Trong các kết quả so sánh sau. Kết quả nào đúng? A. 3 10 B. 3 − 27 − 4 C. 4 + 3 6 D. 5 3 − 8 = 3
Câu 11: Kết quả thực hiện phép tính 2 − 18 là ? A. − 2 B. − 2 2 C. − 3 2 D. − 4 2
Câu 12: Tìm x để căn thức sau xác định 2 1− 4x ? A. x 0 B. 1 1 −1 1 x C. x D. x 4 2 2 2
PHẦN II. TỰ LUẬN (7,0 điểm)
Bài 1. (2,0 điểm) Rút gọn các biểu thức: Trang 11 2 + 2 2 − 2
a) A = 3 + 12 − 48 b) B = 3− 3 + 2 +1 2 −1
Bài 2. (3,0 điểm)
1) (2,0 điểm) Giải các phương trình và hệ phương trình sau 2x − y = 4
a) (3x − 2)(2x + ) 1 = 0 b) x + 2y = −3
2) (1,0 điểm) Một người đi xe máy từ địa điểm A đến địa điểm B cách nhau 60km. Khi từ
B trở về A, do trời mưa người đó giảm tốc độ 10km/h so với lúc đi nên thời gian về nhiều
hơn thời gian đi là 30 phút. Tính tốc độ lúc về của người đó.
Bài 3. (2,0điểm)
a) Giải bất phương trình sau: x − 3 x −1 x + 2 − 3 6 4
b) Cho a b . Chứng minh 3a + 2 a + 2b +1 -----HẾT----- ĐÁP ÁN
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Mỗi câu đúng được 0,25 điểm
Bảng đáp án trắc nghiệm: Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp D A B A C B D D A D B D án
PHẦN II. TỰ LUẬN (7,0 điểm) Biểu Bài Đáp án điểm
A = 3 + 12 − 48 = 3 + 4 3 . − 16 3 . 0,25 1a = 3 + 22 3 . − 42 3 . 0,25 (1) = 0,25 3 + 2 3 − 4 3 0,25
= (1+ 2 − 4) 3 = − 3 2 + 2 2 − 2 2( 2 + ) 1 2( 2 − ) 1 0,5 b B = 3 − 3 + = 3 − . 3 + 2 +1 2 −1 2 +1 2 −1 (1đ) 0,5
= (3− 2)(.3+ 2)= 9 − 2 = 7
Để giải phương trình đã cho ta giải hai phương trình sau: 0,25 2
*)3x − 2 = 0 3x = 2 x = 0,25 2.1a 3−1 (1đ)
*) 2x +1 = 0 2x = 1 − x = 2 0,25 0,25 Trang 12 2 x = −1
Vậy phương trình đã cho có hai nghiệm là 3 và x = 2 2x − y = 4 4x − 2y = 8 0,25 x + 2y = −3
x + 2y = −3 5x = 5 x = 1 0,25 2.1b x + 2y = −3 1+ 2y = −3 (1đ) x =1 x =1 0,25 2y = −4 y = −2 0,25
Vậy hệ đã cho có nghiệm duy nhất ( ; x y) = ( ; 1 −2)
Gọi tốc độ của xe máy lúc về là x(km/h), x > 0
Tốc độ của xe máy lúc đi là: x + 10 (km/h) 60
Thời gian của xe máy lúc đi là (h) x +10 60
Thời gian của xe máy lúc về là (h) x 0,25
Theo bài ra ta có phương trình: 60 60 1 − = 0,25 x x +10 2 2.2 120x +1200 120x x(x +10) (1đ) − = 2x(x +10)
2x(x +10) 2x(x +10)
120 x +1200 −120 x = x(x +10) 2 x + 10x = 1200 2
x +10x + 25 = 1225 (x + 5)2 = 1225 x + 5 = 35 x = 30 0,25 x + 5 = −35 x = −40
Đối chiếu điều kiện, ta có: x = 30 thỏa mãn. 0,25
Vậy tốc độ của xe máy lúc về là 30km/h. x − 3 x −1 x + 2
4x −12 2x − 2 3x + 6 − − 0,25 3a 3 6 4 12 12 12 0,25
4x −12 − 2x + 2 3x + 6 0,25 (1đ)
−x 16 x 16
Vậy nghiệm của bất phương trình đã cho là x 16 0,25 3b Ta có:
a b 2a b 2 0,25 (1đ) a 3 a + b 2 Trang 13
3a + 2 a + 2b + 2 (1) 0,25
Mà a + 2b + 2 a + 2b +1 (2) 0,25
Từ (1) và (2) suy ra 3a + 2 a + 2b +1 0,25 -----HẾT----- ĐỀ 3
ĐỀ KIỂM TRA GIỮA HỌC KỲ I MÔN: TOÁN 9 Thời gian: 90 phút
A. TRẮC NGHIỆM (3,0 điểm)
Phần 1. Câu trắc nghiệm nhiều phương án lựa chọn. Học sinh trả lời từ câu 1 đến câu 6
và ghi 1 đáp án đúng vào bài làm.
Câu 1. Trong các phương trình sau phương trình nào không phải là phương trình bậc nhất hai ẩn ?
A. 2x - 3y = 5.
B. 0x + 2y = 4.
C. 2x - 0y = 3.
D. 0x - 0y = 6.
Câu 2. Hệ phương trình nào dưới đây là hệ hai phương trình bậc nhất hai ẩn? 2 ìï 2x + 3y = 1
ìï 0, 5x - 0,2y = - 0,1
ìï - 4x + 7y = - 10 ìï x + 3y = 2 A. ï ï ï ï í B. C. D. ï í í í - 3x = 18. 2 2 ï
ï 0x + 0y = - 0, 4.
ï 3x + 8y = - 19.
ï 31x + 5y = - 1. ïî ïî ïî ïî
Câu 3. Trong các hệ hai phương trình bậc nhất hai ẩn sau, hệ phương trình nào nhận cặp số (- 1;- 2) là nghiệm?
ìï 12x - 3y = - 6
ìï 0,2x - 3y = 0, 7 ìï - x + y = 1 ìï x + 3y = 2 A. ï ï ï ï í B. C. D. ï í í í - 5x = 5. ï
ï - x - 0, 8y = 2. ï 3x + y = - 2.
ï 31x + 5y = -1. î ïî ïî ïî
Câu 4. Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn? A. 2
- 2x + 5 > 0 .
B. 3x - y £ 0 .
C. - 4x - 2 < 0 .
D. 5 + 0x ³ - 7 .
Câu 5. Cho hai số a, b được biểu diễn trên trục số như Hình 3. Phát biểu nào sau đây là đúng?
A. a < b và b < 0 .
B. 0 < b và b < a . C. a < 0 và 0 < b .
D. 0 < a và a < b .
Câu 6. Cho tam giác A BC vuông tại A . Ta có sin B bằng AB A C AB AC A. . B. . C. . D. . AC A B BC BC
Phần 2. Câu hỏi trắc nghiệm đúng sai. (Chỉ ghi đúng hoặc sai vào bài làm) Trang 14
Câu 7. Cho a > b. Xét tính đúng/ sai của các khẳng định sau a) a + 2 > b + 2 b) 3.a < 3.b c) -5a < -5b d) a + 3 > b – 2
Phần 3. Câu trắc nghiệm trả lời ngắn.
Câu 8. Giá trị của biểu thức N là bao nhiêu (chỉ ghi đáp án vào bài làm, không cần trình bày lời giải chi tiết) 0 sin 58 0 0 0 0 N =
- cos 60 + tan 37 . tan 53 + sin 30 0 cos 32
B. TỰ LUẬN (7,0 điểm). Câu 9. (1,5 điểm).
1. Viết số nghiệm có thể của một hệ hai phương trình bậc nhất hai ẩn? ìï 3
ï (x - 7) = 4(y - 5)
2. Giải HPT sau: í
ï 4x - 3y + 8 = 0. ïî
Câu 10. (1,0 điểm). Hai người thợ cùng xây một bức tường trong 3 giờ 45 phút thì xong.
Nhưng họ chỉ làm chung trong ba giờ thì người thứ nhất được điều đi làm việc khác, người
thứ hai xây tiếp bức tường còn lại trong 2 giờ nữa thì xong. Hỏi nếu làm một mình thì mỗi
người xây xong bức tường trong bao lâu?
Câu 11. (1,0 điểm). Giải PT và BPT sau: a) x - 3 1 - 2x
(2 - 3x )(4x + 5) = 0 b) < 6 - 5 3
Câu 12. (1,0 điểm). Viết bất đẳng thức để mô tả tình huống sau:
a) Bạn An ít nhất 18 tuổi mới được đi bầu cử đại biểu Quốc hội.
b) Một thang máy chở được tối đa 700kg.
c) Bạn phải mua hàng có tổng trị giá ít nhất 1 triệu đồng mới được giảm giá.
d) Bạn ném vào rổ ít nhất 5 quả bóng mới vào được đội tuyển bóng rổ.
Câu 13. (2,0 điểm).
1. Hãy giải thích tại sao 0 0 0 0
sin 35 = cos 55 ; t an 35 = cot 55 Trang 15
2. Cho tam giác A BC vuông tại A có cạnh huyền bằng 20 cm, µ 36o B = . Hãy giải thích vì
sao A B » 16,18 cm
Câu 14. (0,5 điểm). Người ta làm một con đường gồm ba đoạn thẳng A B,BC ,CD bao
quanh hồ nước như hình vẽ sau. Tính khoảng cách A D .
-------- Hết -------- ĐỀ 4
ĐỀ KIỂM TRA GIỮA HỌC KỲ I MÔN: TOÁN 9 Thời gian: 90 phút
I. TRẮC NGHIỆM (3,0 điểm) Chỉ chọn một chữ cái đứng trước câu trả lời đúng.
Câu 1. Trong các phương trình sau phương trình nào là phương trình bậc nhất hai ẩn ?
A. 2x - 3y = 5. 2 B. 2 x + 2x - 1 = 0. C. 3 2x - 3 = 0. D. - x = 6. x
Câu 2. Hệ phương trình nào dưới đây là hệ hai phương trình bậc nhất hai ẩn? 2 ìï x + y = 3 ìï x - y = 1
ìï - 4x + 7y = - 10 ìï x + 3y = 2 A. ï ï ï ï í B. ï C. D. ï í í í - 3x = 18. 2 2 2 ï ï x - 2y = 0.
ï 3x + 8y = - 19.
ï 31x + 5y = - 1. ïî ïî ïî ïî
ìï 12x - 3y = - 6
Câu 3. Cho hệ phương trình ïí
cặp số nào sau đây là nghiệm của HPT? ï - 5x = 5. ïî A. (- 1;- 2) B. (- 1; ) 2 C. (1;- 2) D. (1; ) 2
Câu 4. Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn? A. 2
- 2x + 5 > 0 .
B. 3x - y £ 0 .
C. 5 + 0x ³ - 7 .
D. - 4x - 2 < 0 .
Câu 5. Cho hai số a, b được biểu diễn trên trục số như Hình 3. Phát biểu nào sau đây là đúng? A. B. C. D.
a < b 0 < b a < 0 0 < a và và và và
b < 0b < a 0 < ba < b . . . . Trang 16
Câu 6. Cho a > b. kết luận nào sau đây không đúng?
A. 2a > 2b .
B. - a < - b .
C. a - b > 0 .
D. a - 2 < b - 2 .
Câu 7. Cho tam giác A BC vuông tại A . Ta có sin B bằng: AB A C AB AC A. . B. . C. . D. . AC A B BC BC Câu 8. µ
Cho tam giác A BC vuông tại A có 0
B = 55 số đo góc C bằng: µ µ µ µ A. 0 C = 35 . B. 0 C = 40 . C. 0 C = 45 . D. 0 C = 50 .
Câu 9. Cho tam giác MNP vuông tại M có MN = 5;MP = 12;NP = 13. cosN = ? 13 5 12 5 A. . B. . C. . D. . 5 13 5 12
Câu 10. Tỉ số lượng giác nào sau đây bằng 0 Sin 40 A. 0 Sin 50 . B. 0 cos 50 . C. 0 t an 50 . D. 0 cot 50 .
Câu 11. Giá trị của 0 sin 30 là bao nhiêu ? A. 0 . B. 1 C. 0, 5 . D. - 0, 5 .
Câu 12. Giá trị của biểu thức 2 0 2 0
sin 25 + cos 25 bằng bao nhiêu ? A. 0 . B. 1 C. 2 . D. 3 .
II. TỰ LUẬN (7,0 điểm).
Câu 13 (NB). (1,0 điểm). 2 5
2. Tìm điều kiện xác định của phương trình = x x - 2 3. Trong các cặp số (6; ) 1 , (2; ) 1 , (- 1;- ) 4 , (0; )
3 , cho biết cặp số nào là nghiệm của phương trình x + y = 3 .
Câu 14 (TH). (1,0 điểm). Cho a > b so sánh
a) a + 1 và b + 1 b) 2a và a + b
Câu 15 (VDT). (1,0 điểm).
Tìm số tự nhiên có hai chữ số, biết rằng tổng các chữ số của nó bằng 14 và nếu đổi
chỗ hai chữ số của nó thì được số nhỏ hơn số ban đầu 18 đơn vị.
Câu 16 (VDT). (1,0 điểm). Giải PT và BPT sau:
a) (3 - 2x)(5x + 4)= 0
b) −3x + 22 −8x +17
Câu 17 (TH). (1,5 điểm). Viết bất đẳng thức để mô tả tình huống sau:
a) Bạn An ít nhất 18 tuổi mới được đi bầu cử đại biểu Quốc hội.
b) Một thang máy chở được tối đa 800kg. Trang 17
c) Giá trị của biểu thức 2x − 3 lớn hơn giá trị biểu thức −7x + 2
Câu 18. (1,5 điểm).
a. Cho tam giác ABC vuông tại A, AB = 6cm; AC = 8cm. Tính độ dài cạnh BC và các tỉ số
lượng giác của góc B? (0,5đ - TH) B
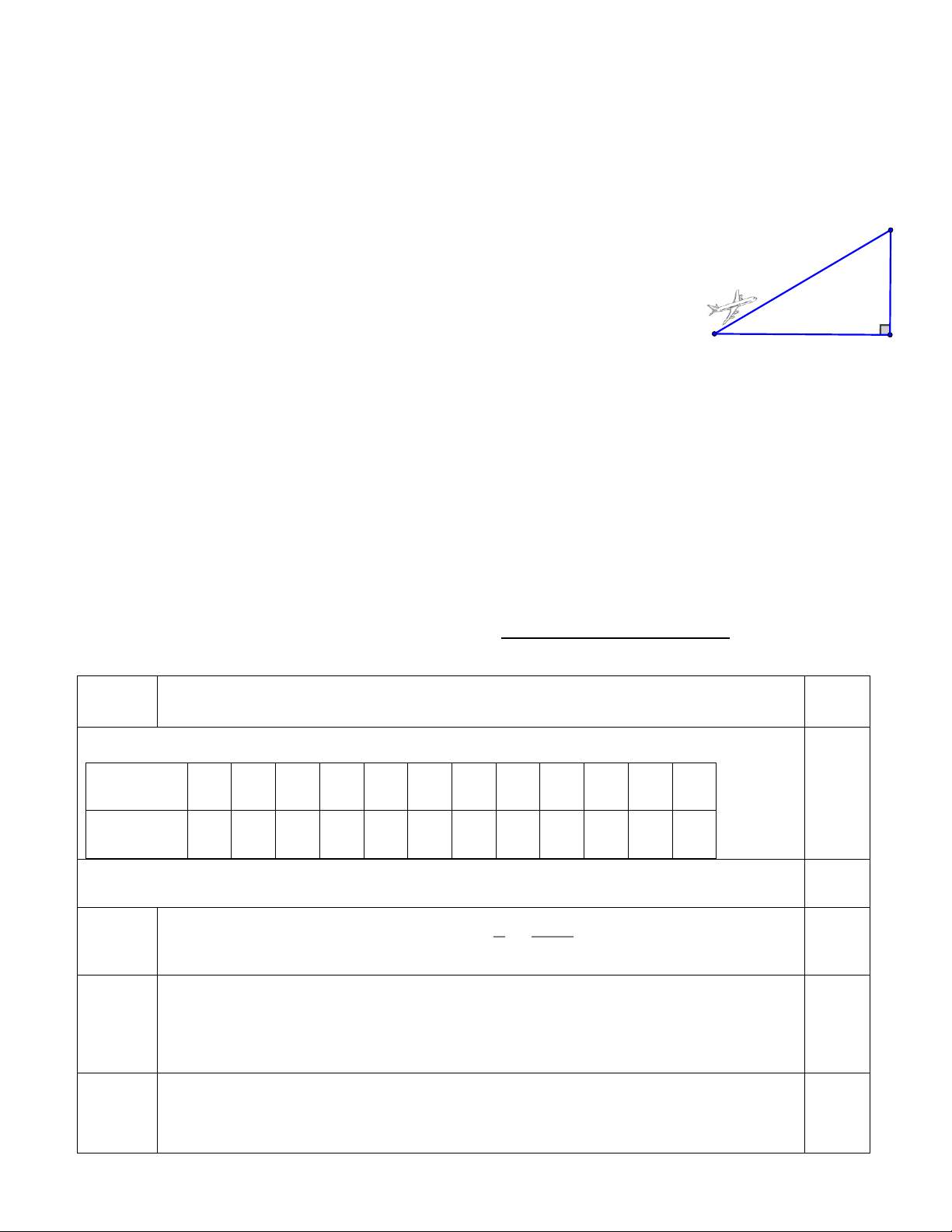
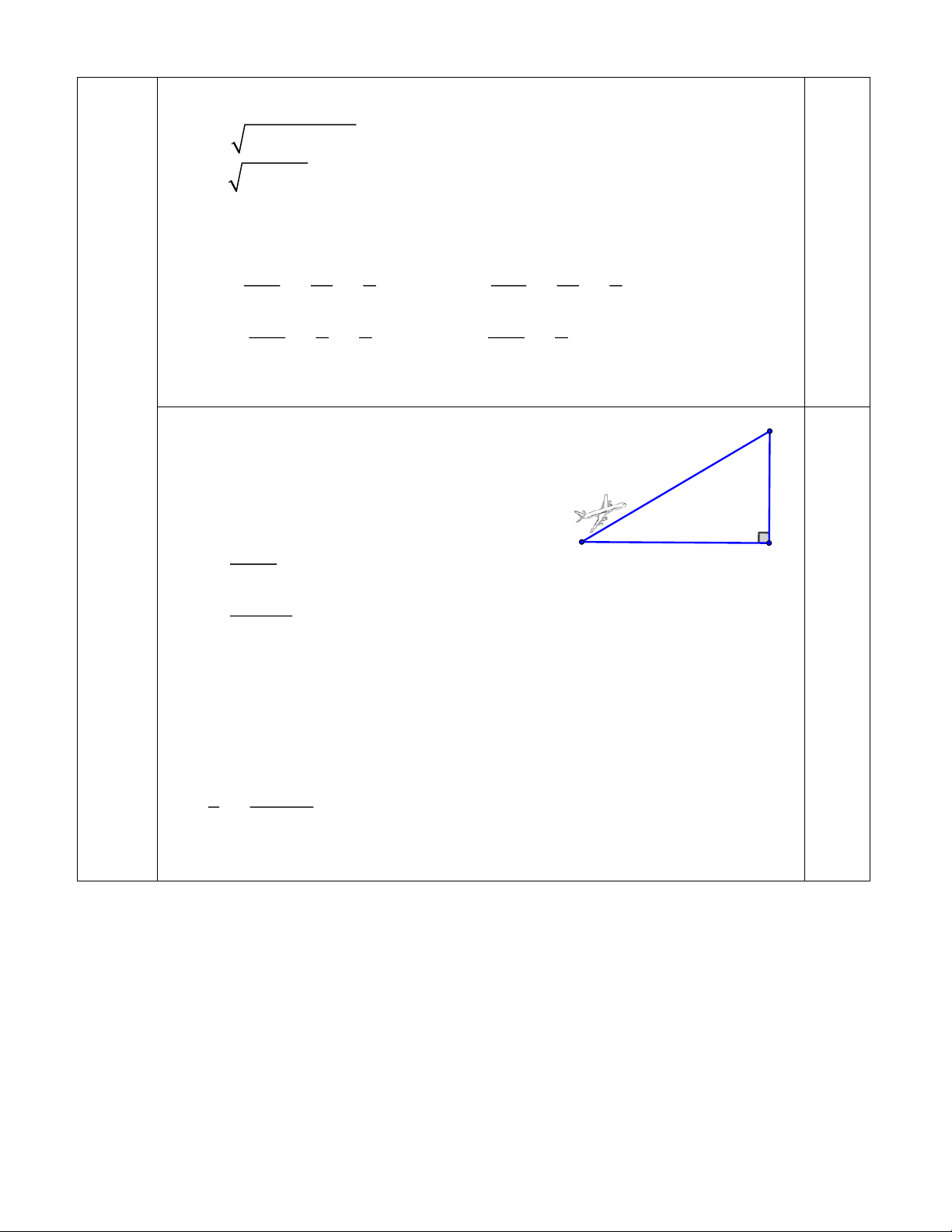
b. Một máy bay cất cánh từ vị trí A, bay lên theo đường AB tạo với phương nằm ngang một góc 0
= 30 , sau một khoảng thời gian 30 giây máy bay
đạt được độ cao là BH = 2,8 km. 30°
Tính vận tốc trung bình của máy bay.( 1,0đ - VDC) A H
-------- Hết --------
HƯỚNG DẪN CHẤM KIỂM TRA GIỮA HỌC KỲ I
Năm học: 2024 - 2025 Bài Đáp án Điểm I.
PHẦN TRẮC NGHIỆM ( mỗi câu trả lời đúng được 0,25 điểm) Câu 1 2 3 4 5 6 7 8 9 10 11 12 03 Đáp án A C A D C D D A B B C B II. PHẦN TỰ LUẬN 07 0,5 13a
Điều kiện xác định của phương trình 2 5 =
là x ¹ 0;x ¹ 2 x x - 2
Cặp số (1; 2) là nghiệm của PT x + y = 3 vì VT = 1 + 2 = 3 = VP 0,25 13b
Cặp số (0; 3) là nghiệm của PT x + y = 3 vì VT = 0 + 3 = 3 = VP 0,25 Vì a > b 0,25 14a
nên a + 1 > b + 1 0,25 Trang 18 Vì a > b 0,25 14b
nên a + a > a + b 0,25
Hay 2a > a + b
Gọi số cần tìm là ab , điều kiện: 1 a 9 ; 0 b 9 ; a;b N 0,25
Vì tổng hai chữ số của nó là 14 nên ta có PT: a + b = 14 (1)
Do đổi chỗ hai chữ số của số ab thì ta được số mới nhỏ hơn số ban đầu
18 đơn vị nên ta có phương trình: 0,25 ab − ba = 18 15
10a + b −10b − a = 18 Hay a – b = 2 (2)
Kết hợp (1) và (2) ta có hệ phương trình: a + b =14 a = 8(tmdk) 0,25 giải HPT ta được a − b = 2 b = 6(tmdk)
Vậy số cần tìm là số 86 0,25
(3 - 2x)(5x + 4)= 0 0,25
3 - 2x = 0 hoặc 5x + 4 = 0 16a 3 x = hoặc - 4 x = 2 5 0,25 ìï ü Vậy PT có tập nghiệm 3 - 4ï S ï ; ï = í ý ï 2 5 ï ïî ïþ
−3x + 22 −8x +17
−3x + 8x 17 − 22 16b 5x 5 − 0,25
x −1. Vậy BPT có nghiệm là x −1 0,25
Gọi x là số tuổi bạn An 0,5 17a Ta có BĐT x 18
Gọi y là khối lượng tối đa thang máy chở được 0,5 17b Ta có BĐT y 800 17c 2x − 3 7 − x + 2 0,5 Trang 19
Tam giác ABC vuông tại A, áp dụng Định lí Pitago ta được : 2 2 0,25 BC = A B + A C 2 2 = 6 + 8 = 10 0,25 A C 8 4 A B 6 3 sin B = = = ; co s B = = = 0,25 BC 10 5 BC 10 5 A C 8 4 A B 3 t an B = = = ; cot B = = A B 6 3 A C 4 0,25 Tam giác AHB có · 0 A HB = 90 (gt) B
Áp dụng hệ thức lượng trong tam giác vuông ta có : 0,25 30° HB A A B = H sin A 2, 8 A B = 0,25 0 sin 30 A B = 5, 6
Sau 30 giây cất cánh máy bay bay được 5,6km
Vận tốc trung bình của máy bay là : đổi 30s » 0, 0083h 0,25 s 5, 6 v = =
» 674, 7 (km / h) t 0, 0083 0,25 Trang 20 ĐỀ 5
ĐỀ KIỂM TRA GIỮA HỌC KỲ I MÔN: TOÁN 9 Thời gian: 90 phút
A. PHẦN TRẮC NGHIỆM: (3 điểm) Khoanh tròn vào chữ cái đứng trước câu trả lời
mà em cho là đúng nhất
Câu 1: Cho số thực a > 0. Số nào sau đây là căn bậc hai số học của a? A. a B. − a C. 2a D. 2 a
Câu 2. Điều kiện xác định của biểu thức 2x − 8 là: A. x = 4 B. x 4 C. x 4 D. x 4
Câu 3: Cho a là số không âm, b là số dương. Khẳng định nào sau đây là đúng? a a a a a − a a a A. = B. = C. = D. = b b b b b b b b
Câu 4: Chọn khẳng định đúng A. 3 27 = 9 B. 3 27 = 3 − C. 3 27 = 3 D. 3 27 = 9 −
Câu 5: “Trong tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng…”. Cụm
từ thích hợp điền vào chỗ trống là:
A. Tích hai cạnh góc vuông
B. Tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền
C. Tích cạnh huyền và 1 cạnh góc vuông
D. Tổng nghịch đảo các bình phương của hai cạnh góc vuông.
Câu 6: Cho hình vẽ sau: Khi đó, SinC bằng A B C AC AB AC AB A. B. C. D. BC BC AB AC
Câu 7. So sánh 5 với 2 6 ta có kết luận: A. 5> 2 6
B. 5< 2 6 C. 5 = 2 6 D. 5 2 6
Câu 8. Tam giác MPQ vuông tại P. Ta có: MP PQ MP MQ A. sinM = ; B. sinM = ; C. sinM = ; D. sinM = MQ MQ QP MP
Câu 9. Cho tam giác ABC vuông tại A, có AB = 6cm, C = 300. độ dài cạnh BC là:
A . 12 cm. B. 4 3 cm C. 10 cm. D. 6 cm. Trang 21
Câu 10. Rút gọn M = 3 3 1 − 25 − 27 ta được: A. M = 8 B. M = - 2 C. M = 2 D. M = - 8
Câu 11. Biểu thức M = 4 − 2 3 có giá trị rút gọn bằng bao nhiêu?
A. 2 − 3 B. 1− 3 C. 3 −1 D. 3 − 2
Câu 12. Tam giác ABC vuông tại A (hình 2), đường cao AH chia cạnh huyền thành hai
đoạn . BH = 3(cm) và HC = 9(cm). Độ dài cạnh góc vuông AB là: A. 6(cm); B. 3 3 (cm); A C. 3.9 (cm); D. 2 2 3 + 9 (cm). c b h Hình 2 c' b' B H C
Phần II: Tự luận (7.0 đ) a
Câu 7 (1 điểm): Thực hiện các phép tính sau: a) 16.121 b) 2 2 + 3 50 − 7 8
Câu 8 (1 điểm). Giải phương trình: 2 3x − 5 3x + 7 3x = 12
Câu 9 (1 điểm): Trục căn thức ở mẫu: 1 4 a) b) 3 2 3 − 5 2 4x −12x + 9
Câu 10 (1 điểm): Cho biểu thức A = 7x − ( 3 x ) 2x − 3 2 a) Rút gọn biểu thức A
b) Tìm x để biểu thức A có giá trị bằng 5
Câu 11 (1 điểm): Một cây cau có chiều cao 6m. Để hái một buồn cau xuống, phải đặt thang
tre sao cho đầu thang tre đạt độ cao đó, khi đó góc của thang tre với mặt đất là bao nhiêu,
biết chiếc thang dài 8m (làm tròn đến phút) Trang 22
Câu 12 (2,0 điểm) Cho tam giác ABC vuông tại A. Biết góc 0 B = 60 , cạnh AB = 10cm.
a) Hãy giải tam giác vuông ABC.
b) Vẽ đường cao AH. Tính độ dài AH, BH ------ Hết ----- HƯỚNG DẪN CHẤM
Phần I. Trắc nghiệm(4 điểm).
Mỗi câu đúng cho 0,25 điểm. Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp án A C B C B B A B A D A A
Phần II: Tự luận (7.0 đ) CÂU ĐÁP ÁN BIỂU ĐIỂM 13 a) 16.121 (1đ) =4. 11 0,25đ =44 0,25đ b) 2 2 + 3 50 − 7 8 = 0,25đ = 0,25đ 14
2 3x − 5 3x + 7 3x = 12 (1đ) 0,25đ - Tìm được x không âm 0,5đ - Tìm được đúng x 0,25đ
- Đối chiếu đk và kết luận 15 1 0,5đ (1đ) a) Tính đúng 3 2 4 0,5đ b) Tính đúng 3 − 5 16 2 4x −12x + 9 (1,25đ) A = 7x − ( 3 x ) 2x − 3 2 a) Rút gọn biểu thức A 1,0đ - Rút gọn đúng Trang 23
b) Tìm x để biểu thức A có giá trị bằng 5 0,25đ - Tìm đúng x - Nhận xét kết luận 17
- Vẽ đúng hình biểu diễn (1đ) - Tính đúng góc 0,75đ - Kết luận đúng 0,25đ 18
Cho tam giác ABC vuông tại A. Biết góc 0 B = 60 , cạnh (1,75đ) AB = 10cm.
a) Hãy giải tam giác vuông ABC. - Tính đúng BC 0,5đ - Tính đúng AC 0,25đ
- Tính đúng số đo góc C 0,5đ
b) Vẽ đường cao AH. Tính độ dài AH, BH - Tính đúng AH 0,5đ
(Học sinh làm theo cách khác đúng vẫn cho điểm tối đa) ĐỀ 6
ĐỀ KIỂM TRA GIỮA HỌC KỲ I MÔN: TOÁN 9 Thời gian: 90 phút
I. PHẦN TRẮC NGHIỆM: (3 điểm)
Chọn chữ cái trước câu trả lời đúng trong các phương án ở mỗi câu hỏi.
Câu 1. Nghiệm của phương trình (2x- ) 1 (x + ) 3 = 0 là: A. 1 x = B. 1 x = hoặc x = - 3 C. x = 3 D. 1 x = và x = 3 2 2 2
Câu 2. Nghiệm của phương trình 2 3 = là: x + 2 x - 1 A. 41 x = × B. x = - 8. C. 41 x = × D. x = 5. 3 4
Câu 3. Nếu tam giác ABC vuông tại A , AB=5, BC = 13 thì cosC bằng: A. 5 B. 3 C. 12 D. 3 3 5 13 4 Trang 24