



Preview text:
ĐỀ 1
ĐỀ ÔN TẬP GIỮA HỌC KỲ I NĂM HỌC 2025-2026
MÔN: TOÁN 10-CHÂN TRỜI SÁNG TẠO
Phần I. Câu trắc nghiệm nhiều phương án lực chọn (6 điểm). Học sinh trả lới từ câu 1 đến câu 20.Mỗi
câu hỏi thí sinh chỉ chọn một phương án.
Câu 1: Với DE (khác vectơ - không) thì độ dài đoạn ED được gọi là A. Giá của . ED B. Độ dài của . ED C. Phương của . ED D. Hướng của . ED
Câu 2: Trong các câu sau, câu nào không phải là mệnh đề?
A. Băng Cốc là thủ đô của Mianma.
B. 8 là số chính phương. C. Buồn ngủ quá!
D. Hình thoi có hai đường chéo vuông góc với nhau.
2x − 5y −1 0
Câu 3: Cho hệ bất phương trình
. Trong các điểm sau, điểm nào thuộc miền nghiệm
2x + y + 5 0
x + y +1 0
của hệ bất phương trình?
A. M (1;0).
B. O(0;0).
C. P(0;2). D. N (0; 2 − ).
Câu 4: Cho hai điểm A và B phân biệt. Điều kiện để I là trung điểm AB là:
A. IA = I . B
B. IA = −I . B
C. IA = I . B
D. AI = BI.
x + y −1 0
Câu 5: Miền nghiệm của hệ bất phương trình
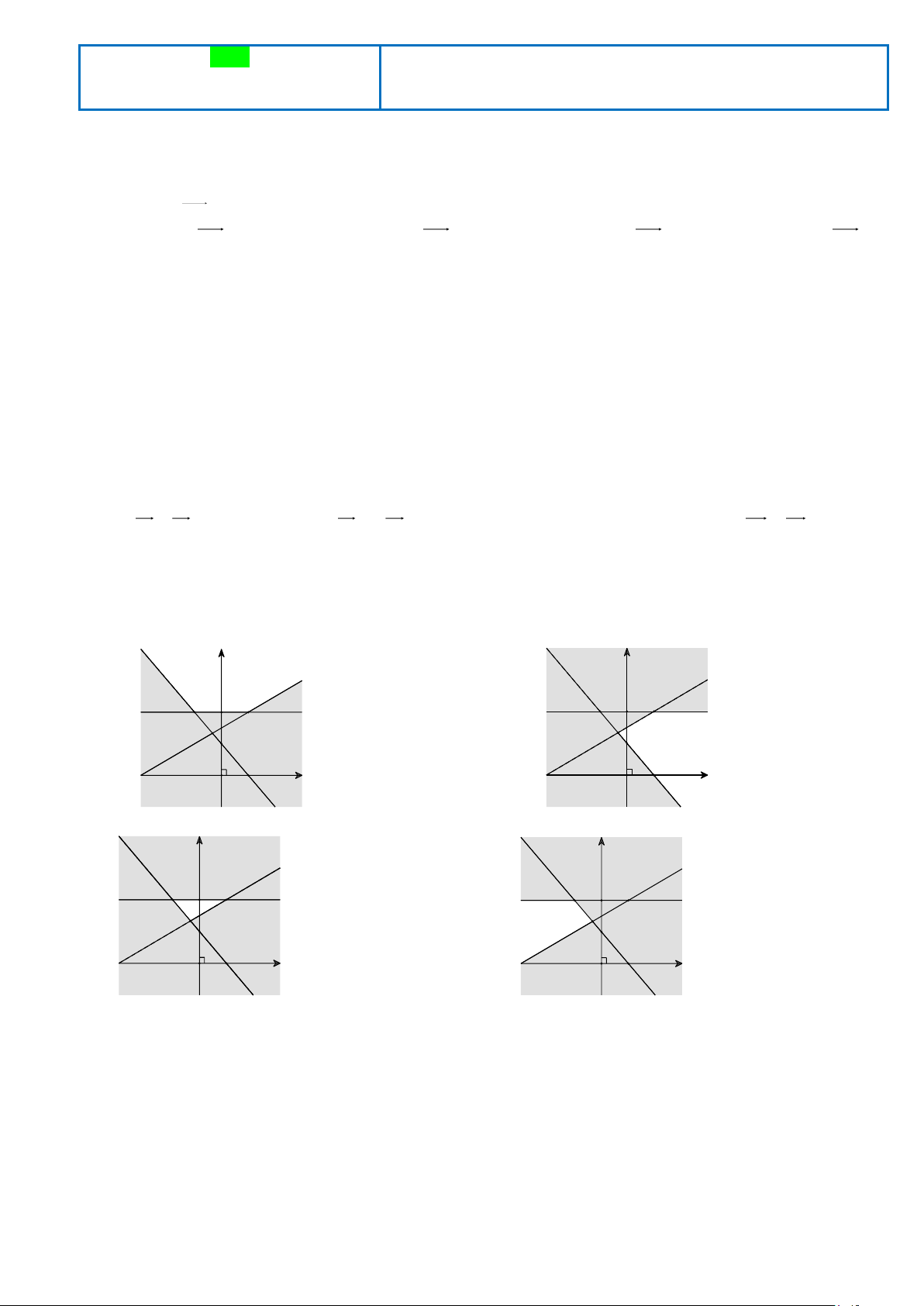
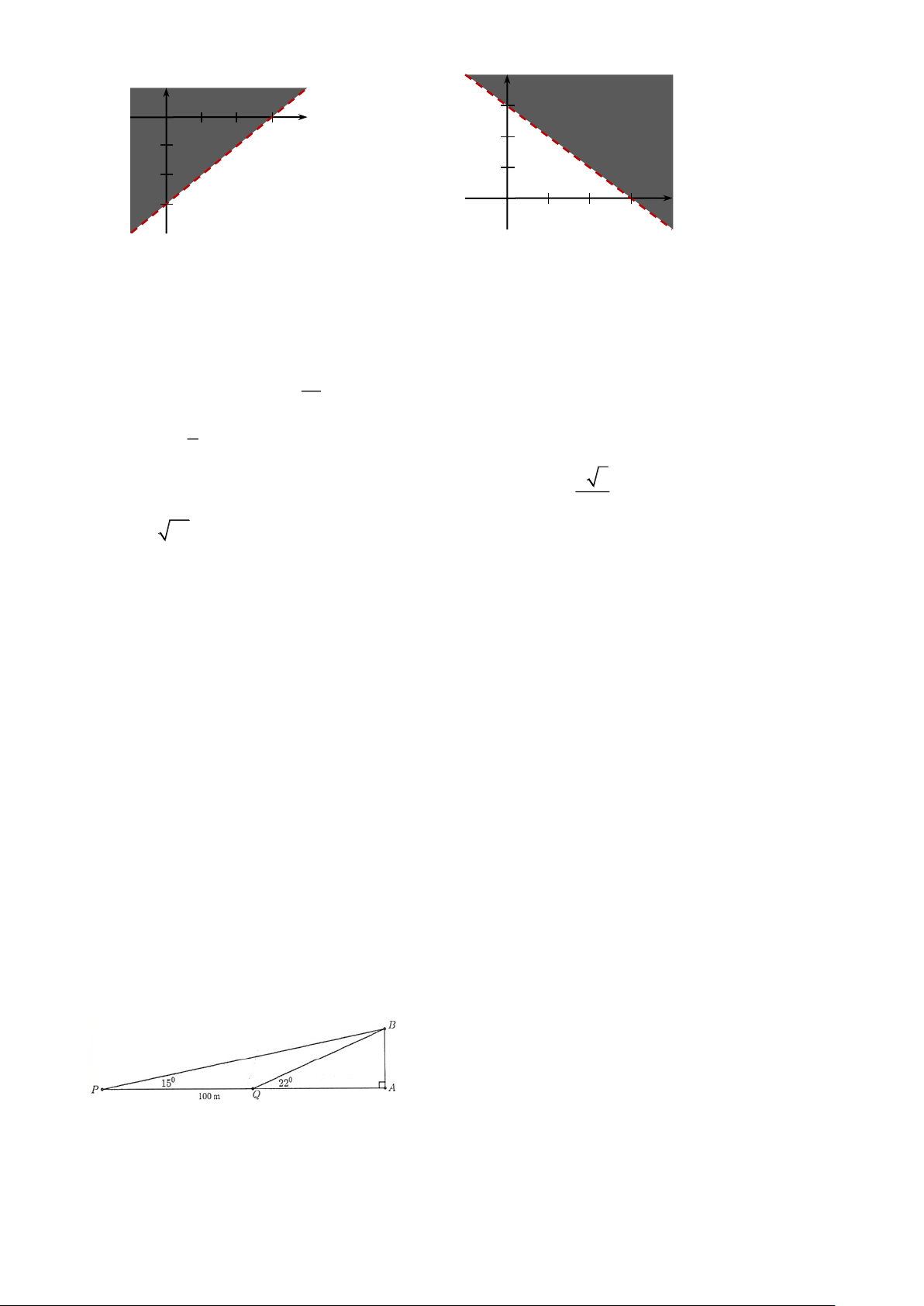
là phần không tô đậm của hình vẽ nào y 2
−x + 2y 3 trong các hình vẽ sau? y y 2 2 1 1 x 1 x 1 -3 O -3 O A. B. y y 2 2 1 1 x 1 x 1 -3 O -3 O C. D.
Câu 6: Cặp số nào sau đây không là nghiệm của bất phương trình 5x − 2( y − ) 1 0 ? A. ( 1 − ;0) . B. (1;3). C. ( 1 − ; ) 1 . D. (0; ) 1 .
Câu 7: Cho hệ bất phương trình x + 3y − 2 0
. Trong các điểm sau, điểm nào thuộc miền nghiệm của
2x + y + 1 0 hệ bất phương trình? A. M (0; ) 1 . B. N ( –1; ) 1 .
C. Q(–1;0). D. P(1;3). Trang 1
Câu 8: Cho hai vectơ a và b không cùng phương. Hai vectơ nào sau đây cùng phương? 1 1 A. 3
− a +b và − a + 6b .
B. − a − b và 2a + b . 2 2 1 1 1
C. a + b và a − 2b .
D. a − b và − a + b . 2 2 2
Câu 9: Cặp số (1; ) 1
− là nghiệm của bất phương trình nào sau đây?
A. x + 3y +1 0 .
B. −x − 3y −1 0 .
C. x + y − 3 0 .
D. −x − y 0 .
Câu 10: Cho lục giác đều ABCDEF có tâm .
O Đẳng thức nào sau đây sai?
A. OD = B . C
B. OB = O . E
C. AB = AF .
D. AB = E . D
Câu 11: Miền nghiệm của bất phương trình 2x + y 1 không chứa điểm nào sau đây? A. D( 1 − ;− ) 1 .
B. B(2;2) .
C. C (3;3) . D. A(1; ) 1 .
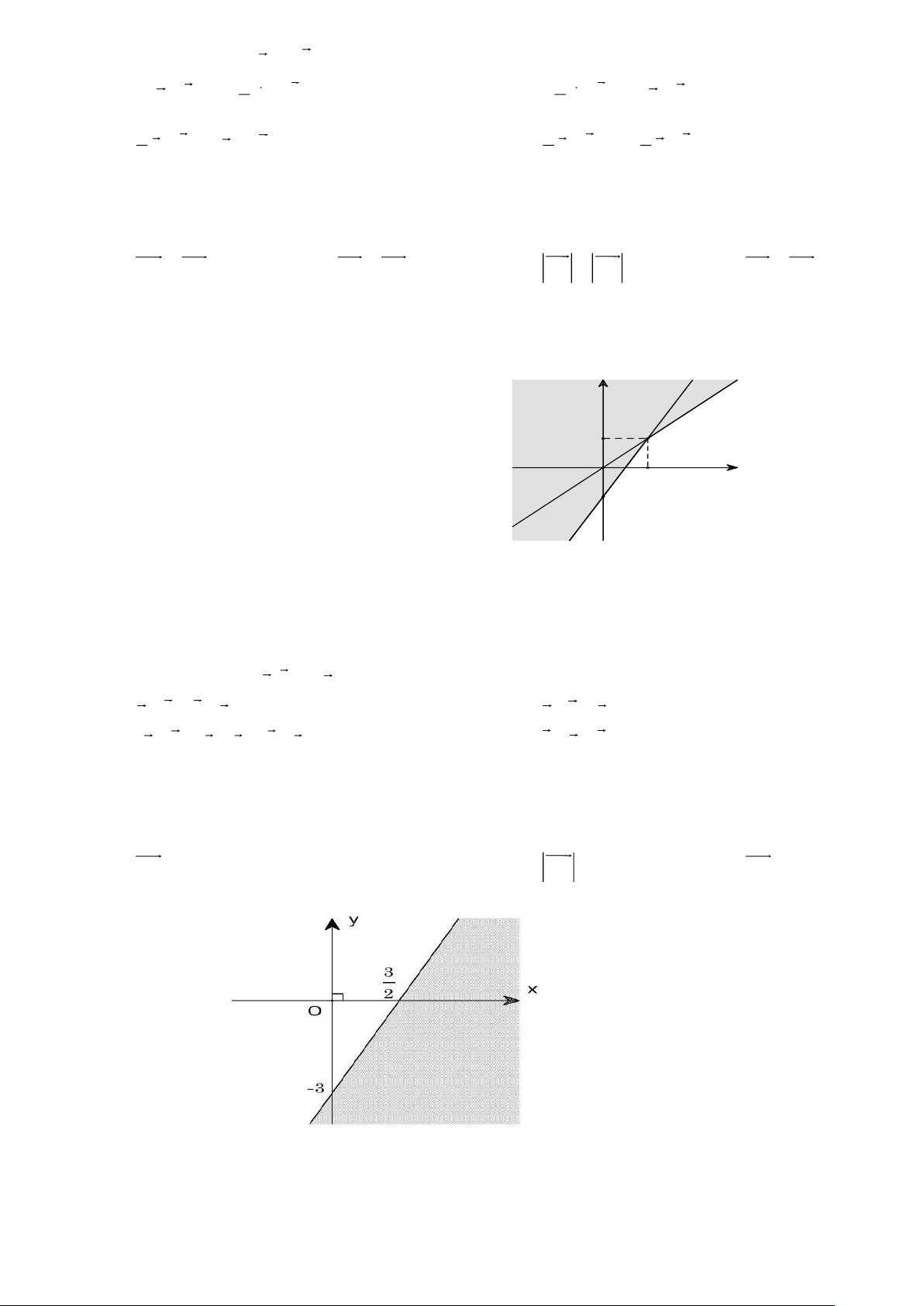
Câu 12: Phần không tô đậm trong hình vẽ dưới đây (không chứa biên), biểu diễn tập nghiệm của hệ bất y 1 x O 1 - 1
phương trình nào trong các hệ bất phương trình sau? x − y 0
A. x − y 0 x − y x − y . B. 0 . C. . D. 0 .
2x − 3y 1
2x − y 1
2x − y 1
2x − y 1
Câu 13: Trong các bất phương trình sau, bất phương trình nào là bất phương trình bậc nhất hai ẩn?
A. 3x − 8y 2025 .
B. x − 4y − 9z 2024 . C. 2
4x + 3y 0 . D. 2
x − 2x + 5 0 .
Câu 14: Cho ba vectơ a,b và c khác vectơ-không. Trong các khẳng định sau, khẳng định nào sai?
A. a + b = b + a .
B. a + 0 = a .
C. (a +b) + c = a + (b + c). D. 0 + a = 0 .
Câu 15: Sử dụng các kí hiệu khoảng, đoạn để viết tập hợp A = xR∣ 4 x 9 :
A. A = (4;9) .
B. A = 4;9.
C. A = (4;9.
D. A = 4;9) .
Câu 16: Vectơ có điểm đầu là D , điểm cuối là E được kí hiệu là A. . ED B. . DE C. DE . D. DE.
Câu 17: Phần tô đậm trong hình vẽ sau, biểu diễn tập nghiệm của bất phương trình nào trong các bất phương trình sau?
A. x − 2y 3 .
B. 2x − y 3 .
C. x − 2y 3 − .
D. 2x − y 3 .
Câu 18: Mệnh đề nào sau đây sai? Trang 2
A. AB 0.
B. 0 cùng phương với mọi vectơ.
C. 0 cùng hướng với mọi vectơ. D. AA = 0.
Câu 19: Nửa mặt phẳng không bị gạch( kể cả đường thẳng d ) ở hình bên là miền nghiệm của bất
phương trình nào sau đây?
A. x + 3y 3.
B. x + 3y 3.
C. 3x + y 3.
D. 3x + y 3 .
Câu 20: Mệnh đề P( x) 2 :" x
, x − x + 7 0". Phủ định của mệnh đề P là A. 2 x
, x − x + 7 0. B. 2 x
, x − x + 7 0. C. 2 x
, x − x + 7 0. D. 2 x
, x − x + 7 0.
Phần II. Tự luận (4 điểm). Học sinh làm bài chi tiết từ câu 1 đến câu 4.
Câu 1 (1 điểm): Thực hiện phép toán vectơ sau: a) 2(a + b) ; b) 2a − (a − 2b) .
Câu 2 (1 điểm): Tìm các tập hợp sau: a) A=4;
9 (9;2024] ; b) B=(- ¥ ; ] 2 Ç(- 6;+ ¥ ).
Câu 3 (1 điểm): Cho hình vuông ABCD có tâm O,cạnh a. Tính a) AB + D
A ; b) OA − CB .
Câu 4 (1 điểm): Lớp 10A có 45 học sinh, trong đó có 15 học sinh được xếp loại học lực giỏi, 20 học
sinh được xếp loại hạnh kiểm tốt, 10 em vừa xếp loại học lực giỏi, vừa có hạnh kiểm tốt. Hỏi có bao
nhiêu học sinh xếp loại học lực giỏi hoặc có hạnh kiểm tốt?
------ HẾT ------ ĐÁP ÁN
Phần I. Câu trắc nghiệm nhiều phương án lực chọn. (Mỗi câu học sinh được 0,3 điểm) Câu 1 2 3 4 5 6 7 8 9 10 Chọn B C D B A B B D A B Câu 11 12 13 14 15 16 17 18 19 20 Chọn A B A D B D B A C A
II. Tự luận (4,0 điểm)
Câu 1:Thực hiện phép toán vectơ sau: a) 2(a + b) ; b) 2a − (a − 2b) Trang 3 Ý Nội dung Điểm a
2(a + b) = 2a + 2b 0,5 b
2a − (a − 2b) = 2a − a + 2b = a + 2b 0,5
Câu 2:Tìm các tập hợp sau: a) A=4;
9 (9;2024] b) B=(- ¥ ; ] 2 Ç(- 6;+ ¥ ). Ý Nội dung Điểm a A=4;
9 (9;2024] = [4; 2024] 0,5 b B=(- ¥ ; ]
2 Ç(- 6;+ ¥ ) = (- 6;2] 0,5
Câu 3: Cho hình vuông ABCD có tâm O, cạnh a. Tính a) AB + D
A ; b) OA − CB Ý Nội dung Điểm a
AB + D
A = AC = AC = a 2 0,25 Vậy AB + D A = a 2 0,25 b
a 2 0,25
OA − CB = CO − CB = BO = BO = ` 2
a 2
Vậy OA − CB = 0,25 2
Câu 4: . Lớp 10A có 45 học sinh, trong đó có 15 học sinh được xếp loại học lực giỏi, 20 học sinh được
xếp loại hạnh kiểm tốt, 10 em vừa xếp loại học lực giỏi, vừa có hạnh kiểm tốt. Hỏi có bao nhiêu học sinh
xếp loại học lực giỏi hoặc có hạnh kiểm tốt? Ý Nội dung Điểm
Gọi A là tập hợp học sinh lớp 10A; B là tập hợp học sinh có học lực giỏi; C là 0,25
tập hợp các học sinh có hạnh kiểm tốt. Khi đó tập hợp cần tìm là tập B C . 0,25
Tập này có 15+ 20−10 = 25 học sinh. Được thể hiện trong biểu đồ Ven như sau: 0,25 10 C A 10 20 B 5
Vậy học sinh xếp loại học lực giỏi hoặc có hạnh kiểm tốt là 25 0,25 ĐỀ 2
ĐỀ ÔN TẬP GIỮA HỌC KỲ I Trang 4 NĂM HỌC 2025-2026
MÔN: TOÁN 10-CHÂN TRỜI SÁNG TẠO
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN: (20 câu – 7,0 điểm)
Học sinh chọn một phương án đúng trong mỗi câu sau.
Câu 1. Điểm nào dưới đây thuộc miền nghiệm của bất phương trình 2x + y −1 0 ?
A. N (1;0). B. Q(1 ) ;1 . C. M (1; 2 − ). D. P(2; 2 − ).
Câu 2. Trong các tập hợp sau, tập hợp nào khác rỗng? A. A = 2
x x + x +1 = 0 . B. B = 2
x x − 2 = 0 .
C. C = x ( 3 x )( 2 – 3 x + ) 1 = 0 .
D. D = x (x − )( 2 2 x + 3) = 0 . 1
Câu 3. Cho biết góc α thỏa 0 0
0 < α < 180 và cos α =
. Giá trị của biểu thức 2 2
P = sin + 3cos là 3 10 11 4 1 A. . B. . C. . D. . 9 9 3 3
Câu 4. Cho hai tập hợp ,
A B . Hãy chọn khẳng định đúng trong các khẳng định sau:
A. B = ( A B)( A\ B) . B. B = ( A B)( A\ B) . C. A = ( A B)( A \ B). D.
A = ( A B)( A\ B) .
Câu 5. Trong các bất phương trình sau, bất phương trình nào là bất phương trình bậc nhất hai ẩn?
A. 2x − 5y + 3z 0 . B. 2
3x + 2x − 4 0 . C. 2
2x + 5y 3 .
D. 2x + 3y 5.
Câu 6. Cho hai góc ( 0 0 , 0 ;180 ), 0 0
α ¹ 90 , β ¹ 90 và , là 2 góc bù nhau. Mệnh đề nào sau đây đúng?
A. cosa + cosb = 0
B. tan a - tan b = 0
C. sina + sinb = 0 D.
cot a - cot b = 0 .
Câu 7. Sử dụng các kí hiệu khoảng, đoạn để viết tập hợp C A với A = x 4 x 9 : ¡ A. (4; 9 . B. 4;9). C. (− ; 4) 9;+). D. (− ; 4 (9;+).
Câu 8. Cho mệnh đề A : “2024 là hợp số”, phủ định của mệnh đề A là
A. 2024 không là hợp số.
B. 2024 là một số chẵn.
C. 2024 là một số chính phương.
D. 2024 là một số lẻ.
Câu 9. Viết mệnh đề sau bằng cách sử dụng kí hiệu hoặc : “Có một số nguyên bằng bình phương của chính nó”. A. 2 x
, x = x . B. 2 x
, x = x . C. 2 x
, x − x = 0. D. 2 x
, x = x .
2x + 3y − 6 0
Câu 10. Miền nghiệm của hệ bất phương trình x 0
chứa điểm nào sau đây?
2x −3y −1 0 A. 1 D 0 ; − .
B. B(0 ; 2). C. C ( 1 − ; 3) .
D. A(1 ; 2). 3
Câu 11. Lớp 10/n trường THPT Phan Châu Trinh chuẩn bị một tiết mục cho Hội diễn văn nghệ SHINE
Tỏa sáng tài năng 2024. Tiết mục này có 15 học sinh hát, 10 học sinh múa phụ họa, trong đó có 5 học
sinh vừa hát vừa múa phụ họa, 3 học sinh làm công tác hậu cần (3 học sinh làm công tác hậu cần không
tham gia múa và hát). Số học sinh của lớp chuẩn bị cho tiết mục văn nghệ nói trên là A. 46 . B. 20 . C. 23. D. 25 . Trang 5
Câu 12. Cho mệnh đề: “Nếu một tứ giác là hình chữ nhật thì tứ giác đó có hai đường chéo bằng nhau”.
Phát biểu nào sau đây đúng?
A. Điều kiện đủ để tứ giác có hai đường chéo bằng nhau là tứ giác đó là hình chữ nhật.
B. Tứ giác là hình chữ nhật là điều kiện cần để tứ giác đó có hai đường chéo bằng nhau.
C. Điều kiện cần và đủ để tứ giác là hình chữ nhật là tứ giác đó có hai đường chéo bằng nhau.
D. Tứ giác có hai đường chéo bằng nhau là điều kiện đủ để tứ giác đó là hình chữ nhật .
Câu 13. Cho B là tập hợp các hình bình hành, V là tập hợp các hình vuông, N là tập hợp các hình chữ
nhật, T là tập hợp các hình thoi. Hãy chọn kết quả đúng trong các kết quả sau.
A. T N B
B. V T B
C. B V T .
D. N T B
Câu 14. Cho tam giác ABC nội tiếp đường tròn bán kính R, AB = R, AC = R 2. Tính số đo góc A biết
A là góc tù. A. 135 . B. 105 . C. 120 . D. 150 .
Câu 15. Một người bắt đầu từ vị trí A đi trong rừng theo hướng N30 W
với vận tốc trung bình 4 km/h,
sau 30 phút đến vị trí B . Từ B , người đó chuyển sang hướng N80E và đi tiếp với vận tốc không đổi
thêm 1h để đến vị trí C . Vị trí C cách vị trí A bao nhiêu km (tính theo đường chim bay)? (làm tròn kết
quả đến một chữ số thập phân).
A. 3,9 km .
B. 4 km .
C. 3,5 km . D. 3,8km .
Câu 16. Tam giác ABC có các góc B = 30 ,
C = 45 , AB = 3. Khi đó cạnh AC bằng 2 6 A. . B. 3 6 . C. 3 2 . D. 6 . 3 2 2
Câu 17. Cho tam giác ABC , mệnh đề nào sau đây sai?
A. Nếu góc A vuông thì 2 2 2
b +c = a .
B. Nếu góc A nhọn thì 2 2 2
b +c a .
C. Nếu góc A nhọn thì 2 2 2 b +c a .
D. Nếu góc A tù thì 2 2 2
b +c a .
Câu 18. Cho tam giác ABC có diện tích S , bán kính đường tròn ngoại tiếp R, bán kính đường tròn nội a + b + c
tiếp r, BC = a, AB = c, AC = , b p =
. Mệnh đề nào dưới đây sai? 2 abc 1 A. = 4R .
B. S = ab sin C . S 2
C. S = pr . D. 2
S = ( p − a)( p − b)( p − c) . 2sin x + cos x
Câu 19. Cho góc x sao cho 0 0 tan x = 2
− , 0 x 180 . Tính giá trị của biểu thức P = sin x − cos x A. 2 − . B. 2 .
C. −1 . D. 1.
Câu 20. Cho các tập hợp ,
A B,C được minh họa bằng biểu đồ Ven như hình bên. Phần tô xám trong hình
là biểu diễn của tập nào sau đây? Trang 6
A. ( A B) \ C
B. A B C
C. ( A \ C) ( A \ B)
D. ( A B) \ C
PHẦN II: TỰ LUẬN (3 câu – 3,0 điểm)
Câu 21. (1 điểm) Cho ba tập hợp A = 2
− ;5) , B = (0;7, C = 0;1;2;3;4; 5 . Tìm A ,
B C B, C \ A, ( AC) \ B .
Câu 22. (1 điểm) Chị Trang là sinh viên đi học xa nhà, chị ấy rất hài lòng khi kiếm được việc làm thêm.
Để đảm bảo việc học tập, chị ấy làm thêm không quá 10 giờ mỗi tuần cho hai công việc. Với công việc
trợ giảng chị ấy kiếm được 120 nghìn đồng mỗi giờ và với công việc thu ngân chị ấy kiếm được 50 nghìn
đồng mỗi giờ. Chị Trang cần kiếm ít nhất 800 nghìn đồng mỗi tuần để trang trải những chi tiêu của mình.
a) Gọi x, y lần lượt là số giờ làm trợ giảng và số giờ làm thu ngân trong một tuần của chị Trang . Viết hệ
bất phương trình biểu diễn các điều kiện của x, y .
b) Biểu diễn miền nghiệm của hệ bất phương trình trong câu a (chỉ cần vẽ hình đúng và ghi các dữ kiện
đúng lên hình, không cần trình bày cách xác định miền nghiệm của hệ ).
c) Hãy chỉ ra hai cách khả thi mà chị Trang có thể phân chia thời gian của mình cho hai công việc và chị
ấy muốn thời gian làm trợ giảng nhiều hơn thời gian làm thu ngân, hơn nữa số giờ phải là các số nguyên.
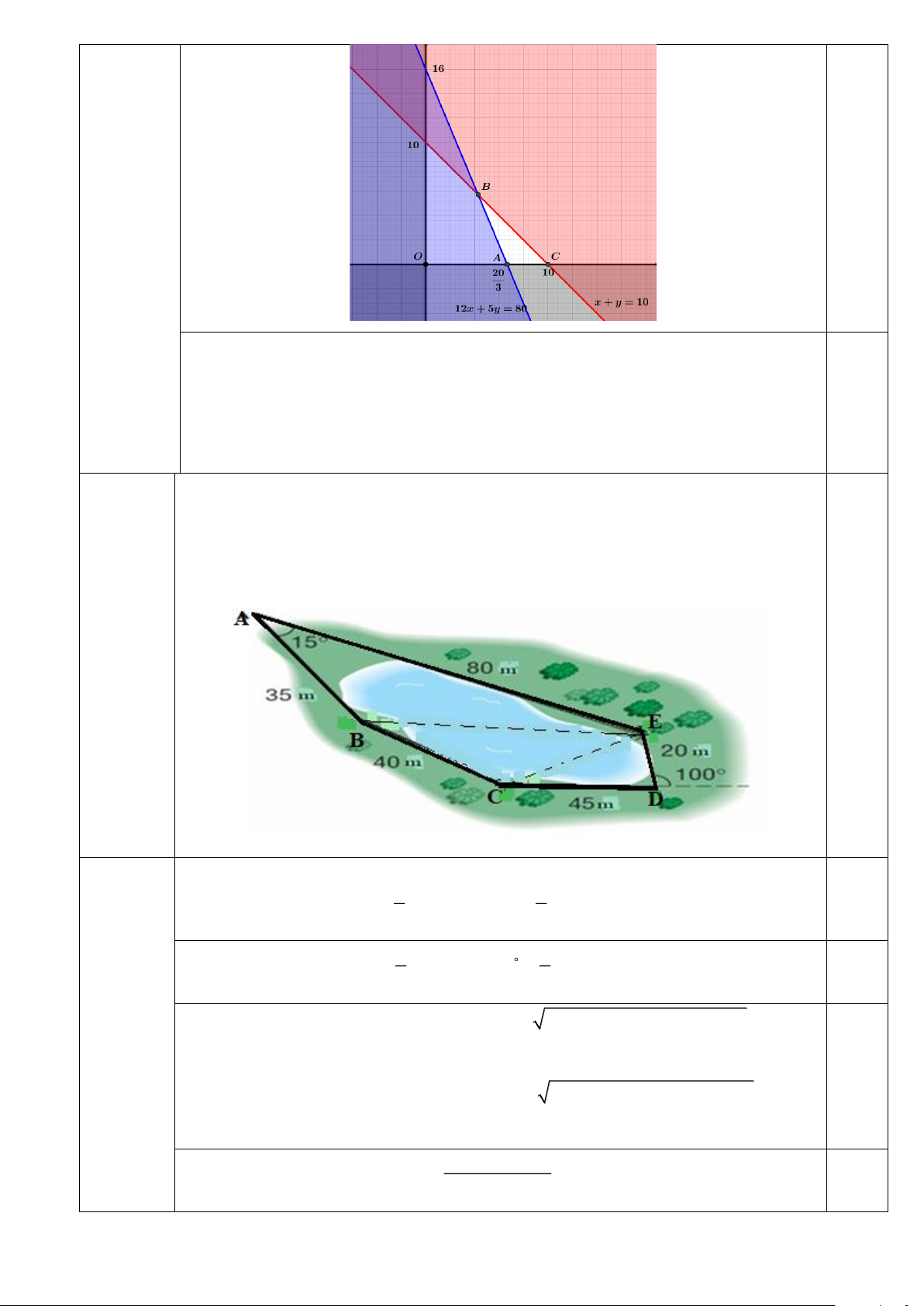
Câu 23. (1 điểm) Để tính gần đúng diện tích của một mặt hồ, nhân viên trắc địa đi vòng quanh hồ và đo
đạc được các số liệu như trong hình vẽ. Với cách đo này, diện tích của mặt hồ xấp xĩ diện tích của ngũ
giác ABCDE , tính diện tích đó (các phép tính trung gian làm tròn đến 1 chữ số thập phân, kết quả cuối
cùng làm tròn đến hàng đơn vị). -------- HẾT-------- Trang 7 BẢNG ĐÁP ÁN
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN: (20 câu – 7,0 điểm) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 C D B C D A C A B A C A B B D C B D D A
PHẦN II: TỰ LUẬN (3 câu – 3,0 điểm) Câu 21.
Cho ba tập hợp A = 2
− ;5) , B = (0;7, C = 0;1;2;3;4; 5 .
( 1 điểm) Tìm A ,
B C B, C \ A, ( AC) \ B .
A B = (0;5) 0.25 đ C B = (− ; 0(7;+ 0.25 ) đ C \ A = 5 0.25 đ
(AC) \ B = 2 − ; 5 \ (0;7 = 2 − ;0 0.25 đ
Chị Trang là sinh viên đi học xa nhà, chị ấy rất hài lòng khi kiếm được việc làm
thêm. Để đảm bảo việc học tập, chị ấy làm thêm không quá 10 giờ mỗi tuần cho
hai công việc. Với công việc trợ giảng chị ấy kiếm được 120 nghìn đồng mỗi giờ và Câu 22.
với công việc thu ngân chị ấy kiếm được 50 nghìn đồng mỗi giờ. Chị Trang cần
( 1 điểm) kiếm ít nhất 800 nghìn đồng mỗi tuần để trang trải những chi tiêu của mình.
a) Gọi x, y lần lượt là số giờ làm trợ giảng và số giờ làm thu ngân của chị Trang
trong một tuần. Viết hệ bất phương trình biểu diễn các điều kiện của x, y .
b) Biểu diễn miền nghiệm của hệ bất phương trình trong câu a (chỉ cần vẽ hình
đúng và ghi đúng các dữ kiện lên hình, không cần trình bày cách xác định miền nghiệm).
c) Hãy chỉ ra hai cách khả thi mà chị Trang có thể phân chia thời gian của mình cho
hai công việc và chị ấy muốn thời gian làm trợ giảng nhiều hơn thời gian làm thu
ngân, hơn nữa số giờ phải là các số nguyên. x 0 x 0 y 0 y 0
a) Theo đề bài có hệ bất phương trình: . x + y 10 (3) x + y 10 0.5 đ 120
x + 50y 800 (4) 12
x + 5y 80
HS đưa ra đươc 2 trong 4 bất phương trình của hệ ( phải có bpt (3) hoặc (4) ) được 0,25 đ
b) Miền nghiệm của hệ bất phương trình là phần không bị gạch ( tam giác ABC ) như hình vẽ: 0.25 đ Trang 8
c) Hai cách khả thi để có thể phân chia thời gian cho hai công việc theo yêu cầu đề bài: Cách 1:
8 giờ làm việc trợ giảng, 1 giờ làm việc thu ngân.
Cách 2: 7 giờ làm việc trợ giảng, 2 giờ làm việc thu ngân. 0.25
HS có thể cho đáp án khác miễn là ( ;
x y) thuộc miền nghiệm của hệ bất phương đ
trình và x y, x, y nguyên.
Để tính gần đúng diện tích của một mặt hồ, nhân viên trắc địa đi vòng quanh hồ và
đo đạc được các số liệu như trong hình vẽ. Với cách đo này, diện tích của mặt hồ xấp
xĩ diện tích của ngũ giác ABCDE , tính diện tích đó (các phép tính trung gian làm
tròn đến 1 chữ số thập phân, kết quả cuối cùng làm tròn đến hàng đơn vị). Câu 23 ( 1 điểm) 1 0.25
Tam giác ABE có: S = . AB AE.sin15 1
= .35.80.sin15 362,3 ( 2 m ) ABE 2 2 đ 1 0.25
Tam giác CDE có: S
= DC.DE.sin 80 1
= .45.20.sin 80 443, 2 ( 2 m ) C DE 2 2 đ 2 2 2 0 2 2
BE = AB + AE − 2A .
B AE.cos15 BE = 35 + 80 − 2.35.80.cos15 47,1 0.25 (m) đ 2 2 2
CE = CD + DE − 2 . CD DE.cos80 2 2
CE = 45 + 20 − 2.45.20.cos80 46 (m).
BC + CE + BE
Tam giác BCE có nửa chu vi p = 66,6 . 2 Trang 9 S
= p ( p − BC)( p − CE)( p − BE ( 2 m ) 0.25 ) 843,6 BCE đ
Vậy diện tích gần đúng của mặt hồ là: 362,3 + 443, 2 + 843,6 1649 ( 2 m ) . ĐỀ 3
ĐỀ ÔN TẬP GIỮA HỌC KỲ I NĂM HỌC 2025-2026
MÔN: TOÁN 10-CHÂN TRỜI SÁNG TẠO
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu
hỏi thí sinh chỉ chọn một phương án. (3.0 điểm)
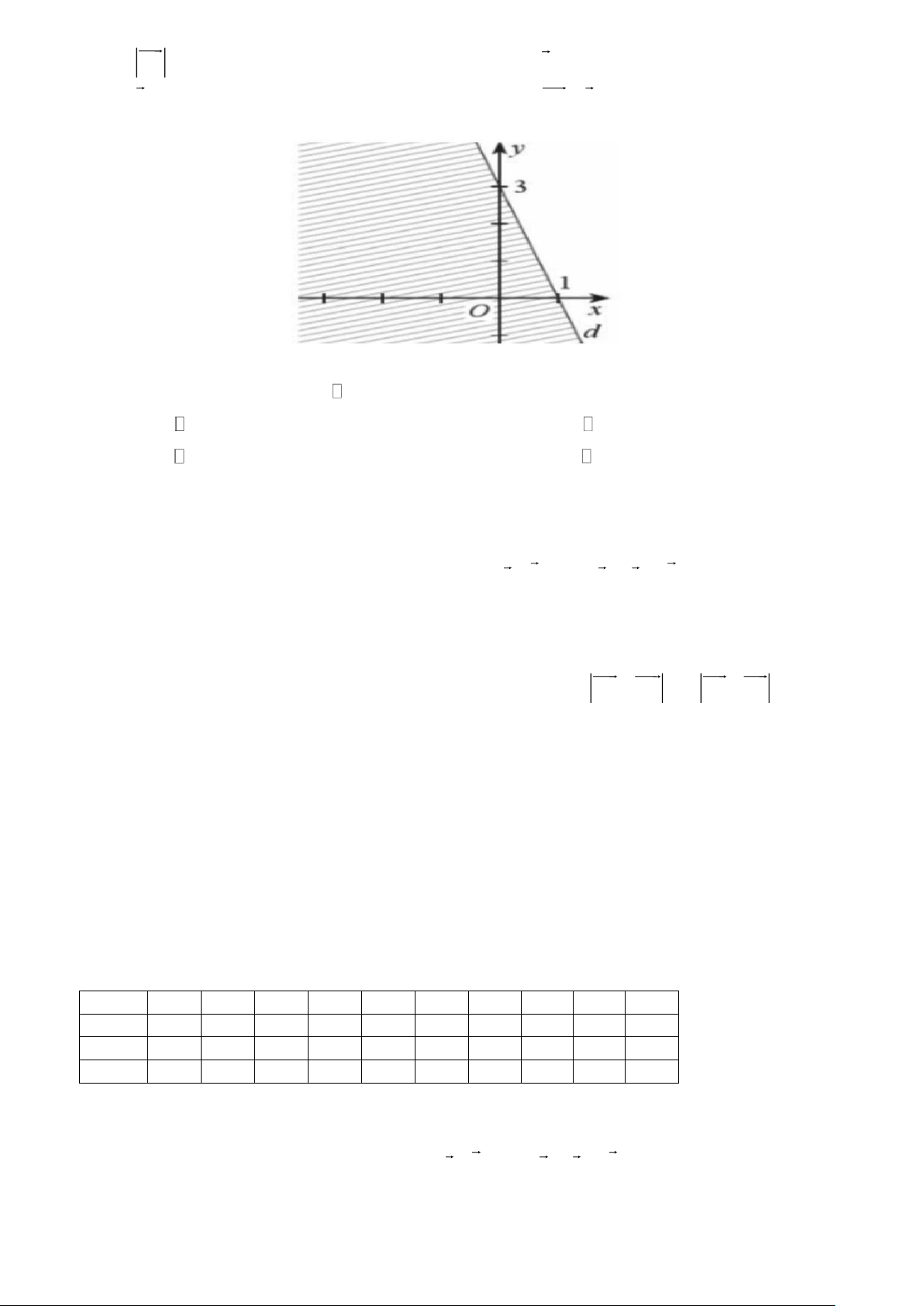
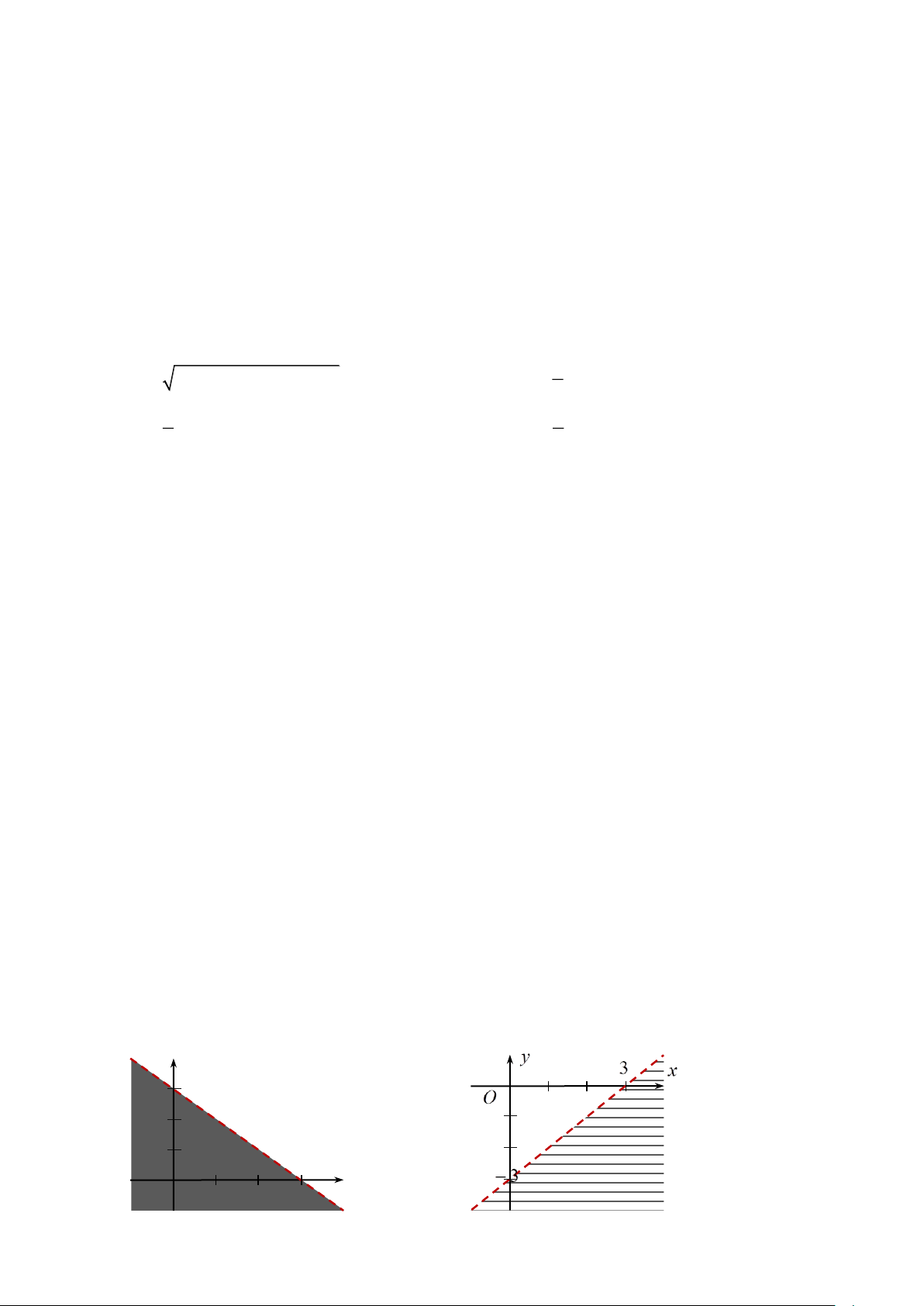
Câu 1: Trong mặt phẳng Oxy, phần nửa mặt phẳng không tô đậm (kể cả đường thẳng) trong hình vẽ bên
là biểu diễn hình học tập nghiệm của bất phương trình nào dưới đây? y _32 x O -3
A. x − 2y 3.
B. x − 2y 3.
C. 2x − y 3.
D. 2x − y 3.
Câu 2: Cho hai tập hợp A = ( 1 − ;
5 , B = (2;9). Khi đó, A \ B bằng A. (2; 5 . B. ( 1 − ;9). C. ( 1 − ;2. D. ( 1 − ;2) .
Câu 3: Xét tam giác ABC tùy ý, có độ dài cạnh BC = a và R là độ dài bán kính đường tròn ngoại tiếp.
Mệnh đề nào dưới đây đúng? a a a a R A. = 2 . R B. = . R C. = 4 . R D. = . sin A sin A sin A sin A 2
Câu 4: Cho tam giác ABC có độ dài cạnh AB = 8cm , AC = 18cm và có diện tích bằng 64 2 cm . Khi đó,
giá trị sin A là 4 8 4 3 A. . B. . C. . D. . 9 9 5 2
Câu 5: Điểm nào dưới đây không thuộc miền nghiệm của bất phương trình 2x + y 1? A. Q(1; ) 1 . B. N ( 2 − ; ) 1 .
C. M (1; − 2) . D. P( 1 − ; − 2) .
Câu 6: Cho tập hợp A = 3
− ;5). Khi đó, C A bằng A. (− ; −
3 5;+). B. (5;+). C. (− ; − ) 3 5,+). D. (− ; − 3 . Câu 7: Với 0 0
90 180 , đẳng thức nào sau đây sai? A. 0
cos(180 −) = −cos . B. 0
cot(180 −) = −cot . C. 0
sin(180 −) = −sin . D. 0
tan(180 −) = − tan .
Câu 8: Câu nào sau đây không phải là mệnh đề? A. Phương trình 2
x + x + 7 = 0 có nghiệm thực.
B. Tam giác đều là tam giác có ba cạnh bằng nhau. Trang 10
C. Bạn có chăm học không?
D. là một số hữu tỉ.
Câu 9: Cho hai tập hợp A = 2 − ; 1 − ;3;5; 7 , B = 2 − ;5;7;13;1
5 . Tìm A B .
A. A B = 13;1 5 .
B. A B = 2 − ;5; 7 .
C. A B = 2 − ; 1 − ;3;5;7;13;1 5 .
D. A B = 1 − ; 3 .
Câu 10: Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất 2 ẩn? 2xy 1 2x 0 2
−x + 2y 2 2x + y 1 A. B. C. D.
x − 2y 2
−x + 2y 2
3x − y 6 −
3x − z 6 −
Câu 11: Cho tập hợp A = 2
x | 2x + 3x − 5 =
0 . Liệt kê các phần tử của tập A . 5 5
A. A = − . B. A = 1 . C. A = 1 ;− . D. A = . 2 2
Câu 12: Cho tam giác ABC có các cạnh BC = 6cm , AC = 7 cm , AB = 5cm . Tính cos B . 1 19
A. cos B = . B. cos B = . 5 35 1 5
C. cos B = . D. cos B = . 15 7
PHẦN II: Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở
mỗi câu, thí sinh chọn đúng hoặc sai. (4.0 điểm) Câu 1: a) n
, n(n +1) + 4 chia hết cho 2. b) 2 x
,4x −1 = 0.
c) Một tứ giác là hình thoi khi và chỉ khi nó có hai đường chéo vuông góc với nhau.
d) 10 là số chính phương.
−x + 2y 0
Câu 2: Cho hệ bất phương trình 2x − y 0
x + y −3 0 Trang 11
a) Hệ bất phương trình đã cho là hệ bất phương trình bậc nhất hai ẩn.
b) Điểm (3;2) thuộc miền nghiệm của hệ bất phương trình đã cho.
c) Miền nghiệm là miền tam giác .
d) Với (x; y) thỏa mãn hệ đã cho, giá trị lớn nhất của F ( ;
x y) = 3x + y bằng 5.
Câu 3: Cho hai tập hợp A = ( 4 − ;4) , B = 1 − ; 1 .
a) A B = 4 − ; 4 .
b) A B = ( 1 − ;1) . c) C B = (− ; − 1 1;+ . )
d) B \ A = .
Câu 4: Cho tam giác ABC , biết AB =13cm, BC =15cm , 0 B = 60 . 1
a) Công thức tính diện tích tam giác ABC là S = . BA BC.sin A . 2 195 3
b) Diện tích tam giác ABC là 2 S = (cm ) . 4
c) Độ dài cạnh AC = 199 (cm) .
d) Độ dài bán kính đường tròn nội tiếp của tam giác ABC là r = 2 + 3 (cm).
PHẦN III. TỰ LUẬN. (3.0 điểm)
Câu 1: Một lớp có 40 học sinh, trong đó có 20 học sinh thích môn Toán, 5 học sinh thích cả 2 môn Toán
và Văn, 4 học sinh không thích cả 2 môn Toán và Văn.
a) Tính số học sinh chỉ thích môn văn.
b) Tính số học sinh thích môn văn.
Câu 2: Một phân xưởng sản xuất hai loại giỏ xách tay loại I và loại II. Thời gian để làm ra một cái giỏ
loại I nhiều gấp hai lần thời gian làm ra một cái giỏ loại II. Nếu chỉ sản xuất toàn giỏ loại II thì trong 1 giờ
phân xưởng làm được 60 cái. Phân xưởng làm việc không quá 8 tiếng mỗi ngày và thị trường tiêu thụ tối
đa mỗi ngày là 200 cái giỏ loại I và 240 cái giỏ loại II. Tiền lãi khi bán một cái giỏ loại I là 24 nghìn
đồng, một cái giỏ loại II là 15 nghìn đồng. Tính số lượng giỏ loại I và loại II trong một ngày mà phân
xưởng cần sản xuất để tiền lãi thu được là cao nhất.
Câu 3: Hai bạn Oanh, Cường lần lượt đứng tại vị trí O,C của một tòa nhà. Hai bạn An, Bình lần lượt
đứng trên mặt đất tại vị trí ,
A B mà tại đó nhìn các điểm C,O các góc lần lượt bằng 0 0 = 30 , = 50 1 2 và 0 0
= 70 , = 80 so với phương nằm ngang. Gọi H là hình chiếu của O trên đường thẳng AB , giả 1 2
sử O,C, H thẳng hàng và biết khoảng cách giữa hai điểm ,
A B là l = 20 m (Hình vẽ dưới). Tính khoảng
cách h giữa vị trí đứng của Oanh và Cường (làm tròn đến hàng phần trăm). O h C β2 α2 β1 α1 H l A B Trang 12
-------------HẾT------------- ĐÁP ÁN
PHẦN I: Trắc nghiệm nhiều lựa chọn
- Mỗi câu đúng được 0,25 điểm. 1 D 2 C 3 A 4 B 5 A 6 C 7 C 8 C 9 B 10 B 11 B 12 A
PHẦN II: Trắc nghiệm đúng sai
- Điểm tối đa mỗi câu là 1 điểm.
- Đúng 1 câu được 0,1 điểm; đúng 2 câu được 0,25 điểm; đúng 3 câu được 0,5 điểm; đúng 4 câu được 1 điểm. Câu 1 Câu 2 Câu 3 Câu 4
a)Đ - b)S - c)S - d)S a)Đ - b)S - c)Đ - d)S
a)S - b)S - c)S - d)Đ a)S – b)Đ – c)Đ – d)S
Phần III: Đáp án tự luận Câu 1
Một lớp có 40 học sinh, trong đó có 20 học sinh thích môn Toán, 5 học 1,0 điểm
sinh thích cả 2 môn Toán và Văn, 4 học sinh không thích cả 2 môn Toán và Văn.
a) Tính số học sinh chỉ thích môn văn.
b) Tính số học sinh thích môn văn. HS lớp: 40 HS thích Văn 4 Hs thích Toán: 20 5 0.5
a) Dựa vào biểu đồ ven, ta suy ra số học sinh chỉ thích môn văn là: 40-4-20=16
b) Số học sinh thích môn văn: 16+5=21 0.5 Câu 2
Một phân xưởng sản xuất hai loại giỏ xách tay loại I và loại II. Thời 1,0 điểm
gian để làm ra một cái giỏ loại I nhiều gấp hai lần thời gian làm ra một
cái giỏ loại II. Nếu chỉ sản xuất toàn giỏ loại II thì trong 1 giờ phân
xưởng làm được 60 cái. Phân xưởng làm việc không quá 8 tiếng mỗi
ngày và thị trường tiêu thụ tối đa mỗi ngày là 200 cái giỏ loại I và 240
cái giỏ loại II. Tiền lãi khi bán một cái giỏ loại I là 24 nghìn đồng, một Trang 13
cái giỏ loại II là 15 nghìn đồng. Tính số lượng giỏ loại I và loại II trong
một ngày mà phân xưởng cần sản xuất để tiền lãi thu được là cao nhất.
Gọi x, y lần lượt là số lượng giỏ loại I và loại II mà phân xưởng sản xuất 0.25
được trong một ngày. (Điều kiện: x, y )
Từ giả thiết suy ra được hệ bất phương trình: 0 x 200 0 x 200
0 y 240 0 y 240 (I) x y
2x + y 480 8 + 30 60
Tổng số tiền lãi là: T = 24x +15y (nghìn đồng) 0.25
Xác định được miền nghiệm của hệ bất phương trình (I) là miền ngũ giác 0.25
ACDEO với A(0; 240), C(120; 240), D(200; 80), E(200; 0), O(0; 0).
- Tại đỉnh A: T = 24. 0+15.240 = 3 600 0.25
- Tại đỉnh C : T = 24.120 +15. 240 = 6 480
- Tại đỉnh D: T = 24.200 +15.80 = 6 000
- Tại đỉnh E : T = 24.200+15.0 = 4 800
- Tại đỉnh O: T = 0
Có 0 < 3 600 < 4 800 < 6 000 < 6 480
Vậy T đạt giá trị lớn nhất bằng 6 480 khi x = 120, y = 240 . Vậy để tiền lãi
thu được là cao nhất, trong một ngày xưởng cần sản xuất 120 cái giỏ loại I và 240 cái giỏ loại II. Câu 3
Hai bạn Oanh, Cường lần lượt đứng tại vị trí O,C của một tòa nhà. 1.0 điểm
Hai bạn An, Bình lần lượt đứng trên mặt đất tại vị trí ,
A B mà tại đó
nhìn các điểm C,O các góc lần lượt bằng 0 0
= 30 , = 50 và 1 2 0 0
= 70 , = 80 so với phương nằm ngang. Gọi H là hình chiếu của 1 2
O trên đường thẳng AB , giả sử O,C, H thẳng hàng và biết khoảng
cách giữa hai điểm ,
A B là l = 20 m (Hình vẽ dưới). Gọi h = OC là
khoảng cách giữa vị trí đứng của Oanh và Cường. Tìm h (làm tròn
đến hàng phần trăm). Trang 14 O h C β2 α2 β1 α1 H l A B Có 0 CAH = = 30 , 0 CBH = = 70 1 1 0
ACB = CBH − CAH = 40 .
Áp dụng định lí sin vào ABC , ta có: 0.25 BC AB 20.sin ( 0 30 ) = = BC m sin CAH sin ACB sin ( 15,56 0 40 ) Xét H
BC vuông tại H , ta có: CH sin CBH =
CH = BC.sin CBH 14,62m BC 0.25 Có 0 OAH = = 50 , 0 OBH = = 80 0 AOB = 30 0.25 2 2
Áp dụng định lí sin vào ABO , ta có: BO AB 20.sin ( 0 50 ) = = BO m sin OAH sin AOB sin ( 30,64 0 30 ) Xét H
BO vuông tại H , ta có: 0.25 HO sin OBH = HO = B .
O sin OBH 30,17 m BO
Vậy h = OC = HO − CH 15,55m .
Nếu giải theo cách khác, kết quả đúng vẫn cho điểm tối đa ĐỀ 4
ĐỀ ÔN TẬP GIỮA HỌC KỲ I NĂM HỌC 2025-2026
MÔN: TOÁN 10-CHÂN TRỜI SÁNG TẠO
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi
thí sinh chỉ chọn một phương án.
Câu 1: Cho tập hợp H = {0;1;2; }
3 . Tập hợp nào dưới đây là tập con của tập hợp H ? A. {- 3;0;1; } 2 B. {0;1;2} C. {0;1;2; } 6 D. {0;2;3;4} Trang 15
Câu 2: Phủ định của mệnh đề “1+ 2 = 3” là mệnh đề A. 1+ 2 3. B. 1+ 2 3. C. 1+ 2 3. D. 1+ 2 3.
Câu 3: Cho 0 90. Khẳng định nào sau đây đúng?
A. tan 0;cot 0
B. tan 0; cot 0
C. tan 0;cot 0
D. tan 0;cot 0
Câu 4: Hệ bất phương trình nào sau đây là hệ bất phương trình bật nhất hai ẩn? 3
−x + y 4 3 3 x + y 0 x − y 0 x + 2y 0 A. B. C. D. x + 2y 1 x + y 3 2y 0 2 y + 3 0
Câu 5: Cho tam giác ABC có BC=a, AC=b, AB=c, h là độ dài đường cao xuất phát từ A, p là nửa chu a
vi. Chọn khẳng định sai trong các khẳng định sau? 1
A. S = p( p − a)( p − )
b ( p − c) B. S = . a h 2 a 1 1 C. S = . a . b sin A D. S = . a . c sin B 2 2
Câu 6: Cho hai tập: A = 3
− ;7, B =2;+) . Xác định A B . A. 7;+) B. 2;7 C. ( 3; − +) D. 3; − +)
Câu 7: Cho tam giác ABC , mệnh đề nào sau đây đúng? A. 2 2 2
a = b + c − 2bc cos B B. 2 2 2
a = b + c − 2bc cos A C. 2 2 2
a = b + c − 2bc cosC D. 2 2 2
a = b + c + 2bc cos A
Câu 8: Trong các bất phương trình sau, bất phương trình nào là bất phương trình bậc nhất hai ẩn? A. 3
x + y 3
B. xy + x 5 C. 2
2x + 3y 4 D. 2 3
3 x + 4 y 6
Câu 9: Cho hai mệnh đề P :"DABC cân " và Q :"DABC có hai đường cao bằng nhau”. Phát biểu
mệnh đề "P Þ Q" bằng cách dùng điều kiện đủ.
A. DABC cân là điều kiện đủ để DABC có hai đường cao bằng nhau.
B. DABC có hai đường cao bằng nhau là điều kiện đủ để DABC cân.
C. DABC cân là điều kiện cần để DABC có hai đường cao bằng nhau.
D. DABC có hai đường cao bằng nhau là điều kiện cần để DABC cân.
Câu 10: Cho 0 90.Mệnh đề nào sau đây đúng?
A. tan(90o −) = tan
B. cos(90o −) = o c s
C. tan(90o −) = cot
D. sin(90o −) = sin
Câu 11: Cho x là một phần tử của tập hợp X. Mệnh đề nào sau đây là đúng? A. x X. B. x X. C. X . x
D. x X.
Câu 12: Hình nào sau đây biểu diễn miền nghiệm của bất phương trình x − y 3? y 3 3 x O A. B. Trang 16 y y x 3 O 3 3 − O x 3 C. D.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở
mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1: Cho tam giác ABC có a=5, b=7, 0 C = 60 35
a) Diện tích tam giác S = 4 b) 1 sin C = 2 7 3
c) Độ dài đường cao xuất phát từ đỉnh A của tam giác ABC là 2 d) c = 39 0 y 5 x 0
Câu 2: Cho hệ bất phương trình có miền nghiệm là S
x + y − 2 0
x − y − 2 0
a) (1; 2) S
b) (2; 2) S c) Cặp số ( ;
x y) S làm biểu thức F=x-2y đạt giá trị nhỏ nhất là bằng -12
d) Miền nghiệm S là miền tam giác
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 4.
Câu 1: Cho hai tập hợp khác rỗng A = [m +1; 2m −1], B = (0;6) . Có bao nhiêu giá trị m nguyên để A B .
Câu 2: Cho hai tập hợp A = ( ;
m m +1) và B = [ 1
− ;3] . Tìm tất cả các giá trị của m ∈[−2024;2019) để A B = .
Câu 3: Hai chiếc tàu thủy P và Q cách nhau 100 m . Từ P và Q thẳng hàng với
chân A của tháp hải đăng AB ở trên bờ biển người ta nhìn chiều cao AB của tháp dưới các góc BPA 15 = và BQA 22 =
. Tính chiều cao AB của tháp làm tròn đến hàng phần mười?
Câu 4: Bác Năm dự định trồng ngô và đậu xanh trên một mảnh đất có diện tích 8 hecta (ha). Nếu trồng 1
ha ngô thì cần 20 ngày công và thu được 40 triệu đồng. Nếu trồng 1 ha đậu xanh thì cần 30 ngày công và
thu được 50 triệu đồng. Bác Năm cần trồng x ha ngô và y ha đậu xanh để thu được nhiều tiền nhất? Biết Trang 17
rằng, bác Năm chỉ có thể sử dụng không quá 180 ngày công cho việc trồng ngô và đậu xanh. Khi đó x+y bằng bao nhiêu? PHẦN IV: TỰ LUẬN
Câu 1 (1 điểm): Biểu diễn miền nghiệm của bất phương trình: x + 2 y 4
Câu 2 (1 điểm): Cho tam giác ABC có AC = 4 cm , góc A = 60 , B = 45 .
a) Tính độ dài cạnh BC.
b) Tính diện tích tam giác ABC. Câu 3 (0,5 điểm):
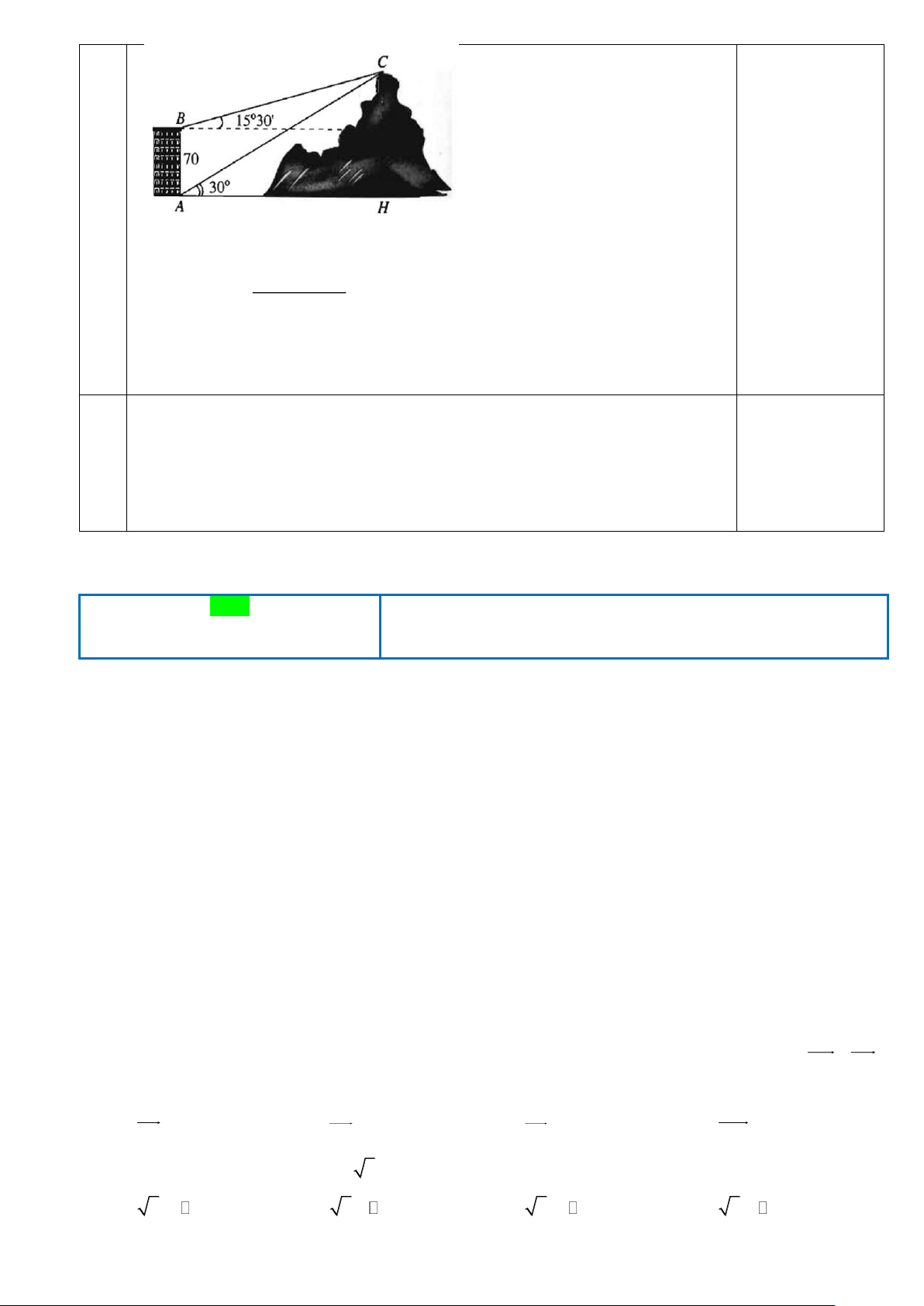
Từ hai vị trí A và B của một tòa nhà, người ta quan sát đỉnh C
của ngọn núi. Biết rằng độ cao AB = 70 m, phương nhìn AC
tạo với phương nằm ngang góc 30, phương nhìn BC tạo với phương nằm ngang góc ' 15 30
. Tính chiều cao của ngọn núi
(làm tròn đến hàng đơn vị)
Câu 4 (0,5 điểm): Lớp 10A có 45 học sinh, trong đó có 23 học sinh tham gia câu lạc bộ thể thao, 17 học
sinh tham gia câu lạc bộ âm nhạc, trong đó có 5 học sinh tham gia cả hai câu lạc bộ thể thao và âm nhạc.
Hỏi có bao nhiêu học sinh của lớp không tham gia cả hai câu lạc bộ thể thao và âm nhạc?
-------------- HẾT ---------------
- Thí sinh không được sử dụng tài liệu;
- Cán bộ coi thi không giải thích gì thêm. ĐÁP ÁN MÔN TOÁN LỚP 10 Câu Nội dung Điểm
Câu + Đường thẳng (d): x + 2 y = 4 đi qua 2 điểm A(4;0) và B(0;2). 0,25 1
+ Thay (0;0) vào bất phương trình x + 2 y 4 (*)ta thấy (0;0) không phải là nghiệm của bpt (*). 0,25 0,25
Vậy miền nghiệm của bpt (*) là miền 0,25
không gạch bỏ (không kể đường thẳng d)
Câu a) Áp dụng định lý hàm số Sin trong tam giác ABC ta có: 2 0 AC.sin A 4.sin 60 0,25+0,25 BC = = = 2 6 0 sin B sin 45 0,25+0,25 1
b) Diện tích tam giác ABC: S = . CA .
CB sin C = 6 + 2 3 2 Trang 18 Câu 3 0.25 0 0 0 0 0 0 0 0.25
BAC = 90 − 30 = 60 , CBA =90 +15,5 =105,5 suy ra BCA = 14,5 A . B sin ABC AC = = ..... 269,407 sin ACB CH = CA. 0 sin 30 134,7034 135m
Vậy chiều cao của ngọn núi là 135 mét Câu
- Vì có 5 hs tham gia cả hai câu lạc bộ thể thao và âm nhạc. 4
- Do đó có 18 HS tham gia CLB thể thao và kg tham gia CLB âm nhạc. 0,25
12 HS HS tham gia CLB âm nhạc và kg tham gia CLB thể thao. 0,25
- Vậy có 10 HS không tham gia CLB nào . ĐỀ 5
ĐỀ ÔN TẬP GIỮA HỌC KỲ I NĂM HỌC 2025-2026
MÔN: TOÁN 10-CHÂN TRỜI SÁNG TẠO
PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1. Trong các câu sau, câu nào là mệnh đề?
A. Các bạn hãy làm bài đi!
B. 2022 là số tự nhiên lẻ.
C. An học lớp mấy?
D. Các bạn có chăm học không?
Câu 2. Trong các cặp số sau đây, cặp nào không là nghiệm của bất phương trình 2x + y 1? A. (3; 7 − ). B. (0; ) 1 . C. (0;0) . D. ( 2 − ; ) 1 .
Câu 3. Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
A. x + y ³ 0. B. 2 x + 2 y < 2. C. x + 2 y ³ 0. D. 2
2x + 3y > 0.
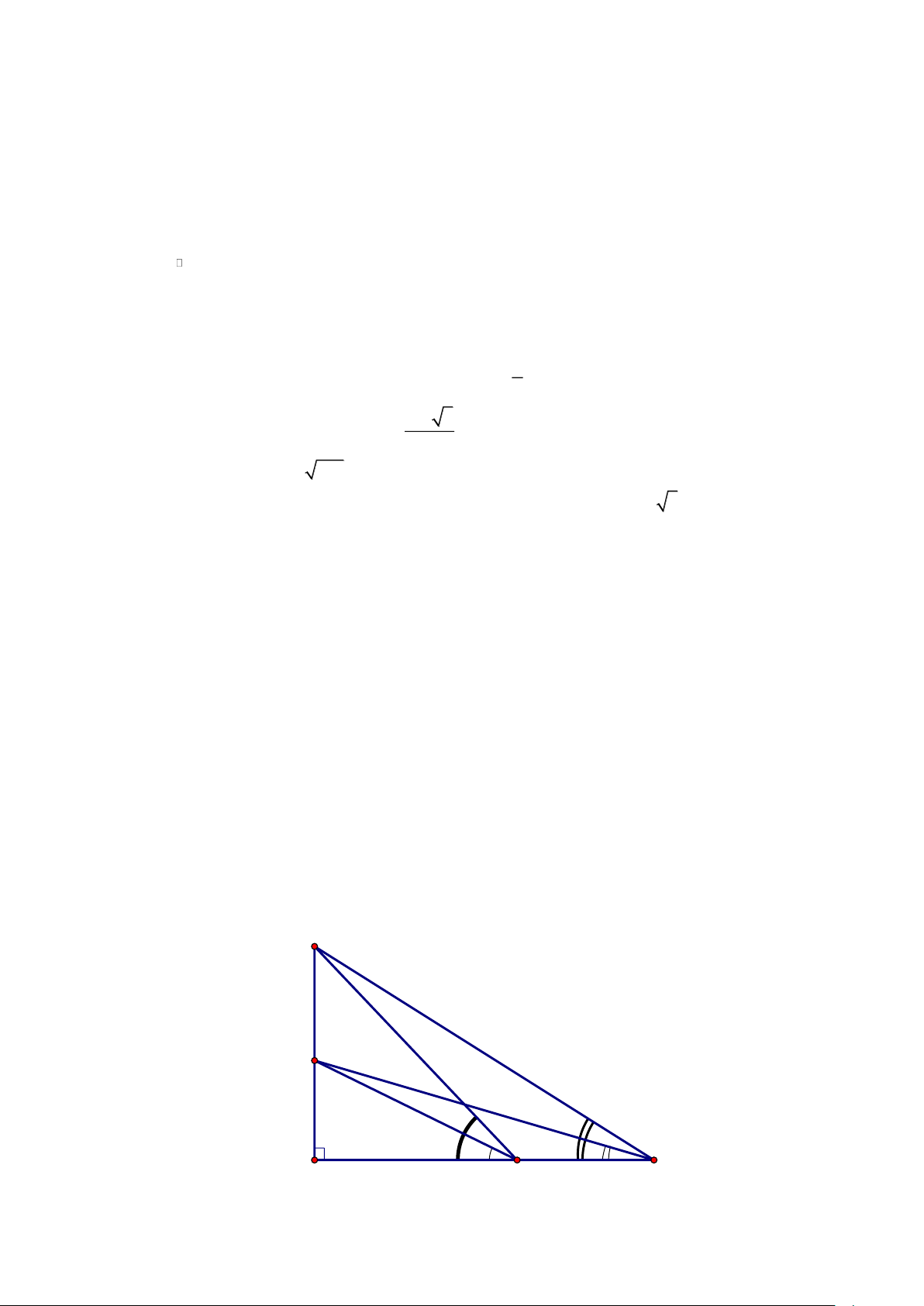
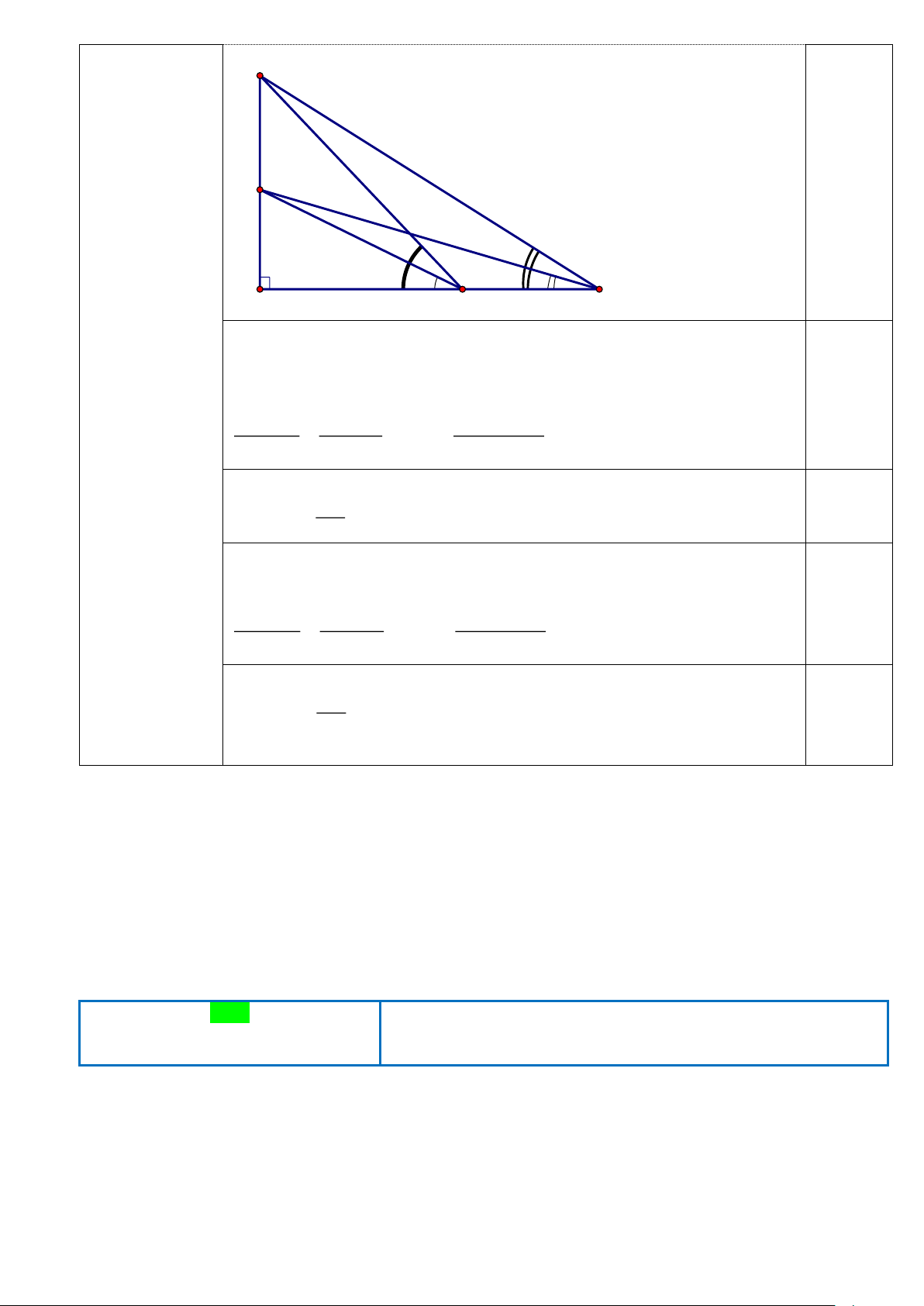
Câu 4. Cho tam giác ABC . Gọi M , N, P lần lượt là trung điểm của AB, BC,CA . Vectơ tổng MP + NP bằng A. CP . B. PA . C. BP . D. MN .
Câu 5. Ký hiệu nào sau đây để chỉ 5 không phải là một số hữu tỉ? A. 5 B. 5 C. 5 D. 5 Trang 19
Câu 6. Cho I là trung điểm của đoạn thẳng AB . Với điểm M bất kỳ, ta luôn có:
1
A. MA+ MB = 3MI
B. MA + MB = MI 2
C. MA + MB = MI
D. MA + MB = 2MI
Câu 7. Vectơ có điểm đầu là A , điểm cuối là B được kí hiệu là: A. BA . B. AB . C. AB . D. AB .
Câu 8. Cho hình bình hành ABCD. Vectơ tổng CB + CD bằng A. AC . B. DB . C. CA . D. BD .
Câu 9. Trong các câu sau đây câu nào không phải là mệnh đề?
A. Nha Trang là thành phố của Khánh Hòa. B. 2 +3 = 6.
C. Một năm có 365 ngày.
D. Học lớp 10 thật vui.
Câu 10. Phần không tô đậm trong hình vẽ dưới đây (không chứa biên), biểu diễn tập nghiệm của hệ bất phương trình nào trong
các hệ bất phương trình y sau? 1 x O 1 -1
ìï x - y > 0
ìï x - y < 0
ìï x - y < 0 ìï x - y ³ 0 A. ïí . B. ïí . C. ïí . D. ïí . ï 2x - y > 1 ïî ï 2x - y > 1 ïî ï 2x - y < 1 ïî ï 2x - y ³ 1 ïî
x + y − 2 0
Câu 11. Trong các cặp số sau, cặp nào không là nghiệm của hệ bất phương trình là
2x − 3y + 2 0 A. ( 1 − ;− )1. B. (0;0) . C. (1; ) 1 . D. ( 1 − ; ) 1 .
Câu 12. Khẳng định nào sau đây đúng?
A. Hai vectơ a và b được gọi là bằng nhau nếu chúng cùng hướng và cùng độ dài.
B. Hai vectơ a và b được gọi là bằng nhau nếu chúng cùng phương và cùng độ dài.
C. Hai vectơ a và b được gọi là bằng nhau nếu chúng cùng độ dài. Trang 20




