




Preview text:
Luyện thi ĐGNL ĐHQGHN VNES
Tự tin - Tiến bước - Khẳng định bản thân
Họ và tên: ................................................................... Đề ôn luyện 01
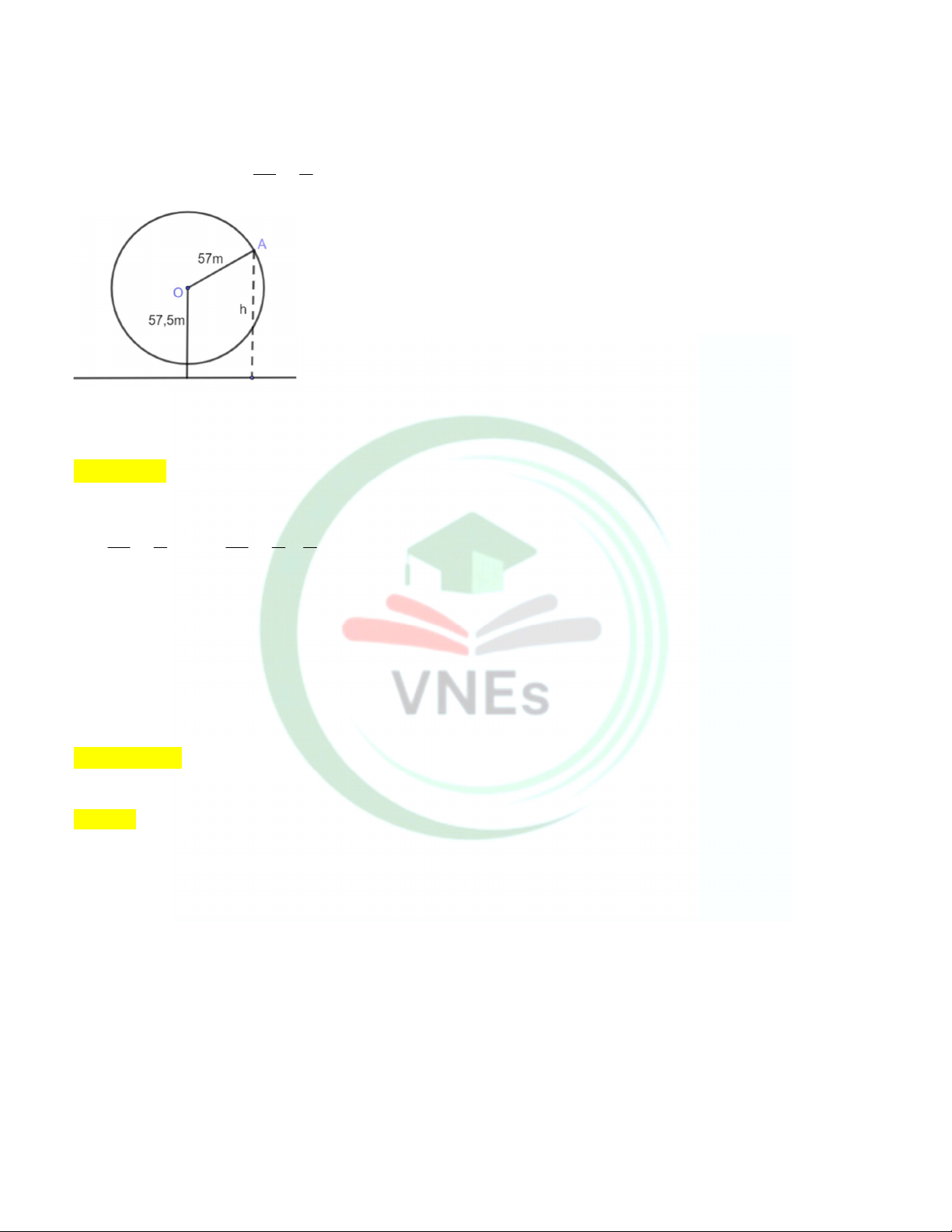
Câu 1. Một vòng quay trò chơi có bán kính 57m , trục quay cách mặt đất 57,5m , quay đều mỗi vòng hết 15 phút.
Khi vòng quay quay đều, khoảng cách hm từ một cabin gắn tại điểm A của vòng quay đến mặt đất được tính bởi công thức: ht 2 57sin t 57,5
với t là thời gian quay tính bằng phút t 0 15 2
Khi quay một vòng lần thứ nhất tính tại thời điểm t 0 ( phút), tại thời điểm nào của t thì cabin ở vị trí cao nhất? Lời giải Đáp án: 7,5
Khi quay một vòng, cabin ở vị trí cao nhất khi 2 2 sin t 1 t k2 k Z 15 2 15 2 2
t 7,5 15k k Z
Vì 0 t 15 nên t 7,5 (phút). Câu 2. Cho hàm số 2
f (x) mx 2mx m 1. Có bao nhiêu giá trị nguyên của tham số m trên đoạn [ 2025; 2025] để f (x) 0, m ? A. 2026 . B. 2025 . C. 4051. D. 4050 . Lời giải Chọn A.
TH1. m 0 .Khi đó: f x 1 0, x . a m 0 m 0 TH2. m 0 Khi đó: 2
f (x) mx 2mx m 1 0,x m 0 . 2 m m m 1 0 m 0
Vậy m 0 thỏa mãn bài toán.
Mà m [ 2025;2025] nên m{0;1;2;...2025}
Vậy có 2026 giá trị nguyên của tham số m
Luyện thi ĐGNL ĐHQGHN VNES
Tự tin - Tiến bước - Khẳng định bản thân
Câu 3. Một người làm việc cho một công ty. Theo hợp đồng trong năm đầu tiên, tháng lương thứ nhất là 8 triệu đồng
và tháng lương sau cao hơn tháng lương trước là 300 ngàn đồng. Hỏi theo hợp đồng tổng số lương người đó nhận
được trong một năm là bao nhiêu triệu đồng (Làm tròn đến hàng phần chục) Lời giải Đáp án: 115,8
Theo hợp đồng trong năm đầu tiên, lương của mỗi tháng lập thành cấp số cộng có số hạng đầu 6 u 8.10 và công sai 1 5 d 3.10 .
Vậy, theo hợp đồng tổng số lương người đó nhận được trong một năm là: 12.11 6 12.11 5 6 S 12.u .d 12.8.10
.3.10 115,8.10 = 115,8 triệu. 12 1 2 2
Câu 4. Biết bốn số hạng liên tiếp của một cấp số cộng biết tổng của chúng bằng 20 và tổng bình phương của chúng
bằng 120. Tổng bình phương của số hạng đầu tiên và số hạng cuối cùng bằng bao nhiêu? Lời giải Trả lời: 68
Gọi 4 số hạng liên tiếp của cấp số cộng cần tìm là u 3d,u d,u d,u 3d, 1 1 1 1 u
3d u d u d u 3d 20 u 5 u 5 Theo bài ra ta có 1 1 1 1 1 1 2 2 2 2 2 2
(u 3d ) (u d) (u d ) (u 3d ) 120 4u 20d 120 d 1 1 1 1 1 1
Vậy 4 số hạng liên tiếp của một cấp số cộng cần tìm là: 2, 4, 6, 8 hoặc 8, 6, 4, 2
Vậy tổng bình phương của số hạng đầu tiên và số hạng cuối cùng bằng 2 2 S 2 8 68
Câu 5. Để dự báo dân số của một quốc gia, người ta sử dụng công thức . nr S
A e , trong đó A là dân số của năm lấy
làm mốc tính, S là dân số sau n năm, r là tỉ lệ gia tăng dân số hằng năm, năm 2017, dân số Việt Nam là 93 671 600
người (Tổng cục Thống kê, Niên giám thống kê 2017, Nhà xuất bản thống kê Tr.79). Giả sử tỉ lệ tăng dân số hằng
năm không đổi là 0,81% , dự báo dân số Việt Nam năm 2035 là bao nhiêu người (kết quả làm tròn đến chữ số hàng trăm)? A. 108311100 . B. 109256100. C. 107500500. D. 108374700. Lời giải Chọn D
Từ năm 2017 đến năm 2035, số năm là: n 2035 2017 18
Dân số Việt Nam năm 2035 là: 18.0,0081 S 93671600.e 108374700 (người).
Luyện thi ĐGNL ĐHQGHN VNES
Tự tin - Tiến bước - Khẳng định bản thân 1
Câu 6. Tính đạo hàm của hàm số 2 y sin x . 2 3 2 1 2 2 1 A. y ' x cos x . B. y ' x cos x . C. 2 y x cos x . D. 2 y ' x cos x . 3 2 3 3 2 3 Lời giải Chọn A 1 Ta có 2 2 y ' . x '.cos x 2 y ' . x cos x . 2 3 3 3 Câu 7. Cho phương trình 2
4log x (m3)log x2m 0 ( m là tham số thực ). Có bao nhiêu giá trị nguyên của 2 2
m để phương trình đã cho có hai nghiệm thực phân biệt thuộc đoạn [1; 8] ? Lời giải Trả lời: 3 Điều kiện: x 0 . 2 Ta có 2
4log x (m3)log x2m 0 1 4 log x
(m3)log x 2m 0 2 2 2 2 2 log x 1 x 2 2
log x(m3)log x2m 0 2 2 2 log x 2m log x 2 . m 1 2 2
Phương trình đã cho có hai nghiệm thực phân biệt thuộc đoạn [1; 8] khi và chỉ khi
1 có một nghiệm thuộc đoạn 0 2m3 1 m2 [1; 8] \ {2} tức 2m1 m . 1
Vậy có 3 giá trị nguyên của m thỏa mãn bài toán.
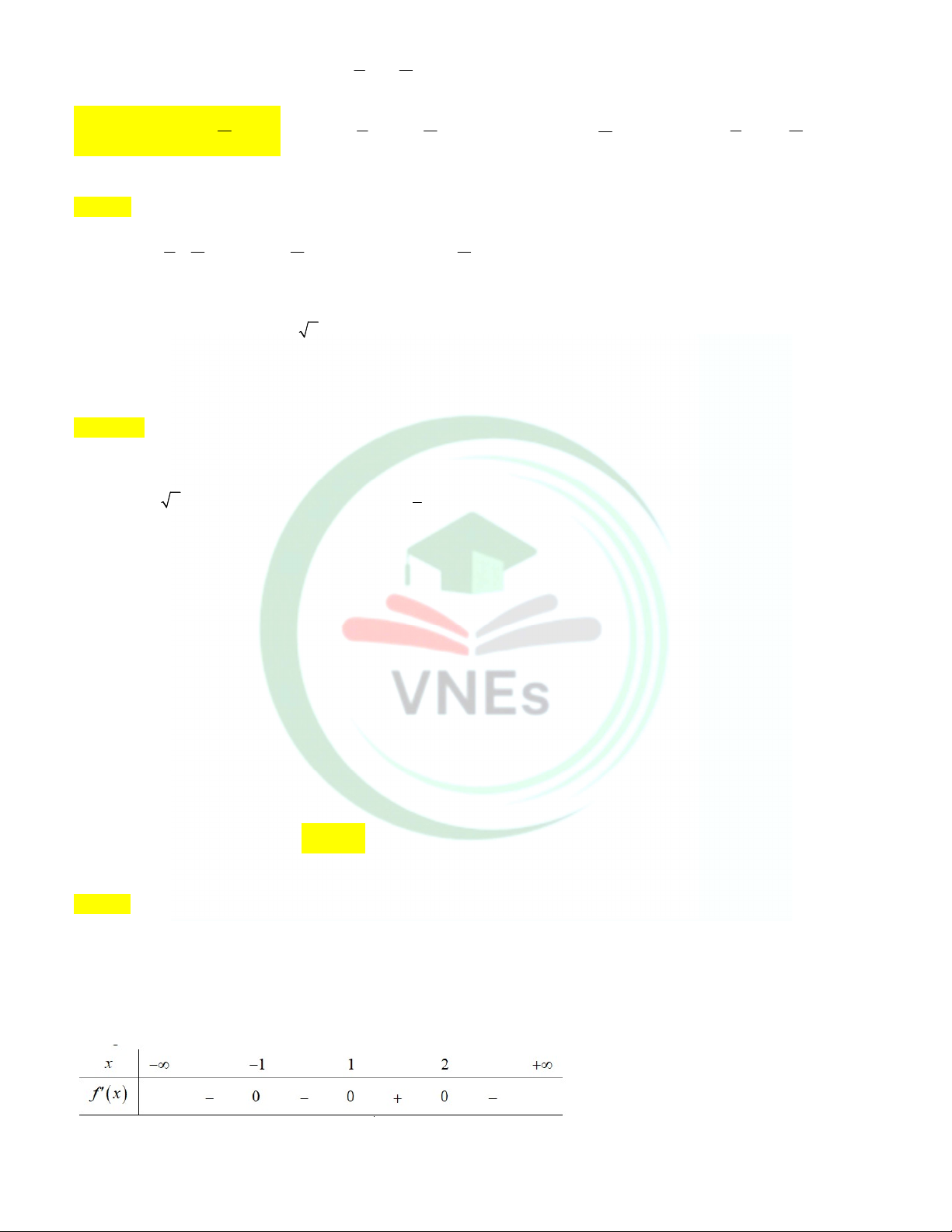
Câu 8. Cho hàm số f x có đạo hàm f x x 2 x 3 1
1 2 x . Hàm số f x đồng biến trên khoảng nào dưới đây?. A. 1 ; 1 . B. 1;2 . C. ; 1 . D. 2; . Lời giải Chọn B x 1
Ta có f x 0 x 2 x 3 1 1 2 x 0 x 1 . x 2 Ta có bảng xét dấu
Từ bảng xét dấu ta có f x 0 với x 1;2 .
Luyện thi ĐGNL ĐHQGHN VNES
Tự tin - Tiến bước - Khẳng định bản thân 4
Câu 9. Trên mặt phẳng toạ độ Oxy, tiếp tuyến của đồ thị hàm số y
tại điểm có hoành độ x 1 và cắt hai x 1
trục toạ độ tại A và B. tính diện tích tam giác OAB? Lời giải Trả lời: 4,5 4 4 Ta có: y . y 1 x 2 1 1 1 2 1
Do đó, phương trình tiếp tuyến của đồ thị hàm số đi qua điểm M 1
; 2 và nhận y làm hệ số góc là: 1 1 y 2 1 x 1 y x 3.
Giao điểm với trục hoành Ox là: y 0 x 3 0 x 3 A(3;0) OA 3
Giao điểm với trục hoành Oy là: x 0 y 0 3 3 B(0; 3) OB 3 1 1 9
Diện tích tam giác OAB bằng: S O . A OB .3.3 4,5 2 2 2
Câu 10. Cho hàm số y f x liên tục, có đạo hàm trên . Đồ thị hàm số y f x như hình vẽ. y y=f'(x) -1 1 4 O x
Hàm số y f 4 x nghịch biến trên khoảng nào dưới đây? A. ; 1 . B. 0;3 . C. 3; . D. 1 ; 1 . Lời giải
Hàm số y f 4 x có y f 4 x .
Khi đó hàm số y f 4 x nghịch biến khi y 0 f 4 x 0 f 4 x 0 . x x
Dựa vào đồ thị hàm số y f x ta có: f x 1 4 1 3 5 4 0 4 x 4 x 0
Vậy hàm số y f 4 x nghịch biến trên các khoảng ; 0 và 3;5 .
Luyện thi ĐGNL ĐHQGHN VNES
Tự tin - Tiến bước - Khẳng định bản thân
Câu 11. Cho hàm số y f x có đạo hàm f x x x 2 x 2 2
5 . Hàm số g x f 10 5x có bao nhiêu điểm cực tiểu? A. 0 . B. 2 . C. 1. D. 3 . Lời giải
Ta có g x 10 5x
f 10 5x x x 2 x 2 5. 10 5 10 5 2 10 5 5 .
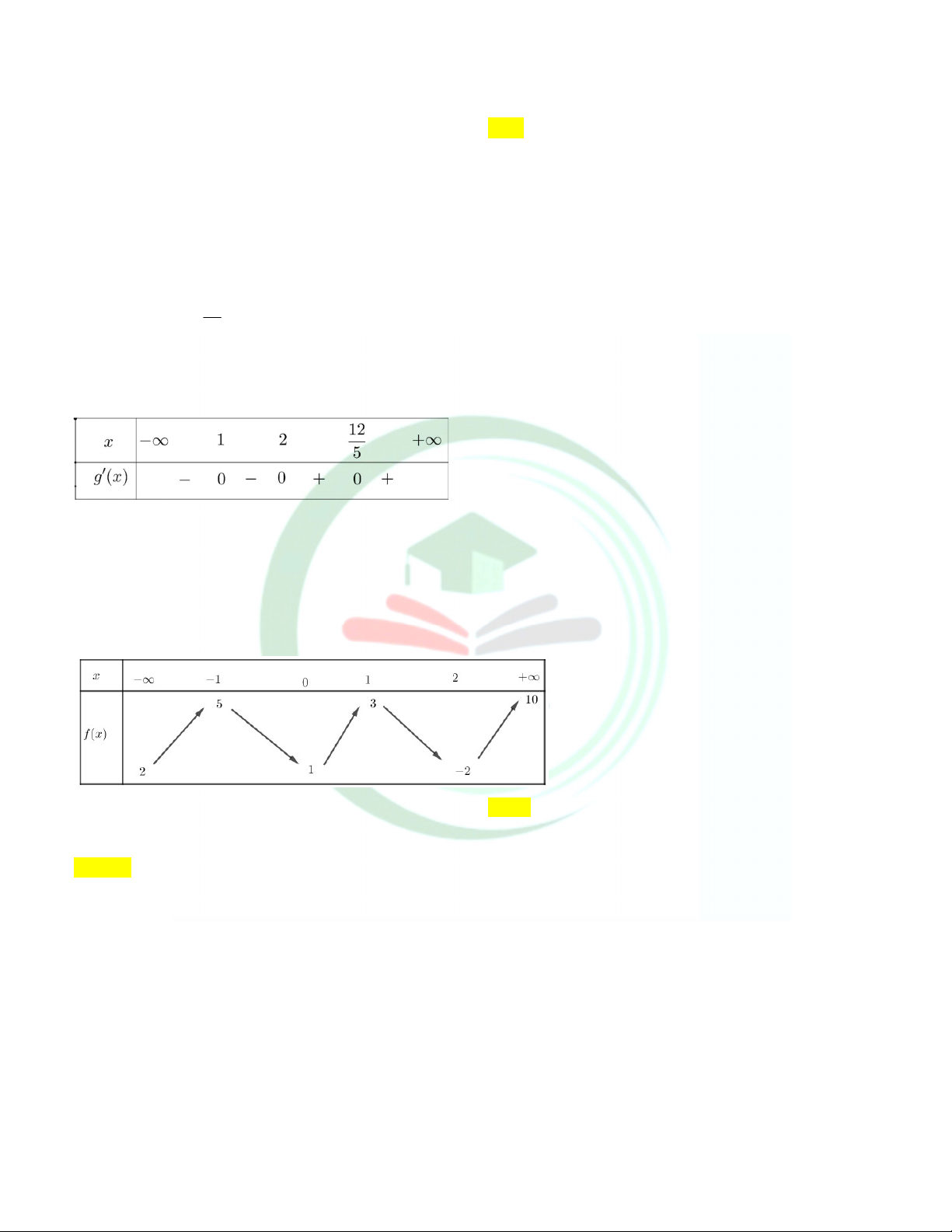
Hay g x x x 2 x 2 5 5 10 5 12 5 5 . x 2 g x 12 0 x . 5 x 1
Bảng xét dấu g x
Vậy hàm số g x có 1 điểm cực tiểu.
Câu 12. Cho hàm số y f x liên tục và có bảng biến thiên trên như hình vẽ bên. Tìm giá trị nhỏ nhất của hàm
số y f cos x 1 . A. 1. B. 3. C. 10. D. 5. Lời giải Chọn C Đặt t cos x 1 . Do 1
cos x 1 0 cos x 1 2
Suy ra điều kiện của t 0;2 .
Khi đó yêu cầu bài toán trở thành: “Tìm giá trị nhỏ nhất của hàm y f t trên đoạn 0; 2 ”.
Dựa vào bảng biến thiên ta thấy hàm y f t với t 0;
2 thì có: min f t 2 0;2
Luyện thi ĐGNL ĐHQGHN VNES
Tự tin - Tiến bước - Khẳng định bản thân 1
Câu 13. Tìm tất cả các giá trị của tham số m để hàm số: 3 y x m 2
1 x 1 3m x 2 có cực đại và cực tiểu. 3 m 5 m 5 A 5 m 0 . B. 5 m 0 . C. . D. . m 0 m 0 Lời giải Chọn C
Ta có tập xác định của hàm số là: D . Và đạo hàm: 2 y ' x 2 m 1 x 1 3m .
Hàm số có cực đại và cực tiểu khi và chỉ khi phương trình y' 0 có hai nghiệm phân biệt m
' 0 m 2 1 1 3m 0 2
0 m 5m 0 m 5
Câu 14. Nguyên hàm của hàm số 2 1 y x 3x là x 3 2 x 3x 3 2 x 3x 1 3 2 x 3x 3 2 x 3x A. ln x C . B. C . C. ln x C . D. ln x C . 3 2 2 3 2 x 3 2 3 2 Lời giải Chọn D 3 2 1 x 3x
Áp dụng công thức nguyên hàm ta có 2 x 3x dx ln x C . x 3 2 2 x x 3
Câu 15. Giá trị của m để y mx 2 là tiệm cận xiên của đồ thị hàm số y bằng x 3 A. 2 . B. 1. C. 1 . D. 2 . Lời giải Chọn B 2 x x 3 9 Ta có lim x 2 lim 0
, do đó y x 2 là tiệm cận xiên của đồ thị hàm số trên m 1 x x 3 x x 3
Luyện thi ĐGNL ĐHQGHN VNES
Tự tin - Tiến bước - Khẳng định bản thân
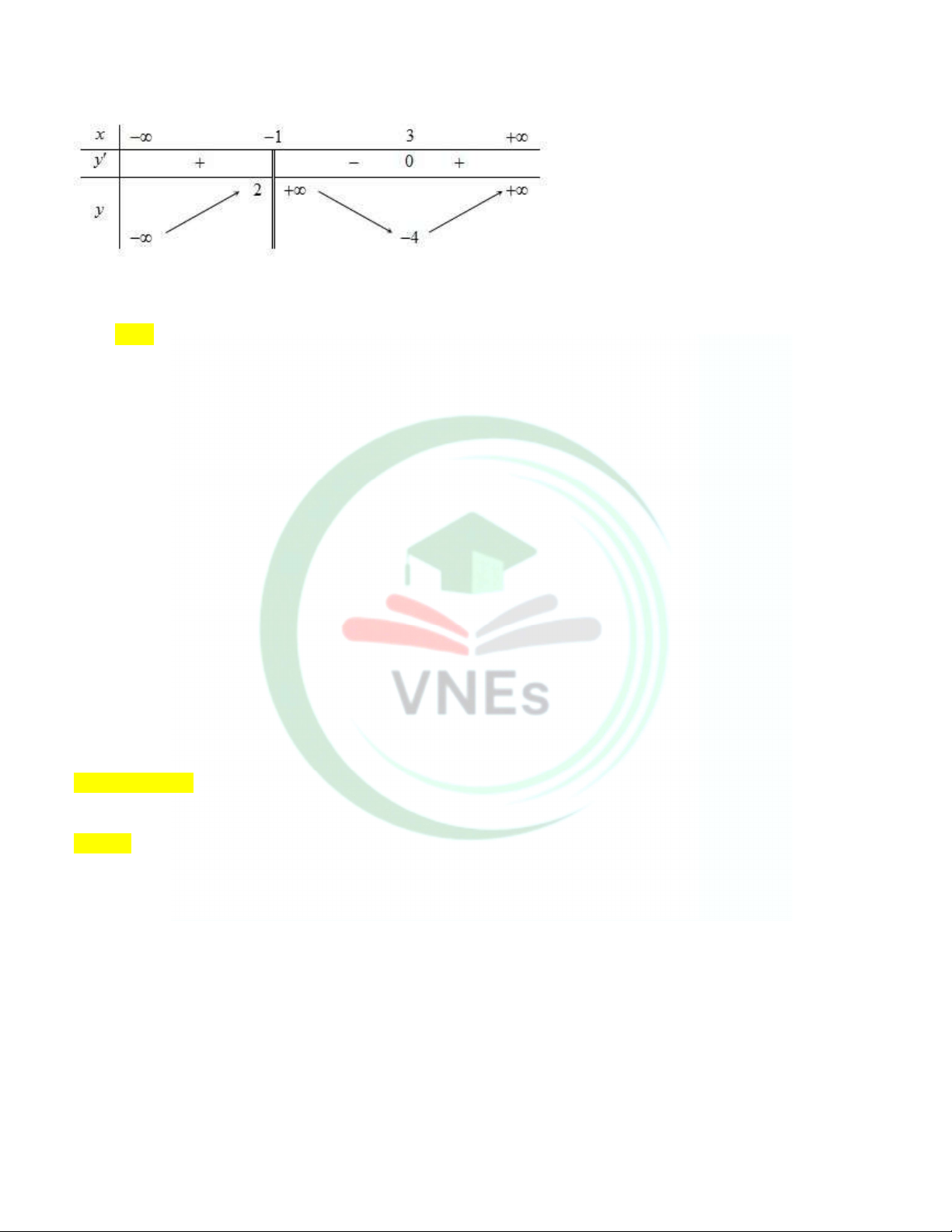
Câu 16. Cho hàm số y f x xác định trên \ 1
, liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình sau
Số nghiệm của phương trình 2
f x 5 f x 4 là A. 5 . B. 6 . C. 4 . D. 7 . Lời giải. f x 1 Phương trình 2
f x 5 f x 4 f x 4
Số nghiệm phương trình f x 1
là số giao điểm của hai đồ thị hàm số y f x và y 1 nên phương trình có 3 nghiệm
Số nghiệm phương trình f x 1
là số giao điểm của hai đồ thị hàm số y f x và y 4 nên phương trình có 2 nghiệm
Vậy số nghiệm của phương trình 2
f x 5 f x 4 là 5 nghiệm
Câu 17. Một ô tô đang chạy với vận tốc 20m/s thì người lái xe đạp phanh. Sau khi đạp phanh, ô tô chuyển động
chậm dần đều với vận tốc v t 4t 20 m/s , trong đó t là khoảng thời gian tính bằng giây kể từ lúc bắt đầu đạp
phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển được bao nhiêu mét? A. 5 0 mét B. 100 mét. C. 5 mét. D. 150 mét. Lời giải Chọn A
Khi xe dừng hẳn thì vận tốc bằng 0 nên ta có t 5 . 5
Vậy quãng đường mà xe di chuyển được kể từ lúc đạp phanh đến khi dừng hẳn là S 4t 20dt 50 m . 0
Luyện thi ĐGNL ĐHQGHN VNES
Tự tin - Tiến bước - Khẳng định bản thân
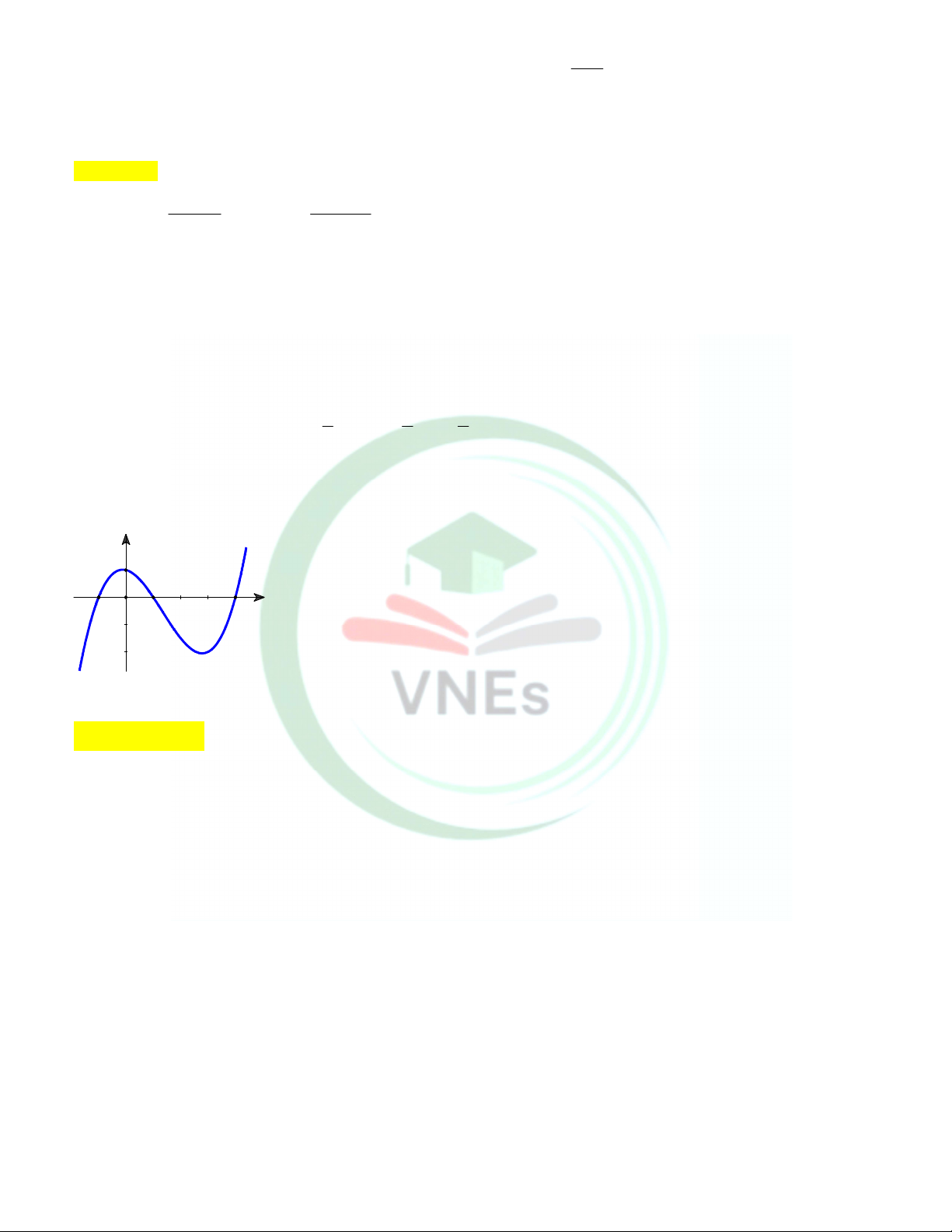
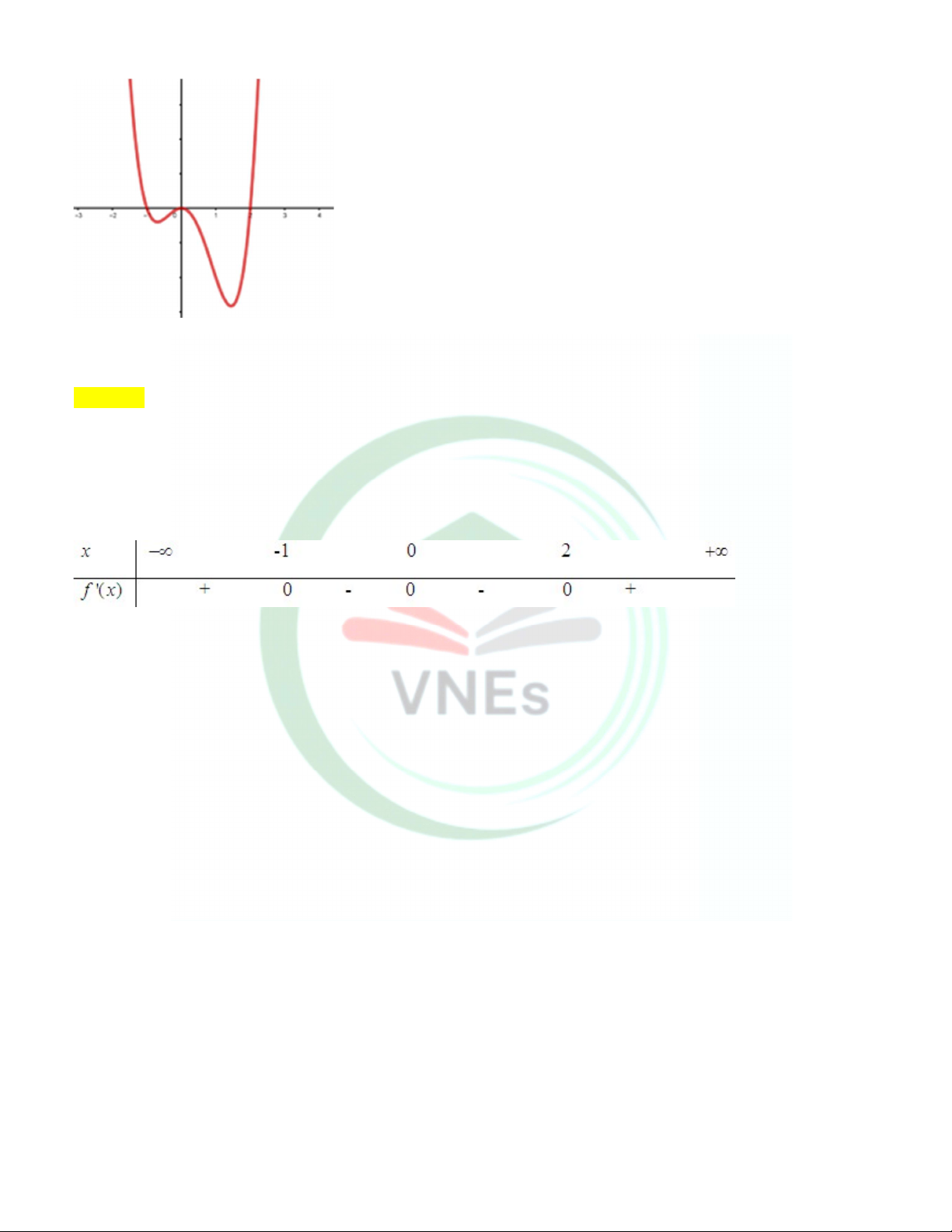
Câu 18. Cho hàm số y f (x) có đồ thị f ( x) như hình vẽ:
Số điểm cực trị của hàm số đã cho là bao nhiêu? Lời giải Trả lời: 2 x 1 Từ đồ thị của f (
x) ta có f (x) 0 x 0 x 2 Bảng xét dấu:
Từ bảng xét dấu của f (
x) ta có f (x) đổi dấu hai lần qua các điểm x 1
; x 2 nên hàm số đã cho có 2 điểm cực trị
Luyện thi ĐGNL ĐHQGHN VNES
Tự tin - Tiến bước - Khẳng định bản thân
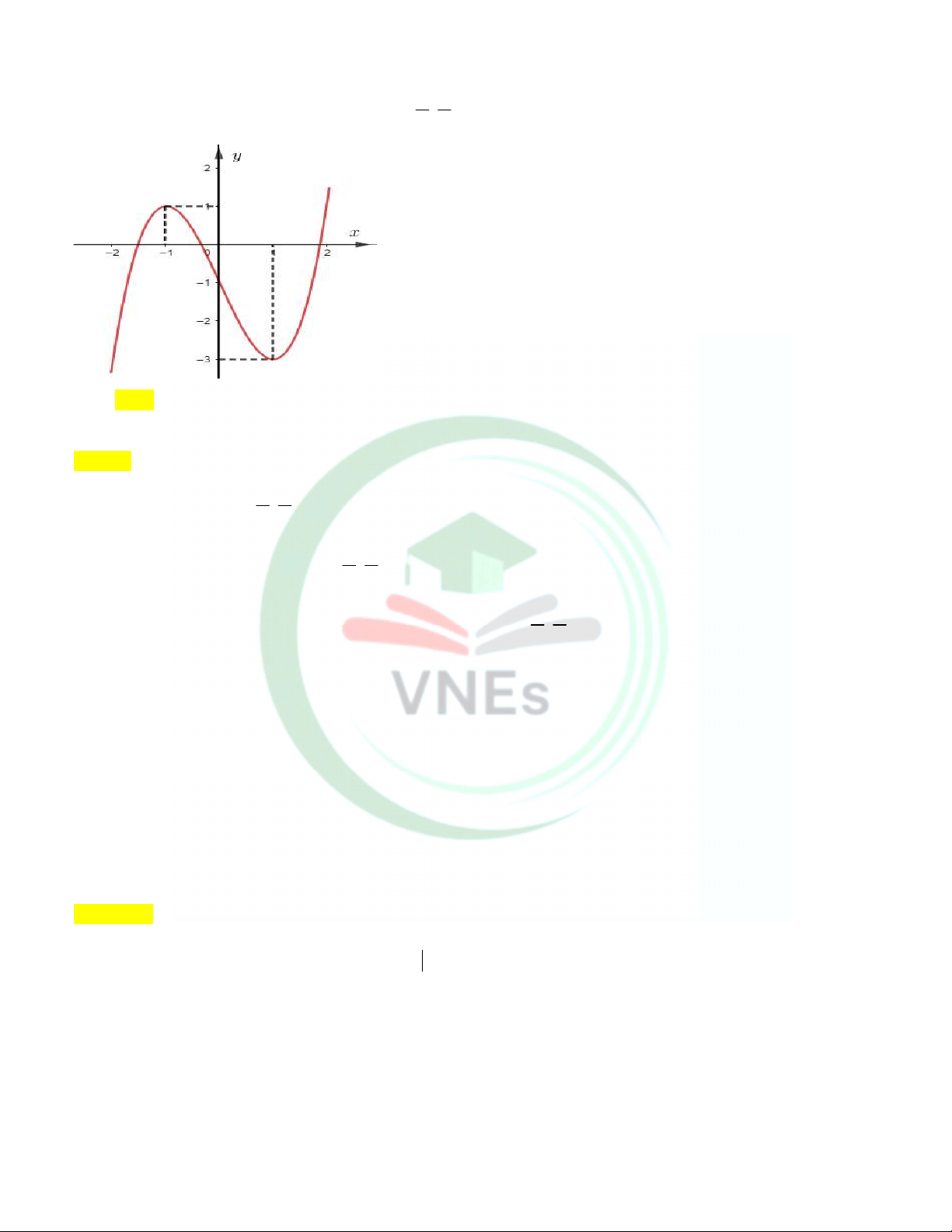
Câu 19. Cho hàm số y f x liên tục trên và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên m để phương trình f 2cos x
1 m có hai nghiệm thuộc ; ? 2 2 A. 3 . B. 2 . C. 4 . D. 5 . Lời giải Chọn A
Đặt 2cos x 1 t ; x ; t 1 ; 1 . 2 2 Ta có: t 1 ; 1 cho 2 nghiệm x ; . 2 2
Do đó phương trình f 2cos x
1 m có hai nghiệm thuộc ;
khi phương trình f t m có một nghiệm 2 2 thuộc 1 ; 1 .
Từ đồ thị ta thấy f t m có một nghiệm thuộc 1 ; 1 m 3 ; 1 .
Vậy tập hợp số nguyên m thỏa mãn yêu cầu bài toán là S 2 ;1;0 . 5 2 Câu 20. Cho f
xdx 10. Kết quả 24 f xdx bằng bao nhiêu? 2 5 Lời giải Trả lời: 34 2 2 2 5 Tacó 2 4 f 5 xdx 2 dx 4 f
xdx 2x 4 f xdx 2
.5 2 4.10 34 . 2 5 5 5 2
Luyện thi ĐGNL ĐHQGHN VNES
Tự tin - Tiến bước - Khẳng định bản thân
Câu 21. Trong không gian với hệ tọa độ Oxyz , cho mặt cầu S 2 2 2
: x y z 2x 4y 6z 0 . Trong các điểm
O0;0;0 , A1;2;3 , B2;1;
1 có bao nhiêu điểm thuộc mặt cầu S ? A. 1. B. 0 . C. 3 . D. 2 . Lời giải Ta có mặt cầu S 2 2 2
: x y z 2x 4y 6z 0 x 2 y 2 z 2 1 2 3 14 .
Điểm O0;0;0S vì 2 2 2 0 1 0 2
0 3 14 14 14 (luôn đúng).
Điểm A1;2;3S vì 2 2 2 1 1 2 2
3 3 14 0 14 (vô lý). Điểm B 2;1;
1 S vì 2 2 2 2 1 1 2
1 3 14 26 14 (vô lý).
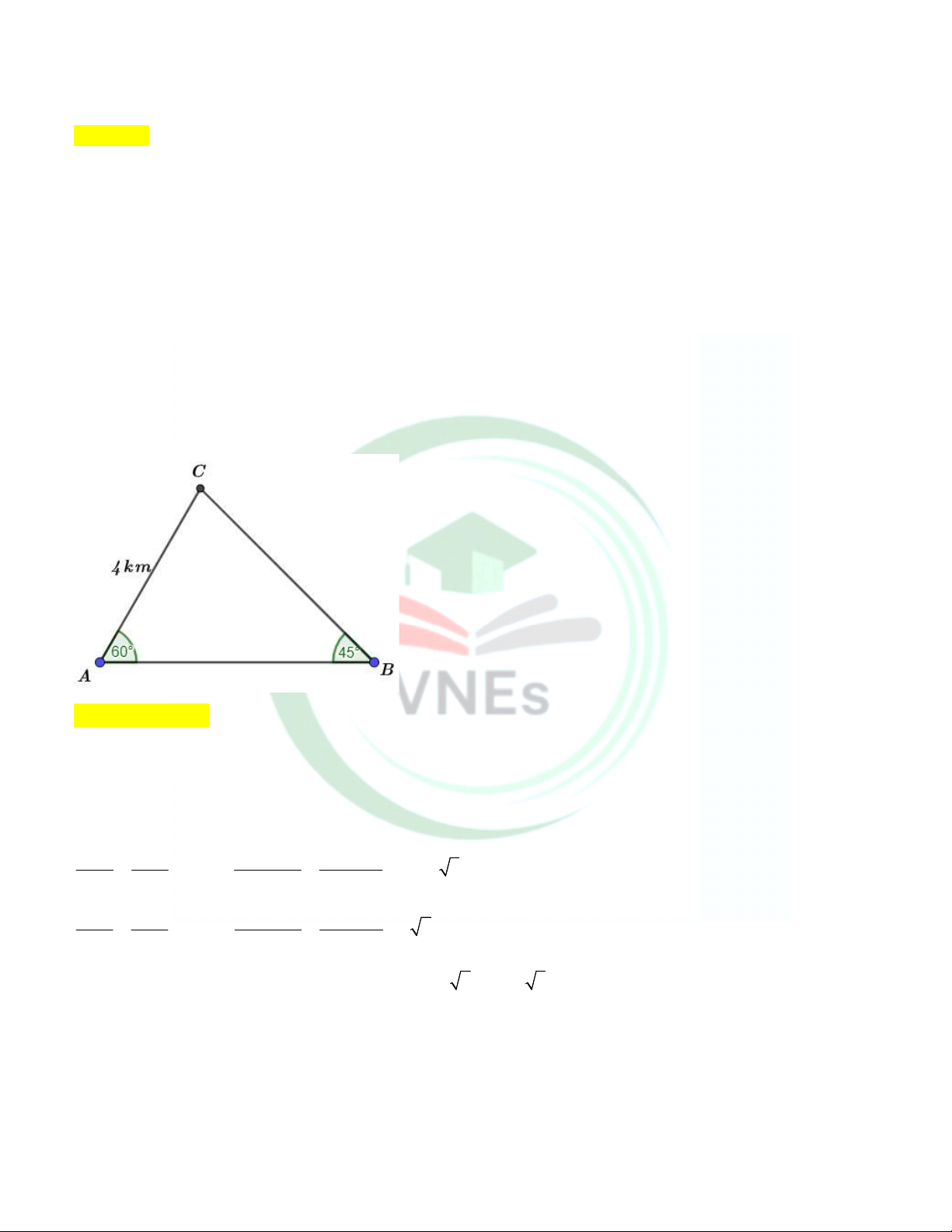
Câu 22. Một người đàn ông bắt đầu đi bộ buổi sáng từ điểm A lần lượt đến điểm B và C rồi quay lại A . Biết BAC 60 và
ABC 45 , AC 4km , tính quãng đường anh ta đi bộ buổi sáng. A. 14,36(k ) m . B. 13, 46 (km) C. 16,34 (km) D. 16, 43(km) Lời giải Ta có
ACB 180 60 45 75
Áp dụng định lí Sin cho tam giác ABC ta có: AB AC AC.sin C 4sin 75 AB 21 3. sin C sin B sin B sin 45 BC AC AC.sin A 4sin 60 BC 2 6 . sin A sin B sin B sin 45
Quãng đường người đàn ông đi bộ buổi sáng là: 4 2 6 21 3 14.36km
Luyện thi ĐGNL ĐHQGHN VNES
Tự tin - Tiến bước - Khẳng định bản thân
Câu 23. Diện tích hình phẳng giới hạn bởi hai đường cong 2 y x 2x và 2 y 2x x 2 là Lời giải Trả lời: 4,5 x 1
Phương trình hoành độ giao điểm 2 2 2
x 2x 2x x 2 x x 2 0 x 2 1 9 Vậy 2 S x x 2 dx = 4,5 2 2
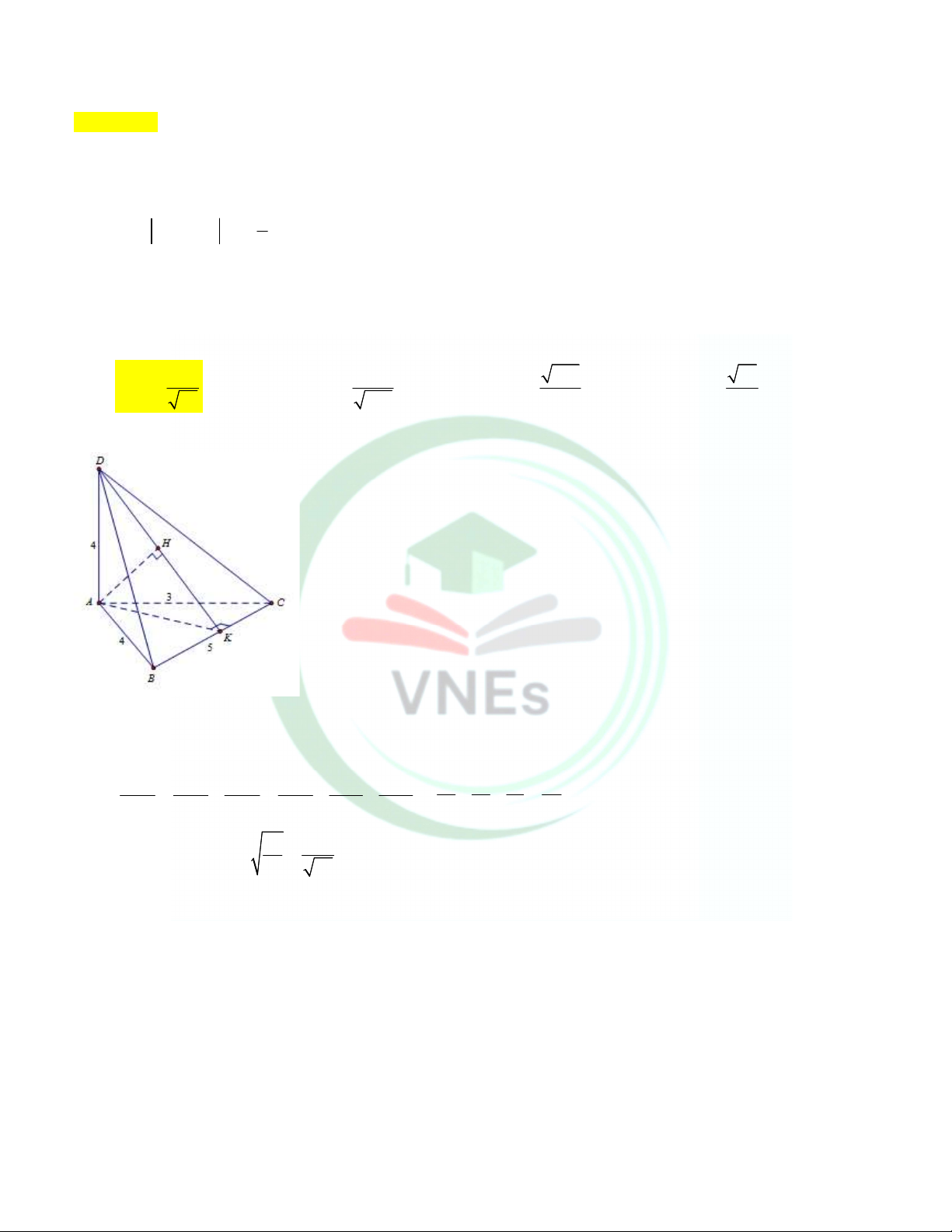
Câu 24. Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC), AC = AD = 4, AB = 3, BC = 5. Tính
khoảng cách d từ điểm A đến mặt phẳng BCD 12 60 769 34 A. d B. d C. d D. d 34 769 60 12 Lời giải Vì 2 2 2
BC BA AC nên tam giác ABC vuông tại A
Gọi K là hình chiếu của A lên Bc, H là hình chiếu của A lên DK. 1 1 1 1 1 1 1 1 1 17 Ta có 2 2 2 2 2 2 AH AD AK AD AB AC 2 2 2 4 4 3 72 17 12 d A; BCD AH 72 34
Luyện thi ĐGNL ĐHQGHN VNES
Tự tin - Tiến bước - Khẳng định bản thân
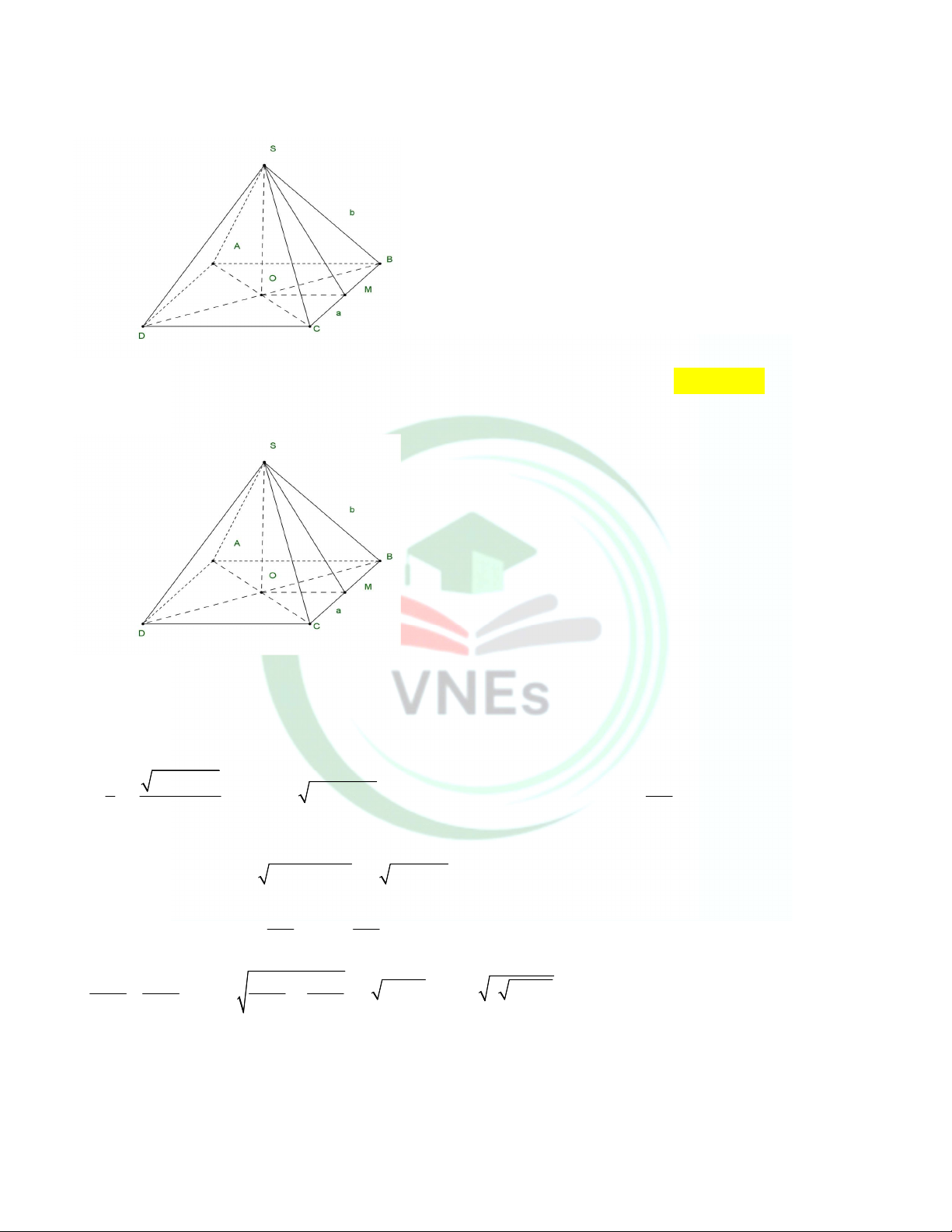
Câu 25. Người ta cần chế tạo các món quà lưu niệm bằng đồng có dạng khối chóp tứ giác đều, được mạ vàng bốn
mặt bên và có thể tích bằng 3
16cm . Diện tích mạ vàng nhỏ nhất của khối chóp bằng bao nhiêu 2 cm (kết quả làm tròn đến hàng đơn vị). A. 2 31(cm ) . B. 2 27 (cm ) . C. 2 33(cm ) . D. 2 29(cm ) . Lời giải
Gọi O , N lần lượt là trung điểm của AC , BC . Gọi a b 2 2 ,
a 0, b 0, 4b 2a 0 lần lượt là độ dài cạnh của hinh
vuông và cạnh bên của hình chóp tứ giác đều. Theo bài ra 2 2 1 4b 2a V a .
16 a 4b 2a 96 a 4b 2a 2 2 2 2 2 4 2 2 2 2 96 2 96 4b 2a . 4 3 2 a
Hình chóp tứ giác đều có tất cả các mặt bên bằng nhau nên diện tích của 4 mặt bằng 2 2 2 2 S 4S
2BC.SM 2a SO OM a 4b a SBC S a 4b a 2 2 96 96 2 2 2 2 2 2 4 a a a 4 2 a a 4608 4608 4608 4608 4 4 3 2 3 2 2 3 a 3 a
3 4608 S 3 4608 29cm . 2 2 2 2 a a a a
Luyện thi ĐGNL ĐHQGHN VNES
Tự tin - Tiến bước - Khẳng định bản thân
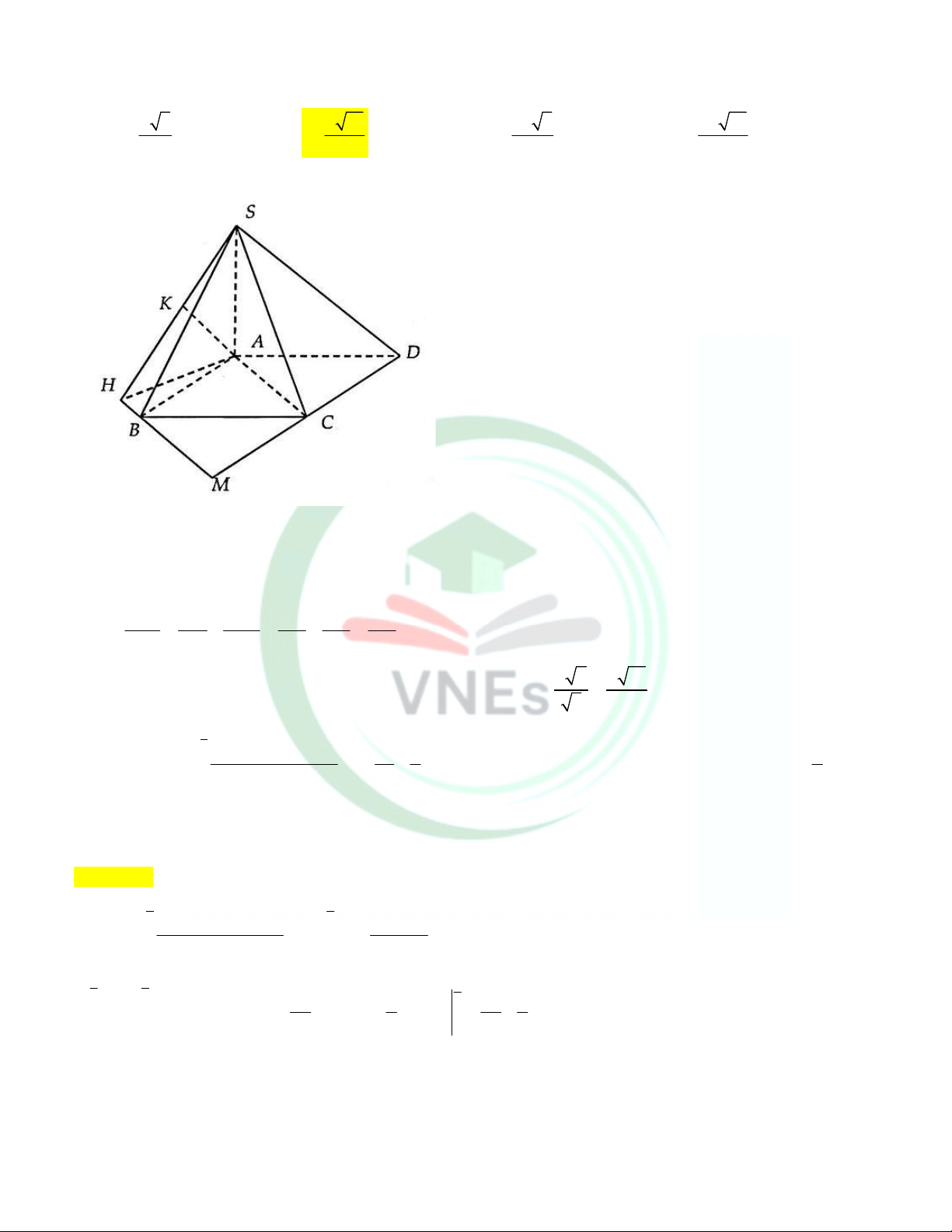
Câu 26. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA (ABCD), góc giữa đường thẳng SC và
mặt phẳng (ABCD) bằng 450. Tính khoảng cách giữa hai đường thẳng SB, AC. a 5 a 10 2a 5 2a 10 A. B. C. D. 5 5 5 5 Lời giải
Gọi M sao cho ABMC là hình bình hành
Vẽ AH vuông góc với BM tại H, AK vuông góc SH tại K Suy ra, AK vuông góc (SBM) 1 1 1 1 4 5 Ta có: 2 2 2 2 2 2 AK SA AH 2a 2a 2a a a
Vì AC song song (SBM) suy ra d AC SB d A SBM 2 10 , ; AK 5 5 π 2 3 2 x x cos x sin x π b b Câu 27. Biết I dx
. Trong đó a , b , c là các số nguyên dương, phân số tối giản. 1 cos x a c c 0 Tính 2 2 2 T a b c . Lời giải Trả lời: 69 2 3 x x cos x sin x 2 3 sin x Ta có I dx x dx 1 cos x 1 cos x 0 0 2 2 2 2 2 1 1 d x x 1cos xsin d x x 2 cos x cos x . 8 2 8 2 0 0 0
Như vậy a 8 , b 1, c 2 . Vậy 2 2 2 T a b c 69 .
Luyện thi ĐGNL ĐHQGHN VNES
Tự tin - Tiến bước - Khẳng định bản thân
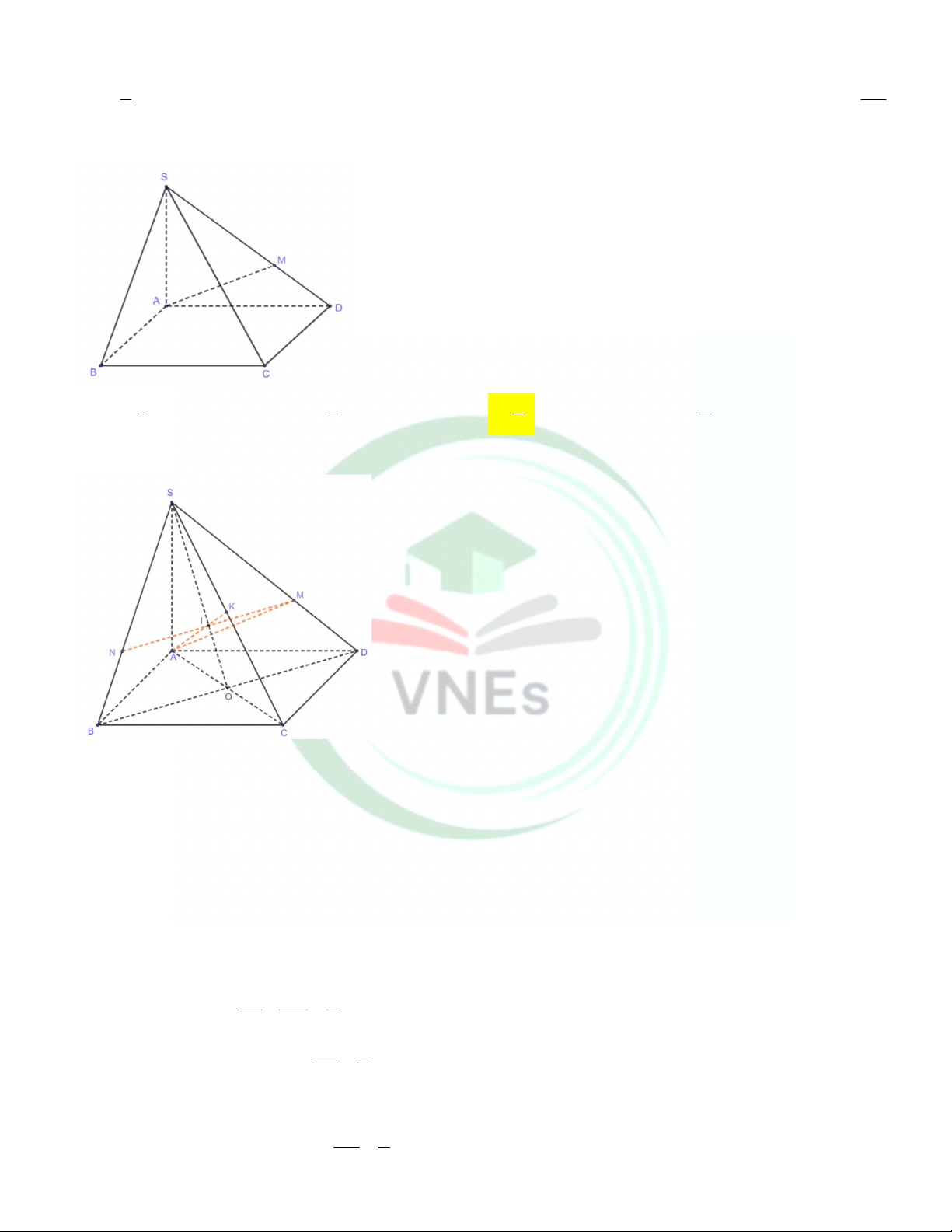
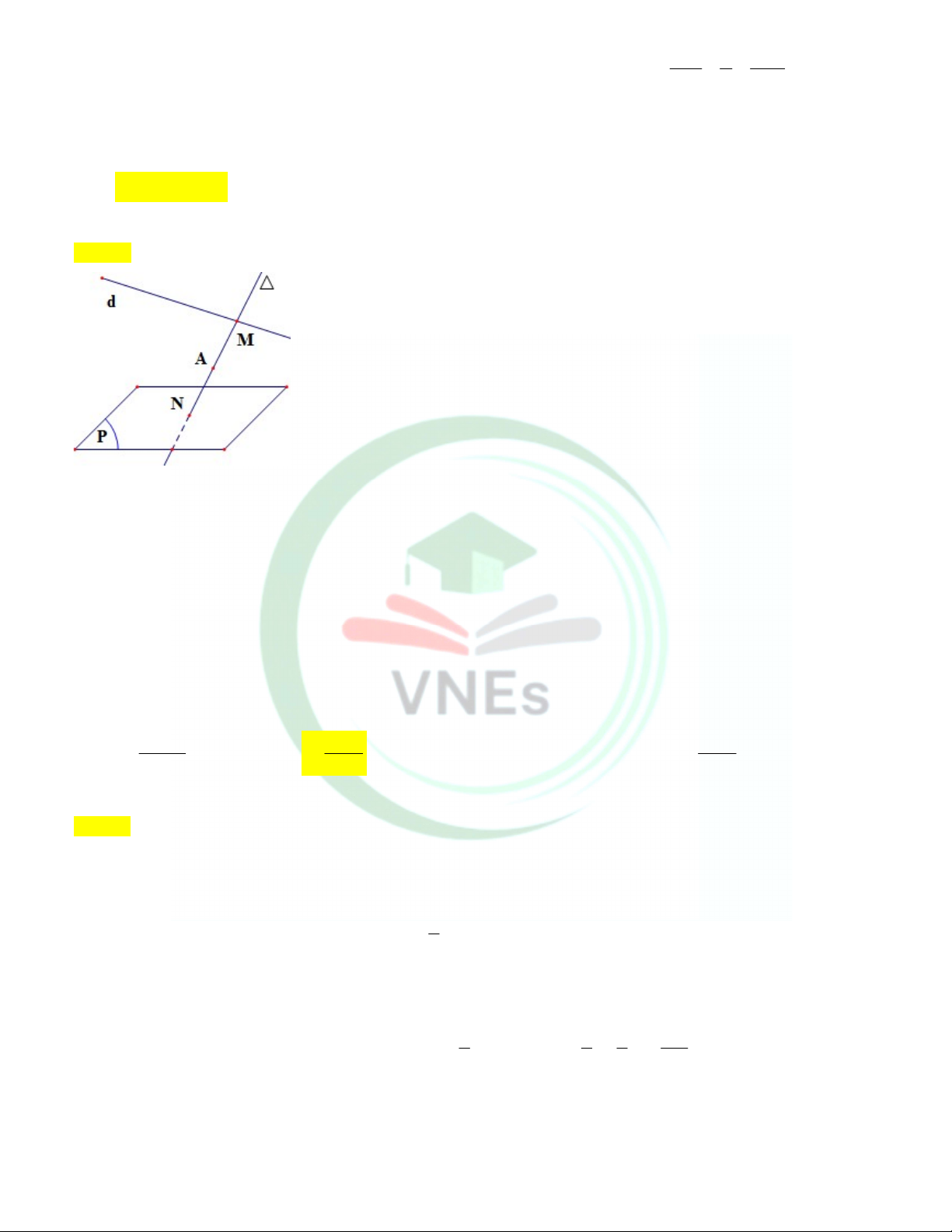
Câu 28. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là điểm thuộc cạnh SD sao cho 2 SM
SD (minh hoạ như hình vẽ). Mặt phẳng chứa AM và song song với BD cắt cạnh SC tại K . Tỷ số SK 3 SC bằng A. 1. B. 2 . C. 1 . D. 3 . 3 3 2 4 Lời giải
Trong mặt phẳng SBD qua M vẽ đường thẳng song song với BD cắt SB tại N .
Trong mặt phẳng ABC D gọi O AC BD
Trong mặt phẳng SBD gọi I SO MN
Trong mặt phẳng SAC gọi K AI SC K AI AMN K SC AMN K SC S OD có SI SM 2 MI //DO SO SD 3
SAC có SO là trung tuyến và SI 2
I là trọng tâm tam giác SAC . SO 3
Nên AK là đường trung tuyến của SAC .
Do đó K là trung điểm của SC SK 1 . SC 2
Luyện thi ĐGNL ĐHQGHN VNES
Tự tin - Tiến bước - Khẳng định bản thân
Câu 29. Đường tròn đi qua 3 điểm A11;8, B13;8, C 14;7 có bán kính R k . Khi đó k ............... Lời giải Trả lời: 5 Gọi C 2 2 2 2
: x y ax by c 0 (dk : a b 4c 0) . 1 1a 8b c 185 a 24
Đường tròn đi qua 3 điểm A11;8, B13;8, C 14;7 nên ta có: 1
3a 8b c 233 b 12 1 4a 7b c 245 c 175 Vậy đường tròn C 2 2
: x y 24x 12y 175 0 có tâm I 1; 1 Ta có 2 2 R a b c 5
Vậy phương trình đường tròn đi qua 3 điểm A11;8, B13;8, C 14;7 có bán kính là R 5 .
Câu 30. Trong không gian với hệ tọa độ Oxyz , cho 3 điểm M 2;3; 1 , N 1 ;1;
1 , P 1;m 1;2 . Với giá trị nào
của m thì tam giác MNP vuông tại N ? Lời giải Trả lời: 0
Ta có MN 3;2;2, NP 2;m2; 1 .
Tam giác MNP vuông tại N khi MN.NP 0 62m2 2.1 0 m 0 .
Câu 31. Trong không gian với hệ tọa độ Oxyz , cho điểm M 2;1;
1 . Viết phương trình mặt phẳng P đi qua M và
cắt ba tia Ox , Oy , Oz lần lượt tại các điểm A , B , C khác gốc O sao cho thể tích khối tứ diện OABC nhỏ nhất.
A. 2x y 2z 3 0 .
B. 4x y z 6 0 .
C. 2x y 2z 6 0 .
D. x 2 y 2z 6 0 . Lời giải Chọn D Gọi A ; a 0;0 , B0; ;
b 0 , C 0;0;c , do A , B , C thuộc ba tia Ox , Oy , Oz nên a , b , c 0 . x y z
P theo đoạn chắn có dạng 1. Do M P 2 1 1 2;1;1 1. a b c a b c 2 1 1 2 1 1 2
Áp dụng Cauchy cho 3 số dương , , ta có 3 1 3 a b c a b c abc abc 2 1 1 1 a 6 V
9 . Dấu bằng xảy ra khi . OABC 6 a b c 3 b c 3 x y z
Vậy P : 1 x 2y 2z 6 0 . 6 3 3
Luyện thi ĐGNL ĐHQGHN VNES
Tự tin - Tiến bước - Khẳng định bản thân
Câu 32. Trong không gian Oxyz , mặt phẳng P đi qua hai điểm M 2; 3; 1 , N 3; 2; 1 và vuông góc với mặt
phẳng Q :3x 2 y z 15 0 có phương trình là
A. 3x 7 y 5z 10 0 . B. 3x 7 y 5z 10 0 . C. 3x 7 y 5z 10 0 . D. 3x 7 y 5z 10 0 . Lời giải
Ta có: MN 1;1; 2 , n n Q MN
Q 3 ; 2 ;1 , , 3;7;5 .
Mặt phẳng P đi qua hai điểm M 2; 3; 1 , N 3; 2;
1 và vuông góc với mặt phẳng Q :3x 2 y z 15 0
nên mặt phẳng P có véctơ pháp tuyến là nQ, MN 3;7;5 .
Phương trình mặt phẳng P đi qua điểm M 2; 3;
1 và có véctơ pháp tuyến nP 3;7;5 là:
3 x 2 7 y 3 5 z
1 0 hay 3x 7 y 5z 10 0 .
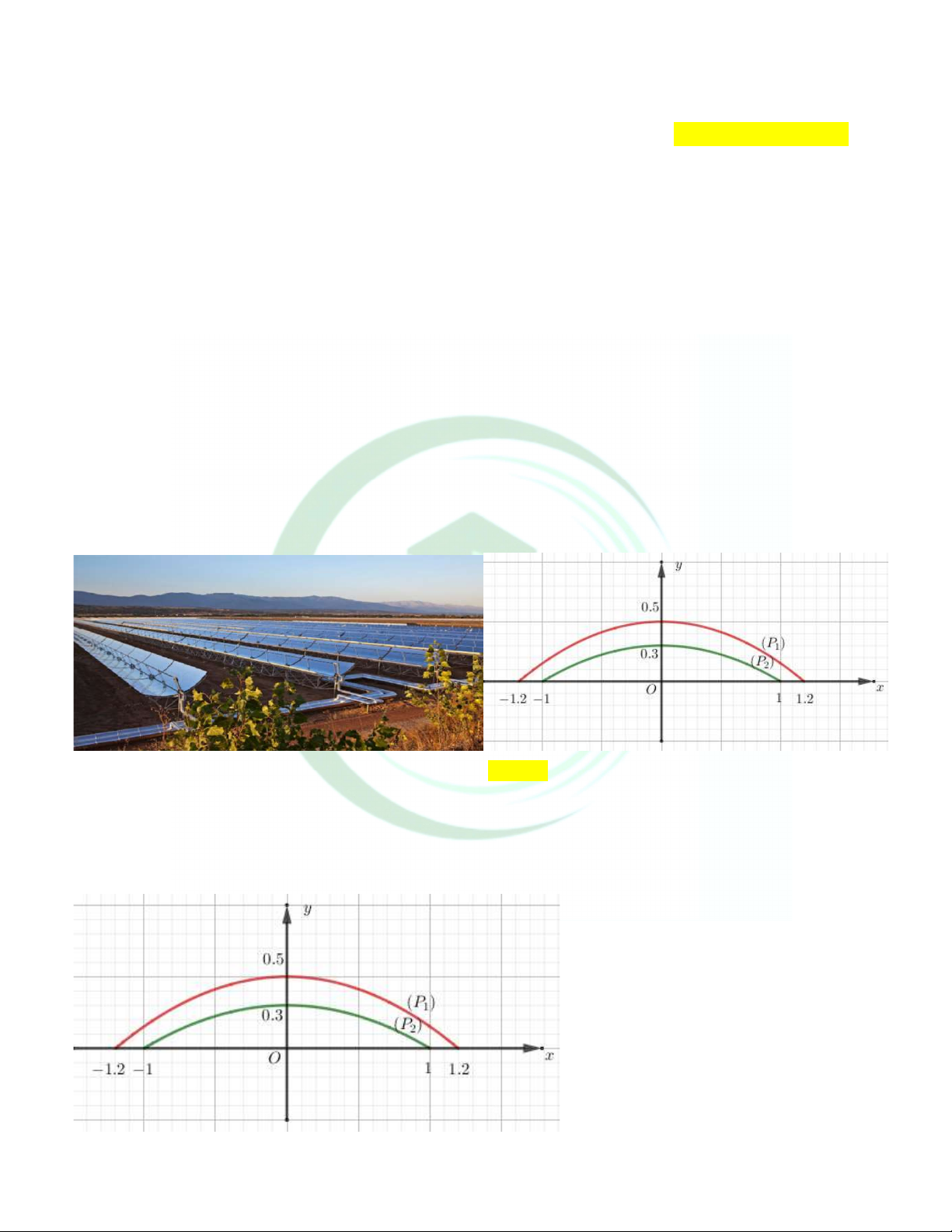
Câu 33. Một nhà máy nhiệt điện sử dụng 90 máng Parabol thu nhiệt năng lượng mặt trời có cùng kích thước, bề mặt
cong đều nhau (tham khảo hình vẽ). Mỗi máng có chiều rộng 2m , bề dày của khối silic làm mặt máng là 2dm , chiều
dài 3m . Đặt máng tiếp giáp mặt đất có điểm cao nhất của khối silic làm mặt máng so với mặt đất là 5dm . Khi đó thể tích (tính theo đơn vị 3
m ) của khối silic làm 90 mặt máng là bao nhiêu (Làm tròn đến hàng đơn vị) A. 107 . B. 1 0 6 . C. 1 08 . D. 1 0 9 . Lời giải
Gọi đường cong tương ứng với vành trên và vành dưới của máng lần lượt là P và P . 2 1
Xét hệ trục tọa độ Oxy như hình vẽ
Khi đó Parabol P và P đều có dạng 2 y ax b . 2 1
Luyện thi ĐGNL ĐHQGHN VNES
Tự tin - Tiến bước - Khẳng định bản thân
P đi qua các điểm có tọa độ 1,2;0;1,2;0; 0;0,5. 1
P đi qua các điểm có tọa độ 1;0 ;1;0 ; 0;0,3. 2 25 1 3 3 Suy ra P 2 : y x và P : y x . 2 2 1 72 2 10 10 1,2 1 25 1 3 3 2
Diện tích mặt cắt của máng Parabol là 2 2 S 2 x dx x dx 2 m . 72 2 10 10 5 0 0 2
Vậy thể tích của khối silic làm 90 mặt máng là V 90. .3 108 3 m . 5
Câu 34. Trong không gian với hệ tọa độ Oxyz cho mặt phẳng (P) : x y z 4 0 và hai đường thẳng x y 3 z 1 x 4 y z 3 d : ; d :
đường thẳng d có véc tơ chỉ phương u (a; ;
b 2) nằm trong mặt phẳng 1 1 2 3 2 1 1 2
và cắt cả d , d . Tính T a b 1 2 A. T 2 . B. T 10 . C. T 4 . D. T 3 Lời giải Chọn A
Giả sử d cắt d , d lần lượt tại (
A t;3 2t; 1 3t), B(4 t '; t ';3 2t ') 1 2
Ta có véc tơ chỉ phương của đường thẳng d là: u AB (t t ' 4; 2t t ' 3; 3t 2t ' 4) t 1
(t t ' 4).1 (2t t ' 3).1 (3t 2t ' 4).(1) 0 Theo đề bài ta có: 5 3t 2t ' 4 2 t ' 2 11 7 11 7 Khi đó u AB ( ; ; 2) a ;b T a b 2 . 2 2 2 2
Luyện thi ĐGNL ĐHQGHN VNES
Tự tin - Tiến bước - Khẳng định bản thân x 1 y z 2
Câu 35. Trong không gian với hệ tọa độ Oxyz ,cho đường thẳng d : , mặt phẳng 2 1 1
(P) : x y 2z 5 0 và điểm A1; 1
;2. Đường thẳng cắt d và P lần lượt tại M và N sao cho A là trung
điểm của đoạn thẳng MN . Một vectơ chỉ phương của là A. u B. u C. u D. u 4;5; 13 3;5; 1 1; 1;2 2;3;2 Lời giải Chọn A M d M 1 2t;t;2 t
A là trung điểm của MN N 3 2t; 2 t;2 t
Lại có N (P) 3 2t 2 t 4 2t 5 0 t 2
M 3;2;4 vec-tơ chỉ phương là u AM 2;3;2
Câu 36. Trong không gian Oxyz cho ba điểm A2;0;0 , B0;3;0 , C 2;3;6 . Thể tích khối cầu ngoại tiếp tứ diện OABC là 1372 343 341 A. B. C. 49 D. 3 6 6 Lời giải Chọn B
Giả sử mặt cầu ngoại tiếp tứ diện OABC có phương trình là 2 2 2
x y z 2ax 2by 2cz d 0 . a 1 4 4a d 0 3 9 6b d 0 b Ta có 2
4 9 36 4a 6b 12c d 0 c 3 d 0 d 0 7 3 4 7 343
Vậy bán kính mặt cầu ngoại tiếp tứ diện OABC là r suy ra V . 2 OABC 3 2 6
Luyện thi ĐGNL ĐHQGHN VNES
Tự tin - Tiến bước - Khẳng định bản thân MA 2
Câu 37. Trong không gian Oxyz , cho điểm A2;2; 2 , B 3; 3;3 , điểm M trong không gian thỏa mãn MB 3
. Độ dài OM lớn nhất bằng m 3 . Khi đó m = ..................... Lời giải Trả lời: 12
Gọi M x; y; z MA 2
x;2 y; 2 z,MB 3 x; 3 y;3 z . 2 Vì MA MB 3MA 2MB 2 2 9MA 4MB . 3 9 2
x2 92 y2 9 2
z2 43 x2 4 3
y2 43 z2 2 2 2
x y z 12x 12y 12z 0.
M mặt cầu S có tâm I 6;6; 6 bán kính R 6 3 .
OM lớn nhất khi và chỉ khi OM OI R OM 6 3 6 3 12 3 . Vậy m = 12
Câu 38. Thời gian chạy 50m của 20 học sinh được ghi lại trong bảng dưới đây: Thời gian (giây) 8,3 8,4 8,5 8,7 8,8 Tần số 2 3 9 5 1
Hỏi trung bình mỗi học sinh chạy 50m hết bao lâu ? (Làm tròn đến số thập phân thứ hai) Lời giải Trả lời: 8,53
8,3.2 8, 4.3 8,5.9 8,7.5 8,8
Thời gian trung bình để mỗi học sinh chạy được 50m là x 8,53. 20
Câu 39. Một nhóm gồm 2 học sinh lớp 10A, 2 học sinh lớp 11A và 2 học sinh lớp 12A xếp thành hai hàng ngang để
chụp ảnh, mỗi hàng 3 người. Hỏi có bao nhiêu cách xếp sao cho hai học sinh cùng lớp thì không đứng chung một hàng? A. 108 B. 216 C. 432 D. 36 Lời giải
Chọn 3 học sinh gồm 1 học sinh lớp 10A ; 1 học sinh lớp 11A ; 1 học sinh lớp 12A có 1 1 1 C .C .C 6 cách. 2 2 2
Xếp 3 học sinh vừa chọn đứng vào hàng thứ nhất có: 3! 6 cách.
Xếp 3 học sinh còn lại đứng vào hàng thứ hai có: 3! 6 cách.
Vậy có: 6.6.6 216 cách xếp học sinh thỏa mãn ycbt.
Luyện thi ĐGNL ĐHQGHN VNES
Tự tin - Tiến bước - Khẳng định bản thân
Câu 40. Bảng số liệu dưới đây thẻ hiện cân nặng (kg) của các thành viên trong một câu lạc bộ thể thao. Tìm trung vị
của mẫu số liệu ghép nhóm này. Làm tròn đến chữ số thập phân thứ nhất. Cân nặng 40;50 50;60 60;70 70;80 80;90 90;100 Tần số 6 8 12 14 7 3 A. 68, 3 . B. 6 7 , 8 . C. 6 9, 2 . D. 6 9, 4 . Lời giải
Cỡ mẫu là n 6 8 12 14 7 3 50 .
Gọi x ,..., x là cân nặng của 50 thành viên và giả sử dãy này đã được xếp theo thứ tự tăng dần. Khi đó trung vị sẽ 1 50 x x nằm ở vị trí 25
26 . Do 2 giá trị x , x thuộc nhóm 60;70 nên nhóm này chứa trung vị. 2 25 26
Ta có p 3;a 60;m 12;m m 6 8 14;a a 70 60 10 3 3 1 2 4 3 50 14 Trung vị 2 M 60 .10 69.2 . e 12
Câu 41. Cả hai xạ thủ cùng bắn vào bia. Xác suất người thứ nhất bắn trúng bia là 0,9 , người thứ hai bắn trúng bia là
0, 7 . Xác suất để có ít nhất một người bắn trúng bia là A. 0,97 . B. 0, 26 . C. 0,85 . D. 0,72 . Lời giải
Gọi A : “Người thứ nhất bắn trúng bia”.
B : “Người thứ hai bắn trúng bia”.
C : “Có ít nhất một người bắn trúng bia”. Suy ra C . A B . Vì hai biến cố ,
A B độc lập với nhau nên ta có P C P A.PB 10,9.10,7 0,97 .
Do đó, xác suất để có ít nhất một người bắn trúng bia là P C 1 PC 1 0,03 0,97 .
Câu 42. Một lớp có 35 học sinh, trong đó có 14 em thích học môn Toán, 13 em thích học môn Ngữ Văn và 5 bạn
thích học môn Toán và môn Ngữ Văn. Chọn ngẫu nhiên một học sinh trong lớp. Tính xác suất để học sinh đó thích
học môn Toán hoặc môn Ngữ Văn. 22 109 27 32 A. . B. . C. . D. . 35 175 35 35 Lời giải
Gọi biến cố A là “học sinh thích học môn Toán”, biến cố B là “học sinh thích học môn Toán”, biến cố A B là
“học sinh thích học môn Toán và môn Ngữ Văn”, biến cố C là “học sinh thích học môn Toán hoặc môn Ngữ Văn”
Ta có: C A B ; P A 14 ; P B 13 ; P A B 5 . . 35 35 35
Vậy ta có: P C P A B P A PB P A 14 13 5 22 B . 35 35 35 35




