12 phương pháp giải và biện luận phương trình chứa căn thức
Tài liệu gồm 93 trang trình bày 12 phương pháp giải và biện luận phương trình chứa căn thức, đi kèm với đó là các ví dụ minh họa có lời giải chi tiết với nhiều biến dạng và độ khó tăng dần.
Các phương pháp giải và biện luận phương trình chứa căn thức được trình bày trong tài liệu gồm:
+ Phương pháp 1. Lũy thừa hai vế và sử dụng các công thức cơ bản.
+ Phương pháp 2. Đưa về dạng tích.
+ Phương pháp 3. Đặt ẩn phụ toàn phần.
+ Phương pháp 4. Đặt ẩn phụ không hoàn toàn.
+ Phương pháp 5. Đặt hai ẩn đưa về phương trình tích hoặc tổng các đại lượng không âm.
+ Phương pháp 6. Đặt ẩn phụ đưa về hệ phương trình.
+ Phương pháp 7. Phương pháp lượng giác hóa.
+ Phương pháp 8. Dùng phương pháp đối lập.
+ Phương pháp 9. Phương pháp khảo sát hàm số.
+ Phương pháp 10. Phương pháp đồ thị.
+ Phương pháp 11. Phương pháp tam thức bậc hai.
+ Phương pháp 12. Phương pháp vectơ.
Chủ đề: Tài liệu chung Toán 10 397 tài liệu
Môn: Toán 10 2.9 K tài liệu
Tác giả:
Preview text:
PHNG TRÌNH CHA CN THC Chuy˚n đề 1:
Lũy thừa hai vế vš d•ng n cŸc c“ng n thức cơ ơ bản 1 2 3 4 5 6 7 8 9 10 11 12
Chuy˚n đề 2: Đưa về t˝ch 13 14 15 16 17 Chuy˚n đề 3: Đ
ặt ẩn phụ tošn p hần 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 Chuy˚n đề 3: Đ
ặt ẩn phụ kh“ng n hošn tošn 35 36 Chuy˚n đề 4: Đ
ặt hai ẩn đưa về p hương
n tr˜nh t˝ch hoặc tổng n cŸc đại lượn ợ g n kh“ng n Žm 37 38 39 40 41 42 Chuy˚n đề 5: Đ
ặt ẩn phụ đưa về hệ p hươn ơ g n tr˜nh 43 44 45 46 47 48 49 50 51 52 53 54 55
Chuy˚n đề 6: Phươn ơ g n phŸp Ÿ lượn ợ g n g iŸc h‚a 56 57 58 59 60
Chuy˚n đề 7: D•ng p hươn ơ g p hŸp Ÿ đối lập ậ 61 62 63 64 65 66
Chuy˚n đề 8: Phươn ơ g n phŸp
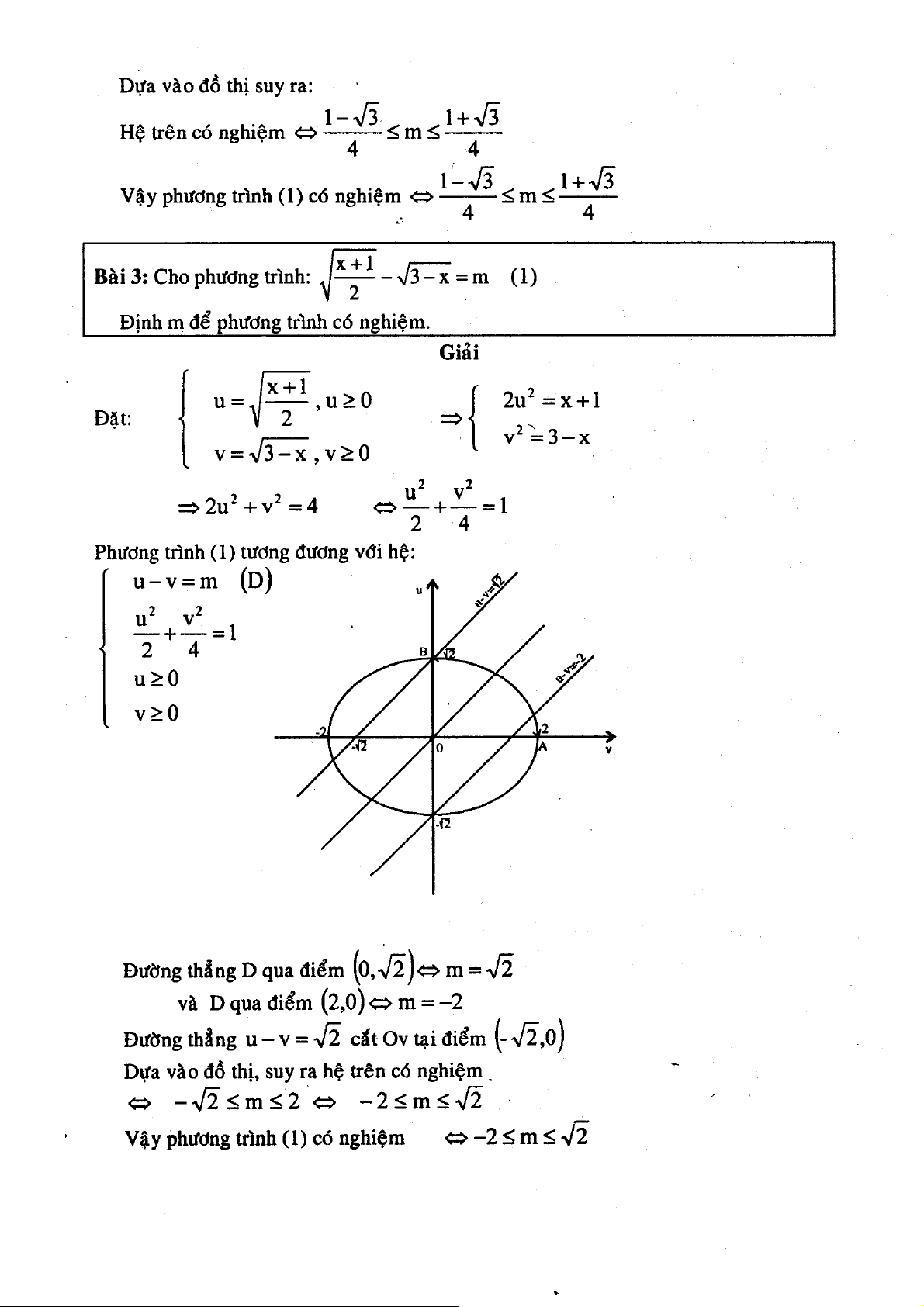
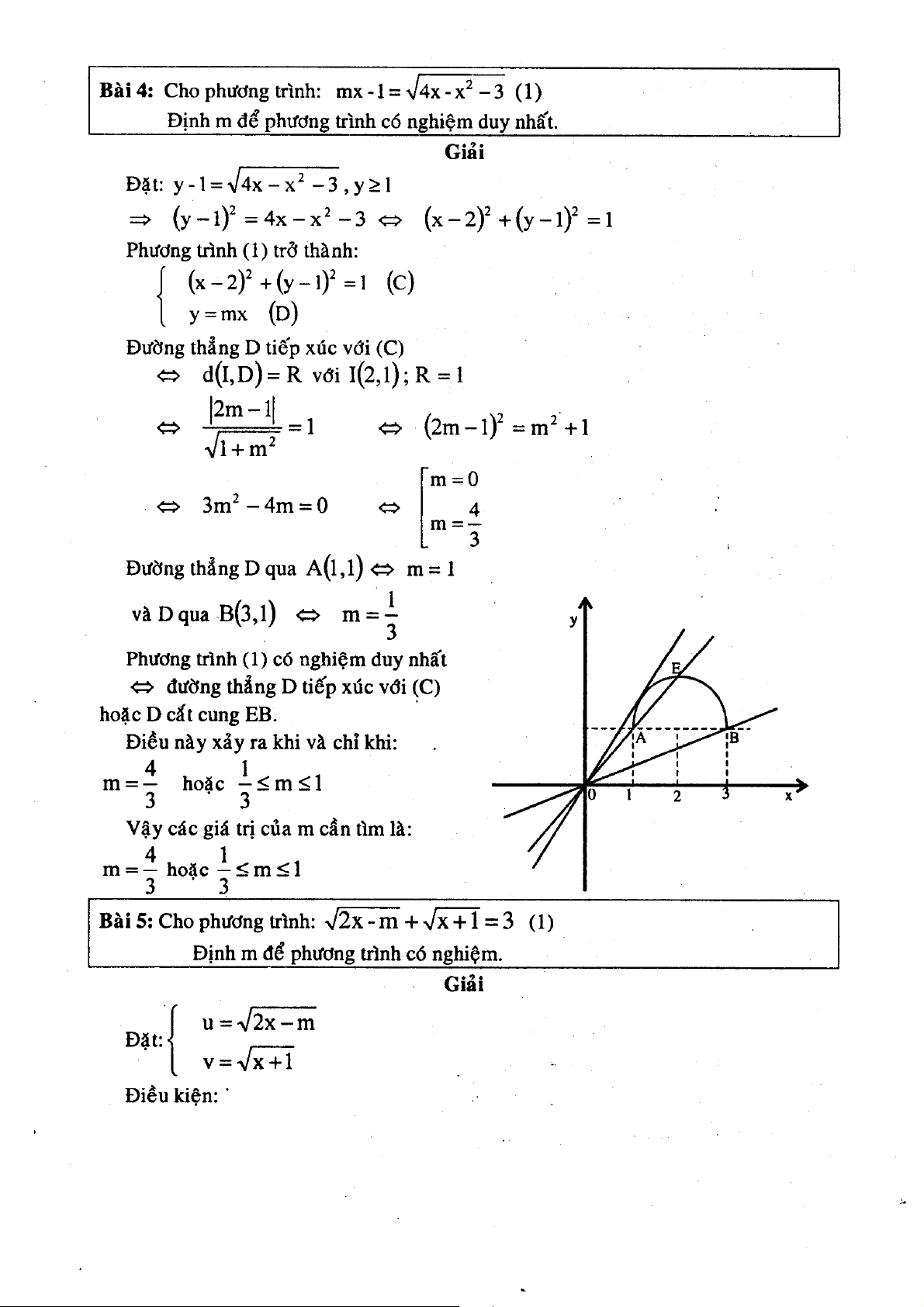
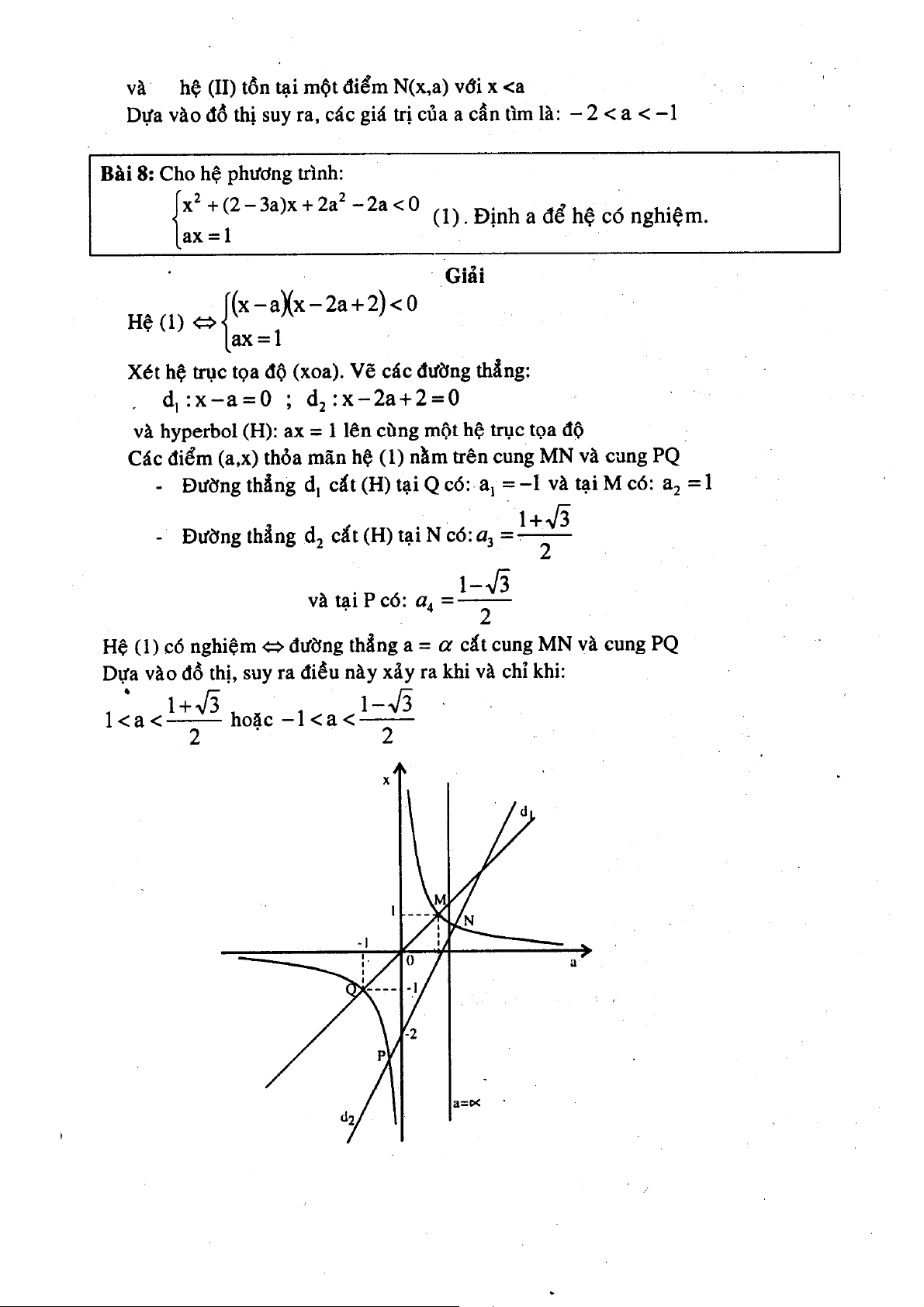
Ÿ khảo sŸt hšm số 67 68 69 70 71 72 73 74 75 Chuy˚n đề ề 9: 9 Phươn ơ g n phŸp Ÿ đồ thị 76 77 78 79 80 81 82
Chuy˚n đề 10: Phương n p hŸp
Ÿ tam thức bậc hai 83 84 85
Chuy˚n đề 11: Phương n p hŸp Ÿ vectơ 86 87 88 89 90 91 92