










Preview text:
TỔNG ÔN HÌNH HỌC 10 – VECTOR
THẦY LÂM PHONG (SÀI GÒN – 0933524179)
TỔNG ÔN TRẮC NGHIỆM VỀ VECTƠ – HÌNH HỌC 10
Sưu tầm và biên soạn: Thầy Hứa Lâm Phong
Vấn đề 1: Nhận biết và xác định Vectơ, hai vectơ cùng phương, hai vectơ bằng nhau.
Câu 1. Khẳng định nào sau đây là đúng ?
A. Giá của vectơ AB là đoạn thẳng đi qua hai điểm A và B.
B. Mỗi vectơ đều có duy nhất một giá của nó.
C. Hai vectơ bằng nhau là hai vectơ có cùng phương và cùng độ dài.
D. Vectơ là một đoạn thẳng có định hướng.
Câu 2. Hai vectơ được gọi là bằng nhau nếu :
A. Chúng có độ dài bằng nhau và cùng phương .
B. Chúng có độ dài bằng nhau và cùng hướng.
C. Chúng có độ dài bằng nhau.
D. Chúng có độ dài bằng nhau và ngược hướng.
Câu 3. Khẳng định nào sau đây sai?
A. Hai vector bằng nhau thì chúng cùng hướng và có cùng độ dài bằng nhau.
B. Hai vector cùng hướng thì chúng cùng phương.
C. Vector không cùng phương với mọi vector khác không.
D. Hai vector có cùng phương thì cùng nằm trên cùng một đường thẳng.
Câu 4. Mệnh đề nào sau đây là đúng ?
A. Hai vectơ cùng phương với một vectơ thứ ba thì cùng phương.
B. Hai vectơ cùng phương với một vectơ thứ ba khác 0 thì cùng phương.
C. Hai vectơ cùng phương với một vectơ thứ ba thì cùng hướng.
D. Hai vectơ ngược hướng với một vectơ thứ ba thì cùng hướng.
Câu 5. Véctơ có điểm đầu và điểm cuối trùng nhau được gọi là
A. vectơ không và kí hiệu 0 .
B. vectơ có phương tùy ý.
C. vectơ có độ dài không xác định. D. vectơ suy biến.
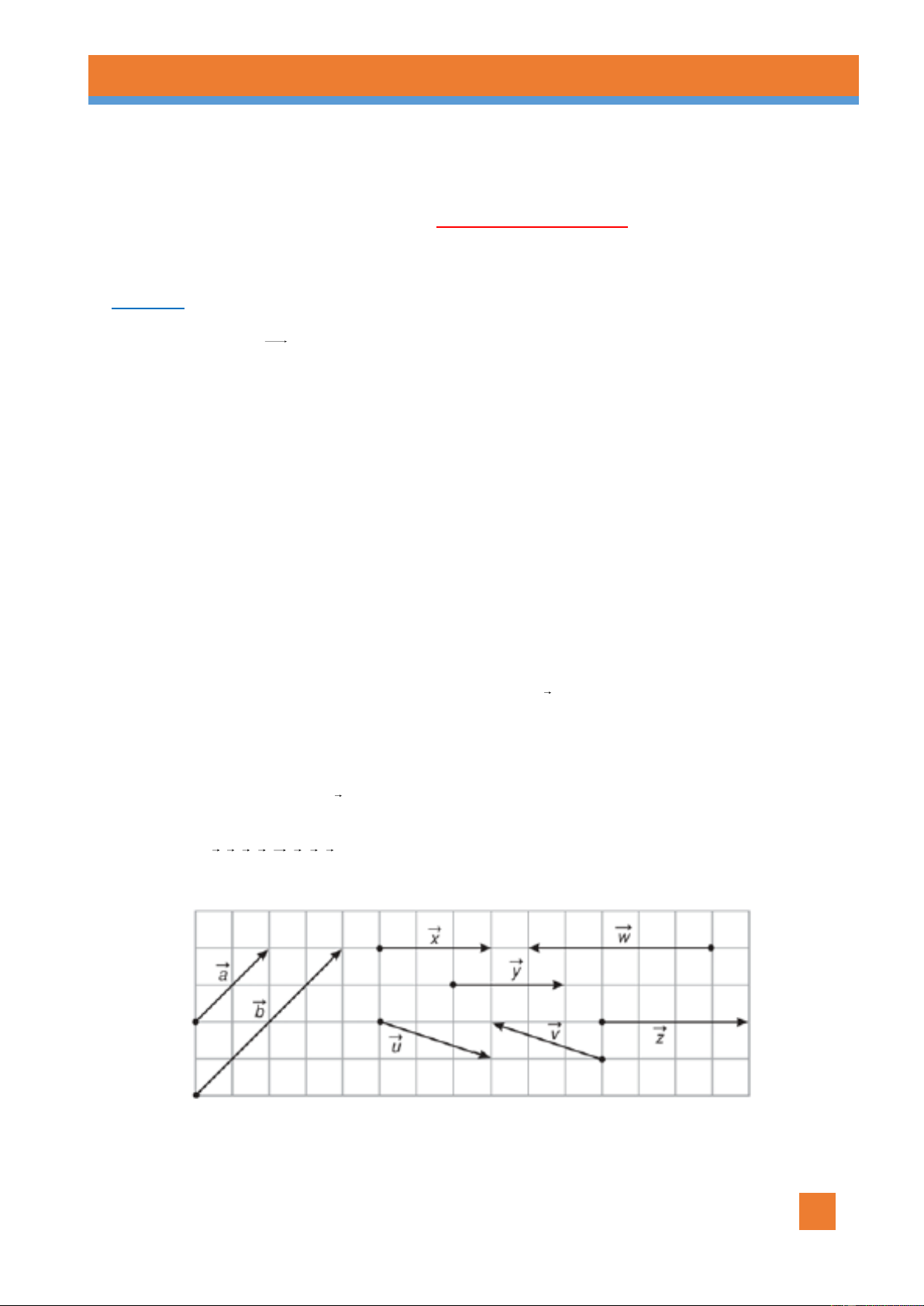
Cho các vectơ a,b,u, v, w, x, y, z thỏa mãn hình 1 sau. Hình 1
ĐĂNG KÝ LỚP OFF TẠI 106/G26 LẠC LONG QUÂN P3 Q11 1
TỔNG ÔN HÌNH HỌC 10 – VECTOR
THẦY LÂM PHONG (SÀI GÒN – 0933524179)
Câu 6. Trong hình 1, vectơ x cùng hướng với vectơ nào sau đây ? A. y, z . B. y, w .
C. w, z . D. b,u .
Câu 7. Trong hình 1, có bao nhiêu cặp vectơ bằng nhau ? A. 0 . B. 2 . C. 1 . D. 3.
Câu 8. Dựa vào hình 1, có bao nhiêu cặp vectơ ngược hướng ? A. 1. B. 2. C. 3 . D. 4.
Câu 9. Dựa vào hình 1, có bao nhiêu cặp vectơ cùng hướng ? A. 1. B. 2. C. 3 . D. 4.
Câu 10. Dựa vào hình 1, cặp vectơ nào sau đây có cùng giá ?
A. a và b .
B. u và v .
C. x và w .
D. y và z .
Câu 11. Dựa vào hình 1, tìm khẳng định đúng ?
A. b 2a .
B. u v .
C. x 4 z .
D. w 5 y . 3 3
Câu 12. Dựa vào hình 1, tìm khẳng định sai ?
A. x y .
B. y 3 z .
C. u v .
D. z 4 w . 4 5
Câu 13. Mệnh đề nào sau đây là đúng ?
A. Có duy nhất một vectơ cùng phương với mọi vectơ.
B. Có ít nhất hai vectơ cùng phương với mọi vectơ.
C. Có vô số vectơ cùng phương với mọi vectơ.
D. Không có vectơ nào cùng phương với mọi vectơ.
Câu 14. Chọn khẳng định sai. Nếu hai vectơ khác 0 bằng nhau thì chúng luôn có đặc điểm là
A. cùng điểm gốc . B. cùng phương.
C. cùng hướng . D. cùng độ dài.
Câu 15. Cho tam giác ABC, có thể xác định bao nhiêu vectơ khác vectơ 0 có điểm đầu và điểm
cuối là đỉnh A, B, C ? A. 3 B. 6 C. 4 D. 9
Câu 16. Cho tứ giác ABCD. Số các vectơ khác 0 có điểm đầu và cuối là đỉnh của tứ giác bằng: A. 4 B. 6 C. 8 D. 12
Câu 17. Cho lục giác đều ABCDEF tâm O. Số các vectơ khác 0 cùng phương với OC có điểm
đầu và cuối là đỉnh của lục giác là: A. 4 B. 6 C. 7 D. 9
Câu 18. Cho lục giác đều ABCDEF tâm O. Ba vectơ bằng vecto BA là: A. OF, DE,OC B. CA,OF, DE C. OF, DE,CO D. OF, ED,OC
Câu 19. Cho lục giác đều ABCDEF tâm O. Số các vectơ bằng OC có điểm đầu và cuối là đỉnh của lục giác là: A. 4 B. 6 C. 2 D. 3
Câu 20. Cho 5 điểm A, B, C, D, E. Có bao nhiêu vectơ khác vectơ không có điểm đầu và điểm
cuối là hai điểm trong các điểm đó? A. 24. B. 30. C. 20 D. 10
Câu 21. Cho hình bình hành ABCD có tâm O. Số vectơ hình thành từ 2 điểm phân biệt trong 5
điểm A, B, C, D, O có độ dài bằng OB là A. 4. B. 3. C. 2 D. 6
ĐĂNG KÝ LỚP OFF TẠI 106/G26 LẠC LONG QUÂN P3 Q11 2
TỔNG ÔN HÌNH HỌC 10 – VECTOR
THẦY LÂM PHONG (SÀI GÒN – 0933524179)
Câu 22. Cho AB ≠ 0 và một điểm C, có bao nhiêu điểm D thỏa mãn: AB CD A. 0 B. 1 C. 2 D. vô số.
Câu 23. Cho AB ≠ 0 và một điểm C, có bao nhiêu điểm D thỏa mãn: AB CD A. 0 B. 1 C. 2 D. vô số.
Câu 24. Cho hình bình hành ABCD. Trong các khẳng định sau, hãy tìm khẳng định sai.
A. AD CB .
B. AD CB .
C. AB DC
D. AB CD
Câu 25. Cho hình vuông ABCD. Trong các khẳng định sau, hãy tìm khẳng định đúng.
A. AC BD .
B. AB, AC cùng hướng. C. AB BC
D. AB CD .
Câu 26. Cho hình thoi ABCD. Trong các khẳng định sau, hãy tìm khẳng định đúng.
A. BA DC .
B. AB AD .
C. BD AC
D. AB CD .
Câu 27. Cho tứ giác ABCD. Gọi M, N, P,Q lần lượt là trung điểm AB, BC, CD, DA . Khẳng
định nào sau đây là sai ?
A. MN QP .
B. MQ NP .
C. PQ MN
D. MN AC .
Câu 28. Điều kiện nào là điều kiện cần và đủ để AB CD :
A. ABCD là hình bình hành.
B. ABDC là hình bình hành.
C. AD và BC có cùng trung điểm.
D. AB CD và AB / /CD .
Câu 29. Cho ABC. Đặt a BC,b AC . Các cặp vectơ nào sau cùng phương?
A. 2a b, a b 2 .
B. a 2b, 2a b . C. a
5 b,10a b 2
D. a b,a b
Câu 30. Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của BC, CA và AB. Các vectơ bằng với CM là A. MB, PN,CN . B. BM, NC, NP . C. BM, PN, NC D. MB, NP,CM
Câu 31. Cho điểm M thuộc đoạn thẳng AB sao cho 3MA 2MB . Khi đó ta có :
A. MA 2 AB .
B. MA 2 MB .
C. MA 3 AB
D. MA 2 AB 5 3 5 5
Câu 32. Cho tam giác ABC, gọi N là điểm trên cạnh AC sao cho NC 2NA . Biểu diễn NA theo AC
A. NA 2 AC .
B. NA 1 AC .
C. NA AC
D. NA 2AC 3 3
Câu 33. Cho tam giác ABC, gọi M là điểm trên cạnh BC sao cho MB 2MC . Biểu diễn
AM 1 AB theo AC 3 2 A. AC .
B. NA 1 AC . C. 0 D. 2AC 3 3
Câu 34. Cho ba điểm A, B, C phân biệt. Điều kiện cần và đủ để ba điểm thẳng hàng là:
A. AC AB BC B. M
: MA MC MB C. k
: AB kAC D. M
: MA MB MC 0
Câu 35. Cho ba điểm M, N, P thẳng hàng, trong đó điểm N nằm giữa hai điểm M và P. Khi đó
các cặp vecto nào sau đây cùng hướng ?
A. MN và PN
B. MN và MP
C. MP và PN
D. NM và NP
ĐĂNG KÝ LỚP OFF TẠI 106/G26 LẠC LONG QUÂN P3 Q11 3
TỔNG ÔN HÌNH HỌC 10 – VECTOR
THẦY LÂM PHONG (SÀI GÒN – 0933524179)
Câu 36. Cho hai vectơ a và b không cùng phương. Hai vectơ nào sau đây là cùng phương ? 1 3
A. u 2a b 3 và v a 3b B. u a b
3 và v a 3 2 b 2 5 5 2 1 1 C. u a b
3 và v 2a b 9
D. u a 3 2
b và v a b 3 2 3 4
Câu 37. Cho hai vectơ a và b không cùng nhưng hai vec tơ 2a b
3 và a x 1 b cùng
phương. Khi đó giá trị của x là: 1 3 A. B. 3 C. 1 D. 2 2 2 2
Câu 38. Điểm P được xác định: MN 4PN . Điểm P được xác định đúng trong hình vẽ nào sau đây: M P N N M P H1 H2 N M P M P N H3 H4 A. H4 B. H1 C. H3 D. H2
Câu 39. Điểm P được xác định: NM 3PM . Điểm P được xác định đúng trong hình vẽ nào sau đây: M P N N M P H1 H2 N M P M P N H3 H4 A. H4 B. H1 C. H3 D. H2
Câu 40. Cho 3 điểm M, N, P thẳng hàng thỏa mãn hình vẽ sau: N M P
Khẳng định nào sau đây là đúng ?
A. MP 2MN
B. PN 3MN
C. NM 1 PM
D. MN 1 PN 2 3
Câu 41. Cho tam giác ABC nội tiếp đường tròn tâm O có trực tâm H. D là điểm đối xứng với B
qua O. Tìm khẳng định đúng trong các khẳng định sau.
A. HA CD và AD CH .
B. HA CD và AD HC
C. HA CD và AC CH .
D. HC AD và OD OB
Câu 42. Cho tam giác ABC nội tiếp đường tròn tâm O có trực tâm H và trọng tâm G. . Tìm khẳng
định đúng trong các khẳng định sau.
A. 3 điểm O, H, G thẳng hàng vì OH O 2 G .
B. 3 điểm O, H, G thẳng hàng vì OH O 3 G .
C. 3 điểm O, H, G thẳng hàng vì OH O 2 G .
D. 3 điểm O, H, G thẳng hàng vì OH 3 OG . 2
Vấn đề 2: Dựng và tính tổng – hiệu của hai vectơ.
ĐĂNG KÝ LỚP OFF TẠI 106/G26 LẠC LONG QUÂN P3 Q11 4
TỔNG ÔN HÌNH HỌC 10 – VECTOR
THẦY LÂM PHONG (SÀI GÒN – 0933524179)
Câu 43. Phát biểu nào sau đây là đúng.
A. Hai vectơ không bằng nhau thì có độ dài không bằng nhau.
B. Hiệu của 2 vectơ có độ dài bằng nhau là vectơ – không.
C. Tổng của hai vectơ khác vectơ –không là 1 vectơ khác vectơ –không.
D. Hai vectơ cùng phương với 1 vec tơ khác 0 thì 2 vec tơ đó cùng phương với nhau.
Câu 44. Cho hai vecto a,b khác vectơ 0 , không cùng phương và có độ dài bằng nhau. Khi đó
giá của hai vectơ a b và a b : A. Song song.
B. Cắt và không vuông góc. C. Trùng nhau.
D. Vuông góc với nhau.
Câu 45. Cho hai vectơ a và b đều khác 0 . Tìm khẳng định đúng trong các khẳng định sau:
A. a b a b a và b cùng phương.
B. a b a b a và b cùng hướng.
C. a b a b a và b ngược hướng.
D. a b a b a và b cùng phương.
Câu 46. Cho hai vectơ a và b khác vectơ 0 . Khẳng định nào sau đây sai ?
A. a là vectơ đối của b thì a b .
B. a và b ngược hướng là điều kiện cần để a là vectơ đối của b .
C. a là vectơ đối của b nếu a b .
D. a là vectơ đối của b thì a b 0 .
Câu 47. Cho 4 điểm bất kỳ A, B, C, D. Đẳng thức nào sau đây là đúng
A. OA CA CO
B. BC AC AB 0
C. BA OB OA
D. OA OB BA
Câu 48. Cho v AC DB CD BA . Khẳng định nào sau đây là đúng ?
A. v AB .
B. v BA .
C. v CB D. v 0
Câu 49. Cho ba điểm phân biệt A, B, C . Đẳng thức nào đúng?
A. CA BA BC .
B. AB AC BC .
C. AB CA CB
D. AB BC CA
Câu 50. Cho hai điểm A và B phân biệt. Điều kiện để I là trung điểm AB là:
A. IA IB .
B. IA IB .
C. IA IB
D. AI BI Câu 51. Cho A
BC cân tại A, đường cao AH . Câu nào sau đây sai ?
A. AB AC .
B. HC HB .
C. AB AC
D. AB AC
Câu 52. Cho đường tròn tâm O và hai tiếp tuyến song song với nhau tiếp xúc với (O) tại hai
điểm A và B . Câu nào sau đây đúng ?
A. OA O B .
B. AB O B .
C. OA O B
D. AB BA Câu 53. Cho A
BC đều. Câu nào sau đây đúng ?
A. AB BC CA .
B. CA AB .
C. AB BC CA
D. CA BC
Câu 54. Cho đường tròn tâm O , và điểm M nằm ngoài đường tròn O, kẻ hai tiếp tuyến MT,
MT' (T và T ' là hai tiếp điểm) . Câu nào sau đây đúng ?
A. MT MT' .
B. MT MT' TT" .
C. MT MT'
D. OT O T' Câu 55. Cho A
BC , với M là trung điểm của BC . Tìm câu đúng.
A. AM MB BA 0 .
B. MA MB AB .
C. MA MB MC
D. AB AC AM Câu 56. Cho A
BC với M, N, P lần lượt là trung điểm của BC, CA, AB . Tìm câu sai.
ĐĂNG KÝ LỚP OFF TẠI 106/G26 LẠC LONG QUÂN P3 Q11 5
TỔNG ÔN HÌNH HỌC 10 – VECTOR
THẦY LÂM PHONG (SÀI GÒN – 0933524179)
A. AB BC AC 0 .
B. AP BM CN 0 .
C. MN NP PM 0 D. PB MC MP
Câu 57. Gọi O là tâm của hình vuông ABCD. Vectơ nào trong các vectơ dưới đây bằng CA ?
A. AB BC . B. O A OC .
C. BD DA
D. DC CB
Câu 58. Cho tam giác ABC. Trong các mệnh đề sau, tìm mệnh đề đúng.
A. AB BC AC .
B. AB BC CA 0 .
C. AB BC CA BC .
D. AB CA BC .
Câu 59. Cho hình bình hành ABCD, O là giao điểm hai đường chéo. Khi đó hãy tính tổng
OA OB OC OD . A. 0 .
B. AC BD .
C. CA BD .
D. CA DB .
Câu 60. Cho tứ giác ABCD. Trong các mệnh đề sau, tìm mệnh đề đúng.
A. AB CD AD CB .
B. AB BC CD DA .
C. AB BC CD DA .
D. AB AD CD CB Câu 61. Cho A
BC và một điểm M thoả mãn điều kiện MA MB MC 0 . Trong các mệnh
đề sau tìm đề sai :
A. MABC là hình bình hành.
B. AM AB AC .
C. BA BC BM
D. MA BC
Câu 62. Cho hình bình hành ABCD tâm I . Câu nào sau đây sai ?
A. AB AD AC .
B. AB BC 2AI .
C. AB CD 0
D. AB AC BC
Câu 63. Cho hình bình hành ABCD . Gọi M, N lần lượt là trung điểm của AB, CD. Tổng
AM AD bằng : A. NC . B. BN . C. MC D. NA
Câu 64. Cho tam giác ABC , I là trung điểm của AB, M là điểm tùy ý. Xét v MA MB 2MC .
Tìm khẳng định đúng.
A. v 2IC .
B. v CA CB .
C. v CA CB
D. v CI
Câu 65. Cho tam giác ABC có trong tâm G. Gọi M, N, P lần lượt là trung điểm của BC, CA, AB.
Chọn khẳng định sai
A. GM GN GP 0 .
B. AG BG CG 0 .
C. AM BN CP 0 . D. GC G 2 P .
Câu 66. Cho tam giác ABC, có trung tuyến AM và trọng tâm G. Khẳng định nào sau đây là đúng
A. AM G 3 M .
B. AM ( 2 AB AC) . 1
C. MG (
3 MA MB MC) .
D. AG ( AB AC) . 3
Câu 67. Cho hình bình hành ABCD có O là giao điểm hai đường chéo. Tìm khẳng định đúng:
A. AO BO BD
B. AO BO CD
C. AB AC DA
D. AO AC BO
Câu 68. Cho bốn điểm A, B, C, D. Gọi I, J lần lượt là trung điểm của các đoạn thẳng AB và CD.
Trong các đẳng thức sau đẳng thức nào sai ?
A. AC BD 2IJ
B. AB CD 2IJ
C. AD BC 2IJ
D. 2IJ DB CA 0
Câu 69. Cho ABC. Gọi I là trung điểm của BC, H là điểm đối xứng của I qua C. AH bằng:
A. AH AC AI
B. AH 2AC AI
C. AH 2AC AB
D. AH AB AC AI
Câu 70. Cho hai vectơ a và b bất kì. Mệnh đề nào sau đây đúng ?
ĐĂNG KÝ LỚP OFF TẠI 106/G26 LẠC LONG QUÂN P3 Q11 6
TỔNG ÔN HÌNH HỌC 10 – VECTOR
THẦY LÂM PHONG (SÀI GÒN – 0933524179)
A. a b a b
B. a b a b
C. a b a b
D. a b a b
Vấn đề 3: Tích vectơ với một số thực.
Câu 71. Cho A
BC có G là trọng tâm, I là trung điểm BC. Đẳng thức nào đúng?
A. GA G 2 I .
B. IG 1 IA .
C. GB GC G 2 I
D. GB GC GA 3 Câu 72. Cho A
BC có trọng tâm G và M là trung điểm BC. Khẳng định nào sau đây là sai ?
A. AG 2 AM .
B. AB AC 3AG .
C. GA BG CG
D. GB GC GM 3
Câu 73. Cho hình bình hành ABCD. Đẳng thức nào đúng?
A. AC BD 2BC .
B. AC BC AB .
C. AC BD C 2 D
D. AC AD CD Câu 74. Cho A
BC vuông tại A với M là trung điểm của BC. Câu nào sau đây đúng ? BC
A. AM MB MC .
B. MB MC .
C. MB MC D. AM 2 Câu 75. Cho A
BC . Gọi M và N lần lượt là trung điểm của AB và AC. Trong các mệnh đề sau tìm mệnh đề sai.
A. AB 2AM .
B. AC 2NC .
C. BC 2MN
D. CN 1 AC 2
Câu 76. Cho hình vuông ABCD có tâm là O. Trong các mệnh đề sau, tìm mệnh đề sai.
A. AB AD 2AO .
B. AD DO 1 CA .
C. OA OB 1 CB
D. AC DB 4AB 2 2
Câu 77. Cho tam giác ABC, có bao nhiêu điểm M thoả mãn : MA MB MC 1 A. 0. B. 1. C. 2 D. vô số.
Câu 78. Cho hình bình hành ABCD, có M là giao điểm của hai đường chéo. Trong các mệnh đề
sau, tìm mệnh đề sai:
A. AB BC AC .
B. AB AD AC .
C. BA BC 2BM
D. MA MB MC MD
Câu 79. Cho G là trọng tâm của A
BC . Trong các mệnh đề sau, tìm mệnh đề đúng :
A. AB BC 2 AG .
B. BA BC 3BG .
C. CA CB CG
D. AB AC BC 0 3
Câu 80. Cho tam giác ABC điểm I thoả: IA 2IB . Chọn mệnh đề đúng. CA CB CA CB CA C 2 B A. CI 2 . B. CI 2 .
C. CI C A C 2 B D. CI 3 3 3
Câu 81. Nhân vectơ a khác 0 với số thực 3 ta được một vectơ :
A. Cùng hướng với a .
B. Không cùng phương với a .
C. Có độ dài gấp 3 lần độ dài vectơ a .
D. Có độ dài bằng độ dài vectơ a .
Vấn đề 4: Tính độ dài của vectơ theo một cạnh cho trước.
Câu 82. Cho hình chữ nhật ABCD có AB 3, BC 4 . Độ dài của AC là: A. 5. B. 6. C. 7 . D. 9.
Câu 83. Cho hình bình hành ABCDi có AD 2, AB 4, BD 5 . Tính độ dài BA DA A. 3. B. 4. C. 5. D. 6.
ĐĂNG KÝ LỚP OFF TẠI 106/G26 LẠC LONG QUÂN P3 Q11 7
TỔNG ÔN HÌNH HỌC 10 – VECTOR
THẦY LÂM PHONG (SÀI GÒN – 0933524179)
Câu 84. Cho hai vectơ a và b có giá vuông góc với nhau và a 4, a b 5 . Tính độ dài b A. 1. B. 9. C. 3. D. 41 .
Câu 85. Cho tam giác ABC đều có cạnh bằng a . Độ dài của AB AC bằng a 3 A. 2a . B. a . C. a 3 D. 2
Câu 86. Cho tam giác ABC vuông cân tại A có AB AC a . Độ dài của AB AC bằng a 2 A. a 2 . B. . C. 2a D. a 2
Câu 87. Cho tam giác ABC vuông cân tại A có AB 3, AC 4 . Độ dài của CB AB bằng A. 2 . B. 2 13 . C. 4 D. 13
Câu 88. Cho tam giác ABC đều cạnh là a . Tính AB CA bằng : a 3 A. 0 . B. 2a . C. D. a 3 2
Câu 89. Cho tam giác ABC đều cạnh là a , H là trung điểm của cạnh BC. Tính CA HC bằng : a 3a 2a 3 a 7 A. . B. . C. D. 2 2 3 2
Câu 90. Cho tam giác ABC vuông tại A có AB 3, AC 4 . Tính AB AC bằng : A. 1. B. 5 . C. 7 D. 7
Câu 91. Cho tam giác ABC vuông tại C có BC a, AC a 3 . Tính CA CB bằng : A. 2a . B. a .
C. a 1 3 D. a2 4
Câu 92. Gọi G là trọng tâm tam giác vuông ABC với cạnh huyền BC 12 . Tính GB GC . A. 2 . B. 2 3 . C. 8 D. 4
Câu 93. Cho hình vuông ABCD cạnh a. Tính AB AC theo a. a A. a . B. 2a . C. 0 D. 2
Câu 94. Cho hai lực F F 100 N có điểm đặt tại O và tạo với nhau một góc 0 60 . Cường độ 1 2
lực tổng hợp của hai lực ấy bằng bao nhiêu ?
A. 100 3 N . B. 50 3 N . C. 100 N . D. 200 N .
Câu 95. Cho hai lực F 30 N, F 40 N có điểm đặt tại O và tạo với nhau một góc 0 90 . Cường 1 2
độ lực tổng hợp của hai lực ấy bằng bao nhiêu ? A. 10 N . B. 70 N . C. 50 N . D. 35 N .
Câu 96. Cho hai lực F F 200 N có điểm đặt tại O và tạo với nhau một góc 0 120 . Cường độ 1 2
lực tổng hợp của hai lực ấy bằng bao nhiêu ?
A. 400 N . B. 200 N . C. 200 3 N . D. 100 2 N .
ĐĂNG KÝ LỚP OFF TẠI 106/G26 LẠC LONG QUÂN P3 Q11 8
TỔNG ÔN HÌNH HỌC 10 – VECTOR
THẦY LÂM PHONG (SÀI GÒN – 0933524179)
Câu 97. Cho hai lực F 100 N, F 150 N . Cường độ lực tổng hợp của hai lực có thể là giá trị 1 2
nào trong các giá trị sau đây ? A. 40 N. B. 270 N . C. 170 N . D. 30 N .
Câu 98. Cho hai lực F 30 N, F 80 N có điểm đặt tại O . Cường độ lực tổng hợp của hai lực 1 2
không thể là giá trị nào trong các giá trị sau đây ? A. 40 N. B. 110 N . C. 70 N . D. 50 N .
Câu 99. Cho ba lực F1 MA, F2 MB, F3 MC A
cùng tác động vào một vật tại điểm M và vật F1
đứng yên. Cho biết cường độ của F1 , F2 đều
bằng 25 N và góc AMB 0 60 . Khi đó cường độ C M lực của F là: F3 3 F2 A. 25 3 N B. 50 3 N B C. 50 2 N D. 100 3 N
Câu 100. Cho hình chữ nhật ABCD tâm O, AB 12a, AD 5a . Tính AD AO theo a 13a A. 13a . B. 6a . C. D. 3a 2
Câu 101. Cho hình thang ABCD (AB // CD) có cạnh AB a
3 ,CD 6a . Tính AB CD theo a A. 3a . B. 9a . C. 0 D. 6a
Câu 102. Cho tam giác đều ABC cạnh 2a. Gọi G là trọng tâm. Khi đó giá trị AB GC là: a 3 2a 3 4a 3 2a A. B. C. D. 3 3 3 3
Câu 103. Cho hình thang ABCD có AB song song CD. Cho AB 2a,CD a . Gọi O là trung điểm
của AD. Tính OB OC 3a A. B. a C. 2a D. 3a 2 21 5
Câu 104. Cho tam giác OAB vuông cân tại O và OA a . Độ dài của u OA OB là 4 2 a 321 a 520 a 541 a 41 A. B. C. D. 4 4 4 4 11 3
Câu 105. Cho tam giác OAB vuông cân tại O và OA a . Độ dài của v OA OB là 4 7 65a 89a a 6073 A. 2a B. C. D. 28 28 28
Câu 106. Cho tam giác ABC biết AB 8, AC 9, BC 11 . M là trung điểm BC, N là điểm trên
đoạn AC sao cho AN x 0 x 9. Hệ thức nào sau đây là đúng ? 1 x 1 1 x 1 A. MN AC AB . B. MN AC BA . 2 9 2 2 9 2
ĐĂNG KÝ LỚP OFF TẠI 106/G26 LẠC LONG QUÂN P3 Q11 9
TỔNG ÔN HÌNH HỌC 10 – VECTOR
THẦY LÂM PHONG (SÀI GÒN – 0933524179) 1 x 1 x 1 1 C. MN AC AB . D. MN AC BA . 2 9 2 9 2 2
Vấn đề 5: Biểu thị một vectơ theo hai vectơ không cùng phương.
Câu 107. Cho tam giác ABC cạnh BC 4 , M thuộc đoạn BC sao cho MC 1 . Cặp số m; n thỏa
AM mAB nAC bằng : 1 3 1 3 1 3 1 3 A. ; . B. ; . C. ; D. ; 2 2 2 2 4 4 4 4
Câu 108. Cho hình bình hành ABCD có AB a , AD b . Gọi M là trung điểm của CD , N là trung
điểm của BM . Tính AN theo a,b . 3 1 3 1 1 3
A. a 1 b . B. a b . C. a b D. a b 2 4 2 8 2 2 4
Câu 109. Cho tam giác ABC và điểm I sao cho IA 2IB . Biểu thị vecto CI theo hai vecto CA và CB như sau: CA CB CA CB CA C 2 B A. CI 2 .
B. CI C A C 2 B . C. CI 2 D. CI 3 3 3
Câu 110. Cho tam giác ABC và điểm I sao cho IA 2IB 0 . Biểu thị vecto CI theo hai vecto CA và CB như sau: CA CB CA CB CA C 2 B A. CI 2 .
B. CI C A C 2 B . C. CI 2 D. CI 3 3 3
Câu 111. Cho tam giác ABC và trọng tâm G. Đặt CA a,CB b Biểu thị vecto AG theo hai vecto
a và b như sau: a b a b a b a b A. AG 2 . B. AG 2 . C. AG 2 D. AG 2 3 3 3 3
Câu 112. Cho tam giác ABC và trọng tâm G. Đặt CA a,CB b Biểu thị vecto CG theo hai vecto
a và b như sau: a b a b a b a b A. CG . B. CG 2 2 . C. CG D. CG 2 2 3 3 3 3
Câu 113. Cho hình bình hành ABCD tâm O. Tìm m và n sao cho BC mOA nOB
A. m n 1 .
B. m n 1 .
C. m , 1 n 1
D. m , 1 n 1
Câu 114. Cho tam giác ABC. Gọi M là điểm sao cho BM 2MC . Các số m, n thỏa mãn
AM mAB nAC . Giá trị của m n là A. 0 . B. 1. C. 2 D. 3
Câu 115. Cho hình bình hành ABCD tâm O. Gọi I là trung điểm của BC. Tìm m, n thỏa mãn
AI mAD nAB . 1 A. m ,n 1 .
B. m ,n 1 1 .
C. m n 1
D. m ,n 1 1 2 2 2
Câu 116. Cho tam giác ABC. Điểm I thuộc đoạn AC sao cho AC 4IC . Tìm m, n thỏa mãn
BI mAC nAB
ĐĂNG KÝ LỚP OFF TẠI 106/G26 LẠC LONG QUÂN P3 Q11 1 0
TỔNG ÔN HÌNH HỌC 10 – VECTOR
THẦY LÂM PHONG (SÀI GÒN – 0933524179) 1 3 1 3 A. m ,n 1 . B. m ,n 1 . C. m ,n 1 D. m ,n 1 2 4 2 4
Câu 117. Cho hình chữ nhật ABCD có tâm O, điểm M là điểm bất kỳ. Tìm số thực m thỏa mãn
điều kiện MA MB MC MD mMO A. 2 . B. 4 . C. 6 D. 8
Câu 118. Cho tam giác ABC và các điểm D, E thỏa AD 2AB và AE 2 AC . Nếu 5
DE mAB nAC, m,n . Tính tích giá trị P m.n
A. P 2 .
B. P 4 . C. P 4 D. P 2 5 5 5 5
Câu 119. Cho tam giác ABC. Gọi M là điểm trên cạnh AB: MB = 4MC. Khi đó, biễu diễn AM theo AB và AC là: 4 4 1 4 1
A. AM 4AB AC B. AM AB 0 AC C. AM AB
AC D. AM AB AC 5 5 5 5 5
Vấn đề 6: Tìm quỹ tích của một điểm thỏa mãn tính chất cho trước.
Câu 120. Cho tam gíac ABC và điểm M thỏa MA MB MC 0 . Vị trí điểm M đối với tam giác ABC là:
A. trực tâm của A BC .
B. tâm đường tròn ngoại tiếp A BC .
C. trọng tâm của A BC .
D. tâm đường tròn nội tiếp A BC .
Câu 121. Cho tam giác ABC và điểm M thỏa MA MB MC 0 thì mệnh đề nào sau đây đúng?
A. M là trọng tâm tam giác ABC.
B. M là trung điểm của AC.
C. ABMC là hình bình hành.
D. ACBM là hình bình hành.
Câu 122. Cho tam giác ABC. Tìm điểm K thỏa mãn KA 2KB CB
A. K là trung điểm của AB.
B. K là trung điểm của BC.
C. K là trọng tâm tam giác ABC.
D. K là trung điểm của AC.
Câu 123. Cho ΔABC có G là trọng tâm. Tìm tập hợp các điểm M thỏa mãn MB MC BC
A. Đường tròn đường kính BC.
B. Đường tròn có tâm C bán kính BC.
C. Đường tròn có tâm B, bán kính BC.
D. Đường tròn có tâm A bán kính BC.
Câu 124. Cho tam giác ABC và điểm M thỏa mãn 2 MA MB MC 3 MB MC . Tập hợp điểm M là
A. một đường thẳng
B. một đường tròn
C. một đoạn thẳng
D. nửa đường thẳng
Câu 125. Cho hình chữ nhật ABCD tâm O; AB 8 cm , AD 6 cm. Tập hợp điểm M thỏa
AO AD MO là
A. Đường tròn tâm O có bán kính 10 cm .
B. Đường tròn tâm O có bán kính 5 cm .
C. Đường thẳng BD.
D. Đường thẳng AC.
Câu 126. Cho tam giác ABC. Tập hợp những điểm M sao cho: MA MB MC MB là:
A. M nằm trên đường tròn tâm I, bán kính R 2AC với I nằm trên cạnh AB sao cho IA 2IB .
B. M nằm trên đường tròn tâm I, bán kính R 2AB với I nằm trên cạnh AB sao cho IA 2IB .
ĐĂNG KÝ LỚP OFF TẠI 106/G26 LẠC LONG QUÂN P3 Q11 1 1
TỔNG ÔN HÌNH HỌC 10 – VECTOR
THẦY LÂM PHONG (SÀI GÒN – 0933524179)
C. M nằm trên đường trung trực của IJ với I, J lần lượt là trung điểm của AB và BC.
D. M nằm trên đường trung trực của BC.
Câu 127. Hãy xác định các điểm I thoả mãn đẳng thức sau: 2IB 3IC 0 IC
A. I là trung điểm BC.
B. I thuộc cạnh BC và BI 3 . 2
C. I nằm trên BC ngoài đoạn BC.
D. I không thuộc BC.
Câu 128. Cho tứ giác ABCD và điểm M tùy ý. Khi đó vectơ u MA 4MB 3MC bằng:
A. u BA 3BC
B. u 3AC AB
C. u 2BI với I là trung điểm của AC.
D. u 2AI với I là trung điểm BC
ĐĂNG KÝ LỚP OFF TẠI 106/G26 LẠC LONG QUÂN P3 Q11 1 2




