











Preview text:
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO KỲ THI CHỌN HỌC SINH GIỎI CẤP HUYỆN Môn: Toán 8
Thời gian: 120 phút (không kể thời gian phát đề) Đề chính thức
Khóa thi: Ngày 2/05/2019 Bài 1. (6,0 điểm)
a. Phân tích các đa thức sau thành nhân tử: 3 2
A = x + 2019x + 2019x + 2018
b. Tìm các giá trị x và y thỏa mãn: 2 2
x + y − 4x − 2y + 5 = 0
c. Chứng minh rằng với mọi số tự nhiên n thì : A = 5n+2 + 26.5n + 82n+1 59 Bài 2. (4,0 điểm) a. Chứng minh 2 2 2
a + b + c 2(ab + bc + ca) với mọi số thực a, b, c.
b. Chứng minh rằng với mọi số nguyên x thì biểu thức P một số chính phương.
P = (x+5)(x+7)( x + 9)( x + ) 11 + 16.
Bài 3 (3.0 điểm): Cho biểu thức: 1 1 1 1 1 P = + + + + 2 2 2 2 2 x − x
x − 3x + 2 x − 5x + 6 x − 7x +12 x − 9x + 20
a) Tìm điều kiện của x để biểu thức P có giá trị.
b) Rút gọn biểu thức P. Bài 4. (5,0 điểm)
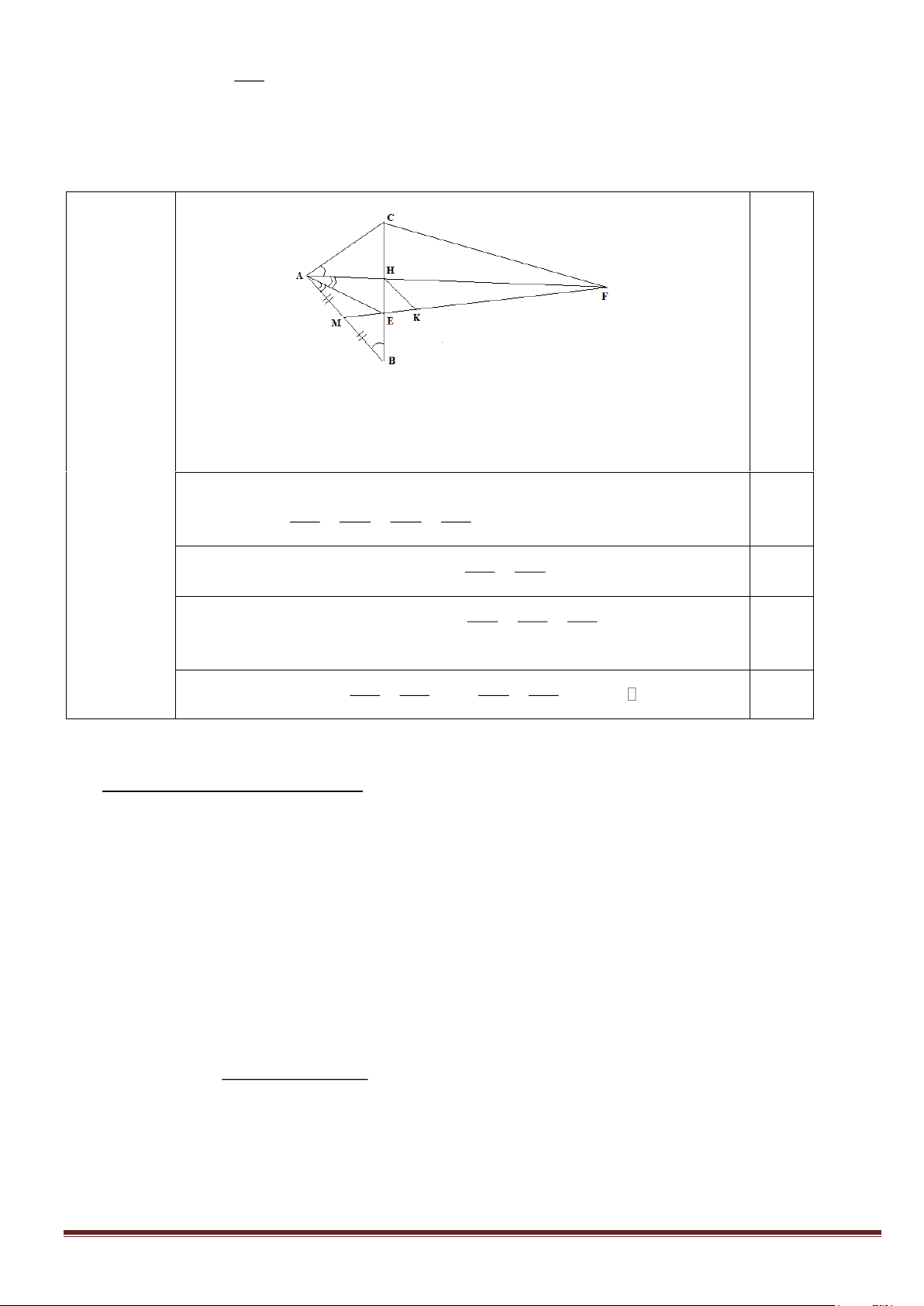
Cho tam giác ABC vuông tại A (AC AB). Vẽ đường cao AH (H BC) . Trên tia
đối của tia BC lấy điểm K sao cho KH = HA. Qua K kẻ đường thẳng song song với AH, cắt đường thẳng AC tại P.
a.Chứng minh: Tam giác ABC Đồng dạng với tam giác KPC.
b. Gọi Q là trung điểm của BP. Chứng minh: QH là đường trung trực của đoạn thẳng AK.
Bài 5 (2.0 điểm): Cho tam giác ABC có ˆ ˆ
A B . Trên cạnh BC lấy điểm H sao cho ˆ ˆ
HAC = ABC . Đường phân giác của góc ˆ
BAH cắt BH ở E. Từ trung điểm M của AB kẽ ME cắt đường thẳng AH tại
F. Chứng minh rằng: CF // AE.
________________Hết________________ \ĐÁP ÁN
Câu 1: a. Phân tích các đa thức sau thành nhân tử: 3 2
A = x + 2019x + 2019x + 2018 3 2
A = x + 2019x + 2019x + 2018 3 2
A = x −1+ 2019(x + x + 2019) 2 2
A = (x - 1)(x + x +1) + 2019(x + x +1) ( 2 A = x + x + ) 1 (x −1+ 2019) 2
A = (x + x + 1 )(x + 2018)
b. Tìm các giá trị x và y thỏa mãn: 2 2
x + y − 4x − 2y + 5 = 0 2 2 2 2
x + y − 4x − 2y + 5 = 0 (x − 4x + 4) + ( y − 2y +1) = 0 2 2
(x − 2) + (y −1) = 0
x = 2 và y = 1
c. Chứng minh rằng với mọi số tự nhiên n thì A = 5n+2 + 26.5n + 82n+1 59
5n+2 + 26.5n + 82n+1 = 25.5n + 26.5n + 8.82n =
5n(59 – 8) + 8.64n = 59.5n + 8(64n – 5n)
59.5n 59 vaø 8(64n – 5n) (64 – 5) = 59
vaäy 5n+2 + 26.5n + 82n+1 59 Câu 2: a. Chứng minh 2 2 2
a + b + c 2(ab + bc + ca) với mọi số thực a, b, c.
Vì a, b, c là độ dài ba cạnh của một tam giác nên ta có: 2
0 a b + c a ab + ca ; 2
0 b c + a b bc + ab 2
0 c a + b c ca + bc Do đó, suy ra: 2 2 2
a + b + c 2(ab + bc + ca)
b. Chứng minh rằng với mọi số nguyên x thì biểu thức P một số chính phương.
Ta có: P = (x+5)(x+7)(x + 9)(x + ) 11 + 16.
P = (x + 5)(x +11)(x + 7)(x + 9) + 16. 2 2
P = (x +16x + 55)(x +16x + 63)+ 16. 2 2 2
P = (x +16x + 55) + 8(x +16x + 55)+ 16. 2 2 2 2
P = (x +16x + 55) + 2(x +16x + 55).4+ 4 . 2 2
P = (x +16x + 59) .Vơi x là số nguyên thì P là một số CP.
Bài 4 (3.0 điểm): Cho biểu thức: 1 1 1 1 1 P = + + + + 2 2 2 2 2 x − x
x − 3x + 2 x − 5x + 6 x − 7x +12 x − 9x + 20
a) Tìm điều kiện của x để biểu thức P có giá trị.
b) Rút gọn biểu thức P.
a) Tìm điều kiện đúng: x 0; x 1; x 2; x 3; x 4; x 5 b) Rút gọn đúng: 1 1 1 1 1 P = + + + +
x(x −1) (x −1)(x − 2) (x − 2)(x − 3) (x − 3)(x − 4) (x − 4)(x −5) = 1 1 1 1 1 1 1 1 1 1 − + − + − + − + −
x −1 x x − 2 x −1 x −3 x − 2 x − 4 x −3 x −5 x − 4 1 1 5 = − = x − 5 x x ( x − 5) I K B 1 H Q 1 P S Câu 4 A
C Chứng minh: ABC KPC ( G.G)
b. Gọi Q là trung điểm của BP. Chứng minh: QH là đường trung trực của đoạn thẳng AK. Trang 2 PB
Ta có: AQ = KQ =
(Trung tuyến ứng với nửa cạnh huyền trong tam giác vuông). 2
Lại có: HK = HA (Giả thiết). Do đó: QH là đường trung trực của AK. Ta có: ˆ ˆ ˆ ˆ ˆ ˆ = + = + = 5 CEA B BAE HAC EAH CAE 0,5đ cân ở C (2đ) CAE CA = CE (1)
Qua H kẽ đường thẳng song song với AB cắt MF ở K. Ta có: BE MB MA FA = = = (2) 0,5đ EH KH KH FH
AE là phân giác của ABH BE AB = (3) 0,25 EH AH đ
CAH và CBA đồng dạng AB CA CE = = (theo (1)) 0,25 AH CH CH (4) đ Từ (2), (3), (4) FA CE = hay AH EH =
AE CF (đpcm) 0,5đ FH CH FH CH PHÒNG GD&ĐT HUYỆN HL
KỲ THI CHỌN HỌC SINH GIỎI LỚP 8 TRƯỜNG THCS NG
NĂM HỌC: 2019 – 2020 Môn thi: TOÁN
Thời gian làm bài: 120 phút.
Câu 1. (3,0 điểm). Phân tích các đa thức sau thành nhân tử: 2 a) 5 4 x + x +1 b) ( )2 2 x – 8 + 36 c) ( 2 − + ) ( 2 + ) 2 x x 1 – 5x x – x 1 + 4x
Câu 2. (3,0 điểm).
a) Rút gọn biểu thức: A = ( − + )2 − ( − )2 a b c b c + 2ab − 2ac 2 x + x − 6 b) Rút gọn: 3 2 x − 4x −18x + 9
c) Chứng minh giá trị của biểu thức sau không phụ thuộc vào biến:
( − )2 −( − )2 + ( − )( + ) −( + )2 3 x 1 1 x 2 x 3 x 3 2x 3 − (5 −16x)
Câu 3. (4,0 điểm). Trang 3 1) Giải phương trình: a) 3 2 x + 5x − 4x − 20 = 0 2 1 2x −1 b) = + . 2 3 x − x +1 x +1 x +1
2) Một người đi xe đạp, một người đi xe máy, một người đi ô tô xuất phát từ địa điểm A lần lượt lúc
8 giờ, 9 giờ, 10 giờ cùng ngày với vận tốc theo thứ tự lần lượt là 10km/h, 30km/h, 50km/h. Hỏi đến
mấy giờ thì ô tô ở vị trí cách đều xe đạp và xe máy?
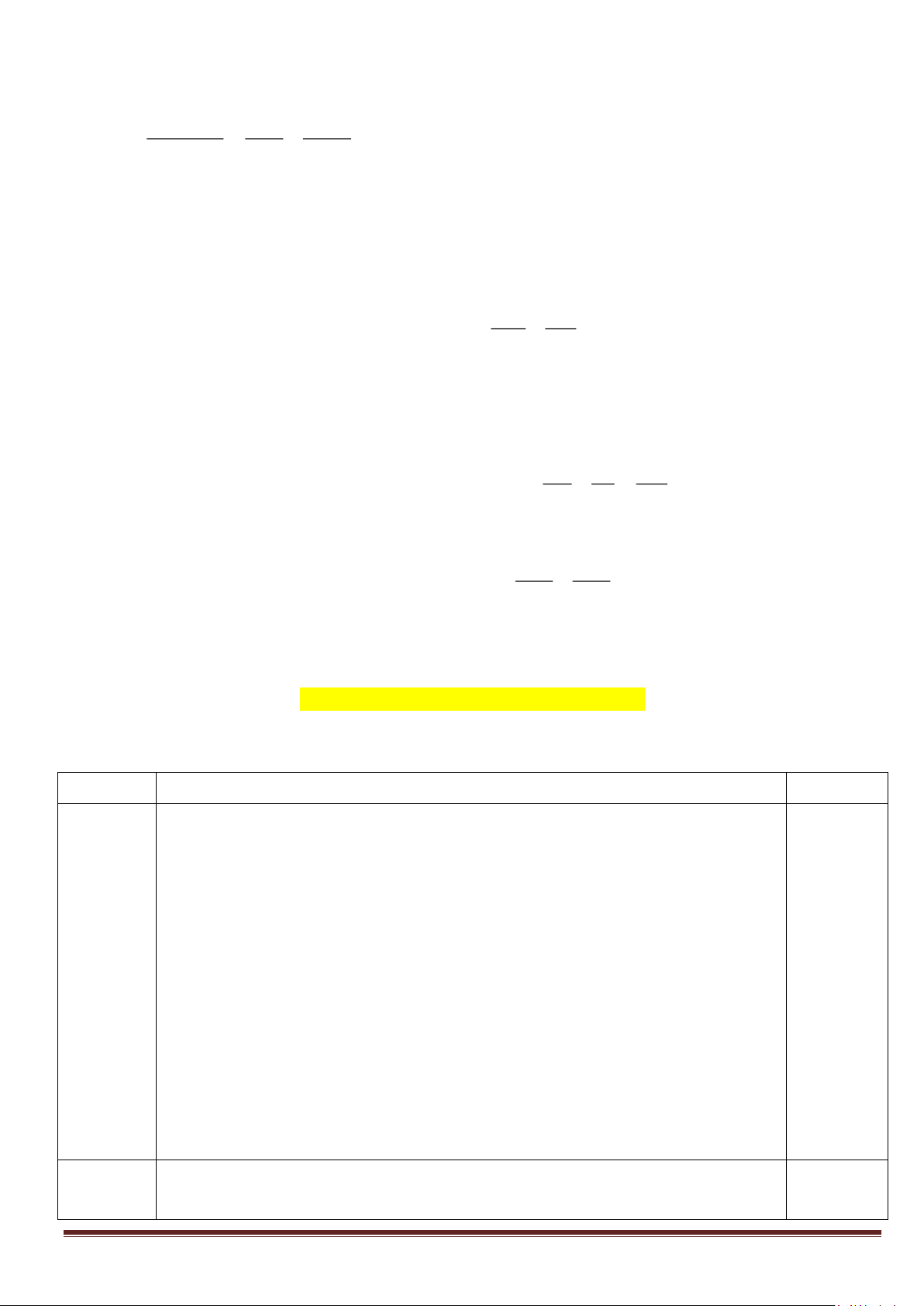
Câu 4. (2,0 điểm). Cho tam giác ABC, trung tuyến AD, trọng tâm G. Đường thẳng d bất kỳ đi qua G AB AC
và cắt AB, AC lần lượt tại M, N. Chứng minh rằng: + = 3 . AM AN
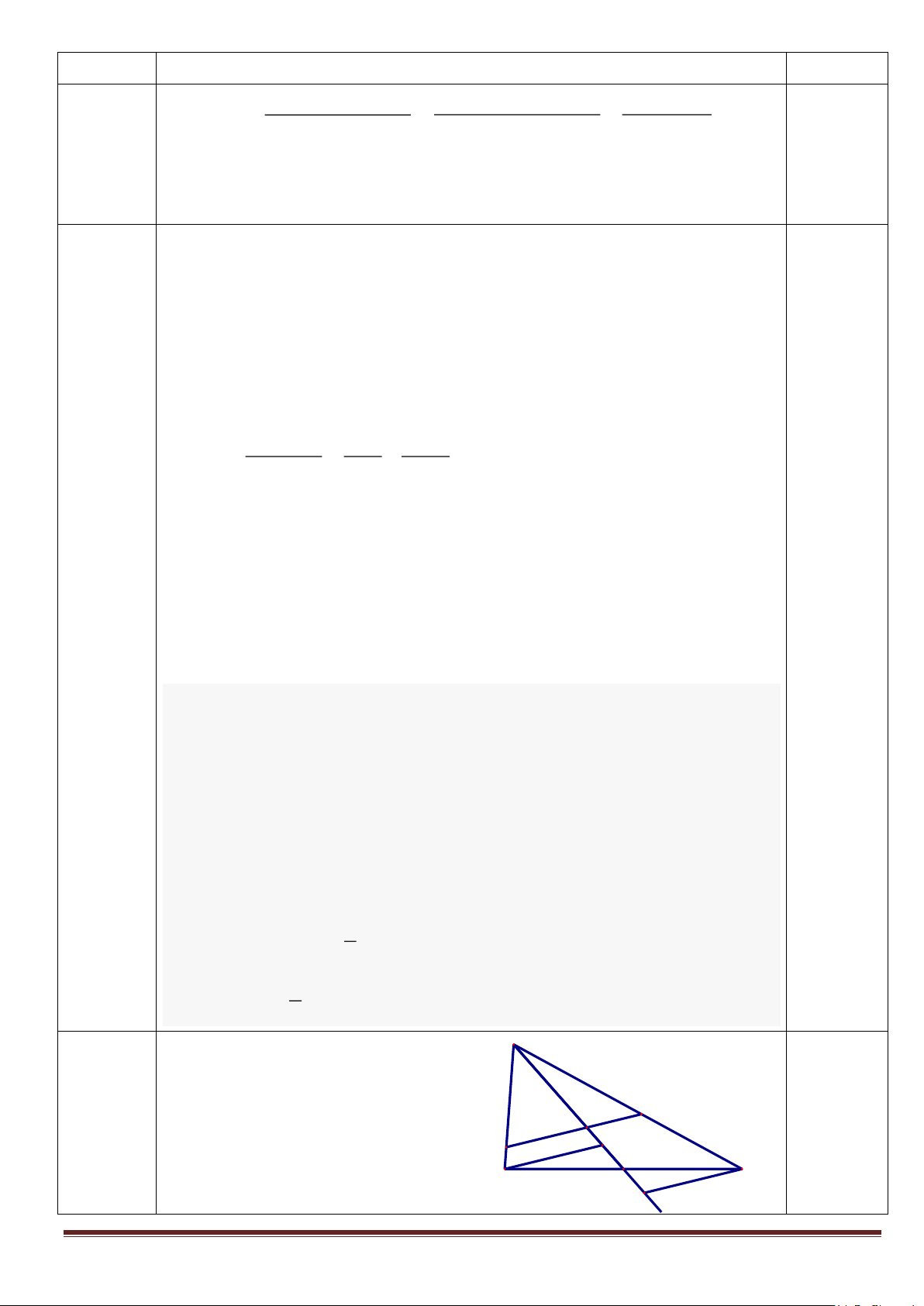
Câu 5. (6,0 điểm). Cho ABC cân tại A, hai đường cao AI và BD cắt nhau tại H. a) Chứng minh rằng: A IC ∽ B DC
b) Gọi E giao điểm của CH và AB. Chứng minh: 2 BE.BA + CH.CE = BC 1 1 2
c) Gọi T là giao điểm của DE và AH. Chứng minh: + = AT AI AH
Câu 6. (2,0 điểm). Tìm giá trị nhỏ nhất của biểu thức: 2 2 x y a) 2 2 A = (x − 2019) + (x + 2020) b) B = + (x, y ) 1 y −1 x −1
----------------Hết-----------------
(Học sinh không được sử dụng máy tính) HƯỚNG DẪN CHẤM Câu Hướng dẫn chấm Điểm Câu 1
Phân tích các đa thức sau thành nhân tử: 3 điểm a) 5 4 x + x +1 5 2 4 2 2 = x − x + x + 2x +1− x ( ) ( )2 2 3 2 2 x x 1 x 1 x = − + − − = ( 2 + + )( 3 x x 1 x − x + ) 1 1 điểm b) ( )2 2 x – 8 + 36 4 2 = x −16x +100 4 2 2 = x + 20x +100 −16x = ( 2 − + ) ( 2 x 4x 10 . x + 4x +10) 1 điểm 2 c) ( 2 + ) ( 2 + ) 2
x – x 1 – 5x x – x 1 + 4x = ( 2 − + ) ( 2 x x 1 . 5x − 6x + ) 1 = ( 2 x − x + ) 1 .(x − ) 1 .(5x − ) 1 1 điểm Câu 2
a) Rút gọn biểu thức: A = ( − + )2 − ( − )2 a b c b c + 2ab − 2ac 2 = ... = a 1 điểm 3 điểm Trang 4 Câu Hướng dẫn chấm Điểm 2 x + x − 6 (x + 3).(x − 2) x − 2 1 điểm b) Rút gọn: = = 3 2 x − 4x −18x + 9 (x + 3).( 2 x − 7x + 3) 2 x − 7x + 3
c) Chứng minh giá trị của biểu thức sau không phụ thuộc vào biến: ( 1 điểm
− )2 − ( − )2 + ( − )( + ) − ( + )2 3 x 1 1 x 2 x 3 x 3
2x 3 − (5 −16x) = ... = −30 Câu 3 1) Giải phương trình: 4 điểm a) 3 2 x + 5x − 4x − 20 = 0 2
x (x + 5) − 4(x + 5) = 0 ( + ) ( 2 x 5 . x − 4) = 0 x = 5 − ; x = 2
Vậy pt có tập nghiệm S = 5 − ; 2 1 điểm 2 1 2x −1 b) = + . (ĐK: x −1) 2 3 x − x +1 x +1 x +1 ( + ) 2
2 x 1 = x − x +1+ 2x −1 2 x − x − 2 = 0
x = 2 (tm) hoặc x = −1 (loại)
Vậy pt có tập nghiệm S = 2 1 điểm
2) Gọi thời gian từ khi ô tô xuất phát đến khi cách đều xe đạp và xe máy là: x (giờ; x 0 )
Thì thời gian xe đạp đã đi là: x + 2 (giờ)
Thời gian xe máy đã đi là: x + 1 (giờ)
Quãng đường ô tô đi là: 50x (km);
Xe máy đã đi là: 30.(x+1) (km); Xe đạp đã đi là: 10.(x+2) (km)
Vì ô tô cách đều xe đạp và xe máy nên quãng đường ô tô đi nhiều hơn xe
đạp bằng quãng đường xe máy đi nhiều hơn ô tô. Ta có phương trình:
50x −10(x + 2)=30(x + 2) − 50x ... 4 x = (tm) 3 4
Vậy đến 10h + h = 11h20' thì ô tô cách đều xe đạp và xe máy 2 điểm 3 Câu 4 A HV: 0,5 2 điểm điểm N G E M - Kẻ BE, CF//MN D C B F Trang 5 Câu Hướng dẫn chấm Điểm AB AC AE AF AE + AF 2AD 1 điểm + = + = = = 3 AM AN AG AG AG AG Câu 5 HV: 0,5 6 điểm A điểm a) Chứng minh được A IC ∽ B DC (g-g) 1 điểm b)
- Chứng minh được: BE.BA = BH.BD = BI.BC T CH.CE = CI.CB E D + = ( + ) 2 BE.BA CH.CE BC. BI IC = BC H 2,5 điểm B I C 1 1 2
c) Gọi T là giao điểm của DE và AH. Chứng minh: + = AT AI AH
- Chứng minh được EH; EA là phân giác trong, ngoài của ETI tại đỉnh E AT HT ET = = AI HI EI HT HI = HT HI − = 0 HT HI +1+1− = 2 AT AI AT AI AT AI + − HT AT AI HI + = 2 AT AI AH AH + = 2 AT AI 2 điểm 1 1 2 + = AT AI AH Câu 6
Tìm giá trị nhỏ nhất của biểu thức: 2 điểm a) = ( − )2 ( + )2 A x 2019 x 2020 2 1 2 =
... = 2x + 2x + 8156761 = 2 x + + 8156760,5 8156760,5 2 1
Dấu “=” xảy ra x = − 1 điểm 2 2 2 x y b) B = + (x;y ) 1 y −1 x −1 a = x −1 Đặt (a;b 0) b = y −1 ( + )2 ( + )2 a 1 b 1 4a 4b a b B = + + = 4 + 4.2 = 8 b a b a b a
Dấu “=” xảy ra a = b = 1 x = y = 2 1 điểm Trang 6
PHÒNG GD & ĐT KÌ THI KHẢO SÁT CHẤT LƯỢNG HỌC SINH MŨI NHỌN
Đề thi chính thức Môn : Toán lớp 8
Thời gian làm bài 120 phút Số báo Đề thi này có 5 câu danh: .......................
Câu 1(4.0 điểm) : Cho biểu thức A = x 3 − 3x x + 4 − + 2 3
x +1 x − x +1 x +1
a) Rút gọn biểu thức A
b) Chứng minh rằng giá trị của A luôn dương với mọi x ≠ - 1
Câu 2(4.0 điểm): Giải phương trình: a) 2
x − 3x + 2 + x −1 = 0 2 2 2 b) 1 1 1 1 8 x + + 4 x + − 4 x + x + = (x + 4)2 2 2 2 2 x x x x
Câu 3(3.0 điểm) : Cho xy ≠ 0 và x + y = 1. x y 2(xy − 2) Chứng minh rằng: + − = 0 3 3 2 2 y −1 x −1 x y + 3
Câu 4(3.0 điểm): Chứng minh rằng: Với mọi x Q thì giá trị của đa thức :
M = (x + 2)(x + 4)(x + 6)(x +8) +16 là bình phương của một số hữu tỉ.
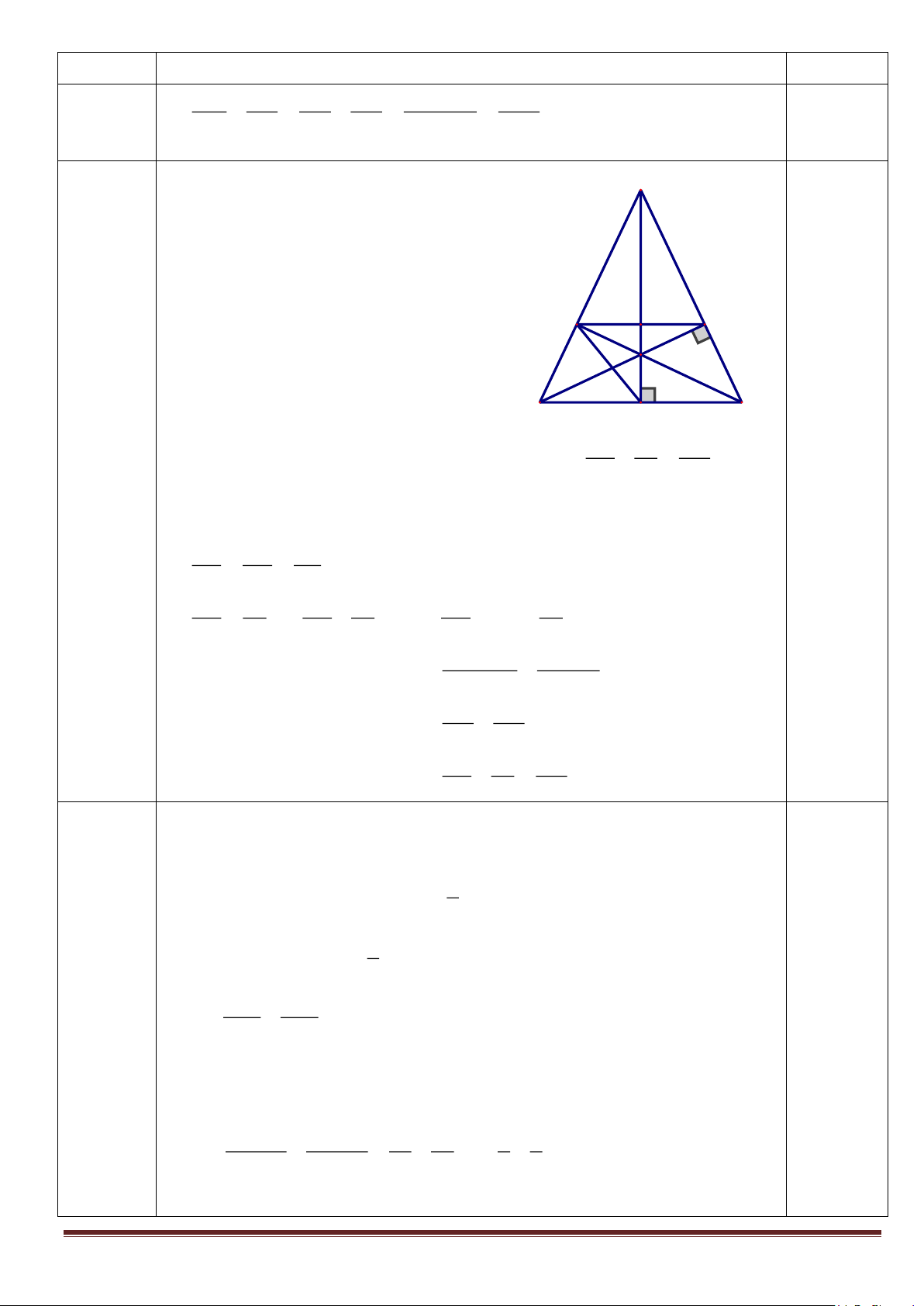
Câu 5 (6.0 điểm) : Cho tam giác ABC vuông tại A (AC > AB), đường cao AH (HBC).
Trên tia HC lấy điểm D sao cho HD = HA. Đường vuông góc với BC tại D cắt AC tại E.
1. Chứng minh rằng hai tam giác BEC và ADC đồng dạng. Tính độ dài đoạn BE
theo m = AB .
2. Gọi M là trung điểm của đoạn BE. Chứng minh rằng hai tam giác BHM và BEC
đồng dạng. Tính số đo của góc AHM
3. Tia AM cắt BC tại G. Chứng minh: GB HD = . BC AH + HC
HƯỚNG DẪN CHẤM TOÁN 8 Câu Nội dung Điểm 1 x ( 2 x − x + ) 1 − ( x + )
1 (3 − 3x) + x + 4 1điểm
- Rút gọn: A = x 3 − 3x x + 4 − + = a 2 3
x +1 x − x +1 x +1
(x + )1( 2x − x + )1 Trang 7 + 2 + 2 +1 (x + )1( 2 3 2 x + x x x x + ) 2 1 1điểm = x + x +1 = = ( x + ) 1 ( 2 x − x + ) 1 (x + ) 1 ( 2 x − x + ) 2 1 x − x +1 2 1 3 x + + 2
Với mọi x ≠ - 1 thì A = x + x +1 = 2 4 1điểm 2 x − x +1 2 1 3 b x − + 2 4 2 2 Vì 1 3 1 3 x + + 0; x − + 0, x 1
− A 0, x 1 − 2 4 2 4 1điểm 2
* Với x 1 (*) x - 1 0 x −1 = x −1 ta có phương trình x2 -3x + 2 + x-1 = 0 1điểm
x − x + = (x − )2 2 2 1 0
1 = 0 x = 1 ( Thoả mãn điều kiện *)
* Với x< 1 (**) x - 1 0 x −1 =1− x ta có phương trình a
x2 -3x + 2 + 1 - x = 0 2
x − 4x + 3 = 0 (x − ) 1 ( x − 3) = 0
+ x - 1 = 0 x = 1( Không thỏa mãn điều kiện **)
+ x - 3 = 0 x = 3 ( Không thoả mãn điều kiện **) 1điểm
Vậy nghiệm của phương trình là : x = 1
* Điều kiện x ≠ 0 (1) 0.5điể 2 2 m * pt 1 1 1 1 8 x + + 4 x + x + − x + = ( x + 4)2 2 2 2 2 x x x x 2 1 1 1 1 8 x + + 2 + 4 x + x + − x + = ( x + 4)2 2 2 2 2 2 2 b x x x x 1điểm = (x + )2 16
4 x ( x + 8) = 0 x = 0 hoặc x = -8
So sánh với điều kiện (1) , suy ra nghiệm của phương trình là x = - 8 0.5điể m Ta có 3
y − = ( y − )( 2
y + y + ) = −x( 2 1 1 1 y + y + )
1 vì xy 0 x, y 0 x, y 0
y-1 0 và x-1 0 1điểm 3 Trang 8 x 1 − = 3 2 y −1 y + y +1 1điểm y 1 − 3
x −1 = ( x − ) 1 ( 2 x − x + ) 1 = − y ( 2 x − x + ) 1 = 3 2 x −1 x + x +1 x y 1 − 1 − + = + 3 3 2 2 y −1 x −1
y + y +1 x + x +1
x + x +1+ y + y +1 (x + y)2 2 2
− 2xy + (x + y) + 2 = − 1điểm ( = − 2 x + x + ) 1 ( 2 y + y + ) 2 2 1 x y +
(x + y)2 − 2xy + xy(x + y)+ xy + (x + y)+1 4 − 2xy x y 2( xy − 2) = − + − = 0 2 2 3 3 2 2 x y + 3 y −1 x −1 x y + 3 Ta có: M = ( 2 x − x + )( 2 10
16 x −10x + 24) +16 1điểm 4
Đặt a = x2 - 10x + 16 suy ra M = a( a+8) + 16 = a2 + 8a + 16 = ( a+ 4)2 1điểm
M = x2 - 10x + 20 )2 ( đpcm) 1điểm 5
+ Hai tam giác ADC và BEC có: Góc C chung. CD CA = (Hai tam giác vuông CE CB
CDE và CAB đồng dạng) 1.5điể a
Do đó, chúng dồng dạng (c.g.c). m Suy ra: 0
BEC = ADC = 135 (vì tam giác AHD vuông cân tại H theo giả thiết). Nên 0
AEB = 45 do đó tam giác ABE vuông cân tại A. Suy ra: 1điểm
BE = AB 2 = m 2
Ta có: BM 1 BE 1 AD = = (do BEC ADC ) BC 2 BC 2 AC 1.5điể
mà AD = AH 2 (tam giác AHD vuông vân tại H) BM AD AH BH BH m b nên 1 1 2 = = = = (do AB H C BA ) BC 2 AC 2 AC AB 2 BE Do đó BHM BEC (c.g.c), suy ra: 0 0
BHM = BEC = 135 AHM = 45 1điểm
Tam giác ABE vuông cân tại A, nên tia AM còn là phân giác góc BAC. 1điểm AB ED AH HD c Suy ra: GB AB = , mà = ( A BC D EC) = (ED// AH ) = GC AC AC DC HC HC Do đó: GB HD GB HD GB HD = = = GC HC GB + GC HD + HC BC AH + HC Trang 9
ĐỀ THI CHỌN HỌC SINH GIỎI MÔN: TOÁN - LỚP 8
THỜI GIAN LÀM BÀI: 150 phút
(không kể thời gian phát đề) ĐỀ BÀI
Bài 1 (4 điểm) 3 2 1− x 1− x − Cho biểu thức A = x : 2 3 1− x
1− x − x + x với x khác -1 và 1.
a, Rút gọn biểu thức A.
b, Tính giá trị của biểu thức A tại x 2 = 1 − . 3
c, Tìm giá trị của x để A < 0.
Bài 2 (3 điểm) 2 2 2 2 2 2
Cho (a − b) + (b − c) + (c − a) = (.
4 a + b + c − ab − ac − bc).
Chứng minh rằng a = b = c .
Bài 3 (3 điểm)
Giải bài toán bằng cách lập phương trình.
Một phân số có tử số bé hơn mẫu số là 11. Nếu bớt tử số đi 7 đơn vị và tăng mẫu lên 4
đơn vị thì sẽ được phân số nghịch đảo của phân số đã cho. Tìm phân số đó.
Bài 4 (2 điểm) 4 3 2
Tìm giá trị nhỏ nhất của biểu thức A = a − 2a + 3a − 4a + 5.
Bài 5 (3 điểm)
Cho tam giác ABC vuông tại A có góc ABC bằng 600, phân giác BD. Gọi M,N,I theo
thứ tự là trung điểm của BD, BC, CD.
a, Tứ giác AMNI là hình gì? Chứng minh.
b, Cho AB = 4cm. Tính các cạnh của tứ giác AMNI.
Bài 6 (5 điểm)
Hình thang ABCD (AB // CD) có hai đường chéo cắt nhau tại O. Đường thẳng qua O và
song song với đáy AB cắt các cạnh bên AD, BC theo thứ tự ở M và N.
a, Chứng minh rằng OM = ON. b, Chứng minh rằng 1 1 2 + = . AB CD MN
c, Biết SAOB= 20082 (đơn vị diện tích); SCOD= 20092 (đơn vị diện tích). Tính SABCD.
HƯỚNG DẪN CHẤM THI HỌC SINH GIỎI
Bài 1( 4 điểm ) a, ( 2 điểm ) Với x khác -1 và 1 thì : 0,5đ Trang 10 3 2
A=1− x − x + x 1 ( − x 1 )( + x) : 1− x 1 ( + x 1 )( 2
− x + x ) − x 1 ( + x) 2 = 1 ( − x 1
)( + x + x − x) 1 ( − x 1 )( + x) : 0,5đ 1− x 1 ( + x 1 )( − 2 2 x + x ) = 1 1 ( 2 + x ) : 0,5đ 1 ( − x) = 1 ( 2 + x 1 )( − x) 0,5đ KL b, (1 điểm) Tại x = 2 − 5 5 2 5 1 = − thì A = 1+ (− ) − 1− (− ) 0,25đ 3 3 3 3 = 25 5 1 ( + 1 )( + ) 0,25đ 9 3 34 8 272 2 = . = = 10 0,5đ 9 3 27 27 KL c, (1điểm)
Với x khác -1 và 1 thì A<0 khi và chỉ khi 1 ( 2 + x 1 )( − x) 0 (1) 0,25đ Vì 1 2
+ x 0 với mọi x nên (1) xảy ra khi và chỉ khi 1− x 0 x 1 0,5đ KL 0,25đ Bài 2 (3 điểm)
Biến đổi đẳng thức để được 0,5đ
a2 + b2 − 2ab + b2 + c2 − bc 2
+ c2 + a2 + 2ac = 4a2 + b 4 2 + c
4 2 − 4ab − 4ac − bc 4 Biến đổi để có ( 2 2
a + b − 2ac) + ( 2 2
b + c − 2bc) + ( 2 2
a + c − 2ac) = 0 0,5đ
Biến đổi để có (a − b)2 + (b − c)2 + (a − c)2 = 0 (*) 0,5đ
Vì (a − b)2 0 ; (b − c)2 0 ; (a − c)2 0; với mọi a, b, c 0,5đ
nên (*) xảy ra khi và chỉ khi (a − b)2 = 0 ; (b − c)2 = 0 và (a − c)2 = 0 ; 0,5đ Từ đó suy ra a = b = c 0,5đ Bài 3 (3 điểm) 0,5đ
Gọi tử số của phân số cần tìm là x thì mẫu số của phân số cần tìm là x+11. Phân số
cần tìm là x (x là số nguyên khác -11) x +11
Khi bớt tử số đi 7 đơn vị và tăng mẫu số 4 đơn vị ta được phân số x − 7 0,5đ x +15 (x khác -15)
Theo bài ra ta có phương trình x = x +15 0,5đ x +11 x − 7
Giải phương trình và tìm được x= -5 (thoả mãn) 1đ
Từ đó tìm được phân số 5 − 0,5đ 6 KL Trang 11 Bài 4 (2 điểm) 0,5đ Biến đổi để có A= 2 a ( 2 a + ) 2 − 2a( 2 a + ) 2 + ( 2 a + ) 2 + 3 = ( 2 a + )( 2 2 a − 2a + ) 1 + 3 = ( 2 a + )( 2 a − ) 1 2 + 3 0,5đ Vì 2 a + 2 0 a và (a − ) 1 2 0 a
nên (a2 + 2)(a − ) 1 2 0 a do đó 0,5đ (a2 + )( 2 a − ) 1 2 + 3 3 a
Dấu = xảy ra khi và chỉ khi a −1 = 0 a = 1 0,25đ KL 0,25đ Bài 5 (3 điểm) B N M A D I C a,(1 điểm)
Chứng minh được tứ giác AMNI là hình thang 0,5đ
Chứng minh được AN=MI, từ đó suy ra tứ giác AMNI là hình thang cân 0,5đ b,(2điểm) 0,5đ Tính được AD = 4 3 8 3 cm ; BD = 2AD = cm 3 3 AM = 1 4 3 BD = cm 2 3 0,5đ
Tính được NI = AM = 4 3 cm 3 0,5đ DC = BC = 8 3 1 4 3 cm , MN = DC = cm 3 2 3 0,5đ
Tính được AI = 8 3 cm 3 Bài 6 (5 điểm) A B O N M D C a, (1,5 điểm) Trang 12
Lập luận để có OM OD = , ON OC = 0,5đ AB BD AB AC
Lập luận để có OD OC = 0,5đ DB AC OM ON = OM = ON 0,5đ AB AB b, (1,5 điểm) Xét OM DM OM AM ABD để có =
(1), xét ADC để có = (2) 0,5đ AB AD DC AD Từ (1) và (2) AM + OM.( 1 1 + ) = DM = AD =1 AB CD AD AD
Chứng minh tương tự ON. 1 1 ( + ) = 1 0,5đ AB CD từ đó có (OM + ON). 1 1 1 1 2 ( + ) = 2 + = 0,5đ AB CD AB CD MN b, (2 điểm) S S S S BOC OB AOB OB = , =
AOB = BOC S S . = S S . 0,5đ S OD S OD S S AOB DOC BOC AOD AOD DOC AOD DOC Chứng minh được S = S 0,5đ AOD BOC 2 S .S = (S ) 0,5đ AOB DOC AOD
Thay số để có 20082.20092 = (SAOD)2 SAOD = 2008.2009
Do đó SABCD= 20082 + 2.2008.2009 + 20092 = (2008 + 2009)2 = 40172 (đơn vị 0,5đ DT)
TRƯỜNG THCS PHAN BỘI
KỲ THI CHỌN HỌC SINH GIỎI LỚP 8 CHÂU
NĂM HỌC 2019 – 2020 Đề thi thử 1 Môn thi: TOÁN
Thời gian: 120 phút (không kể thời gian giao đề)
Câu 1. (4,0 điểm). Phân tích các đa thức sau thành nhân tử: 1) x2 + 6x + 5 2) (x2 – 8)2 + 36
3) (x2 – x + 1)2 – 5x(x2 – x + 1) + 4x2
Câu 2. (3,0 điểm).
1) Rút gọn biểu thức: A = (a− b+ c)2 − (b− c)2 + 2ab− 2ac 2 x + x − 6 2) Rút gọn : 3 2
x − 4x −18x + 9
3) Chứng minh giá trị của biểu thức sau không phụ thuộc vào biến:
(x − )2 −(x − )2 + (x − )(x + )−( x + )2 3 1 1 2 3 3 2 3 − (5 − 20x)
Câu 3. (4,0 điểm). 1) Giải phương trình: a) 3 2
x + 5x − 4x − 20 = 0
x − 971 x − 973 x − 975 x − 977
x − 972 x − 970 x − 968 x − 966 b) + + + = + + + 972 970 968 966 971 973 975 977 Trang 13 − c) 2 1 2x 1 = + . 2 3 x − x +1 x +1 x +1
2) Hai người làm chung công việc trong 4 ngày thì xong . Nhưng chỉ làm được trong 2 ngày ,
người kia đi làm công việc khác , người thứ hai làm tiếp trong 6 ngày nữa thì xong . Hỏi mỗi
người làm một mình thì bao lâu xong công việc ?
Câu 4. (2,0 điểm). Cho tam giác ABC, trung tuyến AD, trọng tâm G. Đường thẳng d qua G cắt AB AC
AB,AC lần lượt tại M, N. Chứng minh rằng: + = 3. AM AN
Câu 5. (5,0 điểm). Cho hình bình hành ABCD (AC > BD). Gọi E, F lần lượt là hình chiếu của B, D
lên AC; H, K lần lượt là hình chiếu của C trên AB và AD.
a) Tứ giác DFBE là hình gì? Vì sao?
b) Chứng minh: CHK ∽ BCA
c) Chứng minh: AC2 = AB. AH + AD.AK
Câu 6. (2,0 điểm).
1) Chứng minh rằng n5 – 5n3 + 4n 120 với n N x + 2 2) Cho biÓu thøc A =
. T×m gi¸ trÞ nguyªn cña x ®Ó A nhËn gi¸ trÞ nguyªn 2 x + 2x + 2
3) Tìm giá trị nhỏ nhất của biểu thức: 2 2
P = (x − 2012) + (x + 2013)
----------------Hết-----------------
(Học sinh không được sử dụng máy tính)
ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM Câu 1 a) 2 2
2x + 5x − 3 = 2x + 6x − x − 3 0,5 4 điểm
= 2x(x + 3) −(x + 3) = (x + 3)(2x − ) 1 0,5 b) 4 2 4 2 2
x + 2009x + 2008x + 2009 = x + x +1+ 2008x + 2008x + 2008 0,5 2 2 2
= (x + x +1)(x − x +1) + 2008(x + x +1) 0,5 2 2 2 2 = 0,5
(x + x +1)(x − x +1+ 2008) = (x + x +1)(x − x + 2009)
c) (x + 2)(x + 4)(x + 6)(x + 8) +16 = (x + 2)(x + 8)(x + 4)(x + 6) +16 = ( 0,5 2 x + x + )( 2 10
16 x +10x + 24) +16 2 + + = Đặt x 10x 20 t = (t − )(t + ) 2 2 4
4 +16 = t −16 +16 = t 0,5 0,5 = (x + x + )2 2 10 20 Câu 2 2 2
1) ( x − y + z) + ( z − y) + ( x − y + z)(2y − 2z) 3 điểm 0,5 0,5 Trang 14
= (x − y + z)2 + 2(x − y + z)( y − z) + ( y − z)2 0,5
= (x − y + z + y − z)2 2 = x 2 + 2) 1 1 1 1 1 x 5x + + + + . 2 2 2 2 2
x + x x + 3x + 2 x + 5x + 6 x + 7x +12 x + 9x + 20 5 0,5 2 1 1 1 1 1 x + 5x = + + + + 0,5 x ( x
) (x )(x ) (x )(x ) (x )(x ) (x )(x ) . 1 1 2 2 3 3 4 4 5 + + + + + + + + + 5 2 1 1 1 1 1 1 1 1 1 1 x + 5x = − + − + − + − + − .
x x +1 x +1 x + 2 x + 2 x + 3 x + 3 x + 4 x + 4 x + 5 5 0,25 2 1 1 x + 5x = − . 0,25 x x + 5 5 5 x ( x + 5) = = x ( x + ) . 1 5 5 Câu 3 1) 4 điểm a) 2
3x + x − 6 − 2 = 0 2
3x − 6 + x − 2 = 0 3( 2
x − 2) + (x − 2) = 0
3(x − 2)(x + 2)+ (x − 2) = 0 0,25 (x − 2)3 ( x + 2 ) +1 = 0
(x − 2)(3x +3 2 + ) 1 = 0 0,25 x − 2 = 0 3x + 3 2 +1 = 0 x = 2 −3 2 −1 x = 3 0,25 3 − 2 −1
Vậy tập nghiệm của phương trình là S = 2; 3 − b) 2 1 2x 1 = + 2 3 x − x +1 x +1 x +1 0,25 x −1 ĐKXĐ: 2( x + ) 2
1 = x − x +1+ 2x −1 2
2x + 2 = x + x 0,25 2
x − x − 2 = 0 (x + ) 1 ( x − 2) = 0 x = 1 − (l)
x = 2(n) 0,25 S = 2 Trang 15 0,25
2) Gọi số phải tìm là x (x > 0)
Vì phần nguyên x có một chữ số nên khi viết thêm chữ số 2 vào bên trái thì 0,25
số đó tăng thêm 20 đơn vị, nghĩa là ta có số có giá trị là 20 + x
Vì khi dịch dấu phẩy sang trái một chữ số thì số đó giảm đi 10 lần, nên khi
dịch dấu phẩy của số có giá trị 20 + x sang trái thì được số có giá trị là 0,25 20 + x 10 0,25
Số mới nhận được bằng 9 số ban đầu nên ta có phương trình 10 20 + x 9 = x 10 10 x = 2,5(n)
Vậy số phải tìm là 2,5 0,25 0,25 Câu 4 2 điểm 1)
Do ADC = B + BAD B ADC 0,25
Lấy E trên AC sao cho ADE = B . Khi đó AE < AC 0,25
ADE và ABD đồng dạng (g-g) 0,25 AD AE 2 = AD = A . B AE A . B AC A AB AD 0,25 E B C D 2) A' A B H C B' H' C'
Gọi k là tỉ số đồng dạng của ABC và A ' B 'C ' 0,25 Ta có AB BC = = k (1) A' B ' B 'C '
Xét ABH và A' B ' H ' có: 0
H = H ' = 90 (GT)
B = B '(GT ) Trang 16
Suy ra ABH và A' B ' H '(g-g) 0,25 AB AH = = k (2) A' B ' A' H ' 0,25 1 AH.BC S ABC 2 2 =
= k.k = k 0,25 S 1 A'B 'C '
A' H '.B 'C ' 2 Câu 5 H 5 điểm C B F O E A K D
a) Ta có : BE ⊥ AC (gt); DF ⊥ AC (gt) => BE // DF 0,5 Chứng minh : BEO
= DFO(g − c − g) => BE = DF 0,5
Suy ra : Tứ giác : BEDF là hình bình hành. 0,5
b) Ta có: ABC = ADC HBC = KDC Chứng minh : C BH C
DK(g − g) 0,5 CH CK =
CH.CD = CK.CB CB CD 0,5 c) Chứng minh : A FD A
KC(g − g) 0,5 0,5 AF AK = A .
D AK = AF.AC AD AC Chứng minh : C FD AH
C(g − g) 0,5 CF AH = CD AC 0,5 Mà : CD = AB CF AH = A .
B AH = CF.AC AB AC 0,5
Suy ra : AB.AH + AD.AK = CF.AC + AF.AC = (CF + AF).AC = AC2 . Câu 6 1) 2 điểm Ta có 0,25 2 2 2
a = 13k + 2 a = 13 k + 2.13k.2 + 4 0,25 2 2 2
b = 13l + 3 b = 13 l + 2.13l.3 + 9 2 2 a + b = 13( 2 2
13k + 4k +13l + 6l ) +13 13 0,5
2) Tìm giá trị nhỏ nhất của biểu thức:
A = x ( x + )( 2
x + x − ) = ( 2 x + x)( 2 1 4 x + x − 4) 0,25 Trang 17 Đặt x2 + x – 2 = t
A = (t + )(t − ) 2 2 2 = t − 4 4 − 0,25
Vậy giá trị nhỏ nhất của A là -4 0,25
Dấu bằng xảy ra khi và chỉ khi t = 0 2
x + x − 2 = 0 ( x − ) 1 ( x + 2) = 0 x = 1 x = −2 0,25
HS có thể làm cách khác, nhưng sử dụng phù hợp kiến thức chương trình vẫn chấm điểm tối đa.
TRƯỜNG THCS PHAN BỘI
KỲ THI CHỌN HỌC SINH GIỎI LỚP 8 CHÂU
NĂM HỌC 2019 – 2020 Đề Thi Thử 2 Môn thi: TOÁN
Thời gian: 120 phút (không kể thời gian giao đề)
Câu 1. (4,0 điểm). Phân tích các đa thức sau thành nhân tử: 2) 2 2x + 5x − 3. 3) 4 2
x + 2009x + 2008x + 2009.
4) ( x + 2)( x + 4)(x + 6)(x + 8) +16.
Câu 2. (3,0 điểm). 4) Rút gọn biểu thức:
(x − y + z)2 +(z − y)2 +(x − y + z)(2y − 2z).
5) Chứng minh giá trị của biểu thức sau không phụ thuộc vào biến: 2 1 1 1 1 1 x + 5x + + + + . . 2 2 2 2 2
x + x x + 3x + 2 x + 5x + 6 x + 7x +12 x + 9x + 20 5
Câu 3. (4,0 điểm). 3) Giải phương trình: d) 2
3x + x − 6 − 2 = 0. − e) 2 1 2x 1 = + . 2 3 x − x +1 x +1 x +1
4) Một số thập phân có phần nguyên là số có một chữ số. Nếu viết thêm chữ số 2 vào bên trái số
đó, sau đó chuyển dấu phẩy sang trái 1 chữ số thì được số mới bằng 9 số ban đầu. Tìm số 10 thập phân ban đầu.
Câu 4. (2,0 điểm).
1) Cho tam giác ABC, đường phân giác AD. Chứng minh rằng: 2 AD A . B AC.
2) Chứng minh rằng tỉ số diện tích của hai tam giác đồng dạng bằng bình phương tỉ số đồng dạng. Trang 18
Câu 5. (5,0 điểm). Cho hình bình hành ABCD có đường chéo AC lớn hơn đường chéo BD. Gọi E, F
lần lượt là hình chiếu của B và D xuống đường thẳng AC. Gọi H và K lần lượt là hình chiếu của C
xuống đường thẳng AB và AD.
a) Tứ giác BEDF là hình gì ? Hãy chứng minh điều đó ?
b) Chứng minh rằng : CH.CD = CB.CK.
c) Chứng minh rằng : AB.AH + AD.AK = AC2.
Câu 6. (2,0 điểm).
4) Cho a,b . Chứng minh rằng nếu a chia 13 dư 2 và b chia 13 dư 3 thì 2 2
a + b chia hết cho 13.
5) Tìm giá trị nhỏ nhất của biểu thức:
A = x ( x + )( 2 1 x + x − 4).
----------------Hết-----------------
(Học sinh không được sử dụng máy tính)
ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM Câu 1 d) 2 2
2x + 5x − 3 = 2x + 6x − x − 3 0,5 4
= 2x(x + 3) −(x + 3) = (x + 3)(2x − ) 1 0,5 điểm e) 4 2 4 2 2
x + 2009x + 2008x + 2009 = x + x +1+ 2008x + 2008x + 2008 0,5 2 2 2
= (x + x +1)(x − x +1) + 2008(x + x +1) 0,5 0,5 2 2 2 2
= (x + x +1)(x − x +1+ 2008) = (x + x +1)(x − x + 2009)
f) (x + 2)(x + 4)(x + 6)(x + 8) +16 = (x + 2)(x + 8)(x + 4)(x + 6) +16 0,5 = ( 2 x + x + )( 2 10
16 x +10x + 24) +16 2 + + = Đặt x 10x 20 t = (t − )(t + ) 2 2 4
4 +16 = t −16 +16 = t 0,5 0,5 = (x + x + )2 2 10 20 Câu 2 2 2
3) ( x − y + z) + ( z − y) + ( x − y + z)(2y − 2z) 3 0,5
= (x − y + z)2 + 2(x − y + z)( y − z) + ( y − z)2 điểm
= (x − y + z + y − z)2 0,5 0,5 2 = x 2 + 4) 1 1 1 1 1 x 5x + + + + . 2 2 2 2 2
x + x x + 3x + 2 x + 5x + 6 x + 7x +12 x + 9x + 20 5 0,5 0,5 Trang 19 2 1 1 1 1 1 x + 5x 0,25 = + + + + x ( x
) (x )(x ) (x )(x ) (x )(x ) (x )(x ) . 1 1 2 2 3 3 4 4 5 + + + + + + + + + 5 0,25 2 1 1 1 1 1 1 1 1 1 1 x + 5x = − + − + − + − + − .
x x +1 x +1 x + 2 x + 2 x + 3 x + 3 x + 4 x + 4 x + 5 5 2 1 1 x + 5x = − . x x + 5 5 5 x ( x + 5) = = x ( x + ) . 1 5 5 Câu 3 3) 4 c) 2
3x + x − 6 − 2 = 0 điểm 2
3x − 6 + x − 2 = 0 3( 2
x − 2) + (x − 2) = 0
3(x − 2)(x + 2)+(x − 2) = 0 0,25 (x − 2)3 ( x + 2 ) +1 = 0
(x − 2)(3x +3 2 + ) 1 = 0 0,25 x − 2 = 0 3x + 3 2 +1 = 0 x = 2 −3 2 −1 x = 3 0,25 3 − 2 −1
Vậy tập nghiệm của phương trình là S = 2; 3 − d) 2 1 2x 1 = + 2 3 x − x +1 x +1 x +1 0,25 x −1 ĐKXĐ: 2( x + ) 2
1 = x − x +1+ 2x −1 2
2x + 2 = x + x 0,25 2
x − x − 2 = 0 (x + ) 1 ( x − 2) = 0 x = 1 − (l) 0,25 x = 2(n) S = 2 0,25
4) Gọi số phải tìm là x (x > 0)
Vì phần nguyên x có một chữ số nên khi viết thêm chữ số 2 vào bên 0,25
trái thì số đó tăng thêm 20 đơn vị, nghĩa là ta có số có giá trị là 20 + x
Vì khi dịch dấu phẩy sang trái một chữ số thì số đó giảm đi 10 lần,
nên khi dịch dấu phẩy của số có giá trị 20 + x sang trái thì được số có 0,25 Trang 20




