











Preview text:
ĐỀ 1
ĐỀ ÔN TẬP GIỮA HỌC KỲ I NĂM HỌC 2025-2026 MÔN: TOÁN 11-CTST
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi
câu hỏi, thí sinh chỉ chọn 1 phương án.
Câu 1: Trên đường tròn lượng giác, góc lượng giác có số đo 510 có cùng điểm biểu diễn với góc nào dưới đây? A. 240. B. 150 . C. 210. D. 360 .
Câu 2: Khẳng định nào sau đây là đúng khi nói về '' đường tròn lượng giác '' ?
A. Mỗi đường tròn là một đường tròn lượng giác.
B. Mỗi đường tròn có bán kính bằng 1 là một đường tròn lượng giác.
C. Mỗi đường tròn có bán kính bằng 1, có tâm tại gốc tọa độ là một đường tròn lượng giác.
D. Mỗi đường tròn được định hướng, có bán kính bằng 1, có tâm tại gốc tọa độ và lấy điểm
A (1;0) là điểm gốc của đường tròn là một đường tròn lượng giác. 3
Câu 3: Cho sin x = với
x , khi đó tan x + bằng 5 2 4 2 1 2 1 A. . B. - . C. - . D. . 7 7 7 7
Câu 4: Tập xác định của hàm số y = tan x là k A. \ 0 . B. \
+ k , k .C. \
k,k . D. \ , k . 2 2
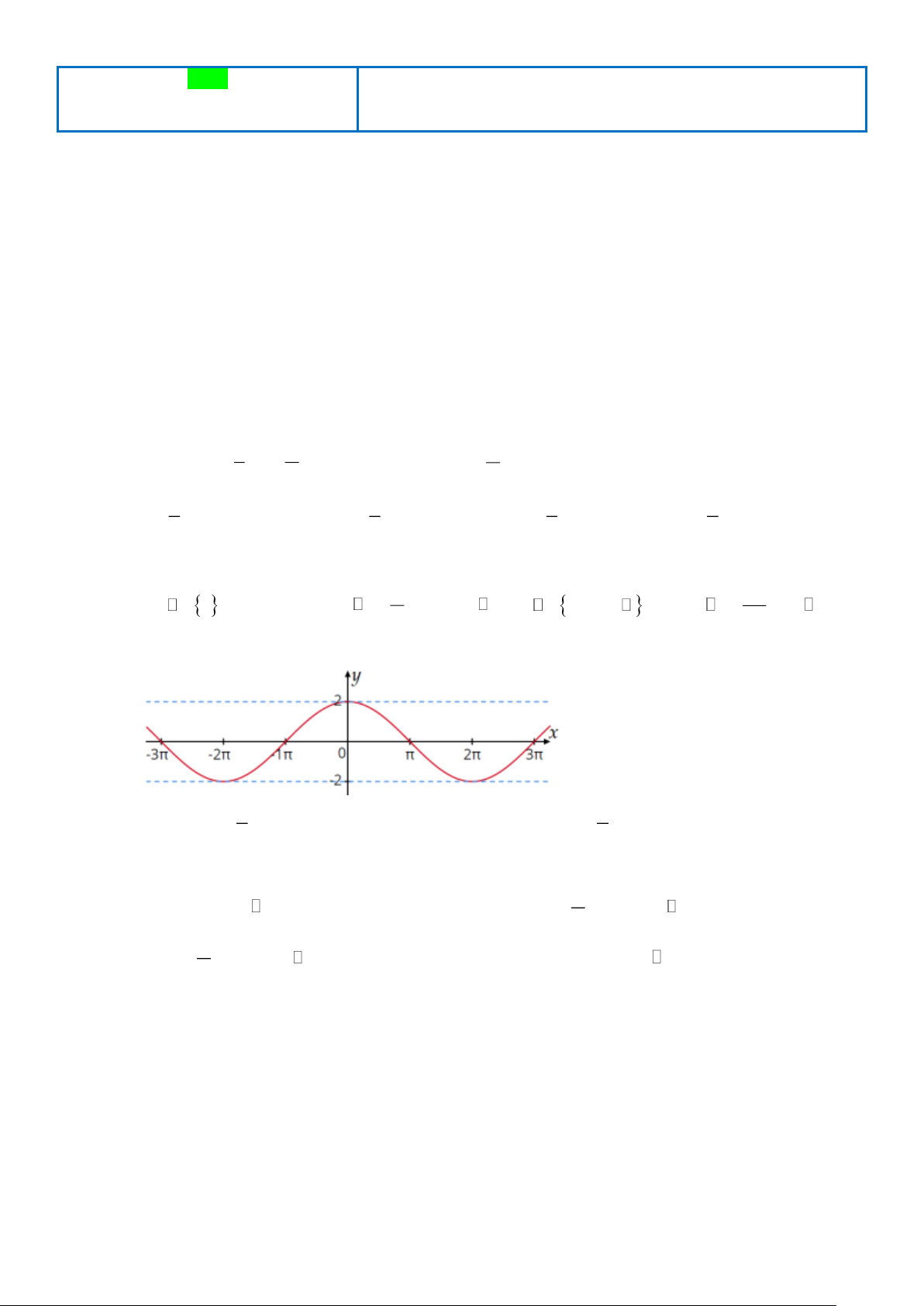
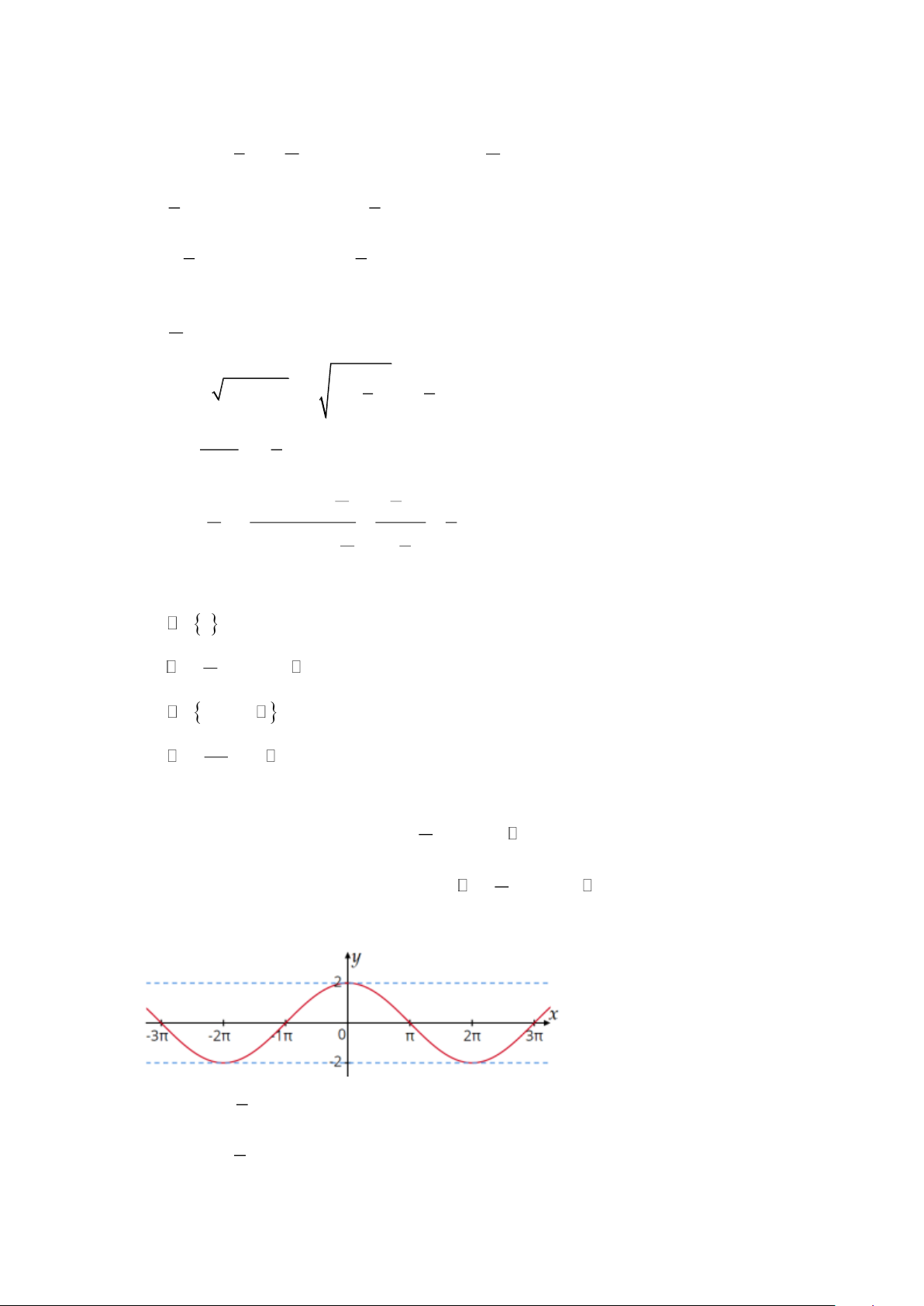
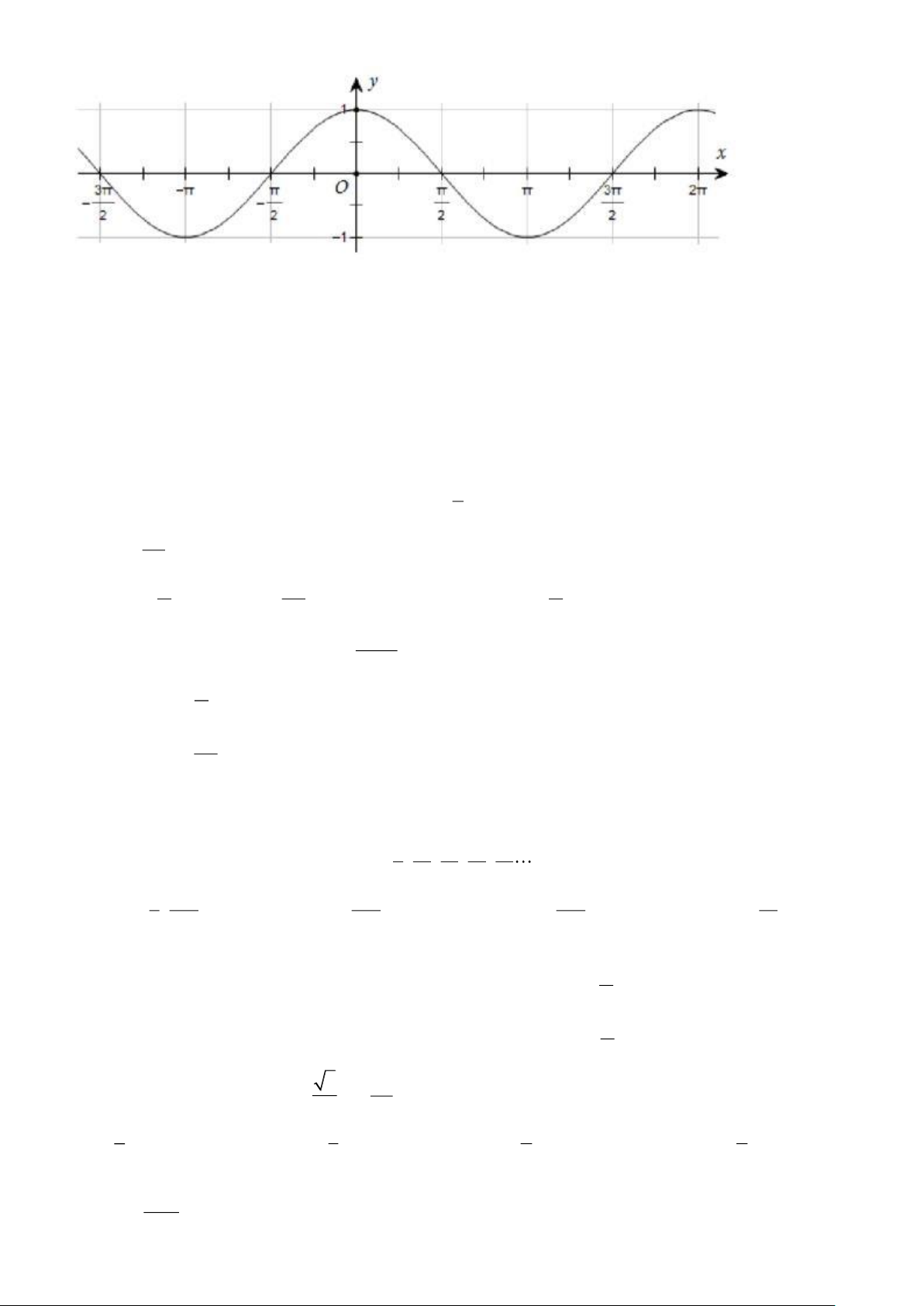
Câu 5: Hàm số nào dưới đây có đồ thị như hình vẽ? x x A. y = 2 cos .
B. y = sin x + 2 . C. y = 2sin .
D. y = 1+ 2 cos x . 2 2
Câu 6: Phương trình sin x = 1 − có nghiệm là
A. x = k , k .
B. x = − + k2 , k . 2 C. x =
+ k2 , k .
D. x = + k2 , k . 2
Câu 7: Dãy số gồm tất cả các số tự nhiên lẻ nhỏ hơn 20, theo thứ tự tăng dần là
A. 1,3,5,7,9,11,13,15,17,19 .
B. 19,17,15,13,11,9,7,5,3,1 . C. 1,3,5,7,....
D. 1, 2,5,7,9,11,13,15,17,19 .
Câu 8: Số hạng tổng quát của cấp số cộng (u biết số hạng đầu u = 5, công sai d = 2 là n ) 1
A. u = 1+ 4n .
B. u = 5n . C. u = 3+ 2n .
D. u = 2 + 3n . n n n n Trang 1
Câu 9: Công bội của cấp số nhân (u biết u = 4 và u = 8 là n ) 3 4 1 A. q = 2 .
B. u = . C. q = 4 . D. q = −4 . n 2
Câu 10: Câu khẳng định nào sau đây sai? 1 A. lim
= 0 với k là số nguyên dương. k n
B. limC = C với C là hằng số. C. lim n
q = 0 với q 1. D. lim n q = 0 với 1 − q 1. Câu 11: Tính lim ( 2 3 − x + 2x − ) 1 bằng x 1 →− A. 0 . B. 1. C. 6 − . D. 3 − .
Câu 12: Hàm số y = f (x) được gọi là liên tục trên đoạna;b nếu nó liên tục trên khoảng ( ; a b) và
A. lim f (x) = f (a) , lim f (x) = f (b) . x a+ → x b+ →
B. lim f (x) = f (a) , lim f (x) = f (b) . x a+ → x b− →
C. lim f (x) = f (a) , lim f (x) = f (b) . x a− → x b+ →
D. lim f (x) = f (a) , lim f (x) = f (b) . x a− → x b− →
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 13 đến câu 16. Trong mỗi ý a), b), c),
d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13: An đi học bằng xe đạp với vận tốc không đổi, biết rằng bánh xe đạp có đường kính 680 mm và
quay được 10 vòng trong 5 giây. Khoảng cách từ nhà An đến trường là 6,5 km và trường của
An vào học lúc 6 giờ 45 phút.
a) Trong một giây bánh xe của An quay được 720 .
b) Độ dài quãng đường An đi được trong một phút bằng 81, 6 m.
c) Vận tốc xe của An nhỏ hơn 16 km/h (kết quả làm tròn đến hàng phần trăm).
d) An đi học lúc 6 giờ 30 phút, thì không muộn học.
Câu 14: Cho phương trình sin 2x + cos3x = 0. Phát biểu sau đúng hay sai? 3 a) x =
là một nghiệm của phương trình. 10
b) Phương trình tương đương với sin 2x = cos( 3 − x).
c) Phương trình tương đương với sin 2x = sin 3x − . 2
d) Tổng các nghiệm của phương trình trong 3 − ; 3 bằng 0.
Câu 15: Cho dãy số (u với u = 3n + 2024 (n ,n ) 1 . n ) n a) u = 2024 . 1
b) (u là cấp số cộng với công sai d = 3. n )
c) Số 2324 là số hạng thứ 98 của dãy.
d) Tổng các số hạng kể từ số hạng thứ 100 đến số hạng thứ 200 là 15150. Trang 2 2
x − 3x −10 khi x 2 −
Câu 16: Cho hàm số f ( x) = x + 2 (m là tham số thực). mx −1 khi x 2 −
a) Hàm số liên tục trên khoảng (− ; − 2). b) f ( 2 − ) = 5.
c) lim f (x) = 5 x 2+ →−
d) Hàm số đã cho liên tục trên tập số thực khi m =1.
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 17 đến câu 22 a
Câu 17: Biết hàm số y = 2cos x − −1
đạt giá trị nhỏ nhất tại điểm x = + k2 , k , với a;b là 3 b a
các số nguyên, là phân số tối giản. Tính giá trị 2
S = a + ab . b
Câu 18: Có bao nhiêu giá trị nguyên của tham số m để phương trình cos 3x − − m = 0 có nghiệm? 5
Câu 19: Độ cao h (m) của một cabin trên vòng quay vào thời điểm t giây sau khi bắt đầu chuyển động
được cho bởi công thức h(t) = 30 + 20sin t +
. Sau bao nhiêu giây thì cabin đạt độ cao 25 3
40 m lần đầu tiên? (làm tròn kết quả đến hàng phần mười). u + u + u = 9
Câu 20: Tính tổng 10 số hạng đầu tiên của cấp số cộng (u , biết công sai dương và 1 2 3 . n ) 2 2 2 u + u + u = 35 1 2 3
Câu 21: Trong năm đầu tiên đi làm, anh A được nhận lương là 10 triệu đồng mỗi tháng. Cứ hết một
năm, anh A lại được tăng lương, mỗi tháng năm sau tăng 12% so với mỗi tháng năm trước. Mỗi
khi lĩnh lương anh A đều cất đi phần lương tăng so với năm ngay trước để tiết kiệm mua ô tô.
Hỏi sau ít nhất bao nhiêu năm thì anh A mua được ô tô giá 500 triệu biết rằng anh A được gia
đình hỗ trợ 32% giá trị chiếc xe?
Câu 22: Cho các số thực a,b, c thỏa mãn 9a + c 27 +3b và a +b + c 1
− . Khi đó số nghiệm thực
phân biệt của phương trình 3 2
x + ax + bx + c = 0 bằng bao nhiêu?
ĐÁP ÁN, HƯỚNG DẪN GIẢI
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn.
Câu 1: Trên đường tròn lượng giác, góc lượng giác có số đo 510 có cùng điểm biểu diễn với góc nào dưới đây? A. 240. B. 150 . C. 210. D. 360. Lời giải.
Vì 510 =150 + 360 nên góc 510 có cùng điểm biểu diễn với góc 150 .
Câu 2: Khẳng định nào sau đây là đúng khi nói về '' đường tròn lượng giác '' ?
A. Mỗi đường tròn là một đường tròn lượng giác.
B. Mỗi đường tròn có bán kính bằng 1 là một đường tròn lượng giác.
C. Mỗi đường tròn có bán kính bằng 1, có tâm tại gốc tọa độ là một đường tròn lượng giác.
D. Mỗi đường tròn được định hướng, có bán kính bằng 1, có tâm tại gốc tọa độ và lấy điểm
A(1;0) là điểm gốc của đường tròn là một đường tròn lượng giác. Lời giải. Trang 3
Theo định nghĩa đường tròn lượng giác là đường tròn có tâm tại gốc tọa độ, bán kính bằng 1,
được định hướng và lấy điểm A(1;0) là điểm gốc của đường tròn. 3
Câu 3: Cho sin x = với
x , khi đó tan x + bằng 5 2 4 2 1 A. . B. - . 7 7 2 1 C. - . D. . 7 7 Lời giải. Vì
x nên cos x 0. 2 2 3 4 2
cos x = − 1− sin x = − 1− = − . 5 5 sin x 3 tan x = = − . cos x 4 3 tan x + tan − +1 1 4 4 tan x + = = = . 4 3 7 1− tan . x tan 1+ .1 4 4
Câu 4: Tập xác định của hàm số y = tan x là A. \ 0 . B. \
+ k , k . 2 C. \
k,k . k D. \ , k . 2 Lời giải
Điều kiện xác định: cos x 0 x
+ k , k . 2
Vậy tập xác định của hàm số y = tan x là \
+ k , k . 2
Câu 5: Hàm số nào dưới đây có đồ thị như hình vẽ? x A. y = 2 cos .
B. y = sin x + 2 . 2 x C. y = 2sin .
D. y = 1+ 2 cos x . 2 Lời giải
Dựa vào đồ thị hàm số ta có: y( ) = y( − ) = 0 . Trang 4 x
Trong các hàm số ở bốn phương án thì chỉ có hàm số y = 2 cos thỏa mãn điều kiện này. 2
Câu 6: Phương trình sin x = 1 − có nghiệm là
A. x = k , k .
B. x = − + k2 , k . 2 C. x =
+ k2 , k . 2
D. x = + k2 , k . Lời giải Ta có sin x = 1
− x = − + k2 , k . 2
Câu 7: Dãy số gồm tất cả các số tự nhiên lẻ nhỏ hơn 20, theo thứ tự tăng dần là
A. 1,3,5,7,9,11,13,15,17,19 .
B. 19,17,15,13,11,9,7,5,3,1 . C. 1,3,5,7,....
D. 1, 2,5,7,9,11,13,15,17,19 . Lời giải
Các số hạng của dãy số là: 1,3,5,7,9,11,13,15,17,19 .
Câu 8: Số hạng tổng quát của cấp số cộng (u biết số hạng đầu u = 5, công sai d = 2 là n ) 1
A. u = 1+ 4n .
B. u = 5n . n n
C. u = 3+ 2n .
D. u = 2 + 3n . n n Lời giải
Ta có: u = u + n −1 d = 5+ n −1 2 = 2n + 3. n 1 ( ) ( )
Câu 9: Công bội của cấp số nhân (u biết u = 4 và u = 8 là n ) 3 4 1 A. q = 2 . B. u = . n 2 C. q = 4 . D. q = −4 . Lời giải u 8 Ta có: 4 q = = = 2. u 4 3
Câu 10: Câu khẳng định nào sau đây sai? 1 A. lim
= 0 với k là số nguyên dương. k n
B. limC = C với C là hằng số. C. lim n
q = 0 với q 1. D. lim n q = 0 với 1 − q 1. Lời giải Ta có lim n
q = + với q 1. Câu 11: Tính lim ( 2 3 − x + 2x − ) 1 bằng x 1 →− Trang 5 A. 0 . B. 1. C. 6 − . D. 3 − . Lời giải Ta có: lim ( 3 − x + 2x − ) 1 = 3. − (− )2 2 1 + 2.(− ) 1 −1 = 6 − . x 1 →−
Câu 12: Hàm số y = f (x) được gọi là liên tục trên đoạna;b nếu nó liên tục trên khoảng ( ; a b) và
A. lim f (x) = f (a) , lim f (x) = f (b) . x a+ → x b+ →
B. lim f (x) = f (a) , lim f (x) = f (b) . x a+ → x b− →
C. lim f (x) = f (a) , lim f (x) = f (b) . x a− → x b+ →
D. lim f (x) = f (a) , lim f (x) = f (b) . x a− → x b− → Lời giải
Hàm số y = f (x) được gọi là liên tục trên đoạna;b nếu nó liên tục trên khoảng ( ; a b) và
lim f (x) = f (a) , lim f (x) = f (b) . x a+ → x b− →
☞Phần 2. Trắc nghiệm lựa chọn đúng sai.
Câu 13: An đi học bằng xe đạp với vận tốc không đổi, biết rằng bánh xe đạp có đường kính 680 mm và
quay được 10 vòng trong 5 giây. Khoảng cách từ nhà An đến trường là 6,5 km và trường của
An vào học lúc 6 giờ 45 phút.
a) Trong một giây bánh xe của An quay được 720 .
b) Độ dài quãng đường An đi được trong một phút bằng 81, 6 m.
c) Vận tốc xe của An nhỏ hơn 16 km/h (kết quả làm tròn đến hàng phần trăm).
d) An đi học lúc 6 giờ 30 phút, thì không muộn học. Lời giải a) Đúng. 10
Một giây bánh xe của An quay được = 2 vòng. 5
Vì một vòng bánh xe quay được một góc 360.
Nên trong 1 giây bánh xe quay được 2.360 = 720 . b) Sai.
Ta có 1 phút bằng 60 giây.
Trong một phút bánh xe quay được 60.2 =120 vòng
Chu vi bánh xe (chiều dài một vòng) là d = 680 mm = 0, 68 m.
Độ dài quãng đường bánh xe quay được trong một phút là 120.0, 68 m = 81, 6 m. c) Đúng. 1 Trong 1 phút =
giờ, An đi được quãng đường 81, 6 m = 0,0816 km. 60 s 0,0816
Vận tốc xe cuả An là v = = 15,38 km/h. t 1 60 d) Sai. s 6,5
Thời gian để An đi từ nhà đến trường là t = = giờ 25,36 phút. v 15,38
An đến trường lúc 6 gời 30 phút + 25,36 phút = 6 giờ 55,36 phút. Trang 6
Vậy An đi học muộn 10,36 phút.
Câu 14: Cho phương trình sin 2x + cos3x = 0. Phát biểu sau đúng hay sai? 3 a) x =
là một nghiệm của phương trình. 10
b) Phương trình tương đương với sin 2x = cos( 3 − x).
c) Phương trình tương đương với sin 2x = sin 3x − . 2
d) Tổng các nghiệm của phương trình trong 3 − ; 3 bằng 0. Lời giải
Phương trình: sin 2x + cos3x = 0
sin 2x = −cos3x
sin 2x = cos( −3x) sin 2x = sin − ( − 3x) 2
sin 2x = sin 3x − 2 2x = 3x − + k2 x = − k2 2 2 , ( k ) 3 3 2 2x = − 3x + k2 = + x k 2 10 5 9 3 7 Với x 3 − ; 3 x − ; − ; − ; ; ; 10 2 10 10 2 10 9 3 7
Tổng các nghiệm trên đoạn 3 − ; 3 là − − − + + + = 0 10 2 10 10 2 10
Vậy: a) Đúng, b) Sai, c) Đúng, d) Đúng.
Câu 15: Cho dãy số (u với u = 3n + 2024 (n ,n ) 1 . n ) n a) u = 2024 . 1
b) (u là cấp số cộng với công sai d = 3. n )
c) Số 2324 là số hạng thứ 98 của dãy.
d) Tổng các số hạng kể từ số hạng thứ 100 đến số hạng thứ 200 là 15150. Lời giải a) Sai.
Ta có u = 3.1+ 2024 = 2027 . 1 b) Đúng.
Ta có: u −u = 3 n +1 + 2024 − 3n + 2024 = 3 (không đổi). n 1 + n ( ) ( )
Suy ra (u là cấp số cộng với công sai d = 3. n ) c) Sai.
Số hạng thứ 98 của dãy là u = 3.98 + 2024 = 2318 2324 . 98 d) Sai. Ta có u
= 3.200 + 2024 = 2624, u = 3.99 + 2024 = 2321. 200 99 Trang 7
Tổng các số hạng kể từ số hạng thứ 100 đến số hạng thứ 200 là (u +u .200 u + u .99 1 200 ) ( 1 99) S − S = − 200 99 2 2
(2027 + 2624).200−(2027 + 232 ) 1 .99 = = 249874 . 2 2
x − 3x −10 khi x 2 −
Câu 16: Cho hàm số f ( x) = x + 2 (m là tham số thực). mx −1 khi x 2 −
a) Hàm số liên tục trên khoảng (− ; − 2). b) f ( 2 − ) = 5.
c) lim f (x) = 5 x 2− →−
d) Hàm số đã cho liên tục trên tập số thực khi m =1. Lời giải a) Đúng 2 x − 3x −10 Với x 2
− ta có f ( x) =
là hàm số liên tục trên (− ; − 2). x + 2 b) Sai Với x = 2
− ta có f (x) = mx −1 f ( 2 − ) = . m ( 2 − ) −1= 2 − m −1. c) Sai 2 − − (x + 2)(x −5) f ( x) x 3x 10 lim = lim = lim = lim (x −5) = 2 − −5 = 7 − . x 2− x 2− →− →− x + 2 x 2− →− x + 2 x 2− →− d) Sai
lim f (x) = lim (mx − ) 1 = 2 − m −1. x 2+ →− x 2+ →− Với x 2
− ta có f (x) = mx −1 là hàm số đa thức liên tục trên ( 2; − + ).
Hàm số f (x) đã cho liên tục trên các khoảng (− ; − 2) và ( 2; − + ).
Hàm số f (x) đã cho liên tục trên khi và chỉ khi lim f (x) = f ( 2 − ) x 2 →−
lim f (x) = lim f (x) = f ( 2 − ) x 2+ x 2− →− →−
☞Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. a
Câu 17: Biết hàm số y = 2cos x − −1
đạt giá trị nhỏ nhất tại điểm x = + k2 , k , với a;b là 3 b a
các số nguyên, là phân số tối giản. Tính giá trị 2
S = a + ab . b Lời giải Đáp số: 40.
Xét hàm số y = 2cos x − −1 . 3 TXĐ: D = . Ta có: 1 − cos x − 1, x 3 Trang 8 2 − 2cos x − 2, x
−3 2cos x − −1 1, x 3 3 4 min y = 3 − cos x −
= −1 x − = + k2 x = + k2 ,k . R 3 3 3 Vậy 2
a = 4;b = 3 a + . a b = 40 .
Câu 18: Có bao nhiêu giá trị nguyên của tham số m để phương trình cos 3x − − m = 0 có nghiệm? 5 Lời giải Đáp số: 3. Ta có cos 3x −
− m = 0 cos 3x − = m có nghiệm 1 − m 1. 5 5
Vì m m 1 − ;0; 1 .
Câu 19: Độ cao h (m) của một cabin trên vòng quay vào thời điểm t giây sau khi bắt đầu chuyển động
được cho bởi công thức h(t) = 30 + 20sin t +
. Sau bao nhiêu giây thì cabin đạt độ cao 25 3
40 m lần đầu tiên? (làm tròn kết quả đến hàng phần mười). Lời giải Đáp số: 12,5 . 1
Ta có h(t) = 40 30 + 20sin t + = 40 sin t + = . 25 3 25 3 2 25 − t + = + k2 t = + 50k 25 3 6 6 (k ) . 5 25 t k2 + = + t = + 50k 25 3 6 2
Cabin đạt độ cao 40 m lần đầu tiên ứng với nghiệm t dương nhỏ nhất của phương trình là t = 12,5.
Vậy sau 12,5 giây thì Cabin đạt độ cao 40 m lần đầu tiên. u + u + u = 9
Câu 20: Tính tổng 10 số hạng đầu tiên của cấp số cộng (u , biết công sai dương và 1 2 3 . n ) 2 2 2 u + u + u = 35 1 2 3 Lời giải Đáp số: 100. u + u + u = 9 u
+ u + d + u + 2d = 9 Ta có 1 2 3 1 1 1 2 2 2 2 u + u + u = 35 u
+ u + d + u + 2d = 35 1 2 3 1 ( 1 )2 ( 1 )2 u = 3− d = − 1 u 3 d u = 3− d 1 1 ( 3− d ) . 2 2 + 3 + (3+ d )2 2 = 35 d = 4 d = 2
Vì công sai dương nên chọn d = 2, từ đó tính được u = 1. 1
Tổng 10 số hạng đầu tiên của cấp số cộng (u là: n ) Trang 9 10 S =
2u + 9d = 5 2.1+ 9.2 = 100 . 10 ( 1 ) ( ) 2
Câu 21: Trong năm đầu tiên đi làm, anh A được nhận lương là 10 triệu đồng mỗi tháng. Cứ hết một
năm, anh A lại được tăng lương, mỗi tháng năm sau tăng 12% so với mỗi tháng năm trước. Mỗi
khi lĩnh lương anh A đều cất đi phần lương tăng so với năm ngay trước để tiết kiệm mua ô tô.
Hỏi sau ít nhất bao nhiêu năm thì anh A mua được ô tô giá 500 triệu biết rằng anh A được gia
đình hỗ trợ 32% giá trị chiếc xe? Lời giải Đáp số: 13năm
Số tiền anh A cần tiết kiệm là 500 − 500.0,32 = 340 (triệu).
Gọi số tiền mà anh A nhận được ở mỗi tháng trong năm đầu tiên là u = 10 (triệu). 1
Thì số tiền mà anh A nhận được ở mỗi tháng trong năm thứ hai là
u = u . 1+ 0,12 = u .1,12 (triệu). 2 1 ( ) 1
Số tiền mà anh A nhận được ở mỗi tháng trong năm thứ ba là
u = u .(1+ 0,12)2 = u .(1,12)2 (triệu). 3 1 1 …
Số tiền mà anh A nhận được ở mỗi tháng trong năm thứ n là u u . − = + . 1,12 n u − = (triệu). 1 ( ) 1 n (1 0,12)n 1 1 Vậy số tiền mà anh A tiết kiệm được sau n năm là
12.(u −u +u −u ++ u −u +u −u
=12.(u −u =12. . 1,12 n u − −u 1 ( ) 1 n 1 ) 2 1 3 2 n 1 − n−2 n n 1 − ) 1 .
Cho 12. u .(1,12)n 1− −u = 340 n− =
n 12,86 n =13. 1 1 ( ) 1 23 1,12 6
Vậy sau ít nhất 13 năm thì anh A sẽ tiết kiệm đủ tiền để mua ô tô.
Câu 22: Cho các số thực a,b, c thỏa mãn 9a + c 27 +3b và a +b + c 1
− . Khi đó số nghiệm thực
phân biệt của phương trình 3 2
x + ax + bx + c = 0 bằng Lời giải Trả lời: 3 Xét phương trình 3 2
x + ax + bx + c = 0 (1). Đặt ( ) 3 2
f x = x + ax + bx + c . (Hàm số liên tục trên R ) 9
a + c 27 + 3b 2
− 7 + 9a − 3b + c 0 f ( 3 − ) 0. Từ giả thiết
a + b + c 1
− 1+ a + b + c 0 f ( ) 1 0. Do đó f (− ) 3 . f ( )
1 0 nên phương trình (1) có ít nhất một nghiệm trong ( 3 − ; ) 1 . Ta nhận thấy:
lim f (x) = − mà f ( 3
− ) 0 nên phương trình (1) có ít nhất một nghiệm (− ; − ) 3 . x→− Trang 10
Tương tự: lim f (x) = + mà f ( )
1 0 nên phương trình (1) có ít nhất một nghiệm x→+ (1;+).
Như vậy phương trình đã cho có ít nhất ba nghiệm thực phân biệt, mặt khác phương trình bậc 3 có tối đa ba nghiệm. Vậy phương trình 3 2
x + ax + bx + c = 0 có ba nghiệm thực phân biệt. ĐỀ 2
ĐỀ ÔN TẬP GIỮA HỌC KỲ I NĂM HỌC 2025-2026 MÔN: TOÁN 11-CTST
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi
thí sinh chỉ chọn một phương án.
Câu 1. Phương trình nào sau đây có nghiệm 1 A. sin x = 2 − .
B. sin x = .
C. sin x = 2. D. cos x = 2. 2 1
Câu 2. Cho tan = và 0 . Tính cot. 3 2 2 2 2 2 A. cot = 3. B. cot = 3 − . C. cot = − . D. cot = . 3 3
Câu 3. Cho dãy số ( u ) với u = ( 5
− )n . Tìm u ? n n 4 A. u = 20 − . B. u = 625 − .
C. u = 625. D. u = 20. 4 4 4 4
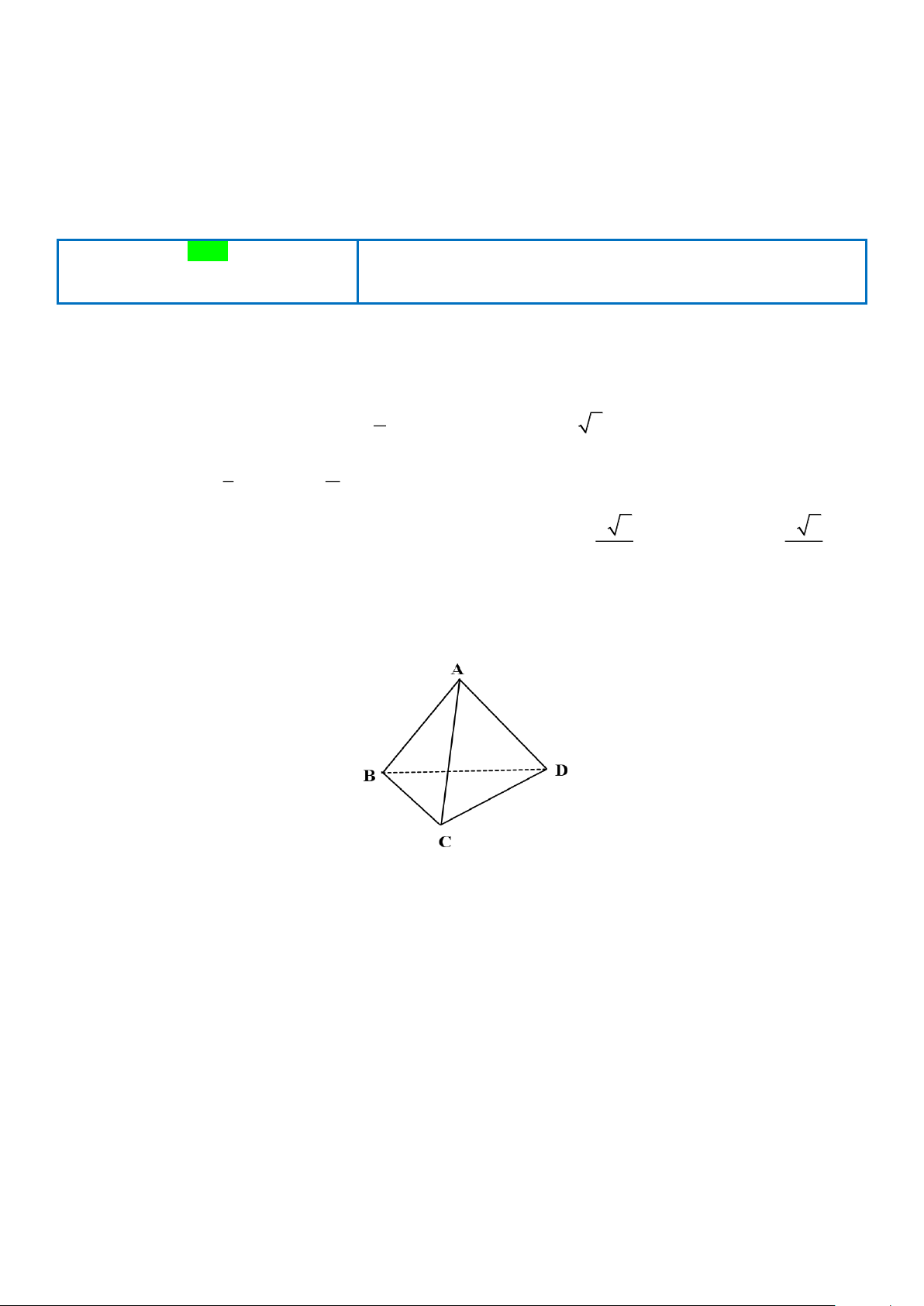
Câu 4. Cho tứ diện ABCD . Lấy điểm M là trung điểm AB . Mệnh đề nào sau đây đúng ?
A. M ( ACD).
B. M BC.
C. M (BCD).
D. M ( ABC).
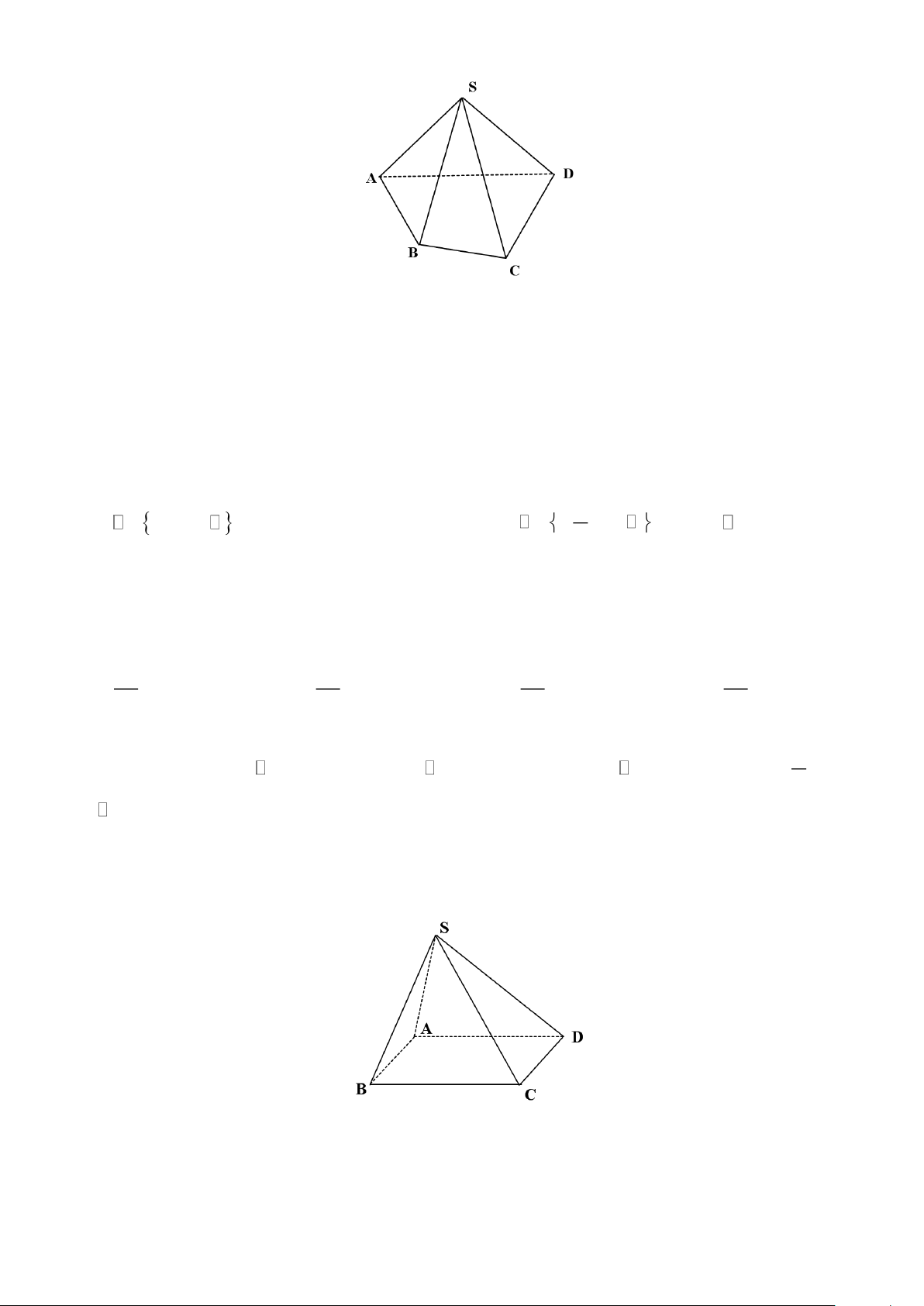
Câu 5. Cho hình chóp tứ giác S.ABCD . Khẳng định nào sau đây là sai?
A. Đỉnh S của hình chóp không nằm trong mặt phẳng ( ABCD) .
B. Hình chóp có mặt đáy ABCD là hình vuông.
C. Hình chóp có 4 mặt bên đều là các tam giác.
D. Hình chóp có tất cả 4 cạnh bên.
Câu 6. Cho hình chóp S.ABCD . Gọi I, J lần lượt là trung điểm S ,
A SC . Trong các đường thẳng sau,
đường thẳng nào song song với IJ ? Trang 11 A. BD. B. AD. C. AB. D. AC.
Câu 7. Cho cấp số nhân (u có số hạng đầu u = 2 và u = 8. Tìm công bội của cấp số nhân. n ) 1 2
A. q = 2.
B. q = 4.
C. q = 6. D. q = 4. −
Câu 8. Trong các công thức sau, công thức nào sai?
A. sin 2a = 2sin a cos . a B. 2 cos2a = 1− 2sin . a C. 2
cos2a = 2cos a −1. D. 2 2
cos2a = sin a − cos . a
Câu 9. Tìm tập giá trị của hàm số y = sin x A. \
k,k . B. [ −1;1].
C. \ k ,k . D. . 2
Câu 10. Cho cấp số nhân (u có số hạng đầu u = 12 và công bội q = −2 . Số hạng thứ sáu của cấp số n ) 1
nhân đã cho có giá trị bằng A. −24 . B. 384 − . C. 2 . D. 34 − .
Câu 11. Đổi số đo góc 135 ra số đo rađian 3 3 3 5 A. . B. . C. . D. . 2 4 5 6
Câu 12. Nghiệm của phương trình cos x = 1 − là:
A. x = + k2 , k . B. x = k2 , k .
C. x = k , k . D. x = + k , 2 k .
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1. Cho hình chóp S.ABCD có đáy là hình bình hành ABCD tâm .
O Gọi M là trung điểm SA.
Xét tính đúng sai của các khẳng định sau
a) Hình chóp S.ABCD có 10 cạnh.
b) Đường thẳng AD và SC chéo nhau.
c) MO / /SC.
d) Giao tuyến của hai mặt phẳng (SAC) và (SBD) là đường thẳng . SO Trang 12
Câu 2. Cho hàm số lượng giác y = f ( x) = cos x +
. Xét tính đúng sai của các khẳng định sau 4
a) Hàm số có tập xác định là .
b) Phương trình f ( x) 1
= tương đương với phương trình cos x + = cos . 2 4 3 7
c) Nghiệm của phương trình f ( x) 1 = là: x = + k2 , x =
+ k2 , k . 2 12 12
d) Phương trình f ( x) 1
= có đúng 2 nghiệm phân biệt thuộc khoảng ( − ; ). 2
Câu 3. Cho dãy số (u với u = 3n + 5. Xét tính đúng sai của các khẳng định sau n ) n
a) Dãy số (u là dãy số tăng. n )
b) Số hạng thứ tám của dãy số là u = 24. 8
c) Dãy số (u là cấp số cộng với công sai d = 2. n )
d) Tổng của 12 số hạng đầu cấp số cộng bằng 294. 1
Câu 4. Cho biết sin = và
. Xét tính đúng sai của các khẳng định sau 2 2
a) cot 0. b) 2 3 cos = . 4 3 c) cos = . 2 3 d) tan = − . 3
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6. sin x + sin 4x ax a
Câu 1. Rút gọn biểu thức A =
ta được kết quả bằng tan (với là phân số tối giản). cos x + cos4x b b Tính a + 2 . b
Câu 2. Chuông đồng hồ ở một toà tháp đánh số tiếng đúng bằng số giờ và cứ mỗi 30 phút không phải là
giờ đúng thì đánh 1 tiếng chuông. Hỏi bắt đầu từ lúc 1 giờ đêm đến 12 giờ trưa, chuông đồng hồ đó đã
đánh tất cả bao nhiêu tiếng?
Câu 3. Hằng ngày mực nước của con kênh lên xuống theo thủy triều. Độ sâu h (mét) của mực nước trong t
kênh được tính tại thời điểm t (giờ, 0 t 24) trong một ngày bởi công thức h = 3cos + +12 . 8 4
Tìm độ sâu của mực nước trong kênh lớn nhất. 3 3 2025
Câu 4. Cho góc thỏa mãn
và sin = − . Tính P = sin − . 2 5 2
Câu 5. Cho hình vuông ban đầu có cạnh bằng 16 cm. Người ta thực hiện tô màu vào các tam giác bằng hai bước sau
Bước 1: Vẽ một hình vuông mới được hình thành bằng cách nối trung điểm của các cạnh hình vuông ban đầu.
Bước 2: Tô màu hai tam giác đối diện nhau trong bốn tam giác được vẽ (tham khảo hình bên dưới). Trang 13
Nếu quá trình này được lặp lại mười lần, hãy xác định tổng diện tích của vùng được tô màu (đơn vị 2 cm ,
kết quả làm tròn đến hàng đơn vị).
Câu 6. Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M là trung điểm của SC . Gọi I giao
điểm của đường thẳng AM và mặt phẳng (SB ) D . Tìm *
k thỏa IA = kIM. ----------- HẾT ---------- ĐÁP ÁN Phần I Phần II Phần III 1 2 3 4 Câu 1. 9 Câu 2. 89 a) S Đ Đ S 1.B 2.A 3.C 4.D Câu 3. 15 5.B 6.D 7.B 8.D Câu 4. -0,8 b) Đ Đ S Đ 9.B 10.B 11.B 12.A Câu 5. 128 Câu 6. 2 c) Đ S S S d) Đ Đ Đ Đ HƯỚNG DẪN CHẤM
Câu 1. Chuông đồng hồ ở một toà tháp đánh số tiếng đúng bằng số giờ và cứ mỗi 30 phút không phải là
giờ đúng thì đánh 1 tiếng chuông. Hỏi bắt đầu từ lúc 1 giờ đêm đến 12 giờ trưa, chuông đồng hồ đó đã
đánh tất cả bao nhiêu tiếng? Lời giải
Số tiếng chuông đánh từ 1 giờ đêm đến 12 giờ trưa theo giờ đúng là cấp số cộng có 12 số hạng với u = 1 1 và công sai d =1. Tổng số tiếng c
huông đánh từ 1 giờ đêm đến 12 giờ trưa mỗi 30 phút không phải là giờ đúng thì có 11 tiếng chuông. 12(2.1 +11.1)
Vậy số tiếng chuông đã đánh là: +11 = 89. 2
Câu 2. Cho hình vuông ban đầu có cạnh bằng 16 cm. Người ta thực hiện tô màu vào các tam giác bằng hai bước sau
Bước 1: Vẽ một hình vuông mới được hình thành bằng cách nối trung điểm của các cạnh hình vuông ban đầu.
Bước 2: Tô màu hai tam giác đối diện nhau trong bốn tam giác được vẽ (tham khảo hình bên dưới).
Nếu quá trình này được lặp lại mười lần, hãy xác định tổng diện tích của vùng được tô màu (đơn vị 2 cm ,
kết quả làm tròn đến hàng đơn vị). Lời giải
Gọi u là diện tích hai tam giác được tô màu ở lần thực hiện thứ n . n Trang 14 16 1
Ở lần 1 thì độ dài cạnh tam giác vuông cân là = 8 nên 2 u = 2 .8 = 64. 2 1 2 2 1
Ở lần 2 thì độ dài cạnh tam giác vuông cân là 8
= 4 2 nên u = 2. . 4 2 = 32. 2 ( )2 2 2 2 1
Ở lần 3 thì độ dài cạnh tam giác vuông cân là 4 2 = 4 nên 2 u = 2. .4 = 16. … 2 3 2 1
Như vậy, dãy số (u là cấp số nhân với u = 64 và công bội q = . n ) 1 2 10 1 1 −
Vậy tổng diện tích sau mười lần thực hiện là 2 S 64 = 128 cm . 10 ( 2) 1 1 − 2 ĐỀ 3
ĐỀ ÔN TẬP GIỮA HỌC KỲ I NĂM HỌC 2025-2026 MÔN: TOÁN 11-CTST
Phần I. Câu trắc nghiệm nhiều phương án lực chọn (6 điểm). Học sinh trả lới từ câu 1 đến câu 20.Mỗi
câu hỏi thí sinh chỉ chọn một phương án.
Câu 1: Một mặt phẳng hoàn toàn được xác định nếu có điều kiện nào sau đây?
A. Ba điểm không thẳng hàng.
B. Ba điểm mà nó đi qua.
C. Một đường thẳng và một điểm thuộc nó.
D. Hai đường thẳng thuộc mặt phẳng.
Câu 2: Gọi S là tập nghiệm của phương trình 2cos x − 3 = 0. Khẳng định nào sau đây là đúng? 11 13 13 5 A. S. B. S. C. − S. D. S. 6 6 6 6 3 1 Câu 3: Cho ,
x y là các góc nhọn, cotx = ,coty = . Tổng x + y bằng 4 7 3 A. . B. − . C. . D. . 4 4 4
Câu 4: Giá trị lớn nhất của biểu thức 2 2
M = 7cos x − 2sin x là A. 5 . B. 16 . C. -2 . D. 7 .
Câu 5: Góc có số đo 108 đổi ra rađian là 3 3 A. . B. . C. . D. . 2 10 5 4 k
Câu 6: Trên đường tròn lượng giác, góc có số đo +
(k Z) được biểu diễn bởi bao nhiêu điểm? 4 2 A. 3 . B. 1. C. 2 . D. 4 .
Câu 7: Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D. Trang 15
Hỏi hàm số đó là hàm số nào?
A. y = cosx .
B. y = −cosx .
C. y = 1+ sin2x . D. y = sin − x .
Câu 8: Cho dãy số (u với u = 2n . Tìm số hạng u . n ) n n 1 + A. u = 2 n +1 . B. u = 2n 2. C. u = 2n + 2 . D. u = 2n +1. n 1 + ( ) n 1 + n 1 + n 1 +
Câu 9: Cho thuộc góc phần phần tư thứ hai của đường tròn lượng giác. Khẳng định nào sau đây là đúng?
A. sin 0;cos 0 .
B. sin 0;cos 0 . C. sin 0;cos x 0 . D. sin 0;cos 0 . 3
Câu 10: Tất cả nghiệm của phương trình sin2x = − là 2 5 A. x = + k2 ,k Z
B. Phương trình vô nghiệm. 6 7 C. x = − + k2 và x =
+ k2 ,k Z . D. x =
+ k2 ,k Z . 6 6 6 2 +1
Câu 11: Tập xác định của hàm số = x y là cosx
A. D = R ‚ + k ,k Z. B. D = . R 2 k
C. D = R ‚ , k Z..
D. D = R ‚ k ,k Z . 2
Câu 12: : Biểu thức sin c
x osy − cos sin x y bằng
A. sin ( y − x) .
B. cos(x − y) .
C. sin (x − y) .
D. cos(x + y) . 1 1 1 1 1
Câu 13: Cho dãy số có các số hạng đầu là: ; ; ; ;
Số hạng tổng quát của dãy số này là 2 3 4 5 3 3 3 3 3 1 1 1 1 1 A. u = . B. u = . C. u = . D. u = . n n 1 3 3 + n n 1 3 − n n 1 3 + n 3n
Câu 14: Tập xác định của hàm số y = tanx là
A. D = R ‚ k ,k Z .
B. D = R ‚ + k2 ,k Z. 2
C. D = R ‚ k2,k Z .
D. D = R ‚ + k ,k Z . 2 5 3 Câu 15: Tính in s biết cos = và 2 . 3 2 1 1 2 2 A. . B. − . C. . D. − . 3 3 3 3
Câu 16: Hàm số nào sau đây là hàm số lẻ? cos A. = x y .
B. y = cos3x .
C. y = 2x + cosx . D. 2
y = x cos(x + ) 3 . 3 x Trang 16
Câu 17: : Cho cấp số cộng với u = 3 và u = 9 . Công sai của cấp số cộng đã cho bằng 1 2 A. -6 . B. 3 . C. 6 . D. 12 .
Câu 18: Trong các dãy số sau đây, dãy số nào là một cấp số cộng? A. 1; 3 − ; 5 − ; 7 − ; 9 − ;. B. 1; 3 − ; 7 − ; 1 − 1; 1 − 5;. C. 1; 3 − ; 6 − ; 9 − ; 12 − ;. D. 1; 2 − ; 4 − ; 6 − ; 8 − ;.
Câu 19: Bất đẳng thức nào dưới đây là đúng? A. cos150 cos120 . B. sin90 sin150 . C. ' ' sin90 15 sin150 30 . D. ' cos90 30 > cos100 .
Câu 20: Cho cấp số cộng (u có các số hạng đầu lần lượt là 5;9;13;17;. Tìm số hạng tổng quát u n ) n của cấp số cộng.
A. u = 5n −1.
B. u = 5n +1.
C. u = 4n +1.
D. u = 4n −1. n n n n
Phần II. Tự luận (4 điểm). Học sinh làm bài chi tiết từ câu 1 đến câu 4.
Câu 1 (1 điểm): Tính P= 2cos2x +3sin3x, Biết x= 0 45 3
Câu 2 (1 điểm): Cho sin x = x
. Tính giá trị lượng giác của cot x 5 2
Câu 3 (1 điểm): Cho tứ diện A.BCD, gọi I, J lần lượt là là trung điểm cạnh BC và AD. Điểm K thuộc 1
cạnh CD sao cho đoạn CK =
CD . Tìm giao tuyến của hai mặt phẳng (IJK) với (ACD) ? 4
Câu 4 (1 điểm): Người ta trồng 2145 cây theo hình một tam giác như sau: hàng thứ nhất có 1 cây, hàng
thứ hai có 2 cây, hàng thứ ba có 3 cây,… Hỏi có tất cả bao nhiêu hàng cây?
------ HẾT ------ ĐÁP ÁN
Phần I. Câu trắc nghiệm nhiều phương án lực chọn. (Mỗi câu học sinh được 0,3 điểm ) Câu 1 2 3 4 5 6 7 8 9 10 Chọn A A D D C D A B B B Câu 11 12 13 14 15 16 17 18 19 20 Chọn A C D D D A C B D C
II. Tự luận (4,0 điểm)
Câu 1: Tính P= 2cos2x +3sin3x, Biết x= 0 45 Ý Nội dung Điểm P= 2cos2x +3sin3x = 2cos(2. 0 45 ) +3sin(3. 0 45 ) 0,25 2 3 2 0,5 =2.0 +3. = 2 2 3 2 0,25 Vậy P= 2 3
Câu 2: Cho sin x = x
. Tính giá trị lượng giác của cot x 5 2 Ý Nội dung Điểm Trang 17 2 3 16 4 Ta có 2 2
sin x + cos x = 1 2 2
cos x =1− sin x =1− = cos x = 0,5 5 25 5 0,25 4
x cos x 0 , chọn cos x = − . 2 5 4 − cos x 4 5 cot x = = = − sin x 3 3 0,25 5
Câu 3: Cho tứ diện A.BCD, gọi I, J lần lượt là là trung điểm cạnh BC và AD. Điểm K thuộc cạnh CD 1 sao cho đoạn CK =
CD . Tìm giao tuyến của hai mặt phẳng (IJK) với (ACD) ? 4 Ý Nội dung Điểm A 0,25 J B D I K C K DC (CDA) 0,25 K (IKJ) J DA (CDA) 0,25 J (IKJ)
Vậy giao tuyến của hai mặt phẳng (IJK) với (ACD) là KJ 0,25
Câu 4: Người ta trồng 2145 cây theo hình một tam giác như sau: hàng thứ nhất có 1 cây, hàng thứ hai có
2 cây, hàng thứ ba có 3 cây,… Hỏi có tất cả bao nhiêu hàng cây? Ý Nội dung Điểm
Gọi số hàng cây là n , hàng thứ n có n cây. 0,25
Ta có 1+ 2 +3+...+ n = 2145 0,25 n(n + ) 1 = 2145. 2 0,25 n = 65 Vậy có 65 hàng cây. 0,25 ĐỀ 4
ĐỀ ÔN TẬP GIỮA HỌC KỲ I NĂM HỌC 2025-2026 MÔN: TOÁN 11-CTST Trang 18
PHẦN I: Câu trắc nghiệm nhiều phương án lựa chọn (3 điểm)
Học sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi học sinh chỉ chọn một phương án.
Câu 1. Khẳng định nào sau đây đúng ?
A. Giá trị lớn nhất của hàm số y=sin(2024x) bằng 2024.
B. Giá trị nhỏ nhất của hàm số y=cos(2024x) bằng −2024.
C. Hàm số y= 3sin2x có tập giá trị là [0 ;3].
D. Hàm số y= 2cos2x có tập giá trị là [−2 ;2].
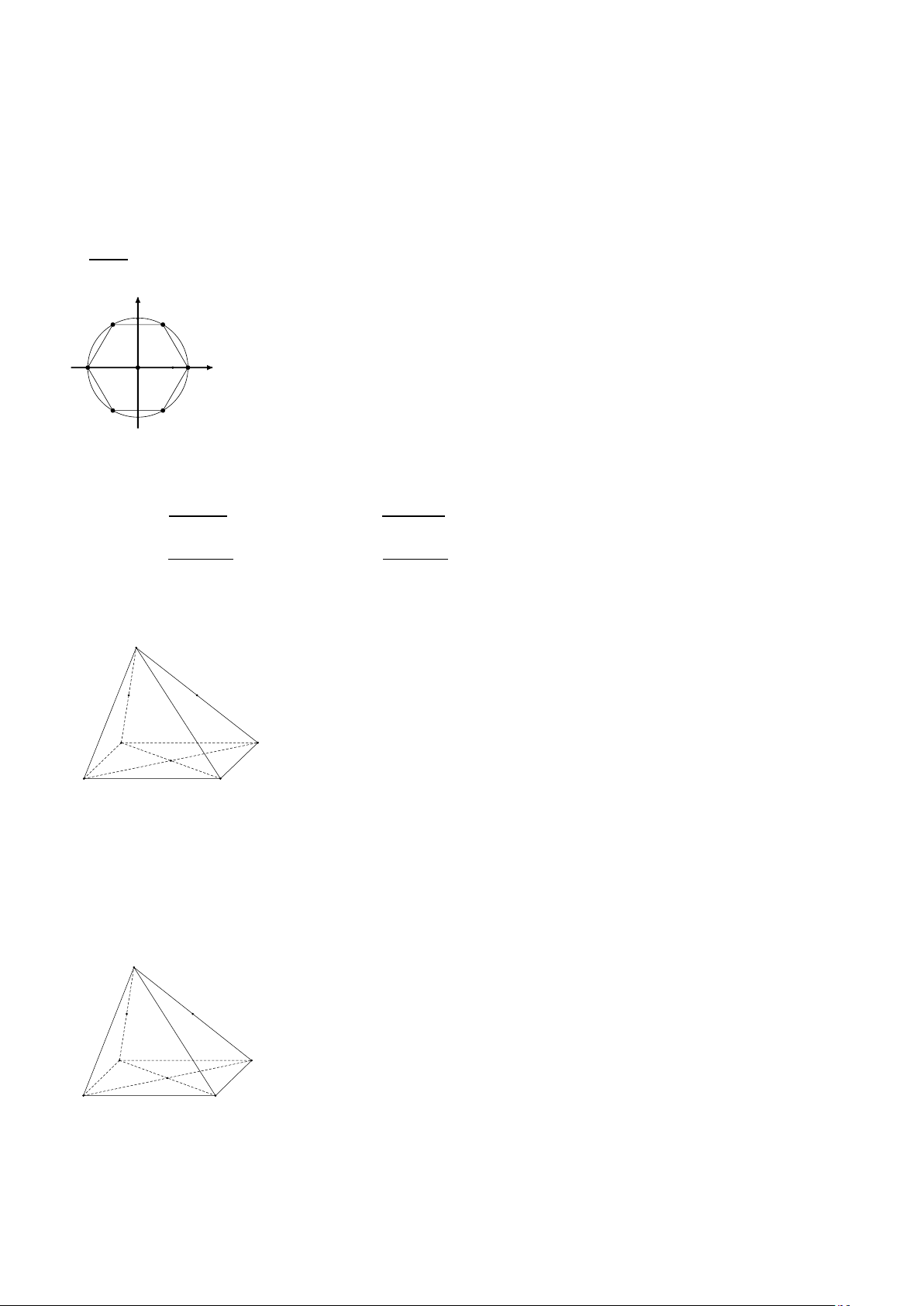
Câu 2. Trên đường tròn lượng giác, cho lục giác đều ABCDEF như hình vẽ. Khi đó góc lượng giác có số −19π
đo 3 có điểm biểu diễn là: y C B D A O x E F A. Điểm B B. Điểm E C. Điểm F D. Điểm C
Câu 3. Hàm số nào sau đây có tập xác định là tập số thực R? 2cotx sinx A. y= cosx −2 B. y= 2cosx−1 2 2cosx C. y= 2sinx −3 D. y= 3sinx −2
Câu 4. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm
SA, SD. Khẳng định nào sau đây sai ? S M N A D O B C
A. Hai đường thẳng OM và SC song song nhau.
B. Hai đường thẳng MN và BC song song nhau.
C. Hai đường thẳng ON và SB song song nhau.
D. Hai mặt phẳng (SAB) và (SCD) cắt nhau theo theo giao tuyến là đường thẳng đi qua điểm S và
song song với hai đường thẳng MB, NC.
Câu 5. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm
SA, SD. Khẳng định nào sau đây đúng ? S M N A D O B C
A. Hai mặt phẳng (SAD) và (SBC) cắt nhau theo theo giao tuyến là đường thẳng đi qua điểm S và
song song với hai đường thẳng AB, CD.
B. Hai mặt phẳng (SAD) và (SBC) cắt nhau theo theo giao tuyến là đường thẳng SO.
C. Hai mặt phẳng (SAD) và (SBC) cắt nhau theo theo giao tuyến là đường thẳng đi qua điểm S và
song song với đường thẳng MN. Trang 19
D. Hai mặt phẳng (SAD) và (SBC) cắt nhau theo theo giao tuyến là đường thẳng đi qua điểm S và
song song với hai đường thẳng MC, NB.
Câu 6. Để tặng quà sinh nhật cho bạn Bình vào ngày thứ bảy, bạn An quyết định để dành tiền mua quà
sinh nhật liên tục từ thứ hai đến thứ sáu theo một cấp số cộng. Biết rằng thứ hai bạn An để dành 30 nghìn
đồng, thứ ba bạn An để dành 50 nghìn đồng. Hỏi thứ sáu bạn An để dành bao nhiêu tiền? A. 90 nghìn đồng. B. 110 nghìn đồng. C. 130 nghìn đồng. D. 70 nghìn đồng. 1
Câu 7. Cho dãy số (un) với un= 3 + 2n +1. Khẳng định nào sau đây đúng?
A. Dãy số (un) giảm và bị chặn.
B. Dãy số (un) tăng và chỉ bị chặn trên.
C. Dãy số (un) giảm và chỉ bị chặn dưới.
D. Dãy số (un) tăng và bị chặn. 5 12 4 3
Câu 8. Cho sina= 13; cosa=13; sinb=5 và cosb= 5. Khẳng định nào sau đây đúng? 33 56 A. cos(a+b)= − 65 B. cos(a+b)= 65 16 63 C. cos(a+b)= 65 D. cos(a+b)= 65
Câu 9. Khẳng định nào sau đây sai ?
A. sin5a +sin3a = 2sin4a.cosa, aR. 1
B. sin5a.sin3a = 2(cos8a –cos2a), aR. a a
C. sina =2sin(2).cos(2)‚aR.
D. cos4a =2cos22a −1, aR. 3 3π
Câu 10. Cho cosa= − 5 với π3 3 A. cota= 4 B. cota= −4 4 4 C. cota= −3 D. cota = 3
Câu 11. Trong các dãy số hữu hạn sau, dãy nào không là cấp số cộng: A. 3; 6; 8; 10; 12. B. 3; 8; 13; 18; 23.
C. 2024; 2023; 2022; 2021; 2020
D. 2024; 2024; 2024; 2024; 2024.
Câu 12. Cho hình chóp S.ABCD, gọi E là giao điểm của AB và CD, F là giao điểm cũa BC và AD.
Khẳng định nào sau đây sai? S A D F C BE
A. Giao tuyến của hai mặt phẳng (SAB) và (SAC) là cạnh SA.
B. Giao tuyến của hai mặt phẳng (SAB) và (SCD) là đường thẳng SE.
C. Hai đường thẳng SC và AD không có điểm chung.
D. Giao tuyến của hai mặt phẳng (SAD) và (SBC) là đường thẳng SF.
PHẦN II: Câu trắc nghiệm dạng đúng sai (4 điểm)
Học sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, học sinh chọn đúng hoặc sai 10
Câu 1: Cho hàm số f(x) = 3cosx +5 Trang 20




