20 Đề Thi Giữa Học Kỳ 1 Toán 9 Năm 2025-2026 Có Lời Giải
Hải đăng Đa Lát là một trong những ngọn hải đăng cao nhất Việt Nam, được đặt trên đảo Đá Lát ở vị trí cực Tây Quần đảo, thuộc xã đảo Trường Sa, huyện Trường Sa, tỉnh Khánh Hòa. Ngọn hải đăng được xây dựng năm 1994, cao 42 mét, có tác dụng chỉ vị trí đảo, giúp tàu thuyền hoạt động trong vùng biển Trường Sa định hướng và xác định được vị trí của mình. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Chủ đề: Đề giữa HK1 Toán 9 300 tài liệu
Môn: Toán 9 2.8 K tài liệu
Tác giả:
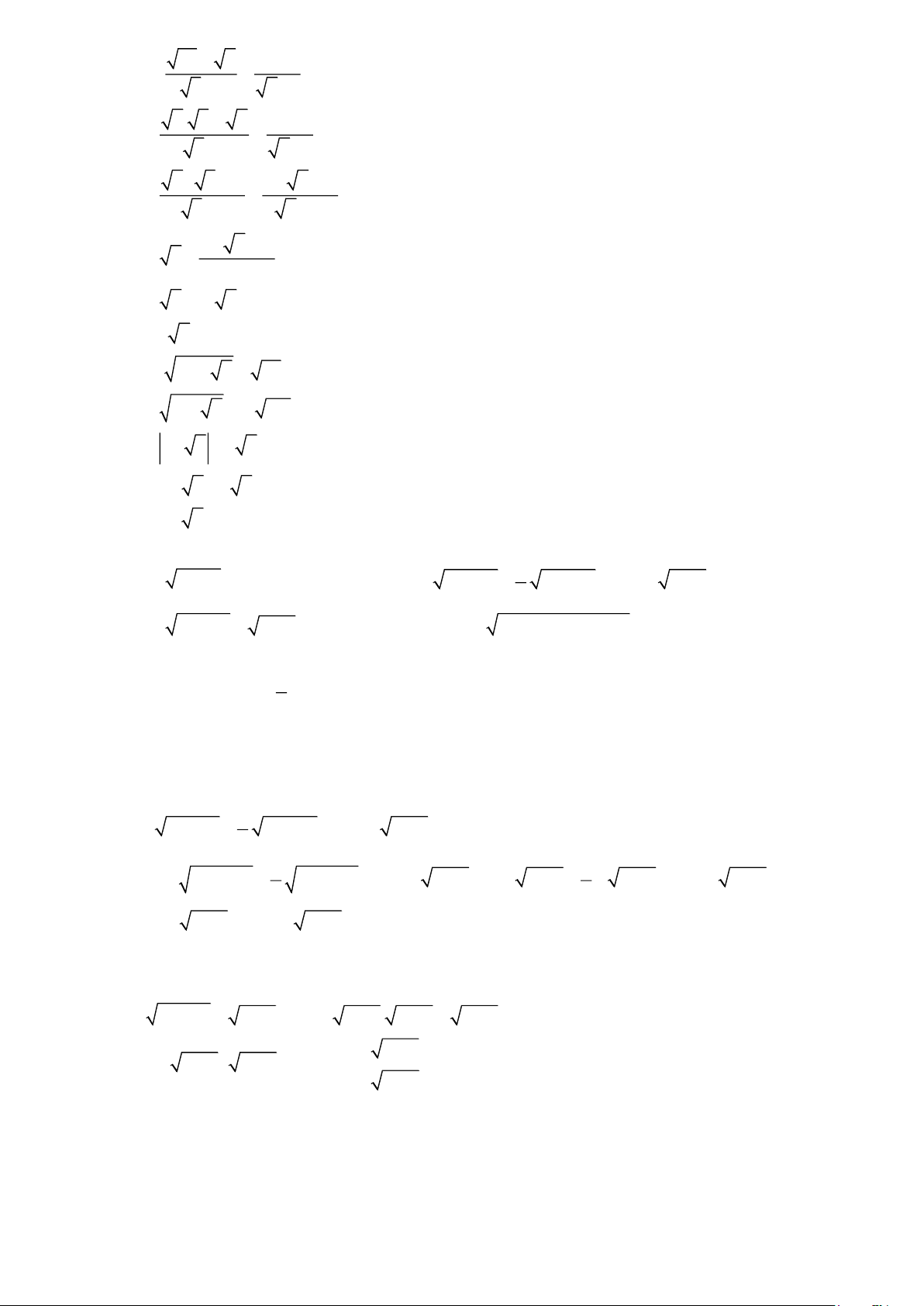
Preview text:
ĐỀ KIỂM TRA GIỮA HỌC KỲ I (ĐỀ 1) MÔN: TOÁN 9
Bài 1(2,5 điểm) Cho hai biểu thức x + 2 x + 5 2 x - 9 x + 3 2 x + 1 A = và B = - -
với (x ³ 0, x ¹ 4, x ¹ 9) x - 3 x - 5 x + 6 x - 2 3- x
a) Tính giá trị của A khi x = 16.
b) Rút gọn biểu thức B
c) Biết rằng P = A : B . Tìm giá trị nhỏ nhất của P
Bài 2(3,0 điểm) Giải các phương trình sau: a) x - 5 = 2 b) 2 x - 6x + 9 = 5 c) 2
4x - 4x + 1 = x + 1 d) 2 2
x - 4x + 4 = 4x - 12x + 9
Bài 3( 3,5 điểm) Cho tam giác ABC vuông tại A ( AB > AC ), đường cao AH ( H Î BC ). Vẽ phân giác
AD của góc BAH ( D Î BH ). Cho M là trung điểm của BA .
a) Cho AC = 3cm ; AB = 4cm . Hãy giải tam giác ABC ?(Làm tròn đến độ)
b) Tính diện tích tam giác AHC DH HC c) Chứng minh rằng: = DB AC
d) Gọi E là giao điểm của DM và AH . Chứng minh: S = S DA C E DDEC
Bài 4(1,0 điểm)
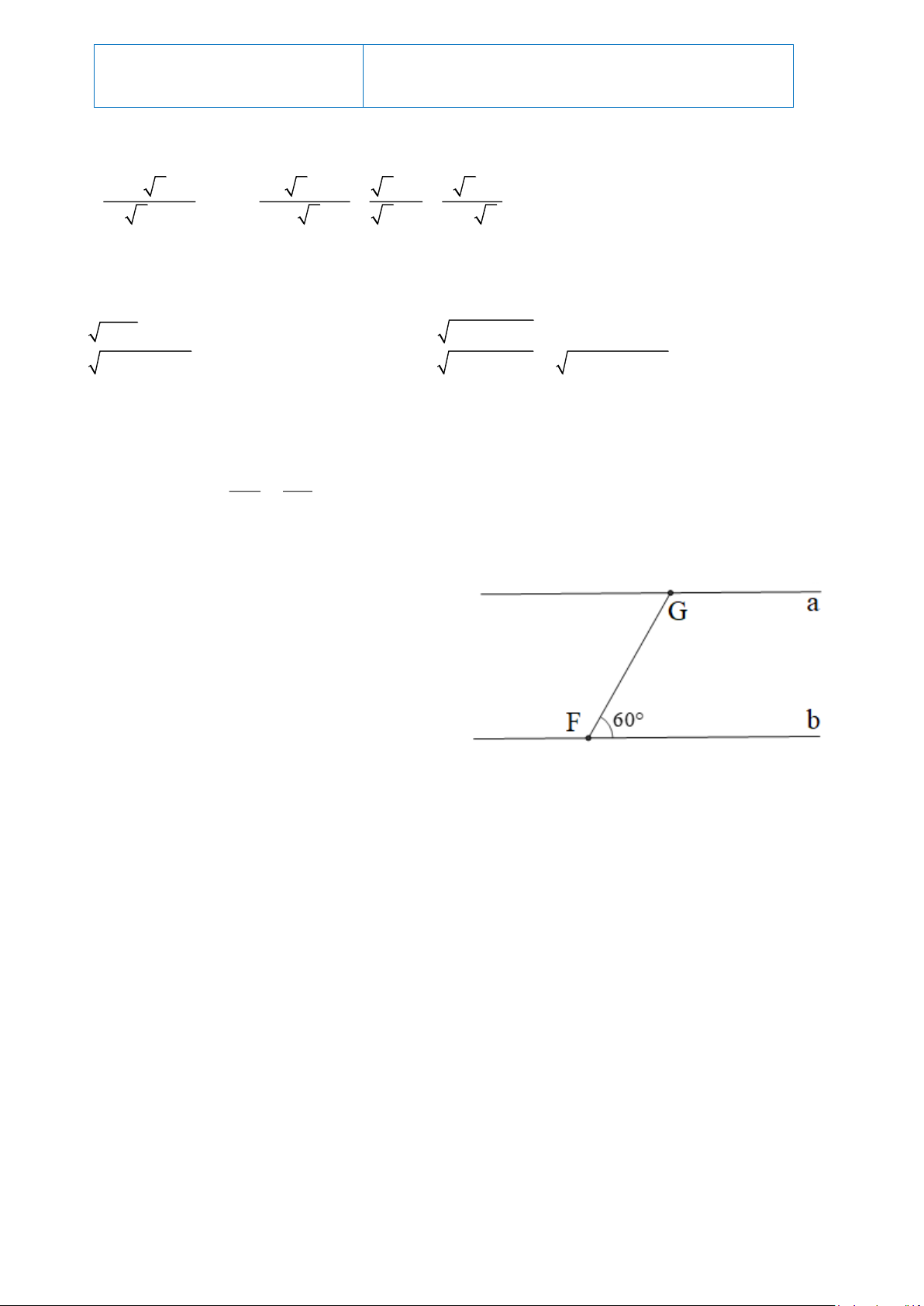
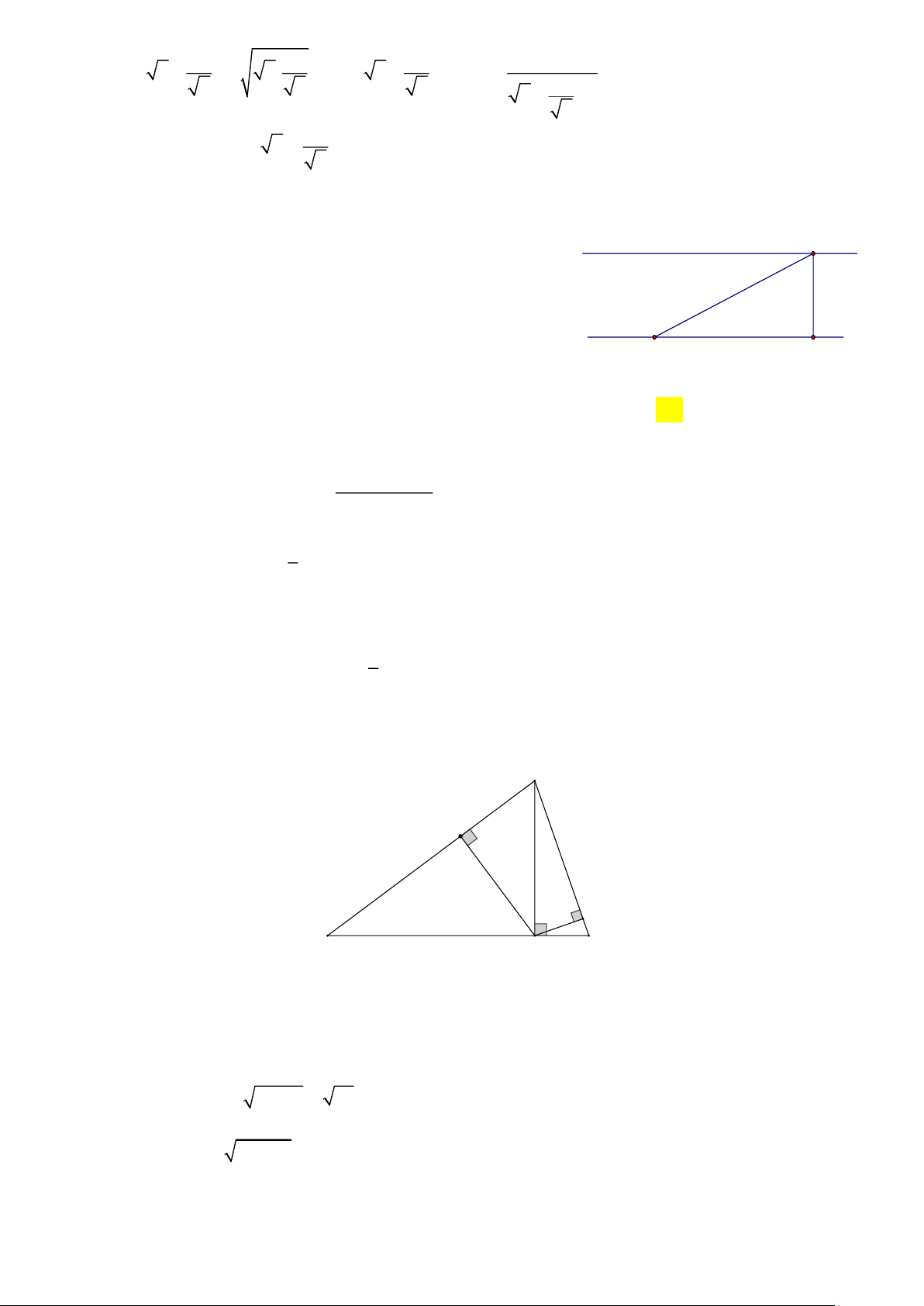
Một con thuyền ở địa điểm F di chuyển từ bờ
sông b sang bờ sông a với vận tốc trung bình là 6
km/h, vượt qua khúc sông nước chảy mạnh trong
5 phút. Biết đường đi của con thuyền là FG , tạo
với bờ sông một góc 60° . a) Tính FG
b) Tính chiều rộng của khúc sông (làm tròn đến mét) ----------Hết----------
Học sinh không sử dụng tài liệu, giáo viên coi
kiểm tra không giải thích gì thêm Trang 1 HƯỚNG DẪN
Câu 1. (2,5 điểm) Cho hai biểu thức x + 2 x + 5 2 x - 9 x + 3 2 x + 1 A = và B = - -
với (x ³ 0, x ¹ 4, x ¹ 9) x - 3 x- 5 x + 6 x - 2 3- x
a) Tính giá trị của A khi x = 16.
b) Rút gọn biểu thức B
c) Biết rằng P = A : B . Tìm giá trị nhỏ nhất của P Lời giải
a) Ta có x = 16 (thỏa mãn điều kiện), thay vào biểu thức A ta có: 16 + 2 16 + 5 29 A = = = 29 16 - 3 1
Vậy khi x = 16 thì A = 29 b) Ta có: 2 x - 9 x + 3 2 x + 1 B = - - x - 5 x + 6 x - 2 3- x 2 x - 9 x + 3 2 x + 1 = ( - + x - ) 2 ( x - ) 3 x - 2 x - 3 2 x - 9- ( x + ) 3 ( x - ) 3 + (2 x + ) 1 ( x - ) 2 = ( x - ) 2 ( x - ) 3
2 x - 9- x + 9 + 2x - 3 x - 2 = ( x - ) 2 ( x - ) 3 ( x - ) 2 ( x x x + - - )1 2 x + 1 = ( = = x - ) 2 ( x - ) 3 ( x - ) 2 ( x - ) 3 x - 3 x + 1 Vậy B =
, (x ³ 0, x ¹ 4, x ¹ 9) x - 3 + + + + + ( x x x x x x + )2 1 + 4 2 5 1 2 5 4
c) Ta có P = A : B = : = = = x + 1+ x - 3 x - 3 x + 1 x + 1 x + 1 Do x ³ 0 Þ x ³ 0 Þ x + 1> 0 4
Áp dụng bất đẳng thức Cô si cho 2 số dương x + 1và ta có: x + 1 4 P = x + + ³ ( x + ) 4 1 2 1 = 4 x + 1 x + 1 4 Dấu bằng xảy ra Û x + 1= Û x + 1= 2 Û
x = 1Û x = 1(thỏa mãn điều kiện) x + 1
Vậy min P = 4 khi x = 1
Câu 2. (3,0 điểm) Giải các phương trình sau: a) x - 5 = 2 b) 2 x - 6x + 9 = 5 c) 2
4x - 4x + 1 = x + 1 d) 2 2
x - 4x + 4 = 4x - 12x + 9 Lời giải Trang 2 a) x - 5 = 2 .
Điều kiện xác định x ³ 5
Ta có: x - 5 = 2 Û x - 5 = 4 Û x = 9 (thỏa mãn x ³ 5 )
Vậy tập nghiệm của phương trình là S = { } 9 . b) 2 x - 6x + 9 = 5 x é - 3 = 5 x é = 8
Ta có: x - 6x + 9 = 5 Û (x- )2 2
3 = 5 Û x - 3 = 5 Û ê Û ê x ê - 3 = - 5 x ê = - 2 ë ë
Vậy tập nghiệm của phương trình là S = {8;- } 2 . c) 2
4x - 4x + 1 = x + 1 Ta có: ìï x + 1³ 0 ìï x ³ - 1 ï ï ï ï
4x - 4x + 1 = x + 1 Û (2x- )2 2
1 = x + 1 Û 2x - 1 = x + 1 ï Û í 2 é x- 1= x + 1 ï Û í x é = 2(nhaä) n ï ê ê ï
ïï 2êx- 1= - x- 1 ïï xê = 0 ïî ë ï ê (nhaä) n î ë
Vậy tập nghiệm của phương trình là S = {2; } 0 . d) 2 2
x - 4x + 4 = 4x - 12x + 9 Ta có: x - x + = x -
x + Û (x- )2 = ( x- )2 2 2 4 4 4 12 9 2 2
3 Û x - 2 = 2x- 3 x é = 1 x é - 2 = 2x- 3 é- x = - 1 ê Û ê Û ê Û ê 5 x ê - 2 = - 2x + 3 3 ê x = 5 x ê = ë ë êë 3 ìï 5ü
Vậy tập nghiệm của phương trình là S ï 1; ï = í ý . ïî 3ï ï ïþ
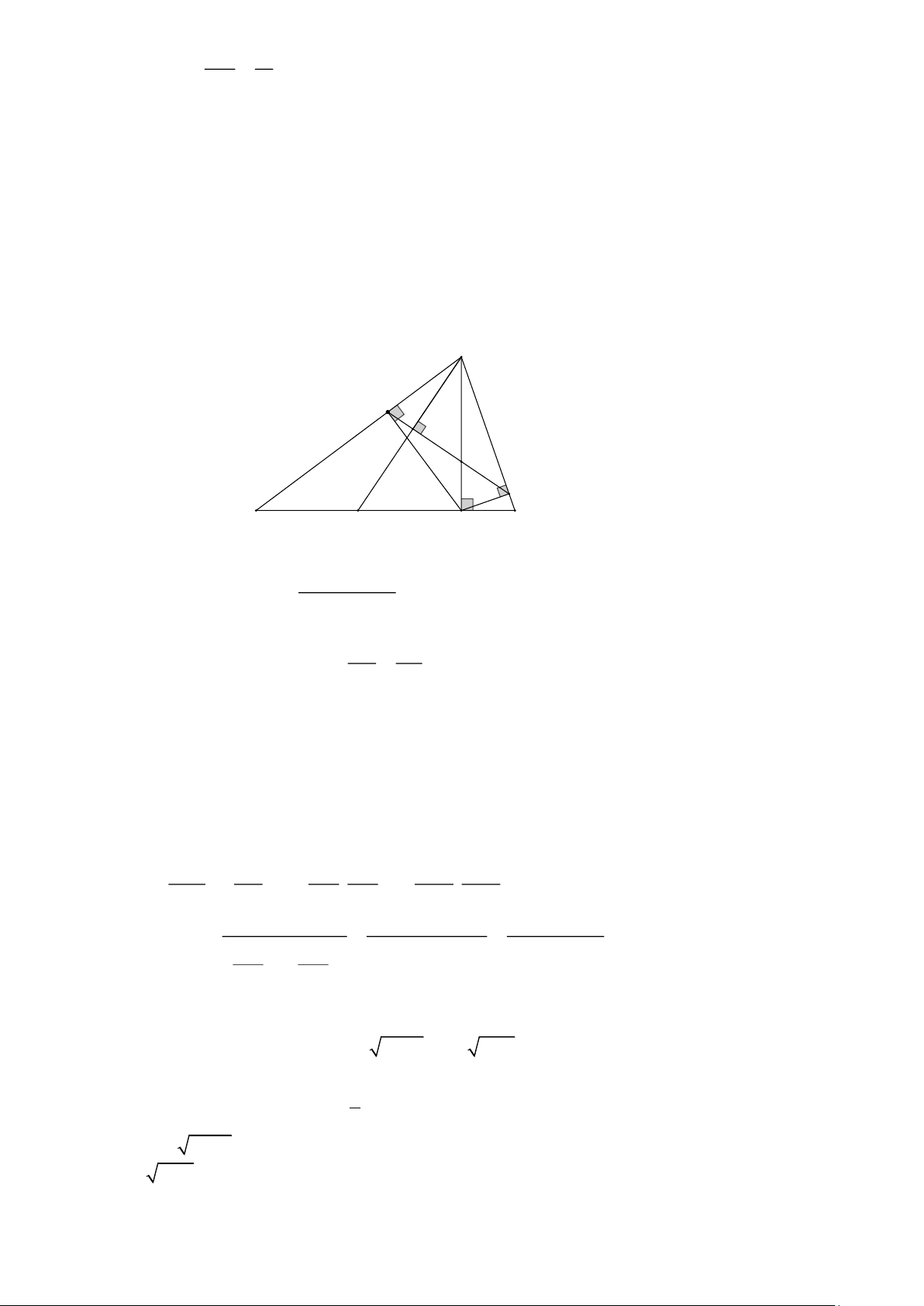
Câu 3. ( 3,5 điểm) Cho tam giác ABC vuông tại A ( AB > AC ), đường cao AH ( H Î BC ). Vẽ phân
giác AD của góc BAH ( D Î BH ). Cho M là trung điểm của BA .
a) Cho AC = 3cm ; AB = 4cm . Hãy giải tam giác ABC ?. Làm tròn đến độ
b) Tính diện tích tam giác AHC DH HC c) Chứng minh rằng: = DB AC
d) Gọi E là giao điểm của DM và AH . Chứng minnh: S = S DA C E DDEC Lời giải E B G D M H 2 1 A C
a) Xét D ABC vuông tại A (gt) có: Trang 3 2 2 2
AB + AC = BC (định lí Pytago) 2 2 2 Þ 4 + 3 = BC 2 Þ BC = 25 Þ BC = 5 (cm) AC 3 Ta có: µ sin B = = Þ B » 37° BC 5 µ µ B + C = 90° µ Þ C » 53°
b) Áp dụng hệ thức lượng vào D ABC vuông tại A , đường cao AH ta có: AH.BC = . AB AC A . B AC 4.3 Û AH = = = 2, 4 (cm) BC 5 2 3 9 Lại có: 2
AC = CH.BC Û CH = = = 1,8 (cm) BC 5
Diện tích tam giác AHC là: 1 1 .HC.AH = .2, 4.1,8 = 2,16( 2 cm ) 2 2
c) Xét D ABH có phân giác AD (giả thuyết) DH AH Þ =
(tính chất phân giác trong tam giác) DB AB
DAHB ” DCHA (g-g) AH HC Þ = (hai góc tương ứng) AB AC DH HC æ AH ö Þ = ç ÷ = ç ÷(đpcm) DB AC çè AB ÷ ø
d) Kẻ HG // AB Xét D ABD có · ADC là góc ngoài · · ¶
Þ ADC = ABD + A 2 Mà · µ ·
DAC = A + HAC 1 Lại có · · ABD = HAC · · Þ ADC = DAC
Þ DACD cân tại C (dhnb)
Þ AC = DC (tính chất) DH HC HC Þ = = (1) DB AC DC EH HG
Xét D AEM , có GH // AB Þ = (định lí Ta lét) EA AM EH HG
Vì M là trung điểm của AB (gt) Þ AM = BM Þ = EA BM DH HG
Xét D DGH , có GH / / AB Þ = (định lí Ta lét) DB BM EH DH Þ = (2) EA DB HC HE Từ (1);(2) Þ =
Þ HC.AE = DC.HE DC AE 1 1 Ta có S = CH.AE , S = EH.DC ACE 2 DEC 2 S CH.AE ACE Þ = = 1 S EH.DC DEC Trang 4 Vậy S = S DA C E DDEC
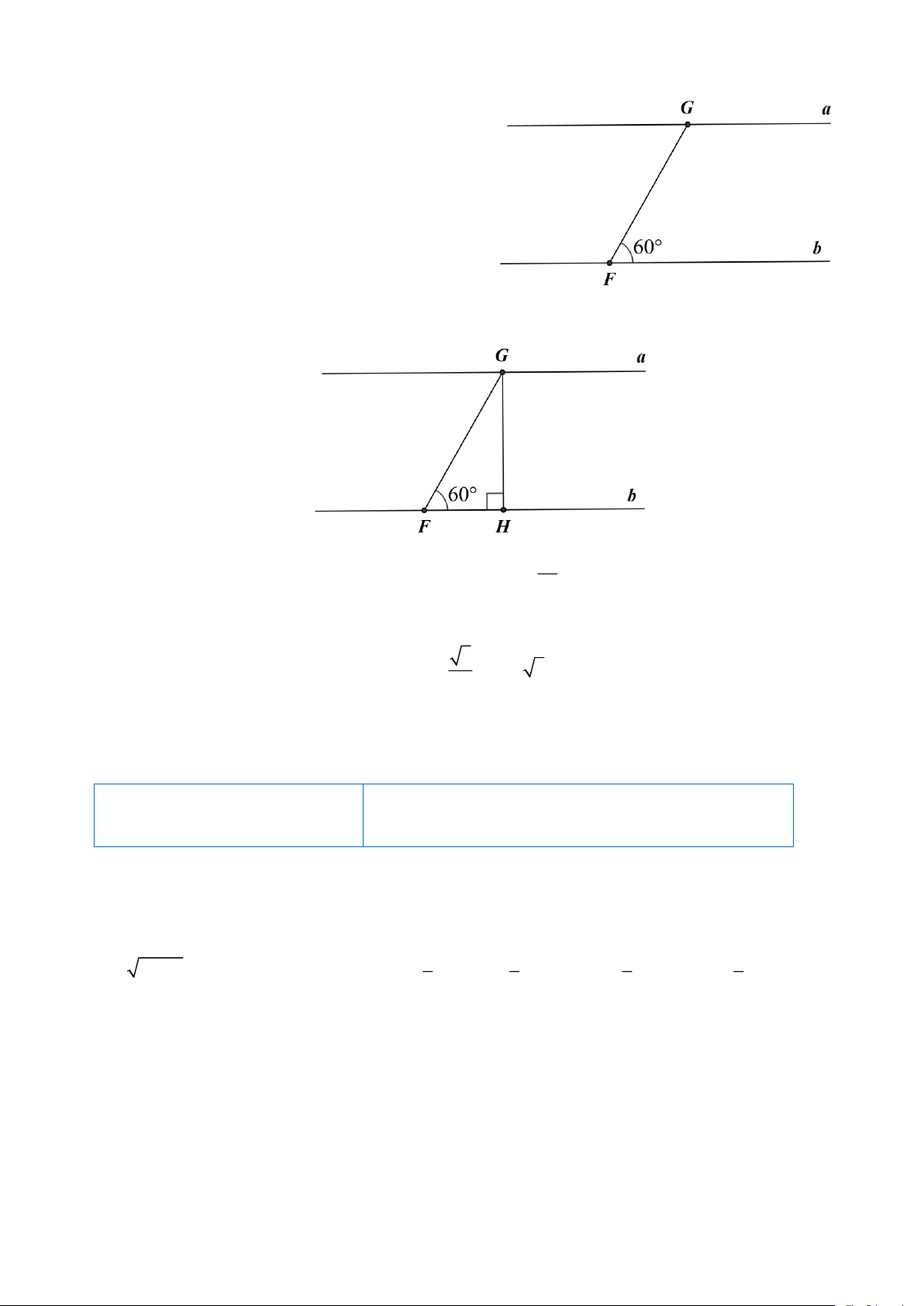
Câu 4. (1,0 điểm)
Một con thuyền ở địa điểm F di chuyển từ
bờ sông b sang bờ sông a với vận tốc trung
bình là 6 km/h, vượt qua khúc sông nước
chảy mạnh trong 5 phút. Biết đường đi của
con thuyền là FG , tạo với bờ sông một góc 60° . a) Tính FG
b) Tính chiều rộng của khúc sông (làm tròn đến mét) Lời giải 5
a) FG là quãng đường đi được của thuyền. FG = 6.
= 0,5km = 500 m . 60
b) Gọi GH là chiều rộng của khúc sông.
Xét D GHF vuông tại H, áp dụng hệ thức về cạnh và góc trong tam giác vuông ta có: · 3 GH = F .
G sin GFB = 500.sin 60° = 500. = 250 3 » 433 m. 2
Vậy, chiều rộng của khúc sông xấp xỉ 433 m.
ĐỀ KIỂM TRA GIỮA HỌC KỲ I (ĐỀ 2) MÔN: TOÁN 9
I. PHẦN TRẮC NGHIỆM ( 1 điểm ) Chọn đáp án đúng trong mỗi câu sau
Câu 1: Căn bậc hai của 9 là: A. 3 . B. 3 . C. 3 − . D. 81. 3 3 3 3
Câu 2: 3 − 5x xác định khi và chỉ khi A. x . B. x . C. x .
D. x . 5 5 5 5
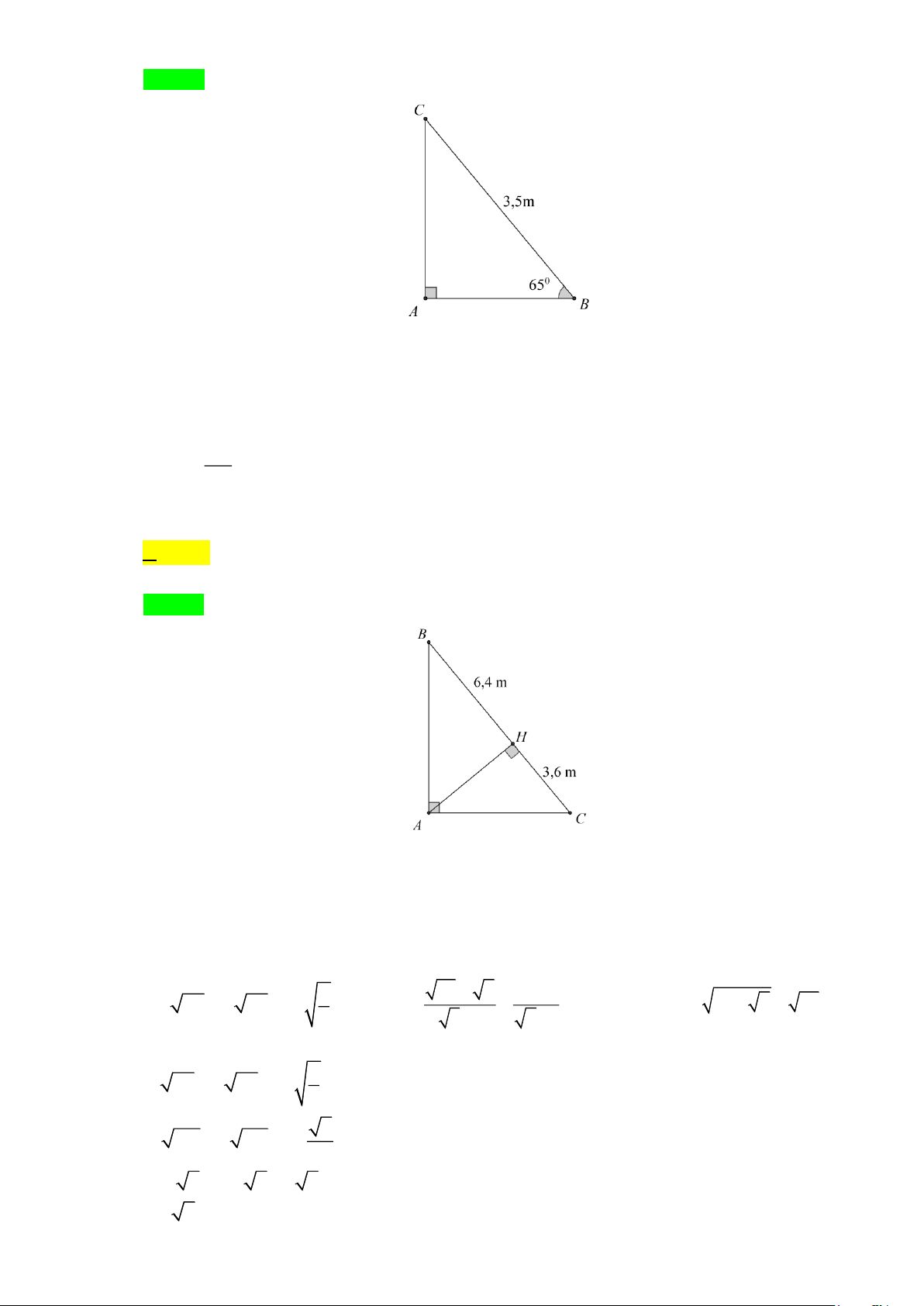
Câu 3: Một cái thang dài 3,5 m đặt dựa vào tường, góc “an toàn” giữa thang và mặt đất để thang không
đổ khi người trèo lên là 65 . Khoảng cách “an toàn” từ chân tường đến chân thang (Kết quả làm tròn đến
chữ số thập phân thứ nhất) là : A. 1, 4 m B. 1, 48 m C. 1m D. 1,5 m
Câu 4: Tam giác ABC vuông tại A , có đường cao AH chia cạnh huyền thành hai đoạn thẳng có độ dài
3, 6 cm và 6, 4 cm . Độ dài một trong các cạnh góc vuông là A. 8 cm . B. 4,8 cm . C. 64 cm . D. 10 cm .
II. PHẦN TỰ LUẬN ( 9 điểm)
Bài 1(1,5 điểm) Thực hiện phép tính. Trang 5 1 35 − 7 12 a). 20 + 2 45 −15 . b). + . c). 8 + 2 7 − 28 . 5 5 −1 7 −1
Bài 2(2 điểm) Giải các phương trình sau: 7 a) 7x − 3 = 5 . b) 5 4x −16 −
9x − 36 = 36 − 3 x − 4 . 3 c) 2
x − 36 − x − 6 = 0 . d) 2 2 3
x + 2 = 3 − 4x + 2x + 4x .
Bài 3(2 điểm) x −1 x − 2 2 + 8 x 2 Cho biểu thức M = và P = + −
với x 0; x 1; x 5 x x +1 x −1 1− x x + 6
a) Tính giá trị của M khi x = 9 . b) Chứng minh P = . x −1 x − 5
c) Đặt Q = M.P +
. Hãy so sánh Q với 3. x
Bài 4(3,5 điểm) Cho tam giác ABC nhọn , đường cao AK . BC
a) Giải tam giác ACK biết C = 30 ,
AK = 3cm . b) Chứng minh AK = . cot B + cot C
c) Biết BC = 5cm, B = 68 ,
C = 30 . Tính diện tích tam giác ABC ( kết quả làm tròn chữ số thập phân thứ nhất). 2 1 cot ACB 1
d) Vẽ hình chữ nhật CKAD , DB cắt AK tại N . Chứng minh rằng = + . 2 2 2 AK DN DB
I. PHẦN TRẮC NGHIỆM BẢNG TRẢ LỜI
Câu 1 Câu 2 Câu 3 Câu 4 B C D A HƯỚNG DẪN
Câu 1. Căn bậc hai của 9 là A. 3 . B. 3 . C. 3 − . D. 81. Lời giải Chọn B
Căn bậc hai của số 9 là 3 . Câu 2.
3 − 5x xác định khi và chỉ khi 3 3 3 3 A. x . B. x . C. x . D. x . 5 5 5 5 Lời giải Chọn C 3
Biểu thức xác định khi 3 − 5x 0 x 5
Câu 3. Một cái thang dài 3,5 m đặt dựa vào tường, góc “an toàn” giữa thang và mặt đất để thang
không đổ khi người trèo lên là 65 . Khoảng cách “an toàn” từ chân tường đến chân thang (Kết
quả làm tròn đến chữ số thập phân thứ nhất) là : A. 1, 4 m . B. 1, 48 m . C. 1m . D. 1,5 m . Trang 6 Lời giải Chọn D
Chiều dài thang là BC = 3,5m .
Góc “an toàn” là ABC = 56 .
Khoảng cách an toàn là AB .
Áp dụng tỉ số lượng giác của góc nhọn cho tam giác vuông ABC ta có: AB cos B =
AB = BC.cos B = 3,5.cos65 1,5m . BC
Câu 4. Tam giác ABC vuông tại A , có đường cao AH chia cạnh huyền thành hai đoạn thẳng có độ
dài 3, 6 cm và 6, 4 cm . Độ dài một trong các cạnh góc vuông là A. 8 cm . B. 4,8 cm . C. 64 cm . D. 10 cm . Lời giải Chọn A
Giả sử HC = 3,6 cm và HB = 6, 4 cm BC = HC + HB = 10 cm .
Áp dụng hệ thức lượng cho tam giác vuông ABC ta có: 2
AB = BH.BC = 6, 4.10 = 64 AB = 8 cm II. PHẦN TỰ LUẬN
Câu 1. (1,5 điểm) Thực hiện phép tính. 1 35 − 7 12 a). 20 + 2 45 −15 b). + c). 8 + 2 7 − 28 5 5 −1 7 −1 Lời giải 1 a) 20 + 2 45 −15 5 5 = 4.5 + 2 9.5 −15 5 = 2. 5 + 2.3 5 − 3 5 = 5 5 . Trang 7 35 − 7 12 b). + 5 −1 7 −1 7. 5 − 7 12 = + 5 −1 7 −1 7.( 5 −1) 12( 7 +1) = + 2 5 −1 ( 7) −1 12( 7 +1) = 7 + 6 = 7 + 2( 7 +1) = 3 7 + 2 . c). 8 + 2 7 − 28 2 = (1+ 7 ) − 4.7 = 1+ 7 − 2 7 =1+ 7 − 2 7 = 1− 7 .
Câu 2. (2 điểm) Giải các phương trình sau: 7 a) 7x − 3 = 5 b) 5 4x −16 −
9x − 36 = 36 − 3 x − 4 3 c) 2
x − 36 − x − 6 = 0 d) 2 2 3
x + 2 = 3 − 4x + 2x + 4x Lời giải 3
a) Điều kiện: x . 7
Bình phương hai vế của phương trình ta được: 7x − 3 = 25 x = 4 ( thỏa mãn điều kiện) .
Vậy tập nghiệm của phương trình là: S = 4 .
b) Điều kiện: x 4 . 7 5 4x −16 −
9x − 36 = 36 − 3 x − 4 3 (x − ) 7 − (x − ) 7 5 4 4 9
4 = 36 − 3 x − 4 10 x − 4 − .3 x − 4 = 36 − 3 x − 4 3 3
6 x − 4 = 36 x − 4 = 6 x − 4 = 36 x = 40 ( thỏa mãn điều kiện) .
Vậy tập nghiệm của phương trình là: S = 40 .
c) Điều kiện: x 6 . 2
x − 36 − x − 6 = 0 x − 6. x + 6 − x − 6 = 0 x − = x = tm
x − 6 ( x + 6 − ) 6 0 6( ) 1 = 0 . x + 6 =1 x = 5 − (L)
Vậy tập nghiệm của phương trình là: S = 6 . d) Điều kiện: 2 3
3 − 4x + 2x + 4x 0 .
Bình phương hai vế của phương trình ta được: 4 2 2 3 4 3 2
x + 4x + 4 = 3 − 4x + 2x + 4x x − 4x + 2x + 4x +1 = 0 ( ) 1 Trang 8
Nhận xét: x = 0 không phải là nghiệm của phương trình ( )
1 , chia cả hai vế của phương trình ( ) 1 cho 2 x ta được: 4 1 1 1 2 2 x − 4x + 2 + + = 0 x + − 4 x − + 2 = 0 2 . 2 2 ( ) x x x x 1 1 1 Đặt 2 2 2 2
x − = a a = x + − 2 x + = a + 2. 2 2 x x x
Phương trình (2) trở thành: a + − a + = (a − )2 2 2 4 2 0 2 = 0 a = 2 . 1
Với a = 2 x − = 2 x − 2x −1 = 0 (x − )2 2
1 = 2 x = 1 2 ( thỏa mãn điều kiện) x
Vậy tập nghiệm của phương trình là: S = 1− 2; 1+ 2. x −1 x − 2 2 + 8 x 2
Câu 3. (2 điểm) Cho biểu thức M = và P = + −
với x 0; x 1; x 5 x x +1 x −1 1− x
a) Tính giá trị của M khi x = 9 . x + 6 b) Chứng minh P = . x −1 x − 5
c) Đặt Q = M.P +
. Hãy so sánh Q với 3. x Lời giải
a) Thay x = 9 ( thỏa mãn điều kiện) vào M ta được: 9 −1 3 −1 2 2 M = =
= . Vậy x = 9 thì M = . 9 3 3 3 b) Ta có:
( x −2)( x − )1+2+8 x +2( x x x + − + )1 2 2 8 2 P = + + = x +1 ( x − ) 1 ( x + ) 1 x −1
( x − )1( x + )1 x − x + + + x + x + x + x + ( x + )1( x +6 3 2 2 8 2 2 7 6 ) x +6 = ( = = = x − ) 1 ( x + ) 1
( x − )1( x + )1 ( x − )1( x + )1 x −1
( điều phải chứng minh) . x + 6 Vậy P = . x −1 c) Ta có: x − 5 x −1 x + 6 x − 5 x + 6 x − 5 x + x +1 Q = M.P + = . + = + = . x x x −1 x x x x ( x x x x x − + + − + )2 1 1 2 1 Xét Q − 3 = − 3 = =
0 với mọi x 0; x 1. x x x Do đó Q 3 .
Câu 4. (3,5 điểm)
Cho tam giác ABC nhọn , đường cao AK .
a) Giải tam giác ACK biết C = 30 , AK = 3cm . BC b) Chứng minh AK = . cot B + cot C Trang 9
c) Biết BC = 5cm, B = 68 ,
C = 30 . Tính diện tích tam giác ABC ( kết quả làm tròn chữ số thập phân thứ nhất). 2 1 cot ACB 1
d) Vẽ hình chữ nhật CKAD , DB cắt AK tại N . Chứng minh rằng = + . 2 2 2 AK DN DB Lời giải
a) Xét tam giác ACK vuông tại K có C = 30 B = 60 ( theo định lí tổng ba góc trong tam giác). AK 3 1 3 Sin C = Sin 30 = = AC = 6 (cm) AC AC 2 AC
Theo định lí Pitago trong tam giác vuông ACK ta có 2 2 2 2
KC = AC − AK = 6 − 3 = 27 = 3 3 (cm). BK
b) Xét tam giác vuông AKB ta có cot B = AK KC
Xét tam giác vuông AKC ta có cot C = AK BK KC BK + KC BC
Nên cot B + cot C = + = = AK AK AK AK BC Vậy AK = (đpcm). cot B + cot C AK
c) Xét tam giác vuông AKB ta có tan B = AK = tan . B BK BK AK
Xét tam giác vuông AKC ta có tan C =
AK = tan C.CK CK tan B KC tan 68 KC KC 43 Từ đó ta có tan .
B BK = tan C.KC = = 4,3 = . tan C BK tan 30 BK BK 10 5 − BK 43 5 53
Mà KC = BC − BK = 5 − BK = = . BK 10 BK 10
Vậy BK = 0,9; KC = 4,1.
Xét tam giác vuông AKC có AK AK 3 AK 3 tan C = tan 30 = = AK = .CK = 2, 4 (cm). CK CK 3 CK 3 1 1 Vậy S
= AK.BC = .2,4.5 = 6 . ABC ( 2 cm ) 2 2
d) Kẻ DI ⊥ BD tại D khi đó ADN = CDI ( cùng phụ với CDN ), Khi đó A
DN ∽ CD
I ( g − g ) Trang 10 2 2 AD AN DN DN AD ND AD Suy ra = = A .
D DI = DN.DC = = 2 2 CD CI DI DI DC DI DC
Vì AK = DC ( tính chất hcn) 2 2 AD ND 2 2
ACB = DAC cot ACB = cot DAC = = 2 2 DC DI
Điều cần chứng minh tương đương với 2 1 ND 1 1 1 1 = + = +
(luôn đúng theo hệ thức lượng trong tam giác 2 2 2 2 2 2 2 DC DI .DN DB DC DI . DB
vuông BDI có đường cao DC ). (Đpcm).
ĐỀ KIỂM TRA GIỮA HỌC KỲ I (ĐỀ 3) MÔN: TOÁN 9
Bài 1(2 điểm) Thực hiện phép tính a) A = + ( − )2 3 125 2 5 + b) B = ( + ) 20 5 2 7 11− 4 7 − 5 + 2 0 cot 32 c) 2 0 2 0 0 0
C = sin 25 + sin 65 − tan 35 + cot 55 − 0 tan 58 Bài 2(1,5 điểm).
Giải các phương trình sau:
a) 9x − 27 − x − 3 = 6 . b) 2
x + 2x +1 − x +1 = 0 Bài 3(2,5 điểm) x − 2 2 x 5 x − 2 x +1
Cho hai biểu thức A = và B = − −
với x 0; x 4 x + x +1
x − 2 x − 2 x x
1) Tính giá trị biểu thức A khi x = 9 .
2) Rút gọn biểu thức B . 1
3) Tìm các giá trị của x để B − . 2 6A
4) Tìm giá trị lớn nhất của biểu thức M = B Bài 4(3,5 điểm)
1) Một con thuyền đi qua một khúc sông theo hướng từ B đến
C (như hình vẽ) với vận tốc 3,5km / h trong 12 phút. Biết rằng
đường đi của thuyền tạo với bờ sông một góc 25 . Hãy tính
chiều rộng của khúc sông ? (Kết quả tính theo đơn vị km ,làm
tròn kết quả đến chữ số thập phân thứ hai).
2) Cho tam giác ABC nhọn có đường cao AH . Gọi E là hình
chiếu của H trên AB .
a. Biết AE = 3,6cm ; BE = 6, 4cm . Tính AH , EH và góc B. (Số đo góc làm tròn đến độ)
b. Kẻ HF vuông góc với AC tại F. Chứng minh .
AB AE = AC.AF.
c. Đường thẳng qua A và vuông góc với EF cắt BC tại D ; EF cắt AH tại O. S Chứng minh rằng AOE S = ADC 2 2 sin . B sin C
Bài 5(0,5 điểm) Giải phương trình 3
2 2x −1 = 8 − x + 3 .
----------------HẾT---------------- Trang 11 HƯỚNG DẪN
Câu 1. (2 điểm) Thực hiện phép tính a) A = + ( − )2 3 125 2 5 + b) B = ( + ) 20 5 2 7 11− 4 7 − 5 + 2 0 cot 32 c) 2 0 2 0 0 0
C = sin 25 + sin 65 − tan 35 + cot 55 − 0 tan 58 Lời giải 2
a) A = 3 125 + (2 − 5) =15 5 + 2 − 5 =15 5 + 5 − 2 = 2(8 5 − ) 1 b) + B = ( + ) 20 5 2 7 11− 4 7 − 5 + 2 2 ( + = 2 + 7 ) (2− 7)2 2 5 ( 5) − ( 5+2) ( + = 2 + 7 ) 5 (2 5 ) 2 − 7 − ( 5 + 2) = (2+ 7)( 7 − 2)− 5 = 7 − 4 − 5 = 3 − 5 0 cot 32 c) 2 0 2 0 0 0
C = sin 25 + sin 65 − tan 35 + cot 55 − 0 tan 58 0 cot 32 2 0 2 0 0 0
C = sin 25 + cos 25 − tan 35 + tan 35 − =1+ 0 −1 = 0 . 0 cot 32 Câu 2. (1,5 điểm).
Giải các phương trình sau:
a) 9x − 27 − x − 3 = 6 . b) 2
x + 2x +1 − x +1 = 0 Lời giải
a) 9x − 27 − x − 3 = 6 (ĐKXĐ: x 3 )
3 x − 3 − x − 3 = 6 2 x − 3 = 6 x − 3 = 3 x − 3 = 9
x =12 (thỏa mãn ĐKXĐ)
Kết luận: x 12 b) 2
x + 2x +1 − x +1 = 0 (ĐKXĐ: x −1) (x + )2 1 − x +1 = 0
x +1( x +1− ) 1 = 0 x +1 = 0 x +1 = 0
x = −1 (TM ) x +1 −1 = 0 x +1 = 1 x = 0 (TM ) Trang 12
Kết luận: x 1 − ; 0 Câu 3. (2,5 điểm) x − 2 2 x 5 x − 2 x +1
Cho hai biểu thức A = và B = − −
với x 0; x 4 x + x +1
x − 2 x − 2 x x
1) Tính giá trị biểu thức A khi x = 9 .
2) Rút gọn biểu thức B . 1
3) Tìm các giá trị của x để B − . 2 6A
4) Tìm giá trị lớn nhất của biểu thức M = B Lời giải
1) Khi x = 9 x = 3 thỏa mãn điều kiện.Thay vào biểu thức A ta được: 3 − 2 1 1 A = =
.Vậy khi x = 9 thì A = 9 + 3 +1 13 13 2 x 5 x − 2 x +1
2) Với x 0; x 4 ta có: B = − −
x − 2 x − 2 x x 2 x 5 x − 2 x +1 = − − x − 2 x ( x − 2) x x x x − ( x + )1( x −2 2 . 5 2 ) = − − x ( x − 2) x ( x − 2) x ( x − 2)
2x − (5 x − 2) −( x + ) 1 ( x − 2) = x ( x − 2)
2x − 5 x + 2 − x + x + 2 = x ( x − 2) ( x x x − − + )2 2 4 4 x − 2 = = = x ( x − 2) x ( x − 2) x x − 2 Vậy B =
với x 0; x 4 x 1 x − 2 1 x − 2 1 2 x − 4 + x
3) Với x 0; x 4 để B − − + 0 0 2 x 2 x 2 2 x 3 x − 4 4 16
0 mà 2 x 0 nên 3 x − 4 0 3 x 4 x x 2 x 3 9 16 1
Kết hợp với điều kiện ta được 0 x thì B − 9 2 6 A ( x −2) 6 x − ( x −2 6 2 ) x 6 x d) Ta có: M = = : = . = B x + x +1 x x + x +1 x − 2 x + x +1 6 1 M =
do x 0 x 0;
0 . Áp dụng bất đẳng thức Cô si với 2 số dương 1 x + +1 x x ta được: Trang 13 1 1 1 6 x + 2 x. = 2 x + +1 3 2 hay M 2 x x x 1 x + +1 x 1 Dấu "=: xảy ra x =
x =1( thỏa mãn đk) x
Vậy Max M = 2 x = 1 Câu 4. (3,5 điểm)
1) Một con thuyền đi qua một khúc sông theo hướng từ C
B đến C (như hình vẽ) với vận tốc 3,5km / h trong 12
phút. Biết rằng đường đi của thuyền tạo với bờ sông
một góc 25 . Hãy tính chiều rộng của khúc sông ? (Kết
quả tính theo đơn vị km ,làm tròn kết quả đến chữ số 25° thập phân thứ hai). B H
2) Cho tam giác ABC nhọn có đường cao AH . Gọi E
là hình chiếu của H trên AB .
a. Biết AE = 3,6cm ; BE = 6, 4cm . Tính AH , EH và góc B. (Số đo góc làm tròn đến độ)
b. Kẻ HF vuông góc với AC tại F. Chứng minh .
AB AE = AC.AF.
c. Đường thẳng qua A và vuông góc với EF cắt BC tại D ; EF cắt AH tại O. S Chứng minh rằng AOE S = ADC 2 2 sin . B sin C Lời giải 1 1) Đổi: 12 phút = giờ 5
Gọi chiều rộng của khúc sông là CH . Đường đi của con thuyền là BK suy ra 0 CH ⊥ BK , CBH = 25 1
Quãng đường BC dài là: 3,5. = 0,7 (km) 5
Xét BHC vuông tại H có: 0 0
CH = sin 25 . BC =sin 25 .0,7 0, 29 (km)
Vậy chiều rộng khúc sông khoảng 0,29 (km). A 3,6 E 6,4 F B H C 2)
a. Biết AE = 3,6cm ; BE = 6, 4cm . Tính AH , EH và góc B. (Số đo làm tròn đến độ)
Ta có: AB = AE + EB = 3,6 + 6, 4 = 10cm
Áp dụng hệ thức lượng trong tam giác vuông AHB có AHB = 90 ; HE ⊥ AB Ta có: 2
AH = AE.AB
AH = 3,6.10 = 36 = 6cm Và: 2
EH = AE.EB
EH = 3,6.6, 4 = 4,8cm Trang 14 AH 6 Sin B = = = 0,6 AB 10 B 36 52 ' b. Chứng minh .
AB AE = AC.AF
Xét ABH có : AHB = 90 ; HE ⊥ AB
Áp dụng hệ thức lượng trong tam giác vuông ta có: 2 A . B AE = AH (1)
Áp dụng hệ thức lượng trong tam giác vuông AHC có: AHC = 90 ; HF ⊥ AC 2
AF.AC = AH (2) Từ (1) và (2) .
AB AE = AC.AF (dpcm). c) A 3,6 E I 6,4 O F B D H C S Chứng minh: AOE S = ADC 2 2 sin . B sin C
Gọi I là giao điểm của AD và EF AE AF
Ta có: AE.AB = AF.AC = AC AB
Dễ dàng chứng minh được E A F ∽ A CB ( . c g.c)
AFI = ABH;ACD = AEO (1) Mà 0 CAD + AFI = 90 0 EAO + ABH = 90
EAO = CAD (2) Từ (1);(2) AD C ∽ AO E (g.g) 2 2 2 2 S AC AC AH AC AH ADC = = . = . 2 2 S AE AH AE AH AE AOE S S S AOE AOE AOE S = = = ADC 2 2 2 2 2 2
AH AE sin C. os c EAO sin C.sin B .
AC AH (đpcm)
Câu 5. (0,5 điểm) Giải phương trình 3
2 2x −1 = 8 − x + 3 . Lời giải 1
Điều kiện 2x −1 0 x . 2 Đặt 2
2x −1 = u u = 2x −1. 3 3 3
x + 3 = v v = x + 3 2v = 2x + 6 . 3 2
2v − u = 2x + 6 − (2x − ) 1 = 7 Trang 15 3 2
2v − u − 7 = 0 8 − v Mà 3
2 2x −1 = 8 − x + 3 2u = 8 − v u = . 2 2 8 − v 3 2v − − 7 = 0 2 2 64 −16v + v 3 2v − − 7 = 0 4 3 2
8v − 64 +16v − v − 28 = 0 3 2
8v − v +16v − 92 = 0 (v − )( 2
2 8v +15v + 46) = 0 v = 2 x + 3 = 8
x = 5 (thỏa mãn điều kiện). Vậy x = 5 .
ĐỀ KIỂM TRA GIỮA HỌC KỲ I (ĐỀ 4) MÔN: TOÁN 9
Bài 1(2,5 điểm) x +1 x − 3 1 2
Cho hai biểu thức A = và B = + −
với x 0 ; x 9 . x − 3 x − 9 x + 3 3 − x
a) Tính giá trị của biểu thức A với x = 0, 25 .
b) Rút gọn biểu thức B . c) Cho = B P
. Chứng minh rằng P 1 với mọi giá trị x thỏa mãn điều kiện. A
Bài 2(2,0 điểm)Tìm x , biết x + 3 a) 25x + 75 +15. = 2 + 4 x + 3 b) 2
x − 2x +1 = 2x + 3 25 Bài 3(1,5 điểm)
Một chiếc thang dài 3,5 m. Cần đặt chân thang cách tường một khoảng bằng bao nhiêu để nó tạo
với phương nằm ngang của mặt đất một góc an toàn 65 . (làm tròn kết quả đến chữ số thập phân thứ hai) Bài 4(3,5 điểm)
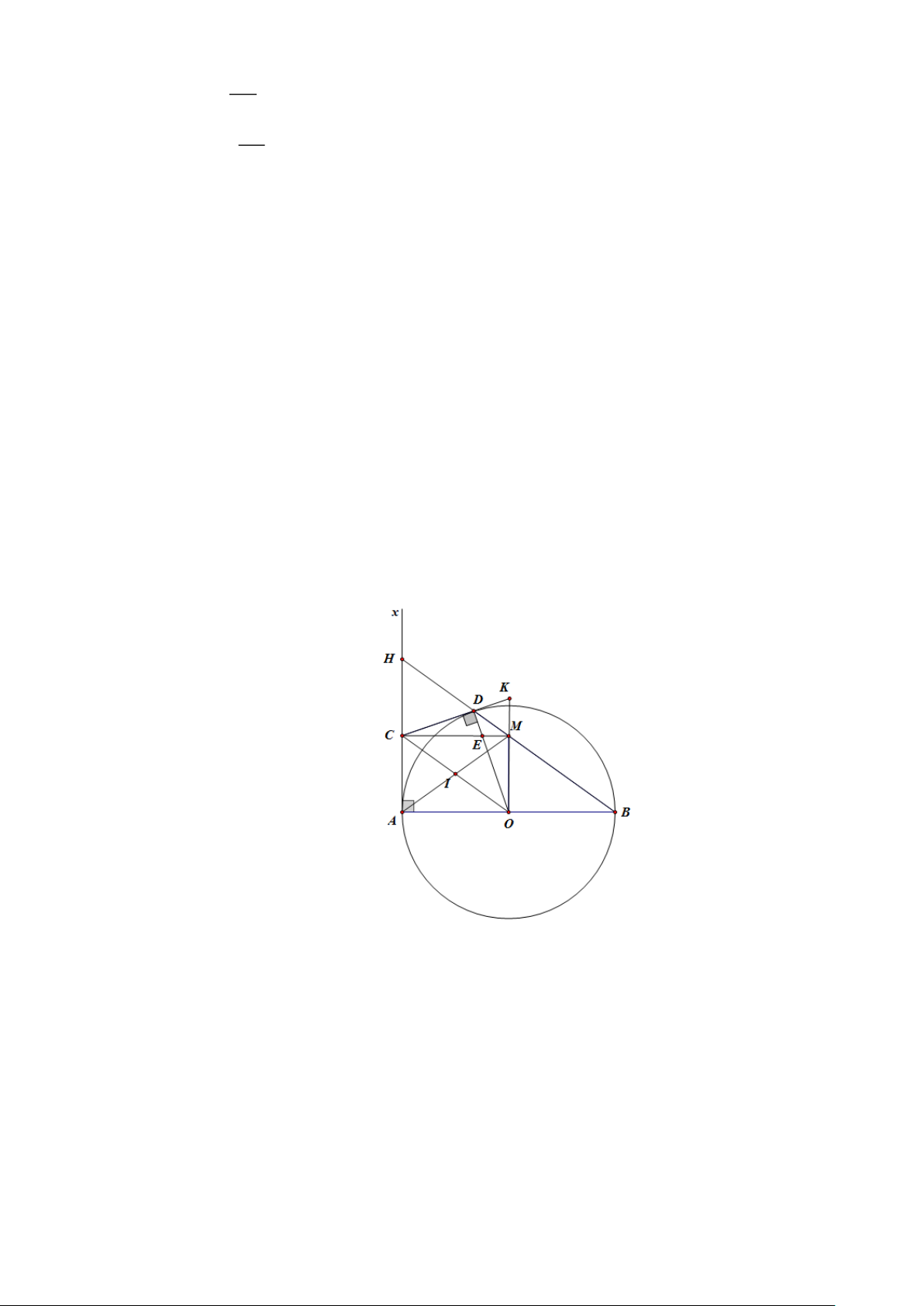
Cho đường tròn (O; R) , đường kính AB . Kẻ tiếp tuyến Ax , lấy điểm C trên Ax(AC R) . Từ C
kẻ tiếp tuyến tại CD với (O) (D là tiếp điểm ) .
a) Chứng minh bốn điểm A,C, D,O cùng thuộc một đường tròn.
b) Chứng minh OC // BD .
c) Đường thẳng vuông góc với A B tại O cắt tia BD tại M . Chứng minh OMCD là hình bình hành.
d) Gọi K là giao điểm của CD và OM , E là giao điểm của CD và OD ; I là giao điểm của AM
và OC . Chứng minh E , K , I thẳng hàng. Bài 5(0,5 điểm) Trang 16
Cho x , y , z là các số thực không âm thỏa mãn x + y + z = 1. Tính giá trị biểu thức 2 2 2
P = 2x + x +1 + 2y + y +1 + 2z + z +1
----------------Hết---------------
Giám thị không giải thích gì thêm HƯỚNG DẪN
Câu 1: (2,5 điểm) x +1 x − 3 1 2
Cho hai biểu thức A = và B = + −
với x 0 ; x 9 . x − 3 x − 9 x + 3 3 − x
a) Tính giá trị của biểu thức A với x = 0, 25 .
b) Rút gọn biểu thức B . c) Cho = B P
. Chứng minh rằng P 1 với mọi giá trị x thỏa mãn điều kiện. A Lời giải
a) Tính giá trị của biểu thức A với x = 0, 25 .
Thay x = 0, 25 (tmdk) vào biểu thức A ta được: x +1 0, 25 +1 0,5 +1 1,5 3 A = = = = = − x − 3 0, 25 − 3 0,5 − 3 2 − ,5 5
b) Rút gọn biểu thức B . x − 3 1 2 B = + −
với x 0 ; x 9 . x − 9 x + 3 3 − x x − 3 1 2 B = ( + + x + 3)( x −3) x + 3 x − 3
x − 3 + x − 3 + 2( x + 3) x + x x ( x +3 3 ) B = ( = = x + 3)( x −3)
( x +3)( x −3) ( x +3)( x −3) = x B . x − 3 c) Cho = B P
. Chứng minh rằng P 1 với mọi giá trị x thỏa mãn điều kiện: x 0 ; x 9 . A B x x + x ( x −3 1 ) = = x P : = = A x − 3
x − 3 ( x −3)( x + ) 1 x +1 x 1 − Xét P −1 = −1 = x +1 x +1 1 −
Vì x +1 0 ; −1 0 nên
0 với x 0 ; x 9 . x +1
P −1 0 với x 0 ; x 9 . P 1. Câu 2: (2,0 điểm) Tìm x , biết Trang 17 x + 3 a) 25x + 75 +15. = 2 + 4 x + 3 25 b) 2
x − 2x +1 = 2x + 3 Lời giải x + 3 a) 25x + 75 +15. = 2 + 4 x + 3 25
5 x + 3 + 3. x + 3 = 2 + 4 x + 3
5 x + 3 + 3. x + 3 − 4 x + 3 = 2
4 x + 3 = 2 (đk: x −3 ) 1 x + 3 = 2 1 x + 3 = 4 11 − x = (thỏa mãn) 4 11 −
Vậy phương trình có nghiệm x = 4 3 b) 2
x − 2x +1 = 2x + 3 (đk: x − ) 2 (x − )2 1 = 2x + 3
x −1 = 2x + 3
x −1 = 2x + 3 x −1 = 2 − x − 3
x −1 = 2x + 3 x −1 = 2 − x − 3 x = 4 − 3x = 2 x = 4 − (L) 2 x = (TM ) 3 2
Vậy phương trình có nghiệm x = 3 Câu 3: (1,5 điểm)
Một chiếc thang dài 3,5 m. Cần đặt chân thang cách tường một
khoảng bằng bao nhiêu để nó tạo với phương nằm ngang của mặt đất C
một góc an toàn 65 . (làm tròn kết quả đến chữ số thập phân thứ hai) Lời giải 3,5m
Theo đề bài ta có hình vẽ sau
Ta có BC = 3,5 m; ABC = 65 Trang 18 65o B A
Xét ABC vuông tại A , có: cos = AB ABC
(hệ thức lượng trong tam giác vuông) BC cos65 = AB 3,5 AB = 3,5.cos 65 AB 1, 48 m
Vậy cần đặt thang sao cho chân thang cách tường khoảng 1, 48 m Câu 4: (3,5 điểm)
Cho đường tròn (O; R) , đường kính AB . Kẻ tiếp tuyến Ax , lấy điểm C trên Ax(AC R) . Từ
C kẻ tiếp tuyến tại CD với (O) (D là tiếp điểm ) .
a) Chứng minh bốn điểm A,C, D,O cùng thuộc một đường tròn.
b) Chứng minh OC / /BD .
c) Đường thẳng vuông góc với A B tại O cắt tia BD tại M . Chứng minh OMCD là hình bình hành.
d) Gọi K là giao điểm của CD và OM , E là giao điểm của CD và OD ; I là giao điểm của
AM và OC . Chứng minh E, K, I thẳng hàng. Lời giải
a) Chứng minh tam giác AOC vuông tại A nên A thuộc đường tròn đường kính OC
Chứng minh tam giác DOC vuông tại D nên D thuộc đường tròn đường kính OC
Do đó bốn điểm A , C , D , O cùng thuộc một đường tròn đường kính OC .
b) Xét (O) có: CA , CD là 2 tiếp tuyến cắt nhau tại C ( gt)
Suy ra: CA = CD (tính chất 2 tiếp tuyến cắt nhau)
Suy ra: C thuộc trung trực của AD (1)
Lại có: OA = OD = R
Suy ra O thuộc đường tròn đường kính AD (2)
Từ (1) và (2) suy ra: OC là đường trung trực của AD
Suy ra: OC ⊥ AD Trang 19
Ta lại chứng minh được : BD ⊥ AD OC //BD
c) Kéo dài BD cắt AC tại H OA = OB Do
CA = CH CO//BD
CM tương tự M là trung điểm của HB
Xét tam giác AHB có OA = OB 1
CO = HB CA = CH 2 MB = CO Mà MB//CO
Suy ra OMCD là hình bình hành.
d) Chứng minh AOMC là hình chữ nhật
KMC = KDO KC = KO KOC cân tại K OD ⊥ OB Mà CM ⊥ KO
EK ⊥ CO
CM DO E
KOC cân tại K; IC = IO; EK ⊥ CO nên E , K , I thẳng hàng. Câu 5: (0,5 điểm)
Cho x, y, z là các số thực không âm thỏa mãn x + y + z = 1. Tính giá trị lớn nhất biểu thức : 2 2 2
P = 2x + x +1 + 2y + y +1 + 2z + z +1 Lời giải
Do x + y + z 1và x, y, z là các số thực không âm 2 2 2 2 2 2
0 x 1 x x x + x + x +1 x + x + x +1 2x + x +1 (x +1) Tương tự: 2 2
0 y 1 2y + y +1 (y +1) 2 2
0 z 1 2z + z +1 (z+1) Nên 2 2 2
P = 2x + x +1 + 2y + y +1 + 2z + z +1 x +1+ y +1+ z +1
P (x + y + z) + 3 = 4 P = 4 max
Dấu “=” xảy ra x = y = 0; z = 1 hoặc x = z = 0; y = 1 hoặc y = z = 0; x = 1
ĐỀ KIỂM TRA GIỮA HỌC KỲ I (ĐỀ 5) MÔN: TOÁN 9 Bài 1(2 điểm): Tính. 2 2 a) 2 9 + 6 4 − 3 25 . b) ( 3 − 2) − ( 3 + 2) . 5 + 5 3 + 3 2 1 6 c) + − ( 3 + 5) d) − + 5 3 +1 3 +1 3 − 2 3 + 3
Bài 2(2 điểm): Giải phương trình Trang 20