200 Câu Trắc Nghiệm Và Tự Luận Ôn Tập Toán 9 Giữa Học Kỳ 1 Năm 2025-2026
Một chiếc thang dài 4m. Để thang tạo được với mặt đất một góc “an toàn” là 65° (tức là đảm bảo thang không bị đổ khi sử dụng). Vậy ta cần đặt chân thang cách chân tường một khoảng cách bằng (kết quả làm tròn đến chữ số thập phân thứ hai). Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Chủ đề: Đề giữa HK1 Toán 9 299 tài liệu
Môn: Toán 9 2.8 K tài liệu
Tác giả:
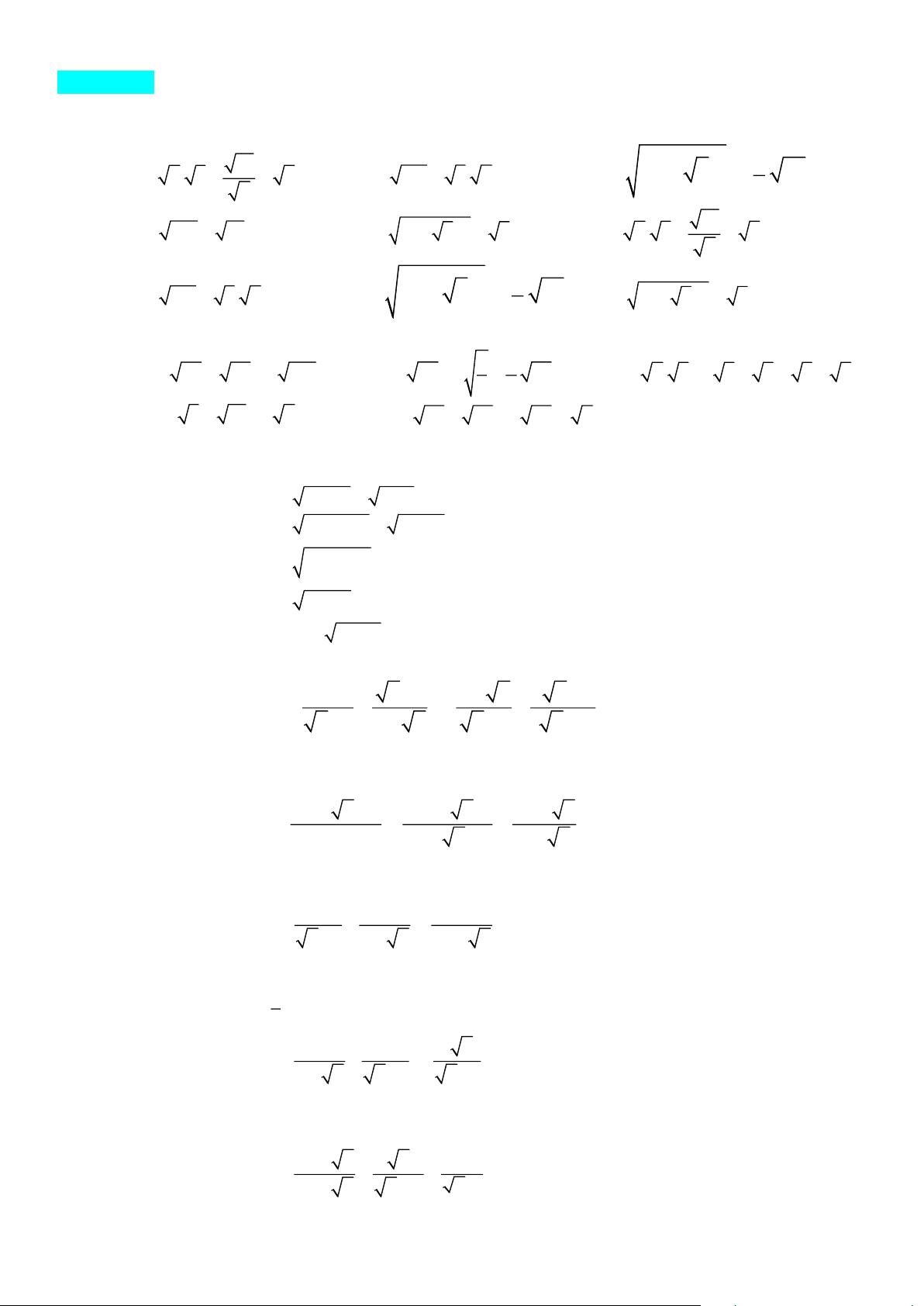
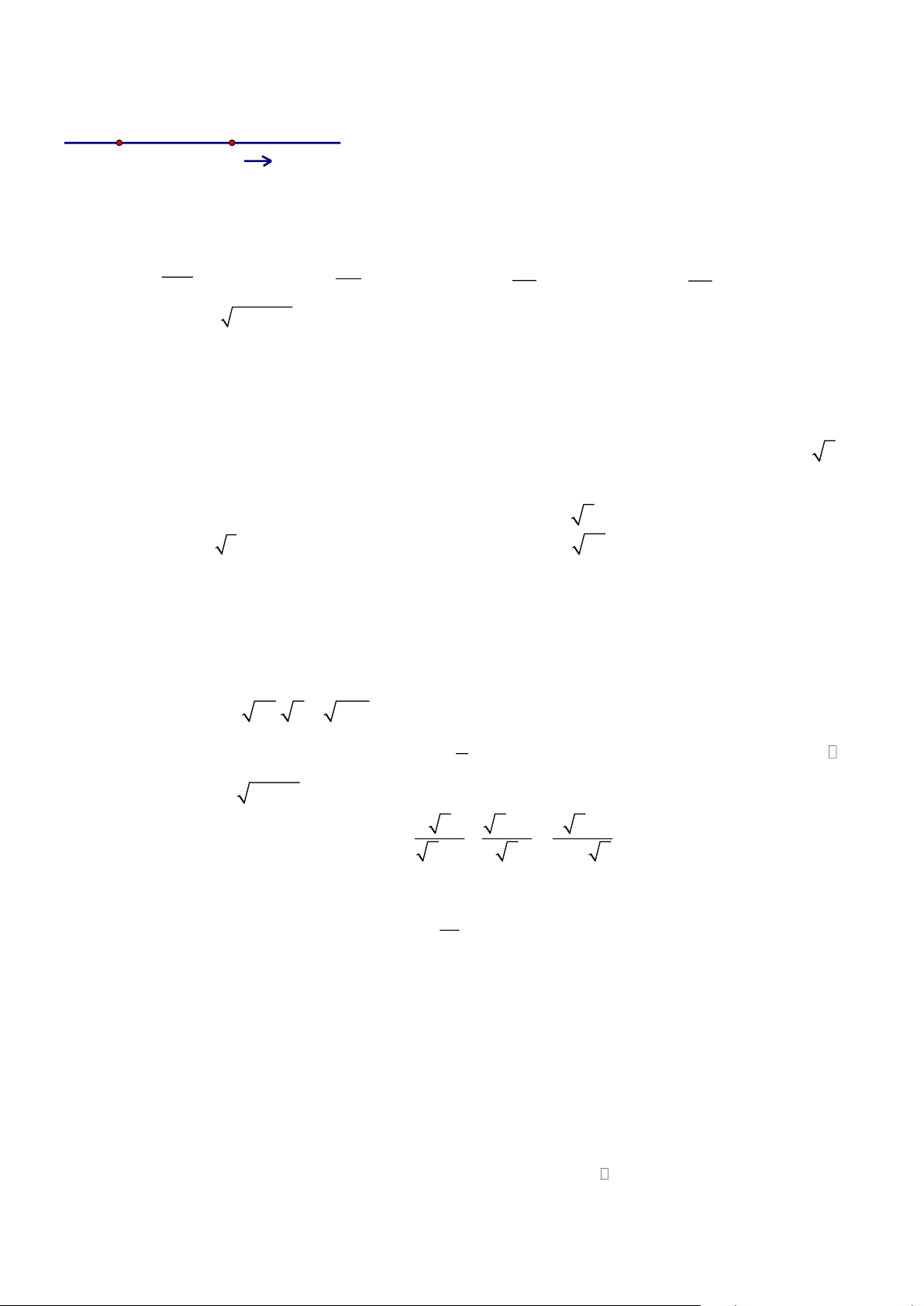
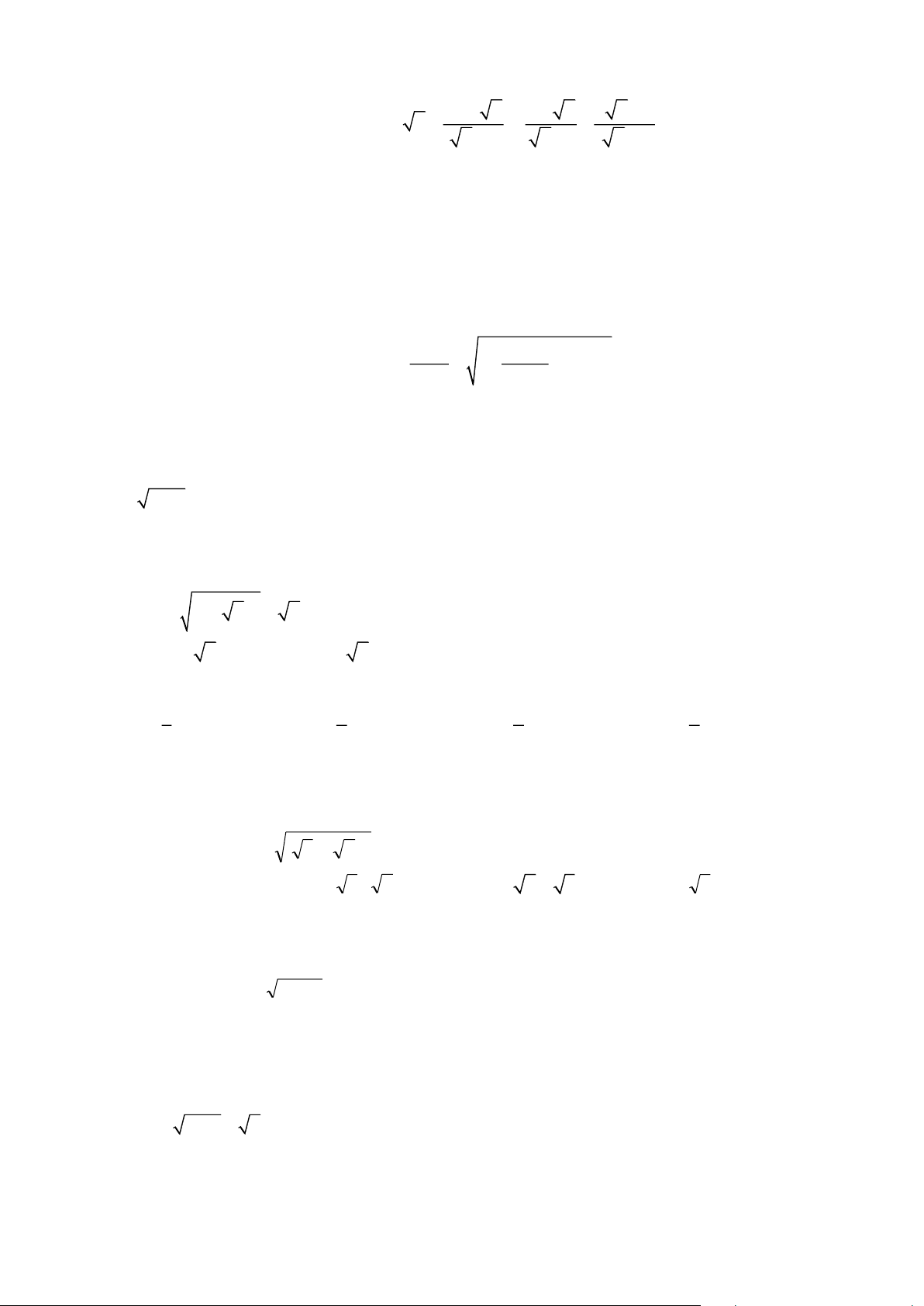
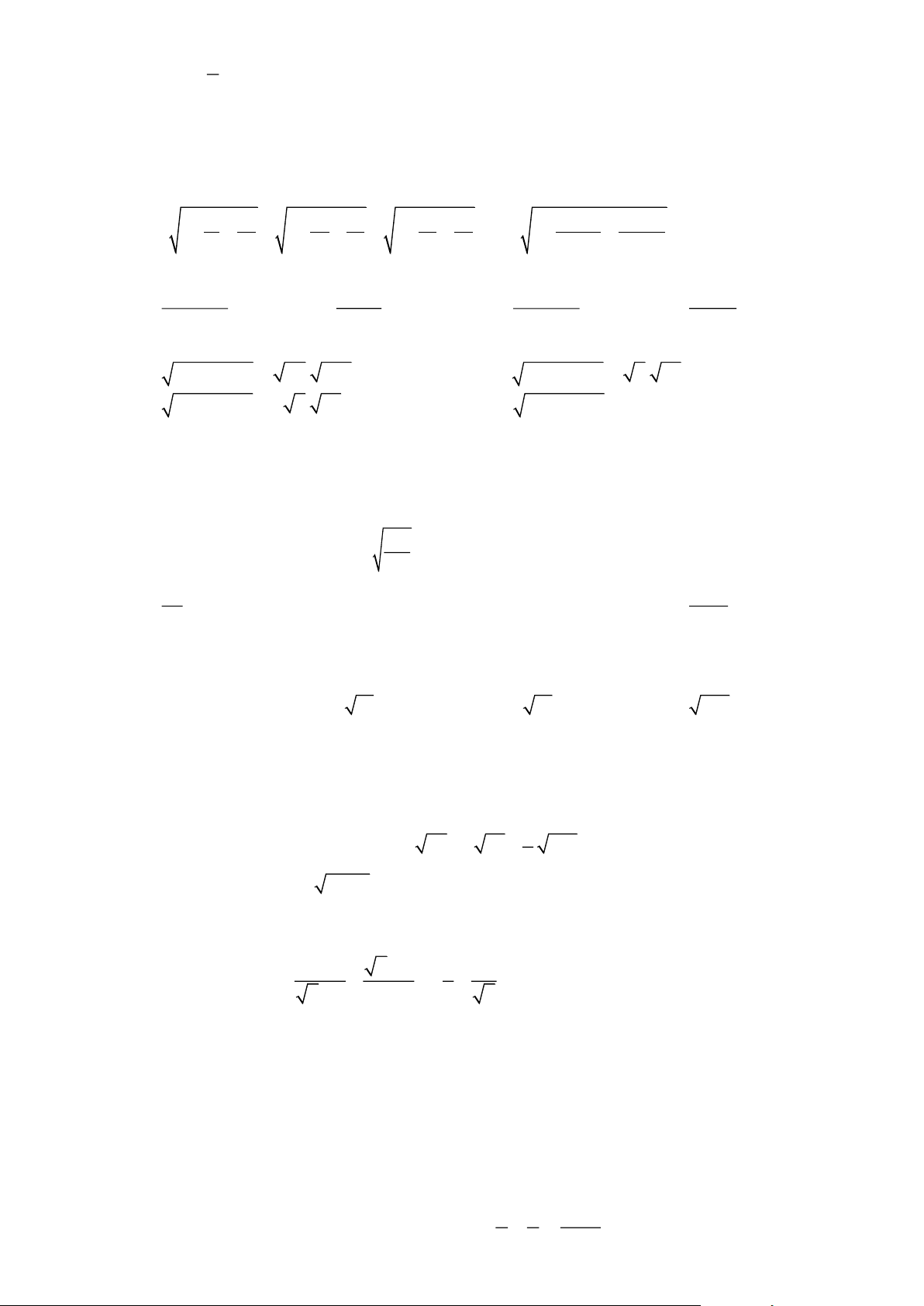
Preview text:
ÔN TẬP GIỮA HỌC KỲ I MÔN TOÁN LỚP 9 A. Trắc nghiệm.
Dạng 1. Căn bậc hai, căn bậc ba.
Câu 1. Căn bậc hai số học của 9 là: A. -3 B. 3 C. ± 3 D. 81
Câu 2. Căn bậc ba của −125 là : A. 5 B. 5 − C. 5 D. −25 −
Câu 3. Kết quả của phép tính 5 5 bằng 5 −1 A. 5. B. 5 5. C. 5 D. -5 Câu 4.
x − 5 xác định khi và chỉ khi: A. x ≥ 5 B. x < 5 C. x ≥ -5 D. x >5 1 1 +
Câu 5. Giá trị biểu thức 2 + 3 2 − 3 bằng: A. -2 1 3 B. 4 C. 0 D. 2
Câu 6. Đưa thừa số ra ngoài dấu căn của biểu thức 2
4(x −1) ta được kết quả bằng A. 2(x −1). B. 2(1− x). C. 2 x −1 . D. 4 x −1 .
Câu 7. So sánh 6 với 2 7 ta có kết luận sau: A. 6 > 2 7 B. 6 < 2 7 C. 6 = 2 7 D. 6 2 7
Câu 8. Với x − 2 − 2 = 0 thì x có giá trị bằng A. −4. B. 4. C. −2. D. 2. 17 −12 2
Câu 9. Thực hiện phép tính ta có kết quả 3 − 2 2 A. 3 + 2 2 B. 1+ 2 C. 2 −1 D. 2 − 2 Câu 10. : 2
−x + 2x −1 xác định khi và chỉ khi:
A. x R B. x = 1 C. x D. x 1
Câu 11. Phương trình 3.x = 12 có nghiệm là A. x=4 B. x=36 C. x=6 D. x=2 1 1 1 1
Câu 12. Rút gọn biểu thức A = + + + ... + 2 1 +1 2 3 2 + 2 3 4 3 + 3 4 2021 2020 + 2020 2021 ta được: 1 1 1 1 A. 1− B. C. 1− D. 2020 2020 2021 2021
Câu 13. Nếu x 2 và x − 2 = 1 thì x +1 bằng A. 6. B. 0. C. 4. D. 3.
Câu 14. Nếu x 2 và x − 2 = 1 thì x +1 bằng A. 6. B. 0. C. 4. D. 3.
Câu 15. Rút gọn biểu thức 2 4x − 4 +
36x − 36 − 2 9x − 9 với x 1 ta được kết quả là 3 A. 0. B. x −1. C. 2 x −1. D. 10 x −1.
Câu 16. Căn bậc hai số học của 36 là A. −6.
B. −6 hoặc 6.
C. −6 và 6. D. 6.
Câu 17. Tất cả các giá trị của x để −2x có nghĩa là A. x 0. B. x 0. C. x 2. D. x 2. Trang 1 −
Câu 18. Kết quả của phép tính 2 2 bằng 2 −1 A. 2 2. B. 2. C. − 2. D. −2 2.
Câu 19. Số nào sau đây có căn bậc hai số học bằng 4 ? A. 2. B. 2 4 . C. −2. D. 16.
Câu 20. Với x 6 và x − 6 − 10 = 0 thì x có giá trị bằng A. −4. B. 4. C. 16. D. 2. Câu 21. Cho 1 1 1 1 + + ++
= a b − c với a, b, c là các số tự nhiên 2 +1 3 + 2 4 + 3 101 + 100
và b là số nguyên tố. Giá trị của a + b + c bằng: A. 100. B. 103. C. 101. D. 104.
Dạng 2. Hàm số bậc nhất.
y = f (x) = (m − 2) x + Câu 22. Cho hàm số
3 biết f (1) = 2 khi đó A. m = 2. B. m = −1. C. m = 1. D. m = −2.
Câu 23. Cho hàm số y = f (x) là hàm số nghịch biến trên R. khẳng định nào sau đây là đúng
A. f (2) f (3) .
B. f (2) = f (3).
C. f (2) f (3).
D. f (2) f (3)
Câu 24. Cho hàm số f(x) = 3 – x2.Khi đó f(-1) bằng A. -2 B. -1 C. 1 D. 2
Câu 25. Gọi a là hệ số góc, b là tung độ gốc của đường thẳng y = 3 − 2 .
x Khi đó biểu thức 2a + b có giá trị bằng A. 10. B. 1. C. 4. D. −1.
Câu 26. Trong các hàm số sau, hàm số nào đồng biến trên R ? A. 1 y = x −1.
B. y = 2019 − 2020 .
x C. y = 2 − x + 3.
D. y = −2(1+ x). 2
Câu 27. Tất cả các giá trị của tham số m để hàm số y = (2 − m) x + m −1 là hàm số bậc nhất là A. m = 2. B. m 1. C. m 2. D. m = 1.
Câu 28. Hệ số góc của đường thẳng 3y − 6x = 8 là A. 2. B. −2. C. −6. D. 1 . 2
Câu 29. Hàm số y = (2m + 4) x + 3m (với m là tham số) nghịch biến trên khi A. m < 0. B. m 2. C. m −2. D. m −2.
Câu 30. Hàm số y = (3− 2m) x + m ( m là tham số) là hàm số bậc nhất khi A. m 0. B. 3 m . C. 3 m = . D. m = 0. 2 2
Câu 31. Giá trị của tham số m để hàm số y = m − 3.x + 3 là hàm số bậc nhất ? A. m 3. B. m −3. C. m 3. D. m 3.
Câu 32. Trong mặt phẳng tọa độ Oxy, đường thẳng y = (m-1)x - 1(d) đi qua điểm A(1; 3) khi đó
giá trị của m là: A. 5. B. 4. C. 2. D. 3.
Câu 33. Trong các hàm số sau, hàm số nào có đồ thị cắt trục tung tại điểm có tung độ bằng 3 ? A. 1 y = x − 3. B. 1 y = 3x − . C. 1 y = x + 2. D. 1 y = x + 3. 2 2 3 2
Câu 34. Đồ thị hàm số y = 3x + 2 cắt trục tung và trục hoành lần lượt tại A và B . Diện tích tam
giác OAB có giá trị bằng (đơn vị đo trên các trục tọa độ là centimet ). A. 4 2 − cm . B. 2 4 2 2 cm . C. 2 cm . D. 2 − cm . 3 3 3 3
Dạng 3. Hệ thức lượng trong tam giác vuông. Trang 2
Câu 35. Cho tam giác ABC vuông tại A , đường cao AH . Biết HB = 2cm, HC = 6cm . Độ dài cạnh AB là A. 6 . cm B. 12 . cm C. 4 . cm D. 8 . cm
Câu 36. Tỉ số giữa hai cạnh góc vuông của một tam giác vuông bằng 15 :13 . Tìm số đo góc nhỏ
nhất của tam giác đó. (Làm tròn đến độ) A. 0 90 . B. 0 50 . C. 0 49 . D. 0 41 .
Câu 37. Cho tam giác ABC vuông tại A có AB = 2cm, BC = 5c .
m Khi đó tanC bằng A. 1 . B. 2 . C. 2. D. 1 . 2 5 5
Câu 38. Cho tam giác ABC vuông tại A , đường cao AH . Biết BH = 4cm, B C = 9cm . Độ dài cạnh
AB là: A. 36cm. B. 6cm. C. 13 . cm D. 97 . cm
Câu 39. Tam giác DEF vuông tại D . Khi đó tan E bằng A. DE DF DE DF . B. . C. . D. . DF DE EF EF
Câu 40. Một chiếc thang dài 4m. Để thang tạo được với mặt đất một góc “an toàn” là 65° (tức là
đảm bảo thang không bị đổ khi sử dụng). Vậy ta cần đặt chân thang cách chân tường một khoảng
cách bằng (kết quả làm tròn đến chữ số thập phân thứ hai) A. 1,76 m B. 1,71 m C. 1,68 m D. 1,69 m
Câu 41. Cho góc nhọn α biết rằng cosα - sinα = 1/3. Giá trị của sinα.cosα là A. 3 B. 1 C. 3 D. 4 2 3 2 9
Câu 42. Cho tam giác ABC vuông tại A , đường cao AH . Biết BH = 2c ,
m H C = 8cm . Độ dài đường cao AH là: A. 5 2 . cm B. 16cm. C. 4 5 . cm D. 4cm.
Câu 43. Tam giác DEF vuông tại D . Khi đó cos E bằng DF DE DE DF . . . . A. EF B. DF C. EF D. DE
Câu 44. Một cột điện cao 5m có bóng trên mặt đất dài 4 .
m Khi đó tia nắng tạo với mặt đất một góc xấp xỉ bằng A. 0 38 40'. B. 0 53 8'. C. 0 51 20'. D. 0 36 52'.
Câu 45. Nếu tam giác MNP vuông tại M thì MP bằng A. N . P cos N. B. N . P sin N.
C. MN.cot N. D. N . P sin . P
Câu 46. Nếu một tam giác vuông có các cạnh góc vuông có độ dài là 2cm và 3cm thì độ dài đường
cao tương ứng với cạnh huyền bằng 6 36 A. . cm B. . cm C. 13 . cm D. 13 . cm 13 13 36 6
Dạng 4. Đường tròn:
Câu 47. Cho đường tròn ( ;10 O
cm) . Lấy một điểm I sao cho OI = 6c ,
m kẻ dây AB vuông góc với
OI tại I. Độ dài dây AB bằng A. 8 . cm B. 16 . cm C. 14 . cm D. 4 . cm
Câu 48. Cho đường tròn (O; 3cm). Khi đó dây lớn nhất của đường tròn (O; 3cm) có độ dài bằng A. 8cm. B. 6cm. C. 5 . cm D. 9 . cm
Câu 49. Cho đường tròn (O;13cm) , dây AB cách tâm O một khoảng bằng 5cm có độ dài là A. 3cm. B. 6cm. C. 24cm. D. 12cm.
Câu 50. Cho đường tròn (O;34cm) có OI vuông góc với dây MN (I Î MN) sao cho OI = 30cm , thì độ dài MN bằng Trang 3 A. 17 . cm B. 32 . cm C. 256 . cm D. 16 . cm B. Tự luận.
Dạng 1. Thực hiện phép tính. Tính giá trị của biểu thức.
Câu 51. Thực hiện phép tính: a) 12 2. 3 − + 9 . b) 121 − 8. 2 c) ( - )2 1 2 5 - 20 2 2 d) 144 − 81 e) 2 (3 − 5) + 5 f) 12 2. 3 − + 9 2 g) 121 − 8. 2 h) ( - )2 1 2 5 - 20 i) 2 (3 − 5) + 5 2
Câu 52. Tính giá trị của biểu thức: 1 1 3 3 3 A = 27 + 64 − 2 125. B = 27 + 3 − 48.
P = 2. 8 − ( 3 + 5)( 3 − 5). 3 2
E = 2 8 + 18 − 5 2 D = ( 50 − 32 + 2 72): 2.
Dạng 2. Giải phương trình.
Câu 53. Giải phương trình: 9x + 9 + x +1 = 12
Câu 54. Giải phương trình: 25x + 25 − 9x + 9 = 6 ( x − )2 3 2 = 7
Câu 55. Giải phương trình: .
Câu 56. Giải phương trình: 4x + 4 − 3 = 7
Câu 57. Giải phương trình sau: 9x − 9 −12 = 0
Dạng 3. Rút gọn biểu thức và bài toán liên quan. 2
x +1 x + x 2 x − 2 − . − − − + −
Câu 58. Cho biểu thức A = x 1 x x x 1 x 1
(với x 0; x 1) a) Rút gọn biểu thức A
b) Tìm các giá trị của x để A có giá trị âm
Câu 59. Cho biểu thức x + 2 x + 1 x - x x - 2 x A = + -
với x > 0 , x ¹ 1. x - 1 x - 2 x + 1 x - x
a) Rút gọn biểu thức A .
b) Tìm các giá trị của x để biểu thức A có giá trị bằng 2. 1 1 x − 4 P = − :
Câu 60. Cho biểu thức
x −1 x − x x − 2 x với x > 0; x ¹ 1; x ¹ 4.
a) Rút gọn biểu thức P. b) Tìm x để 1 P . 3 1 1 5 x A = + .
Câu 61. Cho biểu thức x − x x −1
x +1 (với x 0; x 1)
a) Rút gọn biểu thức A.
b) Tìm các giá trị nguyên của x để biểu thức A nhận giá trị nguyên. x + 2 x x 1 A = + . − − x 1 +
Câu 62. Cho biểu thức x 2 x x 2
(với x 0; x 4 )
a) Rút gọn biểu thức A. Trang 4
b) Tìm x để A 0. 1 1 x − 4 A = − .
Câu 63. Cho biểu thức x − 2 x + 2
x + 3 (với x 0; x 4)
a) Rút gọn biểu thức A. b) Tìm x để 1 A . 2 x + 2 x x
Câu 64. Cho biểu thức: A = + : x +1
(với x > 0 và x 4 ) x 2 x x 2 − − a) Rút gọn biểu thứcA.
b) Tính giá trị của biểu thức A khi x = 8.
Dạng 4. Các bài toán về hàm số bậc nhất.
Câu 65. Hàm số y = (45 − 2023)x + 2 là hàm số đồng biến hay nghịch biến trên ? Vì sao ?
Câu 66. Hàm số y = (2 2 − 3) x +1 là hàm số đồng biến hay nghịch biến trên ? Vì sao?
Câu 67. Hàm số y = (89− 2 2023) x − 2022 là hàm số đồng biến hay nghịch biến trên ? Vì sao ?
Câu 68. Tìm giá trị của m để đồ thị của hàm số bậc nhất y = (2m +1)x − 5 cắt trục hoành tại điểm có hoành độ bằng −5.
Câu 69. Tìm hệ số b khi biết đường thẳng y = 3 x + b đi qua điểm M ( 1 − ;2).
Câu 70. Tìm các giá trị của m để đường thẳng (d): y = mx − 3 (với m 0 ) đi qua điểm ( A −1; 2).
Câu 71. Cho hai đường thẳng y = 2
− m x − 3, (m 0) và 5
y = (3m − 5)x +1, (m ). Tìm giá trị của 3
m để hai đường thẳng đã cho song song với nhau
Câu 72. Cho hai hàm số bậc nhất y = 5m x −1 và y = (m −1)x + 3. Tìm giá trị của m để đồ thị của
hai hàm số đã cho là hai đường thẳng cắt nhau.
Câu 73. Tìm các giá trị của m để đường thẳng (d ): y = (m + )
1 x − 3 − m cắt trục hoành tại điểm có hoành độ bằng 2.
Dạng 5. Các bài toán hình học.
Câu 74. Cho ABC vuông tại A, đường cao AH. Biết BH = 18 cm; HC = 32 cm.
a) Tính độ dài AH, số đo góc B và góc C ( kết quả làm tròn đến phút).
b) Tia phân giác của góc BAC cắt BC tại D. Tính độ dài AD ( kết quả làm tròn đến số thập phân thứ
Câu 75. Cho ABC có ba góc nhọn nội tiếp đường tròn (O;R) và AB < AC. Kẻ đường kính AD
của đường tròn. Gọi H là trực tâm của ABC . a) Tính ACD .
b) Chứng minh tứ giác BHCD là hình bình hành.
Câu 76. Cho tam giác ABC có AB = 15 cm, AC =20 cm, BC = 25 cm.
a) Chứng minh tam giác ABC vuông tạiA. Tính độ dài đường cao AH.
b) Đường phân giác của góc A cắt BC tạiD. Từ D kẻ DE và DF lần lượt vuông góc với AB và
AC(E AB , F AC ). Tứ giác AEDF là hình gì? Vì sao? Tính diện tích tứ giác AEDF.
Câu 77. 1) Cho ABC vuông tại A., đường cao AH. Biết AC = 12 cm; BC = 13 cm.
a) Tính số đo góc B, góc C ( kết quả làm tròn đến phút).
b) Tính độ dài đường cao AH.
2) Cho đường tròn tâm O , bán kính R =10cm. Kẻ dây cung AB =16 cm. Tính khoảng
cách từ tâm O đến dây cung AB
Dạng 6. Bài tập nâng cao. Trang 5 2 2022 2022
Câu 78. Chứng minh rằng A = 2 1+ 2022 + +
có giá trị là số tự nhiên. 2 2023 2023
Câu 79. Giải phương trình x−2+ 10 3 − x 5 = − . x 4(x + 2020 1)x − 2019 2x + 2x +
Câu 80. Tính giá trị của biểu thức = 1 1 3 P với x = − . 2 2x + 3x 2 3 − 2 2 3 + 2
Câu 81. Cho a, b,c là ba số hữu tỉ thoả mãn điều kiện ab + bc + ca = 1. Chứng minh rằng 2 2 2
P = (a +1)(b +1)(c +1) là một số hữu tỉ.
MỘT SỐ ĐỀ THAM KHẢO: Đề 1:
PHẦN TRẮC NGHIỆM (3,0 điểm).
Câu 1. Giá trị của m để hàm số y = (m + 2)x −1 đồng biến trên R là: A. m −2 B. m −2 C. m −2 D. m −2
Câu 2. Cho ABC vuông tại A, biết BC = 15cm; AC = 8cm. SinB bằng: A. 15 B. 15 C. 8 D. 8 8 17 15 17
Câu 3. Điểm thuộc đồ thị hàm số y = 3x - 5 là A. (1; 2 − ) B. (1;2) C. ( 2 − ; ) 1 D. (2;− ) 1
Câu 4. Hàm số nào dưới đây đồng biến trên R ? 1
A. y = 4x −1. B. y = 5 − . x 2
C. y = −3x +1.
D. y = 1− 2x .
Câu 5. Căn bậc hai của 16 là: A. 196 B. 4 C. -4 D. ± 4
Câu 6. Các tia nắng tạo với mặt đất một góc 45 . Nếu một người cao 1,6 m thì bóng của người đó
trên mặt đất (đơn vị theo m) là: A. 0,8 B. 1,2 C. 1 D. 1,6 Câu 7.
x − 5 xác định khi và chỉ khi: A. x < 5 B. x >5 C. x ≥ -5 D. x ≥ 5
Câu 8. Cho hai đường thẳng d: y= x - 2 và d′: y = 2x + m ( m là tham số khác 0). Giá trị của m để
đường thẳng (d′) cắt đường thẳng (d ) tại một điểm trên trục tung là: A. m 2 B. m = −2 C. m = 2 D. m = 2;
Câu 9. Nếu 5 + x = 4 thì x bằng: A. x = 121 B. x = 11 C. x = 4 D. x = - 1 Câu 10. Cho 1 1 1 1 + + ++
= a b − c với a, b, c là các số tự nhiên 2 +1 3 + 2 4 + 3 101 + 100
và b là số nguyên tố. Giá trị của a + b + c bằng: A. 100. B. 103. C. 101. D. 104. 2
Câu 11. (2x +1) bằng: A. − 2x +1 B. 2x +1 C. - (2x+1) D. 2x+1 Câu 12. Tính ( − )2
3 2 − 2 có kết quả là: A. 3 B. − 3 C. 3 − 4 D. 4 − 3 Trang 6 2 2
Câu 13. Giá trị biểu thức + bằng: 3 + 2 2 3 − 2 2 A. 8 2 B. -12 C. 12 D. -8 2
Câu 14. Nếu hai đường tròn (O) và đường tròn (O’) có bán kính lần lượt là 5 cm và 3 cm, khoảng
cách hai tâm OO’= 7 cm thì hai đường tròn
A. không có điểm chung B. cắt nhau C. tiếp xúc ngoài D. tiếp xúc trong
Câu 15. Cho ( O; 5cm ), một dây cung AB= 6 cm. Khoảng cách từ O đến dây AB là A. 8 cm B. 3 cm C. 4 cm D. 5 cm
Câu 16. Căn bậc ba của -125 là:
A. không tồn tại căn bậc ba của -125. B. -5 C. 5 . D. 5. 2 x − 2x +1
Câu 17. Khi x 1 rút gọn biểu thức A = ta được kết quả là x −1 A. A = 1 B. A = 2.
C. A = x −1. D. A = −1.
Câu 18. Cho tam giác ABC vuông tại A ( AB AC), đường cao AH . Biết AH = 6c , m B C = 13cm .
Độ dài cạnh AC là: A. 7 cm. B. 2 13 . cm C. 205 . cm D. 3 13 cm. 2
Câu 19. x = 5 thì x bằng: A. ±5 B. 25 C. ± 25 D. 5
Câu 20. Trong các điểm sau điểm nào thuộc đồ thị hàm số y =2x - 1. A. (−2;−3) B. (2;1) C. (−1;−3) D. (−3;−1)
PHẦN TỰ LUẬN (7,0 điểm).
Câu 21. (3,0 điểm):
1) Tính giá trị của biểu thức: 8 + 72 − 2 18
2) Giải phương trình: 4x − 4 + 9x − 9 =10
3) Tìm các giá trị của m để đường thẳng (d): y = (m −1)x − 3 (với m 1) song song với
đường thẳng y = 2x +1. −
Câu 22. (1,5 điểm): Cho biểu thức 1 2 x 3 P = − . ( x , 0 x 9 )
x − 3 x − 9 x +1 1) Rút gọn P. 2) Tìm x để 1 P = . 5
Câu 23. (2,0 điểm):
1) Cho ABC vuông tại A đường cao AH. Biết BH = 18 cm; HC = 32 cm.
a. Tính độ dài AH ; AB.
b. Tính số đo góc B và gócC.
2) Cho đường tròn (O;R). Từ một điểm A bên ngoài đường tròn kẻ tiếp tuyến AB với
đường tròn (B là tiếp điểm). Trên đường tròn lấy điểm C ( C khác B) sao cho AB=AC.
Chứng minh AC là tiếp tuyến của đường tròn (O;R).
x x − 2x + 2 x +14
Câu 24. (0,5 điểm): Cho x 0 tìm giá trị nhỏ nhất của biểu thức P = + 2016. x +1 Đề 2:
PHẦN I. TRẮC NGHIỆM (3,0 điểm) Trang 7
Câu 1. Một mảnh đất hình vuông có diện tích 2
600m . Độ dài cạnh của hình vuông (kết quả làm
tròn đến chữ số thập phân thứ nhất) là A. 24,5m B. 24, 4m C. 10 6m D. 24m
Câu 2. Các căn bậc hai của 64 là A. 8 B. −8 C. 8 D. 64
Câu 3. Biểu thức x + 6 xác định khi và chỉ khi A. x −6 B. x 0 C. x 36 D. x 0
Câu 4. Số nhỏ nhất trong các số 5 2;2 6;3 5;4 3 là A. 3 5 B. 4 3 C. 5 2 D. 2 6 1 −
Câu 5. Cho hàm số y = f (x) =
x + 3. Khẳng định sau đây là sai? 2
A. f (6) f (7) B. f (2) = 2 C. f ( ) 7 1 = D. f (− ) 7 1 = 2 2
Câu 6. Rút gọn biểu thức ( − )2 2 3 được kết quả là A. 3 − 2 B. 2 − 3 C. 3 + 2 D. 4 − 2 3
Câu 7. Căn bậc ba của −8 là A. 2 B. 2 C. −2 D. −8
Câu 8. Tập nghiệm của bất phương trình x +1 2 là
A. x | x 3 B. x | 1 − x 3 C. x | 1 − x 1 D. x | 1 − x 5 b
Câu 9. Rút gọn biểu thức 2 2a
− 4a b với a 0,b 0 được kết quả là 4 A. a b B. −a b C. 3a b D. −1,5a b
Câu 10. Cho đường tròn (O; R) . Khẳng định nào là đúng?
A. Đường tròn là hình có vô số tâm đối xứng
B. Đường tròn là hình có vô số trục đối xứng
C. Nếu điểm A nằm trong đường tròn thì đoạn OA = R
D. Nếu ba điểm A, B, C thuộc đường tròn thì tam giác ABC là tam giác vuông
Câu 11. Trong các hàm số sau, hàm số nào là hàm số bậc nhất một ẩn?
A. y = 3 x + 2 B. 2 y = x − 2
C. y = 7 − x
D. y = mx + 6 với m . R
Câu 12. Cho đường thẳng (d ) : y = 3x + 4 , kết luận nào sau đây đúng ?
A. Đường thẳng (d ) luôn song song với trục hoành
B. Đường thẳng (d ) luôn đi qua gốc tọa độ.
C. Đường thẳng (d ) có hệ số góc là 4 .
D. Đường thẳng (d ) có hệ số góc là 3.
Câu 13. Cho tam giác ABC vuông tại A, đường cao AH. Khẳng định nào sau đây là đúng? A. 2
AB = BC.HC. B. 2
AC = BC.BH. C. 2 AH = A . B AC.
D. AH.BC = . AB AC.
Câu 14. Khẳng định nào sau đây là sai ? A. 2 0 2 0 cos 10 + cos 80 =1. B. 0 0 sin10 = cos80 . C. 0 0 tan80 = cot10 . D. 0 0 tan10 cot80 =1. Trang 8
Câu 15. Khoảng cách từ A đến B là 12km , một người đi xe máy từ B ngược với chiều từ B đến A
với vận tốc 30km / h . Sau t giờ (t 0) , người đó cách A một quãng đường là S . Khi đó mối quan
hệ của hàm số S và biến t là A 12 km B
A. S = 5t + 3
B. S = 12t + 30
C. S = 30t +12
D. S = 30t
Câu 16. Cho tam giác ABC vuông tạiA. Giá trị của tanC là AB A. B. AB C. AC D. AC AC BC AB BC
Câu 17. Biểu thức 10 − 2x xác định khi và chỉ khi A. x 5 B. x 5 C. x 5 D. x 10
Câu 18. Một cột điện cao thế cao 20m có bóng trên mặt đất dài 8m . Góc mà tia sáng Mặt Trời tạo
với mặt đất (làm tròn đến độ) là A. 0 69 B. 0 68 C. 0 22 D. 0 90
Câu 19. Cho đường tròn ( ;
O 5cm), đường kính AB vuông góc với dây CD tại H. Biết OH = 5cm . Khẳng định đúng là?
A. AB CD
B. CD = 2 5cm
C. CD = 4 5cm .
D. CD = 2 30cm .
Câu 20. Với giá trị nào của m thì đường thẳng y = (m – 3) x + 6 (với m 3) song song với đường
thẳng y = 2 − x ? A. m = 1. B. m = 2 C. m = 5 D. m = −2
Phần II. TỰ LUẬN (7 điểm)
Câu 21. (3 điểm) 1) Rút gọn: 3 A = 25. 9 − 27 − . 1
2) Cho hàm số y = (4m − 2) x +1 với m . Tìm tham số m để hàm số ngịch biến trên . 2
3) Tìm x , biết 4x − 4 − 9 = 0 . − −
Câu 22. (1,5 điểm) Rút gọn biểu thức x x 3 3 x 9 A = − :
với x 0, x 9 . x 3 x + x + 3 x
Câu 23. (2 điểm) Cho tam giác ABC vuông tại A, kẻ đường cao AH. Biết AB = 4c , m AC = 7,5cm .
1)Tính BC, CotB và chứng minh 2 8 AB = BC.AH . 15
2)Vẽ đường tròn tâm I đường kính BH, vẽ đường tròn tâm J đường kính CH. Hãy xác định vị
trí tương đối của hai đường tròn (I ),( J ) ?
Câu 24. (0,5 điểm) Sự tương quan giữa nhiệt độ C và nhiệt độ F là một hàm số bậc nhất:
t = at + b . Biết rằng nước đóng băng ở 320F và sôi ở 2120F. Hỏi 1000F ứng với bao nhiêu độ C? F C
----------------Hết---------------- Đề 3:
PHẦN I. TRẮC NGHIỆM (3 điểm)
Câu 1. Hàm số y = mx + m − 2 (với m là tham số) đồng biến trên khi A. m 0. B. m 2. C. m 2. D. m 0. Trang 9 −
Câu 2. Tung độ gốc của đường thẳng 3 5 y = x + bằng 4 2 − − − A. 5. B. 3. C. 3 . x D. 5 . 2 4 4 2
Câu 3. Nếu tam giác MNP vuông tại M thì cos N bằng A. MN MP MN MP . B. . C. . D. . PN PN PM MN
Câu 4. Đường tròn là hình
A. Có hai trục đối xứng
B. Có vô số trục đối xứng
C. Có một trục đối xứng
D. Không có trục đối xứng
Câu 5. Đường thẳng a cách tâm O của đường tròn (O; R) một khoảng bằng d. Đường thẳng a là
tiếp tuyến của (O; R) khi A. d = . R B. d . R C. d . R D. d . R
Câu 6. Nếu một tam giác vuông có các cạnh góc vuông dài là 4,5cm và 6cm thì độ dài đường
cao tương ứng với cạnh huyền bằng A. 7,5 cm B. 3,5 cm C. 3,6 cm D. 5 cm
Câu 7. Căn bậc hai của 36 là A. 6 và -6 B. -6 C. 36 D. 6
Câu 8. Trong các hàm số sau, hàm số nào nghịch biến trên R ? A. 1 y = x +1 . B. y = 7 − 5 . x
C. y = 3x − 5
D. y = −2(1− x). 2 1 Câu 9. Biểu thức có nghĩa khi nào? a A. a ≠ 0 B. a ≥ 0 C. a > 0 D. a ≤ 0
Câu 10. Căn bậc ba của -125 là A. 5 B. 25 C. -5 D. -25
Câu 11. Cho ABC vuông tạiA. Khẳng định nào sau đây là đúng?
A. sin B = cosC
B.sin B = sin C .
C. cot B = cosC D. tanB = tanC .
Câu 12. Kết quả đưa thừa số vào trong dấu căn của biều thức x y với x 0, y 0 là
A. − | x | y B. 2 x y C. 2 − x y
D. | x | y
Câu 13. Cho tam giác ABC vuông tại A, đường cao AH (H BC). Trong các hệ thức sau hệ thức nào sai? A. 2
AB = BC.BH B. 2
AC = BC.BH C. 2
AH = BH.CH D. .
AB AC = BC.AH
Câu 14. Kết quả khai căn của biểu thức: 2 ( 3 −1) là A. 1- 3 B. -1- 3 C. 3 + 1 D. 3 -1
Câu 15. Tâm của đường tròn ngoại tiếp tam giác là giao điểm của
A. Ba đường cao của tam giác đó.
C. Ba đường phân giác của tam giác đó.
B. Ba đường trung tuyến của tam giác đó.
D. Ba đường trung trực của tam giác đó.
PHẦN II. TỰ LUẬN (7 điểm)
Câu 16. (3điểm).
1. Tính giá trị của biểu thức A = 3. 27 − 50 : 2.
2. Hàm số y = (45− 2023) x − 2024 là hàm số đồng biến hay nghịch biến trên ? Tại sao? Trang 10
3. Viết các tỉ số lượng giác sau thành tỉ số lượng giác của góc nhỏ hơn 450
cos650; tan 470; sin730; cot520 + − +
Câu 17. (1 điểm). Rút gọn biểu thức 6 2 x x x 2 x 2 A = x + −
với x 0; x 1. x 3 x 1 x 1 + − +
Câu 18. (2,5 điểm)
Cho ABC vuông tại A, đường cao AH chia cạnh huyền BC thành hai đoạn BH = 3,6cm và
HC = 6,4 cm. Trên cạnh AClấy điểm M (M ,
A M C ) . Kẻ AD vuông góc với MB tạiD.
1. Tính AB; AC; góc B; góc C (số đo góc làm tròn đến phút)
2. Chứng minh BD.BM=BH.BC.
3. Chứng minh 4 điểm A; B; H; D cùng thuộc một đường tròn. Chứng minh AC là tiếp tuyến của đường tròn đó 2 2022 2022
Câu 19. (0.5điểm) Thu gọn biểu thức: 2 P = + 1+ + 2022 . 2 2023 2023
………………………. Hết……………………. Đề 4:
PHẦN TRẮC NGHIỆM (3,0 điểm). Câu 1.
x + 5 xác định khi và chỉ khi: A. x ≥ 5 B. x < 5 C. x ≥ -5 D. x >5
Câu 2. Căn bậc hai số học của 16 là: A. -4 B. 4 C. ± 4 D. 196 Câu 3. Tính ( − )2 1 2 − 2 có kết quả là: A. 1− 2 2 B. 2 2 −1 C. 1 D. 1 −
Câu 4. Cho tam giác ABC vuông tại A , có BC =10c ,
m AC = 8cm . Sin ABC bằng: A. 3 B. 4 C. 3 D. 4 5 5 4 3
Câu 5. Cho hai đường thẳng d: y=4x+7 và d′: y = m2x + m+5 ( m là tham số khác 0). Giá trị của
m để đường thẳng (d′) song song với đường thẳng (d ) là: A. m = 4. B. m = 2 C. m = −2. D. m = 2 ;
Câu 6. Giá trị biểu thức ( 3 − )2 2 bằng: A. 1 B. 3 - 2 C. 2 − 3 D. 5
Câu 7. Cho đường thẳng a và một điểm O cách a là 5cm. Số điểm chung của đường thẳng a và đường tròn (O;5cm) là: A. 0 B. 1 C. 2 D. 3
Câu 8. Giá trị của x để 2x +1 = 3 là: A. x = 13 B. x =14 C. x =1 D. x =4
Câu 9. Cho hàm số y = f ( x) = 3x − 2, biết y = 4 thì x bằng: A. 4 B. −4 C. −2 D. 2
Câu 10. Với x − 2 − 2 = 0 thì x có giá trị bằng A. −4. B. 4. C. −2. D. 2.
Câu 11. Căn bậc ba của 64 là : A. 8 B. -8 C. 4 D. 4
Câu 12. Hàm số nào dưới đây đồng biến trên R ? Trang 11 1 A. y = − . x
B. y = 2x −1.
y = − x D. y = −3x +1. 2 C. 1 2
Câu 13. Một cái cây có bóng trên mặt đất dài 8m, biết tại thời điểm đó tia sáng mặt trời tạo với mặt
đất một góc bằng 500. Chiều cao của cây đó là ( kết quả làm tròn đến số thập phân thứ hai): A. 9,53 m B. 8 m C. 6,13 m D. 5,14 m
Câu 14. Cho biểu thức 1 1 1 1 1 1 1 1 E = 1+ + + 1+ + + 1+ + +...+ 1+ + 2 2 2 2 2 2 2 2 1 2 2 3 3 4 2021 2022
Giá trị của biểu thức E bằng: 2 2 A. 4088483 B. 2021 C. 4088483 D. 2022 2021 2022 2022 2021
Câu 15. Khẳng định nào đúng ? A. ( 4) − .( 25 − ) = 4 − . 25 − . B. ( 4 − ).( 2 − 5) = 4. 25. C. ( 4) − .( 25 − ) = − 4. 25. D. ( 4 − ).( 2 − 5) = −(4.25).
Câu 16. Giá trị của m để hàm số y = (m − 2)x − 2 nghịch biến trên R là:
A. m 2
B. m 2
C. m 2 D. m 2
Câu 17. Cho ( O ; 5cm ), một dây cung cách tâm O là 3cm. Độ dài của dây đó là : A. 8 cm B. 3 cm C. 4 cm D. 5 cm 4
Câu 18. Kết quả rút gọn biểu thức a 2 2b với b < 0 là: 2 4b 2 a 2 2 a b A. B. a2b C. -a2b D. 2 2 b
Câu 19. Cho tam giác ABC vuông tại A ( AB AC ) , đường cao AH . Biết AH = 6c , m B C = 13cm .
Độ dài cạnh AC là: A. 7 cm. B. 3 13 cm. C. 2 13 . cm D. 205 . cm
Câu 20. Trong các điểm sau điểm nào thuộc đồ thị hàm số y =2x+1. A. (1;3) B. (3;1) C. (−1;−3) D. (−3;−1)
PHẦN TỰ LUẬN (7,0 điểm).
Câu 21. (3,0 điểm)
1) Tính giá trị của biểu thức: 1 A = 6 27 − 2 75 − 300. 2
2) Giải phương trình: 2x −1 +1 = 6
3) Tìm các giá trị của m để đường thẳng (d): y = mx − 3 (với m 0 ) đi qua điểm ( A 1; 2).
Câu 22. (1,5 điểm) + Cho biểu thức 5 x 2 1 1 P = − −
với x 0; x 4 x − 2 x − 4 2 x
1) Rút gọn biểu thức P.
2) Tìm x nguyên để P nhận giá trị nguyên.
Câu 23. (2,0 điểm):
1) Cho ABC vuông tại A., đường cao AH. Biết AC = 12 cm; BC = 13 cm.
a) Tính số đo góc B, góc C ( kết quả làm tròn đến phút).
b) Tính độ dài đường cao AH.
2) Cho đường tròn tâm O , bán kính R =10cm. Kẻ dây cung AB =16 cm. Tính khoảng
cách từ tâm O đến dây cung AB 1 1 1
Câu 24. (0,5 điểm): Cho x 2021; y 2021 thỏa mãn: + = . x y 2021 Trang 12 x + y Chứng minh rằng: = 1 x − 2021+ y − 2021
----------------Hết---------------- Trang 13