































































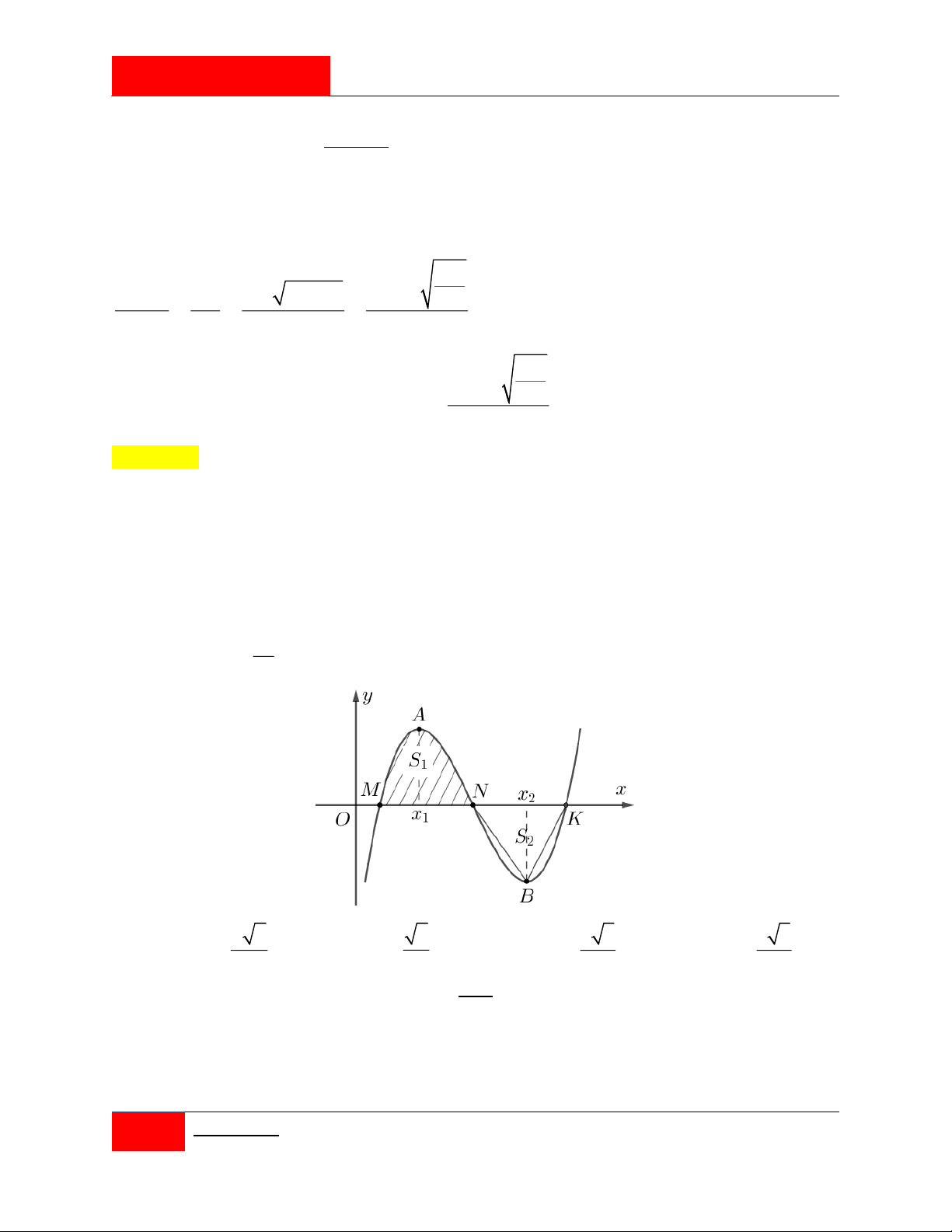
















































Preview text:
201 câu hỏ i hay Phầ n 2 Câu hỏ i
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
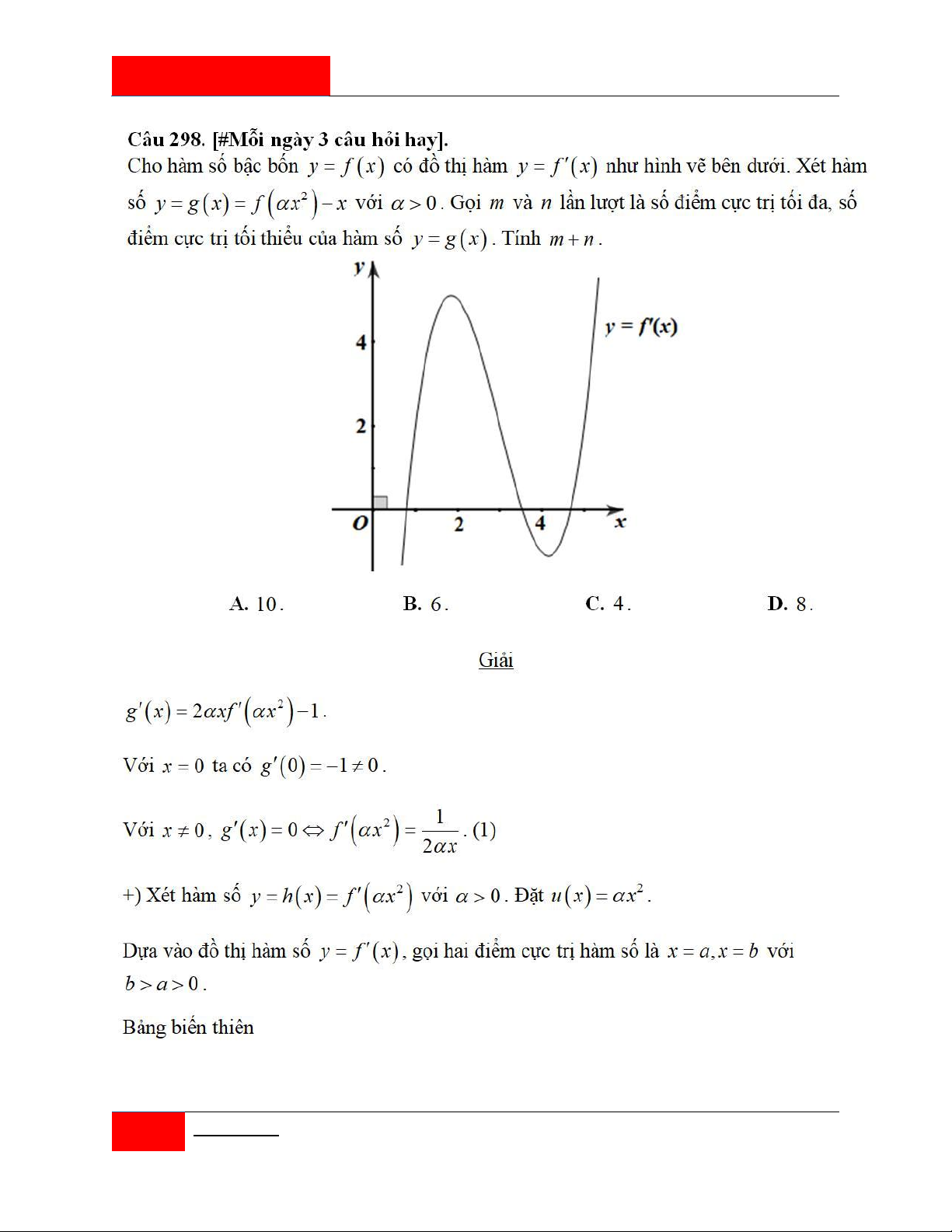
Câu 202. [#Mỗi ngày 3 câu hỏi hay].
Trong các số phức z dưới đây, số phức nào thỏa mãn z 1 và 3
z z 2 đạt giá trị lớn nhất? 1 3 1 3 2 5 2 5 A. z . i B. z . i C. z . i D. z . i 2 2 2 2 3 3 3 3
Câu 203. [#Mỗi ngày 3 câu hỏi hay].
Gọi S là tập hợp tất cả các số phức z thoả mãn z 1 34 và z 1 mi z m 2i . Gọi z , z S 1
2 là hai số phức thuộc sao cho z
z nhỏ nhất, giá trị của z z bằng? 1 2 1 2 A. 2. B. 2 3 . C. 2 . D. 3 2 .
Câu 204. [#Mỗi ngày 3 câu hỏi hay].
Xét số phức z có phần thực dương và ba điểm ,
A B, C lần lượt là điểm biểu diễn của các 2 1 1 1
số phức z, và z . Biết tứ giác OABC là một hình bình hành, giá trị nhỏ nhất của z z z z bằng? A. 2. B. 2. C. 2 2. D. 4.
Câu 205. [#Mỗi ngày 3 câu hỏi hay].
Một trang giấy A4 kích thức 21 cm x 29,7 cm có thể viết được 50 dòng, mỗi dòng có 75
chữ số (chữ số trong hệ thập phân). Ngày 25 / 01 / 2013 , người ta đã tìm được số nguyên 57885161 tố Mersenne 2
1 . Nếu viết số nguyên tố này theo hệ thập phân trên trang giấy
A4 nói trên thì cần bao nhiêu tờ giấy A4, biết rằng mỗi tờ giấy tương ứng với 2 trang? A. 2324 tờ. B. 2315 tờ. C. 2323 tờ. D. 2316 tờ.
Câu 206. [#Mỗi ngày 3 câu hỏi hay]. Cho dãy số u
u u u u u n thỏa mãn 10 2 20 2 1 , với mọi số nguyên n 10 n n 1 u n 1 10
n 2 . Tìm số tự nhiên n u 0 nhỏ nhất để 2019 2019 . 0 n
A. n 22168 .
B. n 22167 .
C. n 22178 .
D. n 22177 . 0 0 0 0
Bài tập tương tự ln 2 2
u u 10 ln 2u 6u 1 2 1 2
Câu 1. Cho dãy số u u u u n thỏa mãn và 2 1 với n2 n n 1
mọi n 1. Giá trị nhỏ nhất của n để u 5050 bằng? n A. 100 . B. 99 . C. 101. D. 102 .
1 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] 1 n 1 u u u
Câu 2. Cho dãy số u 2 3 10
n xác định bởi: u ;u u S u ... 1 n 1 . Tổng n 3 n 3 1 2 3 10 bằng? 3280 29524 25942 1 A. . B. . C. . D. . 6561 59049 59049 243
Câu 3. Cho dãy số u u u u u . Đặ n thỏa mãn , 6 2 và log log 8 11 t n n 1 n 2 5 9 2
S u u ... u . Tìm số tự nhiên n nhỏ nhất thỏa mãn S 20172018 . n 1 2 n n A. 2587 . B. 2590 . C. 2593 . D. 2584 .
Câu 4. Cho dãy số u
log 2u 63 2log u 8n 8 , n N n thỏa mãn n * 3 5 4 . Đặt u .S 148
S u u ... u . Tìm số nguyên dương lớn nhất n thỏa mãn n 2n . n 1 2 n u .S 75 2n n A. 18 . B. 17 . C. 16 . D. 19 .
Câu 207. [#Mỗi ngày 3 câu hỏi hay].
Trong không gian với hệ tọa độ Oxyz , cho mặt cầu S 2 2 2
: x y z 4x 4 y 2z 7 0
và đường thẳng d là giao tuyến của hai mặt phẳng x1 2m y 4mz 4 0 và m
2x my 2m
1 8 0 . Khi m thay đổi các giao điểm của d và S nằm trên một m
đường tròn cố định. Tính bán kính r của đường tròn đó. 142 92 23 586 A. r . B. r . C. r . D. r . 15 3 3 15
Câu 208. [#Mỗi ngày 3 câu hỏi hay].
Trong không gian Oxyz , cho ba điểm A0;0; 4, B 3; 2;6,C 3; 2
;6. Gọi M là điểm di
động trên mặt cầu S 2 2 2
: x y z 4. Giá trị nhỏ nhất của biểu thức MA MB MC bằng? A. 2 34 . B. 6 5 . C. 4 10 . D. 2 29 .
Câu 209. [#Mỗi ngày 3 câu hỏi hay].
Cho hàm số f x liên tục và nhận giá trị không âm trên đoạn 0;
1 . Giá trị nhỏ nhất của 2 1
biểu thức M 2 f x 3x f xdx 4 f x x xf xdx bằng? 0 0 1 1 1 1 A. . B. . C. . D. . 24 8 12 6
2 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Câu 210. [#Mỗi ngày 3 câu hỏi hay].
Cho hàm số y f x có đạo hàm liên tục trên R thỏa mãn 2
xf x f x 2 . '
f x x, x
và f 2 1. Tích phân 2
f x dx bằng? 0 3 4 A. . B. . C. 2 . D. 4 . 2 3
Câu 211. [#Mỗi ngày 3 câu hỏi hay].
Trong không gian Oxyz , cho hai mặt cầu S 2 2 2
: x y z 2x 4 y 2z 2 0 và 1 S 2 2 2
: x y z 2x 4 y 2z 4 0 . Xét tứ diện ABCD có hai đỉnh , A B nằm trên 2
S ; hai đỉnh C,D nằm trên S . Thể tích khối tứ diện ABCD có giá trị lớn nhất bằng 2 1 A. 3 2 . B. 2 3 . C. 6 3 . D. 6 2 .
Câu 212. [#Mỗi ngày 3 câu hỏi hay].
Gọi S là tập hợp các số phức z có phần thực và phần ảo đều là các số nguyên đồng thời
thoả mãn hai điều kiện: z 3 4i 2 và z z z z . Số phần tử của tập S bằng? A. 11. B. 12 . C. 13 . D. 10 .
Câu 213. [#Mỗi ngày 3 câu hỏi hay].
S x 2 y 2 z 2 : 1 1 1 12
Trong không gian Oxyz , cho mặt cầu và mặt phẳng
P: x 2y 2z 11 0. P
Xét điểm M di động trên ; các điểm ,
A B, C phân biệt di S S ABC động trên
sao cho AM , BM , CM là các tiếp tuyến của . Mặt phẳng
luôn đi qua điểm cố định nào dưới đây? 1 1 1 3 A. ; ; . B. 0; 1 ;3 . C. ; 0; 2 . D. 0;3; 1 . 4 2 2 2
Câu 214. [#Mỗi ngày 3 câu hỏi hay]. x 1 Cho hàm số y
có đồ thị C . Biết rằng C có tiệm cận ngang và tồn tại tiếp 2 ax 1
tuyến của C song song và cách tiệm cận ngang của C một khoảng bằng 3 . Mệnh đề nào dưới đây đúng ?
3 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] 1 3 1 3 A. a ;1 . B. a 1; . C. a 0; . D. a ; 2 . 2 2 2 2
Câu 215. [#Mỗi ngày 3 câu hỏi hay].
Xét số phức z có phần thực dương và ba điểm ,
A B, C lần lượt là điểm biểu diễn của các 2 1 1 1
số phức z, và z . Biết tứ giác OABC là một hình bình hành, giá trị nhỏ nhất của z z z z bằng? A. 2. B. 2 . C. 2 2. D. 4 .
Câu 216. [#Mỗi ngày 3 câu hỏi hay].
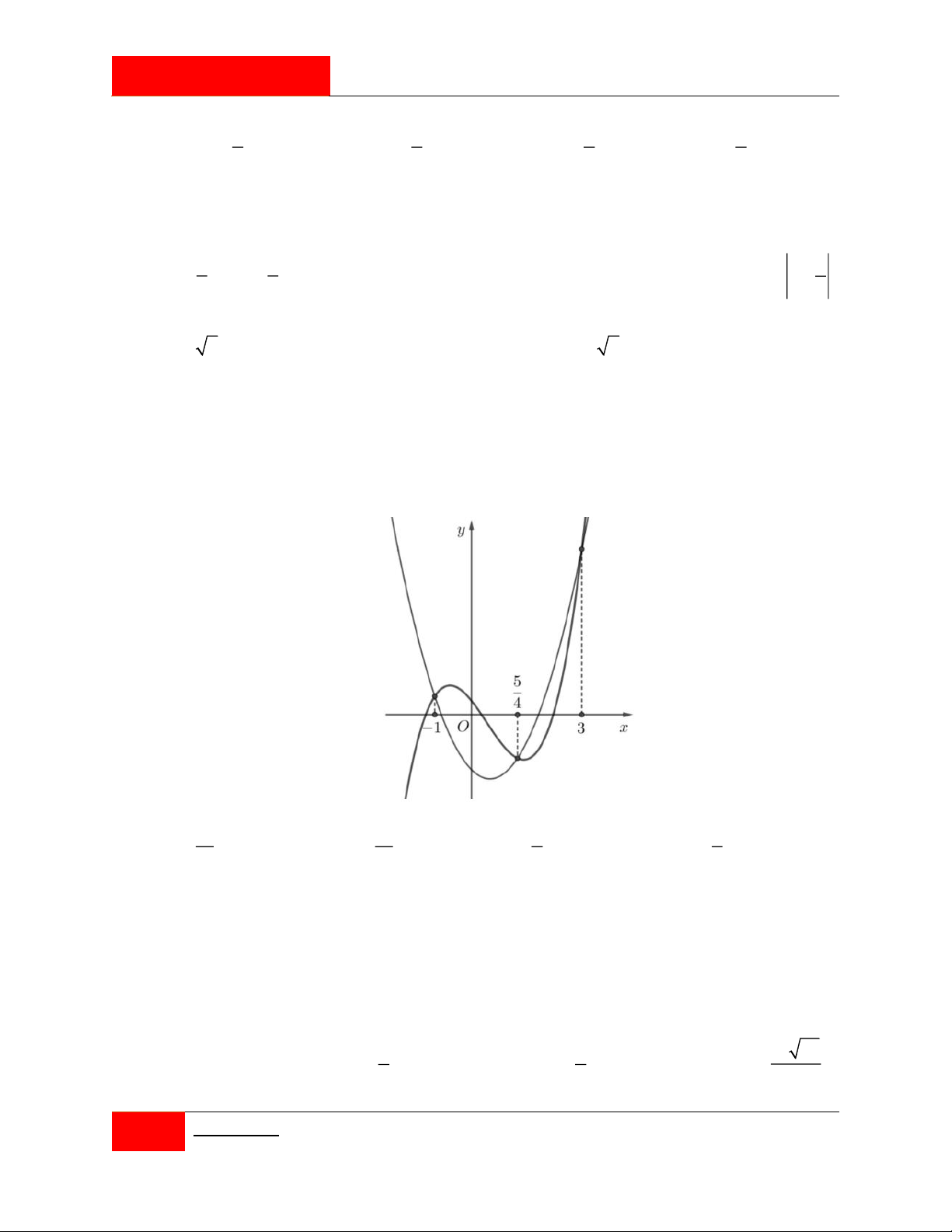
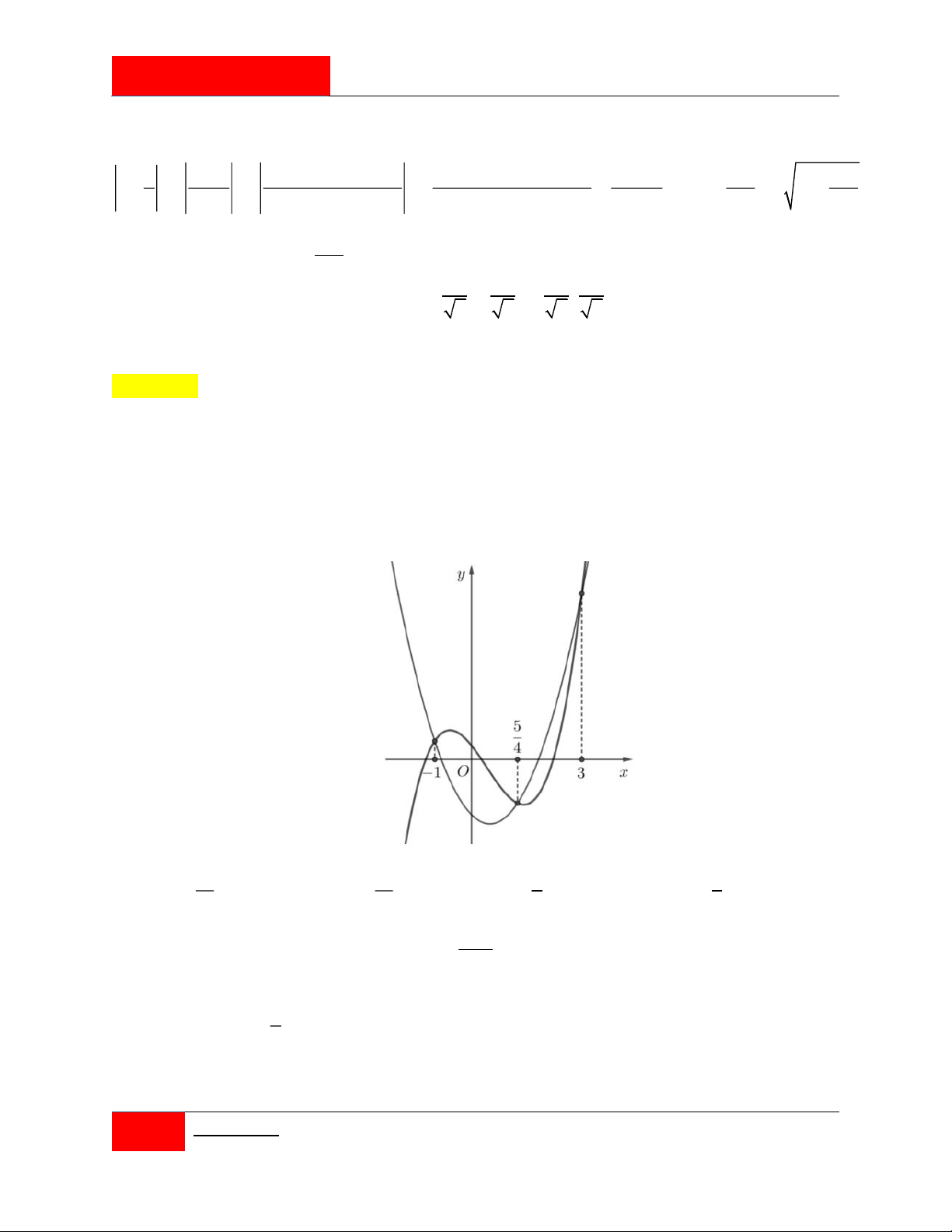
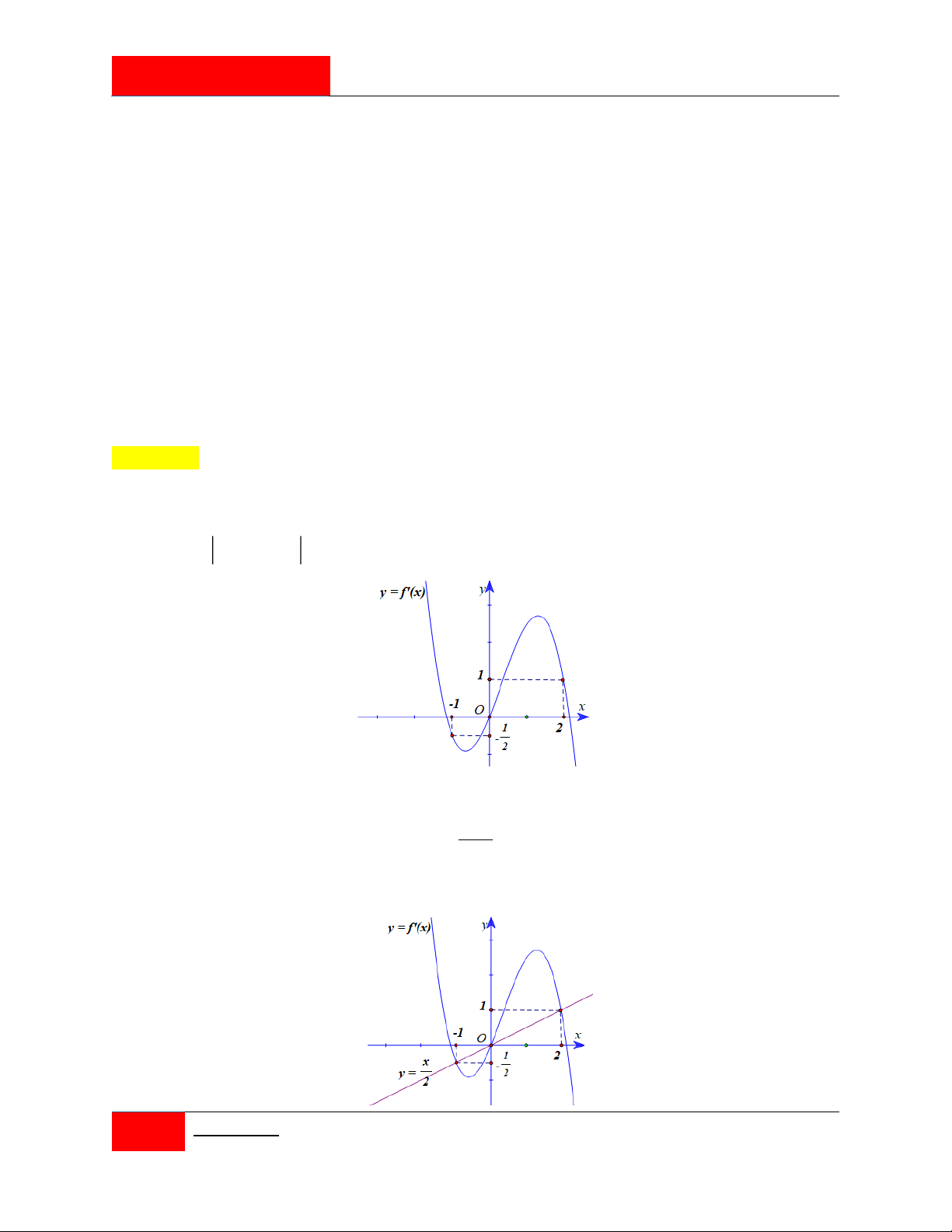
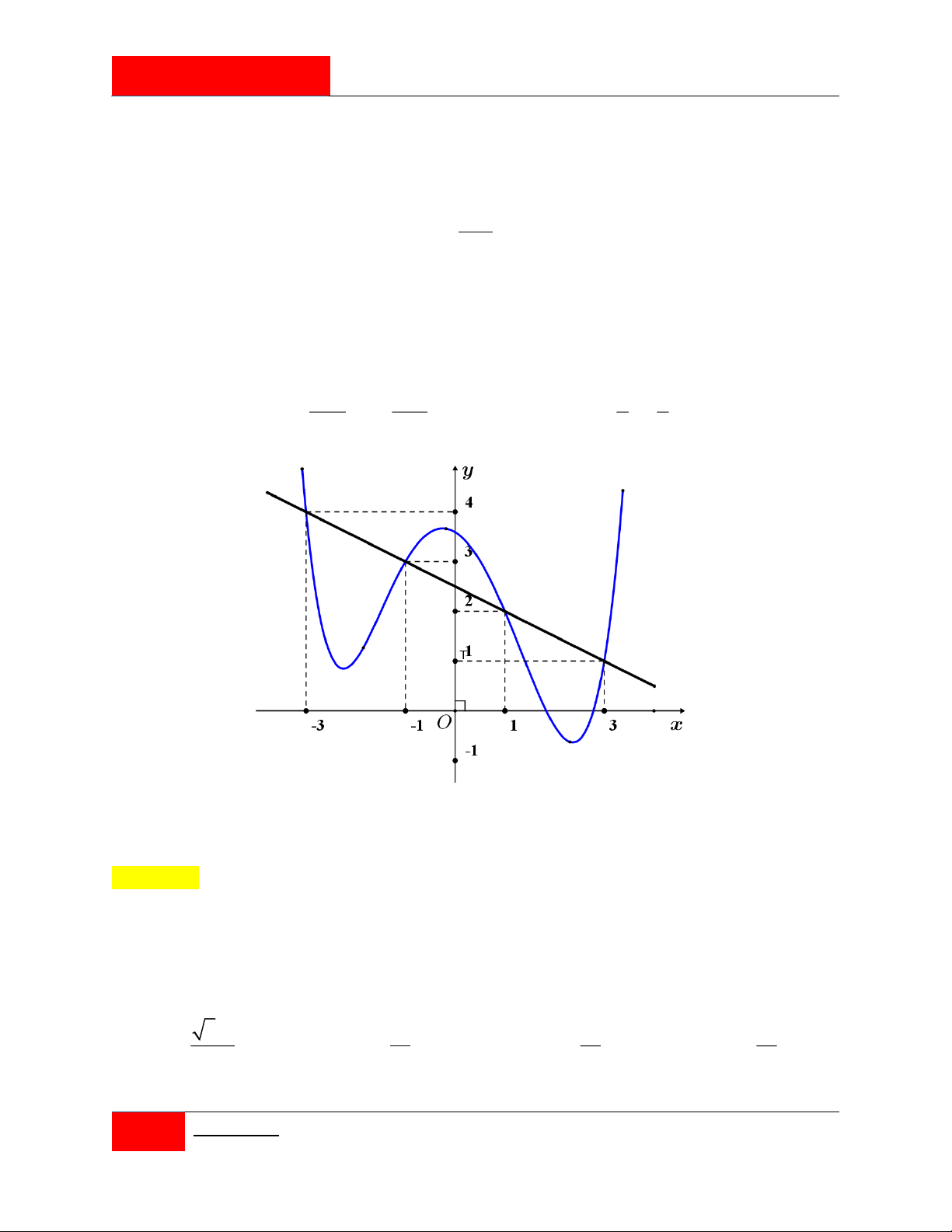
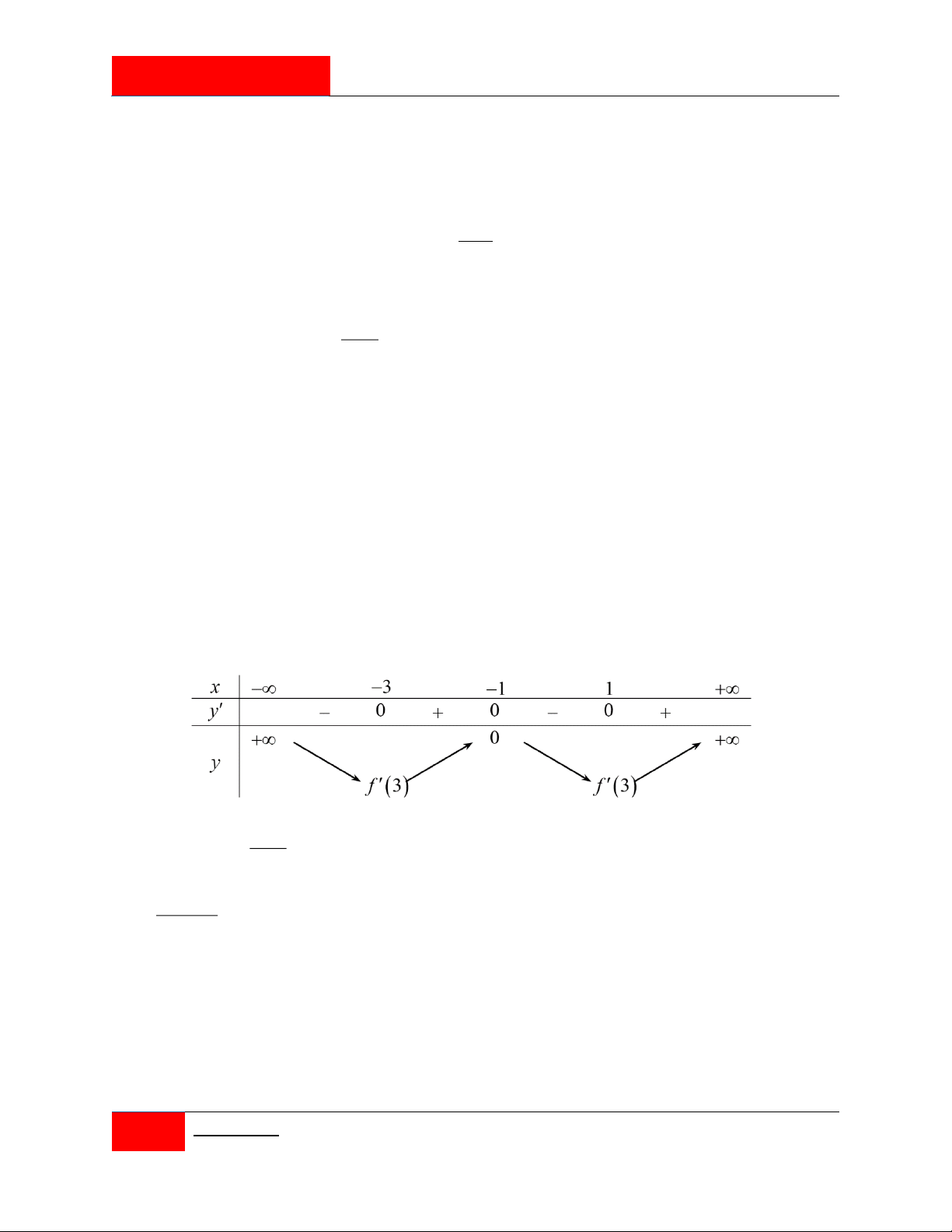
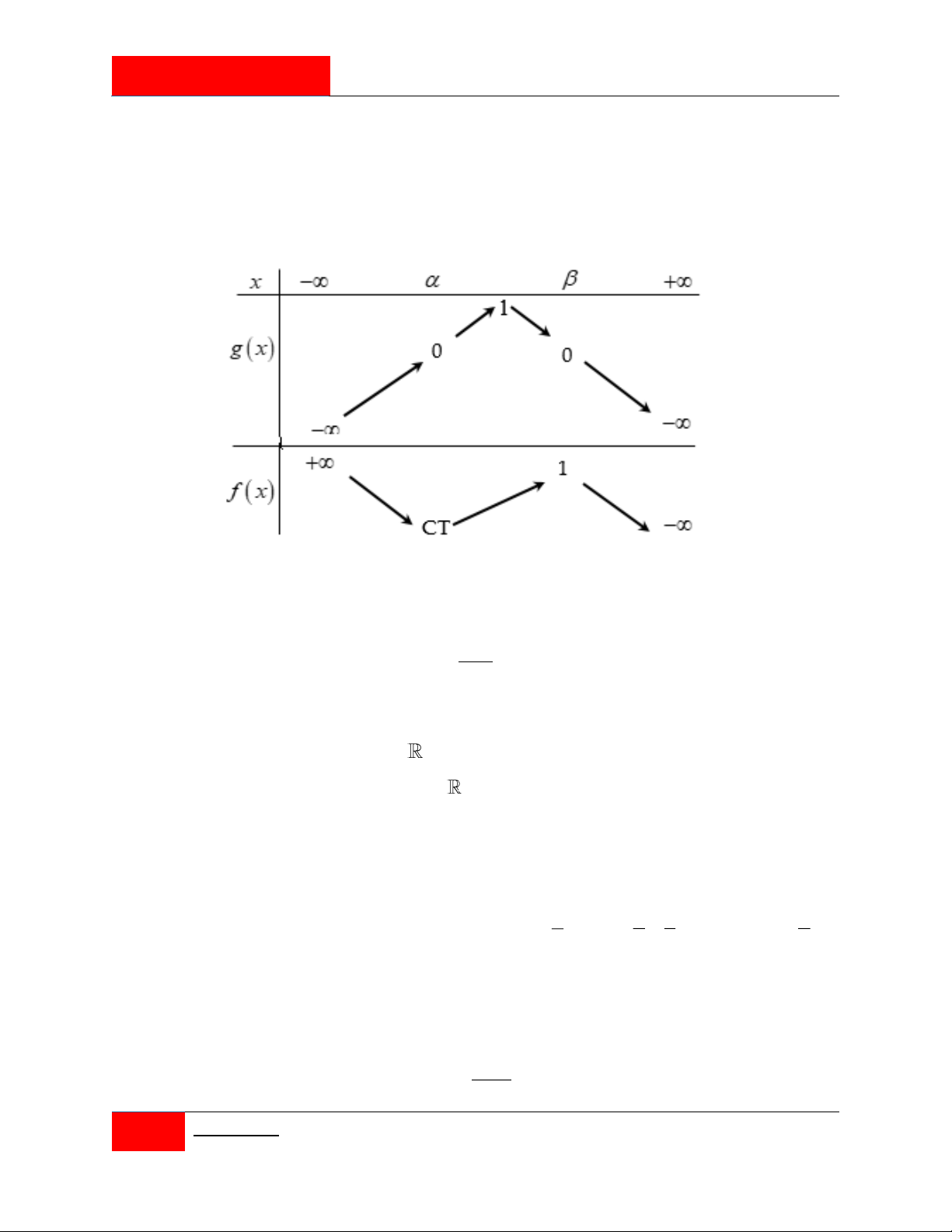
Cho hai hàm số f x 4 3 2
ax bx cx dx e và g x 3 2
mx nx px 1 với
a, b, c, d, ,
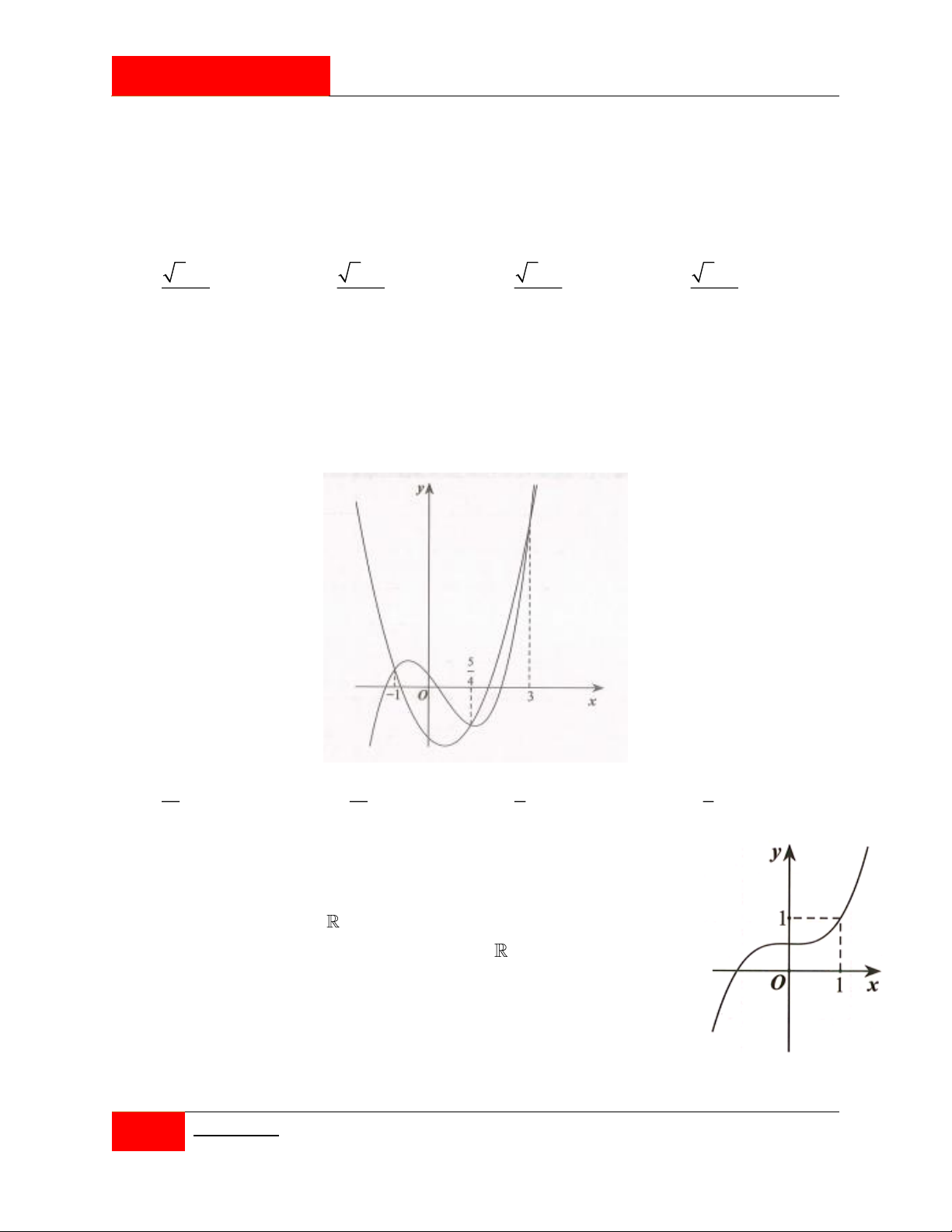
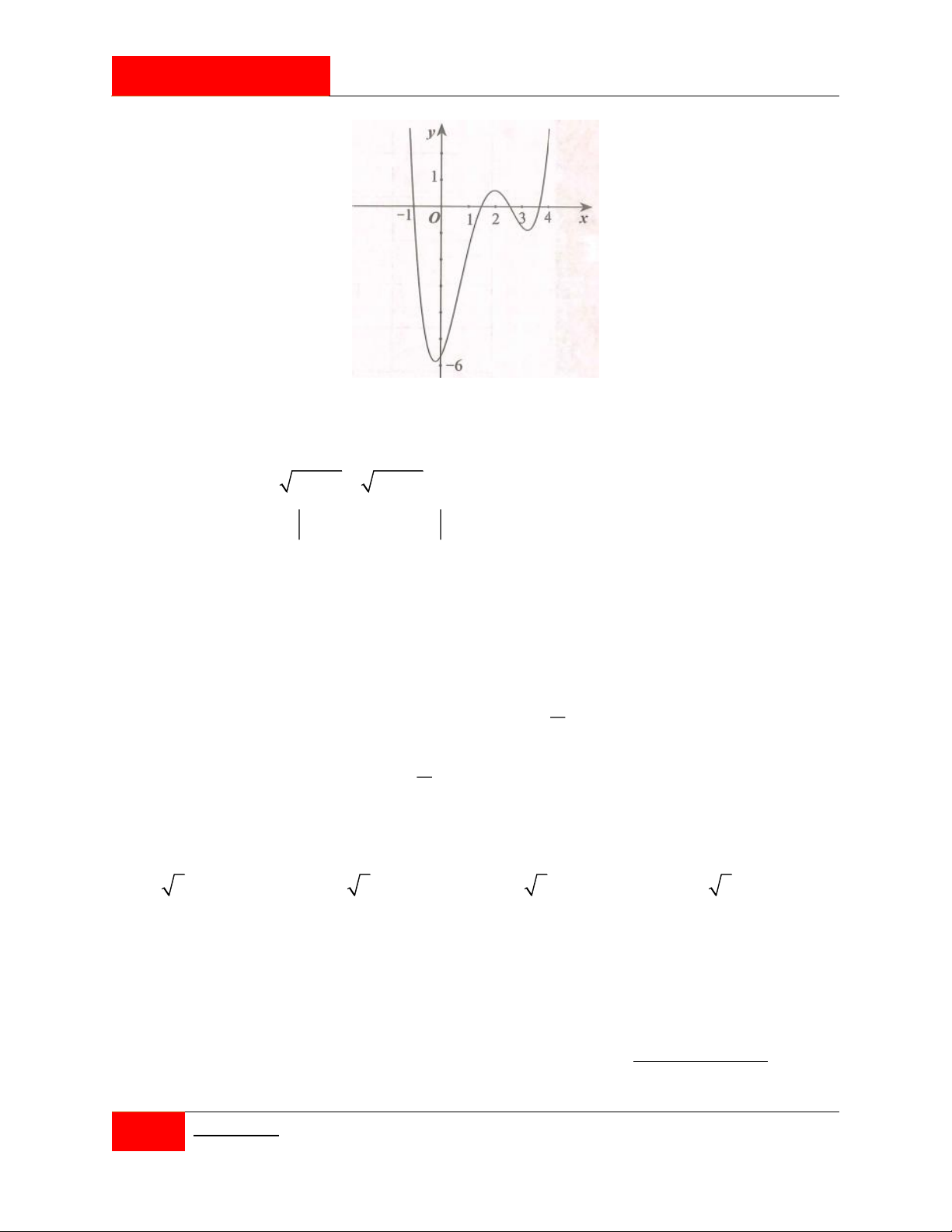
e m, n, p, q là các số thực. Đồ thị của hai hàm số y f 'x; y g 'x như
hình vẽ bên. Tổng các nghiệm của phương trình f x q g x e bằng 13 13 4 4 A. . B. . C. . D. . 3 3 3 3
Câu 217. [#Mỗi ngày 3 câu hỏi hay].
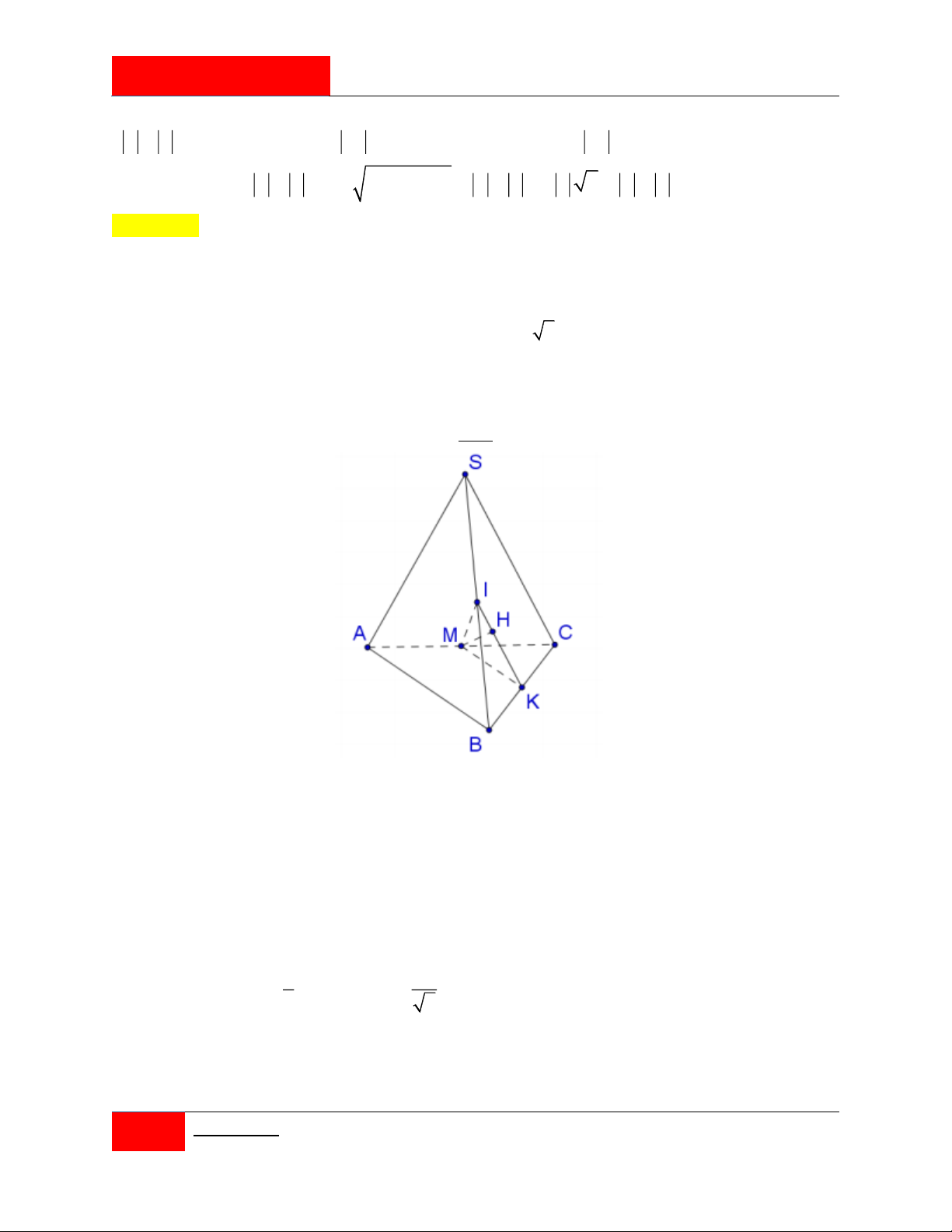
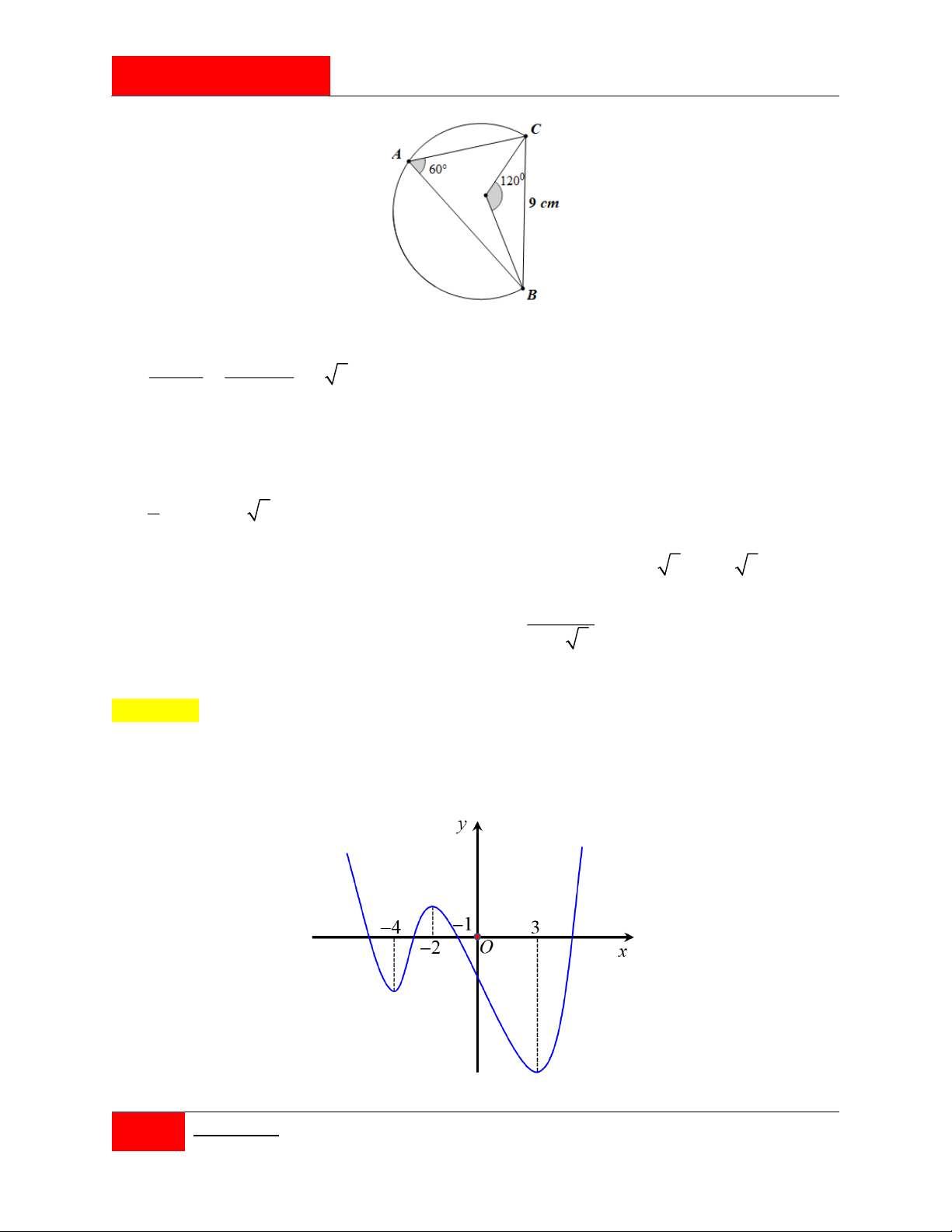
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , AB 6 , BC 8 . Biết
SA 8 và SA ( ABC) . Một khối cầu có tâm thuộc phần không gian bên trong của khối
chóp và tiếp xúc với tất cả các mặt của hình chóp S.ABC . Tính khoảng cách d từ tâm
của khối cầu đến mặt phẳng SBC . 4 3 12 34
A. d 6 . B. d . C. d . D. d . 3 2 17
4 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Câu 218. [#Mỗi ngày 3 câu hỏi hay].
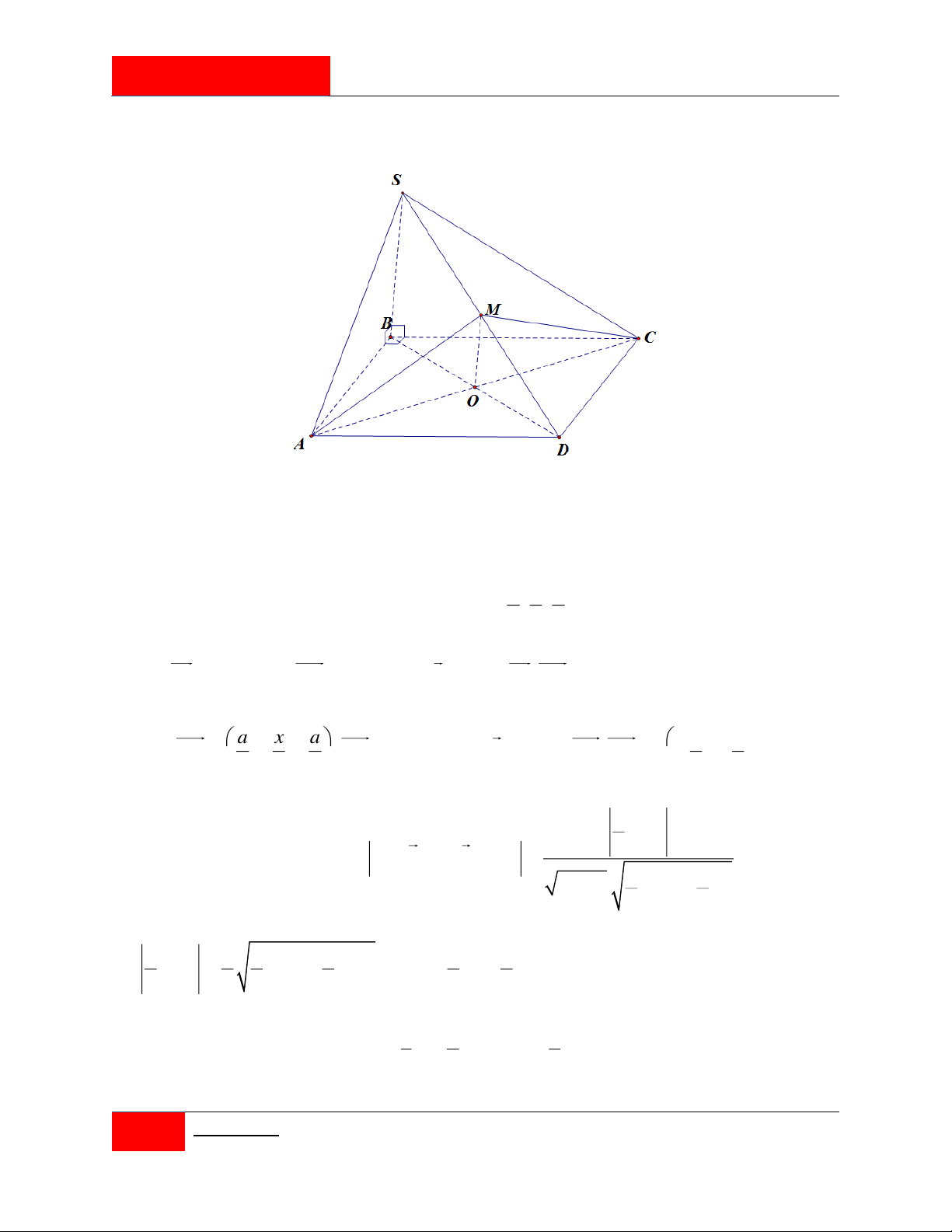
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a , góc 60o ABC cạnh bên
SD a 2 . Hình chiếu vuông góc của S trên mặt phẳng ABCD là điểm H thuộc đoạn
BD sao cho HD 3
HB . Gọi M là trung điểm của cạnh SD . Tính khoảng cách giữa hai
đường thẳng CM và SB . a 30 a 7 30a a 30 A. . B. . C. . D. . 8 4 7 5
Câu 219. [#Mỗi ngày 3 câu hỏi hay].
Trong mặt phẳng tạo độ Oxyz , cho bốn điểm A0; 1 ;2 , B2; 3 ;0 ,C 2 ;1 ;1 , D 0; 1 ;3 .
Gọi L là tập hợp tất cả các điểm M trong không gian thỏa mãn đẳng thức M .
A MB MC.MD 1 . Biết rằng L là một đường tròn, đường tròn đó có bán kính r bằng bao nhiêu? 11 7 3 5 A. r . B. r . C. r . D. r . 2 2 2 2
Câu 220. [#Mỗi ngày 3 câu hỏi hay].
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC vuông tại C, có 0 ABC 60 ; x y x
AB 3 2. Đường thẳng AB có phương trình 3 4 8
, đường thẳng AC 1 1 4
nằm trên mặt phẳng : x z 1 0. Biết điểm B là điểm có hoành độ dương, gọi
a,b,c là tọa độ của điểm C. Giá trị a b c bằng? A. 2. B. 3. C. 4. D. 7.
Câu 221. [#Mỗi ngày 3 câu hỏi hay].
Một hộp có 6 viên bi xanh, 5 viên bi đỏ và 4 viên bi vàng. Chọn ngẫu nhiên 5 viên bi
sao cho có đủ cả ba màu. Số cách chọn là? A. 2163. B. 2170. C. 3003. D. 3843.
Câu 222. [#Mỗi ngày 3 câu hỏi hay].
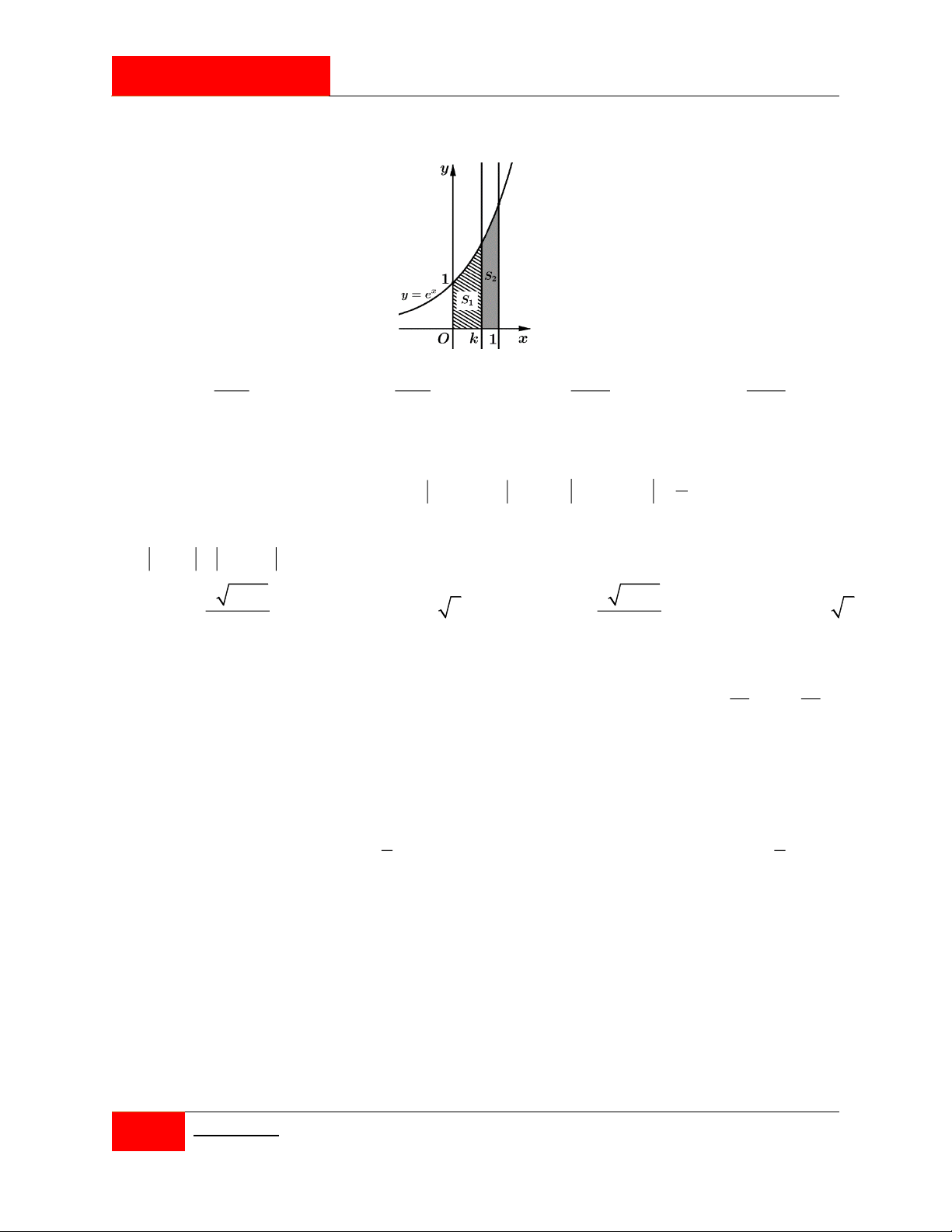
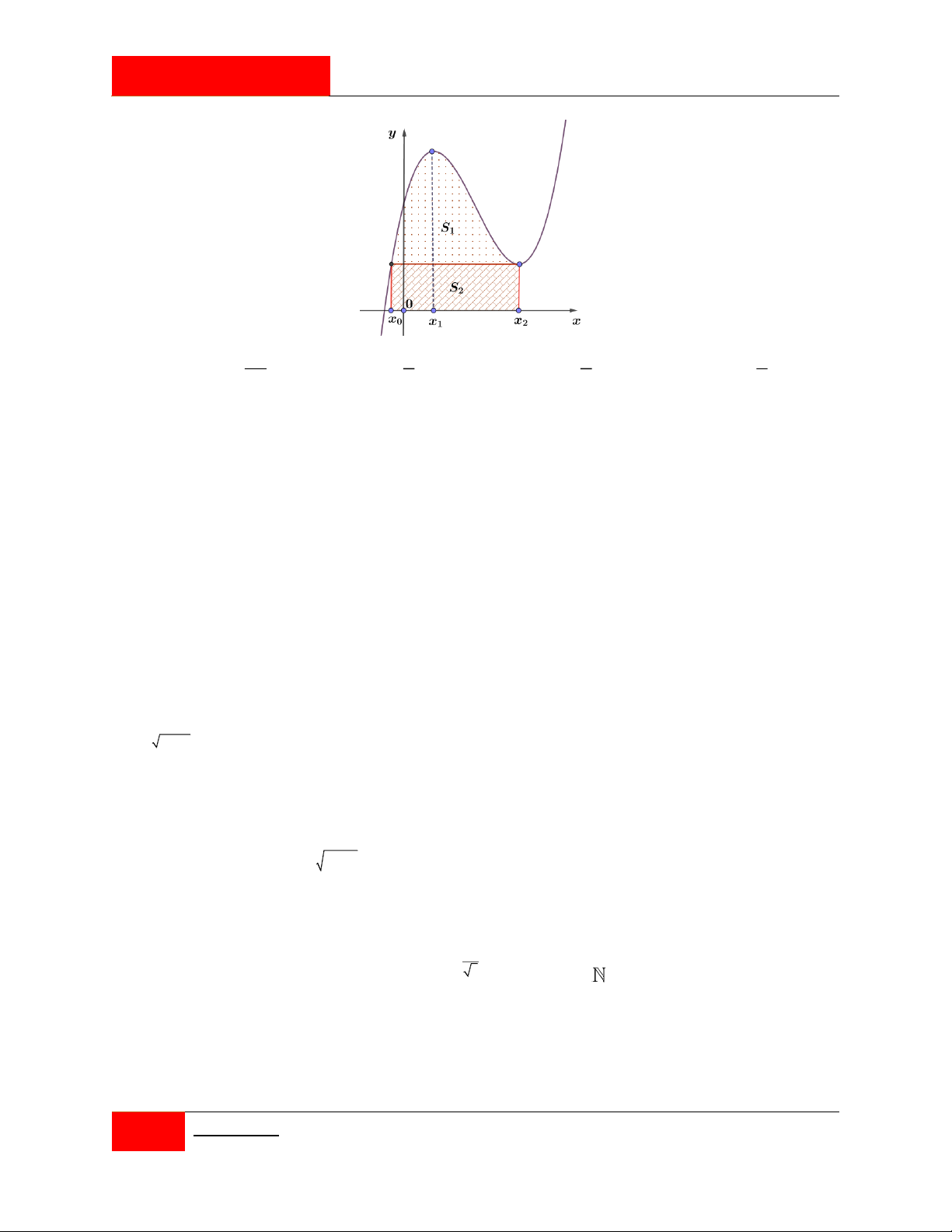
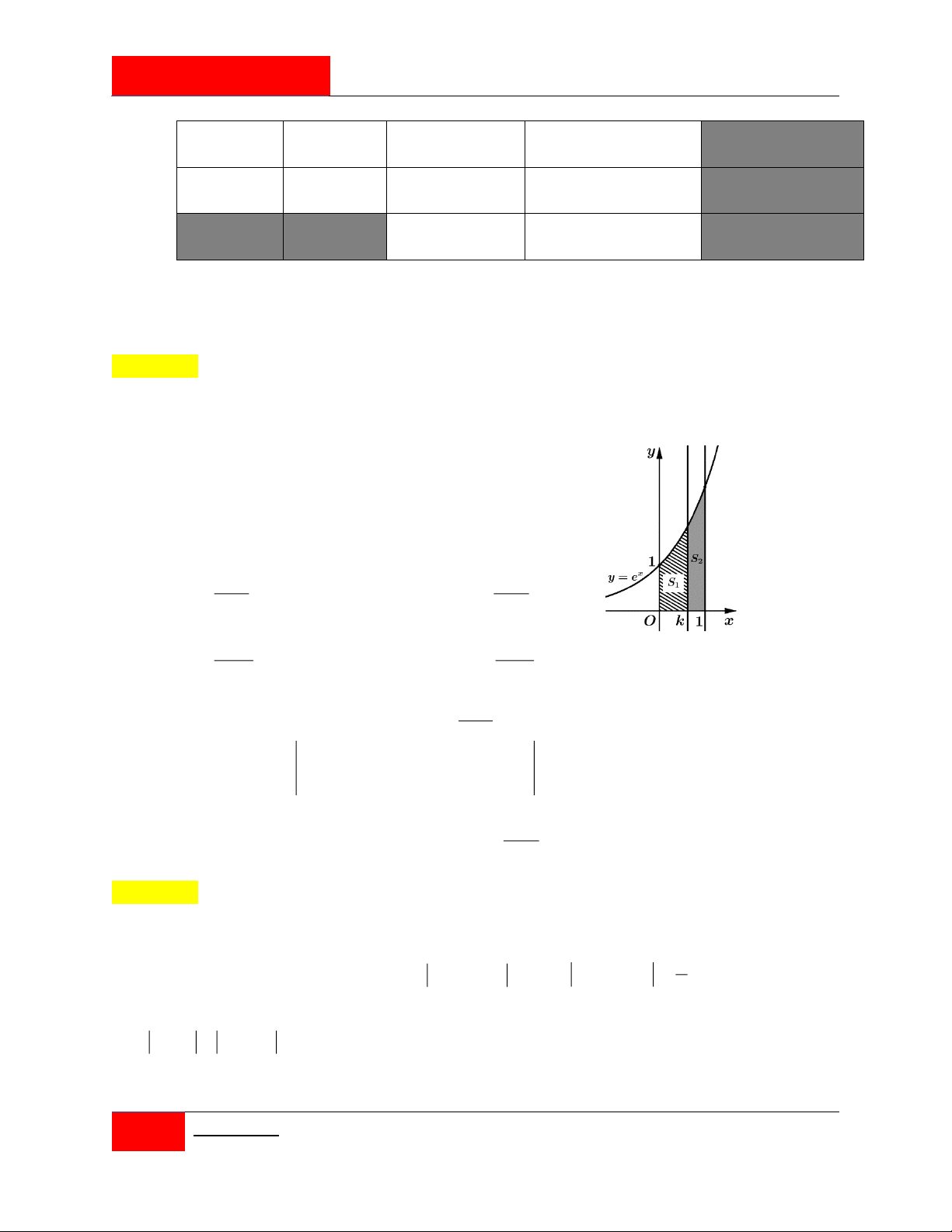
Kí hiệu H là hình phẳng giới hạn bởi các đường x y
e , y 0, x 0 và x 1.
Đường thẳng x k 0 k
1 chia H thành hai phần có diện tích tương ứng S , S 1 2
5 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
như hình vẽ bên, biết S S . Mệnh đề nào sau đây là đúng? 1 2 k e k e k e k e 1 1 2 3 A. e . B. e . C. e . D. e . 2 2 2 2
Câu 223. [#Mỗi ngày 3 câu hỏi hay]. 1
Biết rằng hai số phức z , z thỏa mãn z 3 4i 1 và z 3 4i . Số phức z có 1 2 1 2 2
phần thực là a và phần ảo là b thỏa mãn 3a 2b 12. Giá trị nhỏ nhất của biểu thức
P z z z 2z 2 bằng? 1 2 3 1105 3 1105 A. P . B. P 5 2 3 . C. P . D. P 5 2 5 . min 11 min min 13 min
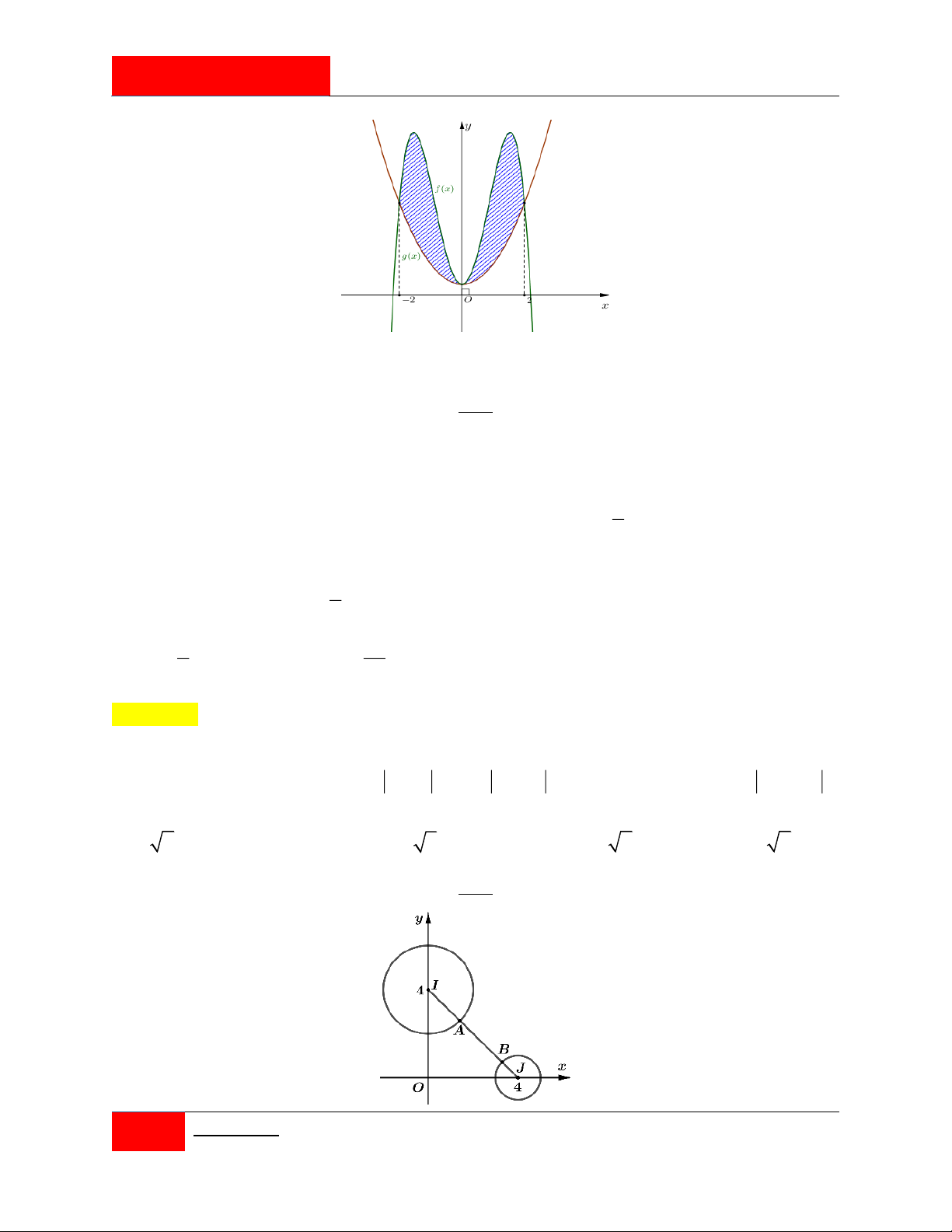
Câu 224. [#Mỗi ngày 3 câu hỏi hay]. 2 2 x x
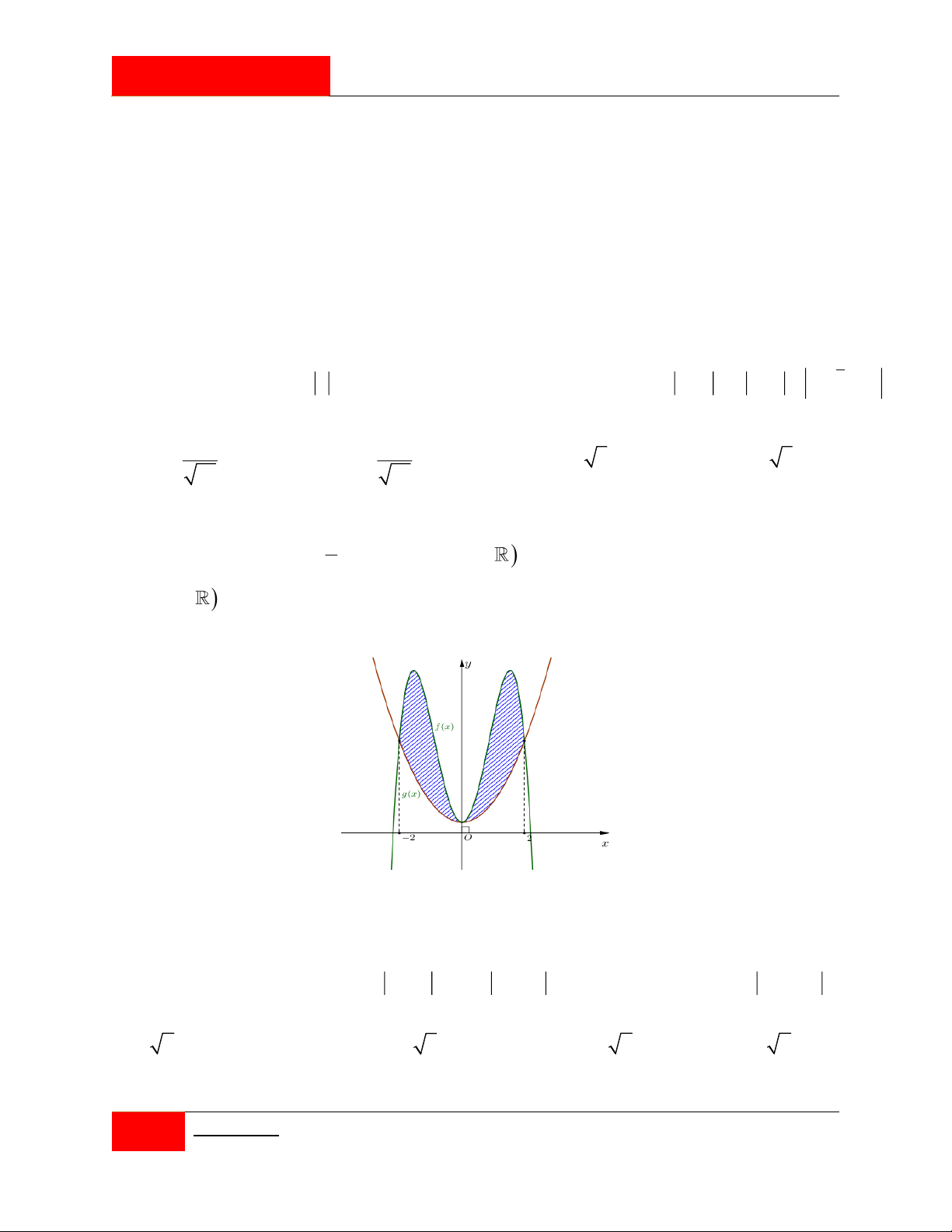
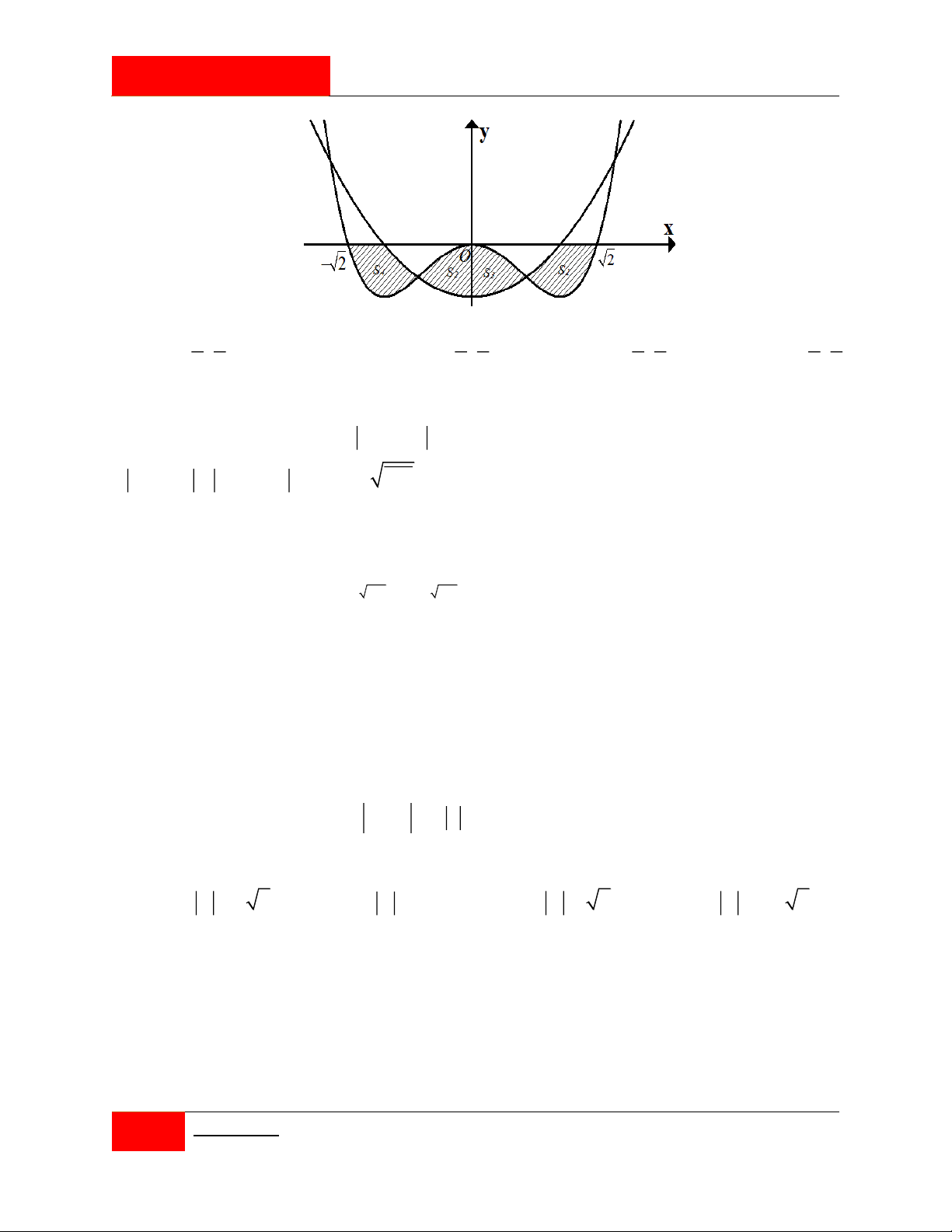
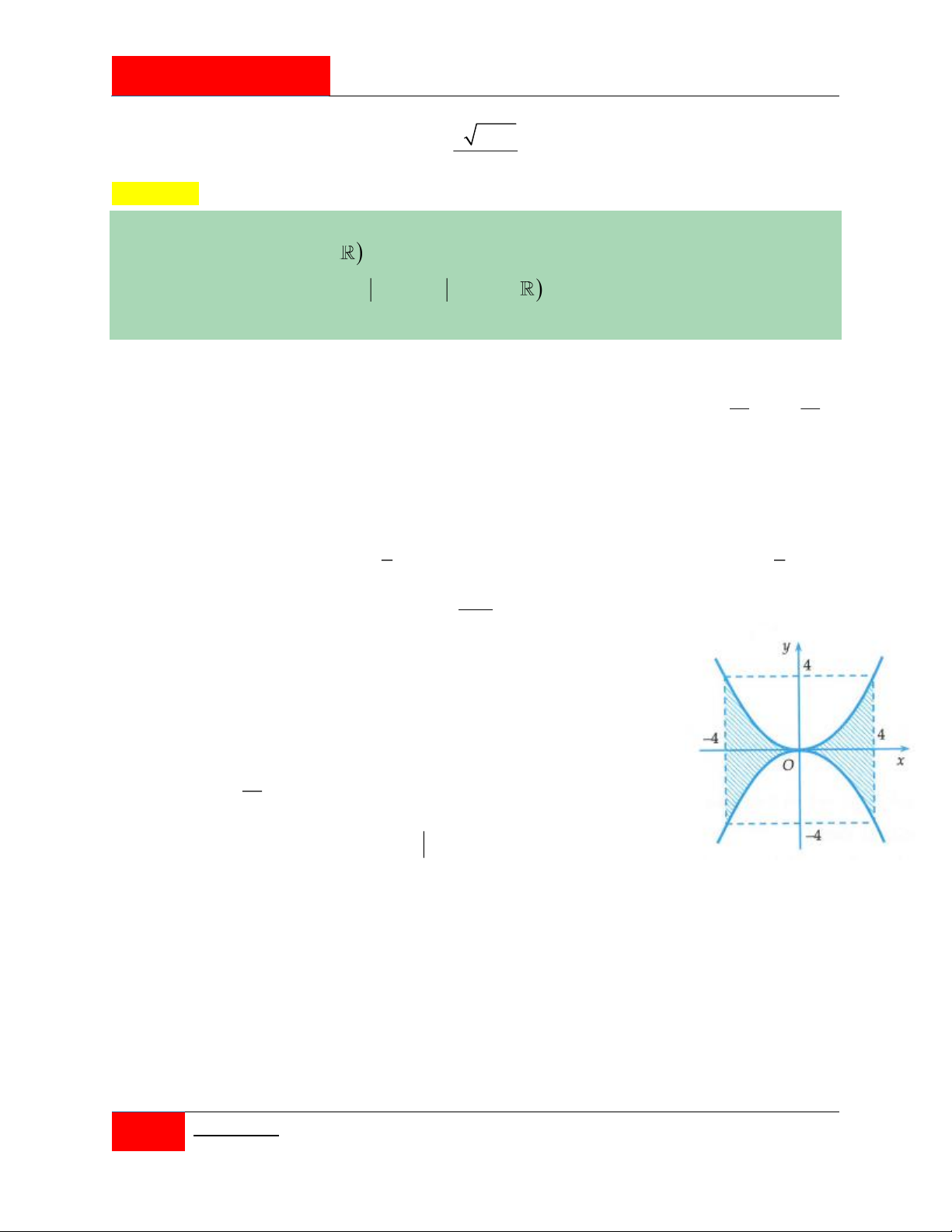
Trong mặt phang tọa độ Oxy , gọi là hình phẳng giới hạn bởi các đường y ; y , 4 4
x 4, x 4 và hình H
là hình gồm các điểm ;
x y thỏa x y
x y 2 2 2 2 16, 2 4. 2
Cho H và H quay quanh trục Oy ta được các vật thể có thể tích lần lượt là V ,V . 2 1 1 2
Đẳng thức nào dưới đây đúng 1 2
A. V V .
B. V V .
C. V 2V .
D. V V . 1 2 1 2 2 1 2 1 2 3
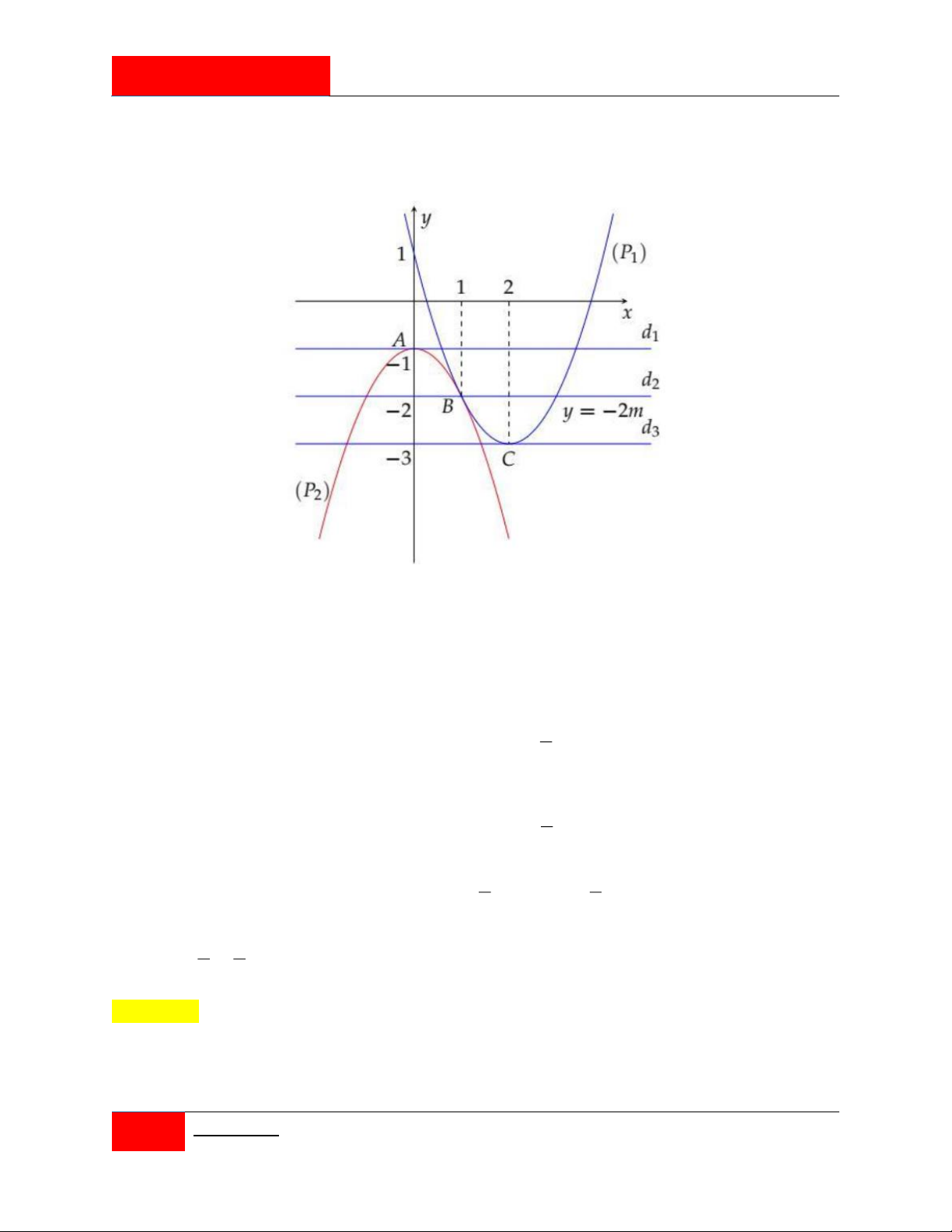
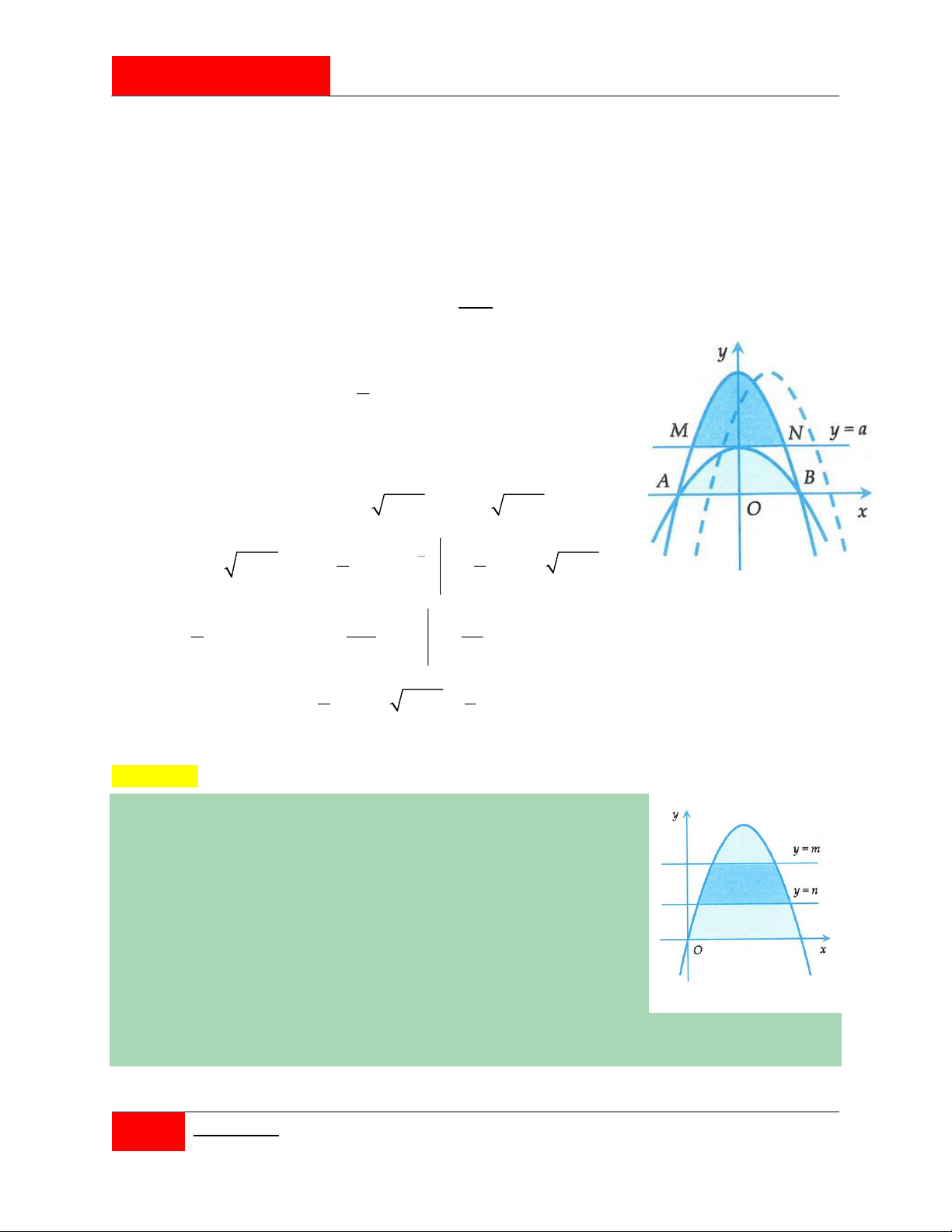
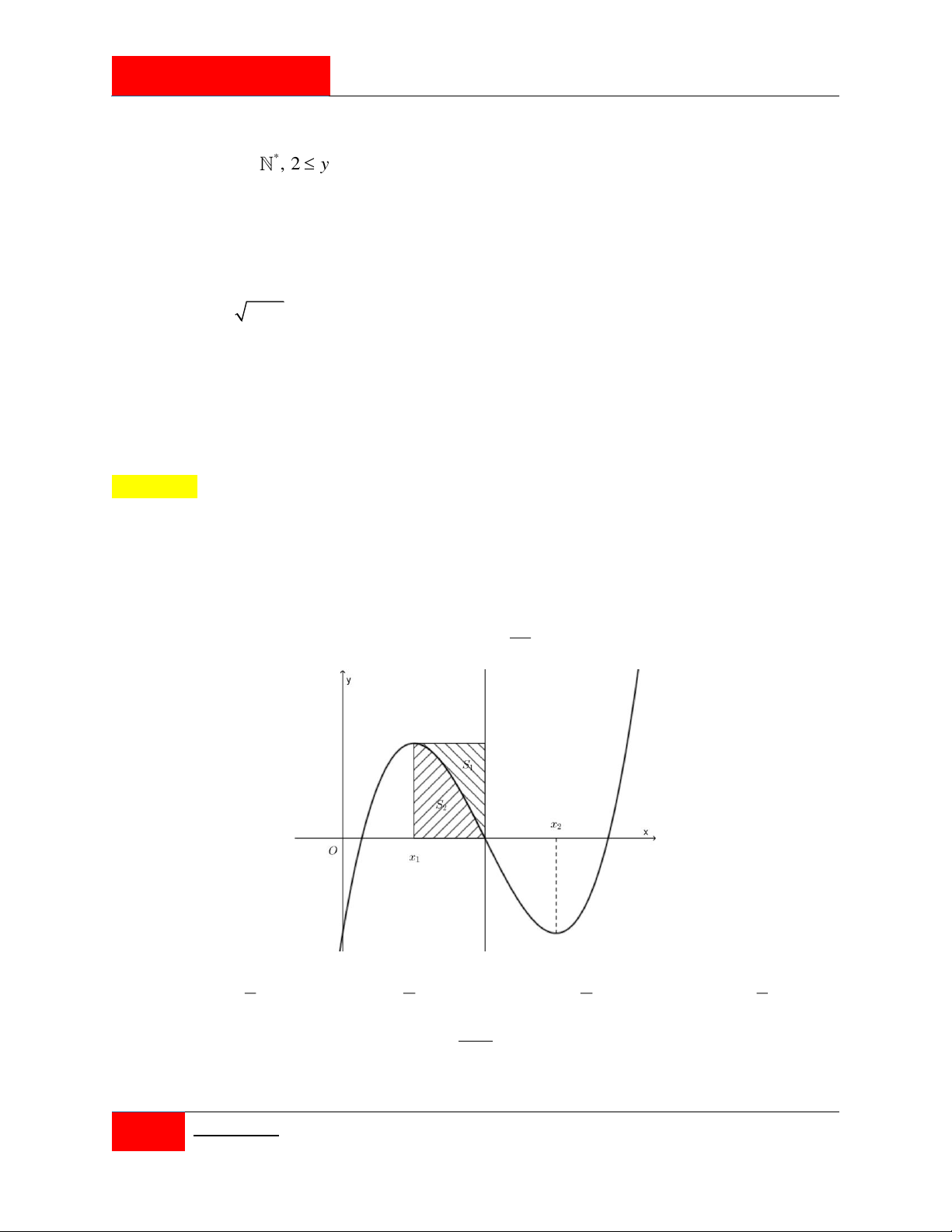
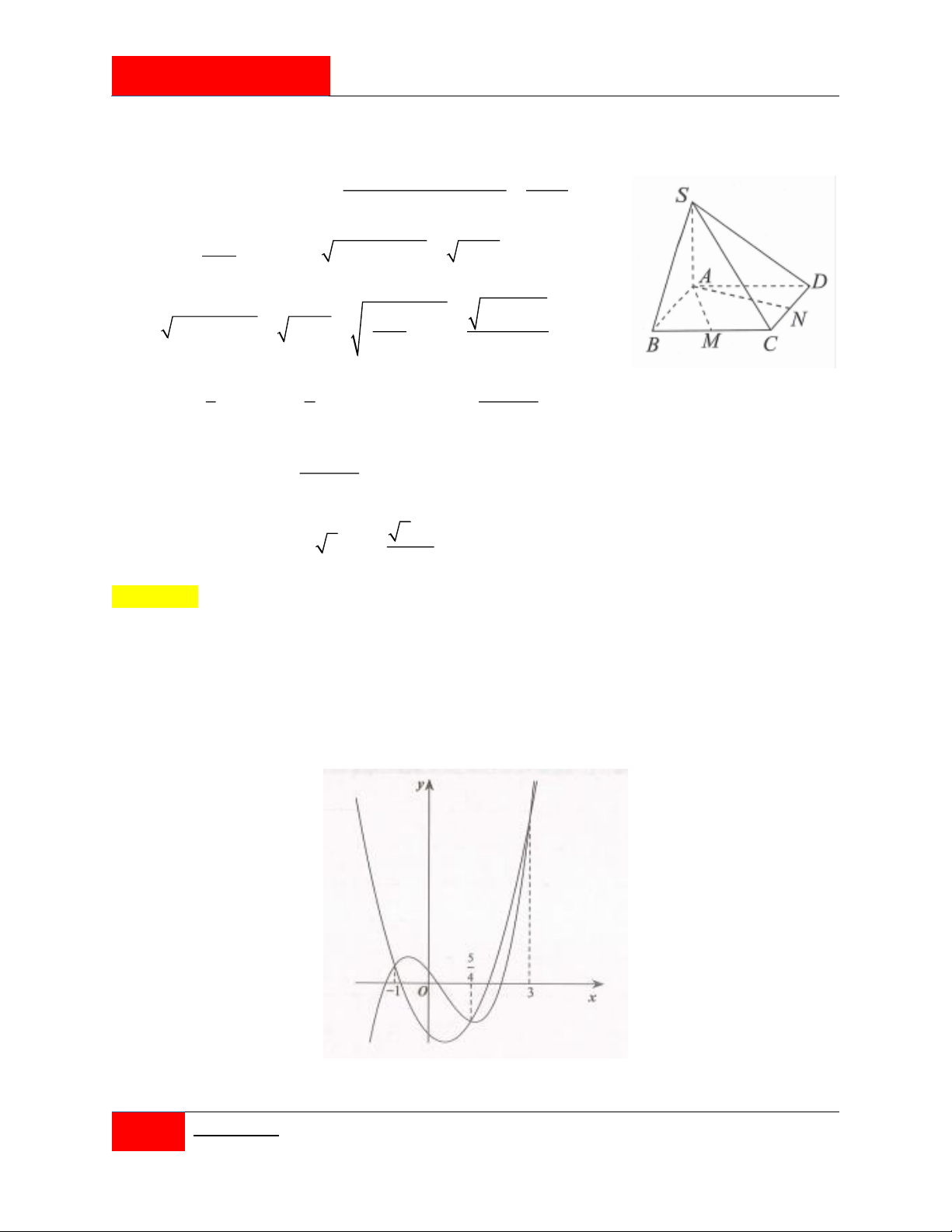
Câu 225. [#Mỗi ngày 3 câu hỏi hay]. Cho parabol P 2
: y x 2x 3 cắt trục hoành tại hai điểm A, B và đường thẳng 1
d : y a 0 a 4 . Xét parabol P đi qua A, B và có đỉnh thuộc đường thẳng y a . 2
Gọi S là diện tích hình phẳng giới hạn bởi P và d . S là diện tích hình phẳng giới 1 1 2
hạn bởi P và trục hoành. Biết S S , tính 3 2
T a 8a 48a . 2 1 2 A. T 99 . B. T 64 . C. T 32 . D. T 72 .
6 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Câu 226. [#Mỗi ngày 3 câu hỏi hay].
Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng P : x y z 1 0 , đường thẳng x 15 y 22 z 37 d : và mặt cầu 2 2 2
(S) : x y z 8x 6 y 4z 4 0 . Một đường 1 2 2
thẳng thay đổi cắt mặt cầu S tại hai điểm A, B sao cho AB 8 . Gọi A , B là hai
điểm lần lượt thuộc mặt phẳng P sao cho AA , BB cùng song song với d . Giá trị lớn
nhất của biểu thức AA BB là 8 30 3 24 18 3 12 9 3 16 60 3 A. B. C. D. 9 5 5 9
Câu 227. [#Mỗi ngày 3 câu hỏi hay].
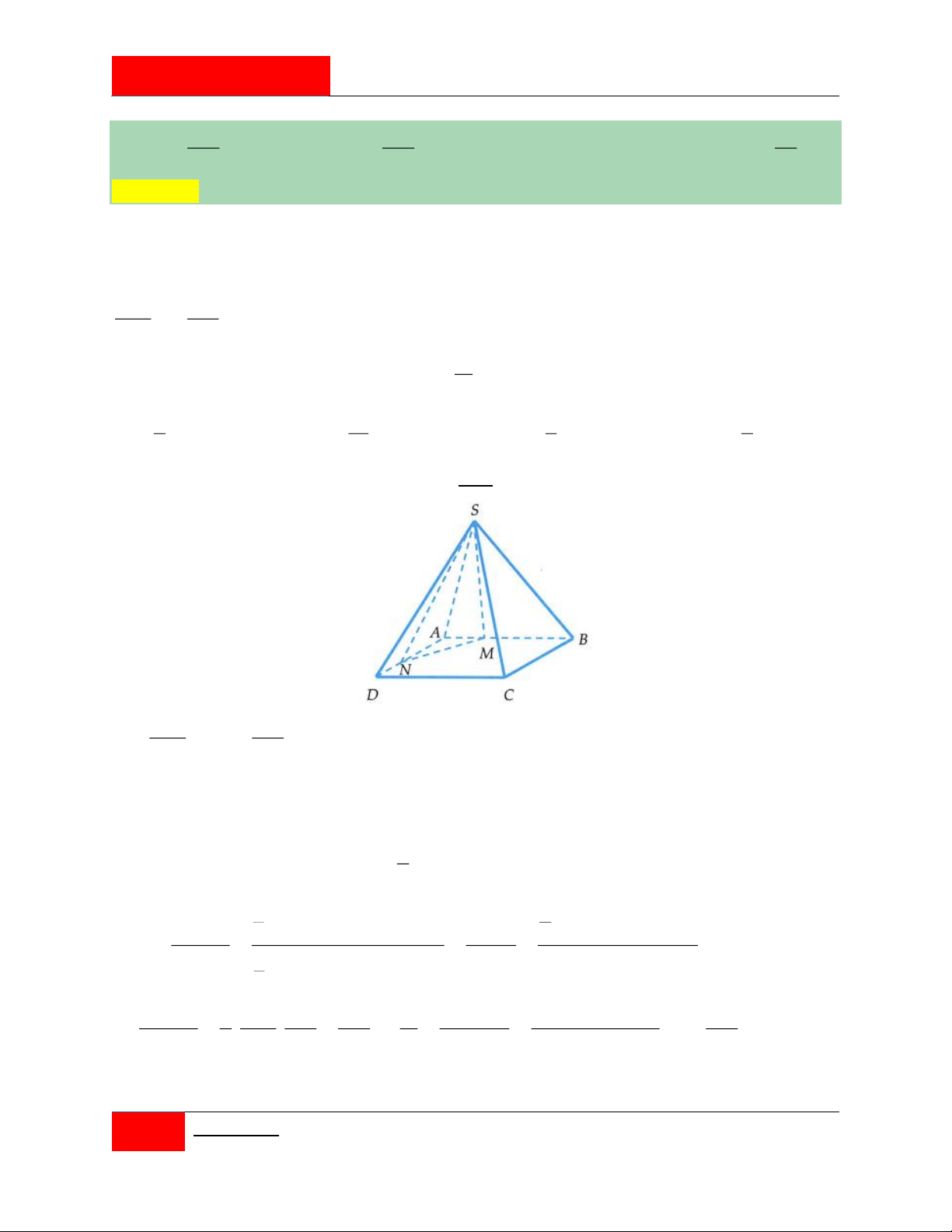
Cho hình chóp S.ABCD có đáy là ABCD là hình bình hành. Hai điểm M, N lần lượt AB AD
thuộc các đoạn thẳng AB và AD ( M và N không trùng với A ) sao cho 2. 4. AM AN Ký hiệu V , S ABCD S MBCDN 1
V lần lượt là thể tích của các khối chóp . và . . Tìm giá trị lớn nhất của tỉ số 1 V V 3 17 1 2 A. . B. . C. . D. . 4 14 6 3
Câu 228. [#Mỗi ngày 3 câu hỏi hay].
Trong không gian với hệ tọa độ Oxyz , cho hai điểm A0; 2; 2, B2; 2
;0 . Gọi I 1;1; 1 1
và I (3;1;1) là tâm của hai đường tròn nằm trên hai mặt phẳng khác nhau và có chung một 2
dây cung AB . Biết rằng luôn có một mặt cầu S đi qua cả hai đường tròn ấy. Tính bán
kính R của S . 219 129 A. R . B. R 2 2 . C. R . D. R 2 6 . 3 3
Câu 229. [#Mỗi ngày 3 câu hỏi hay].
Cho số phức z thỏa mãn đồng thời hai điều kiện z i 1 và z 2m 2 với m là
tham số thực. Tập hợp các giá trị thực của tham số m để tồn tại hai số phức thỏa mãn các điều kiện trên là? A. 2 ;2 \ 0 . B. 2;2 . C. 2 ;2 \ 0 . D. 2;2 .
7 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Câu 230. [#Mỗi ngày 3 câu hỏi hay].
Cho hàm số f x 3 2
x 3x m . Hỏi có bao nhiêu giá trị nguyên của tham số mm 2018 để
với mọi bộ ba số phân biệt a,b, c thì f a, f b, f c là độ dài ba cạnh của một tam giác. A. 2011 . B. 2012 . C. 2010 . D. 2018 .
Câu 231. [#Mỗi ngày 3 câu hỏi hay]. 2 2
Trong không gian với hệ tọa độ Oxyz , cho mặt cầu S : x 2
1 y z 2 9 ngoại
tiếp khối bát hiện H được ghép từ hai khối chóp tứ giác đều S.ABCD và S .ABCD
(đều có đáy là tứ giác ABCD ). Biết rằng đường tròn ngoại tiếp của tứ giác ABCD là
giao tuyến của mặt cầu S và mặt phẳng P : 2x 2 y z 8 0 . Tính thể tích khối bát diện H . 34 665 68 1330 A. V . B. V . C. V . D. V . H H H H 9 81 9 81
Câu 232. [#Mỗi ngày 3 câu hỏi hay]. Cho m
ab với a 1, b 1 và 2
P log b 2 27 log a 4 . Biết rằng P đạt giá a 3 log a b c d 3
trị nhỏ nhất khi m
c,d,e . Tính c d S . e e 2 1
A. Vô số giá trị.
B. S 0. C. S . D. S . 3 3
Câu 234. [#Mỗi ngày 3 câu hỏi hay]. 3
Cho hàm số f x có đạo hàm liên tục trên đoạn 0; 1 thỏa mãn 2
f (x) 6x f 3 x . 3x 1 2 x
Giá trị x
1 f ' dx bằng? 2 0 8 4 12 2 A. . B. . C. . D. . 5 5 5 5
Câu 235. [#Mỗi ngày 3 câu hỏi hay].
Cho z x yi với x, y
là số phức thỏa mãn điều kiện z 2 3i z i 2 5 .
Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 2 2
P x y 8x 6 y . Tính M m . 156 156 A. 60 2 10 . B. 20 10 . C. 60 2 10 . D. 20 10 . 5 5
8 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Câu 236. [#Mỗi ngày 3 câu hỏi hay].
Gọi z , z , z , z là các nghiệm của phương trình 4 3 2
z 4z 3z 3z 3 0 . Tính giá trị 1 2 3 4 biểu thức T 2 z 2z 2 2 z 2z 2 2 z 2z 2 2 z 2z 2 1 1 2 2 3 3 4 4
A. T 102 .
B. T 101.
C. T 99 . D. T 100 .
Câu 237. [#Mỗi ngày 3 câu hỏi hay]. Biết phương trình 1 2 log 2x 3 log 1980 2 x x
có 2 nghiệm x , x . Tính x x . 2 2 1 2 1 2 A. log 10. B. log 11. C. log 12. D. log 13. 2 2 2 2
Câu 238. [#Mỗi ngày 3 câu hỏi hay].
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P : 4x 7 y z 25 0 và đường x 1 y z 1 thẳng d :
. Gọi d là hình chiếu vuông góc của d lên mặt phẳng P . 1 1 1 2 1 1
Đường thẳng d nằm trên P tạo với d ,d các góc bằng nhau, d có vectơ chỉ phương 2 1 1 2 a 2b u ; a ; b c . Tính 2 c a 2b 2 a 2b a 2b 1 a 2b A. . B. 0 . C. . D. 1. c 3 c c 3 c
Câu 239. [#Mỗi ngày 3 câu hỏi hay].
Trong không gian Oxyz, cho hai điểm A6; 3 ;4 , B ; a ;
b c . Gọi M,N,P lần lượt là giao
điểm của đường thẳng AB với các mặt phẳng tọa độ Oxy,Oxz,Oyz. Biết rằng M,N,P
nằm trên đoạn AB sao cho AM = MN = NP = PB. Tính giá trị của tổng a b c .
A. a b c 11.
B. a b c 11.
C. a b c 17 .
D. a b c 17 .
Câu 240. [#Mỗi ngày 3 câu hỏi hay].
Trong không gian với hệ tọa độ Oxyz, cho các điểm A 2
;0;0 , B0;4;2 ,C 2;2; 2 . Gọi
d là đường thẳng đi qua A và vuông góc với mặt phẳng (ABC), S là điểm di động trên
đường thẳng d, G và H lần lượt là trọng tâm của ABC , trực tâm của SBC . Đường
thẳng GH cắt đường thẳng d tại S . Tính tích S . A S A . 3 9 A. S . A S A . B. S . A S A . C. S . A S A 12 . D. . SA S A 6 . 2 2
Câu 241. [#Mỗi ngày 3 câu hỏi hay].
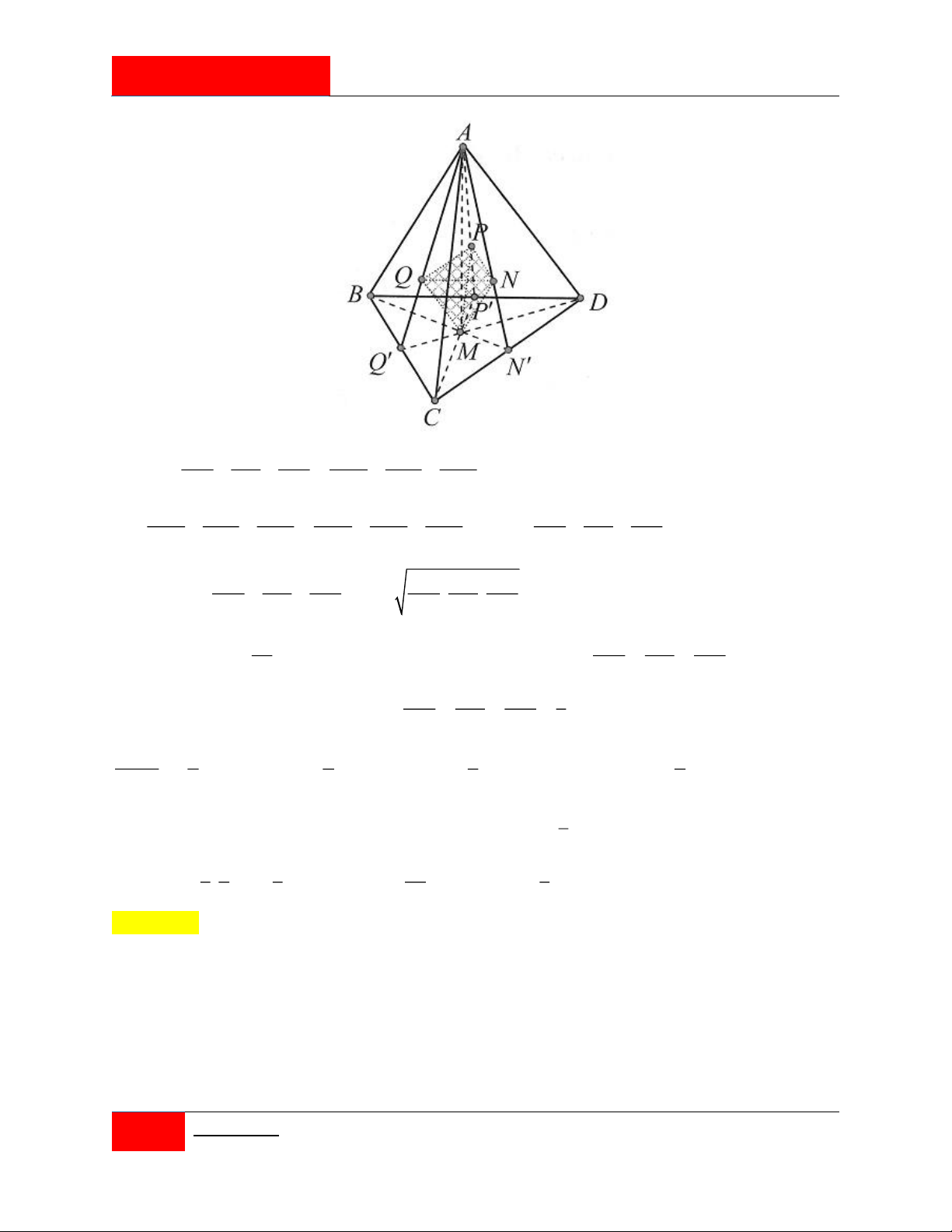
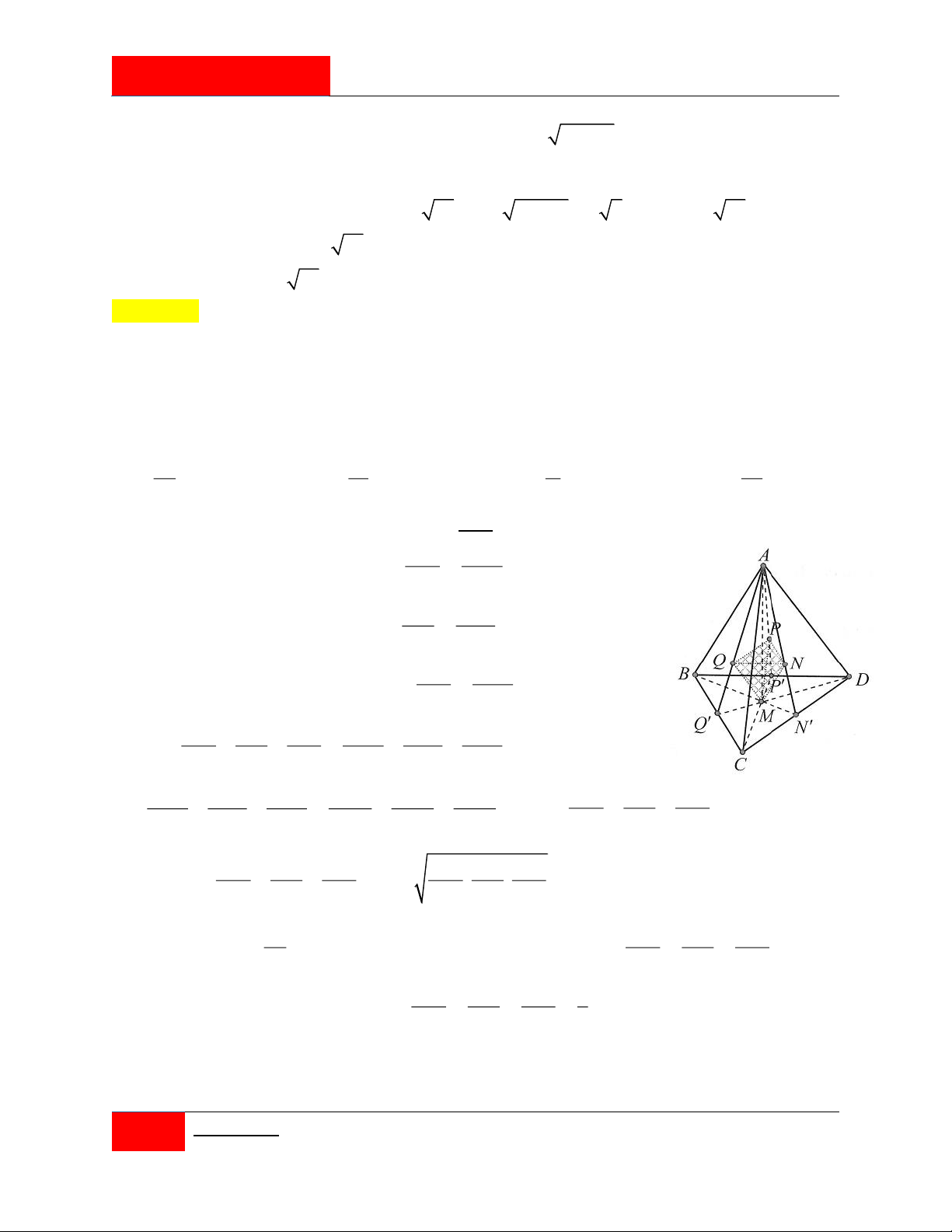
Cho tứ diện ABCD có thể tích là V . Điểm M thay đổi trong tam giác BCD . Các đường
thẳng qua M và song song với AB, AC, AD lần lượt cắt các mặt phẳng ACD , ABD ,
9 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
ABC tại N,P,Q. Giá trị lớn nhất của khối MNPQ là: V V V V A. . B. . C. . D. . 27 16 8 54
Câu 242. [#Mỗi ngày 3 câu hỏi hay].
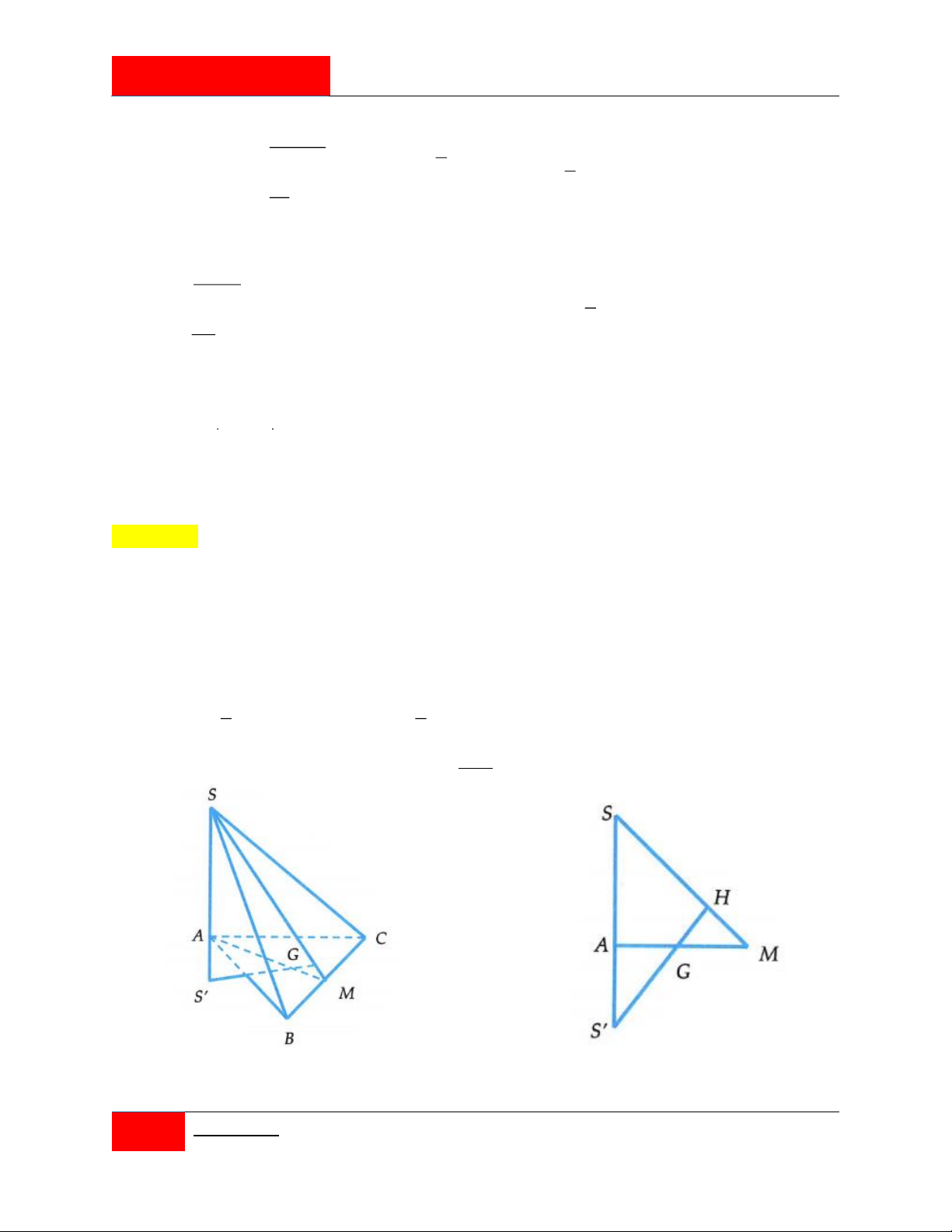
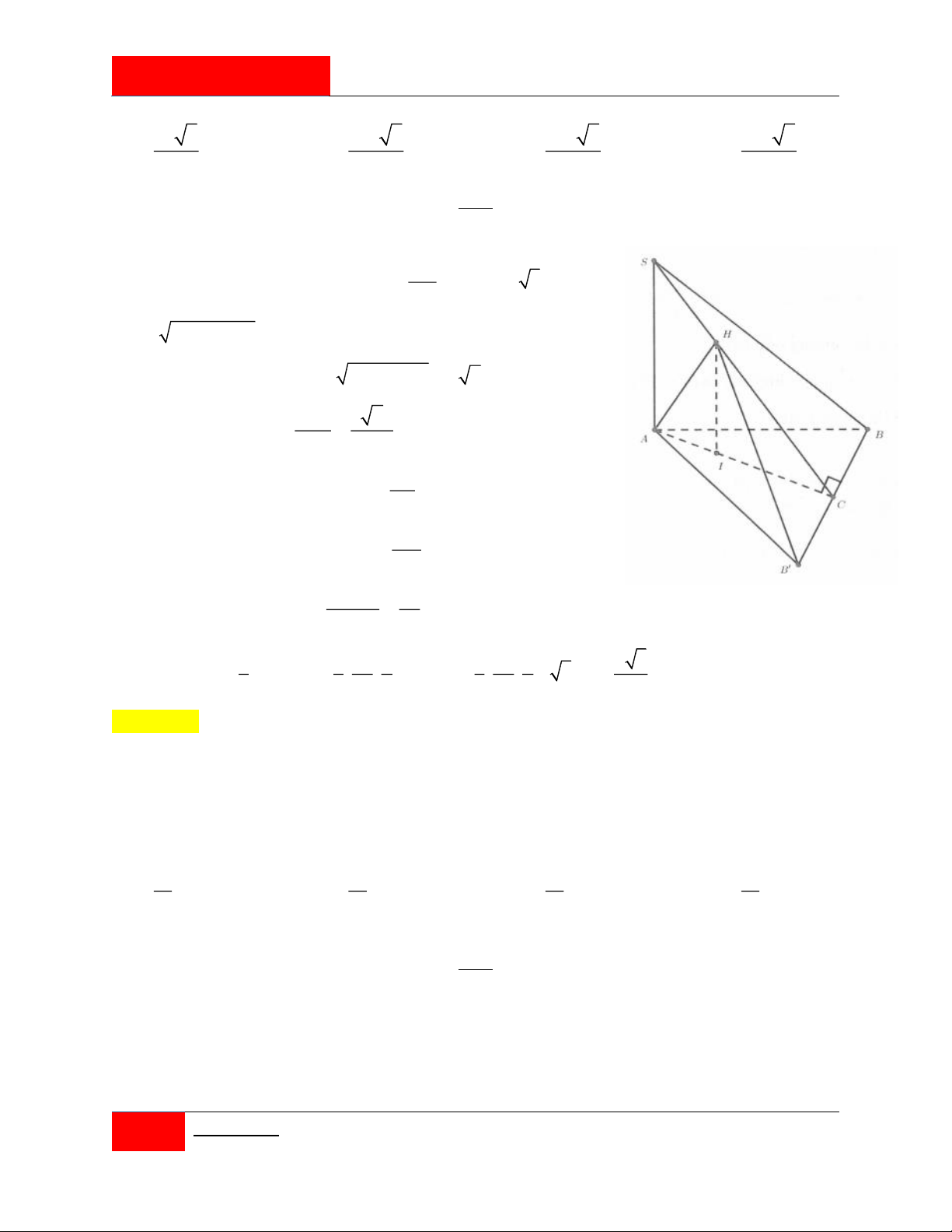
Cho hình chóp S.ABC có đường cao SA 2a , tam giác ABC vuông tại C , 0
AB 2a,CAB 30 . Gọi H là hình chiếu của A trên SC, B ' là điểm đối xứng của B
qua mặt phẳng SAC . Thể tích của khối chóp H.AB ' B bằng 3 a 3 3 6a 3 3 4a 3 3 2a 3 A. . B. . C. . D. . 7 7 7 7
Câu 243. [#Mỗi ngày 3 câu hỏi hay].
Cho tứ diện ABCD và các điểm M, N, P thuộc các cạnh BC, BD, AC sao cho
BC 4BM , AC 3AP , BD 2BN . Tính tỉ số thể tích hai phần của khối tứ diện ABCD
được phân chia bởi mặt phẳng MNP . 7 7 8 8 A. . B. . C. . D. . 13 15 15 13
Câu 244. [#Mỗi ngày 3 câu hỏi hay].
Cho số phức z a bi; a,b . Nhận xét nào sau đây luôn đúng? A. z 2a b . B. z 2 a b . C. z 2 a b . D. z 2 a b .
Câu 245. [#Mỗi ngày 3 câu hỏi hay].
Cho hình chóp S.ABC có ABC là tam giác vuông cân tại B, AB BC 2a, SAB SCB 90 .
Và khoảng cách từ A đến mặt phẳng SBC bằng a 2. Tính diện tích mặt cầu ngoại tiếp
S.ABC theo a. A. 2 6 a . B. 2 3 a . C. 2 4 a . D. 2 12 a .
Câu 246. [#Mỗi ngày 3 câu hỏi hay].
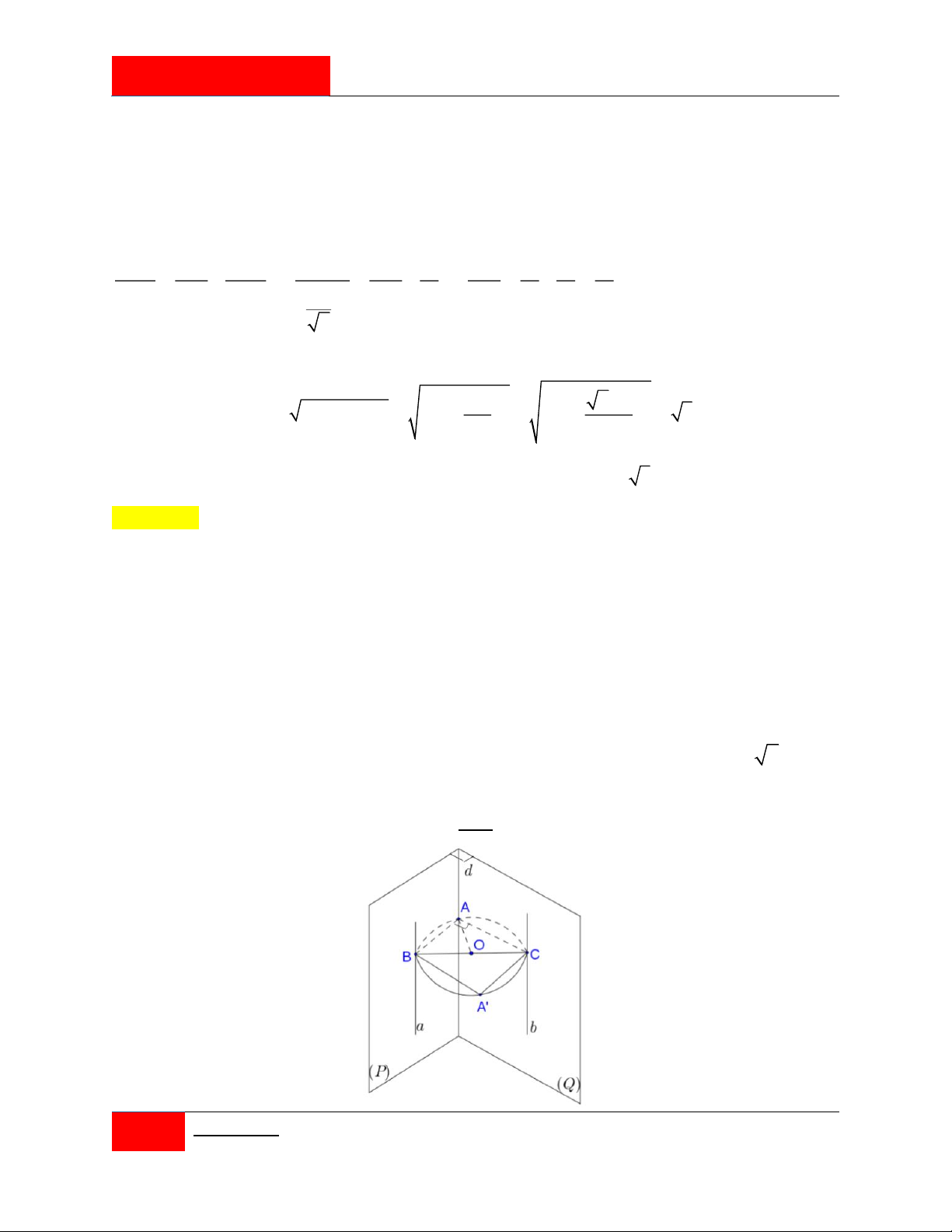
Cho hai đường thẳng a, b cố định, song song với nhau và khoảng cách giữa chúng bằng
4 . Hai mặt phẳng P, Q thay đổi vuông góc với nhau lần lượt chứa hai đường thẳng
a, b . Gọi d là giao tuyến của P, Q . Khẳng định nào sau đây là đúng?
A. d thuộc 1 mặt trụ cố định có khoảng cách giữa đường sinh và trục bằng 4 .
B. d thuộc 1 mặt nón cố định
10 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
C. d thuộc 1 mặt trụ cố định có khoảng cách giữa đường sinh và trục bằng 2 2 .
D. d thuộc 1 mặt trụ cố định có khoảng cách giữa đường sinh và trục bằng 2 .
Câu 247. [Mỗi ngày 3 câu hỏi hay].
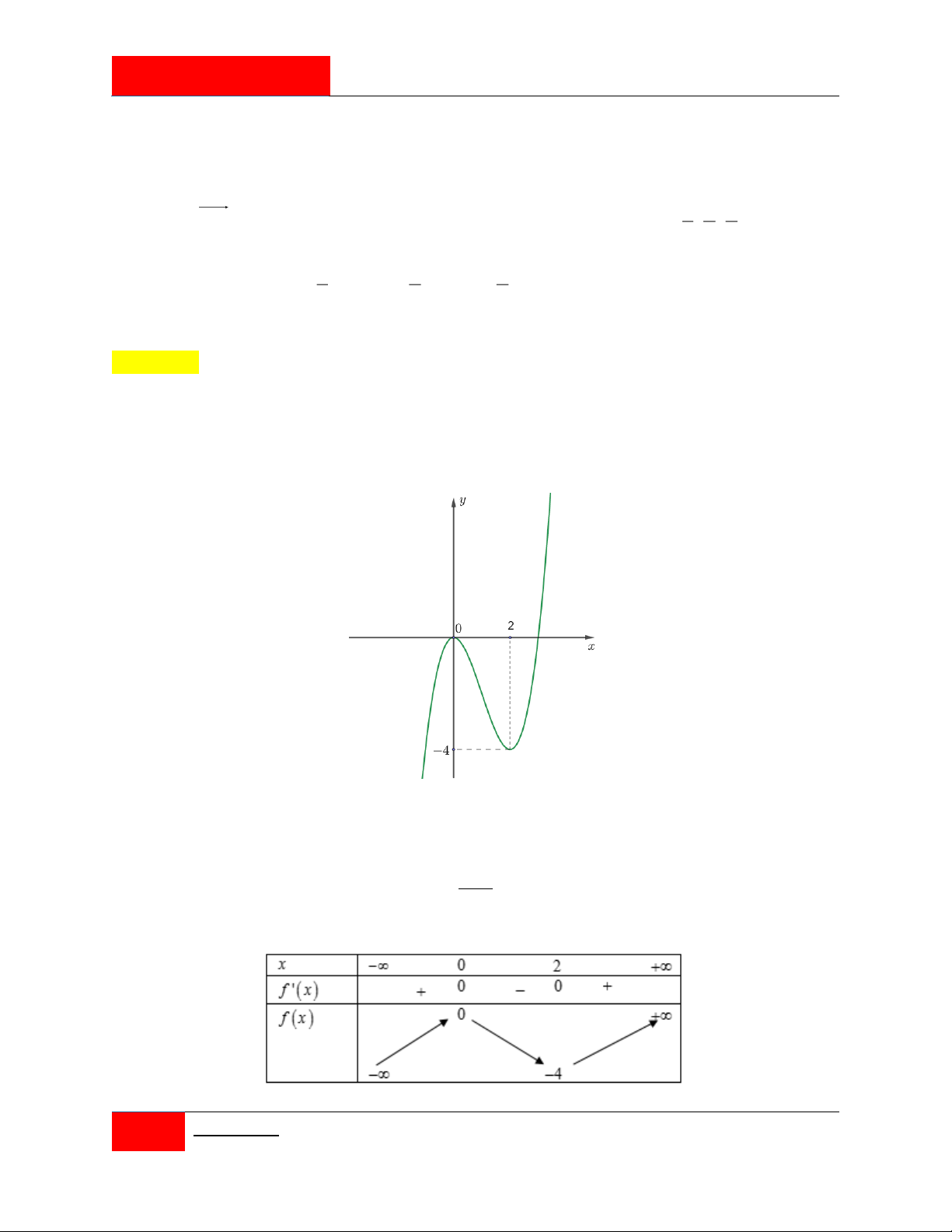
Cho hàm số f x 4 3 2
ax bx cx dx e ( ae 0 ). Đồ thị hàm số y f x như hình bên. Hàm số y f x 2 4
x có bao nhiêu điểm cực tiểu A. 3 . B. 5 . C. 4 . D. 2 .
Câu 248. [#Mỗi ngày 3 câu hỏi hay].
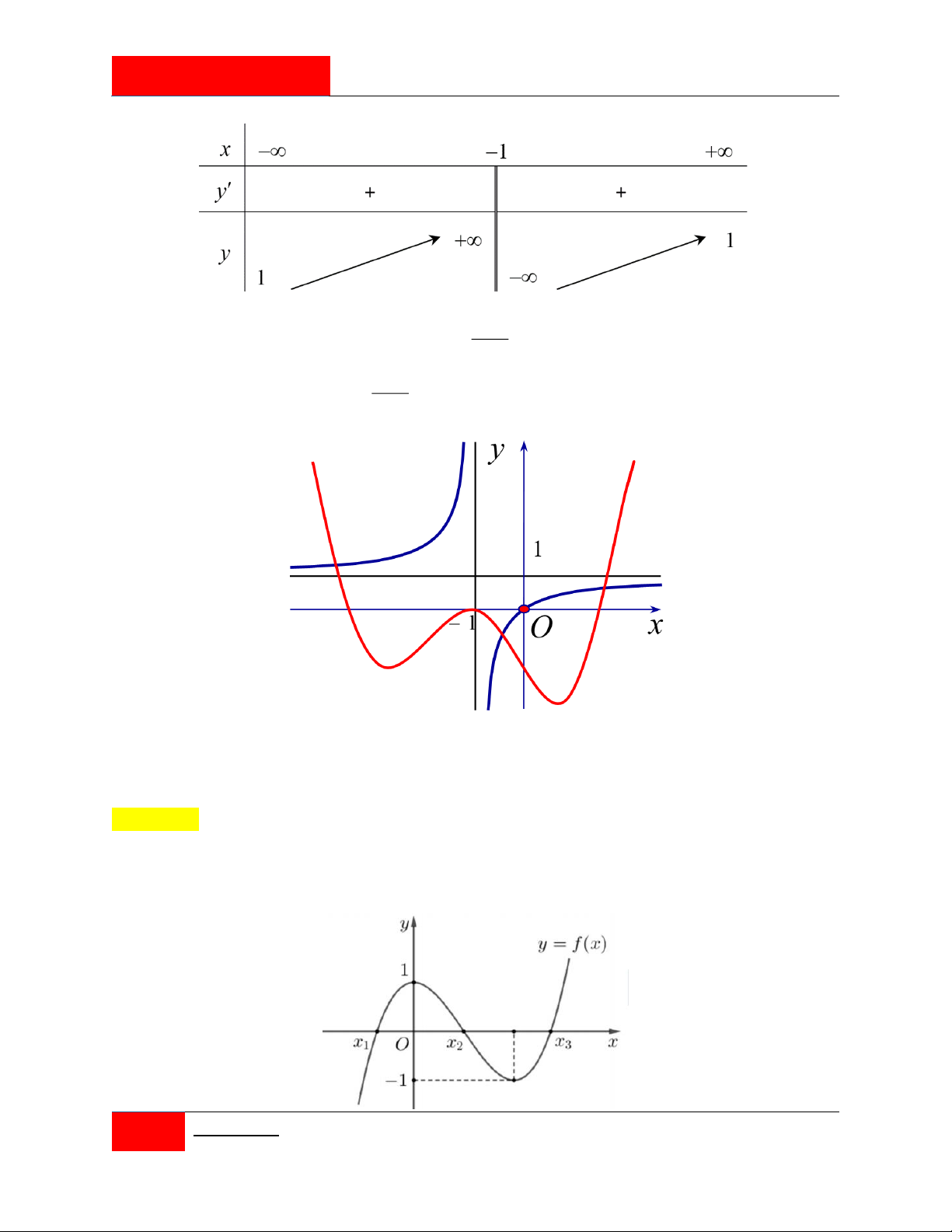
Cho hàm số bậc năm f x . Hàm số y f x có đồ thị là đường cong trong hình bên.
Hàm số g x f x x 2 7 2
1 đồng biến trên khoảng nào dưới đây?
A. 2;0 . B. 3; 1 .
C. 3; . D. 2;3 .
11 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Câu 249. [Mỗi ngày 3 câu hỏi hay].
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB a, SB a và
SB ABCD . Gọi M là trung điểm của SD . Biết rằng góc giữa hai mặt phẳng ACM
và SAD bằng 60 . Thể tích khối chóp S.BCD bằng? 3 3a 3 a 3 a 3 a A. . B. . C. . D. . 3 2 6 3
Câu 250. [#Mỗi ngày 3 câu hỏi hay].
Cho z x yi với x, y
là số phức thỏa mãn điều kiện z 2 3i z i 2 5 .
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 2 2
P x y 8x 6 y . Tính M m . 156 156 A. 60 2 10 . B. 20 10 . C. 60 2 10 . D. 20 10 . 5 5
Câu 251. [#Mỗi ngày 3 câu hỏi hay].
Cho tứ diện ABCD có thể tích là V . Điểm M thay đổi trong tam giác BCD . Các đường
thẳng qua M và song song với AB, AC, AD lần lượt cắt các mặt phẳng ACD , ABD ,
ABC tại N, P, Q . Giá trị lớn nhất của khối MNPQ là: V V V V A. . B. . C. . D. . 27 16 8 54
Câu 252. [#Mỗi ngày 3 câu hỏi hay].
Cho tam giác ABC có BC a , 0
BAC 135 . Trên đường thẳng vuông góc với ABC
tại A lấy điểm S thỏa mãn SA a 2 . Hình chiếu vuông góc của A trên SB, SC lần
lượt là M , N . Góc giữa hai mặt phẳng ABC và AMN là? A. 30 . B. 45 . C. 60 . D. 75 .
Câu 253. [#Mỗi ngày 3 câu hỏi hay].
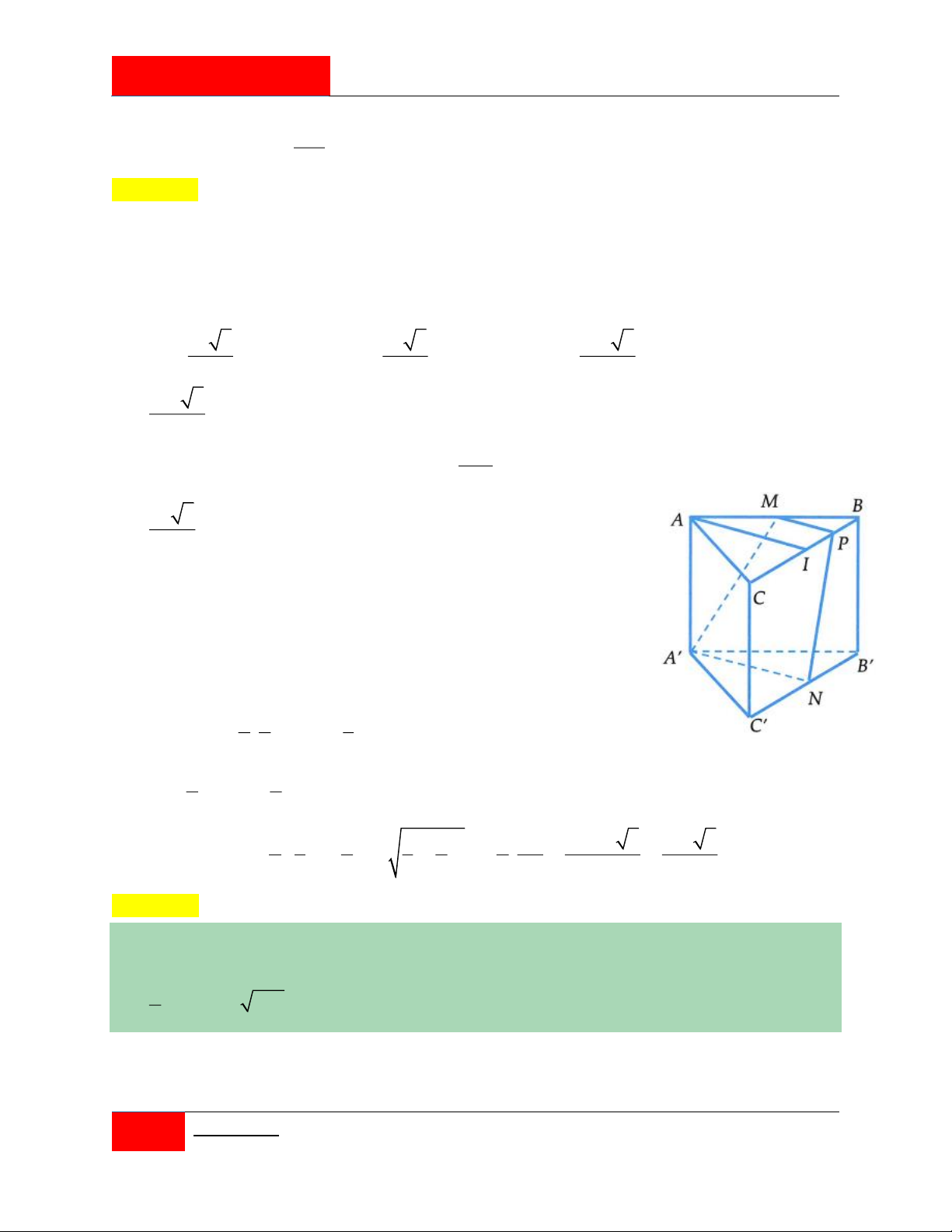
Cho hình lăng trụ tam giác đều ABC.
A BC có tất cả các cạnh đều bằng a . Gọi M , N
lần lượt là trung điểm của các cạnh AB và BC . Mặt phẳng
A MN cắt cạnh BC tại
P . Tính thể tích V của khối đa diện MBPA BN. 3 3 3 3 3 7 3 3 7 3 A. a V . B. a V . C. a V . D. a V . 36 12 96 48
Câu 254. [#Mỗi ngày 3 câu hỏi hay].
Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng P : x y z 1 0 , đường thẳng
12 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] x 15 y 22 z 37 d :
và mặt cầu S 2 2 2
: x y z 8x 6 y 4z 4 0 . Một đường 1 2 2
thẳng thay đổi cắt mặt cầu S tại hai điểm A, B sao cho AB 8 . Gọi A , B là hai
điểm lần lượt thuộc mặt phẳng P sao cho AA , BB cùng song song với d . Giá trị lớn
nhất của biểu thức AA BB là 8 30 3 24 18 3 12 9 3 16 60 3 A. . B. . C. . D. . 9 5 5 9
Câu 255. [#Mỗi ngày 3 câu hỏi hay]. 2
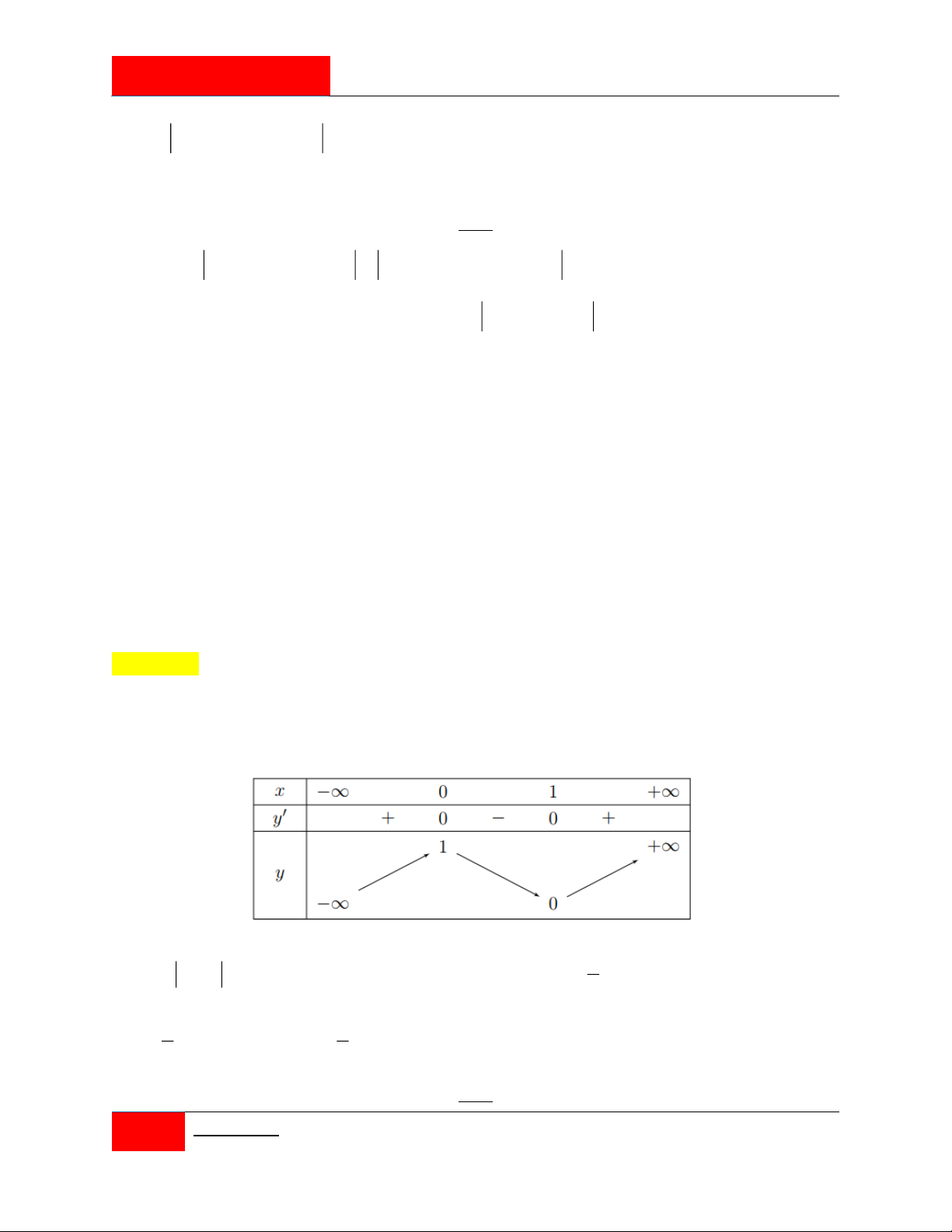
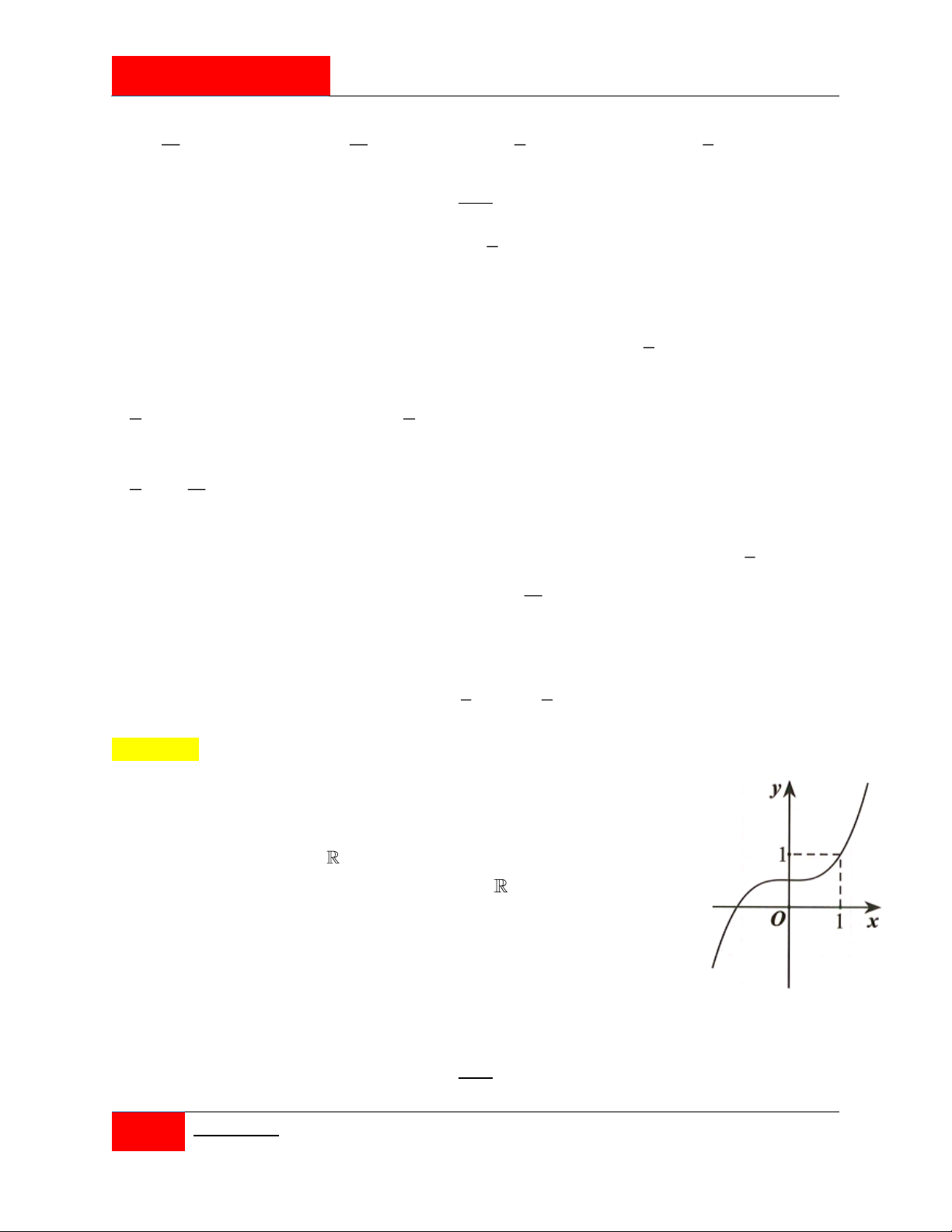
Cho hàm số y f x có đạo hàm trên và f x 4 x
2x , x 0 và 2 x f 1 1
. Khẳng định nào sau đây đúng?
A. Phương trình f x 0 có 1 nghiệm trên 0; 1 .
B. Phương trình f x 0 có 3 nghiệm trên 0;
C. Phương trình f x 0 có 1 nghiệm trên 1;2 .
D. Phương trình f x 0 có 1 nghiệm trên 2;5 .
Câu 256. [#Mỗi ngày 3 câu hỏi hay]. 2
x x Biết 4 4 1
x , x là hai nghiệm của phương trình 2 log
4x 1 6x và 1 2 7 2 x 1 x 2x
a b với a, b là hai số nguyên dương. Tính a b . 1 2 4
A. a b 13 .
B. a b 11 .
C. a b 16 .
D. a b 14 .
Câu 257. [#Mỗi ngày 3 câu hỏi hay]. x y
Cho hai số thực x, y thỏa mãn log
xx 3 y y 3 xy . Tìm giá 3 2 2
x y xy 2
trị nhỏ nhất của biểu thức P x 2 5
y xy 3y . A. 8 . B. 5. C. 7. D. 6 .
Câu 258. [#Mỗi ngày 3 câu hỏi hay].
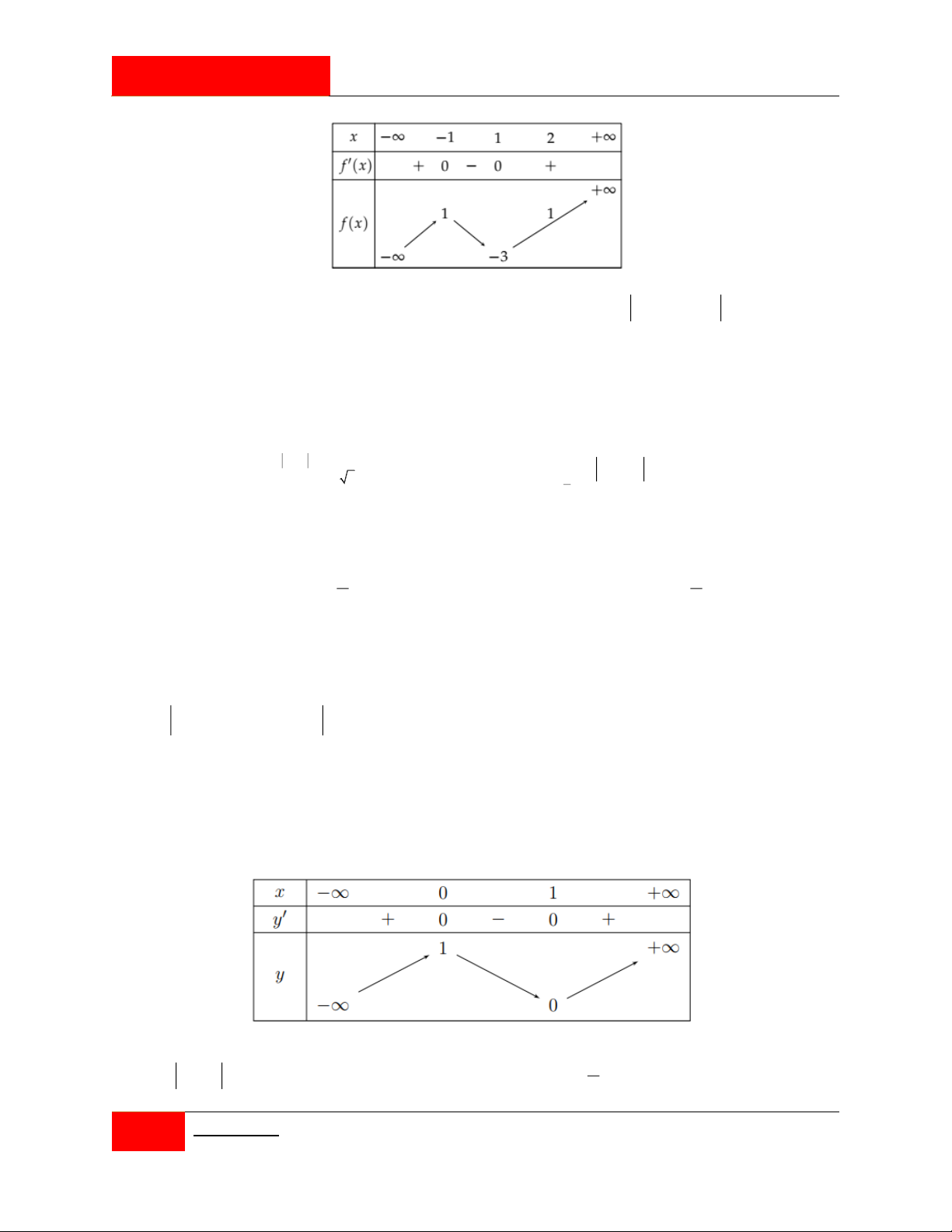
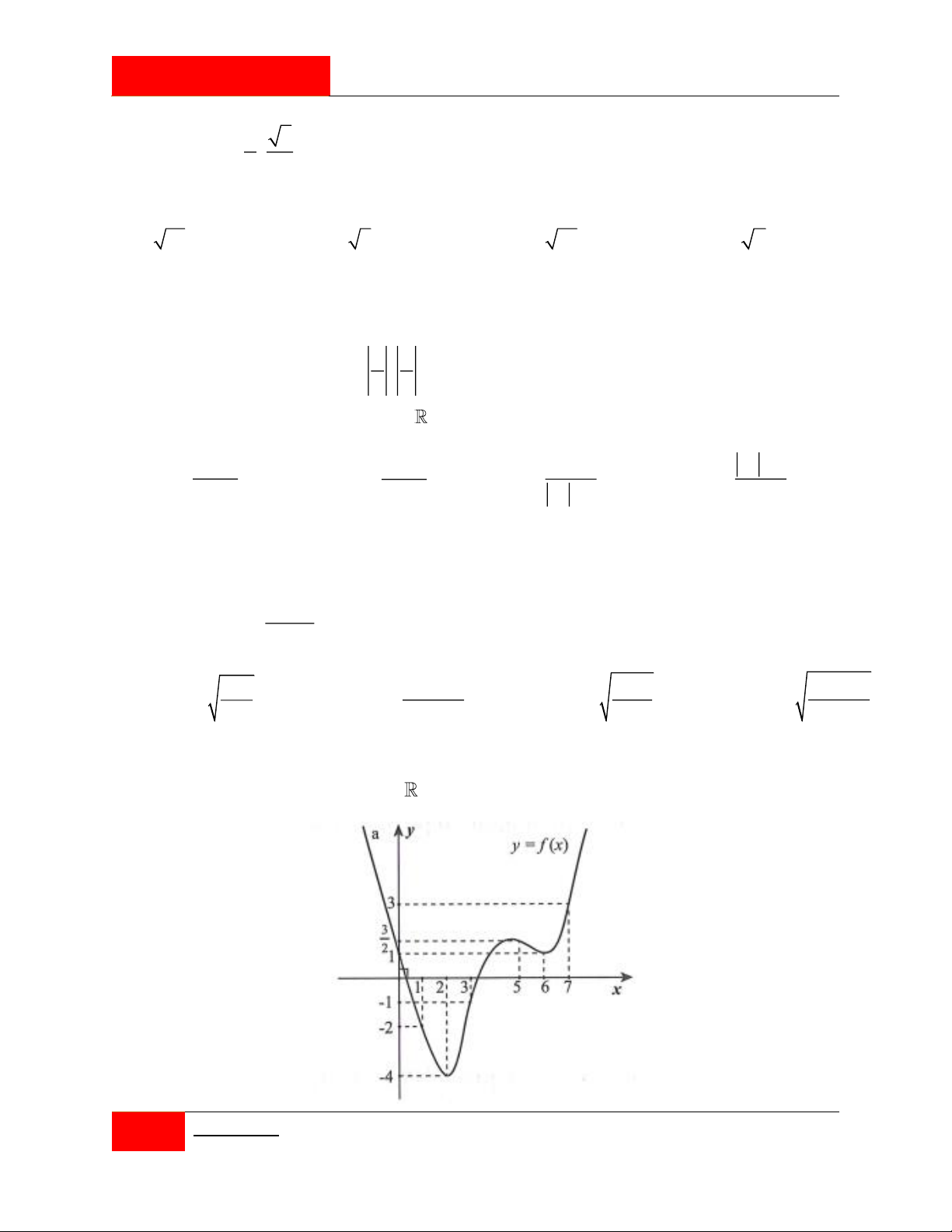
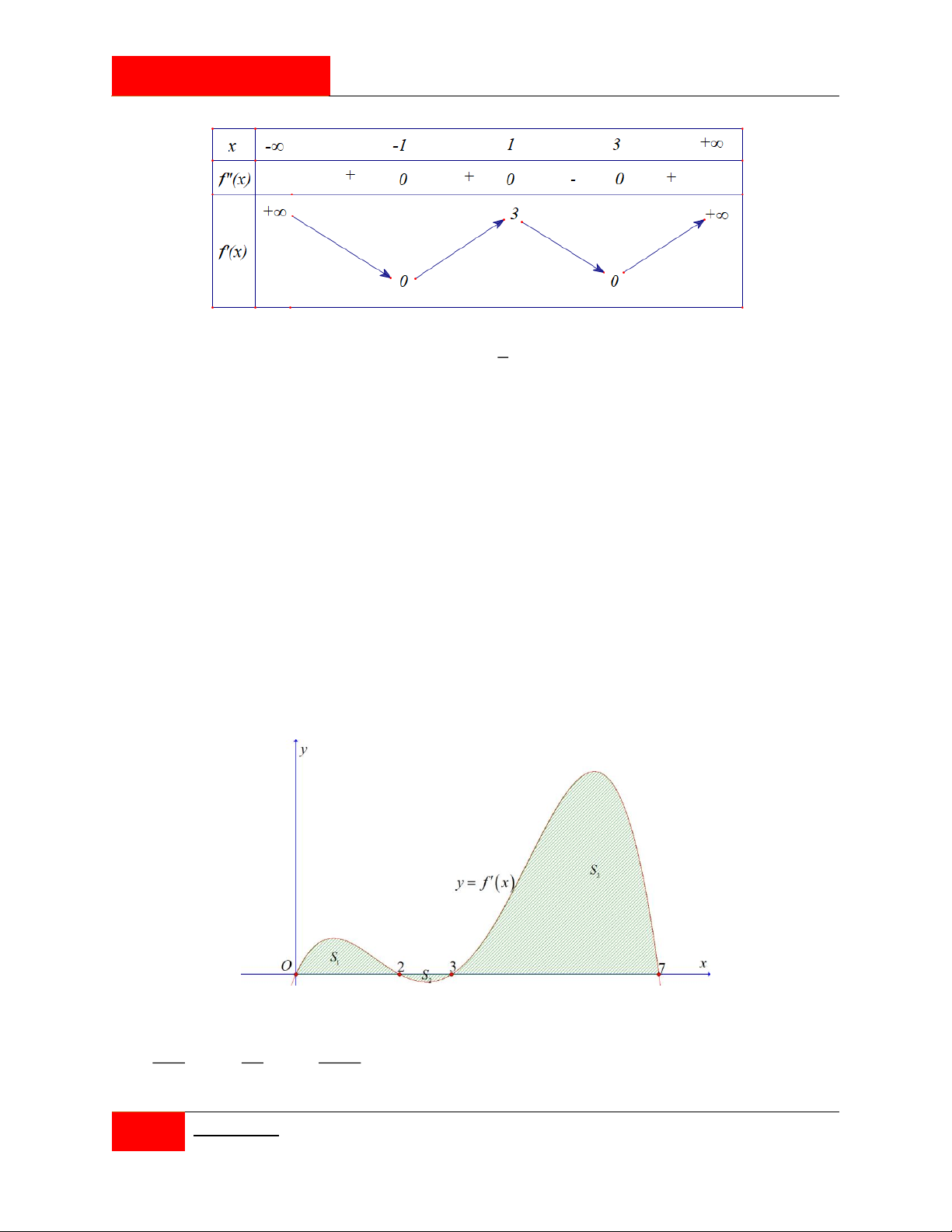
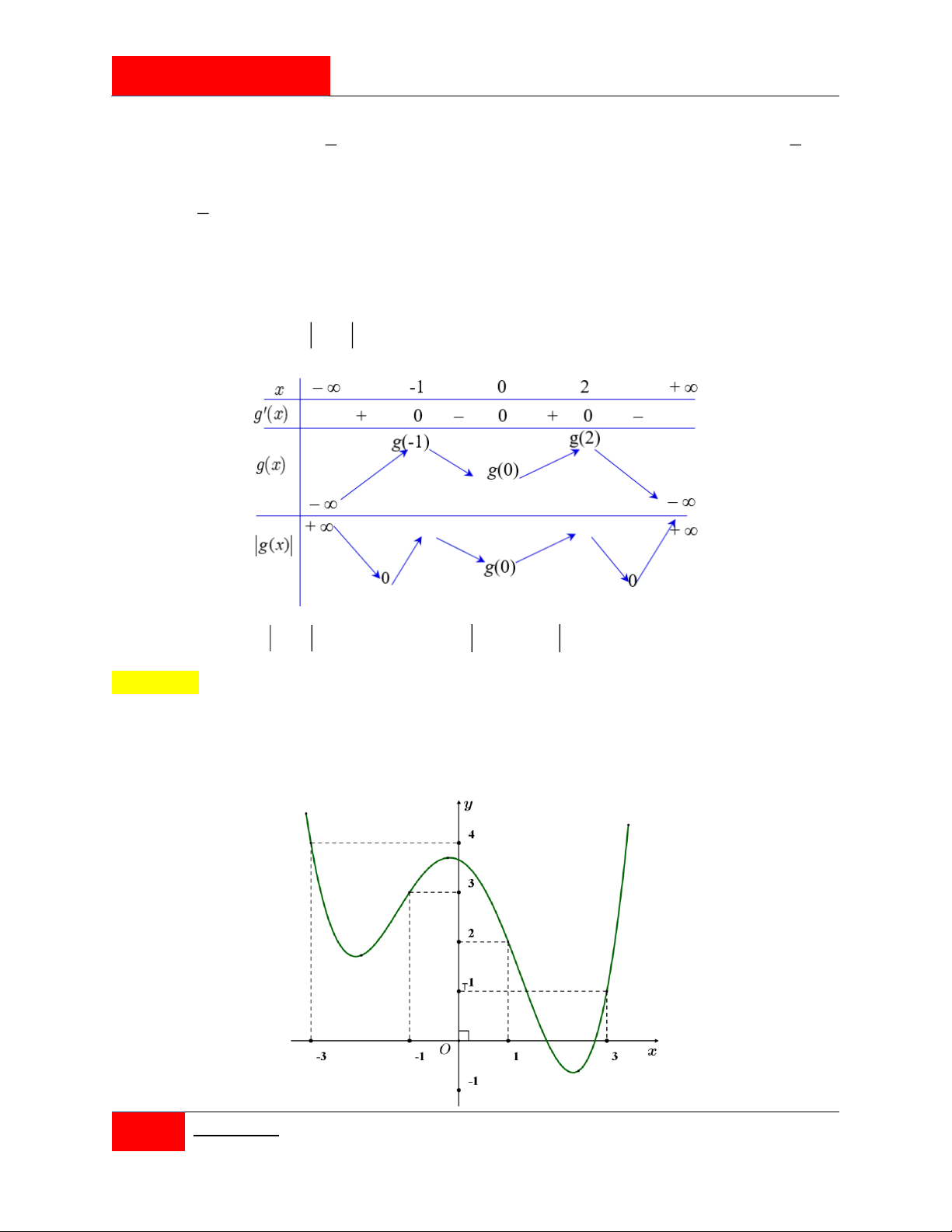
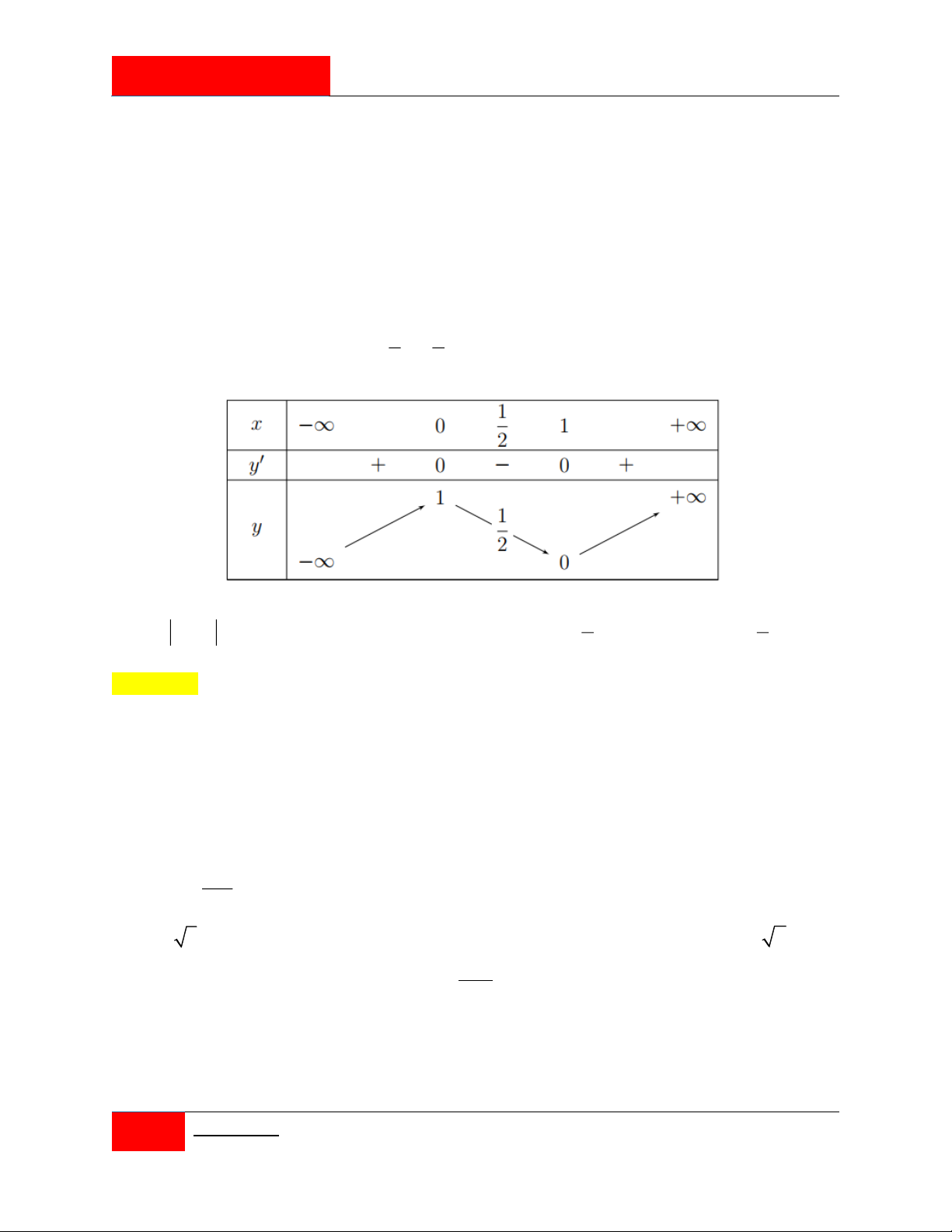
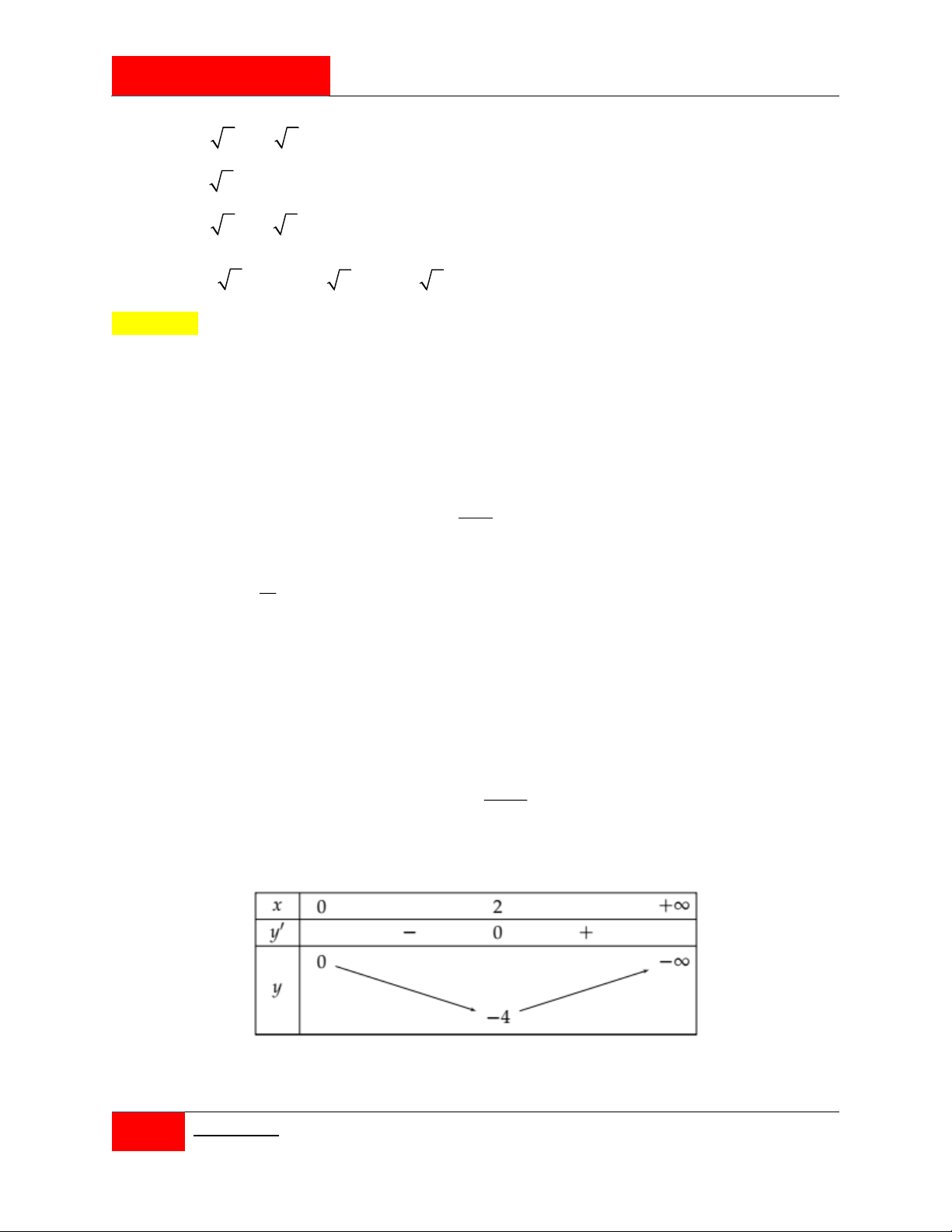
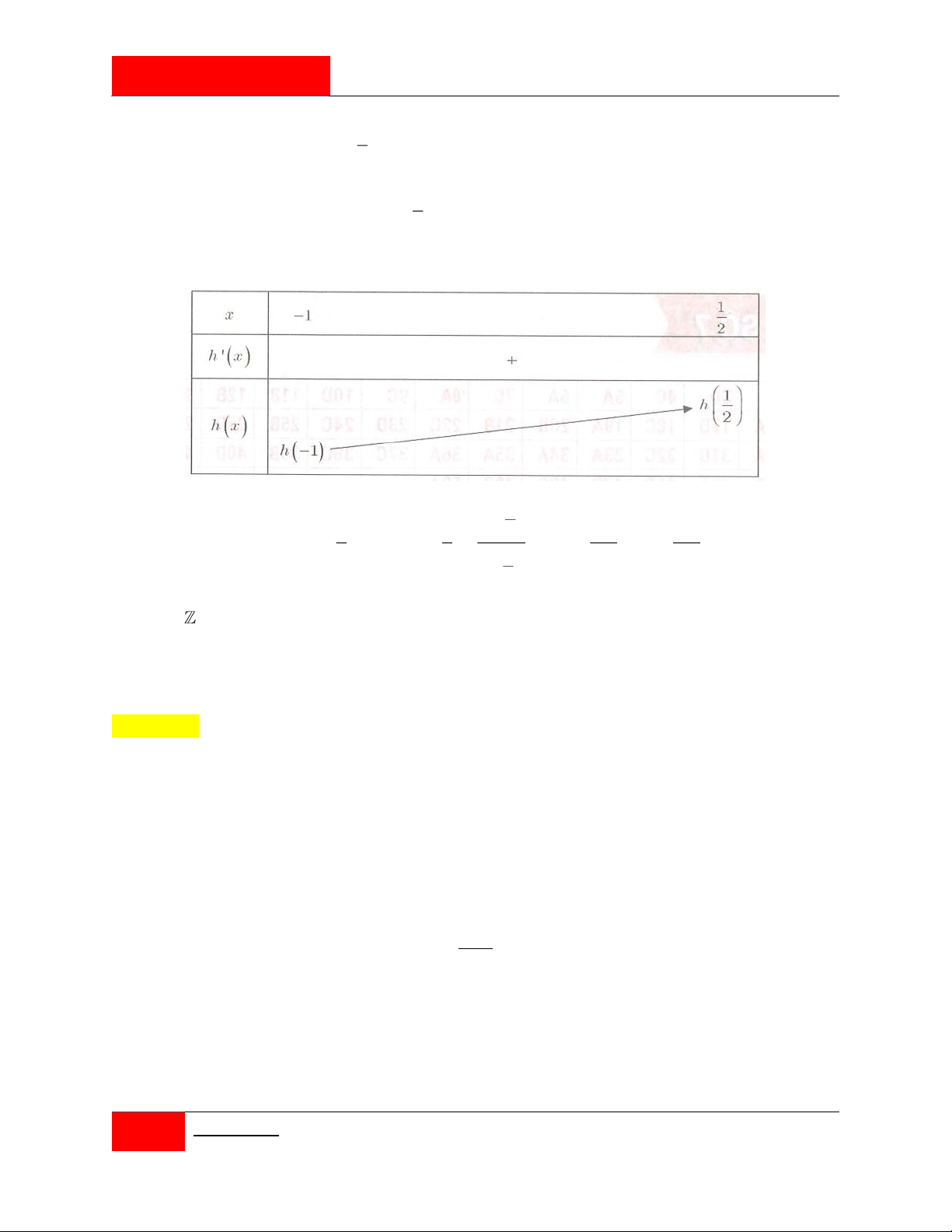
Cho hàm số y f x liên tục trên có bảng biến thiên như hình vẽ.
13 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Có bao nhiêu giá trị nguyên của tham số m để phương trình f 2 f x m 1 có đúng 2 nghiệm trên 1 ; 1 ? A. 13 . B. 9 . C. 4 . D. 5 .
Câu 259. [#Mỗi ngày 3 câu hỏi hay].
Cho phương trình xm x 4 log 2 3 2 2 2 2 x x x log
2 x m 2 0 . Gọi S là tập 1 2 2
hợp tất cả các giá trị của m để phương trình có 3 nghiệm thực phân biệt. Tổng các phần tử của S bằng: 1 3 A. 3 . B. . C. 2 . D. . 2 2
Câu 260. [#Mỗi ngày 3 câu hỏi hay].
Gọi S là tập hợp tất cả các giá trị của tham số thực m sao cho giá trị nhỏ nhất của hàm số 4
y sin x cos 2x m bằng 2 . Số phần tử của S là: A. 4. B. 3. C. 1. D. 2.
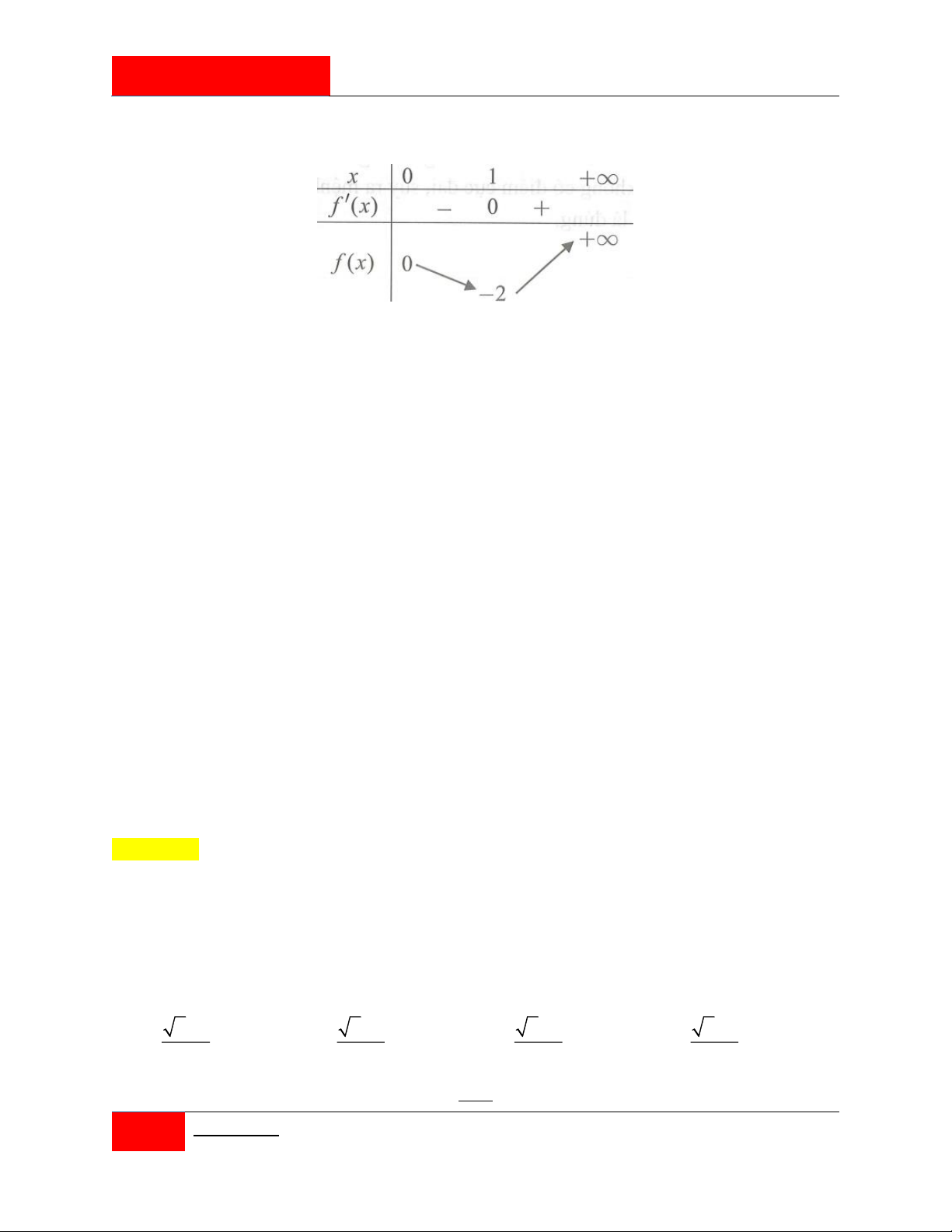
Câu 261. [#Mỗi ngày 3 câu hỏi hay]. Cho hàm số y f x 3 2
ax bx cx d có bảng biến thiên như sau: Khi đó 1
f x m có bốn nghiệm phân biệt x x x
x khi và chỉ khi: 1 2 3 4 2
14 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] 1 1 A. m 1. B. m 1.
C. 0 m 1.
D. 0 m 1. 2 2
Câu 262. [#Mỗi ngày 3 câu hỏi hay].
Trong không gian với hệ trục tọa độ Oxyz , cho ba mặt phẳng P : x 2y z 1 0 ,
Q: x 2y z 8 0 và R: x 2y z 4 0. Một đường thẳng d thay đổi cắt ba
mặt phẳng P, Q, R lần lượt tại ,
A B, C .
Tìm giá trị nhỏ nhất của biểu thức 2 144 T AB AC A. 3 72 3 . B. 96 . C. 108 . D. 3 72 4 .
Câu 263. [#Mỗi ngày 3 câu hỏi hay]. Cho parabol P 2
: y x 2x 3 cắt trục hoành tại hai điểm ,
A B và đường thẳng 1
d : y a 0 a 4 . Xét parabol P đi qua ,
A B và có đỉnh thuộc đường thẳng y a . 2
Gọi S là diện tích hình phẳng giới hạn bởi P và d . S là diện tích hình phẳng giới 1 1 2
hạn bởi P và trục hoành. Biết S S , tính 3 2
T a 8a 48a . 2 1 2 A. T 99 . B. T 64 . C. T 32 . D. T 72 .
Câu 264. [#Mỗi ngày 3 câu hỏi hay].
Cho hình chóp S.ABCD có đáy là ABCD là hình bình hành. Hai điểm M , N lần lượt
thuộc các đoạn thẳng AB và AD ( M và N không trùng với A ) sao cho AB AD 2.
4. Ký hiệu V ,V lần lượt là thể tích của các khối chóp S.ABCD và AM AN 1 V
S.MBCDN . Tìm giá trị lớn nhất của tỉ số 1 V 3 17 1 2 A. . B. . C. . D. . 4 14 6 3
Câu 265. [#Mỗi ngày 3 câu hỏi hay].
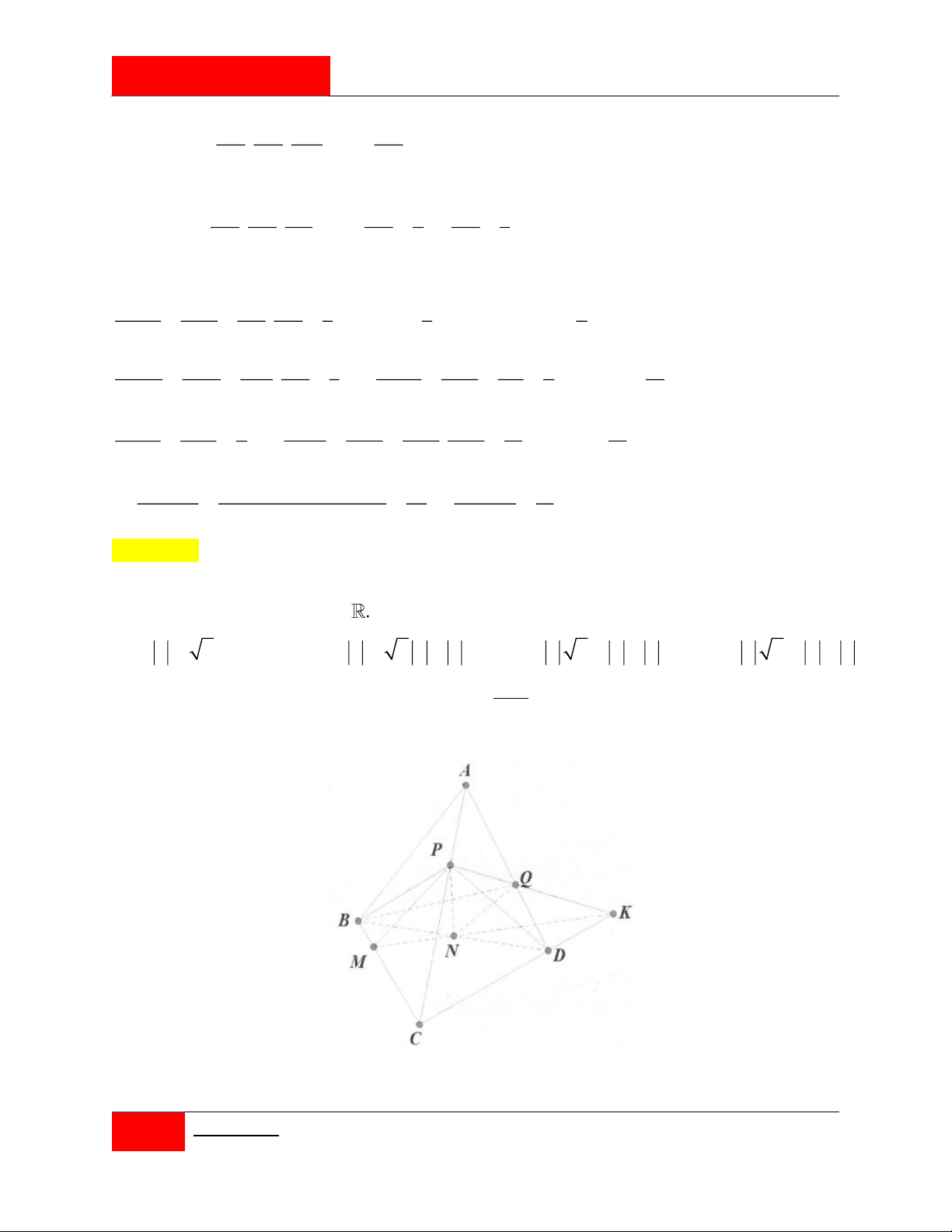
Trong không gian Oxyz , cho bốn điểm A3 1
; ;0 , B 2;0;
1 , C 0;2;
1 , D 0;0; 2 . Với
mỗi điểm M tùy ý, đặt T MA MB MC MD . Gọi M
a;b;c sao cho T đạt giá trị 0
nhỏ nhất. Lúc đó, tổng a 5b c bằng? A. 3 . B. 13 . C. 7 . D. 4 .
15 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Câu 266. [#Mỗi ngày 3 câu hỏi hay].
Trong không gian Oxyz , cho hai mặt phẳng : x my z 6m 3 0 và
: mx y mz 3m 8 0 (với m là tham số thực); hai mặt phẳng này cắt nhau theo
giao tuyến là đuờng thẳng . Gọi ' là hình chiếu của lên mặt phẳng Oxy . Biết rằng
khi m thay đổi thì đường thẳng ' luôn tiếp xúc với một mặt cầu cố định có tâm I ; a ;
b c thuộc mặt phẳng Oxy . Tính giá trị biểu thức 2 2 2
P 10a b 3c ? A. P 56 . B. P 9 . C. P 41 . D. P 73 .
Câu 267. [#Mỗi ngày 3 câu hỏi hay].
Cho số phức z thỏa mãn z 2 . Giá trị nhỏ nhất của biểu thức: P 2 z 1 2 z 1 z z 4i bằng: 14 7 A. 4 . B. 2 . C. 4 2 3 . D. 2 3 . 15 15
Câu 268. [#Mỗi ngày 3 câu hỏi hay]. 1
Cho hàm số y f x 4 2
x ax b a,b có đồ thịvà y g x 2 x m nx p 2 , m n, p
có đồ thị Pnhư hình vẽ. Diện tích hình phẳng giới hạn bởi C và Pcó
giá trị nằm trong khoảng nào sau đây? A. 4;4 ,1 . B. 4, 2;4,3 . C. 4,3;4, 4 . D. 4,1;4, 2 .
Câu 269. [#Mỗi ngày 3 câu hỏi hay]. Xét các số phức z z
z 4 1 và iz 2 1. Giá trị nhỏ nhất của z 2z 1 , 2 thỏa mãn 1 2 1 2 bằng A. 4 2 3 B. 2 5 2 C. 4 2 D. 4 2 3
16 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Câu 270. [#Mỗi ngày 3 câu hỏi hay].
Trong không gian Oxyz , cho hai điểm A0;8;2 , B 9; 7
;23 và mặt cầu S có
phương trình S x 2 y 2 z 2 : 5 3 7
72. Mặt phẳng P : x by cz d 0
đi qua điểm A và tiếp xúc với mặt cầu S sao cho khoảng cách từ B đến mặt phẳng
P lớn nhất. Giá trị của b c d khi đó là
A. b c d 2 .
B. b c d 4 .
C. b c d 3.
D. b c d 1.
Câu 271. [#Mỗi ngày 3 câu hỏi hay]. 2 x 1 x 1 Biết phương trình log 2log
có một nghiệm dạng x a b 2 5 3 x 2 2 x
trong đó a, b là các số nguyên. Tính T 2a . b A. 3 . B. 8 . C. 4 . D. 5 .
Câu 272. [#Mỗi ngày 3 câu hỏi hay].
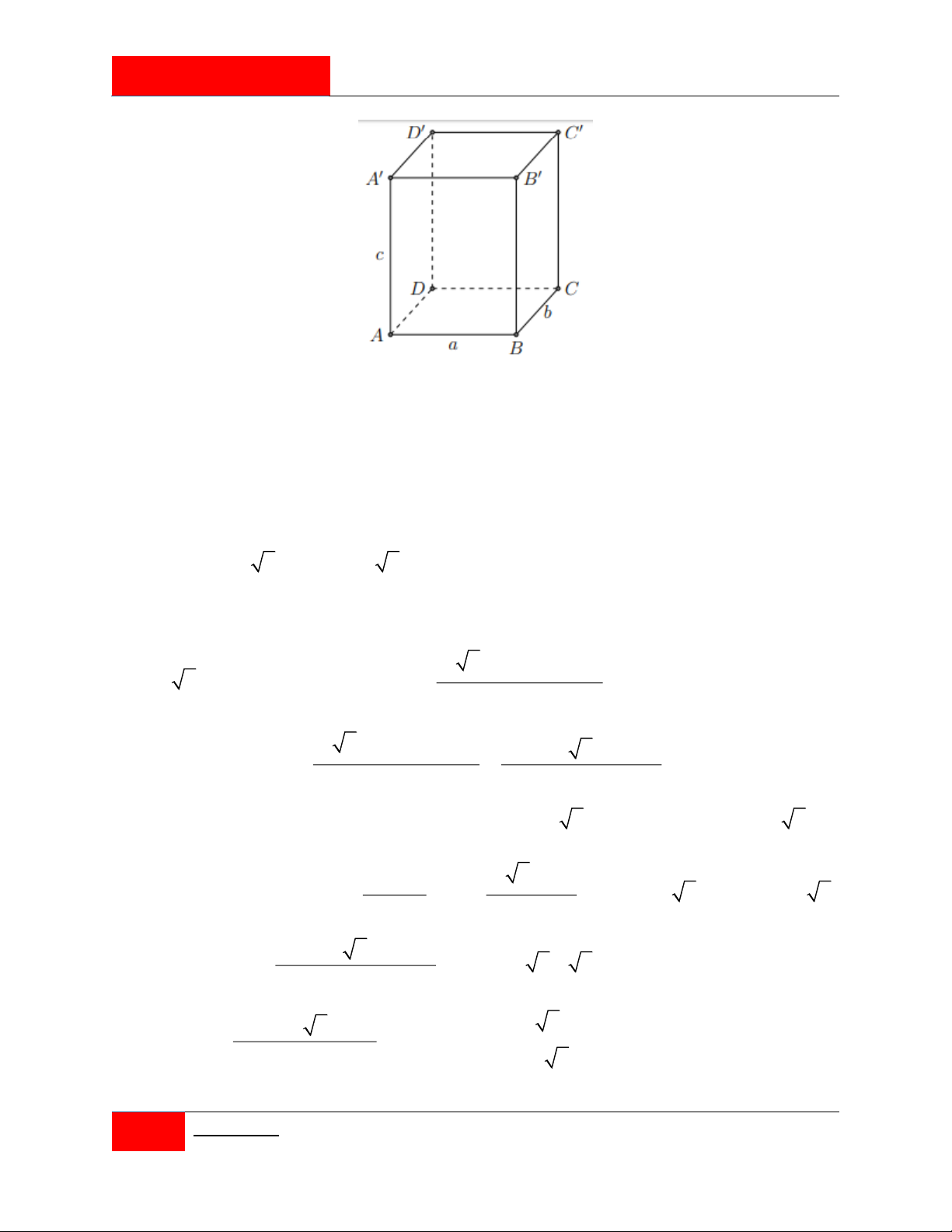
Cho hình hộp chữ nhật AB . CD
A BCD có tổng diện tích của tất cả các mặt là 36, độ dài
đường chéo AC bằng 6. Hỏi thể tích của khối hộp lớn nhất là bao nhiêu? A. 8 . B. 8 2 . C. 16 2 . D. 24 3 .
Câu 273. [#Mỗi ngày 3 câu hỏi hay].
Có bao nhiêu số nguyên của m để phương trình log 2x m 2
2log x x 4x 2m 1 2 2
có 2 nghiệm thực phân biệt. A. 2 . B. 3 . C. 1 . D. 4 .
Câu 274. [#Mỗi ngày 3 câu hỏi hay].
Trong tất cả các cặp số thực ; x y thỏa mãn log
2x 2 y 5 1. Có bao nhiêu giá 2 2 x y 3
trị thực của m để tồn tại duy nhất cặp số thực ; x y sao cho 2 2
x y 4x 6 y 13 m 0 . A. 3 . B. 1 . C. 2 . D. 0 .
Câu 275. [#Mỗi ngày 3 câu hỏi hay]. x y 1
Cho các số thực x, y, z thỏa mãn các điều kiện x 0, y 0, z 1 và log 2x y . 2 4x y 3
17 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] 2 2 x z y Khi đó giá trị ( 1) ( 2)
nhỏ nhất của biểu thức T tương ứng bằng: 3x y x 2z 3 A. 4 2 . B. 6 . C. 6 3 . D. 4 .
Câu 276. [#Mỗi ngày 3 câu hỏi hay].
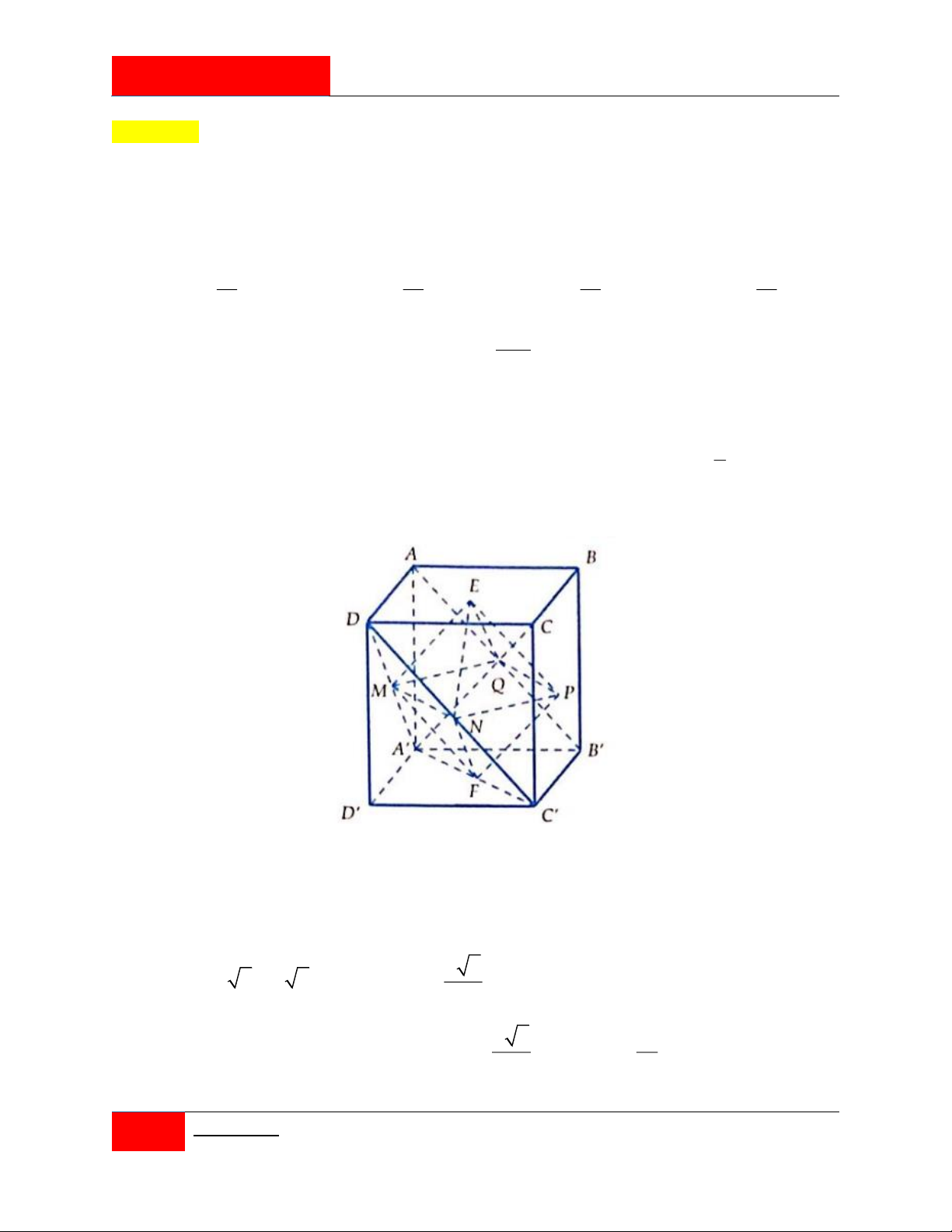
Cho hình lập phương AB . CD
A BCD .Gọi E, F , M , N , P,Q lần lượt là tâm của các mặt AB ;
CD A' B 'C ' D '; ADD ' A'; DCC ' D ';CBB 'C '; ABB ' A' . Biết cạnh khối lập phương bằng
a ,khi đó thể tích của khối tám mặt đều nội tiếp khối lập phương trên là 3 a 3 a 3 a 3 a A. . B. . C. . D. . 8 12 4 6
Câu 277. [#Mỗi ngày 3 câu hỏi hay].
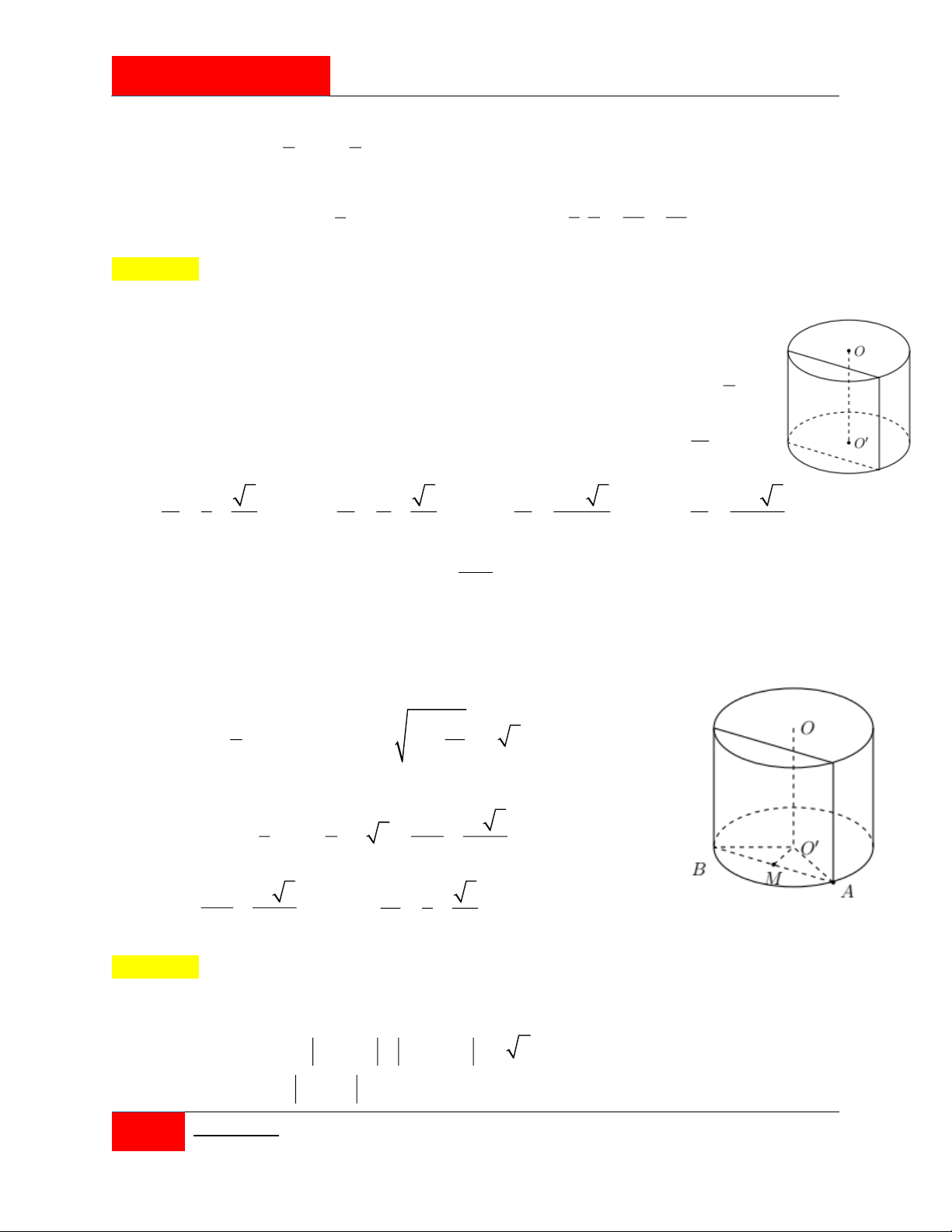
Cho khối trụ T có trục OO , bán kính r và thể tích V. Cắt khối trụ T thành hai r
phần bởi mặt phẳng P song song với trục và cách trục một khoảng bằng 2 V
(như hình vẽ). Gọi V là thể tích phần không chứa trục OO . Tính tỉ số 1 . 1 V V 1 3 V 3 V 3 V 4 3 A. 1 . B. 1 . C. 1 . D. 1 . V 3 4 V 4 3 V 2 V 4
Câu 278. [#Mỗi ngày 3 câu hỏi hay].
Xét số phức z thỏa mãn z 2 i z 4 7i 6 2. Gọi m, M lần lượt là giá trị nhỏ nhất
cả giá trị lớn nhất của z 1 i . Tính P m M. 5 2 2 73 5 2 73
A. P 13 73 . B. P P P 2 . C. 5 2 73 . D. 2 .
Câu 279. [#Mỗi ngày 3 câu hỏi hay]. Phương trình 3
x m x x x 2 3 3 2
x x x m 2 1 2 6 9 2
2 1 có 3 nghiệm phân biệt khi và chỉ khi m ; a b , đặt 2 2
T b a thì: A. T 36 . B. T 48 . C. T 64 . D. T 72 .
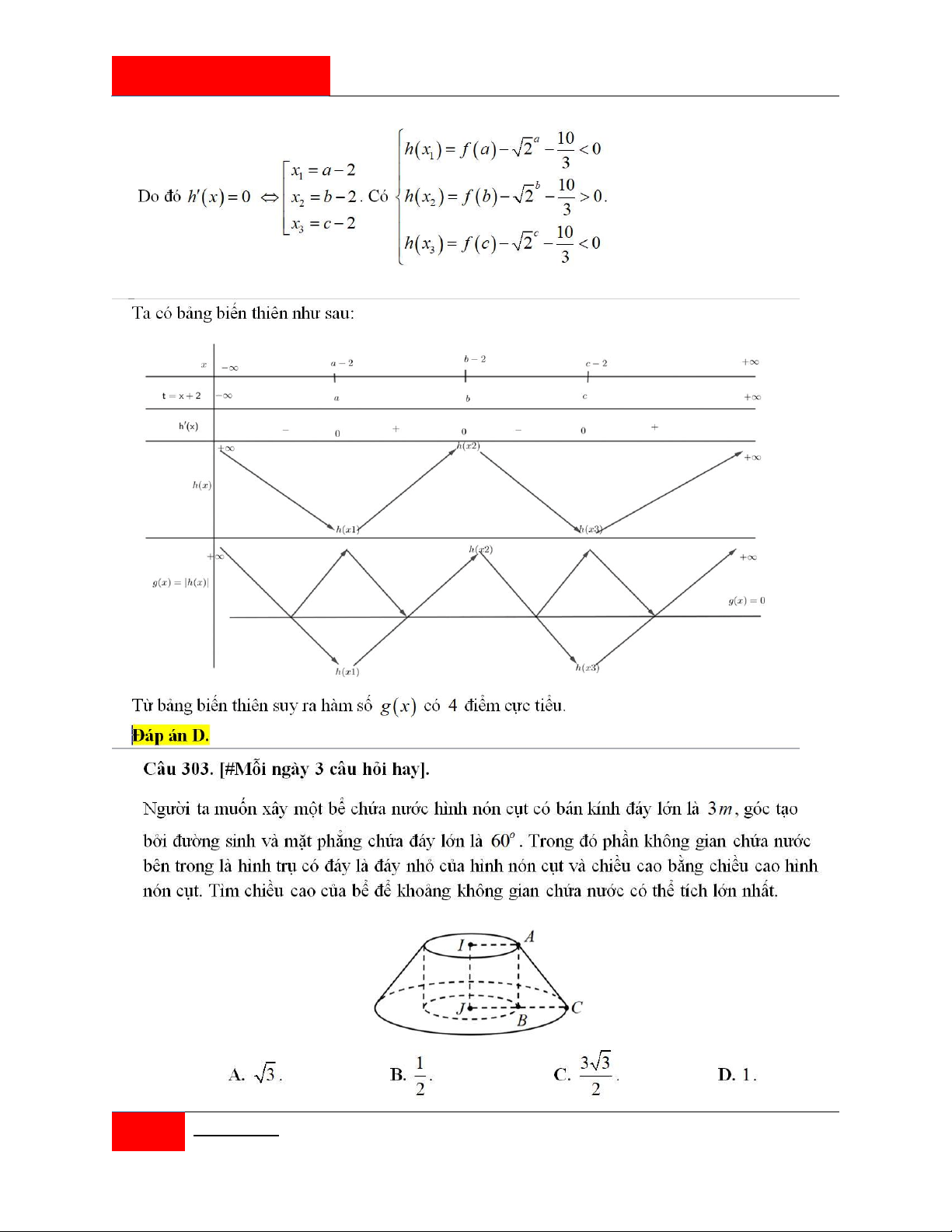
Câu 280. [#Mỗi ngày 3 câu hỏi hay].
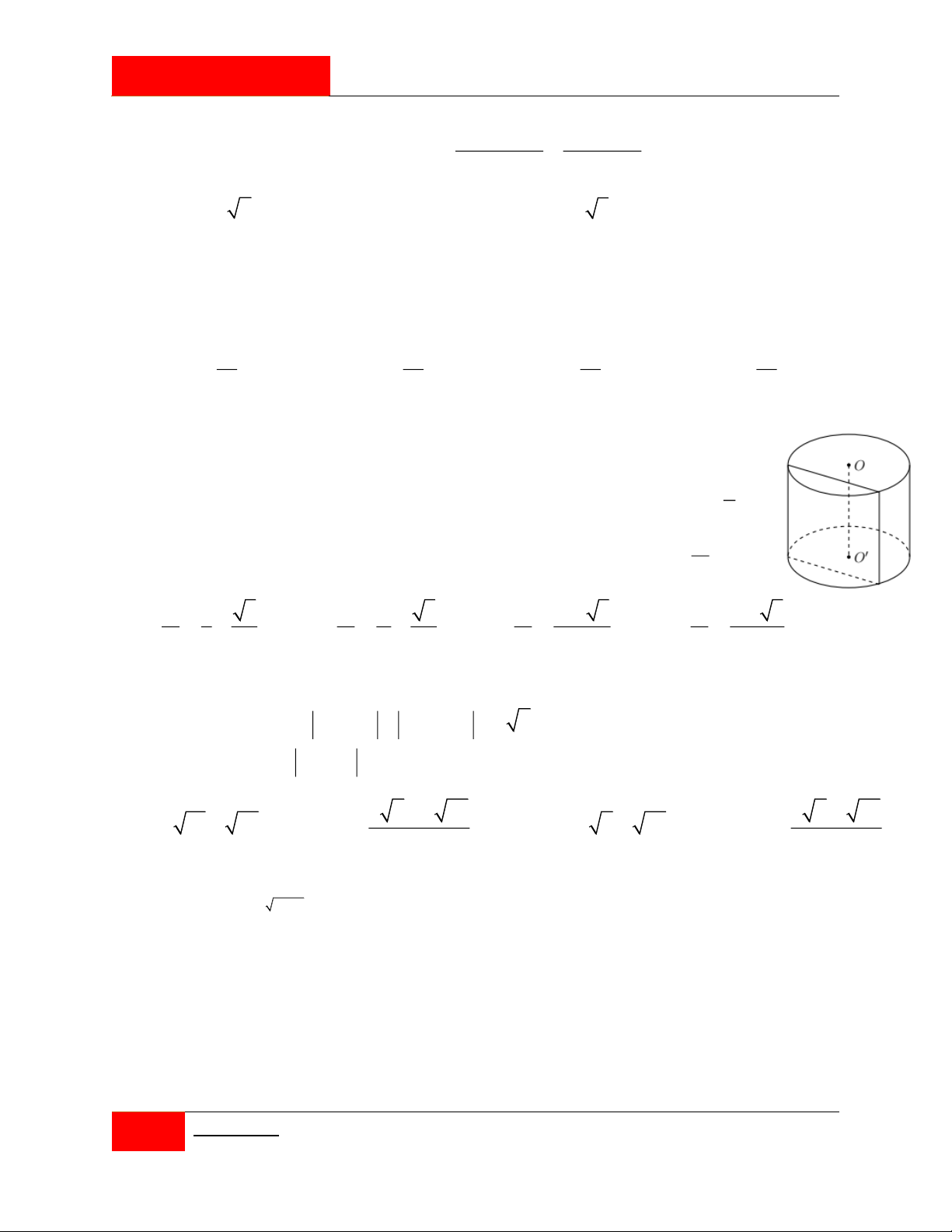
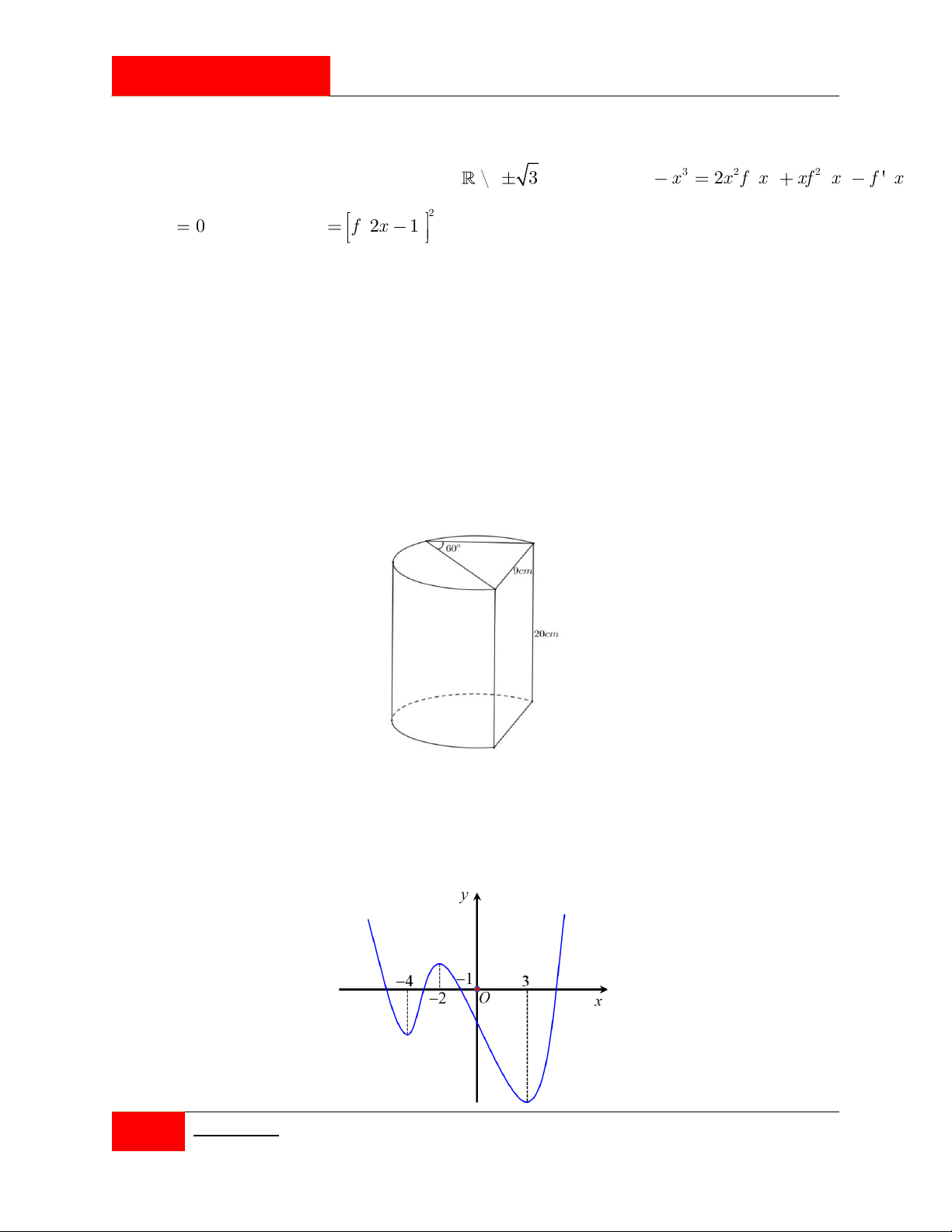
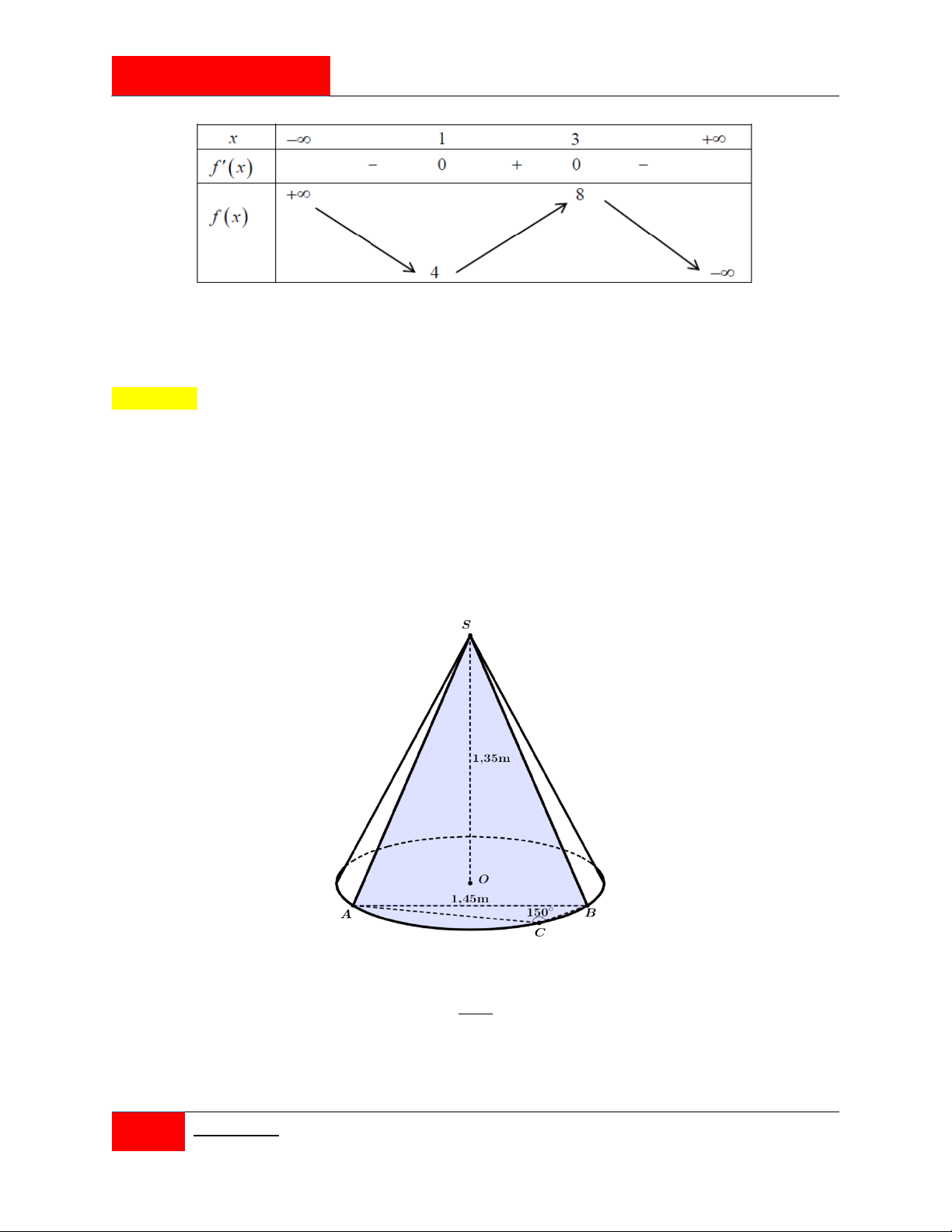
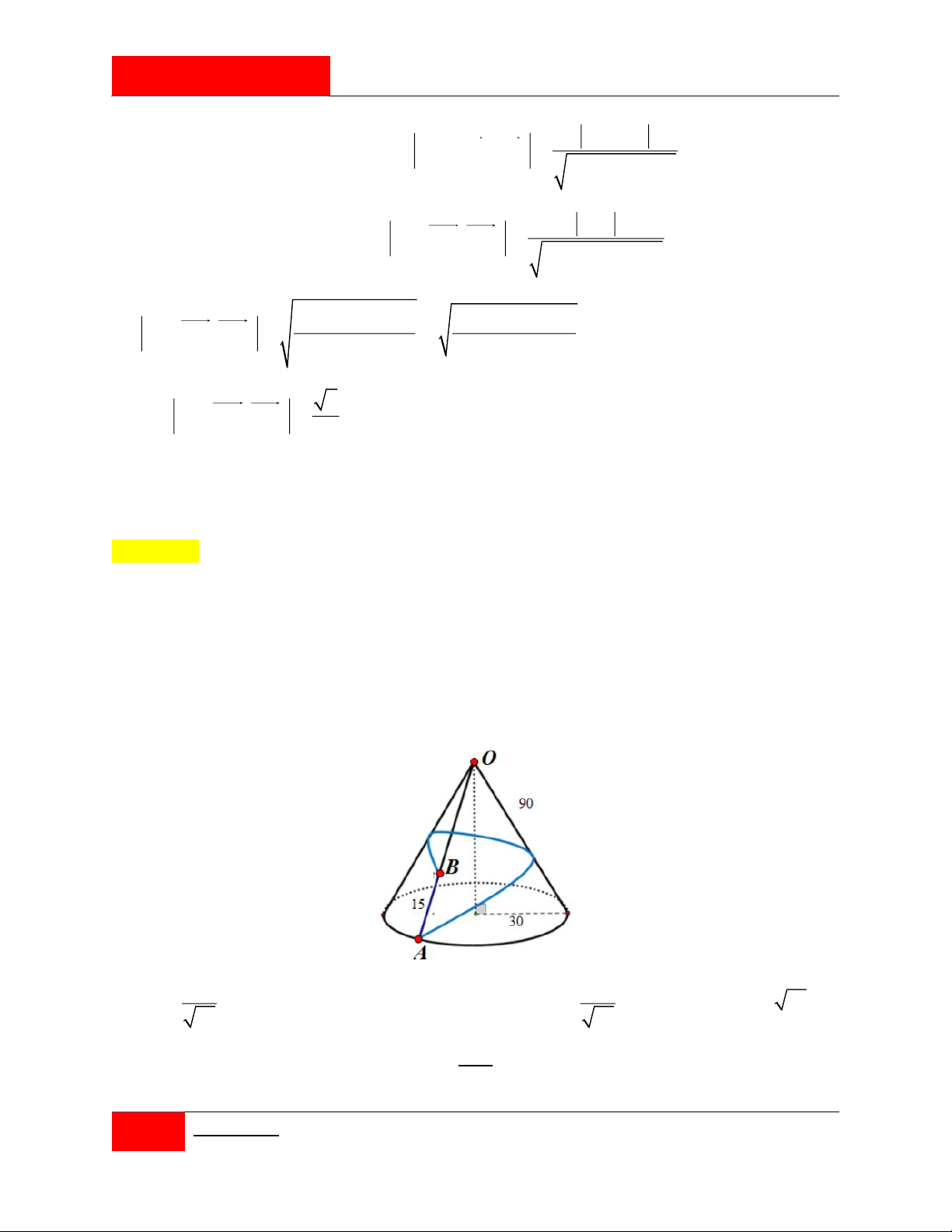
Nhân dịp quảng bá chiếc nón lá Việt Nam, một cửa hàng có đặt trước sảnh một cái nón lớn
với chiều cao 1,35m . Cửa hàng có sơn cách điệu hoa văn trang trí một phần của hình nón
18 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
ứng với cung AB như hình vẽ. Biết AB 1, 45m , ACB 150 và giá tiền để trang trí 2 1m
là 2.000.000 đồng. Hỏi số tiền (làm tròn đến hàng nghìn) mà cửa hàng cần dùng để trang
trí mặt trước của nón là bao nhiêu? A. 4.510.000 đồng. B. 3.021.000 đồng. C. 3.010.000 đồng. D. 3.008.000 đồng.
Câu 281. [#Mỗi ngày 3 câu hỏi hay].
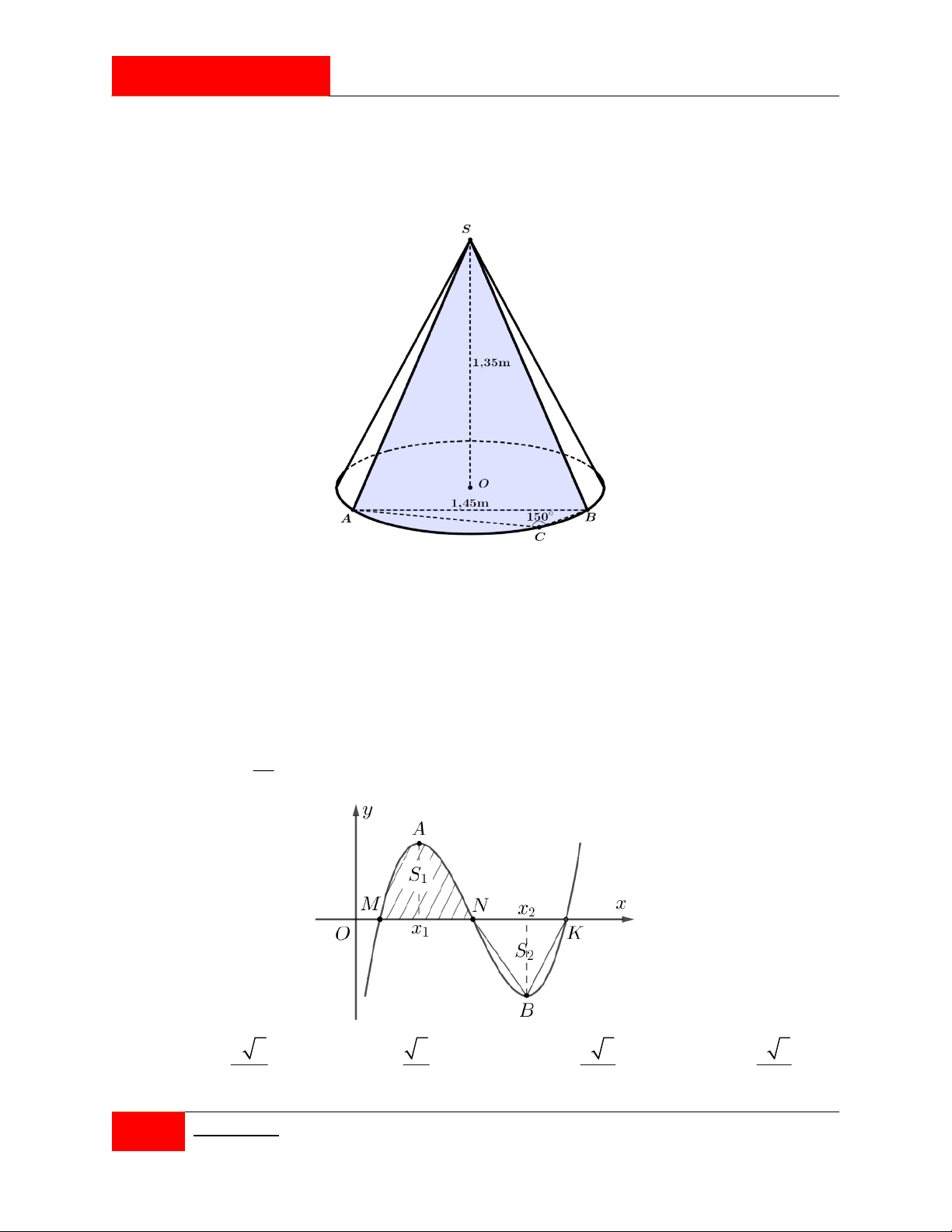
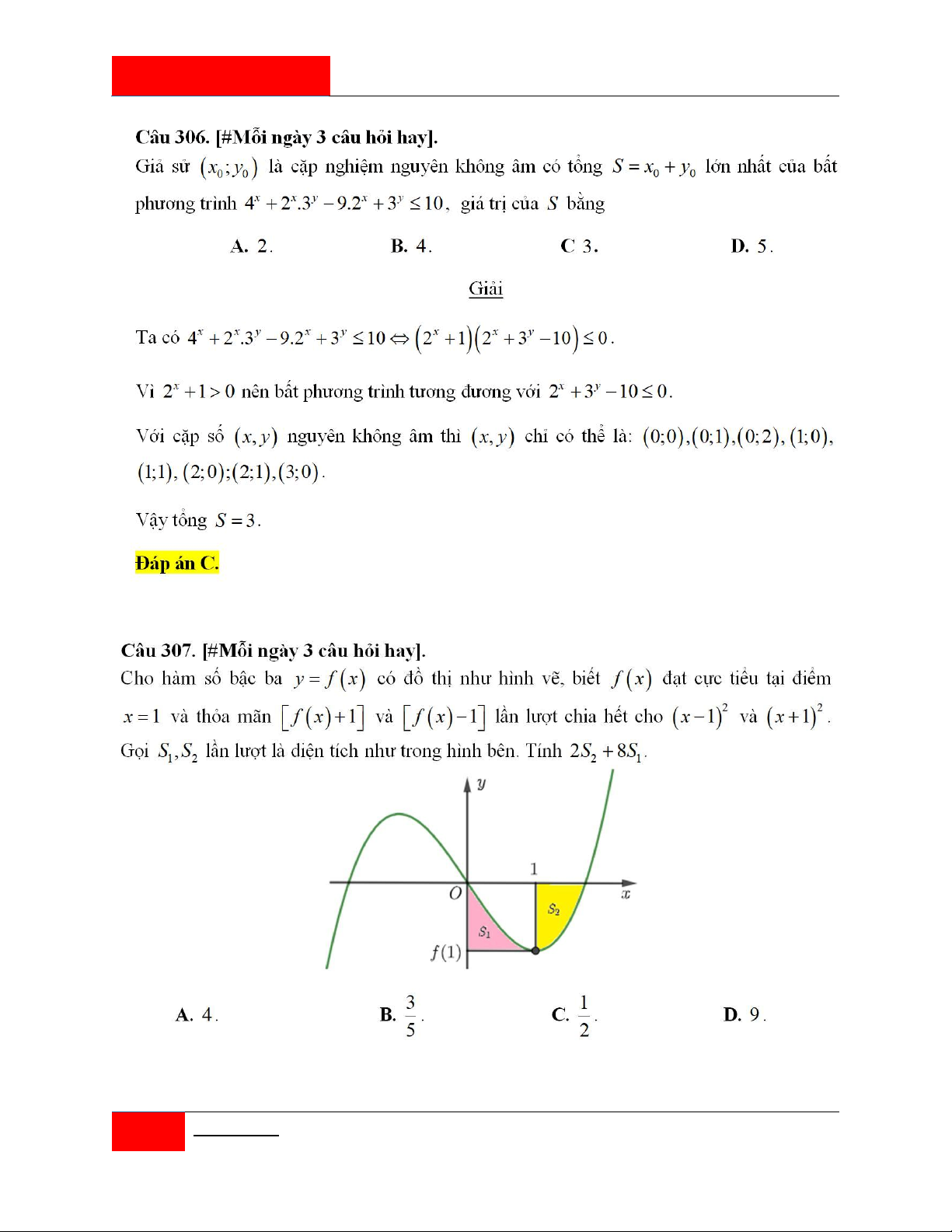
Cho hàm số bậc ba y f x có đồ thị là đường cong C trong hình bên. Hàm số f x
đạt cực trị tại hai điểm x , x thỏa f x f x 0 . Gọi ,
A B là hai điểm cực trị của đồ 1 2 1 2
thị C ; M , N, K là giao điểm của C với trục hoành; S là diện tích của hình phẳng
được gạch trong hình, S là diện tích tam giác NBK . Biết tứ giác MAKB nội tiếp đường 2 tròn, khi đó tỉ S số 1 bằng S2 2 6 6 5 3 3 3 A. . B. . C. . D. . 3 2 6 4
19 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
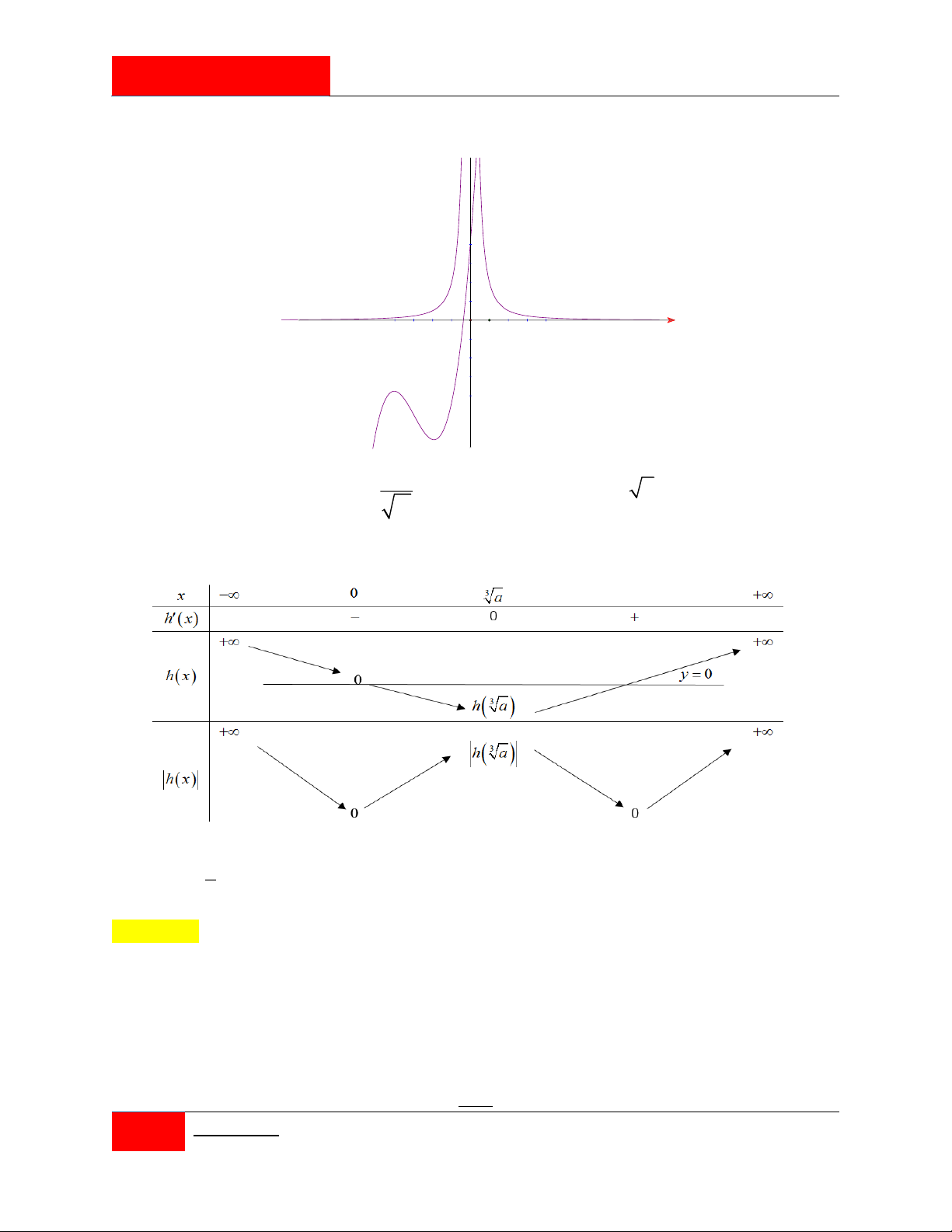
Câu 282. [#Mỗi ngày 3 câu hỏi hay].
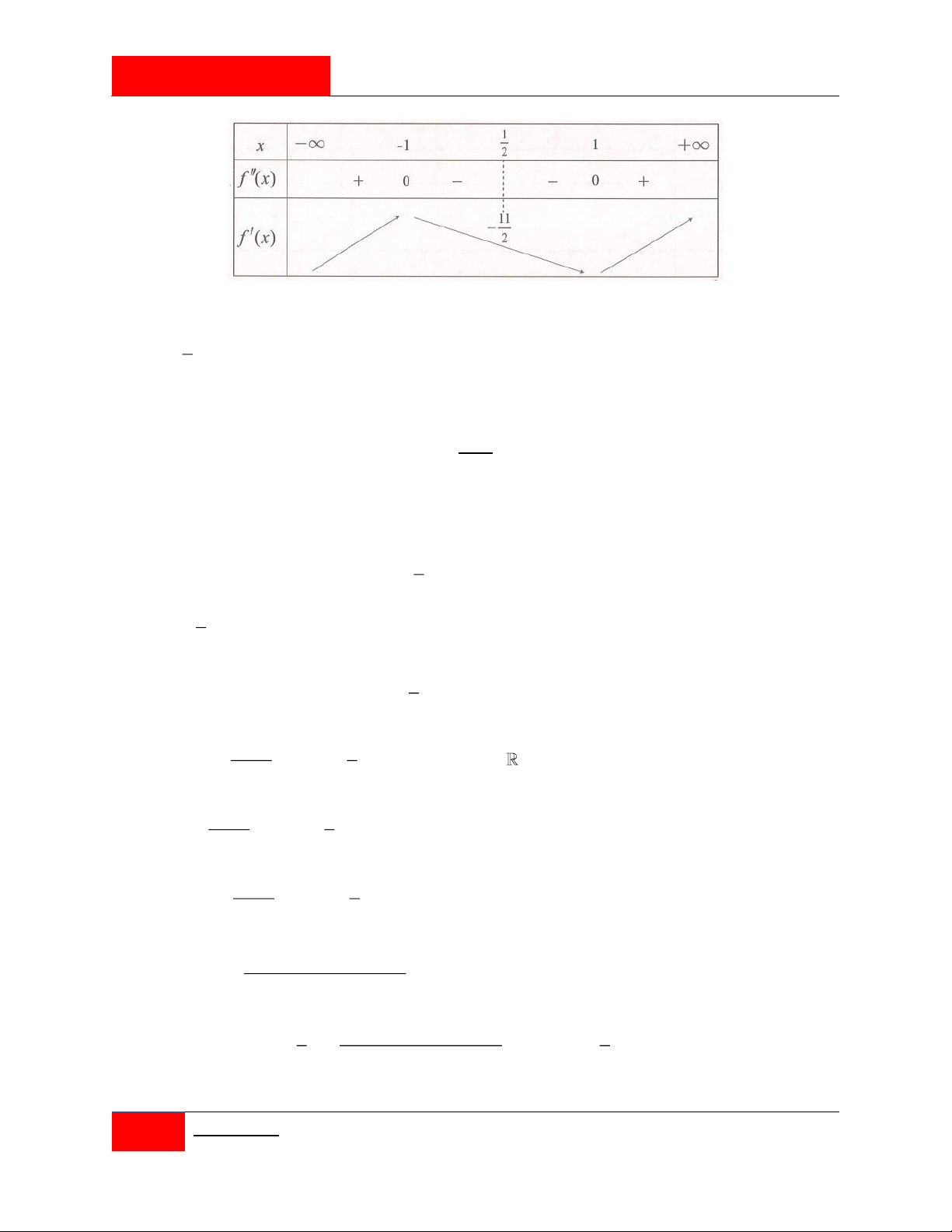
Cho hàm số f x xác định và liên tục trên \ 3 , thỏa mãn 3 2 2 1 x 2x f x xf x f ' x 2 và f 1 0 . Hàm số g x f 2x
1 có bao nhiêu điểm cực tiểu ? A. 0 . B. 1 . C. 2 . D. 3 .
Câu 283. [#Mỗi ngày 3 câu hỏi hay].
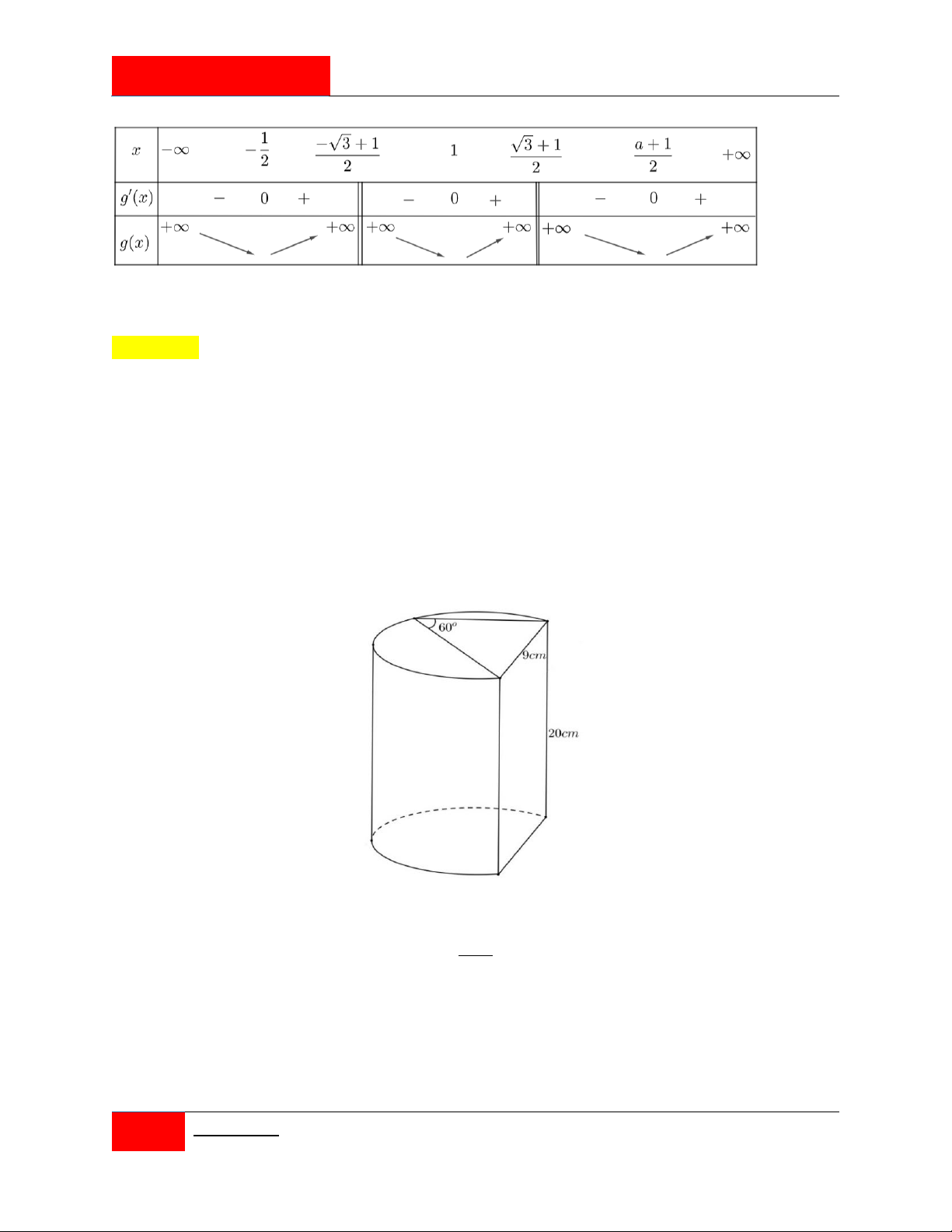
Một bác thợ hàn làm ra những chi tiết trang trí giống nhau có dạng là một phần của mặt
xung quanh hình trụ như hình vẽ. Để làm ra sản phẩm đó bác thợ hàn cắt ra từ một tấm kim
loại phẳng hình chữ nhật kích thước 120 cm 240 cm thành những miếng kim loại hình chữ
nhật bằng nhau, một cạnh 20 cm , cạnh còn lại có độ dài L . Sau đó bác thợ hàn uốn cong
những miếng kim loại nhỏ đó thì được sản phẩm cần làm. Hỏi từ tấm kim loại ban đầu bác
thợ hàn có thể làm được tối đa bao nhiêu sản phẩm như vậy. Giả sử hao phí nguyên vật
liệu là không đáng kể. A. 60 . B. 72 . C. 66 . D. 80 .
Câu 284. [#Mỗi ngày 3 câu hỏi hay].
Cho hàm số y f x là đa thức bậc 5 có đồ thị f x như hình vẽ.
20 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Hàm số g x f 2 x x 2 2
x có bao nhiêu điểm cực trị? A. 3 . B. 2 . C. 4 . D. 1 .
Câu 285. [#Mỗi ngày 3 câu hỏi hay].
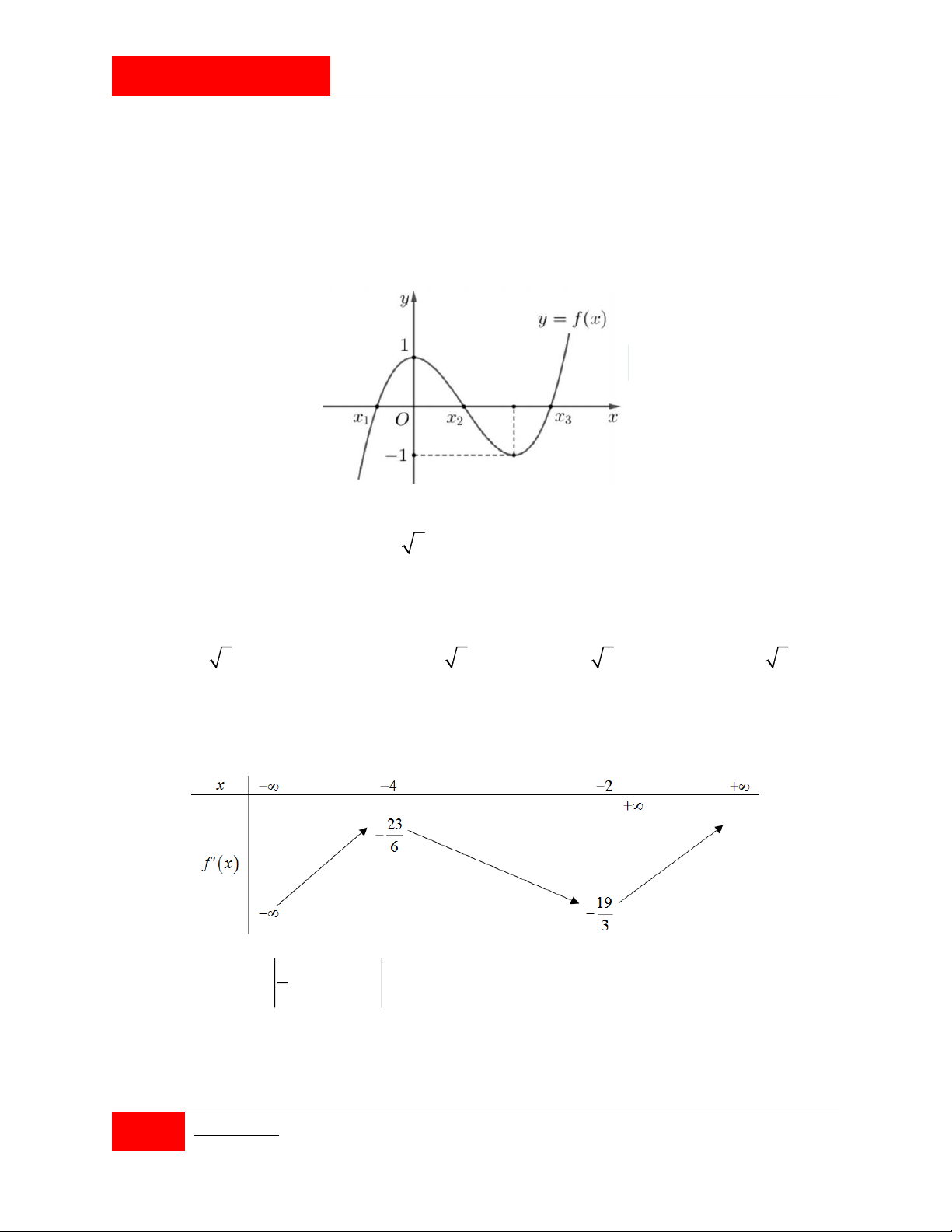
Cho hàm số bậc ba y f x có đồ thị C như hình vẽ.
Biết rằng đồ thị hàm số đã cho cắt trục Ox tại ba điểm có hoành độ x , x , x theo thứ tự 1 2 3
lập thành cấp số cộng và x x 2 3 . Gọi diện tích hình phẳng giới hạn bởi C và 3 1
trục Ox là S , diện tích S của hình phẳng giới hạn bởi các đường y f x 1, 1
y f x 1, x x và x x bằng 1 3
A. S 2 3 .
B. S 4 3 . C. 4 3 . D. 8 3 .
Câu 286. [#Mỗi ngày 3 câu hỏi hay].
Cho hàm bậc bốn và f 0 0 . Hàm số f ' x có bảng biến thiên như sau 1
Hỏi hàm số g x f 3
x 2x có bao nhiêu điểm cực trị 3 A. 1 . B. 2 . C. 3 . D. 4 .
21 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Câu 287. [#Mỗi ngày 3 câu hỏi hay].
Có bao nhiêu cặp số ;
x y thỏa mãn tính chất x x x y 2021 2021 log log , ở đó là số thực y
dương, y là số nguyên dương nhỏ hơn 2021 ? A. 4038 . B. 6057 . C. 6060 . D. 4040 .
Câu 288. [#Mỗi ngày 3 câu hỏi hay].
Cho f x là hàm bậc ba có đồ thị như hình vẽ. Biết hàm số f x đạt cực trị tại x ; x 1 2
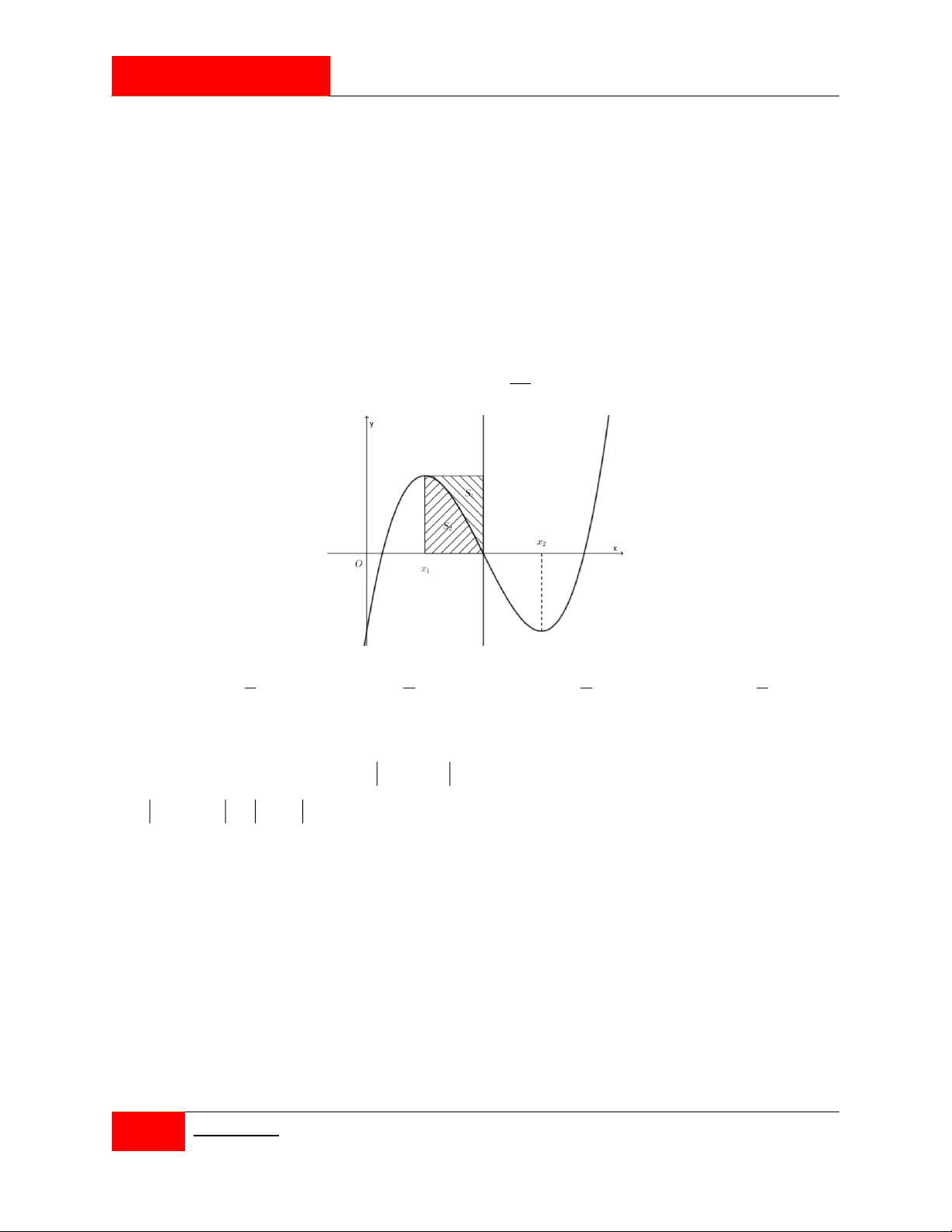
thỏa mãn x x 4 và tâm đối xứng của đồ thị hàm số nằm trên trục hoành. Gọi S ; S 2 1 1 2 S
là diện tích hình phẳng như trong hình vẽ. Tỷ số 1 bằng: S2 3 3 4 5 A. . B. . C. . D. . 5 4 3 3
Câu 289. [#Mỗi ngày 3 câu hỏi hay].
Cho số phức z thoả mãn z 1 2i 2 . Tìm giá trị lớn nhất của biểu thức 2 2
P z 2 3i z 5i . A. P 96 . B. P 66 . C. P 152 . D. P 132 . max max max max
Câu 290. [#Mỗi ngày 3 câu hỏi hay]. 2 2 2
Trong không gian với hệ tọa độ Oxyz , cho mặt cầu S : x 1
y 2 z 3 16
và các điểm A1;0;2 , B 1
;2;2. Gọi P là mặt phẳng đi qua hai điểm A, B sao cho
thiết diện của P với mặt cầu S có diện tích nhỏ nhất. Khi viết phương trình P dưới
dạng P : ax by cz 3 0 . Tính T a b c . A. 3 . B. 3 . C. 0 . D. 2 .
22 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Câu 291. [#Mỗi ngày 3 câu hỏi hay]. x 2 y 1 z 1
Trong không gian Oxyz, cho đường thẳng d : và mặt phẳng 1 2 2
P: x y z 6 0. Gọi là mặt phẳng đi qua đường thẳng d và tạo với P một
góc nhỏ nhất. Khi đó dạng phương trình tổng quát của là ax by z d 0. Khi đó
giá trị của a b d bằng: A. 6. B. 7. C. 5. D. 3.
Câu 292. [#Mỗi ngày 3 câu hỏi hay].
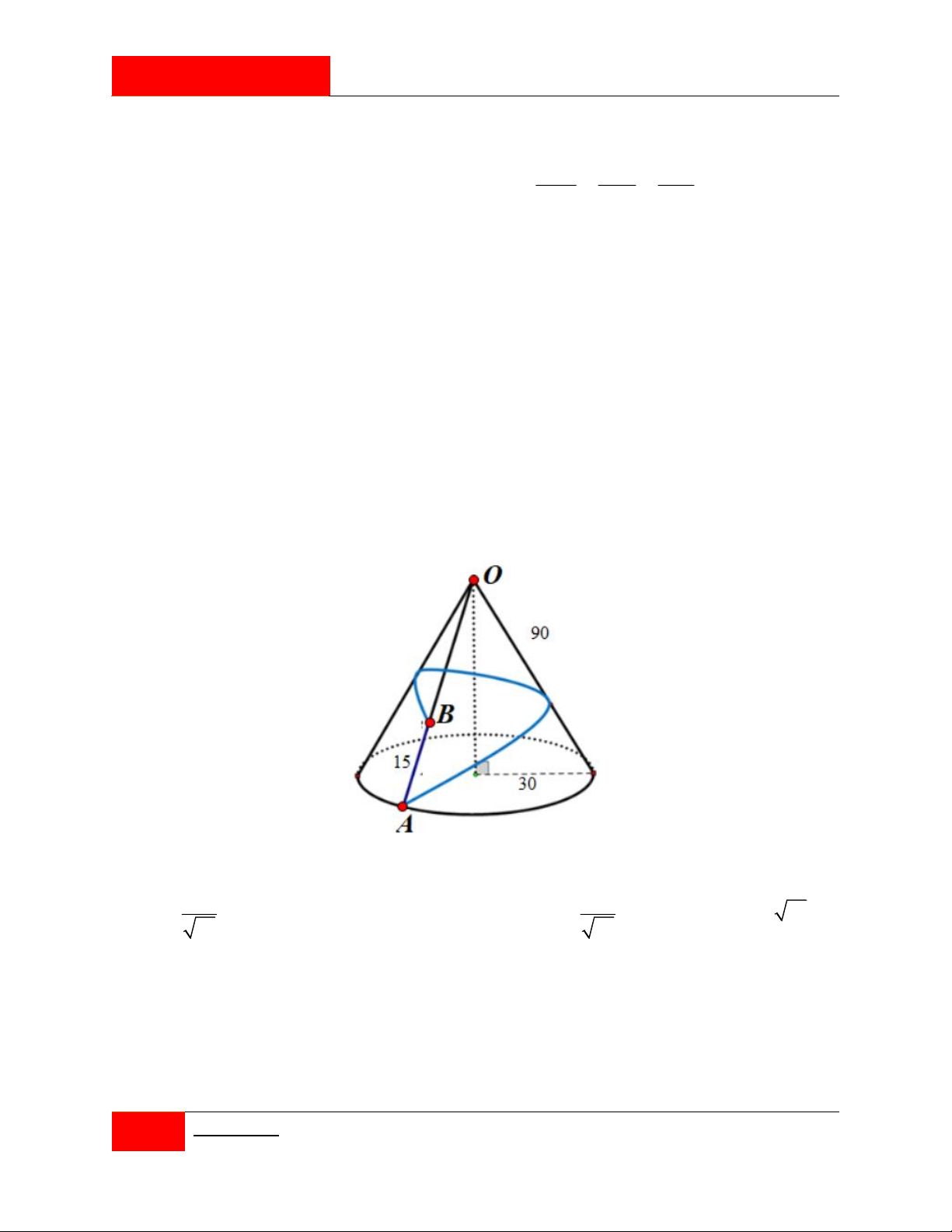
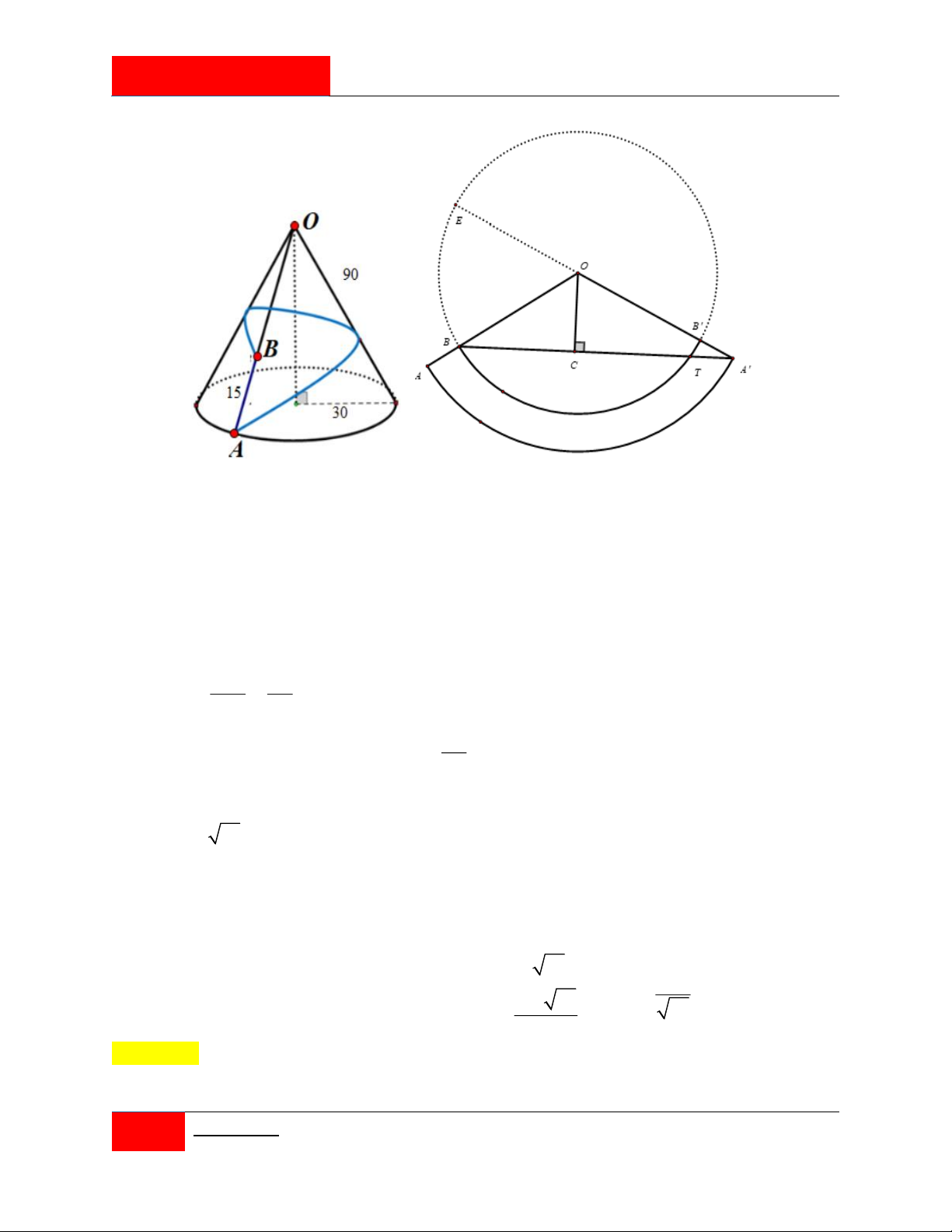
Hình vẽ dưới đây mô tả một ngọn núi có dạng hình nón. Nhà đầu tư du lịch dự định xây
dựng một con đường nhằm phục vụ việc chuyên chở khách du lịch tham quan ngắm cảnh
vòng quanh ngọn núi bắt đầu từ vị trí A và dừng ở vị trí B . Biết rằng người ta đã chọn xây
dựng đường đi ngắn nhất vòng quanh núi từ A đến B , đoạn đường đầu là phần lên dốc từ
A và đoạn sau sẽ xuống dốc đến B . Tính quãng đường xuống dốc khi đi từ A đến B . 400 600 A. . B. 0 . C. . D. 15 91 . 91 91
Câu 293. [#Mỗi ngày 3 câu hỏi hay].
Cho hàm số y f x 3 2
ax 2x bx 1 và y g x 2
cx 4x d có bảng biến thiên
dưới đây. Biết đồ thị hàm số y f x và y g x cắt nhau tại ba điểm phân biệt có
hoành độ lần lượt là x , x , x thỏa mãn x x x 9. Giá trị của P 3a b c 2d là 1 2 3 1 2 3
23 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] A. 1 . B. 0 . C. 2 . D. 3 .
Câu 294. [#Mỗi ngày 3 câu hỏi hay].
Cho các số thực x, y, z thỏa mãn log 2 2
2x y log 3 3 x 2 y
log z . Có bao giá trị 3 7
nguyên của z để có đúng hai cặp x, y thỏa mãn đẳng thức trên ? A. 2 . B. 211. C. 99 . D. 4.
Câu 295. [#Mỗi ngày 3 câu hỏi hay].
Một gia đình có bồn tắm có bề mặt phẳng và lòng trong như hình vẽ, lòng trong của bồn tắm có
hình dạng bán cầu, mất đi chỏm cầu. Biết thể tích khối chỏm cầu được tính bởi công thức 2 2 h V h R
với R là bán kính khối cầu, h là chiều cao của chỏm cầu và OH m . 3 2 Thể tích 3
m lòng trong của bồn tắm là
24 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] 8 5 2 10 2 5 2 10 2 A. . B. . C. . D. . 24 3 12 3
Câu 296. [#Mỗi ngày 3 câu hỏi hay].
Cho mặt cầu S có tâm I 3;2;2 bán kính R 2 , mặt cầu S có tâm I 1;0;1 bán 2 2 1 1 1
kính R 1. Phương trình mặt phẳng P đồng thời tiếp xúc với S và S và cắt đoạn 2 1 2
I I có dạng 2x by cz d 0 . Tính T b c d . 1 2 A. 5 . B. 1. C. 3 . D. 2 .
Câu 297. [#Mỗi ngày 3 câu hỏi hay].
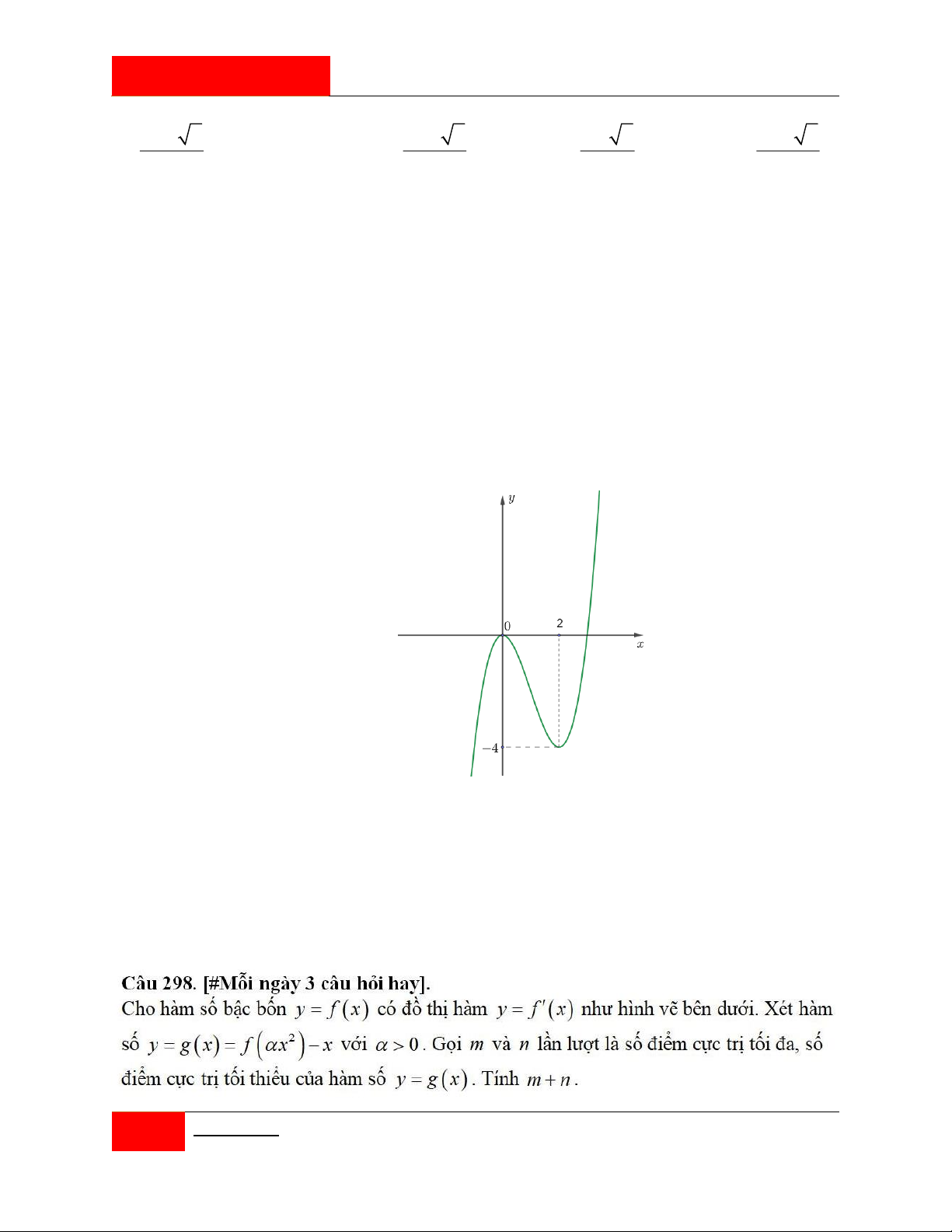
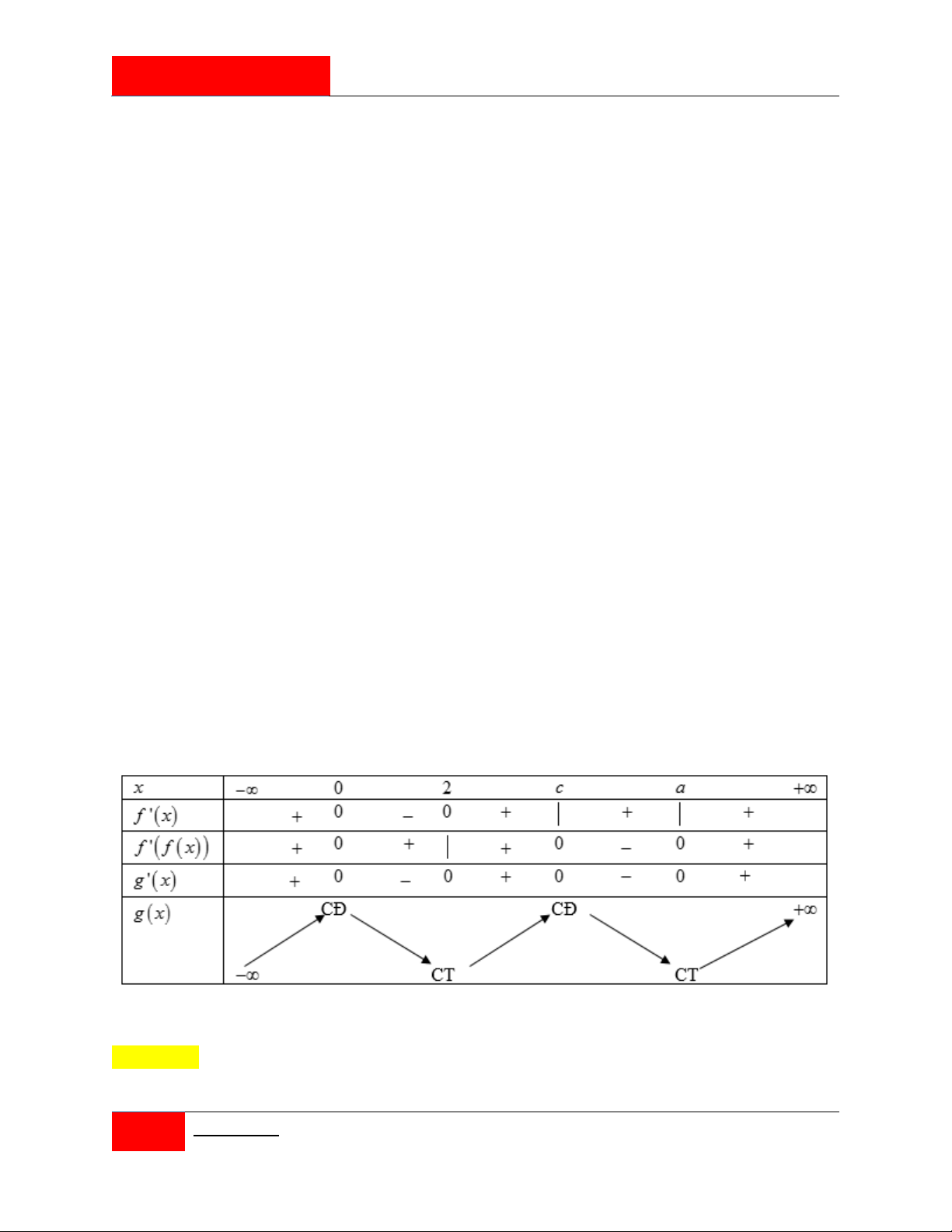
Cho hàm số bậc ba y f x có đồ thị hàm số như hình vẽ sau.
Hàm số y g x f f x 1202 có
A. 3 điểm cực đại, 2 điểm cực tiểu.
B. 2 điểm cực đại, 3 điểm cực tiểu.
C. 2 điểm cực đại, 2 điểm cực tiểu.
D. 1 điểm cực đại, 1 điểm cực tiểu.
25 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
26 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
27 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
28 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
29 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
30 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
31 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
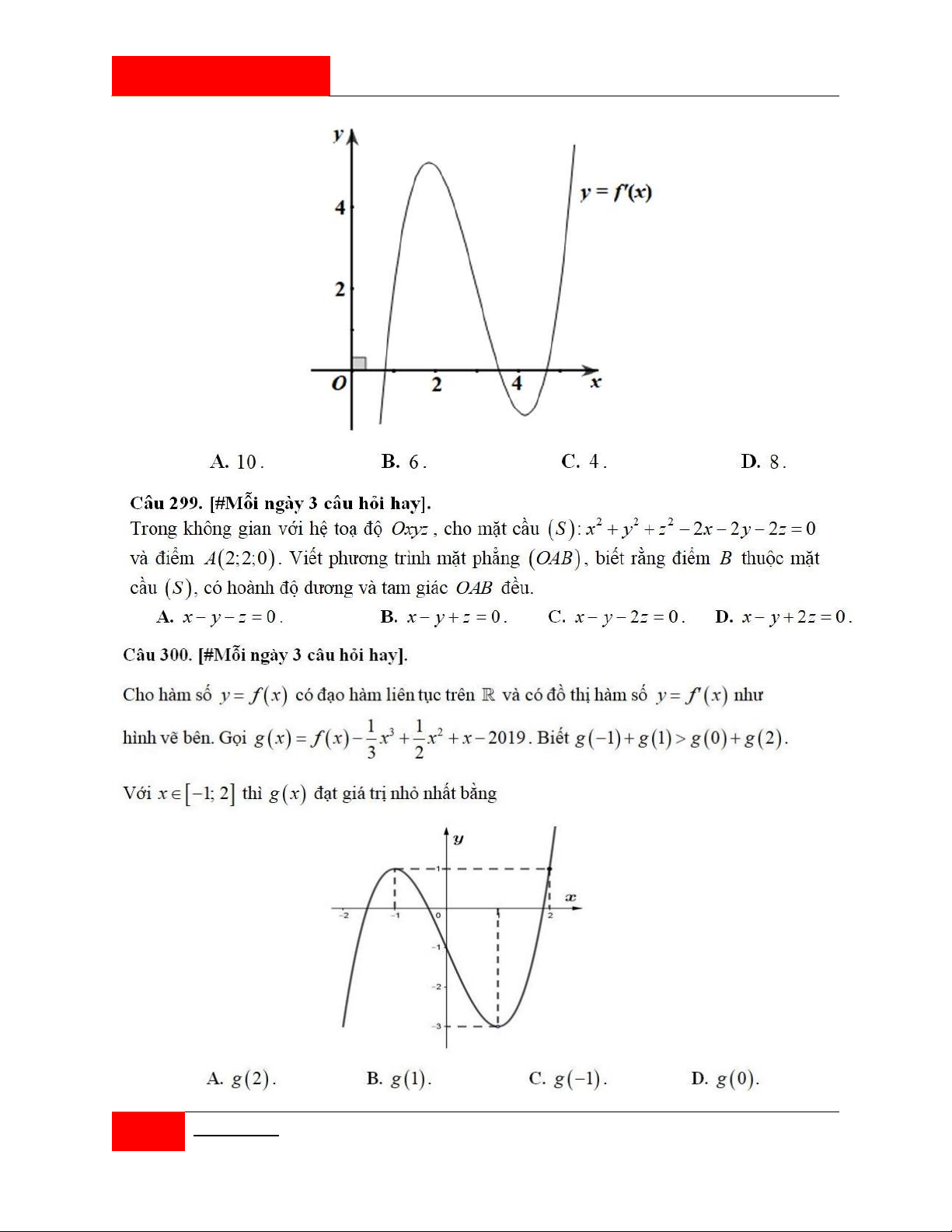
Câu 319. [#Mỗi ngày 3 câu hỏi hay].
Cho x, y 0;2 thỏa mãn x 3 x 8 eyey
11 . Giá trị lớn nhất của P ln x 1 ln y bằng:
A. 1 ln 3 ln 2. B. 2 ln 3 ln 2. C. 1 ln 3 ln 2. D. 1 ln 2.
Câu 320. [#Mỗi ngày 3 câu hỏi hay].
Cho hàm số y f x có đạo hàm liên tục trên đoạn 0;
1 và thỏa mãn f 0 0 . Biết 1 9 1 x 3 1 2
f x dx
và f ' xcos dx
. Tích phân f x dx bằng. 2 2 4 0 0 0 6 2 4 1 A. . B. C. D. . . .
Câu 321. [#Mỗi ngày 3 câu hỏi hay].
Cho hàm số y f x và f x 0, x
. Biết hàm số y f 'x có bảng biến thiên như 1 137 hình vẽ và f . 2 16
Có bao nhiêu giá trị nguyên của 2 m 20
20;2020 để hàm số g x x 4mx5 e
. f x đồng biến 1 trên 1 ; . 2 A. 4040. B. 4041. C. 2019. D. 2020.
Câu 322. [#Mỗi ngày 3 câu hỏi hay].
Cho cấp số cộng a , cấp số nhân b thỏa mãn a a 0, b b 1 và hàm số n n 2 1 2 1 f x 3
x 3x sao cho f a 2 f a và f log b 2 f log b . Tìm số nguyên dương n 2 2 2 1 2 1
nhỏ nhất sao cho b 2019a . n n A. 17. B. 14. C. 15. D. 16.
32 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
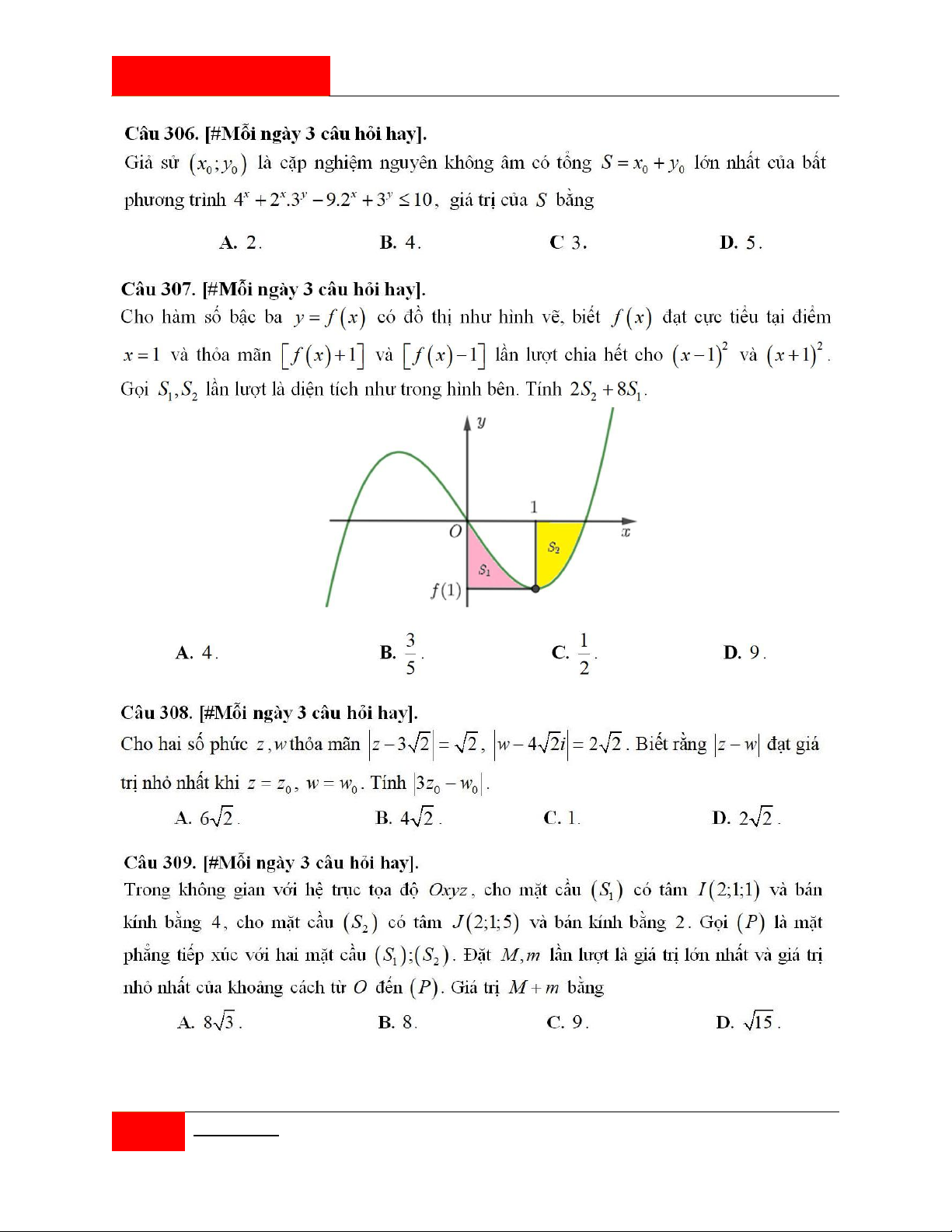
Câu 323. [#Mỗi ngày 3 câu hỏi hay].
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, AB 1, cạnh bên SA 1 và vuông
góc với mặt phẳng đáy ABCD . Kí hiệu M là điểm di động trên đoạn CD và N là điểm
di động trên đoạn CB sao cho MAN 45 . Thể tích nhỏ nhất của khối chóp S.AMN là? 2 1 2 1 2 1 2 1 A. . B. . C. . D. . 9 3 6 9
Câu 324. [#Mỗi ngày 3 câu hỏi hay]. Cho hai hàm số 4 3 2
f x ax bx cx dx e và g x 3 2
mx nx px 1 với a, b, c, d, e,
m, n, p, q là các số thực. Đồ thị của hai hàm số y f x; y g x như hình vẽ dưới.
Tổng các nghiệm của phương trình f x q g x e bằng 13 13 4 4 A. . B. . C. . D. . 3 3 3 3
Câu 325. [#Mỗi ngày 3 câu hỏi hay]. Cho hàm số 3 2
f x ax bx cx d có đồ thị như hình vẽ. Gọi S là tập
hợp các giá trị của m ( m ) sao cho x 3
1 m f 2x
1 mf x f x 1 0, x
. Số phần tử của tập S là A. 2 B. 0 C. 3 D. 1
33 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Câu 326. [#Mỗi ngày 3 câu hỏi hay].
Gọi S là tập hợp tất cả các giá trị thực của m để tồn tại 4 số phức z thỏa mãn
z z z z 2 và z z 2 z z m là số thuần ảo. Tổng các phần tử của S là: 2 1 2 1 1 A. 2 1 B. C. D. 2 2 2
Câu 327. [#Mỗi ngày 3 câu hỏi hay]. Cho phương trình: 3m m e e 2 x x 2 2 1
1 x 1 x . Tìm tất cả các giá trị thực của tham
số m để phương trình đã cho có nghiệm. 1 1 1 1 A. ln 2; . B. 0; ln 2 . C. ; ln 2 . D. 0; . 2 2 2 e
Câu 328. [#Mỗi ngày 3 câu hỏi hay].
Cho hàm số có đạo hàm liên tục trên khoảng 1; và thỏa mãn
xf x f x 3 2
ln x x f x, x
1; ; biết f 3 e 3e . Giá trị f 2 thuộc khoảng nào dưới đây? 25 A. 12; . 2
Câu 329. [#Mỗi ngày 3 câu hỏi hay].
x y z
Tổng giá trị lớn nhất và nhỏ nhất của biểu thức F
bằng bao nhiêu, biết rằng x,
x y z
x y z
y, z là các số thực thỏa mãn log
x x 2 y y 2 z z 2 . 16 2 2 2
2x 2y 2z 1 1 2 2 1 A. . B. . C. . D. . 3 3 3 3
Câu 330. [#Mỗi ngày 3 câu hỏi hay].
Cho các số thực dương x, y thỏa mãn 2 2 x y 1 2 log 2 2
x y 1 3. Biết giá trị lớn nhất 3 của biểu thức a 6 3 3
S x y x y là
với a, b là các số nguyên dương và phân số a b b
tối giản. Tính giá trị biểu thức T 2a b .
34 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] A. T 25. B. T 34. C. T 32. D. T 41.
Câu 331. [#Mỗi ngày 3 câu hỏi hay]. z i a
Cho số thực a thay đổi và số phức z thỏa mãn . Trên mặt phẳng 2
1 a a 2 1 i a
tọa độ, gọi M là điểm biểu diễn số phức z. Khoảng cách ngắn nhất giữa hai điểm M và
I 3; 4 (khi a thay đổi) là: A. 4. B. 3. C. 5. D. 6.
Câu 332. [#Mỗi ngày 3 câu hỏi hay].
Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình sau có bốn nghiệm phân biệt: 4 2 x
x m 2 16 8 1
x m 2m 1 0 . A. 4. B. 7. C. 6. D. 5.
Câu 333. [#Mỗi ngày 3 câu hỏi hay].
Cho hàm số f x có đạo hàm xác định trên và thỏa mãn f x 2
x f x2019 4x 6x.e
0 và f 0 2019
. Số nghiệm nguyên dương của bất
phương trình f x 7 là A. 91. B. 46. C. 45. D. 44.
Câu 334. [#Mỗi ngày 3 câu hỏi hay].
Xét số phức z có phần thực dương và ba điểm A, B, C lần lượt là điểm biểu diễn của các 1 1 số phức z, và z
. Biết tứ giác OABC là một hình bình hành, giá trị nhỏ nhất của z z 2 1 z bằng z A. 2 . B. 2. C. 2 2 . D. 4.
Câu 335. [#Mỗi ngày 3 câu hỏi hay]. 2 2 x 5y
Cho x, y là các số dương thỏa mãn 2 2 log
1 x 10xy 9y 0 . Gọi M, m lần 2 2 2
x 10xy y 2 2 lượ x xy 9 y
t là giá trị lớn nhất, giá trị nhỏ nhất của P
. Tính T 10M m . 2 xy y
35 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] A. T 60 . B. T 94 . C. T 104 . D. T 50 .
Câu 336. [#Mỗi ngày 3 câu hỏi hay].
Cho hình lăng trụ tam giác đều ABC.AB C
có cạnh đáy bằng a và cạnh bên bằng a 2 . AM A N 1
Lấy M, N lần lượt trên cạnh AB , A C sao cho AB A C
. Tính thể tích V của khối 3 BMNC C . 3 a 6 3 2a 6 3 3a 6 3 a 6 A. . B. . C. . D. . 108 27 108 27
Câu 337. [#Mỗi ngày 3 câu hỏi hay]. Cho hàm số 3 2
y f (x) x 3x 2 và phương trình f (x) m m n có 8 nghiệm phân biệt với m ( 6 ; 2)
. Khẳng định nào sau đây đúng? 6 m 4 3 m 2 A. . B. . 2 n 6 2m
6 2m n 2 3 m 2 3 m 2 C. .
D. 0 n 6 2m . m n
2 n m
Câu 338. [#Mỗi ngày 3 câu hỏi hay]. m 2 6i Cho số phức z , m
nguyên dương. Có bao nhiêu giá trị m 1;50 để z là số 3 i thuần ảo? A. 25. B. 50. C. 26. D. 24.
Câu 339. [#Mỗi ngày 3 câu hỏi hay].
Tìm tất cả các giá trị nguyên của m để hệ phương trình sau có nghiệm: 2 x x 1 2 x 1 3 3
2017x 2017 1 . 2 x
m 2 x 2m 3 0 2 A. m 3. B. m 3. C. m 2. D. m 2.
Câu 340. [#Mỗi ngày 3 câu hỏi hay].
Cho các hàm số f x, f x , f x ,... biết: o 1 2
36 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] f x x x x f x f x n o
ln ln 2019 ln 2019 , 1, . n 1 n
Số nghiệm của phương trình f x 0 là 2020 A. 6058. B. 6057. C. 6059. D. 6063.
Câu 341. [#Mỗi ngày 3 câu hỏi hay]. x y z
Cho các số thực x, y, z thỏa mãn log log log
3. Tính giá trị nhỏ nhất 2 3 5 4 9 25 của S log . x log . y log z. 2001 2018 2019
A. min S 27.log 2.log 3.log 5. 2001 2018 2019
B. min S 44.log 2.log 3.log 5. 2001 2018 2019
C. min S 88.log 2.log 3.log 5. 2001 2018 2019 289 D. min S .log 2.log 3.log 5. 2001 2018 2019 8
Câu 342. [#Mỗi ngày 3 câu hỏi hay].
Cho hàm số f x nhận giá trị dương trên [0;1] , có đạo hàm dương và liên tục trên [0;1] , 1 1 1 3
thỏa mãn f 0 1 và 3
f x 4 f '
x dx 3 f ' x 2
. f xd . I x Tính
f xd .x 0 0 0 1 2 1
A. I 2 e 1 . B. I 2 2 e 1 . C. e I . D. e I . 2 2
Câu 343. [#Mỗi ngày 3 câu hỏi hay].
Với a là tham số thực để bất phương trình 2x 3x ax 2 có tập nghiệm là khi đó
A. a ;0 .
B. a 1;3 .
C. a 3; .
D. a 0; 1
Câu 344. [#Mỗi ngày 3 câu hỏi hay].
Trong không gian với hệ tọa độ Oxyz, cho ba điểm P, Q, R lần lượt di động trên ba trục 1 1 1 1
tọa độ Ox, Oy, Oz (không trùng với gốc tọa độ O) sao cho . Biết 2 2 2 OP OQ OR 8
mặt phẳng PQR luôn tiếp xúc với mặt cầu S cố định. Đường thẳng d thay đổi nhưng
37 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] luôn đi qua 1 3 M ;
;0 và cắt S tại hai điểm A, B phân biệt. Diện tích lớn nhất của 2 2 tam giác AOB là A. 15 . B. 5 . C. 17 . D. 7 .
Câu 345. [#Mỗi ngày 3 câu hỏi hay].
Giả sử x là nghiệm của phương trình 2
ax bx c 0 a 0 . Cho hàm số o b c
y f x Mx với M max ;
. Tìm các giá trị của tham số a sao cho hàm số a a
g x f x ax nghịch biến trên . 2 x x 1 2 x x 1 A. a o .
B. a o . C. a o .
D. a o . x 1 x x 1 x o o o o
Câu 346. [#Mỗi ngày 3 câu hỏi hay].
Cho hàm số f x nhận giá trị dương và có đạo hàm f x liên tục trên 0 ;1 thỏa mãn 1 1 dx 2 f 1 . e f 0 và
f x dx 2
. Mệnh đề nào sau đây đúng? 2 f x 0 0 e 2 e 2 2e 2 e 2 A. f 2 1 . B. f 1 . C. f 2 1 . D. f 1 . e 1 e 1 2 e 1 e 1
Câu 347. [#Mỗi ngày 3 câu hỏi hay].
Cho hàm số y f x liên tục trên và có đồ thị như hình vẽ.
38 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] 2
3x 2x 3
Tìm tất cả các giá trị m để phương trình f
m có nghiệm. 2 2x 2
A. 4 m 2 .
B. 4 m 2 .
C. 2 m 4 .
D. 2 m 4 .
Câu 348. [#Mỗi ngày 3 câu hỏi hay].
Có bao nhiêu số nguyên m để phương trình 2 9.3 x 4 2 4
2 1 3 3.3x m x x m 1 0
có đúng 3 nghiệm phân biệt? A. Vô số. B. 3. C. 1. D. 2.
Câu 349. [#Mỗi ngày 3 câu hỏi hay].
Cho khối chóp S.ABC có SA SB SC a , ASB 60 , BSC 90 ,
ASC 120 . Gọi CN AM
M, N lần lượt là các điểm trên cạnh AB và SC sao cho . Khi khoảng cách giữa SC AB
M và N nhỏ nhất, tính thể tích V của khối chóp S.AMN. 3 2a 3 5 2a 3 5 2a 3 2a A. . B. . C. . D. . 72 72 432 432
Câu 350. [#Mỗi ngày 3 câu hỏi hay].
Cho một đa giác đều H có 15 đỉnh. Người ta lập một tứ giác có 4 đỉnh là 4 đỉnh của
H . Tính số tứ giác được lập thành mà không có cạnh nào là cạnh của H . A. 4950. B. 1800. C. 30. D. 450.
Câu 351. [#Mỗi ngày 3 câu hỏi hay].
Cho hàm số đa thức f x 5 4 3 2
mx nx px qx hx r , ,
m n, p, q, , h r . Đồ thị 3 5 11
hàm số y f x cắt trục hoành tại các điểm có hoành độ lần lượt là –1; ; ; . Số 2 2 3
điểm cực trị của hàm số g x f x m n p q h r là
39 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] A. 6. B. 7. C. 8. D. 9.
Câu 352. [#Mỗi ngày 3 câu hỏi hay].
Cho hàm số f x 3 3
7 3x 7 3x 2019 .
x Gọi S là tập hợp các giá trị nguyên của m
thỏa mãn điều kiện f 3 2
x x x m f 2 2 3
2x 2x 5 0, x 0; 1 . Số phần tử của S là? A. 7. B. 3. C. 9. D. 5.
Câu 353. [#Mỗi ngày 3 câu hỏi hay].
Cho hình hộp chữ nhật ABC . D
A BC ' D có AB BC, BC 3c . m Hai mặt phẳng ACC
A và BD
D B hợp với nhau góc 0 .
Đường chéo BD hợp với mặt 2
phẳng CDDC một góc β 0 .
Hai góc , thay đổi nhưng thỏa mãn hình 2
hộp ADDA .BCCB luôn là hình lăng trụ đều. Giá trị lớn nhất của thể tích khối hộp ABC . D
A BCD là A. 3 3cm . B. 3 2 3cm . C. 3 6 3cm . D. 3 12 3cm .
Câu 354. [#Mỗi ngày 3 câu hỏi hay].
Cho hàm số f x nhận giá trị dương, có đạo hàm liên tục trên 0;2. Biết f 0 1 và 3 2 2
x 3x . f x 2 2 4 . 2 x x f x f x e
với mọi x 0;2. Tính tích phân I . dx f x 0
40 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] 14 32 16 16 A. I . B. I . C. I . D. I . 3 5 3 5
Câu 355. [#Mỗi ngày 3 câu hỏi hay].
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S 2 2 2
: x y z 4x 4 y 2z 7 0 và đường thẳng d là giao tuyến của hai mặt m
phẳng x 1 2m y 4mz 4 0 và 2x my 2m
1 8 0 . Khi m thay đổi các giao
điểm của d và S nằm trên một đường tròn cố định. Tính bán kính r của đường tròn m đó. 142 92 23 586 A. r . B. r . C. r . D. r . 15 3 3 15
Câu 356. [#Mỗi ngày 3 câu hỏi hay].
Trong không gian Oxyz, cho điểm M 2; 3
;4. Gọi P là mặt phẳng đi qua M và cắt các trục
x 'Ox, y 'Oy, z 'Oz lần lượt tại các điểm D, E, F sao cho
OD OE 2 2
m 2m 2OF 0 , trong đó m là tham số thực. Gọi S là tập hợp các giá
trị của m để chỉ có đúng ba mặt phẳng P thỏa mãn yêu cầu trên.
Tập hợp S có bao nhiêu tập hợp con khác rỗng? A. 7. B. 3. C. 15. D. 4.
Câu 357. [#Mỗi ngày 3 câu hỏi hay]. z 4 3i
Cho z x yi x, y là số phức thỏa mãn điều kiện z 3 2i 5 và 1. z 3 2i
Gọi M , m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức 2 2
T x y 8x 4 y . Tính M m A. 18 . B. 4 . C. 20 . D. 2 .
Bài tập tương tự
Cho z x yi x, y là số phức thỏa mãn điều kiện z 2 3i z i 2 5 . Gọi
M , m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức 2 2
P x y 8x 6 y . Tính M m 156 165 A. 20 10 .
B. 60 20 10 . C.
20 10 . D. 60 20 10 . 5 5
41 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Câu 358. [#Mỗi ngày 3 câu hỏi hay].
Cho hình chóp S.ABCD có đáy là ABCD là hình bình hành. Hai điểm M, N lần lượt thuộc các đoạ AB AD
n thẳng AB và AD (M và N không trùng với A) sao cho 2. 4. Ký AM AN
hiệu V ,V lần lượt là thể tích của các khối chóp S.ABCD và S.MBCDN. Tìm giá trị lớn 1 V
nhất của tỉ số 1 V 3 17 1 2 A. . B. . C. . D. . 4 14 6 3
Câu 359. [#Mỗi ngày 3 câu hỏi hay].
Từ hai chữ số 0 và 1 tạo ra được bao nhiêu số có 2018 chữ số chia hết cho 5, đồng thời
tổng của các chữ số là một số chẵn A. 2018 2 . B. 2017 2 . C. 2015 2 . D. 2016 2 .
Câu 360. [#Mỗi ngày 3 câu hỏi hay].
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Dựng mặt phẳng (P) cách đều
năm điểm A, B, C, D và S. Hỏi có tất cả bao nhiêu mặt phẳng (P) như vậy? A. 1 mặt phẳng. B. 2 mặt phẳng. C. 4 mặt phẳng. D. 5 mặt phẳng.
Câu 361. [#Mỗi ngày 3 câu hỏi hay]. 3 2 7
Cho hàm số f x có đạo hàm liên tục trên 0;
3 thỏa mãn f 3 0 , '
f x dx 6 0 3 7 3 và f x dx
. Tích phân f xdx bằng: x 1 3 0 0 7 97 7 7 A. . B. . C. . D. . 3 30 6 6
Câu 362. [#Mỗi ngày 3 câu hỏi hay].
Trong không gian Oxyz , cho hai điểm A0;1;2 và B 3;1;3 thoả mãn AB BC AB ; AD AD
BC . Gọi (S ) là mặt cầu có đường kính AB , đường thẳng CD di động
và luôn tiếp xúc với mặt cầu (S) . Gọi E AB, F CD và EF là đoạn vuông góc chung
của AB và CD . Biết rằng đường thẳng là tiếp tuyến của mặt cầu S và thỏa mãn () ;
EF () AB và d ;
A 3 . Khoảng cách giữa và CD lớn nhất bằng 3 2 3 3 A. . B. 2 . C. . D. 3 . 2 2
42 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Câu 363. [#Mỗi ngày 3 câu hỏi hay].
Xét các số phức z 1 i, z 1 3i, z 4 i và số phức z thay đổi. Biết rằng tồn tại số 1 2 3 z z z z z z z z z z z z
phức z , z , z mà 4 2 5 3 6 1 , , là các số thực, còn 4 5 6 , , 4 5 6 z z z z z z z z z z z z 4 3 5 1 6 2 2 3 3 1 1 2 2 2 2
thuần ảo. Tìm giá trị nhỏ nhất của T z z
z z z z . 4 5 6 72 72 18 A. . B. 3. C. . D. . 5 25 25
Câu 364. [#Mỗi ngày 3 câu hỏi hay].
Gieo một con súc sắc cân đối và đồng chất ba lần liên tiếp. Gọi P là tích ba số ở ba lần
tung (mỗi số là số chấm trên mặt xuất hiện ở mỗi lần tung), tính xác suất sao cho P không chia hết cho 6 . 82 90 83 60 A. . B. . C. . D. . 216 216 216 216
Câu 365. [#Mỗi ngày 3 câu hỏi hay].
Cho hai số phức z, w thỏa mãn z 2w 3, 2z 3w 6 và z 4w 7. Tính giá trị của
biểu thức P z.w z. . w A. P 14 . i B. P 28 . i C. P 14. D. P 28.
Câu 366. [#Mỗi ngày 3 câu hỏi hay].
Cho hàm số f x có đọa hàm liên tục trên đoạn 0
;1 đồng thời thỏa mãn f 0 9 và
f x f x 2 9 x 9
. Tính T f 1 f 0 . 1
A. T 2 9 ln 2 .
B. T 9 . C. T 9ln 2 .
D. T 2 9 ln 2 . 2
Câu 367. [#Mỗi ngày 3 câu hỏi hay].
Xét các số phức z a bi a,b thỏa mãn z 3 2i 2 . Tính a b khi
z 1 2i 2 z 2 5i đạt giá trị nhỏ nhất. A. 4 3 . B. 2 3 . C. 3. D. 4 3 .
Câu 368. [#Mỗi ngày 3 câu hỏi hay].
Tìm số nguyên dương n thỏa mãn 0 1 2
2C 5C 8C ... n C . n n n 3 2 n 1600 n A. n 5 . B. n 7 . C. n 10 . D. n 8 .
Câu 369. [#Mỗi ngày 3 câu hỏi hay].
43 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để phương trình m
1 .16x 2.25x x 1 log
5 .4x 1 m 2 4 x 2.25x x 5.20
có hai nghiệm thực phân biệt. Số phần tử của S bằng A. 4 . B. 3 . C. 1 . D. 2 .
Câu 370. [#Mỗi ngày 3 câu hỏi hay].
Cho hàm số f x liên tục trên . Biết rằng phương trình f x 0 có 8 nghiệm dương
phân biệt không nguyên, phương trình f 3 2
2x 3x
1 0 có 20 nghiệm phân biệt, phương trình f 4 2
x 2x 2 0 có 8 nghiệm phân biệt. Hỏi phương trình f x 0 có
bao nhiêu nghiệm thuộc khoảng 2; ? A. 0 . B. 1 . C. 2 . D. 4 .
Câu 371. [#Mỗi ngày 3 câu hỏi hay]. Cho hàm số 2
y x có đồ thị C , biết rằng tồn tại hai điểm A , B thuộc đồ thị C sao
cho tiếp tuyến tại A , B và đường thẳng pháp tuyến của hai tiếp tuyến đó tạo thành một
hình chữ nhật có chiều dài gấp đôi chiều rộng. Gọi S là diện tích giới hạn bởi đồ thị C 1
và hai tiếp tuyến, S là diện tích hình chữ nhật giới hạn bởi các tiếp tuyến và pháp tuyến 2 S tại ,
A B . Tính tỉ số 1 ? S2 1 1 125 125 A. . B. . C. . D. . 6 3 768 128
Câu 372. [#Mỗi ngày 3 câu hỏi hay].
Cho số phức z thỏa z 1 z 1 z z 4 6 và z 5i 2 thì giá trị nhỏ nhất của 1 1 1 1 2
z z m . Khẳng định đúng là 1 2
A. m 0;2 .
B. m 2;4 .
C. m 4;5 .
D. m 5;7 .
Câu 373. [#Mỗi ngày 3 câu hỏi hay].
Cho hàm số y f x 4 2
x 2x và hàm số y g x 2 2
x m , với 0 m 2 là tham số
thực. Gọi S , S , S , S là diện tích các miền gạch chéo được cho trên hình vẽ. Ta có diện tích 1 2 3 4
S S S S tại m . Chọn mệnh đề đúng. 1 4 2 3 0
44 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] 1 2 2 7 7 5 5 3 A. m ; . B. m ; . C. m ; . D. m ; . 0 2 3 0 3 6 0 6 4 0 4 2
Câu 374. [#Mỗi ngày 3 câu hỏi hay].
Giả sử z là số phức thỏa mãn iz 2 i 3 . Giá trị lớn nhất của biểu thức
2 z 4 i z 5 8i có dạng abc . Khi đó a b c bằng A. 6 . B. 9 . C. 12 . D. 15 .
Câu 375. [#Mỗi ngày 3 câu hỏi hay]. 2 x x 1 2 x 1 3 3
2020x 2020 0
Cho hệ bất phương trình
( m là tham số). Gọi S là 2 x m 2 2
x m 3 0
tập tất cả các giá trị nguyên của tham số m để hệ bất phương trình đã cho có nghiệm.
Tính tổng các phần tử của S . A. 10 . B. 15 . C. 6 . D. 3 .
Câu 376. [#Mỗi ngày 3 câu hỏi hay].
Trong các số phức z thỏa mãn 2
z 1 2 z gọi z và z lần lượt là các số phức có 1 2
môđun nhỏ nhất và lớn nhất. Khi đó môđun của số phức w z z là 1 2 A. w 2 2 . B. w 2 . C. w 2 .
D. w 1 2 .
Câu 377. [#Mỗi ngày 3 câu hỏi hay].
Trong không gian với hệ toạ độ Oxyz , cho mặt cầu S 2 2 2
: x y z 3 . Một mặt phẳng
tiếp xúc với mặt cầu S và cắt các tia Ox,Oy,Oz lần lượt tại các điểm , A B,C thoả mãn 2 2 2
OA OB OC 27 . Diện tích của tam giác ABC bằng
45 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] 9 3 3 3 A. . B. 3 3 . C. 9 3 . D. . 2 2
Câu 378. [#Mỗi ngày 3 câu hỏi hay].
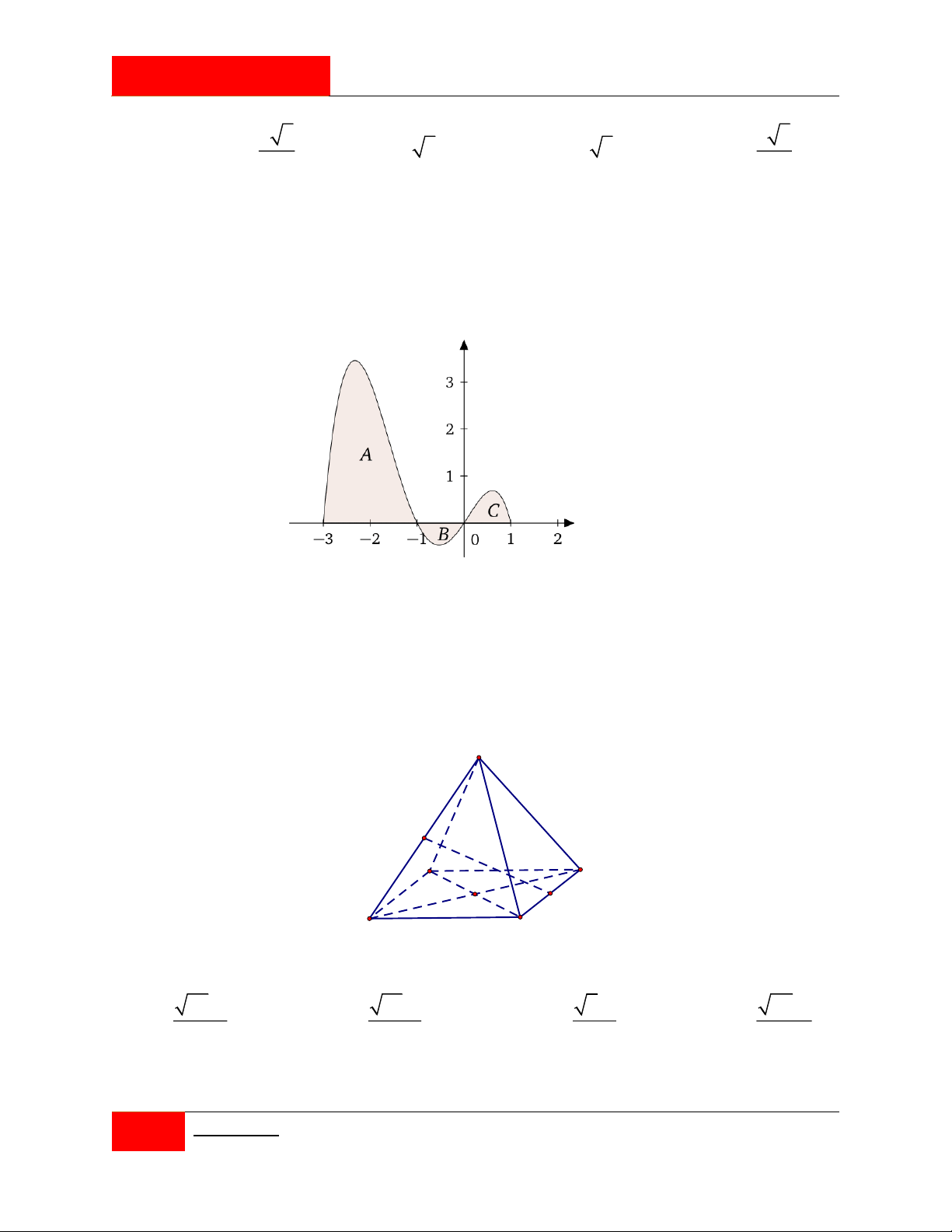
Cho hàm số y f x liên tục trên đoạn 3 ;
1 và có đồ thị như hình vẽ dưới. Biết diện 2 tích các hình ,
A B,C lần lượt là 27, 2 và 3. Tính tích phân I 3
x xf 2 x 3dx. 0 A. 14 . B. 32 . C. 32 . D. 28 .
Câu 379. [#Mỗi ngày 3 câu hỏi hay].
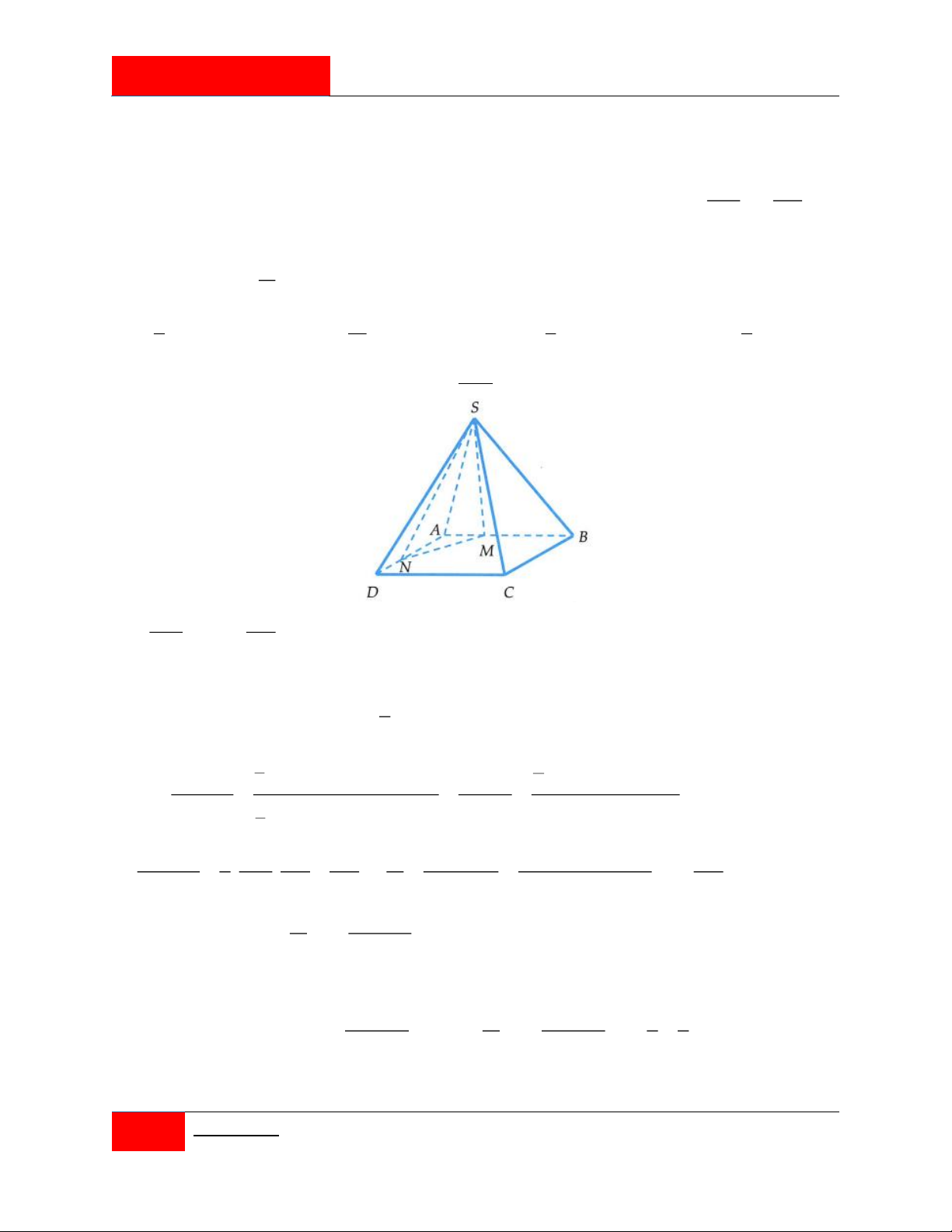
Cho hình chóp đều S.ABCD có cạnh đáy bằng a . Gọi M , N lần lượt là trung điểm của các cạnh S ,
A CD . Biết góc giữa đường thẳng MN với mặt phẳng SBD bằng 30 (như hình vẽ). S M D C N A B
Thể tích của khối chóp đều S.ABCD là: 3 30 3 21 3 5 3 22 A. a V . B. a V . C. a V . D. a V . 18 6 3 6
Câu 380. [#Mỗi ngày 3 câu hỏi hay].
46 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Trong không gian với hệ tọa độ Oxyz , cho hai mặt cầu S : x 4 y z 16 , 1 2 2 2
S :x 42 2 2
y z 36 và điểm A4;0;0 . Đường thẳng 2
di động nhưng luôn tiếp
xúc với (S ) , đồng thời cắt S tại hai điểm B C . Tam giác 2 1 ,
ABC có thể có diện tích lớn nhất là bao nhiêu? A. 24 5 . B. 48. C.7 2. D. 28 5 .
Câu 381. [#Mỗi ngày 3 câu hỏi hay].
Cho hàm số f x 4 3 2
2x 8x 16x 1 m (m là tham số). Biết rằng khi m thay đổi thì
số điểm cực trị của hàm số có thể là a hoặc b hoặc c . Giá trị a b c bằng A. 12. B. 16. C. 15. D. 13.
Câu 382. [#Mỗi ngày 3 câu hỏi hay].
Cho hàm số y f (x) có đạo hàm liên tục trên , f 6
0 và bảng xét dấu đạo hàm Hàm số y f 4 2
x x 6 4 2 3 4
6 2x 3x 12x có tất cả bao nhiêu điểm cực trị? A. 7 . B. 4 . C. 1 . D. 5 .
Câu 383. [#Mỗi ngày 3 câu hỏi hay].
Cho đồ thị C 3 2
: y x 3x mx 3 và đường thẳng d : y ax với m, a là các tham số
và a 0 . Biết rằng ,
A B là hai điểm cực trị của C và d cắt C tại hai điểm C, D
sao cho CD 4 2 và ACBD là hình bình hành. Tính diện tích của ACBD . A. 12 . B. 16 . C. 9 . D. 4 10 .
Câu 384. [#Mỗi ngày 3 câu hỏi hay].
Cho hàm số y f x có đạo hàm liên tục trên
. Biết y f x có bảng biến thiên như hình vẽ
47 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] 1
Có bao nhiêu số tự nhiên n sao cho ln f x 3 2
x 3x 9x m
n có nghiệm với 3 x 1
;3 và m0; 13 A. 3 . B. 2 . C. 5 . D. 7 .
Câu 385. [#Mỗi ngày 3 câu hỏi hay]. 2020
Gọi S là tập hợp các số tự nhiên n có 4 chữ số thỏa mãn 2020 2020 2 3 2 n n n 3 .
Số phần tử của S là A. 8999 . B. 2019 . C. 1010 . D. 7979 .
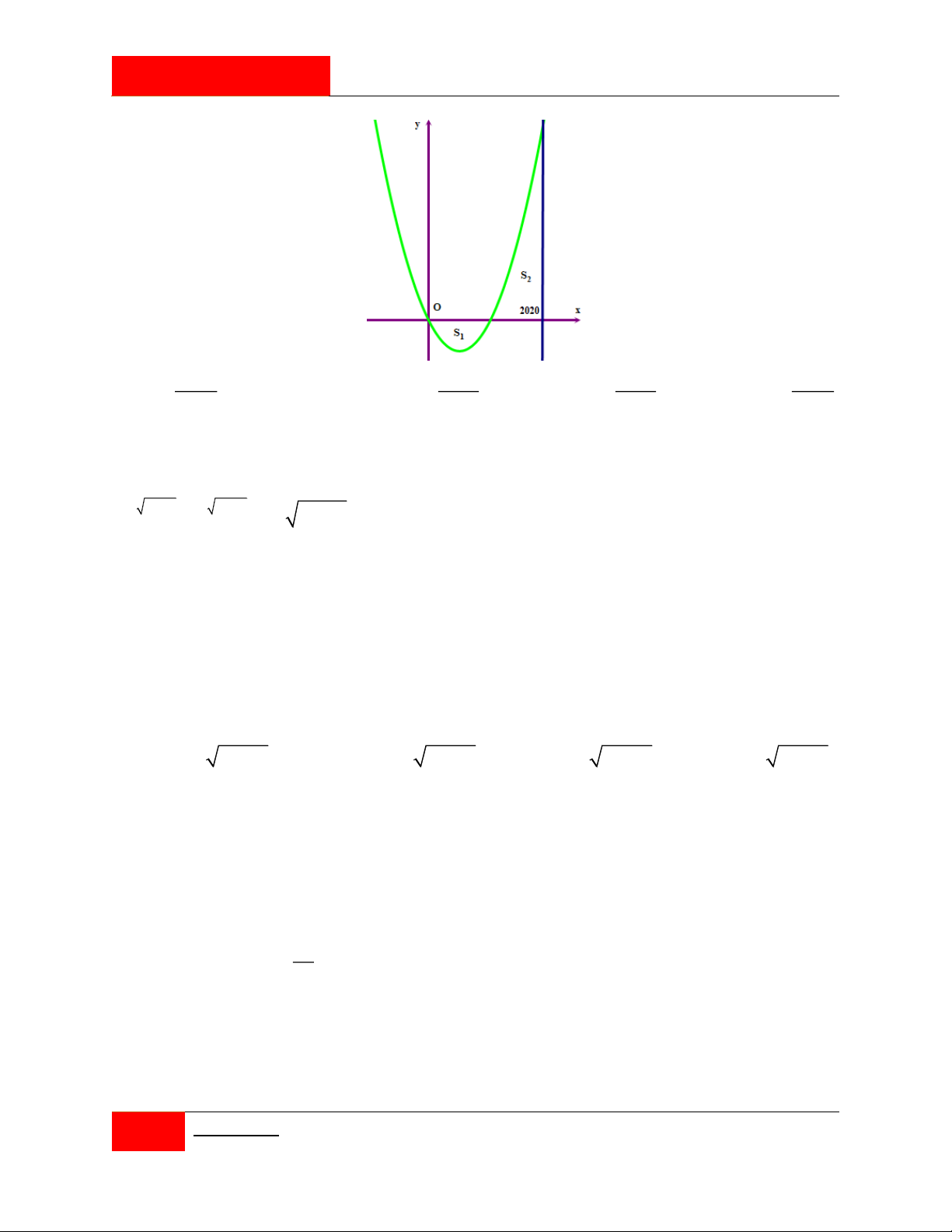
Câu 386. [#Mỗi ngày 3 câu hỏi hay].
Cho hàm số y f x có đạo hàm liên tục trên đoạn 0;7 và có đồ thị hàm số
y f x trên đoạn 0;7 như hình vẽ.
Đặt g x f 2x
1 , biết rằng diện tích các hình phẳng trong hình vẽ lần lượt là 244 28 2528 S , S , S
và f 0 1, tính g 4 . 1 15 2 15 3 15
48 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] 2759 2744 5518 563 A. . B. . C. . D. . 15 15 15 3
Câu 387. [#Mỗi ngày 3 câu hỏi hay].
Trong không gian với hệ tọa độ Oxyz , cho hình chóp M .ABCD có đỉnh M thay đổi 2 2 2
luôn nằm trên mặt cầu S : x 2 y
1 z 6 1, đáy ABCD là hình vuông có
tâm H 1;2;3 , A3;2;
1 . Thể tích lớn nhất của khối chóp M .ABCD bằng 32 128 64 A. 64 . B. . C. . D. . 3 3 3
Câu 388. [#Mỗi ngày 3 câu hỏi hay].
Có tất cả bao nhiêu giá trị nguyên của y để phương trình
ln log y ln log y sin x sin x có nghiệm? 5 5 A. 10 . B. 11 . C. 42 . D. 43 .
Câu 389. [#Mỗi ngày 3 câu hỏi hay].
Xét hai số phức z , z , thỏa mãn z 1 1, z 2 3 và z z 1 6 . Giá trị lớn 1 2 1 2 1 2
nhất của 5z z 7 3i bằng 1 2 A. 3 2 3 . B. 2 2 3 . C. 3 3 . D. 2 3 2 .
Câu 390. [#Mỗi ngày 3 câu hỏi hay]. 2 2 2
Trong không gian với hệ tọa độ Oxyz , mặt cầu S : x 3 y 2 z 1 75 và
mặt phẳng P 2
m m x 2
m m y m 2 : 2 4 1 2 3
1 z m 1 0 . A là điểm thuộc
mặt cầu S . Khi khoảng cách từ A đến mặt phẳng P đạt giá trị lớn nhất thì khối nón
có đỉnh là A , đường tròn đáy là giao tuyến của P và S có thể tích bằng bao nhiêu? A. 128 3 . B. 75 3 . C. 32 3 . D. 64 3 .
Câu 391. [#Mỗi ngày 3 câu hỏi hay]. Cho hàm số 2
y x mx 0 m 2020 có đồ thị C . Gọi S S là diện tích của hình 1 2
phẳng giới hạn bởi C , trục hoành, trục tung và đường thẳng x 2020 . Giá trị của m sao
cho S S là 2 1
49 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] 4040 4041 2021 2020 A. m B. m C. m D. m 3 3 3 3
Câu 392. [#Mỗi ngày 3 câu hỏi hay].
Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng 2000 ; 2000 để log b log 4 a a b a b
m log b 3 với mọi a,b 1; a A. 2199 . B. 2000 . C. 2001 . D. 1999 .
Câu 393. [#Mỗi ngày 3 câu hỏi hay].
Trong không gian với hệ tọa độ Oxyz cho ba điểm A2;0;0 , B0;4;0 , C 0;0;6 . Điểm
M thay đổi trên mặt phẳng ABC và N là điểm trên tia OM sao cho OM .ON 2020 .
Biết rằng khi M thay đổi, điểm N luôn thuộc một mặt cầu S cố định. Đường thẳng đi
qua D 0;202;10 cắt S theo một dây cung EF ,khi đó EF có độ dài ngắn nhất là. A. 4 10226 . B. 2 10226 . C. 3 10226 . D. 5 10226 .
Câu 394. [#Mỗi ngày 3 câu hỏi hay].
Cho hàm số bậc ba y f x có đồ thị là đường cong ở hình bên dưới. Gọi x , x lần lượt 1 2
là hai điểm cực trị thỏa mãn x x 2 và f x 3 f x 0. Đường thẳng song song 1 2 2 1
với trục Ox và qua điểm cực tiểu cắt đồ thị hàm số tại điểm thứ hai có hoành độ x và 0 S
x x 1. Tính tỉ số 1 ( S và S lần lượt là diện tích hai hình phẳng được gạch ở hình 1 0 1 2 S2 bên dưới).
50 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] 27 5 3 3 A. . B. . C. . D. . 8 8 8 5
Câu 395. [#Mỗi ngày 3 câu hỏi hay].
Trong không gian Oxyz, cho hai điểm A2;3; 1 ; B 1;3; 2 và mặt cầu S 2 2 2
: x y z 2x 4 y 2z 3 0 . Xét khối nón N có đỉnh là tâm I của mặt cầu
và đường tròn đáy nằm trên mặt cầu S . Khi N có thể tích lớn nhất thì mặt phẳng chứa
đường tròn đáy của N và đi qua hai điểm ,
A B có phương trình dạng 2x by cz d 0
và y mz e 0 . Giá trị của b c d e bằng A. 15. B. 12. C. 14. D. 13.
Câu 396. [#Mỗi ngày 3 câu hỏi hay]. Tổng tất cả các giá trị nguyên của m để phương trình 3
x3 m3x 3 2 x3 3 9 24 .3 3x x x x m
1 có 3 nghiệm phân biệt là A. 45 . B. 34 . C. 27 . D. 38 .
Câu 397. [#Mỗi_ngày_3_câu_hỏi_hay]. 2 x Cho biểu thức 1 4 P 2 2 y
trong đó x, y là 2 số thực thỏa mãn 3
y y x 3 26 3 2
x 3xyx y . 1
Biết rằng giá trị lớn nhất của P có dạng . c a b
với a, b, c
. Giá trị của biểu thức
a b c là? A. 3 . B. 2 . C. 4 . D. 5 .
Câu 398. [#Mỗi_ngày_3_câu_hỏi_hay].
51 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
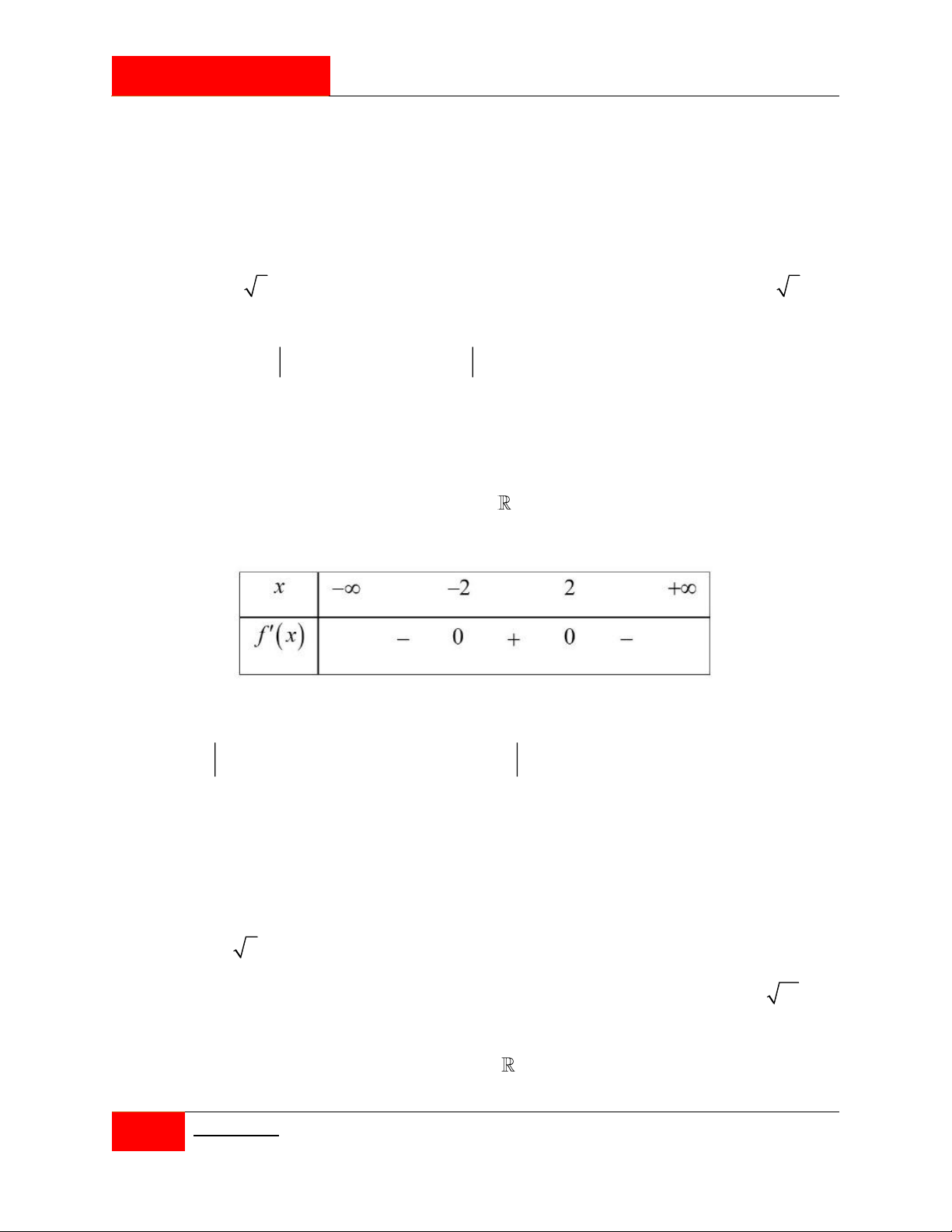
Trong một hình tứ diện ta tô màu các đỉnh, trung điểm các cạnh, trọng tâm các mặt và
trọng tâm tứ diện. Chọn ngẫu nhiên 4 điểm trong số các điểm đã tô màu, xác suất để 4
điểm được chọn có thế tạo thành bốn đỉnh của một tứ diện là 188 1009 245 136 A. . B. . C. . D. . 273 1365 273 195
Câu 399. [#Mỗi_ngày_3_hỏi_hay].
Trong không gian Oxyz, biết rằng với mọi tham số thực a thay đổi thì mặt phẳng P :
2sina cosa x 2sina cosa y 6 cosaz sina 3cosa 2 0 luôn tiếp xúc với
một mặt cầu cố định có bán kính R là? 2 2 1 A. R . B. R 2 . C. R . D. R . 2 4 2
Câu 400. [#Mỗi ngày 3 câu hỏi hay].
Cho hàm số y f x liên tục trên M và có đồ thị C . Biết hai tiếp tuyến với C tại
điểm x 1 tạo với nhau một góc 45°, hai tiếp tuyến này cùng với trục hoành tạo thành 0
một tam giác nhọn có số đo ba góc lập thành một cấp số cộng. Biết rằng biểu thức
f x f 2 x A lim
dương. Khi đó giá trị của A bằng x 1 x 1 A. 2. B. 2 2 3 . C. 3 2 . D. 3 1.
Câu 401. [#Mỗi_ngày_3_câu_hỏi_hay].
Trong không gian Oxyz, cho mặt cầu S có tâm I 2;1;0 , bán kính bằng 3 và mặt cầu 1
S có tâm J 0;1;0 , bán kính bằng 2. Đường thẳng thay đổi tiếp xúc với cả hai mặt 2
cầu S , S . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của khoảng cách 2 1
từ điểm A1;1;
1 đến đường thẳng . Giá trị tổng M m bằng A. 5 . B. 5 2 . C. 6 . D. 6 2 .
Câu 402. [#Mỗi ngày 3 câu hỏi hay].
f 3 x. f x 1
Cho hàm số y f x có đạo hàm trên 0; 3 , thỏa mãn với mọi
f x 1
52 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] 3 x 0; 3 và f 1 0 . Tính tích phân xf x I dx . 2 f x 2 2 0 1 3 . f x 1 3 5 A. I . B. I 1. C. I . D. I . 2 2 2 -----THE END-----
53 I can’t??? I can!! | ▫▪ 201 câu hỏ i hay Phầ n 2 Đáp án
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Câu 202. [#Mỗi ngày 3 câu hỏi hay].
Trong các số phức z dưới đây, số phức nào thỏa mãn z 1 và 3
z z 2 đạt giá trị lớn nhất? 1 3 1 3 2 5 2 5 A. z . i B. z . i C. z . i D. z . i 2 2 2 2 3 3 3 3 Giải
Đặt z x yi x, y . Ta có: 3 3 z z
x x y 2 2 4 4 2
4x 2i (do z 1).
z z x x 2 x 2 3 3 2 2 x 3 2 2 4 4 2 4 2 1
16x 4x 16x 8.
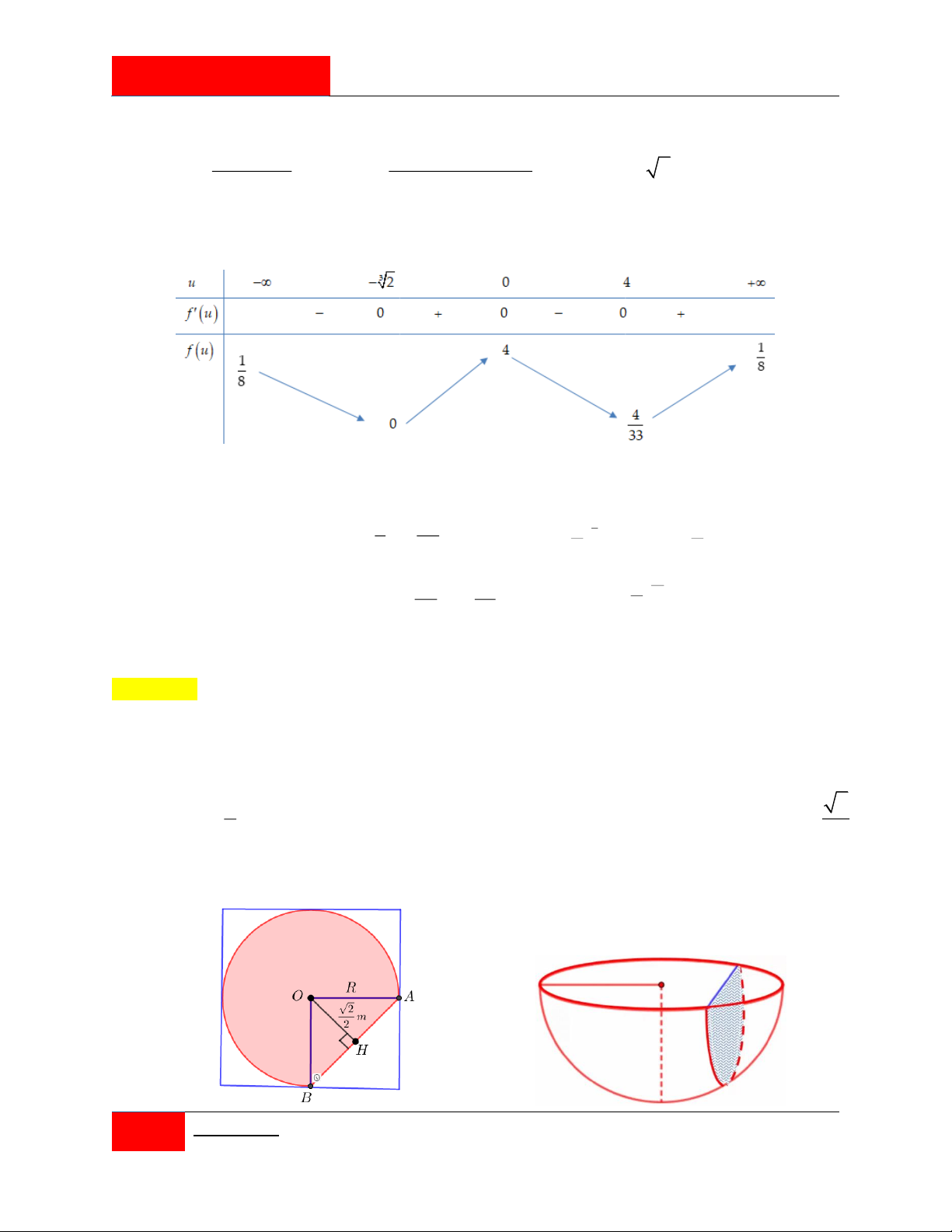
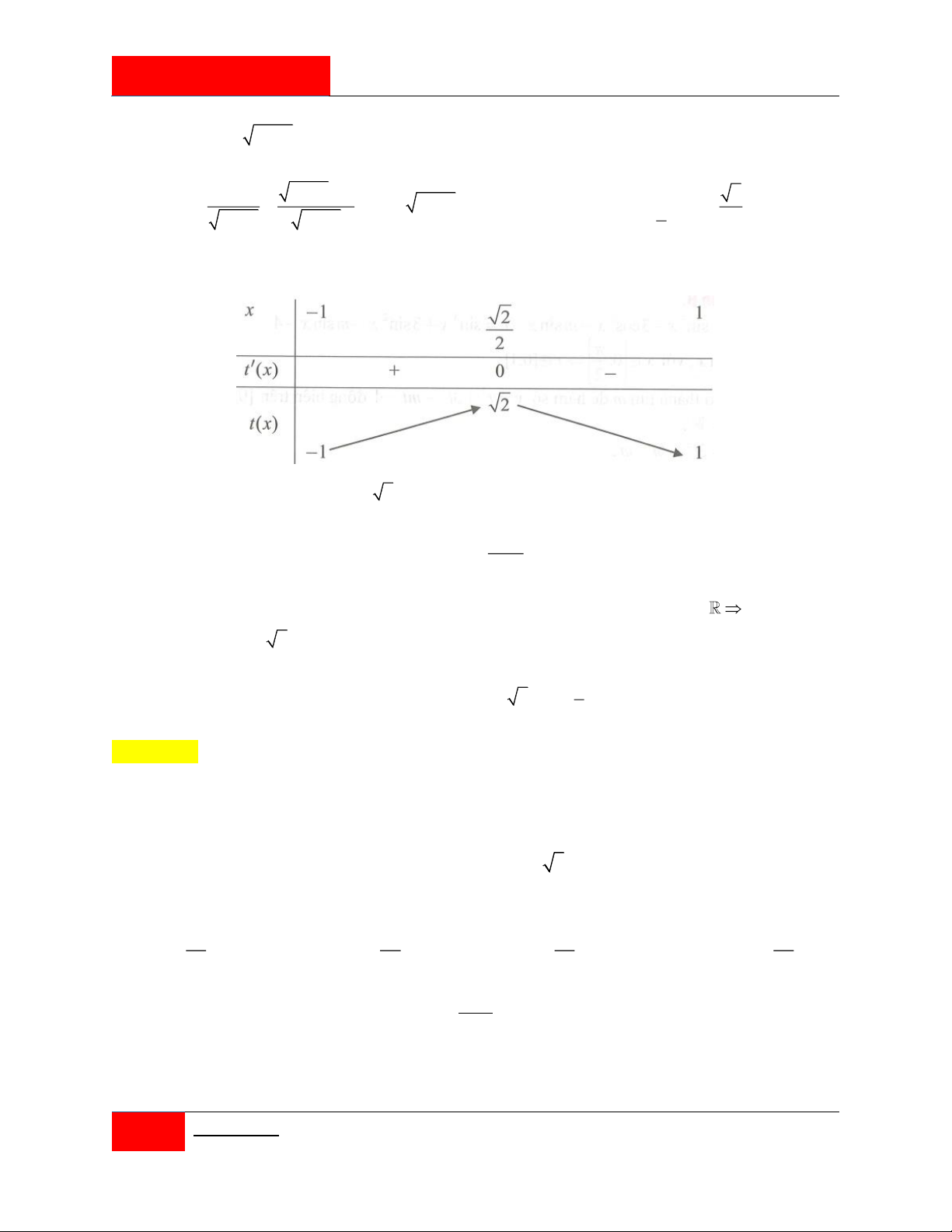
Xét hàm số f x 3 2
16x 4x 16x 8, x 1 ; 1 . 2 1
Ta có: f x 2
48x 8x 16 0 x hay x . 3 2 1 2 8 Tính f 1 4, f 13, f , f 1 4. 2 3 27 1 3
Dựa vào kết quả trên ta thấy 3
max z z 2 13 z . i z 1 2 2 Đáp án A.
Câu 203. [#Mỗi ngày 3 câu hỏi hay].
Gọi S là tập hợp tất cả các số phức z thoả mãn z 1 34 và z 1 mi z m 2i . Gọi z , z S 1
2 là hai số phức thuộc sao cho z
z nhỏ nhất, giá trị của z z bằng? 1 2 1 2 A. 2. B. 2 3 . C. 2 . D. 3 2 . Giải
Đặt z x yi theo giả thiết có: 2 2 2 2
(x 1) y 34
(x 1) y 34(1) . 2 2 2 2
(x 1) (y ) m (x ) m (y 2) (
2m 2)x (2m 4)y 3 0(2)
Ta có (1) là đường tròn (C) có tâm I (1;0), R 34;(2) là đường thẳng Δ.
Vì vậy có tối đa 2 số phức z thoả mãn và gọi A z , B z ta có 1 2 2 2 2
AB 2 R d (I , ) 2 34 d (I , ) AB d(I, ) . min max
1 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] 1(2m 2) 3 34 13
Ta có d (I, ) d(I,) m . max 2 2 2 8 (2m 2) (2m 4) 2 2
(x 1) y 34, Khi đó
z z 3 2. 5 3 1 2 x y 3 0 4 4 Đáp án D.
Câu 204. [#Mỗi ngày 3 câu hỏi hay].
Xét số phức z có phần thực dương và ba điểm ,
A B, C lần lượt là điểm biểu diễn của các 2 1 1 1
số phức z, và z . Biết tứ giác OABC là một hình bình hành, giá trị nhỏ nhất của z z z z bằng? A. 2. B. 2. C. 2 2. D. 4. Giải 1 1 1 1
Ta có OA z , AB
z , BC z
z ,OC z . z z z z
Vì OABC là một hình bình hành nên z z 2 2 OA BC 1 1 1 z 1 z 2 2
z z 1 z 1 1 1 z AB OC z z z z z z z z Đặt 2 2 2
z x yi z x y 2xy .
i vậy điều kiện trở thành: 2 2
z z 2 2
x y xyi 2 2 1 1 1 2 x y 1 2xyi
x y 2 x y x y 2 x y x y 2 x y 2 2 2 2 2 2 2 2 2 2 2 2 2 1 4 1 4 1 1 2 2 2 2
x y 1 x y 1 2 2 2 2
x y 0 y x 2 2 2 2
x y 1 (x y 1) Khi đó 2 2 2 2 2 2 2 2 2 2 2 4 1 1 z
(x y 1) 2xyi
(x y 1) 4x y 1 4x 1 1 2 2 z 2x 2 2x . 2. 2 2 2 2 2 z z x yi x y 2x 2x 2x
2 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] 1 2 2x 2 2 x Dấu bằng đạt tại 1 1 1 1 2 2 y x ( ; x y) ; ; ; 2 2 2 2 x 0 Đáp án B.
Câu 205. [#Mỗi ngày 3 câu hỏi hay].
Một trang giấy A4 kích thức 21 cm x 29,7 cm có thể viết được 50 dòng, mỗi dòng có 75
chữ số (chữ số trong hệ thập phân). Ngày 25 / 01 / 2013 , người ta đã tìm được số nguyên 57885161 tố Mersenne 2
1 . Nếu viết số nguyên tố này theo hệ thập phân trên trang giấy
A4 nói trên thì cần bao nhiêu tờ giấy A4, biết rằng mỗi tờ giấy tương ứng với 2 trang? A. 2324 tờ. B. 2315 tờ. C. 2323 tờ. D. 2316 tờ. Giải Đặ 57885161 57885161 t p 2 1 thì p 1 2
Suy ra: log p
1 57.885.161log 2 17.425.169, 76 Hay 1742516976 17425169 17425170 p 1 10 10 p 1 10
Do đó, viết trong hệ thập phân thì p có 17425170 chữ số. 17.425.170 Ta có:
2323,356 nên số tờ giấy A4 cần dùng để viết số nguyên tố đã cho là 50.75.2 2324 . Đáp án A.
Câu 206. [#Mỗi ngày 3 câu hỏi hay]. Cho dãy số u
u u u u u n thỏa mãn 10 2 20 2 1 , với mọi số nguyên n 10 n n 1 u n 1 10
n 2 . Tìm số tự nhiên n u 0 nhỏ nhất để 2019 2019 . 0 n
A. n 22168 .
B. n 22167 .
C. n 22178 .
D. n 22177 . 0 0 0 0 Giải u 2u Điề 0 u kiện: n n1 . 2u 1 0 10
Từ giả thiết ta có: 10u u u 2u
20u 2u 1 n 10 n n 1 n 1 10
u 2u (20 u 2u 2) u n n 2 1 21 0 n n 1 1 10
3 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] 2 Vì u 2u ; 0 20 u 2u 2 ; 0 nên suy ra: n n 1 u n n 1 2 1 10 1 0 u ; 1 u 2u , 2 10 n n 1 n Do đó, u q
n là cấp số nhân công bội 2 . 9 9 9 n 1 n 1 0
l u 2 .u u 2 u 2 .2 2 10 1 1 n 2019 n 1 0 2019 u 2019 2 2019
n 10 2019log 2019 n 2
n 22167,45947 n 22178 0 Đáp án D. Bài tập tương tự ln 2 2
u u 10 ln 2u 6u 1 2 1 2
Câu 1. Cho dãy số u u u u n thỏa mãn và 2 1 với n2 n n 1
mọi n 1. Giá trị nhỏ nhất của n để u 5050 bằng? n A. 100 . B. 99 . C. 101. D. 102 . 1 n 1 u u u
Câu 2. Cho dãy số u 2 3 10
n xác định bởi: u ;u u S u ... 1 n 1 . Tổng n 3 n 3 1 2 3 10 bằng? 3280 29524 25942 1 A. . B. . C. . D. . 6561 59049 59049 243
Câu 3. Cho dãy số u u u u u . Đặ n thỏa mãn , 6 2 và log log 8 11 t n n 1 n 2 5 9 2
S u u ... u . Tìm số tự nhiên n nhỏ nhất thỏa mãn S 20172018 . n 1 2 n n A. 2587 . B. 2590 . C. 2593 . D. 2584 .
Câu 4. Cho dãy số u
log 2u 63 2log u 8n 8 , n N n thỏa mãn n * 3 5 4 . Đặt u .S 148
S u u ... u . Tìm số nguyên dương lớn nhất n thỏa mãn n 2n . n 1 2 n u .S 75 2n n A. 18 . B. 17 . C. 16 . D. 19 .
Đáp án: 1D; 2B; 3C; 4A.
Câu 207. [#Mỗi ngày 3 câu hỏi hay].
Trong không gian với hệ tọa độ Oxyz , cho mặt cầu S 2 2 2
: x y z 4x 4 y 2z 7 0
và đường thẳng d là giao tuyến của hai mặt phẳng x1 2m y 4mz 4 0 và m
2x my 2m
1 8 0 . Khi m thay đổi các giao điểm của d và S nằm trên một m
đường tròn cố định. Tính bán kính r của đường tròn đó.
4 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] 142 92 23 586 A. r . B. r . C. r . D. r . 15 3 3 15 Giải
S có tâm I 2; 2
;1 , bán kính R 4 .
Các điểm d có tọa độ thỏa mãn x 1 2m y 4mz 4 0 và 2x my 2m 1 z 8 0 m Do đó: x
12m y 4mz 4 22x my
2m 1 z 8 0
5x y 2z 20 0
Suy ra d luôn nằm trong mp P : 5x y 2z 20 0 cố định khi m thay đổi. m 14
Mà d I,P
4 P cắt S theo giao tuyến là đường tròn tâm H bán kính 30 196 142 2 2 r
R d I,P 16 225 15 Đáp án A. Note:
Với hai mặt phẳng P : a x b y c z d 0 ; Q : a x b y c z d 0 1 1 1 1 2 2 2 2
Khi đó, giao tuyến của P , Q luôn nằm trên mặt phẳng có phương trình:
a x b y c z d a x b y c z d 0 với 2 2 0 . 1 1 1 1 1 1 1 1
Câu 208. [#Mỗi ngày 3 câu hỏi hay].
Trong không gian Oxyz , cho ba điểm A0;0; 4, B 3; 2;6,C 3; 2
;6. Gọi M là điểm di
động trên mặt cầu S 2 2 2
: x y z 4. Giá trị nhỏ nhất của biểu thức MA MB MC bằng? A. 2 34 . B. 6 5 . C. 4 10 . D. 2 29 . Giải Với điểm M ;
x y; z S thì 2 2 2
x y z 4 0 và điểm I 3;0;6 là trung điểm BC và
MA MB MC MA 2 MI MA 2MI 2 2 2 2 2 2
x y (z 4) 2 (x 3) y (z 6) 2 2 2 2 2 2 2 2 2
x y (z 4) 3x y z 4 2 (x 3) y (z 6)
5 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] 2 2 2 2 2 2 2 x y (z 1) (x 3) y (z 6) 2 2 2
2 (x 3 x) (y y) (z 1 6 z) 2 34 x z 1 k 0 3 x 6 z 3 127 15 9 5 127
Dấu bằng đạt tại: y 0 ;
x y; z ; 0; 34 34 2 2 2
x y z 4 Đáp án A.
Câu 209. [#Mỗi ngày 3 câu hỏi hay].
Cho hàm số f x liên tục và nhận giá trị không âm trên đoạn 0;
1 . Giá trị nhỏ nhất của 2 1
biểu thức M 2 f x 3x f xdx 4 f x x xf xdx bằng? 0 0 1 1 1 1 A. . B. . C. . D. . 24 8 12 6 Giải
Để cho đơn giản đặt a f x ta có: 1 M 1
2 f x 3x f x dx 4 f x x xf xdx 0 0 1 1
2a3xadx
4a x xadx 0 0 1 x
2a 4a xa 3ax x xa 1 2 1 2 dx dx . 8 24 0 0 2 x 1 Vì 2
2a 3ax 4a ax x ax
2 a x 4 0. 8 8 Dấu bằng đạt tại: x x 2 a
x 4a x a
f x . 4 4 Đáp án A.
Câu 210. [#Mỗi ngày 3 câu hỏi hay].
6 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Cho hàm số y f x có đạo hàm liên tục trên R thỏa mãn 2
xf x f x 2 . '
f x x, x
và f 2 1. Tích phân 2
f x dx bằng? 0 3 4 A. . B. . C. 2 . D. 4 . 2 3 Giải 2 2 2
Lấy tích phân hai vế trên đoạn 0;2 có xf
x.f 'x 2 dx
f (x)dx xd . x 0 0 0
Tích phân từng phần có: 2 2 2 2 x xf x f ' x 1 2 1 1 2 dx xd f x 2 f x 2 f x 2 dx f 2 2 f
xd .x 2 2 0 2 2 0 0 0 0 2 2 f 2 xdx 2 2 2 2 2 1 1 2 Vậy 2 f 2 2 f x 2 dx f x 2 dx xdx f x 0 dx 2. 2 3 3 0 0 0 0 2 2 Đáp án C.
Câu 211. [#Mỗi ngày 3 câu hỏi hay].
Trong không gian Oxyz , cho hai mặt cầu S 2 2 2
: x y z 2x 4 y 2z 2 0 và 1 S 2 2 2
: x y z 2x 4 y 2z 4 0 . Xét tứ diện ABCD có hai đỉnh , A B nằm trên 2
S ; hai đỉnh C,D nằm trên S . Thể tích khối tứ diện ABCD có giá trị lớn nhất bằng 2 1 A. 3 2 . B. 2 3 . C. 6 3 . D. 6 2 . Giải
Mặt cầu S có tâm I 1; 2 ;
1 , R 2 . Mặt cầu S có tâm I (1; 2 ;1), R 10. 2 1 1 2
Gọi a, b lần lượt là khoảng cách từ tâm I đến hai đường thẳng AB, CD . Ta có: 2 2 2 2 2 2
AB 2 R a 2 4 a ; CD 2 R b 2 10 b 1 2
và d AB,CD d I, AB d I,CD a b và sin AB,CD 1.
Do đó theo công thức tính thể tích tứ diện cho trường hợp đặc biệt có: 1 V AB CD d AB CD AB CD a b a b ABCD 2 . . , .sin , 2 2 4 . 10 6 2. 6 3
7 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Dấu bằng đạt tại a;b 1;2. Đáp án D.
Câu 212. [#Mỗi ngày 3 câu hỏi hay].
Gọi S là tập hợp các số phức z có phần thực và phần ảo đều là các số nguyên đồng thời
thoả mãn hai điều kiện: z 3 4i 2 và z z z z . Số phần tử của tập S bằng? A. 11. B. 12 . C. 13 . D. 10 . Giải
a 32 b 42 4
a 32 b 42 4 Đặt:
z a bi theo giả thiết có 2 2 2a 2b a b . a, b a, b
Ta phải có: a 2 3 4 2
a 3 2 1 a 5 .
4b 42 +) Nếu 4 a 1 b 4 ; a b 1; 4; 2 1 b
4 b 42 +) Nếu 4 a 2 b 3;4;
5 a;b 2;3;2; 4;2;5; 2 4 b
4 b 42 +) Nếu 4 a 3 b 3;4;5;
6 a;b 3;3; 3; 4; 3;5; 3;6 . 2 9 b
4 b 42 +) Nếu 4 a 4 b 4;
5 a;b 4; 4; 4;5 2 16 b
4 b 42 +) Nếu 4 a 5 VN . 2 25 b
Vậy có tất cả 10 số phức thoả mãn. Đáp án D.
Câu 213. [#Mỗi ngày 3 câu hỏi hay].
S x 2 y 2 z 2 : 1 1 1 12
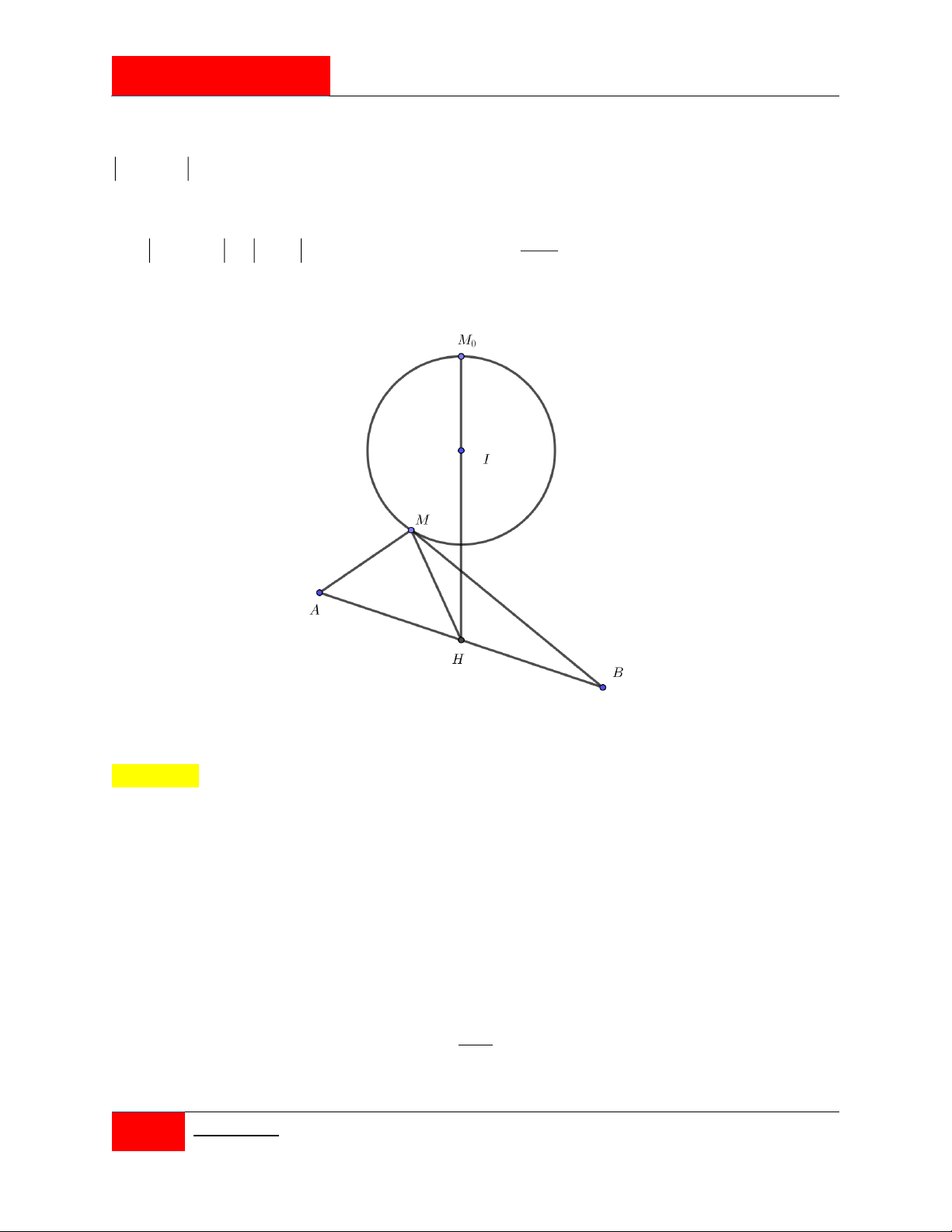
Trong không gian Oxyz , cho mặt cầu và mặt phẳng
P: x 2y 2z 11 0. P
Xét điểm M di động trên ; các điểm ,
A B, C phân biệt di S S ABC động trên
sao cho AM , BM , CM là các tiếp tuyến của . Mặt phẳng
luôn đi qua điểm cố định nào dưới đây?
8 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] 1 1 1 3 A. ; ; . B. 0; 1 ;3 . C. ; 0; 2 . D. 0;3; 1 . 4 2 2 2 Giải
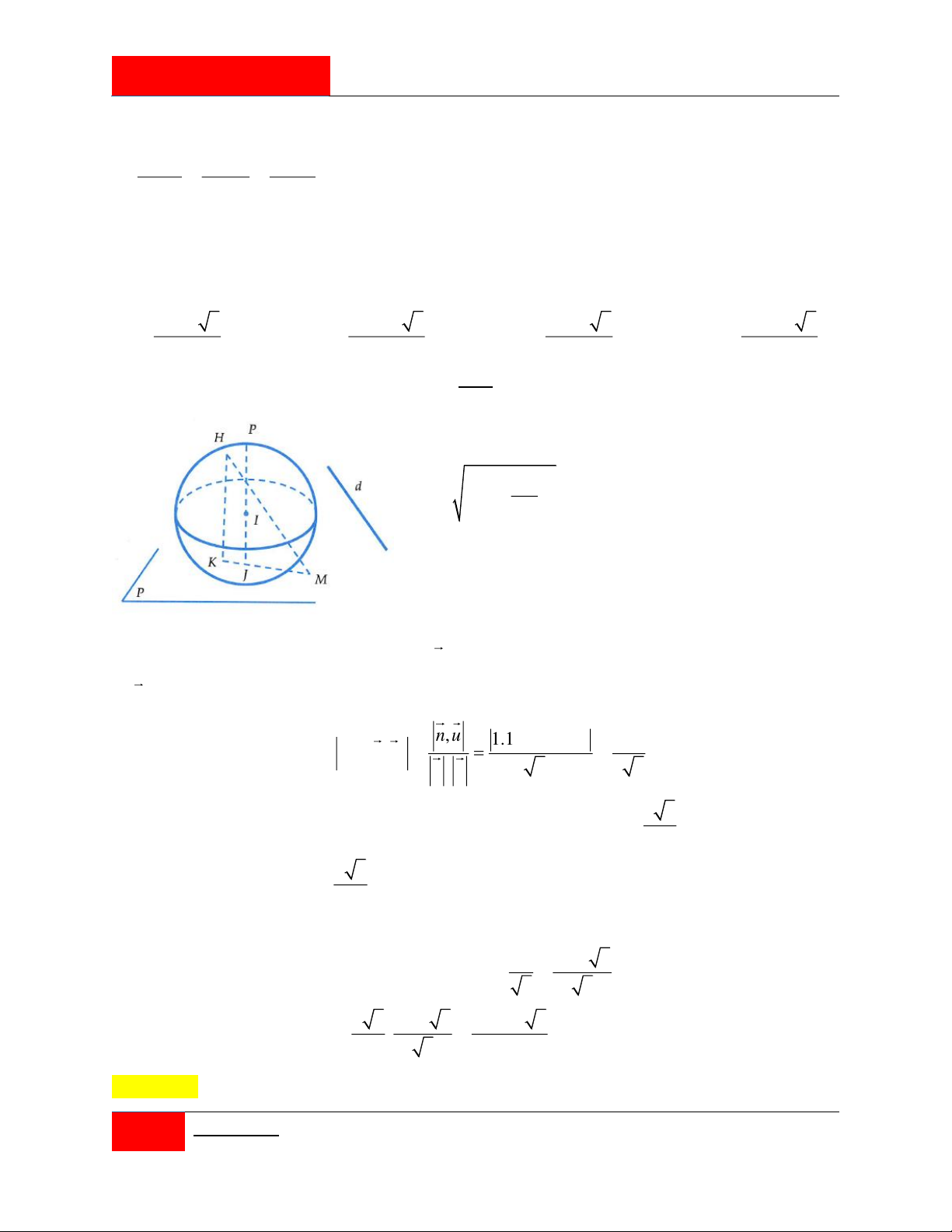
Mặt cầu S có tâm I 1;1;
1 bán kính R 2 3. Xét điểm M ; a ;
b c và A ;
x y; z ta có hệ điều kiện: A(S) x 2 1 y 2 1 z 2 1 12 0 2 2 2
IAM 90 AI AM IM M P
a 2b 2c 11 0 x 2 1 y 2 1 z 2 1 12 1 1
2 x a2 y b2 z c2 a 2 1 b 2 1 c 2 1 2
a 2b 2c 11 0 3 Lấy 1 – 2 theo vế có:
x 2 y 2 z 2 xa2 yb2 z c2 a 2 b 2 c 2 1 1 1 12 12 1 1 1 a
1 x b
1 y c
1 z a b c 9 0
Vậy mặt phẳng qua ba tiếp điểm là
Q:a
1 x b
1 y c
1 z a b c 9 0.
Kết hợp với 3 suy ra mặt phẳng này luôn đi qua điểm cố định 0;3; 1 . Đáp án D.
Câu 214. [#Mỗi ngày 3 câu hỏi hay]. x 1 Cho hàm số y
có đồ thị C . Biết rằng C có tiệm cận ngang và tồn tại tiếp 2 ax 1
tuyến của C song song và cách tiệm cận ngang của C một khoảng bằng 3 . Mệnh đề nào dưới đây đúng ? 1 3 1 3 A. a ;1 . B. a 1; . C. a 0; . D. a ; 2 . 2 2 2 2 Giải
Điều kiện để đường cong C có tiệm cận ngang khi và chỉ khi: 1 1
a 0 TCN : y ; y a a
9 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] ax 2
ax 1 x 1 2 ax 1 1 ax Ta có: y ' . 2 ax 1 ax 3 2 1
Để tiếp tuyến của C tại điểm M song song với tiệm cận ngang thì: y x ax x M M 1 1 1 ' 0 1 0 M M ; 1 . a a a 1 1 1 3 a a
Khi đó d t TCN d M TCN a M 9 ; , . 16 1 1 1 3 a a Đáp án A.
Câu 215. [#Mỗi ngày 3 câu hỏi hay].
Xét số phức z có phần thực dương và ba điểm ,
A B, C lần lượt là điểm biểu diễn của các 2 1 1 1
số phức z, và z . Biết tứ giác OABC là một hình bình hành, giá trị nhỏ nhất của z z z z bằng? A. 2. B. 2 . C. 2 2. D. 4 . Giải 1 1 1 1
Ta có: OA z , AB
z , BC z
z ,OC z . z z z z
Vì OABC là một hình bình hành nên z z 2 2 OA BC 1 1 1 z 1 z 2 2
z z 1 z 1 1 1 z AB OC z z z z z z z z Đặt 2 2 2
z x yi z x y 2xyi , vậy điều kiện trở thành: 2 2
z z 2 2
x y xyi 2 2 1 1 1 2 x y 1 2xyi
x y 2 x y x y 2 x y x y 2 x y 2 2 2 2 2 2 2 2 2 2 2 2 2 1 4 1 4 1 1 2 2 2 2
x y 1 x y 1 2 2 2 2
x y 0 y x 2 2 2 2
x y 1 (x y 1)
10 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] Khi đó: 2 2 2 2 2 2 2 2 2 2 2 4 1 1 z
(x y 1) 2xyi
(x y 1) 4x y 1 4x 1 1 2 2 z 2x 2 2x . 2. 2 2 2 2 2 z z x yi x y 2x 2x 2x 1 2 2x 2 2 x Dấu bằng đạt tại: 1 1 1 1 2 2 y x ; x y ; ; ; 2 2 2 2 x 0 Đáp án B.
Câu 216. [#Mỗi ngày 3 câu hỏi hay].
Cho hai hàm số f x 4 3 2
ax bx cx dx e và g x 3 2
mx nx px 1 với
a, b, c, d, ,
e m, n, p, q là các số thực. Đồ thị của hai hàm số y f 'x; y g 'x như
hình vẽ bên. Tổng các nghiệm của phương trình f x q g x e bằng 13 13 4 4 A. . B. . C. . D. . 3 3 3 3 Giải
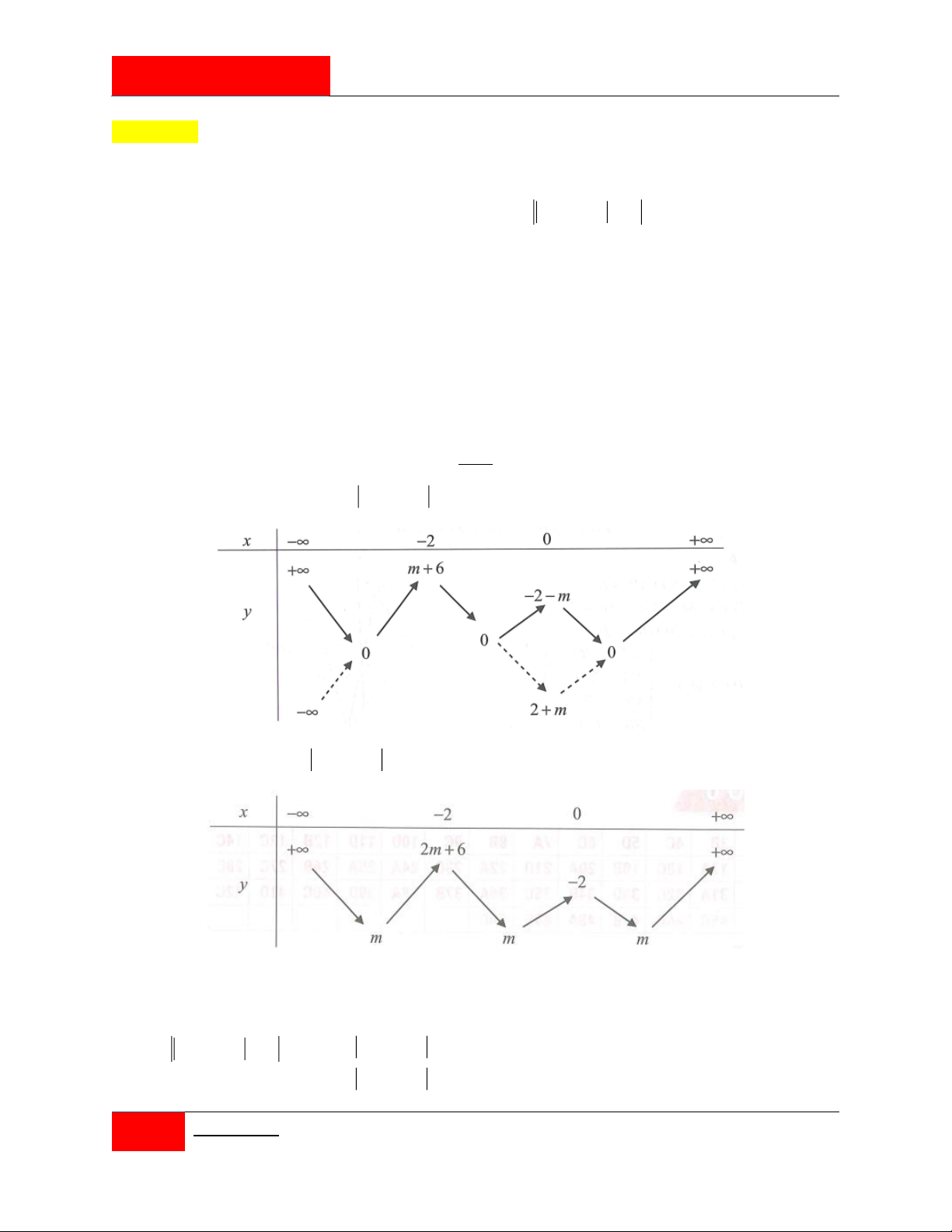
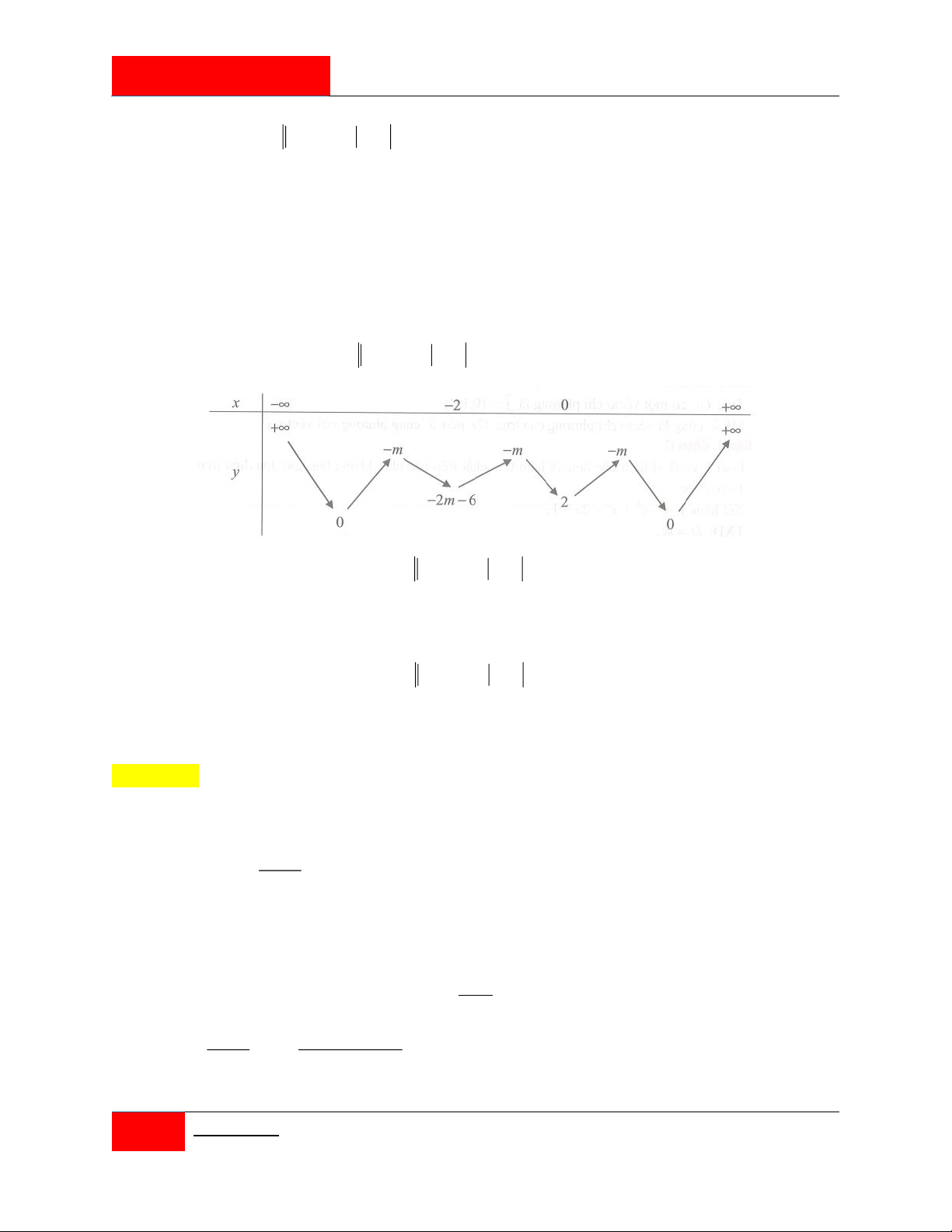
Đặt: h x f x g x có:
h x k x 5 ' 1 x
x 3 k 0;h0 f 0 g 0 e . q 4 Do đó
11 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] x x
h x h x h h h xdx e q kx 5 0 0 ' 1 x
x 3dx e . q 4 0 0 x x k k
x 14x5x3dxeq 3 2
4x 13x 2x 15dx e . q 4 4 0 0 k 13 4 3 2 x
x x 15x e . q 4 3
Phương trình tương đương với: 5 x 3 h x 13 4 3 2
e q x
x x 15x 0 x 0 . 3 x 3
Tổng các nghiệm của phương trình bằng 5 4 0 3 . 3 3 Đáp án C.
Câu 217. [#Mỗi ngày 3 câu hỏi hay].
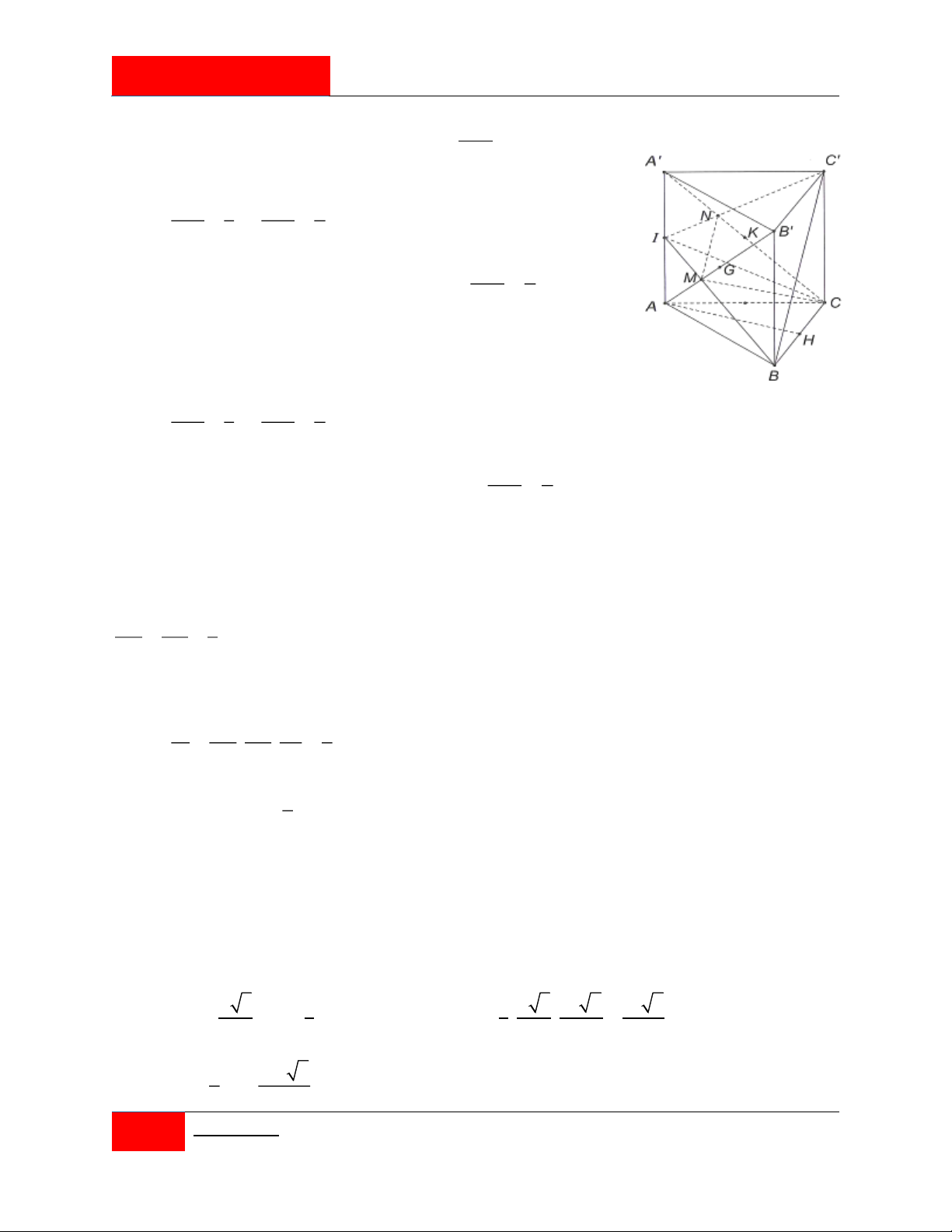
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , AB 6 , BC 8 . Biết
SA 8 và SA ( ABC) . Một khối cầu có tâm thuộc phần không gian bên trong của khối
chóp và tiếp xúc với tất cả các mặt của hình chóp S.ABC . Tính khoảng cách d từ tâm
của khối cầu đến mặt phẳng SBC . 4 3 12 34
A. d 6 . B. d . C. d . D. d . 3 2 17 Giải
Phân tích hướng giải:
Chúng ta thấy thật khó khăn khi dựng được tâm của mặt cầu như giả thiết! Vậy có cách
nào khác mà ta có thể tính được khoảng cách này mà không cần xác định tâm của mặt cầu?
Nhận xét: Khoảng cách cần tìm là bán kính của mặt cầu và là đường cao của khối chóp
có đỉnh là tâm của mặt cầu và đáy là một mặt của khối chóp đã cho.
Các mặt của hình chóp đã cho đều là các tam giác vuông. Hướng dẫn giải.
Gọi I , r lần lượt là tâm và bán kính của khối cầu trên.
Ta có: r d I;SBC d I; ABC d I;SAB d I;SAC . 1 1 V V V V V V r. S S S S r.S S . ABC I. ABC I. ASB I. ASC I.S BC ABC SAB SAC SBC 3 3 tp
12 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
SBC 3V r d I , Stp 1 1 Mà: V .S . A S
.8.24 64 và S 24 24 40 40 128 3 ABC 3 tp V
Vậy r d I SBC 3 3.64 3 , . S 128 2 tp Đáp án C.
Câu 218. [#Mỗi ngày 3 câu hỏi hay].
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a , góc 60o ABC cạnh bên
SD a 2 . Hình chiếu vuông góc của S trên mặt phẳng ABCD là điểm H thuộc đoạn
BD sao cho HD 3
HB . Gọi M là trung điểm của cạnh SD . Tính khoảng cách giữa hai
đường thẳng CM và SB . a 30 a 7 30a a 30 A. . B. . C. . D. . 8 4 7 5 Giải
Phân tích hướng giải:
Ta thấy CM và SB là hai đường thẳng chéo nhau và không vuông góc.
Ta tìm mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.
Khi đó bài toán trở thành tính khoảng cách từ đường thẳng và mặt phẳng song song.
Hướng khác: phương pháp tọa độ trong không gian.
Đường thẳng d đi qua A và có vectơ chỉ phương a .
Đường thẳng d ' đi qua A' và có vectơ chỉ phương a '. AA a a
Khoảng cách giữa d và d ' là d d d . , ' ; ' a,a ' Hướng dẫn giải.
Cách 1: Sử dụng thể tích 2 2 a 3 a 3 Ta có: S 2S 2.
(tam giác ABC đều) ABCD ABC 4 2 27 a 5 3 3 a 3 3a 3 2 2 2 2 SH
SD HD 2a a
HD OD . 16 4 2 2 2 4 2 3 1 1 a 5 a 3 a 15 V SH.S . . S .ABCD 3 ABCD 3 4 2 24
13 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] Ta lại có:
SB//OM SB// MAC d ;
SB CM d ;
SB (MAC) d(S;MAC ) d D;MAC 1 1 1 a V d ABCD S d ABCD S V . CD ACD 3 1 1 15 M; . . S; . M.A ABCD S. 3 3 2 2 4 ABCD 96 3 a 15 1 3V a 30 Mặt khác: V d D MAC S d D MAC . CD CD MAC M.A 32 ; . ; M.A 2 3 S a MAC 2 8 8 Đáp án A.
Cách 2: Tính trực tiếp
Dựng MI // SH và IK OM . Ta có:
MAC MIO AC OI;AC MI
MAC MIO OM IK OM IK MAC
SB//OM SB// MAC d(S ;
B CM ) d (S ;
B (MAC)) d S;MAC d D;MAC 4d I;MAC 4IK 1 a 3 OI OD 4 8 27 a 5 1 a 5 2 2 2 2 SH
SD HD 2a a
IM SH 16 4 2 8 1 1 1 64 64 512 30a a 30 a 30 IK d S ;
B CM 4IK 4. . 2 2 2 2 2 2 IK IO IM 3a 5a 15a 32 32 8
Cách 3: Phương pháp tọa độ (Cách này tính toán khá phức tạp nên chỉ
nêu ra để học sinh thấy không phải bài toán nào cũng dùng phương pháp
tọa độ cũng nhanh nhất).
Ta chọn hệ trục tọa độ như hình vẽ và chọn a 1. 5 3 1 3 3 3 5 Ta có: S ;0;0 ;B 0; ;0 ;C ; ;0 ;M 0; ; . 4 4 2 4 8 8
Câu 219. [#Mỗi ngày 3 câu hỏi hay].
Trong mặt phẳng tạo độ Oxyz , cho bốn điểm A0; 1 ;2 , B2; 3 ;0 ,C 2 ;1 ;1 , D 0; 1 ;3 .
Gọi L là tập hợp tất cả các điểm M trong không gian thỏa mãn đẳng thức
14 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] M .
A MB MC.MD 1 . Biết rằng L là một đường tròn, đường tròn đó có bán kính r bằng bao nhiêu? 11 7 3 5 A. r . B. r . C. r . D. r . 2 2 2 2 Giải
Phân tích hướng giải: . MA MB 1
Ta tìm tọa độ của điểm M thỏa hệ phương trình: .
MA MB MC.MD 1 MC.MD 1 Hướng dẫn giải.
Gọi M x; y;z là tập hợp các điểm thỏa mãn yêu cầu bài toán. Ta có:
MA x; y1; z 2, BM x 2; y 3; z,CM x 2; y 1; z 1 , DM ;
x y 1; z 3 . MA MB 1 Từ giả thiết: .
MA MB MC.MD 1 . MC.MD 1
xx 2 y
1 y 3 z z 2 2 2 2 1
x y z 2x 4y 2z 2 0 x
x 2 y 1 y 1 z 1 z 3 2 2 2 1
x y z 2x 4z 1 0
Cách 1: Suy ra tập hợp điểm M là đường tròn giao tuyến của mặt cầu tâm I 1; 2
;1 , R 2 và mặt cầu tâm I 1 ;0;2 , R 2 2 1 1 1 Ta có: I I 3 ; 1 2 2 I I 9 7 Dễ thấy: 2 1 2 r R 4 . 1 2 4 2 Đáp án B. 2 2 2 2 2 2
x y z 2x 4y 2z 2 0
x y z 2x 4y 2z 2 0 S Cách 2: 2 2 2
x y z 2x 4z 1 0
4x 4y 2z 1 0 P S 4 8 2 1 3 có tâm I 1; 2
;1 ; R 2; d I;P . 2 2 2 2 4 4 2 9 7 2 2 r
R d 4 4 2 Đáp án B.
Câu 220. [#Mỗi ngày 3 câu hỏi hay].
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC vuông tại C, có 0 ABC 60 ;
15 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] x y x
AB 3 2. Đường thẳng AB có phương trình 3 4 8
, đường thẳng AC nằm 1 1 4
trên mặt phẳng : x z 1 0. Biết điểm B là điểm có hoành độ dương, gọi a,b,c
là tọa độ của điểm C. Giá trị a b c bằng? A. 2. B. 3. C. 4. D. 7. Giải x 3 y 4 x 8
Tọa độ điểm A là nghiệm của hệ: 1 1 4 A1;2;0.
x z 1 0 Gọi B 3 ; m 4 ; m 8
4m A .
B Vì x 0 m 3. B m loaïi 2 3 Từ 2
AB 3 2 AB 18 18m 2 18 B2;3; 4 . m 1 C
a c 1 0 3 6 2 2 27 Ta có: 0 AC A . B sin 60 a 1 b 2 2 c 2 2 BC.AC 0 a 2 a
1 b 3b 2 c c 4 0 7 5
Giải hệ trên ta được a
; b 3; c . Vậy a b c 4. 2 2 Đáp án C.
Câu 221. [#Mỗi ngày 3 câu hỏi hay].
Một hộp có 6 viên bi xanh, 5 viên bi đỏ và 4 viên bi vàng. Chọn ngẫu nhiên 5 viên bi
sao cho có đủ cả ba màu. Số cách chọn là? A. 2163. B. 2170. C. 3003. D. 3843. Giải
Số cách chọn 5 viên bi bất kì trong hộp là: 5 C cách. 15
Khi chọn bất kỳ thì bao gồm các trường hợp sau: Chỉ có một màu Chỉ có hai màu Có đủ ba màu
16 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] Xanh: 5 C cách. Xanh – Đỏ: 5 5 5
C C C cách. 6 11 6 5 Đỏ: 5 C cách. Đỏ - Vàng: 5 5 C C cách. 5 9 5 Xanh – Vàng: 5 5 C C cách. 10 6
Suy ra số cách chọn thỏa mãn yêu cầu bài toán (có đủ ba màu) là: 5 C 5 5
C C 5 5 5
C C C
C C C C 2170. 1 6 5 5 5 9 5 5 5 15 6 5 1 0 1 6 Đáp án B.
Câu 222. [#Mỗi ngày 3 câu hỏi hay].
Kí hiệu H là hình phẳng giới hạn bởi các đường x y e ,
y 0, x 0 và x 1. Đường thẳng x k 0 k 1 chia
H thành hai phần có diện tích tương ứng S , S như hình 1 2
vẽ bên, biết S S . Mệnh đề nào sau đây là đúng? 1 2 k e k e 1 1 A. e . B. e . 2 2 k e k e 2 3 C. e . D. e . 2 2 Giải k k 1 1 Ta có: xd x k S e x e e 1
và S e dx e e e . x x k 1 2 0 0 k k k k k e 1
Theo giả thiết: S S e 1 e e e . 1 2 2 Đáp án B.
Câu 223. [#Mỗi ngày 3 câu hỏi hay]. 1
Biết rằng hai số phức z , z thỏa mãn z 3 4i 1 và z 3 4i . Số phức z có 1 2 1 2 2
phần thực là a và phần ảo là b thỏa mãn 3a 2b 12. Giá trị nhỏ nhất của biểu thức
P z z z 2z 2 bằng? 1 2
17 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] 3 1105 3 1105 A. P . B. P 5 2 3 . C. P . D. P 5 2 5 . min 11 min min 13 min Giải
Gọi M , M , M lần lượt là điểm biểu diễn của các số phức z , 2z , z trên mặt phẳng tọa 1 2 1 2 độ Oxy .
Do z 3 4i 1 nên quỹ tích điểm M là đường tròn C có tâm I 3;4 và bán kính 1 1 1 1 R 1 1
Do z 3 4i
2z 6 8i 1 nên quỹ tích điểm M là đường tròn C có tâm 2 2 2 2 2 I
6;8 và bán kính R 1 2
Ta có điểm M a;b thỏa mãn 3a 2b 12 nên quỹ tích điểm M là đường thẳng
d : 3x 2 y 12 0
Khi đó P z z z 2z 2 MM MM 2 1 2 1 2
Gọi C là đường tròn đối xứng với đường tròn C qua đường thẳng d. Ta tìm được 2 3 138 64
tâm của C là I ;
và bán kính R 1 3 3 13 13
Khi đó P MM MM 2 MM MM 2 AB 2 với M C và A, B lần lượt 3 3 1 2 1 3
là giao điểm của đường thẳng I I với hai đường tròn C , C (quan sát hình vẽ). 1 3 1 3
Dấu "=" xảy ra khi và chỉ khi M A và M B 1 3
18 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] 3 1105 Vậy P
AB 2 I I 2R 2 I I . min 1 3 1 3 13 Đáp án C. Note:
* Số phức z x yi, x, y có điểm biểu diễn trên hệ trục tọa độ Oxy là M ; x y . *
Nếu số phức z thỏa mãn z a bi k k thì tập hợp các điểm biểu diễn số
phức z là đường tròn có tâm I a;b và bán kính R k.
Câu 224. [#Mỗi ngày 3 câu hỏi hay]. 2 2 x x
Trong mặt phang tọa độ Oxy , gọi là hình phẳng giới hạn bởi các đường y ; y , 4 4
x 4, x 4 và hình H
là hình gồm các điểm ;
x y thỏa x y
x y 2 2 2 2 16, 2 4. 2
Cho H và H quay quanh trục Oy ta được các vật thể có thể tích lần lượt là V ,V . 2 1 1 2
Đẳng thức nào dưới đây đúng 1 2
A. V V .
B. V V .
C. V 2V .
D. V V . 1 2 1 2 1 2 2 1 2 3 Giải
* Hình phẳng H được biểu diễn bằng miền tô đậm trong hình vẽ 1 bên.
Thể tích khối trụ bán kính r 4, chiều cao h 8 là 2 2
V r h .4 .8 128 (đvtt).
Thể tích của khối tròn xoay thu được khi quay hình phẳng giới hạn 2 x bởi parabol y
, trục hoành, đường thẳng y 4 xung quanh trục 4 4 4 4 tung là: 2 2 V x dy 4 ydy 2 y 32 (đvtt). P 0 0 0
Suy ra thể tích của khối tròn xoay thu được khi quay H quanh trục Oy là: 1
V V 2V
128 2.32 64 (đvtt). 1 P
* Hình phẳng H được biểu diễn bằng miền tô đậm trong hình vẽ bên. 2
19 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] 4 4 256
Thể tích khối cầu lớn bán kính R 4 là 3 3 V R .4 (đvtt) L 3 3 3 4 4 32
Thể tích khối cầu nhỏ bán kính r 2 là 3 3 V r .2 N 3 3 3
Suy ra thể tích của khối tròn xoay thu được khi quay H quanh trục Oy là 2 256 32
V V 2V 2 64 (đvtt) 2 L N 3 3 V 64 Vậy 1
1V V . 1 2 V 64 2 Đáp án A.
Câu 225. [#Mỗi ngày 3 câu hỏi hay]. Cho parabol P 2
: y x 2x 3 cắt trục hoành tại hai điểm A, B và đường thẳng 1
d : y a 0 a 4 . Xét parabol P đi qua A, B và có đỉnh thuộc đường thẳng y a . 2
Gọi S là diện tích hình phẳng giới hạn bởi P và d . S là diện tích hình phẳng giới 1 1 2
hạn bởi P và trục hoành. Biết S S , tính 3 2
T a 8a 48a . 2 1 2 A. T 99 . B. T 64 . C. T 32 . D. T 72 . Giải
Để việc tính toán trở nên đơn giản, ta tịnh tiến hai parabol sang trái
một đơn vị. Khi đó, phương trình các parabol mới là P a 2
: y x 4, P 2 : y x a . 1 2 4
Gọi A, B là các giao điểm của P và trục 1 Ox A 2
;0, B2;0 AB 4 . Gọi M, N là giao điểm của P 1
và đường thẳng d M 4 a;a, N 4 a;a . 4 4 3 4 4 Ta có S 2
4 y.dy 4 y2 4 a 4 a . 1 3 3 a a 3 2 a ax 8a 2 S 2
x a .dx 2 ax 2 4 12 3 0 4 8
Theo giả thiết S S 4 a 4 a 4 a3 2 3 2
4a a 8a 48a 64 . 1 2 3 3 Vậy T 64 . Đáp án B.
Câu 226. [#Mỗi ngày 3 câu hỏi hay].
20 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng P : x y z 1 0 , đường thẳng x 15 y 22 z 37 d : và mặt cầu 2 2 2
(S) : x y z 8x 6 y 4z 4 0 . Một đường 1 2 2
thẳng thay đổi cắt mặt cầu S tại hai điểm A, B sao cho AB 8 . Gọi A , B là hai
điểm lần lượt thuộc mặt phẳng P sao cho AA , BB cùng song song với d . Giá trị lớn
nhất của biểu thức AA BB là 8 30 3 24 18 3 12 9 3 16 60 3 A. B. C. D. 9 5 5 9 Giải
Mặt cầu S có tâm I 4; 3; 2
và bán kính R 5
Gọi H là trung điểm của AB thì IH AB và 2 AB 2 IH R 3 2
Gọi M là trung điểm của AB , do AA ' //BB ' //d nên
tứ giác AABB là hình thang và AA BB 2HM
(tính chất đường trung bình của hình thang), M P
Mặt phẳng P có vectơ pháp tuyến là n 1;1
;1 và đường thẳng d có vectơ chỉ phương
là u 1; 2; 2 n u Suy ra:
d P n u , 1.1 1.2 1.2 5 sin , sin cos , n . u 3.3 3 3 3 3
Gọi K là hình chiếu của H lên P thì HK HM.sin HM HK 5 Khi đó: 6 3
AA BB 2HM HK 5
Để AA BB lớn nhất thì HK lớn nhất 4 4 3 3
HK đi qua I hay HK
IH d I; P 3 max 3 3 6 3 4 3 3 24 18 3
Vậy AA BB lớn nhất bằng . . 5 3 5 Đáp án B.
21 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Câu 227. [#Mỗi ngày 3 câu hỏi hay].
Cho hình chóp S.ABCD có đáy là ABCD là hình bình hành. Hai điểm M, N lần lượt AB AD
thuộc các đoạn thẳng AB và AD ( M và N không trùng với A ) sao cho 2. 4. AM AN Ký hiệu V , S ABCD S MBCDN 1
V lần lượt là thể tích của các khối chóp . và . . Tìm giá trị lớn nhất của tỉ số 1 V V 3 17 1 2 A. . B. . C. . D. . 4 14 6 3 Giải Đặ AB AD t x và
y x, y
1 . Từ giả thiết ta có x 2 y 4 1 AM AN 1 x 2
2y 4 x 2 Suy ra: 2 .
x 4 2y 1 1 y 3
1 d S ABCD 1 . ; .S .AM .AN.sin AMN DAB V S Ta có: S.AMN 3 AMN 2 V 1 S.ABCD
d S ABCD S A . B A . D sin DAB . ; . ABCD S 3 ABCD V AM AN V V V S. 1 1 AMN 1 S.MBCDN S.ABCD S V . 1 . . AMN 1 2 S V . 2 AB AD 2 ABCD xy V S V .ABCD S V , 2 ABCD xy V Từ 1 và 2 suy ra 1 1 1 V x x . 4
Áp dụng bất đẳng thức cho hai số dương x và 4 – x ta có: 2
x x x 4 x 1 V 1 1 3 4 4 1 V
x x 1 . 2 4 4 4
Dấu “” xảy ra khi và chỉ khi x 4 x x 2 y 1 .
22 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] Đáp án A.
Câu 228. [#Mỗi ngày 3 câu hỏi hay].
Trong không gian với hệ tọa độ Oxyz , cho hai điểm A0; 2; 2, B2; 2
;0 . Gọi I 1;1; 1 1
và I (3;1;1) là tâm của hai đường tròn nằm trên hai mặt phẳng khác nhau và có chung một 2
dây cung AB . Biết rằng luôn có một mặt cầu S đi qua cả hai đường tròn ấy. Tính bán
kính R của S . 219 129 A. R . B. R 2 2 . C. R . D. R 2 6 . 3 3 Giải
Gọi d là đường thẳng đi qua I vuông góc với mặt phẳng 1 1
I AB , khi đó d chứa tâm các mặt cầu đi qua đường tròn tâm 1 1
I ; d là đường thẳng đi qua I và vuông góc với mặt phẳng 1 2 2
I AB , khi đó d chứa tâm các mặt cầu đi qua đường tròn tâm 2 2
I . Do đó, mặt cầu S đi qua cả hai đường tròn tâm I và 1 2
I có tâm I là giao điểm của d và d và bán kính R = IA. 2 1 2 Ta có I A 1 ;1;3 , I B 1; 3 ;1 I ; A I B 10; 4; 2 d có vec tơ chỉ 1 1 1 1 nên đường thẳng 1
phương là u 5;2;1 cùng phương với vec tơ I ; A I B 1 1 1
x 1 5t1 Phương trình đườ
ng thẳng d là y 1 2t t 1 1 1 z 1 t 1 Ta có I A 3 ;1;1 , I B 1 ; 3 ; 1 I ; A I B 2; 4 ;10 d có vec tơ 2 2 2 2 . Đường thẳng 2
chỉ phương là u 1; 2
;5 cùng phương với vectơ I ; A I B 2 2 2
x 3 t2 Phương trình đườ
ng thẳng d là y 1 2t t 2 2 2 z 15t 2 1 1
5t 3 t 1 2 t 1 3 8 5 2 Xét hệ phương trình 1
2t 1 2t . Suy ra I ; ; 1 2 1 3 3 3 1
t 1 5t t 2 1 2 3
23 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] 2 2 2 8 5 2 129
Bán kính mặt cầu S là R IA 0 2 2 . 3 3 3 3 Đáp án C.
Câu 229. [#Mỗi ngày 3 câu hỏi hay].
Cho số phức z thỏa mãn đồng thời hai điều kiện z i 1 và z 2m 2 với m là
tham số thực. Tập hợp các giá trị thực của tham số m để tồn tại hai số phức thỏa mãn các điều kiện trên là? A. 2 ;2 \ 0 . B. 2;2 . C. 2 ;2 \ 0 . D. 2;2 . Giải Gọi M ;
x y là điểm biểu diễn z x iy x, y trên mặt phẳng phức.
Từ z i x y 2 2 1 1
1 M đường tròn C có tâm I 0;1 , bán kính R 1. Từ 1 1 1 z m
x m2 2 2 2 2
y 4 M đường tròn C có tâm I 2 ; m 0 , bán kính 2 2 R 2 . 2
Để tồn tại hai số phức thỏa mãn các điều kiện đã cho khi và chỉ khi tồn tại hai điểm M,
tức là C và C cắt nhau tại hai điểm phân biệt khi và chỉ khi: 2 1
R R I I R R 1 2m2 2
1 3 0 m 4 m 2 ;2 \ 0 . 1 2 1 2 1 2 Đáp án A.
Câu 230. [#Mỗi ngày 3 câu hỏi hay].
Cho hàm số f x 3 2
x 3x m . Hỏi có bao nhiêu giá trị nguyên của tham số
m m 2018 để với mọi bộ ba số phân biệt a,b,c thì f a, f b, f c là độ dài ba cạnh của một tam giác. A. 2011 . B. 2012 . C. 2010 . D. 2018 . Giải
Do f a, f b, f c là độ dài ba cạnh của một tam giác nên f a f b f c 3 2
a a m 3 2
b b m 3 2 3 3
c 3c m với mọi a,b,c 1; 3 3 2
a a 3 2
b b 3 2 3 3
c 3c m với mọi a,b,c 1; 3 Do đó 3 2
a a 3 2
b b 3 2 min 3 3
c 3c
m với mọi a,b, c 1; 3 Ta cần tìm 3 2 a a 3 2 min 3 b 3b 3 2
và maxc 3c với mọi a,b,c 1; 3
24 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Xét hàm số f x 3 2
x 3x trên 1; 3 . x 0
Ta có f x 2 3x 6 ; x f x 2
0 3x 6x 0 . x 2
Do x [1;3] nên x 2 . Ta có: f 1 2 , f 2 4 , f 3 0
max f x f 3 0 [1;3] Suy ra: max
f x f 2 4 [1;3] Suy ra: 3 2
a a 3 2
b b 3 2 min 3 3
c 3c 4 4 0 8
Đẳng thức xảy ra khi a b 2, c 3 hoặc a c 2, b 3 hoặc b c 2, a 3.
Do đó 8 m m 8 . Mà m 2018 và m nguyên nên m 9;..;201 8
Vậy có 2018 9 1 2010 giá trị m thỏa mãn. Đáp án C.
Câu 231. [#Mỗi ngày 3 câu hỏi hay]. 2 2
Trong không gian với hệ tọa độ Oxyz , cho mặt cầu S : x 2
1 y z 2 9 ngoại
tiếp khối bát hiện H được ghép từ hai khối chóp tứ giác đều S.ABCD và S .ABCD
(đều có đáy là tứ giác ABCD ). Biết rằng đường tròn ngoại tiếp của tứ giác ABCD là
giao tuyến của mặt cầu S và mặt phẳng P : 2x 2 y z 8 0 . Tính thể tích khối bát diện H . 34 665 68 1330 A. V . B. V . C. V . D. V . H H H H 9 81 9 81 Giải
Mặt cầu S có tâm I 1;0;2 , bán kính R 3. Nhận xét thấy S, I , S thẳng hàng và S
S AB D
C . Khi đó SS 2R 6 . 1 1 Ta có: V V V d S ABC S
d S ABCD S H S ABC S ; D . ; . . D . AB D C AB DC AB D 3 3 C 1
d S ABC d S ABC 1 ; D ; D .S . S S .S 2S . AB D C AB D C AB D 3 3 C
Từ giả thiết suy ra ABCD là hình vuông, gọi a là cạnh của hình vuông đó.
25 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Mặt phẳng P cắt mặt cầu S theo giao tuyến là một
đường tròn có bán kính bằng r và ngoại tiếp hình vuông ABCD.
Suy ra 2r AC a 2 2 a r . 2
Từ d I P 2 2 2 ; r R 2 a r R
d I P 2 2 2 8 17 2 ; 3 3 3 2 2 17 a . 3 2 2 2 17 68 Vậy 2 V . H 2S 2a 2. ABC D 3 2 9 Đáp án C.
Câu 232. [#Mỗi ngày 3 câu hỏi hay]. Cho m
ab với a 1, b 1 và 2
P log b 2 27 log a 4 . Biết rằng P đạt giá a 3 log a b c d 3
trị nhỏ nhất khi m
c,d,e . Tính c d S . e e 2 1
A. Vô số giá trị.
B. S 0. C. S . D. S . 3 3 Giải
Phân tích: Ta có thể biểu thức 2
P log b 2 27 log a 4 theo log b a b a
Vậy cần tính log b theo m . a Hướng dẫn giải. 1 1
Theo giả thiết ta có m log ab b b m . a
1 loga log 3 1 3 3 a Suy ra: P b P m a 2 2 2 27 2 27 log 4 3 1 4 log b 3m 1 a
P m 2 27 27 3 1
4. Vì a 1, b 1 nên log b 3m 1 0. 3m 1 3m 1 a
Áp dụng bất đẳng thức Cauchy cho ba số dương, ta có:
26 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
P m 2 27 27 3m 2 27 3 1 4 3. P 3 1 . 3m 1 3m 1 3m 4 13. 2 1
Dấu bằng xảy ra khi và chỉ khi: m 2 27 3 1 3m 3 1
27 3m 1 3 3m 1 1 3 1 1 3 1.k 1 .k 3 m k 0 3 3 3.k
Có vô số các số c, d , e thỏa bài toán đó là: a k; d k; e 3k k 0 c d k Nhưng c d k 2 S
có giá trị duy nhất là S . e e 3k 3 Đáp án C.
Câu 234. [#Mỗi ngày 3 câu hỏi hay]. 3
Cho hàm số f x có đạo hàm liên tục trên đoạn 0; 1 thỏa mãn 2
f (x) 6x f 3 x . 3x 1 2 x
Giá trị x
1 f ' dx bằng? 2 0 8 4 12 2 A. . B. . C. . D. . 5 5 5 5 Giải
Phân tích: Đây là bài toán tổng hợp về tích phân. Học sinh cần lưu ý một số điểm nhận dạng phương pháp sau: Xuất hiện tích phân . ' ,
g x f x dx ta nghĩ đến phương pháp từng phần. Xuất hiện tích phân ,
f x dx ta nghĩ đến phương pháp đổi biến số.
Trên đây, chính là hai phương pháp để tính tích phân.
Nhắc lại công thức. x u 2 2 x du
Công thức đổi biến số
f u dx f u . u ' 1 x u 1 x b b b
Công thức từng phần udv uv vd . u a a a
27 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] Hướng dẫn giải:
Biến đổi theo phương pháp tích phân từng phần kết hợp đổi biến ta có: 2 1 2 I
x x x x x 1 f ' dx
x 12 f 2 x 2 1 f 2
f dx 0 2 2 2 2 0 0 0 1 1 du 6 f 1 2 f 0 2
f u 6 f 1 2 f 0 4 f xdx 1 0 0 2 6
Sử dụng kỹ thuật đổi biến số xử lý dữ liệu f x 2 6x f 3 x để xuất hiện 3x 1 1 ,
f x dx ta cần lấy tích phân hai vế. Khi đó: 0 1 1 1 1 1 1 2 du f x dx 6
x f 3x 6 2 dx dx 6 x f u
4 2 f xdx 4 f xdx 4 2 3x 1 3x 0 0 0 0 0 0
Để tính f 0, f
1 ta thay lần lượt x 1, x 0 vào đẳng thức f 1 6 f 1 3 f 3 1 f x 2 x f 3 x 6 6 . Ta được: 5 . 3x 1 f 0 6 f 0 6 1 18 2
Vậy I 6 f
1 2 f 0 4 f xdx 12 16 . 5 5 0 Đáp án D.
Câu 235. [#Mỗi ngày 3 câu hỏi hay].
Cho z x yi với x, y
là số phức thỏa mãn điều kiện z 2 3i z i 2 5 .
Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 2 2
P x y 8x 6 y . Tính M m . 156 156 A. 60 2 10 . B. 20 10 . C. 60 2 10 . D. 20 10 . 5 5 Giải Phân tích:
28 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
2x y 2 0
Từ giả thiết z 2 3i z i 2 5 ta biến đổi x 2 2 y 2 1 25 - Gọi A2; 6
, B 2;2 là các giao điểm của đường thắng 2x y 2 0 và đường tròn
C x 2 y 2 ' : 2 1 25. Ta có: 2 2
P x y 8x 6 y
x 2 y 2 4 3 P 25.
Gọi C là đường tròn tâm J 4 ; 3
, bán kính R P 25. Hướng dẫn giải.
- Theo bài ra: z 2 3i z i 2 5
x 2 y 2 x 2 y 2 2 3 2 1 5
2x y 2 0 x 2 2 y 2 1 25
2x y 2 0
Tập hợp điểm biểu diễn số phức z là miền mặt phẳng T thỏa mãn: x 2 2 y 2 1 25 - Gọi A2; 6 , B 2
; 2 là các giao điểm của đường thẳng 2x y 2 0 và đường tròn
C x 2 y 2 ' : 2 1 25. - Ta có: 2 2 2 2
P x y 8x 6 y (x 4) ( y 3) P 25.
Gọi C là đường tròn tâm J 4 ; 3
, bán kính R P 25.
- Đường tròn C cắt miền T khi và chỉ khi:
JK R JA IJ IK R IA 2 10 5
25 P 3 5 40 20 10 P 20
M 20 và m 40 20 10.
Vậy M m 60 20 10. Đáp án C.
Câu 236. [#Mỗi ngày 3 câu hỏi hay].
Gọi z , z , z , z là các nghiệm của phương trình 4 3 2
z 4z 3z 3z 3 0 . Tính giá trị 1 2 3 4 biểu thức T 2 z 2z 2 2 z 2z 2 2 z 2z 2 2 z 2z 2 1 1 2 2 3 3 4 4
A. T 102 .
B. T 101.
C. T 99 . D. T 100 .
29 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] Giải Đặt f z 4 3 2
z 4z 3z 3z 3 f z z z z z z z z z 1 2 3 4 Do 2 z 2z 2 z 1 i z 1 i nên 1 1 1 1 T 2 z 2z 2 2 z 2z 2 2 z 2z 2 2 z 2z 2 f 1 i f 1
i 10 i 10 i 101 1 1 2 2 3 3 4 4 Đáp án D.
Câu 237. [#Mỗi ngày 3 câu hỏi hay]. Biết phương trình 1 2 log 2x 3 log 1980 2 x x
có 2 nghiệm x , x . Tính x x . 2 2 1 2 1 2 A. log 10. B. log 11. C. log 12. D. log 13. 2 2 2 2 Giải
Đặt 2x t, t 0 . Suy ra x log t. 2 2x 32 t 22 Ta có: 2 x 1 log
2t t 3954t 11 0 * 2 x 1980 2 1 1980 t
Vì phương trình đã cho có hai nghiệm x , x nên phương trình * có hai nghiệm t ,t . 1 2 1 2
Theo Viète: t t 11 x x log t log t log t t log 11. 1 2 1 2 2 1 2 2 2 1 2 2 Đáp án B.
Câu 238. [#Mỗi ngày 3 câu hỏi hay].
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P : 4x 7 y z 25 0 và đường x 1 y z 1 thẳng d :
. Gọi d là hình chiếu vuông góc của d lên mặt phẳng P . 1 1 1 2 1 1
Đường thẳng d nằm trên P tạo với d ,d các góc bằng nhau, d có vectơ chỉ phương 2 1 1 2 a 2b u ; a ; b c . Tính 2 c a 2b 2 a 2b a 2b 1 a 2b A. . B. 0 . C. . D. 1. c 3 c c 3 c Giải Cách 1:
Gọi Q d,d khi đó Q có vectơ pháp tuyến n n ,u 5;5;15 Q P 1 1 .
Đường thẳng d có vectơ chỉ phương u n , n 22;11; 1 1 1 P Q 1 hay một vectơ chỉ
phương khác u2;1; 1 .
30 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Vì n ,u 0 4a 7b c 0 c 7b 4a u ; a ;
b 7b 4a . P 2 2
Ta lại có d ,d d ,d cos u ,u cos
u ,u . 1 2 1 2 1 2 1 2
a 2b 4a 7b 2a b 4a 7b 5a 5b 6a 6b a b 0 a b a 2b
Chọn a 1 b 1, c 3 1 c Cách 2:
Gọi Q d,d khi đó P Q . Các đường thẳng nằm trong P mà vuông góc với 3
Q thì vuông góc với tất cả các đường thẳng trong Q hay chúng cùng tạo với d ,d 1 1 các góc 0
90 . Do đó, các đường thẳng này thỏa mãn yêu cầu đề bài. Chúng có vectơ chỉ a b
phương u n 2 1;1;3 1. Q c Đáp án D.
Câu 239. [#Mỗi ngày 3 câu hỏi hay].
Trong không gian Oxyz, cho hai điểm A6; 3 ;4 , B ; a ;
b c . Gọi M,N,P lần lượt là giao
điểm của đường thẳng AB với các mặt phẳng tọa độ Oxy,Oxz,Oyz. Biết rằng M,N,P
nằm trên đoạn AB sao cho AM = MN = NP = PB. Tính giá trị của tổng a b c .
A. a b c 11.
B. a b c 11.
C. a b c 17 .
D. a b c 17 . Giải
Các phương trình Oxy : z 0 ; Oyz : x 0 ; Oxz : y 0 . Giả sử M x ; y ;0 , M M
N x ;0; z
, P 0; y ; z . Theo giả thiết ta có M là trung điểm của AN nên ta có: P P N N 6 x 3 4 z N M ; ; N . 2 2 2 4 z Do z 0 nên
N 0 z 4 3
M x ; ; 0 và N x ;0; 4 . N M 2 N M 2 x 2 y 3 z
Lại có N là trung điểm của MP nên M N ; P ; P . 2 4 2
31 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] 2y 3 P 0 3 y 0 y Mà N nên 4 P 2 Khi đó 3 P 0; ; 8 . z 4 z 2 N P 4 z 8 P 2 6 xN x M x x x 3 Từ 2 2 6 M N 4 M . Vậy M 4; ;0 , N 2;0; 4 . x x 2x 0 x 2 2 M x M N N N 2 x 6 2 B 2 6 a 2
Mặt khác AB 2AN y 3 2 B 2
;3 12 b 3 . B 0 3 z 4 2 c 12 B 4 4
Vậy a b c 2 3 12 11. Đáp án B.
Câu 240. [#Mỗi ngày 3 câu hỏi hay].
Trong không gian với hệ tọa độ Oxyz, cho các điểm A 2
;0;0 , B0;4;2 ,C 2;2; 2 . Gọi
d là đường thẳng đi qua A và vuông góc với mặt phẳng (ABC), S là điểm di động trên
đường thẳng d, G và H lần lượt là trọng tâm của ABC , trực tâm của SBC . Đường
thẳng GH cắt đường thẳng d tại S . Tính tích S . A S A . 3 9 A. S . A S A . B. S . A S A . C. S . A S A 12 . D. . SA S A 6 . 2 2 Giải
32 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Nhận thấy AB BC CA 2 6 nên ABC đều. Do G là trọng tâm của ABC nên
CG AB , mà CG SA CG SAB CG SB . Lại có CH SB (H là trực tâm của
SBC ) nên SB CHG . Suy ra SB GH .
Gọi M là trung điểm của BC.
Ta có BC SA , BC AM BC SAM BC GH .
Như vậy GH SBC GH SM hay S H
SM SS H SMA . Suy ra AS G
∾ AMS AS AG AM AS 2 2 2 2 AB 3 2 2 6. 3
AS .AS AM .AG AM . AM . . 12 . 3 3 2 3 2 Đáp án C.
Câu 241. [#Mỗi ngày 3 câu hỏi hay].
Cho tứ diện ABCD có thể tích là V . Điểm M thay đổi trong tam giác BCD . Các đường
thẳng qua M và song song với AB, AC, AD lần lượt cắt các mặt phẳng ACD , ABD ,
ABC tại N,P,Q . Giá trị lớn nhất của khối MNPQ là: V V V V A. . B. . C. . D. . 27 16 8 54 Giải MN N M
Tam giác ABN có MN / / AB . AB N B MP P M
Tam giác ACP có MP / / AC . AC P C MQ Q M
Tam giác ADQ có QM / / AD . AD Q D
33 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] Khi đó: MN MP MQ N M P M Q M AB AC AD N B P C Q D N M P M Q M S S S MN MP MQ Mà MCD MBD MBC 1 N B P C Q D nên 1 S S S AB AC AD BCD BCD BCD 3 3 MN MP MQ MN MP MQ Lại có 3 3 1 3 . . (Cauchy) AB AC AD AB AC AD 1 MN MP MQ MN.M . P MQ A .
B AC.AD MN.M . P MQ lớn nhất khi 27 AB AC AD MN MP MQ 1
M là trọng tâm tam giác BCD
NPQ / / BCD, AB AC AD 3 2 S NPQ 2 1 1 1 , Mà S
d M , NPQ d , A BCD S nên S S và S N P Q BCD NPQ BCD 3 4 9 2 N P Q 1
Vậy giá trị lớn nhất của khối tứ diện MNPQ là V S .d M NPQ MNPQ NPQ , 3 1 1 1 V 1 V . S . d A BCD với V .S .d , A BCD V AB D C BCD MNPQ BCD , , 3 9 3 27 3 Đáp án A.
Câu 242. [#Mỗi ngày 3 câu hỏi hay].
Cho hình chóp S.ABC có đường cao SA 2a , tam giác ABC vuông tại C , 0
AB 2a,CAB 30 . Gọi H là hình chiếu của A trên SC, B ' là điểm đối xứng của B
qua mặt phẳng SAC . Thể tích của khối chóp H.AB ' B bằng
34 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] 3 a 3 3 6a 3 3 4a 3 3 2a 3 A. . B. . C. . D. . 7 7 7 7 Giải AC
Xét tam giác ABC , ta có: cosCAB
AC a 3 và AB 2 2 BC AB AC . a
Xét tam giác SAC có 2 2 SC
SA AC a 7 và 2 AC 3 7a 2
HC.SC AC HC SC 7
Xét tam giác SAC ta có sin SA SCA 1 SC
Xét tam giác HIC ta có sin HI HCI 2 HC S . A HC 6a Từ
1 và 2 ta có: HI . SC 7 1 1 6a 1 1 6a 1 2 3 Ta có: 3 V HI.S . . AC.BB' . . .a 3.2a a .
H . AB ' B AB ' 3 B 3 7 2 3 7 2 7 Đáp án D.
Câu 243. [#Mỗi ngày 3 câu hỏi hay].
Cho tứ diện ABCD và các điểm M, N, P thuộc các cạnh BC, BD, AC sao cho
BC 4BM , AC 3AP , BD 2BN . Tính tỉ số thể tích hai phần của khối tứ diện ABCD
được phân chia bởi mặt phẳng MNP . 7 7 8 8 A. . B. . C. . D. . 13 15 15 13 Giải
Trong mặt phẳng DBC vẽ MN cắt CD tại K .
Trong mặt phẳng ACD vẽ PK cắt AD tại Q .
Theo định lí Mennelaus cho tam giác BCD cát tuyến
35 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] MNK KC ND MB KC ta có . . 1 3. KD NB MC KD
Theo định lí Mennelaus cho tam giác ACD cát tuyến PKQ KC QD PA QA 3 QA 3 ta có . . 1 . KD QA PC QD 2 AD 5 Đặt V V , ta có ABCD V S B.APQ APQ AP AQ 1 1 4 . V V V V . B. APQ B. ACD B. V S AC AD 5 5 PQDC 5 B.ACD ACD V S BM BN 1 V S CP 2 1 P.BMN BMN . và P.BCD CPD V V . V S BC BD 8 P. V S CA 3 BMN 12 P.BCD BCD ACD V V S S Q.PBN S 1 BQPD DQP DQP S 2 1 PBN và . ADP V V . V S 2 V S S S 15 QPBN 15 Q.PBD PBD ACD DAP ACD V V V V V AB.MNPQ . A BPQ P.BNM Q.PBN 7 AB.MNPQ 7 . V V 20 V 13 CD.MNPQ Đáp án A.
Câu 244. [#Mỗi ngày 3 câu hỏi hay].
Cho số phức z a bi; a,b . Nhận xét nào sau đây luôn đúng? A. z 2a b . B. z 2 a b . C. z 2 a b . D. z 2 a b . Giải
36 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] a b2 2 2 2 2 2 2
0 a b 2 ab 2a 2b a b 2 ab
2a b a b 2 2 2 2 2 2
a b a b z 2 a b Đáp án D.
Câu 245. [#Mỗi ngày 3 câu hỏi hay].
Cho hình chóp S.ABC có ABC là tam giác vuông cân tại B, AB BC 2a, SAB SCB 90 .
Và khoảng cách từ A đến mặt phẳng SBC bằng a 2. Tính diện tích mặt cầu ngoại tiếp
S.ABC theo a. A. 2 6 a . B. 2 3 a . C. 2 4 a . D. 2 12 a . Giải
Gọi K là trung điểm của BC .
Do SCB SAB 90 nên dễ dàng nhận thấy trung điểm I của SB là tâm mặt cầu ngoại tiếp chóp SABC .
Gọi M là trung điểm của AC . Tam giác ABC vuông tại B , ta có MA MB MC, mặt
khác IA IB IC, do đó IM là trục của đường tròn ngoại tiếp tam giác ABC hay IM ABC 1 a
Ta có d M,SBC d A,SBC 2 2
Trong tam giác IMK , kẻ MH IK 1 .
37 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] BC IM
BC IMK BC MH2 BC MK Từ
1 , 2 suy ra MH SBC.
Xét tam giác vuông IMK , ta có: 1 1 1 1 1 1 1 2 1 1 2 MI a 2 2 2 2 2 2 2 2 2 2 MH MI MK a MI a MI a a a 2
Xét tam giác vuông IMA , ta có: 2 2 AC 2.2a 2 2 2 2 IA IM MA a a 3a 2 2
Vậy diện tích mặt cầu ngoại tiếp chóp SABC là: 2 2 2 S 4 R 4 3a 1 a . Đáp án D.
Câu 246. [#Mỗi ngày 3 câu hỏi hay].
Cho hai đường thẳng a, b cố định, song song với nhau và khoảng cách giữa chúng bằng
4 . Hai mặt phẳng P, Q thay đổi vuông góc với nhau lần lượt chứa hai đường thẳng
a, b . Gọi d là giao tuyến của P, Q . Khẳng định nào sau đây là đúng?
A. d thuộc 1 mặt trụ cố định có khoảng cách giữa đường sinh và trục bằng 4 .
B. d thuộc 1 mặt nón cố định
C. d thuộc 1 mặt trụ cố định có khoảng cách giữa đường sinh và trục bằng 2 2 .
D. d thuộc 1 mặt trụ cố định có khoảng cách giữa đường sinh và trục bằng 2 . Giải
38 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
AB d, B a
Lấy A là 1 điểm bất kì thuộc d . Từ A kẻ
AC d,C b
Vì P Q BAC 90 1
Ta đi chứng minh BC chính là khoảng cách giữa hai đường thẳng a và b, BC = 4: AB d Ta có
d ABC d BC AC d
Mà a//b//d , suy ra BC a, b BC 4 2 Từ
1 2 suy ra A thuộc đường tròn đường kính BC bằng 4 không đổi
Do đó d thuộc mặt trụ có khoảng cách giữa đường sinh và trục bằng 2. Đáp án D.
Câu 247. [Mỗi ngày 3 câu hỏi hay].
Cho hàm số f x 4 3 2
ax bx cx dx e ( ae 0 ). Đồ thị hàm số y f x như hình bên. Hàm số y f x 2 4
x có bao nhiêu điểm cực tiểu A. 3 . B. 5 . C. 4 . D. 2 . Giải
Đặt g x f x 2 4
x . Ta có: gx 4 f x 2x 22 f x x .
39 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] x
Ta có 0 x g x f x
. Dựa vào đồ thị hàm số y f x và đường thẳng y suy 2 2 x 1 x
ra f x x 0 . 2 x 2
Theo hình vẽ ta có a 0 , mà ae 0 e 0 suy ra g 0 4 f 0 4e 0 .
Bảng biến thiên của y g x như sau:
Dựa vào đồ thị y g x suy ra hàm số y f x 2 4
x có 3 điểm cực tiểu. Đáp án A.
Câu 248. [#Mỗi ngày 3 câu hỏi hay].
Cho hàm số bậc năm f x . Hàm số y f x có đồ thị là đường cong trong hình bên.
40 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Hàm số g x f x x 2 7 2
1 đồng biến trên khoảng nào dưới đây?
A. 2;0 . B. 3; 1 .
C. 3; . D. 2;3 . Giải
Ta có: g x f x x 2 7 2
1 g x 2
f 7 2x 2x 1 .
Hàm số g x f x x 2 7 2
1 đồng biến khi và chỉ khi:
g x 0 2
f 7 2x 2x
1 0 f 7 2x x 1 1 . t Đặ 7 5 t
t t 7 2x x 1 1
. Suy ra: f t 1 5 1 : t . 2 2 2 2 3 t 1 3 7 2x 1 4 x 5 Từ đồ thị suy ra: . 1 t 3 1 7 2x 3 2 x 3 Đáp án D.
Câu 249. [Mỗi ngày 3 câu hỏi hay].
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB a, SB a và
SB ABCD . Gọi M là trung điểm của SD . Biết rằng góc giữa hai mặt phẳng ACM
và SAD bằng 60 . Thể tích khối chóp S.BCD bằng? 3 3a 3 a 3 a 3 a A. . B. . C. . D. . 3 2 6 3
41 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] Giải
Đặt AD x .
Chọn hệ trục tọa độ sao cho B O 0;0;0,Ox B ;
A Oy BC;Oz BS khi đó A a x a ;
a 0;0, S 0;0;a,C 0; ;
x 0 D ; a ; x 0, M ; ; . 2 2 2 Ta có: SA ;
a 0; a; AD 0; ;
x 0 nSAD S ,
A AD a ; x 0; ax . a x a 1 1 Lại có: MA ; ; ; AC
a; ;x0 nCAM 2 M ,
A AC a ; x a ;0 . 2 2 2 2 2 1 2 2 a x Khi đó:
SAD CAM 2 cos ;
cos nSAD, nCAM cos60 . 2 2 1 2 2 1 4 2a x . a x a 4 4 1 2 2 1 1 4 4 1 6 2 2 1 2 1 2 a x a x a x x x
a x a . 2 2 2 2 2 2 1 1 1
Thể tích khối chóp S.BCD là: 3 V .S . B , A . B AD a . 3 2 6
42 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] Đáp án C.
Câu 250. [#Mỗi ngày 3 câu hỏi hay].
Cho z x yi với x, y
là số phức thỏa mãn điều kiện z 2 3i z i 2 5 .
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 2 2
P x y 8x 6 y . Tính M m . 156 156 A. 60 2 10 . B. 20 10 . C. 60 2 10 . D. 20 10 . 5 5 Giải Phân tích:
2x y 2 0
Từ giả thiết z 2 3i z i 2 5 ta biến đổi x 2 2 y 2 1 25 - Gọi A2; 6
, B 2;2 là các giao điểm của đường thắng 2x y 2 0 và đường 2 2
tròn C ' : x 2 y 1 25. Ta có: 2 2
P x y 8x 6 y
x 2 y 2 4 3 P 25.
Gọi C là đường tròn tâm J 4 ; 3
, bán kính R P 25. Hướng dẫn giải.
- Theo bài ra: z 2 3i z i 2 5
x 2 y 2 x 2 y 2 2 3 2 1 5
2x y 2 0 x 2 2 y 2 1 25
tập hợp điểm biểu diễn số phức z là miền mặt phẳng T thỏa mãn:
2x y 2 0 x 2 2 y 2 1 25 - Gọi A2; 6 , B 2
; 2 là các giao điểm của đường thẳng 2x y 2 0 và đường 2 2
tròn C ' : x 2 y 1 25. - Ta có: 2 2 2 2
P x y 8x 6 y (x 4) ( y 3) P 25.
43 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Gọi C là đường tròn tâm J 4 ; 3
, bán kính R P 25.
- Đường tròn C cắt miền T khi và chỉ khi:
JK R JA IJ IK R IA 2 10 5
25 P 3 5 40 20 10 P 20
M 20 và m 40 20 10.
Vậy M m 60 20 10. Đáp án C.
Câu 251. [#Mỗi ngày 3 câu hỏi hay].
Cho tứ diện ABCD có thể tích là V . Điểm M thay đổi trong tam giác BCD . Các đường
thẳng qua M và song song với AB, AC, AD lần lượt cắt các mặt phẳng ACD , ABD ,
ABC tại N, P, Q . Giá trị lớn nhất của khối MNPQ là: V V V V A. . B. . C. . D. . 27 16 8 54 Giải MN N M
Tam giác ABN có MN / / AB . AB NB MP P M
Tam giác ACP có MP / / AC . AC P C MQ Q M
Tam giác ADQ có QM / / AD . AD Q D MN MP MQ NM P M Khi đó: Q M AB AC AD NB P C Q D NM P M Q M S S S MN MP MQ Mà
MCD MBD MBC 1 nên 1 NB P C Q D S S S AB AC AD BCD BCD BCD 3 3 MN MP MQ MN MP MQ Lại có 3 3 1 3 . . (Cauchy) AB AC AD AB AC AD 1 MN MP MQ MN.M . P MQ A .
B AC.AD MN.M . P MQ lớn nhất khi 27 AB AC AD MN MP MQ 1
M là trọng tâm tam giác BCD
NPQ / /BCD, AB AC AD 3
44 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] 2 SNPQ 2 1 1 , Mà S S nên S S và N P S Q 4 BCD NPQ 9 BCD
N PQ 3
d M NPQ 1 , d , A BCD 2 1
Vậy giá trị lớn nhất của khối tứ diện MNPQ là V S .d M NPQ MNPQ NPQ , 3 1 1 1 V 1 V . S . d A BCD với V .S .d , A BCD V . AB D C BCD MNPQ BCD , , 3 9 3 27 3 Đáp án A.
Câu 252. [#Mỗi ngày 3 câu hỏi hay].
Cho tam giác ABC có BC a , 0
BAC 135 . Trên đường thẳng vuông góc với ABC
tại A lấy điểm S thỏa mãn SA a 2 . Hình chiếu vuông góc của A trên SB, SC lần
lượt là M , N . Góc giữa hai mặt phẳng ABC và AMN là? A. 30 . B. 45 . C. 60 . D. 75 . Giải Hướng dẫn giải.
Gọi AD là đường kính của đường tròn tâm O ngoại tiếp tam giác ABC . SA DC Khi đó, ta có:
DC SAC AC DC DC AN
AN SDC AN SD (1). SC AN SA DB Tương tự:
DB (SAB) AB DB DB AM
AM SBD AM SD (2). SB AM Từ
1 và 2 suy ra SD AMN .
Suy ra ABC; AMN S ; A SD AS . D BC
Ta có: AD 2R a 2. sin A
45 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] AD ASD có: 0 tan ASD 1 ASD 45 . SA Đáp án B.
Câu 253. [#Mỗi ngày 3 câu hỏi hay].
Cho hình lăng trụ tam giác đều ABC.
A BC có tất cả các cạnh đều bằng a . Gọi M , N
lần lượt là trung điểm của các cạnh AB và BC . Mặt phẳng
A MN cắt cạnh BC tại
P . Tính thể tích V của khối đa diện MBPA BN. 3 3 3 3 3 7 3 A. a V . B. a V . C. a V . D. 36 12 96 3 7 3 a V . 48 Giải
Hình lăng trụ ABC.
A BC có h
AA a và diện tích đáy 2 3 a B . 4
Gọi I là trung điểm của BC và P là trung điểm của BI MP//A N.
Suy ra, P là giao điểm của BC và A MN .
Ta có MBP ∽
A BN nên khối đa diện
MBPA BN là một khối chóp cụt. 1 1 1 Ta có: S . .S B MBP 2 4 ABC 8 1 1 S S B A B . N 2 ABC 2 2 3 h Do đó: 1 1 1 1 h 7B .7. a a 3 7a 3 V B B B B MBP A B N . . . . 3 8 2 8 2 3 8 3.8.4 96 Đáp án C. Study tips:
Thể tích khối chóp cụt có chiều cao h và diện tích hai đáy là B và B : h V
B B B B. 3
Câu 254. [#Mỗi ngày 3 câu hỏi hay].
Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng P : x y z 1 0 , đường thẳng
46 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] x 15 y 22 z 37 d :
và mặt cầu S 2 2 2
: x y z 8x 6 y 4z 4 0 . Một đường 1 2 2
thẳng thay đổi cắt mặt cầu S tại hai điểm A, B sao cho AB 8 . Gọi A , B là hai
điểm lần lượt thuộc mặt phẳng P sao cho AA , BB cùng song song với d . Giá trị lớn
nhất của biểu thức AA BB là 8 30 3 24 18 3 12 9 3 16 60 3 A. . B. . C. . D. . 9 5 5 9 Giải
Mặt cầu S có tâm I 4;3; 2
và bán kính R 5
Gọi H là trung điểm của AB thì IH AB và 2 AB 2 IH R 3 2
Gọi M là trung điểm của AB , do A
A //BB//d nên
tứ giác AABB là hình thang và AA BB 2HM
(tính chất đường trung bình của hình thang), M P
Mặt phẳng P có vectơ pháp tuyến là n 1;1
;1 và đường thẳng d có vectơ chỉ phương
là u 1; 2; 2 n u Suy ra:
d P n u , 1.1 1.2 1.2 5 sin , sin cos , n . u 3.3 3 3 3 3
Gọi K là hình chiếu của H lên P thì HK HM.sin HM HK 5 Khi đó: 6 3
AA BB 2HM HK 5
Để AA BB lớn nhất thì HK lớn nhất 4 4 3 3
HK đi qua I hay HK
IH d I; P 3 max 3 3 6 3 4 3 3 24 18 3
Vậy AA BB lớn nhất bằng . . 5 3 5 Đáp án B. Study tips:
47 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Đường thẳng d có vec tơ chỉ phương u và mặt phẳng (P) có vec tơ pháp tuyến n . Gọi u n
là góc tạo bởi đường thẳng d và mặt phẳng (P) thì u n , sin cos , u . n
Câu 255. [#Mỗi ngày 3 câu hỏi hay]. 2
Cho hàm số y f x có đạo hàm trên và f x 4 x
2x , x 0 và 2 x f 1 1
. Khẳng định nào sau đây đúng?
A. Phương trình f x 0 có 1 nghiệm trên 0; 1 .
B. Phương trình f x 0 có 3 nghiệm trên 0;
C. Phương trình f x 0 có 1 nghiệm trên 1;2 .
D. Phương trình f x 0 có 1 nghiệm trên 2;5 . Giải x 1 1 x x 4 2 2 2 2 3 6 3
Ta có: f x x 2x 0,x 0 2 2 2 x x x
Hàm số y f x đồng biến trên 0;
Phương trình f x 0có nhiều nhất một nghiệm trên khoảng 0; 1 2 2 2 2 21
Từ f x 4 x
2x 0,x 0 suy ra f x 4 dx x 2x dx 2 x 2 x 5 1 1
f f 21 f f 21 21 f 17 2 1 (2) 1 1 2 5 5 5 5
Kết hợp giả thiết ta có hàm số y f x liên tục trên [1; 2] và f 2. f 1 02 Từ
1 và 2 suy ra phương trình f x 0 có đúng một nghiệm trên 1;2 . Đáp án C. Study tips:
Để giải được bài toán ở câu 41, ta cần lưu ý đến các kiến thức đã học sau đây:
1. Nếu hàm số f x liên tục và đơn điệu trên D thì phương trình f x 0 có nhiều nhất một nghiệm trên D
2. Nếu hàm số y f x liên tục trên đoạn [a; b] và f a. f b 0 thì tồn tại ít nhất
một điểm c a,b sao cho f c 0
48 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] b b
3. Nếu f x g x,x a,b f xdx
f xdx a a
Câu 256. [#Mỗi ngày 3 câu hỏi hay]. 2
x x Biết 4 4 1
x , x là hai nghiệm của phương trình 2 log
4x 1 6x và 1 2 7 2 x 1 x 2x
a b với a, b là hai số nguyên dương. Tính a b . 1 2 4
A. a b 13 .
B. a b 11 .
C. a b 16 .
D. a b 14 . Giải
Điều kiện: x 0, n 0. 2 2
4x 4x 1
4x 4x 1 Ta có: 2 2 log
4x 1 6x log
4x 4x 1 log 2x 2 . x 7 7 7 2x 2 x
Xét hàm số f t log t t có f t 1
1 0t 0 nên hàm số đồng biến trên 0; . 7 t ln 7 Do đó ta có: 2 2 3 5
4x 4x 1 2x 4x 6x 1 0 x . 4 3 5 3 5 1 3 5 3 5 1 x 2x 2.
9 5 hoặc x 2x 2. . 9 5 . 1 2 1 2 4 4 4 4 4 4 3 5 3 5 Vậy x ; x
. Do đó a 9;b 5 và a b 9 5 14. 1 2 4 4 Đáp án D.
Câu 257. [#Mỗi ngày 3 câu hỏi hay]. x y
Cho hai số thực x, y thỏa mãn log
xx 3 y y 3 xy . Tìm giá 3 2 2
x y xy 2
trị nhỏ nhất của biểu thức P x 2 5
y xy 3y . A. 8 . B. 5. C. 7. D. 6 . Giải
49 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] x Điề y u kiện:
0 x y 0 . 2 2
x y xy 2 x y Ta có log
xx 3 y y 3 xy 3 2 2
x y xy 2
2log x y 2log 2 2
x y xy 2 2 2
x y xy 3x 3y 3 3
2log x y 2 2log 2 2
x y xy 2 2 2
x y xy 2 3x 3y 3 3
2log 3x 3y 3x 3y 2log 2 2
x y xy 3 2 2
x y xy 2 (*). 3 3 2
Xét hàm đặc trưng f t 2log t t,t 0; , ta có f t
1 0,t 0;. 3 t.ln 3
Suy ra hàm f t đồng biến trên khoảng 0; .
Phương trình (*) f
y f 2 2
x y xy 2 2 3x 3
2 x y xy 2 3x 3y 2 2
y xy 3y x 3x 2
P x y xy y x x x 2 2 2 5 ( 3 ) 2 7 1 6 6 Đáp án D.
Câu 258. [#Mỗi ngày 3 câu hỏi hay].
Cho hàm số y f x liên tục trên có bảng biến thiên
như hình vẽ. Có bao nhiêu giá trị nguyên của tham số m
để phương trình f 2 f x m 1 có đúng 2 nghiệm trên 1 ; 1 ? A. 13 . B. 9 . C. 4 . D. 5 . Giải 2 f x m
2 f x m 1 VN 2 f x m 2 2
Ta có: f 2 f x m 1
2 f x m 2 2
f x m 2 f x 2 m 2
50 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] 2 m 3 1 0 m 8 2
Dựa vào bảng biến thiên, ta suy ra: ycbt 0 m 4 . 2 m 4 m 4 3 1 2
Vậy có 5 giá trị nguyên của tham số m thỏa yêu cầu đề bài. Đáp án D.
Câu 259. [#Mỗi ngày 3 câu hỏi hay].
Cho phương trình xm x 4 log 2 3 2 2 2 2 x x x log
2 x m 2 0 . Gọi S là tập 1 2 2
hợp tất cả các giá trị của m để phương trình có 3 nghiệm thực phân biệt. Tổng các phần tử của S bằng: 1 3 A. 3 . B. . C. 2 . D. . 2 2 Giải
Điều kiện xác định: x .
Xét phương trình xm x 4 log 2 3 2 2 2 2 x x x log
2 x m 2 0 1 1 2 2 x x xm 1 2 .log
x 2x 2 2 1 2 1 2 1 2 2 .log 2 x m 2 2 2 2 x 2 x 1 x 2 .og m 2 x 2x 2 1 2 2 .log 2 x m 2 2 2 2 Xét hàm số: 2t f t log
t 2 , t 2. 2 t t 1
Ta có f 't 2 .ln 2.log t 2 2 . 0 t 0. 2 t 2ln2
Mà f t liên tục trên 0; suy ra f t đồng biến trên 0; .
Phương trình (2) có dạng f 2 x 2x
1 f 2 x m và 2
x 2x 1 x
1 0; 2 x m 0, x . 2
x 2x 1 2x m 2
x 4x 1 2 m * Do đó 2 2
x 2x 1 2 x m 2
x 2x 1 2 m x 2 x 1 2 m **
51 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Phương trình (1) có 3 nghiệm thực phân biệt khi và chỉ khi (2) có 3 nghiệm phân biệt. Dựng các parabol: 2
y x 4x 1 P và 2
y x 1 P trên cùng 1 hệ trục tọa độ. 2 1
Số lượng nghiệm của * và ** bằng số giao điểm của đường thẳng d : y 2 m lần
lượt với các đồ thị P và P . Dựa vào đồ thị có thể thấy phương trình đã cho có đúng 2 1
3 nghiệm phân biệt thì d phải nằm ở các vị trí của d , d , d . 1 2 3 Tương ứng khi đó: 1 2 m 1 m 2 2 m 2 m 1 3 2 m 3 m 2 1 3
Do đó có 3 giá trị m thỏa mãn yêu cầu: m ; m 1; m . 2 2 1 3
Vậy S ;1; . 2 2 Đáp án A.
Câu 260. [#Mỗi ngày 3 câu hỏi hay].
Gọi S là tập hợp tất cả các giá trị của tham số thực m sao cho giá trị nhỏ nhất của hàm
52 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] số 4
y sin x cos 2x m bằng 2 . Số phần tử của S là: A. 4. B. 3. C. 1. D. 2. Giải Ta có: 4 4 2
y sin x cos 2x m sin x 2sin x m 1 . Đặt 2
t sin x, t 0; 1 , hàm số trở thành 2
y t 2t m 1 .
Xét hàm f t 2
t 2t m 1, với t 0;
1 . Ta có f 't 2t 2 0 , với t 0; 1 , suy
ra hàm số nghịch biến trên 0; 1 . Do đó f
1 f t f 0 m f t m 1.
Xét các trường hợp sau:
+ m 1 0 m 1. Khi đó, y m 1. Theo giả thiết m 1 2 m 3 (thỏa mãn).
+ 1 m 0 . Khi đó, min y 0 (loại).
+ m 0 . Khi đó, min y m . Theo giả thiết m 2 (thỏa mãn).
Vậy tập hợp S có 2 phần tử. Đáp án D.
Câu 261. [#Mỗi ngày 3 câu hỏi hay]. Cho hàm số y f x 3 2
ax bx cx d có bảng biến thiên như sau: Khi đó 1
f x m có bốn nghiệm phân biệt x x x
x khi và chỉ khi: 1 2 3 4 2 1 1 A. m 1. B. m 1.
C. 0 m 1.
D. 0 m 1. 2 2 Giải
53 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Ta có: f x 2 '
3ax 2bx c . Từ bảng biến thiên của hàm số f x , ta có: f 0 1 d 1 a 2 f 1 0
a b c d 0 b 3 f ' 0 . 0 c 0 c 0 f 3
a 2b c 0 d 1 ' 1 0
Như vậy f x 3 2 1 1
2x 3x 1, f . 2 2 Do đó 1 1
f x m có bốn nghiệm phân biệt x x x
x khi và chỉ khi m 1. 1 2 3 4 2 2 Đáp án B.
Câu 262. [#Mỗi ngày 3 câu hỏi hay].
Trong không gian với hệ trục tọa độ Oxyz , cho ba mặt phẳng P : x 2y z 1 0 ,
Q: x 2y z 8 0 và R: x 2y z 4 0. Một đường thẳng d thay đổi cắt ba
mặt phẳng P, Q, R lần lượt tại ,
A B, C . Tìm giá trị nhỏ nhất của biểu thức 2 144 T AB AC A. 3 72 3 . B. 96 . C. 108 . D. 3 72 4 . Giải
Dễ thấy mặt phẳng P nằm giữa hai mặt phẳng Q và R ; ba mặt phẳng
P, Q, R đôi một song song với nhau.
Trên mặt phẳng P lấy điểm M 1;0;0.
54 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] Gọi ’
B , C’ , lần lượt là hình chiếu của A trên hai mặt phẳng Q và R. Ta có:
AB d A Q d M Q 1 2.0 0 8 3 6 ' ; ; . 6 2
AC d A R d M R 1 2.0 0 4 6 ' ; ; . 6 2 AB ' BB '
Suy ra AB ' 3AC 3 . AC ' CC '
Đặt: CC ' x x 0 BB' 3 . x 2 2 2 27 2 3
AB AB ' BB ' 9x và 2 2 AC
AC ' CC '2 x . 2 2 Khi đó: 2 144 27 2 144 3 2 72 72 T AB 9x 9 x AC 2 3 2 2 3 2 3 2 x x x 2 2 2 3 2 72 72 T 3. 9 x . . 108. 3 2 3 2 3 2 x x 2 2 3 72 72
Giải thích: Ta áp dụng bất đẳng thức Cauchy cho ba số dương 2 9 x , , 2 3 2 3 2 x x 2 2 3 72 10 Dấu ‘ ’
xảy ra khi và chỉ khi 2 9 x x . 2 3 2 2 x 2 Đáp án C.
Câu 263. [#Mỗi ngày 3 câu hỏi hay].
55 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] Cho parabol P 2
: y x 2x 3 cắt trục hoành tại hai điểm ,
A B và đường thẳng 1
d : y a 0 a 4 . Xét parabol P đi qua ,
A B và có đỉnh thuộc đường thẳng y a . 2
Gọi S là diện tích hình phẳng giới hạn bởi P và d . S là diện tích hình phẳng giới 1 1 2
hạn bởi P và trục hoành. Biết S S , tính 3 2
T a 8a 48a . 2 1 2 A. T 99 . B. T 64 . C. T 32 . D. T 72 . Giải
Để việc tính toán trở nên đơn giản, ta tịnh tiến hai parabol sang
trái một đơn vị. Khi đó, phương trình các parabol mới là 2 a
P : y x 4, P 2 : y x a . 1 2 4 Gọi ,
A B là các giao điểm của P và trục 1 Ox A 2
;0, B2;0 AB 4 . Gọi M , N là giao điểm của
P và đường thẳng d M 4a;a, N 4a;a. 1 4 4 3 4 4 Ta có S 2
4 y.dy 4 y2 4 a 4 a . 1 3 a 3 a 3 2 a ax 2 8 a S 2
x a .dx 2 ax 2 4 12 3 0 4 8
Theo giả thiết S S
4 a 4 a 4 a3 2 3 2
4a a 8a 48a 64 . 1 2 3 3 Vậy T 64 . Đáp án B.
Note: Bài toán được lấy ý tưởng từ bài toán vô cùng quen thuộc:
Bài tập tương tự
Gọi H là hình phẳng giới hạn bởi đồ thị hàm số 2
y x 4x
và trục hoành. Hai đường thẳng y m và y n chia H thành
3 phần có diện tích bằng nhau. Tính giá trị của biểu thức
T m3 n3 4 4 .
56 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] 320 512 75 A. T . B. T .
C. T 405 . D. T . 9 15 2 Đáp án A.
Câu 264. [#Mỗi ngày 3 câu hỏi hay].
Cho hình chóp S.ABCD có đáy là ABCD là hình bình hành. Hai điểm M , N lần lượt
thuộc các đoạn thẳng AB và AD ( M và N không trùng với A ) sao cho AB AD 2.
4. Ký hiệu V ,V lần lượt là thể tích của các khối chóp S.ABCD và AM AN 1 V
S.MBCDN . Tìm giá trị lớn nhất của tỉ số 1 V 3 17 1 2 A. . B. . C. . D. . 4 14 6 3 Giải AB AD Đặt x và
y x, y 1 . AM AN
Từ giả thiết ta có x 2 y 4 1 1 x 2
2y 4 x 2 Suy ra: 2 .
x 4 2y 1 1 y 3
1 d S ABCD 1 . ; .S .AM .AN.sin DAB AMN V S Ta có: S.AMN 3 AMN 2 V 1 S A . B A . D sin DAB S. ABCD
.d S; ABCD. ABCD S 3 ABCD V 1 AM AN 1 V V V V 1 S. AMN 1 S.MBCDN S. ABCD S. . . AMN 1 2 V 2 AB AD 2xy V V V 2xy S. ABCD S. ABCD S , ABCD
57 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] V 1 Từ
1 và 2 suy ra 1 1 V x x . 4
Áp dụng bất đẳng thức cho hai số dương x và 4 – x ta có: 2
x x V x 4 x 4 1 1 3 1 4 1 V
x x 1 . 2 4 4 4
Dấu “” xảy ra khi và chỉ khi x 4 x x 2 y 1. Đáp án A.
Note: Bất đẳng thức Cauchy áp dụng cho n số thực không âm a , a ,..., a (n 2, n ) 1 2 n a a n ... an
là a a ... a .n
n a .a ..a hay 1 2 a a ...a . 1 2 n 1 2 n 1 2 n n
Dấu “=” xảy ra khi và chỉ khi a a ... a . 1 2 n
Câu 265. [#Mỗi ngày 3 câu hỏi hay].
Trong không gian Oxyz , cho bốn điểm A3 1
; ;0 , B 2;0;
1 , C 0;2;
1 , D 0;0; 2 . Với
mỗi điểm M tùy ý, đặt T MA MB MC MD . Gọi M
a;b;c sao cho T đạt giá trị 0
nhỏ nhất. Lúc đó, tổng a 5b c bằng? A. 3 . B. 13 . C. 7 . D. 4 . Giải Ta có AB 1 ; 1 ; 1 ; AC 3 1 ; ; 1 và AD 3 ; 1 ; 2 .
Mà AB; AC .AD 0
nên A, B, C, D đồng phẳng và tạo thành tứ giác ABCD có hai x 3t
x 2 t đườ 3 1
ng chéo AD : y t
và BC : y t cắt nhau tại điểm I ; ; 1 . 2 2 z 2 2 t z 1
Mặt khác, MA MD AD và MB MC BC nên T MA MB MC MD AD BC . Do đó 3 1 T
AD BC 14 2 2 khi M I . Suy ra M ; ; 1 . min 0 2 2
Vậy a 5b c 3 . Đáp án A.
Câu 266. [#Mỗi ngày 3 câu hỏi hay].
Trong không gian Oxyz , cho hai mặt phẳng : x my z 6m 3 0 và
: mx y mz 3m 8 0 (với m là tham số thực); hai mặt phẳng này cắt nhau theo
giao tuyến là đuờng thẳng . Gọi ' là hình chiếu của lên mặt phẳng Oxy . Biết rằng
58 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
khi m thay đổi thì đường thẳng ' luôn tiếp xúc với một mặt cầu cố định có tâm I ; a ;
b c thuộc mặt phẳng Oxy . Tính giá trị biểu thức 2 2 2
P 10a b 3c ? A. P 56 . B. P 9 . C. P 41 . D. P 73 . Giải
Mặt phẳng : x my z 6m 3 0 có một véc tơ pháp tuyến là n l; ; m l , và 1
mặt phẳng : mx y mz 3m 8 0 có một véc tơ pháp tuyến là n ; m 1; m 2 4 4 Ta có: M 3 m 3;0; 3 m m m
có một véc tơ chỉ phương là u n ;n 2 2 m 1; 2 ; m m 1 1 2
Gọi P là mặt phẳng chứa đường thẳng và vuông góc với mặt phẳng Oxy. Khi đó
P có một véc tơ pháp tuyến là n u k 2 ; 2 ;
m l m ;0 (với k 0;0; 1 . )
Phương trình mặt phẳng P là mx 2 m 2 2 1
y 6m 6m 8 0. Vì I ; a ;
b c Oxy nên I ; a ; b 0
Theo giả thiết ta suy ra P là tiếp diện của mặt cầu S d I; P R (cố định) 2ma 2 1 m 2
b 6m 6m 8
R 0 (cố định)
4m 1 m 2 2 2
2m a 3 6 b 2 m b 8
2m a 3 6 b 2
m b 8 R 2 m 1 R 0 2 m 1
2ma 3 6 b 2
m b 8 R 2 m 1
2a 3 0
6 b R a 3 b 8 R
6 b b 8 R 0
R 6 b 0 2 a 3 0 a 3
6 b R
6 b b 8 b 8 R
R 6 b 0 R 0
59 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] a 3 Suy ra . Vậy I 3 ;7;0, do đó 2 2 2
P 10a b 3c 41. b 7 Đáp án C.
Câu 267. [#Mỗi ngày 3 câu hỏi hay].
Cho số phức z thỏa mãn z 2 . Giá trị nhỏ nhất của biểu thức: P 2 z 1 2 z 1 z z 4i bằng: 14 7 A. 4 . B. 2 . C. 4 2 3 . D. 2 3 . 15 15 Giải
Gọi z x yi, x, y . Theo giả thiết, ta có: 2 2
z 2 x y 4 . Suy ra
2 x, y 2 . Khi đó 2 2 : P z
z z z i x 2
y x 2 2 1 2 1 4 2 1
1 y y 2
P x 2 y x2 2 2
y y 2 2 1 1 2
2 2 1 y 2 y
Dấu “” xảy ra khi x 0 .
Xét hàm số f y 2
2 1 y 2 y trên đoạn 2;2 , ta có: 2 f y 2 y 2 y 1 y f y 1 1 ; 0 y . 2 2 1 y 1 y 3 1 Ta có: f 2 3; f 2
4 2 5; f 2 2 5 . 3 1
Suy ra: min f y 2 3 khi y . 2 ;2 3 1
Do đó: P 22 3 4 2 3 . Vậy P 4 2 3 khi z i . min 3 Đáp án C.
Câu 268. [#Mỗi ngày 3 câu hỏi hay]. 1
Cho hàm số y f x 4 2
x ax b a,b có đồ thịvà y g x 2 x m nx p 2 , m n, p
có đồ thị Pnhư hình vẽ. Diện tích hình phẳng giới hạn bởi C và Pcó
giá trị nằm trong khoảng nào sau đây?
60 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] A. 4;4 ,1 . B. 4, 2;4,3 . C. 4,3;4, 4 . D. 4,1;4, 2 . Giải 2
Diện tích hình phẳng giới hạn bởi C và P : S
f x gxdx . 2 1
h x f x g x là hàm bậc bốn có hệ số bậc bốn bằng , có hai nghiệm đơn 2
x 2 , x 2 và một nghiệm kép x=0
hx f x g x 1 2
x x 2x 2 2 2 1 2 S
x x x 64 2 2 dx 4,266.. 2 15 2 Đáp án B.
Câu 269. [#Mỗi ngày 3 câu hỏi hay]. Xét các số phức z z
z 4 1 và iz 2 1. Giá trị nhỏ nhất của z 2z 1 , 2 thỏa mãn 1 2 1 2 bằng A. 4 2 3 B. 2 5 2 C. 4 2 D. 4 2 3 Giải
61 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] Đặt z 2
z , suy ra P z 2z z ( 2
z ) z z . 3 2 1 2 1 2 1 3 1 1 Và z
z thế vào iz 2 1 iz 2 1 z 4i 2. 2 3 2 2 3 3 2 Gọi ,
A B là hai điểm biểu diễn cho hai số phức z , z . 3 1
z 4i 2 A thuộc đường tròn tâm I (0; 4), R 2. 3 3
z 4 1 B thuộc đường tròn tâm J (4;0), R 1. 1 1
P IJ R R 4 2 3 min 1 3
P z z AB . 1 3 P
IJ R R 4 2 3 max 1 3 Đáp án D.
Câu 270. [#Mỗi ngày 3 câu hỏi hay].
Trong không gian Oxyz , cho hai điểm A0;8;2 , B 9; 7
;23 và mặt cầu S có
phương trình S x 2 y 2 z 2 : 5 3 7
72. Mặt phẳng P : x by cz d 0
đi qua điểm A và tiếp xúc với mặt cầu S sao cho khoảng cách từ B đến mặt phẳng
P lớn nhất. Giá trị của b c d khi đó là
A. b c d 2 .
B. b c d 4 .
C. b c d 3.
D. b c d 1. Giải
Vì A P nên ta 8b 2c d 0 d 8
b 2c P : x by cz 8b 2c 0. 5 11b 5c
Do P tiếp xúc với mặt cầu S nên d I; P R 6 2 . 2 2 1 b c
9 7b 23c 8b 2c
5 11b 5c 4 1 b 4c
Ta có: d B; P 2 2 2 2 1 b c 1 b c b 1 4c B P 5 11b 5c 1 b 4c d ; 4 d ;
B P 6 2 4 2 2 2 2 1 b c 1 b c 2 2 1 b c CosiSvac 1116 2 2
1 b c d ;
B P 6 2 4 d ;
B P 18 2 . 2 2 1 b c c 1 b b 1 4 Dấu “=” xảy ra khi c 4 . 5 11b 5 c 6 2 d 0 2 2
1 b c
62 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] Vậy P
18 2 khi b c d 3. max Đáp án C.
Câu 271. [#Mỗi ngày 3 câu hỏi hay]. 2 x 1 x 1 Biết phương trình log 2log
có một nghiệm dạng x a b 2 5 3 x 2 2 x
trong đó a, b là các số nguyên. Tính T 2a . b A. 3 . B. 8 . C. 4 . D. 5 . Giải 2 x 1 x 1 2 x 1 x 1 Ta có: log 2log log 2log 5 2 5 3 x 2 2 x x 2 x
Điều kiện xác định: x 1. 1 log
2 x 1 2log 2 x log x 2log x 1 * 5 3 5 3
Xét hàm số f t log t 2log t 1 với t 1. 5 3 1 2
Ta có: f t
với t > 1 suy ra f t đồng biến trên 1; . t t 0 ln 5 1 ln 3
Từ * ta có f 2 x
1 f x nên suy ra
x x x 2 2 1
2 x 1 0 x 1 2 ( do x > 1)
Suy ra x 3 2 2 a 3;b 2 2a b 8. Đáp án B.
Câu 272. [#Mỗi ngày 3 câu hỏi hay].
Cho hình hộp chữ nhật AB . CD
A BCD có tổng diện tích của tất cả các mặt là 36, độ dài
đường chéo AC bằng 6. Hỏi thể tích của khối hộp lớn nhất là bao nhiêu? A. 8 . B. 8 2 . C. 16 2 . D. 24 3 . Giải
63 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Gọi độ dài AB a, BC b, A A . c
ab bc ca 18 Khi đó theo đề ta có 2 2 2
a b c 36 2
Suy ra a b c 2 2 2
a b c 2ab bc ca 72.
Hay a b c 6 2 b c 6 2 . a
Ta có: . b c a
b c2 2 2 2 2 36
2bc a 36 . 6 2 a a 36 Hay 6 2 a 2 2 2 2
2bc a 36 bc . 2 a2 2 a 3 2 6 2 36
2a 12 2a 36a
Từ đó ta có V abc . a 2 2
Không mất tổng quát, giả sử a maxa,b,
c , khi đó 6 2 a b c 3a a 2 2 . 6 2 a b c 2 2 2 2 2 2 2 Lại có 2
36 a b c a a
3a 12 2a 0 a 4 2 . 2 2 Xét hàm số 3 2 2 12 2 36 a a a f a
với a [2 2; 4 2] . 2 2 a 2 6 24 2 36 L a a
Ta có f a
, f a 0 . 2 a 3 2 N
64 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] f 2 2 4 2
Ta có f 3 2 0
f 4 2 8 2 Vậy V
8 2 khi a 4 2,b c 2. max Đáp án B.
Câu 273. [#Mỗi ngày 3 câu hỏi hay].
Có bao nhiêu số nguyên của m để phương trình log 2x m 2
2log x x 4x 2m 1 2 2
có 2 nghiệm thực phân biệt. A. 2 . B. 3 . C. 1 . D. 4 . Giải x 0 Điều kiện: . x m 2 log 2x m 2
2log x x 4x 2m 1 log 2x m 2
2log x x 2 2x m 1 2 2 2
log 2x m 22x m 2 2
1 log x x log 2x m 2 2x m log x x 2 2 2 2 2 2
f u f v
Xét f u log u u, u 0 ; ta có: f u 1 1 0 . 2 u ln 2
Xét hàm số f x 2
x 2x,x 0.
Phương trình có 2 nghiệm dương khi 4 2m 0 2 m 0 suy ra có 1 giá trị nguyên.
65 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] Đáp án C.
Câu 274. [#Mỗi ngày 3 câu hỏi hay].
Trong tất cả các cặp số thực ; x y thỏa mãn log
2x 2 y 5 1. Có bao nhiêu giá 2 2 x y 3
trị thực của m để tồn tại duy nhất cặp số thực ; x y sao cho 2 2
x y 4x 6 y 13 m 0 . A. 3 . B. 1 . C. 2 . D. 0 . Giải Ta có: log 2x 2 y 5 1 ⇔ 2 2
2x 2 y 5 x y 3 ⇔ 2 2 x y 2 x 2y 2 0 1 2 2 x y 3
⇒ Tập hợp các cặp số thực ; x y thỏa mãn log 2x 2 y 5 1 là hình tròn 2 2 x y 3 C 2 2 : x y 2
x 2y 2 0 (tính cả biên). 1 2 2 Xét 2 2
x y 4x 6 y 13 m 0 x 2 y 3 . m x 2
TH1: m 0 , không thỏa mãn (1). y 3
TH2: m 0 , khi đó tập hợp các cặp số thực ; x y thỏa mãn 2 2
x y 4x 6 y 13 m 0 là đường tròn C 2 2 : x y 4
x 6y 13 m 0. 2
Để tồn tại duy nhất cặp số thực ;
x y thỏa mãn yêu cầu bài toán thì hai đường tròn C1
và C tiếp xúc ngoài với nhau hoặc hai đường tròn C và C tiếp xúc trong và đường 2 1 2
tròn C có bán kính lớn hơn đường tròn C . C có tâm I 1;1 , bán kính R 2. 1 1 1 2 1
C có tâm I 2 ; 3
, bán kính R m m 0 . 2 2 2
Để C và C tiếp xúc ngoài thì I I R R . 2 1 1 2 1 2
⇔ 2 2 3
4 2 m ⇔ 5 2 m m 9 tm
Để đường tròn C và C tiếp xúc trong và đường tròn C có bán kính lớn hơn đường 2 2 1
tròn C . ⇒ R R I I ⇔ m 2 2 2
3 4 ⇔m = 49 ( tm ) 1 2 1 1 2
Vậy có 2 giá trị của m thỏa mãn yêu cầu bài toán.
66 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] Đáp án C.
Câu 275. [#Mỗi ngày 3 câu hỏi hay]. x y 1
Cho các số thực x, y, z thỏa mãn các điều kiện x 0, y 0, z 1 và log 2x y . 2 4x y 3 2 2 x z y Khi đó giá trị ( 1) ( 2)
nhỏ nhất của biểu thức T tương ứng bằng: 3x y x 2z 3 A. 4 2 . B. 6 . C. 6 3 . D. 4 . Giải Từ giả thiết ta có: x y 1 x y 1 log
2x y 1 log
2x y 1 2 2 4x y 3 4x y 3 2x 2 y 2 log
4x y 3 2x 2y 2 2 4x y 3
f 2x 2y 2 f 4x y 3 2x 2y 2 4x y 3 y 2x 1
(Với hàm f t log t t là đơn điệu trên 0; ) 2
x z 2 y 2 x z 2 x 2 1 2 1 2 3
Thay vào biểu thức T ta được: T 3x y x 2z 3 5x y x 2z 3
x z 2 x 2 x z 2 1 x z 2 1 2 3 3 4 3 4
Áp dụng bất đẳng thức: T . 5x y x 2z 3 6x 2z 4 2 3x z 2 Đặ 1 4 1 4
t t 3x z 2 T t 4
2 t. 4 4 2 t 2 t y 2x 1 y 2x 1
x z 0 x z 0
Dấu " " xảy ra khi t 2 3x z 2
: t 2 3x z 2 y 1 y 1 x z 1 2x 3 x z 1 2x 3 5x 1 x 2z 3 5x 1 x 2z 3
Suy ra giá trị nhỏ nhất của biểu thức T 4 .
67 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] Đáp án D.
Câu 276. [#Mỗi ngày 3 câu hỏi hay].
Cho hình lập phương AB . CD
A BCD .Gọi E, F , M , N , P,Q lần lượt là tâm của các mặt AB ;
CD A' B 'C ' D '; ADD ' A'; DCC ' D ';CBB 'C '; ABB ' A' . Biết cạnh khối lập phương bằng
a ,khi đó thể tích của khối tám mặt đều nội tiếp khối lập phương trên là 3 a 3 a 3 a 3 a A. . B. . C. . D. . 8 12 4 6 Giải
Ta thấy khối tám mặt đều đó thực chất là 2 khối chóp có chung đáy EMNPQF được
đánh dấu như hình trên. 1
Xét A' DC ' có: M , N lần lượt là trung điểm của DA' và DC ' MN A'C ' 2 Do ABC .
D A' B 'C ' D ' là khối lập phương cạnh a .
A'B 'C 'D ' là hình vuông cạnh a . 2
A'C ' AB 2 a 2 . Do vậy a MN 2 a 2 2 a
+) Nhận thấy MNPQ là một hình vuông cạnh S 2 MNPQ 2
68 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
+) d E MNPQ 1 1 ; .EF a 2 2 1 2 3 1 1 a a V 2.V
2. d E, MNPQ .S 2. . . . a . EMNPQF E.MNPQ 3 MNPQ 3 2 2 6 Đáp án D.
Câu 277. [#Mỗi ngày 3 câu hỏi hay].
Cho khối trụ T có trục OO , bán kính r và thể tích V. Cắt khối trụ T thành hai r
phần bởi mặt phẳng P song song với trục và cách trục một khoảng bằng 2 V
(như hình vẽ). Gọi V là thể tích phần không chứa trục OO . Tính tỉ số 1 . 1 V V 1 3 V 3 V 3 V 4 3 A. 1 . B. 1 . C. 1 . D. 1 . V 3 4 V 4 3 V 2 V 4 Giải
Gọi h là chiều cao của khối trụ T . Thể tích khối trụ đã cho là 2 V . h r .
Gọi A và B là giao điểm của mặt phẳng P với đường tròn đáy tâm O và M là trung điểm của AB. 2 r r Ta có: 2 O M
AB 2AM 2 r
r 3 A O B 120 . 2 4
Diện tích đáy phần khối trụ không chứa trục là 2 2 1 2 1 r r 3
S S S r r r . q AO . . . 3 1 B 3 2 3 4 2 2 r r 3 V 1 3 V . h . Suy ra 1 . 1 3 4 V 3 4 2 Đáp án A.
Câu 278. [#Mỗi ngày 3 câu hỏi hay].
Xét số phức z thỏa mãn z 2 i z 4 7i 6 2. Gọi m, M lần lượt là giá trị nhỏ nhất
cả giá trị lớn nhất của z 1 i . Tính P m M.
69 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] 5 2 2 73 5 2 73
A. P 13 73 . B. P P P 2 . C. 5 2 73 . D. 2 . Giải
Gọi A là điểm biểu diễn số phức z , F 2 ;1 , F 4;7 N 1; 1 . 1 2 và
Từ z 2 i z 4 7i 6 2 và F F 6 2 F F 1 2
nên ta có A là đoạn thẳng 1 2 . Gọi H là 3 3 5 2 2 73
hình chiếu của N lên F F H ; P NH NF . 1 2 , ta có 2 2 . Suy ra 2 2 Đáp án B.
Câu 279. [#Mỗi ngày 3 câu hỏi hay]. Phương trình 3
x m x x x 2 3 3 2
x x x m 2 1 2 6 9 2
2 1 có 3 nghiệm phân biệt khi và chỉ khi m ; a b , đặt 2 2
T b a thì: A. T 36 . B. T 48 . C. T 64 . D. T 72 . Giải 3
x m x x x Ta có: 2 3 3 2
x x x m 2 1 2 6 9 2 2 1
3 m x 3 3 3 2 2 2
8 3 2 2 x x m x 3 m x x m x x3 3 2 2 3 2 2 .
Xét hàm f t t 3 2 t trên .
Ta có: f t t 2
2 .ln 2 3t 0,t nên hàm số liên tục và đồng biến trên . Do đó từ
1 suy ra m x x3 3 2 2 3
m 8 9x 6x x .
Xét hàm số f x 3 2
x 6x 9x 8 trên . x
Ta có: f x 2 3
x 12x 9 ; f x 3 0 . x 1 Bảng biến thiên
70 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Dựa vào bảng biến thiên ta có, phương trình có 3 nghiệm phân biệt khi 4 m 8 .
Suy ra a 4; b 8 2 2
T b a 48 . Đáp án B.
Câu 280. [#Mỗi ngày 3 câu hỏi hay].
Nhân dịp quảng bá chiếc nón lá Việt Nam, một cửa hàng có đặt trước sảnh một cái nón lớn
với chiều cao 1,35m . Cửa hàng có sơn cách điệu hoa văn trang trí một phần của hình nón
ứng với cung AB như hình vẽ. Biết AB 1, 45m , ACB 150 và giá tiền để trang trí 2 1m
là 2.000.000 đồng. Hỏi số tiền (làm tròn đến hàng nghìn) mà cửa hàng cần dùng để trang
trí mặt trước của nón là bao nhiêu? A. 4.510.000 đồng. B. 3.021.000 đồng. C. 3.010.000 đồng. D. 3.008.000 đồng. Giải
Gọi r là bán kính đường tròn đáy của hình nón.
71 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] 1, 45
Áp dụng định lý sin ta có
2r r 1,45m . sin150
Suy ra góc ở tâm của hình nón ứng với cung AB là 60 .
Diện tích phần mặt nón mà cửa hàng cần sơn và trang trí là 157 2 2 .1, 45
rl.60 rl .r. r h 40 . 360 6 6 6 157 .1,45 40
Số tiền cửa hàng cần bỏ ra để trang trí là
.2000000 3.008.000 đồng. 6 Đáp án D.
Câu 281. [#Mỗi ngày 3 câu hỏi hay].
Cho hàm số bậc ba y f x có đồ thị là đường cong C trong hình bên. Hàm số f x
đạt cực trị tại hai điểm x , x thỏa f x f x 0 . Gọi ,
A B là hai điểm cực trị của đồ 1 2 1 2
thị C ; M , N, K là giao điểm của C với trục hoành; S là diện tích của hình phẳng
được gạch trong hình, S là diện tích tam giác NBK . Biết tứ giác MAKB nội tiếp đường 2 tròn, khi đó tỉ S số 1 bằng S2 2 6 6 5 3 3 3 A. . B. . C. . D. . 3 2 6 4 Giải
Kết quả bài toán không thay đổi khi ta tịnh tiến đồ thị đồ thị C sang trái sao cho điểm
uốn trùng với gốc tọa độ O . (như hình dưới)
72 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Do f x là hàm số bậc ba, nhận gốc tọa độ là tâm đối xứng O N .
Đặt x a, x a , với a 0 f x k 2 2 '
x a với k 0 1 2 f x 1 3 2 k x
a x x a 3, x a 3 M K 3
Có MAKB nội tiếp đường tròn tâm O OA OM a 3 1 3 2 Có f x 2 2
OA x f a 3 3
a 2 k a a a 2 k 1 1 2 3 2a
f x 3 2 1 3 2 x a x 2 2a 3 0 0
S f x 2 3 2 1 a 4 2 9 2 2 dx x x a 1 2 2a 12 2 8 a 3 a 3 1 S S
f a MO a a a AMO 1 6 2 . 2. 3 2 2 2 2 S 3 3 Vậy 1 . S 4 2 Đáp án D.
Câu 282. [#Mỗi ngày 3 câu hỏi hay].
Cho hàm số f x xác định và liên tục trên \ 3 , thỏa mãn 3 2 2 1 x 2x f x xf x f ' x 2 và f 1 0. Hàm số g x f 2x
1 có bao nhiêu điểm cực tiểu ? A. 0 . B. 1 . C. 2 . D. 3 . Giải Ta có: 2 3 2 2 2 2 1 x 2x f x xf x f ' x 1 f ' x x x 2xf x f x x x f x
73 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] 2 1 f ' x 1 f ' x 1 x x dx xdx C 2 2 x f x 2 x f x x f x 1 1 3 Do f 1 0 C C 1 f 1 2 2 2 Khi đó: 1 x 3 2 4x f x x f ' x 1 2 2 x f x 2 x 3 2 x 3 Suy ra: 2 2 3 f x 0 x x 3x 2 0 x 1 x 2 0 x 1 x 2 2 x 3 2 x 1 2 4 2 4 2 f ' x 0 4x x 3 4x x 6x 9 x 6x 4x 9 0 x a 2 1 2 1 2 x x 2 Khi đó: g ' x 4f ' 2x 1 f 2x 1 0 2x 1 1 x 1 2x 1 a a 1 3 x 2 2 Ta có:
f x không xác định khi x 3
g x không xác định khi 3 1 2x 1 3 x 2 4 8 Mặt khác: g ' 1 4.f ' 3 .f 3 4. . 0 và 3 3 lim g x , lim g x , lim g x , lim g x , 3 1 3 1 3 1 3 1 x x x x 2 2 2 2 lim g x , lim g x x x Ta có bảng biến thiên:
74 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Từ bảng biến thiên suy ra g x có 3 điểm cực tiểu. Đáp án D.
Câu 283. [#Mỗi ngày 3 câu hỏi hay].
Một bác thợ hàn làm ra những chi tiết trang trí giống nhau có dạng là một phần của mặt
xung quanh hình trụ như hình vẽ. Để làm ra sản phẩm đó bác thợ hàn cắt ra từ một tấm kim
loại phẳng hình chữ nhật kích thước 120 cm 240 cm thành những miếng kim loại hình chữ
nhật bằng nhau, một cạnh 20 cm , cạnh còn lại có độ dài L . Sau đó bác thợ hàn uốn cong
những miếng kim loại nhỏ đó thì được sản phẩm cần làm. Hỏi từ tấm kim loại ban đầu bác
thợ hàn có thể làm được tối đa bao nhiêu sản phẩm như vậy. Giả sử hao phí nguyên vật
liệu là không đáng kể. A. 60 . B. 72 . C. 66 . D. 80 . Giải
Sản phẩm bác thợ hàn làm ra là một phần của mặt xung quanh hình trụ có đáy là một phần
của đường tròn ngoại tiếp tam giác ABC như hình vẽ.
75 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Gọi R là bán kính đường tròn đó, áp dụng định lí sin trong tam giác ABC ta có BC 9 R 3 3 cm 0 2sin A 2sin 60
Gọi L là độ dài phần cung tròn đó.
Dễ thấy góc ở tâm của đường tròn ngoại tiếp tam giác ABC bẳng 0 120 nên ta có 2 L
.2 R 4 3 cm . 3
Do đó diện tích xung quanh của sản phẩm đó là 2 S
20.L 20.4 3 80 3 cm xq 240.120
Số sản phẩm tối đa bác thợ hàn có thể làm được là 66,16 80 3
Vậy tối đa bác thợ hàn có thể làm được 66 sản phẩm. Đáp án C.
Câu 284. [#Mỗi ngày 3 câu hỏi hay].
Cho hàm số y f x là đa thức bậc 5 có đồ thị f x như hình vẽ.
76 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Hàm số g x f 2 x x 2 2
x có bao nhiêu điểm cực trị? A. 3 . B. 2 . C. 4 . D. 1 . Giải
Ta có: g x x f 2 2 2 .
x 2x 2x . x
g x f 2 0 x 2x
, do x 1 không phải là nghiệm phương trình. x 1
Xét hàm số : y f 2 x 2x .
y x f 2 2 2 x 2x . x 1 x 1 2 x 2x 4 Khi đó, y 0 x 1 . 2 x 2x 2 x 3 2
x 2x 3 Bảng biến thiên : x Xét hàm số: y . x 1 1 y x . x 0, 1 2 1 Bảng biến thiên :
77 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] x
Số nghiệm của phương trình: f 2 x 2x
chính bằng số giao điểm của hai đồ thị x 1 x
hàm số y f 2
x 2x và y . x 1
Từ đồ thị suy ra phương trình g x 0 có 3 nghiệm đơn, nên hàm số g x có 3 điểm cực trị. Đáp án A.
Câu 285. [#Mỗi ngày 3 câu hỏi hay].
Cho hàm số bậc ba y f x có đồ thị C như hình vẽ.
78 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Biết rằng đồ thị hàm số đã cho cắt trục Ox tại ba điểm có hoành độ x , x , x theo thứ tự 1 2 3
lập thành cấp số cộng và x x 2 3 . Gọi diện tích hình phẳng giới hạn bởi C và 3 1
trục Ox là S , diện tích S của hình phẳng giới hạn bởi các đường y f x 1, 1
y f x 1, x x và x x bằng 1 3
A. S 2 3 .
B. S 4 3 . C. 4 3 . D. 8 3 . Giải
Ta có: “ x , x , x theo thứ tự lập thành cấp số cộng” 1 3 x x x 1 2 3 2 2
Ta có: “Gọi diện tích hình phẳng giới hạn bởi C và trục Ox là S ” 2 x 3 x
Vây dựa vào hình ảnh, ta có: S
f x dx
f xdx 1 x 2 x 2 x 3 x
Do f x làm hàm số bậc 3 nên ta có:
f x dx
f xdx 1 1 x 2 x
Ta có: “diện tích S của hình phẳng giới hạn bởi các đường y f x 1, y f x 1, 1
x x và x x ” 1 3 3 x x x x S
f x 1 f x 1 dx
2 f x 2 dx 2.
f x 1 dx 2. f x 1 dx 1 3 3 3 1 x 1 x 1 x 1 x
Dựa vào đồ thị ta có thể thấy rằng, khi x x ; x thì đồ thị y f x nằm phía trên đồ 1 3 thị y 1 3 x x x x
S 2. f x 1
dx 2. f x 1 dx 2 f x dx 1. dx 1 3 3 3 x x x x 1 1 1 1 3 x x Trong đó: 3 1.dx x
x x 2 3 3 1 x 1 x 1 3 x 2 x 3 x
Trong đó: f xdx f xdx
f xdx 1 x 1 x 2 x
79 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] 3 x 3 x 3 x Mà theo
1 thì ta có: f xdx f xdx f xdx 0 1 x 2 x 2 x 3x 3 x
Vậy ta có: S 2 f x dx 1.
dx 2. 0 2 3 4 3 . 1 x x 1 1 Đáp án C.
Câu 286. [#Mỗi ngày 3 câu hỏi hay].
Cho hàm bậc bốn và f 0 0 . Hàm số f ' x có bảng biến thiên như sau 1
Hỏi hàm số g x f 3
x 2x có bao nhiêu điểm cực trị 3 A. 1 . B. 2 . C. 3 . D. 4 . Giải Xét hàm số h x 1 f 3
x x h x 2 x f 3
x h x f 3 x 2 2 2 ' 0 ,x 0 1 2 3 x Đặ 2 2 4 t 3
t x f t
. Ta xét hàm số k t
kt 3 2 t 3 2 3 5 t 3 t
80 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] y Ta có đồ thị hàm số x O 1 2
Từ đồ thị hàm số ta thấy f t tại 3 3
a 0 a x x a 0 3 2 t Ta có bảng biến thiên 1 (Vì h0
f 0 2.0 0 0 0 ). Từ bảng biến thiên ta thấy hàm số có 3 điểm cực trị. 3 Đáp án C.
Câu 287. [#Mỗi ngày 3 câu hỏi hay].
Có bao nhiêu cặp số ;
x y thỏa mãn tính chất x x x y 2021 2021 log log , ở đó là số thực y
dương, y là số nguyên dương nhỏ hơn 2021 ? A. 4038 . B. 6057 . C. 6060 . D. 4040 . Giải
81 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] x 0 Điều kiện: * y , 2 y 2020 x y log x x x x y log 0 2021 log y logy 2021 2021 2021.log 0 y 2020 log x y 2021 x 1 x 1 2020 log x 2021 a 1 a x y y
Với x 1 y 2;3;4;...;202 0 có 2019 cặp ; x y a x y
, có 2 y 2020 có 2019.2 4038 cặp ; x y Vậy có 6057 . Đáp án B.
Câu 288. [#Mỗi ngày 3 câu hỏi hay].
Cho f x là hàm bậc ba có đồ thị như hình vẽ. Biết hàm số f x đạt cực trị tại x ; x 1 2
thỏa mãn x x 4 và tâm đối xứng của đồ thị hàm số nằm trên trục hoành. Gọi S ; S 2 1 1 2 S
là diện tích hình phẳng như trong hình vẽ. Tỷ số 1 bằng: S2 3 3 4 5 A. . B. . C. . D. . 5 4 3 3 Giải
82 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Gọi I là điểm uốn của đồ thị hàm số
Tịnh tiến đồ thị theo vector IO ta được đồ thị hàm số y g x có điểm uốn là gốc tọa
độ O và hai điểm cực trị x 2 , x 1. 3 4
g 'x 3ax 2x 2 a 2 3
x 4 với a 0 .
Từ đó ta có g x a 3
x 12x d .
Do g x đi qua gốc tọa độ O nên d 0 g x a 3 x 12x. 0 x 0
Ta có S a x 12x 4 3 2 dx a 6x 20a . 2 4 2 2
Lại có: S S bằng diện tích của hình chữ nhật có các cạnh là 2 và g 2 16a 1 2
S S 32a . Do đó S 32a 20a 12a . 1 2 1 S 12a 3 Vậy 1 . S 20a 5 2 Đáp án A.
Câu 289. [#Mỗi ngày 3 câu hỏi hay].
Cho số phức z thoả mãn z 1 2i 2 . Tìm giá trị lớn nhất của biểu thức 2 2
P z 2 3i z 5i . A. P 96 . B. P 66 . C. P 152 . D. P 132 . max max max max Giải
83 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] Gọi M ;
x y ; I 1; 2
lần lượt là điểm biểu diễn của các số phức z và 1 2i .
z 1 2i 2 M thuộc đường tròn tâm I , bán kính R 2 .
Gọi A2;3; B 0;5 lần lượt là điểm biểu diễn của các số phức 2 3i và 5i . 2 2 2 2 2 AB
P z 2 3i z 5i MA MB 2 2MH
(với H 1;4 là trung điểm của 2 AB ). P HM
HM HI R 8 2 P 2.8 4 132. max max max Đáp án D.
Câu 290. [#Mỗi ngày 3 câu hỏi hay]. 2 2 2
Trong không gian với hệ tọa độ Oxyz , cho mặt cầu S : x
1 y 2 z 3 16
và các điểm A1;0;2 , B 1
;2;2. Gọi P là mặt phẳng đi qua hai điểm A, B sao cho
thiết diện của P với mặt cầu S có diện tích nhỏ nhất. Khi viết phương trình P dưới
dạng P : ax by cz 3 0 . Tính T a b c . A. 3 . B. 3 . C. 0 . D. 2 . Giải
84 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] I B H A K
Mặt cầu có tâm I 1;2;3 bán kính là R 4 .
Ta có A , B nằm trong mặt cầu. Gọi K là hình chiếu của I trên AB và H là hình chiếu
của I lên thiết diện.
Ta có diện tích thiết diện bằng 2 2 2 S r R IH .
Do đó diện tích thiết diện nhỏ nhất khi IH lớn nhất.
Mà IH IK suy ra P qua ,
A B và vuông góc với IK .
Ta có IA IB 5 suy ra K là trung điểm của AB . Vậy K 0;1;2 và KI 1;1; 1 .
Vậy P : x
1 y z 2 0 x y z 3 0 . Vậy T 3 . Đáp án B.
Câu 291. [#Mỗi ngày 3 câu hỏi hay]. x 2 y 1 z 1
Trong không gian Oxyz, cho đường thẳng d : và mặt phẳng 1 2 2
P: x y z 6 0. Gọi là mặt phẳng đi qua đường thẳng d và tạo với P một
góc nhỏ nhất. Khi đó dạng phương trình tổng quát của là ax by z d 0. Khi đó
giá trị của a b d bằng: A. 6. B. 7. C. 5. D. 3. Giải
VTPT của mặt phẳng là n ; a ; b 1 .
Do đường thẳng d nằm trong mặt phẳng suy ra a 2b 2 0 1
85 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] a b 1
Góc tạo bởi và P lớn nhất cosn ;n đạt GTNN. ( P) ( ) 3 2 2 a b 1 1 b Từ
1 suy ra a 2 2b thế vào: cos n ;n . ( P) ( ) 3 2
5b 8b 5 b b b n n . P 1 2 2 1 2 cos ; ( ) ( ) 3 2
5b 8b 5 2
15b 24b 15 6 min cos n ; n b 1 . ( P) ( ) 9
Suy ra mặt phẳng : 4x y z d 0. Vì M 2;1;
1 d d 6 .
a b d 3. Đáp án D.
Câu 292. [#Mỗi ngày 3 câu hỏi hay].
Hình vẽ dưới đây mô tả một ngọn núi có dạng hình nón. Nhà đầu tư du lịch dự định xây
dựng một con đường nhằm phục vụ việc chuyên chở khách du lịch tham quan ngắm cảnh
vòng quanh ngọn núi bắt đầu từ vị trí A và dừng ở vị trí B . Biết rằng người ta đã chọn xây
dựng đường đi ngắn nhất vòng quanh núi từ A đến B , đoạn đường đầu là phần lên dốc từ
A và đoạn sau sẽ xuống dốc đến B . Tính quãng đường xuống dốc khi đi từ A đến B . 400 600 A. . B. 0 . C. . D. 15 91 . 91 91 Giải
86 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Trải phẳng: Cắt mặt nón theo đường sinh đi qua điểm A , trải phẳng như hình vẽ.
Gọi C là đỉnh dốc, do người ta đã chọn xây dựng đường đi ngắn nhất vòng quanh núi từ
A đến B nên B , C , A thẳng hàng.
Ta có OA 90 , OB 75 , B A
15 , bán kính đường tròn đáy hình nón R 30 .
Chu vi đường tròn chân núi l 2.R 2.30 60 .
Đường tròn tâm O , bán kính OA 90 có chiều dài cung AA là 60 .
Góc ở đỉnh của đường tròn tâm O , khi trải phẳng 60 2 Có AOB
(công thức tính chiều dài cung l R ). 90 3 2
AOB có OB 75 , OA 90 , A O B . 3 2 2 2 A B
OA OB 2OA .O . B cos A O B 20475
AB 15 91 .
Điểm C AB , C là đỉnh cao nhất của dốc khi OC ngắn nhất OC AB .
Đoạn xuống dốc là CB . Ta có 2 2 2 2 2 2 2 2 2
OC OA CA OB BC CA CB OA OB 2475 CA CB 15 91 600
CA CBCA CB 2475 165 91 CB . CA CB 91 91 Đáp án C.
87 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Câu 293. [#Mỗi ngày 3 câu hỏi hay].
Cho hàm số y f x 3 2
ax 2x bx 1 và y g x 2
cx 4x d có bảng biến thiên
dưới đây. Biết đồ thị hàm số y f x và y g x cắt nhau tại ba điểm phân biệt có
hoành độ lần lượt là x , x , x thỏa mãn x x x 9. Giá trị của P 3a b c 2d là 1 2 3 1 2 3 A. 1 . B. 0 . C. 2 . D. 3 . Giải
Ta có f x 2 '
3ax 4x b là hàm số bậc hai, cùng bậc với g x .
Mà từ đồ thị ta có hàm số f x đạt cực trị tại hai điểm là nghiệm của phương trình
g x 0 nên f ' x k.g x, x k 0. 2
ax x b k 2 3 4
cx 4x d , x 3 a kc k 1 4 4k 3
a c 1 b kd b d Đồ 2 4 8 4
thị hàm số g x có tung độ đỉnh bằng 1 nên g 1
d 1 d 1 2 . c c c c
Phương trình hoành độ giao điểm của đồ thị hai hàm số f x và g x : 3 2 2 3
ax x bx cx x d ax c 2 2 1 4 2
x b 4 x 1 d 0 * .
Theo giả thiết, phương trình * có 3 nghiệm x , x , x thỏa mãn x x x 9 nên theo 1 2 3 1 2 3 đị c 2
nh lí Vietè cho phương trình bậc ba, ta có
9 c 2 9a 3. a
88 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] 3 a c 3 a c 1 a b d b d 3 Từ
1 , 2 và 3 ta có hệ phương trình: b 3 4 4 . d 1 d 1 c 1 c c
c 2 9a
c 2 3c d 3
Với các giá trị trên thay vào * thì thỏa mãn phương trình có 3 nghiệm phân biệt có tổng bằng 9 . 1
Vậy P 3a b c 2d 3. 3 1 6 1. 3 Đáp án A.
Câu 294. [#Mỗi ngày 3 câu hỏi hay].
Cho các số thực x, y, z thỏa mãn log 2 2
2x y log 3 3 x 2 y
log z . Có bao giá trị 3 7
nguyên của z để có đúng hai cặp x, y thỏa mãn đẳng thức trên ? A. 2 . B. 211. C. 99 . D. 4. Giải 2 2
2x y 3t 1 Ta có: log 2 2
2x y log 3 3 x 2 y 3 3
log z t x 2y 7t 2 . 3 7 z 10t 3 t 2t log 3 2 3 + Nếu y 0 3
2 x 7 thay vào 1 ta được 3 2.7
3t t log 2 do đó 49 z 10 . 3 3 49 + Nếu y 0 2 3 x 2x y
3 27t x 2y 2 2 2 2 3 3 t t 49 y 49 Từ 1 & 2 suy ra , * . x 2 y 49t 2 2 3 3 x y 3 3 2 2 27 27 2 x 2 2 1 y Đặ x t 3
u,u 2 . y
89 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] u u 22 0 3 6u 3
u 2u 4
Xét f u f u 3 u . 2u 0 2 3 1 2u 4 2 2 1 u 4 Ta có bảng biến thiên
Nhận xét với mỗi giá trị u tương ứng với duy nhất 1 cặp x, y thỏa mãn bài toán do đó t 1 1 49 log49 log 49 4 4 8 27 27 8 27 10 z 10
Yêu cầu bài toán tương đương . t 4 log 49 4 49 33 0 27 0 z 10 27 33
Vì z là số nguyên nên có 211 giá trị thỏa mãn. Đáp án B.
Câu 295. [#Mỗi ngày 3 câu hỏi hay].
Một gia đình có bồn tắm có bề mặt phẳng và lòng trong như hình vẽ, lòng trong của bồn tắm có
hình dạng bán cầu, mất đi chỏm cầu. Biết thể tích khối chỏm cầu được tính bởi công thức 2 2 h V h R
với R là bán kính khối cầu, h là chiều cao của chỏm cầu và OH m . 3 2 Thể tích 3
m lòng trong của bồn tắm là
90 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] 8 5 2 10 2 5 2 10 2 A. . B. . C. . D. . 24 3 12 3 Giải
Khối cầu S có tâm là O và bán kính là R OH. 2 1m . 2
Suy ra chiều cao chỏm cầu là h 1 m . 2 1 4 h 8 5 2
Vậy thể tích bồn tắm là 3 2
R h R . 2 3 3 24 Đáp án A.
Câu 296. [#Mỗi ngày 3 câu hỏi hay].
Cho mặt cầu S có tâm I 3;2;2 bán kính R 2 , mặt cầu S có tâm I 1;0;1 bán 2 2 1 1 1
kính R 1. Phương trình mặt phẳng P đồng thời tiếp xúc với S và S và cắt đoạn 2 1 2
I I có dạng 2x by cz d 0 . Tính T b c d . 1 2 A. 5 . B. 1. C. 3 . D. 2 . Giải Ta có I I 2 ; 2 ; 1
I I 3 R R nên hai mặt cầu S và S tiếp xúc ngoài 2 1 1 2 1 2 1 2
với nhau tại M nằm trên đoạn I I MI R 2;MI R 1 và thoả mãn 1 1 2 2 1 2 MI 2 MI 1 . 1 2 Gọi M ;
x y; z .Ta có MI 3 ;
x 2 y; 2 z và MI 1 ;
x y;1 z 2 1 5 x 3 x 2 2x 3 Từ 2 5 2 4
1 ta có hệ 2 y 2 y
y M ; ; . 3 3 3 3 2 z 2 2z 4 z 3
91 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Mặt phẳng P cần tìm tiếp xúc với S và S đồng thời cắt đoạn I I tại N 2 1 1 2
I N I N I I mà NI R 2; NI R 1 nên N M . Khi ấy, I I P nên 1 2 1 2 1 2 1 1 2 2
P nhận I I 2 ; 2 ; 1
làm vectơ pháp tuyến và P đi qua 5 2 4 M ; ; . Vậy P 1 2 3 3 3 có phương trình: 5 2 4 2 x 2 y 1 z 0 2
x 2y z 6 0 3 3 3
2x 2y z 6 0 b 2;c 1;d 6
T b c d 3 . Đáp án C.
Câu 297. [#Mỗi ngày 3 câu hỏi hay].
Cho hàm số bậc ba y f x có đồ thị hàm số như hình vẽ sau. Hàm số y g x f f x 1202 có
A. 3 điểm cực đại, 2 điểm cực tiểu.
B. 2 điểm cực đại, 3 điểm cực tiểu.
C. 2 điểm cực đại, 2 điểm cực tiểu.
D. 1 điểm cực đại, 1 điểm cực tiểu. Giải
Bảng biến thiên cùa hàm số y f x có dạng:
92 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Xét g x f f x 1202 .
Suy ra g ' x f ' x. f ' f x . x 0 x 0
f ' x 0 x 2 x 2
Với g ' x 0 . f ' f x
f x 0 0 x c 2 f x 2
x a c 2
Với x 0 là nghiệm bội 3 .
Với x 0 , f x 0 .
Với 0 x 2 thì f x 0 .
Với x 2, f x 0 .
Với x 0 thì f x 0 , suy ra f f x 0 .
Với 0 x c thì f x 0 suy ra f f x 0 .
Với c x a thì 0 f x 2 suy ra f f x 0 .
Với x a thì f x 2 suy ra f f x 0 .
Nên, ta có bảng biến thiên hàm số y g x như sau:
Vậy hàm số có 2 điểm cực đại, 2 điểm cực tiểu. Đáp án C.
93 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
94 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Xem thêm hình bên dưới:
95 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
96 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
97 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
98 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
99 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
100 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
101 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
102 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
103 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
104 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
105 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
106 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
107 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
108 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
109 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
110 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
111 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
112 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
113 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
114 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
115 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
116 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
117 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
118 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
119 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Do đó ta có được một biểu thức tương đương dưới đây:
120 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
121 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
122 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Câu 319. [#Mỗi ngày 3 câu hỏi hay].
Cho x, y 0;2 thỏa mãn x 3 x 8 eyey
11 . Giá trị lớn nhất của P ln x 1 ln y bằng:
A. 1 ln 3 ln 2. B. 2 ln 3 ln 2. C. 1 ln 3 ln 2. D. 1 ln 2. Giải Điề 1
u kiện: x 1, y . e
Phương trình tương đương với: 2 2 2 2 2 x x
e y ey e y ey 2 5 24 11 11
x 5x 24 0 *
Ta có: x 2 2 5 0, x 1. 11 2x 5 x 8 ey y Do đó: ey x 8 2 e * 11 2x 5 .
ey 3 x 3 x y ey 2 e x 8 x 8 9 + Với y 0;2 (vì 2 ). e e e 3 x + Với y
0;2 (vì 1 x 2). e Cách 1:
Khi đó, ta được: P ln x ln3 x trên 1;2 . 1 1 Ta có: P'
0 3 x ln3 x x ln x ** . 2x ln x
2 3 x ln 3 x 1
Xét hàm f t t ln t trên 1; , có f 't ln t 0, t 1; . 2 ln t
Khi đó f x f x 3 ** 3
3 x x x . 2 Bảng biến thiên:
123 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] 3 3
Dựa vào bảng biến thiên, suy ra P
2 ln3 ln 2 khi x ;y . max 2 2e Cách 2:
Khi đó, ta được: P ln x ln3 x trên 1;2 . 2
x x
P ln x ln 3 x 2 3 2
2 ln x ln
3 x 2lnx
3 x 2 ln 4 ln3ln2, x 1;2 . 2
ln x ln3 x 3
Dấu “=” xảy ra khi x 3 x x . x 2 1;2 3 3 Vậy từ đó P
2 ln3 ln 2 khi x ;y . max 2 2e Đáp án B.
Câu 320. [#Mỗi ngày 3 câu hỏi hay].
Cho hàm số y f x có đạo hàm liên tục trên đoạn 0;
1 và thỏa mãn f 0 0 . Biết 1 9 1 x 3 1 2
f x dx
và f ' xcos dx
. Tích phân f x dx bằng. 2 2 4 0 0 0 6 2 4 1 A. . B. C. D. . . . Giải x x Đặ u cos du sin dx t 2 2 2 . dv f '
xdx v f x
124 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] 1 1 1 x x x Suy ra f '
xcos dx cos f x f
xsin dx 2 2 2 2 0 0 0 1 x f 1 .cos f 0.cos0 f
xsin dx 2 2 2 0 1 1 f x x 3 dx f x x 3 sin sin dx . 2 2 4 2 2 0 0 2 1 x Xét tích phân f
x ksin dx 0 2 0 1 x x 2 f
x 2kf x 2 2 sin k sin dx 0 2 2 0 1 1 1 x x 9 3 1 2 f
xdx 2k f x 2 2 2 sin k sin dx 0
2k k 0 k 3 . 2 2 2 2 2 0 0 0 2 1
Khi đó ta có: x x x f x 3sin dx 0 f x3sin
0 f x 3sin . 2 2 2 0 1 x 1 1 cos 1 x 6 x 6 6 Vậy f x 2 dx 3 sin dx 3. cos cos cos0 . 2 2 2 0 0 0 0 2 Đáp án A. Chú ý: 1 x 3
Sử dụng phương pháp từng phần đối với tích phân f ' xcos dx . 2 4 0 2 1 x x 1 1 x Xét f
x ksin dx 0
, tìm k, từ đó suy ra f x k sin . f
xdx ksin dx . 2 2 2 0 0 0
Câu 321. [#Mỗi ngày 3 câu hỏi hay].
Cho hàm số y f x và f x 0, x
. Biết hàm số y f 'x có bảng biến thiên như 1 137 hình vẽ và f . 2 16
125 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Có bao nhiêu giá trị nguyên của 2 m 20
20;2020 để hàm số g x x 4mx5 e
. f x đồng biến 1 trên 1 ; . 2 A. 4040. B. 4041. C. 2019. D. 2020. Giải 2 2 Ta có:
g ' x 2x 4m x 4mx5 .e . f x x 4mx5 e . f ' x
g 'x 2x 4m. f x f 'x 2 x 4mx5 .e .
Yêu cầu bài toán g x 1 ' 0, x 1 ;
và g ' x 0 chỉ xảy ra tại một số hữu hạn điểm 2 1 thuộc 1 ; . 2 2
x m f x f x 1 2 4 . ' 0, x 1 ; (vì x 4mx 5 e 0 ) 2 f ' x 1 2
x 4m
(vì f x 0, x )
f x , x 1; , 2 f ' x 1
4m 2x
f x , x 1; *. 2 f ' x 1 Xét h x 2x
f x , x 1; . 2
f '' x. f x f ' x 2
Ta có h' x 2 . 2 f x f ' x 0 1 f '
x.f x f ' x 2 1 Mà f x , x 1; 0, x 1; . 2 0 2 f (x) 2
126 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Từ đó suy ra h x 1 ' 0, x 1 ; . 2 1
Vậy hàm số h x đồng biến trên 1 ; . 2 Bảng biến thiên: 1 f ' 1 1 2 225 225
Vậy điều kiện * 4m h 4m 2. 4m m . 2 2 1 137 548 f 2 m Mà m
m 1;2;3;...;202 0 . 2020;2020
Vậy có 2020 giá trị nguyên của m thỏa mãn yêu cầu bài toán. Đáp án D.
Câu 322. [#Mỗi ngày 3 câu hỏi hay].
Cho cấp số cộng a , cấp số nhân b thỏa mãn a a 0, b b 1 và hàm số n n 2 1 2 1 f x 3
x 3x sao cho f a 2 f a và f log b 2 f log b . Tìm số nguyên dương n 2 2 2 1 2 1
nhỏ nhất sao cho b 2019a . n n A. 17. B. 14. C. 15. D. 16. Giải
Xét hàm số f x 3
x 3x trên 0; .
x 10;
Ta có f ' x 2
3x 3 0 x . 1 0;
127 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Bảng biến thiên hàm số f x trên 0; như sau:
Vì a 0 nên f a 2
f a f a 2 0 1 . 2 1 2 2
Giả sử a 1 , vì f x đồng biến trên 1; nên f a f a suy ra f a 2 f a vô 2 1 2 1 1 lý.
Vậy a 0;1 do đó 2
f a 0 2 . 1 1 f a 0 a 0 1 Từ (1), (2) ta có: 1 f . a 2 a 1 2 2
Vậy số hạng tổng quát của dãy cấp số cộng a là: a n 1. n n Đặ t log b t 1 2 1
, suy ra: f t f t 2 , vì 1 b b nên 0 t t , theo lập luận trên ta có: 1 2 t log b 1 2 1 2 2 2 2 t 0 log b 0 b 1 1 2 1 1 . t 1 log b 1 b 2 2 2 2 2
Vậy số hạng tổng quát của dãy cấp số nhân b là 1 b 2n . n n Do đó n 1 b 2019a 2 2019 n . n n 1 *
Trong 4 đáp án n 16 là số nguyên dương nhỏ nhất thỏa mãn (*). Đáp án D.
Câu 323. [#Mỗi ngày 3 câu hỏi hay].
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, AB 1, cạnh bên SA 1 và vuông
góc với mặt phẳng đáy ABCD . Kí hiệu M là điểm di động trên đoạn CD và N là điểm
di động trên đoạn CB sao cho MAN 45 . Thể tích nhỏ nhất của khối chóp S.AMN là? 2 1 2 1 2 1 2 1 A. . B. . C. . D. . 9 3 6 9 Giải
128 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Đặt DM x, BN y ta có DAM BAN tan DAM tan BAN x y tan 45 tan .
1 tan DAM .tan BAN 1 xy 1 x Suy ra y và 2 2 2 AM AD DM x 1 , 1 x 2 2 2 x x 1 1 2 2 2 AN
AB BN 1 y 1 . 1 x x 1 2 1 1 x 1
Vì vậy V S . A S S .
A AM .AN.sin 45 . 3 AMN 6 6 x 1 2 x 1
Xét hàm số y f x . 6 x 1
Khảo sát ta có f x f 2 1 2 1 . 3 Đáp án B.
Câu 324. [#Mỗi ngày 3 câu hỏi hay]. Cho hai hàm số 4 3 2
f x ax bx cx dx e và g x 3 2
mx nx px 1 với a, b, c, d, e,
m, n, p, q là các số thực. Đồ thị của hai hàm số y f x; y g x như hình vẽ dưới.
Tổng các nghiệm của phương trình f x q g x e bằng
129 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] 13 13 4 4 A. . B. . C. . D. . 3 3 3 3 Giải Đặ 5
t h x f x g x có h x k x 1 x
x 3 (với k 0 ) và 4
h 0 f 0 g 0 e q . x x Do đó
h x h x h h h
xdxeq kx 5 0 0 1 x
x 3dx e q 4 0 0 x x k k
x 1 4x 5 x 3 dx e q 3 2
4x 13x 2x 15dx e q 4 4 0 0 k 13 4 3 2 x
x x 15x e q . 4 2 5 x 3
Phương trình tương đương vớ 13 i: h x 4 3 2
e q x
x x 15x 0 x 0 . 3 x 3 5 4
Tổng các nghiệm của phương trình bằng 0 3 . 3 3 Đáp án C.
Câu 325. [#Mỗi ngày 3 câu hỏi hay]. Cho hàm số 3 2
f x ax bx cx d có đồ thị như hình vẽ. Gọi S là tập
hợp các giá trị của m ( m ) sao cho x 3
1 m f 2x
1 mf x f x 1 0, x
. Số phần tử của tập S là A. 2 B. 0 C. 3 D. 1 Giải
130 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] m 0
Từ giả thiết suy ra: g 3
1 0 m m 0 m 1 . m 1
Với m 0 ta có: x 1 f
x 1 0 x (đúng) 1
Với m 1 ta có: 2x 1 1 f 2x 1 1 0 x (đúng) 2 Với m 1. f 2x 1 1
Xét x 1 ta có: lim x f x 4 2
1, đủ lớn sao cho f 2
1 1 2 f
1 f 2
1 1 2 f 0
(mâu thuẫn (*)) m 1 (loại). Vậy m 0 ;1 . Đáp án A.
Câu 326. [#Mỗi ngày 3 câu hỏi hay].
Gọi S là tập hợp tất cả các giá trị thực của m để tồn tại 4 số phức z thỏa mãn
z z z z 2 và z z 2 z z m là số thuần ảo. Tổng các phần tử của S là: 2 1 2 1 1 A. 2 1 B. C. D. 2 2 2 Giải
Gọi z x yi z x yi
Ta có: z z z z 2
x yi x yi x yi x yi 2
2x 2yi 2 x y 1 (*)
131 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
x y 1 khi x 0, y 0 d1
x y 1 khi x 0, y 0 d2
x y 1 khi x 0, y 0 d3 x y 1
khi x 0, y 0 d4
Ta lại có z z 2 z z m x yix yi 2 x yi x yi m
xx 2
2 y xy xy 2yi 2x m 2 2
x y m 2yi là số thuần ảo 2 2 2 2
x y m 0 x y m C
Tập hợp các điểm biểu diễn số phức z thỏa mãn (*) là hình vuông
Để tồn tại 4 số phức z thì C phải cắt cả 4 cạnh của hình vuông ABCD tại 4 điểm phân biệt. 0 0 1 1 Ta có d ; O d 1 2 2 1 1 2 1 R m Để
C cắt ở 4 cạnh của hình vuông ABCD tại 4 điểm phân biệt thì C 2 R m 1 C 1 1 2 1 S
;1 Tổng các phần tử của S là 1 . 2 2 2 Đáp án B.
Câu 327. [#Mỗi ngày 3 câu hỏi hay]. Cho phương trình: 3m m e e 2 x x 2 2 1
1 x 1 x . Tìm tất cả các giá trị thực của tham
số m để phương trình đã cho có nghiệm. 1 1 1 1 A. ln 2; . B. 0; ln 2 . C. ; ln 2 . D. 0; . 2 2 2 e Giải Điều kiện: 2 1 x 0 1 x 1. 2 Đặ t 1 t 2 2 2 2 2 2 2
x 1 x t t x 1 x 2x 1 x 1 2x 1 x x 1 x . 2
132 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Ta có: t x 2
x 1 x , x 1 ; 1 . x 0 x x x x t 'x 2 1 0 2 2 1
0 1 x x 1 x . 2 2 2 2 2 1 x 1 x 1 x x x 2 2 Bảng biến thiên:
Từ bảng biến thiên ta có: t 1 ; 2 . 2 Khi đó phương trình trở t m m 1 thành: 3 e e 2t 1 t 2 t 3
1 t t * . 2 Xét hàm số 3
f t t t ta có f t 2 '
3t 1 0, t
Hàm số đồng biến trên Hàm số đồng biến trên 1 ; 2 .
Từ m m f e
f t e t m t m 1 * ln 0;ln 2 0; ln 2 . 2 Đáp án B.
Câu 328. [#Mỗi ngày 3 câu hỏi hay].
Cho hàm số có đạo hàm liên tục trên khoảng 1; và thỏa mãn
xf x f x 3 2
ln x x f x, x
1; ; biết f 3 e 3e . Giá trị f 2 thuộc khoảng nào dưới đây? 25 27 23 29 A. 12; . B. 13; . C. ;12 . D. 14; . 2 2 2 2 Giải
Vì x 1; nên ta có 2
x f x xf x 4 2
ln x x xf x
133 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] 2
x f x 2xf x f x ln x 1 4 3 x x
f x f x
f x f x ln x 1
ln xdx 1 dx 2 3 2 3 x x x x
f x ln x f x f x dx x dx C 2 3 3 x x x
f x ln x f x 2 ln x x x C x C
x C f x . 2 2 x x ln x 3 Theo đề x 8 23
bài f 3 e 3e C 0 f x f 2 ;12 . ln x ln 2 2 Đáp án C.
Câu 329. [#Mỗi ngày 3 câu hỏi hay].
x y z
Tổng giá trị lớn nhất và nhỏ nhất của biểu thức F
bằng bao nhiêu, biết rằng x,
x y z
x y z
y, z là các số thực thỏa mãn log
x x 2 y y 2 z z 2 . 16 2 2 2
2x 2y 2z 1 1 2 2 1 A. . B. . C. . D. . 3 3 3 3 Giải
x y z Ta có: log
x x 2 y y 2 z z 2 16 2 2 2
2x 2y 2z 1
log x y z 2x y z log 2 2 2
2x 2 y 2z 1 2 2 2
2x 2 y 2z 1 16 16
log 4x y z 4x y z log 2 2 2
2x 2 y 2z 1 2 2 2
2x 2 y 2z 1 4 4
Xét hàm số: f t log t t t 0 . 4
Hàm số luôn đồng biến trên tập xác định.
Suy ra: f x y z f 2 2 2 4
2x 2 y 2z 1
134 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
4x y z 1 2 2 2 2 2 2
2x 2y 2z 1 x y z 2x 2y 2z 0 S . 2
Ta có mặt cầu S có tọa độ tâm và bán kính là: I 10 1;1;1 , R . 2
x y z Ta có: F F
1 x F
1 y F
1 z 0 P .
x y z
Mặt phẳng P và mặt cầu S có điểm chung điều kiện cần và đủ là
d I P
F 1 F 1 F 1 10 , R
F 2 F 2 2 2 1 1 1 2 10 1 2 10 2
3F 2F 13 0 F . 3 3
x y z 2
Tổng giá trị lớn nhất và nhỏ nhất của biểu thức F bằng .
x y z 3 Đáp án B.
Câu 330. [#Mỗi ngày 3 câu hỏi hay].
Cho các số thực dương x, y thỏa mãn 2 2 x y 1 2 log 2 2
x y 1 3. Biết giá trị lớn nhất 3 của biểu thức a 6 3 3
S x y x y là
với a, b là các số nguyên dương và phân số a b b
tối giản. Tính giá trị biểu thức T 2a b . A. T 25. B. T 34. C. T 32. D. T 41. Giải Nhận xét hàm số t 1 f (t) 2
log (t 1) đồng biến và f (2) 3, từ đó 3 2 2 x y 1 2 log 2 2 x y 2 2
1 3 x y 2 3 3 3
S x y x y x y 2 2
1 x y xy 2 2 2 2
S (x y) (3 xy) (2 2xy)(3 xy) . 2 2 x Đặt y
t xy do xy
1 nên t [1;1] . 2
135 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] Xét hàm số 1 512 2
g(t) (2 2t)(3 t) trên [1;1] được max g(t) g . t 1 ; 1 3 27 512 16 6 Do S 0 nên 2 S S . 27 9 Vậy T 34 . Đáp án B.
Câu 331. [#Mỗi ngày 3 câu hỏi hay]. z i a
Cho số thực a thay đổi và số phức z thỏa mãn . Trên mặt phẳng 2
1 a a 2 1 i a
tọa độ, gọi M là điểm biểu diễn số phức z. Khoảng cách ngắn nhất giữa hai điểm M và
I 3; 4 (khi a thay đổi) là: A. 4. B. 3. C. 5. D. 6. Giải Ta có: z i a i a 2 z a
1 a a 2i 1 2 2 1 a 2 1 ai a 2 2 i a a 1
a 1 a i 2 z a z a i 1 2 2 2 a i a i 2
a 1a i a i a 1 z z i 2 2 2 2 a i a 1 a 1 a 1 a 1
M là điểm biểu diễn số phức z M , . 2 2 a 1 a 1 2 2 2 a 1 a 1 Ta có: 1. 2 2 2 a a a 1 1 1
Suy ra tập hợp các điểm biểu diễn số phức z là đường tròn 2 2
x y 1 có tâm O 0;0 bán kính R 1 . Khi đó IM
IO R 3 2 2 4 1 5 1 4 . min
136 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] Đáp án A.
Câu 332. [#Mỗi ngày 3 câu hỏi hay].
Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình sau có bốn nghiệm phân biệt: 4 2 x
x m 2 16 8 1
x m 2m 1 0 . A. 4. B. 7. C. 6. D. 5. Giải Ta có: 4 2 x
x m 2 16 8 1
x m 2m 1 0 .
x x m x m2 m2 4 2
x m 4 2 16 8 1 1 0 1 8 1
x 16x 0 .
Đặt 1 m M , phương trình trở thành: 2 4 2
M 8xM x 16x 0 * . x x x x . M 2 4 2 4 ' 4 16 0
TH1: x 0 , Phương trình (*) có nghiệm kép M 4x 0 1 m 0 m 1. x 0
Khi đó phương trình ban đầu trở thành: 4 2 2
x 16x 0 x 2
x 16 0 . x 4
Phương trình có 3 nghiệm phân biệt m 1 không thỏa mãn.
TH2: x 0 Phương trình (*) có 2 nghiệm phân biệt: 2 2
M 4x x x 4x M 0 1
(1), (2) là phương trình bậc hai nên có tối đa 2 2 2
M 4x x x 4x M 0 2 nghiệm.
Do đó, để phương trình ban đầu có 4 nghiệm phân biệt thì (1), (2) đều có 2 nghiệm phân
biệt, và 4 nghiệm này phân biệt nhau ' 0 4 M 0 M 4 1 4 M 4 ' 0 4 M 0 M 4 2 4
m m 4 5 m 3 3 m 5 .
Kết hợp điều kiện m m 2 , 1 ,0,2,3, 4 . Thử lại m 2 x 2
2;2 6 (thỏa mãn).
137 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] m 1 x 2
6;2 2 (thỏa mãn).
m 0 x 2 5;2 3 (thỏa mãn).
m 2 x 2
3;2 5 (thỏa mãn).
m 3 x 2
2;2 6 (thỏa mãn).
m 4 x 1 ; 3
;2 7 (thỏa mãn).
Vậy có 6 giá trị nguyên của tham số m thỏa mãn yêu cầu bài toán. Đáp án C.
Câu 333. [#Mỗi ngày 3 câu hỏi hay].
Cho hàm số f x có đạo hàm xác định trên và thỏa mãn f x 2
x f x2019 4x 6x.e
0 và f 0 2019
. Số nghiệm nguyên dương của bất
phương trình f x 7 là A. 91. B. 46. C. 45. D. 44. Giải Cách 1: Theo giả thiết f x 2
x f x 2 2019
x f x e 2019 4x 6x. 0 6x 1 e
2x fx,x (1). 2
x f x TH1: Nếu 2019 1 e 0 thì 2
x f x
f x 2 2019 0
x 2019 ta có (1)
đúng với mọi x .
Do đó f x 2 2
7 x 2019 7 x 2026 2026 x 2026 .
Vì x nguyên dương nên x 1;2;3;...; 45 .
Trong trường hợp này có 45 giá trị nguyên dương của x thỏa mãn yêu cầu đề bài. 2
x f x TH2: Nếu 2019 1 e
0 thì ta có thể giả sử rằng tồn tại hàm số f x có đạo hàm
xác định trên và thỏa mãn yêu cầu đề bài.
138 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] 2 Khi đó, tạ
x f x
i x 0 ta có f 0 2019 nên 2019 1 e 0 (mâu thuẫn).
Vậy có tất cả 45 giá trị nguyên dương của x thỏa mãn yêu cầu đề bài. Cách 2: Theo giả thiết f x 2
x f x e
f x f x 2 2 2019 2x 3x 2019 4x 6x. 0 4x e 6x.e ,x . 2 2 2 2 f x f x Suy ra f x 2x 3x 2019 2x 3x 2019 4x.e x d 6x.e x d e e C . f 0 Mà f 0 2019 nên 2019 e e
C C 0 .
Do đó f x 2 2 2x 3x 2019 e e hay f x 2 x 2019 .
Khi đó f x 2 2
7 x 2019 7 x 2026 2026 x 2026 .
Vì x nguyên dương nên x 1;2;3;...; 45 .
Vậy có 45 giá trị nguyên dương của x thỏa mãn yêu cầu đề bài. Đáp án C.
Câu 334. [#Mỗi ngày 3 câu hỏi hay].
Xét số phức z có phần thực dương và ba điểm A, B, C lần lượt là điểm biểu diễn của các 1 1 số phức z, và z
. Biết tứ giác OABC là một hình bình hành, giá trị nhỏ nhất của z z 2 1 z bằng z A. 2 . B. 2. C. 2 2 . D. 4. Giải 1 1 1 1
Ta có OA z , AB
z , BC z
z , OC z . z z z z
Vì OABC là một hình bình hành nên
139 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] z z 2 2 OA BC 1 1 1 z 1 z 2 2
z z 1 z 1 1 1 z AB OC z z z z z z z z Đặt 2 2 2
z x yi z x y 2xyi vậy điều kiện trở thành: 2 2
z z 2 2
x y yi 2 2 1 1 1 2x x y 1 2xyi
x y 2
y x y 2
y x y 2 x y 2 2 2 2 2 2 2 2 2 2 2 2 2 1 4x 1 4x 1 1 2 2 2 2
x y 1 x y 1
x y y x .
x y 1
x y 2 2 2 2 0 2 2 2 2 1 2 2 1 1 z
x y 2 1 2xyi
x y 2 2 2 2 2 2 2 2 1 4x y Khi đó z 2 2 z z x yi x y 2 1 2 1 2x 2 2x . 2 2 2 2x 2x 2 1 2x 2 2 x 1 1 1 1 Dấu bằng xảy ra tại 2 2 y x ; x y ; , ; . 2 2 2 2 x 0 Đáp án B.
Câu 335. [#Mỗi ngày 3 câu hỏi hay]. 2 2 x 5y
Cho x, y là các số dương thỏa mãn 2 2 log
1 x 10xy 9y 0 . Gọi M, m lần 2 2 2
x 10xy y 2 2 lượ x xy 9 y
t là giá trị lớn nhất, giá trị nhỏ nhất của P
. Tính T 10M m . 2 xy y A. T 60 . B. T 94 . C. T 104 . D. T 50 . Giải
Bất phương trình tương đương với:
140 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] log 2 2
x 5y log 2 2
x 10xy y log 2 2 2 2
x 5y 2 2
x 10xy y 0 2 2 2 log 2 2
2x 10 y 2 2 2
x 5y log 2 2
x 10xy y 2 2
x 10xy y 2 2 2 2 2 2
2x 10y x 10xy y 2 x x x 2 2
x 10xy 9y 0 10 9 0 1 9 y y y 2 x x 9 2 2 Khi đó: x xy 9 y y y P 2 xy y x 1 y Đặ x t t
(với 1 t 9 ). y t t
Xét hàm số: f t 2 9 . t 1 2 t 2t 8 t 4
Ta có: f t . t 0 2 1 t 2 11 99 Ta lại có: f 1
; f 2 5; f 9 . 2 10 99 Nên M , m 5. 10
Vậy T 10M m 94 . Đáp án B.
Câu 336. [#Mỗi ngày 3 câu hỏi hay].
Cho hình lăng trụ tam giác đều ABC.AB C
có cạnh đáy bằng a và cạnh bên bằng a 2 . AM A N 1
Lấy M, N lần lượt trên cạnh AB , A C sao cho AB A C
. Tính thể tích V của khối 3 BMNC C . 3 a 6 3 2a 6 3 3a 6 3 a 6 A. . B. . C. . D. . 108 27 108 27
141 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] Giải
Gọi G, K lần lượt là tâm các hình chữ nhật ABB A
và AAC C . AM 1 AM 2 Ta có: AB
(do G là trung điểm AB ). 3 AG 3 AM 2
Xét tam giác ABA có AG là trung tuyến và . AG 3
Suy ra M là trọng tâm tam giác ABA .
Do đó BM đi qua trung điểm I của AA . A N 1 A N 2 Ta có: ). A C 3 A K
(do K là trung điểm A C 3 AN 2
Xét tam giác AAC có AK là trung tuyến và A
, suy ra N là trọng tâm của tam K 3
giác AAC . Do đó C N
đi qua trung điểm I của AA .
Từ M là trọng tâm tam giác ABA và N trọng tâm của tam giác AAC , suy ra: IM IN 1 IB IC . 3
Gọi V , V lần lượt là thể tích các khối chóp IMNC; IBCC . 1 2 V IM IN IC 1 Ta có: 1 . . V IB IC . IC 9 2 8
Mà V V V V V . 1 2 2 9
Hạ AH vuông góc với BC tại H thuộc BC.
Ta được AH vuông góc với mặt phẳng BB C C
, AA song song với mặt phẳng BB C C
nên khoảng cách từ I đến mặt phẳng BB C C
bằng khoảng cách từ A đến BB C C và bằng AH. a 3 1 1 a 3 a 2 a 6 Ta có: AH , V
d I;(BB C C ) 2 3 .S . . . 2 2 3 BCC 3 2 2 12 3 8 2a 6
Suy ra: V V . 2 9 27
142 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] Đáp án B.
Câu 337. [#Mỗi ngày 3 câu hỏi hay]. Cho hàm số 3 2
y f (x) x 3x 2 và phương trình f (x) m m n có 8 nghiệm phân biệt với m ( 6 ; 2)
. Khẳng định nào sau đây đúng? 6 m 4 3 m 2 A. . B. . 2 n 6 2m
6 2m n 2 3 m 2 3 m 2 C. .
D. 0 n 6 2m . m n
2 n m Giải
Ta có bảng biến thiên của y f (x) m
Bảng biến thiên của y f (x) m m
TH1: 2m 6 0 m 3 n 0
Ta có: f (x) m m n f (x) m m n .
f (x) m m n
143 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Suy ra phương trình f (x) m m n có 8 nghiệm phân biệt khi: 3 m 2 3 m 2 3 m 2
0 n 2m 60 n 2m 6
0 n 2m 6
n 2m 6
n 2m 6 2 n m
m n 2
2 n m
TH2: 2m 6 0 m 3
Ta có bảng biến thiên của y f (x) m m như sau:
+ Nếu 2m 6 2 4 m 3 thì f (x) m m n có 8 nghiệm phân biệt khi 4 m 3
2 n m hay .
2 n m
+ Nếu 2m 6 2 6 m 4 thì f (x) m m n có 8 nghiệm phân biệt khi 6 m 4 2
m 6 n m 0 n m hay .
0 n m Đáp án D.
Câu 338. [#Mỗi ngày 3 câu hỏi hay]. m 2 6i Cho số phức z , m
nguyên dương. Có bao nhiêu giá trị m 1;50 để z là số 3 i thuần ảo? A. 25. B. 50. C. 26. D. 24. Giải m m 2 6i
26i3i m Ta có: z 2i 2m. m i 3 i
3 i3 i
144 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
+ Với m 4k k thì 2m z
+ Với m 4k 2k thì 2m z
+ Với m 4k 1k thì 2m z .i
+ Với m 4k 3k thì 2m z .i m 4k 1
Vậy để z là số thuần ảo thì k mà 1 m 50
m 4k 3 1 4k 1 50 0 4k 49 0 k 12,25 k 0;1;2;3;...;1 2 Nên
1 4k 3 50 2 4k 47
0,5 k 11,75 k 0;1;2;....;1 1
Vậy có tất cả 13 12 25 giá trị của k thỏa mãn điều kiện, tức cũng có 25 giá trị của m
thỏa mãn điều kiện đề bài. Đáp án A.
Câu 339. [#Mỗi ngày 3 câu hỏi hay].
Tìm tất cả các giá trị nguyên của m để hệ phương trình sau có nghiệm: 2 x x 1 2 x 1 3 3
2017x 2017 1 . 2 x
m 2 x 2m 3 0 2 A. m 3. B. m 3. C. m 2. D. m 2. Giải Điều kiện: x 1 . Ta có: 2 x x 1 2 x 1 x x x 1 1 3 .3 3 .3 2017 2017 9 9 3 20171 x . VT x x 1 9 9 3 0 TH1: 1
x 1 thì VP x . 2017 1 0 Suy ra x x 1 9 9 3
20171 x có nghiệm với 1 x 1.
TH2: x 1 thì VT VP .
145 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] VT x x 1 9 9 3 0
TH3: x 1 thì VP x . 2017 1 0 Suy ra x x 1 9 9 3
20171 x vô nghiệm. Vậy (1) có nghiệm với: 1 x 1. x x Ta có: 2 2 3 2 m (với 1 x 1). x 2 2 Để x 2x 3
bất phương trình có nghiệm trên 1; 1 thì: m min 2 . Vậy m 2 . 1 ; 1 x 2 Đáp án C.
Câu 340. [#Mỗi ngày 3 câu hỏi hay].
Cho các hàm số f x, f x , f x ,... biết: o 1 2 f x x x x f x f x n o
ln ln 2019 ln 2019 , 1, . n 1 n
Số nghiệm của phương trình f x 0 là 2020 A. 6058. B. 6057. C. 6059. D. 6063. Giải Ta có: f x o 0 f x 0 f x 1 f x 2018 2017 2 f x 0 f x 1 o 2020 2019 f x 2 f x 3 .... 2018 2017 f x o 2020 1 2019 ;0 x e 2019
ln x 4038;0 x e x 1
Xét hàm số y f x x e x e ta có: 2019 2019
y ' ;e x e o 2019 2019 ln ; , x 2019
ln x 4038; x e 1 2019 ; x e x
BBT hàm số y f x o
146 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] x 0 2019 e 2019 e y’ + - + y 2019 -2019
Vậy số nghiệm của phương trình là: 2019.3 2 6059 . Đáp án C.
Câu 341. [#Mỗi ngày 3 câu hỏi hay]. x y z
Cho các số thực x, y, z thỏa mãn log log log
3. Tính giá trị nhỏ nhất 2 3 5 4 9 25 của S log . x log . y log z. 2001 2018 2019
A. min S 27.log 2.log 3.log 5. 2001 2018 2019
B. min S 44.log 2.log 3.log 5. 2001 2018 2019
C. min S 88.log 2.log 3.log 5. 2001 2018 2019 289 D. min S .log 2.log 3.log 5. 2001 2018 2019 8 Giải
Điều kiện: x 4; y 9; z 25. x 2 x 2 2 a log a log
a log x 2 log x a 2 2 2 2 2 4 4 Đặ y t 2 b log
log y b 2 3 3 9 z 2 c log
log z c 2 5 5 25
Khi đó a,b,b 0 và a b c 3
147 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] log x log 2.log x 2 a 2 .log 2 2001 2001 2 2001 Ta có: log y 2 b 2 .log 3 2018 2018 log z 2c 2 .log 5 2019 2019 Suy ra S 2 a 2 2 b 2 2 c 1 .log 2.log 3.log 5. 2001 2018 2019 P a b
Ta có: a b a b a b a b 2 2 2 2 2 2 2 2 2 2 1 1 3 3 2 (Bunhiacopxki)
a b 3
a b2 1 2 2 3 3 a b2 2 2 1 2 2 P
a b c 1 2 2 2 3 a b2 2 2 2 1 2 c 2 2
a b2 a b2 a b a b 3 1 c 1 2 1 3 c 3
a b c2 2 27 4 4 2 2
P 27 khi a b c 1 hay x 8, y 27, z 125 Suy ra S 27.log 2.log 3.log 5 min 2001 2018 2019 Đáp án A.
Câu 342. [#Mỗi ngày 3 câu hỏi hay].
Cho hàm số f x nhận giá trị dương trên [0;1] , có đạo hàm dương và liên tục trên [0;1] , 1 1 1 3
thỏa mãn f 0 1 và 3
f x 4 f '
x dx 3 f ' x 2
. f xd . I x Tính
f xd .x 0 0 0 1 2 1
A. I 2 e 1 . B. I 2 2 e 1 . C. e I . D. e I . 2 2 Giải
Áp dụng bất đẳng thức AM-GM cho ba số dương ta có
148 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2] 3 3 3 3 f x f x f x f x 3
f x 4[ f ' x 3
] 4[ f ' x 3 3 ]
3 4[ f 'x 3 ] . . 2 2 2 2
3 f 'x 2 . f x 1 1 Suy ra 3
f x 4[ f 'x 3]dx 3 f ' x 2 . f x dx . 0 0 1 1 Mà 3
f x 4[ f ' x 3
] dx 3 f ' x 2
. f xdx nên dấu “=” xảy ra, tức là 0 0 3 3 f x f x f x 3 f x 1 4[ ' ] ' f x 2 2 2 f ' x 1 f ' x 1 1 1 dx dx f x
x C f x x C e f x 2 f x ln 2 2 2 1 1 x
Theo giả thiết f 0 1 C 0 f x 2
e f xdx 2 e 1. 0 Đáp án A.
Câu 343. [#Mỗi ngày 3 câu hỏi hay].
Với a là tham số thực để bất phương trình 2x 3x ax 2 có tập nghiệm là khi đó
A. a ;0 .
B. a 1;3 .
C. a 3; .
D. a 0; 1 Giải
Xét trường hợp a 0 , phương trình không nhận các giá trị âm của x làm nghiệm.
Thật vậy, khi đó 2x 3x 2 mà ax 2 2 .
Suy ra loại a 0 .
Xét trường hợp a 0 2x 3x
2 2x 3x ax ax 2 0 .
Đặt 2x 3x f x
ax 2 , x .
Khi đó 2x ln 2 3x f x
ln 3 a , x .
0 2x ln 2 3x f x ln 3 a 1 .
149 I can’t??? I can!! | ▫▪
Nhóm Toán anh Dúi [201 CÂU HỎI HAY PHẦN 2]
Đặt 2x ln 2 3x g x ln 3 , x . g x x 2 x 2
2 ln 2 3 ln 3 0 , x .
Suy ra hàm số g x đồng biến trên .
Lại có lim g x và lim g x 0 . x x
Suy ra với mỗi giá trị a 0 thì phương trình
1 luôn có nghiệm duy nhất là x . 0
Ta có phương trình f x 0 có nghiệm duy nhất là x . 0
Mà lim f x và lim f x a 0 nên f x 0 , x x và f x 0 , 0 x x x x 0 Bảng biến thiên x x 0 f x – + f x f x 0
Dựa vào bảng biến thiên ta thấy f x đạt giá trị nhỏ nhất tại x , ta kết hợp với điều kiện 0
đề bài là f x 0 , x và f 0 0 suy ra x 0 và x 0 là giá trị duy nhất để 0 0
f x 0 .
Suy ra x 0 là giá trị duy nhất để f x 0 0 0
f 0 ln 2 ln3 a 0 .
Suy ra a ln 2 ln 3 ln 6 .
Như vậy a là giá trị duy nhất thỏa mãn yêu cầu bài toán.
Suy ra mệnh đề đúng là a 1;3 . Đáp án C.
150 I can’t??? I can!! | ▫▪
Document Outline
- 201 câu hỏi hay Phần 2 - chính thức - đề
- 201 câu hỏi hay Phần 2




