94 bài tập trắc nghiệm tích vô hướng của hai vectơ có đáp án và lời giải

Tài liệu gồm 41 trang, được biên soạn bởi thầy giáo Lê Bá Bảo, tuyển chọn 94 bài tập trắc nghiệm tích vô hướng của hai vectơ có đáp án và lời giải chi tiết, phù hợp với chương trình sách giáo khóa Toán 10 mới: Cánh Diều, Chân Trời Sáng Tạo, Kết Nối Tri Thức Với Cuộc Sống.

162 81 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 4: Vectơ (KNTT)

Môn: Toán 10

Thông tin:

41 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
Luyện tập VECTƠ
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề: TÍCH VÔ HƯỚNG CỦA 2 VECTƠ
I. TÓM TẮT LÝ THUYẾT
1. Định nghĩa góc giữa hai vectơ
A
O
B
Cho hai vectơ
u
và
v
khác vectơ
0
. Từ một điểm O tuỳ ý, vẽ các vec tơ
OA u
và
OB v
. Khi đó
số đo của góc
được gọi là số đo của góc giữa hai vectơ
,uv
, kí hiệu là
,.uv
Chú ý
Quy ước rằng góc giữa hai vectơ
u
và
0
có thể nhận một giá trị tuỳ ý từ
0
đến
180 .
Nếu
, 90uv
thì ta nói rằng
u
và
v
vuông góc với nhau, kí hiệu là
uv
hoặc
.vu
Đặc biệt: Vectơ
0
vuông góc với mọi vectơ.
2. Tích vô hướng của hai vectơ khác vectơ-không
u
và
v
là một số, kí hiệu là
.uv
được xác định bởi
công thức sau:
. . . , .u v u v cos u v
Chú ý
.0 u v u v
Tích
.uu
còn được viết là
2
u
và được gọi là bình phương vô hướng của
.u
Ta có
2
2
. .cos0 . u u u u
3. Biểu thức toạ độ và tính chất của tích vô hướng
Tích vô hướng của hai vectơ
( ; )u x y
và
( ; )v x y

được tính theo công thức:
. . .
u v x x u u
Nhận xét
Hai vectơ
u
và
v
vuông góc với nhau khi và chỉ khi
. . 0.x x y y


Bình phương vô hướng của vectơ
( ; )u x y
là
2 2 2
.u x y
Nếu
0u
và
0v
thì
2 2 2 2
.
cos ,
.
.




u v xx yy
uv
uv
x y x y
Tính chất
Với ba vectơ
, , u v w
bất kì và mọi số thực k ta có:
..u v v u
( tính chất giao hoán);
. . .u v w u v u w
( Tính chất phân phối đối với phép cộng);
. . . .ku v k u v u kv
u
v
Luyện tập VECTƠ
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
II. BÀI TẬP TRẮC NGHIỆM
Dạng 1: GÓC GIỮA HAI VECTO
Câu 1. Cho tam giác
ABC
như hình vẽ.
Xác định góc
,AB AC
.
A.
45
. B.
120
. C.
15
. D.
165
.
Câu 2. Cho tam giác
ABC
đều. Góc giữa hai vectơ
AB
và
AC
bằng
A.
60 .
B.
120
. C.
150
. D.
30
.
Câu 3. Cho tam giác
ABC
đều. Góc giữa hai vectơ
AB
và
BC
bằng
A.
60 .
B.
120
. C.
150
. D.
30
.
Câu 4. Cho tam giác
ABC
đều. Góc giữa hai vectơ
AB
và
CB
bằng
A.
60 .
B.
120
. C.
150
. D.
30
.
Câu 5. Cho hình bình hành
ABCD
. Góc giữa 2 vectơ
AB
và
BC
là
A.
BAC
. B.
ADC
. C.
BAD
. D.
ABC
.
Câu 6. Cho tam giác
ABC
cân tại
A
, góc
100BAC
. Số đo góc giữa hai véctơ
AB
và
BC
là
A.
140
. B.
80
. C.
40
. D.
100
.
Câu 7. Cho hai vectơ
a
;
b
khác vectơ
0
thỏa mãn
1
..
2
a b a b
. Khi đó góc giữa hai vectơ
a
;
b
bằn
A.
60 .
B.
120
. C.
150
. D.
30
.
Câu 8. Cho hai vec tơ
a
và
b
biết
6, 12ab
và
10ab
. Khi đó,
cosin
của góc giữa hai vectơ
a
và
ab
bằng
A.
1
18
. B.
2
3
. C.
1
15
. D.
1
15
.
Câu 9. Cho hai vecto
a
,
b
sao cho
a
2
,
2b
và hai vectơ
x a b
,
2y a b
vuông góc với
nhau. Tính góc giữa hai véc tơ
a
và
b
.
A.
120
. B.
60
. C.
90
. D.
30
.
Dạng 2: TÍNH TÍCH VÔ HƯỚNG
Câu 10. Trong các công thức sau, công thức nào xác định tích vô hướng của hai vectơ
,ab
cùng khác
0
?
A.
. . . ,a b a b cos a b
. B.
. . . ,a b a b cos a b
.
C.
. . .sin ,a b a b a b
. D.
..a b a b
.
Câu 11. Cho hai vectơ
a
và
b
. Đẳng thức nào sau đây sai?
Luyện tập VECTƠ
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
A.
. . .cos ,a b a b a b
. B.
2 2 2
..a b a b
.
C.
2 2 2
1
.
2
a b a b a b
. D.
2
2
aa
.
Câu 12. Cho hai véctơ
,ab
khác véctơ-không thỏa mãn
..a b a b
. Khi đó, góc giữa hai vectơ
,ab
bằng
A.
45 .
B.
0.
C.
D.
90 .
Câu 13. Cho hai vectơ
a
và
b
. Đẳng thức nào sau đây sai?
A.
2 2 2
1
..
2
a b a b a b
. B.
2 2 2
1
. . .
2
a b a b a b
C.
22
1
..
2
a b a b a b
. D.
22
1
. . .
4
a b a b a b
Câu 14. Cho
3a
,
5b
,
o
, 45ab
. Tích vô hướng của
a
và
b
bằng
A.
15
2
. B.
15 3
2
. C.
15
2
. D.
15
2
.
Câu 15. Cho hai vectơ
a
và
b
. Biết
2, 3ab
và
, 30ab 
. Tính
ab
.
A.
11
. B.
13
. C.
12
. D.
14
.
Câu 16. Cho
,ab
có
4; 5.ab
và
. 10.ab
Tính
cos ; .ab
A.
3
cos ; .
2
ab
B.
2
cos ; .
2
ab
C.
1
cos ; .
2
ab
D.
1
cos ; .
2
ab
Câu 17. Cho hai véctơ
,ab
thỏa mãn:
4; 3; 4a b a b
. Gọi
là góc giữa hai véctơ
,ab
. Khẳng
định nào dưới đây đúng?
A.
0
60
. B.
0
30
. C.
1
cos
3
. D.
3
cos
8
.
Câu 18. Cho tam giác
ABC
có
30 ,ABC
5, 8AB BC
. Tính
.BA BC
.
A.
20.
B.
20 3.
C.
20 2.
D.
40 3.
Câu 19. Cho hình vuông
ABCD
cạnh
2a
. Khi đó
.AB AC
bằng
A.
2
4a
. B.
2
2a
. C.
2
2
2
a
. D.
2
a
.
Câu 20. Cho tam giác vuông cân
ABC
có
AB AC a
. Tính
..AB AC
A.
2
a
. B.
2
2
a
. C.
0
. D.
2
3
2
a
.
Câu 21. Cho tam giác
ABC
vuông tại
A
,
,2AB a BC a
. Tích vô hướng
.BA B C
bằng
A.
2
a
. B.
2
1
2
a
. C.
2
3a
. D.
2
a
.
Câu 22. Cho tam giác
ABC
vuông cân tại
,A
có
.AB a
Tích vô hướng
.BA B C
bằng
A.
2
.a
B.
2
.
2
a
C.
2
.
2
a
D.
2
.a
Luyện tập VECTƠ
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 23. Cho tam giác
ABC
có
0
ˆ
90A
,
0
ˆ
60B
và
AB a
. Khi đó,
.AC CB
bằng
A.
2
2a
. B.
2
2a
. C.
2
3a
. D.
2
3a
.
Câu 24. Cho
ABC
vuông cân tại
A
, cạnh
5AB
. Tích vô hướng
.BC BA
bằng
A.
52
. B.
25
. C.
20
. D.
20
.
Câu 25. Góc tạo bởi
m
và
n
là
90
và
2021m
,
2022n
. Khi đó,
.mn
bằng
A.
4086462
. B.
0
. C.
4086462
. D.
1
.
Câu 26. Cho hai véc tơ
a
,
b
thỏa mãn
3, 4ab
và
( , ) 60ab 
. Tích vô hướng
.ab
bằng
A.
6
. B.
63
. C.
12
. D.
43
.
Câu 27. Cho hình bình hành
ABCD
, với
2AB
,
1BC
,
60BAD 
. Tích vô hướng
.AB AD
bằng
A.
1
. B.
1
. C.
1
2
. D.
1
2
.
Câu 28. Cho tam giác
ABC
vuông tại
A
có
;3AB a AC a
và
AM
là trung tuyến. Tính tích vô
hướng
..BA AM
A.
2
.
2
a
B.
2
.a
C.
2
.a
D.
2
.
2
a
Câu 29. Cho hình bình hành
ABCD
, với
2AB
,
1AD
,
60BAD 
. Tích vô hướng
.AB AD
bằng
A.
1
. B.
1
. C.
1
2
. D.
1
2
.
Câu 30. Cho hình bình hành
ABCD
, với
2AB
,
1AD
,
60BAD 
. Tích vô hướng
.BA BC
bằng
A.
1
. B.
1
2
C.
1
. D.
1
2
.
Câu 31. Cho hình bình hành
ABCD
, với
2AB
,
1AD
,
60BAD 
. Độ dài đường chéo
AC
bằng
A.
5
. B.
7
. C.
5
. D.
7
2
.
Câu 32. Cho hình bình hành
ABCD
, với
2AB
,
1AD
,
60BAD 
. Độ dài đường chéo
BD
bằng
A.
3
. B.
5
. C.
5
. D.
3
.
Câu 33. Cho hình vuông
ABCD
cạnh bằng 3, gọi
E
là điểm đối xứng của
D
qua
C
. Giá trị
.AE CD
bằng
A.
18
. B.
93
. C.
95
. D.
18
.
Câu 34. Cho hình bình hành
ABCD
có
2 , 3 , 60AB a AD a BAD
. Điểm
K
thuộc
AD
thỏa mãn
2AK DK
. Tính tích vô hướng
.BK A C
A.
2
3a
. B.
2
6a
. C.
0
. D.
2
a
.
Câu 35. Cho hình vuông
ABCD
cạnh
5
. Khi đó,
.AB AC
bằng
A.
25.
B.
25 2.
C.
25 2
.
2
D.
25
2
.
Câu 36. Cho tam giác
ABC
đều cạnh
a
. Tính
..AB AC
A.
2
3
..
2
a
AB AC
B.
2
..
2
a
AB AC
C.
2
..AB AC a
D.
2
. 2 .AB AC a
Luyện tập VECTƠ
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 37. Cho hình vuông
ABCD
cạnh
2a
,
M
là trung điểm của cạnh
CD
. Chọn khẳng định đúng.
A.
2
.
2
a
AM DC
. B.
.0AM DC
. C.
2
.AM DC a
. D.
2
.2AM DC a
.
Câu 38. Cho hình vuông
ABCD
có độ dài cạnh bằng
10
. Tính giá trị
.AB CD
.
A.
100
. B.
10
. C.
0
. D.
100
.
Câu 39. Cho tam giác đều
ABC
có độ dài cạnh bằng 4 và điểm
M
thỏa mãn
1
2
BM BC
. Tính
.BM BA
.
A.
.4BM BA
. B.
.4BM BA 
. C.
. 4 3BM BA
. D.
. 4 3BM BA 
.
Câu 40. Cho hình vuông
ABCD
có độ dài các cạnh bằng
a
. Tính
.A C BD
.
A.
2
.2AC BD a
. B.
.0AC BD
. C.
.0AC BD
. D.
2
.2AC BD a
.
Câu 41. Cho tam giác đều
có trọng tâm
G
và độ dài cạnh bằng
a
. Tính
..AB AG
A.
2
3
6
a
. B.
2
3
4
a
. C.
2
3
4
a
. D.
2
2
a
.
Câu 42. Cho tam giác đều ABC cạnh a, đường cao AH. Tính
.AC AC AB
A.
2
2
2
a
. B.
2
3
2
a
. C.
2
2
a
. D.
2
2
a
.
Câu 43. Cho hình thoi
ABCD
tâm
O
có cạnh bằng
2a
và
60ABD 
. Gọi
I
là điểm thỏa mãn
20IC ID
. Tính tích vô hướng
.AO BI
.
A.
2
2
2
a
. B.
2
3
2
a
. C.
2
2
a
. D.
2; 3u 
Câu 44. Cho tam giác
ABC
vuông tại
A
có
3; 4AB AC
. Trên đoạn thẳng
BC
lấy điểm
M
sao
cho
2MB MC
. Tính tích vô hướng
.AM BC
.
A.
23
3
. B.
41
3
. C.
8
. D.
23
.
Câu 45. Cho hình vuông
ABCD
cạnh bằng 5. Tính
.. AB AC BC BD BA
A.
10 2
. B.
50
. C.
0
. D.
75
.
Câu 46. Cho hai vectơ
a
và
b
có
4a
,
5b
và
0
, 120ab
. Tính
ab
.
A.
21
. B.
21
. C.
41
. D.
41
.
Dạng 3: TÍNH TÍCH VÔ HƯỚNG BẰNG BIỂU THỨC TỌA ĐỘ
Câu 47. Cho hai vectơ
2; 1u 
,
3;4v 
. Tích
.uv
bằng
A.
11.
B.
10.
C.
5.
D.
2.
Câu 48. Trong mặt phẳng toạ độ
Oxy
, cho
(1;4)a
,
( 1;3)b 
. Khi đó giá trị tích vô hướng của hai
véctơ
a
và
b
là
A.
12
. B.
11.
C.
0.
D.
11.
Câu 49. Trong mặt phẳng tọa độ
Oxy
, cho hai vectơ
3u i j
và
22v j i
. Tính
.uv
.
A.
.4uv
. B.
.4uv
. C.
.2uv
. D.
.2uv
.
Câu 50. Cho
0; 3A
;
4;0B
;
2; 5C 
. Tính
.AB BC
.
Luyện tập VECTƠ
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
A.
16
. B.
9
. C.
10
. D.
9.
Câu 51. Cho
2; 3u
. Với giá trị nào của
m
thì
3;vm
vuông góc với
u
?
A.
1m
. B.
2m
. C.
1m
. D.
2m
.
Câu 52. Trong mặt phẳng tọa độ
Oxy
cho các vectơ
1; 3a
,
2;5b
. Tính tích vô hướng của
.ab
.
A.
7
. B.
13
. C.
17
. D.
13
.
Câu 53. Trong mặt phẳng tọa độ
Oxy
, cho
2; 5a 
và
;2b m m
. Tìm
m
biết
a
và
b
vuông
góc.
A.
10
3
m 
. B.
10
3
m 
. C.
10
7
m 
. D.
10
7
m
.
Câu 54. Trong mặt phẳng toạ độ
Oxy
, cho
(1;4)a
;
(4;0).b
Khi đó, cosin góc giữa hai vecto
a
và
b
là
A.
17
17
. B.
17
.
17
C.
0.
D.
2.
Câu 55. Trên mặt phẳng
,Oxy
cho hai vectơ
2;1a
và
2; 4 .b 
Khi đó góc giữa hai vectơ
a
và
b
bằng
A.
30
. B.
45
. C.
90
. D.
60
.
Câu 56. Cho hai vectơ
3;1a
,
3; 3b 
. Góc giữa hai vectơ
a
và
b
bằng
A.
15
. B.
30
. C.
45
. D.
60
.
Câu 57. Trong mặt phẳng
Oxy
, cho
1;2 , 4;1 , 5;4A B C
. Tính góc
.BAC
A.
45 .
B.
90
. C.
30
. D.
60
.
Câu 58. Trong mặt phẳng tọa độ
Oxy
, cho tam giác
ABC
biết
(1;2)A
,
(4;1)B
,
(5;4)C
. Tính góc
A
của
tam giác
ABC
.
A.
60
. B.
45
. C.
90
. D.
120
.
Câu 59. Tam giác
ABC
có
1;2A
,
0;4B
,
3;1C
. Góc
BAC
của tam giác
ABC
gần với giá trị nào
dưới đây?
A.
90
. B.
36 52
. C.
143 7
. D.
53 7
.
Câu 60. Trong mặt phẳng
Oxy
cho các điểm
1; 1 ; 3;1 ; 6;0A B C
. Khẳng định nào sau đây
đúng:
A.
4; 2 ; 3;1AB BC
. B.
o
135B
.
C.
20AB
. D.
3BC
.
Câu 61. Trong mặt phẳng
Oxy
cho các điểm
1;2 ; 5;8AB
. Điểm
M Ox
sao cho tam giác
MAB
vuông tại
A
. Diện tích tam giác
MAB
bằng
A.
10
. B.
18
. C.
24
. D.
12
.
Câu 62. Trong mặt phẳng tọa độ
Oxy
, cho điểm
2; 3A
. Tìm tọa độ điểm
B
thuộc trục tung, biết
khoảng cách giữa hai điểm
A
và
B
bằng
25
và điểm
B
có tung độ dương.
A.
0;1B
. B.
0;7B
. C.
2;0B
. D.
7;0B
.
Luyện tập VECTƠ
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 63. Trong mặt phẳng
Oxy
, cho hai điểm
3 ; 4A
và
2; 5B
. Tọa độ điểm
M
thuộc trục
Ox
cách đều hai điểm
;AB
là
A.
2
;0
5



. B.
2
;0
5



. C.
19
;
22



. D.
1
;0
2



.
Câu 64. Trong hệ toạ độ
Oxy
, cho hai điểm
(1; 1)A
và
( 2; 2)B 
. Điểm
C
thuộc trục
Ox
sao cho tam
giác
ABC
cân tại
A
là
A.
( 2;0)C
. B.
(0; 2)C
. C.
(4;0)C
. D.
(2;0)C
.
Câu 65. Trong mặt phẳng tọa độ
Oxy
cho hai điểm
1;2A
;
1;1B
. Điểm
M
thuộc trục
Oy
thỏa
mãn tam giác
MAB
cân tại
M
. Khi đó, độ dài đoạn
OM
bằng
A.
5
2
. B.
3
2
. C.
1
2
. D.
7
2
.
Câu 66. Trong mặt phẳng tọa độ
Oxy
, cho tam giác
ABC
có
1; 1A
,
4;1B
,
5; 7C
. Tính diện
tích
S
của tam giác
ABC
.
A.
26S
. B.
13S
. C.
3 13 65S 
. D.
3 13
2
S
.
Câu 67. Trong mặt phẳng với hệ tọa độ
Oxy
, cho hai điểm
3;2 ,A
4;3B
. Điểm
M
thuộc tia
Ox
.
Khẳng định nào dưới đây đúng?
A.
7;0M
. B.
5;0M
. C.
9;0M
. D.
2;0M
.
Câu 68. Cho hai điểm
1;3 , 8;2AB
. Gọi
C
là điểm thuộc trục hoành sao cho tam giác
ABC
vuông
tại
C
và
6OC
. Giá trị của biểu thức
22
5
CC
xy
là
A.
9
. B.
14
. C.
21
. D.
30
.
Câu 69. Trong mặt phẳng
Oxy
, cho hai điểm
1;2 , 3;1 .AB
Tìm tọa độ điểm
C
trên trục
Oy
sao
cho tam giác
ABC
vuông tại
A
.
A.
6;0C
. B.
0;6C
. C.
6;0C
. D.
0; 6C
.
Câu 70. Cho tam giác
ABC
có
1;2 , 0;3 ,C 5; 2 .AB
Tìm tọa độ chân đường cao hạ từ đỉnh
A
của
tam giác
ABC
.
A.
0;3
. B.
0; 3
. C.
3;0
. D.
3;0
.
Câu 71. Trong mặt phẳng
Oxy
, cho tam giác
ABC
biết
1;1A
,
3;1B
và
2;4C
. Tìm tọa độ trực
tâm
H
của tam giác
ABC
A.
1;1H
. B.
2;1H
. C.
1;2H
. D.
2;2H
.
Câu 72. Cho tam giác
ABC
có
1;3 , 3; 4AB
và
6;2C
. Trực tâm của tam giác
ABC
là
;H a b
.
Tính giá trị biểu thức
2T a b
.
A.
10
. B.
6
. C.
8
. D.
7
.
Câu 73. Trong mặt phẳng tọa độ
Oxy
cho tam giác
.ABC
Biết
3; 1 , 1;2AB
và
1; 1I
là trọng tâm
tam giác
.ABC
Trực tâm
H
của tam giác
ABC
có tọa độ
;.ab
Tính
3.ab
A.
2
3.
3
ab
B.
4
3.
3
ab
C.
3 1.ab
D.
3 2.ab
Luyện tập VECTƠ
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 74. Trong mặt phẳng tọa độ
Oxy
, cho hình thang cân
ABCD
với các đáy là
AB
và
CD
. Biết
1;2A
,
2; 3B
, điểm
C
nằm trên trục tung, điểm
D
nằm trên trục hoành. Tính
OC OD
.
A.
4
3
. B.
2
. C.
6
. D.
26
3
.
Câu 75. Trong mặt phẳng
Oxy
, cho bốn điểm
2;3 , 2;4 , 3;0 , 1; 1 .A B C D
Có bao nhiêu
điểm
M
thuộc đường thẳng
: 2 1d y x
sao cho
. 3?MA MB MC MD
A. 0. B. 1. C. 2. D. 3.
Câu 76. Trong mặt phẳng tọa độ
Oxy
cho hai điểm
3; 1A 
và
5;0B
. Biết có hai điểm
C
nằm
trên parabol
2
:2P y x x
sao cho tam giác
ABC
vuông tại
C
là
1 1 1 2 2 2
; , ;C x y C x y
.
Tính giá trị biểu thức
1 2 2 1
T x y x y
.
A.
4
. B.
5
. C.
6
. D.
5
.
Câu 77. Trong mặt phẳng
Oxy
, cho tam giác
ABC
với
2;4 , 1;1 , 7; 1A B C
. Biết
;0M a b a
là điểm nằm trong mặt phẳng
Oxy
thoả mãn tam giác
ABM
vuông cân tại
B
. Tính giá trị
34T a b
.
A.
2T
. B.
2T 
. C.
12T
. D.
12T 
.
Câu 78. Trong mặt phẳng tọa độ
Oxy
, cho
4;6A
;
5;1B
;
;3Cn
. Tìm
m
,
n
để
1
;
2
Im



là tâm
đường tròn ngoại tiếp tam giác
ABC
.
A.
5
2
m 
;
1n 
B.
5
2
m
;
1n 
. C.
5
2
m
;
1
2
n
n

. D.
5
2
m 
;
1
2
n
n

.
Câu 79. Trong mặt phẳng tọa độ
Oxy
, cho tam giác
ABC
, biết
;H a b
là toạ độ chân đường cao đỉnh
A
của tam giác
ABC
, biết toạ độ
3;1 , 4; 4BC
và trọng tâm
G
của tam giác
ABC
có toạ
độ
4;0G
. Tính
ab
.
A.
2
13
. B.
33
13
. C.
35
13
. D.
68
13
.
Dạng 4: CÁC BÀI TOÁN KHÁC
Câu 80. Cho
a
,
b
có
2ab
vuông góc với vectơ
54ab
và
ab
. Tính góc giữa vectơ
a
và
b
.
A.
30
. B.
45
. C.
90
. D.
60
.
Câu 81. Cho biết
; 120ab 
;
3; 3ab
. Độ dài của véctơ
ab
bằng
A.
33
. B.
32
. C.
3
2
. D.
33
2
.
Câu 82. Trong mặt phẳng tọa độ
Oxy
, cho ba điểm
3;4 , 2;1 , 2; 3M N P 
. Tìm điểm
I
trên
đường thẳng
NP
sao cho góc
135MIN 
.
A.
3;2I
. B.
2;3I
. C.
5;4I
. D.
4;5I
.
Câu 83. Cho tam giác đều
ABC
cạnh
3a
,
0a
. Lấy các điểm
M
,
N
,
P
lần lượt trên các cạnh
BC
,
CA
,
AB
sao cho
BM a
,
2CN a
,
AP x
03xa
. Tìm
x
để
AM PN
.
Luyện tập VECTƠ
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
A.
3
5
a
x
. B.
2
5
a
x
. C.
4
5
a
x
. D.
.
Câu 84. Cho tam giác
ABC
đều cạnh
a
. Trên các cạnh
,,BC CA AB
lần lượt lấy các điểm
,,M N P
sao
cho
2MC MB
,
1
2
NA NC
và
AP x
. Tìm
x
để
AM
vuông góc với
PN
.
A.
4
15
a
. B.
3
a
. C.
2 6 3
39
a
. D.
1 3 3
39
a
.
Câu 85. Cho hình chữ nhật
ABCD
thỏa
2AB a
,
AD a
. Gọi
,MN
là hai điểm thỏa mãn
2DM MC
,
AN xAB
,
x
. Tìm
x
để
AM
và
DN
vuông góc.
A.
3
7
x
. B.
3
8
x
. C.
1
2
x
. D.
2
5
x
.
Câu 86. Cho hình thoi
ABCD
có cạnh bằng
a
và
60BAD 
. Quỹ tích các điểm
M
thỏa mãn
2
.MA MC a
là đường tròn có bán kính bằng
A.
2a
. B.
7
2
a
. C.
3
2
a
. D.
a
.
Câu 87. Cho ba điểm không thẳng hàng
,,A B C
.Điều kiện cần và đủ để ba điểm
,,A B C
thỏa mãn điều
kiện
( ). 0CA CB AB
là:
A.
ABC
đều. B.
ABC
cân tại
C
.
C.
ABC
vuông tại
C
. D.
ABC
vuông cân tại
C
.
Câu 88. Cho hình thang vuông
ABCD
với đường cao
2,AB a
các cạnh đáy
AD a
và
3.BC a
Gọi
M
là điểm trên đoạn
AC
sao cho
..AM k AC
Tìm
k
để
BM
và
CD
vuông góc.
A.
4
.
9
B.
3
.
7
C.
1
.
3
D.
2
.
5
Câu 89. Cho hai điểm
,BC
phân biệt. Tập hợp những điểm
M
thỏa mãn
2
. CM CB CM
là
A. đường tròn đường kính
BC
. B. đường tròn
;B BC
.
C. đường tròn
;C CB
. D. đường tròn
;2C CB
.
Câu 90. Cho ba điểm
,,A B C
phân biệt. Tập hợp những điểm
M
mà
..CM CB CACB
là
A. đường tròn đường kính
AB
.
B. đường thẳng đi qua
A
và vuông góc với
BC
.
C. đường thẳng đi qua
B
và vuông góc với
AC
.
D. đường thẳng đi qua
C
và vuông góc với
AB
.
Câu 91. Cho tam giác
ABC
, điểm
J
thỏa mãn
3AK KJ
,
I
là trung điểm của cạnh
AB
,điểm
K
thỏa
mãn
20KA KB KC
. Một điểm
M
thay đổi thỏa mãn
3 . 2 0MK AK MA MB MC
.
Tập hợp điểm
M
là
A. đường tròn đường kính
IJ
. B. đường tròn đường kính
IK
.
C. đường tròn đường kính
JK
. D. đường trung trực đoạn
JK
.
Câu 92. Cho tam giác
ABC
có
G
là trọng tâm. Tập hợp các điểm
M
trong mặt phẳng thoả mãn
2 2 2 2 2 2
4MA MB MC GA GB GC
là
A. Đường tròn tâm
G
bán kính bằng
GB
. B. Đường tròn tâm
G
bán kính bằng
GA
.
C. Đường tròn tâm
G
bán kính bằng
GC
. D. Đường tròn tâm
G
bán kính bằng
4GA
.
Luyện tập VECTƠ
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 93. Cho
ABC
đều, cạnh bằng
0a
. Tìm quỹ tích điểm
M
thỏa mãn
2
7
. . .
4
a
MAMB MB MC MC MA
.
A. Quỹ tích điểm
M
là đường trung trực của
AB
.
B. Quỹ tích điểm
M
là đường thẳng đi qua trọng tâm của
ABC
và song song với
BC
.
C. Quỹ tích điểm
M
là đường tròn có bán kính bằng
6
2
a
.
D. Quỹ tích điểm
M
là đường tròn có bán kính bằng
3
2
a
.
Câu 94. Cho tam giác
ABC
đều cạnh
a
. Điểm
M
là một điểm thỏa mãn đẳng
thức
2
. . .
6
a
MAMB MB MC MC MA
. Biết tập hợp điểm
M
là một đường tròn. Bán kính
đường tròn đó là
A.
2R
. B.
3
a
R
. C.
4
a
R
. D.
2
a
R
.
_____________________HẾT_____________________
Huế, 10h00’ Ngày 02 tháng 12 năm 2022
Luyện tập VECTƠ
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
III. LỜI GIẢI BÀI TẬP TRẮC NGHIỆM
Dạng 1: GÓC GIỮA HAI VECTO
Câu 1. Cho tam giác
ABC
như hình vẽ.
Xác định góc
,AB AC
.
A.
45
. B.
120
. C.
15
. D.
165
.
Lời giải:
Ta có:
, 180 120 45 15 . AB AC BAC
Câu 2. Cho tam giác
ABC
đều. Góc giữa hai vectơ
AB
và
AC
bằng
A.
60
. B.
120
. C.
150
. D.
30
.
Lời giải:
C
B
A
Ta có
; 60 .AB AC BAC
Câu 3. Cho tam giác
ABC
đều. Góc giữa hai vectơ
AB
và
BC
bằng
A.
60
. B.
120
. C.
150
. D.
30
.
Lời giải:
C'
C
B
A
Ta có
; 180 120 .AB BC BAC
Câu 4. Cho tam giác
ABC
đều. Góc giữa hai vectơ
AB
và
CB
bằng
A.
60
. B.
120
. C.
150
. D.
30
.
Lời giải:
Luyện tập VECTƠ
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
C'
C
B
A
Ta có
; 60 .AB AC BAC
Câu 5. Cho hình bình hành
ABCD
. Góc giữa 2 vectơ
AB
và
BC
là
A.
BAC
. B.
ADC
. C.
BAD
. D.
ABC
.
Lời giải:
Theo tính chất hình bình hành ta có
BC AD
.
Vậy
,,AB BC AB AD BAD
.
Câu 6. Cho tam giác
ABC
cân tại
A
, góc
100BAC
. Số đo góc giữa hai véctơ
AB
và
BC
là
A.
140
. B.
80
. C.
40
. D.
100
.
Lời giải:
Xét tam giác
ABC
cân tại
A
, góc
0
100BAC
suy ra
0
40ABC ACB
.
Dựng
BM AB
, khi đó,
,,AB BC BM BC
00
180 140MBC ABC
.
Câu 7. Cho hai vectơ
a
;
b
khác vectơ
0
thỏa mãn
1
..
2
a b a b
. Khi đó góc giữa hai vectơ
a
;
b
bằn
A.
60
. B.
120
. C.
150
. D.
30
.
Lời giải:
Ta có
aa
.
Luyện tập VECTƠ
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Vậy
. . cos ,a b a b a b
1
.
2
ab
1
cos ,
2
ab
, 60ab
.
Câu 8. Cho hai vec tơ
a
và
b
biết
6, 12ab
và
10ab
. Khi đó,
cosin
của góc giữa hai vectơ
a
và
ab
bằng
A.
1
18
. B.
2
3
. C.
1
15
. D.
1
15
.
Lời giải:
Dựng
,AB a BC b
. Khi đó
a b AC
.
Ta được tam giác
ABC
có
6, 12, 10AB BC AC
và
,,a a b AB AC
.
2 2 2 2 2 2
2
2
10 6 12
.4
22
AC AB BC
BC AC AB BC AC AB AC AB
.
Vậy
. 4 1
cos ,
. 6.10 15
AB A C
AB AC
AB AC
.
Câu 9. Cho hai vecto
a
,
b
sao cho
a
2
,
2b
và hai vectơ
x a b
,
2y a b
vuông góc với
nhau. Tính góc giữa hai véc tơ
a
và
b
.
A.
120
. B.
60
. C.
90
. D.
30
.
Lời giải:
Vì hai véc tơ
x a b
,
2y a b
vuông góc với nhau nên
. 2 0a b a b
22
2 . 0a b a b
22
2. . .cos , 0a b a b a b
2
2
2. 2 2 2.2.cos , 0ab
cos , 0 , 90a b a b
.
Dạng 2: TÍNH TÍCH VÔ HƯỚNG
Câu 10. Trong các công thức sau, công thức nào xác định tích vô hướng của hai vectơ
,ab
cùng khác
0
?
A.
. . . ,a b a b cos a b
. B.
. . . ,a b a b cos a b
.
C.
. . .sin ,a b a b a b
. D.
..a b a b
.
Câu 11. Cho hai vectơ
a
và
b
. Đẳng thức nào sau đây sai?
A.
. . .cos ,a b a b a b
. B.
2 2 2
..a b a b
.
Luyện tập VECTƠ
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
C.
2 2 2
1
.
2
a b a b a b
. D.
2
2
aa
.
Lời giải:
Câu A, C, D: Đúng.
Câu B sai vì
2 2 2
2
. . .cos ,a b a b a b
.
Câu 12. Cho hai véctơ
,ab
khác véctơ-không thỏa mãn
..a b a b
. Khi đó, góc giữa hai vectơ
,ab
bằng
A.
45 .
B.
0.
C.
D.
90 .
Lời giải:
Ta có:
..
. . cos ,


a b a b
a b a b a b
0
cos ; 1 ; 180 a b a b
.
Câu 13. Cho hai vectơ
a
và
b
. Đẳng thức nào sau đây sai?
A.
2 2 2
1
..
2
a b a b a b
. B.
2 2 2
1
. . .
2
a b a b a b
C.
22
1
..
2
a b a b a b
. D.
22
1
. . .
4
a b a b a b
Lời giải:
Nhận thấy C và D chỉ khác nhau về hệ số
1
2
và
1
4
nên đáp án sai sẽ rơi vào C hoặcD.
D đúng, Ta có :
22
2 2 2 2
1
. . . 4 .. .. .
4
a b a b a b a b a b a b a b a b
A đúng, vì
22 22
. . . . . 2 .a b a b a b a a a b b a b b a b ab ba
2 2 2
1
.. .
2
a b a b a b
B đúng, vì
22 22
. . . . . 2 .a b a b a b a a a b b a b b a b ab ba
2 2 2
1
..
2
a b a b a b
.
Câu 14. Cho
3a
,
5b
,
o
, 45ab
. Tích vô hướng của
a
và
b
bằng
A.
15
2
. B.
15 3
2
. C.
15
2
. D.
15
2
.
Lời giải:
Ta có
o
15
. . .cos , 3.5.cos45
2
a b a b a b
.
Câu 15. Cho hai vectơ
a
và
b
. Biết
2, 3ab
và
, 30ab 
. Tính
ab
.
A.
11
. B.
13
. C.
12
. D.
14
.
Lời giải:
Luyện tập VECTƠ
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Ta có:
2
2 2 2 2
2 2 . .cos , a b a b ab a b a b a b
,
2
0
4 3 2.2. 3.cos30 13ab
13ab
.
Câu 16. Cho
,ab
có
4; 5.ab
và
. 10.ab
Tính
cos ; .ab
A.
3
cos ; .
2
ab
B.
2
cos ; .
2
ab
C.
1
cos ; .
2
ab
D.
1
cos ; .
2
ab
Lời giải:
Ta có
.1
cos ;
2
.

ab
ab
ab
.
Câu 17. Cho hai véctơ
,ab
thỏa mãn:
4; 3; 4a b a b
. Gọi
là góc giữa hai véctơ
,ab
. Khẳng
định nào dưới đây đúng?
A.
0
60
. B.
0
30
. C.
1
cos
3
. D.
3
cos
8
.
Lời giải:
Ta có:
2
22
4 16 2 . 16a b a b a a b b
22
3
4 2.4.3.cos 3 16 cos .
8

Câu 18. Cho tam giác
ABC
có
30 ,ABC
5, 8AB BC
. Tính
.BA BC
.
A.
20.
B.
20 3.
C.
20 2.
D.
40 3.
Lời giải:
Ta có
. . .cos 5.8.cos30 20 3.BA BC BA BC ABC
Vậy
. 20 3.BA BC
Câu 19. Cho hình vuông
ABCD
cạnh
2a
. Khi đó
.AB AC
bằng
A.
2
4a
. B.
2
2a
. C.
2
2
2
a
. D.
2
a
.
Lời giải:
Ta có
2
. .cos , 2 .2 2.cos45 4AB AC AB AC AB AC a a a
.
Câu 20. Cho tam giác vuông cân
ABC
có
AB AC a
. Tính
..AB AC
A.
2
a
. B.
2
2
a
. C.
0
. D.
2
3
2
a
.
Luyện tập VECTƠ
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Lời giải:
Tam giác
ABC
vuông cân tại
A
.
Câu 21. Cho tam giác
ABC
vuông tại
A
,
,2AB a BC a
. Tích vô hướng
.BA BC
bằng
A.
2
a
. B.
2
1
2
a
. C.
2
3a
. D.
2
a
.
Lời giải:
2
. . .cos .2 .
2
a
BA BC BA BC B a a a
a
.
Câu 22. Cho tam giác
ABC
vuông cân tại
,A
có
.AB a
Tích vô hướng
.BA B C
bằng
A.
2
.a
B.
2
.
2
a
C.
2
.
2
a
D.
2
.a
Lời giải:
Tam giác
ABC
vuông cân tại
,A
có
2.AB a BC a
2
, 45 . . .cos , . 2.cos45 .BA BC BA BC BA BC BA BC a a a
Câu 23. Cho tam giác
ABC
có
0
ˆ
90A
,
0
ˆ
60B
và
AB a
. Khi đó,
.AC CB
bằng
A.
2
2a
. B.
2
2a
. C.
2
3a
. D.
2
3a
.
Lời giải:
Luyện tập VECTƠ
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Gọi
D
là điểm đối xứng với
A
qua
C
.
Khi đó:
.AC CB
. . .cos150CD CB CD CB
2
3
3.2 . 3
2
a a a




.
Câu 24. Cho
ABC
vuông cân tại
A
, cạnh
5AB
. Tích vô hướng
.BC BA
bằng
A.
52
. B.
25
. C.
20
. D.
20
.
Lời giải:
Xét
ABC
vuông cân tại
A
, cạnh
5AB
suy ra
52BC
và
45ABC 
.
Ta có
. . .cos ; . .cos 5.5 2.cos45 25BC BA BC BA BC BA BC BA ABC
.
Câu 25. Góc tạo bởi
m
và
n
là
90
và
2021m
,
2022n
. Khi đó,
.mn
bằng
A.
4086462
. B.
0
. C.
4086462
. D.
1
.
Lời giải:
Ta có
. . .cos ; 2021.2022.cos90 0m n m n m n
.
Vậy
.0mn
.
Câu 26. Cho hai véc tơ
a
,
b
thỏa mãn
3, 4ab
và
( , ) 60ab 
. Tích vô hướng
.ab
bằng
A.
6
. B.
63
. C.
12
. D.
43
.
Lời giải:
Ta có
. . .cos( , ) 3.4.cos60 6a b a b a b
.
Câu 27. Cho hình bình hành
ABCD
, với
2AB
,
1BC
,
60BAD 
. Tích vô hướng
.AB AD
bằng
A.
1
. B.
1
. C.
1
2
. D.
1
2
.
Lời giải:
B
A
C
Luyện tập VECTƠ
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
. . .cos ; . .cos 2.1.cos60 1AB AD AB AD AB AD AB AD BAD
.
Câu 28. Cho tam giác
ABC
vuông tại
A
có
;3AB a AC a
và
AM
là trung tuyến. Tính tích vô
hướng
..B A AM
A.
2
.
2
a
B.
2
.a
C.
2
.a
D.
2
.
2
a
Lời giải:
C
B
A
M
Ta có tam giác
ABC
vuông tại
A
và có
AM
là trung tuyến nên
2
BC
AM
.
2 2 2 2
3
2 2 2
BC AB AC a a
AM a

.
Tam giác
AMB
có
AB BM AM a
nên là tam giác đều. Suy ra góc
60MAB 
.
Ta có
2
. . . .cos( , ) . .cos60
2
a
BA AM AB AM AB AM AB AM a a
.
Câu 29. Cho hình bình hành
ABCD
, với
2AB
,
1AD
,
60BAD 
. Tích vô hướng
.AB AD
bằng
A.
1
. B.
1
. C.
1
2
. D.
1
2
.
Lời giải:
B
D
C
A
. . .cos ; . .cos 2.1.cos60 1AB AD AB AD AB AD AB AD BAD
.
Câu 30. Cho hình bình hành
ABCD
, với
2AB
,
1AD
,
60BAD 
. Tích vô hướng
.BA BC
bằng
A.
1
. B.
1
2
C.
1
. D.
1
2
.
Lời giải:
Luyện tập VECTƠ
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
B
D
C
A
Theo giả thiết:
60 120BAD ABC
.
. . .cos ; . .cos 2.1.cos120 1BA BC BA BC BA BC AB BC ABC
.
Câu 31. Cho hình bình hành
ABCD
, với
2AB
,
1AD
,
60BAD 
. Độ dài đường chéo
AC
bằng
A.
5
. B.
7
. C.
5
. D.
7
2
.
Lời giải:
B
D
C
A
Ta có:
222
2 2 2
2 . 2 1 2.1 7AC AB AD AC AB AD AB AD AC AC
.
Câu 32. Cho hình bình hành
ABCD
, với
2AB
,
1AD
,
60BAD 
. Độ dài đường chéo
BD
bằng
A.
3
. B.
5
. C.
5
. D.
3
.
Lời giải:
B
D
C
A
2 2 2
2 2 2
2 . 2 1 2. 1BD BA BC BD BA BC BA BC BD
3BD
.
Câu 33. Cho hình vuông
ABCD
cạnh bằng 3, gọi
E
là điểm đối xứng của
D
qua
C
. Giá trị
.AE CD
bằng
A.
18
. B.
93
. C.
95
. D.
18
.
Lời giải:
Luyện tập VECTƠ
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Ta có
C
là trung điểm của
DE
nên
2.3 6DE 
.
Khi đó:
. . . .AE CD AD DE CD AD CD DE CD
0
0 . .cos180 6.3. 1 18DE CD
.
Câu 34. Cho hình bình hành
ABCD
có
2 , 3 , 60AB a AD a BAD
. Điểm
K
thuộc
AD
thỏa mãn
2AK DK
. Tính tích vô hướng
.BK A C
A.
2
3a
. B.
2
6a
. C.
0
. D.
2
a
.
Lời giải:
O
B
C
A
D
K
Ta có
2
3
BK AB AD
;
AC AB AD
Khi đó:
22
2 2 1
. ( )( )
3 3 3
BK AC AB AD AB AD AB AD ABAD
2 2 2
21
. 4 .9 2 .3 . 60
33
BK AC a a a a cos a
Câu 35. Cho hình vuông
ABCD
cạnh
5
. Khi đó,
.AB AC
bằng
A.
25.
B.
25 2.
C.
25 2
.
2
D.
25
2
.
Lời giải:
Ta có
ABCD
là hình vuông nên
52AC
; góc
0
45BAC
;
Tích vô hướng
0
. . .cos ; 5.5 2.cos45 25AB AC AB AC AB AC
.
Câu 36. Cho tam giác
ABC
đều cạnh
a
. Tính
..AB AC
A.
2
3
..
2
a
AB AC
B.
2
..
2
a
AB AC
C.
2
..AB AC a
D.
2
. 2 .AB AC a
Lời giải:
Tam giác
AB AC a
và
60BAC 
.
2
. . .cos . .cos60
2
a
AB AC AB AC A a a
.
Câu 37. Cho hình vuông
ABCD
cạnh
2a
,
M
là trung điểm của cạnh
CD
. Chọn khẳng định đúng.
Luyện tập VECTƠ
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
A.
2
.
2
a
AM DC
. B.
.0AM DC
. C.
2
.AM DC a
. D.
2
.2AM DC a
.
Lời giải:
Ta có
. ( ). . .AM DC AD DM DC AD DC DM DC
Mà
0
. . .cos90 0AD DC AD DC
Và
02
. . .cos0 .2 .1 2DM DC DM DC a a a
Vậy
2
. . 2AM DC DM DC a
.
Câu 38. Cho hình vuông
ABCD
có độ dài cạnh bằng
10
. Tính giá trị
.A B CD
.
A.
100
. B.
10
. C.
0
. D.
100
.
Lời giải:
Ta có
. . .cos , . .cos180 10.10. 1 100 ABCD AB CD AB CD ABCD
.
Câu 39. Cho tam giác đều
ABC
có độ dài cạnh bằng 4 và điểm
M
thỏa mãn
1
2
BM BC
. Tính
.BM B A
.
A.
.4BM BA
. B.
.4BM BA 
. C.
. 4 3BM BA
. D.
. 4 3BM BA 
.
Lời giải:
Ta có
11
2
22
BM BC BM BC
.
Khi đó
0
. . .cos ; 2.4.cos120 4BM BA BM BA BM BA
.
Câu 40. Cho hình vuông
ABCD
có độ dài các cạnh bằng
a
. Tính
.AC BD
.
A.
2
.2AC BD a
. B.
.0AC BD
. C.
.0AC BD
. D.
2
.2AC BD a
.
Lời giải:
Vì
ABCD
là hình vuông nên hai đường chéo
AC
và
BD
vuông góc nhau.
Hay
AC BD
nên
.0AC BD
.
Câu 41. Cho tam giác đều
có trọng tâm
G
và độ dài cạnh bằng
a
. Tính
..AB AG
A.
2
3
6
a
. B.
2
3
4
a
. C.
2
3
4
a
. D.
2
2
a
.
Luyện tập VECTƠ
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Lời giải:
Ta có
. .cos ,AB AG AB AG AB AG
; với
0
3
; ; , 30
3
a
AB AB a AG AG AB AG
.
Vậy
2
0
3
. . .cos30
32
aa
AB AG a
.
Câu 42. Cho tam giác đều ABC cạnh a, đường cao AH. Tính
.AC AC AB
A.
2
2
2
a
. B.
2
3
2
a
. C.
2
2
a
. D.
2
2
a
.
Lời giải:
Ta có
2
0
a
AC AC AB AC.BC CA.CB CA.CB.cosC a.a.cos60
2
.
Câu 43. Cho hình thoi
ABCD
tâm
O
có cạnh bằng
2a
và
60ABD 
. Gọi
I
là điểm thỏa mãn
20IC ID
. Tính tích vô hướng
.AO BI
.
A.
2
2
2
a
. B.
2
3
2
a
. C.
2
2
a
. D.
2; 3u 
Lời giải:
O
I
C
B
A
D
Do
ABCD
là hình thoi có cạnh bằng
a
và
60ABD 
nên
ABD
và
BCD
là các tam giác đều
cạnh
a
.
Ta có:
. . . D .AO BI AO BD DI AO B AO DI
22
..
33
AO DC AO AB




2
2 2. 3 2
. . .cos30
3 2 2
aa
a
. Vậy,
2
2
.
2
a
AO BI
.
Câu 44. Cho tam giác
ABC
vuông tại
A
có
3; 4AB AC
. Trên đoạn thẳng
BC
lấy điểm
M
sao
cho
2MB MC
. Tính tích vô hướng
.AM BC
.
Luyện tập VECTƠ
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
A.
23
3
. B.
41
3
. C.
8
. D.
23
.
Lời giải:
Ta có
1
22
3
MB MC AM AB AC
, do đó
1
.2
3
AM BC AB AC AC AB
.
Vì tam giác
ABC
vuông tại
A
nên
.0AB AC
.
Vậy
22
22
1 1 1 23
. 2 2 2.
3 3 3 3
AM BC AB AC AC AB AC AB AC AB
.
Câu 45. Cho hình vuông
ABCD
cạnh bằng 5. Tính
.. AB AC BC BD BA
A.
10 2
. B.
50
. C.
0
. D.
75
.
Lời giải:
Ta có:
.AB AC BC BD BA
.2AB AC BD
(Vì
BC BA BD
)
2 . .AB BD AC BD
2.AB BD
(Vì
. 0)AC BD
2 . .AB BA AB AD
2.AB BA
(Vì
.0AB AD
)
2
2. .cos180AB
50
.
Câu 46. Cho hai vectơ
a
và
b
có
4a
,
5b
và
0
, 120ab
. Tính
ab
.
A.
21
. B.
21
. C.
41
. D.
41
.
Lời giải:
Ta có
2
22
22
2 . 2 cos , 21a b a b a b a b a b a b a b
.
Dạng 3: TÍNH TÍCH VÔ HƯỚNG BẰNG BIỂU THỨC TỌA ĐỘ
Câu 47. Cho hai vectơ
2; 1u 
,
3;4v 
. Tích
.uv
bằng
A.
11.
B.
10.
C.
5.
D.
2.
Lời giải:
Với
2; 1
. 2. 3 1 4 10.
3;4
u
uv
v


Câu 48. Trong mặt phẳng toạ độ
Oxy
, cho
(1;4)a
,
( 1;3)b 
. Khi đó giá trị tích vô hướng của hai
véctơ
a
và
b
là
A.
12
. B.
11.
C.
0.
D.
11.
Lời giải:
Ta có:
. 1.( 1) 4.3 11ab
.
Luyện tập VECTƠ
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 49. Trong mặt phẳng tọa độ
Oxy
, cho hai vectơ
3u i j
và
22v j i
. Tính
.uv
.
A.
.4uv
. B.
.4uv
. C.
.2uv
. D.
.2uv
.
Lời giải:
Theo giả thiết ta có
1;3u
và
2;2v 
.
Khi đó
. 1. 2 3.2 4uv
.
Câu 50. Cho
0; 3A
;
4;0B
;
2; 5C 
. Tính
.AB BC
.
A.
16
. B.
9
. C.
10
. D.
9
.
Lời giải:
Ta có
4; 3AB 
;
6; 5BC
Vậy
.AB BC
4. 6 3 . 5 9
.
Câu 51. Cho
2; 3u
. Với giá trị nào của
m
thì
3;vm
vuông góc với
u
?
A.
1m
. B.
2m
. C.
1m
. D.
2m
.
Lời giải:
Ta có:
2. 3 3 . 0 2 v u m m
.
Câu 52. Trong mặt phẳng tọa độ
Oxy
cho các vectơ
1; 3a
,
2;5b
. Tính tích vô hướng của
.ab
.
A.
7
. B.
13
. C.
17
. D.
13
.
Lời giải:
Ta có
. 1.2 3 .5 13ab
.
Câu 53. Trong mặt phẳng tọa độ
Oxy
, cho
2; 5a 
và
;2b m m
. Tìm
m
biết
a
và
b
vuông
góc.
A.
10
3
m 
. B.
10
3
m 
. C.
10
7
m 
. D.
10
7
m
.
Lời giải:
Để
ab
thì
10
. 0 2 5 2 0
3
a b m m m
.
Câu 54. Trong mặt phẳng toạ độ
Oxy
, cho
(1;4)a
;
(4;0).b
Khi đó, cosin góc giữa hai vecto
a
và
b
là
A.
17
17
. B.
17
.
17
C.
0.
D.
2.
Lời giải:
Ta có:
. 4 17
cos( , )
17
17. 16
.
ab
ab
ab
.
Câu 55. Trên mặt phẳng
,Oxy
cho hai vectơ
2;1a
và
2; 4 .b 
Khi đó góc giữa hai vectơ
a
và
b
bằng
A.
30
. B.
45
. C.
90
. D.
60
.
Lời giải:
Luyện tập VECTƠ
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
.
. . .cos , cos , 0 , 90
.
ab
a b a b a b a b a b
ab
Câu 56. Cho hai vectơ
3;1a
,
3; 3b 
. Góc giữa hai vectơ
a
và
b
bằng
A.
15
. B.
30
. C.
45
. D.
60
.
Lời giải:
Ta có:
.
cos ;
.
ab
ab
ab
3 3 3 1
2
2.2 3

; 60ab
.
Câu 57. Trong mặt phẳng
Oxy
, cho
1;2 , 4;1 , 5;4A B C
. Tính góc
.BAC
A.
45 .
B.
90
. C.
30
. D.
60
.
Lời giải:
Ta có:
3; 1AB 
,
4;2AC
.
Khi đó:
2
2 2 2
3.4 1 .2
.2
cos cos ,
2
.
3 1 . 4 2
AB AC
BAC AB AC
AB AC

.
Suy ra
45
o
BAC
.
Câu 58. Trong mặt phẳng tọa độ
Oxy
, cho tam giác
ABC
biết
(1;2)A
,
(4;1)B
,
(5;4)C
. Tính góc
A
của
tam giác
ABC
.
A.
60
. B.
45
. C.
90
. D.
120
.
Lời giải:
Ta có:
(3; 1)AB 
,
(4;2)AC
. 3.4 ( 1).2 10AB AC
,
10AB
,
25AC
.
. 10 2
cos( ) cos( , )
.2
10.2 5
AB AC
A AB AC
AB AC
45A
.
Câu 59. Tam giác
ABC
có
1;2A
,
0;4B
,
3;1C
. Góc
BAC
của tam giác
ABC
gần với giá trị nào
dưới đây?
A.
90
. B.
36 52
. C.
143 7
. D.
53 7
.
Lời giải:
Ta có
1;2 ; 2; 1AB AC
.
. 2 2 4
cos
5
5. 5
.
AB AC
BAC
AB AC
143 7BAC
.
Câu 60. Trong mặt phẳng
Oxy
cho các điểm
1; 1 ; 3;1 ; 6;0A B C
. Khẳng định nào sau đây
đúng:
A.
4; 2 ; 3;1AB BC
. B.
o
135B
.
C.
20AB
. D.
3BC
.
Lời giải:
4; 2 ; 3; 1BA BC
Luyện tập VECTƠ
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
2 2 2 2
4.3 2 . 1
.2
cos cos ;
2
.
4 2 . 3 1
BA BC
B BA BC
BA BC

o
135B
.
Câu 61. Trong mặt phẳng
Oxy
cho các điểm
1;2 ; 5;8AB
. Điểm
M Ox
sao cho tam giác
MAB
vuông tại
A
. Diện tích tam giác
MAB
bằng
A.
10
. B.
18
. C.
24
. D.
12
.
Lời giải:
Vì
M Ox
nên có tọa độ
;0Ma
, ta có
1; 2 ; 6;6AM a AB
.
Tam giác
MAB
vuông tại
A
. 0 6 1 12 0 1AB AM a a
1;0M
.
Ta có
22
1 1 0 2 2 2AM
;
22
5 1 8 2 6 2AB
.
Vậy
11
. . .2 2.6 2 12
22
ABM
S AM AB
.
Câu 62. Trong mặt phẳng tọa độ
Oxy
, cho điểm
2; 3A
. Tìm tọa độ điểm
B
thuộc trục tung, biết
khoảng cách giữa hai điểm
A
và
B
bằng
25
và điểm
B
có tung độ dương.
A.
0;1B
. B.
0;7B
. C.
2;0B
. D.
7;0B
.
Lời giải:
Ta có
B
thuộc trục tung nên gọi
0,Bb
,
0b
.
Ta có
2; 3AB b
.
Theo giả thiết
2
22
22
1( )
2 5 2 3 20 6 7 0
7( )
b TM
AB b b b
bL

.
Vậy
0;1B
.
Câu 63. Trong mặt phẳng
Oxy
, cho hai điểm
3 ; 4A
và
2; 5B
. Tọa độ điểm
M
thuộc trục
Ox
cách đều hai điểm
;AB
là
A.
2
;0
5



. B.
2
;0
5



. C.
19
;
22



. D.
1
;0
2



.
Lời giải:
Vì
M Ox
nên
;0Mx
.
Ta có:
3; 4AM x
;
2; 5BM x
.
Để
M
cách đều
;AB
thì
AM BM
2 2 2 2
3 4 2 5xx
2
5
x
Vậy
2
;0
5
M



.
Câu 64. Trong hệ toạ độ
Oxy
, cho hai điểm
(1; 1)A
và
( 2; 2)B 
. Điểm
C
thuộc trục
Ox
sao cho tam
giác
ABC
cân tại
A
là
A.
( 2;0)C
. B.
(0; 2)C
. C.
(4;0)C
. D.
(2;0)C
.
Lời giải:
Luyện tập VECTƠ
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Ta có
22
( 2 1) ( 2 1) 10AB
Do điểm
( ; )C a b
thuộc trục
Ox
nên
( ;0)Ca
suy ra
22
( 1) (0 1)AC a
Tam giác
ABC
cân tại
A
AB AC
22
4
10 ( 1) (0 1)
2
a
a
a

Với
(4;0)C
, ta có
( 3; 1), (3;1)AB AC
suy ra 3 điểm
,,A B C
thẳng hàng, loại trường hợp này.
Với
( 2;0)C
, kiểm tra tương tự thấy thoả mãn. Vậy
( 2;0)C
.
Câu 65. Trong mặt phẳng tọa độ
Oxy
cho hai điểm
1;2A
;
1;1B
. Điểm
M
thuộc trục
Oy
thỏa
mãn tam giác
MAB
cân tại
M
. Khi đó, độ dài đoạn
OM
bằng
A.
5
2
. B.
3
2
. C.
1
2
. D.
7
2
.
Lời giải:
Điểm
M
thuộc trục
Oy
0;My
.
Ta có tam giác
MAB
cân tại
M
MA MB
2 2 2
2
1 2 1 1yy
4 4 1 2yy
3
2
y
.
Vậy
3
2
OM
.
Câu 66. Trong mặt phẳng tọa độ
Oxy
, cho tam giác
ABC
có
1; 1A
,
4;1B
,
5; 7C
. Tính diện
tích
S
của tam giác
ABC
.
A.
26S
. B.
13S
. C.
3 13 65S 
. D.
3 13
2
S
.
Lời giải:
Ta có:
3;2AB
,
4; 6AC
.0AB AC AB AC
1 1 1
. 9 4. 16 36 2.13 13
2 2 2
ABC
S AB AC
.
Câu 67. Trong mặt phẳng với hệ tọa độ
Oxy
, cho hai điểm
3;2 ,A
4;3B
. Điểm
M
thuộc tia
Ox
.
Khẳng định nào dưới đây đúng?
A.
7;0M
. B.
5;0M
. C.
9;0M
. D.
2;0M
.
Lời giải:
;0M Ox M x
(theo giả thiết thì
0x
).
Ta có
3; 2 ,AM x
4; 3BM x
Tam giác
ABM
vuông tại
M
.0AM BM
3 4 2 3 0xx
2
60xx
2 ( )
3 ( )
x TM
xL

.
Vậy
2x
thỏa mãn yêu cầu bài toán.
Câu 68. Cho hai điểm
1;3 , 8;2AB
. Gọi
C
là điểm thuộc trục hoành sao cho tam giác
ABC
vuông
tại
C
và
6OC
. Giá trị của biểu thức
22
5
CC
xy
là
Luyện tập VECTƠ
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
A.
9
. B.
14
. C.
21
. D.
30
.
Lời giải:
Gọi
;0Cx
là điểm thuộc trục hoành. Ta có:
1; 3 , 8; 2AC x BC x
.
Do tam giác
ABC
vuông tại
C
nên
.0AC BC
2
7
1 . 8 3 . 2 0 9 14 0
2
x
x x x x
x
Vì
6OC
nên ta chọn
2x
. Suy ra
2;0C
. Vậy
22
59
CC
xy
.
Câu 69. Trong mặt phẳng
Oxy
, cho hai điểm
1;2 , 3;1 .AB
Tìm tọa độ điểm
C
trên trục
Oy
sao
cho tam giác
ABC
vuông tại
A
.
A.
6;0C
. B.
0;6C
. C.
6;0C
. D.
0; 6C
.
Lời giải:
C Oy
0;Cy
4; 1AB
,
1; 2AC y
.
Ba điểm
A
,
B
,
C
tạo thành một tam giác vuông tại
A
0
0
AB
AC
AB AC
.0AB AC
6.y
Vậy
0;6 .C
Câu 70. Cho tam giác
ABC
có
1;2 , 0;3 ,C 5; 2 .AB
Tìm tọa độ chân đường cao hạ từ đỉnh
A
của
tam giác
ABC
.
A.
0;3
. B.
0; 3
. C.
3;0
. D.
3;0
.
Lời giải:
A
B
C
Ta có
1;1 ; 6; 4 ; 5; 5 .AB AC BC
Nhận thấy rằng
. 1.5 1.( 5) 0AB BC
nên tam giác
ABC
vuông tại
.B
Vậy chân đường cao hạ từ đỉnh
A
của tam giác
ABC
trùng với đỉnh
0; 3 .B
Câu 71. Trong mặt phẳng
Oxy
, cho tam giác
ABC
biết
1;1A
,
3;1B
và
2;4C
. Tìm tọa độ trực
tâm
H
của tam giác
ABC
A.
1;1H
. B.
2;1H
. C.
1;2H
. D.
2;2H
.
Lời giải:
Gọi
;H x y
.
Luyện tập VECTƠ
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Vì
H
là trực tâm của tam giác
ABC
nên ta có
.0
.0
AH BC
BH AC
(1)
Mà
1; 1AH x y
,
1;3BC 
,
3; 1BH x y
,
3;3AC
.
Do đó
1. 1 3 1 0
2
1
2
3 3 3 1 0
xy
x
y
xy


. Vậy
2;2H
.
Câu 72. Cho tam giác
ABC
có
1;3 , 3; 4AB
và
6;2C
. Trực tâm của tam giác
ABC
là
;H a b
.
Tính giá trị biểu thức
2T a b
.
A.
10
. B.
6
. C.
8
. D.
7
.
Lời giải:
Ta có:
1; 3
3;6
3; 4
5; 1
AH a b
BC
BH a b
AC

.
Theo giả thiết
H
là trực tâm tam giác
ABC
nên ta có
AH BC
BH AC
45
3 1 6 3 0
. 0 2 7
11
5 19 16
5 3 1 4 0
.0
11
a
ab
BC AH a b
ab
ab
AC BH
b

.
Suy ra
45 16
;
11 11
H



và
45 16
27
11 11
T



.
Câu 73. Trong mặt phẳng tọa độ
Oxy
cho tam giác
.ABC
Biết
3; 1 , 1;2AB
và
1; 1I
là trọng tâm
tam giác
.ABC
Trực tâm
H
của tam giác
ABC
có tọa độ
;.ab
Tính
3.ab
A.
2
3.
3
ab
B.
4
3.
3
ab
C.
3 1.ab
D.
3 2.ab
Lời giải:
C
B
A
H
Giả sử
;
CC
C x y
và
;y
HH
Hx
. Có I là trọng tâm tam giác ABC nên ta có
Luyện tập VECTƠ
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
1
3
4
3
A B C
I
C
C
A B C
I
x x x
x
x
y
y y y
y





1; 4C
Ta có
3; 1 ; 2; 6
HH
AH x y BC
;
1; 2 ; 2; 3
HH
BH x y AC
H
là trực tâm tam giác
ABC
nên
10
2 3 6 1 0
.0
3
8
2 1 3 2 0
.0
9
H
HH
HH
H
x
xy
AH BC
xy
BH AC
y



10 8
;
39
ab
2
3
S
.
Câu 74. Trong mặt phẳng tọa độ
Oxy
, cho hình thang cân
ABCD
với các đáy là
AB
và
CD
. Biết
1;2A
,
2; 3B
, điểm
C
nằm trên trục tung, điểm
D
nằm trên trục hoành. Tính
OC OD
.
A.
4
3
. B.
2
. C.
6
. D.
26
3
.
Lời giải:
Tứ giác
ABCD
là hình thang cân có các đáy là
AB
và
CD
CD t AB
với
0t
.
Vì
C Oy
nên
0;Cc
,
D Ox
nên
;0Dd
.
Ta có
1; 5 ; ;AB CD d c
.
.
55
d t d t
CD t AB
c t c t



.
Vì
ABCD
là hình thang cân nên
AC BD
22
AC BD
2 2 2 2
0 1 2 2 0 3 *cd
.
Thay
5ct
dt
vào
*
ta được:
22
1 5 2 2 9tt
2
24 16 8 0tt
1
1
3
t ktm
t tm

. Với
15
0;
33
tC



và
1
;0
3
D



.
Vậy
51
2
33
OC OD
.
Câu 75. Trong mặt phẳng
Oxy
, cho bốn điểm
2;3 , 2;4 , 3;0 , 1; 1 .A B C D
Có bao nhiêu
điểm
M
thuộc đường thẳng
: 2 1d y x
sao cho
. 3?MA MB MC MD
A. 0. B. 1. C. 2. D. 3.
Lời giải:
Luyện tập VECTƠ
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Gọi
;M a b
là tọa độ điểm cần tìm.
Ta có:
. 3 . 3.MA MB MC MD AM BM CM DM
Lại có:
;M a b
thuộc đường thẳng
: 2 1 2 1 ;2 1 .d y x b a M a a
Khi đó:
2;2 4
2;2 5 3 3;6 10
3;2 1
AM a a
BM a a AM BM CM a a
CM a a
1;2DM a a
Mà
.3AM BM CM DM
2
0
3 3 . 1 6 10 .2 3 15 20 0
4
3
a
a a a a a a
a
.
Vậy
45
0;1 hay ; .
33
MM



Câu 76. Trong mặt phẳng tọa độ
Oxy
cho hai điểm
3; 1A 
và
5;0B
. Biết có hai điểm
C
nằm
trên parabol
2
:2P y x x
sao cho tam giác
ABC
vuông tại
C
là
1 1 1 2 2 2
; , ;C x y C x y
.
Tính giá trị biểu thức
1 2 2 1
T x y x y
.
A.
4
. B.
5
. C.
6
. D.
5
.
Lời giải:
Gọi
2
;2C x x x
2
2
3 ; 1 2
5 ; 2
CA x x x
CB x x x
.
Do tam giác
ABC
vuông tại
C
nên ta có
.0CACB
22
3 5 1 2 2 0x x x x x x
432
4 6 4 15 0x x x x
2
22
2
2 3 0 1
2 3 2 5 0
2 5 0 2
xx
x x x x
xx
.
Giải (1) được
1
2
1 1;3
3 3;3
xC
xC

.
Luyện tập VECTƠ
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Giải (2): Vô nghiệm.
Vậy có hai điểm thỏa mãn yêu cầu bài toán và
1 .3 3.3 6T
.
Câu 77. Trong mặt phẳng
Oxy
, cho tam giác
ABC
với
2;4 , 1;1 , 7; 1A B C
. Biết
;0M a b a
là điểm nằm trong mặt phẳng
Oxy
thoả mãn tam giác
ABM
vuông cân tại
B
. Tính giá trị
34T a b
.
A.
2T
. B.
2T 
. C.
12T
. D.
12T 
.
Lời giải:
Ta có
1;3 ; 1; 1B abA BM 
Vì tam giác
ABM
vuông cân tại
B
, suy ra:
22
22
22
1
3 4 0
.0
2 2 8 0
1 3 1 0
113 1
ab
BM BA
a b a b
AB
a
ab
B
b
M



2
2
2
43
43
2
0
0
4 3 4 3 2 8 0
2
2
4
b
ab
ab
a
b
b
b b bb
b
l
a






.
Vậy toạ độ điểm
2;2M
, suy ra
3 4 2T a b
.
Câu 78. Trong mặt phẳng tọa độ
Oxy
, cho
4;6A
;
5;1B
;
;3Cn
. Tìm
m
,
n
để
1
;
2
Im



là tâm
đường tròn ngoại tiếp tam giác
ABC
.
A.
5
2
m 
;
1n 
B.
5
2
m
;
1n 
. C.
5
2
m
;
1
2
n
n

. D.
5
2
m 
;
1
2
n
n

.
Lời giải:
1; 5AB 
,
4; 9AC n
.
,,A B C
là
3
đỉnh của một tam giác
AB
và
AC
không cùng
phương
9 11
4
55
nn
.
Ta có:
9
;6
2
IA m


;
11
;1
2
IB m


;
1
;3
2
IC n m


.
I
là tâm đường tròn ngoại tiếp tam giác
ABC
khi
22
22
IA IB
IA IC
22
22
22
22
9 11
61
22
91
63
22
mm
m n m
Luyện tập VECTƠ
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
22
22
25 10 0
91
63
22
m
m n m

5
5
2
2
13
1
22
/
1 3 2
22
m
m
n
n
tm
n
n







.
Vậy
5
2
m
;
1
2
n
n

.
Câu 79. Trong mặt phẳng tọa độ
Oxy
, cho tam giác
ABC
, biết
;H a b
là toạ độ chân đường cao đỉnh
A
của tam giác
ABC
, biết toạ độ
3;1 , 4; 4BC
và trọng tâm
G
của tam giác
ABC
có toạ
độ
4;0G
. Tính
ab
.
A.
2
13
, B.
33
13
. C.
35
13
. D.
68
13
.
Lời giải:
4;0G
là trọng tâm tam giác
ABC
, suy ra
5
3
3
3
A B C
G
A
A
A B C
G
xxx
x
x
y
yyy
y



Gọi
;H x y
là chân đường cao đỉnh
A
, suy ra
. 0 1 5 5 3 0 5 10 0 1AH BC x y x y
Vì
H BC
nên
;BH BC
cùng phương, suy ra
31
5 16 0 2
15
xy
xy

Từ
1
và
2
ta có hệ
35
5 10
13
5 16 33
13
x
xy
xy
y


.
Toạ độ điểm
35 33
;
13 13
H



, suy ra
68
13
ab
.
Dạng 4: CÁC BÀI TOÁN KHÁC
Câu 80. Cho
a
,
b
có
2ab
vuông góc với vectơ
54ab
và
ab
. Tính góc giữa vectơ
a
và
b
.
A.
30
. B.
45
. C.
90
. D.
60
.
Lời giải:
+ Vì
2ab
vuông góc với vectơ
54ab
nên
2 . 5 4 0 a b a b
.
22
5 8 6 . 0 a b a b
22
58
.
6

ab
ab
22
58
.
6

ab
ab
(1)
Luyện tập VECTƠ
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
+ Theo đề
22
a b a b
.
+ Từ (1) ta được
2
.
2
a
ab
+ Ta có
2
0
2
.1
2
cos , , 60
2
a
ab
a b a b
ab
a
.
+ Kết luận: Góc giữa vectơ
a
và
b
bằng
0
60
.
Câu 81. Cho biết
; 120ab 
;
3; 3ab
. Độ dài của véctơ
ab
bằng
A.
33
. B.
32
. C.
3
2
. D.
33
2
.
Lời giải:
Ta có
2
2 2 2
22
2. . 2. . . ;a b a b a a b b a b a b cos a b
1
9 9 2.3.3. 27
2



.
Suy ra:
33ab
.
Câu 82. Trong mặt phẳng tọa độ
Oxy
, cho ba điểm
3;4 , 2;1 , 2; 3M N P 
. Tìm điểm
I
trên
đường thẳng
NP
sao cho góc
135MIN 
.
A.
3;2I
. B.
2;3I
. C.
5;4I
. D.
4;5I
.
Lời giải:
+) Ta có
4; 4NP
;
Gọi
; 2 ; 1I x y IN x y
.
Vì
,I NP IN NP
là hai vectơ cùng phương
21
1 ; 1 .
44
xy
y x I x x


+) Ta có
.
cos = cos , (1).
.
IM NP
MIN IM NP
IM NP
Vì
135MIN 
và
3 ; 5 ; 4; 4IM x x NP
nên từ
1
ta có:
2
28
1
2
2 16 34. 2
x
xx


22
5 5; 4
2 8 2 16 34 8 15 0
3 3; 2
xI
x x x x x
xI


+) Trường hợp 1:
os os
.1
5; 4 2;0 ; 3; 3 ,
2
.
IM IN
I IM IN c MIN c IM IN
IM IN
45MIN 
(loại).
+) Trường hợp 2:
os os
.1
3;2 0; 2 ; 1; 1 ,
2
.
IM IN
I IM IN c MIN c IM IN
IM IN
135MIN 
(TM).
Vậy điểm cần tìm là
3;2 .I
Luyện tập VECTƠ
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 83. Cho tam giác đều
ABC
cạnh
3a
,
0a
. Lấy các điểm
M
,
N
,
P
lần lượt trên các cạnh
BC
,
CA
,
AB
sao cho
BM a
,
2CN a
,
AP x
03xa
. Tìm
x
để
AM PN
.
A.
3
5
a
x
. B.
2
5
a
x
. C.
4
5
a
x
. D.
.
Lời giải:
Ta có
1
3
AM AB BM AB BC
1 2 1
3 3 3
AB AC AB AB AC
.
Ta có
1
33
x
PN AN AP AC AB
a
.
Để
AM PN
thì
2 1 1
. 0 0
3 3 3 3
x
AM PN AB AC AC AB
a
22
2 2 1
. . 0
9 9 9 9
xx
AB AC AB AC AB AC
aa
.
22
2 2 1
. .cos60 3 3 . .cos60 0
9 9 9 9
xx
AB AC a a AB AC
aa
22
2 1 2 1 1
3 3 9 9 3 3 0
9 2 9 9 9 2
xx
a a a a a a
aa
2
54
20
25
a
a ax x
.
Vậy
4
5
a
x
thì
AM PN
.
Câu 84. Cho tam giác
ABC
đều cạnh
a
. Trên các cạnh
,,BC CA AB
lần lượt lấy các điểm
,,M N P
sao
cho
2MC MB
,
1
2
NA NC
và
AP x
. Tìm
x
để
AM
vuông góc với
PN
.
A.
4
15
a
. B.
3
a
. C.
2 6 3
39
a
. D.
1 3 3
39
a
.
Lời giải:
Luyện tập VECTƠ
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Đặt
,AB b AC c
Ta có
1 1 1 2
3 3 3 3
AM AB BM AB BC AB AC AB c b
1
3
x
PN AN AP c b
a
Để
1 2 1
. 0 0
3 3 3
x
AM PN AM PN c b c b
a
22
2 3 0 . 3 . 2 . . 6 . 0c b ac xb a c xb c a b c x b
22
. 2 3 . 6 . 0a c a x b c x b
2 0 2
. 2 3 . . .cos60 6 . 0a a a x a a x a
2
3
60
2
x
a a a x



15 4
20
2 15
a
a x x
.
Câu 85. Cho hình chữ nhật
ABCD
thỏa
2AB a
,
AD a
. Gọi
,MN
là hai điểm thỏa mãn
2DM MC
,
AN xAB
,
x
. Tìm
x
để
AM
và
DN
vuông góc.
A.
3
7
x
. B.
3
8
x
. C.
1
2
x
. D.
2
5
x
.
Lời giải:
N
M
D
C
B
A
Cách 1. Xét tam giác vuông
DAN
có
tan
AN
ADN
AD
Xét tam giác vuông
ADM
có
cot
AD
MAD
DM
Vì
AM DN
nên
90ADN MAD
.
Do đó
3 3 3
tan cot .
2
2 2 4 4
3
AN AD AD a
ADN MAD AN a
AD DM a
DC
.
Suy ra
3 1 3 3
.
4 2 8 8
AN a
AN AB
AB a
. Vậy
3
8
x
.
Cách 2.
Ta có
22
33
AM AD DM AD DC AD AB
Ta có
DN AN AD xAB AD
.
Ta có
2
. 0 . 0
3
AM DN AB AD xAB AD



Luyện tập VECTƠ
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
22
22
. . 0
33
xAB AB AD xAD AB AD
22
23
.4 0
38
x a a x
.
Cách 3. Chọn hệ trục tọa độ
Oxy
với
0;0D
,
2 ;0Ca
;
0;Aa
;
2;B a a
.
Ta suy ra
4
;0
3
a
M



,
; , 0 2N t a t a
;
4
;
3
a
AM a



;
;DN t a
.
Ta có
2
43
. 0 0
34
aa
AM DN AM DN t a t
.
Do đó
33
; ; ;0 ; 2 ;0
44
aa
N a AN AB a

.Ta có
3
8
AN AB
. Vậy
3
8
x
.
Câu 86. Cho hình thoi
ABCD
có cạnh bằng
a
và
60BAD 
. Quỹ tích các điểm
M
thỏa mãn
2
.MA MC a
là đường tròn có bán kính bằng
A.
2a
. B.
7
2
a
. C.
3
2
a
. D.
a
.
Lời giải:
a
60
°
O
C
D
A
B
Gọi
O
là giao của hai đường chéo
AC
và
BD
.
Ta có:
.MA MC MO OA MO OC MO OA MO OA
2
2
22
22
33
24
aa
MO OA MO MO




Do đó
2
22
77
.
42
aa
MA MC a MO MO
.
Vậy tập hợp các điểm
M
thỏa mãn yên cầu bài toán là đường tròn tâm
O
bán kính bằng
7
2
a
.
Câu 87. Cho ba điểm không thẳng hàng
,,A B C
.Điều kiện cần và đủ để ba điểm
,,A B C
thỏa mãn điều
kiện
( ). 0CA CB AB
là:
A.
ABC
đều. B.
ABC
cân tại
C
.
C.
ABC
vuông tại
C
. D.
ABC
vuông cân tại
C
.
Lời giải:
Gọi
M
là trung điểm của
AB
Luyện tập VECTƠ
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Ta có
2CA CB CM
. Nên
( ). 0 2 . 0 .CA CB AB CM AB CM AB
Vậy
ABC
cân tại
C
.
Câu 88. Cho hình thang vuông
ABCD
với đường cao
2,AB a
các cạnh đáy
AD a
và
3.BC a
Gọi
M
là điểm trên đoạn
AC
sao cho
..AM k AC
Tìm
k
để
BM
và
CD
vuông góc.
A.
4
.
9
B.
3
.
7
C.
1
.
3
D.
2
.
5
Lời giải:
H
M
D
C
B
A
Hạ
DH BC
dễ thấy
ABHD
là hình chữ nhật và
.BH a
Từ giả thiết
..AM k AC AB BM k AB BC
1 . . .BM k AB k BC
Mặt khác:
.DC DH HC
Theo chứng minh trên ta có
DH AB
và
2
3
HC BC
nên
2
.
3
DC AB BC
. 0 * .BM CD BM DC
Do giả thiết ta có
.0AB BC
nên
2
* 1 . . . 0
3
k AB k BC AB BC



2 2 2 2
22
1 . . . 0 4 1 . .9 0
33
k
k AB k BC k a a
2
4 4 6 0 .
5
k k k
Câu 89. Cho hai điểm
,BC
phân biệt. Tập hợp những điểm
M
thỏa mãn
2
. CM CB CM
là
A. đường tròn đường kính
BC
. B. đường tròn
;B BC
.
C. đường tròn
;C CB
. D. đường tròn
;2C CB
.
Lời giải:
22
. . 0 . 0 CM CB CM CM CB CM CM MB
.
Tập hợp điểm
M
là đường tròn đường kính
BC
.
Câu 90. Cho ba điểm
,,A B C
phân biệt. Tập hợp những điểm
M
mà
..CM CB CACB
là
A. đường tròn đường kính
AB
.
B. đường thẳng đi qua
A
và vuông góc với
BC
.
C. đường thẳng đi qua
B
và vuông góc với
AC
.
D. đường thẳng đi qua
C
và vuông góc với
AB
.
Lời giải:
. . . . 0 . 0 . 0 CM CB CACB CM CB CACB CM CA CB AM CB
.
Tập hợp điểm
M
là đường thẳng đi qua
A
và vuông góc với
BC
.
Luyện tập VECTƠ
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 91. Cho tam giác
ABC
, điểm
J
thỏa mãn
3AK KJ
,
I
là trung điểm của cạnh
AB
,điểm
K
thỏa
mãn
20KA KB KC
. Một điểm
M
thay đổi thỏa mãn
3 . 2 0MK AK MA MB MC
.
Tập hợp điểm
M
là
A. đường tròn đường kính
IJ
. B. đường tròn đường kính
IK
.
C. đường tròn đường kính
JK
. D. đường trung trực đoạn
JK
.
Lời giải:
J
K
I
C
B
A
Ta có:
2 4 2 4MA MB MC MK KA KB KC MK
.
Lấy điểm
J
thỏa mãn
3AK KJ
. Ta có
1
2 4 2
AB AC
AK AI AC
, mà
3AK KJ
nên
1 4 1 2
3 3 3 3
AJ AK KJ AK AK AK AB AC
.
Lại có
1 2 2 2 2
3 3 3 3 3
BJ AJ AB AB AC AB AB AC BC
.
Suy ra
J
là điểm cố định nằm trên đoạn thẳng
BC
xác định bởi hệ thức
2
3
BJ BC
.
Ta có
3 3 3 3MK AK MK KJ MJ
.
Như vậy
3 . 2 0 3 . 4 0 . 0MK AK MA MB MC MJ MK MJ MK
.
Từ đó suy ra điểm
M
thuộc đường tròn đường kính .
Vì , là các điểm cố định nên điểm luôn thuộc một đường tròn đường kính là đường tròn cố
định.
Câu 92. Cho tam giác
ABC
có
G
là trọng tâm. Tập hợp các điểm
M
trong mặt phẳng thoả mãn
2 2 2 2 2 2
4MA MB MC GA GB GC
là
A. Đường tròn tâm
G
bán kính bằng
GB
. B. Đường tròn tâm
G
bán kính bằng
GA
.
C. Đường tròn tâm
G
bán kính bằng
GC
. D. Đường tròn tâm
G
bán kính bằng
4GA
.
Lời giải:
Ta có
G
là trọng tâm tam giác
ABC
nên
0GA GB GC
.
Khi đó
2 2 2
2 2 2
2 2 2
2 2 2 2
2 2 2 2
32
3
MA MB MC MA MB MC
MG GA MG MG
GA GB GC MG GA GB GC
GA GBM GC
GB GC
MG
G
Suy ra
2 2 2 2 2 2
4MA MB MC GA GB GC
2 2 2 2 2 2 2
34MG GA GB GC GA GB GC
Luyện tập VECTƠ
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
22
33MG GA MG GA
Do điểm
G
cố định và độ dài
GA
không đổi nên điểm
M
thuộc đường tròn tâm
G
bán kính
bằng
GA
.
Vậy tập hợp điểm
M
thoả mãn đề bài là đường tròn tâm
G
bán kính bằng
GA
.
Câu 93. Cho
ABC
đều, cạnh bằng
0a
. Tìm quỹ tích điểm
M
thỏa mãn
2
7
. . .
4
a
MAMB MB MC MC MA
.
A. Quỹ tích điểm
M
là đường trung trực của
AB
.
B. Quỹ tích điểm
M
là đường thẳng đi qua trọng tâm của
ABC
và song song với
BC
.
C. Quỹ tích điểm
M
là đường tròn có bán kính bằng
6
2
a
.
D. Quỹ tích điểm
M
là đường tròn có bán kính bằng
3
2
a
.
Lời giải:
Gọi
O
là trọng tâm của
ABC
, ta có:
3MA MB MC MO
22
9.MA MB MC MO
2 2 2 2
2 . . . 9MA MB MC MA MB MB MC MC MA MO
Mà:
2 2 2
2 2 2
2 2 2
MA MB MC MA MB MC MO OA MO OB MO OC
2 2 2 2 2 2
3 2 . 3MO OA OB OC OA OB OC MO MO a
Từ đó, ta có:
2 2 2 2
2 2 2
9
67
. . .
2 2 4
MO MA MB MC
MO a a
MAMB MB MC MC MA
2
2
33
42
aa
MO MO
.
Vậy quỹ tích điểm
M
là đường tròn tâm
O
,
bán kính bằng
3
2
a
.
Câu 94. Cho tam giác
ABC
đều cạnh
a
. Điểm
M
là một điểm thỏa mãn đẳng
thức
2
. . .
6
a
MAMB MB MC MC MA
. Biết tập hợp điểm
M
là một đường tròn. Bán kính
đường tròn đó là
A.
2R
. B.
3
a
R
. C.
4
a
R
. D.
2
a
R
.
Lời giải:
Gọi
G
là trọng tâm tam giác
ABC
,
I
là trung điểm
BC
. Khi đó ta có:
2
2
39MA MB MC MG MA MB MC MG
2 2 2
2
2 . . . 9MA MB MC MAMB MB MC MC MA MG
2
2 2 2
2
9
3
a
MG GA MG GB MG GC MG
Luyện tập VECTƠ
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
2
2 2 2 2
2
3 2 9
3
a
MG MG GA GB GC GA GB GC MG
22
2 2 2 2
4
6 3 6 3.
3 9 3
aa
MG GA MG AI
2
2
2
43
6.
3 2 3 3
a a a
MG MG




.
Vậy tập hợp điểm
M
là đường tròn tâm
G
bán kính
3
a
R
.
_____________________HẾT_____________________
Huế, 10h00’ Ngày 02 tháng 12 năm 2022
| 1/41
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Luyện tập VECTƠ Chủ đề:
TÍCH VÔ HƯỚNG CỦA 2 VECTƠ I. TÓM TẮT LÝ THUYẾT
1. Định nghĩa góc giữa hai vectơ A B u O v
Cho hai vectơ u và v khác vectơ 0 . Từ một điểm O tuỳ ý, vẽ các vec tơ OA u và OB v . Khi đó
số đo của góc AOB được gọi là số đo của góc giữa hai vectơ u, v , kí hiệu là u, v . Chú ý
Quy ước rằng góc giữa hai vectơ u và 0 có thể nhận một giá trị tuỳ ý từ 0 đến 180 . 
Nếu u, v   90 thì ta nói rằng u và v vuông góc với nhau, kí hiệu là u v hoặc v u.
Đặc biệt: Vectơ 0 vuông góc với mọi vectơ.
2. Tích vô hướng của hai vectơ khác vectơ-không u và v là một số, kí hiệu là .
u v được xác định bởi
công thức sau: u.v u . v .cos u,v . Chú ý
u v u.v  0  2 Tích .
u u còn được viết là u và được gọi là bình phương vô hướng của u.  2 Ta có 2
u u . u .cos 0  u .
3. Biểu thức toạ độ và tính chất của tích vô hướng
Tích vô hướng của hai vectơ u ( ;
x y) và v(x ; y ) được tính theo công thức: u.v  .
x x  u.u Nhận xét
Hai vectơ u và v vuông góc với nhau khi và chỉ khi . x x  . y y  0.
Bình phương vô hướng của vectơ u( ; x y) là 2 2 2
u x y . u.v xx  yyu v  
Nếu u  0 và v  0 thì cos  ,  2 2 2 2 u . v
x y . x  yTính chất
Với ba vectơ u, v, w bất kì và mọi số thực k ta có: . u v  .
v u ( tính chất giao hoán); .
u v w  . u v  .
u w ( Tính chất phân phối đối với phép cộng);
ku.vk .uv .ukv .
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Luyện tập VECTƠ
II. BÀI TẬP TRẮC NGHIỆM
Dạng 1: GÓC GIỮA HAI VECTO Câu 1.
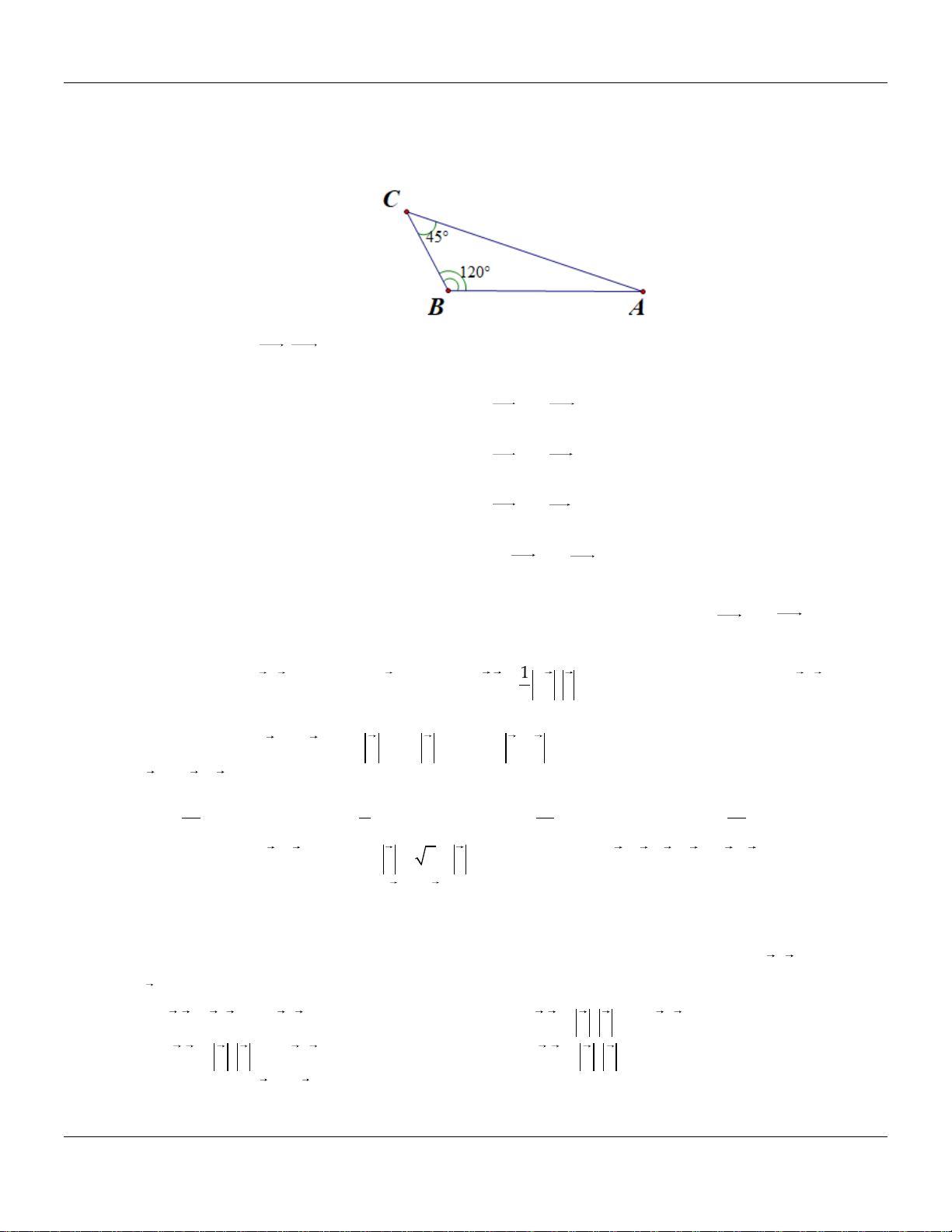
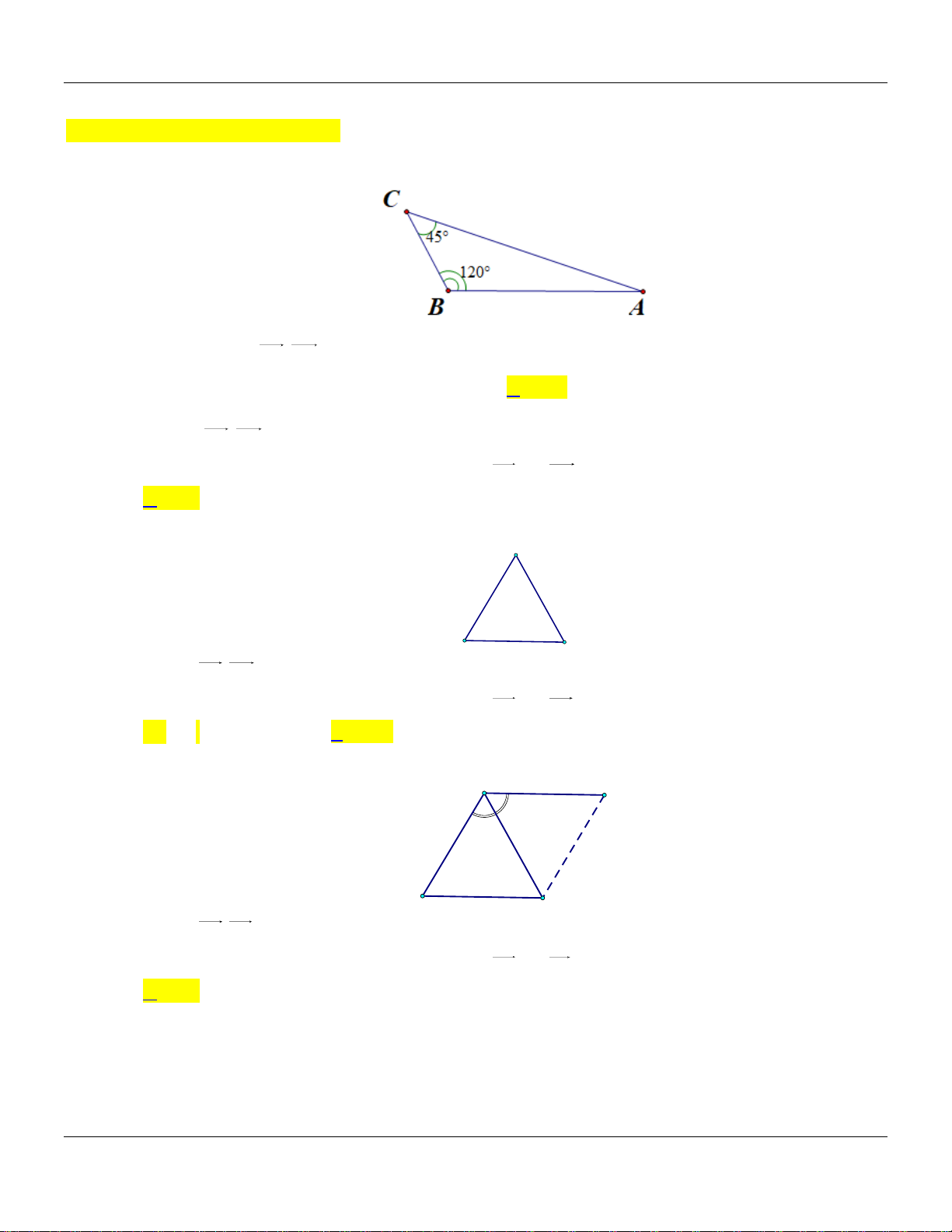
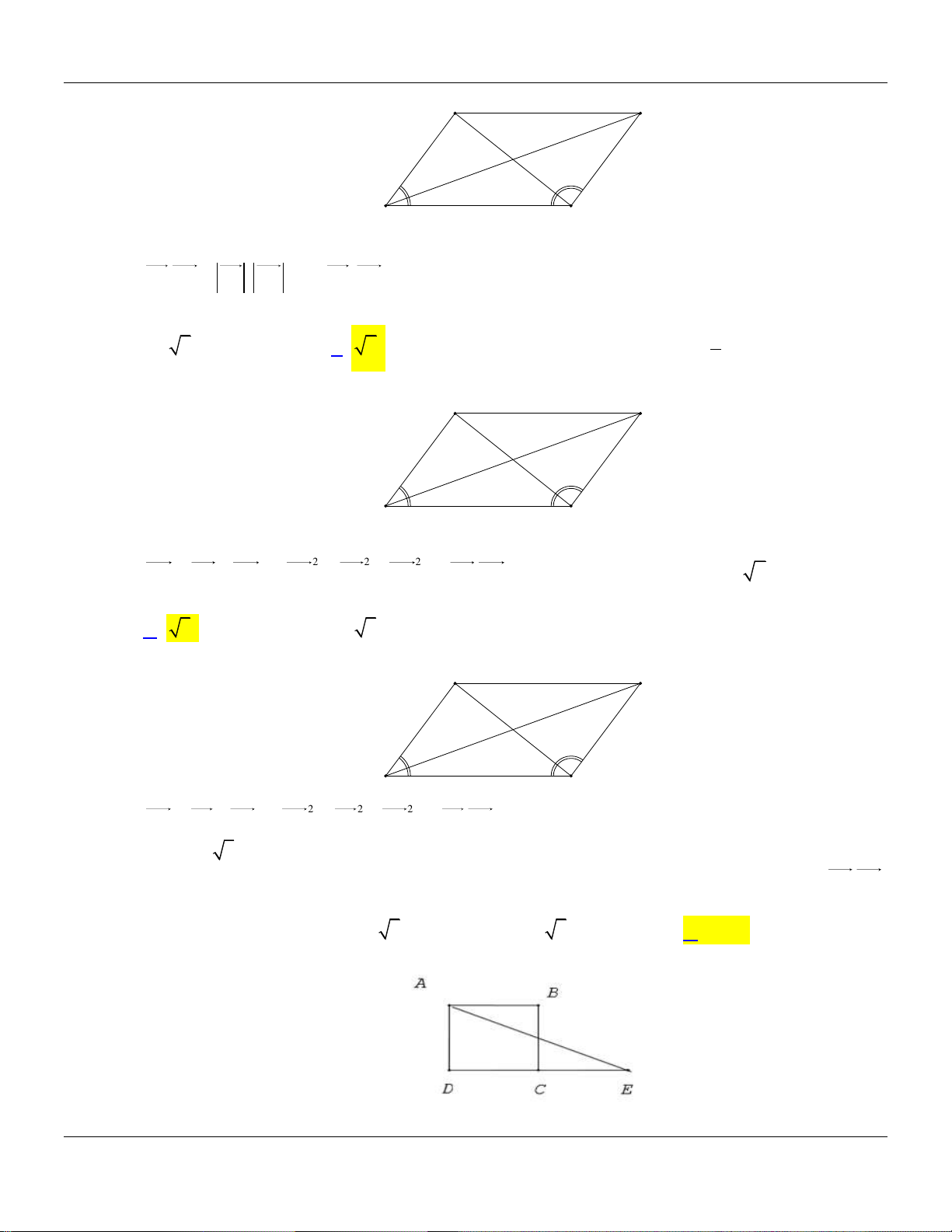
Cho tam giác ABC như hình vẽ.
Xác định góc  AB, AC . A. 45 . B. 120 . C. 15 . D. 165 . Câu 2.
Cho tam giác ABC đều. Góc giữa hai vectơ AB và AC bằng A. 60 .  B. 120 . C. 150 . D. 30 . Câu 3.
Cho tam giác ABC đều. Góc giữa hai vectơ AB và BC bằng A. 60 .  B. 120 . C. 150 . D. 30 . Câu 4.
Cho tam giác ABC đều. Góc giữa hai vectơ AB và CB bằng A. 60 .  B. 120 . C. 150 . D. 30 . Câu 5.
Cho hình bình hành ABCD . Góc giữa 2 vectơ AB và BC là A. BAC . B. ADC . C. BAD . D. ABC . Câu 6.
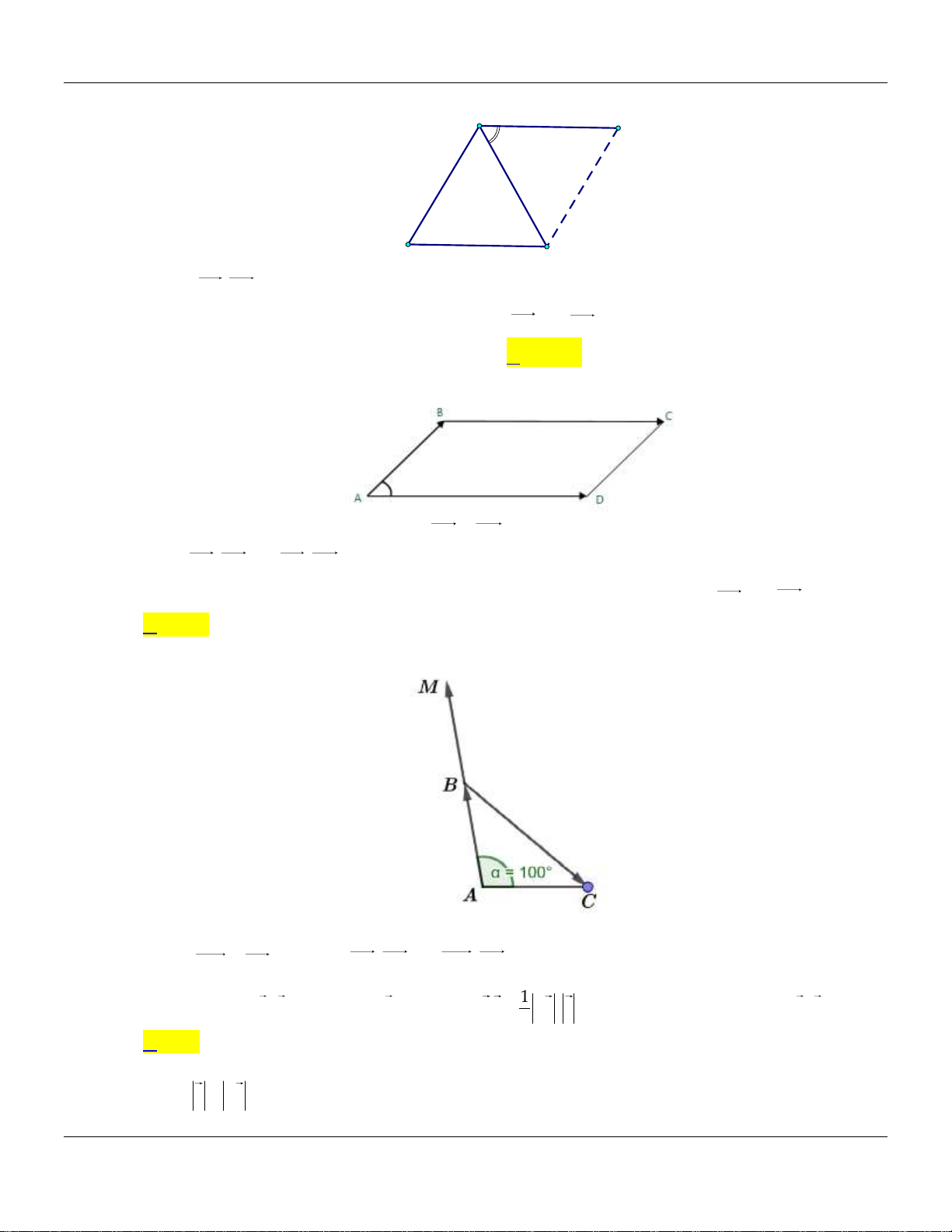
Cho tam giác ABC cân tại A , góc BAC  100 . Số đo góc giữa hai véctơ AB và BC là A. 140 . B. 80 . C. 40 . D. 100 . 1 Câu 7.
Cho hai vectơ a ; b khác vectơ 0 thỏa mãn . a b
a . b . Khi đó góc giữa hai vectơ a ; b bằn 2 A. 60 .  B. 120 . C. 150 . D. 30 . Câu 8.
Cho hai vec tơ a và b biết a  6, b  12 và a b  10 . Khi đó, cosin của góc giữa hai vectơ
a và a b bằng 1 2 1 1 A.  . B. . C. . D.  . 18 3 15 15 Câu 9.
Cho hai vecto a , b sao cho a  2 , b  2 và hai vectơ x a b , y  2a b vuông góc với
nhau. Tính góc giữa hai véc tơ a và b . A. 120 . B. 60 . C. 90 . D. 30 .
Dạng 2: TÍNH TÍCH VÔ HƯỚNG
Câu 10. Trong các công thức sau, công thức nào xác định tích vô hướng của hai vectơ a ,b cùng khác 0 ? A. .
a b a .b.cos a ,b . B. .
a b a . b .cos a ,b . C. .
a b a . b .sin a ,b . D. .
a b a . b .
Câu 11. Cho hai vectơ a và b . Đẳng thức nào sau đây sai?
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Luyện tập VECTƠ 2 2 2 A. .
a b a . b .cos a,b.
B. a . b  . a b . 2 2 2 1 2 2 C. . a b
a b a b .
D. a a . 2  
Câu 12. Cho hai véctơ a, b khác véctơ-không thỏa mãn a.b   a . b . Khi đó, góc giữa hai vectơ a, b bằng A. 45 .  B. 0 .  C. 180 .  D. 90 . 
Câu 13. Cho hai vectơ a và b . Đẳng thức nào sau đây sai? 2 2 2 1 2 2 2 1 A. . a b
a.b a b . B. . a b
a b a b 2  . . 2  2 2 1 2 2 1 C. . a b
a.b ab . D. . a b
a b a b 4  . . 2 
Câu 14. Cho a  3 , b  5 , a b o ,
 45 . Tích vô hướng của a và b bằng 15 15 3 15 15 A. . B. . C.  . D.  . 2 2 2 2
Câu 15. Cho hai vectơ a và b . Biết a  2, b  3 và a,b  30 . Tính a b . A. 11 . B. 13 . C. 12 . D. 14 .
Câu 16. Cho a, b có a  4; b  5. và a.b  10. Tính cos a;b . A. a b 3 cos ;  . B. a b 2 cos ;  . C. a b 1 cos ;   . D. a b 1 cos ;  . 2 2 2 2
Câu 17. Cho hai véctơ a,b thỏa mãn: a  4; b  3; a b  4 . Gọi  là góc giữa hai véctơ a,b . Khẳng
định nào dưới đây đúng? 1 3 A. 0   60 . B. 0   30 . C. cos  . D. cos  . 3 8
Câu 18. Cho tam giác ABC có ABC  30 ,
AB  5, BC  8. Tính B . A BC . A. 20. B. 20 3. C. 20 2. D. 40 3.
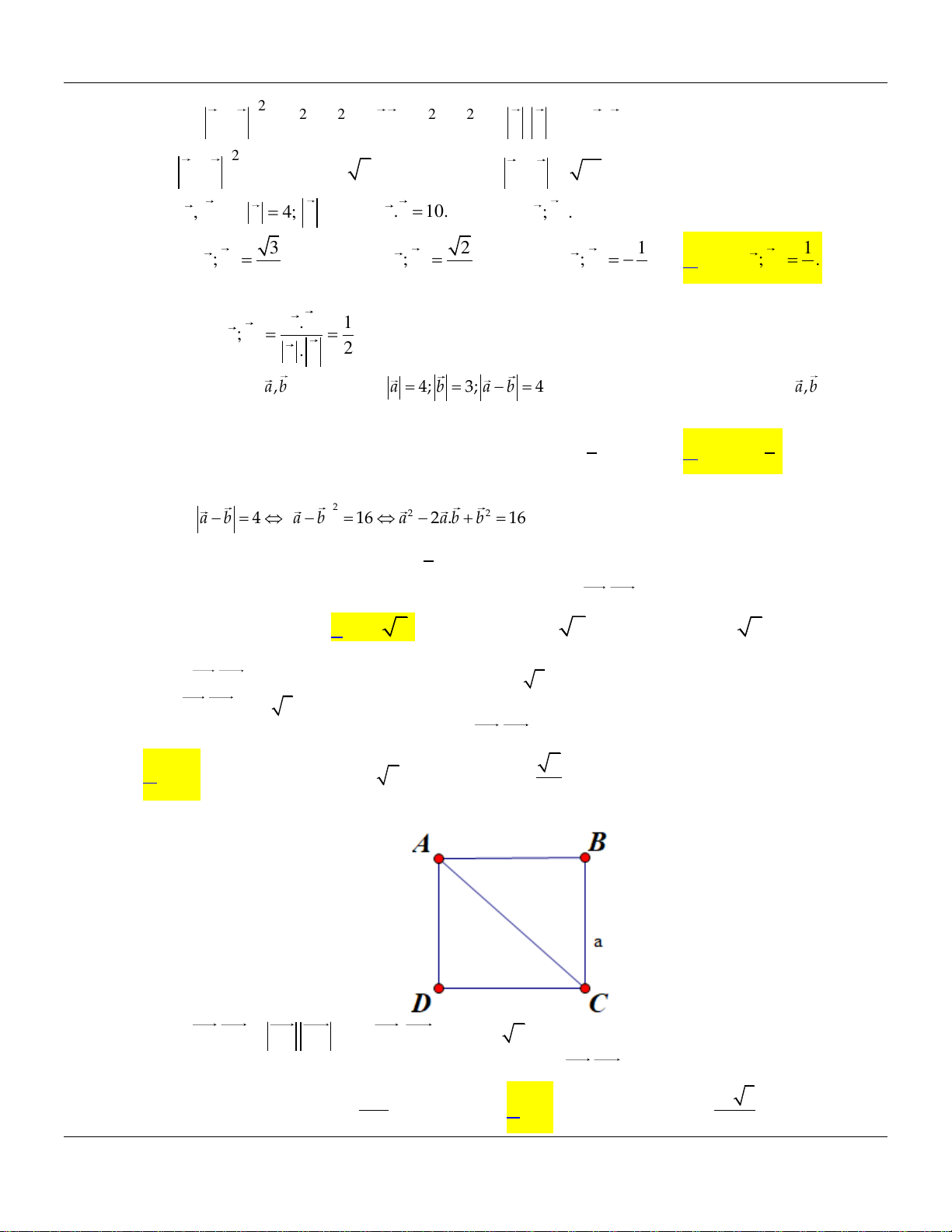
Câu 19. Cho hình vuông ABCD cạnh 2a . Khi đó A . B AC bằng 2 A. 2 4a . B. 2 a 2 . C. 2 a . D. 2 a . 2
Câu 20. Cho tam giác vuông cân ABC có AB AC a . Tính A . B AC. 2 a 2 a 3 A. 2 a . B. . C. 0 . D. . 2 2
Câu 21. Cho tam giác ABC vuông tại A , AB a, BC  2a . Tích vô hướng B . A BC bằng 1 A. 2 a . B. 2 a . C. 2 a 3 . D. 2 a . 2
Câu 22. Cho tam giác ABC vuông cân tại , A có AB  .
a Tích vô hướng B . A BC bằng 2 a 2 a A. 2 a . B.  . C. . D. 2 a . 2 2
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Luyện tập VECTƠ
Câu 23. Cho tam giác ABC có 0 ˆ A  90 , 0
ˆB  60 và AB a . Khi đó, AC.CB bằng A. 2 2a . B. 2 2a . C. 2 3a . D. 2 3a .
Câu 24. Cho ABC vuông cân tại A , cạnh AB  5 . Tích vô hướng BC.BA bằng A. 5 2 . B. 25 . C. 20 . D. 20 .
Câu 25. Góc tạo bởi m và n là 90 và m  2021, n  2022 . Khi đó, . m n bằng A. 4086462 . B. 0 . C. 4086462  . D. 1.
Câu 26. Cho hai véc tơ a , b thỏa mãn a  3, b  4 và (a,b)  60 . Tích vô hướng . a b bằng A. 6 . B. 6 3 . C. 12 . D. 4 3 .
Câu 27. Cho hình bình hành ABCD , với AB  2 , BC  1 , BAD  60 . Tích vô hướng A . B AD bằng 1 1 A. 1  . B. 1. C.  . D. . 2 2
Câu 28. Cho tam giác ABC vuông tại A có AB  ;
a AC a 3 và AM là trung tuyến. Tính tích vô hướng B . A AM . 2 a 2 a A. . B. 2 a . C. 2 a . D.  . 2 2
Câu 29. Cho hình bình hành ABCD , với AB  2 , AD  1 , BAD  60 . Tích vô hướng A . B AD bằng 1 1 A. 1  . B. 1. C.  . D. . 2 2
Câu 30. Cho hình bình hành ABCD , với AB  2 , AD  1 , BAD  60 . Tích vô hướng B . A BC bằng 1 1 A. 1  . B. C. 1  . D.  . 2 2
Câu 31. Cho hình bình hành ABCD , với AB  2 , AD  1 , BAD  60 . Độ dài đường chéo AC bằng 7 A. 5 . B. 7 . C. 5 . D. . 2
Câu 32. Cho hình bình hành ABCD , với AB  2 , AD  1 , BAD  60 . Độ dài đường chéo BD bằng A. 3 . B. 5 . C. 5 . D. 3 .
Câu 33. Cho hình vuông ABCD cạnh bằng 3, gọi E là điểm đối xứng của D qua C . Giá trị AE.CD bằng A. 18 . B. 9 3 . C. 9 5 . D. 18 .
Câu 34. Cho hình bình hành ABCD có AB  2a, AD  3a, BAD  60 . Điểm K thuộc AD thỏa mãn
AK  2DK . Tính tích vô hướng BK.AC A. 2 3a . B. 2 6a . C. 0 . D. 2 a .
Câu 35. Cho hình vuông ABCD cạnh 5 . Khi đó, A . B AC bằng 25 2 25 A. 25. B. 25 2. C. . D. . 2 2
Câu 36. Cho tam giác ABC đều cạnh a . Tính A . B AC. 2 3 2 A. .  a AB AC . B. .  a AB AC . C. 2 . AB AC a . D. 2 . AB AC  2a . 2 2
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Luyện tập VECTƠ
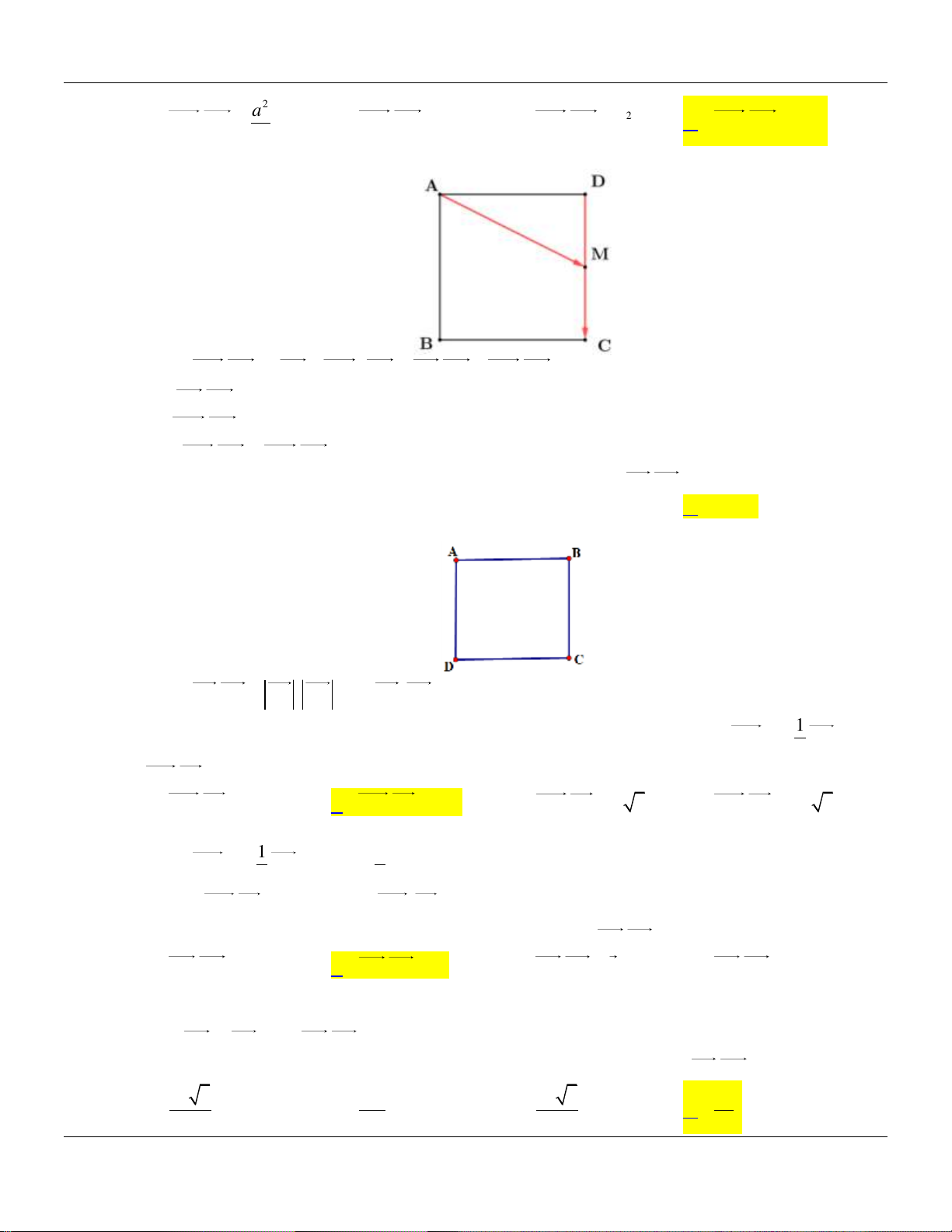
Câu 37. Cho hình vuông ABCD cạnh 2a , M là trung điểm của cạnh CD . Chọn khẳng định đúng. 2 a
A. AM .DC  .
B. AM .DC  0 . C. 2
AM .DC a . D. 2
AM .DC  2a . 2
Câu 38. Cho hình vuông ABCD có độ dài cạnh bằng 10 . Tính giá trị A . B CD . A. 100 . B. 10 . C. 0 . D. 100 . 1
Câu 39. Cho tam giác đều ABC có độ dài cạnh bằng 4 và điểm M thỏa mãn BM   BC . Tính 2 BM .BA .
A. BM .BA  4 .
B. BM .BA  4 .
C. BM .BA  4 3 .
D. BM .BA  4 3 .
Câu 40. Cho hình vuông ABCD có độ dài các cạnh bằng a . Tính AC.BD . A. 2
AC.BD  2a .
B. AC.BD  0 .
C. AC.BD  0 . D. 2
AC.BD  2a .
Câu 41. Cho tam giác đều ABC có trọng tâm G và độ dài cạnh bằng a . Tính A . B AG. 2 a 3 2 3a 2 a 3 2 a A. . B. . C. . D. . 6 4 4 2
Câu 42. Cho tam giác đều ABC cạnh a, đường cao AH. Tính AC AC AB. 2 a 2 2 a 3 2 a 2 a A.  . B. . C. . D. . 2 2 2 2
Câu 43. Cho hình thoi ABCD tâm O có cạnh bằng a 2 và ABD  60 . Gọi I là điểm thỏa mãn
2IC ID  0 . Tính tích vô hướng A . O BI . 2 a 2 2 a 3 2 a A. . B. . C. .
D. u  2; 3   2 2 2
Câu 44. Cho tam giác ABC vuông tại A có AB  3; AC  4 . Trên đoạn thẳng BC lấy điểm M sao
cho MB  2MC . Tính tích vô hướng AM .BC . 23 41 A. . B. . C. 8 . D. 23 . 3 3
Câu 45. Cho hình vuông ABCD cạnh bằng 5. Tính  AB AC.BC BD BA. A. 10 2 . B. 50 . C. 0 . D. 75 .
Câu 46. Cho hai vectơ a và b có a
4 , b  5 và a b 0 ,
120 . Tính a b . A. 21 . B. 21 . C. 41 . D. 41 .
Dạng 3: TÍNH TÍCH VÔ HƯỚNG BẰNG BIỂU THỨC TỌA ĐỘ
Câu 47. Cho hai vectơ u  2;   1 , v   3
 ;4 . Tích u.v bằng A. 11. B. 10. C. 5.
D. 2.
Câu 48. Trong mặt phẳng toạ độ Oxy , cho a  (1; 4) , b  ( 1
 ;3) . Khi đó giá trị tích vô hướng của hai
véctơ a và b là A. 12 . B. 11. C. 0. D. 11.
Câu 49. Trong mặt phẳng tọa độ Oxy , cho hai vectơ u i  3j và v  2j  2i . Tính . u v . A. . u v  4 . B. . u v  4 . C. . u v  2 . D. . u v  2 .
Câu 50. Cho A0; 3 ; B4;0 ; C  2  ; 5   . Tính A . B BC .
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Luyện tập VECTƠ A. 16 . B. 9 . C. 10 . D. 9.
Câu 51. Cho u  2; 3
  . Với giá trị nào của m thì v   3;
m vuông góc với u ?
A. m  1.
B. m  2 .
C. m  1.
D. m  2 .
Câu 52. Trong mặt phẳng tọa độ Oxy cho các vectơ a 1; 3 , b 2;5 . Tính tích vô hướng của . a b . A. 7 . B. 13 . C. 17 . D. 13 .
Câu 53. Trong mặt phẳng tọa độ Oxy , cho a  2;  5 và b  m; m  2 . Tìm m biết a và b vuông góc. 10 10 10 10 A. m   .
B. m   .
C. m   . D. m  . 3 3 7 7
Câu 54. Trong mặt phẳng toạ độ Oxy , cho a  (1; 4) ; b  (4;0). Khi đó, cosin góc giữa hai vecto a và b là  17 17 A. . B. . C. 0. D. 2. 17 17
Câu 55. Trên mặt phẳng Oxy, cho hai vectơ a  2;  1 và b  2; 4
 . Khi đó góc giữa hai vectơ a và b bằng A. 30 . B. 45 . C. 90 . D. 60 .
Câu 56. Cho hai vectơ a   3 
;1 , b  3; 3. Góc giữa hai vectơ a và b bằng A. 15 . B. 30 . C. 45 . D. 60 .
Câu 57. Trong mặt phẳng Oxy , cho A1; 2, B 4 
;1 , C 5; 4 . Tính góc BAC. A. 45 .  B. 90 . C. 30 . D. 60 .
Câu 58. Trong mặt phẳng tọa độ Oxy , cho tam giác ABC biết (
A 1; 2) , B(4;1) , C(5; 4) . Tính góc A của tam giác ABC . A. 60 . B. 45 . C. 90 . D. 120 .
Câu 59. Tam giác ABC có A1; 2 , B 0; 4 , C 3; 
1 . Góc BAC của tam giác ABC gần với giá trị nào dưới đây? A. 90 . B. 36 5  2 . C. 143 7   . D. 53 7   .
Câu 60. Trong mặt phẳng Oxy cho các điểm A 1  ;  1 ; B 3 
;1 ; C 6;0 . Khẳng định nào sau đây đúng: A. AB   4  ; 2  ; BC   3   ;1 . B. o B  135 .
C. AB  20 . D. BC  3.
Câu 61. Trong mặt phẳng Oxy cho các điểm A 1
 ;2; B5;8 . Điểm M Ox sao cho tam giác MAB
vuông tại A . Diện tích tam giác MAB bằng A. 10 . B. 18 . C. 24 . D. 12 .
Câu 62. Trong mặt phẳng tọa độ Oxy , cho điểm A2; 3 . Tìm tọa độ điểm B thuộc trục tung, biết
khoảng cách giữa hai điểm A và B bằng 2 5 và điểm B có tung độ dương. A. B 0;  1 .
B. B 0;7 .
C. B 2;0 .
D. B 7;0 .
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Luyện tập VECTƠ
Câu 63. Trong mặt phẳng Oxy , cho hai điểm A3 ; 4 và B  2
 ; 5 . Tọa độ điểm M thuộc trục Ox cách đều hai điểm ; A B là  2   2   1 9   1  A.  ;0   . B. ; 0   . C. ;   . D. ; 0   .  5   5   2 2   2 
Câu 64. Trong hệ toạ độ Oxy , cho hai điểm (
A 1; 1) và B( 2  ; 2)
 . Điểm C thuộc trục Ox sao cho tam
giác ABC cân tại A là
A. C(2; 0) .
B. C(0; 2) .
C. C(4; 0) .
D. C(2; 0) .
Câu 65. Trong mặt phẳng tọa độ Oxy cho hai điểm A1; 2 ; B 1; 
1 . Điểm M thuộc trục Oy thỏa
mãn tam giác MAB cân tại M . Khi đó, độ dài đoạn OM bằng 5 3 1 7 A. . B. . C. . D. . 2 2 2 2
Câu 66. Trong mặt phẳng tọa độ Oxy , cho tam giác ABC có A1;   1 , B 4; 
1 , C 5; 7 . Tính diện
tích S của tam giác ABC . 3 13
A. S  26 .
B. S  13 .
C. S  3 13  65 . D. S  . 2
Câu 67. Trong mặt phẳng với hệ tọa độ Oxy , cho hai điểm A3; 2, B 4;3 . Điểm M thuộc tia Ox .
Khẳng định nào dưới đây đúng?
A. M  7;0 .
B. M  5;0 .
C. M  9;0 .
D. M  2;0 .
Câu 68. Cho hai điểm A1;3, B 8; 2 . Gọi C là điểm thuộc trục hoành sao cho tam giác ABC vuông
tại C và OC  6 . Giá trị của biểu thức 2 2
x y  5 là C C A. 9 . B. 14 . C. 21 . D. 30 .
Câu 69. Trong mặt phẳng Oxy , cho hai điểm A1; 2 ,B 3
 ;1. Tìm tọa độ điểm C trên trục Oy sao
cho tam giác ABC vuông tại A .
A. C 6;0 .
B. C 0;6 .
C. C 6;0 .
D. C 0; 6 .
Câu 70. Cho tam giác ABC có A 1
 ;2,B0;3,C5; 2. Tìm tọa độ chân đường cao hạ từ đỉnh A của tam giác ABC . A. 0; 3 .
B. 0;  3 . C. 3;0 . D.  3  ;0 .
Câu 71. Trong mặt phẳng Oxy , cho tam giác ABC biết A1;  1 , B 3; 
1 và C 2; 4 . Tìm tọa độ trực
tâm H của tam giác ABC A. H 1;  1 . B. H 2;  1 .
C. H 1; 2 .
D. H 2; 2 .
Câu 72. Cho tam giác ABC có A1;3, B 3;  4 và C 6; 2 . Trực tâm của tam giác ABC là H a;b .
Tính giá trị biểu thức T a  2b . A. 10 . B. 6 . C. 8 . D. 7 .
Câu 73. Trong mặt phẳng tọa độ Oxy cho tam giác ABC. Biết A3; 1  ,B 1
 ;2 và I 1;1 là trọng tâm
tam giác ABC. Trực tâm H của tam giác ABC có tọa độ a;b. Tính a  3 . b 2 4
A. a  3b  .
B. a  3b   .
C. a  3b  1.
D. a  3b  2. 3 3
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Luyện tập VECTƠ
Câu 74. Trong mặt phẳng tọa độ Oxy , cho hình thang cân ABCD với các đáy là AB và CD . Biết
A1; 2 , B 2; 3 , điểm C nằm trên trục tung, điểm D nằm trên trục hoành. Tính OC OD . 4 26 A. . B. 2 . C. 6 . D. . 3 3
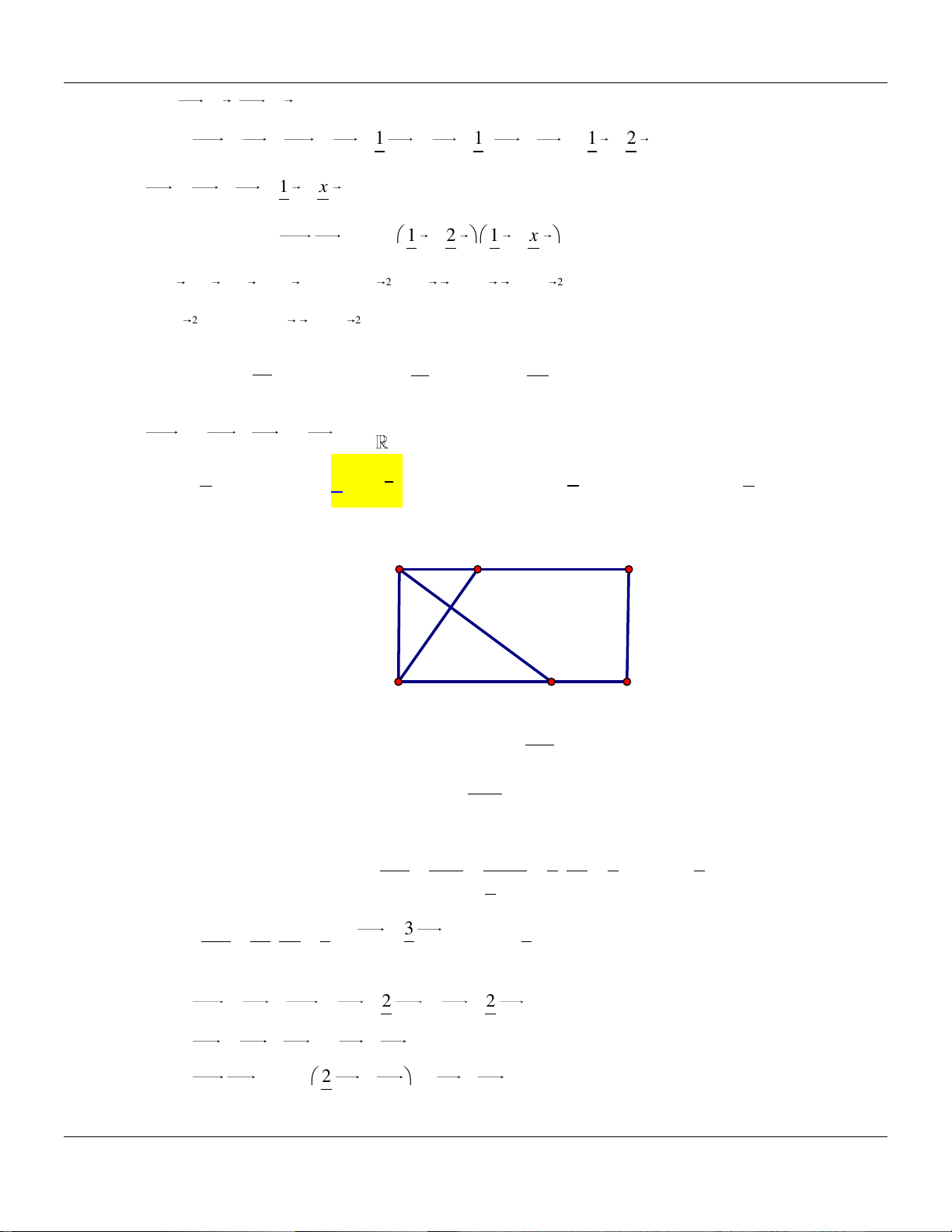
Câu 75. Trong mặt phẳng Oxy , cho bốn điểm A 2
 ;3, B2;4, C 3;0, D 1  ;  1 . Có bao nhiêu
điểm M thuộc đường thẳng d : y  2x 1 sao cho MA MB MC.MD  3  ? A. 0. B. 1. C. 2. D. 3.
Câu 76. Trong mặt phẳng tọa độ Oxy cho hai điểm A 3  ; 
1 và B 5;0 . Biết có hai điểm C nằm trên parabol  P 2
: y x  2x sao cho tam giác ABC vuông tại C là C x ; y ,C x ; y . 1  1 1  2  2 2 
Tính giá trị biểu thức T x y x y . 1 2 2 1 A. 4 . B. 5 . C. 6 . D. 5  .
Câu 77. Trong mặt phẳng Oxy , cho tam giác ABC với A2; 4, B 1  ;1 , C 7;   1 . Biết M  ;
a b a  0
là điểm nằm trong mặt phẳng Oxy thoả mãn tam giác ABM vuông cân tại B . Tính giá trị
T  3a  4b .
A. T  2 .
B. T  2 .
C. T  12 .
D. T  12 .  1 
Câu 78. Trong mặt phẳng tọa độ Oxy , cho A4;6 ; B 5;  1 ; C  ;
n 3 . Tìm m , n để I  ; m   là tâm  2 
đường tròn ngoại tiếp tam giác ABC . 5 5 5  n  1 5  n  1 A. m   ; n  1 B. m  ; n  1 . C. m  ;  .
D. m   ;  . 2 2 2 n  2  2 n  2 
Câu 79. Trong mặt phẳng tọa độ Oxy , cho tam giác ABC , biết H a;b là toạ độ chân đường cao đỉnh
A của tam giác ABC , biết toạ độ B 3  ;1 , C 4; 4
  và trọng tâm G của tam giác ABC có toạ
độ G 4;0 . Tính a b . 2 33 35 68 A. . B. . C. . D. . 13 13 13 13
Dạng 4: CÁC BÀI TOÁN KHÁC
Câu 80. Cho a , b có a  2b vuông góc với vectơ 5a  4b và a b . Tính góc giữa vectơ a và b . A. 30 . B. 45 . C. 90 . D. 60 .
Câu 81. Cho biết  ;
a b 120 ; a  3; b  3. Độ dài của véctơ a b bằng 3 3 3 A. 3 3 . B. 3 2 . C. . D. . 2 2
Câu 82. Trong mặt phẳng tọa độ Oxy , cho ba điểm M 3; 4, N 2  ;1 , P  2  ; 3
  . Tìm điểm I trên
đường thẳng NP sao cho góc MIN  135 . A. I 3; 2 .
B. I 2;3 .
C. I 5; 4 .
D. I 4;5 .
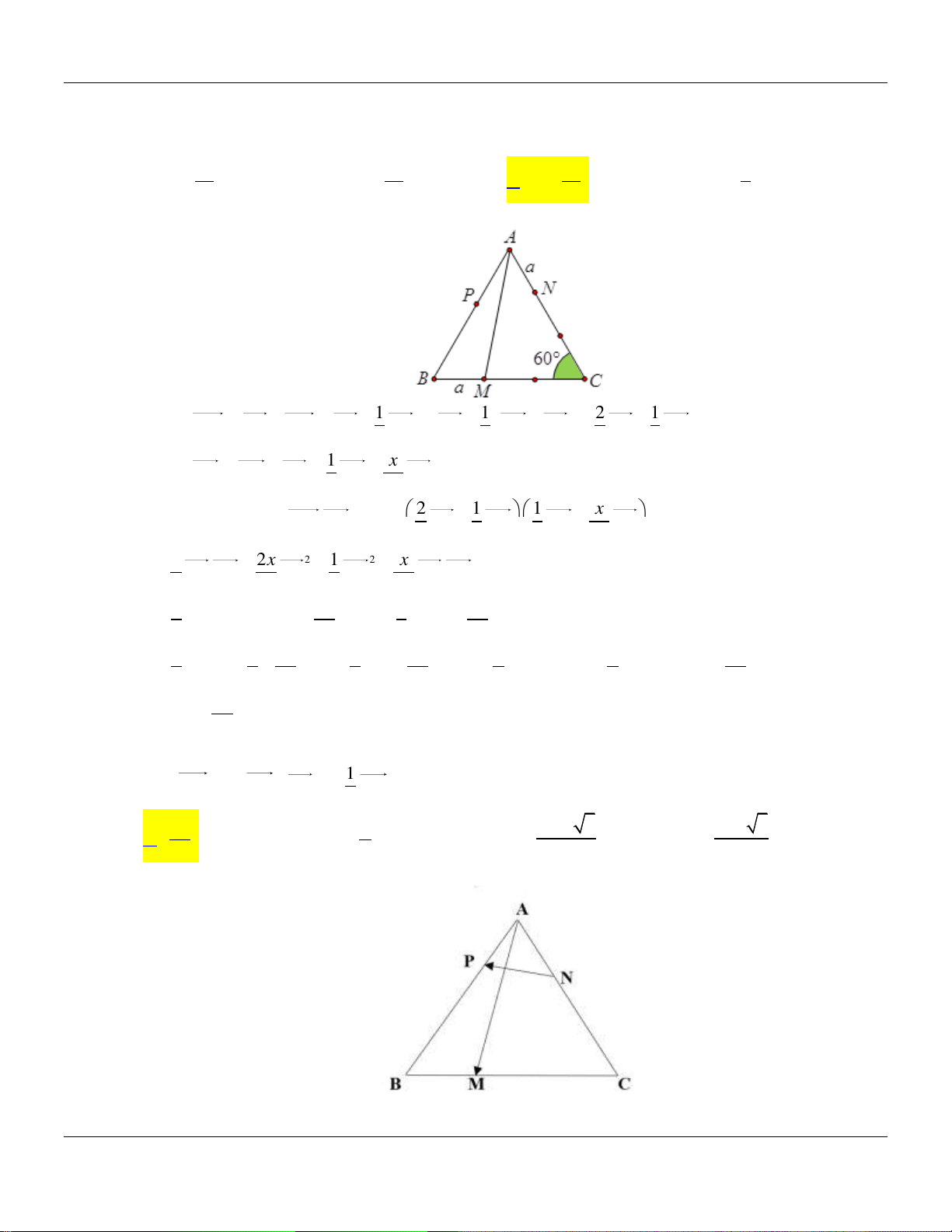
Câu 83. Cho tam giác đều ABC cạnh 3a , a  0 . Lấy các điểm M , N , P lần lượt trên các cạnh BC ,
CA , AB sao cho BM a , CN  2a , AP x 0  x  3a . Tìm x để AM PN .
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Luyện tập VECTƠ 3a 2a 4a a A. x  . B. x  . C. x  . D. x  . 5 5 5 5
Câu 84. Cho tam giác ABC đều cạnh a . Trên các cạnh BC,C ,
A AB lần lượt lấy các điểm M , N , P sao 1
cho MC  2MB , NA   NC và AP x . Tìm x để AM vuông góc với PN . 2 4a a 2  6 3 1 3 3 A. . B. . C. a . D. a . 15 3 39 39
Câu 85. Cho hình chữ nhật ABCD thỏa AB  2a , AD a . Gọi M , N là hai điểm thỏa mãn
DM  2MC , AN x AB , x
. Tìm x để AM và DN vuông góc. 3 3 1 2 A. x  .
B. x  . C. x  . D. x  . 7 8 2 5
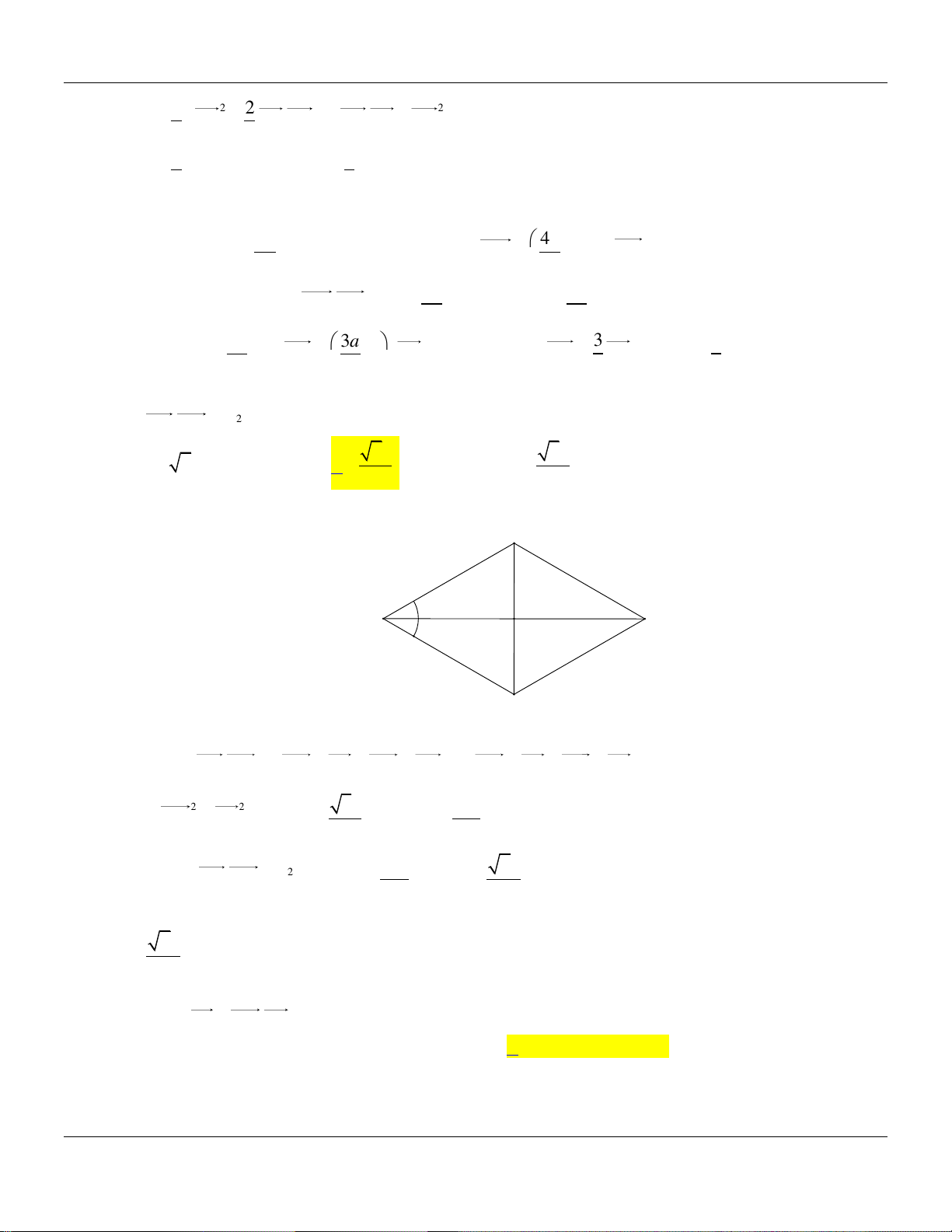
Câu 86. Cho hình thoi ABCD có cạnh bằng a và BAD  60 . Quỹ tích các điểm M thỏa mãn 2 M .
A MC a là đường tròn có bán kính bằng 7a 3a A. 2a . B. . C. . D. a . 2 2
Câu 87. Cho ba điểm không thẳng hàng ,
A B, C .Điều kiện cần và đủ để ba điểm ,
A B, C thỏa mãn điều
kiện (CA CB).AB  0 là:
A. ABC đều.
B. ABC cân tại C .
C. ABC vuông tại C .
D. ABC vuông cân tại C .
Câu 88. Cho hình thang vuông ABCD với đường cao AB  2a, các cạnh đáy AD a và BC  3 . a Gọi
M là điểm trên đoạn AC sao cho AM k.AC. Tìm k để BM và CD vuông góc. 4 3 1 2 A. . B. . C. . D. . 9 7 3 5 2
Câu 89. Cho hai điểm B, C phân biệt. Tập hợp những điểm M thỏa mãn CM .CB CM là
A. đường tròn đường kính BC .
B. đường tròn  B; BC  .
C. đường tròn C;CB .
D. đường tròn C; 2CB .
Câu 90. Cho ba điểm ,
A B, C phân biệt. Tập hợp những điểm M mà CM .CB  . CA CB là
A. đường tròn đường kính AB .
B. đường thẳng đi qua A và vuông góc với BC .
C. đường thẳng đi qua B và vuông góc với AC .
D. đường thẳng đi qua C và vuông góc với AB .
Câu 91. Cho tam giác ABC , điểm J thỏa mãn AK  3KJ , I là trung điểm của cạnh AB ,điểm K thỏa
mãn KA KB  2KC  0 . Một điểm M thay đổi thỏa mãn 3MK AK.MA MB  2MC  0 .
Tập hợp điểm M là
A. đường tròn đường kính IJ .
B. đường tròn đường kính IK .
C. đường tròn đường kính JK .
D. đường trung trực đoạn JK .
Câu 92. Cho tam giác ABC có G là trọng tâm. Tập hợp các điểm M trong mặt phẳng thoả mãn 2 2 2 2 2 2
MA MB MC  4GA GB GC là
A. Đường tròn tâm G bán kính bằng GB .
B. Đường tròn tâm G bán kính bằng GA .
C. Đường tròn tâm G bán kính bằng GC .
D. Đường tròn tâm G bán kính bằng 4GA .
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
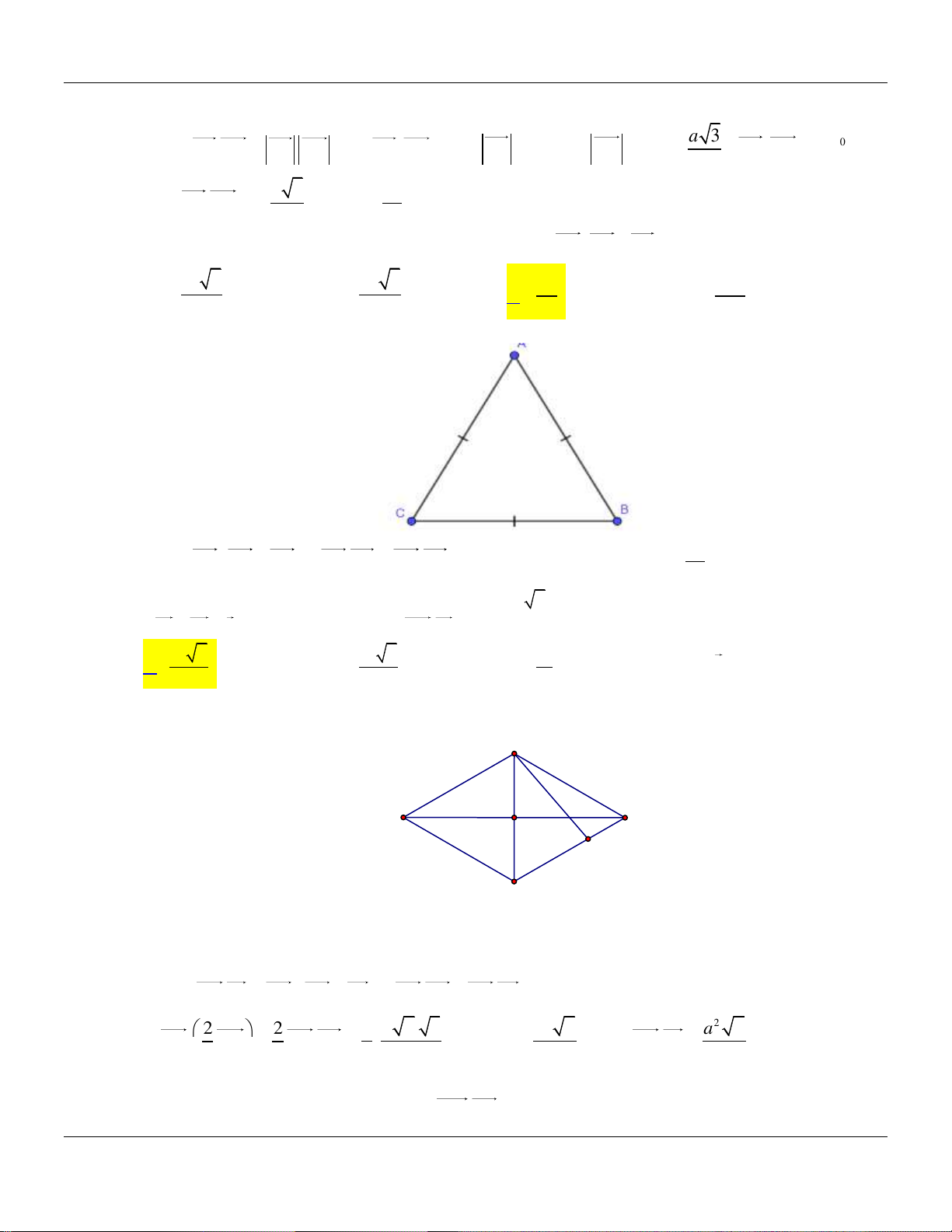
Luyện tập VECTƠ Câu 93. Cho
ABC đều, cạnh bằng a  0 . Tìm quỹ tích điểm M thỏa mãn 2 7a M . A MB M .
B MC MC.MA  . 4
A. Quỹ tích điểm M là đường trung trực của AB .
B. Quỹ tích điểm M là đường thẳng đi qua trọng tâm của ABC và song song với BC . 6a
C. Quỹ tích điểm M là đường tròn có bán kính bằng . 2 3a
D. Quỹ tích điểm M là đường tròn có bán kính bằng . 2
Câu 94. Cho tam giác ABC đều cạnh a . Điểm M là một điểm thỏa mãn đẳng 2 a thức M . A MB M .
B MC MC.MA  
. Biết tập hợp điểm M là một đường tròn. Bán kính 6 đường tròn đó là a a a
A. R  2 . B. R  . C. R  . D. R  . 3 4 2
_____________________HẾT_____________________
Huế, 10h00’ Ngày 02 tháng 12 năm 2022
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Luyện tập VECTƠ
III. LỜI GIẢI BÀI TẬP TRẮC NGHIỆM
Dạng 1: GÓC GIỮA HAI VECTO Câu 1.
Cho tam giác ABC như hình vẽ.
Xác định góc  AB, AC . A. 45 . B. 120 . C. 15 . D. 165 . Lời giải:
Ta có:  AB, AC  BAC 180  120  45 15 .  Câu 2.
Cho tam giác ABC đều. Góc giữa hai vectơ AB và AC bằng A. 60 . B. 120 . C. 150 . D. 30 . Lời giải: A C B Ta có A ;
B AC  BAC  60 . Câu 3.
Cho tam giác ABC đều. Góc giữa hai vectơ AB và BC bằng A. 60 . B. 120 . C. 150 . D. 30 . Lời giải: A C' B C Ta có A ;
B BC  180  BAC  120 . Câu 4.
Cho tam giác ABC đều. Góc giữa hai vectơ AB và CB bằng A. 60 . B. 120 . C. 150 . D. 30 . Lời giải:
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Luyện tập VECTƠ A C' C B Ta có A ;
B AC  BAC  60 . Câu 5.
Cho hình bình hành ABCD . Góc giữa 2 vectơ AB và BC là A. BAC . B. ADC . C. BAD . D. ABC . Lời giải:
Theo tính chất hình bình hành ta có BC AD .
Vậy  AB, BC   AB, AD  BAD . Câu 6.
Cho tam giác ABC cân tại A , góc BAC  100 . Số đo góc giữa hai véctơ AB và BC là A. 140 . B. 80 . C. 40 . D. 100 . Lời giải:
Xét tam giác ABC cân tại A , góc 0 BAC  100 suy ra 0
ABC ACB  40 .
Dựng BM AB , khi đó,  AB, BC  BM , BC 0 0
MBC 180  ABC  140 . 1 Câu 7.
Cho hai vectơ a ; b khác vectơ 0 thỏa mãn . a b
a . b . Khi đó góc giữa hai vectơ a ; b bằn 2 A. 60 . B. 120 . C. 150 . D. 30 . Lời giải:
Ta có a  a .
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Luyện tập VECTƠ Vậy . a b  1
a . b cos a,b  a . b  a b 1 cos ,
  a,b  60. 2 2 Câu 8.
Cho hai vec tơ a và b biết a  6, b  12 và a b  10 . Khi đó, cosin của góc giữa hai vectơ
a và a b bằng 1 2 1 1 A.  . B. . C. . D.  . 18 3 15 15 Lời giải:
Dựng AB a, BC b . Khi đó a b AC .
Ta được tam giác ABC có AB  6, BC  12, AC  10 và  a, a b   AB , AC . 2    
BC AC AB BC   AC AB 2 2 2 2 2 2 2 AC AB BC 10 6 12  AC.AB    4  . 2 2 AB AC  Vậy AB AC . 4 1 cos ,     . A . B AC 6.10 15 Câu 9.
Cho hai vecto a , b sao cho a  2 , b  2 và hai vectơ x a b , y  2a b vuông góc với
nhau. Tính góc giữa hai véc tơ a và b . A. 120 . B. 60 . C. 90 . D. 30 . Lời giải:
Vì hai véc tơ x a b , y  2a b vuông góc với nhau nên  2 2
a b.2a b  2 2
0  2a b  .
a b  0  2. a b a . b .cosa,b  0   2 2 2. 2
 2  2.2.cosa,b  0  cosa,b  0  a,b  90.
Dạng 2: TÍNH TÍCH VÔ HƯỚNG
Câu 10. Trong các công thức sau, công thức nào xác định tích vô hướng của hai vectơ a ,b cùng khác 0 ? A. .
a b a .b.cos a ,b . B. .
a b a . b .cos a ,b . C. .
a b a . b .sin a ,b . D. .
a b a . b .
Câu 11. Cho hai vectơ a và b . Đẳng thức nào sau đây sai? 2 2 2 A. .
a b a . b .cos a,b.
B. a . b  . a b .
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Luyện tập VECTƠ 2 2 2 1 2 2 C. . a b
a b a b .
D. a a . 2   Lời giải: Câu A, C, D: Đúng. 2 2 2 Câu B sai vì 2 .
a b a . b .cos a,b .
Câu 12. Cho hai véctơ a, b khác véctơ-không thỏa mãn a.b   a . b . Khi đó, góc giữa hai vectơ a, b bằng A. 45 .  B. 0 .  C. 180 .  D. 90 .  Lời giải:  . a b   a .  b Ta có:  
a b    a b 0 cos ; 1 ; 180 .  .
a b   a . b cos  a,b
Câu 13. Cho hai vectơ a và b . Đẳng thức nào sau đây sai? 2 2 2 1 2 2 2 1 A. . a b
a.b a b . B. . a b
a b a b 2  . . 2  2 2 1 2 2 1 C. . a b
a.b ab . D. . a b
a b a b 4  . . 2  Lời giải: 1 1
Nhận thấy C và D chỉ khác nhau về hệ số và nên đáp án sai sẽ rơi vào C hoặcD. 2 4 2 2 2 2 2 2 1
D đúng, Ta có : a  .b a b  a .b  a .b  4 . a .b  . a .b
a.b ab 4  2 2 2 2 A đúng, vì a b a b a b . a b . a a . a b . b a . b b a b 2 . a b a b   2 2 2 1 ..
a  .b a b 2  2 2 2 2 B đúng, vì a b a b a b . a b . a a . a b . b a . b b a b 2 . a b a b   2 2 2 1 ..
a b a b . 2 
Câu 14. Cho a  3 , b  5 , a b o ,
 45 . Tích vô hướng của a và b bằng 15 15 3 15 15 A. . B. . C.  . D.  . 2 2 2 2 Lời giải: 15 Ta có .
a b a . b .cos a,b o  3.5.cos 45  . 2
Câu 15. Cho hai vectơ a và b . Biết a  2, b  3 và a,b  30 . Tính a b . A. 11 . B. 13 . C. 12 . D. 14 . Lời giải:
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Luyện tập VECTƠ 2
Ta có:  a b  2 2 2 2
a b  2ab a b  2 a . b .cosa,b ,
  a b 2 0
 4  3  2.2. 3.cos30 13  a b  13 .
Câu 16. Cho a, b có a  4; b  5. và a.b  10. Tính cos a;b . A. a b 3 cos ;  . B. a b 2 cos ;  . C. a b 1 cos ;   . D. a b 1 cos ;  . 2 2 2 2 Lời giải: a b Ta có a b . 1 cos ;   . a . b 2
Câu 17. Cho hai véctơ a,b thỏa mãn: a  4; b  3; a b  4 . Gọi  là góc giữa hai véctơ a,b . Khẳng
định nào dưới đây đúng? 1 3 A. 0   60 . B. 0   30 . C. cos  . D. cos  . 3 8 Lời giải:
Ta có: a b   a b2 2 2 4
 16  a  2a.b b  16 2 2 3
 4  2.4.3.cos  3  16  cos  . 8
Câu 18. Cho tam giác ABC có ABC  30 ,
AB  5, BC  8. Tính B . A BC . A. 20. B. 20 3. C. 20 2. D. 40 3. Lời giải: Ta có B . A BC B .
A BC.cos ABC  5.8.cos 30  20 3. Vậy . BA BC  20 3.
Câu 19. Cho hình vuông ABCD cạnh 2a . Khi đó A . B AC bằng 2 A. 2 4a . B. 2 a 2 . C. 2 a . D. 2 a . 2 Lời giải:
Ta có AB AC AB ACAB AC 2 . .cos ,  2 .
a 2a 2.cos 45  4a .
Câu 20. Cho tam giác vuông cân ABC có AB AC a . Tính A . B AC. 2 a 2 a 3 A. 2 a . B. . C. 0 . D. . 2 2
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Luyện tập VECTƠ Lời giải:
Tam giác ABC vuông cân tại A .
Câu 21. Cho tam giác ABC vuông tại A , AB a, BC  2a . Tích vô hướng B . A BC bằng 1 A. 2 a . B. 2 a . C. 2 a 3 . D. 2 a . 2 Lời giải: a 2 B . A BC B . A BC.cos B  . a 2 . aa . 2a
Câu 22. Cho tam giác ABC vuông cân tại , A có AB  .
a Tích vô hướng B . A BC bằng 2 a 2 a A. 2 a . B.  . C. . D. 2 a . 2 2 Lời giải:
Tam giác ABC vuông cân tại ,
A có AB a BC a 2.
BA BC  BABC BA BC BA BC 2 , 45 . . .cos ,  .
a a 2.cos 45  a .
Câu 23. Cho tam giác ABC có 0 ˆ A  90 , 0
ˆB  60 và AB a . Khi đó, AC.CB bằng A. 2 2a . B. 2 2a . C. 2 3a . D. 2 3a . Lời giải:
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Luyện tập VECTƠ
Gọi D là điểm đối xứng với A qua C .  3 
Khi đó: AC.CB  . CD CB  . CD . CB cos150 2  a 3.2 . a     3  a  . 2   
Câu 24. Cho ABC vuông cân tại A , cạnh AB  5 . Tích vô hướng BC.BA bằng A. 5 2 . B. 25 . C. 20 . D. 20 . Lời giải: B A C
Xét ABC vuông cân tại A , cạnh AB  5 suy ra BC  5 2 và ABC  45 .
Ta có BC.BA BC . BA .cosBC;BA  BC.B .
A cos ABC  5.5 2.cos 45  25 .
Câu 25. Góc tạo bởi m và n là 90 và m  2021, n  2022 . Khi đó, . m n bằng A. 4086462 . B. 0 . C. 4086462  . D. 1. Lời giải: Ta có .
m n m . n .cos ;
m n  2021.2022.cos90  0 . Vậy . m n  0 .
Câu 26. Cho hai véc tơ a , b thỏa mãn a  3, b  4 và (a,b)  60 . Tích vô hướng . a b bằng A. 6 . B. 6 3 . C. 12 . D. 4 3 . Lời giải: Ta có .
a b a . b .cos(a, b)  3.4.cos 60  6 .
Câu 27. Cho hình bình hành ABCD , với AB  2 , BC  1 , BAD  60 . Tích vô hướng A . B AD bằng 1 1 A. 1  . B. 1. C.  . D. . 2 2 Lời giải:
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Luyện tập VECTƠ A .
B AD AB . AD .cos  A ; B AD  A . B A .
D cos BAD  2.1.cos 60  1 .
Câu 28. Cho tam giác ABC vuông tại A có AB  ;
a AC a 3 và AM là trung tuyến. Tính tích vô hướng B . A AM . 2 a 2 a A. . B. 2 a . C. 2 a . D.  . 2 2
Lời giải: A B C M
Ta có tam giác ABC vuông tại A và có AM là trung tuyến nên BC 2 2 2 2 BC AB AC a  3a AM  . AM     a . 2 2 2 2
Tam giác AMB có AB BM AM a nên là tam giác đều. Suy ra góc MAB  60 . 2 a Ta có B . A AM   A .
B AM   AB . AM .cos ( AB , AM )   . a . a cos 60   . 2
Câu 29. Cho hình bình hành ABCD , với AB  2 , AD  1 , BAD  60 . Tích vô hướng A . B AD bằng 1 1 A. 1  . B. 1. C.  . D. . 2 2
Lời giải: D C A B A .
B AD AB . AD .cos  A ; B AD  A . B A .
D cos BAD  2.1.cos 60  1 .
Câu 30. Cho hình bình hành ABCD , với AB  2 , AD  1 , BAD  60 . Tích vô hướng B . A BC bằng 1 1 A. 1  . B. C. 1  . D.  . 2 2
Lời giải:
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Luyện tập VECTƠ D C A B
Theo giả thiết: BAD  60  ABC  120 . B .
A BC BA . BC .cos B ; A BC   A .
B BC.cos ABC  2.1.cos120  1  .
Câu 31. Cho hình bình hành ABCD , với AB  2 , AD  1 , BAD  60 . Độ dài đường chéo AC bằng 7 A. 5 . B. 7 . C. 5 . D. . 2
Lời giải: D C A B Ta có: 2 2 2 2 2 2
AC AB AD AC AB AD  2A .
B AD AC  2 1  2.1  AC  7 .
Câu 32. Cho hình bình hành ABCD , với AB  2 , AD  1 , BAD  60 . Độ dài đường chéo BD bằng A. 3 . B. 5 . C. 5 . D. 3 .
Lời giải: D C A B 2 2 2 2 2 2
BD BA BC BD BA BC  2B .
A BC BD  2 1  2.  1  BD  3 .
Câu 33. Cho hình vuông ABCD cạnh bằng 3, gọi E là điểm đối xứng của D qua C . Giá trị AE.CD bằng A. 18 . B. 9 3 . C. 9 5 . D. 18 . Lời giải:
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Luyện tập VECTƠ
Ta có C là trung điểm của DE nên DE  2.3  6 .
Khi đó: AE.CD   AD DE.CD A .
D CD DE.CD 0  0  DE. .
CD cos180  6.3.  1  18  .
Câu 34. Cho hình bình hành ABCD có AB  2a, AD  3a, BAD  60 . Điểm K thuộc AD thỏa mãn
AK  2DK . Tính tích vô hướng BK.AC A. 2 3a . B. 2 6a . C. 0 . D. 2 a . Lời giải: B C O A K D 2
Ta có BK   AB
AD ; AC AB AD 3 2 2 1 Khi đó: 2 2
BK.AC  ( AB
AD)( AB AD)   AB AD AB AD 3 3 3 2 1 2 2 2 BK.AC  4
a  .9a  2 . a 3 .
a cos60  a 3 3
Câu 35. Cho hình vuông ABCD cạnh 5 . Khi đó, A . B AC bằng 25 2 25 A. 25. B. 25 2. C. . D. . 2 2 Lời giải:
Ta có ABCD là hình vuông nên AC  5 2 ; góc 0 BAC  45 ;
Tích vô hướng AB AC AB ACAB AC 0 . . .cos ;  5.5 2.cos 45  25 .
Câu 36. Cho tam giác ABC đều cạnh a . Tính A . B AC. 2 3 2 A. .  a AB AC . B. .  a AB AC . C. 2 . AB AC a . D. 2 . AB AC  2a . 2 2 Lời giải:
Tam giác AB AC a và BAC  60 . 2 a A .
B AC AB . AC .cos A  . a . a cos 60  . 2
Câu 37. Cho hình vuông ABCD cạnh 2a , M là trung điểm của cạnh CD . Chọn khẳng định đúng.
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Luyện tập VECTƠ 2 a
A. AM .DC  .
B. AM .DC  0 . C. 2
AM .DC a . D. 2
AM .DC  2a . 2 Lời giải:
Ta có AM .DC  ( AD DM ).DC A .
D DC DM .DC Mà 0 A . D DC A . D DC.cos 90  0 Và 0 2
DM .DC DM .DC.cos 0  .2 a .1 a  2a Vậy 2
AM .DC DM .DC  2a .
Câu 38. Cho hình vuông ABCD có độ dài cạnh bằng 10 . Tính giá trị A . B CD . A. 100 . B. 10 . C. 0 . D. 100 . Lời giải: Ta có A .
B CD AB . CD .cos  AB,CD  A . B .
CD cos180  10.10.  1  1  00 . 1
Câu 39. Cho tam giác đều ABC có độ dài cạnh bằng 4 và điểm M thỏa mãn BM   BC . Tính 2 BM .BA .
A. BM .BA  4 .
B. BM .BA  4 .
C. BM .BA  4 3 .
D. BM .BA  4 3 . Lời giải: 1 1
Ta có BM   BC BM BC  2 . 2 2
Khi đó BM BA BM BABM BA 0 . . .cos ;  2.4.cos120  4  .
Câu 40. Cho hình vuông ABCD có độ dài các cạnh bằng a . Tính AC.BD . A. 2
AC.BD  2a .
B. AC.BD  0 .
C. AC.BD  0 . D. 2
AC.BD  2a . Lời giải:
Vì ABCD là hình vuông nên hai đường chéo AC và BD vuông góc nhau.
Hay AC BD nên AC.BD  0 .
Câu 41. Cho tam giác đều ABC có trọng tâm G và độ dài cạnh bằng a . Tính A . B AG. 2 a 3 2 3a 2 a 3 2 a A. . B. . C. . D. . 6 4 4 2
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Luyện tập VECTƠ Lời giải: a 3 Ta có A .
B AG AB AG .cos  AB, AG ; với AB AB  ; a AG AG  ; AB, AG 0  30 . 3 2 a 3 a Vậy 0 A . B AG  . a .cos 30  . 3 2
Câu 42. Cho tam giác đều ABC cạnh a, đường cao AH. Tính AC AC AB. 2 a 2 2 a 3 2 a 2 a A.  . B. . C. . D. . 2 2 2 2 Lời giải: a Ta có ACAC  AB 2 0
 AC.BC  CA.CB  CA.CB.cosC  a.a.cos60  . 2
Câu 43. Cho hình thoi ABCD tâm O có cạnh bằng a 2 và ABD  60 . Gọi I là điểm thỏa mãn
2IC ID  0 . Tính tích vô hướng A . O BI . 2 a 2 2 a 3 2 a A. . B. . C. .
D. u  2; 3   2 2 2 Lời giải: B A C O I D
Do ABCD là hình thoi có cạnh bằng a và ABD  60 nên ABD và BCD là các tam giác đều cạnh a . Ta có: A . O BI A .
O BD DI   A . O D B A . O DI  2  2 2 2  2 a 2. 3 a 2 a 2 A . O DC A . O AB    . . . a cos 30  . Vậy, A . O BI   . 3  3 3 2 2 2
Câu 44. Cho tam giác ABC vuông tại A có AB  3; AC  4 . Trên đoạn thẳng BC lấy điểm M sao
cho MB  2MC . Tính tích vô hướng AM .BC .
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Luyện tập VECTƠ 23 41 A. . B. . C. 8 . D. 23 . 3 3 Lời giải: 1 1 Ta có MB  2
MC AM  AB  2AC , do đó AM.BC  AB  2ACAC AB. 3 3
Vì tam giác ABC vuông tại A nên . AB AC  0 . 2 2 1 1 1 23
Vậy AM .BC   AB  2AC AC AB  2AC AB    2 2
2.AC AB   . 3 3 3 3
Câu 45. Cho hình vuông ABCD cạnh bằng 5. Tính  AB AC.BC BD BA. A. 10 2 . B. 50 . C. 0 . D. 75 . Lời giải:
Ta có:  AB AC.BC BD BA   AB AC.2BD (Vì BC BA BD )  2 A .
B BD AC.BD  2 A .
B BD (Vì AC.BD  0)  2 A . B BA A .
B AD  2 A . B BA (Vì . AB AD  0 ) 2
 2.AB .cos180  50 .
Câu 46. Cho hai vectơ a và b có a
4 , b  5 và a b 0 ,
120 . Tính a b . A. 21 . B. 21 . C. 41 . D. 41 . Lời giải: 2 2 2 2 2
Ta có a b  a b  a b  2 . a b
a b  2 a b cos a,b  21 .
Dạng 3: TÍNH TÍCH VÔ HƯỚNG BẰNG BIỂU THỨC TỌA ĐỘ
Câu 47. Cho hai vectơ u  2;   1 , v   3
 ;4 . Tích u.v bằng A. 11. B. 10. C. 5.
D. 2. Lời giải: u    2;  1 Với 
u.v  2.3      v     1 4 10. 3; 4
Câu 48. Trong mặt phẳng toạ độ Oxy , cho a  (1; 4) , b  ( 1
 ;3) . Khi đó giá trị tích vô hướng của hai
véctơ a và b là A. 12 . B. 11. C. 0. D. 11. Lời giải: Ta có: . a b  1.( 1  )  4.3  11.
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Luyện tập VECTƠ
Câu 49. Trong mặt phẳng tọa độ Oxy , cho hai vectơ u i  3j và v  2j  2i . Tính . u v . A. . u v  4 . B. . u v  4 . C. . u v  2 . D. . u v  2 . Lời giải:
Theo giả thiết ta có u  1; 3 và v   2  ;2 . Khi đó . u v  1. 2    3.2  4 .
Câu 50. Cho A0; 3 ; B4;0 ; C  2  ; 5   . Tính A . B BC . A. 16 . B. 9 . C. 10 . D. 9  . Lời giải:
Ta có AB  4;  3 ; BC   6  ; 5 Vậy A . B BC  4. 6     3  . 5    9  .
Câu 51. Cho u  2; 3
  . Với giá trị nào của m thì v   3;
m vuông góc với u ?
A. m  1.
B. m  2 .
C. m  1.
D. m  2 . Lời giải:
Ta có: v u  2. 3     3
 .m  0  m  2  .
Câu 52. Trong mặt phẳng tọa độ Oxy cho các vectơ a 1; 3 , b 2;5 . Tính tích vô hướng của . a b . A. 7 . B. 13 . C. 17 . D. 13 . Lời giải: Ta có . a b  1.2   3  .5  1  3.
Câu 53. Trong mặt phẳng tọa độ Oxy , cho a  2;  5 và b  m; m  2 . Tìm m biết a và b vuông góc. 10 10 10 10 A. m   .
B. m   .
C. m   . D. m  . 3 3 7 7 Lời giải:
Để a b thì a b
m  m   10 . 0 2 5 2  0  m   . 3
Câu 54. Trong mặt phẳng toạ độ Oxy , cho a  (1; 4) ; b  (4;0). Khi đó, cosin góc giữa hai vecto a và b là  17 17 A. . B. . C. 0. D. 2. 17 17 Lời giải: . a b 4 17
Ta có: cos(a, b)    . a . b 17. 16 17
Câu 55. Trên mặt phẳng Oxy, cho hai vectơ a  2;  1 và b  2; 4
 . Khi đó góc giữa hai vectơ a và b bằng A. 30 . B. 45 . C. 90 . D. 60 . Lời giải:
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Luyện tập VECTƠ b a b
a b a ba.b a. . .cos , cos , 
 0  a,b  90 a . b
Câu 56. Cho hai vectơ a   3 
;1 , b  3; 3. Góc giữa hai vectơ a và b bằng A. 15 . B. 30 . C. 45 . D. 60 . Lời giải: a b  Ta có: a b . cos ;  3 3 3 1 
   ;ab  60. a . b 2.2 3 2
Câu 57. Trong mặt phẳng Oxy , cho A1; 2, B 4 
;1 , C 5; 4 . Tính góc BAC. A. 45 .  B. 90 . C. 30 . D. 60 . Lời giải:
Ta có: AB  3;  1 , AC  4;2 . . AB AC 3.4  1  .2 2
Khi đó: cos BAC  cos  AB, AC      . AB . AC 3   2 2 2 2 2 1 . 4  2 Suy ra 45o BAC  .
Câu 58. Trong mặt phẳng tọa độ Oxy , cho tam giác ABC biết (
A 1; 2) , B(4;1) , C(5; 4) . Tính góc A của tam giác ABC . A. 60 . B. 45 . C. 90 . D. 120 . Lời giải: Ta có: AB  (3; 1
 ) , AC  (4;2)  . AB AC  3.4  ( 1
 ).2  10 , AB  10 , AC  2 5 . A . B AC 10 2 cos( ) A  cos( A , B AC)     A  45 . A . B AC 10.2 5 2
Câu 59. Tam giác ABC có A1; 2 , B 0; 4 , C 3; 
1 . Góc BAC của tam giác ABC gần với giá trị nào dưới đây? A. 90 . B. 36 5  2 . C. 143 7   . D. 53 7   . Lời giải:
Ta có AB   1
 ;2; AC  2;  1 . . AB AC 2   2 4  cos BAC     BAC 143 7   . AB . AC 5. 5 5
Câu 60. Trong mặt phẳng Oxy cho các điểm A 1  ;  1 ; B 3 
;1 ; C 6;0 . Khẳng định nào sau đây đúng: A. AB   4  ; 2  ; BC   3   ;1 . B. o B  135 .
C. AB  20 . D. BC  3. Lời giải: BA   4  ; 2
 ; BC  3;  1
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Luyện tập VECTƠ      B  BA BC . BA BC 4.3  2.  1 2 cos cos ;    2 2 2 2 BA . BC   2 4 2 . 3 1 o  B 135 .
Câu 61. Trong mặt phẳng Oxy cho các điểm A 1
 ;2; B5;8 . Điểm M Ox sao cho tam giác MAB
vuông tại A . Diện tích tam giác MAB bằng A. 10 . B. 18 . C. 24 . D. 12 . Lời giải:
Vì M Ox nên có tọa độ M a;0 , ta có AM  a 1; 2
 ; AB  6;6 .
Tam giác MAB vuông tại A A .
B AM  0  6 a  
1 12  0  a  1  M 1;0 . 2 2 2 2
Ta có AM  1 
1  0  2  2 2 ; AB  5   1  8  2  6 2 . 1 1 Vậy S
 .AM.AB  .2 2.6 2 12 . ABM  2 2
Câu 62. Trong mặt phẳng tọa độ Oxy , cho điểm A2; 3 . Tìm tọa độ điểm B thuộc trục tung, biết
khoảng cách giữa hai điểm A và B bằng 2 5 và điểm B có tung độ dương. A. B 0;  1 .
B. B 0;7 .
C. B 2;0 .
D. B 7;0 . Lời giải:
Ta có B thuộc trục tung nên gọi B 0,b , b  0 . Ta có AB   2  ;b  3 . 2   2 2 b 1(TM ) Theo giả thiết 2
AB  2 5   2
   b  3 2
 20  b  6b  7  0   . b  7  (L) Vậy B 0;  1 .
Câu 63. Trong mặt phẳng Oxy , cho hai điểm A3 ; 4 và B  2
 ; 5 . Tọa độ điểm M thuộc trục Ox cách đều hai điểm ; A B là  2   2   1 9   1  A.  ;0   . B. ; 0   . C. ;   . D. ; 0   .  5   5   2 2   2  Lời giải:
Vì M Ox nên M  ; x 0 .
Ta có: AM   x  3; 4
  ; BM  x  2; 5   . Để M cách đều ;
A B thì AM BM   2
x  2   2   x  2   2 3 4 2 5  x   5  2  Vậy M  ;0   .  5 
Câu 64. Trong hệ toạ độ Oxy , cho hai điểm (
A 1; 1) và B( 2  ; 2)
 . Điểm C thuộc trục Ox sao cho tam
giác ABC cân tại A là
A. C(2; 0) .
B. C(0; 2) .
C. C(4; 0) .
D. C(2; 0) . Lời giải:
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Luyện tập VECTƠ Ta có 2 2 AB  ( 2  1)  ( 2  1)  10
Do điểm C(a;b) thuộc trục Ox nên C(a; 0) suy ra 2 2
AC  (a 1)  (0 1)
Tam giác ABC cân tại A AB AC a  4 2 2
 10  (a 1)  (0 1)  
Với C(4; 0) , ta có AB( 3  ; 1
 ), AC(3;1) suy ra 3 điểm a  2  ,
A B, C thẳng hàng, loại trường hợp này.
Với C(2; 0) , kiểm tra tương tự thấy thoả mãn. Vậy C(2; 0) .
Câu 65. Trong mặt phẳng tọa độ Oxy cho hai điểm A1; 2 ; B 1; 
1 . Điểm M thuộc trục Oy thỏa
mãn tam giác MAB cân tại M . Khi đó, độ dài đoạn OM bằng 5 3 1 7 A. . B. . C. . D. . 2 2 2 2 Lời giải:
Điểm M thuộc trục Oy M 0; y .
Ta có tam giác MAB cân tại M MA MB
   y2   2    y2 2 1 2 1 1  4  4y  1 3 2 y y  . 2 3 Vậy OM  . 2
Câu 66. Trong mặt phẳng tọa độ Oxy , cho tam giác ABC có A1;   1 , B 4; 
1 , C 5; 7 . Tính diện
tích S của tam giác ABC . 3 13
A. S  26 .
B. S  13 .
C. S  3 13  65 . D. S  . 2 Lời giải:
Ta có: AB 3; 2 , AC 4; 6    .
AB AC  0  AB AC 1 1 1  SA . B AC  9  4. 16  36  2.13  13 . ABC  2 2 2
Câu 67. Trong mặt phẳng với hệ tọa độ Oxy , cho hai điểm A3; 2, B 4;3 . Điểm M thuộc tia Ox .
Khẳng định nào dưới đây đúng?
A. M  7;0 .
B. M  5;0 .
C. M  9;0 .
D. M  2;0 . Lời giải:
M Ox M  ;
x 0 (theo giả thiết thì x  0 ).
Ta có AM   x  3; 2
 , BM  x  4; 3  
Tam giác ABM vuông tại M AM .BM  0   x  3 x  4   2   3    0 x  2 (TM ) 2
x x  6  0   . x  3  (L)
Vậy x  2 thỏa mãn yêu cầu bài toán.
Câu 68. Cho hai điểm A1;3, B 8; 2 . Gọi C là điểm thuộc trục hoành sao cho tam giác ABC vuông
tại C và OC  6 . Giá trị của biểu thức 2 2
x y  5 là C C
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Luyện tập VECTƠ A. 9 . B. 14 . C. 21 . D. 30 . Lời giải:
Gọi C x ;0 là điểm thuộc trục hoành. Ta có: AC   x 1;  3, BC   x  8;  2 .
Do tam giác ABC vuông tại C nên AC.BC  0  x   x
1 . x  8   3  . 2   7 2
 0  x  9x 14  0   x  2
Vì OC  6 nên ta chọn x  2 . Suy ra C 2;0 . Vậy 2 2
x y  5  9 . C C
Câu 69. Trong mặt phẳng Oxy , cho hai điểm A1; 2 ,B 3
 ;1. Tìm tọa độ điểm C trên trục Oy sao
cho tam giác ABC vuông tại A .
A. C 6;0 .
B. C 0;6 .
C. C 6;0 .
D. C 0; 6 . Lời giải:
C Oy C 0; yAB   4  ; 1   , AC   1  ; y  2. AB  0 
Ba điểm A , B , C tạo thành một tam giác vuông tại A  AC  0  A .
B AC  0  y  6. AB AC  Vậy C 0;6.
Câu 70. Cho tam giác ABC có A 1
 ;2,B0;3,C5; 2. Tìm tọa độ chân đường cao hạ từ đỉnh A của tam giác ABC . A. 0; 3 .
B. 0;  3 . C. 3;0 . D.  3  ;0 . Lời giải: A B C
Ta có AB  1;1; AC  6;  4; BC  5;  5.
Nhận thấy rằng A . B BC  1.5  1.( 5
 )  0 nên tam giác ABC vuông tại B.
Vậy chân đường cao hạ từ đỉnh A của tam giác ABC trùng với đỉnh B0; 3.
Câu 71. Trong mặt phẳng Oxy , cho tam giác ABC biết A1;  1 , B 3; 
1 và C 2; 4 . Tìm tọa độ trực
tâm H của tam giác ABC A. H 1;  1 . B. H 2;  1 .
C. H 1; 2 .
D. H 2; 2 . Lời giải: Gọi H  ; x y  .
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Luyện tập VECTƠ
AH.BC  0
Vì H là trực tâm của tam giác ABC nên ta có  (1)
BH.AC  0
Mà AH   x 1; y   1 , BC   1
 ;3 , BH  x  3; y   1 , AC  3;3 . 1.  x   1  3 y   1  0 x  2 Do đó   1     . Vậy H 2; 2 . 3
  x  3  3 y   1  0  y  2
Câu 72. Cho tam giác ABC có A1;3, B 3;  4 và C 6; 2 . Trực tâm của tam giác ABC là H a;b .
Tính giá trị biểu thức T a  2b . A. 10 . B. 6 . C. 8 . D. 7 . Lời giải:
AH  a 1;b 3  BC   3;6 Ta có:  .
BH  a  3;b  4  AC   5;  1 AH BC
Theo giả thiết H là trực tâm tam giác ABC nên ta có  BH AC  45 a
BC.AH  0 3  a  
1  6 b  3  0
a  2b  7  11         .
AC.BH  0 5
 a 3 1b  4  0 5
a b 19 16 b    11  45 16  45 16  Suy ra H ;   và T   2  7   .  11 11  11  11 
Câu 73. Trong mặt phẳng tọa độ Oxy cho tam giác ABC. Biết A3; 1  ,B 1
 ;2 và I 1;1 là trọng tâm
tam giác ABC. Trực tâm H của tam giác ABC có tọa độ a;b. Tính a  3 . b 2 4
A. a  3b  .
B. a  3b   .
C. a  3b  1.
D. a  3b  2. 3 3 Lời giải: A H B C
Giả sử C x ; y và H x ; y
. Có I là trọng tâm tam giác ABC nên ta có H H C C
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Luyện tập VECTƠ
x x x A B C   xI   x  1 3 C     C1; 4  
y y y  y  4  A B CCy  3 I
Ta có AH  x  3; y  1; BC  2; 6
 ; BH  x  1; y  2; AC   2  ; 3  H HH H
H là trực tâm tam giác ABC nên  
AH.BC  0  x    y   10 2 3 6 1  0 xHH H 3       10 8 a  ; b   2  S  . BH.AC  0   2 
 x  1  y   3 9 3 H  3 2 H  0 8 y   H  9
Câu 74. Trong mặt phẳng tọa độ Oxy , cho hình thang cân ABCD với các đáy là AB và CD . Biết
A1; 2 , B 2; 3 , điểm C nằm trên trục tung, điểm D nằm trên trục hoành. Tính OC OD . 4 26 A. . B. 2 . C. 6 . D. . 3 3 Lời giải:
Tứ giác ABCD là hình thang cân có các đáy là AB và CD CD t AB với t  0 .
Vì C Oy nên C 0;c , D Ox nên D d ;0 .
Ta có AB  1;  5;CD  d ;  c . d td t
CD t.AB     . c  5  tc  5t
Vì ABCD là hình thang cân nên AC BD 2 2  AC BD
   2  c  2  d  2    2 0 1 2 2 0 3 *. c  5t Thay 
vào * ta được:   t  2  t  2 1 5 2 2  9 d tt  1 ktm     2   1 5 1
24t 16t  8  0  1 
. Với t    C 0;    và D  ;0   . t   tm      3 3 3  3 5 1
Vậy OC OD    2 . 3 3
Câu 75. Trong mặt phẳng Oxy , cho bốn điểm A 2
 ;3, B2;4, C 3;0, D 1  ;  1 . Có bao nhiêu
điểm M thuộc đường thẳng d : y  2x 1 sao cho MA MB MC.MD  3  ? A. 0. B. 1. C. 2. D. 3. Lời giải:
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Luyện tập VECTƠ
Gọi M a;b là tọa độ điểm cần tìm.
Ta có: MA MB MC.MD  3
  AM BM CM .DM  3  .
Lại có: M a;b thuộc đường thẳng d : y  2x 1  b  2a 1  M  ; a 2a   1 .
AM  a  2;2a  4 
Khi đó: BM  a  2; 2a  5  AM BM CM  3a  3;6a 10
CM  a3;2a   1 
DM  a 1; 2a
Mà  AM BM CM .DM  3  a  0  
 3a  3.a   1  6a 10 2 .2a  3
  15a  20a  0  4  . a   3   Vậy M   4 5 0;1 hay M ; .    3 3 
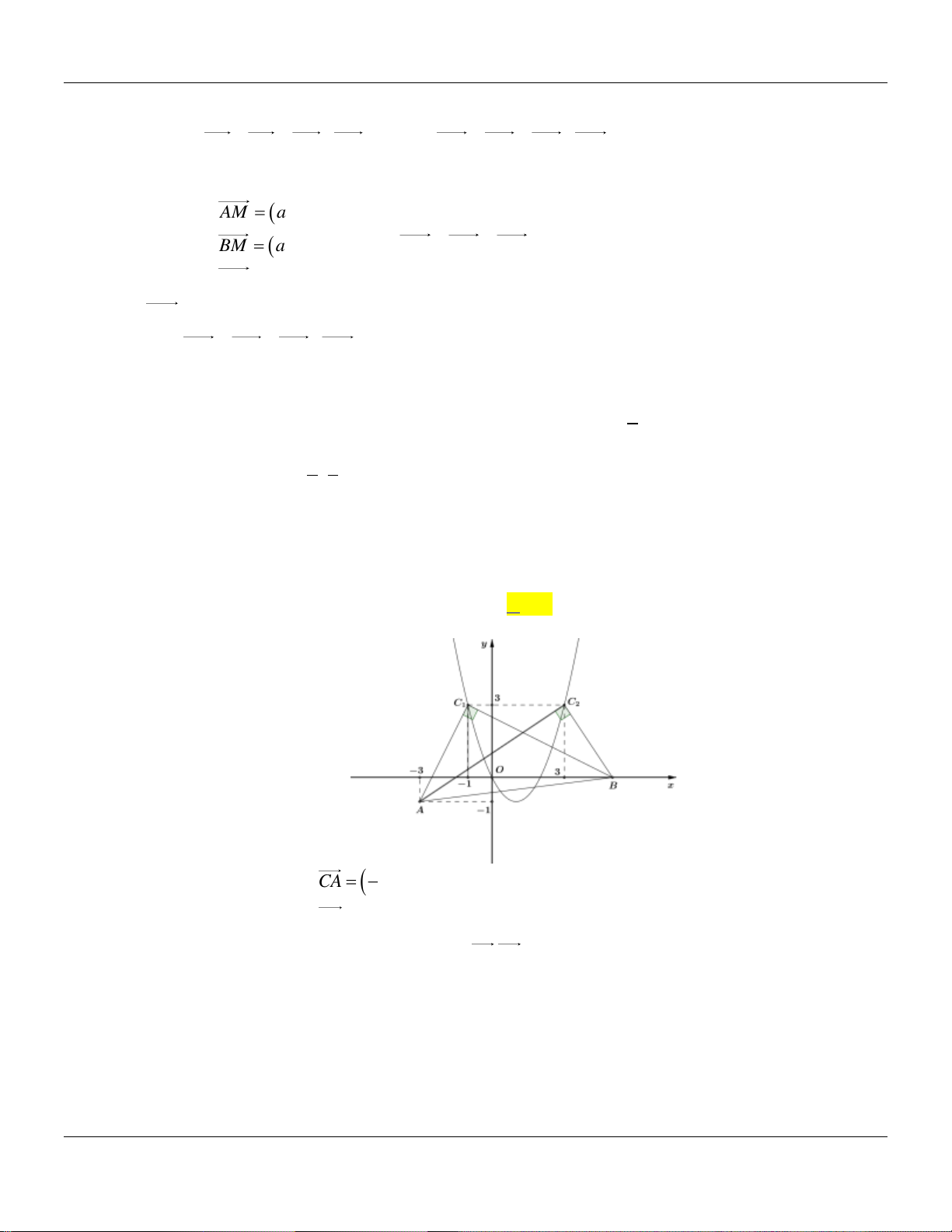
Câu 76. Trong mặt phẳng tọa độ Oxy cho hai điểm A 3  ; 
1 và B 5;0 . Biết có hai điểm C nằm trên parabol  P 2
: y x  2x sao cho tam giác ABC vuông tại C là C x ; y ,C x ; y . 1  1 1  2  2 2 
Tính giá trị biểu thức T x y x y . 1 2 2 1 A. 4 . B. 5 . C. 6 . D. 5  . Lời giải: CA    2 3   ;
x 1 x  2x Gọi C  2 ;
x x  2x   . CB    2 5  ;
x x  2x
Do tam giác ABC vuông tại C nên ta có C . A CB  0
   x  x   2
  x x 2 3 5 1 2
x  2x  0 2
x  2x  3  0 1 4 3 2
x  4x  6x  4x 15  0   2
x  2x  3 2
x  2x  5    0   . 2
x  2x  5  0  2
x  1 C 1;3 1   Giải (1) được  .
x  3  C 3;3  2  
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Luyện tập VECTƠ Giải (2): Vô nghiệm.
Vậy có hai điểm thỏa mãn yêu cầu bài toán và T    1 .3  3.3  6 .
Câu 77. Trong mặt phẳng Oxy , cho tam giác ABC với A2; 4, B 1  ;1 , C 7;   1 . Biết M  ;
a b a  0
là điểm nằm trong mặt phẳng Oxy thoả mãn tam giác ABM vuông cân tại B . Tính giá trị
T  3a  4b .
A. T  2 .
B. T  2 .
C. T  12 .
D. T  12 . Lời giải:
Ta có BA  1;3; BM  a 1;b   1
Vì tam giác ABM vuông cân tại B , suy ra: 1   a   1  3b   1  0 BM .BA  0 
a  3b  4  0      2 2 AB B M
 1  3  1 a2  1 b2 2 2
a b  2a  2b  8  0   b   2
a  4  3b 
a  4  3b   a  2         b .  4  3b   0 2 2
b  24  3b  2b 8  0   b   0 b  2  l a  4 
Vậy toạ độ điểm M  2
 ;2 , suy ra T  3a  4b  2 .  1 
Câu 78. Trong mặt phẳng tọa độ Oxy , cho A4;6 ; B 5;  1 ; C  ;
n 3 . Tìm m , n để I  ; m   là tâm  2 
đường tròn ngoại tiếp tam giác ABC . 5 5 5  n  1 5  n  1 A. m   ; n  1 B. m  ; n  1 . C. m  ;  .
D. m   ;  . 2 2 2 n  2  2 n  2  Lời giải:
AB  1; 5 , AC  n  4; 9 . ,
A B, C là 3 đỉnh của một tam giác  AB và AC không cùng 9 11
phương  n  4   n   . 5 5  9  11   1  Ta có: IA ; 6  m   ; IB ;1 m   ; IC n  ; 3   m   .  2   2   2  2 2 IA IB
I là tâm đường tròn ngoại tiếp tam giác ABC khi  2 2 IA IC 2 2   9          m2 11 6     1 m2   2   2    2 2   9          m2 1 6  n     3 m2   2   2 
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Luyện tập VECTƠ  5 m     5 25 10m  0 2  m     1 3  2 2 2   9    n      .         m2 1 6  n      3   m2  n  1 2 2       t / m 2   2   1 3   n  2  n      2 2 5  n  1 Vậy m  ;  . 2 n  2 
Câu 79. Trong mặt phẳng tọa độ Oxy , cho tam giác ABC , biết H a;b là toạ độ chân đường cao đỉnh
A của tam giác ABC , biết toạ độ B 3  ;1 , C 4; 4
  và trọng tâm G của tam giác ABC có toạ
độ G 4;0 . Tính a b . 2 33 35 68 A. , B. . C. . D. . 13 13 13 13 Lời giải:
x x x A B C x   G  x  5 3
G 4;0 là trọng tâm tam giác ABC , suy ra A   
y y y y  3   A B C A y G  3 Gọi H  ; x y  là chân đường cao đỉnh A , suy ra
AH.BC  0  1 x  5  5 y  3  0  x  5y 10  0   1 x  3 y 1
Vì H BC nên BH ; BC cùng phương, suy ra 
 5x y 16  0 2 1 5   35 x
x  5y  1  0  13 Từ   1 và 2 ta có hệ    . 5
x y 16 33 y   13  35 33  68 Toạ độ điểm H ; 
 , suy ra a b  .  13 13  13
Dạng 4: CÁC BÀI TOÁN KHÁC
Câu 80. Cho a , b có a  2b vuông góc với vectơ 5a  4b và a b . Tính góc giữa vectơ a và b . A. 30 . B. 45 . C. 90 . D. 60 . Lời giải:
+ Vì a  2b vuông góc với vectơ 5a  4b nên a  2b.5a  4b  0 . 2 2
 5a  8b  6 . a b  0 2 2 5   8  .  a b a b 6 2 2 5  a  8 b  . a b  (1) 6
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Luyện tập VECTƠ 2 2
+ Theo đề a b a b . 2 a + Từ (1) ta được . a b  2 2 a . a b 1 + Ta có a b 2 cos ,  
  a,b 0  60 . 2 a b 2 a
+ Kết luận: Góc giữa vectơ a và b bằng 0 60 .
Câu 81. Cho biết  ;
a b 120 ; a  3; b  3. Độ dài của véctơ a b bằng 3 3 3 A. 3 3 . B. 3 2 . C. . D. . 2 2 Lời giải: 2 2 2 2 2 2   
Ta có a b  a b  a  2. .
a b b a b  1
2. a . b .cos a;b  9  9  2.3.3.  27   .  2 
Suy ra: a b  3 3 .
Câu 82. Trong mặt phẳng tọa độ Oxy , cho ba điểm M 3; 4, N 2  ;1 , P  2  ; 3
  . Tìm điểm I trên
đường thẳng NP sao cho góc MIN  135 . A. I 3; 2 .
B. I 2;3 .
C. I 5; 4 .
D. I 4;5 . Lời giải:
+) Ta có NP   4  ; 4 ; Gọi I  ;
x y   IN  2  ; x 1 y  . 2  x 1 y
Vì I NP IN , NP là hai vectơ cùng phương  
y x 1 I  ; x x   1 . 4  4  IM NP +) Ta có MINIM NP . cos = cos ,  (1). IM . NP Vì MIN  135 và IM  3  ;
x 5  x; NP   4  ;  4 nên từ   1 ta có: 2  x  8 1
x  5  I 5; 4  2 2  2
x  8  2x 16x  34  x  8x 15  0   2
2x 16x  34. 2 2 x  3  I  3; 2 IM.IN 1
+) Trường hợp 1: I 5; 4  IM  2  ;0; IN  3;
  3  cosMIN cosIM, IN   IM . IN 2
MIN  45 (loại). IM.IN 1 
+) Trường hợp 2: I 3; 2  IM 0; 2; IN  1
 ;  1  cosMIN cosIM, IN   IM . IN 2
MIN  135(TM).
Vậy điểm cần tìm là I 3; 2.
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Luyện tập VECTƠ
Câu 83. Cho tam giác đều ABC cạnh 3a , a  0 . Lấy các điểm M , N , P lần lượt trên các cạnh BC ,
CA , AB sao cho BM a , CN  2a , AP x 0  x  3a . Tìm x để AM PN . 3a 2a 4a a A. x  . B. x  . C. x  . D. x  . 5 5 5 5 Lời giải: 1 1 2 1
Ta có AM AB BM AB BC AB   AC AB  AB AC . 3 3 3 3 1 x
Ta có PN AN AP AC AB . 3 3a  2 1  1 x
Để AM PN thì AM .PN  0  AB AC AC AB  0     3 3  3 3a  2 2 2 2x 1 xA . B AC AB AC A . B AC  0 . 9 9a 9 9a 2 2xB AC    a2 1 x A . .cos 60 3  3a2  A . B AC.cos 60  0 9 9a 9 9a 2 1 2x 1 x 1 5 4a 2 2
 3a 3a   9a  9a
3a 3a   0 2
 2a ax  0  x  . 9 2 9a 9 9a 2 2 5 4a Vậy x
thì AM PN . 5
Câu 84. Cho tam giác ABC đều cạnh a . Trên các cạnh BC,C ,
A AB lần lượt lấy các điểm M , N , P sao 1
cho MC  2MB , NA   NC và AP x . Tìm x để AM vuông góc với PN . 2 4a a 2  6 3 1 3 3 A. . B. . C. a . D. a . 15 3 39 39 Lời giải:
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Luyện tập VECTƠ Đặt AB  , b AC c 1 1 1 2
Ta có AM AB BM AB BC AB   AC AB  c b 3 3 3 3 1 x
PN AN AP c b 3 a  1 2  1 x
Để AM PN AM .PN  0  c b c b  0     3 3  3 a
 c bac xb 2 2 2 3  0  . a c  3 . xb c  2 . a . b c  6 . x b  0 2
a c   a x 2 . 2 3 . b c  6 . x b  0 2
a a   a x 0 2 . 2 3 . . a . a cos 60  6 . x a  0  3x  2  15 4a a a a   6x  0    2a
x  0  x  .  2  2 15
Câu 85. Cho hình chữ nhật ABCD thỏa AB  2a , AD a . Gọi M , N là hai điểm thỏa mãn
DM  2MC , AN x AB , x
. Tìm x để AM và DN vuông góc. 3 3 1 2 A. x  .
B. x  . C. x  . D. x  . 7 8 2 5 Lời giải: A N B D C M AN
Cách 1. Xét tam giác vuông DAN có tan ADN AD AD
Xét tam giác vuông ADM có cot MAD DM
Vì AM DN nên ADN MAD  90 . AN AD AD 3 a 3 3
Do đó tan ADN  cot MAD     .
  AN a . AD DM 2 2 2a 4 4 DC 3 AN 3a 1 3 3 3 Suy ra  .
  AN AB . Vậy x  . AB 4 2a 8 8 8 Cách 2. 2 2
Ta có AM AD DM AD DC AD AB 3 3
Ta có DN AN AD x AB AD .  2 
Ta có AM .DN  0  AB AD . 
 xAB AD  0  3 
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Luyện tập VECTƠ 2 2 2 2  xAB A . B AD x A .
D AB AD  0 3 3 2 3 2 2  .4
x a a  0  x  . 3 8
Cách 3. Chọn hệ trục tọa độ Oxy với D 0;0 , C 2a;0 ; A0; a ; B 2a; a .  4a   4a  Ta suy ra M ; 0 
 , N t;a,0  t  2a ; AM  ; a
 ; DN  t;a .  3   3  4a 3a Ta có 2
AM DN AM .DN  0 
t a  0  t  . 3 4  3a   3a  3 3 Do đó N ; a ; AN  ;0 ; AB     
2 ;a0.Ta có AN AB . Vậy x  .  4   4  8 8
Câu 86. Cho hình thoi ABCD có cạnh bằng a và BAD  60 . Quỹ tích các điểm M thỏa mãn 2 M .
A MC a là đường tròn có bán kính bằng 7a 3a A. 2a . B. . C. . D. a . 2 2 Lời giải: B A C 60° O a D
Gọi O là giao của hai đường chéo AC và BD . Ta có: M .
A MC  MO OAMO OC  MO OAMO OA 2 2   2 2 3a 3a 2 2
MO OA MO     MO    2 4   2 7a 7a Do đó 2 2 M .
A MC a MO   MO  . 4 2
Vậy tập hợp các điểm M thỏa mãn yên cầu bài toán là đường tròn tâm O bán kính bằng 7a . 2
Câu 87. Cho ba điểm không thẳng hàng ,
A B, C .Điều kiện cần và đủ để ba điểm ,
A B, C thỏa mãn điều
kiện (CA CB).AB  0 là:
A. ABC đều.
B. ABC cân tại C .
C. ABC vuông tại C .
D. ABC vuông cân tại C . Lời giải:
Gọi M là trung điểm của AB
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Luyện tập VECTƠ
Ta có CA CB  2CM . Nên (CA CB).AB  0  2CM .AB  0  CM  . AB
Vậy ABC cân tại C .
Câu 88. Cho hình thang vuông ABCD với đường cao AB  2a, các cạnh đáy AD a và BC  3 . a Gọi
M là điểm trên đoạn AC sao cho AM k.AC. Tìm k để BM và CD vuông góc. 4 3 1 2 A. . B. . C. . D. . 9 7 3 5 Lời giải: B A M D H C
Hạ DH BC dễ thấy ABHD là hình chữ nhật và BH  . a
Từ giả thiết AM k.AC   AB BM   k. AB BC  BM  k  
1 .AB k.B . C
Mặt khác: DC DH HC. 2 2
Theo chứng minh trên ta có DH AB và HC
BC nên DC AB BC. 3 3
BM CD BM .DC  0 *.   Do giả thiết ta có .
AB BC  0 nên     k   AB k BC 2 * 1 . . . AB BC  0    3   k   2 2k 2 2 1 .AB
.k.BC  0  4 k   2 2 1 .a  .9a  2
0  4k  4  6k  0  k  . 3 3 5 2
Câu 89. Cho hai điểm B, C phân biệt. Tập hợp những điểm M thỏa mãn CM .CB CM là
A. đường tròn đường kính BC .
B. đường tròn  B; BC  .
C. đường tròn C;CB .
D. đường tròn C; 2CB . Lời giải: 2 2
CM .CB CM CM .CB CM  0  CM .MB  0 .
Tập hợp điểm M là đường tròn đường kính BC .
Câu 90. Cho ba điểm ,
A B, C phân biệt. Tập hợp những điểm M mà CM .CB  . CA CB là
A. đường tròn đường kính AB .
B. đường thẳng đi qua A và vuông góc với BC .
C. đường thẳng đi qua B và vuông góc với AC .
D. đường thẳng đi qua C và vuông góc với AB . Lời giải: CM .CB  .
CA CB CM .CB  .
CA CB  0  CM CA.CB  0  AM.CB  0 .
Tập hợp điểm M là đường thẳng đi qua A và vuông góc với BC .
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Luyện tập VECTƠ
Câu 91. Cho tam giác ABC , điểm J thỏa mãn AK  3KJ , I là trung điểm của cạnh AB ,điểm K thỏa
mãn KA KB  2KC  0 . Một điểm M thay đổi thỏa mãn 3MK AK.MA MB  2MC  0 .
Tập hợp điểm M là
A. đường tròn đường kính IJ .
B. đường tròn đường kính IK .
C. đường tròn đường kính JK .
D. đường trung trực đoạn JK . Lời giải: A I K J C B
Ta có: MA MB  2MC  4MK KA KB  2KC  4MK . 1 AB AC
Lấy điểm J thỏa mãn AK  3KJ . Ta có AK  AI AC  
, mà AK  3KJ nên 2 4 2 1 4 1 2
AJ AK KJ AK AK AK AB AC . 3 3 3 3 1 2 2 2 2
Lại có BJ AJ AB AB AC AB   AB AC BC . 3 3 3 3 3 2
Suy ra J là điểm cố định nằm trên đoạn thẳng BC xác định bởi hệ thức BJ BC . 3
Ta có 3MK AK  3MK  3KJ  3MJ .
Như vậy 3MK AK.MA MB  2MC  0  3MJ .4MK   0  MJ.MK  0 .
Từ đó suy ra điểm M thuộc đường tròn đường kính .
Vì , là các điểm cố định nên điểm luôn thuộc một đường tròn đường kính là đường tròn cố định.
Câu 92. Cho tam giác ABC có G là trọng tâm. Tập hợp các điểm M trong mặt phẳng thoả mãn 2 2 2 2 2 2
MA MB MC  4GA GB GC là
A. Đường tròn tâm G bán kính bằng GB .
B. Đường tròn tâm G bán kính bằng GA .
C. Đường tròn tâm G bán kính bằng GC .
D. Đường tròn tâm G bán kính bằng 4GA . Lời giải:
Ta có G là trọng tâm tam giác ABC nên GA GB GC  0 . Khi đó 2 2 2 2 2 2
MA MB MC MA MB MC
 MG GA2 MG GB2 MG GC2 2 2 2 2
 3MG GA GB GC  2MG GAGB GC 2 2 2 2
 3MG GA GB GC Suy ra 2 2 2 2 2 2
MA MB MC  4GA GB GC 2 2 2 2 2 2 2
 3MG GA GB GC  4GA GB GC
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Luyện tập VECTƠ 2 2
 3MG  3GA MG GA
Do điểm G cố định và độ dài GA không đổi nên điểm M thuộc đường tròn tâm G bán kính bằng GA .
Vậy tập hợp điểm M thoả mãn đề bài là đường tròn tâm G bán kính bằng GA . Câu 93. Cho
ABC đều, cạnh bằng a  0 . Tìm quỹ tích điểm M thỏa mãn 2 7a M . A MB M .
B MC MC.MA  . 4
A. Quỹ tích điểm M là đường trung trực của AB .
B. Quỹ tích điểm M là đường thẳng đi qua trọng tâm của ABC và song song với BC . 6a
C. Quỹ tích điểm M là đường tròn có bán kính bằng . 2 3a
D. Quỹ tích điểm M là đường tròn có bán kính bằng . 2 Lời giải:
Gọi O là trọng tâm của ABC , ta có: 2 2
MA MB MC  3MO  MA MB MC  9.MO  2 2 2
MA MB MC  MA MB MB MC MC MA 2 2 . . .  9MO 2 2 2 2 2 2 Mà: 2 2 2
MA MB MC MA MB MC  MO OA  MO OB  MO OC  2 2 2 2
MO OA OB OC  OAOB OC 2 2 3 2
.MO  3MO a 2 MO   2 2 2
MA MB MC  2 2 2 9 6MO a 7a Từ đó, ta có: M . A MB M .
B MC MC.MA    2 2 4 2  3a 3a 2 MO   MO  . 4 2 3a
Vậy quỹ tích điểm M là đường tròn tâm O , bán kính bằng . 2
Câu 94. Cho tam giác ABC đều cạnh a . Điểm M là một điểm thỏa mãn đẳng 2 a thức M . A MB M .
B MC MC.MA  
. Biết tập hợp điểm M là một đường tròn. Bán kính 6 đường tròn đó là a a a
A. R  2 . B. R  . C. R  . D. R  . 3 4 2 Lời giải:
Gọi G là trọng tâm tam giác ABC , I là trung điểm BC . Khi đó ta có:
MA MB MC MG  MA MB MC2 2 3  9MG 2 2 2
MA MB MC  MA MB MB MC MC MA 2 2 . . .  9MG
 MG GA MG GB MG GC 2 2 2 2 a 2   9MG 3
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Luyện tập VECTƠ
MG MG GAGB GC 2 2 2 2 2 a 2 3 2
GA GB GC   9MG 3 2 2 a 4 a 2 2 2 2
 6MG  3GA
 6MG  3. AI  3 9 3 2 2 4  a 3  a a 2  6MG  .    MG    . 3 2 3 3   a
Vậy tập hợp điểm M là đường tròn tâm G bán kính R  . 3
_____________________HẾT_____________________
Huế, 10h00’ Ngày 02 tháng 12 năm 2022
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115