AI và Mô Hình Hồi Quy - Khoa CNTT, Trường ĐH Phenikaa. Môn Nhập môn AI | Đại học Trường Đại học Phenika.

lOMoAR cPSD| 59561309
AI với mô hình hồi quy (regression)
Khoa Công nghệ Thông ,n – Trường Đại học Phenikaa lOMoAR cPSD| 59561309 Nội dung lOMoAR cPSD| 59561309
Các khái niệm về mô hình hồi quy
•Mô hình hồi quy là gì?
• Mô hình hồi quy là một phương pháp trong thống kê và học máy
(machine learning) sử dụng để xác định mối quan hệ giữa một
hoặc nhiều biến độc lập (hoặc biến giải thích) và một biến phụ
thuộc (hoặc biến phản ứng).
• Mục Uêu của mô hình hồi quy là dự đoán giá trị của biến phụ
thuộc dựa trên giá trị của các biến độc lập. lOMoAR cPSD| 59561309
Các khái niệm về mô hình hồi quy
• Các ứng dụng mô hình hồi quy Ứng dụng rộng rãi trong nhiều lĩnh vực:
• Tài Chính và Kinh Doanh:
• Dự đoán giá chứng khoán dựa trên các biến như lợi suất, thông =n kinh tế.
• Ước lượng tác động của các chiến lược kinh doanh đối với doanh số bán hàng. • Y Tế:
• Dự đoán các chỉ số sức khỏe dựa trên các yếu tố như lối sống, chế độ dinh dưỡng. lOMoAR cPSD| 59561309
• Đánh giá tác động của các yếu tố đối với kết quả điều trị.
Các khái niệm về mô hình hồi quy
•Các ứng dụng mô hình hồi quy (<) •Marke&ng:
• Dự đoán doanh số bán hàng dựa trên chiến lược Uếp thị • Phân
\ch tác động của chiến lược quảng cáo đối với doanh số . •Nông nghiệp:
• Dự đoán sản lượng cây trồng dựa trên điều kiện thời Uết và thổ nhưỡng .
• Đánh giá tác động của phân bón và thuốc trừ sâu. lOMoAR cPSD| 59561309
Các khái niệm về mô hình hồi quy
•Các ứng dụng mô hình hồi quy (<)
•Lĩnh vực Môi trường:
• Dự đoán mức độ ô nhiễm dựa trên các yếu tố môi trường
• Đánh giá tác động của biện pháp bảo vệ môi trường .
•Trong lĩnh vực Giáo dục:
• Dự đoán hiệu suất học tập dựa trên các yếu tố như thời gian học .
• Đánh giá tác động của các chương trình giáo dục •... lOMoAR cPSD| 59561309
Các kỹ thuật hồi quy
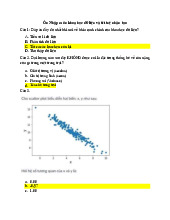
• Hồi quy tuyến /nh - Linear regression: dự đoán một giá trị của Y
(mang giá trị liên tuc), Linear regression là một hàm tuyến \nh của
một hay nhiều biến độc lập.
• Hồi quy phi tuyến – Nonlinear regression: dự đoán một giá trị của
Y (mang giá trị liên tuc), Nonlinear regression là một hàm phi tuyến
\nh của một hay nhiều biến độc lập.
• Hồi quy logis5c – LogisUc regression dự đoán xác suất của Y (giá trị
nhị phân hoặc theo thứ tự), xác suất sẽ thu được từ một hàm của
một hay nhiều biến độc lập. lOMoAR cPSD| 59561309
Các kỹ thuật hồi quy
Hồi quy tuyến tính •Hồi tuyến Fnh lOMoAR cPSD| 59561309
• Là phương pháp học máy có giám sát đơn giản, được sử dụng để dự
đoán (predict) giá trị đầu ra (liên tục, dạng số).
• Là phương pháp dựa trên thống kê để thiết lập mối quan hệ giữa một
biến phụ thuộc và một nhóm tập hợp các biến độc lập.
•Hồi quy tuyến Fnh có thể chia làm 2 loại
• Hồi quy tuyến Unh đơn biến (đơn giản - Simple linear regression) • Hồi quy tuyến Unh đa biến
Hồi quy tuyến tính
•Hồi tuyến Fnh đơn giản
• Định lượng được mối quan hệ giữa hai biến liên tục lOMoAR cPSD| 59561309
• Dự đoán giá trị của một biến từ việc HIỂU về giá trị của một biến khác
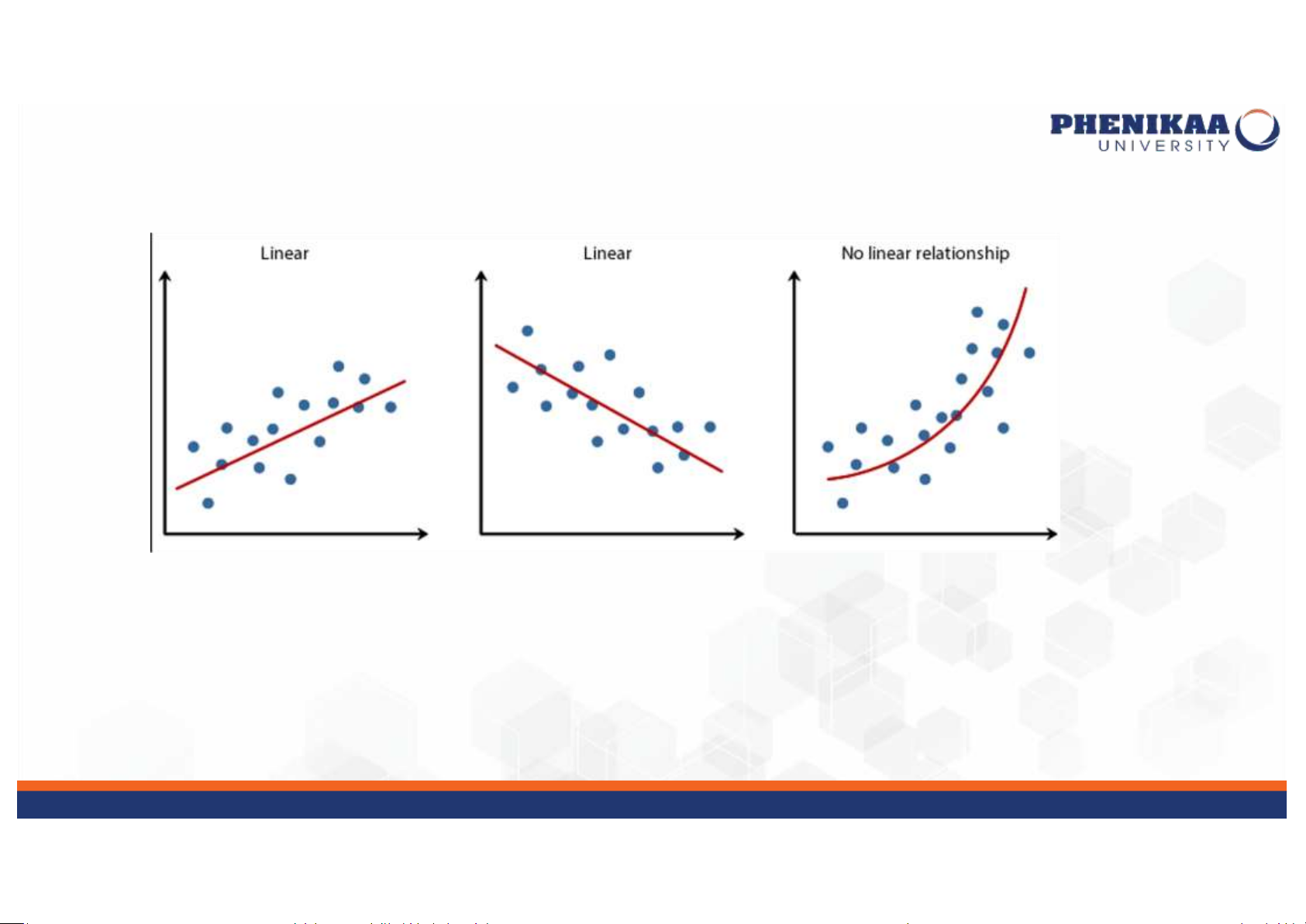
• Trong Simple Linear Regression, dễ dàng tạo ra một phương trình để dnh
giá trị của một biến phụ thuộc (Y) từ một biến độc lập (X).
• Là phương pháp dựa trên thống kê để thiết lập mối quan hệ giữa một
biến phụ thuộc và một nhóm tập hợp các biến độc lập. Hồi quy tuyến Dnh
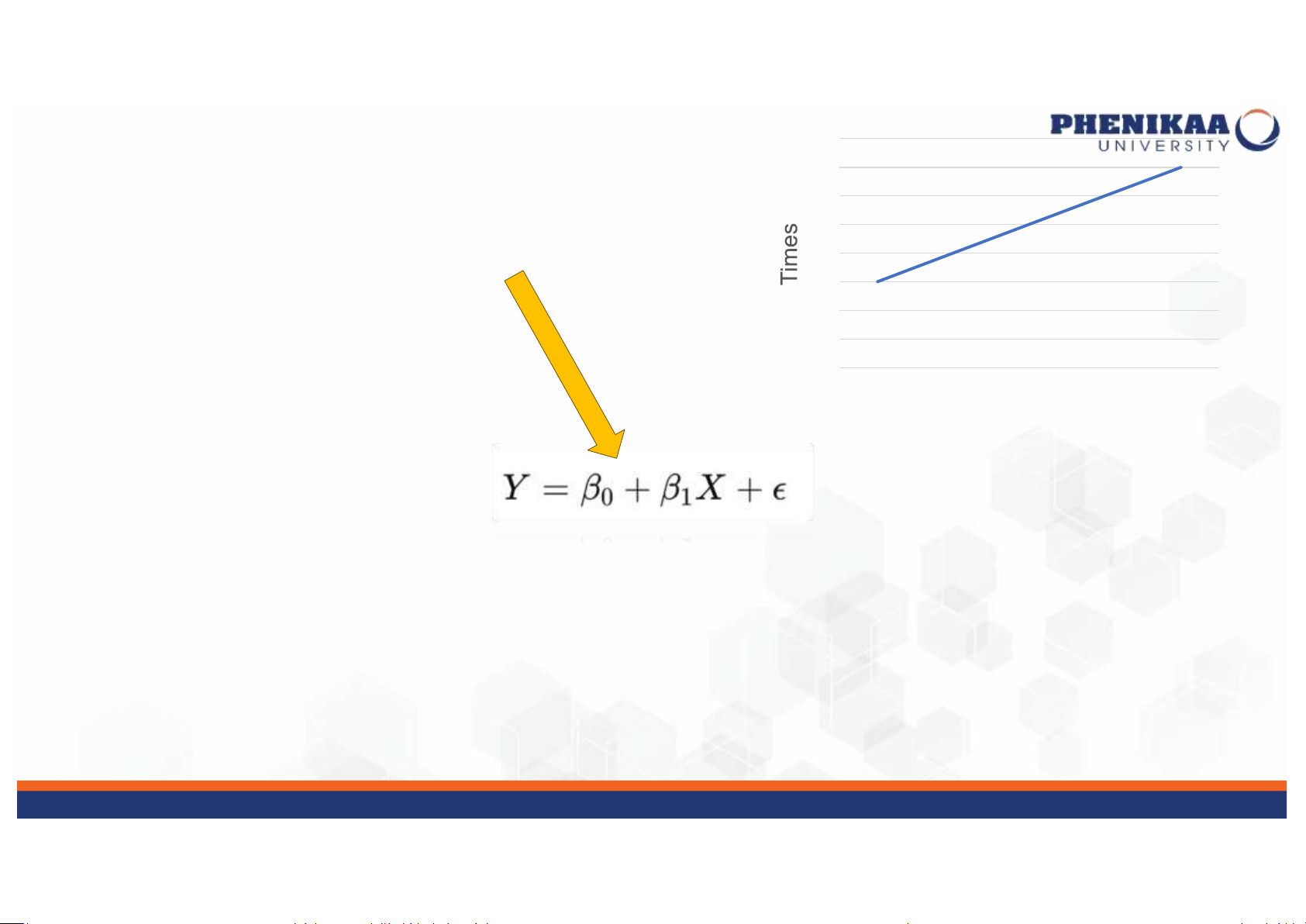
•Hồi tuyến Fnh đơn giản
• Biểu diễn mô hình hồi quy tuyến Unh đơn giản (đơn biến) lOMoAR cPSD| 59561309 Hồi quy tuyến Dnh
• Hồi tuyến 6nh đa biến
• Biểu diễn mô hình hồi quy tuyến đa biến lOMoAR cPSD| 59561309
Nhiệm vụ chính là ước lượng các hệ số sao cho mô
hình dự đoán Y gần giống nhẩt có thể với giá trị thực tế lOMoAR cPSD| 59561309 Hồi quy tuyến Dnh •Ví dụ minh họa
• Lái xe đi làm với vận tốc trung bình 60km/giờ
• Mô hình toán học diễn tả được mối quan hệ giữa hai biến: quãng đường
(distance) và thời gian (rme). Time = 1 * distance (1) Time = 1 x distance • Hay: 8 Y = a*X 6 4 2 0 lOMoAR cPSD| 59561309 1 2 3 4 5 6 7 8 Km(s) Hồi quy tuyến Dnh •Ví dụ minh họa
• Tuy nhiên: Nếu mất thêm 3 phút mỗi ngày từ nhà tới nơi để xe. Sau đấy mới lái tới công ty • Vậy mô hình (1) sẽ thành Time = 3 + 1 * distance (2) • Hay: Y = b + a*X Y = 3 + 1*X Time = 3 + 1 x distance lOMoAR cPSD| 59561309 8 7 6 5 4 3 2 1 0 1 2 3 4 5 Km(s) Hồi quy tuyến Dnh •Ví dụ minh họa
• Tuy nhiên: Quãng đường đi làm cho mỗi phút là không chính xác
bởi vì Time = 3 + 1 x distance lOMoAR cPSD| 59561309
giao th ô ng, l à m đ ư ờ ng,.... L ú c n à y m ô 8 h ì nh (2) tr ở th à nh: 7
Time = 3 + 1 * distance + randomEffect (3) 6 • 5 Hay: Y = b + a*X + e 4 3 với: 2 b=3 1 a = 1 0 e: hệ số lỗi 1 2 3 4 5 Km(s) Hồi quy tuyến Dnh
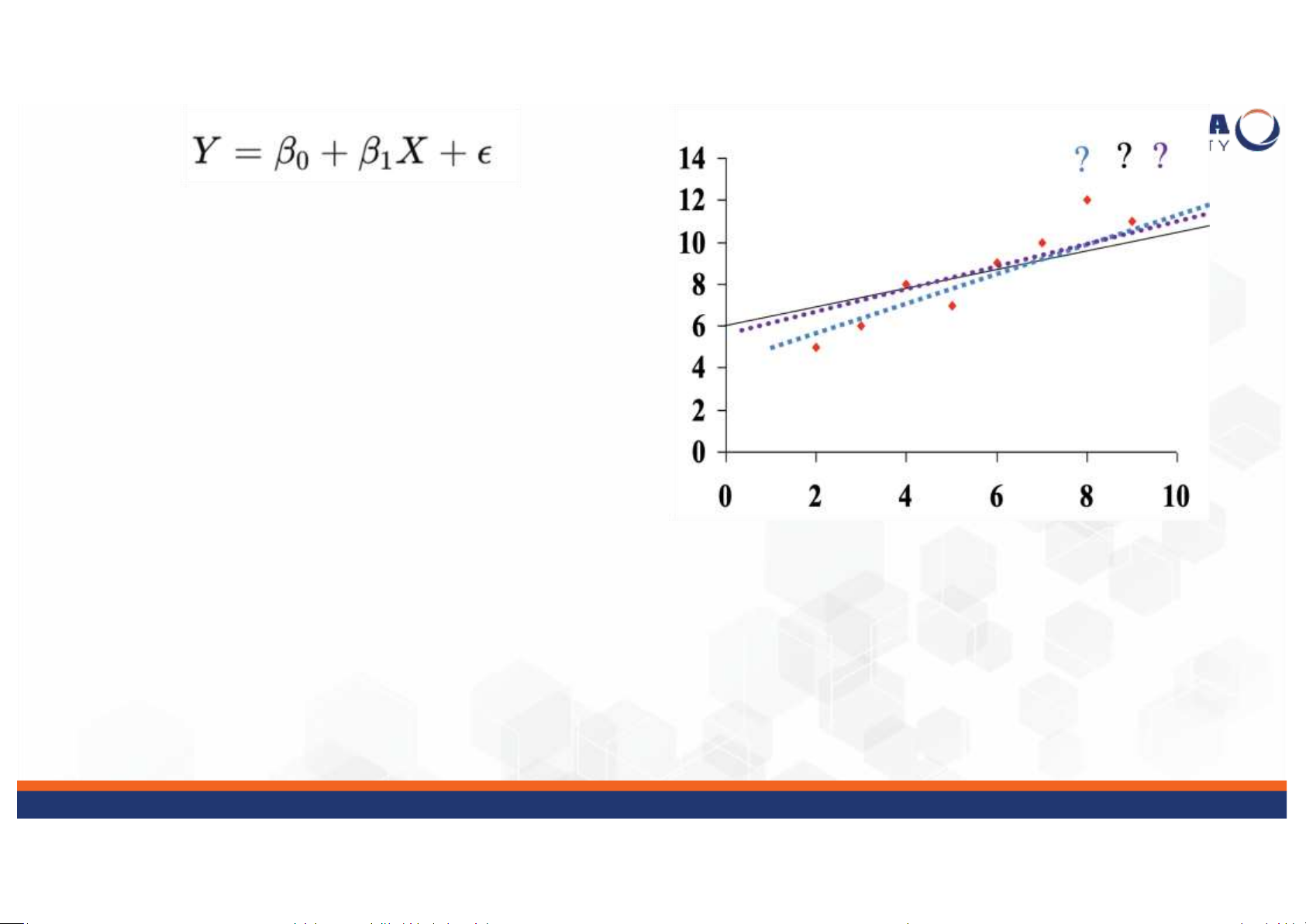
• Nhiệm vụ: chọn tham số cho mô hình lOMoAR cPSD| 59561309 • Tìm đường phù hợp
với dữ liệu nhất (The line best fit) lOMoAR cPSD| 59561309 Hồi quy tuyến Dnh
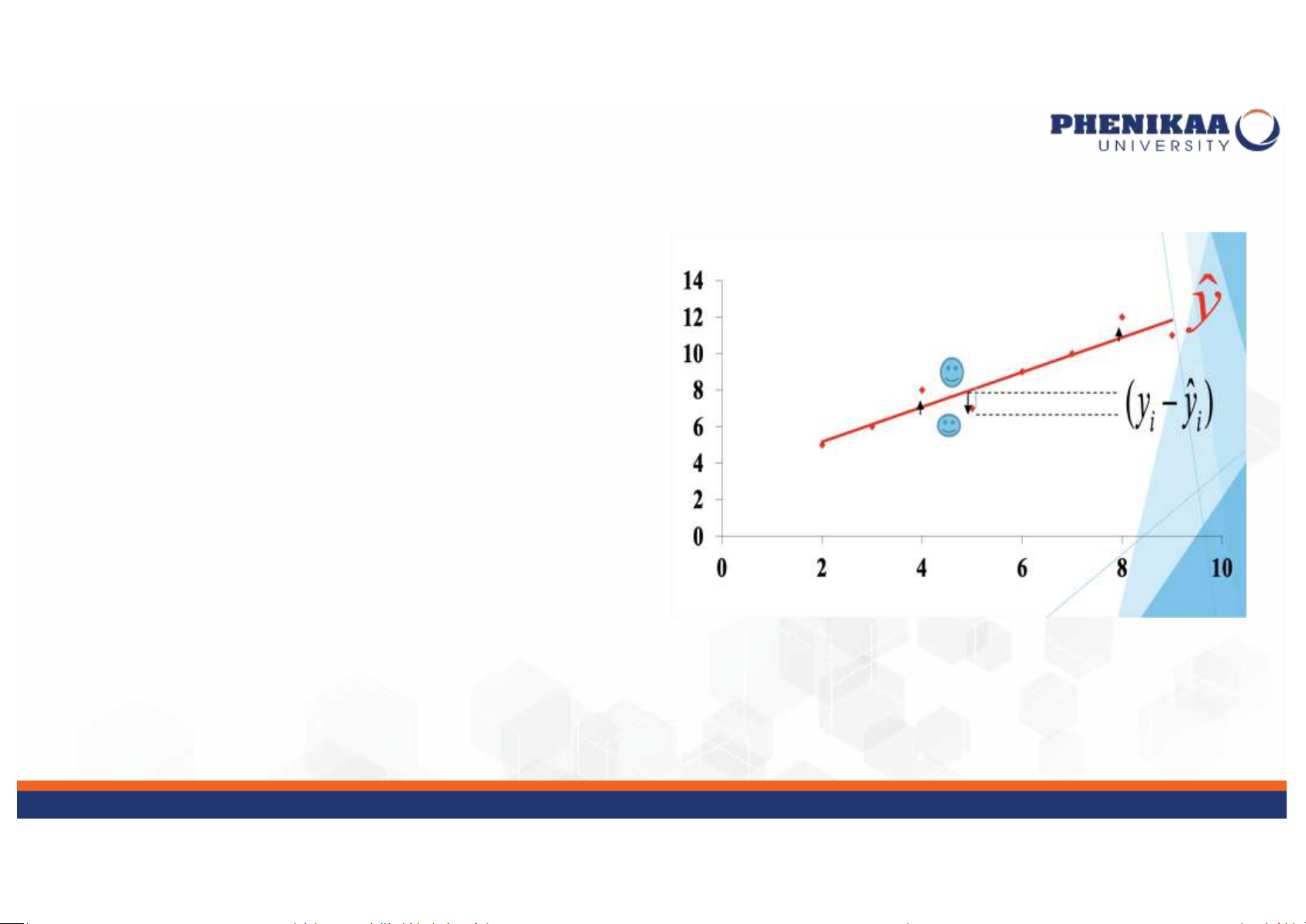
• Rõ ràng, đường thằng rất hiếm phù hợp (chạy qua) toàn bộ dữ liệu
một cách chính xác, do đó
luôn tồn tại lỗi (sai số) liên quan đến đường này
• Như vậy, chúng ta có thể
xem ”The line of best fit” là đường
phù hợp nhất là đường giảm tối
đa sự mở rộng của các lỗi Hồi quy tuyến Dnh
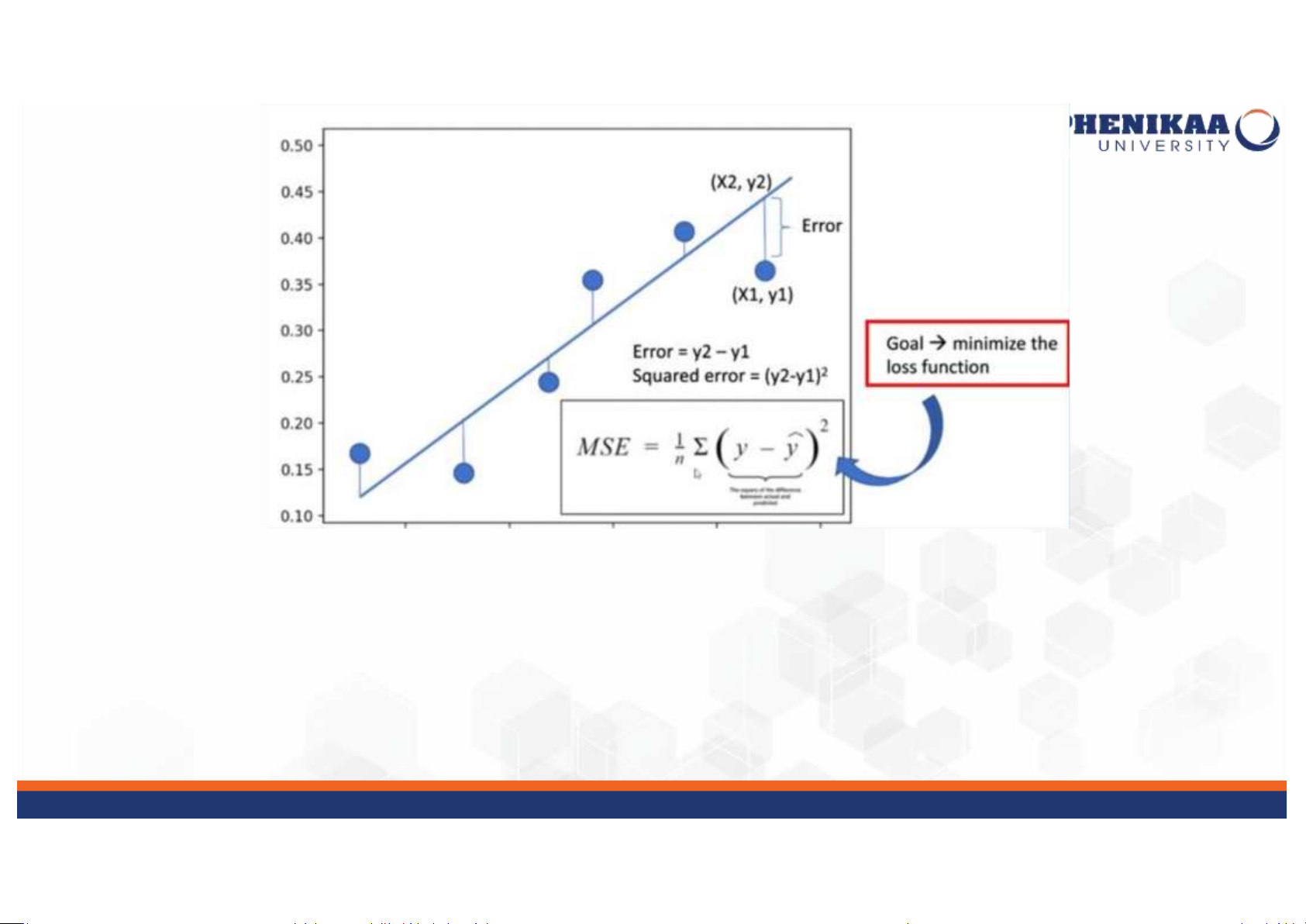
• Hàm mất mát (Lost Funciton): lOMoAR cPSD| 59561309 lOMoAR cPSD| 59561309
Hồi quy tuyến tính
• Hàm mất mát (Lost Funciton):
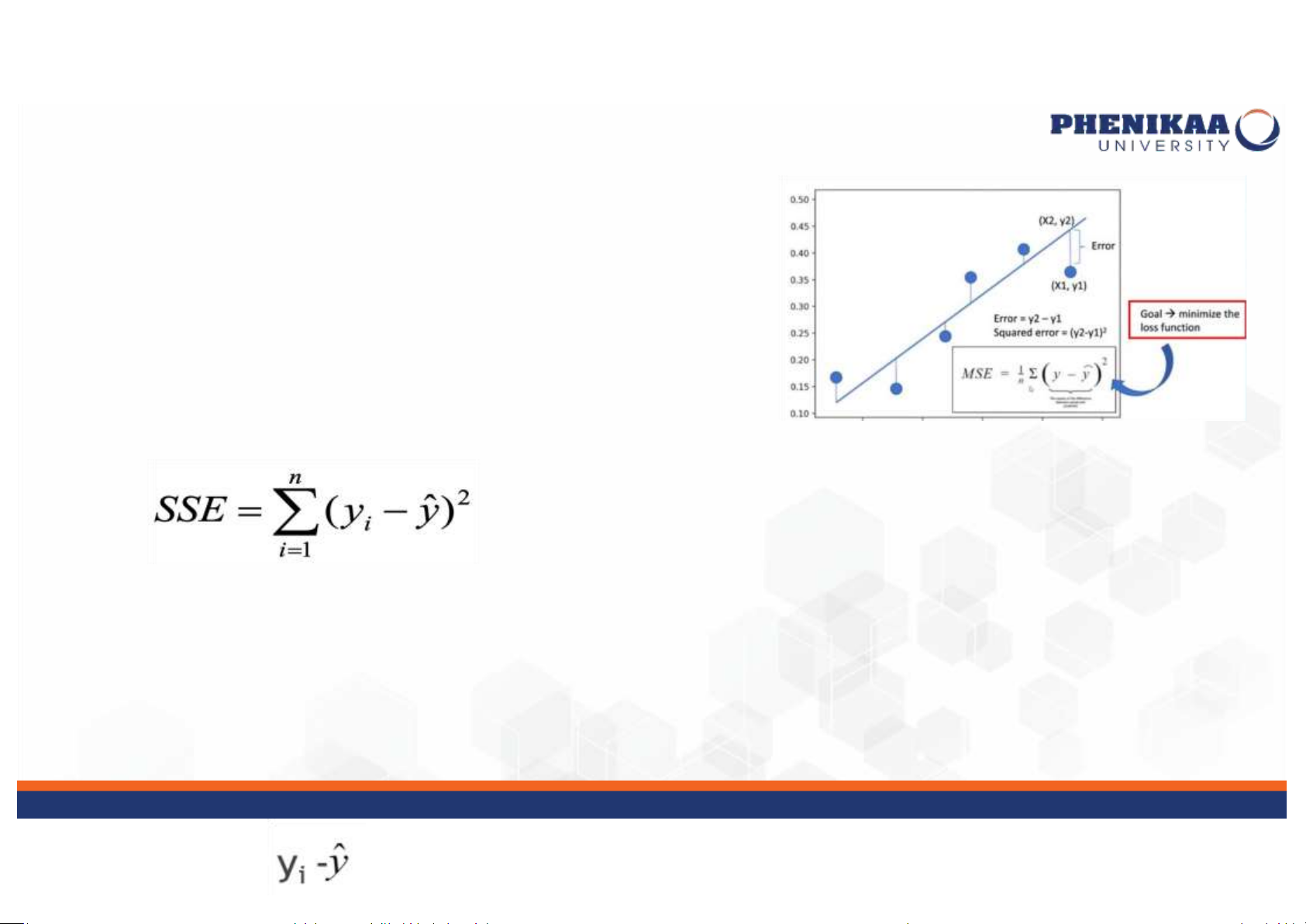
• Trong đó được gọi là lỗi (error) hay phần dư thừa (residual)
• Đường line of best fit sẽ xác định được khi
tổng lỗi bình phương (SSE) được giảm tối đa:
• Trong đó SSE ( Sum of the Squared Errors): Tổng lỗi bình phương