APPLIED STATISTICS COURSE CODE: ENEE1006IU Lecture 13:
Chapter 7: Analysis of Variance (ANOVA)
(3 credits: 2 is for lecture, 1 is for lab-work)
Instructor: TRAN THANH TU Email: tttu@hcmiu.edu.vn tttu@hcmiu.edu.vn 1
CHAPTER 7: ANALYSIS OF VARIANCE (ANOVA)
•7.1. Inferences about a population variance
•7.2. Inferences about two population variances
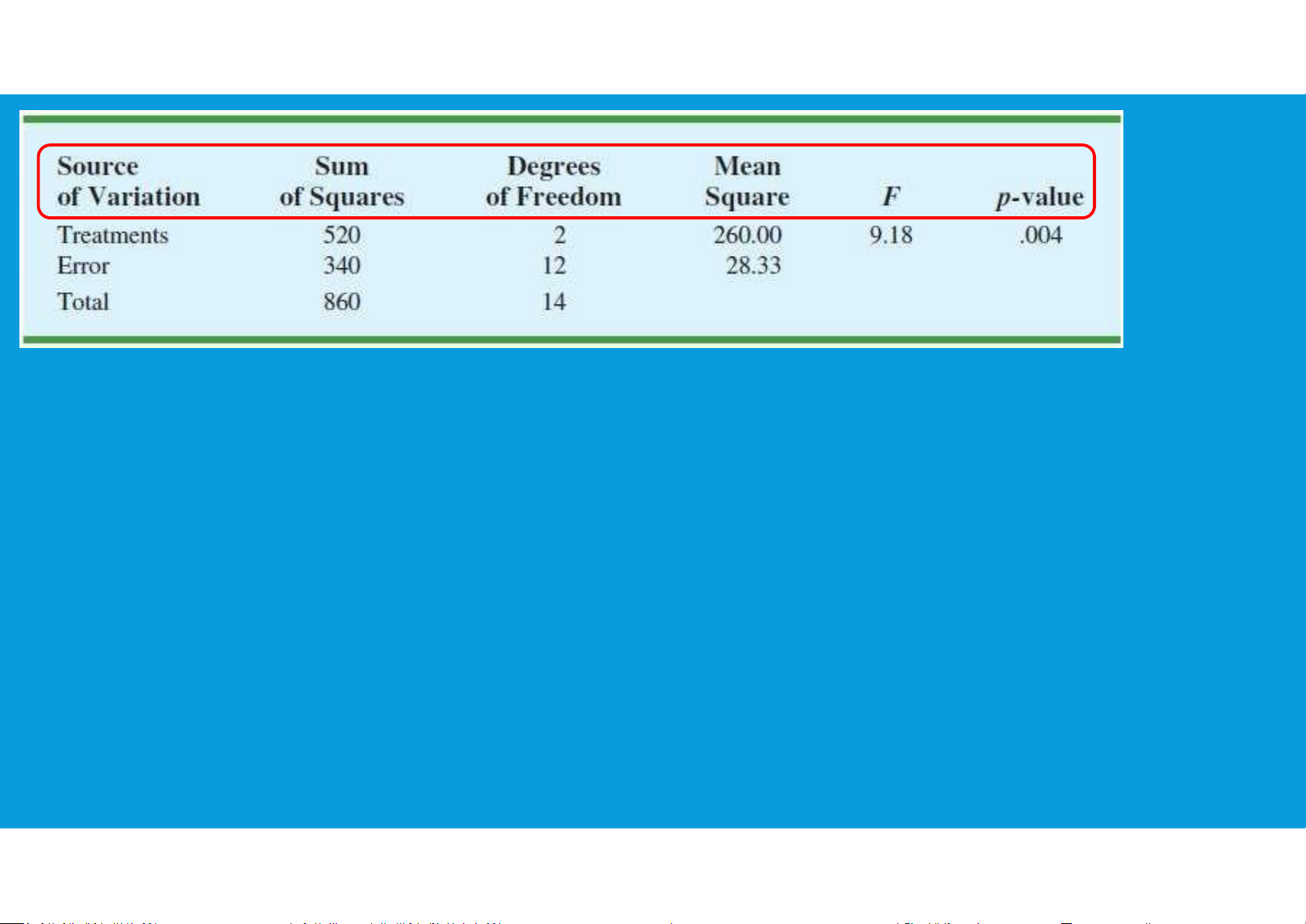
•7.3. Assumptions for analysis of variance •7.4. A conceptual overview •7.5. ANOVA table •7.6. ANOVA procedure 7.5. ANOVA TABLE •Total Sum Square (TSS): tttu@hcmiu.edu.vn 2 SSTR (sum of squares due to treatments) the degrees of freedom tttu@hcmiu.edu.vn 3 7.5. ANOVA TABLE •Total Sum Square (TSS):
•The analysis of variance can be viewed as the process of partitioning the total sum
of squares and the degrees of freedom into their corresponding sources: treatments and error.
•Dividing the sum of squares by the appropriate degrees of freedom provides the
variance estimates, the F value, and the p-value used to test the hypothesis of equal population means. •ANOVA TABLE: tttu@hcmiu.edu.vn 4
MULTIPLE COMPARISON PROCEDURES
•When we use analysis of variance to test whether the means of k populations are
equal, rejection of the null hypothesis allows us to conclude only that the
population means are not all equal.
•In some cases we will want to go a step further and determine where the
differences among means occur. tttu@hcmiu.edu.vn 5
•The purpose of this section is to show how multiple comparison procedures can
be used to conduct statistical comparisons between pairs of population means.
Fisher’s least significant difference (LSD) procedure can be used to determine
where the differences occur (pairwise comparisons)
MULTIPLE COMPARISON PROCEDURES
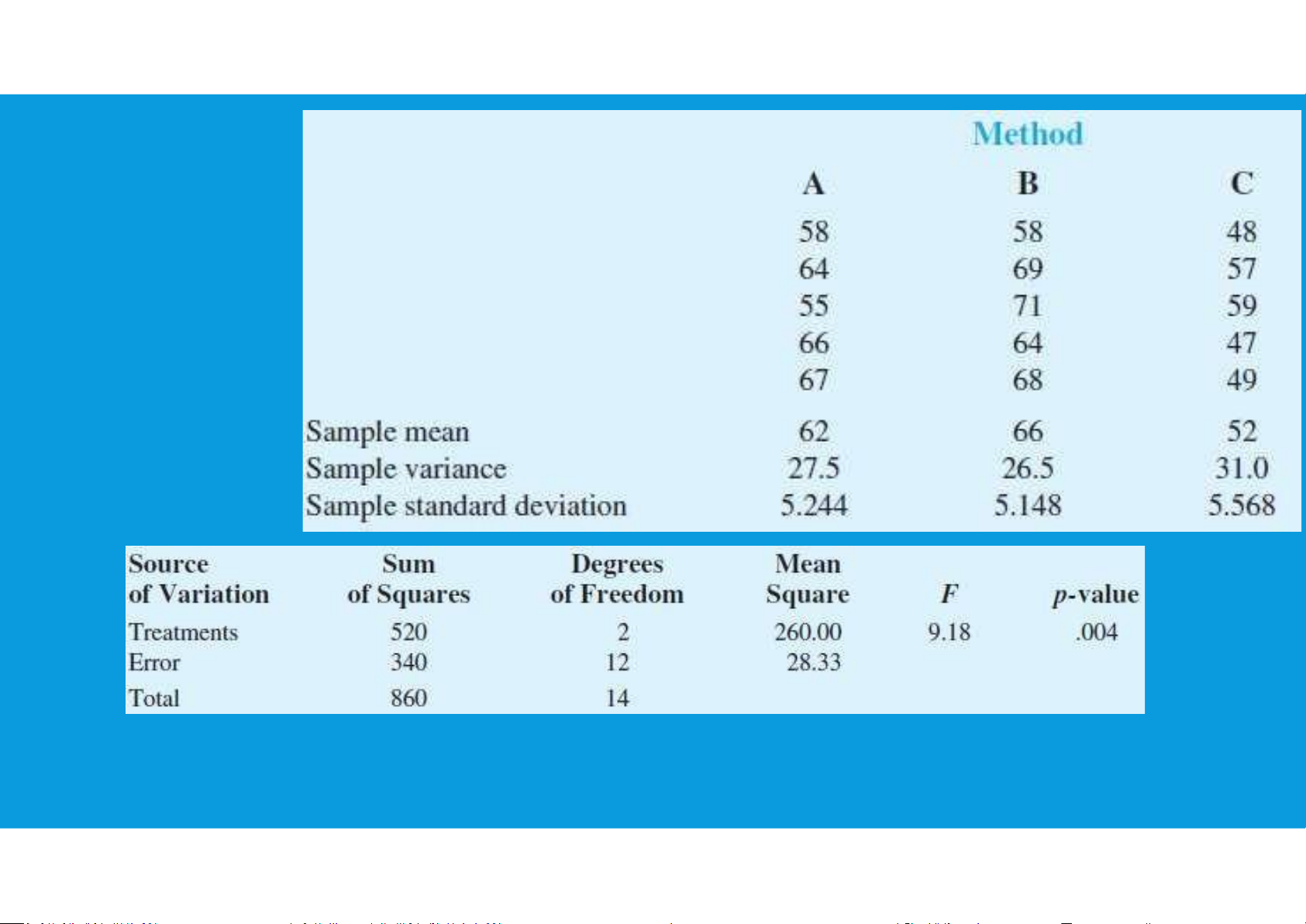
Fisher’s least significant difference (LSD) procedure: tttu@hcmiu.edu.vn 6 tttu@hcmiu.edu.vn 7
MULTIPLE COMPARISON PROCEDURES
Fisher’s least significant difference (LSD) procedure: tttu@hcmiu.edu.vn 8 EXAMPLE tttu@hcmiu.edu.vn 9 tttu@hcmiu.edu.vn 10
MULTIPLE COMPARISON PROCEDURES
- If the confidence interval includes the value zero, we cannot reject the
hypothesis that the two population means are equal. tttu@hcmiu.edu.vn 11
- If the confidence interval does not include the value zero, we conclude that
there is a difference between the population means. tttu@hcmiu.edu.vn 12
cannot reject the hypothesis that the two population means of A and B are equal tttu@hcmiu.edu.vn 13 lOMoARcPSD|47231818 PAIRWISE COMPARISONS
• In discussing multiple comparison procedures we refer to this probability of a Type I error (α
= 0.05) as the comparisonwise Type I error rate;
• Comparisonwise Type I error rates indicate the level of significance associated with a single pairwise comparison.
• What is the probability that in making three pairwise comparisons, we will commit a Type I
error on at least one of the three tests?
• The probability that we will not make a Type I error on any of the three tests is (0.95)(0.95)(0.95) = 0.8574 14 lOMoARcPSD|47231818
the probability of making at least one Type I error is 1 − 0.8574 = 0.1426 overall or
experimentwise Type i error rate ( tttu@hcmiu.edu.vn PAIRWISE COMPARISONS
•The experimentwise Type I error rate gets larger for problems with more populations.
should look for alternatives that provide better control over the experimentwise error rate
Bonferroni adjustment: involves using a smaller comparisonwise error rate for each test: 15 lOMoARcPSD|47231818
•If we want to test C pairwise comparisons and want the maximum probability
of making a Type I error for the overall experiment to be , we simply use a
comparisonwise error rate equal to /C tttu@hcmiu.edu.vn
7.6. ANOVA PROCEDURE – RANDOMIZED BLOCK DESIGN
•Randomized block design: Its purpose is to control some of the extraneous
sources of variation by removing such variation from the MSE tttu@hcmiu.edu.vn 16 lOMoARcPSD|47231818 17 lOMoARcPSD|47231818
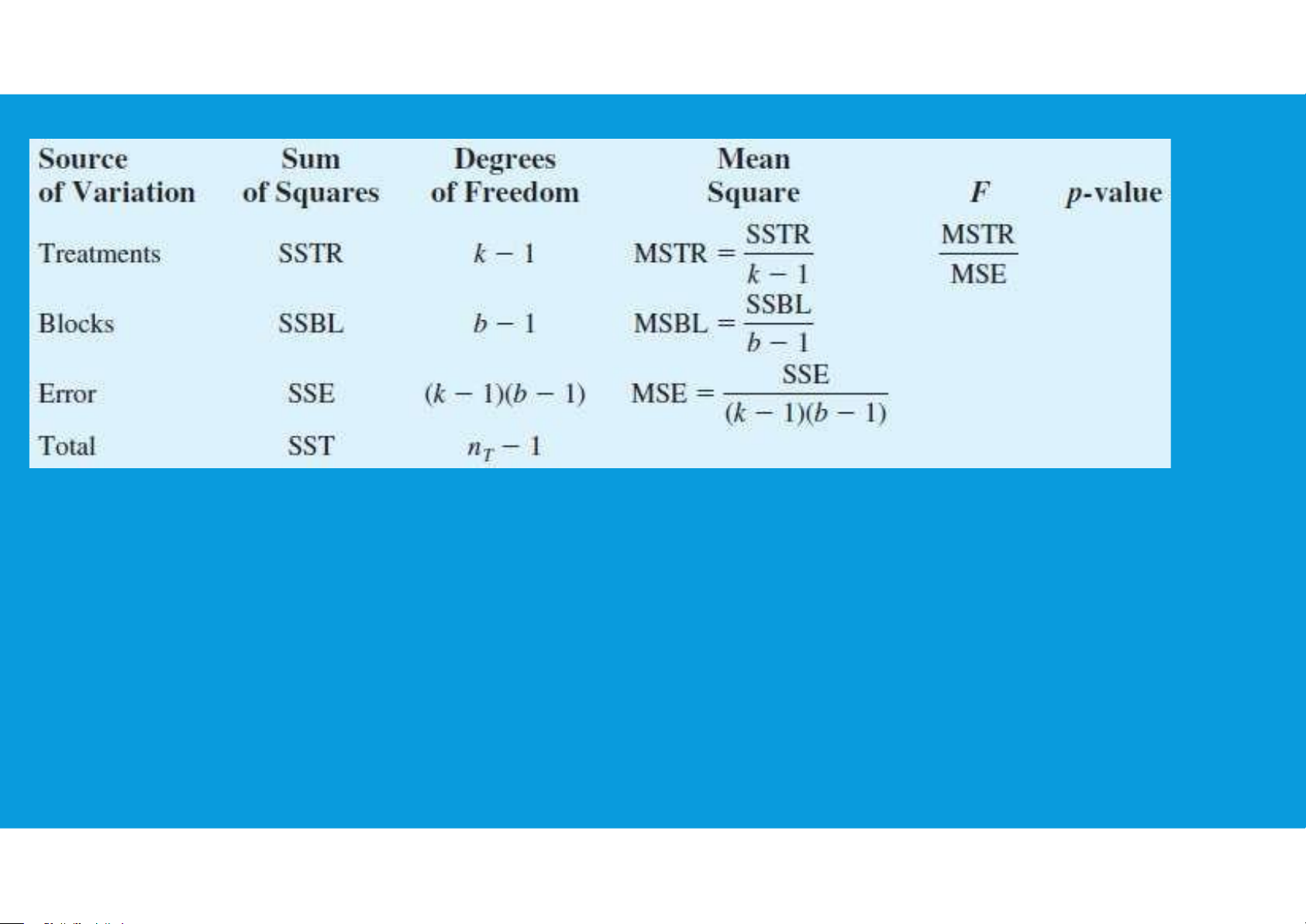
7.6. ANOVA PROCEDURE – RANDOMIZED BLOCK DESIGN
•The ANOVA procedure for the randomized block design requires us to partition
the sum of squares total (SST) into three groups: sum of squares due to
treatments (SSTR), sum of squares due to blocks (SSBL), and sum of squares due to error (SSE): tttu@hcmiu.edu.vn 18 lOMoARcPSD|47231818
•ANOVA table for the randomized block design with k treatments and b blocks: tttu@hcmiu.edu.vn 19 lOMoARcPSD|47231818 7.6. ANOVA PROCEDURE tttu@hcmiu.edu.vn 20