Bài 1: Định nghĩa đạo hàm. Ý nghĩa hình học của đạo hàm | Giáo án Toán 11 Cánh diều

Trường THPT số 1 Si Ma Cai
Họ và tên giáo viên: Trần Mạnh Hùng Tổ Toán Tin NN
KẾ HOẠCH BÀI DẠY
TÊN BÀI DẠY: ĐỊNH NGHĨA ĐẠO HÀM. Ý NGHĨA HÌNH HỌC CỦA ĐẠO HÀM
Môn học/Hoạt động giáo dục: Toán; lớp: 11
Thời gian thực hiện: (02 tiết) I. Mục tiêu 1. Về kiến thức:
- Đạo hàm tại 1 điểm, các bài toán dẫn dắt khái niệm
- Phương pháp tính đạo hàm tại 1 điểm bằng định nghĩa
- Ý nghĩa của đạo hàm: Hình học và vật lí 2. Về năng lực:
- Năng lực tư duy và lập luận Toán học: Trong tiếp cận ý nghĩa hình học và vật lí đạo hàm
- Năng lực mô hình hóa Toán học: Trong các bài toán thực tế.
- Năng lực giải quyết vấn đề Toán học: Trong các lời giải của các bài tập.
- Năng lực giao tiếp Toán học: Trong các định lý, ví dụ, bài tập.
- Năng lực sử dụng công cụ, phương tiện để học Toán: Sử dụng máy tính cầm tay. 3. Về phẩm chất:
- Chăm chỉ, hoàn thành các nhiệm vụ được giao.
- Trách nhiệm, cố gắng chiếm lĩnh kiến thức mới, cố gắng làm đúng các bài tập.
- Có thế giới quan khoa học
II. Thiết bị dạy học và học liệu
- Kế hoạch bài dạy, SGK, phiếu học tập, phấn, thước kẻ, máy chiếu, phần mềm GSP…
III. Tiến trình dạy học Tiết 1.
1. Hoạt động 1: Khởi động
a) Mục tiêu: Tạo tâm thế học tập cho học sinh, giúp các em ý thức được nhiệm vụ học tập,
sự cần thiết phải tìm hiểu về các vấn đề đã nêu ra, từ đó gây được hứng thú với việc học bài mới.
b) Nội dung: Tên lửa vũ trụ là phương tiện được chế tạo đặc biệt giúp con người thực hiện
các sứ mệnh trong không gian như: tiếp cận đến các hành tinh ngoài Trái Đất, vận chuyển con
người và thiết bị lên vũ trụ
Câu hỏi: Nếu quỹ đạo chuyển động của tên lửa được miêu tả bằng hàm số theo thời gian
thì đại lượng nào biểu thị độ nhanh chậm của chuyển động tại một thời điểm? 2
c) Sản phẩm: Câu trả lời của học sinh d) Tổ chức thực hiện:
Chuyển giao
* Giáo viên trình chiếu hình ảnh - HS quan sát.
- HS tìm câu trả lời, tuy nhiên sẽ khó để giải quyết được câu hỏi trọn vẹn.
Thực hiện
- Mong đợi: Kích thích sự tò mò của HS :
+ Đưa ra một số nhận định theo tìm hiểu của bản thân
Báo cáo thảo luận * Đại diện nhóm báo cáo, các nhóm còn lại theo dõi thảo luận.
- GV nhận xét thái độ làm việc, phương án trả lời của học sinh, ghi nhận
Đánh giá, nhận xét, và tuyên dương học sinh có câu trả lời tốt nhất. Động viên các học sinh còn
tổng hợp
lại tích cực, cố gắng hơn trong các hoạt động học tiếp theo - Chốt kiến thức
2. Hoạt động 2: Hình thành kiến thức mới
I. Đạo hàm tại một điểm
Hoạt động 2.1. Các bài toán dẫn đến khái niệm đạo hàm
a) Mục tiêu: Học sinh tiếp cận bài toán dẫn tới khái niệm đạo hàm b) Nội dung:
- Đưa ra bài toán: Tính vận tốc trung bình của chuyển động trong các khoảng đưa ra
c) Sản phẩm: Bảng tính toán vận tốc trung bình theo thời gian
- Học sinh nhận ra được dãy số vận tốc trung bình tính được dần đến 1 giá trị
d) Tổ chức thực hiện: Học sinh thảo luận cặp đôi
Một đoàn tàu chuyển động thẳng khởi hành từ một nhà ga. Quãng đường
s (mét) đi được của đoàn tàu là một hàm số của thời gian t (phút). Ở ( ) 2 f t = t
những phút đầu tiên hàm số đó là . [t ;t] 0
Chuyển giao
H1: Hãy tính vận tốc trung bình của chuyển động trong khoảng với
t = 3,t = 2,t = 2,5,t = 2,9,t = 2,99,t = 2,999 0 ?
H2: Nhận xét gì về các giá trị vận tốc trung bình khi t càng gần với t 0
H3: Giá trị nào trong các giá trị trong bảng phản ánh đúng nhất vận tốc
trung bình của tàu tại thời điểm t0 3 - Tìm câu trả lời H1: t D = t -t s 0 ( ) 0,5 0,1 0,01 0,001
Thực hiện v ( ) m 5,5 5,9 5,99 5,999 tb
H2: Gần giá trị 6, tiến dần về 6. H3; Giá trị 6
- HS làm việc cặp đôi theo bàn.
Báo cáo thảo luận * Đại diện nhóm báo cáo, các nhóm còn lại theo dõi thảo luận.
- GV nhận xét thái độ làm việc, phương án trả lời của học sinh, ghi nhận
và tuyên dương học sinh có câu trả lời tốt nhất. Động viên các học sinh còn
lại tích cực, cố gắng hơn trong các hoạt động học tiếp theo - Chốt kiến thức
f (t) - f (t0 )
Đánh giá, nhận xét,
t - t càng nhỏ thì tỉ số
càng phản ánh chính xác sự nhanh 0 t - t
tổng hợp 0
f (t) - f (t0 )
chậm của tàu. Từ đó xem giới hạn
là vận tốc tức thời tại t t - t 0 0
f (t) - f (t0 ) kí hiệu v(t lim = v(t0 ) 0 ) hay
gọi là đạo hàm của hàm số t® 0t t - t0
y = f (t).
Hoạt động 2.2. Định nghĩa đạo hàm tại một điểm và cách tính đạo hàm bằng định nghĩa
a) Mục tiêu: Định nghĩa đạo hàm tại 1 điểm, liên hệ với giới hạn hàm số, tính đạo hàm của hàm
số tại 1 điểm bằng định nghĩa b) Nội dung:
2. Định nghĩa đạo hàm tại một điểm
ĐN1: Cho hàm số y = f (x) xác định trên ( ;
a b) và điểm x Î ; a b 0 ( ).
f ( x) - f (x0 )
Nếu tồn tại giới hạn hữu hạn lim
thì giới hạn đó gọi là đạo hàm của hàm số x® 0 x x - x0
f (x) tại x 0
Kí hiệu: f ¢(x y¢ 0 ) hoặc x0
Trong định nghĩa trên: x
D = x - x là số gia của biến số tại x 0 0 y
D = f (x + x D )- f (x x D x
0 ) gọi là số gia của hàm số tương ứng với số gia tại điểm 0 y D Tóm lại: f ¢( x = lim 0 ) x D ®0 x D
3. Các bước tính đạo hàm bằng định nghĩa B1: Xét x
D là số gia của biến số tại x . Tính y
D = f (x + x D - f x 0 ) ( 0) 0 y D B2: Rút gọn x D y D B3: Tính lim x D ®0 x D 4 y D Kết luận: Nếu lim
= a Þ f ¢(x = a 0 ) x D ®0 x D Phiếu học tập
Bài 1: Tính đạo hàm của hàm số ( ) 2
f x = x bằng định nghĩa a. Tại điểm x = 2 b. Tại điểm bất kì 0
Bài 2: Bài tập 1 – Sgk 63
Bài 3: Bài tập 2 – Sgk 63
c) Sản phẩm: Hình thành định nghĩa và phương pháp tìm đạo hàm bằng định nghĩa
d) Tổ chức thực hiện: Học sinh thảo luận cặp đôi; hoạt động nhóm lớn;
Giáo viên nêu định nghĩa hoặc học sinh tổng quát từ 2.1
H1? Nêu khái niệm đạo hàm tại điểm x của hàm số f (x)? 0
H2? Nêu các bước tính đạo hàm bằng định nghĩa? Cần lưu ý những gì ?
H3? Yêu cầu học sinh đọc ví dụ 1 – Sgk63 sau đó thực hiện phiếu học tập
Chuyển giao
* Trên cơ sở câu trả lời của học sinh, giáo viên chuẩn hóa kiến thức, từ
đó nhấn mạnh việc tìm đạo hàm bằng định nghĩa cần lưu ý hàm số xác
định và giới hạn hữu hạn. GV chia lớp thành 6 nhóm và giao nhiệm vụ cho các nhóm: Nhóm 1+2: Ví dụ 1a Nhóm 3+4: BT1-Sgk 63
Nhóm 5+6 (Khá): Ví dụ 1b, BT2 – Sgk63
* Học sinh từ định nghĩa vận tốc tức thời đưa ra định nghĩa tổng quát cho
đạo hàm, giáo viên nhấn mạnh, khắc sâu.
Học sinh làm việc theo nhóm lần lượt giải quyết các câu hỏi. Mong đợi Nhóm 1+2: 2 y D D x + 4 x D + 4 - 4 = = x D + 4 x D x D
Thực hiện y D lim
= 4 Þ f ¢(2) = 4 x D ®0 x D Nhóm 3+4: y D 3( x D + )3 1 - 3 = = 3( 2 D x + 3 x D + 3) x D x D y D lim = 9 Þ f ¢( ) 1 = 9 x D ®0 x D Nhóm 5+6: 5 2 2 2 y D D x + 2D .
x x + x - x = = x D + 2x x D x D y D lim
= 2x Þ f ¢(x) = 2x x D ®0 x D
BT2: Hàm số xác định tại x = 0 0 y D 0 + x D - 0 x D = = x D x D x D y D y D lim =1 ¹ lim = 1
- . Do đó không tồn tại giới hạn, không tồn tại x 0+ D x 0 x - D ® D ® x D đạo hàm. y D x + x D - x x + x D - x Với x > 0: 0 0 0 0 = = = 1 0 x D x D x D y D lim =1 x D ®0 x D y D x + x D - x -x - x D - (-x ) x < 0 : 0 0 0 0 = = = - 1 0 x D x D x D y D lim = - 1 x D ®0 x D Do có thể chọn x
D đủ nhỏ để x ; x + x
D cùng dấu nhau trong mỗi 0 0
trường hợp trên. Do đó tồn tại đạo hàm với mọi x ¹ 0
Báo cáo thảo luận * Đại diện nhóm báo cáo, các nhóm còn lại theo dõi thảo luận.
- GV nhận xét thái độ làm việc, phương án trả lời của học sinh, ghi nhận
và tuyên dương học sinh có câu trả lời tốt nhất. Động viên các học sinh còn
Đánh giá, nhận xét, lại tích cực, cố gắng hơn trong các hoạt động học tiếp theo
tổng hợp
- Chốt kiến thức: Hàm số y = f (x) có đạo hàm trên ( ; a b) nếu có đạo
hàm tại mọi x trên khoảng đó Tiết 2.
Ý nghĩa vật lý và ý nghĩa hình học của đạo hàm
1. Hoạt động 2: Hình thành kiến thức
4. Ý nghĩa vật lí đạo hàm
Hoạt động 2.1: Ý nghĩa vật lí đạo hàm
a) Mục tiêu: Thấy được ý nghĩa đạo hàm trong các bài toán vật lí b) Nội dung:
Phiếu học tập: Một viên đạn bắn đi theo phương thẳng đứng với phương trình 2
s = 200t - 5t (mét). Tính vận tốc tức thời của viên đạn tại các thời điểm t = 3,5,9.
c) Sản phẩm: Câu trả lời của học sinh (hoặc kết quả hoạt động nhóm của học sinh) d) Tổ chức thực hiện:
Chuyển giao
- Yêu cầu học sinh nhắc lại bài toán mở đầu 6
Cần nêu bật được: Đạo hàm của hàm số tại các điểm trên chính là vận tốc
tức thời của chuyển động hay v(t = s¢ t 0 ) ( 0) - Tìm câu trả lời
Thực hiện
- HS làm việc theo nhóm lần lượt giải quyết các câu hỏi.
- GV theo dõi, hỗ trợ, hướng dẫn các nhóm
Báo cáo thảo luận * Đại diện nhóm báo cáo, các nhóm còn lại theo dõi thảo luận.
- GV nhận xét thái độ làm việc, phương án trả lời của học sinh, ghi nhận
Đánh giá, nhận xét, và tuyên dương học sinh có câu trả lời tốt nhất. Động viên các học sinh còn
tổng hợp
lại tích cực, cố gắng hơn trong các hoạt động học tiếp theo - Chốt kiến thức
II. Ý nghĩa hình học của đạo hàm
Hoạt động 2.2: Ý nghĩa hình học của đạo hàm
a) Mục tiêu: Hiểu được ý nghĩa hình học của đạo hàm, hệ số góc và phương trình tiếp tuyến
b) Nội dung: Sử dụng mô hình hình học động Geogebra để xây dựng khái niệm
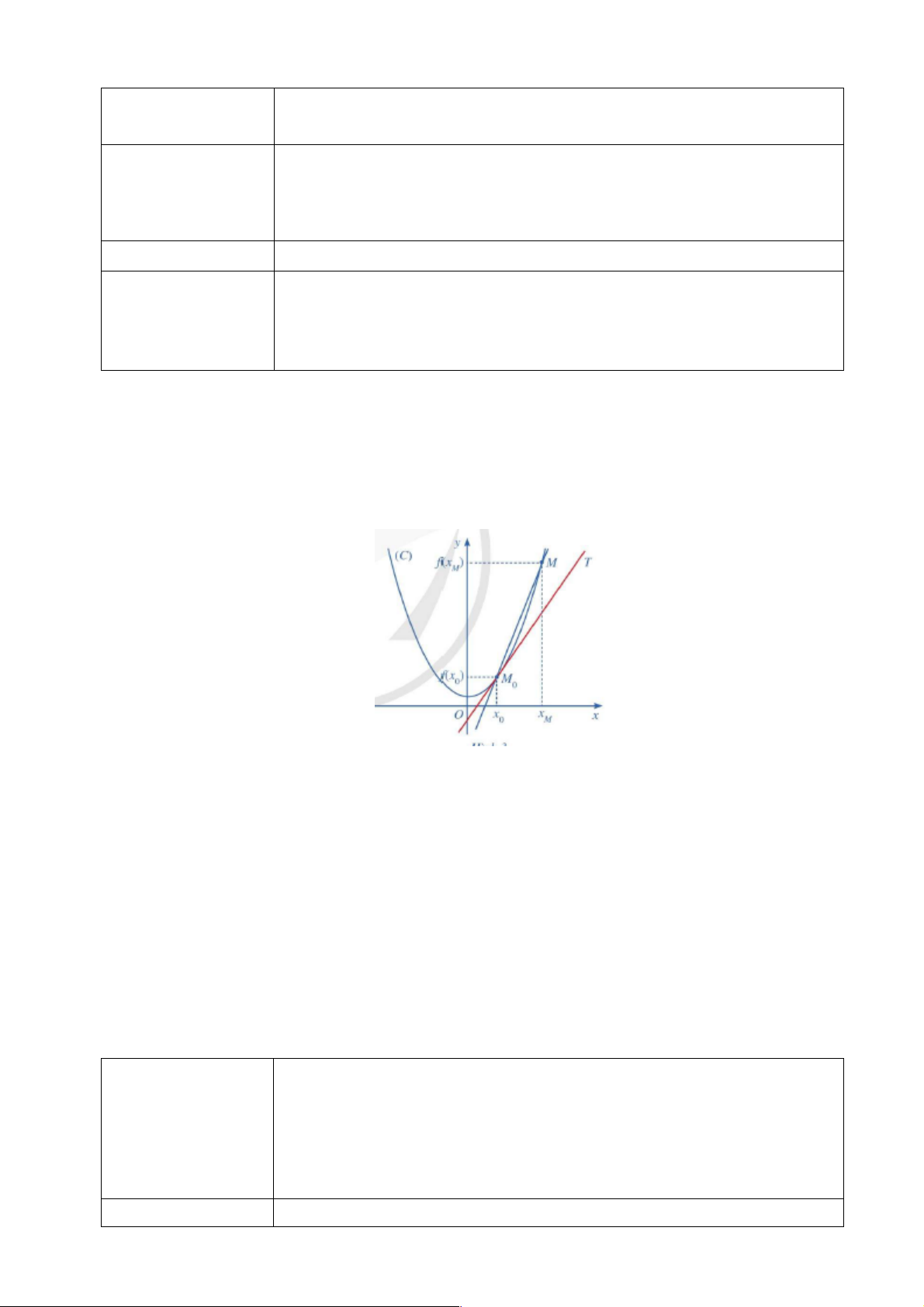
Cho hàm số y = f (x) có đồ thị (C), một điểm M cố định thuộc (C) có hoành độ x . Với 0 0
mỗi điểm M thuộc (C) khác M , kí hiệu x là hoành độ của M và k là hệ số góc của cát 0 M M
tuyến M M . Giả sử tồn tại giới hạn hữu hạn k = lim k , khi đó ta coi đường thẳng M T đi 0 0 M ® 0 M x 0 x
qua M và có hệ số góc k là vị trí giới hạn của cát tuyến M M khi M di chuyển theo (C) dần 0 0 0 tới M . 0
Đường thẳng M T gọi là tiếp tuyến của (C) tại điểm M 0 0
M gọi là tiếp điểm. 0
c) Sản phẩm: Câu trả lời của học sinh
d) Tổ chức thực hiện: Học sinh làm việc theo nhóm (6-7 học sinh).
* GV tổ chức hoạt động trao đổi thảo luận của các nhóm.
H1: Nhắc lại khái niệm hệ số góc của đường thẳng ?
Chuyển giao
H2: Xác định hệ số góc k của tiếp tuyến M T theo x ? 0 0 0
H3: Lập phương trình tiếp tuyến tại M ? 0
Thực hiện
- HS thảo luận theo nhóm thực hiện nhiệm vụ 7
- GV theo dõi, hỗ trợ, hướng dẫn các nhóm
f (x - f x M ) ( 0)
H2: k = lim k = lim = f ¢ x 0 M ( 0) ® ® M x 0 x M x 0 x x - x M 0
H3: Đường thẳng qua M và có hệ số góc là f ¢(x0 ) 0
y = f ¢(x
x - x + f x 0 ) ( 0 ) ( 0)
- Học sinh tổ chức phản biện
Báo cáo thảo luận * Đại diện nhóm báo cáo, các nhóm còn lại theo dõi thảo luận.
- GV nhận xét thái độ làm việc, phương án trả lời của học sinh, ghi nhận
Đánh giá, nhận xét, và tuyên dương học sinh có câu trả lời tốt nhất. Động viên các học sinh còn
tổng hợp
lại tích cực, cố gắng hơn trong các hoạt động học tiếp theo - Chốt kiến thức
2. Hoạt động 3: Luyện tập
a) Mục tiêu: Xác định hệ số góc, lập phương trình tiếp tuyến của đồ thị hàm số tại 1 điểm b) Nội dung: BT1: Cho hàm số 2 y = x - ( 1 C)
a. Xác định hệ số góc của tiếp tuyến đồ thị (C) tại điểm có hoành độ bằng 2
b. Viết phương trình tiếp tuyến tại điểm M(2;3)
BT2: - Bài tập 3 - Sgk
c) Sản phẩm: Bài làm của học sinh
d) Tổ chức thực hiện: Làm việc theo nhóm đôi
* GV đề nghị hs nêu cách giải từng phần và lời giải chi tiết.
Chuyển giao
* GV nhận xét và chuẩn hóa lời giải
* HS suy nghĩ đưa ra lời giải.
* Thảo luận theo nhóm đôi
Thực hiện
Phân chia theo các nhóm: Mỗi nhóm thực hiện 01 bài tập (BT1 hoặc BT2)
* Đại diện nhóm báo cáo, các nhóm còn lại theo dõi thảo luận.
BT1: a. Hệ số góc: k = 4
Báo cáo thảo luận b. Phương trình tiếp tuyến: y = 4x - 5
BT2: a. Hệ số góc: k = 7 -
b. Phương trình tiếp tuyến: y = 7 - x + 8
- GV nhận xét thái độ làm việc, phương án trả lời của học sinh, ghi nhận
Đánh giá, nhận xét, và tuyên dương học sinh có câu trả lời tốt nhất. Động viên các học sinh còn
tổng hợp
lại tích cực, cố gắng hơn trong các hoạt động học tiếp theo - Chốt kiến thức
3. Hoạt động 4: Vận dụng
a) Mục tiêu: Vận dụng ý nghĩa hình học và vật lí của đạo hàm vào bài toán thực tiễn 8
b) Nội dung: Bài tập 4- Sgk
Giả sử chi phí C (USD) để sản xuất Q máy vô tuyến là C (Q) 2 = Q +80Q +3500
a. Ta gọi chi phí biên là chi phí gia tăng để sản xuất thêm 1 sản phẩm từ Q sản phẩm
lên Q+1 sản phẩm. Giả sử chi phí biên được xác định là C¢(Q). Tìm hàm chi phí biên
b. Tìm C¢(90) và giải thích ý nghĩa kết quả tìm được
c. Hãy tính chi phí sản xuất máy vô tuyến thứ 100
c) Sản phẩm: Kết quả bài làm của học sinh.
d) Tổ chức thực hiện: Thảo luận cặp đôi, theo nhóm.
- GV hướng dẫn học sinh tiếp cận vấn đề và giao nhiệm vụ
Chuyển giao
- GV đề nghị HS nêu cách giải từng phần và lời giải chi tiết.
- GV nhận xét và chuẩn hóa lời giải
- HS suy nghĩ đưa ra lời giải.
- Thảo luận theo nhóm đôi Mong muốn: 2 C D 2 . Q Q D + D Q +80 Q D a. = = 2Q + Q D +80 Q D Q D C D
Thực hiện lim
= 2Q + 80 ®hàm chi phí biên Q D ®0 Q D
b. C¢(90) = 2.90+80 = 260 nghĩa là nếu tăng số lượng sản phẩm từ 90
lên 91 thì chi phí gia tăng theo là 260 USD và do hàm chi phí biên bậc
nhất đồng biến nên số sản phẩm càng tăng cao thì chi phí gia tăng trên
mỗi sản phẩm càng lớn (mỗi sp sau cao hơn sp trước là 2 USD)
c. Chi phí sản xuất máy vô tuyến thứ 100 là C ( ) 2
100 =100 +80.100 +3500 = 21500 (USD)
Báo cáo thảo luận * Đại diện nhóm báo cáo, các nhóm còn lại theo dõi thảo luận.
- GV nhận xét thái độ làm việc, phương án trả lời của học sinh, ghi nhận
Đánh giá, nhận xét, và tuyên dương học sinh có câu trả lời tốt nhất. Động viên các học sinh còn
tổng hợp
lại tích cực, cố gắng hơn trong các hoạt động học tiếp theo - Chốt kiến thức