lOMoAR cPSD| 44919514 Bài giảng lOMoAR cPSD| 44919514 TOÁN CHO CÁC NHÀ KINH TẾ
Chương 6: GIẢI TÍCH NHIỀU BIẾN Mục tiêu:
Giới thiệu các khái niệm cơ bản về hàm số nhiều biến, các đạo hàm riêng
và tối ưu hoá hàm nhiều biến.
Cách giải các bài toán tối ưu hoá tổng quát và các bài toán tối ưu hoá ứng dụng trong kinh tế.
Các ứng dụng của hàm số nhiều biến trong phân tích kinh doanh, kinh tế
và các bài toán khoa học xã hội. Nội dung: 2 lOMoAR cPSD| 44919514 1. Hàm số nhiều biến 2. Đạo hàm riêng
3. Tối ưu hoá hàm số hai biến
4. Cực trị có điều kiện ràng buộc: Phương pháp nhân tử Lagrange lOMoAR cPSD| 44919514 Bài giảng 4 lOMoAR cPSD| 44919514 TOÁN CHO CÁC NHÀ KINH TẾ
Chương 6: GIẢI TÍCH NHIỀU BIẾN
Bài 1: Hàm số nhiều biến
Khái niệm và ví dụ hàm nhiều biến.
Đồ thị và đường mức hàm hai biến số.
Hàm sản xuất Cobb-Douglas, đường đẳng lượng và đường
bàng quan trong kinh tế học. lOMoAR cPSD| 44919514
Tổng doanh thu của một loại hàng hóa
nếu bán được đơn vị sản phẩm ở thị
trường nội địa với giá $90 mỗi đơn vị và
đơn vị sản phẩm ở thị trường nước
ngoài với giá $110 mỗi đơn vị là:
Thể tích V và diện tích bề mặt S của một
hộp đựng tài liệu dài feet, rộng feet và sâu và 1 6 lOMoAR cPSD| 44919514 Ví dụ: Giả sử Định nghĩa a)
Tìm Hàm số hai biến: Hàm số với hai biến tập
độc lập và là một quy tắc cho tương xác định của
ứng với mỗi cặp số theo thứ tự
trong một tập hợp (miền xác định của
) đã cho với một và chỉ một số hàm b) Tính
thực, được ký hiệu là
Nếu không được chỉ định cụ thể , ta sẽ
quy ước miền xác định của hàm là tập
hợp của tất cả các cặp giá trịlàm cho biểu thức xác định. 1 7 lOMoAR cPSD| 44919514 Ví dụ:
Doanh thu dưới dạng hàm của hai biến số. Một
cửa hàng thể thao bán hai loại vợt tennis, nhãn
hiệu Serena Williams và Maria Sharapova.
Nếu mỗi vợt nhãn hiệu Williams và Sharapova
được bán với giá lần lượt là đô la và đô la
thì cầu tương ứng đối với mỗi và
Hãy biểu diễn tổng doanh thu hàng năm từ việc
bán các loại vợt này như là một hàm của và . 8 lOMoAR cPSD| 44919514 Định nghĩa
Đồ thị của hàm số hai biến là tập
hợp của tất cả các bộ ba số sao chonằm
trong miền xác định của
Để vẽ đồ thị hàm số như vậy, chúng
ta cần xây dựng một hệ tọa độ ba chiều.
2. Đồ thị và đường mức hàm hai biến số
Một số mặt cong trong không gian ba chiều 9 lOMoAR cPSD| 44919514
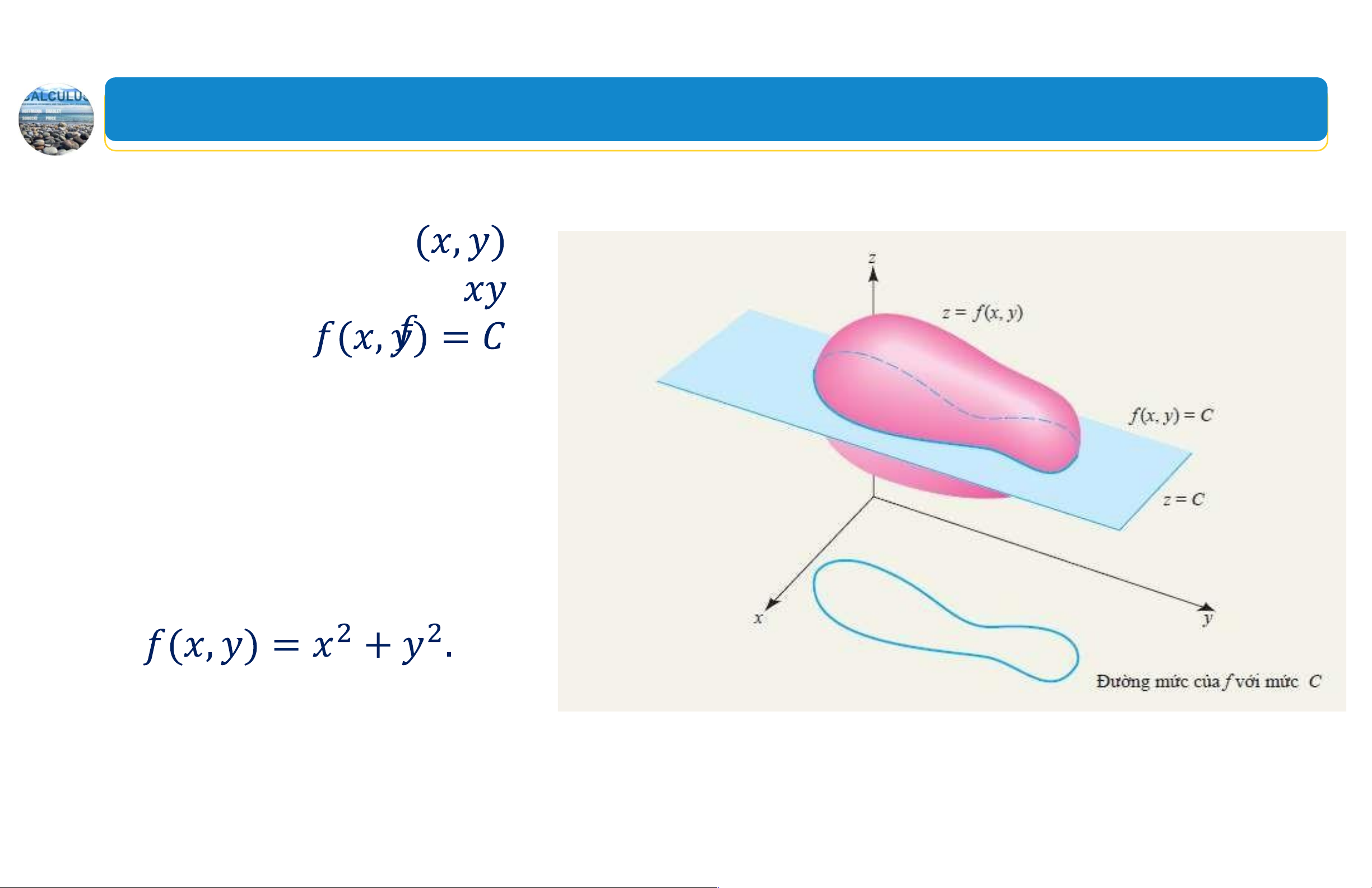
2. Đồ thị và đường mức hàm hai biến số Định nghĩa Minh họa
Tập hợp các điểm trong mặt
phẳng thỏa mãn được gọi
là đường mức của tại mức C. Ví dụ: Xem xét các
đường mức của hàm số
giống như một ngọn núi. 10 lOMoAR cPSD| 44919514 2 b)Các đường mứ11 c lOMoAR cPSD| 44919514 cung cấp bản đồ địa hình của 12 lOMoAR cPSD| 44919514
3. Hàm sản xuất Cobb-Douglas
Ví dụ: Giả sử sản lượng của một nhà máy được Định nghĩa
cho bởi hàm sản xuất Cobb-Douglas Hàm sản lượng có , trong đó là vốn dạng:
đầu tư được đo bằng đơn vị $1,000 và là lượng
lao động được đo bằng số giờ làm việc. là
a. Tính sản lượng của nhà máy khi đầutư vốn các hằng số dương với
là $512,000 và 1,000 giờ lao động được sử dụng. , được gọi là
b. Chứng minh sản lượng ở phần (a)sẽ tăng dạng hàm sản xuất
gấp đôi nếu cả đầu tư vốn và quy mô lao động Cobb-Douglas. được nhân đôi. 13 lOMoAR cPSD| 44919514
4. Đường đẳng lượng và đường bàng quan Định nghĩa Đường mức của hàm sản lượng được gọi là
đường cong sản lượng không đổi C hoặc một đường đẳng lượng. Hàm lợi ích
là mức độ hài lòng (hoặc lợi ích) của người
tiêu dùng khi mua đơn vị hàng hóa thứ nhất và đơn vị hàng hóa thứ hai. Đường mức
của hàm lợi ích được gọi là đường bàng quan.
4. Đường đẳng lượng và đường bàng quan – Ví dụ
Ví dụ: Giả sử lợi ích của người tiêu dùng khi mua đơn vị hàng hóa thứ
nhất và đơn vị của hàng hóa thứ hai là 14 lOMoAR cPSD| 44919514
Nếu người tiêu dùng mua đơn vị hàng hóa đầu tiên và đơn vị
hàng hóa thứ hai, tìm lợi ích hiện tại của người tiêu dùng và vẽ đường
bàng quan tương ứng với mức lợi ích đó.
4. Đường đẳng lượng và đường bàng quan – Ví dụ
Ví dụ: Khi sử dụng lao động lành nghề và lao động giản đơn, một nhà máy
sản xuất đượcđơn vị sản phẩm mỗi ngày. Hiện tại có 10 lao động lành nghề
và 20 lao động giản đơn. a. Tính mức sản lượng hàng ngày hiện tại.
b. Tìm một phương trình thể hiện mối liên hệ giữa số lao động lành nghềvà
số lao động giản đơn khi sản lượng hàng ngày được giữ như mức hiện tại.
c. Vẽ đường đẳng lượng (đường sản xuất không đổi) tương ứng với mứcsản lượng hiện tại.
d. Ta nên thay đổi lượng lao động giản đơn như thế nào để vẫn giữ được
mức sản lượng như hiện tại khi số lao động lành nghề tăng thêm 2? 15 lOMoAR cPSD| 44919514 Bài giảng
Downloaded by Trang Thu (htttc1k21@gmail.com) lOMoAR cPSD| 44919514 TOÁN CHO CÁC NHÀ KINH TẾ
Chương 6: GIẢI TÍCH HÀM NHIỀU BIẾN
Bài 2: Đạo hàm riêng và vi phân
Tính toán và giải thích các đạo hàm riêng.
Ứng dụng đạo hàm riêng để tìm hiểu bài toán phân tích cận biên trong kinh tế học.
Tính đạo hàm riêng bậc hai. 17
Downloaded by Trang Thu (htttc1k21@gmail.com) lOMoAR cPSD| 44919514
Sử dụng quy tắc đạo hàm của hàm hợp để tìm tốc độ thay đổi và tính xấp xỉ số gia 1. Đạo hàm riêng
Định nghĩa: Cho hàm hai biến
Đạo hàm riêng của theo
được ký hiệu bởi hoặc
là hàm có được bằng cách lấy đạo hàm theo , coi là một hằng số.
Đạo hàm riêng của theo được ký hiệu bởi hoặc
là hàm có được bằng cách lấy đạo hàm , coi là một hằng số.
Ví dụ: Tìm các đạo hàm riêng và với 18
Downloaded by Trang Thu (htttc1k21@gmail.com) lOMoAR cPSD| 44919514 1
Theo định nghĩa, đạo hàm riêng và được xác định bởi: và 1
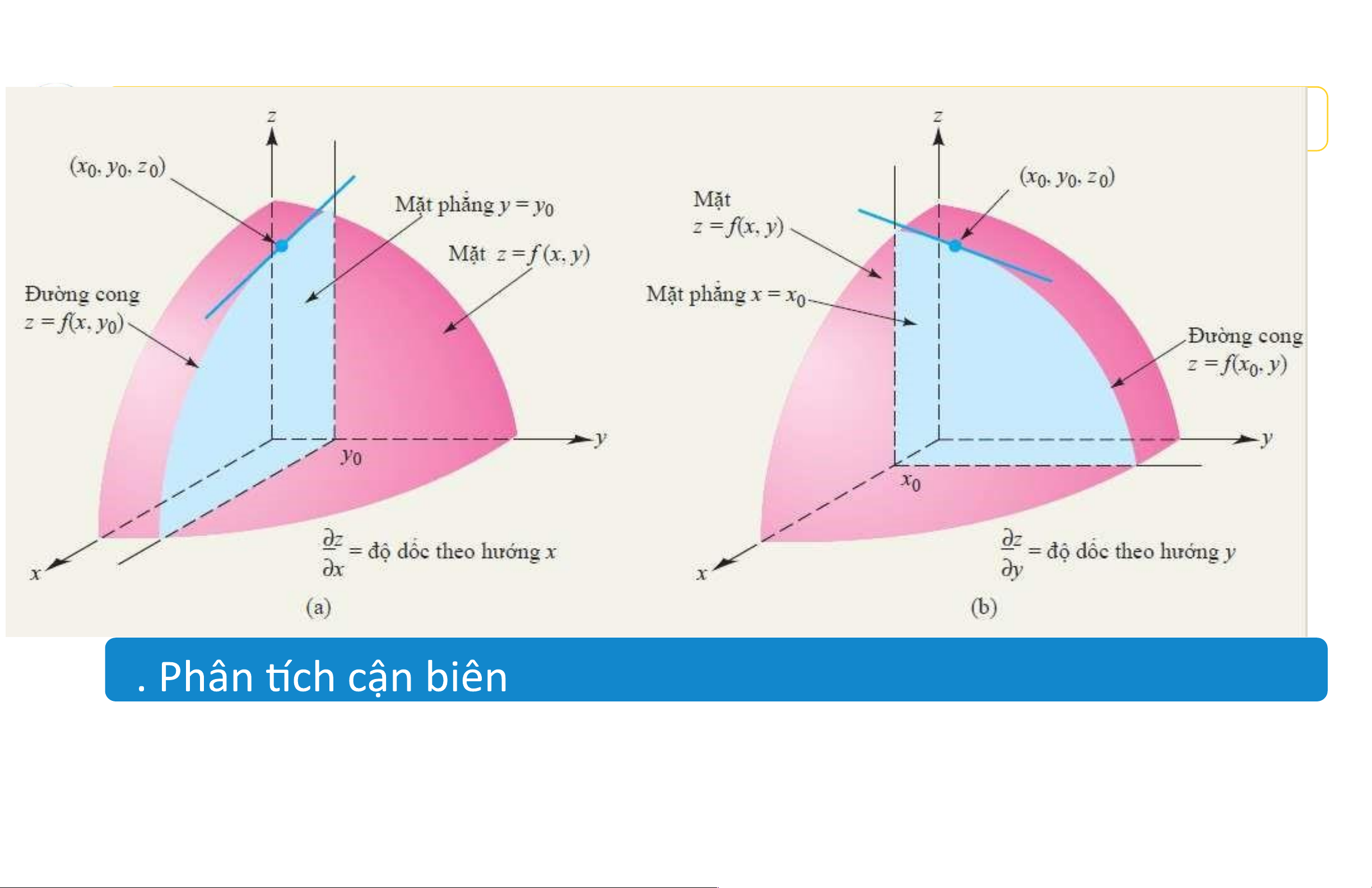
Giải thích hình học của đạo hàm riêng 19
Downloaded by Trang Thu (htttc1k21@gmail.com) lOMoAR cPSD| 44919514 2 20
Downloaded by Trang Thu (htttc1k21@gmail.com)