




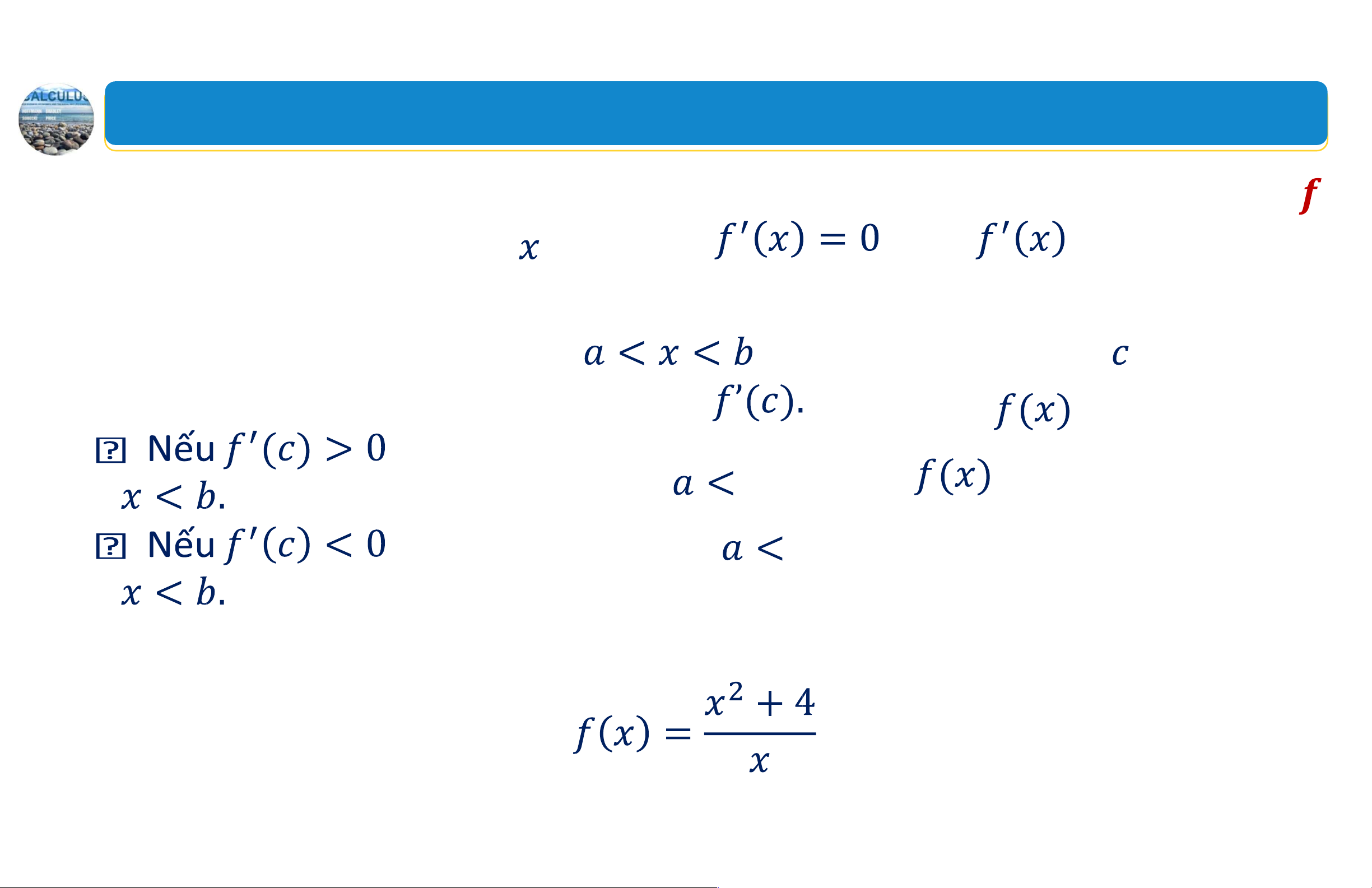





Preview text:
lOMoAR cPSD| 44919514 Bài giảng lOMoAR cPSD| 44919514 TOÁN CHO CÁC NHÀ KINH TẾ
Chương 3: MỘT SỐ ỨNG DỤNG CỦA ĐẠO HÀM Mục tiêu:
Giới thiệu các khái niệm hàm tăng, hàm giảm, cực trị tương đối, tính
lõm và điểm uốn, bài toán tối ưu hoá, phân tích cận biên, độ co dãn của cầu.
Đề cập các ứng dụng của đạo hàm trong phân tích kinh doanh, kinh
tế và các bài toán khoa học xã hội. Nội dung: 2 lOMoAR cPSD| 44919514
1. Hàm tăng và hàm giảm; Cực trị tương đối
2. Tính lõm và điểm uốn
3. Vẽ đồ thị của hàm số
4. Tối ưu hoá; Độ co giãn của cầu
5. Các bài toán tối ưu hoá ứng dụng khác lOMoAR cPSD| 44919514 Bài giảng 4 lOMoAR cPSD| 44919514 TOÁN CHO CÁC NHÀ KINH TẾ
Chương 3: MỘT SỐ ỨNG DỤNG CỦA ĐẠO HÀM
Bài 1: Hàm tăng và hàm giảm; cực trị tương đối
Tìm hiểu về hàm tăng và hàm giảm Tìm các điểm
tới hạn và cực trị tương đối.
Sử dụng đạo hàm cấp một để tìm cực trị tương đối
và vẽ đồ thị của một hàm số lOMoAR cPSD| 44919514 1 6 lOMoAR cPSD| 44919514 Định nghĩa
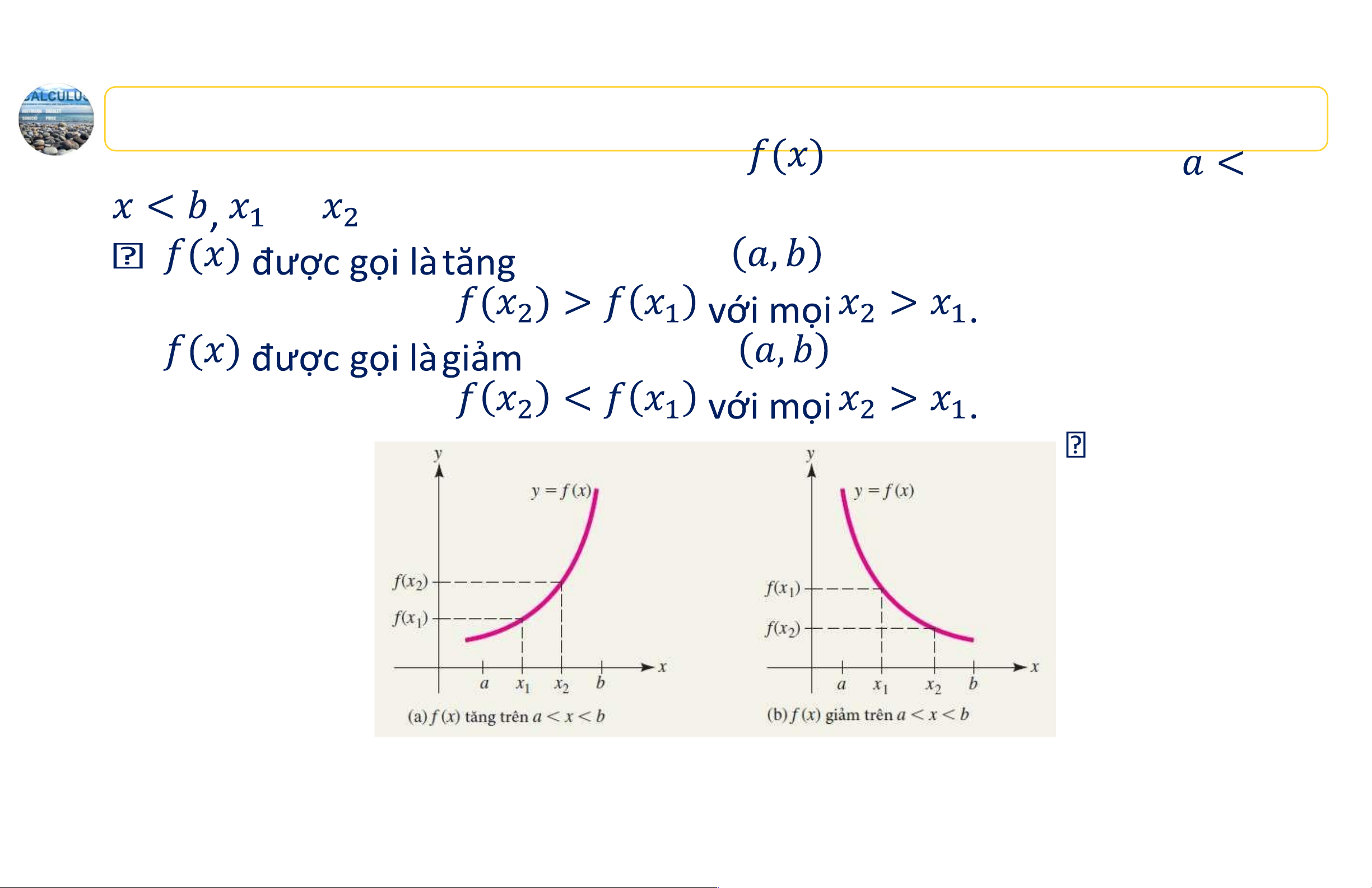
Hàm tăng và hàm giảm. Giả sử hàm số xác định trên khoảng và là hai số bất kỳ trên khoảng nếu: trên khoảng này. Khi đó trên khoảng nếu: 7 lOMoAR cPSD| 44919514 1 Minh họa
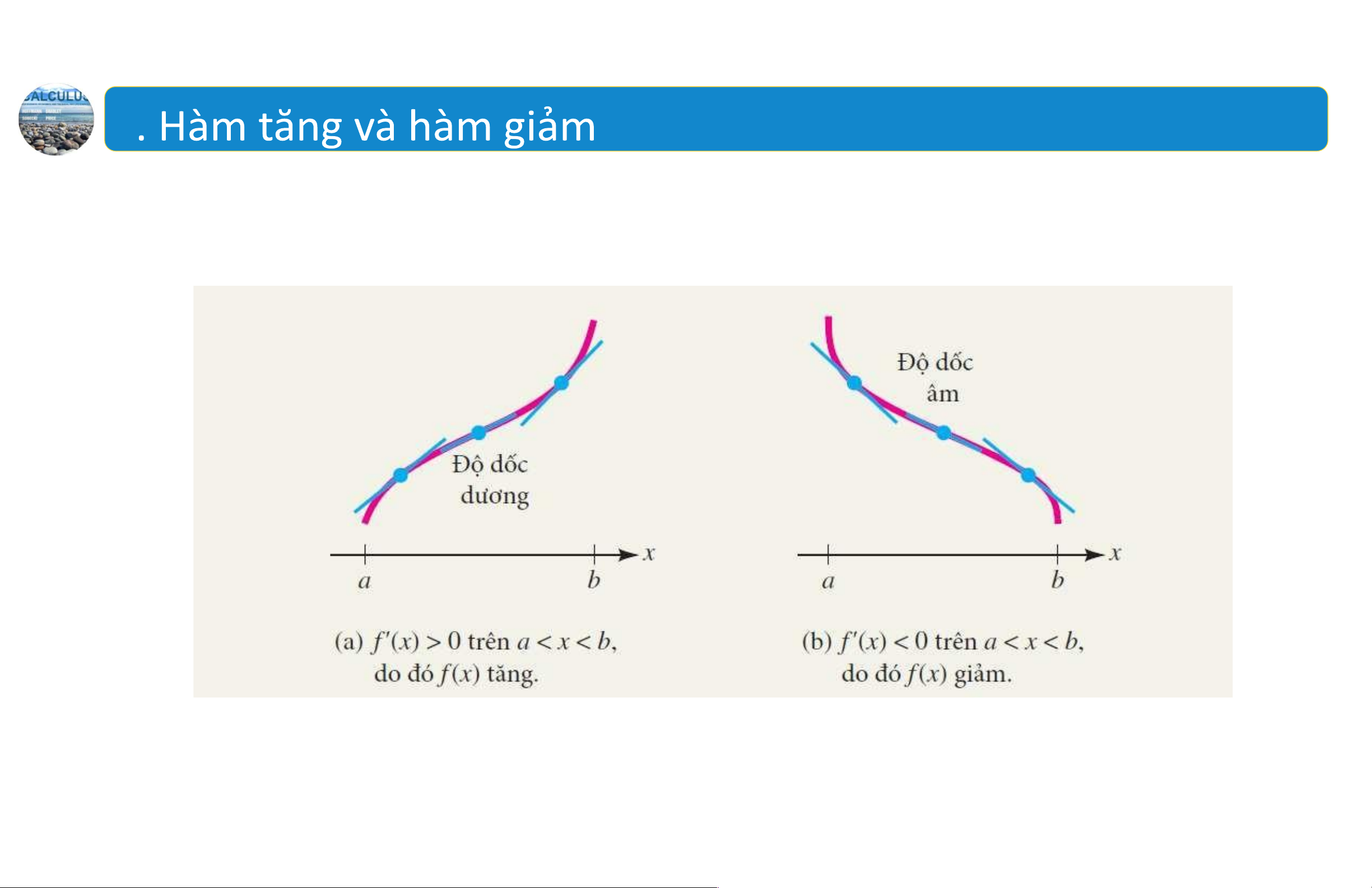
Đạo hàm của các hàm số tăng và giảm 8 lOMoAR cPSD| 44919514 1. Hàm tăng và hàm giảm
Quy trình sử dụng đạo hàm để tìm các khoảng tăng, giảm của hàm số .
Bước 1. Tìm tất cả giá trị của thỏa mãn hoặc không liên
tục. Các giá trị này chia trục số thành các khoảng rời nhau.
Bước 2. Trong mỗi khoảng con được xác định ở Bước 1, chọn số bất kỳ trong
khoảng đó và tính Khi đó: thì hàm số tăng (đồ thị đi lên) trên khoảng thì hàm số giảm (đồ thị đi xuống) trên khoảng
Ví dụ: Tìm các khoảng tăng, giảm của hàm số: 9 lOMoAR cPSD| 44919514 2 Định nghĩa
Hàm số được gọi là có một cực đại tương đối tại nếu với mọi thuộc một khoảng chứa c
Hàm số được gọi là có một cực tiểu tương đối tại nếu với mọi thuộc một khoảng chứa c .
Cực đại tương đối và cực tiểu tương đối của được gọi là cực trị tương đối của nó.
Một số trong miền xác định của hàm
được gọi là một số tới hạn nếu hoặc
không tồn tại, điểm tương ứng trên đồ thị của
được gọi là một điểm tới hạn của 10 lOMoAR cPSD| 44919514
Lưu ý: Cực trị tương đối chỉ có thể xảy ra tại các điểm tới hạn, nhưng không
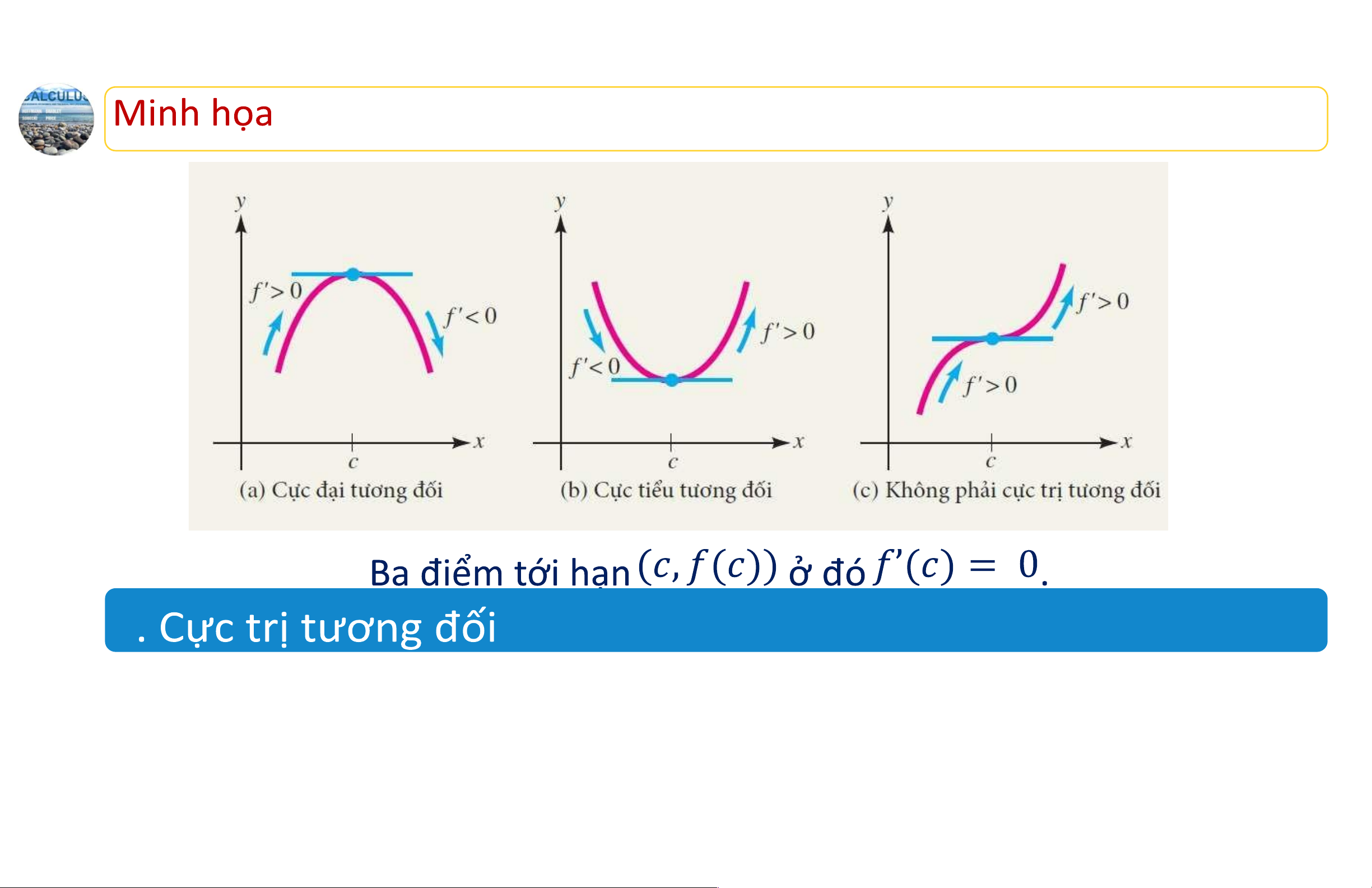
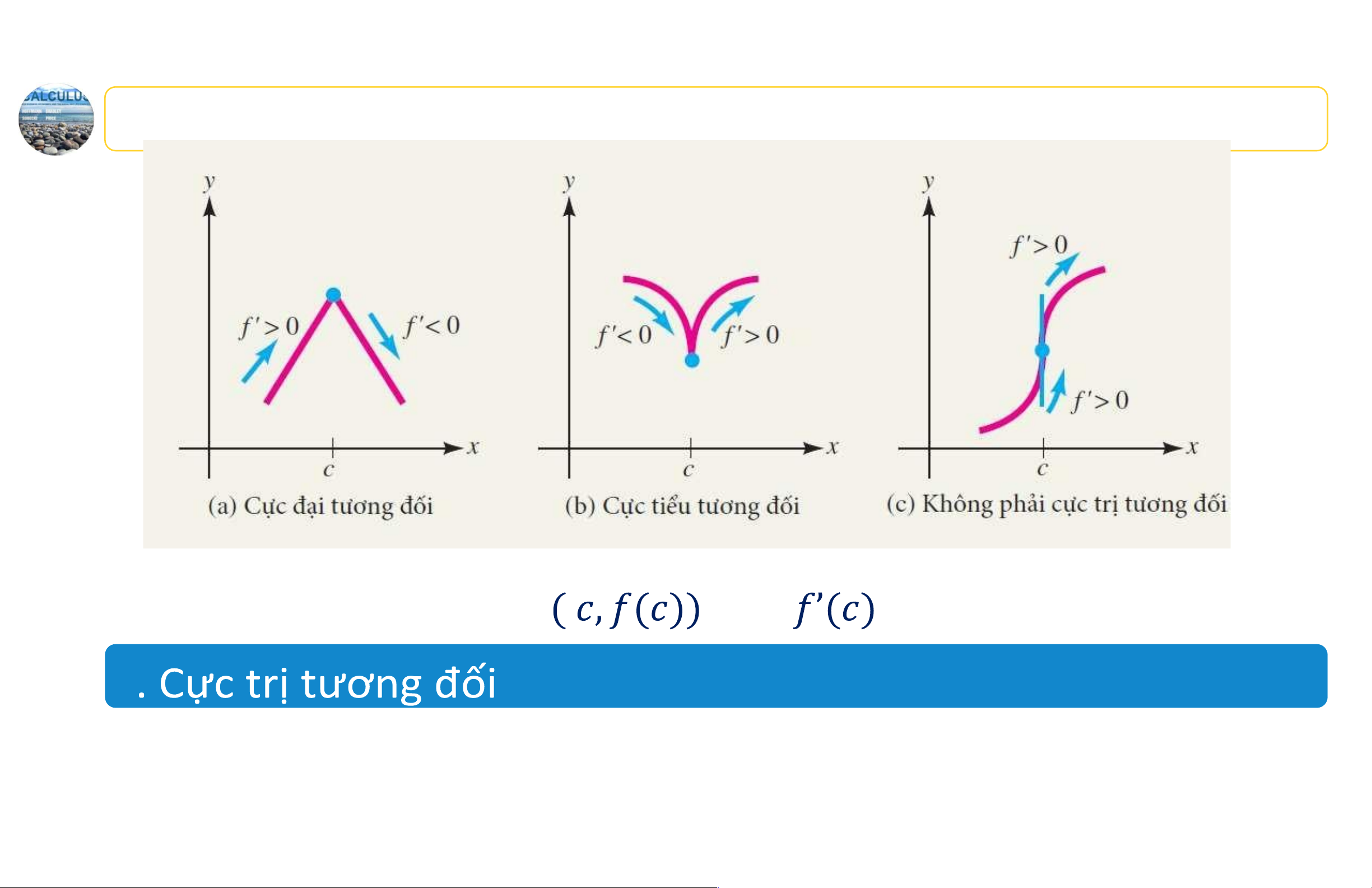
phải tất cả các điểm tới hạn đều tương ứng với cực trị tương đối. 2 11 lOMoAR cPSD| 44919514 2 12 lOMoAR cPSD| 44919514 Minh họa Ba điểm tới hạn ở đó không xác định. 2 13 lOMoAR cPSD| 44919514
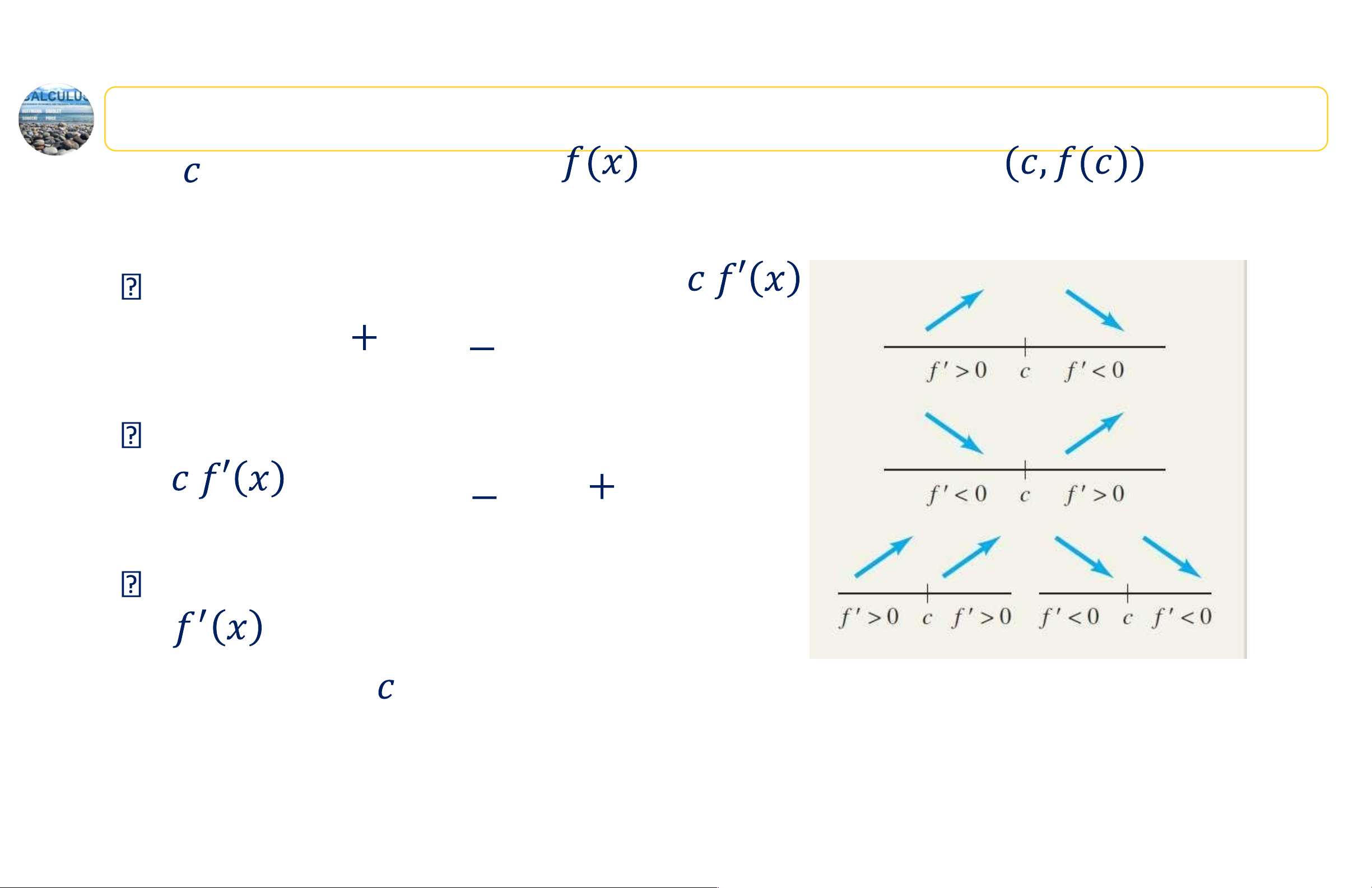
Kiểm tra cực trị tương đối bằng đạo hàm cấp một
Cho là một số tới hạn của
. Khi đó, điểm tới hạn là:
một cực đại tương đối nếu qua đổi dấu từ sang
một cực tiểu tương đối nếu qua đổi dấu từ sang
Không phải là cực trị tương đối nếu
có cùng một dấu ở cả hai phía của 14 lOMoAR cPSD| 44919514 2. Cực trị tương đối
tuần kể từ khi được đưa ra thị
trường được cho bởi công thức:
Ví dụ: Tìm các số tới hạn của hàm số
triệu đô-la. Thời điểm nào doanh
và phân loại các điểm tới hạn.
thu đạt tối đa? Doanh thu tối đa
Ví dụ: Doanh thu từ việc bán bằng bao nhiêu.
một số áo cho mùa hè mới sau
3. Phác họa đồ thị của hàm số
Quy trình phác họa đồ thị của hàm liên tục trên miền xác định sử dụng đạo hàm
Bước 1. Tìm miền xác định của . 15 lOMoAR cPSD| 44919514 Bước 2. Tính
tìm các số tới hạn của
và xác định các khoảng tăng, giảm của
trong miền xác định của nó.
Bước 3. Biểu diễn các điểm tới hạn
trên mặt phẳng tọa độ với
hình "chóp mũ“nếu nó là cực đại tương đối và hình "đáy cốc"
nếu nó là cực tiểu tương đối, tìm các giao điểm với các trục tọa độ
và một số điểm đặc biệt khác.
Bước 4. Phác họa đồ thị của là một đường cong trơn nối các điểm tới
hạn, sao cho đồ thị đi lên nếu
và có tiếp tuyến nằm ngang tại các điểm mà
3. Phác họa đồ thị của hàm số
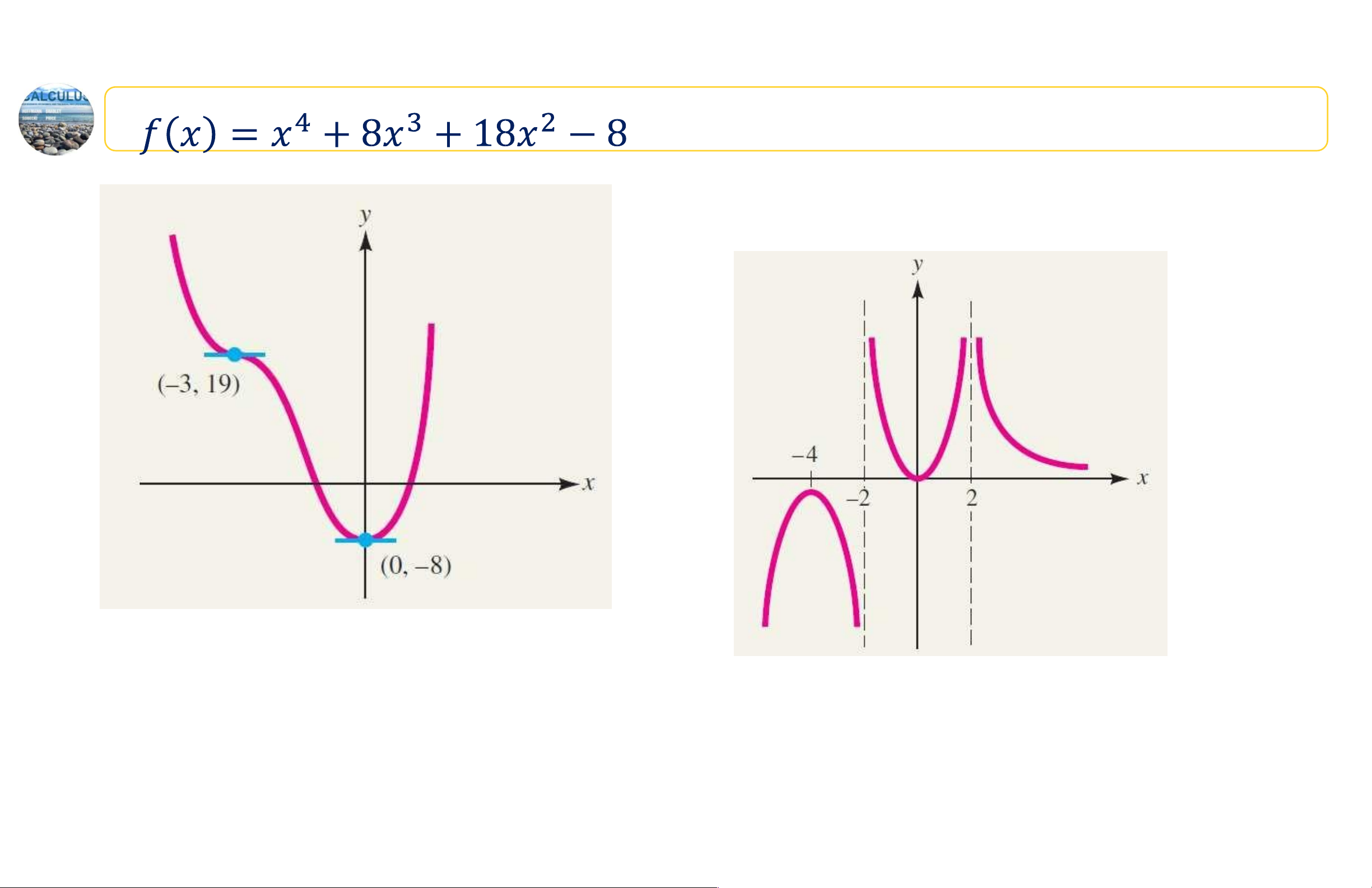
Ví dụ: Vẽ đồ thị của hàm số
Ví dụ thực hành từ đồ thị Dựa 16 lOMoAR cPSD| 44919514
vào đồ thị hàm số, hãy tìm các khoảng
mà đạo hàm của hàm số đã cho có giá trị dương? giá trị âm? 17 lOMoAR cPSD| 44919514 Bài giảng
Downloaded by Trang Thu (htttc1k21@gmail.com) lOMoAR cPSD| 44919514 TOÁN CHO CÁC NHÀ KINH TẾ
Chương 3: MỘT SỐ ỨNG DỤNG CỦA ĐẠO HÀM
Bài 2: Tính lõm và Điểm uốn Tìm hiểu về tính lõm.
Sử dụng dấu của đạo hàm cấp hai để tìm các khoảng lõm Tìm các điểm uốn. 19
Downloaded by Trang Thu (htttc1k21@gmail.com) lOMoAR cPSD| 44919514
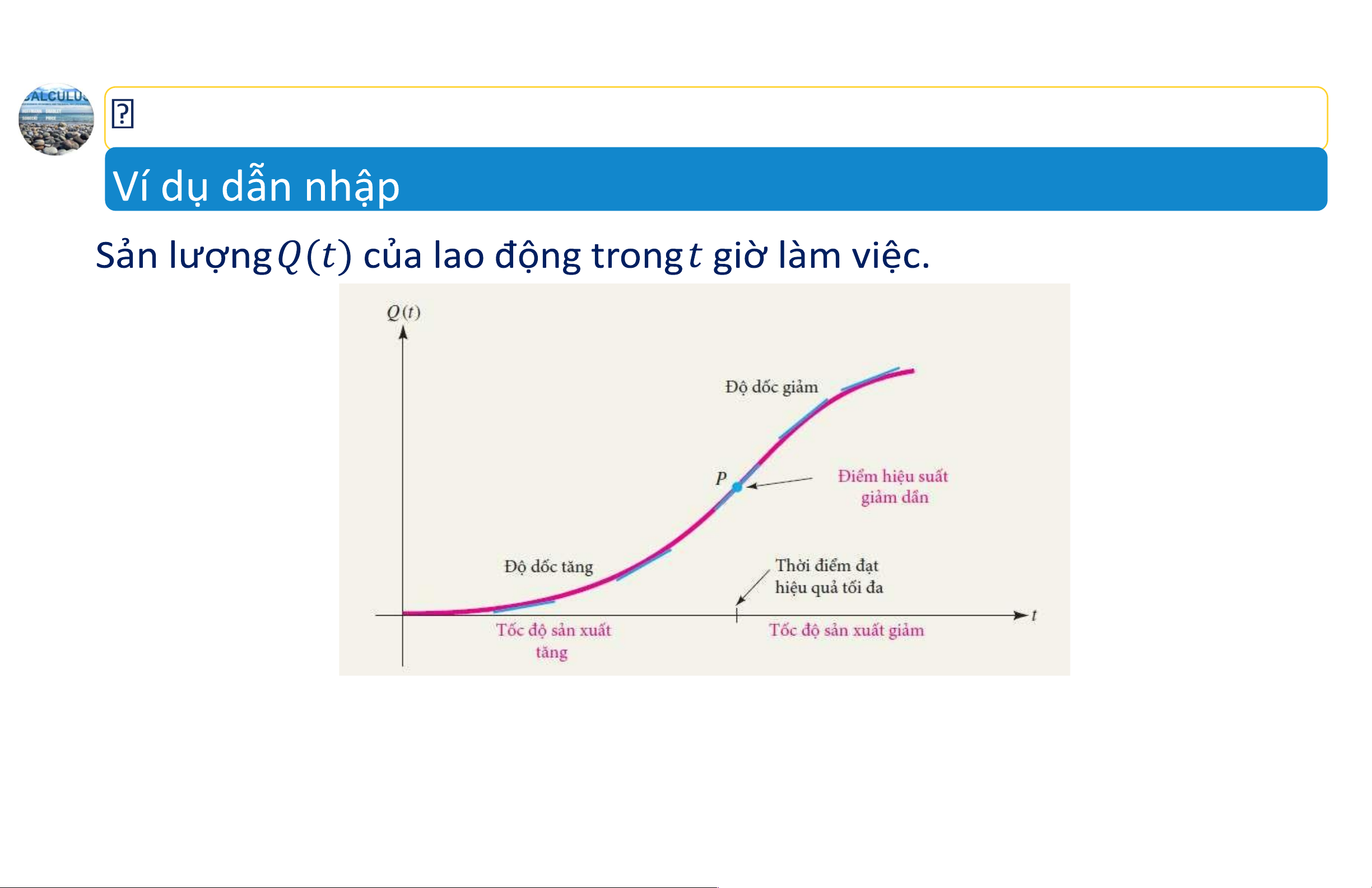
Sử dụng đạo hàm cấp hai để kiểm tra cực trị tương đối.
Điểm P được gọi là điểm hiệu suất giảm dần. 20
Downloaded by Trang Thu (htttc1k21@gmail.com)




