Bài 1 môn xác suất thống kê| Đại học Kinh tế Quốc Dân

Đại học Kinh tế Quốc dân với những kiến thức và thông tin bổ ích giúp các bạn định hướng và họp tập dễ dàng hơn. Mời bạn đọc đón xem. Chúc bạn ôn luyện thật tốt và đạt điểm cao trong kì thi sắp tới

18 9 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Xác suất thống kê (XSTK021)

Trường: Đại học Kinh Tế Quốc Dân

Thông tin:

6 trang 6 tháng trước

Tác giả:

Profile Hà Việt Anh
BÀI T P TH NG KÊ TOÁN Ậ Ố
BÀI 1. KHÁI NI N ỆM CƠ BẢ
TT
Nội dung
Giải
1
Xác định tổng thể, mẫu, quan sát, biến trong mỗi câu sau:
a. Điề ều tra 40 sinh viên K62 NEU v giới tính, quê quán, điểm
Toán đầu vào đạ ọc, điể ết năm họi h m tổng k c thức nhất.
b. Khảo sát 80 khách nam và 70 khách n v ữ ề đánh giá (từ 1 sao đến
5 sao) c a h i v i ch ng s n ph m, ch ng d ch v ủ ọ đố ớ ất lượ ả ẩ ất lượ ị ụ
giao hàng, ch ng d ch v sau bán hàng c a 1 c a hàng bán ất lượ ị ụ ủ ử
hàng online.
2
Kết qu ả nào sau đây là thống kê mô t , th ng kê suy di n, gi i thích? ả ố ễ ả
a. Điể ủm thi trung bình môn Toán c a 30 học sinh là 7,3.
b. Nhìn chung, điểm thi THPT môn Toán năm nay cao hơn năm
trước.
c. Có th cho r ng thu nh p trung bình c ng cể ằ ậ ủa người lao độ ủa
công ty đã tăng lên.
d. Độ phân tán v chi u cao c a t t c hề ề ủ ấ ả ọc sinh trường A là 7,2 cm.
3
Một siêu th ghi l i nh ng thông tin sau c a m i khách hàng s hị ạ ữ ủ ỗ ở ữu
thẻ thành viên:
a. Giới tính c a khách ủ
b. n/huy Khu v a khách (quực cư trú củ ậ ện nào)
c. Loạ ẻ ữ ạ ại th khách sở h u (b c, vàng, b ch kim)
d. T ổng số đơn hàng khách đã mua
e. Số ấ n nhtiền khách đã chi cho hóa đơn gầ t
Hãy phân lo i các biạ ến tương ứ ới các thông tin trên (địng v nh danh,
thứ b ng) ậc, định lượ
4
Mỗi người tham gia phỏng vấn nhân viên của một công ty phải trả
lời câu h i c a 2 giám kh o. T l ỏ ủ ả ỉ ệ chấm đạt c a giám kh o A là 70%, ủ ả
của giám khảo B là 60%. T lỉ ệ người thi bị cả hai giám khảo chấm
không đạt là 14%.
a. Hai bi n c ế ố “giám khảo A chấm đạt” và “giám khảo B chấm đạt”
có độc lập không? Có xung khắc không? Chứng minh.
b. Những người được c hai giám kh o chả ả ấm đạt thì được thi vòng
tiế ỷ ệ đượ ếp theo. Tìm t l c thi vòng ti p theo.
c. Tìm t l i thi b giám kh o B ch t bi t rỉ ệ ngườ ị ả ấm không đạ ế ằng
giám kh ảo A đã chấm đạt.
5
Lô hàng có 10 h p s n ph p s n ph m c a nhà ộ ả ẩm, trong đó có 3 hộ ả ẩ ủ
máy A, còn l i là h p s n ph m c a nhà máy B. M i h u có 12 ạ ộ ả ẩ ủ ỗ ộp đề
sản phẩm.
Mỗi h p s n ph m c a nhà máy A có 2 ph ph m. ộ ả ẩ ủ ế ẩ
Mỗi h p s n ph m c a nhà máy B có 3 ph phộ ả ẩ ủ ế ẩm.
a. Lấy 1 hộp rồi t y 1 sừ đó lấ ản phẩm. Tìm xác suất l c ph ấy đượ ế
phẩm.
b. L ấy 1 h p r i t ộ ồ ừ đó lấy 1 sản ph m thì ẩ được ph m. Tìm xác ế phẩ
suất đã lấy được hộp sản phẩm của nhà máy A.
c. Lấy 1 h p r i t ộ ồ ừ đó lấ ẩm thì đượy 1 sản ph c phế phẩm. L y tiấ ếp
1 s n ph m n a (không hoàn l i s n phả ẩ ữ ạ ả ẩm trước đó). Tìm xác
suấ ế ụ ế ẩt ti p t c l c phấy đượ ph m.
6
X, Y l t là t t l i nhu i c phi u A và ần lượ ỉ suấ ợ ận khi đầu tư vào 2 lợ ổ ế
B. Bi c l p và có phân ph i xác su ết X và Y độ ậ ố ất:
X (%)
-5
0
5
10
P
0,2
0,3
0,4
0,1
Y (%)
-4
0
4
8
P
0,18
0,3
0,4
0,12
a. Nếu mu n khố ả năng đạt tỉ suấ ật lợi nhu n t i thiố ểu là 3% cao hơn
thì nên mua c phi u nào? ổ ế
b. N ếu muốn tỉ suất l i nhu ợ ận trung bình cao hơn thì nên mua cổ
phiếu nào?
c. Nếu mu n r i ro ố ủ – đo bởi phương sai của t t l i nhu n ỉ suấ ợ ậ – thấp
hơn thì nên mua cổ phiếu nào?
d. N ếu muốn rủi ro thấp nhất thì chia vốn để mua c hai lo i c ả ạ ổ
phiếu theo t lỉ ệ nào?
7
Tỉ lệ khách vào c a hàng quy nh mua hàng là 35%. Quan sát ử ết đị
ngẫu nhiên 25 khách vào cửa hàng.
a. Tìm xác su t có ít nh t là 2 khách mua hàng. ấ ấ
b. Số khách mua hàng trung bình là bao nhiêu?
c. Số ả khách mua hàng có kh năng xảy ra cao nhất là mấy người?
Tìm xác su t c a giá tr này. ấ ủ ị
8
Lương tháng của nhân viên (đơn vị ập đoàn : nghìn USD) của một t
lớn là bi n ng u nhiên liên t c có hàm m xác suế ẫ ụ ật độ ất:
𝑓
(
𝑥
)
={
(𝑥 − 1)/2 ; 𝑥∈[1;2]
(5 − 𝑥)/6 ; 𝑥∈
[ ]
2;5
0 ; 𝑥∉
[ ]
1;5
a. Tình lương trung bình của người lao động
b. Tìm t lỉ ệ c trung bình người lao động có lương cao hơn mứ
9
Cân n ng c a s n ph m phân ph i chu n v i trung bình 400g và ặ ủ ả ẩ ố ẩ ớ
phương sai là 900g
2
.
a. Tìm t l s n ph m n ỉ ệ ả ẩ ặng hơn 355g.
b. Tìm t lỉ ệ sản phẩm nhẹ hơn 445g.
c. Tìm t l s n ph m có cân n ng sai l ch so v i m c trung bình ỉ ệ ả ẩ ặ ệ ớ ứ
không quá 30g.
d. Biết cân nặng của các s n ph c lả ẩm độ ập v i nhau. Tìm xác suớ ất
để ổ ặ ủ ả t ng cân n ng c a 2 s n ph t quá 850g. ẩm vượ
10
X là s i c a h hàng tháng ố ngườ ủ ộ gia đình, Y là chi tiêu trung bình
của h ộ gia đình (triệu đồng) ở một khu v c. Cho b ng phân ph i xác ự ả ố
suất đồ ời sau đây:ng th
6
10
15
20
0,1
0,2
0
0
0,02
0,18
0,15
0,05
0
0,05
0,12
0,03
0
0,02
0,04
0,04
a. Có th dùng giá tr i di n cho chi tiêu c a h gia ể ị nào để đạ ệ ủ ộ
đình bất kì ở khu vực này?
b. Tìm chi tiêu trung bình của hộ gia đình có từ 3 đến 4 người.
c. Số người và chi tiêu c a h v i nhau ủ ộ gia đình có liên hệ ớ
không? N u có thì liên h t ch n m c nào? ế ệ chặ ẽ đế ứ
| 1/6
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

BÀI TẬP THỐNG KÊ TOÁN
BÀI 1. KHÁI NIỆM CƠ BẢN TT Nội dung Giải 1
Xác định tổng thể, mẫu, quan sát, biến trong mỗi câu sau:
a. Điều tra 40 sinh viên K62 NEU về giới tính, quê quán, điểm
Toán đầu vào đại học, điểm tổng kết năm học thức nhất.
b. Khảo sát 80 khách nam và 70 khách nữ về đánh giá (từ 1 sao đến
5 sao) của họ đối với chất lượng sản phẩm, chất lượng dịch vụ
giao hàng, chất lượng dịch vụ sau bán hàng của 1 cửa hàng bán hàng online. 2
Kết quả nào sau đây là thống kê mô tả, thống kê suy diễn, giải thích?
a. Điểm thi trung bình môn Toán của 30 học sinh là 7,3.
b. Nhìn chung, điểm thi THPT môn Toán năm nay cao hơn năm trước.
c. Có thể cho rằng thu nhập trung bình của người lao động của công ty đã tăng lên.
d. Độ phân tán về chiều cao của tất cả học sinh trường A là 7,2 cm. 3
Một siêu thị ghi lại những thông tin sau của mỗi khách hàng sở hữu thẻ thành viên: a. Giới tính của khách
b. Khu vực cư trú của khách (quận/huyện nào)
c. Loại thẻ khách sở hữu (bạc, vàng, bạch kim)
d. Tổng số đơn hàng khách đã mua
e. Số tiền khách đã chi cho hóa đơn gần nhất
Hãy phân loại các biến tương ứng với các thông tin trên (định danh,
thứ bậc, định lượng) 4
Mỗi người tham gia phỏng vấn nhân viên của một công ty phải trả
lời câu hỏi của 2 giám khảo. Tỉ lệ chấm đạt của giám khảo A là 70%,
của giám khảo B là 60%. Tỉ lệ người thi bị cả hai giám khảo chấm không đạt là 14%.
a. Hai biến cố “giám khảo A chấm đạt” và “giám khảo B chấm đạt”
có độc lập không? Có xung khắc không? Chứng minh.
b. Những người được cả hai giám khảo chấm đạt thì được thi vòng
tiếp theo. Tìm tỷ lệ được thi vòng tiếp theo.
c. Tìm tỉ lệ người thi bị giám khảo B chấm không đạt biết rằng
giám khảo A đã chấm đạt. 5
Lô hàng có 10 hộp sản phẩm, trong đó có 3 hộp sản phẩm của nhà
máy A, còn lại là hộp sản phẩm của nhà máy B. Mỗi hộp đều có 12 sản phẩm.
Mỗi hộp sản phẩm của nhà máy A có 2 phế phẩm.
Mỗi hộp sản phẩm của nhà máy B có 3 phế phẩm.
a. Lấy 1 hộp rồi từ đó lấy 1 sản phẩm. Tìm xác suất lấy được phế phẩm.
b. Lấy 1 hộp rồi từ đó lấy 1 sản phẩm thì được phế phẩm. Tìm xác
suất đã lấy được hộp sản phẩm của nhà máy A.
c. Lấy 1 hộp rồi từ đó lấy 1 sản phẩm thì được phế phẩm. Lấy tiếp
1 sản phẩm nữa (không hoàn lại sản phẩm trước đó). Tìm xác
suất tiếp tục lấy được phế phẩm. 6
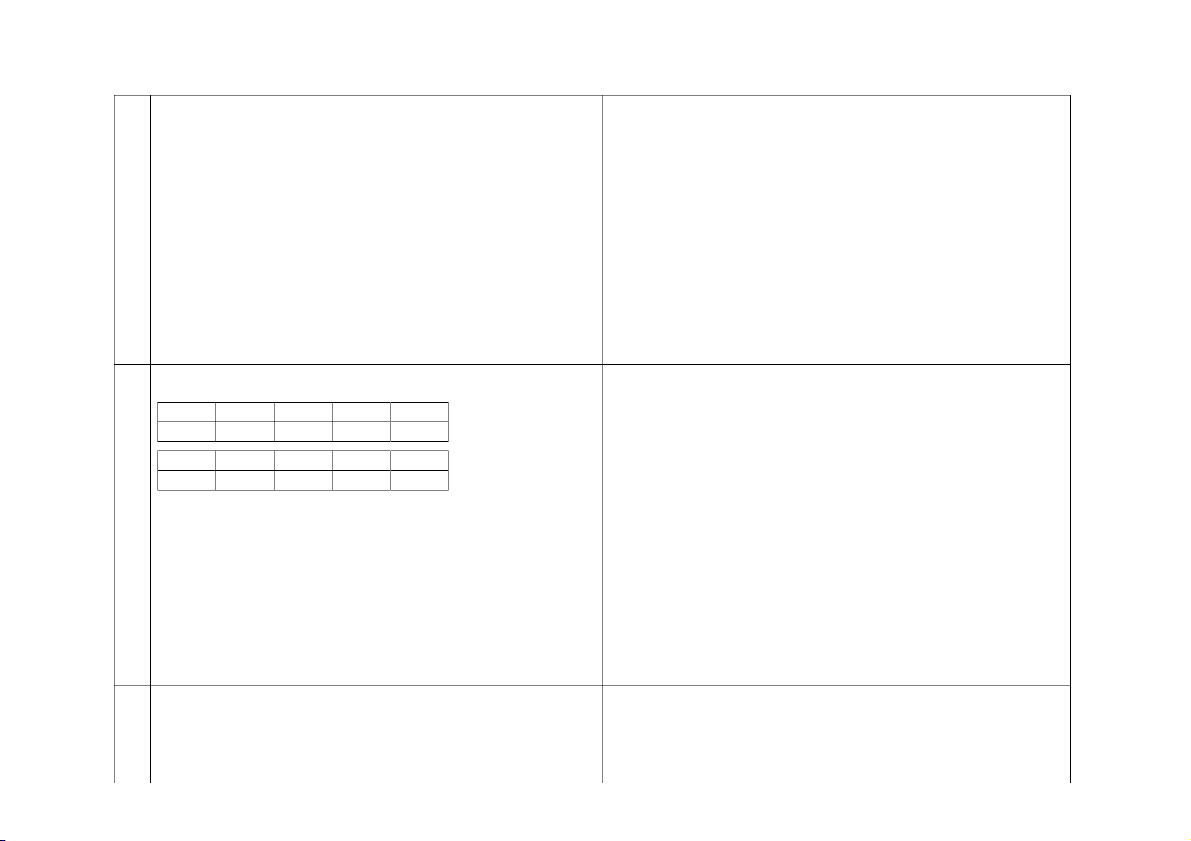
X, Y lần lượt là tỉ suất lợi nhuận khi đầu tư vào 2 lợi cổ phiếu A và
B. Biết X và Y độc lập và có phân phối xác suất: X (%) -5 0 5 10 P 0,2 0,3 0,4 0,1 Y (%) -4 0 4 8 P 0,18 0,3 0,4 0,12
a. Nếu muốn khả năng đạt tỉ suất lợi nhuận tối thiểu là 3% cao hơn
thì nên mua cổ phiếu nào?
b. Nếu muốn tỉ suất lợi nhuận trung bình cao hơn thì nên mua cổ phiếu nào?
c. Nếu muốn rủi ro – đo bởi phương sai của tỉ suất lợi nhuận – thấp
hơn thì nên mua cổ phiếu nào?
d. Nếu muốn rủi ro thấp nhất thì chia vốn để mua cả hai loại cổ phiếu theo tỉ lệ nào? 7
Tỉ lệ khách vào cửa hàng quyết định mua hàng là 35%. Quan sát
ngẫu nhiên 25 khách vào cửa hàng.
a. Tìm xác suất có ít nhất là 2 khách mua hàng.
b. Số khách mua hàng trung bình là bao nhiêu?
c. Số khách mua hàng có khả năng xảy ra cao nhất là mấy người?
Tìm xác suất của giá trị này. 8
Lương tháng của nhân viên (đơn vị: nghìn USD) của một tập đoàn
lớn là biến ngẫu nhiên liên tục có hàm mật độ xác suất:
(𝑥 − 1)/2 ; 𝑥 ∈ [1; 2]
𝑓(𝑥) = {(5 − 𝑥)/6 ; 𝑥 ∈ [2; 5] 0 ; 𝑥 ∉ [1; 5]
a. Tình lương trung bình của người lao động
b. Tìm tỉ lệ người lao động có lương cao hơn mức trung bình 9
Cân nặng của sản phẩm phân phối chuẩn với trung bình 400g và phương sai là 900g2.
a. Tìm tỉ lệ sản phẩm nặng hơn 355g.
b. Tìm tỉ lệ sản phẩm nhẹ hơn 445g.
c. Tìm tỉ lệ sản phẩm có cân nặng sai lệch so với mức trung bình không quá 30g.
d. Biết cân nặng của các sản phẩm độc lập với nhau. Tìm xác suất
để tổng cân nặng của 2 sản phẩm vượt quá 850g.
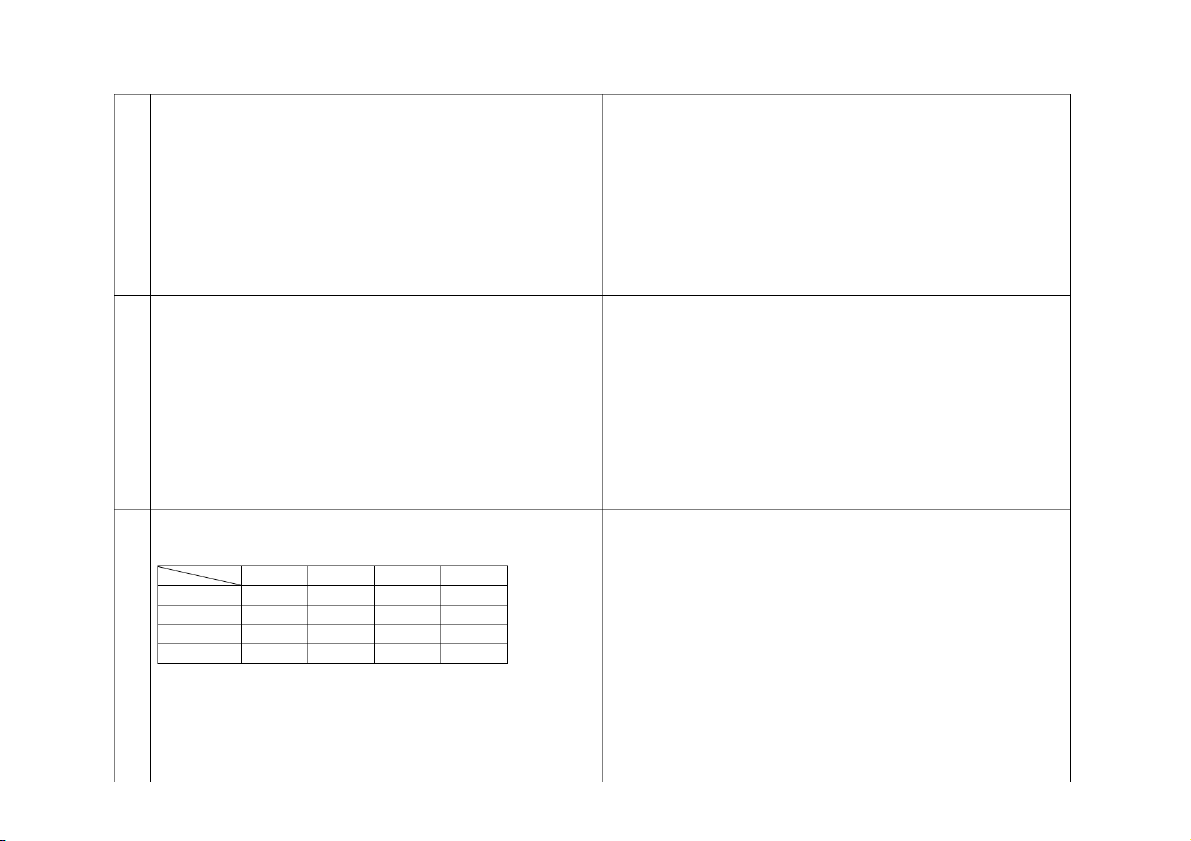
10 X là số người của hộ gia đình, Y là chi tiêu trung bình hàng tháng
của hộ gia đình (triệu đồng) ở một khu vực. Cho bảng phân phối xác
suất đồng thời sau đây: X Y 6 10 15 20 1 – 2 0,1 0,2 0 0 3 – 4 0,02 0,18 0,15 0,05 5 – 6 0 0,05 0,12 0,03 7 – 10 0 0,02 0,04 0,04
a. Có thể dùng giá trị nào để đại diện cho chi tiêu của hộ gia
đình bất kì ở khu vực này?
b. Tìm chi tiêu trung bình của hộ gia đình có từ 3 đến 4 người.
c. Số người và chi tiêu của hộ gia đình có liên hệ với nhau
không? Nếu có thì liên hệ chặt chẽ đến mức nào?