Bài 14: Phương trình vi phân và lý thuyết chuối | Giải tích 3 | Đại học Bách Khoa Hà Nội

PGS. TS. Nguyễn Xuân Thảo thaonx-fami@mail.hut.edu.vn
PHƯƠNG TRÌNH VI PHÂN VÀ LÍ THUYẾT CHUỖI BÀI 14
§3.3. Phép tịnh tiến và phân thức đơn giản
 Quy tắc phân thức đơn giản
 Giải PTVPTT hệ số hằng bậc lớn hơn hay bằng 3
 Sự cộng hưởng và nhân tử tích lặp bậc hai 1. Mở đầu.
Phương trình vi phân tuyến tính với hệ số hằng có
nghiệm là biến đổi Laplace nghịch đảo của hàm hữu P(s) tỉ R(s )  ( Q s)
Cần đưa ra kĩ thuật cho phép tính 1 L R(s ) được thuận lợi.
PGS. TS. Nguyễn Xuân Thảo thaonx-fami@mail.hut.edu.vn
2. quy tắc phân thức đơn giản
a) Quy tắc 1. Phân thức đơn giản tuyến tính Nếu n
Q(s) có s  a thì R s  có các số hạng sau 1 A  2 A  ...  n A , A  i , i  1,n s  a s  a2 s  an
b) Quy tắc 2. Phân thức đơn giản bậc hai n Nếu 2
Qs có s  a  2
b  thì R s có dạng A s  B A s  B A s  1 1  2 2  B ...  n n s  a2  2 2 b s a2 n 2  b s a2 2         b 
ở đó A , B  , i  1, i i n
PGS. TS. Nguyễn Xuân Thảo thaonx-fami@mail.hut.edu.vn
Định lí 1. Biến đổi trên trục s Nếu F(s)  L f (t 
) tồn tại với s  c, thì tồn tại L  at e f (t  ) với s  a  c và có L  at e f (t 
)  F (s  a)  L f t s  a. Hay tương đương với 1 L F s a  at at    e f t  1 ( )
( ) e L F st  Chứng minh. Ta có      sa  t F s a e f t   dt   st  at e e f t   dt 0 0  L  at
e f t , s  a  c
Từ kết quả này và từ bảng 4.1.2 có
PGS. TS. Nguyễn Xuân Thảo thaonx-fami@mail.hut.edu.vn f t  F s n! at n , s  a e t  (2.1) s  an1 s  a at , s  e cos(kt ) a  (2.2) s  a2  2 k k at , s  e sin(kt ) a  (2.3) s  a2  2 k
PGS. TS. Nguyễn Xuân Thảo thaonx-fami@mail.hut.edu.vn
Ví dụ 1. Tìm phép biến đổi Laplace ngược của 2 s  1 a) R(s)  3 s  2 2s  8s 2 s  1      A  B  C R s s s  2 s  4 s s  2 s  4  2 s 1  (
A s  2)(s  4)  Bs(s  4) Cs(s  2).
 Thay s  0, s  2, và s  4 ta có 1 5 17
8A  1, 12B  5, 24C  17  A   ; B  ; C  8 12 24 1 1 5 1 17 1  R s   .  .  . , 8 s 12 s  2 24 s  4 1 1 5 2 17 t 4t .  L R s      e  e 8 12 24
PGS. TS. Nguyễn Xuân Thảo thaonx-fami@mail.hut.edu.vn 2 s 2 b (K54) 1)     s F s 4 s  2 5s  4 1
(f t   2cost  sint  2cos2t  2sin2t ) 3 2 s 2 2)     s F s 4 s  2 3s  2
(f t   2cost  sint  2cos 2t  2 sin 2t ) c (K60) 1)    s F s s  2 ( 3)  4 3 (   3t   cos(2 )  3t f t e t e sin(2t )) 2 t 2) Tính L e t   2 (s)  
PGS. TS. Nguyễn Xuân Thảo thaonx-fami@mail.hut.edu.vn 1 2 2 (   ,s  2) s  3 2 s (s  2 1) 3t 
3) Tính L e sin(t  )(s) 4 1 1 s  3 ( [  ],s  3) 2 (s  2 3)  1 (s  2 3)  1 GIẢI 2)
PGS. TS. Nguyễn Xuân Thảo thaonx-fami@mail.hut.edu.vn 2 +) L 
 t    L  2t  t e t s e te  t  2 ( ) 2 (s)  L  2t L  t e s te  s  L  2 ( ) 2 ( ) t (s) 1 2 1 +)    2 ,s  2. s  3 2 s (s  2 1) 1)
PGS. TS. Nguyễn Xuân Thảo thaonx-fami@mail.hut.edu.vn +) 1 L F s     s  (t )  1 L  (t ) (s  2 3)  4    1 s  3    1 3  = L  (t)  L  (t) (s  2 3)  4  (s  2 3)  4    1 s  3  3   2  = L  (t)  1 L  (t ) (s  2 3)  4  2 (s  2 3)  4  3t 1  s  3 3t 1  2  = e L  (t )  e L  (t )  2 s  4  2  2 s  4    3t 3 e [cos(2t )  sin(2t )]. 2
PGS. TS. Nguyễn Xuân Thảo thaonx-fami@mail.hut.edu.vn d (K64) 1) L  t
e [sin(2t )  3 cos(2t ) ](t) 3s  1 ( ,s  1) 2 s  2s  5 1  s 1  2) Tính   L  (t)  2 s  6s  13  ( 3t  3 os(2 ) 2 t e c t e sin(2t )) 1 13s  14 3) Tính    L  (t) ( 2 -3e t +3et ) (s  2 2) (s  1) GIẢI d1
PGS. TS. Nguyễn Xuân Thảo thaonx-fami@mail.hut.edu.vn +) L  t
e [sin(2t )  3 cos(2t ) ](t)  = L  t sin(2  ) ( )  3L  t e t s e cos(2t  ) (t ) = L sin(2t 
) (s  1)  3L cos(2t  ) (s  1) 2 s  1 3s 1 +)   3  ,s  1 (s  2 1)  4 (s  2 1)  4 (s  2 1)  4 2)
PGS. TS. Nguyễn Xuân Thảo thaonx-fami@mail.hut.edu.vn 1  s  1    1 s  3  4  L  (t)  L  (t)  2 s  6s  13  (s  2 3)  4    1 s  3    2  = L  (t)  1 2L  (t) (s  2 3)  4  (s  2 3)  4  3t 1  s  3t 1  2    = e L  (t )  2e L  (t )  2 s  4   2 s  4   3t e [cos(2t )  2 sin(2t )].
Ví dụ 2. Giải bài toán giá trị ban đầu
PGS. TS. Nguyễn Xuân Thảo thaonx-fami@mail.hut.edu.vn y  y  y  2 4 4 t ; y(0)  y (0)  0.
 Tác động phép biến đổi Laplace ta có 2 2 s Y( ) s  4sY( ) s  4Y( ) s  . 3 s 2  A B C D E Y(s)       3 s (s  2 3 2 2) s s s s  22 s  2
 Đồng nhất các hệ số ta có 1 1 3 1 3 Y s  2  2  8  4 ( )  8 3 2 s s s s 2 s   2 2 1 1 3 1 t 3  2 2  ( )      2t y t t t te e . 4 2 8 4 8
PGS. TS. Nguyễn Xuân Thảo thaonx-fami@mail.hut.edu.vn 1
Ví dụ 3. Xét một hệ con lắc lò xo với m  , k  17, 2
c  3 đơn vị (mét, kilôgam, giây). x(t ) là khoảng dịch
chuyển của khối lượng m từ vị trí cân bằng của nó.
Nếu khối lượng được đặt ở vị trí x(0)  3, x '(0)  1.
Tìm x(t) là hàm của dao động tự do tắt dần.
Hình 4.3.1. Hệ khối lượng-lò xo và vật cản của Ví dụ 1
PGS. TS. Nguyễn Xuân Thảo thaonx-fami@mail.hut.edu.vn
 Ta có phương trình vi phân tương ứng với bài 1
toán là: x  3x 17x  0 2
với điều kiện ban đầu x(0)  3; x(0)  1
 Tác động phép biến đổi Laplace vào hai vế, chú ý L   0  0 ta có  2 s X(s)  3s  
1  6sX(s)  3  34 X(s)    0  3s  19 s  3 5 X (s)   3.  2 2 s  6s  34 s  32  25 s  32  25
 Sử dụng (2.2), (2.3) có 3t x(t)  e 3cos5t  2sin5t 
PGS. TS. Nguyễn Xuân Thảo thaonx-fami@mail.hut.edu.vn
Hình 4.3.2. Hàm vị trí x(t ) trong Ví dụ 1.
Từ hình ta thấy đồ thị của dao động tắt dần.
3. Giải PTVP tuyến tính bậc lớn hơn hay bằng 3 với hệ số hằng
Ví dụ 4. a) Xét hệ con lắc lò xo - giảm xóc như trong x(0)  x(0)  0
Ví dụ 3, tuy nhiên với điều kiện và
PGS. TS. Nguyễn Xuân Thảo thaonx-fami@mail.hut.edu.vn
với một lực tác động bên ngoài F(t )  15 sin2t . Tìm
chuyển động tức thời và ổn định của khối lượng đó.
 Ta cần giải bài toán với giá trị ban đầu
x " 6x ' 34x  30 sin 2t ; x(0)  x '(0)  0.
 Tác động phép biến đổi Laplace vào ta có 2 60
s X (s)  6sX (s)  34 X (s)  2 s  4 60 As  B Cs   D X s   . 2 s  4   (s  2 3)  2  2 5 s  4 s  2 3    25 10 50 10
 Đồng nhất ta có A   , B  , C  D  . 29 29 29 Vì vậy,
PGS. TS. Nguyễn Xuân Thảo thaonx-fami@mail.hut.edu.vn   1 10s  50 10s  10  X s     29  2 s  4 s  32    25   
1 10s  25.2 10(s  3)  4.5    . 29  2 s  4 s  32    25   Do đó 5 ( )  2cos2 5sin2  2      3t x t t t e 5cos5t  2sin5t  29 29 b) 3 x
 x  6x  0, x 0  0, x0  x 0  1 +)  3
s X s  s     2 1 s X s   1  6sX s  0 s 2 1  5 1 6  +) X s        3 2  15  3 2 
PGS. TS. Nguyễn Xuân Thảo thaonx-fami@mail.hut.edu.vn 1 +)  5L  1 L      3t   6L  2t e e  15 1 L  2t   6  3t e e  5  15  1 +)    2t   6  3t x t e e  5 15
c) x  6x  8x  2, x 0  0  x0 1 (    1 2 2 t  4t x t e e  4 d)    4   8  t x x x
e , x 0  x0  0 1 (   t   2  2t x t e e
2cos2t  sin2t ) 10 4        3           e) x x 0 x 0 1 x 0 x 0 x 0 0
PGS. TS. Nguyễn Xuân Thảo thaonx-fami@mail.hut.edu.vn 1
(x t   cosh t  cos t ) 2 f)   4 x   x  x x    x     x      3 13 36 0, 0 0 0, 0 2, x   0 13 1 1
( x t   sin2t  sin3t ) 2 3
g) 4  2    2t x x x e , x 0   x 0   x 0 3  x 0  0 1 (     2 2 t x t e
 10t  2cost  5t  14 sint ) 50 h)  x  6  x  18 x  cos 2 , t x 0  1,  x 0  1 1 1 (     3t x t e 489cos3t 307sin3t  7cos2t 6sin2t) 510 170
PGS. TS. Nguyễn Xuân Thảo thaonx-fami@mail.hut.edu.vn i (K54) 1) 3 x
 x 12x  0, x 0  0, x0  x 0  1 1 5 t 1 (   3      4t x t e e ) 6 21 14 2) 3 x
 x  20x  0, x 0  0, x0  x 0  1 1 1 1 (   4t      5t x t e e ) 10 6 15 j (K55) 1/   4 x 3  x  4x  0, x  0   x   0   x   0  0,  x   0 1 1 1 1 ( 2t   sin   2t t e e ) 5 20 20 2/   4 x 8 
x  9x  0, x0   x 0   x 0  0,  x 0 1
PGS. TS. Nguyễn Xuân Thảo thaonx-fami@mail.hut.edu.vn 1 1 t 1 ( 3   sin   3t t e e ) 10 60 60 k (K56) 1/   6   4 k x  4x  x  4x  sinh2t, x 0  0, k  0, 5 sinh2t  sin2t sinht  sint (  ) 20 15 2/ 6  4 x  4x  x  4x  sin2t ,  k x 0  0, k  0, 5. sinh2t  sin2t sinht  sint (  ) 20 15 l (K58) 1/   4 x
 4x  0, x(0)  0  x0  x(0), x(0)  1. 1 i i h2 sin sinh2 ( ) t t
PGS. TS. Nguyễn Xuân Thảo thaonx-fami@mail.hut.edu.vn m (K60) 1/   3       2t x x x x
e , x(0)  0  x0  x(0). 1 t 1 t 1 t 1 ( 2     t e e te e ) 3 12 2 4 2/ 4 x
 8x  9x  0, x(0)  0  x0, x(0)  x(0)  1. 1 t 1 1 ( e  o c s3t  sin3t ) 10 10 30 3/ 3 x
 5x  28x  34x  0, x(0)  0  x0, x(0)  1. 1 1 4 ( t 3t   e c  3 os5 t e t e sin5t )
PGS. TS. Nguyễn Xuân Thảo thaonx-fami@mail.hut.edu.vn l (K62) 1/   3 y
 2y  y  4, y(0)  0,y(0)  2,y (0)  2. (4  3  2 t t e ) 2/ 3 x
 x  6x  0, x(0)  1,x0  2, x(0)  3. 1 9 1 ( 2t    3t e e ) 6 10 15 o (K63)   3 x
 2x 16x  0, x(0)  x(0)  0,x(0)  20. ( 2t e  2t e [ cos(2t )  2 sin(2t )]) GIẢI
PGS. TS. Nguyễn Xuân Thảo thaonx-fami@mail.hut.edu.vn +) L x(t 
) (s)  X(s); L x(t 
) (s)  sX(s)  x(0)  sX (s) L x t  s  2 s X s  sx  x  2 ( ) ( ) ( ) (0) (0) s X(s); L x t  s  3 s X s  2 ( ) ( )
( ) s x(0)  sx(0)  x(0)   3 s X s   3 s  2 ( ) 20 ( 2s  16)X(s)  20 20  X (s)  3 s  2 2s  16 20 +) 1 x(t ) = L X(s     1 ) (t) =L (t)   (s  2)[(s  2 2)  4] 1  1    1 s  6  = L  (t)  L  (t) s  2  (s  2 2)  4 
PGS. TS. Nguyễn Xuân Thảo thaonx-fami@mail.hut.edu.vn 2t   1 s  2    2  = e  L  (t )  1 2L  (t ) (s  2 2)  4  (s  2 2)  4  2t 2t 1  s  1  2  = e  e L  (t )  2L  (t )  2 s  4   2 s  4    2t  2t e e [cos(2t )  2 sin(2t )] p (K64) 1)4 x  4  x  4x  0, (0) x   x (0)  0, 
x (0)  1, x(0)  2. 2 2 ( t sin(t 2)  sin( 2t) t 2 o c s t ) ( 2)
PGS. TS. Nguyễn Xuân Thảo thaonx-fami@mail.hut.edu.vn 2)   3    t y y
e , y(0)  y 0  y  0. t e o c s t  sin (1  t ) 2 2 3)   3 x   x  6  x  0, (0) x  0, x0   x (0)  2. 2 4 t 2 ( 2     3t e e ) 3 5 15 4) (4) 3 y  4y
 6y  4y  y  0, y(0)  0  y(0), 1 y    (3) 0 1 y (0). ( t e (3t  2 3t  3 2t )) 3 GIẢI
PGS. TS. Nguyễn Xuân Thảo thaonx-fami@mail.hut.edu.vn 1) +) L x(t 
) (s)  X(s); L x(t 
) (s)  sX(s)  x(0)  sX (s) L x t  s  2 s X s  sx  x  2 ( ) ( ) ( ) (0) (0) s X(s); L  (4) x t  s  4 s X s  3 s x  2 ( ) ( ) ( )
(0) s x(0)  sx(0)  x(0)  4 s X(s)  s  2  4 2 s  2
 (s  4s  4)X(s)  s  2  X(s)  4 s  2 4s  4 1 1 s  2 +)   x(t)=L X(s     ) (t)=L  (t)  2 (s  2 2) 
PGS. TS. Nguyễn Xuân Thảo thaonx-fami@mail.hut.edu.vn   s  1   1  = L  (t)  1 2L  (t)  2 (s  2 2)   2 (s  2 2)  1 2  t sin( 2t )  [ sin( 2t )  2t cos( 2t )] 3 2 2 2( 2) 1 1  t sin( 2t )  [ sin( 2t )  2t cos( 2t )] 2 2 2 2 q (K66) 1) 3 y  4 
x  4, y(0)  y(0)  0, y (0)  4. 1 ( sinh(2t)  c s o h(2t )  t  1) 2
PGS. TS. Nguyễn Xuân Thảo thaonx-fami@mail.hut.edu.vn
4. Sự cộng hưởng và nhân tử tích lặp bậc hai
Hay dùng hai phép biến đổi Laplace ngược của hàm
phân thức đơn giản trong trường hợp phân tích lặp
bậc hai (nhận được khi sử dụng kỹ thuật như ở Ví dụ 5, Bài 13)   1  s  1 L  (t )  t sin(kt ); 2  2 s  2 2k  k     1  1  1 L  (t )  [sin(kt )  kt cos(kt )] 2 3  2 s  2 2k  k  
PGS. TS. Nguyễn Xuân Thảo thaonx-fami@mail.hut.edu.vn
Ví dụ 5. Sử dụng phép biến đổi Laplace để giải bài
toán với giá trị ban đầu  x  2x  F  0
0 sin t ; x(0)  0  x(0)
 Tác động phép biến đổi Laplace vào có 2 2 F  s X (s )   X (s )  0 0 2 s  2 F   X(s)  0  2 s   2  2 s   2 0  F   1 1   0   ,    2  2  2 0 s  2 2 s 2     0  0   tìm được x t 
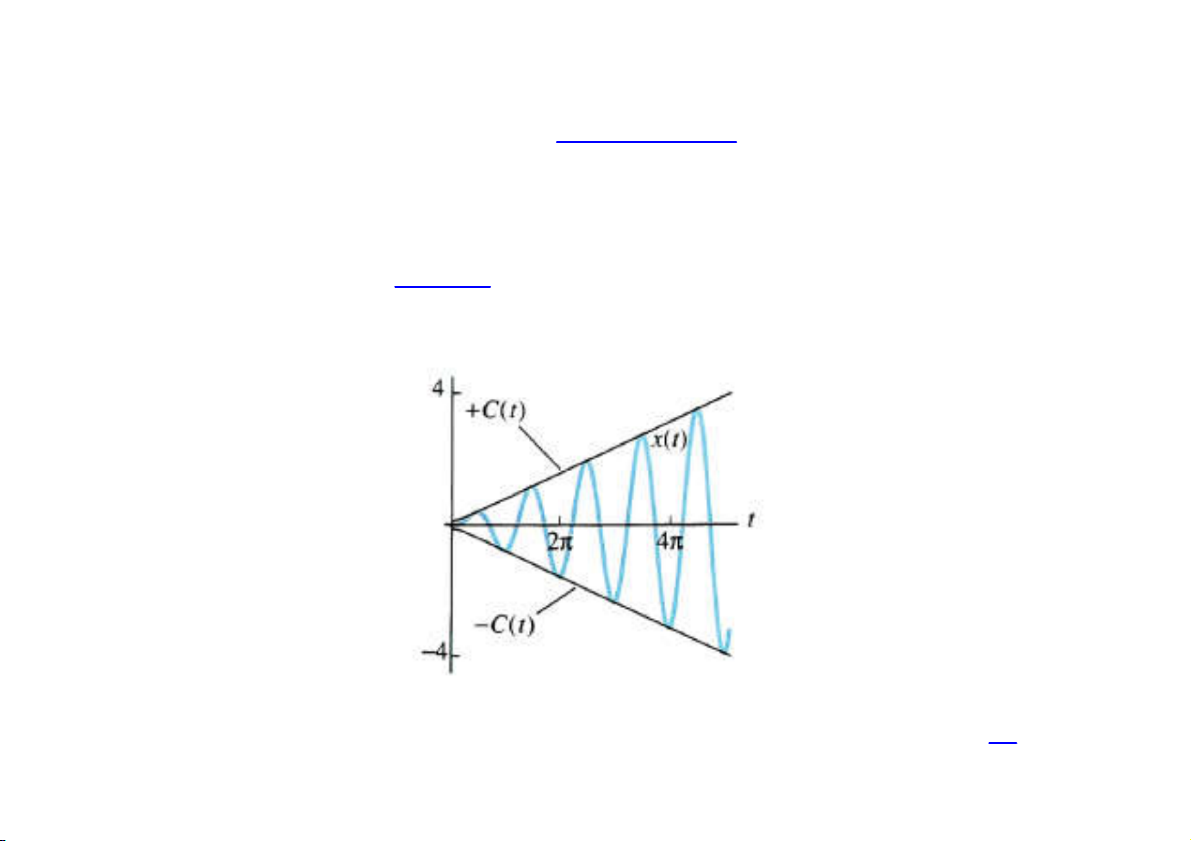
PGS. TS. Nguyễn Xuân Thảo thaonx-fami@mail.hut.edu.vn  Nếu    F  0 0 0 ta có X (s)  , khi đó  2 2 s  20  ( )  0 F x t si  n t   t cos 0 0 0t   2 2 0 1
Hình 4.3.4. Nghiệm cộng hưởng trong (18) với   0 và F  0 1 x  C(t )
, cùng với đường bao của nó
PGS. TS. Nguyễn Xuân Thảo thaonx-fami@mail.hut.edu.vn
Ví dụ 6. Giải bài toán với giá trị ban đầu 4 2 "  4 t y y y te ; y  y  y  (3) (0) '(0) "(0) y (0)  0.  Có 4 L y t   2 ( ) s Y (s),   L y t   4 ( ) s Y (s), L  t te  1  . s  2 1
 Tác động phép biến đổi Laplace vào có  4 4 s  2 2s   1 Y(s)  . s  2 1
PGS. TS. Nguyễn Xuân Thảo thaonx-fami@mail.hut.edu.vn 4  Y(s)  (s  2 2 1) (s  2 1) A B Cs  D E s      F (s  2 1) s  1 s 2 2 2 s   1 1
 Dùng hệ số bất định có Y s  1 2 2s 2s  1     s  2 s 1 1  2 2 2 s   s  1 1  Do đó ( )  (  2) t y t t e  t   1 sint  2cost . HA H V A E V E A A G O G OD O D U N U DE D RS E TA T N A D N IN D G! G
PGS. TS. Nguyễn Xuân Thảo thaonx-fami@mail.hut.edu.vn
Họ và tên: .......................................... Lớp: .............
- Em có thích môn học này không? Vì sao?
- Em thấy cần bổ sung thêm gì để bài giảng tốt hơn?