Bài 2: Các phép biến đổi lượng giác | Giáo án Toán 11 Cánh diều

Ngày soạn: .../.../... Ngày dạy: .../.../...
BÀI 2: CÁC PHÉP BIẾN ĐỔI LƯỢNG GIÁC (3 TIẾT) I. MỤC TIÊU:
1. Kiến thức, kĩ năng:
Học xong bài này, HS đạt các yêu cầu sau:
- Nhận biết, mô tả được các phép biến đổi lượng giác cơ bản: công thức cộng;
công thức góc nhân đôi; công thức biến đổi tích thành tổng và công thức biến đổi tổng thành tích.
- Vận dụng được công thức cộng, công thức góc nhân đôi để giải các bài toán
như tính giá trị lượng giác của một góc, rút gọn những biểu thức lượng giác
đơn giản và chứng minh một số bất đẳng thức. 2. Năng lực
Năng lực chung:
- Năng lực tự chủ và tự học trong tìm tòi khám phá
- Năng lực giao tiếp và hợp tác trong trình bày, thảo luận và làm việc nhóm
- Năng lực giải quyết vấn đề và sáng tạo trong thực hành, vận dụng.
Năng lực riêng:
- Tư duy và lập luận toán học: So sánh, phân tích dữ liệu tìm ra mối liên hệ
giữa các đối tượng đã cho và nội dung bài học, từ đó có thể áp dụng kiến thức
đã học để giải quyết các bài toán.
- Mô hình hóa toán học, giải quyết vấn đề toán học thông qua các bài toán thực
tiễn gắn với giá trị lượng giác của góc lượng giác và các phép biến đổi lượng giác.
- Sử dụng công cụ, phương tiện học toán. 3. Phẩm chất
- Có ý thức học tập, ý thức tìm tòi, khám phá và sáng tạo, có ý thức làm việc
nhóm, tôn trọng ý kiến các thành viên khi hợp tác.
- Chăm chỉ tích cực xây dựng bài, có trách nhiệm, chủ động chiếm lĩnh kiến
thức theo sự hướng dẫn của GV.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU
1. Đối với GV: SGK, Tài liệu giảng dạy, giáo án, đồ dùng dạy học.
2. Đối với HS: SGK, SBT, vở ghi, giấy nháp, đồ dùng học tập (bút, thước...), bảng
nhóm, bút viết bảng nhóm.
III. TIẾN TRÌNH DẠY HỌC
A. HOẠT ĐỘNG 1: KHỞI ĐỘNG (MỞ ĐẦU) a) Mục tiêu:
- Tạo hứng thú, thu hút HS tìm hiểu nội dung bài học.
b) Nội dung: HS đọc tình huống mở đầu, suy nghĩ trả lời câu hỏi.
c) Sản phẩm: HS đưa ra những nhận định ban đầu về công thức tính toán, biến đổi
chứa giá trị lượng giác.
d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ:
- GV yêu cầu HS đọc phần tình huống mở đầu:
Ở lớp dưới, ta đã làm quen với một số phép tính trong tập hợp các số thực, chẳng
hạn: phép tính luỹ thừa với số mũ tự nhiên và những công thức để tính toán hay biến
đổi những biểu thức chứa các luỹ thừa như vậy. Việc lấy các giá trị lượng giác của
góc lượng giác đã hình thành nên những phép tính mới trong tập hợp các số thực, đó
là những phép tính lượng giác.
Có hay không những công thức để tính toán hay biến đổi những biểu thức chứa giá trị lượng giác?
Bước 2: Thực hiện nhiệm vụ: HS quan sát và chú ý lắng nghe, thảo luận nhóm hoàn thành yêu cầu.
Bước 3: Báo cáo, thảo luận: GV gọi một số HS trả lời, HS khác nhận xét, bổ sung.
Bước 4: Kết luận, nhận định: GV đánh giá kết quả của HS, trên cơ sở đó dẫn dắt
HS vào bài học mới: “Việc lấy các giá trị lượng giác của góc lượng giác đã hình
thành nên những phép tính mới trong tập hợp các số thực. Bài học hôm nay, chúng
ta cùng đi tìm hiểu một số phép tính lượng giác.”
Bài mới: Các phép biến đổi lượng giác.
B. HOẠT ĐỘNG 2: HÌNH THÀNH KIẾN THỨC MỚI
Hoạt động 2.1: Công thức cộng a) Mục tiêu:
- Nhận biết được công thức cộng.
- Vận dụng được công thức cộng để giải quyết các bài tính giá trị lượng giác, chứng
minh đẳng thức lượng giác. b) Nội dung:
HS đọc SGK, nghe giảng, thực hiện các nhiệm vụ được giao, suy nghĩ trả lời câu
hỏi, thực hiện các HĐ 1, 2, 3, Luyện tập 1, 2, 3, đọc hiểu ví dụ.
c) Sản phẩm: HS hình thành được kiến thức bài học, câu trả lời của HS cho các câu
hỏi. HS nhận biết được công thức cộng và sử dụng để tính được giá trị lượng giác của góc.
d) Tổ chức thực hiện: HĐ CỦA GV VÀ HS
SẢN PHẨM DỰ KIẾN
Bước 1: Chuyển giao nhiệm vụ: 1. Công thức cộng
- GV triển khai HĐ1 cho HS thực hiện HĐ1
+ Phần a, GV chỉ định 2 HS đứng tại a) Với 𝑎 = ! ta có sin 𝑎 = sin ! = #; " " $
chỗ trình bày kết quả.
Với 𝑏 = ! ta có sin 𝑏 = sin ! = √%
+ Tính giá trị lượng giác của các góc % % $
theo đề bài, từ đó rút ra đẳng thức về cos 𝑏 = cos ! = # % $
𝑠𝑖𝑛(𝑎 + 𝑏) và 𝑠𝑖𝑛(𝑎 − 𝑏).
Ta có sin(𝑎 + 𝑏) = sin 1! + !2 = sin ! = 1 " % $
sin 𝑎 cos 𝑏 + cos 𝑎 sin 𝑏 = # . # + √% . √% $ $ $ $
Do đó sin(𝑎 + 𝑏) = sin 𝑎 𝑐𝑜𝑠𝑏 + cos 𝑎 sin 𝑏 (vì cùng bằng 1).
b) Ta có: sin(𝑎 − 𝑏) = sin[𝑎 + (−𝑏)]
= sin 𝑎 cos(−𝑏) + cos 𝑎 sin(−𝑏)
= sin 𝑎 cos 𝑏 + cos 𝑎 (− sin 𝑏)
+ Phần b, GV chỉ định 1 HS nhắc lại = sin 𝑎 cos 𝑏 − cos 𝑎 sin 𝑏
công thức giá trị lượng giác của hai Công thức cộng góc đối nhau.
+ sin(𝑎 − 𝑏) = sin 𝑎 sin 𝑏 + cos 𝑎 sin 𝑏
+ sin(𝑎 + 𝑏) = sin 𝑎 cos 𝑏 − cos 𝑎 sin 𝑏
- GV giới thiệu và trình bày công thức
cộng trong trường hợp tổng quát cho
HS: Trong trường hợp tổng quát, với
các góc lượng giác a, b, ta có các công Ví dụ 1: (SGk – tr.16)
thức sau (thường được gọi chung là Hướng dẫn giải (SGK – tr.16).
công thức cộng đối với sin).
- GV cho HS thực hiện Ví dụ 1. GV có Luyện tập 1
thể hướng dẫn cho HS cách làm:
Áp dụng công thức cộng ta có:
+ Tách 𝑠𝑖𝑛 75' = 𝑠𝑖𝑛(30' + 45') sin ! = sin 1$! − !2 #$ % (
- GV cho HS tự thực hiện Luyện tập 1 = sin!cos! − cos!sin!
và GV chỉ định 1 HS đứng tại chỗ trình % ( % ( bày cách làm. = √% . %√$ − # . √$ $ $ $ $
+ ! có thể tách thành tổng hay hiệu #$
của những số nào? HĐ2
a) Ta có: cos(a + b) = sin @) − (a + b)A $
- GV triển khai phần HĐ2 cho HS thực hiện. = sin @1) − a2 − bA $
+ GV đặt câu hỏi: Nhắc lại công thức = sin 1) − a2 . cos b − cos 1) − a2 . sin b $ $
giá trị lượng giác giữa hai góc phụ = cosa.cosb − sina.sinb
nhau, hai góc đối nhau?
Vậy cos(a + b) = cos a cos b − sin a sin b.
b) Ta có: cos(a − b) = cos[a + (−b)] = cos a cos b + sin a sin b
+ GV mời 2 HS lên bảng trình bày và Vậy cos(a − b) = cos a cos b + sin a sin b.
rút ra kết luận cho trường hợp tổng quát Công thức
về công thức cộng đối với côsin.
+ cos(𝑎 + 𝑏) = cos 𝑎 cos 𝑏 − sin 𝑎 sin 𝑏
+ cos(𝑎 − 𝑏) = cos 𝑎 cos 𝑏 + sin 𝑎 sin 𝑏
Ví dụ 2: (SGK – tr.17).
Hướng dẫn giải (SGK – tr.17). Luyện tập 2
Áp dụng công thức cộng, ta có:
- GV ghi bảng công thức cộng với cos 15' = cos(45' − 30')
côsin và đề nghị HS ghi bài và học = cos 45' . cos 30' + sin 45' . sin 30' thuộc công thức.
= √$ . √% + √$ . # = √"/√$
- GV cho HS đọc – hiểu phần Ví dụ 2 $ $ $ $ ( HĐ3
và trình bày lại cách làm.
a) Khi các biểu thức đều có nghĩa, ta có:
- HS làm phần Luyện tập 2 theo nhóm đôi. tan(a + b) = *+,(4/5) 23*(4/5)
+ GV đặt câu hỏi cho HS: Ta có thể
!"# $ %&! '(%&! $ !"# ' = *+,423*5/23*4*+,5 = %&! $ %&! ' (
%&! $ %&! '*!"# $ !"# ')
biến đổi cos 15' thành cos của tổng 23* 4 23* 56*+, 4 *+, 5 %&! $ %&! '
hai góc lượng giác nào? = 74,4/74,5 #674, 4 74, 5
Vậy tan(a + b) = 74, 4/74, 5
- GV gợi ý cho HS thực hiện phần HĐ3 #674, 4 74, 5
b) Khi các biểu thức đều có nghĩa, ta có:
+ HS thảo luận nhóm 2 người và thảo tan(a − b) = tan[a + (−b)] luận theo gợi ý của GV → GV gợi ý: = 74,4/74,(65) = 74,4674,5 #674, 4 74,(65) #/74, 4 74, 5
+ Phần a, ta cần sử dụng công thức Vậy
biến đổi của tan(𝑎 + 𝑏) = *+,(./0), tan(a − b) = tan(a − b) = 74,4674,5 23*(./0) #/74, 4 74, 5
sau đó áp dụng công thức cộng của sin Công thức
và cos để hoàn thành phần a.
+ tan(𝑎 + 𝑏) = 74, ./74, 0 #674, . 74, 0
+ Phần b, ta biến đổi (a – b) thành + tan(𝑎 − 𝑏) = 74, . #/74, . 74, 0
[a + (-b)] để áp dụng được kết quả câu
(Khi các biểu thức đều có nghĩa) a.
Ví dụ 3: (SGK – tr.17)
Hướng dẫn giải (SGK – tr.17). Luyện tập 3
+ GV trình bày công thức cộng đối với Áp dụng công thức cộng, ta có:
tang trong khung kiến thức trọng tâm tan 165' = tan(120' + 45')
và yêu cầu HS ghi bài cần thận.
= 74,#$8,674,(9, = √%/# = #6√% #674, #$8, 74, (9, #6:6√%;.# √%
- GV cho HS đọc – hiểu Ví dụ 3 sau đó
mời 1 HS đứng tại chỗ trình bày và giải
thích cách làm của Ví dụ.
- GV gọi 1 HS đứng tại chỗ trình bày
hướng làm phần Luyện tập 3, và mời
1 HS khác lên bảng trình bày đáp án.
Bước 2: Thực hiện nhiệm vụ:
- HS theo dõi SGK, chú ý nghe, tiếp
nhận kiến thức, hoàn thành các yêu cầu, thảo luận nhóm. - GV quan sát hỗ trợ.
Bước 3: Báo cáo, thảo luận:
- HS giơ tay phát biểu, lên bảng trình bày
- Một số HS khác nhận xét, bổ sung cho bạn.
Bước 4: Kết luận, nhận định: GV
tổng quát lưu ý lại kiến thức trọng tâm:
+ Công thức cộng đối với sin, côsin, tang.
+ Cách đọc để nhớ được công thức nhanh.
Hoạt động 2.2: Công thức nhân đôi a) Mục tiêu:
- HS phát biểu được công thức nhân đôi.
- HS vận dụng công thức nhân đôi trong tính toán giá trị lượng giác của góc lượng giác.
b) Nội dung: HS đọc SGK để tìm hiểu nội dung kiến thức theo yêu cầu của GV, chú
ý nghe giảng, thực hiện hoạt động 4, Luyện tập 4, 5, ví dụ.
c) Sản phẩm: HS hình thành được kiến thức bài học, câu trả lời của HS cho các câu
hỏi. HS nhận biết được công thức nhân đôi để từ đó tính giá trị lượng giác của các góc.
d) Tổ chức thực hiện:
HOẠT ĐỘNG CỦA GV VÀ HS
SẢN PHẨM DỰ KIẾN
Bước 1: Chuyển giao nhiệm vụ:
2. Công thức nhân đôi
- GV cho HS thảo luận nhóm đôi và gợi HĐ4
ý cho HS thực hiện HĐ4. Ta có:
+ Các em viết lại công thức công của + sin 2𝑎 = sin(𝑎 + 𝑎)
sin, côsin và tang nhưng thay b bằng a = sin 𝑎 cos 𝑎 + cos 𝑎 sin 𝑎 = 2 sin 𝑎 cos 𝑎 để thực hiện. = cos(𝑎 + 3𝑎)
+ GV mời 1 HS lên bảng trình bày đáp = cos 𝑎 cos 𝑎 − sin 𝑎 sin 𝑎 = cos$ 𝑎 − sin$ 𝑎 án.
+ Khi các biểu thức đều có nghĩa thì:
tan 2𝑎 = tan(𝑎 + 𝑎) = 74,./74,. #674, . 74, . = $74,. #674,- $. Công thức
- GV chính xác hóa đáp án và giới thiệu + sin 2𝑎 = 2 sin 𝑎 cos 𝑎
công thức nhân đôi trong khung kiến + cos 2𝑎 = cos$ 𝑎 − sin$ 𝑎
thức trọng tâm cho HS.
+ tan 2𝑎 = $ 74, %. #674,- . Nhận xét
- GV đặt câu hỏi thêm cho HS:
+ cos 3𝑎 = cos$ 𝑎 − sin$ 𝑎 = 2 cos$ 𝑎 − 1 . = 1 − 2 sin$ 𝑎
+ Từ biểu thức mới, hãy rút ra cos$ 𝑎 + cos$ 𝑎 = #/23*$.; sin$ 𝑎 = #623*$. (công và sin$ 𝑎? $ $ thức hạ bậc).
+ GV yêu cầu 2 HS lên bảng thực hiện
và chính xác hóa bằng phần Nhận xét.
- GV hướng dẫn cho HS thực hiện Ví dụ 4.
Ví dụ 4: (SGK – tr.18).
+ Phần a, bình phương hai vế sẽ xuất
Hướng dẫn giải (SGK – tr.18).
hiện hằng đẳng thức. Sau khai triển sẽ
có được 2 𝑠𝑖𝑛 𝑎 𝑐𝑜𝑠 𝑎 chính là bằng 𝑠𝑖𝑛 2𝑎 .
+ Phần b, áp dụng công thức nhân đôi.
- HS tự thảo luận và thực hiện với bạn
cùng bàn để hoàn thành Luyện tập 4. Luyện tập 4
+ GV chỉ định 1 HS đứng tại chỗ nêu
Áp dụng công thức nhân đôi, ta có: đáp án. $ 74,.
- GV yêu cầu HS đọc – hiểu phần Ví tan . = - = $.(6$) = ( $ #674,-. #6(6$)- % -
dụ 5 sau đó trình bày lại cách thực hiện Ví dụ 5: (SGK – tr.18). Ví dụ này.
Hướng dẫn giải (SGK – tr.18).
- HS thảo luận nhóm ba người theo gợi
ý của GV thực hiện Luyện tập 5. Luyện tập 5
+ Áp dụng công thức hạ bậc cho Áp dụng công thức hạ bậc, ta có:
sin$ ! và cos$ ! để thực hiện tính toán. = = #623*>$./? + sin$ ! = 0 = $6√$ = $ $
Bước 2: Thực hiện nhiệm vụ:
Mà sin ! > 0 nên sin ! = G$6√$ = @$6√$ = = ( $
- HS theo dõi SGK, chú ý nghe, tiếp #/23*>$./? #/23*/ #/√-
nhận kiến thức, suy nghĩ trả lời câu hỏi, + cos$ ! = 0 = 1 = - = $/√$ = $ $ $ $ hoàn thành các yêu cầu. nên cos ! = @$9/√$
- GV: quan sát và trợ giúp HS. = $
Bước 3: Báo cáo, thảo luận:
- HS giơ tay phát biểu, lên bảng trình bày
- Một số HS khác nhận xét, bổ sung cho bạn.
Bước 4: Kết luận, nhận định: GV
tổng quát lưu ý lại kiến thức trọng tâm
và yêu cầu HS ghi chép đầy đủ vào vở: + Công thức nhân đôi.
+ Công thức hạ bậc nâng cung.
Hoạt động 2.3: Công thức biến đổi tích thành tổng. a) Mục tiêu:
- HS phát biểu được công thức biến đổi tích thành tổng.
- HS vận dụng công thức biến đổi tích thành tổng trong tính toán giá trị lượng giác của góc lượng giác. b) Nội dung:
HS đọc SGK, nghe giảng, thực hiện các nhiệm vụ được giao, suy nghĩ trả lời câu
hỏi, thực hiện các hoạt động 5, Luyện tập 6, ví dụ.
c) Sản phẩm: HS hình thành được kiến thức bài học, câu trả lời của HS cho các câu hỏi.
HS nhận biết công thức biến tích thành tổng và áp dụng tính giá trị lượng giác của
góc lượng giác, tính giá trị biểu thức lượng giác.
d) Tổ chức thực hiện: HĐ CỦA GV VÀ HS
SẢN PHẨM DỰ KIẾN
Bước 1: Chuyển giao nhiệm vụ:
3. Công thức biến đổi tích thành tổng
- GV yêu cầu HS thảo luận nhóm 4, HĐ5.
theo phương pháp khăn trải bàn làm Ta có: thực hiện HĐ5. + cos(a + b) + cos(a − b)
+ HS trao đổi, tranh luận về rút gọn = (cos a cos b − sin a sin b) + (cos a cos b +
mỗi biểu thức trong HĐ. sin a sin b)
+ GV chỉ định 3 HS lên bảng trình = cos a cos b − sin a sin b + cos a cos b + bày lời giải. sin a sin b
= cos a cos b − sin a sin b − cos a cos b − sin a sin b = −2 sin a sin b + sin(a + b) + sin(a − b)
= (sin a cos b + cos a sin b) + (sin a cos b − cos a sin b)
= sin a cos b + cos a sin b + sin a cos b − cos a sin b = 2 sin a cos b
Vậy cos(a + b) + cos(a − b) = 2 cos a cos b
+ GV yêu cầu các HS dưới lớp thực cos(a − b) + cos(a − b) = −2 sin a sin b
hiện thêm hoạt động sau:
sin(a − b) + sin(a − b) = 2 sin a cos b
Từ những biểu thức vừa rút gọn, các Công thức biến đổi tích thành tổng em hãy rút ra:
cos 𝑎 cos 𝑏 = # [cos(𝑎 − 𝑏) + cos(𝑎 − 𝑏)]
𝑐𝑜𝑠 𝑎 𝑐𝑜𝑠 𝑏 ; 𝑠𝑖𝑛 𝑎 𝑠𝑖𝑛 𝑏 ; 𝑠𝑖𝑛 𝑎 𝑐𝑜𝑠 𝑏 $
→ GV chính xác hóa câu trả lời bằng sin 𝑎 sin 𝑏 = − # [cos(𝑎 + 𝑏) − cos(𝑎 − 𝑏)] $
phần công thức trong khung kiến thức trọng tâm.
Ví dụ 6: (SGK – tr.19).
Hướng dẫn giải (SGK – tr.19).
- HS đọc phần Ví dụ 6 và thực hiện Câu hỏi phụ
câu hỏi phụ của GV như sau:
D = cos x cos(x + 603) cos(x − 603)
Biến đổi tích thành tổng của biểu D = cos x . # (cos 1203 + cos 2x) $ thức sau: = # cos x 1− # + cos 𝑥2
𝐷 = 𝑐𝑜𝑠 𝑥 𝑐𝑜𝑠(𝑥 + 60') 𝑐𝑜𝑠(𝑥 − $ $ 60')
= − # cos x + # cos 2x cos x ( $
= − # cos x + # cos 3x + # cos x ( ( ( Luyện tập 6
Áp dụng công thức biến đổi tích thành tổng, ta
- GV cho HS thực hiện Luyện tập 6 có:
+ Để tính được B cần sử dụng công B = cos 4cos 4
thức nào? Và phải tính được giá trị $ $ nào?
= # Ncos 1%4 + 42 + cos 1%4 − 42O $ $ $ $ $
(Công thức cos a cos b và tính giá trị = # (cos 2a + cos a) $ cos 2a).
Bước 2: Thực hiện nhiệm vụ:
- HS theo dõi SGK, chú ý nghe, tiếp
nhận kiến thức, hoàn thành các yêu cầu, thảo luận nhóm. - GV quan sát hỗ trợ.
Bước 3: Báo cáo, thảo luận:
- HS giơ tay phát biểu, lên bảng trình bày
- Một số HS khác nhận xét, bổ sung cho bạn.
Bước 4: Kết luận, nhận định: GV
tổng quát lưu ý lại kiến thức trọng tâm:
+ Công thức biến tích thành tổng.
Hoạt động 2.4: Công thức biến đổi tổng thành tích. a) Mục tiêu:
- HS phát biểu được công thức biến đổi tổng thành tích.
- HS vận dụng công thức biến đổi tổng thành tích trong tính toán giá trị lượng giác của góc lượng giác. b) Nội dung:
HS đọc SGK, nghe giảng, thực hiện các nhiệm vụ được giao, suy nghĩ trả lời câu
hỏi, thực hiện các hoạt động 6, Luyện tập 7, ví dụ.
c) Sản phẩm: HS hình thành được kiến thức bài học, câu trả lời của HS cho các câu hỏi.
HS nhận biết công thức biến tổng thành tích và áp dụng tính giá trị lượng giác của
góc lượng giác, tính giá trị biểu thức lượng giác.
d) Tổ chức thực hiện: HĐ CỦA GV VÀ HS
SẢN PHẨM DỰ KIẾN
Bước 1: Chuyển giao nhiệm vụ:
4. Công thức biến đổi tổng thành tích
- GV triển khai HĐ6 thành phiếu bài HĐ6.
tập cho HS thực hiện theo nhóm 4 HS
sử dụng phương pháp khăn trải bàn để
thực hiện và hoàn thành. → GV hướng dẫn:
+ Từ 𝑎 + 𝑏 = 𝑢 và 𝑎 − 𝑏 = 𝑣 tìm ra a và b theo u và v.
+ Thay (𝑎 + 𝑏) = 𝑢; (𝑎 − 𝑏) = 𝑣
vào công thức biến đổi tích thành tổng
theo 𝑐𝑜𝑠 𝑎 𝑐𝑜𝑠 𝑏.
- GV cho HS trình bày kết quả phiếu Công thức biến đổi tổng thành tích
học tập, từ đó giới thiệu công thức biến + 𝑐𝑜𝑠 𝑢 + 𝑐𝑜𝑠 𝑣 = 2 𝑐𝑜𝑠 A/B 𝑐𝑜𝑠 A6B $ $ đổi tổng thành tích.
+ 𝑐𝑜𝑠 𝑢 − 𝑐𝑜𝑠 𝑣 = −2 𝑠𝑖𝑛 A/B 𝑠𝑖𝑛 A6B $ $
- GV có thể lưu ý mối quan hệ của hai + 𝑠𝑖𝑛 𝑢 + 𝑠𝑖𝑛 𝑣 = 2 𝑠𝑖𝑛 (A/B) 𝑐𝑜𝑠 A6B $ $
loại công thức: biến tổng thành tích và Ví dụ 7: (SGK – tr.19).
tích thành tổng để HS dễ nhớ hơn.
Hướng dẫn giải (SGK – tr.19, 20).
- HS đọc, trình bày lại Ví dụ 7, giải Luyện tập 7
thích công thức đã sử dụng.
Áp dụng công thức biến đổi tổng thành tích ta
- HS làm Luyện tập 7: trình bày cách có: làm. 34/4 3464 5 5 5 5 + sin C) + sin ) = 2 sin cos D D $ $ = 2 sin () cos ) D % 34/4 3464
− cos ) = −2 sin 5 5 sin 5 5 + cos C) D D $ $ $ *+,14 23*4 Khi đó: D = 5 6 = − cot ) = − √% 6$ *+,14 *+,4 % %
- HS đọc Ví dụ 8. 5 6
+ Nêu các rút gọn biểu thức tích 𝑢. 𝑖?
Ví dụ 8: (SGK – tr.20).
Bước 2: Thực hiện nhiệm vụ:
Hướng dẫn giải (SGK – tr.20).
- HS theo dõi SGK, chú ý nghe, tiếp
nhận kiến thức, hoàn thành các yêu cầu, thảo luận nhóm. - GV quan sát hỗ trợ.
Bước 3: Báo cáo, thảo luận:
- HS giơ tay phát biểu, lên bảng trình bày
- Một số HS khác nhận xét, bổ sung cho bạn.
Bước 4: Kết luận, nhận định: GV
tổng quát lưu ý lại kiến thức trọng tâm:
+ Công thức biến tổng thành tích.
C. HOẠT ĐỘNG 3: LUYỆN TẬP
a) Mục tiêu: Học sinh củng cố lại kiến thức đã học.
b) Nội dung: HS vận dụng các kiến thức của bài học làm bài tập trắc nghiệm và bài
1, 2, 3, 4, 5, 6, 7, 8 (SGK – tr.20, 21).
c) Sản phẩm học tập: Câu trả lời của HS. HS vận dụng các phép biến đổi lượng
giác để tính giá trị lượng giác của góc lượng giác, tính giá trị biểu thức, rút gọn biểu thức.
d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ:
- GV cho HS thực hiện bài trắc nghiệm
Câu 1. Giá trị của sin (C%! là? " A. √% B. − √% C. √$ D. − # $ $ $ $
Câu 2. Tích số cos 10' . cos 30' . cos 50' . cos 70' bằng A. # B. # C. % D. # #" = #" (
Câu 3. Biểu thức 𝐴 = #
− 2𝑠𝑖𝑛 70' có giá trị bằng? $ FGH #$, A. 1 B. -1 C. 2 D. -2
Câu 4. Giá trị của 𝐴 = cos 2𝑥 + % với 𝑥 = ! *+,- I ( A. 4 B. 6 C. -6 D. -4
Câu 5. Cho A, B, C là các góc nhọn và tan 𝐴 = # ; tan 𝐵 = # ; tan 𝐶 = #. Tổng A + $ 9 = B + C bằng? A. ! B. ! C. ! D. ! " 9 ( %
- GV tổ chức cho HS hoạt động thực hiện Bài 1, 2, 3, 4, 5, 6, 7, 8 (SGK – tr.20, 21).
Bước 2: Thực hiện nhiệm vụ: HS quan sát và chú ý lắng nghe, thảo luận nhóm,
hoàn thành các bài tập GV yêu cầu.
- GV quan sát và hỗ trợ.
Bước 3: Báo cáo, thảo luận:
- Câu hỏi trắc nghiệm: HS trả lời nhanh, giải thích, các HS chú ý lắng nghe sửa lỗi sai.
- Mỗi bài tập GV mời HS trình bày. Các HS khác chú ý chữa bài, theo dõi nhận xét bài trên bảng.
Bước 4: Kết luận, nhận định:
- GV chữa bài, chốt đáp án, tuyên dương các hoạt động tốt, nhanh và chính xác. Kết quả:
Đáp án trắc nghiệm 1 2 3 4 5 A B C D C Bài 1. $
cos a = % ⇒ sin a = G1 − 1%2 = ( (do sin a > 0) 9 9 9 π π π 3 + 4√3
sin 1a + 2 = sin a cos + cos a sin = 6 6 6 10 π π π 3 + 4√3
cos 1a − 2 = cos a cos + sin a sin = 3 3 3 10 π π tan a + tan tan 1a + 2 = 4 = −7 4 π 1 − tan a . tan 4 Bài 2.
A = sin(a − 17∘) cos(a + 13∘) − sin(a + 13∘) cos(a − 17∘) 1
= sin(a − 17∘ − a − 13∘) = sin(−30∘) = − 2 π π π π
B = cos 1b + 2 cos 1 − b2 − sin 1b + 2 sin 1 − b2 3 6 3 6
= cos 1b + ) + ) − b2 = cos ) = 0 % " $ Bài 3.
tan 2 a = tan[ (a + b) + (a − b)] = 74,(4/5)/74,(465) = %/$ = −1 #674,(4/5) 74,(465) #6%.$
tan 2 b = tan[ (a + b) − (a − b)] = 74,(4/5)674,(465) = %6$ = # #/74,(4/5) 74,(465) #/%.$ C Bài 4. $
cos 2a = 1 − 2 sin$ a = 1 − 2. 1 " 2 = 6% √9 9 $
cos 4 a = 2 cos$ 2 a − 1 = 1− % 2 − 1 = 6C $9 $9 Bài 5. Có: sin a + cos a = 1
⟺ (sin a + cos a)$ = 1$ ⟺ sin$ a + 2 sin a cos a + cos$ a = 1 Bài 6.
Ta có: ) < a < π ⇒ sin α > 0, cos α < 0 $ #/7 cos$ a = #/23*$4 =
6 = $ → cos α = 6(√" (do cos a < 0) $ $ % % #67 sin$ a = #623*$4 =
6 = # → sin α = √$% (do sin a > 0) $ $ % % √6
tan 𝑎 = *+,. = 6 = − √$ 23* . 6√8 $ 6 Bài 7.
A = cos 1x + )2 cos 1x − )2 = # Ncos 1x + ) + x − )2 + cos 1x + ) − x + )2O " " $ " " " " = # Ncos 2 x + cos )O = % $ % =
B = sin 1x + )2 sin 1x − )2 = 6# Ncos 1x + ) + x − )2 − cos 1x + ) − x + )2O % % $ % % % %
= 6# Ncos 2 x − cos $)O = − # @# − 1− #2A = − %. $ % $ ( $ = Bài 8.
A = *+,$K/(*+,K/*+,%K) = *+,$K/$*+,$K23*K 23* $K/(23* K/23* %K) 23* $K/$ 23* $K 23* K
= *+,$K(#/$23*K) = *+,$K = tan 2 x 23* $K(#/$ 23* K) 23* $K
D. HOẠT ĐỘNG 4: VẬN DỤNG a) Mục tiêu:
- Học sinh thực hiện làm bài tập vận dụng để nắm vững kiến thức.
b) Nội dung: HS sử dụng SGK và vận dụng kiến thức đã học để làm bài tập 9,10 (SGK – tr.21)
c) Sản phẩm: Kết quả thực hiện các bài tập. HS vận dụng phép biến đổi lượng giác
giải quyết một số vấn đề thực tiễn gắn với giá trị lượng giác của góc lượng giác.
d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ
- GV yêu cầu HS hoạt động hoàn thành bài tập 9,10 (SGK – tr.21).
Bước 2: Thực hiện nhiệm vụ
- HS suy nghĩ, trao đổi, thảo luận thực hiện nhiệm vụ.
- GV điều hành, quan sát, hỗ trợ.
Bước 3: Báo cáo, thảo luận
- Bài tập: đại diện HS trình bày kết quả, các HS khác theo dõi, đưa ý kiến.
Bước 4: Kết luận, nhận định
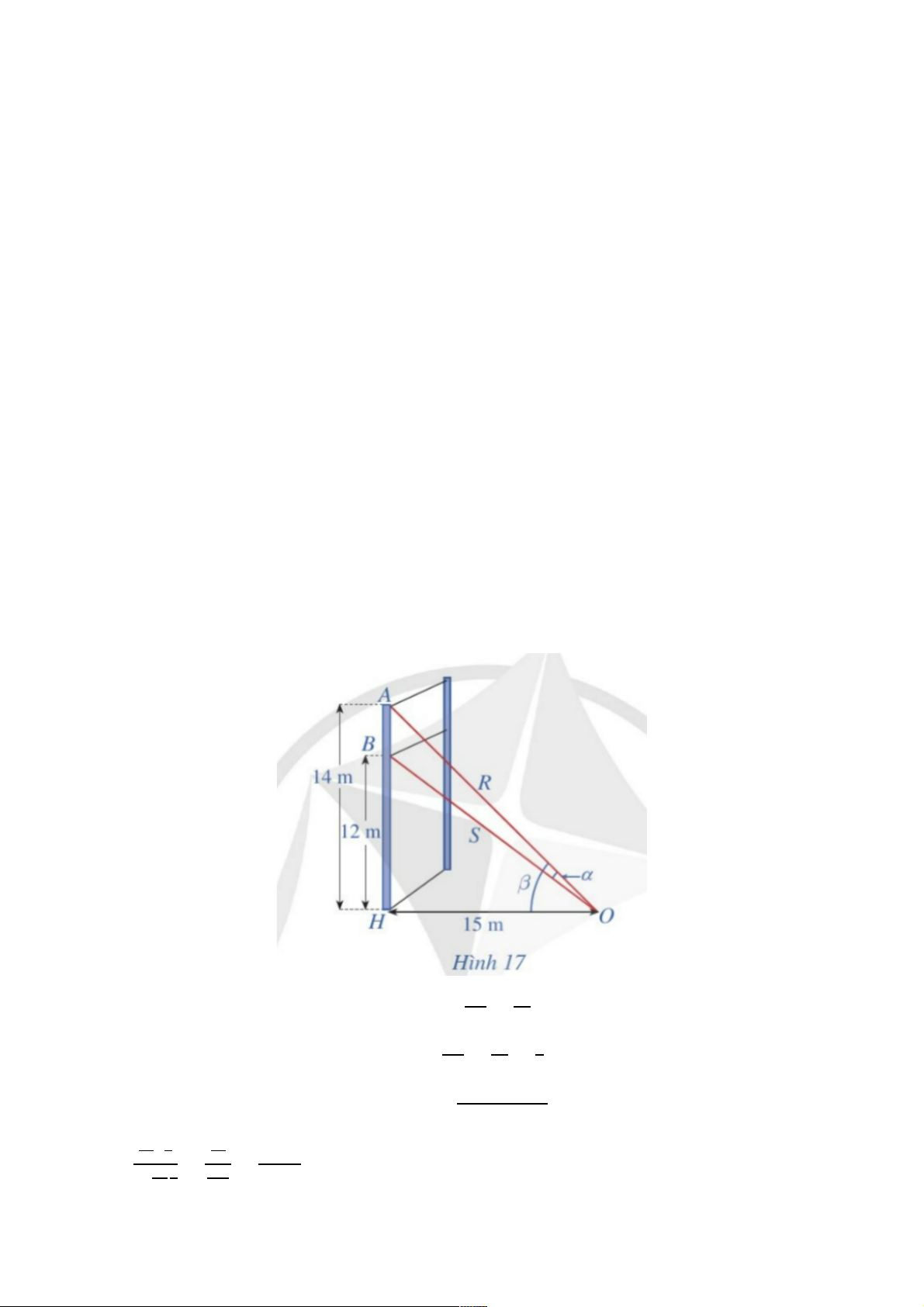
- GV nhận xét, đánh giá, đưa ra đáp án đúng, chú ý các lỗi sai của học sinh hay mắc phải. Gợi ý đáp án: Bài 9.
a) Xét ∆AOH vuông tại H, ta có : tan β = LM = #( MN #9
Xét ∆BOH vuông tại H, ta có : tan γ = OM = #$ = ( MN #9 9 tan α = tanbβ − BOH
cd = tan(β − γ) = 74,P674,Q #/74, P 74, Q 7161 - = 79 9 = 79 = #888 #/71.1 767 #$%%# 79 9 39
b) Từ tan α = #8 , để tìm số đo góc α, ta sử dụng máy tính cầm tay ấn lần lượt các #%# nút:
Ta được kết quả làm tròn kết quả đến hàng đơn vị theo đơn vị độ là 4°. Vậy α ≈ 4°. Bài 10.
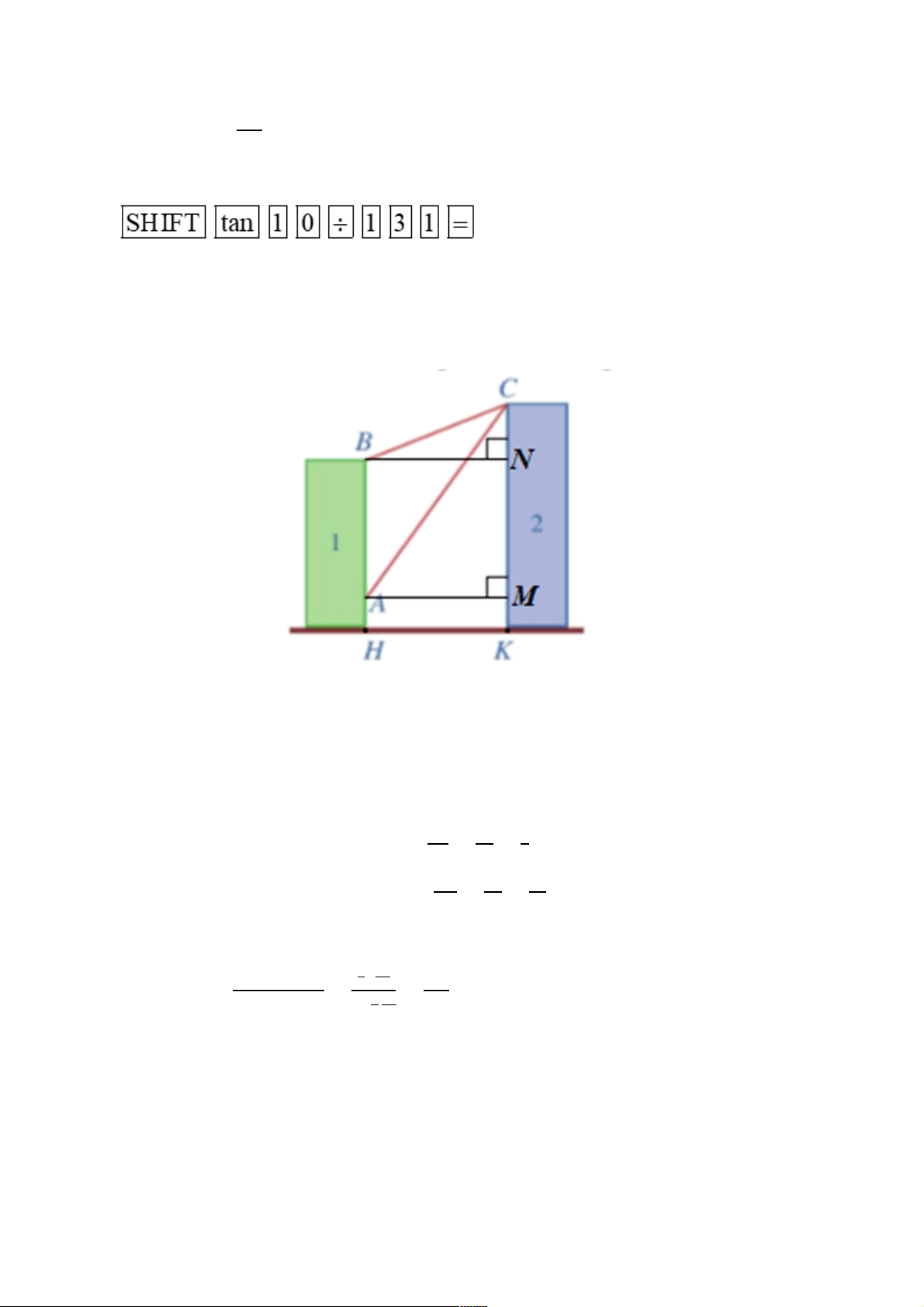
Kẻ AM ⊥ CK, BN ⊥ CK ta có : BN = AM = HK = 20 (m);
MN = AB = BH – AH = 24 – 6 = 18 (m);
CM = CN + MN = 8 + 18 = 26 (m).
+ Xét ∆BCN vuông tại N có: tan α = OR = $8 = 9 SR = $
+ Xét ∆ACM vuông tại M có: tan β = LT = $8 = #8; ST $" #% Ta có: tan ACB j = tanbBCN c − ACM cd = tan(α − β) 967: → tan ACB j = 74,U674,P = - 76 = ((9 #/74, U 74, P #/9.7: C#" - 76 → ACB j ≈ 0,013
Vậy góc ACB (phạm vi camera có thể quan sát được ở chung cư thứ nhất) có số đo xấp xỉ 0,01°.
* HƯỚNG DẪN VỀ NHÀ
• Ghi nhớ kiến thức trong bài.
• Hoàn thành các bài tập trong SBT
• Chuẩn bị bài mới: "Hàm số lượng giác và đồ thị".