Bài 2: Các quy tắc tính đạo hàm | Giáo án Toán 11 Cánh diều

Trường THPT số 1 Si Ma Cai
Họ và tên giáo viên: Lê Thị Phượng
Tổ : Toán – Tin - NN
KẾ HOẠCH BÀI DẠY
TÊN BÀI DẠY: QUY TẮC TÍNH ĐẠO HÀM
Môn học/Hoạt động giáo dục: Toán; lớp: 11
Thời gian thực hiện: (03 tiết) I. Mục tiêu 1. Về kiến thức:
- Đạo hàm của các hàm sơ cấp cơ bản
- Đạo hàm của các hàm tổng hiệu tích thương. 2. Về năng lực:
- Năng lực tư duy và lập luận Toán học: Trong áp dụng tính toán đạo hàm của các hàm số theo yêu cầu.
- Năng lực mô hình hóa Toán học: Trong các bài toán thực tế về chuyển động, về mạch điện.
- Năng lực giải quyết vấn đề Toán học: Trong các lời giải của các bài tập.
- Năng lực giao tiếp Toán học: Trong các định lý, ví dụ, bài tập.
- Năng lực sử dụng công cụ, phương tiện để học Toán: Sử dụng máy tính cầm tay. 3. Về phẩm chất:
- Chăm chỉ, hoàn thành các nhiệm vụ được giao.
- Trách nhiệm, cố gắng chiếm lĩnh kiến thức mới, cố gắng làm đúng các bài tập.
- Có thế giới quan khoa học
II. Thiết bị dạy học và học liệu
- Kế hoạch bài dạy, SGK, phiếu học tập, phấn, thước kẻ, máy chiếu, phần mềm GSP…
III. Tiến trình dạy học Tiết 1.
1. Hoạt động 1: Khởi động
a) Mục tiêu: Tạo tâm thế học tập cho học sinh, giúp các em ý thức được nhiệm vụ học tập,
sự cần thiết phải tìm hiểu về các vấn đề đã nêu ra, từ đó gây được hứng thú với việc học bài mới. b) Nội dung:
Câu 1: Đưa ra thời gian tính đạo hàm tại một điểm khi làm bài tập 1,3 của bài Định nghĩa
đạo hàm. Ý nghĩa của đạo hàm trang 63.
Câu 2: Dựa vào định nghĩa thì ta thấy việc tính đạo hàm như thế nào ?
Câu 3: Để có thể tính đạo hàm nhanh và gọn đối với một số hàm sơ cấp cơ bản, cần có một
quy tắc để tính ? Những hàm sơ cấp cơ bản làm hàm nào ?
c) Sản phẩm: Câu trả lời của học sinh
d) Tổ chức thực hiện:
* Giáo viên cho học sinh chia nhóm 4 người phỏng vấn việc làm bài tập
Chuyển giao
và nhận xét việc tính đạo hàm tại một điểm bằng định nghĩa.
- HS thực hiện nhóm 4 người đưa ra nhận xét.
- HS nhận định được việc tìm đạo hàm theo định nghĩa là phức tạp và mất thời gian.
Thực hiện
- Mong đợi: Kích thích sự tò mò của HS :
+ Nêu các hàm số có quy tắc tính thì nhanh gọn hơn.
+ Qua việc đọc trước bài ở nhà, học sinh nêu các hàm sơ cấp cơ bản có quy tắc tính đạo hàm.
Báo cáo thảo luận * Đại diện nhóm báo cáo, các nhóm còn lại theo dõi thảo luận.
- GV nhận xét thái độ làm việc, phương án trả lời của học sinh, ghi nhận
Đánh giá, nhận xét, và tuyên dương học sinh có câu trả lời tốt nhất. Động viên các học sinh còn
tổng hợp
lại tích cực, cố gắng hơn trong các hoạt động học tiếp theo - Chốt kiến thức 2
2. Hoạt động 2: Hình thành kiến thức mới
I. Đạo hàm của một số hàm sơ cấp cơ bản
Hoạt động 2.1. Đạo hàm của hàm số n
y = x (n Î • ,n > 1)
a) Mục tiêu: Học sinh biết quy tắc tính đạo hàm của các hàm số dạng n
y = x (n Î • ,n > 1) . b) Nội dung: Hàm số n
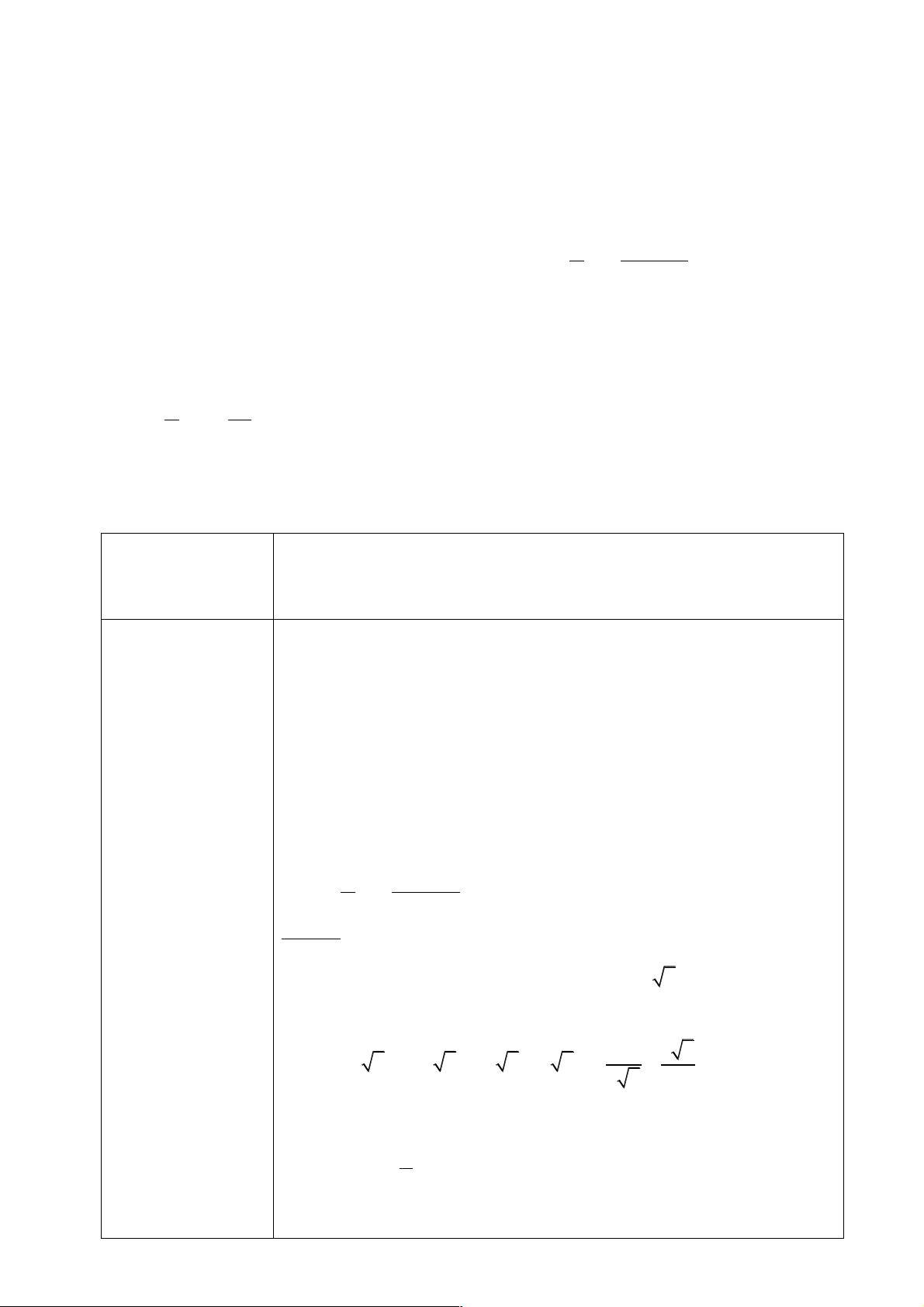
y = x (n Î • ,n > 1) có đạo hàm tại mọi x Î ! và ( n x ) n 1 ' . n x - = Đạo hàm của n
y = x (n Î • ,n > 1), y = x, y = c Ví dụ 1 ( sgk)
Luyện tập 1: Cho hàm số 22 y = x .
a) Tính đạo hàm của hàm số trên tại điểm x bất kì.
b) Tính đạo hàm của hàm số trên tại điểm x = 1 - . 0
c) Sản phẩm: Câu trả lời của học sinh.
d) Tổ chức thực hiện: Học sinh thực hiện nhiệm vụ cá nhân.
Yêu cầu học sinh thực hiện
H1: Tính đạo hàm của hàm số 2
y = x tại điểm x bất kì bằng định nghĩa. 0
Chuyển giao
H2: Dự đoán đạo hàm của hàm số n
y = x tại điểm x bất kì. Nghiên cứu ví dụ 1
Làm bài tập tự luyện 1
- Tính đạo hàm của hàm số 2
y = x tại điểm x bất kì bằng định nghĩa ở 0
nhà. Nhận xét kết quả. - Dự đoán đạo hàm n
y = x thông qua kết quả trên. Ví dụ 1: ( Sgk )
Thực hiện Luyện tập 1: Cho hàm số 22 y = x . a) Ta có: y = ( 22 x )¢ 21 ' = 22.x .
b) Đạo hàm của hàm số tại điểm x = - 1 là: y - = (- )21 '( 1) 22. 1 = 2 - 2 0
Báo cáo thảo luận Báo cáo kết quả thực hiện.
- GV nhận xét thái độ làm việc, phương án trả lời của học sinh, ghi nhận và
Đánh giá, nhận xét, tuyên dương học sinh có câu trả lời tốt nhất. Động viên các học sinh còn lại
tổng hợp
tích cực, cố gắng hơn trong các hoạt động học tiếp theo - Chốt kiến thức
Hoạt động 2.2. Đạo hàm của hàm số y = x
a) Mục tiêu: Tính đạo hàm y = x 1
b) Nội dung: Hàm số y = x có đạo hàm tại mọi x Î ! , x > 0 và ( x)¢ = . 2 x
H2: Tính đạo hàm của hàm số y = x tại điểm x =
1 bằng định nghĩa 0 Ví dụ 2: Sgk
Luyện tập 2: Tính đạo hàm của hàm số f (x) = x tại điểm x = 9. 0
c) Sản phẩm: Công thức đạo hàm của hàm số y = x .
d) Tổ chức thực hiện: Học sinh thảo luận cặp đôi
H1? Tập xác định của hàm số y = x ?
Chuyển giao
H2 HS tự tính đạo hàm của hàm y = x bằng định nghĩa tại x = 1 ? 0
Ví dụ 2. HS nghiên cứu kiến thức SGK
Luyện tập 2: HS làm và thảo chia sẻ nhóm đôi. 3 1 H2: y ' = ( )1 2
* Học sinh đưa ra kết luận dựa vào kiến thức sgk. 1
Hàm số y = x có đạo hàm tại mọi x Î ! , x > 0 và ( x)¢ = . 2 x
Thực hiện Ví dụ 2. Sgk 1
Luyện tập 2: Ta có: f ( ¢ x) = với x > 0. 2 x 1 1
Vậy đạo hàm của hàm số trên tại điểm x = 9 là: f (4 ¢ ) = = . 0 2 9 6
Báo cáo thảo luận * Đại diện học sinh báo cáo, các HS còn lại theo dõi thảo luận.
- GV nhận xét thái độ làm việc, phương án trả lời của học sinh, ghi nhận
Đánh giá, nhận xét, và tuyên dương học sinh có câu trả lời tốt nhất. Động viên các học sinh
tổng hợp
còn lại tích cực, cố gắng hơn trong các hoạt động học tiếp theo - Chốt kiến thức
Hoạt động 2.3. Đạo hàm của hàm số lượng giác.
a) Mục tiêu: Học sinh biết đạo hàm của các hàm lượng giác cơ bản. b) Nội dung:
* Đạo hàm các hàm số y = sin , x y = cos , x y = tan , x y = cot x Ví dụ 3,4,5,6 Sgk Luyện tập 3,4,5,6
c) Sản phẩm: Công thức đạo hàm các hàm lượng giác và làm rõ các ví dụ.
d) Tổ chức thực hiện: Học sinh thảo luận, hoạt động nhóm lớn ( lớp chia 8 nhóm )
GV Phân công nhiệm vụ
Nhóm 1+5: Đạo hàm của hàm y = sin x, luyện tập 3.
Nhóm 2+6: Đạo hàm của hàm y = cos x , luyện tập 4.
Chuyển giao
Nhóm 3+7: Đạo hàm của hàm y = tan x, luyện tập 5.
Nhóm 4+8: Đạo hàm của hàm y = cot x , luyện tập 6.
Ví dụ 3,4,5,6 HS nghiên cứu SGK để định hướng lời giải. - Tìm câu trả lời
a. Hàm số y = sin x có đạo hàm tại mọi x Î ! và (sin x)¢ = cos x. Ví dụ 3 Sgk p
Luyện tập 3 Tính đạo hàm của hàm số f (x) = sin x tại điểm x = . 0 2 Ta có: f ( ¢ x) = cos x . p
Đạo hàm của hàm số trên tại điểm x = là: 0 2 æ p ö p
Thực hiện f ¢ = cos = 0. ç ÷ è 2 ø 2
b. Hàm số y = cos x có đạo hàm tại mọi x Î ! và (cos x)¢ = -sin x. Ví dụ 4 Sgk
Luyện tập 4 Một vật dao động theo phương trình f (x) = cos x , trong đó
x là thời gian tính theo giây. Tính vận tốc tức thời của vật tại thời điểm x = 2( s) . 0
Ta có: v(t) = f (¢x) = -sin x.
Vận tốc của vật tại thời điểm x = 2 là: 0 4 v(2) = - i s n 2 p
c.Hàm số y = tan x có đạo hàm tại mọi x ¹
+ kp ,k Î ! và 2 1 (tan x)¢ = . 2 cos x Ví dụ 5 Sgk p
Luyện tập 5 Tính đạo hàm của hàm số f (x) = tan x tại điểm x = - . 0 6 1 æ p ö Ta có: f ( ¢ x) = x ¹ + kp ,k Î ! . 2 ç ÷ cos x è 2 øp
Đạo hàm của hàm số trên tại điểm x = - là: 0 6 æ p ö 1 4 f ¢ - = = ç ÷ è 6 ø æ p 2 ö 3 cos - ç ÷ è 6 ø
d. Hàm số y = cot x có đạo hàm tại mọi x ¹ kp ,k Î ! và 1 (cot x)¢ = - 2 sin x Ví dụ 6 Sgk p
Luyện tập 6 Tính đạo hàm của hàm số f (x) = cot x tại điểm x = - . 0 3 1
Ta có: f (¢x) = -
(x ¹ kp , k Î !). 2 sin x p
Đạo hàm của hàm số trên tại điểm x = - là: 0 3 æ p ö 1 4 f ¢ - = - = - . ç ÷ è 3 ø æ p 2 ö 3 sin - ç ÷ è 3 ø
* Đại diện nhóm báo cáo theo nội dung được phân công , các nhóm còn
Báo cáo thảo luận lại theo dõi thảo luận.
- GV nhận xét thái độ làm việc, phương án trả lời của học sinh, ghi nhận
Đánh giá, nhận xét, và tuyên dương học sinh có câu trả lời tốt nhất. Động viên các học sinh còn
tổng hợp
lại tích cực, cố gắng hơn trong các hoạt động học tiếp theo - Chốt kiến thức
Hoạt động 2.4: Đạo hàm của hàm số mũ.
a) Mục tiêu: Học sinh biết đạo hàm của hàm số x y = e , x y = a . b) Nội dung:
Đạo hàm của hàm số x y = e , x y = a . Ví dụ 7.
c) Sản phẩm: Kết quả thực hiện của học sinh
d) Tổ chức thực hiện: Hoạt động cá nhân.
GV yêu cầu học sinh nêu công thức đạo hàm của hàm x y = e , x y = a .
Chuyển giao Nghiên cứu VD7
Thực thực hiện luyện tập 7 Hàm số x
y = e có đạo hàm tại mọi x Î ! và ( x ) x e ¢ = e
Thực hiện Tổng quát: Hàm số x
y = a (a > 0,a ¹ )
1 có đạo hàm tại mọi x Î ! và 5 ( x)¢ x a = a ln a Ví dụ 7 Sgk
Luyện tập 7 Tính đạo hàm của hàm số ( ) 10x f x = tại điểm x = 1 - . 0 Ta có: ¢( ) =10x f x ln10 . - ln10
Đạo hàm của hàm số trên tại điểm x = 1 - là: f ¢(- ) 1 1 =10 ln10 = 0 10
Báo cáo thảo luận * Đại diện HS báo cáo, các HS còn lại theo dõi thảo luận.
- GV nhận xét thái độ làm việc, phương án trả lời của học sinh, ghi nhận
Đánh giá, nhận xét, và tuyên dương học sinh có câu trả lời tốt nhất. Động viên các học sinh còn
tổng hợp
lại tích cực, cố gắng hơn trong các hoạt động học tiếp theo - Chốt kiến thức
Hoạt động 2.5: Đạo hàm của hàm số lôgarit
a) Mục tiêu: Học sinh đạo hàm của hàm số y = ln x , y = log x a > a ¹ a ( 0, )1. b) Nội dung:
Đạo hàm của hàm số y = ln x , y = log x a > a ¹ a ( 0, )1. Ví dụ 8
c) Sản phẩm: Kết quả thực hiện của học sinh
d) Tổ chức thực hiện: Hoạt động cá nhân.
GV yêu cầu học sinh đưa ra kết quả tính đạo hàm của hàm số y = ln x ,
y = log x a > a ¹ a ( 0, )
Chuyển giao
1 dựa vào kiến thức sgk trình bày ? Nghiên cứu Ví dụ 8 Thực hiện luyện tập 8
Hàm số y = ln x có đạo hàm tại mọi x dương và ( ) 1 ln x ¢ = x Tổng quát:
Hàm số y = log x a > a ¹ x a ( 0,
)1 có đạo hàm tại mọi dương và ( x ¢ = a ) 1 log x ln a Ví dụ 8 Sgk 1
Thực hiện
Luyện tập 8 Tính đạo hàm của hàm số f (x) = log x tại điểm x = . 0 2 1
Ta có: f ¢( x) = (x > 0). .l x n10 1
Đạo hàm của hàm số trên tại điểm x = là: 0 2 æ 1 ö 1 2 f ¢ = = . ç ÷ è 2 1 ø ln10 ln10 2
Báo cáo thảo luận * Đại diện HS báo cáo, các HS còn lại theo dõi thảo luận.
- GV nhận xét thái độ làm việc, phương án trả lời của học sinh, ghi nhận
Đánh giá, nhận xét, và tuyên dương học sinh có câu trả lời tốt nhất. Động viên các học sinh còn
tổng hợp
lại tích cực, cố gắng hơn trong các hoạt động học tiếp theo - Chốt kiến thức Tiết 2:
II. Đạo hàm của tổng, hiệu, tích, thương và đạo hàm của hàm hợp.
Hoạt động 2.5: Đạo hàm của tổng, hiệu, tích, thương.
a) Mục tiêu: Học sinh biết công thức đạo hàm của tổng, hiệu, tích, thương 6 b) Nội dung:
Định lí công thức đạo hàm.
Giả sử f = f (x), g = g (x) là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định. Ta có:
( f + g)¢ = f ¢+ g¢
( f - g)¢ = f ¢- g¢ ¢ ( æ f ö f g¢ - fg¢
fg)¢ = f g¢ + fg¢ = g = g x ¹ 0 ç ÷ 2 ( ( ) ) è g ø g
Hệ quả Nhận định với c là một hằng số nên c ' = 0
Cho f = f (x) là hàm số có đạo hàm tại điểm x thuộc khoảng xác định
Nếu c là một hằng số thì (cf )¢ = cf ¢. æ 1 ¢ö f ¢ = - f = f x ¹ 0 ç ÷ 2 ( ( ) ). è f ø f Ví dụ 9, 10 Sgk Ví dụ 10
c) Sản phẩm: Câu trả lời của học sinh
d) Tổ chức thực hiện: Học sinh làm việc theo nhóm đôi.
* GV yêu cầu học sinh thực hiện thảo luận nhóm đôi, đưa ra nhận định về
đạo hàm tổng, hiệu, tích, thương theo định lí và hệ quả.
Chuyển giao
* Trên cơ sở câu trả lời của học sinh, giáo viên chuẩn hóa kiến thức, yêu
cầu học sinh nghiên cứu VD 9, 10 và thực hiện luyện tập 9,10 - Nhận định:
Định lý: Đối với hàm tổng, hiệu thực hiện bình thường.
Hàm thương tử gần giống tích thay bởi dấu trừ và có mẫu.
Giả sử f = f (x), g = g (x) là các hàm số có đạo hàm tại điểm x
thuộc khoảng xác định. Ta có:
( f + g)¢ = f ¢+ g¢
( f - g)¢ = f ¢- g¢
( fg)¢ = f g¢ + fg¢ æ f ¢ö f g¢ - fg¢ = g = g x ¹ 0 ç ÷ 2 ( ( ) ) è g ø g
Thực hiện Hệ quả: Sgk Ví dụ 9 Sgk
Luyện tập 9 Tính đạo hàm của hàm số f (x) = x x tại điểm x dương bất kì.
Học sinh thực hiện nhiệm vụ cá nhân
x = (x x ) = x x + x ( x ) 1 3 x f '( ) ' ' . ' = x + . x = 2 x 2 Ví dụ 10 Sgk
Luyện tập 10 Tính đạo hàm của hàm số f (x) = tan x + cot x tại điểm p x = . 0 3
Học sinh thảo luận nhóm đôi, nhận dạng biểu thức f , g áp dụng tính và đưa và đáp án. 7 Ta có: f (x) = ( x + x) = ( x) + ( x) 1 1 ' tan cot ' tan ' cot ' = - . 2 2 cos x sin x æ p ö 1 1 4 8 f ' = - = 4 - = ç ÷ è 3 ø æ p ö æ p 2 2 ö 3 3 cos sin ç ÷ ç ÷ è 3 ø è 3 ø
* Đại diện HS và nhóm báo cáo, các HS, nhóm còn lại theo dõi thảo
Báo cáo thảo luận luận.
- GV nhận xét thái độ làm việc, phương án trả lời của học sinh, ghi nhận
Đánh giá, nhận xét, và tuyên dương học sinh có câu trả lời tốt nhất. Động viên các học sinh còn
tổng hợp
lại tích cực, cố gắng hơn trong các hoạt động học tiếp theo - Chốt kiến thức
Hoạt động 2.6: Đạo hàm của hàm hợp.
a) Mục tiêu: Học sinh biết hàm hợp, quy tắc tính đạo hàm của hàm hợp
b) Nội dung: Hàm hợp
Cho hàm số y = f (u) =
u u = g (x) 2 sin ; = x .
a) Bằng cách thay u bởi 2
x trong biểu thức sin u , hãy biểu thị giá trị của y theo biến số x .
b) Xác định hàm số y = f (g (x)).
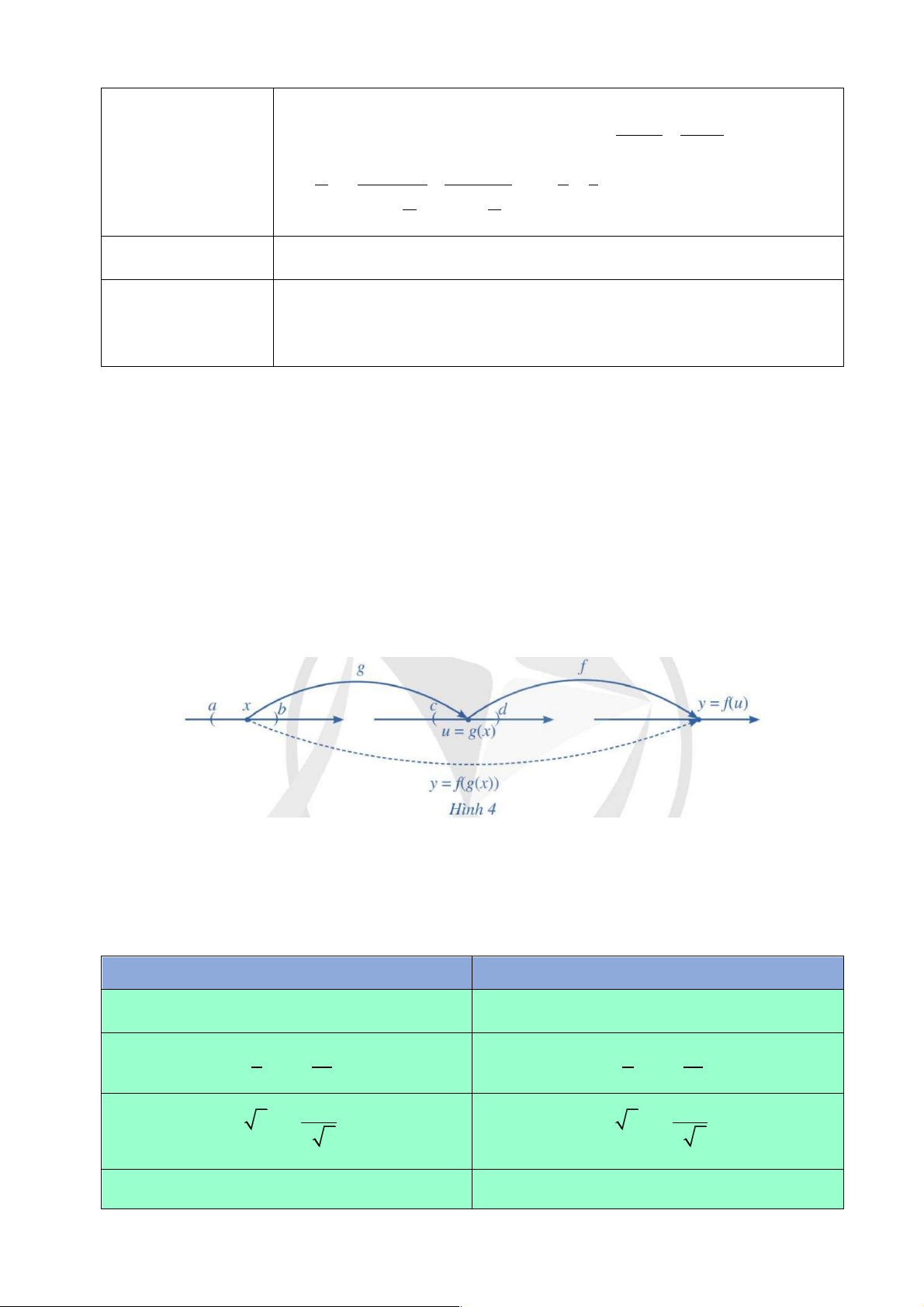
Giả sử hàm số u = g (x) xác định trên ( ;
a b) và lấy giá trị trên ( ;
c d)); y = f (u) là
hàm số của u , xác định trên ( ;
c d ) và lấy giá trị trên ! . Khi đó, ta có thể lập được
một hàm số mới xác định trên ( ;
a b) và lấy giá trị trên ! theo quy tắc như Hình 4.
Hàm số y = f (g (x)) được gọi là hàm hợp của hai hàm số y = f (u),u = g (x).
Quy tắc tính đạo hàm của hàm hợp Hệ quả Ví dụ 11,12 Sgk Luyện tập 11, 12
Chốt bảng tổng hợp quy tắc đạo hàm
Đạo hàm của hàm số sơ cấp cơ bản thường gặp
Đạo hàm của hàm hợp ( ở đây u = u (x) ( nx )¢ n 1 = . n x - ( nu )¢ n 1 = . n x - .u¢ 1 ¢ æ ö 1 ¢ æ ö ¢ = - 1 u = - ç ÷ 2 ç ÷ è x ø x 2 è u ø u ( ¢ ¢ u¢ x ) 1 = ( u) = 2 x 2 u
(sin x)¢ = cos x
(sinu)¢ = u .¢cosu 8
(cos x)¢ = -sin x (cosu)¢ = u - .¢sinu ( u¢ x) 1 tan ¢ = (tanu)¢ = 2 cos x 2 cos u ( u¢ x) 1 cot ¢ = - (cotu)¢ = - 2 sin x 2 sin u ( x )¢ x e = e ( u )¢ = . u e u¢ e ( x )¢ x a = a .ln a ( u )¢ = . u a
u¢ a .ln u ( ) 1 u¢ ln x ¢ = (lnu)¢ = x u ( ¢ u¢ x ¢ = (log u = a ) a ) 1 log x ln a u ln a
c) Sản phẩm: Câu trả lời của học sinh
d) Tổ chức thực hiện: Học sinh làm việc theo nhóm đôi.
* GV yêu cầu học sinh thực hiện thảo luận nhóm đôi, đưa ra hiểu biết về
hàm hợp, lấy ví dụ hàm hợp.
Chuyển giao
* Dựa vào quy tắc thực hiện VD 11,12 học sinh thực hiện cá nhân.
Tự nghiên cứu VD 13 và thực hiện nhóm đôi luyện tập 11, 12
- Nhận định: Hàm hợp: Cho hàm số y = f (u) =
u u = g (x) 2 sin ; = x .
Bằng cách thay u bởi 2
x trong biểu thức sin u , được hàm số 2 y = sin x
- Quy tắc: Nếu hàm số u = g(x) có đạo hàm tại x là u¢ x
và hàm số y = f (u) có đạo hàm tại u là y¢ thì hàm hợp y = f (g(x)) có u
đạo hàm tại x là y¢ = y¢ .u¢ x u x Ví dụ 11, 12 Sgk
Luyện tập 11 Hàm số y = log 3x +1 2 (
) là hàm hợp của hai hàm số nào ?
Thực hiện
Giải Ta có: y = f (g (x)). f = log g x
g (x) = 3x +1 2 ( ( )) và
Luyện tập 11 Tìm đạo hàm của mỗi hàm số sau: a) 3x 1 y e + =
b) y = log 2x - 3 3 ( ) Giải: a) y ( 3x 1
e + ) ( x ) 3x 1+ 3x 1 ' ' 3 1 '.e 3.e + = = + = 2x - 3 ' 2
b) y ' = (log 2x - 3 ' = = 3 ( )) ( )
(2x -3)ln3 (2x -3).ln3
* Đại diện HS và nhóm báo cáo, các HS, nhóm còn lại theo dõi thảo
Báo cáo thảo luận luận.
- GV nhận xét thái độ làm việc, phương án trả lời của học sinh, ghi nhận
Đánh giá, nhận xét, và tuyên dương học sinh có câu trả lời tốt nhất. Động viên các học sinh còn
tổng hợp
lại tích cực, cố gắng hơn trong các hoạt động học tiếp theo - Chốt kiến thức Tiết 3
3. Hoạt động 3: Luyện tập
a) Mục tiêu: bước đầu biết vận dụng quy tắc tính đạo hàm của hàm sơ cấp cơ bản, hàm
tổng, hiệu, tích, thương và hàm hợp và làm bài tập 9 b) Nội dung:
Bài 1: Phát biểu đúng a) (u + v + )
w ¢ = u¢ + v¢ + w¢ b) (u + v - )
w ¢ = u¢ + v¢ - w¢; ¢ æ ö ¢
Phát biểu sai: c) (uv)¢ = u u u v ¢ ¢ d) =
với v = v(x) ¹ 0,v¢ = v ( ¢ x) ¹ 0. ç ÷ è v ø v¢
Bài 2: Cho u = u(x),v = v(x), w = (
w x) là các hàm số có đạo hàm tại điểm x thuộc khoảng xác
định. Chứng minh rằng ( . u . v ) w ¢ = u .¢ . v w + . u v .¢w + . u . v w¢. Ta có: ( . u . v ) w ¢ = (( . u v). ) w ¢ = ( . u v)'.w+( .
u v).w' = ( u'v + . u v').w)+( .
u v).w' = u .¢ .vw+ . u v .¢w + . u . v w¢
Bài 3: Tìm đạo hàm của mỗi hàm số sau: a) y = ( 3 2
x - x + x + ) = ( 3 x ) -( 2 x ) +( x) 2 ' 4 3 2 10 ' 4 ' 3
' 2 '+10' =12x - 6x + 2; æ x +1ö
(x + )1'(x - )1-(x + )1(x - )1' x -1-(x + )1 2 - b) y ' = ' = = = ç ÷ è x -1ø (x - )2 1 (x - )2 1 (x - )2 1 x
c) y = (- x x) = (- x) x +(- x) 2 ' 2 ' 2 '. 2 x ' = 2 - x - = 4 - x 2 x 1
d) y ' = (3sin x)'+ (4cos x)'- (tan x)' = 3cos x - 4sin x - 2 cos x
e) ' = (4x + 2 x )' = (4x )'+(2ex )' = 4x ln4+2ex y e
g) y = (x x) = x
x + x ( x) 1 ' ln ' 'ln . ln ' =1.ln x + . x = ln x +1 x Bài 4: Cho hàm số 3 2 ( ) 2 x f x + = .
a) Hàm số f (x) là hàm hợp của các hàm số nào? ( ) 2u f x =
, f (u) = 3x + 2
b) Tìm đạo hàm của f x = ( 3x+2 ) = ( x + ) 3x+2 3x+2 ( )' 2 ' 3 2 '.2 = 3.2 .
Bài 5: Tìm đạo hàm của mỗi hàm số sau: a) y = ( 2 x + x) = ( x) +( 2 ' sin3 sin '
sin3 ' sin x)' = (3x)'cos3x + 2sin x(sin x)' = 3cos3x + 2sin . x cos x - x+ - x+ 2 b) ' ( 2 1 log (2 1) 3 ' log 2 1 ' 3 ' 2.3- x y x x + = + + = + + = - .ln 3 2 ) ( 2( )) ( 2 1) 2 1 . (2x + )1ln2
Bài 6. Viết phương trình tiếp tuyến của đồ thị mỗi hàm số sau: a) 3 2
y = x - 3x + 4 tại điểm có hoành độ x = 2 0 y = ( 3 2 x - x + ) 2 ' 3 4 ' = 3x - 6x y( ) = ( 3 2 2 2 -3.2 + 4) = 0 2 y ' = 3.2 - 6.2 (2)
Phương trình tiếp tuyến: y = y '
(x- x + y Û y = 0. x-2 +0 Û y = 0 x 0 ) 0 ( ) ( 0)
b) y = ln x tại điểm có hoành độ x = e 0 y = ( x) 1 ' ln ' = x 1 y ' = , y = e = e (ln ) 1 (e) e ( ) 2 1 e -1
Phương trình tiếp tuyến: y = y '
(x - x + y Û y =1. x -e + Û y = x - x 0 ) 0 ( ) ( 0) e e c) x
y = e tại điểm có hoành độ x = 0. 0 10 ' x y = e , 0 y = e = , 1 0 y ' = e = ( 1 0) (0)
Phương trình tiếp tuyến: y = y '
(x- x + y Û y =1. x-0 +1Û y = x+1 x 0 ) 0 ( ) ( 0)
c) Sản phẩm: Bài làm của học sinh
d) Tổ chức thực hiện: Làm việc theo nhóm đôi
* GV đề nghị hs nêu cách giải từng phần và lời giải chi tiết.
Chuyển giao
* GV nhận xét và chuẩn hóa lời giải
Bài 1: học sinh làm cá nhân
Bài 2: Học sinh thảo luận nhóm đôi Chia lớp thành 10 nhóm: Nhóm 1,2 làm bài 3 a,b,c
Thực hiện Nhóm 3,4 làm bài 3 d,e,g Nhóm 5,6 làm bài 4 Nhóm 7,8 làm bài 5 Nhóm 9, 10 làm bài 6
* Đại diện HS, nhóm báo cáo, các HS, nhóm còn lại theo dõi thảo luận.
Báo cáo thảo luận * Yêu cầu làm rõ những nội dung có nhóm, HS còn thắc mắc.
- GV nhận xét thái độ làm việc, phương án trả lời của học sinh, ghi nhận
Đánh giá, nhận xét, và tuyên dương học sinh có câu trả lời tốt nhất. Động viên các học sinh còn
tổng hợp
lại tích cực, cố gắng hơn trong các hoạt động học tiếp theo - Chốt kiến thức
4. Hoạt động 4: Vận dụng
a) Mục tiêu: Vận dụng ứng dụng hình học, vật lý và quy tắc tính đạo để giải quyết các bài toán thực tế. b) Nội dung: Bài tập 7,8
Bài 7: Một viên đạn được bắn lên từ mặt đất theo phương thẳng đứng với tốc độ ban đầu
v = 196 m / s (bỏ qua sức cản của không khí). Tìm thời điểm tại đó tốc độ của viên đạn bằng 0 . 0
Khi đó viên đạn cách mặt đất bao nhiêu mét (lấy 2 g = 9,8 m / s )? 1 1
Hướng dẫn: Phương trình chuyển động của viên đạn 2 2
h = h + v .t - g.t = 196t - .9.8.t 0 0 2 2
Vận tốc của viên đạn tại thời điểm t : v(t) = h(t)' =196-.9.8.t
Vận tốc bằng 0: v(t) 196
= 0 Û196 - 9.8t = 0 Û t = Û t = 20 9,8 1
Khoảng cách giữa viên đạn và mặt đất 2
h =196.20 - .9.8.20 =1960m 2
Bài 8: Cho mạch điện như Hình 5. Lúc đầu tụ điện có điện tích Q . Khi đóng khoá K , 0
tụ điện phóng điện qua cuộn dây; điện tích q của tụ điện phụ thuộc vào thời gian t
theo công thức q(t) = Q sinwt, trong đó w là tốc độ góc. Biết rằng cường độ I (t) 0
của dòng điện tại thời điểm t được tính theo công thức I (t) = q (¢t). Cho biết -8 Q = 10 (C) và 6
w =10 p(rad / s). Tính cường độ của dòng điện tại thời điểm 0
t = 6( s) (tính chính xác đến 5 10- ( mA)).
Hướng dẫn: Phương trình điện tích q(t) 8 - 6 = Q .sin t w =10 .sin10 pt 0
Cường độ dòng điện I (t) = q (t) = ( 8- 6pt) 2 - 6 ' 10 .sin10 ' =10 .cos10 pt
Tại thời điểm t = 6( s) ta có I ( ) 2 - 6
6 =10 .p.cos10 p.6 » 0,0314( A)
c) Sản phẩm: Kết quả bài làm của học sinh.
d) Tổ chức thực hiện: Thảo luận theo nhóm ( giáo viên hướng dẫn về nhà đối với HS yếu ).
- GV hướng dẫn học sinh tiếp cận vấn đề và giao nhiệm vụ
Chuyển giao
- GV đề nghị HS nêu cách giải từng phần và lời giải chi tiết. 11
- GV nhận xét và chuẩn hóa lời giải
- HS suy nghĩ đưa ra lời giải.
Thực hiện
- Thảo luận theo nhóm 4 học sinh.
Báo cáo thảo luận * Đại diện nhóm báo cáo, các nhóm còn lại theo dõi thảo luận.
- GV nhận xét thái độ làm việc, phương án trả lời của học sinh, ghi nhận
Đánh giá, nhận xét, và tuyên dương học sinh có câu trả lời tốt nhất. Động viên các học sinh còn
tổng hợp
lại tích cực, cố gắng hơn trong các hoạt động học tiếp theo - Chốt kiến thức