BÀI 2 CÂY QUYẾT ĐỊNH (DECISION TREE

BÀI 2 CÂY QUYẾT ĐỊNH (DECISION TREE)
Giảng viên: TS. Hoàng Văn Thông
Email: thonghv@utc.edu.vn – ĐT: 0988.113.679 1 NỘI DUNG I. BÀI TOÁN PHÂN LỚP II. ỨNG DỤNG CỦA PHÂN LỚP
III. PHÂN LỚP DỰA TRÊN CÂY QUYẾT ĐỊNH IV. BÀI TẬP 2
I. BÀI TOÁN PHÂN LỚP
• Cho một tập mẫu dữ liệu D ={ (x , C ), i = 1,..,N }, x là một véc tơ n i i i
chiều có dạng (x , x ,.., x ), x U là miền xác định của các biến i1 i2 in ij j
(thuộc tính) 𝔛 của bài toán, với j = 1,..,n, C  C tập các nhãn có m j i
lớp, i = 1,.., m, N là số mẫu dữ liệu.
• Từ tập mẫu dữ liệu D xây dựng một mô hình cho phép phân lớp
bất kỳ mẫu dữ liệu p  U = U  ...  U . 1 n
• Mô hình là một ánh xạ f từ U vào C 3
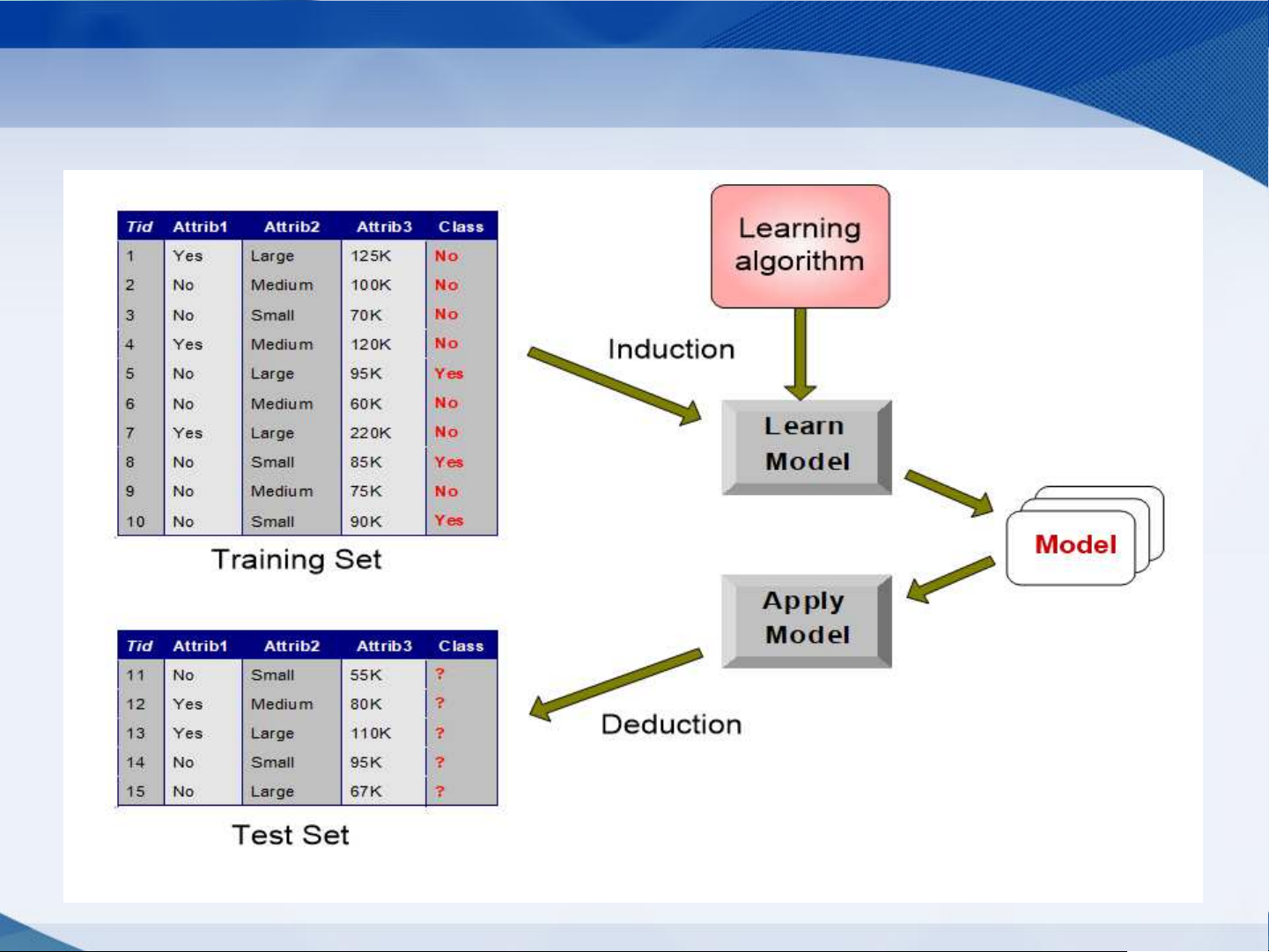
Minh họa bài toán phân lớp 4
Các phương pháp phân lớp cơ bản 1. Decision Tree based Methods 2. Rule-based Methods
3. Naïve Bayes and Bayesian Belief Networks 4. Support Vector Machines 5
II. ỨNG DỤNG PHÂN LỚP
– Trong y học: chẩn đoán bệnh (dựa trên các triệu chứng, kết
quả xét nghiệm phân loại bệnh)
– Trong sinh học: xác định loài
– Trong sản xuất: phân loại sản phẩm
– Trên web: phân lớp email, phân lớp website,...
– Nhận dạng: chữ viết, hình ảnh,... 6
III. PHÂN LỚP DỰA TRÊN CÂY QUYẾT ĐỊNH 1. Cây quyết định 2. Một số khái niệm 3.
Các thuật toán xây dựng cây quyết 4.
Thuật toán xây dựng cây quyết định tổng quát 5.
Cây quyết định ID3 6.
Cây quyết định C4.5 7.
Cây quyết định CART 8.
Kiểu dữ liệu của thuộc tính 9. Cắt tỉa cây
10. Rừng ngẫy nhiên 7
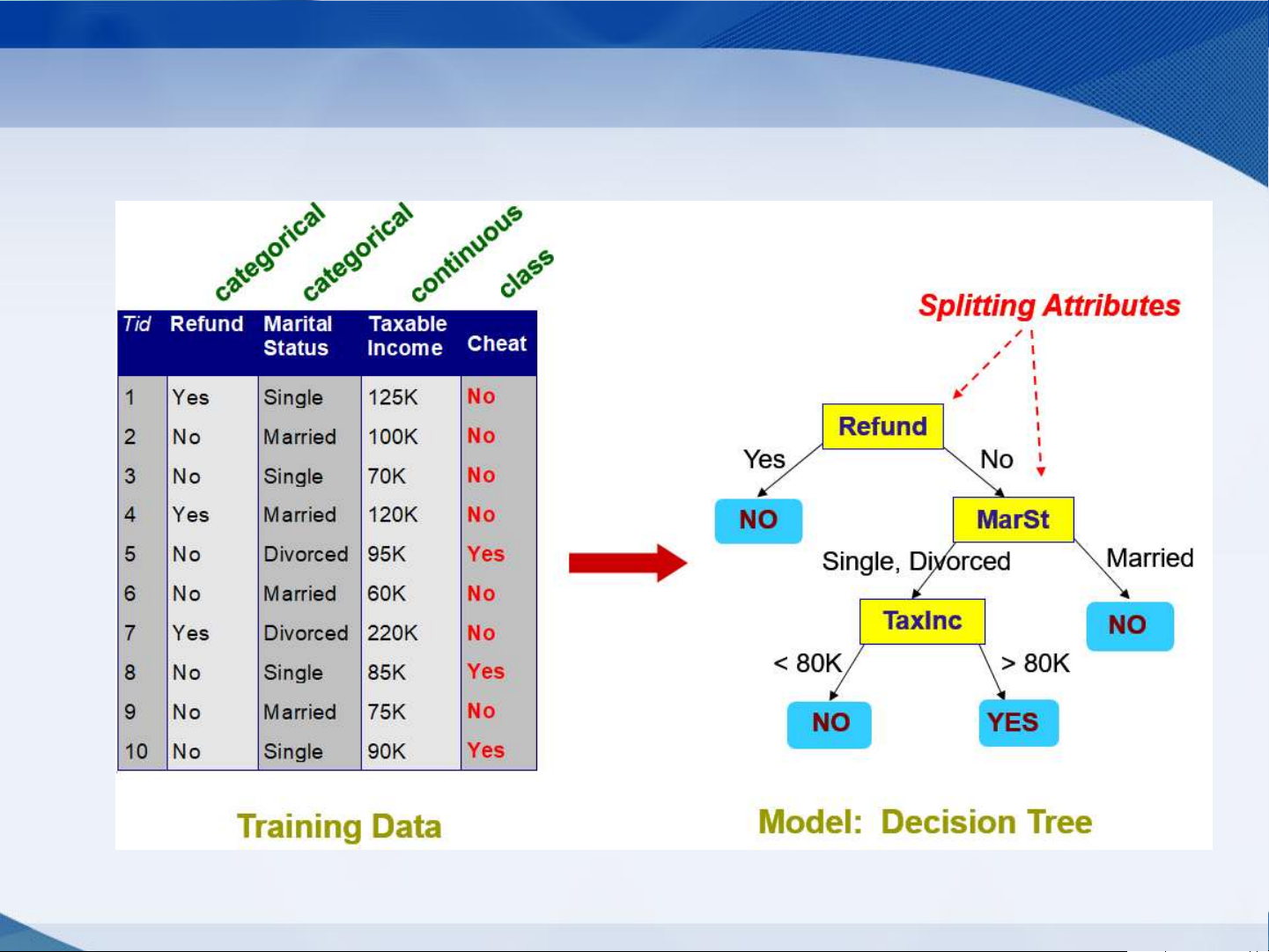
1. Cây QĐ sinh ra từ dữ liệu
• Mỗi cây quyết định cho môt tâp quy tắc phân lớp:
• Mỗi đường di từ gốc đến là cho 1 luật
• Mỗi nút ≠ lá biểu thị một thuộc tính/điều kiện kiểm tra
• Mỗi cạnh biểu thị giá trị kiểm tra của thuộc tính tương ứng
• Mỗi lá cho một giá trị nhãn xác định bởi luật 8
Ví dụ Cây QĐ sinh ra từ dữ liệu 9
2. Một số khái niệm
• Độ trong suốt (pure) của DB: một DB có độ trong suốt cao nếu nó
có ít lớp (trong trường hợp lý tưởng là có 1 lớp).
• Độ đo lựa chọn thuộc tính (Attribute selection measure): là độ
đo của mỗi thuộc tính dùng để lựa chọn thuộc tính phân hoạch tập
dữ liệu có độ trong suốt cao nhất. 10
3. Các thuật toán xây dựng cây quyết định
• Dựa trên đô đo lựa chọn thuộc tính ta có các thuật toán
– ID3 - Iterative Dichotomise, tác giả J. Ross Quinlan (1970s-1980s), sử dụng độ đo Gain Information
– C4.5 (Khắc phục nhược điểm ID3), tác giả J. Ross Quinlan (1993), sử dụng độ
đo Gain ratio (hiện tại có phiên bản C5.0)
– CART - Classification and Regression Trees , tác giả L. Breiman, J. Friedman, R.
Olshen, and C. Stone (1984), sử dụng độ đo Gini index
– Một số độ đo khác: CHAID, C-SEP, MDL 11
4. Thuật toán xây dựng cây quyết định tổng quát 12 5. Cây quyết định ID3
Độ đo lựa chọn thuộc tính Infomation Gain (Gain)
- Dựa trên lý thuyết thông tin của Claude Shannon
- Một thuộc tính được chọn nếu nó có giá trị Gain lớn nhất Ta có:
- 𝐼𝑛𝑓𝑜 𝐷 = − 𝑚
𝑖=1 𝑝𝑖 × 𝑙𝑜𝑔2 𝑝𝑖 trong đó 𝑝𝑖 = |𝐷 𝐶𝑖 | |𝐷| -
Thuộc tính A có các giá trị là {a , a , ..., a } 1 2 v - 𝐼𝑛𝑓𝑜 𝑣 |𝐷𝑗| 𝐴 𝐷 = 𝑗=1 × 𝑖𝑛𝑓𝑜 𝐷 |𝐷| 𝑗
- Độ đo Infomation gain của A
𝐺𝑎𝑖𝑛 𝐴 = 𝐼𝑛𝑓𝑜 𝐷 − 𝐼𝑛𝑓𝑜𝐴 𝐷
- Nhược điểm của độ đo này là có xu hướng lựa chọn thuộc tính có
nhiều giá trị => khả năng tạo ra các phân hoạch dữ liệu có tính trong
suốt cao => có Gain->min. (Ví dụ: thuộc tính ID) 13
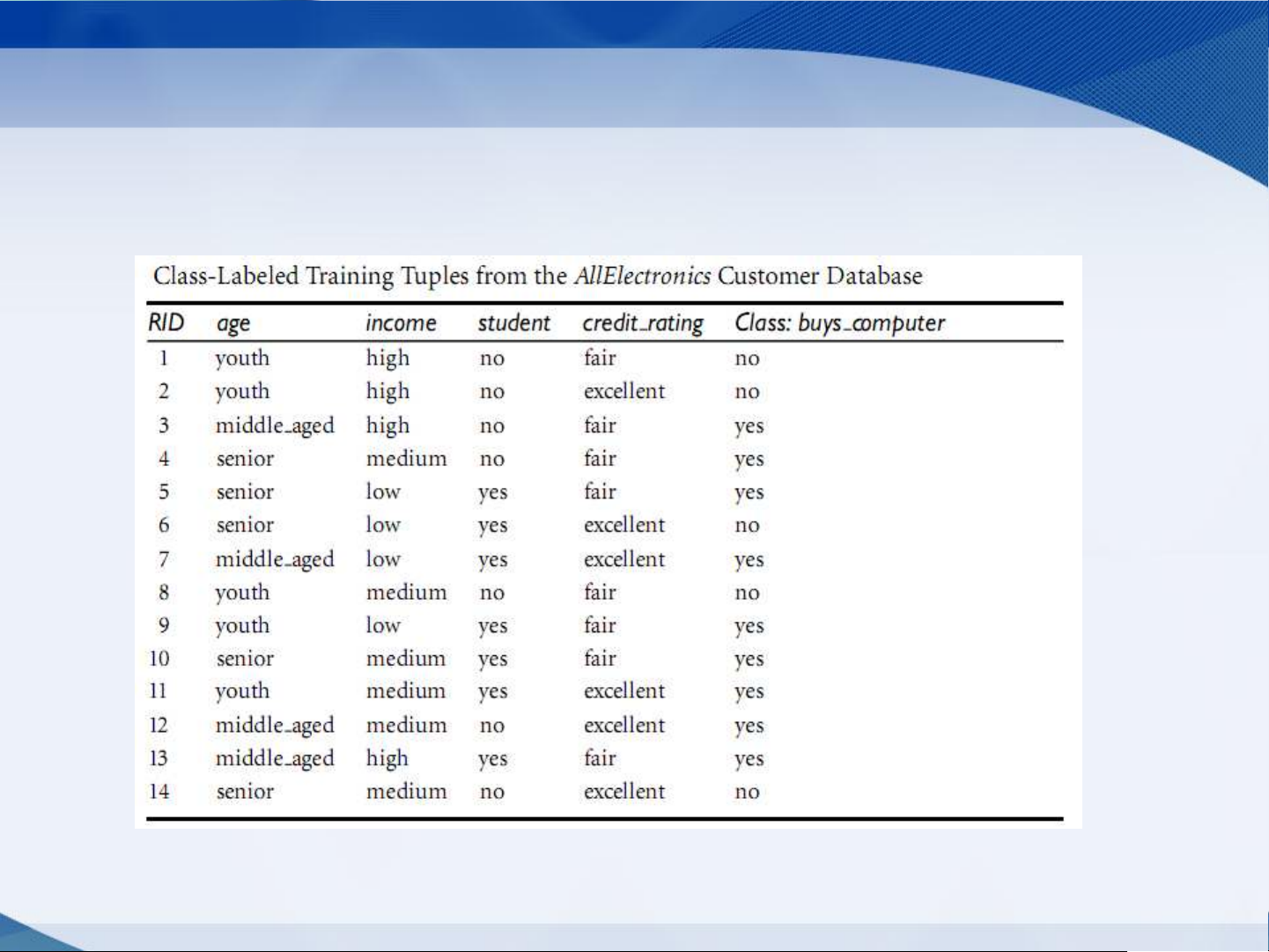
Ví dụ: Xây dựng cây ID3 cho bài toán sau đây 14
6. Cây quyết đinh C4.5
Độ đo lựa chọn thuộc tính Gain ratio
- Khắc phục nhược điểm của độ đo Infomation gain
- Một thuộc tính A được chọn nếu nó có giá trị Gain Ratio lớn nhất Tính:
𝑆𝑝𝑙𝑖𝑡𝐼𝑛𝑓𝑜 𝑣 |𝐷𝑗| |𝐷𝑗| 𝐴 𝐷 = − 𝑗=1 × 𝑙𝑜𝑔 |𝐷| 2 |𝐷|
𝑮𝒂𝒊𝒏𝑹𝒂𝒕𝒊𝒐 𝑨 = 𝑮𝒂𝒊𝒏(𝑨)
𝑺𝒑𝒍𝒊𝒕𝑰𝒏𝒇𝒐𝑨(𝑫) 15
7. Cây quyết định CART
Độ đo lựa chọn thuộc tính Gini index
- Gini index đo độ không trong suốt của tập dữ liệu D - Tính:
𝐺𝑖𝑛𝑖 𝐷 = 1 − 𝑚 2 𝑖=1 𝑝𝑖
Trong đó p là xác suất một bộ trong D thuộc lớp C , được tính 𝑝 i i 𝑖 = |𝐷 𝐶𝑖 | |𝐷| -
Thuộc tính A có các giá trị là {a , a , ..., a } 1 2 v - 𝐺𝑖𝑛𝑖 𝑣 |𝐷𝑗| 𝐴 𝐷 = 𝑗=1 × 𝐺𝑖𝑛𝑖 𝐷 |𝐷| 𝑗
- Độ đo Infomation gain của A
∆𝐺𝑖𝑛𝑖 𝐴 = 𝐺𝑖𝑛𝑖 𝐷 − 𝐺𝑖𝑛𝑖𝐴 𝐷 16
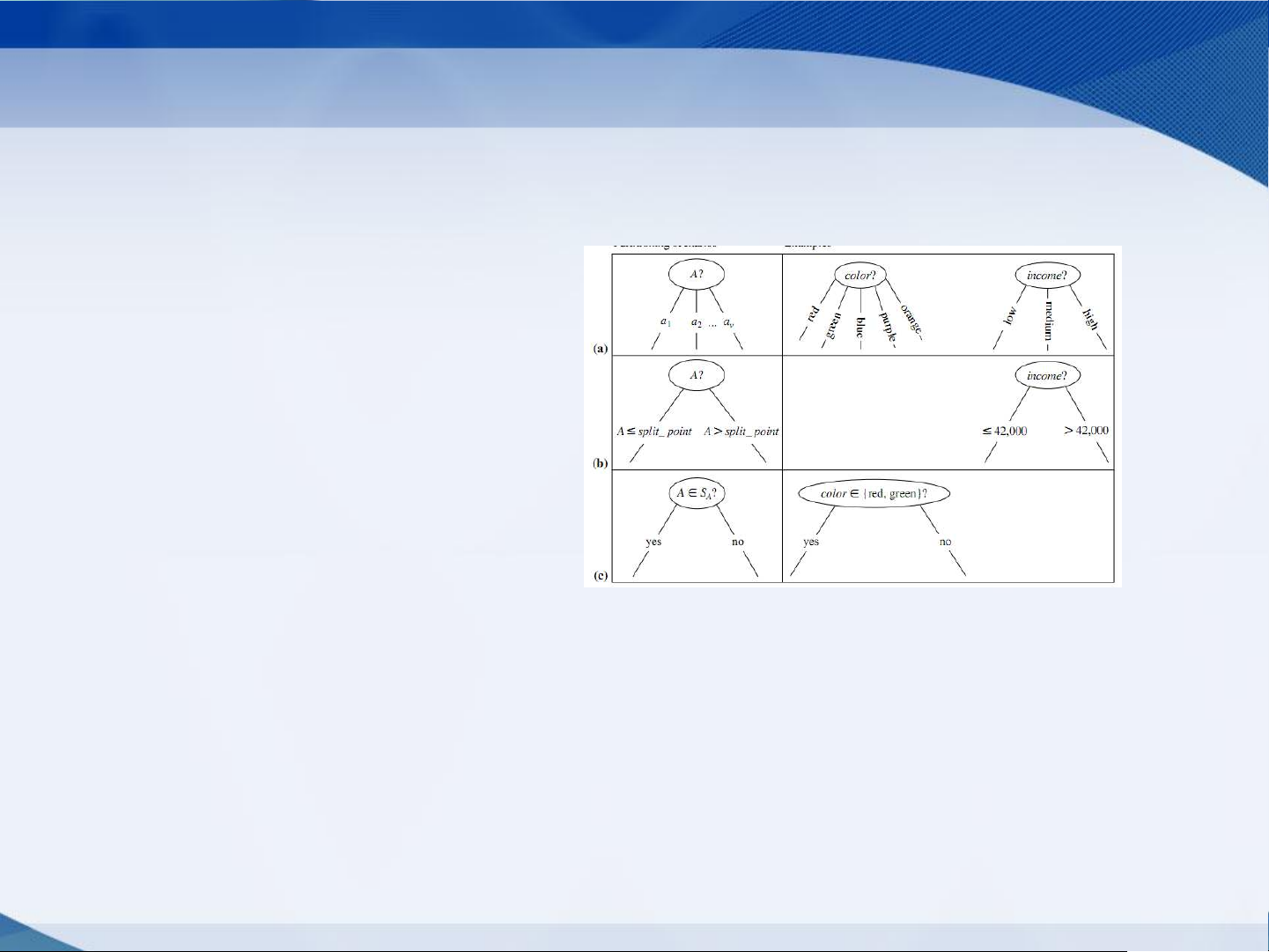
8. Các kiểu dữ liệu của thuộc tính • Kiểu thuộc tính – Định danh – Thứ tự – Dữ liệu liên tục • Các cách chia – 2-way split – Multi-way split 17 Cách phân chia
• Multi-way split: Sử dụng một số giá trị khác nhau CarType Family Luxury Sports
• Binary split: Chia giá trị thành 2 tập con. CarType CarType Hoặc {Sports, {Family, Luxury} {Family} Luxury} {Sports} 18 Dữ liệu liên tục
• Có 2 cách để giải quyết
– Rời rạc hóa để hình thành thuộc tính phân loại
• Tĩnh: Rời rạc hóa ngay từ đầu
• Động: Các khoảng có thể được xác định: khoảng bằng nhau, tần xuất bằng
nhau (phần trăm) hoặc phân cụm
– Phân chia nhị phân: (A < v) or (A  v)
• Xem xét tất cả các khả năng chia để tìm điểm chia tốt nhất 19 9. Cắt tỉa cây
- Lý do phải cắt tỉa
- Một số nhánh cây bất thường (do dữ liệu bị nhiễu, phần tử ngoại lai)
- Giải quyết vấn đề quá khớp dữ liệu (overfitting data)
- Làm cho cây trở nên đơn giản hơn => dễ hiểu với người dùng
- Các hướng tiếp cận
- Cắt tỉa trước (prepruning): dừng (halting) sơm trong quá trình
xây dựng cây, không phân hoạch tiếp mà tạo ra nút lá với nhãn
là lớp có số lượng cao nhất
- Dừng lại khi cây đạt độ cao cho trước
- Dừng lại khi độ đo lựa chọn thuộc tính < ngưỡng cho trước
- Cắt tỉa sau (postpruning): cắt tỉa sau khi cây đã phát triển đầy đủ.
- Thay thế một cây con bằng một nút lá có nhãn là lớp chủ yếu của cây con 20