


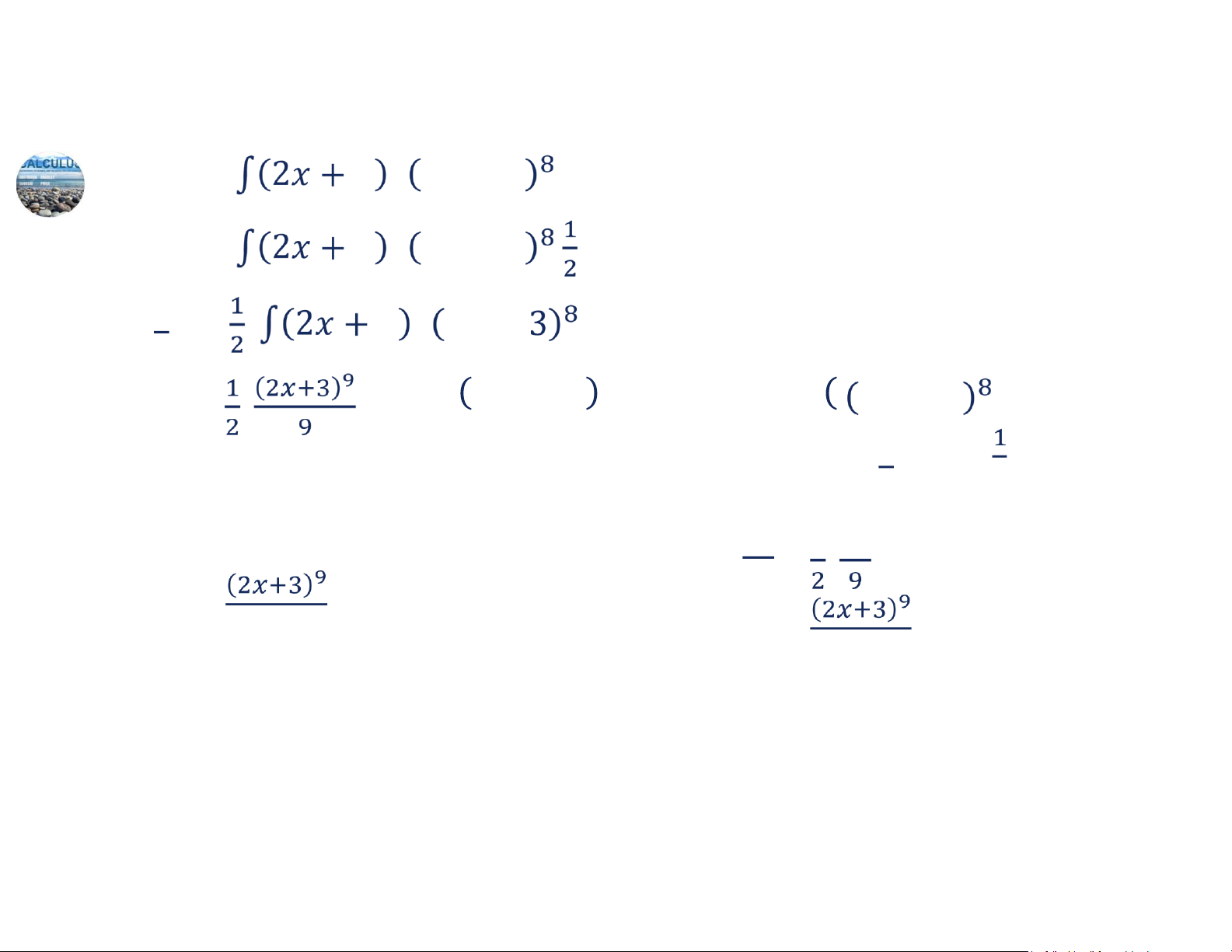






Preview text:
lOMoAR cPSD| 44919514 Bài giảng
KHOA TOÁN KINH T Ế
B Ộ MÔN TOÁN C Ơ B Ả N lOMoAR cPSD| 44919514
TOÁN CHO CÁC NHÀ KINH TẾ
Chương 4: PHÉP TOÁN TÍCH PHÂN
Bài 2: Tính tích phân bằng
phương pháp đổi biến
M ụ ctiêuh ọ ct ậ p
❖ Sử dụng phương pháp ổi biến ể tính tích phân bất ịnh.
❖ Giải bài toán giá trị ban ầu của phương trình vi phân bằng phương pháp ổi biến. lOMoAR cPSD| 44919514
❖ Khám phá mô hình iều chỉnh giá trong kinh tế. ❖Bài tập yêu cầu: 2
1. Phương pháp đổi biến
❖ Tính bất biến của biểu thức tích phân: Nếu 𝑓 𝑥 𝑑𝑥 𝐹 𝑥 𝐶 thì 𝑓 𝑢 𝑑𝑢 𝐹 𝑢 𝐶 vớ i 𝑢 𝑢 𝑥 . lOMoAR cPSD| 44919514 ❖ Ví
dụ: 3 𝑑𝑥 ❖ Cách trình bày khác: Đặt 𝑢 2𝑥 3 ⇒ 𝑑𝑢 2𝑑𝑥 3 2𝑑𝑥 ⇒ 𝑑𝑥 𝑑𝑢 𝑑 2𝑥 3 Khi ó: 2𝑥 3 𝑑𝑥 𝑢 𝑑𝑢 𝑢 𝑑𝑢 𝐶 𝐶 𝐶 𝐶 𝐶 3 lOMoAR cPSD| 44919514
1. Phươngpháp ổ ibi ến
Côngth ứ cng ắ ng ọ n: 4 lOMoAR cPSD| 44919514
Ví dụ: Tính tích phân bằng phương pháp ổi biến
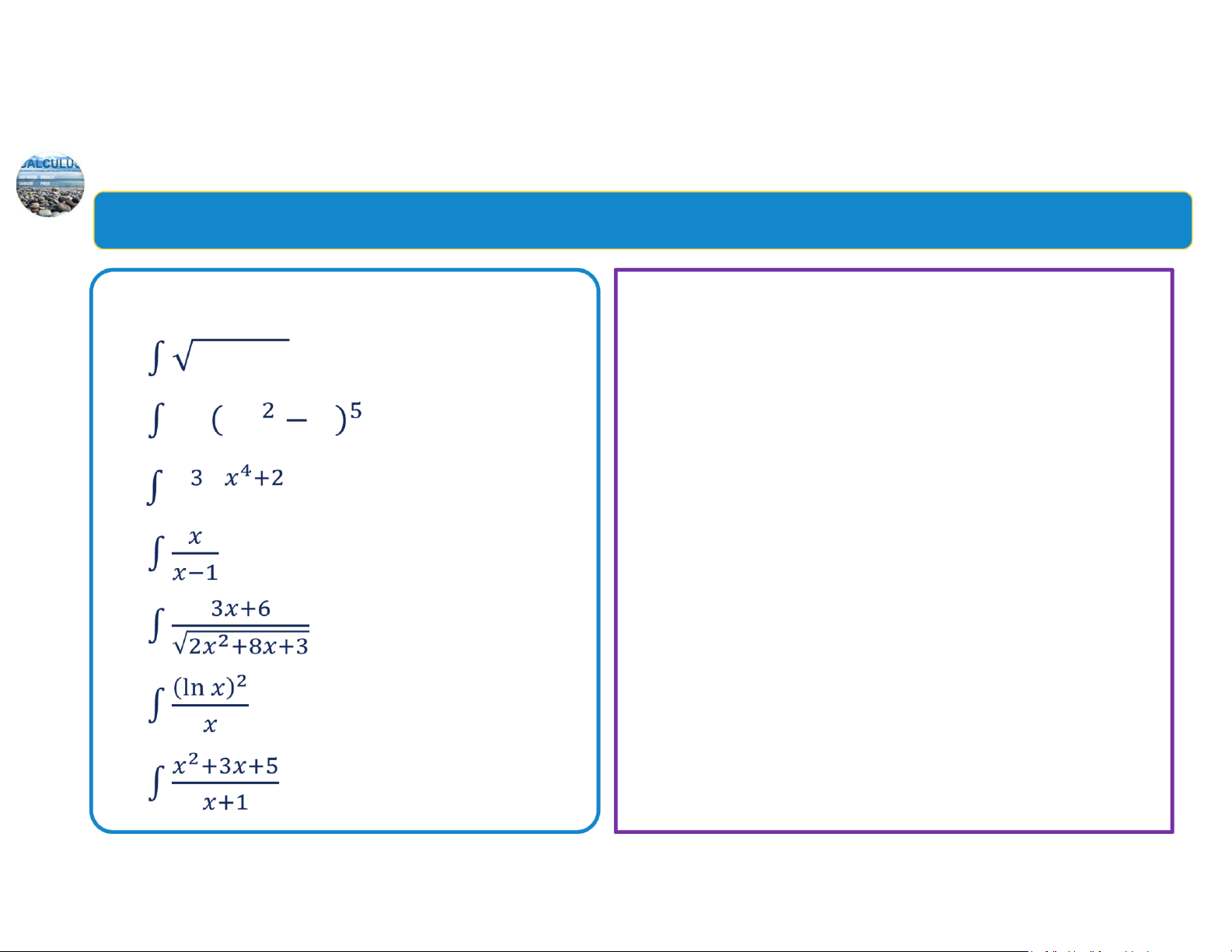
Tính các tích phân: 1. Chọn 𝑢 sao cho 𝑢′ là một phần của hàm lấy tích phân 𝑓 𝑥 . a. 2𝑥 7 𝑑𝑥
2. Chọn 𝑢 là một phần của 𝑓 𝑥
b. 8𝑥 4𝑥 3 𝑑𝑥 (phần làm cho tích phân khó tính trực tiếp), như: biểu thức
c. 𝑥 𝑒 𝑑𝑥 dưới dấu căn, phần mẫu của
phân thức, phần mũ của hàm d. 𝑑𝑥 mũ,… e.
𝑑𝑥 3. Không nênlấy tích phân vì nhặt 𝑢 là toàn bư vậy
thộườhàmng dẫn ến một tích phân phức tạp f. 𝑑𝑥 hơn. lOMoAR cPSD| 44919514 g.
𝑑𝑥 4. Hãy kiên trì và thbiến khác nhau. ử các phép ổi 5
Downloaded by Trang Thu (htttc1k21@gmail.com) lOMoAR cPSD| 44919514 lOMoAR cPSD| 44919514
Ví dụ: Tìm giá từ tốc ộ thay ổi giá
Người ta ước lượng được tốc độ thay đổi mức giá 𝑝
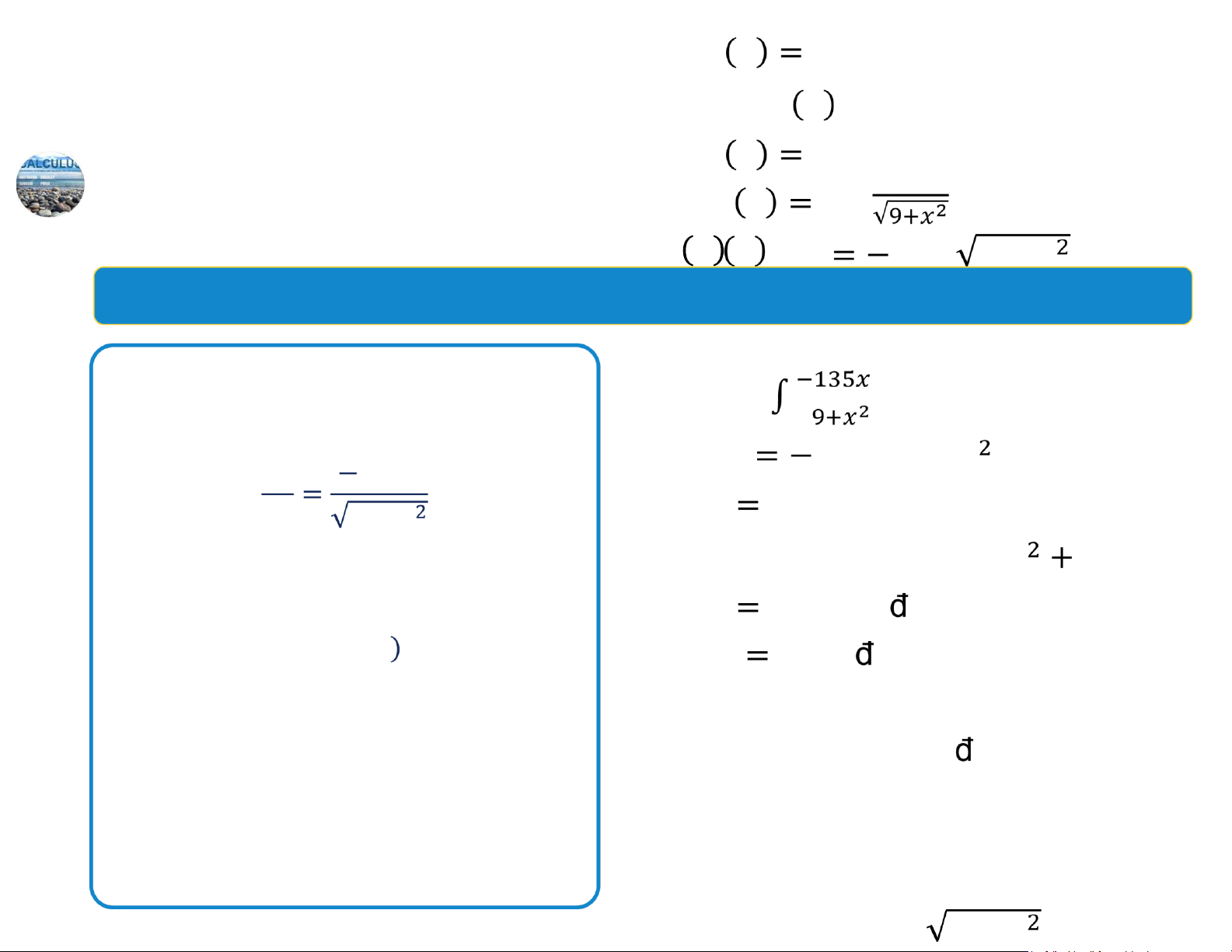
a. Tìm hàm cầu 𝑝 𝑥 . c. 𝑝 𝑥 a. 𝑝 𝑥 𝑑𝑥
(đô la) của mỗi đơn vị một loại hàng hóa là: 𝑑𝑝 135𝑥 135 9 𝑥 𝐶 𝑑𝑥 9𝑥 𝑝 4 30 ⇒ 𝐶 705
với 𝑥 đo bằng (trăm) đơn vị là lượng cầu Vậy 𝑝 𝑥 135 9 𝑥 705
của người tiêu dùng (số lượng hàng hóa được mua ở 132.24 ( ô la)
mức giá đó). Giả sử lượng b. 𝑝 3 cầu là 400 đơn vị 𝑥4 300 ( ô la)
khi giá là 30 đô 𝑝 0 la mỗi đơn vị. 20 ⇒ 𝑥 4.09
b. Với mức giá nào thì lượng cầu là 300
Vậy ở mức giá 20 ô la thì lượng
đơn vị? Ở mức giá nào thì lượng cầu bị cầu xấp xỉ 409 ơn vị sản phẩm. triệt tiêu?
c. Lượng cầu là bao nhiêu ở mức giá 20 đô la mỗi đơn vị? 7
Downloaded by Trang Thu (htttc1k21@gmail.com) lOMoAR cPSD| 44919514
3. Mô hình điều chỉnh giá
❖ Xét thị trường một loại hàng hóa: 𝑝 :
giá mỗi ơn vị hàng hóa.
𝑆 𝑝 : lượng cung hàng hóa tại mức giá 𝑝.
𝐷 𝑝 : lượng cầu hàng hóa tại mức giá 𝑝.
❖ Trong phân tích ộng các mô hình kinh tế, các ại lượng ều thay ổi
theo thời gian: 𝑝 𝑡 , 𝑆 𝑝 𝑡 , 𝐷 𝑝 𝑡 .
❖ Mô hình iều chỉnh giá Evans: giả thiết tốc ộ thay ổi của giá 𝑝
theo thời gian tỷ lệ thuận với lượng thiếu hụt 𝐷 𝑆, tức là: 𝑑𝑝 𝑘𝐷 𝑆 ; 𝑘 0 𝑑𝑡 Downloaded by Trang Thu (htttc1k21@gmail.com) lOMoAR cPSD| 44919514 8
Ví dụ: Nghiên cứu mô hình iều chỉnh giá
Byung‐Soon là người quản lý bán hàng một loại
chứng tỏ rằng 𝑝 𝑡 tiệm cận về 𝑝 trong dài hạn (khi
sản phẩm với mức giá ban đầu là $5 mỗi đơn 𝑡 → ∞).
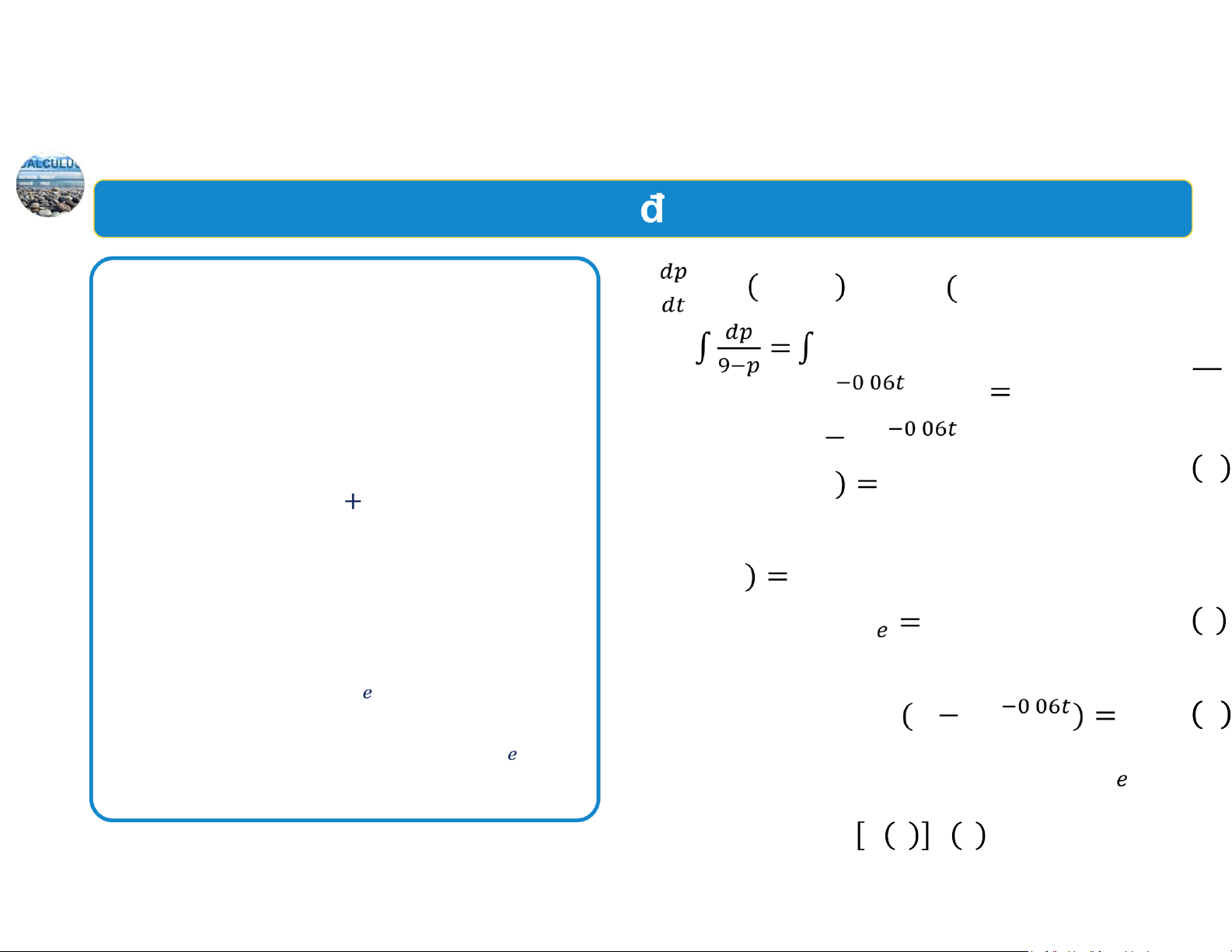
vị. Cô ấy dự kiến sau 𝑡 tháng, tốc độ thay đổi a. 𝑘𝐷 𝑆 0.06 9 𝑝
giá 𝑝 𝑡 bằng 2% của mức thiếu hụt 𝐷 𝑆, trong
đó lượng cung 𝑆 𝑝 và lượng cầu 𝐷 𝑝 sản phẩm ⇒ 0.06𝑑𝑡
(tính theo nghìn đơn vị) được cho bởi: ⇒𝑝 9 𝐶𝑒 . ; 𝑝 0 5 ⇒ 𝐶 4 𝐷 50𝑝
và 𝑆 23 2𝑝 với 0 𝑝9.
a. Thiết lập và giải bài toán giá trị ban đầu để Vậy 𝑝 𝑡 9 4𝑒 . (đô la). tìm mức giá 𝑝 𝑡 . b. Khi 𝑡 6: 𝑝 6 6.21
b. Doanh thu Byung‐Soon dự kiến thu được
từ việc bán sản phẩm này 6 tháng sau là 𝑅 𝑡 1,000𝐷 𝑝 𝑡 𝑝 𝑡 bao nhiêu? ⇒ 𝑅 6 271,936 (đô la).
c. Mức giá cân bằng 𝑝 (mức giá để lượng
cung bằng lượng cầu) là bao nhiêu? Hãy
c. D 𝑝 𝑆 𝑝 ⇒ 𝑝 9 (đô la) Mặt khác:
Downloaded by Trang Thu (htttc1k21@gmail.com) lOMoAR cPSD| 44919514 lim 𝑝 𝑡 lim 9 4𝑒 . 9
Vậy trong dài hạn 𝑝 𝑡 tiệm cận với 𝑝 . →→ 9
Bài tập: Kế hoạch ầu tư
Một nhà ầu tư thực hiện gửi tiết kiệm ều ặn số tiền 𝐷 ô la mỗi năm vào một
tài khoản ể kiếm lời với lãi suất tính gộp liên tục hàng năm là 𝑟.
a. Giải thích tại sao tài khoản tăng với tốc ộ 𝑟𝑉 𝐷, với 𝑉 𝑡 là giá trị của tài
khoản sau 𝑡 năm tính từ lần gửi ầu tiên. Giải phương trình vi phân ể tìm 𝑉 𝑡 .
b. Amanda muốn nghỉ hưu sau 20 năm nữa. Để xây dựng quỹ hưu cho mình,
cô ấy gửi ều ặn hàng năm số tiền 8,000 ô la. Nếu lãi suất hiện hành ổn
ịnh ở mức 4%/năm và ược tính gộp liên tục thì cô ấy sẽ có bao nhiêu tiền
trong tài khoản sau 20 năm nữa?
c. Anibal ước tính rằng anh ấy cần 800,000 ô la ể nghỉ hưu. Nếu tỷ lệ lãi
suất hiện hành là 5%/năm và ược tính gộp liên tục thì anh ấy cần gửi ều
ặn hàng năm bao nhiêu tiền ể có thể về hưu sau 30 năm nữa? 10 Downloaded by Trang Thu (htttc1k21@gmail.com) lOMoAR cPSD| 44919514 Tô
i t i n r ằ ng kho ả ng
m ộ tn ử an h ữ ng gì
khác bi ệ tg i ữ a
doanh nhân thành đ ạ t và
khôn g t hàn h đ ạ tl à
s ự kiên trì t uy ệ t đ ố i . Steve Jobs
Downloaded by Trang Thu (htttc1k21@gmail.com)




