Bài 3: Hàm số mũ. Hàm số lôgarit | Giáo án Toán 11 Cánh diều

Trường THPT số 1 Bắc Hà
Họ và tên giáo viên: Hoàng Văn Dũng
Tổ: Khoa học tự nhiên Đỗ Hải Yến
KẾ HOẠCH BÀI DẠY
TÊN BÀI DẠY: BÀI 3. HÀM SỐ MŨ. HÀM SỐ LOGARIT
Môn học/Hoạt động giáo dục: Toán; lớp: 11
Thời gian thực hiện: (03 tiết) I. MỤC TIÊU:
1. Kiến thức, kĩ năng:
Học xong bài này, HS đạt các yêu cầu sau:
- HS ôn tập lại các kiến thức trọng tâm trong: Phép tính lũy thừa với số mũ thực; phép
tính lôgarit; hàm số mũ, hàm số lôgarit; phương trình, bất phương trình mũ và lôgarit.
- Vận dụng, giải quyết một số vấn đề toán học và thực tiễn gắn với các kiến thức có trong chương VI. 2. Năng lực
Năng lực chung:
- Năng lực tự chủ và tự học trong tìm tòi khám phá
- Năng lực giao tiếp và hợp tác trong trình bày, thảo luận và làm việc nhóm
- Năng lực giải quyết vấn đề và sáng tạo trong thực hành, vận dụng.
Năng lực riêng:
- Tư duy và lập luận toán học: HS sẽ được đặt vào các tình huống thực tế liên quan đến
hàm số mũ và hàm số lôgarit. Bằng cách áp dụng tư duy logic và lập luận toán học, HS sẽ phân
tích và suy luận để hiểu rõ hơn về các khái niệm và quy tắc trong lĩnh vực này.
- Mô hình hóa toán học, giải quyết vấn đề toán học: HS sẽ được thách thức trong việc
xây dựng các mô hình toán học để mô phỏng và giải quyết các bài toán liên quan đến hàm số mũ
và hàm số lôgarit. Bằng cách áp dụng kiến thức đã học, HS sẽ tìm ra cách giải quyết các vấn đề
và khám phá mối quan hệ giữa các yếu tố trong các bài toán này.
- Giao tiếp toán học: HS được khuyến khích tham gia vào các hoạt động nhóm, trao đổi ý
kiến và thảo luận với nhau về các khái niệm và phương pháp giải quyết trong các bài toán liên
quan đến hàm số mũ, hàm số lôgarit; phương trình, bất phương trình mũ và lôgarit. Điều này
giúp các em rèn kỹ năng giao tiếp toán học, trình bày ý tưởng và thảo luận với nhóm để tìm ra
các cách tiếp cận tốt nhất.
- Sử dụng công cụ, phương tiện học toán: Xuyên suốt bài học. 3. Phẩm chất
- Có ý thức học tập, ý thức tìm tòi, khám phá và sáng tạo, có ý thức làm việc nhóm, tôn
trọng ý kiến các thành viên khi hợp tác.
- Chăm chỉ tích cực xây dựng bài, có trách nhiệm, chủ động chiếm lĩnh kiến thức theo sự hướng dẫn của GV.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU
1. Đối với GV: SGK, Tài liệu giảng dạy, giáo án, đồ dùng dạy học.
2. Đối với HS: SGK, SBT, vở ghi, giấy nháp, đồ dùng học tập (bút, thước...), bảng nhóm, bút viết bảng nhóm.
III. TIẾN TRÌNH DẠY HỌC
1. HOẠT ĐỘNG 1. KHỞI ĐỘNG a) Mục tiêu:
- Tạo hứng thú, thu hút HS tìm hiểu nội dung bài học.
b) Nội dung: Một doanh nghiệp gửi ngân hàng 1 tỉ đồng với kì hạn 1 năm, lãi suất 6,2%/năm.
Giả sử trong suốt n năm ( *
nΕ ), doanh nghiệp đó không rút tiền ra và số tiền lãi sau mỗi năm
sẽ được nhập vào vốn ban đầu. Biết rằng lãi suất không thay đổi trong thời gian này.
Mối liên hệ giũa số tiền doanh nghiệp đó có đượ (cả gốc và lãi) với số năm gửi ngân hàng gợi
nên hàm số nào trong toán học?
c) Sản phẩm: HS trả lời được hàm số liên quan.
d) Tổ chức thực hiện:
Chuyển giao
- GV cho học sinh chép đề suy nghĩ về câu hỏi trên - HS suy nghĩ
Thực hiện - HS tìm câu trả lời
- Mong đợi: Kích thích sự tò mò của HS
Báo cáo thảo
GV gọi một số HS trả lời, HS khác nhận xét, bổ sung. luận
GV đánh giá kết quả của HS, trên cơ sở đó dẫn dắt HS vào bài học mới:
Đánh giá, nhận “Mối liên hệ giữa số tiền gửi và số năm gửi, lãi suất chính là hàm số mũ.
xét, tổng hợp
Đó là hàm số mà hôm nay chúng ta cùng tìm hiều”
Bài mới: Hàm số mũ. Hàm số logarit
2. HOẠT ĐỘNG 2. HÌNH THÀNH KIẾN THỨC MỚI I. HÀM SỐ MŨ 1. Định nghĩa
Hoạt động 2.1: Hình thành công thức tính tiền gửi ngân hàng trong 1 bài toán khởi động
a) Mục tiêu: Học sinh tính được số tiền cả gốc và lãi gửi ngân hàng sau 1, 2 năm từ đó xây
dựng nên công thức tính tiền gửi tổng quát. b) Nội dung
Vẫn bài toán khởi động. Em hãy trả lời câu hỏi sau
CH1: Tính số tiền doanh nghiệp đó có được sau 1 năm, 2 năm, 3 năm;
CH2: Dự đoán công thức tính số tiền doanh nghiệp đó có được sau n năm.
c) Sản phẩm: HS trả lời được câu hỏi 1, 2
d) Tổ chức thực hiện: Hoạt động nhóm
Chuyển giao
- GV cho học sinh chép đề suy nghĩ về câu hỏi trên - HS suy nghĩ
- HS tìm câu trả lời, tuy nhiên sẽ khó để giải quyết câu hỏi 2.
Thực hiện
- Mong đợi: Kích thích sự tò mò của HS khi giải quyết câu 2
+ Huy động các kiến thức đã học để để suy luận ở bài toán đối với số năm là n.
Báo cáo thảo
GV gọi một số HS trả lời, HS khác nhận xét, bổ sung. luận
GV đánh giá kết quả của HS, trên cơ sở đó dẫn dắt HS vào bài học mới:
“Mối liên hệ giữa số tiền gửi và số năm gửi, lãi suất chính là hàm số mũ
Đánh giá, nhận hay là công thức tổng quát mà các em vừa suy nghĩ tìm ra. Đó là hàm số mà
xét, tổng hợp
hôm nay chúng ta cùng tìm hiều”
Nhận xét: Tương ứng mỗi giá trị x với giá trị (1,062)x y = xác định một
hàm số, hàm số đó gọi là hàm số mũ cơ số 1,062
Hoạt động 2.2: Định nghĩa, tập xác định hàm số mũ
a. Mục tiêu: Học sinh biết được định nghĩa, tập xác định của hàm số mũ. b. Nội dung
Cho số thực a(a > 0, a ¹ 1). Hàm số x
y = a được gọi là hàm số mũ cở số a .
Tập xác định của hàm số mũ x
y = a (a > 0, a ¹ 1) là ! .
Ví dụ 1. Trong các hàm số sau, hàm số nào là hàm số mũ? a) 2 y = x b) ( 3)x y = ; 1 c) y = x d) 5 y = x .
c) Sản phẩm: HS trả lời được đâu là hàm số mũ (Đáp án B)
d) Tổ chức thực hiện:
- GV cho học sinh đọc sgk và phát biểu định nghĩa hàm số mũ, tập xác
Chuyển giao định
Sau đó nêu ra ví dụ 1 để học sinh làm - HS đọc SGK
Thực hiện
- HS phát biểu trả lời câu hỏi của giáo viên, nêu định nghĩa
Vận dụng định nghĩa, suy nghĩ giải quyết ví dụ 1
Báo cáo thảo luận GV gọi một số HS trả lời, HS khác nhận xét, bổ sung.
Đánh giá, nhận
GV đánh giá kết quả của HS
xét, tổng hợp
Hoạt động 2.3: Đồ thị và tính chất
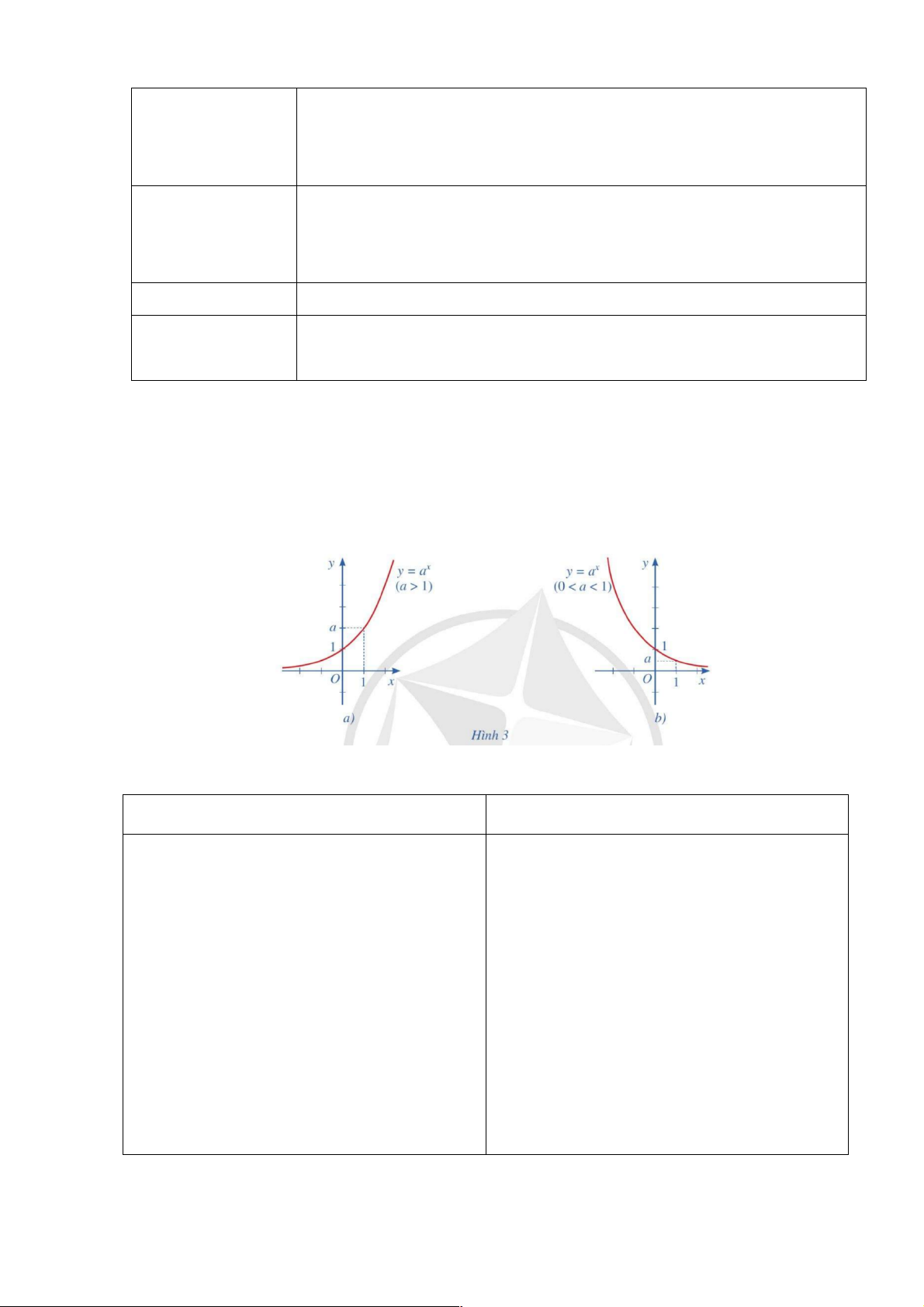
a. Mục tiêu: Học sinh biết được đồ thị và tính chất của hàm số mũ b. Nội dung Đồ thị hàm số x
y = a (a > 0, a ¹ 1) là một đường cong liền nét, cắt trục tung tại điểm
có tung độ bằng 1 , nằm ở phía trên trục hoành và đi lên nếu a > 1, đi xuống nếu 0 < a < 1.
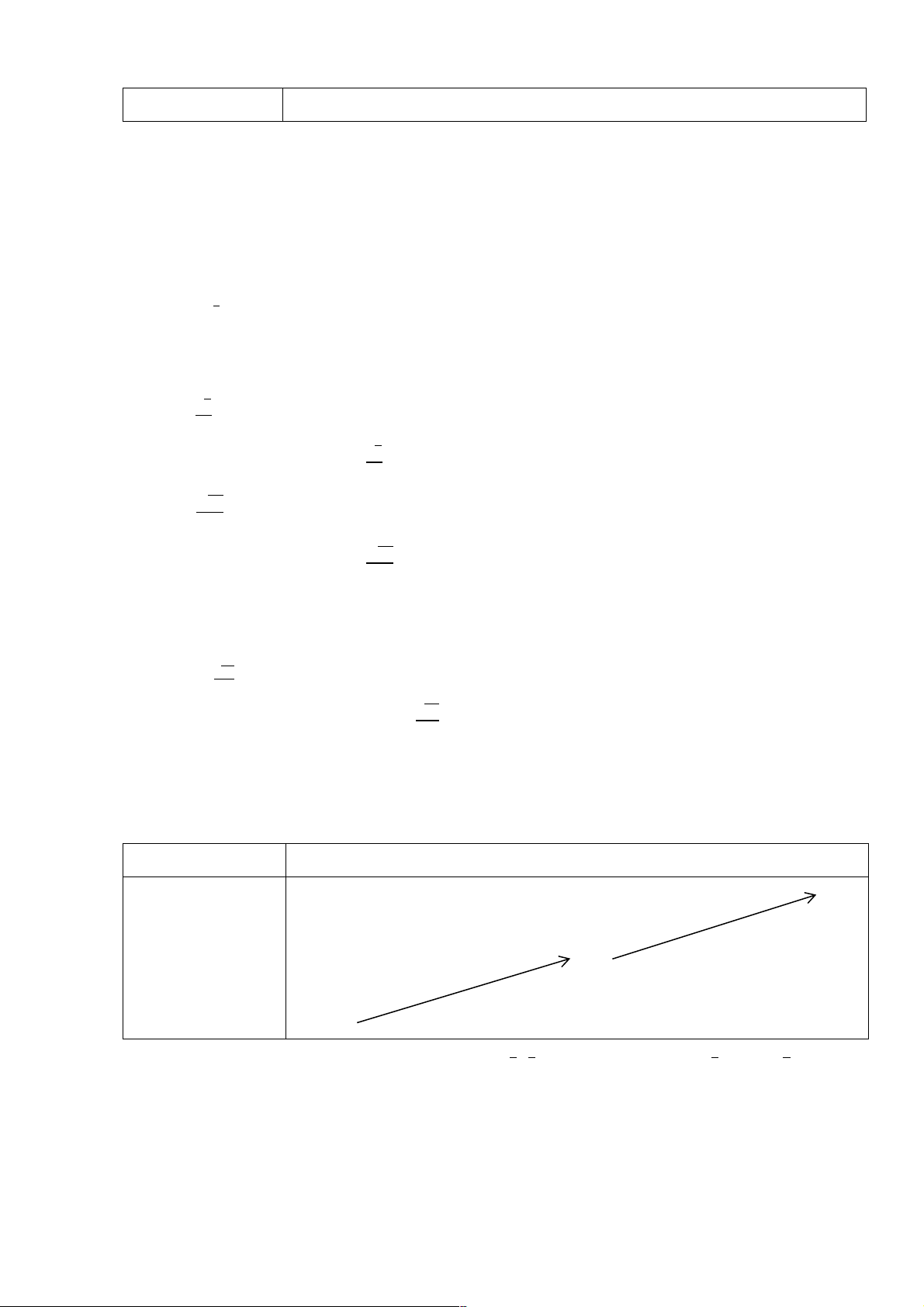
Nhận xét : Cho hàm số mũ x
y = a (a > 0, a ¹ 1). x
y = a (a >1) x
y = a (0 < a <1)
• Tập xác định: R ; tập giá trị: (0; ¥ + ).
• Tập xác định: R ; tập giá trị: (0; ¥ + ). • Tính liên tục • Tính liên tục Hàm số x
y = a (a >1) là hàm số liên Hàm số x
y = a (0 < a <1) là hàm số tục trên R . liên tục trên R .
• Giới hạn đặc biệt
• Giới hạn đặc biệt lim x a = 0, lim x a = ¥ + . lim x a = ¥ + , lim x a = 0. x ¥ ®- x® ¥ + x ¥ ®- x® ¥ + • Sự biến thiên • Sự biến thiên
Hàm số đồng biến trên R .
Hàm số nghịch biến trên R . • Bảng biến thiên • Bảng biến thiên Chú ý :
Từ tính liên tục và sự biến thiên của hàm số mũ, ta có thể chứng minh được mệnh đề sau:
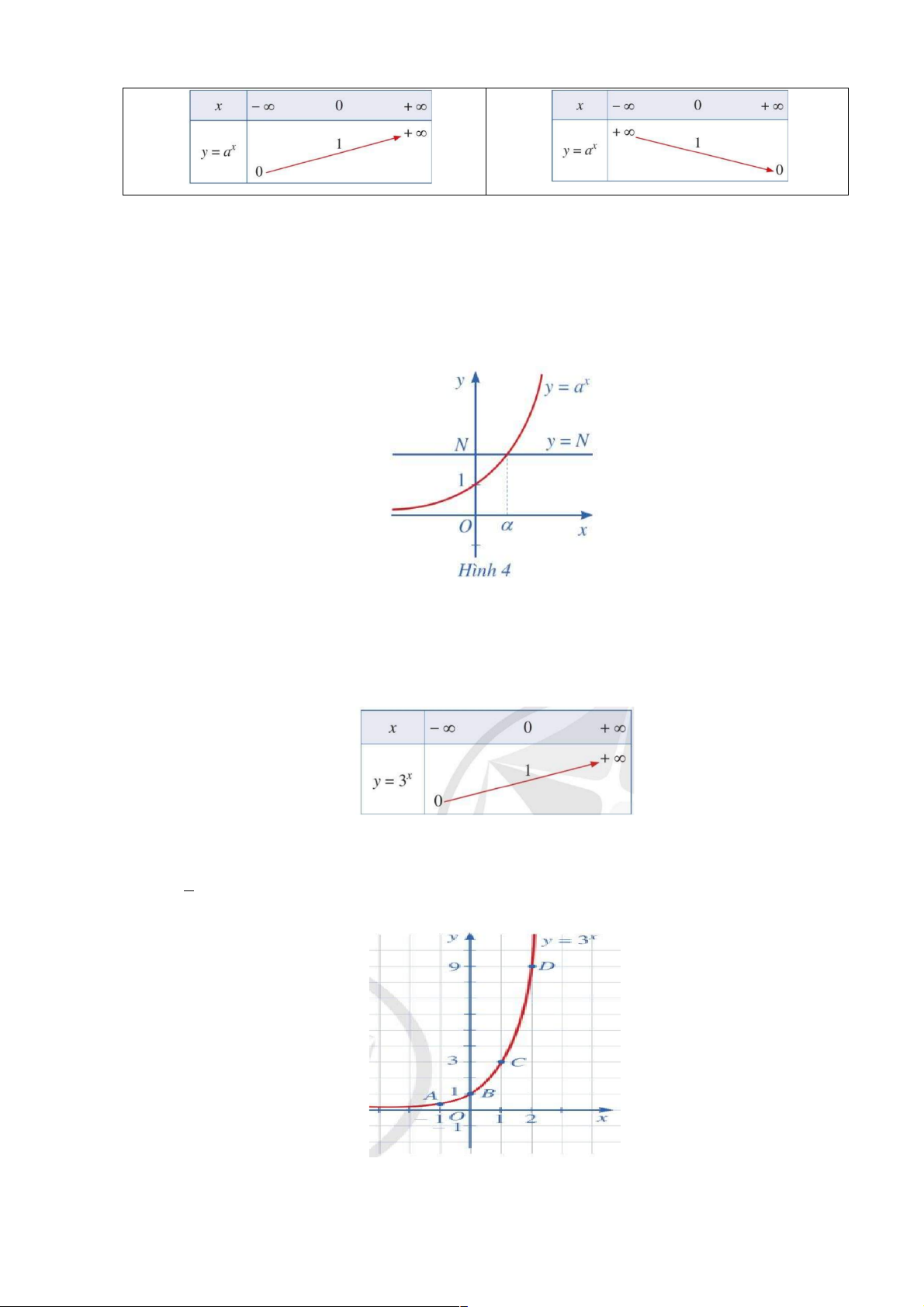
Với mỗi N > 0, đường thẳng y = N cắt đồ thị hàm số mũ x
y = a (a > 0, a ¹ 1) tại một và chỉ
một điểm (Hình 4). Nói cách khác, ta có: Với mỗi N > 0, tồn tại duy nhất số thực a sao cho aa = N . Ví dụ 2 :
Lập bảng biến thiên và vẽ đồ thị hàm số: 3x y = Giải Vì hàm số 3x
y = có cở số 3 > 1 nên ta có bảng biến thiên như sau: Đồ thị của hàm số 3x
y = là một đường cong liền nét đi qua các điểm æ 1 ö A 1 - ; , B ç ÷ (0 )
;1 ,C (1;3), D(2;9) (Hình 5). è 3 ø Ví dụ 3 :
Trong Vật lí, sự phân rã của các chất phóng xạ được cho bởi công thức: t ( ) æ 1 T ö m t = m .
; trong đó m là khối lượng chất phóng xạ bạn đầu (tại thời điểm t = 0 ), m(t) 0 ç ÷ è 2 ø 0
là khối lượng chất phóng xạ tại thời điểm t và T là chu kì bán rã ( Nguồn: Giải tích 12,
NXBGD Việt Nam, 2021). Hạt nhân Poloni ( Po) là chất phóng xạ a có chu kì bán rã là 138
ngày ( Nguồn: Vật lí 12 , NXBGD Việt Nam, 2021). Giả sử lúc đầu có 100 gam Poloni. Tính
khối lượng Poloni còn lại sau 100 ngày theo đơn vị gam (làm tròn kết quả đến hàng phần mười). Giải:
Khối lượng Poloni còn lại sau 100 ngày là : 100 138 æ 1 ö m(100) =100. » 60,5 ç ÷ ( g) è 2 ø
c) Sản phẩm: học sinh nêu được dáng điệu, tính chất của hàm số mũ trong các trường hợp, giải
quyết được ví dụ 2, ví dụ 3
d) Tổ chức thực hiện: Cho hàm số mũ 2x y = .
a) Tìm giá trị y tương ứng với giá trị của x trong bảng sau:
b) Trong mặt phẳng tọa độ Oxy , hãy biểu diễn các điểm trong bảng giá trị ở câu a.
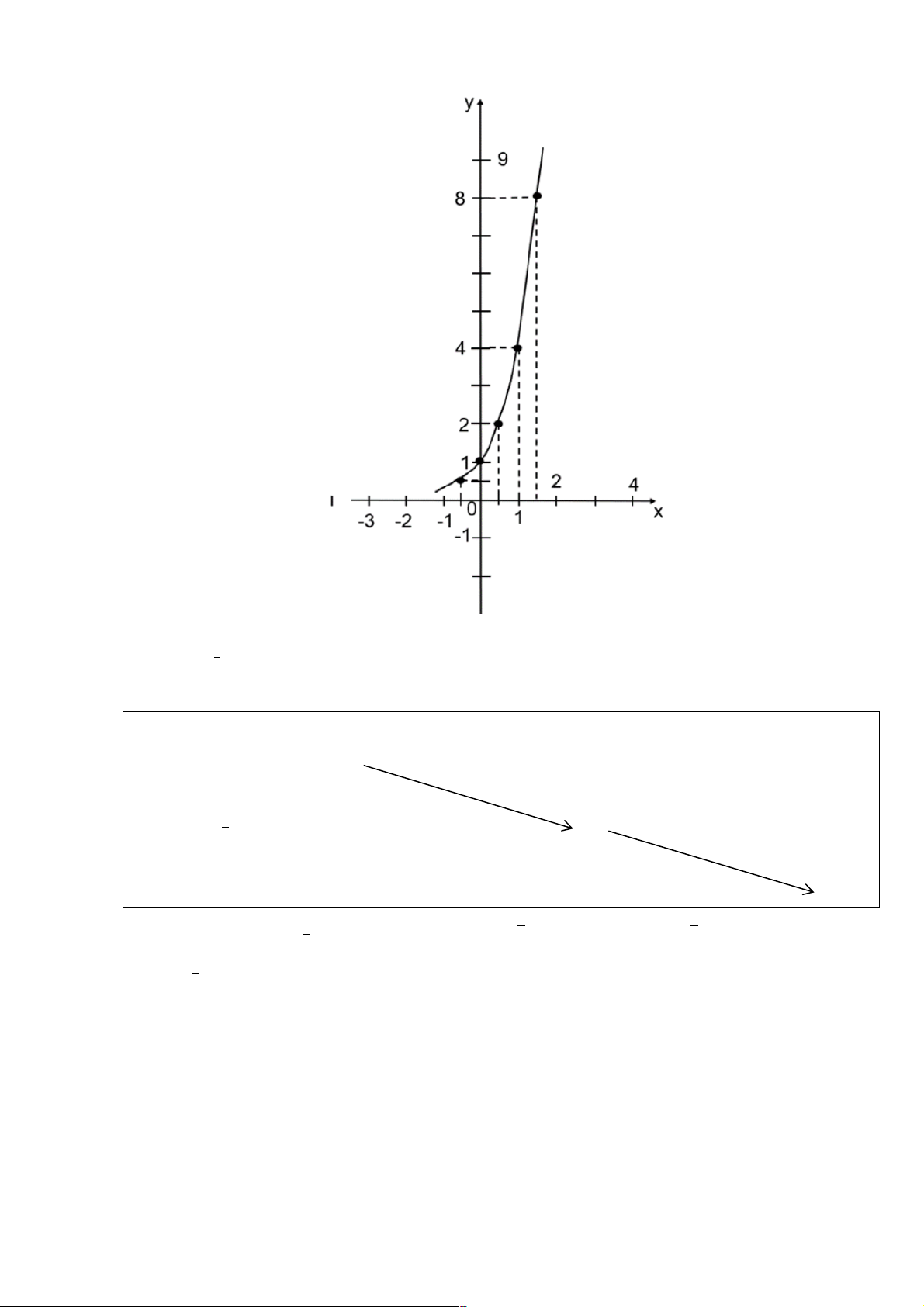
Bằng cách làm tương tự, lấy nhiều điểm ( ;2x x
) với xÎR và nối lại, ta
được đồ thị hàm số 2x y = (Hình 1).
Chuyển giao
c) Cho biết tọa độ giao điểm của đồ thị hàm số 2x y =
với trục tung và vị trí
của đồ thị hàm số đó so với trục hoành.
d) Quan sát đồ thị hàm số 2x y = , nêu nhận xét về: • lim 2x, lim 2x x ¥ ®- x®+¥ •
Sự biến thiên của hàm số 2x y =
và lập bảng biến thiên của hàm số đó. Nêu nhận xét? æ 1 x ö
3. Cho hàm số mũ y = . ç ÷ è 2 ø
a) Tìm giá trị y tương ứng với giá trị của x trong bảng sau: x 3 - 2 - 1 - 0 1 y ? ? ? ? ?
b) Trong mặt phẳng tọa độ Oxy , hãy biểu diễn các điểm ( ; x y) trong bảng giá trị ở câu a. æ 1 x ö æ ö
Bằng cách làm tương tự, lấy nhiều điểm ç ;
x ç ÷ ÷ với xÎR và nối lại, ta ç 2 ÷ è ø è ø æ 1 x ö
được đồ thị hàm số y = (Hình 2). ç ÷ è 2 ø æ 1 x ö
c) Cho biết tọa độ giao điểm của đồ thị hàm số y = với trục tung và ç ÷ è 2 ø
vị trí của đồ thị hàm số đó so với trục hoành. æ 1 x ö
d) Quan sát đồ thị hàm số y = , nêu nhận xét về: ç ÷ è 2 ø æ 1 x ö æ 1 x ö • lim , lim ç ÷ ç ÷ x ¥ ®- è 2 x®+¥ ø è 2 ø æ 1 x ö •
Sự biến thiên của hàm số y =
và lập bảng biến thiên ç ÷ è 2 ø của hàm số đó Nêu nhận xét?
Nêu ra ví dụ 2, Ví dụ 3 - HS quan sát, suy nghĩ
- HS phát biểu trả lời câu hỏi của giáo viên
Nhận xét: Đồ thị hàm số 2x y =
là một đường cong liền nét, cắt trục tung
tại điểm có tung độ bằng 1 , nằm ở phía trên trục hoành và đi lên kể từ trái sang phải.
Thực hiện æ 1 x ö
Nhận xét: Đồ thị hàm số y =
là một đường cong liền nét, cắt trục ç ÷ è 2 ø
tung tại điểm có tung độ bằng 1, nằm ở phía trên trục hoành và đi xuống kể từ trái sang phải.
Vận dụng định nghĩa, suy nghĩ giải quyết ví dụ 2,3
Báo cáo thảo
* Đại diện nhóm báo cáo, các nhóm còn lại theo dõi thảo luận. luận
- GV nhận xét thái độ làm việc, phương án trả lời của học sinh, ghi nhận và
Đánh giá, nhận tuyên dương học sinh có câu trả lời tốt nhất. Động viên các học sinh còn lại
xét, tổng hợp
tích cực, cố gắng hơn trong các hoạt động học tiếp theo - Chốt kiến thức TIẾT 2.
1. HOẠT ĐỘNG 1. MỞ ĐẦU a) Mục tiêu:
- Tạo hứng thú, giúp học sinh nhớ lại những phần kiến thức bổ trợ quan trong liên quan đến
logarit để cho bài học mới được thuận lợi.
b) Nội dung: HS thực hoàn thiện các công thức về logarit đã học được để dưới dạng điền khuyết. Phiếu học tập
Với số thực dương a khác 1, số thực dương b , ta có log 1 = ....; log a = .... log c
a = .....; loga b a = .... a a a
Với ba số thực dương a, ,
m n và a ¹ 1, ta có: log mn = a ( ) ...... æ m ö log = ..... a ç ÷ è n ø
Cho a > 0, a ¹ 1,b > 0. Với mọi số thực a , ta có: log ba = ..... a
Cho a > 0, a ¹ 1,b > 0. Với mọi số nguyên dương n ³ 2 , ta có: log n b = .... . a log b
Với a,c là hai số thực dương khác 1 và b là số thực dương, ta có: ....... c = log a c
Với a > 0 và a ¹ 1,b > 0 và b ¹ 1,c > 0,a ¹ 0, ta có những công thức sau:
- log b×log c = .....; a b 1 - ..... = ; log a b - log = a b ...... a
c) Sản phẩm: HS hoàn thiện đầy đủ công thức, ghi nhớ công thức.
d) Tổ chức thực hiện: Tham gia dưới dạng 4 đội chơi thi xem đội nào nhanh nhất và trả lời
đúng nhiều nhất có thưởng.
- GV triển khai cuộc chơi và phát phiếu cho 4 đội (mỗi đội có 2 thành viên)
- Yêu cầu các đội hoàn thành phiếu trong thời gian nhanh nhất và đội nào
trả lời đúng và nhanh nhất sẽ có 1 phần thưởng. Hs không tham gia làm
Chuyển giao
khán giả cũng làm ra nháp để nhận xét và cũng có phần thưởng nếu nhận xét đúng.
Thời gian thi là tối đa là 3p
Ban giám khảo sẽ là các bạn có năng lực và giáo viên
Khi có hiệu lệnh các đội bắt đầu
Thực hiện
HS giám khảo quan sát Hs còn lại làm ra nháp để chuẩn bị nhận xét
GV gọi một số HS nhận xét, bổ sung. Sau đó là đánh giá của ban giám
Báo cáo thảo luận khảo. Chọn ra đội thắng cuộc
GV đánh giá tinh thần, ý thức của các đội chơi và khán giả , tuyên dương
những bạn nắm vững kiến thức, tự tin,
Đánh giá, nhận
“Để bài học hôm nay các em nắm kiến thức được thông suốt thì các em cần
xét, tổng hợp
nắm chắc kiến thức, công thức mà các em đã vừa ôn lại thông qua trò chơi ”
Vào bài mới: Hàm số mũ.Hàm số logarit (Phần hàm số logarit)
2. HOẠT ĐỘNG 2. HÌNH THÀNH KIẾN THỨC II. HÀM SỐ LÔGARIT 1. Định nghĩa
Hoạt động 2.1: Bài toán tìm giá trị tương ứng
a) Mục tiêu: Học sinh tính giá trị y tương ứng với giá trị x cho trước thông qua bảng b) Nội dung
Tìm giá trị y tương ứng với giá trị x trong bảng sau: x 1 2 4 8 y = log x ? ? ? ? 2
c) Sản phẩm: HS tìm được các giá trị y và điền vào bảng
d) Tổ chức thực hiện: Hoạt động nhóm
Chuyển giao
- GV cho học sinh chép đề suy nghĩ về câu hỏi trên - HS suy nghĩ
Thực hiện
- Mong đợi: Hs sử dụng kiến thức biến đổi logarit đã học để trả lời đúng
Báo cáo thảo
GV gọi một số HS trả lời, HS khác nhận xét, bổ sung. luận
GV đánh giá kết quả của HS, trên cơ sở đó dẫn dắt HS vào bài học mới:
Nhận xét: Tương ứng với mỗi giá trị x dương với giá trị y = log x xác
Đánh giá, nhận 2
định một hàm số, hàm số đó gọi là hàm số logarit cơ số 2
xét, tổng hợp
Dẫn dắt “Để hiểu rõ hơn thế nào là hàm số logarit ta đi vào tìm hiểu định nghĩa”
Hoạt động 2.2: Định nghĩa, tập xác định hàm số logarit
a) Mục tiêu: Học sinh nắm được định nghĩa, tập xác định hàm số logarit b) Nội dung
Cho số thực a(a > 0,a ¹ )
1 . Hàm số y = log x được gọi là hàm số lôgarit cơ số a a
Tập xác định của hàm số lôgarit y = log x a > a ¹ (0;+¥) a ( 0, )1 là
Ví dụ 4: Trong các hàm số sau, hàm số nào là hàm số lôgarit? a) y = log 5; b) y = log e; x x c) y = log x ; d) 5 y = x . 5 Giải
Trong các hàm số đã cho, chỉ có hàm số y = log x là có dạng hàm số lôgarit y = log x 5 a
(a = 5 > 0,a ¹ )1. Vậy hàm số y = log x là hàm số lôgarit. 5
c) Sản phẩm: HS nêu được đinh nghĩa, tập xác định, vân dụng trả lời được ví dụ 1
d) Tổ chức thực hiện:
- GV cho học sinh đọc SGK sau đó nêu định nghĩa, tập xác định
Chuyển giao
- Đưa ra ví dụ 1, yêu cầu các em suy nghĩ trả lời - HS suy nghĩ, trả lời
Thực hiện
Hs sử dụng kiến thức định nghĩa để làm ví dụ 1
Báo cáo thảo
GV gọi một số HS trả lời, HS khác nhận xét, bổ sung. luận
Đánh giá, nhận GV đánh giá kết quả của HS
xét, tổng hợp
Hoạt động 2.3: Đồ thị và tính chất
a) Mục tiêu: Học sinh biết được đồ thị và tính chất của hàm số logarit b) Nội dung
Đồ thị hàm số y = log x (a > 0,a ¹ )
1 là một đường cong liền nét, cắt trục hoành tại a
điểm có hoành độ bằng 1, nằm ở phía bên phải trục tung và đi lên nếu a > 1, đi xuống nếu
0 < a < 1 .
Nhận xét: Đồ thị hàm số y = log x là một đường cong liền nét, cắt trục hoành tại điểm có 1 2
hoành độ bằng 1, nằm ở phía bên phải trục tung và đi lên kể từ trái sang phải.
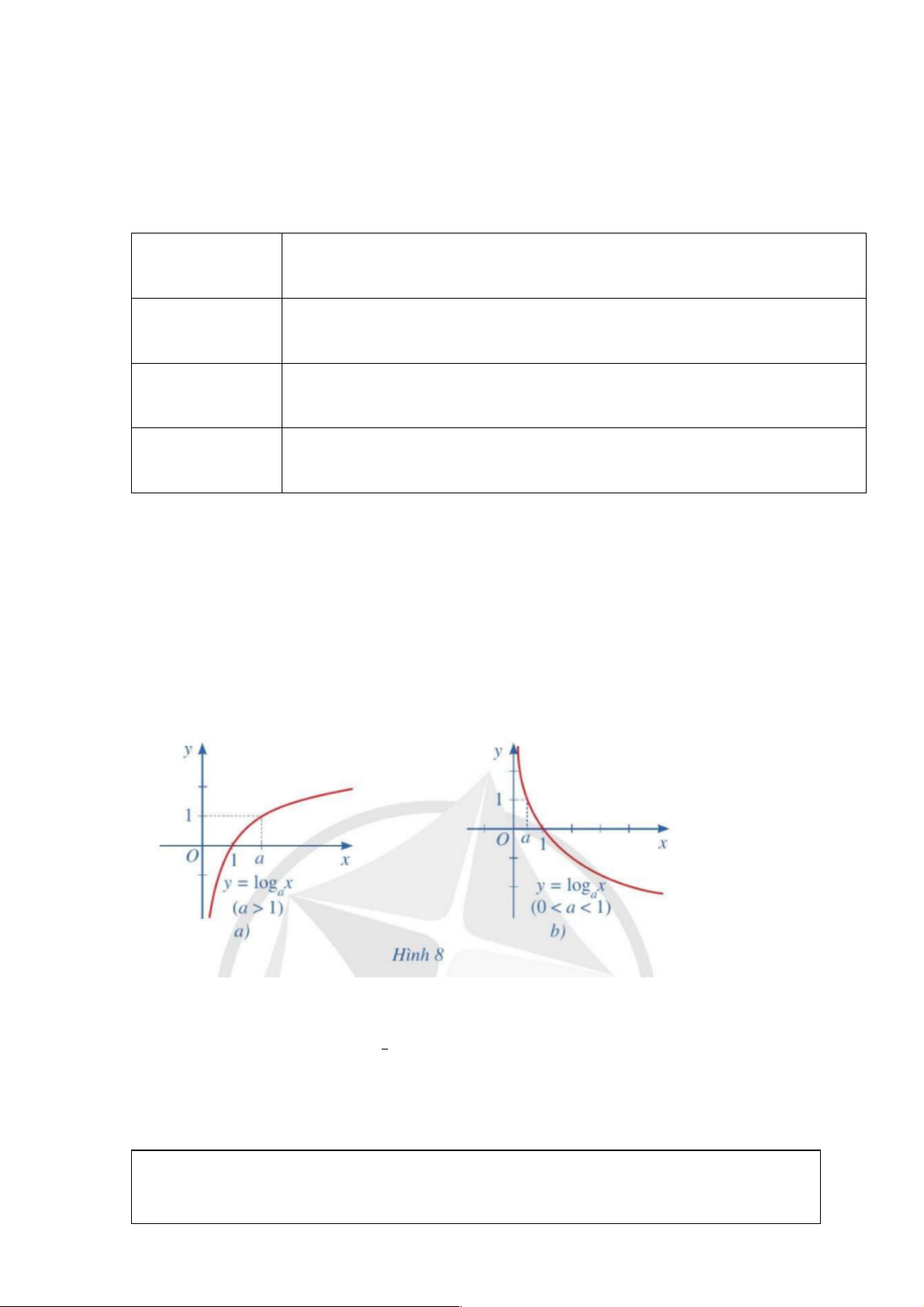
Trong trường hợp tổng quát ta có nhận xét sau (Hình 8):
Đồ thị hàm số y = log x (a > 0,a ¹ )
1 là một đường cong liền nét, cắt trục hoành tại a
điểm có hoành độ bằng 1, nằm ở phía bên phải trục tung và đi lên nếu a > 1, đi xuống
nếu 0 < a < 1 .
Nhận xét: Cho hàm số lôgarit y = log x với a > 0, a ¹ 1. a y = log , x a > y = log , x < a < a (0 )1 a ( )1
1. 1. Tập xác định: (0;+¥)
1. 1. Tập xác định: (0;+¥)
2. 2. Sự biến thiên. 2. 2. Sự biến thiên. 1 1 y ' = > 0, x " > 0 y ' = < 0, x " > 0 x ln a x ln a
®hàm số luôn đồng biến trên (0;+¥)
® hàm số luôn nghịch biến (0;+¥) Giới hạn đặc biệt: Giới hạn đặc biệt: lim log x = - , ¥ lim log x = + . ¥ lim log x = + , ¥ lim log x = - . ¥ + a a + a a x 0 ® x®+¥ x 0 ® x®+¥
Tiệm cận: Oy là tiệm cận đứng
Tiệm cận: Oy là tiệm cận đứng.
3. 3. Bảng biến thiên. 3. 3. Bảng biến thiên. 4. 4. Đồ thị 2. 3. 4. Đồ thị
c) Sản phẩm: HS biết được các dáng điệu đồ thị trong 2 trường hợp và tính chất của đồ thị
d) Tổ chức thực hiện:
Cho hàm số lôgarit y = log x. 2
Chuyển giao
a) Tìm giá trị y tương ứng với giá trị x trong bảng sau: x 0,5 1 2 4 8 y ? ? ? ? ?
b) Trong mặt phẳng tọa độ Oxy, biểu diễn điểm ( ; x y) trong
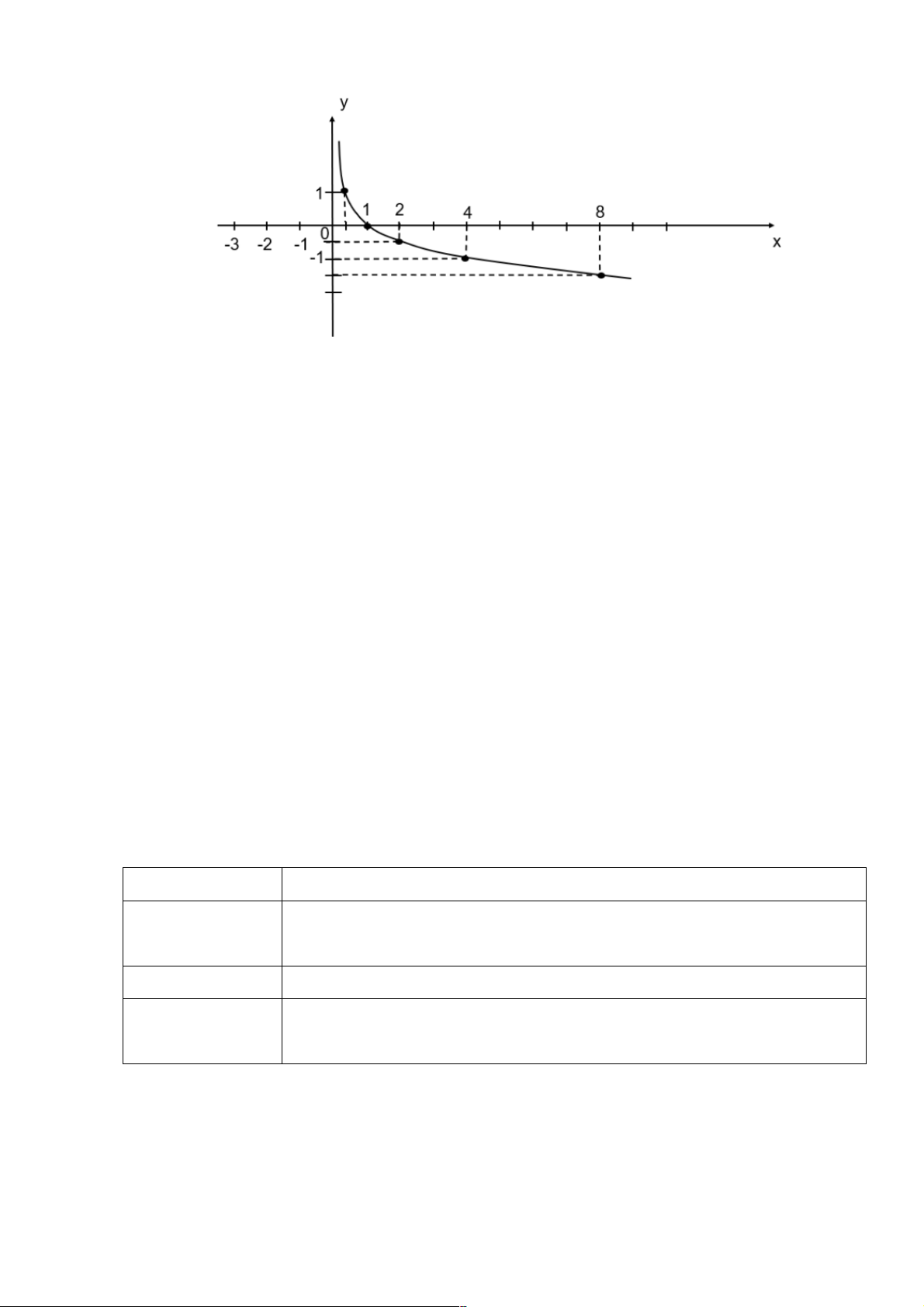
bảng giá trị ở câu a. Bằng cách làm tương ứng, lấy nhiều điểm ( ;l x og x x Î(0;+¥) 2 ) với
và nối lại, ta được đồ thị hàm số
y = log x (Hình 6). 2
c) Cho biết tọa độ giao điểm đồ thị hàm số y = log x với trục 2
hoanhfvaf vị trí của đồ thị hàm số đó so với trục tung.
d ) Quan sát đồ thị hàm số y = log x, nêu nhận xét về: 2 • lim log , x lim log ; x + 2 2 x 0 ® x®+¥ •
Sự biến thiên của hàm số y = log x và lập bảng biến thiên 2 của hàm số đó. Nêu nhận xét?
Cho hàm số lôgarit y = log x . 1 2 a)
Tìm giá trị y tương ứng với
giá trị x trong bảng sau: x 0,5 1 2 4 8 y ? ? ? ? ?
b) Trong mặt phẳng tọa độ Oxy, biểu diễn điểm ( ; x y) trong
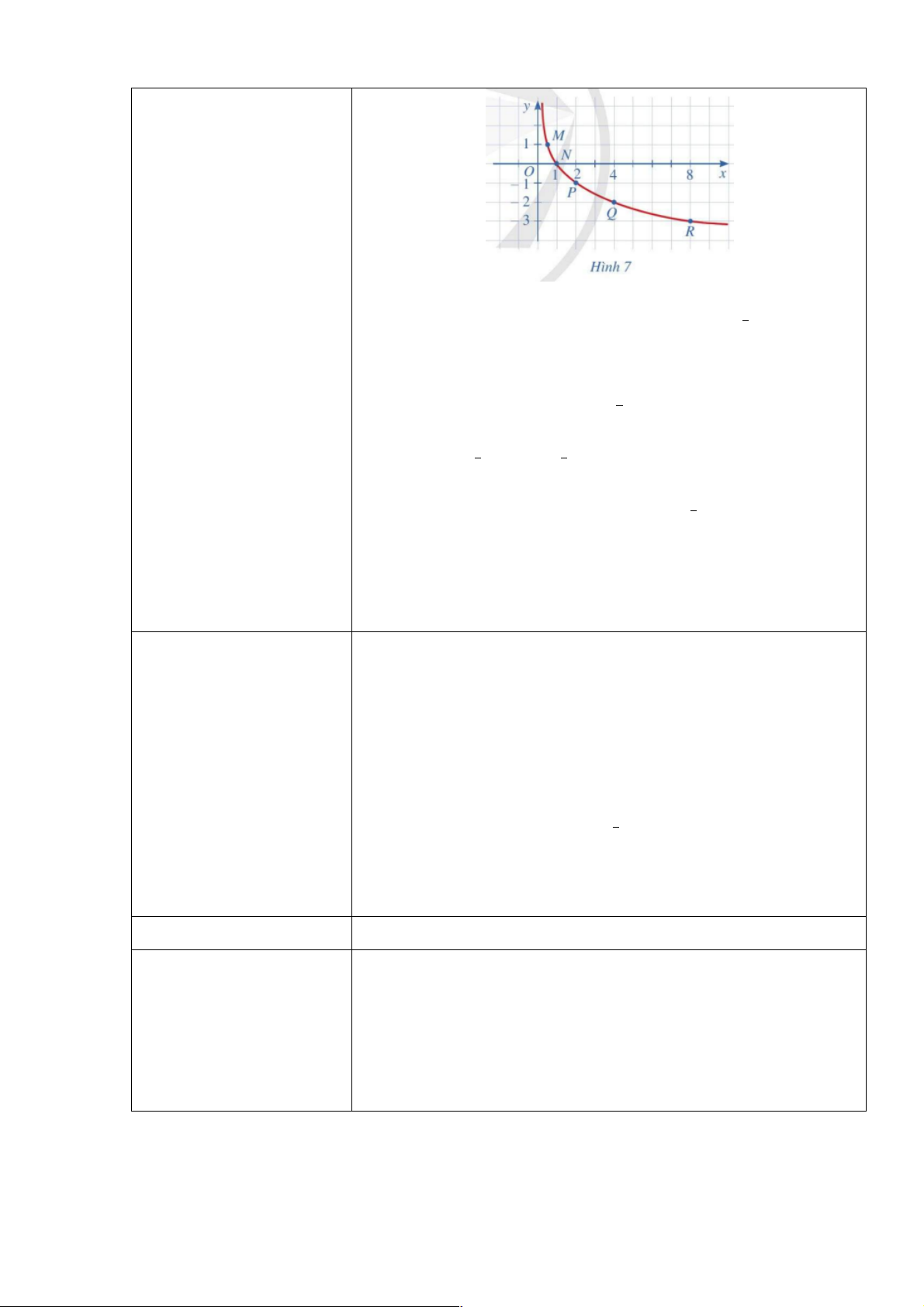
bảng giá trị ở câu a. Bằng cách làm tương ứng, lấy nhiều điểm æ ö ç ;l
x og x với x Î(0;+¥) và nối lại, ta được đồ thị hàm số 1 ÷ è 2 ø
y = log x (Hình 7). 1 2
c) Cho biết tọa độ giao điểm đồ thị hàm số y = log x với trục 1 2
hoành và vị trí của đồ thị hàm số đó so với trục tung.
d) Quan sát đồ thị hàm số y = log x , nêu nhận xét về: 1 2 • lim log , x lim log ; x + 1 1 x®0 x®+¥ 2 2 •
Sự biến thiên của hàm số y = log x và lập bảng biến 1 2 thiên của hàm số đó. Nêu nhận xét? - HS quan sát, suy nghĩ
- HS phát biểu trả lời câu hỏi của giáo viên
Nhận xét: Đồ thị hàm số y = log x là một đường cong liền nét, 2
cắt trục hoành tại điểm có hoành độ bằng 1, nằm ở phía bên phải
Thực hiện
trục tung và đi lên kể từ trái sang phải.
Nhận xét: Đồ thị hàm số y = log x là một đường cong liền nét, 1 2
cắt trục hoành tại điểm có hoành độ bằng 1, nằm ở phía bên phải
trục tung và đi lên kể từ trái sang phải.
Báo cáo thảo luận
* Đại diện nhóm báo cáo, các nhóm còn lại theo dõi thảo luận.
- GV nhận xét thái độ làm việc, phương án trả lời của học sinh,
ghi nhận và tuyên dương học sinh có câu trả lời tốt nhất. Động
Đánh giá, nhận xét, tổng viên các học sinh còn lại tích cực, cố gắng hơn trong các hoạt hợp động học tiếp theo - Chốt kiến thức
3. HOẠT ĐỘNG 3. LUYỆN TẬP
a) Mục tiêu: Học sinh củng cố lại kiến thức đã học.
b) Nội dung: HS vận dụng các kiến thức của bài học làm bài tập
Bài 1. Lập bảng biến thiên và vẽ đồ thị hàm số: y = log . x 3
Bài 2. Lốc xoáy là hiện tượng một luồng không khí xoáy tròn mở rộng ra từ một đám mây dông
xuống tới mặt đất (Hình 10). Các cơn lốc xoáy thường có sức tàn phá rất lớn. Tốc độ của gió
(đơn vị: dặm/giờ) gần tâm của một cơn lốc xoáy được tính bởi công thức: S = 93logd + 65,
(Nguồn: Ron Larson, Intermediate Algebra, Cengage) trong đó d (đơn vị: dặm) là quãng đường
cơn lốc xoáy di chuyển được.
Hãy tính tốc độ của gió ở gần tâm (làm tròn kết quả đến hàng đơn vị) khi cơn lốc xoáy di chuyển
được quãng đường là: a) 5 dặm; b) 10 dặm. Giải
a) Tốc độ của gió ở gần tâm khi cơn lốc xoáy di chuyển được quãng đường 5 dặm là:
S = 93log5 + 65 »130 dặm/ giờ
b) Tốc độ của gió ở gần tâm khi cơn lốc xoáy di chuyển được quãng đường 10 dặm là: S = 93log10 + 65 =158 d ặm/ giờ
c) Sản phẩm học tập: Lời giải bài tập 1, 2.
d) Tổ chức thực hiện:
Chuyển giao
- GV cho HS thực hiện bài tập.
- HS quan sát và chú ý lắng nghe, thảo luận nhóm, hoàn thành các bài tập
Thực hiện GV yêu cầu.
- GV quan sát và hỗ trợ.
- Mỗi bài tập GV mời HS trình bày. Các HS khác chú ý chữa bài, theo dõi
Báo cáo thảo luận nhận xét bài trên bảng.
Đánh giá, nhận
- GV chữa bài, chốt đáp án, tuyên dương các hoạt động tốt, nhanh và chính
xét, tổng hợp xác. TIẾT 3.
1. HOẠT ĐỘNG 1. MỞ ĐẦU a) Mục tiêu:
- Tạo hứng thú, thu hút HS tìm hiểu nội dung bài học.
b) Nội dung: HS thực hiện làm và trả lời nhanh phần bài tập trắc nghiệm theo sự hướng dẫn của GV.
c) Sản phẩm: HS trả lười được đáp án và giải thích được tại sao chọn đáp án đó.
d) Tổ chức thực hiện:
- GV trình chiếu câu hỏi trắc nghiệm.
Chuyển giao
- GV cho HS trả lời nhanh các câu hỏi trắc nghiệm.
Thực hiện
HS quan sát và chú ý lắng nghe, thảo luận nhóm hoàn thành yêu cầu.
Báo cáo thảo luận GV gọi một số HS trả lời, HS khác nhận xét, bổ sung.
GV đánh giá kết quả của HS, trên cơ sở đó dẫn dắt HS vào bài học mới:
Đánh giá, nhận
“Để giúp các em tổng kết lại các kiến thức về hàm số mũ và hàm số lôgarit,
xét, tổng hợp
tiết học ngày hôm nay chúng ta sẽ đi vào luyện tập và vận dụng kiến thức
qua các bài toán cơ bản và nâng cao.”
Câu hỏi trắc nghiệm:
Câu 1. Trong các hàm số sau, hàm số nào là hàm số mũ? # A. 𝑦 = 4𝑥! B. 𝑦 = "
C. 𝑦 = %"&
D. 𝑦 = 𝑥√&' #! $
Câu 2. Trong các hàm số sau, hàm số nào là hàm số lôgarit?
A. 𝑦 = 𝑙𝑜𝑔#𝑒!
B. 𝑦 = 𝑙𝑜𝑔#√3
C. 𝑦 = 𝑙𝑜𝑔(𝑥$ D. 𝑦 = 𝑥(
Câu 3. Tập giá trị của hàm số 𝑦 = 𝑎#(𝑎 > 0, 𝑎 ≠ 1) là : A. (0; +∞) B. [0; +∞) C. ℝ ∖ {0} D. ℝ
Câu 4. Tập giá trị của hàm số 𝑦 = 𝑙𝑜𝑔)𝑥(𝑎 > 0, 𝑎 ≠ 1) là : A. (0; +∞) B. [0; +∞) C. ℝ ∖ {0} D. ℝ
Câu 5. Khẳng định nào sau đây là đúng?
A. Hàm số 𝑦 = 𝑎#(𝑎 > 0, 𝑎 > 1, 𝑎 ≠ 1) nghịch biến trên ℝ.
B. Hàm số 𝑦 = 𝑎#(0 < 𝑎 < 1, 𝑎 ≠ 1) nghịch biến trên ℝ.
C. Hàm số 𝑦 = 𝑙𝑜𝑔)𝑥(𝑎 > 0, 𝑎 > 1, 𝑎 ≠ 1) nghịch biến trên (0; +∞).
D. Hàm số 𝑦 = 𝑙𝑜𝑔)𝑥(0 < 𝑎 < 1, 𝑎 ≠ 1) đồng biến trên (0; +∞). Đáp án Câu 1 2 3 4 5 Đáp án C C D A B
2. HOẠT ĐỘNG 2. HÌNH THÀNH KIẾN THỨC a) Mục tiêu:
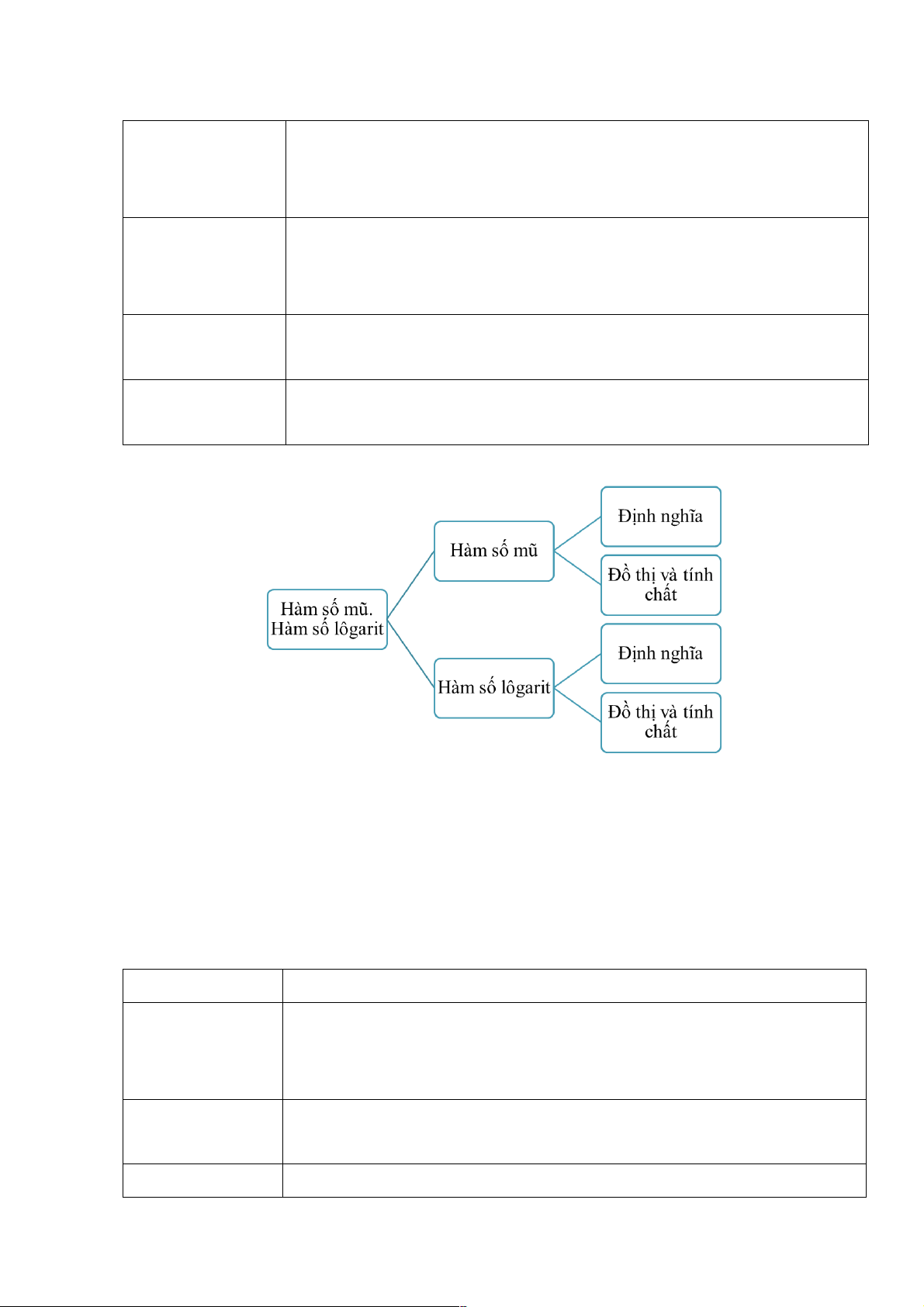
- HS nắm vững và hệ thống hóa được kiến thức của Bài 3. Hàm số mũ. Hàm số lôgarit theo sơ
đồ tư duy hoặc sơ đồ cây. b) Nội dung:
- HS hệ thống hóa kiến thức trong bài theo yêu cầu, dẫn dắt của GV.
c) Sản phẩm: HS ghi nhớ và vận dụng kiến bài để thực hành làm các bài tập SGK và của GV.
Sơ đồ hệ thống hóa kiến thức tham khảo.
d) Tổ chức thực hiện:
- GV cho HS thực hiện hệ thống hóa kiến thức thức của Bài 3. Hàm số mũ.
Chuyển giao
Hàm số lôgarit theo sơ đồ tư duy hoặc sơ đồ cây.
- HS thực hiện nhiệm vụ theo nhóm đôi.
- HS theo dõi SGK, chú ý nghe, tiếp nhận kiến thức, hoàn thành các yêu
Thực hiện cầu, thảo luận nhóm. - GV quan sát hỗ trợ.
- HS giơ tay phát biểu, lên bảng trình bày
Báo cáo thảo luận - Một số HS khác nhận xét, bổ sung cho bạn.
Đánh giá, nhận
GV tổng quát, nhận xét quá trình hoạt động của các HS, cho HS nhắc lại
xét, tổng hợp
kiến thức trọng tâm của bài. Sơ đồ:
3. HOẠT ĐỘNG 3. LUYỆN TẬP
a) Mục tiêu: Học sinh củng cố lại kiến thức đã học.
b) Nội dung: HS vận dụng các kiến thức của bài học làm bài tập 1, 2, 3, 4 (SGK – tr.47).
c) Sản phẩm học tập: Câu trả lời của HS. HS vận dụng kiến thức đã học về hàm số mũ, hàm số
lôgarit để giải các bài tập 1, 2, 3, 4 (SGK – tr.47).
d) Tổ chức thực hiện:
Chuyển giao
- GV cho HS thực hiện bài tập.
- HS quan sát và chú ý lắng nghe, thảo luận nhóm, hoàn thành các bài tập
Thực hiện GV yêu cầu.
- GV quan sát và hỗ trợ.
- Mỗi bài tập GV mời HS trình bày. Các HS khác chú ý chữa bài, theo dõi
Báo cáo thảo luận nhận xét bài trên bảng.
Đánh giá, nhận
- GV chữa bài, chốt đáp án, tuyên dương các hoạt động tốt, nhanh và chính
xét, tổng hợp xác. Bài 1. a) 𝑦 = 12# TXĐ: 𝐷 = ℝ
b) 𝑦 = 𝑙𝑜𝑔!(2𝑥 − 3) TXĐ: 𝐷 = (0; +∞)
c) 𝑦 = 𝑙𝑜𝑔"(−𝑥$ + 4) # TXĐ: 𝐷 = (0; +∞) Bài 2. # a) 𝑦 = %√"& $
Hàm số nghịch biến trên ℝ. Vì √" < 1 $ $ # b) 𝑦 = A √$*B $ $
Hàm số nghịch biến trên ℝ. Vì √$* < 1 $ c) 𝑦 = 𝑙𝑜𝑔+𝑥
Hàm số đồng biến trên (0; +∞). Vì 𝜋 > 1 d) 𝑦 = 𝑙𝑜𝑔 𝑥 √"# &
Hàm số nghịch biến trên (0; +∞). Vì √&! < 1 , Bài 3. a) 𝑦 = 4# Bảng biến thiên 𝑥 −∞ 0 + ∞ +∞ 𝑦 = 4# 1 0
Đồ thị hàm số 𝑦 = 4# là đường thẳng đi qua 𝐴 %− & ; &&, 𝐵(0; 1), 𝐶(1; 4), 𝐷 %& ; 2&, 𝐸 %" ; 8& $ $ $ $ b) 𝑦 = 𝑙𝑜𝑔"𝑥 & Bảng biến thiên 𝑥 −∞ 0 + ∞ 0 𝑦 = 𝑙𝑜𝑔&𝑥 0 , −∞
Đồ thị hàm số 𝑦 = 𝑙𝑜𝑔"𝑥 là đường thẳng đi qua 𝐴 %& ; 1&, 𝐵(1; 0), 𝐶 %2; − &&, 𝐷(4; −1), & , $ 𝐸 %8; − "& $ Bài 4.
Ta có: 𝑆 = 𝐴. 𝑒𝑟𝑡 Trong đó:
𝑆 là dân số của Việt Nam năm 2030 (cần dự đoán).
𝐴 là dân số của Việt Nam năm 2021, đã biết là 98,564,407 người.
𝑟 là tỉ lệ tăng dân số hàng năm, đã biết là 0,93%
𝑡 là số năm từ năm 2021 đến năm 2030, tức là 𝑡 = 2030 − 2021 = 9 năm.
Thay các giá trị vào công thức, ta có: 𝑆 = 98,564,407 . 𝑒(',''/"./)
Sau khi tính toán, ta có kết quả: 𝑆 ≈ 107 169 341 người.
Vậy dự đoán dân số Việt Nam năm 2030 là khoảng 107 triệu người.
4. HOẠT ĐỘNG 4. VẬN DỤNG a) Mục tiêu:
- Học sinh thực hiện làm bài tập vận dụng để nắm vững kiến thức.
b) Nội dung: HS sử dụng SGK và vận dụng kiến thức đã học để làm bài tập.
c) Sản phẩm: Kết quả thực hiện các bài tập.
d) Tổ chức thực hiện:
Chuyển giao
- GV yêu cầu HS hoạt động hoàn thành bài tập 5, 6, 7 (SGK -tr.47).
- HS suy nghĩ, trao đổi, thảo luận thực hiện nhiệm vụ.
Thực hiện
- GV điều hành, quan sát, hỗ trợ
Báo cáo thảo luận - Bài tập: Đại diện HS trình bày kết quả, các HS khác theo dõi, đưa ý kiến.
Đánh giá, nhận
- GV nhận xét, đánh giá, đưa ra đáp án đúng, chú ý các lỗi sai của học sinh
xét, tổng hợp hay mắc phải. Bài 5.
Để tính số đơn vị kiến thức học sinh đã học được sau một số ngày nhất định, ta chỉ cần thay giá
trị của t vào công thức 𝑓(𝑡) = 𝑐(1 − 𝑒234), trong đó:
Số đơn vị kiến thức học sinh đã học được sau 2 ngày: Thay t = 2 vào công thức 𝑓(𝑡) = 𝑐(1 −
𝑒234) và biết rằng 𝑓(𝑡) = 25 (số đơn vị kiến thức đã học được), k = 0.2 (tốc độ tiếp thu), ta
có: 𝑓(𝑡) = 25(1 − 𝑒2',$$) => 𝑓(2) ≈ 8,24
Tương tự: 𝑓(8) ≈ 19,95 Bài 6.
Độ 𝑝𝐻 của mẫu 1 là:
𝑝𝐻 = −𝑙𝑜𝑔[8. 102(] = −(𝑙𝑜𝑔8 + 𝑙𝑜𝑔102() = −(𝑙𝑜𝑔8 − 7𝑙𝑜𝑔10) = 7 − 𝑙𝑜𝑔8 = 7 − 3𝑙𝑜𝑔2
Độ 𝑝𝐻 của mẫu 2 là:
𝑝𝐻 = −𝑙𝑜𝑔[2. 102/] = −(𝑙𝑜𝑔2 + 𝑙𝑜𝑔102/) = 9 − 𝑙𝑜𝑔2
Nhận thấy 7 − 3𝑙𝑜𝑔2 < 9 − 𝑙𝑜𝑔2 Bài 7. Có 𝑦 = 𝑙𝑜𝑔 &! &,'* ≈ 7 &'
Vậy sau ít nhất 7 năm thì cô Yên có thể rút ra được số tiền 15 triệu đồng từ tài khoản tiết kiệm đó
* HƯỚNG DẪN VỀ NHÀ
• Ghi nhớ kiến thức trong bài.
• Hoàn thành các bài tập trong SBT.
• Chuẩn bị bài mới: "Bài 4. Phương trình, bất phương trình mũ và lôgarit".