










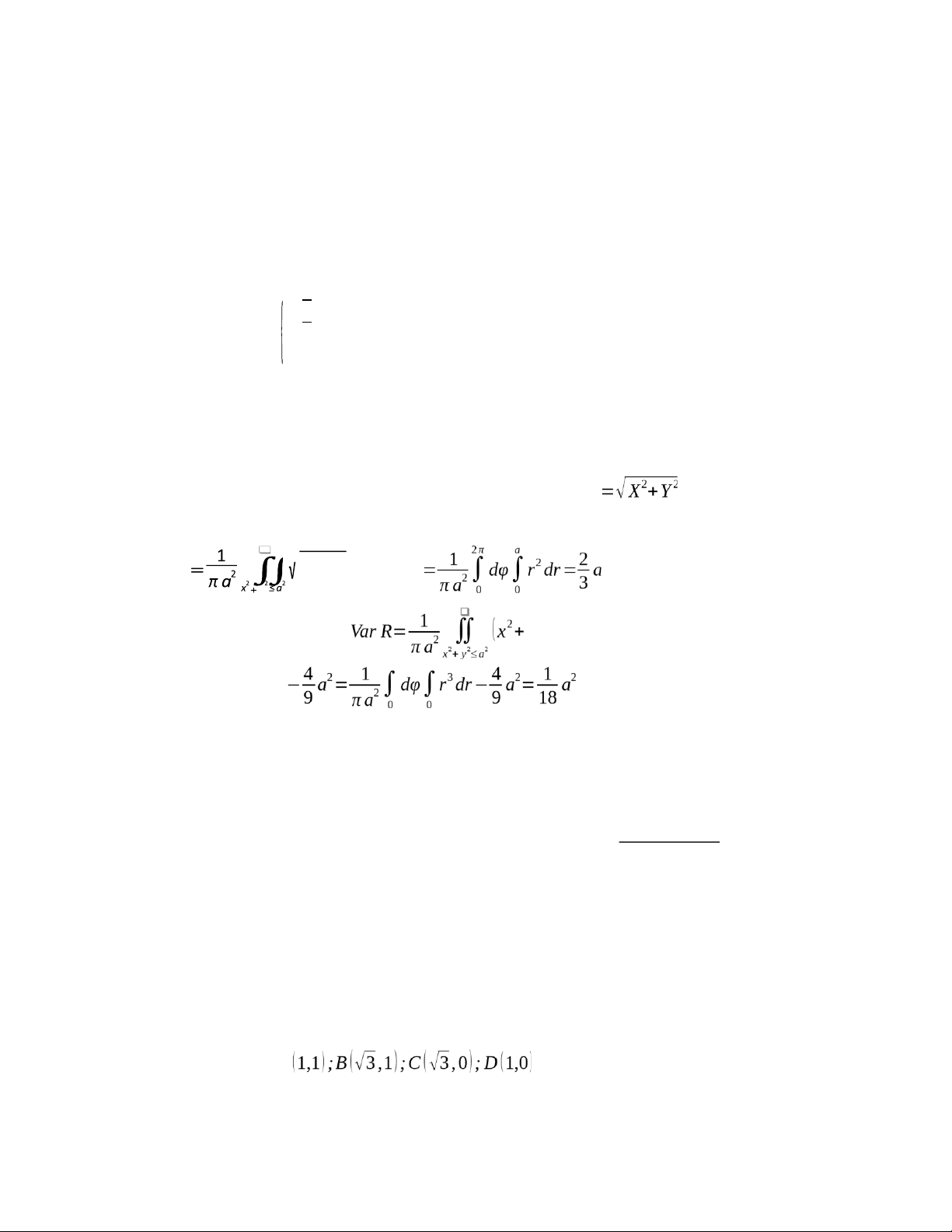







Preview text:
lOMoAR cPSD| 59285474
BÀI 4. BIẾN NGẪU NHIÊN NHIỀU CHIỀU (VECTƠ NGẪU NHIÊN).
• Vectơ ngẫu nhiên và hàm phân phối xác suất.
Cho X1=X1 (ω) , X2=X2(ω),…, Xn=Xn (ω);ω∈Ω là các biến ngẫu nhiên tạo nên vectơ ngẫu nhiên n chiều,
X (ω)=( X1, X2,…, Xn): Ω→Rn.
Hàm phân phối xác suất của vectơ ngẫu nhiên n chiều X (ω) , xác định bởi;
FX ( x )=FX (
1, X2,…,Xn x1,x2,…, xn)
¿ P{ω:( X1 (ω)<x1,X2(ω)<x2,…, Xn (ω)<xn)}
¿ P (X1<x1, X2<x2,…,X n<xn).
(Hàm phân phối xác suất của vectơ ngẫu nhiên n chiều X (ω) , xác định như trên
thường được gọi là hàm phân phối đồng thời – joint distribution). Nói một cách
tổng quát, độ đo xác định trên các tập Borel B trong Rn :
μX1,X2, …, Xn ( B )=P({ω:(X1 (ω)<x1, X2 (ω)<x2,…, Xn (ω)<xn)∈B})
được gọi là hàm phân phối xác suất đồng thời của các biến ngẫu nhiên
X1 (ω), X2 (ω)…, Xn (ω).
Khi n = 2, ta có trường hợp riêng là biến ngẫu nhiên 2 chiều:
F ( X,Y ) (x , y)=P (ω:(X (ω)<x ,Y ( ω)<y))=P ( X<x ,Y < y ).
• Vectơ ngẫu nhiên liên tục và rời rạc.
Đại lượng ngẫu nhiên n chiều được gọi là liên tục (có hàm phân phối xác
suất liên tục) nếu hàm phân phối FX ( x) liên tục khắp nơi và nếu hàm mật độ: ∂n F X ( 1, X2,…,Xn
x1, x2,…, xn) f X (x 1,X2,…,X n 1,x2,…,xn)= ∂ x1∂
x2…∂ xn tồn tại và liên tục từng khúc. FX (
1,X2,…,Xn x1,x2,…,xn)=¿ x1 x2 xn 1 lOMoAR cPSD| 59285474
¿∫∫ …∫ f X (
1,X2,…,Xn t1,t2,…,tn)dt1dt2…dtn. . −∞ −∞ −∞
Đại lượng ngẫu nhiên n chiều được gọi là rời rạc (có hàm phân phối xác suất
rời rạc) nếu các đại lượng ngẫu nhiên thành phần xi;i=1,2,…,n là rời rạc, khi
đó hàm mật độ rời rạc được xác định bởi xác suất điểm f X1,X2,…,X
(nx1,x2,…,xn)=P( X1=x1,X2=x2,…, Xn=xn).
• Phân phối xác suất của biến ngẫu nhiên thành phần
Hàm phân phối xác suất của biến ngẫu nhiên thành phần xk, (với mỗi k, nguyên,
dương ≤n xác định) còn gọi là phân phối lề (marginal distribution). Cụ thể là: k F (⏞
X ( x )∶=F
+∞,+∞,...,+∞,x ,+∞,…,+∞). k
X1,X2,…,Xn
Hàm mật độ thành phần tương ứng sẽ là:
d f Xi (x)=dx F Xi ( x ).
• Một số đặc tính của hàm phân phối đồng thời.
Hàm phân phối đồng thời của biến ngẫu nhiên n chiều có các tính chất:
1) Không giảm đối với mỗi biến số.
2) Liên tục phải đối với mỗi biến số.
3) FX1,X2,…,X n (+∞,+∞,...,+∞)=1 FX ( (
1,X2,…,X n −∞, x2,…, xn)=F X1,X2,…, Xn x1,−∞,…, xn)=…=¿ ¿ FX (
1,X2,…,X n x1,x2,…,xn−1,−∞)=0.
∑∑ …∑ P (X1=x1, X2=x2,…, Xn=xn)=1;nếu X (ω) rờirạc , (X ) ( ) ( ) 1 X2 X n ,…,X (x n
1,x2,…, xn)d x1d x2…d xn=1;nếu X (ω)liêntục.
• Kỳ vọng (giá trị trung bình ngẫu nhiên).
Kỳ vọng của hàm φ( X1, X2,…, Xn) ta ký hiệu là Eφ (X1, X2,…, Xn). Kỳ
vọng của phân phối rời rạc: 2 lOMoAR cPSD| 59285474
Eφ (X1, X2,…, Xn)
,…, xn) p(x1, x2,…, xn),
trong đó mỗi tổng ∑ (…) , được lấy theo tất cả các giá trị mà X có thể nhận i (X ) i
và p(x1, x2,…, xn)=P (X1=x1, X2=x2,…, X n=xn).
Kỳ vọng của phân phối liên tục:
Eφ (X1, X2,…, Xn)=¿ ¿ ,…,xn)f X (
1,X2,…,X n x1,x2,…,xn)d x1d x2…d xn .
• Các momen gốc và momen trung tâm. Momen gốc mα
được định nghĩa qua kỳ vọng của [( X 1α2…αn
1)α1( X2)α2…( Xn)αn] mα ∶ ( ].
1α2…α n =E [( X1)α1 X2)α2…(X n)αn Momen trung tâm μα
được định nghĩa qua kỳ vọng của tích, 1α2…αn
[( X1−E X1)α ( ] , Cụ
1 X2−E X2)α2…( Xn−E Xn)αn thể là: μα ∶ ( ]
1α2…αn =E [( X1−E X1)α1 X2−E X2)α2…( Xn−E X n)αn .
• Momen tương quan và hệ số tương quan.
Momen tương quan Cov ( X ,Y )(hay còn gọi là hiệp phương sai – covariance)
của hai biến ngẫu nhiên X và Y được xác định bởi:
Cov ( X ,Y )=E [( X−EX ) (Y −EY )]=E ( XY )−EX. EY .
Hệ số tương quan ρ (correlation coefficient) giữa hai biến ngẫu nhiên X XY
và Y được xác định bởi: Cov ( X ,Y ) ;
Hệ số tương quan có các đặc tính sau: 3 lOMoAR cPSD| 59285474 1) ρXY =ρYX 2) −1≤ρXY ≤1.
3) Nếu X và Y là các đại lượng ngẫu nhiên độc lập thí: ρXY =0.
4) Nếu ρXY >0, thì X và Y đồng biến, nếu ρXY <0, thì X và Y nghịch biến.
Ma trận vuông có các phần tử là các Cov ( Xi, X j), được gọi là ma trận tương
quan (hay ma trận hiệp phương sai).
Ma trận tương quan luôn là một ma trận đối xứng (suy từ định nghĩa).
MỘT SỐ CÔNG THỨC CẦN NHỚ VỀ BIẾN 2 CHIỀU
Liên hệ giữa hàm phân phối đồng thời(F X,Y) và các hàm phân phối thành phần(F X);(FY ) )
FX ( x )=lim F X ,Y ( x , y y →∞ )
FY ( y )=lim F X,Y ( x , y x→∞
Liên hệ giữa hàm mật độ đồng thời(f X,Y) và các hàm mật độ thành phần(f X);(f Y ) +∞
f X ( x )=∫ f X ,Y (x , y ) dy f Y
f X, Y ( x, y ) dx
Liên hệ giữa hàm phân phối đồng thời (F X,Y)và hàm mật độ đồng thời (f X,Y) x y FX ,Y
f X ,Y (t1,t2)d t1dt2 ∂2 F (x , y ) y f X,Y y
Cách tính mật độ xác suất có điều kiện
Nếu X và Y là các biến liên tục 4 lOMoAR cPSD| 59285474
f X,Y ( x|y)= f
Xf,YY((xy,) y ) =+∞ f
X ,Y ( x, y) f X ,Y ( x, y) dx
f X,Y ( y|x)=
f Xf,YX((xx,) y ) =+∞ f X ,Y ( x, y)
f X ,Y ( x, y) dy
Nếu X và Y là các biến rời rạc )
P (X=xi,Y=y j
P (X=xi|Y =y j )=
; ∀i=1,n;i=1,m
P(Y =y j) )
P (X=xi,Y=y j
P (Y= y j|X=xi )=
; ∀i=1,n;i=1,m P (X=xi)
Điều kiện để X và Y là các biến thành phần độc lập
Nếu X và Y là các biến liên tục, điều kiện chúng là các biến độc lập là
f X,Y ( x, y )=f X ( x ) .f Y ( y ), hoặc FX ,Y ( x, y)=F X ( x ). FY ( y),
Nếu X và Y là các biến rời rạc, điều kiện chúng là các biến độc lập là P
(X=xi ,Y=y j)=P (X=xi) P (Y= y j);∀i=1,n;i=1,m
MỘT SỐ PHÂN PHỐI XÁC SUẤT NHIỀU CHIỀU (Vectơ ngẫu nhiên)
1. PHÂN PHỐI CHUẦN N-CHIỀU (Multivariate Normal Distribution)
Vectơ ngẫu nhiên X (X1, X2,…, Xn), được gọi là có phân phối chuẩn n chiều nếu nó có hàm mật độ n 5 lOMoAR cPSD| 59285474
f (x1,x2,…,xn) , trong đó:
E Xi=ai ;i=1,2,…,n.
kij=cov( Xi , X j), là các phần tử của ma trận tương quan không suy biến K. k k … k ∆=det K=≠0. k là các
phần tử của ma trận đảo K−1.
• Khi n=2, ta có phân phối chuẩn hai chiều với hàm mật độ tương ứng là: f ¿, trong đó:
μX=EX; μY =EY ; σ2X=Var X ; σ2Y =VarY ; ρ=ρX,Y= E ( )( ) X−σμ X X σ YY−μY ;
Với ( X ,Y ) phân phối chuẩn hai chiều như trên, ta sẽ có các phân phối thành
phần (còn gọi là phân phối lề hoặc phân phối biên) tương ứng là các phân phối chuẩn:
X N (μX ,σ2X );Y N( μY ,σ2Y );
Các hàm mật độ phân phối thành phần f X f Y
Hàm mật độ phân phối có điều kiện f . 6 lOMoAR cPSD| 59285474
σ X √2 π(1−ρ¿¿2)exp¿¿
Các kỳ vọng có điều kiện.
σ X E ( X /Y
=a)=μ X+ρ σY (a−μY ) ,
E(( X−μX )2/Y=a)=σ2X (1−ρ¿¿2)¿.
2. PHÂN PHỐI ĐA THỨC (Multinomial Distribution)
Vectơ ngẫu nhiên X (X1, X2,…, Xk ), được gọi là có phân phối đa thức k chiều với các
tham số dương: n, p1, p2,…, pk;n∈N ;0<pi<1;i=1,2,…,k; nếu với mọi mi k k
nguyên, dương và ∑ mi=n;∑ pi=1;ta có: i=1 i=1
P ( X=m)=P( X1=m1, X2=m2,…, Xk =mk ) n!mk ¿
m1!m2!…mk ! p…pk . • Các số đặc trưng
E Xi=n pi;i=1,2,…,k
Var Xi=n pi (1−pi);i=1,2,…,k
Cov ( Xi, X j)=−n pi pj ;i≠ j;i, j=1,2,…,k.
3. PHÂN PHỐI BERNOULLI HAI CHIỀU ( Bivariate Bernoulli Distribution)
Vectơ ngẫu nhiên X ( X ,Y ), được gọi là có phân phối Bernoulli hai chiều với các
tham số dương p1, p2;;0<p1<1;0<p2<1;0<p1+p2≤1 nếu với mọi m1,m2chỉ nhận các
giá trị 0 hoặc 1 và m1+m2≤1, với các xác suất tương ứng: 1 m1 m2 1−m1−m
P (X=m1,Y=m2)=
m1!m2!(1−m1−m2)! p1 p2 (1−p1−p2) 2 • Các số đặc trưng
EX=p1;EY=p2; 7 lOMoAR cPSD| 59285474
Var X=p1 (1−p1);Var Y=p2 (1−p2);
Cov ( X ,Y )=−p1 p2.
• Xác suất có điều kiện
P (Y=m2/X=m1)=
P ( X=m1,Y
=m2)= P ( X=m1,Y =m2) ; P (X=m1)
P ( X=0)+P ( X=0)
trong đó: m1,m2=¿0 hoặc 1 và m1+m2≤1.
• Kỳ vọng có điều kiện
E ( X /y )=
p1 (1−y) ;E (Y /x )= p2(1−x) (1−p2) (1−p1)
Var ( X/ y)=
p1 (1−y )(1−p21−p2) ;Var (Y /x )=
p2(1−x )(1−p21−p2) (1−p2) (1−p1)
4. PHÂN PHỐI NHỊ THỨC HAI CHIỀU ( Bivariate Binomial Distribution)
Vectơ ngẫu nhiên X ( X ,Y ), được gọi là có phân phối nhị thức hai chiều với các tham số dương n, p nguyên, dương và
1, p2;n∈N ;0<p1+p2<1 nếu với mọi m1,m1
m1+m2≤n, ta có xác suất: n! m1 m2
n−m1−m
P (X=m1,Y=m2)=
m1!m2!(n−m1−m2)! p1 p2 (1−p1−p2) 2 • Các số đặc trưng
EX=np1;EY=n p2;
Var X=n p1 (1−p1);Var Y=np2(1−p2);
Cov ( X ,Y )=−np1 p2.
• Xác suất có điều kiện )
P (Y=m2/X=m1)=
P ( X=m1,Y =m2 =¿ P (X=m1) ¿(1−p1)m (
1−nCmn−2 m1 pm2 2 1−p1−p2)n−m1−m2. 8 lOMoAR cPSD| 59285474
• Kỳ vọng có điều kiện
p1 (n−y )
p2 (n−x )
E ( X /y )=
; E (Y /x )= (1−p2) (1−p1)
p1 (n−y ) (1−p1−p2)
p2 (n−x ) (1−p1−p2)
Var ( X/ y)=
2 ;Var (Y /x )= 2 (1−p2) (1−p1)
5. PHÂN PHỐI HÌNH HỌC HAI CHIỀU ( Bivariate Geometric Distribution)
Vectơ ngẫu nhiên X ( X ,Y ), được gọi là có phân phối hình học hai chiều với các tham số dương p1,
p2;;0<p1<1;0<p2<1;0<p1+p2≤1 nếu với mọi
m1,m1nguyên,dương(m1,m2=0,1,…)ta có: P −p1−p2) • Các số đặc trưng p1 p2 EX= ;EY = ; 1−p1−p2 1−p1−p2 Var X=
p1 (1−p2) 2 ;Var X=
p2 (1−p1) 2 ; (1−p1−p2) (1−p1−p2) p1 p2 Cov ( X ,Y )= 2 (1−p1−p2)
• Xác suất có điều kiện
P (Y=m2/X=m1)=
(Mm11+!Mm22)!! pm2 (21−p2)m1+1.
• Kỳ vọng có điều kiện
E ( X /y )=
p1 (1+ y ) ;E (Y /x )=
p2(1+x ) ; (1−p1) (1−p2)
Var ( X/ y)=
p1 (1+y2) ;Var (Y /x )=
p2 (1+x2) ; 9 lOMoAR cPSD| 59285474 (1−p2) (1−p1)
6. PHÂN PHỐI SIÊU BỘI HAI CHIỀU ( Bivariate Hypergeometric Distribution)
Vectơ ngẫu nhiên X ( X ,Y ), được gọi là có phân phối nhị siêu bội hai chiều với các
tham số nguyên, dương r,n1,n2,n3, nếu với mọi m1,m2=0,1,…,r ; sao cho,
m1≤n1;m2≤n2; r−m1−m2<n3; ta có xác suất: 1 m m
r−m −m P Cn 1+n2+n3 • Các số đặc trưng r n1 EX= n1+n2+n3 r n2 EY= n1+n2+n3 Var X= (rnn (
1+1(nn22++nn33))2
nn11++nn22++nn33−−1r)
rn2(n1+n3) n1+n2+n3−r Var Y= (n ( 1+n2+n3)2
n1+n2+n3−1) Cov XY = (n1+r nn ( 12+n2n3)2
nn11++nn22++nn33−−1r)
• Xác suất có điều kiện 1 m2
r−m1−m2
P (Y=m2/X=m1)= r−m ; 1 Cn2 Cn3 Cn2+n3
• Kỳ vọng có điều kiện 10 lOMoAR cPSD| 59285474
E ( X /y )=
n1(r−y ) ;E (Y /x )=
n2(r−x ) ; (n1+n3) (n2+n3)
Var (Y /x)= n2n3 ( )
n1+n2+n3−x )( x−n1 ; n2+n3−1 n2+n3 n2+n3
Var ( X/ y)= n1n3 ( )
n1+n2+n3−y )( y−n2 n2+n3−1 n2+n3 n2+n3
7. PHÂN PHỐI CAUCHY HAI CHIỀU ( Bivariate Cauchy Distribution)
Vectơ ngẫu nhiên X ( X ,Y ), được gọi là có phân phối Cauchy hai chiều với các
tham số dương θvà các hằng số thực α ,β, nếu hàm mật độ cùa nó có dạng: θ f ( x , y)=
;x∈R , y ∈R.
• Các số đặc trưng EX ,EY ,Var X,Var Y ,Cov ( X ,Y ) đều không tồn tại. Hàm mật độ có điều kiện
θ2+( y−β )2
f ( y/x )=
[θ2+( x−α )2+( y−β )2]
• Kỳ vọng có điều kiện
E ( X /y )=α
E (Y /x)=β 11 lOMoAR cPSD| 59285474
VÍ DỤ VÀ BÀI TẬP VỀ BIẾN NGẪU NHIÊN NHIỀU CHIỀU BÀI TẬP 1
Một vết đen có thể xuất hiện một cách ngẫu nhiên trên một màn hình rađa tròn có bán
kính bằng a, biết rằng tọa độ ( X ,Y ) của vết đen có hàm mật độ phân phối đồng thời xác định bởi: 1 2 2 2 2 ;nếux +y ≤a f ( x , y)=π a
0;nếu x2+y2>a2
Hãy tính kỳ vọng và phương sai của khoảng cách R, từ tâm đường tròn đến vết đen.
Hướng dẫn giải
Ta tính kỳ vọng và phương sai của đại lượng ngẫu nhiên R như của một hàm 2
biến có phân phối đều trên hình tròn bán kính a. Ta sẽ thu được kết quả sau: ER y
x2+ y2dxdy . 2π a y2)dxdy . BÀI TẬP 2 A
Cho biến ngẫu nhiên hai chiều với hảm mật độ có dạng f ( x , y )= 2 2 (1+x )(1+y )
a) Hãy xác định hằng số A
b) Tìm hảm phân phối đồng thời của ( X ,Y )
c) Tìm hảm phân phối thành phần của X và của Y.
d) Các biến ngẫu nhiên X và Y có độc lập không.
e) Tìm xác suất để ( X ,Y ) thuộc miền chữ nhật ABCD với A ; .
Hướng dẫn giải 12 lOMoAR cPSD| 59285474
a) Áp dụng công thức (5) cho biến ( X ,Y ) ta có dxdy=1 ⇒ A. dxdy=1
Mặt khác khi tính tích phân trên ta sẽ có dxdy −∞ −∞ ¿
Vậy ta có A= ;
b) Hảm phân phối đồng thời tương ứng của ( X ,Y ) sẽ là x y x y FX ,Yf X ,Y, −∞ −∞ 1 2 ¿ ;
c) Hàm phân phối của X và Y có thể tìm bằng cách
FX ( x)=lim F X ,Y ( x ,
y)=¿(arctg x+),¿ y →∞ FY
( y)=lim F X,Y ( x , y )=¿(arctg y+).¿ x→∞
d) Ta có X và Y là hai đại lượng ngẫu nhiên độc lập
(xem tính chất thứ 6) của hàm phân phối nhiều chiều)
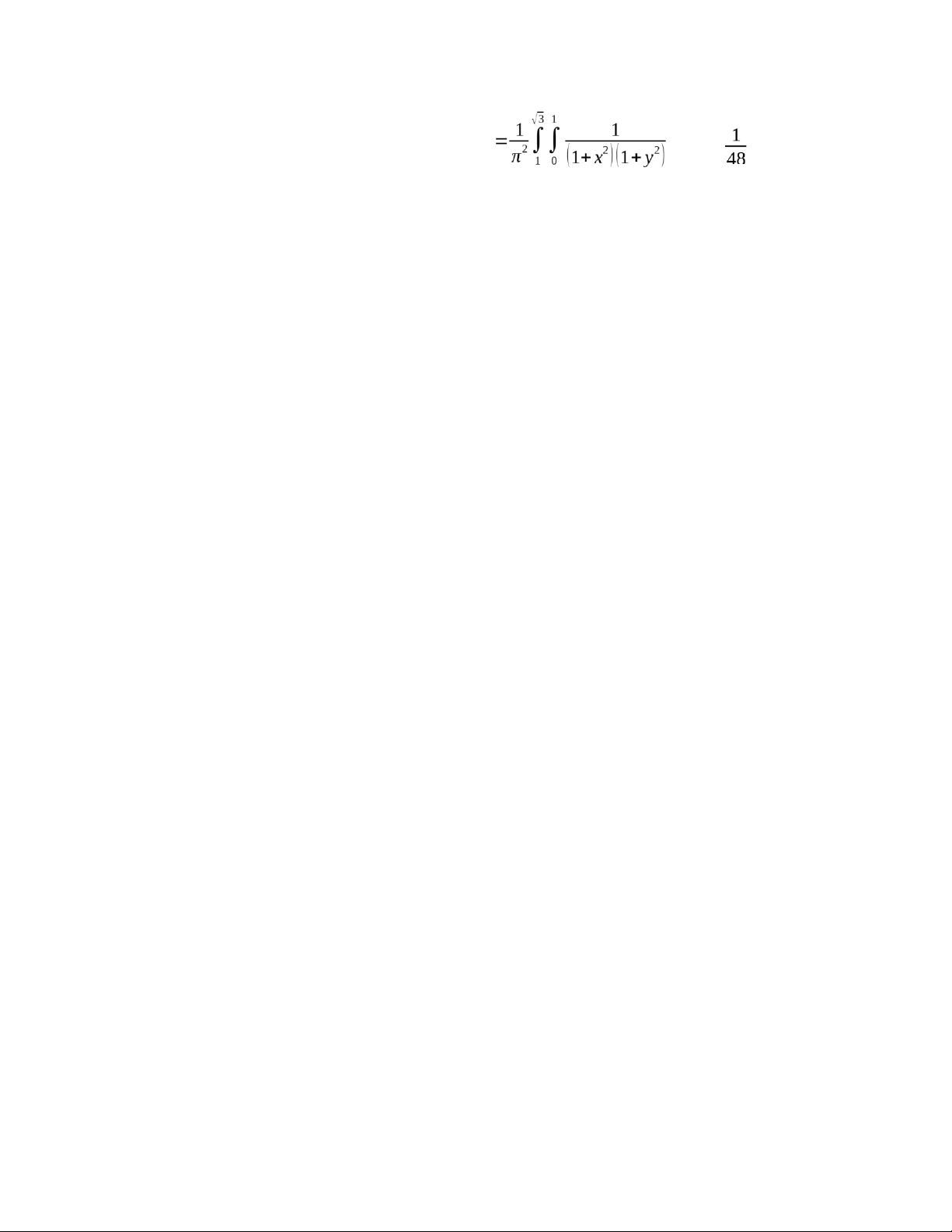
e) Áp dụng công thức (6) ta sẽ có 13 lOMoAR cPSD| 59285474 ❑
P (( XY ) ∈ ABCD)= ∬ f ( x , y ) dxdy dxdy= ; ( XY )∈ ABCD BÀI TẬP 3 14 lOMoAR cPSD| 59285474 15 lOMoAR cPSD| 59285474 16 lOMoAR cPSD| 59285474 17 lOMoAR cPSD| 59285474 18 lOMoAR cPSD| 59285474
BÀI TẬP 4 Cho biến ngẫu nhiên hai chiều ( X ,Y ) , với bảng phân phối xác suất Gía trị Y Gía trị X 1 2 3 1 0,17 0,13 0,25 2 0,10 0,30 0,05
Từ đó ta thấy rằng các biến ngẫu nhiên thành phần X, và Y đều là rời rạc có các
xác suất tương ứng với các giá trị của chúng là P j=1 j=1 3 3
P ( X=2 )=∑ P ( X=2,Y= j)=∑ p2 j=0,10+0,30+0,05=0,45 j=1 j=1
Từ đó suy ra kỳ vọng của X bằng
EX=1.0,55+2.0,45=1,45. ⇒ E X2=1.0,55+22.0,45=2,35.
Phương sai của X sẽ bắng
Var X=E X2−( EX )2=2,35−(1,45)2=0,2475
Tương tự như vậy ta sẽ tính được các xác suất tương ứng với các giá trị của Y theo bảng sau Giá trị của Y 1 2 3 Xác suất tương ứng 0,27 0,43 0,30
Từ đó suy ra kỳ vọng của Y bằng
EY=1.0,27+2.0,43+3.0,30=2,03
⇒ EY2=1.0,27+22.0,43+32.0,30=4,69
Phương sai của Y sẽ bắng
VarY=EY2−(EY )2=4,69−(2,03 )2=0,5691. Mặt khác ta sẽ có
E(XY)=1.0,17+1.2.0,13+1.3.0,25+2.1.0,10+2.2.0,30+2.3.0,05=2,88.
Theo công thức (10) ta sẽ thu được 19 lOMoAR cPSD| 59285474
Cov XY =E ( XY )−EX .EY=2,88−1,45.2,03=−0,0635.
Từ đây ta có thể kết luận: Hai biến ngẫu nhiên X và Y không độc lập với nhau,
(momen tương quan khác không).
Trong ví dụ này ta được ma trận hiệp phương sai là ( 0,2475 −0,0635) −0,0635 0,5691
Hệ số tương quan tương ứng ta tính theo công thức (12) sẽ thu được
BÀI TẬP VỀ NHÀ
• Bài tập 4.1
Cho hàm phân phối xác suất đồng thời của X,Y là
FX ,Y ( x, y )={(1−e−x )(1−e−y),nếu x>0, y>0
0,trongcác trườnghợpkhác
a) Hãy tính hàm mật độ phân phối thành phần cùa X và Y,
b) Tìm xác suất P (1< X<3,1<Y <2) .
• Bài tập 4.2
Cho hàm mật đô đồng thời của X,Y là 3 f X,Y ( x,
y )=4 (2−x−y ) ,nếu0<x, y<2;0<x+ y<2
0,trongcáctrườnghợpkhác
Hãy tính xác suất có điều kiện: P ( X<1∨Y <1 )
• Bài tập 4.3
Cho X,Y có hàm mật độ đồng thời là 5 2
x y nếu0<x , y<2;
f X,Y ( x, y)=16
0,trongcáctrườnghợpkhác
Hãy tìm hàm mật độ thành phần của X.
• Bài tập 4.4 20



