BÀI 7 MẪU NGẪU Nhiên - Lý thuyết về Xác Suất Thống kê cùng với một bài tập ví dụ. Môn Xác suất thống kê(XSTK) | Đại học Trường Đại học Công nghệ thông tin, Đại học Quốc gia Thành phố Hồ Chí Minh.

lOMoAR cPSD| 59285474
BÀI 7 KHÁI NIỆM VỀ MẪU NGẪU NHIÊN VÀ SUY DIỄN THỐNG KÊ
7.1 KHÁI NIỆM VỀ MẪU NGẪU NHIÊN
7.1.1 Tổng thể và mẫu ngẫu nhiên
Trong thực tế ta thường phải phân tích và nghiên cứu một tổng thể gồm các phần tử có
chung một hay một vài dấu hiệu định tính hoặc định lượng cần quan tâm. Tổng thề đó có
thể hữu hạn hay vô hạn các phần tử.
Dấu hiệu nghiên cứu của tổng thể thể hiện và thay đổi khác nhau trên mỗi phần tử, được
mô tả như một biến ngẫu nhiên X có mật độ phân phối xác suất f ( x ) nào đó có thề có như
phân phối chuẩn, phân phối nhị thức,….Chẳng hạn ta xét tổng thể là sản phẩm của nhà
máy ta có thể quan tâm đến số lượng sản phẩm thông qua giá trị trung bình, và chất lượng
sản phẩm thông qua số phế phẩm thường được tính qua đặc trưng của phân phối nhị thức.
Tóm lại ta có thể đi đến các định nghĩa sau.
Định nghĩa 7.1 Tập hợp các phần tử có chung một hay một vài dấu hiệu định tính hoặc
định lượng nào đó được gọi là tổng thể nghiên cứu (hay đơn giản là tổng thể hoặc còn gọi là dân số).
Thông thường với mỗi tổng thể ta không nghiên cứu trực tiếp toàn thể các phần tử của nó
mà thông qua một số phần tử đại diện mà ta gọi là sử dụng phương pháp mẫu.
Định nghĩa 7.2 Mẫu ngẫu nhiên kích thước n (hay còn gọi là cỡ n) của tổng thể X có phân
phối xác suất f ( x ) là biến ngẫu nhiên n-chiều (X 1, X2 ,…, Xn), với các thành phần Xi độc
lập có cùng phân phối xác suất của X. Mẫu cụ thể là một giá trị của mẫu ngẫu nhiên ta ký
hiệu là (x1 ,x2 ,… ,xn).
Ngoài việc cho các giá trị của mẫu dưới dạng cụ thể nêu trên, mẫu còn được mô tả dưới
dạng phân phối tần suất thực nghiệm như sau.
Với mẫu cụ thể (x1,x2,… ,xk), trong đó xi có ni ;i=1,2,…,k; giá trị. Giả sử x1<x2<…<xk; và
n1+n2+…+nk=n;
Khi đó ta có bảng phân phối tần suất thực nghiệm
xi x1 x2 … xn f i f 1 f 2 … f n 1 lOMoAR cPSD| 59285474 ni
x1,x2,…,xn) của mẫu ngẫu nhiên
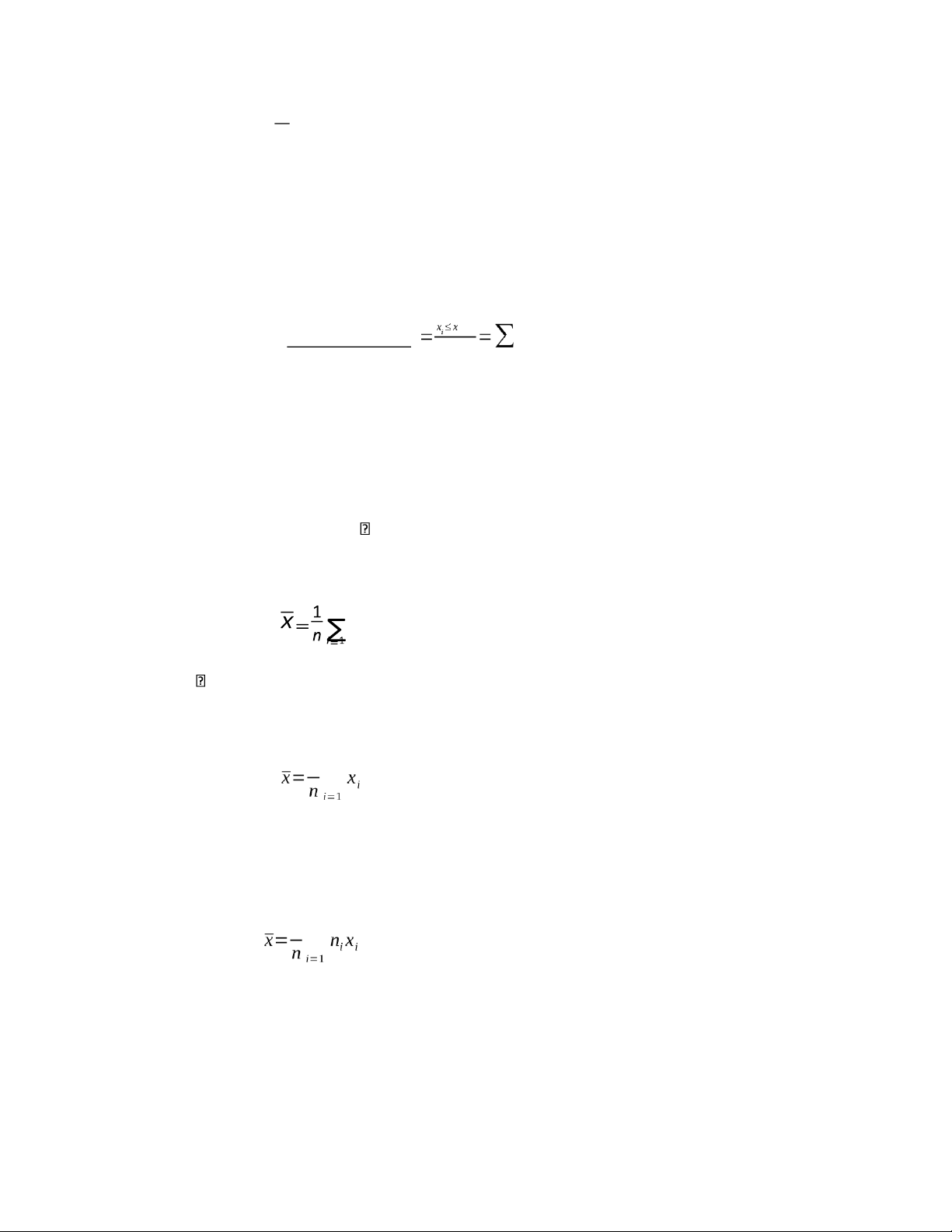
Ta sẽ có: f i= n ⇔f 1+f 2+…+f k=1.Từ mẫu cụ thể (
(X 1, X2 ,…, Xn), ta xác định hàm phân phối mẫu bởi hệ thức
Số phầntử xi≤ x ∑ ni Fn( x ) ∶= n n xi ≤ x f i
Trong phần các định lý giới hạn xác suất ta biết rằng theo luật số lớn Bernoulli, khi n→∞ ta sẽ có
Fn( x) P F ( x)=P ( X ≤ x ). →
7.1.2 Các số đặc trưng của mẫu Trung bình mẫu, trung bình điều hòa và trung bình nhân
Trung bình mẫu của X là n Xi .
Giả sử ta có mẫu cụ thể là (x1,x2,…,xn) trung bình mẫu cụ thể (hay còn gọi là trung
bình mẫu thực nghiệm) của X sẽ là 1 n ∑ .
+ Nếu trong mẫu chỉ có các giá trị khác nhau là x1, x2,…, xk với các tần số tương ứng
là n1,n2,…,nk, thỏa điều kiện n1+n2+…+nk=n, khi đó trung bình mẫu thực nghiệm được
xác định bằng biểu thức 1 ∑k .
+ Trường hợp mẫu chia khoảng: X ¿ ¿ ……. ¿ n ……. i n1 n2 nk 2 lOMoAR cPSD| 59285474
trong đó: n1+n2+…+nk=n.
Ta sẽ xác định trung bình mẫu thực nghiệm là k niθi trong đó θ ai+1
i là điểm giữa của khoàng (ak ,ak+1]bằng: θi= ai+2 ;
Trung bình điều hòa μh
Nếu trong mẫu chỉ có các giá trị khác nhau là x1, x2,…, xk với các tần số tương ứng
là n1 ,n2 ,… ,nk , thỏa điều kiện n1+n2+…+nk=n, khi đó trung bình điều hòa được xác
định bằng biểu thức n μh= k ni ; ∑i=1 xi
Trung bình nhân μt được xác định bởi
μt=√n x1. x2.….xn .
Nếu trong mẫu chỉ có các giá trị khác nhau là x1, x2,…, xk với các tần số tương ứng
là n1 ,n2 ,… ,nk , thỏa điều kiện n1+n2+…+nk=n, khi đó trung bình nhân được xác định bằng biểu thức .
Ví dụ 7.1 Hai công nhân cùng thực hiện việc lắp ráp một loại sản phẩm. Người thứ nhất
lắp một sản phẩm hết 12 phút, người thứ hai lắp một sản phẩm hết 10 phút. Nếu trong một
ca máy (là 4 giờ) thì hãy tìm thời gian trung bình để họ lắp ráp được một sản phẩm. Trong
trường hợp này để tính thời gian trung bình để họ lắp ráp được một sản phẩm, trước hết
ta cần lấy tổng thời gian của họ (trong một ca máy) chia cho số sản phẩm họ lắp được, đó
chính là trung bình điều hòa, nó sẽ bằng
2 n 60×4 + 60×4 phút. 3 lOMoAR cPSD| 59285474 i=1 xi
Ví dụ 7.2 Trong thời gian 15 năm, tốc độ tăng trưởng thu nhập bình quân đầu người của
một huyện ghi nhận được như sau: có 6 năm tốc độ tăng so với năm trước là 115%, có 2
năm tốc độ tăng so với năm trước là 120%, có 7 năm tốc độ tăng so với năm trước là 125%.
Tính tốc độ tăng trưởng trung bình hàng năm của huyện đó trong 15 năm.
Trong ví dụ này tốc độ tăng trưởng so sánh các năm với gốc khác nhau nên ta phải tính
trung bình nhân để được tốc độ tăng trung bình. Từ đó ta có ⇒
⇒lnμt=0,184347 ⇒ μt ≈1,2028
Vậy tốc độ tăng trung bình của huyện trong 15 năm ≈120%.
Ví dụ 7.3 Trong thời gian 10 năm, tốc độ tăng giá trị sản lượng của một xí nghiệp như sau:
Có 5 năm tốc độ tăng so với năm trước là 110%; có 2 năm tốc độ tăng so với năm trước
là 125%;và có 3 năm tốc độ tăng so với năm trước là 115%; Tìm tốc độ tăng trưởng trung
bình hàng năm của xí nghiệp đó.
Trong ví dụ này tốc độ tăng trưởng so sánh các năm với gốc khác nhau nên ta phải tính
trung bình nhân để được tốc độ tăng trung bình. Từ đó ta có ⇒
⇒μt=0,144 ⇒ μt ≈114,4%
Chú ý: + Trung bình mẫu X là loại thường gặp nhất trong các vấn đề về thống kê. + Trong
kinh tế và xã hội trung bình nhân thường chỉ dùng trong tính tốc độ tăng trưởng
bình quân như trong ví dụ 7.2.
Phương sai mẫu
Phương sai mẫu của X là n
S2 ∶=n−1 1 ∑i=1 (Xi −X )2 . 4 lOMoAR cPSD| 59285474
Phương sai mẫu chưa hiệu chỉnh là n ^S . n i=1
Với kỳ vọng và phương sai mẫu nêu trên, độ lệch chuẩn của mẫu là
E (S2)=σ2; S ;
Kỳ vọng của phương sai mẫu chưa hiệu chỉnh sẽ là 2
E (^S2)=n−1 σ . n
Phương sai mẫu cụ thể (hay còn gọi là phương sai mẫu thực nghiệm) n s2 1 2 .
Phương sai mẫu thực nghiệm chưa hiệu chỉnh n s^ .
Một số tính chất của trung bình mẫu X:
Cho X1 , X2 ,…, Xn, là mẫu cỡ n, từ dân số có phân phối FX, với kỳ vọng μ, và phương sai σ2, khi đó ta sẽ có:
E ( X )=μ; σ 2 Var ( X )= ; n 3
E (( X )3)=m3+3 (n−1) m2 μ+2 (n−1) (n−2) μ ;mi=E X i;i=2,3. n ∑
Một số tính chất của phương sai mẫu: S2= i =n1 ( Xn2i −−1X)2 5 lOMoAR cPSD| 59285474
E (S2)=σ2 2 μ4 3−n 2 i
Var (S )= n + n (n−1) μ2;μi=E ( X−μ) ;i=2,3,4,…
7.2 PHÂN PHỐI MẪU TỪ DÂN SỐ CHUẨN
7.2.1 Một số phân phối xác suất thông dụng trong thống kê
• Phân phối Chi bình phương, χ2(Chi square- Distribution)
Biến ngẫu nhiên ξđược gọi là có phân phối χ2 (n) chi bình phương với n bậc tự do nếu
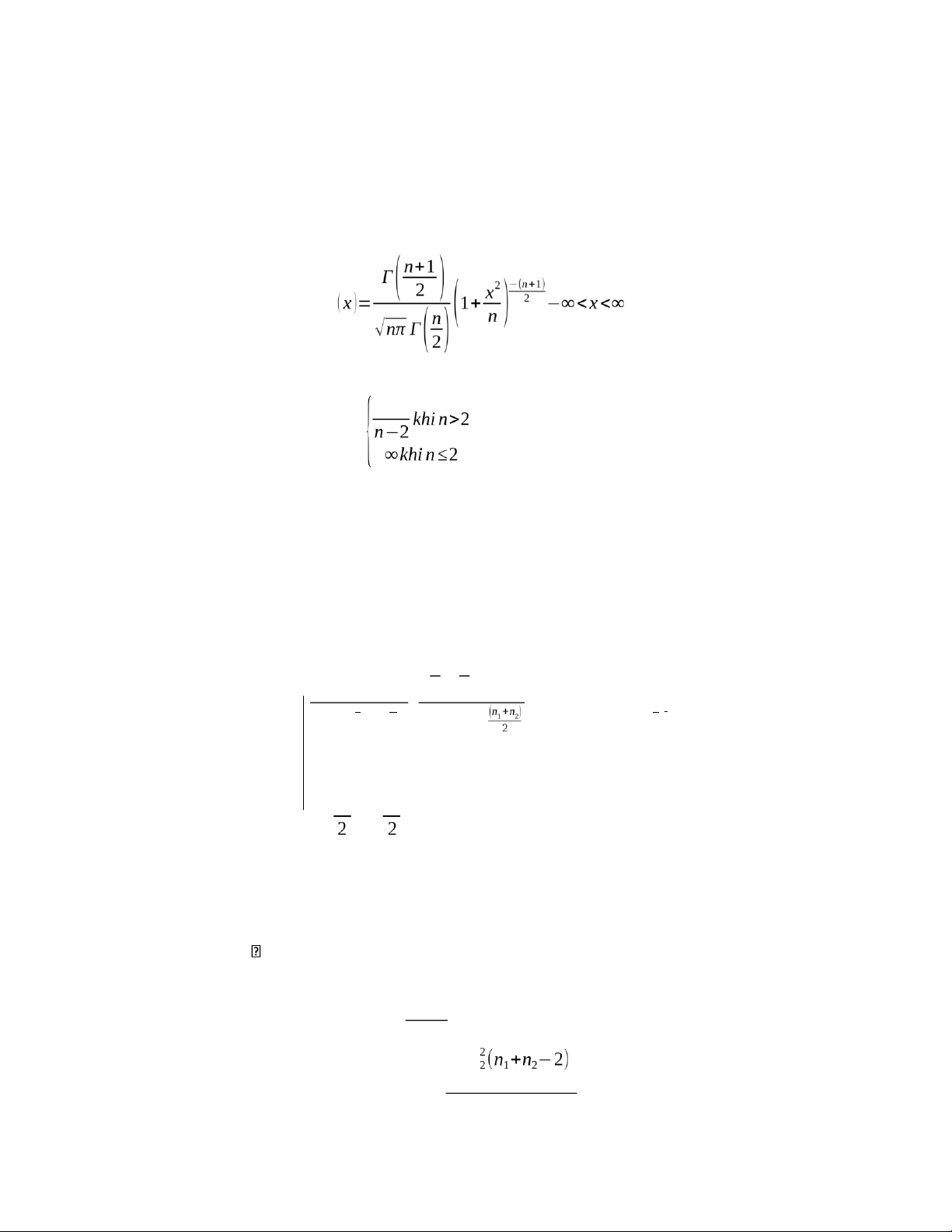
nó có hàm mật độ: 0;khix ≤0 , { f ( x )= ;k hix>0.
Các số đặc trưng: Eξ=n. Var ξ=2n.
Trường hợp đặc biệt: Nếu ξ1,ξ2,…,ξn là các biến ngẫu nhiên độc lập và cùng có phân phối
chuẩn tương ứng {N (ai ,σ2)};i=1,2,…,n. Khi đó, biến ngẫu nhiên: 1 n 2 i 1 n
sẽ có phân phối “chi bình phương lệch” với n bậc tự do,tham số lệch là¿ 2 . σ i=1
Các số đặc trưng của phân phối “chi bình phương lệch” là: 6 lOMoAR cPSD| 59285474
Eξ=m+n;Varξ=4m+2n.
• Phân phối Student hay còn gọi là phân phối t
Biến ngẫu nhiên ξđược gọi là có phân phối Student với n bậc tự do - T (n) nếu nó có hàm mật độ: f
Các số đặc trưng n Eξ=0;Var ξ=
• Phân phối F (F- Phân phối - Fisher - Snedecor)
Biến ngẫu nhiên ξđược gọi là có phân phối F với các bậc tự do (n1,n2) nếu nó có hàm mật độ: Γ(n ) 1+2n2
n1n21 .n2n22 . x(n21−1) .;nếux ≥0, f
( x )=n1 n2 Γ(
)Γ() (n2+n1 x) 0;nếux<0,
ta ký hiệu nó bởi F (n1,n2). Các số đặc trưng n2
+ Nếu n2>2:Eξ= n2−2 2n
+ Nếu n2>4: Var ξ= 2 7 lOMoAR cPSD| 59285474
n1(n2−2) (n2−4)
7.2.2 Các phân phối xác suất của các thống kê từ dân số chuẩn
Cho một mẫu ngẫu nhiênX1, X2,…, Xn từ một tập hợp X có phân phối xác suất f (x; θ), trong
đó θ là một tham số, một thống kê là một hàm T củaX1 , X2 ,…, Xn, nghĩa là
T=T ( X1, X2,…, Xn),
không có tham số θ. Nếu phân phối của dân số đã biết, thì đôi khi có thể tìm thấy phân
phối xác suất của thống kê T. Phân phối chung của các biến ngẫu nhiên X1 , X2 ,…, Xn
được gọi là phân phối của mẫu. Mật độ đồng thời của mẫu là n
f (x1 ,x2 ,…,xn ,θ)=f (x1,θ) f ( x2 ,θ)…f (xn ,θ )=∏ f (xi ,θ ), i=1
trong đó các biến ngẫu nhiên X1, X2,…, Xn là độc lập và có cùng phân phối.
• Định lý 7.1 Cho X
N (μ,σ2), và X1 , X2 ,…, Xn là mẫu ngẫu nhiên từ dân số X, khi đó 2 phân phối của
tổng sẽ là phân phối chi bình phương với n bậc tự do.
Chứng minh: Ta sử dụng tính chất của hàm sinh momen để chứng minh định lý này.
Trước hết ta có nhận xét: Vì Xi N (μ ,σ2), nên Y i σ ,…,n.
Từ đó phân phối của z1=(Y i)2trong đó Y i là biến ngẫu nhiên chuẩn N (0,1) sẽ là:
Fz1 ( x)=P{(Y i )2<x}={FY i (√x)−FYi (−√x+0,);nếux>0.
Gọi f Y ( x) là hàm mật độ của Y i
1, ta sẽ suy ra hàm mật độ của z1 là: 0;nếu x<0,
f z;nếu x>0. ⇒ 8 lOMoAR cPSD| 59285474 0;nếu x<0, f z1 ( x )=1 x 2 e 2 ;nếu x>0. (1)
Vậy z1=(Y i)2 , có phân phối chi bình phương với bậc tự do bằng một (n=1).
Mặt khác ta biết rằng hàm sinh momen của phân phối chi bình phương với 1 bậc tự do được xác định bởi:
Mz (t )=(1−2t )−1/2. 1
Từ đó theo tính chất hàm sinh của tổng các đại lượng ngẫu nhiên độc lập {(Y i)2};i=1,2,…,nsẽ bằng n
tích các hàm sinh, do đó ta thu được hàm sinh của Zn=∑ (Y i)2 : i=1 −n
M Z (t)=(1−2t ) 2 . n
Vậy phân phối của tổng Zn=¿
là phân phối chi bình phương với n bậc tự do.
• Định lý 7.2 Cho X
N (μ,σ2), và X1 , X2 ,…, Xn là mẫu ngẫu nhiên từ dân số X, khi đó 2 biến ngẫu nhiên:
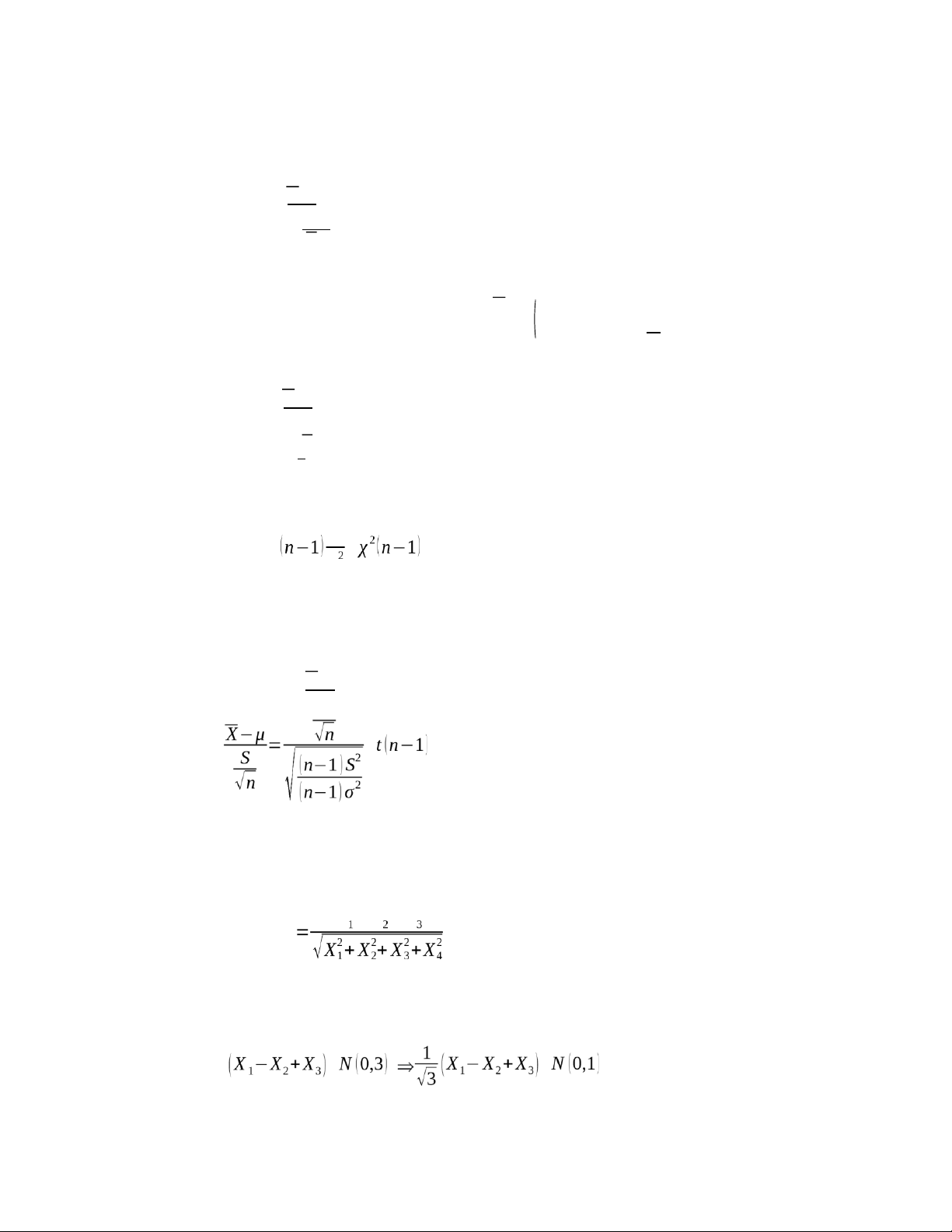
sẽ có phân phối chi bình phương với (n−1)bậc tự do.
Chứng minh: Trước hết sử dụng kết quả của định lý 7.1, ta có ∑ χ 2(1) , I
Vậy hàm sinh momen của các đại lượng đó tương ứng sẽ là n
X −μ 2 −n M; M ;
Mặt khác X và S2 là độc lập với nhau, và ta có biểu diễn 9 lOMoAR cPSD| 59285474 ∑ I Từ đó suy ra E ¿ E , Do đó ta có −n −1 2
(1−2t ) 2 =(1−2t ) 2 E[exp (n−1 S
) σ2 t];t<12 ; S2 Vậy
hàm sinh momen của (n−1) 2 sẽ là: σ ] S 2 2 −n −1 ,
Eexp (n−1) 2 t =(1−2t ) σ
Và đó cũng chính là hàm sinh momen của χ2 (n−1 ), từ đó theo tính duy nhất của hàm sinh ta suy ra điều phải chứng minh. ∎
• Định lý 7.3 NếuZ N (0,1)và U χ2 (n) , ngoài ra, Z và U độc lập, thì biến ngẫu nhiên W Z W= được xác định bởi:
U ; sẽ có phân phối Student với n bậc tự do. √ n U Z Z θ= ;⇒W= = ; 10 lOMoAR cPSD| 59285474
Chứng minh: Ta ký hiệu √ n Khi đó ta có FW
f z( x) f θ ( y ) dxdy. Mặt khác ta biết rằng: . Vì vậy: FW f Z , θ( x ,
y )dydx . θ −∞ zy 0 −∞
Lấy vi phân biểu thức trên theo z, ta sẽ thu được hàm mật độ f W |y|dy
Mặt khác ta biết rằng U
χ2 (n) , vậy
sẽ có phân phối chi với n bậc tự do, nghĩa là
, vậy nó có hàm mật độ phân phối tương ứng là n−1 ;nếu y≥0, f 0;nếu y<0. U
Sử dụng tính độc lập của Z và
√ cùng tính chất của hàm gamma là n −y
e β dy=Г (α ) βα ; Ta sẽ thu được 11 lOMoAR cPSD| 59285474
Đây chính là hàm mật độ của phân phối Student với n bậc tự do. ∎
• Định lý 7.4 Cho X
N (μ,σ2), và X1 , X2 ,…, Xn là mẫu ngẫu nhiên từ dân số X, khi đó X−μ
phân phối của S sẽ có phân phối Student với (n−1)bậc tự do. √n 2
Chứng minh: Vì mỗi X
i N (μ ,σ2); nên ta sẽ có: X Nμ, σ ), từ đó suy ra n X−μ N (0,1). S √n
Hơn nữa, từ định lý 7.5, ta biết rằng S2 . σ Vì vậy: X−μ S
. (Theo định lý 7.6). ∎
Ví dụ 7.4 Cho X1 , X2 , X3, X 4 , là một mẫu ngẫu nhiên có cỡ (n=4 ) và từ dân số có phân
phối chuẩn tắc N (0,1) . Ta quan tâm đến hàm thống kê xác định bởi
X −X +X W ;
Hãy tính kỳ vọng của W .
Theo giả thuyết ta có: Xi N (0,1);i=1,2,3,4. Suy ra: . 12 lOMoAR cPSD| 59285474
Mặt khác theo định lý 7.1, biến ngẫu nhiên ( X21+X22+X23+X24), sẽ có phân phối chi bình
phương với 4 bậc tự do: ( X21+X22+X23+X 24) χ2 (4 ). Từ đó suy ra
W t ( 4). (Theo định lý 7.3)
Khi tìm kỳ vọng của W , ta cần biến đổi một chút EW
Phân phối F và các thống kê từ dân số chuẩn
Trong chương 3 ta đã giới thiệu về phân phối F đó là phân phối xác suất của tỷ số X X .n2
= ; trong đó X ,Y là các biến ngẫu nhiên
có phân phối chi bình phương với Y Y .n1 các bậc tự
do tương ứng là n1,n2. Phân phối F (n1,n2) đó có hàm mật độ Γ(n ) 1+n2
n21 .n2n22 . x( n21−1) 2 n1
.;nếux ≥0, f ( x )=n1 n2 Γ(
)Γ() (n2+n1 x) 0;nếux<0.
Ngoài ra phân phối F (n1,n2) còn có các tính chất đặc biệt sau: 1 a) Nếu X
F (n1,n2), thì khi đó X F (n2,n1). b) Nếu X
N (m1 ,σ 21),và X1, X2,…, Xn là mẫu ngẫu nhiên cỡ n, từ dân số X . Cho 13 lOMoAR cPSD| 59285474
Y N(m2,σ22) và Y 1 ,Y 2,…,Y m là mẫu ngẫu nhiên cỡ m, từ dân số Y . Khi đó hàm S thống kê
sẽ có phân phối F
(n−1,m−1). S
Ví dụ 7.5 Cho X1, X2, X3, X4 và Y1,Y 2,Y3,Y 4,Y5 là 2 mẫu ngẫu nhiên cỡ 4 và 5 từ dân số chuẩn
tắc (N(0,1) ¿. Hãy tính phương sai của hàm thống kê: 2 5 XX 4
T=4 Y 21+Y 22+Y 23+Y 24+Y 25 ;
Do X có phân phối chuẩn tắc (N(0,1) ¿, nên ta sẽ có
( X21+X22+X23+X24) χ2 (4 )
(Y 21+Y 22+Y 23+Y 24+Y 25) χ2(5 )
Do đó, theo phần lý thuyết nêu trên, ta sẽ thu được T
7.2 MẪU NGẪU NHIÊN HAI CHIỀU
Giả sử trên cùng một tổng thề phải nghiên cứu đồng thời hai dấu hiệu định tính hoặc định
lượng, trong đó dấu hiệu nghiên cứu thứ nhất có thể xem như biến ngẫu nhiên X, còn dấu
hiệu nghiên cứu thứ hai có thể xem như biến ngẫu nhiên Y. Lúc đó việc nghiên cứu đồng
thời hai dấu hiệu trong tổng thể tương tự như việc nghiên cứu một biến ngẫu nhiên hai chiều.
Định nghĩa: Mẫu ngâu nhiên hai chiều kích thước n là tập hợp của n biến ngẫu nhiên độc
lập (X i,Y i);i=1,2,… ,n được thành lập từ n biến ngẫu nhiên 2 chiều ( X ,Y )và có cùng quy
luật phân phối xác suất với ( X ,Y ) . 14 lOMoAR cPSD| 59285474
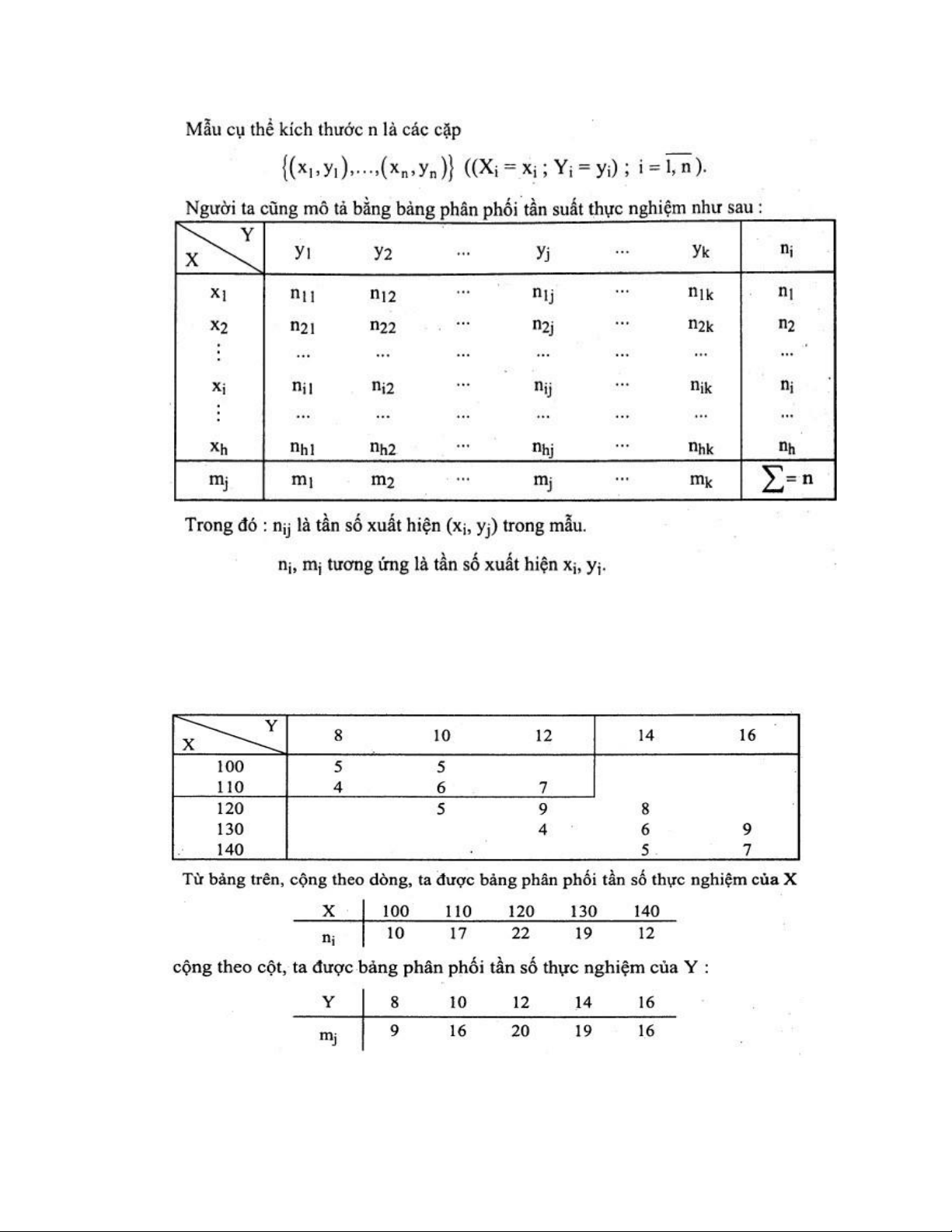
Ví dụ 7.6 Điều tra về hai chỉ tiêu chiều dài X (cm) và hàm lượng chất Y(%) các sản phẩm
của một xí nghiệp ta có kết quả 15 lOMoAR cPSD| 59285474 BÀI TẬP Bài tập 7.1
Cho bảng phân phối thực nghiệm
Hãy tính trung bình, phương sai và độ lệch chuẩn của mẫu nêu trên.
Ta biểu diễn bảng dữ liệu nêu trên dưới dạng sau
Khi đó ta thấy rằng trung bình, phương sai và độ lệch chuẩn của mẫu tương ứng là 16 lOMoAR cPSD| 59285474 Bài tập 7.2
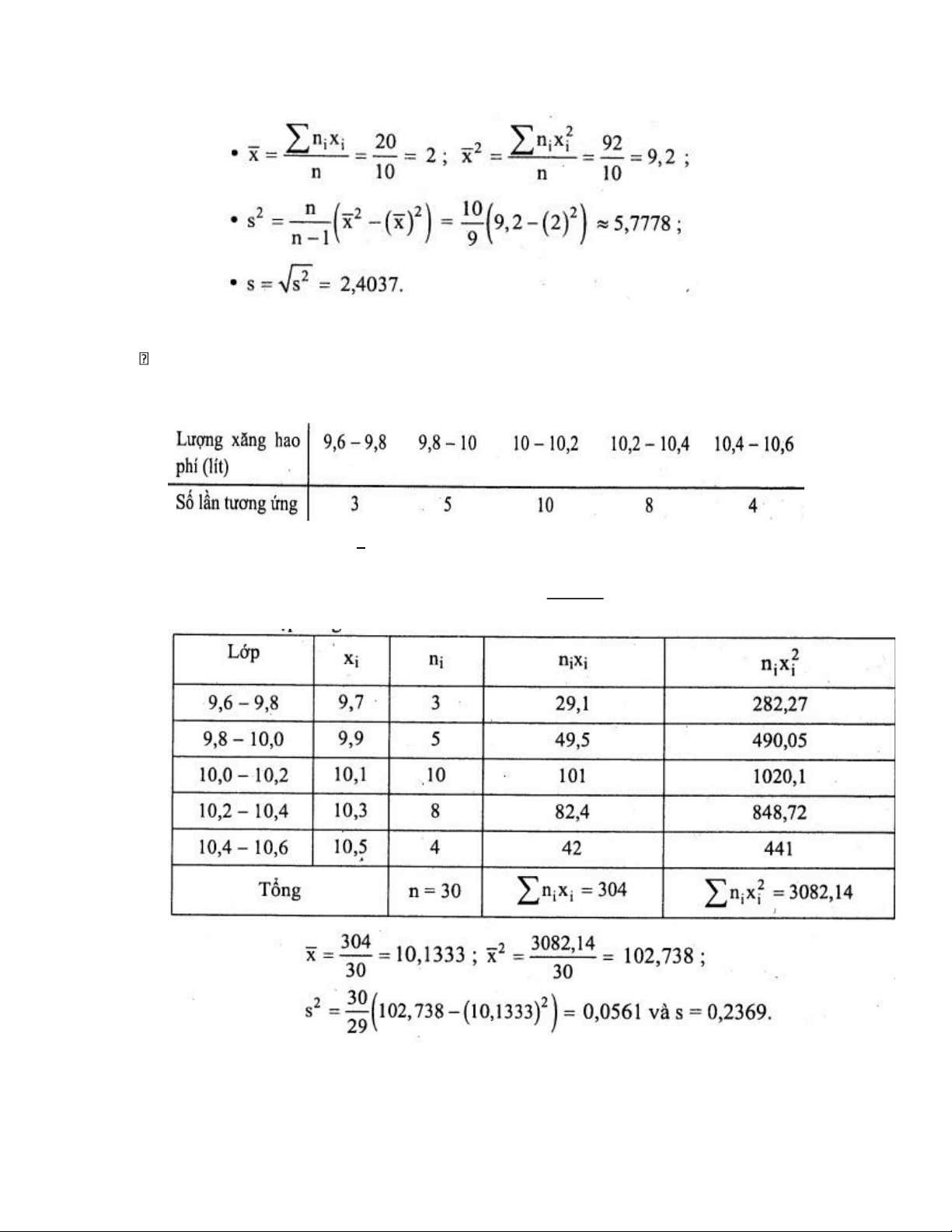
Lượng xăng hao phí của một ô tô đi từ A đến B sau 30 lần chạy được cho trong bảng
Hãy tính trung bình mẫu x(kỳ vọng mẫu) và phương sai mẫu s2 tương ứng với số liệu trên.
Ta lập bảng phân phối mới bằng các đại diện: x' +xi i=
xi−12 để tính 17