13 trang 2 lượt tải

Bài tập xác suất thống kê - Lớp CN1 . Môn Xác suất thống kê(XSTK) | Đại học Trường Đại học Công nghệ thông tin, Đại học Quốc gia Thành phố Hồ Chí Minh.

3/ Xác suất (probability):

Cho bài toán: từ một hộp bi có: 8 bi ỏ + 12 bi xanh + 6 bi vàng + 14 bi en; ta lấy ra ngẫu nhiên cùng lúc 5 viên bi. Biết rằng các viên bi có cùng kích cỡ, hình dáng và trọng lượng.

Tính khả năng ể trong 5 viên bi lấy ra, a/ Có úng 4 bi ỏ;

b/ Có ít nhất 3 bi ỏ, ít nhất 1 bi xanh; c/ Có ít nhất 2 bi ỏ và ít nhất 2 bi vàng; d/ Có ủ 4 màu bi.

Tài liệu gồm 13 trang giúp bạn tham khảo, củng cố kiến thức và ôn tập đạt kết quả cao trong kỳ thi sắp tới. Mời bạn đọc đón xem!

Môn: Xác suất thống kê(XSTK) 16 tài liệu

Trường: Trường Đại học Công nghệ Thông tin, Đại học Quốc gia Thành phố Hồ Chí Minh 557 tài liệu

Tác giả:

trang le

3 ngày trước

Danh sách Quiz

lOMoARcPSD| 59285474

Bui 02 – Ngy 13-10-2024 – môn Xác suất thống kê – lớp CN1.K2023.3

3/ Xc sut (probability):

Cho bi ton: t mt hp bi c: 8 bi  + 12 bi xanh + 6 bi vng + 14 bi en; ta lấy ra ngu

nhiên cng lc 5 viên bi. Bit rng các viên bi c cng kch c, hnh dáng v trng lưng.

Tnh kh năng  trong 5 viên bi lấy ra, a/

C ng 4 bi ;

b/ C t nhất 3 bi , t nhất 1 bi xanh; c/

C t nhất 2 bi  v t nhất 2 bi vng; d/

C  4 mu bi.

Ta c xác suất ca s kin A l kh năng xy ra ca A khi ta thc hin php th, v k

hiu l

P A( )

| A|

(%) | |

với | A| = số cách xy ra s kin A

| | = số cách xy ra trưng hp tng quát. Tnh cht:

(Kolmogorov)

i/ Ta c: 0 P A( ) 1; ii/ P(

=) 1; iii/ P( ) = 0;

iv/ P A() = −1 P A( ), với A l s kin ối lập ca s kin A.

Gợi ý:

Mt cách chn 5 bi t hp c 40 bi l 1 mu c 5:

+ không

thứ t;

+ không

lặp (mỗi viên bi ều khác nhau)

lOMoARcPSD| 59285474

 Đây l t hp.

a/ Gi A = “C ng 4 bi ”

Ta c xác suất ca A l: P A( )

| A|

C C

100

2240

100 0,34% | | C

658008

b/ Gi B = {c t nhất 3 bi , t nhất 1 bi xanh} Các

trưng hp c th xy ra l:

Trưng

hp

Bi  (c tất

c 8 bi)

Bi xanh (c

tất c 12 bi)

Bi khác  v khác

xanh (c tất c 20 bi)

Kt qu

C C C83 121

201

C C83 122

C C

Đáp số = C C C83 + + 121201 C C583 122 C C84 121 = 13440

+3696 +840 0,0273 2,73%

658008

(TH sai lầm: chn 3 bi ; 1 bi xanh; v chn tip 1 bi còn thiu t 36 bi

C C C83 121 361

 áp số =

100 3,6766% ).

C40

c/ Gi C = {c t nhất 2 bi  v t nhất 2 bi vng} Các

trưng hp c th xy ra l:

Trưng

hp

Bi  (c tất

c 8 bi)

Bi vng (c

tất c 6 bi)

Bi khác  v khác

vng (c tất c 26 bi)

Kt qu

C C C82 62

261

lOMoARcPSD| 59285474

C C

Đáp số = C C C82 + + 62261 C C C C582 63 83 62 =

10920+560+840 0,0187 1,87%

658008

d/ Gi D = {c  4 mu bi}

Các trưng hp c th xy ra l:

Trưng

hp

Bi  (c tất

c 8 bi)

Bi xanh (c

tất c 12 bi)

Bi vng (c

tất c 6 bi)

Bi en (c

tất c 14 bi)

Kt qu

C C C C81 121

61 142

C C C C81 121

62 141

C C C C81 122

61 141

C C C C82 121

61 141

C C81 + + + 121 C C61 142 C C81 121 C C62 141 C C81

122 C C61 141 C C82 121 C C61 1

Đáp số

= 0,2206 22,06%

4/ Cc công thc tnh xc sut:

a/ Công thc cng xc sut:

Ta c: P(A + B) = P(A) + P(B) – P(AB);

Nu A, B xung khắc nhau, nghĩa l AB = . Khi , ta c P(AB) = P( ) = 0, nên

lOMoARcPSD| 59285474

P(A + B) = P(A) + P(B).

Suy ra, kh năng  c hai A, B không xy ra l: P( AB. ) = 1 – P(A + B).

P(A + B + C) = P(A) + P(B) + P(C) – P(AB) – P(BC) – P(AC) + P(ABC) = xác suất 

c t nhất 1 trong 3 s kin A, B, C xy ra.

Suy ra, kh năng  c 3 s kin không xy ra l: P( ABC. . ) = 1 – P(A + B + C).

b/ S c lp theo xc sut:

Hai s kin A, B ưc gi l c lập nhau theo xác suất, nu:

P(AB) = P(A).P(B)

Ba s kin A, B, C ưc gi l c lập nhau theo xác suất, nu:

P(AB) = P(A).P(B);

P(AC) = P(A).P(C);

P(BC) = P(B).P(C).

P(ABC) = P(A).P(B).P(C)

c/ Công thc xc sut c iu kin: (các s kin diễn ra theo trnh t thi gian)

Xác suất xy ra ca A với iều kin s kin B  xy ra trước  ưc k hiu l:

P A B( |) = P AB( . )

P B()

(B  xy ra trước A)

d/ Công thc nhân xc sut: (các s kin diễn ra theo trnh t thi gian)

P(AB) = P(A).P(B|A), nu A xy ra trước B;

= P(B).P(A|B), nu B xy ra trước A;

V P(ABC) = P(A).P(B|A).P(C|AB), nu A xy ra trước, ri n B, n C;

= P(A).P(C|A).P(B|AC), nu A xy ra trước, ri n C, n B;

= P(B).P(A|B).P(C|BA), nu B xy ra trước, ri n A, n C;

lOMoARcPSD| 59285474

= P(B).P(C|B).P(A|BC), nu B xy ra trước, ri n C, n A;

= P(C).P(A|C).P(B|CA), nu C xy ra trước, ri n A, n B;

= P(C).P(B|C).P(A|CB), nu C xy ra trước, ri n B, n A.

e/ Công thc xc sut ton phn (công thức xác suất ầy ):

Gi A

, A

, …, A

l mt nhm ầy , v

A = s kin cần quan tâm.

Ta c: P A P A P A A( ) = (

). ( |

)+P A P A A(

). (|

) + +P A P A A(

). ( |

) .

Ngoi ra, ta c:

P A A( j. )P A P A A( j ). (

| j )

P A A( j | ) = =

P A( ) P A P A A(

) ( |

)

+P A P A A(

) ( |

)

+ +P A P A A(

) ( |

) Ta gi ây l công thức BAYES.

V d 1: bi 3/ trang 5

Mt hp c 14 lá thăm, trong  c 4 lá trng thưng v 10 lá không trng thưng.

Cho SV A lên bắt thăm ầu tiên.

SV B lên bắt thăm tip theo.

Hi trò chơi ny c công bng hay không? V sao?

Gii:

Gi A = {SV A bắt thăm trng thưng}

B = {SV B bắt thăm trng thưng}

Suy ra A = {SV A bắt thăm không trng thưng}

Ta c: P(A) = C141 = =4 2 , suy ra P A( ) 1 = −P A( ) 1= − =2 5 .

14 7 7 7

Theo công thức xác suất ầy  (xác suất ton phần), ta c:

lOMoARcPSD| 59285474

P(B) = P(A).P(B|A) + P A P B A( ). ( | )

= 2 C13

+ 5 C14

= 2 + 3 5 4 = 26 = 2

7 C

7 13 7 13 7 13 7

Cho nên ta c P(A) = P(B) = 2/7, nên trò chơi l công bng.

V d 2: bi 8/ trang 5

Gi C = {ngưi bnh b cht}, suy ra C = {ngưi bnh không cht}

LNT = {ngưi bnh b lit na thân}

L2C = {ngưi bnh b lit 2 chân}

KB = {ngưi bnh khi bnh hon ton}. a/ Tnh

xác suất  ngưi bnh không cht.

Cách 1: P(C ) = 1 – P(C) = 1 – 0,1 = 0,9 = 90%

Cách 2: P(C ) = P(LNT) + P(L2C) + P(KB) = 0,3 + 0,2 + 0,4 = 0,9 = 90%. b/

Nu bit rng ngưi bnh không cht, tnh xác suất ngưi  b tật.

Theo công thức Bayes, ta c:

P(b tật| C ) = P LNT P L C() + ( 2 ) = 0,3+ 0,2 = 5 55,56%.

P C() 0,9 9

V d 3: bi 11/ trang 6

Gi Nam = {ngưi i khám bnh l nam}

N = {ngưi i khám bnh l n}

LS = {ngưi i khám bnh mắc bnh lon sắc}

[Ta c Nam.N = ; v

Nam + N = ton b dân cư trong vng =

Suy ra: Nam, N to thnh mt nhm ầy ]. a/

Theo công thức xác suất ầy , ta c:

P(LS) = P(Nam).P(LS|Nam) + P(N).P(LS|N)

lOMoARcPSD| 59285474

= 0,4*0,1 + 0,6*0,15 = 0,04+0,09 = 0,13 = 13%. b/

Nu ngưi ny b lon sắc, tnh xác suất ngưi ny l nam.

Ta c công thức Bayes:

P(Nam|LS) = P Nam P LS Nam( ). ( | ) =

0,4 0,1

30,77%.

P LS( ) 0,13 13

V d 4: bi 27/ trang 8

Gi TQ = {sa Trung Quốc},

TL = {sa Thái Lan},

NZ = {sa New Zealand}.

M = {sa b nhiễm Melamine}.

[ Ta c: TQ.TL = ;

TQ.NZ = ;

TL.NZ = ;

TQ + TL + NZ = ton b sa trong thng = .

Suy ra, TQ, TL, NZ to thnh 1 nhm ầy ]. a/

Theo công thức xác suất ầy , ta c:

P(M) = P(TQ).P(M|TQ) + P(TL).P(M|TL) + P(NZ).P(M|NZ)

= 0,35*0,2 + 0,2*0,15 + 0,45*0,4 = 0,28 = 28% b/ Theo công

thức xác suất Bayes, ta c:

P(NZ|M) = = 64,29%.

c/ Gi s hp sa kim tra không b nhiễm Melamine, tnh kh năng  hp sa ny không

phi l sa Trung Quốc.

Cách 1: lm thao cách a Ảnh

Cách 2: xác suất sa không b nhiễm Melamine l:

lOMoARcPSD| 59285474

P M() = −1 P M() = −10,28 = 0,72 = 72%. Theo công thức Bayes, ta c:

P(không phi sa TQ|không nhiễm Melamine)

= PTQ M( |) = PTL P M TL P NZ P M NZ( ). (

| ) + (). ( | )

0,72

= 0,2 0,85+ 0,45 0,6 = 11 61,11%

0,72 18

Bi: 15/ trang 6,

Gi n l số lần cần bắn ca tên la (n > 0).

Ta c P(tên la bắn trng mc tiêu trong n lần) >= 90%.

P(c t nhất 1 lần trng trong n lần bắn) >= 0,9.

P(số lần bắn trng l >=1 trong n lần bắn) >= 0,9.

1 – P(số lần bắn trng < 1 trong n lần bắn) >= 0,9.

1 – P(số lần bắn trng = 0 trong n lần bắn) >= 0,9.

1 – P(c n lần bắn ều sai) >= 0,9.

1 – (0,4)

>= 0,9.

(0,4)

0,1 log

0,4

(0,4)

log

0,4

(0,1) n 2,5129, nên n = 3.

Vậy cần bắn t nhất l 3 tên la.

Bi: 20/ trang 7

Gi A = “x th thứ nhất bắn trng”

B = “x th thứ hai bắn trng”

C = “bia chỉ b bắn trng 1 viên”.

Ta c kh năng xy ra ca C l:

P(C) = P AB P AB( . ) + ( . ) = 0,7 + 0,4 0,3 0,6 = 46% .

Theo công thức Bayes, ta c:

lOMoARcPSD| 59285474

P B C( | ) = 39,13% .

Bi 1: bi 67/ trang 12

Bi 2: bi 69/ trang 12-13.

Bi 3: bi 70/ trang 13.

Bi 4: bi 114/ trang 19.

Bi 5: bi 143/ trang 23

Bi 6: bi 152 trang 24

Bi 7: bi 160 trang 25

Bi 8: bi 167 trang 26.

Chương 2: BIN NGU NHIÊN

1/ Mt s khi nim:

Bin ngu nhiên l mt ánh x:

X: →

nghĩa l X l mt loi bin nhận giá tr thc ca mnh mt cách ngu nhiên, ty thuc

vo kt qu xy ra khi ta thc hin php th.

* Phân loi bin ngu nhiên (BNN): BNN ưc chia thnh 2 loi

a/ BNN ri rc (discrete random variable): l loi bin c tập hp các giá tr l nhng

i lưng ri rc, m ưc, c hu hn phần t.

b/ BNN liên tc (continuous random variable): l loi bin c tập hp các giá tr l mt

on no  trên trc số, không m ưc, c vô hn phần t.

V d 1: Tui th ca con ngưi ( ơn v tnh l “năm”), l BNN liên tc, ưc tnh t lc con

ngưi sinh ra n lc qua i.

0 tui 1 tui 2 tui

lOMoARcPSD| 59285474

V d 2: (Bi toán tung ng xu ăn tiền). Mt ngưi chơi khi tham gia trò chơi ny s thy

2 ng xu. (Bit rng kh năng xuất hin mặt sấp ca mỗi ng xu l 30%). Nu ng xu xuất

hin mặt sấp th ngưi chơi thắng 5000 ng, còn nu ng xu ra mặt nga th thua 3000 ng.

Gi X l số tiền (thắng hoặc thua) ca ngưi chơi sau khi thy 2 ng xu.  X l mt BNN

ri rc.

Các giá tr m X nhận ưc l ph thuc vo kt qu xy ra khi ta thy 2 ng xu.

TH1: ng xu xuất hin 2 mặt sấp (SS)

 X = 2*5000 ng = 10000 ng, với xác suất l:

P(X = 10000 ng) = P(SS) = 0,3*0,3 = 0,09 = 9%.

TH2: ng xu xuất 1 sấp, 1 nga (SN + NS)

 X = 5000 ng – 3000 ng = 2000 ng, với xác suất l:

P(X = 2000 ng) = P(SN + NS) = P(SN) + P(NS) = 0,3*0,7+0,7*0,3

= 0,42 = 42%.

TH3: ng xu xuất hin 2 mặt nga (NN)

 X = 2*(– 3000 ng) = – 6000 ng, với xác suất l:

P(X = – 6000 ng) = P(NN) = 0,7*0,7 = 0,49 = 49%.

Như vậy:

10000 voi xs 0,09

X = 2000 voi xs 0,42

−6000 voi xs 0,49

2/ Bng phân phi xc sut ca BNN ri rc (probability distribution table of discrete

random variable): l bng c cấu trc sau:

…

Trong :

lOMoARcPSD| 59285474

;

, x

,…, x

l các giá tr thc m X c th nhận ưc khi ta thc hin php th; p P

X x

= ( = =

) kh năng m X nhận giá tr l x

khi ta thc hin php th.

Ta c:

V d mu 1: lập bng phân phối xác suất cho X l BNN th hin cho số tiền thu ưc ca

ngưi chơi trong trò chơi tung 2 ng xu ăn tiền nêu trên.

Gii:

T các trưng hp phân tch giá tr ca X nêu trên, ta c bng phân phân phối (xs):

Ta c mod(X) = -6000 ng do xác suất lc ny l 0,49 l cao nhất trong tất c các xác

suất nhận ưc, nghĩa l kh năng cao nhất l ngưi chơi thua 6000 ng.

Mod(X) l giá tr m X c nhiều kh năng nhận ưc nhất khi ta thc hin php th, nghĩa

l xác suất ca X khi  l lớn nhất.

Ta c số tiền trung bnh m ngưi chơi nhận ưc ( 1 ván) khi tham gia trò chơi ny l:

E(X) =

= −6000*0.49+ 2000*0,42+10000*0,09 =−1200 ng.

(nghĩa l trung bnh 1 ván ngưi chơi thua lỗ 1200 ng).

Gi : bi 22/ trang 35:

Gi T l số tiền ngưi chơi nhận ưc khi ặt 10000 ng vo mặt “bầu” trong trò chơi

lắc bầu cua.

TH1: c 0 mặt bầu => T = - 10000 ng, với xác suất l:

P(T=-10000) = 5 5 5* *

125

6 6 6 216

TH2: c 1 mặt bầu => T = 10000 ng, với xác suất l:

P(T = 10000 ng) = 1 * 5 * 5 + 5 * 1 * 5 + 5 * 5 * 1 = 75

+ + + =p

6000

−

2000

10000

,49

,42

,09

lOMoARcPSD| 59285474

6 6 6 6 6 6 6 6 6 216

TH3: c 2 mặt bầu => T = 20000 ng, với xác suất l:

P(T = 20000 ng) =…..

TH4: c 3 mặt bầu => T = 30000 ng, với xác suất l:

P(T = 30000 ng) = ….

Nên ta c bng phân phối xác suất ca T l

-10000

10000

20000

30000

b/ Tiền trung bnh (k vng) m ngưi chơi thu ưc trong 1 ván l:

E(T) = T =−10000*

125

+10000*

+ 20000* +30000* = ...

216 216

(ta c Mod(X) = -10000 ng).

------------------------------------------------------

V d mu 2: bi 27/ trang 36

Gi X l số lưng máy b hng trong khong thi gian t.

Các giá tr m X c th nhận ưc l:

TH1: c 0 máy b hng => X = 0, với xác suất l:

P(X = 0) = 0,8*0,9*0,7 = 0,504 = 50,4%

TH2: c 1 máy b hng => X = 1, với xác suất l:

P(X = 1) = 0,2*0,9*0,7 + 0,8*0,1*0,7 + 0,8*0,9*0,3 = 0,398=39,8%

TH3: c 2 máy b hng => X = 2, với xác suất l:

P(X = 2) = 0,2*0,1*0,7 + 0,2*0,9*0,3 + 0,8*0,1*0,3 = 0,092 = 9,2%

TH4: c 3 máy b hng => X = 3, với xác suất l:

P(X = 3) = 0,2*0,1*0,3 = 0,006

Nên ta c bng phân phối xác suất ca X l

lOMoARcPSD| 59285474

0,504

0,398

0,092

0,006

Suy ra, Mod(X) = 0, nghĩa l kh năng nhiều nhất l không c máy hng trong khong

thi gian t.

b/ K vng ca X l:

E(X) = [0*0,504+1*0,398+2*0,092+3*0,006] = [0,6] = 1 máy

(với [x] = php toán lấy phần nguyên ca số thc x,

= số nguyên nh nhất, c giá tr >= số thc

x, v d: [1,25] = 2; [10,004] = 11; [12,8] = 13; [9] = 9,…).

Phương sai ca X l:

Var(X) = D(X) = (0 – 0,6)

*0,504 + (1 – 0,6)

*0,398 + (2 – 0,6)

*0,092 + (3 –

0,6)

*0,006 = 0,46.

Var = Variance =  sai lch

D(X) = Dispersion =  phân tán.

Cách 2: Var(X) = D(X) = E(X

) – [E(X)]

= X

−

( )

Với E X(

) = =X

0 *0,504 1 *0,398

+2 *0,092

*0,006

=0,82

v E X( ) = =X 0,6

Suy ra, Var(X) = D(X) = 0,82 – 0,6*0,6 = 0,46

Bấm Tải xuống để xem toàn bộ.

Preview text:

lOMoAR cPSD| 59285474
Buổi 02 – Ngày 13-10-2024 – môn Xác suất thống kê – lớp CN1.K2023.3
3/ Xác suất (probability):
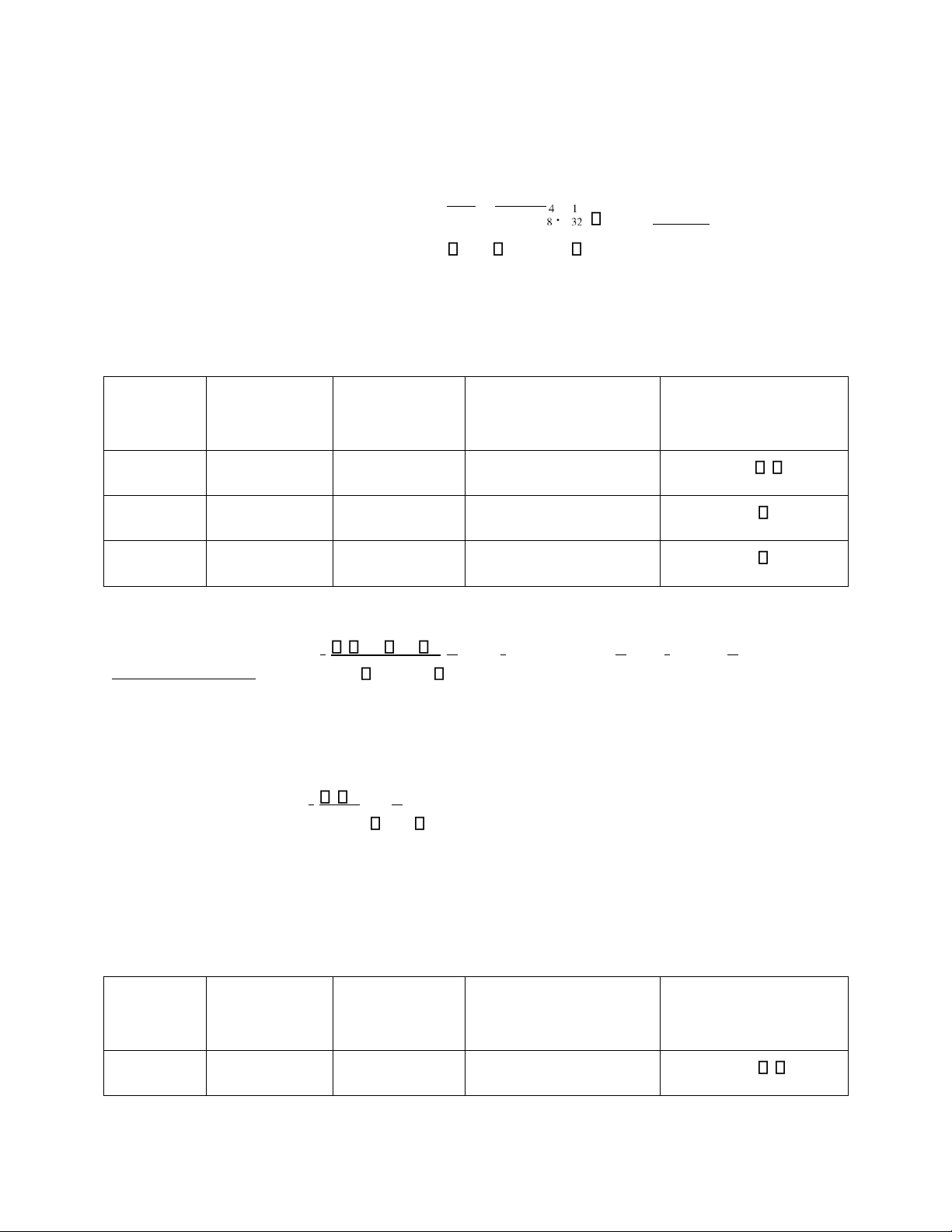
Cho bài toán: từ một hộp bi có: 8 bi ỏ + 12 bi xanh + 6 bi vàng + 14 bi en; ta lấy ra ngẫu
nhiên cùng lúc 5 viên bi. Biết rằng các viên bi có cùng kích cỡ, hình dáng và trọng lượng.
Tính khả năng ể trong 5 viên bi lấy ra, a/ Có úng 4 bi ỏ;
b/ Có ít nhất 3 bi ỏ, ít nhất 1 bi xanh; c/
Có ít nhất 2 bi ỏ và ít nhất 2 bi vàng; d/ Có ủ 4 màu bi.
Ta có xác suất của sự kiện A là khả năng xảy ra của A khi ta thực hiện phép thử, và ký hiệu là = P A( ) | A| (%) | |
với | A| = số cách xảy ra sự kiện A
| | = số cách xảy ra trường hợp tổng quát. Tính chất: (Kolmogorov)
i/ Ta có: 0 P A( ) 1; ii/ P( =) 1; iii/ P( ) = 0;
iv/ P A() = −1 P A( ), với A là sự kiện ối lập của sự kiện A. Gợi ý:
Một cách chọn 5 bi từ hộp có 40 bi là 1 mẫu cỡ 5: + không thứ tự; + không
lặp (mỗi viên bi ều khác nhau) lOMoAR cPSD| 59285474  Đây là tổ hợp.
a/ Gọi A = “Có úng 4 bi ỏ” = =
Ta có xác suất của A là: P A( ) | A| =C C 2240 5 100 100 0,34% | | C40 658008
b/ Gọi B = {có ít nhất 3 bi ỏ, ít nhất 1 bi xanh} Các
trường hợp có thể xảy ra là: Trường Bi ỏ (có tất Bi xanh (có Bi khác ỏ và khác Kết quả hợp cả 8 bi)
tất cả 12 bi) xanh (có tất cả 20 bi) 1 3 1 1 C C C83 121 201 2 3 2 0 C C83 122 3 4 1 0 C C84 121
Đáp số = C C C83 + + 121201 C C583 122 C C84 121 = 13440 +3696 +840 0,0273 2,73% C40 658008
(TH sai lầm: chọn 3 bi ỏ; 1 bi xanh; và chọn tiếp 1 bi còn thiếu từ 36 bi C C C83 121 361  áp số = 5 100 3,6766% ). C40
c/ Gọi C = {có ít nhất 2 bi ỏ và ít nhất 2 bi vàng} Các
trường hợp có thể xảy ra là: Trường Bi ỏ (có tất Bi vàng (có Bi khác ỏ và khác Kết quả hợp cả 8 bi) tất cả 6 bi)
vàng (có tất cả 26 bi) 1 2 2 1 C C C82 62 261 lOMoAR cPSD| 59285474 2 2 3 0 C C82 63 3 3 2 0 C C83 62
Đáp số = C C C82 + + 62261 C C C C582 63 83 62 = 10920+560+840 0,0187 1,87% C40 658008
d/ Gọi D = {có ủ 4 màu bi}
Các trường hợp có thể xảy ra là: Trường Bi ỏ (có tất Bi xanh (có Bi vàng (có Bi en (có Kết quả hợp cả 8 bi)
tất cả 12 bi) tất cả 6 bi) tất cả 14 bi) 1 1 1 1 2 C C C C81 121 61 142 2 1 1 2 1 C C C C81 121 62 141 3 1 2 1 1 C C C C81 122 61 141 4 2 1 1 1 C C C C82 121 61 141
C C81 + + + 121 C C61 142 C C81 121 C C62 141 C C81 122 C C61 141 C C82 121 C C61 1 = 5 14 Đáp số C40 = 0,2206 22,06%
4/ Các công thức tính xác suất:
a/ Công thức cộng xác suất:
Ta có: P(A + B) = P(A) + P(B) – P(AB);
Nếu A, B xung khắc nhau, nghĩa là AB = . Khi ó, ta có P(AB) = P( ) = 0, nên lOMoAR cPSD| 59285474 P(A + B) = P(A) + P(B).
Suy ra, khả năng ể cả hai A, B không xảy ra là: P( AB. ) = 1 – P(A + B).
P(A + B + C) = P(A) + P(B) + P(C) – P(AB) – P(BC) – P(AC) + P(ABC) = xác suất ể
có ít nhất 1 trong 3 sự kiện A, B, C xảy ra.
Suy ra, khả năng ể cả 3 sự kiện không xảy ra là: P( ABC. . ) = 1 – P(A + B + C).
b/ Sự ộc lập theo xác suất:
Hai sự kiện A, B ược gọi là ộc lập nhau theo xác suất, nếu: P(AB) = P(A).P(B)
Ba sự kiện A, B, C ược gọi là ộc lập nhau theo xác suất, nếu: P(AB) = P(A).P(B); P(AC) = P(A).P(C); P(BC) = P(B).P(C). P(ABC) = P(A).P(B).P(C)
c/ Công thức xác suất có iều kiện: (các sự kiện diễn ra theo trình tự thời gian)
Xác suất xảy ra của A với iều kiện sự kiện B ã xảy ra trước ó ược ký hiệu là: P A B( |) = P AB( . ) P B() (B ã xảy ra trước A)
d/ Công thức nhân xác suất: (các sự kiện diễn ra theo trình tự thời gian)
P(AB) = P(A).P(B|A), nếu A xảy ra trước B;
= P(B).P(A|B), nếu B xảy ra trước A;
Và P(ABC) = P(A).P(B|A).P(C|AB), nếu A xảy ra trước, rồi ến B, ến C;
= P(A).P(C|A).P(B|AC), nếu A xảy ra trước, rồi ến C, ến B;
= P(B).P(A|B).P(C|BA), nếu B xảy ra trước, rồi ến A, ến C; lOMoAR cPSD| 59285474
= P(B).P(C|B).P(A|BC), nếu B xảy ra trước, rồi ến C, ến A;
= P(C).P(A|C).P(B|CA), nếu C xảy ra trước, rồi ến A, ến B;
= P(C).P(B|C).P(A|CB), nếu C xảy ra trước, rồi ến B, ến A.
e/ Công thức xác suất toàn phần (công thức xác suất ầy ủ):
Gọi A1, A2, …, An là một nhóm ầy ủ, và
A = sự kiện cần quan tâm.
Ta có: P A P A P A A( ) = ( 1). (
| 1)+P A P A A( 2). (| 2) + +P A P A A( n). ( | n) . Ngoài ra, ta có: P A A( j. )P A P A A( j ). ( | j ) P A A( j | ) = =
P A( ) P A P A A( ) )
1) ( | 1 +P A P A A( 2) ( | 2 + +P A P A A( n) ( |
n) Ta gọi ây là công thức BAYES. Ví dụ 1: bài 3/ trang 5
Một hộp có 14 lá thăm, trong ó có 4 lá trúng thưởng và 10 lá không trúng thưởng.
Cho SV A lên bắt thăm ầu tiên.
SV B lên bắt thăm tiếp theo.
Hỏi trò chơi này có công bằng hay không? Vì sao? Giải:
Gọi A = {SV A bắt thăm trúng thưởng}
B = {SV B bắt thăm trúng thưởng}
Suy ra A = {SV A bắt thăm không trúng thưởng}
Ta có: P(A) = C141 = =4 2 , suy ra P A( ) 1 = −P A( ) 1= − =2 5 . C14 14 7 7 7
Theo công thức xác suất ầy ủ (xác suất toàn phần), ta có: lOMoAR cPSD| 59285474
P(B) = P(A).P(B|A) + P A P B A( ). ( | ) = 2 C 1 1 13 + 5 C14 = 2 + 3 5 4 = 26 = 2 7 C13 7 C13 7 13 7 13 7 13 7
Cho nên ta có P(A) = P(B) = 2/7, nên trò chơi là công bằng. Ví dụ 2: bài 8/ trang 5
Gọi C = {người bệnh bị chết}, suy ra C = {người bệnh không chết}
LNT = {người bệnh bị liệt nửa thân}
L2C = {người bệnh bị liệt 2 chân}
KB = {người bệnh khỏi bệnh hoàn toàn}. a/ Tính
xác suất ể người bệnh không chết.
Cách 1: P(C ) = 1 – P(C) = 1 – 0,1 = 0,9 = 90%
Cách 2: P(C ) = P(LNT) + P(L2C) + P(KB) = 0,3 + 0,2 + 0,4 = 0,9 = 90%. b/
Nếu biết rằng người bệnh không chết, tính xác suất người ó bị tật.
Theo công thức Bayes, ta có:
P(bị tật| C ) = P LNT P L C() + ( 2 ) = 0,3+ 0,2 = 5 55,56%. P C() 0,9 9
Ví dụ 3: bài 11/ trang 6
Gọi Nam = {người i khám bệnh là nam}
Nữ = {người i khám bệnh là nữ}
LS = {người i khám bệnh mắc bệnh loạn sắc} [Ta có Nam.Nữ = ; và
Nam + Nữ = toàn bộ dân cư trong vùng =
Suy ra: Nam, Nữ tạo thành một nhóm ầy ủ]. a/
Theo công thức xác suất ầy ủ, ta có:
P(LS) = P(Nam).P(LS|Nam) + P(Nữ).P(LS|Nữ) lOMoAR cPSD| 59285474
= 0,4*0,1 + 0,6*0,15 = 0,04+0,09 = 0,13 = 13%. b/
Nếu người này bị loạn sắc, tính xác suất người này là nam. Ta có công thức Bayes:
P(Nam|LS) = P Nam P LS Nam( ). ( | ) = 0,4 0,1 = 4 30,77%. P LS( ) 0,13 13
Ví dụ 4: bài 27/ trang 8
Gọi TQ = {sữa Trung Quốc}, TL = {sữa Thái Lan}, NZ = {sữa New Zealand}.
M = {sữa bị nhiễm Melamine}. [ Ta có: TQ.TL = ; TQ.NZ = ; TL.NZ = ;
TQ + TL + NZ = toàn bộ sữa trong thùng = .
Suy ra, TQ, TL, NZ tạo thành 1 nhóm ầy ủ]. a/
Theo công thức xác suất ầy ủ, ta có:
P(M) = P(TQ).P(M|TQ) + P(TL).P(M|TL) + P(NZ).P(M|NZ)
= 0,35*0,2 + 0,2*0,15 + 0,45*0,4 = 0,28 = 28% b/ Theo công
thức xác suất Bayes, ta có: P(NZ|M) = = 64,29%.
c/ Giả sử hộp sữa kiểm tra không bị nhiễm Melamine, tính khả năng ể hộp sữa này không
phải là sữa Trung Quốc.
Cách 1: làm thao cách a Ảnh
Cách 2: xác suất sữa không bị nhiễm Melamine là: lOMoAR cPSD| 59285474
P M() = −1 P M() = −10,28 = 0,72 = 72%. Theo công thức Bayes, ta có:
P(không phải sữa TQ|không nhiễm Melamine) = PTQ M(
|) = PTL P M TL P NZ P M NZ( ). ( | ) + (). ( | ) 0,72
= 0,2 0,85+ 0,45 0,6 = 11 61,11% 0,72 18 Bài: 15/ trang 6,
Gọi n là số lần cần bắn của tên lửa (n > 0).
Ta có P(tên lửa bắn trúng mục tiêu trong n lần) >= 90%.
P(có ít nhất 1 lần trúng trong n lần bắn) >= 0,9.
P(số lần bắn trúng là >=1 trong n lần bắn) >= 0,9.
1 – P(số lần bắn trúng < 1 trong n lần bắn) >= 0,9.
1 – P(số lần bắn trúng = 0 trong n lần bắn) >= 0,9.
1 – P(cả n lần bắn ều sai) >= 0,9.
1 – (0,4)n >= 0,9.
(0,4)n 0,1 log0,4(0,4)n log0,4(0,1) n 2,5129, nên n = 3.
Vậy cần bắn ít nhất là 3 tên lửa. Bài: 20/ trang 7
Gọi A = “xạ thủ thứ nhất bắn trúng”
B = “xạ thủ thứ hai bắn trúng”
C = “bia chỉ bị bắn trúng 1 viên”.
Ta có khả năng xảy ra của C là: P(C) = P AB P AB( . ) + ( . ) = 0,7 + 0,4 0,3 0,6 = 46% .
Theo công thức Bayes, ta có: lOMoAR cPSD| 59285474 P B C( | ) = 39,13% . Bài 1: bài 67/ trang 12
Bài 2: bài 69/ trang 12-13. Bài 3: bài 70/ trang 13. Bài 4: bài 114/ trang 19. Bài 5: bài 143/ trang 23 Bài 6: bài 152 trang 24 Bài 7: bài 160 trang 25 Bài 8: bài 167 trang 26.
Chương 2: BIẾN NGẪU NHIÊN
1/ Một số khái niệm:
Biến ngẫu nhiên là một ánh xạ: X: →
nghĩa là X là một loại biến nhận giá trị thực của mình một cách ngẫu nhiên, tùy thuộc
vào kết quả xảy ra khi ta thực hiện phép thử.
* Phân loại biến ngẫu nhiên (BNN): BNN ược chia thành 2 loại
a/ BNN rời rạc (discrete random variable): là loại biến có tập hợp các giá trị là những
ại lượng rời rạc, ếm ược, có hữu hạn phần tử.
b/ BNN liên tục (continuous random variable): là loại biến có tập hợp các giá trị là một
oạn nào ó trên trục số, không ếm ược, có vô hạn phần tử.
Ví dụ 1: Tuổi thọ của con người ( ơn vị tính là “năm”), là BNN liên tục, ược tính từ lúc con
người sinh ra ến lúc qua ời.
0 tuổi 1 tuổi 2 tuổi lOMoAR cPSD| 59285474
Ví dụ 2: (Bài toán tung ồng xu ăn tiền). Một người chơi khi tham gia trò chơi này sẽ thảy
2 ồng xu. (Biết rằng khả năng xuất hiện mặt sấp của mỗi ồng xu là 30%). Nếu ồng xu xuất
hiện mặt sấp thì người chơi thắng 5000 ồng, còn nếu ồng xu ra mặt ngửa thì thua 3000 ồng.
Gọi X là số tiền (thắng hoặc thua) của người chơi sau khi thảy 2 ồng xu.  X là một BNN rời rạc.
Các giá trị mà X nhận ược là phụ thuộc vào kết quả xảy ra khi ta thảy 2 ồng xu.
TH1: ồng xu xuất hiện 2 mặt sấp (SS)
 X = 2*5000 ồng = 10000 ồng, với xác suất là:
P(X = 10000 ồng) = P(SS) = 0,3*0,3 = 0,09 = 9%.
TH2: ồng xu xuất 1 sấp, 1 ngửa (SN + NS)
 X = 5000 ồng – 3000 ồng = 2000 ồng, với xác suất là:
P(X = 2000 ồng) = P(SN + NS) = P(SN) + P(NS) = 0,3*0,7+0,7*0,3 = 0,42 = 42%.
TH3: ồng xu xuất hiện 2 mặt ngửa (NN)
 X = 2*(– 3000 ồng) = – 6000 ồng, với xác suất là:
P(X = – 6000 ồng) = P(NN) = 0,7*0,7 = 0,49 = 49%. Như vậy: 10000 voi xs 0,09 X = 2000 voi xs 0,42 −6000 voi xs 0,49
2/ Bảng phân phối xác suất của BNN rời rạc (probability distribution table of discrete
random variable): là bảng có cấu trúc sau: X x1 x2 … xn P p1 p2 … pn Trong ó: lOMoAR cPSD| 59285474
x1 x2 xn ;
x1, x2,…, xn là các giá trị thực mà X có thể nhận ược khi ta thực hiện phép thử; p P
X xi = ( = =i ) khả năng mà X nhận giá trị là xi khi ta thực hiện phép thử.
Ta có: p1 + + + =p2 pn 1.
Ví dụ mẫu 1: lập bảng phân phối xác suất cho X là BNN thể hiện cho số tiền thu ược của
người chơi trong trò chơi tung 2 ồng xu ăn tiền nêu trên. Giải:
Từ các trường hợp phân tích giá trị của X nêu trên, ta có bảng phân phân phối (xs): X 6000 − 2000 10000 P 0 ,49 ,42 0 0 ,09
Ta có mod(X) = -6000 ồng do xác suất lúc này là 0,49 là cao nhất trong tất cả các xác
suất nhận ược, nghĩa là khả năng cao nhất là người chơi thua 6000 ồng.
Mod(X) là giá trị mà X có nhiều khả năng nhận ược nhất khi ta thực hiện phép thử, nghĩa
là xác suất của X khi ó là lớn nhất.
Ta có số tiền trung bình mà người chơi nhận ược (ở 1 ván) khi tham gia trò chơi này là:
E(X) = X = −6000*0.49+ 2000*0,42+10000*0,09 =−1200 ồng.
(nghĩa là trung bình 1 ván người chơi thua lỗ 1200 ồng).
Gợi ý: bài 22/ trang 35:
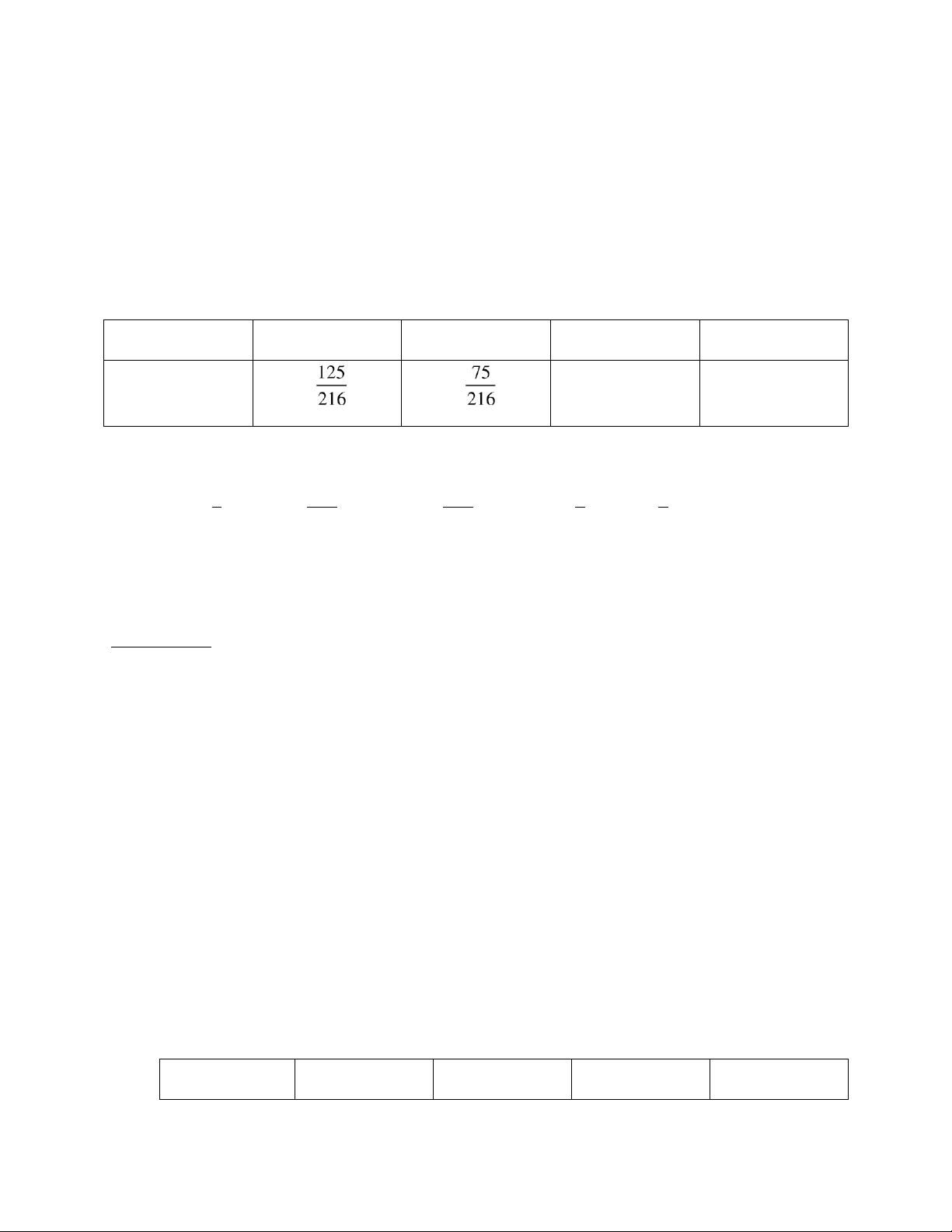
Gọi T là số tiền người chơi nhận ược khi ặt 10000 ồng vào mặt “bầu” trong trò chơi lắc bầu cua.
TH1: có 0 mặt bầu => T = - 10000 ồng, với xác suất là: = P(T=-10000) = 5 5 5* * 125 6 6 6 216
TH2: có 1 mặt bầu => T = 10000 ồng, với xác suất là:
P(T = 10000 ồng) = 1 * 5 * 5 + 5 * 1 * 5 + 5 * 5 * 1 = 75 lOMoAR cPSD| 59285474 6 6 6 6 6 6 6 6 6 216
TH3: có 2 mặt bầu => T = 20000 ồng, với xác suất là: P(T = 20000 ồng) =…..
TH4: có 3 mặt bầu => T = 30000 ồng, với xác suất là: P(T = 30000 ồng) = ….
Nên ta có bảng phân phối xác suất của T là T -10000 10000 20000 30000 P
b/ Tiền trung bình (kỳ vọng) mà người chơi thu ược trong 1 ván là: E(T) = T =−10000*
125 +10000* 75 + 20000* +30000* = ... 216 216
(ta có Mod(X) = -10000 ồng).
------------------------------------------------------
Ví dụ mẫu 2: bài 27/ trang 36
Gọi X là số lượng máy bị hỏng trong khoảng thời gian t.
Các giá trị mà X có thể nhận ược là:
TH1: có 0 máy bị hỏng => X = 0, với xác suất là:
P(X = 0) = 0,8*0,9*0,7 = 0,504 = 50,4%
TH2: có 1 máy bị hỏng => X = 1, với xác suất là:
P(X = 1) = 0,2*0,9*0,7 + 0,8*0,1*0,7 + 0,8*0,9*0,3 = 0,398=39,8%
TH3: có 2 máy bị hỏng => X = 2, với xác suất là:
P(X = 2) = 0,2*0,1*0,7 + 0,2*0,9*0,3 + 0,8*0,1*0,3 = 0,092 = 9,2%
TH4: có 3 máy bị hỏng => X = 3, với xác suất là:
P(X = 3) = 0,2*0,1*0,3 = 0,006
Nên ta có bảng phân phối xác suất của X là X 0 1 2 3 lOMoAR cPSD| 59285474 P 0,504 0,398 0,092 0,006
Suy ra, Mod(X) = 0, nghĩa là khả năng nhiều nhất là không có máy hỏng trong khoảng thời gian t. b/ Kỳ vọng của X là:
E(X) = [0*0,504+1*0,398+2*0,092+3*0,006] = [0,6] = 1 máy
(với [x] = phép toán lấy phần nguyên của số thực x,
= số nguyên nhỏ nhất, có giá trị >= số thực
x, ví dụ: [1,25] = 2; [10,004] = 11; [12,8] = 13; [9] = 9,…). Phương sai của X là:
Var(X) = D(X) = (0 – 0,6)2*0,504 + (1 – 0,6)2*0,398 + (2 – 0,6)2*0,092 + (3 – 0,6)2*0,006 = 0,46.
Var = Variance = ộ sai lệch
D(X) = Dispersion = ộ phân tán. −
Cách 2: Var(X) = D(X) = E(X2) – [E(X)]2 = X2 ( )X 2
Với E X( 2) = =X 2 0 *0,504 1 *0,3982 + 2 +2 *0,0922 +3 *0,0062=0,82
và E X( ) = =X 0,6
Suy ra, Var(X) = D(X) = 0,82 – 0,6*0,6 = 0,46

Bài tập xác suất thống kê - Lớp CN1 . Môn Xác suất thống kê(XSTK) | Đại học Trường Đại học Công nghệ thông tin, Đại học Quốc gia Thành phố Hồ Chí Minh.

Tài liệu liên quan:

Tai Lieu GK SXTK Va Bang Gia Tri. Môn Xác suất thống kê(XSTK) | Đại học Trường Đại học Công nghệ thông tin, Đại học Quốc gia Thành phố Hồ Chí Minh.

BÀI 4. BIẾN NGẪU Nhiên NHIỀU CHIỀU 26. Môn Xác suất thống kê(XSTK) | Đại học Trường Đại học Công nghệ thông tin, Đại học Quốc gia Thành phố Hồ Chí Minh.

BÀI 7 MẪU NGẪU Nhiên - Lý thuyết về Xác Suất Thống kê cùng với một bài tập ví dụ. Môn Xác suất thống kê(XSTK) | Đại học Trường Đại học Công nghệ thông tin, Đại học Quốc gia Thành phố Hồ Chí Minh.

Giải bài tập - giai bai tap. Môn Xác suất thống kê(XSTK) | Đại học Trường Đại học Công nghệ thông tin, Đại học Quốc gia Thành phố Hồ Chí Minh.