Bài 4: Phương trình lượng giác cơ bản | Giáo án Toán 11 Cánh diều

Trường: THPT Chuyên Lào Cai Họ và tên giáo viên: Tổ: TOÁN - TIN
Cao Thị Hồng Tuyết = Nguyễn Bá Hoàng
Ngày soạn: 27/8/2023
BÀI 4: PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN
Môn học/Hoạt động giáo dục: Toán – ĐS-GT: 11
Thời gian thực hiện: 03 tiết I. MỤC TIÊU 1. Kiến thức
- Biết phương trình lượng giác cơ bản sin x = ; a cos x = ; a tan x = ;
a cot x = a và công thức nghiệm.
- Nắm được điều kiện của a để các phương trình sin x = ;
a cos x = a có nghiệm.
- Biết cách sử dụng các kí hiệu arcsin , a arccos ,
a arctan a,arccot . a 2. Năng lực
- Năng lực tự học:Học sinh xác định đúng đắn động cơ thái độ học tập; tự đánh giá và điều chỉnh
được kế hoạch học tập; tự nhận ra được sai sót và cách khắc phục sai sót.
- Năng lực giải quyết vấn đề: Biết tiếp nhận câu hỏi, bài tập có vấn đề hoặc đặt ra câu hỏi. Phân tích
được các tình huống trong học tập.
- Năng lực tự quản lý: Làm chủ cảm xúc của bản thân trong quá trình học tập vào trong cuộc sống;
trưởng nhóm biết quản lý nhóm mình, phân công nhiệm vụ cụ thể cho từng thành viên nhóm, các
thành viên tự ý thức được nhiệm vụ của mình và hoàn thành được nhiệm vụ được giao.
- Năng lực giao tiếp: Tiếp thu kiến thức trao đổi học hỏi bạn bè thông qua hoạt động nhóm; có thái
độ tôn trọng, lắng nghe, có phản ứng tích cực trong giao tiếp.
- Năng lực hợp tác: Xác định nhiệm vụ của nhóm, trách nhiệm của bản thân đưa ra ý kiến đóng góp
hoàn thành nhiệm vụ của chủ đề.
- Năng lực sử dụng ngôn ngữ: Học sinh nói và viết chính xác bằng ngôn ngữ Toán học.
3. Phẩm chất:
- Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
- Chăm chỉ tích cực xây dựng bài, chủ động chiếm lĩnh kiến thức theo sự hướng dẫn của GV.
- Năng động, trung thực, sáng tạo trong quá trình tiếp cận tri thức mới ,biết quy lạ về quen, có tinh
thần hợp tác xây dựng cao.
- Hình thành tư duy logic, lập luận chặt chẽ, và linh hoạt trong quá trình suy nghĩ.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU
- Các kiến thức về công thức lượng giác - Ti vi, máy tính - Phiếu học tập
III. TIẾN TRÌNH DẠY HỌC :
1. HOẠT ĐỘNG 1: MỞ ĐẦU
a) Mục tiêu: tiếp cận phương trình lượng giác cơ bản
b) Nội dung: Ta xét bài toán sau:
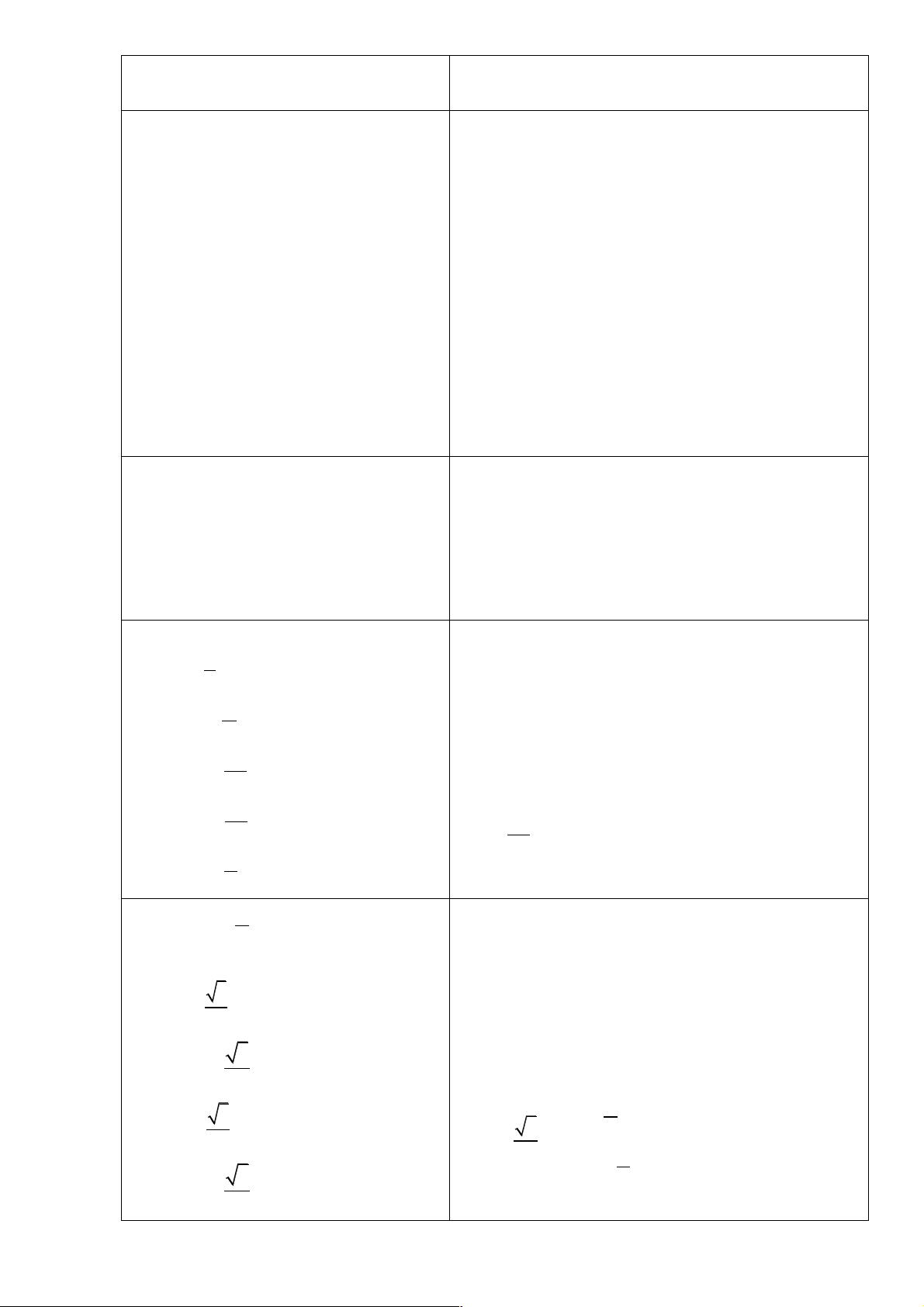
Một vệ tinh nhân tạo bay quanh Trái đất theo quỹ đạo hình elíp (hình dưới). Độ cao h (tính bằng π
km) của vệ tinh so với bề mặt trái đất được xác định bởi công thức h = 550 + 450cos t , trong đó 50
t là thời gian tính bằng phút kể từ lúc vệ tinh bay vào quỹ đạo. Người ta cần thực hiện một thí
nghiệm khoa học khi vệ tinh cách mặt đất 250 km. Hãy tìm các thời điểm để có thể thực hiện thí nghiệm đó. c) Sản phẩm: π π 2
Bài toán này dẫn đến việc giải phương trình 550 + 450cos t = 250 Û cos t = - 50 50 3 2 Nếu đặt = π x
t thì phương trình trên có dạng cos x = - . 50 3
d) Tổ chức thực hiện:
*) Chuyển giao nhiệm vụ : GV nêu và trình chiếu câu hỏi, yêu cầu HS làm việc cá nhân để hoàn
thành hệ thống câu hỏi.
*) Thực hiện: Yêu cầu HS suy nghĩ, trao đổi tích cực
GV gợi ý bằng cách đưa ra các các câu hỏi:
- Câu hỏi 1: Nêu yêu cầu của bài toán này?
- Câu hỏi 2: Nếu đặt = π x
t thì hãy viết lại phương trình theo x ? 50
*) Báo cáo, thảo luận:
- GV gọi lần lượt 2 HS lên bảng trình bày câu trả lời của mình.
- Các học sinh khác nhận xét, bổ sung để hoàn thiện câu trả lời.
*) Đánh giá, nhận xét, tổng hợp:
- GV nhận xét, đánh giá phần trả lời của HS.
- GV nhấn mạnh kết quả: “ tìm x 2 để cos x = - ” 3
Trong thực tế có nhiều bài toán dẫn đến việc giải các phương trình có dạng:
sin x = a, cos x = a, tan x = a,cot x = a với x là ẩn, a là tham số.
Các phương trình trên gọi là phương trình lượng giác cơ bản.
2.HOẠT ĐỘNG 2: HÌNH THÀNH KIẾN THỨC MỚ
HĐ1: Phương trình sin x = a
a) Mục tiêu: Hình thành công thức và biết vận dụng giải phương trình sin x = a b)Nội dung
H1: Tìm công thức nghiệm của phương trình sin x = a và các trường hợp đặc biệt của nó
H2: Ví dụ 1: Giải các phương trình sau 1 2 - 3 - 2 0 a)sin x = , b)sin x = , c)sin(x +15 ) = , d)sin5x = 2 5 2 2 c) Sản phẩm:
Phương trình sin x = a (1)
+ a > 1: phương trình ( ) 1 vô nghiệm.
+ a £ 1: Gọi sina = a , phương trình ( ) 1 có nghiệm là: éx = a + k2p sin x = sina Û ;k Î ê ¢
ëx = p - a + k2p Chú ý. é x = b ! + k360! + sin x = sin b ! Û ê , k Î Z 0
ëx =180 - b ! + k360! ì p p ï- £ a £ + í 2
2 Þ a = arcsina , phương trình (1) có ïî sina = a
éx = arcsina + k2p nghiệm: ;k Î ê ¢
ëx = p - arcsina + k2p
é f (x) = g(x) + k2p
+ sin f (x) = sin g(x) Û , k Î Z ê
ë f (x) = p - g(x) + k2p • Đặc biệt: p
* sin x =1 Û x = + k2p,k Î! 2 p * sin x = 1
- Û x = - + k2p,k Î! 2
* sin x = 0 Û x = kp , k Î! Ví dụ 1: é p é p x = + k2p x = + k2p 1 p ê 6 ê 6 a)sin x = = sin Û ê Û ê , k Î Z 2 6 p 5p êx p k2p ê = - + x = + k2p êë 6 êë 6 é 2 x = arcsin + k2p 2 ê 5 b)sin x = Û ê , k Î Z 5 2
êx = p -arcsin + k2p êë 5 - 3 éx + = - + k éx = - + k c)sin(x +15 ) = = sin ( 60 - ) 0 0 0 0 0 15 60 360 75 360 0 0 Û ê Û ê , k Î Z 0 0 0 0 0 0 2
êëx +15 =180 + 60 + k360 ëx = 225 + k360 é p - é p x = + k2p x = - + k2p - 2 p ê 4 ê 4 d)sin x = = sin(- ) Û ê Û ê
, k Î Z 2 4 p 5p êx p k2p ê = + + x = + k2p êë 4 êë 4
d) Tổ chức thực hiện
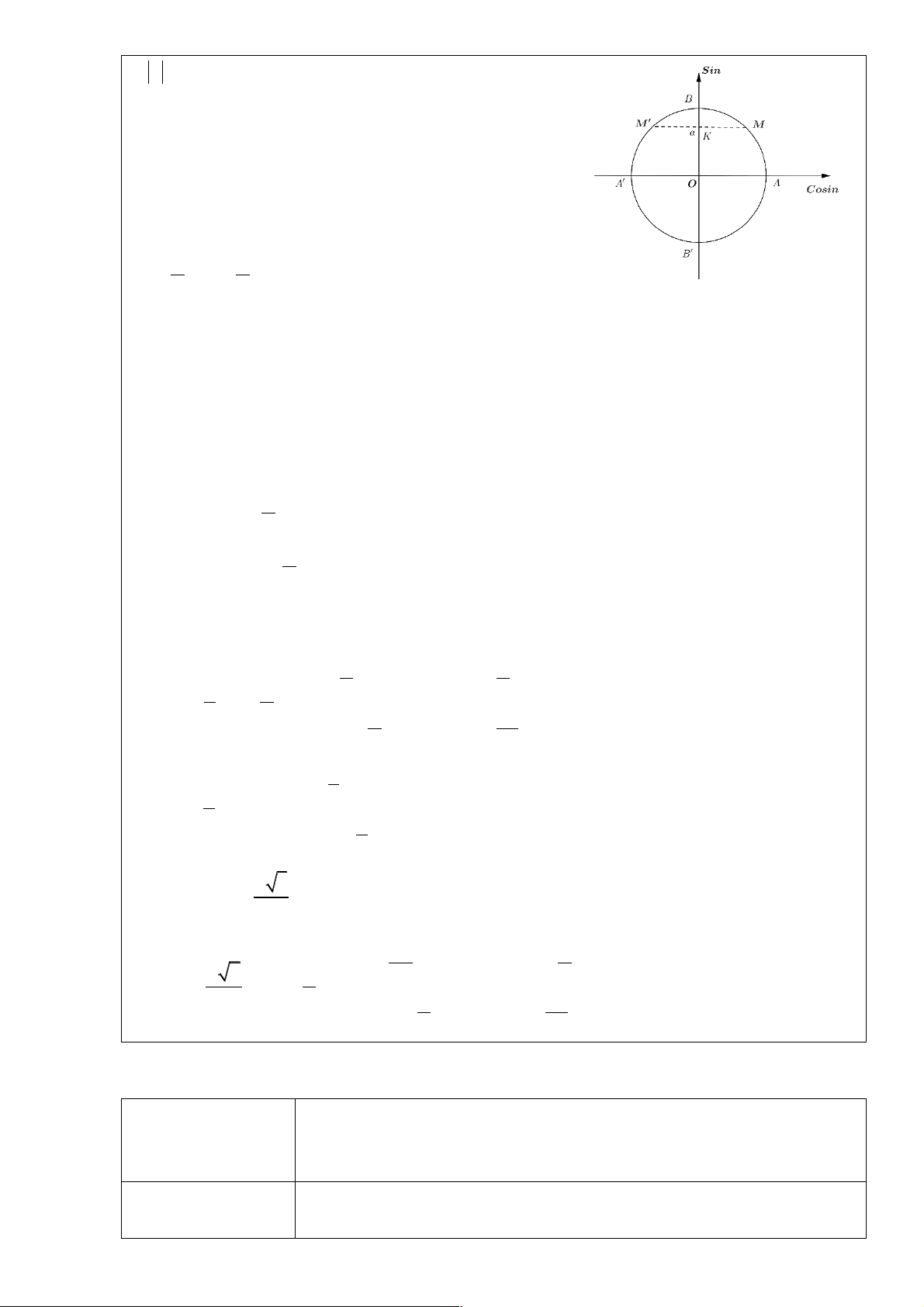
- GV trình chiếu hình vẽ trong SGK ® đặt vấn đề nghiên cứu công thức
Chuyển giao nghiệm
- HS vẽ hình và nhớ lại tính tuần hoàn của hàm số sin
- HS thảo luận cặp đôi thực hiện nhiệm vụ
Thực hiện
- GV theo dõi, hỗ trợ , hướng dẫn các nhóm
- HS nắm được công thức nghiệm của phương trình sin x = a và các trường
hợp đặc biệt của nó.
- Phân biệt các trường hợp của công thức để vận dụng giải toán.
Báo cáo thảo luận - Trong công thức nghiệm không thể chứa cùng lúc 2 đơn vị radian và độ
- GV gọi 4HS lên bảng trình bày lời giải cho VD1
- HS khác theo dõi, nhận xét, hoàn thiện sản phẩm
- GV nhận xét thái độ làm việc, phương án trả lời của học sinh, ghi nhận
Đánh giá, nhận xét, và tuyên dương học sinh có câu trả lời tốt nhất. Động viên các học sinh còn
tổng hợp
lại tích cực, cố gắng hơn trong các hoạt động học tiếp theo
- Chốt kiến thức và các bước giải phương trình
HĐ2. Phương trình cos x = a
a) Mục tiêu: Hình thành công thức và biết vận dụng giải phương trình sin x = a . b) Nội dung:
H1: Tìm công thức nghiệm của phương trình cos x = a và các trường hợp đặc biệt của nó
H2: Ví dụ 2: Giải các phương trình sau æ 3p ö 3 - - p a) cos x + = , b) cos ç ÷ ( 1 4 0 2x + 5 ) = , c) cos3x = , d) cos 2x = cos è 8 ø 2 2 5 10 c) Sản phẩm:
Phương trình cos x = a (2) + a > :
1 phương trình (2) vô nghiệm.
+ a £ 1: Gọi cosa = a , phương trình (2)có nghiệm là: é x = a + k2p , k Î!. ê ëx = a - + k2p Chú ý. é x = a + k2p + cos x = cosa Û , k Î Z ê ëx = a - + k2p é = b ! + ! + x k360 cos x = cos b ! Û ê , k Î Z
ëx = -b ! + k360! ì0 £ a £ p + í
Þ a = arccosa , phương trình (2) có nghiệm: x = ± arccos a + k2p ,k Î! îcosa = a
é f (x) = g(x) + k2p
+ cos f (x) = cos g(x) Û , k Î Z ê
ë f (x) = -g(x) + k2p • Đặc biệt:
+ cos x =1 Û x = k2p , k Î Z + cos x = 1
- Û x = p + k2p , k Î Z p
+ cos x = 0 Û x = + kp , k Î Z 2 Ví dụ 2:
a) Phương trình vô nghiệm vì 3 - Ï[ 1 - ] ;1 2 0 é 115 0 0 0 0 x = + 180 k - é ê b) 1
2x + 5 = 120 + k360 0 0 2 cos(2x + 5 ) = = cos120 Û ê Û ê
, k Î Z 0 0 0 0 2 ë2x + 5 = 120 - + k360 ê 125 - 0 x = + 180 k êë 2 c) 4 4 1 4 k2p cos3x =
Û 3x = arccos + k2p Û x = arccos +
, k Î Z 5 5 3 5 3 d) p p p cos 2x = cos Û 2x = ± + k2p Û x = ±
+ kp ,k Î Z 10 10 20
d) Tổ chức thực hiện
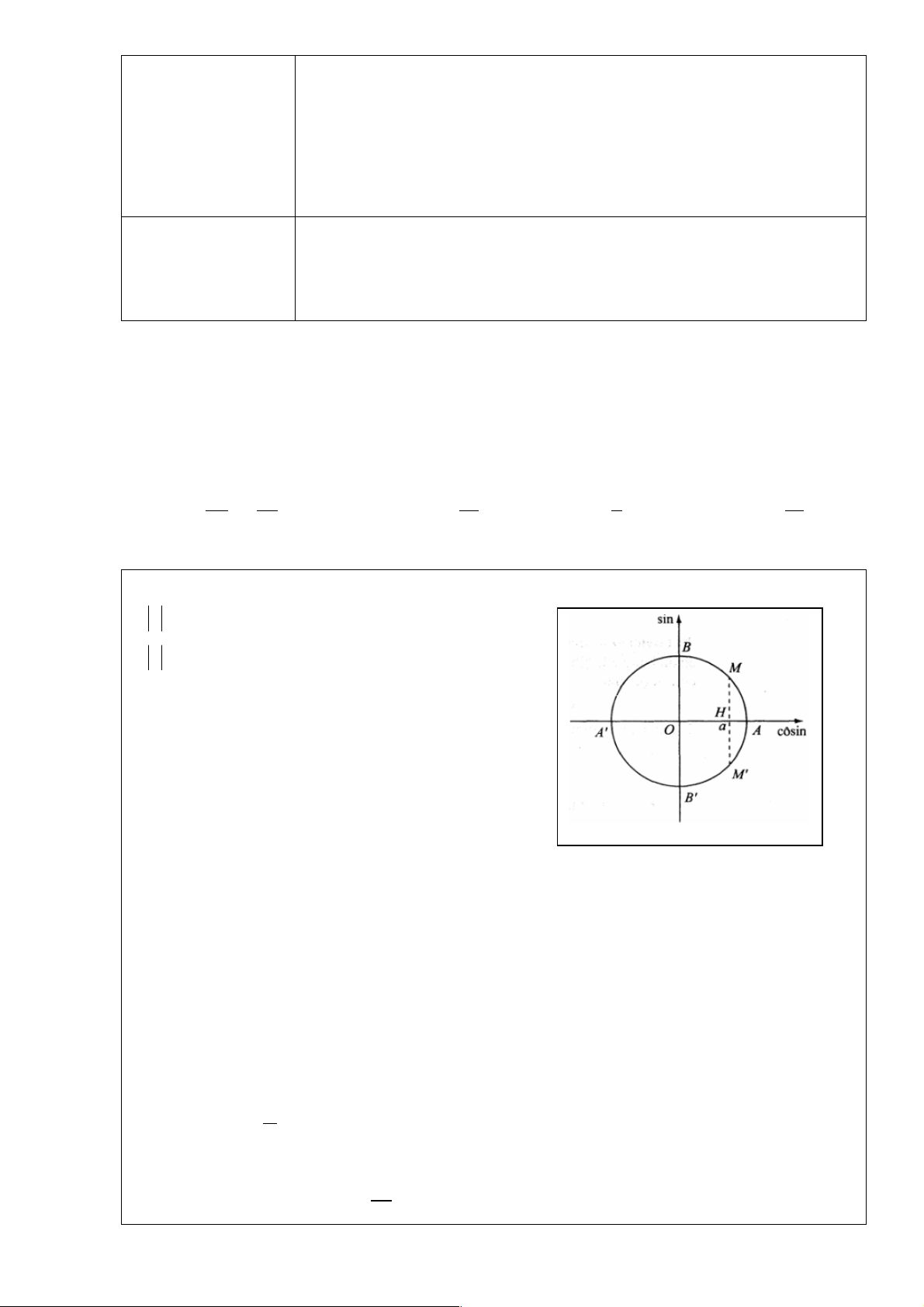
- GV trình chiếu hình vẽ trong SGK ® đặt vấn đề nghiên cứu công thức
Chuyển giao nghiệm
- HS vẽ hình và nhớ lại tính tuần hoàn của hàm số cos
- HS thảo luận cặp đôi thực hiện nhiệm vụ
Thực hiện
- GV theo dõi, hỗ trợ , hướng dẫn các nhóm
- HS nắm được công thức nghiệm của phương trình cos x = a và các trường
hợp đặc biệt của nó.
- Phân biệt các trường hợp của công thức để vận dụng giải toán.
Báo cáo thảo luận - Trong công thức nghiệm không thể chứa cùng lúc 2 đơn vị radian và độ
- GV gọi 4HS lên bảng trình bày lời giải cho VD2
- HS khác theo dõi, nhận xét, hoàn thiện sản phẩm
- GV nhận xét thái độ làm việc, phương án trả lời của học sinh, ghi nhận và
Đánh giá, nhận xét, tuyên dương học sinh có câu trả lời tốt nhất. Động viên các học sinh còn lại
tổng hợp
tích cực, cố gắng hơn trong các hoạt động học tiếp theo
- Chốt kiến thức và các bước giải phương trình
HĐ 3. Phương trình tan x = a
a) Mục tiêu: Hình thành công thức và biết vận dụng giải phương trình tan x = a . b) Nội dung:
H1: Tìm công thức nghiệm của phương trình tan x = a và các trường hợp đặc biệt của nó
H2: Ví dụ 2: Giải các phương trình sau 2p 0 a) tan x = tan , b) tan x = 5 - ,
c) tan(x - 35 ) = 3 , d) tan 4x = 1 - 5 c) Sản phẩm:
Phương trình tan x = a (3)
Điều kiện của phương trình là: p
x ¹ + kp (k Î Z). 2
- Gọi x1 là hoành độ giao điểm( tan x = .
a )thỏa mãn điều kiện 1 p p - < x < . 1 2 2
Kí hiệu x = arctan a. Khi đó, nghiệm của phương trình là: x = arctan a + kp (k ÎZ ) 1
* Chú ý: a) Phương trình tan x = tana Þ x = a + kp (k Î Z)
Tổng quát: tan f (x) = tan g (x) Þ f (x) = g (x) + kp(k ÎZ) b) Phương trình 0 0 0
tan x = tan b Þ x = b + 1
k 80 (k ÎZ)
c) Các trường hợp đặc biệt: • p
tan x =1Þ x = + kp (k Î Z) 4 • p tan x = 1
- Þ x = - + kp (k Î Z) 4
• tan x = 0 Þ x = kp (k Î Z) Ví dụ 3: 2p 2p a) tan x = tan Û x = + kp , k Î Z 5 5 ) b tan x = 5 - Û x = arctan( 5 - ) + kp, k ÎZ 0 0 0 0 0 0
c) tan(x - 35 ) = 3 Û x - 35 = 60 + 1
k 80 Û x = 95 + 1 k 80 k Î Z p - p - kp d) tan 4x = 1 - Û 4x = + kp Û x = + , k Î Z 4 16 4
d) Tổ chức thực hiện
- GV trình chiếu hình vẽ trong SGK ® đặt vấn đề nghiên cứu công thức nghiệm
Chuyển giao
- HS vẽ hình và quan sát sự tương giao của đồ thị hàm số y = tan x và
đường thẳng y = a . Từ đó hình thành công thức nghiệm
- HS thảo luận cặp đôi thực hiện nhiệm vụ.
Thực hiện
- GV quan sát, theo dõi các nhóm. Giải thích câu hỏi nếu các nhóm chưa
hiểu rõ nội dung vấn đề nêu ra
- HS nắm được công thức nghiệm của phương trình tan x = a và các trường
hợp đặc biệt của nó.
- Phân biệt các trường hợp của công thức để vận dụng giải toán.
Báo cáo thảo luận - Trong công thức nghiệm không thể chứa cùng lúc 2 đơn vị radian và độ
- GV gọi 4HS lên bảng trình bày lời giải cho VD3
- HS khác theo dõi, nhận xét, hoàn thiện sản phẩm
- GV nhận xét thái độ làm việc, phương án trả lời của học sinh, ghi nhận và
Đánh giá, nhận xét, tuyên dương học sinh có câu trả lời tốt nhất. Động viên các học sinh còn lại
tổng hợp
tích cực, cố gắng hơn trong các hoạt động học tiếp theo
- Chốt kiến thức và các bước giải phương trình
HĐ 4. Phương trình cot x = a
a) Mục tiêu: Hình thành công thức và biết vận dụng giải phương trình cot x = a . b)Nội dung:
H1: Tìm công thức nghiệm của phương trình cot x = a và các trường hợp đặc biệt của nó
H2: Ví dụ 2: Giải các phương trình sau p 1 - æ p 0 ö a)cot x = cot , b)cot(x + 5 ) = , c)cot - 2x = 1 - , d)cot 2x = 7 ç ÷ 5 3 è 4 ø c) Sản phẩm:
Phương trình cot x = a (4)
- Điều kiện của phương trình là: x ¹ p k , (k ÎZ) - Gọi x = < <
1 là hoành độ giao điểm( cot x .
a )thỏa mãn điều kiện 0 x p. 1 1
Kí hiệu x = arccot a. Khi đó, nghiệm của phương trình là: x = arccot a + kp (k ÎZ ) 1
* Chú ý: a) Phương trình cot x = cota Þ x = a + kp (k Î Z)
Tổng quát: cot f (x) = cot g (x) Þ f (x) = g (x) + kp(k ÎZ) b) Phương trình 0 0 0
cot x = cot b Þ x = b + 1
k 80 (k ÎZ)
c) Các trường hợp đặc biệt: • p cot x = 1Þ x =
+ kp (k Î Z) 4 • p cot x = 1
- Þ x = - + kp (k Î Z) 4 • p cot x = 0 Þ x =
+ kp (k Î Z) 2 Ví dụ 4: p p a) cot x = cot Û x = + kp , k Î Z 5 5 1 - 0 0 0 0 0 0 b)cot(x + 5 ) = Û x + 5 = 6 - 0 + 1 k 80 Û x = 6 - 5 + 1 k 80 , k Î Z 3 æ p ö p p - p kp c)cot - 2x = 1 - Û - 2x = + kp Û x = + , k Î Z ç ÷ è 4 ø 4 4 4 2 1 kp
d) cot 2x = 7 Û 2x = arccot 7 + kp Û x = arccot 7 + , k Î Z 2 2
d) Tổ chức thực hiện
- GV trình chiếu hình vẽ trong SGK ® đặt vấn đề nghiên cứu công thức nghiệm
Chuyển giao
- HS vẽ hình và quan sát sự tương giao của đồ thị hàm số y = cot x và
đường thẳng y = a . Từ đó hình thành công thức nghiệm
- HS thảo luận cặp đôi thực hiện nhiệm vụ.
Thực hiện
- GV quan sát, theo dõi các nhóm. Giải thích câu hỏi nếu các nhóm chưa
hiểu rõ nội dung vấn đề nêu ra
- HS nắm được công thức nghiệm của phương trình cot x = a và các trường
Báo cáo thảo luận hợp đặc biệt của nó.
- Phân biệt các trường hợp của công thức để vận dụng giải toán.
- Trong công thức nghiệm không thể chứa cùng lúc 2 đơn vị radian và độ
- GV gọi 4HS lên bảng trình bày lời giải cho VD4
- HS khác theo dõi, nhận xét, hoàn thiện sản phẩm
- GV nhận xét thái độ làm việc, phương án trả lời của học sinh, ghi nhận và
Đánh giá, nhận
tuyên dương học sinh có câu trả lời tốt nhất. Động viên các học sinh còn lại
xét, tổng hợp
tích cực, cố gắng hơn trong các hoạt động học tiếp theo
- Chốt kiến thức và các bước giải phương trình
3. HOẠT ĐỘNG 3: LUYỆN TẬP
a) Mục tiêu: Học sinh biết áp dụng các kiến thức về phương trình lượng giác vào các dạng bài tập cụ thể. b) Nội dung: PHIẾU HỌC TẬP 1 Câu hỏi
Lời giải chi tiết
Câu 1: Trong các phương trình sau, phương
………………………………………………….
trình nào vô nghiệm ?
…………………………………………………. A. cot x = 2 - .
………………………………………………….
B. sin(x -p ) =1 .
………………………………………………….
…………………………………………………. p C. cos 2x = .
…………………………………………………. 3 3
………………………………………………….
D. 2sin x = . 2
Câu 2: Nghiệm đặc biệt nào sau đây là sai ?
…………………………………………………. p A. sin x = 1
- Û x = - + k2p
…………………………………………………. . 2
………………………………………………….
B. sin x = 0 Û x = kp.
………………………………………………….
C. sin x = 0 Û x = k2p.
…………………………………………………. p
D. sin x =1 Û x = + k2p
…………………………………………………. . 2
………………………………………………….
Câu 3: Phương trình tan x = 4 có nghiệm là
…………………………………………………. A. vô nghiệm .
…………………………………………………. p B. x = + kp , k Î Z.
…………………………………………………. 4
………………………………………………….
C. x = arctan 4 + kp , k Î Z .
………………………………………………….
D. x = arctan 4 + k2p , k Î Z .
………………………………………………….
Câu 4: Chọn đáp án đúng trong các câu sau.
………………………………………………….
éx = y + k2p
………………………………………………….
A. sin x = sin y Û (k Î ) Z ê
ëx = p - y + k2p
………………………………………………….
………………………………………………….
éx = y + kp
B. sin x = sin y Û (k Î Z). ê
………………………………………………….
ëx = p - y + kp
………………………………………………….
éx = y + k2p
C. sin x = sin y Û (k Î Z).
…………………………………………………. ê
ëx = -y + k2p
………………………………………………….
…………………………………………………
éx = y + kp
D. sin x = sin y Û (k Î ) Z . ê
ëx = -y + kp
Câu 5: Tìm các giá trị của m để phương trình
………………………………………………….
cos 2x = m có nghiệm.
…………………………………………………. A. 2 - £ m £ 2.
………………………………………………….
B. m £ 1.
…………………………………………………. C. 1 - £ m £ 1.
………………………………………………….
D. m < 2.
………………………………………………….
Câu 6: Nghiệm của phương trình 1
…………………………………………………. cos x = - 2
…………………………………………………. là
…………………………………………………. p
A. x = ± + k2p , k Î . Z
…………………………………………………. 3
…………………………………………………. p B. 2 x = ± + kp , k Î . Z
…………………………………………………. 3
…………………………………………………. p C. 2 x = ± + k2p , k Î . Z
…………………………………………………. 3
…………………………………………………. p
D. x = ± + k2p , k Î . Z
…………………………………………………. 6 p
Câu 7. x = - + k2p là họ nghiệm của …………………………………………………. 6
………………………………………………….
phương trình nào sau đây ?
…………………………………………………. 3
…………………………………………………. A. sin x = . 2
………………………………………………….
…………………………………………………. 3 B. sin x = - .
…………………………………………………. 2
…………………………………………………. 3 C. cosx = .
…………………………………………………. 2
…………………………………………………. 3
…………………………………………………. D. cosx = - . 2
Câu 8: Nghiệm của phương trình
…………………………………………………. cot 2x = - 3 là
………………………………………………….
…………………………………………………. p p A. x = -
+ k ,k Î Z.
…………………………………………………. 6 2
…………………………………………………. p B. x = -
+ kp ,k Î Z.
…………………………………………………. 12
…………………………………………………. p p
…………………………………………………. C. x = -
+ k ,k Î Z.
…………………………………………………. 12 2
…………………………………………………. 3 D. x = arccot(-
) + kp ,k Î Z.
…………………………………………………. 2
Câu 9: Số nghiệm của phương trình
…………………………………………………. 0 sin(2x -30 ) = 1 trong khoảng 0 0 ( 1
- 80 ;180 ) là …………………………………………………. A. 0
…………………………………………………. B. 1.
…………………………………………………. C. 2.
…………………………………………………. D. 3.
………………………………………………….
………………………………………………….
Câu 10: Phương trình
…………………………………………………. 2 2 3 o
c s 2x + 2sin x -5
…………………………………………………. = 0 có nghiệm là
…………………………………………………. 1-sin x
A. x = kp .
………………………………………………….
…………………………………………………. p B. x = + kp . 2
………………………………………………….
C. x = p + k2p
…………………………………………………. p
………………………………………………….
D. x = - + k2p . 2 c) Sản phẩm:
- Học sinh viết bài làm ra phiếu học tập cá nhân.
- Học sinh thể hiện trên bảng nhóm kết quả bài làm của mình. Dự kiến Câu hỏi
Lời giải chi tiết
Câu 1: Trong các phương trình sau,
phương trình nào vô nghiệm ? A. cot x = 2 - .
B. sin(x -p ) =1 . p cos 2x = > 1 3 p C. cos 2x = .
Vậy phương trình vô nghiệm. 3 3 Đáp án C
D. 2sin x = . 2
Câu 2: Nghiệm đặc biệt nào sau đây là sai ? p A. sin x = 1
- Û x = - + k2p. 2 Đáp án C
B. sin x = 0 Û x = kp.
C. sin x = 0 Û x = k2p. p
D. sin x =1 Û x = + k2p . 2
Câu 3: Phương trình tan x = 4 có nghiệm là A. vô nghiệm . p B. x = + kp , k Î Z. Đáp án C. 4
x = arctan 4 + kp
C. x = arctan 4 + kp , k Î Z .
D. x = arctan 4 + k2p , k Î Z .
Câu 4: Chọn đáp án đúng trong các câu sau. A. Đáp án A
éx = y + k2p sin x = sin y Û (k Î ) Z é = + p ê x y k2 sin x = sin y Û (k Î ) Z
ëx = p - y + k2p ê
ëx = p - y + k2p B.
éx = y + kp sin x = sin y Û (k Î Z). ê
ëx = p - y + kp
éx = y + k2p
C. sin x = sin y Û (k Î Z). ê
ëx = -y + k2p
éx = y + kp
D. sin x = sin y Û (k Î ) Z . ê
ëx = -y + kp
Câu 5: Tìm các giá trị của m để phương
trình cos 2x = m có nghiệm. A. 2 - £ m £ 2.
B. m £ 1. Đáp án C C. 1 - £ m £ 1. 1 - £ m £ 1.
D. m < 2.
Câu 6: Nghiệm của phương trình 1 cos x = - là 2 p
A. x = ± + k2p , k Î . Z 3 p B. 2 x = ± + kp , k Î . Z 3 Đáp án C p C. 2 x = ± + k2p , k Î . Z 2p 3 x = ± + k2p p 3
D. x = ± + k2p , k Î . Z 6 p
Câu 7. x = - + k2p là họ nghiệm của 6
phương trình nào sau đây ? 3 A. sin x = . 2 3 B. sin x = - . Đáp án C 2 é p 3 x = + k2p C. cosx = . 3 ê 6 cosx = Û ê 2 2 p êx = - + k2p 3 êë D. cosx = - . 6 2
Câu 8: Nghiệm của phương trình cot 2x = - 3 là p p A. x = -
+ k ,k Î Z. 6 2 p B. x = -
+ kp ,k Î Z. Đáp án C 12 p = - Û = - + p p p cot 2x 3 2x k 6 C. x = -
+ k ,k Î Z. p kp 12 2 Û x = - + 3 12 2 D. x = arccot(-
) + kp ,k Î Z. 2
Câu 9: Số nghiệm của phương trình Đáp án C 0 sin(2x -30 ) = 1 trong khoảng 0 0 0 0
sin(2x - 30 ) = 1 Û 2x - 30 = 90 + k360 0 0 ( 1 - 80 ;180 ) là 0 0 Û x = 60 + 180 k A. 0 x Î( 0 0 - )Þ xÎ{ 0 0 180 ;180 120 - ;60 } B. 1. C. 2. Vậy có hai nghiệm. D. 3. Câu 10: Phương trình Đáp án D 2 2 3 o
c s 2x + 2sin x -5 2 2 2 = 0 3 os c 2x + 2sin x - 5 3
ì cos 2x - cos 2x - 4 = 0 có nghiệm là = 0 Û 1-sin x í 1- sin x si î n x ¹ 1
A. x = kp . ìécos 2x = 1 - p ïê ì2x = p + k2p B. x = + kp . ï 4 ï 2 Û ê í cos 2x = Û í p ë 3 x ¹ + k2p
C. x = p + k2p ï ïî 2 si ïî n x ¹1 p
D. x = - + k2p . p 2 Û x = - + k2p 2
d) Tổ chức thực hiện
GV: Chia lớp thành 4 nhóm. Phát phiếu học tập 1
Chuyển giao
HS: Nhận nhiệm vụ : làm bài vào phiếu học tập cá nhân trong 15 phút.
Học sinh thảo luận nhóm viết vào phiếu học tập trong 7 phút
GV: điều hành, quan sát, hỗ trợ
Thực hiện
HS: 4 nhóm tự phân công nhóm trưởng, hợp tác thảo luận thực hiện nhiệm
vụ. Ghi kết quả vào bảng nhóm.
Đại diện nhóm trình bày kết quả thảo luận
Báo cáo thảo luận Các nhóm khác theo dõi, nhận xét, đưa ra ý kiến phản biện để làm rõ hơn các vấn đề
GV nhận xét thái độ làm việc, phương án trả lời của các nhóm học sinh, ghi
Đánh giá, nhận
nhận và tuyên dương nhóm học sinh có câu trả lời tốt nhất.
xét, tổng hợp
Hướng dẫn HS chuẩn bị cho nhiệm vụ tiếp theo
4. HOẠT ĐỘNG 4: VẬN DỤNG.
a) Mục tiêu: Giải quyết một số bài toán ứng dụng phương trình lượng giác cơ bản trong thực tế. b) Nội dung PHIẾU HỌC TẬP 2 Vận dụng 1:
Một vệ tinh nhân tạo bay quanh trái đất theo một quỹ đạo hình elip. Chiều cao h (tính theo đơn vị p
kilomet) của vệ tinh so với bề mặt trái đất xác định bởi công thức h = 550 + 450cos t , 50
trong đó t là thời gian tính bằng phút kể từ vệ tinh bay vào quỹ đạo. Người ta cần thực hiện một thí
nghiệm khoa học khi vệ tinh cách mặt đất 250km . Hãy tìm các thời điểm để có thể thực hiện thí nghiệm đó. Vận dụng 2:
Số giờ có ánh sáng mặt trời của một thành phố A ở vĩ độ 400 bắc trong ngày thứ t của một năm Èp ˘
không nhuận được cho bởi hàm số d(t) = 3 sin Í
(t - 80)˙+ 12 với t Z
Œ ;0 < t £ 365. Thành phố A có 182 Í ˙ Î ˚
đúng 12 giờ ánh sáng mặt trời vào ngày nào trong năm? Vận dụng 3:
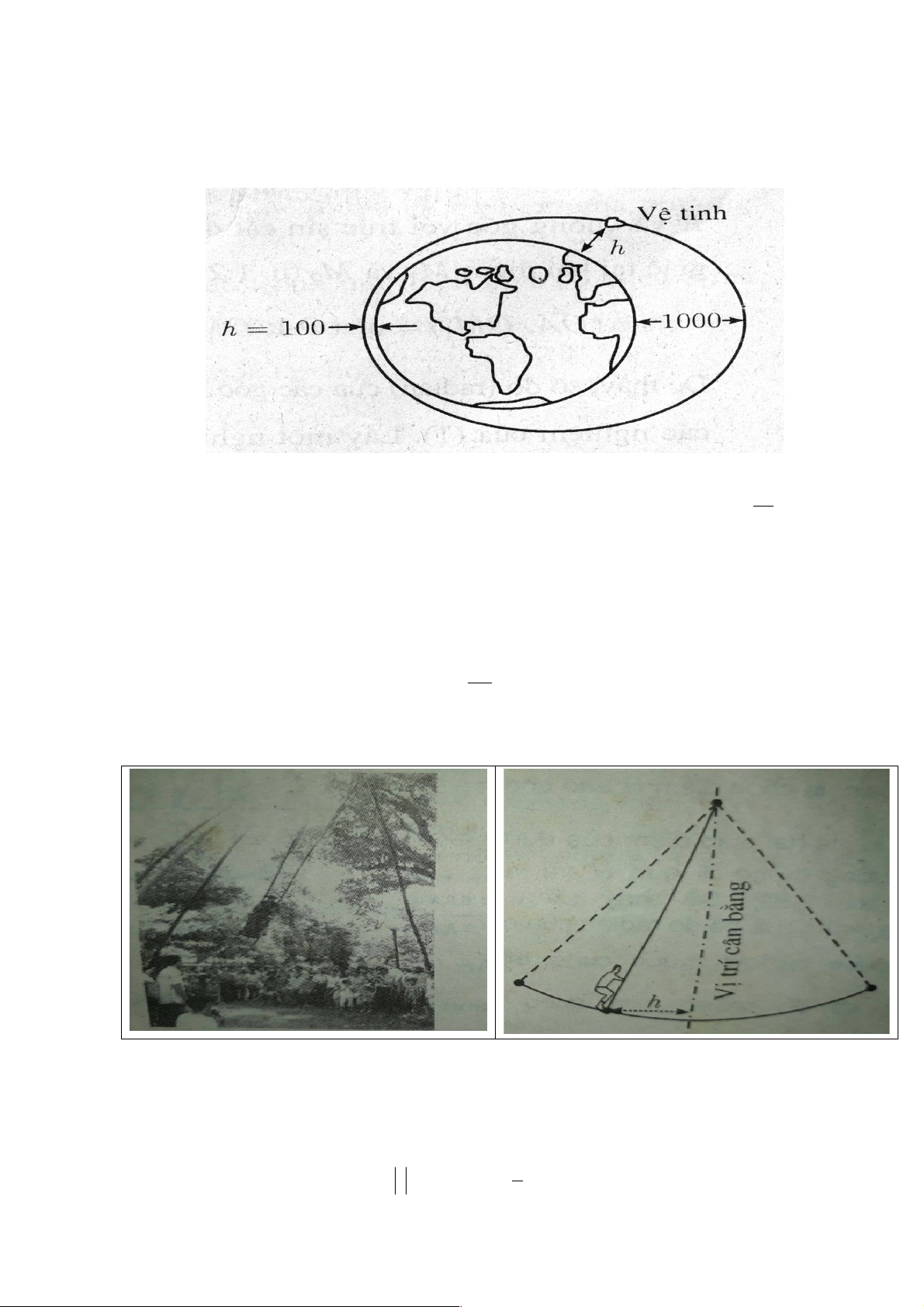
Mùa xuân ở hội Lim( tỉnh Bắc Ninh) thường có trò chơi đu. Khi người chơi đu nhún đều , cây đu sẽ
đưa người chơi đu qua lại vị trí cân bằng . Nghiên cứu trò chơi này, người ta thấy khoảng cách h (
tính bằng mét) thì người chơi đu đến vị trí cân bằng (H2) được biểu diễn qua thời gian t (t ≥ ) 0 và p È ˘
được tính bằng giây bởi hệ thức h = d với d = 3 cos Í (2t - 1) ,
˙ trong đó ta quy ước rằng d > 0 khi vị Í3 ˙ Î ˚
trí cân bằng ở về phía sau lưng người chơi đu và d < 0 trong trường hợp ngược lại.Tìm các thời điểm
trong vòng 2 giây đầu tiên mà người chơi đu cách vị trí cân bằng 2 mét .
c) Sản phẩm: Sản phẩm trình bày của 4 nhóm học sinh
d) Tổ chức thực hiện
GV: Chia lớp thành 4 nhóm. Phát phiếu học tập 2
Chuyển giao
HS: Nhận nhiệm vụ
Các nhóm HS thực hiện tìm tòi, nghiên cứu và làm bài
Thực hiện
Chú ý: Việc tìm kết quả tích phân có thể sử dụng máy tính cầm tay
HS cử đại diện nhóm trình bày sản phẩm
Báo cáo thảo luận Các nhóm khác theo dõi, nhận xét, đưa ra ý kiến phản biện để làm rõ hơn các vấn đề.
GV nhận xét thái độ làm việc, phương án trả lời của các nhóm học sinh, ghi
nhận và tuyên dương nhóm học sinh có câu trả lời tốt nhất.
Đánh giá, nhận
- Chốt kiến thức tổng thể trong bài học.
xét, tổng hợp
- Hướng dẫn HS về nhà tự xây dựng tổng quan kiến thức đã học bằng sơ đồ tư duy.
*Hướng dẫn làm bài Vận dụng 1: Tìm t thỏa mãn é 50 æ 2 ö t = arccos - + 1 k 00 ê ç ÷ p p p 2 p è 3 ø h = 550 + 450cos t = 250 Û cos t = - Û ê , k Î ! 50 50 3 ê 50 æ 2 ö t = - arccos - + 1 k 00 ê ç ÷ p ë p è 3 ø Vận dụng 2: æ p ö p 3sin ç (t -80) +12 =12 Û ÷
(t -80) = kp Û t -80 =180k Û t = 80+180k è180 ø 180 Vậy t = 260 Vận dụng 3: ép ê ( æ ö t - ) 2 2 1 = arccos + k2 ç ÷ p æ p ö æ p ö è ø 3cosç (2t - ) 1 = 2 Û cos ÷ ç (2t - ) 2 3 3 1 = Û ê ÷ è 3 ø è 3 ø 3 êp ê ( æ ö t - ) 2 2 1 = - arccos + k2 ç ÷ p ë 3 è 3 ø é 3 æ 2 ö t = 1+ arccos + 6k ê ç ÷ p è 3 ø Û êê 3 æ 2 ö t = 1- arccos + 6k ê ç ÷ ë p è 3 ø