BÀI 5 PHÉP NHÂN MA TR N VÀ MA TR N NGH CH Đ O ThS. Vũ Quỳnh Anh
Trường Đại học Kinh tế quốc dân v1.0014105206 1
TÌNH HUỐNG KH I Đ NG: Tính doanh thu c a m t cửa hàng
Một cửa hàng gạo chuyên kinh doanh ba mặt hàng: gạo Bắc Hương, gạo Tám Điện Biên
và gạo Tám Thái Lan với giá tương ng là 18.000 đồng/1kg; 20.000 đồng/1kg và 19.000 đồng/1kg.
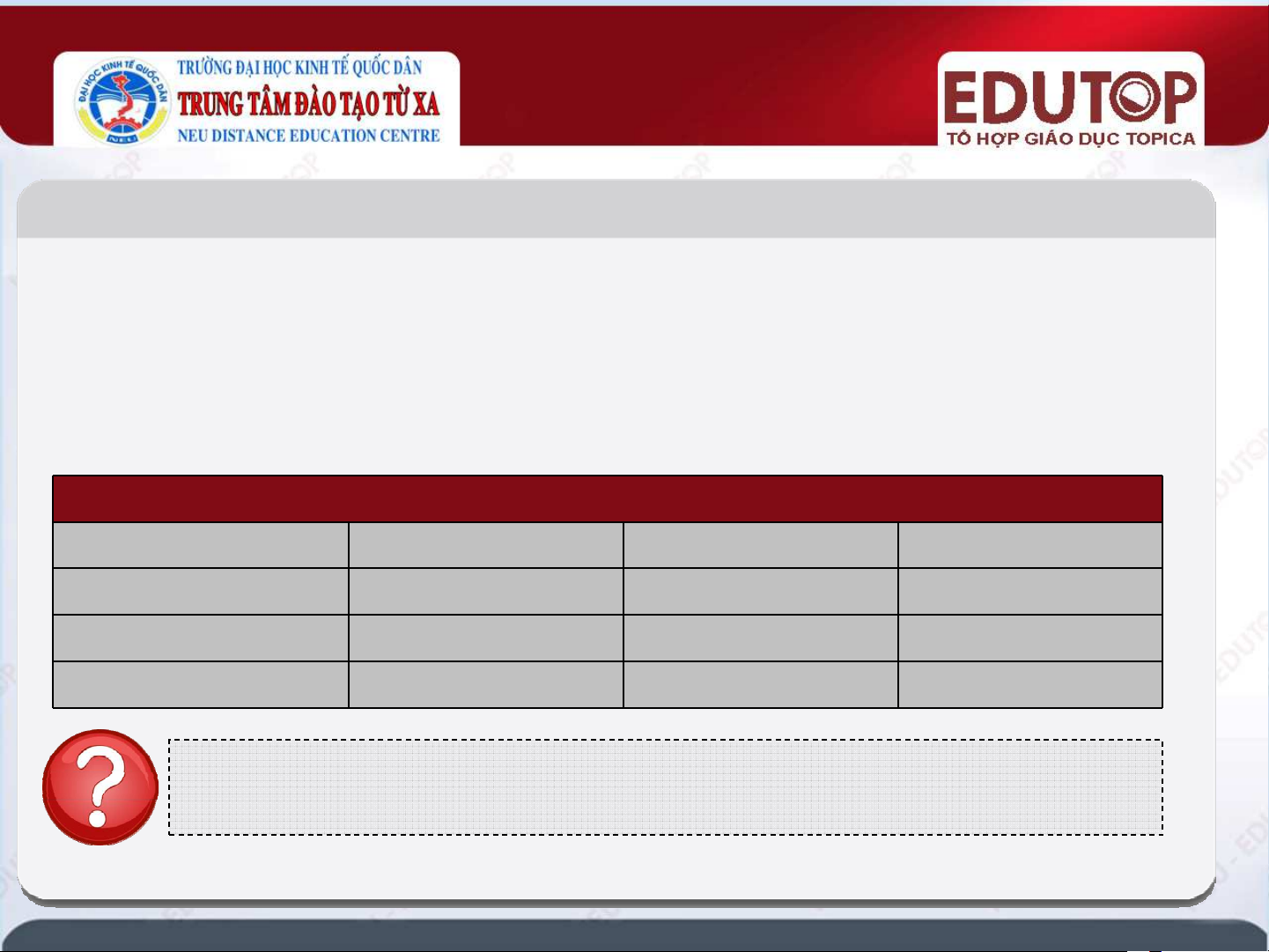
Trong 3 tháng đầu năm, cửa hàng bán đư c số lư ng c thể như sau: Đơn vị: kg Tháng Loại gạo 1 2 3 Bắc Hương 345 340 350 Tám Điện Biên 315 330 370 Tám Thái Lan 430 425 425
Hãy sử d ng ma tr n, tính doanh thu c a cửa hàng trong từng tháng. v1.0014105206 2 M C TIÊU •
Sinh viên nắm đư c cách nhân hai ma tr n, các tính chất c a phép nhân. •
Nắm đư c định nghĩa và các tính chất c a ma tr n ph h p, nghịch đảo. •
Tính đư c ma tr n ph h p, ma tr n nghịch đảo c a một ma tr n vuông. •
Biết sử d ng ma tr n nghịch đảo trong việc giải phương trình ma tr n. v1.0014105206 3 N I DUNG
Phép nhân ma tr n với ma tr n Ma tr n nghịch đảo
ng d ng c a ma tr n nghịch đảo v1.0014105206 4
1. PHÉP NHÂN MA TR N V I MA TR N
1.1. Định nghĩa phép nhân hai ma tr n
1.2. Các tính chất cơ bản c a phép nhân hai ma tr n v1.0014105206 5
1.1. Đ NH NGHƾA PHÉP NHÂN HAI MA TR N
Cho ma tr n A cấp mn và B cấp np . A = (a ) B =(b ) ij mn jk np
Tích c a A với B là một ma tr n cấp mp ký hiệu: AB = (c ) ik mp đư c xác định như sau: b  1k   b d c 2k c  A .B  (a ,a , ,  a ).
  a b  a b  a b ik i k i1 i2 in i1 1k i2 2k in nk      b  nk  v1.0014105206 6 VÍ D 1 Cho 2 ma tr n:  2  3 1  1 3 2     A  , B    4  0 3 4 0 3       2 3 4     Tính AB. Gi i: c c c  11 12 13 A B  (c )  ik 23   23 33 c c c  21 22 23  v1.0014105206 7 VÍ D 1 2 2 d c c A B 1 3 2 4 2 12 4 18 c 4 0 3 4 8 0 6 14 11 1 1    21     
        
             2   2       3   3  d c c A B 1 3 2 0 3 0 6 9 c 4 0 3 0 12 0 9 21 12 1 2    22                      3  3     1 1 d c c A B 1 3 2 3 1 9 8 2 c 4 0 3 3  4  0 12  8 13 1 3    23                  4    4 18 9 2  AB    14 21 8 v1.0014105206 8 VÍ D 2  2  3 1  1 3 2     Cho 2 ma tr n A  , B    4  0 3 4 0 3       2 3 4     Tính BA’ Gi i:   2 3 1   1 4      B A '   4 0 3 3 0      2 3 4   2 3           2  9  2  8  0  3   5  1 1        4  0  6
 1 6  0  9   1 0  2 5      2 9 8 8 0 1 2   1 5 4            v1.0014105206 9 CHÚ Ý
1. Tồn tại tích AB khi và chỉ khi số cột c a A bằng số dòng c a B.
2. Tồn tại cả hai tích AB và BA khi A có cấp mn thì B phải có cấp nm.
3. Phép nhân ma tr n không có tính chất giao hoán, nói chung AB ≠ BA.
4. A nhân đư c với A khi A là ma tr n vuông. v1.0014105206 10
1.2. CÁC TÍNH CH T CƠ B N C A PHÉP NHÂN HAI MA TR N
1. Tính chất kết h p: (AB)C = A(BC)
2. Tính chất phân phối đối với phép cộng:
A(B + C) = AB + AC, (B + C)D = BD + CD
3. Với A, B là hai ma tr n sao cho tích AB có nghĩa và α là một số bất kỳ ta luôn có: α(AB) = (αA)B = A(αB).
4. Mọi ma tr n đều không thay đổi khi nhân với ma tr n đơn vị E (nếu phép nhân có ý nghĩa): AE = A, EB = B 5. (AB)’ = B’A’.
6. A và B là các ma tr n vuông cùng cấp. Khi đó: |AB|= |A|.|B| v1.0014105206 11 2. MA TR N NGH CH Đ O
2.1. Khái niệm ma tr n nghịch đảo
2.2. Ma tr n ph h p c a ma tr n vuông
2.3. Điều kiện tồn tại và công th c tìm ma tr n nghịch đảo
2.4. Các tính chất cơ bản c a ma tr n nghịch đảo v1.0014105206 12
2.1. KHÁI NI M MA TR N NGH CH Đ O •
Đ nh nghƿa: Ma tr n nghịch đảo c a một ma tr n vuông A là một ma tr n vuông X
(cùng cấp với A) thỏa mãn điều kiện: AX = XA = E •
Ký hi u: Ma tr n nghịch đảo c a A là A–1 Chú ý: •
Khái niệm ma tr n nghịch đảo chỉ áp d ng cho ma tr n vuông. •
Ma tr n nghịch đảo c a A (nếu có) là duy nhất. v1.0014105206 13 2.2. MA TR N PH H P C A MA TR N VUÔNG •
Đ nh nghƿa: Cho ma tr n A vuông cấp n: A = (a )ijnn • Ký hi u: A A  A  11 21 n1   A A  A * 12 22 n2 A            A A  A  1n 2n nn n n 
A = (-1)i+j M là phần bù đại số c a a ij ij ij
A* gọi là MA TR N PH H P c a ma tr n A. v1.0014105206 14 VÍ D 2 5
Tính ma tr n ph h p c a ma tr n A    1 3   Gi i: 2 3 A  ( 1  )  3  3 A  ( 1  ) 5  5  11 21 3 4 A  ( 1  ) 1 1  A  ( 1  )  2  2 12 22  A A   3 5   11 21 A*       A A 1    2 12 22  v1.0014105206 15 VÍ D 1 2 3     Tính ma tr n ph h p A  2 3 1   3 2 2     3 1  2 3  2 A   ( 1  )  ( 6   2)  8  3 A   ( 1  )  (  4   6)  2  11 2 2  21  2 2    2 1   1 3   3 4 Cột 1 A   ( 1  )  (  4   3)  7 A   ( 1  )  ( 2   9)  7 12 Cột 2 3 2   22 3 2    2 3  1 2 4 A  ( 1  )  (4  9)  5  5 A  ( 1  )  (  2  6)  4 13 3 2  23 3 2  v1.0014105206 16 VÍ D  2 3  4 A   ( 1  )  (2  9)  11 31 3 1   1 3   Cột 3 5 A   ( 1  )  (  1 6)  7  32 2 1   1 2 6 A  ( 1  )  (3  4)  1  33 2 3   A A A   8  2  11 11 21 31      A*  A A A  7 7 7  12 22 32      A A A   5 4 1     13 23 33  v1.0014105206 17 BÀI T P 1 2 3     Cho ma tr n A  2 3 1   3 2 2    Tính: det(A), A.A*, A*.A Gi i: det(A) = 21 21 0 0  21 0 0  *   *   AA  0 21 0 A A  0 21 0      0 0 21  0 0 21     v1.0014105206 18 2.2. MA TR N PH
H P C A MA TR N VUÔNG (ti p theo) Tính ch t:  d 0  0    0 d  0 * * AA  A A  dE    (d  A )        0 0  d   v1.0014105206 19
2.3. ĐI U KI N TỒN TẠI VÀ CÔNG TH C TÌM MA TR N NGH CH Đ O •
Đ nh lý: Điều kiện cần và đ để một ma tr n vuông A có ma tr n nghịch đảo là d = |A| ≠ 0 1 Khi đó: 1 A   A * d •
Đ nh nghƿa: Ma tr n vuông có định th c khác 0 đư c gọi là ma tr n không suy bi n.
Ma tr n có ma tr n nghịch đảo còn đư c gọi là ma tr n kh ngh ch hay ma tr n kh đ o. v1.0014105206 20