










Preview text:
School of Industrial Engineering and Management
International University-VNU HCM PROJECT
Deterministic Models in Operations Research Group 6 1. Nguyễn Hà An IELSIU20001 2. Hồ Nguyễn Phương Anh IELSIU20252 3. Đỗ Trần Nhật Ánh IELSIU20007
4. Nguyễn Ngọc Khánh Ngân IELSIU20137 5. Lưu Nguyễn Minh Thư IELSIU20124 6. Lê Hoàng Yến IELSIU20087 TABLE OF CONTENTS
I. INTRODUCTION .......................................................................................................................................... 3
1. Background of study .................................................................................................................................................... 3
2. Problem statement ....................................................................................................................................................... 4
II. MATHEMATICAL MODEL/ ALGORITHMS ....................................................................... 6
1. Parameters .................................................................................................................................................................... 6
2. Decision variables ......................................................................................................................................................... 7
3. Objective function ........................................................................................................................................................ 7
4. Constraints .................................................................................................................................................................... 7
III. PROBLEM SOLVING ............................................................................................................................. 8
1. CPLEX Code ................................................................................................................................................................ 8
2. Data input ................................................................................................................................................................. 9
3. Processing and result analysis: ............................................................................................................................. 10
IV. RESULT ANALYSIS AND DISCUSSION .............................................................................. 12
1. Sensitivity Analysis ..................................................................................................................................................... 12
2. Solution Discussion..................................................................................................................................................... 21
3. Future Development ............................................................................................................................................... 22
V. REFERENCES ............................................................................................................................................... 24
VI. CONTRIBUTION FORM ................................................................................................................... 24 LISTS OF FIGURES
Figure 1.1 Door positions……………………………………………………………………………. 5
Figure 3.1. Data input………………………………………………………………………………. 10
Figure 3.2. Results of xim and yjn…………………………………………………………………… 11
Figure 4.1. Decrease to 12 forklifts………………………………………………………………... 13
Figure 4.2. Decrease to 9 forklifts…………………………………………………………………. 14 1
Figure 4.3. Increase to 18 forklifts………………………………………………………………… 16
Figure 4.4. Increase to 21 forklifts…………………………………………………………………. 17
Figure 4.6. Increase forklift’s capacity to 250 orders……………………………………………… 20 2 LISTS OF TABLES
Table 1.1. Distances from R to S……………………………………………………………………. 5
Table 1.2. Forklifts…………………………………………………………………………………... 5
Table 1.3. Orders flow………………………………………………………………………………. 6
Table 1.4. Forklift trips……………………………………………………………………………… 6
Table 4.1. Forklifts…………………………………………………………………………………. 12
Table 4.2. Forklift trips…………………………………………………………………………….. 12
Table 4.3. Forklifts…………………………………………………………………………………. 14
Table 4.4. Forklift trips…………………………………………………………………………….. 14
Table 4.5. Forklifts………………………………………………………………………………… 15
Table 4.6. Forklift trips…………………………………………………………………………….. 15
Table 4.7. Forklift………………………………………………………………………………….. 17
Table 4.8. Forklift trips…………………………………………………………………………….. 17
Table 4.9. The change in total travel distance……………………………………………………… 18
Table 4.10. Forklifts………………………………………………………………………………... 19
Table 4.11. Forklift trips…………………………………………………………………………… 19
Table 4.12. Comparison between the number of 3 - ton forklifts and 5 - ton forklifts in terms of
travelled distance and total costs ………………………………………………………………….. 21
Chart 4.1. The change in total travel distance relative to the quantity of forklifts…………………. 19
Chart 4.2. The relationship between cost and decrease in total travel distance…………………… 22 I. Introduction 1. Background of study
Cross-docking facility is now utilized in supply chains to minimize space of warehousing.
Goods arrive, then are quickly sorted in accordance with inbound and outbound shipments
and then immediately transported, often within 24 hours. In traditional warehouse
management, inventory is unloaded from inbound railcars or semi-trailers and stored in the
warehouse. They are then repackaged and shipped. However, with a cross-docking system,
orders are fulfilled faster. This supply chain model is utilized when dealing with perishable items or various suppliers. 3
A large shipping company has multiple freight yards located in several locations around the
country. Inbound trucks transport shipments from vendors' end/or other freight yards to the
yard, where the shipments are sorted by destination and loaded onto outward trucks for
delivering to customers. One side of the dock is assigned for arriving vehicles, while the other
side is designated for departing trucks. The truck driver leaves the yard with another trailer
for his next assignment after dropping the trailer end. Each trailer has a forklift driver who
oversees unloading the contents and loading them into different empty trailers based on their
destination. The empty trailers are parked at the shipping doors, each of which has a specific
destination allocated to it. When the trailer is filled, it is taken away and replaced with an
empty trailer bound for the same location. As a result, the time it takes to process each trailer
differs widely depending on the distance between the receiving door and the shipping door.
Because the freight yard has no storage, all goods must be processed the day they arrive and
moved directly from the inbound trailer to the outbound trailer to minimize damage or loss.
The longer it takes to unload the trailer, the more forklifts will be needed, and the more
crowded dock will get. Therefore, the optimal solution for dock door assignment is critical to
operate the dock smoothly and efficiently. 2. Problem statement
In this project, our group will analyze the dock door assignment problem of ABC Shipping
Company. ABC Company receives 100,000 orders a day on average, and there are 15 forklifts
in use. ABC consists of 5 inbound doors and 5 outbound doors. The sorting center receives
orders from 3 origins O1, O2, O3, and delivers to 4 other destinations D1, D2, D3, D4.
We assume that the doors at inbound and outbound are R (receiving) and S (shipping),
respectively. Figure 1 shows the position of the doors. Outbound
S1 S2 S3 S4 S5 4
R1 R2 R3 R4 R5 Inbound
Figure 1.1 Door positions
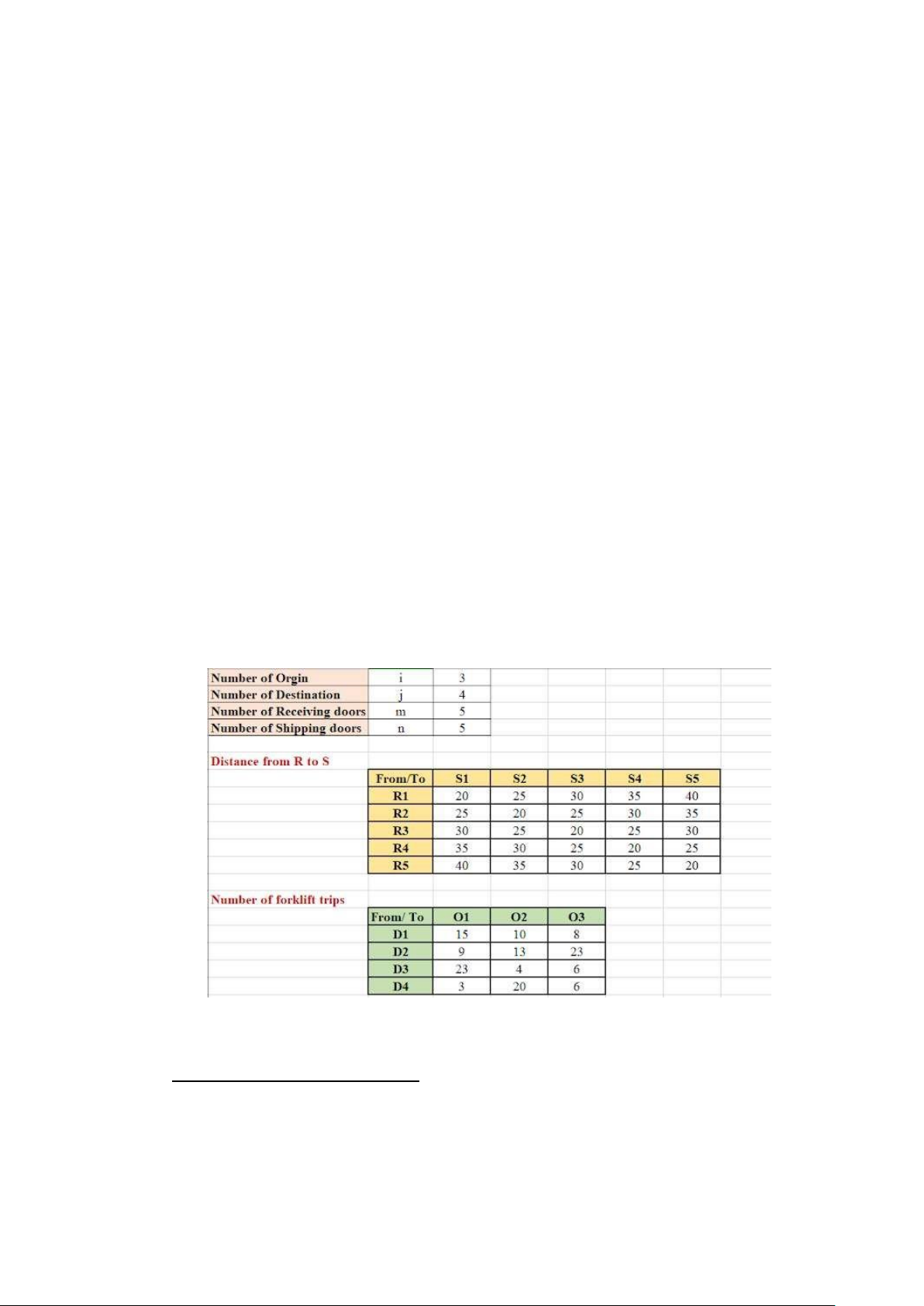
We have collected data about the distance of goods flow from one R to another S From/To S1 S2 S3 S4 S5 R1 20 25 30 35 40 R2 25 20 25 30 35 R3 30 25 20 25 30 R4 35 30 25 20 25 R5 40 35 30 25 20
Table 1.1. Distances from R to S
Table 2 shows the details of the kind of forklift available.
Quantity Orders per loading Total time (minutes) Forklifts 15 150 10
Table 1.2. Forklifts
Table 3 provides information about the quantity of order flow from 3 origins to each
destination, whose total is 100,000 orders. From/ To O1 O2 O3 D1 11,000 7,000 5,500 D2 6,700 9,200 16,800 D3 17,000 2,400 4,400 D4 1,800 14,300 3,900 5
Table 1.3. Orders flow
Table 4 illustrates the number of forklift trips required to move the items from origin i to destination j From/ To O1 O2 O3 D1 15 10 8 D2 9 13 23 D3 23 4 6 D4 3 20 6
Table 1.4. Forklift trips
With the given problem and the collected data, this project will develop a solution for the
issue of assignment of dock doors to incoming and outgoing trucks at ABC freight yard to
increase the efficiency of the dock operation, which means minimizing the distance between
receiving and leaving doors. Besides, the goal of this project is using CPLEX software to
solve the mathematical model which has been built in response to the aforementioned problem.
In addition, the sensitivity analysis has been applied to check the validity of all coefficients.
The foremost outcome of the project will be a promising solution for ABC Company on the dock door assignment problem.
II. Mathematical Model/ Algorithms
There are 5 receiving doors, namely R1, R2, R3, R4, R5, and 5 shipping doors, namely S1, S2, S3, S4, S5, at the dock.
There are 3 origins, namely O1, O2, O3, and 4 destinations, namely D1, D2, D3, D4, for the goods. 1. Parameters
Let dmn be the distance between receiving door m and shipping door n and wij be the number
of forklift trips required to move the items from origin i to destination j 6 2. Decision variables
Let xim = 1, if products from origin i are assigned to receiving door m
xim = 0, otherwise and yjn = 1, if products to destination j are assigned
to shipping door n yjn = 0, otherwise 3. Objective function
The objective is to allocate receiving doors to origins and shipping doors to destinations such
that the total distance travelled by forklifts is minimized.
So, the objective function is formulated as follows:
Minimize f(X,Y)= ∑ ∑ ∑𝑖 𝑗
𝑚 ∑𝑛 𝑤𝑖𝑗𝑑𝑚𝑛𝑥𝑖𝑚𝑦𝑗𝑛
Because there are wij forklift trips from origin i to destination j, the total distance travelled
will be wijdmn if origin i is allocated to receiving door m and destination j is assigned to
shipping door. So, the objective function adds the total distance travelled from all receiving
doors to all shipping doors based on the door assignment X and Y. 4. Constraints •
Constraint 1 ensures that each origin is allocated to at least one receiving door
∑𝑚 𝑥𝑖𝑚 ≥1 for i = 1, 2, 3 •
Constraint 2 ensures that each receiving door is allocated to only one origin
∑𝑖 𝑥𝑖𝑚 =1 for m = 1, 2, 3, 4, 5 •
Constraint 3 ensures that each destination is allocated to at least one shipping door
∑𝑛 𝑦𝑗𝑛 ≥ 1 for j = 1, 2, 3, 4 •
Constraint 4 ensures that each shipping door is allocated to only one destination
∑𝑛 𝑦𝑗𝑛 = 1 for n = 1, 2, 3, 4, 5 •
Constraint 5 restricts that all variables are equal to 1 or 0
∑ 𝑥𝑖𝑚 = 0 or 1 for all i, m
∑ 𝑦𝑗𝑛 = 0 or 1 for all j, n 7 III. Problem solving 1. CPLEX Code int numOrigin=...; int numDestination=...; int numReceiving=...; int numShipping=...; range Origin=1..numOrigin; range
Destination=1..numDestination; range
Receiving=1..numReceiving; range
Shipping=1..numShipping; float D[Receiving][Shipping]; float
W[Origin][Destination]; dvar boolean
x[Origin][Receiving]; dvar boolean y[Destination][Shipping];
minimize sum(i in Origin, j in Destination, m in Receiving, n in
Shipping)W[i][j]*D[m][n]*x[i][m]*y[j][n]; subject to { forall (m in Receiving) { sum(i in Origin)x[i][m]==1; } forall (i in Origin) {
sum(m in Receiving)x[i][m]>=1; } 8 forall (n in Shipping) {
sum(j in Destination)y[j][n]==1; } forall (j in Destination){ sum(n in Shipping)y[j][n]>=1; }
} execute Write_Result{ writeln("Optimal total distance
traveled: ",cplex.getObjValue()); writeln("Part 1: Origin -
Receiving door"); writeln(""); for (var i in Origin) for
(var m in Receiving) if (x[i][m]==1){ writeln("Origin
" +i+ " assigned to Receiving door " +m); writeln(); }
writeln("Part 2: Destination - Shipping door");
writeln(""); for (var j in Destination) for (var n in
Shipping) if (y[j][n]==1){ writeln("Destination " +j+ "
assigned to Shipping door " +n); writeln(); } } 2. Data input
In this project, we are given data on the number of inbound doors, outbound doors, origins,
and destinations. Then, we decided to let dmn be the distance between receiving door m and
shipping door n and wij be the number of forklift trips required to move the items from origin
i to destination j, whose data are already collected. Regarding our decision variables, we noted
xim =1, if products from origin i are assigned to receiving door m and yjn =1, if products to 9
destination j are assigned to shipping door n. We decided to put them into the Excel file and
then connect to the data file in Cplex by using the function “SheetConnection”. • CPLEX Code
SheetConnection my_data("OR_Project.xlsx"); numOrigin from
SheetRead(my_data,"'Main Problem'!C1"); numDestination from
SheetRead(my_data,"'Main Problem'!C2"); numReceiving from
SheetRead(my_data,"'Main Problem'!C3"); numShipping from
SheetRead(my_data,"'Main Problem'!C4"); D from
SheetRead(my_data,"'Main Problem'!C8:G12");
W from SheetRead(my_data,"'Main Problem'!C16:E19");
x to SheetWrite(my_data,"'Result'!C3:G5"); y
to SheetWrite(my_data,"'Result'!C8:G12"); Figure 3.1. Data input
3. Processing and result analysis:
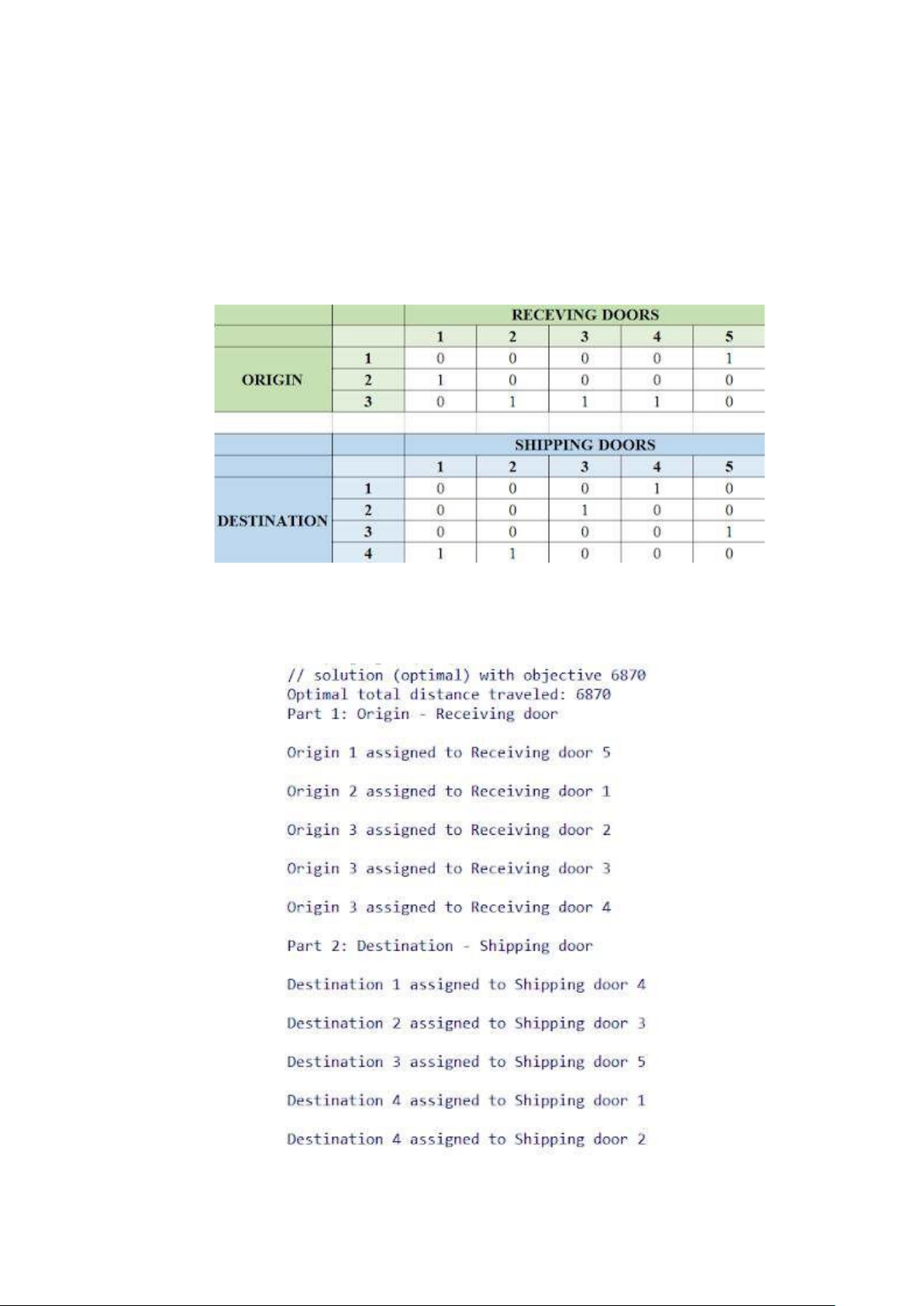
The outcome of running CPLEX with the objective function and all constraints are included
in the tables below. From table 1, if xim = 1, products from origin i are assigned to receiving 10
door m. We can see that Origin 1 is only assigned to Receiving door 5, Origin 2 is assigned
to Receiving door 1, and Origin 3 is assigned to Receiving door 2,3,4.
Similarly, if yjn = 1, products to destination j are assigned to shipping door n. Table 2 displays
that Destination 1 is assigned to Shipping door 4, Destination 2 is assigned to Shipping door
3, Destination 3 is assigned to Shipping door 5 and Destination 4 is assigned to Shipping door 1, 2.
Figure 3.2. Results of x and y im jn
Finally, the optimal distance traveled is 6870 . 11 0
IV. Result analysis and Discussion 1. Sensitivity Analysis
a. Change in forklift quantity
Sensitivity analysis is an important step to recognize the effects of the parameters on the
decision. To test the sensitivity of the mathematical model, we will adjust the value of the
parameters in the objective function to see the change in the total travel distance.
Case 1: Decreasing the forklift quantity
Case 1.1: Using 12 forklifts
For this case, we tried to decrease the number of forklifts from 15 to 12, which means that we
decreased 3 forklifts in total and 1 forklift for each origin O1, O2, O3.
Quantity Orders per loading Total time (minutes) Forklifts 12 150 10
Table 4.1. Forklifts
Since altering forklift quantity, we could have the different number of forklift trips required
to move the items from origin i to destination j: From/ To O1 O2 O3 D1 19 12 10 D2 12 16 28 D3 29 4 8 D4 3 24 7
Table 4.2. Forklift trips
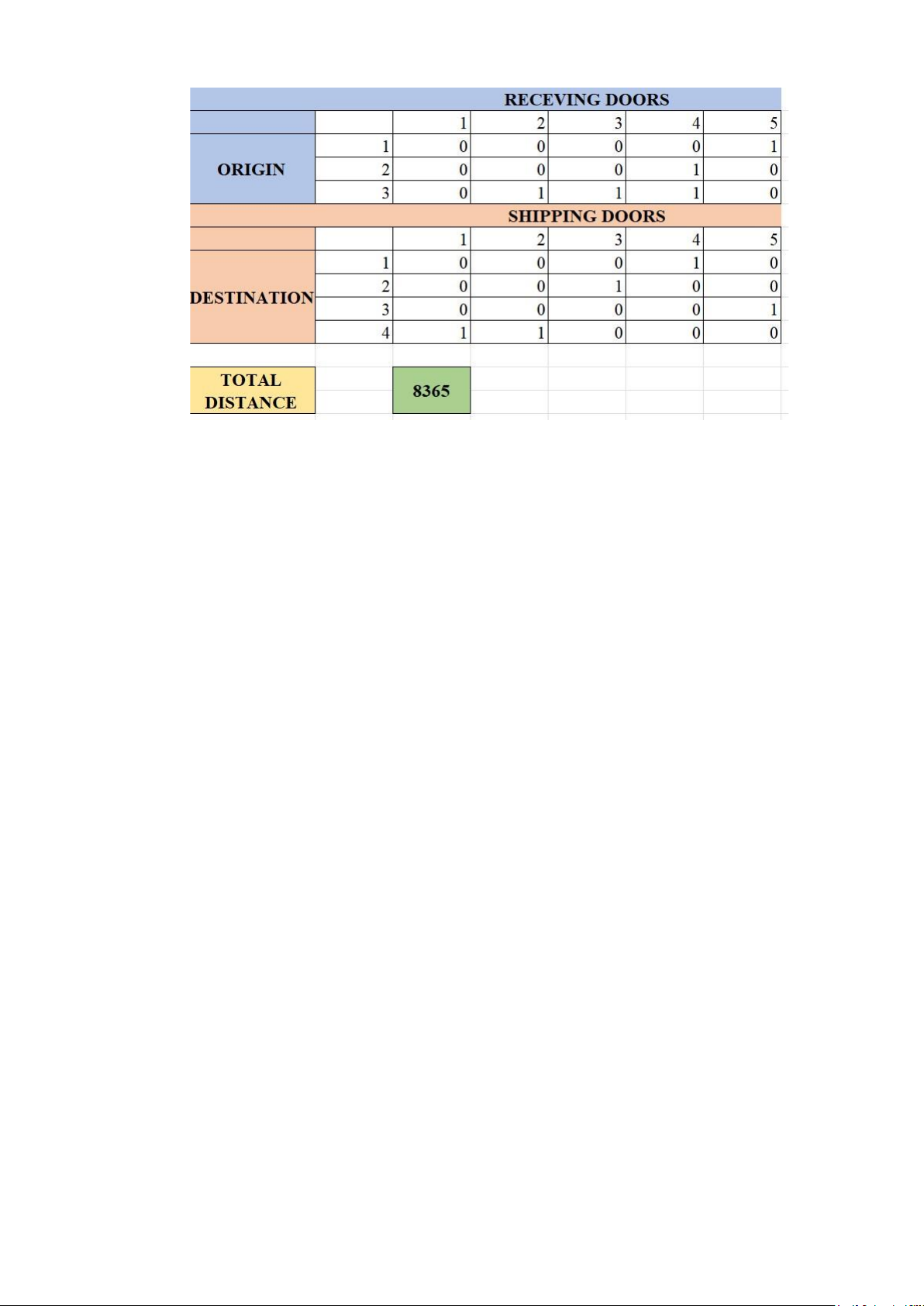
After running the code for this case, we can have the result with the optimal objective is 8365: 12
Figure 4.1. Decrease to 12 forklifts
Part 1: Origin - Receiving door
Origin 1 assigned to Receiving door 5
Origin 2 assigned to Receiving door 4
Origin 3 assigned to Receiving door 2
Origin 3 assigned to Receiving door 3
Origin 3 assigned to Receiving door 1
Part 2: Destination - Shipping door
Destination 1 assigned to Shipping door 4
Destination 2 assigned to Shipping door 3
Destination 3 assigned to Shipping door 5
Destination 4 assigned to Shipping door 1
Destination 4 assigned to Shipping door 2
Case 1.2: Using 9 forklifts
For this case, we tried to decrease the number of forklifts from 15 to 9, which means that we
decreased 6 forklifts in total and 2 forklifts for each origin O1, O2, O3. 13
Quantity Orders per loading Total time (minutes) Forklifts 9 150 10
Table 4.3. Forklifts
Since altering forklifts quantity, we could have the different number of forklift trips required
to move the items from origin i to destination j: From/ To O1 O2 O3 D1 25 16 13 D2 15 21 38 D3 38 6 10 D4 4 32 9
Table 4.4. Forklift trips
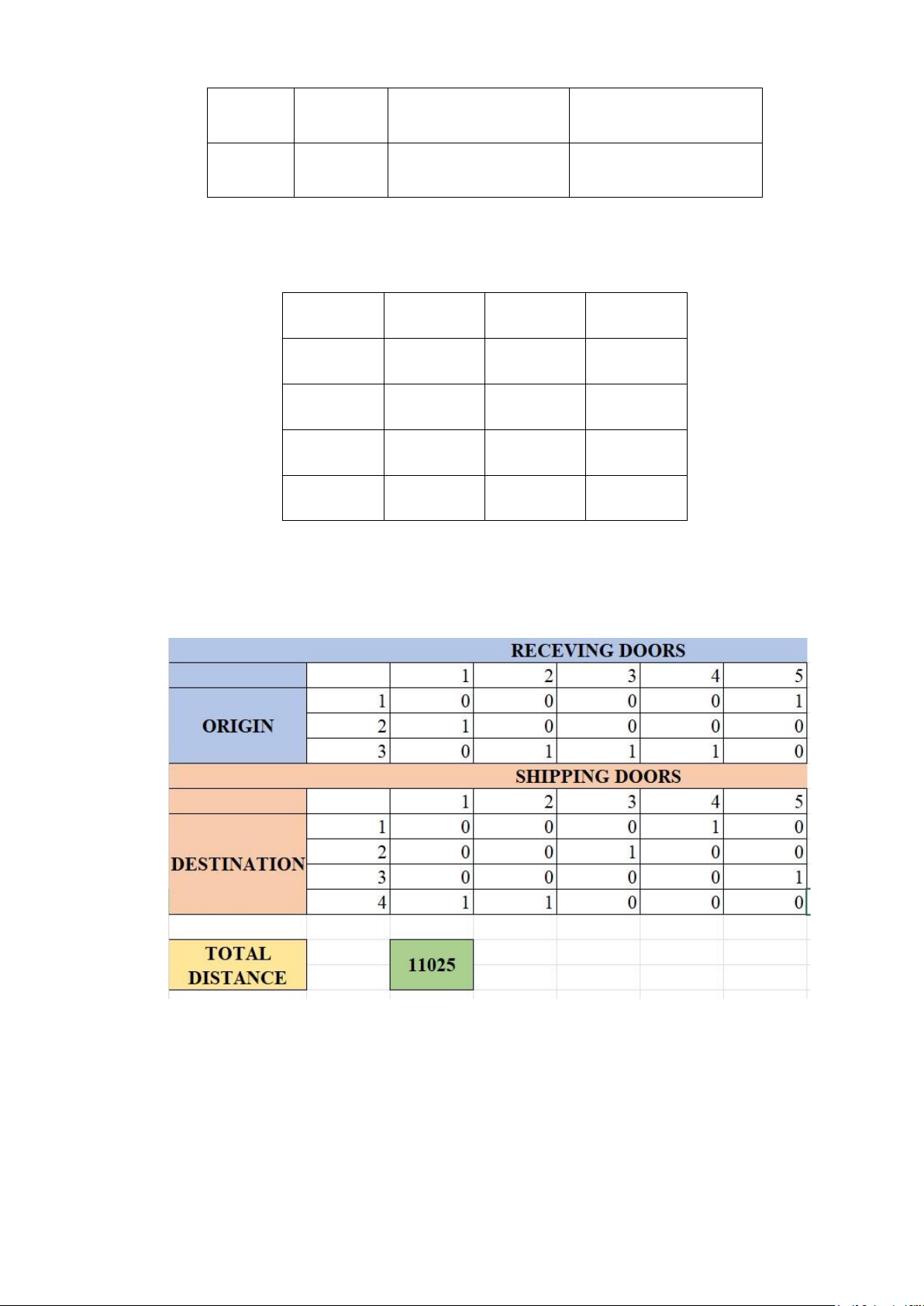
After running the code for this case, we can have the result with the optimal objective is 11205:
Figure 4.2. Decrease to 9 forklifts
Part 1: Origin - Receiving door
Origin 1 assigned to Receiving door 5
Origin 2 assigned to Receiving door 4 14
Origin 3 assigned to Receiving door 2
Origin 3 assigned to Receiving door 3
Origin 3 assigned to Receiving door 1
Part 2: Destination - Shipping door
Destination 1 assigned to Shipping door 4
Destination 2 assigned to Shipping door 3
Destination 3 assigned to Shipping door 5
Destination 4 assigned to Shipping door 1
Destination 4 assigned to Shipping door 2
Case 2: Increasing forklift quantity
Case 2.1: Using 18 forklifts
For this case, we tried to increase the number of forklifts from 15 to 18, which means that we
raised 3 forklifts in total and 1 forklift for each origin O1, O2, O3.
Quantity Orders per loading Total time (minutes) Forklifts 18 150 10
Table 4.5. Forklifts
Since altering forklift quantity, we could have the different number of forklift trips required
to move the items from origin i to destination j: From/ To O1 O2 O3 D1 13 8 7 D2 8 11 19 D3 19 3 5 D4 2 16 5
Table 4.6. Forklift trips
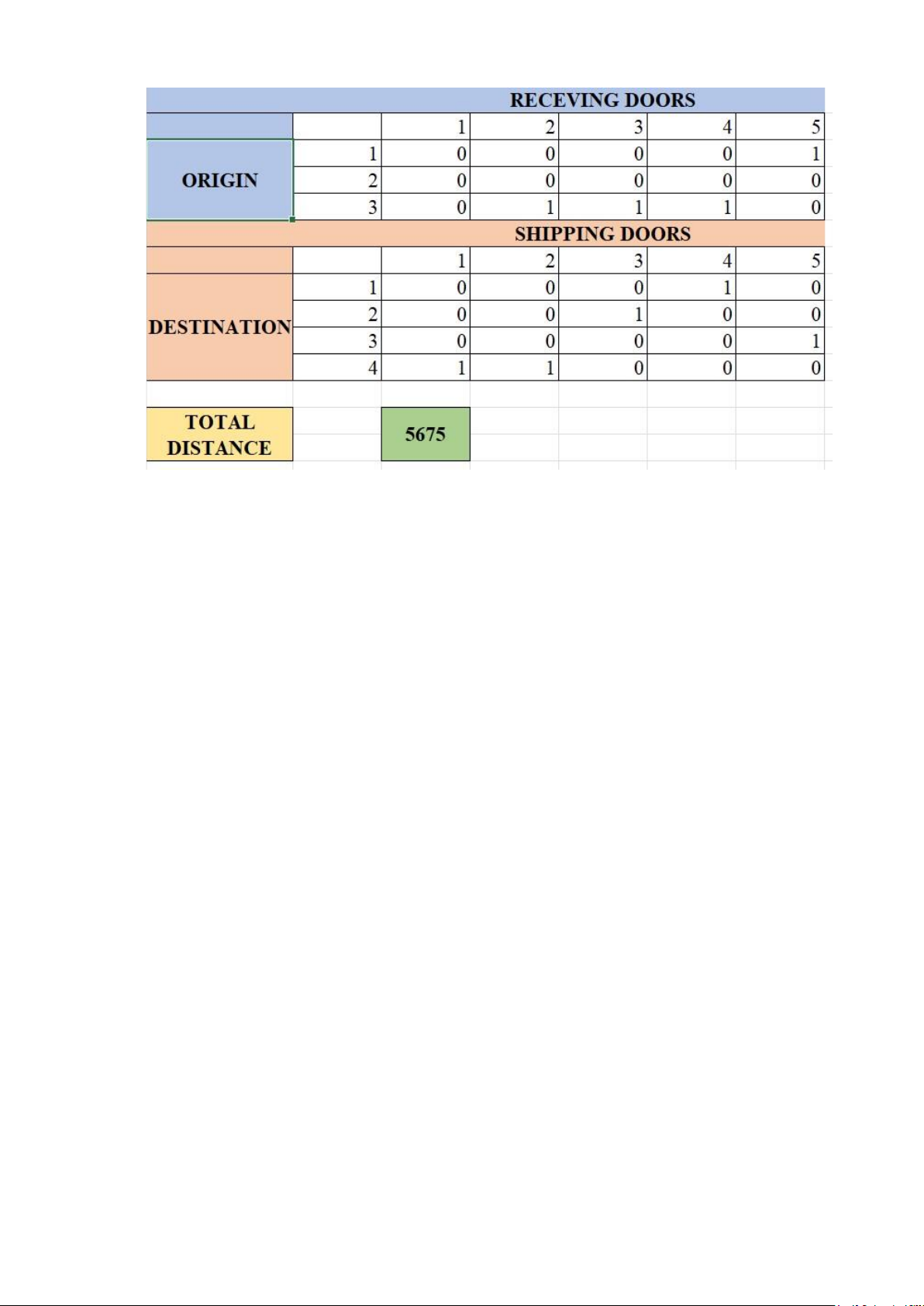
After running the code, we can have the below result with the optimal objective is 5675: 15
Figure 4.3. Increase to 18 forklifts
Part 1: Origin - Receiving door
Origin 1 assigned to Receiving door 5
Origin 2 assigned to Receiving door 4
Origin 3 assigned to Receiving door 2
Origin 3 assigned to Receiving door 3
Origin 3 assigned to Receiving door 1
Part 2: Destination - Shipping door
Destination 1 assigned to Shipping door 4
Destination 2 assigned to Shipping door 3
Destination 3 assigned to Shipping door 5
Destination 4 assigned to Shipping door 1
Destination 4 assigned to Shipping door 2 16
Case 2.2: Using 21 forklifts
For this case, we tried to increase the number of forklifts from 15 to 21, which means that we
raised 6 forklifts in total and 2 forklifts for each origin O1, O2, O3.
Quantity Orders per loading Total time (minutes) Forklifts 21 150 10
Table 4.7. Forklift
Since altering forklift quantity, we could have the different number of forklift trips required
to move the items from origin i to destination j: From/ To O1 O2 O3 D1 11 7 6 D2 7 9 16 D3 17 3 5 D4 2 14 4
Table 4.8. Forklift trips
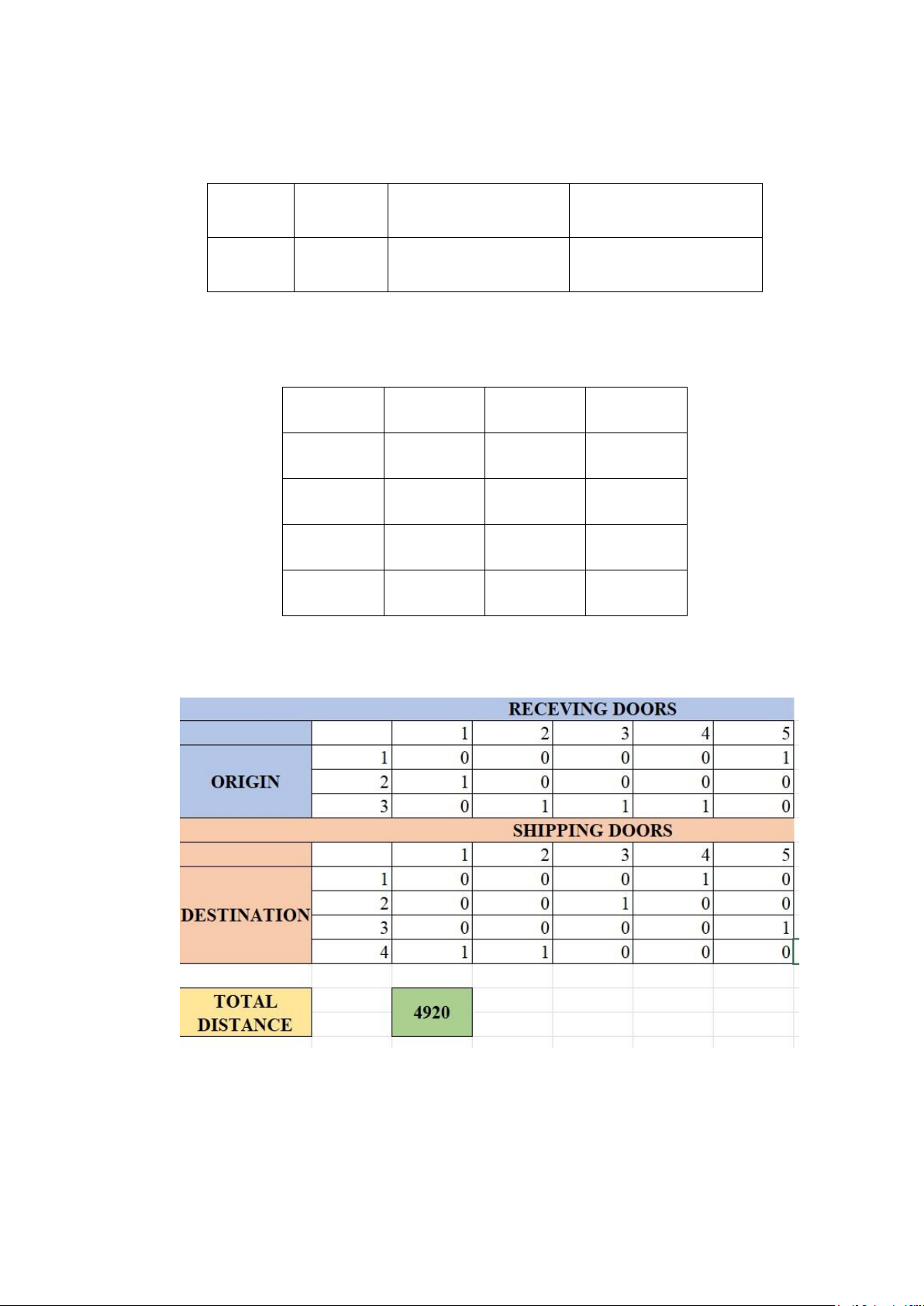
After running the code, we can have the below result with the optimal objective 4920:
Figure 4.4. Increase to 21 forklifts
Part 1: Origin - Receiving door
Origin 1 assigned to Receiving door 5 17
Origin 2 assigned to Receiving door 4
Origin 3 assigned to Receiving door 2
Origin 3 assigned to Receiving door 3
Origin 3 assigned to Receiving door 1
Part 2: Destination - Shipping door
Destination 1 assigned to Shipping door 4
Destination 2 assigned to Shipping door 3
Destination 3 assigned to Shipping door 5
Destination 4 assigned to Shipping door 1
Destination 4 assigned to Shipping door 2
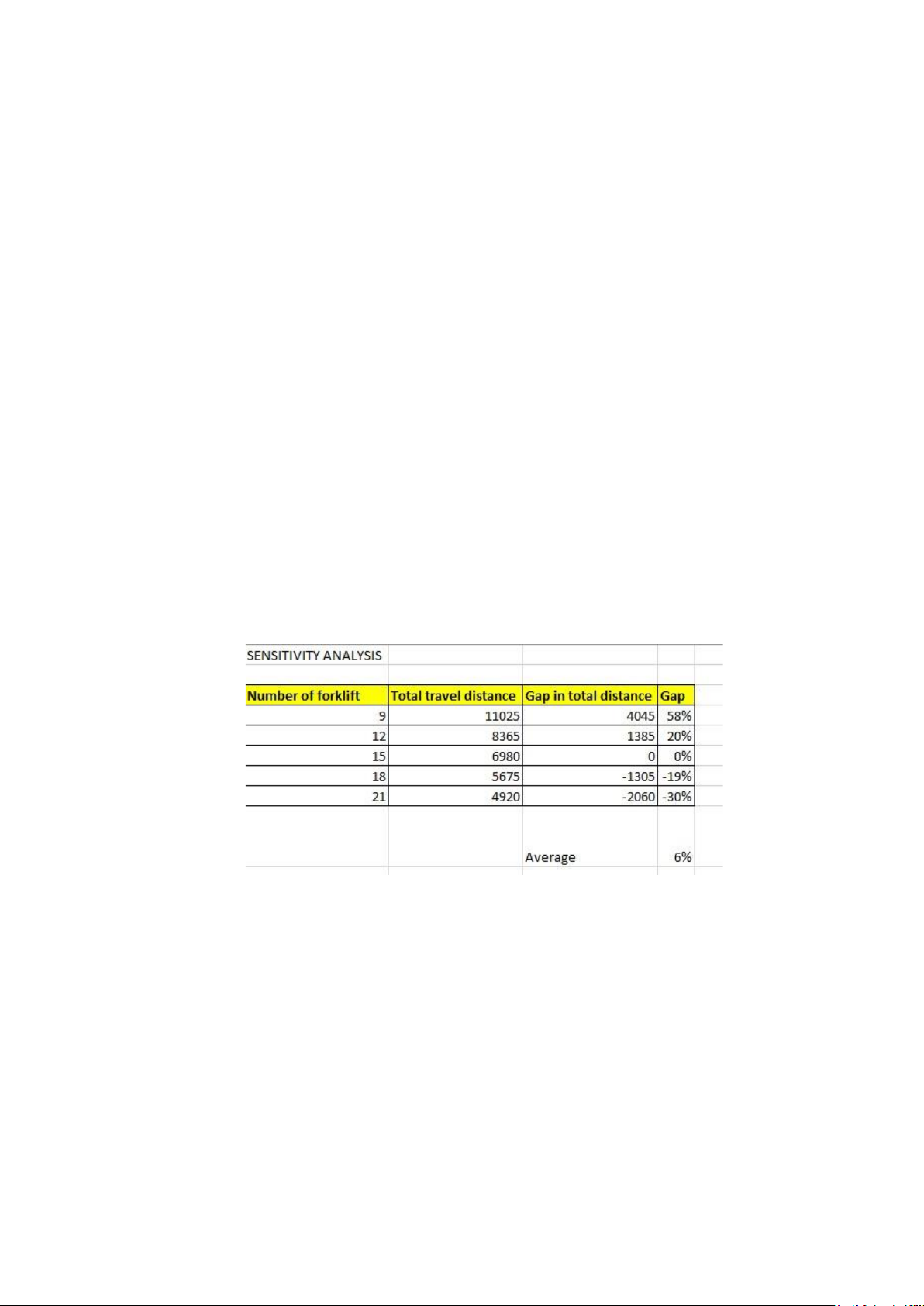
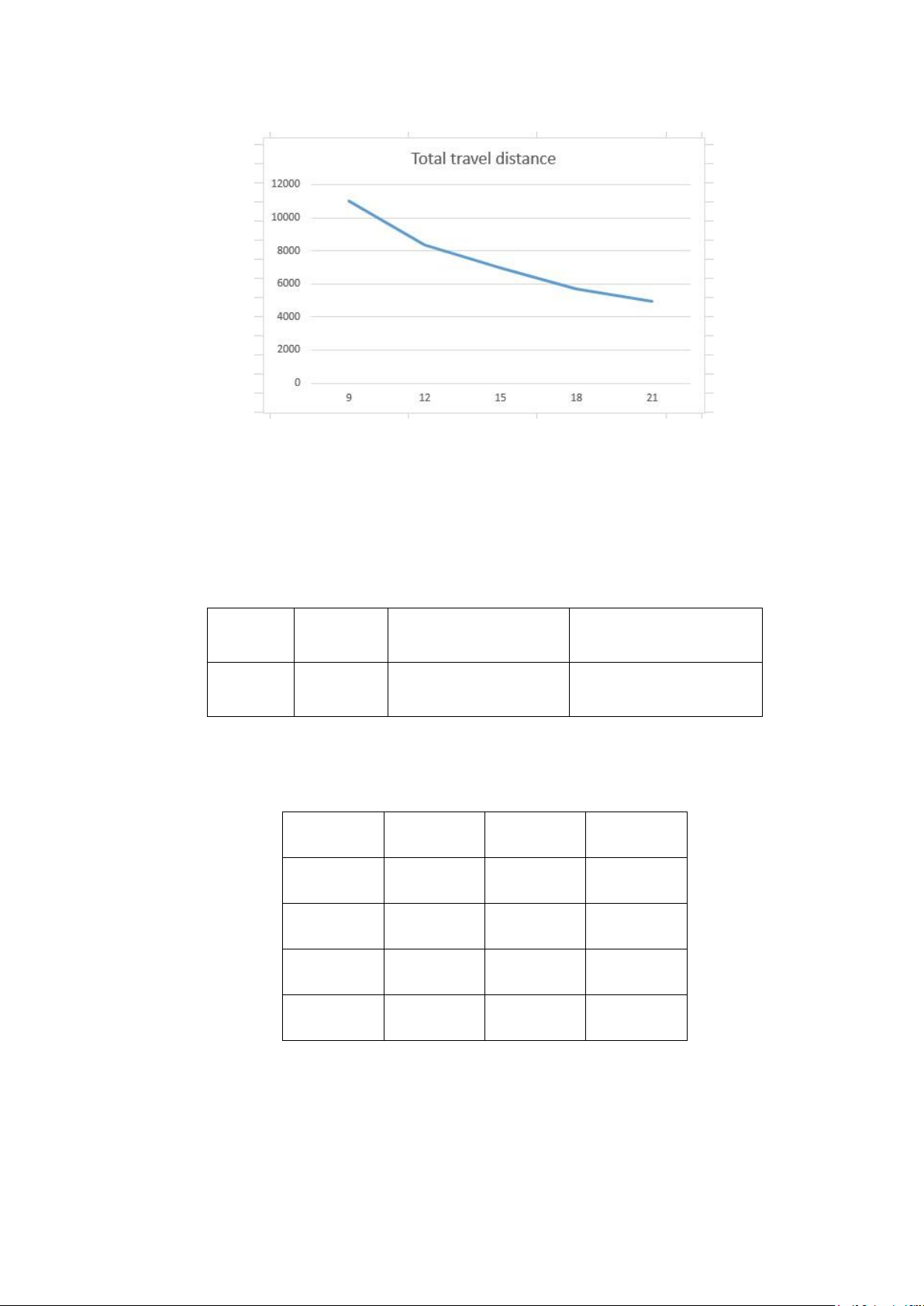
After running the CPLEX code for 4 cases, we summarize the change in total travel distance in the below table: 18
Table 4.9. The change in total travel distance
Chart 4.1. The change in total travel distance relative to the quantity of forklifts
b. Change in forklift capacity
After changing the forklift quantity, we also tried to alter the forklift capacity as well. To be
more specific, we are going to increase the capacity of the forklift from 150 to 250 and modify
the forklift from 3-ton to 5-ton forklifts.
Quantity Orders per loading Total time (minutes) Forklifts 15 250 10
Table 4.10. Forklifts
Since altering forklift quantity, we could have the different number of forklift trips required
to move the items from origin i to destination j: From/ To O1 O2 O3 D1 9 6 5 D2 6 8 14 D3 14 2 4 D4 2 12 4
Table 4.11. Forklift trips
After running the code, we can have the below result with the optimal objective 4280: 19




