Bài giảng cấp số cộng

Tài liệu gồm 43 trang, tóm tắt lý thuyết trọng tâm, các dạng toán và bài tập chủ đề cấp số cộng, có đáp án và lời giải chi tiết, giúp học sinh lớp 11 tham khảo khi học chương trình Đại số và Giải tích 11 chương 3: Dãy Số, Cấp Số Cộng Và Cấp Số Nhân.

84 42 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 2: Dãy số. Cấp số cộng và cấp số nhân (KNTT)

Môn: Toán 11

Thông tin:

29 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
Trang 1
CHUYÊN ĐỀ
BÀI GIẢNG CẤP SỐ CỘNG
Mục tiêu
Kiến thức
+ Hiểu được khái niệm cấp số cộng.
+ Nắm được công thức tổng quát, tổng n số hạng đầu tiên của cấp số cộng.
+ Biết được số hạng đầu và công sai của cấp số cộng.
Kĩ năng
+ Tìm được các yế
u tố còn lại khi biết 3 trong 5 yếu tố: số hạng đầu, số hạng thứ k, công sai, số
số hạng, tổng n số hạng đầu của cấp số cộng.
+ Liên hệ được kiến thức về cấp số cộng để giải những bài toán thực tế.
TOANMATH.co
m
Trang 2
I. LÍ THUYẾT TRỌNG TÂM
Định nghĩa
Cấp số cộng là một dãy số (vô hạn hay hữu hạn) mà trong đó, kể từ số hạng thứ hai, mỗi số hạng đều
bằng tổng của số hạng đứng ngay trước nó với một số d không đổi, nghĩa là

n
u
là cấp số cộng
1
2, .
nn
nuud

Số d được gọi là công sai của cấp số cộng.
Định lí 1
Nếu

n
u
là một cấp số cộng thì kể từ số hạng thứ hai, mỗi số hạng (trừ số hạng cuối đối với cấp số cộng
hữu hạn) đều là trung bình cộng của hai số hạng đứng kề nó trong dãy, tức là
11
.
2
kk
k
uu
u

Hệ quả: Ba số a, b, c (theo thứ tự đó) lập thành một cấp số cộng khi và chỉ khi a + c = 2b.
Định lí 2
Nếu một cấp số cộng có số hạng đầu
1
u
và công sai d thì số hạng tổng quát
n
u
của nó được xác định bởi
công thức sau:

1
1
n
uu n d
.
Định lí 3
Giả sử

n
u
là một cấp số cộng có công sai d.
Gọi
12
1
...
n
nk n
k
Suuu u

(
n
S là tổng của n số hạng đầu tiên của cấp số cộng).
Ta có
1
1
21
.
22
n
n
nu n d
nu u
S




SƠ ĐỒ HỆ THỐNG HÓA
1nn
uu d

2n
Nhận diện cấp số cộng
là hằng số
Số hạng tổng quát
Tổng n số hạng đầu tiên
Số hạng thứ k
Ba số a, b, c theo thứ
tự lập thành cấp số
cộng khi và chỉ khi
CẤP SỐ CỘNG
Hệ quả
TOANMATH.co
m
Trang 3
II. CÁC DẠNG BÀI TẬP
Dạng 1: Nhận dạng một dãy số là cấp số cộng
Phương pháp giải
Sử dụng định nghĩa

n
u
là một cấp số cộng khi và chỉ khi
1
,
nn
uud

với d là một hằng số.
Để chứng minh dãy số

n
u
là một cấp số cộng, ta xét
1nn
du u

Nếu d là hằng số thì

n
u
là một cấp số cộng với công sai d.
Nếu d phụ thuộc vào n thì

n
u
không là cấp số cộng.
Ví dụ mẫu
Ví dụ 1.
Chứng minh các dãy số sau là cấp số cộng.
a) Dãy số
n
u
với
2020 2021.
n
un
b) Dãy số
n
u
với
25.
n
un
Hướng dẫn giải
a) Dãy số
n
u
với 2020 2021.
n
un
Ta có

1
2020 1 2021 2020 2021 2020.
nn
uu n n

Vậy

n
u
là một cấp số cộng với công sai
2020.d
b) Dãy số

n
u
với 2 5.
n
un
Ta có
1
215252.
nn
uu n n

Vậy
n
u
là một cấp số cộng với công sai
2.d 
Ví dụ 2. Chứng minh các dãy số sau không phải là cấp số cộng.
a) Dãy số
n
u
với
2
1.
n
unn
b) Dãy số
n
u
với

13.
n
n
un
Hướng dẫn giải
a) Dãy số
n
u
với
2
1.
n
unn
Ta có

2
2
1
111 122
nn
uun n nn n

phụ thuộc vào n.
Vậy

n
u
không là cấp số cộng.
b) Dãy số
n
u
với

13.
n
n
un
Ta có
    
1
1
131 13 131321
nnnnn
nn
uu n n

 

phụ thuộc vào n.
TOANMATH.co
m
Trang 4
Vậy

n
u
không là cấp số cộng.
Bài tập tự luyện dạng 1
Câu 1:
Dãy số nào sau đây là cấp số cộng?
A. 1; 3; 6; 9; 12. B. 1; 4; 7; 10; 14. C. 1; 2; 4; 8; 16. D. 0; 4; 8; 12; 16.
Câu 2: Trong các dãy sau đây, dãy nào là cấp số cộng?
A.
3.
n
n
u
B.

1
3.
n
n
u

C. 31.
n
un D.
2
5.
n
unn
Câu 3: Một cấp số cộng
n
u
với
1
11
,
22
ud
có dạng khai triển nào sau đây?
A.
11
; 0; 1; ; 1;...
22
B.
11 1
; 0; ; 0; ;...
22 2

C.
13 5
; 1; ; 2; ;...
22 2
D.
113
; 0; ; 1; ;...
222
Câu 4: Trong các dãy số sau, dãy số nào là một cấp số cộng
A. 1; -2; -4; -6; -8. B. 1; -3; -6; -9; -12. C. 1; -3; -7; -11; -15. D. 1; -3; -5; -7; -9.
Câu 5: Trong các dãy số sau đây dãy số nào là cấp số cộng?
A.
1, 1.
n
unn
B. 23, 1.
n
unn C.
2
1, 1.
n
un n D.

1
2,1.
n
n
un

Câu 6: Trong các dãy số sau đây, dãy số nào là cấp số cộng?
A.
2
3 2020.
n
un
B.
3 2020.
n
un
C.
3.
n
n
u
D.

1
3.
n
n
u

Câu 7: Trong các dãy số

n
u
sau đây, dãy số nào không phải là cấp số cộng?
A. 31.
n
un B.
21.
n
n
u 
C.

2
2
1.
n
un n
D.
1
1
3
1, 1.
nn
u
uun

Câu 8: Các dãy số sau có số dạng tổng quát
n
u
, dãy số nào
không phải là cấp số cộng?
A. 1; 3; 5; 7; 9. B. 13; 17; 21; 25; 29. C.
13.
n
n
u 
D.

2
2
3.
n
un n
Câu 9: Trong các dãy số sau đây dãy số nào là cấp số cộng?
A.
1
1
1
.
21
nn
u
uu


B.
1
1
1
.
1
nn
u
uu


C.
2
.
n
un
D.

3
1.
n
un
Câu 10: Dãy số nào dưới đây là cấp số cộng?
A.
*
2, .
n
n
un n
B.

*
31, .
n
unn
C.

*
3, .
n
n
un
D.

*
31
,.
2
n
n
un
n

Câu 11: Khẳng định nào sau đây sai?
A. Dãy số 0,1; 0,01; 0,001; 0,0001;… không phải là một cấp số cộng.
B. Dãy số
113
;0; ;1; ;...
222
là một cấp số cộng với
1
1
2
1.
1
2
u
d

TOANMATH.co
m
Trang 5
C. Dãy số
23
11 1
; ; ;...
22 2
là một cấp số cộng có ba số hạng và
1
1
2
.
1
2
u
d
D. Dãy số -2; -2; -2; -2;… là một cấp số cộng
1
2
.
0
u
d

Câu 12: Cho dãy số có các số hạng đầu là 8; 15; 22; 29; 36;… Viết công thức số hạng tổng quát?
A. 77.
n
un B. 7.
n
un
C.
Không viết được dưới dạng công thức. D. 71.
n
un
Câu 13: Cho 2 cấp số cộng hữu hạn 4; 7; 10; 13; 16;… và 1; 6; 11; 16; 21;…; mỗi cấp số cộng có 100 số
hạng. Hỏi có tất cả bao nhiêu số có mặt trong cả hai cấp số trên?
A. 21. B. 20. C. 18. D. 19.
Câu 14: Trong các dãy số dưới đây, dãy số nào là cấp số cộng?
A. Dãy số
,
n
a
với

2
2*
25 4, .
n
an nn
B. Dãy số
,
n
b
với
*
11
1, 3 4, .
nn
bb b n

C. Dãy số
,
n
c
với
*
2019 , .
n
n
cn
D. Dãy số
,
n
d
với
*
11
2020
1, , .
1
n
n
dd n
d

Dạng 2: Tìm số hạng đầu tiên, công sai của cấp số cộng, tìm số hạng thứ k của cấp số cộng, tính
tổng k số hạng đầu tiên.
Phương pháp giải
Ta lập hệ phương trình gồm hai ẩn
1
u và
.d
Sau đó giải hệ phương trình này tìm được
1
u và
.d
Muốn tìm
số hạng thứ
,k
trước tiên ta phải tìm
1
u và
.d
Sau đó áp dụng công thức
1
1.
k
uu k d
Muốn tính tổng
của k số hạng đầu tiên, ta phải tìm
1
u và
.d
Sau đó áp dụng công thức


1
1
21
.
22
k
k
ku k d
ku u
S




Ví dụ mẫu
Ví dụ 1.
Tìm số hạng đầu và công sai của cấp số cộng
123
222
123
9
.
35
uuu
uuu


Hướng dẫn giải
Cách 1.
Ta có

11 1
123
22
222
2
123
11 1
29
9
35
235
uudu d
uuu
uuu
uud ud





 

1
1
1
22
2
2
3
3
3
.
2
4
33335
ud
ud
ud
d
d
dd







Với
1
21.du
Với
1
25.du
Cách 2. Đặt
123
;; .uxdxxuxd 
Áp dụng công thức

1
1
n
uu n d
lập hệ phương trình
gồm hai ẩn
1
u và
.d
TOANMATH.co
m
Trang 6
Ta có

123
22
222
2
123
9
9
35
35
xd xxd
uuu
uuu
xd x xd







22
2
2
3
3
3
.
2
4
33335
x
x
x
d
d
dd




Với
1
21.du
Với
1
25.du
Ví dụ 2. Tìm bốn số hạng liên tiếp của một cấp số cộng biết tổng của chúng
bằng 20 và tổng các bình phương của chúng bằng 120.
Hướng dẫn giải
Giả sử bốn số hạng
3; ; ; 3axaxaxax
lập thành cấp số cộng với công
sai là
2.dx
Khi đó ta có

222 2
3320
3 3 120
ax ax ax ax
ax ax ax ax


22
420
5
.
1
4 20 120
a
a
x
ax




Vậy bốn số cần tìm là 2; 4; 6; 8.
- Nếu số số hạng của cấp số
cộng là lẻ thì gọi công sai
,dx
là chẵn thì gọi công
sai
2dx
rồi viết các số
hạng dưới dạng đối xứng.
- Nếu cấp số cộng
n
a
thỏa
mãn
12
22 22
12
...
...
n
n
aa a p
aa as


thì
1
1
1
.
2
nn
ap d
n




và

22
22
12
.
1
ns p
d
nn

Ví dụ 3. Tìm số hạng đầu tiên, công sai, số hạng thứ 50 và tổng của 20 số
hạng đầu tiên của cấp số cộng ,
n
u biết rằng
5
9
19
.
35
u
u
Hướng dẫn giải
Áp dụng công thức

1
1,
n
uu n d
ta có
5
1
1
91
19
419
3
.
35 8 35
4
u
ud
u
uud
d




Vậy số hạng đầu tiên
1
3,u công sai
4.d
Số hạng thứ 50 là
50 1
49 3 49.4 199.uu d
Tổng của 20 số hạng đầu tiên là

1
50
50 2 49
25. 2.3 49.4 5050.
2
ud
S

Áp dụng công thức

1
1
n
uu n d
Lập được hệ phương trình
gồm hai ẩn
1
u và
.d
Để tính tổng k số hạng đầu
tiên, ta áp dụng công thức
1
21
.
2
k
ku k d
S



Ví dụ 4.
Tìm số hạng đầu và công sai của các cấp số cộng
TOANMATH.co
m
Trang 7
a)
12
18
34
.
45
S
S
b)
4
1234
20
.
111125
24
S
uuuu

Hướng dẫn giải
a) Ta có

1
1
12
1
18 1
1
12 2 11
31
34
34 6 33 17
9
2
.
45
2175 1
18 2 17
45
9
2
ud
u
Sud
S
ud
ud
d







b)
1
4
1234
1234
22 3 20
20
111125
111125
24
24
ud
S
uuuu
uuuu







1
*
3
5
2
.
11 1 125
33 3 3
24
55 5253
22 2 2
ud
ddddddd



Áp dụng công thức

1
21
2
k
ku k d
S



Biểu diễn được
4
S
theo hai
ẩn
1
u và
.d
Áp dụng công thức

1
1
n
uu n d
Lập được hệ phương trình
gồm hai ẩn
1
u và
.d

*
22
1 1 1 1 25 10 10 25
.
33
9
24 24
55 55
25 25
22 22
44
dd
dd
dd








Đặt
2
;0,
4
d
tt
ta được


225 225 9
10 10 25 5
25 9 25 24 25 9 25 24
tt
tt tt





2
100 20 5
24 20 4 25 9 25
25 9 25 24
145
9 154 145 0 .
9
1
t
ttt
tt
t
tt
t



Nếu
2
145 145 145
.
99 3
td d
Với
1
145 145
5.
32
du
Với
1
145 145
5.
32
du
Nếu
2
t1 d 1 1.d 
Với
1
37
15 .
22
du
TOANMATH.co
m
Trang 8
Với
1
313
15 .
22
du
Ví dụ 5. Biết
4 8 12 16
224.uuu u
Tính
19
.S
Hướng dẫn giải
Ta có
481216
224uuu u
111 1 1 1
3 7 11 15 224 4 36 224 9 56.ududu du d u d ud   
Ta có

19 1 1
19
2 18 19 9 19.56 1064.
2
Sudud
Ví dụ 6. Cho cấp số cộng
n
u
biết 9 5 .
n
un Tìm
100
.S
Hướng dẫn giải
Ta có

*
1
95 1 95 5, .
nn
uu n n n



Suy ra
1
5, 4.du
Vậy
1
100
2 1 100 2.4 99. 5
24350.
22
nu n d
S


Bài tập tự luyện dạng 2
Câu 1:
Số hạng đầu
1
u và công sai d của cấp số cộng
n
u
có
23
7; 4uulà
A.
1
1; 3 .ud B.
1
10; 3.ud C.
1
4; 3.ud D.
1
4; 3.ud
Câu 2: Cho cấp số cộng
n
u
với số hạng đầu là
1
15u và công sai
2.d 
Số hạng thứ 8 của cấp số
cộng là
A.
8
1.u
B.
8
1.u 
C.
8
103.u
D.
8
64.u
Câu 3: Cho cấp số cộng
n
u
có
1
1; 2; 483.
n
udS Giá trị của n là
A.
20.n
B.
21.n
C.
22.n
D.
23.n
Câu 4: Cho cấp số cộng
n
u
xác định bởi
1
1
2
.
3
nn
u
uu


Số 70 là số hạng thứ bao nhiêu của cấp số
cộng?
A. 15. B. 23. C. 25. D. 205.
Câu 5: Cho một cấp số cộng
n
u
có
1
5u và tổng của 50 số hạng đầu bằng 5150. Công thức của số hạng
tổng quát
n
u là
A. 14.
n
un B. 5.
n
un C. 32.
n
un D. 23.
n
un
Câu 6: Cho cấp số cộng
n
u
có 2 3.
n
un Biết 320,
n
S giá trị của n là
A.
16n
hoặc
20.n 
B.
15.n
C.
20.n
D.
16.n
Câu 7: Cho dãy số
n
u
biết 2 5.
n
un Chọn khẳng định đúng.
A.
n
u
là một cấp số cộng với công sai
2.d
B.
n
u
là một cấp số cộng với công sai
2.d 
C.
n
u
là một cấp số cộng với công sai
5.d
D.
n
u
là một cấp số cộng với công sai
5.d 
TOANMATH.co
m
Trang 9
Câu 8: Cho cấp số cộng
n
u
biết
1
7u và
4.d
Lựa chọn kết quả đúng trong các kết quả sau
A.
15 3
46.uu B.
29 22
28.uu C.
17 13
18.uu D.
1000 100
350.uu
Câu 9: Cho dãy số
n
u
là một cấp số cộng có công sai
3.d
Chọn khẳng định đúng trong các khẳng
định sau
A. Dãy số
10 20 30 10
;;;...; , 1
n
uuu u n theo thứ tự lập thành một cấp số cộng với công sai là 10.
B. Dãy số
10 20 30 10
;;;...; , 1
n
uuu u n theo thứ tự lập thành một cấp số cộng với công sai là 20.
C. Dãy số
10 20 30 10
;;;...; , 1
n
uuu u n theo thứ tự lập thành một cấp số cộng với công sai là 30.
D. Dãy số
10 20 30 10
;;;...; , 1
n
uuu u n theo thứ tự lập thành một cấp số cộng với công sai là 15.
Câu 10: Cho cấp số cộng
n
u
có công sai d. Gọi
n
S là tổng của n số hạng đầu tiên. Hãy chỉ ra hệ thức sai
trong các hệ thức sau.
A.
38 56
.uuuu B.
59 7
2.uu u C.
2
49 6
..uu u
D.
35 4
2.SS Sd
Câu 11: Cho cấp số cộng
n
u
, biết
15
4
20
14
uu
S

. Số hạng đầu
1
u và công sai d là
A.
1
8; 3.ud B.
1
8; 2.ud C.
1
8; 3.ud  D.
1
8; 2.ud
Câu 12: Số hạng đầu
1
u và công sai d của cấp số cộng
n
u
có
153
16
10
7
uuu
uu


là
A.
1
33; 12.ud
B.
1
36; 13.ud
C.
1
35; 13.ud
D.
1
34; 13.ud
Câu 13: Cấp số cộng
n
u
có
610
18, 110SSthì tổng 20 số hạng đầu tiên là
A. 620. B. 280. C. 360. D. 153.
Câu 14: Cho cấp số cộng 5 2.
n
un Biết 16040,
n
S số số hạng của cấp số cộng là
A. 79. B. 3024. C. 80. D. 100.
Câu 15: Chọn khẳng định đúng trong các khẳng định sau. Nếu 3 số
,,abc
khác 0 lập thành cấp số cộng
thì
A. nghịch đảo của chúng cũng lập thành một cấp số cộng.
B. bình phương của chúng cũng lập thành cấp số cộng.
C. c, b, a theo thứ tự đó cũng lập thành cấp số cộng.
D. Tất cả các khẳng định trên đều sai.
Câu 16: Cho cấp số cộng có
10 15
85, 240,SS  khi đó
20
S bằng
A. -325. B. -170. C. -395. D. -470.
Câu 17: Tổng tất cả các số tự nhiên chẵn nhỏ hơn 555 là
A. 77145. B. 77284. C. 76450. D. 77006.
Câu 18: Cho cấp số cộng có
1
11
,.
44
ud
Chọn khẳng định đúng trong các khẳng định sau đây?
A.
5
5
.
4
S
B.
5
4
.
5
S
C.
5
5
.
4
S 
D.
5
4
.
5
S 
TOANMATH.co
m
Trang 10
Câu 19: Cho cấp số cộng
,
n
u
với
1
2, 3.ud Kết quả nào sau đây đúng?
A.
3
1.u  B.
3
7.u  C.
4
7.u  D.
6
0.u
Câu 20: Cho cấp số cộng có
222
60.uu
Tổng của 23 số hạng đầu là
A. 690. B. 680. C. 600. D. 500.
Câu 21: Công sai d của một cấp số cộng hữu hạn có số hạng đầu
1
10u và số hạng cuối
21
50u là
A.
4.d
B.
2.d
C.
2.d
D.
2.d 
Câu 22: Tổng 10 số hạng đầu của cấp số cộng có
110
8, 62uulà
A.
10
175.S B.
10
350.S C.
10
700.S D.
10
1400.S
Câu 23: Cho cấp số cộng có
1
1, 2, 483.
n
udS Số các số hạng của cấp số cộng đó là
A.
20.n
B.
21.n
C.
22.n
D.
23.n
Câu 24: Cho cấp số cộng có tổng 4 số hạng bằng 22, tổng bình phương của chúng bằng 166. Bốn số hạng
của cấp số cộng này là
A. 1; 4; 7; 10. B. 1; 4; 5; 10. C. 2; 3; 5; 10. D. 2; 3; 4; 5.
Câu 25: Cho cấp số cộng
n
u
thỏa mãn
25
310
42
.
66
uu
uu


Tổng của 346 số hạng đầu là
A. 242546. B. 242000. C. 241000. D. 240000.
Câu 26: Cho cấp số cộng
n
u
có
5
18u
và
2
4.
nn
SS
Số hạng đầu tiên
1
u
và công sai d của cấp số cộng
là
A.
1
2; 4.ud B.
1
2; 3.ud
C.
1
2; 2.ud
D.
1
3; 2.ud
Câu 27: Cho cấp số cộng gồm 4 số hạng
1, , 7, .ab
Giá trị của
,ab
là
A.
3, 11.ab
B.
2, 9.ab
C.
4, 12.ab
D.
7, 1.ab
Câu 28: Cho dãy số
n
a
có tổng n số hạng đầu tiên là
2
23.
n
Snn
Khi đó
A.
n
a
là một cấp số cộng với công sai bằng 4. B.
n
a
là một cấp số cộng với công sai bằng 2.
C.
n
a
là một cấp số cộng với công sai bằng 1. D.
n
a
là một cấp số cộng với công sai bằng 8.
Câu 29: Cho cấp số cộng
n
u
với số hạng đầu là
1
6u  và công sai
4.d
Tổng 14 số hạng đầu tiên
của cấp số cộng đó bằng
A. 280. B. 308. C. 644. D. 46.
Câu 30: Cho cấp số cộng
n
u
gồm 4 số hạng
2, ,6, .ab
Tích
.ab
bằng
A. 12. B. 32. C. 40. D. 22.
Câu 31: Cho cấp số cộng có tổng n số hạng đầu là
2*
34, .
n
Snnn
Giá trị số hạng thứ 10 của cấp
số cộng là
A.
10
55.u B.
10
67.u C.
10
61.u D.
10
59.u
TOANMATH.co
m
Trang 11
Câu 32: Thêm 6 số xen giữa hai số 3 và 24 ta được một cấp số cộng có 8 số hạng. Khi đó tổng các số
hạng là
A. 110. B. 107. C. 106. D. 108.
Câu 33:
Thêm 5 số xen giữa hai số 25 và 1 ta được một cấp số cộng có 7 số hạng. Số hạng thứ 50 là
A. -169. B. 169. C. -171. D. 171.
Câu 34: Cho một cấp số cộng
n
u
có
1
1u và tổng 100 số hạng đầu bằng 24850. Giá trị biểu thức
12 23 4950
11 1
...S
uu uu u u

là
A.
9
.
246
S
B.
4
.
23
S
C.
123.S
D.
49
.
246
S
Câu 35:
Cho cấp số cộng
n
u
thỏa mãn
532
74
321
.
32 34
uuu
uu


Giá trị của biểu thức
45 30
...Su u u là
A. -1242. B. -1222. C. -1276. D. -1286.
Dạng 3: Dựa vào tính chất của cấp số cộng: chứng minh đẳng thức, giải phương trình và các bài
toán thực tế
Phương pháp giải
Nếu
n
u
là một cấp số cộng thì kể từ số hạng thứ hai, mỗi số hạng (trừ số hạng cuối cùng đối với cấp số
cộng hữu hạn) đều là trung bình cộng của hai số hạng đứng kề nó trong dãy, tức là
11
.
2
kk
k
uu
u

Hệ quả: Ba số
,,abc
(theo thứ tự đó) lập thành một cấp số cộng khi và chỉ khi
2.ac b
Ví dụ mẫu
Ví dụ 1.
Cho
,,abc
là ba số hạng liên tiếp của một cấp số cộng, chứng minh rằng
a)
22
22.abccab
b)

2
2
82 .abcbc
Hướng dẫn giải
Vì
,,abc
là ba số hạng liên tiếp của một cấp số cộng nên
22.ac b a bc
a) Ta có

2
2222
22 22.44 42aabbc bcbbbccbbc
2
= c 2 .bc
Vậy
22 22
22 22.a ab c bc a bc c ab
b) Ta có

2
222
82 844 8abcbc bcbbccbc

2
22
= 4 4 2 .bbcc bc
Ví dụ 2. Một tam giác vuông có chu vi bằng 3a và ba cạnh lập thành một cấp số cộng. Tính độ dài ba
cạnh của tam giác theo a.
Hướng dẫn giải
Gọi
,,
x
yz
theo thứ tự là độ dài ba cạnh của tam giác
.
x
yz
TOANMATH.co
m
Trang 12
Chu vi của tam giác là
3. 1xyz a
Theo tính chất của cấp số cộng, ta có

2. 2xz y
Tam giác đã cho vuông nên

222
.3xyz
Thay (2) và (1), ta được
33 .ya ya
Thay
ya
vào (2), ta được
22.
x
zaxaz
Thay
2
az
và
y
a
vào (3), ta được

2
22 2
53
2540 .
44
aa
az a z a az z x
Vậy độ dài ba cạnh của tam giác là
35
,, .
44
aa
a
Ví dụ 3. Cho
222
,,abclập thành một cấp số cộng có công sai khác 0.
Chứng minh rằng
111
;;
bccaab
cũng lập thành một cấp số cộng.
Ta sẽ chứng minh
112
.
ab bc ca


Hướng dẫn giải
Theo giả thiết, ta có
22 2
2.ac b
Ta phải chứng minh
11 2
.
bc ab ca


Ta có
22 22 22 22
0acbb abbc

ab bc
abab bcbc
bc ab






ac bc ab ca
ab bc
bcca abca bcca abca
 


 

ac bc ab ca
acca bcca abca abca
 

 
11 11 11 2
bc ca ca ab ab bc ca


(điều phải chứng minh).
Ví dụ 4. Cho tam giác ABC có
tan , tan ,tan ,
222
A
BC
theo thứ tự đó lập thành
cấp số cộng. Chứng minh cosA, cosB, cosC theo thứ tự cũng lập thành cấp số
cộng.
Ta sẽ chứng minh
cosA + cosC = 2cosB
Hướng dẫn giải
Ta có
sin sin sin
22 2
tan tan 2 tan 2.
22 2
cos cos cos
22 2
A
CB
AC B
A
CB

TOANMATH.co
m
Trang 13
sin .cos sin .cos sin
22 22 2
2.
cos .cos cos
22 2
A
CCA B
A
CB

sin
sin cos sin
22
22 2
22.
cos .cos cos cos .cos cos
22 2 22 2
AC
B
BB
A
CBAC B




2
cos 2.cos .cos .sin
2222
BACB

1cos
cos cos .sin .
2222
B
AC AC B






1cos
cos .sin sin .sin
22222
BACBBB

2
1cos
cos .cos sin
2 222
BACAC B


1cos 1 1cos
cos cosA
22 2
BB
C



1 cos cos cos 1 cos
B
CA B
cos cos 2cos
A
CB
cos ,cos ,cos
A
BC
theo thứ tự đó lập thành một cấp số cộng.
Ví dụ 5. Cho các số dương a; b; c theo thứ tự lập thành cấp số cộng. Chứng
minh rằng
111
;;
bccaab
theo thứ tự đó cũng lập thành cấp số cộng.
Ta sẽ chứng minh
11
2
bc ab
ca

Hướng dẫn giải
Vì
,,abc
lập thành cấp số cộng nên
2.ac b
Ta cần chứng minh
11 2
.
bc ab ca


Ta có
2ac b abbc a b a b b c b c 





11 11 11 2
ab bc ab bc
bc ab
bcca abca
ac bc ba ca
bcca abca
bc ca ca ab bc ab ca




 




TOANMATH.co
m
Trang 14
111
;;
bccaab

theo thứ tự đó lập thành cấp số cộng.
Ví dụ 6. Tìm giá trị của m để phương trình
2
23 2 0xx xm
có 3 nghiệm phân biệt lập thành
một cấp số cộng có công sai lớn hơn 2.
Hướng dẫn giải
Ta có


2
1
23 2 0 3.
2
x
xx xm x
x
m

Ba nghiệm này lập thành một cấp số cộng có công sai lớn hơn 2 nên có 3 trường hợp.
Trường hợp 1: Ba nghiệm thứ tự là
-3;1; 2 .m
Suy ra
5
4;
2
dm
(thỏa mãn).
Trường hợp 2: Ba nghiệm thứ tự
3; 2 ;1.m
Suy ra
1
2;
2
dm
(loại).
Trường hợp 3: Ba nghiệm thứ tự
2;3;1.m
Suy ra
7
4;
2
dm
(thỏa mãn).
Vậy các giá trị m cần tìm là
75
;.
22
m




Ví dụ 7. Tìm m để phương trình

2
42
20 1 0xxm
có bốn nghiệm phân biệt lập thành cấp số cộng.
Hướng dẫn giải
Đặt
2
,0.txt Phương trình trở thành

2
2
20 1 0 1 .ttm
Phương trình đã cho có bốn nghiệm phân biệt khi và chỉ khi phương trình (1) có hai nghiệm dương
12
,tt
phân biệt
12
0 tt


'2
2
02990
911
0200 .*
1
0
10
mm
m
S
m
P
m






Bốn nghiệm của phương trình lập thành cấp số cộng là
2112
,,,.tttt
Ta có
21 1
1221
12 1
2
39.
2
tt t
tttt
tt t



Theo Định lí Vi-ét, ta có
 
21 1
12 2
22
12
92
20 18 .
.1 136
tt t
tt t
tt m m







 


TOANMATH.co
m
Trang 15
Suy ra
7m
hoặc
5m 
(thỏa mãn (*)).
Vậy các giá trị m cần tìm là
5; 7 .m
Ví dụ 8. Chứng minh rằng: Nếu phương trình
32
--0xax bxc
có ba nghiệm lập thành cấp số cộng thì
3
9227.ab a c
Hướng dẫn giải
Giả sử phương trình có ba nghiệm
123
,,
x
xx lập thành cấp số cộng.
Suy ra
13 2
2. 1xx x
Mặt khác

32
123
-
x
ax bx c x x x x x x
32
123 122331 123
x
x x x x xx xx xx x xxx
Suy ra

123
.2xxxa
Từ (1) và (2), suy ra
2
3
x
a hay
2
.
3
a
x
Phương trình đã cho có nghiệm
2
,
3
a
x
tức là
32
0
333
aaa
abc
  

  
  
3
3
2
09 2 27
27 3
aba
cabac
(điều phải chứng minh).
Ví dụ 9. Cho
22
1
;;
2
x
y
theo thứ tự lập thành một cấp số cộng.
Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
2
3.Px
yy

Hướng dẫn giải
Ta có
22
1
;;
2
x
y
theo thứ tự lập thành một cấp số cộng nên
22
1.xy
Đặt
sin , cos .xy

Ta có
22
31cos2
3 3sin .cos cos sin 2
22
Pxyy


213sin2cos2.P

Phương trình
2 1 3 sin 2 cos2P
 theo biến
có nghiệm


2
2
2
13
21 3 1 .
22
PP
Vậy
3
max .
2
P
Đẳng thức khi và chỉ khi 3 sin 2 cos 2 2



sin 2 1 .
66
kk






TOANMATH.co
m
Trang 16
1
.
2
MinP 
Đẳng thức khi và chỉ khi 3 sin 2 cos 2 2



sin 2 1 .
63
kk






Bài tập tự luyện dạng 3
Câu 1:
Cho tổng
1 6 11 16 ... 970.x
Giá trị của
x
là
A. 96. B. 69. C. 97. D. 7.
Câu 2: Biết
1 4 7 ... 28 155.xx x x
Giá trị của x là
A.
1.x
B.
1.x 
C.
2.x
D.
3.x 
Câu 3: Với giá trị nào của x thì
2
13; 5;1
x
xxlập thành cấp số cộng?
A.
0.x
B.
1.x 
C. 2.x  D.
.x 
Câu 4: Chu vi của một đa giác là 158 cm, số đo các cạnh lập thành một cấp số cộng với công sai
3d
cm. Biết cạnh lớn nhất là 44 cm. Số cạnh của đa giác đó là
A. 6. B. 3. C. 5. D. 4.
Câu 5: Phương trình
42
10 0xxm
có 4 nghiệm phân biệt lập thành một cấp số cộng. Khi đó m thuộc
khoảng nào sau đây?
A.
0;5 .m
B.
5;15 .m
C.
25;0 .m 
D.
15;25 .m
Câu 6: Cho tam giác
A
BC
có ba góc
,,
A
BC
theo thứ tự đó lập thành cấp số cộng và 𝐶
󰆹
5𝐴
󰆹
. Số đo các
góc
,,
A
BC
lần lượt là
A.
10 ,120 ,50 .
B.
15 ,105 ,60 .
C.
5,60,25.
D.
20 ,60 ,100 .
Câu 7: Một công ty thực hiện việc trả lương cho các kĩ sư theo phương thức như sau: Mức lương của quý
làm việc đầu tiên cho công ty là 15 triệu đồng/quý và kể từ quý làm việc thứ hai mức lương sẽ được tăng
thêm 1,5 triệu đồng mỗi quý. Tổng số tiền lương một kĩ sư được nhận sau 3 năm làm việc cho công ty là
A. 495 triệu đồng. B. 279 triệu đồng. C. 384 triệu đồng. D. 558 triệu đồng.
Câu 8: Cho tam giác vuông có độ dài ba cạnh lập thành một cấp số cộng với công sai
2.d
Bán kính
đường tròn ngoại tiếp
R
của tam giác đó là
A.
3.R
B.
4.R
C.
1.R 
D.
5.R
Câu 9: Độ dài ba cạnh của một tam giác vuông lập thành một cấp số cộng. Nếu cạnh trung bình bằng 6
thì công sai của cấp số cộng này là
A. 7,5. B. 4,5. C. 0,5. D. 1,5.
Câu 10: Giá trị
,ab
để phương trình
3
0xaxb
có ba nghiệm phân biệt lập thành cấp số cộng là
A.
0, 0.ba
B.
0, 0.ba
C.
0, 0.ba
D.
0, 1.ba
Câu 11: Một em học sinh dùng các que diêm để xếp thành hình tháp có quy luật được thể hiện như trong
hình dưới.
TOANMATH.co
m
Trang 17
Số que diêm để xếp thành hình tháp 10 tầng là
A. 69 que. B. 39 que. C. 420 que. D. 210 que.
Câu 12: Tam giác
A
BC
có ba cạnh
,,abc
thỏa mãn
222
,,abctheo thứ tự đó lập thành một cấp số cộng.
Chọn khẳng định đúng trong các khẳng định sau
A.
222
tan ,tan ,tan
A
BC theo thứ tự đó lập thành một cấp số cộng.
B.
222
cot ,cot , cot
A
BC theo thứ tự đó lập thành một cấp số cộng.
C.
cos , cos ,cos
A
BC
theo thứ tự đó lập thành một cấp số cộng.
D.
222
sin ,sin ,sin
A
BC theo thứ tự đó lập thành một cấp số cộng.
Câu 13: Số đo các góc của một tứ giác lồi lập thành một cấp số cộng và góc lớn nhất gấp 5 lần góc nhỏ
nhất. Số đo góc nhỏ nhất bằng
A.
25 .
B.
30 .
C.
45 .
D.
35 .
Câu 14: Người ta trồng 3420 cây theo một hình tam giác như sau: hàng thứ nhất trồng 1 cây, kể từ hàng
thứ 2 trở đi số cây trồng mỗi hàng nhiều hơn 1 cây so với hàng liền trước nó. Hỏi có tất cả bao nhiêu hàng
cây?
A. 81. B. 82. C. 80. D. 79.
Câu 15: Chu vi một đa giác là 158 cm, các cạnh của đa giác này lập thành một cấp số cộng với công sai
3.dcm
Biết cạnh lớn nhất có độ dài là 44 cm, độ dài cạnh nhỏ nhất của đa giác là
A. 32 cm. B. 33 cm. C. 38 cm. D. 35 cm.
Câu 16: Giá trị của n để
123
,,
nnn
CCC
theo thứ tự lập thành một cấp số cộng là
A.
9.n
B.
6.n
C.
2.n
D.
7.n
Câu 17: Giá trị của x để
2; 2 1;5x
theo thứ tự lập thành một cấp số cộng là
A.
1
.
4
x 
B.
1
.
3
x 
C.
1
.
4
x
D.
1.x
Câu 18: Cho
,,,
A
BCD
là bốn số thực dương lập thành một cấp số cộng. Giá trị biểu thức
22
22
DA
CB
bằng
A. 1. B. 0. C. 3. D. -1.
Câu 19: Cho
12
,
x
x là nghiệm của phương trình
2
30xxa
và
12
,yylà nghiệm của phương trình
2
11 0.xxb
Nếu
1212
,,,
x
xyy theo thứ tự lập thành một cấp số cộng thì tích ab có giá trị là
A.
1.ab 
B.
585
.
8
ab 
C.
585
.
8
ab
D.
54.ab
TOANMATH.co
m
Trang 18
Câu 20: Tìm m để phương trình
32
21 90xmxx
có ba nghiệm phân biệt lập thành một cấp số
cộng, ta được
,
a
m
b
với
,,ab
phân số
a
b
tối giản. Giá trị biểu thức
22
Pa b
là
A.
13.P
B.
20.P
C.
5.P
D.
10.P
Câu 21: Cho tam giác đều
111
A
BC
có độ dài cạnh bằng 4. Trung điểm các cạnh của tam giác
111
A
BC
tạo
thành tam giác
222
,
A
BC trung điểm các cạnh của tam giác
222
A
BC tạo thành tam giác
333
,...ABC Gọi
123
,P , ,...
P
P
lần lượt là chu vi của tam giác
111 2 2 2 3 3 3
,,,...ABC ABC ABC
Giá trị biểu thức
123
...PPPP
là
A.
8.P
B.
24.P
C.
6.P
D.
18.P
Câu 22: Cửa hàng xếp 1089 hộp sơn theo số lượng 1; 3; 5; … (hộp) từ trên xuống dưới (số hộp sơn trên
mỗi hàng xếp từ trên xuống dưới là các số lẻ liên tiếp như hình bên dưới). Hàng cuối cùng có bao nhiêu
hộp sơn?
A. 63. B. 65. C. 67. D. 69.
Câu 23: Một đội công nhân trồng cây xanh từ kilômet số 6 đến kilômet số 8. Cứ 20m trồng một cây. Hỏi
có bao nhiêu cây được trồng?
A. 100. B. 200. C. 250. D. 101.
Câu 24: An từ thành phố về quê thăm ông bà trên quãng đường 54 km. Biết giờ đầu tiên An đi được
15km và mỗi giờ sau An đi kém hơn giờ trước 1km. Thời gian An đi từ nhà về quê là
A. 27 giờ. B. 4 giờ. C. 3 giờ. D. 15 giờ
Câu 25: Ngày thứ nhất cửa hàng bán được 10 cốc nước mía, ngày sau bán nhiều hơn ngày hôm trước đó
1 cốc nước mía. Hỏi ngày thứ 10 cửa hàng sẽ bán được bao nhiêu cốc nước mía?
A. 15 cốc. B. 17 cốc. C. 19 cốc. D. 21 cốc.
Câu 26: Một nhóm gồm 3003 người xếp thành hình tam giác như sau: hàng thứ nhất có 1 người, hàng thứ
hai có 2 người, hàng thứ ba có 3 người,… Hỏi có bao nhiêu hàng?
A. 75. B. 76. C. 77. D. 78.
Câu 27: Tổng tất cả các giá trị m để phương trình

42
21 210xmxm
có bốn nghiệm phân biệt
lập thành một cấp số cộng là
A.
40
.
9
B.
40
.
9
C.
32
.
9
D.
32
.
9
ĐÁP ÁN
Dạng 1. Nhận dạng một dãy số là cấp số cộng
TOANMATH.co
m
Trang 19
1 - D 2 - C 3 - D 4 - C 5 - B 6 - B 7 - B 8 - C 9 - B 10 - B
11 - C 12 - D 13 - B 14 - A
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1.
Dãy số 0; 4; 8; 12; 16 là cấp số cộng có số hạng đầu là
1
0u
và công sai
4.d
Câu 2.
Ta có 3 1
n
un là một cấp số cộng vì
1
311313.
nn
uu n n



Câu 3.
Ta có
12345
113
, 0, , 1, ,...
222
uuuuu
Câu 4.
Dãy số
n
u
có tính chất
1nn
uud
thì được gọi là một cấp số cộng.
Ta thấy dãy số 1; -3; -7; -11; -15 là một cấp số cộng có số hạng đầu là 1 và công sai bằng -4.
Câu 5.
Ta có

1
213232, 1.
nn
uu n n n

Do đó dãy số trong đáp án
B là cấp số cộng theo định nghĩa.
Câu 6.
Ta có
1 1
3 1 2020 3 2020 3 3.
nn n n
uu n n uu
 
Vậy dãy số trên là cấp số cộng có công sai
3.d
Câu 7.
Ta có
21
n
n
u 
không là cấp số cộng vì
1
1
22.
nn
nn
uu

Câu 8.
Xét dãy số
13,
n
n
u 
suy ra
1
1
13.
n
n
u

Ta có
*
1
2.3 , .
n
nn
uu n

Do đó
13.
n
n
u 
không phải là cấp số cộng.
Câu 9.
Ta có
1
1
1
1
nn
u
uu


là cấp số cộng vì
1
1
1
1
1.
1
nn
nn
u
uu
uu



Câu 10.
Ta có

*
31
n
unn
là cấp số cộng vì
1
311313
nn
uu n n
 
là hằng số.
Câu 11.
Xét đáp án C.
23
11511
2.
22822

nên dãy số
23
11 1
; ; ;...
22 2
không là cấp số cộng.
Câu 12.
TOANMATH.co
m
Trang 20
Dãy số 8; 15; 22; 29; 36; … là một cấp số cộng với
1
8
7
u
d
công thức tổng quát là
71.
n
un
Câu 13.
Gọi cấp số cộng thứ nhất là
n
u
và cấp số cộng thứ hai là
.
n
v
Ta có
 
1
1431 31;
nn
uu n d n u n
1
1151 54.
kk
vv k d k v k
Với
, ,1 100,1 100.kn n k
Ta có
315 4 3 5 1.
nk
uv n k n k
Mà 3 và 5 là hai số nguyên tố cùng nhau nên n chia hết cho 5.
Đặt
5, 3 1.ntt kt
Do
1 100,1 100nk 
nên
1;2;3;...;20 .t
Câu 14.
Ta có

2
2* *
25 4, 2025, .
nn
an nn an n
Do đó
*
1
20,
nn
aa n

nên
n
a
là cấp số cộng với công sai
20.d
Dạng 2. Tìm số hạng đầu tiên, công sai của cấp số cộng, tìm số hạng thứ k của cấp số cộng, tính tổng
k số hạng đầu tiên
1 – B 2 – A 3 – D 4 – C 5 – A 6 – D 7 – A 8 – B 9 – C 10 – C
11 – A 12 – B 13 – A 14 – C 15 – C 16 – C 17 – D 18 – C 19 – C 20 – A
21 – C 22 – B 23 – D 24 – A 25 – A 26 – A 27 – A 28 – A 29 – A 30 – B
31 – C 32 – D 33 – C 34 – D 35 – A
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1.
Ta có
23
7; 4uu suy ra
3.d 
từ đó
1
7 ( 3) 10.u 
Câu 2.
Ta có
181
1 7 15 7.( 2) 1.
n
uu n duu d
Câu 3.
Ta có


1
2
21
23
2.483 . 2. 1 1 .2 2 483 0 .
21
2
n
nu n d
n
Snnnn
n





Do
*
n
nên
23.n
Câu 4.
Ta có
1
1
1
2
2; 3.
3
nn
u
ud
uu



Suy ra
23 1 3 5.
n
unn
TOANMATH.co
m
Trang 21
Từ đó
70 3 5 25.nn
Câu 5.
Ta có

50 1
50
2 49 5150 4.
2
Sud d
Số hạng tổng quát của cấp số cộng bằng
1
114.
n
uu n d n
Câu 6.
Ta có
1
5u suy ra
2
52 3
4.
2
n
nn
Snn


Câu 7.
1
21
2
3
25 2.
1
n
u
un duu
u



Câu 8.
15 3 1 1
14 2 12 48 6uuu du d d
loại A;
29 22 1 1
28 21 7 28uuu du d d 
chọn B;
17 13 1 1
16 12 4 16 18uuududd 
loại C;
1000 100
900 350uu d loại D.
Câu 9.
Gọi
n
a
là cấp số cộng theo thứ tự
10 20 30 10
; ; ;...; , 1,
n
uuu u n
lúc đó ta có
1101
21
2201
9
' 10 30.
19
au u d
daa d
au u d



Câu 10.
Ta có
22
49 1 1 1 1
.382411.uuududu d ud

2
222
61 1 1
52510.uudu d ud
Suy ra
2
49 6
..uu u
Câu 11.
Ta có

11
15 1
1
1
4
1
240
20
380
8
.
237
14
3
22 3 14
uud
uu
ud
u
ud
S
d
ud








Câu 12.
Ta có

11 1
153
1
1
16 1
11
4210
10
210
36
.
7257
13
57
uudud
uuu
ud
u
uu u d
d
uud
 








Câu 13.
Ta có

1
6
1
1
10 1
1
32 5 18
18
256
7
.
110 2 9 22
4
52 9 110
ud
S
ud
u
Sud
d
ud








TOANMATH.co
m
Trang 22
Từ đó mà
20 1
10 2 19 10 2. 7 19.4 620.Sud
Câu 14.
Ta có cấp số cộng: 5 2
n
un nên
12
3, 8,... 5.uu d
 
1
2
16040 2 1 16040 2.3 1 .5 16040
22
80
5 32080 0 80.
401
(loai)
5
n
nn
Sund n
n
nn n
n





Câu 15.
Không mất tổng quát giả sử
abc cbbad
với d là công sai.
Khi đó
 
111 1 11
2
dd
ab aad aad bc ada d
 

nên loại A.
22 2 22 2
223ba add cb ad d
nên loại B.
Nếu
,,abc
lập thành cấp số cộng với công sai d thì
,,cba
cũng lập thành cấp số cộng với công sai –d.
Câu 16.
10 1
1
20 1
15 1
985
194
19 395.
14 240
31
SSd
S
SS d
SS d
d





Câu 17.
Theo giả thiết
278.554
2 4 ... 552 554 77006.
2

Câu 18.
Theo giả thiết
51
115
5105.10. .
444
Su d




Câu 19.
Ta có
41 61
3 2 3. 3 7, 5 2 5. 3 13.uu d uu d 
Câu 20.

222 1 23 1
23 23.60
60 2 22 60 2 22 690.
22
uu u d S u d
Câu 21.
Ta có
11
1
21 1
10 10
10
50 20 50
2.
uu
u
uud
d






Câu 22.
Ta có
1
1
1
10 1
8
8
8
62 9 62
6.
u
u
u
uud
d



Suy ra
10 1
5 2 9 5 2.8 9.6 350.Sud
TOANMATH.co
m
Trang 23
Câu 23.



1
2
483 2 1 483 2. 1 1 .2 483
22
23
2 483 0 23.
21( )
n
nn
Sund n
n
nn n
n loai
 




Câu 24.
1234
1
1
2222 2 2
1234 1 1
22
4622
1
3
166 4 12 14 166
uuuu
ud
u
d
uuuu u ud d





hoặc
1
10
.
3
u
d

Câu 25.

25
1
1
346
310 1
42
2542
11
346
2.11 345.4 242546.
66 2 11 66
42
uu
ud
u
S
uu u d
d





Câu 26.
Ta có
51
18 4 18 1 .uud

21 1
111
1221
44 2
22
42 222 2 02.
nn
nn d n n d
S S nu nu
unddundd ud




 
Từ (1) và (2) suy ra
1
2; 4.ud
Câu 27.
Ta có
1 7 3;7 7 14 3 11.aaaabb 
Câu 28.
Ta có số hạng thứ n của dãy là

2
2
1
23213141.
nnn
aSS n n n n n

Suy ra
1
45.
n
an

Khi đó
1
4
nn n
aa a

là một cấp số cộng với công sai là 4.
Câu 29.
Ta có

14 1
2 1 280.
2
n
Sund

Câu 30.
Ta có
2 6 4;6 6 8 . 32.aaaabbab 
Câu 31.
Từ giả thiết ta có
2
11
3.1 4.1 7.Su
Ta có
2
10
86 76 1
34 61 61.
22
nn
nnnn
Snn un u


Cách khác
22
110109
3.10 4.10 3.9 4.9 61.
nnn
uSS u SS

Câu 32.
TOANMATH.co
m
Trang 24
Xen giữa hai số 3 và 24 thêm 6 số để được cấp số cộng có 8 số hạng thì

18
8
83248
108.
22
uu
S


Câu 33.
Ta có
125
4.
6
d

Do đó
50 1
49 25 49.4 171.uu d
Câu 34.
Gọi d là công sai của cấp số đã cho.
Ta có

1
100 1
497 2
50 2 99 24850 5
99
u
Sud d

12 23 4950
55 5
5 ...S
uu uu u u

32 5049
21
12 23 4950
1 2 2 3 48 49 49 50
150 11
...
1111 1 1 1 1
...
1 1 1 1 245 49
.
49 246 246
uu u u
uu
uu uu u u
uuuu u u u u
S
uu uu d



 
Câu 35.
Ta có

111
532
1
1
74 1
11
43 2 21
321
39 21
2
.
3 2 34 12 34
3
3623 34
ud udud
uuu
ud
u
uu u d
d
ud ud







 




4 5 30 30 3
30 3
... 2.2 29. 3 2.2 2.3 1242.
22
Su u u S S
Dạng 3. Dựa vào tính chất của cấp số cộng: chứng minh đẳng thức, giải phương trình và các bài
toán thực tế
1 – A 2 – A 3 – D 4 – D 5 – B 6 – D 7 – B 8 – D 9 – D 10 – C
11 – D 12 – D 13 – B 14 – C 15 – D 16 – D 17 – C 18 – C 19 – B 20 – C
21 – B 22 – B 23 – D 24 – B 25 – D 26 – C 27 - D
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1.
Giả sử .
n
x
u Khi đó cấp số cộng có công sai
5.d
Do đó
1
21215
1 6 11 ... . . 970
22
und n
xnn
 

2
20
5 3 1940 0 .
97
5
n
nn
n


Ta có
20 1
19 1 19.5 96.xu u d
Câu 2.
TOANMATH.co
m
Trang 25
Ta có
1 4 7 ... 28 155.xx x x
Do đó
128
.10 155 2 29 31 1.
2
xx
xx


Câu 3.
Để 3 số
2
13; 5;1
x
xx lập thành cấp số cộng thì
2
2. 5 1 3 1
x
xx
2
2280xx
(phương trình vô nghiệm)
Không tìm được x thỏa yêu cầu.
Câu 4.
Ta có
158 44 41 38 35
nên đa giác có 4 cạnh.
Câu 5.
42
10 0. 1xxm
Đặt
2
,0,txt phương trình (1) trở thành
2
10 0. 2ttm
Phương trình (1) có 4 nghiệm là 4 số hạng liên tiếp của một cấp số cộng khi và chỉ khi phương trình (2)
có 2 nghiệm dương phân biệt thỏa mãn
*
21 21
9, .tt tt
Điều kiện phương trình (2) có 2 nghiệm dương phân biệt
'25 0
0025.
10 0
m
Pm m
S

 

Theo định lý Vi-ét


**
21
***
21
10
.
.
tt
tt m

Từ

*
và

**
suy ra
12
1, 9tt thế vào

***
ta được
9m
(nhận).
Câu 6.
A
BC
có ba góc
,,
A
BC
theo thứ tự đó lập thành cấp số cộng
𝐴
󰆹
𝐶
󰆹
2𝐵
.
Ta có
󰇱
𝐴
󰆹
𝐵
𝐶
󰆹
180
𝐴
󰆹
𝐶
󰆹
2𝐵
𝐶
󰆹
5𝐴
󰆹
󰇱
𝐴
󰆹
20
𝐵
60
𝐶
󰆹
100
Câu 7.
Gọi
n
u (triệu đồng)

*
nN
là mức lương của kỹ sư ở quý làm việc thứ n.
Ta có
1
15; 1,5.ud Đến quý thứ 12 mức lương của kỹ sư là
12 1
11 31,5uu d (triệu đồng).
Vậy tổng số tiền nhận được của kỹ sư sau 3 năm là
12 1 2 12
12 15 31,5
... 279
2
Suu u

(triệu đồng).
Câu 8.
Gọi độ dài 3 cạnh của tam giác cần tìm là
,2,4 0.aa a a
TOANMATH.co
m
Trang 26
Theo bài ra, ta có

22
22
6
24-4-120 .
-2
a
aa a aa
a

Suy ra độ dài cạnh huyền là
6 4 10.
Vậy
5.R
Câu 9.
Theo giả thiết

22
2
36 3
6- 6 6 36-12 12 .
24 2
ddddd
Câu 10.
Giả sử phương trình đã cho có ba nghiệm phân biệt là
123
,,
x
xx theo thứ tự đó lập thành một cấp số cộng.
Suy ra
213
2.
x
xx
Mặt khác
32
1 2 3 1 2 3 12 23 31 123
---0- - 0.xx xx xx x x x x x xx xx xx xxxx
Đồng nhất với phương trình
3
0.xaxb
Suy ra
123 2
00.xxx x
Thay
2
0x vào phương trình đã cho, ta được
0.b
Phương trình đã cho trở thành

3
2
0
0.
01
x
xax
xa


Để phương trình đã cho có 3 nghiệm phân biệt thì phương trình (1) có hai nghiệm phân biệt
0.a
Vậy
0,a 0.b 
Câu 11.
Ta có số que diêm để xếp được tầng đế của tháp là một cấp số cộng với
1
3; 4.ud
Suy ra số que diêm để xếp được tầng đế của tháp 10 là
10 1
9 39.uud
Từ đó số que diêm để xếp được hình tháp 10 tầng là
10 1 2 10
10 3 39
... 210
2
Suu u

que
Câu 12.
Áp dụng định lý sin trong tam giác
A
BC
ta có
2sin, 2sin, 2sin.aRAbRBcRC
Theo giả thiết
222
,,abc theo thứ tự đó lập thành cấp số cộng nên
22 2
2ac b
22 22 22 2 2 2
4 .sin 4 .sin 2.4 .sin sin sin 2.sin .RARCRB AC B
Vậy
222
sin ,sin ,sin
A
BCtheo thứ tự đó lập thành cấp số cộng.
Câu 13.
Gọi góc nhỏ nhất là x, ta có bốn góc là
,,2,3
x
xdx dx d
(với d là công sai).
Ta có hệ

23360
35
xxdxdxd
xd x
 

TOANMATH.co
m
Trang 27
Giải hệ ta tìm được
30 .x 
Câu 14.
Giả sử trồng được n hàng cây
1, .nn
Số cây ở mỗi hàng lập thành cấp số cộng có
1
1u và công sai
1.d
Theo giả thiết
 
2
1
80
3240 2 1 3240 1 6480 6480 0 .
81
2
n
n
n
Sundnnnn
n
 


Kết hợp với điều kiện, ta được
80.n
Vậy có tất cả 80 hàng cây.
Câu 15.
Giả sử đa giác có n cạnh; độ dài các cạnh thứ tự lập thành cấp số cộng với công sai
3dcm
là
12
; ;...; .
n
uu u
Từ giả thiết ta có


1
1
1
2
1
1
44
347
47 3
44
35
.
44 316
158
4
3 91 316 0
158
2
n
n
n
n
u
un
un
u
u
uun
nu
S
n
nn







Câu 16.
Ta có

13 2
23
nn n
CC Cn
  

2
7
!! !
9140 7 3.
2
1! 3!. 3! 2!. 2!
n
nn n
nn n don
n
nn n


Câu 17.
Ta có
2; 2 1;5x
theo thứ tự lập thành một cấp số cộng nên

1
21 2521 .
4
xxx
Câu 18.
Ta có
,2,3.BAdCA dDA d  
Khi đó


2
2
22 2
22
22 2
3
69
3.
23
2
Ad A
DA Add
CB Add
Ad Ad





Câu 19.
Phương trình
2
30xxa
(có 2 nghiệm khi
9
4
a
).
Theo định lý Vi-ét, ta có
12
12
3
.
.
xx
x
xa

Phương trình
2
11 0xxb
(có 2 nghiệm khi
121
4
b
).
TOANMATH.co
m
Trang 28
Theo định lý Vi-ét, ta có
12
12
11
.
.
yy
yy b


Theo bài ra
121 2
,,,
x
xyy theo thứ tự lập thành một cấp số cộng với công sai là d nên
1
1
1
1
23
.
2
2511
2
xd
x
xd
d



Suy ra
1 5 9 13 585
.... .
292 2 8
ab 
Câu 20.
Ta có


32
2
0
21 90 1 .
21 90 2
x
xmxx
xmx


Phương trình (2) luôn có hai nghiệm trái dấu
12
,
x
x do
1. 9 9 0.ac 
Do đó phương trình (1) luôn có ba nghiệm phân biệt
12
0.
x
x
Để ba nghiệm trên lập thành một cấp số cộng thì
12
1
2.0 2 1 0 .
2
xx m m
Vậy
5.P
Câu 21.
Ta có
21321431 1
1
11111 1
; ; ...; .
22428 2
n
n
P
PP P PP P P P P

Vậy
1
123 1 1 1 1 1
111
... ... 2 24.
1
248
1
2
P
PPPP P P P P P
Câu 22.
Giả sử 1089 được xếp thành n hàng. Từ giả thiết ta có số hộp sơn trên mỗi hàng là số hạng của một cấp số
cộng
n
u
với số hạng đầu
1
1u
công sai
2.d
Do đó
1089 1 1089 33.
n
Snnn n
Vậy số hộp sơn ở hàng cuối cùng là
33
1 32.2 65u  (hộp sơn).
Câu 23.
Khoảng cách từ các cây đến mốc 6 ki-lô-mét tạo thành cấp số cộng có công sai
20 .dm
TOANMATH.co
m
Trang 29
Ta có
 
1
1 6000 1 20.
n
uu n d n
Cây cuối cùng ở vị trí 8 ki-lô-mét nên ta có

8000 6000 1 20 101.nn
Câu 24.
Quãng đường An đi được trong mỗi giờ là một cấp số cộng.
Ta có
 
2
1
4
2 1 54 30 1 . 1 31 108 0 .
27
22
n
n
nn
Sund n nn
n



Với
27n
thì
27 1
27 1 11uu d
nên vô lý.
Vậy An đi từ nhà về quê hết 4 giờ.
Câu 25.
Số cốc nước bán được trong các ngày lập thành một cấp số cộng với công sai
1d
.
Số cốc nước bán trong ngày thứ 10 là
10 1
9 10 9.1 19.uud
Câu 26.
Gọi n là số hàng cần tìm, ta có
77
1
1 2 3 ... 3003 3003 77.
78
2
n
nn
nn
n
 

Câu 27.
Đặt
2
,0,txt ta thu được phương trình

2
21210.2tmtm
Điều kiện để phương trình ban đầu có bốn nghiệm phân biệt là phương trình (2) có hai nghiệm dương
12
,tt
12
tt
hay
0
.
1
2
m
m

Khi đó bốn nghiệm là
2112
,,,.tttt
Điều kiện để bốn nghiệm trên lập thành cấp số cộng là
21 1
2tt t hay
21
9.tt
Kết hợp định lý Vi-ét tìm được
4
4, .
9
mm
Từ đó ra tổng các giá trị của m bằng
32
.
9
| 1/29
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

CHUYÊN ĐỀ
BÀI GIẢNG CẤP SỐ CỘNG Mục tiêu Kiến thức
+ Hiểu được khái niệm cấp số cộng.
+ Nắm được công thức tổng quát, tổng n số hạng đầu tiên của cấp số cộng.
+ Biết được số hạng đầu và công sai của cấp số cộng. Kĩ năng
+ Tìm được các yếu tố còn lại khi biết 3 trong 5 yếu tố: số hạng đầu, số hạng thứ k, công sai, số
số hạng, tổng n số hạng đầu của cấp số cộng.
+ Liên hệ được kiến thức về cấp số cộng để giải những bài toán thực tế. Trang 1
I. LÍ THUYẾT TRỌNG TÂM Định nghĩa
Cấp số cộng là một dãy số (vô hạn hay hữu hạn) mà trong đó, kể từ số hạng thứ hai, mỗi số hạng đều
bằng tổng của số hạng đứng ngay trước nó với một số d không đổi, nghĩa là
u là cấp số cộng  n
  2,u u d. n n n 1 
Số d được gọi là công sai của cấp số cộng. Định lí 1
Nếu u là một cấp số cộng thì kể từ số hạng thứ hai, mỗi số hạng (trừ số hạng cuối đối với cấp số cộng n uu
hữu hạn) đều là trung bình cộng của hai số hạng đứng kề nó trong dãy, tức là k 1 k 1 u    . k 2
Hệ quả: Ba số a, b, c (theo thứ tự đó) lập thành một cấp số cộng khi và chỉ khi a + c = 2b. Định lí 2
Nếu một cấp số cộng có số hạng đầu u và công sai d thì số hạng tổng quát u của nó được xác định bởi 1 n
công thức sau: u u n 1 d . n 1   Định lí 3
Giả sử u là một cấp số cộng có công sai d. n n
Gọi S  u u u ... u n k 1 2 n k 1 
( S là tổng của n số hạng đầu tiên của cấp số cộng). n
nu u
n 2u n 1 d  1 n   1   Ta có S    . n 2 2
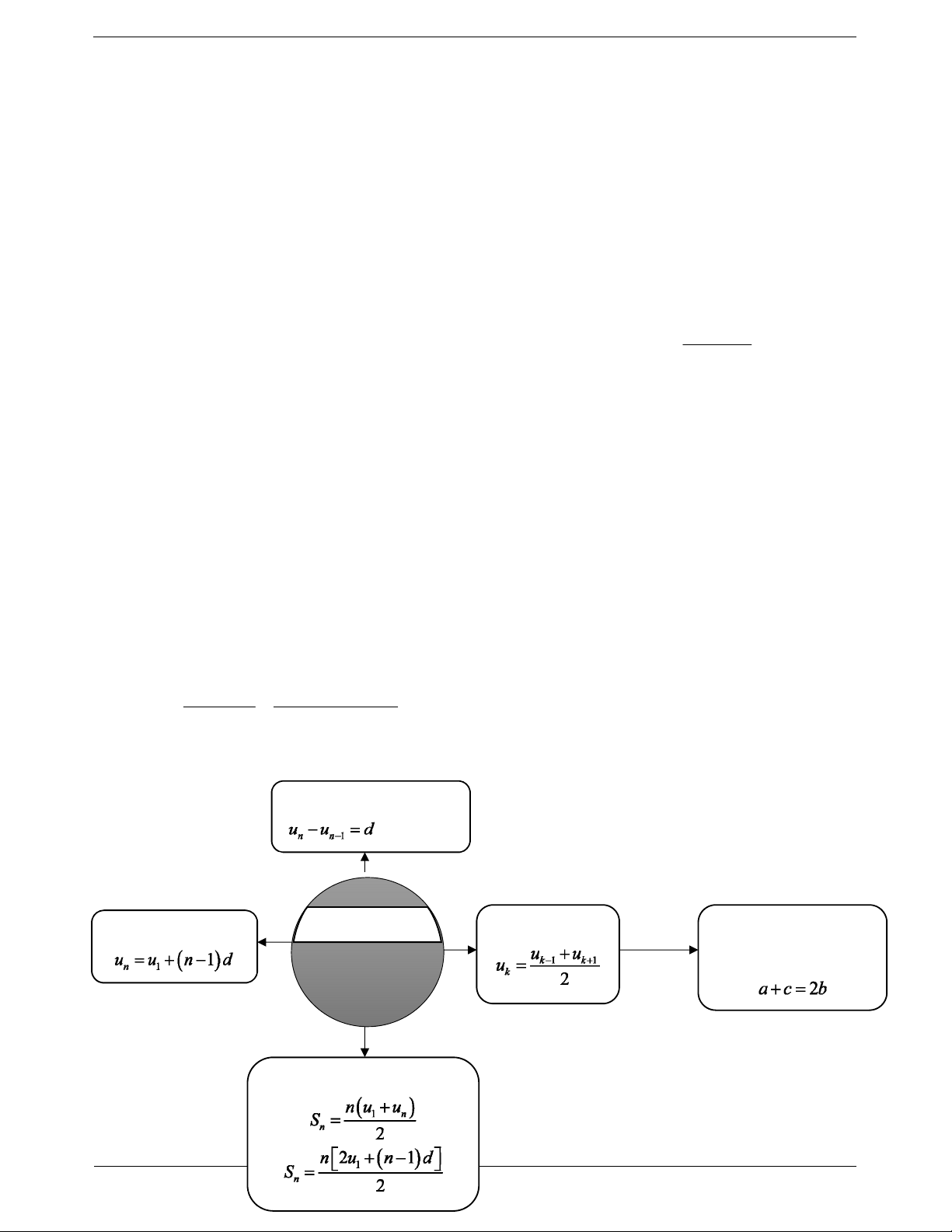
SƠ ĐỒ HỆ THỐNG HÓA
Nhận diện cấp số cộng là hằng số
Số hạng tổng quát CẤP SỐ CỘNG Số hạng thứ k
Ba số a, b, c theo thứ Hệ quả tự lập thành cấp số u ud n n 1  cộng khi và chỉ khi  n  2
Tổng n số hạng đầu tiên TOANMATH.com Trang 2
II. CÁC DẠNG BÀI TẬP
Dạng 1: Nhận dạng một dãy số là cấp số cộng Phương pháp giải
Sử dụng định nghĩa u là một cấp số cộng khi và chỉ khi u u d, với d là một hằng số. n n 1  n
Để chứng minh dãy số u là một cấp số cộng, ta xét d u u n n 1  n
 Nếu d là hằng số thì u là một cấp số cộng với công sai d. n
 Nếu d phụ thuộc vào n thì u không là cấp số cộng. n Ví dụ mẫu
Ví dụ 1. Chứng minh các dãy số sau là cấp số cộng.
a) Dãy số u với u  2020n  2021. n n
b) Dãy số u với u  2  n  5. n n
Hướng dẫn giải
a) Dãy số u với 2
u  020n  2021. n n Ta có u
u  2020 n 1  2021 2020n  2021  2020. n 1  n    
Vậy u là một cấp số cộng với công sai d  2020. n
b) Dãy số u với 2
u   n  5. n n Ta có u
u  2 n 1  5  2n  5  2. n 1  n    
Vậy u là một cấp số cộng với công sai d  2.  n
Ví dụ 2. Chứng minh các dãy số sau không phải là cấp số cộng.
a) Dãy số u với 2
u n n 1. n n
b) Dãy số u với u    n n   1 n 3 . n
Hướng dẫn giải
a) Dãy số u với 2
u n n 1. n n Ta có uu n
n    n n   n   phụ thuộc vào n. n  2 1  1 1  2 1 2 2 n 1 
Vậy u không là cấp số cộng. n
b) Dãy số u với u    n n   1 n 3 . n  Ta có uu     n      n           n  n 1 1 3 1 1 n 3 1 n 3 1 n 3 2 1 n n 1             phụ thuộc vào n. TOANMATH.com Trang 3
Vậy u không là cấp số cộng. n
Bài tập tự luyện dạng 1
Câu 1: Dãy số nào sau đây là cấp số cộng?
A. 1; 3; 6; 9; 12. B. 1; 4; 7; 10; 14. C. 1; 2; 4; 8; 16. D. 0; 4; 8; 12; 16.
Câu 2: Trong các dãy sau đây, dãy nào là cấp số cộng?
A. u  3n. B. u    C.
u  3n 1. D. 2 u  5n  . n n  n 1 3 . n n n 1 1
Câu 3: Một cấp số cộng u với u   ,d  có dạng khai triển nào sau đây? n  1 2 2 1 1 1 1 1
A.  ; 0; 1; ; 1;... B.  ; 0; ; 0;  ;... 2 2 2 2 2 1 3 5 1 1 3 C. ; 1; ;
2; ;... D.  ; 0; ; 1; ;... 2 2 2 2 2 2
Câu 4: Trong các dãy số sau, dãy số nào là một cấp số cộng
A. 1; -2; -4; -6; -8. B. 1; -3; -6; -9; -12. C. 1; -3; -7; -11; -15. D. 1; -3; -5; -7; -9.
Câu 5: Trong các dãy số sau đây dãy số nào là cấp số cộng?
A. u n 1, n  1. B. u  2n  3, n  1. C. 2
u n 1, n  1. D. u    n n  n 1 2 , 1. n n n
Câu 6: Trong các dãy số sau đây, dãy số nào là cấp số cộng? A. 2
u  3n  2020. B. u  3n  2020. C. u  3n. D. u    n  n 1 3 . n n n
Câu 7: Trong các dãy số u sau đây, dãy số nào không phải là cấp số cộng? n u   3 A.
u  3n 1. B. u  2n 1. C. u n   n D. 1 n  2 2 1 . n n
u u 1,n 1.  n 1 n
Câu 8: Các dãy số sau có số dạng tổng quát u , dãy số nào không phải là cấp số cộng? n
A. 1; 3; 5; 7; 9. B. 13; 17; 21; 25; 29. C. u  1 3n. D. u n   n n  2 2 3 . n
Câu 9: Trong các dãy số sau đây dãy số nào là cấp số cộng? u   1  u   1  A. 1  . B. 1  . C. 2
u n . D. u n n  3 1 . u  2u 1  uu 1 n n 1  nn 1 n
Câu 10: Dãy số nào dưới đây là cấp số cộng? 3n 1 A. n u n n  
B. u n n   C. n u n   D. u  , n   n  * . n  * 3 , . n  * 3 1, . n  * 2 , . n  2
Câu 11: Khẳng định nào sau đây sai?
A. Dãy số 0,1; 0,01; 0,001; 0,0001;… không phải là một cấp số cộng.  1 u   1 1 3  1 
B. Dãy số  ;0; ;1; ;...là một cấp số cộng với 2 1 . 2 2 2 1 d   2 TOANMATH.com Trang 4  1 u  1 1 1  1  C. Dãy số ; ;
;... là một cấp số cộng có ba số hạng và 2  . 2 3 2 2 2 1 d   2 u   2 
D. Dãy số -2; -2; -2; -2;… là một cấp số cộng 1  . d  0
Câu 12: Cho dãy số có các số hạng đầu là 8; 15; 22; 29; 36;… Viết công thức số hạng tổng quát?
A. u  7n  7. B. u  7 . n n n
C. Không viết được dưới dạng công thức. D. u  7n 1. n
Câu 13: Cho 2 cấp số cộng hữu hạn 4; 7; 10; 13; 16;… và 1; 6; 11; 16; 21;…; mỗi cấp số cộng có 100 số
hạng. Hỏi có tất cả bao nhiêu số có mặt trong cả hai cấp số trên?
A. 21. B. 20. C. 18. D. 19.
Câu 14: Trong các dãy số dưới đây, dãy số nào là cấp số cộng?
A. Dãy số a , với a n   n n
   B. Dãy số b với * b  1,b  3b  4, n    . n  , n  2 2 * 2 5 4 , . n 1 n 1  n 2020
C. Dãy số c , với n * c  2019 , n
   . D. Dãy số d với * d  1, d  , n    . n  , n n 1 n 1  d 1 n
Dạng 2: Tìm số hạng đầu tiên, công sai của cấp số cộng, tìm số hạng thứ k của cấp số cộng, tính
tổng k số hạng đầu tiên. Phương pháp giải
Ta lập hệ phương trình gồm hai ẩn u và d. Sau đó giải hệ phương trình này tìm được u và d. Muốn tìm 1 1
số hạng thứ k, trước tiên ta phải tìm u và d. Sau đó áp dụng công thức u u k 1 d. Muốn tính tổng k 1   1
của k số hạng đầu tiên, ta phải tìm u và d. Sau đó áp dụng công thức 1
k u u
k 2u k 1 d  1 k   1   S    . k 2 2 Ví dụ mẫu u
  u u  9 
Ví dụ 1. Tìm số hạng đầu và công sai của cấp số cộng 1 2 3  . 2 2 2 u
  u u  35  1 2 3
Hướng dẫn giải u
  u u  9 u
  u d u  2d  9  Cách 1. Ta có 1 2 3 1 1 1    2 2 2 2 u
  u u  35  u
  u d u  2d  35 1 2 3  1  1 2  1 2 Áp dụng công thức u   3  d    
u u n 1 d n 1   1 u 3 d u   3  d 1 1         3  d   . 2 2
 3  3 d 2 2  35 d  4 d  2  lập hệ phương trình
Với d  2  u  1.
gồm hai ẩn u và d. 1 1 Với d  2   u  5. 1
Cách 2. Đặt u x d; x  ;
x u x d. 1 2 3 TOANMATH.com Trang 5 u
  u u  9
x d x x d  9  Ta có 1 2 3    u
  u u  35    x d
2  x x d2 2 2 2 2  35 1 2 3 x  3  x  3 x  3        3  d  . 2 2
 3  3 d 2 2  35 d  4 d  2 
Với d  2  u  1. 1 Với d  2   u  5. 1
Ví dụ 2. Tìm bốn số hạng liên tiếp của một cấp số cộng biết tổng của chúng -
Nếu số số hạng của cấp số
bằng 20 và tổng các bình phương của chúng bằng 120.
cộng là lẻ thì gọi công sai d  , x
Hướng dẫn giải
là chẵn thì gọi công
Giả sử bốn số hạng a  3 ; x a  ; x a  ;
x a  3x lập thành cấp số cộng với công sai d
2x rồi viết các số
hạng dưới dạng đối xứng. sai là d  2 . x
- Nếu cấp số cộng a thỏa n    a  3x
a x a xa 3x  20 Khi đó ta có mãn    a  3x
2 a x2 a x2 a 3x2 120
a a  ... a p  1 2 nthì 4a  20 a  5 2 2 2 2
a a  ... a s  1 2 n     . 2 2
4a  20x 120 x  1  1  nn   1  a p  .d  
Vậy bốn số cần tìm là 2; 4; 6; 8. 1 n 2   12 2 2 ns p và d   . 2 n  2 n   1
Ví dụ 3. Tìm số hạng đầu tiên, công sai, số hạng thứ 50 và tổng của 20 số u  19
Áp dụng công thức
hạng đầu tiên của cấp số cộng , u biết rằng 5  . n u  35
u u n 1 d n 1    9
Lập được hệ phương trình
Hướng dẫn giải
gồm hai ẩn u và d.
Áp dụng công thức u u n 1 d, 1 n 1  
Để tính tổng k số hạng đầu u  19 u   4d 19 u   3
tiên, ta áp dụng công thức ta có 5 1 1      . u  35 u  8d  35   d  4 9 1
k 2u k 1 d   1   S   . k
Vậy số hạng đầu tiên u  3, công sai d  4. 2 1
Số hạng thứ 50 là u u  49d  3  49.4  199. 50 1
Tổng của 20 số hạng đầu tiên là 502u  49d 1  S
 25. 2.3  49.4  5050. 50   2
Ví dụ 4. Tìm số hạng đầu và công sai của các cấp số cộng TOANMATH.com Trang 6 S  20 S  34 4  a) 12  . b)  1 1 1 1 25 . S  45      18 u u u u 24  1 2 3 4
Hướng dẫn giải 12  2u 11d  31 1  34 u          1 S 34 6u 33d 17  a) Ta có 12 2 1 9        . S  45  18 2u 17d 2u 17d  5 1 18   1   1  45 d    2  9 S  20
2 2u  3d  20
Áp dụng công thức 4  1   
k 2u k 1 d   1   b)  1 1 1 1 25   1 1 1 1 25          S k u u u u 24  2  u u u u 24 1 2 3 4  1 2 3 4
Biểu diễn được S theo hai 4  3 ẩn u và d. u  5  d  1 1 2 
Áp dụng công thức  1 1 1 1 25
u u n 1 d n 1         . *  3 3 3 3 24
Lập được hệ phương trình
5  d 5  d d 5  d  2d 5  d  3d  2 2 2 2
gồm hai ẩn u và d. 1       1 1   1 1  25 10 10 25 *              . 2 2 3 3 d d 24 9d d 24
 5  d 5  d   5  5   25  25   2 2   2 2  4 4 2 d Đặt
t;t  0, ta được 4 10 10 25
225  t  225  9t 5    
25  9t 25  t 24
259t25t 24 100  20t 5      t   tt
25  9t 25  t
2420 4  25 9 25  24  145 t  2 9t 154t 145 0       9 .  t  1 145 145 145 Nếu 2 t   d   d   . 9 9 3  145 145 Với d   u  5  . 1 3 2  145 145 Với d    u  5  . 1 3 2 Nếu 2
t 1  d 1  d  1  .  3 7
Với d 1 u  5   . 1 2 2 TOANMATH.com Trang 7  3 13 Với d  1   u  5   . 1 2 2
Ví dụ 5. Biết u u u u  224. Tính S . 4 8 12 16 19
Hướng dẫn giải
Ta có u u u u  224 4 8 12 16
u  3d u  7d u 11d u 15d  224  4u  36d  224  u  9d  56. 1 1 1 1 1 1 19 Ta có S
2u 18d 19 u  9d  19.56 1064. 19  1   1  2
Ví dụ 6. Cho cấp số cộng u biết 9 u   5 . n Tìm S . n n 100
Hướng dẫn giải Ta có u
u  9  5 n     n   n
   Suy ra d  5,  u  4.  n    1  9 5  * 5, . n 1 1
n 2u n 1 d 100 2.4  99. 5 1       Vậy S    24350. 100 2 2
Bài tập tự luyện dạng 2
Câu 1: Số hạng đầu u và công sai d của cấp số cộng u có u  7;u  4 là n  1 2 3
A. u  1; d  3. B. u  10; d  3
 . C. u  4;d  3
 . D. u  4;d  3  . 1 1 1 1
Câu 2: Cho cấp số cộng u với số hạng đầu là u 15 và công sai d  2.Số hạng thứ 8 của cấp số n  1 cộng là
A. u 1. B. u  1.
C. u  103. D. u  64. 8 8 8 8
Câu 3: Cho cấp số cộng u có u  1
 ;d  2; S  483. Giá trị của n là n  1 n
A. n  20. B. n  21. C. n  22. D. n  23. u   2 
Câu 4: Cho cấp số cộng u xác định bởi 1 
. Số 70 là số hạng thứ bao nhiêu của cấp số n uu  3  n 1 n cộng?
A. 15. B. 23. C. 25. D. 205.
Câu 5: Cho một cấp số cộng u có u  5và tổng của 50 số hạng đầu bằng 5150. Công thức của số hạng n  1 tổng quát u là n A. u  1 4 . n B. u  5 . n C. u  3  2 . n D. u  2  3 . n n n n n
Câu 6: Cho cấp số cộng u có u  2n  3. Biết 320 S
, giá trị của n là n n n
A. n  16 hoặc n  20. B. n  15. C. n  20. D. n  16.
Câu 7: Cho dãy số u biết 2
u n  5. Chọn khẳng định đúng. n n
A.u là một cấp số cộng với công sai d  2. B.u là một cấp số cộng với công sai d  2. n n
C.u là một cấp số cộng với công sai d  5. D.u là một cấp số cộng với công sai d  5. n n  TOANMATH.com Trang 8
Câu 8: Cho cấp số cộng u biết u  7 và d  4. Lựa chọn kết quả đúng trong các kết quả sau n  1
A. u u  46. B. u u  28. C. u u  18. D. uu  350. 15 3 29 22 17 13 1000 100
Câu 9: Cho dãy số u là một cấp số cộng có công sai d  3.Chọn khẳng định đúng trong các khẳng n  định sau
A. Dãy số u ;u ;u ;...;u , n
 1 theo thứ tự lập thành một cấp số cộng với công sai là 10. 10 20 30 10n
B. Dãy số u ;u ;u ;...;u , n
 1 theo thứ tự lập thành một cấp số cộng với công sai là 20. 10 20 30 10n
C. Dãy số u ;u ;u ;...;u , n
 1 theo thứ tự lập thành một cấp số cộng với công sai là 30. 10 20 30 10n
D. Dãy số u ;u ;u ;...;u , n
 1 theo thứ tự lập thành một cấp số cộng với công sai là 15. 10 20 30 10n
Câu 10: Cho cấp số cộng u có công sai d. Gọi S là tổng của n số hạng đầu tiên. Hãy chỉ ra hệ thức sai n n trong các hệ thức sau.
A. u u u u . B. u u  2u . C. 2
u .u u . D. S S  2S d. 3 8 5 6 5 9 7 4 9 6 3 5 4 u   2u  0
Câu 11: Cho cấp số cộng u , biết 1 5
. Số hạng đầu u và công sai d là n  S 14  1 4
A. u  8; d  3
 . B. u  8;d  2. C. u  8;d  3. D. u  8;  d  2. 1 1 1 1 u
  u u 10
Câu 12: Số hạng đầu u và công sai d của cấp số cộng u có 1 5 3 là n  1 u u  7  1 6
A. u  33; d  12. B. u  36; d  13. C. u  35; d  13. D. u  34; d  13. 1 1 1 1
Câu 13: Cấp số cộng u có S 18, S 110 thì tổng 20 số hạng đầu tiên là n  6 10
A. 620. B. 280. C. 360. D. 153.
Câu 14: Cho cấp số cộng 5
u n  2. Biết 16 S
040, số số hạng của cấp số cộng là n n
A. 79. B. 3024. C. 80. D. 100.
Câu 15: Chọn khẳng định đúng trong các khẳng định sau. Nếu 3 số , a ,
b c khác 0 lập thành cấp số cộng thì
A. nghịch đảo của chúng cũng lập thành một cấp số cộng.
B. bình phương của chúng cũng lập thành cấp số cộng.
C. c, b, a theo thứ tự đó cũng lập thành cấp số cộng.
D. Tất cả các khẳng định trên đều sai.
Câu 16: Cho cấp số cộng có S  85  , S  240  , khi đó S bằng 10 15 20
A. -325. B. -170. C. -395. D. -470.
Câu 17: Tổng tất cả các số tự nhiên chẵn nhỏ hơn 555 là
A. 77145. B. 77284. C. 76450. D. 77006. 1 1
Câu 18: Cho cấp số cộng có u  , d   . Chọn khẳng định đúng trong các khẳng định sau đây? 1 4 4 5 4 5 4
A. S  . B. S  . C. S   . D. S   . 5 4 5 5 5 4 5 5 TOANMATH.com Trang 9
Câu 19: Cho cấp số cộng u , với u  2, d  3
 . Kết quả nào sau đây đúng? n 1 A. u  1.  B. u  7.  C. u  7.
D. u  0. 3 3 4 6
Câu 20: Cho cấp số cộng có u u  60. Tổng của 23 số hạng đầu là 2 22
A. 690. B. 680. C. 600. D. 500.
Câu 21: Công sai d của một cấp số cộng hữu hạn có số hạng đầu u  10 và số hạng cuối u  50 là 1 21
A. d  4. B. d  2. C. d  2. D. d  2.
Câu 22: Tổng 10 số hạng đầu của cấp số cộng có u  8,u  62 là 1 10
A. S  175. B. S  350. C. S  700. D. S  1400. 10 10 10 10
Câu 23: Cho cấp số cộng có u  1
 ,d  2, S  483. Số các số hạng của cấp số cộng đó là 1 n
A. n  20. B. n  21. C. n  22. D. n  23.
Câu 24: Cho cấp số cộng có tổng 4 số hạng bằng 22, tổng bình phương của chúng bằng 166. Bốn số hạng
của cấp số cộng này là
A. 1; 4; 7; 10. B. 1; 4; 5; 10. C. 2; 3; 5; 10. D. 2; 3; 4; 5. u   u  42
Câu 25: Cho cấp số cộng u thỏa mãn 2 5 
. Tổng của 346 số hạng đầu là n u u  66  3 10
A. 242546. B. 242000. C. 241000. D. 240000.
Câu 26: Cho cấp số cộng u có u  18 và 4S S . Số hạng đầu tiên u và công sai d của cấp số cộng n  5 n 2n 1 là
A. u  2;d  4.
B. u  2;d  3. 1 1
C. u  2;d  2.
D. u  3; d  2. 1 1
Câu 27: Cho cấp số cộng gồm 4 số hạng 1,  a,7, . b Giá trị của , a b là
A. a  3,b 11.
B. a  2,b  9.
C. a  4,b 12.
D. a  7,b  1  .
Câu 28: Cho dãy số a có tổng n số hạng đầu tiên là 2 S  2n  3 . n Khi đó n n
A.a là một cấp số cộng với công sai bằng 4. B.a là một cấp số cộng với công sai bằng 2. n n
C.a là một cấp số cộng với công sai bằng 1. D.a là một cấp số cộng với công sai bằng 8. n n
Câu 29: Cho cấp số cộng u với số hạng đầu là u  6 và công sai d  4. Tổng 14 số hạng đầu tiên n  1
của cấp số cộng đó bằng
A. 280. B. 308. C. 644. D. 46.
Câu 30: Cho cấp số cộng u gồm 4 số hạng 2, , a 6, .
b Tích a.b bằng n
A. 12. B. 32. C. 40. D. 22.
Câu 31: Cho cấp số cộng có tổng n số hạng đầu là 2 *
S  3n  4n, n   . Giá trị số hạng thứ 10 của cấp n số cộng là
A. u  55. B. u  67. C. u  61. D. u  59. 10 10 10 10 TOANMATH.com Trang 10
Câu 32: Thêm 6 số xen giữa hai số 3 và 24 ta được một cấp số cộng có 8 số hạng. Khi đó tổng các số hạng là
A. 110. B. 107. C. 106. D. 108.
Câu 33: Thêm 5 số xen giữa hai số 25 và 1 ta được một cấp số cộng có 7 số hạng. Số hạng thứ 50 là
A. -169. B. 169. C. -171. D. 171.
Câu 34: Cho một cấp số cộng u có u 1 và tổng 100 số hạng đầu bằng 24850. Giá trị biểu thức n  1 1 1 1 S    ... là u u u u u u 1 2 2 3 49 50 9 4 49 A. S  . B. S
. C. S  123. D. S  . 246 23 246 u
  3u u  2  1
Câu 35: Cho cấp số cộng u thỏa mãn 5 3 2 
. Giá trị của biểu thức S u u  ... u là n  3u  2u  3  4  4 5 30 7 4
A. -1242. B. -1222. C. -1276. D. -1286.
Dạng 3: Dựa vào tính chất của cấp số cộng: chứng minh đẳng thức, giải phương trình và các bài toán thực tế Phương pháp giải
Nếu u là một cấp số cộng thì kể từ số hạng thứ hai, mỗi số hạng (trừ số hạng cuối cùng đối với cấp số n uu
cộng hữu hạn) đều là trung bình cộng của hai số hạng đứng kề nó trong dãy, tức là k 1 k 1 u    . k 2
Hệ quả: Ba số a, ,
b c (theo thứ tự đó) lập thành một cấp số cộng khi và chỉ khi a c  2 . b Ví dụ mẫu
Ví dụ 1. Cho a, ,
b c là ba số hạng liên tiếp của một cấp số cộng, chứng minh rằng a) 2 2
a  2bc c  2a . b b)
a bc   b c2 2 8 2 .
Hướng dẫn giải Vì a, ,
b c là ba số hạng liên tiếp của một cấp số cộng nên a c  2b a  2b  . c
a) Ta có a ab   b c2 2
  b c 2 2 2 2 2 2 2
.b  4b  4bc c  4b  2bc 2 = c  2 . bc Vậy 2 2 2 2
a  2ab c  2bc a  2bc c  2 . ab
b) Ta có a bc   b c2 2 2 2 8 2
 8bc  4b  4bc c  8bc
b bc c   b c2 2 2 = 4 4 2 .
Ví dụ 2. Một tam giác vuông có chu vi bằng 3a và ba cạnh lập thành một cấp số cộng. Tính độ dài ba
cạnh của tam giác theo a.
Hướng dẫn giải
Gọi x, y, z theo thứ tự là độ dài ba cạnh của tam giác  x y z. TOANMATH.com Trang 11
Chu vi của tam giác là x y z  3a.   1
Theo tính chất của cấp số cộng, ta có x z  2 y. 2
Tam giác đã cho vuông nên 2 2 2
x y z . 3
Thay (2) và (1), ta được 3y  3a y  . a
Thay y a vào (2), ta được x z  2a x  2a z.
Thay x  2a z và y a vào (3), ta được 5a 3a
2a z2 2 2 2
a z  5a  4az  0  z   x  . 4 4 3a 5a
Vậy độ dài ba cạnh của tam giác là , a, . 4 4 Ví dụ 3. Cho 2 2 2
a ,b ,c lập thành một cấp số cộng có công sai khác 0. Ta sẽ chứng minh 1 1 2 1 1 1   . Chứng minh rằng ; ;
cũng lập thành một cấp số cộng.
a b b c c a
b c c a a b
Hướng dẫn giải Theo giả thiết, ta có 2 2 2
a c  2b . 1 1 2 Ta phải chứng minh   .
b c a b c a Ta có 2 2 2 2 2 2 2 2
a c b b a b b c  0
            a b b c a b a b b c b c   b c a b a b b c
a cb c a bc a     
b cc a a bc a
b cc a
a bc aa c b c a b c a     
a cc a b cc a a bc a a bc a 1 1 1 1 1 1 2       
(điều phải chứng minh).
b c c a
c a a b
a b b c c a A B C
Ví dụ 4. Cho tam giác ABC có tan , tan , tan
, theo thứ tự đó lập thành 2 2 2 Ta sẽ chứng minh
cấp số cộng. Chứng minh cosA, cosB, cosC theo thứ tự cũng lập thành cấp số
cosA + cosC = 2cosB cộng.
Hướng dẫn giải A C B sin sin sin A C B Ta có 2 2 2 tan  tan  2 tan    2. 2 2 2 A C B cos cos cos 2 2 2 TOANMATH.com Trang 12 A C C A B sin .cos  sin .cos sin 2 2 2 2 2   2. A C B cos .cos cos 2 2 2  A C  sin B B B    sin cos sin  2 2  2 2 2   2   2. A C B A C B cos .cos cos cos .cos cos 2 2 2 2 2 2 B A C B 2  cos  2.cos .cos .sin 2 2 2 2 1 cos B   A C
A C  B   cos  cos .sin .      2  2 2      2 1 cos B A C B B B   cos .sin  sin .sin 2 2 2 2 2 1 cos B A C A C B 2   cos .cos  sin 2 2 2 2 1 cos B 1      C   1 cos B cos  cosA  2 2  2
 1 cos B  cos C  cos A 1 cos B
 cos A  cos C  2 cos B  cos , A cos ,
B cosC theo thứ tự đó lập thành một cấp số cộng.
Ví dụ 5. Cho các số dương a; b; c theo thứ tự lập thành cấp số cộng. Chứng Ta sẽ chứng minh minh rằng 1 1  1 1 1 b c a b ; ;
theo thứ tự đó cũng lập thành cấp số cộng. 2 b c c a a bc a
Hướng dẫn giải Vì , a ,
b c lập thành cấp số cộng nên a c  2 . b 1 1 2 Ta cần chứng minh   . b c a b c a
Ta có a c  2b a b b c   a b a b   b c  b c a b b c a b b c     b c a b
b c c a  a b c a
a c b c  b a c a   
b c  c a
a b c a 1 1 1 1 1 1 2        b c c a c a a b b c a b c a TOANMATH.com Trang 13 1 1 1  ; ;
theo thứ tự đó lập thành cấp số cộng. b c c a a b
Ví dụ 6. Tìm giá trị của m để phương trình  2
x  2x  3x  2m  0 có 3 nghiệm phân biệt lập thành
một cấp số cộng có công sai lớn hơn 2.
Hướng dẫn giải x 1 Ta có  2 x
2x 3x 2m 0       x  3  .  x  2m
Ba nghiệm này lập thành một cấp số cộng có công sai lớn hơn 2 nên có 3 trường hợp.
Trường hợp 1: Ba nghiệm thứ tự là -3;1;2 . m 5
Suy ra d  4;m  (thỏa mãn). 2 1
Trường hợp 2: Ba nghiệm thứ tự 3;  2 ;
m 1. Suy ra d  2;m   (loại). 2
Trường hợp 3: Ba nghiệm thứ tự 2 ; m 3  ;1. 7
Suy ra d  4;m   (thỏa mãn). 2  7 5 
Vậy các giá trị m cần tìm là m   ; .  2 2
Ví dụ 7. Tìm m để phương trình x
x  m  2 4 2 20
1  0 có bốn nghiệm phân biệt lập thành cấp số cộng.
Hướng dẫn giải Đặt 2
t x ,t  0. Phương trình trở thành t
t  m  2 2 20 1  0   1 .
Phương trình đã cho có bốn nghiệm phân biệt khi và chỉ khi phương trình (1) có hai nghiệm dương t ,t 1 2
phân biệt 0  t t 1 2  ' 2   0
m  2m  99  0   9  m  11
 S  0  20  0   . *   m  1 P  0    m   2 1  0
Bốn nghiệm của phương trình lập thành cấp số cộng là  t ,  t , t , t . 2 1 1 2
 t t  2  t  Ta có 2 1 1 
 3 t t t  9t . 1 2 2 1
 t t  2 t  1 2 1 t 9t t    2 2 1 1    
Theo Định lí Vi-ét, ta có t t  20  t   18 . 1 2 2   t .t   m  2 1   m   2 1  36 1 2 TOANMATH.com Trang 14
Suy ra m  7 hoặc m  5 (thỏa mãn (*)).
Vậy các giá trị m cần tìm là m 5;  7 .
Ví dụ 8. Chứng minh rằng: Nếu phương trình 3 2
x - ax bx - c  0 có ba nghiệm lập thành cấp số cộng thì 3
9ab  2a  27 . c
Hướng dẫn giải
Giả sử phương trình có ba nghiệm x , x , x lập thành cấp số cộng. 1 2 3
Suy ra x x  2x . 1 1 3 2   Mặt khác 3 2
x - ax bx c   x x x x x x 1   2   3  3
x   x x x  2
x x x x x x x x x x x 1 2 3  1 2 2 3 3 1 1 2 3
Suy ra x x x  . a 2 1 2 3   a
Từ (1) và (2), suy ra 3x a hay x  . 2 2 3 a 3 2  a   a   a
Phương trình đã cho có nghiệm x  , tức là  abc  0 2       3  3   3   3  3 2a ba 3   
c  0  9ab  2a  27c (điều phải chứng minh). 27 3 1 Ví dụ 9. Cho 2 2
x ; ; y theo thứ tự lập thành một cấp số cộng. 2
Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 2
P  3xy y .
Hướng dẫn giải 1 Ta có 2 2
x ; ; y theo thứ tự lập thành một cấp số cộng nên 2 2 x y  1. 2
Đặt x  sin, y  cos. Ta có 3 1 cos 2 2 2 P 3xy y 3 sin.cos cos  sin 2        2 2
 2P 1  3 sin 2  cos 2.
Phương trình 2P 1  3 sin 2  cos 2 theo biến  có nghiệm  2P   1   32 2 1 3 2
1    P  . 2 2 3
Vậy max P  . Đẳng thức khi và chỉ khi 3 sin 2  cos 2  2 2      sin 2 
 1     k k    .  6  6 TOANMATH.com Trang 15 1
MinP   . Đẳng thức khi và chỉ khi 3 sin 2  cos 2  2  2      sin 2 
 1      k k    .  6  3
Bài tập tự luyện dạng 3
Câu 1: Cho tổng 1 6 1116  ...  x  970. Giá trị của x là
A. 96. B. 69. C. 97. D. 7.
Câu 2: Biết  x  
1   x  4   x  7  ...  x  28  155. Giá trị của x là
A. x  1. B. x  1. C. x  2. D. x  3.
Câu 3: Với giá trị nào của x thì 2 1 3 ;
x x  5;1 x lập thành cấp số cộng?
A. x  0. B. x  1. C. x   2. D. x . 
Câu 4: Chu vi của một đa giác là 158 cm, số đo các cạnh lập thành một cấp số cộng với công sai d  3
cm. Biết cạnh lớn nhất là 44 cm. Số cạnh của đa giác đó là
A. 6. B. 3. C. 5. D. 4.
Câu 5: Phương trình 4 2
x 10x m  0 có 4 nghiệm phân biệt lập thành một cấp số cộng. Khi đó m thuộc khoảng nào sau đây?
A. m  0;5. B. m 5;15. C. m 25;0. D. m 15;25.
Câu 6: Cho tam giác ABC có ba góc ,
A B,C theo thứ tự đó lập thành cấp số cộng và 𝐶 5𝐴. Số đo các góc ,
A B,C lần lượt là A. 10 ,  120 ,  50 .  B. 15 ,  105 ,  60 .  C. 5 ,  60 ,25 .  D. 20 ,  60 ,  100 . 
Câu 7: Một công ty thực hiện việc trả lương cho các kĩ sư theo phương thức như sau: Mức lương của quý
làm việc đầu tiên cho công ty là 15 triệu đồng/quý và kể từ quý làm việc thứ hai mức lương sẽ được tăng
thêm 1,5 triệu đồng mỗi quý. Tổng số tiền lương một kĩ sư được nhận sau 3 năm làm việc cho công ty là
A. 495 triệu đồng. B. 279 triệu đồng. C. 384 triệu đồng. D. 558 triệu đồng.
Câu 8: Cho tam giác vuông có độ dài ba cạnh lập thành một cấp số cộng với công sai d  2. Bán kính
đường tròn ngoại tiếp R của tam giác đó là
A. R  3. B. R  4. C. R  1. D. R  5.
Câu 9: Độ dài ba cạnh của một tam giác vuông lập thành một cấp số cộng. Nếu cạnh trung bình bằng 6
thì công sai của cấp số cộng này là
A. 7,5. B. 4,5. C. 0,5. D. 1,5. Câu 10: Giá trị ,
a b để phương trình 3
x ax b  0 có ba nghiệm phân biệt lập thành cấp số cộng là
A. b  0, a  0.
B. b  0, a  0.
C. b  0, a  0.
D. b  0, a 1.
Câu 11: Một em học sinh dùng các que diêm để xếp thành hình tháp có quy luật được thể hiện như trong hình dưới. TOANMATH.com Trang 16
Số que diêm để xếp thành hình tháp 10 tầng là
A. 69 que. B. 39 que. C. 420 que. D. 210 que.
Câu 12: Tam giác ABC có ba cạnh a, , b c thỏa mãn 2 2 2
a ,b ,c theo thứ tự đó lập thành một cấp số cộng.
Chọn khẳng định đúng trong các khẳng định sau A. 2 2 2 tan ,
A tan B, tan C theo thứ tự đó lập thành một cấp số cộng. B. 2 2 2 cot ,
A cot B,cot C theo thứ tự đó lập thành một cấp số cộng. C. cos , A cos ,
B cosC theo thứ tự đó lập thành một cấp số cộng. D. 2 2 2 sin ,
A sin B,sin C theo thứ tự đó lập thành một cấp số cộng.
Câu 13: Số đo các góc của một tứ giác lồi lập thành một cấp số cộng và góc lớn nhất gấp 5 lần góc nhỏ
nhất. Số đo góc nhỏ nhất bằng
A. 25. B. 30 .
C. 45. D. 35.
Câu 14: Người ta trồng 3420 cây theo một hình tam giác như sau: hàng thứ nhất trồng 1 cây, kể từ hàng
thứ 2 trở đi số cây trồng mỗi hàng nhiều hơn 1 cây so với hàng liền trước nó. Hỏi có tất cả bao nhiêu hàng cây?
A. 81. B. 82. C. 80. D. 79.
Câu 15: Chu vi một đa giác là 158 cm, các cạnh của đa giác này lập thành một cấp số cộng với công sai d  3c .
m Biết cạnh lớn nhất có độ dài là 44 cm, độ dài cạnh nhỏ nhất của đa giác là
A. 32 cm. B. 33 cm. C. 38 cm. D. 35 cm.
Câu 16: Giá trị của n để 1 2 3
C ,C ,C theo thứ tự lập thành một cấp số cộng là n n n
A. n  9. B. n  6. C. n  2. D. n  7.
Câu 17: Giá trị của x để 2;
 2x 1;5 theo thứ tự lập thành một cấp số cộng là 1 1 1
A. x   . B. x   . C. x  . D. x  1. 4 3 4 2 2 D A Câu 18: Cho ,
A B,C, D là bốn số thực dương lập thành một cấp số cộng. Giá trị biểu thức bằng 2 2 C B
A. 1. B. 0. C. 3. D. -1.
Câu 19: Cho x , x là nghiệm của phương trình 2
x  3x a  0 và y , y là nghiệm của phương trình 1 2 1 2 2
x 11x b  0. Nếu x , x , y , y theo thứ tự lập thành một cấp số cộng thì tích ab có giá trị là 1 2 1 2 585 585
A. ab  1. B. ab   . C. ab  . D. ab  54. 8 8 TOANMATH.com Trang 17
Câu 20: Tìm m để phương trình 3
x   m   2 2
1 x  9x  0 có ba nghiệm phân biệt lập thành một cấp số a a
cộng, ta được m  , với a,b ,
 phân số tối giản. Giá trị biểu thức 2 2
P a b là b b
A. P  13. B. P  20. C. P  5. D. P  10.
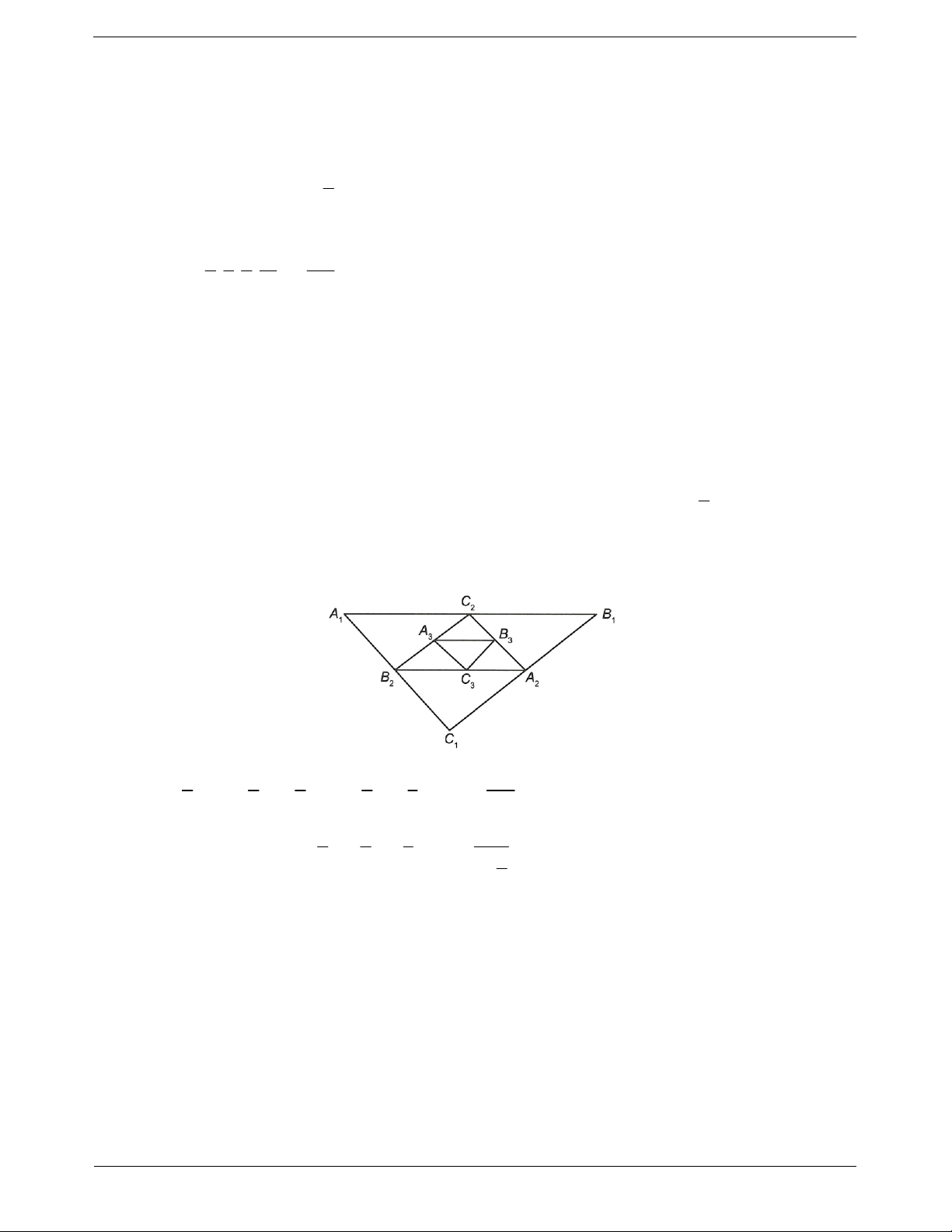
Câu 21: Cho tam giác đều A B C có độ dài cạnh bằng 4. Trung điểm các cạnh của tam giác A B C tạo 1 1 1 1 1 1
thành tam giác A B C , trung điểm các cạnh của tam giác A B C tạo thành tam giác A B C ,... Gọi 2 2 2 2 2 2 3 3 3
P , P , P ,... lần lượt là chu vi của tam giác A B C , A B C , A B C ,... Giá trị biểu thức P P P P  ... 1 2 3 1 1 1 2 2 2 3 3 3 1 2 3 là
A. P  8. B. P  24. C. P  6. D. P  18.
Câu 22: Cửa hàng xếp 1089 hộp sơn theo số lượng 1; 3; 5; … (hộp) từ trên xuống dưới (số hộp sơn trên
mỗi hàng xếp từ trên xuống dưới là các số lẻ liên tiếp như hình bên dưới). Hàng cuối cùng có bao nhiêu hộp sơn?
A. 63. B. 65. C. 67. D. 69.
Câu 23: Một đội công nhân trồng cây xanh từ kilômet số 6 đến kilômet số 8. Cứ 20m trồng một cây. Hỏi
có bao nhiêu cây được trồng?
A. 100. B. 200. C. 250. D. 101.
Câu 24: An từ thành phố về quê thăm ông bà trên quãng đường 54 km. Biết giờ đầu tiên An đi được
15km và mỗi giờ sau An đi kém hơn giờ trước 1km. Thời gian An đi từ nhà về quê là
A. 27 giờ. B. 4 giờ. C. 3 giờ. D. 15 giờ
Câu 25: Ngày thứ nhất cửa hàng bán được 10 cốc nước mía, ngày sau bán nhiều hơn ngày hôm trước đó
1 cốc nước mía. Hỏi ngày thứ 10 cửa hàng sẽ bán được bao nhiêu cốc nước mía?
A. 15 cốc. B. 17 cốc. C. 19 cốc. D. 21 cốc.
Câu 26: Một nhóm gồm 3003 người xếp thành hình tam giác như sau: hàng thứ nhất có 1 người, hàng thứ
hai có 2 người, hàng thứ ba có 3 người,… Hỏi có bao nhiêu hàng?
A. 75. B. 76. C. 77. D. 78.
Câu 27: Tổng tất cả các giá trị m để phương trình 4
x  m   2 2
1 x  2m 1  0 có bốn nghiệm phân biệt
lập thành một cấp số cộng là 40 40 32 32 A.  . B. . C.  . D. . 9 9 9 9 ĐÁP ÁN
Dạng 1. Nhận dạng một dãy số là cấp số cộng TOANMATH.com Trang 18 1 - D 2 - C 3 - D 4 - C 5 - B 6 - B 7 - B 8 - C 9 - B 10 - B 11 - C 12 - D 13 - B 14 - A
HƯỚNG DẪN GIẢI CHI TIẾT Câu 1.
Dãy số 0; 4; 8; 12; 16 là cấp số cộng có số hạng đầu là u  0 và công sai d  4. 1 Câu 2.
Ta có u  3n 1 là một cấp số cộng vì u
u  3 n 1 1  3n 1  3. n 1  n       n Câu 3. 1 1 3
Ta có u   ,u  0,u  ,u  1,u  ,... 1 2 3 4 5 2 2 2 Câu 4.
Dãy số u có tính chất u u d thì được gọi là một cấp số cộng. n n 1  n
Ta thấy dãy số 1; -3; -7; -11; -15 là một cấp số cộng có số hạng đầu là 1 và công sai bằng -4. Câu 5. Ta có u
u  2 n 1  3  2n  3  2,n  1. n 1  n  
Do đó dãy số trong đáp án B là cấp số cộng theo định nghĩa. Câu 6. Ta có u
u  3 n 1  2020  3n  2020  3  uu  3. n 1  n     n 1  n
Vậy dãy số trên là cấp số cộng có công sai d  3. Câu 7.
Ta có u  2n 1 không là cấp số cộng vì n 1 u
u  2   2n. n n 1  n Câu 8.
Xét dãy số u  1 3n , suy ra n 1 u  1 3  . Ta có n * u
u  2.3 ,n   . n n 1  n 1  n
Do đó u  1 3n. không phải là cấp số cộng. n Câu 9. u   1  u   1  Ta có 1  là cấp số cộng vì 1 
u u 1. uu 1  1 uu 1 nn n 1  nn 1 n Câu 10.
Ta có u n   * 3
1 n   là cấp số cộng vì u
u  3 n 1 1 3n 1  3 là hằng số. n 1  n   nCâu 11. 1 1 5 1 1 1 1 1 Xét đáp án C. 2.     nên dãy số ; ;
;... không là cấp số cộng. 2 3 2 2 8 2 2 2 3 2 2 2 Câu 12. TOANMATH.com Trang 19 u   8
Dãy số 8; 15; 22; 29; 36; … là một cấp số cộng với 1 
 công thức tổng quát là u  7n 1. d  7 n Câu 13.
Gọi cấp số cộng thứ nhất là u và cấp số cộng thứ hai là v n . n
Ta có u u n 1 d  4  3 n 1  u  3n 1; n 1     n
v v k 1 d  1 5 k 1  v  5k  4. k 1     k Với k, n ,
 1 n 100,1 k 100.
Ta có u v  3n 1  5k  4  3n  5k   1 . n k
Mà 3 và 5 là hai số nguyên tố cùng nhau nên n chia hết cho 5.
Đặt n  5t,t   k  3t 1.
Do 1 n 100,1 k 100 nên t 1;2;3;...;2  0 . Câu 14.
Ta có a   n  2 2 * * 2
5  4n ,n    a  20n  25, n    . n n Do đó * aa  20, n
   nên a là cấp số cộng với công sai d  20. n n 1  n
Dạng 2. Tìm số hạng đầu tiên, công sai của cấp số cộng, tìm số hạng thứ k của cấp số cộng, tính tổng
k số hạng đầu tiên 1 – B 2 – A 3 – D 4 – C 5 – A 6 – D 7 – A 8 – B 9 – C 10 – C 11 – A 12 – B 13 – A 14 – C 15 – C 16 – C 17 – D 18 – C 19 – C 20 – A 21 – C 22 – B 23 – D 24 – A 25 – A 26 – A 27 – A 28 – A 29 – A 30 – B 31 – C 32 – D 33 – C 34 – D 35 – A
HƯỚNG DẪN GIẢI CHI TIẾT Câu 1.
Ta có u  7;u  4 suy ra d  3. từ đó u  7  ( 3  ) 10. 2 3 1 Câu 2.
Ta có u u n 1 d u u  7d  15  7.(2)  1. n 1   8 1 Câu 3.
n 2u n 1 d    n  23 1   Ta có S   2.483  . n   n   n n    n 2. 1  1.2 2 2 483 0 . 2  n  21  Do *
n nên n  23. Câu 4. u   2  Ta có 1   u  2;
d  3. Suy ra u  2  3 n   n n   1 3 5. 1 uu  3  n 1 n TOANMATH.com Trang 20
Từ đó 70  3n  5  n  25. Câu 5. 50 Ta có S
2u  49d  5150  d  4. 50  1  2
Số hạng tổng quát của cấp số cộng bằng u u n 1 d  1 4 . n n 1   Câu 6.
n 5  2n  3 Ta có u  5 suy ra 2 S   n  4 . n 1 n 2 Câu 7. u   3  1
u  2n  5  
d u u  2. n 2 1 u  1   2 Câu 8.
u u u 14d u  2d  12d  48  6 loại A; 15 3 1  1 
u u u  28d u  21d  7d  28 chọn B; 29 22 1  1 
u u u 16d u 12d  4d  16  18 loại C; 17 13 1  1  u
u  900d  350 loại D. 1000 100 Câu 9.
Gọi a là cấp số cộng theo thứ tự u ;u ;u ;...;u , n   1, lúc đó ta có n  10 20 30 10n
a u u  9d 1 10 1 
d '  a a 10d  30. 2 1
a u u 19d  2 20 1 Câu 10.
Ta có u .u  u  3d u  8d  2 2
u  24d 11u d. 4 9 1 1 1 1
u  u  5d 2 2 2 2
u  25d 10u d. Suy ra 2
u .u u . 6 1 1 1 4 9 6 Câu 11. u   2u  0 u
  2 u  4d  0  3
u  8d  0 u   8 1 5 1  1  Ta có 1 1        . S  14 
2 2u  3d  14 2u  3d  7   d  3  4  1  1 Câu 12. u
  u u  10 u
  u  4d u  2d  10  u   2d 10 u   36 1 5 3 1  1   1  Ta có 1 1        . u u  7  u
  u  5d  7 2u  5d  7   d  13  1 6 1  1  1 Câu 13. S 18 3
 2u  5d 18 
2u  5d  6 u   7  6  1  Ta có 1 1        . S  110  5
 2u  9d 110 2u  9d  22   d  4 10  1  1 TOANMATH.com Trang 21
Từ đó mà S  10 2u 19d  10 2. 7 19.4  620. 20  1      Câu 14. Ta có cấp số cộng: 5
u n  2 nên u  3,u  8,...  d  5. n 1 2 n n
S  16040  2u n 1 d   16040  2.3  n 1 .5  16040 n  1       2 2  n  80 2 5n n 32080 0       401  n  80. n   (loai)  5 Câu 15.
Không mất tổng quát giả sử a b c c b b a d với d là công sai. 1 1 1 1 d 1 1 d Khi đó        nên loại A. a b a a d
a a d b c a d a  2d   2 2 2
b a ad d    2 2 2 2
c b  2ad  3d  nên loại B. Nếu , a ,
b c lập thành cấp số cộng với công sai d thì c, ,
b a cũng lập thành cấp số cộng với công sai –d. Câu 16.
S S  9d  8  5 S 194 10 1 1   
S S 19d  39  5. 20 1
S S 14d  2  40  d  31  15 1 Câu 17. 278.554
Theo giả thiết 2  4  ...  552  554   77006. 2 Câu 18. 1  1  5
Theo giả thiết S  5u 10d  5. 10.    . 5 1   4  4  4 Câu 19.
Ta có u u  3d  2  3. 3  7,u u  5d  2  5. 3  13. 4 1   6 1   Câu 20. 23 23.60
u u  60  2u  22d  60  S  2u  22d   690. 2 22 1 23  1  2 2 Câu 21. u  10 u  10 u  10 Ta có 1 1 1      u  50 u  20d  50   d  2. 21 1 Câu 22. u   8 u   8 u   8 Ta có 1 1 1      u  62 u  9d  62   d  6. 10 1
Suy ra S  5 2u  9d  5 2.8  9.6  350. 10  1    TOANMATH.com Trang 22 Câu 23. n n S  483 
u n d      n    n 2 1 483 2. 1 1 .2 483 1         2 2  n  23 2
n  2n  483  0   n  23.  n  21  (loai) Câu 24. u
  u u u  22 
4u  6d  22   u   10 1 2 3 4 u 1 1 1      hoặc 1  . 2 2 2 2 2 2 u
  u u u  166
4u 12u d 14d  166   d  3 d  3  1 2 3 4 1 1 Câu 25. u   u  42
2u  5d  42 u  11 2 5 1 1 346       S  2.11 345.4  242546. 346   u u  66 2u 11d  66   d  4 2 3 10 1 Câu 26.
Ta có u  18  u  4d  18 1 . 5 1    n n   1 d   2n 2n   1 d
4S S  4 nu   2nu n 2n  1   1  2 2    
 4u  2nd  2d  2u  2nd d  2u d  0 2 . 1 1 1  
Từ (1) và (2) suy ra u  2;d  4. 1 Câu 27.
Ta có a 1  7  a a  3;7  a b  7  b 14  3 11. Câu 28.
Ta có số hạng thứ n của dãy là a S S
 2n  3n  2       n 2 2 1 3 n 1 4n 1. n n n 1   Suy ra a  4n  5. n 1  Khi đó aa  4 
a là một cấp số cộng với công sai là 4. n 1  nn Câu 29. n
Ta có S  2u n 1 d   280. 14  1   2  Câu 30.
Ta có a  2  6  a a  4;6  a b  6  b  8  . a b  32. Câu 31. Từ giả thiết ta có 2
S u  3.1  4.1  7. 1 1 n 8  6n n 7  6n 1 2    
Ta có S  3n  4n  
u  6n 1 u  61. n n 10 2 2 Cách khác 2
u S S
u S S  3.10  4.10      2 3.9 4.9 61. n n n 1 10 10 9  Câu 32. TOANMATH.com Trang 23
u u 8 3 24 8 1 8   
Xen giữa hai số 3 và 24 thêm 6 số để được cấp số cộng có 8 số hạng thì S    108. 8 2 2 Câu 33. 1 25 Ta có d   4.
 Do đó u u  49d  25  49.4  171.  6 50 1 Câu 34.
Gọi d là công sai của cấp số đã cho. 497  2u Ta có S
 502u  99d  1  24850  d   5 100 1 99 5 5 5  5S    ... u u u u u u 1 2 2 3 49 50 u u u u u u 2 1 3 2 50 49    ... u u u u u u 1 2 2 3 49 50 1 1 1 1 1 1 1 1      ...    u u u u u u u u 1 2 2 3 48 49 49 50 1 1 1 1 245 49       S  . u u u u  49d 246 246 1 50 1 1 Câu 35. u
  3u u  2  1 u
  4d  3 u  2d u d  2  1  3
u  9d  2  1 u   2 5 3 2 1  1   1  Ta có 1 1        . 3u  2u  3  4  3
u  6d  2 u  3d  3  4
u 12d  34   d  3 7 4  1   1  1 30 3
S u u ... u S S  2.2  29. 3   2.2  2.3  1242.  4 5 30 30 3      2 2
Dạng 3. Dựa vào tính chất của cấp số cộng: chứng minh đẳng thức, giải phương trình và các bài toán thực tế 1 – A 2 – A 3 – D 4 – D 5 – B 6 – D 7 – B 8 – D 9 – D 10 – C 11 – D 12 – D 13 – B 14 – C 15 – D 16 – D 17 – C 18 – C 19 – B 20 – C 21 – B 22 – B 23 – D 24 – B 25 – D 26 – C 27 - D
HƯỚNG DẪN GIẢI CHI TIẾT Câu 1.
Giả sử x u . Khi đó cấp số cộng có công sai d  5. n
2u n 1 d 2  n 1 5 1    
Do đó 1 6 11 ...  x  .n  .n  970 2 2 n  20 2 5n 3n 1940 0       97 .        Ta có x u
u 19d 1 19.5 96. n   20 1  5 Câu 2. TOANMATH.com Trang 24 Ta có  x  
1   x  4   x  7  ...  x  28  155.
x 1 x  28 Do đó
.10  155  2x  29  31 x 1. 2 Câu 3. Để 3 số 2 1 3 ;
x x  5;1 x lập thành cấp số cộng thì  2
2. x  5  1 3x  1 x 2
 2x  2x 8  0 (phương trình vô nghiệm)
 Không tìm được x thỏa yêu cầu. Câu 4.
Ta có 158  44  41 38  35 nên đa giác có 4 cạnh. Câu 5. 4 2
x 10x m  0.   1 Đặt 2
t x ,t  0, phương trình (1) trở thành 2
t 10t m  0. 2
Phương trình (1) có 4 nghiệm là 4 số hạng liên tiếp của một cấp số cộng khi và chỉ khi phương trình (2)
có 2 nghiệm dương phân biệt thỏa mãn t  9t  * , t t . 2 1   2 1
 '  25  m  0 
Điều kiện phương trình (2) có 2 nghiệm dương phân biệt P m  0  0  m  25. S 10  0  t   t 10  ** 2 1  Theo định lý Vi-ét  t  .t m   . *** 2 1 
Từ *  và **  suy ra t 1,t  9 thế vào ***  ta được m  9 (nhận). 1 2 Câu 6.
ABC có ba góc ,
A B,C theo thứ tự đó lập thành cấp số cộng  𝐴 𝐶 2𝐵. 𝐴 𝐵 𝐶 180 𝐴 20 Ta có 𝐴 𝐶 2𝐵  𝐵 60 𝐶 5𝐴 𝐶 100 Câu 7.
Gọi u (triệu đồng)  *
n N  là mức lương của kỹ sư ở quý làm việc thứ n. n
Ta có u  15; d  1,5. Đến quý thứ 12 mức lương của kỹ sư là u u 11d  31,5 (triệu đồng). 1 12 1
Vậy tổng số tiền nhận được của kỹ sư sau 3 năm là 1215  31,5
S u u  ...  u   279 (triệu đồng). 12 1 2 12 2 Câu 8.
Gọi độ dài 3 cạnh của tam giác cần tìm là a, a  2, a  4a  0. TOANMATH.com Trang 25 a  6
Theo bài ra, ta có a  a  22  a  42 2 2
a - 4a -12  0  .  a  -2
Suy ra độ dài cạnh huyền là 6  4  10. Vậy R  5. Câu 9. 36 3
Theo giả thiết 6 - d 2  6  6  d 2 2
 36 -12d 12d d   . 24 2 Câu 10.
Giả sử phương trình đã cho có ba nghiệm phân biệt là x , x , x theo thứ tự đó lập thành một cấp số cộng. 1 2 3
Suy ra 2x x x . 2 1 3
Mặt khác  x - x  x - x  x - x  3
 0  x -  x x x  2
x x x x x x x x - x x x  0. 1 2 3 1 2 3  1 2 2 3 3 1 1 2 3
Đồng nhất với phương trình 3
x ax b  0.
Suy ra x x x  0  x  0. 1 2 3 2
Thay x  0 vào phương trình đã cho, ta được b  0. 2 x  0
Phương trình đã cho trở thành 3
x ax  0   . 2 x a  0    1
Để phương trình đã cho có 3 nghiệm phân biệt thì phương trình (1) có hai nghiệm phân biệt
a  0. Vậy b  0,a  0. Câu 11.
Ta có số que diêm để xếp được tầng đế của tháp là một cấp số cộng với u  3; d  4. 1
Suy ra số que diêm để xếp được tầng đế của tháp 10 là u u  9d  39. 10 1
Từ đó số que diêm để xếp được hình tháp 10 tầng là 103 39
S u u ... u   210 que 10 1 2 10 2 Câu 12.
Áp dụng định lý sin trong tam giác ABC ta có a  2Rsin , A b  2Rsin ,
B c  2Rsin C. Theo giả thiết 2 2 2
a ,b ,c theo thứ tự đó lập thành cấp số cộng nên 2 2 2
a c  2b 2 2 2 2 2 2 2 2 2
 4R .sin A 4R .sin C  2.4R .sin B  sin A sin C  2.sin . B Vậy 2 2 2 sin ,
A sin B,sin C theo thứ tự đó lập thành cấp số cộng. Câu 13.
Gọi góc nhỏ nhất là x, ta có bốn góc là ,
x x d, x  2d, x  3d (với d là công sai).
x  x d   x  2d   x  3d   360 Ta có hệ 
x  3d  5x TOANMATH.com Trang 26
Giải hệ ta tìm được x  30 .  Câu 14.
Giả sử trồng được n hàng cây n  1, n  .
Số cây ở mỗi hàng lập thành cấp số cộng có u  1 và công sai d  1. 1 Theo giả thiết nn  80
S  3240  2u n d    n n    n n    n   1 3240    2 1 6480 6480 0 . 1 2  n  81 
Kết hợp với điều kiện, ta được n  80.
Vậy có tất cả 80 hàng cây. Câu 15.
Giả sử đa giác có n cạnh; độ dài các cạnh thứ tự lập thành cấp số cộng với công sai d  3cm là
u ;u ;...;u . 1 2 n Từ giả thiết ta có u   44 u   44 n u    3n  47  u   47  3n u   35 n
 u u n       . 1 n  1 1 1 S  158    n u     n n   n n 158  44 316 3 91 316 0 4 1  2  2 Câu 16. Ta có 1 3 2
C C  2C n  3 n n nn! n! n! n  7 2             n   n n n do n
1 ! 3!.n  3! 2!.n  2 9 14 0 7   3. ! n  2 Câu 17. Ta có 2;
 2x 1;5theo thứ tự lập thành một cấp số cộng nên x       x   1 2 1 2 5 2 1  x  . 4 Câu 18.
Ta có B A d,C A  2d, D A  3d. 2 2 D AA3d 2 2 2  A 6Ad  9d Khi đó    3. 2 2 C B
A 2d2  Ad2 2 2Ad  3d Câu 19. 9 Phương trình 2
x  3x a  0 (có 2 nghiệm khi a  ). 4 x x  3
Theo định lý Vi-ét, ta có 1 2  .
x .x a  1 2 121  Phương trình 2
x 11x b  0 (có 2 nghiệm khi b  ). 4 TOANMATH.com Trang 27
y y  11
Theo định lý Vi-ét, ta có 1 2  .
y .y  b  1 2
Theo bài ra x , x , y , y theo thứ tự lập thành một cấp số cộng với công sai là d nên 1 2 1 2  1
2x d  3 x  1 1    2 . 2x  5d  11  1 d  2 1 5 9 13 585 Suy ra . a b   . . .   . 2 9 2 2 8 Câu 20. x  0 Ta có 3
x  2m   2
1 x  9x  0   1   . 2 x   2m   1 x  9  0 2
Phương trình (2) luôn có hai nghiệm trái dấu x , x do ac  1.9  9  0. 1 2
Do đó phương trình (1) luôn có ba nghiệm phân biệt x  0  x . 1 2 1
Để ba nghiệm trên lập thành một cấp số cộng thì x x  2.0  2m 1  0  m   . 1 2 2 Vậy P  5. Câu 21. 1 1 1 1 1 1
Ta có P P; P P P; P P P...; P P. 2 1 3 2 1 4 3 1 n n 1  1 2 2 4 2 8 2 1 1 1 P Vậy 1
P P P P  ...  P P P P  ...   2P  24. 1 2 3 1 1 1 1 1 2 4 8 1 1 2 Câu 22.
Giả sử 1089 được xếp thành n hàng. Từ giả thiết ta có số hộp sơn trên mỗi hàng là số hạng của một cấp số
cộng u với số hạng đầu u 1 công sai d  2. n  1
Do đó S  1089  n n n  
1  1089  n  33. n
Vậy số hộp sơn ở hàng cuối cùng là u  1 32.2  65 (hộp sơn). 33 Câu 23.
Khoảng cách từ các cây đến mốc 6 ki-lô-mét tạo thành cấp số cộng có công sai d  20 . m TOANMATH.com Trang 28
Ta có u u n 1 d  6000  n 1 20. n 1    
Cây cuối cùng ở vị trí 8 ki-lô-mét nên ta có 8000  6000  n   1 20  n  101. Câu 24.
Quãng đường An đi được trong mỗi giờ là một cấp số cộng. n nn  4
Ta có S  2u n d      n
   n n    n   1 54 30     1 .  2 1 31 108 0 . 1 2 2   n  27
Với n  27 thì u u  27 1 d  11 nên vô lý. 27 1  
Vậy An đi từ nhà về quê hết 4 giờ. Câu 25.
Số cốc nước bán được trong các ngày lập thành một cấp số cộng với công sai d  1 .
Số cốc nước bán trong ngày thứ 10 là u u  9d  10  9.1  19. 10 1 Câu 26.
Gọi n là số hàng cần tìm, ta có n n   1 n  77
1 2  3  ...  n  3003   3003   n  77. 2  n  78  Câu 27. Đặt 2
t x ,t  0, ta thu được phương trình 2
t  2m  
1 t  2m 1  0. 2
Điều kiện để phương trình ban đầu có bốn nghiệm phân biệt là phương trình (2) có hai nghiệm dương m  0 
t ,t t t hay  1 . 1 2  1 2 m    2
Khi đó bốn nghiệm là  t ,  t , t , t . 2 1 1 2
Điều kiện để bốn nghiệm trên lập thành cấp số cộng là t t  2 t hay t  9t . 2 1 1 2 1 4
Kết hợp định lý Vi-ét tìm được m  4, m   . 9 32
Từ đó ra tổng các giá trị của m bằng . 9 TOANMATH.com Trang 29