Bài giảng cấp số nhân

Tài liệu gồm 37 trang, tóm tắt lý thuyết trọng tâm, các dạng toán và bài tập chủ đề cấp số nhân, có đáp án và lời giải chi tiết, giúp học sinh lớp 11 tham khảo khi học chương trình Đại số và Giải tích 11 chương 3: Dãy Số, Cấp Số Cộng Và Cấp Số Nhân.

75 38 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 2: Dãy số. Cấp số cộng và cấp số nhân (KNTT)

Môn: Toán 11

Thông tin:

37 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
Trang 1
CHUYÊN ĐỀ
BÀI GIẢNG CẤP SỐ NHÂN
Mục tiêu
Kiến thức
+ Nắm vững khái niệm cấp số nhân
+ Nắm được tính chất 3 số hạng liên tiếp của một cấp số nhân
+ Nắm được công thức tổng quát, công thức tính tổng n số hạng đầu của một cấp số nhân
Kĩ năng
+ Nhận biết được mộ
t cấp số nhân dựa vào định nghĩa
+ Tìm được yếu tố còn lại khi biết 3 trong 5 yếu tố: số hạng đầu, số hạng thứ k, tổng n số hạng
đầu tiên, công bội, số số hạng của cấp số nhân
+ Áp dụng tính chất cấp số nhân vào các bài toán giải phương trình, chứng minh đẳng thức, bất
đẳng thức
+ ứng dụng vào các bài toán thực tế
TOANMATH.co
m
Trang 2
I. LÍ THUYẾT TRỌNG TÂM
Định nghĩa
Cấp số nhân là một dãy sô (hữu hạn hoặc vô hạn), trong đó kể từ số hạng thứ hai, mỗi số hạng đều là tích
của số hạng đứng ngay trước nó với một số không đổi q
Số q được gọi là công bội của cấp số nhân
Nếu

n
u là cấp số nhân với công bội q, ta có công thức truy hồi
1
.
nn
uuq
với
*
n
Đặc biệt:
Khi 0q , cấp số nhân có dạng
1
,0,0,...,0,...u
Khi 1q , cấp số nhân có dạng
111 1
, , ,..., ,...uuu u
Khi
1
0u thì với mọi q, cấp số nhân có dạng 0,0,0,...,0,...
Số hạng tổng quát
Định lí 1.
Nếu cấp số nhân có số hạng đầu
1
u và công bội q thì số hạng tổng quát
n
u được xác định bởi
công thức
1
1
.
n
n
uuq
với
2n
Tính chất
Định lí 2.
Trong một cấp số nhân, bình phương của mỗi số hạng (trừ số hạng đầu và cuối) đều là tích của
hai số hạng đứng kề với nó, nghĩa là
2
11
.
kkk
uuu

với
2k
Tổng n số hạng đầu tiên của cấp số nhân
Định lí 3.
Cho cấp số nhân

n
u với công bội 1q
Đặt
12
...
nn
Suu u. Khi đó
1
1
1
n
n
uq
S
q
Chú ý: Nếu 1q thì cấp số nhân là
111 1
, , ,..., ,...uuu u khi đó
1n
Snu
SƠ ĐỒ HỆ THỐNG HÓA
TOANMATH.co
m
Trang 3
II. CÁC DẠNG BÀI TẬP
Dạng 1: Chứng minh một dãy

n
u là cấp số nhân
Phương pháp giải
Chứng minh
1
., 1
nn
uuqn
 trong đó q là một số không đổi
Nếu
*
0,
n
un
thì ta lập tỉ số
1n
n
u
k
u
* k là hằng số thì

n
u là cấp số nhân có công bội qk
* k phụ thuộc vào n thì

n
u không là cấp số nhân
Để chứng minh dãy
n
u không phải là cấp số nhân, ta chỉ cần chỉ ra ba số hạng liên tiếp không
tạo thành cấp số nhân, chẳng hạn
3
2
21
u
u
uu
Để chứng minh a, b, c theo thứ tự đó lập thành cấp số nhân, ta chứng minh
2
ac b hoặc bac
Ví dụ mẫu
Ví dụ 1.
Xét trong các dãy số sau, dãy số nào là cấp số nhân? Tìm công bội của cấp số nhân đó
a)

21
4
n
n
u
 b)

31
7.5
n
n
n
u

Hướng dẫn giải
CẤP SỐ NHÂN
1
.
nn
uuq
Số hạng tổng quát
1
1
.
n
n
uuq
2n
Số hạng thứ k
2
11
.
kkk
uuu

2k
Tổng n số hạng đầu tiên
1n
Snu khi 1q
1
1
1
n
n
uq
S
q
khi
1q
TOANMATH.co
m
Trang 4
a) Ta có



23
2
1
21
4
416
4
n
n
n
n
u
u

là số không đổi nên
n
u
là cấp số nhân với công bội q = 16
b) Ta có



1
311
3
1
31
7.5
7.5 875
7.5
n
n
n
n
n
n
u
u


không đổi nên
n
u
là cấp số nhân với công bội
875q 
Ví dụ 2. Xét trong các dãy số sau, dãy số nào là cấp số nhân? Tìm công bội của cấp số nhân đó
a)
1
1
3
9
n
n
u
u
u
b)
1
2
1
2
nn
u
uu
Hướng dẫn giải
Ta có
11
11
1
9
,2
9
nnn
nn
nn
n
uuu
uun
uu
u



Do đó có
135 21
246 2
... ...
... ...
n
n
uuu u
uuu u



1
2
Theo đề bài ta có
12
1
9
33uu
u
 (3)
Từ (1), (2), (3) suy ra
12345 2 21
... ...
nn
uuuuu u u

Do đó
n
u
là cấp số nhân với công bội q = 1
b) Ta có
22 2
21 32 43
4, 16, 256uu uu uu  
suy ra
2
1
4
2
2
u
u

và
424
313
256
16
16
uuu
uuu

Do đó
n
u
không là cấp số nhân
Ví dụ 3. Cho
n
u
là cấp số nhân có công bội
1
0; 0qu
. Chứng minh rằng dãy số

n
v
với
2
.
nnn
vuu cũng là một cấp số nhân
Hướng dẫn giải
Ta có

121
3
2
11
223
11 1 1
21
.
...
....
nn
nnn
nn
nn
n
vuu
uq uq
q
vuu uquq



 nên
n
v là cấp số nhân với công bội là
3
q
Ví dụ 4. Cho dãy số
n
u được xác định bởi
1
1
2
,1
49
nn
u
n
uu


. Chứng minh rằng dãy số

n
v xác
định bởi 3, 1
nn
vu n là một cấp số nhân. Hãy xác định số hạng đầu và công bội của cấp số nhân
đó
TOANMATH.co
m
Trang 5
Hướng dẫn giải
Ta có 3
nn
vu (1)
11
3
nn
vu

 (2)
Theo đề ra
11
49 34 3
nn n n
uu u u

 (3)
Thay (1) và (2) vào (3) ta được
1
1
4, 1 4
n
nn
n
v
vvn
v

(không đổi)
Suy ra
n
v
là cấp số nhân với công bội q = 4 và số hạng đầu
11
35vu
Bài tập tự luyện dạng 1
Câu 1:
Trong các dãy số sau, dãy số nào là cấp số nhân?
A.
1
2
1
1
2
nn
u
uu
.
B.
1nn
unu
. C.
1
1
2
5
nn
u
uu

. D.
11
3
nn
uu

.
Câu 2: Trong các dãy số sau, dãy số nào là cấp số nhân?
A.
1
1
3
n
n
u 
.
B.
2
1
3
n
n
u
.
C.
1
3
n
un
.
D.
2
1
3
n
un
.
Câu 3: Trong các dãy số sau, dãy số nào là cấp số nhân?
A.
1
3
1
3
nn
u
uu
.
B.
1nn
uu
. C.
1
1
1
6
nn
u
uu
.
D.
1
23
nn
uu
.
Câu 4: Dãy số nào sau đây là cấp số nhân?
A.
1
2
3
n
un. B.
2
2
n
un. C.
2
3
n
n
u . D.
2
1
n
un.
Câu 5: Trong các dãy số sau, dãy nào là cấp số nhân?
A.
1
4
3
n
n
u . B.
2
1
5
n
n
u
. C.
1
2
3
n
un. D.
2
1
3
n
un.
Câu 6: Dãy số nào trong các dãy số sau vừa là một cấp số cộng, vừa là một cấp số nhân?
A. 1; 1; 1; 1; 1; ... B. 1;0; 0;0;0;... C. 3; 2;1;0; 1;... D. 1;1;1;1;1; ...
Câu 7: Cho cấp số nhân có
1
0u và công bội 0q . Trong các nhận xét sau, nhận xét nào đúng?
A. 0
n
u với mọi n. B. 0
n
u với mọi n lẻ và 0
n
u với mọi n chẵn.
C.
0
n
u
với mọi n.
D.
0
n
u
với mọi n chẵn và
0
n
u
với mọi n lẻ.
Câu 8: Hỏi
1
2
,
1
4
,
1
8
,
1
32
là bốn số hạng đầu của dãy số nào sau đây?
A.
1
2
n
u
n
. B.
1
21
n
u
n
. C.
1
2
n
n
u . D.
2
1
n
u
n
.
Câu 9: Dãy số nào dưới đây không là cấp số nhân?
A.
11 1
1; ; ;
5 25 125
 . B.
111
;;;1
842
 .
C.
4444
2;2 2;4 2;8 2 . D.
11 1
1; ; ;
3927
.
TOANMATH.co
m
Trang 6
Câu 10: Trong các dãy số sau, dãy nào là cấp số nhân?
A.
21
n
n
u 
. B.
1
1
2
1
3
nn
u
uu
.
C.
23
5
n
n
u
.
D.
1
1
n
n
u
n
.
Câu 11: Trong các dãy số sau, dãy nào là cấp số nhân?
A.
1
2
1
1
2
nn
u
uu
.
B.
1
1
1
2
2.
nn
u
uu

. C.
2
1
n
un. D.
12
11
1; 2
.
nnn
uu
uuu


.
Câu 12: Trong các dãy số sau, dãy nào là cấp số nhân?
A.
1
31
n
n
u
. B.
2
1
3
n
n
u
 . C.
1
2
3
n
un . D.
3
1
n
un.
Câu 13: Cho dãy số
n
u là một cấp số nhân với
0,
n
un

. Dãy số nào sau đây không phải là cấp số
nhân?
A.
135
; ; ;...uuu B.
123
3 ;3 ;3 ;...uuu C.
123
111
; ; ;...
uuu
D.
123
1; 1; 1; . ..uuu
Câu 14: Cho dãy số
n
u được xác định bởi
11
2; 2 3 1
nn
uuu n
 . Công thức số hạng tổng quát của
dãy số đã cho là biểu thức có dạng .2
n
abnc, với a, b, c là các số nguyên với 2;nn . Khi đó
tổng a + b + c có giá trị bằng
A. – 4 . B. 4. C. – 3 . D. 3.
Câu 15: Cho dãy số
n
u có các số hạng đầu là 5, 10, 15, 20, 25,… Số hạng tổng quát của dãy là
A. 5( 1)
n
un. B. 5
n
un . C. 5
n
un. D. 51
n
un.
ĐÁP ÁN VÀ LỜI GIẢI BẢI TẬP TỰ LUYỆN DẠNG 1
1-C 2-B 3-C 4-C 5-B 6-D 7-B 8-C 9-B 10-B
11-B 12-B 13-D 14-C 15-B
Câu 1:
Ta có

1
1
1
2
5
5
n
n
nn
n
u
u
u
uu
u


là cấp số nhân có số hạng đầu
1
2u và công bội 5q 
Câu 2:
Xét
1
21
11
33
nn
nn
uu


Ta có
*
1
12
111
:,
33 3
n
nn
n
u
u


Vậy
n
u là cấp số nhân có công bội
1
3
q
Câu 3:
TOANMATH.co
m
Trang 7
Xét
1
6
n
n
u
u
nên
n
u
là cấp số nhân có công bội
6q
Câu 4:
Vì
2
2
22
1
3
39
3
n
n
n
n
u
u
 nên
2
3
n
n
u là cấp số nhân có công bội 9q
Câu 5:
Vì
2
1
3
1
1
5
1
5
5
n
n
n
n
u
u

nên
2
1
5
n
n
u
là cấp số nhân có công bội
1
5
q
Câu 6:
Dãy số 1; 1; 1; 1; 1;… vừa là cấp số cộng công sai là 0, số hạng đầu là 1 vừa là cấp số nhân số hạng đầu
là 1, công bội là 1
Câu 7:
Vì
2
12131
0; 0 . 0; . 0uq uuquuq
Hay
21 2
21 211
.0; .0
nn
nn
uuq u uq

Câu 8:
Xét cấp số nhân
n
u với
1
11
,
22
uq
Ta có
1
1
1
11 1
..
22 2
n
n
n
n
uuq




Câu 9:
Dãy
111
;;;1
842
 có
2
11
.1
24




nên không là cấp số nhân
Câu 10:
Dãy số
1
1
1
2
1
1
3
3
n
n
nn
u
u
u
uu

là cấp số nhân với
1
1
2,
3
uq
Câu 11:
Dãy số
1
1
1
2
2.
nn
u
uu

có
1
2
n
n
u
u

nên là một cấp số nhân với công bội là
2q 
Câu 12:
Ta có
223
1
1111
:
3333
n
n
nnn
n
u
u
u





TOANMATH.co
m
Trang 8
Suy ra
2
1
3
n
n
u

là một cấp số nhân với công bội là
1
3
q
Câu 13:
Dãy
135
; ; ;...uuu
là cấp số nhân công bội
2
q
Dãy
123
3 ;3 ;3 ;...uu u là cấp số nhân công bội 3q
Dãy
123
111
; ; ;...
uuu
là cấp số nhân công bội
1
q
Dãy
123
1; 1; 1; . ..uuu không phải là cấp số nhân
Câu 14:
Ta có
11
231 352 315
nn n n
uu n un u n




với 2;nn
Đặt 3 5
nn
vu n, ta có
1
2
nn
vv
với 2;nn
Như vậy

n
v là cấp số nhân với công bội q = 2 và
1
10v
Do đó
1
10.2 5.2
nn
n
v

Suy ra 3 5 5.2
n
n
un hay 5.2 3 5
n
n
un với 2;nn
Vậy
5, 3, 5ab c
nên
53 53abc
Câu 15:
Ta có
12 3
5; 10 5.2; 15 5.3;... 5.
n
uu u un
Dạng 2: Xác định số hạng đầu, số hạng thứ k, công bội, tổng n số hạng đầu tiên của cấp số nhân
Phương pháp giải
Dựa vào giả thuyết, ta lập một hệ phương trình chứa công bội q và số hạng đầu
1
u . Giải hệ phương
trình này tìm được q và
1
u
Nếu cấp số nhân
n
u có số hạng đầu
1
u và công bội q thì số hạng tổng quát
n
u được xác định bởi
công thức
1
1
.2
n
n
uuq n

Tổng của n số hạng đầu tiên

1
1
1
1
n
n
n
Snu
uq
S
q
khi
khi
1
1
q
q
Ví dụ mẫu
Ví dụ 1.
Tìm số hạng đầu và công bội của cấp số nhân, biết
a)
15
26
51
102
uu
uu


b)
2
3
6
43
u
S
Hướng dẫn giải
TOANMATH.co
m
Trang 9
a) Ta có



4
4
1
15
11
5
4
26
11
1
151
51 *
.51
102 **
102
1 102
uq
uu
uuq
uu
uq uq
uq q








Chia từng vế của (**) cho (*) ta được

4
1
4
1
1
102
51
1
uq q
uq
1
4
51 51
23
117
qu
q

Vậy
1
3u và q = 2
b)



1
1
2
3
2
31
1
6
6
6*
1
43 1 43 **
43
1
uq
uq
u
q
Suqq
u
q




chia từng vế của (*) cho (**) ta được

1
2
1
6
43
1
uq
uqq


22
6
43 6 1 6 37 6 0
1
6
q
qqqqq
q

Với
1
61qu
Với
1
1
36
6
qu
Vậy
1
6
1
q
u
hoặc
1
1
6
36
q
u
Ví dụ 2. Cho cấp số nhân
n
u có công bội nguyên và các số hạng thỏa
mãn
24
135
10
21
uu
uuu


a) Tìm số hạng đầu và công bội của cấp số nhân
b) Tổng của bao nhiêu số hạng đầu tiện bằng 1365?
c) Số 4096 là số hạng thứ mấy của cấp số nhân?
a) Ta có

3
3
24
1
11
3
24
24
11 1
1
51
..10
121
10
.21
121
uqq
uq uq
qq
qq
uuq uq
uqq







432 2
2
11
10 21 10 21 10 0 10 21 10 0qqqq q q
qq

 


Đặt
22
2
11
2qtt q
qq

. Ta có phương trình
Sử dụng công thức
1
1
.
k
k
uuq
Đưa hệ phương trình
về hệ phương trình
hai ẩn q và
1
u
Sử dụng công thức
1
1
.
k
k
uuq
Và
1
1
.,1
1
n
n
q
Su q
q

Đưa hệ phương trình
về hệ phương trình
hai ẩn q và
1
u
Sử dụng công thức
1
1
.
k
k
uuq
Đưa hệ phương trình
về hệ phương trình
hai ẩn q và
1
u
TOANMATH.co
m
Trang 10

22
5
2
10 2 21 10 0 10 21 10 0
2
5
t
tt tt
t

Với
2
2
515
2520
1
22
2
q
tq qq
q
q

 

Mà q nguyên nên
2q 
Với
2
212
5250
55
tq qq
q
 (vô nghiệm)
Ta có
1
3
10
21qu
qq
 
Vậy
1
2; 1qu 
b) Ta có
1
1
1365 . 1365
1
n
n
q
Su
q



12
1 . 1365 2 4096 12
12
n
n
n


Vậy tổng của 12 số hạng đầu tiên bằng 1365
c) Ta có

1
1
1
4096 . 4096 1 2 4096
k
k
k
uuq
 
1112
2 4096 2 2 1 12 13
kk
kk

 
Vậy số 4096 là số hạng thứ 13 của cấp số nhân
Ví dụ 3. Tính các tổng sau
a)
23
11 1 1
...
22 2 2
n
n
S 
b)
22 2
11 1
3 9 ... 3
39 3
n
n
n
S

 


Hướng dẫn giải
a) Ta có dãy số
23
11 1 1
; ; ;...;
22 2 2
n
là một cấp số nhân với n số hạng, số hạng đầu
1
1
2
u
và công bội
2
1
1
2
1
2
2
q 
Do đó
1
1
1
11 1
2
.. 1
1
12 2
1
2
n
n
n
n
q
Su
q




TOANMATH.co
m
Trang 11
b)
22 2
11 1
3 9 ... 3
39 3
n
n
n
S

 


24 2
24 2
11 1
3 2 3 2 ... 3 2
33 3
n
n
  

24 2
24 2
11 1
3 3 ... 3 ... 2 2 2 ... 2
33 3
n
n

  



n soá 2
Dãy số
24 2
3 ;3 ;...;3
n
là cấp số nhân với n số hạng, có số hạng đầu
2
1
3u
và công bội
4
2
3
9
3
q 
Do đó

11
1199
.9. 91
1198
nn
n
q
Su
q



Dãy số
24 2
11 1
...
33 3
n
 là cấp số nhân với n số hạng, số hạng đầu
1
2
1
3
u và công bội
1
9
q
Do đó
21
1
1
11 1191
9
.. 1
1
19 898.9
1
9
nn
n
nn
q
Su
q





Vậy

1
919 1
991
91 2 2
88.9 8.9
nn
n
n
n
nn
Snn


Ví dụ 4. Tính tổng sau
a) 1 11 111 ... 111...1
n
S 
n soá 1
b) 6 66 666 ... 666...6
n
S 

n soá 6
Hướng dẫn giải
a) Ta có
1
1 11 111 ... 111...1 9 99 999 ... 999...9
9
n
S





n soá 1 n soá 9


23
1
10 1 10 1 10 1 ... 10 1
9
n




23
1
10 10 10 ... 10 1 1 ... 1
9
n









n soá 1
1
10 1 10
110910
9 1 10 81
n
n
n
n






Vậy
1
10 9 1 1
81
n
n
n
S

b)
6
6 66 666 ... 666...6 9 99 999 ... 999...9
9
n
S




 
n soá 6 n soá 9


2
10 1 100 1 1000 1 ... 10 1
3
n


TOANMATH.co
m
Trang 12

23
22101202
10 10 10 ... 10 10. 10 1
33101273
n
nn
n
nn






Vậy

20 2
10 1
27 3
n
n
n
S 
Bài tập tự luyện dạng 2
Câu 1:
Cho các cấp số nhân với
17
1
;32
2
uu
.Công bội của cấp số nhân là
A.
1
2
.
B. 4 . C. 2 . D. 1 .
Câu 2: Cấp số nhân
n
u có
3
.2
5
n
n
u . Số hạng đầu tiên và công bội của cấp số nhân là
A.
1
6
,3
5
uq
.
B.
1
6
,2
5
uq
.
C.
1
6
,2
5
uq
.
D.
1
6
,5
5
uq
.
Câu 3: Cho cấp số nhân có
1
1
1;
10
uq

. Số
103
1
10
là số hạng thứ bao nhiêu của cấp số nhân?
A. Số hạng thứ 103. B. Số hạng thứ 104. C. Số hạng thứ 105. D. Số hạng thứ 106.
Câu 4. Cho các khẳng định sau
1. Tồn tại một cấp số nhân
n
u có
5
0u
và
75
0u
2. Nếu các số thực a, b, c theo thứ tự đó lập thành một cấp số cộng có công sai khác 0 thì các số
222
,,abctheo thứ tự đó cũng lập thành một cấp số cộng
3. Nếu các số thực a, b, c theo thứ tự đó lập thành một cấp số nhân thì các số
222
,,abctheo thứ tự đó
cũng lập thành một cấp số nhân
Số khẳng địn đúng là
A. 1 B. 2 C. 3 D. 0
Câu 5: Cho cấp số nhân có
16
1, 0,00001uu . Khi đó công bội q và số hạng tổng quát
n
u là
A.
1
11
,
10 10
n
n
qu

B.
1
1
,10
10
n
n
qu

C.
1
11
,
10 10
n
n
qu

D.

1
1
1
,
10 10
n
n
n
qu

Câu 6: Cho cấp số nhân
2; 4; 8;...
Tổng n số hạng đầu tiên của cấp số nhân là
A.


21 2
12
n




B.

21 2
12
n



C.


2
21 2
12
n




D.

2
21 2
12
n



Câu 7: Cho cấp số nhân biết
1
1; 2uq. Số hạng thứ 11 là
A. 20 B. 1024 C. 22 D. 2008
Câu 8: Nếu cấp số nhân
n
u có
1
3u và công bội 3q thì giá trị
7
u là
A.
6
3 B.
7
3 C. 21 D.
8
3
Câu 9: Cấp số nhân
n
u có
3
.2
5
n
n
u
. Số hạng đầu tiên và công bội q là
TOANMATH.co
m
Trang 13
A.
1
6
,3
5
uq
B.
1
6
,2
5
uq
C.
1
6
,2
5
uq
D.
1
6
,5
5
uq
Câu 10: Cho cấp số nhân có
25
1
,16
4
uu
. Công bội và số hạng đầu tiên của cấp số nhân là
A.
1
11
;,
22
qu
B.
1
11
;,
22
qu 
C.
1
1
4; ,
16
qu
D.
1
1
4; ,
16
qu 
Câu 11:
Cho cấp số nhân với
1
3, 2uq
. Số 192 là số hạng thứ mấy của cấp số nhân?
A.
7
u
B.
6
u
C.
8
u
D. Không thuộc cấp số trên
Câu 12: Tổng 10 số hạng đầu của một cấp số nhân có
110
4, 2048uulà
A.
10
8184S B.
10
4092S C.
10
12276S D.
10
6138S
Câu 13: Cho cấp số nhân với
1
4, 4uq. Ba số tiếp theo của cấp số nhân là
A. 16;64; 256 B. 16; 64; 256 C. 16;64;256 D. 16;64;256
Câu 14: Cho dãy số xác định bởi
*
11
2
11
1, 2 ;
332
nn
n
uu u n
nn





. Khi đó
2018
u bằng
A.
2016
2018
2017
21
3 2019
u  B.
2018
2018
2017
21
3 2019
u  C.
2017
2018
2018
21
3 2019
u  D.
2017
2018
2018
21
3 2019
u 
Câu 15: Cho
2
3 3.2 3.2 ... 3.2
n
S 
. Khẳng định nào sau đây đúng với mọi n nguyên dương?
A.
32 1
n
S  B.

1
32 1
n
S
 C.

1
32 1
n
S
 D.
1
32 1
n
S

Câu 16: Cho một cấp số nhân biết
1
3, 2uq. Tổng của 10 số hạng đầu tiên của cấp số nhân là
A.
9
3. 1 2 B.

10
3. 1 2 C.
9
3. 2 1 D.
10
3. 2 1
Câu 17: Cho cấp số nhân
n
u , biết
2017 2020
1, 1000uu. Tổng 10 số hạng đầu tiên của cấp số nhân
bằng
A.
10
2016
10 1
9.10
B.
10
2016
91
8.9
C.
10
2016
110
9.10
D.
10
2019
10 1
9.10
Câu 18: Tổng
23 100
1 2 2 2 ... 2
bằng
A.
100
12 B.
100
21 C.
101
12 D.
101
21
Câu 19: Cấp số nhân 5; 10; …; 1280 có bao nhiêu số hạng?
A. 9 B. 7 C. 8 D. 10
Câu 20: Số hạng thứ 5 của cấp số nhân 2; 6; … là
A. 48 B. 486 C. 81 D. 162
Câu 21: Cho cấp số nhân có
1
1, 3uq. Số hạng thứ 9 của cấp số nhân là
A. 6561 B. 19683 C. 2187 D. 729
Câu 22: Dãy số có số hạng tổng quát
2
1
3
n
n
u



là một cấp số nhân có công bội q bằng
A.
1
3
B. 3 C.
1
9
D.
1
3
TOANMATH.co
m
Trang 14
Câu 23: Tổng
11 1
... ...
416 4
n




bằng
A.
1
2
B.
2
9
C.
1
3
D.
2
3
Câu 24: Cho cấp số nhân lùi vô hạn
n
u
với
1
1
3
n
n
u




. Tổng của cấp số nhân đó là
A.
1
6
B.
1
4
C.
1
12
D.
1
12
Câu 25: Tổng
111
1 ...
248
S  có giá trị
A. 1 B. 2 C. 4 D.

Câu 26: Cho cấp số nhân
n
u biết
123
13
31
26
uuu
uu


. Giá trị
1
u và q là
A.
1
2; 5uq hoặc
1
1
25;
5
uq B.
1
5; 1uq hoặc
1
1
25;
5
uq
C.
1
25; 5uq
hoặc
1
1
1;
5
uq
D.
1
1; 5uq
hoặc
1
1
25;
5
uq
Câu 27: Cấp số nhân
n
u
có
6
.2
5
n
n
u . Số hạng đầu tiên và công bội q là
A.
1
6
,2
5
uq B.
1
6
,2
5
uq C.
1
12
,2
5
uq D.
1
12
,5
5
uq
Câu 28: Cho cấp số nhân
n
u có
2
2u  và
5
54u . Khi đó tổng 1000 số hạng đầu tiên của cấp số nhân
đó bằng
A.
1000
13
4
B.
1000
31
2
C.
1000
31
6
D.
1000
31
3
Câu 29: Số hạng đầu và công bội của cấp số nhân thỏa mãn
52
64
36
48
uu
uu


là
A.
1
4, 4uq B.
1
2, 4uq C.
1
2, 2uq D.
1
4, 2uq
Câu 30: Tổng
234
122 2 2S  là một số chia hết cho
A. 21 B. 41 C. 51 D. 31
Câu 31: Cho cấp số nhân
n
u
có
3
24u và
4
48u . Tổng năm số hạng đầu tiên của cấp số nhân đó bằng
A. 168 B. 186 C. – 186 D. 196
Câu 32: Cho cấp số nhân với
1
1
3,
2
uq. Số 222 là số hạng thứ mấy của cấp số nhân?
A. Số hạng thứ 11 B. Số hạng thứ 9
C.
Số hạng thứ 12 D. Không thuộc cấp số nhân
Câu 33: Cho cấp số nhân có
42
53
54
108
uu
uu


. Số hạng đầu tiên
1
u và công bội q của cấp số nhân là
TOANMATH.co
m
Trang 15
A.
1
9u
và
2
q
B.
1
9u
và
2
q 
C.
1
9u 
và
2
q
D.
1
9u 
và
2
q
Câu 34: Cho cấp số nhân có
42
53
54
108
uu
uu


. Giá trị
1
u và q của cấp số nhân là
A.
1
9u và 2q B.
1
9u và 2q  C.
1
9u  và 2q D.
1
9u  và 2q 
Câu 35: Cho cấp số nhân có
1
3; 2uq. Số 192 là số hạng thứ bao nhiêu của cấp số nhân?
A. Số hạng thứ 5 B. Số hạng thứ 6 C. Số hạng thứ 7 D. Số hạng thứ 8
Câu 36: Cho cấp số nhân
n
u
có công bội 1q và
13
22
13
3
5
uu
uu


. Tổng 10 số hạng đầu tien của cấp số
nhân là
A.
10
31 2 2
16
S
B.

10
31 1 2S  C.
10
31 2 1S  D.
10
31 2 1S 
Câu 37: Cho cấp số nhân
n
u
có tổng n số hạng đầu tiên là
1
31
3
n
n
n
S
. Số hạng thứ 5 của cấp số nhân là
A.
5
4
2
3
u B.
5
5
1
3
u C.
5
5
3u D.
5
5
5
3
u
Câu 38: Cho cấp số nhân có
16
1; 0.00001uu . Khi đó công bội q và số hạng tổng quát là
A.
1
11
,
10 10
n
n
qu

B.
1
1
,10
10
n
n
qu
 
C.
1
11
,
10 10
n
n
qu

D.

1
1
1
,
10 10
n
n
n
qu

Câu 39: Cho dãy số
n
u
xác định bởi
1
1
3
u
và
1
1
.
3
nn
n
uu
n
. Giá trị tổng
310
2
1
...
23 10
uu
u
Su
là
A.
3280
6561
B.
29524
59049
C.
25942
59049
D.
1
243
Câu 40: Cho cấp số nhân
n
u có
4
11
24; 16384
n
u
u
u
. Số hạn thứ 17 của cấp số nhân là
A.
3
67108864
B.
3
268435456
C.
3
536870912
D.
3
214783648
ĐÁP ÁN VÀ LỜI GIẢI BẢI TẬP TỰ LUYỆN DẠNG 2
1-C 2-C 3-B 4-A 5-D 6-A 7-B 8-B 9-C 10-C
11-A 12-B 13-A 14-A 15-C 16-D 17-A 18-D 19-A 20-D
21-A 22-D 23-C 24-D 25-B 26-D 27-C 28-D 29-C 30-D
31-B 32-D 33-A 34-A 35-C 36-C 37-A 38-D 39-B 40-C
Câu 1:
Ta có
66
71
1
32 2
2
uuq q q
TOANMATH.co
m
Trang 16
Câu 2:
Ta có
1
6
1
5
nu
và
1
1
3
.2
5
2
3
.2
5
n
n
n
n
u
u

Câu 3:
Giả sử
103
1
10
n
u
ta có
1103 1
1
1
103
11 11
. 1. 1 103 104
10 10 10 10
nn
n
n
uuq n n

 

 
 
Câu 4:
1. Sai
Ta có
474
51 751
.,uuqu uq. Do đó
5
u và
75
u cùng dấu
2. Sai
Vì a, b, c theo thứ tự đó lập thành một cấp số cộng có công sai d khác 0 nên b = a + d, c = a + 2d
Suy ra
22 222 2 22 2
2, 44 2ba addca add ac b  
Vậy
222
,,abc theo thứ tự không lập thành cấp số cộng
3. Đúng
Vì a, b, c theo thứ tự đó lập thành một cấp số nhân có công bội d khác 0 nên
2
., .badcad
Suy ra
2
222224 22 2
,badcad ac b
Vậy
222
,,abc theo thứ tự lập thành cấp số nhân
Câu 5:
Ta có
5
16
5
0,00001 1 1
1, 0,00001
110 10
uu q q  
Vậy số hạng tổng quát

1
1
1
1
1.
10 10
n
n
n
n
u




Câu 6:
Ta có
1
2u  và 2q 
Tổng n số hạng đầu tiên của cấp số nhân là
 


21 2
2
12
12 3
n
n
n
S





Câu 7:
Ta có
10 10
11 1
. 1.2 1024uuq
Câu 8:
Ta có
667
71
.3.33uuq
TOANMATH.co
m
Trang 17
Câu 9:
Ta có
12 32
3
2
12 3
12
36 36 36
.2 , .2 .2, .2 .2 2, 2
55 55 55
u
u
uu u
uu

Vậy cấp số nhân cần tìm có
1
6
,2
5
uq
Câu 10:
Ta có
3
5
2
1
2
1
1
4
64 4
416
u
u
qqu
uq

Câu 11:
Số hạng tổng quát của cấp số nhân là

1
3. 2
n
n
u

Ta cần tìm n sao cho

1
192 3. 2 192 7
n
n
un
 
Câu 12:
Ta có
9
10 1
.2uuq q. Do đó
10
10 1
1
.4092
1
q
Su
q

Câu 13:
Ta có
21 32 43
. 16; . 64; . 256uuq uuq uuq .
Câu 14:
Ta có
1 1
2
11132 121
22
332321 231
nn n n n
n
uu u u u
nn n n n n

 



(1)
Đặt
1
1
nn
vu
n

, từ (1) ta suy ra
1
2
3
nn
vv
Do đó
n
v là cấp số nhân với
11
11
22
vu, công bội
1
2
q
Suy ra
111
1
1
12 1 12 12 1
...
23 123 23 1
nnn
n
nnn
vvq u u
nn

  

  

  
Vậy
2017
2016
2018
2017
12 1 2 1
.
2 3 2019 3 2019
u




Câu 15:
Ta có
2
1,2,2 ,...,2
n
là cấp số nhân với
1
1
2
u
q
nên
1
21
12
122 ...2 2 1
12
n
nn

21
3 1 2 2 ... 2 3 2 1
nn
S

Câu 16:
Ta có

10 10
10
10 1
112
.3.3.21
112
q
Su
q



TOANMATH.co
m
Trang 18
Câu 17:
Ta có
33
2017
2020 2017 1
2016
2016
1
. 1000 10
10
u
uuqq q u
u

10 10 10
10 1
2016 2016
11101101
..
110 9 9.10
q
Su
q


Câu 18:
Xét cấp số nhân
n
u với
1
2, 2uq
Ta có
100
2 3 100 101
100
2. 1 2
1 2 2 2 ... 2 1 1 2 1
12
S

Câu 19:
Xét cấp số nhân
n
u
với
1
5, 2uq
Ta có
1118
1
. 1280 5.2 2 2 9
nnn
n
uuq n


Vậy cấp số nhân đã cho có 9 số hạng
Câu 20:
Xét cấp số nhân
n
u với
1
2, 3uq. Suy ra
44
51
. 2.3 162uuq
Câu 21:
Ta có
88
91
. 1.3 6561uuq
Câu 22:
Ta có
12
11 1
,
39 3
uu q
Câu 23:
Xét cấp số nhân với
1
11
,
44
uq
có 1q nên
1
1
1
4
1
13
1
4
u
S
q

Câu 24:
Ta có
1
1
1
11 1
9
,
1
93 1 12
1
3
u
uq S
q





Câu 25:
Ta có
1
1
11
1, 2
1
21
1
2
u
uq S
q

Câu 26:
TOANMATH.co
m
Trang 19
Ta có




2
22
1
123
22
2
13
1
1
2
26 31
131
11
31
26 1 31 1
26
26
126
1
uqq
qqq
uuu
qq q
uu
uq
u
q









1
2
1
5
1
52650
1
25
5
q
u
qq
u
q

Câu 27:
Ta có
12
12 24
,2
55
uu q
Câu 28:
Ta có
2
1
4
5
1
1
3
2
2
2
54
54
3
q
u
uq
u
uq
u







Vậy
1000 1000
1000
21 3 3 1
.
32 3
S


Câu 29:
Ta có


4
1
52
453
53
64
1
36
36
48 36
48
48
uq q
uu
qq qq
uu
uq q








453543 2
4433 34340 1 23 20qqqq qqqq qq q qq
2
0
1
2
2
320
q
q
q
q
qq



(do
1
4
36
0; 1) 2
qq u
qq

Câu 30:
Ta có
1234
1; 2 ; 2 ; 2 ; 2 là một cấp số nhân với
1
1; 2uq có 5 số hạng
5
5
1
121
1. 2 1 31 31
121
n
q
Su
q



Câu 31:
Từ giả thiết
3
24u và
4
48u suy ra 2q
Lại có
3
1
2
24
6
4
u
u
q

Vậy
5
51
131
6. 186
11
q
Su
q



Câu 32:
TOANMATH.co
m
Trang 20
Giả sử số 222 là số hạng thứ n
Ta có
11
1
1
11
222 3. 74
22
nn
n
n
uuq

 

 
 
(không tồn tại
n
thỏa mãn)
Vậy 222 không là số hạng của cấp số nhân
Câu 33:


2
3
1
42
11
2
42
22
53 1
1
11
1
154
2
54
2
54
108 1 54
9
108
1 108
uq q
q
uu
q
uq uq
uu uqq
u
uq uq
uq q









Câu 34:

3
42
11
42
53
11
54 1
54
108 2
108
uu
uq uq
uu
uq uq





Ta thấy
3
11
0uq uq nên chia phương trình (2) cho phương trình (1) ta được q = 2
Thay q = 2 vào phương trình (1) ta tìm được
1
9u
Câu 35:
Có

1
11
1
1
192
.2647
3
n
nn
n
n
u
uuq q n
u


Câu 36:
Ta có

1
13
3
13 13
2
22
13 13
1
13 13
3
2
3
1
33
5.2
1
2. 5
2
u
uu
u
uu uu
uu uu
u
uu uu
u


 







Trường hợp 1.
1
2
3
3
1
1
22
2
u
u
qq
u
u

(do 1q )
Với
2q thì

10 5
1
10
11.12
31 2 1
1
12
uq
S
q


Trường hợp 2.
1
2
3
3
1
1
2
1
2
1
1
2
2
q
u
u
q
u
u
q


(loại do 1q )
Câu 37:
1
11
31 2.1
33
31
11
3
3. 1
33
nn
n
n
n
n
n
S

 


 

 


Vậy
4
151
4
12
2; .
33
uq uuq
TOANMATH.co
m
Trang 21
Câu 38:
Ta có
55
61
1
0.00001 . 0.00001 1. 0.00001
10
uuq qq
Mặt khác

1
1
1
1
1
1
.1.
10 10
n
n
n
n
n
uuq




Câu 39:
Theo đề ta có
1
1
11
.
313
nn
nn
uu
n
uu
nnn

Mà
1
1
3
u nên
223 10
310
2
11 1 1 1 1 1
. ; . ;...;
233 3 333 3 10 3
uu
u
   

   
   
Do đó dãy
n
u
n



là một cấp số nhân có số hạng đầu
1
1
3
u
, công bội
1
3
q
Khi đó
10
310
2
1
10 10
3 1 59048 29524
...
2 3 10 2.3 2.3 59049
uu
u
Su

Câu 40:
Từ
7
7
4
7
11
111
16384 16384
44
u
qq
uq




Ta có 24
n
u tương ứng khi n = 1
Số hạng thứ 17 của cấp số nhân là
16
17
13
24.
4 536870912
u




Dạng 3: Dựa vào tính chất của cấp số nhân, chứng minh đẳng thức, giải phương trình và ứng dụng
bài toán thực tế
Phương pháp giải
Áp dụng tính chất : Ba số a, b, c theo thứ tự đó lập thành cấp số nhân thì
2
ac b hoặc bac
Nếu cấp số nhân
n
u có số hạng đầu
1
u và công bội q thì số hạng tổng quát
n
u được xác định bởi công
thức
1
1
.2
n
n
uuq n

Tổng của n số hạng đầu tiên

1
1
1
1
n
n
n
Snu
uq
S
q
khi
khi
1
1
q
q
Ví dụ mẫu
Ví dụ 1.
Tìm x, y biết 5 ;2 3 ; 2
x
yx yx y theo thứ tự lập thành cấp số cộng và các số

22
1; 1; 1yxyx
theo thứ tự lập thành cấp số nhân
Hướng dẫn giải
TOANMATH.co
m
Trang 22
Ba số
5;23;2
x
yx yx y
theo thứ tự lập thành cấp số cộng nên

2
22 3 5 2
5
x
yxyxyyx (*)
Ba số

22
1; 1; 1yxyx
theo thứ tự lập thành cấp số nhân nên

222 2 2
111 1 1xy y x xy xy x y  
Trường hợp 1.
112xy xyxy xy (**)
Từ (*) và (**) suy ra
10 4
;
33
xy
Trường hợp 2. 1 1 2 0xy xy x y xy x y  (***)
Từ (*) và (***) suy ra
2
0; 0
43
0
33
55
;
410
xy
xx
xy


 
Vậy các cặp số
;
x
y
cần tìm là
 
33 104
;;;0;0;;
410 33
xy







Ví dụ 2. Cho a, b, c là ba số hạng liên tiếp của một cấp số nhân. Chứng minh
a)

33
ab bc ca abc a b c
b)

2
2222
abbc abbc
c)
222
abcabc a b c 
Hướng dẫn giải
Vì a, b, c là ba số hạng liên tiếp của một cấp số nhân nên
2
bac
a) Ta có


3
33 3
32
abcabc babc abb bc abbcca  (điều phải chứng minh)
b) Ta có
2 2 2 2 22 22 4 22 22 4 22
2abbc abacbbc ab bbc 

2
22 22
2.a b ab bc b c ab bc (điều phải chứng minh)
c) Ta có
  
2
2
abcabc ac b ac b ac b 


2 222 222222
22a accba bcbabc   (điều phải chứng minh)
Ví dụ 3. Số đo bốn góc của một tứ giác lập thành cấp số nhân và góc cuối gấp 9 lần góc thứ hai. Tìm số
đo của góc thứ nhất
Hướng dẫn giải
Gọi A, B, C, D theo thứ tự đó là bốn đỉnh của tứ giác thỏa mãn đề bài
Theo bài ra ta có
23
;;
B
Aq C Aq D Aq
Mặt khác
32
9993DBAq Aqq q
Với
330qBA  (loại)
TOANMATH.co
m
Trang 23
Với q = 3 ta có
000
360 3 9 27 360 9ABCD A A A A A
Ví dụ 4. Cho a, b, c là các số nguyên dương thỏa mãn
b
a
là một số nguyên. Các số a, b, c theo thứ tự lập
thành một cấp số nhân và
2
3
abc
b


. Tìm a
Hướng dẫn giải
Vì a, b, c theo thứ tự lập thành một cấp số nhân nên
2
.; .baqcaq
Vì
b
a
là một số nguyên mà a, b là số nguyên dương nên q là số nguyên dương
Ta có

2
2
23616
3
abc
b a aq aq aq a q


Vì a, q nguyên dương nên ta có bảng sau
a 1 2 3 6

2
1q
6 3 2 1
q
61 31
21
2
Kết luận Loại Loại Loại Thỏa mãn
Vậy a = 6
Ví dụ 5. Tìm m để phương trình
32
31 5 4 80xmxmx (1) có 3 nghiệm lập thành một cấp số
nhân
Hướng dẫn giải
Giả sử
123
;;
x
xx
là ba nghiệm của phương trình (1)
123
0xx xx xx
32
123 122331 123
0x xxxx xxxxxxxxxx
Suy ra
123
8xxx
Lại có ba nghiệm
123
;;
x
xx lập thành một cấp số nhân nên
23
213 2123 2
82xxx xxxx x
Mà
2
x
là nghiệm của phương trình (1) nên
32
231.254.280 2mm m
Thử lại với m = 2 thì phương trình (1) trở thành
TOANMATH.co
m
Trang 24
32
1
71480 2
4
x
xx x x
x

(thỏa mãn)
Vậy m = 2 là giá trị cần tìm
Ví dụ 6. Cho 3 số dương có tổng là 65 lập thành một cấp số nhân tăng. Nếu bớt một đơn vị ở số hạng thứ
nhất và 19 đơn vị ở số hạng thứ ba ta được một cấp số cộng. Tìm 3 số đó
Hướng dẫn giải
Gọi
123
,,uu u theo thứ tự đó lập thành một cấp số nhân
Theo đề bài
123
1, , 19uuutheo thứ tự đó lập thành một cấp số cộng
Ta có
123 123
13 2123
65 65
1192 2 20
uuu uu u
uu uuuu
 





2
2
1
11 1
2
2
11 1
1
165
..65
2. 20
12 20
uqq
uuquq
uuquq
uqq







1
2
Chia vế với vế của (1) cho (2), ta được
2
2
16513
12 20 4
qq
qq




222
3
41 131 2 9 30 9 0
1
3
q
qq qq q q
q
 
Vì
123
,,uu u theo thứ tự lập thành một cấp số nhân tăng dần nên
1
35qu
Vậy 3 số cần tìm là 5; 15; 45
Ví dụ 7. Cho tam giác ABC vuông tại A có ba cạnh CA, AB, BC theo thứ tự lập thành một cấp số nhân
có công bội là q. Tìm q
Hướng dẫn giải
Vì tam giác ABC vuông tại A nên
222
BC AB AC
Theo giả thiết ta có ba cạnh CA, AB, BC theo thứ tự lập thành một cấp số nhân có công bội là q nên
2
.BC q AC
và
.
A
BqAC
Do đó
2224222242
.. 10BC AB AC q AC q AC AC q q
2
2
2
15
15
2
2
15
2
q
q
q

(do
2
225
0)
2
qq

Vì 0q nên
225
2
q
TOANMATH.co
m
Trang 25
Ví dụ 8. Cho hình vuông
1
C
có cạnh bằng 1,
2
C
là hình vuông có các đỉnh là các trung điểm của cạnh
hình vuông
1
C . Tương tự, gọi
3
C là hình vuông có các đỉnh là trung điểm của các cạnh hình vuông
2
C .
Tiếp tục như vậy ta được một dãy các hình vuông
123
, , ,..., ,...
n
CCC C
Tính tổng diện tích của 10 hình
vuông đầu tiên của dãy
Hướng dẫn giải
Diện tích của hình vuông
1
C là 1
Độ dài đường chéo hình vuông
1
C là 2
Hình vuông
2
C có cạnh bằng
1
2
đường chéo hình vuông
1
C
Diện tích của hình vuông
2
C là
2
2
2




Hình vuông
3
C có cạnh bằng
1
2
đường chéo hình vuông
2
C
Diện tích của hình vuông
3
C là
4
2
2




Hình vuông
n
C có cạnh bằng
1
2
đường chéo hình vuông
1n
C
Diện tích của hình vuông
n
C là

21
2
2
n




Do đó, dãy diện tích các hình vuông
123
, , ,..., ,...
n
CCC C lập thành cấp số nhân với số hạng đầu
2
10
1101
2 1 1 1023
1, .
2 2 1 512
q
uq Su
q





Ví dụ 9. Để tiết kiệm năng lượng, một công ty điện lực đề xuất bán điện sinh hoạt cho người dân theo
hình thức lũy tiến (bậc thang) như sau: Mỗi bậc gồm 10 số; bậc 1 từ số thứ 1 đến số thứ 10, bậc 2 từ số 11
đến số 20, bậc 3 từ số thứ 21 đến số thứ 30,…Bậc 1 có giá là 1500 đồng/1 số, giá của mỗi số ở
bậc thứ
TOANMATH.co
m
Trang 26
1
n
tăng so với giá của mỗi số ở bậc thứ n là 2,5%. Gia đình ông An sử dụng hết 345 số trong tháng 1,
hỏi tháng 1 ông An phải đóng bao nhiêu tiền?
Hướng dẫn giải
Gọi
1
u là số tiền phải trả cho 10 số điện đầu tiên
Suy ra
1
10.1500 15000u 
(đồng)
2
u là số tiền phải trả cho các số điện từ 11 đến 20
Suy ra
21
1 0,025uu
....................................................................................
34
u là số tiền phải trả cho các số điện từ 331 đến 340
Suy ra

33
34 1
1 0,025uu
Số tiền phải trả cho 340 số điện đầu tiên là




34 34
11 1
1 1 0,025 1 1 0,025
. 15000. 789193, 28
1 1 0,025 1 1 0,025
Su S
 

 
Số tiền ông An phải trả cho các số điện từ 341 đến 345 là

34
2
5.1500 1 0,025 17364,92S 
Vậy tháng 1 gia đình ông An phải trả số tiền là:
12
806558SS S
(đồng)
Ví dụ 10. Từ độ cao 55,8m của tháp nghiêng Pisa nước Italia, người ta thả một quả bóng cao su chạm
xuống đất. Giả sự mỗi lần chạm đất quả bóng lại nảy lên độ cao bằng
1
10
độ cao mà quả bóng đạt trước
đó. Tính tổng độ dài hành trình của quả bóng được thả từ lúc ban đầu cho đến khi nó nằm yên trên mặt
đất
Hướng dẫn giải
Gọi
n
h là độ dài đường đi của quả bóng ở lần rơi xuống thứ n

*
n
Gọi
n
l
là độ dài đường đi của quả bóng ở lần nảy lên thứ n
*
n
Theo bài ra ta có
11
1
55,8, .55,8 5,58
10
hl và các dãy số
n
h ,
n
l là các cấp số nhân lùi vô hạn với
công bội
1
10
q
Suy ra tổng độ dài đường đi của quả bóng là

11
11
10
68,2( )
11
9
11
10 10
hl
Shlm


Bài tập tự luyện dạng 3
TOANMATH.co
m
Trang 27
Câu 1: Ba số
2,3 3,5 5
x
xx
theo thứ tự là ba số hạng liên tiếp của một cấp số nhân. Biết
1
x 
, số
hạng tiếp theo của cấp số nhân đó là
A.
250
3
B.
250
3
C.
250
D.
250
Câu 2: Cho cấp số nhân 4; ; 9xthì giá trị x là
A. 5 B.
6,5
C. 6 D. 36
Câu 3: Cho cấp số nhân có bốn số hạng 2; ; 18;
x
y . Hãy chọn kết quả đúng
A. 6; 54xy B. 6; 54xy C. 6; 54xy  D. 10; 26xy 
Câu 4: Giá trị của x để 3 số 21;;21
x
xx theo thứ tự lập thành cấp số nhân là
A.
1
3
x  B. 3x  C.
1
3
x  D. 1x 
Câu 5: Ba số x, y, z theo thứ tự lập thành một cấp số nhân với công bội q khác 1 đồng thời các số
x; 2y; 3z theo thứ tự lập thành một cấp số cộng với công sai khác 0. Giá trị của q là
A.
1
3
q
B.
1
9
q
C.
1
3
q 
D. 3q 
Câu 6: Nếu ba số
;;
x
ax bx c
theo thứ tự lập thành một cấp số nhân thì giá trị của x tính theo a, b, c
là
A.
2
2
abc
x
abc

B.
2
2
cab
x
ab c

C.
2
2
bac
x
abc

D.
222
abc
x
abc


Câu 7: Cho cấp số nhân
11
,,
5125
x

. Giá trị của x là
A.
1
5
B.
1
25
C.
1
5
D.
5
Câu 8: Với giá trị nào của x thì 3 số 2; 1;3
x
xx lập thành cấp số nhân?
A. 1 B. 2 C. 3 D. Không có giá trị nào
Câu 9: Bốn số a, b, c, d theo thứ tự lập thành một cấp số cộng và bốn số
1, 1, 3, 9abc d
theo thứ tự
lập thành một cấp số nhân. Tổng a + d bằng
A. 6 B. 8 C. 10 D. 12
Câu 10: Có bao nhiêu cấp số nhân gồm bốn phần tử mà tổng của chúng bằng 45 và số hạng thứ tư bằng
bốn lần số hạng thứ 2?
A. 1 B. 2 C. 3 D. 4
Câu 11: Trong một cấp số nhân có các số hạng đều dương, hiệu của số hạng thứ năm và thứ tư là 576,
hiệu của số hạng thứ hai và số hạng đầu là 9. Tổng 5 số hạng đầu tiên của cấp số nhân đó bằng
A. 768 B. 1024 C. 1023 D. 1061
Câu 12: Ba số ;3;
x
y theo thứ tự lập thành cấp số cộng, ba số 1, ,
x
y theo thứ tự lập thành một cấp số
nhân. Biết rằng
0x , khi đó tích
.
x
y
bằng
A. 8 B. – 27 C. – 8 D. 5
TOANMATH.co
m
Trang 28
Câu 13: Cho bộ số
000
,,
x
yz là nghiệm của hệ phương trình
4
2222
32312
xyza
xy z a
x
yz a



. Các giá trị dương của
a để
000
,,
x
yz
lập thành một cấp số nhân là
A.
1a
B.
2a
C.
3a
D.
4a
Câu 14: Tất cả các giá trị thực của tham số m để phương trình
32
3120xmxmx
có ba nghiệm
phân biệt lập thành một cấp số nhân là
A.
3
5
21
m 
B.
3
5
32 1
m 
C.
3
5
32 1
m
D.
3
5
32 1
m
Câu 15: Ba số a, b, c theo thứ tự là số hạng thứ nhất, số hạng thứ hai và số hạng thứ ba của một cấp số
nhân, đồng thời cũng lần lượt là số hạng thứ nhất, số hạng thứ hai và số hạng thứ tư của một cấp số cộng
có công sai bằng 10. Giá trị của a là
A.
5
a
B.
10
3
a
C.
10
a
D.
10
3
a 
Câu 16: Cho ba số
sin
,cos ,tan
6
theo thứ tự lập thành một cấp số nhân, với 0
2
. Khi đó giá
trị
cos 2
bằng
A.
1
2
B.
3
2
C.
3
2
D.
1
2
Câu 17: Cho hình vuông
1
C có cạnh bằng a. Người ta chia mỗi
cạnh của hình vuông thành bốn phần bằng nhau và nối các điểm
chia một cách thích hợp để có hình vuông
2
C
như hình vẽ
Từ hình vuông
2
C
lại tiếp tục làm như trên ta nhận được dãy
các hình vuông
123
, , ,...,
n
CCC C. Gọi
i
S là diện tích của hình
vuông
1, 2,3,...
i
Ci . Đặt
123
... ...
n
TSS S S
Biết
32
3
T
Giá trị của a là
A. 2a B.
5
2
a C. 2a D. 22a
Câu 18: Người ta thiết kế một cái tháp gồm 11 tầng. Diện tích bề mặt trên của mỗi tầng bằng nửa diện
tích mặt trên của tầng ngay bên dưới và diện tích mặt trên của tầng 1 bằng nửa diện tích đế tháp. Biết diện
tích đáy tháp là
2
12288m , diện tích mặt trên cùng bằng
A.
2
8m
B.
2
6m
C.
2
12m
D.
2
10m
Câu 19: Một khu rừng có trữ lượng gỗ là
53
6.10 m . Biết tốc độ sinh trưởng của các cây trong rừng là
4,5% mỗi năm. Hỏi sau 10 năm, khu rừng đó sẽ có bao nhiêu
3
m gỗ (làm tròn đến hàng đơn vị)?
A.
3
931782m B.
3
931781m C.
3
891657m D.
3
891658m
TOANMATH.co
m
Trang 29
Câu 20: Bạn An thả quả bóng cao su từ độ cao 10m theo phương thẳng đứng. Mỗi khi chạm đất nó lại
nảy lên theo phương thẳng đứng với độ cao bằng
3
4
độ cao trước đó. Tổng quãng đường bóng đi được đến
khi bóng dừng hẳn là
A. 40 m B. 70 m C. 50 m D. 80 m
Câu 21: Cho ba số thực dương a, b, c là ba số hạng liên tiếp của một cấp số nhân đồng thời thỏa mãn điều
kiện
222
333
4
abc
abc

. Giá trị của biểu thức
333
111
P
abc

là
A.
4
P
B.
2
P
C.
1
2
P
D.
1
4
P
Câu 22: Cho tam giác ABC cân tại đỉnh A, biết độ dài cạng đáy BC, đường cao AH và cạnh bên AB theo
thứ tự lập thành cấp số nhân với công bội a. Giá trị của
2
q bằng
A.
22
2
B.
22
2
C.
21
2
D.
21
2
Câu 23: Cho bốn số a, b, c, d theo thứ tự đó tạo thành cấp số nhân với công bội khác 1. Biết tổng ba số
hạng đầu bằng
148
9
, đồng thời theo thứ tự đó chúng lần lượt là số hạng thứ nhất, thứ tư và thứ tám của
một cấp số cộng. Giá trị biểu thức
Tabcdlà
A.
101
27
T
B.
100
27
T
C.
100
27
T 
D.
101
27
T 
Câu 24: Tam giác mà ba đỉnh của nó là ba trung điểm ba cạnh của tam giác ABC được gọi là tam giác
trung bình của tam giác ABC. Ta xây dựng dãy các tam giác
111 2 2 2 3 3 3
, , ,...ABC ABC ABC sao cho
111
A
BC là
một tam giác đều cạnh bằng 3 và với mỗi số nguyên dương
2n , tam giác
nnn
A
BC là tam giác trung
bình của tam giác
111nnn
A
BC

. Với mỗi số nguyên dương n, kí hiệu
n
S tương ứng là diện tích hình tròn
ngoại tiếp tam giác
nnn
A
BC . Giá trị tổng
12
...
n
SS S S
A.
15
4
S
B. 4S
C.
9
2
S
D. 5S
Câu 25: Cho hình vuông ABCD có các cạnh bằng a và có diện tích
1
S
Nối 4 trung điểm
111 1
,,,
A
BCD
theo thứ tự của 4 cạnh AB, BC, CD, DA
ta được hình vuông thứ hai có diện tích
2
S . Tiếp tục làm như thế,
ta được hình vuông thứ ba là
222 2
,,,
A
BCD có diện tích
3
S ,...
và cứ tiếp tục làm như thế, ta tính được các hình vuông lần lượt
có diện tích có diện tích
045 10
,...,, SSS (tham khảo hình vẽ bên).
Giá trị tổng có diện tích
1 2 3 100
...SS S S S là
A.

2100
100
21
2
a
S
B.

2100
99
21
2
a
S
C.
2
100
2
a
S
D.
299
98
21
2
a
S
TOANMATH.co
m
Trang 30
Câu 26:
Tổng cấp số nhân lùi vô hạn
n
u có
1
1u và
134
,,uuu theo thứ tự là ba số hạng liên tiếp trong
một cấp số cộng là
A.
51
2
B.
51
2
C.
1
51
D. 2
Câu 27: Với giá trị nào của tham số m thì phương trình
32
680xmx x
có ba nghiệm thực lập thành
một cấp số nhân?
A.
1m
B.
3m 
C.
3m
D.
4m 
Câu 28: Các giá trị m để phương trình
32
21210xxmxm có ba nghiệm lập thành một cấp
số nhân là
A. 1, 3, 4mmm  B. 1, 13, 4mmm 
C.
1, 3, 4mm m D. Không có giá trị của m
ĐÁP ÁN VÀ LỜI GIẢI BẢI TẬP TỰ LUYỆN DẠNG 3
1-B 2-C 3-C 4-C 5-A 6-C 7-B 8-D 9-B 10-C
11-C 12-C 13-C 14-B 15-C 16-D 17-A 18-B 19-A 20-B
21-D 22-C 23-C 24-B 25-B 26-B 27-B 28-D
Câu 1:
Ba số
2;3 3;5 5
x
xx theo thứ tự là ba số hạng liên tiếp của một cấp số nhân nên

2
2
1
25 5 3 3 8 90 9
9
x
xx x x x x
x


(do 1)
x
Với x = 9, suy ra
3.9 3 30 5
2.9 18 3
q

Số hạng tiếp theo của cấp số nhân đó là

5 250
5.9 5 .
33

Câu 2:
Ta có
2
4936 6xx
Câu 3:
Ta có


2
2
6
21836 6
54
6
18 324
54
x
xx
y
x
xy
y






Câu 4:
TOANMATH.co
m
Trang 31
Ta có
22 2
1
4131
3
xx x x
Câu 5:
Vì x, y, z theo thứ tự lập thành một cấp số nhân với công bội q khác 1 nên
2
.; .yxqzxq(1)
Các số x, 2y, 3z theo thứ tự lập thành một cấp số nhân nên
34
x
zy (2)
Thay (1) vào (2) được

22 2
1
3 4 34103410
1
3
q
xxq xqxqq qq
q

Vì
1q nên
1
3
q
Câu 6:
Để ba số ;;
x
ax bx c theo thứ tự lập thành cấp số nhân thì
 
2
2
222 2
22
2
bac
xb xaxc x bxb x acxac bacx acb x
abc


Câu 7:
11
;;
5 125
x

là cấp số nhân khi và chỉ khi
2
11 1
.
5 125 25
xx
Câu 8:
3 số 2; 1;3
x
xxlà cấp số nhân khi và chỉ khi

2
123
x
xx
22 2
21 56 2 370xx xx xx (vô nghiệm)
Vậy không có giá trị x thỏa mãn đề bài
Câu 9:
Gọi m là công sai của cấp số cộng
Khi đó
;2, 3bamca mda m  
Do 1, 1, 3, 9
abc d theo thứ tự lập thành một cấp số nhân nên


2
2
13 1
19 3
ac b
bd c


Thay ; 2 , 3
bamca md a m   vào hệ trên và rút gọn ta được
2
2
1
22
2
4
2
a
am
m
am
m



Thử lại ta thấy chỉ có trường hợp
1, 2am
thỏa mãn
Vậy
23 8ad a m
Câu 10:
TOANMATH.co
m
Trang 32
Ta có
4
1
1
4
1
42
3
1
11
2
1
.45
0; 45
1
45
2; 3
4
0
2; 95
.4.
4
q
u
qu
q
S
qu
uu
q
qu
uq uq
q



 

Câu 11:
43
43
54
3
11
1
21
11
576
..576
576
64 4 3
9
19
.9
uu
uq uq
qq
qqu
uu
q
uq u






Vậy tổng 5 số hạng đầu là
5
51
1
1023
1
q
Su
q

Câu 12:
Ba số
,3,
x
y theo thứ tự lập thành cấp số cộng nên 6xy (1)
Ba số
1, ,
x
y
theo thứ tự lập thành cấp số nhân nên
2
x
y (2)
Từ (1), (2) và
0x suy ra
2
.8
4
x
xy
y


Câu 13:
Giải hệ phương trình ta được
000
359
;2;
66
aa
xyz


Để
000
,,
x
yz theo thứ tự lập thành một cấp số nhân thì
2
00 0
.
x
zy
2
3
35 9
. 4 5 24 117 0
39
66
5
a
aa
aa
a



Do
0a nên 3a
Câu 14:
Giả sử phương trình đã cho có ba nghiệm phân biệt
123
,,
x
xx
Khi đó
123
2xxx . Mà
2
13 2
x
xx
nên
3
2
2x
Do đó ta có
3
3
5
142.3
32 1
mmm
Thử lại với
3
5
32 1
m 
thấy thỏa mãn
Vậy
3
5
32 1
m 
Câu 15:
Theo đề bài ta có
121 41
;10;30aubu u cu u
Theo tính chất cấp số nhân, ta có

2
2
111 1
.10 301010bac u uu u a
Câu 16:
TOANMATH.co
m
Trang 33
Theo giả thiết ta có


 
2
2232
sin
sin 1
.tan cos cos 6. cos cos 1 0 cos
66.cos 2


Từ đó

2
1
cos 2 2 cos 1
2


Câu 17:
Cạnh của hình vuông

2
C là
22
2
31 10
44 4
a
aaa




Do đó diện tích
2
21
55
88
SaS
Cạnh của hình vuông

3
C là
2
22
2
32 2 2
10
31 10
44 4 4
a
aa a a








Do đó diện tích
2
2
32
55
88
SaS




Lý luận tương tự ta có các
123
; ; ;...; ...
n
SSS S tạo thành một dãy cấp số nhân lùi vô hạn có
11
uS và công
bội
5
8
q
Vậy
2
2
1
832
42
133
Sa
Taa
q

(do 0)a
Câu 18:
Ta nhận thấy diện tích các mặt trên của mỗi tầng lập thành 1 cấp số nhân với công bội
1
2
q
Số hạng đầu
1
12288u . Khi đó mặt trên cùng tầng 11 ứng với
12
u
Do đó
11
11
12 1
1
. 1288. 6
2
uuq




Câu 19:
Đặt
5
0
6.10u
và
4,5% 0, 045r 
Gọi
n
u là trữ lượng gỗ của khu rừng sau năm thứ n. Khi đó ta có
1
1,
nn
uu rn

Suy ra
n
u là cấp số nhân với số hạng đầu
0
u và công bội 1qr
Do đó số hạng tổng quát của cấp số nhân
n
u là

0
1
n
n
uu r
Sau 10 năm, khu rừng đó sẽ có

10
10 5 3 3
10 0
. 6.10 . 1 0,045 931781,653 931782uuq m m gỗ
Câu 20:
Các quãng đường khi bóng đi xuống tạo thành một cấp số nhân lùi vô hạn có
1
10u
và
3
4
q
TOANMATH.co
m
Trang 34
Tổng các quãng đường khi bóng đi xuống là
1
10
40
3
1
1
4
u
S
q

Tổng quãng đường bóng đi được (cả lên và xuống) đến khi bóng dừng hẳn là 2 10 80 10 70( )Sm
Câu 21:
Ta có
222 3 3 3
333 222 22 22 22
1
4
4
abc a b c a b c
a b c abc bc ca ab



Mặt khác a, b, c là ba số hạng liên tiếp của một cấp số nhân nên
2
ac b
Do đó
22 2 2 22 3 4 3 3 3 3
11111
44
abcabc
P
bc ca ab ac b ac a b c

Câu 22:
Đặt
;;BC a AB AC b AH h
. Theo giả thiết ta có a, h, b lập thành cấp số nhân, suy ra
2
hab
Mặt khác, tam giác ABC cân tại đỉnh A nên
22 2
22
24
a
bb a
hm

Do đó

22 2
22
440 222
24
bb a
ab a ab b a b

Lại có
2
bqa nên
2
122221
42
22 2
b
q
a


Câu 23:
Ta có
2
2
148
9
ac b
bd c
abc



1
2
3
Cấp số cộng có
148
,,uaubuc. Gọi x là công sai của cấp số cộng. Vì cấp số nhân có công bội khác
1 nên
0x
Ta có
3
7
ba x
ca x


(4)
Từ (1) và (4) suy ra

2
2
73 90aa x a x ax x 
Do
0x nên 9ax
Từ (3) và (4), suy ra
148
310
9
ax
TOANMATH.co
m
Trang 35
Do đó
16
3
4
64
4
9
9
256
27
b
a
c
x
d







Vậy
100
27
Tabcd

Câu 24:
Vì dãy các tam giác
111 2 2 2 3 3 3
, , ,...ABC A BC ABC là các tam giác đều nên bán kính đường tròn ngoại tiếp các
tam giác bằng cạnh nhân
3
3
Với n = 1 thì tam giác đều
111
A
BC
có cạnh bằng 3 nên đường tròn ngoại tiếp tam giác
111
A
BC
có bán kính
2
11
33
3. . 3.
33
RS





Với n = 2 thì tam giác đều
222
A
BC có cạnh bằng
3
2
nên đường tròn ngoại tiếp tam giác
222
A
BC có bán
kính
2
22
13 13
3. . . 3. .
23 23
RS





Với n = 3 thì tam giác đều
333
A
BC có cạnh bằng
3
4
nên đường tròn ngoại tiếp tam giác
333
A
BC có bán
kính
2
33
13 13
3. . . 3. .
43 43
RS





...............................................................................
Như vậy tam giác đều
nnn
A
BC có cạnh bằng
1
1
3.
2
n



nên đường tròn ngoại tiếp tam giác
nnn
A
BC có bán
kính
2
11
13 13
3. . . 3. .
23 23
nn
nn
RS


 


 

 

Khi đó ta được dãy
123
; ; ;...; ...
n
SSS S là một cấp số nhân lùi vô hạn với số hạng đầu
11
3uS
 và công
bội
1
4
q
Do đó tổng
1
12
... ... 4
1
n
u
SS S S
q

Câu 25:
Ta có
222
12 3
11
; ; ,...
24
SaS aS a
TOANMATH.co
m
Trang 36
Do đó
123 100
, , ,...,SS S S
là cấp số nhân với số hạng đầu
2
11
uSa
và công bội
1
2
q
Suy ra
2100
123 100 1
99
21
1
... .
12
n
a
q
SS S S S S
q

Câu 26:
n
u là cấp số nhân lùi vô hạn có công bội q, suy ra 1q và
22 33
31 41
.;.uuq quuqq
Mà và
134
,,uuu theo thứ tự là ba số hạng liên tiếp trong một cấp số cộng nên
14 3
2.uu u
Từ đó ta có
3232 2 2
12. 2.10 1 10 10qqqq qqq qq  
15
15
2
2
15
2
q
q
q

(vì
1q )
Vậy
1
1251
12
1515
1
2
u
S
q


Câu 27:
Ta chứng minh nếu
123
;;
x
xx
là nghiệm của phương trình
32
680xmx x
thì
123
123
8
x
xxm
xxx

Thật vậy
32
123
68
x
mx x x x x x x x

123
32 3 2
123 122331 123
123
68
8
x
xxm
xmx x x xxxx xxxxxxxxxx
xxx

 
Điều kiện cần: Phương trình
32
680xmx xcó ba nghiệm thực
123
x
xx lập thành một cấp số
nhân
233
13 2 123 2 2 2
...8 2xx x xxx x x x
Vậy phương trình
32
680xmx xphải có nghiệm bằng 2
Thay
2x vào phương trình ta có 3m 
Điều kiện đủ: Thử lại với
3m  ta có
32
4
3680 2
1
x
xxx x
x



(thỏa yêu cầu bài toán)
Câu 28:
Giả sử phương trình có ba nghiệm phân biệt lập thành cấp số nhân
Khi đó
2
13 2
123 2
12 23 31
1
2
2
1
xx x
m
xxx x
xx xx xx m


Thay vào phương trình ta được 1, 3, 4mmm 
TOANMATH.co
m
Trang 37
Thay từng giá trị của m vào phương trình ta thấy không có giá trị nào của m thỏa mãn yêu cầu bài toán
| 1/37
| | Tải xuống

Có thể bạn quan tâm:

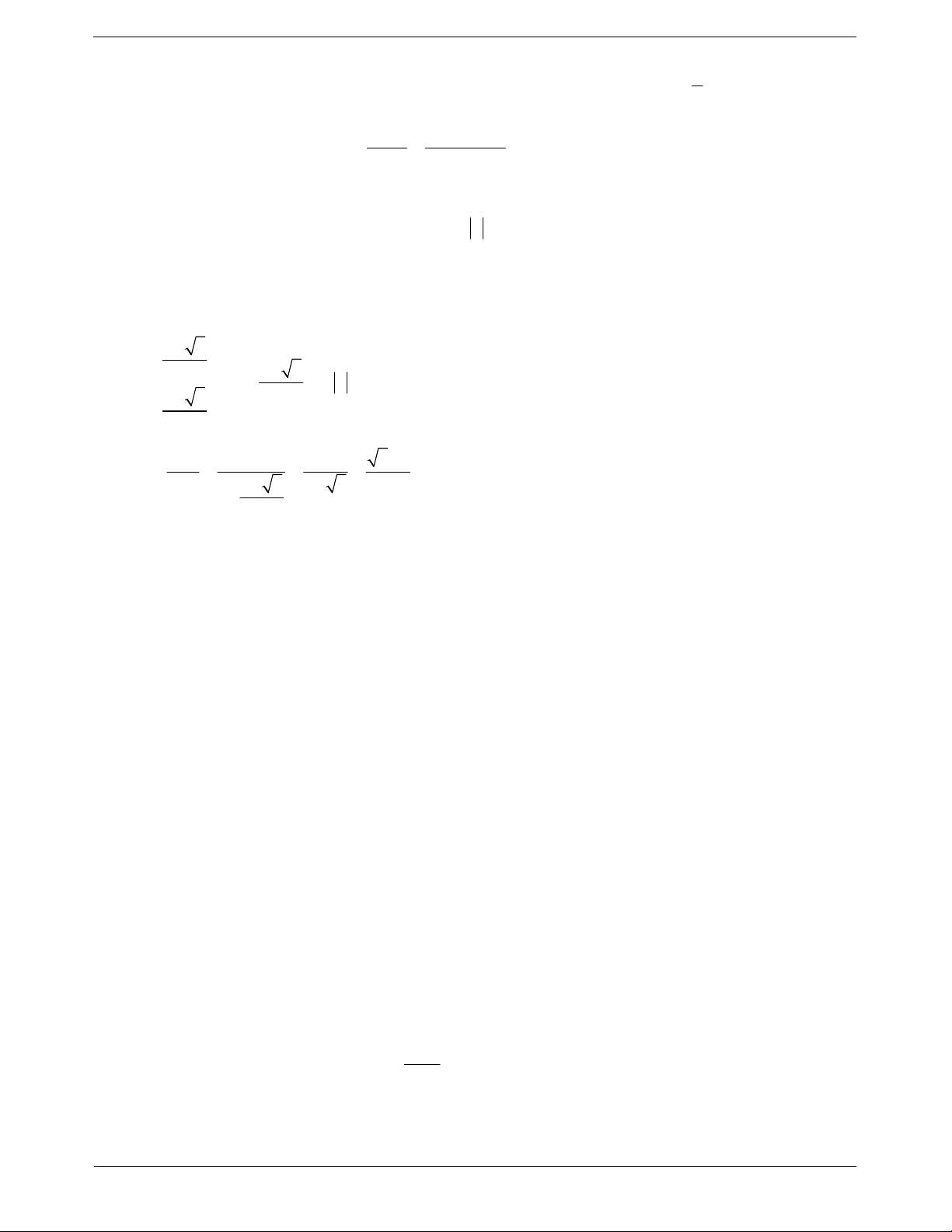
Preview text:

CHUYÊN ĐỀ
BÀI GIẢNG CẤP SỐ NHÂN Mục tiêu Kiến thức
+ Nắm vững khái niệm cấp số nhân
+ Nắm được tính chất 3 số hạng liên tiếp của một cấp số nhân
+ Nắm được công thức tổng quát, công thức tính tổng n số hạng đầu của một cấp số nhân  Kĩ năng
+ Nhận biết được một cấp số nhân dựa vào định nghĩa
+ Tìm được yếu tố còn lại khi biết 3 trong 5 yếu tố: số hạng đầu, số hạng thứ k, tổng n số hạng
đầu tiên, công bội, số số hạng của cấp số nhân
+ Áp dụng tính chất cấp số nhân vào các bài toán giải phương trình, chứng minh đẳng thức, bất đẳng thức
+ ứng dụng vào các bài toán thực tế Trang 1
I. LÍ THUYẾT TRỌNG TÂM Định nghĩa
Cấp số nhân là một dãy sô (hữu hạn hoặc vô hạn), trong đó kể từ số hạng thứ hai, mỗi số hạng đều là tích
của số hạng đứng ngay trước nó với một số không đổi q
Số q được gọi là công bội của cấp số nhân
Nếu u là cấp số nhân với công bội q, ta có công thức truy hồi u u .q với * n   n n 1  n Đặc biệt:
 Khi q  0 , cấp số nhân có dạng u ,0,0,...,0,... 1
 Khi q 1, cấp số nhân có dạng u ,u ,u ,...,u ,... 1 1 1 1
 Khi u  0 thì với mọi q, cấp số nhân có dạng 0,0,0,...,0,... 1
Số hạng tổng quát
Định lí 1. Nếu cấp số nhân có số hạng đầu u và công bội q thì số hạng tổng quát u được xác định bởi 1 n công thức 1 u u . n q   với n  2 n 1 Tính chất
Định lí 2. Trong một cấp số nhân, bình phương của mỗi số hạng (trừ số hạng đầu và cuối) đều là tích của
hai số hạng đứng kề với nó, nghĩa là 2
u u .u với k  2 k k 1  k 1 
Tổng n số hạng đầu tiên của cấp số nhân
Định lí 3. Cho cấp số nhân u với công bội q  1 n u 1 nq 1  
Đặt S u u  ...  u . Khi đó S n 1 2 n n 1 q Chú ý: Nếu 1
q  thì cấp số nhân là u ,u ,u ,...,u ,... khi đó S nu 1 1 1 1 n 1
SƠ ĐỒ HỆ THỐNG HÓA TOANMATH.com Trang 2
Số hạng tổng quát Số hạng thứ k 2 1 u u . n q   CẤP SỐ NHÂN
u u .u k k 1  k 1  n 1
u u .q k  2 n  2 n n 1    Tổng n số h ạng đầu tiên S nu khi q  1 n 1 u 1 nq 1   S  khi q  1 n 1 q
II. CÁC DẠNG BÀI TẬP
Dạng 1: Chứng minh một dãy u là cấp số nhân n Phương pháp giải Chứng minh u
u .q, n
 1 trong đó q là một số không đổi n 1  n u Nếu * u  0, n
   thì ta lập tỉ số n 1  k n un
* k là hằng số thì u là cấp số nhân có công bội q k n
* k phụ thuộc vào n thì u không là cấp số nhân n
Để chứng minh dãy u không phải là cấp số nhân, ta chỉ cần chỉ ra ba số hạng liên tiếp không n u u
tạo thành cấp số nhân, chẳng hạn 3 2  u u 2 1
Để chứng minh a, b, c theo thứ tự đó lập thành cấp số nhân, ta chứng minh 2
ac b hoặc b ac Ví dụ mẫu
Ví dụ 1. Xét trong các dãy số sau, dãy số nào là cấp số nhân? Tìm công bội của cấp số nhân đó a) u  2 1 4 n   b) u    n  n 3n 1 7 .5 n Hướng dẫn giải TOANMATH.com Trang 3 un  42n 3 a) Ta có   4 
16 là số không đổi nên u là cấp số nhân với công bội q = 16 n  2n 1   2 1 un  4  u 7 n  .5 n  n 1    1 3 1 1 b) Ta có 3   7.5   875 
không đổi nên u là cấp số nhân với công bội n u   n  7n 3n 1 .5 q  875 
Ví dụ 2. Xét trong các dãy số sau, dãy số nào là cấp số nhân? Tìm công bội của cấp số nhân đó  u  3 1   u  2 a)  9 b) 1  u  2 uu n 1   u   n 1  n n Hướng dẫn giải 9 u u u Ta có n 1  n n 1   
u u , n   2 n 1  n 1 u 9 un n un 1
u u u  ...  u ...   1 Do đó có 1 3 5 2n 1  
u u u  ...  u  ...  2 2 4 6 2n 9
Theo đề bài ta có u  3  u   3 (3) 1 2 u1
Từ (1), (2), (3) suy ra u u u u u  ...  u u ... 1 2 3 4 5 2n 2n 1 
Do đó u là cấp số nhân với công bội q = 1 n  b) Ta có 2 2 2
u u  4,u u  16,u u  256 2 1 3 2 4 3 u 4 u 256 u u suy ra 2   2 và 4 2 4  16   u 2 u 16 u u 1 3 1 3
Do đó u không là cấp số nhân n
Ví dụ 3. Cho u là cấp số nhân có công bội q  0;u  0 . Chứng minh rằng dãy số v với n n  1
v u .u cũng là một cấp số nhân n n 2n Hướng dẫn giải n 1  2n 1 v u .u
u .q .u .q  Ta có n n 2n 1 1 3  
q nên v là cấp số nhân với công bội là 3 q n n2 2n3 v u .u
u .q .u .q n 1  n 1  2n  1 1 1  u  2
Ví dụ 4. Cho dãy số u được xác định bởi 1  , n
 1. Chứng minh rằng dãy số v xác n n u  4u  9  n 1 n định bởi 3
v u  , n
 1 là một cấp số nhân. Hãy xác định số hạng đầu và công bội của cấp số nhân n n đó TOANMATH.com Trang 4 Hướng dẫn giải
Ta có v u  3 (1)  vu  3 (2) n n n 1  n 1  Theo đề ra u
 4u  9  u  3  4 u  3 (3) n 1  n n 1   n v
Thay (1) và (2) vào (3) ta được n 1 v  4v , n   1    4 (không đổi) n 1  n vn
Suy ra v là cấp số nhân với công bội q = 4 và số hạng đầu v u  3  5 n  1 1
Bài tập tự luyện dạng 1
Câu 1: Trong các dãy số sau, dãy số nào là cấp số nhân?  1 u  u  2 A. 1  2 . B. unu . C. 1 . D. uu  3 . n 1  nu  5  u n 1  n 1  2 u u   n 1  n n 1  n
Câu 2: Trong các dãy số sau, dãy số nào là cấp số nhân? 1 1 1 1 A. u  1. B. u
. C. u n  . D. 2 u n  . n 3n n n2 3 n 3 n 3
Câu 3: Trong các dãy số sau, dãy số nào là cấp số nhân? u   3 u   1 A. 1  . B. uu . C. 1  . D. u  2u  3. 3 uu n 1  n n 1  nu  6u n 1  nn 1 n
Câu 4: Dãy số nào sau đây là cấp số nhân? 1
A. u n  2 . B. 2
u n  2 . C. 2
u  3 n . D. 2 u n 1. n 3 n n n
Câu 5: Trong các dãy số sau, dãy nào là cấp số nhân? 1 1 1 1 A. u   4. B. u
. C. u  2n  . D. 2 u n  . n 3n n n2 5 n 3 n 3
Câu 6: Dãy số nào trong các dãy số sau vừa là một cấp số cộng, vừa là một cấp số nhân? A. 1; 1;  1;  1  ; 1;
 ... B. 1;0;0;0;0;... C. 3;2;1;0; 1
 ;... D. 1;1;1;1;1;...
Câu 7: Cho cấp số nhân có u  0 và công bội 0
q  . Trong các nhận xét sau, nhận xét nào đúng? 1
A. u  0 với mọi n.
B. u  0 với mọi n lẻ và u  0 với mọi n chẵn. n n n
C. u  0 với mọi n.
D. u  0 với mọi n chẵn và u  0 với mọi n lẻ. n n n 1 1 1 1 Câu 8: Hỏi , , ,
là bốn số hạng đầu của dãy số nào sau đây? 2 4 8 32 1 1 1 1 A. u  . B. u  . C. u  . D. u  . n 2n n 2n 1 n 2n n 2 n
Câu 9: Dãy số nào dưới đây không là cấp số nhân? 1 1 1 1 1 1 A. 1;   ; ; 
. B.  ;  ;  ;1. 5 25 125 8 4 2 1 1 1 C. 4 4 4 4 2; 2 2;4 2;8 2 . D. 1; ; ; . 3 9 27 TOANMATH.com Trang 5
Câu 10: Trong các dãy số sau, dãy nào là cấp số nhân? u   2 1  2n  3 n 1
A. u  2n 1. B. . C. u  . D. u  . n  1 uu n n  5 n 1 n 1   3 n
Câu 11: Trong các dãy số sau, dãy nào là cấp số nhân?  1  1 u   u   u  1;u  2 A. 1  2 . B. 1  2 . C. 2
u n 1. D. 1 2 . n     2 u u .u uu   u   2.un 1 n 1  n n 1  nn 1 n
Câu 12: Trong các dãy số sau, dãy nào là cấp số nhân? 1 1 1 A. u  . B. u  
. C. u   2n . D. 3 u n 1. n 3n 1 n n2 3 n 3 n
Câu 13: Cho dãy số u là một cấp số nhân với u 0, n  
  . Dãy số nào sau đây không phải là cấp số n n nhân? 1 1 1
A. u ;u ;u ;... B. 3u ;3u ;3u ;... C. ; ;
;... D. u 1;u 1;u 1;... 1 3 5 1 2 3 u u u 1 2 3 1 2 3
Câu 14: Cho dãy số u được xác định bởi u  2;u  2u  3n 1. Công thức số hạng tổng quát của n  1 n n 1 
dãy số đã cho là biểu thức có dạng .2n a
bn c , với a, b, c là các số nguyên với n  2;n   . Khi đó
tổng a + b + c có giá trị bằng A. – 4 . B.
4. C. – 3 . D. 3.
Câu 15: Cho dãy số u có các số hạng đầu là 5, 10, 15, 20, 25,… Số hạng tổng quát của dãy là n A. 5(
u n 1) . B. u  5n . C. u  5  n . D. u  5n 1. n n n n
ĐÁP ÁN VÀ LỜI GIẢI BẢI TẬP TỰ LUYỆN DẠNG 1
1-C 2-B 3-C 4-C 5-B 6-D 7-B 8-C 9-B 10-B 11-B 12-B 13-D 14-C 15-B Câu 1:u  2 u Ta có 1 n 1     5
  u là cấp số nhân có số hạng đầu u  2 và công bội 5 q   n u  5  u  1  u n 1 n n Câu 2: 1 1 Xét u   u n n2 n 1  n 1 3 3  u 1 1 1 Ta có n 1  *  :  ,  n 1  n2 u 3 3 3 n 1
Vậy u là cấp số nhân có công bội q n  3 Câu 3: TOANMATH.com Trang 6 u Xét n 1
  6 nên u là cấp số nhân có công bội q  6 n un Câu 4: 2 u 3 n Vì n 2   3  9 nên 2
u  3 n là cấp số nhân có công bội q  9 2n2 u 3 n n 1  Câu 5: 1 n2 u 1 1 1 Vì n 5   nên u
là cấp số nhân có công bội q u 1 5 n n2 5 5 n 1  n3 5 Câu 6:
Dãy số 1; 1; 1; 1; 1;… vừa là cấp số cộng công sai là 0, số hạng đầu là 1 vừa là cấp số nhân số hạng đầu là 1, công bội là 1 Câu 7: Vì 2
u  0;q  0  u u .q  0;u u .q  0 1 2 1 3 1 Hay 2n 1  2
u u .q  0;uu . n q  0 2n 1 2n 1  1 Câu 8: 1 1
Xét cấp số nhân u với u  , q n  1 2 2 n 1  n 1  1  1 Ta có 1
u u .q  .  n 1   2  2  2n Câu 9: 1 1 1 2  1  1
Dãy  ;  ;  ;1 có    .1  
nên không là cấp số nhân 8 4 2  2  4 Câu 10:u  2 1  u 1 1 Dãy số n 1  1  
 là cấp số nhân với u  2,q uu u 3 1  3 n 1   3 n n Câu 11:  1 u   u Dãy số 1  2 có n 1
   2 nên là một cấp số nhân với công bội là q   2 u u    2.un n 1  n Câu 12: 1 u  1   1  1 Ta có n u      :   n n2  n2   n3  3 u  3   3  3 n 1  TOANMATH.com Trang 7 1 1 Suy ra u  
là một cấp số nhân với công bội là q n n2 3 3 Câu 13:
Dãy u ;u ;u ;... là cấp số nhân công bội 2 q 1 3 5
Dãy 3u ;3u ;3u ;... là cấp số nhân công bội 3q 1 2 3 1 1 1 1 Dãy ; ;
;... là cấp số nhân công bội u u u q 1 2 3
Dãy u 1;u 1;u 1;... không phải là cấp số nhân 1 2 3 Câu 14: Ta có u  2u
 3n 1  u  3n  5  2 u  3 n 1  5 n n   n n 1  nn 1    với 2; Đặt 3
v u n  5 , ta có v  2v với n  2; n   n n n n 1 
Như vậy v là cấp số nhân với công bội q = 2 và v 10 n  1 Do đó n 1 v 10.2    5.2n n
Suy ra u  3n  5  5.2n hay u  5.2n  3n  5 với 2
n  ; n   n n
Vậy a  5,b  3  ,c  5
 nên a b c  5   3     5    3  Câu 15:
Ta có u  5;u  10  5.2;u  15  5.3;...  u  5.n 1 2 3 n
Dạng 2: Xác định số hạng đầu, số hạng thứ k, công bội, tổng n số hạng đầu tiên của cấp số nhân Phương pháp giải
Dựa vào giả thuyết, ta lập một hệ phương trình chứa công bội q và số hạng đầu u . Giải hệ phương 1
trình này tìm được q và u 1
Nếu cấp số nhân u có số hạng đầu u và công bội q thì số hạng tổng quát u được xác định bởi n  1 n công thức n 1 u u .q   n  2 n 1  
Tổng của n số hạng đầu tiên  S nu n 1  khi q  1 u 1 nq  1   S   khi q  1 n  1 q Ví dụ mẫu
Ví dụ 1. Tìm số hạng đầu và công bội của cấp số nhân, biết
u u  51  u  6 a) 1 5  b) 2  u u  102  S  43 2 6  3 Hướng dẫn giải TOANMATH.com Trang 8  Sử dụng công thức u u  51
u u .q  51  u   4 4 1 q  51 1  * 1 5 1 1   a) Ta có      5 u u  102 1 
u q u q  102  uq u u . k q     4 1 q  102 ** 2 6 1 1 k 1 1    Đưa hệ phương trình u q  4 1 q 1  102
Chia từng vế của (**) cho (*) ta được  về hệ phương trình u  4 1 q 51 1  hai ẩn q và u 1 51 51
q  2  u    3 1 4 1 q 17 Vậy u  3và q = 2 1  u q  6 1  u  6  u q  6   Sử dụng công thức 1 * 2   b) 3    1 q   S  43 u  43
u 1 q q  43 **  1  u u . k q   1   2 3 1     1 q k 1 Và u q 6
chia từng vế của (*) cho (**) ta được  n u  1 2 1 q q 43 1 q 1  S u . , q  1 n 1 1 qq  6 Đưa hệ phương trình 43q 6 2 1 q q  2 6q 37q 6 0           1  q   về hệ phương trình 6 hai ẩn q và u
 Với q  6  u 1 1 1  1
Với q   u  36 1 6  1 q  6  q  Vậy  hoặc  6 u  1  1 u   36  1
Ví dụ 2. Cho cấp số nhân u có công bội nguyên và các số hạng thỏa Sử dụng công thức n  1 u u . k q  
u u  10 k 1 mãn 2 4 
u u u  21   Đưa hệ phương trình 1 3 5
a) Tìm số hạng đầu và công bội của cấp số nhân về hệ phương trình
b) Tổng của bao nhiêu số hạng đầu tiện bằng 1365? hai ẩn q và u 1
c) Số 4096 là số hạng thứ mấy của cấp số nhân? a) Ta có  .  .  10  u   3 3 q q u q u q   51 2 4 1 1 q q 2  1 1 1      2 4
u u q u .q  2  1  u   2 4
1 q q  2  1 q q 10 1 1 1 1  3  1   1  4 3 2 2
 10q  21q 10q  21q 10  0  10 q   21 q  10  0  2     q   q  1 1 Đặt 2 2
q   t t  2  q  . Ta có phương trình 2 q q TOANMATH.com Trang 9  5  t    2 t   2 2 10
2  21t 10  0  10t  21t 10  0   2  t   5  q  2   5 1 5 Với 2 t q 2q 5q 2 0             1 2 q 2 q    2
Mà q nguyên nên q  2   2 1 2 Với 2
t   q    5q  2q  5  0 (vô nghiệm) 5 q 5 10 Ta có q  2   u   1  1 3 q q Vậy q  2;  u  1  1 1 nq
b) Ta có S  1365  u . 1365 n 1 1 q n   1 2   1 .
1365  2n  4096  n  12 1 2
Vậy tổng của 12 số hạng đầu tiên bằng 1365 c) Ta có u 4096 u . k q 4096           k  1 2k 1 1 4096 1 k 1  k 1  12
 2  4096  2  2  k 1 12  k 13
Vậy số 4096 là số hạng thứ 13 của cấp số nhân
Ví dụ 3. Tính các tổng sau 1 1 1 1 a) S    ... n 2 3 2 2 2 2n 2 2 2  1   1   n 1  b) S  3   9   ... 3  n        3   9   3n Hướng dẫn giải 1 1 1 1 1 a) Ta có dãy số ; ; ;...;
là một cấp số nhân với n số hạng, số hạng đầu u  và công bội 2 3 2 2 2 2n 1 2 1 2 1 2 q   1 2 2  1 n  1 1 n q 1     2  1
Do đó S u .  . 1 n 1 1 q 2 1 2n 1 2 TOANMATH.com Trang 10 2 2 2  1   1   n 1  b) S  3   9   ... 3  n        3   9   3n  1 1 n 1 2 4 2  3  2   3  2  ... 3  2  2 4 2 3 3 3 nn  1 1 1 2 4 2 
 3  3  ... 3    ...  2  2  2  ... 2  2 4 2   3 3
3 n   n soá 2 4 3 Dãy số 2 4 2
3 ;3 ;...;3 n là cấp số nhân với n số hạng, có số hạng đầu 2
u  3 và công bội q   9 1 2 3 1 nq 1 9n 9
Do đó S u .  9.  9n 1 1 1   1 q 1 9 8 1 1 1 1 1 Dãy số  ...
là cấp số nhân với n số hạng, số hạng đầu u  và công bội q  2 4 2 3 3 3 n 1 2 3 9 1 n 1 1 q 1 1  1  9n n 1 Do đó 9 S u .  .  1  2 1   1 q 9 1 8  9n  8.9n 1 9 n n 1  9 9n    n 1 9 1 9 1 Vậy S     n   n n 9     1 2 2 8 8.9n 8.9n
Ví dụ 4. Tính tổng sau a) 1
S  11111 ...111...1 b)
S  6  66  666  ...  666...6 n  n  n soá 1 n soá 6 Hướng dẫn giải 1  
a) Ta có S  111111 ...111...1  
9  99  999 ... 999...9 n   9 n soá 1  n soá 9  1  10 1 2 10   1   3 10   1  ...  10n      1 9 1      2 3
10 10 10  ...10n  11...1   9   n soá 1  1   n    n 1 10 1 10 10   9n 10    n  9  110  81   n 1
10   9n   1 1 Vậy S n 81 6  
b) S  6  66  666  ... 666...6  
9  99  999 ... 999...9 n   9 n soá 6  n soá 9 
2 10 1 100 1 1000 1 ...  10n           1 3 TOANMATH.com Trang 11 2 2  10n   n n 1 20 n 2 2 3  10
 10 10 ...10  n  10.  n      10  1 3 3  10 1  27 3 20 n n 2 Vậy S    n 10 1 27 3
Bài tập tự luyện dạng 2 1 
Câu 1: Cho các cấp số nhân với u  ;u  3
 2 .Công bội của cấp số nhân là 1 7 2 1 A.  . B. 4  . C. 2  . D. 1  . 2 3
Câu 2: Cấp số nhân u có u  .2n . Số hạng đầu tiên và công bội của cấp số nhân là n n 5 6 6 6 6
A. u  , q  3 . B. u  , q  2
 . C. u  ,q  2 . D. u  ,q  5 . 1 5 1 5 1 5 1 5 1  1
Câu 3: Cho cấp số nhân có u  1;  q  . Số
là số hạng thứ bao nhiêu của cấp số nhân? 1 10 103 10
A. Số hạng thứ 103. B. Số hạng thứ 104. C. Số hạng thứ 105. D. Số hạng thứ 106.
Câu 4. Cho các khẳng định sau
1. Tồn tại một cấp số nhân u có u  0 và u  0 n  5 75
2. Nếu các số thực a, b, c theo thứ tự đó lập thành một cấp số cộng có công sai khác 0 thì các số 2 2 2
a ,b , c theo thứ tự đó cũng lập thành một cấp số cộng
3. Nếu các số thực a, b, c theo thứ tự đó lập thành một cấp số nhân thì các số 2 2 2
a ,b , c theo thứ tự đó
cũng lập thành một cấp số nhân
Số khẳng địn đúng là
A. 1 B. 2 C. 3 D. 0
Câu 5: Cho cấp số nhân có u  1
 ,u  0,00001. Khi đó công bội q và số hạng tổng quát u là 1 6 n 1 1  1  1  1 1    1 n A. q  ,u B. n 1 q  ,u  1
 0  C. q  ,u D. q  ,u n n 1 10 10  10 n n n 1 10 10  n n 1 10 10 
Câu 6: Cho cấp số nhân 2;  4; 8
 ;... Tổng n số hạng đầu tiên của cấp số nhân là 2  1  2  n   2  1 2n      2 2 1 2 n      2 2 1 2 n   A.   B.   C.   D.   1  2   1 2 1  2   1 2
Câu 7: Cho cấp số nhân biết u  1;q  2 . Số hạng thứ 11 là 1
A. 20 B. 1024 C. 22 D. 2008
Câu 8: Nếu cấp số nhân u có u  3và công bội 3
q  thì giá trị u là n  1 7 A. 6 3 B. 7 3 C. 21 D. 8 3 3
Câu 9: Cấp số nhân u có u  .2n . Số hạng đầu tiên và công bội q là n n 5 TOANMATH.com Trang 12 6 6 6 6
A. u  , q  3 B. u  , q  2
C. u  ,q  2 D. u  ,q  5 1 5 1 5 1 5 1 5 1
Câu 10: Cho cấp số nhân có u  ,u  16 . Công bội và số hạng đầu tiên của cấp số nhân là 2 5 4 1 1 1 1 1 1
A. q  ;u  , B. q   ;u   , C. q  4;u  , D. q  4;  u   , 1 2 2 1 2 2 1 16 1 16
Câu 11: Cho cấp số nhân với u  3, q  2
 . Số 192 là số hạng thứ mấy của cấp số nhân? 1
A. u B. u C. u D. Không thuộc cấp số trên 7 6 8
Câu 12: Tổng 10 số hạng đầu của một cấp số nhân có u  4,u  2048là 1 10
A. S  8184 B. S  4092 C. S  12276 D. S  6138 10 10 10 10
Câu 13: Cho cấp số nhân với u  4, q  4
 . Ba số tiếp theo của cấp số nhân là 1 A. 1  6;64; 256  B. 16  ; 6  4; 256 
C. 16;64; 256 D. 16  ;64;256 1  n 1 
Câu 14: Cho dãy số xác định bởi * u  1,u  2u
; n   . Khi đó u bằng 1 n 1   n 2  3 
n  3n  2  2018 2016 2 1 2018 2 1 2017 2 1 2017 2 1 A. u   B. u   C. u   D. u   2018 2017 3 2019 2018 2017 3 2019 2018 2018 3 2019 2018 2018 3 2019 Câu 15: Cho 2 3 3.2 3.2 ... 3.2n S     
. Khẳng định nào sau đây đúng với mọi n nguyên dương? A. 32n S    1 B. Sn 1 3 2     1 C. Sn 1 3 2     1 D. Sn 1 3 2     1
Câu 16: Cho một cấp số nhân biết u  3, q  2 . Tổng của 10 số hạng đầu tiên của cấp số nhân là 1 A.  9 3. 1 2  B.  10
3. 1 2  C.   9 3. 2   1 D.  10 3. 2   1
Câu 17: Cho cấp số nhân u , biết u 1,u
 1000 . Tổng 10 số hạng đầu tiên của cấp số nhân n  2017 2020 bằng 10 10 1 10 9 1 10 110 10 10 1 A. B. C. D. 2016 9.10 2016 8.9 2016 9.10 2019 9.10 Câu 18: Tổng 2 3 100
1 2  2  2  ... 2 bằng A. 100 1 2 B. 100 2 1 C. 101 1 2 D. 101 2 1
Câu 19: Cấp số nhân 5; 10; …; 1280 có bao nhiêu số hạng?
A. 9 B. 7 C. 8 D. 10
Câu 20: Số hạng thứ 5 của cấp số nhân 2; 6; … là
A. 48 B. 486 C. 81 D. 162
Câu 21: Cho cấp số nhân có u  1, q  3 . Số hạng thứ 9 của cấp số nhân là 1
A. 6561 B. 19683 C. 2187 D. 729 2  1 n
Câu 22: Dãy số có số hạng tổng quát u
là một cấp số nhân có công bội q bằng n    3  1 1 1 A.
B. 3 C. D. 3 9 3 TOANMATH.com Trang 13 1 1 1 n   Câu 23: Tổng  ...  ...   bằng 4 16  4  1 2 1 2
A. B. C. D. 2 9 3 3 n 1 1   
Câu 24: Cho cấp số nhân lùi vô hạn u với u  
. Tổng của cấp số nhân đó là n n    3  1 1 1 1
A. B. C. D. 6 4 12 12 1 1 1
Câu 25: Tổng S  1    ... có giá trị 2 4 8
A. 1 B. 2 C. 4 D. 
u u u  31
Câu 26: Cho cấp số nhân u biết 1 2 3
. Giá trị u và q là n
u u  26  1 1 3 1 1
A. u  2; q  5 hoặc u  25;q B. u  5; q  1 hoặc u  25;q 1 1 5 1 1 5 1 1
C. u  25; q  5 hoặc u  1;q D. u  1;q  5 hoặc u  25;q  1 1 5 1 1 5 6
Câu 27: Cấp số nhân u có u  .2n . Số hạng đầu tiên và công bội q là n n 5 6 6 12 12
A. u  , q  2 B. u  , q  2  C. u
, q  2 D. u  , q  5 1 5 1 5 1 5 1 5
Câu 28: Cho cấp số nhân u có u  2
 và u  54 . Khi đó tổng 1000 số hạng đầu tiên của cấp số nhân n  2 5 đó bằng 1000 1 3 1000 3 1 1000 3 1 1000 3 1 A. B. C. D. 4 2 6 3
u u  36
Câu 29: Số hạng đầu và công bội của cấp số nhân thỏa mãn 5 2  là u u  48  6 4
A. u  4, q  4 B. u  2, q  4 C. u  2, q  2 D. u  4, q  2 1 1 1 1 Câu 30: Tổng 2 3 4
S  1 2  2  2  2 là một số chia hết cho
A. 21 B. 41 C. 51 D. 31
Câu 31: Cho cấp số nhân u có u  24 và u  48 . Tổng năm số hạng đầu tiên của cấp số nhân đó bằng n  3 4
A. 168 B. 186 C. – 186 D. 196 1
Câu 32: Cho cấp số nhân với u  3, q   . Số 222 là số hạng thứ mấy của cấp số nhân? 1 2
A. Số hạng thứ 11
B. Số hạng thứ 9
C. Số hạng thứ 12
D. Không thuộc cấp số nhân
u u  54
Câu 33: Cho cấp số nhân có 4 2 
. Số hạng đầu tiên u và công bội q của cấp số nhân là u u  108  1 5 3 TOANMATH.com Trang 14
A. u  9 và q  2 B. u  9 và q  2  C. u  9
 và q  2 D. u  9  và q  2 1 1 1 1
u u  54
Câu 34: Cho cấp số nhân có 4 2 
. Giá trị u và q của cấp số nhân là u u  108  1 5 3 A. u  9 và 2
q B. u  9 và 2
q   C. u  9  và 2
q D. u  9  và 2 q   1 1 1 1
Câu 35: Cho cấp số nhân có u  3; q  2
 . Số 192 là số hạng thứ bao nhiêu của cấp số nhân? 1
A. Số hạng thứ 5 B. Số hạng thứ 6 C. Số hạng thứ 7 D. Số hạng thứ 8
u u  3
Câu 36: Cho cấp số nhân u có công bội 1 q  và 1 3
. Tổng 10 số hạng đầu tien của cấp số n   2 2 u u  5  1 3 nhân là 312  2 A. S
B. S  31 1 2 C. S  31 2 1 D. S  31 2 1 10   10   10   10 16 3n 1
Câu 37: Cho cấp số nhân u có tổng n số hạng đầu tiên là S
. Số hạng thứ 5 của cấp số nhân là n n n 1 3  2 1 5 A. u B. u C. 5
u  3 D. u  5 4 3 5 5 3 5 5 5 3
Câu 38: Cho cấp số nhân có u  1
 ;u  0.00001. Khi đó công bội q và số hạng tổng quát là 1 6 1 1  1 1 1 1   1 n A. q  ,u B. n 1 q ,u 10      C. q   ,u D. q   ,u n n 1 10 10  10 n n n 1 10 10  n n 1 10 10  1 n 1 u u u
Câu 39: Cho dãy số u xác định bởi u  và u  .u . Giá trị tổng 2 3 10 S u   ... là n  1 3 n 1  3 n n 1 2 3 10 3280 29524 25942 1 A. B. C. D. 6561 59049 59049 243 u
Câu 40: Cho cấp số nhân u có 4 u  24;
16384 . Số hạn thứ 17 của cấp số nhân là n n u11 3 3 3 3 A. B. C. D. 67108864 268435456 536870912 214783648
ĐÁP ÁN VÀ LỜI GIẢI BẢI TẬP TỰ LUYỆN DẠNG 2
1-C 2-C 3-B 4-A 5-D 6-A 7-B 8-B 9-C 10-C
11-A 12-B 13-A 14-A 15-C 16-D 17-A 18-D 19-A 20-D
21-A 22-D 23-C 24-D 25-B 26-D 27-C 28-D 29-C 30-D
31-B 32-D 33-A 34-A 35-C 36-C 37-A 38-D 39-B 40-C Câu 1: 1 Ta có 6 6 u u q  32
   q q  2  7 1 2 TOANMATH.com Trang 15 Câu 2: 3 n 6 .2 u
Ta có n  1 u  và n 5   2 1 5 u 3 n 1 n 1 .2   5 Câu 3: 1 Giả sử  u 103 10 n n 1  103 n 1  n 1  1   1   1  ta có 1
u u .q   1  .     
n 1  103  n  104 n 1 103       10  10   10   10  Câu 4: 1. Sai Ta có 4 74
u u .q ,u u q . Do đó u và u cùng dấu 5 1 75 1 5 75 2. Sai
Vì a, b, c theo thứ tự đó lập thành một cấp số cộng có công sai d khác 0 nên b = a + d, c = a + 2d Suy ra 2 2 2 2 2 2 2 2 2
b a  2ad d ,c a  4ad  4d a c  2b Vậy 2 2 2
a ,b ,c theo thứ tự không lập thành cấp số cộng 3. Đúng
Vì a, b, c theo thứ tự đó lập thành một cấp số nhân có công bội d khác 0 nên 2 b  . a d,c  . a d
Suy ra b a d c a d a c  b 2 2 2 2 2 2 4 2 2 2 , Vậy 2 2 2
a ,b ,c theo thứ tự lập thành cấp số nhân Câu 5: 0,00001 1 1 Ta có 5 u  1
 ,u  0,00001 q     q   1 6 5 1  10 10 n 1  1      1 n
Vậy số hạng tổng quát u  1.   n   n 1  10  10  Câu 6: Ta có u  2  và q  2 1  2  1 2  n  2
Tổng n số hạng đầu tiên của cấp số nhân là n S        n 1  2   1  2 3   Câu 7: Ta có 10 10
u u .q  1.2  1024 11 1 Câu 8: Ta có 6 6 7
u u .q  3.3  3 7 1 TOANMATH.com Trang 16 Câu 9: 3 6 3 6 3 6 u u Ta có 1 2 3 2 2 3
u  .2  ,u  .2  .2,u  .2  .2   2,  2 1 2 3 5 5 5 5 5 5 u u 1 2 6
Vậy cấp số nhân cần tìm có u  , q  2 1 5 Câu 10: 1 u u 1 Ta có 3 5 2 4 q
 64  q  4  u    1 u q 4 16 2 Câu 11:
Số hạng tổng quát của cấp số nhân là u   1 3. 2 n   n
Ta cần tìm n sao cho u       n n  n 1 192 3. 2 192 7 Câu 12: 10 q 1 Ta có 9
u u .q q  2 . Do đó S u .  4092 10 1 10 1 q 1 Câu 13:
Ta có u u .q  1
 6;u u .q  64;u u .q  2  56 . 2 1 3 2 4 3 Câu 14: 1  n 1  1  3 2  1 2  1  Ta có u  2u   2u    u   u  (1) n 1   n 2   nn 1   3 
n  3n  2  3  n  2 n 1   n  2 3 nn 1 1 2
Đặt v u  , từ (1) ta suy ra vv n n n 1 n 1  3 n 1 1 1
Do đó v là cấp số nhân với v u   , công bội q n  1 1 2 2 2 n 1  n 1  n 1  n 1  2  1 1  2  1  2  1 Suy ra 1 v v q  .  u   .  u  .  n 1       2  3 nn 1 2  3 n  2  3  n 1 2017 2016 1  2  1 2 1 Vậy u  .    2018   2017 2  3  2019 3 2019 Câu 15: u  1 n 1   n 1 2 Ta có 2
1, 2, 2 ,..., 2n là cấp số nhân với 1  nên 2 n 1 1 2  2  ... 2   2  1 q  2 1 2 S  2 n   n 1 3 1 2 2 ... 2 3 2          1 Câu 16: 10 10 1 q 1 2 Ta có S u .  3.  3. 10 2 1 10 1  1 q 1 2 TOANMATH.com Trang 17 Câu 17: u 1 Ta có 3 3 2017 uu
.q q  1000  q  10  u   2020 2017 1 2016 u 10 2016 10 10 10 q 1 1 10 1 10 1  S u .  .  10 1 2016 2016 q 1 10 9 9.10 Câu 18:
Xét cấp số nhân u với u  2, q  2 n  1 2. 100 1 2 2 3 100  Ta có 101
1 2  2  2  ... 2  1 S  1  2 1 100 1 2 Câu 19:
Xét cấp số nhân u với u  5, q  2 n  1 Ta có n 1  n 1  n 1  8
u u .q
 1280  5.2  2  2  n  9 n 1
Vậy cấp số nhân đã cho có 9 số hạng Câu 20:
Xét cấp số nhân u với u  2, q  3 . Suy ra 4 4
u u .q  2.3  162 n  1 5 1 Câu 21: Ta có 8 8
u u .q  1.3  6561 9 1 Câu 22: 1 1 1
Ta có u  ,u   q  1 2 3 9 3 Câu 23: 1 1 1 u 1
Xét cấp số nhân với u  , q  có q  1 nên 1 4 S    1 4 4 1 q 1 3 1 4 Câu 24: 1 1 1 u 1 Ta có 1 9
u  , q    S    1 9 3 1 q  1  12 1     3  Câu 25: 1 u 1 Ta có 1
u  1, q   S    2 1 2 1 q 1 1 2 Câu 26: TOANMATH.com Trang 18  26 31    u
  u u  31 u   2 1 q q  2 2  31    1 1 q 1 q q  Ta có 1 2 3       26 2
1 q q   31 2 1 q u u  26   u   2 26 1 3 1 q  26 1   u  1   2 1 q  q  5  u  1 2 1 5q 26q 5 0       1    q u  25  1  5 Câu 27: 12 24 Ta có u  ,u   q  2 1 2 5 5 Câu 28:  q  3  u   2   u q  2   Ta có 2 1      4 2 u  54 u q  54   u  5 1  1   3 1000 1000 2 1 3 3 1 Vậy S  .  1000 3 2  3 Câu 29:
u u  36 u   4 q q  36 1  Ta có 5 2     48 4
q q  36 5 3 q q u u  48  u     5 3 6 4 q q  48 1  4 5 3 5 4 3
q q q q q q q q   q q  q   2 4 4 3 3 3 4 3 4 0 1
2 3q q  2  0  q  0  q  1    36
q  2 (do q  0;q  1)  u   2  q  2 1 4 q q  2
3q q  2  0 Câu 30: Ta có 1 2 3 4
1; 2 ;2 ; 2 ; 2 là một cấp số nhân với u  1; q  2 có 5 số hạng 1 n 5 q 1 2 1 5  S u 1.  2 1  3131 1 q 1 2 1 Câu 31:
Từ giả thiết u  24 và u  48 suy ra q  2 3 4 u 24 Lại có 3 u    6 1 2 q 4 5 1 q 3  1 Vậy S u  6.  186 5 1 1 q 1  Câu 32: TOANMATH.com Trang 19
Giả sử số 222 là số hạng thứ n n 1  n 1  n  1   1  Ta có 1 u u q  222  3.   
 74 (không tồn tại n   thỏa mãn) n 1      2   2 
Vậy 222 không là số hạng của cấp số nhân Câu 33:
u u  54
u q u q  54  u q   2 3 q 1  54  q  2 1    q  2 4 2 1 1          4 2 2 u u  108 
u q u q  108  uq q 1  108 u q q 1  54 u  9 1 1     1  2 5 3  1  2  1 Câu 34: 3
u u  54
u q u q  54 1 4 2 1 1      4 2 u u  108 
u q u q  108 2 5 3  1 1   Ta thấy 3
u q u q  0 nên chia phương trình (2) cho phương trình (1) ta được q = 2 1 1
Thay q = 2 vào phương trình (1) ta tìm được u  9 1 Câu 35: u n n n    192 Có u u . n qq       n n  2 1 1 1 64 7 1 u 3 1 Câu 36:u   2 1 
u u  3  u u  3  u   u  3 u  1  Ta có 1 3 1 3 1 3 3       2 2 u u  5   u u  2u .u  5 u .u  2      1 3  u 1 1 3 2 1 3 1 3 1   u  2  3  u 1  u Trường hợp 1. 1 2 3   q
 2  q  2 (do q 1 ) u  2  u 3 1 u  10 1 q  1. 5 1 2 1 
Với q  2 thì S    31 2 1 10   1 q 1 2  1 q  u 2    u 1 2 Trường hợp 2. 1 2 3   q     (loại do q  1) u  1  u 2  1 3 1 q    2 Câu 37:     n  1 n   1 n
3 1    2.1    3n 1  3   3      S        n n 1 3  n 1 1 3 . 1 3 3 1 2 Vậy 4
u  2;q   u u .q  1 5 1 4 3 3 TOANMATH.com Trang 20 Câu 38: 1 Ta có 5 5
u  0.00001  u .q  0.00001  1.
q  0.00001  q   6 1 10 n 1     n 1 1 n 1  
Mặt khác u u .q  1  .   n 1   n 1  10  10  Câu 39: n 1 u 1 u Theo đề ta có n 1 u  .  n u   n 1  3 n n n 1 3 n 1 2 2 3 10 u 1 1  1  u 1  1   1  u  1  Mà u  nên 2 3 10  .  ;  .  ;...;  1         3 2 3 3  3  3 3  3   3  10  3   u  1 1 Do đó dãy n
 là một cấp số nhân có số hạng đầu u  , công bội q   n  1 3 3 10 u u u 3 1 59048 29524 Khi đó 2 3 10 S u   ...    1 10 10 2 3 10 2.3 2.3 59049 Câu 40: 7 u 1  1  1 Từ 4 7  16384  16384  q   q  7   u q  4  4 11
Ta có u  24 tương ứng khi n = 1 n 16  1  3
Số hạng thứ 17 của cấp số nhân là u  24.  17    4  536870912
Dạng 3: Dựa vào tính chất của cấp số nhân, chứng minh đẳng thức, giải phương trình và ứng dụng bài toán thực tế Phương pháp giải
Áp dụng tính chất : Ba số a, b, c theo thứ tự đó lập thành cấp số nhân thì 2
ac b hoặc b ac
Nếu cấp số nhân u có số hạng đầu u và công bội q thì số hạng tổng quát u được xác định bởi công n  1 n thức n 1 u u .q   n  2 n 1  
Tổng của n số hạng đầu tiên  S nu n 1  khi q  1 u 1 nq  1   S   khi q  1 n  1 q Ví dụ mẫu
Ví dụ 1. Tìm x, y biết 5x y;2x  3y; x  2 y theo thứ tự lập thành cấp số cộng và các số
y  2 xy  x  2 1 ; 1;
1 theo thứ tự lập thành cấp số nhân Hướng dẫn giải TOANMATH.com Trang 21
Ba số 5x y;2x  3y; x  2y theo thứ tự lập thành cấp số cộng nên
x y   x yx y 2 2 2 3 5 2  y x (*) 5
Ba số  y  2 xy   x  2 1 ; 1;
1 theo thứ tự lập thành cấp số nhân nên
xy  2   y  2 x  2  xy  2  xy x y  2 1 1 1 1 1
Trường hợp 1. xy 1  xy x y 1  x y  2 (**) 10 4
Từ (*) và (**) suy ra x  ; y  3 3
Trường hợp 2. xy 1  xy x y 1  2xy x y  0 (***)
x  0; y  0 4 3 Từ (*) và (***) suy ra 2 x x 0     3 3 5 5
x   ; y    4 10  3 3  10 4  Vậy các cặp số  ;
x y cần tìm là  ; x y   ; ;   0;0; ;    4 10   3 3 
Ví dụ 2. Cho a, b, c là ba số hạng liên tiếp của một cấp số nhân. Chứng minh a)    3     3 ab bc ca abc a b c
b)         2 2 2 2 2 a b b c ab bc
c)        2 2 2
a b c a b c a b c Hướng dẫn giải
Vì a, b, c là ba số hạng liên tiếp của một cấp số nhân nên 2 b ac 3 a) Ta có
   3     3          3 3 2 abc a b c b a b c ab b bc
ab bc ca (điều phải chứng minh) b) Ta có  2 2 a b  2 2 b c  2 2 2 2 4 2 2 2 2 4 2 2
a b a c b b c a b  2b b c
a b ab bc b c  ab bc2 2 2 2 2 2 .
(điều phải chứng minh)
c) Ta có                         2 2 a b c a b c a c b a c b a c b 2 2 2 2 2 2 2 2 2 2
a  2ac c b a  2b c b a b c (điều phải chứng minh)
Ví dụ 3. Số đo bốn góc của một tứ giác lập thành cấp số nhân và góc cuối gấp 9 lần góc thứ hai. Tìm số đo của góc thứ nhất Hướng dẫn giải
Gọi A, B, C, D theo thứ tự đó là bốn đỉnh của tứ giác thỏa mãn đề bài Theo bài ra ta có     2   3
B Aq;C Aq ; D Aq Mặt khác    3  2
D  9B Aq  9Aq q  9  q  3  Với q  3   B  3  A  0 (loại) TOANMATH.com Trang 22
Với q = 3 ta có     0     0  0
A B C D  360  A  3A  9A  27A  360  A  9 b
Ví dụ 4. Cho a, b, c là các số nguyên dương thỏa mãn là một số nguyên. Các số a, b, c theo thứ tự lập a
a b c
thành một cấp số nhân và  b  2 . Tìm a 3 Hướng dẫn giải
Vì a, b, c theo thứ tự lập thành một cấp số nhân nên 2 b  . a ; q c  . a q b
Vì là một số nguyên mà a, b là số nguyên dương nên q là số nguyên dương a
a b c Ta có
b   a aq aq aq   aq  2 2 2 3 6 1  6 3
Vì a, q nguyên dương nên ta có bảng sau a 1 2 3 6 q  2 1 6 3 2 1 q 6 1 3 1 2 1 2
Kết luận Loại Loại Loại Thỏa mãn Vậy a = 6
Ví dụ 5. Tìm m để phương trình 3
x   m   2 3
1 x  5m  4 x 8  0 (1) có 3 nghiệm lập thành một cấp số nhân Hướng dẫn giải
Giả sử x ; x ; x là ba nghiệm của phương trình (1) 1 2 3
x x x x x x  0 1   2   3  3
x   x x x  2
x x x x x x x x x x x  0 1 2 3  1 2 2 3 3 1 1 2 3 Suy ra x x x  8 1 2 3
Lại có ba nghiệm x ; x ; x lập thành một cấp số nhân nên 1 2 3 2 3
x x x x x x x  8  x  2  2 1 3 2 1 2 3 2
Mà x là nghiệm của phương trình (1) nên 2 3   m   2 2 3
1 .2  5m  4.2  8  0  m  2
Thử lại với m = 2 thì phương trình (1) trở thành TOANMATH.com Trang 23 x  1 3 2 x 7x 14x 8 0       x  2  (thỏa mãn) x  4 
Vậy m = 2 là giá trị cần tìm
Ví dụ 6. Cho 3 số dương có tổng là 65 lập thành một cấp số nhân tăng. Nếu bớt một đơn vị ở số hạng thứ
nhất và 19 đơn vị ở số hạng thứ ba ta được một cấp số cộng. Tìm 3 số đó Hướng dẫn giải
Gọi u ,u ,u theo thứ tự đó lập thành một cấp số nhân 1 2 3
Theo đề bài u 1,u ,u 19 theo thứ tự đó lập thành một cấp số cộng 1 2 3
u u u  65
u u u  65 Ta có 1 2 3 1 2 3   
u 1 u 19  2u
u  2u u  20  1 3 2  1 2 3   u
u u q u q    2 2
1 q q  65 . . 65 1    1 1 1 1     2
u  2u .q u q  20  u  2   2 1 1 1
1 2q q  20 1  2 1 q q 65 13
Chia vế với vế của (1) cho (2), ta được   2 1 2q q 20 4 q  3 4 2 1 q q  13 2 1 2q q  2 9q 30q 9 0             1  q   3
Vì u ,u ,u theo thứ tự lập thành một cấp số nhân tăng dần nên q  3  u  5 1 2 3 1
Vậy 3 số cần tìm là 5; 15; 45
Ví dụ 7. Cho tam giác ABC vuông tại A có ba cạnh CA, AB, BC theo thứ tự lập thành một cấp số nhân có công bội là q. Tìm q Hướng dẫn giải
Vì tam giác ABC vuông tại A nên 2 2 2
BC AB AC
Theo giả thiết ta có ba cạnh CA, AB, BC theo thứ tự lập thành một cấp số nhân có công bội là q nên 2
BC q .AC và AB  . q AC Do đó 2 2 2 4 2 2 2 2 4 2
BC AB AC q .AC q .AC AC q q 1  0  1 5 2 q  2 1 5 2  2 5 2    q  (do 2
q  0)  q    1 5 2 2 2 q   2 2  2 5 Vì 0 q  nên q  2 TOANMATH.com Trang 24
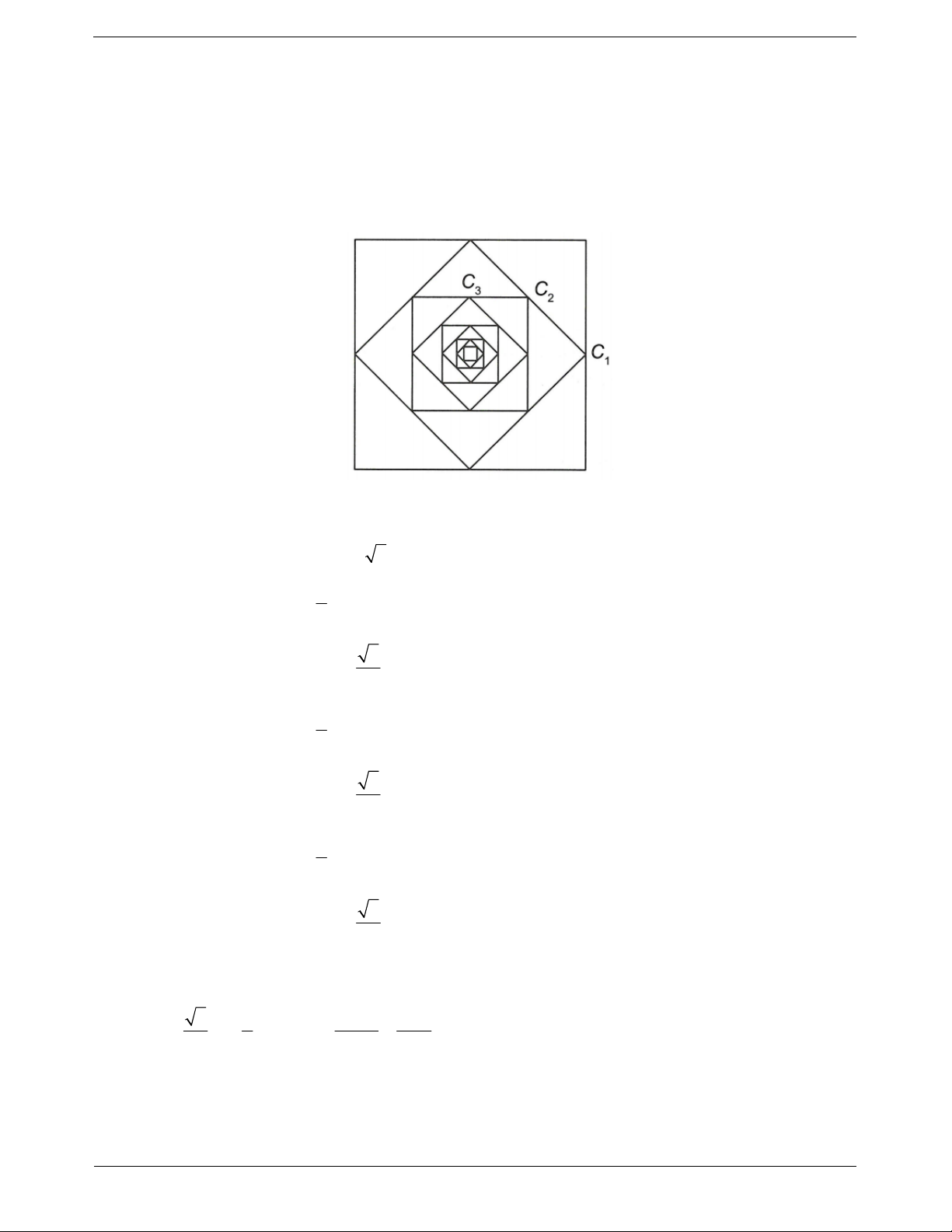
Ví dụ 8. Cho hình vuông C có cạnh bằng 1, C là hình vuông có các đỉnh là các trung điểm của cạnh 1 2
hình vuông C . Tương tự, gọi C là hình vuông có các đỉnh là trung điểm của các cạnh hình vuông C . 1 3 2
Tiếp tục như vậy ta được một dãy các hình vuông C ,C ,C ,...,C ,... Tính tổng diện tích của 10 hình 1 2 3 n
vuông đầu tiên của dãy Hướng dẫn giải
Diện tích của hình vuông C là 1 1
Độ dài đường chéo hình vuông C là 2 1 1
Hình vuông C có cạnh bằng đường chéo hình vuông C 2 2 1 2    2
Diện tích của hình vuông C là 2    2    1
Hình vuông C có cạnh bằng đường chéo hình vuông C 3 2 2 4    2
Diện tích của hình vuông C là 3    2    1
Hình vuông C có cạnh bằng đường chéo hình vuông C n 2 n 1  2n  1    2
Diện tích của hình vuông C là n    2   
Do đó, dãy diện tích các hình vuông C ,C ,C ,...,C ,... lập thành cấp số nhân với số hạng đầu 1 2 3 n 2 10  2  1 q 1 1023
u  1, q  
   S u .  1 10 1  2  2 q 1 512  
Ví dụ 9. Để tiết kiệm năng lượng, một công ty điện lực đề xuất bán điện sinh hoạt cho người dân theo
hình thức lũy tiến (bậc thang) như sau: Mỗi bậc gồm 10 số; bậc 1 từ số thứ 1 đến số thứ 10, bậc 2 từ số 11
đến số 20, bậc 3 từ số thứ 21 đến số thứ 30,…Bậc 1 có giá là 1500 đồng/1 số, giá của mỗi số ở bậc thứ TOANMATH.com Trang 25
n 1 tăng so với giá của mỗi số ở bậc thứ n là 2,5%. Gia đình ông An sử dụng hết 345 số trong tháng 1,
hỏi tháng 1 ông An phải đóng bao nhiêu tiền? Hướng dẫn giải
Gọi u là số tiền phải trả cho 10 số điện đầu tiên 1
Suy ra u  10.1500  15000 (đồng) 1
u là số tiền phải trả cho các số điện từ 11 đến 20 2
Suy ra u u 1 0,025 2 1  
....................................................................................
u là số tiền phải trả cho các số điện từ 331 đến 340 34
Suy ra u u 1 0,02533 34 1
Số tiền phải trả cho 340 số điện đầu tiên là 1 1 0,02534 1 1 0,02534 S u .  S  15000.  789193,28 1 1 1 1 0,025 1 1 1 0,025
Số tiền ông An phải trả cho các số điện từ 341 đến 345 là
S  5.15001 0,02534 17364,92 2
Vậy tháng 1 gia đình ông An phải trả số tiền là: S S S  806558 (đồng) 1 2
Ví dụ 10. Từ độ cao 55,8m của tháp nghiêng Pisa nước Italia, người ta thả một quả bóng cao su chạm 1
xuống đất. Giả sự mỗi lần chạm đất quả bóng lại nảy lên độ cao bằng
độ cao mà quả bóng đạt trước 10
đó. Tính tổng độ dài hành trình của quả bóng được thả từ lúc ban đầu cho đến khi nó nằm yên trên mặt đất Hướng dẫn giải
Gọi h là độ dài đường đi của quả bóng ở lần rơi xuống thứ n  * n    n
Gọi l là độ dài đường đi của quả bóng ở lần nảy lên thứ n  * n    n 1
Theo bài ra ta có h  55,8,l
.55,8  5,58 và các dãy số h ,l là các cấp số nhân lùi vô hạn với n  1 1 10 n 1 công bội q  10
Suy ra tổng độ dài đường đi của quả bóng là h l 10 1 1 S   
h l  68,2(m) 1 1  1 1 9 1 1 10 10
Bài tập tự luyện dạng 3 TOANMATH.com Trang 26
Câu 1: Ba số 2x,3x  3,5x  5 theo thứ tự là ba số hạng liên tiếp của một cấp số nhân. Biết x  1  , số
hạng tiếp theo của cấp số nhân đó là 250 250 A. B.
C. 250 D. 250 3 3
Câu 2: Cho cấp số nhân 4;  ; x 9  thì giá trị x là A. 5 B. 6,
 5 C. 6 D. 36
Câu 3: Cho cấp số nhân có bốn số hạng 2  ; ; x 1
 8; y . Hãy chọn kết quả đúng A. 6;
x   y  54 B. 6; x y  5  4 C. 6;
x   y  5  4 D. 10
x   ; y  2  6
Câu 4: Giá trị của x để 3 số 2x 1; ;
x 2x 1 theo thứ tự lập thành cấp số nhân là 1 1
A. x   B. x   3 C. x   D. x  1  3 3
Câu 5: Ba số x, y, z theo thứ tự lập thành một cấp số nhân với công bội q khác 1 đồng thời các số
x; 2y; 3z theo thứ tự lập thành một cấp số cộng với công sai khác 0. Giá trị của q là 1 1 1
A. q B. q C. q   D. q  3  3 9 3
Câu 6: Nếu ba số x  ; a x  ;
b x c theo thứ tự lập thành một cấp số nhân thì giá trị của x tính theo a, b, c là 2 a bc 2 c ab 2 b ac 2 2 2
a b c A. x B. x C. x D. x
2a b c
a b  2c
a  2b c
a b c 1  1 
Câu 7: Cho cấp số nhân , x, . Giá trị của x là 5 125 1 1 1 A. B.
C. D. 5 5 25 5
Câu 8: Với giá trị nào của x thì 3 số 2;
x x 1;3  x lập thành cấp số nhân? A. 1  B. 2 C. 3
D. Không có giá trị nào
Câu 9: Bốn số a, b, c, d theo thứ tự lập thành một cấp số cộng và bốn số a 1,b 1,c  3, d  9 theo thứ tự
lập thành một cấp số nhân. Tổng a + d bằng
A. 6 B. 8 C. 10 D. 12
Câu 10: Có bao nhiêu cấp số nhân gồm bốn phần tử mà tổng của chúng bằng 45 và số hạng thứ tư bằng
bốn lần số hạng thứ 2?
A. 1 B. 2 C. 3 D. 4
Câu 11: Trong một cấp số nhân có các số hạng đều dương, hiệu của số hạng thứ năm và thứ tư là 576,
hiệu của số hạng thứ hai và số hạng đầu là 9. Tổng 5 số hạng đầu tiên của cấp số nhân đó bằng
A. 768 B. 1024 C. 1023 D. 1061 Câu 12: Ba số  ;3
x ; y theo thứ tự lập thành cấp số cộng, ba số 1, x, y theo thứ tự lập thành một cấp số
nhân. Biết rằng x  0 , khi đó tích . x y bằng
A. 8 B. – 27 C. – 8 D. 5 TOANMATH.com Trang 27
x y z a  4 
Câu 13: Cho bộ số x , y , z là nghiệm của hệ phương trình 2x y  2z  2a  2 . Các giá trị dương của 0 0 0
3x  2y 3z 1 2a
a để x , y , z lập thành một cấp số nhân là 0 0 0
A. a  1 B. a  2 C. a  3 D. a  4
Câu 14: Tất cả các giá trị thực của tham số m để phương trình 3 2
x  3mx  m  
1 x  2  0 có ba nghiệm
phân biệt lập thành một cấp số nhân là 5 5 5 5 A. m   B. m   C. m D. m  3 2 1 3 3 2 1 3 3 2 1 3 3 2 1
Câu 15: Ba số a, b, c theo thứ tự là số hạng thứ nhất, số hạng thứ hai và số hạng thứ ba của một cấp số
nhân, đồng thời cũng lần lượt là số hạng thứ nhất, số hạng thứ hai và số hạng thứ tư của một cấp số cộng
có công sai bằng 10. Giá trị của a là 10 10
A. a  5 B. a
C. a  10 D. a   3 3 sin  Câu 16: Cho ba số
,cos, tan theo thứ tự lập thành một cấp số nhân, với     0 . Khi đó giá 6 2 trị cos 2 bằng 1 3 3 1 A. B. C. D.  2 2 2 2
Câu 17: Cho hình vuông C có cạnh bằng a. Người ta chia mỗi 1 
cạnh của hình vuông thành bốn phần bằng nhau và nối các điểm
chia một cách thích hợp để có hình vuông C như hình vẽ 2 
Từ hình vuông C lại tiếp tục làm như trên ta nhận được dãy 2 
các hình vuông C ,C ,C ,...,C . Gọi S là diện tích của hình 1 2 3 n i
vuông C i 1,2,3, 
... . Đặt T S S S  ... S  ... i  1 2 3 n 32 Biết T  3 Giá trị của a là 5
A. a  2 B. a
C. a  2 D. a  2 2 2
Câu 18: Người ta thiết kế một cái tháp gồm 11 tầng. Diện tích bề mặt trên của mỗi tầng bằng nửa diện
tích mặt trên của tầng ngay bên dưới và diện tích mặt trên của tầng 1 bằng nửa diện tích đế tháp. Biết diện tích đáy tháp là 2
12288m , diện tích mặt trên cùng bằng A. 2 8m B. 2 6m C. 2 12m D. 2 10m
Câu 19: Một khu rừng có trữ lượng gỗ là 5  3
6.10 m . Biết tốc độ sinh trưởng của các cây trong rừng là
4,5% mỗi năm. Hỏi sau 10 năm, khu rừng đó sẽ có bao nhiêu 3
m gỗ (làm tròn đến hàng đơn vị)? A. 3 931782m B. 3 931781m C. 3 891657m D. 3 891658m TOANMATH.com Trang 28
Câu 20: Bạn An thả quả bóng cao su từ độ cao 10m theo phương thẳng đứng. Mỗi khi chạm đất nó lại 3
nảy lên theo phương thẳng đứng với độ cao bằng độ cao trước đó. Tổng quãng đường bóng đi được đến 4 khi bóng dừng hẳn là
A. 40 m B. 70 m C. 50 m D. 80 m
Câu 21: Cho ba số thực dương a, b, c là ba số hạng liên tiếp của một cấp số nhân đồng thời thỏa mãn điều 2 2 2 a b c 1 1 1 kiện
 4 . Giá trị của biểu thức P    là 3 3 3
a b c 3 3 3 a b c 1 1
A. P  4 B. P  2 C. P D. P  2 4
Câu 22: Cho tam giác ABC cân tại đỉnh A, biết độ dài cạng đáy BC, đường cao AH và cạnh bên AB theo
thứ tự lập thành cấp số nhân với công bội a. Giá trị của 2 q bằng 2  2 2  2 2 1 2 1 A. B. C. D. 2 2 2 2
Câu 23: Cho bốn số a, b, c, d theo thứ tự đó tạo thành cấp số nhân với công bội khác 1. Biết tổng ba số 148 hạng đầu bằng
, đồng thời theo thứ tự đó chúng lần lượt là số hạng thứ nhất, thứ tư và thứ tám của 9
một cấp số cộng. Giá trị biểu thức T a b c d là 101 100 100 101 A. T B. T C. T   D. T   27 27 27 27
Câu 24: Tam giác mà ba đỉnh của nó là ba trung điểm ba cạnh của tam giác ABC được gọi là tam giác
trung bình của tam giác ABC. Ta xây dựng dãy các tam giác A B C , A B C , A B C ,... sao cho A B C là 1 1 1 2 2 2 3 3 3 1 1 1
một tam giác đều cạnh bằng 3 và với mỗi số nguyên dương n  2 , tam giác A B C là tam giác trung n n n
bình của tam giác A B C . Với mỗi số nguyên dương n, kí hiệu S tương ứng là diện tích hình tròn n 1  n 1  n 1  n
ngoại tiếp tam giác A B C . Giá trị tổng S S S  ... S n n n 1 2 n 15 9 A. S
B. S  4 C. S D. S  5 4 2
Câu 25: Cho hình vuông ABCD có các cạnh bằng a và có diện tích S 1
Nối 4 trung điểm A , B ,C , D theo thứ tự của 4 cạnh AB, BC, CD, DA 1 1 1 1
ta được hình vuông thứ hai có diện tích S . Tiếp tục làm như thế, 2
ta được hình vuông thứ ba là A , B ,C , D có diện tích S ,... 2 2 2 2 3
và cứ tiếp tục làm như thế, ta tính được các hình vuông lần lượt
có diện tích có diện tích S , S ,..., S (tham khảo hình vẽ bên). 4 5 100
Giá trị tổng có diện tích S S S S  ...  S là 1 2 3 100 2 a  100 2   1 2 a  100 2   1 A. S B. S 100 2 99 2 2 a 2 a  99 2   1 C. S D. S  100 2 98 2 TOANMATH.com Trang 29
Câu 26: Tổng cấp số nhân lùi vô hạn u có u 1và u ,u ,u theo thứ tự là ba số hạng liên tiếp trong n  1 1 3 4 một cấp số cộng là 5 1 5 1 1 A. B. C. D. 2 2 2 5 1
Câu 27: Với giá trị nào của tham số m thì phương trình 3 2
x mx  6x  8  0 có ba nghiệm thực lập thành một cấp số nhân?
A. m  1 B. m  3 C. m  3 D. m  4
Câu 28: Các giá trị m để phương trình 3 2
x  2x  m  
1 x  2m  
1  0 có ba nghiệm lập thành một cấp số nhân là A. m  1,  m  3  ,m  4  B. m  1,
m 13,m  4 
C. m  1, m  3, m  4
D. Không có giá trị của m
ĐÁP ÁN VÀ LỜI GIẢI BẢI TẬP TỰ LUYỆN DẠNG 3
1-B 2-C 3-C 4-C 5-A 6-C 7-B 8-D 9-B 10-C
11-C 12-C 13-C 14-B 15-C 16-D 17-A 18-B 19-A 20-B
21-D 22-C 23-C 24-B 25-B 26-B 27-B 28-D Câu 1: Ba số 2 ;
x 3x  3;5x  5 theo thứ tự là ba số hạng liên tiếp của một cấp số nhân nên x  
2x 5x  5  3x  32 1 2
x 8x  9  0   x  9  (do x  1)  x  9 3.9  3 30 5
Với x = 9, suy ra q    2.9 18 3
Số hạng tiếp theo của cấp số nhân đó là    5 250 5.9 5 .  3 3 Câu 2: Ta có 2 x  4 9
   36  x  6 Câu 3:   x  6 2   x    2   1
 8  36  x  6   y  54 Ta có    xy    18  2  324  x  6   y  54  Câu 4: TOANMATH.com Trang 30 1 Ta có 2 2 2
x  4x 1  3x  1  x   3 Câu 5:
Vì x, y, z theo thứ tự lập thành một cấp số nhân với công bội q khác 1 nên 2 y  . x ; q z  . x q (1)
Các số x, 2y, 3z theo thứ tự lập thành một cấp số nhân nên x  3z  4y (2)  q 1 Thay (1) vào (2) được 2 x 3xq 4xq x  2 3q 4q  2 1 0 3q 4q 1 0             1  q   3 1
Vì q  1 nên q  3 Câu 6: Để ba số x  ; a x  ;
b x c theo thứ tự lập thành cấp số nhân thì 2  
x b2   x a x cb ac 2 2 2
x bx b x  a cx ac   b a c 2 2 2
x ac b x
a  2b c Câu 7: 1  1  1 1 1 ; ; x
là cấp số nhân khi và chỉ khi 2 x  .  x   5 125 5 125 25 Câu 8: 3 số 2;
x x 1;3  x là cấp số nhân khi và chỉ khi  x  2
1   x  23  x 2 2 2
x  2x 1  x  5x  6  2x  3x  7  0 (vô nghiệm)
Vậy không có giá trị x thỏa mãn đề bài Câu 9:
Gọi m là công sai của cấp số cộng
Khi đó b a  ;
m c a  2 ,
m d a  3m
a  1c 3  b  2 1 Do 1,
a b 1, c  3, d  9 theo thứ tự lập thành một cấp số nhân nên  b  
1 d  9  c  32  a  1 2
2a  2  m  Thay ;
b a m c a  2 ,
m d a  3m vào hệ trên và rút gọn ta được    m  2 2  4a m  m  2 
Thử lại ta thấy chỉ có trường hợp a  1, m  2 thỏa mãn
Vậy a d  2a  3m  8 Câu 10: TOANMATH.com Trang 31 4  q 1 u .  45 
q  0;u  45 1 1  S  45  q 1 Ta có 4      q  2;u  3 1 u 4u   q 0    4 2  3
u .q  4u .q  q  2;  u  9  5 1 1  2  1  q  4 Câu 11: 4 3 4 3
u u  576 u
 .q u .q  576  5 4 q q 576 1 1 3     
q  64  q  4  u  3 1 u u  9 
u .q u  9 q 1 9 2 1  1 1 5 q 1
Vậy tổng 5 số hạng đầu là S u  1023 5 1 q 1 Câu 12:
Ba số x,3, y theo thứ tự lập thành cấp số cộng nên x y  6 (1)
Ba số 1, x, y theo thứ tự lập thành cấp số nhân nên 2 x y (2) x  2 
Từ (1), (2) và x  0 suy ra   . x y  8   y  4 Câu 13: a  3 5a  9
Giải hệ phương trình ta được x  ; y  2; z  0 0 0 6 6
Để x , y , z theo thứ tự lập thành một cấp số nhân thì 2
x .z y 0 0 0 0 0 0  a  3 a  3 5a  9 2 . 4 5a 24a 117 0         39 6 6 a    5
Do a  0 nên a  3 Câu 14:
Giả sử phương trình đã cho có ba nghiệm phân biệt x , x , x 1 2 3
Khi đó x x x  2 . Mà 2 x x x nên 3 x  2 1 2 3 1 3 2 2 5 Do đó ta có 3
m 1  4 2.3m m   3 3 2 1 5
Thử lại với m   thấy thỏa mãn 3 3 2 1 5 Vậy m   3 3 2 1 Câu 15:
Theo đề bài ta có a u ;b u u 10;c u u  30 1 2 1 4 1
Theo tính chất cấp số nhân, ta có b  .
a c  u 102 2
u u  30  u 10  a 10 1 1  1  1 Câu 16: TOANMATH.com Trang 32 Theo giả thiết ta có 2 sin       2 sin      2    3    2 1 .tan cos cos 6. cos cos 1  0  cos  6 6.cos 2 Từ đó     2 1 cos 2 2 cos 1   2 Câu 17: 2 2  3   1  a 10
Cạnh của hình vuông C là a a a  2  2      4   4  4 5 5 Do đó diện tích 2
S a S 2 1 8 8 2 2 2  3   1  a 10  10 
Cạnh của hình vuông C là 2 a aa   a 3  3  2   2  2   4 4 4  4        2  5  5 Do đó diện tích 2 S a S 3   2  8  8
Lý luận tương tự ta có các S ; S ; S ;...; S ... tạo thành một dãy cấp số nhân lùi vô hạn có u S và công 1 2 3 n 1 1 5 bội q  8 2 S 8a 32 Vậy 1 2 T   
a  4  a  2 (do a  0) 1 q 3 3 Câu 18: 1
Ta nhận thấy diện tích các mặt trên của mỗi tầng lập thành 1 cấp số nhân với công bội q  2
Số hạng đầu u  12288 . Khi đó mặt trên cùng tầng 11 ứng với u 1 12 11  1  Do đó 11
u u .q  1288.  6 12 1    2  Câu 19: Đặt 5
u  6.10 và r  4,5%  0,045 0
Gọi u là trữ lượng gỗ của khu rừng sau năm thứ n. Khi đó ta có u
u 1 r , n   n 1  n   n
Suy ra u là cấp số nhân với số hạng đầu u và công bội q 1 r n  0
Do đó số hạng tổng quát của cấp số nhân u là u u 1 nr n 0   n
Sau 10 năm, khu rừng đó sẽ có u u .q  6.10 .1 0,04510 10 5  931781,653 3 m   931782 3 m gỗ 10 0  Câu 20: 3
Các quãng đường khi bóng đi xuống tạo thành một cấp số nhân lùi vô hạn có u  10 và q  1 4 TOANMATH.com Trang 33 u 10
Tổng các quãng đường khi bóng đi xuống là 1 S    40 1 q 3 1 4
Tổng quãng đường bóng đi được (cả lên và xuống) đến khi bóng dừng hẳn là 2S 10  80 10  70(m) Câu 21: 2 2 2 3 3 3 a b c 1
a b c a b c Ta có  4      3 3 3 2 2 2 2 2 2 2 2 2
a b c 4 a b c b c c a a b
Mặt khác a, b, c là ba số hạng liên tiếp của một cấp số nhân nên 2 ac b 1 a b c a b c 1 1 1 1 Do đó           P  2 2 2 2 2 2 3 4 3 3 3 3 4 b c c a a b ac b a c a b c 4 Câu 22: Đặt BC  ;
a AB AC  ;
b AH h . Theo giả thiết ta có a, h, b lập thành cấp số nhân, suy ra 2 h ab 2 2 2 b b a
Mặt khác, tam giác ABC cân tại đỉnh A nên 2 2 h m   a 2 4 2 2 2 b b a Do đó 2 2 
ab a  4ab  4b  0  a  2 2  2b 2 4 b 1 2 2  2 2 1 Lại có 2
b q a nên 2 q     a 2 2  2 4 2 Câu 23:  2  ac b   1  Ta có 2  bd c 2  148 3
a b c   9
Cấp số cộng có u a,u  ,
b u c . Gọi x là công sai của cấp số cộng. Vì cấp số nhân có công bội khác 1 4 8 1 nên x  0
b a  3x Ta có  (4)
c a  7x
Từ (1) và (4) suy ra a a x  a x2 2 7 3
ax  9x  0
Do x  0 nên a  9x 148
Từ (3) và (4), suy ra 3a 10x  9 TOANMATH.com Trang 34   16 b    3 a  4    64 Do đó  4   c x  9  9    256 d      27 10  0
Vậy T a b c d  27 Câu 24:
Vì dãy các tam giác A B C , A B C , A B C ,... là các tam giác đều nên bán kính đường tròn ngoại tiếp các 1 1 1 2 2 2 3 3 3 3 tam giác bằng cạnh nhân 3
Với n = 1 thì tam giác đều A B C có cạnh bằng 3 nên đường tròn ngoại tiếp tam giác A B C có bán kính 1 1 1 1 1 1 2 3  3  R  3.  S  .3. 1 1  3  3    3
Với n = 2 thì tam giác đều A B C có cạnh bằng nên đường tròn ngoại tiếp tam giác A B C có bán 2 2 2 2 2 2 2 2 1 3  1 3  kính R  3. .  S  .3. . 2 2  2 3  2 3    3
Với n = 3 thì tam giác đều A B C có cạnh bằng nên đường tròn ngoại tiếp tam giác A B C có bán 3 3 3 4 3 3 3 2 1 3  1 3  kính R  3. .  S  .3. . 3 3  4 3  4 3   
............................................................................... n 1 1   
Như vậy tam giác đều A B C có cạnh bằng 3.
nên đường tròn ngoại tiếp tam giác A B C có bán n n n    2  n n n 2 n 1  n 1 1 3 1   3      kính R  3. .  S  .   3. .    n 2 3 n  2 3       
Khi đó ta được dãy S ; S ; S ;...; S ... là một cấp số nhân lùi vô hạn với số hạng đầu u S  3 và công 1 2 3 n 1 1 1 bội q  4 u Do đó tổng 1
S S S  ...  S ...   4 1 2 n 1 q Câu 25: 1 1 Ta có 2 2 2
S a ; S a ; S a ,... 1 2 3 2 4 TOANMATH.com Trang 35 1
Do đó S , S , S ,..., S là cấp số nhân với số hạng đầu 2
u S a và công bội q  1 2 3 100 1 1 2 2 1 nq a  100 2   1
Suy ra S S S S  ...  SS .  1 2 3 100 1 99 1 q 2 Câu 26:
u là cấp số nhân lùi vô hạn có công bội q, suy ra q 1và 2 2 3 3
u u .q q ;u u .q q n  3 1 4 1
Mà và u ,u ,u theo thứ tự là ba số hạng liên tiếp trong một cấp số cộng nên u u  2.u 1 3 4 1 4 3 Từ đó ta có 3 2 3 2
q q q q    q   2 q q   2 1 2. 2. 1 0 1
1  0  q q 1  0  1 5 q  2 1 5    q  (vì q  1 )  1 5 2 q   2 u 1 2 5 1 Vậy 1 S     1 q 1 5 1 5 2 1 2 Câu 27:
x x x m
Ta chứng minh nếu x ; x ; x là nghiệm của phương trình 3 2
x mx  6x  8  0 thì 1 2 3 1 2 3  x x x  8  1 2 3 Thật vậy 3 2
x mx  6x  8   x x x x x x 1   2   3 
x x x m 3 2 3
x mx  6x  8  x  x x x  2
x x x x x x x x x x x  1 2 3  1 2 2 3 3 1 1 2 3 1 2 3  x x x  8  1 2 3
Điều kiện cần: Phương trình 3 2
x mx  6x  8  0 có ba nghiệm thực x x x lập thành một cấp số 1 2 3 nhân 2 3 3
x .x x x .x .x x  8  x x  2 1 3 2 1 2 3 2 2 2 Vậy phương trình 3 2
x mx  6x  8  0 phải có nghiệm bằng 2
Thay x  2 vào phương trình ta có m  3  x  4 
Điều kiện đủ: Thử lại với m  3  ta có 3 2 x 3x 6x 8 0       x  2 
(thỏa yêu cầu bài toán) x  1   Câu 28:
Giả sử phương trình có ba nghiệm phân biệt lập thành cấp số nhân 2  x x x 1 3 2  m 1 Khi đó 
x x x  2   x   1 2 3 2 2
x x x x x x m 1  1 2 2 3 3 1
Thay vào phương trình ta được 1
m   , m  3, m  4  TOANMATH.com Trang 36
Thay từng giá trị của m vào phương trình ta thấy không có giá trị nào của m thỏa mãn yêu cầu bài toán TOANMATH.com Trang 37