-
Thông tin
-
Quiz
Bài giảng chi tiết và bài tập luyện tập - Xác suất thống kê | Học viện Chính sách và Phát triển
Bài giảng chi tiết và bài tập luyện tập - Xác suất thống kê | Học viện Chính sách và Phát triển được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn sinh viên cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!
Xác suất thống kê (CSPT) 16 tài liệu
Học viện Chính sách và Phát triển 360 tài liệu
Bài giảng chi tiết và bài tập luyện tập - Xác suất thống kê | Học viện Chính sách và Phát triển
Bài giảng chi tiết và bài tập luyện tập - Xác suất thống kê | Học viện Chính sách và Phát triển được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn sinh viên cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!
Môn: Xác suất thống kê (CSPT) 16 tài liệu
Trường: Học viện Chính sách và Phát triển 360 tài liệu
Thông tin:
Tác giả:
Preview text:
BÀI GIẢNG
XÁC SUẤT VÀ THỐNG KÊ TOÁN
GIẢNG VIÊN: TRẦN ĐÌNH SƠN Mobile: 0974500322
Tài liệu học tập Giáo trình
1. Nguyễn Cao Văn, Ngô văn Thứ, Trần Thái Ninh. Giáo trình lý thuyết xác
suất và thống kê toán. NXB Đại học Kinh tế Quốc dân, 2017 Tài liệu tham khảo
1.Nguyễn Văn Cường, Bùi Đức Dương. Giáo trình lý thuyết xác suất và thống
kê toán, NXB Thống kê, 2010
2. Đào Hữu Hồ. Hướng dẫn giải các bài toán Xác xuất – Thống kê. NXB Đại
học Quốc gia Hà Nội, 2015
3. Nguyễn Cao Văn, Trần Thái Ninh. Bài tập lý thuyết xác suất và thống kê
toán, NXB Giáo dục, Hà Nội 2005
Chương I. Biến cố ngẫu nhiên và xác suất
1.1 Phép thử và các biến cố 1.1.1. Phép thử
Việc thực hiện một nhóm các đk cơ bản để quan sát một hiện tượng có thể xảy
ra hay không gọi là phép thử. 1.1.2. Biến cố
Hiện tượng có thể xảy ra trong kết quả của phép thử gọi là biến cố.
VD : - Gieo một con xúc xắc là một phép thử.
- Việc xuất hiện một mặt nào đó gọi là biến cố. 1.1.3. Các loại biến cố
+ Biến cố chắc chắn ( ký hiệu là U ): Là biến cố nhất định xảy ra khi thực hiện một phép thử.
+ Biến cố không thể có ( ký hiệu V): Là biến cố không thể xảy ra khi thực hiện một phép thử.
+ Biến cố ngẫu nhiên ( ký hiệu A,B,C…): Là biến cố có thể xảy ra hoặc không
xảy ra khi thực hiện một phép thử.
VD : Khi gieo một con xúc xắc
+ Biến cố: Xuất hiện mặt có số chấm là biến cố chắc chắn.
+Biến cố xuất hiện mặt có 7 chấm là biến cố không thể.
+ Biến cố xuất hiện mặt có 2 chấm là biến cố ngẫu nhiên.
1.2. Xác xuất của biến cố 1.2.1. Khái niệm
Xác suất của một biến cố là một số đặc trưng cho khả năng khách quan
xuất hiện biến cố đó khi thực hiện phép thử.
1.2.2. Định nghĩa cổ điển về xác suất
a. Định nghĩa: Xác suất xuất hiện biến cố A trong một phép thử là tỷ số giữa
số kết cục thuận lợi cho A và tổng số các kết cục duy nhất đồng khả năng
có thể xảy ra khi thực hiện phép thử.
Ký hiệu P(A) là XS của biến cố A
m là số kết cục thuận lợi cho biến cố A
n là số kết cục duy nhất đồng khả năng của phép thử thì P(A) = (1.1)
b. Các tính chất của xác xuất. 0 < P(A) < 1 P(U) =1 P(V)= 0. Như vậy : 0 (1.2)
Chú ý: + P(A) = 1 chưa chắc A=U + P(A) = 0 chưa chắc A=V
c. Các phương pháp tính xác xuất bằng định nghĩa cổ điển. 1. Suy luận trực tiếp.
Số kết cục trong phép thử là nhỏ, suy luận đơn giản.
VD. Trong bình có a quả cầu trắng, b quả cầu đen. Tìm xác suất để lấy được quả cầu trắng. Giải
+ Gọi A là biến cố lây được quả cầu trắng.
+ Số kết cục thuận lợi cho A là: m = a
+ Số kết cục xảy ra là n=a+b 2. Dùng sơ đồ Ven
Số kết cục là lớn, suy đoán phức tạp thì có thể dùng sơ đồ Ven. Sơ đồ hình cây
VD: Giả sử xác suất sinh con trai,con gái là bằng nhau và bằng 0,5. Một gia
đình có 3 con. Tìm xác suất để gia đình đó có có 2 con gái. Giải.
+ Gọi A là biến cố gđ có 2 con gái Con đầu + Ta lập sơ đồ
Nhìn vào sơ đồ ta thấy có: G T G G 8 kết cục: TTT, TTG, TGT, T T TGG, GTT, GTG, GGT, GGG T
Có 3 kết cục 2 gái ( TGG, G T T G T G G GTG, GGT) P(A) = 3/8 Sơ đồ bảng
VD: Gieo con xúc xắc 2 lần. Tìm xác suất trong đó có một lần được 6 chấm Giải.
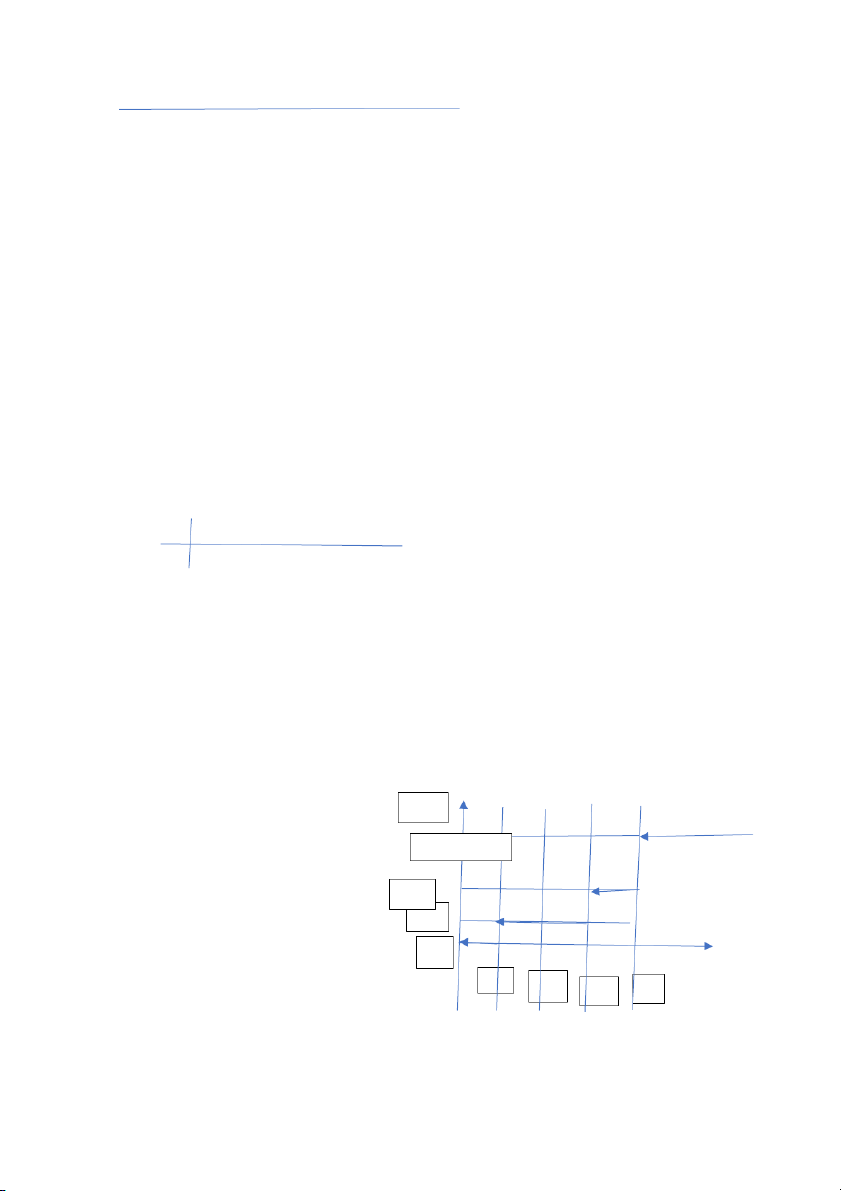
+ Gọi A là biến cố “ Trong 2 lần gieo có đúng một lần được 6 chấm” + Lập bảng 2 1 2 3 4 5 6 1 1 1 1 1 2 1 3 1 4 1 5 1 6 2 2 1 2 2 2 3 2 4 2 5 2 6 3 3 1 3 2 3 3 3 4 3 4 3 6 4 4 1 4 2 4 3 4 4 4 5 4 6 5 5 1 5 2 5 3 5 4 5 5 5 6 6 6 1 6 2 6 3 6 4 6 5 6 6
+ Nhìn vào bảng ta thấy: n=36; m=10 P(A)=10/36=5/6 Sơ đồ dạng tập hợp
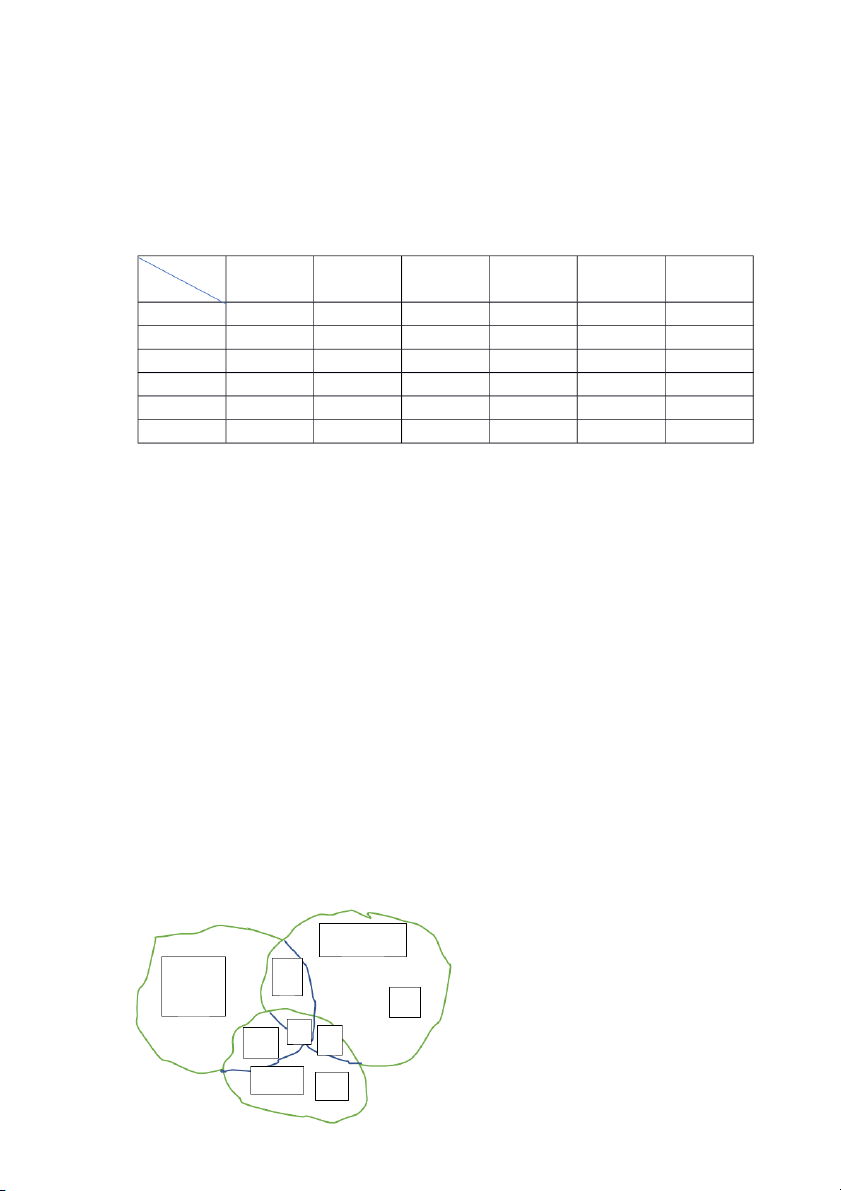
VD: Lớp có 50 học sinh, trong đó: 20 người chơi bóng đá
15 người chơi bóng chuyền 10 người chơi bóng rổ
8 người chơi bóng đá và bóng chuyền
5 người chơi bóng đá và bóng rổ
3 người chơi bóng chuyền và bóng rổ
1 người chơi bóng đá, bóng chuyền và bóng rổ.
Lấy ngẫu nhiên một học sinh. Tìm xác suất để người đó chơi ít nhất một trong các môn bóng trên. Giải
+ Gọi A là biến cố “ để học sinh chơi một trong các môn bóng trên”. + Ta lập sơ đồ sau b.chuyền B đá 7 8 5 1 4 2 + n= 50; m b.rổ 30/50 = 3/5 3
3. Dùng công thức của giải tích tổ hợp
Phép thử lớn, không thể suy đoán trực tiếp được
VD. Một hộp có 10 sp , trong đó có 6 chính phẩm, 4 phế phẩm. Lấy ngẫu nhiên 3 sp. Tìm xác suất để: a) Cả 3 sp là chính phẩm
b) Trong 3sp có đúng 2 chính phẩm Giải
a) Gọi A là biến cố :”lấy được 3 chính phẩm”
Ta thấy có: khả năng lấy 3 sp n= 120 Số kết cục của A là Vậy P(A) = m/n= 1/6
b) Gọi B là biến cố :” Trong 3 sp có đúng 2 chính phẩm” + Vẫn có n=120
+ Số kết cục thuận lợi cho B là m= =60 =
1.2.3. Định nghĩa thống kê về xác suất
1. Định nghĩa 1. Tần suất xuất hiện biến cố trong n phép thử là tỷ số giữa số
phép thử trong đó biến cố xuất hiện và tổng số phép thử được thực hiện.
+ Số phép thử là n; Số lần xuất hiện biến cố A là k
+ Tần suất xuất hiện biến cố A là: f(A) = (1.3)
2. Định nghĩa 2. Xác xuất xuất hiện biến cố A trong một phép thử là số p
không đổi mà f(A) trong n phép thử sẽ dao động rất ít quanh số p khi số
phép thử tăng lên vô hạn. P(A)
1.2.4. Định nghĩa hình học về xác suất
Xác suất để một điểm ngẫu nhiên rơi vào một phần nào đó của một miền cho
trước tỷ lệ với độ đo của miền đó ( độ dài, diện tích…) và không phụ thuộc vào
vị trí, dạng kích thước của miền đó.
Độ đo của miền cho trước là S, độ đo hình học của một phần A nào đó là SA thì
xác suất để một điểm ngẫu nhiên rơi vào phần A là: p=SA/S
1.2.5. Nguyên lý xác suất lớn và xác suất nhỏ
1. Nếu một biến cố có xác xuất rất nhỏ thì thực tế có thể cho rằng, trong một
phép thử biến cố đó sẽ không xảy ra.
Chú ý: Quy định mức rất nhỏ tùy thuộc vào từng bài toán.
2. Nếu biến cố ngẫu nhiên có xác suất gần bằng 1 thì thực tế có thể cho rằng
biến cố đó sẽ xảy ra trong một phép thử.
1.3. Mối quan hệ giữa các biến cố. Định lý cộng xác suất.
1.3.1. ĐN 1. Biến cố C gọi là tổng của 2 biến cố A và B, ký hiệu C=A+B nếu C
chỉ xảy ra khi có ít nhất 1 trong 2 biến cố A và B xảy ra.
VD 1. A là bc “người 1 bắn trúng bia”
B là bc “người 2 bắn trúng bia”
C là bc “bia trúng đạn” Thì C=A+B
VD 2. A là bc “xuất hiện mặt 6 chấm”
B là bc “xuất hiện mặt 5 chấm”
C là bc “ được ít nhất 5 chấm” Thì C=A+B
1.3.2. ĐN 2. Biến cố A gọi là tổng các bc A1,A2,…,An nếu A xảy ra khi có ít nhất
một trong các bc đó xảy ra.
Ký hiệu A = A1 + A2 +…+ An
1.3.3. ĐN 3. Hai bc A và B gọi là xung khắc với nhau nếu chúng không thể đồng
thời xảy ra trong một phép thử.
VD 3. + Trong VD 1 A, B là không xung khắc.
+ Trong VD 2 A, B là xung khắc.
VD 4. Có 3 loại cầu: trắng, xanh, đỏ trong bình. Lấy ngẫu nhiên một quả cầu.
A là bc “ lấy được quả cầu trắng”
B là bc “ lấy được quả cầu xanh”
C là bc “ lấy được quả cầu đỏ”
A, B, C là các bc xung khắc
1.3.4. ĐN 4. Nhóm n bc A1,A2,…,An được gọi là xung khắc từng đôi nếu bất kỳ
2 bc nào trong nhóm này cũng xung khắc với nhau.
1.3.5. Định lý. Xác suất của tổng 2 bc xung khắc bằng tổng xác suất của 2 bc đó.
A, B xung khắc thì: P(A+B)=P(A)+P(B) (1.4) Chứng minh
+ Gọi n là số kết cục đồng khả năng có thể xảy ra khi phép thử thực hiện
+ m1 là số kết cục thuận lợi cho bc A xảy ra
+ m2 là số kết cục thuận lợi cho bc B xảy ra
Vậy kết cục thuận lợi cho A hoặc B là m1 + m2 P(A+B)= = Hệ quả
Hệ quả 1. A1, A2,…,An xung khắc từng đôi thì: P( (1.5)
VD. XS để một xạ thủ bắn trúng điểm 10 là 0,1; điểm 9 là 0,2; điểm 8 là 0,25; ít
hơn 8 là 0,45. Xạ thủ bắn 1 viên đạn, tìm XS để xạ thủ được ít nhất 9 điểm. Giải
+ Gọi A là bc “ bắn trúng điểm 10”
+ Gọi B là bc “bắn trúng điểm 9”
+ Gọi C là bc “bắn ít nhất điểm 9”
C=A+B, A, B là 2 bc xung khắc P(C)= P(A)+P(B)= 0,3
ĐN 5. Các bc A1,A2,…,An được gọi là một nhóm đầy đủ các bc nếu trong một
phép thử sẽ xảy ra chỉ một trong các bc đó
(chúng xung khắc từng đôi và A1+A2+…+An là bc chắc chắn)
VD. Gieo con xúc xắc, Ai (i=1,2,…,6) là bc xuất hiện mặt i chấm thì A1,A2,…,A6
là một nhóm đầy đủ các bc.
Hệ quả 2. Nếu A1,A2,…,An tạo nên một nhóm đầy đủ các bc thì tổng XS của chúng bằng 1
ĐN 6. Hai bc A và là đối lập với nhau nếu chúng tạo nên một nhóm đầy đủ các bc VD. +A là bc bắn trúng bia + là bc bắn trượt bia
A và là hai bc đối lập với nhau.
VD. Một hòm gồm a chính phẩm, b phế phẩm. Lấy ngẫu nhiên từ hòm đó n sp.
Gọi A là bc “ trong n sp lấy ra có ít nhất 1 chính phẩm”, là bc “ trong n sp lấy ra
không có chính phẩm nào” thì A và là các bc đối lập nhau. Hệ quả 3. P(A)+P( (1.7)
VD. XS để sản xuất ra một chính phẩm là 0,9.Tìm XS để sản xuất ra một phế phẩm. Giải
+ Gọi A là bc “ sản xuất ra một chính phẩm”
+ Gọi là bc “ sản xuất ra một phế phẩm”
A, là đối lập nhau P(A)+P( P(=1-P(A) = 0,1
VD. Trong hòm có n sp, có m chính phẩm. Lấy ngẫu nhiên k sp (k . Tìm XS
trong đó có ít nhất 1 chính phẩm. Giải
+ Gọi A là bc “ trong k sp lấy ra có ít nhất 1 chính phẩm”
+ Gọi là bc “ trong k sp lấy ra không có chính phẩm nào”
Dễ thấy A và đối lập P(A)=1-P(
+ Khi k > n – m thì P(A)=1. +Khi k - Có cách lấy k sp
- Số phế phẩm n – m, kết cục thuận lợi cho là - P( - P(A)= 1 – P( =1 -
VD. Hòm có 10 chi tiết , trong đó có 2 chi tiết hỏng. Tìm XS để khi lấy ngẫu
nhiên 6 chi tiết thì có không quá 1 chi tiết hỏng. Giải
+ Gọi A0 là bc “ trong 6 chi tiết không có chi tiết nào hỏng”
+ A1 là bc “ trong 6 chi tiết có một chi tiết hỏng”
+ A là bc “trong 6 chi tiết có không quá một chi tiết hỏng”
A = A0 + A1 ; A0, A1 xung khắc P(A)= P(A0) + P(A1) Ta có P(A0) = ; P(A1) = P(A)=
1.4. Một số định lý và công thức thức tính XS 1.4.1. XS có điều kiện
ĐN. XS của bc A được tính với đk của bc B đã xảy ra gọi là XS có điều kiện
của A. Ký hiệu là P(A/B).
VD. Trong bình có 5 quả cầu trắng, 3 quả cầu đen. Lấy ngẫu nhiên lần lượt 2
quả cầu. Tìm XS để lần thứ 2 lấy được quả càu trắng (bc B) nếu biết lần thứ nhất
đã lấy được quả cầu trắng (bc A). Giải
Sau khi lấy lần thứ nhất (A đã xảy ra) thì trong bình chỉ còn 4 quả cầu trắng, 3 quả cầu đen P(B/A) = 4/7. 1.4.2. Định lý nhân XS
ĐN 1. Biến cố C gọi là tích của hai biến cố A và B nếu C xảy ra khi chỉ khi A và
B cũng xảy ra đồng thời. Ký hiệu C=A.B
VD. Hai hộp. Mỗi hộp đều đựng cầu trắng và cầu đen
A là bc “lấy được cầu trắng ở hộp thứ nhất”
B là bc “ lấy được cầu trắng ở hộp thứ hai”
C là bc “lấy được 2 cầu trắng” C= A.B
ĐN 2. A là tích của các bc A1,A2,…,An nếu A xảy ra khi và chỉ khi cả n bc A1,A2,
…,An xảy ra. Ký hiệu A= A1.A2…An=
ĐN 3. Hai bc A, B gọi là độc lập với nhau nếu việc xảy ra hay không xảy ra của
bc này không làm thay đổi XS của bc kia và ngược lại.
Khi việc xảy ra hay không xảy ra của bc này làm thay đổi XS của biến cố kia
thì hai bc gọi là phụ thuộc nhau.
VD. Trong bình có 3 cầu trắng, 2 cầu đen. Lấy ngẫu nhiên 1 quả. A là bc lấy
được cầu trắng P(A)= 3/5. Quả cầu bỏ lại vào bình, tiếp tục lấy 1 quả cầu, B
là bc lần 2 lấy được cầu trắng P(B) = 3/5 A, B độc lập
VD như trên , nhưng không hoàn lại thì P(B) = 2/4=1/2 ( lần 1 lấy được cầu trắng)
Nếu lần 1 lấy được cầu đen thì P(B) = 3/4 - A, B phụ thuộc nhau.
ĐN 4. Các bc A1,A2,…,An gọi là độc lập từng đôi với nhau nếu mỗi cặp trong n
bc đó độc lập với nhau.
VD: Gieo đồng xu 3 lần, gọi Ai (i=1,2,3) là bc được mặt sấp ở lần gieo thứ i. Rõ
ràng A1 độc lập với A2, A3 ; A2 đl với A3.
ĐN 5. Các bc A1,A2,…,An gọi là độc lập toàn phần với nhau nếu mỗi bc độc lập
với một tổ hợp bất kỳ các bc còn lại.
A1,A2,A3 đl toàn phần với nhau nếu A1 đl với A2, A3 ; A2 đl với A3
A1 đl với tích A2.A3 ; A2 đl với tích A1.A3; A3 đl với tích A1.A2
Chú ý: Các bc độc lập từng đôi chưa chắc đã độc lập toàn phần.
Nhiều khi phải biểu diễn bc phức tạp dưới dạng tích các bc đơn giản. VD. Sản xuất ra 3 sp
+ A1 là sp 1 chính phẩm ; là sp 1 phế phẩm
+ A2 là sp 2 chính phẩm ; là sp 2 phế phẩm
+ A3 là sp 3 chính phẩm ; là sp 3 phế phẩm
+ C là bc trong 3 sp đó có ít nhất 2 chính phẩm thì
C = A1A2 + A1A3 +A2A3 + A1A2A3
1. Định lý 1. Nếu 2 bc A và B độc lập thì P(AB)=P(A)P(B) (1.8)
Hẹ quả 1. A,B độc lập thì:
P(A) = P(AB)/P(B) ; P(B)=P(AB)/P(A) (1.9)
Hệ quả 2. A1,A2,…,An đl toàn phần thì P() (1.10)
VD. Hộp 1 đựng 10 ốc trong đó có 6 cái tốt
Hộp 2 đựng 15 vít trong đó có 9 cái tốt
Lấy ngẫu nhiên mỗi hộp 1 chi tiết. Tìm XS để lấy được một bộ tốt Giải
+ Gọi A1 là bc “lấy ốc tốt”
+ Gọi A2 là bc “lấy vit tốt”
+ A là bc “lây được bộ tốt”
Vì A1,A2 đl với nhau P(A)=P(A1A2)=P(A1)P(A2)= =
2. Định lý 2. XS tích của hai bc phụ thuộc A và B bằng tích của một trong
hai bc đó với XS có đk của bc còn lại.
P(AB)=P(A)P(B/A) = P(B)P(A/B) (1.11)
Hệ quả 1: Nếu P(B)>0 thì: P(A/B) = P(AB)/P(B) (1.12)
P(A)>0 thì: P(B/A) = P(AB)/P(A) (1.13)
Hệ quả 2: Nếu A1,A2,…,An phụ thuộc thì
P(A1A2…An)= P(A1).P(A2/A1)…P(An/ A1A2…An-1) (1.14)
Hệ quả 3. Nếu A và B đl thì
P(A/B)=P(A) ; P(B/A) = P(B) (1.15)
VD. Trong hòm có 7 chính phẩm, 3 phế phẩm. Tìm XS để 2 lần lấy đều là chính phẩm. Giải
+ Goi A1 là bc “lần 1 lấy chính phẩm”
+Gọi A2 là bc “ lần 2 lấy chính phẩm”
+ Gọi A là bc cả 2 lần lấy là chính phẩm
A=A1A2 ; A1, A2 là 2 bc phụ thuộc
P(A) = P(A1A2) = P(A1)P(A2/A1)= 7/10. 6/9 = 7/15
3. Định lý 3. Nếu A, B là hai bc không xung khắc thì:
P(A+B)=P(A)+P(B) – P(AB) (1.16)
Hệ quả 1. A1,A2,…,An không xung khắc thì: P( (1.17) Hệ quả 2. P()= (1.18)
4. Định lý 4. Nếu A1,A2,…,An không xung khắc và độc lập toàn phần với nhau thì: P( 1 - P( ) (1.19)
VD. Hai máy bay ném bom một mục tiêu, mỗi máy bay ném một quả với XS
trúng là 0,7 và 0,8. Tìm XS để mục tiêu bị trúng bom Giải
+A là bc “mục tiêu trúng bom”
+ A1 là bc “quả 1 trúng”
+ A2 là bc “quả 2 trúng”
Ta có A= A1+A2; A1 , A2 không xung khắc P(A)= P(A1)+P(A2) – P(A1A2)
A1, A2 đl với nhau nên: P(A1A2)=P(A1)P(A2)
P(A)= P(A1)+P(A2) – P(A1)P(A2) = 0,7+0,8 – 0,7.0,8= 0,94 1.4.3. Công thức Bernoulli
+ Các phép thử đl : XS để xảy ra một bc không phụ thuộc vào các phép thử trước + Có n phép thử đl
+ Mỗi phép thử chỉ có A xảy ra hoặc không xảy ra. XS để A xảy ra trong mỗi phép thử đều là p
Bài toán thỏa mãn 3 đk trên là tuân theo lược đồ Bernoulli. Lúc đó XS để trong
n phép thử đl nói trên, bc A xuất hiện đúng x lần, ký hiệu Pn(x) được tính theo công thức Bernoulli: Pn(x) = (1.21)
VD. Phân xưởng có 5 máy hoạt động, XS trong ca mỗi máy bị hỏng là 0,1. Tìm
XS để trong ca có đúng 2 máy bị hỏng. Giải
+ Hoạt động của mỗi máy là 1 phép thử có 5 phép thử đl
+ Mỗi phép thử có 2 trường hợp : - máy hỏng. - - Máy tôt + XS hỏng đều bằng 0,1
thỏa mãn lược đồ Bernoulli P5(2)=
1.4.4. Công thức XS đầy đủ, công thức Bayes
1. Công thức XS đầy đủ
A là bc có thể xảy ra đồng thời với một trong các bc H1, H2,…,Hn. Nhóm H1,
H2,…,Hn là một nhóm đầy đủ các bc. Khi đó: P(A) = (1.22).
H1, H2,…,Hn thường gọi là các giả thuyết.
VD. Có 3 hộp giống nhau. Hộp 1 đựng 10 sp, có 6 chính phẩm. Hộp 2 đựng 15
sp, có 10 chính phẩm. Hộp 3 đựng 20 sp có 15 chinh phẩm. Lấy ngẫu nhiên một
hộp, từ đó lấy ngẫu nhiên 1 sp. Tìm XS để lấy được chính phẩm. Giải
+ A là bc lấy được chính phẩm. A có thể xảy ra đồng thời với một trong 3 bc sau
. H1 là sp lấy ra từ hộp 1
. H2 là sp lấy ra từ hộp 2
. H3 là sp lấy ra từ hộp 3
Theo gt, H1, H2, H3 là đồng khả năng P(H1)=P(H2)=P(H3)=1/3
XS có đk của bc A khi Hi xảy ra là:
P(A/H1)=6/10; P(A/H2)=10/15; P(A/H3)=15/20
Do đó: P(A) = P(H1)P(A/H1) + P(H2)P(A/H2) + P(H3)P(A/H3) = 31/45
VD. Hộp 1 có 10 sp trong đó có 9 chính phẩm
Hộp 2 có 20 sp trong đó có 18 chính phẩm
Từ hộp 1 lấy ngẫu nhiên 1 sp rồi bỏ vào hộp 2. Tìm XS lấy ngẫu nhiên 1 sp từ
hộp 2 được chính phẩm. Giải
+ A là bc lấy được chính phẩm từ hộp 2. Biến cố A có thể xảy ra đồng thời với 1
trong 2 bc sau đây tạo thành nhóm đầy đủ các bc
. H1 là sp bỏ từ hộp 1 sang là chính phẩm. P(H1)=9/10.
. H2 là sp bỏ từ hộp 1 sang là phế phẩm. P(H2)=1/10.
Có P(A/H1)=19/21; P(A/H2)=18/21
P(A) = P(H1)P(A/H1) + P(H2)P(A/H2) = 0,9. 2. Công thức Bayes
+ Giả sử bc A có thể xảy ra đồng thời với một trong n các bc H1, H2, …, Hn tạo
nên một nhóm đầy đủ các bc. + Lúc đó: P(Hi/A) = (i=1,2,..,n) (1.23) Chú ý:
+ H1, H2,… gọi là giả thuyết
+P(Hi) được xác định trước khi phép thử tiến hành nên gọi là XS tiên nghiệm.
+ P(Hi/A): Xác định sau khi phép thử thực hiện nên gọi là XS hậu nghiệm.
+ Như vậy công thức Bayes cho phép đánh giá lại XS xảy ra các giả thuyết sau
khi biết phép thử bc A xảy ra.
VD. Dây chuyền lắp ráp các chi tiết do 2 máy SX. Trung bình máy 1 cung cấp
60% chi tiết, máy hai 40% chi tiết. Khoảng 90% chi tiết do máy 1 SX đạt tiêu
chuẩn, 85% chi tiết do máy 2 SX đạt tiêu chuẩn. Lấy ngẫu nhiên từ dây chuyền
1 sp thấy nó đạt tiêu chuẩn. Tìm XS để sp đó do máy 1 SX ra. Giải
+ A – bc “ Lấy từ dây chuyền đạt tiêu chuẩn”
+H1 – bc “ chi tiết do máy 1 SX”.
+ H2 – bc “ chi tiết do máy 2 SX”.
XS để chi tiết do máy 1 SX: P(H1/A)= Theo đk bài toán P(H1)= 0,6 P(A/H1)=0,9 P(H2)=0,4 P(A/H2)=0,85
P(H1/A)= 0,6.0,9/(0,6.0,9+0,4.0,85)= 0,614
VD. Khi đưa sp ra thị trường, người ta đã phỏng vấn ngẫu nhiên 200 khách
hàng. Thấy 34 người nói “sẽ mua”, 96 người trả lời “có thể sẽ mua”, 70 người
trả lời “không mua”. Kinh nghiệm cho thấy tỷ lệ khách hàng thực sự sẽ mua sp
tương ứng với cách trả lời là: 40%, 20%, 1%
a. Hãy đánh giá thị trường tiềm năng của sp
b. Trong số khách hàng thực sự mua sp thì có bao nhiêu % trả lời sẽ mua. Giải.
a. Thị trường tiềm năng của sp chính là tỷ lệ khách hàng thực sự mua sp ấy.
Vì vậy, gọi A là bc “lấy ngẫu nhiên 1 khách hàng thì người đó thực sự mua”
+ H1 – Người đó trả lời sẽ mua
+H2 – Người đó trả lời “có thể sẽ mua”
+H3 – Người đó trả lời “không mua”
Theo công thức XS đầy đủ:
P(A)= P(H1)P(A/H1) + P(H2)P(A/H2) + P(H3)P(A/H3) =
= (34/200).0,4 + (96/200).0,2 + (70/200).0,01 = 0,1675
Vậy thị trường tiềm năng của sp là: 16,75% b. Theo công thức Bayes P(H1/A) = = = =
Chương II. Biến ngẫu nhiên và quy luật phân phối xác suất
2.1. Định nghĩa và phân loại biến ngẫu nhiên 1. Định nghĩa
Một biến cố gọi là biến ngẫu nhiên nếu trong kết quả của phép thử nó sẽ
nhận một và chỉ một trong các giá trị có thể có của nó, tùy thuộc vào sự tác
động của các nhân tố ngẫu nhiên.
Biến ngẫu nhiên ký hiệu là X , Y, Z hay X1, X2,… các giá trị có thể có của
chúng ký hiệu là x1 , x2,…
Nói X là biến ngẫu nhiên, vì trước khi thử ta không biết chắc chắn nó nhận
giá trị bao nhiêu, mà chỉ có thể dự đoán điều đó với một XS nhất định. VD.
+ Gieo một con xúc xắc. Gọi X là “số chấm xuất hiện”. X là biến ngẫu nhiên
(vì trong kết quả có thể nhận 6 giá trị).
+ X là số con trai trong 100 trẻ sắp sinh ở nhà hộ sinh. X là biến ngẫu nhiên
+ Y là khoảng cách từ điểm chạm của viên đạn đến tâm bia. Y là biến ngẫu nhiên.
2. Phân loại biến ngẫu nhiên
+ Biến ngấu nhiên gọi là rời rạc nếu các giá trị có thể có của nó lập nên một
tập hữu hạn hoặc đếm được ( có thể liệt kê được) VD.
- X là “số chấm xuất hiện khi gieo xúc xắc” – là biến ngẫu nhiên rời rạc vì đó là tập hữu hạn
- Phân xưởng có 5 máy. X là “số máy hỏng trong một ca”. X là biến ngẫu
nhiên rời rạc vì các giá trị có thể có là: 0, 1, 2, 3, 4, 5
+ Biến ngẫu nhiên liên tục là các giá trị có thể có của nó lấp đầy một khoảng trên trục số.
VD. Bắn bia. X là “khoảng cách từ điểm chạm đến tâm bia”. X là biến ngẫu
nhiên liên tục vì không thể liệt kê được các giá trị có thể có của X.
2.2 Quy luật phân phối XS của biến ngẫu nhiên
ĐN. Quy luật phân phối XS của biến ngẫu nhiên là sự tương ứng giữa các
giá trị có thể có của nó và các XS tương ứng với các giá trị đó. Thực tế thường dùng + Bảng phân phối XS + Hàm phân bố XS. + Hàm mật độ XS 2.2.1. Bảng phân phối XS
+ Dùng để mô tả quy luật phân phối XS của các biến ngẫu nhiên rời rạc.
+ X là biến ngẫu nhiên rời rạc có các giá trị: x1, x2,… +XS tương ứng p1, p2, …
+ Bảng phân phối của biến ngẫu nhiên rời rạc X sẽ là: X x1 x2 …. xn P p1 p2 ….pn
VD. Gieo con xúc xắc. X là “số chấm xuất hiện”. Tìm quy luật phân phối của X Giải
X = 1, 2, 3, 4, 5, 6. XS tương ứng đều bằng 1/6 bảng phân phối XS là: X 1 2 3 4 5 6 P
Kiểm tra: 1/6+1/6+1/6+1/6+1/6+1/6 = 1
VD. Một hộp có 10 sp. Trong đó có 6 chính phẩm. Lấy ngẫu nhiên 2 sp. Tìm
quy luật phân phối XS của số chính phẩm lấy ra. Giải
+ Gọi Y là “số chính phẩm lấy ra trong 2 sp”. Y = 0, 1, 2 + Ta có P(0)= ; P(1) =; P(2)= Bảng phân phối XS là:
X 0 1 2 Kiểm tra: 2/15+8/15+5/15 = 1 P
VD. XS để xạ thủ bắn trúng bia là 0,8. Xạ thủ được phát từng viên đạn để bắn
cho đến trúng bia thì thôi. Tìm quy luật phân phối XS (PPXS) của số viên đạn được phát. Giải.
+ Gọi X là “số viên đạn được phát”. X là biến ngẫu nhiên nhận các giá trị X=1, 2,…,k, … + Các XS tương ứng:
P(X=1) là XS để số viên đạn phát là 1. Ngay viên đầu đã trúng, do đó P(1)=0,8.
P(X=2) là XS để số viên đạn phát là 2 xảy ra 2 bc: phát đầu bắn trượt, phát 2
bắn trúng. Theo định lý nhân XS P(X=2)=0,2.0,8
Tổng quát: P(X=k)=(0,2)k-10,8 Bảng PPXS: X 1 2…………… k…….. P 0,8 0,2.0,8 (0,2)k-10,8 Kiểm tra = =1
2.2.2. Hàm phân bố xác suất (PBXS)
Áp dụng cho cả biến ngẫu nhiên rời rạc và liên tục 1. ĐN
Hàm PBXS của biến ngẫu nhiên X, ký hiệu F(x), là XS để biến ngẫu
nhiên X nhận giá trị nhỏ hơn x, với x là một số thực bất kỳ.
F(x) = P(XChú ý: Đây là định nghĩa tổng quat của hàm PBXS. Với từng loại biến ngẫu
nhiên hàm PBXS được tính theo công thức riêng.
Nếu X là biến ngẫu nhiên rời rạc thì hàm PBXS xác định theo công thức: F(x) =
VD. Biến ngẫu nhiên rời rạc có bảng PPXS X 1 3 4 P 0,1 0,5 0,4
Tìm hàm PBXS và vẽ đồ thị. Giải.
+ Nếu x (X< x): là bc không thể có F(x)=0
+ Nếu 1+ Nếu 3+ Nếu x>4. Bc (X0,1+0,5+0,4 =1 F(x) Vậy: 1 F(x) = 0,6
Đồ thị F(x) có dạng như hình vẽ 0,1 0 1 2 3 4
2. Các tính chất của hàm PBXS
a. Tính chất 1. Hàm PBXS luôn nhận giá trị trong [0 , 1] 0
b. Tính chất 2. x2 > x1 thì F(x2 F(x1) Hệ quả 1. P(a
Hệ quả 2. XS để biến ngẫu nhiên liên tục X nhận một giá trị xác định bằng 0. P(X=x) = 0 (2.5)
Hệ quả 3. Với biến ngẫu nhiên liên tục ta có: P(a
Vậy việc xét XS để biến ngẫu nhiên liên tục nhận 1 giá trị xác định là không
ý nghĩa. Nhưng việc tìm XS để nó nhận giá trị trong một khoảng là có giá trị. c. Tính chất 3.
Hệ quả: Nếu biến ngẫu nhiên chỉ nhận giá trị trong đoạn [a , b] thì : xb, F(x) = 1. 3. Ý nghĩa của hàm PBXS
Từ F(x) = P(Xtrái một số thực nào đó.
Toàn bộ XS của biến ngẫu nhiên bằng 1,do đó giá trị của hàm PBXS tại một
điểm x cho biết có bao nhiêu phần của một đơn vị XS phân bố trong đoạn (.
VD. Biến ngẫu nhiên có hàm PBXS F(x) =
Tìm XS để trong kết quả của phép thử, X nhận giá trị trong khoảng [0; 1/3] Giải P(0 2.2.3. Hàm mật độ XS
1. ĐN. Hàm mật độ XS của biến ngẫu nhiên liên tục X là đạo hàm bậc nhất
của hàm PBXS của biến ngẫu nhiên đó. f(x) = F’(x) (2.8) b. Tìm hàm PBXS F(x)
c. Tìm XS để biến ngẫu nhiên nhận giá trị trong (0 ; ) Giải.
a. Theo tính chất của hàm mật độ XS ta có a=1/2 b. F(x) = Với x : F(x) =0 Với - : F(x) = Với x> : F(x) ==++=1 Vậy: F(x) =
c. P(0VD. Hàm mật độ XS của biến ngẫu nhiên X có dạng f(x) =
Tìm XS để tiến hành 3 phép thử độc lập có hai lần X nhận giá trị trong khoảng (-1;1). Giải
+ XS để tiến hành một phép thử biến ngẫu nhiên nhận kết quả trong (- 1;1):
P(-1+ Theo đề bài: Thực hiện 3 phép thử độc lập, trong mỗi phép thử chỉ có
hai khả năng: X nhận giá trị trong (-1 ; 1) (bc A), hoặc không nhận giá trị
trong khoảng đó ( bc ). XS để trong mỗi phép thử biến ngẫu nhiên X
nhận trong khoảng (-1 ; 1) đều bằng 0,5. Do đó theo công thức Bernoulli,
XS để trong 3 phép thử có 2 lần X nhận giá trị trong ( -1 ; 1 ) là: P3(2) = = 0,375.
3. Ý nghĩa của hàm mật độ XS
Hàm mật độ XS của biến ngẫu nhiên X tại điểm x cho biết mức độ tập trung XS tại điểm đó.
2.3 Các tham số đặc trưng của biến ngẫu nhiên
Những thông tin cô đọng phản ánh từng phần về biến ngẫu nhiên gọi là các tham số đặ trưng
+Các tham số đặc trưng cho xu hướng trung tâm của biến ngẫu nhiên: Kỳ vọng, trung vị, môt,…
+ Các tham số đặc trưng cho sự phân tán của biến ngẫu nhiên: Phương sai,
độ lệch chuẩn, hệ số biến thiên.
+ Các tham số đặc trưng cho phân phối XS 2.3.1. Kỳ vọng toán 1. ĐN
Các biến ngẫu nhiên rời rạc X nhận các giá trị x1,x2,..., XS tương ứng
p1,p2,.. Kỳ vọng toán của biến ngẫu nhiên rời rạc X, ký hiệu E(X) là: E(X) = (2.14)
+ Nếu X là biến ngẫu nhiên liên tục thì: E(X) = (2.15)
VD.Biến ngẫu nhiên X có hàm mật độ XS: f(x) = Tìm E(X) Giải. E(X) = = + + = = = 2. Tính chất.
Tính chất 1. Nếu C= const thì E(C) =C
Tính chất 2. C=const, X là biến ngẫu nhiên thì E(CX)= CE(X) (2.16)
Hai biến ngn gọi là độc lập với nhau nếu quy luật phân phối XS của biến ngn
này không phụ thuộc gì vào việc biến ngn kia nhận giá trị bằng bao nhiêu.
X, Y là biến ngn.Tổng của X và Y là X+Y mà các giá trị có thể có của nó là
tổng mỗi giá trị có thể có của X và mỗi giá trị có thể có của Y.
Khi X, Y độc lập thì P(X+Y)=P(X)P(Y)
Khi X,Y phụ thuộc thì P(X+Y)=P(X)P(Y/X)=P(Y)P(X/Y)
Tính chất 3. E(X+Y)=E(X) + E(Y) Hệ quả: E( = (2.18)
Tích của 2 biến ngn độc lập X, Y là biến ngn XY mà các giá trị có thể có của
nó là tích giữa mỗi giá trị có thể có của X và mỗi giá trị có thể có của Y.các
XS tương ứng là tích của các XS thành phần.
Tính chất 4. Nếu X,Y độc lập thì E(XY)=E(X)E(Y) (2.19) Hệ quả: E( (2.20)
3. Bản chất và ý nghĩa của kỳ vọng toán
+ Kỳ vọng toán của biến ngn gần bằng trung bình số học của các giá trị quan
sát được của biến ngn. Nó phản ánh giá trị trung tâm của PPXS của biến ngn.
VD. Thời gian xếp hàng chờ mua hàng là biến ngn liên tục T có hàm mật độ XS như sau. f(t) =
Tìm thời gian xếp hàng trung bình của khách hàng Giải.
Thời gian xếp hàng trung bình chính là kỳ vọng toán E(T) = = + + = = = = 2,4 phút.
VD. XS để một nhà máy sản xuất ra phế phẩm bằng p. Máy sửa chữa ngay sau khi làm ra phế phẩm.
Tìm số sp được sản xuất ra giữa hai lần sửa chữa. Giải.
Gọi X là số sp được sản xuất ra giữa hai lần sửa chữa. X có bảng PPXS sau: X 1 2 3 ….. k …… P p qp q2p ….. qk-1p …..
Trong đó q=1-p ( XS để sx ra chính phẩm)
Số sp trung bình sx ra là kỳ vọng toán E(X) E(X) = = = = = E(X) = p.
4. Ứng dụng của kỳ vọng toán.
Tiêu chuẩn này thường được biểu diễn dưới dạng lợi nhuận kỳ vọng, hay
doanh số kỳ vọng để làm căn cứ lựa chọn chiến lược kinh doanh. 2.3.2. Trung vị
+ Ký hiệu là md là giá trị nằm chính giữa PPXS biến ngn. Nó là giá trị chia
phân phối của biến ngn thành hai phần bằng nhau.
+ X là biến ngn rời rạc thì Xi là trung vị nếu nó thỏa mãn F(Xi) F(Xi+1) (2.24)
+ X là biến ngn liên tục thì md thỏa mãn: (2.25) 2.3.3. Mốt (Mode)
+Ký hiệu m0 là giá trị của biến ngn tương ứng với :
1. XS lớn nhất nếu là biến ngn rời rạc
2. Cực đại của hàm mật độ XS nếu là biến ngn liên tục
VD Tìm trung vị và mốt của biến ngn có bảng PPXS sau X 20 21 22 23 24 25 P 0,3 0,25 0,18 0,14 0,1 0,03 Giải Ta xây dựng hàm PBXS F(x)=
Từ đó ta thấy: md = 21 ; m0 = 20 2.3.4. Phương sai
1. ĐN. Phương sai của biến ngn X, ký hiệu V(X) là kỳ vọng toán của bình
phương sai lệch của biến ngn so với kỳ vọng toán của nó V(X)=E[X – E(X)]2 (2.26)
+ Với X là biến ngn rời rạc thì: V(X)= (2.27)
+ Với X là biến ngn liên tục: V(X) = (2.28)
+ Thường tính phương sai bằng công thức:
V(X) = E(X2) – [E(X)]2 (2.29) CM
V(X)=E[X – E(X)]2 = E[X2 – 2XE(X) + (E(X))2] = E(X2) – 2E(X)E(X) + (E(X))2 = E(X2) – [E(X)]2 Từ đó
+ Với biến ngn rời rạc : V(X) = – [E(X)]2 (2.30)
+ Với biến ngn liên tục: V(X)= – [E(X)]2 (2.31)
VD. Cho biến ngẫu nhiên rời rạc X 1 3 4 P 0,1 0,5 0,4 Tìm V(X). Giải
E(X) = 1.0,1 + 3.0,5 + 4.0,4 = 3,2
E(X2) = 12.0,1 + 32.0,5 +42.0,4 = 11
V(X) = E(X2) – [E(X)]2 = 11 – (3,2)2 = 0,76
VD. Biến ngn liên tục có mật độ XS f(x) = Tính V(X). Giải E(X)= E(X2)= V(X) = E(X2) – [E(X)]2 =
2. Các tính chất của phương sai
Tính chất 1. C= const thì V(C) = 0 (2.32)
Tính chất 2. V(CX) = C2V(X) (2.33)
Tính chất 3. X, Y độc lập thì V(X+Y) = V(X) + V(Y) (2.34)
Hệ quả 1. Nếu X1, X2, ..., Xn độc lập với nhau thì: V( (2.35)
Hệ quả 2. C=const thì V(C+X) = V(X) (2.36)
Hệ quả 3. X, Y độc lập thì V(X – Y) = V(X) + V(Y) (2.37)
3. Bản chất và ý nghĩa của phương sai
+ Phương sai là trung bình số học của bình phương các sai lệch giữa các giá trị
có thể có của biến ngn so với giá trị trung bình của các giá trị đó.
+ Phản ánh mức độ phân tán của các giá trị của biến ngẫu nhiên xung quanh giá
trị trung bình của nó là kỳ vọng toán.
VD. Gieo n con xúc xắc. Tìm phương sai tổng số điểm thu được. Giải.
+ Gọi Xi là số điểm thu được ở con xúc xắc thứ i (i=1,2...,n)
+ Gọi X là tổng số điểm thu được ở cả n con xúc xắc X =
+ Các Xi là độc lập, nên V(X)= V( +Ta có V(X 2 i) = E(Xi ) – [E(Xi)]2 Xi có bảng PPXS Xi 1 2 3 4 5 6 P 1/6 1/6 1/6 1/6 1/6 1/6 Từ đó tính được:
E(Xi) = 1/6(1+2 +3 +4 +5 +6) = 7/2 E(X 2 2 2 2 2 2 2
i ) = 1/6(1 + 2 +3 +4 +5 +6 ) = 91/6 V(X 2 2
i) = E(Xi ) – [E(Xi)]2 =91/6 – (7/2) = 35/2 V(X) =
VD. XS để một máy SX ra phế phẩm bằng p. Máy sẽ được sửa chữa ngay sau
khi làm ra phế phẩm. Tìm phương sai của số sp được sx giữa hai lần sửa chữa. Giải
+ Ta có bảng PPXS của X ( số sp giữa 2 lần sửa chữa) X 1 2 3 ,,,,,,, k.....
P p qp q2p.....qk-1p.... q=1-p + Dễ tính E(X) = 1/p + E(X2) = + Ta đã biết: = V(X) = E(X2) – [E(X)]2 =
4. Ứng dụng của phương sai
+ Trong kỹ thuật, Phương sai đặc trưng cho độ phân tán của các chi tiết gia công
hay sai số của thiết bị.
+ Trong kinh tế đặc trưng cho sự rủi ro của các quyết định.
2.3.5. Độ lệch chuẩn, hệ số biến thiên, giá trị tới hạn 1. Độ lệch chuẩn
ĐN. Độ lệch chuẩn của biến ngn X là: (2.38) 2. Hệ số biến thiên
ĐN. Hệ số biến thiên xác định theo công thức: CV=.100% Nếu E(X) (2.39).
+ CV dùng để đo mức độ thuần nhất của một phân phối. CV càng nhỏ thì mức
độ thuần nhất càng lớn
+ CV cũng dùng để so sánh mức độ phân tán của 2 phân phối mà kỳ vọng toán
và độ lệch chuẩn không nhất thiết phải như nhau. 3. Giá trị tới hạn
ĐN. Giá trị tới hạn mức của biến ngn X ký hiệu là là giá trị của X thỏa mãn đk P(X> =
Trên đồ thị giá trị tới hạn mô tả như hình vẽ f(x)
Vậy giá trị tới hạn là giá trị
sao cho diện tích gh bởi trục hoành,
đường cong mật độ XS và đường thẳng bằng x
2.3.6. Hệ số nhọn, hệ số bất đối xứng ( đọc thêm)
Chương III. Một số quy luật phân phối XS thông dụng
3.1. Quy luật không – một A(p) (Quy luật Bernoulli)
Một bình có M quả cầu trắng, N – M quả cầu đen.
Lấy ngn 1 quả cầu. A là bc “cầu trắng”, là bc “cầu đen” + XS để có A là p = M/N
+ XS để có là q= (N – M )/N = 1 – M/N = 1 – p
Tổng quát: Có phép thử, bc A xảy ra với XS p. Gọi X là số lần xuất hiện bc A
trong phép thử đó. Vậy X là biến ngn rời rạc với 2 giá trị có thể có bằng 1( xuất
hiện), bằng 0 ( không xuất hiện). XS để X nhận một trong hai giá trị đó là: P x
x = p q1-x với x = 0, 1 (3.1)
1.ĐN. Biến ngn rời rạc nhận một trong hai giá trị có thể có X =0, 1 với các XS
tương ứng tính bằng biểu thức (3.1) gọi là phân phối theo quy luật không – một
(quy luật Bernoulli) với tham số là p.
Ký hiệu quy luật này : A(p)
Bảng PPXS của biến ngn phân phối theo quy luật không – một : X 0 1 q=1 – p P q p
2.Các tham số đặc trưng của quy luật A(p)
+ Kỳ vọng : E(X) = 0.q + 1.p = p
+ Phương sai: V(X) = E(X2) – [E(X)]2 = [02.q + 12.p] – p2 = p(1 – p ) = pq + Độ lệch chuẩn:
3.2. Quy luật nhị thức – B(n,p)
Xét VD: Hộp có M cầu trắng, N – M cầu đen. Lấy lần lượt ra n quả cầu theo phương thức hoàn lại.
A – là bc “cầu trắng”, là bc “cầu đen” + XS để có A là p = M/N
+ XS để có là q= (N – M )/N = 1 – M/N = 1 – p
Những đk này dẫn đến lược đồ Bernoulli
Tổng quát: Có lược đồ Bernoulli, có n phép thử độc lập, mỗi phép thử chỉ cho
hai trường hợp A xuất hiện hoặc A không xuất hiện . XS đê có A: p, XS để là q = 1 – p
Gọi X là số lần xuất hiện biến cố A trong n phép thử độc lập nói trên. X là biến
ngn rời rạc với các giá trị có thể có X = 0,1,2,…,n. XS để X nhận các giá trị
tương ứng tính bằng công thức Bernoulli:
px = với x=0,1,2,…,n (3.2)
1.ĐN. Biến ngẫu nhiên rời rạc X nhận một trong các giá trị có thể có X =
0,1,2…,n với các XS tương ứng tính theo công thức (3.2) gọi là phân phối theo
quy luật nhị thức với tham số là n,p.
Ký hiệu quy luật nhị thức là: B(n,p)
Bảng PPXS của biến ngn X phân phối theo quy luật nhị thức: X 0 1 … x … n P
Khi tính XS để biến ngn X phân phối theo quy luật nhị thức nhận giá trị trong
khoảng [x , x + h], h nguyên dương (hP(x px + px+1 +….+ px+h (3.3) Dễ dàng chứng minh: px = (3.4)
VD. Phân xưởng có 5 máy độc lập. XS trong một ngày mỗi máy bị hỏng đều là 0,1. Tìm XS để
a. Một ngày có 2 máy hỏng
b. Một ngày có không quá 2 máy hỏng. Giải.
+ Mỗi máy hoạt động là một phép thử, có 5 phép thử độc lập. Mỗi phép thử chỉ
có 2 khả năng: Máy hỏng hoặc tốt. XS hỏng đều bằng 0,1 có lược đồ
Bernoulli. Gọi X là bc “số máy hỏng trong một ngày”, X phân phối theo quy
luật B(n,p) với n=5, p=0,1.
+ XS 1 ngày có 2 máy hỏng : p2 =
+XS một ngày có không quá 2 máy hỏng: P(0
2.Các tham số của quy luật nhị thức + Kỳ vọng: E(X) = np (3.5)
+ Phương sai: V(X) = npq (3.6) + Độ lệch chuẩn:
VD. Một nhân viên bán hàng, mỗi ngày đi chào hàng ở 10 nơi với XS bán được
hàng mỗi nơi là 0,2. Vậy nếu người đó đi bán 300 ngày thì trung bình sẽ có
khoảng bao nhiêu ngày người đó bản được hàng. Giải.
+ Xét một ngày nào đó, ta có lược đồ Bernoulli. Gọi X là số lần bán được hàng
trong ngày của người dó sẽ tuân theo luật nhị thức với n=10, p=0,2.
XS để người đó bán được hàng trong ngày là:
P = P(X = 1 – P(X=0) =1 - = 1 – (0,8)10 = 0,8926
+ Xét trong một năm ta có lược đồ Bernoulli. Gọi Y là số ngày bán được hàng
trong một năm, Y tuân theo quy luật nhị thức với n=300, p = 0,8926. Số ngày
trung bình một năm bán được là:
E(Y) = np = 300.0,8926 = 267,78 ngày
Chú ý: Nếu X tuân theo quy luật nhị thức thì mot (m0) thỏa mãn: np – q np + p (3.7)
3.Quy luật PPXS của tần suất
+ Nhiều khi quan tâm đến tỷ lệ xuất hiện bc A trong lược đồ Bernoulli. Ta biến
đổi X thành tần suất xuất hiện bc A trong n phép thử: f = X/n
+ Bảng PPXS của f có dạng: f 0 1/n … x/n … 1 P
E(f) = E(X/n) =E(X)/n = np/n = p (3.8) V(f) = V(X/n) = (3.9) (3.10) 3.3. Quy luật Poisson – P(
+ Nếu X là biến ngẫu nhiên PP theo quy luật nhị thức, XS để X nhận một trong
các giá trị có thể có của nó tính bằng công thức Bernoulli
+ Nếu n quá lớn, p quá nhỏ thì có thể chứng minh:
px =P(X=x)= (3.11) ( Chú ý np = const = )
(3.11) là công thức Poisson.
Thực tế công thức Poisson có thể thay cho công thức Bernoulli với n20; p0,1 ( np
1. ĐN. Biến ngn rời rạc X nhận một trong các giá trị có thể có X=0, 1, 2,…
với các XS tương ứng được tính theo (3.11) gọi là phân bố theo quy luật Poisson với tham số
Quy luật Poisson ký hiệu là: P(
Bảng PPXS theo quy luật Poisson X 0 1 …. x …. P …. ….
+ Nếu X phân phối theo quy luật Poisson thì:
P(x= px + px+1 +….+ px+h (3.12) + Ta có : px = (3.13)
VD. Một máy có 5000 ống sợi, XS để 1 phút ống sợi bị đứt bằng 0,0002. Tìm
XS để trong một phút có không quá 2 ống sợi bị đứt. Giải.
+ Bài toán thỏa mãn lược đồ Bernoulli, do n lớn, p quá nhỏ, np = 5000.0,0002
=1. Do đó nếu gọi X là số ống sợi bị đứt trong 1 phút thì X PP theo quy luật Poisson.
+ Ta có : P(0= p0 + p1 + p2 = += = += 0,9225
2. Các tham số đặc trưng của quy luật Poisson + Kỳ vọng: E(X) = (3.14) + Phương sai: V(X) = (3.15)
+ Mốt mo thỏa mãn: . Từ đây thấy nếu nguyên thì m0 cùng lúc nhận 2 giá trị
nguyên m0 = và m0 =. Còn là số thập phân thì mốt sẽ là số nguyên nằm trong
khoảng 2 số thập phân -1 và
VD.XS vận chuyển mà mỗi chai bị vỡ là 0,001. Vận chuyển 2000 chai
a. Tìm số chai vỡ trung bình
b. Số chai vỡ nhiều nhất khi vận chuyển. Giải.
+ Bài toán thỏa mãn lược đồ Bernoulli. n=2000 là lớn, p=0,001 là nhỏ np = 2
+ Gọi X là bc “số chai vỡ khi vận chuyển”, X là biến ngn PP theo quy luật Poisson
+ Số chai vỡ trung bình là: E(X) = =2
+ Số chai vỡ nhiều nhất là giá trị mốt m0 số chai vỡ nhiều nhất là 1 hoặc 2 chai.
3.4. Quy luật PP đều – U(a;b) (đọc thêm)
Biến ngẫu nhiên (BNN) liên tục gọi là phân phối đều trên (a,b), ký hiệu U(a,b),
nếu hàm mật độ XS có dạng: F(x) = + Kỳ vọng: E[X]= (a+b)/2
+ Phương sai: V[X] = (b-a)2/12.
3.5. Quy luật PP chuẩn – N(
1. ĐN. BNN liên tục X nhận giá trị trên R được gọi là có PP chuẩn ( hay PP
theo luật chuẩn) với tham số và nếu hàm mật độ XS của nó có dạng: f(x) = = (3.16)
Khảo sát hàm số trên thấy: + TXĐ: R
+ f(x) > 0 ; 0x là tiệm cận ngang;
+ f(x) có cực đại tại x0 =; f(x0) =
+ Đồ thị nhận đường thẳng x = là trục đối xứng.
Đồ thị f(x) có dạng như hình vẽ f(x) _ _ . | | |
Từ hàm mật độ XS hàm PBXS của BNN theo quy luật chuẩn: F(X) = (3.17)
2.Các tham số đặc trưng của quy luật chuẩn + Kỳ vọng: E(X)= (3.18) + Phương sai: V(X) = (3.19) (3.20)
3.Quy luật chuẩn hóa (chuẩn tắc)
BNN X phân phối chuẩn với E(X) = , độ lệch chuẩn là . Xét BNN ( trong thống
kê gọi là chuẩn hóa BNN X) U = gọi là phép chuẩn hóa BNN X
ĐN. BNN U nhận giá trị trên R gọi là tuân theo quy luật chuẩn hóa nếu hàm mật độ XS của nó có dạng: (3.21)
Đồ thị của hàm có dạng như hình vẽ. | . | -1 0 1 u
+ Hàm PBXS của BNN U PP chuẩn hóa có dạng: (3.22) + Kỳ vọng: E(U) = E()= + Phương sai: V(U)=V(
+ Phân phối chuẩn hóa ký hiệu : N(0;1)
4.Giá trị tới hạn chuẩn ( phân vị mức
ĐN. Giá trị tới hạn chuẩn mức ( ký hiệu là ) là giá trị của BNN U có PP chuẩn
hóa thỏa mãn đk P(U> =
Do U PP chuẩn hóa , nên hàm mật độ XS của U là: P(U> = | . | u 5.Công thức tính XS
a. Công thức tính XS để BNN nhận giá trị trong (a;b)
+ BNN X có hàm mật độ XS f(x) thì XS để X nhận giá trị trong (a;b) là:
P(a P(a+ Bằng cách đặt Z = , sau khi biến đổi chúng ta tính được: P(aTrong đó có tính chất: + + Với mọi u>5 thì
VD. Một cơ sở cần mua một loại gioăng cao su có độ dày từ 0,118cm đến
0,122cm. Có 2 cửa hàng cùng bán loại gioăng này với độ dày là BNN PP chuẩn
với các đặc trưng cho trong bảng sau: Độ dày trung bình Độ lệch chuẩn Giá bán Cửa hàng A 0,12 0,001 3USD/hộp/1000c Cửa hàng B 0,12 0,0015 2,6USD/hộp/1000c
Hỏi nên mua cửa hàng nào? Giải.
+ Cần xác định tỷ lệ gioăng đáp ứng yêu cầu.
+ Gọi XA , XB là độ dày gioăng của cửa hàng A và B
+ Theo gt, XA , XB đều là phân phối chuản P(0,118 2
P(0,118+ Vậy giá bán mỗi chiếc gioăng dùng được ở cửa hàng A, B lần lượt là:
3/954,4= 0,00314 USD ; 2,6/816,4 = 0,00318 USD
+ Từ đó thấy nên mua ở cửa hàng A
b.XS sự sai lệch giữa BNN và kỳ vọng toán của nó.
+BNN phân phối chuẩn X. Tìm XS để BNN nhận giá trị sao cho: |X - P(|X - )=P(= = Vậy: P(|X - (2.24)
6.Quy tắc hai xích ma và ba xích ma
+Trong công thức P(|X - ta đặt P(|X - (3.25)
Công thức (3.25) gọi là quy tắc hai xích ma
+ Tương tự, nếu thì ta có: P(|X - (3.26)
Công thức (3.26) gọi là quy tắc ba xích ma. Từ đó thấy:
+ XS đẻ BNN PP chuẩn lấy giá trị trong khoảng là 0,9544 hay 95,44%
+ XS đẻ BNN PP chuẩn lấy giá trị trong khoảng là 0,9973 hay 99,73%
…………………………………f(x)
……………………………………………………………………………………
……………………………………………………………………………………
……………………………………………………………………………………
……………………………………………………………………………………
…………………………………………………. 95,44% 99,73%
7. Phân phối XS của tổng các BNN độc lập tuân theo cùng quy luật
+X1 là BNN tuân theo quy luật chuẩn E(X1)= ; V(X1)=
+ X2 là BNN tuân theo quy luật chuẩn E(X2)= ; V(X2)=
Thì X=X1+X2 cũng PP theo quy luật chuẩn E(X)= , V(X)=
+ Nếu X1,X2,…, Xn là BNN độc lập lẫn nhau, cùng tuân theo một quy luật PPXS
nào đó (không nhất thiết là quy luật chuẩn) với các kỳ vọng toán E(X1), E(X2),
… phương sai V(X1),V(X2),.. thì BNN X= sẽ PP xấp xỉ chuẩn với: E(X)= ; V(X) = Khi n khá lớn (n>30).
8. Sự hội tụ của quy luật nhị thức và quy luật Poisson về quy luật chuẩn.
+ Khi dùng quy luật nhị thức , nếu n khá lớn thì tính theo công thức Bernoulli sẽ
khó khăn. Khi đó, nếu p nhỏ đến mức np thì dùng quy luật Poisson. Nhưng nếu
p không nhỏ (p>0,1) thì không dùng phân phối Poisson được. Lúc đó có thể
dùng quy luật chuẩn để thay thế cho quy luật nhị thức.
Quy luật chuẩn có thể thay thế cho quy luật nhị thức,nếu thỏa mãn đồng thời 2 đk: n > 5 và
Khi đó BNN X PP nhị thức có thể coi là PP xấp xỉ chuẩn với: E(X)= ; V(X) = = npq P(X=x)= (3.27)
(3.27) gọi là định lý địa phương Laplace. + Ta có: P(x (3.28)
(3.28) gọi là tích phân Laplace.
Chú ý: Với quy luật Poisson thì hội tụ về quy luật chuẩn khi . Vậy nếu X PP
Poisson song thì có thể xem X là PP chuẩn với E(X)=; V(X) =
VD. XS để sản phẩm sau khi sản xuất không được kiểm tra chất lượng là 0,2.
Tìm XS để 400 sp được sản xuất ra có
a. 80 sp không được kiểm tra
b. Có từ 70 đến 100 sp không được kiểm tra. Giải.
+ Gọi X là số sp không được kiểm tra: X + n=400>5 và Nên có thể coi X a.P(X=80)=
Với u= = 0 P(X=80)= = =0,04986 b.P(70X100)= == = 0,8882 Chú ý
+ Quy luật chuẩn có nhiều ứng dụng
+ Hầu hết tuân theo quy luật chuẩn.
+ Nếu BNN là một tổng số lớn các BNN độc lập và giá trị mỗi biến chỉ chiếm vị
trí nhỏ trong tổng số thì X sẽ có PP xấp xỉ chuẩn.
3.6. Quy luật khi bình phương - (đọc thêm)
3.7. Quy luật Student – T(n) (đọc thêm)
3.8. Quy luật Fisher – Snedecor – F(n1,n2) (đọc thêm)
Chương IV. Biến ngẫu nhiên hai chiều
4.1 Khái niệm về biến ngẫu nhiên hai chiều.
+ Các chương trước chỉ xét BNN là một số. Đó là BNN một chiều
+ Thực tế BNN có thể biểu diễn bằng nhiều số (2,3,… số). BNN như vậy gọi là BNN nhiều chiều
VD> Xét một sp công nghiệp
+ Nếu để ý đến chiều dai BNN một chiều
+ Nếu để ý đến chiều dài, chiều rộng BNN hai chiều.
+ Nếu để ý đến chiều dài, chiều rộng và chiều cao BNN ba chiều
BNN nhiều chiều cũng có 2 loại: Rời rạc , liên tục
4.1 Bảng PPXS của BNN rời rạc hai chiều
Bảng PPXS đồng thời của BNN 2 chiều rời rạc liệt kê các giá trị có thể có của
nó và các XS tương ứng. Nó có dạng: X x1 x2 … xi … xn Y y1 P(x1,y1) P(x2,y1) … P(xi,y1) … P(xn,y1) y2 P(x1,y2) P(x2,y2) … P(xi,y2) … P(xn,y2) … … … … … … … yi P(x1,yi) P(x2,yi) … P(xi,yi) … P(xn,yi) … … … … … … … yn P(x1,yn) P(x2,yn) … P(xi,yn) … P(xn,yn)
xi (i=1,2,..,n) là các giá trị có thể có của X.
yj(j=1,2,…,n) là các giá trị có thể có của Y
P(xi,yj)- là XS đồng thời để BNN hai chiều (X,Y) nhận giá trị (xi,xj) Chú ý: (4.1) 4.2.2 Bảng PPXS biên
Bảng PPXS biên của thành phần X có dạng X x1 x2 …. xn P P(x!) P(x2) …. P(xn)
Trong đó: P(xi) = i=1,2,… (4.2) Rỗ ràng:
Bảng PPXS biên của thành phần Y có dạng X y1 y2 …. yn P P(y1) P(y2) …. P(yn)
Trong đó: P(yi) = i=1,2,… (4.3) Rỗ ràng:
VD. Cho bảng PPXS đồng thời của BNN hai chiều X 26 30 41 50 Y 2,3 0,05 0,08 0,12 0,04 2,7 0,09 0,30 0,11 0,21
Tìm bảng PPXS biên của thành phần X và Y Giải.
Bảng PPXS biên của thành phần X và Y là X 26 30 41 50 P 0,14 0,38 0,23 0,25 Y 2,3 2,7 P 0,29 0,71
4.3.3. Bảng PPXS có điều kiện
Xét BNN rời rạc (X,Y) trong dó giá trị có thể có của X,Y là: x1, x2,…,xn; y1, y2, …,ym
P(xi/yj) (i= là XS có đk để X nhận giá trị xi với đk Y nhận giá trị yj
Bảng PPXS có đk của thành phần X với đk Y=yj là X/yj x1 x2 … xn
P P(x1/yj) P(x2/yj) … P(xn/yj) Trong đó: P(xi/yj)= (4.4) Chú ý: =
Tức là cũng thỏa mãn các yêu cầu của một quy luật PPXS.
Tương tự bảng PPXS có đk của thành phần Y đối với X là Y/xi y1 y2 … ym
P P(y1/xi) P(y2/xi) … P(ym/xi) P(yj/xi)= (i= (4.5) Và =
VD. PPXS của lương tháng Y ( triệu đồng) và giới tính X của công nhân một công ty như sau: Y 0,5 1 1,5 X Nữ : 0 0,1 0,3 0,2 Nam: 1 0,06 0,18 0,16
Tìm PPXS của lương tháng của nữ công nhân. Giải. P(x1)=P(0)= 0,1+0,3+0,2=0,6 P(y1/x1)= P(y2/x1)= P(y3/x1)=
Vậy BPPXS lương tháng của nữ công nhân là: Y/X=x1 0,5 1 1,5 P 1/6 1/2 1/3
4.3. Các tham số đặc trưng của BNN rời rạc hai chiều.
4.3.1. Kỳ vọng toán và phương sai của các thành phần.
Kỳ vọng toán của các thành phần xác định theo công thức:
+Nếu X, Y là BNN rời rạc thì: E(X) = (4.6) E(Y) = (4.7)
+Nếu X,Y là BNN liên tục thì: E(X) = (4.8) E(Y) = (4.9)
Phương sai được xác định theo công thức
+Nếu X, Y là BNN rời rạc thì: V(X) = (4.10) V(Y)= (4.11)
+Nếu X,Y là BNN liên tục thì: V(X)=(4.12) V(Y)= (4.13)
4.3.2. Kỳ vọng có điều kiện
Kỳ vọng toán có đk của BNN rời rạc Y với đk X=x ( 1 giá trị xác định của X) là
tổng các tích giữa các giá trị có thể có của Y với XS có đk tương ứng: E(Y/X=x)= (4.14) Nếu BNN liên tục thì: E(Y/X=x)= (4.15)
Tương tự kỳ vọng toán có đk của X khi Y=y:
+ BNN rời rạc: E(X/Y=y)= (4.16)
+ BNN liên tục: E(X/Y=y)= (4.17)
Hàm hồi quy của X đối với Y là kỳ vọng toán có đk của X đối với Y f(y) = E(X/y) (4.18)
VD. Thống kê dân số của một nước ở độ tuổi trưởng thành theo trình độ học vấn X và lứa tuổi Y như sau: Y 25 – 35 35 – 55 55 – 100 X 30 45 70 Thất học: 0 0,01 0,02 0,05 Tiểu học: 1 0,03 0,06 0,10 Trung học: 2 0,18 0,21 0,15 Đại học: 3 0,07 0,08 0,04
Tìm học vấn trung bình theo lứa tuổi. Giải.
Học vấn trung bình theo lứa tuổi là kỳ vọng toán có đk của X theo Y.
Với Y=30 ta có bảng PPXS sau X/Y=30 0 1 2 3
P 0, 01/0,29 0,03/0,29 0,18/0,29 0,07/0,29 E(X/Y=30) = 2,069
Tương tự: E(X/Y=45)=1,946 ; E(X/Y=70) = 1,569
Chương V. Các định lý giới hạn – Luật số lớn
5.1. Bất đẳng thức Trebưsep
Định lý: Nếu X là BNN có kỳ vọng toán và phương sai hữu hạn thì >0 tùy ý ta có: P(|X – E(X)| < ) (5.1) CM
Ta chứng minh cho trương hợp X là BNN rời rạc
Giả sử X là BNN rời rạc với các giá trị có thể có là x1, x2,… với các XS tương
ứng p1, p2,… Giả thiết k giá trị đầu tiên thỏa mãn |xi – E(X)|<, n-k giá trị còn lại thỏa mãn |xi – E(X)|.
Do các bc để |X – E(X)|<, |xi – E(X)| đối lập nhau, nên:
P(|X – E(X)| < )=1 - P(|X – E(X)| ) (*) Ta có: V(X) = [x 2 2 2 2
1 – E(X)] p1 +…+ [xk – E(X)] pk +[xk+1 – E(X)] pk+1 +…+[xn – E(X)] pn Các số hạng đều nên: V(X) [x 2 2
k+1 – E(X)] pk+1 +…+[xn – E(X)] pn
Chú ý với xi (i=k+1,k+2,..,n) đều có |xi – E(X)| nên V(X) (pk+1 + …+pn)
Theo định lý cộng XS thì pk+1+…+ pn là XS để BNN X nhận một trong các giá
trị xk+1 +…+ xn song mọi giá trị này đều thỏa mãn |xi – E(X)| Từ đó
pk+1 + …+pn = P(|X – E(X)| )
V(X) P(|X – E(X)| ) P(|X – E(X)| ) (5.2)
Từ (*) và (5.2) P(|X – E(X)| < )
Chú ý: (5.2) cũng được sử dụng như là một dạng khác của bất đẳng thức Trebưsep
VD. Thu nhập trung bình hàng năm của dân cư một vùng là 700USD, độ lệch
chuẩn là 120 USD. Hãy xác định một khoảng thu nhập hàng năm xung quanh
giá trị trung bình của ít nhất 95% dân cư vùng đó. Giải
+ X là thu nhập hàng năm của dân cư vùng này
+ Theo đề bài: E(X) = 700;
+ Theo bất đẳng thức Trebưsep:
P(|X – E(X)| < ) = = 0,95
Vậy ít nhất 95% dân cư vùng này có thu nhập hàng năm trong khoảng : ( 700 –
536,656; 700 + 536,656) khỏang (163,344 ; 1236,656). 5.2. Định lý Trebưsep
Định lý: Nếu các BNN X1,X2,…,Xn,… độc lập từng đôi, có các kỳ vọng toán
hữu hạn và các phương sai bị chặn trên bởi hằng số C ( V(Xi) ; i=1,2…,n) thì với
mọi số dương bé tùy ý ta có: (5.3) CM. +Xét BNN +E()= E( +V()= V(
Theo bất đẳng thức Trebưsep, ta có: P(| – E()| < )
Do V(Xi)< C P(| – E()| < ) Do nên
+ Nếu X1,X2,… độc lập từng đôi, có cùng kỳ vọng toán (E(Xi) = m), các phương
sai cùng bị chặn trên (V(Xi) thì: (5.4)
Định lý Treebưsep còn gọi là luật số lớn Trebưsep. 5.3. Định lý Bernoulli
Định lý: Nếu f là tần suất xuất hieenjbieens cố A trong n phép thử độc lập và p là
XS xuất hienj biến cố đó trong mỗi phép thử thì bé tùy ý ta có: (5.5) CM.
+ Xét BNN f = là tần suất xuất hiện bc A trong n phép thử độc lập. E(f) = E( V(f) = V(
X là số lần xuất hiện bc A trong n phép thử độc lập, mà theo giả thiết XS xuất
hiện bc trong mỗi phép thử là p. Vậy X phân phối theo quy luật nhị thức với
tham số n, p E(X) =np, V(X) = np(1-p) E(f) = V(f) =
Áp dụng bất đẳng thức Trebưsep ]=1 Do
Định lý này gọi là luật số lớn của Bernoulli
Định lý Bernoulli có thể viết ngắn gọn: f
5.4. Định lý giới hạn trung tâm 1. Hàm đặc trưng.
a. ĐN. Hàm đặc trưng của BNN X là kỳ vọng toán của BNN ó thể viết exp(itx)). Ký hiệu: Từ ĐN
+Nếu X là BNN rời rạc thì:
+Nếu X là BNN liên tục thì: .
b.Các tính chất của hàm đặc trưng b1. | Thật vậy, do |, nên b2.Nếu Y=ax+b thì theo định nghĩa:
b3.F(X) xác định một cách duy nhất hàm đặc trưng
b4.Nếu X1,X2,…,Xn là các BNN độc lập thì:
Thật vậy, vì X1,X2,… độc lập nên: = = ]=
b5.Nếu E|X|k thì cũng đạo hàm đén bậc k tại mọi điểm t
Hệ quả: E|X|k thì có khai triển Taylor + 0(
b6. Nếu { Fn(x)} là dãy hàm PBXS và {} là dãy các hàm đặc trưng tương ứng thì
đk cần và đủ để { Fn(x)} hội tụ yếu ( tức là hội tụ tại các điểm Fn(x) liên tục) tới
hàm PBXS F(x) là {} hội tụ tại mọi t đến hàm đặc trưng tương ứng tương ứng với F(x) VD. Cho BNN X Tìm Giải. Theo quy luật B(n,p) ta có: Px = =E(eitx) = = VD. Cho BNN X Tìm Giải.
+Theo quy luật Poisson: Px = x=0,1,2,… + == + Có thể CM X : N(0,1) thì
2. Định lý giới hạn trung tâm
. ( Định lý Lindenberg – Lewi)
Định lý: Nếu X1,X2,…,Xn,… là một dãy các BNN độc lập cùng tuân theo một
quy luật PPXS nào đó với kỳ vọng toán và phương sai hữu hạn: E(Xk) = a ; V(Xk) =
thì quy luật PPXS của BNN:
sẽ hội tụ khi n về quy luật chuẩn hóa N(0,1). Tức là: P( CM.
Theo tính chất của hàm đặc trưng, ta chỉ cần chỉ ra rằng hội tụ đến hàm đặc
trưng của PP chuẩn là khi n Xét BNN:
Un – E(Un) = (X1 – E(X1)) + (X2 – E(X2)) +…+ (Xn – E(Xn))
Ký hiệu Yk = Xk – E(Xk) thì
Un – E(Un) = Y1 + Y2 +…+ Yn Mặt khác E(Yk) = E[xk – E(Xk)] =0 V(Yk) = E(
Đặt thì từ hệ quả suy ra: Do Un – E(Un) = nên =
Từ đó theo tính chất của hàm đặc trưng ta thu được hàm đặc trưng của là Do đó : = =
Về thực hành : Với n đủ lớn có thể cho rằng : P( Hoặc
P(aVD. Chọn ngẫu nhiên 192 số trên đoạn [0;1] tìm XS để tổng điểm thu được (X)
nằm trong khoảng ( 88; 104). Giải.
+ Có thể coi: X = , trong đó mọi BNN Xi độc lập và cùng theo quy luật PP đều
U(0,1) E(Xi) = ½ ; V(Xi)=1/12 E(X) = nE(Xi) = 96 ; V(X)=nV(Xi)= 16 = 4
P(88VD. Cho X. Tìm XS để X nhận giá trị trong khoảng (40; 50). Giải.
+ Coi X = , trong đó Xi độc lập cùng PP A(p=0,02). Từ định lý giới hạn trung tâm: X, do đó P(40