Bài giảng chương 1 môn Toán cao cấp | Trường Quốc tế - Đại học Quốc gia Hà Nội

02/15/2024 TOÁN CAO CẤP 2
TS. NGUYỄN NGỌC GIANG LOGO
CHƯƠNG 1. HÀM SỐ, ĐỒ THỊ VÀ GIỚI HẠN 1 Hàm số 2 Hàm số sơ cấp 3
Vô cùng bé, vô cùng lớn 4
Tính liên tục của hàm số 5 TS. NGUYỄN NGỌC GIANG 1 02/15/2024
CHƯƠNG 1. HÀM SỐ, ĐỒ THỊ VÀ GIỚI HẠN 1. HÀM SỐ
Hàm là một quy tắc cho tương ứng mỗi phần tử thuộc tập hợp A với một
và chỉ một phần tử thuộc tập hợp B. Tập A được gọi là tập xác định của
hàm, tập B được gọi là tập giá trị.
Ta thường kí hiệu hàm số bằng chữ f, chẳng hạn hàm f(x). 3 5 TS. NGUYỄN NGỌC GIANG
CHƯƠNG 1. HÀM SỐ, ĐỒ THỊ VÀ GIỚI HẠN
CÁC HÀM SỐ SƠ CẤP CƠ BẢN
Các hàm số quen thuộc sau đây được gọi là các hàm số sơ cấp cơ bản: +) Hàm hằng; +) Hàm lũy thừa  f (x) x ,     ; +) Hàm mũ ( ) x
f x 3 a , 0  a  1;
+) Hàm logarith f (x)  log , x 0  a  1; a
+) Các hàm lượng giác f (x)  sin ; x cos ; x tan ; x cot . x
+) Các hàm lượng giác ngược f 5 (x)  arcsin ; x arccos ; x arctan ; x arccot . x
Hàm số sơ cấp là hàm số thu được từ các hàm số sơ cấp cơ bản bằng
cách sử dụng hữu hạn các phép toán: cộng, trừ, nhân, chia và phép hợp. Ví dụ 3
f (x)  tan(x  2x). TS. NGUYỄN NGỌC GIANG 2 02/15/2024
CHƯƠNG 1. HÀM SỐ, ĐỒ THỊ VÀ GIỚI HẠN
1.1. Hàm lũy thừa:y x  y  1 Tập xác định:  0, 1 Nhận xét: 3 Tăng:   0 0   1 Giảm:   0   0 5 x TS. NGUYỄN NGỌC GIANG
CHƯƠNG 1. HÀM SỐ, ĐỒ THỊ VÀ GIỚI HẠN 1.2. Hàm mũ x
y  a 0  a   1 y
Tập xác định: , 0  a  1 a  1 Nhận xét: 3 Tăng: a  1 Giảm: 0  a 1 5 x TS. NGUYỄN NGỌC GIANG 3 02/15/2024
CHƯƠNG 1. HÀM SỐ, ĐỒ THỊ VÀ GIỚI HẠN 1.2. Hàm mũ x
y  a 0  a   1
Tập giá trị : 0,  x x a 0 x x x x a  1 3 x a  2 1 2 1 2 1 1 x x2  a a a a   1 1 x  2 x  a x2 a x x a  a    x x x a b ab    x 5 b  b  TS. NGUYỄN NGỌC GIANG
CHƯƠNG 1. HÀM SỐ, ĐỒ THỊ VÀ GIỚI HẠN
1.3. Hàm logarity  log x 0  a   1 a y
Tập xác định: 0,  Nhận xét: a  1 3 Tăng: a 1
Giảm: 0  a  1 x 5 0  a  1 TS. NGUYỄN NGỌC GIANG 4 02/15/2024
CHƯƠNG 1. HÀM SỐ, ĐỒ THỊ VÀ GIỚI HẠN log 1  0 log x  ln x a e
log x x  log x  log x a 1 2  a  1  a  2   x  3 1 1 log  log    x  log x
log x  log  x a a 1  a  2  x  a a  2  log x 5log x   log x  log . b log x a a a a b TS. NGUYỄN NGỌC GIANG
CHƯƠNG 1. HÀM SỐ, ĐỒ THỊ VÀ GIỚI HẠN
1.4. Hàm lượng giác
Hàm sin : y  sin x Tập XĐ :  ,   3 Tập GT:  1  ;  1 5 TS. NGUYỄN NGỌC GIANG 5 02/15/2024
CHƯƠNG 1. HÀM SỐ, ĐỒ THỊ VÀ GIỚI HẠN
1.4. Hàm lượng giác
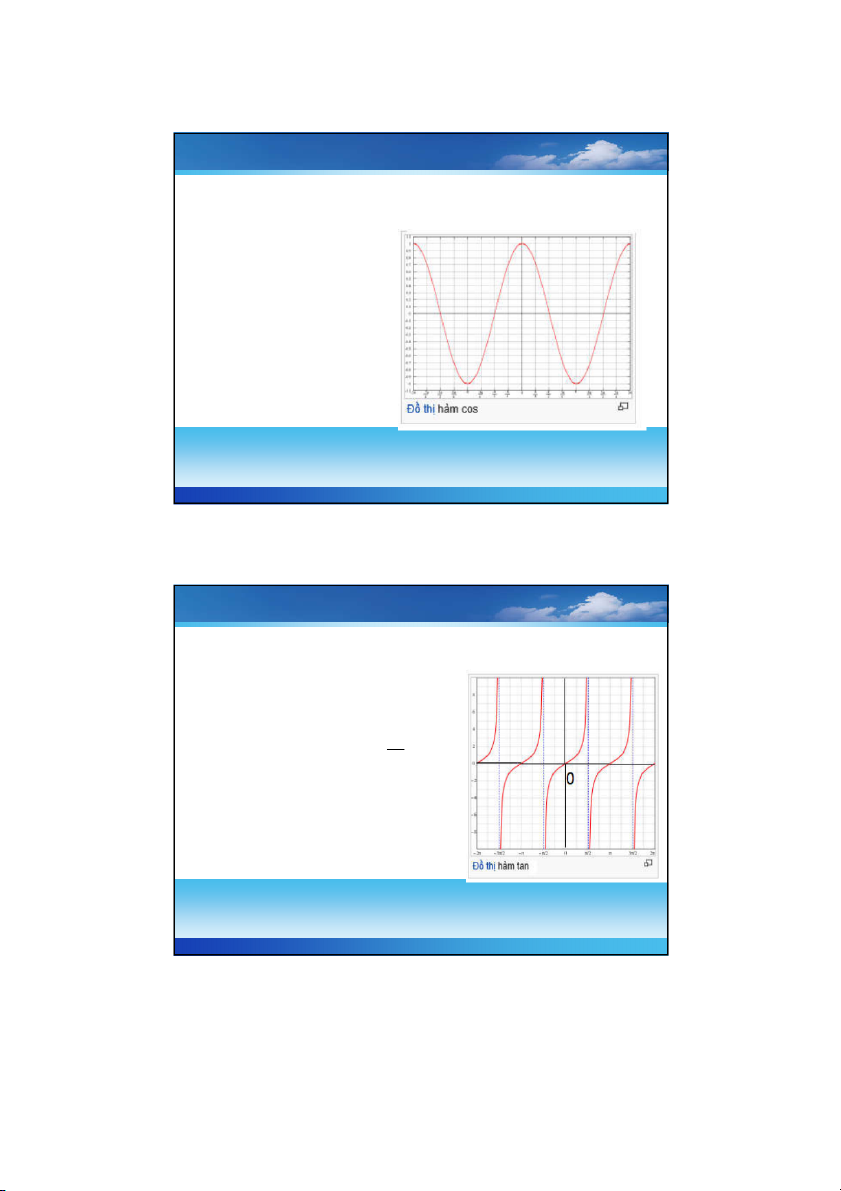
Hàm cos : y  cos x
Tập XĐ : , 3 Tập GT:  1  ;  1 5 TS. NGUYỄN NGỌC GIANG
CHƯƠNG 1. HÀM SỐ, ĐỒ THỊ VÀ GIỚI HẠN
1.4. Hàm lượng giác
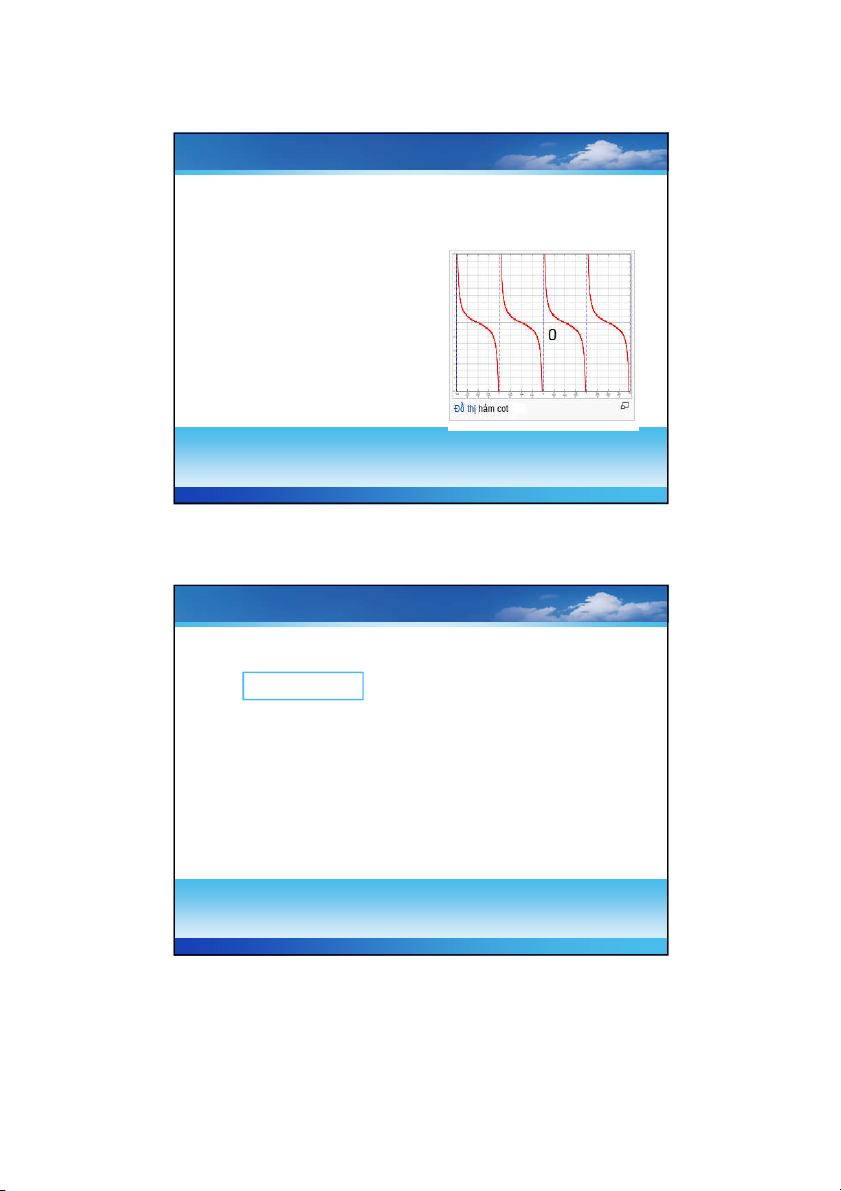
Hàm tan : y  tan x   
Tập XĐ : , \   k  3  2  Tập GT:  ,   5 TS. NGUYỄN NGỌC GIANG 6 02/15/2024
CHƯƠNG 1. HÀM SỐ, ĐỒ THỊ VÀ GIỚI HẠN
1.4. Hàm lượng giác
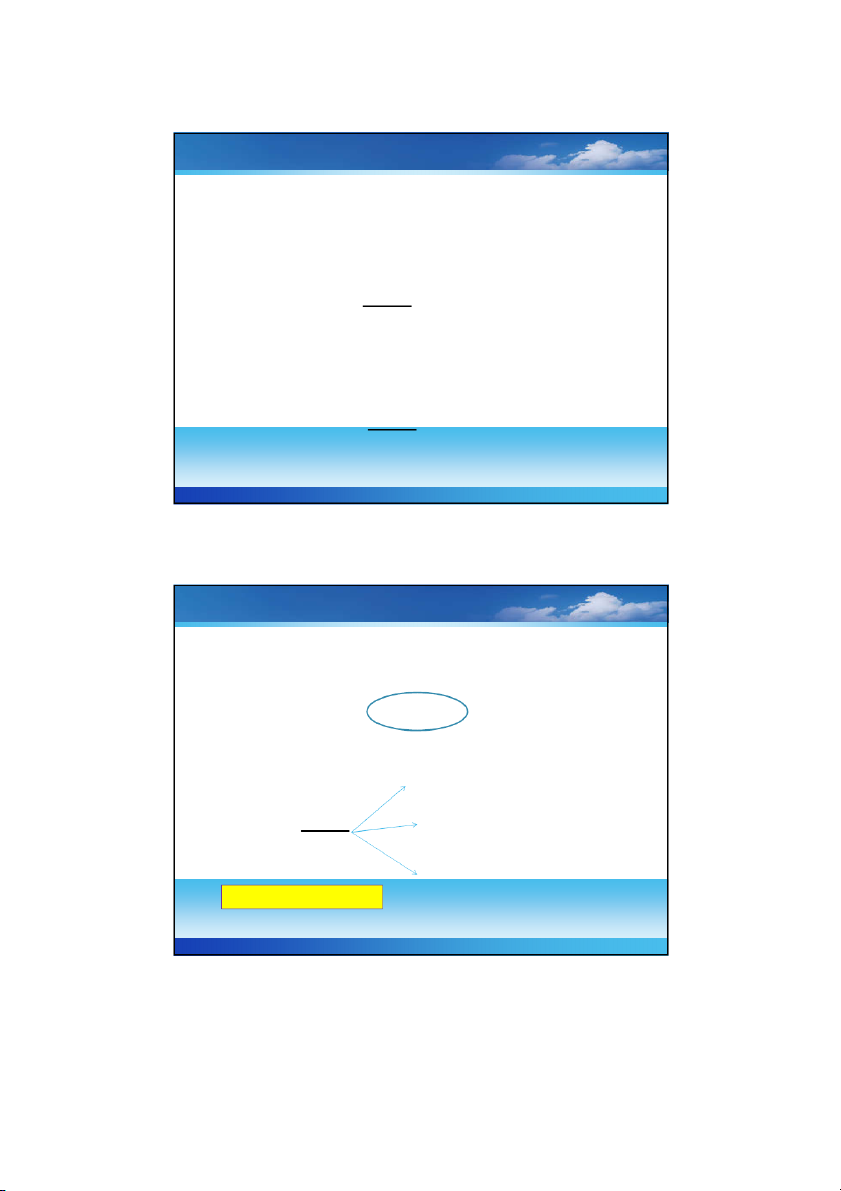
Hàm cot : y  cot x
Tập XĐ :, \k 3 Tập GT:  ,   5 TS. NGUYỄN NGỌC GIANG
CHƯƠNG 1. HÀM SỐ, ĐỒ THỊ VÀ GIỚI HẠN
1.5. Hàm lượng giác ngược: y  arcsin x
TXÑ :D  1,    1
TGT : T    / 2, / 2 3   Ví dụ: Vì : arcsin  1      / 2 sin   / 2  1  arcs 5 in 1   / 2 sin  / 2 1 arcsin 1/ 2    / 6 sin  / 6  1/ 2 TS. NGUYỄN NGỌC GIANG 7 02/15/2024
CHƯƠNG 1. HÀM SỐ, ĐỒ THỊ VÀ GIỚI HẠN
1.5. Hàm lượng giác ngược: y  arccos x
TXÑ :D   1,    1
TGT : T    0,  3   Ví dụ: Vì : arccos  1   cos   1  arccos  1  0 cos0  1 5 arccos1/ 2   / 3 cos / 3 1/ 2 TS. NGUYỄN NGỌC GIANG
CHƯƠNG 1. HÀM SỐ, ĐỒ THỊ VÀ GIỚI HẠN
1.5. Hàm lượng giác ngược: y  arctan x
TXÑ :D  , 
3 TGT : T   / 2, / 2 Ví dụ: Vì : arctan 1    / 4 tan   / 4  1  arctan51   / 4 tan / 4 1
arctan 1/ 3  / 6 tan  / 6 1/ 3 TS. NGUYỄN NGỌC GIANG 8 02/15/2024
CHƯƠNG 1. HÀM SỐ, ĐỒ THỊ VÀ GIỚI HẠN
1.5. Hàm lượng giác ngược: y  arccot x
TXÑ :D  ,
TGT : T  0,  3  Ví dụ:    3 arccot 1  Vì :  3 cot   1 4  4        arccot  1  cot  1 5 4  4    arccot 1/ 3   / 3 cot /  3  1/ 3 TS. NGUYỄN NGỌC GIANG
CHƯƠNG 1. HÀM SỐ, ĐỒ THỊ VÀ GIỚI HẠN
2. Giới hạn của hàm số, các dạng vô định
2.1. Định nghĩa: Cho hàm số y = f (x) xác định trong khoảng (a, b). 3 lim f x  L xc  
   0,  0 : 5
x  c    f  x  L   TS. NGUYỄN NGỌC GIANG 9 02/15/2024
CHƯƠNG 1. HÀM SỐ, ĐỒ THỊ VÀ GIỚI HẠN
2.2. Các giới hạn cơ bản sin x tan 1.lim  lim x 1 5.lim x e   x 0  x 0 x  x x arcsin x arctan x 2.lim  lim 1 6.lim x e  0 x0 3 x0 x x x  1 3.lim  0  7.limln x      0 x 0  x x 5 8.lim ln x  
4.lim x     0 x x TS. NGUYỄN NGỌC GIANG
CHƯƠNG 1. HÀM SỐ, ĐỒ THỊ VÀ GIỚI HẠN
2.2. Các giới hạn cơ bản ( tt)  1 x x 9.lim 1    lim e 1  
1 x1x  e 12.lim  1 x x 0  x  x 0 x ln1 x 3  x a 1 10.lim  1 13.lim  lna x 0  x x 0 x log   x 1 x   1 a 1  1 11.lim  14.lim    5 x 0 x lna x 0 x TS. NGUYỄN NGỌC GIANG 10 02/15/2024
CHƯƠNG 1. HÀM SỐ, ĐỒ THỊ VÀ GIỚI HẠN
3. Giới hạn của hàm số, các dạng vô định
4. Các dạng vô định: 0.    0 3 0 7 dạng 1  5 0  0 0  TS. NGUYỄN NGỌC GIANG
CHƯƠNG 1. HÀM SỐ, ĐỒ THỊ VÀ GIỚI HẠN
5. Vô cùng bé (VCB) – Vô cùng lớn ( VCL) 5.1. Vô cùng bé:
Định nghĩa: f(x) gọi là VCB trong quá trìnhx  x0 3  lim f x  x   0 x 0 Ví dụ: Khi x  0 5 sin , tan , x x
x e 1, ln  x   1 ,...:VCB TS. NGUYỄN NGỌC GIANG 11 02/15/2024
CHƯƠNG 1. HÀM SỐ, ĐỒ THỊ VÀ GIỚI HẠN
Định lý: Trong cùng một quá trìnhx  x0
1) Nếu hàm f (x) là một VCB và f (x) khác 0 thì 1 :VCL 3 f x 
2) Nếu hàm f (x) là một VCL và f (x) khác 0 thì 5 1   :VCB f x TS. NGUYỄN NGỌC GIANG
CHƯƠNG 1. HÀM SỐ, ĐỒ THỊ VÀ GIỚI HẠN
5.2. Vô cùng bé (VCB) – Vô cùng lớn ( VCL)
a) So sánh các VCB trong cùng một quá trình:   x 0x f x   VCB x 0 x
 g  x 3
L  0  f x   0 g x  f  x   L  lim L A VCB cùng x  0 x cấp 5 g x 
L    g x   0 f x
L  A  1  f  g TS. NGUYỄN NGỌC GIANG 12 02/15/2024
CHƯƠNG 1. HÀM SỐ, ĐỒ THỊ VÀ GIỚI HẠN Đặc biệt: f x  L  lim
1  f x  g x xx0 g  x
b) Bảng các VCB tương đương thường gặp: x  0 1) sin x  x 2) tan x  x 3 3) ln x   1  x 4) x e 1  x 2 x 5)    1 n x x 1  nx
6) e  x 1 2 2 7) ln  5 1    x x x 3  2 8) sin   x x x 3 6 9) tan   x 2 x x x 3 10) 1 cosx  2 TS. NGUYỄN NGỌC GIANG
CHƯƠNG 1. HÀM SỐ, ĐỒ THỊ VÀ GIỚI HẠN
5.3. Vô cùng bé (VCB) – Vô cùng lớn ( VCL)
a) Quy tắc ngắt bỏ VCB cấp cao.   x x f x  xx 3 0  VCB 0
 g  x
f x    0 g x  5
 f x g x  g x TS. NGUYỄN NGỌC GIANG 13 02/15/2024
CHƯƠNG 1. HÀM SỐ, ĐỒ THỊ VÀ GIỚI HẠN Ví dụ 1: tanx  sin  lim x I sin x  x x 0  2x tan x  x x  x  I  lim 3 x0 2x  I 1 5 TS. NGUYỄN NGỌC GIANG
CHƯƠNG 1. HÀM SỐ, ĐỒ THỊ VÀ GIỚI HẠN Ví dụ 2: 3
tan 2x  sin 2x  sin  lim x I 3 x 0 2x 3
2x  2x  x 3  I  lim 3 x0 2x 1  I  5 2 TS. NGUYỄN NGỌC GIANG 14 02/15/2024
CHƯƠNG 1. HÀM SỐ, ĐỒ THỊ VÀ GIỚI HẠN 1
Ví dụ 3: I  limcos x 2 tan x x 0 I 1    x 0   x   1 cos 1 x  
I  lim 1  cos x   2 1 tan cosx 1 1    x0   3 2  x       x   1 2 lim cos 1 lim  2  2 x 0 x 0 tan x x  e  e 5 1 2  e TS. NGUYỄN NGỌC GIANG
CHƯƠNG 1. HÀM SỐ, ĐỒ THỊ VÀ GIỚI HẠN
b) Vô cùng bé (VCB) – Vô cùng lớn ( VCL)
5. So sánh các VCL trong cùng một quá trình:   x 0x f x   xx VCL 0  g  x 3
L  0  Cấp của f thấp hơn g f x 
L  A  Cấp của g bằng cấp f L  lim
xx0 g  5 x  Cấp của g thấp hơn f L   
L  A  1  f  g TS. NGUYỄN NGỌC GIANG 15 02/15/2024
CHƯƠNG 1. HÀM SỐ, ĐỒ THỊ VÀ GIỚI HẠN
c) Vô cùng bé (VCB) – Vô cùng lớn ( VCL)
d) Quy tắc ngắt bỏ VCL cấp thấp.
Cấp của f(x) nhỏ hơn cấp của g(x) 3 f  x x x   0   VCL x 0 x
 g x 5
 f x g x  g x TS. NGUYỄN NGỌC GIANG
CHƯƠNG 1. HÀM SỐ, ĐỒ THỊ VÀ GIỚI HẠN Ví dụ 1: 2 2x  3x 5 I  lim x 2 x 1  3 2 2
Ngắt VCL cấp thấp  2x  3x  5  2x 2 2 x 2 x 2  lim  lim  x
2x 5 x 2x 2 TS. NGUYỄN NGỌC GIANG 16 02/15/2024
CHƯƠNG 1. HÀM SỐ, ĐỒ THỊ VÀ GIỚI HẠN Ví dụ 2: 4 x  x 1 I  lim Ngắt VCL cấp thấp x 3 2 x
x  x  x 1 4 4
x  x 1  x 3 3 2 3 x
x  x  x 1  x x 4   lim x I  lim x    3 x x 5 x x TS. NGUYỄN NGỌC GIANG
CHƯƠNG 1. HÀM SỐ, ĐỒ THỊ VÀ GIỚI HẠN
TÍNH LIÊN TỤC CỦA HÀM SỐ 1. Định lí
Giới hạn tồn tại khi và chỉ khi lim f (x) và tồn tại và lim f (x) lim f (x )  x x  bằng nhau. x 0 x x 0 x 0 Khi đó
lim f (x)  lim f (x)  lim f (x) x x      30 x 0 x x 0 x
Giới hạn một phía thường được dùng để tính giới hạn trong các trường
hợp hàm chứa giá trị tuyệt đối, chứa căn bậc chẵn, hoặc hàm ghép. 2. Định nghĩa
Hàm số f được gọi5là liên tục tại x0 nếu f xác định tại x và 0
lim f (x)  f (x ). 0 x 0 x
Nếu f không liên tục tại x0, ta nói f gián đoạn tại x0. TS. NGUYỄN NGỌC GIANG 17 02/15/2024
CHƯƠNG 1. HÀM SỐ, ĐỒ THỊ VÀ GIỚI HẠN Định lí
Hàm số sơ cấp liên tục trên miền xác định của nó. Ví dụ 1 1
Xét tính liên tục của hàm số tại điểm f (x)  x  0. 3x 0 Vì 1 1 3 lim   ; lim      x 0  x x 0 3  3x
nên là điểm gián đoạn. x  0 0 5 TS. NGUYỄN NGỌC GIANG HẾT CHƯƠNG 1 LOGO 18