Bài giảng Chương 2: Biến ngẫu nhiên | Học viện Báo chí và Tuyên truyền

Chương 2: Biến ngẫu nhiên Phan Thị Khánh Vân
E-mail: khanhvanphan@hcmut.edu.vn Ngày 9 tháng 9 năm 2024 (Phan Thị Khánh Vân)
Chương 2: Biến ngẫu nhiên Ngày 9 tháng 9 năm 2024 1 / 32 Nội dung 1
Biến ngẫu nhiên. Hàm xác suất. Hàm mật độ xác suất. Hàm phân phối xác suất
Biến ngẫu nhiên rời rạc
Biến ngẫu nhiên liên tục 2
Một số đại lượng đặc trưng của BNN
Một số đại lượng đặc trưng của BNN rời rạc
Đặc trưng của BNN liên tục. 3
Véc tơ ngẫu nhiên rời rạc và các đặc trưng 4
Phân phối XS có điều kiện (Phan Thị Khánh Vân)
Chương 2: Biến ngẫu nhiên Ngày 9 tháng 9 năm 2024 2 / 32 Biến ngẫu nhiên
Biến ngẫu nhiên là một hàm số nhận giá trị thực ứng với mỗi kết quả trong không gian
mẫu của một thí nghiệm ngẫu nhiên.
Tung 3 đồng xu, gọi X là số mặt sấp thu được. SSS 3 mặt sấp: X = 3 SSN 2 mặt sấp: X = 2 SNS 2 mặt sấp: X = 2 SNN 1 mặt sấp: X = 1 NSS 2 mặt sấp: X = 2 NSN 1 mặt sấp: X = 1 NNS 1 mặt sấp: X = 1 NNN 0 mặt sấp: X = 0
Biến ngẫu nhiên: X : Ω → {0, 1, 2, 3} ⊂ R.
Tập giá trị của BNN X : R = {0, 1, 2, 3} là một tập rời rạc, ta gọi X là một BNN rời rạc. (Phan Thị Khánh Vân)
Chương 2: Biến ngẫu nhiên Ngày 9 tháng 9 năm 2024 3 / 32
Biến ngẫu nhiên liên tục và rời rạc
Một BNN rời rạc là một BNN với tập giá trị là một tập hữu hạn hoặc vô hạn đếm được.
Một BNN liên tục là một BNN với tập giá trị là một khoảng/ đoạn trong tập số thực.
Khối lượng của một quả dưa hấu được chọn ngẫu nhiên: BNN liên tục
Tình trạng hôn nhân: Không phải BNN
Thời gian gây ra một vụ cháy: BNN liên tục
Số lượng cuộc gọi khẩn cấp trong một giờ: BNN rời rạc
Độ dài của một nhánh cây tulip được chọn ngẫu nhiên: BNN liên tục
Màu sắc của một bông tulip: Không phải BNN (Phan Thị Khánh Vân)
Chương 2: Biến ngẫu nhiên Ngày 9 tháng 9 năm 2024 4 / 32
BNN rời rạc. Phân phối xác suất. Hàm xác suất X 0 1 2 3
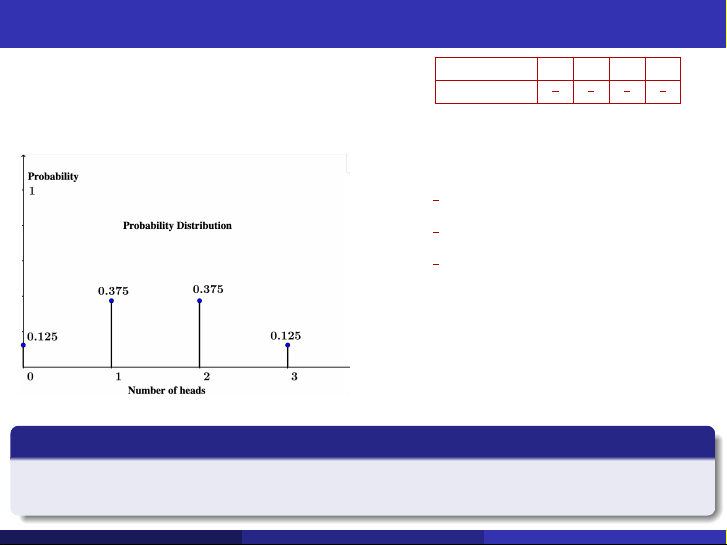
Tung một đồng xu cân bằng 3 lần. X là số mặt sấp. - P(X = x ) 1 3 3 1 8 8 8 8 Phân phối xác suất
f (x ) = P(X = x ): Hàm xác suất. f (0) = 1 , 8 f (1) = 3 = f (2), 8 f (3) = 1 . 8
f (0) + f (1) + f (2) + f (3) = 1 Phân phối xác suất
Phân phối xác suất của một BNN X là một mô tả các xác suất tương ứng với các giá trị của X . (Phan Thị Khánh Vân)
Chương 2: Biến ngẫu nhiên Ngày 9 tháng 9 năm 2024 5 / 32 Hàm xác suất (PMF)
Với một BNN rời rạc X nhận các giá trị x1, x2, ..., xn, hàm xác suất đặc trưng cho phân
phối xác suất tại mỗi giá trị, thỏa mãn các điều kiện sau: f (xi ) ≥ 0 n P f (xi ) = 1 i =1 f (xi ) = P(X = xi )
Kiểm tra đèn flash của máy ảnh
Thời gian sạc lại đèn flash được thử nghiệm trên ba máy ảnh điện thoại. Xác suất để một
máy ảnh vượt qua bài kiểm tra là 0.8 và các máy ảnh thực hiện độc lập. Xét X là số
lượng máy ảnh vượt qua bài kiểm tra.
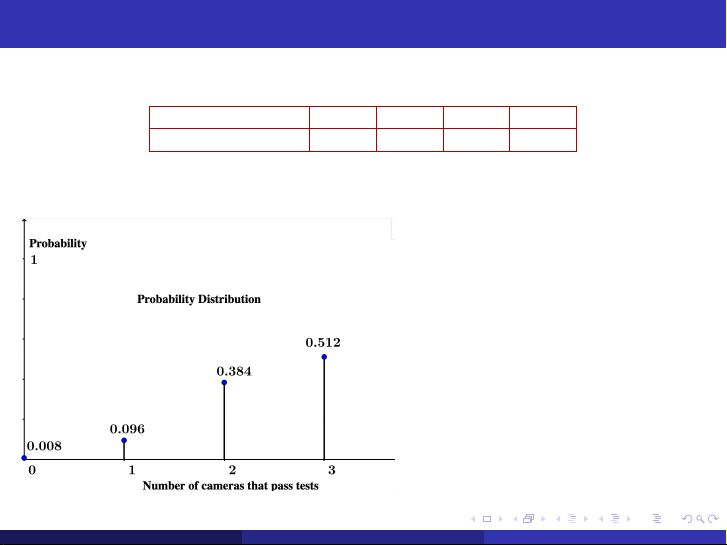
Phân phối xác suất của BNN X : X 0 1 2 3 P(X = x ) 0.23 C 1 3 0.220.8 C 2 3 0.2 ∗ 0.82 0.83 (Phan Thị Khánh Vân)
Chương 2: Biến ngẫu nhiên Ngày 9 tháng 9 năm 2024 6 / 32
BNN rời rạc. Hàm phân phối xác suất (CDF)
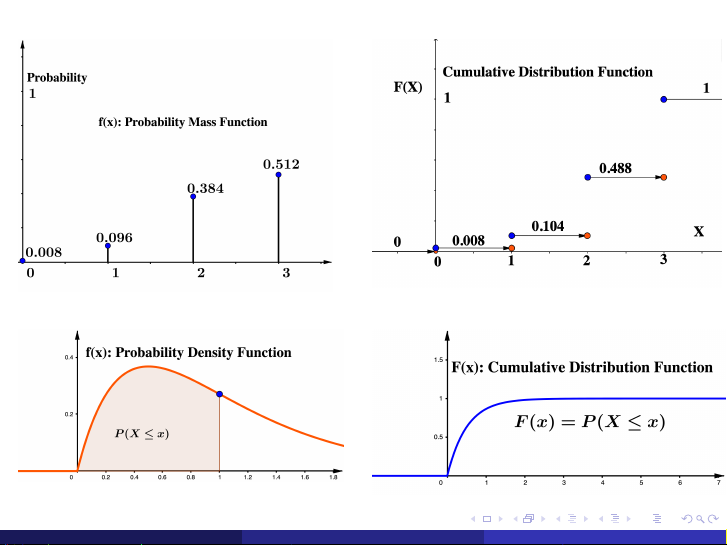
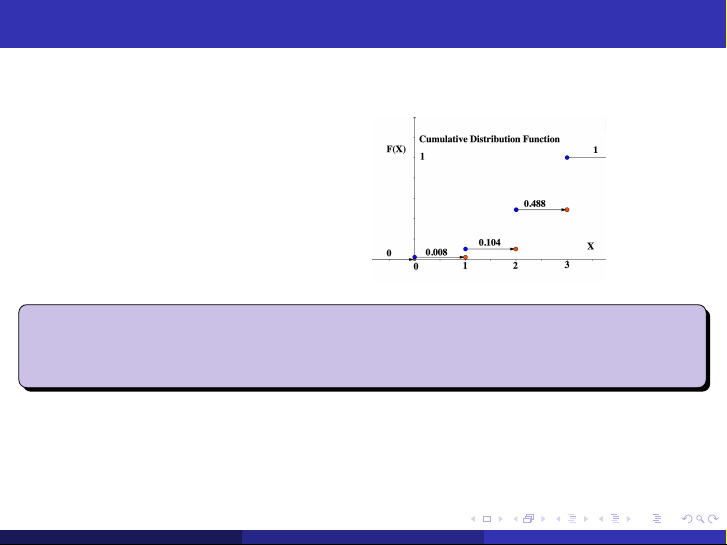
Xét X là số máy ảnh vượt qua bài kiểm tra X 0 1 2 3 f (x ) = P(X = x ) 0.008 0.096 0.384 0.512
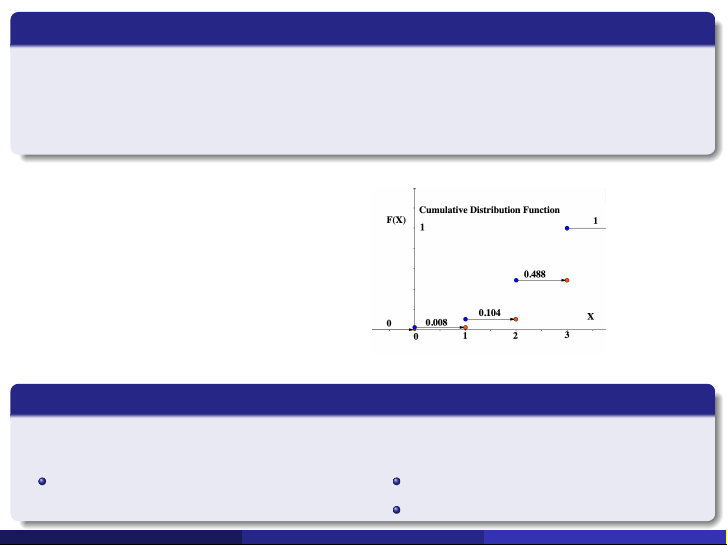
Xét: F (2.5) = P(X ≤ 2.5) = 0.008 + 0.096 + 0.384 = 0.488 F (x ) = P(X ≤ x ) 0, nếu x < 0,     0.008, nếu 0 ≤ x < 1,   = 0.104, nếu 1 ≤ x < 2,   0.488, nếu 2 ≤ x < 3,    1, nếu 3 ≤ x.
- Hàm phân phối xác suất (Phan Thị Khánh Vân)
Chương 2: Biến ngẫu nhiên Ngày 9 tháng 9 năm 2024 7 / 32
Hàm phân phối xác suất (CDF)
Hàm phân phối xác suất đặc trưng cho mức độ tập trung xác suất của BNN X ở phía
bên trái của số thực x, hàm được xác định bởi
F (x ) = P(X ≤ x ) = P f (xi ) xi ≤x 0, nếu x < 0,     0.008, nếu 0 ≤ x < 1,   F (x ) = 0.104, nếu 1 ≤ x < 2,   0.488, nếu 2 ≤ x < 3,    1, nếu 3 ≤ x. Tính chất
Với một BNN rời rạc X , F (x) thỏa
F (x ) = P(X ≤ x ) = P f (xi ). 0 ≤ F (x) ≤ 1. xi ≤x F (x ) là một hàm tăng. (Phan Thị Khánh Vân)
Chương 2: Biến ngẫu nhiên Ngày 9 tháng 9 năm 2024 8 / 32 Ví dụ
Xét một BNN rời rạc X : Ω → {1, 2, 3, 4}.
Hàm xác suất: f (xi ) = c.xi , với xi = 1, 2, 3, 4, c = const. a. Tìm c.
b. Tìm hàm phân phối xác suất F (x). c. Tìm P(X ≤ 3). d. Tìm P(X ≤ 3|X ≥ 2).
a. Ta có P f (xi ) = c(1 + 2 + 3 + 4) = 10c = 1, suy ra c = 0.1. X 1 2 3 4 f (x ) = P(X = x ) 0.1 0.2 0.3 0.4 b. 0, nếu x < 1,     0.1, nếu 1 ≤ x < 2,   F (x ) = P(X ≤ x ) = 0.3, nếu 2 ≤ x < 3,   0.6, nếu 3 ≤ x < 4,    1, nếu x ≥ 4
c. P(X ≤ 3) = P(X = 1) + P(X = 2) + P(X = 3) = 0.6 P(2 ≤ X ≤ 3) d. P(X ≤ 3|X ≥ 2) = = 5 . P(X ≥ 2) 9 (Phan Thị Khánh Vân)
Chương 2: Biến ngẫu nhiên Ngày 9 tháng 9 năm 2024 9 / 32
Hàm phân phối xác suất và hàm xác suất
Giả sử ta cần tìm hàm xác suất f (x) của BNN X khi biết hàm phân phối xác suất: 0, nếu x < 0,     0.008, nếu 0 ≤ x < 1,   F (x ) = 0.104, nếu 1 ≤ x < 2,   0.488, nếu 2 ≤ x < 3,    1, nếu 3 ≤ x.
Chú ý: f (x ) = P(X = x ) = P(X ≤ x ) − P(X < x ) nên nếu F (x ) liên tục tại x0, thì f (x0) = P(X = x0) = 0.
Từ đồ thị ta thấy F (x) không liên tục tại 4 điểm 0, 1, 2, 3: X chỉ nhận 4 giá trị này. f (0) = 0.008 − 0 = 0.008;
f (2) = 0.488 − 0.104 = 0.384;
f (1) = 0.104 − 0.008 = 0.096; f (3) = 1 − 0.488 = 0.512. (Phan Thị Khánh Vân)
Chương 2: Biến ngẫu nhiên Ngày 9 tháng 9 năm 2024 10 / 32
Biến ngẫu nhiên liên tục: Hàm mật độ xác suất
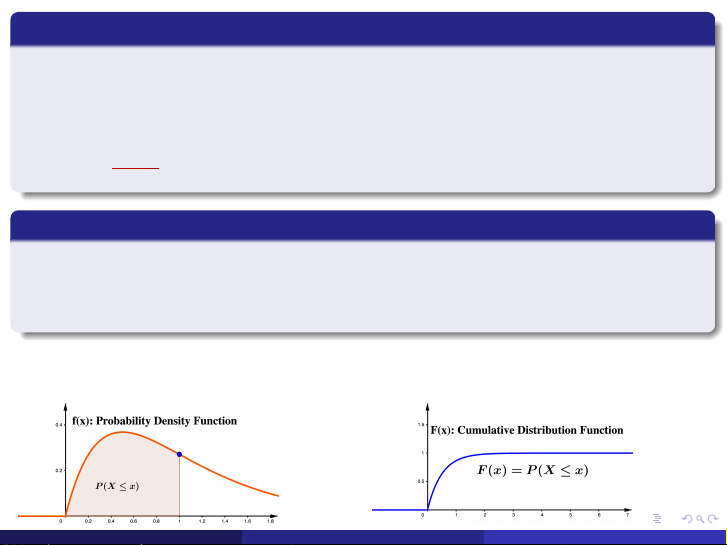
Hàm mật độ xác suất (PDF)
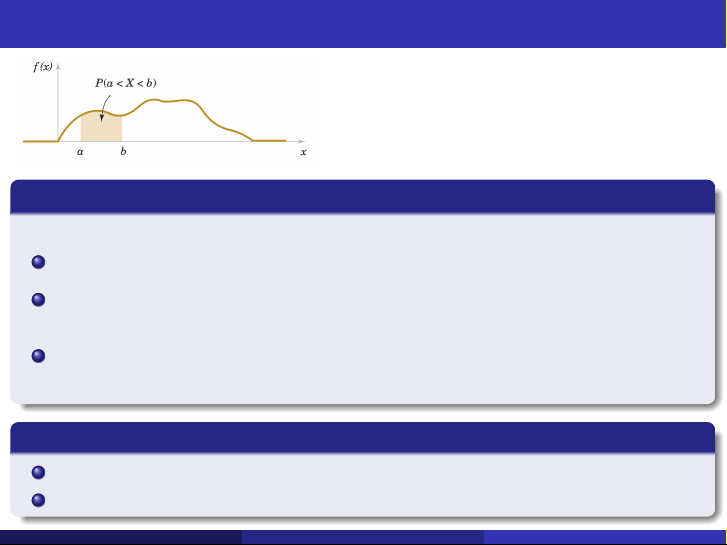
biểu thị mức độ tập trung xác suất của BNN liên tục trong lân cận của một điểm, thỏa 1 f (x ) ≥ 0 ∞ R 2 f (x )dx = 1 −∞ b R 3 P(a ≤ X ≤ b) =
f (x )dx : diện tích miền nằm dưới đồ thị hàm f (x ) từ a đến b với a mọi a, b. Chú ý 1
Với một BNN liên tục X thì P(X = x) = 0 với mọi x. 2
P(a ≤ X ≤ b) = P(a < X < b). (Phan Thị Khánh Vân)
Chương 2: Biến ngẫu nhiên Ngày 9 tháng 9 năm 2024 11 / 32 Cường độ dòng điện
BNN liên tục X biểu thị cường độ dòng điện đo được trong một sợi dây đồng mỏng tính
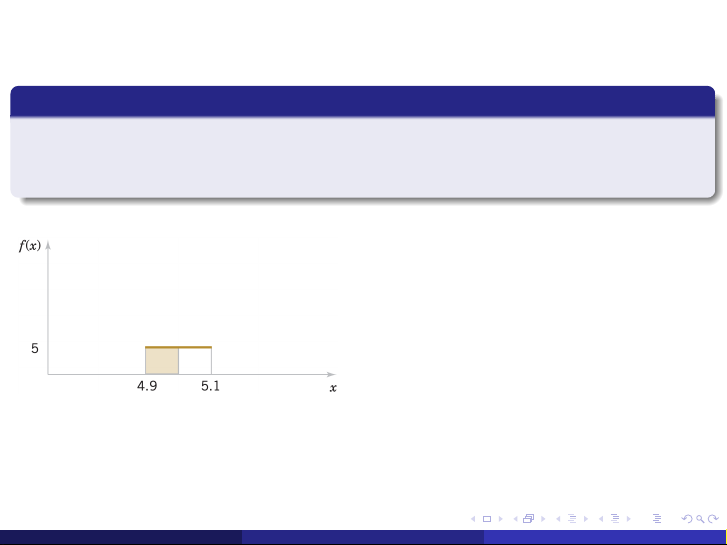
bằng mA. Giả sử rằng giá trị của X thuộc [4.9, 5.1] mA và hàm mật độ xác suất của X
là f (x) = 5 với 4.9 ≤ x ≤ 5.1. Tính xác suất để cường độ dòng điện nhỏ hơn 5 mA. 5 5
P(X < 5) = R f (x )dx = R 5dx = 0.5. −∞ 4.9 (Phan Thị Khánh Vân)
Chương 2: Biến ngẫu nhiên Ngày 9 tháng 9 năm 2024 12 / 32 Đường kính lỗ khoan
X biểu thị đường kính của lỗ được khoan trên một bộ phận có dạng tấm kim loại. Đường
kính mục tiêu là 12, 5 mm. Dữ liệu lịch sử cho thấy rằng phân phối của X có thể được
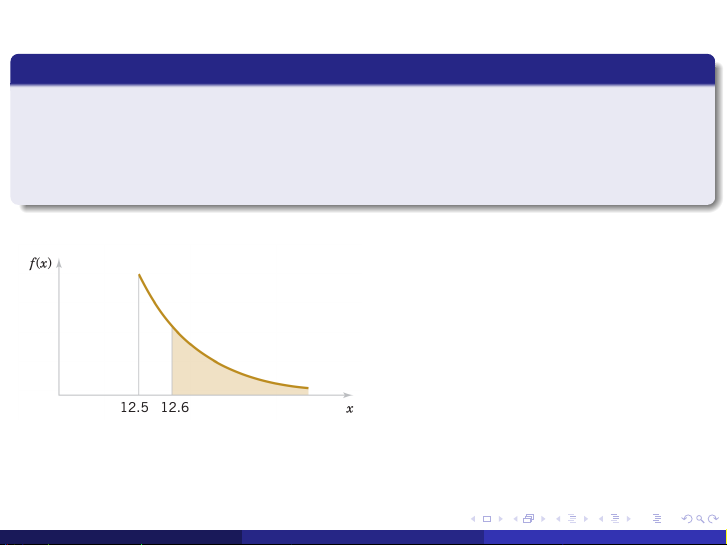
lập mô hình bằng hàm mật độ xác suất f (x) = 20e−20(x−12.5), với x ≥ 12.5. Nếu một bộ
phận có đường kính lớn hơn 12.60 mm sẽ bị loại bỏ, thì tỷ lệ bộ phận bị loại bỏ là bao nhiêu? ∞ Z P(X > 12.6) = f (x )dx 12.6 ∞ Z = 20e−20(x−12.5)dx 12.6 = e−2. (Phan Thị Khánh Vân)
Chương 2: Biến ngẫu nhiên Ngày 9 tháng 9 năm 2024 13 / 32
Hàm phân phối xác suất (CDF)
Hàm phân phối xác suất của một BNN liên tục X được xác định bởi x
F (x ) = P(X ≤ x ) = R f (u)du, với −∞ < x < ∞. −∞ dF (x ) Tính chất:
= f (x ) (nếu đạo hàm tồn tại). dx Ví dụ
Tìm hàm mật độ xác suất PDF , biết hàm phân phối xác suất CDF : (0, nếu x < 0, F (x ) = 1 − e−x2 , nếu x > 0. (0, nếu x < 0, f (x ) = 2xe−x2 , nếu x > 0. (Phan Thị Khánh Vân)
Chương 2: Biến ngẫu nhiên Ngày 9 tháng 9 năm 2024 14 / 32 (Phan Thị Khánh Vân)
Chương 2: Biến ngẫu nhiên Ngày 9 tháng 9 năm 2024 15 / 32 Ví dụ
Xét một BNN liên tục X : Ω → [0, 4]. Hàm mật độ xác suất: 0, nếu x / ∈ [2, 4]   f (x ) = c.x , nếu x ∈ [0, 2]  1 − cx nếu x ∈ [2, 4]. a. Tìm c. c. Tìm P(X > 3).
b. Tìm hàm phân phối xác suất F (x). d. Tìm P(X ≤ 3|X ≥ 1). ∞ 2 4
a. Ta có R f (x)dx = 1 ⇔ R cxdx + R (1 − cx)dx = 1 ⇔ c = 0.25. −∞ 0 2 b. 0, nếu x < 0,    0.25 R x tdt = 0.125x 2, nếu 0 ≤ x ≤ 2, F (x ) = 0
0.25 R 2 tdt + R x (1 − 0.25t)dt = −0.125x2 + x − 1, nếu 2 ≤ x ≤ 4,   0 2  1, nếu x > 4.
c. P(X > 3) = 1 − P(X ≤ 3) = 1 − F (3) = 0.125. P(1 ≤ X ≤ 3) d. P(X ≤ 3|X ≥ 1) =
= F(3)−F(1) = 0.875−0.125 = 0.8571. P(X ≥ 1) 1−F (1) 1−0.125 (Phan Thị Khánh Vân)
Chương 2: Biến ngẫu nhiên Ngày 9 tháng 9 năm 2024 16 / 32
Kỳ vọng, phương sai, độ lệch chuẩn
Chi tiêu của một hộ gia đình từ 2013-2018 Năm 2013 2014 2015 2016 2017 2018 Mức chi tiêu $54, 720 $51, 095 $60, 000 $55, 524 $70, 373 $60, 000 54.72 + 51.095 + ... + 60
Mức chi tiêu trung bình (kỳ vọng): µ = = 58.619 (ngàn đô). 6
(54.72 − µ)2 + ... + (60 − µ)2 Phương sai: σ2 = = 32.227 ((ngàn đô)2). 6 √ Độ lệch chuẩn: σ = σ2 = 6.1014 (ngàn đô).
Số tin nhắn nhận được mỗi giờ có phân phối xác suất như sau X : số tin nhắn 10 11 12 13 14 15 f (x ) = P(X = x ) 0.08 0.15 0.3 0.2 0.2 0.07
Số tin nhắn trung bình (kỳ vọng):
E(X ) = P xf (x ) = 10 × 0.08 + 11 × 0.15 + · · · + 15 × 0.07 = 12.5 (tin nhắn). x
Phương sai: V(X ) = P(x − µ)2f (x) = (10 − 12.5)20.08 + · · · + (15 − 12.5)20.07 x = 1.85 (tin nhắn2) (Phan Thị Khánh Vân)
Chương 2: Biến ngẫu nhiên Ngày 9 tháng 9 năm 2024 17 / 32
Kỳ vọng (Giá trị trung bình)
Kỳ vọng của một BNN X là giá trị trung bình theo xác suất của X .
µ = E(X ) = P xi f (xi ) = P xi P(X = xi ). i i
Phương sai và độ lệch chuẩn
Phương sai là trung bình của bình phương sai lệch giữa BNN X với kỳ vọng của nó
σ2 = V(X ) = E(X − µ)2 = P(xi − µ)2f (xi ) = P x2if (xi ) − µ2 = E(X 2) − (E(X ))2. i i √ Độ lệch chuẩn: σ = σ2.
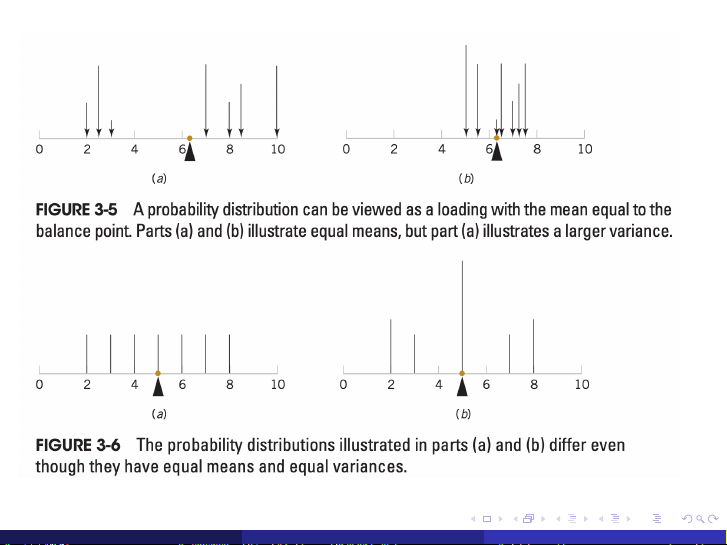
Phương sai đặc trưng cho sự phân tán của BNN X xung quanh kỳ vọng của nó. Trong kỹ
thuật, phương sai thường đặc trưng cho mức độ phân tán của kích thước các chi tiết gia
công hay sai số của thiết bị. Phương sai cho biết sự ổn định của thiết bị. Trong nông
nghiệp, phương sai đặc trưng cho mức độ đồng đều của vật nuôi hay cây trồng. Trong
quản lý và kinh doanh, nó đặc trưng cho mức độ rủi ro của các quyết định.
Độ lệch chuẩn thường được sử dụng để đánh giá mức độ phân tán thay vì phương sai, vì nó cùng đơn vị với X . (Phan Thị Khánh Vân)
Chương 2: Biến ngẫu nhiên Ngày 9 tháng 9 năm 2024 18 / 32 (Phan Thị Khánh Vân)
Chương 2: Biến ngẫu nhiên Ngày 9 tháng 9 năm 2024 19 / 32 Ví dụ
Người ta muốn xét nghiệm 5000 người để lọc ra những người bị COVID 19. Biết rằng tỉ
lệ người bị COVID là p = 5%. Người ta có 2 phương pháp như sau:
1. Xét nghiệm từng người: Cần 5000 bộ kit xét nghiệm.
2. Xét nghiệm bằng cách gộp một mẫu gồm nhóm 5 người, nếu kết quả âm tính thì dừng
xét nghiệm, nếu kết quả dương tính thì xét nghiệm lại từng người.
Tính số lần xét nghiệm trung bình của phương pháp 2, so sánh với phương pháp 1.
Gọi X là số xét nghiệm cần làm cho 1 nhóm 5 người. Ta có bảng phân phối XS: x 1 6 f (x ) 0.955 1 − 0.955
E(X ) = 1 ∗ 0.955 + 6 ∗ (1 − 0.955) = 2.1311.
Số lần xét nghiệm trung bình cho 5000 người: 1000 ∗ E(X ) ≈ 2131 (lần).
So sánh ta thấy phương pháp thứ 2 tiết kiệm chi phí hơn, đặc biệt khi xác xuất bị bệnh p càng nhỏ. (Phan Thị Khánh Vân)
Chương 2: Biến ngẫu nhiên Ngày 9 tháng 9 năm 2024 20 / 32