Bài giảng chương 7: Lý thuyết đồng dư môn Toán rời rạc | Đại học Kỹ thuật - Công nghệ Cần Thơ
Bài giảng chương 7: Lý thuyết đồng dư môn Toán rời rạc | Đại học Kỹ thuật - Công nghệ Cần Thơ. Tài liệu được biên soạn dưới dạng file PDF gồm 18 trang, giúp bạn tham khảo, ôn tập và đạt kết quả cao trong kì thi sắp tới. Mời bạn đọc đón xem!
Môn: Toán rời rạc (CT)
Trường: Đại học Kỹ thuật - Công nghệ Cần Thơ
Thông tin:
Tác giả:
Tài liệu liên quan:
Preview text:
Chương 7: LÝ THUYẾT ĐỒNG DƯ ´ Quan hệ đồng dư
´ Phương trình đồng dư bậc nhất một ẩn
´ Hệ phương trình đồng dư
´ Phương trình đồng dư bậc cao một ẩn Quan hệ đồng dư
´Cho a và b là hai số nguyên, m là số nguyên dương. Khi đó a và b được gọi là
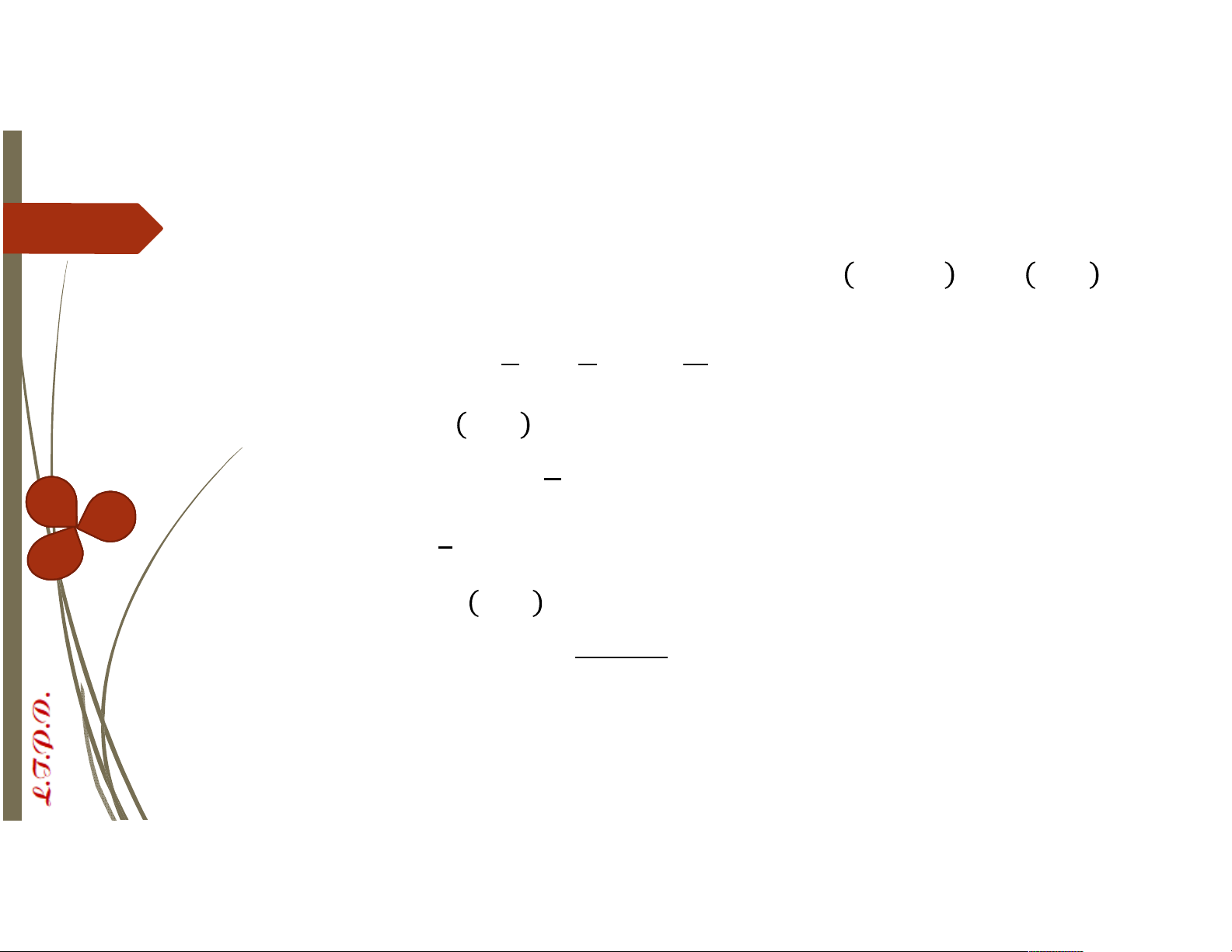
đồng dư theo modulo m, ký hiệu a ≡ (
) nếu a và b có cùng số dư khi chia cho m. Ta có a ≡ ( ) khi và chỉ khi a − ⋮ ´VD: 16 ≡ 11 5 ; −7 ≡ 5 ( 3)
´Cho a và b là hai số nguyên, m là số nguyên dương, các mệnh đề sau tương đương nhau ´a ≡ ( ) ´a = + ∈ ℤ ´a − ≡ 0 ( )
´Các tính chất của đồng dư 1. Nếu a ≡ , ∀ = 1,2, … , thì ´ a a … a ≡ … ´ a +a + ⋯ +a ≡ + + ⋯ + Quan hệ đồng dư 2. ≡ ⇔ ± ≡ ± , với mọi ∈ ℤ 3. ≡ ⇔ ≡ + , với mọi ∈ ℤ 4. Nếu ≡ thì ≡
, với là số nguyên dương 5. Nếu ≡ thì ≡
với mọi ∈ ℤ. Trường hợp , = 1 ta có ≡ ⇔ ≡
6. Nếu là số nguyên dương thì ≡ ( ) ⇔ ≡ ( )
7. Nếu > 0 là UC của , , thì ≡ ( ) ⇔ ≡ ( )
8. Nếu là UC của , và d, m = 1 thì ≡ ( ) ⇔ ≡ ( ) 9. Nếu ≡ , ∀ = 1,2, … , và = [ , , … , ] thì ≡ 10. Nếu ≡
và > 0 là ước của thì ≡ 11. Nếu ≡
và là UC của a, thì là ước của 12. Nếu ≡ thì , = ( , ) Quan hệ đồng dư
Phi hàm Euler: Với m là số nguyên dương, ta gọi ( ) là số các
số nguyên dương không vượt quá m và nguyên tố cùng nhau với m. VD: 1 = 1, 2 = 1, 3 = 2, 4 = 2 Quan hệ đồng dư
Phương trình đồng dư bậc nhất một ẩn
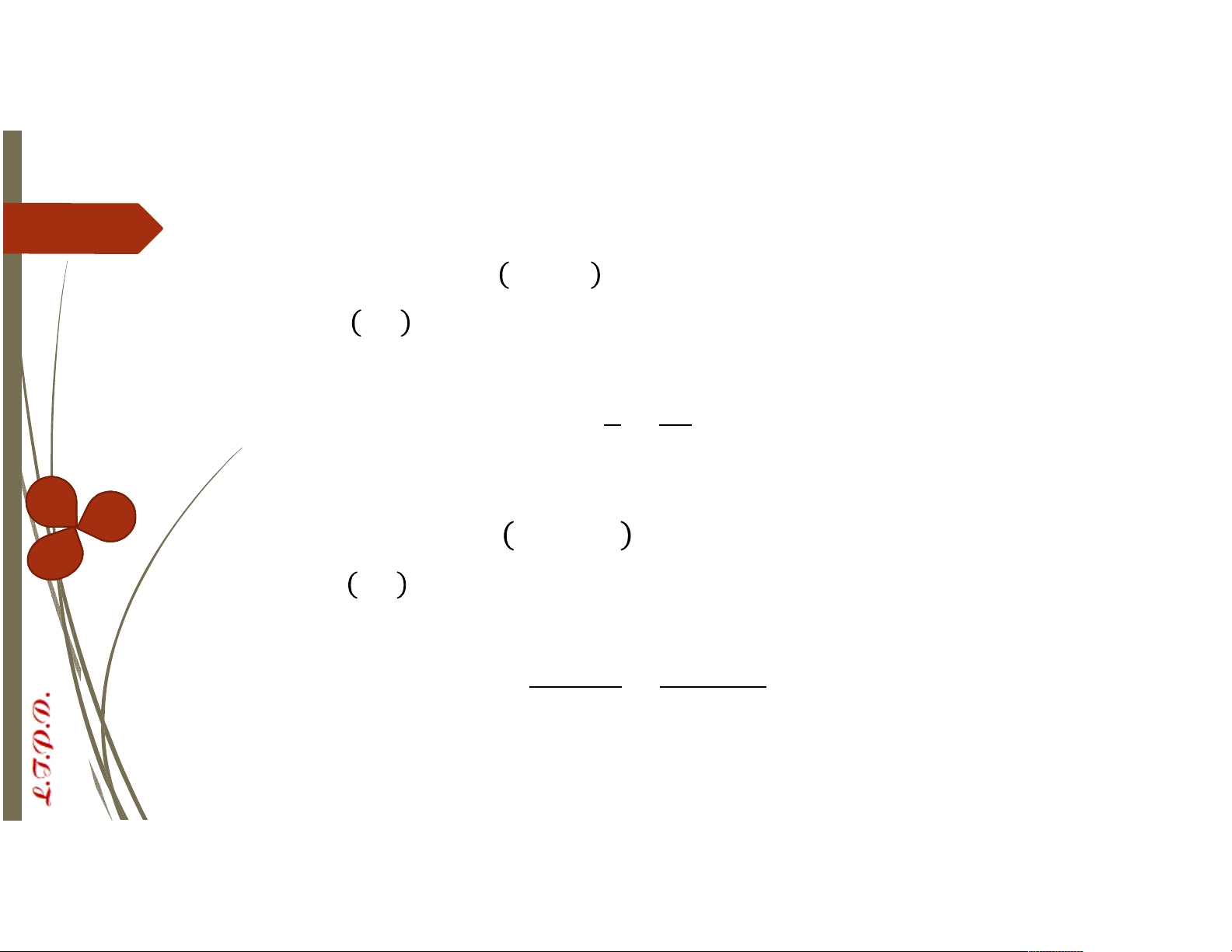
´Cho , , ∈ ℤ, > 0. Một phương trình có dạng ≡ , trong
đó là ẩn số nhận giá trị nguyên, được gọi là pt đồng dư bậc nhất một ẩn ´VD: 9 ≡ 6 15 ´ ≡ (∗∗) ´Đặt d = ,
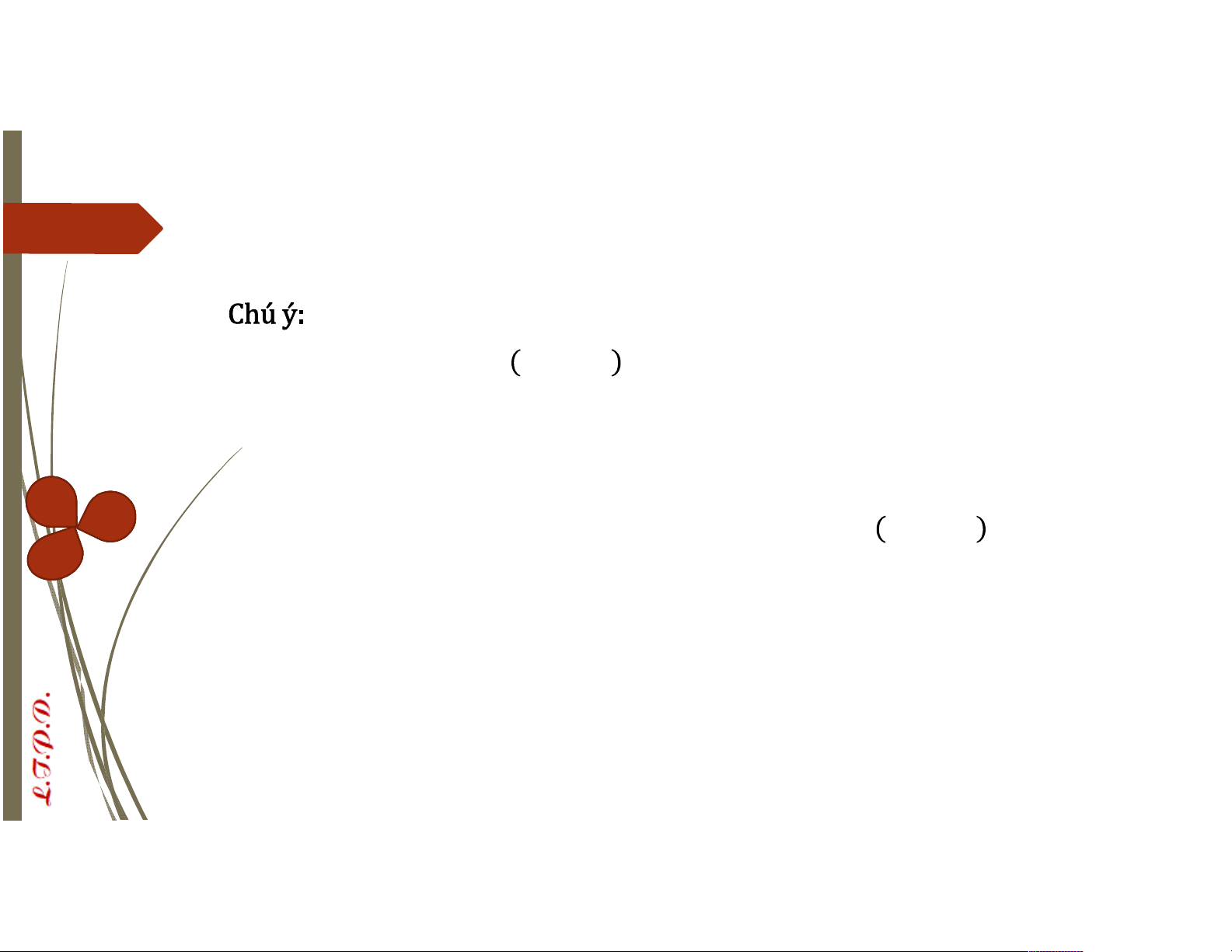
´Nếu d ∤ thì (∗∗) vô nghiệm
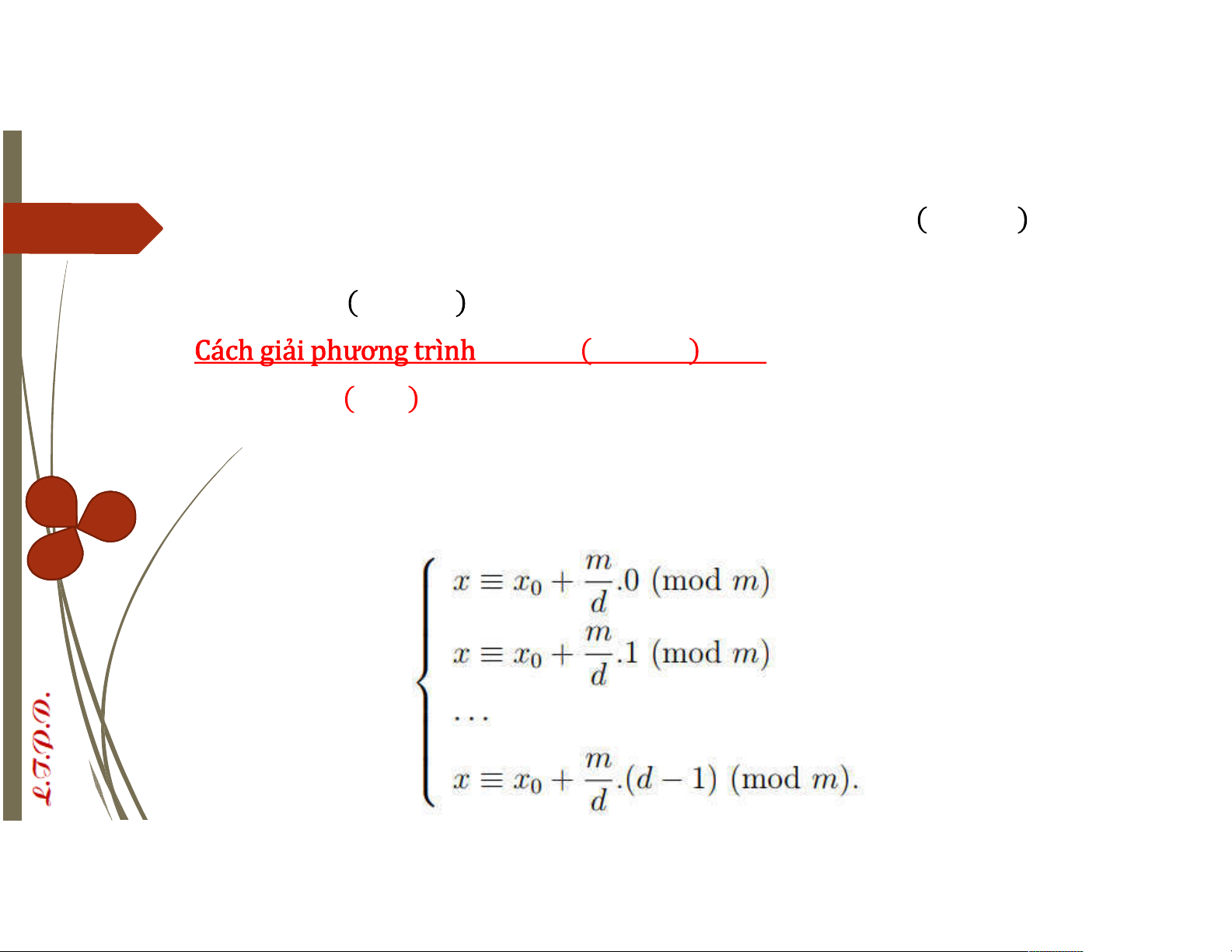
´Nếu | thì (∗∗) có nghiệm không đồng dư theo modulo . Nếu là
một nghiệm của (∗∗) thì nghiệm của (∗∗) được xác định như sau:
Phương trình đồng dư bậc nhất một ẩn
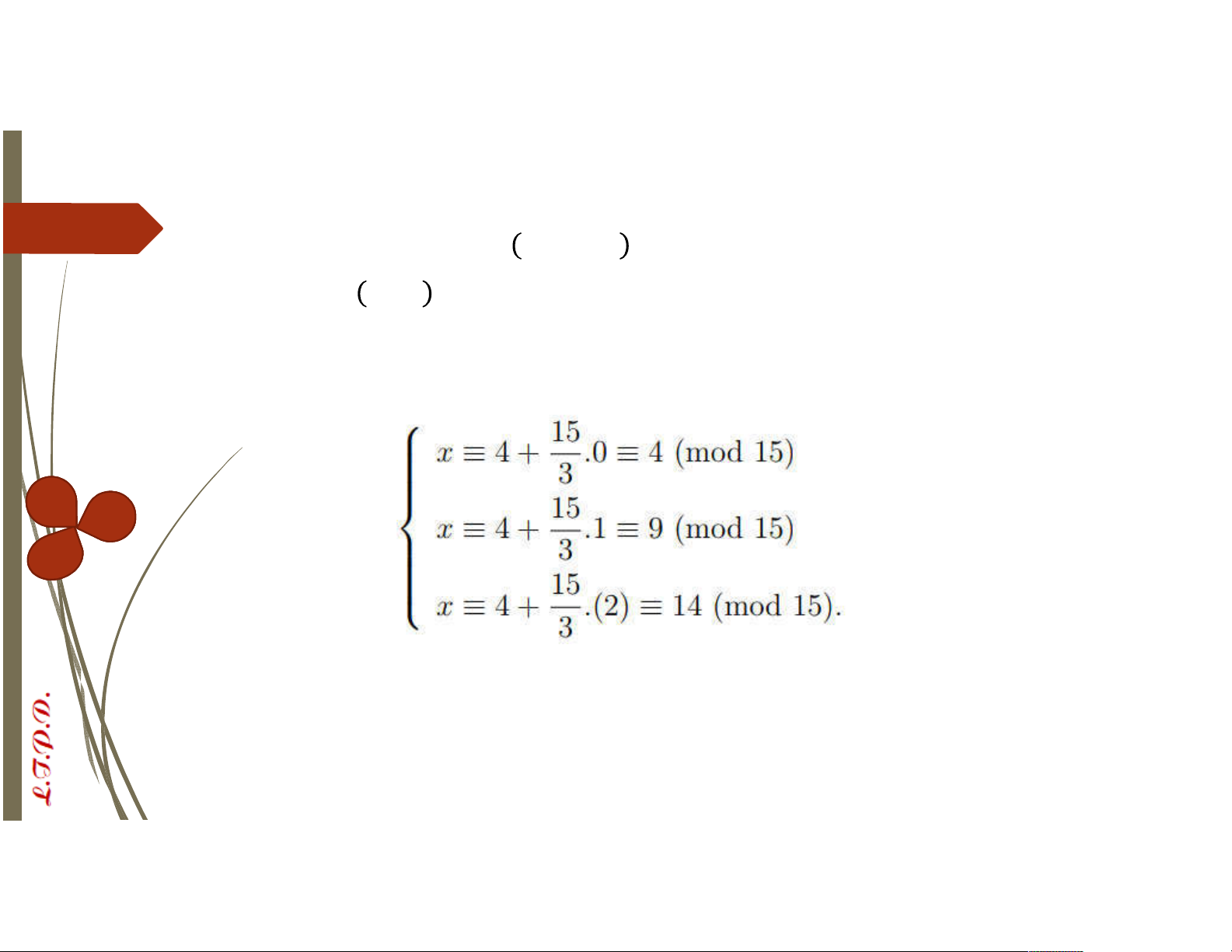
´Giải phương trình 9 ≡ 6 15
´Ta có d = 9,15 = 3|6. Do đó pt có 3 nghiệm không đồng dư theo modulo 15. Ta thấy
= 4 là một nghiệm của . Vậy 3 nghiệm của
được xác định như sau:
Phương trình đồng dư bậc nhất một ẩn
´Cách tìm nghiệm riêng : Xét phương trình ≡ , d = , | .
Giả sử d=1, vì nếu d ≠ 1 thì ta chia a, b, m cho d ta được ≡ ( ) ´TH1: Nếu | , vì ,
= 1 nên chia hai vế của pt cho , ta được ≡ ( ) Khi đó, ta có = là một nghiệm của pt. ´TH2: Nếu ∤ , vì , nên pt ±
= luôn có nghiệm. Khi đó: + = là một nghiệm của pt
Phương trình đồng dư bậc nhất một ẩn ´VD: Giải pt 4 ≡ 12 7
´ d = 4,7 = 1|12. Do đó pt có một nghiệm theo modulo 7
´Tìm nghiệm riêng: Vì 4 |12 nên ta được một nghiệm của pt là 12 = = 4 = 3
´Vậy một nghiệm của pt là ≡ 3 ( 7) ´VD: Giải pt 3 ≡ 4 11
´d = 3,7 = 1|4. Do đó pt có một nghiệm theo modulo 11
´Tìm nghiệm riêng: Vì 3 ∤ 4 nên một nghiệm riêng của pt là + 4 + 11.1 = = 3 = 5
´ Vậy một nghiệm của pt là ≡ 5 ( 11)
Phương trình đồng dư bậc nhất một ẩn ´ ´Pt đồng dư ≡
có nghiệm khi và chỉ khi pt Diophante + = có nghiệm ´Nếu pt +
= có nghiệm thì ta dùng thuật toán Euclide để tìm hai số nguyên , thỏa + = ´Khi đó,
là một nghiệm của pt đồng dư ≡
Phương trình đồng dư bậc nhất một ẩn VD: CMR 1997 − 1997 chia hết cho 4
´Ta có: 1997 ≡ 4.499 + 1 ≡ 1 4 ´Do đó: 1997 ≡ 1 ≡ 1 (mod 4) ´Và: 1997 ≡ 1 ≡ 1 (mod 4) ´Khi đó: 1997 − 1997 ≡ 1 − 1 ≡ 0(mod 4)
´Vậy biểu thức đã cho chia hết cho 4
Phương trình đồng dư bậc nhất một ẩn
VD: Tìm số dư khi chia 1532 − 1 cho 9 ´Ta có: 1532 ≡ 2 9 ´Suy ra: 1532 ≡ 2 ≡ 5 9
´Do đó: 1532 − 1 ≡ 5 − 1 ≡ 4 9
Phương trình đồng dư bậc nhất một ẩn VD: CMR 4 + 3
chia hết cho 13 với mọi số tự nhiên n
´Ta có: 4(4 ) + 9.3 ≡ 4.16 −4.3 ≡ 4.3 − 4.3 ≡ 0 13 ⇒ đccm VD: CMR Nếu , 7 = 1 thì − 1 chia hết cho 7
´Vì , 7 = 1 và 7 là số nguyên tố nên theo đl Fermat bé: ≡ 1 (mod 7) ´Ta có a ≡ ≡ 1 ≡ 1 (mod 7) ´Do đó − 1 ≡ 1 − 1 ≡0 (mod 7)
Hệ phương trình đồng dư
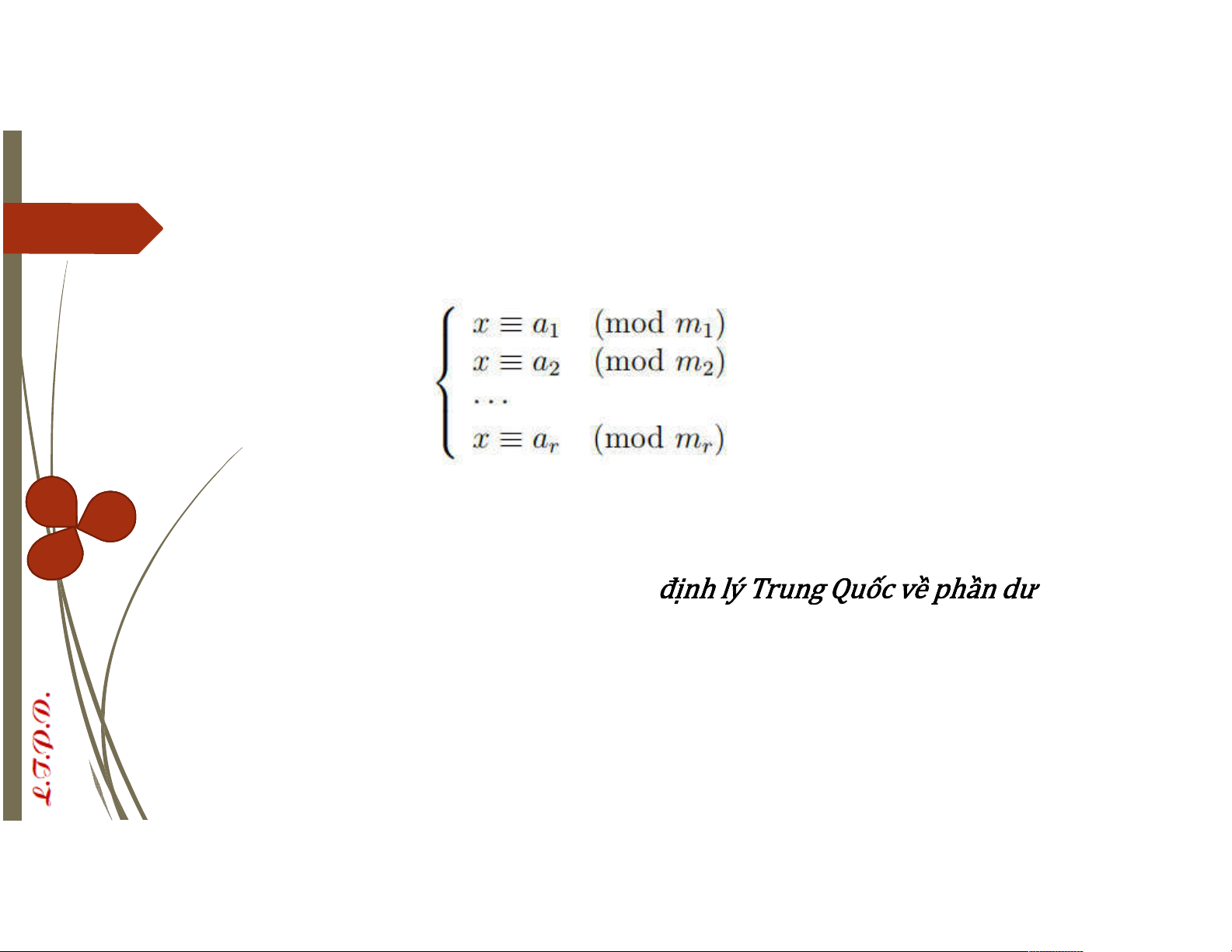
´Hệ phương trình sau đây được gọi là htp đồng dư bậc nhất một ẩn ´Nếu
là một nghiệm của hpt thì mọi số nguyên đồng dư với theo modulo = [ , , … ,
] đều là nghiệm của hpt
´Tìm nghiệm của hpt đồng dư theo : Nếu hpt đồng dư có , , … ,
là các số nguyên tố cùng nhau từng đôi thì hpt có
duy nhất nghiệm theo modulo M = …
Hệ phương trình đồng dư
´Cách giải hpt đồng dư theo : ´Điều kiện áp dụng: , , … ,
là các số nguyên tố sánh đôi ´Đặt = …
´Với mỗi ∈ {1,2, … , } ´Đặt = = … … ´Giải pt đồng dư ≡ 1 ( ) tìm ´Khi đó: ≡ + + ⋯ + ( ) là nghiệm của hpt
Hệ phương trình đồng dư ´ Đặt = …
´ Với mỗi ∈ {1,2, … , } ´ Đặt = = … …
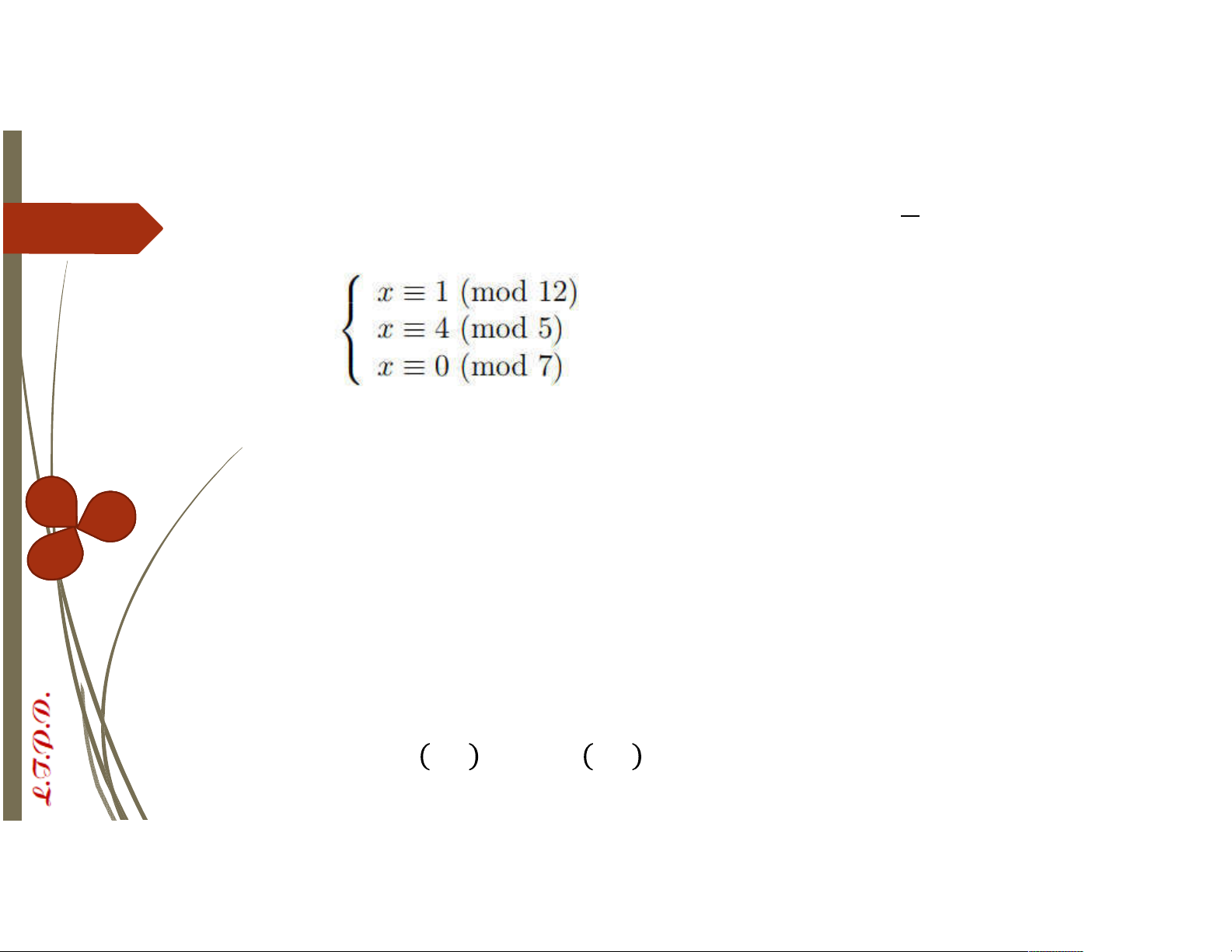
VD: Tìm nghiệm của hpt đồng dư ´ Giải pt đồng dư ≡ 1 ( ) ´ ≡ + + ⋯ + ( ) là nghiệm ´Vì = 12, = 5,
= 7 là các số nguyên tố sánh đôi thỏa mãn đk đl TQ ´Đặt = = 12.5.7 = 420; = 35; = 84; = 60 ´Giải các pt đồng dư ´35 ≡ 1 ( 12) có nghiệm là ≡ −1 ( 12) ´84 ≡ 1 ( 5) có nghiệm là ≡ −1 ( 5) ´60 ≡ 1 ( 7) có nghiệm là ≡ 2 ( 7) ´Vậy nghiệm của hpt là
≡ 1.35. −1 + 4.84. −1 + 0.60.2 ≡ 49 ( 420)
Hệ phương trình đồng dư
´Nếu hệ phương trình không thể áp dụng định lý TQ thì ta có thể sử dụng phương
pháp thế hoặc đưa về dạng định lý TQ để giải ≡ 1 12 (1) ´VD: ≡ 4 5 (2) ≡ 7 14 (3) (3) ⟺ = 7 + 14
Thế ( ) vào (1) ta được: 7 + 14 ≡ 1 12
⟺ 2 ≡ −6 mod 12 ⟺ ≡ −3 ≡ 3 6 ⟺ = 3 + 6 ( )
Thế ( ) vào ( ) ta được: = 7 + 14 3 + 6 = 49 + 84 ( )
Thế ( ) vào (2) ta được: 49 + 84 ≡ 4 5 ⟺ k ≡ 0 5 ⟺ = 5ℎ ( )
Thế ( ) vào ( ) ta được: = 49 + 84.5ℎ = 49 + 420h ⟺ x ≡ 49 (mod 420)
Hệ phương trình đồng dư
´Nếu hệ phương trình không thể áp dụng định lý TQ thì ta có thể sử dụng phương
pháp thế hoặc đưa về dạng định lý TQ để giải ≡ 1 12 (1) ´VD: ≡ 4 5 (2) ≡ 7 14 (3) (1) ⟺ ≡ 1 3 1a ≡ 1 4 (1 ) (3) ⟺ ≡ 7 2 ≡ 7 7 ⟺ ≡ 1 2 (3 ) ≡ 0 7 (3 )
Ta thấy nếu (1b) thỏa thì (3a) cũng thỏa nên giữ lại pt (1b) và bỏ đi pt hệ quả (3a) ≡ 1 3 (1′) ℎ ⟺ ≡ 1 4 (2′) ≡ 4 5
(3′) Áp dụng đl TQ giải được nghiệm: x ≡ 49 (mod 420) ≡ 0 7 (4′)