Bài giảng Chương I: Biến cố và xác suất của biến cố môn Xác suất thống kê | Học viện Ngân hàng

XÁC SUẤT VÀ THỐNG KÊ Giáo trình:
David R. Anderson, Dennis J. Sweeney, Thomas A. Williams (2023), Thống kê trong kinh tế và kinh doanh,
Nhà xuất bản Kinh tế TP. Hồ Chí Minh. Tham khảo: 1.
Basic business Statistics Concepts and Applications; Berenson • Levine • Szabat 2.
Statisics for Business and Economics: David R. Anderson – Dennis I. Sweeney – Thomas R. William. 3.
Nguyễn Mạnh Thế, Phạm Ngọc Hưng, Bùi Dương Hải (2020), Giáo trình lí thuyết xác suất trong kinh
tế và tài chính, Nhà xuất bản Đại học Kinh tế quốc dân. 4.
Đặng Hùng Thắng (2022), Mở đầu về lí thuyết xác suất và các ứng dụng, Nhà xuất bản Giáo dục. 5.
Đặng Hùng Thắng (2022), Thống kê và ứng dụng, Nhà xuất bản Giáo dục.
Thiết bị: Máy tính Casio fx – 570ES PLUS, 580 VNX..; Phần mềm: R; Excel 1 hvnh.edu.vn
XÁC SUẤT VÀ THỐNG KÊ
1. Chương I: Biến cố và xác suất của biến cố
2. Chương II: Biến ngẫu nhiên
3. Chương III: Một số quy luật phân phối xác suất thông dụng
4. Chương IV: Cơ sở lý thuyết mẫu
5. Chương V: Ước lượng tham số
6. Chương VI: Kiểm định giả thuyết thống kê hvnh.edu.vn 2
Chương I: Biến cố và xác suất của biến cố
1. Phép thử ngẫu nhiên và không gian mẫu;
2. Biến cố và mối quan hệ giữa chúng;
3. Xác suất của một biến cố;
4. Các quy tắc tính xác suất. hvnh.edu.vn 3
1. Phép thử ngẫu nhiên và không gian mẫu
Một (dãy) hành động mà kết quả không thể biết chắc chắn (chỉ có thể dự báo) trước
được gọi là một “phép thử ngẫu nhiên”.
Mỗi kết quả của một hành động không biết chắc chắn trước kết quả: biến cố đơn;
Mỗi kết quả của một dãy hành động đều không biết chắc chắn trước kết quả: biến cố phức hợp.
Quy ước: ta sẽ quan tâm tới phép thử nói chung.
 Ký hiệu phép thử ngẫu nhiên: τ
 Tập hợp tất cả các kết quả của phép thử τ gọi là Không gian mẫu, ký hiệu là Ω:
Ω = tập tất cả các kết quả có thể xảy ra của τ hvnh.edu.vn 4
2. Biến cố và mối quan hệ giữa chúng
2.1. Biến cố: Một biến cố là kết quả của 1 phép thử (biến cố đơn) hoặc 1 dãy
phép thử (biến cố phức hợp).
Ký hiệu biến cố: thường ký hiệu
Chữ (ký tự) = ”kết quả của phép thử”
 Một kết quả của τ được gọi là “kết quả thuận lợi” cho biến cố A nếu A
xảy ra khi kết quả đó xảy ra. Tập các kết quả thuận lợi cho A ký hiệu là ΩA .
2.2. Mối quan hệ giữa các biến cố (kéo theo, tương đương, đối)
2.3. Các phép toán trên biến cố (phép hợp, phép giao) hvnh.edu.vn 5
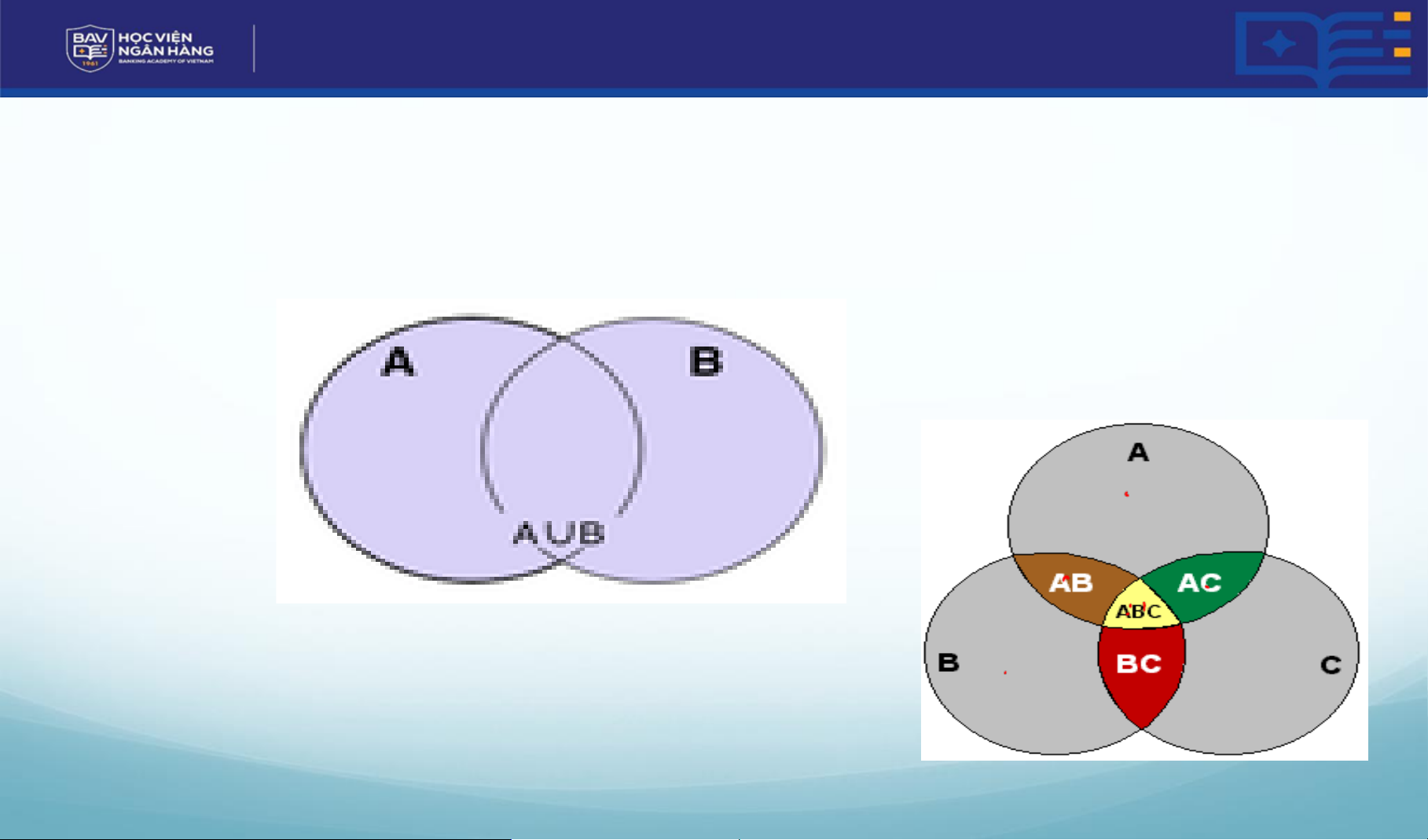
 Phép hợp các biến cố: ký hiệu A U B
ĐN: AB xảy ra khi có ít nhất một trong hai biến cố A, B xảy ra.
 Phép giao của các biến cố: A.B.
ĐN: A.B xảy ra  cả A và B cũng xảy ra. hvnh.edu.vn 6
Ví dụ 1: Có 3 người cùng bắn vào 1 mục tiêu một cách độc lập.
Hãy xây dựng các biến cố sau:
a. Chỉ có người thứ 1 bắn trúng mục tiêu;
b. Chỉ có 1 người bắn trúng mục tiêu;
c. Chỉ có 2 người bắn trúng mục tiêu;
d. Có người bắn trúng mục tiêu.
Ak= “người thứ k bắn trúng mục tiêu”: hvnh.edu.vn 7
 Tính chất chung của các phép toán hvnh.edu.vn 8
3. Xác suất của biến cố a.
Định nghĩa cổ điển về xác suất
Giả sử 1 phép thử τ có tất cả n kết quả đồng khả năng, trong đó có m kết quả thuận lợi cho A. Khi đó. P(A) = m/n
b. Định nghĩa xác suất theo nghĩa hình học
Ví dụ 2: giả sử người ta bắn vào một cái bia ở tầm gần, sao cho việc trúng mỗi điểm trên bia là như nhau. Tính xác suất
bắn trúng hồng tâm (vòng 10)?
ĐN: Giả sử phép thử T có vô số kết cục đồng khả năng, có thể biểu diễn như là điểm của miền hình học Ω nào đó, các kết
quả thuận lợi cho biến cố A được biểu diễn như là điểm của miền hình học ΩA nào đó. Khi đó
P(A) = độ đo của ΩA / độ đo của Ω
c. Định nghĩa xác suất theo nghĩa thống kê
Việc tính khả năng để một máy nào đó sản xuất ra phế phẩm, ta không thể dùng 2 ĐN trên mà phải dựa vào quan sát thực
tế => định nghĩa xác suất theo nghĩa thống kê
ĐN: Giả sử phép thử τ được lặp đi, lặp lại nhiều lần trong những điều kiện giống hệt nhau. Nếu trong n lần thực hiện τ có
m lần xuất hiện biến cố A, thì hvnh.edu.vn 9 P(A) ≈ f(A) =m/n
4. Các quy tắc tính xác suất
4.1. Quy tắc cộng: giúp ta tính xác xuất để ít nhất 1 trong 2 (n) biến cố có thể xảy ra.
Định nghĩa: Biến cố A và B được gọi là xung khắc nếu A.B = Ø
Nếu các biến cố Ai: i = 1..n liên quan tới phép thử τ là các biến cố xung khắc từng đôi một thì n n 𝑃(ራ Ai) = ෍ P(Ai) i=1 i=1 Tính chất:  P(A) = 1 – P(Ā) (1); P(ĀB) = P(B) – P(AB) (2);  Câu hỏi: P(AഥB) =??? hvnh.edu.vn 10
Nếu không có điều kiện xung khắc từng đôi. Ta có công thức cộng xs TQ: n n
P ራ Ai = ෍ P(Ai) − ෍ 𝑃 AiAj + ෍
P AiAjAk + ⋯ + −1 n−1P(A1A2 … An) i=1 i=1
1≤i1≤iVí dụ 3: Một công ty QC một loại dịch vụ: 40% người biết qua truyền hình, 35% qua truyền thanh và
10% qua cả 2 hình thức thông tin. Tính tỷ lệ khách hàng nắm được thông tin?
Ví dụ 4: Xét số liệu về tỷ suất sinh lợi sau 1 năm và sau 5 năm của 30 quỹ ĐTCK lớn nhất tính đến ngày
(31/3/2000) (cite Wall stress Journal). Quy ước rằng nếu tỷ suất sinh lợi sau 1 năm vượt qua 50% được
gọi là cao, nếu tỷ suất sinh lợi sau 5 năm vượt qua 300% cũng được gọi là cao. 9 trong số các quỹ được
xét có tỷ suất sinh lợi sau 1 năm > 50%, 7 quỹ trong số đó có tỷ suất sinh lợi sau 5 năm vượt qua 300%; 5
trong số các quỹ đó có tỷ suất sinh lợi sau 1 năm > 50%, và tỷ suất sinh lợi sau 5 năm vượt qua 300%. 1.
Tính xác suất để 1 quỹ đầu tư ck có tỷ suất sinh lợi cao?
2. Tính xs để 1 quỹ đầu tư chứng khoán có tỷ suất lợi nhuận cao cả sau 1 năm và sau 5 năm? 3.
Tính xs để 1 quỹ đầu tư chứng khoán có tỷ suất lợi nhuận đều không cao cả sau 1 năm và sau 5 năm? hvnh.edu.vn 11
4.2. Xác suất có điều kiện
ĐN: Giả sử P(A) > 0. Xác suất của biến cố B với điều kiện biến cố A đã xảy ra là
một số không âm ký hiệu P(B|A), nó biểu thị khả năng xảy ra của biến cố B khi biến cố A đã xảy ra: P(B|A) = P(A.B)/P(A) Chú ý:
 Ta có P(A|B) = 1 – P(Ā|B);
Nếu A kéo theo B thì P(B|A) = 1;
 Nếu B kéo theo A thì A.B = B => P(B|A) = P(B)/P(A) (**). hvnh.edu.vn 12
Ví dụ 5: Một cuộc khảo sát khách hang của Morgan Stanley, lấy mẫu cả nam lẫn nữ để hỏi
về việc họ thích ướng nước tinh khiết đóng chai hơn hay các loại nước uống thể thao
hơn. Giả sử có 200 nam và 200 nữ tham gia trả lời cuộc khảo sát, trong đó có 280 người trả
lời thích uống nước tinh khiết đóng chai. Trong nhóm trả lời họ thích nước cho thể thao hơn, có 80 nam và 40 nữ.
M = “khách hang là nam”; W = ” KH là nữ”; B = “KH thích nước đóng chai hơn”; S = “KH
thích dung nước thể thao hơn”.
a. Tính P(M|S), P(W|S), P(M.S), P(W.S)?
b. Nếu biết 1 KH là nam, tính xác suất để KH này thích các loại nước uống thể thao hơn?
c. Nếu biết 1 KH là nữ, tính xác suất để KH này thích các loại nước uống thể thao hơn?
d. Việc thích uống nước thể thao hơn có độc lập với việc khách hang là nam hay nữ hay
không? Giair thích câu trả lời bang xác suất.(không, P(S|M) khác P(S)) hvnh.edu.vn 13
4.3. Quy tắc nhân xác suất
ĐN: Hai bc A và B đgl độc lập với nhau nếu P(Ā|B) = P(Ā) hoặc P(B|A) = P(B)
(A xảy ra hay không cũng không ảnh hưởng gì tới B).
 Nếu A, B độc lập thì P(AB) = P(A).P(B)
 Nếu A, B phụ thuộc và A tác động tới B: P(AB) = P(A).P(B|A)
 Trong trường hợp họ các biến cố là phụ thuộc:
P(A1…An) = P(A1)P(A2|A1)P(A3|A1A2)…P(An|A1A2…An-1) hvnh.edu.vn 14
Ví dụ 6: Bắn liên tiếp vào mục tiêu, cho đến khi có 1 viên đạn đầu tiên trúng thì
dừng lại. Tìm xác suất để sao cho phải bắn tới viên thứ 4. Biết rằng xác suất bắn
trúng của mỗi lần là như nhau, bằng 0,3. Công thức nhân:
 Nhắc lại: Hai biến cố A.B độc lập thì P(AB) = P(A)P(B)
 Họ {Ai: i = 1…n} đgl độc lập toàn phần nếu nó độc lập từng đôi một và mỗi
biến cố độc lập với giao của một số tuỳ ý các biến cố còn lại.
P(A1A2…An) = P(A1)P(A2)…P(An) hvnh.edu.vn 15
Ví dụ 7: Một tờ tiền giả lần lượt được 2 người A, B kiểm tra. Xác suất để người A
phát hiện ra tờ tiền giả là 0.85. Nếu người A nói tờ tiền là giả thì người B cũng
nhận định vậy với xác suất là 0.9. Ngược lại, nếu người A cho rằng tờ tiền là tiền
thật thì người B cũng nhận định như thế với xác suất 0.4.
a. Tính xác suất để có ít nhất một người nhận định tờ tiền là giả?
b. Biết tờ tiền đó đã bị ít nhất một người phát hiện là giả. Tính xác suất để A phát hiện ra nó? hvnh.edu.vn 16
4.4. Công thức xác suất đầy đủ
ĐN: Họ các biến cố {H1, H2, … , Hn} được gọi là nhóm đầy đủ các biến cố nếu nó
thoả mãn 2 điều kiện sau: H n
i.Hj =  với mọi i khác j; ڂi=1 Hi = Ω
Định lý: (CT XS đầy đủ) Giả sử có nhóm đầy đủ các biến cố {H1, H2, … , Hn} có
xác suất khác 0. A là biến cố nào đó trong cùng một phép thử. Khi đó: n P A = ෍ P(Hi)P(A|Hi) i=1 hvnh.edu.vn 17
Ví dụ 18: Có 3 hộp đựng sản phẩm như sau:
Hộp 1: 6 chính phẩm; 4 phế phẩm;
Hộp 2: 10 chính phẩm; 5 phế phẩm;
Hộp 3: 15 chính phẩm; 5 phế phẩm.
Lấy ngẫu nhiên 1 hộp, từ đó lấy ngẫu nhiên 2 sp. Tìm xác suất 2 sản phẩm lấy ra
có 1 chính phẩm và 1 phế phẩm? hvnh.edu.vn 18
Ví dụ 9: Trong 1 trạm cấp cứu bỏng, thấy 80% bỏng do nóng; 20% bỏng do hoá chất.
Loại bỏng do nóng có 30% bị biến chứng, bỏng do hoá chất có 50% bị biến chứng. Từ
tập hồ sơ bệnh án, rút ngẫu nhiên 1 bệnh án. Tìm xác suất để rút được bệnh án của bệnh nhân bị biến chứng?
Ví dụ 10: Một nhà phân phối sản phẩm của hang Apple nghiên cứu sở thích của khách
hàng. Ông ta thấy từ số lieu thống kê là: 80% khách hàng thích iphone. Khi một khách
hàng đã thích iphone, thì khả năng người ấy thích ipad là 85%. Khi một khách hàng
không thích iphone thì khả năng người ấy thích ipad là 45%.
a. Tính tỷ lệ khách hàng thích cả iphone và ipad?
b. Giả sử một khách hang không thích ipad, tính xác suất để người ấy thích iphone?
c. Tính tỷ lệ khách hang chỉ thích 1 trong 2 loại Iphone hoặc Ipad?
d. Tính tỷ lệ khách hàng thích ít nhất một trong hai loai Iphone hoặc Ipad? hvnh.edu.vn 19 4.5. Công thức Bayes
Định lý Bayes được sử dung rất rộng rãi trong các phân tích để ra quyết định lựa chọn. Xác suất tiên nghiệm
P(H_i) thường được phán đoán chủ quan bởi người ra QĐ. Sau đó các thông tin thu thập được từ viêc
chọn mẫu và các xác suất hậu nghiệm được tính làm cơ sở đưa ra các QĐ tốt nhất.
Định lý: Giả sử biến cố A có thể xảy ra đồng thời với 1 trong n biến cố H1, H2,…,Hn, và nhóm này tạo nên
nhóm đầy đủ các biến cố . Khi đó P H P H i . P(A|Hi) i A = σni=1 P Hj . P(A|Hj) Nhận xét: -
{Hi}- giả thiết, P(Hi) – được xác định trước khi phép thử được tiến hành – xác suất tiên nghiệm; -
P(Hi|A) – được xác định sau khi phép thử được tiến hành – xác suất hậu nghiệm.
Công thức Bayes đánh giá lại xác suất xảy ra các giả thiết khi đã biết kết quả của phép thử là biến cố A đã xảy ra. hvnh.edu.vn 20