Bài giảng chương V Cảm ứng điện từ môn Vật lý đại cương 2 | Trường Đại học Bách Khoa Hà Nội

TRƯỜNG ĐẠI HỌC BÁCH KHOA HÀ NỘI HANOI UNIVERSITY OF SCIENCE AND TECHNOLOGY (HUST) Viện Vật lý Kỹ thuật CHƯƠN Sc G hool V of Engineering Physics (SEP) CẢM ỨNG ĐIỆN TỪ
1. Hiện tượng cảm ứng điện từ 2. Hiện tượng tự cảm
3. Năng lượng từ trường 1
1. Hiện tượng cảm ứng điện từ 1. Thí nghiệm Faraday S vN v Michael Faraday (1791-1867) Khái niệm:
Là hiện tượng xuất hiện dòng điện cảm ứng trong một vòng
dây dẫn khép kín (hay mạch kín) khi từ thông qua mạch đó biến thiên theo thời gian. 2
1. Hiện tượng cảm ứng điện từ
1. Thí nghiệm Faraday (tiếp) v v v S S v N N N N S S ' B ' B ' B ' B II II
Đặc điểm dòng điện cảm ứng:
Chỉ tồn tại trong thời gian từ thông B gửi qua mạch thay đổi; thay đổi B
Có cường độ tỉ lệ thuận với tốc độ Tăng dần
biến đổi của từ thông; I I
Có chiều phụ thuộc vào từ thông ' B
gửi qua mạch tăng hay giảm. 3
1. Hiện tượng cảm ứng điện từ
2. Định luật Lenz xác định chiều dòng cảm ứng Nội dung.
Dòng cảm ứng có chiều sao cho từ
trường do nó sinh ra chống lại sự biến
thiên của từ thông sinh ra nó. Ví dụ:
Khi cực Bắc (N) tiến vào vòng dây Heinrich Lenz từ thông mdo từ trường Bcủa nam (1804-1865)
châm gửi qua cuộn dây có chiều từ trên S v
xuống và tăng dần dòng cảm ứng IC N
tạo ra B’cảm ứng ngược chiều B B’ v B S từ thông
’mcủa B’chống lại sự tăng m
IC.ngược chiều kim đồng hồ. N của B B ’
Rút thanh nam châm ra khỏi vòng IC
dây hiện tượng ngược lại. IC 4 30-Oct-19
1. Hiện tượng cảm ứng điện từ
3. Sức điện động cảm ứng
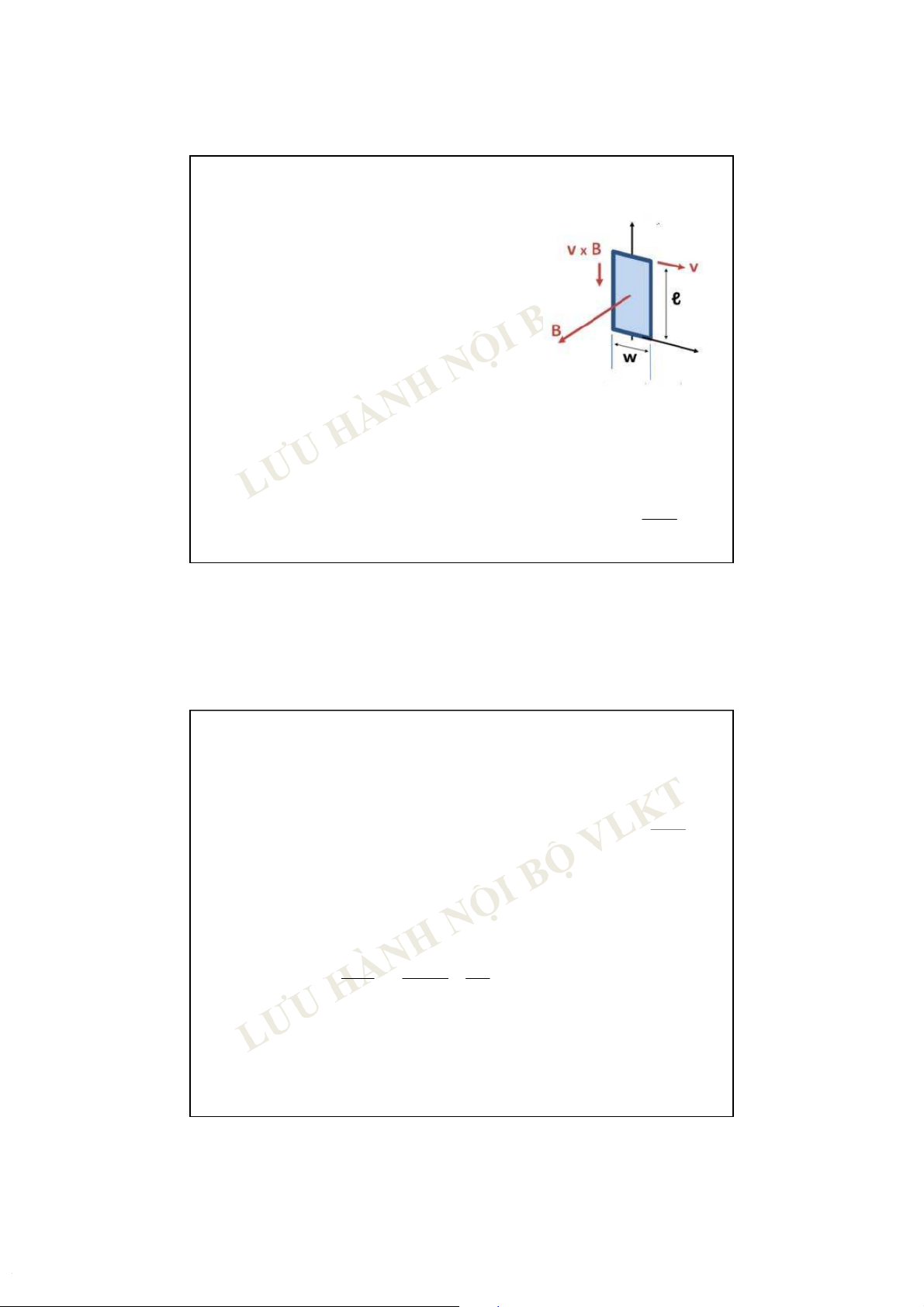
Xét vòng dây dẫn kín di chuyển trong B d
m là biến thiên từ thông gửi qua
vòng dây trong thời gian dt gây ra
dòng cảm ứng Ictheo đ/l Lenz có
nguồn gốc từ một nguồn điện cảm ứng
đặc trưng bởi s.đ.đ cảm ứng Ec.
Công của từ lực để di chuyển vòng dây: dA =Ic.d m
đ/l Lenz: từ lực tác dụng lên Icngăn cản sự di chuyển của vòng
dây (là nguyên nhân sinh ra Ic) công cản: dA’ = - dA = - Ic d . m
đ/l bảo toàn năng lượng: dA ’ chuyển thành NL của Ic dA’ = -I d c.d m= E c.Ic.dt (NL của Ic) m EC dt 5
1. Hiện tượng cảm ứng điện từ
3. Sức điện động cảm ứng (tiếp)
Từ định luật cơ bản của hiện tượng cảm ứng điện từ, suy ra: dA’ = -I dm c.d m= E c.Ic.dt (NL của Ic) EC dt
Sức điện động cảm ứng trong một mạch kín bất kỳ bằng về trị số
nhưng khác dấu với tốc độ thay đổi của từ thông qua mạch.
Định nghĩa đơn vị từ thông
Nếu từ thông gửi qua diện tích mạch kín giảm từ giá trị mvề 0: m m d 0 m E m= E c. t C dt t t Với t = 1 s, E c= 1 V m= 1 (V) . 1 (s) = 1 Webe (Wb)
Webe là từ thông gây ra trong một vòng dây dẫn bao quanh
nó một sức điện động cảm ứng bằng 1 V khi từ thông đó giảm
đều xuống giá trị 0 trong thời gian 1 s 6 30-Oct-19
1. Hiện tượng cảm ứng điện từ
4. Máy phát điện xoay chiều Khung dây (Nvòng dây) IC n diện tích Squay trong từ O
trường đều (B const ) với vận B tốc góc .
Vị trí ban đầu của khung Chổi than tương ứng góc giữa pháp
tuyến mặt phẳng khung n và B Cổ góp Sau khoảng thời gian t ~
vị trí khung ứng với góc: = t +
Từ thông gửi qua khung sau khoảng thời gian t: m= N.B.S.cos =N.B.S.cos( t+ ) 7
1. Hiện tượng cảm ứng điện từ
4. Máy phát điện xoay chiều (tiếp)
Vị trí khung dây trong từ trường B Khi khung quay đều trong
từ trường xuất hiện 1 s.đ.đ
cảm ứng xoay chiều hình sin m,Ec, C E NB.S.ωB. ω S. t m= NB.S.cos t theo đ/l Lenz: N.B. . S . E sin tdΦm C dt Đặt E cmax. = si N.B.S. n t E Ec ω α C max
Chu kỳ = chu kỳ quay của khung: 2π T ω E c NBSω Dòng cảm ứng I c sin ωt R R NBSω Ic= I0.sin t Đặt: I I cmax 0 R 8 30-Oct-19
1. Hiện tượng cảm ứng điện từ
5. Dòng xoáy (dòng Foucault/ eddy current)
Dòng cảm ứng (có dạng xoáy) xuất hiện
trên bề mặt vật dẫn khi đặt trong từ trường: E ICF R Hệ quả:
Xuất hiện từ trường riêng Léon Foucault (1819-1868) của dòng cảm ứng IF Từ trường
Dòng cảm ứng xuất hiện Cuộn dây cuộn dây
trên bề mặt vật dẫn sẽ bị tiêu
tán dưới dạng nhiệt tiêu hao Từ trường năng lượng vô ích giảm dòng xoáy Dòng xoáy
hiệu suất thiết bị (đặc biệt với các động cơ). Vật dẫn 9
1. Hiện tượng cảm ứng điện từ
5. Dòng xoáy (dòng Foucault/ eddy current) (tiếp)
Do có từ trường của dòng cảm ứng xuất hiện trên bề mặt vật
dẫn ứng dụng trong các thiết bị dò tìm kim loại. Báo động Dòng cảm Dòng tạo ứng do từ từ trường trường dòng xoáy Dòng xoáy Cuộn phát Cuộn thu Dòng xoáy Cửa an ninh (security gate)
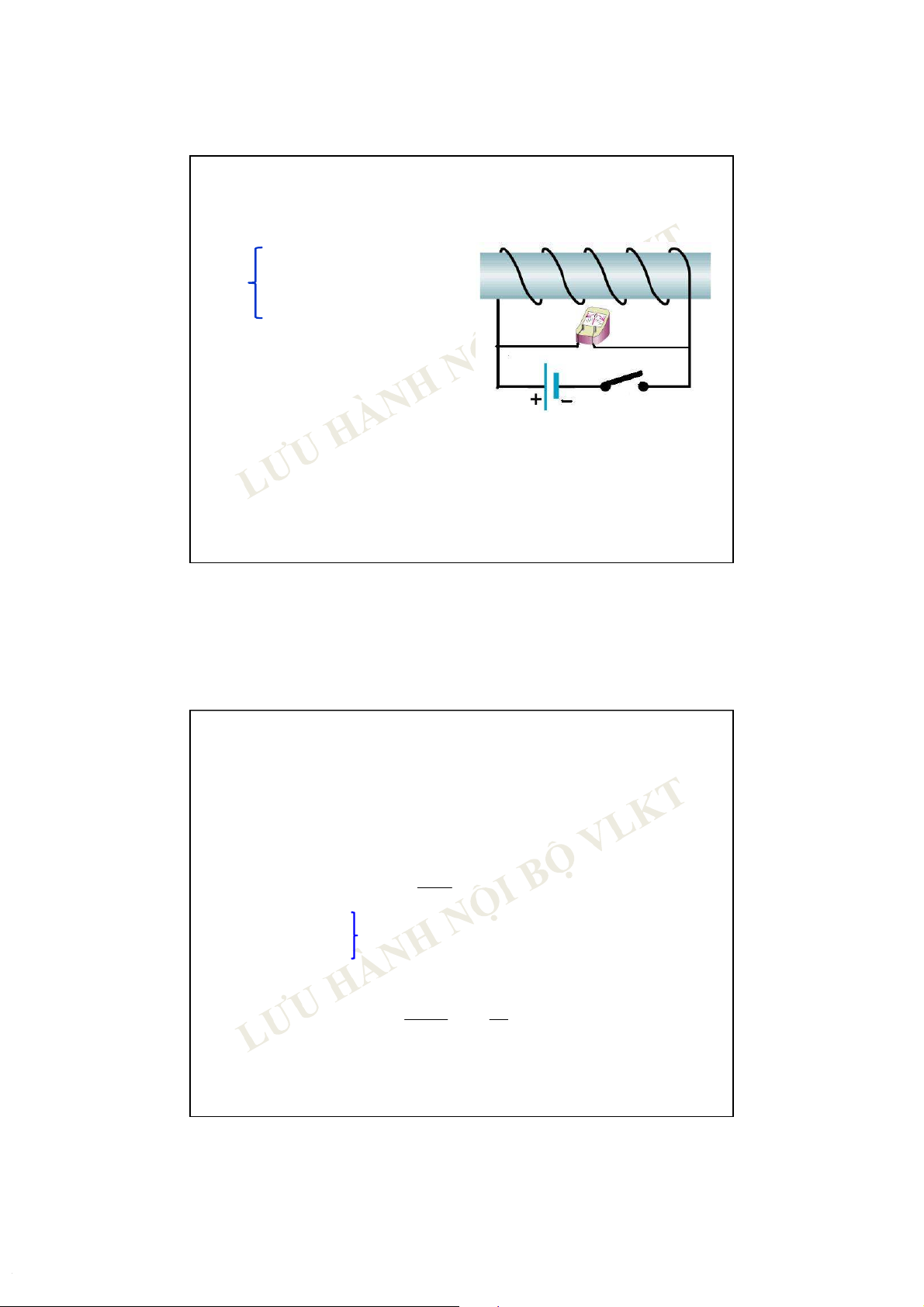
Thiết bị dò mìn (mine detector) 10 30-Oct-19 2. Hiện tượng tự cảm 1. Hiện tượng Xét mạch điện với: + nguồn điện (E); + điện kế (G); + ống dây có lõi sắt.
Trường hợp ngắt mạch (mở K): G
Kim G không về vị trí 0 mà
lệch theo chiều ngược lại; K
Kim G trở về 0 sau khoảng E thời gian t.
Giải thích: trong khoảng thời gian t, từ thông qua cuộn dây giảm
từ m 0 xuất hiện dòng cảm ứng Iccó độ lớn và chiều ngược
với dòng ban đầu, theo đ/l Lenz, như được hiển thị trên G.
Trường hợp đóng mạch quá trình ngược lại. 11 2. Hiện tượng tự cảm Khái niệm:
Là hiện tượng xuất hiện dòng điện trong một mạch điện có
cuộn dây (hay ống dây), khi từ thông gửi qua cuộn dây bởi dòng
điện của mạch đó thay đổi.
2. Suất điện động tự cảmdm Theo đ/l Lenz: Etc dt Có: m B m I viết được: m= L.I và: B I
Kết luận: đ/v mạch đứng yên và giữ nguyên hình dạng, có: ( ) tc d LI dI E L
(L:gọi là hệ số tự cảm) dt dt
Trong mạch điện đứng yên và không thay đổi hình dạng, sức
điện động tự cảm luôn tỷ lệ với tốc độ biến thiên cường độ dòng điện trong mạch. 12 30-Oct-19 2. Hiện tượng tự cảm 3. Hệ số tự cảm
Định nghĩa đơn vị đo hệ số tự cảm (L) Đơn vị : Henry (H), 1Wb Wb 1H 1 1A A
H là hệ số tự cảm của 1 mạch
kín, khi có dòng điện cường độ 1 A
chạy qua mạch đó thì sinh ra trong l S
chân không, từ thông bằng 1 Wb.
Trường hợp ống dây có lõi sắt (vật dẫn): Φ N.B.S n2 S . .I n 2 S . L 0 0 I I I.l l Do lõi sắt lớn
đơn vị Hlớn thực tế chỉ dùng đơn vị
mH = 10-3 H, hoặc 1 H = 10-6 H 13 2. Hiện tượng tự cảm
Ứng dụng hiện tượng tự cảm
Vòng dây cảm ứng (Inductive Loop Detector - ILD) đóng vai trò như một
loại cảm biến điện từ ứng dụng trong lĩnh vực giao thông vận tải.
Nguyên lý: xe cộ là các vật dẫn chạy vào khu vực có các vòng dây chôn phía
dưới (đã có dòng điện) Lvòng dây thay đổi Ivòng dây thay đổi tín hiệu được
đưa vào máy tính để hệ thống nhận biết cho mục đích quản lý phương tiện lưu
thông trên đường hoặc điều khiển quá trình đóng/mở thanh chắn tại các lối
vào/ra bãi đỗ hay đóng phí đường bộ tự động,… Vòng dây phía dưới Máy tính mặt đường hệ thống Từ trường Nguồn điện có đồng hồ đo 14 30-Oct-19 2. Hiện tượng tự cảm 4. Hiệu ứng bề mặt
Khi cho dòng điện cao tần chạy qua 1 dây dẫn dòng tự cảm chỉ B
xuất hiện ở bề mặt dây dẫn Tần số f= 103Hz dòng tự
cảm chạy trong lớp vật liệu bề mặt ~ 2 mm
Tần số f= 105Hz dòng tự cảm chỉ chạy trong lớp vật liệu bề mặt ~ 0,2 mm
Ứng dụng trong công nghệ:
Dùng dây dẫn rỗng để tải dòng cao tần
Kỹ thuật tôi bề mặt hợp kim bằng dòng cao tần 15
3. Năng lượng từ trường
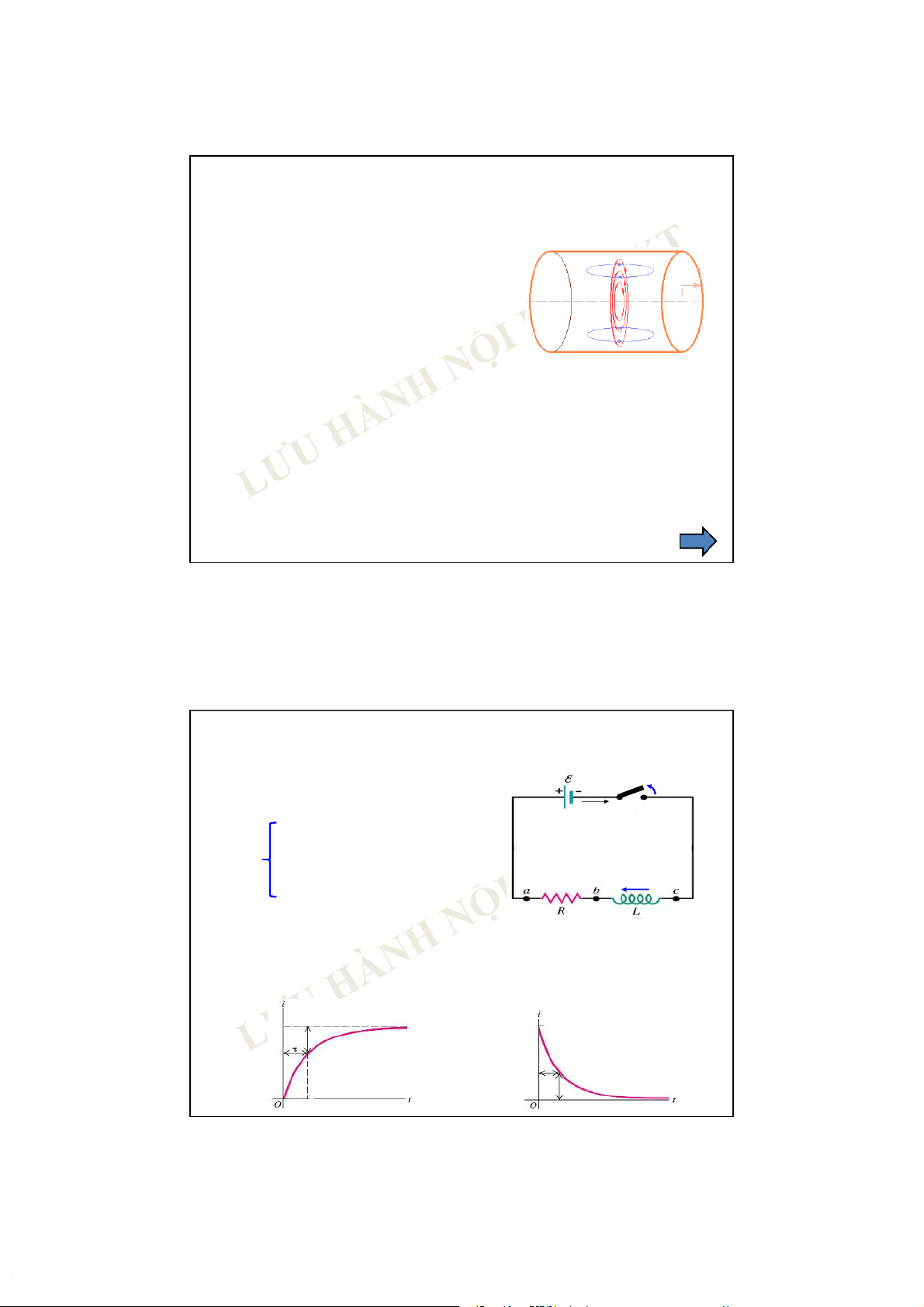
1. Năng lượng từ trường của một ống dây Mạch điện có khóa K: K i0
+ Sức điện động E,dòng i0;
+Ống dây: hệ số tự cảm L và điện trở R. itc Khi đóng mạch i B Khi ngắt mạch i B& & mgửi qua L itc ngược mgửi qua L itc cùng chiều i0 i = i0- itc NL chiều i0 i = i0+ itc NL
nguồn (~ i02) > NL mạch (~ i2).
nguồn (~ i02) < NL mạch (~ i2). i0i0 16 30-Oct-19
3. Năng lượng từ trường
1. Năng lượng từ trường của một ống dây (tiếp) dI = L/R I(t) 100 (U) t UE R L IR L dt 0 0 1 0.632 x Us/R 2 0.865 x Us/R U 3 0.950 x Us/R 4 0.981 x Us/R % Imax (US/R) R t U t U 5 0.992 x Us/R L S 012345 ( ) 1 I t1 Se e R R = L/R I(t) 100 0 Vs/R 1 0. 368 x Us/R U 2 0.135 x Us/R 3 0.05 x Us/R R % Imax (US/R) I t U t L ( ) Se 4 0.019 x Us/R R 5 0.008 x Us/R 0 12 3 45 17
3. Năng lượng từ trường
1. Năng lượng từ trường của một ống dây (tiếp)
Áp dụng đ/l Ohm trong quá trình hình thành dòng điện i: E + E =R.i tc di Hay: E R.i L dt Nhân 2 vế với idt: E idt =R.i2dt + L.i.di NL nguồn NL nhiệt NL từ trường
NL từ trường khi thiết lập dòng điện trong ống dây:dW =L.i.di W i I 1 2 W dW L.i.di L.I 2 0 i 0 18 30-Oct-19
3. Năng lượng từ trường
2. Mật độ năng lượng từ trường l
Xét ống dây có thể tích: V = l.S
Mật độ NL từ trường trong ống dây: 2 1 n S 2 1 2 μμ I L.I 0 W 2 l 2 wm V l.S l.S 2 1 n 2 μμ I 2 1 B 0 2 2 l w (trong ống dây: B=const) n mμμ 2 B 0 0 μμ I l
wmcũng được áp dụng để xác định mật độ NL cho từ trường bất kỳ! 19
3. Năng lượng từ trường
3. Năng lượng từ trường không gian
Chia không gian từ trường thành những thể tích vô cùng nhỏ
dV sao cho B = const trong mỗi dV.
Năng lượng từ trường trong mỗi thể tích dV: 1 B2 mdW m w dV dV 2 0
Năng lượng từ trường trong cả không gian: 1dV B 2 W dW m m 2 V V0 W 1BHdV B m H 2 V 0 20