Bài giảng công thức lượng giác cần nhớ | Toán 11

[Công thức lượng giác cần nhớ - Tài liệu tặng miễn phí cho học sinh] CÔNG TH C L NG GIÁC C N NH 1. Công th c l
ng giác cơ bản nên nh 2 2 sin   cos   1 3 3
sin   cos   (sin  cos )(1 sin cos ) 1  3 3 2
sin   cos   (sin  cos )(1 sin cos ) 1 tan   ,   k,k  2 cos  2 4 4 2 2
sin   cos   1 2sin  cos  1 2 1 cot  
,  k , k  4 4 2 2           2 sin cos sin cos cos 2 sin  6 6 2 2         sin cos 1 3sin cos
tan .cot  1,  k , k  2 6 6 2 2
sin   cos    cos 2 (1 sin  cos  ) 2. Giá trị l
ng giác c a cung có liên quan đặc biệt
Cung đối nhau:  và  
Cung bù nhau:  và  
Cung hơn kém  :  và                cos( ) cos sin( ) sin sin( ) sin sin(   )  sin
cos(  )   cos
cos(   )   cos tan(   )   tan
tan(  )   tan tan(   )  tan cot(   )  cot
cot(  )   cot cot(   )  cot  
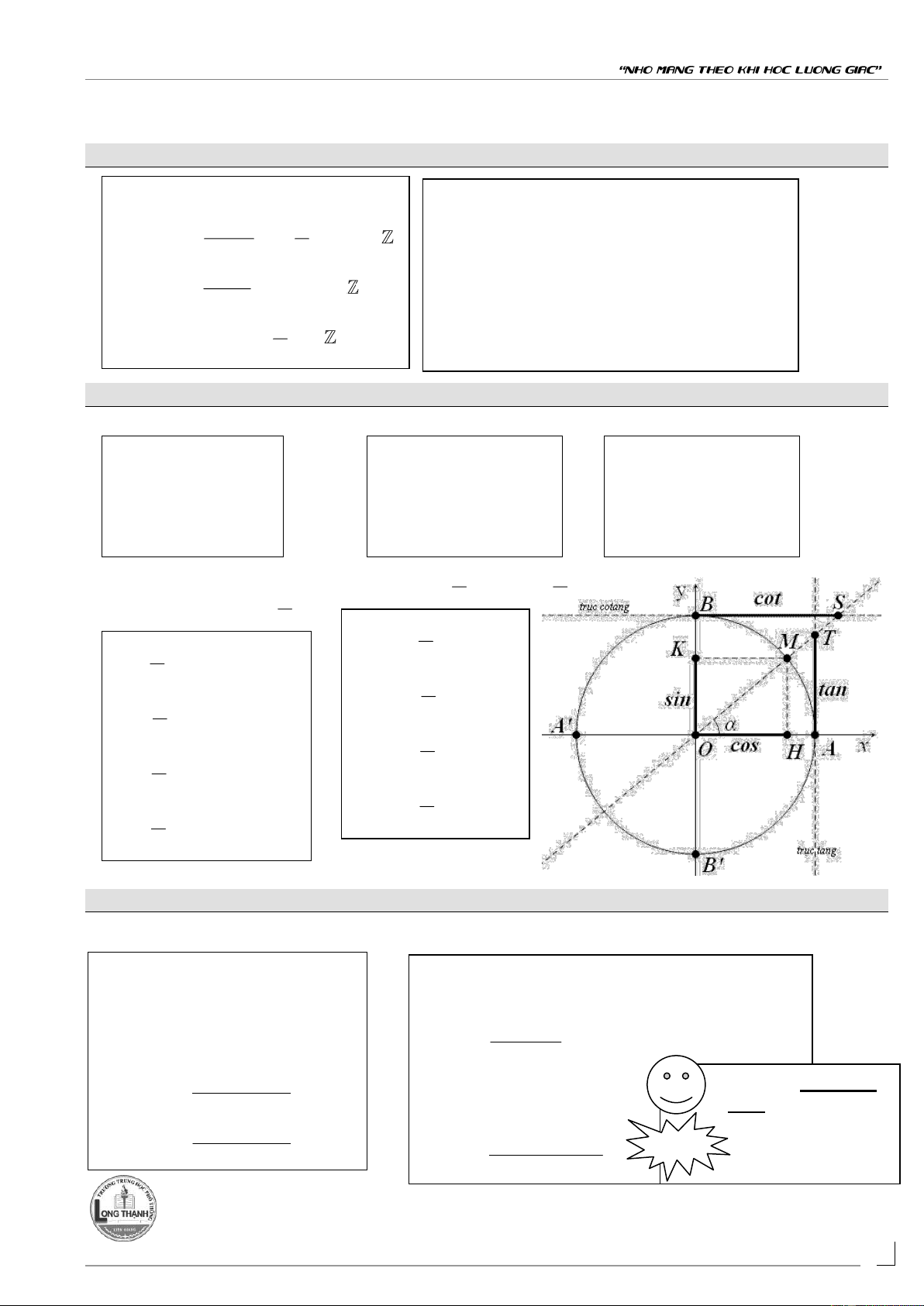
Đường tròn lượng giác 
Cung hơn kém :  và   2 2
Cung phụ nhau:  và  2    sin     cos    sin     cos 2   2        
cos     sin cos     sin 2   2     
tan     cot    tan     cot 2   2        
cot      tan cot     tan 2   2   3. Công th c l ng giác
Công thức cộng
Công thức nhân đôi, nhân ba
cos(a  b)  cos a cosb  sin asin b sin 2  2sin cos
cos(a b)  cosacosb sin asinb 2 2 2 2            cos 2 cos sin 2 cos 1 1 2 sin
sin(a  b)  sin a cos b  cos a sin b 2 tan  tan 2 
sin(a  b)  sin a cosb  cos a sin b 2 1 tan  tan a  tan b 3
sin 3  3sin  4sin 
Cần nhớ công thức
tan(a  b)  1 tanatanb 3
cộng cho chắc chắn.
cos 3  4cos   3cos 
Từ công thức cộng ta tan a tan b tan(a  b)  3 3 tan   tan  Bí quyết
có thể suy ra những 1 tan a tan b tan 3  2 1 3tan 
công thức còn lại.
 Name:…………………………………………… class:………..
[Biên soạn gv Đặng Trung Hiếu – 0939.239.628 – www.gvhieu.wordpress.com] aug-2012 1
[Công thức lượng giác cần nhớ - Tài liệu tặng miễn phí cho học sinh]
Công thức hạ bậc
Công thức biến tích thành tổng 1
cos a cos b  cos(a  b)  cos(a  b) 1 cos 2 3cos  cos3 2 3 cos   ; cos   2 2 4 1
sin a sin b  cos(a b)  cos(a  b) 1 cos 2 3sin   sin 3 2 3 2 sin   ; sin   2 4 1  
sin a cos b  sin(a  b)  sin(a  b) 1 cos 2 2 tan   2 1 cos 2
Công thức biến đổi tổng thành tích
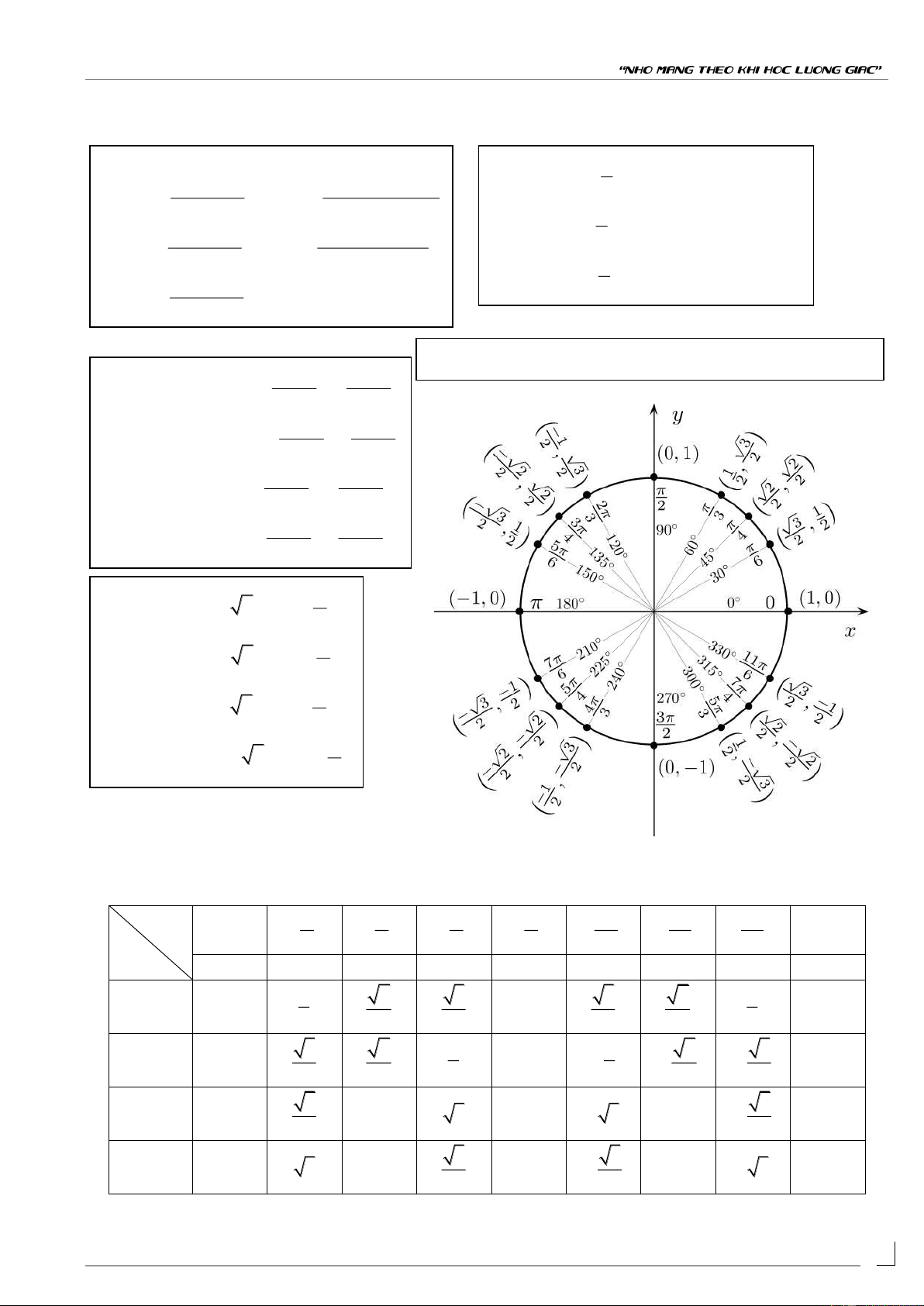
Tọa đ điểm M (cos ; sin) trên đ ờng tròn l ng giác       cos  cos   2cos cos 2 2       cos  cos   2  sin sin 2 2       sin   sin   2sin cos 2 2       sin   sin   2cos sin 2 2 
sin   cos  2 sin(  ) 4  2 cos(  ) 4 
sin   cos  2 sin(  ) 4    2 cos(  ) 4 Giá trị l
ng giác c a m t số cung đặc biệt c n ghi nh     2 3 5  0  6 4 3 2 3 4 6 00 0 30 0 45 0 60 0 90 0 120 0 135 0 150 0 180 1 3 3 2 1 sin 0 2 1 0 2 2 2 2 2 2 3 2 1 1 2 3 cos 1 0    -1 2 2 2 2 2 2 3 3 tan 0 1 3 ||  3 -1  0 3 3 3 3 cot || 3 1 0  -1  3 || 3 3
[Biên soạn gv Đặng Trung Hiếu – 0939.239.628 – www.gvhieu.wordpress.com] aug-2012 2