


















Preview text:
CHÀO MỪNG CÁC EM
ĐẾN VỚI BÀI GIẢNG HÔM NAY KHỞI ĐỘNG
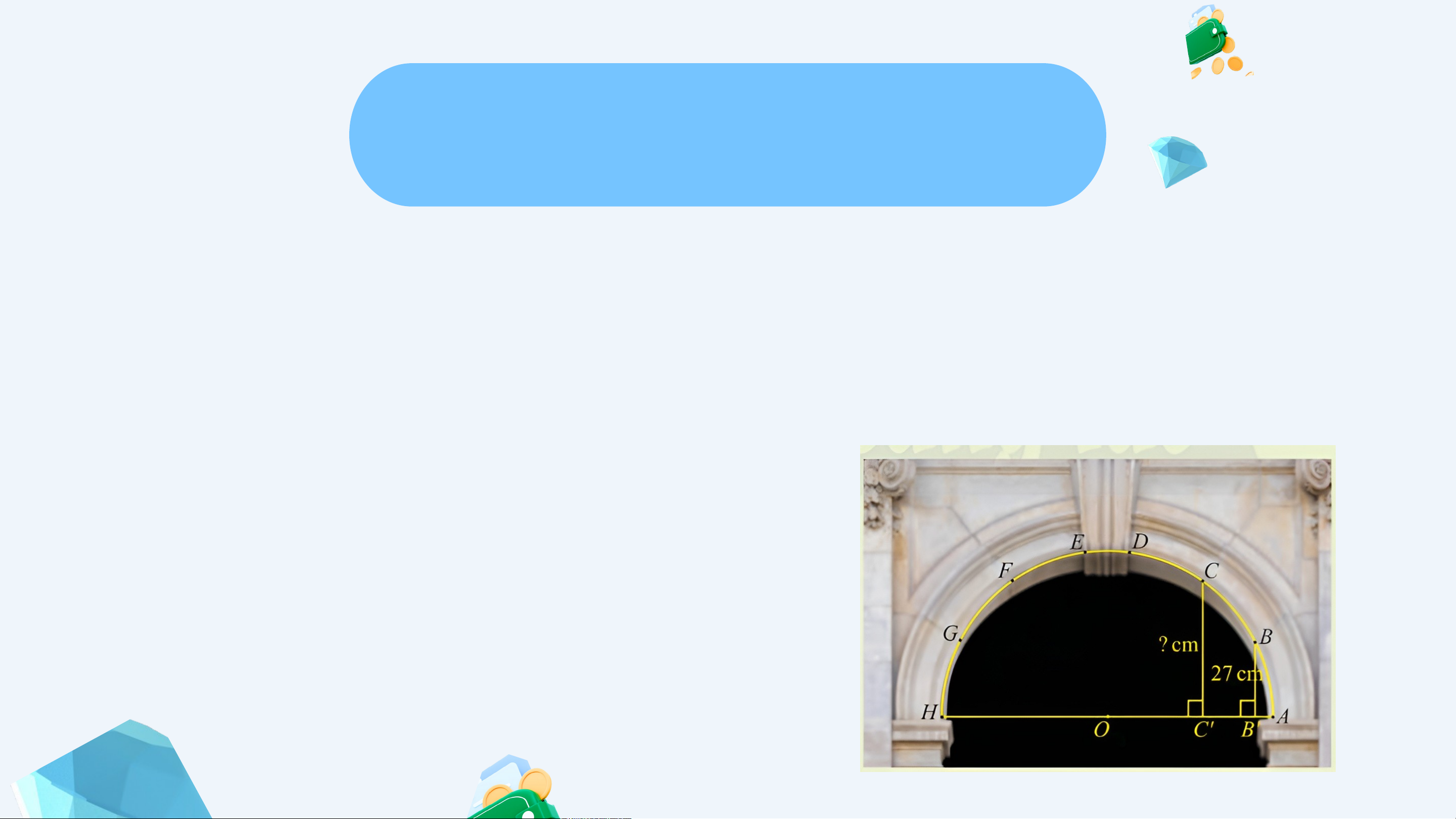
Trong kiến trúc, các vòm cổng bằng đá thường có hình nửa đường tròn để có
thể chịu lực tốt. Trong hình bên, vòm cổng được ghép bởi sáu phiến đã hai bên
tạo thành các cung AB, BC, CD, EF, GH bằng nhau và một phiến đá chốt ở đỉnh.
Nếu biết chiều rộng cổng và khoảng cách từ
điểm B đến đường kính AH, làm thế nào để
tính được khoảng cách từ điểm C đến AH? KHỞI ĐỘNG Gợi ý
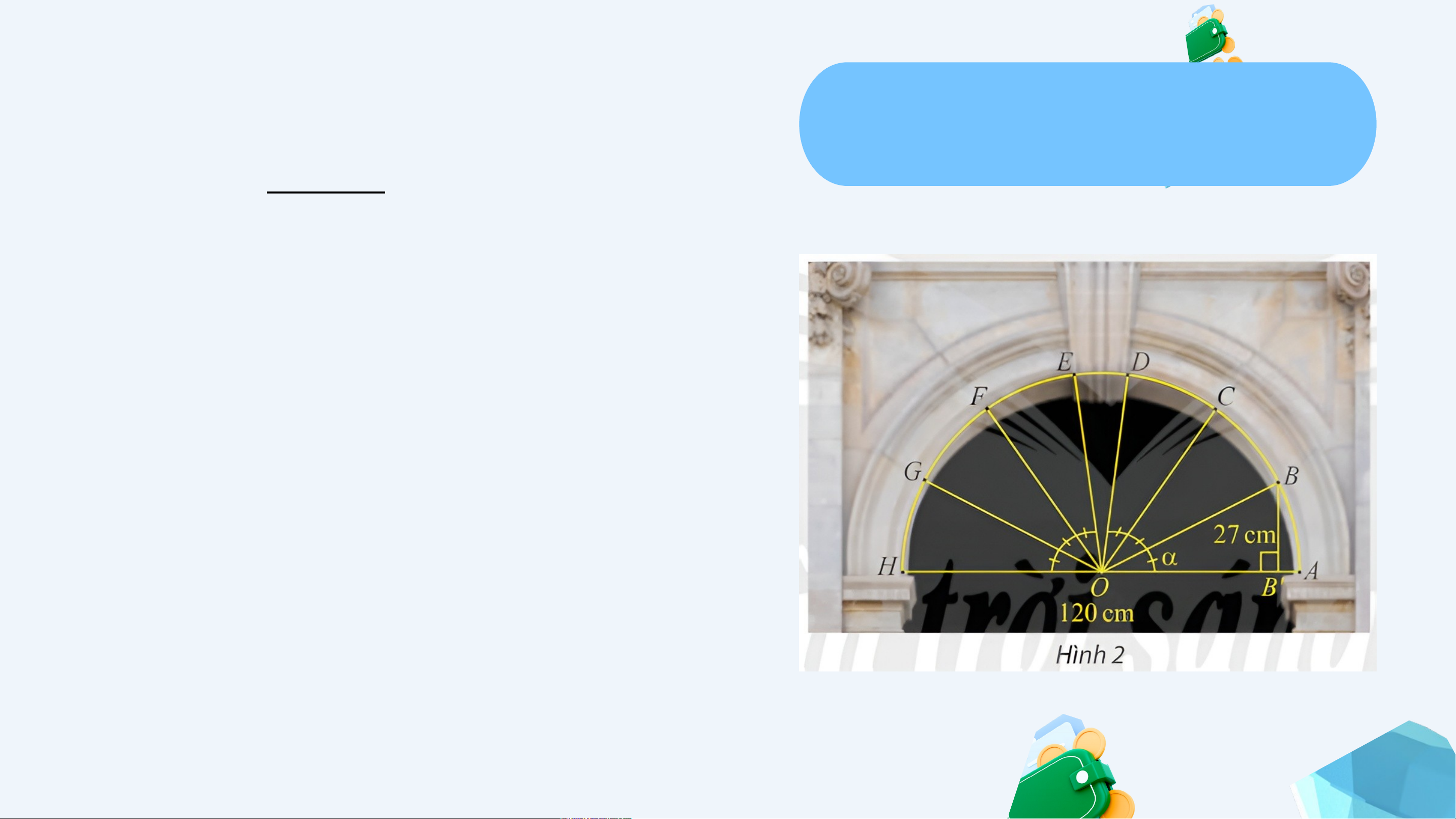
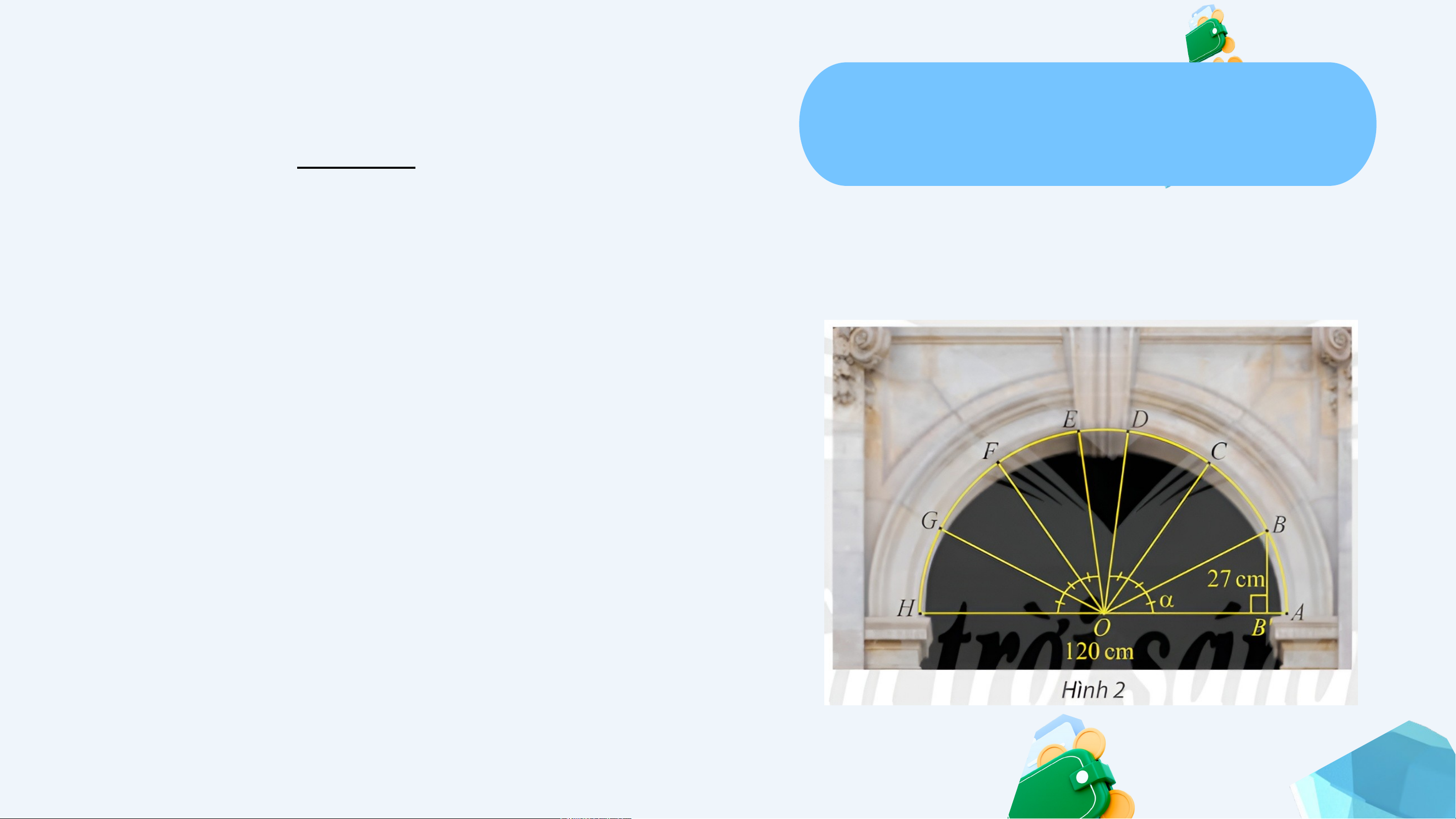
+ Chiều rộng cổng , khoảng cách từ
điểm B đến đường kính AH là
+ Giả sử . Ta có khoảng cách từ đến bằng nên . Gợi ý KHỞI ĐỘNG
Với là góc nhọn nên có thể tính được tất cả các giá tri lượg giác của góc .
Mặt khác, các cung và bằng nhau nên và
khoảng cách từ đến là .
Do đó để tính được khoảng cách từ đến ,
cần có công thức biểu diễn qua các giá trị lượng giác của góc . BÀI 3:
CÁC CÔNG THỨC LƯỢNG GIÁC NỘI DUNG BÀI HỌC 1 Công thức cộng
2 Công thức góc nhân đôi C
3 ông thức biến đổi tích thành tổng Cô
4 ng thức biến đổi tổng thành tích 1. CÔNG THỨC CỘNG
Thảo luận nhóm đôi, hoàn thành HĐKP1. HĐKP1:
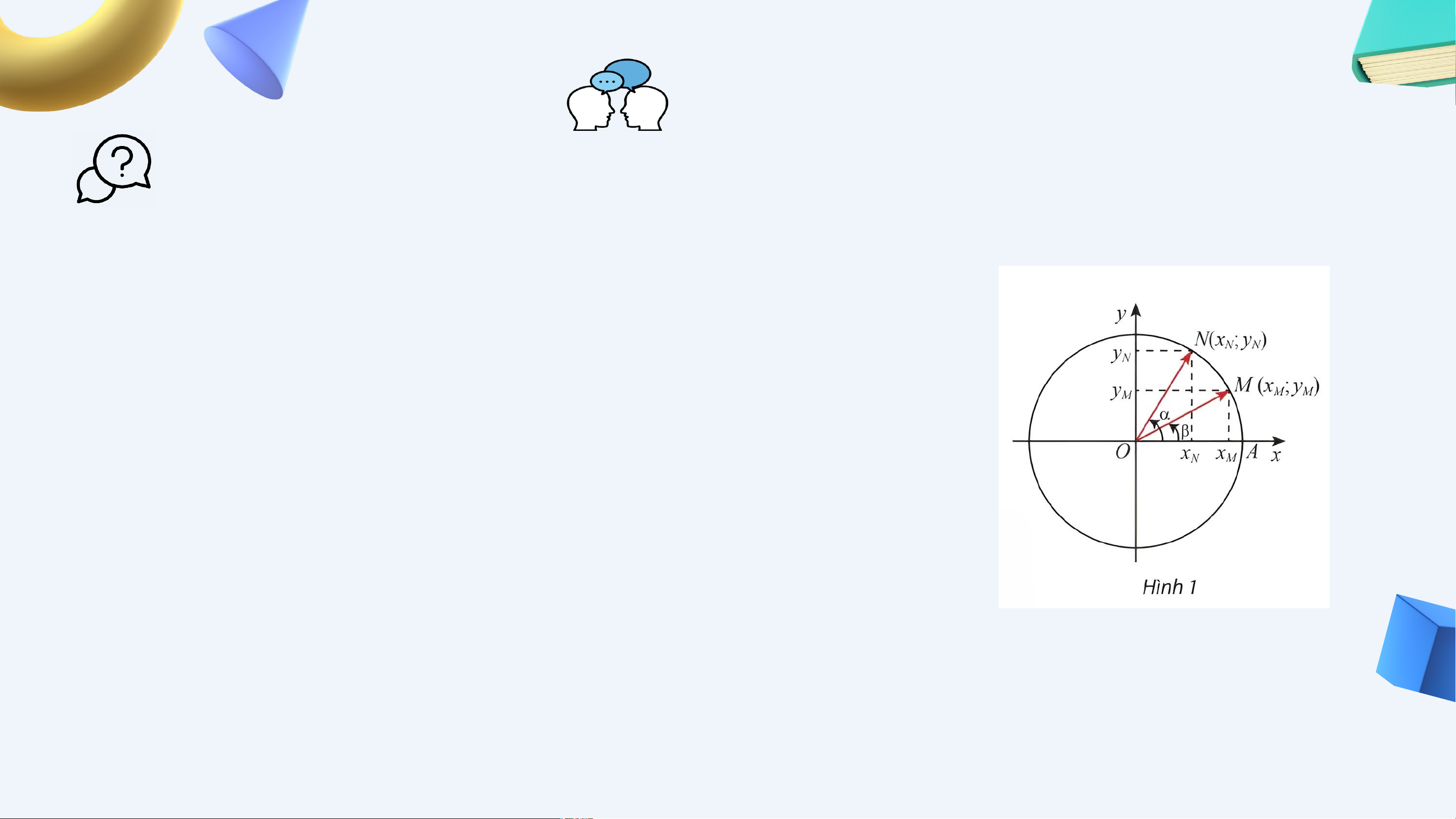
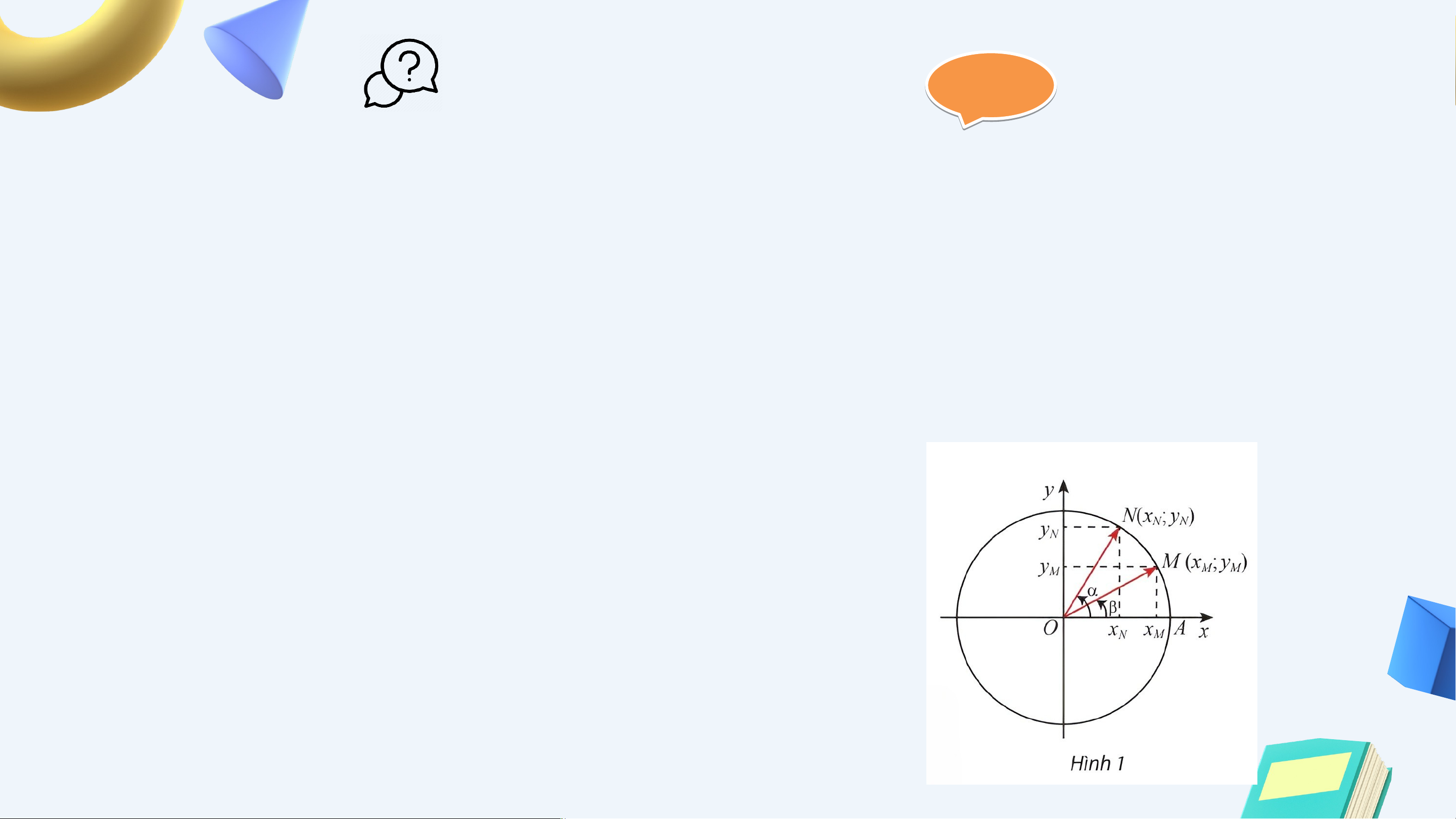
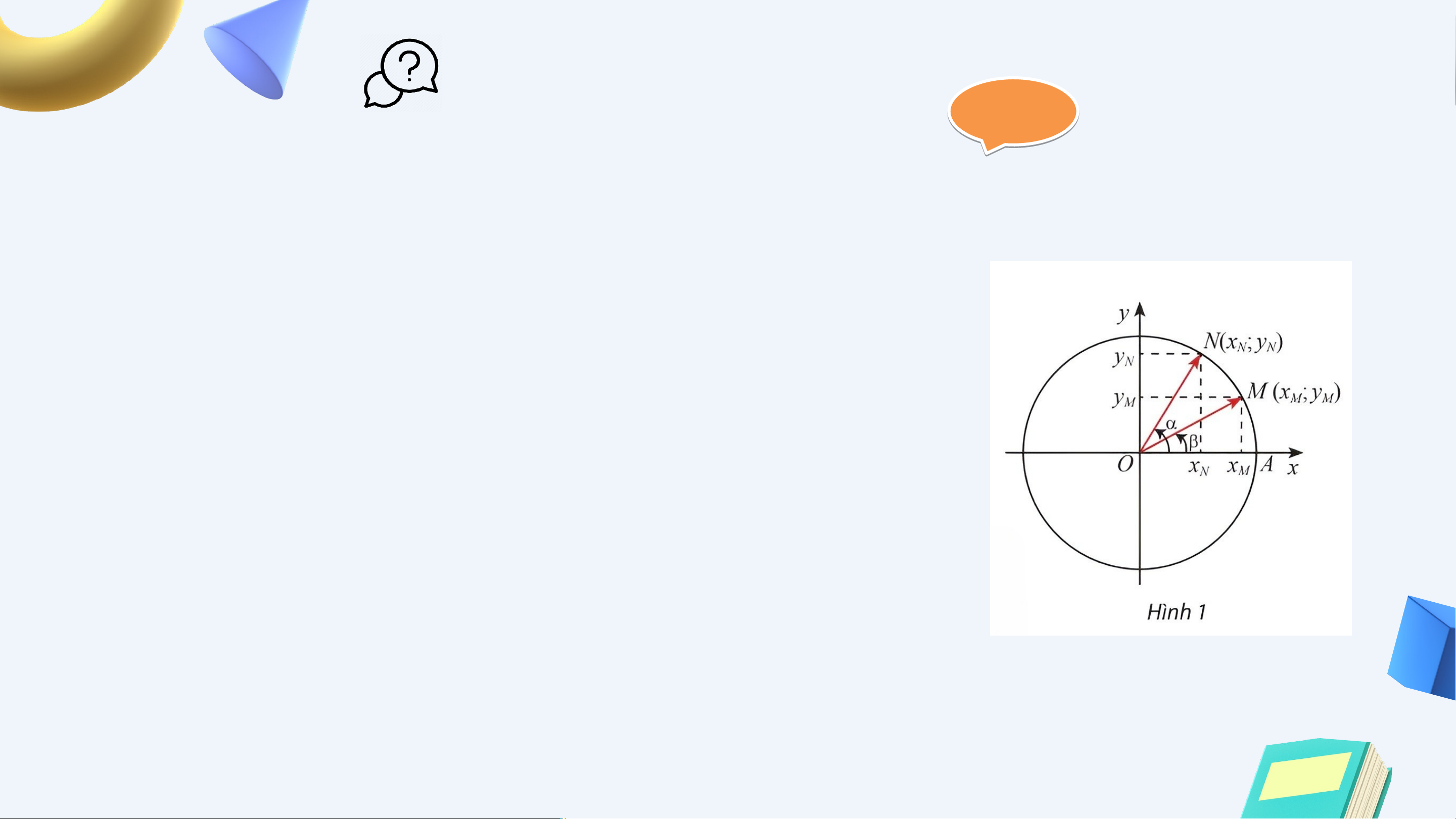
Quan sát Hình 1. Từ hai cách tính tích vô
hướng của vectơ và sau đây:
Hãy suy ra công thức tính theo các giá trị lượng giác của và. Từ đó, hãy suy ra
công thức bằng cách thay bằng HĐKP1: Giải ả
(định nghĩa của tích vô hướng)
Vì và lần lượt là điểm biểu diễn của các
góc lượng giác và trên đường tròn
lượng giác, nên toạ độ của các điểm này là và . HĐKP1: Giải sin sin 𝛼cos 𝛽 tan 𝛼 tan (𝛼+𝛽)
+cos 𝛼 sin 𝛽 +tan 𝛽 ( 𝛼+𝛽)= = =
cos (𝛼+ 𝛽) cos 𝛼cos 𝛽 −sin𝛼sin 𝛽 1−tan 𝛼tan 𝛽 tan 𝛼
tan 𝛼−tan 𝛽 tan +tan (− 𝛽)
( 𝛼− 𝛽)=tan [𝛼 +(− 𝛽)]= =
1−tan 𝛼 tan (−𝛽) 1+tan𝛼 tan 𝛽 KẾT LUẬN
Công thức cộng
cos(𝛼+𝛽)=cos𝛼cos 𝛽−sin𝛼sin 𝛽 cos(𝛼− 𝛽)=cos𝛼cos 𝛽+sin𝛼sin 𝛽
sin(𝛼+ 𝛽)=sin𝛼 cos 𝛽+c 𝑜𝑠𝛼sin 𝛽 sin(𝛼− 𝛽)=sin𝛼cos 𝛽−c𝑜𝑠𝛼sin 𝛽 tan 𝛼
tan 𝛼−tan 𝛽 tan +tan 𝛽 ( 𝛼+𝛽)= tan(𝛼− 𝛽)=
1−tan 𝛼tan 𝛽
1+tan 𝛼tan 𝛽
Ví dụ 1: SGK – tr.21 Tính giá trị của Giả i i ả Thực hành 1 Tính và Giả i i
2. HIỆU CỦA HAI BÌNH PHƯƠNG HĐKP2:
Hãy áp dụng công thức cộng cho trường hợp và tính các giá trị lượng giác của góc Giải ả
+¿cos 2𝛼=cos(𝛼+𝛼)=cos𝛼 cos𝛼−sin 𝛼sin 𝛼=cos2𝛼−sin2𝛼 Mà . Hoặc . . . KẾT LUẬN
Công thức góc nhân đôi
cos2𝛼=cos2𝛼−sin2𝛼=2cos2𝛼−1=1−2𝛼
sin2𝛼=2sin𝛼cos 𝛼 2tan 𝛼
tan2𝛼=1−tan2𝛼
Ví dụ 2: SGK – tr.22 Tính Giả i i ả Ta có Suy ra Vì nên . Suy ra 1 LUYỆN TẬP NHÀ SƯU TẬP ĐẠI DƯƠNG Câu hỏi 1: Biến đổi thành tổng A. C. B. B. D. Bài ài 6. 6 ( SG S K C K – hứ t – r n . r 24)
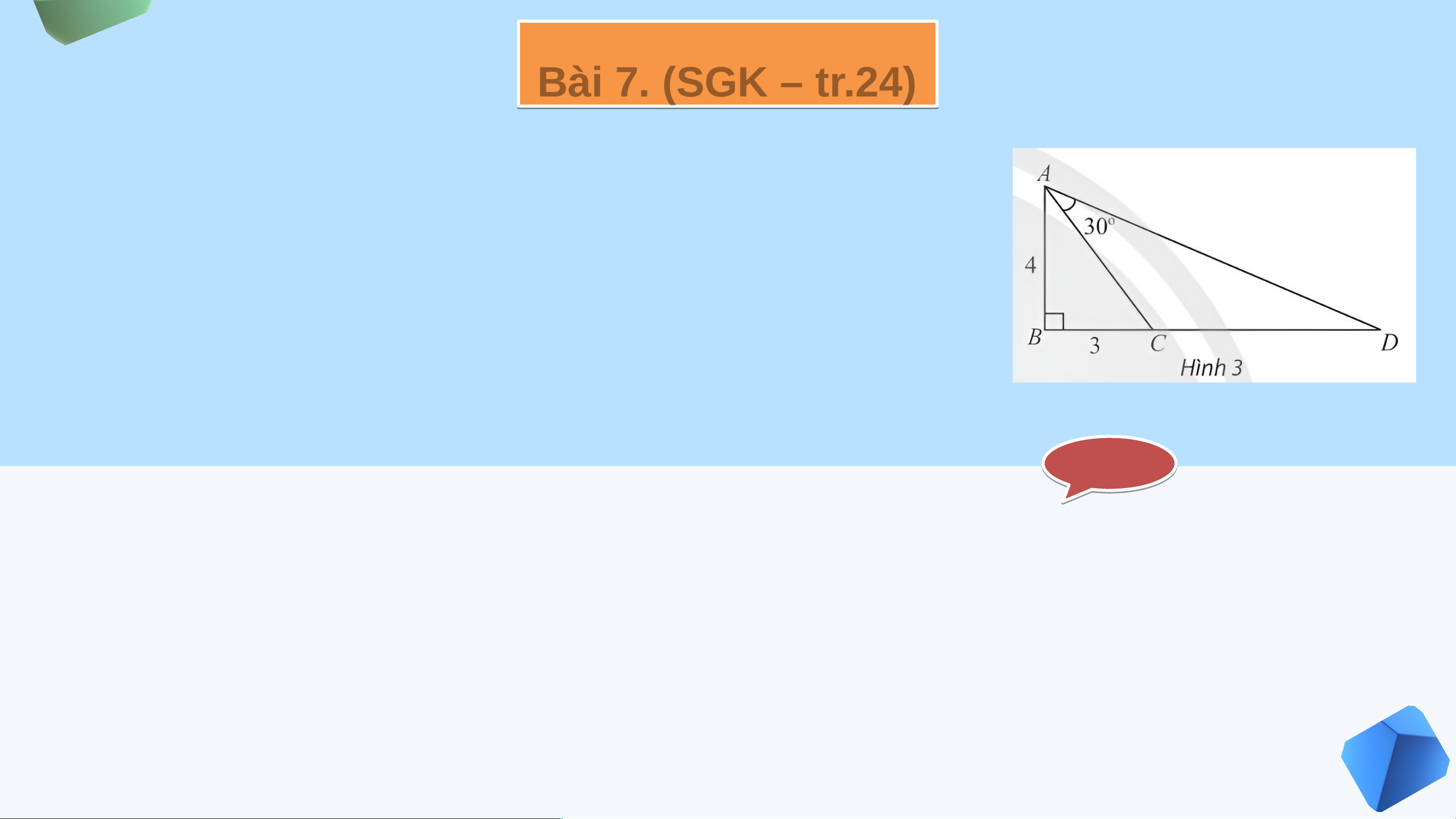
.g minh rằng trong tam giác , ta có Giả i i ả Trong tam giác , ta có . Do đó . 1 VẬN DỤNG Bà B i i7. (SG K (SG – tr. tr 24) .
Trong Hình 3, tam giác vuông tại và có hai
cạnh góc vuông là , . Vẽ điểm nằm trên tia
đối của tiathỏa mãn . Tính từ đó tính độ dài cạnh . Giải ả
Đặt . Vì tam giác vuông tại nên tan . Suy ra . Bài 9 i . (SGK – tr.24 tr +25) Giả i i
Khoảng cách từ đến mặt đất là .
Khoảng cách từ đến mặt đất là .
HƯỚNG DẪN VỀ NHÀ
Chuẩn bị trước “Bài Ghi nhớ Hoàn thành bài tập 4. Hàm số lượng kiến thức trong bài. trong SBT
giác và đồ thị”
BÀI HỌC KẾT THÚC,
CẢM ƠN CÁC EM ĐÃ LẮNG NGHE
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28



