Chuyên đề bài tập Lượng Giác | Toán 11

11/7/2016
Công thức lượng giác tổng hợp toàn tập ­ Toán Học Toán Học
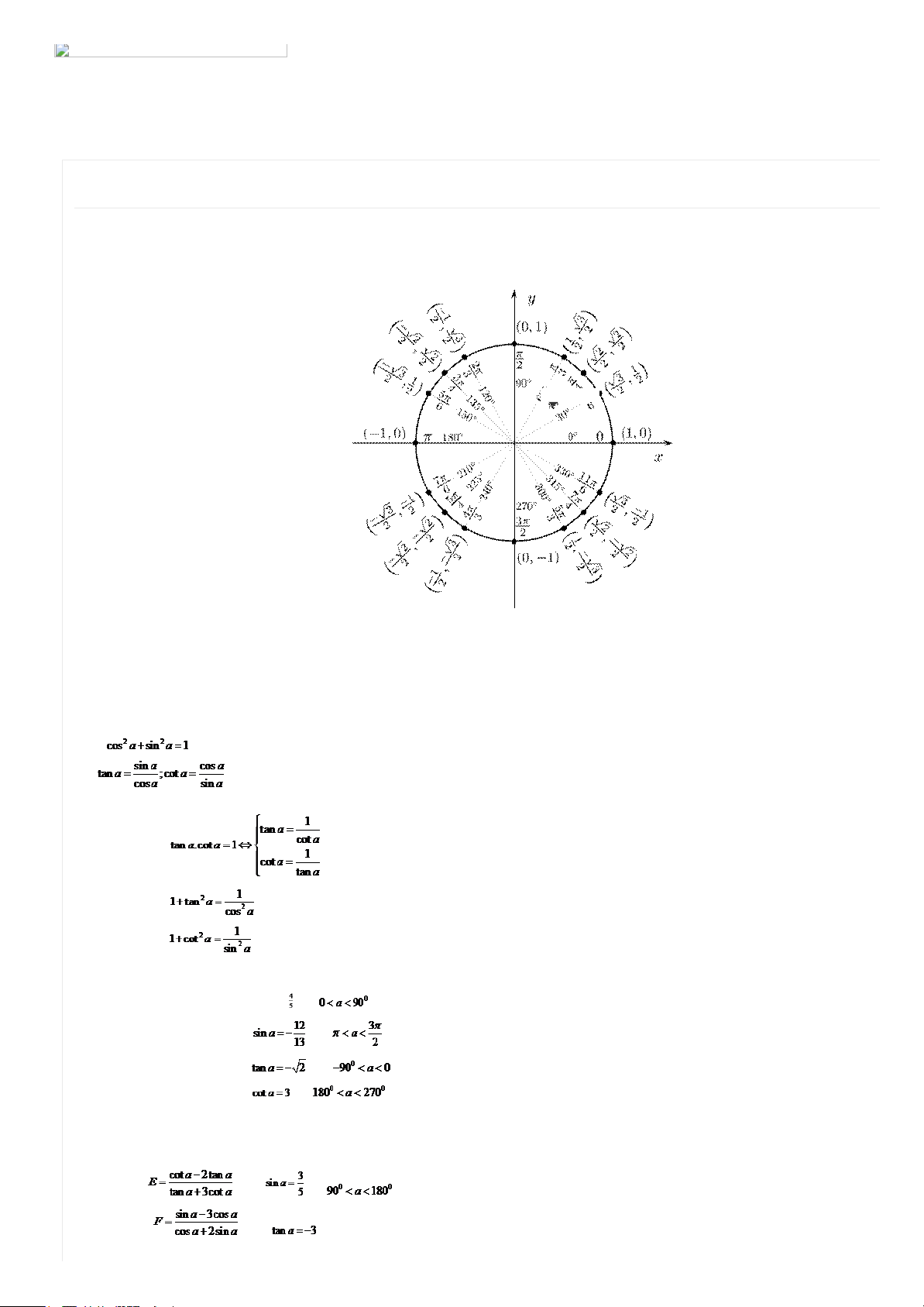
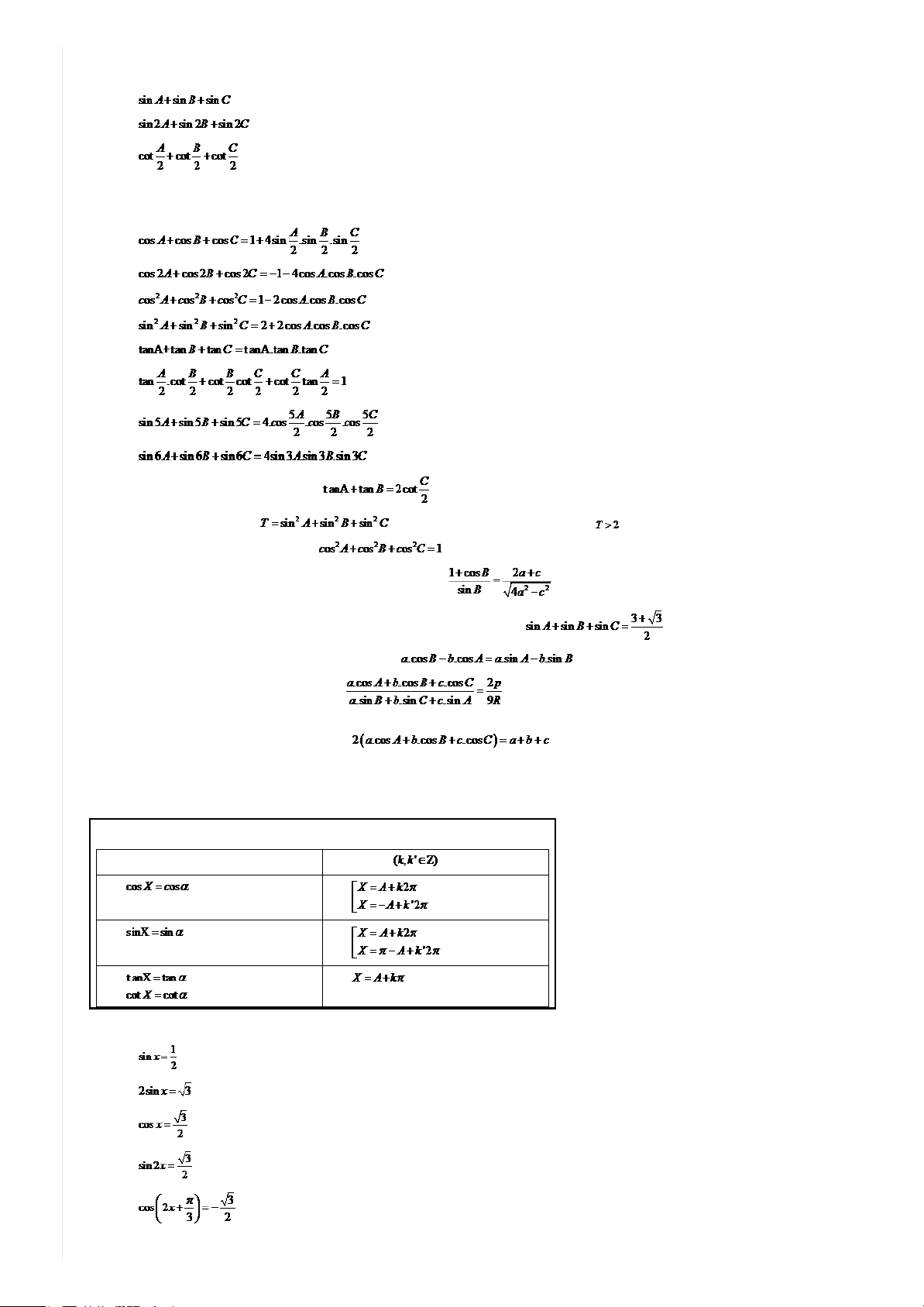
Công thức lượng giác tổng hợp toàn tập CHUYểN Đ BÀI T P L NG GIÁC Print this post V n đ 1 : H Th c L ng C B n Ki n th c c b n Hệ quả 1 : Hệ quả 2 : B. TOÁN TệNH GIÁ TR L NG GIÁC C A 1 CUNG
1) a.Tính sina , tana, cota biết cosa = và
2) b.Tính cosa, tana, cota biết và
3) c.Tính cosa, sina, cota biết và
4) d.Tính sina, cosa, tana biết và TệNH GIÁ TR L
NG GIÁC B NG SỬ D NG CÔNG TH C C B N. 5) a.tính biết và 6) b.Tính biết
ht p:/ www.toanhoc.edu.vn/2015/02/cong­thuc­luong­giac­tong­hop­toan­tap.html 1/16 11/7/2016
Công thức lượng giác tổng hợp toàn tập ­ Toán Học 7) c.Tính biết 8) d.Tính biết 9) e. Tính biết 10) tính 11) a.Tính , , biết b.Tính , biết Đ N GI N BI U TH C 12) . 13) . 14) 15) 16) 17) 18) 19) 20)
CH NG MINH CÁC H NG Đ NG TH C L NG GIÁC 21) . 22) . 23) 24) 25) 26) 27) . 28) . 29) . CH NG MINH MỘT BI U TH C L
NG GIÁC KHÔNG PH THUỘC VÀO X 30) a. 31) b. 32) c.
ht p:/ www.toanhoc.edu.vn/2015/02/cong­thuc­luong­giac­tong­hop­toan­tap.html 2/16 11/7/2016
Công thức lượng giác tổng hợp toàn tập ­ Toán Học 33) d. 34) 35)
V N Đ 2 : CUNG ( GịC) Cị LIểN QUAN ĐẶC BI T (Cung liên k t). STT Hai cung Gọi lƠ hai Công th c cung Cách nh 1 Đối nhau Cos đối 2 Bù nhau Sin bù 3 Phụ nhau Phụ chéo Sai kém Sai tan, 4 cot 2 cung sai Sai kém kém thì 5 sin ( cung lớn) = cos ( cung nhỏ)
H qu : A , B , C là 3 góc trong 1 tam giác a. Ta có : A + B + C = (phụ) Ch ng minh r ng: 36) 37) 38) 39) 40) 41)
ht p:/ www.toanhoc.edu.vn/2015/02/cong­thuc­luong­giac­tong­hop­toan­tap.html 3/16 11/7/2016
Công thức lượng giác tổng hợp toàn tập ­ Toán Học 42) Tính giá tr bi u th c : 43) 44) 45) 46) 47) Đ n gi n bi u th c sau : 48) 49) 50) V N Đ 3 : CÔNG TH C CỘNG KI N TH C C B N
Hệ quả : Biến đổi biểu thức về dạng tích số i. Giả sử
( và a và b không đồng thời triệt tiêu) Ta có :
Áp dụng kết quả trên ta có :
ht p:/ www.toanhoc.edu.vn/2015/02/cong­thuc­luong­giac­tong­hop­toan­tap.html 4/16 11/7/2016
Công thức lượng giác tổng hợp toàn tập ­ Toán Học
Rút gọn các bi u th c sau : 51) 52) 53) 54) 55) 56) 57) 58) 59) Ch ng minh r ng : 60) 61) 62) 63)
64) Chứng minh các biểu thức sau không phụ thuộc vào x : 65) 66) 67)
Các bƠi toán liên quan đ n tam giác :
68) Chứng minh rằng với mọi tam giác ABC (không vuông) ta đều có : 69)
70) Chứng minh rằng với mọi tam giác ABC ta đều có : 71)
72) Cho tam giác ABC. Tìm giá trị nhỏ nhất của biểu thức : 73)
và xác định hình tính của tam giác ABC trong trường hợp này. 74)
75) Cho tam giác ABC có 3 góc nhọn và trực tâm H chia đường cao theo tỉ số .Tính
theo m và chứng minh rằng :
76) Cho tam giác ABC thỏa mãn : . CMR tam giác ABC cân.
Các bƠi toán liên quan khác
77) Cho x và y là hai số thay đổi và là nghiệm đúng của phương trình
. Tìm giá trị nhỏ nhất và giá trị lớn nhất của phương trình
ht p:/ www.toanhoc.edu.vn/2015/02/cong­thuc­luong­giac­tong­hop­toan­tap.html 5/16 11/7/2016
Công thức lượng giác tổng hợp toàn tập ­ Toán Học
78) Cho bốn số thay đổi a, b, x, y thỏa mãn và . CMR :
79) Tìm giá trị lớn nhất và nhỏ nhất của biểu thức
biết x và y là hai số thay đổi thỏa mãn :
80) Cho hai số x và y thay đổi sao cho
. Tìm giá trị lớn nhất và nhỏ nhất của biểu thức : V N Đ 4 : CÔNG TH C NHỂN A.KI N TH C C B N Công th c nhơn đôi Hệ quả Đặt , ta có : Công th c nhơn 3 81) Tính biết 82) Tính Tính giá tr bi u th c sau: 83) 84) 85) 86) 87) 88) 89) Ch ng minh r ng : 90) 91) 92) 93) 94)
ht p:/ www.toanhoc.edu.vn/2015/02/cong­thuc­luong­giac­tong­hop­toan­tap.html 6/16 11/7/2016
Công thức lượng giác tổng hợp toàn tập ­ Toán Học 95) 96) 97) 98) 99)
100) Cho tam giác cân có góc ở đỉnh bằng
, cạnh bên bằng b và cạnh đáy băng a. CMR Tính giá tr bi u th c sau : 101) nếu 102) nếu 103) nếu
V N Đ 5 : BI N Đ I TệCH THÀNH T NG
Bi n đ i các bi u th c sau thƠnh t ng : 104) 105) 106)
Ch ng minh các đ ng th c sau: 107) 108) 109) 110) Cho tam giác ABC có
V N Đ 6: BI N Đ I T NG THÀNH TệCH KI N TH C C B N H qu :
ht p:/ www.toanhoc.edu.vn/2015/02/cong­thuc­luong­giac­tong­hop­toan­tap.html 7/16 11/7/2016
Công thức lượng giác tổng hợp toàn tập ­ Toán Học
Bi n đ i các bi u th c sau v d ng tích : 111) 112) 113) 114) Đ n gi n các bi u th c sau: 115) 116) Ch ng minh r ng : 117) 118)
V N Đ 7 : CÁC BI N Đ I V GịC TRONG TAM GIÁC
A, B , C là 3 góc trong 1 tam giác , ta có : vậy : (bù) ( phụ) B t đ ng th c côsi Cho a ,b >0 ta luôn có hay Tổng quát : ta luôn có B t đ ng th c BOUNHIACOSKY hay Đ nh lí hƠm s sin Đ nh lí hƠm s cosin
ht p:/ www.toanhoc.edu.vn/2015/02/cong­thuc­luong­giac­tong­hop­toan­tap.html 8/16 11/7/2016
Công thức lượng giác tổng hợp toàn tập ­ Toán Học
Cho tam giác ABC bi n đ i các bi u th c sau v d ng tích : 119) 120) 121)
A , B , C lƠ 3 góc c a 1 tam giác. Ch ng minh r ng : 122) 123) 124) 125) 126) 127) 128) 129)
130) Chứng tỏ rằng nếu tam giác ABC có
thì tam giác ABC là 1 tam giác cân.
131) Cho tam giác ABC , đặt
. Chứng minh rằng tam giác ABC nhọn .
132) Hãy nhận dạng tam giác ABC biết : .
133) Cho tam giác ABC có các cạnh và các góc thỏa mãn hệ thức :
Chứng minh tam giác ABC cân.
134) Số đo 3 góc của tam giác ABC lập thành 1 cấp số cộng và thỏa mãn hệ thức : . Tính các góc A, B , C.
135) Chứng minh rằng tam giác ABC cân khi và chỉ khi : .
136) Chứng minh rằng nếu tam giác ABC có :
(trong đó p là nửa chu vi. R là bán kính đường tròn ngoại tiếp tam giác). Thì tam giác ABC là tam giác đều.
137) Giả sử tam giác ABC thỏa mãn điều kiện :
. Thì tam giác ABC là tam giác đều. V N Đ 8 : PH NG TRỊNH L NG GIÁC C B N KI N TH C C B N Lo i 1 : PH NG TRỊNH C B N Phương trình Lời giải Gi i các ph ng trình sau : 138) 139) 140) 141) 142)
ht p:/ www.toanhoc.edu.vn/2015/02/cong­thuc­luong­giac­tong­hop­toan­tap.html 9/16 11/7/2016
Công thức lượng giác tổng hợp toàn tập ­ Toán Học 143) 144) 145) 146) 147) 148) 149) 150) 151) 152) 153) 154) 155) 156) 157) 158) 159) 160) 161) 162) 163) 164) 165) 166) 167) 168) 169) 170) 171) 172) 173) 174) 175) 176) 177) 178) 179)
ht p:/ www.toanhoc.edu.vn/2015/02/cong­thuc­luong­giac­tong­hop­toan­tap.html 10/16 11/7/2016
Công thức lượng giác tổng hợp toàn tập ­ Toán Học 180) 181) 182) 183) 184) 185) 186) 187) 188) 189) 190) 191) 192) 193) 194) 195) 196) 197)
Tính giá tr g n đúng các nghi m ph ng trình sau: 198) trong khoảng 199) trong khoảng 200) trong khoảng 201) trong đoạn 202) trong khoảng 203) trong khoảng 204) trong khoảng GI I VÀ BI N LU N PH NG TRỊNH: 205) 206)
207) Tìm tất cả giá trị của m để phương trình sau có 1 và chỉ 1 nghiệm
208) Tìm tất cả giá trị của m để phương trình sau có nghiệm
209) Tìm tất cả giá trị của m để phương trình sau có nghiệm LO I 2 Lo i 2 : PH NG TRỊNH Cách giải :
ht p:/ www.toanhoc.edu.vn/2015/02/cong­thuc­luong­giac­tong­hop­toan­tap.html 11/16 11/7/2016
Công thức lượng giác tổng hợp toàn tập ­ Toán Học
(điều kiện để phương trình có nghiệm ) Gi i các ph ng trình sau : 210) 211) 212) 213) 214) 215) 216) 217) 218) 219) 220) 221) 222) 223) 224) 225) 226) 227) 228) 229) 230) 231) 232) 233)
234) Tìm các giá trị của để phương trình : có nghiệm
235) Tìm các giá trị của để phương trình : 236) trong khoảng
Gi i vƠ bi n lu n ph ng trình theo tham s m : 237) Cho phương trình :
.Chứng minh rằng phương trình trên luôn có nghiệm. 238) Cho phương trình :
.Giải và biện luận phương trình theo tham số m.
ht p:/ www.toanhoc.edu.vn/2015/02/cong­thuc­luong­giac­tong­hop­toan­tap.html 12/16 11/7/2016
Công thức lượng giác tổng hợp toàn tập ­ Toán Học
239) Tìm các giá trị của
thỏa mãn phương trình sau với mọi m:
240) Tìm m để phương trình có nghiệm : LO I 3
Phương trình chứa tổng và tích của sinx và cosx
:A(sinx+cosx)+Bsinxcosx+C=0 (1) Đặt
Thay vào phương trình (1), ta có : Gi i các ph ng trình sau : 241) 242) 243) 244) 245) 246) 247) 248) 249) 250) 251) 252) 253) 254) 255) 256) 257) 258) Cho phương trình :
a)Chứng minh rằng phương trình có ít nhất một nghiệm trong khoảng
b) Xác định a để phương trình có duy nhất một nghiệm trong khoảng
c)Xác định a để phương trình có 2 nghiệm trong khoảng 259) Cho phương trình :
. Xác định m để phương trình có nghiệm trong khoảng LO I 4 :PH
NG TRỊNH THU N NH T Đ I V I SINX VÀ COSX Cách 1 :
Bước 1 : kiểm tra cosx = 0 có phải là nghiệm đúng của phương trình hay không ?
Bước 2 : chia hai vế của phương trình cho
ta được phương trình bậc hai có ẩn số phụ t = tanx. . Cách 2 :
ht p:/ www.toanhoc.edu.vn/2015/02/cong­thuc­luong­giac­tong­hop­toan­tap.html 13/16 11/7/2016
Công thức lượng giác tổng hợp toàn tập ­ Toán Học Dùng công thức :
Để biến đổi phương trình về dạng bậc nhất đối với sin2x và cos2x (Acos2x + Bsin2x = C). GI I CÁC PH NG TRỊNH SAU : 260) 261) 262) 263) 264) 265) 266) 267) 268) 269) 270) 271) 272) 273) 274) 275) 276)
277) Số đo của một trong các góc của tam giác vuông ABC là nghiệm của phương trình :
. Chứng minh rằng tam giác ABC là tam giác vuông.
V N Đ 9 : GI I VÀ BI N LU N PH NG TRỊNH L NG GIÁC
278) Cho phương trình lượng giác :
279) Giải phương trình với
280) Tìm m để phương trình có nghiệm
281) Cho phương trình lượng giác :
. Xác định a để phương trình có nghiệm. 282) Cho phương trình :
. Với giá trị nào của m thì phương trình có nghiệm. 283) Cho phương trình :
a) Giải phương trình khi a = 1.
b) Tìm a để phương trình có ít nhất 1 nghiệm . 284) Cho phương trình :
a) Giải phương trình với k = 2.
b) Giải và biện luận phương trình trong trường hợp tổng quát. 285) Cho phương trình :
. Xác định a để phương trình có nhiều hơn 1 nghiệm trong khoảng .
286) Tìm số dương a nhỏ nhất thỏa mãn điều kiện :
ht p:/ www.toanhoc.edu.vn/2015/02/cong­thuc­luong­giac­tong­hop­toan­tap.html 14/16 11/7/2016
Công thức lượng giác tổng hợp toàn tập ­ Toán Học V N Đ 10 ­ MỘT S PH NG TRỊNH L NG GIÁC KHÔNG MẪU MỰC 287) Giải phương trình : 288) Giải phương trình : 289) Giải phương trình : . 290) Giải phương trình : 291) Giải phương trình : . 292) Giải phương trình : .
293) Chứng minh rằng phương trình sau vô nghiệm : . 294) Giải phương trình : . 295) Giải phương trình : 296) Giải phương trình : . 297) Giải phương trình : V N Đ 11 ­ H PH NG TRỊNH L NG GIÁC
298) Giải hệ phương trình :
299) Giải hệ phương trình :
300) Giải hệ phương trình :
301) Giải hệ phương trình :
302) Giải hệ phương trình : 303) Giải hệ khi m = 0.
304) Xác định m để hệ phương trình có nghiệm.
305) Tìm m để hệ phương trình sau có nghiệm :
306) Giải hệ phương trình :
307) Giải hệ phương trình :
308) Giải hệ phương trình :
309) Tìm m để hệ phương trình có nghiệm.
310) Tìm m để hệ phương trình :
có nghiệm. Tìm nghiệm đó.
ht p:/ www.toanhoc.edu.vn/2015/02/cong­thuc­luong­giac­tong­hop­toan­tap.html 15/16 11/7/2016
Công thức lượng giác tổng hợp toàn tập ­ Toán Học
311) Giải và biện luận phương trình: . V N Đ 12 ­ B T PH NG TRỊNH L NG GIÁC
Gi i các b t ph ng trình l ng giác sau: 312) 313) 314) 315) 316) 317) 318) 319) 320) 321) 322) 323) 324) 325) 326) Xác định
sao cho phương trình sau có nghiệm :
327) Tìm các giá trị của a để phương trình sau vô nghiệm :
328) Giải bất phương trình : .
329) Giải bất phương trình : .
330) Giải bất phương trình :
331) Tìm tất cả giá trị của m để bất phương trình sau có nghiệm đúng với mọi x:
ht p:/ www.toanhoc.edu.vn/2015/02/cong­thuc­luong­giac­tong­hop­toan­tap.html 16/16