


























































































Preview text:
LỚP TOÁN THẦY CƯ- TP HUẾ
CS 1: TRUNG TÂM MASTER EDUCATIPM- 25 THẠCH HÃN
CS 2: TRUNG TÂM 133 XUÂN 68
CS 3: TRUNG TÂM 168 MAI THÚC LOAN
CS 4: TRUNG TÂM TRƯỜNG NGUYỄN TRƯỜNG TỘ TOÁN 11- CÁNH DIỀU
TÀI LIỆU DÀNH CHO HỌC SINH LỚP TOÁN THẦY CƯ-TP HUẾ
(Chiêu sinh thường xuyên, bổ trợ kiến thức kịp thời)
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com Mục lục
BÀI 1: DÃY SỐ ................................................................................................................................ 3
A. TÓM TẮT KIẾN THỨC CƠ BẢN CẦN NẮM .................................................................... 3
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP............................................................ 4
Dạng 1. Tìm số hạng của dãy số ............................................................................................................. 4
1. Phương pháp .................................................................................................................... 4
2. Các ví dụ .......................................................................................................................... 4
Dạng 2. Tính tăng giảm của dãy số ....................................................................................................... 5
1. Phương pháp .................................................................................................................... 5
2. Các ví dụ .......................................................................................................................... 5
Dạng 3. Dãy số bị chặn ............................................................................................................................. 9
1. Phương pháp .................................................................................................................... 9
2. Các ví dụ .......................................................................................................................... 9
C. GIẢI BÀI TẬP SÁCH GIÁO KHOA.................................................................................... 16 GV: TR
D. BÀI TẬP TRẮC NGHIỆM ..................................................................................................... 19 Ầ N
BÀI 2: CẤP SỐ CỘNG ................................................................................................................. 35 Đ ÌN
A. TÓM TẮT KIẾN THỨC CƠ BẢN CẦN NẮM H
.................................................................. 35 C Ư
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP.......................................................... 35 – 0834
Dạng 1. Nhận dạng 1 dãy số là cấp số cộng ...................................................................................... 35 3321
1. Phương pháp ............................................................................................................... 35 33
2. Các ví dụ rèn luyện kĩ năng ........................................................................................ 35
Dạng 2. Xác định số hạng , công sai và số hạng tổng quát của cấp số cộng .............................. 36
1. Phương pháp ............................................................................................................... 36
2. Các ví dụ rèn luyện kĩ năng ........................................................................................ 36
Dạng 3. Tính tổng các số hạng trong một cấp số cộng .................................................................... 37
1. Phương pháp ............................................................................................................... 37
2. Các ví dụ rèn luyện kĩ năng ........................................................................................... 37
Dạng 4: Giải phương trình ( tìm x trong cấp số cộng) ................................................................... 38
1. Phương pháp ................................................................................................................... 38
2. Các ví dụ rèn luyện kĩ năng ............................................................................................. 38
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 1
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
Dạng 5. Chứng minh một hệ thức trong cấp số cộng lập thành cấp số cộng, bài toán có sử dụng yếu
tố cấp số cộng ........................................................................................................................................... 39
1. Phương pháp .................................................................................................................. 39
2. Các ví dụ rèn luyện kĩ năng ........................................................................................... 39
C. GIẢI BÀI TẬP SÁCH GIÁO KHOA.................................................................................... 41
D. BÀI TẬP TRẮC NGHIỆM ..................................................................................................... 45
BÀI 3: CẤP SỐ NHÂN ................................................................................................................. 55
A. TÓM TẮT KIẾN THỨC CƠ BẢN CẦN NẮM .................................................................. 55
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP.......................................................... 56
Dạng 1. Chứng mình một dãy số là cấp số nhân .............................................................................. 56
1. Phương pháp .................................................................................................................. 56
2. Các ví dụ rèn luyện kĩ năng ........................................................................................... 56
Dạng 2. Xác định các số hạng của cấp số nhân, tổng của cấp số nhân ....................................... 58
1. Phương pháp .................................................................................................................. 58
2. Các ví dụ rèn luyện kĩ năng ........................................................................................ 58 GV: TR
Dạng 3. Các bài toán thực tế ............................................................................................................... 70 Ầ
C. GIẢI BÀI TẬP SÁCH GIÁO KHOA.................................................................................... 72 N Đ ÌN
D. BÀI TẬP TRẮC NGHIỆM ..................................................................................................... 75 H C Ư
ÔN TẬP CHƯƠNG 2 .................................................................................................................... 92 – 0834
PHẦN 1: GIẢI BÀI TẬP SÁCH GIÁO KHOA ................................................................................. 92 3321
PHẦN 2: BÀI TẬP TỔNG ÔN CHƯƠNG 2 .................................................................................... 100 33
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 2
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
CHƯƠNG II: DÃY SỐ. CẤP SỐ CỘNG VÀ CẤP SỐ NHÂN BÀI 1: DÃY SỐ
A. TÓM TẮT KIẾN THỨC CƠ BẢN CẦN NẮM I. Khái niệm Ta có khái niệm sau: -Mỗi hàm số u m * : 1; 2;3; ;
m được gọi là một dãy số hữu hạn. Do mỗi số nguyên
dương k 1 k m tương ứng với đúng một số u nên ta có thể viết dãy số đó dưới dạng khai k
triển: u ,u ,u ,,u . 1 2 3 m
-Số u gọi là số hạng đầu, số u gọi là số hạng cuối của dãy số đó. 1 m
Ta có khái niệm về dãy số vô hạn (gọi tắt là dãy số) như sau: -Mỗi hàm số *
u : được gọi là một dãy số vô hạn.
Do mỗi số nguyên dương n tương ứng với đúng một số u nên ta có thể viết dãy số đó dưới n
dạng khai triển: u ,u , u ,,u , 1 2 3 n
-Dãy số đó còn được viết tắt là u . n
-Số u gọi là số hạng thứ nhất (hay số hạng đầu), số u gọi là số hạng thứ hai, ..., số u gọi là 1 2 n
số hạng thứ n và là số hạng tổng quát của dãy số đó. GV: TR Chú ý:
Dãy số không đổi là dãy số có tất cả các số hạng đều bằng nhau. Ầ N
II. CÁCH CHỌN MỘT DÃY SỐ Đ ÌN H
Ta có thể cho dãy số bằng một trong những cách sau: C Ư
- Liệt kê các số hạng của dãy số đó (với những dãy số hữu hạn và có ít số hạng). – 0834
- Diễn đạt bằng lời cách xác định mỗi số hạng của dãy số đó.
- Cho công thức của số hạng tổng quát của dãy số đó. 3321
- Cho bằng phương pháp truy hồi. 33
III. DÃY SỐ TĂNG, DÃY SỐ GIẢM
- Dãy số u được gọi là dãy số tăng nếu u u với mọi * n . n n 1 n
- Dãy số u được gọi là dãy số giảm nếu u u với mọi * n . n n 1 n Chú ý:
Không phải mọi dãy số đều là dãy số tăng hay dãy số giảm. Chẳng hạn, dãy số u với n u ( 1
)n có dạng khai triển: 1,1, 1,1, 1, không là dãy số tăng, cũng không là dãy số n giảm. IV. DÃY SỐ BỊ CHẶN
- Dãy số u được gọi là bị chặn trên nếu tồn tại một số M sao cho u M với mọi * n . n n
- Dãy số u được gọi là bị chặn duới nếu tồn tại một số m sao cho u m với mọi * n . n n
- Dãy số u được gọi là bị chặn nếu nó vừa bị chặn trên, vừa bị chặn dưới; tức là tồn tại các số n
m và M sao cho m u M với mọi * n . n
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 3
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
Dạng 1. Tìm số hạng của dãy số 1. Phương pháp
Một dãy số có thể cho bằng:
- Liệt kê các số hạng (chỉ dùng cho các dãy hữu hạn và có ít số hạng);
- Công thức của số hạng tồng quát; - Phương pháp mô tả; - Phương pháp truy hồi. 2. Các ví dụ n (1)n
Ví dụ 1. Cho dãy số ( u ) xác định bởi u
. Tìm 5 số hạng đầu tiên của dãy số. n n 2n 1 Lời giải n (1)n 3 2 5 4 Ta có u
u 0;u ;u ;u ;u . n 1 2 3 4 5 2n 1 5 7 9 11
Ví dụ 2. Cho dãy số u , từ đó dự đoán u n n GV: TR u 5 u 3 a) u 1 : ; b) u : n 1 n u u 3 u 4u n 1 n n 1 n Ầ N Lời giải Đ ÌN a) Ta có: H C u 5 Ư 1 – u 5 1.3 0834 2 u 5 2.3 3 3321 u 5 3.3 4 33 ... u 5 n 1 .3 * n b) Ta có u 3 1 u 3.4 2 2 u 3.4 3 3 u 3.4 4 ... n 1 u 3.4 * n
Ví dụ 3. Cho dãy số u , từ đó dự đoán u n n u 1 u 3 a) u 1 : ; b) u : n 1 n u 2u 3 2 n 1 n u 1 u n 1 n Lời giải
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 4
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com a) Ta có: 2 u 1 2 3 1 3 u 5 2 3 2 4 u 13 2 3 3 5 u 29 2 3 4 ... n 1 u 2 3 * n b) Ta có 2 u 3 3 0 1 2 u 10 3 1 2 2 u 11 3 2 3 2 u 12 3 3 4 ... 3 u 3 n 1 * n
Dạng 2. Tính tăng giảm của dãy số 1. Phương pháp
(un) là dãy số tăng un+1 > un, n N*. GV: TR u u n
n+1 – un > 0 , n N*
1 1,n N* ( un > 0). Ầ un N Đ ÌN (un) là dãy số giảm
un+1 < un với n N*. H C Ư – u n 0834
un+1 – un< 0 , n N*
1 1, n N* (un > 0). un 3321 2. Các ví dụ 33
Ví dụ 1. Xét tính đơn điệu của dãy số sau: n
a) u 2n 3 b) u n n 2n Lời giải
a) Ta có: u 2n 3;u
2(n 1) 3 2n 5 u
u (2n 5) (2n 3) 0 n n 1 n 1 n Suy ra u
u dãy số đã cho là dãy tăng. n 1 n n n 1 u n 1 2n 1 n 1 1 n 1 b) Ta có: n 1 u ;u n n n 1 n 1 n 1 2 2 u 2 n 2 n 2 n n u 1 n 1 1 n 1 Giả sử: n 1 1
1 n 1 4n 3n 1 vô lý. u 2 n 4 n n
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 5
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com u Vậy n 1 1 u
u dãy số đã cho là dãy số giảm. n 1 n un
Ví dụ 2. Xét tính đơn điệu của dãy số sau: n n 1 n a) u b) u n 2 n 1 n n Lời giải n n 1 n 1 a) Ta có: u ;u n 2 n 1 2 2 n 1 (n 1) 1 n 2n 2 (n 1) n n 2 n 1 n 2 n 2n 2 1 u u n 1 n 2 2 n 2n 2 n 1 2 n 1 2
n 2n 2 3 2 3 2 2
n n n 1 n 2n 2n n n 1 0 n
1 u là dãy số giảm. n 2 n 1 2
n 2n 2 2 n 1 2
n 2n 2 n 1 n n 1 n 2 b) u 1 u 1 n n 1 n n n 1 Khi đó ta có: n 2 n 1 n 2 n 1
n n 2 (n 1) n 1 GV: TR u u 1 1 n 1 n n 1 n n 1 n n(n 1) Ầ N Giả sử: u
u 0 n n 2 (n 1) n 1 0 n n 2 (n 1) n 1 n 1 n Đ ÌN 2 3 3 2 3 2 2 H
n (n 2) (n 1) n 2n n 3n 3n 1 n 3n 1 0 vô lý. C Ư Vậy là dãy số giảm. – u
u 0 u n 1 n n 0834
Ví dụ 3. Xét tính đơn điệu của dãy số sau: 3321 1 n 1 33 a) u 2 b) u n n n n 1 Lời giải 1 1 1 1 1 a) u 2 u 2 u u 2 2 0 u u n n 1 n 1 n n 1 n n 1 n nn n 1 1 n
Vậy dãy số u là dãy số giảm. n n 1 2 b) u 1 n n 1 n 1 2 2 2 2 Khi đó: u 1 u u 1 1 0 u u n 1 n 1 n 2 n n 2 n 1 n 1 n 2 n 1 n
Vậy dãy số u là dãy số tăng. n
Ví dụ 4. Xét tính đơn điệu của các dãy số sau:
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 6
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com 2n 1 a) u b) 2 u 2n 5 n 5n 2 n Lời giải 2n 1 2 1 2 1 a) u u n 5n 2 3 55n 2 n 1 5 55n 7 2 1 2 1 1 Khi đó: u u 0 u u . n 1 n
5 55n 7 5 55n 2
5n 25n 7 n 1 n
Vậy u là dãy số giảm. n
b) u 2n 5 u 2n 2 2 1 5 n n 1 Khi đó u
u 2 n n n u u u là dãy số tăng n 2 1 5 2 2 5 4 2 0 n 1 n 1 n n
Ví dụ 5. Xét tính đơn điệu của dãy số sau: 2 2n 1 a) u
b) u n 1 n n 2 n 1 n Lời giải 2 2n 1 3 3 a) u 2 u 2 n 2 2 n 1 2 n 1 n 1 GV: TR n 1 1 2 1 1 3 3 * 2 Ầ
Với n N n 1 n 2 2 u u N 2 2 2 2 n 1 n Đ n 1 1 n 1 n 1 1 n 1 ÌN H C
u là dãy số tăng. n Ư – 0834 1 1
b) u n 1 n u n n 1 n n 1
n 1 n 2 3321 1 1 33
Do n * nên n 2 n 1 n 1 n u u n 1 n
n 2 n 1 n 1 n u
u u là dãy số giảm. n 1 n n
Ví dụ 6. Xét tính đơn điệu của các dãy số sau: 2 3n 2n 1 n 1 1 a) u b) u n n 1 n n Lời giải 2 3n 2n 1 6 6 a) u 3n 5 u 3n 2 n n 1 n 1 n 1 n 1 6 6 6 Khi đó: u
u 3n 2 3n 5 3 n 1 n n 2 n 1
(n 1)(n 2)
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 7
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com n 1 6 6 Với
(n 1)(n 2) 6 1 3 2 u u 1 n N
(n 1)(n 2)
(n 1)(n 2) n n
u là dãy số tăng. n n 1 1 n 1 b) Ta có: u n n
n n 1 1 n 1 1
Khi n tăng thì dễ thấy mẫu số tăng, phân số giảm nên dãy số đã cho là dãy số giảm. 3n
Ví dụ 7. Xét tính tăng - giảm của dãy số u với u . n n n 1 2 Lời giải n 1 n 1 n 1 3 u 3 2 3 Ta có: n 1 u 1 n 1 n2 n2 2 u 2 3n 2 n Do * * u 0, n u u , n u tăng. n n 1 n n n
Ví dụ 8. Xét tính tăng - giảm của dãy số u với u . n n 2n Lời giải GV: TR n 1 u n 1 2n 1 n 1 1 1 Ta có: n 1 u 1 n 1 n 1 n 1 2 u 2 n 2 n 2 n n Ầ N Đ 1 u 1 ÌN Với * n 1 n n 1 1 2 1 H n u 2 C n Ư * * – Mà u 0, n u u , n u giảm. n n 1 n n 0834 3321 3n
Ví dụ 9. Xét tính tăng - giảm của dãy số u với u . n n 2 n 33 Lời giải 2 2 n 1 n 1 2 3 u 3 n n u 1 1 Ta có: n 1 u 3 n 1 n 1 2 2 (n 1) u (n 1) 3n n 1 u 3 n n n 1 u 1 1 1 Khi đó: n 1 1 3 3 1 n mà *
n n 1 . u n n n 3 1 1 u 1 1 1 n 1 1 3 3 1 n mà *
n n 2 . u n n n 3 1 1 u
u n 1 Hơn nữa *
u 0,n nên n 1 n n
u u n 2 n 1 n
Do đó u u và u u u u u
không tăng và cũng không giảm. 2 3 n n 1 n 1 2
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 8
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
Ví dụ 10. Xét tính tăng - giảm của dãy số u với u n n 1 . n n Lời giải Ta có: u
n 1 n u u
n 1 2 n n 1 . n 1 n 1 n 2 2
Lại có: n n n 2 n
n n 2 n n * 1 1 2 2 2 1 4 2 1 0, n * *
n 1 n 1 2 n, n u u 0, n u giảm. n 1 n n na 2
Ví dụ 11. Với giá trị nào của a thì dãy số u , với u n n n 1 a) là dãy số tăng. b) là dãy số giảm Lời giải na 2 2 a 2 a a 2 Ta có: u a u 2 u u . n n 1 n 1 n 1 n 1 n 2 n n 1 n 2 a 2
a) Để u là dãy số tăng thì u u 0 a 2 . n n 1 n n 1 n 2 a 2 GV: TR
b) Để u là dãy số giảm thì u u 0 a 2 n n 1 n n 1 n 2 Ầ N
Dạng 3. Dãy số bị chặn Đ ÌN 1. Phương pháp H C Ư
(un) là dãy số bị chăn trên M R: un M, n N*. – 0834
(un) là dãy số bị chặn dưới m R: un m, n N*. 3321
(un) là dãy số bị chặn m, M R: m un M, n N*. Chú ý: 33
+) Trong các điều kiện về bị chặn ở trên thì không nhất thiết phải xuất hiện dấu ‘ ’
+) Nếu một dãy số tăng thì luôn bị chặn dưới bởi u ; còn dãy số giảm thì bị chặn trên bởi u . 1 1 2. Các ví dụ
Ví dụ 1. Xét tính bị chặn của các dãy số sau: 2 n 1 7n 5 a) u b) u n 2 2n 3 n 5n 7 Lời giải 3 2 n 5 1 5
a) Viết lại u dưới dạng: 2 u n n 2 2n 3 2 2 2n 3 2 2 2 2n 3
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 9
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com 1
n 0 u 0 3
Với n 1 u 2 u 2 1 n 1 2 n
2 2n 3 0 u n 2 2 2 u
(n 1) 1 2n 3 Xét: n 1 2 2 u 2(n 1) 3 n 1 n u Nhận thấy u 0 thì n 1 1 2
n 2n 2 2 2n 3 2 n 1 2
2n 4n 1 n un 4 2 3 2 4 3 2 2 2 2
4n 3n 4n 6n 4n 6 4n 4n n 2n 4n 1 n 6n 6 n 4n 1 0 10n 5 * n Do đó: u
u u 1 n 1 n 2 Vậy 2
u 1 u bị chặn. n n 7 24 (5n 7) 7n 5 7 24 7 5
b) Viết lại u dưới dạng 5 5 u n u n n 5n 7 5n 7 5 5(5n 7) 5 n 7 5 7 Do đó, u u bị chặn GV: TR n n 7 5 Ầ
Ví dụ 2. Xét tính bị chặn của các dãy số sau: N Đ 1 ÌN 1 a) u b) u H n 2 n C 2n 3 n n 1 Ư – Lời giải 0834 1 3321
n 0 u 0 3 33 a) Với
n 1 u 1 u 1 1 n 2 n
2 2n 3 0, u 0 n 2 u 2n 3 Xét n 1
1 n n 1 2 u 2(n 1) 3 n 1 1
Do đó, suy ra: u u u . Vậy 1 u u bị chặn. n n n n 1 2 5 5 b) Ta dễ dàng thấy:
u 0 do đó nó bị chặn dưới. n 1
Vì n(n 1) 2 u
do đó nó bị chặn trên. n 2
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 10
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com 1
Vậy ta được 0 u , do đó nó bị chặn. n 2
Ví dụ 3. Xét tính bị chặn của các dãy số sau: 1 n 1 a) u b) u n 2 2n 1 n 2 n 1 Lời giải a) Với * 2
n 0 u 1 n
N : 2n 1 0 nên u 0 0 n do đó: u 1 n n 2 u 2n 1 Xét n 1
1 n n 1 2 u 2(n 1) 1 n
Do đó, suy ra u u
u u 1 n n 1 2 1 Vậy 1
u 1 u bị chặn. n n b) Với *
n 0 u 1 n N : n 1 0 và 2
n 1 0 nên u 0 0 n do đó u 1 n n n 1 Và n , 1 , vậy 1
u 1 u bị chặn. n n 2 GV: TR n 1
Ví dụ 4. Xét tính bị chặn của các dãy số sau: Ầ N Đ 2 2n 2 2n 2n 1 ÌN a) u . b) u . n 2 n 2 H n 1 n n 4 C Ư Lời giải – 0834 2 2n 0 a) Vì n
N u 0 3321 2 n n 1 0 33 2 2n 1 2 2 Mặt khác, u 2
2. Vậy 0 u 2 u bị chặn. n n n 2 2 n 1 n 1 2
2n 2n 1 2 2 n 1 1 0 b) Vì n
N u 0 n 2
n n 4 n(n 1) 4 0 2 n n 2 2
n n 4 7 2 2 1 7 Mặt khác, u 2 2 n 2 2 2 n n 4 n n 4 n n 4
Vậy 0 u 2 u bị chặn. n n 3n (1)n
Ví dụ 5. Cho dãy số u , với u n n n 1 4n (1)
a) Tính 6 số hạng dầu tiên của dãy, nêu nhận xét về tính đơn điệu của dãy số.
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 11
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com 3n 4
b) Tính u và u
. Chứng minh rằng 0 u . 2n 2n 1 n 4n 1 Lời giải 2 8 13 16 19
a) Ta có: u ;u 1;u ;u ;u ;u
, nhận xét thấy dãy số không tăng cũng 1 2 3 4 5 6 5 13 15 21 23 không giảm. 6n 1 u 2n b) Ta có 8n 1 6n 2 u 2n 1 8n 5 3n 1 3n 1
Tổng quát, với n 2k(k 1, k Z ) u 0 u n 4n 1 n 4n 1 u 0 3n 1 n 3n 4
Vói n 2k 1(k 0, k Z ) u n n n u n 3 1 3 4 3 4 0 4n 1 n u 4n 1 n 4n 1 4n 1 4n 1 3n 4
Vậy với mọi n thì 0 u n 4n 1
Ví dụ 6. Xét tính bị chặn trên, bị chặn dưới, bị chặn của các dãy số ( u ) cho bởi: n GV: TR 2n 3 1 a) u b) u Ầ n n N n 2 n(n 1) Đ ÌN Lời giải H C Ư 2n 5 2n 3 1 – a) u u
0 nên dãy là dãy tăng. n 1 n 0834 n 3 n 2
(n 3)(n 2) 3321 2n 3 2(n 2) 1 1 5 Hơn nữa u 2
1 u bị chặn trên bởi 2, chặn dưới bởi u . n n 2 n 2 n 2 n 1 3 33
Vậy dãy đã cho bị chặn. u n(n 1) n 1 b) n1
1 dãy là dãy giảm và bị chặn trên bởi u . u
(n 1)(n 2) n 2 1 2 n
Ví dụ 7. Xét tính bị chặn trên, bị chặn dưới, bị chặn của các dãy số u cho bởi: n 2 n 2n n a) u b) u n 2 n n 1 n 2
n 2n n Lời giải 2 2 2 2
n 2n 1 2n 2 n 2n n 4n 3 n 2n a) u u 0 và n 1 n 2 2 2 2
n 2n 1 n 1 1 n n 1 n 3n 3 n n 1 2 2 n 2n
n n 1 n n u 1 1 n 2 2 2 n n 1 n n 1 n n 1
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 12
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
Nên dãy đã cho là dãy tăng, bị chặn dưới bởi 1. 2 2 n
n( n 2n n)
n 2n n b) Ta có u 0 . Lại có n 2 2n 2
n 2n n 2 u
n 4n 3 n 1 n 1 2 2 1
n 4n 3 n 2n 1 2 un
n 2n n 2 2 2 2 2 2
n 4n 3 n 2n 1 2 n 2n n 1
n 2n n 2n 1 n 2n (*) 1
Do (*) hiển nhiên đúng nên ta có dãy đã cho là dãy tăng, và bị chặn dưới bởi u . 1 3 1 n n Hơn nữa u
1 u bị chặn trên bởi 1. Vậy dãy đã cho bị chặn. n 2 n 2 n n n n n 3
Ví dụ 8. Chứng minh rằng dãy số u giảm và bị chặn. n n 1 Lời giải n 4 n 3
n 4n
1 n 2n 3 Xét: u u n 1 n n 2 n 1
n 2n 1 2 2
n 5n 4 n 5n 6 2 GV: TR =
n 2n 1
n 2n 1 Ầ N Nhận thấy u
u 0 u
u , do đó, dãy số u giảm n 1 n n 1 n n Đ ÌN H 2 C
Viết lại u dưới dạng u 1 1 u bị chặn dưới n n n Ư n 1 – 0834 1 1 1 1
Ví dụ 9. Chứng minh rằng dãy số u tăng và bị chặn trên. n 3321 1.2 2.3 3.4 n(n 1) 33 Lời giải
Viết lại u dưới dạng n 2 1 3 2 4 3 (n 1) n 1 1 1 1 1 1 1 1 u 1 1 n 1.2 2.3 3.4 n(n 1) 2 2 3 3 4 n n 1 n 1 1 1 1 1 Xét hiệu: u u 1 1 0 u tăng n 1 n n n 2 n 1 n 1 n 2 1
Nhận thấy u 1 1 u bị chặn trên. n n n 1 2 n 1
Ví dụ 10. Chứng minh rằng dãy số u
là một dãy số bị chặn. n 2 2n 3 Lời giải
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 13
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com 3 2 n 5 1 5
Viết lại u dưới dạng 2 u n n 2 2n 3 2 2 2n 3 2 2 2 2n 3 1
n 0 u 0 3 Với
n 1 u 2 u 2 1 n 1 2 n
2 2n 3 0 u n 2 2 2 u (n 1) 1 2n 3 Xét n 1 2 2 u 2(n 1) 3 n 1 n u Nhận thấy: với u
0 thì n1 1 2
n 2n 2 2 2n 3 2 n 1 2
2n 4n 1 n un 4 2 3 2 4 3 2 2 2 2
4n 3n 4n 6n 4n 6 4n 4n n 2n 4n 1 n 6n 6 n 4n 1 0 10n 5 n N Do đó, u
u u 1. Vậy 2 u 1 u bị chặn n n n 1 n 2 u 0 1
Ví dụ 11. Chứng minh rằng dãy số 1 GV: TR u u 4 n 1 2 n Ầ N
a) Chúng minh rằng u 8 . Đ n ÌN H
a) Giả sử tồn tại u 8 u 2 u 4 8 n n 1 n C Ư – Lời giải 0834
Như vậy nếu tồn tại u 8 thì u 8, cũng suy ra u ,u
u ,u 8 Vô lí do u 0 8. Nên 3321 n n 1 n 2 n 3 2 1 1
điều giả sử là sai. Suy ra u 8 33 n 1 u 8 u b) Xét u u
u 4 u 4 n n 0 u u n 1 n n n n 1 2 2 2 n
Suy ra dãy tăng. Mà u 8 và u 0 u 0. Suy ra dãy bị chặn dưới. n 1 n
Vậy dãy tăng và bị chặn. u 1 1
Ví dụ 12. Chứng minh rằng dãy số u 2 n u n 1 u 1 n
a) Tìm 5 số hạng đầu tiên của dãy số 3
b) Chứng minh rằng dãy số bị chặn dưới bởi 1 và bị chặn trên bởi 2 Lời giải
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 14
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com 3 7 17 2 2 2 1 2 3 7 17 41 a) 2 5 12 u 1;u ;u ;u ;u 1 2 3 4 5 1 1 2 3 5 7 12 17 29 1 1 1 2 5 12 1
b) u 1 0 u 0 suy ra u 1 1 1 n n 1 u 1 n v 1 2 1
Đặt u v 2 , ta có n n v 2 2 v (1 2) 1 1 1 2 v 2 n n v n 1 n 1 v 2 1 v 1 2 v v n n n 1 2 1 n 1 x 1 2 Đặt 1 x n vn x 1
2 (1 2)x n 1 n 2 (1 2) 1 2 y Đặt 1 y x n n 2 2
y (1 2)y n 1 n 2 n 1 (1 2) n (1 2)
Do y là cấp số nhân công bội 1 1 2 y (1 2) n n 2 2 n 1 GV: TR 1 2 (1 2) 2 2 Suy ra x v u 2 n n n1 n n 1 2 2 1 2 (1 2) 1 2 (1 2) Ầ N Đ Vậy ta có đpcm. ÌN H C u 2 Ư
Ví dụ 13. Chứng minh rằng dãy số 1
tăng và bị chăn trên bởi 2. – 0834 u u 2 n 1 n 3321 Lời giải 33 Ta có u 1 n
Giả sử tồn tại u 2 u 2 2 u 2 n n 1 n 1
Như vậy, nếu tồn tại u 2 thì suy ra u
2 , từ đó cũng suy ra được u ,u u ,u 2 vô n n 1 n 2 n 3 2 1 lý
Do u 2 2. Nên điều giả sử là sai. 1 Suy ra u 2 n 2 u 2 u 2 u u n n n 1 n Xét u
u u 2 u 0 n 1 n n n u 2 u u 2 u n n n n Suy ra u
u , nên đây là dãy tăng. n 1 n
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 15
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
Vậy dãy đã cho tăng và bị chặn trên bởi 2.
C. GIẢI BÀI TẬP SÁCH GIÁO KHOA
Bài 1. Viết năm số hạng đầu của mỗi dãy số có số hạng tổng quát u cho bởi công thức sau: n n (1)n 2n 1 a) 2 u 2n 1 b) u c) u d) u 1 . n n 2n 1 n n n n Lời giải
a) Ta có: 5 số hạng đầu tiên của dãy u là: 2 2
u 21 1 3;u 2 2 1 9 ; n 1 2 2 2 2
u 2.3 1 19;u 2.4 1 33;u 2.5 1 51. 3 4 5 (1)n
b) Ta có 5 số hạng đầu của dãy u là: n 2n 1 1 3 5 (1) 1 ( 1 ) 1 (1) 1 u 1 u ; u ; 1 3 5 2 11 1 2.3 1 5 2.5 1 9 2 4 (1) 1 (1) 1 u ; u ; 2 4 2 2 1 3 2.4 1 7 2n
c) Ta có 5 số hàng đầu của dãy u là: n n 1 3 5 2 2 2 u 2; u 8; u 32 1 3 5 1 1 1 2 4 2 2 GV: TR u 4; u 16; . 2 4 1 1 Ầ N n Đ 1 ÌN
d) Ta có 5 số hạng đầu của dãy u 1 là: n n H C Ư – 0834 3321 33 1 3 5 1 1 64 1 7776 u 1 2; u 1 ; u 1 1 3 5 1 3 27 5 3125 2 4 1 9 1 625 u 1 ; u 1 ; 2 4 2 4 4 256
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 16
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
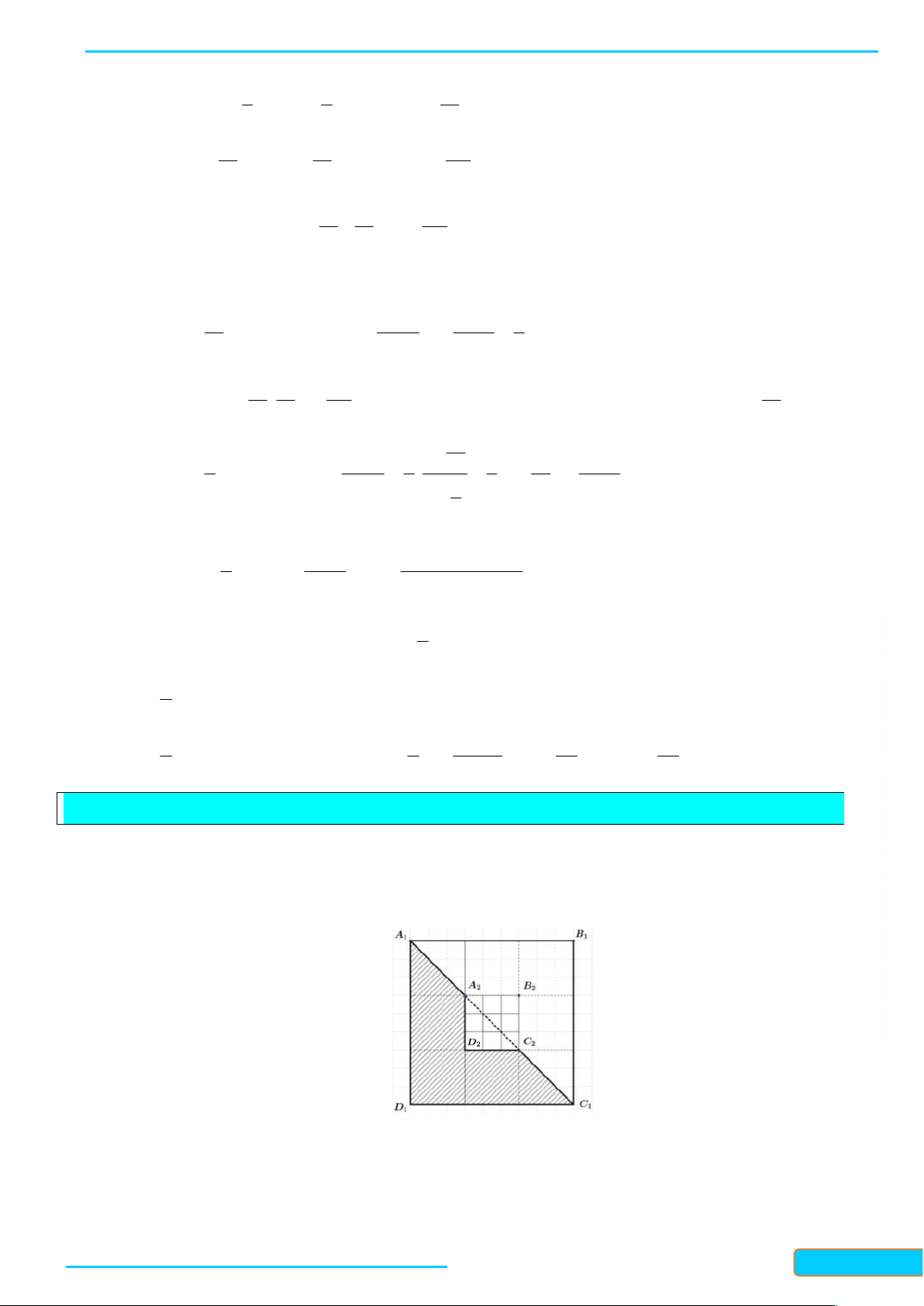
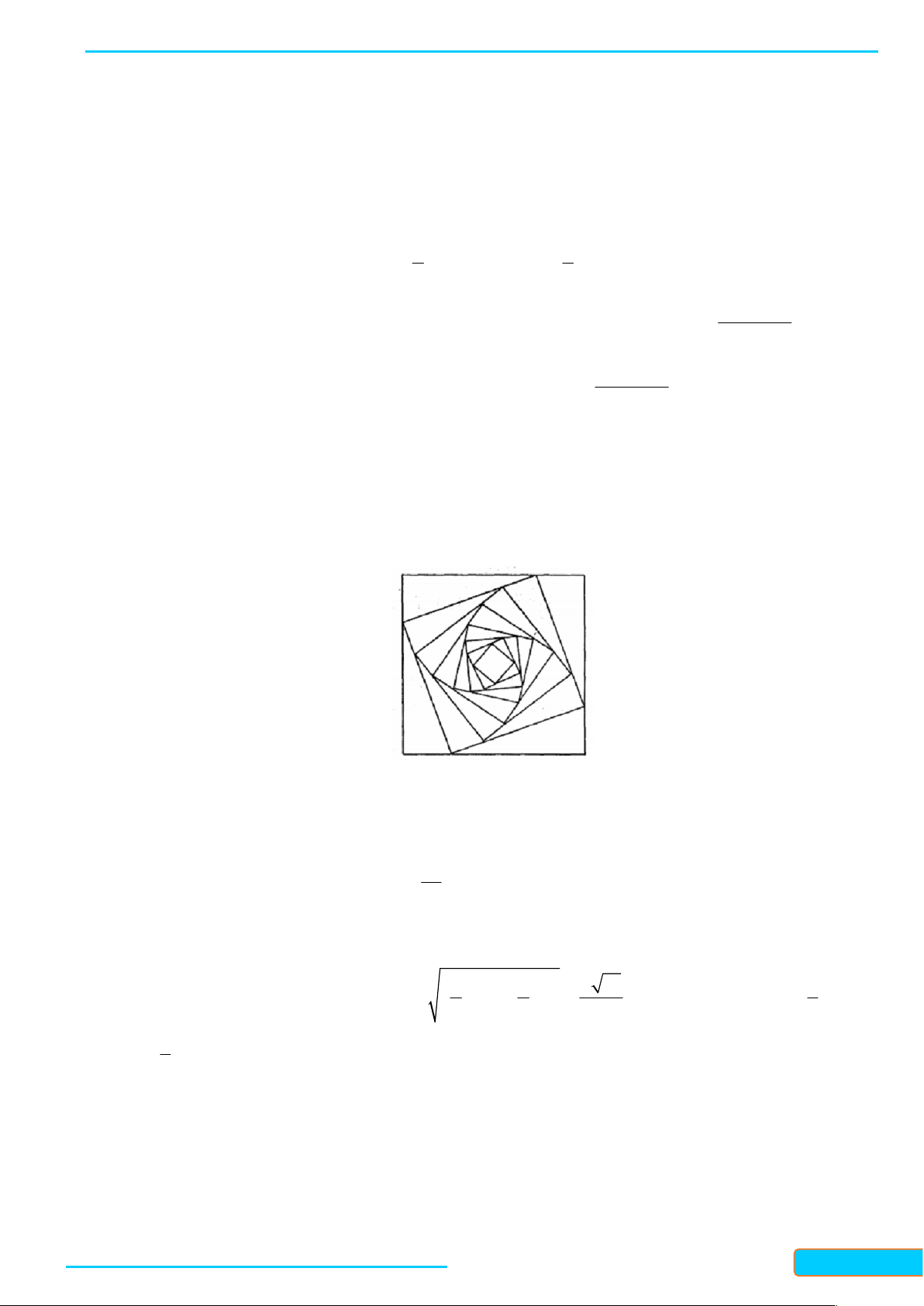
Bài 2.a) Gọi u là số chấm ở hàng thứ n trong Hình 1. Dự đoán công thức của số hạng tổng quát cho n dãy số u . n
b) Gọi v là tổng diện tích của các hình tô màu ở hàng thứ n trong Hình 2 (mỗi ô vuông nhỏ là một n
đơn vị diện tích). Dự đoán công thức của số hạng tổng quát cho dãy số v . n Lời giải
a)Số chấm ở hàng thứ nhất là: u 1 ; 1
Số chấm ở hàng thứ hai là: u 2 ; 2
Số chấm ở hàng thứ ba là: u 3 ; 3
Số chấm ở hàng thứ tư là: u 4 ; 4
Vậy số chấm ở hàng thứ n là: u n . n
b) Diện tích của các ô màu ở hàng thứ nhất là: v vi = 1 = 13; GV: TR
Diện tích của các ô màu ở hàng thứ hai là: 3 v 8 2 ; 2 Ầ
Diện tích của các ô màu ở hàng thứ ba là: 3 v 27 3 ; 3 N Đ
Diện tích của các ô màu ở hàng thứ tư là: 3 v 64 4 ; ÌN 4 H C
Vậy diện tích của các ô màu ở hàng thứ n là: 3 v n . n Ư –
Bài 3. Xét tính tăng, giảm của mỗi dãy số u , biết: n 0834 n 3 3321 a) u n n 2 n 33 3 b) u n 2n n! c) u ( 1
)n 2n n 1 Lời giải n 1 3 n 2 a) Ta có: u n 1 n 1 2 n 3 n 2 n 3 2 2
n 4 n 9 5 Xét hiệu u u * 0, n . n 1 n n 3 n 2
n 3n 2
n 3n 2 Suy ra u u n 1 n
Vì vậy dãy số đa cho là dãy số tăng. n 1 3 3 3n 3 b) Ta có: u u n 1 n 1 2 n 1 ! 2 n 1 2n n! 2 n 1 n 3 3 Vìn * nên suy ra u u . 2n 1 2 n 1 n
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 17
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
Vì vậy dãy số đã cho là dãy số giảm. c) Ta có: n 1 u ( 1 ) n n 1 2 1 1 +) Nếu n n chẵn thì u
2.2n 1 và u 2 1. Do đó u u . n 1 n n 1 n
Vì vậy với n chẵn thì dãy số đã cho là dãy giảm. +) Nếu n n lẻ thì u
2 2 1 và u 2n . Do đó u u . n 1 n 1 n 1 n
Vì vậy với n chã̃n thì dãy số đã cho là dãy tăng.
Bài 4. Trong các dãy số u được xác định như sau, dãy số nào bị chặn dưới, bị chặn trên, bị chặn? n a) 2 u n 2 n
b) u 2n 1 n 1 c) u . n 2 n n Lời giải a) Ta có: *
n nên n 1 suy ra 2 n 2 3 Do đó u 3 n
Vậy dãy số (un) bị chặn dưới bởi 3. b) Ta có: *
n nên n 1 suy ra u 2n 1 1 n Do đó u 1. n
Vậy dãy số ( u ) bị chặn trên bởi 1. n GV: TR 1 1 1 1 c) Ta có: u n 2 n n nn 1 n n 1 Ầ N Đ 1 1 1 1 Vì *
n nên n 1 suy ra u 0 ÌN n n 1 n n n 1 H C Ư 1 1 1 1 1 1 1 Ta lại có: 1 và suy ra u 1 – n n n 1 2 n n 1 2 2 0834 1 Do đó 0 u 3321 n 2 33
Vậy dãy số u bị chặn. n
Bài 5. Cho dãy số thực dương u . Chứng minh rằng dãy số u là dãy số tăng khi và chỉ khi n n un 1 1 với mọi * n un Lời giải u +) Nếu n 1 1 với mọi * n thì u
u . Do đó dãy số u là dãy số tăng. n u n 1 n n u
+) Nếu u là dãy số tăng thì u
u do đó n 1 1. n n 1 n un
Bài 6. Chị Mai gửi tiền tiết kiệm vào ngân hàng theo thể thức lãi kép như sau: Lần đầu chị gửi 100
triệu đồng. Sau đó, cứ hết 1 tháng chị lại gửi thêm vào ngân hàng 6 triệu đồng. Biết lãi suất của ngân
hàng là 0,5% một tháng. Gọi P (triệu đồng) là số tiền chị có trong ngân hàng sau n tháng. n
a) Tính số tiền chị có trong ngân hàng sau 1 tháng.
b) Tính số tiền chị có trong ngân hàng sau 3 tháng.
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 18
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
c) Dự đoán công thức của P tính theo n . n Lời giải
a) Số tiền chị có trong ngân hàng sau 1 tháng là:
P 100 100.0, 5% 6 100, 5 6 (triệu đồng). 1
b) Số tiền chị có trong ngân hàng sau 2 tháng là:
P 100, 5 6 100, 5 6 0, 5% 6 100, 5 6 1 0, 5% 6 100, 5 1 0, 5% 6. 1 0,5% 6 (triệu đồng). 2
Số tiền chị có trong ngân hàng sau 3 tháng là:
P 100,5 6 1 0,5% 6 100,5 6 1 0,5% 6 0, 5% 6 3 2 2
100, 5 (1 0, 5%) 6(1 0, 5%) 6 1 0,5% 6 (triệu đồng).
c) Số tiền chị có trong ngân hàng sau 4 tháng là: P 100,5 6 2
(1 0,5%) 6 1 0,5% 6 100,5 6 2
(1 0, 5%) 6 (1 0, 5%) 6]0,5% 6 4 3 3 2
100,5 (1 0, 5%) 6 (1 0,5%) 6(1 0,5%) 6 1 0,5% 6
Số tiền chị có trong ngân hàng sau n tháng là: n 1 n 1 n2 n3
P 100,5 (1 0,5%) 6(1 0,5%) 6(1 0,5%) 6 (1 0,5%) 6 với mọi * n . n D. BÀI TẬP TRẮC NGHIỆM n
Câu 1: Cho dãy số u , biết u
. Năm số hạng đầu tiên của dãy số đó lần lượt là những n n GV: TR n 1 số nào dưới đây? Ầ N 1 2 3 4 5 2 3 4 5 6 Đ
A. ; ; ; ; .
B. ; ; ; ; . ÌN 2 3 4 5 6 3 4 5 6 7 H C 1 2 3 4 5 2 3 4 5 6 Ư C. ; ; ; ; . D. ; ; ; ; . – 2 3 4 5 6 3 4 5 6 7 0834 Lời giải 3321 Chọn A 33 1 2 3 4 5
Ta có u ;u ;u ;u ;u . 1 2 3 4 5 2 3 4 5 6
Nhận xét: (i) Dùng MTCT chức năng CALC để kiểm tra (tính) nhanh. n
Câu 2: Cho dãy số u , biết u
. Ba số hạng đầu tiên của dãy số đó lần lượt là những n n 3n 1 số nào dưới đây? 1 1 1 1 1 3 1 1 1 1 2 3 A. ; ; . B. ; ; . C. ; ; . D. ; ; . 2 4 8 2 4 26 2 4 16 2 3 4 Lời giải Chọn B
Dùng MTCT chức năng CALC: ta có
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 19
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com 1 2 2 1 3 3 u ;u ;u . 1 2 2 3 3 2 3 1 8 4 3 1 26 u 1
Câu 3: Cho dãy số u , biết 1
với n 0 . Ba số hạng đầu tiên của dãy số đó là lần n u u 3 n 1 n
lượt là những số nào dưới đây? A. 1 ;2;5. B. 1;4;7. C. 4;7;10. D. 1 ;3; 7. Lời giải Chọn A
Ta có u 1; u u 3 2; u u 3 5. 1 2 1 3 2 2 2n 1
Câu 4: Cho dãy số u , biết u . Tìm số hạng u . n n 2 n 3 5 1 17 7 71 A. u . B. u . C. u . D. u . 5 4 5 12 5 4 5 39 Lời giải Chọn C 2
Thế trực tiếp hoặc dùng chức năng CALC: 2.5 1 49 7 u . 5 2 5 3 28 4 GV: TR Câu 5: n
Cho dãy số u , biết u
n Mệnh đề nào sau đây sai? n 1 .2 . n Ầ N Đ A. u 2. B. u 4. C. u 6. D. u 8. 1 2 3 4 ÌN H C Lời giải Ư – 0834 Chọn D 3321
Thay trực tiếp hoặc dùng chức năng CALC: 33 u 2. 1 2
; u 1 .2.2 4, u 1 2.3 6; u 1 2.4 8 . 1 2 2 3 3 4 4
Nhận xét: Dễ thấy u 0 khi n chẵn và ngược lại nên đáp án D sai. n n 2n
Câu 6: Cho dãy số u , biết u Tìm số hạng u . n 1 . . n n 3 8 8 A. u . B. u 2. C. u 2. D. u . 3 3 3 3 3 3 Lời giải Chọn D 3
Thay trực tiếp hoặc dùng chức năng CALC: u 3 2 8 1 . . 3 3 3
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 20
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com u 2 1
Câu 7: Cho dãy số u xác định bởi . Tìm số hạng u . n 1 u u 1 4 n 1 n 3 5 2 14 A. u . B. u 1. C. u . D. u . 4 9 4 4 3 4 27 Lời giải Chọn A Ta có 1 1 1 2 1 1 2 5 u u 1 2 1 1; u u 1 ; u
u 1 1 . 2 1 3 2 4 3 3 3 3 3 3 3 3 9
Nhận xét: Có thể dùng chức năng “lặp” trong MTCT để tính nhanh. u 3 1
Câu 8: Cho dãy u xác định bởi
. Mệnh đề nào sau đây sai? n un u 2 n 1 2 5 15 31 63 A. u . B. u . C. u . D. u . 2 2 3 4 4 8 5 16 Lời giải GV: TR Chọn A Ầ u 3 7 u 7 15 1 2 N u
2 2 ; u 2 2 2 3 Đ Ta có 2 2 2 2 4 4 ÌN u 15 31 u 31 63 3 4 H u 2 2 ; u 2 2 . 4 5 C 2 8 8 2 16 16 Ư – 0834
Nhận xét: Dùng chức năng “lặp” trong MTCT để tính nhanh. 3321 n 1 8
Câu 9: Cho dãy số u , biết u . Số
là số hạng thứ mấy của dãy số? n n 2n 1 15 33 A. 8. B. 6. C. 5. D. 7. Lời giải Chọn D Ta cần tìm n n sao cho 1 8 u
15n 15 16n 8 n 7. n 2n 1 15
Nhận xét: Có thể dùng chức năng CALC để kiểm tra nhanh. 2n 5 7
Câu 10: Cho dãy số u , biết u . Số
là số hạng thứ mấy của dãy số? n n 5n 4 12 A. 8. B. 6. C. 9. D. 10. Lời giải Chọn A
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 21
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
Dùng chức năng “lặp” để kiểm tra đáp án. Hoặc giải cụ thể như sau: 2n 5 7 u
24n 60 35n 28 11n 88 n 8. n 5n 4 12
Câu 11: Cho dãy số u , biết u 2 .n Tìm số hạng u . n n n 1 A. u 2 .2 n . B. u 2n 1. C. u 2 n 1 . D. u 2n 2. n 1 n 1 n 1 n 1 Lời giải Chọn A
Thay n bằng n 1 trong công thức u ta được: n 1 u 2 2.2n . n n 1
Câu 12: Cho dãy số u , biết u 3 .n Tìm số hạng u . n n 2n 1 A. 2 u 3 .3n 1. B. n n 1 u 3 .3 . C. 2 u 3 n 1. D. 2n 1 u 3 . 2n 1 2n 1 2n 1 2 n 1 Lời giải Chọn B Ta có n n2n 1 2n 1 n n 1 u 3 u 3 3 .3 . n 2n 1
Câu 13: Cho dãy số u , với n 1 u 5 . Tìm số hạng u . n n n 1 n n n GV: TR A. 1 u 5 . B. u 5 . n C. 1 u 5.5 . D. 1 u 5.5 . n 1 n 1 n 1 n 1 Lời giải Ầ N Đ ÌN Chọn B H C n 1 nn 1 n 1 1 u 5 u 5 5n. Ư n n 1 – 0834 2n3 n 1 Câu 14:
Cho dãy số u , với u . Tìm số hạng u . n n n 1 3321 n 1 2n 1 3 2n 1 3 33 n 1 n 1 A. u . B. u . n 1 n 1 n 1 n 1 2n3 2n5 n n C. u . D. u . n 1 n 1 n 2 n 2 Lời giải Chọn D n n n n 1 n 2 1 3 2 3 2 5 1 1 n n n 1 u u . n n 1 n 1 n 1 1 n 2 1 2 3 4
Câu 15: Dãy số có các số hạng cho bởi: 0; ; ; ; ;. có số hạng tổng quát là công thức nào 2 3 4 5 dưới đây?
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 22
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com n 1 n n 1 2 n n A. u . B. u . C. u . D. u . n n n n 1 n n n n 1 Lời giải Chọn C
Vì u 0 nên loại các đáp án A và B 1 Ta kiểm tra 1 u ở các đáp án C, D: 2 2 Xét đáp án C: n 1 1 u u n 2 n 2 2 Xét đáp án D: n n 2 1 u u loại n 2 n 1 3 2 Nhận xét: 1 1 1 2 1 2 3 1 n u 0 ; u ; u ,... nên đoán 1 u . 1 2 3 1 2 2 3 3 n n
Câu 16: Dãy số có các số hạnh cho bởi: 1 ;1; 1 ;1; 1
;. có số hạng tổng quát là công thức nào dưới đây? A. n n u 1. B. u 1. C. u D. u n 1 1 . n 1 . n n Lời giải GV: TR Chọn C Ầ
Vì dãy số đa cho không phải là dãy hằng nên loại các đáp án A và B N Đ ÌN Ta kiểm tra u 1 ở các đáp án C, D: 1 H C n Ư
Xét đáp án C: u u n 1 1 1 – 0834 Xét đáp án D: u u loại D n n 1 1 2 1 1 1 1 3321
Câu 17: Cho dãy số có các số hạng đầu là: 2
;0; 2; 4;6;. Số hạng tổng quát của dãy số này là 33
công thức nào dưới đây? A. u 2 . n
B. u n 2.
C. u 2 n
D. u 2n 4. n 1 . n n n Lời giải Chọn D
Kiểm tra u 2 ta loại các đáp án B, C 1
Ta kiểm tra u 0 ở các đáp án A, D: 2
Xét đáp án A: u 2n u 4 0 loại A n 2
Xét đáp án D: u 2n4 2.24 0 n
Nhận xét: Dãy 2; 4;6;... có công thức là *
2n n nên dãy 2;0;2;4;6; . có được bằng cách
“tịnh tiến” 2n sang trái 4 đớn vị, tức là 2n 4.
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 23
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com u 2
Câu 18: Cho dãy số u , được xác định 1
. Số hạng tổng quát u của dãy số là số hạng n u 2u n n 1 n nào dưới đây? A. n 1 u n . B. u 2 . n C. n 1 u 2 . D. u 2. n n n n Lời giải Chọn B u 2 1 u 2 Từ công thức 1 u
2u 2.2 4. 2 1 u 2u n 1 n u
2u 2.4 8 3 2 Xét đáp án A với 1 1 0 n 1 u 1 1 1 A loại. 1
Xét đáp án B, ta thấy đều thỏa mãn. Xét đáp án C với 1 1 2 n 1 u 2 2 4 C loại. 1
Dễ thấy đáp án D không thỏa mãn. 1 u
Câu 19: Cho dãy số
u , được xác định 1 2
. Số hạng tổng quát u của dãy số là số hạng n n u u 2 n 1 n GV: TR nào dưới đây? A. 1 1 u 2 n
B. u 2 n C. 1 u 2 . n D. 1 u 2 . n n 1 . n 1 . n n Ầ 2 2 2 2 N Đ ÌN Lời giải H C Ư Chọn B – 0834 1 u 1 3321 2 1 Từ công thức u 1 3 1 2 u
u 2 2 . 2 1 33 2 2 u u 2 n 1 n 3 7 u
u 2 2 3 2 2 2 Xét đáp án A với 1 5 n 2
u 2 2 1 A loại. 2 2 2
Xét đáp án B, ta thấy đều thỏa mãn. Xét đáp án C với 1 1 7 n 2
u 2.2 4 C loại. 2 2 2 2 Xét đáp án D với 1 5 n 1
u 2.1 D loại. 1 2 2 u 2
Câu 20: Cho dãy số
u , được xác định 1
. Số hạng tổng quát u của dãy số là số n u u 2n 1 n n 1 n hạng nào dưới đây?
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 24
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
A. u n 2 2 1 . B. 2 u 2 n .
C. u n
D. u n n 2 2 1 . n 2 2 1 . n n Lời giải Chọn A
Kiểm tra u 2 ta loại các đáp án B và C 1
Ta có u u 2.11 3. 2 1
Xét đáp án A: u 2 n 2 1 u 3 n 2 Hoặc kiểm tra: u
u n n n n 2 2 1 2 1. n 1
Xét đáp án D: u 2n 2 1 u 1 loại D n 2 Hoặc kiểm tra: u u n
n n n n 2 2 1 2 1 2 1. n 1 u 1
Câu 21: Cho dãy số
u , được xác định 1
. Số hạng tổng quát u của dãy số là số hạng n 2 u u n n n 1 n nào dưới đây? A. n(n 1)(2n 1) n n n u 1 . B. ( 1)(2 2) u 1 . n 6 n 6 n n n n n n GV: TR C. ( 1)(2 1) u 1 . D. ( 1)(2 2) u 1 . n 6 n 6 Ầ Lời giải N Đ ÌN Chọn C H C Ư
Kiểm tra u 1 ta loại đáp án A 1 – 0834 Ta có 2
u u 1 2. 2 1 3321 Xét đáp án B: n(n 1)(2n 2) 2.1.6 u 1 u 1 3 2 B loại. n 2 33 6 6 Xét đáp án C:
n(n 1)(2n 1) 2.1.3 u u 1 u 1 2 n n 2 6 6 Xét đáp án D: n(n 1)(2n 2) 2.3.2 u 1 . u 1 3 2 D loại. n 2 6 6 u 2 1 Câu 22:
Cho dãy số u , được xác định
1 . Số hạng tổng quát u của dãy số là số n u 2 n n 1 u n hạng nào dưới đây? A. n 1 n n n u . B. 1 u . C. 1 u . D. u . n n n n n n n n 1 Lời giải Chọn C
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 25
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
Kiểm tra u 2 ta loại các đáp án A, B 1 Ta có 1 3 u 2 . 2 u 2 1 Xét đáp án C: n 1 3 u u n 2 n 2 Xét đáp án D : n 2 u u D loại. n 2 n 1 3 u 1
Câu 23: Cho dãy số 1
u , được xác định
. Số hạng tổng quát u của dãy số là số n n u u n n 2n 1 1 hạng nào dưới đây? A. n u 1 . n B. u 1 . n C. u D. u . n n 2 1 1 . n n n Lời giải Chọn D
Kiểm tra u 1 ta loại đáp án A, B và C 1
Câu 24: Cho dãy số u có số hạng tổng quát là u 23n với *
n . Công thức truy hồi của dãy n n số đó là: u 6 u 6 u 3 u 3 A. 1 . B. 1 . C. 1 . D. 1 . GV: TR u
6u , n 1 u
3u , n 1 u
3u , n 1 u
6u , n 1 n n 1 n n 1 n n 1 n n 1 Ầ Lời giải N Đ ÌN Chọn B H C Ư Vì 1
u 2.3 6 nên ta loại các đáp án C và D 1 – 0834 Ta có 2 u 2.3 18. 2 3321 u 6 Xét đáp án A: 1
u 6u 6.6 36 A loại. 2 1 33 u
6u , n 1 n n 1 u 6 Xét đáp án B: 1
u 3u 3.6 18 2 1 u
3u , n 1 n n 1 a 3 1
Câu 25: Cho dãy số
a , được xác định
. Mệnh đề nào sau đây sai? n 1 a a , n 1 n 1 2 n A. 93 3
a a a a a . B. a . 1 2 3 4 5 16 10 512 C. 9 a a . D. 3 a . n 1 n 2n n 2n Lời giải Chọn D
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 26
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com Ta có u u u u u u 3 1 2 1 3 1 1 a 3; a ; a ; a ,... u nên suy ra đáp án D sai. 1 2 3 2 4 3 n n 1 n 1 2 2 2 2 2 2 2 Xét đáp án A: 5 1 1 1 1 1 1 2 93
a a a a a 3 1 3. A đúng. 1 2 3 4 5 2 3 4 2 2 2 2 1 16 1 2 Xét đáp án B: 3 3 a B đúng. 10 9 2 512 Xét đáp án C 3 3 3 3.2 9 a a C đúng. n 1 n n n 1 2 2 2n 2n
Câu 26: Cho các dãy số sau. Dãy số nào là dãy số tăng? 1 1 1 1 A. 1; 1; 1; 1; 1; 1; B. 1; ; ; ; ; 2 4 8 16 1 1 1 1 C. 1; 3; 5; 7; 9; D. 1; ; ; ; ; 2 4 8 16 Lời giải Chọn C GV: TR
Xét đáp án A: 1; 1; 1; 1; 1; 1; đây là dãy hằng nên không tăng không giảm. Ầ N 1 1 1 1 Đ
Xét đáp án B: 1; ; ; ; ;
u u u loại B 1 2 3 2 4 8 16 ÌN H C Xét đáp án C: * 1; 3; 5; 7; 9;
u u , n Ư n n 1 – 0834 Xét đáp án D: 1 1 1 1 1; ; ; ; ;
u u u u loại D 1 2 3 2 4 8 16 n 3321 33
Câu 27: Trong các dãy số u
cho bởi số hạng tổng quát u sau, dãy số nào là dãy số tăng? n n A. 1 n n u . B. 1 u . C. 5 u . D. 2 1 u . n 2n n n n 3n 1 n n 1 Lời giải Chọn D
Vì 2n;n là các dãy dương và tăng nên 1 1 ;
là các dãy giảm, do đó loại A,B 2n n 3 u 1 Xét đáp án C: n 5 2 u
u u loại C n 1 2 3n 1 7 u 2 6 Xét đáp án D: 2n 1 3 1 1 u 2 u u 3 0 n n 1 n 1 n 1 n
n 1 n 2
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 27
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
Câu 28: Trong các dãy số u
cho bởi số hạng tổng quát u sau, dãy số nào là dãy số tăng? n n A. 2 n u . B. 3 u . C. u 2n. D. u n 2 . n 3n n n n Lời giải Chọn C Xét đáp án C: n n 1 u 2 u
u 2 2n 2n 0 n n 1 n
Vì 2n;n là các dãy dương và tăng nên 1 1 ;
là các dãy giảm, do đó loại các đáp án A và 2n n B u n 4 Xét đáp án D: u 2 2
u u loại D n 2 3 u 8 3
Câu 29: Trong các dãy số u
cho bởi số hạng tổng quát u sau, dãy số nào là dãy số giảm? n n A. 1 n u . B. 3 1 u . C. 2 u n .
D. u n 2. n 2n n n 1 n n Lời giải Chọn A GV: TR
Vì 2n là dãy dương và tăng nên 1 là dãy giảm 2n Ầ u 1 1 N 3n 1 Đ Xét B: u
u u loại B n 5 1 2 ÌN n 1 u 2 3 H C Ư Hoặc – 0834 3n 2 3n 1 4 u u
0 nên u là dãy tăng. n n 1 n n 2 n 1 n 1 n 2 3321 33
Xét C: u n u u n
n n loại C n 2 2 2 1 2 1 0 n n 1 Xét D: 1 u n 2 u
u n 3 n 2 0 loại D n n 1 n
n 3 n 2
Câu 30: Trong các dãy số u
cho bởi số hạng tổng quát u sau, dãy số nào là dãy số giảm? n n 2 A. n 1 n u sin . n B. u .
C. u n n 1. D. u 1 .2n n 1 . n n n n Lời giải Chọn C A. 1 1
u sin n u
u 2 cosn
sin có thể dương hoặc âm phụ thuộc n nên đáp án A n n 1 n 2 2
sai. Hoặc dễ thấy sin n có dấu thay đổi trên *
nên dãy sin n không tăng, không giảm.
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 28
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com 2 2 B. n 1 1 1 1 n n 1 u n u u 1
0 nên dãy đã cho tăng nên B sai. n n 1 n n n n 1 n nn 1 C. 1
u n n 1
, dãy n n 1 0 là dãy tăng nên suy ra u giảm. n n n n 1
D. u n
1 2n là dãy thay dấu nên không tăng không giảm. n 1 Cách trắc nghiệm.
A. u sin n có dấu thay đổi trên *
nên dãy này không tăng không giảm. n n 1 u 2 2 1 2 B. n 1 n 1 u , ta có
u u u không giảm. n 5 n 1 2 n 2 n u n 2 2 n
1 u 1 C.
u n n 1 , ta có 1
u u nên dự đoán dãy này giảm. n 1 2 n
2 u 2 1 2
D. u n
1 2n là dãy thay dấu nên không tăng không giảm. n 1 Cách CASIO. Các dãy n sin ; 1 2n n 1 có dấu thay đổi trên *
nên các dãy này không tăng không
giảm nên loại các đáp án A, D
Còn lại các đáp án B, C ta chỉ cần kiểm tra một đáp án bằng chức năng TABLE. GV: TR 2
Chẳng hạn kiểm tra đáp án B, ta vào chức năng TABLE nhập F X X 1 với thiết X Ầ N
lập Start 1, End 10, Step 1. Đ ÌN H
Nếu thấy cột F X các giá trị tăng thì loại B và chọn C, nếu ngược lại nếu thấy cột C Ư
F X các giá trị giảm dần thị chọn B và loại C – 0834
Câu 31: Mệnh đề nào sau đây đúng? 3321 A. Dãy số 1 n u 2 là dãy tăng.
B. Dãy số u
1 2n là dãy giảm. n 1 33 n n C. Dãu số n 1 u là dãy giảm. D. Dãy số 1 u 2n cos là dãy tăng. n n 1 n n Lời giải Chọn D Xét đáp án A: 1 1 1 u 2 u u 0 loại A n n 1 n n n 1 n
Xét đáp án B: u n
1 2n là dãy có dấu thay đổi nên không giảm nên loại B n 1 Xét đáp án C: n 1 2 1 1 u 1 u u 2 0 loại C n n 1 n 1 n 1 n
n 1 n 2 Xét đáp án D: 1 1 1 u 2n cos u u 2cos cos 0 nên n n 1 n n n 1 n 2
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 29
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
Câu 32: Mệnh đề nào sau đây sai? A. Dãy số 1 n u là dãy giảm. B. Dãy số 2
u 2n 5 là dãy tăng. n n n n C. Dãy số 1 u 1 là dãy giảm. D. Dãy số 2
u n sin n là dãy tăng. n n n Lời giải Chọn C Xét A: 1 n 1 1 1 u n u u
n n 1 0 nên dãy u là dãy giảm n n n 1 n n n n 1 n nên C đúng. Xét đáp án B: 2
u 2n 5 là dãy tăng vì 2
n là dãy tăng nên B đúng. Hoặc n u
u 2 2n 1 0 nên u là dãy tăng. n n 1 n n n n Xét đáp án C: 1 n 1 u n n n 2 2 1 u 1 0 . 1
u là dãy tăng nên n n n u n 1 n n n Xét đáp án D: 2
u n sin n u u n n nên D đúng. n 2 1 sin 1 2 sin 0 n n 1 Câu 33: n
Cho dãy số u , biết 3 1 u
. Dãy số u bị chặn trên bởi số nào dưới đây? n n n 3n 1 GV: TR A. 1 . B. 1. C. 1 . D. 0. 3 2 Ầ N Đ Lời giải ÌN H C Chọn B Ư – n 5 1 1 0834 Ta có 3 1 2 u 1
1. Mặt khác: u 0 nên suy ra dãy u bị chặn n n 3n 1 3n 1 2 7 2 2 3321 trên bởi số 1. 33
Câu 34: Trong các dãy số u
cho bởi số hạng tổng quát u sau, dãy số nào bị chặn trên? n n A. 2 u n . B. u 2n. C. 1 u .
D. u n 1. n n n n n Lời giải Chọn C Các dãy số 2; 2n n
; n 1 là các dãy tăng đến vô hạn khi n tăng lên vô hạn nên chúng
không bị chặn trên (có thể dùng chức năng TABLE của MTCT để kiểm tra). Nhận xét: 1 u 1 với mọi *
n nên dãy u bị chặn trên bởi 1. n n n
Câu 35: Cho dãy số u , biết u cos n sin .
n Dãy số u
bị chặn trên bởi số nào dưới đây? n n n A. 0. B. 1. C. 2. D. Không bị chặn trên.
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 30
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com Lời giải Chọn C Ta có MTCT u
u sin1 cos11 0 nên loại các đáp án A và B (dùng TABLE của MTCT n 1
để kiểm tra, chỉ cần 1 số hạn nào đó của dãy số lớn hơn thì dãy số đó không thể bị chặn trên bởi . )
Ta có u cos n sin n 2 sinn 2 n 4
Câu 36: Cho dãy số u , biết u sin n cos .
n Dãy số u bị chặn dưới bởi số nào dưới đây? n n n A. 0. B. 1. C. 2. D. Không bị chặn dưới. Lời giải Chọn C MTCT u
u sin 5cos5 1 0
loại A và B (dùng TABLE của MTCT để kiểm tra, n 5
chỉ cần có một số hạng nào đó của dãy số nhỏ hơn thì dãy số đó không thể bị chặn dưới với số . )
Ta có u 2 sinn 2 GV: TR n 4 Ầ
Câu 37: Cho dãy số u , biết u 3 cos n sin .
n Dãy số u
bị chặn dưới và chặn trên lần lượt n n n N Đ
bởi các số m và M nào dưới đây? ÌN H C
A. m 2; M 2. B. 1
m ; M 3 1. Ư 2 – 0834
C. m 3 1; M 3 1. D. 1 1
m ; M . 2 2 3321 Lời giải 33 Chọn A MTCT TABLE 1 u
u 3 1 loại C và D n 1 2 MTCT TABLE 1 u u loại B n 4 2 Vậy Nhận xét: 3 1 u 2
sin n cos n 2sinn 2 u 2. n 2 2 6 n
Câu 38: Cho dãy số n u , biết u
Mệnh đề nào sau đây đúng? n 2n 5 1 .5 . n
A. Dãy số u bị chặn trên và không bị chặn dưới. n
B. Dãy số u bị chặn dưới và không bị chặn trên. n
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 31
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
C. Dãy số u bị chặn. n
D. Dãy số u không bị chặn. n Lời giải Chọn D Nếu n chẵn thì 2n 1 u 5
0 tăng lên vô hạn (dương vô cùng) khi n tăng lên vô hạn nên n
dãy u không bị chặn trên. n Nếu n lẻ thì 2n 1 u 5
0 giảm xuống vô hạn (âm vô cùng) khi n tăng lên vô hạn nên n
dãy u không bị chặn dưới. n
Vậy dãy số đã cho không bị chặn. Câu 39: 1 1 1
Cho dãy số u , với u ... , n 1; 2; 3 .
Mệnh đề nào sau đây đúng? n n 1.4 2.5 nn 3
A. Dãy số u bị chặn trên và không bị chặn dưới. n
B. Dãy số u bị chặn dưới và không bị chặn trên. n
C. Dãy số u bị chặn. n
D. Dãy số u không bị chặn. n GV: TR Lời giải Ầ Chọn C N Đ ÌN Ta có 1 1 1 1 u 0
u bị chặn dưới bởi 0. Mặt khác * k nên n n H k k 3 k k C 1 k k 1 Ư – suy ra: 0834 1 1 1 1 1 1 1 1 1 1 1 1 3321 u
1 1 1 n 1.2 2.3 3.4 nn 1 2 2 3 2 4 n n 1 n 1 33
nên dãy u bị chặn trên, do đó dãy u bị chặn. n n Câu 40: 1 1 1
Cho dãy số u , với u ... , n 2; 3; 4; .
Mệnh đề nào sau đây đúng? n n 2 2 2 2 3 n
A. Dãy số u bị chặn trên và không bị chặn dưới. n
B. Dãy số u bị chặn dưới và không bị chặn trên. n
C. Dãy số u bị chặn. n
D. Dãy số u không bị chặn. n Lời giải Chọn C
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 32
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com Ta có 1 1 1 1 u 0
u bị chặn dưới bởi 0. Mặt khác *
k , k 2 nên 2 n n k k 1 k k 1 k suy ra: 1 1 1 1 1 1 1 1 1 1 1 1 u
1 1 1 n 1.2 2.3 3.4 nn 1 2 2 3 2 4 n n 1 n 1
nên dãy u bị chặn trên, do đó dãy u bị chặn. n n
Câu 41: Trong các dãy số u sau đây, dãy số nào là dãy số bị chặn? n A. n 2 u n 1. B. 1 u n .
C. u 2n 1. D. u . n n n n n n 1 Lời giải Chọn D Các dãy số 2; ; 2n n n
dương và tăng lên vô hạn (dương vô cùng) khi n tăng lên vô hạn, nên các dãy 1 2 1; ; 2n n n
1 cũng tăng lên vô hạn (dương vô cùng), suy ra các dãy này n
không bị chặn trên, do đó chúng không bị chặn. Nhận xét: n 1 0 u 1 1. n n 1 n 1 GV: TR
Câu 42: Trong các dãy số u cho bởi số hạng tổng quát u sau, dãy số nào bị chặn? n n n Ầ A. 1 u . B. u 3 .
C. u n 1. D. 2 u n . n n n n n N 2 Đ ÌN Lời giải H C Ư Chọn A – 0834 Các dãy số 2; ; 3n n n
dương và tăng lên vô hạn (dương vô cùng) khi n tăng lên vô hạn 3321 nên các dãy 2; 1; 3n n n
cũng tăng lên vô hạn (dương vô cùng), suy ra các dãy này 33
không bị chặn trên, do đó chúng không bị chặn. Nhận xét: 1 1 0 u . n 2n 2 u 6
Câu 43: Cho dãy số
u , xác định bởi 1
. Mệnh đề nào sau đây đúng? n * u
6 u , n n 1 n A. 5 6 u . B. 6 u 3. C. 6 u 2. D. 6 u 2 3. n 2 n n n Lời giải Chọn D Ta có 5 u 12 3
2 nên loại các đáp án A, B, C 2 2 Nhận xét: Ta có
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 33
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com u 6 u 6 u 6 1 1 1 u 0 u 6. n n u 6 u u 0 u u n n 6 6 n 1 1 n 1 n
Ta chứng minh quy nạp u 2 3. n
u 2 3;u 2 3 u 6 u
6 2 3 6 6 2 3. 1 k k 1 k 1
Câu 44: Cho dãy số u , với u sin
. Khẳng định nào sau đây là đúng? n n n 1
A. Số hạng thứ n 1 của dãy là u sin . n 1 n 1
B. Dãy số u là dãy số bị chặn. n
C. Dãy số u là một dãy số tăng. n
D. Dãy số u không tăng không giảm. n Lời giải Chọn B u sin u sin sin A sai. n n 1 n 1 n 1 1 n 2 u sin
1 u 1 B đúng. n n 1 n GV: TR u u sin sin 0 0 C, D sai. n 1 n n 2 n 1 n 2 n 1 2 Ầ N Đ
Câu 45: Cho dãy số n u với u
Mệnh đề nào sau đây đúng? n 1 . n , ÌN H C
A. Dãy số u là dãy số tăng.
B. Dãy số u là dãy số giảm. n n Ư –
C. Dãy số u là dãy số bị chặn.
D. Dãy số u là dãy số không bị chặn. n n 0834 3321 Lời giải 33 Chọn C u
là dãy thay dấu nên không tăng, không giảm A, B sai. n n 1
Tập giá trị của dãy u là 1; 1
1 u 1 C đúng. n n 1 n
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 34
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com BÀI 2: CẤP SỐ CỘNG
A. TÓM TẮT KIẾN THỨC CƠ BẢN CẦN NẮM I. ĐỊNH NGHĨA
Cấp số cộng là một dãy số, trong đó kể từ số hạng thứ hai, mỗi số hạng đều bằng tổng của số
hạng đứng ngay trước nó với một số không đổi d , tức là: u u
d ( n 2). n n 1
Số d được gọi là công sai của cấp số cộng.
Nếu u là cấp số cộng với công sai d thì với số tự nhiên n 2 , ta có:u u d. n n n 1 Chú ý:
Khi d 0 thì cấp số cộng là một dãy số không đổi. II.SỐ HẠNG TỔNG QUÁT Nếu cấp số cộng (
) có số hạng đầu và công sai thì số hạng tổng quát được xác định bởi công thức: = + ( − 1) với ≥ 2. Nhận xét: Từ công thức = + ( − 1) , ta có: = + 1 với ≥ 2.
III. TỔNG n SỐ HẠNG ĐẦU CỦA MỘT CẤP SỐ CỘNG
Cho cấp số cộng u có số hạng đầu u và công sai d . Đặt S u u u u . Khi n 1 n 1 2 3 n GV: TR u u n 1 n đó: S . n 2 Ầ N Nhận xét: Đ ÌN
2u n 1 d n 1 H C
Do u u n 1 d nên u u 2u n 1 d . Suy ra S . 1 n 1 n 1 n Ư 2 – 0834
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP 3321
Dạng 1. Nhận dạng 1 dãy số là cấp số cộng 33 1. Phương pháp
Sử dụng định nghĩa u là một cấp số cộng khi và chỉ khi u u d, với d là một hằng số. n n 1 n
Để chứng minh dãy số u là một cấp số cộng, ta xét d u u n n 1 n
Nếu d là hằng số thì u là một cấp số cộng với công sai d. n
Nếu d phụ thuộc vào n thì u không là cấp số cộng. n
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1. Chứng minh các dãy số sau là cấp số cộng.
a) Dãy số u với u 2020n 2021. n n
b) Dãy số u với u 2 n 5. n n Hướng dẫn giải
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 35
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
a) Dãy số u với u 2020n 2021. n n Ta có u
u 2020 n 1 2021 2020n 2021 2020. n 1 n
Vậy u là một cấp số cộng với công sai d 2020. n
b) Dãy số u với u 2 n 5. n n Ta có u
u 2 n 1 5 2n 5 2. n 1 n
Vậy u là một cấp số cộng với công sai d 2 . n
Ví dụ 2. Chứng minh các dãy số sau không phải là cấp số cộng.
a) Dãy số u với 2
u n n 1. n n b) Dãy số n u với u n n 1 3 . n Hướng dẫn giải
a) Dãy số u với 2
u n n 1. n n Ta có u u n n
n n
n phụ thuộc vào n. n 2 1 1 1 2 1 2 2 n 1
Vậy u không là cấp số cộng. n b) Dãy số n u với u n n 1 3 . n n 1 n n n n GV: TR Ta có u u 1 3 n 1 1 3n 1 3 1
3 2 1 phụ thuộc vào n. n 1 n Ầ
Vậy u không là cấp số cộng. n N Đ ÌN H C
Dạng 2. Xác định số hạng , công sai và số hạng tổng quát của cấp số cộng Ư – 0834 1. Phương pháp 3321
Xác định một cấp số cộng là xác định số hạng đầu u và công sai d 1 33
Từ những giải thiết ta thường lập hệ phương trình theo ẩn số u và d rồi giải hệ đó. 1
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1: Cho cấp số cộng u có u 15 và d 2 . Tìm u . n 3 n Lời giải. 15
u u 2d u 19 Ta có 3 1 1
u u n 1 d 2 n 21. n 1 d 2 d 2
Ví dụ 2: Một cấp số cộng có 8 số hạng. Số hạng đầu là 5, số hạng thứ tám là 40. Khi đó công sai
d của cấp số cộng đó là bao nhiêu? Lời giải. u 5 Ta có: 1 d 5
40 u u 7d 8 1
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 36
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
Ví dụ 3: Cho cấp số cộng u
có u 123 và u u 84 . Tìm số hạng u . n 1 3 15 17 Lời giải. u u 84
Ta có công sai của cấp số cộng là 3 15 d 7 . 3 15 12
Suy ra u u (17 1)d 11 . 17 1
Ví dụ 4: Cho cấp số cộng u
có u 123 và u u 84 . Tìm số hạng u . n 1 3 15 17
Cho cấp số cộng u có u 2u 0 và S 14 . Tính số hạng đầu u và công sai d của cấp số n 1 5 4 1 cộng. Lời giải
Ta có u 2u 0 u 2(u 4d ) 0 3u 8d 0 . 1 5 1 1 1 4(2u 3d ) 1 S 14
14 2u 3d 7 4 1 2 3
u 8d 0 u 8 Ta có hệ phương trình 1 1 . 2u 3d 7 d 3 1
Dạng 3. Tính tổng các số hạng trong một cấp số cộng 1. Phương pháp GV: TR n u u n 2u n 1 d 1 n 1
Tính tổng n số hạng đầu tiên nhờ công thức: S n 2 2 Ầ N
2. Các ví dụ rèn luyện kĩ năng Đ ÌN
Ví dụ 1: Cho cấp số cộng u có u 4 và d 5. Tính tổng 100 số hạng đầu tiên của cấp số n 1 H C Ư cộng. – 0834 Lời giải 3321 n n 1 100.99 S nu d S 100u d 24350 n 1 100 1 33 2 2
Ví dụ 2: Xét các số nguyên dương chia hết cho 3. Tính tổng số 50 số nguyên dương đầu tiên Lời giải
Số nguyên dương chia hết cho 3 có dạng *
3n n nên chúng lập thành cấp số cộng u 3 1 50 u 3n S u u 3825 n 50 1 50 u 150 2 50 n n n 1 Chú ý: S u u nu d n . 1 n 1 2 2
Ví dụ 3: Tính tổng S 1 2 3 4 5 ... 2n
1 2n với n 1 và n . Lời giải Với mọi *
n thì 2n 1 2n 1.
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 37
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
Ta có S 1 2 3 4 5 6 2n
1 2n . Do đó ta xem S là tổng của n số
hạng, mà mỗi số hạng đều bằng 1 nên S . n
Nhận xét: Ta có 1;3;5;; 2n 1 và 2; 4;6;; 2n là các cấp số cộng có n số hạng nên
S 1 3 5 2n
1 2 4 6 2n n n
n n 2 n 2 1 2 1 2 2
n n . n 2 2
Ví dụ 4: Cho cấp số cộng u thỏa mãn u u u u 100. Tính tổng 16 số hạng đầu tiên của n 2 8 9 15 cấp số cộng đã cho. Lời giải
Ta có u u u u 100 4u 30d 100 2u 15d 50. 2 8 9 15 1 1 16 Khi đó S u u
8 2u 15d 8.50 400 16 1 16 1 2
Ví dụ 5: Cho cấp số cộng u có công sai d 3 và 2 2 2
u u u đạt giá trị nhỏ nhất. Tính tổng n 2 3 4 S
của 100 số hạng đầu tiên của cấp số cộng đó. 100 Lời giải
Đặt a u thì 1 GV: TR
u u u a d 2 a 2d 2 a 3d 2 3a 36a 126 3a 62 2 2 2 2 18 18 với mọi 2 3 4 Ầ N
a . Dấu bằng xảy ra khi a 6 0 a 6 .Suy ra u 6 . 1 Đ ÌN
100.2u 100 1 d 1 H Ta có S 1 4250 . C 100 2 Ư –
Ví dụ 5. Biết u u u u 224. Tính S . 0834 4 8 12 16 19 3321 Hướng dẫn giải
Ta có u u u u 224 33 4 8 12 16
u 3d u 7d u 11d u 15d 224 4u 36d 224 u 9d 56. 1 1 1 1 1 1 19 Ta có S
2u 18d 19 u 9d 19.56 1064. 19 1 1 2
Dạng 4: Giải phương trình ( tìm x trong cấp số cộng) 1. Phương pháp Ba số a, ,
b c (theo thứ tự đó) lập thành một cấp số cộng khi và chỉ khi a c 2 . b
Sử dụng các tính chất của cấp số cộng
2. Các ví dụ rèn luyện kĩ năng Ví dụ 1: Cho các số 4
;1;6; x theo thứ tự lập thành một cấp số cộng. Tìm . x Lời giải. Vì các số 4
;1;6; x theo thứ tự u ,u ,u , u lập thành cấp số cộng nên 1 2 3 4
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 38
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
u u u u
x 6 6 1 x 11 4 3 3 2
Ví dụ 2: Nếu các số 5 ; m 7 2 ;
m 17 m theo thứ tự lập thành cấp số cộng thì m bằng bao nhiêu? Lời giải. Ba số 5 ; m 7 2 ;
m 17 m theo thứ tự u ,u ,u lập thành cấp số cộng nên 1 2 3
u u 2u 5 m 17 m 2 7 2m m 4 1 3 2
Nhận xét: Ta có thể dùng tính chất u u u u . 3 2 2 1
Ví dụ 3: Với giá trị nào của x và y thì các số 7 ; ;
x 11; y theo thứ tự đó lập thành một cấp số công? Lời giải. Bốn số 7 ; ;
x 11; y theo thứ tự u ,u ,u , u lập thành cấp số cộng nên 1 2 3 4 u
u u u
y 11 11 x
x y 22 x 2 4 3 3 2
u u u u
y 11 x 7
x y 18 y 20 4 3 2 1
Dạng 5. Chứng minh một hệ thức trong cấp số cộng lập thành cấp số cộng, bài toán có sử
dụng yếu tố cấp số cộng 1. Phương pháp GV: TR
Nếu u là một cấp số cộng thì kể từ số hạng thứ hai, mỗi số hạng (trừ số hạng cuối cùng đối n Ầ
với cấp số cộng hữu hạn) đều là trung bình cộng của hai số hạng đứng kề nó trong dãy, tức là N Đ u u k 1 k 1 ÌN u . k H 2 C Ư
Hệ quả: Ba số a, ,
b c (theo thứ tự đó) lập thành một cấp số cộng khi và chỉ khi a c 2 . b – 0834
Sử dụng các tính chất của cấp số cộng 3321
2. Các ví dụ rèn luyện kĩ năng 33
Ví dụ 1: Chứng minh rằng ba số dương a, ,
b c theo thứ tự lập thành một cấp số cộng khi và chỉ 1 1 1 khi các số , ,
theo thứ tự lập thành một cấp số cộng. b c c a a b Lời giải.
Ta sẽ chứng minh bằng phép biến đổi tương đương. 1 1 1 Ba số , ,
lập thành cấp số cộng khi và chỉ khi b c c a a b 1 1 1 1 b a c b c a b c a b c a
( c a )( b c )
( a b )( c a )
( b a )( b a ) ( c b )( c b )
b a c b a, ,
b c theo thứ tự lập thành một cấp số cộng. Ví dụ 2. Cho a, ,
b c là ba số hạng liên tiếp của một cấp số cộng, chứng minh rằng
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 39
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com a) 2 2
a 2bc c 2a . b
b) a bc b c2 2 8 2 . Hướng dẫn giải Vì a, ,
b c là ba số hạng liên tiếp của một cấp số cộng nên a c 2b a 2b . c
a) Ta có a ab b c2 2
b c 2 2 2 2 2 2 2
.b 4b 4bc c 4b 2bc 2 = c 2b . c Vậy 2 2 2 2
a 2ab c 2bc a 2bc c 2a . b
b) Ta có a bc b c2 2 2 2 8 2
8bc 4b 4bc c 8bc
b bc c b c2 2 2 = 4 4 2 .
Ví dụ 3. Một tam giác vuông có chu vi bằng 3a và ba cạnh lập thành một cấp số cộng. Tính độ
dài ba cạnh của tam giác theo a. Hướng dẫn giải
Gọi x, y, z theo thứ tự là độ dài ba cạnh của tam giác x y z.
Chu vi của tam giác là x y z 3 . a 1
Theo tính chất của cấp số cộng, ta có x z 2 y. 2
Tam giác đã cho vuông nên 2 2 2
x y z . 3 GV: TR
Thay (2) và (1), ta được 3y 3a y . a
Thay y a vào (2), ta được x z 2a x 2a z. Ầ N Đ
Thay x 2a z và y a vào (3), ta được ÌN H C 5a 3a Ư 2a z2 2 2 2
a z 5a 4az 0 z x . – 4 4 0834 3a 5a
Vậy độ dài ba cạnh của tam giác là , a, . 3321 4 4 33
Ví dụ 4. Tìm tất cả các giá trị của tham số m để phương trình sau có ba nghiệm phân biệt lập
thành một cấp số cộng: 3 2
x mx m m 2 3 2
4 x 9m m 0 . Lời giải
- Điều kiện cần: Giả sử phương trình đã cho có ba nghiệm phân biệt x , x , x lập thành một cấp 1 2 3
số cộng. Theo định lý Vi-ét đối với phương trình bậc ba, ta có x x x 3m . Vì x , x , x lập 1 2 3 1 2 3
thành cấp số cộng nên x x 2x . Suy ra 3x 3m x m . Thay x m vào phương trình đã 1 3 2 2 2 2 cho, ta được m 0 3 2 m 3 .
m m 2m m 4 2 2
.m 9m m 0 m m 0 m 1 - Điều kiện đủ:
+ Với m 0 thì ta có phương trình 3
x 0 x 0 (phương trình có nghiệm duy nhất). Do đó
m 0 không phải giá trị cần tìm.
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 40
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
+ Với m 1, ta có phương trình 3 2
x 3x 6x 8 0 x 1; x 2; x 4.
Ba nghiệm 2; 1; 4 lập thành một cấp số cộng nên m 1 là giá trị cần tìm.
Ví dụ 5. Tìm giá trị của tham số m để phương trình sau có bốn nghiệm phân biệt lập thành một cấp số cộng: 4 2 2
x 10x 2m 7m 0 . Lời giải. Đặt 2
t x t 0 . Khi đó ta có phương trình: 2 2
t 10t 2m 7m 0 (*) .
Phương trình đã cho có 4 nghiệm phân biệt khi và chỉ khi phương trình (*) có 2 nghiệm dương 2 2 5
(2m 7m) 0 phân biệt 2
0 2m 7m 25. 2
2m 7m 0
(do tổng hai nghiệm bằng 10 0 nên không cần điều kiện này).
+ Với điều kiện trên thì (*) có hai nghiệm dương phân biệt là t , t (t t ) . 1 2 1 2
Khi đó phương trình đã cho có bốn nghiệm phân biệt là t ; t ; t ; t . 2 1 1 2
Bốn nghiệm này lập thành một cấp số cộng khi t t t t
t t t 9t . 1 2 1 1 2 1 2 1
Theo định lý Vi-ét ta có: 2
t t 10; t .t 2m 7m . 1 2 1 2 t 9t t 1 2 1 1 m 1
Suy ra ta có hệ phương trình t t 10 t 9 . 1 2 2 9 GV: TR m 2 2
t .t 2m 7m 2m 7m 9 2 1 2 Ầ N
C. GIẢI BÀI TẬP SÁCH GIÁO KHOA Đ ÌN H
Bài 1. Trong các dãy số sau, dãy số nào là cấp số cộng? Vì sao? C Ư 1 5 11 7 a) ; b) 10, 2 , 1 4, 2 6, 3 8 , , 2, , – 2 4 4 2 0834 c) 1, 2, 3, 4, 5 ; d) 1, 4, 7,10,13 . 3321 Lời giải 33 a)Ta có: 10; 2
; 14; 26; 38 là cấp số cộng có số hạng đầu u 10 và công sai của cấp số 1
cộng là: d 12 1 5 11 7 1 3 b) Ta có: ; ; 2; ;
là cấp số cộng có số hạng đầu là u và công sai d . 2 4 4 2 1 2 4 c)Ta có: 2 2 2 2 2
1 ; 2 ;3 ; 4 ;5 không là cấp số cộng vì 2 2 2 2 2 1 3 2 .
d) Ta có: 1; 4;7;10;13 là cấp số cộng có số hạng đầu là u 1 và công sai d 3 1
Bài 2. Trong các dãy số u với số hạng tổng quát sau, dãy số nào là cấp số cộng? Nếu là cấp n
số cộng, hãy tìm số hạng đầu u và công sai d . 1 3n 7
a) u 3 2n b) u c) u 3n . n n 5 n Lời giải a) Ta có: u
3 2 n 1 3 2n 2 1 2n n 1 Suy ra u
u 1 2n 3 3 . n 1 n
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 41
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
Vì vậy đây là một cấp số cộng có số hạng đầu u 1 và công sai d 2 . 1 3n 1 7 3n 10 b) Ta có: u n 1 5 5 3n 10 3n 7 3 Xét hiệu u u . n 1 n 5 5 5 3
Vì vậy đây là một cấp số cộng có số hạng đầu u 2 và công sai d . 1 5 c) Ta có: n 1 u 3 3.3n n 1 Xét hiệu u
u 3.3n 3n 2.3n . với * n n 1 n
Vì vậy đây không là một cấp số cộng.
Bài 3. Cho cấp số cộng u có số hạng đầu u 3
, công sai d 5 . n 1
a) Viết công thức của số hạng tổng quát u . n
b) Số 492 là số hạng thứ mấy của cấp số cộng trên?
c) Số 300 có là số hạng nào của cấp số cộng trên không? Lời giải
a) Ta có công thức số hạng tổng quát của cấp số cộng u là: u 3 (n 1 .5 ) 5n 8 . n 1 b) Xét u 492 n 5n 8 492 n 100 .
Vậy số 492 là số hạng thứ 100 của cấp số cộng trên. GV: TR c) Xét u 300 n 5n 8 300 Ầ N Đ n 61, 6 ÌN H
Vậy không tồn tại số hạng trong cấp số cộng bằng 300. C Ư
Bài 4. Cho cấp số cộng u có u 4,u 1. Tính u . n 1 2 10 – 0834 Lời giải 3321
Công sai của cấp số cộng u là d = u u 1 4 3 . n 2 1 33
Khi đó số hạng tổng quát của cấp số cộng là: u u n 1 d 4 n 1 (3) n 1
Suy ra u 4 10 1 3 31 . 10 1
Bài 5. Cho cấp số cộng u với u và u u u 1 . n 1 3 1 2 3
a) Tìm công sai d và viết công thức của số hạng tổng quát u . n
b) Số - 67 là số hạng thứ mấy của cấp số cộng trên?
c) Số 7 có phải là một số hạng của cấp số cộng trên không? Lời giải
a) Ta có: u u u 1 1 2 3
u u d u 2d 1 1 1 1
3u 3d 1 1 1 2 Mà u nên d 1 3 3
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 42
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com 1 2 2 1
Khi đó công thức tổng quát của cấp số cộng là: u n n với mọi * n N . n 1 3 3 3 3 2 1
b) Xét u n 6 7 n 3 3 2 202 n 3 3 n 101 Vậy số 67
là số hạng thứ 101 của dãy. c) Xét u 7 n 2 1 n 7 3 3 2 20 n 3 3 n 1 0
Vậy số 7 không phải là một số hạng trong cấp số cộng.
Bài 6. Tính tổng 100 số hạng đầu của dãy số u với u 0,3n 5 với mọi n 1. n n Lời giải Ta có: u
0, 3 n 1 5 0, 3n 5, 3 n 1 Xét hiệu u
u 0,3n 5, 3 0,3n 5 0,3 . GV: TR n 1 n
Do đó u là một cấp số cộng với số hạng đầu u 5,3 và công sai d 0,3. n 1 Ầ
Khi đó số hạng tổng quát của cấp số cộng un là: N
u 5, 3 n 1 .0, 3 n Đ ÌN Suy ra u
5, 3 100 1 0, 3 35 . 100 H C 1005,3 35 Ư
Vậy tổng của 100 số hạng đầu của dãy số là: S 2015 . 100 – 2 0834
Bài 7. Chiều cao (đơn vị: centimét) của một đứa trẻ n tuổi phát triển bình thường được cho bởi 3321 công thức: 33
x 75 5n 1 . n (Nguồn: https:///bibabo.vn)
a) Một đứa trẻ phát triển bình thường có chiều cao năm 3 tuổi là bao nhiêu centimét?
b) Dãy số x có là một cấp số cộng không? Trung bình một năm, chiều cao mỗi đứa trẻ phát n
triển bình thường tăng lên bao nhiêu centimét? Lời giải
a) Chiều cao 3 năm tuổi của một đứa bé phát triển bình thường là:
x 75 5 3 1 85 cm 3 b) Ta có: x
75 5 n 11 75 5n n 1 Xét hiệu x
x 75 5n 75 5 n 1 5 n 1 n
Do đó x là một cấp số cộng có số hạng đầu x 75 và công sai d 5 n 1
Bài 8. Khi kí kết hợp đồng lao động với người lao động, một doanh nghiệp đề xuất hai phương án
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 43
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com trả lương như sau:
Phương án 1: Năm thứ nhất, tiền lương là 120 triệu. Kể từ năm thứ hai trở đi, mỗi năm tiền
lương được tăng 18 triệu.
Phuơng án 2: Quý thứ nhất, tiền lương là 24 triệu. Kể từ quý thứ hai trở đi, mỗi quý tiền lương được tăng 1,8 triệu.
Nếu là người được tuyển dụng vào doanh nghiệp trên, em sẽ chọn phương án nào khi:
a) Kí hợp đồng lao động 3 năm?
b) Kí hợp đồng lao động 10 năm? Lời giải
+) Theo phương án 1: Gọi (un) là dãy số tiền lương của người lao động theo phương án 1 qua mỗi năm.
Dãy số u lập thành một cấp số cộng có số hạng đầu u 120 và công sai d 18 . n 1
Khi đó số hạng tổng quát của cấp số nhân là: u 120 n 1 18 . n
+) Theo phương án 2: Gọi v là dãy số tiền lương của người lao động theo phương án 2 qua n từng quý.
Dãy số v lập thành một cấp số cộng có số hạng đầu v 24 và công sai d 1,8 . n 1
Khi đó số hạng tổng quát của cấp số nhân là v 24 n 1 1,8 . n
a) Khi kí hợp đồng 3 năm tương đương với 12 quý ta có: GV: TR
+) Theo phương án 1: u 120 + (3 - 1).18 = 156 (triệu đồng) 3
Tổng số tiền lương nhận được sau 3 năm là: Ầ N Đ 3120 156 ÌN S 414 (triệu đồng). 3 H 2 C Ư
+) Theo phương án 2: u 24 12 1 1,8 43,8 . 12 – 0834
Tổng số tiền lương nhận được sau 3 năm tương ứng với 12 quý là: 3321 12 24 43,8 S 406,8 (triệu đồng). 12 2 33
Vậy nếu được tuyển dụng vào doanh nghiệp và kí hợp đồng lao động 3 năm thì nên theo phương án 1.
b) Khi kí hợp đồng 10 năm tương đương với 40 quý ta có:
+) Theo phương án 1: u 120 10 1 .18 282 (triệu đồng) 10 10 120 282
Tổng số tiền lương nhận được sau 10 năm là: S 2010 (triệu đồng). 10 2
+) Theo phương án 2: u 24 40 1 1,8 94, 2 (triệu đồng). 40 40 24 94, 2
Tổng số tiền lương nhận được sau 10 năm tương ứng với 40 quý là: S 2364 12 2 (triệu đồng).
Vậy nếu được tuyển dụng vào doanh nghiệp và kí hợp đồng lao động 10 năm thì nên theo phương án 2.
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 44
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com D. BÀI TẬP TRẮC NGHIỆM
Câu 1: Dãy số nào sau đây không phải là cấp số cộng? 2 1 1 2 4 A. ; ;0; ; ;1; .... B. 15 2;12 2;9 2;6 2;.... 3 3 3 3 3 4 7 9 11 1 2 3 4 3 5 C. ;1; ; ; ;.... D. ; ; 3; ; ;... 5 5 5 5 3 3 3 3 Lời giải Chọn C
Chỉ cần tồn tại hai cặp số hạng liên tiếp của dãy số có hiệu khác nhau: u u u u m 1 m k 1 k
thì ta kết luận ngay dãy số đó không phải là cấp số cộng. Xét đáp án A: 2 1 1 2 4 1 ; ;0; ; ;1; ....
u u u u u u loại A 2 1 3 2 4 3 3 3 3 3 3 3 Xét đáp án B: 15 2;12 2;9 2; 6 2;....
3 3 u u u u u u loại B 2 1 3 2 4 3 Xét đáp án C: 4 7 9 11 1 2 ;1; ; ; ;....
u u
u u Chọn C 2 1 3 2 5 5 5 5 5 5 Xét đáp án D: 1 2 3 4 3 5 3 ; ; 3; ; ;...
u u u u u u loại D 2 1 3 2 4 3 3 3 3 3 3 GV: TR 1 1
Câu 2: Cho cấp số cộng có số hạng đầu u , công sai d . Năm số hạng liên tiếp đầu 1 Ầ 2 2 N Đ
tiên của cấp số này là: ÌN H 1 1 1 1 1 1 3 5 1 1 3 C A. ;0;1; ;1. B. ;0; ;0; . C. ;1; ; 2; . D. ;0; ;1; . Ư 2 2 2 2 2 2 2 2 2 2 2 – 0834 Lời giải 3321 Chọn D 33 1 1 n
Ta dùng công thức tổng quát
u u n 1 d n 1 1 , hoặc n 1 2 2 2 1 u
u d u để tính các số hạng của một cấp số cộng. n 1 n n 2 1 u 1 2
u u d 0 2 1 Ta có 1 1 1
u ; d u
u d 1 3 2 2 2 2
u u d 1 4 3 3 u
u d 5 4 2
Nhận xét: Dùng chức năng “lặp” của MTCT để tính: Nhập: 1 X X
(nhập X X d ). 2
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 45
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com Bấm CALC: nhập 1 (nhập u ). 2 1
Để tính 5 số hạng đầu ta bấm dấu “=” liên tiếp để ra kết quả 4 lần nữa!
Câu 3: Viết ba số hạng xen giữa các số 2 và 22 để được một cấp số cộng có năm số hạng. A. 7; 12; 17, B. 6; 10; 14. C. 8; 13; 18. D. 6; 12; 18. Lời giải Chọn A
Giữa 2 và 22 có thêm ba số hạng nữa lập thành cấp số cộng, xem như ta có một cấp số
cộng có 5 số hạng với u 2; u 22; ta cần tìm u , u , u . 1 5 2 3 4 u
u d 7 2 1 Ta có u u 22 2 5 1
u u 4d d 5 u
u 2d 12 5 1 3 1 4 4
u u 3d 17 4 1
Câu 4: Cho hai số 3 và 23. Xen kẽ giữa hai số đã cho n số hạng để tất cả các số đó tạo thành
cấp số cộng có công sai d 2. Tìm n. A. n 12. B. n 13. C. n 14. D. n 15. Lời giải Chọn A GV: TR
Theo giả thiết thì ta được một cấp số cộng có n 2 số hạng với u 3, u 23. 1 n2 u u 23 3 Ầ Khi đó u
u n 1 d n 1 n
13 n 12 A n2 1 2 1 N d 2 Đ ÌN H
Câu 5: Biết các số 1 2 3
C ; C ; C theo thứ tự lập thành một cấp số cộng với n 3. Tìm n. C n n n Ư – A. n 5. B. n 7. C. n 9. D. n 11. 0834 Lời giải 3321 Chọn B 33 Ba số 1 2 3
C ; C ; C theo thứ tự u , u , u lập thành cấp số cộng nên n n n 1 2 3
n2n 1 n n 1 n 1 3 2
u u 2u C C 2C
n 3 n 2. 1 3 2 n n n 6 2 2 n 3n 2 n 2 2 1 n 1
n 9n 14 n 7n 3 . 6 n 7
Nhận xét: Nếu u , u , u
là ba số hạng liên tiếp của một cấp số cộng thì ta có k 1 k k 1 u u 2u . k 1 k 1 k
Câu 6: Cho cấp số cộng u có các số hạng đầu lần lượt là 5; 9; 13; 17; . Tìm số hạng tổng n
quát u của cấp số cộng. n
A. u 5n 1.
B. u 5n 1.
C. u 4n 1.
D. u 4n 1. n n n n Lời giải
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 46
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com Chọn C
Các số 5; 9; 13; 17; theo thứ tự đó lập thành cấp số cộng u nên n u 5 1 CTTQ
u u n
1 d 5 4n 1 4n 1 n 1
d u u 4 2 1 1
Câu 7: Cho cấp số cộng u có u 3 và d . Khẳng định nào sau đây đúng? n 1 2 1 1 A. u 3 n B. u 3 n 1. n 1 . 2 n 2 1 1 C. u 3 n D. u 3 n n 1 . n 1 . 2 4 Lời giải Chọn C u 3 1 Ta có CTTQ 1 1
u u n1 d 3 n 1 n 1 d 2 2
Câu 8: Trong các dãy số được cho dưới đây, dãy số nào là cấp số cộng? 7 A. u 7 3 . n B. u 7 3 . n C. u . D. u 7.3 . n n n n 3n n GV: TR Lời giải Chọn A Ầ N Đ
Dãy u là cấp số cộng u an b ( a,b là hằng số). n n ÌN H C
Câu 9: Trong các dãy số được cho dưới đây, dãy số nào là cấp số cộng? Ư – n u 1 u 1 0834 A. u n B. u sin . C. 1 . D. 1 . n 1 2 1 . n n u u 1 u 2u n n 1 n n 1 3321 Lời giải 33 Chọn C
Dãy u là một cấp số cộng u u d ( d là hằng số). n n n 1
Câu 10: Trong các dãy số được cho dưới đây, dãy số nào không phải là cấp số cộng?
A. u 4n 9. B. u 2 n 19.
C. u 2n 21. D. u 2n 15. n n n n Lời giải Chọn D
Dãy số u 2n 15 không có dạng an b nên có không phải là cấp số cộng. n
Câu 11: Cho cấp số cộng u có u 5 và d 3. Mệnh đề nào sau đây đúng? n 1 A. u 34. B. u 45. C. u 31. D. u 35. 15 15 13 10 Lời giải
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 47
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com Chọn C u 37 15 u 5 1
u 3n8 u 31 n 13 d 3 u 22 10 1 1
Câu 12: Cho cấp số cộng u có u và d . Gọi S là tổng 5 số hạng đầu tiên của cấp n 1 4 4 5
số cộng đã cho. Mệnh đề nào sau đây đúng? 5 4 5 4 A. S . B. S . C. S . D. S . 5 4 5 5 5 4 5 5 Lời giải Chọn A 1 u 1 4 5.4 1 1 5 S 5u d 5. 10. 5 1 1 2 4 4 4 d 5
Câu 13: Cho cấp số cộng u có d 2 và S 72. Tìm số hạng đầu tiên u . n 8 1 1 1 A. u 16. B. u 16. C. u . D. u . 1 1 1 16 1 16 Lời giải GV: TR Chọn A Ầ d 2 N Đ 8.7 72 8u 28. 2 u 16 1 1 ÌN 72 S 8u d 8 1 H 2 C Ư
Câu 14: Một cấp số cộng có số hạng đầu là 1, công sai là 4, tổng của n số hạng đầu là 561. Khi – 0834
đó số hạng thứ n của cấp số cộng đó là u có giá trị là bao nhiêu? n 3321 A. u 57. B. u 61. C. u 65. D. u 69. n n n n 33 Lời giải Chọn C u 1, d 4 1 2 nn n n 2 1 561 n
.4 2n n 561 0 n 17. 5
61 S nu d 2 n 1 2
u u u 16d 116.4 65 C n 17 1
Câu 15: Một cấp số cộng có 12 số hạng. Biết rằng tổng của 12 số hạng đó bằng 144 và số hạng
thứ mười hai bằng 23. Khi đó công sai d của cấp số cộng đã cho là bao nhiêu? A. d 2. B. d 3. C. d 4. D. d 5. Lời giải Chọn A
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 48
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com u 11d 23 u 1 1 1 u 23 12 1 2 u S 144 u u 23 1 144 d 2 12 1 12 2 11 2 3n 19n
Câu 16: Tổng n số hạng đầu tiên của một cấp số cộng là S với *
n . Tìm số hạng n 4
đầu tiên u và công sai d của cấp số cộng đã cho. 1 A. 1 3 3 5 1
u 2; d .
B. u 4; d .
C. u ; d 2.
D. u ; d . 1 2 1 2 1 2 1 2 2 Lời giải Chọn B 2 2 n n n n d d Ta có 3 19 3 19 2 2 n
n S nu d n u n n 1 1 4 4 4 2 2 2 d 3 u 4 1 2 4 3 . d 19 d u 1 2 2 4
Câu 17: Tổng n số hạng đầu tiên của một cấp số cộng là 2
S n 4n với *
n . Tìm số hạng n
tổng quát u của cấp số cộng đã cho. n n 1 8 A. u 2n 3.
B. u 3n 2. C. n 1 u 5.3 . D. u 5. . n n n n GV: TR 5 Lời giải Ầ N Đ Chọn A ÌN H C d 1 Ư d d
n n S n 2 – Ta có 2 2 4 u n n 1 0834 2 2 d u 4 1 2 3321 u 5 1
u 2n 3 33 d 2 n
Câu 18: Cho cấp số cộng u có u 2001 và u 1995 . Khi đó u bằng: n 2 5 1001 A. u 4005. B. u 4003. C. u 3. D. u 1. 1001 1001 1001 1001 Lời giải Chọn C
2001 u u d u 2003 2 1 1 u
u 1000d 3 1001 1 19
95 u u 4d d 2 5 1
Câu 19: Cho cấp số cộng u , biết: u 1,u
8 . Tính công sai d cảu cấp số cộng đó. n n n 1 A. d 9. B. d 7. C. d 7. D. d 9. Lời giải Chọn D
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 49
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com d u u 8 1 9 n 1 n un .
Câu 20: Cho cấp số cộng
Hãy chọn hệ thức đúng trong các hệ thức sau: u u u .u 10 20 u u . 10 30 u . 5 10 20 A. 2 B. u u 2u . u .u u . 90 210 150 C. 10 30 20 D. 2 Lời giải Chọn B u u
u 9d u 29d 10 30 1 1 Xét đáp án A: u 19d 1 2 2 loại u
u u 4d u 9d 2u 13d 5 10 1 1 2 u u
2u 298d 2 u 149d 90 210 2 1 Xét đáp án B:
2u 2 u 159d 150 1
Nhận xét: Có thể lấy một cấp số cộng cụ thể để kiểm tra, ví dụ u n * n . n
Câu 21: Cho cấp số cộng u thỏa mãn u u 60. Tính tổng S của $24$ số hạng đầu tiên n 2 23 24
của cấp số cộng đã cho. A. S 60. B. S 120. C. S 720. D. S 1440. 24 24 24 24 Lời giải GV: TR Chọn C u u
60 u du 22d 60 2u 23d 60. 2 23 1 1 1 Ầ N Đ Khi đó 24 S u u
12 u u 23d 12 2u 23d 12.60 720. 24 1 24 1 1 1 ÌN 2 H C Ư
Câu 22: Một cấp số cộng có 6 số hạng. Biết rằng tổng của số hạng đầu và số hạng cuối bằng – 0834
17; tổng của số hạng thứ hai và số hạng thứ tư bằng 14. Tìm công sai d của câp số 3321 cộng đã cho. A. d 2. B. d 3. C. d 4. D. d 5. 33 Lời giải Chọn B u u 17
2u 5d 17 u 16 1 6 1 1 u u 14
2u 6d 14 d 3 2 4 1 u u 8
Câu 23: Cho cấp số cộng u thỏa mãn 7 3
. Tìm công sai d của câp số cộng đã cho. n u u 75 2 7 1 1 A. d . B. d . C. d 2. D. d 3. 2 3 Lời giải Chọn C
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 50
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com u u 8
u 6d u 2d 8 d 2 7 3 1 1 u u 75
u d u 6d 75
u 2 u 12 75 2 7 1 1 1 1 u u 26
Câu 24: Cho cấp số cộng u thỏa mãn 1 7
. Mệnh đề nào sau đây đúng? n 2 2 u u 466 2 6 u 13 u 10 u 1 u 13 A. 1 . B. 1 . C. 1 . D. 1 . d 3 d 3 d 4 d 4 Lời giải Chọn C u u 26 2
u 6d 26 u 133d (1) Ta có 1 1 1 7 . u u 466
u d2 u 5d2 466
u d 2 u 5d 2 2 2 466 2 2 6 1 1 1 1
Thay (1) và (2) ta được: d2 d2 2 13 2 13 2
466 8d 338 466
d 4 u 1 1
d 4 u 25 1 u
u u 15
Câu 25: Cho cấp số cộng u thỏa mãn 1 3 5
. Chọn khẳng định đúng trong các khẳng n u u 27 1 6 định sau? u 21 u 21 u 18 u 21 GV: TR A. 1 . B. 1 . C. 1 . D. 1 . d 3 d 3 d 3 d 4 Ầ N Lời giải Đ ÌN Chọn B H C Ư
u u u 15
u u 2d u 4d 15
u 2d 15 u 21 1 3 5 1 1 1 1 1 – Ta có . u u u d 0834 27
u u 5d 27 2 5 27 d 3 1 6 1 1 1 3321 u
u u 36
Câu 26: Cho cấp số cộng u thỏa 2 4 6
. Tìm công sai d của cấp số cộng u biết n n 33 u u 54 2 3 d 10. A. d 3. B. d 4. C. d 5. D. d 6. Lời giải Chọn A u
u u 36
u d u 3d u 5d 36 2 4 6 1 1 1 Ta có u u 54
u d u 2d 54 2 3 1 1 u 3d 12 1 1 Từ
. Thay vào 2 , ta được . 1 suy ra u 12 3d
u d u 2d 54 2 1 1 1
d d 2 12 2 12
54 d 18d 45 0 d 3 hoặc d 15 . u
u u 27
Câu 27: Cho cấp số cộng u thỏa 1 2 3 . Tính u . n 2 2 2 2 u
u u 275 1 2 3
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 51
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com A. u 3. B. u 6. C. u 9. D. u 12. 2 2 2 2 Lời giải Chọn C u
u u 27 u
u d u 2d 27 1 1 1 Ta có 1 2 3 2 2 2 2 u
u u 275 1 2 3 u u d u 2d 275 1 1 2 1 2 u d 9 1 1 . u
u d2 u 2d2 2 275 2 1 1 1 Từ
1 suy ra d 9 u . Thay vào 2 , ta được 1
u u 9 u 2 2
u 29u 2 2
275 u 18u 65 0 u 13 u 5 . 1 1 1 1 1 1 1 1 hoặc 1 u 13 u 5 Vậy 1 hoặc 1
u u d 9 d 4 2 1 d 4
Câu 28: Tính tổng T 15 20 25 ... 7515. A. T 5651265. B. T 5651256. C. T 5651625. D. T 5651526. Lời giải Chọn A
Ta thấy các số hạng của tổng T tạo thành một cấp số cộng với số hạng đầu u 15 và 1 GV: TR công sai d 5. Ầ
Giả sử tổng trên có n số hạng thì u 7515 n N Đ ÌN
u n 1 d 7515 15 n 1 5 7515 n 1501 . 1 H C Ư
2u 1500d .1501 2.15 1500.5 .1501 1 Vậy T S 5651265 1501 – 2 2 0834 Câu 29: Tính tổng 2 2 2 2 2 2
T 1000 999 998 997 ... 2 1 . 3321 A. T 500500. B. T 500005. C. T 505000. D. T 500050. 33 Lời giải Chọn A
Ta có T 1.1000 9991.998 997...1.2
1 1999 1995 ... 3.
Ta thấy các số hạng của tổng T tạo thành một cấp số cộng với số hạng đầu u 1999 1 và công sai d 4.
Giả sử tổng trên có n số hạng thì
u 3 u n
1 d 3 1999 n
1 4 3 n 500. n 1 u u .500 1999 3 .500 1 500 Vậy T S 500500 500 2 2
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 52
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
Câu 30: Cho cấp số cộng u ; u ; u ; ; u có công sai $d,$ các số hạng của cấp số cộng đã cho 1 2 3 n 1 1 1 1
đều khác $0.$ Với giá trị nào của d thì dãy số ; ; ; ; là một cấp số cộng? u u u u 1 2 3 n A. d 1. B. d 0. C. d 1. D. d 2. Lời giải Chọn B 1 1 d u
u d u u u u Ta có 2 1 2 1 1 2 . u u d 1 1 d 3 2 u u u u 3 2 2 3
Theo yêu cầu bài toán thì ta phải có 1 1 1 1 u u u u 2 1 3 2 d 0 d 0 1 1 d 0
u u u 2d 1 3 1 u u 1 3
Câu 31: Ba góc của một tam giác vuông tạo thành cấp số cộng. Hai góc nhọn của tam giác có số đo (độ) là: A. 20 và 70 . B. 45 và 45 . C. 20 và 45 . D. 30 và 60 . GV: TR Lời giải Chọn D Ầ N Đ Ba góc ,
A B, C của một tam giác vuông theo thứ tự đó ( A B C ) lập thánh cấp số cộng ÌN H
nên C 90, C A 2B . C Ư A B C 180 3B 180 B 60 – 0834 Ta có
A C 2B
AC 2B A 30 C 90 C 90 C 90 3321 33 Câu 32: Ba góc ,
A B, C A B C của tam giác tạo thành cấp số cộng, biết góc lớn nhất gấp
đôi góc bé nhất. Hiệu số đo độ của góc lớn nhất với góc nhỏ nhất bằng: A. 40 . B. 45 . C. 60 . D. 80 . Lời giải Chọn A Ba góc ,
A B, C của một tam giác theo thứ tự đó lập thành cấp số cộng thỏa yêu cầu, thì C 2 ,
A C A 2B . Ta có 0 0 0 0
A B C 180 3 B 180 B 60 A 40 0 0 0
A C 2B
A C 2B A C 120 B 60
C A 40 . 0 C 2A C 2A C 2A C 80
Câu 33: Một tam giác vuông có chu vi bằng 3 và độ dài các cạnh lập thành một cấp số cộng. Độ
dài các cạnh của tam giác đó là:
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 53
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com 1 3 1 5 3 5 1 7 A. ; 1; . B. ; 1; . C. ; 1; . D. ; 1; . 2 2 3 3 4 4 4 4 Lời giải Chọn C
Ba cạnh a, b, c a b c của một tam giác theo thứ tự đó lập thành một cấp số cộng thỏa 2 2 2 2 2 2 2 2 2
a b c
a b c
a b c yêu cầu thì
a b c 3 3 b 3 b 1 .
a c 2b
a c 2b
a 2bc 2c 3 a 4 Ta có b a b c 2c2 5 2 2 2 1 2
1 c 4c 5 0 c b 1 . a2c 4 5 c 4
Câu 34: Một rạp hát có 30 dãy ghế, dãy đầu tiên có 25 ghế. Mỗi dãy sau có hơn dãy trước 3 ghế.
Hỏi rạp hát có tất cả bao nhiêu ghế? A. 1635. B. 1792. C. 2055. D. 3125. Lời giải Chọn C GV: TR
Số ghế của mỗi dãy (bắt đầu từ dãy đầu tiên) theo thứ tự đó lập thành một cấp số cộng
có 30 số hạng có công sai d 3 và u 25. 1 Ầ N 30.29 Đ
Tổng số ghế là S u u u 30u d 2055 30 1 2 30 1 ÌN 2 H C Câu 35: Ư
Người ta trồng 3003 cây theo một hình tam giác như sau: hàng thứ nhất trồng 1 cây, – 0834
hàng thứ hai trồng 2 cây, hàng thứ ba trồng 3 cây,.Hỏi có tất cả bao nhiêu hàng cây? A. 73. B. 75. C. 77. D. 79. 3321 Lời giải. 33 Chọn C
Số cây mỗi hàng (bắt đầu từ hàng thứ nhất) lập thành một cấp số cộng u có n
u 1, d 1. Giả sử có n hàng cây thì u u u 3003 S . 1 1 2 n n nn 1 Ta có 2
3003 S nu
d n n 6006 0 n 77 n 1 2
Câu 36: Một chiếc đồng hồ đánh chuông, kể từ thời điểm 0 (giờ) thì sau mỗi giờ thì số tiếng
chuông được đánh đúng bằng số giờ mà đồng hồ chỉ tại thời điểm đánh chuông. Hỏi một
ngày đồng hồ đó đánh bao nhiêu tiếng chuông? A. 78. B. 156. C. 300. D. 48. Lời giải Chọn C
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 54
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
Kể từ lúc 1 (giờ) đến 24 (giời) số tiếng chuông được đánh lập thành cấp số cộng có 24 số
hạng với u 1, công sai d 1. Vậy số tiếng chuông được đánh trong 1 ngày là: 1 24 S S u u 12 1 24 300 24 1 24 2
Câu 37: Trên một bàn cờ có nhiều ô vuông, người ta đặt 7 hạt dẻ vào ô đầu tiên, sau đó đặt tiếp
vào ô thứ hai số hạt nhiều hơn ô thứ nhất là 5, tiếp tục đặt vào ô thứ ba số hạt nhiều hơn
ô thứ hai là 5,… và cứ thế tiếp tục đến ô thứ n . Biết rằng đặt hết số ô trên bàn cờ người
ta phải sử dụng 25450 hạt. Hỏi bàn cờ đó có bao nhiêu ô vuông? A. 98. B. 100. C. 102. D. 104. Lời giải Chọn B
Số hạt dẻ trên mỗi ô (bắt đầu từ ô thứ nhất) theo thứ tự đó lập thành cấp số cộng u n
có u 7, d 5. Gọi n là số ô trên bàn cờ thì u u u 25450 S . Ta có 1 1 2 n n nn 2 1 n n
25450 S nu d 7n .5 n 1 2 2 2
5n 9n 50900 0 n 100
Câu 38: Một gia đình cần khoan một cái giếng để lấy nước. Họ thuê một đội khoan giếng nước GV: TR
đến để khoan giếng nước. Biết giá của mét khoan đầu tiên là 80.000 đồng, kể từ mét
khoan thứ 2 giá của mỗi mét khoan tăng thêm 5000 đồng so với giá của mét khoan trước Ầ N
đó. Biết cần phải khoan sâu xuống 50m mới có nước. Vậy hỏi phải trả bao nhiêu tiền Đ ÌN
để khoan cái giếng đó? H C Ư A. 5.2500.000 đồng.
B. 10.125.000 đồng. C. 4.000.000 đồng. D. 4.245.000 đồng. – 0834 Lời giải 3321 Chọn B 33
Giá tiền khoang mỗi mét (bắt đầu từ mét đầu tiên) lập thành cấp số cộng u có n
u 80 000, d 5000. Do cần khoang 50 mét nên tổng số tiền cần trả là 1 50.49
u u u S 50u
d 50.80 000 1225.5000 10125 000 1 2 50 0 5 1 2 BÀI 3: CẤP SỐ NHÂN
A. TÓM TẮT KIẾN THỨC CƠ BẢN CẦN NẮM I. ĐỊNH NGHĨA
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 55
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
Cấp số nhân là một dãy số, trong đó kể từ số hạng thứ hai, mỗi số hạng đều bằng tích của
số hạng đứng ngay trước nó với một số không đổi q , tức là: u u .q n 2 . n n 1
Số q được gọi là công bội của cấp số nhân.
Nếu u là cấp số nhân với công bội q và u 0 với mọi n 1 thì với số tự nhiên n 2 , ta n n u có: n . q un 1 Chú ý:
Khi q 1 thì cấp số nhân là một dãy số không đổi. II. SỐ HẠNG TỔNG QUÁT
Nếu cấp số nhân u có số hạng đầu u và công bội q thì số hạng tổng quát u được xác n 1 n định bởi công thức: n 1 u u q n 2 . n 1
III. TỔNG n SỐ HẠNG ĐẦU CỦA MỘT CẤP SỐ NHÂN
Cho cấp số nhân u có số hạng đầu u và công bội q 1. n 1 u 1 n q 1
Đặt S u u u u . Khi đó: S . n 1 2 3 n n 1 q
Chú ý: Nếu q 1 thì S nu . n 1 GV: TR
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP Ầ
Dạng 1. Chứng mình một dãy số là cấp số nhân N Đ ÌN 1. Phương pháp H C
Xác định một cấp số nhân là xác định số hạng đầu u1 và công bội q Ư –
Từ những giải thiết ta thường lập hệ phương trình theo ẩn số u1 và q rồi giải hệ đó. 0834
2. Các ví dụ rèn luyện kĩ năng 3321 u 2
Ví dụ 1: Cho dãy số 1 . 33 n u xác định bởi u
4u 9, n 1 1 n n
a) Chứng minh dãy số v với v u 3 , n 1 là một cấp số nhân. n n n
b) Tìm công thức tổng quát của dãy số n u . Lời giải v
4u 9 3 4u 3
a) Ta có v u 3 , suy ra v u u n 1 n n . Do đó . n n 1 1 3 4 9 3 n n n 4 v u 3 u 3 n n n
Vậy v là cấp số nhân với số hạng đầu v u và công bội . n 1 1 3 2 3 5 q 4 b) Do v
v là cấp số nhân với 1 5
nên số hạng tổng quát của n 1 n 1 . n v v q q 4 n 1. 5.4
Suy ra công thức tổng quát của dãy số n . n u là 1 u v 3 5.4 3 n n
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 56
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
Ví dụ 2: Xét trong các dãy số số sau, dãy số nào là cấp số nhân, (nếu có) tìm công bối của cấp số nhân đó: a). 2 1 u ( 3) n b). n 3n2 u ( 1 ) .5 n n u 3 u 2 1 c). 1 d). 9 2 u u u n 1 n n 1 u n Lời giải 2n3 u (3) a). Ta có n 1 2
(3) 9 (không đổi). Kết luận u là cấp số nhân với công n 2n 1 u (3) n bội q 9 . n 1 3( n 1 )2 u (1) .5 b). Ta có n 1 3
1.5 125 (không đổi). Kết luận u là cấp số nhân n n 3n2 u (1) .5 n
với công bội q 125 . u 4 u 256 c). Ta có 2 u u 4 , 2
u u 16 , 2
u u 256 , suy ra 2 2 và 4 16 2 1 3 2 4 3 u 2 u 16 1 3 u u 2 4
. Do đó u không là cấp số nhân. n u u 1 3 9 GV: TR u u u d). n 1 n n 1 u u , n 2 . Do đó có: n 1 n 1 u 9 u n n Ầ u N n 1 Đ ÌN
u u u .... u .... (1) 1 3 5 2n 1 H C
Và u u u .... u ... (2) Ư 2 4 6 2n – 0834 9
Theo đề bài có u 3 u 3 (3) 1 2 u1 3321
Từ (1), (2),(3) suy ra u u u u u .... u u
.... Kết luận u là cấp số n 1 2 3 4 5 2n 2n 1 33
nhân với công bội q 1. u 2
Ví dụ 3: Cho dãy số u được xác định bởi 1 , n
1. Chứng minh rằng dãy số v n n u 4u 9 n 1 n
xác định bởi v u 3, n
1 là một cấp số nhân. Hãy xác định số hạng đầu và công bội của cấp n n số nhân đó. Lời giải
Vì có v u 3 (1) v u 3 (2) . n n n 1 n 1 Theo đề u
4u 9 u
3 4 u 3 (3). n 1 n n 1 n v
Thay (1) và (2) vào (3) được: n 1 v 4v , n 1
4 (không đổi). Kết luận v là n n 1 n vn
cấp số nhân với công bội q 4 và số hạng đầu v u 3 5 . 1 1
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 57
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
Ví dụ 4: Cho x, 3, y theo thứ tự lập thành cấp số nhân và 4
x y 3. Tìm x, y. Lời giải 9 Ta có: .
x y 9 y x 9 4 5 Thay vào 4 4
x y 3 x 3 5 x 5 3
. 3 x 3 x 3 x 9 x 3 y 3 3. Kết luận 3 y 3 3
Dạng 2. Xác định các số hạng của cấp số nhân, tổng của cấp số nhân 1. Phương pháp
Dựa vào giả thuyết, ta lập một hệ phương trình chứa công bội q và số hạng đầu u , giải hệ 1
phương trình này tìm được q và u . 1
Để xác định số hạng thứ k, ta sử dụng công thức: 1 u u . k q . k 1 1 n q
Để tính tổng của n số hạng, ta sử dụng công thức: S u .
, q 1 . Nếu q 1 thì n 1 1 q GV: TR
u u u ... u , do đó S nu . 1 2 3 n n 1
2. Các ví dụ rèn luyện kĩ năng Ầ N Đ ÌN
Ví dụ 1: Tìm số hạng đầu và công bội của cấp số nhân, biết: H C u u 51 u
u u 135 u 6 Ư a) 1 5 b) 1 2 3 c) 2 – u u 102
u u u 40 S 43. 2 6 4 5 6 3 0834 3321 Lời giải 4 4 33 u 1 q 51 * u u 51 u u q 51 1 1 5 1 1 a). 5 u u 102 u
q u q 102 u q 4 2 6 1 1 1 q 102 ** 1 ** u q 4 1 q 1 102 51 51 Lấy
q 2 u 3. * 1 u 4 1 q 51 4 1 q 17 1
Kết luận có công bội q 2 và số hạng đầu tiên u 3. 1
Kết luận: u 3 và q 2 1 2 u
u u 135 u
u q u q 135 b) 1 2 3 1 1 1 3 4 5
u u u 40 4 5 6 u
.q u q u q 40 1 1 1
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 58
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com u 2 1 q q 135 * 1 3 u q 2 1 q q 40 ** 1 ** 3 u q 2 1 q q 1 40 8 2 Lấy 3 q q * u 2 1 q q 135 27 3 1 135 1215 u . 1 2 1 q q 19 2 1215
Kết luận có công bội q
và số hạng đầu tiên u . 3 1 19 u 6 u q 6 u q 6 c) 2 1 1 2 S 43
u u u 43 u
u q u q 43 3 1 2 3 1 1 1 u q 6 * 1 * u q 6 1 . Lấy u 2 2 1 q q 43 ** * *
u 1 q q 43 1 1 1 q 2 43
6 1 q q 2
6q 37q 6 0 q 6 q 6 GV: TR 1
Với q 6 u 1. Với q u 36. 1 1 6 Ầ N Đ 1 ÌN q 6 q Kết luận hoặc 6 H C u 1 1 Ư u 36 1 – 0834 u u 51
Ví dụ 2: Cho CSN u có các số hạng thỏa: 1 5 n
u u 102 3321 2 6
a). Tìm số hạng đầu và công bội của CSN. 33
b). Hỏi tổng bao nhiêu số hạng đầu tiên bằng 3069?
c). Số 12288 là số hạng thứ mấy? Lời giải 4 4 u u 51 u u q 51 u
(1 q ) 51 (*) a). Ta có 1 5 1 1 1 5 4 u u 102 2 6 u
q u q 102 u
q(1 q ) 102 (**) 1 1 1 4 (**) u q(1 q ) 102 Lấy 1
q 2 u 3 . 4 1 (*) u (1 q ) 51 1
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 59
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com 1 n q 1 2n
b). Có S 3069 u . 3069 3.
3069 2n 1024 n 10 . Kết luận n 1 1 q 1 2
tổng của 10 số hạng đầu tiên bằng 3069. c).Có k 1 k 1 k 1 12
u 12288 u .q 12288 3.2 12288 2 4096 2 k 1
k 1 12 k 13 . Kết luận số 12288 là số hạng thứ 13.
Ví dụ 3: Cho cấp số nhân u . Tìm u và q, biết rằng: n 1 35
u u u 2 3 4 2
u u u 65 u
u u 42 1) u u 25 2) 1 3 5 3) 2 4 6 1 5 u u 325. u u 20 1 7 3 5
u 0i 1,...,5 i u
u u u 15
4) u u 165;u u 60. 5). 1 2 3 4 1 6 3 4 2 2 2 2 u
u u u 85. 1 2 3 4 u
u u 13 8
u 5 5u 0 6) 1 2 3 7) 2 5
u u u 351 3 3 4 5 6 u u 189 1 3 u u u 1728 u u 3 8) 1 2 3 9). 1 3 2 2 GV: TR
u u u 63 u u 5 1 2 3 1 3 Ầ u
u u 7 N 10). 1 2 3 Đ 2 2 2 ÌN u
u u 21 1 2 3 H C Ư Lời giải – 0834 3321 35
u u u 2 3 4 33 2 35 2 3
u .q u .q u .q 1 1 1 1 1). u u 25 2 1 5 4
u 0 i 1,,,5
u .u .q 25 2 1 1 i 5 2 2 u .q 2 2
5 u .q 5 u thay vào (1) được: 1 1 1 2 q 5 35 1 2 3
q q q 2 2 1 q q 2
79 2q 5q 2 0 q 2 q . 2 q 2 2 5 1
Với q 2 u . Với q u 20. 1 4 1 2 2 4
u u u 65 2 4 u 1 q q 65 1 u
u q u q 65 1 2). 1 3 5 1 1 1 u u 325. 6 6 1 7 u u q 325. u 1 q 325 2 1 1 1
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 60
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com 2 1 325 2 1 q 2 4 6 1 q q q 3 Lấy: 5 6 vi 1+q 1 2 q 2 4 2 4 1 1 q q 65 1 q q 2 2
1 q 5 q 4 q 2. 65 65
Với q 2 u 5 . Với q 2 u 5. 1 2 4 1 1 2 2 1 2 2 2 4 u .q u u u u
q u q u q 2 4 3 5 1 q q 42 1 42 . . . 42. 1 3). 2 4 6 1 1 1 2 4 u u 20 u
.q u .q 20 u .q 2 3 5 1 q 20 2 1 1 1 2 4 1 1 q q 21 Lấy: 2 4 3
10 10q 10q 21 q 21q 2 q 2 1 q 10 21 10 4 3 2 2
10q 21q 10q 21q 10 0 10q 21q 10 10 2 q q 1 1 2 10 q 21 1 10 0 2 q q 2 1 1 1 Đặt: 2 2 2 t q t q q t 2.
Điều kiện t 2 2 GV: TR q q q Ầ 5 2 2 2 N
10t 2 21t 10 0 10t 21t 10 0 t= t (loại). Đ 2 5 ÌN H C 5 1 5 1 Với 2 Ư t q
2q 5q 2 0 q q 2 2 q 2 2 – 0834 1 20 20 3321 Nếu q u 64 1 2 4 2 4 2 q q 1 1 33 2 2 20 20
Nếu q 2 u 1. 1 2 4 2 4 q q 2 2
4). u u 165; u u 60. 1 6 3 4 5 u u q 165 u 1 q 165 1 1 1 1 5 2 3 2 u
q u q 60 1 1 u
q 1 q 60 2 1 1 1 11 1 q 2 3 4 5
1 q q q q q 11 Lấy 2 2 q 1 q 2 4 q 1 q 4 2 3 4
q q q q 2 4 3 2 4 1
11q 4q 4q 7q 4q 4 0
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 61
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com 4 3 2 4q 4q 7q 4q 4 1 1 2 0 4 q 4 q 7 0 2 2 2 2 2 2 q q q q q q q 2 1 1 1 Đặt: 2 2 2 t q t q q t 2.
Điều kiện: t 2. 2 q q q 5 3
4 2t 2 2
4t 7 0 4t 4t 15 0 t t (loại). 2 2 5 1 5 1 Với 2 t q
2q 5q 2 0 q 2 q = 2 q 2 2 165 165 1 165 165
với q 2 u 5 với q u 160. 1 5 2 5 1 q 1 2 1 2 5 2 1 q 1 1 2 u
u u u 15 2 3 u
u q u q u q 15 5). 1 2 3 4 1 1 1 1 2 2 2 2 u
u u u 85. 2 2 2 2 4 6 u
u q u q u q 85. 1 2 3 4 1 1 1 1 2 u 2 2 3 2 2 3
1 q q q 15 u
1 q q q 15 1 1 1 2 u 2 4 6
1 q q q 85. 2 u 2 4 6
1 q q q 85 2 . 1 1 GV: TR 2 1
1 q q q 2 2 3 2 45
1 q q 1 q 45 Lấy 2 4 6 2 4 2 Ầ 2
1 q q q 17 1 q q 1 q 17 N Đ ÌN 2 H 2 2 2 2 2 C
1 q1 q 45
1 q 1 q 45
1 2q q 1 q 45 Ư 2 4 4 4 –
1 q 1 q 17 1 q 17 1 q 17 0834 2 3 2 4 4 3321
171 q 2q 2q q q 451 q 33 4 3 2 28q 34q 34q 34q 28 4 3 2
28q 34q 34q 34q 28 0 0 (vì dễ dàng 2 2 2 2 2 q q q q q thấy q 0 ) 34 1 1 2 2
28q 34q 34
28 0 14 q 17 q 17 0 2 q q q 2 1 1 1 Đặt 2 2 2 t q t q q t 2
. Điều kiện: t 2. 2 q q q 5 9 2t 2 14
2 17t 17 0 14t 17t 45 0 t t (loại) 2 7 5 1 5 1 Với 2 t q
2q 5q 2 0 q 2 q = 2 q 2 2
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 62
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com 1 15
với q 2 u 1. với q u 8. 1 1 2 3 2
1 q q q u u u u 2 1 q q 13 13 1 6). 1 2 3 3
u u u 351 u q 2 4 5 6 1 q q 351 1 13 13 Lấy 3
q 27 q 3 u 1. 1 2 1 q q 1 3 9 8
u 5 5u 0 7). 2 5 1 3 3 u u 189. 1 3 3 8 2 2 3 3 4 8
u q 5 5u q 0 8
5 5q q q 1 1 5 5 5 5 1 u u q 3 3 2 189. 189 1 1 3 u 6 1 q 3 189 u 125 u 5. 1 1 6 1 1 q u u u 1728 8). 1 2 3 1
u u u 63 1 2 3 2 u .u . . q u .q 1728 u q 12 u q 12 1 1 1 1 3 3 1 GV: TR 1 u
u q u q 3 u
1 q q 63 u 2 2 2 1 q q 63 1 1 1 1 1 Ầ N Đ 12 ÌN u 12 1
q 4 u 3 1 q u H 1 C q 1 Ư 12 2 q u 48. 2 1 –
1 q q 63
12q 51q 12 0 4 0834 q 3321 2 u 2 u 3 2 2 u 1 q 3 1 u 1 q 9 1 33 9). 1 3 2 2 4 2 4 u u 5 1 3 u 1 q 5 2 u 1 q 5 1 1 q 2 2 9 Lấy . Đặt: 2
t q ,t 0. 4 1 q 5 1
51 t 2 9 2 1 t 2
4t 10t 4 0 t 2 t = 2
Với t 2 q 2 3 3 q 2 u
1 q 2 u 1 1 2 1 q 1 2 1 q 1 2 Với t q 2 2
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 63
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com 2 3 2 3 q u 2 q u 2. 1 2 2 1 q 1 2 2 1 q 2 u
u u 7
u u q u q 7 1 1 1 10). 1 2 3 2 2 2 2 u 2
u u 21 2 2 u u q u q 21 1 1 1 1 2 3 u
1 q q 7 u
1 q q 2 2 2 2 1 49 1 . Lấy được: 2 u 2 4 1 q q 2 21 u 2 4 1 1 q q 21 1
1 q q 2 2 49 21 2 4 2 3
1 q q 2q 2q 2q 49 2 4 1 q q 2 4 1 q q 21 2 3 4
q q q q 2 4 q q 4 3 2 21 1 2 3 2 49 1
28q 42q 14q 42q 28 0. 4 3 2 28q 42q 14q 42q 28 42 28 2
0 28q 42q 14 0 2 2 2 2 2 2 q q q q q q q 1 1 2 28 q 42 q 14 0 2 2 q q 2 GV: TR 1 1 1 Đặt: 2 2 2 t q t q q t 2
. Điều kiện: t 2 2 q q q Ầ N Đ 5 2 2 2
28 t 2 42t 14 0 28t 42t 70 0 t t 1(loại) ÌN 2 H C Ư 5 1 5 1 – Với 2 t q
2q 5q 2 0 q 2 q = 0834 2 q 2 2 3321 7 1 7
q 2 u 1 q u 4 1 2 1 2 33 1 q q 2 1 q q
Ví dụ 3: Tìm số hạng đầu và công bội của cấp số nhân, biết: u u 72 u
u u 65 u u 90 a) 4 2 b) 1 3 5 c) 3 5 u u 144 u u 325 u u 240 5 3 1 7 2 6 u
u u 21
u u u 14 1 2 3 u
u u u 30 d) 1 2 3 e) 1 1 1 7 f) 1 2 3 4
u .u .u 64 2 2 2 2 u
u u u 340 1 2 3 u u u 12 1 2 3 4 1 2 3 Lời giải u q u u u
q u q 2 3 q 1 72 (1) 72 72 1 a) 4 2 1 1 4 2 2 u u 144 u
q u q 144 u q 2 5 3 q 1 144 (2) 1 1 1
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 64
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
Lấy (2):(1) được: q 2 , thay q 2 vào (1) được u 12 1 2 u q u u u
q u q 2 2 4 1 q 90 (1) 90 90 1 c) 3 5 1 1 5 u u 240 u
q u q 240 u q 4 2 6 1 q 240 (2) 1 1 1 u q 1 q 1 q 1 (2) q 1 4 240 2 2 2 8 1 q 8 Lấy 2 (1) u q 2 1 q 90 q 2 1 q 3 q 3 1 1 2
3q 8q 3 0 q q 3 3 1
Với q thay vào (1) được u 729 . 3 1
Với q 3 thay vào (1) được u 1. 1 u
u u 14 u
u q u q 14 u 2 2 1 q q 14 (1) 1 1 2 3 1 1 1 d) 2
u .u .u 64 u u qu q 64 u q3 1 2 3 1 1 1 64 (2) 1 4 4
(2) u q 4 u , thay vào (1) được 2
1 q q 14 1 1 q q GV: TR 1 2
2q 5q 2 0 q 2 q 2 Ầ N Đ 1 ÌN
Với q 2 u 2 . Với q u 8 . 1 1 H 2 C Ư – 2 2 u u u 21 u
u q u q 21
u 1 q q 21 (1) 0834 1 2 3 1 1 1 1 e) 2 1 1 1 7 1 1 1
7 q q 1 7 3321 2 (2) 2 u u u 12 u u q u q 12 1 2 3 1 1 1 u q 12 1 33 21 21 1 7 2
(1) 1 q q , thay vào (2): u q 36 u q 6 2 1 2 u 1 u u q 12 1 1 1 6 6 1 Với u thay vào (1): 2 1 q q 2
21 2q 5q 2 0 q 2 q 1 q q 2 1
Nếu q 2 u 3 . Nếu q u 12 1 1 2 6
Với u thay vào (1): 1 q 6 9 65 9 65 2 1 q q 2
21 2q 9q 2 0 q q q 4 4
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 65
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com 9 65 27 3 65 9 65 27 3 65 Nếu q u . Nếu q u 1 4 2 1 4 2 2 3 u
u u u 30 u
u q u q u q 30 f) 1 2 3 4 1 1 1 1 2 2 2 2 2 2 2 2 4 2 6 u
u u u 340 u
u q u q u q 340 1 2 3 4 1 1 1 1 u 2 2 3
1 q q q 30
u 1 q 1 q 30 1 1 2 u 2 4 2 2 4 6
1 q q q 340 u 1 q 1 q 340 1 1 2 u 1 q2 2 2 1 q 900 (1) 1 2 u 4 1 q 2 1 q 340 (2) 1 1 q2 2 1 (1) q 45 Lấy
, quy đồng rút gọn được: 4 3 2
14q 17q 17q 17q 14 0 4 (2) 1 q 17 17 14 2
14q 17q 17 0 2 q q 1 1 1 2 14 q 17 q 17 0
. Đặt t q
, điều kiện t 2 2 q q q GV: TR 5 9 2
14t 17t 45 0 t t (loại). 2 7 Ầ N 5 1 5 1 Đ Với 2 t q
2q 5q 2 0 q 2 q ÌN 2 q 2 2 H C Ư 1 –
Với q 2 u 2 . Với q u 16 1 1 0834 2 3321
Ví dụ 4: Tìm a, b biết rằng: 1, a, b là 3 số hạng liên tiếp của cấp số cộng và 2 2
1, a , b là 3 số hạng 33
liên tiếp của một cấp số nhân. Lời giải 1 b 2a 1 b 2a 1
Theo đề bài ta có hệ phương trình: 2 4 b a 2 b a Với 2
b a thay vào (1) được 2 2
1 a 2a a 2a 1 0 a 1 b 1 Với 2
b a thay vào (1) được 2 2
1 a 2a a 2a 1 0 a 1 2 a 1 2 a
b 2 1 2 1 2 b 3 2 2 a
b 2 1 2 1 2 b 3 2 2
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 66
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com a 1 a 1 2 a 1 2 Kết luận
thỏa yêu cầu đề bài. b 1 b 3 2 2 b 3 2 2
Ví dụ 5: Tìm số hạng đầu của CSN biết công bội bằng 3, tổng số các số hạng là 728 và số hạng cuối bằng 486. Lời giải S 728 Theo đề bài ta có: n u 486 n u 1 n q 1 728 n u
u q 728(1 q) 1 1 1 q
u 486q 728(1 q) u 2 1 1 n u q 486q 1 n 1 u q 486 1
Ví dụ 6: Cho 3 số tạo thành một cấp số cộng có tổng 21.Nếu thêm 2, 3, 9 lần lượt vào số thứ nhất,
số thứ hai, số thứ ba tạo thành một cấp số nhân. Tìm 3 số đó. Lời giải
Gọi u ,u ,u thành lập cấp số cộng. 1 2 3 GV: TR
Theo đề bài: u 2;u 3;u 9 là ba số liên tiếp tạo thành cấp số nhân. 1 2 3 Ầ u
u u 21 3 u 21 N 1 2 3 2 Đ ÌN Theo đề bài: u u 2u u u 2u 1 3 2 1 3 2 H 2 2 C
u 2 u 9 u 3
u 2 u 9 u 3 1 3 2 1 3 2 Ư – 0834 u 7 2 3321 u 14 u 1 3 33
14 u 2 u 9 100 3 3
Giải : 16 u u 9 100 2 u
7u 44 0 u 11 u 4 3 3 3 3 3 3
Với u 11 u 3 . Với u 4 u 18. 3 1 3 1
Ví dụ 7: Cho 3 số dương có tổng là 65 lập thành một cấp số nhân tăng, nếu bớt một đơn vị ở số
hạng thứ nhất và 19 đơn vị ở số hạng thứ ba ta được một cấp số cộng. Tìm 3 số đó. Lời giải
Gọi u ,u ,u theo thứ tự đó lập thành một cấp số nhân. 1 2 3
Theo đề: u 1;u 19 theo thứ tự đó lập thành một cấp số cộng. 1 3 u
u u 65 Ta có: 1 2 3
u 1 u 19 2u 1 3 2
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 67
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com 2 u 2
u u 65 u
u .q u .q 65 u 1 q q 65 1 1 1 2 3 1 1 1
u 2u u 20 2 2 1 2 3 u
2u .q u .q 20 u 1 2q q 20 2 1 1 1 1 2 1 1 q q 65 13 Lấy 2
q q 2 4 1
13 1 2q q 2 2 1 2q q 20 4 1 2
9q 30q 9 0 q 3 q 3
Vì u ,u ,u theo thứ tự lập thành cấp số nhân tăng dần nên chọn q 3 u 5 1 2 3 1
Vậy u 5; u 15; u 45. 1 2 3
Ví dụ 8: Tìm 3 số hạng liên tiếp của một cấp số nhân biết tổng của chúng là 19 và tích là 216. Lời giải
Gọi ba số hạng liên tiếp của cấp số nhân là u ,u ,u với công bội là q. Theo đề bài ta có 1 2 3 u 2 2 1 q q 19 ( ) 1 u
u u 19 u
u q u q 19 hệ phương trình: 1 1 1 1 2 3 6
u .u .u 216 u q 6
u q 6 u 1 3 3 1 2 3 1 1 q 6 3 2 GV: TR Thay u vào ( ) được: 2
6q 13q 6 0 q hoặc q . 1 q 2 3 Ầ N 3 Đ Với q
u 4, u 6, u 9 . 1 2 3 ÌN 2 H C 2 Ư Với q
u 9,u 6, u 4 . 1 2 3 – 3 0834 3321
Ví dụ 9: Tìm công bội của một cấp số nhân có số hạng đầu là 7, số hạng cuối là 448 và tổng số các số hạng là 889. 33 Lời giải n u q 1 1 S 889 u q u q n 889 n 889( 1) (1) Theo đề bài ta có 1 1 q 1 u 448 n n u
q 448q (2) 1 n 1 u q 448 1
Thay (2) vào (1) được: 448q 7 889q 889 q 2
Ví dụ 10: Tìm bốn số hạng liên tiếp của một cấp số nhân, trong đó số hạng thứ hai nhỏ hơn số
hạng thứ nhất 35, còn số hạng thứ ba lớn hơn số hạng thứ tư 560. Lời giải
Theo đề bài ta có hệ phương trình: u u 35 u u q 35 u (1 q) 35 (1) 1 2 1 1 1 2 3 2 u u 560
u q u q 560
u q (1 q) 560 (2) 3 4 1 1 1
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 68
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
Thay (1) vào (2) ta được 2
q 16 q 4 35 140 560 2240
Với q 4 thay vào (1) được u
, u u q , u , u 1 3 2 1 3 3 3 3 3
Tìm 3 số hạng đầu của một cấp số nhân, biết rằng khi tăng số thứ hai thêm 2 thì các số
đó tạo thành một cấp số cộng, còn nếu sau đó tăng số cuối thêm 9 thì chúng lại lập
thành một cấp số nhân.
Ví dụ 11: Tìm các số dương a và b sao cho a, a + 2b, 2a + b lập thành một cấp số cộng và (b +
1)2, ab + 5, (a + 1)2 lập thành một cấp số nhân. Lời giải
Theo tính chất của CSC ta có: a (2a b) 2(a 2b) (1)
Theo tính chất của CSN ta có: 2 2 2
(b 1) (a 1) (ab 5) (2)
Từ (1) khai triển rút gọn ta được: a 3b , thay vào (2): 2 2 2 2 2
(b 1) (3b 1) (3b 5) (b 1)(3b 1) (3b 5)
Với b b 2 1 3
1 3b 5 b 1 a 3
Với b b 2 2 1 3 1 3
b 5 6b 4b 6 0 (vô nghiệm). GV: TR
Kết luận a 3,b 1 Ầ N Đ ÌN
Ví dụ 12: Tính các tổng sau: H C a). 2 3
S 2 2 2 2n Ư n – 1 1 1 1 0834 b). S n 2 3 2 2 2 2n 3321 2 2 2 1 1 n 1 c). S 3 9 3 33 n 3 9 3n
d). S 6 66 666 666...6 n n so 6 Lời giải a). Ta có dãy số 2 3 2, 2 , 2 , , 2n
là một cấp số nhân với n số hạng, có số hạng đầu 2 2 1 n q 1 2n
u 2 và công bội q
2 . Do đó S u . 2. 2 2n 1 . n 1 1 2 1 q 1 2 1 1 1 1 b). Ta có dãy số , , , ,
là một cấp số nhân với n số hạng, có số hạng đầu 2 3 2 2 2 2n n 1 1 1 1 2 1 1 n q 1 2 1 u và công bội 2 q
. Do đó S u . . 1 . 1 2 1 2 n 1 1 q 2 1 2n 1 2 2
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 69
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com 2 2 2 1 1 n 1 c). S 3 9 3 n 3 9 3n 1 1 n 1 2 4 2 3 2 3 2 3 2 2 4 2 3 3 3 n n 1 1 1 2 4 2
3 3 3
2 2 2 2 2 4 2 3 3 3 n n • Có dãy số 2 4 2 3 , 3 , , 3 n
là cấp số nhân với n số hạng, có số hạng đầu 2 u 3 và công 1 4 3 1 n q 1 9n 9 bội q
9 . Do đó S u . 9. 9n 1 . 1 1 2 3 1 q 1 9 8 1 1 1 1 • Có dãy số , , ,
là cấp số nhân với n số hạng, có số hạng đầu u và công 2 4 2 3 3 3 n 1 2 3 1 n 1 1 1 q 1 1 1 9n n 1 bội q . Do đó 9 S u . . 1 . 9 1 1 1 q 9 1 8 9n 8.9n 1 9 n n n n 1 9 1 9 1 9 9 1 Vậy S n n . n 9 1 2 2 8 8.9n 8.9n GV: TR 6
d). S 6 66 666 666...6
9 99 999 999...9 n 9 n so 6 n Ầ N 2 Đ
(10 1) (100 1) (1000 1) (10n 1) ÌN 3 H C 2 2 10n n n 1 20 n 2 Ư 2 3 10
10 10 10 n 10. n 10 1 – 3 3 10 1 27 3 0834 3321
Dạng 3. Các bài toán thực tế 33
Câu 1. Với hình vuông A B C D như hình vẽ bên, cách tô màu như phần gạch sọc được gọi là 1 1 1 1
cách tô màu “đẹp”. Một nhà thiết kế tiến hành tô màu cho một hình vuông như hình bên, theo quy trình sau:
Bước 1: Tô màu “đẹp” cho hình vuông A B C D . 1 1 1 1
Bước 2: Tô màu “đẹp” cho hình vuông A B C D là hình vuông ở chính giữa khi chia 2 2 2 2
hình vuông A B C D thành 9 phần bằng nhau như hình vẽ. 1 1 1 1
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 70
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
Bước 3: Tô màu “đẹp” cho hình vuông A B C D là hình vuông ở chính giữa khi chia 3 3 3 3
hình vuông A B C D thành 9 phần bằng nhau. Cứ tiếp tục như vậy. Hỏi cần ít nhất 2 2 2 2
bao nhiêu bước để tổng diện tích phần được tô màu chiếm 49,99% . Lời giải
Gọi diện tích được tô màu ở mỗi bước là u , *
n . Dễ thấy dãy các giá trị u là một n n 4 1
cấp số nhân với số hạng đầu u và công bội q . 1 9 9 k u q 1 1
Gọi S là tổng của k số hạng đầu trong cấp số nhân đang xét thì S . k k q 1 k u q 1 1
Để tổng diện tích phần được tô màu chiếm 49,99% thì
0, 4999 k 3,8 . q 1
Vậy cần ít nhất 4 bước.
Câu 2. Cho hình vuông C a 1 có cạnh bằng
. Người ta chia mỗi cạnh của hình vuông thành bốn
phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông C2 (Hình vẽ). GV: TR Ầ N Đ ÌN H C Ư – 0834 Từ hình vuông C C C
2 lại tiếp tục làm như trên ta nhận được dãy các hình vuông , 1 2 3321
, C ,., C . Gọi S là diện tích của hình vuông C i 1, 2,3,.... . i . Đặt 3 n i 33 32
T S S S ...S ... . Biết T , tính a ? 1 2 3 n 3 Lời giải 2 2 3 1 a 10 5
Cạnh của hình vuông C a a a 2 S a 2 là: . Do đó diện tích 2 2 4 4 4 8 5 S . 1 8
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 71
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com 2 2 2 3 1 a 10 10
Cạnh của hình vuông C 2 a a a a 3 là: . Do đó diện 3 2 2 4 4 4 4 2 5 5 tích 2 S a
S . Lý luận tương tự ta có các S , S , S ,...S .... tạo thành một dãy 3 2 1 2 3 n 8 8 5
cấp số nhân lùi vô hạn có u S và công bội q . 1 1 8 S 2 8a 32 1 T . Với T ta có 2
a 4 a 2 . 1 q 3 3
C. GIẢI BÀI TẬP SÁCH GIÁO KHOA
Bài 1. Trong các dãy số sau, dãy số nào là cấp số nhân? Vì sao? a) 5; 0 ,5;0, 05; 0 , 005; 0, 0005 1 1 b) 9, 3, 1, , ; 3 9 c) 2,8,32, 64, 256 . Lời giải 1
a) Từ số hạng thứ hai của dãy số ta thấy số hạng sau gấp
lần số hạng trước của dãy. 10
Vì vậy dãy trên là cấp số nhân với số hạng đầu u 5 và công bội q 0 ,5. 1 GV: TR 1
b) Từ số hạng thứ hai của dãy số ta thấy số hạng sau gấp số hạng trước của dãy. 3 Ầ N 1 Đ
Vì vậy dãy trên là cấp số nhân với số hạng đầu u 9 và công bội q . 1 ÌN 3 H C 8 32 256 64 c) Ta có: Ư 2 8 64 32 – 0834
Vì vậy dãy trên không là cấp số nhân. 3321
Bài 2. Chứng minh mỗi dãy số u với số hạng tổng quát như sau là cấp số nhân: n 33 3 5 a) u 2n b) u c) n n 4 3n u ( 0 , 75)n n Lời giải 3 a) Ta có: n 1 u 2 n 1 4 u 3 n n 3 Xét 1 1 2 : 2n 2 u 4 4 n
Vì vậy dãy số đã cho là một cấp số nhân. 5 b) Ta có: u n 1 n 1 3 u 5 5 1 Xét n 1 : . n 1 u 3 3n 3 n
Vì vậy dãy số đã cho là một cấp số nhân. c) Ta có: 1 u ( 0 , 75)n . n 1
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 72
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com u Xét n 1 n 1
(0, 75) : (0, 75)n 0, 75 . un
Vì vậy dãy số đã cho là một cấp số nhân.
Bài 3. Cho cấp số nhân u với số hạng đầu u 5
, công bội q 2 . n 1 a) Tìm u . 9
b) Số 320 là số hạng thứ bao nhiêu của cấp số nhân trên?
c) Số 160 có phải là một số hạng của cấp số nhân trên không? Lời giải
a) Ta có u là cấp số nhân có số hạng đầu u 5
và công bội q 2 có số hạng tổng quát là: n 1 1 u 5.2n * n . n b) Xét n 1 u 5.2 3 20 n n 1 2 64 n 1 6 n 7 .
Vậy số 320 là số hạng thứ 7 của cấp số nhân. c) Xét n 1 u 5.2 160 n n 1 2 3 2 n 1 5 n 4 N
Vậy số 160 không phải là một số hạng của cấp số nhân. GV: TR 27
Bài 4. Cho cấp số nhân u với u 3,u . n 1 3 Ầ 4 N Đ
a) Tìm công bội q và viết năm số hạng đầu của cấp số nhân trên. ÌN H
b) Tính tổng 10 số hạng đầu của cấp số nhân trên. C Ư Lời giải – 0834 a) Ta có 2
u u q 3 1 3321 3 q u 27 9 2 33 Xét 2 3 q . u 3 4 3 1 q 2 3
+) Với q ta có năm số hạng đầu của cấp số nhân là: 2 4 27 3 243 u 3; u ; u 3 1 3 5 4 2 16 3 3 9 3 81 u 3
; u 3 ; 2 4 2 4 2 8 3 +) Với q=
ta có năm số hạng đầu của cấp số nhân là: 2
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 73
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com 4 27 3 243 u 3; u ; u 3 . 1 3 5 4 2 16 3 3 9 3 81 u 3 ; u 3 ; 2 4 2 4 2 8 3
b) Tổng của 10 số hạng đầu của cấp số nhân với số hạng đầu u 3 và công bội q là: 1 2 10 3 31 2 S 68 . 10 3 1 2 3
Tổng của 10 số hạng đầu của cấp số nhân với số hạng đầu u 3 và công bội q là: 1 2 10 3 31 2 S 340 . 10 3 1 2
Bài 5. Một tỉnh có 2 triệu dân vào năm 2020 với tỉ lệ tăng dân số là 1% / năm. Gọi u là số dân n
của tỉnh đó sau n năm. Giả sử tỉ lệ tăng dân số là không đổi.
a) Viết công thức tính số dân của tỉnh đó sau n năm kể từ năm 2020.
b) Tính số dân của tỉnh đó sau 10 năm kể từ năm 2020. GV: TR Lời giải Ầ N
a) Ta có dãy u lập thành một cấp số nhân có số hạng đầu là u 2 triệu dân và công sai n o Đ ÌN q 1% . H C Ư
Khi đó số hạng tổng quát của 1
u 2 (11%)n (triệu dân). n – 0834
b) Số dân của tỉnh đó sau 10 năm kể từ năm 2020 là: 3321 10 1 u 2 (1 1%) 2,19 (triệu dân). 10 33
Bài 6. Một gia đình mua một chiếc ô tô giá 800 triệu đồng. Trung bình sau mỗi năm sử dụng,
giá trị còn lại của ô tô giảm đi 4% (so với năm trước đó).
a) Viết công thức tính giá trị của ô tô sau 1 năm, 2 năm sử dụng.
b) Viết công thức tính giá trị của ô tô sau n năm sử dụng.
c) Sau 10 năm, giá trị của ô tô ước tính còn bao nhiêu triệu đồng? Lời giải
a) Sau 1 năm giá trị của ô tô còn lại là: u 800 800.4% 800. 1 4% 768 (triệu đồng). 1
Sau 2 năm giá trị của ô tô còn lại là:
u 800.1 4% 800.1 4% 2
.4% 800.(1 4%) 737, 28 (triệu 1 đồng).
b) Gọi u là giá trị của ô tô sau n năm sử dụng. n
Dãy số u tạo thành một cấp số nhân với số hạng đầu là giá trị đầu n
của ô tô là u 800 triệu đồng và công bội q 1 4% . 0
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 74
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
Khi đó công thức tổng quát để tính u 800.(1 4%)n . n
c) Sau 10 năm sử dụng giá trị của ô tô còn lại là: 10
u 800 (1 4%) 531,87 (triệu đồng). 10
Bài 7. Một người nhảy bungee (một trò chơi mạo hiểm mà người chơi nhảy từ một nơi có địa thế
cao xuống với dây đai an toàn buộc xung quanh người) từ một cây cầu và căng một sợi dây dài
100 m . Sau mỗi lần rơi xuống, nhờ sự đàn hồi của dây, người nhảy được kéo lên một quãng đường
có độ dài bằng 75% so với lần rơi trước đó và lại bị rơi xuống đúng bằng quãng đường vừa được
kéo lên (Hình 3). Tính tổng quãng đường người đó đi được sau 10 lần kéo lên và lại rơi xuống. Lời giải
Gọi u là độ dài dây kéo sau n lần rơi xuống (n ) n Ta có: u 100 m . 0
Sau lần rơi đầu tiên độ dài dây kéo còn lại là: u 100.75% m . 1
Sau cú nhảy tiếp theo độ dài dây kéo còn lại là: u 100.75%.75% 100 . 2 (75%) m . 2
Dãy số này lập thành một cấp số nhân có số hạng đầu là 100 và công bội q 0, 75% , có công thức tổng quát n 1 u 100 (0, 75%) . n m
Tổng quãng đường người đó đi được sau 10 lần kéo lên và lại rơi xuống là: 100 10 1 (75%) S 377, 5 m . 10 1 75% GV: TR D. BÀI TẬP TRẮC NGHIỆM
Câu 1: Trong các dãy số sau, dãy số nào không phải là một cấp số nhân? Ầ N Đ A. 2; 4; 8; 16; B. 1; 1; 1; 1; ÌN 3 5 7 H C. 2 2 2 2 1 ; 2 ; 3 ; 4 ;
D. a; a ; a ; a ; a 0. C Ư – Lời giải 0834 Chọn C 3321 u 9 u 33 Xét đáp án C: 2 2 2 2 2 3 1 ; 2 ; 3 ; 4 ; 4 u 4 u 1 2
Các đáp án A, B, D đều là các cấp số nhân.
Nhận xét: Dãy u với u
0 là cấp số nhân u . n
a q , tức là các số hạng của nó đều n n n
được biểu diễn dưới dạng lũy thừa của cùng một cơ số q (công bội), các số hạng liên
tiếp (kể từ số hạng thứ hai) thì số mũ của chúng cách đều nhau. Ví dụ 2; 4; 8; 16;
là cấp số nhân và u 2n. n n 1; 1; 1; 1;
là cấp số nhân và u n 1 . n 1 n 3 5 7
a; a ; a ; a ; a 0 là cấp số nhân và 2 1 u a a n 2 . . a
Câu 2: Dãy số nào sau đây không phải là cấp số nhân?
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 75
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com A. 1 1 1 1 1; 2; 4; 8; B. 2 3 4 3; 3 ; 3 ; 3 ; C. 1 1 4; 2; ; ; D. ; ; ; ; 2 4 2 4 6 Lời giải Chọn D
Các đáp án A, B, C đều là các cấp số nhân công bội lần lượt là 1 2;3; . 2 Xét đáp án D: 1 1 1 1 u 1 1 u 2 3 ; ; ; ; 2 4 6 2 u u 1 2
Câu 3: Dãy số 1; 2; 4; 8; 16; 32; là một cấp số nhân với:
A. Công bội là 3 và số hạng đầu tiên là 1.
B. Công bội là 2 và số hạng đầu tiên là 1.
C. Công bội là 4 và số hạng đầu tiên là 2.
D. Công bội là 2 và số hạng đầu tiên là 2. Lời giải Chọn B u 1 1 Cấp số nhân: 1; 2; 4; 8; 16; 32; u 2 q 2 u GV: TR 1
Câu 4: Cho cấp số nhân u với u 2 và q 5. Viết bốn số hạng đầu tiên của cấp số nhân. n 1 Ầ N Đ A. 2; 10; 50; 250. B. 2; 10; 50; 250. ÌN H
C. 2; 10; 50; 250. D. 2; 10; 50; 250. C Ư – Lời giải. 0834 Chọn B 3321 33 u 2 1 u 2 u u q 10 1 2 1 q 5 u u q 50 3 2
u u q 250 4 3
Câu 5: Một cấp số nhân có hai số hạng liên tiếp là 16 và 36. Số hạng tiếp theo là: A. 720. B. 81. C. 64. D. 56. Lời giải Chọn B
Ta có cấp số nhân u có: n u 16 u k k 9 1 q u u q 81 k 2 k 1 u 36 u 4 k 1 k
Câu 6: Tìm x để các số 2; 8; x; 128 theo thứ tự đó lập thành một cấp số nhân.
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 76
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com A. x 14. B. x 32. C. x 64. D. x 68. Lời giải Chọn B
Cấp số nhân 2; 8; x; 128 theo thứ tự đó sẽ là u ; u ; u ; u , ta có 1 2 3 4 u u 2 3 8 x x 32 u u x 32 1 2 2 8
x 32 x 32 2 u u 1 28 x x 1024 3 4 x 32 u u x 8 2 3
Câu 7: Tìm tất cả giá trị của x để ba số 2x 1; x; 2x 1 theo thứ tự đó lập thành một cấp số nhân. A. 1 x . B. 1 x . C. x 3. D. x 3. 3 3 Lời giải Chọn A
Cấp số nhân 2x 1; ;
x 2x 1 2x 1 2x 1 2 2
1 x 3x 1 x . 3
Câu 8: Tìm x để ba số 1 x; 9 x; 33 x theo thứ tự đó lập thành một cấp số nhân. GV: TR A. x 1. B. x 3. C. x 7.
D. x 3; x 7. Ầ N Lời giải Đ ÌN H Chọn B C Ư – Cấp số nhân x x x
x x x2 1 ; 9 ; 33 1 33 9 x 3. 0834
Câu 9: Với giá trị ,
x y nào dưới đây thì các số hạng lần lượt là 2; ;
x 18; y theo thứ tự đó lập 3321 thành cấp số nhân? 33 x 6 x 10 x 6 x 6 A. . B. C. D. . . . y 54 y 26 y 54 y 54 Lời giải Chọn C x 18 x 6 Cấp số nhân: 2 x 2 ; ;
x 18; y 324 . Vậy 18 y y 5 4 x x 18 ;
x y 6;54 hoặc ; x y 6 ;54
Câu 10: Cho cấp số nhân có các số hạng lần lượt là x; 12; y; 192. Mệnh đề nào sau đây là đúng?
A. x 1; y 144.
B. x 2; y 72.
C. x 3; y 48.
D. x 4; y 36.
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 77
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com Lời giải Chọn C 12 y 144 x x x 3 Câp số nhân: 12 ;
x 12; y; 192 y . y 192 y 48 2 y 2304 12 y
Câu 11: Thêm hai số thực dương x và y vào giữa hai số 5 và 320 để được bốn số 5; x; y; 320 theo
thứ tự đó lập thành cấp số nhận. Khẳng định nào sau đây là đúng? x 25 x 20 x 15 x 30 A. . B. C. D. . . . y 125 y 80 y 45 y 90 Lời giải Chọn B u 5 1 x q 5 Cấp số nhân: x 20 2
5; x; y; 320 x . 2
y u u q y 80 3 1 5 3 x 3 320
u u q 4 1 25 GV: TR
Câu 12: Ba số hạng đầu của một cấp số nhân là x 6; x và .
y Tìm y , biết rằng công bội của Ầ cấp số nhân là 6. N Đ ÌN A. y 216. B. 324 y . C. 1296 y . D. y 12. H 5 5 C Ư – Lời giải 0834 Chọn C 3321
Cấp số nhân x 6; x và y có công bội q 6 nên ta có 33 36
u x 6, q 6 1 x 5
x u u q 6 x 6 2 1 36 1296 2 y 36.
y u u q 36x 3 2 5 5
Câu 13: Hai số hạng đầu của của một cấp số nhân là 2x 1 và 2
4 x 1. Số hạng thứ ba của cấp số nhân là: A. 2x 1. B. 2x 1. C. 3 2
8x 4 x 2x 1. D. 3 2
8x 4 x 2x 1. Lời giải Chọn C 2
Công bội của cấp số nhân là: 4x 1 q
2x 1. Vậy số hạng thứ ba của cấp số nhân là: 2x 1
2x x 3 2 4 1 2
1 8x 4x 2x 1
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 78
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
Câu 14: Dãy số nào sau đây là cấp số nhân? u 1 u 1 A. 1 . B. 1 . u
u 1, n 1 u
3u , n 1 n 1 n n 1 n u u 2 1 C. 1 2 . D. . u
2u 3, n 1 n 1 n u sin , n 1 n n 1 Lời giải Chọn B
u là cấp số nhân u qu n n 1 n
Câu 15: Cho dãy số u với 3 u
.5n. Khẳng định nào sau đây đúng? n n 2
A. u không phải là cấp số nhân. n B. 3 u
là cấp số nhân có công bội q 5 và số hạng đầu u . n 1 2 C. 15 u
là cấp số nhân có công bội q 5 và số hạng đầu u . n 1 2
D. u là cấp số nhân có công bội 5 q
và số hạng đầu u 3. n 2 1 GV: TR Lời giải Chọn C Ầ N Đ 3 15 n ÌN u
.5 là cấp số nhân công bội q 5 và u n 1 H 2 2 C Ư Câu 16: –
Trong các dãy số u cho bởi số hạng tổng quát u sau, dãy số nào là một cấp số nhân? n n 0834 A. 1 1 u . B. 1 u 1. C. 1 u n . D. 2 u n . n n2 n n n n 3321 3 3 3 3 33 Lời giải Chọn A n u 3 1 Dãy 1 1 u 9.
là cấp số nhân có n 1 n2 3 3 q 3
Câu 17: Trong các dãy số u cho bởi số hạng tổng quát u sau, dãy số nào là một cấp số nhân? n n A. u 73 . n
B. u 73n. C. 7 u . D. u 7.3n. n n n 3n n Lời giải Chọn D u 21 Dãy
u 7.3n là cấp số nhân có 1 n q 3
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 79
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
Câu 18: Cho dãy số u là một cấp số nhân với *
u 0, n . Dãy số nào sau đây không phải là n n cấp số nhân?
A. u ; u ; u ; ...
B. 3u ; 3u ; 3u ; ... 1 3 5 1 2 3 C. 1 1 1 ; ; ; ...
D. u 2; u 2; u 2; ... u u u 1 2 3 1 2 3 Lời giải Chọn D
Giả sử u là cấp số nhân công bội q, thì n
Dãy u ; u ; u ; ... là cấp số nhân công bội 2 q . 1 3 5
Dãy 3u ; 3u ; 3u ; ... là cấp số nhân công bội 2 . q 1 2 3 Dãy 1 1 1 ; ;
; ... là cấp số nhân công bội 1 . u u u q 1 2 3
Dãy u 2; u 2; u 2; ... không phải là cấp số nhân. 1 2 3
Nhận xét: Có thể lấy một cấp số nhân cụ thể để kiểm tra, ví dụ u 2n. n
Câu 19: Cho cấp số nhân có các số hạng lần lượt là 3; 9; 27; 81; ... . Tìm số hạng tổng quát u của n GV: TR cấp số nhân đã cho. A. n 1 u 3 . B. u 3n. C. n 1 u 3 .
D. u 33n. n n n n Ầ N Đ Lời giải ÌN H C Chọn B Ư – 0834 u 3 1 Câp số nhân n 1 n 1 3; 9; 27; 81; ... n 9 u u q 3.3 3 . n 1 3321 q 3 3 33
Câu 20: Một cấp số nhân có 6 số hạng, số hạng đầu bằng 2 và số hạng thứ sáu bằng 486. Tìm
công bội q của cấp số nhân đã cho. A. q 3. B. q 3. C. q 2. D. q 2. Lời giải Chọn A u 2
Theo giải thiết ta có: 1 5 5 5
486 u u q 2q q 243 q 3. 6 1 u 486 6
Câu 21: Cho cấp số nhân u có u 3 và 2 q
. Mệnh đề nào sau đây đúng? n 1 3 A. 27 16 16 27 u . B. u . C. u . D. u . 5 16 5 27 5 27 5 16 Lời giải
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 80
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com Chọn B u 3 4 1 2 16 16 4 2 u u q 3. 3. . 5 1 q 3 81 27 3
Câu 22: Cho cấp số nhân u có u 2 và u 8 . Mệnh đề nào sau đây đúng? n 1 2 A. S 130. B. u 256. C. S 256. D. q 4. 6 5 5 Lời giải Chọn D
u 2 1 q4 u 2 1 q 145 5 1 S u . 2. 410 5 1 u
8 u q 2q 1 q 1 4 2 1 146 S 2. 1638 6 1 4
u u q 2.44 4 512. 5 1
Câu 23: Cho cấp số nhân u có u 3 và q 2 . Số 192 là số hạng thứ mấy của cấp số nhân đã n 1 cho? GV: TR A. Số hạng thứ 5. B. Số hạng thứ 6. Ầ C. Số hạng thứ 7.
D. Không là số hạng của cấp số đã cho. N Đ ÌN Lời giải H C Ư Chọn C – 0834 n n 192 n u u q n n 3. 1 2 1 1 .2n 64 6 1 1 6 1 .2 7. 1 3321 1 33
Câu 24: Cho cấp số nhân u có u 1 và 1 q . Số
là số hạng thứ mấy của cấp số n 1 10 103 10 nhân đã cho? A. Số hạng thứ 103. B. Số hạng thứ 104. C. Số hạng thứ 105.
D. Không là số hạng của cấp số đã cho. Lời giải Chọn B 1 n n 1 n chan n 1 1 1 u u q 1. n 104. 103 n 1 n 1 10 10 10 n1103
Câu 25: Một cấp số nhân có công bội bằng 3 và số hạng đầu bằng 5. Biết số hạng chính giữa là
32805. Hỏi cấp số nhân đã cho có bao nhiêu số hạng? A. 18. B. 17. C. 16. D. 9.
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 81
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com Lời giải Chọn B n 1 n 1 n 1 8
32805 u u q 5.3 3
6561 3 n 9. Vậy u là số hạng chính giữa của cấp số n 1 9
nhân, nên cấp số nhân đã cho có 17 số hạng.
Câu 26: Cho cấp số nhân u có u 81 và u
9. Mệnh đề nào sau đây đúng? n n n 1 A. 1 q . B. q 9. C. q 9. D. 1 q . 9 9 Lời giải Chọn A Công bội un 9 1 1 q u 81 9 n Câu 27: 1
Một dãy số được xác định bởi u 4 và u u , n 2. Số hạng tổng quát u của dãy 1 n n 1 2 n số đó là: n 1 A. 1 n 1 n u 2 . B. u C. u D. u 4 . n n 1 4 2 . n 1 2 . n n 2 Lời giải GV: TR Chọn D Ầ N u 4 u 4 n 1 1 1 Đ n 1 1 1 1 u u q 4. . ÌN n 1 u u q 2 n 1 n H 2 2 C Ư –
Câu 28: Cho cấp số nhân u có u 3 và q 2. Tính tổng 10 số hạng đầu tiên của cấp số n 1 0834 nhân đã cho. 3321 A. S 511. B. S 1025. C. S 1025. D. S 1023. 10 10 10 10 33 Lời giải Chọn D u 3 1 q 1 2 10 10 1 S u . 3. 1023. 10 1 q 2 1 q 1 2
Câu 29: Cho cấp số nhân có các số hạng lần lượt là 1; 4; 16; 64; Gọi S là tổng của n số hạng n
đầu tiên của cấp số nhân đó. Mệnh đề nào sau đây đúng? n n 1 1 4 n 44n 1 A. n 1 S 4 . B. S . C. 4 1 S . D. S . n n 2 n 3 n 3 Lời giải Chọn C
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 82
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com u 1 n n n
Cấp số nhân đã cho có 1 1 q 1 4 4 1 S u . 1. . n 1 q 4 1 q 1 4 3
Câu 30: Một cấp số nhân có 6 số hạng với công bội bằng 2 và tổng số các số hạng bằng 189. Tìm
số hạng cuối u của cấp số nhân đã cho. 6 A. u 32. B. u 104. C. u 48. D. u 96. 6 6 6 6 Lời giải Chọn D q 2 q 2 Theo giả thiết: 5 5 6 6 1 q 1 2
u u q 3.2 96. 6 1
S 189 u u . u 3 6 1 1 1 1 q 1 2
Câu 31: Cho cấp số nhân u có u 6 và q 2. Tổng n số hạng đầu tiên của cấp số nhân đã n 1 cho bằng 2046. Tìm . n A. n 9. B. n 10. C. n 11. D. n 12. Lời giải Chọn B n 1 n q 1 2 Ta có n n
2046 S u . 6. 2 2 1 2 1024 n 10. n 1 GV: TR 1 q 1 2 Câu 32:
n Tìm số hạng thứ 4 của Ầ
Cho cấp số nhân u có tổng n số hạng đầu tiên là S 5 1. n n N Đ cấp số nhân đã cho. ÌN H C A. u 100. B. u 124. C. u 500. D. u 624. 4 4 4 4 Ư – 0834 Lời giải 3321 Chọn C 33 q u u q u n 1 n 1 4 1 1 n Ta có 5 1 S u . q 1 . Khi đó n 1 1 1 1 q q 1 q 5 q 5 3 3
u u q 4.5 50 4 1 n Câu 33: 3 1
Cho cấp số nhân u có tổng n số hạng đầu tiên là S
. Tìm số hạng thứ 5 của n n n 1 3 cấp số nhân đã cho. A. 2 1 5 u . B. u . C. 5 u 3 . D. u . 5 4 3 5 5 3 5 5 5 3 Lời giải Chọn A n u 3 1 q u 2 n 1 1 Ta có 3 1 1 u 1 3 1 S 1 n q Khi đó n n 1 1 . 1 3 3 1 q q q 3 3
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 83
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com 2 4 u u q 5 1 4 3
Câu 34: Một cấp số nhân có số hạng thứ bảy bằng 1 , công bội bằng 1 . Hỏi số hạng đầu tiên của 2 4
cấp số nhân bằng bào nhiêu? A. 4096. B. 2048. C. 1024. D. 1 . 512 Lời giải Chọn B 1 q 6 Ta có 4 4 u 2048 1 1 u 2 6 1
u u q 7 1 6 2 4
Câu 35: Cho cấp số nhân u có u 6 và u 486. Tìm công bội q của cấp số nhân đã cho, n 2 6 biết rằng u 0. 3 A. q 3. B. 1 q . C. 1 q . D. q 3. 3 3 Lời giải Chọn D GV: TR
6 u u q 2 1 4 4
q 81 3 q 3. Ầ 5 4 4 N
486 u u q u . q q 6.q 6 1 1 Đ ÌN H
Câu 36: Cho cấp số nhân u ; u ; u ; với u 1. Tìm công bội q để 4u + 5u đạt giá trị nhỏ 1 2 3 1 2 3 C Ư nhất? – 0834 A. 2 q . B. q 0. C. 2 q . D. q 1. 5 5 3321 Lời giải 33 Chọn A 2 Ta có 2 4 4 2 2
4u 5u 4u q 5u q 5q 4q 5q . Vậy 2 3 1 1 5 5 5 4
min 4u 5u khi 2 q 2 3 5 5
Câu 37: Một cấp số nhân có số hạng thứ hai bằng 4 và số hạng thứ sáu bằng 64, thì số hạng
tổng quát của cấp số nhân đó có thể tính theo công thức nào dưới đây? A. n 1 u 2 . B. u 2n C. n 1 u 2 . D. u 2 . n n n n n Lời giải Chọn B
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 84
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
4 u u q u 2 Ta có 2 1 1 n 1 n 1 u u q 2.2 2n. n 1 5 4 4 64
u u q u . q q 4q q 2 6 1 1
Câu 38: Cho cấp số nhân u có công bội .
q Mệnh đề nào sau đây đúng? n A. u u k 1 u u .q . B. k 1 k 1 u .
C. u u .u .
D. u u k –1 q. k 1 k 1 k 2 k k 1 k 2 Lời giải Chọn A
Câu 39: Cho cấp số nhân u có u 0 và q 0. Đẳng thức nào sau đây là đúng? n 1 A. 3
u u .q . B. 4
u u .q . C. 5
u u .q . D. 6
u u .q . 7 4 7 4 7 4 7 4 Lời giải Chọn A 3 u u q 4 1 u 3 u q 3 3 .q u q 7 1 4 6 u u q 7 1
Câu 40: Cho cấp số nhân u có u 0 và q 0. Với 1 k ,
m đẳng thức nào dưới đây là đúng? n 1
A. u u . k q .
B. u u . m q . C. u u . m k q .
D. u u .qmk . m k m k m k m k Lời giải GV: TR Chọn C Ầ N k 1 m 1 k 1 mk mk Đ u u q u u q u q .q u q k 1 m 1 1 k ÌN H C
Câu 41: Cho một cấp số nhân có n số hạng n k 5
5 . Đẳng thức nào sau đây sai? Ư – 0834
A. u .u u .u .
B. u .u u .u .
C. u .u u .u .
D. u .u u .u . 1 n 2 n 1 1 n 5 n4 1 n 55 n 55 1 n k nk 1 3321 Lời giải 33 Chọn C n 1 u u u .u q u q u q
u u với k m n 1. n
k 1 m 1 . . 1 1 1 1 1 k m u 192
Câu 42: Tìm số hạng đầu
u và công bội q của cấp số nhân u biết 6 . n , 1 u 384 7 u 5 u 6 u 6 u 5 A. 1 . B. 1 . C. 1 . D. 1 . q 2 q 2 q 3 q 3 Lời giải Chọn B 5 q 2 19
2 u u q 6 1 192 . 6 384
u u q u q q 192q u 6 7 1 5 1 1 5 q
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 85
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com u u 36
Câu 43: Cho cấp số nhân u thỏa mãn 4 2
. Chọn khẳng định đúng? n u u 72 5 3 u 4 u 6 u 9 u 9 A. 1 . B. 1 . C. 1 . D. 1 . q 2 q 2 q 2 q 3 Lời giải Chọn B
u u u q 2 q 2 36 q 1 4 2 1 36 . 2 72
u u u q 2 q 1 u q 2 q u 6 1 1 q 36q q 2 5 3 1 1 q 1 u 8u
Câu 44: Cho cấp số nhân u thỏa mãn 20 17
. Chọn khẳng định đúng? n u u 272 1 5 A. q 2. B. q 4. C. q 4. D. q 2. Lời giải Chọn A 3 19 16 q 8 u 8u u q 8u q 1 1 q 2 20 17 272 . u u 272 u 1 q 272 u u 16 1 5 1 4 1 4 1 1 q GV: TR
Câu 45: Một cấp số nhân có năm số hạng mà hai số hạng đầu tiên là các số dương, tích của số Ầ
hạng đầu và số hạng thứ ba bằng 1, tích của số hạng thứ ba và số hạng cuối bằng 1 . N 16 Đ ÌN
Tìm số hạng đầu u và công bội q của cấp số nhân đã cho. 1 H C 1 u 2 u 2 1 Ư u 1 1 u – A. 1 2 . B. 1 . C. 1 . D. 1 2 . 0834 q q q 2 2 2 q 2 3321 Lời giải 33 Chọn B u , u 0, 1 1 1 u 0 q 0 q 2 2 2 2 u .u 1 . u q 1 1 3 1 1 u 2 1 1 . 1 2 6 2 2 4 4 q u u u q u q q q 3 5 1 1 16 16
Câu 46: Cho cấp số nhân u có công bội q và thỏa n 1 1 1 1 1 u
u u u u 49 1 2 3 4 5 u u u u u . 1 2 3 4 5
u u 35 1 3 Tính 2
P u 4q . 1 A. P 24. B. P 29. C. P 34. D. P 39.
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 86
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com Lời giải Chọn B Nhận xét: Nếu 1 1 1 1 1
u , u , u , u , u là một cấp số nhân với công bội q thì , , , , 1 2 3 4 5 u u u u u 1 2 3 4 5
cũng tạo thành cấp số nhân với công bội 1 . q 1 1 5 5 q 1 1 q u . 49 . 1 1
Do đó từ giả thiết ta có q 1 u 1 . 1 1 q 2 u u q 35 2 1 1 5 5 Phương trình q 1 49 q 1 2 4 2 1 u .
u q 49 u q 7 . 1 4 q 1
u q q 1 1 1 1 Với 7 2 u q 7
. Thay vào 2 , ta được u 7 35 u 42 . Suy ra 2 q : vô lý. 1 1 1 42 u 28 u 28 1 1 Với 2
u q 7 . Thay vào 2 , ta được u 7 35 u 28 . Vậy hoặc . Khi đó 1 1 1 1 1 q q 2 2 2
u 4q 29. 1 GV: TR u
u u 26
Câu 47: Cho cấp số nhân
u có công bội q và thỏa 1 2 3
. Tìm q biết rằng q 1. n 2 2 2 u
u u 364 1 2 3 Ầ N Đ A. 5 q . B. q 4. C. 4 q . D. q 3. ÌN 4 3 H C Ư Lời giải – 0834 Chọn D 3321 2 u
u u 26 u 2 1 q q 26 2 u 2 1 q q 2 26 1 1 1 1 2 3 33 Ta có . 2 2 2 2 2 4 u u u 364 2 2 4 u 1 q q 364 2 1 1 2 3 u 1 q q 364 1 Lấy 1 chia 2 , ta
1q q 2 2 2 được 26 1 1 4 3 2 2
3q 7q 4q 7q 3 0 3q 7
q 4 0 . 2 4 2 1 q q 364 q q
t 1 loaïi Đặt 1 t q
, t 2 . Phương trình trở thành 2
3t 7t 10 0 10 . q t 3 Với 10 1 10 t , suy ra 2 q
3q 10q 3 0 q 3 hoặc 1 q
. Vì q 1 nên q 3. 3 q 3 3
Câu 48: Các số x 6y, 5x 2y, 8x y theo thứ tự đó lập thành một cấp số cộng; đồng thời các số
x 1, y 2, x 3y theo thứ tự đó lập thành một cấp số nhân. Tính 2 2 x y .
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 87
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com A. 2 2 x y 40. B. 2 2 x y 25. C. 2 2
x y 100. D. 2 2 x y 10. Lời giải Chọn A
x 6y8x y 25x 2y
Theo giả thiết ta có x
1 x 3y y 22 x 3y x 3y x 6 . 3y
1 3y 3y y 22 0 y 22 y 2 Suy ra 2 2 x y 40.
Câu 49: Ba số x; y; z theo thứ tự lập thành một cấp số nhân với công bội q khác 1; đồng thời các
số x; 2y; 3z theo thứ tự lập thành một cấp số cộng với công sai khác 0. Tìm giá trị của q . A. 1 q . B. 1 q . C. 1 q . D. q 3. 3 9 3 Lời giải Chọn A 2
y xq; z xq x 0 GV: TR 2
x 3xq 4xq x 2
3q 4q x 3z 2 2y 1 0 . 2
3q 4q 1 0 Ầ N
Nếu x 0 y z 0 công sai của cấp số cộng: x; 2 y; 3z bằng 0 (vô lí). Đ ÌN H q 1 C 1 2 Ư
Nếu 3q 4q 1 0 1 q q 1 . q 3 – 3 0834 3321
Câu 50: Cho dãy số tăng a, ,
b c c theo thứ tự lập thành cấp số nhân; đồng thời a, b 8, c 33
theo thứ tự lập thành cấp số cộng và a, b 8, c 64 theo thứ tự lập thành cấp số nhân.
Tính giá trị biểu thức P a b 2c. A. 184 P . B. P 64. C. 92 P . D. P 32. 9 9 Lời giải Chọn B 2 2 ac b ac b 1 Ta có
a c 2b 8
a 2b 16c 2 .
ac 64 b 2 8
ac 64a b 2 8 3
Thay (1) vào (3) ta được: 2 2
b 64a b 16b 64 4a b 4 4.
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 88
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com c 8 a
a 2b 16c
Kết hợp (2) với (4) ta được: 7 5 4a b 4 4c 60 b 7
Thay (5) vào (1) ta được: c 36 7c
8 c 4c 602 2
9c 424c 3600 0
100 c 36 c . c 9
Với c 36 a 4, b 12 P 412 72 64.
Câu 51: Số hạng thứ hai, số hạng đầu và số hạng thứ ba của một cấp số cộng với công sai khác 0
theo thứ tự đó lập thành một cấp số nhân với công bội q . Tìm . q A. q 2. B. q 2. C. 3 q . D. 3 q . 2 2 Lời giải Chọn B
Giả sử ba số hạng a; ;
b c lập thành cấp số cộng thỏa yêu cầu, khi đó ; b ;
a c theo thứ tự đó
lập thành cấp số nhân công bội . q Ta có
a c 2b b 0 GV: TR 2
bq bq 2b . 2 2
a bq; c bq
q q 2 0 Ầ N
Nếu b 0 a b c 0 nên a; ;
b c là cấp số cộng công sai d 0 (vô lí). Đ ÌN H Nếu 2
q q 2 0 q 1 hoặc q 2. Nếu q 1 a b c (vô lí), do đó q 2. C Ư –
Câu 52: Cho bố số a, b, c, d biết rằng a, ,
b c theo thứ tự đó lập thành một cấp số nhân công bội 0834 q 1 ; còn ,
b c, d theo thứ tự đó lập thành cấp số cộng. Tìm q biết rằng a d 14 và 3321 b c 12. 33 A. 18 73 q . B. 19 73 q . C. 20 73 q . D. 21 73 q . 24 24 24 24 Lời giải Chọn B
Giả sử a,b,c lập thành cấp số cộng công bội .
q Khi đó theo giả thiết ta có: 2 b
aq, c aq 2
aq d 2aq 1 b d 2c
a d 14 2 a d 14 a 2
q q 12 3 b c 12
Nếu q 0 b c 0 d (vô lí)
Nếu q 1 b a
;c a b c 0 (vô lí).
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 89
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com Vậy 12 q 0, q
1, từ (2) và (3) ta có: d 14a và a thay vào (1) ta được: 2 q q 2 3 12q 14q 14q 12 24q 3 2
12q 7q 13q 6 0 2 2 2 q q q q q q q 73 1 19 2
12q 19q 6 0 q 24 Vì q 1 nên 19 73 q . 24
Câu 53: Gọi S 111111...111...1 ( n số 1) thì S nhận giá trị nào sau đây? n n A. 10 1 S . B. 10 1 S 10 . 81 81 n n C. 10 1 S 10 . n D. 1 10 1 S 10 n . 81 9 9 Lời giải Chọn D n Ta có 1 1 1 10 S 9 99 999 ... 99...9 . 1 0. n . 9 n so 9 9 1 10 b Câu 54: 21.3 b Biết rằng 2 10
S 1 2.3 3.3 ...11.3 a
. Tính P a . GV: TR 4 4 A. P 1. B. P 2. C. P 3. D. P 4. Ầ N Đ Lời giải ÌN H Chọn C C Ư – Từ giả thiết suy ra 2 3 11 . Do đó 3S 3 2.3 3.3 ... 11.3 0834 11 11 1 3 1 21.3 1 21 3321 2 10 11 11 11
2S S 3S 1 3 3 ... 3 10.3 11.3 S .3 . 1 3 2 2 4 4 33 11 b Vì 1 21.3 21.3 1 1 11 S a
a , b 11 P 3. 4 4 4 4 4 4
Câu 55: Một cấp số nhân có ba số hạng là , a ,
b c (theo thứ tự đó) trong đó các số hạng đều khác
0 và công bội q 0. Mệnh đề nào sau đây là đúng? A. 1 1 1 1 1 1 . B. . C. . D. 1 1 2 . 2 a bc 2 b ac 2 c ba a b c Lời giải Chọn B Ta có 1 1 2 ac b 2 b ac
Câu 56: Bốn góc của một tứ giác tạo thành cấp số nhân và góc lớn nhất gấp 27 lần góc nhỏ nhất.
Tổng của góc lớn nhất và góc bé nhất bằng:
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 90
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com A. 0 56 . B. 0 102 . C. 0 252 . D. 0 168 . Lời giải Chọn C
Giả sử 4 góc A, B, C, D (với A B C D ) theo thứ tự đó lập thành cấp số nhân thỏa yêu cầu với công bội . q Ta có q A B C D 360 A 3 2 3
1 q q q 360 A 9
A D 252. 3 D 27 A Aq 27A 3
D Aq 243
Câu 57: Người ta thiết kế một cái tháp gồm 11 tầng. Diện tích bề mặt trên của mỗi tầng bằng nữa
diện tích của mặt trên của tầng ngay bên dưới và diện tích mặt trên của tầng 1 bằng nửa
diện tích của đế tháp (có diện tích là 2
12 288 m ). Tính diện tích mặt trên cùng. A. 2 6 m . B. 2 8 m . C. 2 10 m . D. 2 12 m . Lời giải Chọn A
Diện tích bề mặt của mỗi tầng (kể từ 1) lập thành một cấp số nhân có công bội 1 q 2 GV: TR và 12 288 u
6 144. Khi đó diện tích mặt trên cùng là 1 2 Ầ 6144 N 10 u u q 6 Đ 11 1 10 2 ÌN H C
Câu 58: Một du khách vào chuồng đua ngựa đặt cược, lần đầu đặt 20000 đồng, mỗi lần sau tiền Ư –
đặt gấp đôi lần tiền đặt cọc trước. Người đó thua 9 lần liên tiếp và thắng ở lần thứ 10. 0834
Hỏi du khác trên thắng hay thua bao nhiêu? 3321 A. Hòa vốn. B. Thua 20000 đồng. 33 C. Thắng 20000 đồng. D. Thua 40000 đồng. Lời giải Chọn C
Số tiền du khác đặt trong mỗi lần (kể từ lần đầu) là một cấp số nhân có u 20 000 và 1 công bội q 2.
Du khách thua trong 9 lần đầu tiên nên tổng số tiền thua là: u 9 1 p 1
S u u ... u 10220000 9 1 2 9 1 p
Số tiền mà du khách thắng trong lần thứ 10 là 9
u u . p 10240000 10 1
Ta có u S 20 000 0 nên du khách thắng 20 000. 10 9
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 91
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com ÔN TẬP CHƯƠNG 2
PHẦN 1: GIẢI BÀI TẬP SÁCH GIÁO KHOA 1 Bài 1:
Cho dãy số u được xác định bởi: u và u 3u với mọi n 2 . Số hạng thứ năm n 1 3 n n 1
của dãy số u là: n A. 27. B. 9. C. 81. D. 243. Lời giải Chọn A u 1
Ta có: n 3. Do đó dãy số u là một cấp số nhân với số hạng đầu u và công n u 1 3 n 1 1
bội q 3 nên ta có số hạng tổng quát là: n 1 n2 u 3 3 với * n . n 3 GV: TR
Do đó số hạng thứ năm của dãy số u là: 52 u 3 27 . n 5 Ầ Bài 2:
Trong các dãy số sau, dãy số nào là cấp số cộng? N Đ ÌN 1 5 11 15 A. 21, 3 , 27, 5 1, 7 5 . B. , , 2, , . H C 2 4 4 4 Ư 1 1 1 1 1 – C. 1, 2, 3, 4, 5 . D. , , , , . 0834 20 30 40 50 60 3321 Lời giải 33 Chọn A Dãy số 21; 3 ; 2 7; 5 1; 7
5 lập thành một cấp số cộng có số hạng đầu là u 21 và 1
công sai d 24 . Bài 3:
Cho cấp số cộng u có số hạng đầu u 5
, công sai d 4 . Công thức của số hạng n 1 tổng quát u là: n
A. u 5 4n .
B. u 1 4n . n n C. 2 u 5 4n .
D. u 9 4n . n n Lời giải Chọn D
Công thức số hạng tổng quát của cấp số cộng u 5 n 1 4 4n 9 . n Bài 4:
Tổng 100 số tự nhiên lẻ đầu tiên tính từ 1 là:
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 92
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com A. 10000. B. 10100. C. 20000. D. 20200. Lời giải Chọn A
Các số tự nhiên lẻ lập thành một cấp số cộng với số hạng đầu u 1và công sai d 2 . 1
Do đó tổng 100 số hạng đầu tiên của cấp số cộng này là: 100.11 99.2 S 10000. 100 2 Bài 5:
Trong các dãy số u cho bằng phương pháp truy hồi sau, dãy số nào là cấp số nhân? n
A. Dãy số u được xác định bởi: u 1 và u u
n 1 với mọi n 2 . n n 1 n 1
B. Dãy số u được xác định bởi: u 1 và u 2u 1 với mọi n 2 . n 1 n n 1
C. Dãy số u được xác định bởi: u 1 và 2 u u với mọi n 2 . n 1 n n 1 1
D. Dãy số u được xác định bởi: u 3 và u u với mọi n 2 . n 1 n n 1 3 Lời giải Chọn D 1
Dãy số u được xác định bởi: u 3 và u u với mọi n 2 là cấp số nhân với n 1 n n 1 GV: TR 3 1
số hạng đầu u 3 và q . 1 Ầ 3 N Đ ÌN 1 1 Bài 6:
Cho cấp số nhân u có u 1
, công bội q . Khi đó là số hạng thứ: H n 1 2017 C 10 10 Ư – A. 2016. B. 2017. C. 2018. D. 2019 0834 Lời giải 3321 Chọn C 33 n 1 1
Số hạng tổng quát của cấp số nhân là: u . n 1 10 n 1 1 1 Xét u n 1 2017 10 10 n 1 2017 1 1 10 10 n 1 2017 n 2018. Bài 7:
Trong các dãy số u sau đây, dãy số nào là dãy số tăng? n 1 A. u sinn . B. u ( n 1 )n . C. u . D. 1 u 2n . n n n n n Lời giải
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 93
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com Chọn D Ta có: n 1 1 n2 u 2 2 n 1 Xét hiệu n2 u u 2
2n 3.2n 0 với mọi * n n 1 n
Vậy dãy số đã cho là dãy số tăng. Bài 8:
Xét tính tăng, giảm và bị chặn của mỗi dãy số u sau, biết số hạng tổng quát: n 2 n 2 a) u ; b) u c) 2 u ( 1 )n n n n n 1 n 5n Lời giải 2 2 (n 1) (n 1) a) Ta có: u n 1 n 1 1 n 2 Xét hiệu 2 2 3 2 (n 1) n
(n 1) n n 2 3 2 3 2
n 3n 3n 1 n 2n u u n 1 n n 2 n 1 n 2n 1
n 2n 1 2 n 3n 1 0 * n N
n 2n 1
Vì vậy dãy số đã cho là dãy số tăng. GV: TR 2 b) Ta có: u n 1 n 1 5 Ầ N 2 2 4 2 8 Đ Xét hiệu u u 0 n 1 n n 1 n n n 1 ÌN 5 5 5 5 5 H C
Vì vậy dãy số đã cho là dãy số giảm. Ư – 0834 Bài 9:
Cho cấp số cộng u . Tìm số hạng đầu u , công sai d trong mỗi trường hợp sau: n 1 3321
a) u u 42 và u u 66 ; b) u u 22 và u u 21. 2 5 4 9 2 4 1 5 33 Lời giải
a) Ta có: u u u d u 3d 42 2 5 1 1 2u 4 d 42 1
Ta lại có: u u u 3 d u 8 d 2u 11 d 66 4 9 1 1 1
Khi đó ta có hệ phương trình: 99 u 1
2u 4d 42 1 7 2u 11d 66 24 1 d 7 99 24
Vậy số hạng đầu của cấp số cộng là: u và công sai d . 1 7 7
b) Ta có: u u u d u 3d 22 2 4 1 1
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 94
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com 2u 4 d 22 1 u 2 d 11 1 u 11 2 d 1
Ta lại có: u .u u u 4d 21. 1 5 1 1
Thay u 11 2d vào biểu thức trên ra được: 1
11 2d 11 2d 4d 21
11 2d 11 2d 21 2 121 4d 21
d 5 hoặc d 5 . Với d 5 thì u 1. 1
Với d 5 thì u 21. 1
Bài 10: Cho cấp số nhân u . Tìm số hạng đầu u , công bội q trong mỗi trường hợp sau: n 1
a) u 192 và u 384 b) u u u 7 và u u 14 . 6 7 1 2 3 5 2 Lời giải a) Ta có 5
u u q 192 và 6
u u q 384 6 1 7 1 5 GV: TR u u q 1 192 1 Xét: 6 1 6 u u q q 384 2 7 1 Ầ N 5 Đ 1 ÌN Suy ra: u 192 : 6144 . 1 H 2 C Ư 1 –
Vậy cấp số nhân có số hạng đầu u u 6144 và công bội q . 1 0834 2 3321 b) Ta có: 2
u u u u u q u q 7 1 2 3 1 1 1 33 u 2 1 q q 7 1 Và 4
u u u q u q 14 5 2 1 1 u q 3 q 1 14 1 u 2 1 q q 1 7 Suy ra: u q 3 q 1 14 1 u 2 1 q q 1 7 u q q 1 2 1 q q 14 1
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 95
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
2 q q 1 2
q q 2 0 q 2 q 1
q 2 thì u 1 1 q 1 thì u 7 1
Bài 11: Tứ giác ABCD có số đo bốn góc ,
A B, C, D theo thứ tự lập thành cấp số cộng. Biết số đo
góc C gấp 5 lần số đo góc A . Tính số đo các góc của tứ giác ABCD theo đơn vị độ. Lời giải
Do A, B, C, D theo thứ tự lập thành một cấp số cộng nên ta có:
B A d;C A 2d; D A 3d Mặt khác:
A B C D 360
A A d A 2d A 3d 360
4 A 6d 360
2 A 3d 180 Ta lại có: GV: TR
A 2d 5A d 2 A Ầ 8A 180 N Đ
A 22, 5 và d 45 ÌN H
B 67, 5 , C 112, 5 , D 157, 5 C Ư –
Bài 12: Người ta trồng cây theo các hàng ngang với quy luật: ở hàng thứ nhất có 1 cây, ở hàng 0834
thứ hai có 2 cây, ở hàng thứ ba có 3 cây,. ở hàng thứ n có n cây. Biết rằng người ta 3321
trồng hết 4950 cây. Hỏi số hàng cây được trồng theo cách trên là bao nhiêu? 33 Lời giải
Giải sử người ta đã trồng được n hàng.
Số cây ở mỗi hàng lập thành một cấp số cộng với u 1 , công sai d 1 1
Tổng số cây ở n hàng cây là: n 1 n n n 1 S 4950 n 2 2 2 n n 9900 0 n 99 ( thảo mãn ) n 100 ( không thảo mãn )
Vậy có 99 hàng cây được trồng theo cách trên.
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 96
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
Bài 13: Một cái tháp có 11 tầng. Diện tích của mặt sàn tầng 2 bằng nửa diện tích của mặt đáy
tháp và diện tích của mặt sàn mỗi tầng bằng nửa diện tích của mặt sàn mỗi tầng ngay
bên dưới. Biết mặt đáy tháp có diện tích là 2
12288 m . Tính diện tích của mặt sàn tầng
trên cùng của tháp theo đơn vị mét vuông. Lời giải
Diện tích mặt đáy tháp là u 12288 2 m . 1 1
Diện tích mặt sàn tầng 2 là: u 12 288. 6144 2 m . 2 2 .
Gọi diện tích mặt sàn tầng n là u với * n . n 1
Dãy u lập thành một cấp số nhân là u 12288 và công bội q , có số hạng tổng n 1 2 n 1 1 quát là: u 12288. . n 2
Diện tích mặt tháp trên cùng chính là mặt tháp thứ 11 nên ta có: 11 1 1 u 12 288. 12 2 m . 11 2 GV: TR
Bài 14: Một khay nước có nhiệt độ 23 C được đặt vào ngăn đá của tủ lạnh. Biết sau mỗi giờ, Ầ
nhiệt độ của nước giảm 20%. Tính nhiệt độ của khay nước đó sau 6 giờ theo đơn vị độ N Đ C . ÌN H C Lời giải Ư –
Gọi u là nhiệt độ của khay nước đó sau n giờ (đơn vị độ C ) với * n N . 0834 n 3321
Ta có: u 23;u 23 23.20% 23.1 20% 2
23.80%;u 23.80%.80% 23.(80%) ; 1 2 3 33
Suy ra dãy u lập thành một cấp số nhân với số hạng đầu u 23 và công bội n 1
q 80% có số hạng tổng quát 1 u 23.(80%)n độ C n
Vậy sau 6 giờ thì nhiệt độ của khay là 5
u 23 (80%) 7,5 C . 6
Bài 15: Cho hình vuông C có cạnh bằng 4. Người ta chia mỗi cạnh hình 1
vuông thành bốn phần bằng nhau và nối các điểm chia một cách
thích hợp để có hình vuông C (Hình 4). Từ hình vuông C lại 2 2
làm tiếp tục như trên để có hình vuông C . Cứ tiếp tục quá trình 3
như trên, ta nhận được dãy các hình vuông C ,C ,C ,,C , 1 2 3 n
Gọi a là độ dài cạnh hình vuông C . Chứng minh rằng dãy số n n
a là cấp số nhân. n Lời giải
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 97
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
Độ dài cạnh của hình vuông đầu tiên là: a 4 . 1
Độ dài cạnh của hình vuông thứ n là: a . n 10
Độ dài cạnh của hình vuông thứ n 1 là: a a . n 1 4 n a 10 Suy ra: n 1 a 4 n 10
Vậy a là một cấp số nhân với số hạng đầu a 4 và công bội q . n 1 4
Bài 16: Ông An vay ngân hàng 1 tỉ đồng với lãi suất 12% / năm. Ông đã trả nợ theo cách: Bắt
đầu từ tháng thứ nhất sau khi vay, cuối mỗi tháng ông trả ngân hàng cùng số tiền là a
(đồng) và đã trả hết nợ sau đúng 2 năm kể từ ngày vay. Hỏi số tiền mỗi tháng mà ông
An phải trả là bao nhiêu đồng (làm tròn kết quả đến hàng nghìn)? Lời giải
Gọi u là số tiền sau mỗi tháng ông An còn nợ ngân hàng. n
Lãi suất mỗi tháng là 1% . Ta có: GV: TR
u 1000000000 đồng. 1 Ầ
u u u 1% a u 11% a (đồng) 2 1 1 1 N Đ ÌN
u u 11% a u 11% a .1% a 3 1 1 H C Ư 2
u (11%) a 11% a 1 – 0834 3321 n 1 n2 n3 n4 u u (11%) a(11%) a(11%) a(11%) a . n 1 33 Ta thấy dãy n2 n3 n4 a(11%) ; a(11%) ; a(11%)
;; a lập thành một cấp số nhân với
số hạng đầu a a và công bội q 11% 99% có tổng n 2 số hạng đầu là: 1 a n2 1 (%) n2 S 100a 1 (99%) . n2 1 99% n 1 n2 Suy ra u u (11%) 100a 1 (99%) n 1
Vì sau 2 năm = 24 tháng thì ông An trả xong số tiền nên n 24 và u 0 . Do đó ta 24 có: 23 22 u
u (11%) 100a 1 (99%) 0 24 1 23 22
1000000000.(99%) 100a 1 (99%) 0 . a 40006888, 25
Vậy mỗi tháng ông An phải trả 40006888,25 đồng.
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 98
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com GV: TR Ầ N Đ ÌN H C Ư – 0834 3321 33
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 99
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
PHẦN 2: BÀI TẬP TỔNG ÔN CHƯƠNG 2 PHẦN 1: TRẮC NGHIỆM
Câu 1: Khẳng định nào sau đây là sai? A. Dãy số có 1 u . a 3n . B. Hiệu số u u 3.a . n 1 n 1 n
C. Với a 0 thì dãy số tăng.
D. Với a 0 thì dãy số giảm. Lời giải Chọn B Ta có n 1 u u .3 a .3n a .3n a 3 1 2 .3n a . n 1 n
Câu 2: Cho dãy số u với u 2n 1. Dãy số u là dãy số n n n
A. Bị chặn trên bởi 1. B. Giảm.
C. Bị chặn dưới bởi 2. D. Tăng. Lời giải Chọn D * n ta có: u
u 2 n 1 1 2n 1 2 0 nên u
u vậy dãy số u tăng. n n 1 n n 1 n
Câu 3: Cho cấp số cộng u có u 3 và công sai d 7 . Hỏi kể từ số hạng thứ mấy trở đi thì n 1 GV: TR
các số hạng của u đều lớn hơn 2018 ? n A. 287 . B. 289 . C. 288 . D. 286 . Ầ N Lời giải Đ ÌN Chọn B H C Ư 2022
Ta có: u u n 1 d 3 7 n 1 7n 4 ; u 2018 7n 4 2018 n – n 1 n 0834 7 Vậy n 289 . 3321
Câu 4: Xác định số hàng đầu u và công sai d của cấp số cộng u có u 5u và u 2u 5 33 n 1 9 2 13 6 .
A. u 3 và d 4 .
B. u 3 và d 5 . C. u 4 và d 5 . D. u 4 và d 3 . 1 1 1 1 Lời giải Chọn A u
8d 5 u d 1 1
Ta có: u u n 1 d . Theo đầu bài ta có hpt: n 1
u 12d 2 u 5d 5 1 1
4u 3d 0 u 3 1 1 . u 2d 5 d 4 1
Câu 5: Cho cấp số cộng u có u 12 , u 18 . Tính tổng 16 số hạng đầu tiên của cấp số n 4 14 cộng này. A. S 24 . B. S 26 . C. S 25 . D. S 24 . 16 16 16 16
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 100
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com Lời giải Chọn D u 3d 12 u 21
Gọi d là công sai của cấp số cộng. Theo giả thiết, ta có 1 1 . u 13d 18 d 3 1 2u 15d .16 1 Khi đó, S
842 45 24 . 16 2
Câu 6: Cho cấp số cộng u biết u 18 và 4S S . Tìm số hạng đầu tiên u và công sai d của n 5 n 2n 1 cấp số cộng.
A. u 2 ; d 4 .
B. u 2 ; d 3 .
C. u 2 ; d 2 .
D. u 3; d 2 . 1 1 1 1 Lời giải Chọn A
Ta có: u 18 u 4d 18 1 . 5 1 n n 1 d 2n 2n 1 d 4S S 4 nu 2nu
4u 2nd 2d 2u 2nd d n 2n 1 1 2 2 1 1
2u d 0 2 . 1 Từ
1 và 2 suy ra u 2 ; d 4 . GV: TR 1
Câu 7: Bốn số tạo thành một cấp số cộng có tổng bằng 28 và tổng các bình phương của chúng Ầ N Đ
bằng 276 . Tích của bốn số đó là : ÌN H A. 585 . B. 161. C. 404 . D. 276 . C Ư – Lời giải 0834 Chọn A 3321 33
Gọi 4 số cần tìm là a 3r , a r , a r , a 3r .
a 3r a r a r a 3r 28 a 7 a 7 Ta có: . a 3r 2
2 a r2 a r 2 a 3r2 276 r 4 r 2
Bốn số cần tìm là 1, 5 , 9 , 13 có tích bằng 585 . u
3u u 2 1
Câu 8: Cho cấp số cộng u thỏa 5 3 2
. Tổng 15 số hạng đầu của cấp số cộng n
3u 2u 3 4 7 4 là. A. 244 . B. 274 . C. 253 . D. 285 . Lời giải Chọn D
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 101
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
Giả sử cấp số cộng có số hạng đầu là u và công sai là d . 1 u
3u u 2 1 u
4d 3 u 2d u d 21 3
u 9d 2 1 1 1 1 Khi đó, 5 3 2 1 3u 2u 3 4 3
u 6d 2 u 3d 34 u 12d 3 4 1 1 7 4 1 u 2 1 . d 3 15 Từ đó suy ra S
. 2.2 15 1 . 3 285 15 2 . u 3
Câu 9: Cho dãy số u biết 1 , * n
. Tìm số hạng tổng quát của dãy số u . n n u 3u n 1 n A. u 3n . B. 1 u 3n . C. 1 u 3n . D. n 1 u n . n n n n Lời giải Chọn A u Ta có n 1 3 . un
Do đó dãy số u là một cấp số nhân với u 3, công bội q 3. n 1
Vậy số hạng tổng quát của cấp số nhân là: 1 u u . n q 1 3.3n 3n . n 1 GV: TR u
u u 13 Ầ
Câu 10: Cho cấp số nhân u thỏa mãn: 1 2 3
. Tổng 8 số hạng đầu của cấp số nhân n N Đ u u 26 4 1 ÌN H u là n C Ư A. . B. . C. . D. . – S 3280 S 9841 S 3820 S 1093 8 8 8 8 0834 Lời giải 3321 Chọn A 33 2 u 3
u u 13 u 1 q q 13 1 q 1 26 Ta có : 1 2 3
q 1 2 q 3 u u 26 2 3
1 q q 13 4 1 u q 1 26 1 u 1. 1 1 8 1 3 S 3280 . 8 1 3 PHẦN 2 : TỰ LUẬN
Câu 11: Tìm giá trị x dương nhỏ nhất thỏa mãn ba số sin x,sin 2x, 3 cos x lập thành cấp số cộng. Lời giải
Theo bài ra, ba số sin x,sin 2x, 3 cos x lập thành cấp số cộng nên suy ra
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 102
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com 1 3
sin x 3 cos x 2sin 2x sin x cos x sin . x cos sin
.cos x sin 2x 2 2 3 3 2x x k 2 x k 2 3 3 sin x sin 2x k Z 3 2 k 2 2x x k 2 x 3 9 3 2
Nghiệm dương x nhỏ nhất sẽ ứng với k 0 . Vậy x hoặc x . 3 9
Câu 12: Chứng minh rằng ba số dương a,b,c theo thứ tự lập thành một cấp số cộng khi và chỉ khi 1 1 1 các số , ,
theo thứ tự lập thành cấp số cộng. b c c a a b Lời giải 1 1 1 Ba số , ,
lập thành cấp số cộng khi và chỉ khi b c c a a b 1 1 1 1 c a b c a b b c b a c b
c a b c a b c a GV: TR
b a b a c b c b Ầ N Đ
b a c b a, ,
b c lập thành cấp số cộng. ÌN H C
Câu 13: Chu vi của một đa giác là 45 cm, số đo các cạnh của nó lập thành một cấp số cộng với Ư –
công sai d 3cm . Biết cạnh lớn nhất là 15 cm, tính số cạnh của đa giác đó. 0834 Lời giải 3321
Gọi cạnh nhỏ nhất của đa giác là u và số cạnh của đa giác là n. 33 1
Ta có 15 u n 1 .3 hay u 18 3n 0 n 6 . 1 1
Tổng các cạnh là 45 cm, ta có
n 15 18 3n 45 hay 2
3n 33n 90 0 . 2 Giải phương trình với *
n N ; n 6 , ta được n 5 .
Câu 14: Tìm ba số hạng liên tiếp của một cấp số cộng, biết rằng:
a) Tổng của chúng bằng 15 và tích của chúng bằng 105.
b) Tổng của chúng bằng 21 và tổng bình phương của chúng bằng 155. Lời giải
Gọi ba số hạng liên tiếp của cấp số cộng là a,b, c a c 2b * .
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 103
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
a b c 15
a b c 15 a) Theo bài ra, ta có
, kết hợp với * , ta được a c 2b abc 105 abc 105 3 b 15 b 5 a 3 a 7
a c 2b c 10 a b 5 hoặc b 5 . abc 105 5 a 10 a 105 c 7 c 3
a b c 21
a b c 21 b) Theo bài ra, ta có
, kết hợp với * , ta được a c 2b 2 2 2
a b c 155 2 2 2
a b c 155 3b 21 b 7 a 5 a 9
a c 2b
c 14 a b 7 hoặc b 7 . 2 2 2
a b c 155 a c 5 14 a2 2 2 c 9 7 155
Câu 15: Cho ba số a,b,c theo thứ tự là ba số hạng liên tiếp của một cấp số cộng. Chứng minh rằng 2 2
a 2bc c 2ab và a bc b c2 2 8 2 . Lời giải
Vì a,b,c theo thứ tự lập thành cấp số cộng suy ra a c 2b . GV: TR Ta có 2 2
a 2bc c 2ab a ca c 2b c a a ca c 2b 0 Ầ N Suy ra 2 2 2 2
a 2bc c 2ab 0 a 2bc c 2ab điều phải chứng minh. Đ ÌN 2 2 2 2 2 2 2 2 H
Lại có a 8bc 2b c a 4a cc a 2c a 4ac 4c a 4ac 4c C Ư 2 2 2 2 –
Suy ra a 8bc 2b c 0 a 8bc 2b c điều phải chứng minh. 0834 3321 u 2 Câu 16: 1
Cho dãy số u xác định bởi . n 33 u
4u 9, n 1 n 1 n
a) Chứng minh dãy số v với v u 3, n 1 là một cấp số nhân. n n n
b) Tìm công thức tổng quát của dãy số u . n Lời giải
a) Ta có v u 3, suy ra v u
3 4u 9 3 . Do đó n 1 n 1 n n n v 4u 9 3 4 u 3 n 1 n n 4 . v u 3 u 3 n n n
Vậy v là cấp số nhân với số hạng đầu v u 3 2 3 5 và công bội q 4 . n 1 1 v 5
b) Do v là cấp số nhân với 1
nên số hạng tổng quát của n 1 n 1 v v .q 5.4 . n q 4 n 1
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 104
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
Suy ra công thức tổng quát của dãy số u là n 1 u v 3 5.4 3 . n n n u u 51
Câu 17: Cho cấp số nhân có 1 5 . u u 102 2 6
a) Tìm số hạng đầu tiên và công bội
b) Tính tổng của 10 số hạng đầu tiên.
c) Tổng của bao nhiêu số hạng đầu sẽ bằng 765.
d) Số 12288 là số hạng thứ mấy? Lời giải u u 51 u u q 51 u 4 4 1 q 51 1 u 3 1 5 Ta có 1 1 1 . 5 u u 102 u
q u q 102 u q 4 1 q 102 q 2 2 6 1 1 1
a) Vậy số hạng đầu u 3 và công bội q 2 . 1 10 10 1 q 1 2
b) Tổng của 10 số hạng đầu tiên S u . 3. 3069 . 10 1 1 q 1 2 GV: TR 1 n q 1 2n
c) Ta có S u . 3.
765 n 8 . Vậy tổng của 8 số hạng đầu tiên n 1 1 q 1 2 Ầ N Đ bằng 765. ÌN H C
d) Giả sử u 12288 . Theo công thức tổng quát của cấp số nhân, ta có Ư n – 0834 n 1 n 1 u u .q 12288 3.2 n 13 . n 1 3321
Vậy 12288 là số hạng thứ 13 của cấp số nhân. 33
Câu 18: Tìm số hạng đầu và công bội của cấp sống nhân n u , biết a) 5 u 1 u 15 u 8u . b) 20 17 . 4 u 2 u 6 3 u 5 u 240 c) 1 u 3 u 5 u 65 u u u 10 . d) 2 4 5 . 1 u 7 u 325 3 u 5 u 6 u 20 Lời giải u 4 4 1 q u u u q u 1 15 1 15 15 a) Ta có 5 1 1 1 . 3 u u 6 u
q u q 6 u q 2 4 2 1 1 1 q 1 6 2
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 105
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com 2 Lấy q 1 15 u 1 chia 2 , ta được 2
2q 5q 2 0 q 2 hoặc 1 q . Vậy 1 1 hoặc q 6 2 q 2 1 u 16 1 . q 2 19 16 3 u 8u u q 8u q q 8 u 12 b) Ta có 20 17 1 1 1 . 2 4 2 4 3 u 5 u 240 q 2 u q u q 240 u q u q 240 1 1 1 1 u 2 4 2 4 1 1 q q u u u u u q u q 65 1 65 65 c) Ta có 1 3 5 1 1 1 . 6 u u 325 u u q 325 u 6 1 7 1 1 1 1 q 325 2 6 1 q Lấy 325 u u 2 chia 1 , ta được 2
1q 5 q 2 . Vậy 1 5 hoặc 1 5 . 2 4 1q q 65 q 2 q 2 u q 2 3 3 4 1 1 q q u u u u q u q u q 10 1 10 10 d) Ta có 2 4 5 1 1 1 . 2 4 5 2 u u u 20 u
q u q u q 20 u q 2 3 3 5 6 1 1 1 1 1 q q 20 2 Lấy u 2 chia
1 , ta được q 2 . Vậy 1 1 . q 2 GV: TR
Câu 19: Tìm số hạng đầu và công bội của cấp sống nhân n u , biết Ầ u 1 N 1 Đ a) S 40 8 . b) 4 . ÌN 3 1 S 8 S 680 H 8 2 C Ư – Lời giải 0834 3321 u 1 1 u 1 1 a) Ta có 1 u 1 8 8 8 3 . 1 q 1 3 1 33 S u . q 3 8 1 2 q 1 2 4 q 1 u . 40 1 1 S 40 b) Ta có 4 q 1 . 8 S 680 8 q 1 u . 680 2 1 q1 8 Lấy u u 2 chia cho 1 , ta được 4 4
q 1 17 q 16 q 2 . Vậy 1 3 hoặc 1 8 . q 2 q 2
Câu 20: Tìm ba số khác nhau tạo thành cấp số cộng có tổng bằng 6, biết rằng nếu hoán đổi vị trí
số hạng thứ nhất và số hạng thứ hai đồng thời giữ nguyên số hạng thứ ba ta được cấp số nhân. Lời giải
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 106
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com Gọi ba số cần tìm là . 1 u , 2 u , 3 u với 1 u 2 u 3 u 1 u ● nên . 1 u , 2 u , 3
u tạo thành cấp số cộng với công sai d 0 1 u , 2 u 1 u d, 3 u 1 u 2d
Hơn nữa, u u u 6 u u du 2d . 1 2 3 1 1 1 6 1 u d 2 ●
tạo thành cấp số nhân 2 u , 1 u , 3
u tạo thành cấp số nhân hay 1 u d, 1 u , 1 u 2d u d u 2 2 1 1 d 1 u
u du d d 2
u u 2 2 1 u 2 2 2 2 u u 2u 8 0 . 1 1 1 1 1 1 1 1 u 4 Với , suy ra : không thỏa mãn. 1 u 2 d 0 Với , suy ra
. Vậy ba số cần tìm là . 1 u 4 d 6 4, 2, 8 GV: TR Ầ N Đ ÌN H C Ư – 0834 3321 33
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 107




