Bài giảng giới hạn của dãy số

Tài liệu gồm 36 trang, tóm tắt lý thuyết SGK, hướng dẫn giải các dạng toán và tuyển chọn các bài tập trắc nghiệm chuyên đề giới hạn của dãy số, có đáp án và lời giải chi tiết; giúp học sinh lớp 11 tham khảo khi học chương trình Đại số và Giải tích 11 chương 4.

63 32 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 2: Dãy số. Cấp số cộng và cấp số nhân (KNTT)

Môn: Toán 11

Thông tin:

55 trang 5 tháng trước

Tác giả:

Profile Kim Oanh
BÀI GIẢNG GIỚI HẠN CỦA HÀM SỐ
A. LÝ THUYẾT
I. ĐỊNH NGHĨA GIỚI HẠN CỦA HÀM SỐ TẠI MỘT ĐIỂM
1. Giới hạn hữu hạn tại một điểm.
Định nghĩa 1:
Cho
( )
;ab
là một khoảng chứa điểm
0
x
và hàm số
( )
y f x=
xác định trên
( )
;ab
hoặc trên
( ) ( )
0
0
; \ . lim
xx
a b x f x L
→
=
với mọi dãy số
n
x
mà
( )
00
; \ ,
nn
x a b x x x→
ta có
Nhận xét:
- Giới hạn của hàm số được định nghĩa thông qua khái niệm giới hạn của dãy số.
- Hàm số không nhất thiết phải xác định tại
0
x
.
Định nghĩa 2 (Giới hạn một bên):
Cho hàm số
( )
y f x=
xác định trên khoảng
( ) ( )
0
0
; . lim
xx
x b f x L
+
→
=
với mọi dãy số
n
x
mà
00
,
nn
x x b x x →
ta có
( )
lim .
n
f x L=
Cho hàm số
( )
y f x=
xác định trên khoảng
( ) ( )
0
0
; . lim
xx
a x f x L
−
→
=
với mọi dãy số
n
x
mà
00
,
nn
a x x x x →
ta có
( )
lim .
n
f x L=
STUDY TIP
0
xx
+
→
nghĩa là
0
xx→
và
0
.xx
0
xx
−
→
nghĩa là
0
xx→
và
0
.xx
Định lí 1
( ) ( ) ( )
0
00
lim lim lim .
xx
x x x x
f x L f x f x L
−+
→
→→
= = =
2. Giới hạn vô cực tại một điểm.
Định nghĩa 3
Cho
( )
;ab
là một khoảng chứa điểm
0
x
và hàm số
( )
y f x=
xác định trên
( )
;ab
hoặc trên
( ) ( )
0
0
; \ . lim
xx
a b x f x
→
= +
với mọi dãy số
n
x
mà
( )
00
; \ ,
nn
x a b x x x→
ta có
( )
.
n
fx = +
Lưu ý:
Các định nghĩa
( ) ( ) ( ) ( )
0
000
lim ; lim ; lim ; lim ;
xx
x x x x x x
f x f x f x f x
++−
→
→→→
= − = + = − = +
( )
0
lim
xx
fx
−
→
= −
được
phát biểu hoàn toàn tương tự.
3. Lưu ý:
a)
( )
fx
không nhất thiết phải xác định tại điểm
0
x
.
b) Ta chỉ xét giới hạn của
( )
fx
tại điểm
0
x
nếu có một khoảng
( )
;ab
(dù nhỏ) chứa
0
x
mà
( )
fx
xác
định trên
( )
;ab
hoặc trên
( )
0
; \ .a b x
Chẳng hạn, hàm số
( )
f x x=
có tập xác định là
)
0;D = +
. Do đó ta không xét giới hạn của hàm số
tại điểm
0
0x =
, do không có một khoảng
( )
;ab
nào chứa điểm
0
mà
( )
fx
xác định trên đó cả. Tương
tự vậy ta cũng không xét giới hạn của
( )
fx
tại mọi điểm
0
0.x
c) Ta chỉ xét giới hạn bên phải của
( )
fx
tại điểm
0
x
nếu có một khoảng
( )
0
;xb
(khoảng nằm bên phải
0
x
) mà
( )
fx
xác định trên đó.
Tương tự, ta chỉ xét giới hạn bên trái của
( )
fx
tại điểm
0
x
nếu có một khoảng
( )
0
;ax
(khoảng nằm bên
trái
0
x
) mà
( )
fx
xác định trên đó.
Chẳng hạn, với hàm số
( )
1f x x=−
, tại điểm
0
1x =
, ta chỉ xét giới hạn bên phải. Với hàm số
( )
1g x x=−
, tại điểm
0
1x =
, ta chỉ xét giới hạn bên trái.
d)
lim ( ) lim ( ) lim ( )
o
oo
xx
x x x x
f x f x f x
−+
→
→→
= + = = +
lim ( ) lim ( ) lim ( )
o
oo
xx
x x x x
f x f x f x
−+
→
→→
= − = = −
II. ĐỊNH NGHĨA GIỚI HẠN CỦA HÀM SỐ TẠI VÔ CỰC
1. Giới hạn hữu hạn tại vô cực.
Định nghĩa 4
Cho hàm số
()y f x=
xác định trên khoảng
( )
; . lim ( )
x
a f x L
→+
+ =
với mọi dãy số
( )
n
x
,
n
xa
và
n
x →+
ta đều có
lim ( )f x L=
.
LƯU Ý: Định nghĩa
lim ( )
x
f x L
→−
=
được phát biểu hoàn toàn tương tự.
2. Giới hạn vô cực tại vô cực.
Định nghĩa 5
Cho hàm số
()y f x=
xác định trên khoảng
( )
; . lim ( )
x
a f x
→+
+ = +
với mọi dãy số
( )
n
x
,
n
xa
và
n
x →+
ta đều có
lim ( )fx= +
.
LƯU Ý: Các định nghĩa:
lim ( ) , lim ( ) , lim ( )
xxx
f x f x f x
→− →+ →−
= + = − = −
được phát biểu hoàn toàn tương
tự.
III. MỘT SỐ GIỚI HẠN ĐẶC BIỆT
a)
lim
o
o
xx
xx
→
=
.
b)
lim ; lim
o
x x x
c c c c
→ →
==
(
c
là hằng số )
c)
lim 0
k
x
c
x
→
=
(
c
là hằng số,
k
nguyên dương ).
d)
lim
k
x
x
→+
= +
với
k
nguyên dương;
lim
k
x
x
→−
= −
nếu
k
là số nguyên lẻ;
lim
k
x
x
→−
= +
nếu
k
là số nguyên chẵn.
Nhận xét:
lim ( ) lim ( )
xx
f x f x
→+ →+

= + − = −

.
IV. ĐỊNH LÍ VỀ GIỚI HẠN HỮU HẠN
Định lí 2
Giả sử
lim ( )
o
xx
f x L
→
=
và
lim ( )
o
xx
g x M
→
=
. Khi đó
a)
lim ( ) ( )
o
xx
f x g x L M
→

=

.
b)
lim ( ) ( )
o
xx
f x g x LM
→

=

;
lim ( )
o
xx
cf x cL
→

=

với
c
là một là một hằng số.
c)
()
lim ( 0)
()
o
xx
f x L
M
g x M
→
=
.
STUDY TIP: Giới hạn hữu hạn, giới hạn của tổng, hiệu, tích, thương của hai hàm số tại một điểm bằng
tổng, hiệu, tích, thương các giới hạn của chúng tại điểm đó (trong trường hợp thương, giới hạn của mẫu
phải khác không).
Định lí 3
Giả sử
lim ( )
o
xx
f x L
→
=
. Khi đó
a)
lim ( )
o
xx
f x L
→
=
.
b)
3
3
lim ( )
o
xx
f x L
→
=
.
c) Nếu
( ) 0fx
với mọi
\
o
Jx
, trong đó
J
là khoảng nào đó chứa
o
x
, thì
0L
và
lim ( )
o
xx
f x L
→
=
.
LƯU Ý: Định lí 2 và định lí 3 vẫn đúng khi thay
o
xx→
bởi
o
xx
−
→
,
o
xx
+
→
.
V. QUY TẮC VỀ GIỚI HẠN VÔ CỰC
Các định lí và quy tắc dưới đây được áp dụng cho mọi trường hợp:
, , ,
o o o
x x x x x x x
−+
→ → → →+
và
x →−
.
Tuyên nhiên, để cho gọn, ta chỉ phát biểu cho trường hợp
o
xx→
.
Quy tắc 1 (Quy tắc tìm giới hạn của tích).
lim ( )
o
xx
L f x
→
=
lim ( )
o
xx
gx
→
lim ( ) ( )
o
xx
f x g x
→


0L
+
+
−
−
0L
+
−
−
+
STUDY TIP: Giới hạn của tích hai hàm số
- Tích của một hàm số có giới hạn hữu hạn khác 0 với một hàm số có giới hạn vô cực là một hàm số có
giới hạn vô cực.
- Dấu của giới hạn theo quy tắc dấu của phép nhân hai số.
Quy tắc 2 (Quy tắc tìm giới hạn của thương)
lim ( )
o
xx
L f x
→
=
lim ( )
o
xx
gx
→
Dấu của
()gx
()
lim
()
o
xx
fx
gx
→
L

Tùy ý
0
0L
0
+
+
-
−
0L
0
+
−
-
+
(Dấu của
( )
gx
xét trên một khoảng K nào đó đang tính giới hạn, với
o
xx
).
STUDY TIP: Giới hạn của thương hai hàm số. Tử thức có giới hạn hữu hạn khác 0:
- Mẫu thức càng tang (dần đến vô cực) thì phân thức càng nhỏ (dần đến 0).
- Mẫu thức càng nhỏ (dần đến 0) thì phân thức có giá trị tuyệt đối càng lớn (dần đến vô cực).
- Dấu của giới hạn theo quy tắc dấu của phép chia hai số.
VI. CÁC DẠNG VÔ ĐỊNH: GỒM
0
, ,0.
0
VÀ
−
.
B. CÁC DẠNG TOÁN VỀ GIỚI HẠN HÀM SỐ
DẠNG 1: TÌM GIỚI HẠN XÁC ĐỊNH BẰNG CÁCH SỬ DỤNG TRỰC TIẾP CÁC ĐỊNH NGHĨA,
ĐỊNH LÍ VÀ QUY TẮC.
Phương pháp:
- Xác định đúng dạng bài toán: giới hạn tại một điểm hay giới hạn tại vô cực? giới
hạn xác định hay vô định?
- với giới hạn hàm số tại một điểm ta cần lưu ý: Cho
()fx
là hàm số sơ cấp xác
định trên khoảng
( )
;ab
chứa điểm
0
x
. Khi đó,
→
=lim ( ) ( )
o
o
xx
f x f x
.
- Với giới hạn hàm số tại vô cực ta “xử lí” tương tự như giới hạn dãy số.
- Với giới hạn xác định, ta áp dụng trực tiếp định nghĩa giới hạn hàm số, các định lí
về giới hạn hữu hạn và các quy tắc về giới hạn vô cực.
STUDY TIP: Dùng định nghĩa chứng minh hàm số
()y f x=
không có giới hạn khi
0
xx→
- Chọn hai dãy số khác nhau
( )
n
a
và
( )
n
b
thỏa mãn
n
a
và
n
b
thuộc tập xác định của hàm số
()y f x=
và khác
0
x
;
00
;
nn
a x b x→→
.
- Chứng minh
( ) ( )
lim lim
nn
f a f b
hoặc chứng minh một trong hai giới hạn này không tồn tại.
- Từ đó suy ra
→
lim ( )
o
xx
fx
không tồn tại. TH
0
xx
→
hoặc
x →
chứng minh tương tự.
Ví dụ 1: Chọn khẳng định đúng trong các khẳng định sau:
A.
→+
=lim sin 1
x
x
B.
→+
=−lim sin 1
x
x
C.
→+
=lim sin 0
x
x
D.
→+
lim sin
x
x
không tồn tại.
Đáp án D
Lời giải
Xét dãy số
()
n
x
với
2
2
n
xn
=+
.
Ta có
n
x →+
và
limsin limsin 2 1
2
n
xn

= + =


.
( )
1
Lại xét dãy số
()
n
y
với
2
2
n
yn
= − +
.
Ta có
n
y →+
và
limsin limsin 2 1
2
n
yn

= − + = −


.
( )
2
Từ
( )
1
và
( )
2
suy ra
→+
lim sin
x
x
không tồn tại. Vậy chọn đáp án D.
Ví dụ 2: Cho hàm số
2
3
1
( ) , lim ( )
2
x
x
f x f x
x
→
+
=
bằng:
A.
+
. B.
0
. C.
53
3
. D.
1
2
.
STUDY TIP: Giới hạn tại một điểm
Nếu
()fx
xác định tại
0
x
và tồn tại một khoảng
( )
;ab
thuộc tập xác định của
()fx
chứa
0
x
thì
→
=lim ( ) ( )
o
o
xx
f x f x
.
- Việc sử dụng hay không sử dụng MTCT để tính
()
o
fx
tùy thuộc vào mức độ phức tạp của
()
o
fx
và
khả năng tính toán của độc giả.
Đáp án C.
Lời giải
Hàm số đã cho xác định trên
( )
0;+
.
Cách 1 (sử dụng định nghĩa):
Giải sử
()
n
x
là một dãy số bất kỳ, thỏa mãn
0, 3
nn
xx
và
3
n
x →
khi
n →+
. Ta có
2
2
1
3 1 5 3
lim ( ) lim
3
2 2 3
n
n
n
x
fx
x
+
+
= = =
( áp dụng quy tắc về giới hạn hữu hạn của dãy số). Do đó
3
53
lim ( )
3
x
fx
→
=
.
Cách 2 (sử dụng định lí về giới hạn hữu hạn):
Theo định lí 1 ta có:
( )
( )
( )
22
2
3 3 3 3 3 3
33
3 3 2 3
3
lim 1 lim lim1 lim .lim lim1
1 3.3 1 5 3
lim lim
3
2 lim2.lim lim2. lim 2 3
lim 2
x x x x x x
xx
x x x x
x
x x x x
x
fx
x x x
x
→ → → → → →
→→
→ → → →
→
+ + +
++
= = = = = =
.
Tuy nhiên trong thực hành, vì là câu hỏi trắc nghiệm nên ta làm như sau.
Cách 3: Vì
( )
fx
là hàm số sơ cấp xác định trên
( )
0;+
chứa điểm
0
3x =
nên
( ) ( )
3
10 5 3
lim 3
3
23
x
f x f
→
= = =
.
Do đó sử dụng MTCT ta làm như cách 4 dưới đây.
Cách 4: Nhập biểu thức của vào màn hình. Bấm phím CALC, máy hỏi X ? nhập 3 = . Máy hiển
thị kết quả như hình:
Do đó chọn đáp án C.
Ví dụ 3: Chọn khẳng định đúng trong các khẳng định dưới đây ?
A.
3
2
lim 1
2
x
x
x
→
+
=
−
. B.
3
2
lim 5
2
x
x
x
→
+
=
−
.
C.
3
2
lim 1
2
x
x
x
→
+
=−
−
. D. Hàm số
( )
2
2
x
fx
x
+
=
−
không có giới hạn khi
3x →
.
Đáp án B
Lời giải
Hàm số
( )
2
2
x
fx
x
+
=
−
xác định trên các khoảng
( )
;2−
và
( )
2;+
. Ta có
( )
3 2; +
.
Cách 1 :
( ) ( )
3
32
lim 3 5
32
x
f x f
→
+
= = =
−
.
Cách 2 : Nhập biểu thức của hàm số
( )
2
2
x
fx
x
+
=
−
và màn hình MTCT. Bấm phím CALC , máy
hỏi X? nhâp 3 =. Máy hiển thị kết quả như hình:
Vậy
3
2
lim 5
2
x
x
x
→
+
=
−
.
Ví dụ 4:
( )
3
lim 2 5
x
xx
→−
−+
bằng:
A.
2−
. B.
3
. C.
+
. D.
−
.
Đáp án C.
Lời giải
Cách 1: Sử dụng MTCT tính giá trị của
( )
3
25f x x x= − +
tại một điểm có giá trị âm rất nhỏ (do
ta đang xét giới hạn của hàm số khi
x →−
), chẳng hạn tại
20
10−
. Máy hiển thị kết quả như
hình:
Đó là một giá trị dương rất lớn. Vậy chọn đáp án C , tức
( )
3
lim 2 5
x
xx
→−
− + = +
.
Cách 2: Ta có
33
2
5
2 5 2x x x
x

− + = − +


.
Vì
3
lim
x
x
→−
= −
và
2
5
lim 2 2 0
x
x
→−

− + = −


nên
3
2
5
lim 2
x
x
x
→−

− + = +


.
Vậy theo Quy tắc 1,
( )
33
2
5
lim 2 5 lim 2
xx
x x x
x
→− →−

− + = − + = +


. Do đó chọn C.
Lưu ý 1:
- Để hiểu tại sao
3
lim
x
x
→−
= −
và
2
5
lim 2 2
x
x
→−

− + = −


xin xem lại phần các giới hạn đặc biệt.
- Bài toán thuộc dạng tính giới hạn hàm số khi
x
dần tới vô cực, nhưng là khi
x →−
. Do đó
không thể áp dụng ngay các kết quả đã biết về giới hạn dãy số, vì giới hạn dãy số được xét khi
n →+
. Ta chỉ có thể áp dụng các kĩ thuật đã biết đối với giới hạn dãy số.
Lưu ý 2: Có thể dễ dàng chứng minh được kết quả như sau :
Cho hàm số
( )
1
1 1 0
... ( 0)
kk
k k k
f x a x a x a x a a
−
−
= + + + +
là một đa thức bậc
k
.
x
k
k
a
Giới hạn của
( )
fx
x →+
Tùy ý
0
k
a
+
0
k
a
−
x →−
k
chẵn
0
k
a
+
0
k
a
−
k
lẻ
0
k
a
−
0
k
a
+
Thật vậy, ta có
( )
10
1
1
...
k
k
k
kk
aa
a
f x x a
x x x
−
−

= + + + +


.
Vì
10
1
1
lim ...
k
kk
kk
x
aa
a
aa
x x x
−
−
→

+ + + + =


và
lim
k
x
x
→+
= +
với
k
tùy ý,
lim
k
x
x
→−
= +
nếu
k
chẵn,
lim
k
x
x
→−
= −
nếu
k
lẻ nên ta dễ dàng suy ra bảng kết quả trên.
Ví dụ 5:
( )
42
lim 3 2 1
x
xx
→−
−+
bằng:
A.
+
. B.
−
. C. 3. D. 2.
Đáp án A
Lời giải
Cách 1: Theo nhận xét trên thì
( )
42
lim 3 2 1
x
xx
→−
− + = +
(
,xk→ −
chẵn và
0
k
a
). Thật
vậy, ta có
4 2 4
24
21
3 2 1 3 .x x x
xx

− + = − +


Vì
4
lim
x
x
→−
= +
và
24
21
lim 3 3 0
x
xx
→

− + =


nên
( )
42
lim 3 2 1
x
xx
→−
− + = +
.
STUDY TIP
- Giới hạn tại vô cực của hàm đa thức là vô cực, chỉ phụ thuộc vào số hạng chứa lũy thừa bậc cao nhất.
- Giới hạn của hàm đa thức tại
+
phụ thuộc vào hệ số của lũy thừa bậc cao nhất. (Giống với
giới hạn của dãy số dạng đa thức).
- Giới hạn của hàm đa thức tại
−
phụ thuộc vào bậc và hệ số của lũy thừa bậc cao nhất.
Cách 2: Sử dụng MTCT tính giá trị hàm số
( )
42
3 2 1f x x x=−+
tại
20
10x =−
, ta được kết quả
như hình :
Kết quả là một số dương rất lớn. Do đó chọn đáp án A,
Ví dụ 6: Cho hàm số
( )
2
25f x x x= − +
. Khẳng định nào dưới đây đúng ?
A.
( )
lim
x
fx
→−
= −
. B.
( )
lim
x
fx
→−
= +
.
C.
( )
lim 1
x
fx
→−
=
. D.
( )
lim
x
fx
→−
không tồn tại.
Đáp án B.
Lời giải
Hàm số
( )
2
25f x x x= − +
xác định trên .
Có thể giải nhanh như sau : Vì
2
25xx−+
là một hàm đa thức của
x
nên có giới hạn tại vô cực.
Mà
2
2 5 0xx− +
với mọi
x
nên giới hạn của
( )
2
25f x x x= − +
tại
−
chắc chắn là
+
.
Thật vậy, ta có
22
22
2 5 2 5
2 5 1 1x x x x
x x x x

− + = − + = − +


.
Vì
lim
x
x
→−
= +
và
2
25
lim 1 1 0
x
xx
→−
− + =
nên
2
lim 2 5
x
xx
→−
− + = +
.
Hoặc ta có thể sử dụng MTCT để tính giá trị của
( )
fx
tại một giá trị âm rất nhỏ của
x
, chẳng
hạn tại
20
10x =−
ta được kết quả như hình:
Kết quả này là một số dương rất lớn. Do đó ta chọn đáp án B. (Dễ thâý kết quả hiển thị trên máy
tính như trên chỉ là kết quả gần đúng do khả năng tính toán hạn chế của MTCT. Tuy nhiên kết
quả đó cũng giúp ta lựa chọn được đáp án chính xác).
STUDY TIP
Ta có
lim
x
x
→
= +
.
Khi
x →−
thì
0x
.
Với
0x
ta có
2
xx=−
.
Cần đặc biệt lưu ý các điều trên khi tính giới hạn tại
−
của hàm chứa căn thức.
Ví dụ 7: Giới hạn của hàm số
( )
22
41f x x x x= − − +
khi
x →−
bằng:
A.
−
. B.
+
. C.
1−
. D. 3.
Đáp án A.
Lời giải
Cách 1: Ta có:
2 2 2 2
22
1 1 1 1
4 1 1 4 1 4x x x x x x x
x x x x
− − + = − − + = − − +
2
11
14x
xx

= − − +



Mà
lim
x
x
→−
= +
và
2
11
lim 1 4 1 2 1 0
x
xx
→

− − + = − = −



.
Vậy
(
)
22
2
11
lim 4 1 lim 1 4
xx
x x x x
xx
→− →−


− − + = − − + = −






.
Lưu ý:
- Độc giả nên đọc lại phần giới hạn dãy số có chứa căn thức để hiểu hơn tại sao lại có định hướng
giải như vậy (mà không đi nhân chia với biểu thức liên hợp).
- Có thể thấy như sau: Vì
22
lim ; lim 4 1
xx
x x x
→− →−
− = + + = +
.
Mà hệ số của
2
x
trong
2
41x +
lớn hơn hệ số của
2
x
trong
2
xx−
nên suy ra
(
)
22
lim 4 1
x
x x x
→−
− − + = −
.
Cách 2: Sử dụng MTCT tính giá trị hàm số tại
10
10x =−
ta được kết quả như hình.
Vậy chọn đáp án A.
Ví dụ 8:
35
2017
lim
35
x
xx
→+
−
bằng:
A.
2017
3
. B.
−
. C.
+
. D. 0.
Đáp án D.
Lời giải
Cách 1: Vì
( )
35
lim 3 5
x
xx
→+
− = −
nên theo quy tắc 2,
35
2017
lim 0
35
x
xx
→+
=
−
.
Cách 2: Sử dụng MTCT tính giá trị hàm số tại
10
10x =
ta được kết quả như hình.
Đó là một kết quả rất gần 0. Do đó chọn đáp án D.
STUDY TIP
Khi hàm số không xác định tại
0
x
thì ta thử áp dụng các quy tắc về giới hạn vô cực. Đó là các
quy tắc áp dụng cho các dạng
. ; ;
0
LL
L
. Lưu ý cách xác định dấu của giới hạn.
- Dạng
L
: giới hạn là 0.
- Dạng
.L
và
0
L
: Giới hạn là vô cực.
Ví dụ 9: Giới hạn bên phải của hàm số
( )
37
2
x
fx
x
−
=
−
khi
2x →
là
A.
+
. B.
−
. C. 3. D.
7
2
.
Đáp án B.
Lời giải
Hàm số
( )
37
2
x
fx
x
−
=
−
xác định trên
( )
; \ 2− +
.
Cách 1: Ta có
( )
2
lim 2 0, 2 0
x
xx
+
→
− = −
với mọi
2x
và
( )
2
lim 3 7 3.2 7 1 0
x
x
+
→
− = − = −
. Do đó
theo quy tắc 2 thì
2
37
lim
2
x
x
x
+
→
−
= −
−
.
Cách 2: Sử dụng MTCT. Tính giá trị của
( )
37
2
x
fx
x
−
=
−
tại
2x =
ta thấy máy báo lỗi Math Error
(do
( )
fx
không xác định tại
2x =
). Quay lại tính giá trị của
( )
fx
tại
10
2 10x
−
=+
(tức
2,0000000001
) là một giá trị của
x
lớn hơn 2 và rất gần 2. Kết quả là một số âm rất nhỏ.
Do đó chọn đáp án B.
Ví dụ 10: Xét bài toán “Tìm
2
2
2
31
lim
2 5 2
x
xx
xx
−
→
+−
−+
”, bạn Hà đã giải như sau:
Bước 1: Vì
( )
2
2
lim 2 5 2 0
x
xx
−
→
− + =
.
Bước 2:
2
2 5 2 0xx− +
với
2x
và
x
đủ gần 2,
Bước 3:
( )
2
2
lim 3 1 13 0
x
xx
−
→
+ − =
Bước 4: nên theo quy tắc 2,
2
2
2
31
lim
2 5 2
x
xx
xx
−
→
+−
= +
−+
.
Hỏi lời giải trên của bạn Hà đã sai từ bước thứ mấy ?
A. Bước 1. B. Bước 2. C. Bước 3. D. Bước 4.
Đáp án B
Lời giải
Xét dấu biểu thức
( )
2
2 5 2g x x x= − +
ta thấy
( )
0gx
với mọi
( )
1;2x
.
Vậy lời giải sai từ bước 2. (Lời giải đúng cho ra kết quả
2
2
2
31
lim
2 5 2
x
xx
xx
−
→
+−
= −
−+
).
STUDY TIP
0
xx
+
→
nghĩa là
0
xx→
và
0
xx
.
0
xx
−
→
nghĩa là
0
xx→
và
0
xx
.
Nếu
0
xx
+
→
thì tính giá trị hàm số tại
0
10
k
xx
−
=+
.
Nếu
0
xx
−
→
thì tính giá trị hàm số tại
0
10
k
xx
−
=−
.
Trong đó
k
là một sô nguyên dương.
Ví dụ 11: Giới hạn
( )
2
4
1
lim
4
x
x
x
→
−
−
bằng:
A. 0. B.
3−
. C.
−
. D.
+
.
Đáp án C.
Lời giải
Cách 1: Ta có
( ) ( )
2
44
lim 1 3 0, lim 4 0
xx
xx
→→
− = − − =
và
( )
2
40x −
với mọi
4x
nên theo quy
tắc 2,
( )
2
4
1
lim
4
x
x
x
→
−
= −
−
. Vậy chọn đáp án C.
Cách 2: Sử dụng MTCT tính giá trị hàm số tại
8
4 10x
−
=+
hoặc tại
8
4 10x
−
=−
ra được các kết
quả như hình
Vậy chọn đáp án C.
Ví dụ 12: Cho hàm số
( )
2
5 2 khi 1
3 khi 1
xx
fx
xx
+
=
−
. Khẳng định nào dưới đây là đúng ?
A.
( )
1
lim 7
x
fx
→
=
. B.
( )
1
lim 2
x
fx
→
=−
.
C.
( )
1
lim 7
x
fx
−
→
=
. D.
( )
1
lim 7
x
fx
+
→
=
.
Đáp án D.
Lời giải
Ta có
( ) ( )
11
lim lim 5 2 5.1 2 7
xx
f x x
++
→→
= + = + =
. Vì chỉ có một đáp án đúng nên chọn đáp án D.
STUDY TIP
Cần xác định đúng biểu thức của
( )
fx
khi
0
xx
+
→
và khi
0
xx
−
→
.
Giải thích thêm : Ta có
( )
( )
22
11
lim lim 3 1 3 2
xx
f x x
−−
→→
= − = − = −
.
Vậy
( ) ( )
11
lim lim
xx
f x f x
−+
→→
nên
( )
1
lim
x
fx
→
không tồn tại.
Các đáp án A, B, C đều sai.
STUDY TIP
( ) ( ) ( )
0
00
lim lim lim
xx
x x x x
f x L f x f x L
−+
→
→→
= = =
.
Ví dụ 13: Cho hàm số
( )
( )
( )
2
2
5 khi 3 1
5
khi 3 2
2
xx
fx
x
x
x
−
=
−
+
.
Trong biểu thức (2) ở trên, cần thay số 5 bằng số nào để hàm số
( )
fx
có giới hạn khi
3x →
?
A. 19. B. 1.
C.
1−
. D. Không có số nào thỏa mãn.
Đáp án C.
Lời giải
Hàm số đã cho các định trên
\2
.
Cách 1: Ta có
( )
22
33
lim lim 5 3 5 2
xx
f x x
++
→→
= − = − =
.
Đặt
( )
2
2
xm
fx
x
−
=
+
khi
3x
(
m
là tham số,
0m
).
Ta có
( )
22
33
39
lim lim
2 3 2 5
xx
x m m m
fx
x
−−
→→
− − −
= = = =
++
.
Để hàm số
( )
fx
có giới hạn khi
3x →
thì
( ) ( )
33
9
lim lim 2 1
5
xx
m
f x f x m
+−
→→
−
= = = −
.
Cách 2: Sử dụng MTCT tính giá trị biểu thức
2
5X −
khi
3X =
được kết quả bằng 2. Sử dụng
MTCT tính giá trị biểu thức
2
2
XA
X
−
+
khi
3X =
và lần lượt nhận các giá trị bằng
19,1
và
1−
. Ta
thấy khi
1A=−
thì biểu thức nhận giá trị bằng 2. Vậy chọn đáp án C.
Ví dụ 14: Cho hàm số
( )
fx
có đồ thị như hình dưới đây:
Quan sát đồ thị và cho biết trong các giới hạn sau, giới hạn nào là
+
?
A.
( )
lim
x
fx
→−
. B.
( )
lim
x
fx
→+
. C.
( )
( )
3
lim
x
fx
+
→−
. D.
( )
3
lim
x
fx
−
→
.
Đáp án C.
Lời giải
Khi
3x
+
→−
, đồ thị hàm số là một đường cong đi lên từ phải qua trái. Do đó
( )
( )
3
lim
x
fx
+
→−
= +
.
Tương tự như vậy ta có
( ) ( ) ( )
3
lim lim 0 ; lim
xx
x
f x f x f x
−
→− →+
→
= = = −
.
Do đó chọn đáp án C.
DẠNG 2: TÌM GIỚI HẠN VÔ ĐỊNH DẠNG
0
.
0
STUDY TIP
Khi tính giới hạn mà không thể áp dụng trực tiếp các định lí về giới hạn hữu hạn hay các quy tắc về giới
hạn vô cực đã biết thì ta gọi đó là các dạng vô định.
Kí hiệu các dạng vô định gồm:
0
, , 0.
0
và
−
. Để tính giới hạn dạng vô định ta phải biến đổi biểu
thức của hàm số về dạng áp dụng được các định lí và quy tắc đã biết. Làm như vậy gọi là “khử dạng vô
định”.
Bài toán:
Tính
( )
( )
0
lim
→xx
fx
gx
khi
( ) ( )
00
lim lim 0
→→
==
x x x x
f x g x
, trong đó
( )
fx
và
( )
gx
là các đa thức hoặc căn thức.
Phương pháp giải (tự luận)
✓ Phân tích tử và mậu thành tích các nhân tử và giản ước. Cụ thể, vì
( ) ( )
00
lim lim 0
→→
==
x x x x
f x g x
nên
( )
fx
và
( )
gx
cùng có nghiệm
0
=xx
. Do đó ta phân tích được
( ) ( ) ( )
0
=−f x x x A x
và
( ) ( ) ( )
0
=−g x x x B x
. Khi đó ta có:
( )
( )
( ) ( )
( ) ( )
( )
( )
0 0 0
0
0
lim lim lim
→ → →
−
==
−
x x x x x x
f x x x A x A x
g x x x B x B x
và công việc còn lại
là đi tính
( )
( )
0
lim
→xx
Ax
Bx
.
✓ Nếu
( )
fx
và
( )
gx
có chứa căn thức thì có thể nhân tử và mẫu với biểu thức liên hợp trước khi phân
tích chúng thành tích để giản ước.
STUDY TIP
Phân tích đa thức thành nhân tử:
✓ Áp dụng hằng đẳng thức đáng nhớ.
✓ Khi đã biết
( )
fx
có nghiệm
0
=xx
, ta sử dụng lược đồ Hooc-ne hoặc chia
( )
fx
cho
0
=xx
được
thương
( )
Ax
. Khi đó
( ) ( ) ( )
0
=−f x x x A x
.
✓ Áp dụng kết quả: nếu phương trình
2
0+ + =ax bx c
có hai nghiệm
12
,xx
thì
( )( )
2
12
+ + = − −ax bx c a x x x x
.
Tổng quát: nếu phương trình
11
1 1 0
... 0
−
−
+ + + + =
kk
kk
a x a x a x a
có các nghiệm thực
12
, ,...,
m
x x x
thì
( ) ( ) ( )
11
1 1 0 1
... ...
−
−
+ + + + = − −
kk
k k k m
a x a x a x a a x x x x A x
, trong đó
( )
Ax
là đa thức bậc
−km
. Tuy nhiên,
trong thực tế, ta dùng kết quả này khi có đủ
k
nghiệm thực, tức
=mk
. Trường hợp ngược lại nên dùng
lược đồ Hooc-ne. (với phương trình bậc hai, bậc ba có thể dùng MTCT để tìm nghiệm)
Ví dụ 1: Tính
2
2
2
4
lim
32
→
−
−+
x
x
xx
.
A. 1. B. 4. C.
2−
. D.
4−
.
Phân tích: Vì
( ) ( )
22
22
lim 4 lim 3 2 0
→→
− = − + =
xx
x x x
nên đây là giới hạn vô định dạng
0
0
. Ta thấy
2
4−x
và
2
32−+xx
đều triệt tiêu tại
2=x
nên
2=x
là nghiệm của
2
4−x
và
2
32−+xx
. Từ
đó ta có cách giải như sau.
Lời giải
Cách 1: Ta có
( )( )
( )( )
2
2
2 2 2
22
4 2 2 2
lim lim lim 4
3 2 2 1 1 2 1
→ → →
−+
− + +
= = = =
− + − − − −
x x x
xx
xx
x x x x x
.
Cách 2: Dử dụng MTCT tính giá trị hàm số
( )
2
2
4
32
−
=
−+
x
fx
xx
tại
2=x
ta thấy máy báo lỗi
Math Error (do hàm số không xác định tại
2=x
). Quay lại tính giá trị hàm số tại
2,0000000001
ta được kết quả như sau:
Lại quay lại tính giá trị hàm số tại 1,9999999999 ta được kết quả như sau:
Vậy chọn đáp án B.
Ví dụ 2: Tính giới hạn
( )
1
lim , *
1
→
−
−
mn
x
xx
mn
x
, ta được kết quả:
A.
+
. B.
−mn
. C.
m
. D.
1
.
Lời giải
Cách 1: Ta có
11
11
lim lim
1 1 1
m n m n
xx
x x x x
x x x
→→

− − −
=−

− − −

.
Lại có
( )
( )
12
11
1 ... 1
1
lim lim
11
−−
→→
− + + + +
−
=
−−
mm
m
xx
x x x x
x
xx
( )
12
1
lim ... 1
−−
→
= + + + + =
mm
x
x x x m
.
Tương tự:
1
1
lim
1
→
−
=
−
n
x
x
n
x
.
Vậy
1 1 1 1
1 1 1 1
lim lim lim lim
1 1 1 1 1
m n m n m n
x x x x
x x x x x x
mn
x x x x x
→ → → →

− − − − −
= − = − = −

− − − − −

.
Cách 2: Cho
m
và
n
các giá trị cụ thể, chẳng hạn
3=m
và
7=m
. Sử dụng MTCT tính
37
1
lim
1
→
−
−
x
xx
x
ta được kết quả
37
1
lim 4
1
→
−
=−
−
x
xx
x
. Vậy đáp án đúng là B.
STUDY TIP
( )
( )
12
1 1 ... 1
−−
− = − + + + +
m m m
x x x x x
1
1
lim
1
→
−
=
−
m
x
x
m
x
1
1
lim
1
→
−
=
−
n
x
x
n
x
Ví dụ 3: Chọn khẳng định đúng trong các khẳng định sau:
A.
3
1
32
lim 0
32
→
+−
=
−+
x
x
xx
. B.
3
1
32
lim
32
→
+−
= +
−+
x
x
xx
.
C.
3
1
32
lim
32
→
+−
= −
−+
x
x
xx
. D.
3
1
32
lim
32
→
+−
−+
x
x
xx
không tồn tại.
Phân tích: Vì
( )
1
lim 3 2 0
→
+ − =
x
x
và
( )
3
1
lim 3 2 0
→
− + =
x
xx
nên đây là dạng vô định
0
0
. Tuy nhiên
ta chưa thể phân tích ngay
32+−x
thành nhân tử mà phải nhân cả tử và mẫu với biểu thức
liên hợp của
32+−x
là
32++x
.
Lời giải
Cách 1: Ta có
3
32
32
x
xx
+−
−+
( )( )
( )
( )
3
3 2 3 2
3 2 3 2
xx
x x x
+ + + −
=
+ + − +
( )
( ) ( )
2
1
3 2 1 2
−
=
+ + − +
x
x x x
( )
( )( )
1
3 2 1 2
=
+ + − +x x x
.
Mà
( )
( )( )
1
1
lim
3 2 1 2
−
→
= −
+ + − +
x
x x x
;
( )
( )( )
1
1
lim
3 2 1 2
+
→
= +
+ + − +
x
x x x
.
Do đó
( )
( )( )
1
1
lim
3 2 1 2
→
+ + − +
x
x x x
không tồn tại.
Suy ra
3
1
32
lim
32
→
+−
−+
x
x
xx
không tồn tại. Vậy chọn đáp án D.
Cách 2: Sử dụng MTCT tính giá trị biểu thức
3
32
32
+−
−+
x
xx
tại
1=x
ta thấy máy báo lỗi Math
Error. Quay lại tính giá trị biểu thức tại
1,000001=x
và tại
0,999999=x
ta được kết quả:
Hai kết quả trên là một số dương rất lớn, một số âm rất nhỏ. Do đó có thể kết luận
3
1
32
lim
32
→
+−
−+
x
x
xx
không tồn tại.
Nhận xét:
- Nếu chỉ tính giá trị biểu thức tại một điểm thì rất dễ chọn đáp án sai.
- Ở đây ta đã chuyển dạng vô định
0
0
về dạng xác định
0
L
.
- Dùng MTCT tìm nghiệm của phương trình
3
3 2 0− + =xx
ta được
12
1, 2= = −xx
. Như vậy
phải có một nghiệm là nghiệm kép do là phương trình bậc ba. Trong trường hợp này, theo Tip
trên đã nêu, ta nên dùng lược đồ Hooc-ne để phân tích đa thức
3
32−+xx
thành nhân tử.
Ví dụ 4: Giới hạn
3
1
2 1 3 2
lim
1
→
− − −
−
x
xx
x
bằng:
A.
1
. B.
0
. C.
+
. D.
1
2
.
Phân tích:
( )
3
1
lim 2 1 3 2 0
→
− − − =
x
xx
và
( )
1
lim 1 0
→
−=
x
x
nên đây là dạng vô định
0
0
. Ta chưa
thể phân tích
( )
3
2 1 3 2= − − −f x x x
thành nhân tử. Mà
( )
fx
lại là hiệu của hai căn thức
không cùng bậc. Ta để ý thấy
21−x
và
3
32−x
đều đạt giá trị bằng 1 tại
1=x
nên ta biến đổi
như sau:
( )
( ) ( )
3
2 1 1 1 3 2= − − + − −f x x x
rồi tiến hành nhân chia với biểu thức liên hợp.
Lời giải
Cách 1: Ta có
33
2 1 3 2 2 1 1 1 3 2
1 1 1
− − − − − − −
=+
− − −
x x x x
x x x
( )
( )
( )
(
)
( )
2
3
3
2 2 3 3
2 1 1 1
1 3 2 3 2 1
−−
=+
− + −
+ − + − −
xx
xx
x x x
( )
2
3
3
23
2 1 1
1 3 2 3 2
=−
−+
+ − + −
x
xx
.
Tac có:
( )
1
2
3
3
23
lim 0
2 1 1
1 3 2 3 2
→


−=

−+
+ − + −

x
x
xx
.
Do đó
3
1
2 1 3 2
lim 0
1
→
− − −
=
−
x
xx
x
.
Cách 2: Sử dụng MTCT tính giá trị biểu thức
3
2 1 3 2
1
− − −
−
xx
x
tại
1=x
ta thấy máy báo lỗi
Math Error. Quay lại tính giá trị biểu thức tại
0,99999999=x
và tại
1,00000001=x
ta được kết
quả:
Do đó chọn đáp án B tức là
3
1
2 1 3 2
lim 0
1
→
− − −
=
−
x
xx
x
.
STUDY TIP
Cho
( )
( ) ( )
3
0
−
=
−
A x B x
fx
xx
(chứa hai căn khác bậc) trong đó
( ) ( )
00
==A x B x m
thì ta biến
đổi như sau:
( )
( ) ( )
3
0
− + −
=
−
A x m m B x
fx
xx
.
Ví dụ 5: Tính giới hạn
( )
3
2
1
6 5 4 3
lim
1
→
− − −
−
x
xx
x
.
A.
0
. B.
2−
. C.
+
. D.
−
.
Lời giải
Cách 1: Đặt
1=−tx
thì
1
1, lim 0
→
= + =
x
x t t
và
( )
3
2
6 5 4 3
1
xx
x
− − −
−
3
2
6 1 4 1tt
t
+ − +
=
( ) ( )
3
22
6 1 2 1 2 1 4 1t t t t
tt
+ − + + − +
=+
( )
( ) ( ) ( )
( )
( )
( )
3 2 2
2
22
2
3
3
6 1 8 12 6 1 4 4 1 4 1
2 1 4 1
6 1 2 1 . 6 1 2 1
+ − + + + + + − +
=+

+ + +
+ + + + + +


t t t t t t t
t t t
t t t t t
( ) ( ) ( )
22
3
3
8 12 4
2 1 4 1
6 1 2 1 . 6 1 2 1
−−
=+
+ + +
+ + + + + +
t
tt
t t t t
.
Vậy
( )
3
2
1
6 5 4 3
lim
1
x
xx
x
→
− − −
−
( ) ( ) ( )
22
0
3
3
8 12 4
lim
2 1 4 1
6 1 2 1 . 6 1 2 1
t
t
tt
t t t t
→

−−

=+

+ + +
+ + + + + +

.
Mà
( ) ( ) ( )
22
0
3
3
8 12 12
lim 4
3
6 1 2 1 . 6 1 2 1
→
−−
= − = −
+ + + + + +
t
t
t t t t
;
0
44
lim 2
2
2 1 4 1
→
==
+ + +
t
tt
.
Vậy
( )
3
2
1
6 5 4 3
lim 4 2 2
1
→
− − −
= − + = −
−
x
xx
x
.
Cách 2: Sử dụng MTCT tính giá trị biểu thức
( )
3
2
6 5 4 3
1
− − −
−
xx
x
tại
0,9999999=x
và tại
1,0000001=x
ta đều được kết quả:
Do đó chọn đáp án B.
Lưu ý:
- Trong cách thứ 2, nếu ta tính giá trị biểu thức tại
0,999999999=x
hoặc tại
1,000000001=x
thì ta được kết quả:
Do vượt quá giới hạn tính toán của máy. Do đó nếu không thử lại với cá trị lớn hơn thì có thể ta
sẽ chọn đáp án A.
ở bài này có nhiều vấn đề cần phân tích thêm. Nếu làm như ví dụ 4 thì ta sẽ biến đổi
( )
3
2
6 5 4 3
1
xx
x
− − −
−
( ) ( )
3
22
6 5 1 1 4 3
11
xx
xx
− − − −
=+
−−
rồi nhân liên hợp để thu được
( )
3
2
6 5 4 3
1
xx
x
− − −
−
( )
( )
( )
( ) ( )
( )
( )
2
3
3
2
3
3
6 1 4 3 4 6 5 6 5 1
1 6 5 6 5 1 1 4 3
x x x
x x x x
+ − − − + − +
=
− − + − + + −
- Ta thấy giới hạn mới thu được vẫn còn là dạng vô định
0
0
nên vẫn tiếp tục phải khử dạng vô định.
Mà việc khử này sẽ rất phức tạp do biểu thức mới thu được khá cồng kềnh. Để giải quyết khó khăn
đó ta thấy trong lời giải trình bày ở trên, ta tiến hành đổi biến để cho mẫu gọn lại và không thêm
bớt 1 trên tử thức mà thêm bớt nhị thức
21+t
. Vậy cơ sở nào để tìm ra nhị thức đó?
Ta mong muốn sau khi thêm bớt tử thức với một lượng
( )
At
nào đó rồi tách ra thành hai phân
thức để nhân liên hợp thì trên tử thức xuất hiện nhân tử
2
t
để giản ước với
2
t
dưới mẫu
( ) ( )
3
3
2 2 2
6 1 4 1
6 1 4 1
+ − − +
+ − +
=+
t A t A t t
tt
t t t
.
Vậy ta phải có
( ) ( )
22
41A t t kt− + =
( )
22
4 1 4A t kt t k = + + =
và
( ) ( ) ( )
2
2
2 1 2 1= + = +A t t A t t
.
- Ở nhiều bài toán giới hạn, ta thấy việc sử dụng MTCT là nhanh hơn giải thông thường. Tuy
nhiên chúng tôi vẫn khuyến nghị độc giả nên nắm vững phương pháp giải thông thường (theo
hình thức tự luận), vì nhiều bài tập không chỉ đơn thuần là tính giới hạn mà người ra đề có thể
hỏi bằng nhiều hình thức khác nhau, đặc biệt có nhiều cách ra đề hạn chế việc sử dụng MTCT
để tìm ra đáp án.
STUDY TIP
Trong nhiều bài toán, không nên chỉ tính giá trị hàm số tại một điểm mà nên tính lại một số điểm
từ lớn đến nhỏ và từ cả hai phía trái, phải của
0
x
.
Ví dụ 6: Giới hạn của hàm số
( )
( )
2
3
21
1
− + + +
=
−
x a x a
fx
x
khi
1→x
bằng
A.
3
−
a
. B.
3
a
. C.
2
3
−−a
. D.
2
3
− a
.
Lời giải
Cách 1:
( )
2
3
1
21
lim
1
x
x a x a
x
→
− + + +
−
( )( )
( )
( )
2
1
11
lim
11
x
x x a
x x x
→
− − −
=
− + +
2
1
1
lim
13
x
x a a
xx
→
−−
= = −
++
Cách 2: (Đặc biệt hóa để sử dụng MTCT) Cho
a
một giá trị bất kì, chẳng hạn
1=a
, thì
( )
2
3
32
1
−+
=
−
xx
fx
x
. Dùng MTCT ta tìm được
2
3
1
3 2 1
lim
1 3 3
→
−+
= − = −
−
x
x x a
x
.
Vậy chọn đáp án A.
Giải thích: phương trình
( )
2
2 1 0− + + + =x a x a
có tổng các hệ số bằng
0
nên ta có một nghiệm
bằng
1
, nghiệm còn lại bằng
1+a
. Do đó ta phân tích được
( ) ( )( )
2
2 1 1 1− + + + = − − −x a x a x x a
.
STUDY TIP
Nếu đa thức có tổng các hệ số bằng
0
thì đa thức có một nghiệm bằng
1
.
Nếu đa thức có tổng các hệ số của các lũy thừa bậc chẵn bằng tổng các hệ số của lũy thừa bậc
lẻ thì đa thức có một nghiệm bằng
1−
.
Ví dụ 7: Giả sử
0
11
lim
2
→
+−
=
x
ax
L
x
. Hệ số
a
bằng bao nhiêu để
3=L
?
A.
6−
. B.
6
. C.
12−
. D.
12
.
Lời giải
Cách 1: Ta có
0
11
lim
2
x
ax
x
→
+−
( )
0
lim
2 1 1
x
ax
x ax
→
=
++
( )
0
lim
4
2 1 1
x
aa
ax
→
==
++
Vậy
4
=
a
L
. Do đó
3 3 12
4
= = =
a
La
. Đáp án đúng là D.
Cách 2: Sử dụng MTCT tìm
0
11
lim
2
→
+−
x
ax
x
lần lượt với
a
bằng
6−
,
6
,
12−
,
12
. Ta thấy với
12=a
thì
0
11
lim
2
→
+−
x
ax
x
bằng
3
. Vậy chọn đáp án D.
STUDY TIP
Một trong các kĩ thuật giải bài toán trắc nghiệm là thử lần lượt các đáp án và chọn ra đáp án thỏa
mãn yêu cầu bài toán.
2. Các bi toán liên quan đn giới hạn đc bit
Trong sách giáo khoa đại số và giải tích 11 có nêu một giới hạn đặc biệt dạng
0
0
Đó là
0
sin
lim 1
x
x
x
→
=
. Sau đây ta xét một số ví dụ áp dụng kết quả này.
Ví dụ 8: Cho
a
và
b
là các số thực khác 0. Khi đó
0
lim
sin
x
ax
bx
→
bằng
A.
a
. B.
b
. C.
a
b
. D.
b
a
.
Lời giải
Đáp án C.
Cách 1: Ta có
0 0 0
lim lim . .lim
sin sin sin
x x x
ax bx a a bx
bx bx b b bx
→ → →
==
Đổi biến
t bx=
ta thấy khi
0x →
thì
0t →
. Do đó
00
lim lim 1
sin sin
xx
bx t
bx t
→→
==
Vậy
0
lim
sin
x
ax a
bx b
→
=
.
Cách 2: Cho
a
và
b
các giá trị cụ thể, chẳng hạn
2, 3ab==
.
Sử dụng MTCT tìm giới hạn
0
2
lim
sin3
x
x
x
→
ta được kết quả bằng
2
3
, tức là bằng
a
b
.
Vậy chọn C.
STUDY TIP
00
sin
lim 1 lim 1
sin
xx
xx
xx
→→
= =
0
sin ( )
lim 1
()
x
Ax
Ax
→
=
, với điều kiện
0
lim ( ) 0
x
Ax
→
=
Ví dụ 9: Cho số thực
a
khác 0. Khi đó
2
0
lim
1 cos
x
x
ax
→
−
bằng
A.
2
2
a
. B.
2
a
. C.
2
2a
. D.
2a
.
Lời giải
Đáp án A
Cách 1: Ta có:
2
2
22
2
2 2 2 2
0 0 0 0
22
2 2 2 2
2
2
lim lim lim . lim .1
1 cos
2sin sin sin
2 2 2
x x x x
ax
ax
xx
ax ax ax
ax a a a a
→ → → →








= = = = =


−




.
Cách 2: Cho a là một giá trị cụ thể, chẳng hạn
2a =
(không nên lấy
1a =
, vì khi đó giá trị của
2
2
a
và
2
a
cũng bằng nhau). Sử dụng MTCT tính giới hạn
2
0
lim
1 cos2
x
x
x
→
−
ta được kết quả bằng
1
2
, tức là bằng
2
2
a
. Vậy chọn đáp án A.
STUDY TIP
( )
( )
0
sin
lim 1
k
k
x
Ax
Ax
→
=
điều kiện
0
lim ( ) 0
x
Ax
→
=
Ví dụ 10:
sin sin
lim
xa
xa
xa
→
−
−
bằng
A.
tana
. B.
cota
. C.
sin a
. D.
cosa
.
Lời giải
Đáp án D
Cách 1: Ta có
2cos sin sin
sin sin
2 2 2
lim lim lim .cos
2
2.
22
x a x a x a
x a x a x a
x a x a
x a x a
xa
→ → →
+ − −


−+
==

−−
−


Mà
sin
2
lim 1
2
xa
xa
xa
→
−
=
−
(xem STUDY TIP trên),
limcos cos
2
xa
xa
a
→
+
=
.
Vậy
sin sin
lim cos
xa
xa
a
xa
→
−
=
−
. Do đó chọn đáp án D.
Cách 2: Sử dụng MTCT tính giới hạn
1
sin sin1
lim
1
x
x
x
→
−
−
(ứng với
1a =
).
So sánh kết quả với
tan1,cot1,sin1,cos1
ta được
1
sin sin1
lim cos1
1
x
x
x
→
−
=
−
.
Vậy chọn đáp án D.
3. Đc thêm
Ví dụ 11: Cho
a
và
b
là các số nguyên dương.
0
15
lim
sin 3
ax
x
e
bx
→
−
=
. Tích
ab
có thể nhận giá trị bằng số nào
trong các số dưới đây?
A. 15. B. 60. C. 240. D. Cả ba đáp án trên.
Lời giải
Đáp án D
Ta có
00
11
lim lim . . 1.1.
sin sin
ax ax
xx
e e bx a a a
bx ax bx b b b
→→

−−
= = =


Vậy để
0
15
lim
sin 3
ax
x
e
bx
→
−
=
thì
5
3
a
b
=
. Vì
a
và
b
là các số nguyên dương nên suy ra
5 , 3a k b k==
với
k
nguyên dương. Do đó
2
15ab k=
.
+
22
15 15 1 1 15.k k k ab= = = =
+
22
15 60 4 2 60.k k k ab= = = =
+
22
15 240 16 4 240k k k ab= = = =
Vậy cả ba đáp án đều đúng. Do đó chọn đáp án D.
STUDY TIP
Ngoài giới hạn
0
sin
lim 1
x
x
x
→
=
, Sách giáo khoa giải tích 12 nâng cao chương 2, 5 cn giới thiệu
thêm các giới hạn:
( )
0
0
1
lim 1,
ln 1
lim 1
x
x
x
e
x
x
x
→
→
−
=
+
=
Ví dụ 12: Cho hàm số
( )
( )
3
ln 1 1
k
x
fx
x
+−
=
, trong đó k là một số nguyên dương. Tìm tất cả các giá trị
của k để
( )
fx
có giới hạn hữu hạn khi x dần tới 0.
A.
,3kk
. B.
,0 3kk
. C.
,3kk
. D.
,0 3kk
.
Lời giải
Đáp án D
Cách 1: Ta có
( ) ( )
33
33
00
ln 1 1 ln 1 1
1
lim lim .
kk
xx
xx
x x x
−
→→

+ − + −

=


Mà
( )
3
3
0
ln 1 1
lim 1
x
x
x
→
+−
=
nên để
( )
fx
có giới hạn hữu hạn khi x dần tới 0 thì hàm số
( )
3
1
k
gx
x
−
=
phải có giới hạn hữu hạn khi x dần tới 0. Muốn vậy thì
3 0 3kk−
. Vì k
nguyên dương nên đáp án là D.
Cách 2: Sử dụng MTTCT tìm giới hạn khi
3k =
, ta được
( )
3
3
0
ln 1 1
lim 1
x
x
x
→
+−
=
.
Vậy ta chỉ xét đáp án C hoặc D. Chẳng hạn với đáp án C, ta sử dụng MTCT tìm giới hạn khi
4k =
. Ta được
( )
3
3
0
ln 1 1
lim
x
x
x
→
+−
= −
. Do đó loại đáp án C. Vậy đáp án đúng là D.
*** Trong chương trình lớp 12 sẽ được học khái niệm căn bậc n.
Định nghĩa
Cho số thực
b
và số nguyên dương
n
( )
2n
. Số
a
được gọi là căn bậc
n
của số
b
nếu
n
ab=
Với
n
chẵn và:
0b+
: Không tồn tạo căn bậc
n
của
b
.
0b+=
: Có một căn bậc
n
của
b
là số 0.
0b+
: Có hai căn trái dấu, kí hiệu giá trị dương là
n
b
, cn giá trị âm là
n
b−
Sau đây ta xét một vài ví dụ liên quan đến căn bậc n.
STUDY TIP
n
n
a b a b= =
-Mọi số thực đều có một căn bậc lẻ và chỉ có một căn bậc lẻ
- Chỉ có số không âm mới có căn bậc chẵn.
Số 0 có một căn bậc chẵn là 0.
Các số dương có hai căn bậc chẵn đối nhau.
Ví dụ 13: Cho
a
là một số thực khác 0 và n là một số nguyên dương,
2n
. Chọn khẳng định đúng
trong các khẳng định sau.
A.
0
11
lim
n
x
ax a
xn
→
+−
=
. B.
0
11
lim
n
x
ax n
xa
→
+−
=
.
C.
0
1 1 1
lim
n
x
ax
xn
→
+−
=
. D.
0
1 1 1
lim
n
x
ax
xa
→
+−
=
.
Lời giải
Đáp án A.
Cách 1: Sử dụng MTCT tìm giới hạn với
5n =
và
3a =
, ta được kết quả
5
0
1 3 1 3
lim
5
x
x
x
→
+−
=
vậy đáp án đúng là A.
Cách 2: Đổi biến đặt
1
11
n
n
n
t
t ax t ax x
a
−
= + = + =
Ta có khi
0x →
thì
1t →
và
( )
( )
12
12
1 1 1 1
1 ... 1
1 ... 1
n
n n n
nn
ax t t a
aa
x t t t t
t t t t
−−
−−
+ − − −
= = =
− + + + +
− + + + +
Mà
12
1
lim
.. 1
nn
x
aa
t t t n
−−
→
=
+ + + +
nên suy ra
0
11
lim
n
x
ax a
xn
→
+−
=
. Vậy chọn A.
STUDY TIP
0
11
lim
n
x
ax a
xn
→
+−
=
( )
( )
1 2 2 1
...
n n n n n n
a b a b a a b ab b
− − − −
− = − + + + +
( )
( )
12
1 1 ... 1
n n n
a a a a a
−−
− = − + + + +
Ví dụ 14: Biết
3
4
8
1 19
lim
82
x
x x a
b
x
→
+ − +
=
+−
trong đó
a
b
là phân số tối giản,
a
và
b
là các số nguyên dương.
Tổng
ab+
bằng
A. 137. B. 138. C. 139. D. 140.
Lời giải
Đáp án C.
Với những bài dạng này, sẽ khó sử dụng MTCT để tìm đáp án đúng.
Đặt
8tx=−
. Suy ra
8xt=+
.
8
lim 0
x
t
→
=
và
( )
3
33
44
4
3
4
3 1 3 1
1 19 9 27
9 27
8 2 16 2
2 1 2
16
1 1 1 1
9 27
3
2
1
16
1
tt
x x t t
x t t
tt
tt
gt
t
t
+ − +
+ − + + − +
==
+ − + −
+−
+ − + −
−
==
+
−
Do đó
3
4
80
1 19
lim lim ( )
82
xt
xx
gt
x
→→
+ − +
=
+−
. p dụng ví dụ 13 Ta có:
3
4
0 0 0
1 1 1
1 1 1 1 1 1
1 1 1
9 27 16
9 27 16
lim ;lim ;lim
2 18 3 81 4 64
t t t
t t t
t t t
→ → →
+ − + − + −
= = = = = =
Vậy
0
11
3 112
18 81
lim ( ) .
1
2 27
64
t
gt
→
−
==
Do đó
3
4
8
1 19 112
lim
27
82
x
xx
x
→
+ − +
=
+−
. Vậy
112, 27ab==
và
139ab+=
*** Tính giới hạn vô định dạng
0
0
bằng đạo hàm (Quy tắc L’Hôpital).
STUDY TIP
*Quy tắc L’Hôpital
( )
( )
00
0
0
'
()
lim lim
()
x x x x
fx
fx
g x g x
→→
=
.
Trong đó
( )
fx
và
( )
gx
xác định trên khoảng
( )
;ab
,
( )
0
;x a b
( ) ( )
00
lim lim 0
x x x x
f x g x
→→
==
(Hoặc
( ) ( )
00
lim lim
x x x x
f x g x
→→
= = 
)
Và
( )
( )
0
'
lim
'
xx
fx
gx
→
tồn tại
Trước khi đọc phần này xin đọc chương đạo hàm trong chương trình lớp 11
Ví dụ 15: Ta xét lại ví dụ 9 đã nêu ở trên.
Cho số thực
a
khác 0. Khi đó
2
0
lim
1 cos
x
x
ax
→
−
bằng
A.
2
2
a
. B.
2
a
. C.
2
2a
. D.
2a
.
Lời giải
Đáp án A
Ngoài hai lời giải đã nêu ở trên ta cn một cách áp dụng Quy tắc L’Hopital như sau:
2
22
0 0 0
2 2 2
lim lim lim
1 cos sin cos
x x x
xx
ax a ax a ax a
→ → →
= = =
−
Ở đây ta áp dụng Quy tắc L’Hopital 2 lần. Cách sử dụng Quy tắc này rất hữu dụng khi giải các
bài toán trắc nghiệm. Tuy nhiên không áp dụng Quy tắc này cho các bài toán tự luận do Quy tắc
L’Hopital không được trình bày trong chương trình THPT.
STUDY TIP
Có thể áp dụng quy tắc L’Hopital nhiều lần để tính giới hạn
Đề nghị: Độc giả hãy vận dụng quy tắc L’Hopital để giải các ví dụ đã nêu ở dạng 2 này.
bài tập dạng trắc nghiệm. Nếu là bài tập dạng tự luận thì các em cần trình bày chi tiết theo
phương pháp đã nêu trên. Riêng A và B, ta giải tự luận như sau:
2
1 1 1
lim lim lim 0
1 ( 1)( 1) 1
x x x
xx
x x x x
→+ →+ →+
−−
= = =
− − + +
5 ( 5)( 5)
lim lim lim ( 5)
55
x x x
x x x
x
xx
→+ →+ →+
− − +
= = + = +
−−
Ví dụ 16: Giới hạn
3
31
lim
52
x
xx
x
→−
−+
−
bằng:
A. 0 B.
3
2
C.
+
D.
−
Đáp án D
Cách 1: Theo kết quả đã nêu ở trên thì
3
2
3 1 1
lim lim
5 2 2
xx
xx
x
x
→− →−
−+
= − = −
−
Cách 2: Sử dụng MTCT
Bổ sung: Nếu là bài toán tự luận ‘Tìm
3
31
lim
52
x
xx
x
→−
−+
−
” thì ta có hai cách giải như sau:
Cách 1: Ta có
2
3
1
3
31
lim lim
5
52
2
xx
x
xx
x
x
x
→− →−
−+
−+
=
−
−
. Mà
2
1
lim ( 3 )
x
x
x
→−
− + = +
;
5
lim ( 2) 2 0
x
x
→−
− = −
nên theo qui tắc 2,
2
3
1
3
31
lim lim
5
52
2
xx
x
xx
x
x
x
→− →−
−+
−+
= = −
−
−
Cách 2 : Ta có
3
23
32
31
1
31
lim lim
52
52
xx
xx
xx
x
xx
→− →−
−+
−+
=
−
−
. Mà
2 3 3 2
3 1 5 2
lim(1 ) 1; lim ( ) 0
xx
x x x x
→− →−
− + = − =
và
32
52
lim 0
x
xx
→−

−


với mọi
0x
nên theo qui tắc 2,
3
23
32
31
1
31
lim lim
52
52
xx
xx
xx
x
xx
→− →−
−+
−+
= = −
−
−
STUDY TIP
k
a
lim
k
x
ax
→−
Chẵn
+
+
-
-
Lẻ
+
-
-
+
Ví dụ 17: Trong các giới hạn sau, giới hạn nào bằng
−
?
A.
53
32
7
lim
2 3 1
x
xx
xx
→−
++
−+
B.
23
2
13
lim
41
x
xx
x
→−
−−
+
C.
34
3
35
lim
1
x
xx
xx
→−
−+
−+
D.
26
2
3
lim
15
x
xx
xx
→−
−
+−
Đáp án C
Lời giải
Cách 1 : Theo cách ghi kết quả ở trên thì
5 3 2 3
22
3 2 2
7 1 1 3 1
lim lim ; lim lim ;
2 3 1 2 4 1 4
x x x x
x x x x
xx
x x x
→− →− →− →−
+ + − −
= = + = − = +
− + +
3 4 2 6
4
35
3 5 3 1
lim 3 lim ; lim lim ;
1 1 5 5
x x x x
x x x x
xx
x x x x
→− →− →− →−
− + −
= = − = = +
− + + −
Cách 2 : sử dụng MTCT tính lần lượt các giới hạn
Khi đến C thấy
34
3
35
lim 3 lim
1
xx
xx
x
xx
→− →−
−+
= = −
−+
nên dừng lại và chọn đáp án C
Ví dụ 4 : Giới hạn
2
41
lim
1
x
xx
x
→−
−+
+
bằng :
A. 2 B. -2 C. 1 D. -1
Đáp án B
Lời giải :
Cách 1 :
2
2 2 2
1 1 1 1 1 1
4 4 4
41
lim lim lim lim 2
1
1 1 1
1
x x x x
xx
xx
x x x x x x
x x x
x
→− →− →− →−
− + − − + − − +
−+
= = = = −
+ + +
+
Vậy chọn đáp án B
Cách 2 : Sử dụng MTCT
Ví dụ 18: Giới hạn
22
41
lim
23
x
x x x
x
→−
− − +
+
bằng :
A.
1
2
−
B.
1
2
C.
−
D.
+
Đáp án B
Lời giải :
Cách 1 : Theo ví dụ đã trình bày ở dạng 1 thì
22
lim( 4 1)
x
x x x
→−
− − + = −
Ta đưa
2
x
ra ngoài căn rồi chia cả tử và mấu cho x. Cụ thể như sau :
22
2
22
11
14
41
lim lim
2 3 2 3
1 1 1 1
1 4 1 4
1
lim lim
3
2 3 2
2
xx
xx
xx
x x x
xx
xx
xx
x x x x
x
x
→− →−
→− →−
− − +
− − +
=
++
− − + + − − + +
= == =
+
+
Vậy đáp án đúng là B
Cách 2 : Sử dụng máy tính tính giá trị hàm số tại
10
10x
−
=
ta được kết quả như hình bên. Vậy
chọn đáp án B
Cách 3 : Ta có thể giải bài này bằng phương pháp loại trừ như sau :
Vì
22
lim( 4 1) ; lim(2 3)
xx
x x x x
→− →−
− − + = − + = −
nên giới hạn cần tìm phải mang dấu
dương. Mặt khác bậc tử và bậc mẫu bằng nhau nên giới hạn cần tìm là hữu hạn.
Đáp án cần tìm là đáp án B
STUDY TIP
Ví dụ 19: Biết
32
21
lim
32
x
xa
x
x x b
→+
+
=
++
trong đó a, b là các số nguyên dương. Giá trị nhỏ nhất của tích
ab bằng :
A. 6 B. 12 C. 18 D. 24
Đáp án C
Lời giải :
Ta có :
32
3 2 3 2
2 1 2 6
lim lim
3 2 3 2 3
xx
x x x
x
x x x x
→+ →+
++
==
+ + + +
Vậy
6
3
a
b
=
Dễ dàng suy ra được tích của ab là 18.
Chú ý : Nếu sử dụng MTCT tính giá trị hàm số tại
10
10x =
thì ta thu được kết quả như hình
bên. Do đó, nếu không có kiến thưc về giới hạn hàm số, rất khó tìm ra được đáp án đúng nếu
chỉ dùng MTCT. Ngược lại nếu có kiến thức vững vàng, bạn đọc sẽ nhanh chóng tìm ra đáp án,
thậm chí là trong chớp mắt ! Vì vậy, tôi xin nhắc lại, tôi khuyến nghị các bạn đọc nên giải bài
tập theo kiểu tự luận một cách căn cơ để có thể đối mặt với các bài toán ‘’chống MTCT’’
STUDY TIP
Dạng 4 : Dạng vô định
0.
Bài toán : Tính giới hạn
0
lim[ ( ) ( )]
xx
u x v x
→
khi
0
lim[ ( )] 0
xx
ux
→
=
và
0
lim[v( )]
xx
x
→
=
Phương pháp : Ta có thể biến đổi
00
()
lim[u(x)v( )] lim
1
()
x x x x
ux
x
vx
→→
=
để đưa về dạng
0
0
hoặc
00
()
lim[u(x)v( )] lim
1
()
x x x x
ux
x
vx
→→
=
để đưa về dạng
.
Tuy nhiên, trong nhiều bài tập, ta chỉ cần biến đổi đơn giản như đưa biểu thức vào trong/ ra
ngoài dâu căn, quy đồng mẫu thức …. Là đưa được về dạng quen thuộc.
Ví dụ 20: Giới hạn
0
11
lim ( 1)
1
x
xx
−
→
−
+
bằng :
A. 0 B. -1 C. 1 D.
−
Đáp án B
Phân tích : Ta có
00
11
lim ; lim( 1) 0
1
xx
xx
−−
→→
= − − =
+
nên chưa có thể áp dụng các định lí, qui tắc để
tính giới hạn.
Lời giải :
Cách 1 : Ta có
0 0 0 0
1 1 1 ( 1) 1
lim ( 1) lim lim lim 1
1 ( 1) ( 1) 1
x x x x
xx
x x x x x x x
− − − −
→ → → →
− + − −
− = = = = −
+ + + +
Cách 2 : Sử dụng MTCT tính giá trị hàm số tại
0,00000001−
ta được kết quả như hình bên. Do
đó chọn đáp án B, tức
0
11
lim ( 1) 1
1
x
xx
−
→
− = −
+
STUDY TIP
Ví dụ 21: Giới hạn
2
2
lim( 2)
4
x
x
x
x
+
→
−
−
bằng :
A.
+
B.
−
C. 0 D. 1
Đáp án C
Phân tích : Vì
2
22
lim( 2) 0; lim
4
xx
x
x
x
++
→→
− = = +
−
nên chưa có thể áp dụng các định lý và qui tắc
để tính giới hạn.
Lời giải :
Cách 1 : Với mọi
2x
ta có :
2
22
( 2) ( 2)
( 2)
4 4 2
x x x x x
x
x x x
−−
− = =
− − +
Do đó
2
22
( 2)
lim( 2) lim 0
42
xx
x x x
x
xx
++
→→
−
− = =
−+
. Vậy chọn đáp án C
Cách 2: Sử dụng MTCT
Ví dụ 22: Giới hạn
3
21
lim ( 1)
52
x
x
x
xx
→−
+
+
++
bằng:
A.
2
2
−
B.
10
5
−
C.
5
5
−
D.
2−
Đáp án B
Phân tích: Ví dụ tương tự đã được nghiên cứu trong phần dạng vô định
Tuy nhiên vì
3
21
lim( 1) ; lim 0
52
xx
x
x
xx
→− →−
+
+ = − =
++
nên giới hạn này cũng có thể coi như dạng
0.
Lời giải
Cách 1: Với
1x −
ta có
10x +
nên
2
1 ( 1)xx+ = − +
. Do đó
2
33
2 1 ( 1) (2 1) 10
lim ( 1) lim
5 2 5 2 5
xx
x x x
x
x x x x
→− →−
+ + +
+ = − = −
+ + + +
Vậy chọn đáp án B
Cách 2: Sử dụng MTCT. Tính giá trị hàm số tại
10
10x
−
=
ta được kết quả như hình bên. So
sánh các đáp số A, B, C, D ta chọn đáp án đúng là B.
STUDY TIP
Ta chỉ quan tâm đến lũy thừa bậc cao nhất là
3
x
. Hệ số của
2
x
trong
2
( 1)x+
là
2
1
do
( )
2
2
1 2 1x x x+ = + +
. Hệ số của x trong 2x + 1 là 2 nên hệ số của
3
x
trên tử là
2
1 .2
. Ở đây
không nhất thiết phải khai triển tích thành đa thức để tìm hệ số của
3
x
.
Ví dụ 23: Giới hạn
1
lim (xsin )
x
x
→+
bằng
A. 0 B. 1 C.
+
D. Không tồn tại
Đáp án B
Phân tích: Vì
1
lim 0
x
x
→+
=
nên
1
lim sin 0
x
x
→+
=
. Ta có dạng
0.
. Lời giải như sau :
Lời giải :
Cách 1 : Ta có :
1
sin
1
lim ( sin ) lim
1
xx
x
x
x
x
→+ →+
=
Đặt
1
t
x
=
và
lim 0
x
t
→+
=
thì
1 sint
lim( sin ) lim 1
xx
x
xt
→+ →+
==
Cách 2: Sử dụng MTCT ( Lưu ý chuyến máy về chế độ Radian)
STUDY TIP
Ở ví dụ 4 ta đã chuyển dạng
0.
thành
0
0
do ta liên tưởng đến giới hạn đặc biệt
0
sinx
lim 1
x
x
→
=
Ví dụ 24: Giới hạn
2
lim ( ) anx
2
x
xt
−

→


−
bằng
A. 1 B. 0 C.
−
D. Không tồn tại
Đáp án A
Phân tích: vì
2 2 2
sinx
lim ( ) 0; lim anx= lim
2 cos
x x x
xt
x
− − −
→ → →
− = = +
nên ta có dạng
0.
Lời giải :
Cách 1 : Đặt
2
tx
=−
thì
2
, lim 0
2
x
x t t
−

→


= − =
và
sin( )
2
( )tan tan( ) t cos
2 2 sin
cos( )
2
t
t
x x t t t
t
t

−
− = − = =
−
. Do đó
2
lim ( )tanx=lim 1
2 sin
to
x
t
x cost
t
−+
→

→


−=
Cách 2 : Sử dụng MTCT
STUDY TIP
22
lim anx=+ ; lim anx=+
xx
tt

−+
→→

. Lưu ý để tránh nhầm lẫn giữa hai giới hạn này
Dạng 5 : Dạng
−
Bài toán : Tính
0
lim[ ( ) ( )]
xx
u x v x
→
−
khi
0
lim ( )
xx
ux
→
= +
và
0
limv( )
xx
x
→
= +
Hoặc tính
0
lim[ ( ) ( )]
xx
u x v x
→
+
khi
0
lim ( )
xx
ux
→
= +
và
0
limv( )
xx
x
→
= −
Phương pháp : Nhân hoặc chia với biểu thức liên hợp (nếu có căn thức) hoặc qui đồng để đưa
về cùng một phân thức ( nếu chứa nhiều phân thức).
Ví dụ 25: Giới hạn
(
)
22
lim 1
x
x x x
→+
+ − +
bằng
A.
1
2
B.
1
4
C.
+
D.
−
Đáp án A
Lời giải :
Cách 1:
Phân tích: Ta thấy
22
lim ; lim 1
xx
x x x
→+ →+
+ = + + = +
nên bài này thuộc dạng
−
. Tương
tự như giới hạn dãy số, ta nhân chia với biểu thưc liên hợp. Lời giải cụ thể như sau:
Ta có:
(
)
22
22
2
1
1
11
lim 1 lim lim
2
11
1
11
x x x
x
x
x x x
x x x
xx
→+ →+ →+
−
−
+ − + = = =
+ + +
+ + +
Cách 2: Sử dụng MTCT
Ví dụ 26: Giới hạn
(
)
2
lim 9 1 3
x
x x x
→−
+ + +
bằng
A.
2
3
B.
2
3
−
C.
1
6
D.
1
6
−
Đáp án D
Lời giải:
Phân tích: Ta có
2
lim 9 1 ; lim(3 )
xx
x x x
→− →−
+ + = + = −
nên bài này thuộc dạng vô
định
−
(mặc dù biểu thức của hàm số lấy giới hạn có hạng tổng). Ta tiến hành nhân chia
với biểu thức liên hợp. Lời giải cụ thể như sau:
Ta có:
(
)
2
2
2
11
lim 9 1 3 lim lim
11
9 1 3
93
xx
x x x
x x x
xx
xx
++
+ + + = =
+ + −
− + + −
2
1
1
11
lim .
3 3 6
11
93
x
x
xx
→+
+
−
= = =
−−
− + + −
Vậy chọn đáp án D.
Cách 2: Sử dụng MTCT tính giá trị hàm số tại
10
10x =−
ta được kết quả như hình bên. Sử
dụng ki thuật tìm dạng phân số của một số thập phân vô hạn tuần hoàn ta được
( )
1
0,1 6
6
−
−=
(xem lại phần giới hạn dãy số). Vậy chọn đáp án D.
Studytip:
Ví dụ 27. Giới hạn
(
)
3
2 3 2
lim 4 3 8 2 1
x
x x x x
→+
+ − + +
bằng:
A.
13
24
B.
7
12
C.
13
24
−
D.
7
12
−
Lời giải
Cách 1: Phân tích:
Vì
3
2 3 2
lim 4 3 ; lim 8 2 1
xx
x x x x
→+ →+
+ = + + + = +
nên đấy cũng là dạng vô định
.−
Tuy
nhiên vì là hiệu của hai căn thức không cùng bậc nên ta chưa thể nhâ chia với biểu thức liên
hợp luôn được. Nhận thấy
0x
thì
3
23
4 8 2x x x==
nên ta thêm bớt
2x
rồi nhân chia liên
hợp.
Với
0x
:
(
)
(
)
33
2 3 2 2 3 2
4 3 8 2 1 4 3 2 2 8 2 1x x x x x x x x x x+ − + + = + − + − + +
2
22
3
3
33
1
2
3
4 3 2
2 1 2 1
4 2 8 8
x
x
x x x
x x x x
+
=−
++

+ + + + + +


Do đó
(
)
3
2 3 2
lim 4 3 8 2 1
x
x x x x
→+
+ − + +
2
2
3
3
33
1
2
3 3 2 7
lim .
2 2 4 4 4 12
3
2 1 2 1
42
4 2 8 8
x
x
x
x x x x
→+


+

= − = − =

+ + +


++
+ + + + + +




Do đó chọn B.
Cách 2: Sử dụng MTCT tính giá trị hàm số tại
10
10x =−
ta được kết quả như hình bên. Sử
dụng ki thuật tìm dạng phân số của một số thập phân vô hạn tuần hoàn ta được
( )
7
0,58 3 .
12
−=
(xem lại phần giới hạn dãy số). Vậy chọn đáp án D.
Studytip:
Lưu ý: Ta xem lại một Ví dụ đã trình bày ở dạng 1 như sau:
Ví dụ 28. Giới hạn của hàm số
( )
22
41f x x x x= − − +
khi
x →+
bằng:
A.
−
B.
+
C.
1−
D.
3
Phân tích: Ví dụ này cũng thuộc dạng
−
nhưng lại không phải là dạng vô định. Bằng các
định lí và quy tắc, ta tính được giới hạn hàm số mà không cần phải nhân chia với biểu thức liên
hợp. Ta xem cách giải cho tiết dưới đây.
Lời giải
2 2 2 2
22
1 1 1 1
4 1 1 4 1 4x x x x x x x
x x x x
− − + = − − + = − − +
2
11
1 4 .x
xx

= − − +



Ta có
lim
x
x
→+
= +
và
2
11
lim 1 4 1 2 1 0.
x
xx
→+
− − + = − = −
Vậy
(
)
22
2
11
lim 4 1 lim 1 4 .
xx
x x x x
xx
→+ →+


− − + = − − + = −






Studytip:
Cũng là
−
nhưng khi nào là xác định, khi nào là vô định? Khi nào phải nhân chia liên hợp,
khi nào thì đưa
n
x
ra ngoài căn rồi đặt nhân tử chung như Ví dụ 4? Để có câu trả lời mời quý
độc giả hãy đọc lại phần giới hạn dãy số có chứa căn.
Ví dụ 29. Trong các giới hạn sau giới hạn nào là hữu hạn:
A.
(
)
2
lim 4 4 3 2 .
x
x x x
→+
+ + +
B.
(
)
2
lim 2 1 3 .
x
x x x
→−
+ + −
C.
(
)
2
lim 1 2 .
x
x x x
→+
− + +
D.
(
)
2
lim 3 2 .
x
x x x
→−
+ + +
Lời giải
Cách 1: Với các kết quả đã biết phần giới hạn dãy số có chứa căn, ta thấy ngay đáp án là D. Thật
vậy:
( )
(
)
22
lim 4 4 3 ; lim 2 lim 4 4 3 2 .
x x x
x x x x x x
→+ →+ →+
+ + = + = + + + + = +
( )
(
)
22
lim 2 1 ; lim 3 lim 2 1 3 .
x x x
x x x x x x
→− →− →−
+ + = + − = + + + − = +
(
)
2
2
11
lim 1 2 lim 1 2
xx
x x x x
xx
→+ →+

− + + = − + + = −



do
2
11
lim ; lim 1 2 1 2 0.
xx
x
xx
→+ →+

= + − + + = −



(
)
2
2
2
2
3
3 2 3
lim 3 2 lim lim .
2
32
32
11
x x x
x
x
x x x
x x x
xx
→− →− →−
+
+−
+ + + = = =
+ + −
+ + −
Cách 2: Sử dụng MTCT để tìm lần lượt các giới hạn.
Ví dụ 30. Giới hạn
2
2
11
lim
42
x
xx
+
→

−

−−

bằng:
A.
+
B.
−
C.
3−
D.
2−
Lời giải
Cách 1: Vì
2
22
11
lim ; lim
42
xx
xx
++
→→
= + = +
−−
nên ta có dạng
.−
Theo phương pháp đã nêu từ đầu, ta đi quy đồng mẫu số các phân thức.
Ta có
( )( ) ( ) ( )( )
2
2 2 2
1 1 1 1 1
lim lim lim .
4 2 2 2 2 2 2
x x x
x
x x x x x x x
+ + +
→ → →

−−

− = − =


− − − + − − +


Vì
( )
( )
22
13
lim 0, lim 2 0
24
xx
x
x
x
++
→→
− − −
= − =
+
và
20x−
với mọi
2x
nên theo quy tắc 2,
( )( )
2
22
1 1 1
lim lim .
4 2 2 2
xx
x
x x x x
++
→→
−−

− = = −

− − − +

Do đó chọn B
Cách 2: Sử dụng MTCT tính giá trị hàm số tại
2,00000001x =
ta được kết quả như hình bên.
Do đó chọn đáp án B, tức là
2
2
11
lim .
42
x
xx
+
→

− = −

−−

Ví dụ 31. Cho
a
và
b
là các số thực khác 0. Tìm hệ thức liên hệ giữa
a
và
b
để giới hạn:
22
2
lim
6 8 5 6
x
ab
x x x x
−
→

−

− + − +

là hữu hạn:
A.
4 0.ab−=
B.
3 0.ab−=
C.
2 0.ab−=
D.
0.ab−=
Lời giải
Cách 1: Ta có
( )( ) ( )( )
22
6 8 5 6 2 4 2 3
a b a b
x x x x x x x x
− = −
− + − + − − − −
( ) ( )
( )( )( )
( )
( )( )( )
34
.
2 3 4 2 3 4
a x b x g x
x x x x x x
− − −
==
− − − − − −
Ta có
( ) ( ) ( ) ( )
2 2 2 2
lim 2 0; lim 3 1; lim 4 2; lim 2 .
x x x x
x x x g x b a
− − − −
→ → → →
− = − = − − = − = −
Do đó nếu
( )
2
lim 0 2 0
x
g x b a
−
→
−
thì giới hạn cần tìm là vô cực theo quy tắc 2.
Từ đó chọn được đáp án đúng là C.
(Thật vậy, nếu
( )
2
lim 2 0
x
g x b a
−
→
= − =
thì
( )( )( ) ( )( )
22
2
6 8 5 6 2 3 4 3 4
a b bx b b
x x x x x x x x x
−
− = =
− + − + − − − − −
Và do đó
( )( )
22
22
lim lim .
6 8 5 6 3 4 2
xx
a b b b
x x x x x x
−−
→→

− = =

− + − + − −

Cách 2: Sử dụng MTCT. Với mỗi đáp án, lấy các giá trị cụ thể của
a
và
b
, thay vào hàm số
rồi tính giới hạn.
Từ đó chọn được đáp án là C.
C. BÀI TẬP RÈN LUYỆN KỸ NĂNG
DẠNG 1. BÀI TẬP TÍNH GIỚI HẠN BẰNG CÁCH SỦ DỤNG ĐỊNH NGHĨA, ĐỊNH LÍ VÀ CÁC
QUY TẮC.
Câu 1: Tìm tất cả các giá trị của tham số thực
m
để
7B
với
( )
32
1
lim 3 2 .
x
B x x m m
→
= + + −
A.
1m
hoặc
3m
B.
1m −
hoặc
3m
C.
13m−
D.
1 3.m
Câu 2: Cho hàm số
( )
2
1
1
.
1
2 2 1
x
khi x
fx
x
x khi x
+
=
−
−
Khi đó
( )
1
lim
x
fx
−
→
bằng:
A.
0
B.
2
C.
−
D.
+
Câu 3: Trong các hầm số sau, hàm số nào có giới hạn tại điểm
1?x =
A.
( )
1
1
fx
x
=
−
B.
( )
1
1
gx
x
=
−
C.
( )
1
1
hx
x
=
−
D.
( )
1
1
tx
x
=
−
Câu 4: Chọn khẳng định đúng.
A.
0
1
limcos 0
x
x
→
=
B.
0
1
limcos 1
x
x
→
=−
C.
0
1
limcos 1
x
x
→
=
D.
0
1
limcos
x
x
→
không tồn
tại.
Câu 5: Trong các giới hạn sau, giới hạn nào bằng
?−
A.
( )
32
lim 5 1 .
x
x x x
→+
− + +
B.
( )
4
lim 2 3 1 .
x
xx
→−
++
C.
( )
23
lim 4 7 2 .
x
xx
→+
−+
D.
( )
5
lim 3 2 .
x
xx
→−
−+
Câu 6: Trong các giới hạn sau, giới hạn nào bằng
?−
A.
(
)
2
lim 4 4 3 2 .
x
x x x
→+
+ + +
B.
(
)
2
lim 4 4 3 2 .
x
x x x
→−
+ + −
C.
(
)
2
lim 4 4 3 .
x
x x x
→+
+ + −
D.
(
)
2
lim 4 4 3 .
x
x x x
→+
− + +
Câu 7: Trong các giới hạn sau, giới hạn nào bằng
?+
A.
( )
2
3
6
lim .
93
x
x
x
+
→−
−
+
B.
( )
1
12
lim .
55
x
x
x
−
→−
−
+
C.
( )
3
4
2
53
lim .
2
x
x
x
→−
−
−
D.
( )
3
2
1
24
lim
1
x
x
x
→−
−
+
Câu 8: Trong các giới hạn sau, giới hạn nào là vô cực?
A.
2
3
2
2
1
lim .
2
x
xx
xx
→
−+
+
B.
( )
( )
32
2
2
2
2
lim .
6
x
xx
xx
+
→−
+
−+
C.
( )
( )
2
4
3
9
lim .
2 1 3
x
xx
xx
−
→
−
−−
D.
( )
2
4
1
21
lim .
1
x
xx
xx
→
−
++
Câu 9: Trong các giới hạn sau, giới hạn nào là vô cực?
A.
2
3
lim .
5 2 4
x
x x x
→−
−
+ + +
B.
( )
3
0
28
lim .
x
x
x
→
−+
C.
( )
2
4
1
23
lim .
x
x x x
xx
−
→−
+ + − −
+
D.
33
5
lim .
42
x
xx
→−
−+
Câu 10: Tìm tất cả các giá trị của tham số thực
m
sao cho hàm số
( )
2
9 3 1f x mx x x= + − +
có giới hạn
hữu hạn khi
.x →+
A.
3m =−
B.
3m −
C.
0m
D.
0m
DẠNG 2. GIỚI HẠN VÔ ĐỊNH DẠNG
0
.
0
Câu 11: Giới hạn
2
36
lim
2
x
x
x
→−
+
+
A. Bằng
3
B. Bằng
3−
C. Bằng
0
D. không tồn tại
Câu 12: Cho
a
là một số thực khác 0. Kết quả đúng của
44
lim
xa
xa
xa
→
−
−
bằng:
A.
3
3a
B.
3
2a
C.
3
a
D.
3
4a
Câu 13: Cho
2
2
1
1
lim ,
1
x
x mx m
Cm
x
→
− + −
=
−
là tham số thực. Tìm
m
để
2.C =
A.
2m =
B.
2m =−
C.
1m =
D.
1m =−
Câu 14: Cho
a
và
b
là các số thực khác
0.
Nếu
2
2
lim 6
2
x
x ax b
x
→
++
=
−
thì
ab+
bằng:
A.
2
B.
4−
C.
6−
D.
8
Câu 15: Cho
a
và
b
là các số thực khác
0.
Giới hạn
0
11
lim
sin
x
ax
bx
→
−+
bằng:
A.
2
a
b
B.
2
a
b
−
C.
2a
b
D.
2a
b
−
Câu 16: Cho
, ,cab
là các số thực khác
0,3 2 0.bc−
Tìm hệ thức liên hệ giữa
,,abc
để:
3
0
tan 1
lim .
2
11
x
ax
bx cx
→
=
+ − +
A.
1
3 2 10
a
bc
=
−
B.
1
3 2 6
a
bc
=
−
C.
1
3 2 2
a
bc
=
−
D.
1
3 2 12
a
bc
=
−
Câu 17: Cho
m
và
n
là các số nguyên dương phân biệt. Giới hạn
( )
1
sin 1
lim
mn
x
x
xx
→
−
−
bằng:
A.
mn−
B.
nm−
C.
1
mn−
D.
1
nm−
Câu 18: Để tính giới hạn
1
5 4 2 1
lim ,
1
x
xx
x
→
− − −
−
bạn Bính đã trình bày bài giải như sau:
Bước 1: Ta có:
1 1 1
5 4 2 1 5 4 1 2 1 1
lim lim lim .
1 1 1
x x x
x x x x
x x x
→ → →
− − − − − − −
=−
− − −
Bước 2:
( )
( )
( )
1 1 1
51
5 4 1 5 5
lim lim lim .
12
5 4 1
1 5 4 1
x x x
x
x
x
x
xx
→ → →
−
−−
= = =
−
−+
− − +
Bước 3:
( )
( )
( )
1 1 1
21
2 1 1 2
lim lim lim 1.
1
2 1 1
1 2 1 1
x x x
x
x
x
x
xx
→ → →
−
−−
= = =
−
−+
− − +
Bước 4:
1
5 4 2 1 5 3
lim 1 .
1 2 2
x
xx
x
→
− − −
= − =
−
Hỏi lời giải của bạn Bính đã mắc lỗi sai ở bước nào?
A. Bước 1. B. Bước 2. C. Bước 3. D. Bước 4.
Câu 19: Biết
3
2
2
8 11 7
lim
32
x
x x m
x x n
→
+ − +
=
−+
trong đó
m
n
là phân số tối giản,
m
và
n
là các số nguyên dương.
Tổng
2mn+
bằng:
A.
68
B.
69
C.
70
D.
71
Câu 20: Biết
( )
( )
3
2
3
6 9 27 54
lim ,
3 3 18
x
x x m
n
x x x
→
− − −
=
− + −
trong đó
m
n
là phân số tối giản,
m
và
n
là các số nguyên
dương. Khi đó
3mn+
bằng:
A.
55
B.
56
C.
57
D.
58
Câu 21: Giới hạn
( )
3
2
1
3 2 5 4
lim
1
x
xx
x
+
→
− − −
−
bằng:
A.
−
B.
+
C.
0
D.
1
Câu 22: Trong bốn giới hạn sau đây, giới hạn nào bằng
0?
A.
3
1
1
lim .
1
x
x
x
→
−
−
B.
( )
2
2
2
1
lim .
32
x
x
xx
+
→−
−
−+
C.
2
2
3
6
lim .
3
x
xx
xx
→−
− − +
+
D.
( )
2
2
32
2
6
lim .
2
x
xx
xx
→−
−−
+
Câu 23: Trong bốn giới hạn sau đây, giới hạn nào khác
0?
A.
2
2
32
lim .
2
x
xx
x
−
→
−+
−
B.
( )
( )
2
2
3
9
lim .
13
x
x
xx
−
→
−
+−
C.
( )
2
2
1
32
lim .
21
x
xx
xx
−
→−
−+
++
D.
3
2
1
1
lim .
1
x
x
x
+
→
−
−
Câu 24: Trong bốn giới hạn sau đây, giới hạn nào không tồn tại?
A.
3
2
2
8
lim .
11 18
x
x
xx
→−
+
++
B.
( )
3
0
3 27
lim .
x
x
x
→
+−
C.
24
0
3
lim .
2
x
xx
x
→
+
D.
( )
2
2
2
lim .
32
x
xx
xx
+
→−
+
++
Câu 25: Trong các giới hạn sau đây, giới hạn nào không hữu hạn?
A.
2
3
2
2 10
lim .
8
x
xx
x
−
→
+−
−
B.
2
2
3
43
lim .
69
x
xx
xx
+
→
−+
−+
C.
2
2
2
lim .
53
x
x
x
+
→
−
+−
D.
2
3
12
lim .
9
x
x
x
−
→
−−
−
DẠNG 3. GIỚI HẠN VÔ ĐỊNH DẠNG
.
Câu 26: Trong bốn giới hạn sau đây, giới hạn nào bằng
1−
?
A.
2
1
lim .
1
x
x
x
→−
−
+
B.
32
23
3
lim .
5
x
xx
xx
→+
−+
−
C.
2
23
lim .
5
x
x
xx
→−
+
−
D.
2
2
21
lim .
3
x
xx
xx
→+
+−
+
Câu 27: Trong các giới hạn hữu hạn sau đây, giới hạn nào là lớn nhất?
A.
( )
( )
( )
3
3
1 3 2 5
lim .
1
x
x x x
xx
→+
+ − −
−
B.
( )( )
( )
( )
22
4
2 1 2
lim .
21
x
x x x
x x x
→−
++
++
C.
( )( )
( )
22
3
1 2 4
lim .
31
x
x x x
xx
→−
+ − +
+
D.
( )( )
( )
( )
23
4
3 1 2
lim .
21
x
xx
x x x
→+
+−
++
Câu 28: Trong các giới hạn sau đây, giới hạn nào là
−
?
A.
2
21
lim .
3
x
xx
x
→−
− + −
+
B.
2
35
lim .
12
x
xx
x
→−
++
+
C.
32
2
13
lim .
52
x
xx
xx
→+
−+
+−
D.
24
2
31
lim .
2
x
xx
xx
→−
−+
−−
Câu 29: Tính giới hạn
2
2
23
lim
4 1 2
x
x x x
xx
→−
++
+ − +
.
A.
1
2
. B.
2
3
. C.
2
3
−
. D.
1
2
−
.
Câu 30: Cho
,,abc
là các số thực khác
0
. Tìm hệ thức liên hệ giữa
,,abc
để
2
92
lim 5
1
x
ax b x
cx
→−
−+
=
+
.
A.
3
5
ab
c
−
=
. B.
3
5
ab
c
−
=−
. C.
3
5
ab
c
+
=
. D.
3
5
ab
c
+
=−
.
Câu 31: Cho
a
và
b
là các tham số thực . Biết rằng
( )
2
4 3 1
lim 0,
1
x
xx
ax b a
cx
→+

++
− + =

+

và
b
thỏa mãn
hệ thức nào trong các hệ thức dưới đây ?
A.
9.ab+=
B.
9.ab+ = −
C.
9.ab−=
D.
9.ab− = −
Câu 32: Trong các giới hạn sau , giới hạn nào là
−
?
A.
4
2
21
lim
2
x
xx
xx
→−
−−
++
. B.
2
52
lim
12
x
xx
x
→−
−+
+
.
C.
5
2
11
lim
21
x
xx
xx
→+
+−
++
. D.
3
32
21
lim
12
x
xx
x
→−
++
−
.
Câu 33: Tìm giới hạn nhỏ nhất trong các giới hạn hữu hạn sau.
A.
6
3
2
lim
31
x
x
x
→−
+
−
. B.
2
3
2
2
lim
83
x
xx
xx
→−
−
−+
.
C.
2
lim
2
x
xx
xx
→+
−+
. D.
2
23
lim
5
x
x
xx
→−
+
++
.
Câu 34: Trong các giới hạn hữu hạn sau , giới hạn nào là lớn nhất?
A.
( )( )
2
3
3
2 5 1
lim
31
x
xx
xx
→+
−−
−+
. B.
( )
2
2
2 1 3
lim
5
x
xx
xx
→−
−−
−
.
C.
( )
( )
42
3
2
lim
1 3 1
x
xx
xx
→+
++
+−
. D.
2
32
lim
1
x
x
xx
→−
−
+−
.
Câu 35: Trong các giới hạn hữu hạn sau , giới hạn nào là nhỏ nhất?
A.
2
2
lim
34
x
x x x
x
→−
−+
−
. B.
( )
3
lim 1 2
1
x
x
x
x
→−
−
−
.
C.
22
41
lim
23
x
x x x
x
→−
− − +
+
. D.
45
54
3 4 2
lim
9 5 4
x
xx
xx
→+
++
++
.
DẠNG 4. GIỚI HẠN VÔ ĐỊNH DẠNG
0.
.
Câu 36: Cho
a
là một số thực dương. Tính giới hạn
( )
2
1 1 1
lim
xa
xa
xa
→

−


−
.
A. bằng
2
1
a
−
. B. là
+
. C. là
−
. D. không tồn tại.
Câu 37: Trong các giới hạn sau , giới hạn nào là hữu hạn ?
A.
( )
3
42
lim 1
21
x
x
x
xx
→+
+
++
. B.
( )
2
3
lim 1
1
→+
+
−
x
x
x
x
.
C.
( )
3
1
lim 2
x
x
x
xx
→+
−
+
+
. D.
( )
2
4
lim 1
21
x
x
x
xx
→+
+
++
.
Câu 38: Trong các giới hạn hữu hạn sau , giới hạn nào là nhỏ nhất?
A.
( )
3
21
lim 1
2
x
x
x
xx
→−
+
+
++
. B.
( )
3
3 11
lim 1 2
1
x
x
x
x
→+
−
−
+
.
C.
( )
3
2
1
lim 1
1
x
x
x
x
+
→
−
−
. D.
( )
3
1
lim 2 3
5 2 1
→−
+
−
++
x
x
x
xx
.
Câu 39: Tính giới hạn
2
3
23
lim
x
xx
x
xx
→+

++
−



.
A.
1
2
. B. 0. C.
+
. D.
−
Câu 40: Tính giới hạn
4
lim tan2 tan
4
x
xx
→

−


.
A.
2
. B. 0. C.
1
2
. D.
1
4
DẠNG 5. DẠNG VÔ ĐỊNH
−
.
Câu 41: Cho
n
là một số nguyên dương. Tính giới hạn
1
1
lim
11
n
x
n
xx
→

−

−−

.
A.
2
n
. B.
1
2
n −
. C.
1
2
n +
. D.
2
2
n +
Câu 42:
Cho hàm số
( )
3
13
1
11
21
khi x
fx
xx
mx khi x
−
=
−−
+
. Với giá trị nào của
m
thì hàm số
( )
fx
có giới hạn
tại điểm
1x =
A. 2. B. -1. C. 1. D. 3
Câu 43: Tìm tất cả các giá trị của tham số thực
k
sao cho giới hạn
2
1
1
lim( )
11
x
k
xx
→
−
−−
là hữu hạn.
A.
2k =
. B.
2k
. C.
2k
. D.
2k
.
Câu 44: Trong các giới hạn sau đây, giới hạn nào là
1−
?
A.
2
lim( 2 )
x
x x x
→−
+−
. B.
2
lim( 2 )
x
x x x
→−
++
.
C.
2
lim( 2 )
x
x x x
→+
++
. D.
2
lim( 2 )
x
x x x
→+
+−
.
Câu 45: Giới hạn
2
lim( 3 5+ax)=+
x
xx
→−
− +
nếu.
A.
1a
. B.
1a
. C.
1a
. D.
1a
.
Câu 46: Cho
a
và
b
là các số thực khác
0
. Biết
2
lim( 2) 3
x
ax x bx
→+
− + + =
, thì tổng
ab+
bằng
A.
2
. B.
6−
. C.
7
. D.
5−
.
Câu 47: Cho
a
và
b
là các số thực khác
0
. Biết
2
lim (ax+b- 6 2) 5
x
xx
→+
− + =
số lớn hơn trong hai số
a
và
b
là số nào trong các số dưới đây?
A.
4
. B.
3
. C.
2
. D.
1
.
Câu 48: Trong các giới hạn dưới đây, giới hạn nào là vô cực?
A.
22
lim( 2 2 3)
x
x x x
→−
+ − +
. B.
2
lim( 4 1 2 )
x
x x x
→−
+ + +
.
C.
2
lim( 9 3 1 5 )
x
x x x
→−
+ + +
. D.
22
lim( 3 1 3 5 )
x
x x x
→−
+ − +
.
Câu 49: Biết
3
2 3 2
lim( 9 2 27 4 5)
x
m
x x x x
n
→−
+ + + + = −
trong đó
m
n
là phân số tối giản,
m
và
n
là các
số nguyên dương. Tìm bội số chung nhỏ nhất của
m
và
n
.
A.
135
. B.
136
. C.
138
. D.
140
.
Câu 50: Cho
a
và
b
là các số nguyên dương. Biết
3
2 3 2
7
lim( 9 + ax 27 5)
27
x
x x bx
→−
+ + + =
, hỏi
a
và
b
thỏa mãn hệ thức nào dưới đây?
A.
2 33ab+=
. B.
2 34ab+=
. C.
2 35ab+=
. D.
2 36ab+=
.
D. HƯỚNG DẪN GIẢI CHI TIẾT
DẠNG 1. BÀI TẬP TÍNH GIỚI HẠN BẰNG CÁCH SỬ DỤNG ĐỊNH NGHĨA, ĐỊNH LÝ VÀ CÁC
QUI TẮC.
Câu 1. Đáp án B.
Cách 1: Ta có
( )
4223lim
222
1
+−=−++=
−→
mmmmxxB
x
.
Do đó
7B
1742
2
−+− mmm
hay
3m
.
Cách 2: Sử dụng MTCT tính B khi
4=m
và
0=m
.
Khi
4=m
thì
712 =B
, do đó chỉ xét A và B.
Khi
0=m
thì
74 =B
, do đó A sai vậy B đúng.
Câu 2. Đáp án D.
Cách 1: Ta có
x
x
xf
xx
−
+
=
−−
−→−→
1
1
lim)(lim
2
11
.
Vì
( )
( )
01lim;21lim
1
2
1
=−=+
−−
−→−→
xx
xx
và
1;01 − xx
nên theo quy tắc 2:
+=
−
+
=
−−
−→−→
x
x
xf
xx
1
1
lim)(lim
2
11
.
Cách 2: Ta có
x
x
xf
xx
−
+
=
−−
−→−→
1
1
lim)(lim
2
11
.
Sử dụng MTCT tính giá trị hàm số tại
99999999,0=x
ta được kết quả
199999998
.
Vậy chọn D.
Câu 3. Đáp án A.
Vì
01lim
1
=−
→
x
x
,
1,01 − xx
nên
+=
−
=
→→
1
1
lim)(lim
11
x
xf
xx
.
Giải thích thêm:
+ Hàm số
1
1
)(
−
=
x
xg
xác định trên khoảng
( )
+;1
nên không tồn tại giới hạn bên trái tại
1=x
, do đó không tồn tại giới hạn tại
1=x
.
+ Hàm số
x
xh
−
=
1
1
)(
xác định trên khoảng
( )
1;−
nên không tồn tại giới hạn bên phải tại
1=x
, do đó không tồn tại giới hạn tại
1=x
.
+ Vì
( )
01lim
1
=−
→
x
x
,
1,01 − xx
,
1,01 − xx
nên
lim ( ) lim
xx
tx
x
−−
→→
= = −
−
11
1
1
,
lim ( ) lim
xx
tx
x
+ +−
→→
= = +
−
11
1
1
.
Vậy
lim ( ) lim ( )
xx
t x t x
−+
→→
11
nên không tồn tại
lim ( )
x
tx
→1
.
Câu 4. Đáp án D.
Xét dãy số
( )
n
x
với
( )
12
1
+
=
n
x
n
. Ta có
0→
n
x
và
( )
112coslim
1
coslim −=+=
n
x
n
(1).
Lại xét dãy số
( )
n
y
với
n
x
n
2
1
=
. Ta có
0→
n
y
và
( )
12coslim
1
coslim ==
n
y
n
(2)
Từ (1) và (2) suy ra
x
x
1
coslim
0→
không tồn tại.
Câu 5. Đáp án C.
Cách 1: Ta có
+=++−
+→
)15(lim
23
xxx
x
,
+=++
−→
)132(lim
4
xx
x
;
−=+−
+→
)274(lim
32
xx
x
;
+=+−
−→
)23(lim
5
xx
x
.
Cách 2: Sử dụng MTCT tính lần lượt các giới hạn cho đến khi tìm được giới hạn bằng
−
.
Câu 6. Đáp án D.
Cách 1: Ta có
+
(
)
+=+++
+→
xxx
x
2344lim
2
,
(
)
+=−++
−→
xxx
x
2344lim
2
+
(
)
+=
−++=−++
+→+→
1
34
4lim344lim
2
2
x
x
xxxx
xx
Do đó
(
)
−=++−
+→
344lim
2
xxx
x
.
Cách 2: Sử dụng MTCT tính lần lượt các giới hạn cho đến khi tìm được giới hạn bằng
−
.
Câu 7. Đáp án C.
Cách 1: Ta có
( )
036lim
2
3
−=−
+
−→
x
x
;
( )
039lim
3
=+
+
−→
x
x
và
3,039 −+ xx
.
Vậy theo quy tắc 2,
−=
+
−
+
−→
x
x
x
39
6
lim
2
3
.
Tương tự:
−=
+
−
−
−→
x
x
x
55
21
lim
1
;
( )
+=
+
−
−→
2
3
2
2
35
lim
x
x
x
;
( )
−=
+
−
−→
2
3
1
1
42
lim
x
x
x
.
Do đó đáp án đúng là C ( Thật ra ta chỉ cần tính đến C là chọn được đáp án đúng).
Cách 2: Sử dụng MTCT tính lần lượt các giới hạn cho đến khi tìm được giới hạn bằng
+
.
Câu 8. Đáp án B.
Cách 1: Các hàm số trong A, C, D đều xác định tại các điểm điểm tính giới hạn. Do đó đáp án là
B.
Thật vậy, ta tính được bằng MTCT:
( )
+=
−−
+
−→
2
2
23
2
6
2
lim
xx
xx
x
.
Cách 2: Sử dụng MTCT tính lần lượt các giới hạn cho đến khi tìm được giới hạn vô cực.
Câu 9. Đáp án C
Cách 1: Ta có
022)32(lim
2
)1(
−=−−++
−
−→
xxx
x
;
0)(lim
4
)1(
=+
−
−→
xx
x
;
1,0)1()(
34
−+=+ xxxxx
.
Vậy
−=
+
−−++
−
−→
xx
xxx
x
4
2
)1(
32
lim
Bổ sung:
+
−=+++−=+++
−→−→
)4
21
5(lim)425(lim
2
2
x
x
xxxx
xx
nên
0
425
3
lim
2
=
+++
−
−→
xxx
x
.
+
( )
12)126(lim
88126
lim
82
lim
2
0
23
0
3
0
=+−=
+−+−
=
+−
→→→
xx
x
xxx
x
x
xxx
.
+
0
24
5
lim)24(lim
23
23
=
+−
−=+−
−→−→
xx
xx
xx
.
Cách 2: Sử dụng MTCT tính lần lượt các giới hạn cho đến khi tìm được giới hạn vô cực.
Câu 10. Đáp án A
Cách 1: Sử dụng MTCT tính toán khi
3−=m
ta được kết quả
2
1
)1393(lim
2
−=+−+−
+→
xxx
x
. Vậy ta chỉ xét các đáp án A và D.
Lại sử dụng MTCT tính toán khi
1−=m
ta được kết quả
+=+−+−
+→
)139(lim
2
xxx
x
. Vậy
loại đáp án D. Do đó đáp án đúng là A.
Cách 2:
)139(lim)(lim
2
+−+=
+→+→
xxmxxf
xx
.
+ Nếu
0m
thì
+=+−+=
+→+→
)139(lim)(lim
2
xxmxxf
xx
.
+ Nếu
0m
thì
lim lim
xx
mx x x x m
x
x
→+ →+


+ − + = + − +





2
2
31
9 3 1 9
.
Ta thấy nếu
3−m
thì
lim
x
m
x
x
→+

+ − +



2
31
90
và do đó
=+−+
+→
)139(lim
2
xxmx
x
.
Ngược lại nếu
3−=m
thì
2
1
)1393(lim
2
−=+−+−
+→
xxx
x
. Vậy đáp án đúng là A.
DẠNG 2. GIỚI HẠN VÔ ĐỊNH DẠNG
0
0
.
Câu 11. Đáp án D.
Ta có
( )
3
2
23
lim
2
63
lim
)2()2(
=
+
+
=
+
+
++
−→−→
x
x
x
x
xx
và
( )
3
2
23
lim
2
63
lim
)2()2(
−=
+
+−
=
+
+
−−
−→−→
x
x
x
x
xx
.
Vậy
2
63
lim
2
63
lim
)2()2(
+
+
+
+
+−
−→−→
x
x
x
x
xx
nên
2
63
lim
2
+
+
−→
x
x
x
không tồn tại.
Câu 12. Đáp án D.
Cách 1: Ta có
33223
32234
4)(lim
))((
limlim aaaxxax
ax
axaaxxax
ax
ax
axaxax
=+++=
−
+++−
=
−
−
→→→
.
Cách 2: Cho
a
một giá trị cụ thể rồi tính giới hạn bằng máy tính cầm tay. Chẳng han với
2=a
ta có
44
3
2
lim 32 4.2
2
xa
x
x
→
−
==
−
. Do đó chọn đáp án D.
Câu 13. Đáp án B.
Cách 1:
2
2
1
1
lim
)1)(1(
)1)(1(
lim
1
1
lim
11
2
2
1
m
x
mx
xx
mxx
x
mmxx
C
xxx
−
=
+
+−
=
+−
+−−
=
−
−+−
=
→→→
Vậy
22 −== mC
.
Cách 2: Thay lần lượt các giá trị của
m
vào, rồi tìm
C
cho đến khi gặp kết quả
2=C
thì dừng
lại.
Câu 14. Đáp án C
Đặt
baxxxg ++=
2
)(
. Rõ ràng là nếu
()g 20
thì
2
)(
lim
2
−
→
x
xg
x
không thể hữu hạn. Do đó điều
kiện đầu tiên là
()g a b= + = −2 0 2 4
.
Khi đó
)
2
)(2()(
b
xxxg −−=
và
2
2)
2
(lim
2
)(
lim
22
bb
x
x
xg
xx
−=−=
−
→→
.
Vậy
.6286
2
26
2
)(
lim
2
−=+=−==−=
−
→
baab
b
x
xg
x
Câu 15. Đáp án B.
Cách 1:
lim lim( . . )
sin sin
xx
ax ax bx
bx x bx b
→→
− + − +
=
00
1 1 1 1 1
.
Mà
lim ;
sin
x
ax a
bx
→
− + −
=
0
11
2
1
sin
lim
0
=
→
bx
bx
x
nên
;
2sin
1
lim
0
b
a
bx
bax
x
−
=
+−
→
Cách 2: Cho
a
và
b
các giá trị cụ thể, thay vào rồi tính giới han. Chẳng hạn với
1== ba
, sử
dụng MTCT ta tính được
0
1 1 1
lim
sin 2
x
x
x
→
−+
=
. Từ đó chọn đáp án đúng là B.
Câu 16. Đáp án D.
Cách 1:
33
tan tan
..
1 x 1 x 1 1
=
+ − + + − +
ax ax x
a
ax
b c bx cx
Lại có
00
tan sina 1
lim lim( . ) 1
cosax
xx
ax x
ax ax
→→
==
3
0
1 x 1 x
lim
x
bc
x
→
+ − +
3
0
1 x 1 1 x 1
lim( )
x
bc
xx
→
+ − + −
=−
32
2 3 6
b c b c−
= − =
Vậy
3
0
tan 6a
lim
32
1 x 1 x
x
ax
bc
bc
→
=
−
+ − +
.
Do đó hệ thức liên hệ giữa
,,abc
là
6a 1 1
3 2 2 3 2 12
a
b c b c
= =
−−
Cách 2: Sử dụng MTCT. Với mỗi đáp án, chọn các giá trị cụ thể của
,,abc
thỏa mãn hệ thức
rồi thay vào để tính giới hạn. Nếu giới hạn tìm được bằng
1
2
thì đó là đáp án đúng.
Chẳng hạn, với đáp án A, chọn
1; 4; 1a b c= = =
, sử dụng MTCT tính được
3
0
tan 3
lim
5
1 4 1
x
x
xx
→
=
+ − +
.
Vậy A không phải là đáp án đúng.
Tương tự vậy B và C cũng không phải là đáp án đúng. Vậy đáp án đúng là D.
Câu 17. Đáp án C.
Cách 1: Ta có
n( 1) sin(x-1) 1
1
m n m n
si x x
x x x x x
−−
==
− − −
Mà
1
lim
1
mn
x
xx
mn
x
→
−
=−
−
;
1
n( 1)
lim 1
1
x
si x
x
→
−
=
−
nên
1
n( 1) 1
lim
mn
x
si x
x x m n
→
−
=
−−
Cách 2: Cho m và n các giá trị cụ thể, thay vào rồi sử dụng MTCT tính giới hạn. Chẳng hạn với
3; 1mn==
ta tính được
3
1
n( 1) 1 1
lim
2
x
si x
x x m n
→
−
==
−−
.
Vậy đáp án đúng là C
Câu 18. Đáp án A.
Vì ta chưa thể biết được các giới hạn
1
5x 4 1
lim
1
x
x
→
−−
−
;
1
2x 4 1
lim
1
x
x
→
−−
−
có hữu hạn hay không
nên chưa thể viết được:
1
5x 4 2x 1
lim
1
x
x
→
− − −
−
1
5x 4 1
lim
1
x
x
→
−−
=
−
1
2x 4 1
lim
1
x
x
→
−−
−
−
Do đó lời giải đã mắc lỗi sai ngay ở bước đầu tiên.
Ta sửa lại như sau:
Bước 1: Ta có
1
5x 4 2x 1
lim
1
x
x
→
− − −
−
1
5x 4 1 2x 1 1
lim( )
11
x
xx
→
− − − −
=−
−−
Câu 19. Đáp án A.
Ta có
3
2
8x 11 x+7
3x 2x
+−
−+
3
22
8x 11 3 7 3
3x 2 3x 2
x
xx
+ − + −
=−
− + − +
2
3
3
22
( 2)( 1)( 7 3)
( 2)( 1)( (8x 11) 3 8 11 9)
xx
x x x
xx
−−
=−
− − + +
− − + + + +
2
3
3
81
( 1)( 7 3)
( 1)( (8x 11) 3 8 11 9)
xx
x
=−
− + +
− + + + +
Ta có
2
2
3
3
88
lim
27
( 1)( (8x 11) 3 8 11 9)
x
x
→
=
− + + + +
;
2
11
lim
6
( 1)( 7 3)
x
xx
→
=
− + +
Do đó
3
2
2
8x 11 x+7 8 1 7
lim
3x 2 27 6 54
x
x
→
+−
= − =
−+
Vậy
7; 54mn==
và
2 68mn+=
.
Câu 20. Đáp án C.
Ta có
3
2
6x 9 27x-54
( 3)( 3x-18)xx
−−
−+
3
2
6x 9 27x-54
( 3) ( 6)xx
−−
=
−+
Sử dụng MTCT ta tính được:
3
2
3
6x 9 27x-54 1
lim
( 3) 6
x
x
→
−−
=
−
;
3
11
lim
69
x
x
→
=
+
nên
3
2
3
6x 9 27x-54 1
lim
( 3)( 3x-18) 54
x
xx
→
−−
=
−+
. Vậy
3 57mn+=
.
Giải tự luận: Đặt
3tx=−
thì
3
lim 0
x
t
→
=
và
3
2
6x 9 27x-54
( 3)x
−−
−
3
2
6 9 27t+27t
t
+−
=
3
22
6 9 ( 3) ( 3) 27 27t t t t
tt
+ − + + − +
=+
( )
( ) ( )
( )
( ) ( )
()
()
t t t
t t t
t t t t t
t
tt
t t t t
−+
=+

+ + +
+ + + + + +


−+
=+
+ + +
+ + + + + +
2 3 2
2
2
22
3
3
2
2
3
3
9
6 9 3
3 3 27 27 27 27
19
6 9 3
3 3 27 27 27 27
Ta có
( )
( ) ( )
lim ;lim
()
tt
t
tt
t t t t
→→
−+
= − =
+ + +
+ + + + + +
2
2
3
00
3
1 1 9 1
63
6 9 3
3 3 27 27 27 27
Vậy
( )
lim .
x
xx
x
→
− − − −
= + =
−
3
2
3
6 9 27 54 1 1 1
6 3 6
3
Mặt khác
lim
x
x
→
=
+
3
11
69
nên
( )
(
)
lim .
x
xx
x x x
→
− − −
=
− + −
3
2
2
3
6 9 27 54 1
54
3 3 18
Lưu ý: Nếu sử dụng MTCT tính giá trị hàm số tại
,x = 3 00000001
và tại
,x = 2 99999999
ta
đều thu được kết quả bằng 0 hoặc máy báo lỗi ( tùy theo loại máy). Điều này là do vượt quá
khả năng tính toán của máy. Ta thay đổi tính giá trị của hàm số tại
,x = 2 99999
thì ta được kết
quả như sau
Kết quả hiển thị trên máy như vậy rất khó để ta tìm ra giới hạn chính xác của hàm số. Tuy
nhiên nếu phân tích kĩ một chút rồi biến đổi như trong lời giải trên thì ta vẫn có thể tìm ra đáp
án đúng chỉ bằng MTCT.
Câu 21. Đáp án A
Bài tập này có dạng tương tự như bài tập trên. Bằng MTCT, không khó để tìm ra đáp án đúng là
A. Tuy nhiên nếu giải tự luận thì có một số vấn đề cần bàn. Đặt
tx=−1
thì
, lim
x
xt
+
→
= + =
1
10
và
( )
− − − + − + + − − +
= = +
−
x x t t t t
t t t
x
3 3 3
2 2 2 2
3 2 5 4 3 1 5 1 3 1 1 1 5 1
1
( )
( )
=+

++
+ + + +


tt
tt
t t t
2
2
2
3
3
35
3 1 1
1 5 1 5 1
( )
( )
( )
( )
t t t
t t t t

+ + + + − + +


=

+ + + + + +


2
3
3
2
3
3
3 1 5 1 5 1 5 3 1 1
3 1 1 1 5 1 5 1
Ta có
( )
( )
( )
( )
lim
t
t t t
t t t t
+
→

+ + + + − + +


= = −

+ + + + + +


2
3
3
2
0
3
3
3 1 5 1 5 1 5 3 1 1
3 1 1 1 5 1 5 1
Vậy
( )
lim .
x
xx
x
+
→
− − −
= −
−
2
2
1
3 2 5 4
1
Ta thấy sau khi đổi biến cho gọn, ta thêm bớt tử với hàng số 1 rồi tách ra thành hai phân thức
và nhân chia liên hợp mà không thêm bớt đa thức. Vậy khi nào thì thêm bớt hằng số, khi nào
thì thêm bớt với đa thức? Quý độc giả hãy nghiên cứu kĩ hai bài tập trên và tự rút ra nhận xét.
Câu 22. Đáp án D
Ta có
(
)
( ) ( )
( )
( ) ( )
lim lim lim .
x x x
xx
x x x x
x x x x x
→− →− →−
−−
− + − +
= = =
++
2
2
2 2 2
3 2 2 2
2 2 2
6
3 2 3 2
0
22
Câu 23. Đáp án C
( ) ( )
( )
( ) ( )
( )( )
( )
lim lim lim lim
x x x x
xx
x x x x x x
x
x
xx
x
− − − −
→ − → − → − → −
++
+ + + + + +
===
+
+
++
+
2 2 2
22
1 1 1 1
12
3 2 3 2 3 2
1
1
21
1
( )
( )
lim .
x
x
−
→−
= − + = −
1
2 1 0
Câu 24. Đáp án C
Ta có
lim lim
xx
x x x x
xx
−−
→→
+ − +
= = −
2 4 2
00
3 3 3
2 2 2
và
lim lim
xx
x x x x
xx
++
→→
++
==
2 4 2
00
3 3 3
2 2 2
Vậy
lim lim
xx
x x x x
xx
−+
→→
++
2 4 2 4
00
33
22
nên
lim
x
xx
x
→
+
24
0
3
2
không tồn tại.
Câu 25. Đáp án B
( )( )
( )
lim lim lim .
x x x
xx
x x x
x
xx
x
+ + +
→ → →
−−
− + −
= = = +
−
−+
−
2
22
3 3 3
13
4 3 1
3
69
3
DẠNG 3. GIỚI HẠN VÔ ĐỊNH DẠNG
.
Câu 26. Đáp án B
+
lim ;
x
x
x
→−
−
= −
+
2
1
1
+
lim ;
x
xx
xx
→+
−+
=−
−
32
23
3
1
5
+
lim ;
x
x
xx
→−
+
=
−
2
23
0
5
+
lim ;
x
xx
xx
→+
+−
=
+
2
2
21
2
3
Câu 27. Đáp án C
+
( )
(
)
(
)
lim .
x
x x x
xx
→+
+ − −
=−
−
3
3
1 3 2 5
5
1
+
(
)
(
)
(
)
( )
lim .
x
x x x
x x x
→−
++
=
++
22
4
2 1 2
0
21
+
(
)
(
)
( )
lim .
x
x x x
xx
→−
+ − +
=
+
22
3
1 2 4
2
3
31
+
(
)
(
)
(
)
( )
lim .
x
xx
x x x
→−
+−
=−
++
23
4
3 1 2
3
2
21
Câu 28. Đáp án B
+
lim .
x
xx
x
→−
− + −
= +
+
2
21
3
+
lim .
x
xx
x
→−
++
= −
+
2
31
12
+
lim .
x
xx
xx
→+
−+
= +
+−
32
2
13
52
+
lim .
x
xx
xx
→−
−+
= +
−−
24
2
31
2
Câu 29. Đáp án C
lim lim lim
x x x
xx
x x x
xx
xx
xx
x
xx
→− →− →−
− + + + +
+ + − +
= = = = −
−−
+ − +
− + − + + − +
2
2
22
22
1 3 1 3
2 3 1 3 2
2 1 3
1 1 2
4 1 2
4 2 4 1
Câu 30. Đáp án C
Ta có
lim lim lim .
x x x
ax bx a b
ax b x a b
xx
cx cx c
c
x
→− →− →−
+ + + +
− + +
= = =
++
+
2
22
22
99
9 2 3
1
11
Do đó
lim .
x
ax b x a b
cx c
→−
− + +
= =
+
2
9 2 3
55
1
Câu 31. Đáp án A
( ) ( ) ( )
lim lim .
xx
xx
ax b x ax b
xx
→ →

+ +
− + = + + − +


++



2
4 3 1 11
45
22
Do đó
( )
lim ; .
x
xx
ax b a b a b
x
→

++
− + = = = − − =

+


2
4 3 1
0 4 5 9
2
Câu 32. Đáp án D
+
lim .
x
xx
xx
→−
−−
= +
++
4
2
21
2
+
lim lim
xx
x x x x
x
x
→− →−
− + − +
= = +
−
+
22
5 2 5 2
12
12
.
+
lim .
x
xx
xx
→+
+−
= +
++
5
2
11
2
+
lim .
x
xx
x
→
++
= −
−
3
32
21
12
Câu 33. Đáp án D
+
lim lim .
xx
x
x
x
xx
→− →−
−+
+
= = −
−−
3
6
6
33
2
1
21
3
3 1 3 1
Ta có
lim lim .
xx
x x x x
x x x x
→− →−
−−
= = − = −
− + − +
22
3
33
22
2 2 1 1
82
8 3 8 3
+
lim .
x
xx
xx
→−
=
−+
2
0
2
+
lim lim .
xx
xx
xx
x
x
x
→+ →+
++
==
++
++
2
2
2 3 2 3
2
15
5
1
Câu 34. Đáp án B
+
( )( )
lim .
x
xx
xx
→+
−−
=
−+
2
3
3
3
2 5 1
2
3
31
+
( )
( )
lim lim .
xx
xx
xx
x
x x x x
→− →−
−−
−−
==
−−
2
2
22
3
2 1 1
2 1 3
2
5
55
+
lim lim .
xx
xx
xx
xx
x
→− →−
−−
==
+−
+−
2
2
3 2 3 2
1
1
1
1
Câu 35. Đáp án A
+
lim lim .
xx
xx
x x x
x
xx
→− →−
− − +
−+
==
−+
2
1
12
21
4
3 4 3 4
+
( )
( )
lim lim
xx
xx
x
x
xx
→− →−
−
− = =
−−
2
33
12
1 2 2
11
(do
,xx−
1
1 2 0
2
).
+
lim .
x
xx
xx
→+
++
=
++
45
54
3 4 2 2
3
9 5 4
DẠNG 4. GIỚI HẠN VÔ ĐỊNH DẠNG
..0
Câu 36. Đáp án D
Cách 1: Ta có
( ) ( )
( )
..
ax
x a ax
ax x a
x a x a
− −
− = =

−

−−
22
1 1 1 1 1
Do đó
( )
( )
lim lim ;
x a x a
xa
ax x a
xa
−−
→→
−
− = = +

−

−
2
1 1 1 1
( )
( )
lim lim ;
x a x a
xa
ax x a
xa
++
→→
−
− = = −

−

−
2
1 1 1 1
Vậy
( ) ( )
lim lim
x a x a
x a x a
x a x a
−+
→→
− −
−−
22
1 1 1 1 1 1
nên
( )
lim
xa
xa
xa
→

−


−
2
1 1 1
không tồn tại.
Cách 2: Cho a một giá trị cụ thể, chẳng hạn
,a = 1
thay vào hàm số rồi sử dụng MTCT để tính
giới hạn. Từ đó ta tìm được đáp án đúng là D.
Câu 37. Đáp án C
+
( )
( )
lim lim .
xx
xx
x
x
x x x x
→+ →+
+
+ = = +
+ + + +
2
3
3
4 2 4 2
1
1
2 1 2 1
+
( )
( )
lim lim .
xx
xx
x
x
xx
→+ →+
+
+ = = +
−−
2
22
31
3
1
11
+
( )
( ) ( )
lim lim .
xx
xx
x
x
x x x x
→+ →+
+−
−
+ = =
++
2
33
21
1
21
+
(
)
(
)
lim lim .
xx
xx
x
x
x x x x
→+ →+
+
+ = = +
+ + + +
2
2
2
4 2 4 2
1
1
2 1 2 1
Câu 38. Đáp án B
+
( )
( )( )
lim lim .
xx
xx
x
x
x x x x
→− →+
++
+
+ = = −
+ + + +
2
33
2 1 1
21
12
22
+
( )
( )( )
lim lim .
xx
xx
x
x
xx
→+ →+
−−
−
− = = −
++
2
22
3 11 1 2
3 11
1 2 2 3
11
+
(
)
(
)
( )
(
)
( )
lim lim lim .
x x x
x x x
x x x x x x x
x x x
x
→+ →+ →+
− = + + − = + + − =
− + +
−
3 2 2
2
1 1 1 1 1 0
1 1 1
1
+
( )
( )( )
lim lim .
xx
xx
x
x
x x x x
→− →−
+−
+
− = =
+ + + +
33
1 2 3
1 3 5
23
5
5 2 1 5 2 1
Câu 39. Đáp án A
Cách 1: Sử dụng MTCT.
Cách 2: Đặt
t
x
=
1
thì
, lim
x
xt
t
→+
==
1
0
và
( ) ( )
t t t t
x x t t
x
xx
t t t

+ − + + − +
+ + + − +
− = = +



3
3
2
2 2 2
1 2 1 1 1 3
2 3 1 2 1 3
( )
( ) ( ) ( )
t
tt
t t t t
−+
=+
+ + +
+ + + + + +
22
3
3
13
1 2 1
1 1 1 3 1 3
Do đó
( )
( ) ( ) ( )
lim lim
xt
x x t
x
xx
tt
t t t t
→+ →


+ + − +

− = +



+ + +


+ + + + + +

2
22
0
3
3
2 3 1 3
1 2 1
1 1 1 3 1 3
Câu 40. Đáp án C
Cách 1: Sử dụng MTCT.
Cách 2: Đặt
π
tx=−
4
thì
→
= − =, lim
π
x
π
x t t
4
0
4
và
− = − = −
tan tan tan tan tan tan
π π π
x x t t t t2 2 2
4 4 2
= = =
cos sin sin cos
cot tan . . .
sin cos sin cos
t t t t t
tt
t t t t t
2 2 2
2
2 2 2
.
Do đó:
sin cos
lim tan tan lim . . .
sin cos
π
t
x
π t t t
xx
t t t
→
→

− = =


0
4
2 2 1
2
4 2 2 2
DẠNG 5. DẠNG VÔ ĐỊNH
.−
Câu 41. Đáp án B
Cách 1: Sử dụng MTCT tính giới hạn với một giá trị cụ thể của
n
rooif so sánh với đáp án.
Chẳng hạn
n = 3
ta có
lim .
x
x
x
→

−=

−
−

3
1
31
1
1
1
Cách 2:
(
)
...
...
n
n
n n n
n x x x
n x x x
x
x x x
−
−
− + + + +
− + − + + −
− = =
−
− − −
21
21
1
1 1 1 1
1
1 1 1
( )
(
)
.... ...
...
n
n
x x x x x x
x x x
−
−
+ + + + + + + + + + +
=
+ + + +
2 2 2
21
1 1 1 1
1
Do đó
lim .
n
x
nn
x
x
→

−
−=

−
−

1
11
12
1
Lưu ý:
lim .
n
x
nn
x
x
→

−
−=

−
−

1
11
12
1
Câu 42. Đáp án B
Theo câu 41, ta có
( )
lim lim lim .
x x x
fx
xx
xx
+ + +
→ → →
= − = − =
−−
−−
33
1 1 1
1 3 3 1
1
11
11
Lại có
( ) ( )
lim lim .
xx
f x mx m
−−
→→
= + = +
11
22
Để
( )
fx
có giới hạn tại điểm
x = 1
thì
( ) ( )
lim lim .
xx
f x f x m m
−+
→→
= + = = −
11
2 1 1
Câu 43. Đáp án A
Ta có
.
k x k
x
xx
+−
−=
−
−−
22
11
1
11
Mà
( )
(
)
→→
+ − = − − =lim ; lim
xx
x k k x
2
11
1 2 1 0
nên để
lim
x
k
x
x
→

−

−
−

2
1
1
1
1
là hữu hạn thì điều kiện cần là
.kk− = =2 0 2
Thật vậy, khi
,.
x
k
xx
xx
−
= − = =
−+
−−
22
1 2 1 1
2
11
11
Nên
lim lim .
xx
k
xx
x
→→

− = =

−+
−

2
11
1 1 1
1 1 2
1
Lưu ý:
lim
n
x
k
x
x
→

−

−
−

1
1
1
1
hữu hạn
.kn=
Câu 44. Đáp án B
Cách 1: Sử dụng MTCT tính lần lượt các giới hạn. Đến ý B ta được giới hạn bằng
1−
. Vậy đáp
án đúng là B.
Cách 2: Ta thấy ngay A và C là các giới hạn vô cực, B và D là dạng vô định
.−
Ta xét giới
hạn ở ý B.
lim .
x
x
x x x
x
x
→−

+ − = = −


− + −
2
2
21
2
11
Vậy đáp án là B.
Bổ sung:
+
lim
x
x x x
→−

+ − = +


2
2
+
lim
x
x x x
→+

+ + = +


2
2
+
lim lim lim .
x x x
x
x x x
x x x
x
→+ →+ →+

+ − = = =


++
++
2
2
22
21
2
2
11
Câu 45. Đáp án D
Cách 1: Sử dụng MTCT tính giới hạn khi
va`aa==10
, ta được
lim ; lim .
xx
x x x x x
→− →−

− + + = − + = +


22
3
3 5 3 5
2
Từ đó suy ra đáp án đúng là D
Cách 2:
lim lim .
xx
x x ax x a
x
x
→− →−


− + + = − − +





2
2
35
3 5 1
Vì
lim
x→−
= −
nên để
lim
x
x x ax
→−

− + + = +


2
35
thì
.aa− 1 0 1
Câu 46. Đáp án D
Ta có
lim lim .
xx
b
ax x bx x a
x
x
→+ →+


− + + = − + +





2
2
2
21
Do đó nếu
a 1
thì
lim .
x
ax x bx
→+

− + + =


2
2
Vậy
.a =1
Khi đó
lim lim .
xx
bx b
x x bx
x x bx
→+ →+
−−

− + + = = −


+ + +
2
2
2
2
2
2
Vậy:
.
b
b− = = −36
2
Do đó
.ab+ = −5
Câu 47. Đáp án C
lim lim .
xx
ax b x x x a b
x
x
→+ →+


+ − − + = − − + +





2
2
62
6 2 1
Do đó nếu
a 1
thì
lim .
x
ax b x x
→+

+ − − + =


2
62
Vậy
.a =1
Khi đó ta có
lim lim .
xx
x
x b x x b b b
x x x
→+ →+
−

+ − − + = + = + = +


+ − +
2
2
6 2 6
6 2 3
2
62
Vậy:
.bb− + = =3 5 2
DO đó số lớn hơn trong hai số
a
và
b
là số 2. Chọn đáp án C.
Câu 48. Đáp án C
Cả bốn giới hạn đều có dạng
−
, tuy nhiên chỉ có giới hạn ở ý C, hệ số trong hai số hạng là
khác nhau.Theo kết quả đã biết thì giới hạn ở ý C chắc chắn là
−
. Do đó đáp án đúng là C,
Thật vậy:
lim lim lim .
x x x
xx
x x x
x x x
x
xx
→− →− →−
−−

+ + − + = = = − = −



+ + +
− + + +



22
22
3 3 1 2
2 2 3
4
22
13
2 2 3
22
lim lim lim .
x x x
xx
x x x
x x x
x
x
x
→− →− →−
++

+ + + + = = = −



+ + −
− + + +



2
2
2
1 1 1
4 1 2
4
11
4 1 2
42
lim lim .
xx
x x x x
x
x
→− →−


+ + + + = − + + + = −





2
2
31
9 3 1 5 9 5
lim lim lim .
x x x
xx
x x x
x x x
x
x
x
→− →− →−
−−

+ + − + = = = =



+ + +
− + + +



22
22
2
1 5 1 5 5 5 3
3 1 3 5
6
23
15
3 1 3 5
33
Câu 49. Đáp án A
Cách 1: Sử dụng MTCT tính giá trị hàm số tại
x =−
10
10
ta được kết quả
p dụng kĩ thuật tìm dạng phân số của số thập phân vô hạn tuần hoàn ta có
( )
,.=
5
0 185
27
Vậy
.
m
n
=
5
27
Từ đó chọn đáp án đúng là A.
Cách 2:
x x x x x x x x x x
+ + + + = + + + + + −
33
2 3 2 2 3 2
9 2 27 4 5 9 2 3 27 4 5 3
(
)
.
xx
x x x
x x x x x x
+
=−
+−
+ + + + + +
2
22
3
3 2 3 2 2
3
2 4 5
9 2 3
27 4 5 3 27 4 5 9
Suy ra
lim .
x
x x x x
→−

+ + + + = + = −

− + +

3
2 3 2
2 4 5
9 2 27 4 5
6 9 9 9 27
Từ đó chọn đáp án đúng là A.
Câu 50. Đáp án B
Làm tương tự như câu 49, ta có:
lim .
x
a b b a
x ax x bx
→−
−−

+ + + + = + =


3
2 3 2
29
9 27 5
6 27 54
Do đó
.ba−=2 9 14
Suy ra
a
là số chẵn. Vậy
ab+2
là số chẵn. Từ đó loại được đáp án A và C.
Giải hệ
ab
ba
+ =
−=
2 34
2 9 14
được
;.ab==2 16
Giải hệ
ab
ba
+ =
−=
2 36
2 9 14
được
a =
11
5
(loại).
Vậy B là đáp án đúng.
_______________ TOANMATH.com _______________
| 1/55
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

BÀI GIẢNG GIỚI HẠN CỦA HÀM SỐ A. LÝ THUYẾT
I. ĐỊNH NGHĨA GIỚI HẠN CỦA HÀM SỐ TẠI MỘT ĐIỂM
1. Giới hạn hữu hạn tại một điểm. Định nghĩa 1: Cho ( ;
a b) là một khoảng chứa điểm x và hàm số y = f ( x) xác định trên ( ; a b) hoặc trên 0
( ;a b) \x . lim f x = L  với mọi dãy số x mà x ( ;ab)\x , x → x ta có lim f (x = L n ) . n 0 n 0  ( ) n 0 x→ 0 x Nhận xét:
- Giới hạn của hàm số được định nghĩa thông qua khái niệm giới hạn của dãy số.
- Hàm số không nhất thiết phải xác định tại x . 0
Định nghĩa 2 (Giới hạn một bên):
Cho hàm số y = f ( x) xác định trên khoảng ( x ; b . lim f x = L  với mọi dãy số x mà n 0 ) ( ) + x→ 0 x x x  ,
b x → x ta có lim f ( x = L n ) . 0 n n 0
Cho hàm số y = f ( x) xác định trên khoảng (a; x . lim f x = L  với mọi dãy số x mà n 0 ) ( ) − x→ 0 x
a x x , x → x ta có lim f ( x = L n ) . n 0 n 0 STUDY TIP x x+
→ nghĩa là x → x và x x . 0 0 0 x x−
→ nghĩa là x → x và x x . 0 0 0 Định lí 1
lim f ( x) = L  lim f ( x) = lim f ( x) = . L x − + → → → 0 x x 0 x x 0 x
2. Giới hạn vô cực tại một điểm. Định nghĩa 3 Cho ( ;
a b) là một khoảng chứa điểm x và hàm số y = f ( x) xác định trên ( ; a b) hoặc trên 0
( ;a b) \x . lim f x = +  với mọi dãy số x mà x ( ;ab)\x , x → x ta có f (x = + n ) . n 0 n 0 ( ) n 0 x→ 0 x Lưu ý:
Các định nghĩa lim f ( x) = − ;
 lim f (x) = + ;
 lim f (x) = − ;
 lim f (x) = + ; 
lim f ( x) = − được x + + − → → → → − → 0 x x 0 x x 0 x x 0 x x 0 x
phát biểu hoàn toàn tương tự. 3. Lưu ý:
a) f ( x) không nhất thiết phải xác định tại điểm x . 0
b) Ta chỉ xét giới hạn của f ( x) tại điểm x nếu có một khoảng ( ;
a b) (dù nhỏ) chứa x mà f ( x) xác 0 0 định trên ( ; a b) hoặc trên ( ; a b) \x . 0
Chẳng hạn, hàm số f ( x) = x có tập xác định là D = 0; + ) . Do đó ta không xét giới hạn của hàm số
tại điểm x = 0 , do không có một khoảng ( ;
a b) nào chứa điểm 0 mà f ( x) xác định trên đó cả. Tương 0
tự vậy ta cũng không xét giới hạn của f ( x) tại mọi điểm x  0. 0
c) Ta chỉ xét giới hạn bên phải của f ( x) tại điểm x nếu có một khoảng ( x ; b (khoảng nằm bên phải 0 ) 0
x ) mà f ( x) xác định trên đó. 0
Tương tự, ta chỉ xét giới hạn bên trái của f ( x) tại điểm x nếu có một khoảng ( ;
a x (khoảng nằm bên 0 ) 0
trái x ) mà f ( x) xác định trên đó. 0
Chẳng hạn, với hàm số f ( x) = x −1 , tại điểm x =1, ta chỉ xét giới hạn bên phải. Với hàm số 0
g ( x) = 1− x , tại điểm x =1, ta chỉ xét giới hạn bên trái. 0
d) lim f (x) = +  lim f (x) = lim f (x) = + x − + → o x x→x o x→x o
lim f (x) = −  lim f (x) = lim f (x) = − x − + → o x x→x o x→x o
II. ĐỊNH NGHĨA GIỚI HẠN CỦA HÀM SỐ TẠI VÔ CỰC
1. Giới hạn hữu hạn tại vô cực. Định nghĩa 4
Cho hàm số y = f (x) xác định trên khoảng ( ;
a +). lim f (x) = L  với mọi dãy số (xn ) x→+ , x a x → + f x = L n và n ta đều có lim ( ) .
LƯU Ý: Định nghĩa lim f (x) = L được phát biểu hoàn toàn tương tự. x→−
2. Giới hạn vô cực tại vô cực. Định nghĩa 5
Cho hàm số y = f (x) xác định trên khoảng ( ;
a +). lim f (x) = +  với mọi dãy số x→+
(x x a x →+ f x = + n ) , n và n ta đều có lim ( ) .
LƯU Ý: Các định nghĩa: lim f (x) = + ,
 lim f (x) = − ,
 lim f (x) = − được phát biểu hoàn toàn tương x→− x→+ x→− tự.
III. MỘT SỐ GIỚI HẠN ĐẶC BIỆT a) lim x = xo . x→xo b) lim c = ;
c lim c = c ( c là hằng số ) x→xo x→ c c) lim
= 0 ( c là hằng số, k nguyên dương ). k x→ x d) lim k
x = + với k nguyên dương; lim k
x = − nếu k là số nguyên lẻ; lim k x = + x→+ x→− x→−
nếu k là số nguyên chẵn.
Nhận xét: lim f (x) = +  lim − f (x) = − x   . →+ x→+
IV. ĐỊNH LÍ VỀ GIỚI HẠN HỮU HẠN Định lí 2
Giả sử lim f (x) = L và lim g(x) = M . Khi đó x→xo x→xo
a) lim  f (x)  (
g x) = L M x   . → o x
b) lim  f (x) ( g x) = LMcf x  = cL x   ; lim ( )  
với c là một là một hằng số. → o x x→ o x f (x) L c) lim = (M  0). x→ o x ( g x) M
STUDY TIP: Giới hạn hữu hạn, giới hạn của tổng, hiệu, tích, thương của hai hàm số tại một điểm bằng
tổng, hiệu, tích, thương các giới hạn của chúng tại điểm đó (trong trường hợp thương, giới hạn của mẫu phải khác không). Định lí 3
Giả sử lim f (x) = L . Khi đó x→xo
a) lim f (x) = L . x→ o x b) 3 3
lim f (x) = L . x→ o x
c) Nếu f (x)  0 với mọi J \ x , trong đó J x L o
là khoảng nào đó chứa o , thì 0 và
lim f (x) = L . x→ o x
LƯU Ý: Định lí 2 và định lí 3 vẫn đúng khi thay x → x x x− → x x+ → o bởi o , o .
V. QUY TẮC VỀ GIỚI HẠN VÔ CỰC
Các định lí và quy tắc dưới đây được áp dụng cho mọi trường hợp: x x ,x x− ,x x+ → → → ,x → + o o o và x →− .
Tuyên nhiên, để cho gọn, ta chỉ phát biểu cho trường hợp x → xo .
Quy tắc 1 (Quy tắc tìm giới hạn của tích).
L = lim f (x) lim g(x) lim  f (x) ( g x) x→x   o x→xo x→ o x L  0 + + − − L  0 + − − +
STUDY TIP: Giới hạn của tích hai hàm số
- Tích của một hàm số có giới hạn hữu hạn khác 0 với một hàm số có giới hạn vô cực là một hàm số có giới hạn vô cực.
- Dấu của giới hạn theo quy tắc dấu của phép nhân hai số.
Quy tắc 2 (Quy tắc tìm giới hạn của thương)
L = lim f (x) lim g(x) Dấu của ( g x) f (x) x→x lim o x→xo x→ o x ( g x) L  Tùy ý 0 L  0 0 + + - − L  0 0 + − - +
(Dấu của g ( x) xét trên một khoảng K nào đó đang tính giới hạn, với x xo ).
STUDY TIP: Giới hạn của thương hai hàm số. Tử thức có giới hạn hữu hạn khác 0:
- Mẫu thức càng tang (dần đến vô cực) thì phân thức càng nhỏ (dần đến 0).
- Mẫu thức càng nhỏ (dần đến 0) thì phân thức có giá trị tuyệt đối càng lớn (dần đến vô cực).
- Dấu của giới hạn theo quy tắc dấu của phép chia hai số. 0 
VI. CÁC DẠNG VÔ ĐỊNH: GỒM , ,0. 0
VÀ  −  .
B. CÁC DẠNG TOÁN VỀ GIỚI HẠN HÀM SỐ
DẠNG 1: TÌM GIỚI HẠN XÁC ĐỊNH BẰNG CÁCH SỬ DỤNG TRỰC TIẾP CÁC ĐỊNH NGHĨA,
ĐỊNH LÍ VÀ QUY TẮC. Phương pháp:
- Xác định đúng dạng bài toán: giới hạn tại một điểm hay giới hạn tại vô cực? giới
hạn xác định hay vô định?
- với giới hạn hàm số tại một điểm ta cần lưu ý: Cho f (x) là hàm số sơ cấp xác định trên khoảng ( ;
a b) chứa điểm x . Khi đó, lim f (x) = f (x ) . 0 → o x xo
- Với giới hạn hàm số tại vô cực ta “xử lí” tương tự như giới hạn dãy số.
- Với giới hạn xác định, ta áp dụng trực tiếp định nghĩa giới hạn hàm số, các định lí
về giới hạn hữu hạn và các quy tắc về giới hạn vô cực.
STUDY TIP: Dùng định nghĩa chứng minh hàm số y = f (x) không có giới hạn khi x → x 0
- Chọn hai dãy số khác nhau (a và (b thỏa mãn a và b thuộc tập xác định của hàm số n ) n ) n n
y = f (x) và khác x ; a → x ;b → x . 0 n 0 n 0
- Chứng minh lim f (a )  lim f b hoặc chứng minh một trong hai giới hạn này không tồn tại. n ( n)
- Từ đó suy ra lim f (x) không tồn tại. TH x x
→ hoặc x → chứng minh tương tự. x→x 0 o
Ví dụ 1: Chọn khẳng định đúng trong các khẳng định sau:
A. lim sin x = 1
B. lim sin x = −1
C. lim sin x = 0
D. lim sin x không tồn tại. x→+ x→+ x→+ x→+ Đáp án D Lời giải
Xét dãy số (x ) với x = + 2n . n n 2   
Ta có x → + và limsin x = limsin + 2n =1. ( ) 1 n n    2  
Lại xét dãy số ( y ) với y = − + 2n . n n 2   
Ta có y → + và limsin y = limsin − + 2n = 1 − . (2) n n    2  Từ ( )
1 và (2) suy ra lim sin x không tồn tại. Vậy chọn đáp án D. x→+ 2 x +1
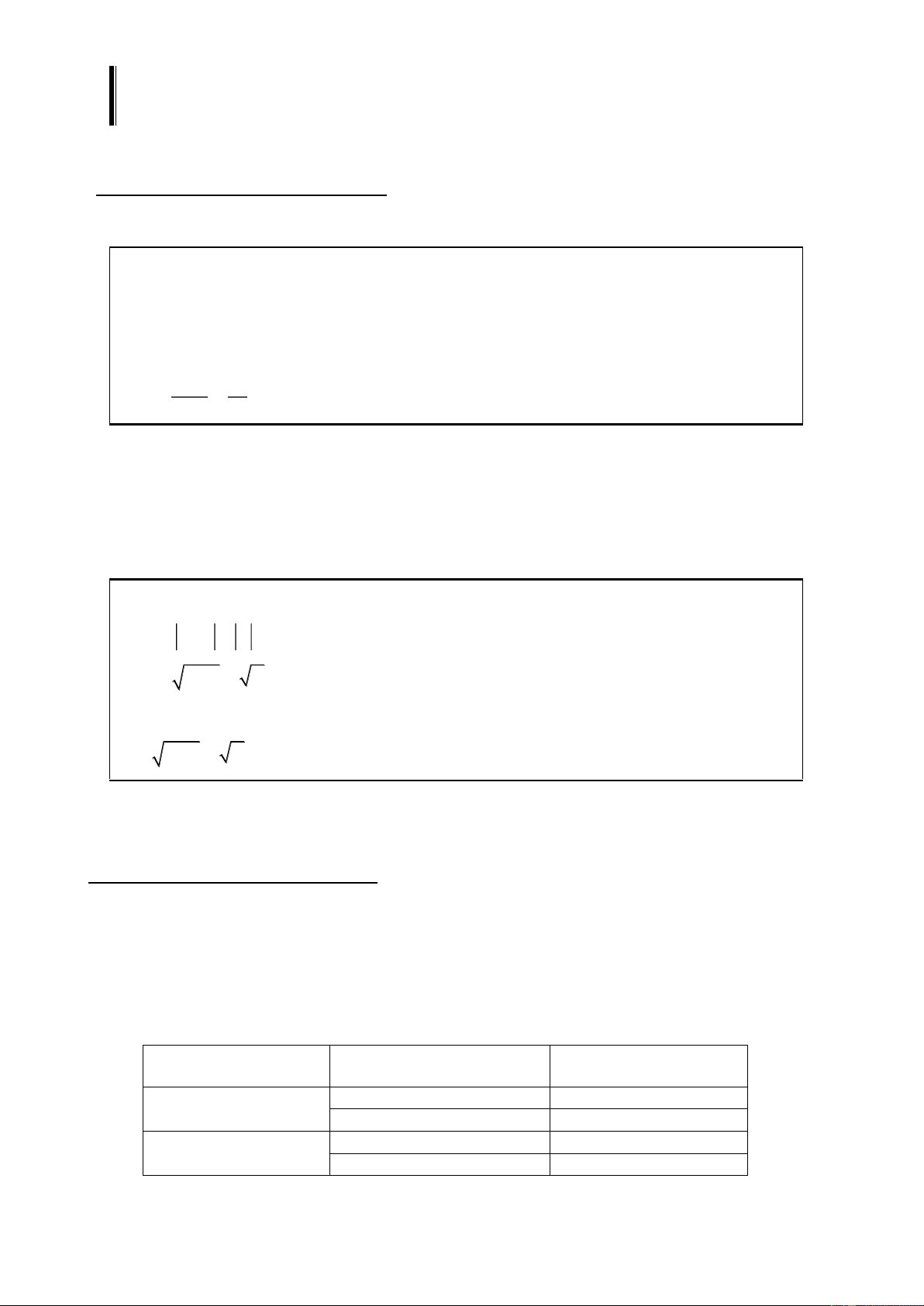
Ví dụ 2: Cho hàm số f (x) =
, lim f (x) bằng: 3 2 x x → 5 3 1 A. +. B. 0 . C. . D. . 3 2
STUDY TIP: Giới hạn tại một điểm
Nếu f (x) xác định tại x và tồn tại một khoảng ( ;
a b) thuộc tập xác định của f (x) chứa x thì 0 0
lim f (x) = f (x ) . → o x xo
- Việc sử dụng hay không sử dụng MTCT để tính f (x ) f x
o tùy thuộc vào mức độ phức tạp của ( ) o và
khả năng tính toán của độc giả. Đáp án C. Lời giải
Hàm số đã cho xác định trên (0;+) .
Cách 1 (sử dụng định nghĩa):
Giải sử (x ) là một dãy số bất kỳ, thỏa mãn x  0, x  3 và x → 3 khi n → +. Ta có n n n n 2 2 x +1 3 +1 5 3
lim f (x ) = lim n = =
( áp dụng quy tắc về giới hạn hữu hạn của dãy số). Do đó n 2 x 2 3 3 n 5 3 lim f (x) = . x 3 → 3
Cách 2 (sử dụng định lí về giới hạn hữu hạn): Theo định lí 1 ta có: 2 lim + ( 2x + ) 2 x + x x + x + lim f ( x) 1 lim lim1 lim .lim lim1 1 3.3 1 5 3 x 3 = lim → x→ x→ x→ x→ x→ = = = = = . x→ x→ 2 x lim → (2 x ) 3 3 3 3 3 3 3 lim 2.lim x lim 2. lim x 2 3 3 x 3 x 3 → x 3 → x→2 x 3 →
Tuy nhiên trong thực hành, vì là câu hỏi trắc nghiệm nên ta làm như sau.
Cách 3: Vì f ( x) là hàm số sơ cấp xác định trên (0;+ ) chứa điểm x = 3 nên 0
f ( x) = f ( ) 10 5 3 lim 3 = = . x 3 → 2 3 3
Do đó sử dụng MTCT ta làm như cách 4 dưới đây.
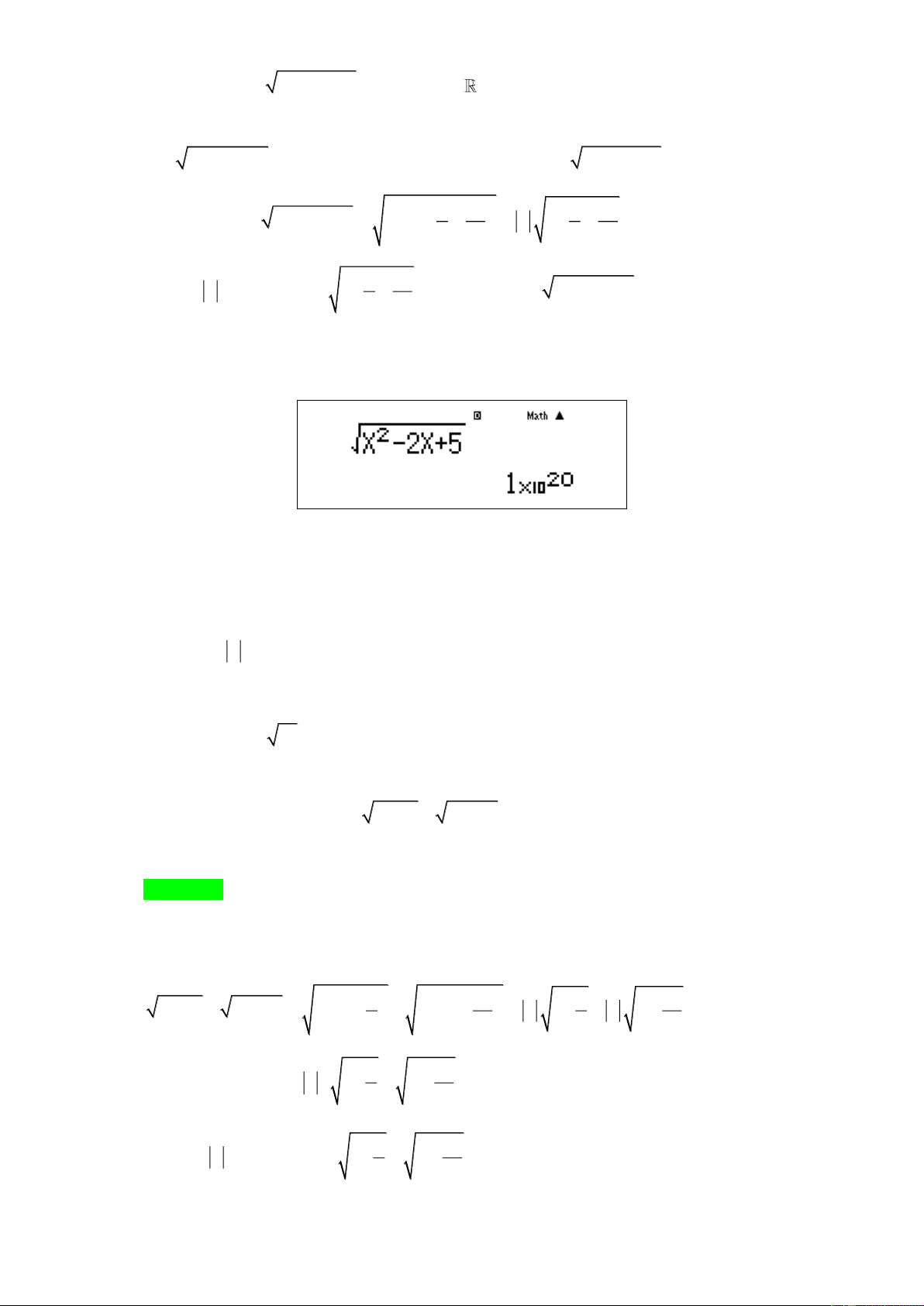
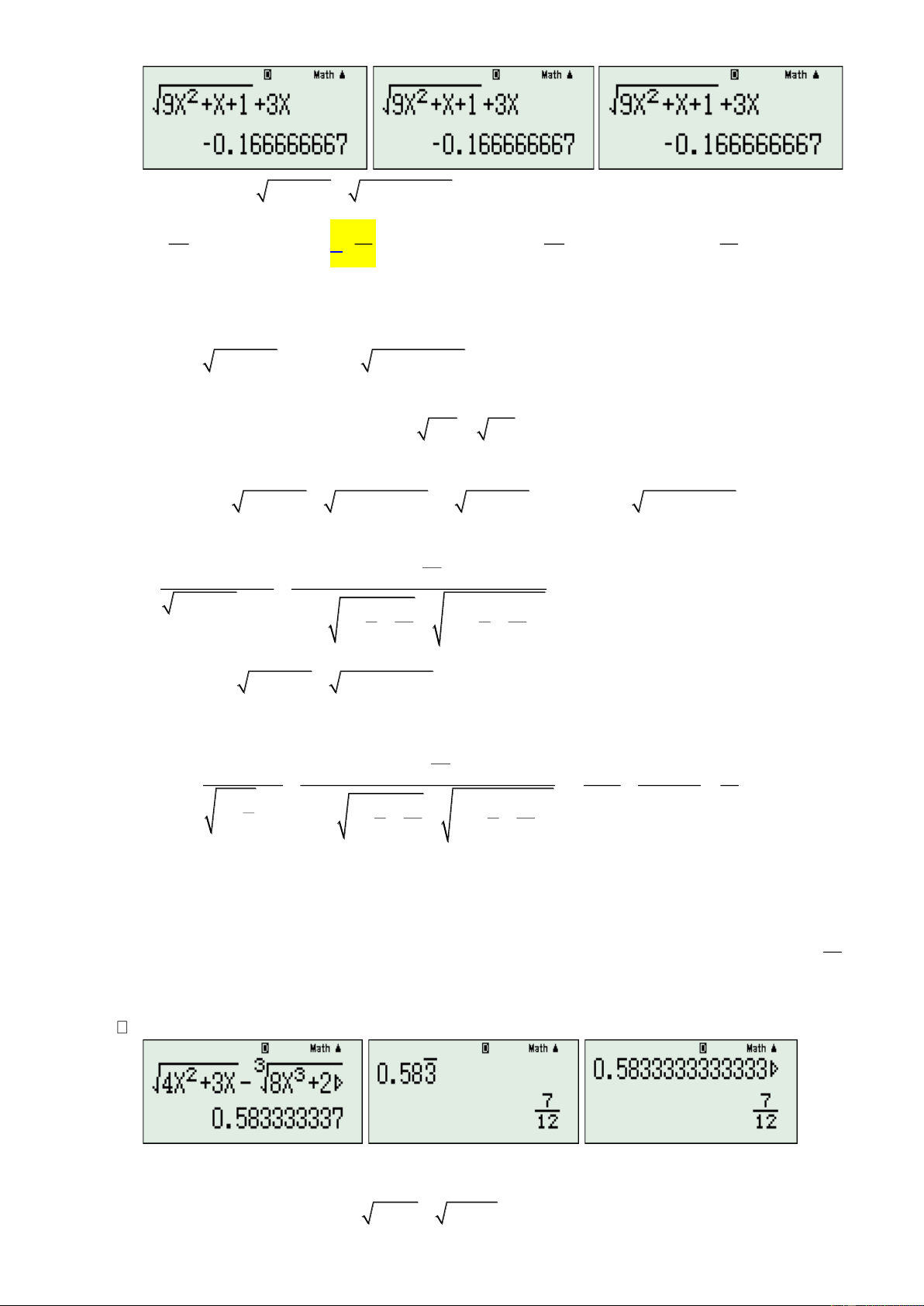
Cách 4: Nhập biểu thức của vào màn hình. Bấm phím CALC, máy hỏi X ? nhập 3 = . Máy hiển thị kết quả như hình: Do đó chọn đáp án C.
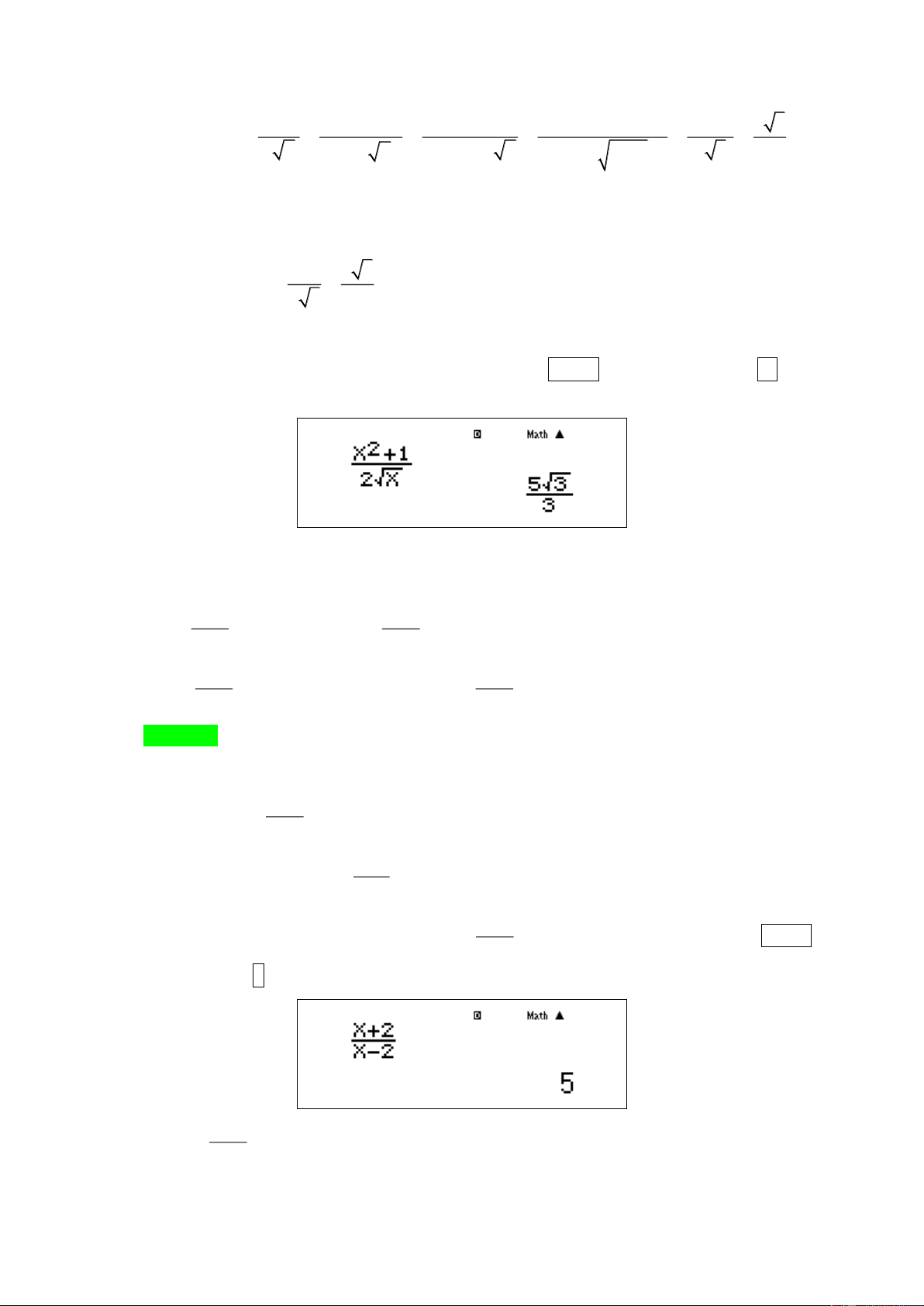
Ví dụ 3: Chọn khẳng định đúng trong các khẳng định dưới đây ? x + 2 x + 2 A. lim =1. B. lim = 5. x→3 x − 2 x→3 x − 2 x + 2 x + C. lim = 1 − f x = x → . x→3 x − . D. Hàm số ( ) 2 2 x − không có giới hạn khi 3 2 Đáp án B Lời giải x + Hàm số f ( x) 2 =
xác định trên các khoảng ( ;
− 2) và (2;+) . Ta có 3(2;+) . x − 2 3 + 2
Cách 1 : lim f ( x) = f (3) = = 5 x→3 3 − . 2 x +
Cách 2 : Nhập biểu thức của hàm số f ( x) 2
= x− và màn hình MTCT. Bấm phím CALC , máy 2
hỏi X? nhâp 3 =. Máy hiển thị kết quả như hình: x + 2 Vậy lim = 5 x→3 x − . 2 Ví dụ 4: ( 3 lim 2
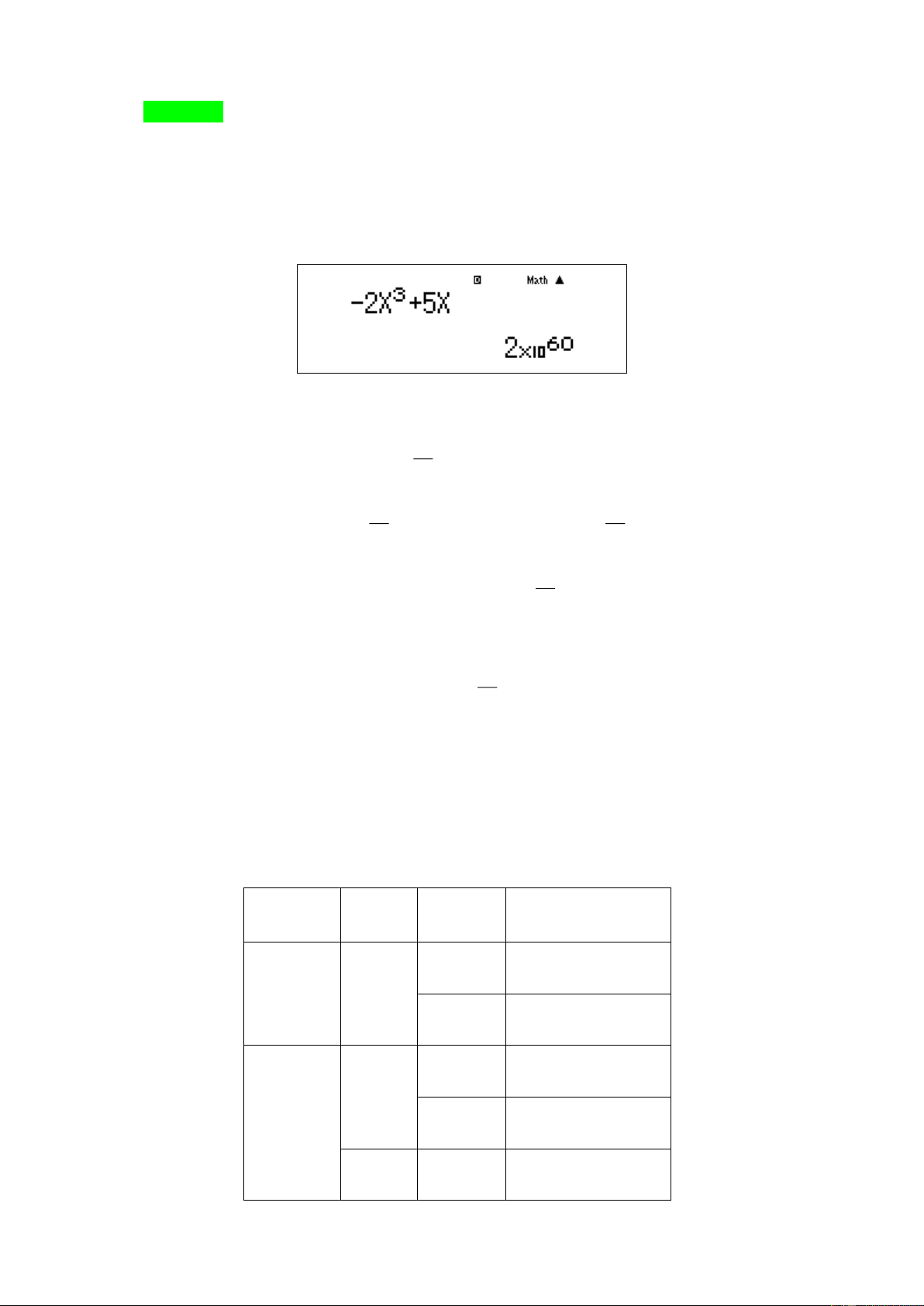
− x + 5x) bằng: x→− A. 2 − . B. 3 . C. +. D. − . Đáp án C. Lời giải
Cách 1: Sử dụng MTCT tính giá trị của f ( x) 3 = 2
− x +5x tại một điểm có giá trị âm rất nhỏ (do
ta đang xét giới hạn của hàm số khi x →−), chẳng hạn tại 20 10 −
. Máy hiển thị kết quả như hình:
Đó là một giá trị dương rất lớn. Vậy chọn đáp án C , tức ( 3 lim 2
− x + 5x) = + . x→−  5  Cách 2: Ta có 3 3 2
− x + 5x = x 2 − +  . 2  x   5   5  Vì 3 lim x = − và lim 2 − + = 2 −  0   nên 3 lim x 2 − + = +   . x→− 2 x→−  x  2 x→−  x   5  Vậy theo Quy tắc 1, lim ( 3 2 − x + 5x) 3 = lim x 2 − + = +   . Do đó chọn C. 2 x→− x→−  x Lưu ý 1:  5  - Để hiểu tại sao 3 lim x = − và lim 2 − + = 2 −  
xin xem lại phần các giới hạn đặc biệt. x→− 2 x→−  x
- Bài toán thuộc dạng tính giới hạn hàm số khi x dần tới vô cực, nhưng là khi x → −. Do đó
không thể áp dụng ngay các kết quả đã biết về giới hạn dãy số, vì giới hạn dãy số được xét khi
n → +. Ta chỉ có thể áp dụng các kĩ thuật đã biết đối với giới hạn dãy số.
Lưu ý 2: Có thể dễ dàng chứng minh được kết quả như sau :
Cho hàm số f ( x) k k 1
= a x + a x − +...+ a x + a (a  0) là một đa thức bậc k . k k 1 − 1 0 k x k a
Giới hạn của f ( x) k a  0 + k x → + Tùy ý a  0 − k a  0 + k k chẵn x → − a  0 − k k lẻ a  0 − k a  0 + ka a a
Thật vậy, ta có f ( x) k k 1 − 1 0 = x a + +...+ +  . kk 1 − kx x x   a a a  Vì k 1 − 1 0 lim a + +...+ + = a  và lim k
x = + với k tùy ý, lim k
x = + nếu k chẵn, kk 1 − k k x→  x x x x→+ x→− lim k
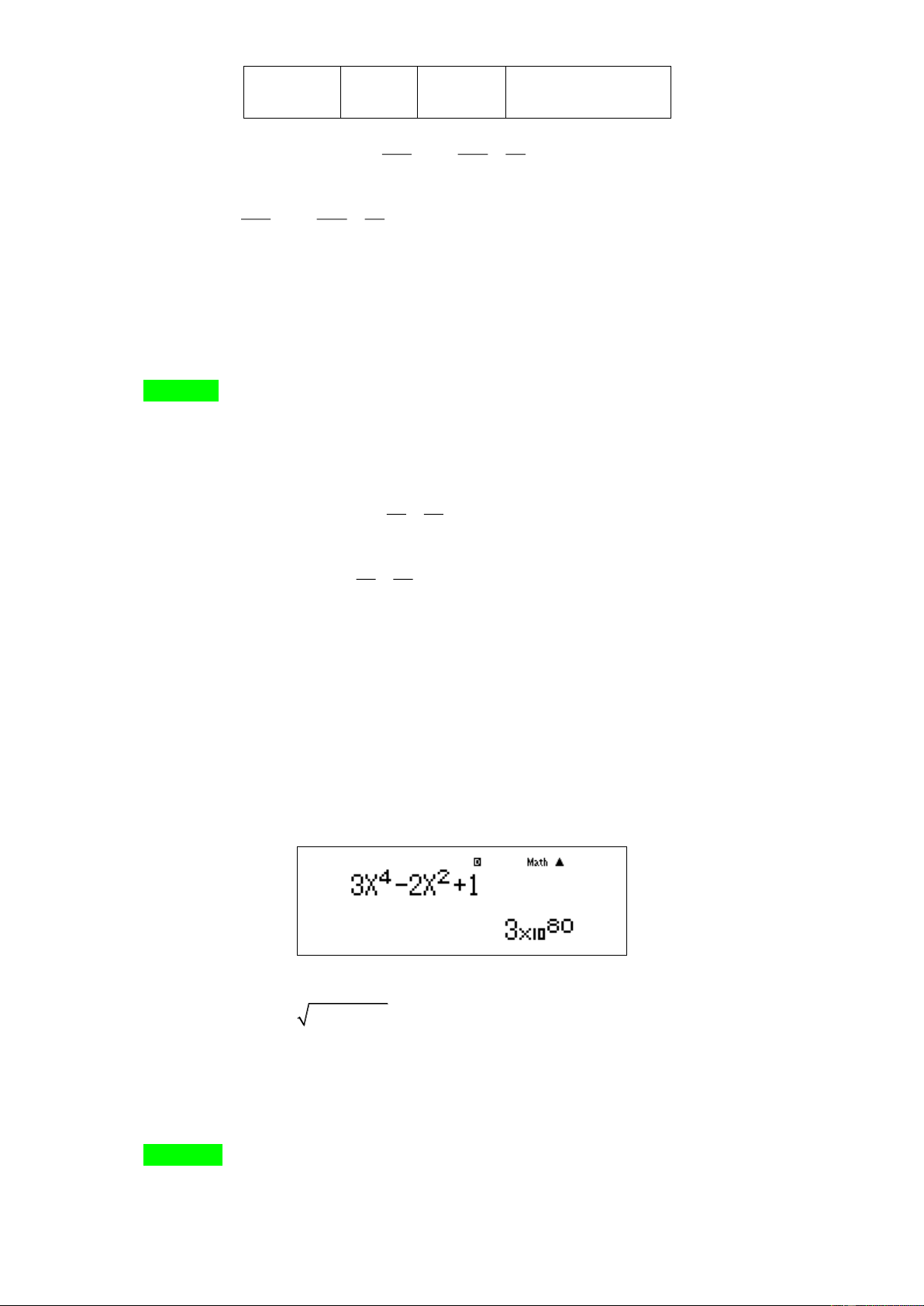
x = − nếu k lẻ nên ta dễ dàng suy ra bảng kết quả trên. x→− Ví dụ 5: ( 4 2
lim 3x − 2x + ) 1 bằng: x→− A. +. B. − . C. 3. D. 2. Đáp án A Lời giải
Cách 1: Theo nhận xét trên thì ( 4 2
lim 3x − 2x + ) 1 = + ( x → − ,
k chẵn và a  0 ). Thật k x→−  2 1  vậy, ta có 4 2 4
3x − 2x +1 = x 3 − + .   2 4  x x   2 1  Vì 4
lim x = + và lim 3 − + = 3  0   nên ( 4 2
lim 3x − 2x + ) 1 = + . x→− 2 4 x→  x x x→− STUDY TIP
- Giới hạn tại vô cực của hàm đa thức là vô cực, chỉ phụ thuộc vào số hạng chứa lũy thừa bậc cao nhất.
- Giới hạn của hàm đa thức tại + phụ thuộc vào hệ số của lũy thừa bậc cao nhất. (Giống với
giới hạn của dãy số dạng đa thức).
- Giới hạn của hàm đa thức tại − phụ thuộc vào bậc và hệ số của lũy thừa bậc cao nhất.
Cách 2: Sử dụng MTCT tính giá trị hàm số f ( x) 4 2
= 3x − 2x +1 tại 20 x = 10 − , ta được kết quả như hình :
Kết quả là một số dương rất lớn. Do đó chọn đáp án A,
Ví dụ 6: Cho hàm số f (x) 2
= x − 2x + 5 . Khẳng định nào dưới đây đúng ?
A. lim f ( x) = − .
B. lim f ( x) = + . x→− x→−
C. lim f ( x) = 1.
D. lim f ( x) không tồn tại. x→− x→− Đáp án B. Lời giải Hàm số f ( x) 2
= x − 2x + 5 xác định trên .
Có thể giải nhanh như sau : Vì 2
x − 2x + 5 là một hàm đa thức của x nên có giới hạn tại vô cực. Mà 2
x − 2x + 5  0 với mọi x nên giới hạn của f ( x) 2
= x − 2x + 5 tại − chắc chắn là +.  2 5  2 5 Thật vậy, ta có 2 2 x − 2x + 5 = x 1− + = x 1− +   . 2 2  x x x x 2 5
Vì lim x = + và lim 1− + =1  0 nên 2 lim
x − 2x + 5 = + . x→− 2 x→− x x x→−
Hoặc ta có thể sử dụng MTCT để tính giá trị của f ( x) tại một giá trị âm rất nhỏ của x , chẳng hạn tại 20 x = 10 −
ta được kết quả như hình:
Kết quả này là một số dương rất lớn. Do đó ta chọn đáp án B. (Dễ thâý kết quả hiển thị trên máy
tính như trên chỉ là kết quả gần đúng do khả năng tính toán hạn chế của MTCT. Tuy nhiên kết
quả đó cũng giúp ta lựa chọn được đáp án chính xác). STUDY TIP Ta có lim x = + . x→
Khi x → − thì x  0 . Với x  0 ta có 2 x = −x .
Cần đặc biệt lưu ý các điều trên khi tính giới hạn tại − của hàm chứa căn thức.
Ví dụ 7: Giới hạn của hàm số f (x) 2 2
= x − x − 4x +1 khi x →− bằng: A. − . B. +. C. 1 − . D. 3. Đáp án A. Lời giải Cách 1: Ta có:  1   1  1 1 2 2 2 2
x − x − 4x +1 = x 1− − x 4 +
= x 1− − x 4 +     2 2  x   x x x  1 1  = x  1− − 4+  2  x x     1 1 
Mà lim x = + và lim  1− − 4 +  =1− 2 = 1 −  0   . x→− 2 x→ x x     1 1  Vậy lim x − x − x + =  x  − − +  = −   . x→− ( 2 2 4 1) lim 1 4 2 x→− x x    Lưu ý:
- Độc giả nên đọc lại phần giới hạn dãy số có chứa căn thức để hiểu hơn tại sao lại có định hướng
giải như vậy (mà không đi nhân chia với biểu thức liên hợp).
- Có thể thấy như sau: Vì 2 2 lim x − x = + ;  lim 4x +1 = + . x→− x→− Mà hệ số của 2 x trong 2
4x +1 lớn hơn hệ số của 2 x trong 2
x − x nên suy ra − − + = −. →− ( 2 2 lim x x 4x 1 x )
Cách 2: Sử dụng MTCT tính giá trị hàm số tại 10 x = 10 −
ta được kết quả như hình. Vậy chọn đáp án A. Ví dụ 8: 2017 lim bằng: 3 5
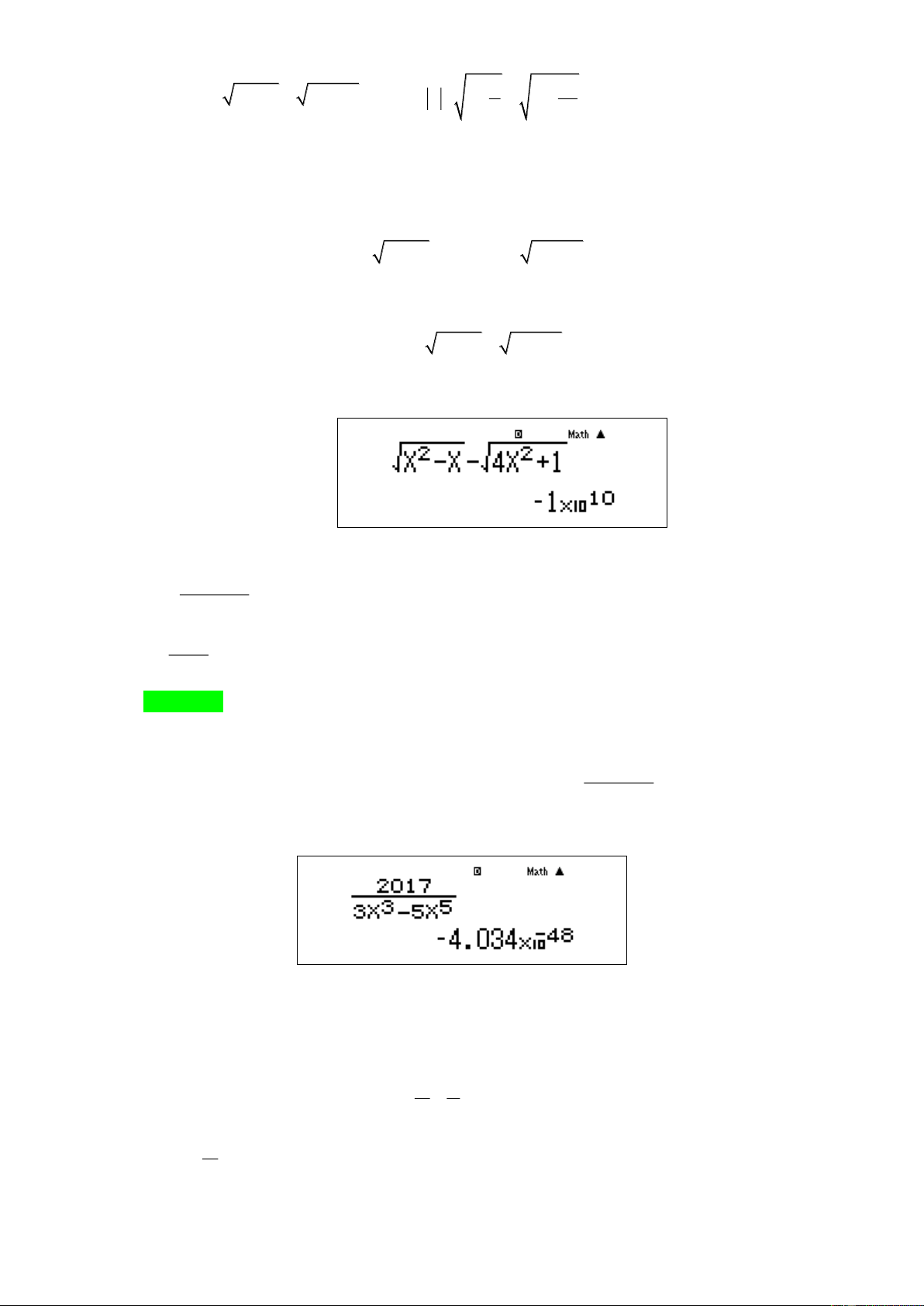
x→+ 3x − 5x 2017 A. . B. − . C. +. D. 0. 3 Đáp án D. Lời giải 2017 Cách 1: Vì ( 3 5
lim 3x − 5x ) = − nên theo quy tắc 2, lim = 0 x→+ 3 5 x→+ 3x − . 5x
Cách 2: Sử dụng MTCT tính giá trị hàm số tại 10
x = 10 ta được kết quả như hình.
Đó là một kết quả rất gần 0. Do đó chọn đáp án D. STUDY TIP
Khi hàm số không xác định tại x thì ta thử áp dụng các quy tắc về giới hạn vô cực. Đó là các 0 L L
quy tắc áp dụng cho các dạng . L  ; ; . Lưu ý cách xác đị  nh dấu của giới hạn. 0 L
- Dạng  : giới hạn là 0. L - Dạng . L  và : Giới hạn là vô cực. 0 − Ví dụ 9: x
Giới hạn bên phải của hàm số f ( x) 3 7 = khi x → 2 là x − 2 7 A. +. B. − . C. 3. D. . 2 Đáp án B. Lời giải x − Hàm số f ( x) 3 7 = xác định trên (− ;  +) \  2 . x − 2
Cách 1: Ta có lim ( x − 2) = 0, x − 2  0 với mọi x  2 và lim (3x − 7) = 3.2 − 7 = 1 −  0 . Do đó + + x→2 x→2 3x − 7 theo quy tắc 2 thì lim = − . + x→2 x − 2 x −
Cách 2: Sử dụng MTCT. Tính giá trị của f ( x) 3 7 =
x = ta thấy máy báo lỗi Math Error x − tại 2 2
(do f ( x) không xác định tại x = 2 ). Quay lại tính giá trị của f ( x) tại 10 x 2 10− = + (tức
2, 0000000001) là một giá trị của x lớn hơn 2 và rất gần 2. Kết quả là một số âm rất nhỏ. Do đó chọn đáp án B. 2 3x + x −1
Ví dụ 10: Xét bài toán “Tìm lim− 2
x→2 2x − 5x +
”, bạn Hà đã giải như sau: 2 Bước 1: Vì lim − + = . − ( 2 2x 5x 2) 0 x→2 Bước 2: 2
2x − 5x + 2  0 với x  2 và x đủ gần 2, Bước 3: lim ( 2 3x + x − =  − )1 13 0 x→2 2 3x + x −1
Bước 4: nên theo quy tắc 2, lim = + − 2 x 2 → 2x − 5x + . 2
Hỏi lời giải trên của bạn Hà đã sai từ bước thứ mấy ? A. Bước 1. B. Bước 2. C. Bước 3. D. Bước 4. Đáp án B Lời giải
Xét dấu biểu thức g ( x) 2
= 2x −5x + 2 ta thấy g (x)  0 với mọi x(1;2) . 2 3x + x −1
Vậy lời giải sai từ bước 2. (Lời giải đúng cho ra kết quả lim = − − 2 x 2 → 2x − 5x + ). 2 STUDY TIP x x+
→ nghĩa là x → x và x x . 0 0 0 x x−
→ nghĩa là x → x và x x . 0 0 0 Nếu x x+
→ thì tính giá trị hàm số tại 10 k x x − = + . 0 0 Nếu x x−
→ thì tính giá trị hàm số tại 10 k x x − = − . 0 0
Trong đó k là một sô nguyên dương. − Ví dụ 11: 1 x Giới hạn lim bằng: x→ (x − 4)2 4 A. 0. B. 3 − . C. − . D. +. Đáp án C. Lời giải
Cách 1: Ta có lim (1− x) = 3
−  0, lim(x − 4)2 = 0 và (x − )2 4
 0 với mọi x  4 nên theo quy x→4 x→4 1− x tắc 2, lim
= − . Vậy chọn đáp án C. x→ (x −4)2 4
Cách 2: Sử dụng MTCT tính giá trị hàm số tại 8 x 4 10− = + hoặc tại 8 x 4 10− = − ra được các kết quả như hình Vậy chọn đáp án C. 5
x + 2 khi x 1
Ví dụ 12: Cho hàm số f ( x) = 
. Khẳng định nào dưới đây là đúng ? 2
x − 3 khi x 1
A. lim f ( x) = 7 .
B. lim f ( x) = 2 − . x 1 → x 1 →
C. lim f ( x) = 7 .
D. lim f ( x) = 7 . − + x 1 → x 1 → Đáp án D. Lời giải
Ta có lim f ( x) = lim (5x + 2) = 5.1+ 2 = 7 . Vì chỉ có một đáp án đúng nên chọn đáp án D. + + x 1 → x 1 → STUDY TIP
Cần xác định đúng biểu thức của f ( x) khi x x+ → và khi x x− → . 0 0
Giải thích thêm : Ta có lim f ( x) = lim − = − = − . − − ( 2 x 3) 2 1 3 2 x 1 → x 1 →
Vậy lim f ( x)  lim f ( x) nên lim f ( x) không tồn tại. − + x 1 → x 1 → x 1 →
Các đáp án A, B, C đều sai. STUDY TIP
lim f ( x) = L  lim f ( x) = lim f (x) = L . x − + → → → 0 x x x x x 0 0 2
x −5 khi x  3 ( ) 1 
Ví dụ 13: Cho hàm số f ( x) = 2  . x − 5  khi x  3 (2)  x + 2
Trong biểu thức (2) ở trên, cần thay số 5 bằng số nào để hàm số f ( x) có giới hạn khi x → 3 ? A. 19. B. 1. C. 1 − .
D. Không có số nào thỏa mãn. Đáp án C. Lời giải
Hàm số đã cho các định trên \   2 .
Cách 1: Ta có lim f ( x) 2 2
= lim x −5 = 3 −5 = 2 . + + x 3 → x 3 → x − m Đặt f (x) 2 =
x  ( m là tham số, m  0 ). x + khi 3 2 x − m 3 − m 9 − m
Ta có lim f ( x) 2 2 = lim = = = − − x 3 → x 3 → x + 2 3 + . 2 5 − Để 9 m
hàm số f ( x) có giới hạn khi x → 3 thì lim f ( x) = lim f ( x)  = 2  m = 1 − . + − x→3 x→3 5
Cách 2: Sử dụng MTCT tính giá trị biểu thức 2
X − 5 khi X = 3 được kết quả bằng 2. Sử dụng 2 X − A
MTCT tính giá trị biểu thức
X = và lần lượt nhận các giá trị bằng 19,1 và 1 − . Ta X + khi 3 2 thấy khi A = 1
− thì biểu thức nhận giá trị bằng 2. Vậy chọn đáp án C.
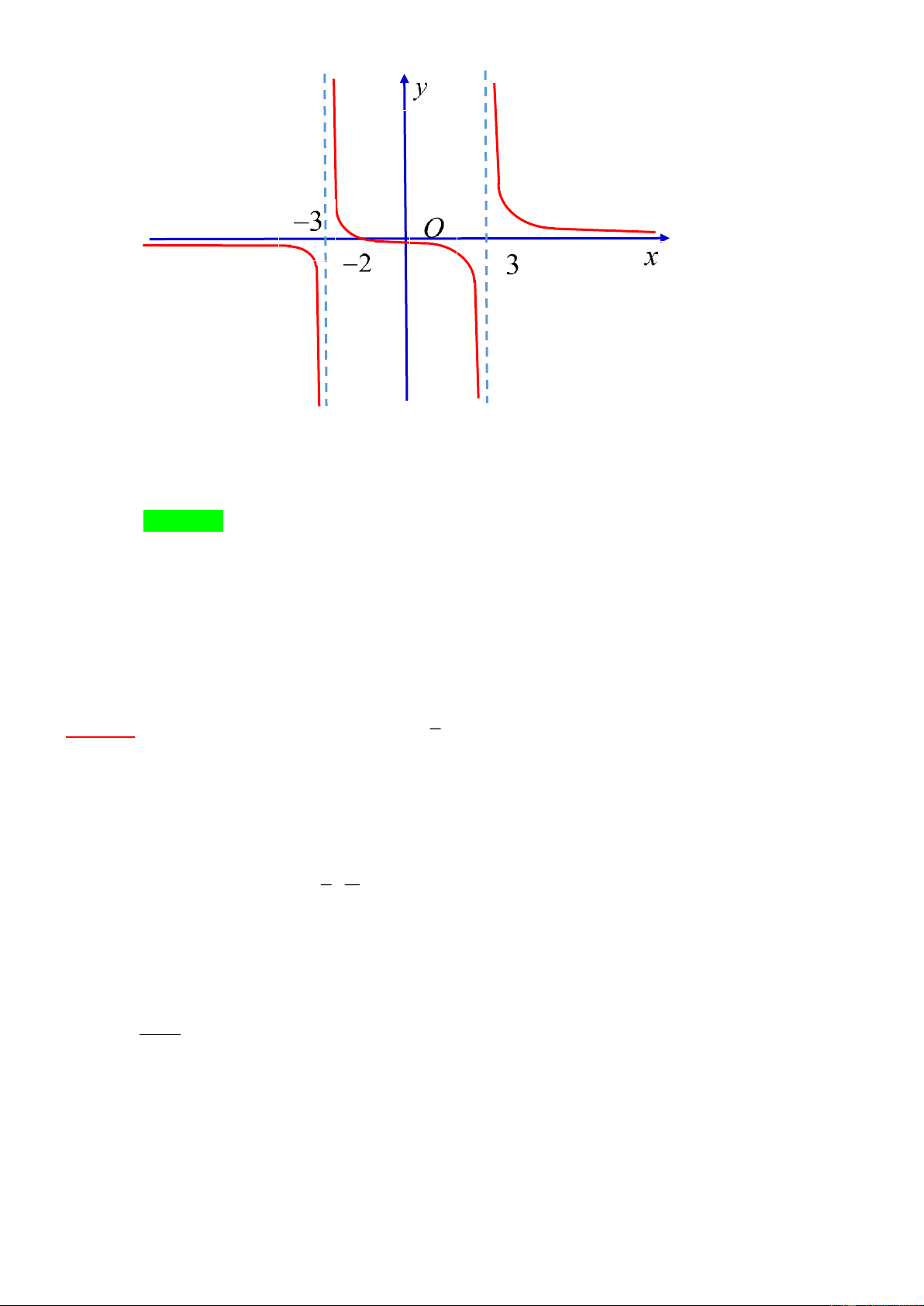
Ví dụ 14: Cho hàm số f (x) có đồ thị như hình dưới đây:
Quan sát đồ thị và cho biết trong các giới hạn sau, giới hạn nào là + ?
A. lim f ( x) .
B. lim f ( x) .
C. lim f ( x) .
D. lim f ( x) . x→− x→+ + − x ( → − ) 3 x 3 → Đáp án C. Lời giải Khi x 3+
→ − , đồ thị hàm số là một đường cong đi lên từ phải qua trái. Do đó lim f (x) = + . + x ( → − ) 3
Tương tự như vậy ta có lim f (x) = lim f (x) = 0 ; lim f (x) = − . x x − →− →+ x 3 → Do đó chọn đáp án C. 0
DẠNG 2: TÌM GIỚI HẠN VÔ ĐỊNH DẠNG . 0 STUDY TIP
 Khi tính giới hạn mà không thể áp dụng trực tiếp các định lí về giới hạn hữu hạn hay các quy tắc về giới
hạn vô cực đã biết thì ta gọi đó là các dạng vô định.   0
Kí hiệu các dạng vô định gồm: , , 0. 0 
và  −  . Để tính giới hạn dạng vô định ta phải biến đổi biểu
thức của hàm số về dạng áp dụng được các định lí và quy tắc đã biết. Làm như vậy gọi là “khử dạng vô định”. Bài toán: f ( x) Tính lim
khi lim f ( x) = lim g ( x) = 0 , trong đó f ( x) và g ( x) là các đa thức hoặc căn thức. x→ x→x x→ 0 x g ( x) 0 0 x
Phương pháp giải (tự luận)
✓ Phân tích tử và mậu thành tích các nhân tử và giản ước. Cụ thể, vì lim f ( x) = lim g ( x) = 0 nên x→x x→ 0 0 x
f ( x) và g ( x) cùng có nghiệm x = x . Do đó ta phân tích được f ( x) = ( x − x A x và 0 ) ( ) 0 f ( x) (x − x A x A x 0 ) ( ) ( )
g ( x) = ( x − x B x . Khi đó ta có: lim = lim = lim và công việc còn lại 0 ) ( ) x→x x→x x→ g x x − 0 ( ) 0 ( x x B x B x 0 ) ( ) 0 ( ) A( x) là đi tính lim . x→ 0 x B ( x)
✓ Nếu f ( x) và g ( x) có chứa căn thức thì có thể nhân tử và mẫu với biểu thức liên hợp trước khi phân
tích chúng thành tích để giản ước. STUDY TIP
Phân tích đa thức thành nhân tử:
✓ Áp dụng hằng đẳng thức đáng nhớ.
✓ Khi đã biết f ( x) có nghiệm x = x , ta sử dụng lược đồ Hooc-ne hoặc chia f ( x) cho x = x được 0 0
thương A( x) . Khi đó f (x) = (x − x A x . 0 ) ( )
✓ Áp dụng kết quả: nếu phương trình 2
ax + bx + c = 0 có hai nghiệm x , x thì 1 2 2
ax + bx + c = a ( x − x x − x . 1 ) ( 2 )
Tổng quát: nếu phương trình k k 1 − 1 a x + a x
+...+ a x + a = 0 có các nghiệm thực x , x ,..., x thì k k 1 − 1 0 1 2 m k k 1 − 1 a x + a x
+...+ a x + a = a x − x ... x − x A x , trong đó A(x) là đa thức bậc k − m. Tuy nhiên, k k 1 − 1 0 k ( 1 ) ( m ) ( )
trong thực tế, ta dùng kết quả này khi có đủ k nghiệm thực, tức m = k . Trường hợp ngược lại nên dùng
lược đồ Hooc-ne. (với phương trình bậc hai, bậc ba có thể dùng MTCT để tìm nghiệm) 2 x − Ví dụ 1: 4 Tính lim . 2
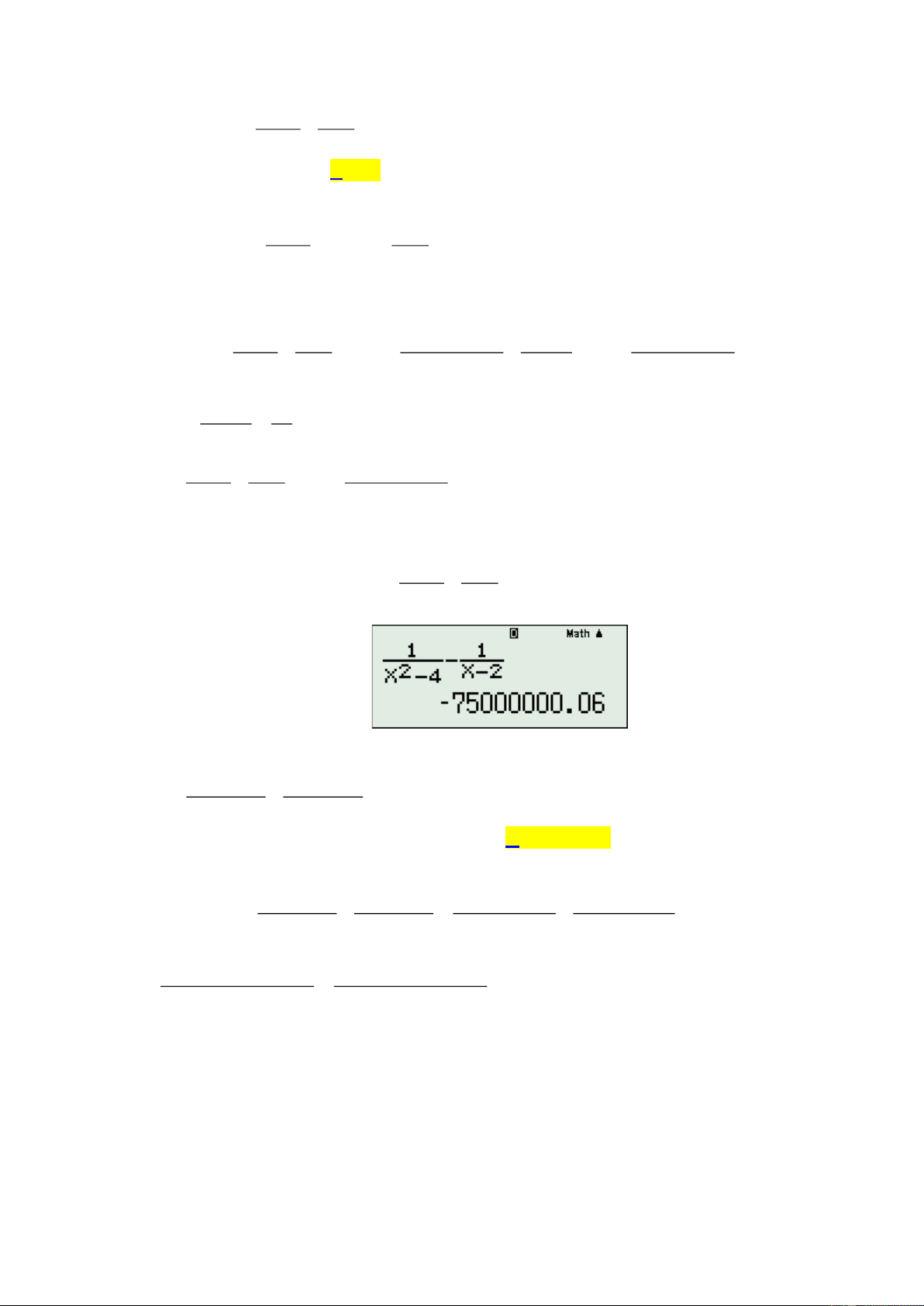
x→2 x − 3x + 2 A. 1. B. 4. C. 2 − . D. 4 − . 0
Phân tích: Vì lim ( 2 x − 4) = lim( 2
x − 3x + 2) = 0 nên đây là giới hạn vô định dạng . Ta thấy x→2 x→2 0 2 x − 4 và 2
x − 3x + 2 đều triệt tiêu tại x = 2 nên x = 2 là nghiệm của 2 x − 4 và 2
x − 3x + 2 . Từ
đó ta có cách giải như sau. Lời giải 2 x − 4 (x −2)(x + 2) x + 2 2 + 2 Cách 1: Ta có lim = lim = lim = = 4 . 2 x→2 x→2 x − 3x + 2
(x − 2)(x − ) x→2 1 x −1 2 −1 x − 4
Cách 2: Dử dụng MTCT tính giá trị hàm số f ( x) 2 =
tại x = 2 ta thấy máy báo lỗi 2 x − 3x + 2
Math Error (do hàm số không xác định tại x = 2 ). Quay lại tính giá trị hàm số tại 2, 0000000001
ta được kết quả như sau:
Lại quay lại tính giá trị hàm số tại 1,9999999999 ta được kết quả như sau: Vậy chọn đáp án B. m x − n Ví dụ 2: x Tính giới hạn lim ( , m n  ) * , ta được kết quả: x 1 → x −1 A. +.
B. m− n. C. m . D. 1. Lời giải m n m x − xx −1 n x −1  Cách 1: Ta có lim = lim −  . x 1 → x 1 x −1 →  x −1 x −1  m x −
(x − )1( m 1− m−2 x + x +...+ x + ) 1 1 Lại có lim = lim = lim ( m 1 − m−2 x + x +...+ x + ) 1 = m . x 1 → x 1 x −1 → x −1 x 1 → n x − Tương tự 1 : lim = n . x 1 → x −1 m n m x − xx −1 n x −1 mx −1 n x −1 Vậy lim = lim −  = lim − lim = m − n . x 1 → x 1 → x 1 → x 1 x −1  x −1 x −1  x −1 → x −1
Cách 2: Cho m và n các giá trị cụ thể, chẳng hạn m = 3 và m = 7 . Sử dụng MTCT tính 3 7 x − x 3 7 x − x lim ta được kết quả lim = 4
− . Vậy đáp án đúng là B. x 1 → x −1 x 1 → x −1 STUDY TIP m
x − = ( x − )( m 1 − m−2 1 1 x + x +...+ x + ) 1 m x −  1 lim = m x 1 → x −1 n x −  1 lim = n x 1 → x −1
Ví dụ 3: Chọn khẳng định đúng trong các khẳng định sau: x + 3 − 2 x + 3 − 2 A. lim = 0 . B. lim = + . 3 x 1 → x − 3x + 2 3 x 1 → x − 3x + 2 x + 3 − 2 x + 3 − 2 C. lim = − . D. lim không tồn tại. 3 x 1 → x − 3x + 2 3 x 1 → x − 3x + 2 0 Phân tích: Vì lim x + − = và lim( 3
x − 3x + 2) = 0 nên đây là dạng vô định . Tuy nhiên x→ ( 3 2) 0 1 x 1 → 0
ta chưa thể phân tích ngay x + 3 − 2 thành nhân tử mà phải nhân cả tử và mẫu với biểu thức
liên hợp của x + 3 − 2 là x + 3 + 2 . Lời giải
( x+3+2)( x+3−2) x + 3 − 2 Cách 1: Ta có = 3 x − 3x + 2
( x+3+2)( 3x −3x+2) x −1 = 1 ( = .
x + 3 + 2)(x − )2 1 ( x + 2)
( x+3+2)(x− )1(x+2) 1 1 Mà lim = −; lim = +. − + x 1
→ ( x +3 + 2)(x − ) 1 ( x + 2) x 1
→ ( x +3 + 2)(x − ) 1 ( x + 2) Do đó 1 lim không tồn tại. x 1
→ ( x +3 + 2)(x − ) 1 ( x + 2) x + 3 − 2 Suy ra lim
không tồn tại. Vậy chọn đáp án D. 3 x 1 → x − 3x + 2 x + 3 − 2
Cách 2: Sử dụng MTCT tính giá trị biểu thức
tại x =1 ta thấy máy báo lỗi Math 3 x − 3x + 2
Error. Quay lại tính giá trị biểu thức tại x = 1, 000001 và tại x = 0,999999 ta được kết quả: x + 3 − 2
Hai kết quả trên là một số dương rất lớn, một số âm rất nhỏ. Do đó có thể kết luận lim 3 x 1 → x − 3x + 2 không tồn tại. Nhận xét:
- Nếu chỉ tính giá trị biểu thức tại một điểm thì rất dễ chọn đáp án sai. 0 L
- Ở đây ta đã chuyển dạng vô định về dạng xác định . 0 0
- Dùng MTCT tìm nghiệm của phương trình 3
x − 3x + 2 = 0 ta được x =1, x = 2 − . Như vậy 1 2
phải có một nghiệm là nghiệm kép do là phương trình bậc ba. Trong trường hợp này, theo Tip
trên đã nêu, ta nên dùng lược đồ Hooc-ne để phân tích đa thức 3
x − 3x + 2 thành nhân tử. 3 x − − x − Ví dụ 4: 2 1 3 2 Giới hạn lim bằng: x 1 → x −1 1 A. 1. B. 0 . C. +. D. . 2 0 Phân tích: lim x − − x − = và lim(x − )
1 = 0 nên đây là dạng vô định . Ta chưa x→ ( 3 2 1 3 2 ) 0 1 x 1 → 0
thể phân tích f ( x) 3
= 2x −1 − 3x − 2 thành nhân tử. Mà f (x) lại là hiệu của hai căn thức
không cùng bậc. Ta để ý thấy 2x −1 và 3 3x − 2 đều đạt giá trị bằng 1 tại x =1 nên ta biến đổi
như sau: f ( x) = ( x − − ) + ( 3 2 1 1
1− 3x − 2 ) rồi tiến hành nhân chia với biểu thức liên hợp. Lời giải 3 3
2x −1 − 3x − 2
2x −1 −1 1− 3x − 2 Cách 1: Ta có = + x −1 x −1 x −1 2x − 2 3 − 3 = x ( + 2x −1 + ) 1 ( x − ) 1 ( 3 3 1+ 3x − 2 + ( 2
3x − 2 ) )(x − ) 1 2 3 = − . 3 2x −1 +1 3 1+ 3x − 2 + ( 2 3x − 2 )   2 3   Tac có: lim − = 0 . x 1 →  x − +  3 2 1 1 3 1+ 3x − 2 + ( 2 3x − 2 )   3 x − − x − Do đó 2 1 3 2 lim = 0 . x 1 → x −1 3
2x −1 − 3x − 2
Cách 2: Sử dụng MTCT tính giá trị biểu thức
tại x =1 ta thấy máy báo lỗi x −1
Math Error. Quay lại tính giá trị biểu thức tại x = 0, 99999999 và tại x = 1, 00000001 ta được kết quả: 3 x − − x −
Do đó chọn đáp án B tứ 2 1 3 2 c là lim = 0 . x 1 → x −1 STUDY TIP 3 A x − B x Cho f ( x) ( ) ( ) =
(chứa hai căn khác bậc) trong đó A( x = B x = m thì ta biến 0 ) ( 0) x − x0 3
A x − m + m − B x
đổi như sau: f (x) ( ) ( ) = . x − x0 3 x − − x − Ví dụ 5: 6 5 4 3 Tính giới hạn lim . x→ (x− )2 1 1 A. 0 . B. 2 − . C. +. D. − . Lời giải
Cách 1: Đặt t = x −1 thì x = t +1, limt = 0 và x 1 →
3 6x − 5 − 4x − 3
3 6t +1 − 4t +1
3 6t +1 − (2t + ) 1 (2t + )− + = 1 4t 1 = + ( 2 2 2 x − )2 1 t t t 6t +1− ( 3 2
8t +12t + 6t + ) 1 ( 2 4t + 4t + ) 1 − (4t + ) 1 = +   3 t
( t + ) +( t + ) t + +( t + ) 2 2 2 2 3
t (2t +1+ 4t +1 6 1 2 1 . 6 1 2 1 )   8 − t −12 4 = + .
3 ( t + )2 + ( t + ) t + + ( t + )2 3 2t +1+ 4t +1 6 1 2 1 . 6 1 2 1  
3 6x − 5 − 4x − 3 8 − t −12 4   Vậy lim = lim + . x→ (x− )2 1 1 t→0  + + + 
3 ( t + )2 + ( t + ) 3 t + + ( t + )2 2t 1 4t 1 6 1 2 1 . 6 1 2 1   8 − t −12 12 4 4 Mà lim = − = 4 − ; lim = = 2. t 0 → t→
3 ( t + )2 + ( t + ) 3 t + + ( t + )2 3 6 1 2 1 . 6 1 2 1 0 2t +1+ 4t +1 2
3 6x − 5 − 4x − 3 Vậy lim = − + = − . x→ (x − ) 4 2 2 2 1 1
3 6x − 5 − 4x − 3
Cách 2: Sử dụng MTCT tính giá trị biểu thức x = ( tại 0, 9999999 và tại x − )2 1
x = 1, 0000001 ta đều được kết quả: Do đó chọn đáp án B. Lưu ý:
- Trong cách thứ 2, nếu ta tính giá trị biểu thức tại x = 0,999999999 hoặc tại x = 1, 000000001 thì ta được kết quả:
Do vượt quá giới hạn tính toán của máy. Do đó nếu không thử lại với cá trị lớn hơn thì có thể ta sẽ chọn đáp án A.
ở bài này có nhiều vấn đề cần phân tích thêm. Nếu làm như ví dụ 4 thì ta sẽ biến đổi
3 6x − 5 − 4x − 3
3 6x − 5 −1 1− 4x − 3 3 − − − = + 6x 5 4x 3 (
rồi nhân liên hợp để thu được 2 2 2 x − )2 1 (x− )1 (x− )1 (x − ) 1
6(1+ 4x − 3) − 4( 3 (6x −5)2 3 + 6x − 5 + )1 = (x − ) 1 ( 3 (6x −5)2 3
+ 6x − 5 + )1(1+ 4x−3) 0
- Ta thấy giới hạn mới thu được vẫn còn là dạng vô định
nên vẫn tiếp tục phải khử dạng vô định. 0
Mà việc khử này sẽ rất phức tạp do biểu thức mới thu được khá cồng kềnh. Để giải quyết khó khăn
đó ta thấy trong lời giải trình bày ở trên, ta tiến hành đổi biến để cho mẫu gọn lại và không thêm
bớt 1 trên tử thức mà thêm bớt nhị thức 2t +1. Vậy cơ sở nào để tìm ra nhị thức đó?
Ta mong muốn sau khi thêm bớt tử thức với một lượng A(t) nào đó rồi tách ra thành hai phân
thức để nhân liên hợp thì trên tử thức xuất hiện nhân tử 2
t để giản ước với 2 t dưới mẫu 3 3 6t +1 − 4t +1
6t +1 − A(t )
A(t ) − 4t +1 = + . 2 2 2 t t t Vậy ta phải có 2
A (t) −( t + ) 2 4 1 = kt 2  A (t) 2
= kt + 4t +1 k = 4 2 và 2
A (t ) = (2t + )
1  A(t ) = 2t +1.
- Ở nhiều bài toán giới hạn, ta thấy việc sử dụng MTCT là nhanh hơn giải thông thường. Tuy
nhiên chúng tôi vẫn khuyến nghị độc giả nên nắm vững phương pháp giải thông thường (theo
hình thức tự luận), vì nhiều bài tập không chỉ đơn thuần là tính giới hạn mà người ra đề có thể
hỏi bằng nhiều hình thức khác nhau, đặc biệt có nhiều cách ra đề hạn chế việc sử dụng MTCT để tìm ra đáp án. STUDY TIP
Trong nhiều bài toán, không nên chỉ tính giá trị hàm số tại một điểm mà nên tính lại một số điểm
từ lớn đến nhỏ và từ cả hai phía trái, phải của x . 0 2
x − a + 2 x + a +1
Ví dụ 6: Giới hạn của hàm số f (x) ( ) = khi x →1 bằng 3 x −1 a −a − 2 2 − a A. − a . B. . C. . D. . 3 3 3 3 Lời giải 2
x − (a + 2) x + a +1 (x − )
1 ( x − a − ) 1 x − a −1 a Cách 1: lim = lim = lim = − 3 2 x 1 → x −1 x→ ( x − ) 1 ( 2 1 x + x + ) 1 x 1 → x + x + 1 3
Cách 2: (Đặc biệt hóa để sử dụng MTCT) Cho a một giá trị bất kì, chẳng hạn a =1, thì 2 x − 3x + 2 1 a f ( x) 2 x − 3x + 2 =
. Dùng MTCT ta tìm được lim = − = − . 3 x −1 3 x 1 → x −1 3 3 Vậy chọn đáp án A.
Giải thích: phương trình 2
x − (a + 2) x + a +1= 0 có tổng các hệ số bằng 0 nên ta có một nghiệm bằng 1, nghiệm còn lại bằng a +1 . Do đó ta phân tích được 2
x − (a + 2) x + a +1 = ( x − )
1 ( x − a − ) 1 . STUDY TIP
 Nếu đa thức có tổng các hệ số bằng 0 thì đa thức có một nghiệm bằng 1.
 Nếu đa thức có tổng các hệ số của các lũy thừa bậc chẵn bằng tổng các hệ số của lũy thừa bậc
lẻ thì đa thức có một nghiệm bằng 1 − . + ax − Ví dụ 7: 1 1 Giả sử lim
= L . Hệ số a bằng bao nhiêu để L = 3 ? x 0 → 2x A. 6 − . B. 6 . C. 12 − . D. 12 . Lời giải 1+ ax −1 ax a a Cách 1: Ta có lim = lim = lim = x 0 → 2x x 0
→ 2x( 1+ ax + ) 1 x 0 → 2( 1+ ax + ) 1 4 a Vậy = a L . Do đó L = 3 
= 3  a = 12. Đáp án đúng là D. 4 4 1+ ax −1
Cách 2: Sử dụng MTCT tìm lim
lần lượt với a bằng 6 − , 6 , 12 − , 12. Ta thấy với x 0 → 2x 1+ ax −1 a =12 thì lim
bằng 3 . Vậy chọn đáp án D. x 0 → 2x STUDY TIP
Một trong các kĩ thuật giải bài toán trắc nghiệm là thử lần lượt các đáp án và chọn ra đáp án thỏa mãn yêu cầu bài toán.
2. Các bài toán liên quan đến giới hạn đặc biệt 0
Trong sách giáo khoa đại số và giải tích 11 có nêu một giới hạn đặc biệt dạng 0 sin x Đó là lim
=1. Sau đây ta xét một số ví dụ áp dụng kết quả này. x 0 → x ax
Ví dụ 8: Cho a và b là các số thực khác 0. Khi đó lim bằng x 0 → sin bx a b A. a . B. b . C. . D. . b a Lời giải Đáp án C. ax bx a a bx
Cách 1: Ta có lim = lim . = .lim x 0 → x 0 → x 0 sin bx sin bx b b → sin bx bx t
Đổi biến t = bx ta thấy khi x → 0 thì t → 0. Do đó lim = lim =1 x 0 → x 0 sin bx → sin t ax a Vậy lim = . x 0 → sin bx b
Cách 2: Cho a và b các giá trị cụ thể, chẳng hạn a = 2,b = 3 . 2x 2 a
Sử dụng MTCT tìm giới hạn lim
ta được kết quả bằng , tức là bằng . x 0 → sin 3x 3 b Vậy chọn C. STUDY TIP sin x x lim =1 lim =1 x 0 → x 0 x → sin x sin ( A x) lim =1, với điều kiện lim ( A x) = 0 x→0 ( A x) x→0 2 x
Ví dụ 9: Cho số thực a khác 0. Khi đó lim x 0 → 1− bằng cos ax 2 2 A. . B. . C. 2 2a . D. 2a . 2 a a Lời giải Đáp án A
Cách 1: Ta có: 2 2  ax     ax      2 2 x x 2 2 2   = =    2 2  2 2 lim lim lim . = lim  = .1 = . 2 2 2 2 x→0 x→0 − ax ax x→0  ax x→0 1 cos  2 2 a a ax a a 2sin sin  sin    2 2  2   
Cách 2: Cho a là một giá trị cụ thể, chẳng hạn a = 2 (không nên lấy a = 1, vì khi đó giá trị của 2 2 2 x và
cũng bằng nhau). Sử dụng MTCT tính giới hạn lim 2 a a x 0 → 1−
ta được kết quả bằng cos 2x 1 2 , tức là bằng
. Vậy chọn đáp án A. 2 2 a STUDY TIP sink A( x) lim =1 0 k x→ A ( x) điều kiện lim ( A x) = 0 x→0 sin x − sin a Ví dụ 10: lim x→a x − bằng a A. tan a . B. cot a . C. sin a . D. cos a . Lời giải Đáp án D x + a x − ax − a  2cos sin sin sin x − sin ax + a Cách 1: Ta có 2 2 2 lim = lim = lim .cos  x→a x→a x − a x − a x→a x − a 2 2.   2  2  x − a sin x + a Mà 2 lim =1 = a . x→a x − (xem STUDY TIP trên), limcos cos a x a → 2 2 sin x − sin a Vậy lim
= cosa . Do đó chọn đáp án D. x a → x − a sin x − sin1
Cách 2: Sử dụng MTCT tính giới hạn lim a = ). x 1 → x − (ứng với 1 1 sin x − sin1
So sánh kết quả với tan1, cot1,sin1, cos1 ta được lim = cos1 x 1 → x − . 1 Vậy chọn đáp án D. 3. Đọc thêm ax e −1 5
Ví dụ 11: Cho a và b là các số nguyên dương. lim
= . Tích ab có thể nhận giá trị bằng số nào x 0 → sin bx 3
trong các số dưới đây? A. 15. B. 60. C. 240.
D. Cả ba đáp án trên. Lời giải Đáp án D ax e −1 ax
e −1 bx a a a Ta có lim = lim . .  =1.1. = x 0 → x 0 sin bx
→  ax sinbx b b b ax e −1 5 a 5 Vậy để lim
= thì = . Vì a và b là các số nguyên dương nên suy ra a = 5k,b = 3k x 0 → sin bx 3 b 3
với k nguyên dương. Do đó 2 ab = 15k . + 2 2
15k = 15  k = 1  k = 1  ab = 15. + 2 2
15k = 60  k = 4  k = 2  ab = 60. + 2 2
15k = 240  k = 16  k = 4  ab = 240
Vậy cả ba đáp án đều đúng. Do đó chọn đáp án D. STUDY TIP sin x Ngoài giới hạn lim
=1, Sách giáo khoa giải tích 12 nâng cao chương 2, 5 còn giới thiệu x 0 → x thêm các giới hạn: x e −1 lim =1, x→0 x ln (1+ x) lim =1 x→0 x ( 3 ln 1 + x ) −1
Ví dụ 12: Cho hàm số f ( x) =
, trong đó k là một số nguyên dương. Tìm tất cả các giá trị k x
của k để f ( x) có giới hạn hữu hạn khi x dần tới 0.
A. k  , k  3 .
B. k  , 0  k  3.
C. k  , k  3 .
D. k  , 0  k  3. Lời giải Đáp án D ln ( 3 1+ x ) −1  ln( 3 1+ x ) −1  1
Cách 1: Ta có lim = lim .  k 3 k 3 x 0 x 0 xx x − → →    ln ( 3 1 + x ) −1 Mà lim
= 1 nên để f (x) có giới hạn hữu hạn khi x dần tới 0 thì hàm số 3 x→0 x g ( x) 1 =
phải có giới hạn hữu hạn khi x dần tới 0. Muốn vậy thì k − 3  0  k  3 . Vì k k 3 x −
nguyên dương nên đáp án là D. ln ( 3 1 + x ) −1
Cách 2: Sử dụng MTTCT tìm giới hạn khi k = 3, ta được lim = 1. 3 x→0 x
Vậy ta chỉ xét đáp án C hoặc D. Chẳng hạn với đáp án C, ta sử dụng MTCT tìm giới hạn khi ln ( 3 1 + x ) −1 k = 4 . Ta được lim
= − . Do đó loại đáp án C. Vậy đáp án đúng là D. 3 x→0 x
*** Trong chương trình lớp 12 sẽ được học khái niệm căn bậc n. Định nghĩa
Cho số thực b và số nguyên dương n (n  2) . Số a được gọi là căn bậc n của số b nếu n a = b Với n chẵn và:
+b  0: Không tồn tạo căn bậc n của b .
+b = 0: Có một căn bậc n của b là số 0.
+b  0: Có hai căn trái dấu, kí hiệu giá trị dương là n b , còn giá trị âm là n − b
Sau đây ta xét một vài ví dụ liên quan đến căn bậc n. STUDY TIP n n
a = b a = b
-Mọi số thực đều có một căn bậc lẻ và chỉ có một căn bậc lẻ
- Chỉ có số không âm mới có căn bậc chẵn.
Số 0 có một căn bậc chẵn là 0.
Các số dương có hai căn bậc chẵn đối nhau.
Ví dụ 13: Cho a là một số thực khác 0 và n là một số nguyên dương, n  2 . Chọn khẳng định đúng
trong các khẳng định sau. n 1+ ax −1 a n 1+ ax −1 n A. lim = . B. lim = . x 0 → x n x 0 → x a n 1+ ax −1 1 n 1+ ax −1 1 C. lim = . D. lim = . x 0 → x n x 0 → x a Lời giải Đáp án A. 5 1+ 3x −1 3
Cách 1: Sử dụng MTCT tìm giới hạn với n = 5 và a = 3, ta được kết quả lim = x 0 → x 5
vậy đáp án đúng là A. n t − n n 1
Cách 2: Đổi biến đặt t = 1+ ax t = 1+ ax x = a
Ta có khi x → 0 thì t →1 và n 1+ ax −1 t −1 t −1 a = a = a = n x t −1 ( − − − − t − ) 1 ( n 1 n 2 t + t + ...+ t + ) n 1 n 2 1 t + t + ...+ t +1 a a n 1+ ax −1 a Mà lim = lim = . Vậy chọn A. n 1 − n−2 x 1 → t + t +..+ t + nên suy ra 1 n x 0 → x n STUDY TIP n 1+ ax −1 a lim = x 0 → x n n n a b
(a b) ( n 1− n−2 n−2 n 1 a a b ... ab b − − = −  + + + + ) n
a − = (a − ) ( n 1 − n−2 1 1 a + a + ...+ a + ) 1 3 x +1 − x +19 a a Ví dụ 14: Biết lim
= trong đó là phân số tối giản, a và b là các số nguyên dương. → 4 x 8 x + 8 − 2 b b
Tổng a + b bằng A. 137. B. 138. C. 139. D. 140. Lời giải Đáp án C.
Với những bài dạng này, sẽ khó sử dụng MTCT để tìm đáp án đúng.
Đặt t = x −8. Suy ra x = t + 8. limt = 0 và x 8 → t t 3 3 1 + − 3 1+ 3 3 x +1 − x +19 t + 9 − t + 27 9 27 = = 4 4 x + 8 − 2 t +16 − 2 t 4 2 1+ − 2 16 t t 3 1+ −1 1+ −1 9 27 − 3 t t = = g (t) 2 t 4 1 + 16 −1 t 3 x +1 − x +19 Do đó lim
= lim g(t) . Áp dụng ví dụ 13 Ta có: → 4 x 8 t 0 x + 8 − 2 → t 1 t 1 t 1 3 4 1+ −1 1+ −1 1+ −1 9 1 9 27 1 27 16 1 16 lim = = ;lim = = ;lim = = t→0 t→0 t→0 t 2 18 t 3 81 t 4 64 1 1 − 3 112 Vậy 18 81 lim g(t) = . = t→0 2 1 27 64 3 x +1 − x +19 112 Do đó lim =
. Vậy a = 112,b = 27 và a + b = 139 → 4 x 8 x + 8 − 2 27 0
*** Tính giới hạn vô định dạng
bằng đạo hàm (Quy tắc L’Hôpital). 0 STUDY TIP
*Quy tắc L’Hôpital f (x) f '( x0 ) lim = lim . x→ → 0 x g(x) x 0 x g ( x0 )
Trong đó f (x) và g (x) xác định trên khoảng ( ; a b) , x  ; a b 0 ( )
lim f ( x) = lim g ( x) = 0 (Hoặc lim f ( x) = lim g ( x) =  ) x→x x→x x→x x→x 0 0 0 0 f '( x) Và lim tồn tại x→ 0 x g '( x)
Trước khi đọc phần này xin đọc chương đạo hàm trong chương trình lớp 11
Ví dụ 15: Ta xét lại ví dụ 9 đã nêu ở trên. 2 x
Cho số thực a khác 0. Khi đó lim x 0 → 1− bằng cos ax 2 2 A. . B. . C. 2 2a . D. 2a . 2 a a Lời giải Đáp án A
Ngoài hai lời giải đã nêu ở trên ta còn một cách áp dụng Quy tắc L’Hopital như sau: 2 x 2x 2 2 lim = lim = lim = 2 2 x 0 → x 0 → x 0 1− cos ax a sin ax → a cos ax a
Ở đây ta áp dụng Quy tắc L’Hopital 2 lần. Cách sử dụng Quy tắc này rất hữu dụng khi giải các
bài toán trắc nghiệm. Tuy nhiên không áp dụng Quy tắc này cho các bài toán tự luận do Quy tắc
L’Hopital không được trình bày trong chương trình THPT. STUDY TIP
Có thể áp dụng quy tắc L’Hopital nhiều lần để tính giới hạn
Đề nghị: Độc giả hãy vận dụng quy tắc L’Hopital để giải các ví dụ đã nêu ở dạng 2 này.
bài tập dạng trắc nghiệm. Nếu là bài tập dạng tự luận thì các em cần trình bày chi tiết theo
phương pháp đã nêu trên. Riêng A và B, ta giải tự luận như sau: x −1 x −1 1 lim = lim = lim = 0 2 x→+ x −1
x→+ (x −1)(x +1) x→+ x +1 x − 5
( x − 5)( x + 5) lim = lim = lim ( x + 5) = + x→+ x − 5 x→+ x − 5 x→+ 3 x − 3x +1 Ví dụ 16: Giới hạn lim bằng: x→− 5 − 2x 3 A. 0 B. C. + D. − 2 Đáp án D 3 x − 3x +1 1
Cách 1: Theo kết quả đã nêu ở trên thì 2 lim = − lim x = − x→− 5 − 2x 2 x→− Cách 2: Sử dụng MTCT 3 x − 3x +1
Bổ sung: Nếu là bài toán tự luận ‘Tìm lim
” thì ta có hai cách giải như sau: x→− 5 − 2x 1 2 − + 3 x 3 x − 3x +1 1 Cách 1: Ta có lim = lim x . Mà 2
lim (x − 3 + ) = + ; x→− 5 − 2 x x →− 5 − x→− x 2 x 1 2 x − 3 + 5 3 x − 3x +1 lim ( − 2) = 2
−  0 nên theo qui tắc 2, lim = lim x = − x→− x x→− 5 − 2 x x →− 5 − 2 x 3 1 − + 3 1 2 3 x − 3x +1 3 1 5 2 Cách 2 : Ta có lim = lim x x . Mà lim (1− + ) = 1; lim ( − ) = 0 và x→− 5 − 2 x x →− 5 2 2 3 3 2 − x→− x x x →− x x 3 2 x x 3 1  1− + 5 2  3 2 3 x − 3x +1 lim −  0  
với mọi x  0 nên theo qui tắc 2, lim = lim x x = − 3 2 x→−  x x x→− 5 − 2 x x →− 5 2 − 3 2 x x STUDY TIP k a lim k ax x→− Chẵn + +  - -  Lẻ + -  - + 
Ví dụ 17: Trong các giới hạn sau, giới hạn nào bằng − ? 5 3 x + x + 7 2 3 1− 3x − x 3 4 x − 3x + 5 2 6 3x − x lim lim lim lim 3 2 2 3 2
A. x→− 2x − 3x +1 B. x→− 4x +1
C. x→− x − x +1
D. x→− 1+ x − 5x Đáp án C Lời giải
Cách 1 : Theo cách ghi kết quả ở trên thì 5 3 2 3 x + x + 7 1 1− 3x − x 1 2 2 lim = lim x = + ;  lim = − lim x = + ;  3 2 2
x→− 2x − 3x +1 2 x→− x→− 4x +1 4 x→− 3 4 2 6 x − 3x + 5 3x − x 1 4 lim = 3 lim x = − ;  lim = lim x = + ;  3 5 x→− x − x +1 x→−
x→− 1+ x − 5x 5 x→−
Cách 2 : sử dụng MTCT tính lần lượt các giới hạn 3 4 − + Khi đế x 3x 5 n C thấy lim
= 3 lim x = − nên dừng lại và chọn đáp án C 3 x→− x − x +1 x→− 2 4x − x +1 Ví dụ 4 : Giới hạn lim bằng : x→− x +1 A. 2 B. -2 C. 1 D. -1 Đáp án B Lời giải : Cách 1 : 1 1 1 1 1 1 − + − − + − − + 2 x 4 x 4 4 2 2 2 4x − x +1 x x x x x x lim = lim = lim = lim = 2 − x→− x +1 x→− x +1 x→− x +1 x→− 1 1+ x Vậy chọn đáp án B Cách 2 : Sử dụng MTCT 2 2
x − x − 4x +1
Ví dụ 18: Giới hạn lim bằng : x→− 2x + 3 1 1 A. − B. C. − D. + 2 2 Đáp án B Lời giải :
Cách 1 : Theo ví dụ đã trình bày ở dạng 1 thì 2 2
lim ( x − x − 4x +1) = − x→− Ta đưa 2
x ra ngoài căn rồi chia cả tử và mấu cho x. Cụ thể như sau : 1 1 − − + 2 2 x 1 x 4 2
x − x − 4x +1 x x lim = lim x→− 2x + 3 x→− 2x + 3 1 1 1 1
−x 1− + x 4 + − 1− + 4 + 2 2 x x x x 1 = lim == lim = x→− 2x + 3 x→− 3 2 2 + x Vậy đáp án đúng là B −
Cách 2 : Sử dụng máy tính tính giá trị hàm số tại 10 x = 10
ta được kết quả như hình bên. Vậy chọn đáp án B
Cách 3 : Ta có thể giải bài này bằng phương pháp loại trừ như sau : Vì 2 2
lim ( x − x − 4x +1) = − ;
 lim (2x +3) = − nên giới hạn cần tìm phải mang dấu x→− x→−
dương. Mặt khác bậc tử và bậc mẫu bằng nhau nên giới hạn cần tìm là hữu hạn.
Đáp án cần tìm là đáp án B STUDY TIP 2x +1 a
Ví dụ 19: Biết lim x =
trong đó a, b là các số nguyên dương. Giá trị nhỏ nhất của tích 3 2 x→+ 3x + x + 2 b ab bằng : A. 6 B. 12 C. 18 D. 24 Đáp án C Lời giải : 3 2 2x +1 2x + x 6 Ta có : lim x = lim = 3 2 3 2 x→+ 3x + x + 2 x→+ 3x + x + 2 3 Vậy a 6 =
Dễ dàng suy ra được tích của ab là 18. b 3
Chú ý : Nếu sử dụng MTCT tính giá trị hàm số tại 10
x = 10 thì ta thu được kết quả như hình
bên. Do đó, nếu không có kiến thưc về giới hạn hàm số, rất khó tìm ra được đáp án đúng nếu
chỉ dùng MTCT. Ngược lại nếu có kiến thức vững vàng, bạn đọc sẽ nhanh chóng tìm ra đáp án,
thậm chí là trong chớp mắt ! Vì vậy, tôi xin nhắc lại, tôi khuyến nghị các bạn đọc nên giải bài
tập theo kiểu tự luận một cách căn cơ để có thể đối mặt với các bài toán ‘’chống MTCT’’ STUDY TIP
Dạng 4 : Dạng vô định 0.
Bài toán : Tính giới hạn lim [u(x)v(x)] khi lim [u(x)] = 0 và lim [v(x)] =  x→ → → 0 x x 0 x x 0 x 0 Phương pháp u(x)
: Ta có thể biến đổi lim [u(x)v(x)] = lim để đưa về dạng hoặc x→x x→x 1 0 0 0 v(x) u(x)  lim [u(x)v(x)] = lim để đưa về dạng x→x x→x 1  . 0 0 v(x)
Tuy nhiên, trong nhiều bài tập, ta chỉ cần biến đổi đơn giản như đưa biểu thức vào trong/ ra
ngoài dâu căn, quy đồng mẫu thức …. Là đưa được về dạng quen thuộc. 1 1 Ví dụ 20: Giới hạn lim ( −1) − x→0 x x + bằng : 1 A. 0 B. -1 C. 1 D. − Đáp án B 1 1 Phân tích : Ta có lim = − ;  lim( −1) = 0 − − x→0 x→0 x x +
nên chưa có thể áp dụng các định lí, qui tắc để 1 tính giới hạn. Lời giải : 1 1 1− (x +1) −x 1 − Cách 1 : Ta có lim ( −1) = lim = lim = lim = 1 − − − − − x 0 → + x 0 → + x 0 → + x 0 x x 1 x(x 1) x(x 1) → x +1
Cách 2 : Sử dụng MTCT tính giá trị hàm số tại 0
− ,00000001 ta được kết quả như hình bên. Do
đó chọn đáp án B, tức 1 1 lim ( −1) = 1 − − x→0 x x +1 STUDY TIP x Ví dụ 21:
Giới hạn lim (x − 2) bằng : + 2 x→2 x − 4 A. + B. − C. 0 D. 1 Đáp án C x
Phân tích : Vì lim (x − 2) = 0; lim
= + nên chưa có thể áp dụng các định lý và qui tắc + + 2 x→2 x→2 x − 4 để tính giới hạn. Lời giải : 2 x (x − 2) x (x − 2)x
Cách 1 : Với mọi x  2 ta có : (x − 2) = = 2 2 x − 4 x − 4 x + 2 − Do đó x (x 2)x lim (x − 2) = lim = 0. Vậy chọn đáp án C + 2 + x→2 − x→2 x 4 x + 2 Cách 2: Sử dụng MTCT 2x +1 Ví dụ 22: Giới hạn lim (x +1) bằng: 3 x→− 5x + x + 2 2 − 10 − 5 − A. 2 B. 5 C. 5 D. − 2 Đáp án B
Phân tích: Ví dụ tương tự đã được nghiên cứu trong phần dạng vô định  2x +1
Tuy nhiên vì lim (x +1) = − ;  lim = 0 3 x→− x→− 5x + x +
nên giới hạn này cũng có thể coi như dạng 2 0. Lời giải Cách 1: Với x  1 − 2
ta có x +1 0 nên x +1 = − (x +1) . Do đó 2 2x +1 (x +1) (2x +1) 10 lim (x +1) = − lim = − 3 3 x→− 5x + x + 2 x→− 5x + x + 2 5 Vậy chọn đáp án B −
Cách 2: Sử dụng MTCT. Tính giá trị hàm số tại 10 x = 10
ta được kết quả như hình bên. So
sánh các đáp số A, B, C, D ta chọn đáp án đúng là B. STUDY TIP
Ta chỉ quan tâm đến lũy thừa bậc cao nhất là 3 x 2 2 . Hệ số của 2
x trong (x +1) là 1 do (x + )2 2 1
= x + 2x +1. Hệ số của x trong 2x + 1 là 2 nên hệ số của 3 x trên tử là 2 1 .2 . Ở đây
không nhất thiết phải khai triển tích thành đa thức để tìm hệ số của 3 x . 1 Ví dụ 23: Giới hạn lim (xsin ) x→+ bằng x A. 0 B. 1 C. + D. Không tồn tại Đáp án B 1 1 Phân tích: Vì lim
= 0 nên lim sin = 0 . Ta có dạng 0. . Lời giải như sau : x→+ x x→+ x Lời giải : 1 sin 1 x
Cách 1 : Ta có : lim (x sin ) = lim x→+ x x →+ 1 x 1 1 sint Đặt t =
và lim t = 0 thì lim (x sin ) = lim =1 x x→+ x→+ x x →+ t
Cách 2: Sử dụng MTCT ( Lưu ý chuyến máy về chế độ Radian) STUDY TIP 0 s inx
Ở ví dụ 4 ta đã chuyển dạng 0. thành do ta liên tưởng đến giới hạn đặc biệt lim =1 0 x→0 xVí dụ 24: Giới hạn lim ( − x) a t nx bằng  −   2 x→   2  A. 1 B. 0 C. − D. Không tồn tại Đáp án A  s inx Phân tích: vì lim ( − x) = 0; lim a t nx= lim
= + nên ta có dạng 0.  − 2  −  −       cos x x→ x→ x→        2   2   2  Lời giải :   Cách 1 : Đặt t =
− x thì x = −t, lim t = 0 và 2 2  −   x→   2   sin( − t)   2 t (
− x) tan x = t tan( − t) = t = cos t . Do đó 2 2  sin t cos( − t) 2  t lim ( − x) t anx= lim cost = 1   −  2 + t o → sin t x→   2  Cách 2 : Sử dụng MTCT STUDY TIP lim a t nx=+ ;  lim a
t nx=+ . Lưu ý để tránh nhầm lẫn giữa hai giới hạn này  −  +     x→ x→      2   2 
Dạng 5 : Dạng  − 
Bài toán : Tính lim [u(x) − v(x)] khi lim u(x) = + và limv(x) = + Hoặc tính x→ → → 0 x x 0 x x 0 x
lim [u(x) + v(x)] khi lim u(x) = + và limv(x) = − x→ → → 0 x x 0 x x 0 x
Phương pháp : Nhân hoặc chia với biểu thức liên hợp (nếu có căn thức) hoặc qui đồng để đưa
về cùng một phân thức ( nếu chứa nhiều phân thức). + − + →+ ( 2 2 lim x x x 1 bằng x ) Ví dụ 25: Giới hạn 1 1 A. B. C. + D. − 2 4 Đáp án A Lời giải : Cách 1: 2 2 Phân tích: Ta thấy lim x + x = + ;
 lim x +1 = + nên bài này thuộc dạng  −  . Tương x→+ x→+
tự như giới hạn dãy số, ta nhân chia với biểu thưc liên hợp. Lời giải cụ thể như sau: 1 − x − lim x
x + x − x + = = = x→+ ( 1 1 1 2 2 1) Ta có: lim lim x→+ 2 2
x + x + x +1 x→+ 1 1 2 1+ + 1+ 2 x x Cách 2: Sử dụng MTCT + + + →− ( 2 lim 9x x 1 3x bằng x ) Ví dụ 26: Giới hạn 2 2 − 1 1 − 3 3 6 6 A. B. C. D. Đáp án D Lời giải: 2 Phân tích: Ta có lim 9x + x +1 = + ;  lim (3 )
x = − nên bài này thuộc dạng vô x→− x→−
định  −  (mặc dù biểu thức của hàm số lấy giới hạn có hạng tổng). Ta tiến hành nhân chia
với biểu thức liên hợp. Lời giải cụ thể như sau: x +1 x +1 Ta có: lim( 2
9x + x +1 + 3x) = lim = lim 2
9x + x +1 − 3x 1 1 −x 9 + + − 3x 2 x x 1 1+ 1 1 − = lim x = =
. Vậy chọn đáp án D. x→+ 1 1 3 − − 3 6 − 9 + + − 3 2 x x
Cách 2: Sử dụng MTCT tính giá trị hàm số tại 10 x = 10 −
ta được kết quả như hình bên. Sử −
dụng ki thuật tìm dạng phân số của một số thập phân vô hạn tuần hoàn ta được − ( ) 1 0,1 6 = 6
(xem lại phần giới hạn dãy số). Vậy chọn đáp án D. Studytip:
Ví dụ 27. Giới hạn + − + + bằng: →+ ( 2 3 3 2 lim 4x 3x 8x 2x 1 x ) 13 7 13 7 A. B. C. − D. − 24 12 24 12 Lời giải
Cách 1: Phân tích: Vì 2 3 3 2 lim 4x + 3x = + ;
 lim 8x + 2x +1 = + nên đấy cũng là dạng vô định − .  Tuy x→+ x→+
nhiên vì là hiệu của hai căn thức không cùng bậc nên ta chưa thể nhâ chia với biểu thức liên
hợp luôn được. Nhận thấy x  0 thì 2 3 3
4x = 8x = 2x nên ta thêm bớt 2x rồi nhân chia liên hợp. Với x  0 : 2 3 3 2 x + x − x + x + = ( 2
x + x − x)+( 3 3 2 4 3 8 2 1 4 3 2
2x − 8x + 2x +1) 1 2 + 2 3x x = − 2 2
4x + 3x + 2x 2 1  2 1  3 3 4 + 2 8 + + + 8 + +   3 3 x xx x  Do đó + − + + →+ ( 2 3 3 2 lim 4x 3x 8x 2x 1 x )    1  2 + 2  3  3 2 7 = lim x − = − = .   x→+ 2 3 2 + 2 4 + 4 + 4 12  2 1  2 1 4 + + 2   3 3 4 + 2 8 + + + 8 + +    3 3 xx x   x x   Do đó chọn B.
Cách 2: Sử dụng MTCT tính giá trị hàm số tại 10 x = 10 −
ta được kết quả như hình bên. Sử
dụng ki thuật tìm dạng phân số của một số thập phân vô hạn tuần hoàn ta được − ( ) 7 0, 58 3 = . 12
(xem lại phần giới hạn dãy số). Vậy chọn đáp án D. Studytip:
Lưu ý: Ta xem lại một Ví dụ đã trình bày ở dạng 1 như sau:
Ví dụ 28. Giới hạn của hàm số f ( x) 2 2
= x − x − 4x +1 khi x → + bằng: A. − B. + C. 1 − D. 3
Phân tích: Ví dụ này cũng thuộc dạng  −  nhưng lại không phải là dạng vô định. Bằng các
định lí và quy tắc, ta tính được giới hạn hàm số mà không cần phải nhân chia với biểu thức liên
hợp. Ta xem cách giải cho tiết dưới đây. Lời giải  1   1   1   1  2 2 2 2
x − x − 4x +1 = x 1− − x 4 + = x 1− − x 4 +         2 2  x   x   x   x   1 1      = x  1− − 4 +     . 2  x x         1   1 
Ta có lim x = + và lim 1− − 4 + =1− 2 = 1 −  0.     x→+ 2 x→+  x   x      1   1  Vậy lim x − x − x + =  x  − − +      = −   x→+ ( 2 2 4 1) lim 1 4 . 2 x→+   x   x     Studytip:
Cũng là  −  nhưng khi nào là xác định, khi nào là vô định? Khi nào phải nhân chia liên hợp, khi nào thì đưa n
x ra ngoài căn rồi đặt nhân tử chung như Ví dụ 4? Để có câu trả lời mời quý
độc giả hãy đọc lại phần giới hạn dãy số có chứa căn.
Ví dụ 29. Trong các giới hạn sau giới hạn nào là hữu hạn: A. ( 2 lim
4x + 4x + 3 + 2x B.
x + x + − x x→− ( 2 lim 2 1 3 ). →+ ). x C. ( 2
lim x − 1+ x + 2x D.
x + x + x + x→− ( 2 lim 3 2 ). →+ ). x Lời giải
Cách 1: Với các kết quả đã biết phần giới hạn dãy số có chứa căn, ta thấy ngay đáp án là D. Thật vậy: 2 x + x + = + ( x) = +  ( 2 lim 4 4 3 ; lim 2 lim
4x + 4x + 3 + 2x = + →+ →+ →+ ) . x x x 2 x + x + = + (− x) = +  ( 2 lim 2 1 ; lim 3 lim
2x + x +1 − 3x = + →− →− →− ) . x x x  1 1  lim x − + x + x = x  − + +  = −   x→+ ( 2 1 2 ) lim 1 2 2 x→+ x x    1 1  do lim x = + ;  lim 1− + + 2  =1− 2  0.  2  x→+ x→+ x x   2 3 + 3x + 2 3 − lim x
x + x + x + = = = x→− ( 2 3 2 ) lim lim . x→− 2 x + 3x + 2 x − x →− 3 2 2 1+ + −1 2 x x
Cách 2: Sử dụng MTCT để tìm lần lượt các giới hạn.   Ví dụ 1 1 30. Giới hạn lim −   bằng: + 2
x→2  x − 4 x − 2  A. + B. − C. 3 − D. 2 − Lời giải 1 1 Cách 1: Vì lim = + ;  lim
= + nên ta có dạng − .  + 2 + x→2 − x→2 x 4 x − 2
Theo phương pháp đã nêu từ đầu, ta đi quy đồng mẫu số các phân thức.  1 1   1 1  −x −1 Ta có lim − = lim    −  = lim . + 2 + + x 2 →  − − x 2 x 4 x 2 → 
(x − 2)(x + 2) (x − 2) x 2 →  (x−2)(x+2) −x −1 3 − Vì lim =  x −
= và x − 2  0 với mọi x  2 nên theo quy tắc 2, + + x→ (x + 2) 0, lim ( 2) 0 2 x→2 4  1 1  −x −1 lim − = lim = − .    Do đó chọn B + 2 + x→2  − − x→2 x 4 x 2  (x −2)(x + 2)
Cách 2: Sử dụng MTCT tính giá trị hàm số tại x = 2, 00000001 ta được kết quả như hình bên.  
Do đó chọn đáp án B, tứ 1 1 c là lim − = − .    + 2
x→2  x − 4 x − 2 
Ví dụ 31. Cho a và b là các số thực khác 0. Tìm hệ thức liên hệ giữa a và b để giới hạn:  a b  lim −   là hữu hạn: − 2 2
x→2  x − 6x + 8 x − 5x + 6 
A. a − 4b = 0.
B. a − 3b = 0.
C. a − 2b = 0.
D. a − b = 0. Lời giải a b a b Cách 1: Ta có − = − 2 2 x − 6x + 8 x − 5x + 6
(x −2)(x −4) (x −2)(x −3)
a ( x − 3) − b( x − 4) g ( x) = ( =
x − )( x − )( x − )
(x − )(x − )(x − ). 2 3 4 2 3 4
Ta có lim ( x − 2) = 0; lim ( x − 3) = 1 − ; lim (x − 4) = 2
− ; lim g (x) = 2b − . a − − − − x→2 x→2 x→2 x→2
Do đó nếu lim g ( x)  0  2b − a  0 thì giới hạn cần tìm là vô cực theo quy tắc 2. − x→2
Từ đó chọn được đáp án đúng là C.
(Thật vậy, nếu lim g ( x) = 2b − a = 0 thì − x→2 a b bx − 2b b − = = 2 2 x − 6x + 8 x − 5x + 6
(x −2)(x −3)(x −4) (x −3)(x −4)   Và do đó a b b b lim − = lim = .   − 2 2 − x→2  − + − + x→2 x 6x 8 x 5x 6 
(x −3)(x −4) 2
Cách 2: Sử dụng MTCT. Với mỗi đáp án, lấy các giá trị cụ thể của a và b , thay vào hàm số rồi tính giới hạn.
Từ đó chọn được đáp án là C.
C. BÀI TẬP RÈN LUYỆN KỸ NĂNG
DẠNG 1. BÀI TẬP TÍNH GIỚI HẠN BẰNG CÁCH SỦ DỤNG ĐỊNH NGHĨA, ĐỊNH LÍ VÀ CÁC QUY TẮC. Câu 1:
Tìm tất cả các giá trị của tham số thực m để B  7 với B = lim( 3 2
x + 3x + m − 2m). x 1 →
A. m  1hoặc m  3 B. m  1
− hoặc m  3 C. 1 −  m  3
D. 1 m  3. 2  x +1  khi x  1 Câu 2:
Cho hàm số f ( x) =  1− x
. Khi đó lim f ( x) bằng:  − x 1 →
2x − 2 khi x  1  A. 0 B. 2 C. − D. + Câu 3:
Trong các hầm số sau, hàm số nào có giới hạn tại điểm x =1? A. f ( x) 1 = B. g ( x) 1 = C. h( x) 1 = D. t ( x) 1 = x −1 x −1 1− x x − 1 Câu 4:
Chọn khẳng định đúng. 1 1 1 1 A. lim cos = 0 B. lim cos = 1 − C. lim cos =1 D. lim cos không tồn x→0 x x→0 x x→0 x x→0 x tại. Câu 5:
Trong các giới hạn sau, giới hạn nào bằng −? A. ( 3 2
lim 5x − x + x + ) 1 . B. ( 4 lim 2x + 3x + ) 1 . x→+ x→− C. ( 2 3
lim 4x − 7x + 2). D. ( 5
lim 3x − x + 2). x→+ x→− Câu 6:
Trong các giới hạn sau, giới hạn nào bằng −? A. ( 2 lim
4x + 4x + 3 + 2x B.
x + x + − x x→− ( 2 lim 4 4 3 2 ). →+ ). x C. ( 2 lim
4x + 4x + 3 − x D. x − x + x + x→+ ( 2 lim 4 4 3). →+ ). x Câu 7:
Trong các giới hạn sau, giới hạn nào bằng +? 2 6 − x 1− 2x 3 5 − 3x 3 2x − 4 A. lim . B. lim . lim . D. lim + − 4 2 x ( → 3 − ) 9 + 3x x ( → − ) 1 5 + C. 5x
x→−2 ( x − 2) x→−1 ( x + ) 1 Câu 8:
Trong các giới hạn sau, giới hạn nào là vô cực? 2 x − x +1 3 2 x + 2x A. 3 lim . lim . 2 x→2 x + B. 2x + x (
→ − ) (x − x + 6)2 2 2 2 9x − x 2 x (2x − ) 1 C. lim D. lim . − 4 x→ (2x − ) 1 ( . 4 3 x − 3) x 1 → x + x +1 Câu 9:
Trong các giới hạn sau, giới hạn nào là vô cực? 3 − (x −2)3 +8 A. lim . B. lim . x→− 2
5x + x + 2 + 4x x→0 x 2
x + x + 2 − 3 − x 5 C. lim . lim . − 3 3 x ( → − ) 4 1 x + D. x
x→− 4x − x + 2
Câu 10: Tìm tất cả các giá trị của tham số thực m sao cho hàm số f ( x) 2
= mx + 9x − 3x +1 có giới hạn
hữu hạn khi x → + .  A. m = 3 − B. m  3 − C. m  0 D. m  0 0
DẠNG 2. GIỚI HẠN VÔ ĐỊNH DẠNG . 0 3x + 6 lim
Câu 11: Giới hạn x 2 →− x + 2 A. Bằng 3 B. Bằng 3 − C. Bằng 0 D. không tồn tại 4 4 x − a
Câu 12: Cho a là một số thực khác 0. Kết quả đúng của lim bằng: x a → x − a A. 3 3a B. 3 2a C. 3 a D. 3 4a 2
x − mx + m −1
Câu 13: Cho C = lim
, m là tham số thực. Tìm m để C = 2. 2 x 1 → x −1 A. m = 2 B. m = 2 − C. m = 1 D. m = 1 − 2
x + ax + b
Câu 14: Cho a và b là các số thực khác 0. Nếu lim
= 6 thì a + b bằng: x 2 → x − 2 A. 2 B. 4 − C. 6 − D. 8 1− ax +1
Câu 15: Cho a và b là các số thực khác 0. Giới hạn lim bằng: x 0 → sin bx a a 2a 2a A. B. − C. D. − 2b 2b b b
Câu 16: Cho a, ,
b c là các số thực khác 0, 3b − 2c  0. Tìm hệ thức liên hệ giữa a, b, c để: tan ax 1 lim = . → 3 x 0 1+ bx − 1+ cx 2 a 1 a 1 a 1 a 1 A. = = = = 3b − B. 2c 10 3b − C. 2c 6 3b − D. 2c 2 3b − 2c 12 sin ( x − ) 1
Câu 17: Cho m và n là các số nguyên dương phân biệt. Giới hạn lim bằng: 1 m n x→ x − x 1 1
A. m− n
B. n − m C. D. m − n n − m
5x − 4 − 2x −1
Câu 18: Để tính giới hạn lim
, bạn Bính đã trình bày bài giải như sau: x 1 → x −1 Bước 1: Ta có:
5x − 4 − 2x −1 5x − 4 −1 2x −1 −1 lim = lim − lim . x 1 → x 1 → x 1 x −1 x −1 → x −1 5x − 4 −1 5( x − ) 1 Bướ 5 5 c 2: lim = lim = lim = . x 1 → x 1 x −1 → (x − )
1 ( 5x − 4 + ) x 1 1 → 5x − 4 +1 2 2x −1 −1 2( x − ) 1 Bướ 2 c 3: lim = lim = lim =1. x 1 → x 1 x −1 → (x − )
1 ( 2x −1 + ) x 1 1 → 2x −1 +1 − − − Bướ 5x 4 2x 1 5 3 c 4: lim = −1= . x 1 → x −1 2 2
Hỏi lời giải của bạn Bính đã mắc lỗi sai ở bước nào? A. Bước 1. B. Bước 2. C. Bước 3. D. Bước 4.
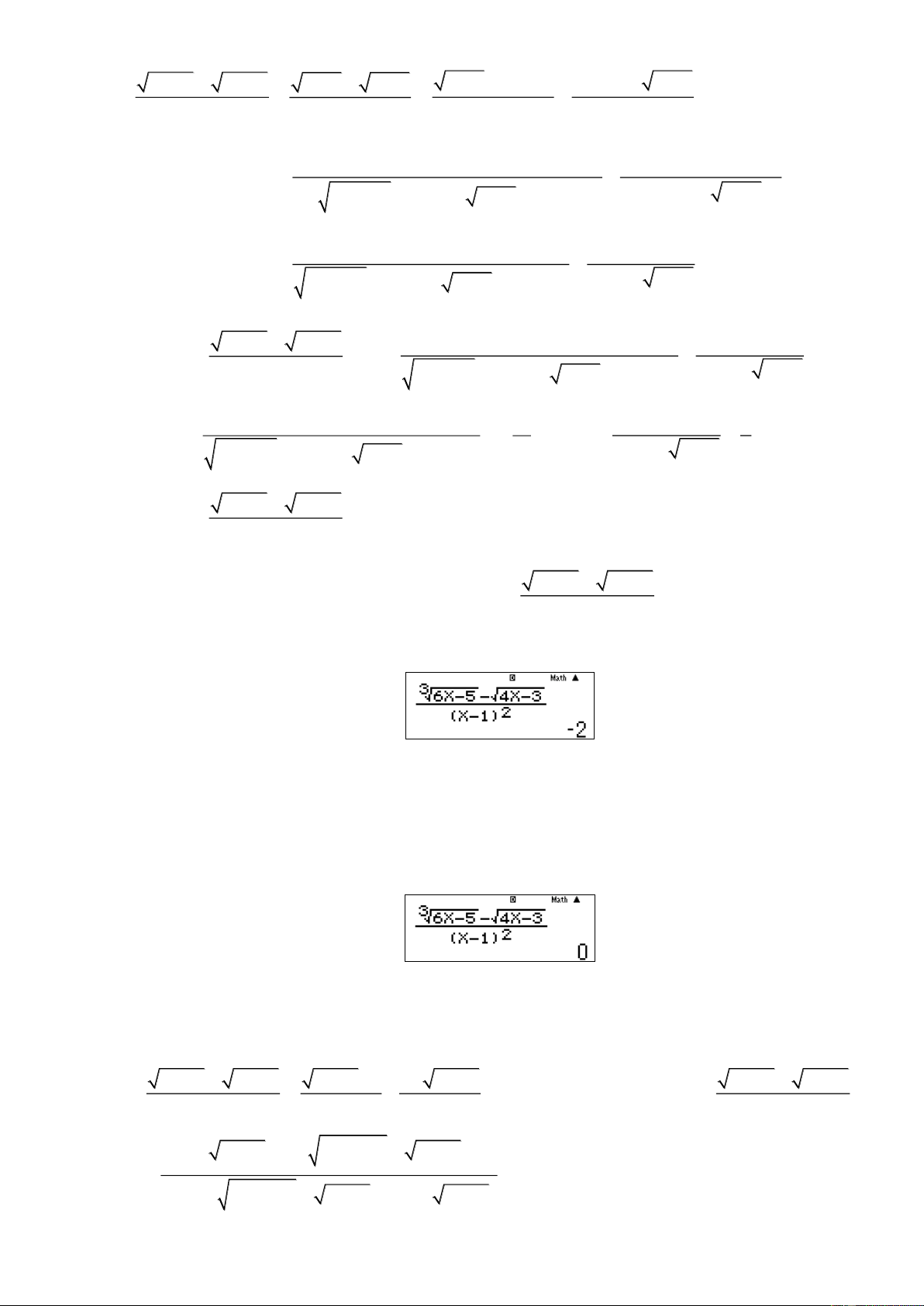
3 8x +11 − x + 7 m Câu 19: Biết lim
= trong đó m là phân số tối giản, m và n là các số nguyên dương. 2 x→2 x − 3x + 2 n n
Tổng 2m + n bằng: A. 68 B. 69 C. 70 D. 71 3
6x − 9 − 27x − 54 m Câu 20: Biết lim =
trong đó m là phân số tối giản, m và n là các số nguyên x→ (x− ) 3 ( , 2 3 x + 3x −18) n n
dương. Khi đó 3m + n bằng: A. 55 B. 56 C. 57 D. 58 3
3x − 2 − 5x − 4
Câu 21: Giới hạn lim bằng: + x→ (x− )2 1 1 A. − B. + C. 0 D. 1
Câu 22: Trong bốn giới hạn sau đây, giới hạn nào bằng 0? (x − x−6)2 2 x −1 2 x −1 2 −x − x + 6 A. lim . lim . C. lim . lim . 3 x 1 → x − B. 1 + 2 3 2 x ( → − ) 2 2 x − 3x + 2 x 3 →− x + D. 3x x 2 →− x + 2x
Câu 23: Trong bốn giới hạn sau đây, giới hạn nào khác 0? 2 x − 3x + 2 2 x − 9 A. lim . B. lim . − − x→2 2 − x x 3 →
( 2x + )1(3− x) 2 x − 3x + 2 3 x −1 C. lim . D. lim . − + x→(− ) 2 1 x + 2x +1 → 2 x 1 x −1
Câu 24: Trong bốn giới hạn sau đây, giới hạn nào không tồn tại? 3 x + 8 (x +3)3 −27 2 4 3x + x x x + 2 A. lim . B. lim . C. lim . D. lim . 2 x 2
→− x +11x +18 x→0 x x→0 2x + x ( → − ) 2 2 x + 3x + 2
Câu 25: Trong các giới hạn sau đây, giới hạn nào không hữu hạn? 2 2x + x −10 2 x − 4x + 3 x − 2 1− x − 2 A. lim . B. lim . C. lim . D. lim . − 3 + 2 + − 2 x 2 → x − 8 x 3 → x − 6x + 9 → 2 x 2 x + 5 − 3 x 3 → x − 9 
DẠNG 3. GIỚI HẠN VÔ ĐỊNH DẠNG . 
Câu 26: Trong bốn giới hạn sau đây, giới hạn nào bằng 1 − ? 2 x −1 3 2 x − x + 3 2x + 3 2 2x + x −1 A. lim . B. lim . C. lim . D. lim . 2 x→− x +1 2 3 x→+ 5x − x
x→− x − 5x 2 x→+ 3x + x
Câu 27: Trong các giới hạn hữu hạn sau đây, giới hạn nào là lớn nhất? (x + ) 1 ( 3
3 − 2x − 5x ) ( 2 2x + ) 1 ( 2 2x + x) A. lim B. lim . x→+ x ( . 3 x − ) 1 x→− ( 4
2x + x)( x + ) 1 ( 2x + )1( 2 2x − x + 4) ( 2 3x + ) 1 ( 3 2 − x ) C. lim . D. lim . 3 x→− x (3x + ) 1 x→+ ( 4
2x + x)( x + ) 1
Câu 28: Trong các giới hạn sau đây, giới hạn nào là − ? 2 2 − x + x −1 2 3x + x + 5 3 2 1− 3x + x 2 4 3x − x +1 A. lim . B. lim . C. lim . D. lim . x→− 3 + x x→− 1+ 2x 2
x→+ 5 + x − 2x 2 x→− 2 − x − x 2
x + 2x + 3x
Câu 29: Tính giới hạn lim . x→− 2 4x +1 − x + 2 1 2 2 1 A. . B. . C. − . D. − . 2 3 3 2
Câu 30: Cho a ,b , c là các số thực khác 0 . Tìm hệ thức liên hệ giữa a ,b , c để 2
ax − b 9x + 2 lim = 5 . x→− cx +1 a − 3b a − 3b a + 3b a + 3b A. = 5. B. = −5. C. = 5. D. = −5. c c c c 2 4x + 3x +1 
Câu 31: Cho a và b là các tham số thực . Biết rằng lim − 
(ax +b) = 0,a  và b thỏa mãn x→+  cx +1 
hệ thức nào trong các hệ thức dưới đây ?
A. a + b = 9.
B. a + b = 9. −
C. a − b = 9.
D. a − b = 9. −
Câu 32: Trong các giới hạn sau , giới hạn nào là − ? 4 2x − x −1 2 x − 5x + 2 A. lim . B. lim 2
x→− x + x + 2 x→− 1+ . 2 x 5 x + x −11 3 3 2 x + 2x +1 C. lim . D. lim . 2 x→+ 2x + x +1 x→− 1− 2x
Câu 33: Tìm giới hạn nhỏ nhất trong các giới hạn hữu hạn sau. 6 x + 2 2 2x − x A. lim . B. 3 lim 3 2
x→− 3x −1 x→− 8x − x + . 3 x x 2 x + 3 C. lim . D. lim . 2
x→+ x − x + 2 x→− 2 x + x + 5
Câu 34: Trong các giới hạn hữu hạn sau , giới hạn nào là lớn nhất?
(2x −5)(1− x)2 (2x − ) 2 1 x − 3 A. 3 lim lim 3 x→+ 3x − x + . B. 1 2 x→− x − . 5x 4 2 x + x + 2 3 − 2 x C. lim . D. lim . x→+
( 3x + )1(3x− )1 x→− 2 x +1 − x
Câu 35: Trong các giới hạn hữu hạn sau , giới hạn nào là nhỏ nhất? 2
x − x + 2x x A. lim lim 1− 2x . x→− 3 − . B. ( ) 4 x 3 x→− x −1 2 2
x − x − 4x +1 4 5 3x + 4x + 2 C. lim . D. lim 5 4 x→− 2x + 3 x→+ 9x + 5x + . 4
DẠNG 4. GIỚI HẠN VÔ ĐỊNH DẠNG 0. .  1 1  1
Câu 36: Cho a là một số thực dương. Tính giới hạn lim −   .
x→a x
a  ( x − a)2 1 A. bằng − . B. là +. C. là − . D. không tồn tại. 2 a
Câu 37: Trong các giới hạn sau , giới hạn nào là hữu hạn ? x 3x A. lim ( x + ) 3 1 lim x +1 . 4 2 x→+
2x + x + . B. ( ) 1 2 x→+ x −1 x −1 x C. lim ( x + 2) 2 lim x +1 3 x→+ x + . D. ( ) x 4 x→+ 2x + x + . 1
Câu 38: Trong các giới hạn hữu hạn sau , giới hạn nào là nhỏ nhất? 2x +1 3x −11 A. lim ( x + ) 1 lim 1− 2x 3 x→− x + x + . B. ( ) 2 3 x→+ x + . 1 x x +1 C. lim − lim 2 − 3x . + ( 3 x )1 2 3 x 1 → x − . D. ( ) 1 x→− 5x + 2x +1  x + 2 x + 3 
Câu 39: Tính giới hạn 2 3 lim x  −    . x→+ x x   1 A. . B. 0. C. +. D. − 2   
Câu 40: Tính giới hạn lim tan 2x tan − x   . x→  4  4 1 1 A. 2 . B. 0. C. . D. 2 4
DẠNG 5. DẠNG VÔ ĐỊNH  −  . n 1 
Câu 41: Cho n là một số nguyên dương. Tính giới hạn lim −   . 1 → 1 n x − x 1− x n n −1 n +1 n + 2 A. . B. . C. . D. 2 2 2 2  1 3  − khi x  1
Câu 42: Cho hàm số f ( x) 3
=  x −1 x −1
. Với giá trị nào của m thì hàm số f ( x) có giới hạn mx + 2 khi x  1 tại điểm x =1 A. 2. B. -1. C. 1. D. 3 1 k
Câu 43: Tìm tất cả các giá trị của tham số thực k sao cho giới hạn lim( − ) là hữu hạn. 2 x 1 → x −1 x −1 A. k = 2 .
B. k  2 . C. k  2 . D. k  2 .
Câu 44: Trong các giới hạn sau đây, giới hạn nào là 1 − ? A. 2
lim ( x + 2x − ) x . B. 2 lim ( x + 2x + ) x . x→− x→− C. 2
lim( x + 2x + x) . D. 2
lim ( x + 2x − ) x . →+ x→+ x Câu 45: Giới hạn 2
lim ( x − 3x + 5+ax) = + nếu. x→− A. a 1 . B. a 1 . C. a 1. D. a 1 .
Câu 46: Cho a và b là các số thực khác 0 . Biết 2
lim (ax − x + bx + 2) = 3 , thì tổng a + b bằng x→+ A. 2 . B. 6 − . C. 7 . D. 5 − .
Câu 47: Cho a và b là các số thực khác 0 . Biết 2
lim (ax+b- x − 6x + 2) = 5 số lớn hơn trong hai số x→+
a và b là số nào trong các số dưới đây? A. 4 . B. 3 . C. 2 . D. 1.
Câu 48: Trong các giới hạn dưới đây, giới hạn nào là vô cực? A. 2 2
lim ( 2x + x − 2x + 3) . B. 2
lim ( 4x + x +1 + 2x) . x→− x→− C. 2
lim ( 9x + 3x +1 + 5 ) x . D. 2 2
lim ( 3x +1 − 3x + 5x) . x→− x→− m Câu 49: Biết 2 3 3 2
lim ( 9x + 2x + 27x + 4x + 5) = −
trong đó m là phân số tối giản, m và n là các x→− n n
số nguyên dương. Tìm bội số chung nhỏ nhất của m và n . A. 135 .
B. 136 . C. 138 . D. 140 . 7
Câu 50: Cho a và b là các số nguyên dương. Biết 2 3 3 2
lim ( 9x + ax + 27x + bx + 5) =
, hỏi a và b x→− 27
thỏa mãn hệ thức nào dưới đây?
A. a + 2b = 33 .
B. a + 2b = 34 .
C. a + 2b = 35 .
D. a + 2b = 36 .
D. HƯỚNG DẪN GIẢI CHI TIẾT
DẠNG 1. BÀI TẬP TÍNH GIỚI HẠN BẰNG CÁCH SỬ DỤNG ĐỊNH NGHĨA, ĐỊNH LÝ VÀ CÁC QUI TẮC. Câu 1. Đáp án B. B = lim ( 2 x + 3 2
x + m − 2m) Cách 1: Ta có 2
= m − 2m + 4 . x→ 1 − Do đó B  7  2
m − 2m + 4  7  m  1 − hay m  3 .
Cách 2: Sử dụng MTCT tính B khi m = 4 và m = 0 .
Khi m = 4 thì B = 12  7 , do đó chỉ xét A và B.
Khi m = 0 thì B = 4  7 , do đó A sai vậy B đúng. Câu 2. Đáp án D. x2 +1
Cách 1: Ta có lim f (x) = lim . − − x − → 1 x − → 1 1− x lim ( 2 x + ) Vì 1 = ;
2 lim (1− x) = 0 và 1− x  ; 0 x  1 − − x→ 1 − x→ 1 − x2 +1
nên theo quy tắc 2: lim f (x) = lim = +. − − x − → 1 x − → 1 1− x x2 +1
Cách 2: Ta có lim f (x) = lim . − − x − → 1 x − → 1 1− x
Sử dụng MTCT tính giá trị hàm số tại x = 99 , 0
999999 ta được kết quả 199999998. Vậy chọn D. Câu 3. Đáp án A. 1
Vì lim x −1 = 0 , x −1  ,
0 x  1nên lim f (x) = lim = + . x 1 → x→1 x→1 x −1 Giải thích thêm: 1
+ Hàm số g(x) =
xác định trên khoảng ( ;
1 +) nên không tồn tại giới hạn bên trái tại x = 1 x −1
, do đó không tồn tại giới hạn tại x = 1. 1
+ Hàm số h(x) =
xác định trên khoảng (−  ) 1
; nên không tồn tại giới hạn bên phải tại 1− x
x = 1, do đó không tồn tại giới hạn tại x = 1. + Vì lim (x − ) 1 = 0 , x −1  ,
0 x  1, x −1  , 0 x  1 x 1 → 1 1 nên lim t( ) x = lim = − , lim ( t ) x = lim = + . − − + +− x→1 x→1 x −1 x→1 x→1 x −1 Vậy lim ( t ) x  lim ( t )
x nên không tồn tại lim ( t ) x . − + x→1 x→1 x→1 Câu 4. Đáp án D. 1 1
Xét dãy số (x với x =
. Ta có x → 0 và lim cos = lim cos (2n + ) 1   = 1 − (1). n ) n (2n + )1 n xn 1 1
Lại xét dãy số (y với x =
. Ta có y → 0 và lim cos = lim co ( s 2  n ) = 1 (2) n ) n 2nn yn 1
Từ (1) và (2) suy ra lim cos không tồn tại. x→0 x Câu 5. Đáp án C. 3 2 4 Cách 1: Ta có lim 5
( x − x + x + )
1 = + , lim (2x + 3x + ) 1 = + ; x→ + x→ − lim (4 2 x − 7 3 x + ) 2 = − 5 ; lim 3 ( x − x + ) 2 = + . x→ + x→ −
Cách 2: Sử dụng MTCT tính lần lượt các giới hạn cho đến khi tìm được giới hạn bằng −  . Câu 6. Đáp án D. Cách 1: Ta có
lim ( 4x2 + 4x + 3 − 2x)
lim ( 4x2 + 4x + 3 + 2x) + = +, = + x→ + x→ − lim ( 4 2
x + 4x + 3 − x)  4 3  + = lim x 4 + + −1 = + x→ + x→ +  2   x x  Do đó lim (x − 4 2
x + 4x + 3)= −. x→ +
Cách 2: Sử dụng MTCT tính lần lượt các giới hạn cho đến khi tìm được giới hạn bằng −  . Câu 7. Đáp án C. lim (6 2 − x ) Cách 1: Ta có = 3
−  0 ; lim (9 + 3x) = 0 và 9 + 3x  , 0 x  3 − . + + x→ 3 − x→ 3 − 6 − x2 Vậy theo quy tắc 2, lim = −. + x − → 3 9 + 3x 1− 2x 5 − 3 3x 3 2x − 4 Tương tự: lim = −; lim = ; lim = . − 2 2 x→ −1 5 + 5x x→−2 (x + 2)
+ x→−1 (x+ ) − 1
Do đó đáp án đúng là C ( Thật ra ta chỉ cần tính đến C là chọn được đáp án đúng).
Cách 2: Sử dụng MTCT tính lần lượt các giới hạn cho đến khi tìm được giới hạn bằng +  . Câu 8. Đáp án B.
Cách 1: Các hàm số trong A, C, D đều xác định tại các điểm điểm tính giới hạn. Do đó đáp án là B. 3 x + 2 2x
Thật vậy, ta tính được bằng MTCT: lim .
x→−2 (x − x − 6) = + 2 2
Cách 2: Sử dụng MTCT tính lần lượt các giới hạn cho đến khi tìm được giới hạn vô cực. Câu 9. Đáp án C Cách 1: Ta có lim ( 2
x + x + 2 − 3 − x) = 2 − 2 0 ; − x ( → − ) 1 lim ( 4 x + x) = 0 ; ( 4 x + ) x = ( 3 x x + ) 1  , 0 x  1 − . − x→(− ) 1
x2 + x + 2 − 3 − Vậy x lim = − − 4 x→(− ) 1 x + x Bổ sung: − 3 2 1 2
+ lim ( 5x + x + 2 + 4x) = lim x(− 5 + + + ) 4 = − nên lim = 0 . x→− x→− 2 x x x→− 5 2
x + x + 2 + 4x (x − 2)3 +8 3 x − 6 2 x +12x − 8 + 8 + lim = lim = lim( 2 x − 6x + ) 12 = 12 . x 0 → x 0 → x 0 → x x 3 2 5
+ lim (4x − x + ) 2 = −  lim = 0 . x→− x→− 4 3 2 x − x + 2
Cách 2: Sử dụng MTCT tính lần lượt các giới hạn cho đến khi tìm được giới hạn vô cực. Câu 10. Đáp án A 2 1
Cách 1: Sử dụng MTCT tính toán khi m = 3
− ta được kết quả lim ( 3
− x + 9x − 3x +1) = − x→+ 2
. Vậy ta chỉ xét các đáp án A và D.
Lại sử dụng MTCT tính toán khi m = 1
− ta được kết quả lim (−x + 9 2 x − 3x + ) 1 = +. Vậy x + →
loại đáp án D. Do đó đáp án đúng là A.
Cách 2: lim f ( )
x = lim (mx + 9 2 x − 3x + ) 1 . x + → x + →
+ Nếu m  0 thì lim f ( )
x = lim (mx + 9 2 x − 3x + ) 1 = +. x + → x + →  3 1  + Nếu  2 
m  0 thì lim  mx + 9x − 3x +1  = lim xm + 9 − +   . 2  x→+   x→+ xx   3 1  Ta thấy nếu m  3
− thì lim m + 9 − +   2 
0 và do đó lim (mx + 9x − 3x + ) 1 =  . 2  x→+ xx x + → Ngược lại nếu 2 1 m = 3 − thì lim ( 3
− x + 9x − 3x +1) = − . Vậy đáp án đúng là A. x→+ 2
DẠNG 2. GIỚI HẠN VÔ ĐỊNH DẠNG 0 . 0 Câu 11. Đáp án D. 3x + 6 (3x + 2) 3x + 6 − ( 3 x + 2) Ta có lim = lim = 3 và lim = lim = 3 − . + + − − x ( → 2 − ) x + 2 x ( → 2 − ) x + 2 x ( → 2 − ) x + 2 x ( → 2 − ) x + 2 3x + 6 3x + 6 3x + 6 Vậy lim  lim nên lim không tồn tại. − + x ( → 2 − ) x + 2 x ( → 2 − ) x + 2 x→ 2 − x + 2 Câu 12. Đáp án D. 4 3 2 2 3 x − a
(x − a)(x + x a + xa + a ) Cách 1: Ta có 3 2 2 3 3 lim = lim
= lim(x + xa + x a + a ) = 4a . x a → x − a x a → x − a x a →
Cách 2: Cho a một giá trị cụ thể rồi tính giới hạn bằng máy tính cầm tay. Chẳng han với 4 4 x − 2 a = 2 3 ta có lim
= 32 = 4.2 . Do đó chọn đáp án D. x→a x − 2 Câu 13. Đáp án B. 2
x − mx + m −1 (x − )( 1 x − m + ) 1 x − m +1 2 − m Cách 1: C = lim = lim = lim = 2 x 1 → x −1 x 1 → (x − )( 1 x + ) 1 x 1 → x +1 2
Vậy C = 2  m = 2 − .
Cách 2: Thay lần lượt các giá trị của m vào, rồi tìm C cho đến khi gặp kết quả C = 2 thì dừng lại. Câu 14. Đáp án C Đặt g(x) g(x = x2 )
+ ax + b. Rõ ràng là nếu ( g ) 2  0 thì lim
không thể hữu hạn. Do đó điều x→2 x − 2 kiện đầu tiên là ( g )
2 = 0  2a + b = −4 . Khi đó b g(x) b b
g(x) = (x − )( 2 x − ) và lim
= lim(x − ) = 2 − . 2 x→2 x − 2 x→2 2 2 Vậy g(x) b lim
= 6 2 − = 6  b = 8
−  a = 2  a + b = − . 6 x→2 x − 2 2 Câu 15. Đáp án B. 1− ax +1 1− ax +1 bx 1 Cách 1: lim = lim( . . ) . x→0 sin bx x→0 x sin bx b 1− ax +1 −a bx 1− ax + b − a Mà lim = ; lim = 1 nên lim = ; x→0 sin bx 2 x→0 sin bx x 0 → sin bx 2b
Cách 2: Cho a và b các giá trị cụ thể, thay vào rồi tính giới han. Chẳng hạn với a = b = 1, sử − + dụng MTCT ta tính được 1 x 1 1 lim
= . Từ đó chọn đáp án đúng là B. x 0 → sin x 2 Câu 16. Đáp án D. tan ax tan ax x Cách 1: = . a . 3 3 1+ x b − 1+ x c ax 1+ bx − 1+ cx tan ax sin ax 1 Lại có lim = lim( . ) = 1 x→0 x→0 ax ax cosax 3 1+ x b − 1+ x c 3 1+ x b −1 1+ x c −1 b c b − c lim = lim( − 3 2 ) = − = x 0 → x x 0 → x x 2 3 6 tan ax 6a Vậy lim = . → 3 x 0 1+ x b − 1+ x c 3b − 2c 6a 1 a 1
Do đó hệ thức liên hệ giữa a,b,c là =  = 3b − 2c 2 3b − 2c 12
Cách 2: Sử dụng MTCT. Với mỗi đáp án, chọn các giá trị cụ thể của a, b, c thỏa mãn hệ thức 1
rồi thay vào để tính giới hạn. Nếu giới hạn tìm được bằng
thì đó là đáp án đúng. 2
Chẳng hạn, với đáp án A, chọn a = 1;b = 4;c = 1, sử dụng MTCT tính được tan x 3 lim = . → 3 x 0 1+ 4x − 1+ x 5
Vậy A không phải là đáp án đúng.
Tương tự vậy B và C cũng không phải là đáp án đúng. Vậy đáp án đúng là D. Câu 17. Đáp án C. si n(x −1) s in(x-1) x −1 Cách 1: Ta có = = m n x − x x −1 m n x − x m n x − x si n(x −1) si n(x −1) 1 Mà lim = m − n lim =1 lim = m n x 1 → x − ; 1 x 1 → x − nên 1 x 1 → x − x m − n
Cách 2: Cho m và n các giá trị cụ thể, thay vào rồi sử dụng MTCT tính giới hạn. Chẳng hạn với si n(x −1) 1 1
m = 3; n = 1ta tính được lim = = 3 x 1 → x − x 2 m − . n Vậy đáp án đúng là C Câu 18. Đáp án A. − − − −
Vì ta chưa thể biết được các giới hạn 5x 4 1 2x 4 1 lim lim x 1 → x − ; 1 x 1 → x − có hữu hạn hay không 1 − − − − − − − nên chưa thể 5x 4 2x 1 5x 4 1 2x 4 1 viết được: lim = lim −lim x 1 → x −1 x 1 → x −1 x 1 → x − 1
Do đó lời giải đã mắc lỗi sai ngay ở bước đầu tiên. Ta sửa lại như sau: − − − − − − − Bướ 5x 4 2x 1 5x 4 1 2x 1 1 c 1: Ta có lim = lim( − ) x 1 → x −1 x 1 → x −1 x − 1 Câu 19. Đáp án A. 3 8x +11 − x+7 3 8x +11 − 3 x + 7 − 3 Ta có = − 2 x − 3x + 2 2 2 x − 3x + 2 x − 3x + 2 x − 2 x − 2 = − 2 3 3
(x − 2)(x −1)( (8x +11) + 3 8 +11 + 9)
(x − 2)(x −1)( x + 7 + 3) 8 1 = − 2 3 3
(x −1)( (8x +11) + 3 8 +11 + 9)
(x −1)( x + 7 + 3) 8 8 1 1 Ta có lim = ; lim = x→2 2 3 3 − + + + + 27 (x 1)( (8x 11) 3 8 11 9)
x→2 (x −1)( x + 7 + 3) 6 3 + − Do đó 8x 11 x+7 8 1 7 lim = − = 2 x→2 x − 3x + 2 27 6 54
Vậy m = 7; n = 54 và 2m + n = 68. Câu 20. Đáp án C. 3 6x − 9 − 27x-54 3 6x − 9 − 27x-54 Ta có = 2
(x − 3)(x + 3x-18) 2 (x − 3) (x + 6)
Sử dụng MTCT ta tính được: 3 6x − 9 − 27x-54 1 1 1 lim = lim = 2 x 3 → (x − ; 3) 6 x→3 x + 6 9 3 6x − 9 − 27x-54 1 nên lim = m + n = . 2 x 3
→ (x − 3)(x + . Vậy 3 57 3x-18) 54
Giải tự luận: Đặt t = x − 3thì lim t = 0 và x→3 3 6x − 9 − 27x-54 3 6t + 9 − 27t+27 3 + − + + − + = 6t 9 (t 3) (t 3) 27t 27 = + 2 (x − 3) 2 t 2 2 t t t − 2 t3 + t2 = + 9 t2 ( t 6 + 9 + t + 3) 2  2 3 3 2  t
(t +3) +(t +3) 27t +27 + (27t +27)     −1 t + = 9 ( + t 6 + 9 + t + 3) ( 2
t + 3) + (t + 3) 3 27t + 27 + 3 (27t + 27)2 −1 1 t + 9 1 Ta có lim = − =
t→0 ( t + +t + ) ; lim 6 t→0 ( 2 3 6 9 3
t + 3) + (t + 3) 3 27t + 27 + 3 (27t + 27)2
6x − 9 − 3 27x − 54 −1 1 1 Vậy lim = + = . x→ ( 2 3 6 3 6 x − 3) 1 1
6x −9 − 3 27x −54 1 Mặt khác lim = nên lim = . x→3 x + 6 9 x→3 ( 2 54
x − 3) (x2 + 3x −18)
Lưu ý: Nếu sử dụng MTCT tính giá trị hàm số tại x = 3,00000001 và tại x = 2,99999999 ta
đều thu được kết quả bằng 0 hoặc máy báo lỗi ( tùy theo loại máy). Điều này là do vượt quá
khả năng tính toán của máy. Ta thay đổi tính giá trị của hàm số tại x = 2,99999 thì ta được kết quả như sau
Kết quả hiển thị trên máy như vậy rất khó để ta tìm ra giới hạn chính xác của hàm số. Tuy
nhiên nếu phân tích kĩ một chút rồi biến đổi như trong lời giải trên thì ta vẫn có thể tìm ra đáp án đúng chỉ bằng MTCT. Câu 21. Đáp án A
Bài tập này có dạng tương tự như bài tập trên. Bằng MTCT, không khó để tìm ra đáp án đúng là
A. Tuy nhiên nếu giải tự luận thì có một số vấn đề cần bàn. Đặt t = x −1 thì x = t + , 1 lim = 0 + x→1 và
3x −2 − 3 5x − 4 t 3 +1 − 3 t 5 +1 t 3 +1 −1 1 − 3 t 5 + = = + 1 ( 2 2 2 2 x −1) t t t = t 3 t 5 t2 ( t 3 +1 +1) + 2  2 t 1+ 3 t 5 +1 + 3 ( t 5 +1)     2  31+ 3 t 5 +1 + 3 ( t 5 +1)  −5( t 3 +1 +1)   =  2  t ( t 3 +1 +1)1+ 3 t 5 +1 + 3 ( t 5 +1)     2  31+ 3 t 5 +1 + 3 ( t 5 +1)  −5( t 3 +1 +1)   Ta có lim = = − + t→0  2  t ( t 3 +1 +1)1+ 3 t 5 +1 + 3 ( t 5 +1)   
3x −2 − 2 5x − 4 Vậy lim = − .  + 2 x→1 (x−1)
Ta thấy sau khi đổi biến cho gọn, ta thêm bớt tử với hàng số 1 rồi tách ra thành hai phân thức
và nhân chia liên hợp mà không thêm bớt đa thức. Vậy khi nào thì thêm bớt hằng số, khi nào
thì thêm bớt với đa thức? Quý độc giả hãy nghiên cứu kĩ hai bài tập trên và tự rút ra nhận xét. Câu 22. Đáp án D ( 2 x2 − x − 6) ( 2 2 2 x − 3) (x + 2) (x−3) (x+2) Ta có lim = lim = = 0 →− x3 + 2x2 →− x2 (x + 2) lim . x x x→− x2 2 2 2 Câu 23. Đáp án C x2 + 3x + 2 x2 + 3x + 2 x2 + 3x + 2 (x+ )1(x+2) lim = lim = lim = lim − − − − 2 2 +1 +1 x ( → − ) 1 + 2 +1 x ( → − ) 1 (x+ ) x 1 ( → − ) 1 x x x x ( → − ) 1 (x )
= − lim (x+2) = −1  . 0 − x ( → − ) 1 Câu 24. Đáp án C 3x2 + x4 −x 3 + x2 3 3x2 + x4 x 3 + x2 3 Ta có lim = lim = − và lim = lim = − − + + x→0 2x x→0 2x 2 x→0 2x x→0 2x 2 3x2 + x4 3x2 + x4 3x2 + x4 Vậy lim  lim nên lim không tồn tại. − + x→0 2x x→0 2x x→0 2x Câu 25. Đáp án B x2 − 4x + 3 (x−1)(x−3) x −1 lim = lim = lim = + .  + 2 + 2 + x→3 − 6 + 9 x→3 ( −3) x→3 x x x − 3 x
DẠNG 3. GIỚI HẠN VÔ ĐỊNH DẠNG .  Câu 26. Đáp án B x2 −1 x3 − x2 + 3 + lim = −; + lim = − ; 1 x→− x + 1
x→+ 5x2 − x3 2x + 3 2x2 + x −1 + lim = ; 0 + lim = ; 2 x→− 2 x2 − 5x x→+ 3x + x Câu 27. Đáp án C
(x+ )1(3−2x−5x3)
(2x2+ )1(2x2+x) + lim = −5 + lim = . 0 →+ x(x3 − ) . x 1
x→− (2x4 + x)(x + ) 1
(x2+ )1(2x2−x+4) (3x2+ )1(2−x3) 2 3 + lim = + lim = − . →− x3 (3x + ) . x 1 3
x→− ( x4 + x)(x+ ) 2 2 1 Câu 28. Đáp án B − x2 2 + x −1 x2 3 + x +1 + lim = + .  + lim = − .  x→− 3 + x x→− 1+ 2x 1 − 3x3 + x2 3x2 − x4 +1 + lim = . + + lim = . +
x→+ 5 + x − 2x2
x→− 2 − x − x2 Câu 29. Đáp án C 2 2 2 −x 1+ + 3x 1+ + 3
x + 2x + 3x −1+ 3 2 lim = lim x = lim x = = − x→− 2 x→− 1 x 1 2 −2 −1 3 4x +1 − x →− + 2 −x 4 + − x +2 4 + −1+ 2 2 x x x Câu 30. Đáp án C 2 2 ax + bx 9 + a + b 9 +
ax − b 9x2 + 2 x2 x2 a + b 3 Ta có lim = lim = lim = . x→− cx +1 x→− cx +1 x→− 1 c c + x − 2 9 + 2 + 3 Do đó ax b x a b lim = 5  = . 5 x→− cx +1 c Câu 31. Đáp án Ax2 4 3x  + +1  11  lim 
−(ax + b) = lim (4x+5)+ − (ax + b) .  x→  x +  2  x→  x + 2    2  4 + 3 +1 Do đó x x lim 
−(ax + b) = 0  a = 4;b = −5  a −b = . 9 x→  x +  2  Câu 32. Đáp án D 2 2 2 x4 − x −1 x − 5x + 2 x − 5x + 2 + lim = . + + lim = lim = + .
x→− x2 + x + 2 x→− 1+ 2 x x→− 1−2x 3 x5 + x −11 x3 + x2 2 +1 + lim = + .  + lim = − . 
x→+ x2 + x + 2 x→ 1−2x Câu 33. Đáp án D − 2 x3 1+ x6 + 6 2 1 + lim = lim x = − . Ta có x→− 3 3 −1 x x →− 3x3 −1 3 2x − x2 2x − x2 1 1 lim 3 = 3 lim = 3 − = − . x→− 2 8 − + 3 x x x
→− 8x2 − x + 3 8 2 x x + lim = . 0
x→− x2 − x + 2 2 x + 3 2 x + 3 + lim = lim = . 2 x→+ 2 x x + x →+ + 1 5 5 x 1+ + x x2 Câu 34. Đáp án B ( 2
2x − 5)(1− x) 2 + lim 3 = 3 . x→+ 3x3 − x +1 3 3 (2 − ) 2 (2x− )1 x 1− x 1 x − 3 2 2 + lim = lim x = . x→− − 2 5 x x x →− x − 5x2 5 3 − 2 x 3 −2 x + lim = lim = . 1 x→− 2 x x + − x →− 1 1 x 1+ − x x2 Câu 35. Đáp án A 1 2 −x 1− +2x
x − x + 2x 1 + lim = lim x = . x→− 3 − 4 x x→− 3 + 4 x 4 2 x 1− 2x x + (1−2x) ( ) lim = lim
= 2 (do − x  , x   1 1 2 0 ). x→− 3 −1 x x →− x3 −1 2 3x4 + 4x5 +2 2 + lim = . x→+ 9x5 + 5x4 + 4 3
DẠNG 4. GIỚI HẠN VÔ ĐỊNH DẠNG . 0 .  Câu 36. Đáp án D  1 1  1 a − x 1 −1 Cách 1: Ta có − = =    x a  ( 2 2 − x − a) .
ax (x −a) ax(x a) .  1 1  1 −1 Do đó lim − = = +   −  x a  ( − → − x − 2 a) lim → ax(x a) ; x a x a  1 1  1 −1 lim − = = −   +  x a  ( + → − x − 2 a) lim → ax(x a) ; x a x a  1 1  1  1 1  1  1 1  1 Vậy lim −  −     nên lim −   không tồn tại. − →  x a  ( − ) lim 2 + 2 x a x a →  x a x a  (x−a)
x→a x a  (x − 2 a)
Cách 2: Cho a một giá trị cụ thể, chẳng hạn a = ,
1 thay vào hàm số rồi sử dụng MTCT để tính
giới hạn. Từ đó ta tìm được đáp án đúng là D. Câu 37. Đáp án C 3 3 2 x x x + 1 + (x+1) ( ) lim = lim = + .  x→+ 4 2 + 2 +1 x x x
→+ 2x4 + x2 +1 2 3x 3x x +1 + (x+1) ( ) lim = lim = + .  x→+ 2 −1 x x →+ x2 −1 2 x −1 x + 2 x −1 + (x+2) ( ) ( ) lim = lim = . 1 x→+ 3 + x x x →+ x3 + x 2 x x2 + 1 2 x + (x + ) ( ) lim 1 = lim = + .  x→+ 4 2 + 2 +1 x x x
→+ 2x4 + x2 +1 Câu 38. Đáp án B 2 2x +1 2x +1 x +1 + (x+1) ( )( ) lim = lim = − 2. x→− 3 + +2 x x x →+ x3 + x + 2 2 3x −11 3x −11 1−2x + (1−2x) ( )( ) lim = lim = −2 3. x→+ 2 +1 x x →+ x2 + 1 + 3 x 2 x 2 x lim (x −1) = lim 1 1 1 1 0 2
(x +x+ )(x− )
= lim (x + x+ ) (x− ) = . x→+ −1 x x →+ x −1 x + 1 x→+ x + 1 x +1 x +1 2 − 3x 3 5 + (2−3x) ( )( ) lim = lim = . x→− 3 5 +2 +1 x x x →− 5x3 + 2x +1 5 Câu 39. Đáp án A Cách 1: Sử dụng MTCT. 1
Cách 2: Đặt t = 1 thì x = , lim t = 0 và x t x→+  3 3 2 x + 2 x + 3  1+ t 2 − 1+ t 3 1+ t 2 − (t + ) 1 (t + )1− 1+ t3 x  −  = = +  x x    t2 t2 t2 −1 t + = + 3 1+ t 2 + (t +1) ( 2 2
t + 1) + (t +1) 3 1+ t 3 + 3 (1+ t 3 ) Do đó    2 x + 2 x + 3   −1 t + 3  lim x  −  = lim +     x→+ x x t→0 1+ t 2 + (t +    )1 ( 2 2 t + ) 1 + (t + ) 3 1 1+ t 3 + 3 (1+ t 3 )    Câu 40. Đáp án C Cách 1: Sử dụng MTCT. π π Cách 2: Đặt t =
− x thì x = − t, lim t = 0 và 4 4 →π x 4  π   π   π  tan2x tan − x = tan2 −t tant = tan −      t 2 tant  4   4   2  = 2 2 2 t 2
t = cos t sin t = t sin t cos t cot tan . . . . sin t 2 cost sin t 2 t 2cost   2 2 1 Do đó π t sin t cos t : lim tan 2x tan − x = lim . . =   . π  4  t→0 sin t 2 t 2cost 2 x→ 4
DẠNG 5. DẠNG VÔ ĐỊNH − .  Câu 41. Đáp án B
Cách 1: Sử dụng MTCT tính giới hạn với một giá trị cụ thể của n rooif so sánh với đáp án.  3 1 
Chẳng hạn n = 3 ta có lim − =   . 1 x→  1− 3 1 1− x x  2 − n − 1
(1+x+x +... n + x 1 2 − n
) 1−x+1−x +... n +1− x 1 Cách 2: − = = n 1− 1− n n x x 1− x 1− x 1+ ( 2 2 −
1+ x) + (1+ x+ x )+....+1+ x+ x +... n + x 2 = 2 − 1+ x + x + ... n + x 1  1  −1 Do đó n n lim − =   . → n x 1 1 − 1− x x  2  1  −1 Lưu ý n n : lim − =   . → n x 1 1 − 1− x x  2 Câu 42. Đáp án B  1 3   3 1 
Theo câu 41, ta có lim f (x) = lim − = lim − =     . 1 + + 3 + 3 x→1 x→1  x −1 −1  x→1  −1 x x x −1
Lại có lim f (x) = lim (mx + 2) = m + .
2 Để f (x) có giới hạn tại điểm x = 1 thì − − x→1 x→1
lim f (x) = lim f (x)  m + 2 = 1  m = − . 1 − + x→1 x→1 Câu 43. Đáp án A 1 k x +1− k Ta có − =
. Mà lim (x +1− k) = 2 − k; lim (x2 − ) 1 = 0 nên để x −1 x2 −1 x2 −1 → x 1 → x 1  1 k  lim − 
 là hữu hạn thì điều kiện cần là 2 − k = 0  k = . 2
x→  x −1 x2 1 −1  1 2 x −1 1  1 k  1 1
Thật vậy, khi k = 2, − = = . Nên lim − = lim =   . x − 2 1 − 2 1 −1 x 2 x x +1 x→1 x −1 −1  x→1 x x +1 2  1  Lưu ý k : lim − 
 hữu hạn  k = . n →1 −1 n x x x −1  Câu 44. Đáp án B
Cách 1: Sử dụng MTCT tính lần lượt các giới hạn. Đến ý B ta được giới hạn bằng 1 − . Vậy đáp án đúng là B.
Cách 2: Ta thấy ngay A và C là các giới hạn vô cực, B và D là dạng vô định − .  Ta xét giới hạn ở ý B.  2  2x
lim  x + 2x − x = = − .
1 Vậy đáp án là B. x→−   − 2 x 1+ −1 x Bổ sung:  2   2 
+ lim  x + 2x − x = + + lim  x + 2x + x = + x→−   x→+    2  2x 2
+ lim  x + 2x − x = lim = lim = . 1 x→+   x→+ 2 x x + x + x →+ + 2 2 1 +1 x Câu 45. Đáp án D
Cách 1: Sử dụng MTCT tính giới hạn khi a = 1 va` a = 0 , ta được  2  3
lim  x − 3x + 5 + x = ; lim
x2 − 3x + 5 = + .
 Từ đó suy ra đáp án đúng là D x→−   2 x→−  3 5   2 
Cách 2: lim  x − 3x + 5 + ax = lim xa − 1− + .  2  x→−   x→− xx   2 
Vì lim = − nên để lim  x − 3x + 5 + ax = + thì a −1  0  a  . 1 x→− x→−   Câu 46. Đáp án D  2 b 2   
Ta có lim  ax − x + bx + 2  = lim xa − 1+ + .  2  x→+   x→+ xx  Do đó  2 
nếu a  1 thì lim  ax − x + bx + 2  = .  Vậy a = . 1 Khi đó x→+    2  −bx −2 b
lim  x − x + bx + 2  = lim = − . x→+   x→+ 2
x + x2 + bx + 2 b Vậy: −
= 3  b = −6. Do đó a + b = − . 5 2 Câu 47. Đáp án C  6 2   2 
lim  ax + b − x − 6x + 2  = lim xa − 1− +  + . b  2  x→+   x→+ xx  Do đó  2 
nếu a  1 thì lim  ax + b − x − 6x + 2  = .  Vậy a = . 1 Khi đó ta có x→+    2  6x −2 6
lim  x + b − x − 6x + 2  = lim
+ b = + b = b + . 3 x→+   x→+ 2
x + x2 − 6x + 2 Vậy: b − + 3 = 5  b = .
2 DO đó số lớn hơn trong hai số a và b là số 2. Chọn đáp án C. Câu 48. Đáp án C
Cả bốn giới hạn đều có dạng  −  , tuy nhiên chỉ có giới hạn ở ý C, hệ số trong hai số hạng là
khác nhau.Theo kết quả đã biết thì giới hạn ở ý C chắc chắn là − . Do đó đáp án đúng là C, Thật vậy:  2 2  x − 3 x − + 3 1 2
lim  2x + x − 2x + 3  = lim = lim = − = − . x→−   x→− 2 2 x  2 2 3 1 3  2 2 4 x + x + x →− + −x 2 + + 2 +   x x     2  x +1 x + + 1 1
lim  4x + x +1 + 2x = lim = lim = − . x→−   x→− 2 x  4 1 2 1 1  4
x + x + − x
→− −x 4+ + +2  x 2   x   3 1   2 
+ lim  9x + 3x +1 +5x = lim x− 9+ + + 5 = − .   2  x→−   x→− xx   2 2  1− 5x 1− 5x + 5 5 3
lim  3x +1 − 3x + 5x  = lim = lim = = . x→−   x→− 2 2 x  3 1 3 5 1 5  2 3 6 x + + x + x
→− −x 3+ + 3+   2 x   xCâu 49. Đáp án A
Cách 1: Sử dụng MTCT tính giá trị hàm số tại x = − 10 10 ta được kết quả
Áp dụng kĩ thuật tìm dạng phân số của số thập phân vô hạn tuần hoàn ta có ,( ) = 5 0 185 . Vậy 27 m = 5 . n 27
Từ đó chọn đáp án đúng là A. 2 3 3 2  2   3 3 2 
Cách 2: 9x + 2x + 27x + 4x + 5 =  9x + 2x + 3x +  27x + 4x + 5 − 3x     2x 4x2 + = − 5 .
9x2 + 2x − 3x 3 ( 2 3 2 3
27x + 4x + 5) +3x 27x3 +4x2 +5 +9x2  2 3 3 2  2 4 5
Suy ra lim  9x + 2x + 27x + 4x + 5  = + = − . x→−   −6 9 + 9 + 9 27
Từ đó chọn đáp án đúng là A. Câu 50. Đáp án B  2 3 3 2  −a b b 2 − a 9
Làm tương tự như câu 49, ta có: lim  9x + ax + 27x + bx + 5  = + = . x→−   6 27 54 Do đó b 2 − a 9 =1 .
4 Suy ra a là số chẵn. Vậy a + b
2 là số chẵn. Từ đó loại được đáp án A và C. a + 2b = 34 Giải hệ  được a = ; 2 b = 1 . 6 b 2 − 9a =  14 a + 2b = 36 Giải hệ 
được a = 11 (loại). b 2 − 9a =  14 5 Vậy B là đáp án đúng.
_______________ TOANMATH.com _______________