










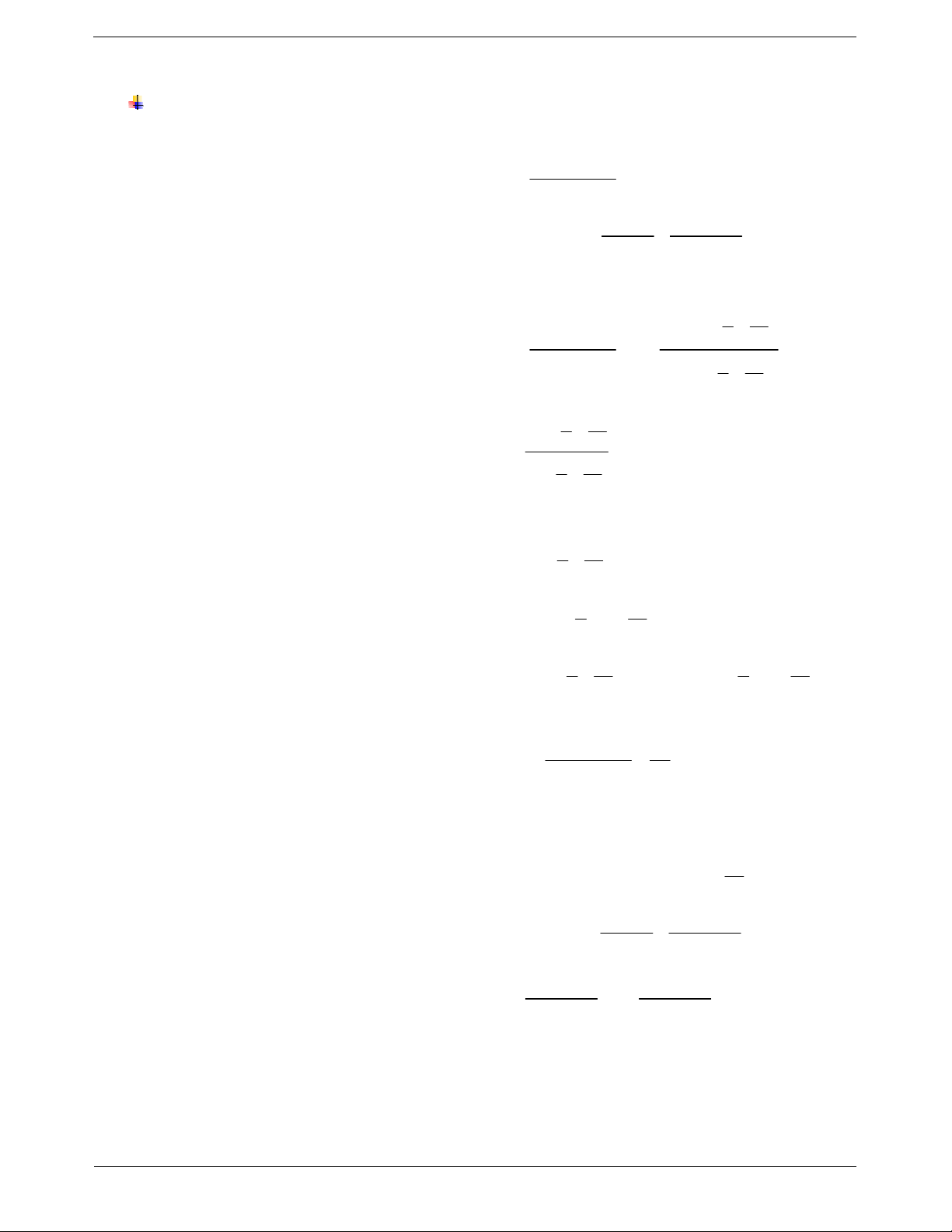
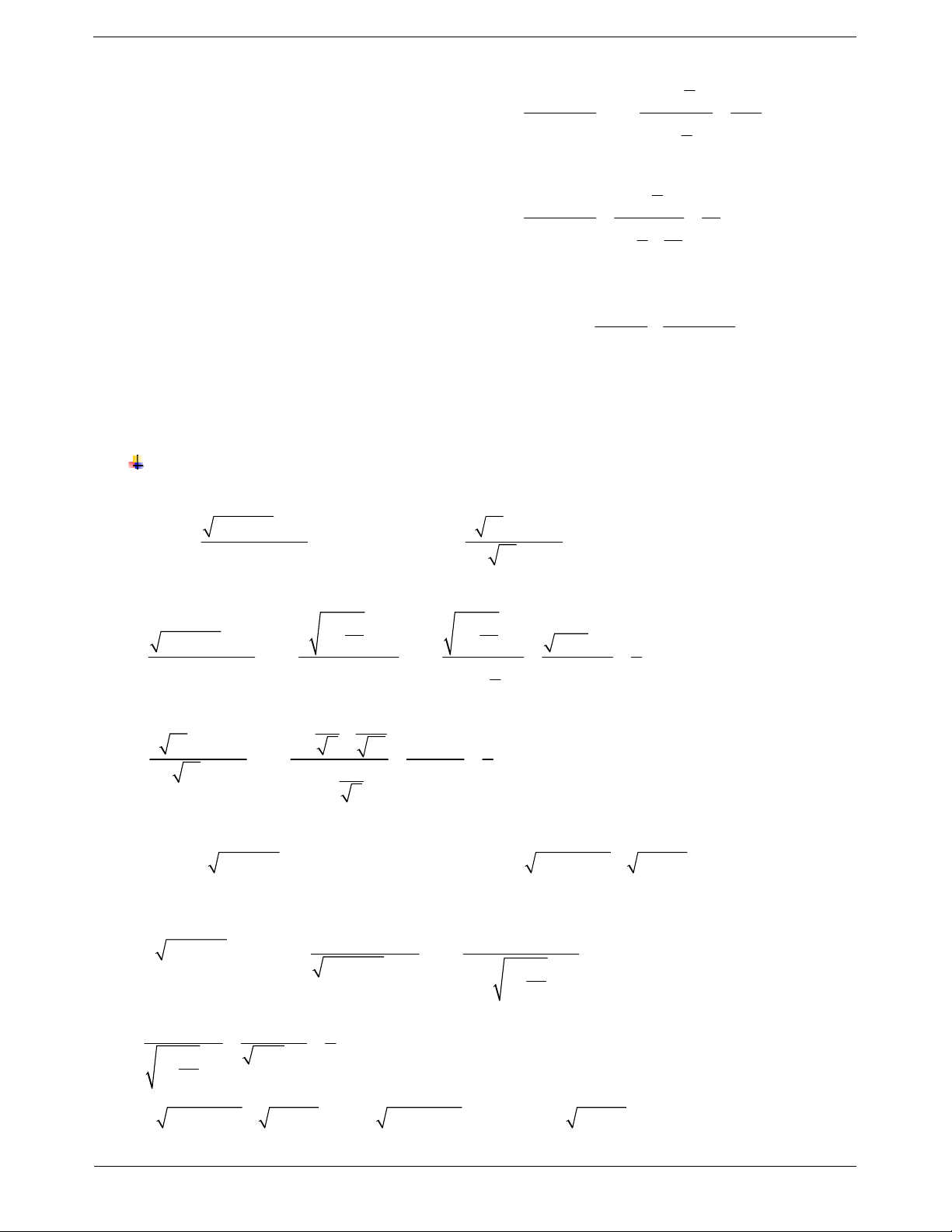









Preview text:
GIỚI HẠN
BÀI GIẢNG GIỚI HẠN DÃY SỐ Mục tiêu Kiến thức
+ Hiểu được khái niệm giới hạn của dãy số.
+ Biết được một số định lí giới hạn của dãy số, cấp số nhân lùi vô hạn. Kĩ năng
+ Áp dụng khái niệm giới hạn dãy số, định lí về giới hạn của dãy số vào giải các bài tập.
+ Biết cách tính giới hạn của dãy số.
+ Biết cách tính tổng của một cấp số nhân lùi vô hạn. Trang 1
I. LÍ THUYẾT TRỌNG TÂM
1. Định nghĩa dãy số có giới hạn 9
1.1. Định nghĩa: Ta có nói rằng dãy số u có giới Nhận xét: n
hạn 0 (hay có giới hạn là 0) nếu với mỗi số dương a) Dãy số u có giới hạn 0 khi và chỉ khi dãy số n
nhỏ tùy ý cho trước, mọi số hạng của dãy số, kể từ u có giới hạn 0. n
một số hạng nào đó trở đi, đều có giá trị tuyệt đối b) Dãy số không đổi u , với u 0 có giới hạn n nhỏ hơn số dương đó. n 0.
Khi đó ta viết: lim u 0 hoặc u 0. n n
(Kí hiệu “ lim u 0 ”, đọc là dãy số u có giới n n n
hạn là 0 khi n dần đến vô cực).
1.2. Một số dãy số có giới hạn 0 thường gặp
Dựa vào định nghĩa, người ta chứng minh được rằng: 1 a) lim 0; n 1 b) lim 0; n 1 c) lim 0; 3 n
d) Dãy số không đổi u với 0
u có giới hạn 0. n n
e) Nếu q 1 thì lim n q 0.
Định lí sau đây thường được sử dụng để chứng minh
một số dãy số có giới hạn 0.
Cho hai dãy số u và v . n n
Nếu u v với mọi n và lim v 0 thì limu 0. n n n n
2. Dãy số có giới hạn hữu hạn Nhận xét:
2.1. Định nghĩa dãy số có giới hạn hữu hạn
- Dãy số u c ó giới hạn là số thực L, khi và chỉ n
Định nghĩa: Ta nói rằng dãy số u có giới hạn là n
khi khoảng cách từ điểm u đến điểm L là u L n n
số thực L nếu lim u L 0. n
gần 0 bao nhiêu cũng được miễn là chọn n đủ
Khi đó ta viết lim u L hoặc . u L
lớn. Tức là khi biểu diễn các số hạng trên trục số n n
Tức là lim u L limu L 0.
ta thấy khi n tăng thì các điểm u tụ tại quanh n n n
2.2. Các định lý cơ bản về giới hạn hàm số điểm L.
- Có những dãy số không có giới hạn hữu hạn.
Định lí 1: Giả sử lim u . L Khi đó: n TOANMATH.com Trang 2
lim u L và 3 3 u L . 1 n n n
Chẳng hạn dãy số , tức là dãy số: Nếu * u 0, n
thì L 0 và lim u L. n n 1; 1; 1 ;1;...
Định lí 2: Giả sử lim u ;
L lim v M và c là một - Nếu C là hằng số thì lim C C. n n hằng số. Khi đó
lim u v L M. limu v L M n n . n n
lim u .v .
L M . lim cu cL n . n n u L lim n (nếu M 0 ). v M n
Định lí 3 (Nguyên lí kẹp giữa): Cho ba dãy số
u ,v , w và số thực L. Nếu u v w với n n n n n n
mọi n và lim u lim w L thì lim v . L n n n Định lí 4:
Một dãy số tăng và bị chặn trên thì có giới hạn.
Một dãy số giảm và bị chặn dưới thì có giới hạn.
2.3. Tổng của cấp số nhân lùi vô hạn
Khái niệm: Cấp số nhân gọi là lùi vô hạn nếu có
công bội q thỏa mãn điều kiện q 1.
Tổng các số hạng: u 2 3 1
S u u u ... u u q u q u q ... , 1 2 3 1 1 1 1 1 q q 1.
3. Dãy số có giới hạn vô cực
Nhận xét: Nếu lim u thì lim u n . n
3.1. Định nghĩa dãy số có giới hạn vô cực Chú ý: Định nghĩa:
Các dãy số có giới hạn là hoặc được
Ta nói rằng dãy số u có giới hạn là nếu với n
gọi chung là các dãy số có giới hạn vô cực hay
mỗi số dương tùy ý cho trước, mọi số hạng của dãy dần đến vô cực.
số, kể từ một số hạng nào đó trở đi, đều lớn hơn số Dãy số có giới hạn là số thực L được gọi là dãy dương đó.
số có giới hạn hữu hạn.
Khi đó ta viết lim u hoặc . u Nhận xét: n n
Ta nói rằng dãy số u có giới hạn là nếu với Từ định nghĩa, ta có kết quả sau: n
a) lim n .
mỗi số âm tùy ý cho trước, mọi số hạng của dãy số,
b) lim n . TOANMATH.com Trang 3
kể từ một số hạn nào đó trở đi, đều nhỏ hơn số âm c) 3 lim n . đó. d) lim k
n k 0.
Khi đó ta viết lim u hoặc u . n n e) lim n
q q 1 . 1
Định lí: Nếu lim u thì lim 0. n un
3.2. Một vài quy tắc tìm giới hạn vô cực Quy tắc 1
Nếu lim u ;
lim v thì limu .v . n n n n
Nếu limu ;
lim v thì limu .v n n . n n
Nếu lim u ;
lim v thì limu .v n n . n n
Nếu limu ;
lim v thì limu .v n n . n n Quy tắc 2
Nếu limu ;
lim v L 0 n n khi L thì u v n n 0 lim . . khi L 0
Nếu lim u ;
lim v L 0 n n khi L thì u v n n 0 lim . . khi L 0 Quy tắc 3
Nếu lim u L 0 , lim v 0 thì n n u
khi v 0, n
Khi lim u L 0 lim n n . n v
khi v 0, n n n u
khi v 0, n
Khi limu L 0 lim n n . n v
khi v 0, n n n
3.3. Một số kết quả Mở rộng: n q n n q k n a) lim và lim 0, với q 1. Ta có lim và lim
0 , với q 1 và k n n q k n n q
b) Cho hai dãy số u và v ,
là một số nguyên dương. n n
Nếu u v với mọi n và lim u thì n n n lim v . n u
Nếu lim u L và lim v thì lim n 0. n n vn TOANMATH.com Trang 4
Nếu lim u (hoặc ) và lim u L thì n n
lim u v (hoặc ). n n
SƠ ĐỒ HỆ THỐNG HÓA DÃY SỐ Định nghĩa
Dãy số u có giới hạn 0 nếu với mọi n CÓ GIỚI HẠN 0
số dương nhỏ tùy ý cho trước, mọi số
hạng của dãy số, kể từ một số hạng nào
đó trở đi, đều có giá trị tuyệt đôi nhỏ hơn số dương đó. 1 lim 0k 0 k n Trường hợp lim n
q 0 với q 1 thường gặp
Cho hai dãy số u và v n n u v n n limu 0 lim v 0 n n TOANMATH.com Trang 5 Dãy số có giới hạn Định nghĩa
Dãy số u có giới hạn là số thực L nếu n hữu hạn
lim u L 0 n
lim u v L M n n
lim u .v . L M n n Phép tính giới hạn
lim cu cL n u L Các định lí lim n M 0 v M n
Cho ba dãy số u ,v , w n n n Nguyên lí u v w Nếu n n n kẹp giữa
lim u lim w L n n
Thì lim v L n
Tổng của cấp số u 2 3 1
S u u q u q q q ... q 1 1 1 1 1 nhân lùi vô hạn 1 q TOANMATH.com Trang 6 Dãy số
Dãy số u có giới hạn là nếu với mỗi số dương tùy ý cho n có giới hạn vô cực
trước, mọi số hạng của dãy kể từ một số hạng nào đó trở đi, đều lớn hơn số dương đó. Định nghĩa
Dãy số u có giới hạn là nếu với mỗi số âm tùy ý cho trước, n
mọi số hạng của dãy kể từ một số hạng nào đó trở đi, đều nhỏ hơn số âm đó. 1
lim u , lim v lim u .v n n n n
lim u , lim v lim u .v n n n n
lim u ,lim v lim u .v n n n n
lim u , lim v lim u .v n n n n 2 lim u khi L 0 n
limu .v n n .
lim v L 0 khi L 0 n Định nghĩa lim u khi L 0 n
limu .v n n .
lim v L 0 khi L 0 n 3 u
khi v 0, n
lim u L 0 lim n n . n v
khi v 0, n n n
lim u L 0 n lim v 0 n u
khi v 0, n
lim u L 0 lim n n . n v
khi v 0, n n n TOANMATH.com Trang 7
II. CÁC DẠNG BÀI TẬP
Dạng 1: Dãy số có giới hạn bằng định nghĩa
Bài toán 1. Chứng minh dãy số có giới hạn 0 bằng định nghĩa Phương pháp giải
Cách 1: Áp dụng định nghĩa.
Ví dụ: Chứng minh các dãy số u sau đây có n
Cách 2: Sử dụng các định lí sau: giới hạn là 0. 1
Nếu k là số thực dương thì lim 0. n k 1 n sin 4n a) u . b) u . n 3n 2 n n 3
Với hai dãy số u và v . n n
hướng dẫn giải
nếu u v với mọi n và lim v 0 và lim u 0. n n n n
a) Với mỗi số dương tùy ý cho trước, ta có
Nếu q 1 thì lim n q 0. 1n 1 1 u n 3n 2 3n 2 3n 1 1 n 2 . 3 1 Đặt n 1 thì *
n và u , n n . 0 3 0 n 0 Vậy lim u 0. n b) Ta có * n thì sin 4n 1 1 1
sin 4n 1 u . n n 3 n 3 n n
Áp dụng cho định lí “Nếu k là một số thực dương 1 1 cho trước thì lim
0 ” ta được lim 0. k n n
Từ đó suy ra lim u 0. n Ví dụ mẫu
Ví dụ 1. Chứng minh các dãy số u sau đây có giới hạn là 0. n 4 1 sin n 1 n 1 a) u . b) u . n 4n 5 n n 1 n 1 2 5
hướng dẫn giải 4 1 sin n 2 2 1 a) Ta có * n thì 4
sin n 1 u . n 4n 5 4n 5 4n 2n TOANMATH.com Trang 8 1 1
Áp dụng định lí “Nếu k là một số thực dương cho trước thì lim
0 ” ta được lim 0. Từ đó suy ra k n n lim u 0. n 1 n 1 1 1 1 1 1 b) Ta có u , n . n n 1 n 1 n 1 n 1 n 1 n 1 2 5 2 5 2 2 2n 1 1 n Vì lim lim 0. 2n 2
Từ đó suy ra limu 0. n
Bài toán 2. Giới hạn của dãy số có số hạng tổng quát dạng phân thức Phương pháp giải
Để tính giới hạn của dãy số có số hạng tổng quát 1
Ví dụ: Chứng minh rằng: lim 0. u n 1
dạng phân thức: lim n . v
Hướng dẫn giải n Nếu ;
u v là hàm đa thức theo biến n thì chia cả 1 1 1 n n Ta có 0 và lim 0. n 1 n n
tử số và mẫu số cho p
n , trong đó p là số mũ lớn Từ đó suy ra điều cần chứng minh. 1
nhất. Sau đó áp dụng: lim
0 (với k 0 ). k n
Nếu u ;v là hàm số mũ thì chia cả tử và mẫu n n cho n
a với a là cơ số lớn nhất. Sau đó sử dụng công thức: lim n
q 0 với q 1.
Chú ý: Thông thường, ta sẽ biến đổi các dãy số
tổng quát về dãy số có giới hạn 0 quen thuộc như trên. Ví dụ mẫu
Ví dụ 1: Chứng minh rằng các dãy số với số hạng tổng quát sau đây có giới hạn 0. a)
u 2n 3 2n.
b) u n 2 n 2 . n n
Hướng dẫn giải 2 2
a) Ta có 2n 3 2n 2n 3 2n 2n 3 2n 3 3
2n 3 2n . 2n 3 2n 3 3 3 3 3 Mà và lim 0. 2n 3 2n 2n 2n 2 2n n n
Từ đó suy ra điều cần chứng minh. TOANMATH.com Trang 9
b) Ta có n 2 n 2 n 2 n 2 n 2 n 2 4 4
n 2 n 2 .
n 2 n 2 4 2 2 Mà và lim 0.
n 2 n 2 n 2 n 2
Từ đó suy ra điều cần chứng minh.
Ví dụ 2: Chứng minh rằng các dãy số với số hạng tổng quát sau có giới hạn 0. n cos n cos a) u . b) 5 u . n n 4 n 4n n
1n cosn sin c) u . d) 5 u . n 2 n 1 n 1,0 1n
Hướng dẫn giải cos n 1 1 1 a) Ta có
và lim 0. Từ đó suy ra điều cần chứng minh. n 4 n 4 n n 1 n cos n cos n 1 1 1 b) Ta có và lim 0. 2 2 2 2 n 1 n 1 n 1 n 2 n
Từ đó suy ra điều cần chứng minh. n cos 1 1 n 1 n 1 c) Ta có 5 và lim 0 (do 1). 4n 4n 4 4 4
Từ đó suy ra điều cần chứng minh. n sin 1 1 n 1 n d) Ta có 5 và lim 0. 1, 0 1 n 1,0 1 n 1,01 1,01
Từ đó suy ra điều cần chứng minh.
Ví dụ 3: Chứng minh rằng các dãy số sau có giới hạn bằng 0. 2n 3n n a a) lim 0. b) lim 0. 4n n!
hướng dẫn giải 2 3 2 n 3 n n n 2 3 a) Ta có lim lim lim 0 0 0 (do 1 và 1). 4n 4 4 4 4
Từ đó suy ra điều cần chứng minh.
b) Gọi m là số tự nhiên thỏa m 1 a . Khi đó với mọi n m 1. TOANMATH.com Trang 10 m nm n a a a a a a a a Ta có 0 . ... . ... . . n! 1 2 m m 1 n m! m 1 nm a m a n a Mà lim 0 và m
a . Từ đó suy ra lim 0. m 1 m! n! n
Ví dụ 4. Cho dãy số u với u . n n 3n u 2 a) Chứng minh rằng n 1 với mọi n. u 3 n 2 n b)
Chứng minh rằng 0 u với mọi n. n 3 c)
Chứng minh rằng dãy số u có giới hạn 0. n
Hướng dẫn giải u
n 1 n n 1 2n 2
a) Với mọi n ta có n 1 : . n 1 u
3 3n 3n 3n 3 n
ta được điều phải chứng minh. 2 n
b) Sử dụng phương pháp quy nạp toán học chứng minh 0 u ; n n * 3 1 2
n 1 ta có 0 u , suy ra (*) đúng với n 1. 1 3 3 k 2 k
Giả sử (*) đúng với n k tức là 0
. Ta phải chứng minh (*) đúng với n k 1. Thật vậy, 3k 3 k 1 k k 1 2 2 2 2 u
0 . Mặt khác u u u . . k 1 k 1 3 k 1 k k 1 3 3 3 3
Ta được điều phải chứung minh. 2 n 2 n c) Do 0 u mà lim 0 nên limu 0. n 3 3 n
Ta được điều phải chứng minh.
CHÚ Ý: MỘT SỐ KỸ THUẬT GIẢI NHANH
Quy ước: Trong máy tính không có biến n nên ta 1
Ví dụ 1. Tính giới hạn sau: lim .
ghi x thay cho n. n 1
Ghi nhớ cách nhập giá trị của x.
Hướng dẫn giải
x thì ta nhập x 9999999999 (10 số 9)
Cách bấm máy:
x thì ta nhập x 9999999999 (10 số 9)
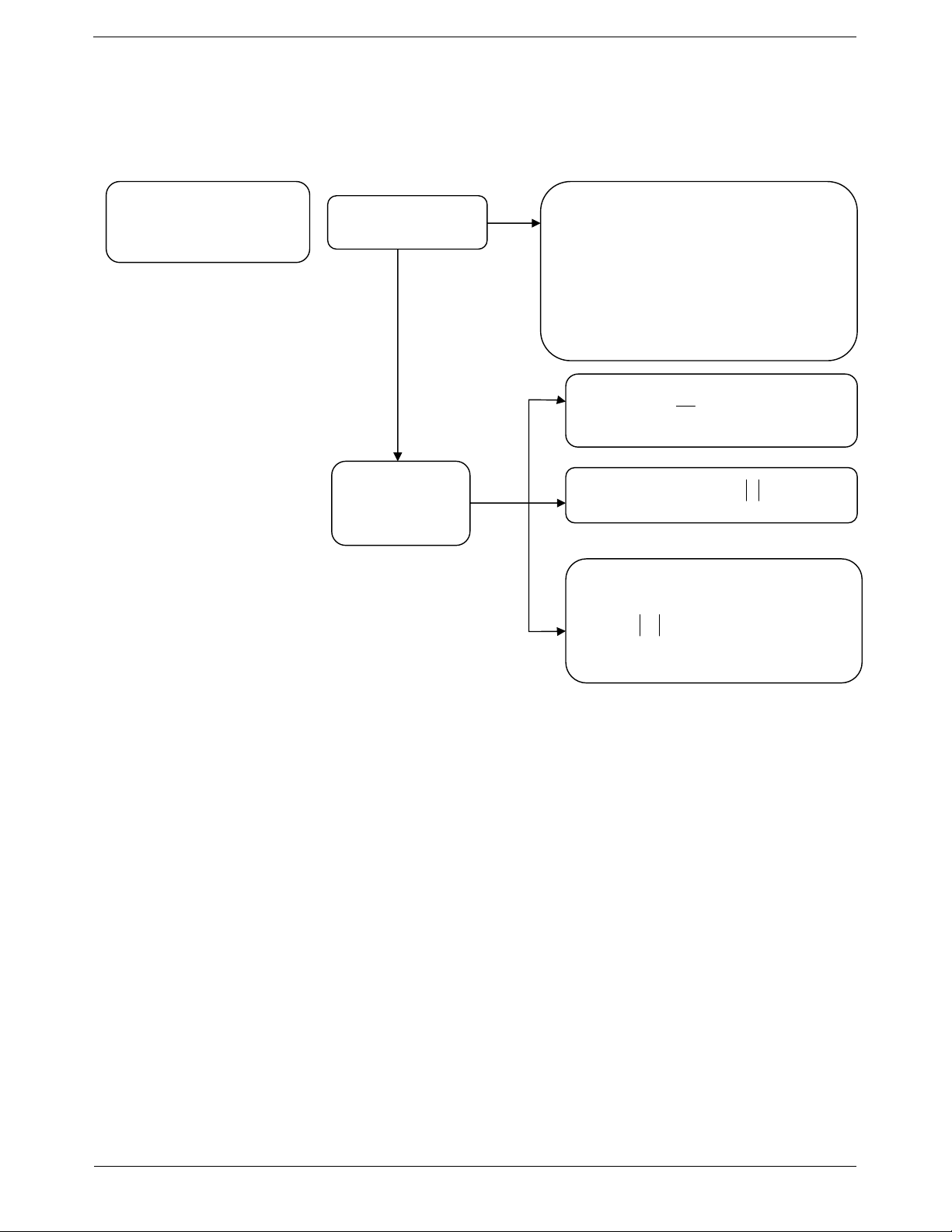
Nhập vào máy tính biểu thức sau:
Đề bài yêu cầu tính lim u thì ta hiểu rằng, biến n TOANMATH.com Trang 11 n .
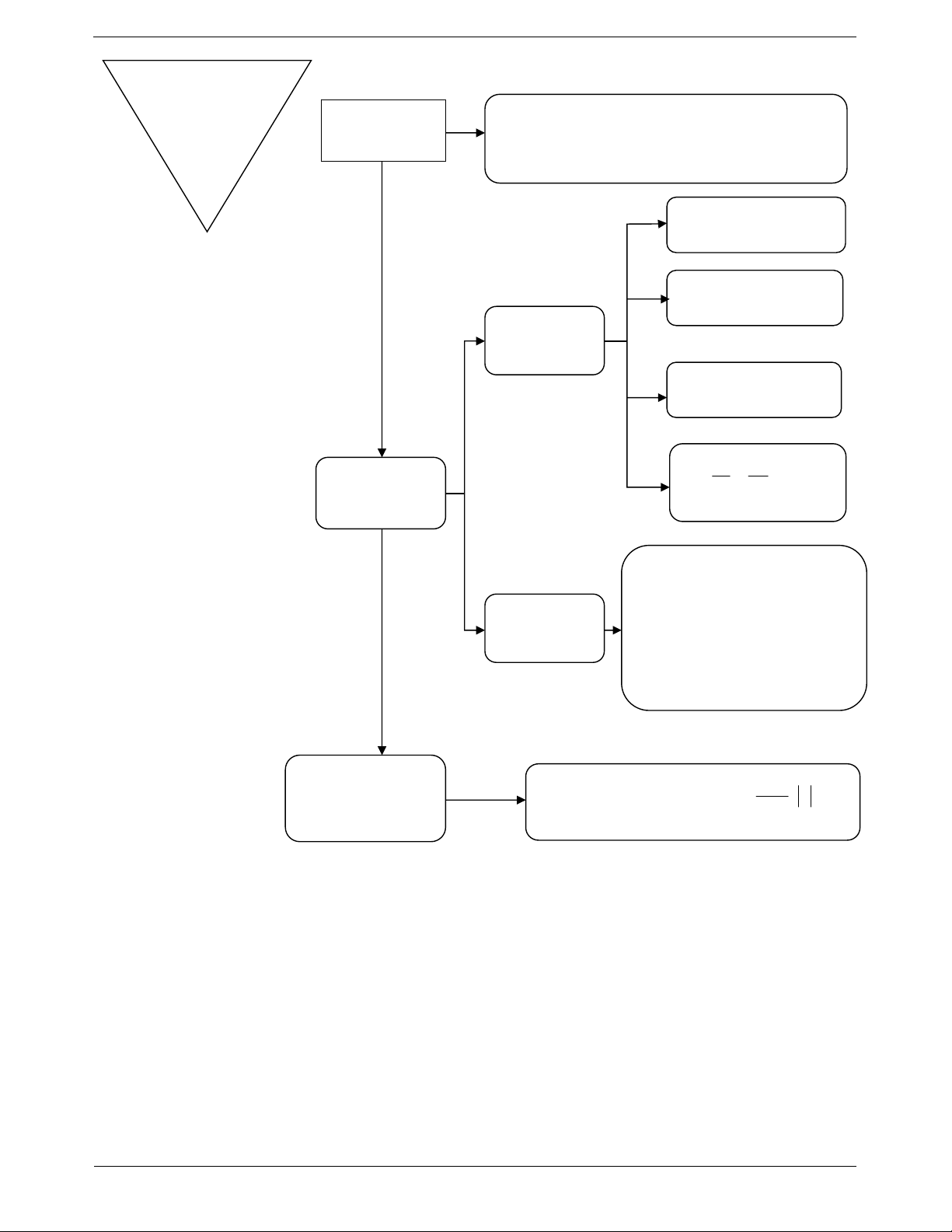
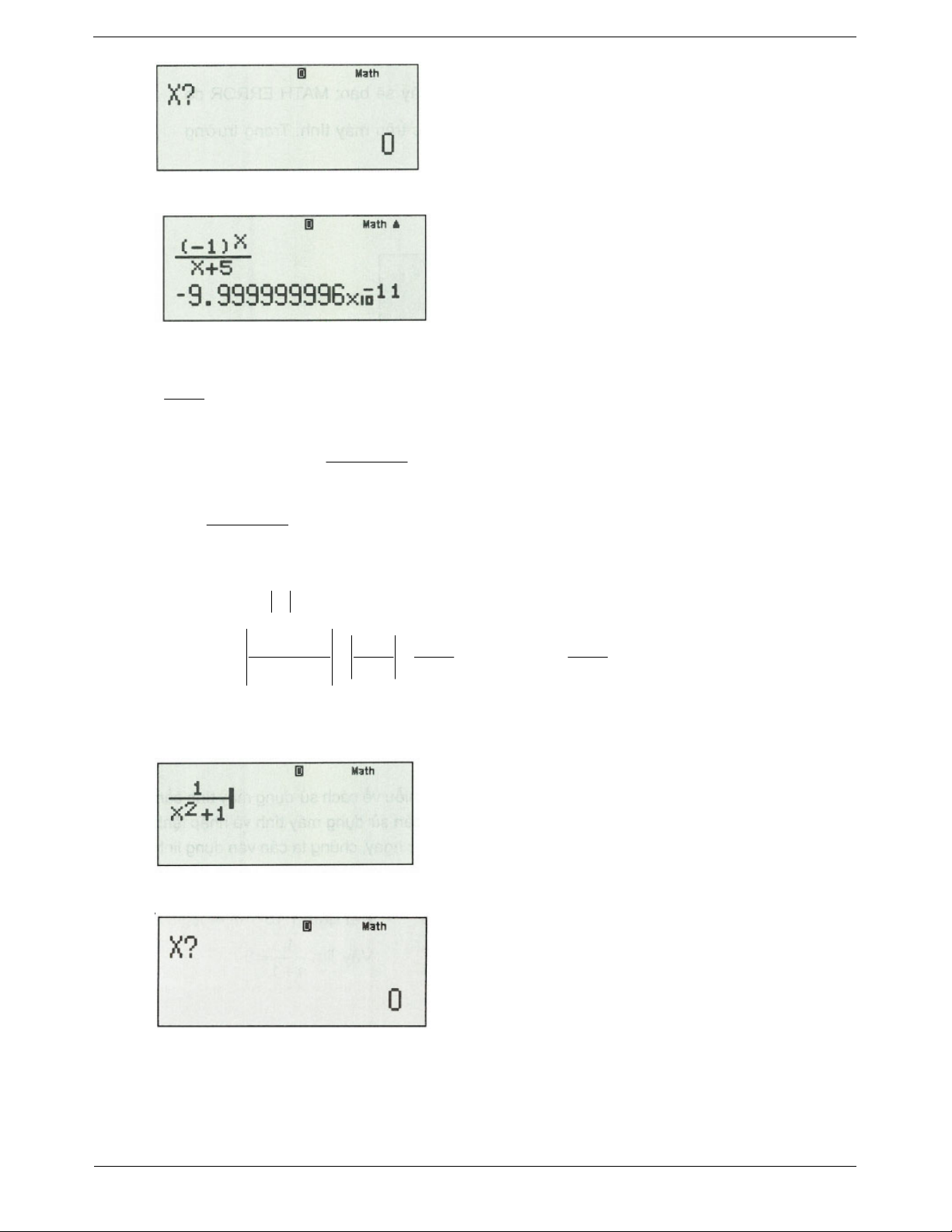
Sau đó bấm CALC, màn hình sẽ xuất hiện như
hình bên. Ta hiểu rằng “Bạn muốn gán x bằng bao nhiêu?”
Ghi nhớ cách hiển thị kết quả
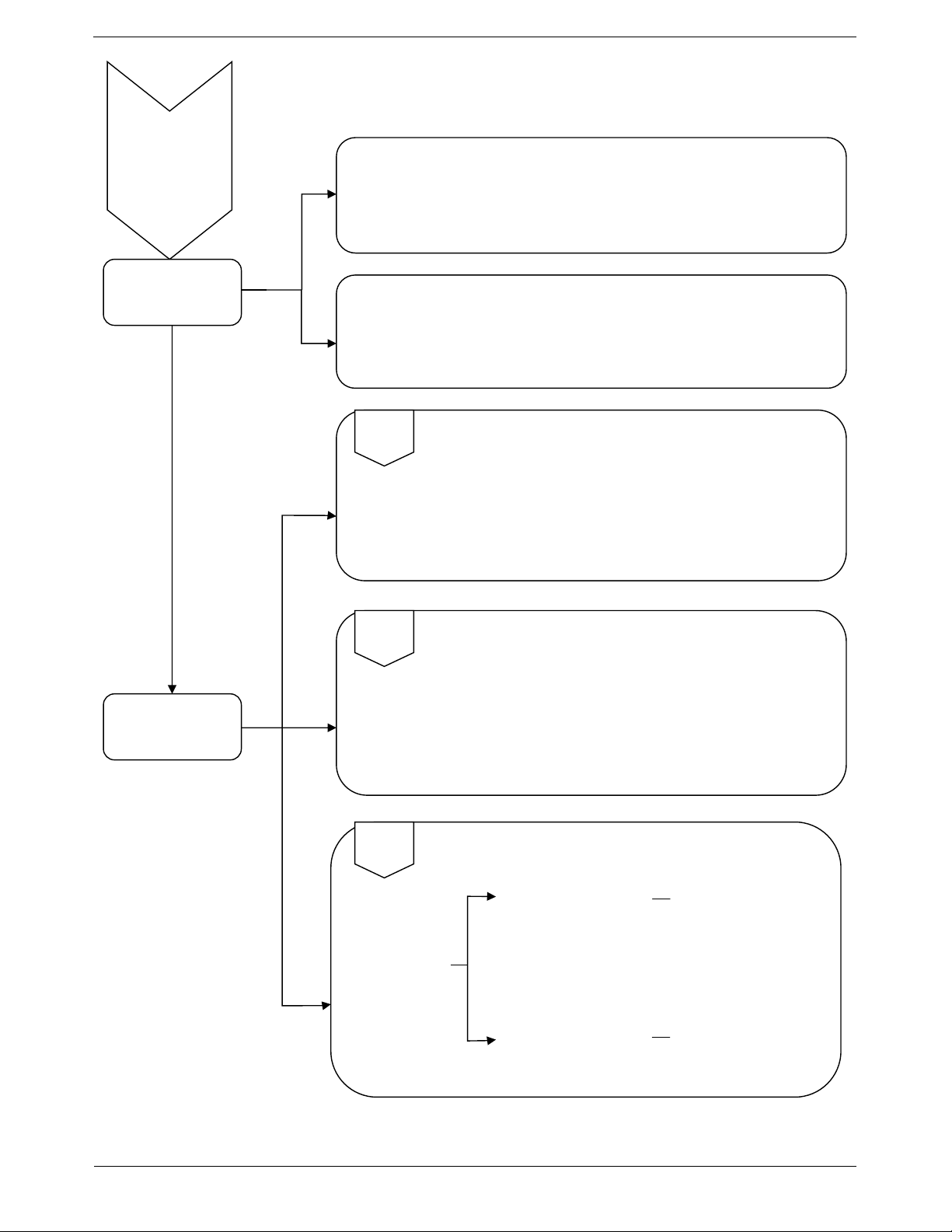
Nhập: x 9999999999 , sau đó bấm “=”, ta được
Gặp hằng số .10n c
(trong đó là số nguyên âm, kết quả: thông thường 10 , 1 2,...) Ví dụ: 12
15.10 là số rất nhỏ và gần bằng 0. Gặp hằng số 10 20 .10 c , .10 c
,... đọc là (dấu của c)
nhân vô cực với c là hằng số (chú ý có thể lớn hơn 10). Ví dụ: 10 5.1 0 là âm vô cực, ghi là 10 ;5
.10 là Kết quả: 10
1.10 là một giá trị rất rất nhỏ gần bằng
dương vô cực, ghi là . 1 0. Vậy lim 0. n 1 VÍ DỤ MINH HỌA 1 n
Ví dụ 1. Tính giới hạn sau: lim . n 5
Hướng dẫn giải
Cách bấm máy:
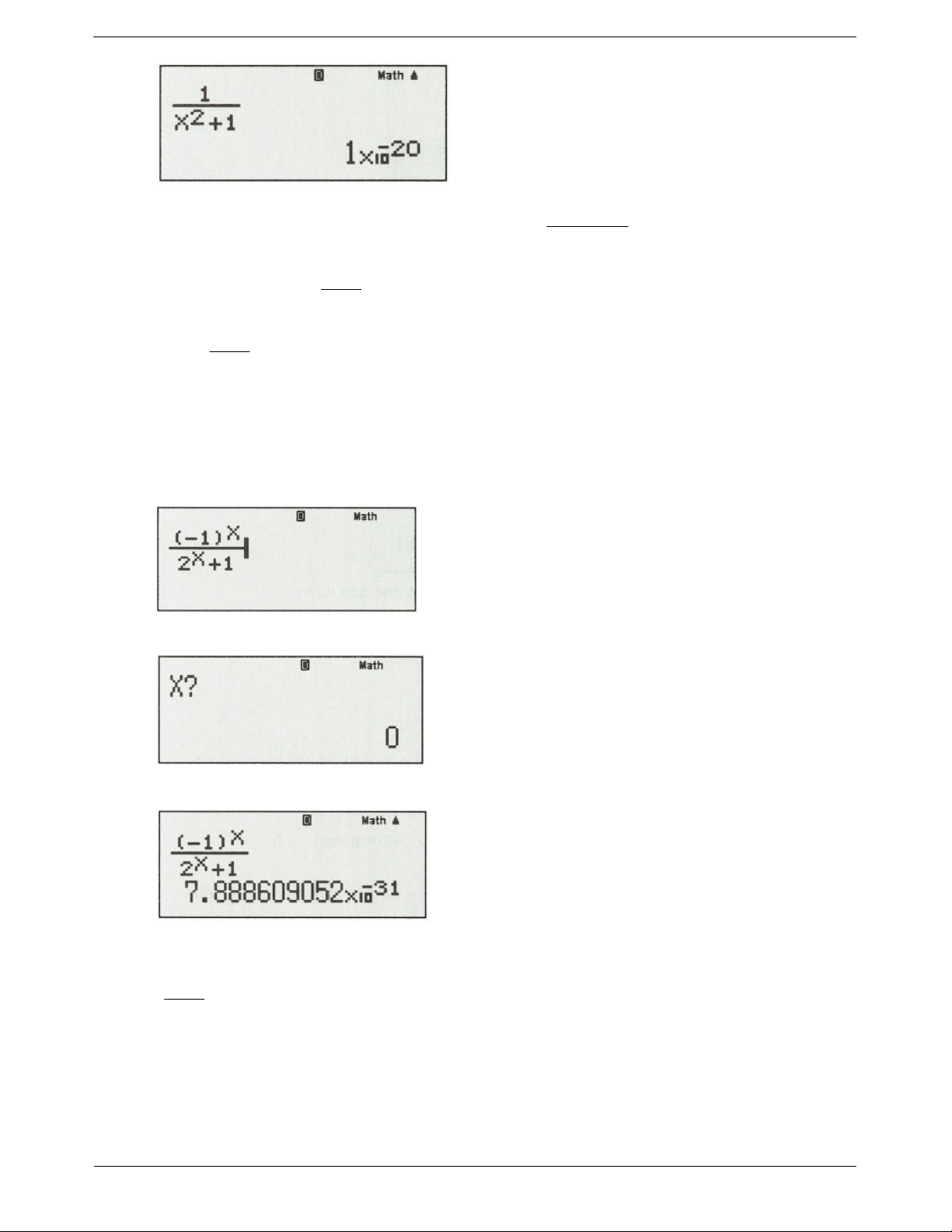
Nhập vào máy tính biểu thức sau: Sau đó bấm CALC. TOANMATH.com Trang 12
Nhập x 9999999999 , sau đó bấm “=”, ta được kết quả: Kết quả: 11 9,999999996.10
là một giá trị rất nhỏ gần bằng 0. 1 n Vậy lim 0. n 5 1 n .cos n
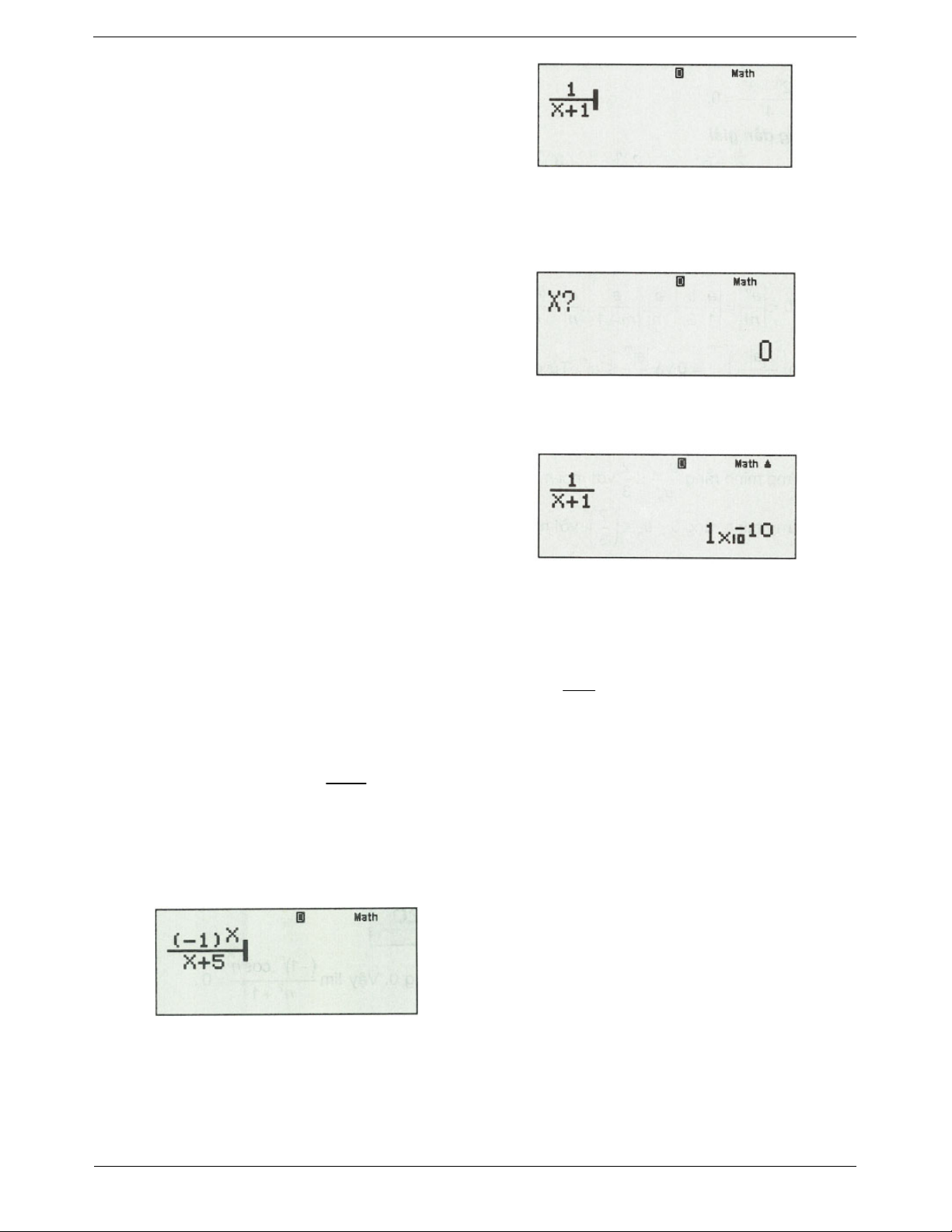
Ví dụ 2. Tính giới hạn sau: lim . 2 n 1
1n .cosn Nếu ta nhập
, sau đó CALC như trên máy sẽ báo: MATH ERROR. 2 n 1
Hướng dẫn giải
Vận dụng định lí 1 nếu u v với mọi n và lim v 0 thì limu 0. n n n n 1 n .cos n cos n 1 1 Ta có đánh giá sau: , ta chỉ cần ghi
vào máy tính là sẽ tính được. 2 2 2 n 1 n 1 n 1 2 n 1
Cách bấm máy:
Nhập vào máy tính biểu thức sau: Sau đó bấm CALC.
Nhập: x 9999999999 , sau đó bấm “=”, ta được kết quả: TOANMATH.com Trang 13
1n .cosn Kết quả: 20
1.10 là một giá trị rất rất nhỏ gần bằng 0. Vậy lim 0. 2 n 1 1n
Ví dụ 3. Tính giới hạn sau lim . 2n 1 1n Nếu ta nhập
, sau đó CALC như trên máy sẽ báo: MATH ERROR do hàm số mũ tăng rất nhanh 2n 1
nên sẽ không tính được trên máy tính. Trong trường hợp này ta sẽ xử lý như sau:
Hướng dẫn giải
Cách bấm máy:
Nhập vào máy tính biểu thức sau: Bấm CALC.
Nhâp: x 100 , sau đó bấm “=”, ta được kết quả: Kết quả: 31
7,888609052.10 là một giá trị rất rất nhỏ gần bằng 0. 1n Vậy lim 0. 2n 1
NHẬN XÉT: Qua 4 ví dụ trên, phần nfao bạn đọc đã hiểu về cách sử dụng máy tính cầm tay (MTCT) để
giải các bài toán về dãy số có giới hạn là 0. Có những bài toán sử dụng máy tính và nhập lệnh CALC
x 9999999999 sẽ ra luôn kết quả, có những bài toán không ra được ngay, chúng ta cần vận dụng linh
hoạt các cách đánh giá cũng như đổi cách bấm máy để ra được kết quả bài toán. Qua đây, đòi hỏi chúng ta TOANMATH.com Trang 14
cần có kiến thức khá chắc chắn về định nghĩa giới hạn dãy số để có thể vận dụng làm các bài tập cho tốt hơn.
Bài tập tự luyện dạng 1
Câu 1: Trong các dãy số sau, dãy số nào có giới hạn 0? n 3 n n n 4 2 5 A. u
. B. u 2 . C. u
. D. u . n 2 n 2 5 n 4 1.cos5n
Câu 2: Dãy số với u có giới hạn bằng n 3n 1 1 A. . B. 1.
C. . D. 0. 3 3 n sin Câu 3: Giới hạn 6 lim bằng 2 3n 1 1 1
A. 0. B. 1. C. . D. . 3 3 n 1 1
Câu 4: Giới hạn lim bằng 3n 5 1 1 1
A. . B. . C. . D. 0. 5 5 3 1n
Câu 5: Giới hạn lim 2 là n 2 1
A. 2. B. . C. 0. D. 1. 2 2 n n 3
Câu 6: Giới hạn lim bằng 3 n 2n 1 1 1
A. . B. 0. C. . D. . 3 2 2
Câu 7: Trong các dãy số dưới đây, dãy số nào có giới hạn 0? 1n sin n cos 2n 2 n 2 1 n .cos n (1): ; (2): ; (3): ; (4): ; (5): . n 5 n 5 n 1 n n 1 2 n 2
A. (1), (2), (3), (4). B. Chỉ (2), (3). C. (1), (2), (3), (5). D. Chỉ (1), (5).
Câu 8: Dãy số nào sau đây có giới hạn khác 0? cos n 1 2n 1 1 A. . B. . C. . D. . n n n n
Câu 9: Xét các câu sau: 1 n (1) Ta có lim 0; 3 TOANMATH.com Trang 15 1 (2) Ta có lim
0 , với k là số nguyên tùy ý. k n
A. Cả hai câu đều đúng. B. Cả hai câu đều sai. C. Chỉ (1) đúng. D. Chỉ (2) sai.
u m, m n 1
Câu 10: Cho dãy số u được xác định . n n n * 2 u
2 u 1 , n n 1 n
Tham số m để dãy số u có giới hạn bằng 0 là n
A. m 1. B. m 2. C. m 3. D. m 4.
Dạng 2: Dãy số có giới hạn hữu hạn
Bài toán 1. Sử dụng định nghĩa chứng minh rằng lim u L n Phương pháp giải
Ta đi chứng minh lim u L 0. 3n 1 3 n
Ví dụ: Chứng minh rằng lim . 2n 1 2
Hướng dẫn giải 3n 1 Đặt u , ta có nhận xét: n 2n 1 3 3n 1 3 5 lim u lim lim 0. n 2 2n 1 2 2n 1 3
Do đó lim u . Ta được điều phải chứng minh. n 2 Ví dụ mẫu 2 n n
Ví dụ 1: Chứng minh rằng lim 1. 2 n 1
Hướng dẫn giải 2 n n 2 n n n 1 Đặt u
, ta có thể nhận xét lim u n 1 lim 1 lim 0. n 2 n 1 2 2 n 1 n 1
Do đó lim u 1. Ta được điều phải chứng minh. n
Bài toán 2: Chứng minh một dãy số có giới hạn Phương pháp giải
Sử dụng nguyên lí kẹp:
Ví dụ: Chứng minh các giới hạn sau:
Cho ba dãy số u ,v , w và số thực L. 3 n n n n a) lim 1 . 3 n 1 Nếu
u v w với mọi n và n n n
lim u lim w L thì lim v . L n n n TOANMATH.com Trang 16 2
n 3n 2 1 b) lim . 2
2n n 2
hướng dẫn giải 3 n 1 a) Ta có lim 1 lim . 3 3 n 1 n 1 1 1 1 xét dãy u u v , n và n 3 n 3 3 n 1 n 1 n n 1 1 lim v lim 0 nên lim 0. n 3 n 3 n 1 3 n Do đó lim 1 . 3 n 1
Ta được điều phải chứng minh. 2
n 3n 2 1 5n 4 b) Ta có lim lim . 2 2n n 2 2 2 2n n 5n 4 Xét dãy u n 2 2 2n n 5n 4 5n 4 5 1 u v n n 2 , . 2 2n n 2 2 4n 4 n n n 5 1 3 Mà lim v lim lim 0 nên lim 0. n 2 4n n 2 2 3n n 2
n 3n 2 1 Do đó lim . 2
2n n 2
Ta được điều phải chứng minh. Ví dụ mẫu
3.3n sin 3n
Ví dụ 1: Chứng minh có giới hạn: lim 3. 3n
Hướng dẫn giải
3.3n sin 3n sin 3n Ta có lim 3 lim . 3n 3n sin 3n 1 1 n 1 n sin 3n Ta lại có n và lim 0 , nên lim 0. 3n 3n 3 3 3n
3.3n sin 3n Do đó lim
3. Ta được điều cần phải chứng minh. 3n TOANMATH.com Trang 17
Bài toán 3. Tính giới hạn của dãy số bằng các định lí về giới hạn Phương pháp giải
Ta lựa chọn một trong hai cách:
Ví dụ: Tìm các giới hạn sau: 2 4
n n 2 a) lim . 2 2n n 1 3 1 b) lim 2n 2 1 . 2 2
n 2n n 3n 1
hướng dẫn giải
Cách 1: Đưa dãy số cần tìm giới hạn về tổng, hiệu, 2 1 2 n 4 2 2
tích, thương của những dãy số mà ta đã biết giới 4
n n 2 n n a) lim lim 2 2n n 1 1 1 hạn. 2 n 2 2 n n Ta có các kết quả sau: 1 2
1. limC C , với C là hằng số. 4 2 lim n n .
2. Kết quả trong định lí 1. 1 1 2 2 n n
3. Kết quả trong định lí 2. Mà 1 1 lim 2 2 n n 1 1 lim 2 lim lim
2 0 0 2 0 . 2 n n 1 2 1 2 lim 4 lim 4 lim lim 2 2 n n n n 4 0 0 4 2 4
n n 2 4 Nên lim 2 . 2 2n n 1 2
Chú ý: Như vậy, để tính các giới hạn trên chúng ta
đã thực hiện phép chia cả tử và mẫu cho bậc cao a
nhất của n và sử dụng kết quả lim 0 với k 0. k n 3 1 a) lim 2n 2 1 2 2
n 2n n 3n 1 32n 2 1 2n 2 1 lim lim . 2 2 n 2n n 3n 1 Mà TOANMATH.com Trang 18 2 1 2 3 2 32n 2 1 n 3.2 lim lim 12. 2 n 2n 2 1 1 n 2 1 2n 2 2 2 1 n 2 lim 4. 2 n 3n 1 3 1 1 1 2 n n
Cách 2: Sử dụng nguyên lí kẹp giữa. Nên 3 1 lim 2n 2 1 12 4 8. 2 2
n 2n n 3n 1
Chú ý: Như vậy, để tính các giới hạn trên chúng ta
đã thực hiện phép tách thành các giới hạn nhỏ. Ví dụ mẫu
Ví dụ 1: Tìm các giới hạn sau: 2
9n 2n 3n 4 5 3 n 4n 2 a) lim . b) lim . 4n 3 4 5 2 n 3n
Hướng dẫn giải 2 2 2 n 9 3n 9 3 2 2
9n 2n 3n n n 9 0 3 0 a) lim lim lim 0. 4n 3 4n 3 3 4 0 4 4 n 4 2 3 4 5 4 4 5 3 n 4n 2 n n 3 0 0 3 b) lim lim . 4 5 3 2 n 3n 2 0 2 2 4 n
ví dụ 2: Tìm các giới hạn sau: a) 2 lim
4n 2n 2n. b) 2 3 2 3 lim
n 2n 3 n n .
hướng dẫn giải
4n 2n 4n 2n
a) lim 4n 2n 2n 2 2 2 lim lim 2
4n 2n 2n 1 2n 1 1 2n 1 1 1 lim . 1 1 0 1 2 1 1 2n b) 2 3 2 3
n n n n
2n n n 3 2 3 lim 2 3 lim 2 3
lim n n n . TOANMATH.com Trang 19 Mà 3 2
n 2n 3 n 2 lim 2 3 2 2 2 lim lim n n n n 1. 2
n 2n 3 n 2 3 11 1 1 2 n n 3 2 3
n n n lim 3 2 3
n n n lim 2 2 3 n .
n n n 2 3 n n 2 3 3 1 1 1 lim . 2 111 3 1 1 3 3 1 1 1 n n 1 2 Vậy lim 2 3 2 3
n 2n 3 n n 1 . 3 3
Chú ý: Để tính các giới hạn trên trước tiên chúng ta cần sử dụng phép nhân liên hợp để khử dạng k và .
Ví dụ 3: Tìm các giới hạn sau: 3n 2.5n 2
1 2 2 ... 2n a) lim . b) lim . 7 3.5n 2
1 3 3 ... 3n
hướng dẫn giải 3 n 2 3n 2.5n 5 0 2 2 a) lim lim 7 3.5n 1 n 7.0 3 3 7. 3 5 n 1 n 1 2 1 2 n n 1 1 2 2 ... 2 2 1 3 3 b) lim lim lim 2. 0. 2 n n 1 n 1 1 3 3 ... 3 3 1 1 1 2 3
Chú ý: Để tính các giới hạn trên chúng ta đã thực hiện phép chia cả tử và mẫu cho cơ số cao nhất và sử
dụng kết quả lim n
q 0 với q 1.
Ví dụ 4. Tìm các giới hạn sau: 1 1 1 a) lim ... n n . 1.3 3.5 2 1 2 1 1 1 1 b) lim 1 1 ... 1 . 2 2 2 2 3 n
Hướng dẫn giải TOANMATH.com Trang 20 1
1 2k 1 2k 1 1 1 1 a) Do
k k . 2 1 2 1 2 2k 1 2k 1
2 2k 1 2k 1 1 1 1 Suy ra lim ... 1.3 3.5
2k 12k 1 1 1 1 1 1 1 1 1 1 1 lim ... lim 1 . 2 1 3 3 5
2n 1 2n 1 2 2n 1 2 1 1 1 1 1 b) Ta có 1 1 1 ...1 1 2 2 2 2 3 4 n 2 2 1 n 1 3 2 4 3 5 n 2 n
n 1 n 1 n 1 . . . . . ... . . . . 2 2 3 3 4 4
n 1 n 1 n n 2n 1 1 1 1 1 n 1 1 Suy ra lim 1 1 ... 1 lim lim n . 2 2 2 2 3 n 2n 2 2
Chú ý: Ta thường gặp giới hạn của một số dãy số sau: P n
Dạng 1: Nếu dãy số u có u
(trong đó P n,Qn là các đa thức của n), thì chia tử và n n Q n mẫu cho k n , với k
n là lũy thừa có số mũ cao nhất của n trong các đa thức P n và Qn , sau đó áp
dụng các định lí về giới hạn hữu hạn.
Dạng 2: Nếu dãy số u có u là biểu thức chứa n dưới dấu căn, thì đưa k
n ra ngoài dấu căn (với k là n n
số cao nhất của n trong dấu căn) rồi áp dụng các định lí. Nếu gặp dạng (vô định) k
n .n với lim u 0 , u n
thì phải nhân và chia với biểu thức liên hợp của biểu thức chứa căn tiến về 0. Cần chú ý các hằng đẳng thức:
a b a b a ;b3 3
a b 3 2 3 3 2
a ab b a .b
Dạng 3: Nếu dãy số u có u là một phân thức mà tử và mẫu là các biểu thức của các lũy thừa có n n dạng n, n
a b ,...n trong đó a, ,
b ... là các hằng số, thì chia cả tử và mẫu cho lũy thừa có cơ số có trị
tuyệt đối lớn nhất trong các lũy thừa ở tử và mẫu, rồi áp dụng các định lí.
Dạng 4: Nếu dãy số u trong đó u là một tổng hoặc một tích của n số hạng (hoặc n thừa số), thì n n
phải rút gọn u rồi tìm lim u theo định lí. n n
Dạng 5: Nếu dãy số u trong đó u được cho bởi một hệ thức truy hồi, thì ta tìm công thức tổng quát n n
của u rồi tìm limu theo định lí. n n
Bài toán 4. Tính tổng của cấp số nhân lùi vô hạn Phương pháp giải TOANMATH.com Trang 21 u
Ví dụ: Tính các tổng sau: Sử dụng công thức: 1
S u u u ... , 1 2 3 1 q 1 1 1 a) S ... ... 2 với q 1. 3 3 3n
b) S 16 8 4 2 ...
Hướng dẫn giải 1 1 1 a) Xét dãy số u là một cấp số n : , ,..., ,... 2 3 3 3n 1 1
nhân có u , q . 1 3 3 n 1 1 1 1 1 1 3 Suy ra S ... 1. 2 3 3 3n 1 1 3 1 Vậy lim S . 2
b) Xét dãy số u :16; 8 ;4; 2; ... là một cấp số n 1
nhân có u 16, q . 1 2 16 32
Suy ra S 16 8 4 2 ... có lim S . 1 3 1 2 Ví dụ mẫu
Ví dụ 1: Hãy biểu diễn các số thập phân vô hạn tuần hoàn sau dưới dạng phân số: a) 0,353535... b) 5,231231...
Hướng dẫn giải 35 2 35 35 35 a) 10
0,353535... 0,35 0,0035 ... ... . 2 4 10 10 1 99 1 2 10 231 231
b) 5, 231231... 5 0, 231 0,000231 ... 5 ... 3 6 10 10 231 3 231 1742 10 5 5 . 1 999 333 1 3 10
Để biểu diễn một số thập phân vô hạn tuần hoàn thành phân số, ta biểu diễn số đó thành tổng của một
cấp số nhân lùi vô hạn và suy ra kết quả.
Cách bấm máy: TOANMATH.com Trang 22 2 n 4n
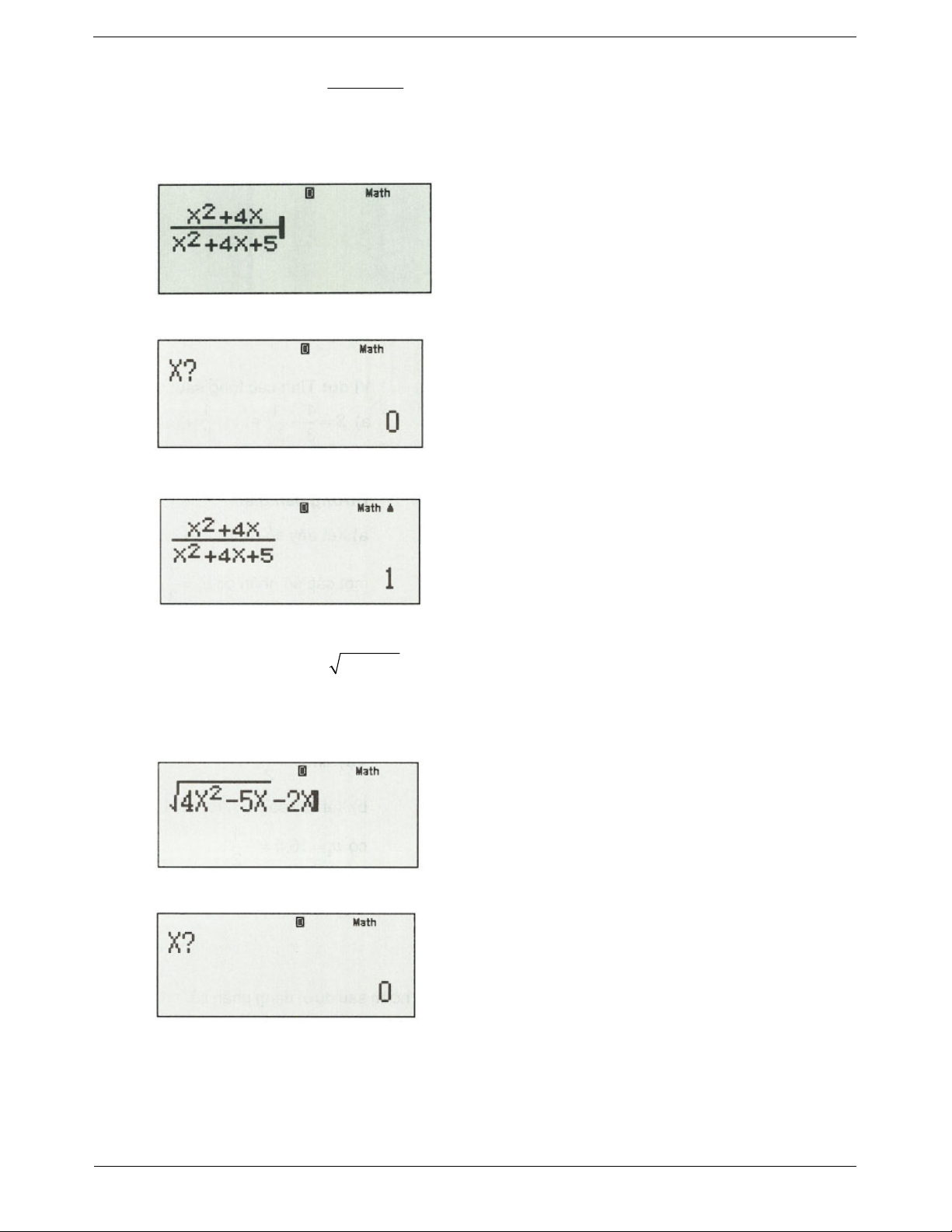
Ví dụ 1: Tính giới hạn sau: lim . 2 n 4n 5
Hướng dẫn giải
Nhập vào máy tính biểu thức sau:
Sau đó bấm CALC.
Nhập x 9999999999 , sau đó bấm “=”, ta được kết quả:
Kết quả: Vậy giới hạn của dãy số bằng 1.
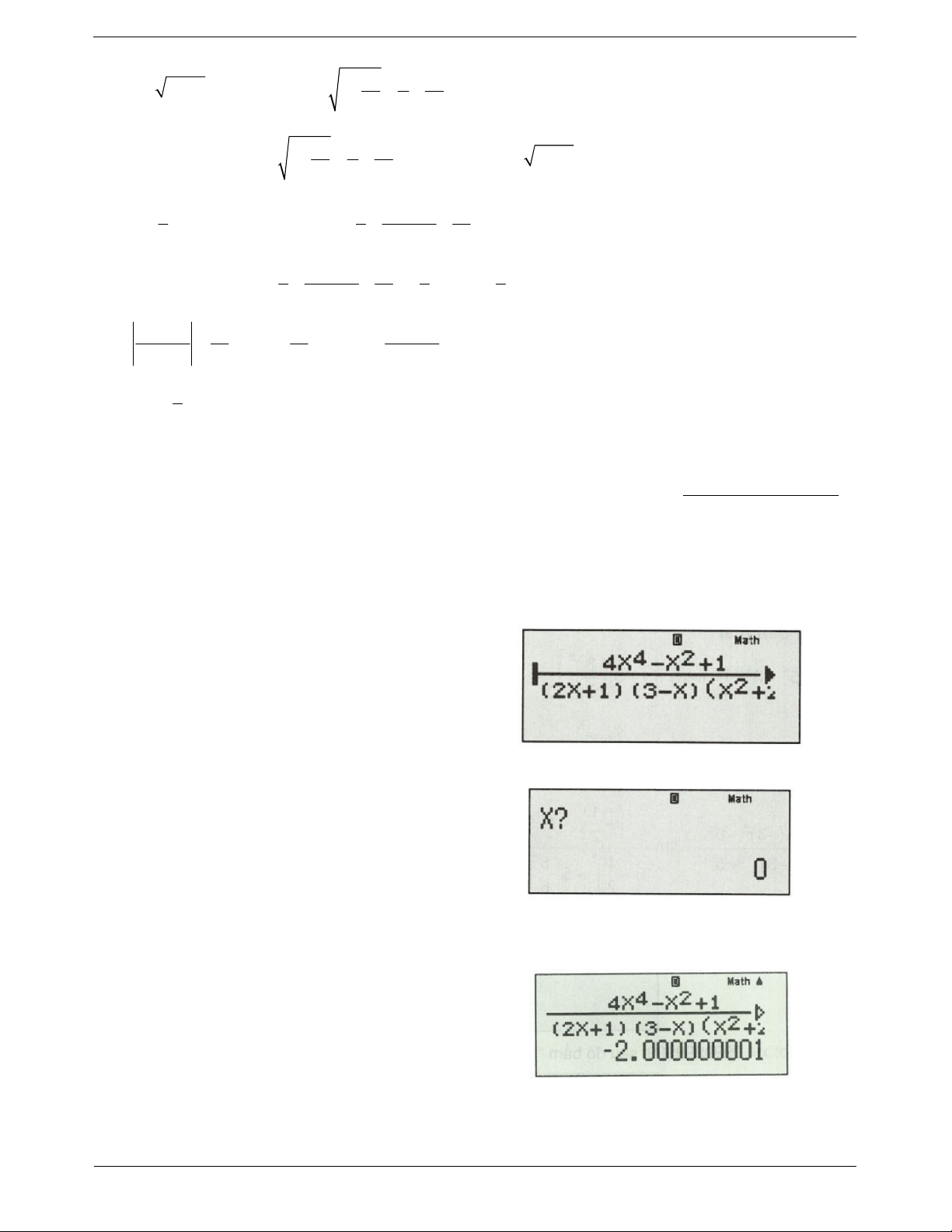
Ví dụ 2: Tính giới hạn sau 2 lim
4n 5n 2n.
Hướng dẫn giải
Nhập vào máy tính biểu thức sau: Sau đó bấm CACL.
Nhập: x 9999999999 , sau đó bấm “=”, ta được kết quả: TOANMATH.com Trang 23 5
Kết quả: Vậy giới hạn của dãy số bằng 1, 25 . 4
NHẬN XÉT: Qua 2 ví dụ trên, phần nào bạn đọc đã hiểu cách sử dụng MTCT để tính toán các bài toán
liên quan đến giới hạn của dãy số (giới hạn là số thực). Tuy nhiên, MTCT không hẳn là một công cụ vạn
năng để chúng ta giải quyết các bài toán phức tạp hay những bài toán hay và khó. Vì vậy, chúng ta cần
phải hiểu sâu bản chất của vấn đề và rèn luyện nhiều dạng bài tập để thao tác nhanh và tập được cách xửl
lí khi gặp một bài toán lạ hay không sử dụng được MTCT. Chúng ta cùng nhau sang các bài tập rèn luyện dưới đây.
Bài tập tự luyện dạng 2 2n 1
Câu 1: Giới hạn lim bằng n 2 3 1 1
A. 2. B. . C. . D. . 2 2 2 n 1
Câu 2: Giới hạn lim bằng 2 n 2 1 1
A. 2. B. . C. 0. D. . 2 6 2 n 1
Câu 3: Giới hạn lim bằng 2n 3 1 2 2
A. 0. B. . C. . D. . 2 3 5 2 3 3
n n 1 n n
Câu 4: Giới hạn lim bằng 2 n n 1 3 1 1 2
A. . B. . C. . D. 1. 2 3 3
Câu 5: Giới hạn 2 3 3
9n 2n 8n 6n 1 n là 1 1 1 1
A. . B. . C. . D. . 6 6 3 3
n n 12 n n 15 2 2
Câu 6: Giới hạn lim bằng 5 n
A. 64. B. 32. C. 16. D. 128. 1 4n
Câu 7: Giới hạn lim là 1 4n TOANMATH.com Trang 24 1 A. 1. B. 1.
C. 0. D. . 3 n n 1 4.3 7
Câu 8: Giới hạn lim là 2.5n 7n
A. 4. B. 2. C. 7. D. 6. 1 1 1
Câu 9: Giới hạn lim ... bằng 2.4 4.6 2n2n 2 1 1 1
A. . B. . C. 2. D. . 3 2 4 1 1 1
Câu 10: Giới hạn lim ... là 1 2 2 1 2 3 3 2 n n 1
n 1 n 3 5 A. 2
B. 1. C. . D. . 2 2
Câu 11: Tổng S 8 88 888 ... 888...8 bằng n chöõ soá 8 A. n 1 10 10 36 . n B. n 1 10 10 54 . n 8 1 C. n 1
10 10 9n . D. n 1
10 10 72n. 81 81 1 1
Câu 12: Tổng S 5 5 1 ... bằng 5 5 25 5 5 25 3 5 A. . B. . 4 4 25 3 5 5 3 5 C. . D. . 4 4
Dạng 3: Dãy số có giới hạn vô cực Phương pháp giải
Đề tỉm giới hạn vô cực của dãy số, ta biến đổi Ví dụ: Tìm các giới hạn sau:
dãy số đã cho về tích hoặc thương của các dãy 5 4
n n n 2 a) lim .
số đã biết giới hạn, rồi dựa theo các quy tắc để 3 2 4n 6n 9
tìm giới hạn vô cực của các dãy số. 3 6 3
n 7n 5n 8 b) lim . n 12
Hướng dẫn giải 5 1 1 2 n 1 5 4 4 5 n n n 2 n n n a) lim lim . 3 2 4n 6n 9 3 6 9 n 4 3 n n TOANMATH.com Trang 25 1 1 2 1 4 5 2 lim . n n n n . 6 9 4 3 n n 1 1 2 1 4 5 1 Mà 2
lim n và lim n n n 0 6 9 4 4 3 n n 5 4
n n n 2 Nên lim . 3 2 4n 6n 9 3 6 3
n 7n 5n 8 b) lim n 12 2 7 5 8 3 n . 1 3 5 6 lim n n n 12 n 1 n 7 5 8 3 1 lim 3 5 6 . n n n n 12 1 n 7 5 8 3 1 3 5 6 n n n 1
Mà lim n và lim 1 0 12 1 1 n 3 6 3
n 7n 5n 8 Nên lim . n 12 Ví dụ mẫu
Ví dụ 1: Tìm các giới hạn sau:
2n 12n3 a)
lim 2n 3 n 1. b) lim . 4 2 n n 1
Hướng dẫn giải a)
n n 3 1 lim 2 3
1 lim n. 2 1 . n n 3 1
Do lim n và lim 2 1 2 1 0. n n
Nên lim 2n 3 n 1 . TOANMATH.com Trang 26 1 3 2 n 1 2n 3 1 2 2 n n b) lim lim . 4 2 n n 1 1 1 1 2 4 6 n n n 1 3 1 1 1 1 1 1 Do lim 1 2 1.2 2 0;lim 0 và 0. 2 2 4 6 n n n n n 2 4 6 n n n
2n 12n3 Nên lim . 4 2 n n 1 Chú ý:
Khi tính các giới hạn phân thức, ta chú ý một số trường hợp sau đây:
Nếu bậc của tử nhỏ hơn bậc của mẫu thì kết quả của giới hạn đó bằng 0.
Nếu bậc của tử bằng bậc của mẫu thì kết quả của giới hạn đó bằng tỉ số các hệ số của lũy thừa cao nhất
của tử và mẫu số.
Nếu bậc của tử lớn hơn bậc của mẫu thì kết quả của giới hạn đó là nếu hệ số cao nhất của tử và mẫu
cùng dấu và kết quả là nếu hệ số cao nhất của tử và mẫu trái dấu.
Ví dụ 2: Tìm các giới hạn sau: 3 n 6n a) n n 1 lim 5 3 . b) lim . 3 n 1 n 1 5
Hướng dẫn giải n n n 3 n a) lim 1 5 3 lim5 . 1 3. . 5 3 n
Do lim 5n và lim 1
3. 1 3.0 1 0 nên n n 1 lim 5 3 . 5 1 n n n 1 3 6 2 b) lim lim . 3 n 1 1 5 1 n 5 n n 3 5 2 6 1 n 1 n 5 n 1 n 5 n Do lim 1 1 0;lim 3 5 0 và 3 5 0 2 2 6 2 6 3 n 6n Nên lim . 3 n 1 n 1 5
Ví dụ 3: Tìm các giới hạn sau: 1 a) 4 lim
n 1 n 1 . b) 3 lim
n 2sin 2n 3 . 3
Hướng dẫn giải TOANMATH.com Trang 27 1 1 1 a) lim 4
n 1 n 2 1 lim n 1 . 4 2 n n n 1 1 1 Do 2
lim n và lim 1 1 0 nên 4 lim
n 1 n 1 . 4 2 n n n 1 1 2sin 2n 3 b) 3 3 lim
n 2sin 2n 3 lim n . 3 3 3 3 n n 1 2sin 2n 3 1 1 Mà 3
lim n và lim 0 0 0. 3 3 3 n n 3 3 2sin 2n 2 2 2sin 2n (do , ; n lim 0 lim 0 ) 3 3 3 3 n n n n 1 Nên 3 lim
n 2sin 2n 3 . 3
MỘT SỐ KỸ THUẬT GIẢI NHANH
Quy ước: Trong máy tính không có biến n nên ta 4 2 4n n 1
Ví dụ: Tính giới hạn sau: lim .
ghi x thay cho n.
2n 13 n 2n 1
Ghi nhớ cách nhập giá trị của x
Hướng dẫn giải
x thì ta nhập x 9999999999 (10 số 9)
Cách bấm máy:
x thì ta nhập x 9999999999 (10 số 9) Nhập vào máy tính biểu thức sau:
Đề bài yêu cầu tính lim u thì ta hiểu rằng, n biến n . Gặp hằng số .10 c
(trong đó là số nguyên
âm, thông thường 10 ; 1 2,...). Sau đó bấm CALC.
Ghi nhớ cách hiển thị kết quả Nhập: 99999999 x
99 , sau đó bấm “=”, ta được Ví dụ: 12
15.10 đọc là 0. kết quả: Gặp hằng số 10 20 .10 c .
c 10 ,... đọc là (dấu của c)
nhân vô cực đối với c là hằng số (chú ý có thể lớn hơn 10). Ví dụ: 10 5.10
đọc là âm vô cực, ghi là ; Kết quả: Vậy giới hạn của dãy số bằng 2. 10
5.10 đọc là dương vô cực, ghi là . TOANMATH.com Trang 28
Kết quả có thể là một số thực cụ thể, đó chính là
giới hạn mà ta cần tìm.
Chú ý: Thông thường, để tính giới hạn của dãy số
(là số thực L), ta cho x , tức là nhập vào
máy tính x 9999999999 (10 số 9).
VÍ DỤ MINH HỌA 2 9n n 1
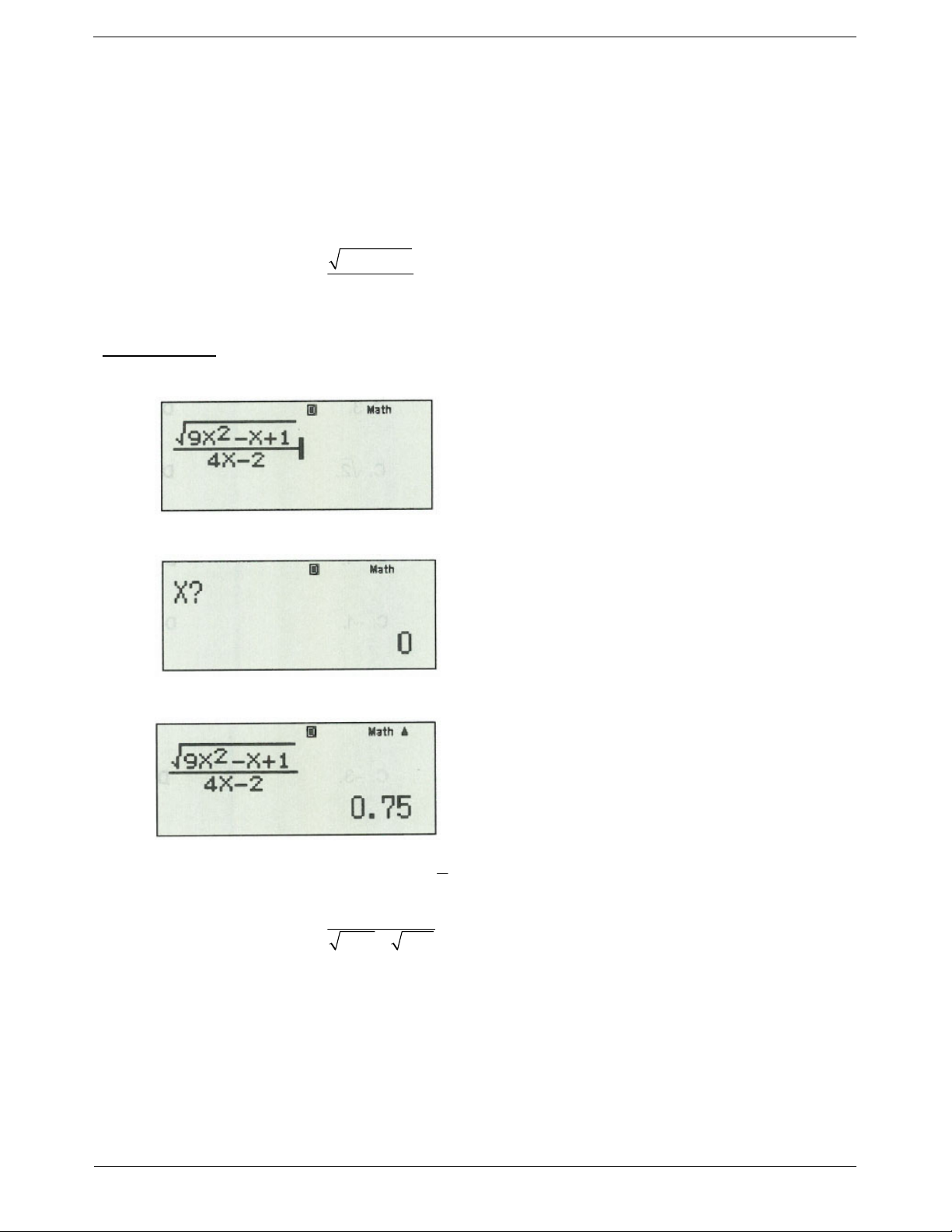
Ví dụ 1: Tính giới hạn sau: lim . 4n 2
Hướng dẫn giải
Cách bấm máy:
Nhập vào máy tính biểu thức sau: Sau đó bấm CALC.
Nhập: x 9999999999 , sau đó bấm “=”, ta được kết quả: 3
Kết quả: Vậy giới hạn của dãy số bằng 0,75 . 4 1
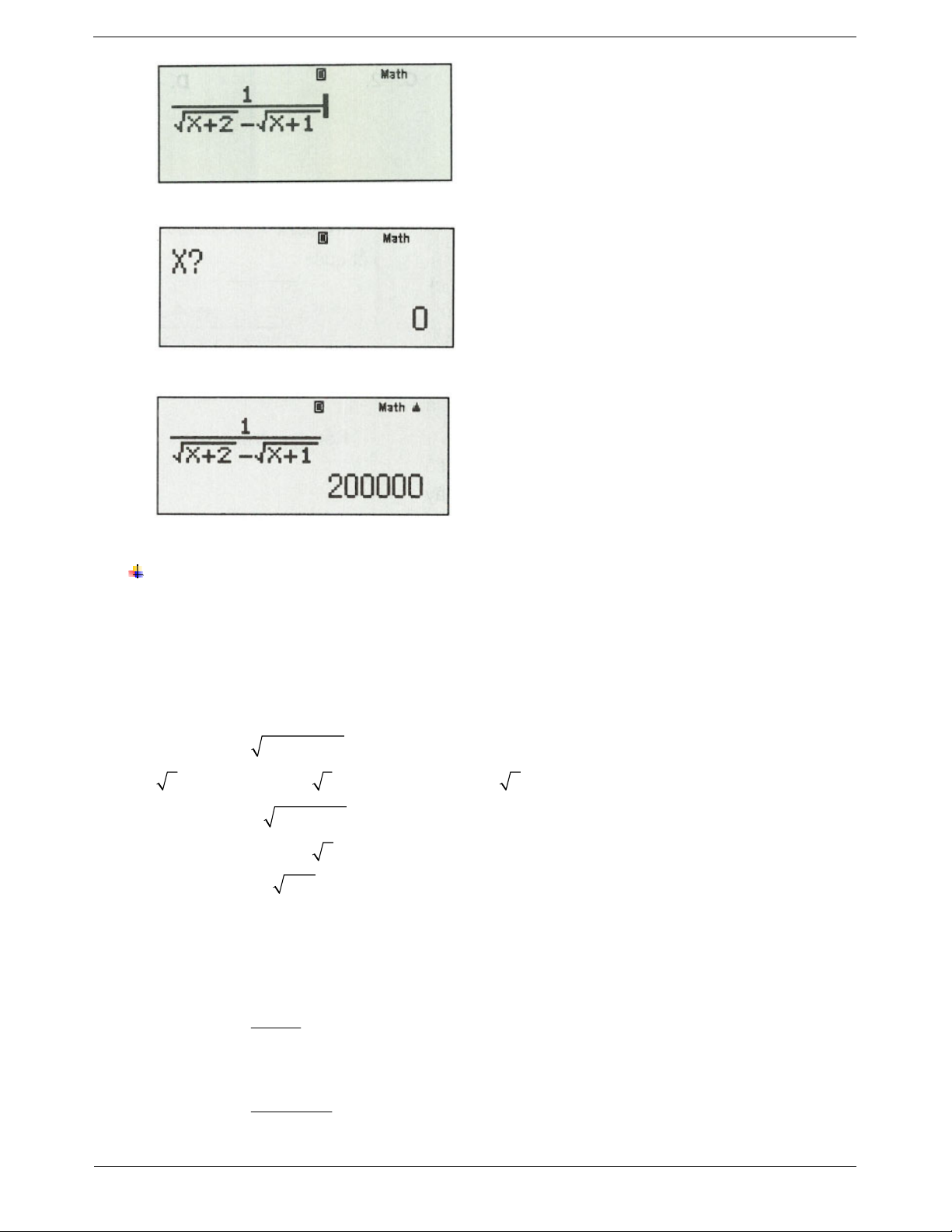
Ví dụ 2: Tính giới hạn sau: lim .
n 2 n 1
Hướng dẫn giải
Cách bấm máy:
Nhập vào máy tính biểu thức sau: TOANMATH.com Trang 29 Sau đó bấm CALC.
Nhập x 9999999999 , sau đó bấm “=”, ta được kết quả:
Kết quả: Vậy giới hạn của dãy số bằng .
Bài tập tự luyện dạng 1 Câu 1: Giới hạn 2
lim 2n n 1 bằng A. .
B. 2. C. 2. D. .
Câu 2: Giá trị của 3 2
lim n 2n 2 bằng A. . B. 3. C. 3. D. . Câu 3: Giới hạn 2
lim 2n 3n 8 bằng
A. 2 2. B. 3. C. 2. D. .
Câu 4: Giá trị của 3 3
lim 1 2n n bằng A. .
B. 3 2. C. 1. D. .
Câu 5: Giá trị của lim n n 1 bằng A. .
B. 1. C. 1. D. . Câu 6: Giới hạn 2 lim 2
5 3n 2n n n bằng A. .
B. 5. C. 5. D. . 3 3n
Câu 7: Giới hạn lim bằng 2 n 1 A. .
B. 3. C. 3. D. . 2 2n 3n 1
Câu 8: Giới hạn lim bằng n 1 TOANMATH.com Trang 30 A. .
B. 3. C. 3. D. .
Câu 9: Giá trị của lim n
n n n n bằng 1 A. . B. .
C. 1. D. . 2
Câu 10: Giá trị của n 2 3 3 lim
n 2n 3 n n bằng 1 A. .
B. . C. 2. D. . 2 2 n 2n 1
Câu 11: Giới hạn lim bằng 3 2 n 2n A. .
B. 2. C. 3. D. . 3 6 3
n 7n 5n 8
Câu 12: Giới hạn lim bằng n 2 A. . B. 7. C. 1. D. . Câu 13: Giới hạn 2
lim n 2 cos3n 2 bằng A. .
B. 3. C. 1 . D. . n cos
Câu 14: Giới hạn lim n bằng 2 n 1
A. 5. B. 0. C. 2. D. . 2 sin n
Câu 15: Giới hạn lim 5 bằng n A. .
B. 5. C. 5. D. .
Đáp án và lời giải
Dạng 1. Dãy số có giới hạn 0 1 – C 2 – D 3 – A 4 – D 5 – A 6 – B 7 – C 8 – C 9 – C 10 – C
HƯỚNG DẪN GIẢI CHI TIẾT Câu 1. 4 4 n Ta có 1 nên lim 0. 2 5 2 5 Câu 2. 1 .cos5n cos5n 1 1 n 1 n 1.cos5n Ta có 0 mà lim 0 nên lim 0. 3n 3n 3n 3 3 3n TOANMATH.com Trang 31 Câu 3. n n sin 1 1 1 sin Ta có 6 0 mà lim 0 nên 6 lim 0. 2 2 2 3n 1 3n 1 3n 2 3n 2 3n 1 Câu 4. n 1 1 1n 1 1 1 n 1 1 Ta có 0 mà lim 0 nên lim 0. 3n 5 3n 5 3n 5 3n 3n 3n 5 Câu 5. 1n 1n 1 n 1 1 Ta có 2 2 mà , n và lim 0. n 2 n 2 n 2 n n 1 n 1 n Suy ra lim 2
2 0 lim 2 2. n 2 n 2 Câu 6. 2 1 3 1 3 n 1 1 3 2 2 1 1 2 n n 3 n n 1 2 1 Ta có .
n n mà lim 0;lim n n 1. 3 n 2n 2 n 2 n 2 3 n 1 1 1 2 2 n n 2 n 2 n n 3 Suy ra lim 0. 3 n 2n Câu 7.
Dễ dàng nhận thấy các các phương án (1); (2); (3); (5) đều có giới hạn là 0, bạn đọc có thể tự chứng minh. Ta xét phương án: 2 2 2 n 1 2 2 2 2 1 1 2 n 2 n 2 n 2 (4): n mà lim n 1. n n , 2 1 n 1 1 1 1 2 n 1 1 1 2 2 n n 2 n
Vậy phương án (4) không thỏa mãn. Câu 8.
Dễ dàng chứng minh được các đáp án A, B và D có giới hạn là 0, bạn đọc có thể tự chứng minh. Ta xét phương án C: 1 n 2 2n 1 n 1 1 2 , mà lim 2 2 0
. Vậy phương án C không thỏa mãn. n n n n Câu 9. 1 1 n
Dễ dàng nhận thấy phương án (1) hoàn toàn chính xác do: 1 nên lim 0. 3 3 TOANMATH.com Trang 32 1
Phương án (2) là sai, vì lim
0 khi k là số nguyên dương k
. Vậy phương án (2) sai. k n Câu 10. n n 1 Ta có 2 u
2 .u 1 u u . n 1 n n 1 n 2n Chứng minh: 1
u 2 n (bằng quy nạp). n * Với n 1 ta có 0
u m 1 2 . 1 * Giả sử 1
u 2 k (với k 1) k * Cần chứng minh: u 2k. k 1 Ta có k 1 u
u 2 2 k 2k 2k . Suy ra điều phải chứng minh. k 1 k 1
Từ đó suy ra u 2n 0 với mọi n u u . n n 1 n 2n 1 1 1 1
Ta có u u ;u u ;u u ;...;u u 2 1 3 2 2 4 3 3 n n 1 n 1 2 2 2 2 1 1 1 1 u u ... . n 1 2 3 n 1 2 2 2 2 n 1 1 1 n 1 1 2 1
Công thức tổng quát u m . m 1 n 2 1 2 2 n 1 u m n 1 lim 0 lim 1 lim 0 2 limm 1 0 m 1.
Dạng 2. Dãy số có giới hạn hữu hạn 1 – A 2 – C 3 – B 4 – D 5 – C 6 – B 7 – B 8 – C 9 – D 10 – B 11 – C 12 – A
HƯỚNG DẪN GIẢI CHI TIẾT Câu 1. 1 2 2n 1 2 Ta có lim lim n 2. n 2 2 1 1 n Câu 2. 1 1 2 n 1 0 Ta có lim lim n n 0. 2 n 2 2 1 1 2 n TOANMATH.com Trang 33 Câu 3. 1 2 1 2 n 1 n 1 1 Ta có lim lim . 2n 3 3 2 2 2 n Câu 4. 1 1 1 3 2 3 3 1 3 6
n n 1 n n n n n 1 Ta có lim lim 1. 2 n n 1 3 1 3 1 1 2 2 n n Câu 5. 1 1 Ta có lim 2 3 3
9n 2n 8n 6n 1 n lim 2
9n 2n 3nlim 3 3
8n 6n 1 2n 0 . 3 3 Câu 6. 5 5
n n 15 n n 15 1 1 2 2 1 1 1 1 2 2 n n Ta có 5 lim lim 2 32. 5 n 1 Câu 7. 1 n 1 1 4n 4 1 Ta có lim lim 1 . 1 4n 1 n 1 1 4 Câu 8. 3 n 4. 7 n n 1 4.3 7 7 7 Ta có lim lim 7. 2.5n 7n 5 n 1 2. 1 7 Câu 9. Ta có 1 1 1 1 1 1 1 1 1 1 1 1 1 1 lim ... n n lim ... lim . 2.4 4.6 2 2 2 2 2 4 4 6 2n 2n 3 2 2 2n 2 4 Câu 10. 1
k k 1 k 1 k 1 1 Ta có
k k 1 k 1 k
k k . 1 k k 1 1 1 Suy ra u limu 1. n 1 n 1 n Câu 11. TOANMATH.com Trang 34 8 8
Ta viết lại S 9 99 999 ...
99...9 10 1100 1...100..0 1 9 n soá 9 9 n soá 0 10. 8 8 10n 1 n 8 1 10 10 8
S 10 100 ...100..00 n S n n 1 n 10 10 9n. 9 9 10 1 9 9 81 n soá 0 Câu 12. 1 1 5 5 5 25 5 5
Ta có S 5 5 1 ... . 5 5 1 1 1 5 4 5
Dạng 3. Dãy số có giới hạn vô cực 1 – D 2 – A 3 – D 4 – A 5 – D 6 – A 7 – A 8 – D 9 – D 10 – D 11 – D 12 – D 13 – D 14 – B 15 – B
HƯỚNG DẪN GIẢI CHI TIẾT Câu 1. 1 1 Ta có lim 2 2n n 2
1 lim n 2 . 2 n n Câu 2. 2 2 Ta có lim 3 2 n 2n 2 3 lim n 1 . 3 n n Câu 3. 3 8 Ta có 2
lim 2n 3n 8 lim n 2 . 2 n n Câu 4. 1 1 Ta có 3 lim 1 2n 3 n 3 lim 1 . 3 2 n n Câu 5. 1
Ta có lim n n 1 lim n n 1 n . Câu 6. 5 n n n 2 n Ta có lim 2 2n 5n 2 lim n 2 và lim 3 2 lim 3 1 . n 3 Nên 2
lim 2 5 3n 2n n n . Câu 7. TOANMATH.com Trang 35 3 3n 3n 3n Ta có lim lim lim lim 3n . 2 n 1 1 1 1 2 n Câu 8. 3 1 2 2 2n 3n 2 1 3 1 1 1 1 1 Ta có lim lim n n . Do lim 2 2 và lim 0 mà 0. n 1 1 1 2 2 2 n n n n n n 2 n n 3 1 2 2 n n Nên lim . 1 1 2 n n Câu 9. 1
Ta có lim n n n n n . 2 Câu 10.
Ta có lim n và 2 2n 3 lim n
n 2n 3 n n 3 n 3 n lim lim 1.
n 2n 3 n 2 2 2 n 3. n n 3
n 3 n 3n Vậy
n 2n n 3 n 3 lim 2 3 n . Câu 11. 2 1 1 1 n . 2 n . 2 2 2 n 2n 1 3 2 2 3 2 2 2 Ta có lim lim n lim n lim 3 2 . n L n 3 2 2 n 2n n 2n 2 2 3 2 2 3 n n . 1 3 3 1 2 n n 2 2 n 1 2 2 2 Do lim n 2 và 3 2
lim n nên L . 2 3 1 2 n Câu 12. Ta có 6 3 n n n 6 7 5 8 2 7 5 8 7 5 8 3 3 n . n . 1 3 3 1 6 3
n 7n 5n 6 3 5 6 8 n n n n 3 5 6 n n n L lim lim lim lim . n n 2 n 2 n 2 2 1 n TOANMATH.com Trang 36 7 5 8 3 1 3 5 6 Ta có n n n lim
1 và lim n . 2 1 n
Từ đó suy ra L . Câu 13. Ta có 2
lim n 2 cos3n 2 . Câu 14. n cos n cos n n n Ta có và lim 0 nên lim n 0. 2 n 2 1 n 1 2 n 1 2 n 1 Câu 15. 2 sin n Ta có lim 5 5. n TOANMATH.com Trang 37




