










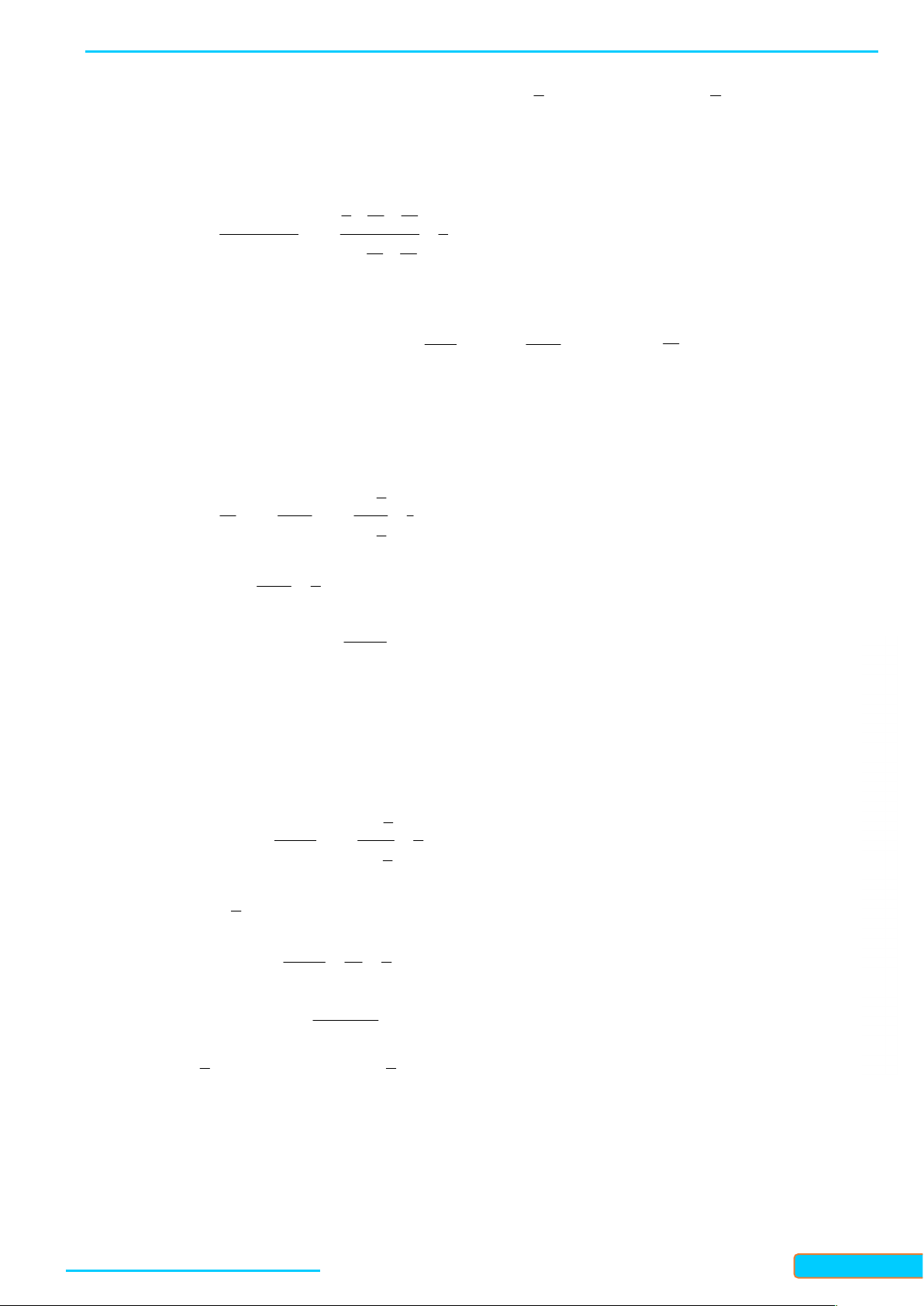

















































































Preview text:
LỚP TOÁN THẦY CƯ- TP HUẾ
CS 1: Trung tâm MASTER EDUCATION- 25 THẠCH HÃN
CS 2: Trung Tâm 133 Xuân 68
CS 3: Trung tâm 168 Mai Thúc Loan
CS4: Trung Tâm THPT Nguyễn Trường Tộ
GIỚI HẠN VÀ HÀM SỐ LIÊN TỤC
TÀI LIỆU DÀNH CHO HỌC SINH LỚP TOÁN THẦY CƯ-TP HUẾ
(Chiêu sinh thường xuyên, bổ trợ kiến thức kịp thời)
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com MỤC LỤC
Chương 3: GIỚI HẠN. HÀM SỐ LIÊN TỤC ....................................................................................................... 3
Bài 1. Giới hạn của dãy số ...................................................................................................................................... 3
A. TÓM TẮT LÝ THUYẾT ............................................................................................................................... 3
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP ................................................................................. 4
Dạng 1. Giới hạn hữu tỉ ....................................................................................................................................... 4
1. Phương pháp .................................................................................................................................................. 4
2. Các ví dụ rèn luyện kĩ năng ........................................................................................................................ 5
Dạng 2. Dãy số chứa căn thức ............................................................................................................................ 6
1. Phương pháp .................................................................................................................................................. 6
2. Các ví dụ rèn luyện kĩ năng ...................................................................................................................... 6
Dạng 3. Tính giới hạn của dãy số chứa hàm mũ ............................................................................................. 7
1. Phương pháp .................................................................................................................................................. 7
2. Các ví dụ rèn luyện kĩ năng ........................................................................................................................ 7
Dạng 4. Tổng của cấp số nhân lùi vô hạn ....................................................................................................... 9
1. Phương pháp .................................................................................................................................................. 9
2. Các ví dụ rèn luyện kĩ năng .................................................................................................................... 9 GV: T
Dạng 5: Phương pháp sai phân và quy nạp tính giới hạn ....................................................................... 10 R Ầ N
1. Phương pháp ............................................................................................................................................ 10 ĐÌN
2. Các ví dụ rèn luyện kĩ năng .................................................................................................................. 12 H CƯ
C. GIẢI BÀI TẬP SÁCH GIÁO KHOA ..................................................................................................... 14 – 0834
D. BÀI TẬP TRẮC NGHIỆM ...................................................................................................................... 17 3321
BÀI 2. GIỚI HẠN CỦA HÀM SỐ ................................................................................................................... 41 33
A. TÓM TẮT KIẾN THỨC CƠ BẢN CẦN NẮM. .................................................................................. 41
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP ........................................................................... 43
Dạng 1: Dãy số có giới hạn hữu hạn ............................................................................................................ 43
1. Phương pháp ............................................................................................................................................ 43
2. Các ví dụ rèn luyện kĩ năng .................................................................................................................. 43
Dạng 2. Giới hạn tại vô cực .......................................................................................................................... 44
1. Phương pháp ............................................................................................................................................ 44
2. Các ví dụ rèn luyện kĩ năng ...................................................................................................................... 45
Dạng 3. giới hạn một bên .................................................................................................................................. 47
1. Phương pháp ................................................................................................................................................ 47
2. Các ví dụ rèn luyện kĩ năng ...................................................................................................................... 47
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 1
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 0 Dạng 3. Dạng vô định
................................................................................................................................... 49 0
1. Phương pháp ................................................................................................................................................ 49
2. Các ví dụ rèn luyện kĩ năng ...................................................................................................................... 49 Dạng 4. Dạng vô định
................................................................................................................................. 56
1. Phương pháp ................................................................................................................................................ 56
2. Các ví dụ rèn luyện kĩ năng ...................................................................................................................... 56
Dạng 5. Dạng vô định , 0. ............................................................................................................... 60
1. Phương pháp ................................................................................................................................................ 60
2. Các ví dụ rèn luyện kĩ năng ...................................................................................................................... 61
C. GIẢI BÀI TẬP SÁCH GIÁO KHOA ......................................................................................................... 63
D. BÀI TẬP TRẮC NGHIỆM .......................................................................................................................... 65
BÀI 3. HÀM SỐ LIÊN TỤC ................................................................................................................................. 85
A. TÓM TẮT LÝ THUYẾT ............................................................................................................................. 85
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP ............................................................................... 86
Dạng 1: Hàm số liên tục tại một điểm ........................................................................................................... 86
1. Phương pháp ............................................................................................................................................ 86 GV: T
2. Các ví dụ rèn luyện kĩ năng .................................................................................................................. 86 R Ầ N
Dạng 2. Hàm số liên tục trên tập xác định ................................................................................................ 88 ĐÌN H CƯ
1. Phương pháp ............................................................................................................................................ 88
2. Các ví dụ rèn luyện kĩ năng .................................................................................................................. 89 – 0834
Dạng 3. Số nghiệm của phương trình trên một khoảng ........................................................................... 90 3321
1. Phương pháp ............................................................................................................................................ 90 33
2. Các ví dụ rèn luyện kĩ năng .................................................................................................................. 90
C. GIẢI BÀI TẬP SÁCH GIÁO KHOA ..................................................................................................... 93
D. BÀI TẬP TRẮC NGHIỆM ...................................................................................................................... 95
BÀI TẬP CUỐI CHƯƠNG III ........................................................................................................................ 107
PHẦN 1: CÂU HỎI TRẮC NGHIỆM ....................................................................................................... 107
BÀI TẬP TỰ LUẬN ..................................................................................................................................... 108
BÀI TẬP TỔNG ÔN CHƯƠNG 3 ................................................................................................................. 113
PHẦN 1: TRẮC NGHIỆM .............................................................................................................................. 113
PHẦN 2: TỰ LUẬN .......................................................................................................................................... 131
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 2
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Chương 3: GIỚI HẠN. HÀM SỐ LIÊN TỤC
Bài 1. Giới hạn của dãy số A. TÓM TẮT LÝ THUYẾT
1. Giới hạn hữu hạn của dãy số
Giới hạn 0 của dãy số
Dãy số u có giới hạn 0 khi n dần tới dương vô cực, nếu u nhỏ hơn một số dương bất kì cho n n
trước, kể từ một số hạng nào đó trở đi, kí hiệu lim u 0 hay u 0 khi n . Ta còn viết là n n n lim u 0 . n
Ta thừa nhận một số giới hạn cơ bản sau đây: 1 lim
0 , với k nguyên dương bất kì. k n lim n
q 0 , với q là số thực thỏa mãn q 1.
Giới hạn hữu hạn của dãy số
Dãy số u có giới hạn hữu hạn là số a ( hay u dần tới a ) khi n dần tiến tới dương vô cực, nếu n n
limu a 0.Khi đó, ta viết lim u a hay lim u a hay u a khi n . n n n n n GV: T
Chú ý: Nếu u c ( c là hằng số) thì lim u limc c . n n R Ầ N ĐÌN
2. Các phép toán về giới hạn hữu hạn của dãy số H CƯ Cho lim u ,
a lim v = b và c là hằng số. Khi đó: n n – 0834
lim u v a b
limu v a b n n n n 3321 33 lim . c u . c a
lim u .v a b n n . n u a lim n b 0 Nếu u 0, n
thì a 0 và lim u a v b n n n
3. Tổng của cấp số nhân lùi vô hạn
Cấp số nhân vô hạn u có công bội q thỏa mãn q 1được gọi là cấp số nhân lùi vô hạn. Cấp n
số nhân lùi vô hạn này có tổng là u 1
S u u ... u ... 1 2 n 1 q 4. Giới hạn vô cực
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 3
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Ta nói dãy số u có giới hạn là nếu u lớn hơn một số dương bất kì, kể từ một số hạng nào đó n n
trở đi, kí hiệu limu hay u khi n + . n n
Ta nói dãy số u có giới hạn là khi n nếu lim u , kí hiệu n n
limu hay u n n
khi n + .
Chú ý: Ta có các kết quả sau:
a) limu khi và chỉ khi lim u ; n n 1
b Nếu limu hoặc limu thì lim 0 ; n n un 1
c) Nếu limu 0 và u 0 với mọi n thì lim . n n un Nhận xét: ) lim k a
n k , k 1 ; ) lim n b
q q 1 .
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP GV: T
Dạng 1. Giới hạn hữu tỉ R 1. Phương pháp Ầ N ĐÌN
Để tính giới hạn của dãy số dạng phân thức, ta chia cà tử thức và mẫu thức cho luỹ thửa cao H CƯ nhất của k
n , với k là bậc cao nhất ở mẫu, rồi áp dụng các quy tắc tinh giới hạn. –
Chú ý : Cho Pn, Qn lần lượt là các đa thức bậc ,
m k theo biến n : 0834 m m 1 3321
Px a n a n
a n a a 0 m m 1 1 0 m Qn k k 1
b n b n b n b b 0 k k 1 1 0 k 33 Pn m Pn m Khi đó a n a n lim m , viết tắt m
, ta có các trường hợp sau : Qn lim k b n Qn k b n k k P n
Nếu « bậc tử » « bậc mẫu ( m k ) thì lim Qn 0. Pn
Nếu « bậc tử » « bậc mẫu ( a
m k ) thì lim m Qn . bk Pn khi a b 0
Nếu « bậc tử » « bậc mẫu ( m k
m k ) thì lim Qn . khi a b 0 m k
Để ý rằng nếu Pn, Qn có chứa « căn » thì ta vẫn tính được bậc của nó. Cụ thể m k k 1
n tì có bậc là . Ví dụ n có bậc là 3 4 ,
n có bậc là 4 ,... n 2 3
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 4
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Trong các bài sau ta có thể dùng dấu hiệu trên để chỉ ra kết quả một cách nhanh chóng !
2. Các ví dụ rèn luyện kĩ năng 3 3n 2 5n 1 Ví dụ 1. Tính lim . 3 2n 2 6n 4n 5 Giải 5 1 3 3 3n 2 5n 3 1 n 3 n lim lim 3 2n 2 6n 4n 6 4 5 5 2 2 2 3 n n n 2 Ví dụ 2: Tính n 2n lim 3 n 3n 1 Lời giải 1 2 2 2 Ta có n 2n 0 lim lim n n 0. 3 n 3n 1 3 1 1 1 2 3 n n
Giải nhanh : Dạng « bậc tử » « bậc mẫu » nên kết quả bằng 0. 7 2 Ví dụ 3: Tính n n lim 3 n 3n 1 GV: T Lời giải 7 2 7 R n n n 4 Ầ lim n N 3 3 n 3n 1 n ĐÌN n b H CƯ
Ví dụ 4: Cho dãy số u với 2 u
trong đó b là tham số thực. Để dãy số u có giới hạn n n n 5n 3 –
hữu hạn, giá trị của b bằng bào nhiêu 0834 Lời giải 3321 b 2 33 Ta có 2n b 2 lim lim lim n u b n 5n 3 3 5 5 n Giải nhanh : 2n b 2n 2
với mọi b . 5n 3 5n 5 2 Ví dụ 5: Cho dãy số 4n n 2 u với u
. Để dãy số đã cho có giới hạn bằng 2 , giá trị của a n n 2 an 5 bằng bao nhiêu Lời giải 1 2 2 4 2 4n n 2 4 2 lim lim lim n n u a a n 0 2. 2 an 5 5 a a 2 n 2 2 Giải nhanh : 4n n 2 4n 4 2 a 2. 2 2 an 5 an a
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 5
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 2 n 2n 3 2n 1 4n 5
Ví dụ 6: Tính giới hạn L lim . 4 n 3n 1 2 3n 7 Lời giải 2 1 5 2 n 2n 3 2n 14n 1 2 4 3 5 n n n 1.2.4 8 L lim lim . 4 n 3n 1 2 3n 7 3 1 7 1.3 3 1 3 3 4 2 n n n 2 n 2n 3 2n 1 4n 2 3 5 Giải nhanh: n .2n .4n 8 . 4 n 3n 1 2 3n 7 4 2 n .3n 3
Dạng 2. Dãy số chứa căn thức 1. Phương pháp
Nếu biểu thức chứa căn thức cần nhân một lượng liên hiệp để đưa về dạng cơ bản. A B
löôïng lieân hieäp laø: A B A B
löôïng lieân hieäp laø: A B A B löôïng lieân hieäp laø: A B 3 3 2 3 2 A B
löôïng lieân hieäp laø: A B A B 3 3 2 3 2 A B
löôïng lieân hieäp laø: A B A B
2. Các ví dụ rèn luyện kĩ năng Ví dụ 1. Tính 2 2 lim n 7 n 5 GV: T Giải R Ầ N 2 2 ĐÌN 2 2 n 7 n 5 2
lim n 7 n 5 lim lim 0 2 2 2 2 H CƯ n 7 n 5 n 7 n 5 – 0834 Ví dụ 2. Tính 2 lim
n n 1 n 3321 Lời giải 33 . 2 2
n n 1 n n n 0
nhân lượng liên hợp : 1 n lim 1 1 1 2 1 lim lim n n n n 2
n n 1 n 1 1 2 1 1 2 n n Giải nhanh : n 1 n 1 2
n n 1 n . 2 2 2 n n 1 n n n Ví dụ 3. Tính 3 2 3 lim
n n n Lời giải 3 2 3 3 3
n n n n n 0
nhân lượng liên hợp :
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 6
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com n
lim n n n 2 1 1 3 2 3 lim lim . 2 3 n n 2 2 3 2 3 2 3 3
n n n n 1 1 3 3 1 1 1 n n 2 2 Giải nhanh : n n 1 3 2 3
n n n . 2 3 2 3 6 3 3 2 3 2 3 2 3 3 n n n n n n
n n n n Ví dụ 4. Tính lim n
n1 n Lời giải
n n 1 n n n n 0
nhân lượng liên hợp :
n n n n 1 1 lim 1 lim lim n 1 n 1 2 1 1 n
Giải nhanh : n n n n n 1 1 . n 1 n n n 2
Dạng 3. Tính giới hạn của dãy số chứa hàm mũ 1. Phương pháp u
Trong tính giới hạn lim n mà u ;v là hàm số mũ thì chia cả tử và mẫu cho n
a với a là cơ số v n n n n GV: T
lớn nhất. Sau đó sử dụng công thức: lim q 0 với q 1. R Ầ
2. Các ví dụ rèn luyện kĩ năng N ĐÌN n n 1 3 2.5 Ví dụ 1: Tính lim H CƯ n 1 2 5n – Lời giải 0834 n n 1 n 1 3 2.5 2.5 3321 Giải nhanh : ~ 10 n 1 2 5n 5n 33 n 3 10 n n 1 3 2.5 5 Cụ thể : lim lim 10. n 1 2 5n n 2 2. 1 5 n n 1 3 4.2 3 Ví dụ 2: Tính lim 3.2n 4n Lời giải n n 1 n 3 4.2 3 3n 3 Giải nhanh : ~ 0. 3.2n 4n 4n 4
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 7
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com n n n 3 1 1 8. 3. n n 1 3 4.2 3 4 2 4 0 Cụ thể : lim lim 0. 3.2n 4n n 1 1 3. 1 2 n 5n1 1 2 Ví dụ 3: Tính lim 5n2 3 Hướng dẫn giải
Cách 1: Giải bằng tự luận n 5n 1 n 1 2 n 2 2 Ta có: lim lim 1 . 0. 5n 2 3 9 3 Cách 2: Mẹo giải nhanh n 5n 1 5n 1 2 n 2 1 . 0. 5n 2 3 3 n n 1 3 4.2 3 Ví dụ 4: Tính lim . n n 3.2 4 Hướng dẫn giải
Cách 1: Giải bằng tự luận n n GV: T 3 2 3 4.2 n n1 3 4.2 4 3 4 4 n R Ta có: (chia tử và mẫu cho 4 n ). Ầ n n n N 3.2 4 2 ĐÌN 3. 1 4 H CƯ n n 1 3 4.2 3 0 lim 0. – Suy ra n n 0834 3.2 4 1 3321 Cách 2: Mẹo giải nhanh n n n 1 n 33 3 4.2 3 3 3 0. n n n 3.2 4 4 4 2
Ví dụ 5: Có bao nhiêu giá trị nguyên của an 1 1
a thuộc 0;20 sao cho lim 3 là một số 2 3 n 2n nguyên. Lời giải 1 2 a 2 an 1 lim lim n a 2 2 3 n 3 Ta có an 1 1 1 2 lim 3 3 a. 2 n 3 n 2n n 1 1 lim lim 0 2n 2 a 0;20, a Ta có a 1;6; 13 . a 3
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 8
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Dạng 4. Tổng của cấp số nhân lùi vô hạn 1. Phương pháp
Cấp số nhân lùi vô hạn là cấp số nhân vô hạn và có công bội là q 1.
Tổng các số hạng của một cấp số nhân lùi vô hạn (un) u1
S u u ... u ... 1 2 n 1 q
Mọi số thập phân đều được biểu diễn dưới dạng luỹ thừa của 10 n a a a 1 2 3 a
X N,a a a ...a ... N ... ... 1 2 3 n 2 3 n 10 10 10 10
2. Các ví dụ rèn luyện kĩ năng n1 1 1 1 1
Ví dụ 1: Tính tổng của cấp số nhân lùi vô hạn 1, , , ,..., ,... 2 4 8 2 Lời giải 1
Theo đề cho ta có: u 1, q . 1 2 u1 1 2 S . 1 q 1 3 1 2 GV: T
Ví dụ 2: Cho số thập phân vô hạn tuần hoàn a 0,212121... (chu kỳ là 21). Tìm a dưới dạng R phân số. Ầ N ĐÌN Lời giải H CƯ
Cách 1: Giải bằng tự luận – Ta có: a 0,212121... 0834
0,21 0,0021 0,000021 ... 3321 1 1 1 21 ... 33 2 4 6 10 10 10 1 1 1 1 1 Tổng S
... là tổng cấp số nhân lùi vô hạn có u , q . 2 4 6 1 10 10 10 2 2 10 10 1 u 2 1 1 10 1 7 S . Do đó A 21. . 1 q 1 99 99 33 1 2 10
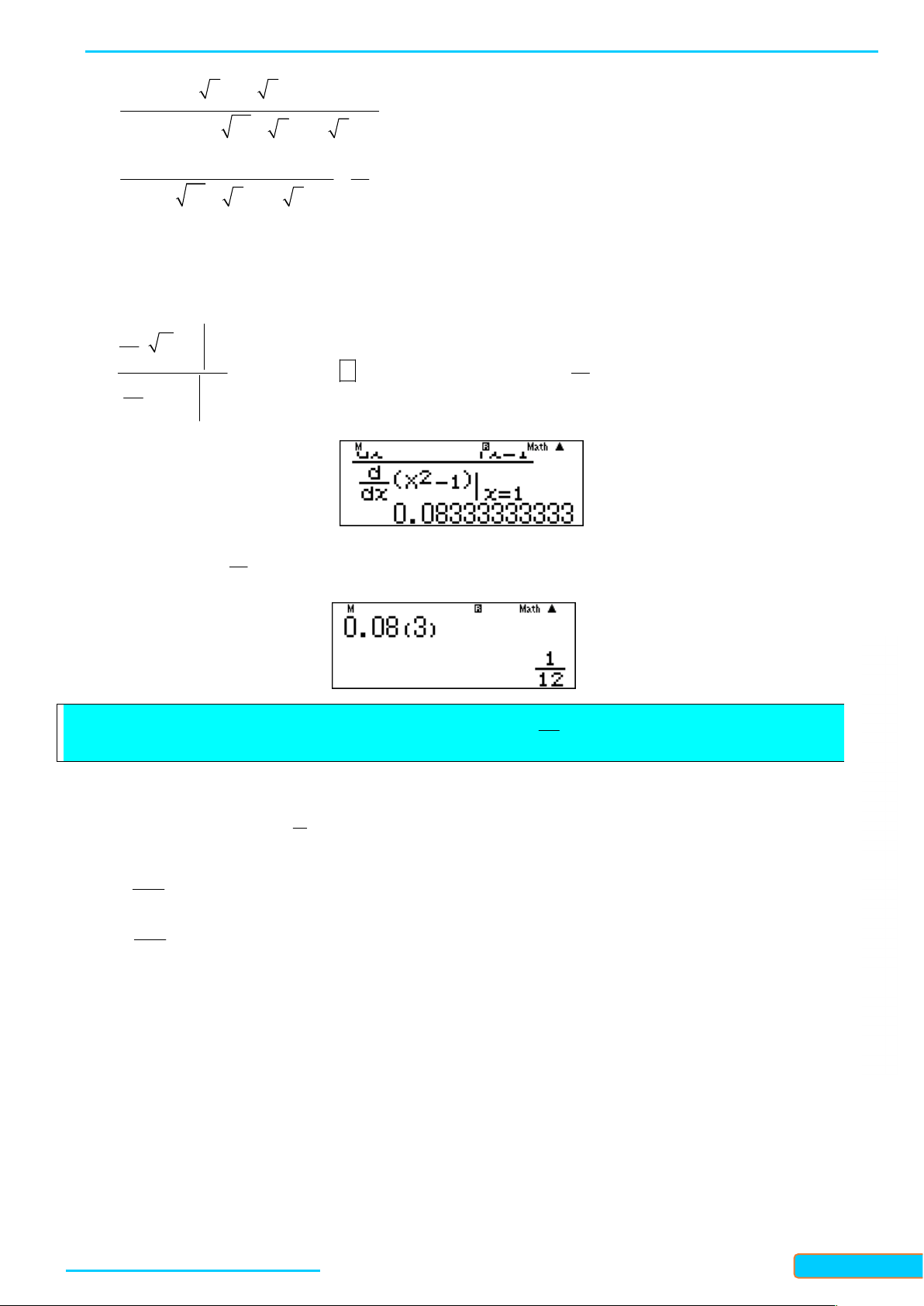
Cách 3: Giải nhanh bằng máy tính 7
Nhập vào màn hình 0,2
1 và ấn phím ta được kết quả . 33
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 9
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Ví dụ 3: Tổng S 1 0,9 0,9 0,9 ... 0,9
... có kết quả bằng bao nhiêu? n 2 3 n1 Hướng dẫn giải
1 0,9 0,92 0,93 ... 0,9n1 S ...
Đây là tổng của cấp số nhân lùi vô hạng có u 1, q 0,9. 1 u1 1 S 10. 1 q 1 0,9
Ví dụ 4: Cho 2 3 S 1 q q q ..., q 1 T 1 Q 2 Q 3 Q ..., Q 1 E 1 qQ 2 2 q Q 3 3 q Q ...
Biểu thị biểu thức E theo S,T Hướng dẫn giải 2 3 S 1 q q
q ..., q 1 là tổng của cấp số nhân lùi vô hạn, có u 1, q q. 1 u 1 S 1 Khi đó: 1 S q . (1) 1 q 1 q S 1 T 1 Tương tự: T Q . (2) 1 Q T 2 2 3 3 GV: T
E 1 q.Q q .Q q .Q ... là tổng của cấp số nhân lùi vô hạng công bội qQ (vì qQ 1 , và u 1). R 1 Ầ N ĐÌN u E 1 (3) H CƯ 1 qQ u ST – Thay (1), (2) vào (3): 1 E E . 0834 T 1 S 1 S T 1 1 . T S 3321 1 33
Ví dụ 5: Tìm số hạng U của cấp số nhân lùi vô hạn, biết S 4; q . 1 2 Hướng dẫn giải u u Ta có: 1 S q 1 1 4 u 2. 1 1 q 1 1 2
Ví dụ 6: Tìm công bội của cấp số nhân lùi vô hạn, biết S 6 ; U 3 . 1 Hướng dẫn giải u 3 1 Ta có: 1 S q 1 6 q . 1 q 1 q 2
Dạng 5: Phương pháp sai phân và quy nạp tính giới hạn 1. Phương pháp
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 10
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
1) Dạng tồng các phân số. 1 1 1 Ví Dụ: A , n 2, n N 2.3 3.4 n(n 1) 1 1 1 Ta phân tích : .(1) k(k 1) k k 1
Để tính A ta thay k từ 2,3,, n vào biểu thức (1) ta tính dễ dàng
2) Dạng tích các phân số: 2 2 2 1 3 1 Ví dụ: B , n 2, n N 2 2 2 3 2 k 1 k 1 k Ta phân tích: : .(2) 2 k k k 1
Để tính B ta thay k từ 2,3,, n vào biểu thức (2) ta tính dễ dàng 3) Dang đa thức:
a) Mỗi đơn thức ở dạng tích:
Ví dụ: C 1.2.3 2.3.4 9 9.100.101 Ta tách:
4k(k 1)(k 2) : 4 k(k 1)(k 2)[(k 3) (k 1)] , k 1, k N
((k 1)k(k 1)(k 2) k(k 1)(k 2)(k 3)) : 4 (3)
Để tính C ta thay k từ : 1,2,3,…, 99 vào biểu thức (3) ta tính được dễ dàng GV: T
Ví dụ: D 3.5.7 5.7.9 (2n 1)(2n 3)(2n 5), n 1, n N R Ầ
Ta tách: (2k 1)(2k 3)(2k 5) (2k 1)(2k 3)(2k 5)[(2k 7) (2k 1)] : 8 N ĐÌN
((2k 1)(2k 3)(2k 5)(2k 7) (2k 1)(2k 1)(2k 3) (2k 5)) : 8 (4) H CƯ
Đề tính D ta thay k từ : 1, 2,3,, n vào biều thức (4) ta tính dễ dàng –
4 ) Đơn thức dạng lũy thừa 0834 Ví Dụ: Tính 3 3 3
E 1 2 n ,
n N.n 1 3321
Ta dùng hẳng đẳng thức : 3 3 2
(x 1) x 3x 3x 1. 33 3 3 2
x 1 2 1 3.1 3.11 3 3 2 x 2
3 2 3 2 3 2 1 … 3 3 2 x n
(n 1) n 3 n 3 n 1 Cộng vế theo vế 3 3 2 2 2 (n 1) 1
3 1 2 n 3(1 2 3 n) n 3n(n 1) 3 2 n 3n 3n 3E n 2 3 2
3 n(n 1)
2n 3n n 3 2
3E n 3n 3n n 2 2
n(n 1)(2n 1) E 6
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 11
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Ngoài ra ta có thể dự đoán được số hạng tổng quát, có thể kết hợp quy nạp để khẳng đinh.
Có thể ùng vòng lặp MTCT để giải quyết các bài toán này.
2. Các ví dụ rèn luyện kĩ năng 1 1 1 Ví dụ 1: Cho u ... . Tính lim u n 1.2 2.3 nn n 1 Lời giải 1 1 1 Ta luôn có: áp dụng vào u : k k n 1 k k 1 1 1 1 1 u ... n 1.2 2.3 3.4 n n 1 1 1 1 1 1 1 1 1 1 ... 1 1 2 2 3 3 4 n n 1 n 1 1 Do đó: lim u lim 1 1. n n 1 1 1 1 1 Ví dụ 2: Cho u ... . Tính lim u n 3.5 5.7 7.9 2n n 1 2n 1 Lời giải 1 1 1 1 Ta luôn có: GV: T . 2k 1 2k 1 2 2k 1 2k 1 R Ầ 1 1 1 1 N u ... ĐÌN n 3.5 5.7 7.9 2n 1 2n 1 H CƯ 1 1 1 1 1 1 1 1 1 1 1 1 ... 2 3 5 2 5 7 2 7 9 2 2n 1 2n 1 – 0834 1 1 1 . 3321 2 3 2n 1 33 1 1 1 1 Do đó lim u lim . n 2 3 2n 1 6 1 2 3 ... n Ví dụ 3: lim bằng bao nhiêu? 2 2n Lời giải nn 1 nn 1 1 2 3 ... n 1
Vì 1 2 3 ... n nên: lim lim . 2 2 2 2n 4n 4 1 1 1
Ví dụ 4: Tính giới hạn: lim 1 1 ... 1 . 2 2 2 2 3 n Lời giải 1 1 1 2 2 2 1 3 2 1 n 1 Ta có: 1 1 ... 1 . ... 2 2 2 2 2 2 2 3 n 2 3 n
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 12
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 2 1 .2 1 .3 1 .3 1 ...n 1 n 1 n 1 . 2 2 2 2 .3 ...n 2n 1 1 1 1 Vậy lim 1 1 ... 1 . 2 2 2 2 3 n 2 U 2 1
Ví dụ 5: Tìm giới hạn của dãy: . U 1 n * U ; n n 1 2 Lời giải
Cách 1: Giải bằng tự luận
Ta chứng minh dãy U là bị chặn: 1 U 2. n n Dãy U là dãy giảm. n U 1 Thật vậy ta xét U U n
U 2U U 1 U 1 (đúng). k1 k k 2 k k k
Vậy dãy U có giới hạn. Đặt limU a . n n U 1 a 1 Ta có: lim U n lim hay a a 1. n1 2 2
Cách 2: Giải nhanh bằng máy tính
Khai báo: 1 X {biến đếm}; 2 A {giá trị u } GV: T 1 A 1 R
Ghi vào màn hình: X X 1: A Ầ 2 N ĐÌN
Ấn CALC và lặp lại phím , quan sát ta thấy dãy giảm và bị chặn dưới bởi 1. Vậy lim U 1. n H CƯ U 2 –
Ví dụ 6: Tìm giới hạn của dãy: 1 . 0834 * U 2 U ; n n 1 n 3321 Lời giải 33
Cách 1: Giải bằng tự luận
Ta sẽ chứng minh dãy bị chặn: 2 U 2 (bằng phương pháp quy nạp). n U 3 (đúng). 1 Giả sử U 2, k 1. k Ta có: U
2 U 2 2 2 k 1 . k 1 k Vậy * U 2 n . k Tương tự: * U 2 n
. Ta chứng minh dãy U là dãy tăng (bằng phương pháp quy nạp). n n
+ U 2; U 2 2 U U . 1 2 1 2 + Giả sử U
U k 2 . Ta xét U U ; k * k1 k k k1
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 13
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com U 2 U 2 U 2 U 2 U U 2 0 k m k k k k
1 U 2 (luôn đúng vì 2 U 2, k * ) k k
Vậy dãy U tăng; bị chặn trên nên có giới hạn, gọi a limU limU . n n n1
Ta có: lim U 2 LimU a 2 a 2 a 2 a n n a 2 (nhaän) 2 a a 2 0 a 1 (loaïi)
Cách 2: Giải nhanh bằng máy tính
Khai báo: 1 X {biến đếm}; 2 A {giá trị u } 1
Ghi vào màn hình: X X 1: A 2 A
Ấn CALC và lặp lại phím , quan sát ta thấy dãy tăng và bị chặn dưới bởi 2. Vậy lim U 2. n U 3 1
Ví dụ 7: Tìm giới hạn của dãy: 1 3 . * U U ; n n 1 n 2 U n Lời giải
Ta có: U 0, n* . n 1 3
Theo bất đẳng thức Cô-si, ta có: * U U 3, n . n 1 n GV: T 2 U n R Vậy U
là dãy bị chặn dưới. Ầ n N ĐÌN 2 1 3 2 1 Un H CƯ Vì U 3 U 3 U U U n n n1 n 2 U 2 n U n n – 0834 1 U U * U , n . n n n 2 3321
Dãy đã cho là giảm. Vậy dãy có giới hạn. Đặt lim U lim U a. n 1 n 33 1 3
Ta có: lim U lim U n n 2 U n 1 3 2 a a a 3 a 3. 2 a
C. GIẢI BÀI TẬP SÁCH GIÁO KHOA
Bài 1. Tìm các giới hạn sau: 2 n 1 2 16n 2 a) lim ; b) lim ; n n 4 2 n 2n 3 c) lim ; d) lim . 2n 1 2 2n Lời giải
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 14
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 2 n 1 1 1 a) lim lim 2 lim 2 lim 2 0 2 . n n n 2 2 16n 2 16n 2 2 2 b) lim lim lim 16 lim16 lim 16 0 4 . 2 2 2 n n n n 4 4 0 c) lim lim n 0 . 2n 1 1 2 0 2 n 2 n 2n 3 1 1 3 1 1 3 1 1 d) lim lim lim lim lim 0 0 . 2 2 2 2n 2 n 2n 2 n 2n 2 2
Bài 2. Tính tổng của các cấp số nhân lùi vô hạn sau: n n 1 1 1 1 1 1 1 1 a) ; b) 2 4 8 2 4 16 64 4 Lời giải 1 n 1 1 1 1 1 a) 2 . 2 4 8 2 1 3 1 2 1 n 1 1 1 1 1 b) 4 . 4 16 64 4 1 3 GV: T 1 4 R Ầ N
Bài 3. Viết số thập phân vô hạn tuần hoàn 0, 444 dưới dạng một phân số. ĐÌN H CƯ Lời giải – 4 0834 0, 444 9 3321
Bài 4. Từ hình vuông đầu tiên có cạnh bằng 1 (đơn vị độ dải), nối các trung điểm của bốn cạnh 33
để có hình vuông thứ hai. Tiếp tục nối các trung điểm của bốn cạnh của hình vuông thứ hai để
được hình vuông thứ ba. Cứ tiếp tục làm như thế, nhận được một dãy hình vuông (xem Hình 5).
a) Kí hiệu a là diện tích của hình vuông thứ n và S là tổng diện tịch của n hình vuông đầu n n
tiên. Viết công thức tính a , S n 1, 2,3, và tìm lim S (giới hạn này nếu có được gọi là tổng n n n
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 15
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
diện tích của các hình vuông).
b) Kí hiệu p là chu vi của hình vuông thứ n và Q là tổng chu vi của n hình vuông đầu tiên. n n
Viết công thức tính p và Q n 1, 2,3, và tìm lim Q (giới hạn này nếu có được gọi là tổng n n n
chu vi của các hình vuông). Lời giải 1 a) a n n 1 2 1 1 1 1 S 1 2 n 2 n 1 2 2 2 1 1 2 1 b) p 4 n n 1 ( 2) 1 1 1 1 Q 4 4 4 4 4 13, 66 n 2 n 1 1 2 ( 2) ( 2) 1 2
Bài 5. Xét quá trình tạo ra hình có chu vi vô cực và diện tích bằng 0 như sau:
Bắt đầu bằng một hình vuông H cạnh bằng 1 đơn vị độ dài (xem Hình 6a ). Chia hình vuông 0
H thành chín hình vuông bằng nhau, bỏ đi bốn hình vuông, nhận được hình H bốn hình 0 1 GV: T
vuông, nhận được hình H (xem Hình 6c ). Tiếp tục quá trình này, ta nhận được một dãy hình 2 R
H n 1, 2,3, . n Ầ N ĐÌN H CƯ – 0834 3321 33
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 16
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 1
Ta có: H có 5 hình vuông, mỗi hình vuông có cạnh bằng ; 1 3 1 1 1 H có 2
5.5 5 hình vuông, mỗi hình vuông có cạnh bằng ;. 2 2 3 3 3 1
Từ đó, nhận được H có 5n hình vuông, mỗi hình vuông có cạnh bằng . n 3n
a) Tính diện tích S của H và tính lim S . n n n
b) Tính chu vi p của H và tính lim p . n n n
(Quá trình trên tạo nên một hình, gọi là một fractal, được coi là có diện tích lim S và chu vi n lim p . n GV: T Lời giải R Ầ N 2 n n n ĐÌN 5 n 1 5 5 a) S 5 limS lim 0 . n n n n H CƯ 3 9 9 9 n n 5 n 1 5 – b) p 5 4 4 limp lim4. . n n n 0834 3 3 3 3321 D. BÀI TẬP TRẮC NGHIỆM 33 3
Câu 1: Giá trị của giới hạn lim là: 2 4n 2n 1 A. 3 . B. . C. 0. D. 1. 4 Lời giải Chọn C 3 2 Ta có 3 0 lim lim n 0. 2 4n 2n 1 2 1 4 4 2 n n
Giải nhanh : Dạng « bậc tử » « bậc mẫu » nên kết quả bằng 0. 3 Câu 2: 3n 2n 1
Giá trị của giới hạn lim là: 4 4n 2n 1
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 17
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com A. . B. 0. C. 2 . D. 3 . 7 4 Lời giải Chọn B 3 2 1 3 2 4 Ta có 3n 2n 1 0 lim lim n n n 0. 4 4n 2n 1 2 1 4 4 3 4 n n
Giải nhanh : Dạng « bậc tử » « bậc mẫu » nên kết quả bằng 0. Câu 3: v
Cho hai dãy số u và v có 1 u và 2 v
. Khi đó lim n có giá trị bằng: n n n n 1 n n 2 un A. 1. B. 2. C. 0. D. 3. Lời giải Chọn A 1 1 Ta có v n 1 1 lim n lim lim n 1. u n 2 2 1 n 1 n Giải nhanh : n 1 n 1. n 2 n
Câu 4: Cho dãy số an u với 4 u
trong đó a là tham số thực. Để dãy số u có giới hạn n n n GV: T 5n 3
bằng 2 , giá trị của a là: R Ầ N A. a 10. B. a 8. C. a 6. D. a 4. ĐÌN H CƯ Lời giải Chọn A – 0834 4 a an 4 a 3321 Ta có lim lim lim n u . Khi đó n 5n 3 3 5 5 33 n a lim u 2 2 a 10 n 5 Giải nhanh : an 4 an a 2 a 10. 5n 3 5n 5 2 Câu 5: n n 5
Tính giới hạn L lim . 2 2n 1 A. 3 L . B. 1 L . C. L 2. D. L 1. 2 2 Lời giải Chọn B
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 18
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 1 5 2 1 2 Ta có n n 5 1 lim lim n n L 2 2n 1 1 2 2 2 n 2 2 Giải nhanh: n n 5 n 1 . 2 2 2n 1 2n 2 2 3 Câu 6: n 3n
Tính giới hạn L lim . 3 2n 5n 2 A. 3 L . B. 1 L . C. 1 L . D. L 0. 2 5 2 Lời giải Chọn A 1 2 3 3 n 3n 3 lim lim n L 3 2n 5n 2 5 2 2 2 2 3 n n 2 3 3 Giải nhanh: n 3n 3n 3 . 3 3 2n 5n 2 2n 2 2 4 Câu 7: 5n 3an
Tìm tất cả các giá trị của tham số a để L lim 1a 0. 4 n 2n 1
A. a 0;a 1. B. 0 a 1.
C. a 0; a 1. D. 0 a 1. Lời giải GV: T Chọn C R Ầ N 5 ĐÌN 2 4 3a 2 5n 3an 3a a 0 lim lim n L 0 . 4 H CƯ 1 an 2n 1 a a 1 a 2 1 1 1 3 4 n n – 0834 3
2n n 2 3n 1
Câu 8: Tính giới hạn L lim . 2n 4 1 n 7 3321 33 A. 3 L . B. L 1. C. L 3. D. L . 2 Lời giải Chọn A Ta có 2 1 2 1 n n 2n n 3n 3 2 3 2 1 . 3 1 3 2 2 2 2 1 n n n n 1.3 3 L lim lim lim . 2n 1 4 n 7 1 7 1 7 4 2.1 2 n2 .n 1 2 1 4 4 n n n n 3
2n n 2 3n 3 2 1 Giải nhanh: n .3n 3 . 2n 1 4 n 7 4 2 . n n 2 3 Câu 9: n 2n
Kết quả của giới hạn lim là: 2 13n
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 19
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com A. 1 . B. . C. . D. 2 . 3 3 Lời giải Chọn C 2 3 2 n 1 3 2 1 2 n 2n n lim lim lim . n n . Ta có 2 1 3n 1 1 2 n 3 3 2 2 n n l im n 2 2 3 1 2 n 2 1 n n 2 1 im lim . n n 2 l im 0 1 3n 1 1 3 3 2 3 n 2 n 3 3 Giải nhanh : n 2n n 1 n . 2 2 13n 3 n 3 3 Câu 10: 2n 3n
Kết quả của giới hạn lim là: 2 4n 2n 1 A. 3 . B. . C. 0 D. 5. 4 7 Lời giải Chọn B 2 GV: T 3 2 n 3 3 2 3 2 2n 3n n lim lim lim . n n . Ta có 2 R 4n 2n 1 2 1 2 1 2 Ầ n 4 4 2 2 N n n n n ĐÌN l im n H CƯ 2 2 3 3 2 2n 3 3 n n 2 3 im lim . n . – n 2 l im 0 4n 2n 1 2 1 0834 2 1 4 4 2 4 n n 2 n n 3321 3 3
Giải nhanh : 2n 3n 3n 3 .n . 33 2 2 4n 2n 1 4n 4 4 Câu 11: 3n n
Kết quả của giới hạn lim là: 4n 5 A. 0. B. . C. . D. 3 . 4 Lời giải Chọn C 3 4 3 n 1 4 3 1 3 3n n n 3 lim lim lim . n n . Ta có 4n 5 5 5 n4 4 n n
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 20
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 3 l imn 3 4 1 3 3 3 1 n n 3 n 3 1 lim l lim n . . l im n 0 4n 5 5 4 5 4 4 n n 4 4 Giải nhanh : 3n n n 1 3 .n . 4n 5 4n 4
Câu 12: Trong các giới hạn sau đây, giới hạn nào bằng 0? 3 2 3 2 4 A. 3 2n 2n 3 2n 3n 2n 3n lim . B. lim . C. lim . D. lim . 2 2n 1 3 2 n 4 2 2 n 1 4 2 2 n n Lời giải Chọn B
. Theo dấu hiệu ở đã nêu ở phần Chú ý trên thì ta chọn giới hạn nào rơi vào trường hợp
« bậc tử » « bậc mẫu » ! 3 3 2n lim
: « bậc tử » « bậc mẫu » và a b 2.2 4 0. 2 2n 1 m k 2 2n 3 lim
0 : « bậc tử » « bậc mẫu ». 3 2 n 4 3 2n 3n lim
: « bậc tử » « bậc mẫu » và a b n k 3 . 2 0. 2 2 n 1 2 4 2n 3n 3 3 a m GV: T lim
: « bậc tử » « bậc mẫu » và 3 3 . 4 2 2 n n 2 2 b 2 2 k R Ầ N
Câu 13: Dãy số nào sau đây có giới hạn là ? ĐÌN 1 2n 3 n 2n 1 2 4 2 2n 3n n 2n H CƯ A. . B. u . C. u . D. u . 2 5n 5n n 3 n 2n n 2 3 n 2n n 5n 1 – Lời giải 0834 Chọn C 3321
Ta chọn đáp án dạng « bậc tử » « bậc mẫu » và a b 0. m k 33 2 4 2n 3n u
: « bậc tử » « bậc mẫu » và a b 3.2 6 0 lim u . n 2 3 n 2n m k n khi a 0 Chú ý : (i) lim m m 1 n a n a n
a n a . m n 1 1 0 khi a 0 n
(ii) Giả sử q max q : i 1;2;m thì i a khi q 1 0 lim . n n n
a q a q a q a
khi a 0, q 1. m m 1 1 0
khi a 0, q1
Ta dùng « dấu hiệu nhanh » này để đưa ra kết quả nhanh chóng cho các bài sau.
Câu 14: Tính giới hạn L 2
lim 3n 5n 3.
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 21
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com A. L 3. B. L . C. L 5. D. L . Lời giải Chọn D 2 lim n . L lim 5 3 2
3n 5n 2 3 lim n 2 vì 5 3 . 2 n n l im 2 2 0 2 n n Giải nhanh : 2 2
3n 5n 3 3n .
Câu 15: Có bao nhiêu giá trị nguyên của tham số a thuộc khoảng 1 0;10 để L n 2 a 3 lim 5 3 2 n . A. 17. B. 3. C. 5. D. 10. Lời giải Chọn A 5 Ta có lim 5n 3 2 a 2 3 n 3 lim n 3 2 a 2 2 n 5 a lim 3 2 2 a 2 2
a 2 0 2 n a 2
Câu 16: Tính giới hạn 4 2
lim 3n 4n n 1 . GV: T A. L 7. B. L . C. L 3. D. L . R Ầ N Lời giải ĐÌN H CƯ Chọn D Ta có – 0834 4 lim n 4 1 1 4 2 4 3321 lim3n 4n n 1 limn 3 vì 4 1 1 . 2 3 4 n n n l im 3 3 0 2 3 4 n n n 33 Giải nhanh : 4 2 4
3n 4n n 1 3n .
Câu 17: Giá trị của giới hạn lim n 5 n 1 bằng: A. 0. B. 1. C. 3. D. 5. Lời giải Chọn A
n 5 n 1 n n 0
nhân lượng liên hợp :
n n 4 lim 5 1 lim 0
n 5 n 1
Câu 18: Giá trị của giới hạn 2 2 lim
n 1 3n 2 là: A. 2. B. 0. C. . D. .
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 22
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Lời giải Chọn C lim 1 2 2 2 n 1
3n 2 limn 1 3 vì 2 2 n n 1 2 lim n , lim 1 3 1 3 0. 2 2 n n Giải nhanh : 2 2 2 2
n 1 3n 2
n 3n 1 3n .
Câu 19: Giá trị của giới hạn 2 2 lim
n 2n n 2n là: A. 1. B. 2. C. 4. D. . Lời giải Chọn B 2 2 2 2
n 2n n 2n n n 0
nhân lượng liên hợp : n lim 4 4 2 2
n 2n n 2n lim lim 2. 2 2
n 2n n 2n 2 2 1 1 n n Giải nhanh : 4n 4n 2 2
n 2n n 2n 2. 2 2 2 2
n 2n n 2n n n 2 2 2 GV: T
Câu 20: Có bao nhiêu giá trị của a để lim n a n n a 2n1 0. R A. 0. B. 2. C. 1. D. 3. Ầ N ĐÌN Lời giải H CƯ Chọn B – 2 2 2
n a n n a 2 2
2 n 1 n n 0
nhân lượng liên hợp: 0834 2 3321 a a 2 n 1 Ta có lim 2 2 2
n a n n a 2n 1 lim 2 2
n n n 1 33 1 2
a a 2 2 a a 2 a 1 lim n 0 . 1 1 2 a 2 1 1 2 n n
Câu 21: Giá trị của giới hạn 2 2 lim
2n n 1 2n 3n 2 là: A. 0. B. 2 . C. . D. . 2 Lời giải Chọn B 2 2 2 2
2n n 1 2n 3n 2 2n 2n 0
nhân lượng liên hợp :
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 23
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com n lim 2 1 2 2
2n n 1 2n 3n 2 lim 2 2
2n n 1 2n 3n 2 1 2 1 lim n . 1 1 3 2 2 2 2 2 2 n n n n Giải nhanh : 2n 1 2n 1 2 2
2n n 1 2n 3n 2 . 2 2 2 2
2n n 1 2n 3n 2 2n 2n 2
Câu 22: Giá trị của giới hạn 2 2 lim
n 2n 1 2n n là: A. 1. B. 1 2. C. . D. . Lời giải Chọn C Giải nhanh : 2 2 2 2
n 2n 1 2n n
n 2n 1 2n . Cụ thể : lim 2 1 1 2 2 n 2n 1
2n n lim .n 1 2 vì 2 n n n 2 1 1 lim n , lim 1 2 1 2 0 2 n n n
Câu 23: Có bao nhiêu giá trị nguyên của a thỏa 2 2 lim
n 8n n a 0 . GV: T A. 0. B. 2. C. 1. D. Vô số. R Ầ N Lời giải ĐÌN H CƯ Chọn B Nếu 2 2 2
n 8n n a n n 0
nhân lượng liên hợp : – 0834 2 2 2a 8 n 2a 8 2 2 3321
Ta có lim n 8n n a lim lim 2
n n n 1 1 1 33 n 2
a 4 0 a 2 .
Câu 24: Giá trị của giới hạn 2 lim
n 2n 3 n là: A. 1. B. 0. C. 1. D. . Lời giải Chọn A 2 2
n 2n 3 n n n 0
nhân lượng liên hợp : 3 n lim 2 2 3 2 2 3 lim lim n n n n 1 2
n 2n 3 n 2 3 1 1 2 n n
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 24
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Giải nhanh : 2n 3 2n 2
n 2n 3 n 1. 2 2
n 2n 3 n n n
Câu 25: Cho dãy số u với 2 2 u
n an 5 n 1 , trong đó a là tham số thực. Tìm a để n n lim u 1. n A. 3. B. 2. C. 2. D. 3. Lời giải Chọn C 2 2 2 2
n an 5 n 1 n n 0
nhân lượng liên hợp : an
1 limu lim n an n n 4 2 2 5 1 lim 2 2
n an 5 n 1 4 a a lim n a 2. a 5 1 2 1 1 2 2 n n n Giải nhanh : an 4 an a 2 2
1 n an 5 n 1 a 2. 2 2 2 2 2 n an 5 n 1 n n
Câu 26: Giá trị của giới hạn lim3 3 3 3
n 1 n 2 bằng: A. 3. B. 2. C. 0. D. 1. GV: T Lời giải R Ầ Chọn C N ĐÌN 3 3 3 3 3 3 3 3
n 1 n 2 n n 0
nhân lượng liên hợp : H CƯ 1 3 3 3 3 – lim n 1 n 2 lim 0. 2 0834 3 3 n 3 3 3 3 3
1 n 1. n 2 3 n 2 3321
Câu 27: Giá trị của giới hạn 3 3 2 lim
n 2n n bằng: 33 A. 1. B. 2 . C. 0. D. 1. 3 3 Lời giải Chọn B 3 3 2 3 3
n 2n n n n 0
nhân lượng liên hợp : n
lim n 2n n 2 2 2 2 3 3 2 lim lim . 3 2 n 2n 2 2 3 3 2 2 3 3 .
n n 2n n 2 2 3 3 1 1 1 n n 2 2 Giải nhanh : 2n 2n 2 3 3 2
n 2n n . 3 2 2 3 6 3 3 2 3 3 2 2 3 3 n . 2 . 2 n n n n n n n n n
Câu 28: Giá trị của giới hạn lim
n n 1 n 1 là:
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 25
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com A. 1. B. . C. 0. D. 1. Lời giải Chọn D
n n 1 n
1 n n n 0
nhân lượng liên hợp :
n n n 2 n 2 lim 1 1 lim lim 1
n 1 n 1 1 1 1 1 n n Giải nhanh : n 2 n 2 n n n 1 1 1.
n 1 n 1 n n
Câu 29: Giá trị của giới hạn n 2 2 lim
n 1 n 3 bằng: A. 1. B. 2. C. 4. D. . Lời giải Chọn B n 2 2
n n n 2 2 1 3
n n 0
nhân lượng liên hợp : n lim n 4 4 2 2
n 1 n 3 lim lim 2 2 2
n 1 n 3 1 3 1 1 2 2 n n Giải nhanh : 4n 4n 2 2 GV: T n n 1 n 3 2. 2 2 2 2
n 1 n 3 n n R Ầ 2 2 N
Câu 30: Giá trị của giới hạn lim n n n 1 n n6 là: ĐÌN H CƯ A. 7 1. B. 3. C. 7 . D. . 2 – Lời giải 0834 Chọn C 3321 2 2 2 2 33
n n n1 n n6 n n n 0
nhân lượng liên hợp : n lim n 7 2 2
n n 1 n n 6 lim 2 2
n n 1 n n 6 7 7 lim . 1 1 1 6 2 1 1 2 2 n n n n Giải nhanh : n 7n 7n 7 2 2
n n 1 n n 6 . 2 2 2 2 2 n n 1 n n 6 n n
Câu 31: Giá trị của giới hạn 1 lim là: 2
n 2 n 4 A. 1. B. 0. C. . D. . Lời giải Chọn C
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 26
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 2 2 2
n 2 n 4 n n 0
nhân lượng liên hợp : 1 1 lim lim 1 2 4 2 2 n 2 n 4 lim . n 1 1 2 2 2 2 2 2 4 n n n n vì 1 2 4 lim n , lim 1 1 1 0 2 2 2 n n Giải nhanh : 1 1 1 2 2 n 2 n 4 2 2 n n n . 2 2 2 n 2 n 4 2
Câu 32: Giá trị của giới hạn 9n n n 2 lim là: 3n 2 A. 1. B. 0. C. 3. D. . Lời giải Chọn A 2 2
9n n n 2 9n 3n 0 giải nhanh : 2 2
9n n n 2 9n 1 3n 2 3n 1 1 2 9 2 2 Cụ thể : 9n n n 2 n n n 9 lim lim 1. 3n 2 2 3 GV: T 3 n R Ầ 1 N
Câu 33: Giá trị của giới hạn lim là: 3 3 ĐÌN n 1 n H CƯ A. 2. B. 0. C. . D. . – Lời giải 0834 Chọn B 3321 3 3 3 3
n 1 n n n 0
nhân lượng liên hợp : 33 lim 1 3 3
n 1 n lim 0 3 n 2 3 3 3 2
1 n n 1 n n2 Câu 34: 2 5
Kết quả của giới hạn lim bằng: 3n 2.5n A. 25 . B. 5 . C. 1. D. 5 . 2 2 2 Lời giải Chọn A n 1 2 25 n2 Cụ thể : 2 5 5 25 lim lim . 3n 2.5n n 3 2 2 5
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 27
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com n2 n2 Giải nhanh : 2 5 5 25 3n 2.5n 2.5n 2 n
Câu 35: Kết quả của giới hạn 3 1 lim bằng: 2n 2.3n 1 A. 1. B. 1 . C. 1 . D. 3 . 2 2 2 Lời giải Chọn B n n Giải nhanh : 3 1 3 1 2n 2.3n 1 2.3n 2 n 1 1 n Cụ thể : 3 1 3 1 lim lim . 2n 2.3n 1 n n 2 1 2 2 3 3 n 5 n 1 2 2 1 Câu 36: 2n 3 a 5 Biết rằng lim
c với a, b, c .
Tính giá trị của biểu thức n n 1 2 n 1 5.2 5 3 b 2 2 2
S a b c . A. S 26. B. S 30. C. S 21. D. S 31. Lời giải GV: T Chọn B n n R 2 1 n 3 Ầ n 1 1 2. 2 N 5 2 2 1 2 2n 3 5 5 ĐÌN lim lim n n n n 5.2n 5 1 2 n 1 1 3 2 1 1 H CƯ 5. 5 . 2 5 5 n – 1 5 0834 2 2. 5 5 3321 Giải nhanh : 33 n n a 5 n 1 1 2 2 1 n 5 2 3 2 2n 1 5 2 2 b 5. n n 5.2n 5 1 2 n 1 3 5 1 2 n 5 5 c 2 Vậy 2 2 2
S 1 5 2 30. n n 2n Câu 37: 3 2
Kết quả của giới hạn lim là: n n 2n2 3 3 2 A. 1. B. 1. C. . D. 1 . 3 4 Lời giải Chọn D n n 2n n n n n Giải nhanh: 3 2 3 4 4 1 n n 2n2 3 3 2 3 n
3n 4.4n 4.4n 4
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 28
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com n n 3 1 n n 2n Cụ thể : 3 2 4 4 1 lim lim . n n 2n2 3 3 2 n n 3 4 3. 3. 4 4 4
Câu 38: Kết quả của giới hạn n
lim 3n 5 là: A. 3. B. 5. C. . D. . Lời giải Chọn D Giải nhanh : Vì n 3 5 nên 3n 5 3n . li m3n n Cụ thể : n 5 n
lim 3n 5 lim 3n 1 vì . 5 3 li m1 1 0 3
Câu 39: Kết quả của giới hạn 4 n 1
lim 3 .2 5.3n là: A. 2 . B. 1. C. . D. 1. 3 3 Lời giải Chọn C Giải nhanh : 4 n 1 3 .2 5.3n 5
.3n 5 0 . GV: T l im3n n R n n n 2 Ầ Cụ thể : 4 1 lim 3 .2 5.3 lim3 16 2.
5 vì n 2 . N ĐÌN 3 lim 162. 5 5 0 3 H CƯ n n 1 3 4.2 3
Câu 40: Kết quả của giới hạn lim là: – n 3.2n 4 0834 A. 0. B. 1. C. . D. . 3321 Lời giải 33 Chọn A 1 n n n n Giải nhanh : 3 4.2 3 3 3 0. 3.2 4n 4n n 4 n n 1 1 n n n n 1 Cụ thể : 3 4.2 3 8.3 3 3 4.2 3 0 24. 0 lim 0. 3.2n 4n 4n 4 3.2n 4n n 1 Câu 41: 2 3n 10
Kết quả của giới hạn lim là: 2 3n n 2 A. . B. 2 . C. 3 . D. . 3 2 Lời giải Chọn A
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 29
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com n n nn 1 n 2 0 3 n Ta có n n k n 3 2
2 C 2 C . Khi đó: n n k 6 6 n 0 2 2 n 2n n lim n 1 2 n 2 3. 10. n 1 2 3n 10 2n 2n 2 n lim lim . vì n 1 . 2 2 2 3. 10. 3n n 2 n 1 2 n 3 2 2 2 2 n n lim 0 1 2 3 3 2 n n n n 1 Câu 42: 4 2 1
Tìm tất cả giá trị nguyên của a thuộc 0;2018 để 4 lim .
3n 4na 1024 A. 2007. B. 2008. C. 2017. D. 2016. Lời giải Chọn B n 1 1 2. n n 1 4 2 2 1 1 1 4 lim lim . 4 3n 4n a n a a 3 4 2a a 2 2 4 4 n n 1 n Giải nhanh: 4 2 4 1 1 4 a 10 4
2 1024 2 a 10. n n 2 3 4 4na 2a 1024 GV: T Mà a 0;20
18 và a nên a 10;20 17
có 2008 giá trị a. R 2 n Ầ n 2n 1 N
Câu 43: Kết quả của giới hạn lim bằng: n ĐÌN 3n 1 3 H CƯ A. 2 . B. 1. C. 1. D. 1 . 3 3 3 – 0834 Lời giải 3321 Chọn C 33 2 n n n 2n 2 1 n 2n 1 Ta có lim lim lim . Ta có 3n 1 3n 3n 1 3n 2 1 2 n 2n n 1 l im lim 3n 1 1 n 2 3 n 2n 1 1 3 lim . n 3n1 3n 3 n n 1 n 1 1 0 0 lim 0 3n 3 3n n 3n 1 cos 3n
Câu 44: Kết quả của giới hạn lim bằng: n 1 A. 3 . B. 3. C. 5. D. 1. 2 Lời giải
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 30
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Chọn B n n 3n 1 cos 3n 3n 1 cos 3n lim lim Ta có : . n 1 n 1 n 3n 3 l im 3 n 1 1 n 3n 1 cos 3n lim 3. n n 1 cos 3n 1 1 cos 3n n 1 0 0 lim 0 n 1 n 1 n 1
Câu 45: Kết quả của giới hạn lim 2.3n n 2 là: A. 0. B. 2. C. 3. D. . Lời giải Chọn D n Ta có n n n 1
lim 2.3 n 2 lim 3 . 2 2. . Vì 3n 3 lim 3n l im 3n n n n 2 n 0 0 lim 0 n , n 2 3 C nn n n 1 1 n 1 3 n lim 2 2. 2 0 3n 3 2 n 1 GV: T lim 0 3 R Ầ
do đó lim 2.3n n 2 . N ĐÌN
Câu 46: Tổng của một cấp số nhân lùi vô hạn bằng 2 , tổng của ba số hạng đầu tiên của cấp số H CƯ
nhân bằng 9 . Số hạng đầu u của cấp số nhân đó là: 1 – 4 0834 A. 9 u 3. B. u 4. C. u . D. u 5. 1 1 1 1 3321 2 33 Lời giải Chọn A
Gọi q là công bội của cấp số nhân, ta có : u 1 1 2 u 2 1q q 1 1 q 2 . 3 1 q 9 2 9 3 1 q 1 S u . u 2 1 3 4 1 3 1 1 q 4 2 1 1 1
Câu 47: Tính tổng S 9 3 1 3 3 9 3n A. 27 S . B. S 14. C. S 16. D. S 15. 2 Lời giải Chọn A
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 31
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Ta có 1 1 1 1 1 1 1 1 27
S 9 3 1 9 1 9 . n 3 2 4 n 1 3 9 3 3 3 3 3 1
2 1 1 CSN lv : h u 1 , q 3 1 3 1 1 1 1 Câu 48:
Tính tổng S 2 1 . 2 4 8 2n A. S 2 1. B. S 2. C. S 2 2. D. 1 S . 2 Lời giải Chọn C Ta có 1 1 1 1 1 S 2 1 2 2 2. 2 4 8 2n 1
1 1 CSN lv : h u 1 , q 2 1 2 2 4 2n
Câu 49: Tính tổng S 1 . 3 9 3n A. S 3. B. S 4. C. S 5. D. S 6. GV: T Lời giải Chọn A R Ầ N ĐÌN Ta có 2 n H CƯ 2 4 2n 2 2 2 1 S 1 1 3. 3 9 3n 3 3 3 2
1 – 2 3 0834 CSN lvh: 1 u 1, q 3 3321 n 1 1 1 1 1
Câu 50: Tổng của cấp số nhân vô hạn , , ,..., ,... bằng: n 1 2 6 18 2.3 33 A. 3 . B. 8. C. 2 . D. 3. 4 3 3 8 Lời giải Chon D . Ta có : n n 1 1 1 1 1 1 1 1 1 1 1 1 3
S 1 . n 1 2 n 1 2 6 18 2.3 2 3 3 3
2 1 8 1 1 CSN : lvh u 1 , q 3 1 3 1 1 1 1 1 1 Câu 51:
Tính tổng S ... ... . 2 3 4 9 2n 3n
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 32
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com A. 1. B. 2 . C. 3 . D. 1 . 3 4 2 Lời giải Chọn D Ta có 1 1 1 1 1 1 S ... ... 2 3 4 9 2n 3n 1 1 1 1 1 1 1 1 1 1 2 3 1 . 2 4
2n 3 9 3n 1 1
2 2 1 1 1 1 CSN l : vh 2 3 1 u q CSN lv : h u q 1 2 3 2 n Câu 52: 1 a a ... a
Giá trị của giới hạn lim
a 1, b 1 bằng: 2
1 b b ... n b A. b a 0. B. 1 . C. 1 . D. Không tồn tại. 1 a 1 b Lời giải Chọn B Ta có 2 1 ... n a a
a là tổng n 1 số hạng đầu tiên của cấp số nhân với số hạng đầu là 1. n 1 1 a n 1 1 a
1 và công bội là a , nên 2
1 a a ... n a . 1 a 1 a GV: T n 1 1 1 b n 1 Tương tự: 1 b 2
1 b b ... n b . R 1 b 1 b Ầ N n 1 ĐÌN 1a 2 n n 1 Do đó 1 a a ... a 1 b 1 a 1 1 b lim lim a lim .
a 1, b 1 . H CƯ 2 n n 1 n 1
1 b b ... b 1b 1 a 1b 1a 1b – 0834 Câu 53: Rút gọn 2 4 6 2 1 cos cos cos c s o n S x x x
x với cos x 1. 3321 A. 2 1 1 S sin x. B. 2 S cos x. C. S . D. S . 2 sin x 2 cos x 33 Lời giải Chọn C Ta có n 1 1 2 4 6 2
S 1 cos x cos x cos x cos x .
2 2 1 cos x sin x 2 CSN : lvh u q x 1 1, cos Câu 54: n Rút gọn 2 4 6 S
x n x sin x 2 1 sin si
1 .sin n x với sin x 1. A. 2 1 S sin x. B. 2 S cos x. C. S . D. 2 S tan x. 2 1 sin x Lời giải Chọn C
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 33
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Ta có n n 1 2 4 6
S 1sin x sin x sin x 2 1 .sin x . 2
1 sin x 2 CSN lvh: 1 u 1, q sin x Câu 55: Thu gọn 2 3
S 1tan tan tan với 0 . 4 A. 1 S . B. cos S . C. tan S . D. 2 S tan . 1 tan 1 tan 2 sin 4 Lời giải Chọn B
Ta có tan 0;
1 với mọi 0; , do đó 4 1 cos cos 2 3
S 1 tan tan tan .
1 tan sin cos CSN : lvh 1 u 1, q tan 2 sin 4 Câu 56: Cho ,
m n là các số thực thuộc 1 ; 1 và các biểu thức: 2 3
M 1 m m m 2 3
N 1 n n n 2 2 3 3
A 1 mn m n m n GV: T
Khẳng định nào dưới đây đúng? R MN MN Ầ A. A . B. A . C. 1 1 1 A . D. 1 1 1 A . N M N 1 M N 1 M N MN M N MN ĐÌN H CƯ Lời giải Chọn A – 0834 1 1 M m 1 3321 Ta có 1 m M , khi đó 1 1 N n 1 33 1 n N 1 1 MN A . 1 mn 1 1 M N 1 1 1 1 M N
Câu 57: Số thập phân vô hạn tuần hoàn 0,5111 được biểu diễn bởi phân số tối giản a . Tính b
tổng T a . b A. 17. B. 68. C. 133. D. 137. Lời giải Chọn B Ta có 2 3 0,5111 0,5 10
10 10n
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 34
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Dãy số 2 3
10 ;10 ;...;10n ;... là một cấp số nhân lùi vô hạn có số hạng đầu bằng 2 u 10 , công 1 2 bội bằng u 10 1 1 q 10 nên 1 S . 1 1 q 110 90 Vậy 46 23 a 23
0,5111... 0,5 S
T a b 68. 90 45 b 45
Câu 58: Số thập phân vô hạn tuần hoàn A 0,353535... được biểu diễn bởi phân số tối giản a . Tính b T a . b A. 3456. B. 3465. C. 3645. D. 3546. Lời giải Chọn B Ta có 35 2 35 35 35 a 35 10
A 0,353535... 0, 35 0, 0035 ... ... T 3465. . 2 4 10 10 1 99 b 99 1 2 10
Câu 59: Số thập phân vô hạn tuần hoàn B 5,231231... được biểu diễn bởi phân số tối giản a . Tính b T a . b A. 1409. B. 1490. C. 1049. D. 1940. GV: T Lời giải R Chọn A Ầ N ĐÌN Ta có H CƯ
B 5, 231231... 5 0, 231 0, 000231... 231 – 3 231 231 231 1742 a 1742 0834 10 5 ... 5 5 T 1409 3 6 10 10 1 999 333 b 333 1 3321 3 10 33
Câu 60: Số thập phân vô hạn tuần hoàn 0,17232323 được biểu diễn bởi phân số tối giản a . b
Khẳng định nào dưới đây đúng? A. 15 a b 2 . B. 14 a b 2 . C. 13 a b 2 . D. 12 a b 2 . Lời giải Chọn D Ta có
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 35
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 1 1 1
0,17232323 0,17 23 4 6 8 1 0 10 10 1 17 17 23 1706 853 10000 23. . 100 1 100 100.99 9900 4950 1100 a 853 12 13
2 T 4097 2 . b 4950
1 3 5 ... 2n 1
Câu 61: Tính giới hạn: lim . 2 3n 4 1 2 A. 0. B. . C. . D. 1. 3 3 Lời giải Chọn B
Ta có: 2 1 3 5 ... 2n 1 n 1 . 2
1 3 5 ... 2n 1 n 1 Vậy: lim lim 2 3n 2 4 3n 4 2 1 2 1 2 n 2n 1 n 1 n lim lim . 2 4 3n 4 3 3 2 GV: T n R 1 1 1 Ầ
Câu 62: Tính giới hạn: lim ... . N 1.2 2.3 ĐÌN nn 1 H CƯ 3 A. 0. B. 1. C. . D. Không có giới 2 – 0834 hạn. 3321 Lời giải 33 Chọn B 1 1 1 1 1 1 1 1 Ta có: lim ... lim 1 ... 1.2 2.3 nn 1 2 2 3 n n 1 1 lim 1 1. n 1 1 1 1
Câu 63: Tính giới hạn: lim ... . 1.3 3.5 n2n 1 2n 1 1 A. 1. B. 0. C. . D. 2. 2 Lời giải Chọn c
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 36
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 1 1 1 Ta có: lim ... 1.3 3.5 n2n 1 2n 1 1 1 1 1 1 1 1 1 1 lim 1 ... lim 1 . 2 3 3 5 2n 1 2n 1 2 2n 1 2 1 1 1
Câu 64: Tính giới hạn: lim ... . 1.3 2.4 nn 2 3 2 A. . B. 1. C. 0. D. . 4 3 Lời giải Chọn A 1 1 1 Ta có: ... 1.3 2.4 n n 2 1 1 1 1 1 1 1 1 1 1 1 ... 2 3 2 4 3 5 n 1 n 1 n n 2 1 1 1 1 1 2 2 n 1 n 2 1 1 1 3 Vậy lim ... . 1.3 2.4 nn 2 4 GV: T 1 1 1 R
Câu 65: Tính giới hạn: lim ... . Ầ N 1.4 2.5 nn 3 ĐÌN 11 3 H CƯ A. . B. 2. C. 1. D. . 18 2 – 0834 Lời giải 3321 Chọn A 33 1 1 1 Ta có: ... 1.4 2.5 n n 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 ... 3 1 4 2 5 3 6 4 7 n 3 n n 2 n 1 n 1 n 2 n n 3 1 1 1 1 1 1 1 3 2 3 n 1 n 2 n 3 1 1 1 11 Vậy: lim ... . 1.4 2.5 nn 3 18 1 2 3 ... n
Câu 66: Cho dãy u với u
. Mệnh đề nào sau đây là mệnh đề đúng? n n 2 n 1 1 A. lim u 0. B. lim u . C. lim u 1. D. lim u không tồn n n 2 n n tại.
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 37
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Lời giải Chọn B
Dãy số 1, 2, 3, …, n là cấp số cộng có số hạng đầu là u 1 số hạng cuối cùng u n , 1 n công sai d 1. nu n n n 1 1
Khi đó S 1 2 3 ... n . n 2 2 n n 1 Viết lại: u n 2 2 n 1 2 1 n 1 n n 1 n 1 lim u lim lim lim . n 2 2 n 1 2 2 2 n 2 2 n 1 U 1 2
Câu 67: Tìm giới hạn của dãy: . 2 1 Un * U ; n n 1 2 2 A. 2. B. 1. C. 2. D. Không có giới hạn. Lời giải GV: T Chọn B 1 5 57 R Ta có: U ; U ; U ;... Ầ 1 2 3 N 2 8 64 ĐÌN
Ta chứng minh: U 1 n * (bằng phương pháp quy nạp). Vậy dãy bị chặn trên. H CƯ n Ta chứng minh U
là dãy tăng. Thật vậy: n – 0834 2 1 Un 3321 Ta có: U U U n1 n n 2 2 33 2 2 U 2U 1 0 U 1 0 luôn đúng * n , vì U 1. n n n n
Vậy dãy có giới hạn. Đặt a lim U lim U . n n1 2 2 1 U 1 a Ta có: lim U lim n a 2a 1 2 a n1 2 2 2 2 2
a 2a 1 0 a 1 . U 5 1
Câu 68: Tìm giới hạn của dãy: 2 2 U . n * U ; n n 1 2U n A. 1. B. 2. C. 3. D. Không có giới hạn. Lời giải
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 38
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Chọn B 1 1 Ta có: U
U 2 (theo bất đẳng thức Cô-si với U 0 ). Vậy U là dãy bị n n1 n U 2 n n chặn dưới.
Dấu “=” không xảy ra, nên * U 2, n . n U 2 2 U 1 1 Lại có: n1 2 n . Vì U 2 U 2 2 2 U n n 2U U 2 n n n 1 1 1 1 1 1 * 1 U U , n . n 1 n 2 2 U 2 U 2 2 2 n n
Vậy dãy giảm, khi đó U có giới hạn. Đặt lim U
lim U a a 0 . n n1 n 2 2 2 U 2 a Ta có: lim U n lim a 2 2a 2 2 a n1 2U 2a n 2
a 2 a 2 (vì a 0 ). U 2 Câu 69:
Tìm giới hạn của dãy: 1 * U 2.U ; n n1 n 1 7 A. 2. B. 1 2. C. . D. Không có giới 2 GV: T hạn. R Lời giải Ầ N ĐÌN Chọn A H CƯ
Ta có: U 2; U 2 2 ;… 1 2 – 0834
Ta sẽ chứng minh U 2 ; n * n
(bằng phương pháp quy nạp). 3321
n 1, U 2 2 . Giả sử U 2, k 1. 1 k 33 Ta có: U 2U 2.2 4 2. k 1 k
Vậy U 2, n . Lại có: * U 0, n . n n U 2U Lại có: n 2 2 1 n 1 dãy tăng. U U U 2 n n n
Vậy dãy đã cho có giới hạn. Đặt lim U lim U a a 0 n1 n Ta có: 2 lim U
lim 2U a 2a a 2a a 2. n 1 n
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 39
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com GV: T R Ầ N ĐÌN H CƯ – 0834 3321 33
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 40
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
BÀI 2. GIỚI HẠN CỦA HÀM SỐ
A. TÓM TẮT KIẾN THỨC CƠ BẢN CẦN NẮM.
1. Giới hạn hữu hạn của hàm số tại một điểm
Cho điểm x thuộc khoảng K và hàm số y f x xác định trên K hoặc K \x . o 0
Ta nói hàm số y f x có giới hạn hữu hạn là số L khi x dần tới x nếu dãy số x bất kì, n 0
x K \ x và x x thì f x L , kí hiệu lim f x L hay f x L khi x x . n n o n 0 0 x 0 x
Nhận xét: lim x x ; lim c= c ( c là hằng số). 0 x 0 x x 0 x
2. Các phép toán về giới hạn hữu hạn của hàm số
a) Cho lim f x L và lim g x M .Khi đó: x 0 x x 0 x
lim f x g x L M
lim f x g x L M xx xx 0 0 f x L
lim f x.g x . L M lim ( với M 0 ). xx x x g x M 0 0 GV: T
b) Nếu f x 0 và lim f x L thì L 0 và lim f x . L x 0 x x 0 x R Ầ N ĐÌN
( Dấu của f x được xét trên khoảng tìm giới hạn, x x ). 0 H CƯ Nhận xét: – 0834 a) lim k k
x x , k là số nguyên dương; o xx 3321 0 33
b) lim cf x c lim f x(c lim f x ). , nếu tồn tại xx xx xx 0 0 0 3. Giới hạn một phía
Cho hàm số y f x xác định trên khoảng x ;b . 0
Ta nói hàm số y f x có giới hạn bên phải là số L khi x dần tới x nếu dãy số x bất kì, n 0
x x b x x b và x x thì f x ,
L kí hiệu lim f x L . 0 n n 0 n 0 n x 0 x
Cho hàm số y f x xác định trên khoảng a, x . o
Ta nói hàm số y f x có giới hạn bên trái là số L khi x dần tới x nếu dãy số x bất kì, n 0
a x x n 0
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 41
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
và x x thì f x ,
L kí hiệu lim f x L . n 0 n x x 0 Chú ý:
a) Ta thừa nhận các kết quả sau:
lim f x L và lim f x L khi và chỉ khi lim f x ; L x x x x xx 0 0 0
Nếu lim f x lim f x thì không tồn tại lim f x . x x x x xx 0 0 0
b) Các phép toán về giới hạn hữu hạn của hàm số ở Mục 2 vẫn đúng khi ta thay x x bằng 0 x x hoặc x x . 0 0
4. Giới hạn hữu hạn của hàm số tại vô cực
Cho hàm số y f x xác định trên khoảng ; a .
Ta nói hàm số y f x có giới hạn hữu hạn là số L khi x nếu dãy số x bất kì, n
x >a và x thì f x L, kí hiệu lim f x L hay f x L khi x +. n n n x
Cho hàm số y f x xác định trên khoảng ; a .
Ta nói hàm số y f x có giới hạn hữu hạn là số L khi x nếu dãy số x bất kì, n GV: T
x thì f x L, kí hiệu lim f x L hay f x L khi x . n n n x R Ầ Chú ý: N ĐÌN c H CƯ
a) Với c là hằng số và k là số nguyên dương, ta luôn có: lim c c và lim 0. k x x x – 0834
b) Các phép toán trên giới hạn hàm số ở Mục 2 vẫn đúng khi thay x x bằng x hoặc 0 3321 x . 33
5. Giới hạn vô cực của hàm số tại một điểm
Cho hàm số y f x xác định trên khoảng x ;b . 0
Ta nói hàm số y f x có giới hạn bên phải là khi x x về bên phải nếu với dãy số xn 0
bất kì, x < x < b và x x thì f x ,
kí hiệu lim f x hay f x khi x x . o n n 0 n 0 x 0 x
Ta nới hàm số y f x có giới hạn bên phải là khi x x về bên phải nếu với dãy số xn 0
bất kì, x < x < b và x x thì f x ,
kí hiệu lim f x hay f x khi x x . o n n 0 n 0 x 0 x Chú ý:
a) Các giới hạn lim f x , lim f x ,
lim f x ,
lim f x ,
lim f x , xx xx x x x 0 0
lim f x được định nghĩa tương tự như trên. x
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 42
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
b) Ta thường có các giới hạn thường dùng sau: 1 1 lim và lim
a ; lim k
x với k nguyên dương; xa xa x a x a x lim k
x với k là số chẵn; lim k
x với k là số lẻ. x x
c) Các phép toán trên giới hạn hàm số ở Mục 2 chỉ áp dụng được khi tất cả các hàm số được xét
có giới hạn hữu hạn. Với giới hạn vô cực, ta có một số quy tắc sau đây.
Nếu lim f x , lim f x L 0 và lim g x thì lim f x.g x được tính theo quy x x 0 x 0 x x 0 x x 0 x tắc cho bởi sau: lim f x lim g x
lim f x.g x x x x x 0 0 x 0 x L 0 L 0
Các quy tắc trên vẫn đúng khi thay x thành x ( hoặc , ). 0 0
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP GV: T R Ầ N
Dạng 1: Dãy số có giới hạn hữu hạn ĐÌN H CƯ 1. Phương pháp –
Nếu hàm số f x xác định trên K x thì lim f x f x . 0 0 0834 xx0 3321
2. Các ví dụ rèn luyện kĩ năng 2 33
Ví dụ 1: Tính lim x x 7. x1 Hướng dẫn giải lim 2
x x 7 11 7 9. x1 4 5 Ví dụ 2: Tính 3x 2x lim 4 6 x 1 5x 3x 1 Hướng dẫn giải 4 5 3x 2x 3 2 1 lim . 4 6 x 1 5x 3x 1 5 3 1 9 Ví dụ 3: Tính 3 lim 4x 2x 3 x1
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 43
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Hướng dẫn giải 3
lim 4x 2x 3 4 2 3 5. x1 3 x 1 Ví dụ 4: Tính lim x 1 3 2 x 3 2 Hướng dẫn giải 3 x 1 1 1 lim 0. x 1 3 3 2 4 2 x 3 2 4 2 x 4x 3 Ví dụ 5: Tính lim 2 x 2 7x 9x 1 Hướng dẫn giải 4 2 x 4x 3 16 16 3 1 lim . 2 x 2 7x 9x 1 28 18 1 3
Dạng 2. Giới hạn tại vô cực 1. Phương pháp GV: T
Giới hạn hữu hạn tại vô cực R Ầ
Cho hàm số y f (x) xác định trên khoảng ;
a . lim f (x) L với mọi dãy số N x ĐÌN x x a x
lim f (x) L n , và ta đều có . n n H CƯ
LƯU Ý: Định nghĩa lim f (x) L được phát biểu hoàn toàn tương tự. x – 0834
Giới hạn vô cực tại vô cực 3321
Cho hàm số y f (x) xác định trên khoảng ;
a . lim f (x) với mọi dãy 33 x
số x , x a và x ta đều có lim f (x) . n n n
LƯU Ý: Các định nghĩa: lim f (x) , lim f (x) , lim f (x) được phát biểu hoàn toàn x x x tương tự.
Một số giới hạn đặc biệt c lim
0 ( c là hằng số, k nguyên dương ). k x x lim k
x với k nguyên dương; lim k
x nếu k là số nguyên lẻ; lim k
x nếu k là số x x x nguyên chẵn.
Nhận xét: lim f (x) lim f (x) . x x
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 44
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
2. Các ví dụ rèn luyện kĩ năng Ví dụ 1: Tính 3
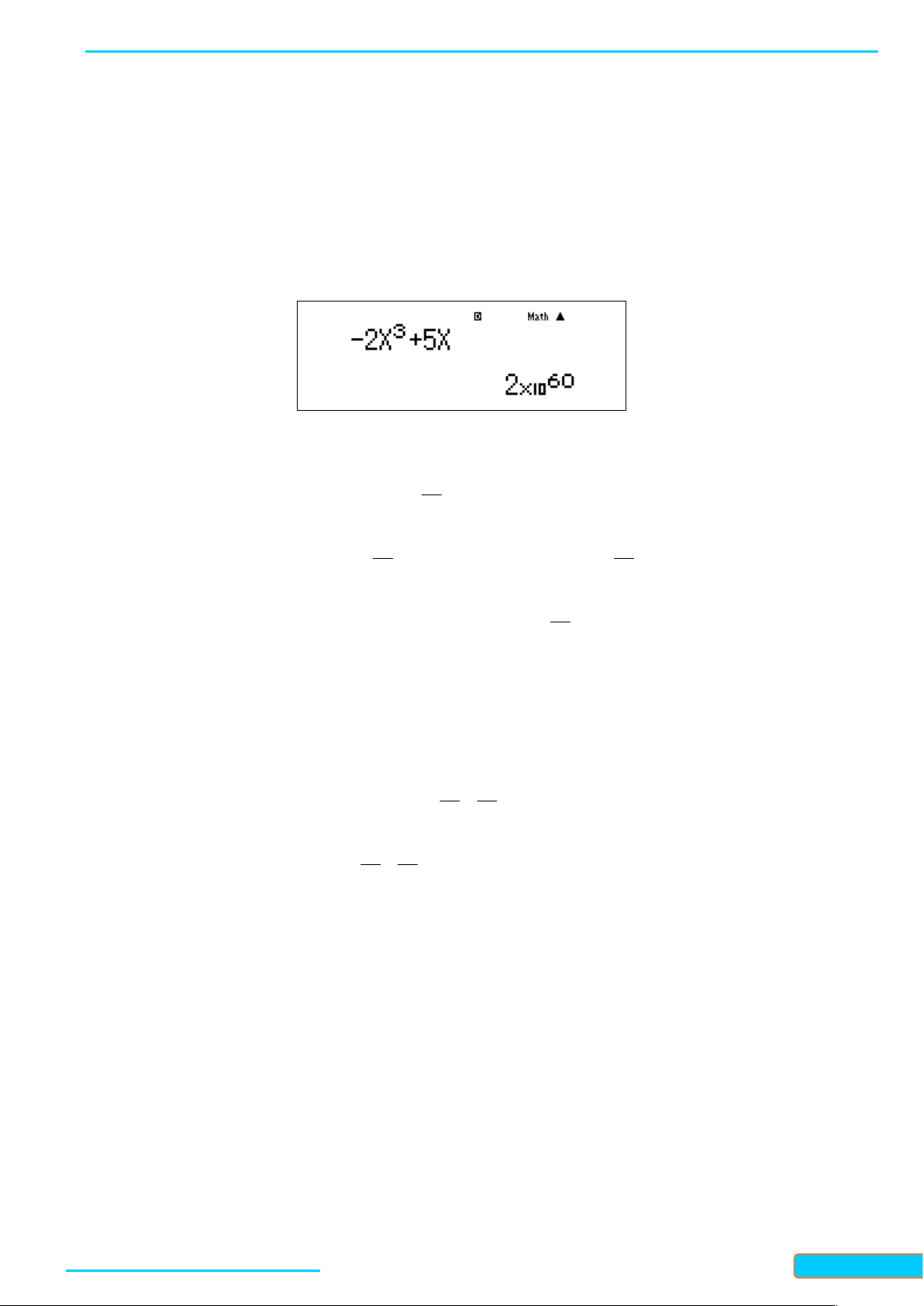
lim 2x 5x x Lời giải
Cách 1: Sử dụng MTCT tính giá trị của f x 3 2
x 5x tại một điểm có giá trị âm rất
nhỏ (do ta đang xét giới hạn của hàm số khi x ), chẳng hạn tại 20 10 . Máy hiển thị kết quả như hình:
Đó là một giá trị dương rất lớn. Vậy chọn đáp án C , tức 3
lim 2x 5x . x 5 Cách 2: Ta có 3 3
2x 5x x 2 . 2 x 5 5 Vì 3
lim x và lim 2 2 0 nên 3 lim x 2 . x 2 x 2 x x x 5 Vậy theo Quy tắc 1, lim 3 2x 5x 3 lim x 2 . 2 x x x GV: T Ví dụ 2: Tính 4 2
lim 3x 2x 1 R x Ầ N ĐÌN Lời giải H CƯ
Cách 1: Theo nhận xét trên thì 4 2
lim 3x 2x
1 ( x , k chẵn và a 0 ). k x – 2 1 4 2 4 0834
Thật vậy, ta có 3x 2x 1 x 3 . 2 4 x x 3321 2 1 Vì 4
lim x và lim 3 3 0 nên 4 2
lim 3x 2x 1 . 33 x 2 4 x x x x Nhận xét:
- Giới hạn tại vô cực của hàm đa thức là vô cực, chỉ phụ thuộc vào số hạng chứa lũy thừa bậc cao nhất.
- Giới hạn của hàm đa thức tại phụ thuộc vào hệ số của lũy thừa bậc cao nhất.
(Giống với giới hạn của dãy số dạng đa thức).
- Giới hạn của hàm đa thức tại phụ thuộc vào bậc và hệ số của lũy thừa bậc cao nhất.
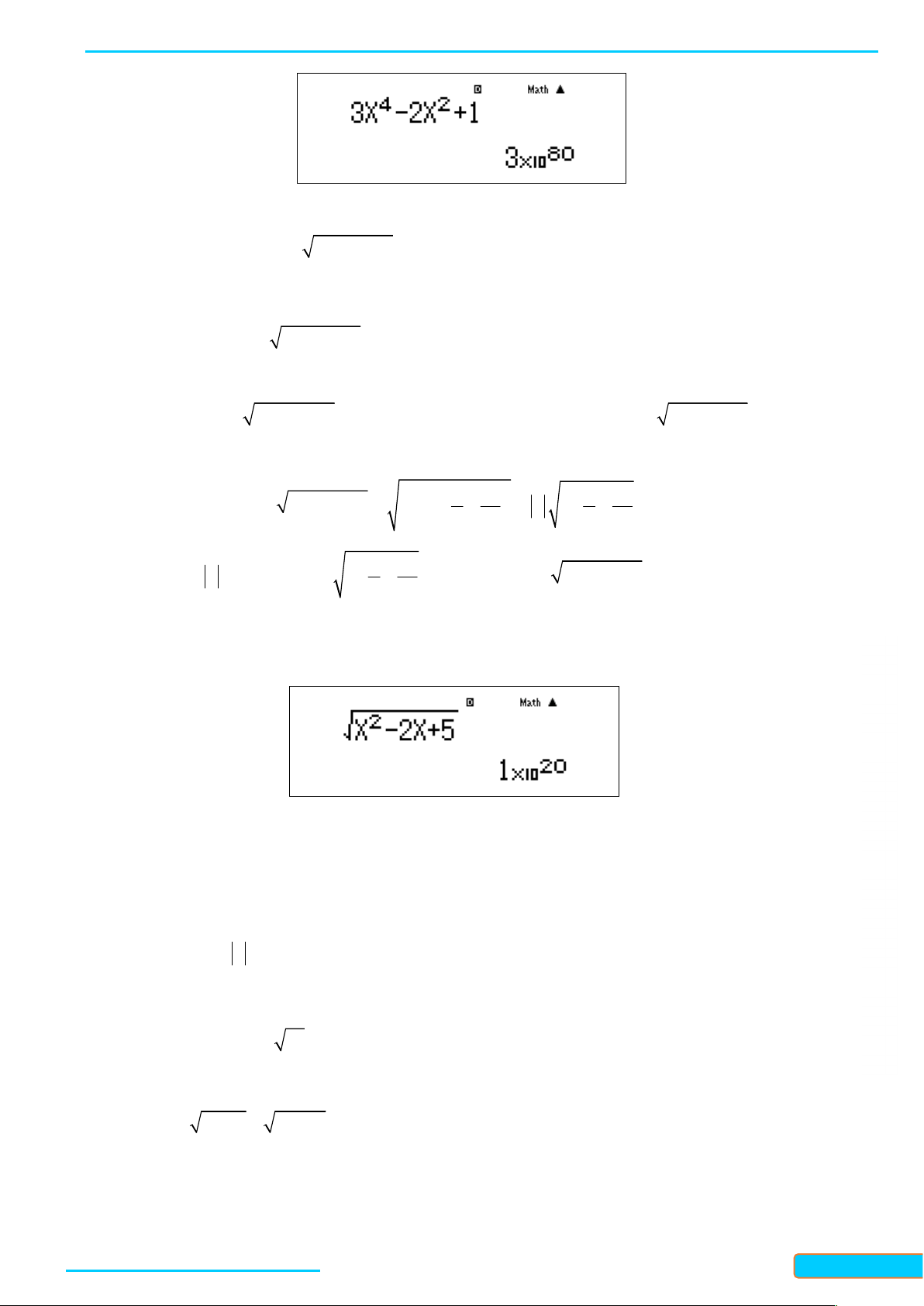
Cách 2: Sử dụng MTCT tính giá trị hàm số f x 4 2
3x 2x 1 tại 20
x 10 , ta được kết quả như hình :
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 45
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Kết quả là một số dương rất lớn. Do đó chọn đáp án A,
Ví dụ 3: Cho hàm số f x 2
x 2x 5 . Tính lim f x x Lời giải
Hàm số f x 2
x 2x 5 xác định trên .
Có thể giải nhanh như sau : Vì 2
x 2x 5 là một hàm đa thức của x nên có giới hạn tại vô cực. Mà 2
x 2x 5 0 với mọi x nên giới hạn của f x 2
x 2x 5 tại chắc chắn là . 2 5 2 5 Thật vậy, ta có 2 2
x 2x 5 x 1 x 1 . 2 2 x x x x 2 5
Vì lim x và lim 1 1 0 nên 2 lim
x 2x 5 . x 2 x x x x
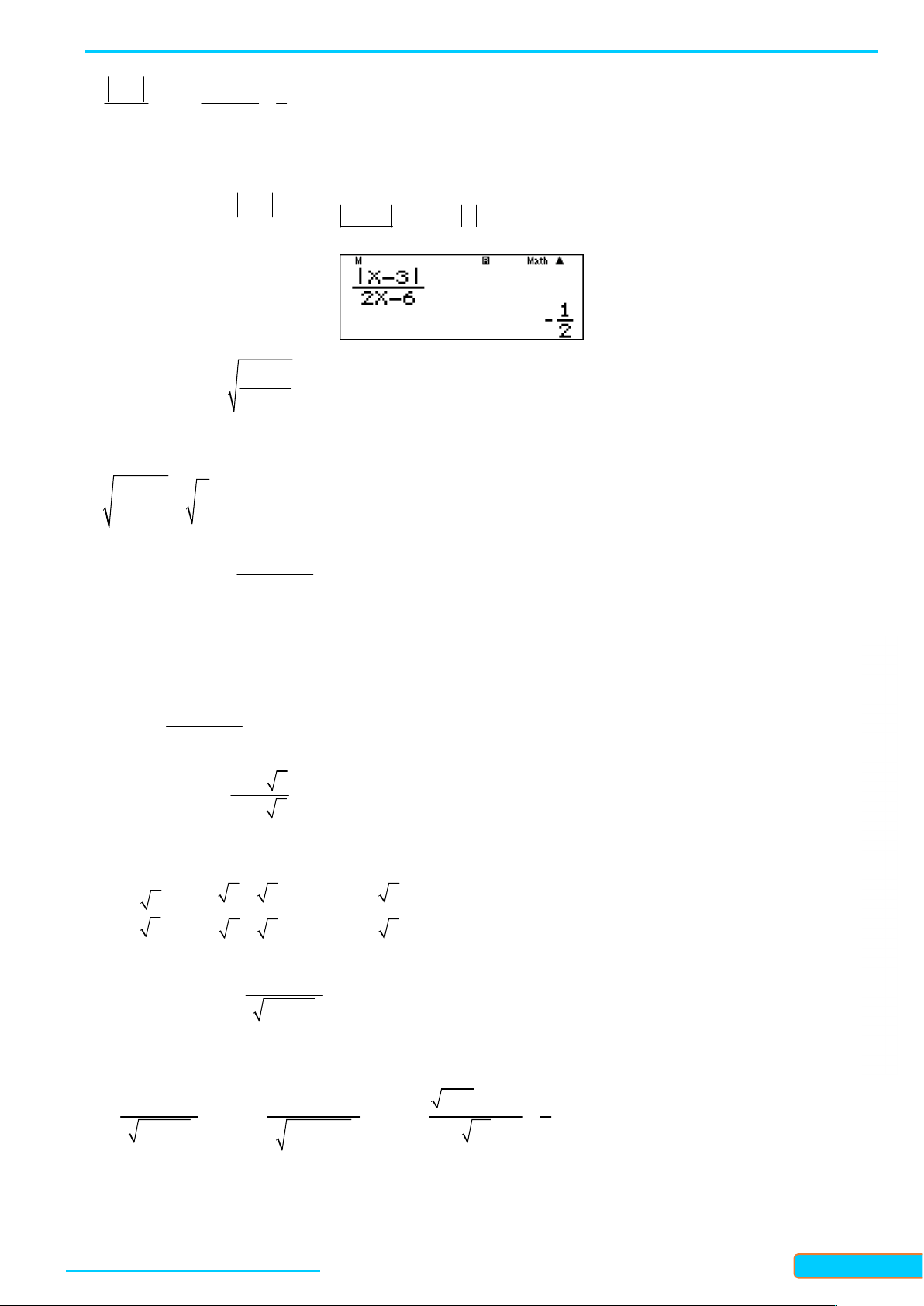
Hoặc ta có thể sử dụng MTCT để tính giá trị của f x tại một giá trị âm rất nhỏ của GV: T
x , chẳng hạn tại 20
x 10 ta được kết quả như hình: R Ầ N ĐÌN H CƯ – 0834
Kết quả này là một số dương rất lớn. Do đó ta chọn đáp án B. (Dễ thâý kết quả hiển 3321
thị trên máy tính như trên chỉ là kết quả gần đúng do khả năng tính toán hạn chế của 33
MTCT. Tuy nhiên kết quả đó cũng giúp ta lựa chọn được đáp án chính xác). Lưu ý:
Ta có lim x . x
Khi x thì x 0 . Với x 0 ta có 2 x x .
Cần đặc biệt lưu ý các điều trên khi tính giới hạn tại của hàm chứa căn thức. Ví dụ 4: 2 2 lim x x 4x 1 x Lời giải Cách 1: Ta có:
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 46
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 1 1 1 1 2 2 2 2
x x 4x 1 x 1 x 4 x 1 x 4 2 2 x x x x 1 1 x 1 4 2 x x 1 1
Mà lim x và lim 1 4 1 2 1 0 . x 2 x x x 1 1 Vậy 2 2 lim
x x 4x 1 lim x 1 4 . x 2 x x x Lưu ý:
- Độc giả nên đọc lại phần giới hạn dãy số có chứa căn thức để hiểu hơn tại sao lại có định
hướng giải như vậy (mà không đi nhân chia với biểu thức liên hợp).
- Có thể thấy như sau: Vì 2 2 lim
x x ; lim 4x 1 . x x Mà hệ số của 2 x trong 2
4x 1 lớn hơn hệ số của 2 x trong 2
x x nên suy ra 2 2 lim
x x 4x 1 . x
Cách 2: Sử dụng MTCT tính giá trị hàm số tại 10
x 10 ta được kết quả như hình. GV: T R Ầ N ĐÌN H CƯ –
Dạng 3. giới hạn một bên 0834 3321 1. Phương pháp 33
Ta cần nắm các tính chất sau
lim f(x) L x ,x x b, lim x x lim f(x ) L n 0 n n 0 n n n x x 0
lim f(x) L x ,a x x , lim x x lim f(x ) L n n 0 n 0 n n n x x 0
lim f(x) lim f(x) L lim f(x) L xx xx xx 0 0 0
2. Các ví dụ rèn luyện kĩ năng x 3 Ví dụ 1: Tính lim x3 2x 6 Hướng dẫn giải
Cách 1: Giải bằng tự luận
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 47
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com x 3 x 3 1 lim lim . x 3 2x 6 x 3 2x 3 2
Cách 2: Giải nhanh bằng máy tính x 3 Nhập vào màn hình và ấn 5 CALC 3 10 ta được kết quả 2x 6 3 1 x Ví dụ 2: Tính lim 2 x 1 3x x Hướng dẫn giải 3 1 x 0 lim 0. 2 x 1 3x x 4 3 x 2x 3 Ví dụ 3: Tính lim 2 x 2 x 2x Hướng dẫn giải GV: T
Tử số có giới hạn là 1
, mẫu số có giới hạn 0 và khi x 2 thì 2 x 2x 0. R Ầ N 3 ĐÌN x 2x 3 Do đó lim . 2 x 2 x 2x H CƯ – 2x x Ví dụ 4: Tính lim 0834 x 0 5x x 3321 Hướng dẫn giải 33 x 2 x 1 2 x 1 2x x 1 lim lim lim 1 . x 0 5x x x 0 x 5 x 1 x 0 5 x 1 1 2 x 4x 3 Ví dụ 5: Tính lim 3 2 x 1 x x Hướng dẫn giải 2 x 1 x 3 x 1x 3 x 4x 3 0 lim lim lim 0. 3 2 x x 2 x x 1 2 1 x 1 x 1 x 1 x
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 48
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 2 x 1 vôùi x 1
Ví dụ 6: Cho hàm số f x 1 x
. Khi đó lim f x bằng bao nhiêu? x 1 2x 2 vôùi x 1 Hướng dẫn giải 2 x 1 lim f x lim
vì tử số có giới hạn là 2, mẫu số có giới hạn 0 và 1 x 0 với x 1. x 1 x 1 1 x 0 Dạng 3. Dạng vô định 0 1. Phương pháp 0 u(x)
Nhận dạng vô định : lim
khi lim u(x) lim u(x) 0. 0 xx v(x) xx xx 0 0 0
Phân tích tử và mẫu thành các nhân tử và giản ước u(x) (x x )A(x) 0 A(x) A(x) lim lim lim vaø tính lim . xx v(x) xx (x x )B(x) xx B(x) xx o o B(x) 0 o o
Nếu phương trình f x 0 có nghiệm là x thì f x x x .g x 0 0 Đặc biệt: 2 GV: T
f(x) ax bx c,maø f(x) 0 coù hai nghieäm phaân bieät x ,x
Nếu tam thức bậc hai 1 2
thì f(x) ñöôïc phaân tích thaønhf(x) ax - x x - x 1 2 R Ầ N ĐÌN
Phương trình bậc 3: 3 2
ax bx cx d 0 (a 0) H CƯ
a b c d 0 thì pt coù moät nghieäm laø x 1, ñeå phaân tích 1 –
thaønh nhaân töû ta duøng pheùp chia ña thöùc hoaëc duøng sô ñoà Hooc-ner 0834 3321
a b c d 0 thì pt coù moät nghieäm laø x 1 , ñeå phaân tích 1
thaønh nhaân töû ta duøng pheùp chia ña thöùc hoaëc duøng sô ñoà Hooc-ner 33
Nếu ux và vx có chứa dấu căn thì có thể nhân tử và mẫu với biểu thức liên hiệp, sau đó
phân tích chúng thành tích để giản ước. A B
löôïng lieân hieäp laø: A B. A B
löôïng lieân hieäp laø: A B.
A B löôïng lieân hieäp laø: A B. 3 3 2 3 2 A B
löôïng lieân hieäp laø: A B A B . 3 3 2 3 2 A B
löôïng lieân hieäp laø: A B A B .
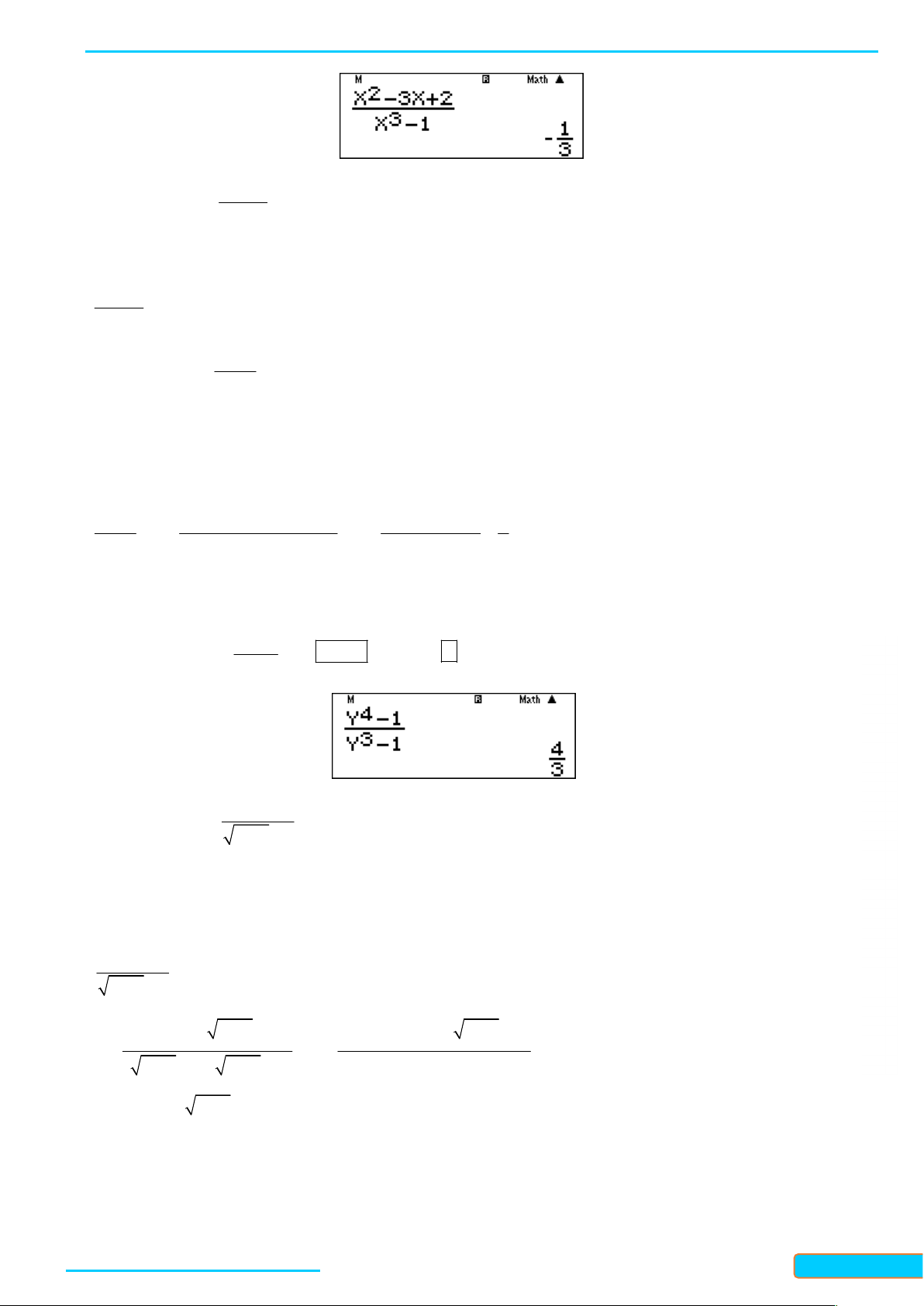
2. Các ví dụ rèn luyện kĩ năng 2 x 3x 2 Ví dụ 1: Tính lim x 1 x 1
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 49
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Hướng dẫn giải
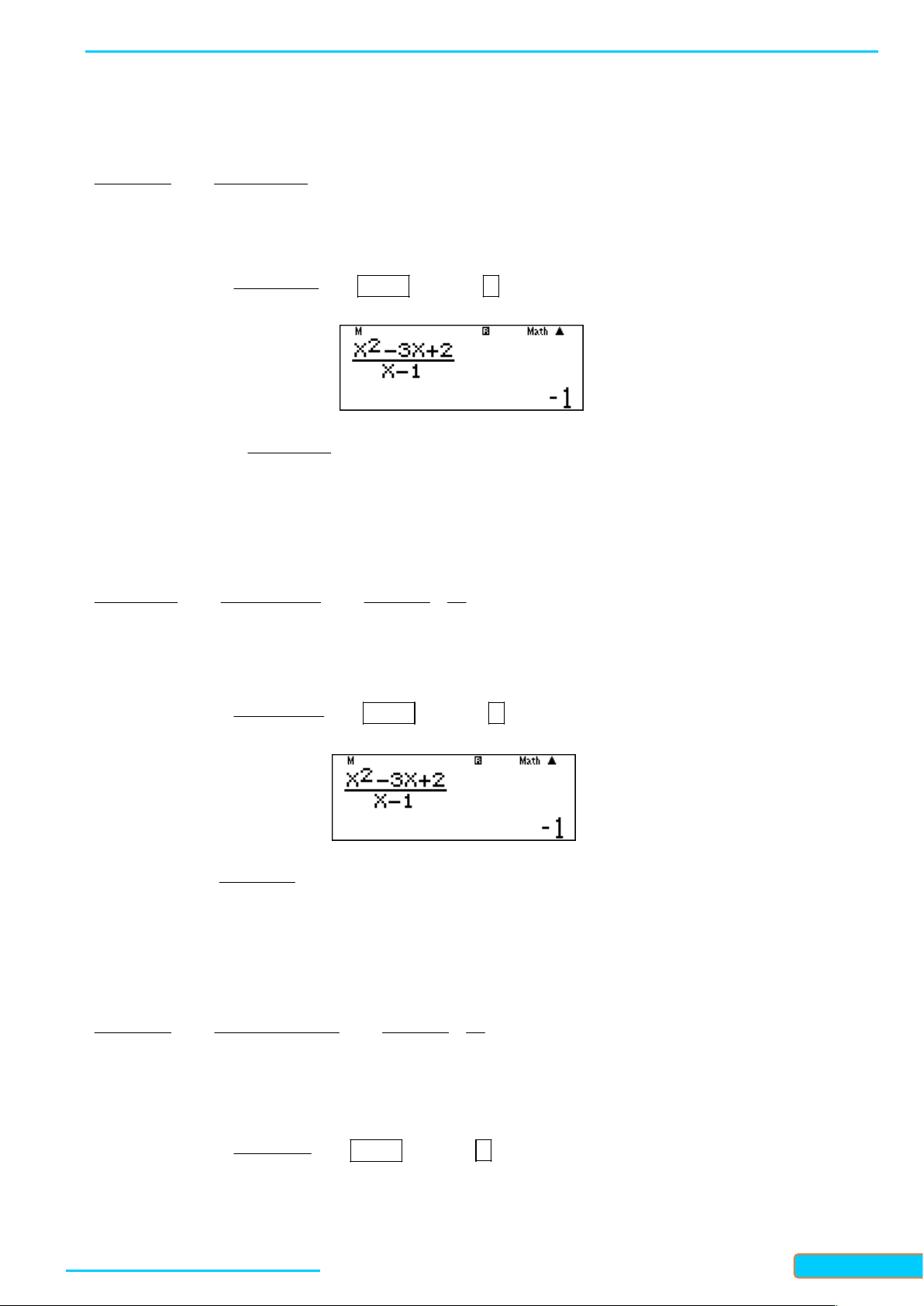
Cách 1: Giải bằng tự luận 2 x 1 x 2 x 3x 2 lim lim
lim x 2 1. x 1 x 1 x 1 x 1 x
Cách 2: Giải nhanh bằng máy tính 2 X 3X 2 Nhập vào màn hình ấn 10 CALC 1 10 ta được kết quả X 1 2 Ví dụ 2: Tính 2x 3x 1 L lim . 2 x 1 1 x Hướng dẫn giải
Cách 1: Giải bằng tự luận 2 2x 1 x 1 2x 1 2x 3x 1 1 lim lim lim . 2 x 1 x 1 1 x 1 x1 x x 1 1 x 2 GV: T
Cách 2: Giải nhanh bằng máy tính R Ầ 2 N 2X 3X 1 ĐÌN Nhập vào màn hình ấn 10 CALC 1 10 ta được kết quả 2 1 X H CƯ – 0834 3321 2 33 Ví dụ 3: Tính x 3x 2 lim 3 x 1 x 1 Hướng dẫn giải
Cách 1: Giải bằng tự luận 2 x 3x 2 x 1 x 2 x 2 1 lim lim lim . 3 x 1 x 1 x 1 x 1 2 x x 2 x 1 1 x x 1 3
Cách 2: Giải nhanh bằng máy tính 2
Nhập vào màn hình x 3x 2 ấn 10 CALC 1 10 ta được kết quả 3 x 1
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 50
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 4 4 t a Ví dụ 4: Tính lim t a t a Hướng dẫn giải 4 4 t a lim lim 3 2 2 3 t t a ta a 3 4a . ta t a ta 4 y 1 Ví dụ 5: Tính lim 3 y 1 y 1 Hướng dẫn giải
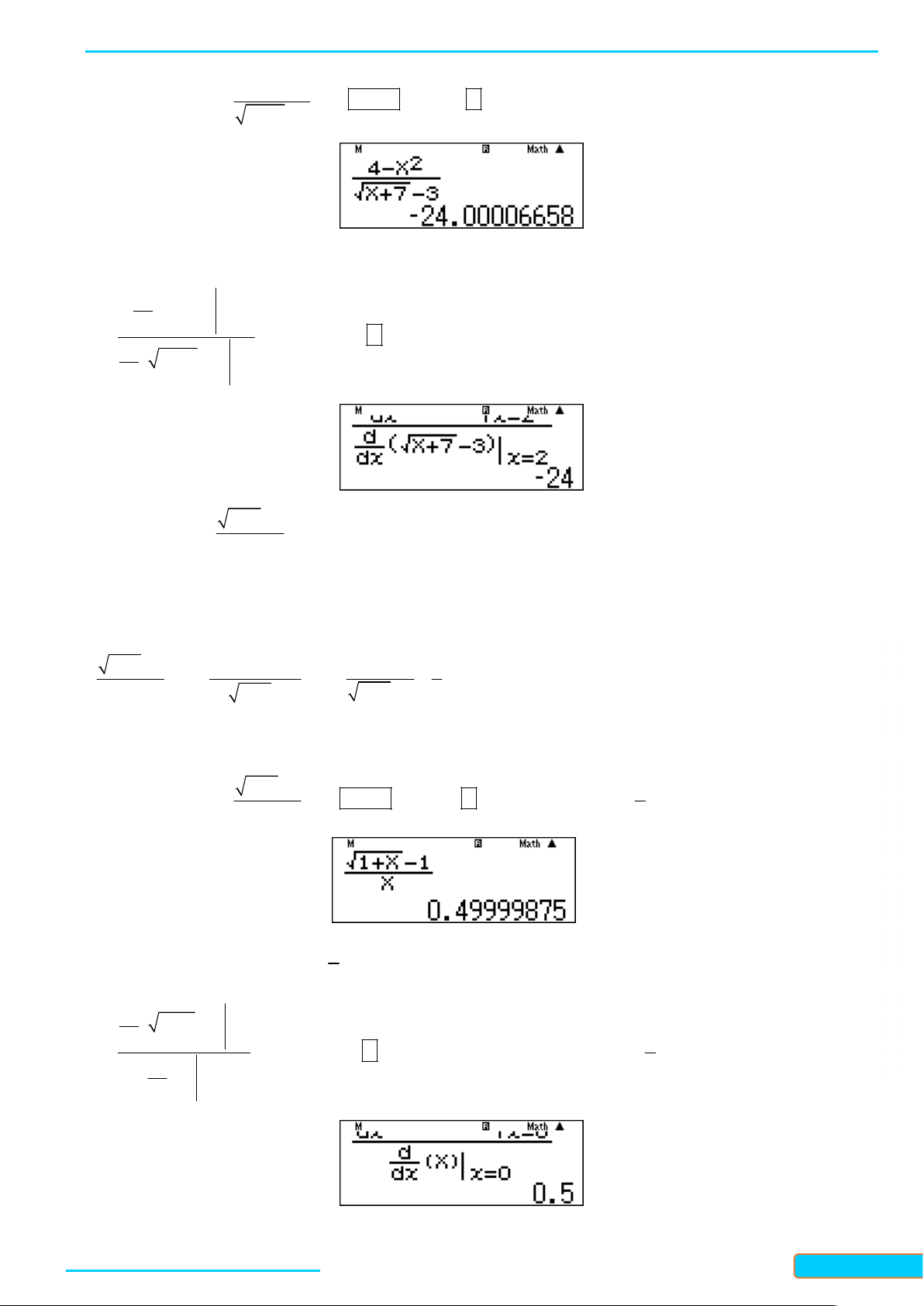
Cách 1: Giải bằng tự luận y 1 y 1 3 2 4 y y y 1 3 2 y y y 1 4 lim lim lim . 3 y 1 y 1 y 1 y 1 2 y y 2 y 1 1 y y 1 3
Cách 2: Giải nhanh bằng máy tính 4 Y 1 GV: T Nhập vào màn hình ấn 10 CALC 1 10 ta được kết quả 3 Y 1 R Ầ N ĐÌN H CƯ – 0834 2 4 x Ví dụ 6: Tính lim 3321 x2 x 7 3 33 Hướng dẫn giải
Cách 1: Giải bằng tự luận 2 4 x lim x2 x 7 3 2 x 4 x 7 3
x 2x 2 x 7 3 lim lim
x2 x2 x 7 9 x 7 3 x 7 3 lim x 2 x 7 3 2 4. x2
Cách 2: Giải nhanh bằng máy tính
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 51
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
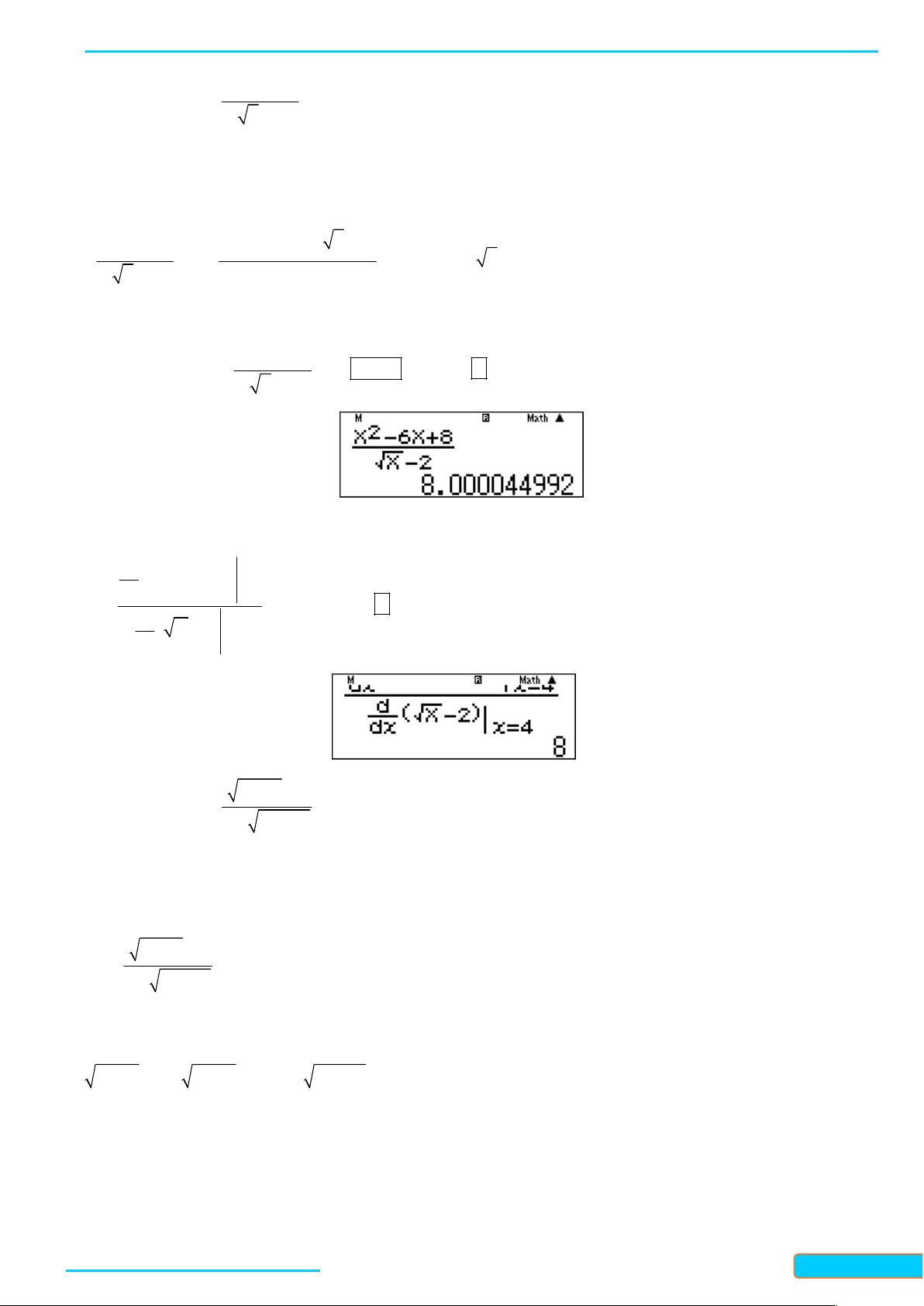
WEB: Toanthaycu.com 2 4 X Nhập vào màn hình ấn 5 CALC 1 10
ta được kết quả 24. X 7 3
Lưu ý: Để ra kết quả chính xác 2
4 ta có thể tính theo quy tắc Lô-pi-tan như sau: d 2 4 X dx Nhập x2
rồi ấn phím ta được kết quả chính xác 24. d X7 3 dx x2 1 x 1 Ví dụ 7: Tính lim x0 x Hướng dẫn giải
Cách 1: Giải bằng tự luận GV: T 1 x 1 1 x 1 1 1 lim lim lim . R x0 x x0 x0 x 1 x 1 1 x 1 2 Ầ N ĐÌN H CƯ
Cách 2: Giải nhanh bằng máy tính – 1 x 1 1 0834 Nhập vào màn hình ấn 5 CALC 0 10
ta được kết quả . x 2 3321 33 1
Lưu ý: Để ra kết quả chính xác ta có thể tính theo quy tắc Lô-pi-tan như sau: 2 d 1 X 1 dx 1 Nhập
x0 rồi ấn phím ta được kết quả chính xác 0,5 . d 2 X dx x0
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 52
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 2 x 6x 8 Ví dụ 8: Tính lim x4 x 2 Hướng dẫn giải
Cách 1: Giải bằng tự luận 2
x 2x 4 x 2 x 6x 8 lim lim
lim x 2 x 2 2 4 8. x4 x4 x 2 x 4 x4
Cách 2: Giải nhanh bằng máy tính 2 x 6x 8 Nhập vào màn hình ấn 5 CALC 4 10
ta được kết quả 8. x 2
Lưu ý: Để ra kết quả chính xác 8 ta có thể tính theo quy tắc Lô-pi-tan như sau: d 2 X 6X 8 dx Nhập
x4 rồi ấn phím ta được kết quả chính xác 8. d X 2 dx GV: T x4 R Ầ N ĐÌN H CƯ – 3 2 x 4 2 0834 Ví dụ 9: Tính lim x2 2 4 2x 8 3321 33 Hướng dẫn giải
Cách 1: Giải bằng tự luận 3 2 x 4 2 E lim x2 2 4 2x 8
Nhân tử và mẫu hai lượng liên hợp: 2 3 2 3 2 2 x 4 2 x 4 4 4 2x 8
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 53
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 2 3 2 3 2 3 2 2 x 4 2 x 4 2 x 4 4 4 2x 8 E lim x2 2 2 2 3 2 3 2
4 2x 8 4 2x 8 x 4 2 x 4 4 2 x 4 8 2 4 2x 8 lim x2 2 2 16 2x 8 3 2 3 2 x 4 2 x 4 4 2 x 4 2 4 2x 8 lim x2 2 2 2x 4 3 2 3 2
x 4 2 x 4 4 2 4 2x 8 8 1 lim . x2 2 24 3 3 2 3 2 2
x 4 2 x 4 4
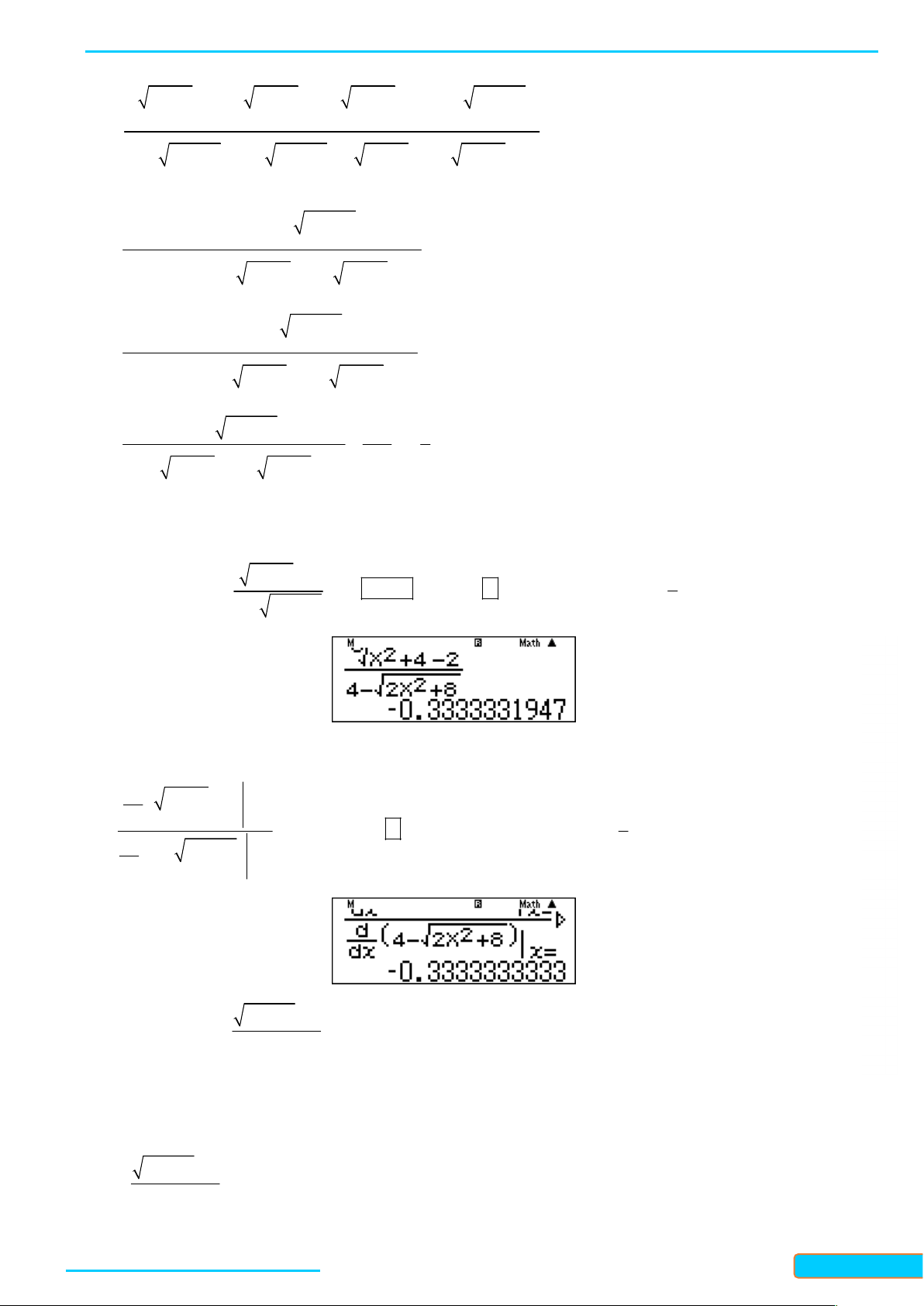
Cách 2: Giải nhanh bằng máy tính 3 2 x 4 2 1 Nhập vào màn hình ấn 5 CALC 4 10
ta được kết quả . 2 4 3 2x 8 GV: T R Ầ N ĐÌN H CƯ
Lời bình: Nếu ta dùng quy tắc Lô-pi-tan – d 3 0834 2 x 4 2 dx x2 3321 Nhập
rồi ấn phím ta được kết quả 1 0, 3 . d 2 3 4 2x 8 33 dx x2 4 2 x 12 2 Ví dụ 10: Tính lim 2 x 2 x 4 Hướng dẫn giải
Cách 1: Giải bằng tự luận 4 2 x 12 2 E lim 2 x 2 x 4
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 54
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 4 2 4 2 x 12 2 x 12 2 lim x2 2 x 4 4 2 x 12 2 2 x 12 4 0 lim
(vẫn còn dạng vô định ) x 2 2 x 4 4 2 0 x 12 2 2 2 x 12 4 x 12 4 lim
x 2 2x 44 2 2 x 12 2 x 12 4 2 x 12 16 lim x 2 2 x 4 4 2 2 x 12 2 x 12 4 1 1 lim . x 2 4 2 2 32
x 12 2 x 12 4
Cách 2: Giải nhanh bằng máy tính Ta dùng quy tắc Lô-pi-tan d 4 2 x 12 2 dx x 1 2 GV: T Nhập
rồi ấn phím ta được kết quả 0,03125 . d 2 32 x 4 R dx Ầ x2 N ĐÌN H CƯ – 0834 6 3321 x 1 Ví dụ 11: Tính lim 2 x 1 x 1 33 Hướng dẫn giải
Cách 1: Giải bằng tự luận 6 x 1 E lim 2 x 1 x 1 6 x 6 2 6 1 x x 1 lim x 1 2 x 6 2 6 1 x x 1 x 1 0 lim (Vẫn dạng vô định ) x 1 2 x 6 2 6 1 0 x x 1
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 55
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com x 1 x 1 lim x 1 x 1 x 6 2 6 1 x x 1 x 1 1 1 lim . x 1 6 2 6 12 x 1 x x 1 x 1
Cách 2: Giải nhanh bằng máy tính Ta dùng quy tắc Lô-pi-tan d 6 X 1 dx Nhập x 1
rồi ấn phím ta được kết quả 1 0,08 3 . d 2 12 x 1 dx x 1 Để chuyển 1 0,08 3 ta bấm như sau 0.08Qs3= 12 GV: T R Ầ N ĐÌN Dạng 4. Dạng vô định H CƯ – 1. Phương pháp 0834
Nhận biết dạng vô định 3321 33 u(x) lim
khi lim u(x) , lim v(x) . xx v(x) xx xx 0 0 0 u(x) lim
khi lim u(x) , lim v(x) . x v(x) xx xx 0 0
Chia tử và mẫu cho n
x với n là số mũ cao nhất của biến ở mẫu ( Hoặc phân tích thành tích chứa nhân tử n x rồi giản ước)
Nếu u(x) hoặc v(x) có chứa biến x trong dấu căn thì đưa xk ra ngoài dấu căn (Với k là mũ
cao nhất của biến x trong dấu căn), sau đó chia tử và mẫu cho luỹ thừa cao nhất của x
(thường là bậc cao nhất ở mẫu).
Cách tính giới hạn dạng này hoàn toàn tương tự giới hạn dãy số.
2. Các ví dụ rèn luyện kĩ năng
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 56
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 4 3 2 Ví dụ 1: Tính 2x x 2x 3 lim 4 x x 2x Hướng dẫn giải
Cách 1: Giải bằng tự luận 1 2 3 4 3 2 2 2 4 2x x 2x 3 x x x lim lim 1. 4 x x 1 x 2x 2 3 x Cách 2: Mẹo giải nhanh 4 3 2 4 2x x 2x 3 2x 1. 4 4 x 2x 2x
Cách 3: Giải nhanh bằng máy tính 4 3 2
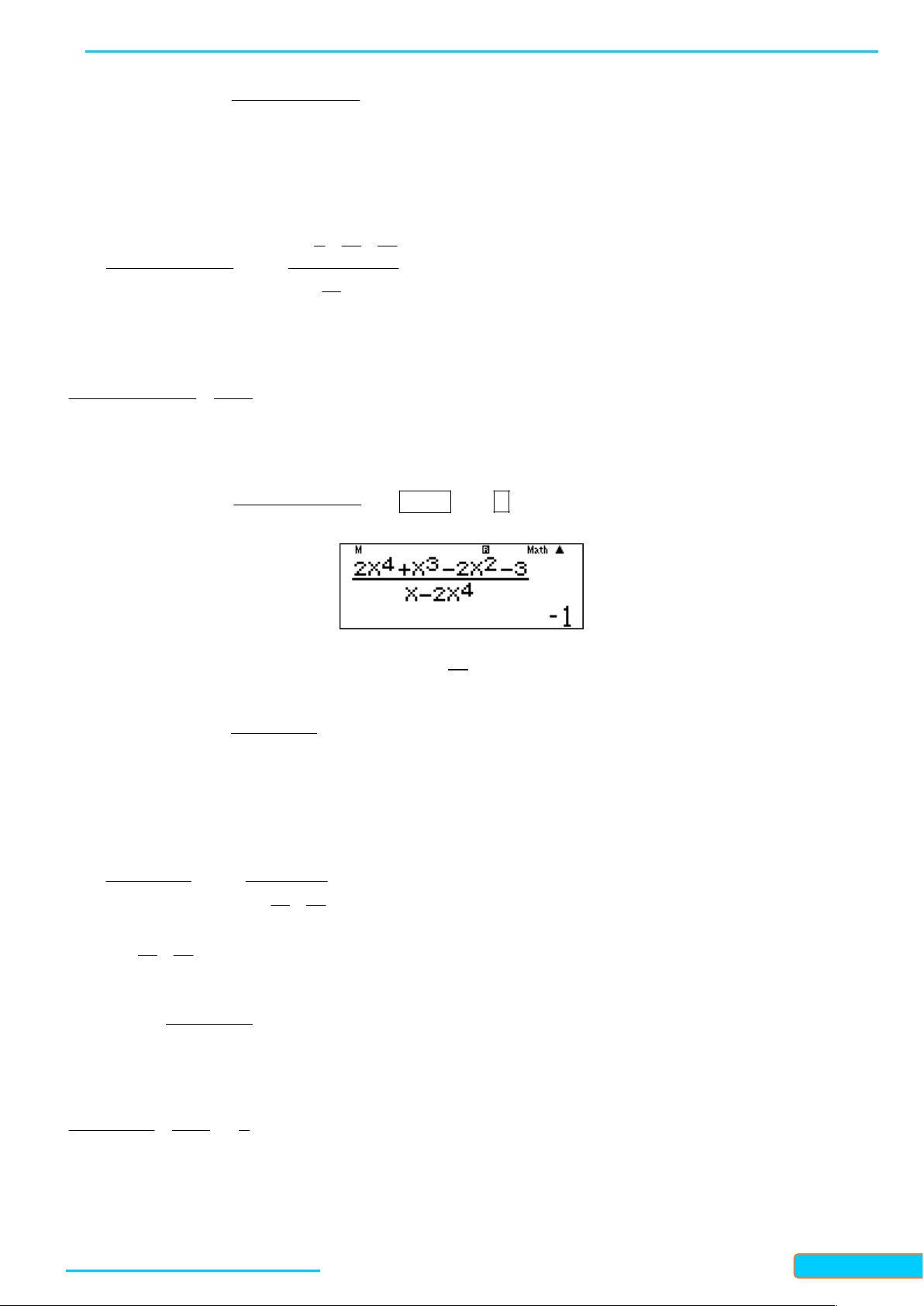
Nhập vào màn hình 2x x 2x 3 ấn 15 CALC 10
ta được kết quả 1. 4 x 2x GV: T 2
Lời bình: “Bậc tử bằng bậc mẫu” nên kết quả 1 . 2 R Ầ N ĐÌN 4 5 Ví dụ 2: Tính 3x 2x lim 4 H CƯ x 5x 3x 2 – Hướng dẫn giải 0834
Cách 1: Giải bằng tự luận 3321 4 5 33 3x 2x 3 2x lim lim 4 x x 3 2 5x 3x 2 5 3 4 x x 3 2 lim 5 5 0; lim 3 2x . 3 4 x x x x 4 5 Do đó: 3x 2x lim . 4 x 5x 3x 2 Cách 2: Mẹo giải nhanh 4 5 5 3x 2x 2x 2 x . 4 4 5x 3x 2 5x 5
Cách 3: Giải nhanh bằng máy tính
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 57
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 4 5
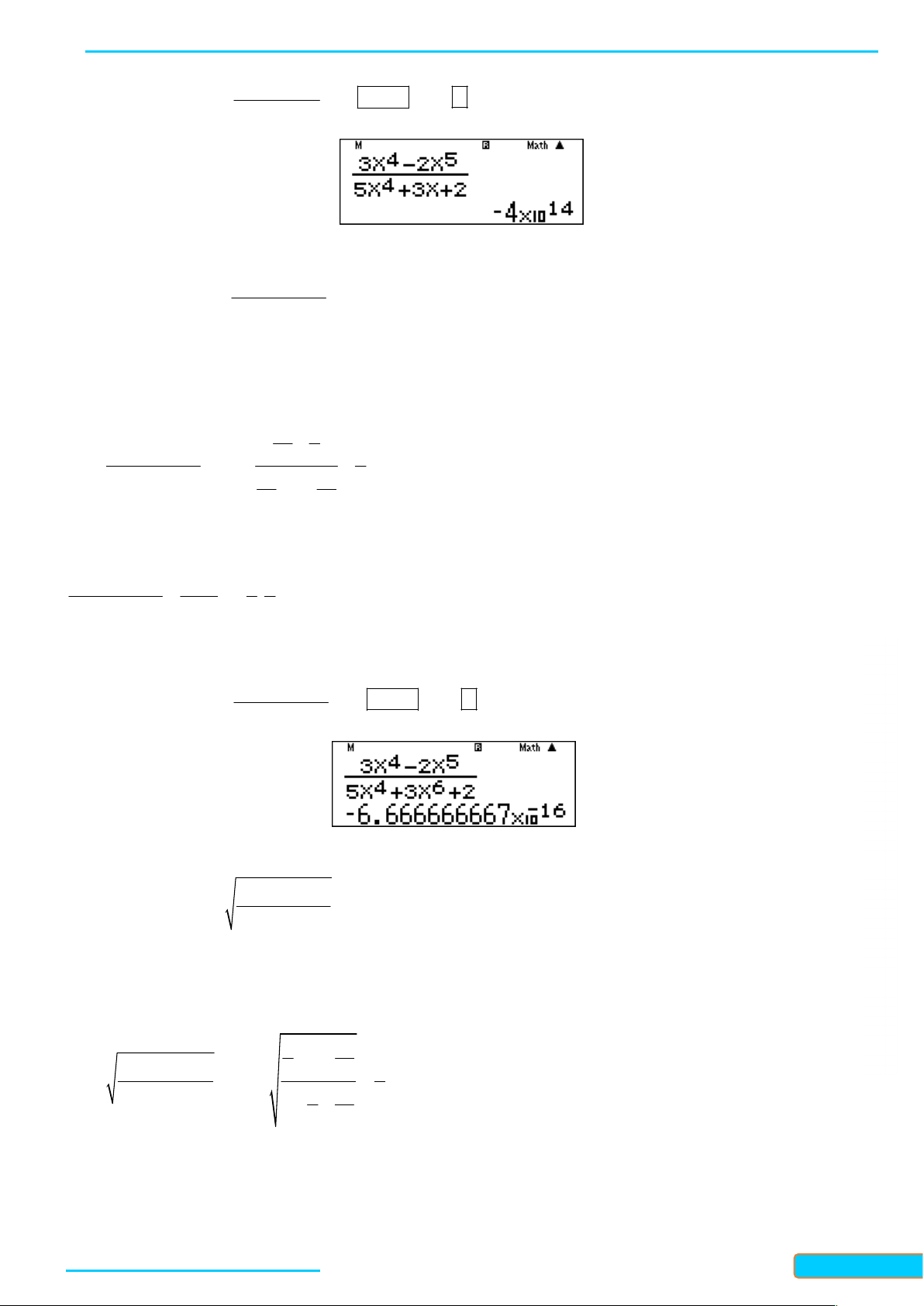
Nhập vào màn hình 3x 2x ấn 15 CALC 10
ta được kết quả . 4 5x 3x 2
Lời bình: Bậc tử lớn hơn bậc mẫu nên kết quả là . 4 5 Ví dụ 3: Tính 3x 2x lim 4 6 x 5x 3x 2 Hướng dẫn giải
Cách 1: Giải bằng tự luận 3 2 4 5 2 3x 2x x x 0 lim lim 0. 4 6 x x 5 2 5x 3x 2 3 3 2 6 x x Cách 2: Mẹo giải nhanh 4 5 5 3x 2x 2x 2 1 . 0. 4 6 6 5x 3x 2 3x 3 x GV: T
Cách 3: Giải nhanh bằng máy tính R 4 5 3x 2x Ầ Nhập vào màn hình ấn 15 CALC 10
ta được kết quả 0. N 4 6 ĐÌN 5x 3x 2 H CƯ – 0834 3321
Lời bình: “Bậc tử bé hơn bậc mẫu” nên kết quả là 0. 33 4 5 3x 4x 2 Ví dụ 4: Tính lim 5 4 x 9x 5x 4 Hướng dẫn giải
Cách 1: Giải bằng tự luận 3 2 4 5 4 5 3x 4x 2 x 2 x lim lim . 5 4 x x 5 4 9x 5x 4 3 9 5 x x Cách 2: Mẹo giải nhanh
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 58
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 4 5 5 3x 4x 2 4x 4 2 . 5 4 5 9x 5x 4 9x 9 3
Cách 3: Giải nhanh bằng máy tính 4 5 3x 4x 2 Nhập vào màn hình ấn 15 CALC 10
ta được kết quả 0. 5 4 9x 5x 4 2 x 2x 3x Ví dụ 5: Tính L lim . x 2 4x 1 x 2 Hướng dẫn giải
Cách 1: Giải bằng tự luận 2 2 2 x 1 3x 1 3 x 2x 3x x x 2 lim lim lim . x 2 x x 1 1 2 3 4x 1 x 2 x 4 x 2 4 1 2 2 x x x GV: T
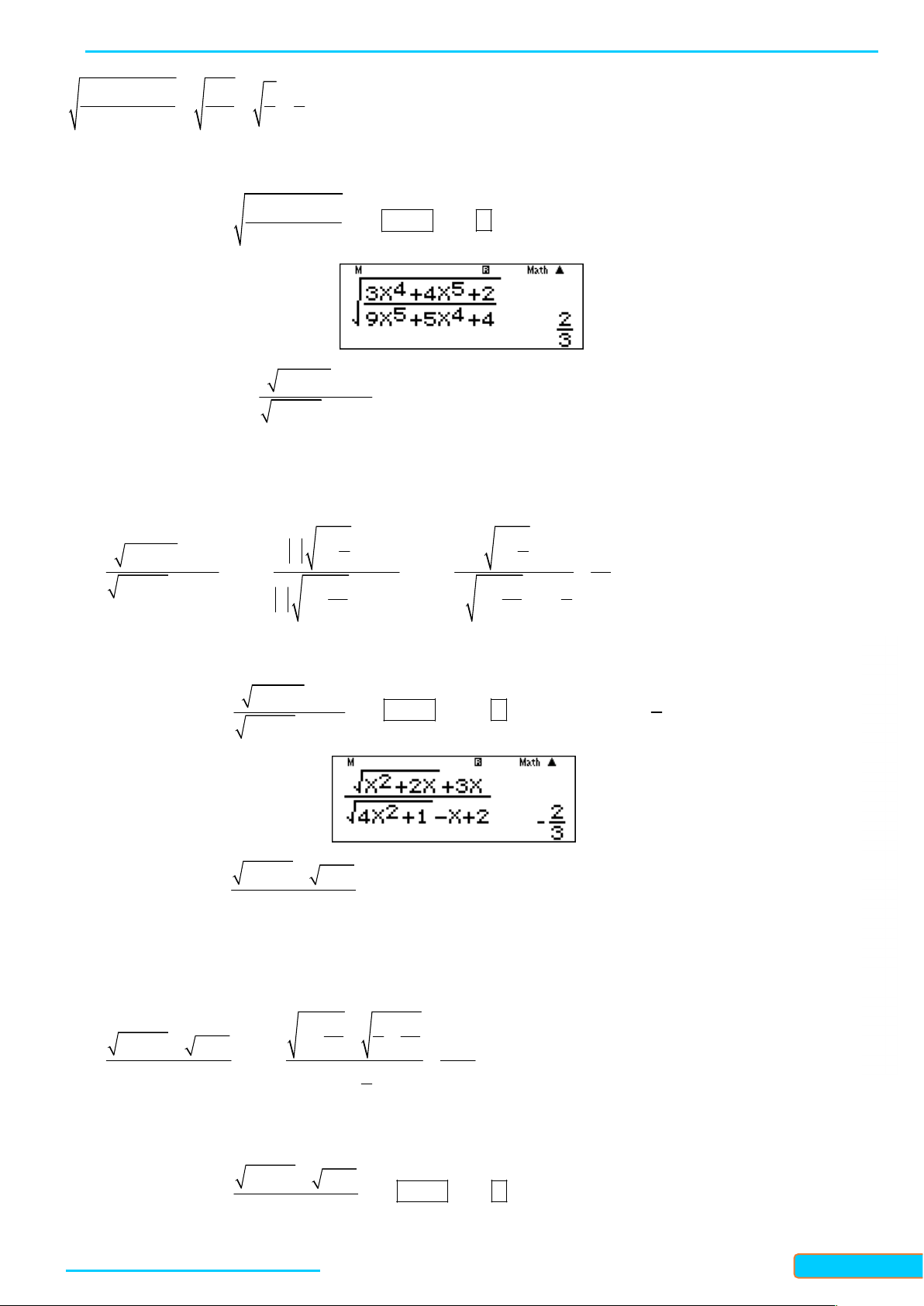
Cách 2: Giải nhanh bằng máy tính R Ầ 2 x 2x 3x 2 N Nhập vào màn hình ấn 15 CALC 10 ta được kết quả . ĐÌN 2 4x 3 1 x 2 H CƯ – 0834 3321 33 2 4x 1 x 5 Ví dụ 6: Tính lim x 2x 7 Hướng dẫn giải
Cách 1: Giải bằng tự luận 1 1 5 4 2 2 2 4x 1 x 5 x x x 2 0 lim lim 1. x 2x 7 x 7 2 0 2 x
Cách 2: Giải nhanh bằng máy tính 2 4x 1 x 5 Nhập vào màn hình ấn 25 CALC 10 ta được kết quả 2x 7
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 59
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com x
Ví dụ 7: Tính lim x 5 3 x x 1 Hướng dẫn giải
Cách 1: Giải bằng tự luận 2 5 x 2 1 x x 5 x lim x 5 lim lim 1. 3 3 x x x 1 x 1 x 1 1 3 x
Cách 2: Giải nhanh bằng máy tính x
Nhập vào màn hình x 5 ấn 25 CALC 10 ta được kết quả 3 x 1 GV: T 3 94 2 R x 1 12x Ầ N Ví dụ 8: Tính lim 100 ĐÌN x 2x 3 H CƯ Hướng dẫn giải – 3 94 0834 1 1 3 2 94 2 x 1 x 2 x 1 1 2x 2 x x 3321 E lim lim 100 x x 2x 3 100 3 33 x 2 100 x 94 3 6 1 94 1 x 1 x 2 2 x x lim x 100 3 x 2 100 x 3 94 1 1 1 2 x x 3 1 . 2 94 2 lim 93 2 . x 3 2 2 100 x
Dạng 5. Dạng vô định , 0. 1. Phương pháp
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 60
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Nếu biểu thức chứa biến số dưới dấu căn thì nhân và chia với biểu thức liên hợp
Nếu biểu thức chứa nhiều phân thức thì quy đồng mẫu và đưa về cùng một biểu thức.
Thông thường, các phép biến đổi này có thể cho ta khử ngay dạng vô định ; 0. hoặc 0
chuyển về dạng vô định ; 0
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1: Tính lim x 1 x 3 x Hướng dẫn giải 4 x 1 x 3 x lim x 1 x 3 lim lim 0. x x x x 1 x 3 1 3 1 1 x x Ví dụ 2: Tính 2 lim x x 5 x x Hướng dẫn giải 2 2 2 x 5 x 5 5
lim x x 5 x lim x lim . GV: T x x 2 x 5 2 x 5 x 1 1 2 x R Ầ N ĐÌN Ví dụ 3: Tính 2 lim x x 5x x H CƯ Hướng dẫn giải – 0834 2 E lim x x 5x 3321 x 33 Nhân và chia liên hợp 2 x x 5x 2 2 x x 5x x x 5x 2 2 x x 5x E lim lim x 2 x 5 x x 5x x x 1 x 5 x lim (Vì lim x lim x ) x 5 x x x x 1 x 5 5 5 lim . x 5 1 1 0 2 1 1 x
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 61
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Ví dụ 4: Tính 1 1 lim 1 x0 x x 1 Hướng dẫn giải 1 1 E lim 1
(Dạng vô định 0. ) x0 x x 1 1 x 1 1 lim lim 1. x0 x x 1 x0 x 1 1 Ví dụ 6: Tính 2 lim x 5 0. x x Hướng dẫn giải 1 2 5 lim x 5 lim 1 1. x x x x Ví dụ 7: Tính 2 lim x x 2 x x Hướng dẫn giải 2 2 2 x 2 x 2 2
lim x x 2 x lim x lim 1 . x x 2 x 2 2 x 2 x 1 1 GV: T 2 x R Ầ 2 x 1 x x 1 N Ví dụ 8: Tính lim ĐÌN x0 x H CƯ Hướng dẫn giải – 0834 2 2 x 1 x x 1 x 1 x x 1 lim lim 3321 x0 x x0 2 x 1 x x 1 33 x 0 lim 0 x0 2 2 x 1 x x 1
Ví dụ 9: Tính lim x 5 x 7 x Hướng dẫn giải x 5 x 7 12 lim x 5 x 7 lim lim x x x x 5 x 7 x 5 x 7 12 x 0 lim 0. x 5 7 2 1 1 x x Ví dụ 10: Tính 2 lim x 5x x . x
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 62
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Hướng dẫn giải 2 2 2 x x x 5 x lim x 5x x lim lim x x 2 x 2 x 5x x x 5x x 5 5 lim . x 5 2 1 1 x 1 Ví dụ 11: Tính 2 lim x 5 1. x x Hướng dẫn giải 5 5 x . 1 x 1 2 2 2 x 5 x x 5 lim lim lim lim 1 1. 2 x x x x x x x x
C. GIẢI BÀI TẬP SÁCH GIÁO KHOA
Bài 1. Tìm các giới hạn sau: x 3 3 x 8 a) lim 2
x 7x 4 ; b) lim ; c) lim . 2 x 2 x 3 x 9 x 1 x 1 Lời giải a) lim 2
x 7x 4 2 2
lim x 7. lim x lim 4 ( 2 ) 7 2 4 22 x 2 x 2 x 2 x 2 GV: T x 3 x 3 1 1 1 R b) lim lim lim 2 Ầ x3 x 9 x 3
x 3 x 3 x3 x 3 3 3 6 N ĐÌN 3 x 8 3 x 8 H CƯ 3 x 8 9 x 8 1 x c) lim lim lim lim x 1 x 1 x 1 x x 1 x 1 1 3 x 8 x 1 3 x 8 x 1 3 x 8 – 0834 1 lim 3321 x 1 3 x 8 33 1 3 1 8 1 6 2 x khi x 1
Bài 2. Cho hàm số f x x khi x 1
Tìm các giới hạn lim f x; lim f x;lim f x (nếu có). x 1 x 1 x 1 Lời giải
lim f x lim x 1, lim f x lim 2 x 1 x 1 x 1 x 1 x 1
Do lim f x lim f x nên không tồn tại lim f x . x 1 x 1 x 1
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 63
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Bài 3. Tìm các giới hạn sau: 4x 3 2 2 x 1 a) lim ; b) lim ; c) lim . x 2x x 3x 1 x x 1 Lời giải 3 4 4x 3 4 0 a) lim lim x 2 . x 2 x x 2 2 2 2 0 b) lim lim x 0 . x 3x 1 x 1 3 0 3 x 1 2 1 2 x 1 x 1 0 c) lim lim 1. x x 1 x 1 1 0 1 x
Bài 4. Tìm các giới hạn sau: 1 x a) lim ; b) 2 lim 1 x ; c) lim . x 1 x 1 x x 3 3 x Lời giải 1 a) lim . GV: T x 1 x 1 R 1 1 2 2 2 Ầ
b) lim 1 x lim x 1 lim x . lim 1 0 1 . 2 2 N x x x x x x ĐÌN x 1 H CƯ c) lim lim . x lim . x 3 3 x x 3 x 3 3 x – 0834
Bài 5. Trong hồ có chứa 6000 lít nước ngọt. Người ta bơm nước biển có nồng độ muối là 3321
30gam / lít vào hồ với tốc độ 15 lít/phút.
a) Chứng tỏ rằng nồng độ muối của nước trong hồ sau t phút kể từ khi bắt đầu bơm là 33 30t C t (gam/lít). 400 t
b) Nồng độ muối trong hồ như thế nào nếu t . Lời giải
a) Sau thời gian t, số lít nước bơm vào hồ là: 15t (lít).
Trong 15t lít nước biển có lượng muối: 30.15t 450t (gam). 450t 30t
Nồng độ muối trong hồ sau thời gian t phút: C t . 6000 15t 400 t 30t 30 30
b) lim C t lim lim 30 . x
x 400 t x 400 0 1 1 t
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 64
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
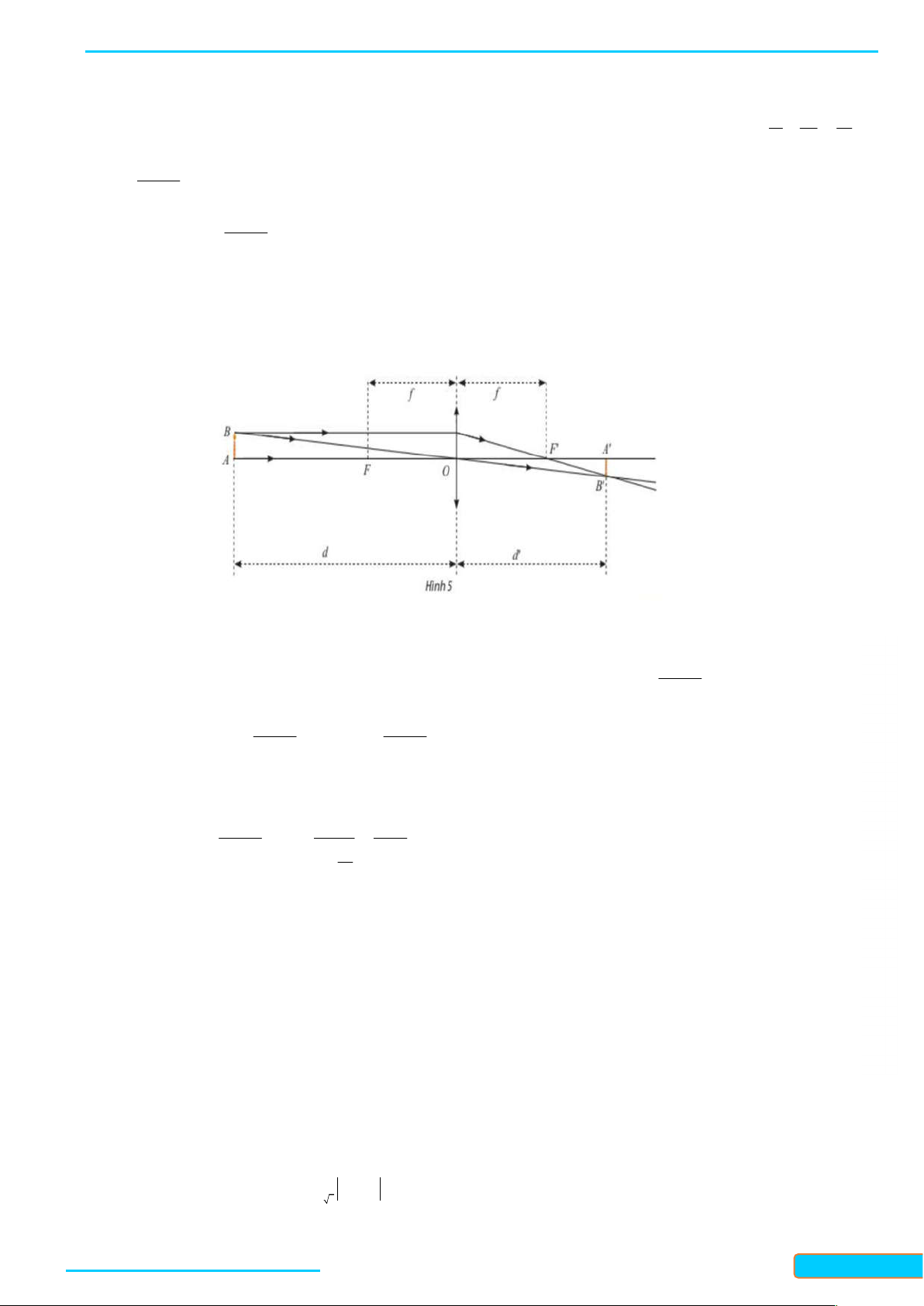
Bài 6. Một thấu kính hội tụ có tiêu cự là f 0 không đổi. Goi d vả d lần lượt lả khoảng cách 1 1 1
từ vật thật và ảnh của nó tới quang tâm O của thấu kính (Hình 5). Ta có công thức: d d f df hay d d f df
Xét hàm số g d
. Tìm các giới hạn sau đây và giải thích ý nghĩa. d f
a) lim g d ;
b) lim g d . d d f Lời giải GV: T 1 a) Ta có: 2 lim df f 0 lim R Ầ d f d f d f N ĐÌN df 1
Suy ra: lim g d lim lim df . H CƯ d f d
f d f d f d f
Vậy khi vật tiến gần tới tiêu điểm thì ảnh càng lớn và tiến tới . – 0834 df f f 3321
b) lim g d lim lim f d d d d f f 1 0 1 33 d
Vậy khi vật ở rất xa, tiến tới
thì ảnh của vật nằm trên tiêu điểm. D. BÀI TẬP TRẮC NGHIỆM
Câu 1: Giá trị của giới hạn lim 2 3x 7x 11 là: x 2 A. 37. B. 38. C. 39. D. 40. Lời giải Chọn A lim 2 3x 7x 2
11 3.2 7.2 11 37 x2
Câu 2: Giá trị của giới hạn 2 lim x 4 là: x 3 A. 0. B. 1. C. 2. D. 3.
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 65
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Lời giải Chọn B
lim x 4 32 2 4 1 x 3 Câu 3: 1
Giá trị của giới hạn 2 lim x sin là: x 0 2 A. 1 sin . B. . C. . D. 0. 2 Lời giải Chọn D Ta có 1 1 2 lim x sin 0.sin 0 x0 2 2 2 Câu 4: x 3
Giá trị của giới hạn lim là: 3 x 1 x 2 A. 1. B. 2. C. 2. D. 3 . 2 Lời giải Chọn B x 3 2 2 1 3 GV: T lim 2 3 x x 2 3 1 1 2 R Ầ 3 N x x ĐÌN
Câu 5: Giá trị của giới hạn lim là: x 2x 1 4 1 x 3 H CƯ A. 1. B. 2. C. 0. D. 3 . 2 – 0834 Lời giải 3321 Chọn C 33 3 3 x x 11 lim 0
x 2x 1 4 x 3 2.1 1 4 1 1 3
Câu 6: Giá trị của giới hạn x 1 lim là: 4
x 1 x x 3 A. 3 . B. 2 . C. 3 . D. 2 . 2 3 2 3 Lời giải Chọn D x 1 1 1 Ta có 2 lim 4
x1 x x 3 1 1 3 3 2 Câu 7: 3x 1 x
Giá trị của giới hạn lim là: x 1 x 1
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 66
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com A. 3 . B. 1 . C. 1 . D. 3 . 2 2 2 2 Lời giải Chọn A 2 Ta có 3x 1 x 3 1 1 3 lim x 1 x 1 1 1 2 2
Câu 8: Giá trị của giới hạn 9x x lim là: x 2x 1 4 3 x 3 A. 1. B. 5. C. 1 . D. 5. 5 5 Lời giải Chọn C 2 2 9x x 9.3 3 1 lim x 2x 1 4 x 3 2.3 1 4 3 3 3 5 2 Câu 9: x x 1
Giá trị của giới hạn 3 lim là: 2 x 2 x 2x A. 1 . B. 1 . C. 1 . D. 1. 4 2 3 5 GV: T Lời giải R Ầ Chọn B N ĐÌN 2 2 x x 1 2 2 1 1 H CƯ 3 lim 2 2 x2 x 2x 2 2.2 2 – 0834 3 2 Câu 10: 3x 4 3x 2
Giá trị của giới hạn lim là: x 2 x 1 3321 A. 3 . B. 2 . C. 0. D. . 33 2 3 Lời giải Chọn C 3 2 3 Ta có: 3x 4 3x 2 12 4 6 2 0 lim 0 x2 x 1 3 3
Câu 11: Giá trị của giới hạn 3
lim x x 1 là: x A. 1. B. . C. 0. D. . Lời giải Chọn D
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 67
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 3 lim x x lim 1 1 3 x x 3 1 lim x 1 vì . 2 3 1 1 x x x x lim 1 1 0 2 3 x x x Giải nhanh: 3 x x 3 1 ~ 1 x
khi x . Câu 12: 3
Giá trị của giới hạn là: 2 lim x 2x 3 x x A. 0. B. . C. 1. D. . Lời giải Chọn B Ta có lim x x x
x x x x x 3 2 3 2 2 3 lim 3 2 2 3 3 lim 1 . 2 x x x x Giải nhanh: 3 3 2
x 2x 3 x ~ x khi x .
Câu 13: Giá trị của giới hạn là: 2 lim x 1 x x A. 0. B. . C. 2 1. D. . Lời giải GV: T Chọn B R Ầ N ĐÌN Giải nhanh: 2 2
x : x 1 x ~
x x 2x . H CƯ
Đặt x làm nhân tử chung: – 0834 lim x x x x 1 2 1 lim 1 1 2 x 3321 x 33 lim x x vì . 1 lim 1 1 2 0 2 x2 x
Câu 14: Giá trị của giới hạn là: 3 3 2 lim 3x 1 x 2 x A. 3 3 1. B. . C. 3 3 1. D. . Lời giải Chọn B Giải nhanh: 3 3 2 3 3 2 x x x x x 3 : 3 1 2 ~ 3 3 1 x .
Đặt x làm nhân tử chung:
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 68
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com lim x x x x 1 2 3 3 2 3 1 2 3 lim 3 1 3 2 x x x lim x x vì . 1 2 3 3 lim 3 1 3 1 0 3 2 x x x
Câu 15: Giá trị của giới hạn x là: 2 lim 4x 7x 2x x A. 4. B. . C. 6. D. . Lời giải Chọn D Đặt 2
x làm nhân tử chung: lim x 7 2 4x 7x 2x 2 lim x 4 2 x x x 2 lim x x vì . 7 lim 4 2 4 0 x x GV: T Giải nhanh: 2 2 2 x : x
4x 7x 2x ~ x
4x 2x 4x . R Ầ N ĐÌN 3 Câu 16: x 8
Giá trị của giới hạn lim là: H CƯ 2 x 2 x 4 A. 0. B. . C. 3. D. Không xác định. – 0834 Lời giải 3321 Chọn C 33 3 2 2 Ta có x 8 (x 2)(x 2x 4) x 2x 4 12 lim lim lim 3 2 x 2 x 2 x 2 x 4
(x 2)(x 2) x 2 4 5 Câu 17: x 1
Giá trị của giới hạn lim là: 3 x 1 x 1 A. 3 . B. 3. C. 5 . D. 5. 5 5 3 3 Lời giải Chọn D x 1 4 3 2 5
x x x x x 4 3 2 1 1
x x x x 1 5 lim lim lim . 3 x x 1 x x 1 2 1 1 x x 2 x 1 1 x x 1 3
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 69
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 3 Câu 18: 2x 6 3 Biết rằng lim a 3 . b Tính 2 2 a b . 2 x 3 3 x A. 9. B. 25. C. 5. D. 13. Lời giải Chọn A 2 2 3 3
x 3 2x 3x 3 2 2 3 x 3x x 3 Ta có lim lim lim 2 x 3 x 3 3 x
3x 3 x x 3 3 x 2 2 3 3. 3 3 18 a 3 2 2 3 3 a b 9 . 3 3 2 3 b 0 2
Câu 19: Giá trị của giới hạn x x 6 lim là: 2 x 3 x 3x A. 1. B. 2 . C. 5. D. 3. 3 3 3 5 Lời giải Chọn C 2 x x 6 x 3 x 2 x 2 3 2 5 lim lim lim . 2 x 3 x 3 x 3x x x x 3 3 x 3 3 GV: T 3 x R
Câu 20: Giá trị của giới hạn lim là: Ầ x 3 3 27 x N ĐÌN A. 1. B. 0. C. 5. D. 3. H CƯ 3 3 5 – Lời giải 0834 Chọn B 3321 33
Ta có 3 x 0 với mọi x 3, do đó: 3 x 3 x lim lim x 3 3 x 3 27 x 3 x 2
9 3x x 3 x 3 3 lim 0. x 3 2 2 9 3x x 9 3.3 3 2 21 x 7 21 12x
Câu 21: Giá trị của giới hạn lim là: x 0 x 21 21 21 21 A. 2 2 2 1 2 . B. . C. . D. . 7 9 5 7 Lời giải Chọn A
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 70
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Ta có 2 21 x 7 21 1 2x 2 21
x 7 1 2x 21 1 2 lim lim lim x . x 0 x 0 x 0 x x 7 2 Câu 22: x x x
Giá trị của giới hạn lim là: 2 x 0 x A. 0. B. . C. 1. D. . Lời giải Chọn D
x x x 2 2
x x x Ta có 1 lim lim lim 2 x 0 x 0 2 x x 2
x x x x0 2
x x x vì 1 0 ; lim 2
x x x và 2
x x x 0 với mọi x 0. 0 x 0 3 Câu 23: x 1
Giá trị của giới hạn lim là: x 1 3 4x 4 2 A. 1. B. 0. C. 1. D. . Lời giải Chọn C GV: T (x 1) x x x 1 3 4 4 2 4 4 4 3 2 3 R Ta có lim lim x 1 3 Ầ x 1 4x 4 2
4x 48 3 2 3 x x 1 N ĐÌN H CƯ 34x42 3
2 4x 4 4 12 lim 1. x 1 3 2 3 –
x x 12 4 1 0834 3 3321 Câu 24: 2 1 x 8 x
Giá trị của giới hạn lim là: x 0 x 33 A. 5 . B. 13 . C. 11 . D. 13 . 6 12 12 12 Lời giải Chọn B 3 3 Ta có 2 1 x 8 x 2 1 x 2 2 8 x lim lim x 0 x 0 x x x 2 1 1 13 lim 1 . x 0 3 x 1 1 3
4 2 8 x 8 x 2 12 12 3 Câu 25: ax 1 1 bx
Biết rằng b 0, a b 5 và lim
2 . Khẳng định nào dưới đây sai? x 0 x A. 1 a 3. B. b 1. C. 2 2 a b 10.
D. a b 0.
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 71
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Lời giải Chọn A 3 3 Ta có ax 1 1 bx ax 1 1 1 1 bx lim lim x 0 x 0 x x x ax bx lim x 0 3 2 3 x1 1 1 1 1 x x x x a b a b lim 2. x 0 3 2 3 1 1 1 1 1 x x x 3 2 a b 5 a b Vậy ta được: 5 a b
a 3, b 2 2 2a 3b 12 3 2 2 Câu 26: 2x 5x 3
Kết quả của giới hạn lim là: 2
x x 6x 3 A. 2. B. . C. 3. D. 2 . Lời giải Chọn D 5 3 2 2 2 Ta có 2x 5x 3 lim lim x x 2 . 2 GV: T
x x 6x 3 x 6 3 1 2 x x R Ầ 2 2 N 2x 5x 3 2x ĐÌN
Giải nhanh : khi x thì : 2. 2 2 x 6x 3 x H CƯ 3 2 Câu 27: 2x 5x 3
Kết quả của giới hạn lim là: 2 – x x 6x 3 0834 A. 2. B. . C. . D. 2 . 3321 Lời giải 33 Chọn C 5 3 3 2 2 3 Ta có: 2x 5x 3 lim lim . x x x . 2 x x 6x 3 x 6 3 1 2 x x 3 2 3 Giải nhanh : khi 2x 5x 3 2x x thì : 2x . 2 2 x 6x 3 x 3 2 Câu 28: 2x 7x 11
Kết quả của giới hạn lim là: 6 5
x 3x 2x 5 A. 2. B. . C. 0. D. . Lời giải Chọn C
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 72
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 2 7 11 3 2 3 4 6 Ta có: 2x 7x 11 0 lim lim x x x 0. 6 5
x 3x 2x 5 x 2 5 3 3 6 x x 3 2 3 Giải nhanh : khi 2x 7x 11 2x 2 1 x thì : . 0. 6 5 6 3 3x 2x 5 3x 3 x Câu 29: 2x 3
Kết quả của giới hạn lim là: x 2 x 1 x A. 2. B. . C. 3. D. 1 . Lời giải Chọn D Khi x thì 2 2 2 x x
x 1 x x x x x 2 x 0 3 2 2x 3
chia cả tử và mẫu cho x , ta được lim lim x 1 . x 2 x 1 x x 1 1 1 2 x
2ax 3 Câu 30: Biết rằng
có giới hạn là khi x (với a là tham số). Tính giá trị nhỏ 2 x 1 x nhất của 2
P a 2a 4. A. P 1. B. P 3. C. P 4. D. P 5. min min min min GV: T Lời giải R Ầ N ĐÌN Chọn B H CƯ Khi x thì 2 2 2 x x
x 1 x x x x x 0 – 0834
Nhân lượng liên hợp: 3321 2 a Ta có x 3 lim lim 2 ax 3 3 1 2 x 1 x 2 lim x 2 a 1 1 . 2 x 2 x x 33 1 x x x x 2 lim x x
2ax 3 Vì lim 1 x 2 lim 1 1 4 0 x 1 x 2 x x 3 lim 2a
2a 0 a 2 . x x Giải nhanh : ta có 2x 3 x 2 x 1 x
ax 2x x ax 2 2 3 1 2 .
x x 22ax a 2 . Khi đó 2
P a 2a 4 a 2
1 3 3, P 3 a 1 2 P 3. min
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 73
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 2 Câu 31: 4x x 1
Kết quả của giới hạn lim là: x x 1 A. 2. B. 1. C. 2. D. . Lời giải Chọn C 2 2 Giải nhanh: khi 4x x 1 4x 2x x 2. x 1 x x 1 1 4 2 2 Cụ thể: 4x x 1 x x 4 lim lim 2. x x 1 x 1 1 1 x 2 Câu 32:
Kết quả của giới hạn 4 x 2x 1 2 x lim là: x 2
9x 3x 2x A. 1 . B. . C. . D. 1 . 5 5 Lời giải Chọn D Giải nhanh : khi 2 2 GV: T
4 x 2x 1 2 x 4 x x 2x x 1 x . 2 2 3x 2x 5 9x 3x 2x 9x 2 x R Ầ N 2 1 2 ĐÌN 4 1 2 2 Cụ thể : 4x 2x 1 2 x x x x 1 lim lim . H CƯ x 2 9x 3x 2 x x 3 5 9 2 x – 0834 2 Câu 33: Biết rằng 4 x 2x 1 2 x L lim
0 là hữu hạn (với a,b là tham số). Khẳng định 3321 x 2
ax 3x bx 33 nào dưới đây đúng. A. a 0. B. 3 L C. 3 L D. b 0. a b b a Lời giải Chọn B Ta phải có 2
ax 3x 0 trên ;
a 0. Ta có 2 2 x
4x 2x 1 2 x 4x x 3 x 0. 2
Như vậy xem như “tử” là một đa thức bậc 1. Khi đó
4 x 2x 1 2 x lim 0 khi và chỉ x 2
ax 3x bx khi 2
ax 3x bx là đa thức bậc 1. Ta có 2 2
ax 3x bx
ax bx a b x
a b 0.
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 74
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 2 Khi đó 4x 2x 1 2 x 3x 3
L 0 b a 0 b a. 2
ax 3x bx
a bx b a 3 3 2 Câu 34:
Kết quả của giới hạn x 2x 1 lim là: x 2 2x 1 A. 2 . B. 0. C. 2 . D. 1. 2 2 Lời giải Chọn C 3 3 2 3 3 Giải nhanh: x 2 x 1 x x 1 x . 2 2 2 x 1 2x 2x 2 2 1 3 1 3 3 2 3 Cụ thể: x 2x 1 x x 1 lim lim . x 2 2x 1 x 1 2 2 2 x
Câu 35: Tìm tất cả các giá trị của a để là . 2 lim 2x 1 ax x A. a 2. B. a 2. C. a 2. D. a 2. Lời giải GV: T Chọn B R Giải nhanh: 2 2 x
2x 1 ax 2x x Ầ N ĐÌN
2x ax a 2x a 2 0 a 2. H CƯ 1 2 –
Cụ thể: vì lim x nên lim 2x 1 ax lim x 2 a 2 x x x 0834 x 3321 1 lim 2 a
a 2 0 a 2. 2 x x 33
Câu 36: Giá trị của giới hạn 3 2
lim 2x x là: x A. 1. B. . C. 1. D. . Lời giải Chọn D Giải nhanh : 3 2 3 x
2x x 2x . 3 lim x x Cụ thể: lim 1 3 2 2x x 3 lim x 2 vì . 1 x x x lim 2 2 0 x x Câu 37: 1 1
Giá trị của giới hạn lim là: 2
x 2 x 2 x 4
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 75
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com A. . B. . C. 0. D. 1. Lời giải Chọn A Ta có 1 1 x 2 1 x 1 lim lim lim 2 2 2 x 2 x 2 x 2 x 2 x 4 x 4 x 4 Vì lim x 1 3 0; lim và 2
x 4 0 với mọi x 2 ;2. 2 x 4 0 x 2 x 2
Câu 38: Kết quả của giới hạn x 15 lim là: x 2 x 2 A. . B. . C. 15 . D. 1. 2 Lời giải Chọn A lim x1 5 13 0 Vì x2 x 15 lim . lim x2 x2
0 & x 2 0, x 2 x 2 x2 Câu 39: x 2
Kết quả của giới hạn lim là: x 2 x 2 A. . B. . GV: T C. 15 . D. Không xác định. 2 R Ầ N Lời giải ĐÌN H CƯ Chọn B –
lim x 2 2 0 x x 2 0834 2 lim . x2
lim x 2 0 & x 2 0, x 2 x 2 3321 x 2 33 3x 6
Câu 40: Kết quả của giới hạn lim là: x 2 x 2 A. . B. 3. C. . D. Không xác định. Lời giải Chọn B
Ta có x 2 x 2 với mọi x 2, do đó : 3x 6 3 x 2 3x 2 lim lim lim lim 3 3 x 2 x 2 x 2 x 2 x 2 x 2 x 2
Câu 41: Kết quả của giới hạn 2 x lim là: 2 x 2 2x 5x 2
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 76
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com A. . B. . C. 1 . D. 1. 3 3 Lời giải Chọn C Ta có 2 x 2 x 1 1 lim lim lim . 2 x 2 x 2 2x 5x 2
2 x12x x 2 1 2x 3 2
Câu 42: Kết quả của giới hạn x 13x 30 lim là: x 3 x 3 2 x 5 A. 2. B. 2. C. 0. D. 2 . 15 Lời giải Chọn C
Ta có x 3 0 với mọi x 3, nên: 2 x 13x 30 x 3 x 1 0 x 3. x 1 0 3 3 3 7 lim lim lim 0 . x 3 x 3 2 x x 3 5 x 3 2 x x 3 2 5 x 5 2 3 5 2x víi x 1
f x 1 x . 2 3x 1 víi x 1 GV: T Câu 43: Cho hàm số
Khi đó lim f x là: x 1 R A. . B. 2. C. 4. D. . Ầ N ĐÌN Lời giải H CƯ Chọn B – 0834 lim f x 2 2
lim 3x 1 3.1 1 2 x 1 x 1 3321 2 x 1 33 víi x 1
Câu 44: Cho hàm số f x 1 x
. Khi đó lim f x là: x 1 2x 2 víi x 1 A. . B. 1. C. 0. D. 1. Lời giải Chọn A 2 2 lim x 1 2 f x x 1 lim lim vì x 1 . x 1 x 1 1 x
lim 1 x 0 & 1 x 0 x 1 x 1 2 Câu 45: Cho hàm số víi f x x 3 x 2
. Khi đó lim f x là:
x 1 víi x 2 x2 A. 1. B. 0. C. 1. D. Không tồn tại. Lời giải
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 77
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Chọn C
lim f x lim 2 x 3 1 Ta có x2 x2
lim f x lim f x 1 lim f x 1.
lim f x lim x x2 x2 x2 1 1 x2 x2 Câu 46: víi Cho hàm số f x x 2 3 x 2
. Tìm a để tồn tại lim f x . ax 1 víi x 2 x 2 A. a 1. B. a 2. C. a 3. D. a 4. Lời giải Chọn B
lim f x lim ax 1 2a 1 Ta có x2 x2 .
lim f x lim x 2 3 3 x2 x2
Khi đó lim f x tồn tại lim f x lim f x 2a 1 3 a 2. x 2 x2 x2 2
x 2x 3 víi x 3 Câu 47: Cho hàm số f x 1
víi x 3. Khẳng định nào dưới đây sai? 2 3 2x víi x 3
A. lim f x 6.
B. Không tồn tại lim f x. x3 x3
C. lim f x 6.
D. lim f x 1 5. x3 x3 GV: T Lời giải R Ầ N Chọn C ĐÌN H CƯ
lim f x lim x x 2 2 3 6 Ta có x3 x3
lim f x lim f x 2 x3 x3 –
lim f x lim x 3 2 15 x3 x3 0834 3321
không tồn tại giới hạn khi x 3. 33
Vậy chỉ có khẳng định C sai. a b b a lim L lim 3 3 Câu 48: Biết rằng x 1 x 1
a b 4 và 1 x 1 x
hữu hạn. Tính giới hạn 1 x 1 x . A. 1. B. 2. C. 1. D. 2. Lời giải Chọn C 2 2 Ta có a b
a ax ax b
a ax ax b lim lim lim . 3 3 x 1 x 1 x x 1 x x 1 x 2 1 1 1
1 x x Khi đó a b lim hữu hạn 2 1 . a 1 .1 a
b 0 2a b 1 . 3 x 1
1 x 1 x
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 78
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com a b 4 a 1 Vậy ta có a b L lim 3 x 1 2a b 1 b 3
1 x 1 x 2 x x 2 x 2 lim lim 1 . x 1 x 2 1 1 x x 2 x 1 1 x x
Câu 49: Giá trị của giới hạn 2 lim
1 2x x là: x A. 0. B. . C. 2 1. D. . Lời giải Chọn B Ta có lim 1 2
1 2x x lim x 2 1 2 x x x Vì 1 lim x ; lim 2 1 2 1 0. 2 x x x Giải nhanh : 2 2 x
1 2x x 2x x 2x x 2 1 x .
Câu 50: Giá trị của giới hạn 2 lim
x 1 x là: x A. 0. B. . C. 1 . D. . 2 Lời giải GV: T Chọn A R Ầ N ĐÌN 2 2 x
x 1 x x x x x 0
Nhân lượng liên hợp. H CƯ Giải nhanh: 1 1 1 2 x
x 1 x 0. 2 2 – 2 1 x x x x x 0834 1 3321 Cụ thể: lim 1 0 2 1 lim lim x x x 0. x x 2 x 1 x x 1 2 33 1 1 2 x Câu 51: Biết rằng
Tính S 5a . b 2 lim 5x 2x
x 5 a 5 .b x A. S 1. B. S 1. C. S 5. D. S 5. Lời giải Chọn A 2 2 x
5x 2x x 5
5x x 5 5x x 5 0
Nhân lượng liên hợp: Giải nhanh: 2 x
5x 2x x 5
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 79
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 2x 2x 2x 1 . 2 2
5x 2x x 5 5x x 5 2 5x 5 Cụ thể: Ta có x lim
x x x x 2 2 5 2 5 lim x 2
5x 2x x 5 1 2 2 1 1 a lim 5 5 S 1. x 2 2 5 5 5 5 5 b 0 x
Câu 52: Giá trị của giới hạn 2 2 lim
x 3x x 4x là: x A. 7 . B. 1 . C. . D. . 2 2 Lời giải Chọn B . Khi 2 2 2 2 x
x 3x x 4x x x 0
Nhân lượng liên hợp: Giải nhanh: 2 2 x
x 3x x 4x x x x 1 . 2 2 2 2 2x 2 x 3x x 4x x x GV: T Cụ thể: 2 2 lim
x 3x x 4x R x Ầ N ĐÌN x 1 1 lim lim . H CƯ x 2 2
x 3x x 4 x x 3 4 2 1 1 x x – 0834
Câu 53: Giá trị của giới hạn 3 3 2 lim
3x 1 x 2 là: x 3321 A. 3 3 1. B. . C. 3 3 1. D. . 33 Lời giải Chọn D lim 1 2 3 3 2
3x 1 x 2 3 lim x 3 1 3 2 x x x x Vì 1 2 3 3 lim x , lim 3 1 3 1 0. 3 2 x x x x Giải nhanh: 3 3 2 3 3 2 x x x x x 3 3 1 2 3 3 1 x .
Câu 54: Giá trị của giới hạn 2 3 3 2 lim
x x x x là: x
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 80
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com A. 5 . B. . C. 1. D. . 6 Lời giải Chọn A Khi 2 3 3 2 2 3 3 x
x x x x x x x x 0
Nhân lượng liên hợp: 2 3 3 2
x x x x 2 3 3 2 lim lim
x x x x x x x x 2 x x 1 1 5 lim . x 2 2 3 x x
x x x 1 3 2 3 6 1 3 x 2 3 1 Giải nhanh: 2 3 3 2 2 3 3 2 x x x x x x x
x x x 2 2 x x x x 2 2 3 x 1 x 1 3 3 2 2 2 3 3 6 6 3 1 x x
x x x x x x x x 1 1 5
x . 2 3 6
Câu 55: Giá trị của giới hạn 3 3 lim
2x 1 2x 1 là: x GV: T A. 0. B. . C. 1. D. . R Ầ N Lời giải ĐÌN H CƯ Chọn A 3 3 3 3 – x 2x 1 2x 1
2x 2x 0
nhân lượng liên hợp: 0834 3321 lim 2 3 3
2x 1 2x 1 lim 0. x x 2x 2 3 1 2x 1 2x 1 2x 2 3 3 1 33 Giải nhanh: 3 3 2 x 1 2 x 1 2 2 2 0. 3 2x 2 3
1 4x 1 2x 2 3 2 3 2 3 2 3 2 3 2 1
4x 4x 4x 3 4x Câu 56:
Kết quả của giới hạn 1 lim x 1 là: x 0 x A. . B. 1. C. 0. D. . Lời giải Chọn B Ta có 1 lim x 1
lim x 1 0 1 1. x 0 x 0 x
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 81
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Câu 57: Kết quả của giới hạn x lim x 2 là: 2 x 2 x 4 A. 1. B. . C. 0. D. . Lời giải Chọn C Ta có x x x 2 . x 0. 2 lim 2 lim 0 . 2 x 2 x 2 x 4 x 2 2
Câu 58: Kết quả của giới hạn 2 x 1 lim x là: 3 2 x 3x x 2 A. 2 . B. 6 . C. . D. . 3 3 Lời giải Chọn B 1 2 2x 1 x x 2 2 1 6 lim lim lim x x . 3 2 3 2 x 3x x 2 x 3x x 2 x 1 2 3 3 3 x x Giải nhanh: 2 x 1 2 x 6 1 6 1 6 x x x . .x . .x . . GV: T 3 2 2 2 3 x x 2 3 x 3 3 x 3 x R Ầ 1 N
Câu 59: Kết quả của giới hạn 2
lim x sin x là: 2 x 0 ĐÌN x H CƯ A. 0. B. 1 . C. . D. . – Lời giải 0834 Chọn B 3321 1 2 2 33
Ta có lim x sin x
lim x sin x 1 1. 2 x 0 x 0 x
Câu 60: Kết quả của giới hạn x lim là: 3 x 1 x 2 1 x 1 A. 3. B. . C. 0. D. . Lời giải Chọn C Với x
x 1; 0 thì x 1 0 và 0 . x 1 x x Do đó lim 3 x 1 lim x 1 2 x x 1 2 x 1 x 1 x 1 x 1 x 1
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 82
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com x lim x 1 2 x x 1 0 x 1 x 1 GV: T R Ầ N ĐÌN H CƯ – 0834 3321 33
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 83
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com GV: T R Ầ N ĐÌN H CƯ – 0834 3321 33
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 84
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com BÀI 3. HÀM SỐ LIÊN TỤC A. TÓM TẮT LÝ THUYẾT
1. Hàm số liên tục tại một điểm
Cho hàm số y f x xác định trên khoảng K và x K . 0
Hàm số y f x được gọi là liên tục tại điểm x nếu lim f x f x . 0 0 x 0 x
Nhận xét: Để hàm số y f x liên tục tại x thì phải có cả ba điều kiện sau: 0
1. Hàm số xác định tại x ;
2. Tồn tại lim f x ;
3. lim f x f x . 0 0 x 0 x x 0 x Chú ý:
Khi hàm số y f x không liên tục tại điểm x thì ta nói f x gián đoạn tại điểm x và x được 0 0 0
gọi là điểm gián đoạn của hàm số f x .
2. Hàm số liên tục trên một khoảng, trên một đoạn
Cho hàm số y f x xác định trên khoảng a;b .
Hàm số y f x được gọi là liên tục trên khoảng a;b nếu f x liên tục tại mọi điểm trong khoảng ấy. GV: T
Cho hàm số y f x xác định trên khoảng a;b . R Ầ N ĐÌN
Hàm số y f x được gọi là liên tục trên đoạn a;b nếu f x liên tục trên khoảng a;b và H CƯ
lim f x f a, lim f x f b. x a x b – 0834
Nhận xét: Đồ thị của hàm số y f x liên tục trên đoạn a;b là một đường liền, có điểm đầu, 3321
điểm cuối (Hình 3). Nếu hai điểm này nằm về hai phía so với trục hoành thì đường liền nói trên luôn cắt trục hoành 33
tại ít nhất một điểm. Điều này còn được phát biểu dưới dạng sau:
Nếu hàm số y f x liên tục trên đoạn a;b và f a. f b 0 thì luôn tồn tại ít nhất một điểm
c a;b sao cho f c 0 .
3. Tính liên tục của hàm sơ cấp
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 85
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Hàm số đa thức y P x , các hàm lượng giác y sin x, y cos x liên tục trên . P x
Hàm số phân thức y
, hàm số căn thức y P x , các hàm số lượng giác y tan x Q x
, y = cot x liên tục trên các khoảng của tập xác định của chúng.
Trong đó P x và Q x là các đa thức.
Nhận xét: Hàm số thuộc những loại trên được gọi chung là hàm số sơ cấp.
4. Tổng, hiệu, tích thương của hàm số liên tục
Cho hai hàm số y f xvà y= g x liên tục tại điểm x . Khi đó: 0
Các hàm số y f x g x, y = f x - g xvà y = f x.g x liên tục tại x . 0 f x Hàm số y
liên tục tại x nếu g x 0 . 0 g x 0
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
Dạng 1: Hàm số liên tục tại một điểm 1. Phương pháp
Ta cần phải nắm vững định nghĩa: GV: T
Cho hàm số y f x xác định trên khoảng K và x K. Hàm số y f x gọi là liên tục tại x nếu 0 0 R Ầ
lim f(x) f(x ) lim f(x) lim f(x) f(x ). 0 0 N xx ĐÌN 0 xx xx o o H CƯ
2. Các ví dụ rèn luyện kĩ năng – Ví dụ 1: Cho
với x 0. Phải bổ sung thêm giá trị f 0 bằng bao nhiêu thì x 2 2 x f x 0834 x hàm số liên tục tại 3321 x 0? Lời giải 33 x 2 2 x x 2 2 x lim f x lim lim x0 x0 x
x0 x 2 2 x 2 1 lim .
x0 x 2 2 x 2
Như vậy để hàm số liên tục tại x 0 thì phải bổ sung thêm giá trị 1 f 0 . 2 2
a x vôùi x 1 vaø a Ví dụ 2: Cho hàm số f x
. Giá trị của a để f x liên tục tại x 1 là bao 3 vôùi x 1 nhiêu? Lời giải TXĐ: D . Ta có:
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 86
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com lim f x lim 2 a x a 1. x 1 x 1
Để hàm số liên tục tại x 1 lim f x f
1 a 1 3 a 4. x 1 2 x 1
Ví dụ 3: Cho hàm số vôùi x 3 vaø x 2 f x 3 . x
Tìm b để f x liên tục tại x 3. x 6 b 3 vôùi x 3 vaø b Lời giải TXĐ: D . Ta có: 2 x 1 3 lim f x lim ; f 3 b 3. 3 x 3 x 3 x x 6 3 3 2 3
Để hàm số liên tục tại x 3 lim f x f 3 b 3 b . x 3 3 3 a 2 khi x 2 Ví dụ 4: Cho hàm số f x .
Với giá trị nào của a thì hàm số liên tục tại x 2. sin khi x 2 x Lời giải TXĐ: D . Ta có f 2 sin 1 2
lim f x lim a 2 a 2 GV: T x 2 x 2 R
lim f x lim sin 1 Ầ 2 N x2 x2 ĐÌN
Hàm số liên tục tại x 2 khi a 1 2 a 3. H CƯ
Ví dụ 5: Tìm số a để hàm số sau liên tục tại điểm x . 0 – 3 0834 3x 2 2 neáu x 2 f x x 2 ; x 2. 0 3321 ax 2 neáu x 2 33 Lời giải TXĐ: D . Ta có: 3 3 x 2 3x 2 2 1 lim f x lim lim . 2 x2 x2 x 2 x2 4
x 23 3x 2 3 2 3x 2 4
lim f x ax 2 2a 2. x 2
Lại có: f 2 2a 2 . 1 7
Hàm số liên tục tại x 2 nếu 2a 2 a . 0 4 8
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 87
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com x 2 vôùi 5 x 4 x 5 Ví dụ 6: Cho hàm số
f x mx 2 vôùi x 4
. Tìm giá trị của m để f x liên tục tại x 4 . x vôùi x 4 3 Lời giải x 2 2 x 2 Ta có: lim f x lim ; lim . x4 x4 x 5 3 x4 3 3 Và f 4 4m 2
Để hàm số liên tục tại x 4 thì lim f x lim f x f 4 x 4 x 4 2 1 4m 2 m . 3 3 2 x 8 3 neáu x 1 Ví dụ 7: Cho hàm số f x 2 x 4x 3
. Tìm giá trị của a để f x liên tục tại x 1. 1 2 cos x a x neáu x 1 6 Lời giải TXĐ: D . 1 1 f 2 2
1 cos a 1 a 1. 6 6 GV: T 1 1 lim f x 2 2 lim cos x a x a 1. R 6 6 Ầ x 1 x 1 N ĐÌN 2 2 2
x 8 3 x 8 3 x 8 3 H CƯ lim f x lim lim 2 x 4x 3 2 x 4x 3 2 x 1 x 1 x 1 x 8 3 – 0834 2 x 1 x 1 x 8 9 3321 lim lim 2 x 4x 3 2 x 8 3 x 1 x 3 2 x 1 x 1 x 8 3 33 x 1 1 lim . 2 x 1 6 x 3 x 8 3
Để hàm số liên tục tại x 1 lim f x lim f x f 1 x 1 x 1 1 2 1 a 1 a 1. 6 6
Dạng 2. Hàm số liên tục trên tập xác định 1. Phương pháp
Để chứng minh hàm số y f x liên tục trên một khoảng, đoạn ta dùng các định nghĩa về
hàm số liên tục trên khoảng, đoạn và các nhận xét để suy ra kết luận.
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 88
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Khi nói xét tính liên tục của hàm số (mà không nói rõ gì hơn) thì ta hiểu phải xét tính liên
tục trên tập xác định của nó.
Tìm các điểm gián đoạn của hàm số tức là xét xem trên tập xác định của nó hàm số không
liên tục tại các điểm nào
Hàm số y f x được gọi là liên tục trên một khoảng nếu nó liên tục tại mọi điểm thuộc khoảng đó.
Hàm số y f x được gọi là liên tục trên đoạn a,b nếu nó liên tục trên và a,b
lim f(x) f(a) , lim f(x) f(b . ) x a x b
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1. Xét tính liên tục của các hàm số sau trên tập xác định của chúng : 2 2 x 4 x 2 khi x 2 khi x 2 a)
f x x 2
b) f x x 2
4 khi x 2 2 2 khi x 2 Lời giải
a) Hàm số f x liên tục với x 2 1 2 x 4
x 2 x 2 GV: T
lim f x lim lim
lim x 2 2 2 4. x 2 x2 x 2 x2 x 2 x 2 R f 2 4
lim f x f 2
f x liên tục tại x 2 2 Ầ x 2 N ĐÌN Từ
1 và 2 ta có f x liên tục trên . H CƯ
b) Hàm số f x liên tục với x 2 1 – 0834 2 x 2 x 2 3321 x 2
lim f x lim lim
lim x 2 2 2 2 2. x 2 x 2 x 2 x 2 x 2 x 2 33
f 2 2 2 lim f x f 2 f x liên tục tại x 2 2 x 2 Từ
1 và 2 ta có f x liên tục trên .
Ví dụ 2. Tìm các giá trị của m để các hàm số sau liên tục trên tập xác định của chúng: 2 2
x x 2
x x khi x 1 khi x 2 a)
f x x 2
b) f x 2 khi x 1
m khi x 2
mx 1 khi x 1 Lời giải
a) Hàm số f x liên tục với x 2 .
Do đó f x liên tục trên f x liên tục tại x 2 lim f x f 2 1 x2
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 89
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 2 x x 2
x 2 x 1
Ta có lim f x lim lim lim x
1 2 1 3; f 2 . m x2 x2 x2 x 2 x 2 x2 Khi đó
1 3 m m 3 .
b) Ta có: lim f x lim mx
1 m 1; lim f x lim 2 x
x 1 1 2; f 1 2. x 1 x 1 x 1 x 1
Từ YCBT lim f x lim f x f
1 m 1 2 m 1. x 1 x 1
Dạng 3. Số nghiệm của phương trình trên một khoảng 1. Phương pháp
Chứng minh phương trình f x 0 có ít nhất một nghiệm
- Tìm hai số a và b sao cho f a.f b 0
- Hàm số f x liên tục trên đoạn a;b
- Phương trình f x 0 có ít nhất một nghiệm x a;b 0
Chứng minh phương trình f x 0 có ít nhất k nghiệm
- Tìm k cặp số a ,b sao cho các khoảng a ;b rời nhau và i i i i
f(a )f(b ) 0, i 1,...,k i i
- Phương trình f x 0 có ít nhất một nghiệm x a ;b . i i i GV: T
Khi phương trình f x 0 có chứa tham số thì cần chọn a, b sao cho : R -
f a , f b không còn chứa tham số hoặc chứa tham số nhưng dấu không đổi. Ầ N ĐÌN
- Hoặc f a, f b còn chứa tham số nhưng tích f(a).f(b) luôn âm. H CƯ
2. Các ví dụ rèn luyện kĩ năng –
Ví dụ 1: Tìm m để phương trình sau có nghiệm: m x 1 x 2 2x 1 0. 0834 3321 Lời giải
Đặt f x mx 1 x 2 2x 1. 33
Tập xác định: D nên hàm số liên tục trên . Ta có: f 1 3; f 2 3 f 1 .f 2 0.
Vậy phương trình đã cho có nghiệm với mọi m.
Ví dụ 2: Chứng minh rằng các phương trình sau luôn có nghiệm với mọi giá trị của tham số:
a) m x 3 2 2 1
1 x x 3 0
b) cos x m cos 2x 0
c) m2cos x 2 2sin5x 1 Lời giải m 1 a) Xét . Phương trình có dạng 2
x x 3 0 nên PT có nghiệm m 1
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 90
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com m 1 Với
giả sử f x m x 3 2 2 1
1 x x 3 m 1
f x liên tục trên R nên f x liên tục trên 1 ;0 Ta có f 2
1 m 1 0; f 0 1
0 f 1 .f 0 0
Do đó PT luôn có nghiệm với mọi giá trị của tham số m
b) Đặt f x cos x mcos 2x f x liên tục trên R 1 3 1 3 Ta có f 0; f 0 f .f 0 4 2 4 2 4 4
Do đó PT luôn có nghiệm với mọi giá trị của tham số m
c) Đặt f x m2cos x 2 2sin5x 1 f x liên tục trên R 3 Ta có f
2 1 0; f 2 1 0 f .f 0 4 4 4 4
Do đó PT luôn có nghiệm với mọi giá trị của tham số m
Ví dụ 3. Chứng minh rằng các phương trình sau có 3 nghiệm phân biệt: a) 3
x 3x 1 0 b) 3
2x 6 1 x 3 Lời giải
a Dễ thấy hàm f x 3
x 3x 1 liên tục trên R . GV: T Ta có: R Ầ N ĐÌN f 2 1
f 2. f
1 0 tồn tại một số a 2; 1 : f a 0 1 . 1 1 H CƯ f 1 3 – f 0 1 0834
f 0. f
1 0 tồn tại một số a 0;1 : f a 0 2 . 2 2 f 1 1 3321 33 f 1 1
f 1 . f 2 0 tồn tại một số a 1; 2 : f a 0 3 . 3 3 f 2 3 Do ba khoảng 2; 1 , 0;
1 và 1; 2 đôi một không giao nhau nên phương trình 3
x 3x 1 0
có ít nhất 3 nghiệm phân biệt.
Mà phương trình bậc 3 thì chỉ có tối đa là 3 nghiệm nên 3
x 3x 1 0 có đúng 3 nghiệm phân biệt. b Đặt 3 3 3
1 x t x 1 t 2t 6t 1 0 .
Xét hàm số f t 3
2t 6t 1 liên tục trên R .
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 91
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
f 2. f 1 3.5 0
Ta có: f 0. f
1 1.3 0 tồn tại 3 số t , t và t lần lượt thuộc 3 khoảng đôi một không 1 2 3 f
1 . f 2 3.5 0 giao nhau là 2; 1 , 0;
1 và 1; 2 sao cho f t f t f t 0 và do đây là phương trình 1 2 3
bậc 3 nên f t 0 có đúng 3 nghiệm phân biệt.
Ứng với mỗi giá trị t , t và t ta tìm được duy nhất một giá trị x thỏa mãn 3
x 1 t và hiển 1 2 3
nhiên 3 giá trị này khác nhau nên PT ban đầu có đúng 3 nghiệm phân biệt.
Ví dụ 4. Chứng minh rằng các phương trình sau luôn có nghiệm: a) 5
x 3x 3 0 b) 4 3 2
x x 3x x 1 0 Lời giải
a Xét f x 5
x 3x 3.
lim f x tồn tại một số x 0 sao cho f x 0. 1 1 x
lim f x tồn tại một số x 0 sao cho f x 0. 2 2 x
Từ đó f x . f x 0 luôn tồn tại một số x x ; x : f x 0 nên phương trình 0 2 1 0 1 2 5
x 3x 3 0 luôn có nghiệm. GV: T
b Xét f x 4 3 2
x x 3x x 1 liên tục trên R R Ta có: f 1 3 0 Ầ N ĐÌN
lim f x tồn tại một số a 0 sao cho f a 0 . x H CƯ 2
x x 3 0 nên luôn tồn tại một số x 0; a thỏa mãn f x 0 nên phương trình 0 0 – 0834 4 3 2
x x 3x x 1 0 luôn có nghiệm. 3321 1
Ví dụ 5. Chứng minh rằng phương trình 2
ax bx c 0 luôn có nghiệm x 0; với a 0 và 33 3
2a 6b 19c 0 . Lời giải Đặt 2
f x ax bx c f x liên tục trên R x 0
Nếu c 0 thì f x 0 có 2 nghiệm là 1 x 3 1 a b 1 c
Nếu c 0 , ta có f 0 ; c f c
2a 6b 18c 3 9 3 18 18 2 1 c 1 f 0.f 0
. Do đó f x 0 có nghiệm trong 0; 3 18 3
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 92
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
C. GIẢI BÀI TẬP SÁCH GIÁO KHOA
Bài 1. Xét tính liên tục của hàm sô: 2
x 1 khi x 0 2
x 2 khi x 1
a) f x
tại điểm x 0 ;
b) f x tạ điểm x 1. 1 x khi x 0 x khi x 1 Lời giải
a) lim f x lim 1 x 1 0 1;
lim f x lim 2 x 2 1 0 1 1 x 0 x 0 x0 x0
Suy ra: lim f x f 0 x0
Vậy hàm số y f x liên tục tại x 0 .
b) lim f x limx 1;
lim f x lim 2 x 2 2 1 2 3 x 1 x 1 x 1 x 1
Suy ra không tồn tại lim f x x 1
Vậy hàm số y f x không liên tục tại x 1. 2 x 4 khi x 2
Bài 2. Cho hàm số f x x 2 a khi x 2
Tìm a để hàm số y f x liên tục trên . GV: T Lời giải R Ầ N Ta có: ĐÌN 2 H CƯ x 4
x 2 x 2
lim f x lim lim
lim x 2 2 2 4; f 2 a x 2 x2 x 2 x 2 x 2 x 2 – 0834
Để hàm số f x liên tục trên thì hàm số f x phải liên tục tại x 2 hay 0 3321
lim f x f 2 . x 2 33 Suy ra: a 4 .
Bài 3. Xét tính liên tục của các hàm số sau: x
a) f x ; b) g x 2 9 x ;
c) h x cosx tanx . 2 x 4 Lời giải x
a) f x
là hàm số phân thức có tập xác định là ; 2 và 2; 2 x 4
Nên hàm số f x liên tục trên các khoảng ; 2 và 2; . b) g x 2
9 x là hàm số căn thức có tập xác định là 3;
3 nên hàm số g x liên tục trên đoạn
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 93
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 3;3. c)
h x cosx tanx là hàm số lượng giác có tập xác định là k 2 Nên hàm số
h x liên tục trên các khoảng k . 2
Bài 4. Cho hàm số f x 2x sinx, g x x 1 . f x
Xét tính liên tục hàm số y f x g x và y . g x Lời giải
Hàm số f x 2x sinx liên tục với mọi x .
Hàm số g x x 1 liên tục trên khoảng 1; .
Suy ra: hàm số y f x.g x liên tục trên khoảng 1;
g x 0 khi x 1. f x Suy ra hàm số y
liên tục trên khoảng 1; . g x
Bài 5. Một bãi đậu xe ô tô đưa ra giá C x (đồng) khi thời gian đậu xe là x (giờ) như sau: GV: T
60000 khi 0 x 2
C x 100000 khi 2 x 4 R Ầ N
200000 khi 4 x 24. ĐÌN H CƯ
Xét tính liên tục của hàm số C x . – 0834 Lời giải 3321
C x 60000 khi x 0; 2 nên hàm số C x liên tục trên (0;2). 33
C x 100000 khi x 2; 4 nên hàm số C x liên tục trên (2;4).
C x 200000 khi x 4; 24 n hàm số C x liên tục trên (4;24). Ta có:
Vậy không tồn tại lim hay hàm số C x không liên tục tại 2. x2
limC x 100000 x4
limC x 200000 x4
Vậy không tồn tại lim hay hàm số C x không liên tục tại 4. x4
Bài 6. Lực hấp dẫn do Trái Đất tác dụng lên một đơn vị khối lượng ở khoảng cách r tính từ tâm của nó là
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 94
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com GMr
khi 0 r R 3 R F r GM khi r R, 2 r
trong đó M là khối lượng, R là bán kính của Trái Đất, G là hằng số hấp dẫn. Hàm số F r có liên tục trên 0; không? Lời giải GMr GMR GM GM GM
lim F r lim , lim F r lim 3 3 2 2 2 rR rR rR rR R R R r R Suy ra: lim
F r F R . Hay hàm số F r liên tục tại r R . r R 0 GMr F r
khi 0 r R nên hàm F r liên tục trên 0; R . 3 R GM F r
khi r R nên hàm F r liên tục trên R; . 3 r
Vậy hàm số F r liên tục trên 0; . D. BÀI TẬP TRẮC NGHIỆM 2
x x 2 Câu 1: khi x 2
Tìm giá trị thực của tham số
m để hàm số f x x 2 liên tục tại x 2. GV: T m khi x 2 R A. m 0. B. m 1. C. m 2. D. m 3. Ầ N ĐÌN Lời giải H CƯ Chọn D – 0834
Tập xác định: D , chứa x 2 . Theo giả thiết thì ta phải có 3321 2
m f f x x x 2 2 lim lim limx 1 3. x2 x2 x2 33 x 2 3 2
x x 2x 2 Câu 2: khi x 1
Tìm giá trị thực của tham số
m để hàm số f x x 1 liên tục tại 3 x m khi x 1 x 1. A. m 0. B. m 2. C. m 4. D. m 6. Lời giải Chọn A
. Hàm số xác định với mọi x . Theo giả thiết ta phải có 2 2 x 1 2 3 2 x x x x 2
3 m f
1 lim f x lim lim lim 2 x 2 3 m 0. x 1 x 1 x 1 x 1 x 1 x 1
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 95
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com x 1 khi x 1
Câu 3: Tìm giá trị thực của tham số k để hàm số y f x x 1
liên tục tại x 1. k 1 khi x 1 1 1 A. k . B. k 2. C. k . D. k 0. 2 2 Lời giải Chọn C
Hàm số f x có TXĐ: D 0;. Điều kiện bài toán tương đương với x 1 1 1 1
Ta có: k 1 y 1 lim y lim lim k . x 1 x 1 x 1 x 1 x 1 2 2 3 x khi x 3
Câu 4: Biết rằng hàm số f x x 1 2
liên tục tại x 3 (với m là tham số). m khi x 3
Khẳng định nào dưới đây đúng? A. m 3 ;0. B. m 3 . C. m 0;5.
D. m 5;. Lời giải Chọn B GV: T
Hàm số f x có tập xác định là 1
; . Theo giả thiết ta phải có R Ầ N ĐÌN x
3 x x 1 2 3
m f 3 lim f x lim lim
lim x 1 2 4. H CƯ x 3 x3 x3 x 3 x 1 2 x 3 – 3 khi x 1 0834 4 x x 3321
Câu 5: Hàm số f x khi x 1
, x 0 liên tục tại: 2 x x 33 1 khi x 0
A. mọi điểm trừ x 0, x 1.
B. mọi điểm x .
C. mọi điểm trừ x 1 . D. mọi điểm trừ x 0. Lời giải Chọn B
Hàm số y f x có TXĐ: D .
Dễ thấy hàm số y f x liên tục trên mỗi khoảng ; 1 , 1
;0 và 0; . (i) Xét tại x 1 , ta có
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 96
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com x x 1 2 4 x x x x 1
lim f x lim lim lim 2
x x 1 3 f 1 . 2 x 1 x 1 x 1 x x x x x 1 1
hàm số y f x liên tục tại x 1 .
(ii) Xét tại x 0 , ta có x x 1 2 4 x x x x 1
lim f x lim lim lim 2
x x 1 1 f 0 . 2 x0 x0 x0 x x x x x0 1
hàm số y f x liên tục tại x 0 . 0,5 khi x 1
x x 1
Câu 6: Số điểm gián đoạn của hàm số f x khi x 1 , x 1 là: 2 x 1 1 khi x 1 A. 0. B. 1. C. 2. D. 3. Lời giải Chọn B
Hàm số y f x có TXĐ D . GV: T x x 1
Hàm số f x
liên tục trên mỗi khoảng ; 1 , 1 ;1 và 1; . 2 x 1 R Ầ N ĐÌN x x 1 x 1 (i) Xét tại x 1
, ta có lim f x lim lim f 1 Hàm số liên 2 x 1 x 1 x 1 H CƯ x 1 x 1 2 tục tại x 1 . – 0834 x x 1 x lim f x lim lim 3321 2 (ii) Xét tại x 1 x 1 x 1 x 1 x 1 x 1 , ta có 33 x x 1 x lim f x lim lim 2 x 1 x 1 x 1 x 1 x 1
Hàm số y f x gián đoạn tại x 1. 2 2 m x khi x 2
Câu 7: Có bao nhiêu giá trị thực của tham số m để hàm số f x liên tục
1 m x khi x 2 trên ? A. 2. B. 1. C. 0. D. 3. Lời giải Chọn A
TXĐ: D . Hàm số liên tục trên mỗi khoảng ; 2 ; 2; .
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 97
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Khi đó f x liên tục trên f x liên tục tại x 2
lim f x f 2 lim f x lim f x f 2. * x 2 x 2 x 2 f 2 2 4m m 1
Ta có lim f x lim 1 m x 21 m * 2 4m 21 m 1 . x2 x2 m f x 2 2 2 2 lim
lim m x 4m x2 x2 x khi x 0; 4
Câu 8: Biết rằng hàm số f x
tục trên 0;6. Khẳng định nào sau đây 1 m khi x 4;6 đúng? A. m 2. B. 2 m 3. C. 3 m 5. D. m 5. Lời giải Chọn A
Dễ thấy f x liên tục trên mỗi khoảng 0;4 và 4;6 . Khi đó hàm số liên tục trên đoạn
0;6 khi và chỉ khi hàm số liên tục tại x 4, x 0, x 6 .
lim f x f 0 x0 GV: T
Tức là ta cần có lim f x f 6 . * x6 R Ầ
lim f x lim f x f 4 N x4 x4 ĐÌN H CƯ
lim f x lim x 0
lim f x lim 1 m 1 m x0 x0 • ; x6 x6 • ; –
f 0 0 0
f 6 1 m 0834 3321
lim f x lim x 2 x4 x4 33
• lim f x lim 1 m 1 m; Khi đó
* trở thành 1 m 2 m 1 2. x4 x4
f 4 1 m 2
x 3x 2 khi x 1
Câu 9: Có bao nhiêu giá trị của tham số
a để hàm số f x x 1 liên tục trên a khi x 1 . A. 1. B. 2. C. 0. D. 3. Lời giải Chọn C
Hàm số f x liên tục trên ;1 và 1;
. Khi đó hàm số đã cho liên tục trên khi
và chỉ khi nó liê tục tại x 1, tức là ta cần có
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 98
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
lim f x f
1 lim f x lim f x f 1 . * x 1 x 1 x 1
x 2 khi x 1
lim f x lim 2 x 1 Ta có f x x 1 x 1 a khi x 1
* không tỏa mãn với mọi
lim f x lim x 2 1 2
x khi x 1 x 1 x 1 a .
Vậy không tồn tại giá trị a thỏa yêu cầu. 2 x 1 khi x 1 Câu 10: Biết rằng
f x x 1
liên tục trên đoạn 0;
1 (với a là tham số). Khẳng định a khi x 1
nào dưới đây về giá trị a là đúng?
A. a là một số nguyên.
B. a là một số vô tỉ. C. a 5. D. a 0. Lời giải Chọn A
Hàm số xác định và liên tục trên 0;
1 . Khi đó f x liên tục trên 0; 1 khi và chỉ khi
lim f x f 1 . * x 1 f 1 a Ta có 2 * a 4. f x x 1 lim lim lim x 1 x 1 4 x 1 x 1 x 1 x 1 GV: T x 1 khi x 1 R
Câu 11: Xét tính liên tục của hàm số
f x
Khẳng định nào dưới đây đúng? Ầ 2 x 1 . N ĐÌN 2x khi x 1 H CƯ
A. f x không liên tục trên .
B. f x không liên tục trên 0;2.
C. f x gián đoạn tại x 1.
D. f x liên tục trên . – 0834 Lời giải 3321 Chọn D 33
f 1 2
Ta có lim f x lim 2 x 2
f x liên tục tại x 1. x 1 x 1 f x x 1 lim lim lim 2 x 1 2 x 1 x 1 x 1 2 x 1
Vậy hàm số f x liên tục trên . 2
x 5x 6 khi x 3
Câu 12: Tìm giá trị nhỏ nhất của
a để hàm số f x 4x 3 x liên tục tại . x 3 2 1 a x khi x 3 A. 2 . B. 2 . C. 4 . D. 4 . 3 3 3 3 Lời giải
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 99
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Chọn A
Điều kiện bài toán trở thành: lim f x lim f x f 3 . * x 3 x 3 f 2 3 13a 2 x 2 4x 3 5 6 x x x
Ta có lim f x lim lim 3 x3 x 3 x 3 4x 3 x 1 x
lim f x lim 2 1 a x 3 1 3a . x3 x 3 * 2 2 a a . min 3 3 3 3x 2 2 khi x 2
Câu 13: Tìm giá trị lớn nhất của
a để hàm số f x x 2 liên tục tại x 2. 1 2 a x khi x 2 4 A. a 3. B. a 0. C. a 1. D. a 2. max max max max Lời giải Chọn C
Ta cần có lim f x lim f x f 2. * x 2 x 2 f 2 7 2 2a GV: T 4 3 Ta có f x 3x 2 2 1 lim lim
* a 1 a 1. R max x2 x 2 x 2 4 Ầ N 1 7 ĐÌN lim f x 2 2 lim a x 2a x 2 x 2 4 4 H CƯ 1
cos x khi x 0 –
Câu 14: Xét tính liên tục của hàm số f x
. Khẳng định nào sau đây đúng? 0834 x 1 khi x 0 3321
A. f x liên tục tại x 0.
B. f x liên tục trên ;1 . 33
C. f x không liên tục trên .
D. f x gián đoạn tại x 1. Lời giải Chọn C
Hàm số xác định với mọi x .
Ta có f x liên tục trên ; 0 và 0; .
f 01
Mặt khác lim f x lim 1cos x 1cos 0 0
f x gián đoạn tại x 0. x 0 x 0
lim f x lim x 1 011 x0 x 0
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 100
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com x x
Câu 15: Tìm các khoảng liên tục của hàm số f x cos khi 1 2
. Mệnh đề nào sau đây là sai?
x1 khi x 1
A. Hàm số liên tục tại x 1 .
B. Hàm số liên tục trên các khoảng , 1 ; 1; .
C. Hàm số liên tục tại x 1 .
D. Hàm số liên tục trên khoảng 1 , 1 . Lời giải Chọn A
Ta có f x liên tục trên ; 1 , 1 ; 1 , 1; . f 1 cos 0 Ta có 2
f x gián đoạn tại x 1.
lim f x lim x 1 2 x 1 x 1 f 1 cos 0 2
Ta có lim f x lim x 1 0
f x liên tục tại x 1. x 1 x 1 x
lim f x lim cos 0 x 1 x 1 2 GV: T
Câu 16: Hàm số f x có đồ thị như hình bên không liên tục tại điểm có hoành độ là bao nhiêu? y R Ầ N ĐÌN 3 H CƯ x 1 – O 1 2 0834 3321 A. x 0. B. x 1. C. x 2. D. x 3. 33 Lời giải Chọn B
Dễ thấy tại điểm có hoành độ x 1 đồ thị của hàm số bị ' đứt ' nên hàm số không liên tục tại đó.
Cụ thể: lim f x 0
3 lim f x nên f x gián đoạn tại x 1. x 1 x 1 2 x
khi x 1, x 0 x Câu 17: Cho hàm số f x 0 khi x 0
. Hàm số f x liên tục tại: x khi x 1
A. mọi điểm thuộc .
B. mọi điểm trừ x 0 .
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 101
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
C. mọi điểm trừ x 1 .
D. mọi điểm trừ x 0 và x 1 . Lời giải Chọn A
Hàm số y f x có TXĐ: D .
Dễ thấy hàm số y f x liên tục trên mỗi khoảng ; 0,0; 1 và 1; .
f 00 2 Ta có x
lim f x lim lim x 0
f x liên tục tại x 0. x0 x 0 x 0 x 2 x
lim f x lim lim x 0 x0 x 0 x 0 x
f 11 2 Ta có x
lim f x lim lim x 1 f x liên tục tại x 1. x 1 x 1 x 1 x
lim f x lim x 1 x 1 x 1
Vậy hàm số y f x liên tục trên . 2 x 1
khi x 3, x 1 x 1 Câu 18: Cho hàm số
f x 4 khi x 1
. Hàm số f x liên tục tại: GV: T
x1 khi x 3 R Ầ N ĐÌN
A. mọi điểm thuộc .
B. mọi điểm trừ x 1 . H CƯ
C. mọi điểm trừ x 3 .
D. mọi điểm trừ x 1 và x 3 . – Lời giải 0834 3321 Chọn D 33
Hàm số y f x có TXĐ: D .
Dễ thấy hàm số y f x liên tục trên mỗi khoảng ; 1 ,1; 3 và 3; . f 1 4 Ta có 2 f x gián đoạn tại x 1. f x x 1 lim lim limx 1 2 x 1 x 1 x 1 x 1 f 3 2 Ta có 2 f x gián đoạn tại x 3. f x x 1 lim lim lim x 1 4 x3 x 3 x 3 x 1 2
x khi x 0
Câu 19: Số điểm gián đoạn của hàm số hx 2
x 1 khi 0 x 2 là:
3x 1 khi x 2 A. 1. B. 2. C. 3. D. 0.
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 102
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Lời giải Chọn A
Hàm số y hx có TXĐ: D .
Dễ thấy hàm số y hx liên tục trên mỗi khoảng ;
0,0;2 và 2; . h 0 1 Ta có
f x không liên tục tại x 0 .
lim h x lim 2x 0 x 0 x 0 h2 5
Ta có lim h x lim x
f x liên tục tại x 2 . 2 1 5 x2 x2
lim h x lim 3x 1 5 x2 x2 2
x x khi x 1 Câu 20: Tính tổng
S gồm tất cả các giá trị m để hàm số f x 2
khi x 1 liên tục tại x 1 2 m
x 1 khi x 1 . A. S 1. B. S 0. C. S 1. D. S 2. Lời giải GV: T Chọn B R Ầ
Hàm số xác định với mọi x . N ĐÌN
Điều kiện bài toán trở thành lim f x lim f x f 1 . * H CƯ x 1 x 1 – f 1 2 0834
Ta có lim f x 2 2
lim m x 1 m 1 * 2 m 1 2 3321 x 1 x 1 2 33
lim f x lim x x 2 x 1 x 1 m 1 S 0.
x cos x khi x 0 2 Câu 21: x Cho hàm số
f x
khi 0 x 1. Hàm số f x liên tục tại: 1 x 3 x khi x 1
A. mọi điểm thuộc x .
B. mọi điểm trừ x 0.
C. mọi điểm trừ x 1.
D. mọi điểm trừ x 0; x 1. Lời giải Chọn C
Hàm số y f x có TXĐ: D .
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 103
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Dễ thấy f x liên tục trên mỗi khoảng ; 0,0; 1 và 1; . f 0 0
Ta có lim f x lim x cos x 0
f x liên tục tại x 0 . x0 x0 2 x
lim f x lim 0 x0 x0 1 x f 1 1 2 x 1
Ta có lim f x lim
f x không liên tục tại x 1 . x 1 x 1 1 x 2
lim f x 3 lim x 1 x 1 x 1
Câu 22: Cho hàm số f x 3 4
x 4x 1. Mệnh đề nào sau đây là sai?
A. Hàm số đã cho liên tục trên .
B. Phương trình f x 0 không có nghiệm trên khoảng ;1 .
C. Phương trình f x 0 có nghiệm trên khoảng 2 ;0. 1 D. Phương trình
f x 0 có ít nhất hai nghiệm trên khoảng 3; . 2 Lời giải GV: T Chọn B R Ầ N ĐÌN
(i) Hàm f x là hàm đa thức nên liên tục trên A đúng. H CƯ f 1 1 0 (ii) Ta có
f x 0 có nghiệm x trên 2 ;1 , mà 1 – f 2 23 0 0834 3321 2 ; 1 2 ; 0 ; 1 B sai và C đúng 33
f 0 1 0 (iii) Ta có f x 0 1 1 có nghiệm
Kết hợp với (1) suy ra x thuộc 1 0; . 2 f 0 2 2 2 1
f x 0 có các nghiệm x , x thỏa: 3 x 1 0 x D đúng. 1 2 1 2 2
Câu 23: Cho phương trình 4 2
2x 5x x 1 0. Mệnh đề nào sau đây là đúng?
A. Phương trình không có nghiệm trong khoảng 1 ;1 .
B. Phương trình không có nghiệm trong khoảng 2 ;0.
C. Phương trình chỉ có một nghiệm trong khoảng 2 ;1 .
D. Phương trình có ít nhất hai nghiệm trong khoảng 0;2. Lời giải
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 104
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Chọn D
Hàm số f x 4 2
2x 5x x 1 là hàm đa thức có tập xác định là nên liên tục trên . Ta có f 0 1 (i) f
1 . f 0 0
f x 0 có ít nhất một nghiệm x thuộc 1 ; 0 . 1 f 1 3 f 0 1 (ii)
f 0. f 1 0
f x 0 có ít nhất một nghiệm x thuộc 0; 1 . 2 f 1 1 f 1 1 (iii) f
1 . f 2 0
f x 0 có ít nhất một nghiệm x thuộc 1; 2. 3 f 2 15
Vậy phương trình f x 0 đã cho có các nghiệm x , x , x thỏa 1 2 3
1 x 0 x 1 x 2 1 2 3 Câu 24: Cho hàm số 3
f (x ) x 3x 1 . Số nghiệm của phương trình f x 0 trên là: A. 0. B. 1. C. 2. D. 3. Lời giải GV: T Chọn D R Ầ N ĐÌN
Hàm số f x 3
x 3x 1 là hàm đa thức có tập xác định là nên liên tục trên . Do H CƯ
đó hàm số liên tục trên mỗi khoảng 2 ; 1 , 1 ;0, 0;2. – 0834 Ta có 3321 f 2 3 f 2 f 1 0
1 có ít nhất một nghiệm thuộc 2 ; 1 . f 1 1 33 f 1 1 f
1 f 0 0
1 có ít nhất một nghiệm thuộc 1 ;0 . f 0 1 f 21
f 2 f 0 0
1 có ít nhất một nghiệm thuộc 0;2 . f 0 1
Như vậy phương trình
1 có ít nhất ba thuộc khoảng 2;2 . Tuy nhiên phương trình
f x 0 là phương trình bậc ba có nhiều nhất ba nghiệm. Vậy phương trình f x 0 có đúng nghiệm trên .
Câu 25: Cho hàm số f x liên tục trên đoạn 1
;4 sao cho f
1 2 , f 4 7 . Có thể nói gì về
số nghiệm của phương trình f x 5 trên đoạn [1;4] : A. Vô nghiệm.
B. Có ít nhất một nghiệm.
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 105
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com C. Có đúng một nghiệm. D. Có đúng hai nghiệm. Lời giải Chọn B
Ta có f x 5 f x5 0 . Đặt gx f x5. Khi đó g 1 f 1 5 2 5 3 g 1 g 4 0.
g4 f 45 75 2
Vậy phương trình gx 0 có ít nhất một nghiệm thuộc khoảng 1;4 hay phương trình
f x 5 có ít nhất một nghiệm thuộc khoảng 1;4 .
Câu 26: Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc khoảng 1
0;10 để phương trình 3 2
x 3x 2m 2x m 3 0 có ba nghiệm phân biệt x , x , x thỏa mãn x 1 x x ? 1 2 3 1 2 3 A. 19. B. 18. C. 4. D. 3. Lời giải Chọn C
Xét hàm số f x 3 2
x 3x 2m2x m3 liên tục trên . GV: T
● Giả sử phương trình có ba nghiệm phân biệt x , x , x sao cho x 1 x x . Khi đó 1 2 3 1 2 3 R
f x x x x x x x . 1 2 3 Ầ N ĐÌN Ta có f 1 1 x 1 x 1
x 0 (do x 1 x x ). 1 2 3 1 2 3 H CƯ Mà f 1 m 5 nên suy ra m
5 0 m 5. – 0834
● Thử lại: Với m 5 , ta có 3321
▪ lim f x nên tồn tại a 1 sao cho f a 0 . 1 33 x
▪ Do m 5 nên f 1 m 5 0 . 2
▪ f 0 m 3 0 . 3
▪ lim f x nên tồn tại b 0 sao cho f b 0 . 4 x Từ
1 và 2 , suy ra phương trình có nghiệm thuộc khoảng ; 1 ; Từ 2 và 3 , suy
ra phương trình có nghiệm thuộc khoảng 1 ;0 ; Từ
3 và 4 , suy ra phương trình có
nghiệm thuộc khoảng 0; .
Vậy khi m 5 thỏa mãn m
m 9;8;7;6 m . 10;10
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 106
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
BÀI TẬP CUỐI CHƯƠNG III
PHẦN 1: CÂU HỎI TRẮC NGHIỆM Câu 1: n 3 lim bằng: 2 n A. 1. B. 0. C. 3. D. 2. Lời giải Chọn B n 3 1 3 1 3 lim lim lim lim 0 0 0 . 2 2 2 n n n n n 1 1 1
Câu 2: Tổng của cấp số nhân lùi vô hạn: M 1 bằng: 2 4 4 4n 3 5 4 6 A. . B. . C. . D. . 4 4 3 5 GV: T Lời giải Chọn C R Ầ N ĐÌN 1 4 M H CƯ 1 3 1 4 – 0834 2 x 9 3321 Câu 3: lim bằng: x3 x 3 33 A. 0. B. 6, C. 3. D. 1. Lời giải Chọn B 2 x 9
x 3 x 3 lim lim li
m x 3 3 3 6 . x3 x3 x3 x 3 x 3 2
x 2x m khi x 2
Câu 4: Hàm số f x
liên tục tại x 2 khi 3 khi x 2 A. m 3 . B. m 5 . C. m 3 . D. m 5 . Lời giải Chọn D
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 107
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
lim f x lim 2 x 2x m 2 2 2.2 m m 8 x2 x2
lim f x lim3 3 x2 x2
Để hàm số f x liên tục tại x 2 thì m 8 3 hay m 5 . 2x 1 Câu 5: lim bằng: x x A. 2. B. -1. C. 0. D. 1. Lời giải Chọn A. 2x 1 1 1 lim lim 2 2 lim 2 0 2 x x x x x x BÀI TẬP TỰ LUẬN
Câu 6: Tìm các giới hạn sau: 3n 1 a) lim ; n 2 n 2 b) lim ; n GV: T R 2 Ầ c) lim ; N ĐÌN 3n 1 H CƯ n 1 2n 2 d) lim . 2 – n 0834 3321 Lời giải 33 3n 1 1 1 a) lim lim 3 3 lim 3 0 3 . n n n 2 2 n 2 n 2 1 1 b) lim lim lim 1 1 lim 1 0 1. 2 2 2 n n n n 2 2 lim 2 0 c) lim lim n n 0 . 3n 1 1 1 3 0 3 3 lim n n n 1 2n 2 2 2n 4n 2 4 2 4 2 d) lim lim lim 2 2 lim lim 2 0 0 2 . 2 2 2 n n 2 n n n n
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 108
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Câu 7: Cho tam giác đều có cạnh bằng a , gọi là tam giác H . Nối các trung điểm của H để tạo 1 1
thành tam giác H . Tiếp theo, nối các trung điểm của H để tạo thành tam giác H 2 2 3
(Hình 1). Cứ tiếp tục như vậy, nhận được dãy tam giác H , H , H ,. Tính tổng chu vi 1 2 3
và tổng diện tích các tam giác của dãy. Lời giải 1 1
Cạnh của các tam giác H , H , H , lần lượt là: ; a a, ; a 1 2 3 2 2 2
Tổng chu vi của các tam giác là: GV: T 1 1 1 1 1
C 3 a 3 a 3
a 3a 1 3a 6a 2 2 2 2 2 2 1 R 1 Ầ 2 N ĐÌN H CƯ 3
Diện tích tam giác H là 2 a . 1 4 – 0834 1 1 3321
Diện tích tam giác H bằng diện tích tam giác H ; Diện tích tam giác H bằng 2 4 1 3 4 33
diện tích tam giác H ; 3
Tổng diện tích các tam giác là: 3 1 1 3 1 3 2 2 2 S a 1 a a 2 4 4 4 4 1 3 1 4
Câu 8: Tìm các giới hạn sau: 2 x 16 3 x 7 a) lim 2
3x x 2 ; b) lim ; c) lim . x 1 x4 x 4 x2 x 2 Lời giải a) lim 2
3x x 2 2 3 (1) 1 2 6 x 1
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 109
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 2 x 16
x 4 x 4 b) lim lim
lim x 4 4 4 8 x4 x4 x4 x 4 x 4 x
3 x 73 x 7 3 7 9 x 7 c) lim lim lim x2 x2 x 2
23 x 7
x2 x 23 x 7 1 1 1 lim . x2 3 x 7 3 2 7 6
Câu 9: Tìm các giới hạn sau: x 2 x 2 a) lim ; b) lim .
x x 1 2 x x Lời giải 2 1 x 2 1 0 a) lim lim x 1 .
x x 1 x 1 1 0 1 x x 2 1 2 1 2 b) lim lim lim lim 0 0 0 . 2 2 2 x x x x x x x x x
Câu 10: Tìm các giới hạn sau: GV: T 1 x a) lim ; b) lim . x 4 x 4 x 2 2 x R Ầ N ĐÌN Lời giải H CƯ 1 x a) lim . b) lim . – x4 x 4 x2 2 x 0834 3321
Câu 11: Xét tính liên tục của hàm số 33 x 4 khi x 0
f x 2cosx khi x 0 Lời giải
Khi x 0 : f x x 4 là hàm căn thức có tập xác định là 4;
nên f x liên tục trên khoảng 0; .
Khi x 0 : f x 2cosx là hàm lượng giác nên f x liên tục trên khoảng ; 0 .
lim f x lim2cosx 2cos0 2 x0 x0
lim f x lim x 4 0 4 2 x0 x0
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 110
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Suy ra: lim f x 2 f 0 hay f x liên tục tại x 0. x0
Vậy hàm số f x liên tục trên . 2 x 25 khi x 5
f x x 5 Câu 12: a khi x 5 Cho hàm số
Tìm a để hàm số y f x liên tục trên . Lời giải 2 x 25
Khi x 5 : f x
là hàm phân thức nên f x liên tục trên các khoảng x 5 ; 5 5;
Để f x liên tục trên thì f x liên tục tại x 5 . Hay lim f x f 5 . x5 2 x 25
x 5 x 5
lim f x lim lim
lim x 5 5 5 10 x5 x5 x5 x5 x 5 x 5
f 5 a GV: T Suy ra: a 10 . R Ầ N
Câu 13: Trong một phòng thí nghiệm, nhiệt độ trong tủ sấy được điều khiển tăng từ 10 C , mỗi ĐÌN
phút tăng 2 C trong 60 phút, sau đó giảm mỗi phút 3 C trong 40 phút. Hàm số biểu H CƯ
thị nhiệt độ (tính theo C ) trong tủ theo thời gian t (tính theo phút) có dạng – 0834 10 2t khi 0 t 60
T t k 3t khi 60 t 100 3321 33
( k là hằng số). Biết rằng, T t là hàm liên tục trên tập xác định. Tìm giá trị của k . Lời giải
T t liên tục trên tập xác định nên T t liên tục tại t 60 . Hay limT t T 60 . t 60
lim T t lim 10 2t 130 t 60 t60
lim T t lim k 3t k 180 t 60 t 60
T 60 10 2.60 130
Suy ra: k 180 130 . Do đó, t 310.
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 111
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com GV: T R Ầ N ĐÌN H CƯ – 0834 3321 33
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 112
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
BÀI TẬP TỔNG ÔN CHƯƠNG 3 PHẦN 1: TRẮC NGHIỆM n n 1 3 4.2 3
Câu 1: Kết quả của lim bằng: 3.2n 4n A. . B. . C. 0 . D. 1. Lời giải Chọn C n n n 3 1 1 n n 1 n n 2. 3. 3 4.2 3 3 2.2 3 4 2 4 lim lim lim 0 3.2n 4n 3.2n 4n n 1 3. 1 2
Câu 2: Giá trị đúng của 2 2 lim
n 1 3n 2 là: A. . B. . C. 0 . D. 1. Lời giải Chọn B lim 1 2 2 2
n 1 3n 2 lim n 1 3 . 2 2 n n GV: T R Ầ 1 2 N
Vì lim n ; lim 1 3 1 3 0 . 2 2 ĐÌN n n H CƯ
Câu 3: Giá trị đúng của lim 3n 5n là: – 0834 A. . B. . C. 2 . D. 2 . 3321 Lời giải 33 Chọn B n n n n 3 lim 3 5 lim 5 1 . 5 n n 3 Vì lim 5 ; lim 1 1 . 5
Câu 4: Tính giới hạn n 1 n n 1 lim 16 4 16 3n T 1 1 1 A. T 0 B. T C. T D. T 4 8 16 Lời giải Chọn C
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 113
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 4n 3n Ta có T n 1 n n 1 lim 16 4 16 3 lim n 1 n n 1 16 4 16 3n n 3 1 4n 3n 4 1 1 lim lim .
16.16n 4n 16.16n 3n n n 1 3 4 4 8 16 16 4 4 3u 1
Câu 5: Cho dãy số u có lim u 2 . Tính giới hạn lim n . n n 2u 5 n 1 3 5 A. B. C. D. 5 2 9 Lời giải Chọn C 3u 1 3.2 1 5
Từ lim u 2 ta có lim n . n 2u 5 2.2 5 9 n 3 2 2n n 4 1 Câu 6: Biết lim
với a là tham số. Khi đó 2 a a bằng 3 an 2 2 A. 12 . B. 2 . C. 0 . D. 6 . Lời giải GV: T Chọn A 1 4 3 R 3 2 n 2 3 Ầ 2n n 4 n n 2 1 N Ta có lim lim . ĐÌN 3 an 2 2 3 a 2
n a 3 H CƯ n
Suy ra a 4 . Khi đó 2 2
a a 4 4 12 . – 0834 1 1 1 Câu 7: Tìm L lim ... 3321 1 1 2
1 2 ... n 5 3 33 A. L . B. L . C. L 2 . D. L . 2 2 Lời giải Chọn C
Ta có 1 2 3 ... k là tổng của cấp số cộng có u 1, d 1 nên 1 1 k k
1 2 3 ... k 2 1 2 2 2 , * k . 1 2 ... k k k 1 k k 1 2 2 2 2 2 2 2 2 2 2 L lim ... lim 2 . 1 2 2 3 3 4 n n 1 1 n 1
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 114
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Câu 8: Tính I n 2 2 lim n 2 n 1 . 3 A. I B. I C. I 1, 499 D. I 0 2 Lời giải Chọn B 3n 3 3 Ta có: I n 2 2 lim n 2 n 1 lim lim 2 2
n 2 n 1 2 1 2 1 1 2 2 n n
Câu 9: Trong các giới hạn hữu hạn sau, giới hạn nào có giá trị khác với các giới hạn còn lại? 3n 1 2n 1 4n 1 n 1 A. lim B. lim C. lim D. lim 3n 1 2n 1 3n 1 n 1 Lời giải Chọn C Ta có 1 1 3 2 3n 1 3 1 2n 1 2 1 lim lim
n 1 vì lim 0 ; lim lim
n 1 vì lim 0 3n 1 1 3 n 2n 1 1 2 n 3 2 n n GV: T R 1 1 Ầ 4 1 N 4n 1 4 n 1 n 1 n 1 ĐÌN lim lim vì lim 0 ; lim lim 1 vì lim 0 . 3n 1 1 3 n n 1 1 n 3 1 H CƯ n n – 2 3 3 0834
Câu 10: Tính lim n 4n 3 8n n. 3321 2 A. . B. 1. C. . D. . 33 3 Lời giải Chọn D Ta có: n 2 3 3 lim
4n 3 8n n n 2 n n 3 3 lim 4 3 2 2n 8n n n 2 n n n 3 3 lim 4 3 2 2n 8n n . 3n 3 3 Ta có: n 2 lim
4n 3 2n lim lim . 2
4n 3 2n 3 4 4 2 2 n
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 115
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 2 n Ta có: n 3 3 lim
2n 8n n lim 2 3
4n 2n 8n n 3 3 8n n2 3 1 1 lim . 2 12 1 1 3 3 4 2 8 8 2 2 n n 3 1 2 Vậy lim n 2 3 3
4n 3 8n n . 4 12 3 x 2
Câu 11: Giới hạn lim bằng 2 x2 x 4 1 A. 2 . B. 4 . C. . D. 0 . 4 Lời giải Chọn C x 2 x 2 1 1 lim lim lim . 2 x2 x2 x 4
x 2 x 2 x2 x 2 4 x 3
Câu 12: Tính giới hạn L lim x3 x 3 GV: T A. L B. L 0 C. L D. L 1 Lời giải R Ầ N ĐÌN Chọn B H CƯ x 3 3 3 Ta có L lim 0 . x3 – x 3 3 3 0834 4x 1 3321 Câu 13: lim bằng
x x 1 33 A. 2 B. 4 C. 1 D. 4 Lời giải Chọn D 1 4 4x 1 lim lim x 4 .
x x 1 x 1 1 x 3x 2 Câu 14: lim bằng
x 2x 4 1 3 3 A. . B. . C. 1. D. . 2 4 2 Lời giải Chọn D
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 116
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 2 3 3x 2 3 Ta có: lim lim x .
x 2x 4 x 4 2 2 x
Câu 15: Trong các mệnh đề sau, mệnh đề nào sai? 1 1 1 1 A. lim . B. lim . C. lim . D. lim . 5 x 0 x x 0 x x0 x x 0 x Lời giải Chọn B 1 Ta có: lim
do lim x 0 và x 0 . Vậy đáp án A đúng. x 0 x x 0 Suy ra đáp án B sai.
Các đáp án C và D đúng. Giải thích tương tự đáp án A . 2x 1
Câu 16: Tính giới hạn lim . x x 1 1 A. . B. 1. C. 2 . D. 1 . 2 Lời giải Chọn C 1 GV: T 2 2x 1 lim lim x 2. R x x 1 Ầ x 1 1 N ĐÌN x H CƯ x
Câu 17: Xác định lim . 2 x0 – x 0834 A. 0 . B. . C. Không tồn tại. D. . 3321 Lời giải 33 Chọn C x x 1 Ta có lim lim lim . 2 2 x 0 x 0 x 0 x x x x x 1 lim lim lim . 2 2 x 0 x 0 x 0 x x x x Vậy không tồn tại lim . 2 x0 x 2
a 2x 3 2017 1
Câu 18: Cho số thực a thỏa mãn lim
. Khi đó giá trị của a là x 2x 2018 2 2 2 1 1 A. a . B. a . C. a . D. a . 2 2 2 2
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 117
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Lời giải Chọn A 3 2017 2 a 2
a 2x 3 2017 1 2 x x 1 a 2 1 2 Ta có: lim lim a . x 2x 2018 2 x 2018 2 2 2 2 2 x
Câu 19: Cho các giới hạn: lim f x 2 ; lim g x 3 , hỏi lim 3 f x 4g x bằng x 0 x x 0 x x 0 x A. 5 . B. 2 . C. 6 . D. 3 . Lời giải Chọn C
Ta có lim 3 f x 4g x
lim 3 f x lim 4g x 3 lim f x 4 lim g x 6 . x xx xx xx xx 0 x 0 0 0 0
Câu 20: Trong các mệnh đề sau, mệnh đề nào đúng? 4 x x 4 x x 4 x x 4 x x A. lim . B. lim 1. C. lim . D. lim 0 . x 1 2x x 1 2x x 1 2x x 1 2x Lời giải Chọn A GV: T 1 1 2 2 R 4 . x x x Ầ x x x x N Vì lim lim lim . Vậy A đúng. ĐÌN x 1 2 x x 1 x 1 x 2x 2x H CƯ x x – x 1 0834
Câu 21: Giới hạn lim bằng
x x 22 2 3321 3 A. . B. . C. 0 . D. . 33 16 Lời giải Chọn A x 1 1 Ta có: lim lim . x 1 . 2 2 x 2 x 2
x2 x 2 1 Do lim
và lim x 1 1 0 .
x x 22 2 x 2 2 3x 1 1 2 x x 2
Câu 22: Cho I lim và J lim
. Tính I J . x0 x x 1 x 1 A. 6. B. 3. C. 6 . D. 0. Lời giải Chọn A
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 118
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Ta có 2 3x 1 1 6x 6 I lim lim lim 3 . x0 x0 x
x 3x 1 x0 1 3x 1 1 2 x x 2 x 1 x 2 J lim lim
lim x 2 3 . x 1 x1 x 1 x 1 x 1
Khi đó I J 6 . 4x 3
Câu 23: Tìm giới hạn lim x 1 x 1 A. . B. 2 . C. . D. 2 . Lời giải Chọn A 4x 3 Ta có lim
vì lim 4x 3 1 , lim x
1 0 , x 1 0 khi x 1 . x 1 x 1 x 1 x 1 cos x
Câu 24: Tìm giới hạn L lim . x 2 x 2 A. L 1 B. L 1 C. L 0 D. L 2 GV: T Lời giải R Ầ Chọn B N ĐÌN H CƯ
Đặt: t x . 2 – 0834 cos t 2 sin t 3321 Khi x
thì t 0 . Vậy L lim lim 1. 2 t0 t0 t t 33
Câu 25: Tìm giới hạn I . 2 lim x 1 x x 2 x A. I 1 2 . B. I 46 31 . C. I 17 11. D. I 3 2 . Lời giải Chọn D 2 2
x x x 2 Ta có: I I lim 1 2 lim x 1 x x 2 x x 2
x x x 2 2 1 x 2 3 I lim x
1 I lim 1 I . x 2
x x x 2 x 1 2 2 1 1 2 x x
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 119
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 3
x 1 x 5
Câu 26: Giới hạn lim bằng x3 x 3 1 1 1 A. 0 . B. . C. . D. . 2 3 6 Lời giải Chọn D 3 3
x 1 x 5
x 12 x 5 2 Ta có: lim lim x3 x 3 x3 x 3 x 1 4 x 5 8 lim lim x
x 3 x 1 2 2 3
x3 x 3 3 x 5 3 2. x 5 4 1 1 1 1 1 lim lim . x 1 2 x x x 52 3 3 3 3 2. x 5 4 4 12 6 4 2020 x a Câu 27: Tính lim . 505 505 xa x a A. 2010 2a . B. 1515 4a . C. . D. 505 4a . Lời giải Chọn B 505 505 2 1010 GV: T 4 2020 x a
x a x a x a lim lim 505 505 505 xa x a 505 xa x a R Ầ N ĐÌN 505 2 1010 2 lim x a x a 505 505 a a 505 a 1010 a 1515 4a . 505 xa H CƯ 2 2x 3x 2 – Câu 28: lim bằng 0834 2 x2 x 4 3321 5 5 1 A. . B. . C. . D. 2 . 4 4 4 33 Lời giải Chọn A 2 2x 3x 2 2x 1 x 2 2x 1 5 Ta có lim lim lim . 2 x2 x 4 x 2
x 2 x 2 x 2 x 2 4 2 x 3x 4 Câu 29: lim bằng. 2 x4 x 4x 5 5 A. 1. B. 1 . C. . D. . 4 4 Lời giải Chọn C
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 120
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 2 x 3x 4 x 1 5 Ta có: lim lim . 2 x4 x 4x x 4 x 4 2x 3 Câu 30: Tính lim . x 2 2x 3 1 1 A. . B. . C. 2 . D. 2 . 2 2 Lời giải Chọn D 3 3 x 2 3 x 2 2 2x 3 x x 2 Ta có: lim lim lim lim x 2 x 2 2x 3 x 3 x 3 x 3 2 . x 2 x 2 2 2 x 2 x 2 x
Câu 31: Trong các mệnh đề sau mệnh đề nào sai 3 A. lim
x x x . B. . 2 lim x x 1 x 2 x x 2 1 2 2 3x 2 3x 2 C. lim . D. lim . x 1 x 1 x 1 x 1 Lời giải Chọn C GV: T 2 2
x x 1 x 4x 4
+ Với đáp án A ta có: lim
x x x x 2 1 2 lim R x 2 Ầ
x x 1 x 2 N ĐÌN H CƯ 3 x 3 3x 3 x 3 lim lim A đúng. – x 2 x 0834
x x 1 x 2 1 1 2 2 x 1 1 2 x x x 3321 33 2 2
x x 1 x 4x 4 2
+ Với đáp án B ta có: lim
x x x x 1 2 lim x 2
x x 1 x 2 3 x 3 3x 3 x 3 lim lim lim B đúng. x 2
x x 1 x 2 x 1 1 2 x 0 x 1 1 2 x x x
+ Với đáp án C ta có lim x
1 0 , x 1 0 với mọi x 1và lim 3x 2 1 0 . x 1 x 1 3x 2 Vậy lim C sai. x 1 x 1
+ Với đáp án D ta có lim x
1 0 , x 1 0 với mọi x 1 và lim 3x 2 1 0 . x 1 x 1
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 121
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 3x 2 Vậy lim D đúng. x 1 x 1 4x 1 1
Câu 32: Tính giới hạn K lim . 2 x0 x 3x 2 2 4 A. K . B. K . C. K . D. K 0 . 3 3 3 Lời giải Chọn A 4x 1 1 4x 4 2 Ta có K lim lim lim . 2 x0 x 3x
x0 x x 3 4x 1 1
x0 x 3 4x 1 1 3 2
ax bx khi x 1
Câu 33: Cho hàm số f (x)
. Để hàm số đã cho có đạo hàm tại x 1 thì 2a b
2x 1 khi x 1 bằng: A. 2 . B. 5 . C. 2 . D. 5 . Lời giải Chọn A
f x f 1 2x 11 GV: T lim lim 2 ; x 1 x 1 x 1 x 1 R Ầ 2 2 N
f x f 1
ax bx a b a x
1 b x 1 x
1 a x 1 b ĐÌN lim lim lim lim x 1 x 1 x 1 x 1 x 1 x 1 x 1 x 1 H CƯ
lim a x 1 b
2a b x 1 – 0834
f x f 1
f x f 1 3321
Theo yêu cầu bài toán: lim lim
2a b 2 . x 1 x 1 x 1 x 1 33 x 1 Câu 34: lim bằng
x 6x 2 1 1 1 A. . B. . C. . D. 1. 2 6 3 Lời giải Chọn B 1 1 x 1 1 Ta có lim lim x .
x 6x 2 x 2 6 6 x Câu 35: Tính 2 lim x 4x 2 x x A. 4 . B. 2 . C. 4 . D. 2 . Lời giải
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 122
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Chọn B 2 2 2 4
x 4x 2 x 4 x 2 lim lim lim x 2 lim x 4x 2 x x
x 2x 4x2x x 2x 4x2x x 4 2 1 1 2 x x 2 . 2 x 4x 4 Câu 36: Tìm lim . x2 x 2 A. Không tồn tại. B. 1 . C. 1 . D. 1. Lời giải Chọn A 2 x 4x 4 x 22 x 2 lim lim lim . x2 x 2 x2 x 2 x2 x 2 Xét: x 2 x 2 lim lim 1. x 2 x 2 x 2 x 2 x 2 x 2 lim lim 1 . x 2 x 2 x 2 x 2 GV: T x 2 x 2 x 2 R Ta có: lim lim nên không tồn tại lim . Ầ x 2 x 2 x2 N x 2 x 2 x 2 ĐÌN H CƯ x 1 Câu 37: Tính lim . 2018 x x 1 – 0834 A. 1 . B. 1. C. 2 . D. 0 . 3321 Lời giải 33 Chọn D 1 1 2 x 1 1 lim lim . x x 0 . 2018 2017 x x 1 x x 1 1 2017 x
Câu 38: Tìm khẳng định đúng trong các khẳng định sau:
I. f x liên tục trên đoạn ;
a b và f a. f b 0 thì phương trình f x 0 có nghiệm.
II. f x không liên tục trên ;
a b và f a. f b 0 thì phương trình f x 0 vô nghiệm. A. Chỉ I đúng. B. Chỉ II đúng.
C. Cả I và II đúng. D. Cả I và II sai. Lời giải Chọn A
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 123
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Câu 39: Tìm khẳng định đúng trong các khẳng định sau: x 1
I . f x
liên tục với mọi x 1. x 1
II . f x sin x liên tục trên . x
III . f x
liên tục tại x 1. x
A. Chỉ I đúng.
B. Chỉ I và II . C. Chỉ I và III . D. Chỉ II và III . Lời giải Chọn D
Ta có II đúng vì hàm số lượng giác liên tục trên từng khoảng của tập xác định.
x , khi x 0 x Ta có x
III đúng vì f x . x x , khi x 0 x
Khi đó lim f x lim f x f 1 1. x 1 x 1 x
Vậy hàm số y f x
liên tục tại x 1. x x 2 khi x 4 Câu 40: x 4
. Khẳng định nào sau đây đúng nhất ? GV: T
Cho hàm số f (x) 1 khi x 4 R 4 Ầ N ĐÌN
A. Hàm số liên tục tại x 4 . H CƯ
B. Hàm số liên tục tại mọi điểm trên tập xác định nhưng gián đoạn tại x 4 .
C. Hàm số không liên tục tại . x 4 – 0834 D. Tất cả đều sai. 3321 Lời giải 33 Chọn A x 2 1 1
Ta có : lim f (x) lim lim f (4) x4 x4 x4 x 4 x 2 4
Hàm số liên tục tại điểm x 4 . 2
x 3x 2 2 khi x 1
Câu 41: Cho hàm số f (x) x 1
. Khẳng định nào sau đây đúng nhất ? 2
3x x 1 khi x 1
A. Hàm số liên tục tại x 1 .
B. Hàm số liên tục tại mọi điểm.
C. Hàm số không liên tục tại x 1 . D. Tất cả đều sai. Lời giải
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 124
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Chọn C
(x 1)(x 2)
lim f (x) lim 2 2 x 1 x 1 x 1
lim f (x) lim 2 3x x 1 3 lim f (x) x 1 x 1 x 1
Hàm số không liên tục tại x 1 .
2 x m khi x 0
Câu 42: Tìm tất cả các giá trị của tham số thực m sao cho hàm số f x liên mx 2 khi x 0 tục trên . A. m 2 . B. m 2 . C. m 2 . D. m 0 . Lời giải Chọn C
Trên khoảng 0; hàm số f x 2 x m là hàm số liên tục. Trên khoảng ;
0 hàm số f x mx 2 là hàm số liên tục.
Ta có lim f x lim
x m m f
và lim f x lim mx 2 2 . 2 0 x0 x0 x 0 x 0
Hàm số f x liên tục trên khi và chỉ khi
lim f x lim f x f 0 m 2 m 2 . x 0 x 0 2
2x 7x 6 GV: T khi x 2 Câu 43:
Cho hàm số y f x x 2
. Biết a là giá trị để hàm số f x liên R 1 x Ầ N a khi x 2 ĐÌN 2 x H CƯ 7
tục tại x 2 , tìm số nghiệm nguyên của bất phương trình 2 x ax 0 . 0 4 – 0834 A. 1. B. 4 . C. 3 . D. 2 . 3321 Lời giải 33 Chọn D
Tại x 2 , ta có: 0 1
f 2 a 4 1 x 1
lim f x lim a a . x 2 x 2 2 x 4 2 2x 7x 6
x 22x 3
lim f x lim lim x 2 x 2 x 2 x 2 x 2
x 22x 3 lim
lim 2x 3 1 . x 2 x 2 x 2
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 125
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Để hàm số liên tục tại x 2 thì f 2 lim f x lim f x 0 x 2 x 2 1 3 a 1 a . 4 4 3 3 7 7
Với a , xét bất phương trình 2 x x 0 x 1 4 4 4 4
Mà x nên x 1 ; 0 .
Vậy bất phương trình đã cho có 2 nghiệm nguyên.
Câu 44: Cho hàm số y f x liên tục trên khoảng ;
a b . Điều kiện cần và đủ để hàm số liên tục trên đoạn ; a b là?
A. lim f x f a và lim f x f b .
B. lim f x f a và lim f x f b . x a x b x a x b
C. lim f x f a và lim f x f b .
D. lim f x f a và lim f x f b . x a x b x a x b Lời giải Chọn A
Hàm số f xác định trên đoạn ;
a b được gọi là liên tục trên đoạn ;
a b nếu nó liên tục trên khoảng ;
a b, đồng thời lim f x f a và lim f x f b . x a x b GV: T
1 x 1 x khi x 0 x R
Câu 45: Tìm tất cả các giá trị của m để hàm số f x liên tục tại Ầ N 1 x ĐÌN m khi x 0 1 x H CƯ x 0 . – A. m 1. B. m 2 . C. m 1. D. m 0 . 0834 Lời giải 3321 Chọn B 33 Ta có 1 x
lim f x lim m m 1 . x 0 x 0 1 x
1 x 1 x 2 x 2
lim f x lim lim lim 1 . x 0 x 0 x x0
x 1 x 1 x x0 1 x 1 x
f 0 m 1
Để hàm liên tục tại x 0 thì lim f x lim f x f 0 m 1 1 m 2 . x 0 x 0
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 126
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 2 x
khi x 1, x 0 x
Câu 46: Cho hàm số f x 0 khi x 0 . Khẳng định nào đúng x khi x 1
A. Hàm số liên tục tại mọi điểm trừ các điểm thuộc đoạn 0 ;1 .
B. Hàm số liên tục tại mọi điểm trừ điểm x 0 .
C. Hàm số liên tục tại mọi điểm thuộc .
D. Hàm số liên tục tại mọi điểm trừ điểm x 1 . Lời giải Chọn C
Tập xác định D .
Nếu x 0 , x 1 thì hàm số y f x liên tục trên mỗi khoảng ; 0,0 ;1 và 1; . 2 2 x x
Nếu x 0 thì f 0 0 và lim f x lim
lim x 0; lim f x lim lim x 0 . x 0 x 0 x 0 x 0 x 0 x 0 x x
Suy ra: lim f x 0 f 0 . x0 GV: T
Do đó, hàm số y f x liên tục tại x 0 . R Ầ N ĐÌN 2 x lim f x lim lim x 1 H CƯ
Nếu x 1 thì f 1 1 và x 1 x 1 x 1 x
lim f x 1 f 1 . x 1 –
lim f x lim x 1 0834 x 1 x 1 3321
Do đó, hàm số y f x liên tục tại x 1 . 33
Vậy hàm số y f x liên tục trên . 1 cos x khi x 0
Câu 47: Cho hàm số f x 2 x . 1 khi x 0
Khẳng định nào đúng trong các khẳng định sau?
A. f x có đạo hàm tại x 0 . B. f 2 0.
C. f x liên tục tại x 0 .
D. f x gián đoạn tại x 0 . Lời giải Chọn D
Hàm số xác định trên
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 127
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com x 2 2sin 1 cos x 1
Ta có f 0 1 và f x 2 lim lim lim 2 2 x0 x0 x0 x x 2 4. 2
Vì f 0 lim f x nên f x gián đoạn tại x 0 . Do đó f x không có đạo hàm tại x0 x 0 . 1 cos x x
0 f x
0 nên f 2 0.VậyA, B,C sai. 2 x 2
x x 2 khi x 1
Câu 48: Cho hàm số f x x 1
. Tìm tất cả các giá trị thực của tham số m để 3 m khi x 1
hàm số gián đoạn tại x 1. A. m 2. B. m 1. C. m 2. D. m 3. Lời giải Chọn B
Tập xác định của hàm số là . 2 x x 2
Hàm số gián đoạn tại x 1 khi lim f x f 1 lim 3m x 1 x 1 x 1 GV: T x 1 x 2 lim
3m lim x 2 3m 3 3m m 1. x 1 x 1 R x 1 Ầ N 2 ĐÌN
x x 12 khi x 4
Câu 49: Tìm tham số thực m để hàm số y f x x 4 liên tục tại điểm H CƯ
mx 1 khi x 4 – 0834 x 4 . 0 3321 A. m 4 . B. m 3 . C. m 2 . D. m 5 . Lời giải 33 Chọn C
Tập xác định: D . Ta có: 2 x x 12
x 3 x 4
+ lim f x lim lim
lim x 3 7 . x 4 x 4 x 4 x 4 x 4 x 4 + f 4 4 m 1.
Hàm số f x liên tục tại điểm x 4
khi và chỉ khi lim f x f 4
4m 1 7 0 x 4 m 2 .
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 128
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 2
x ax b x 1
Câu 50: Cho a,b là hai số thực sao cho hàm số f x x 1
liên tục trên . Tính
2ax 1, x 1 a b . A. 0 B. 1 C. 5 D. 7 Lời giải Chọn D Ta có f 1 2a 1. 2
x ax b
Để hàm số liên tục trên thì phải tồn tại lim
và lim f x f 1 . x 1 x 1 x 1 2
x ax b Để tồn tại lim thì 2
x ax b x 1 1 a b 0 b a 1 . x 1 x 1 2
x ax b x
1 x a 1 Suy ra lim lim
lim x a 1 a 2 . x 1 x 1 x 1 x 1 x 1
Do đó để hàm số liên tục trên thì t . 2 2 x 1 neáu x 1
Câu 51: Giá trị của m sao cho hàm số f x x 1
liên tục tại điểm x 1 là GV: T 3
x m neáu x 1 R Ầ N A. 5 . B. 1. C. 1 . D. 5 . ĐÌN Lời giải H CƯ Chọn B – 0834 2 x 1 Ta có và . 3321 f 1 3 m
lim f x lim lim x 1 2 x 1 x 1 x 1 x 1 33
Hàm số f x liên tục tại điểm x 1 lim f x f
1 3 m 2 m 1 . x 1 2
x 3x 4 khi x 1
Câu 52: Cho hàm số f x x 1
. Xác định a để hàm số liên tục tại điểm 2 ax 1 khi x 1 x 1. A. a 3. B. a 2. C. a 2. D. a 1. Lời giải: Chọn C
Tập xác định D . Ta có f 1 1 2a
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 129
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 2 x 3x 4
và lim f x lim 2 ax
1 1 2a; lim f x lim
lim x 4 5. x 1 x 1 x 1 x 1 x 1 x 1
Hàm số đã cho liên tục tại x 1 f
1 lim f x lim f x 1 2a 5 a 2 . x 1 x 1
Câu 53: Tìm tất cả các giá trị của tham số m để hàm số sau liên tục trên x 1 khi x 1
f x ln x x 1 2 . m e 1 2mx khi x 1 1 A. m 1. B. m 1. C. m . D. m 0 . 2 Lời giải Chọn D
Tập xác định D , f 1 1 m .
Ta thấy hàm số f x liên tục trên các khoảng ; 1 và 1; . x 1 lim f x lim
1, lim f x lim . x 1 2 . m e 1 2mx 1 m x 1 x 1 ln x x 1 x 1
Hàm số f x liên tục trên khi và chỉ khi hàm số f x liên tục tại x 1
lim f x lim f x f 1 . GV: T x 1 x 1 R
1 m 1 m 0 . Ầ N ĐÌN 2
x 4x 3 khi x 1 H CƯ
Câu 54: Tìm m để hàm số f (x) x 1
liên tục tại điểm x 1 . mx 2 khi x 1 – 0834 A. m 2 . B. m 0 . C. m 4 . D. m 4 . 3321 Lời giải 33 Chọn A 2 x 4x 3 x 1 x 3
Ta có: lim f x lim lim
lim x 3 2 . x 1 x 1 x 1 x 1 x 1 x 1
lim f x lim mx 2 m 2 . x 1 x 1 f 1 m 2 .
Để hàm số đã cho liên tục tại điểm x 1 thì lim f x lim f x f 1 x 1 x 1
2 m 2 m 0 .
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 130
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
3x a 1, khi x 0
Câu 55: Cho hàm số f x 1 2x 1
. Tìm tất cả giá trị của a để hàm số đã cho , khi x 0 x
liên tục tại điểm x 0 . A. a 1 . B. a 3 . C. a 2 . D. a 4 . Lời giải Chọn C Ta có:
f 0 lim f x lim 3x a 1 a 1 . x 0 x 0 1 2x 1 2x 2
lim f x lim lim lim 1. x 0 x 0 x x 0
x 1 2x 1 x 0 1 2x 1
Hàm số liên tục tại x 0 f 0 lim f x lim f x a 1 1 a 2 . x 0 x 0 2 2 m x khi x 2
Câu 56: Có bao nhiêu giá trị thực của tham số m để hàm số f x liên tục 1 m
x khi x 2 trên ? GV: T A. 0 . B. 2 . C. 3 . D. 4 . Lời giải R Ầ N ĐÌN Chọn B H CƯ
Ta có hàm số luôn liên tục x 2 . – 0834
Tại x 2 , ta có lim f x lim 1 m x 1 m2 ; x 2 x 2 3321
lim f x lim ; f 2 2 4m . 2 2 m x 2 4m 33 x2 x2
Hàm số liên tục tại x 2 khi và chỉ khi
lim f x lim f x f 2 2
4m 1 m 2
2 4m 2m 2 0 1 x 2 x 2
Phương trình luôn có hai nghiệm thực phân biệt. Vậy có hai giá trị của m . PHẦN 2: TỰ LUẬN
Câu 57: Tính các giới hạn sau 2
3n 4n 1 a) lim . 2 2n 3n 7 3 n 4 b) lim . 3 5n n 8
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 131
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com n 1 2n 1 c) lim .
3n 2n 3 Lời giải 4 1 2 3 2 3
n 4n 1 3 a) lim lim n n . 2 2n 3n 7 3 7 2 2 2 n n 1 3 1 3 n 4 1 b) lim lim n . 3 5n n 8 1 8 5 5 2 3 n n 1 1 1 2 n 1 2n 1 n n 1.2 2 c) lim lim .
3n 2n 3 2 3 3.1 3 3 1 n n
Câu 58: Tính các giới hạn sau 2 2
n n 3 n 1 3 3
8n n 2n 1 2 2
n n 1 2n 3 a) lim . b) lim . c) lim . n 1 3n 1 2 3n n 1 Lời giải 2 2
n n 3 n 1 1 1 1 3 1 GV: T 2 2 2
n n 3 n 1 n n n 1 3 1 a) lim lim lim 4. n 1 1 1 1 R 1 1 Ầ N n n ĐÌN 1 1 H CƯ 3 3 3 8 2 2 2
8n n 2n 1 n n 8 2 4 b) lim lim . – 3n 1 1 3 3 0834 3 n 3321 2 2
n n 1 2n 3 1 3 2 2 1 2 2 2 2 33
n n 1 2n 3 n n n 1 2 c) lim lim lim 1. 2 2 3n n 1 3n n 1 1 1 3 3 2 2 n n n
Câu 59: Tính các giới hạn sau n 2n 1 3n 2 2n
1 n 2 n a) lim . b) lim . 3 6n 3 1 n n Lời giải 1 2 2 3 n 2n 1 3n 2 n n 2.3 1 a) lim lim . 6n 3 3 3 1 1 6 36 6 n
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 132
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 1 1 2 1 2 1 2n 1 n 2 2 n n n n n b) lim lim 0. 3 n n 1 1 2 n
Câu 60: Tính các giới hạn sau 2 2
4n n 3n 2
9n n 3n 1 a) lim . b) lim . 2 n 1 2 n 2 Lời giải 4 1 2 2 3 2 3
4n n 3n a) n n lim lim 3. 2 n 1 1 1 2 n 9 1 3 1 2 2 3 2
9n n 3n 1 b) n n n n lim lim 0. 2 n 2 2 1 2 n
Câu 61: Tính các giới hạn sau n 1 2 2n n 2 n 1 2
3n 2n 3 2 n a) lim . b) lim . n 1 2 n 2 3 3n 3 2n 1 Lời giải GV: T 1 1 1 1 R 2 2 1 2 3 Ầ n
1 2n n n 1 n n n n 1.2 N a) lim lim 1. ĐÌN n 1 2 n 2 3 3n 1 2 1.1 3 1 1 3 2 H CƯ n n – 2 3 1 0834 2 3n 2n 3 2 3 1 2 n n n n b) lim lim 3. 3 3321 2n 1 1 1 3 n 33
Câu 62: Tính các giới hạn sau 1 4n 2n 5.3n 3n 4n a) lim . b) lim . c) lim . 1 4n 3n 1 3n 4n Lời giải 1 n 1 1 4 n 1 a) 4 lim lim 1 1 4n 1 1 1 4n n 2 5 2n 5.3n b) 3 lim lim 5 3n 1 1 1 3n
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 133
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com n 3 1 3n 4n c) 4 lim lim 1 3n 4n n 3 1 4
Câu 63: Tính các giới hạn sau a) 3 3 2 lim
n 3n n. b) 3 3 2 lim
n 3 n 2 . Lời giải 3 2 3
n 3n n 3 a) lim 3 3 2
n 3n n lim lim 3 2 n 3n 2 2 2 3 3 2 3 n . n n 3n 3 3 3 3 1 1 1 n n 2 1 3 3 3 Khi n thì: 3 3 3 lim 0 lim 1 1 lim 1 1 1 1 n n n n Do đó, 3 3 2 lim
n 3n n 3 b) 3 3 2
n n
3 3n n 2 lim 3 2 lim 3
lim n n 2 GV: T R Ầ N ĐÌN H CƯ – 0834 3321 33 3 3 2 2 n 3 n n n 2 3 2 lim lim lim lim 2 2 2 2 3 n 2 3 3 n n 2
n n n 3 n 2 3 3 3 3 n n 2 3 . 3 3 n . n n 3 2 Khi n thì: 3 n 2 3 3
n n n 2 3 lim 3 . 3
; lim n n 2
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 134
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 3 2 lim lim 0. Do đó, 3 3 2 lim
n 3 n 2 0 2 2 3 2 3 3 3 2 3 . 3 n n n n n n
Câu 64: Tính các giới hạn sau 2
n n n a) 2
lim n 1 n n . b) lim . 2
4n 3n 2n Lời giải 1 2 2 1 n 1 n n n 1 1 a) lim 2 1 lim lim lim n n n n 2
n 1 n n
n 1 n n 1 1 1 2 1 1 n n 1 Do đó, lim 2
n 1 n n . 2 3 2 2 2 2 4 2
n n n
n n n
4n 3n 2n 1 n 2 b) lim lim . lim 2 2 2 2
4n 3n 4n 3
4n 3n 2n
n n n 1 3 1 1 n 2
n n n 2 Do đó, lim 2 3
4n 3n 2n GV: T
Câu 65: Tính các giới hạn sau R Ầ 3 2 3 N
2n n n 2 3 2 3 ĐÌN
a) lim 4n n 2n 8n . b) lim . 2
n n n H CƯ Lời giải – 0834 a) 2 3 2 3 n n n n
2n n n 3 2 3 lim 4 2 8 lim 4 2 lim
2n 8n 2n 3321 2 2 2 3 3 33
4n n 4n
2n 8n 8n lim lim 2 2
4n n 2n 2 3 2n 8n 2 3 2 3
3 4n 2n 2n 8n 2 n 2n lim lim 2
4n n 2n 2n 8n 2 2 3 2 3 1 3 3 4n 2 . n 8n 1 4n 1 1 2 1 1 3 3 1 1 lim 4 2 lim 2. 1 2 2 1 n 4n 4n
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 135
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 1 lim 4 2 2 2 0 n 1 Khi n thì: lim 0 2 1 n 3 3 1 1 lim 2. 1 2 2 1 2 2 2 2 4n 4n 1 1 2 1 1 3 3 1 1 lim 4 2 lim 2. 1 2 2 1 n 4n 4n Do đó, 2 3 2 3 lim
4n n 2n 8n 3 2 3 2 3 3 2
2n n n
2n n n
n n n b) lim lim . 2 2 2
n n n
n n n 2 3 2n n 2 2 3 2 3 3
n n 2n n 1 1 n n 1 n 1 1 n n lim lim 2 2 2 2 3 6 2 3 2 2 3 3 n . 1 n . n n 1 3 1 1 1 n n n n 2 GV: T 3 2 2 3 lim 1 1 1 1 11 1 R n n Ầ 1 N Khi n thì: lim 0 ĐÌN n 1 H CƯ lim 1 1 1 n – 0834 1 1 1 3 2 3 3321 n
2n n n lim 1. Do đó, lim 1 2 2
n n n 33 3 2 2 3 1 1 1 n n
Câu 66: Tìm các giới hạn sau 2 x 3x 2 2 x 2x a) lim b) lim x2 x 2 2 x2 2
x 6x 4 3 x 3x 2 3 2
x x x 1 c) lim d) lim 4 x 1 x 4x 3 2 x 1
x 3x 2 Lời giải 2 x 3x 2 x 1 x 2 a) lim lim lim x 1 1 x2 x2 x2 x 2 x 2 2 x 2x x x 2 x x 2 x b) lim lim lim lim 1 2 x
2x 6x 4 x 2 2 2 2
x 3x 2 x2 2 x 1 x 2
x2 2 x 1
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 136
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com x 3x 2 x 2 3 1 x 2 x 2 3 1 c) lim lim lim 4 x 1 x 1 x 4x 3 x 2
1 x 2x 3 2 2 x 1
x 2x 3 6 2
x x x 1 x 2 3 2 1 x 1 x 1 x 1 d) lim lim lim 0 2 x 1 x 1
x 3x 2 x 1 x 2 x 1 x 2
Câu 67: Tìm giới hạn các hàm số sau: 4 2 x x 72 3 2
x 5x 3x 9 a) lim b) lim 2 x3 x 2x 3 4 2 x3 x 8x 9 2 6
x 5x 4x 4 4 x a c) lim d) lim x 1 x2 1 xa x a Lời giải x x x 3 3 2 4 2
x 3x 8x 24 72 3 2
x 3x 8x 24 51 a) lim lim lim 2 x3 x3 x 2x 3 x 1 x 3 x3 x 1 2
x x x x 3 2 3 2 x 2x 3 5 3 9 2 x 2x 3 b) lim lim lim 0 4 2 x x 8x 9 x x 3 3 2 3 3
x 3x x 3 3 2
x3 x 3x x 3 c) GV: T R Ầ N ĐÌN H CƯ – 0834 3321 33 x 1 5 4 3 2 2 6
4x 4x 4x 4 5 4 x x x x x 5 4 3 2
4x 4x 4x 4x x lim lim lim x 1 x2 x 1 x2 1 1 x 1 x 1
x a 3 2 2 3 4 4
x ax a x a x a d) 3 2 2 3
x ax a x a 3 lim lim lim 4a xa xa xa x a x a
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 137
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Câu 68: Tính các giới hạn sau 2 x 16 2 4 x 2 x 3x 2 a) lim b) lim c) lim 2
x4 x x 20 3 x 2 x 8 2 x 2
2x x 6 Lời giải 2 x 16
x 4 x 4 x 4 8 a) lim lim lim 2 x4 x4 x x 20
x 4 x 5 x4 x 5 9 2 4 x
2 x2 x 2 x 1 b) lim lim lim 3 x x 8
x x 2 2 2 2
x 2x 4 2 x 2 x 2x 4 3 2 x 3x 2 x 1 x 2 x 1 1 c) lim lim lim 2 x 2 x2 2x x 6
x 22x 3 x 2 2x 3 9
Câu 69: Tính các giới hạn sau 2 x x 30 2 2x 5x 2 2 2x 3x 1 a) lim b) lim c) lim 2 x 5 2x 9x 5 2 1 2 x 1 x 4x 1
x 4x 5 2 Lời giải 2 x x 30
x 5 x 6 x 6 a) lim lim lim 1 2 x5 x5 2x 9x 5
x 52x x5 1 2x 1 2 2x 5x 2 2x 1 x 2 x 2 3 b) lim lim lim 2 1 1 1 GV: T x 4x 1 x 2x 1 2x 1 x 2x 1 4 2 2 2 R 2 2x 3x 1 2x 1 x 1 Ầ 2x 1 1 N c) lim lim lim 2 ĐÌN x 1 x1
x 4x 5 x 1 5 x x 1 5 x 6 H CƯ
Câu 70: Tính các giới hạn sau – 3 3 2 x 3x 2
x x 2x 4 0834 a) lim b) lim c) 3 2 x 1
x x x 1 2 x1 x 3x 4 3321 4 2 x 6x 27 lim 33 3 2 x 3
x 3x x 3 Lời giải x 3x 2 x 2 3 1 x 2 x 2 3 a) lim lim lim 3 2 x
x x x 1 x x 2 1 1 1 x x 1 1 x 1 2
x x x x 1 2 3 2 x 2x 4 2 4 2 x 2x 4 7 b) lim lim lim 2 x 1 x1 x 3x 4 x 1 x 4 x1 x 4 5 x x 2 x 3 2 x 9 2 4 2
x 3 x 3 6 27 36 c) lim lim lim 3 2 x
x 3x x 3 x 2 3 3 x 1 x 3 2 x 3 x 1 5
Câu 71: Tính các giới hạn sau 3 x 3x 2 2 4x x 18 4 2 x x 72 a) lim b) lim c) lim 4 x 1 x 4x 3 3 x2 x 8 2 x3 x 2x 3
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 138
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Lời giải x 3x 2 x 2 3 1 x 2 x 2 3 1 a) lim lim lim 4 x 1 x 1 x 4x 3 x 2
1 x 2x 3 2 2 x 1 x 2x 3 6 2 2 4x x 18
x 24x 9 4x 9 17 b) lim lim lim 3 x x 8 x x 2 2 2 2
x 2x 4 2
x2 x 2x 4 12 x x 2
x 8 x 3 x 3 2 4 2
x 8 x 3 72 51 c) lim lim lim 2 x3 x3 x 2x 3 x 1 x 3 x3 x 1 2
Câu 72: Tính các giới hạn sau 5 x 1 5 x 1 a) lim b) lim 3 x1 x 1 3 x 1 x 1 3 2
x 5x 3x 9 c) lim 4 2 x3 x 8x 9 Lời giải x 1 4 3 2 5
x x x x x 4 3 2 1 1
x x x x 1 5 a) lim lim lim 3 x x 1 x x 1 2 1 1 x x 2 x1 1 x x 1 3 x 1 4 3 2 5
x x x x x 4 3 2 1 1
x x x x 1 5 b) lim lim lim 3 x x 1 x x 1 2 1 1 x x 2 x 1 1 x x 1 3 GV: T
x x x x 3 2 3 2 x 2x 3 5 3 9 2 x 2x 3 R c) lim lim lim 0 Ầ 4 2 2 2 x3 x3 x3 N x 8x 9 x
1 x 3 x 3 x 1 x 3 ĐÌN H CƯ
Câu 73: Tính các giới hạn sau 2 1 1 3 – a) lim b) lim c) 0834 2 x 1 x 1 x 1 3 x 1 1 x 1 x 3321 1 4 lim 2
x2 x 2 x 4 33 Lời giải 2 1 2 x 1 1 x 1 1 a) lim lim lim lim 2 2 2 x 1 x 1 x 1 x 1 x 1 x 1 x 1 x 1 x 1 2 1 3 2
1 x x 3 x 1 x 2 b) lim lim lim 3 x 1 x 1 x x 1 x 2
1 x x x 1 x 2 1 1 1
1 x x x 2 lim 1 2 x 1
1 x x 1 4 x 2 4 1 1 c) lim lim lim 2 x 2 x 2 x 2 x 4
x 2 x 2 x 2 x 2 4
Câu 74: Tìm giới hạn các hàm số sau
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 139
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com x 3 2 2 x 2 2x 7 3 a) lim b) lim c) lim 2 x7 49 x 2
x2 x 3x 2 3 2 x 1 x 4x 3 Lời giải x
x 3 2 x 3 2 3 2 1 1 a) lim lim lim 2 x7 x7 49 x
x 3 27 x7 x x7 7 x x 3 2 56 x
2 x 22 x 2 2 2 1 1 b) lim lim lim 2 x2 x2 x 3x 2 x
1 x 22 x 2 x2 x 1 2 x 2 4 c) x
2x 7 3 2x 7 3 2 7 3 2 1 lim lim lim 3 2 x 1 x 1 x 4x 3 x 1 2
x 3x 3 2x 7 3 x 1 2
x 3x 3 2x 7 3 15
Câu 75: Tìm giới hạn các hàm số sau 2 1 x 3 4x 1 3 x x 2 a) lim b) lim c) lim 2 x 1
x 3x 2 2 x2 x 4 3 x2 x 8 Lời giải x 2 2 3x 3 2 2 2 x 3 2 3 x 1 1 a) lim lim lim 2 x 1 x 1
x 3x 2 2
x x x x 1 2
x x 2 2 3 3 1 2 2 3 3 2 GV: T 4x 1 3 4x 1 3 R 4x 1 3 4 1 Ầ b) lim lim lim N 2 x2 x2 x2 x 4 6 ĐÌN
x 2 x 2 4x 1 3
x 2 4x 1 3 H CƯ c) – x x 2 x 2 x 2 0834 x x 2 x 1 1 lim lim lim 3 x2 x2 2 x2 2 x 8 16 x 2 x 2x 4 x x 2 x 2x 4 x x 2 3321 33
Câu 76: Tìm giới hạn các hàm số sau 3 x 1 3 1 1 x a) lim b) lim 3
x1 2x 5x 3 2 x0 2x x
3 2x 12 x 4 x 1 c) lim d) lim 2 x 2 x 2x 3 2 x 1 x x 2 Lời giải x
3 x 13 2 3 3 x x.1 1 1 1 a) lim lim lim 1 2 x 1 x 1 2x 5x 3 x
1 2x 3 3 2 3
x x.1 x 1 1
2x 3 3 2 3 x x.1 1
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 140
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com b)
1 1 x 1 1 x 1 x 1 1 x 2 3 3 3 3 1 1 lim lim lim 2 x0 x0 2x x x x x 2 3
1 1 x 1 x 2 0 x 2 3
1 1 x 1 x 2 3 3 6
3 2x 12 x 3 3 2x 12 x x 2 3 2 x 2x 12 x 2 12 c) lim lim 2 x 2 x2 x 2x
x x 2 2 3 3 2
(2x 12) x 2x 12 x x 2 2
x 2x 12 2 x 2x 12 5 lim lim x 2
x x 2 3 3 2 x x x
x x2 2 3 3 2 x x x x 6 2 (2 12) 2 12 (2 12) 2 12 x 4 x 1 4 4 x 1 x x 1 1 d) lim lim 3 2 x 1 x 1 x x 2 x 1 2
x x 2 4 x 1 x 1
x 1 x 1 1 1 lim lim x 1 x 2
x x 4 x x x 1 2
x x 4 x x 12 1 2 1 1 2 1 1
Câu 77: Tính các giới hạn sau
2x 7 x 4 3 x 3x 2 2 3
x 3 x 3x a) lim b) lim c) lim 3 2 x 1 x 4x 3 2 x 1 x 1 x 1 x 1 GV: T Lời giải R 2 Ầ
2x 7 x 4
2x 7 x 4 N a) Ta có lim lim ĐÌN 3 2 x 1 x 1 x 4x 3 3 2 2
x x 3x 3 2x 7 x 4 H CƯ 2
x 10x 9 x 1 9 x – lim x 1 2 2 0834
x 3x
1 2x 7 x 4 x
1 x 3 x
1 2x 7 x 4 3321 9 x 9 1 4 lim x 1 2 33
x x x x 1 3.231 4 15 3 1 2 7 4 2 3 6 6
x 3 x 3x x 3x 2
x 1 3x 3 b) lim lim lim 2 x 1 x 1 x 1 2 x 1 3
x 3x 2 x 1 x 1 x 1 3
x 3x 2 3 x 1 3 x 1 3 x 1 x 1 3 x 1 2 x x 1 3 lim lim x 1 x 1 x 1 3
x 3x 2 x 1 x 1 x 1 3
x 3x 2 3 x 1 2 2 x x 1 3 1 1 1 1 1 3 2.3 3 3 lim x 1 x 3 x x 1 1 1 1 2.2 4 1 3 2 x 3 x 3 3 3 x x x x 2 2 3 2 3 2 6 4 2
x 3 x 6x 9x c) lim lim lim x 1 x 1 x 1 x 1 2 3
x 3 x 3x x 1 x 1 2 3
x 3 x 3x
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 141
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 6 4 2 6 4 4 2 2
x 6x 8x 3
x x 5x 5x 3 3x lim lim x 1 x 1 2 3
x 3 x 3x x 1 x 1 2 3
x 3 x 3x 2 x 1 4 2
x 5x 3 x 1 4 2
x 5x 3 1 1 1 5 3 1 lim lim x 1 x 2 3 x
x x x 1 2 3 x x x 2 1 3 2 1 3 3 3 3
Câu 78: Tính các giới hạn sau 2x 1 2 x 1 x x 1 a) lim b) lim c) lim x x 1 2
x 1 3x 5x 2
x x x 1 Lời giải 1 2 2x 1 2 0 a) lim lim x 2 x x 1 x 1 1 0 1 x 1 2 1 2 x 1 1 0 1 b) lim lim x 2
x 1 3x 5 x x 1 3 0 3.0 5 5 5 2 x x 1 1 2 x x 1 x x 0 0 c) lim lim 0 2
x x x 1 x 1 1 1 0 0 1 2 GV: T x x R
Câu 79: Tính các giới hạn sau Ầ N 2 ĐÌN 3x 2x 1 3 2 3x 2x 1 3 3x 2x 2 a) lim b) lim c) lim 4 3 2 H CƯ
x 5x 1 2 x 2x
x 4x 3x 2
x 2x 2x 1 – Lời giải 0834 3 3321 x 2 x 6 3 2 1 2 6 3.0 6 a) lim lim x 33
x 5x 1 2 x 2x x 1 2 5 01 2.0 5 5 1 x x 3 2 1 3 2 2 4 3x 2x 1 3.0 2.0 0 b) lim lim x x x 0 4
x 4x 3x 2 x 3 2 4 3.0 2.0 4 3 4 x x 2 2 3 3 2 3 3x 2x 2 3 2.0 2.0 3 c) lim lim x x 3 2
x 2x 2x 1 x 2 1 2 2.0 0 2 2 3 x x
Câu 80: Tính các giới hạn sau 2
x 3x 2x 2
x x 2 3x 1 x x 3 a) lim b) lim c) lim x 3x 1 x 2 2
4x 1 1 x x x 1
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 142
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Lời giải
a) Đặt x t
. Với x t 3 2 2 1 2
x 3x 2x
t 3t 2t t 1 3.0 2 1 Khi đó lim lim lim x 3x 1 t 3t 1 t 1 3 0 3 3 t 1 2 1 1 3 2 2
x x 2 3x 1 b) x x x lim lim 4 x 2 4x 1 1 x x 1 1 4 1 2 x x Đặt x t
. Với x t . Khi đó 1 2 1 1 3 2 2 2
x x 2 3x 1
t t 2 3t 1 t t t 2 lim lim lim x 2 t 2
4x 1 1 x 4t 1 1 t t 1 1 3 4 1 2 t t 1 3 2 x x 3 x x 0 3.0 c) lim lim 0 2 x x 1 x 1 1 0 1 2 x
Câu 81: Tính các giới hạn sau GV: T 2 x 4 2 x 2 x R a) lim b) lim c) lim 2 2 Ầ x 2 x 2 x2 2x 5x 2 x2 2x 5x 2 N ĐÌN Lời giải H CƯ 2 x 4 x 2 a) lim lim – x2 x2 0834 x 2 x 2 3321 2 x x 2 1 1 b) lim lim lim 2 x 2 x 2 2x 5x 2
x 22x x 2 1 2x 1 3 33 2 x 2 x 1 1 c) lim lim lim 2 x 2 x 2 2x 5x 2
x 22x x 2 1 2x 1 3
Câu 82: Xét tính liên tục của hàm số tại điểm được chỉ ra : x 3 khi x 1 a)
f x x 1 (tại x 1 ) 1 khi x 1
x 3 2 khi x 1 b) f x x 1 (tại x 1 ) 1 khi x 1 4 Lời giải
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 143
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 1 3
a Ta có: f 1 1 1 1 x 3
lim f x lim 1 f
1 hàm số liên tục tại x 1 x 1 x1 x 1 1
b Ta có : f 1 . 4 x 3 2
x 3 2 x 3 2 1
lim f x lim lim lim f 1 x 1 x 1 x x 1 1 x 1 x 3 2 x 1 x 3 2
Vậy hàm số liên tục tại x 1 .
Câu 83: Xét tính liên tục của hàm số tại điểm được chỉ ra: 2 3
2 7x 5x x khi x 2 a) f x 2 x 3x 2 (tại x 2 ) 1 khi x 2 x 5 khi x 5
b) f x 2x 1 3 (tại x 5 )
x 52 3 khi x 5 Lời giải
a Ta có: f 2 1 GV: T x 2 2 2 3 x 3x x x x 2 1 2 7 5 x 3x 1 Mà lim f x lim lim lim 1 f 2 R 2 Ầ x2 x2 x2 x 3x 2
x 2 x x2 1 x 1 N ĐÌN
Vậy hàm số liên tục tại x 2 H CƯ
b Ta có: f 2 5 5 5 3 3 . – 0834
Lại có lim f x lim x 52 3 3 x 5 x 5 3321 x 5 2x 1 3 33 x 5 2x 1 3 Và lim f x lim lim lim 3 x 5 x 5 x 5 2x 1 3
2x 1 3 2x 1 3 x 5 2
Từ đó f 5 lim f x hàm số liên tục tại x 5 . x 5
Câu 84: Xét tính liên tục của các hàm số sau trên tập xác định của chúng : 3
x x 2 khi x 1 3 a) f x x 1 4
khi x 1 3 2
x 3x 4 khi x 2
b) f x 5 khi x 2
2x 1 khi x 2
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 144
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Lời giải 3 3 x x 2
x 1 x 1 1 4
a lim f x lim lim lim 1 3 3 2 x 1 x 1 x 1 x 1 x 1 x 1 x x 1 3
Do đó, hàm số này liên tục tại x 1 b lim 2 x 3x 4 =2; lim 2x 1 5 x 2 x 2
Mà f x 5 khi x 2 nên lim f x lim f x lim f x x2 x 2 x2
Do đó, hàm số đã cho liên tục khi x 2
Câu 85: Xét tính liên tục của các hàm số sau trên tập xác định của chúng : 2 2 x 4 x 2 khi x 2 khi x 2 a)
f x x 2
b) f x x 2 4 khi x 2 2 2 khi x 2 Lời giải
a Hàm số f x liên tục với x 2 1 2 x 4
x 2 x 2
lim f x lim lim
lim x 2 2 2 4. x 2 x2 x 2 x 2 GV: T x 2 x 2 R f 2 4
lim f x f 2
f x liên tục tại x 2 2 Ầ x 2 N ĐÌN Từ ta có liên tục trên . H CƯ 1 và 2 f x – Hàm số liên tục với b f x x 2 1 0834 3321 2 x
x 2x 2 2
lim f x lim lim lim x 2 2 2 2 2. 33 x 2 x 2 x 2 x 2 x 2 x 2
f 2 2 2 lim f x f 2 f x liên tục tại x 2 2 x 2 Từ
1 và 2 ta có f x liên tục trên .
Câu 86: Chứng minh rằng các phương trình sau có 3 nghiệm phân biệt: a) 3
x 3x 1 0 b) 3
2x 6 1 x 3 Lời giải
a Dễ thấy hàm f x 3
x 3x 1 liên tục trên R . Ta có:
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 145
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com f 2 1
f 2. f
1 0 tồn tại một số a 2 ; 1 : f a 0 1 . 1 1 f 1 3 f 0 1
f 0. f
1 0 tồn tại một số a 0;1 : f a 0 2 . 2 2 f 1 1 f 1 1 f
1 . f 2 0 tồn tại một số a 1; 2 : f a 0 3 . 3 3 f 2 3 Do ba khoảng 2 ; 1 , 0;
1 và 1;2 đôi một không giao nhau nên phương trình 3
x 3x 1 0 có ít nhất 3 nghiệm phân biệt.
Mà phương trình bậc 3 thì chỉ có tối đa là 3 nghiệm nên 3
x 3x 1 0 có đúng 3 nghiệm phân biệt. b Đặt 3 3 3
1 x t x 1 t 2t 6t 1 0 .
Xét hàm số f t 3
2t 6t 1 liên tục trên R .
f 2. f 1 3.5 0
Ta có: f 0. f
1 1.3 0 tồn tại 3 số t , t và t lần lượt thuộc 3 khoảng đôi 1 2 3 f
1 . f 2 3.5 0
một không giao nhau là 2 ; 1 , 0;
1 và 1;2 sao cho f t f t f t 0 và 1 2 3 GV: T
do đây là phương trình bậc 3 nên f t 0 có đúng 3 nghiệm phân biệt. R Ầ
Ứng với mỗi giá trị t , t và t ta tìm được duy nhất một giá trị x thỏa mãn 3 x 1 t 1 2 3 N ĐÌN
và hiển nhiên 3 giá trị này khác nhau nên PT ban đầu có đúng 3 nghiệm phân biệt. H CƯ
Câu 87: Chứng minh rằng các phương trình sau luôn có nghiệm: – 0834 a) 5
x 3x 3 0 b) 4 3 2
x x 3x x 1 0 3321 Lời giải Xét 33 a f x 5
x 3x 3.
lim f x tồn tại một số x 0 sao cho f x 0. 1 1 x
lim f x tồn tại một số x 0 sao cho f x 0. 2 2 x
Từ đó f x . f x 0 luôn tồn tại một số x x ; x : f x 0 nên phương trình 0 2 1 0 1 2 5
x 3x 3 0 luôn có nghiệm.
b Xét f x 4 3 2
x x 3x x 1 liên tục trên R Ta có: f 1 3 0
lim f x tồn tại một số a 0 sao cho f a 0 . x 2
x x 3 0 nên luôn tồn tại một số x 0; a thỏa mãn f x 0 nên phương 0 0 trình 4 3 2
x x 3x x 1 0 luôn có nghiệm.
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 146