



























































































































































Preview text:
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
CHƯƠNG VI. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
A. KIẾN THỨC CƠ BẢN CẦN NẮM
BÀI 1. PHÉP TÍNH LŨY THỪA
Trong khoa học, người ta thường dùng lũy thừa để ghi các số, có thể rất lớn hoặc rất bé. Chẳng
hạn, bảng dưới đây cho một số ví dụ về cách ghi độ dài. Độ dài (m) Ghi bằng lũy thừa (m) Ghi bằng đơn vị 1000000000 9 10 1Gm (gigamét) 1000000 6 10 1 Mm (megamét) 1000 3 10 1 km (kilômét) 0,001 3 10− 1 mm (milimét) 0,000001 6 10− 1μm (micrômét) 0,000000001 9 10− 1 nm (nanomét)
Cách ghi như vậy có tiện ích gì? Từ các lũy thừa quen thuộc ở ba dòng đầu, hãy dự đoán quy
tắc viết lũy thừa ở ba dòng cuối. Lời giải GV
Cách ghi như vậy giúp con số không chứa quá dài, chứa quá nhiều số 0 dẫn đến việc có thể viết thừa : TR hoặc thiếu số 0 ẦN Đ − ÌN
Quy tắc viết luỹ thừa ở ba dòng cuối, số chữ số sau dấu phẩy là n thì số đó được viết là 10 n H CƯ
1. Lũy thừa với số mũ nguyên – 083
Cho biết dãy số (an ) được xác định theo một quy luật nào đó và bốn số hạng đầu tiên của nó được cho 4332133
như ở bảng dưới đây: n 1 2 3 4 5 6 7 an 16 8 4 2 ? ? ?
a) Tìm quy luật của dãy số và tìm ba số hạng tiếp theo của nó.
b) Nếu viết các số hạng của dãy số dưới dạng lũy thừa, thì bốn số hạng đầu tiên có thể viết thành 4 3 2 1
2 ;2 ;2 ;2 . Dự đoán cách viết dưới dạng lũy thừa của ba số hạng tiếp theo của dãy số và giải thích. Lời giải
a) Quy luật của dãy số là kể từ số hạng thứ 2 , mỗi số hạng bằng số liền trước chia cho 2 Ta có: 1 1
a =1;a = ;a = 5 6 7 2 4 b) Ta có 0 1 − 2 a 2 ;a 2 ;a 2− = = = 5 6 7
Do mỗi số hạng bằng số liền trước chia cho 2 nên khi viết dưới dạng luỹ thừa có cơ số là 2 , số mũ của
mỗi số hạng kém số mũ của số hạng liền trước 1 đơn vị.
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 1
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Ở cấp Trung học cơ sở, chúng ta đã biết lũy thừa với số mũ tự nhiên: n
a = a . a . a .... a (n∈ ,n > 0,a ∈ ) 0 ,a =1(a ≠ 0). n thua o s
Phép tính lũy thừa có thể mở rộng với số mũ nguyên bất kì. Lũy thừa với số mũ nguyên âm được định nghĩa như sau: −n 1 a =
Với số nguyên dương n , số thực a ≠ 0 , lũy thừa của a với số mũ −n xác định bởi n a Chú ý: a) 0
a =1 với mọi a ∈,a ≠ 0. b) 0
0 và 0−n (với n > 0 ) không có nghĩa.
Ví dụ 1. Tính giá trị các biểu thức sau: 2 − 2 − a) 4 2− b) 3 9 ⋅ 1 ; c) 0 : ( 3) . 4 2 Lời giải a) 4− 1 1 2 = = 4 2 16 2 − b) 3 1 1 16 9⋅ = 9⋅ = 9⋅ = 9⋅ = 16 ; 2 4 9 G 3 9 V : 16 T 4 RẦ 2 − N 1 1 1 0 Đ c) : ( 3) = :1 = = 4 ÌN 2 2 1 1 H C 4 2 Ư –
Luyện tập 1. Tính giá trị các biểu thức sau: 083 4332133 a) 1 ( 5)− − , 5 − b) 0 1 2 ⋅ ; 2 3 − c) 2− 1 2 6 ⋅ : 2− 3 Lời giải − a) 1 − 1 1 ( 5) − = = 1 ( 5) − 5 5 − b) 0 1 1 1 2 ⋅ = 1⋅ = = 32 5 2 1 1 32 2 3 − c) 2− 1 2 − 1 1 1 1 1 1 1 6 ⋅ : 2 = ⋅ : = ⋅ : = ⋅ 27⋅4 = 3 2 3 2 3 6 1 2 36 1 4 36 27 3
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 2
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Vận dụng 1: Trong khoa học, người ta thường phải ghi các số rất lớn hoặc rất bé. Để tránh phải viết và
đếm quá nhiều chữ số 0 , người ta quy ước cách ghi các số dưới dạng 10m A⋅
, trong đó 1≤ A ≤10 và m là số nguyên.
Khi một số được ghi dưới dạng này, ta nói nó được ghi dưới dạng ki hiệu khoa học.
Chẳng hạn, khoảng cách 149600000 km từ Trái Đất đến Mặt Trời được ghi dưới dạng kí hiệu khoa học là 8 1,496.10 km .
Ghi các đại lượng sau dưới dạng kí hiệu khoa học:
a) Vận tốc ánh sáng trong chân không là 299790000 m / s ;
b) Khối lượng nguyên tử của oxygen là 0,00000000000000000000000002657 kg . Lời giải
a) Vận tốc ánh sáng trong chân không là 8 2,9979.10 m / s
b) Khối lượng nguyên tử oxygen là 26 2,657 10− ⋅ kg 2. Căn bậc n
HĐ 2. Một thùng gỗ hình lập phương có độ dài cạnh a(dm) . Kí hiệu S và V lần lượt là diện tích một
mặt và thể tích của thùng gỗ này.
a) Tính S và V khi a =1dm và khi a = 3dm . b) a bằng bao nhiêu đề 2 S = 25dm ?
c) a bằng bao nhiêu để 3 V = 64dm ? GV: TRẦN ĐÌNH CƯ – 083 Lời giải 4332133 a) Khi a =1dm thì 2 2 3 3
S =1 =1dm ;V =1 =1dm Khi a = 3dm thì 2 2 3 3
S = 3 = 9dm ;V = 3 = 27dm b) Để 2
S = 25dm thì a = 25 = 5dm c) Để 3 V = 64dm thì 3 a = 64dm Trong hoạt động trên:
• Nếu cho biết a , yêu cầu tìm S hay V thì ta dùng phép tính luỹ thừa: 2 3
S = a ,V = a .
• Nếu cho biết S hay V , yêu cầu tìm a thì ta dùng phép tính lấy căn: 3
a = S ,a = V .
Mở rộng phép lấy căn bậc hai, căn bậc ba đã quen thuộc ở cấp Trung học cơ sờ, ta có định nghĩa sau đây: n(n ≥ 2) Cho số nguyên dương
và số thực b bất kì. Nếu có số thực a sao cho n a = b
thì a được gọi là một căn bậc n của b .
Chú ý: Ở cấp Trung học cơ sở ta đã biết:
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 3
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
a) Nếu b > 0 thì b có hai căn bậc hai, kí hiệu là b (gọi là căn bậc hai số học của b ) và − b
b) Số 0 chỉ có duy nhất một căn bậc hai là chính nó;
c) Nếu b < 0 thì b không có căn bậc hai nào;
d) Mọi số thực b có duy nhất một căn bậc ba, kí hiệu là 3 b .
Mở rộng kết quả này, ta có:
Cho n là số nguyên dương (n ≥ 2),b là số thực bất kì. Khi đó:
• Nếu n là số chẵn thì:
• b < 0 : không tồn tại căn bậc n của b .
• b = 0 : có một căn bậc n của b là 0 .
• b > 0 : có hai căn bậc n của b đối nhau, kí hiệu giá trị dương là n b và giá trị âm là n − b .
- Nếu n là số lẻ thì có duy nhất một căn bậc n của b , kí hiệu n b . Chú ý:
a) Nếu n chẵn thì căn thức n b có nghĩa chi khi b ≥ 0 .
b) Nếu n lẻ thì căn thức n b luôn có nghĩa với mọi số thực b .
Ví dụ 2: Tìm các căn bậc bốn của 16 ; căn bậc năm của 4 − 2 . Lời giải Ta có 4
2 =16 . Suy ra 16 có hai căn bậc bốn là 4 16 = 2 và 4 − 16 = 2 − . Ta có 5 4 − 2 = (− 2) GV: T Suy ra 5 4 − 2 = − 2 RẦN ĐÌN
Ta có các tính chất sau đây (với điều kiện các căn thức đều có nghĩa): H CƯ – 083 4332133
Ví dụ 3. Tính giá trị các biểu thức sau: a) ( )4 4 3 −π b) 5 5 8 ⋅ 4 − c) 4 3 2 2 Lời giải a) 4 4
(3−π ) = 3−π = π − 3 (vì π > 3) ; b) 5 5 5 8 ⋅ 4 − = 8⋅( 4 − ) 5 3 2 5 5 5 5 = 2 − ⋅ 2 = 2 − = ( 2) − = 2 − ; c) 4 3 4 3 3 3 4 3 4 3 2 2 = ( 2) ⋅ 2 = ( 2) = 2
Luyện tập 2. Tính giá trị các biểu thức sau: a) 1 4 b) 6 2 ( 8) c) 4 4 3 ⋅ 27 16 Lời giải
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 4
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 4 a) 1 1 1 1 4 = 4 = = 16 2 2 2 b) 6 2 6 2 6 6 ( 8) = 8 = 2 = 2 = 2 c) 4 4 4 4 4 3 ⋅ 27 = 3.27 = 3 = 3 = 3
3. Luỹ thừa với số mũ hữu tỉ
HĐ 3. Cho số thực a > 0 . a) Hai biểu thức 6 4 a và 3 2
a có giá trị bằng nhau không? Giải thích.
b) Chỉ ra ít nhất hai biểu thức khác nhau có giá trị bằng 3 2 a . Lời giải a) Ta có: 6 4 3 2 4 3 2 2 = 2 = 2
b) Các biểu thức khác có giá trị bằng 3 2 2 là 9 6 12 8 2 ; 2
Cho số thực dương a và số hữu tỉ m r = , trong đó ,
m n∈,n > 0 . n G
Luỹ thừa của a với số mũ r , kí hiệu r
a , được xác định bởi V m : T r n n m R
a = a = a . ẦN Đ ÌN
Ví dụ 4. Biểu thị các luỹ thừa sau đây dưới dạng căn thức: H 1 2 CƯ a) 3 2 b) 3 5− . – 083 Lời giải 4332133 1 a) 3 3 2 = 2 2 − b) − 1 1 3 3 2 = = 3 = 3 5 5 . 2 5 25
HĐ 3. Tính giá trị biểu thức sau: 1 1 − a) 2 36 2 25 b) c) 1,5 100 49 Lời giải 1 a) 2 25 = 25 = 5 1 − 1 − b) 2 36 36 1 49 7 = = = = 49 49 36 36 6 49 3 c) 1,5 2 3
100 =100 = 100 = 1000000 =1000 .
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 5
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
HĐ 4. Viết các biểu thức sau dưới dạng lũy thừa với số mũ hữu tỉ: 4 a) 3 1 2 b) 5 c) ( 5 a ) (a > 0) 27 Lời giải 3 a) 3 2 2 = 2 1 b) 5 1 1 5 = 27 27 4 c) 5 4 5
( a) (a > 0) = a
4. Lũy thừa với số mũ thực
Ta biết rằng, 2 là một số vô tỷ có thể biểu diễn dưới dạng số thập phân vô hạn không tuần hoàn: 2 =1,414213562 .
Cũng có thể coi 2 là giới hạn của dãy số hữu tỉ (r : n ) 1,4;1,41;1,414;1,4142......
Từ đây, ta lập dãy số các lũy thừa (3 nr ).
a)Bảng dưới cho biết những số hạng đầu tiên của dãy số (3 nr )( làm tròn đến chữ số thập phân thứ chín).
Sử dụng máy tính cầm tay, hãy tính số hạng thứ 6 và thứ 7 của dãy số này. GV: TRẦN ĐÌNH CƯ – 083 4332133
b) Nêu nhận xét về dãy số (3 nr ). Lời giải a) n r n 3 nr 1 1,4 4,655536722 2 1,41 4,706965002 3 1,414 4,727695035
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 6
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 4 1,4142 4,728733930 5 1,41421 4,728785881 6 1,414213 4,728801466 7 1,4142134 4,728804064
b) Ta thấy dãy số (3 nr ), khi n → ∞ + thì nr 2 3 → 3
Người ta chứng minh được rằng dãy số (3 nr )ở trên có giới hạn khi n → +∞ . Giới hạn đó là một số thực, kí hiệu là 2
3 và gọi là lũy thừa với số mũ 2 . Vậy 2 3 = lim 3 nr . n→+∞
Sử dụng máy tính cầm tay ( làm tròn đến chữ số thập phân thứ chín), ta thấy 2 3 ≈ 4,728804388.
Môt cách tổng quát, với a là số thực dương, α là số vô tỷ bất kỳ, người ta chứng minh được rằng có dãy
số hữu tỉ (r sao cho α = n r
có giới hạn không phụ thuộc vào việc chọn dãy (r . n ) n )
lim r và dãy số (a ) →+∞ n n ( nra ) Giới hạn của dãy số
được gọi là lũy thừa của số thực dương a với số mũ α , kí hiệu là α a G α n r V a = lim a α = lim rn : n→+∞ n→+∞ T với . RẦ N Đ
Chú ý: 1α =1với mọi α ∈ ÌN . H
Ví dụ 5: Sử dụng máy tính cầm tay, tính giá trị các lũy thừa sau, làm tròn đến chữ số thập phân thứ CƯ − 2 – 3 1 sau: 2 ; . 083 2 4332133 Lời giải Ấn lần lượt các phím Ta được 3 2 ≈ 3,321997 . Ấn lần lượt các phím − 2 ta được: 1 ≈ 2,665144 . 2
HĐ 5. Sử dụng máy tính cầm tay, tính các lũy thừa sau đây ( làm tròn đến chữ số thập phân thứ sáu):
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 7
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com a) 1,5 1,2 b) 3 10 c) ( ) 23 0,5 − Lời giải a) 1,5 1,2 =1,314534 b) 3 10 = 53,957374 2 c) − 3 (0,5) = 2,924018
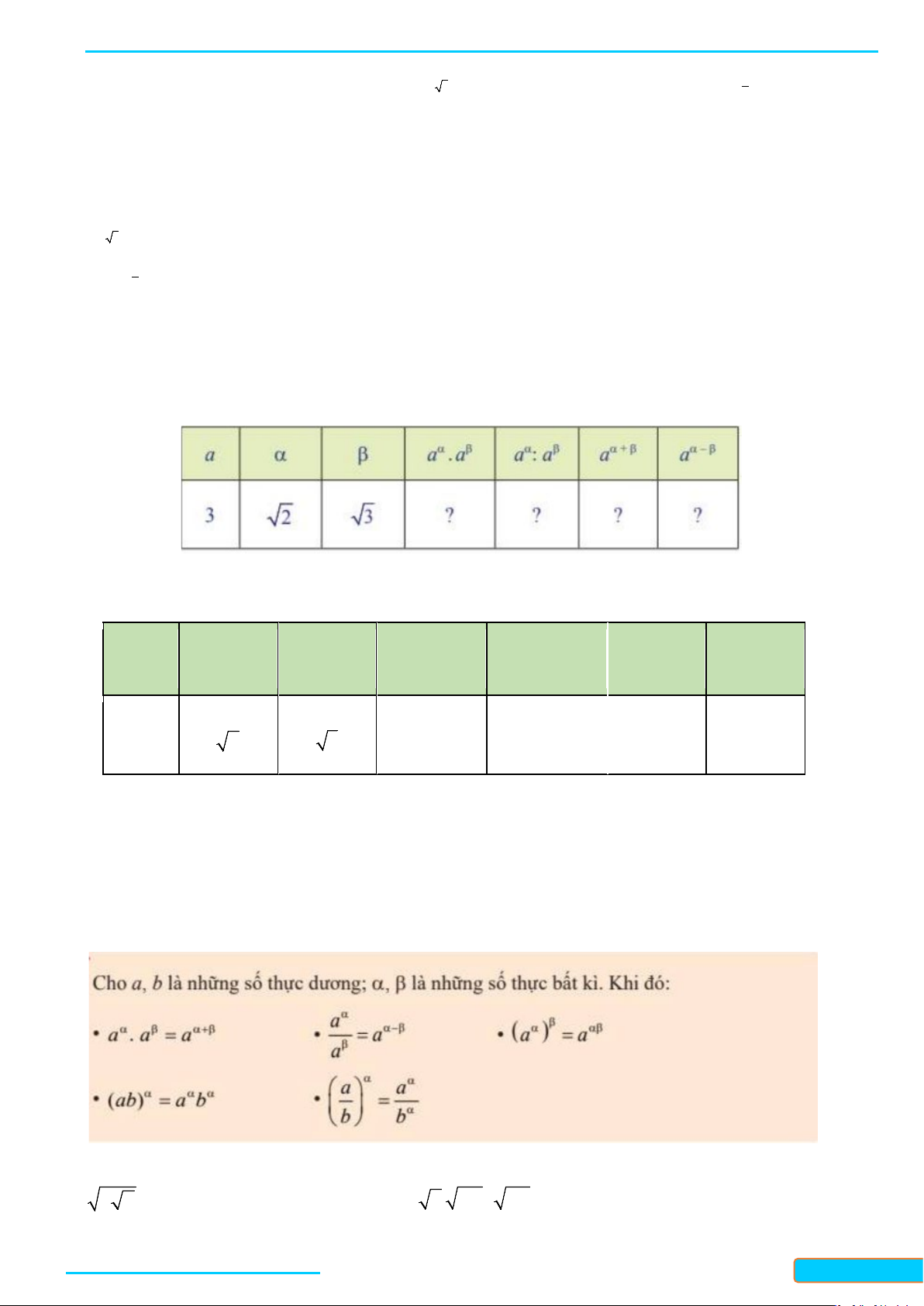
5. Tính chất của phép tính lũy thừa.
a) Sử dụng máy tính cầm tay, hoàn thành bảng sau vào vở( làm tròn kết quả đến chữ sso thập phân thứ năm)
b) Từ kết quả ở câu a, có dự đoán gì về tính chất của phép tính lũy thừa với số mũ thực? Lời giải GV α β α β + − : T α β a ⋅a a : a aα β aα β R a ẦN ĐÌN H 3 31,70659 0,70527 31,70659 0,70527 C 2 3 Ư – 083 4332133
Ta thấ: aα ⋅aβ = aα+β α β α −β a : a = a
Phép tính lũy thừa với số mũ thực có tính chất tương tự như lũy thừa với số mũ tự nhiên.
Ví dụ 6: Viết các biểu thức sau dưới dạng một lũy thừa (a > 0) a) a a b) 3 4 3− 6 1 . : − a a a
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 8
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Lời giải 1 1 1 3 3 1 1 3 3 a) . 2 2 2 3 2 a a = .
a a = a = a = a . 1 3 1 1 3 1 1 b) 3 4 3 6 1 − − − − 3 4 6 3 4 6 4
a. a : a = a .a : − − − a = a = a . 2+ 5 1− 5
Ví dụ 7: Rút gọn biểu thức 6 .2 3+ 5 3 Lời giải 2+ 5 1− 5 6 .2 (2.3)2+ 5 1− 5 .2 2+ 5 2+ 5 1− 5 3 − − 5 2+ 5 1 + − 5 2+ 5−3− 5 3 1 − 8 = = 2 .3 .2 .3 = 2 .3 = 2 .3 = . 3+ 5 3+ 5 3 3 3
HĐ 6. Viết các biểu thức sau dưới dạng một lũy thừa (a > 0) 3 1 2 1 1 a) 5 2 5 . : − a a a b) 2 2 a a a Lời giải 3 1 2 3 1 2 − 3 a) − + − 5 2 5 5 2 5 2
a ⋅a : a = a = a 1 1 1 1 1 1 1 1 1 + 2 2 2 2 2 2 2 2 2 1
b) a ⋅ a ⋅ a = a ⋅ a ⋅a = a ⋅ a = a ⋅ a G 1 1 1 1 1 + V 2 2 2 2 2 :
= a ⋅a = a = a = a T RẦN 2 2 2 Đ
HĐ 7. Rút gọn biểu thức: ( ) (9 − x y y ) ( Với ;xy >0). ÌN H Lời giải CƯ – 2 083 ( 2
x ⋅ y) ⋅( − 2 y ) 2⋅ 2 2 − 2 2 2− 2 2 9 = x ⋅ y ⋅9⋅ y = 9x ⋅ y = 9x 4332133
Vận dụng 2 : Tại một vùng biển , giả sử cường độ ánh sáng I thay đổi theo độ sâu theo công thức 0,3 .10− = d I I
, trong đó d là độ sâu ( tính bằng mét) so với mặt hồ, I là cường độ ánh sáng tại mặt hồ. 0 0
a) Tại độ sâu 1m , cường độ ánh sáng gấp bao nhiêu lần I ? 0
b) Cường độ ánh sáng tại độ sâu 2m gấp bao nhiêu lần so với tại độ sâu 10m ? Làm tròn kết quả đến hai chữ số thập phân. Lời giải a) Tại d =1; ta có 0 − ,31⋅ 0 − ,3 I = I ⋅10 = I ⋅10 . 0 0
Vậy cường độ ánh sáng tại độ sau 1 m gấp 0,3 10− lần I 0
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 9
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com b) Tại d = 2 ; ta có 0 − ,3.2 I = I ⋅10 . 0 Tại d = 10; ta có 0 − ,3.10 I = I ⋅10 0
Cường độ ánh sáng tại độ sau 2 m gấp 0 − ,3.2 0 − ,3.10 0 − ,3.2−( 0 − ,3.10) 0,3.8 10 :10 =10 = 10
= 251,19 lần sao với tại độ sâu 10 m
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
Dạng 1. Rút gọn biểu thức 1. Phương pháp
• Giải bằng phương pháp tự luận (kết hợp nhiều tính chấ của lũy thừa)
• Giải bằng casio (dò tìm đáp án đối với trắc nghiệm)
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1. Rút gọn biểu thức K = ( 4 x − x + )( 4 1 x + x + ) 1 (x − x + ) 1 ta được: A. 2 x +1 B. 2 x + x +1 C. 2
x – x +1 D. 2 x –1 Lời giải Chọn B
Cách 1. Tự luận: Dựa vào hằng đẳng thức thứ ba ta có K ( x x
)( x x )(x x ) ( x )2 4 4 1 1 1 1 X = − + + + − + = + − (x− x + )1 G
= (x + x + )(x − x + ) = (x + )2 2 1 1
1 − x = x + x −1 V . : TRẦ
Cách 2. Casio: Biểu diễn qua 100 N Đ 4 4 Calc ÌN
Nhập ( X − X + ) 1 ( X + X + ) 1 ( X − X + ) 1 →10101 X 100 = H C 2 2 Ư
=100 +100 +1 = x + x +1⇒ B – 083
Cách 3. Casio: Thử lần lượt 4 đáp án. 4332133 Nhập ( 4 X − X + ) 1 ( 4 X + X + )
1 ( X − X + ) 2
1 : X + X +1 Calc →3;3 ⇒ B X 1 = 2 1 1 1 −
Ví dụ 2. Cho x, y là các số thực dương. Rút gọn biểu thức 2 2
= − 1− 2 y y K x y + ? x x A. x B. 2x C. x +1 D. x –1 Lời giải Chọn A
Cách 1. Tự luận: Viết biểu thức K dưới dạng − −
K = ( x − y ) ( x y y )2 2 2 1− = = x ⇒ A 2 x x − y x
Cách 2. Casio: Biểu diễn qua 100 và 0,01
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 10
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 2 1 1 1 − Nhập Y Y 2 2
K = X −Y 1− 2 Calc +
→100 = x ⇒ A X 100 = ;Y =0,01 X X
Cách 3. Casio: Thử lần lượt 4 đáp án. Đáp án đúng là đáp án A. 2 1 1 1 − Nhập Y Y 2 2
K = X −Y 1− 2 + : Calc X →1;1⇒ A X 1 = ;Y =0 X X 1 1 5 3 2 2
a a − a
Ví dụ 3. Cho số thực a > 0 và a ≠ 1. Hãy rút gọn biểu thức P = 1 7 19 4 12 12
a a − a
A. P = 1+ a B. P = 1
C. P = a
D. P = 1− a Lời giải Chọn A 1 1 5 3 1 2 2 1
a a − a 3 2 a a ( 2 1− a ) 5 6 a ( 2 1− a ) Ta có P = = = = 1+ a ⇒ A 1 7 19 1 7 5 4 12 12 4 12
a a − a a a (1− a) 6 a (1− a) 2 3 a (3 2− 3 a − a )
Ví dụ 4. Cho hàm số f (a) =
với a > 0, a ≠ 1. Tính giá trị M = f ( 2018 2017 ) . G 1 V 8 8 3 8 1 − : a a − a T ( ) RẦN A. 2018 M = 2017 +1. B. 1009 2017 . ĐÌNH C. 1009 2017 +1. D. 1009 2017 − −1. CƯ Lời giải – 083 Chọn D 4332133 Cách 1. Tự luận 2 2 2 2 1 3 3 2 − 3 −
a ( a − a) 1 3 3 3 3 − − Ta có f (a) a a a a 1 a 2 = = = = 1 − − a 1 − 8 a ( 3 1 a − a− ) 1 3 1 1 1 8 8 8 8 8 8 2 a a − a a a − a Do đó M = f ( ) = − −( )1 2018 2018 1009 2 2017 1 2017 = 1 − − 2017 .
Cách 2. Casio biểu diễn qua 100 2 3 X (3 2− 3 X − X ) Nhập f ( X ) Cacl = → 11 − = 1 − − 100 = 1 − − X 1 X = 8 X ( 3 1 X − X − ) 100 8 8 Do đó M = f ( 2018 ) 2018 1009 2017 = 1 − − 2017 = 1 − − 2017 .
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 11
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 2 1 x
Ví dụ 5. Cho x, y là các số thực dương và x ≠ y . Biểu thức = ( x x + )2 2 2 2 − 4 x A x y xy bằng A. 2x 2x y − x B. 2x 2x x − y C. ( − )2x x y D. 2x 2x x − y Lời giải Chọn B 4x = + ( )2x 4x + − ( )2x 4x = − ( )2x 4 2 4 2 x S x xy y xy x xy + y = ( − )2 2 2 x x x 2x 2x x y = x − y
Nhận xét: Câu này là câu bẫy với những ai dùng máy tính. Thật vậy 2 1 X Nhập ( X X X +Y )2 2 2 2
− 4 X XY −( 2X 2 X Y − X ) Calc
→0 khoanh đáp án A là sai vì đáp án B mới X =2;Y =3
là đáp án đúng. Để không bị sai khi gặp các đáp án giống nhau mà trong 1 đáp án có dấu trị tuyệt đối thì
ta nên thử với các giá trị đối nhau 2 1 X Nhập ( X X X +Y )2 2 2 2 X 2 X 2 − 4 X Calc
XY − X −Y . { → = = 0 X 2;Y 3 X = 2; − Y = 3 −
Dạng 2. Viết biểu thức dưới dạng lũy thừa 1. Phương pháp GV: T
• Giải bằng phương pháp tự luận (kết hợp nhiều tính chấ của lũy thừa) RẦ
• Giải bằng casio (dò tìm đáp án đối với trắc nghiệm) N ĐÌN
2. Các ví dụ rèn luyện kĩ năng H 11 CƯ
Ví dụ 1. Rút gọn biểu thức 16
x x x x : x ta được: – 083 A. 4 x B. 6 x C. 8 x D. x 4332133 Lời giải Chọn a
Cách 1. Theo nguyên tắc "Chia cộng" từ trong ra ngoài ta có 1 3 3 7 7 15 15 2 2 4 4 8 8 16 x x x x = x x .
x x = x x x = x . x x = x x = .
x x = x = x 11 15 11 1 Do đó 16 16 16 4 4
x x x x : x = x : x = x = x .
Chú ý: Trong quá trình thực hành vì cùng 1 ẩn x nên ta chỉ cần nhẩm theo số mũ cho nhanh.
Cách 2. Thử 4 đáp án. 11 Nhập 16 4 X X X X : Calc
X − X →0 ⇒ A X =2 11 Cách 3. Nhập Calc 1 16 log X X X X − X → ⇒ A X logX X =2 4
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 12
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Ví dụ 2. Biểu thức 2 2 2 3 3 K =
viết dưới dạng luỹ thừa với số mũ hữu tỉ là: 3 3 3 5 1 1 1 A. 18 2 2 2 8 2 6 2 B. C. D. 3 3 3 3 Lời giải Chọn B Cách 1. Coi 2
X = . Theo nguyên tắc "Chia cộng" ta có 3 1 3 1 3 1 3 3 3 3 3 3 3 3 2 2 2 2 2
K = X X X = X X.X = X X = X.X = X = X
Cách 2. Thử 4 đáp án. Nhập 3 3 Calc 1 log X X X → ⇒ B X X =2 2 2
Ví dụ 3. Cho a;b > 0 viết 3
a . a và 3 b b b về dạng x, y
a b ; x, y ∈ .
Khi đó 6x +12y là A. 17. B. 7 . C. 14. D. 7 . 12 6 Lời giải Chọn C GV 2 : T Calc 7 3 → = R log A A x A . A=2 Ầ 6 N Nhập
⇒ 6x +12y =14 . ĐÌN 3 Calc 7 log B B B → = y H B B=2 12 CƯ – 083 4332133
Dạng 3. So sánh 1. Phương pháp
• Giải bằng phương pháp tự luận (kết hợp nhiều tính chấ của lũy thừa)
• Giải bằng casio: Sử dụng chức năng Ture/Fasle hoặc thay giá trị trực tiếp
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1. Cho a 1. Mệnh đề nào sau đây đúng? 3 2 1 A. a 3 1 a 1 1 . B. 1. C. 3 a a . D. . 5 a a 2018 2019 a a Lời giải Chọn A Ta có 1 5 a . 5 a
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 13
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 3 5 1 Lại có 3 5 3 a a a . 5 a 1 a
Ví dụ 2. So sánh ba số: ( )0,3 0,2 , ( )3,2 0,7 và 0,2 3 ta được
A. (0,7)3,2 < (0,2)0,3 0,2 < 3 .
B. (0,2)0,3 < (0,7)3,2 0,2 < 3 . C. 0,2 < ( )0,3 < ( )3,2 3 0,2 0,7 . D. ( )0,3 0,2 < < ( )3,2 0,2 3 0,7 . Lời giải Chọn A 1 3 1 Ta có: ( )0,3 = ( ) = ( )3 10 10 = ( )10 0,2 0,2 0,2 0,008 . 1 ( ) = ( )32 3,2 = ( )32 10 10 0,7 0,7 0,7 . 1 = ( )1 2 0,2 . 10 2 10 3 3 = 3 . Do ( )32 0,7
< 0,008 < 3 nên (0,7)3,2 < (0,2)0,3 0,2 < 3 . 1 1
Ví dụ 3. Nếu (a − )4 < (a − )3 2
2 thì khẳng định nào sau đây là đúng?
A. 2 < a < 3. B. a > 2 . C. a < 3. D. a > 3. GV: Lời giải T RẦ Chọn D N Đ 1 1 ÌN Ta có 1 1
< và (a − )4 < (a − )3 2
2 nên a − 2 >1 ⇔ a > 3. H 4 3 CƯ 3 − 5 − – − 4 < − 4 083
Ví dụ 4. Cho (2m ) 1 (2m )
1 . Khẳng định nào sau đây đúng? 4332133 A. m ≥1.
B. 1 ≤ m ≤1. C. m >1.
D. 1 < m <1. 2 2 Lời giải Chọn D 3 − 5 − Do 3 − 5 − > nên ta có: ( m − ) 1 4 < ( m − ) 4 2 1 2 1
⇔ 0 < 2m −1<1 ⇔ 1< 2m < 2 ⇔ < m <1. 4 4 2 1 1
Ví dụ 5. Nếu (a − )4 < (a − )3 2
2 thì khẳng định nào sau đây là đúng?
A. 2 < a < 3. B. a > 2 . C. a < 3. D. a > 3. Lời giải Chọn D 1 1 Ta có 1 1
< và (a − )4 < (a − )3 2
2 nên a − 2 >1 ⇔ a > 3. 4 3
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 14
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 2018 2019 Ví dụ 6. π π
Cho mệnh đề A: sin sin >
và mệnh đề B : log > . Khẳng định e 2018 loge 2019 12 12 2 2 nào dưới đây đúng?
A. A sai, B sai.
B. A đúng, B đúng.
C. A đúng, B sai.
D. A sai, B đúng. Lời giải Chọn C 2018 2019 Ta có: π π π sin
< 1và 2018 < 2019 nên sin sin > suy ra A đúng. 12 12 12
Tương tự vì e >1và 2018 < 2019 nên log < suy ra B sai. e 2018 loge 2019 2 2 2
Ví dụ 7. Khẳng định nào sau đây đúng? A. 2017 − 2018 ( 5 2) ( 5 2)− + < + . B. 2018 2019 ( 5 + 2) > ( 5 + 2) . C. 2018 2019 ( 5 − 2) > ( 5 − 2) . D. 2018 2019 ( 5 − 2) < ( 5 − 2) . Lời giải Chọn C 0 < 5 − 2 <1 G 2018 2019 ⇒ ( 5 − 2) > ( 5 − 2) ⇒ C đúng. V: < T 2018 2019 RẦN 5 + 2 >1 2017 − 2018 − Đ ⇒ ( 5 + 2) > ( 5 + 2) ⇒ A sai ÌN 2017 − > 2018 − H CƯ 5 + 2 >1 – 2018 2019 ⇒ ( 5 + 2) < ( 5 + 2) ⇒ B sai 083 2018 < 2019 4332133 0 < 5 − 2 <1 2018 2019 ⇒ ( 5 − 2) > ( 5 − 2) ⇒ D sai. 2018 < 2019
Ví dụ 8. Mệnh đề nào dưới đây sai? 2019 2018 A. 2017 2018
( 2 − )1 > ( 2 − )1 . B. 2 2 1− < 1− . 2 2 C. 2018 2017 ( 3 − ) 1 > ( 3 − ) 1 . D. 2 1+ 3 2 > 2 . Lời giải Chọn A 2018 > 2017 2018 2017 Do nên ( 3 − ) 1 < ( 3 − ) 1 . 3 −1 >1
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 15
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
C. GIẢI BÀI TẬP SÁCH GIÁO KHOA
Bài 1. Tính giá trị các biểu thức sau: 2 − a) 3 2 0 .3 .12 ; 4 2 − 2 − b) 1 2 . ; 12 3 c) ( ) 2 2 2 − − ( 5 2 .5 : 5.5− ). Lời giải 2 − a) 3 2 0 1 1 16 ⋅3 ⋅12 = ⋅9⋅1 = ⋅9 = ⋅9 = 16 2 4 9 3 9 16 4 1 − 2 − b) 1 2 1 1 1 9 ⋅ = ⋅ = 12⋅ =12⋅ = 27 2 12 3 1 4 2 4 12 9 3 2 − 2 2 − c) ( ⋅ ) 2 2 2 − − ( 5− ⋅ ) 1 2 1 5 1 2 5 : 5 5 = ⋅ 1 1 16 5 :5⋅ = : 4 4 4 = ⋅5 = ⋅5 = ⋅5 =16 2 5 4 2 5 4 5 2 4 4 2 5 5 5 16 4 G
Bài 2. Viết các biểu thức sau dưới dạng một luỹ thừa (a > 0) : V: T 4 R a) 8 3. 3. 3. 3 ; ẦN ĐÌN b) a a a ; H 3 4 C a. a. a Ư c) . 2 – 3 5 083 ( a) 5.a 4332133 Lời giải 1 1 1 1 1 1 15 1+ + + a) 4 8 2 4 8 2 4 8 8
3⋅ 3 ⋅ 3 ⋅ 3 = 3⋅3 ⋅3 ⋅3 = 3 = 3 1 1 3 3 3 7 7 b) 1+ 1+ 2 2 2
a ⋅ a ⋅ a = a ⋅ a ⋅a = a ⋅ a = a ⋅ a 4 4 4 8
= a ⋅a = a = a = a 1 1 1 1 1 1 13 + + 3 4 13 1 2 3 4 2 3 4 12 ⋅ ⋅ ⋅ ⋅ c) a a a a a a a a 1 − 12 12 = = = = a = a 2 3 2 3 2 + a 5 3 5 5 5 5 5 ( a) ⋅a a ⋅a a
Bài 3. Rút gọn các biểu thức sau (a > 0,b > 0) : 1 1 7 a) 3 2 6 a a a ; 2 1 1 b) 3 4 6 a a : a ; 3 1 1 3 c) 3 − − 1 2 2 2 2
a b − a b . 2 3
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 16
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Lời giải 1 1 7 1 1 7 a) + + 3 2 6 3 2 6 2
a ⋅a ⋅a = a = a 2 1 1 2 1 1 3 b) + − 3 4 6 3 4 6 4
a ⋅a : a = a = a 3 1 1 3 3 1 1 3 c) 3 − − 1 3 1 − + − + 1 2 2 2 2 2 2 2 2 1
a ⋅b − a ⋅b = ⋅ − ⋅ a ⋅b = − a− b 2 3 2 3 2
Bài 4. Với một chỉ vàng, giả sử người thợ lành nghề có thể dát mỏng thành lá vàng rộng 2 1m và dày khoảng 7
1,94.10− m . Đồng xu 5000 đồng dày 3
2,2.10− m . Cần chồng bao nhiêu lá vàng như trên để có độ
dày bằng đồng xu loại 5000đồng? Làm tròn kết quả đến chữ số hàng trăm. Lời giải
Để có độ dày bằng đồng xu loại 5000 đồng ta cần chồng bao nhiêu lá vàng như trên là: ( 3 − ) ( 7
2,2.10 : 1,94.10− ) ≈11300 (lá vàng) t
Bài 5. Tại một xí nghiệp, công thức P(t) 3 1 500. =
được dùng để tính giá trị còn lại ( tính theo triệu 2 G
đồng) của một chiếc máy sau thời gian t ( tính theo năm) kể từ khi đưa vào sử dụng. V: T
a) Tính giá trị còn lại của máy sau 2 năm; sau 2 năm 3 tháng. RẦ
b) Sau 1 năm đưa vào sử dụng, giá trị còn lại của máy bằng bao nhiêu phần trăm so với ban đầu ? N Đ Lời giải ÌN H C 2 Ư 3 1 –
a) Với t = 2 : P(2) = 500⋅ ≈ 314,98 (triệu đồng) 083 2 4332133 2 năm 3 tháng = 2,25 năm. 2,25 3 1
Với t = 2,25: P(2,25) = 500. ≈ 297,3 (triệu đồng) 2 1 b) Với t P( ) 3 1 1: 1 500. = = ≈ 396,85 (triệu đồng) 2
Sau 1 năm đưa vào sử dụng, giá trị còn lại của máy bằng: 396,85:500.100 = 79,37% so với ban đầu.
Bài 6. Biết rằng 10α 2;10β = = 5 . Tính α+β α −β 2α 2 − α β 2 10 ;10 ;10 ;10 ;1000 ;0,01 α a) 16α +16−α ; b) ( α −α + )2 2 2 . Lời giải
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 17
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
10α+β =10α ⋅10β =2⋅5=10 − 10α α β 2 10 = = 10β 5 10 α = (10α )2 2 2 = 2 = 4 2 − α 1 1 10 = = 2 10 α 4 1000 = (10 )β β = (10β )3 3 3 = 5 =125 2α 2α 1 1 1 1 1 1 1 0,01 = = = = = = = 2 100 100 α ( )2α 4 10 α ( α )4 4 2 2 16 10 10
Bài 7. Biết rằng α 1
4 = . Tính giá trị các biểu thức sau: 5 a) 16α +16−α ; b) ( α −α + )2 2 2 . Lời giải 2 a) − 1 + = + = + = + = + = α ( )α α α α 1 (4α α )2 2 1 1 1 626 16 16 16 4 16 ( 4 ) (4α )2 2 2 5 1 25 5 b) GV: T 2 2 2 α −α R α −α α α −α −α 2α 2 − α 2 2 Ầ
(2 +2 ) = (2 ) +2⋅2 ⋅2 +(2 ) = 2 +2+2 = (2 ) +2+(2 ) N Đ α −α α 1 1 1 36 ÌN = 4 + 2 + 4 = 4 + 2 + = + 2 + = H 4α 5 1 5 CƯ 5 – 083
D. BÀI TẬP TRẮC NGHIỆM 4332133 ( a .b )4 4 3 2
Câu 1: Cho a , b là các số thực dương. Rút gọn biểu thức P = được kết quả là 3 12 6 a .b A. 2 ab . B. 2 a b . C. ab . D. 2 2 a b . Lời giải Chọn C ( a .b )4 4 3 2 3 2 Ta có: a .b P = = = . a b . 6 a .b (a .b)6 3 12 6 2 Câu 2: Biểu thức 5 3
T = a a với a > 0 . Viết biểu thức T dưới dạng luỹ thừa với số mũ hữu tỉ là: 3 2 1 4 A. 5 a . B. 15 a . C. 3 a . D. 15 a . Lời giải Chọn D
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 18
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 1 4 4 Ta có 5 3 T = a a 5 5 3 = .aa 3 = a 15 = a . 2
Câu 3: Cho a là số thực dương, khác 1. Khi đó 4 3 a bằng 8 3 A. 3 a . B. 6 a . C. 3 2 a . D. 8 a . Lời giải Chọn B 2 2 1 Ta có 4 3 3.4 6 6
a = a = a = a .
Câu 4: Cho 0 < a ≠ 1. Giá trị của biểu thức P = ( 3 2 log .a a là a ) A. 4 . B. 3 . C. 5 . D. 5 . 3 3 2 Lời giải Chọn C 2 5 Ta có: P = ( 3 2 log .a a 5 3 = log .aa 3 = log a = . a ) a a 3 1
Câu 5: Rút gọn biểu thức 3 6
P = x . x với x > 0 . 1 2 G
A. P = x . B. 8 P = x . C. 9 P = x . D. 2 P = x . V: TR Lời giải ẦN Chọn A ĐÌN 1 1 1 1 1 H 3 6 3 6 2 C
Với x > 0 , ta có P = x .x x + = = x = x . Ư – 3+ 5 083
Câu 6: Tính giá trị của biểu thức 6 A = . 2+ 5 1+ 5 4332133 2 .3 A. 1. B. 5 6− . C. 18 . D. 9 . Lời giải Chọn C 3+ 5 3+ 5 3+ 5 Ta có 6 A 2 .3 = = 3+ 5−2− 5 3+ 5−1− 5 = 2 .3 2 = 2.3 = 18 . 2+ 5 1+ 5 2 .3 2+ 5 1+ 5 2 .3 1
Câu 7: Rút gọn biểu thức 3 4
P = x . x , với x là số thực dương. 1 7 2 2 A. 12 P = x . B. 12 P = x . C. 3 P = x . D. 7 P = x . Lời giải Chọn B 1 1 1 7 3 4 3 4 12
P = x . x = x .x = x .
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 19
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 4 4
Câu 8: Cho x > 0, y > 0 . Viết biểu thức 6 5 5
x . x x về dạng m
x và biểu thức 5 6 5
y : y y về dạng n y .
Tính m − n . A. 11 . B. 8 − . C. 11 − . D. 8 . 6 5 6 5 Lời giải Chọn B
Với x > 0 , y > 0 , ta có 1 4 4 1 6 4 5 1 4 5 1 6 + + 4 5 1 5 5 x . x x 5 5 2 5 6 12 5 6 12
= x . x .x = x .x .x = x ⇒ m = + + . 5 6 12 4 5 6 5
y : y y y = x + 1. Do đó 11 m − n = . 6
Câu 9: Cho a > 0 , b > 0 và x , y là các số thực bất kỳ. Đẳng thức nào sau đúng? x A. ( a + )x x x
a b = a + b . B. x = a . −x b . C. x+y x y a = a + a . D. x
a b = (ab)xy y . b Lời giải Chọn B x x Ta có a a = x . x a b− = . x G b b V: T 3 R 2 5 Ầ
Câu 10: Rút gọn biểu thức P = x . x ? N Đ 4 3 17 13 ÌN A. 7 x . B. 10 x . C. 10 x . D. 2 x . H CƯ Lời giải – 083 Chọn C 4332133 3 3 1 3 1 17 Với x > 0 thì + 2 5 2 5 2 5 10
P = x . x = x .x = x = x . 1 2 2 1
Câu 11: Cho a > 0 , b − 1 a b
> 0 và biểu thức T = 2(a + b) 1 .(ab)2 . 1 + − . Khi đó: 4 b a A. 2 T = . B. 1 T = . C. T = 1. D. 1 T = . 3 2 3 Lời giải Chọn C
Do a > 0 , b > 0 ta có: 1 2 2 2 − a b ab a b ab a − b
T = 2(a + b) .(ab)1 1 1 2 1 2 1 ( ) 2 . 1 + − = . 1+ − 2 + = . 1+ . 4 b a a + b 4 b
a a + b 4 ab 1 (a+b)2 2 2 =
4ab + a − 2ab + b = = 1 . a + b a + b
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 20
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 1 − 3 a (3 3 4 a − a )
Câu 12: Cho hàm số f (a) =
với a > 0,a ≠ 1 . Tính giá trị M = f ( 2016 2017 ) 1 8 a (8 3 8 1 a − a− ) A. 1008 M = 2017 − 1 B. 1008 M = 2017 − − 1 C. 2016 M = 2017 − 1 D. 2016 M = 1− 2017 Lời giải Chọn B 1 − 3 a (3 3 4 a − a ) ( ) 1− a f a = = = 1
− − a nên M = f ( 2016 ) 2016 1008 2017 = 1 − − 2017 = 1 − − 2017 1 − a −1 8 a (8 3 8 1 a − a ) 3+1 2− 3
Câu 13: Rút gọn biểu thức a .a P = với a > 0 ( + a − ) 2 2 2 2
A. P = a B. 3 P = a C. 4 P = a D. 5 P = a Lời giải Chọn D 3+1 2− 3 3 Ta có a .a a 5 P = = = a ( + − 2 −2 ) 2 2 2 4 a a GV: T 1 1 R 3 3 Ầ a b + b a m n N
Câu 14: Cho hai số thực dương a,b. Rút gọn biểu thức A =
ta thu được A = a .b . Tích 6 6 Đ a + b ÌN H của . m n là CƯ – A. 1 B. 1 C. 1 D. 1 083 8 21 9 18 4332133 Lời giải Chọn C 1 1 1 1 1 1 1 1 1 1 3 3 6 6
a .b b + a 1 1 3 3 3 2 3 2
a b + b a a .b + b .a 1 1 3 3 A = = =
= a .b ⇒ m = , 1 n = ⇒ . m n = . 6 6 1 1 1 1 a + b 3 3 9 6 6 6 6 a + b a + b m
Câu 15: Cho biểu thức 5 3 8 2 2 2 n =
, trong đó m là phân số tối giản. Gọi 2 2
P = m + n . Khẳng định n nào sau đây đúng?
A. P ∈(330;340).
B. P ∈(350;360).
C. P ∈(260;370).
D. P ∈(340;350). Lời giải Chọn D 3 1 1 3 1 1 11 Ta có 5 3 5 3 3 + + 5 10 30 5 10 30 15 8 2 2 = 2 2 2 = 2 .2 .2 = 2 = 2
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 21
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com m 11 m = 11 2 2 2 2 ⇒ = ⇒
⇒ P = m + n = 11 + 15 = 346 . n 15 n = 15 11 3 7 3 m
Câu 16: Rút gọn biểu thức a .a A =
với a > 0 ta được kết quả n
A = a trong đó m,n *
∈ N và m là 4 7 5 a . a− n
phân số tối giản. Khẳng định nào sau đây đúng? A. 2 2 m − n = 312 . B. 2 2 m + n = 543. C. 2 2 m − n = 312 − . D. 2 2 m + n = 409. Lời giải Chọn A 11 7 11 3 7 3 3 3 6 19 Ta có: a .a a .a a 7 A = = = = a 5 − 23 4 7 5 a . a− 4 7 7 a .a a m Mà n
A = a , m,n *
∈ N và m là phân số tối giản 2 2
⇒ m = 19,n = 7 ⇒ m − n = 312 n x −x Câu 17: Cho 4x − −
+ 4−x = 2 và biểu thức 4 2 2 a A = = . Tích .
a b có giá trị bằng: 1+ 2x + 2−x b A. 6 . B. 10 − . C. 8 − . D. 8 . Lời giải Chọn A 2 2 x −x x −x x −x x −x x −x G
Ta có: 4 + 4 = 2 ⇔ (2 ) + (2 ) + 2.2 .2 = 4 ⇔ ( + )2 2 2 = 4 ⇔ 2 + 2 = 2 V: TR x −x Ầ x −x 4 − (2 + − − 2 4 2 2 ) 4−2 2 a N Ta có: A = = = = = . Đ 1+ 2x + 2−x 1+ 2x + 2−x 1+ 2 3 b ÌN ( ) H CƯ a = 2 Suy ra: ⇒ . a b = 2.3 = 6 . – = 083 b 3 4332133 4 1 − 2 3 3 3
a a + a
Câu 18: Cho a là số thực dương. Đơn giản biểu thức P = . 1 3 1 − 4 4 4
a a + a
A. P = a(a +1) .
B. P = a −1.
C. P = a .
D. P = a + 1. Lời giải Chọn C 4 1 − 2 3 3 3 + 4 1 − 4 2 a a a 3 3 3 3 2
a .a + a a a + a a(a +1) P = = = = = a . 1 3 1 − 1 3 1 1 − a + 1 a + 1 4 4 4 4 4 4 4
a a + a a .a + a .a
Câu 19: Cho biểu thức 3 4 3
P = x x x , với x > 0 . Mệnh đề nào dưới đây đúng? 1 7 5 7 A. 2 P = x B. 12 P = x 8 24
C. P = x
D. P = x
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 22
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Lời giải Chọn C 1 1 1 7 1 1 1 7 5 Ta có : 3 4 3 3 2 4 3 2 4 3 3 24 8 P = x x x = [ ( x x .x ) ] = [ (
x x ) ] = x .x =x 1 2 2017 Câu 20: Tích ( ) 1 1 1 2017 ! 1 1 ...1 + + +
được viết dưới dạng b
a , khi đó (a, b) là cặp nào 1 2 2017 trong các cặp sau? A. (2018; 2017) . B. (2019; 2018) . C. (2015; 2014) . D. (2016; 2015) . Lời giải Chọn A 1 2 2017 1 2 2016 2017 Ta có ( ) 1 1 1 (
) 2 3 2017 2018 2017 ! 1 1 ... 1 2017 ! ... + + + = 1 2 2017 1 2 2016 2017 = ( ) 2017 1 1 1 1 2018 2017 ! . . ... . 2017 = 2018 . Vậy a = 2018; 2017 b = . 1 2 3 2016 2017 1 1 1+ + m Câu 21: Cho 2 2 ( +1) ( ) = 5 x x f x
. Biết rằng: (1). (2)... (2020) 5n f f f =
với m,n là các số nguyên dương và
phân số m tối giản. Tính 2 m − n n A. 2 m − n = 2021. B. 2 m − n = 1 − . C. 2 m − n = 1 . D. 2
m − n = 2020 . GV Lời giải : TR Chọn B ẦN 2 2 2 2 + + + + 2 1 1
x (x 1) x (x 1) Đ x +x+1 1+ + 1 1 2 2 2 2 1+ − ÌN Ta có: x (x+1) x (x+1) x(x+1) x x+1 f (x) = 5 = 5 = 5 = 5 . H CƯ 2020 1 1 m ∑1 + − m 2020 – x x+1 1 1 m = n x 1 n 083
Do đó: f (1). f (2)... f (2020) = 5 ⇔ 5 = 5 ⇔ ∑ 1+ − = . x=1 x x + 1 n 4332133 1 4084440 m 2 ⇔ 2021− = =
⇒ m = 4084440 = 2021 −1,n = 2021. 2021 2021 n Vậy: 2 m − n = ( 2 − ) 2 2021 1 − 2021 = 1 − . 3
Câu 22: Cho m > 0 , a = m m , m y =
. Mệnh đề nào dưới đây đúng? 2 4 a . m A. 1 y 1 1 1 = . B. y = . C. y = . D. y = . 18 35 a 2 a 9 34 a 6 11 a Lời giải Chọn A 1 1 1 3 1 3 1 1 . 3 13 12 18 m m m a 1 2 18 2 18 12
a = m m = m ⇒ a = m = m , y = = = = = . 2 4 1 2 2 18 35 a . m 2 a a 4 . a a m
Câu 23: Biểu thức C = x x x x x với x > 0 được viết dưới dạng lũy thừa số mũ hữu tỉ là
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 23
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 3 7 15 31 A. 16 x . B. 8 x . C. 16 x . D. 32 x . Lời giải Chọn D Với x > 0 ta có 2 C = x x x x x 4 2
⇔ C = x .x x x x 8 4 2
⇔ C = x .x .x x x 31 16 8 4 2
⇔ C = x .x .x .x x 32 16 8 4 2
⇔ C = x .x .x .x .x 32 31 ⇔ C = x 32 ⇔ C = x . 7 3 5 3 m
Câu 24: Rút gọn biểu thức a .a A =
với a > 0 ta được kết quả n
A = a , trong đó m , *
n∈ và m là 4 7 2 a . a− n
phân số tối giản. Khẳng định nào sau đây đúng? A. 2 2 m − n = 25 . B. 2 2 m + n = 43 . C. 2 3m − 2n = 2 . D. 2 2m + n = 15 . Lời giải Chọn D 7 5 7 3 5 3 3 3 5 7 2 2 m = 2 Ta có: a .a A = a .a = 4 3 3 7 a + − + = 7 = a ⇒ 2
⇒ 2m + n = 15 . 4 7 2 a . a− 2 − n = 7 4 7 a .a 7 2 − 6 3
Câu 25: Cho a,b là hai số thực dương. Thu gọn biểu thức a .b , kết quả nào sau đây là đúng? 6 2 ab G 4 V a 3 : A. . B. ab . C. b . D. a . T R b a b ẦN Lời giải ĐÌNH Chọn D CƯ 7 2 7 2 − − – 6 3 6 3 a .b a .b − a 1 1 083 Ta có: = = a .b = . 1 1 6 2 ab b 4332133 6 3 a .b Câu 26: 2 2 2 P =
. Mệnh đề nào trong các mệnh đề sau là đúng? Cho biểu thức 3 3 3 3 3 1 18 1 1 A. 8 2 18 2 P 2 2 = 2 . B. P = . C. P = . D. P = . 3 3 3 3 Lời giải Chọn D 3 3 1 3 1 . +1 2 2 3 2 2 Ta có: 2 2 2 2 2 2 2 2 3 3 P = 3 3 = 3 3 = = = . 3 3 3 3 3 3 3 3
Câu 27: Cho a là số dương khác 1. Khẳng định nào sau đây là đúng? 2019 2019 A. 2019 − 2019 a = a . B. 2019 − 1 a = − . C. 2019 − 1 a = . D. 2019 − 2019 a = −a . a a Lời giải
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 24
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Chọn C 2019 Ta có: 2019 − 1 1 a = = . 2019 a a ( a .b )4 4 3 2
Câu 28: Cho a , b là các số thực dương. Rút gọn biểu thức P = được kết quả là 3 12 6 a .b A. ab . B. 2 2 a b . C. 2 ab . D. 2 a b . Lời giải Chọn A ( a .b )4 4 3 2 3 2 Ta có: a .b P = = = ab . 6 a .b (a .b)6 3 12 6 2 1 1
Câu 29: Cho biểu thức 2 3 6
P = x .x . x với x > 0 . Mệnh đề nào dưới đây đúng? 11 7 5
A. P = x B. 6 P = x C. 6 P = x D. 6 P = x Lời giải Chọn A 1 1 1 1 1 + + 2 3 6 2 3 6
P = x .x . x = x = x GV 3 : T
Câu 30: Cho a là số thực dương. Viết và rút gọn biểu thức 2018 2018 a .
a dưới dạng lũy thừa với số mũ RẦN
hữu tỉ. Tìm số mũ của biểu thức rút gọn đó. ĐÌN 3 H A. 2 . B. 1 . C. 3 . D. . 2 C 1009 1009 1009 2018 Ư – Lời giải 083 4332133 Chọn A 3 3 1 4 2 2018 2018 2018 2018 2018 1009 a . a = a .a = a = a
. Vậy số mũ của biểu thức rút gọn bằng 2 . 1009
Câu 31: Cho số thực a > 1 và các số thực α , β . Kết luận nào sau đây đúng?
A. aα > 1, α ∀ ∈ .
B. aα > aβ ⇔ α > β . C. 1 < 0, α ∀ ∈ .
D. aα < 1, α ∀ ∈ . aα Lời giải Chọn B
Với a > 1 và α , β ∈ . Ta có: aα > aβ ⇔ α > β . Câu 32: Cho α β
π > π . Kết luận nào sau đây đúng? A. α.β = 1. B. α > β . C. α < β . D. α + β = 0 . Lời giải Chọn B
Vì π ≈ 3,14 > 0 nên α β π > π ⇔ α > β.
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 25
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Câu 33: Với các số thực a , b bất kì, mệnh đề nào sau đây đúng? A. (3 )b a = 3a+b . B. (3 )b a 3ab = . C. (3 )b a = 3a−b . D. (3 )b a 3 ba = . Lời giải Chọn B a a 5 4
Câu 34: Cho a,b là các số thực thỏa điều kiện 3 4 > và 4 3
b > b .Chọn khẳng định đúng trong các 4 5 khẳng định sau?
A. a > 0 và b > 1.
B. a > 0 và 0 < b < 1 .
C. a < 0 và 0 < b < 1 .
D. a < 0 và b > 1. Lời giải Chọn C a a Vì 3 4 > ⇒ a < 0 . 4 5 5 4 Và 4 3
b > b ⇒ 0 < b < 1.
Câu 35: Cho a thuộc khoảng 2 0;
, α và β là những số thực tuỳ ý. Khẳng định nào sau đây là sai? e
A. (aα )b α. a β = .
B. aα > aβ ⇔ a < β . C. aα .aβ = aα+β .
D. aα > aβ ⇔ α > β . GV: Lời giải T RẦ Chọn D N ĐÌN 2 a 0; ∈ ⇒ Hàm số x
y = a nghịch biến.Do đó aα > aβ ⇔ α < β . H e CƯ –
Vậy đáp án sai là D . 083
Câu 36: Trong các khẳng định sau, khẳng định nào sai? 4332133 2017 2018 2018 2017
A. ( 2 −1) > ( 2 −1) .
B. ( 3 −1) > ( 3 −1) . 2018 2017 C. 2 2 2 +1 3 2 > 2 . D. 1− < 1− . 2 2 Lời giải Chọn B 2017 2018 +) 0 < 2 −1 < 1
⇒ ( 2 −1) > ( 2 −1) nên A đúng. 2017 < 2018 2018 2017 +) 0 < 3 −1 < 1
⇒ ( 3 −1) < ( 3 −1) nên B sai. 2018 > 2017 2 > 1 +) 2 +1 3 ⇒ 2 > 2 nên C đúng. 2 + 1 > 3
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 26
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 2 2018 2017 +) 0 < 1− < 1 2 2 2 ⇒ 1− < 1− nên D đúng. 2018 2 2 > 2017
Câu 37: Cho các số thực a; b thỏa mãn 0 < a < 1 < b. Tìm khẳng định đúng:
A. lna > lnb .
B. (0,5)a (0,5)b < .
C. log b < 0. D. 2a 2b > . a Lời giải Chọn B
Do cơ số e ∈(1;+∞) và 0 < a < b nên ta có lna < lnb . Đáp án A sai.
Do cơ số 0,5∈(0;1) và 0 < a < b nên ta có (0,5)a (0,5)b > . Đáp án B sai.
Do cơ số a∈(0;1) và b > 1 nên ta có log b < log 1 ⇔ log b < 0 . Đáp án C đúng. a a a
Do cơ số 2∈(1;+∞) và a < b nên ta có 2a 2b < . Đáp án D sai.
Câu 38: Khẳng định nào sau đây đúng? A. 2017 − 2018 ( 5 2) ( 5 2)− + < + . B. 2018 2019 ( 5 + 2) > ( 5 + 2) . C. 2018 2019 ( 5 − 2) > ( 5 − 2) . D. 2018 2019 ( 5 − 2) < ( 5 − 2) . Lời giải Chọn C G 0 < 5 − 2 < 1 V 2018 2019 ⇒ − > − ⇒ : ( 5 2) ( 5 2) C đúng. T 2018 < 2019 RẦN Đ 5 + 2 > 1 ÌN 2017 − 2018 ⇒ ( 5 + 2) > ( 5 + 2)− ⇒ A sai H 2017 − > 2018 − CƯ – + > 083 5 2 1 2018 2019 ⇒ ( 5 + 2) < ( 5 + 2) ⇒ B sai 4332133 2018 < 2019 0 < 5 − 2 < 1 2018 2019 ⇒ ( 5 − 2) > ( 5 − 2) ⇒ D sai. 2018 < 2019
Câu 39: Khẳng định nào dưới đây là đúng? 3 3 −π −π 2 50 − 100 A. 3 5 > 1 . B. 1 1 < . C. − 2 1 3 < . D. < ( 2) . 7 8 2 3 5 4 Lời giải Chọn B Ta có: 3 3 3 5 3 5 < ⇒ < . Phương án A sai. 7 8 7 8 1 1 1 −π 1 −π > ⇒ <
. Phương án B đúng. 2 3 2 3
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 27
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 2 − 2 − 2 − 2 1 3 5 3 5 3 < ⇒ > ⇒ > . Phương án C sai. 5 50 1 − < ( 2)100 ⇒ (2 ) 50 − − < (2)100 2 100 100 ⇒ 2 <
2 . Phương án D sai. 4
Câu 40: Trong các mệnh đề sau, mệnh đề nào sai? 2019 2018 A. 2+1 3 2 2 2 > 2 . B. 1− < 1− . 2 2 2017 2018 2018 2017
C. ( 2 −1) > ( 2 −1) .
D. ( 3 −1) > ( 3 −1) . Lời giải Chọn D
A đúng vì 2 > 1 và 2 + 1 > 3 nên 2+1 3 2 > 2 . 2019 2018 B đúng vì 2 2 2 1− < 1
và 2019 > 2018 nên 1− < 1− . 2 2 2 2017 2018
C đúng vì ( 2 −1) < 1 và 2017 < 2018 nên ( 2 −1) > ( 2 −1) . 2018 2017
D sai vì 3 −1 < 1 và 2017 < 2018 nên ( 3 −1) < ( 3 −1) . GV: T Câu 41: 3 3
P = x + x y + y + x y và 3 Q = 2 x + y
, với x , y là các số thực khác 0 R Cho 2 4 2 2 2 4 ( )3 3 2 2 ẦN Đ
. So sánh P và Q ta có ÌN H < = = − > A. P Q . B. P Q . C. P Q . D. P Q . CƯ Lời giải – 083 Chọn A 4332133 Ta có 2 x , 2 y , 3 4 2 x y , 3 2 4
x y là những số thực dương. Q = ( 3 2 x + y )3 3 2 2 2 3 4 2 3 2 4 2
= 2 x + 3 x y + 3 x y + y 2 3 4 2 3 2 4 2 2 3 4 2 3 2 4 2
= x + 3 x y + 3 x y + y + x + 3 x y + 3 x y + y 2 3 4 2 3 2 4 2
> x + 3 x y + 3 x y + y 2 3 4 2 3 2 4 2 > x + x y +
x y + y = P
Vậy P < Q .
Câu 42: Tìm tập tất cả các giá trị của a để 21 5 7 2 a > a ? A. a > 0 .
B. 0 < a < 1 . C. a > 1. D. 5 2 < a < . 21 7 Lời giải Chọn B 7 2 21 6
a = a . Ta có 21 5 7 2 21 5 21 6
a > a ⇔ a > a mà 5 < 6 vậy 0 < a < 1 .
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 28
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Câu 43: Tìm khẳng định đúng. 2016 2017 2016 2017
A. (2 − 3) > (2 − 3) .
B. (2 + 3) > (2 + 3) . 2016 − 2017 − 2016 − 2017 − C. −(2 + 3) > −(2 + 3) . D. (2 − 3) > (2 − 3) . Lời giải Chọn A 2016 2017
Có 0 < 2 − 3 < 1 ⇒ (2 − 3) > (2 − 3) .
Câu 44: Cho a > 1. Mệnh đề nào dưới đây là đúng. 3 2 1 A. a 1 1 − 1 > 1 B. < C. 3 a > D. 3 a > a a 2017 2018 a a 5 a Lời giải Chọn C Ta có : − 3 1 a 1 1 > ⇔ > 3 5
⇔ a < a luôn đúng với a > 1. 5 a 3 5 a a 1 1
Câu 45: Cho biết (x − )− − 3 > (x − ) 6 2 2
, khẳng định nào sau đây đúng?
A. 2 < x < 3 .
B. 0 < x < 1. C. x > 2 . D. x > 1. Lời giải GV Chọn A : TR − > ⇔ > Ầ Điều kiện: x 2 0 x 2 . N Đ 1 1 − − ÌN Ta có 1 1
− < − nên (x − ) 3 > (x − ) 6 2 2
⇔ x − 2 < 1 ⇔ x < 3 . Vậy 2 < x < 3 . H 3 6 CƯ U = V = W = X = Y = – Câu 46: Cho 2020 2.2019 , 2020 2019 , 2019 2018.2019 , 2019 5.2019 và 2019 2019 . Số nào 083
trong các số dưới đây là số bé nhất? 4332133
A. X −Y .
B. U − V .
C. V − W .
D. W − X . Lời giải Chọn C Ta có: 2019 X −Y = 4.2019 . 2020 2019 U − V = 2019 = 2019.2019 . 2019 2019 2019
V − W = 2019.2019 − 2018.2019 = 2019 . 2019
W − X = 2013.2019 .
Vậy trong các số trên, số nhỏ nhất là V − W . a b
Câu 47: Tìm tất cả các số thực m sao cho 4 4 +
= 1 với mọi a + b = 1. 4a + 4b m + m A. m = 2 ± . B. m = 4. C. m = 2. D. m = 8 . Lời giải Chọn A
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 29
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com a b
Ta có a + b = 1 ⇔ b = 1− a . Thay vào 4 4 + = 1 ta được 4a + 4b m + m a 1−a a 1 4 4 4 + .4 m + 4 + .4 −a m 2 + = 1 ⇔
= 1 ⇔ m = 4 ⇔ m = 2 ± . a 1−a a 1−a 2 4 + m 4 + m 4 + .4 m + .4 m + m
Câu 48: Gọi x ,x là hai nghiệm của phương trình: 2
x − 6x + 1 = 0 với x > x . Tính giá trị của biểu thức 1 2 1 2 2017 2018 P = x .x 1 2 A. P = 1 B. P = 3 + 2 2
C. P = 3 − 2 2 D. P = ( − )17 3 2 2 Lời giải Chọn C x + x = 6 Ta có 2017 2017 2018 P = x .x = x .x
.x . Theo định lý viet: 1 2 ⇒ P = x 1 2 ( 1 2) 2 2 x .x = 1 1 2 x = 3 + 2 2 Ta có 2 1
x − 6x + 1 = 0 ⇔ ⇒ P = 3 − 2 2 . x = 3 − 2 2 2 2017 2018
Câu 49: Rút gọn biểu thức 3 3 P 9 80 3 9 80 = + ⋅ − + . A. P = 1. B. 3 P = 9 + 80 . C. 3 P = 9 − 80 . D. 4035 3 P 9 80 = + . G V: TR Lời giải ẦN Chọn C ĐÌNH + + − Đặt 3 3 x = 9 80 9 80 ta có CƯ 2 2 – 3 3 3 3 3 083
x = 9 + 80 + 3. 9 + 80 . 9 − 80 + 3. 9 + 80. 9 − 80 + 9 − 80 4332133 3 3 3 3 18 3. 9 80 . 9 80 . 9 80 9 80 = + + − + + − 3 3 = 18 + 3 .
x 9 + 80 . 9 − 80 = 18 + 3x ⇒ x = 3 3 3 ⇒ 3 − 9 + 80 = 9 − 80 2017 2018 2017 2018 Ta có 3 3 P 9 80 3 9 80 = + ⋅ − + 3 3 = 9 80 9 − 80 + ⋅ 2017 3 3 3 = 9 + 80 . 9 − 80
⋅ 9 − 80 = (3 1)2017 3⋅ 9 − 80 3 = 9 − 80 2018 2017
Câu 50: Tính giá trị của biểu thức P = (7 + 4 3) .(7 − 4 3) A. 1. B. 7 − 4 3 . C. 7 + 4 3 . D. ( + )2017 7 4 3 . Lời giải Chọn C 2018 2017 2017
Ta có P (7 4 3) .(7 4 3) (7 4 3 ).(7 4 3 ) = + − = + − (7+4 3)=
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 30
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 2017 = 1 (7+4 3)=7+4 3. GV: TRẦN ĐÌNH CƯ – 083 4332133
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 31
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Bài 2. PHÉP TÍNH LÔGARIT
A. KIẾN THỨC CƠ BẢN CẦN NẮM
Thang Richter được sử dụng để đo độ lớn các trận động đất. Nếu máy đo địa chấn ghi được
biên độ lớn nhất của một trận động đất là 10M A = μm ( 6
1μm = 10− m)thì trận động đất đó có độ lớn bằng
M độ Richter. Người ta chia các trận động đất thành các mức độ như sau:
Biên độ lớn nhất Độ Richter Mức độ
Mô tả ảnh hưởng (μm) 2,9 ≤ 10 ≤ 2,9 rất nhỏ Không cảm nhận được 3 3,9 10 −10 3,0 − 3,9 nhỏ
Cảm nhận được, không gây hại 4 4,9 10 −10 4,0 − 4,9 nhẹ
Đồ đạc rung chuyển, thiệt hại nhỏ 5 5,9 10 −10 5,0 − 5,9
trung bình Gây thiệt hại với kiến trúc yếu 6 6,9 10 −10 6,0 − 6,9 mạnh
Gây thiệt hại tương đối nặng đối với vùng đông dân cư 7 7,9 10 −10 7,0 − 7,9 rất mạnh
Tàn phá nghiệm trọng trên diện tích lớn 8 ≥ 10 ≥ 8,0
cực mạnh Tàn phá cực kì nghiệm trọng trên diện tích lớn
(Theo Britannica)
Đo độ lớn của động đất theo thang Richter có ý nghĩa như thế nào? Lời giải
Theo thang Richter, độ Richter càng lớn thì động đất càng mạnh
1. Khái niệm lôgarit
Độ lớn M (theo độ Richter) của một trận động đất được xác định như .
a) Tìm độ lớn theo thang Richter của các trận động đất có biên độ lớn nhất lần lượt là 3,5 4,3
10 μm;100000 μm;100.10 μm .
b) Một trận động dất có biên độ lớn nhất A = 65000μm thì độ lớn M của nó phải thoả mãn hệ thức nào? Lời giải a) Khi 3,5 A =10 thì M = 3,5 Khi 5
A =100000 =10 thì M = 5
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 1
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Khi 4,3 2 4,3 2+4,3 6,3
A =100⋅10 =10 ⋅10 =10 =10 thì M = 6,3
b) Khi A = 65000 , ta có: A >10000 hay 4
A >10 . Suy ra M > 4 A <100000 hay 5
A <10 . Suy ra M < 5 Suy ra 4 < M < 5
Cho hai số thực dương a,b với a ≠ 1. Số thực α thoả mãn đẳng thức aα = b được gọi là
lôgarit cơ số a của b và kí hiệu là log b . a log b aα α = ⇔ = b . a
Ví dụ 1. Viết các đẳng thức luỹ thừa sau thành đẳng thức lôgarit: a) 5 3 = 243; b) 2 − 1 10 = ; 100 c) ( )0 3 =1. Lời giải a) 5 3 = 243 ⇒ log 243 = 5 ; 3 b) 2 − 1 1 10 = ⇒ log = 2 − ; 10 100 100
c) ( 3)0 =1⇒ log 1= 0. 3 Chú ý
a) Biểu thức log b chỉ có nghĩa khi > ≠ và . a a 0,a 1 b > 0
b) Từ định nghĩa lôgarit, ta có: • log = a 1 0; ( ) 1 • log a = a 1; (2) • log b a = b a ; (3) • loga b a = ; b (4)
Hai công thức (3) và (4) cho thấy phép lấy lôgarit và phép nâng lên luỹ thừa là hai phép hoàn toàn ngược nhau. Ví dụ 2. Tính a) 1 log ; 2 4 b) log35 9 . Lời giải a) 1 2 log log 2− = = 2 − 2 2 4 b) log 5 = ( 2 )log35 2 3 2log3 5 = = ( log35 ) 2 9 3 3 3 = 5 = 25 .
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 2
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Tính a) 3 log 3 ; 3 b) log 8 ; 1 2 log5 4 c) 1 . 25 Lời giải 1 a) 3 1 3 log 3 = log 3 = 3 3 3 3 − b) 3 1 1 log 8 log 2 log log = = = = 3 − 1 1 1 3 − 1 2 2 2 2 2 2 log5 4 c) 1 = ( 2 5 )log54 = ( 2 log − − − 1 5 4 5 ) 2 = 4 = 25 16
2. Tính lôgarit bằng máy tính cầm tay
Sử dụng máy tính cầm tay, ta có thể tính nhanh giá trị của các lôgarit ( thường cần lấy giá trị
gần đúng bằng cách làm tròn đến hàng nào đó). Chú ý
a) Lôgarit cơ số 10 được gọi là lôgarit thập phân. Ta viết log N hoặc lg N thay cho log N . 10
b) Lôgarit cơ số e còn được gọi là lôgarit tự nhiên. Ta viết ln N thay cho log N . e
Ví dụ 3. Sử dụng máy tính cầm tay, tính giá trị các biểu thức sau ( làm tròn kết quả đến chữ số thập phân thứ sáu): a) log 5 ; 3 b) log 0,2 ; c) ln10. Lời giải
a) Ấn lần lượt các phím
ta được kết quả log 5 ≈1,464974 . 3
b) Ấn lần lượt các phím
ta được kết quả log 0,2 ≈ 0 − ,698970.
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 3
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
c) Ấn lần lượt các phím
ta được kết quả ln10 ≈ 2,302585.
Luyện tập 2. Sử dụng máy tính cầm tay, tính giá trị các biểu thức sau ( Làm tròn kết quả đến chữ số thập phân thứ sáu): 3
a) log 0,5 ; b) log 25 ; c) ln . 5 2 Lời giải a) log 0,5 = 0 − ,430676 5 b) log25 =1,397940 c) 3 ln = 0,405465 2
3. Tính chất của phép tính lôgarit.
HĐ 2. Cho các số thực dương a, M , N với a ≠ 1. Bạn Quân đã vẽ sơ đồ và tìm ra công thức biến đổi biểu
thức log MN như sau: a ( )
a) Giải thích cách làm của bạn Quân. M
b) Vẽ sơ đồ tương tự để tìm công thức biến đổi cho log M α α ∈ a và log . a ( ) N Lời giải
a) Áp dụng công thức logab a = b , ta có: logaM log = ; a N a M a = N nên logaM logaN logaM logaN MN a a a + = ⋅ = Mặt khác logaMN a = MN
Suy ra: logaM+logaN logaMN a = a ⇔ log M + N = MN a loga loga b)
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 4
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Tổng kết hoạt động trên, ta nhận được các tính chất:
Cho các số thực dương a, M , N với a ≠ 1, ta có: ● log MN = M + N a ( ) loga loga M ● log = M − N a loga loga N ● log M α = α M α ∈ a loga ( )
Chú ý: Đặc biệt, a, M , N với dương, a ≠ 1, ta có: 1 n 1 ● log = − N log M = M ∈ a log a loga ; ● với n N *. N a n
Ví dụ 4. Tính giá trị biểu thức sau: 2 a) log + log 12 2 2 log 9 .3 log 25 2 2 ; b) ; c) 3 . 3 ( ) 3 5 Lời giải 2 2 a) 3 log + log 12 = log .12 = log 2 = 3log 2 = 3.1 = 3 2 2 2 2 2 . 3 3 b) log ( 2 2 9 .3 ) 2 2 2
= log 9 + log 3 = 2log 3 + 2log 3 = 2.2.log 3+ 2 = 4 + 2 = 6. 3 3 3 3 3 3 1 2 c) 3 2 2 2 3 3
log 25 = log 25 = log 5 = log 5 = .1 = . 5 5 5 5 3 3 3
Ví dụ 5. Trong hóa học, nồng độ pH của một dung dịch được tính theo công thức pH= - log[H+], trong đó
[H+] là nồng độ H+( ion hydro) tính bằng mol/L. Các dung dịch có độ pH bé hơn 7 thì gọi là acid, có pH
lớn hơn 7 thì có tính kiềm, có pH bằng 7 thì trung tính.
a) Tính độ pH của dung dịch có nồng độ H+ là 0,0001 mol/L. Dung dịch này có tính acid, kiềm hay trung tính ?
b) Dung dịch A có nồng độ H+ gấp đôi nồng độ H+ của dung dịch B. Độ pH của dung dịch nào lớn hơn và
lớn hơn bao nhiêu ? Làm tròn kết quả đến hàng nghìn. Lời giải
a) pH = -log0,0001 = - log 10-4 = 4log10=4. Do 4 < 7 nên dung dịch có tính acid.
b) Kí hiệu pHA , pHB lần lượt là độ pH của hai dung dịch A và B ; [H+]A ,[H+]B lần lượt là nồng độ của
hai dung dịch A và B. Ta có
pHA = - log[H+]A = - log(2[H+]B) = - log2 – log[H+]B = -log2 +pHB.
Suy ra pHA – pHB = log2 ≈ 0,301.
Vậy dung dịch B có độ pH lớn hơn và lớn hơn khoảng 0,301.
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 5
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 1
Luyện tập 3. Tính: a) log 4 + log − 5 5
; b) log 28 log 7 ; c) log 1000 . 4 2 2 Lời giải a) 1 1 log 4 log log 4 + = ⋅ = log 1 = 0 5 5 5 5 4 4
b) log 28 − log 7 = log (28: 7) 2 = log 4 = log 2 = 2 2 2 2 2 2 1 c) 1 1 1 3 2 3
log 1000 = log1000 = log1000 = log10 = ⋅3 = 2 2 2 2
Vận dụng: Độ lớn M của một trận động đất theo thang Richter được tính theo công thức = log A M , A0
trong đó A là biên độ lớn nhất ghi được bởi máy đo địa chấn, A0 là biên độ chuẩn được sử dụng để hiệu
chỉnh độ lệch gây ra bởi khoảng cách của máy đo địa chấn so với tâm chấn ( ở ► và ◙1, A0 = 1μm ) .
a) Tính độ lớn của trận động đất có biên độ A bằng i) 5,1 10 A 65000A 0 ; ii) . 0
b) Một trận động đất tại địa điểm N có biên độ lớn nhất gấp ba lần biên độ lớn nhất của trận động đất tại
địa điểm P. So sánh độ lớn của hai trận động đất. Lời giải a) 5,1 i) Khi 5,1
A =10 A . Ta có: 10 A0 5,1 M = log = log10 = 5,1 (Richter) 0 A0
ii) Khi A = 65000A . Ta có: 65000A0 M = log = log65000 = 4,8 (Richter) 0 A0
b) Trận động đất tại điểm P có biên độ lớn nhất là A thì trận động đất tại N có biên độ lớn nhất là 3 A
Ta có độ lớn của hai trận động đất là: A 3A M = M = P log ; N log A A 0 0
Độ lớn trận động đất tại N lớn hơn độ lớn trận động đất tại P là: 3A 3A A A0 M − M = − = = = N P log log log log3 0,5 (Richter) A A A 0 0 A0
4. Công thức đổi cơ số
HĐ 3. Khi chưa có máy tính, người ta thường tính các logarit dựa trên bảng giá trị logarit thập phân đã
được xây dựng sẵn. Chẳng hạn, để tính x = log 15, người ta viết 2x =15, rồi lấy logarit thập phân hai 2 log15
vế, nhận được x log 2 = log15 hay x = . log 2
Sử dụng cách làm này, tính log N theo log a và log N với a, N > 0,a ≠ 1. a Lời giải
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 6
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Ta có x = log N = a hay x a N
Lấy lôgarit thập phân 2 vế, ta được x loga = logN . Suy ra logN x = loga Suy ra log log N N = a loga
Với cách làm như ở HĐ 3, ta nhận được công thức đổi cơ số. log N
Cho các số dương a,b, N (a ≠ 1,b ≠ 1) , ta có log b N = a . log a b Đặc biệt, ta có: 1 1 • log N = N ≠ log α α N = log N ≠ . a a 0 a ( )1; • ( ) log a α N
Ví dụ 6. Tính các giá trị của biểu thức: 1 a) log 27 ; b) log 3.log . 9 2 3 4 Lời giải 3 3 3 a) 3
log 27 = log 3 = log 3 = .1 = ; 2 9 3 3 2 2 2 1 log2 1 b) 4 2 log 3.log log 3. log 2− = = = 2 − log 2 = 2.1 − = 2 − 2 3 2 2 2 . 4 log 3 2
Ví dụ 7. Đặt log 3 = a,log 5 = b . Biểu thị log 10 theo a và b . 2 2 9 Lời giải log 10 log 2.5 log 2 + log 5 1+ b 2 2 ( ) 2 2 log 10 = = = = 9 . 2 log 9 log 3 2log 3 2a 2 2 2
HĐ 4. Tính giá trị các biểu thức sau: a) log 8 1 ; b) log 5.log 6.log 8 . 4 5 6 4 Lời giải 3 − a) log 8 log 2 3 3 2 2 log 8 = = = = 1 2 1 log 2− 2 − 2 4 2 log2 4 3 b) log 5 log 6 log 8 log 8 log 2 3 2 2 2 2 2 log 5⋅log 6⋅log 8 = ⋅ ⋅ = = = 4 5 6 2 log 4 log 5 log 6 log 4 log 2 2 2 2 2 2 2
HĐ 5. Đặt log 2 = a,log 7 = b . Biểu thị log 21 theo a và b . 3 3 12 Lời giải
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 7
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com log 21 log 7.3 3 ( ) log 3+ log 7 1+ b 3 ) log 21 = = = = log 12 log 2 .3 2log 2 + log 3 2a +1 3 ( ) 3 3 12 2 3 3 3
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
Dạng 1. Rút gọn biểu thức 1. Phương pháp
• Sử dụng tư duy tự luận: Kết hợp nhiều tính chất và công thức • Sử dụng Casio
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1. (Trường THPT Lê Quý Đôn – Hà Nội năm 2017) Rút gọn biểu thức 5 3
A log a a a a = với a
a > 0,a ≠ 1 ta được kết quả nào sau đây? A. 7 . B. 5. C. 4 . D. 2. 4 3 3 Lời giải Chọn A Cách 1. Tự luận 1 3 7 Ta có 5 5 5 3 3 7 = = 2 3 4 4
A log a a a a a a a a = a a a = a = a loga . loga . . loga . 4 Cách 2. Casio Nhập 5 3 7 log Calc X X X X − → ⇒ A X 0 X =2 4
Ví dụ 2. (Trường THPT Chuyên Lê Quý Đôn – Bình Thuận năm 2017) Cho a,b > 0 và a,b ≠ 1. Đặt
log b = α , tính theo α biểu thức 3
P = log b − log a a 2 a b 2 − α 2 α − 2 α − 2 α − A. 2 5 P = B. 12 P = C. 4 3 P = D. 3 P = α 2α 2α α Lời giải Chọn B Ta có 3 1 3
P = log b − log a = log b − 2log a 2 a b 2 a b 2 1 1 6 α −12 = log b − a = b − = a 6logb log 2 2 a log b α a 2
Ví dụ 3. (Trường THPT Chuyên Lê Quý Đôn – Bình Thuận năm 2017) Cho x > 0 thỏa mãn
log log x = log log x . Tính (log x 2 )2 2 ( 8 ) 8 ( 2 ) A. 3 B. 3 3 C. 27 D. 9 Lời giải Chọn C
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 8
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Cách 1. Đặt t = log x, ta có 1 t t t 1
log x = log x = .log x = ⇒ log = log t ⇔ log = log t 2 3 8 2 2 2 8 2 2 3 3 3 3 3 t t 3 3 ⇔ log
= log t ⇔ = t ⇔ t = 3 3 ⇒ log x = t = 27 ⇒ C 2 2 ( 2 )2 2 3 3
Cách 2. Nhập log log x − log log Shift+Calc
x →luu A 2 ( 8 ) 8 ( 2 ) x=2
Nhập (log x)2 − 27 Calc →0 ⇒ C 2 X =A
Ví dụ 4. (Trường THPT Lê Quý Đôn – Hà Nội năm 2017) Cho log m = a và A = log m m > m ≠ m 8 ( 0, ) 2 1 .
Khi đó mối quan hệ giữa A và a là: − + A. a a A = (3− a) . a B. 3 A = . C. 3 A = .
D. A = (3+ a) . a a a Lời giải Chọn C
Cách 1. Biến đổi log m theo log m m 8 2 + Ta có 3 3 = log a A + m = + = + ⇔ A = ⇒ C m 8 logm 3logm 2 1 1 a a
Cách 2. Từ giả thiết log m = a rút ra m và thế vào 2 Ta có log = ⇔ = 2a m a m khi đó 2 a 1 3+ = log a A m = = + a = ⇒ C m 8 log a 8.2 log 2 log 2 2 ( ) ( 3 2 2 ) a a
Cách 3. Sử dụng Casio. Không mất tính tổng quát cho m = 2 ⇒ a = log 2 =1 2 + Nhập ( M ) 3 log 8 A Calc − → ⇒ C M 0 M A 2 A = =
Ví dụ 5. (Trường Chuyên Võ Nguyên Giáp – 2017) Cho các số thực dương x, y, z thỏa mãn a 2b 3 = 10 , = 10 , =10 c xy yz zx
(a, ,bc∈ R) . Tính P = log x + log y + log z
A. P = 3abc
B. P = a + 2b + 3c C. a b c P = 6abc D. 2 3 P + + = 2 Lời giải Chọn D Ta có α 2b 3c = = = ⇒ ( )2 a+2b+3 10 , 10 , 10 =10 c xy yz zx xyz . Suy ra ( ) 1 ( )2 1 a 2b 3c a 2b 3 log log log log log log10 c P x y z xyz xyz + + + + = + + = = = = . 2 2 2
Ví dụ 6. (Chuyên Hùng Vương – Gia Lai Lần 1 – 2017) Cho a, b là hai số thực dương khác 1 và thỏa mãn 2 b −
a b = − . Tính giá trị biểu thức P = a ab + a ( 3 log ) a b ( 3 ) 8 log 8log 2017. 3 A. P = 2019. B. P = 2020. C. P = 2017. D. P = 2016. Lời giải Chọn A
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 9
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Cách 1. Ta có 2 1 8 2 8 log b − a + b + = ⇔ b − = ⇔ b = a 8 logb logb 0 loga 0 loga 2 3 3 log b a 4 1 Do đó 4 1 3 3 P = log a + b + = + b + = ⇒ A a loga 2017 .loga 2017 2019 3 3
Cách 2. Không mất tính tổng quát cho a = 2 Nhập ( X )2 − ( 3 8 log 8log 2 Shift Calc X + + → X 4 2 ) X =b=2 3 Nhập P = log ( 3 A AB )+ 2017 Calc → ⇒ B A 2019 A=2;B=4 Nhận xét:
- Thông thường để giải theo kiểu trắc nghiệm ta sẽ cho a hoặc b bằng 1 số thực cụ thể và giải phương
trình theo b hoặc a. Tuy nhiên trong nhiều trường hợp biểu phức tạp khó giải thì ta nên chọn cho a và b
đồng thời các số thực, quan trọng là chọn như thế nào để thoả mãn bài toán, kinh nghiệm ở đây ta thấy
để rút gọn log b thì n
b = a . Theo giả thiết nên ta kiểm tra như sau: a Nhập 2 B − ( 3A B) 8 log 8log Calc + → thoả mãn A B 0 2 A=2;B=2 3 Nhập P = log ( 3 A AB )+ 2017 Calc → A 2019 A=2;B=4
- Ta có thể nhập như sau: (Y )2 − ( 3 X Y ) 8 log 8log Shift+Calc
+ →1,732050808 luu → A X Y Y =3;X =2 3 Nhập P = log ( 3 X XY )+ 2017 Calc → ⇒ B X 2019
X =a=A;Y =3
Ví dụ 7. (Sở GD và ĐT Vĩnh Phúc L2 – 2017) Cho a,b là hai số thực dương, khác 1. Đặt log b = m , tính a
theo m giá trị của 3
P = log b − log a . 2 a b 2 2 2 2 A. 4m −3 − − − B. m 12 C. m 12 D. m 3 2m 2m m 2m Lời giải Chọn B Cách 1. Ta có 3 1
P = log b − log a = log b − 6log a 2 a b 2 a b 2 1 6 1 6 m −12 = log b − = m − = . 2 a log b m m a 2 Cách 2. Ta có log m
b = m ⇔ b = a thay vào ta được a 2 3 m 3 m 6 m −12
P = log b − log a = log a − log a = − = . 2 2 m a b a a 2 m m
Cách 3. Cho a = m = 2 ⇒ b = 4 2 − Nhập 3 m 12
P = log b − log Calc a −
→0 ⇒ B 2 a b a m 2;b 4 2m = = =
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 10
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Ví dụ 8. (Sở GD và Vũng Tàu năm 2017) Cho x, y, z,a,b,c thoả mãn ln x ln y ln z = = = ln t và 2 2 xy = z t . a b c
Tính giá trị của P = a + b − 2c A. 4 B. 1 C. 2 − D. 2 2 Lời giải Chọn D a x = t b x y z y = t Cách 1. ln ln ln a b 2c 2 = = = ln t ⇒
⇒ t .t = t t ⇔ a + b = 2c + 2 c a b c z = t 2 2 xy = z t
⇒ a + b − 2c = 2 .
Chú ý: Có thể đặt ln x ln y ln z = = = ln t = u a b c ln x a = = log x ln t t
Cách 2. ln x ln y ln z ln = = = ln y t ⇔ b = = log y a b c ln t t ln z c = = log z ln t t xy 2
⇒ a + b − 2c = log x + y − z = = t = . t logt 2logt logt logt 2 2 z
Cách 3. Cho a = 2;b = 3;c = 4 thì từ 2 2 6
xy = z t ⇒ t = 4 ln x Calc a = → A 6 ln t x=2;t= 4 Khi đó ln y Calc b =
→ B ⇒ P = a + b − 2c = A + B − 2C = 2 . 6 ln t y=3;t= 4 ln z Calc c = →C 6 ln t z=2;t= 4 2
Ví dụ 9. (Trung Tâm BDVH Lý Tự Trọng) Cho log a logb log c = = = log x ≠ 0; b y
= x . Tính y theo p q r ac
p, q, r . + A. 2
y = q − pr . B. p r y = .
C. y = 2q − p − r .
D. y = 2q − pr . 2q Lời giải
log a = p log x
Theo giả thiết ta có log a logb log c log x = = =
⇒ logb = q log x p q r logc = r log x
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 11
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 2 2 Và b y = ⇔ log b x = log y x ac ac
⇒ y log x = 2logb − log a − log c = 2q log x − p log x − r log x = log x(2q − p − r)
⇒ y = 2q − p − r (do log x ≠ 0 ). Chọn đáp án C
Ví dụ 10. (Chuyên Lương Văn Tuỵ Lần 1 – 2017) Cho x > 0, x ≠ 1 thỏa mãn biểu thức 1 1 1 + + ...+
= M . Chọn khẳng định đúng trong các khẳng định sau: log x log x log x 2 3 2017 A. 2017! = 2017 x B. 2017M x = C. 2017! x = D. M x = 2017! M M Lời giải Chọn D Ta có 1 log b a = ⇒ a = ⇒ M = log + + + x 2
logx 3 ... logx 2017 a .logb 1 logb log a b ⇒ M = log = x ( 2.3.....2017) logx 2017! M ⇒ x = 2017!.
Ví dụ 11. Cho hai số thực dương x và y thỏa mãn log x = log y = log x + y và 4 6 9 ( )
x −a + b = (a,b +
∈ ). Tính tỉ số S = a + b . y 2 A. S = 6 B. S = 8 C. S = 4 D. S =11 Lời giải Chọn A
Theo giả thiết log x = log y = log x + y có hai ẩn ta đưa về 1 ẩn như sau 4 6 9 ( )
log x = log x + y y = 6 x 4 9 ( ) log4 ⇔
log y = log x
log x = log x + 6 x 6 4 4 9 ( log4 )
log X −log X + 6 X Shift+Calc
→5,162430201 luu → A = x 4 ( ) log4( ) 9 ( ) Nhập X =2 log4( X ) 6 Calc →8,385348209 luu → B = y X =A Mod 7 nhập: ( ) = − 2 A f X X
với a = f ( X ),b = X B a =1
Start =1; End = 9;Step =1 và nhìn trên bảng ta được
⇒ a + b = 6 ⇒ A b = 5 x = 4t
Cách 2. Đặt log x = log y = log x + y = t ⇒ y = 6t 4 6 9 ( )
x + y = 9t
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 12
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com x 2 t = y 3 ⇒ − + − + = + a b a t t t 2 t Mod 1 5 1 5 3 4 + 6 − 9 = 0 → = = ⇒
⇒ a + b = 6 ⇒ A 3 2 2 b = 5
Ví dụ 12. Cho a, b, c là các số thực dương thỏa log37 log711 l 11 og 25 a = 27,b = 49,c
= 11 . Tính giá trị biểu thức 2 2 2 log3 7 log711 l 11 og 25 T = a + b + c
A. T = 76 + 11 B. T = 31141 C. T = 2017 D. T = 469 Lời giải Chọn D
Từ giả thiết biến đổi 2 2 2 log 7 log 11 log 25 log 7 log 11 l 11 og 25 = + +
= ( log 7 ) 3 + ( log 11) 7 + ( l 11 og 25 T a b c a b c ) 11 3 7 3 7 = ( ) 7 + ( )log 11 27 49 + ( 11)l 11 og 25 log3 7 (27)log 7 = ( 33)log37 3 3 = ( log37 3 ) 3 = 7 = 343 Ta có ( 49)log 11 = ( 2 7 )log711 2 7 = ( log711 7 ) 2 = 11 =121 . ( 11) l 11 og 25 1 1 1 l 11 og 25 2 = 11 = ( l 11 og 25 11 )2 2 = 25 = 25 = 5
⇒ T = 343+121+ 5 = 469 .
Ví dụ 13. (Sở GD và ĐT Vĩnh Phúc L2 – 2017) Cho x, y,z là ba số thực khác 0 thỏa mãn 2x = 5y =10−z . Giá
trị của biểu thức A = xy + yz + zx bằng? A. 3 B. 0 C. 1 D. 2 Lời giải Chọn B y = = x y − z x y 1 2 10 1 (2 10 x z x z ) 1
Cách 1. Ta có 2 = 5 =10 ⇔ 2 = 5 = ⇔ ⇔ 10z 5 10 y z =1 (5 10 )x y z =1 2 10 xy yz =1 + + ⇔ ⇒ =
= ⇒ A = xy + yz + zx = ⇒ B xy zx (2 10 xy yz )(5 10 xy
zx ) 10xy yz zx 1 0 5 10 =1 = → − y log 4 B Cách 2. Cho y z 5
x = 2 ⇒ 5 =10 = 4 ⇔ z = −log 4 → C 10 Nhập Calc
A = XY +YM + MX →0 ⇒ B
X =2;Y =B;M =C x = log t 2
Cách 3. 2x 5y 10−z t = =
= ⇒ y = log t . Nhập A = xy + yz + zx 5 z = − log t 10
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 13
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
= log M.log M + log M. −log M + −log M .log Calc
M →0 ⇒ B 2 5 5 ( 10 ) ( 10 ) 2 t=M =2 z 2 =10−x z z − −
Cách 4. Ta có 2x = 5y =10−z ⇔ ⇒ 2.5 =10 =10 x y z z ⇔ − − = 1 z − x y 5 =10 y
⇔ xy + yz + zx = 0 ⇒ B 1 2 x = t 1 1 1 1
Cách 5. Ta có x y z y − − x y 1 1 1 2 = 5 =10 = t ⇒ 5 = t ⇒ 2.5 =10 ⇔ t . z
t = t ⇔ + = − x y z 1 10 − z = t
⇔ xy + yz + zx = 0 ⇒ B
Ví dụ 14. Cho ba điểm A( ; b log b B c c , C ( ;
b 3log b với 0 < a ≠ 1, b > 0, c > 0 . Biết B là a ) a ), ( ;2loga )
trọng tâm của tam giác OAC với O là gốc tọa độ. Tính S = 2b + . c A. S = 9. B. S = 7. C. S =11. D. S = 5. Lời giải Chọn A
0 + b + b = c
Vì B là trọng tâm của tam giác OAC nên 3 0 + log b + b a 3loga = 2log c 3 a b + b = 3c 2b = 3c 2b = 3c ⇔ ⇔ ⇔ 2 3 4log b = c b = c a 6loga 2loga 3loga log b = c a loga 27 2 = 3 b b c = c>0 8 ⇔ →
⇒ S = 2b + c = 9. 2 3 b = c 9 c = 4
Dạng 2. Biểu diễn theo lôga 1. Phương pháp
• Sử dụng tư duy tự luận: Kết hợp nhiều tính chất và công thức • Sử dụng Casio
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1. (Đề minh họa 2017) Đặt a = log 3, b = log 3 . Hãy biểu diễn log 45 theo a và b. 2 5 6 2 A. + 2 − log 45 a ab = B. 2 2 log 45 a ab = 6 ab 6 ab 2 C. + 2 − log 45 a ab = D. 2 2 log 45 a ab = 6 ab + b 6 ab + b Lời giải Chọn C
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 14
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Cách 1. Tự luận
Ta có log 45 = log 9 + log 5. 6 6 6 2 2 2 2 log 9 = 2log 3 a = = = = . 6 6 log 6 1+ log 2 1 a +1 3 3 1+ a 1 1 log 5 a = = = vì log 2 b = . 6
log 6 log 3+ log 2 b a +1 5 a 5 5 5 ( ) Vậy 2a a a + 2 log 45 ab = + = . 6
a +1 b(a + ) 1 ab + b
Cách 2. Thử lần lượt 4 đáp án. Đáp án đúng là đáp án C. log 3 → A
Tính và lưu thành hai biến A và B. Tính 2 log 3 → B 5 + Nhập a 2 log 45 ab Calc − →0 ⇒ C 6 a A;b B ab + b = =
Ví dụ 2. (Sở GD và ĐT Vũng Tàu lần 2 năm 2017) Cho a = log 2 và b = log 5 . Tính log 60 theo a và b. 3 3 10 + + + − − + + + A. 2a b 1 . B. 2a b 1 . C. 2a b 1 . D. a b 1 . a + b a + b a + b a + b Lời giải Chọn A Ta có 2 1 1
log 60 = 2log 2 + log 3+ log 5 = + + 10 10 10 10
1+ log 5 log 2 + log 5 1+ log 2 2 3 3 5 2 1 1 2 1 1 2a + b +1 = + + = + + = log 5 . log 2 + log 5 log 2 b a + b a 3 a + b 3 3 3 1+ 1+ 1+ 1+ log 2 log 5 a b 3 3 Ví dụ 3. +
(Sở GD và ĐT Thanh Hoá năm 2017) Cho log , log axy log , trong 54 168 = 1 12 24 = y và 7 12 = x bxy + cx
đó a, b, c là các số nguyên. Tính giá trị biểu thức S = a + 2b + 3 . c A. S = 4. B. S = . 19 C. S = . 10 D. S = . 15 Lời giải Chọn D
Cách 1: Nhận xét về mối quan hệ giữa biểu thức và cơ số để phân tích hợp lí Ta thấy 2 3 3 3
12 = 3.2 ;24 = 3.2 ;54 = 3 .2;168 = 2 .3.7 do đó ta sẽ phân tích theo số 2 và 3. Số 7 làm cơ số trung gian
log 12 = x ⇔ log 3+ 2log 2 = x (1) 7 7 7
xy = log 12.log 24 = log 24 ⇒ log 3+ 3log 2 = xy (2) 7 12 7 7 7
Từ (1) và (2) ta suy ra log 2 = xy − x, log 3 = 3x − 2xy . 7 7 log 168 log ( 3 2 .3.7 7 ) + + + Do đó 3log 2 log 3 1 xy 1 7 log 168 = = = = . log 54 log 3 .2 log 2 + 3log 3 5 − xy + 8x 7 ( ) 7 7 54 3 7 7 7
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 15
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Do đó a =1,b = 5
− ,c = 8 ⇒ S =15 ⇒ D Cách 2: + Ta có xy = log 24 và log 168 log 24 1 7 7 log 168 = = 7 54 log 54 log 54 7 7 + + Do đó log 168 log 24 1 a log 24 1 7 7 7 log 168 = = =
. Đồng nhất hai vế ta được 54 log 54 log 54
blog 24 + c log 12 7 7 7 7 a =1 . Để tìm ,
b c ta có thể làm như sau b log 24+clog 12 = log 54 7 7 7 Cách 2.1: − Dùng mode7 ta có log 54 c log 12 7 7
blog 24 + c log 12 = log 54 ⇔ b = 7 7 7 log 24 7 −
Nhập f (x) log 54 X log 12 7 7 =
(b = f (x);c = X );Start = 9;
− End = 9;Step =1. log 24 7
Ta nhìn bảng trên máy tính. Từ đó suy ra b = 5; − c = 8
Cách 2.2: Giải hệ hai ẩn hai phương trình Mode 5 +1 b
log 24 + c log 12 = log 54 b = 5 − 7 7 7 ⇔
2b + 3c = S −1 c = 8
Dạng 3. So sánh 1. Phương pháp
• Sử dụng tư duy tự luận: Kết hợp nhiều tính chất và công thức • Sử dụng Casio
2. Các ví dụ rèn luyện kĩ năng 5 3 Ví dụ 1. Nếu 5 3 a > a và 4 5 log < thì b log 5 b 6
A. 0 < a <1, 0 < b <1
B. 0 < a <1, 1 b > C. a >1, 1 b >
D. a >1, 0 < b <1 Lời giải Chọn B 5 3 4 5 < < Cách 1. Vì 5 3 5 6
⇒ 0 < a <1 và ⇒ b >1 5 3 4 5 < 5 3 logb log a > a 5 b 6
Cách 2. Vì phép so sánh là dựa vào cơ số nên ta chỉ thử với cơ số lớn hơn 1 và lớn hơn 0 nhỏ hơn 1. Coi
a = X ;b = Y 5 3 Nhập 5 3 Calc
X − X → < 0 ⇒ C, D loại X =2 1 > Nhập 4 5 log − log Calc → < ⇒ B Y Y 0 Y =2 5 6
Ví dụ 2. (Trường THPT Hà Trung lần 3 năm 2017) Cho hai số thực dương a, b khác 1 thỏa mãn: 13 15 1 2 7 8 a > a , log <
Mệnh đề nào dưới đây đúng? b logb . 2 3
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 16
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
A. a<1 và b<1.
B. a >1 và b >1.
C. a >1 và b <1.
D. a <1 và b >1. Lời giải Chọn D 13 15 1 2 7 8 < a > a log b logb Vì 2 3 ⇒ 0 < a <1 13 15 và ⇒ b >1 < 1 2 7 8 < 2 3
Ví dụ 3. (Đề minh họa 2017) Cho hai số thực a và b, với 1< a < b . Khẳng định nào dưới đây là khẳng định đúng? A. log b < < a < b < a a 1 logb B. 1 loga logb C. log a < b < a < < b b loga 1 D. logb 1 loga Lời giải Chọn B
Cách 1. Dựa vào giả thiết 1< a < b nên ta lấy loga hai vế theo cơ số a và b ta được. a,b >1 1 = log a < b a log Vì a ⇒ ⇒ log a < < b b 1 log a < b
log a < log b = 1 a b b
Cách 2. Đặc biệt hoá cho a, b là 1 số cụ thể thoả mãn 1< a < b log 3 =1,584962501 >1
Không mất tính tổng quát cho 2
a = 2 < b = 3 ⇒ ⇒ D log 2 = 0,6309297536 < 1 3
Ví dụ 3. (Chuyên Lam Sơn Lần 1 năm 2017) Cho 0 < x <1; 0 < a; ;
b c ≠ 1 và log x > > x > x so c 0 logb loga
sánh a,b,c ta được kết quả:
A. a > b > c
B. c > a > b
C. c > b > a
D. b > a > c Lời giải Chọn D
Vì 0 < x <1⇒ ln x < 0 . Do đó: ln x ln x ln log x x > > x > x ⇔ > > > ⇒ c < < < c 0 logb loga 0 ln 0 lna lnb lnc lnb ln a
Mà hàm số y = ln x đồng biến trên (0;+∞) nên ta suy ra c < a < b
C. GIẢI BÀI TẬP SÁCH GIÁO KHOA
Bài 1. Tính giá trị các biểu thức sau: a) log 16 b) 1 log c) log1000 d) log312 9 . 2 3 27 Lời giải a) 4 log 16 = log 2 = 4 2 2 b) 1 3 log log 3− = = 3 − 3 3 27
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 17
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com c) 3 log1000 = log10 = 3 d) ( 2 log312 ) 2 3 = 12 =144
Bài 2. Tìm các giá trị của x đề biểu thức sau có nghĩa: a) log (1− 2x) ; b) logx . + 5 3 1 Lời giải
a) Để log 1− 2x có nghĩa thì − > Hay 1 x < 3 ( ) 1 2x 0 2 b) Để log > − x có nghĩa thì Hay + 5 1 x +1 0 x > 1
Bài 3. Sử dụng máy tính cầm tay, tính giá trị các biểu thức sau (làm tròn kết quả đến chữ số thập phân thứ tư): a) log 15 b) log8 − log3; c) 3 3ln 2 Lời giải a) log 15 = 2,4650 3 b) log8 − log3 = 0,4260 c) 3ln2 = 2,0794
Bài 4. Tính giá trị các biểu thức sau: a) log 9 + log 4 b) log 2 − log 50 c) 1 log 5 − log 15 . 6 6 5 5 3 3 2 Lời giải a) log 9 + log 4 = log (9.4) 2 = log 36 = log 6 = 2. 6 6 6 6 6 b) 2 1 2 log 2 log 50 log log log 5− − = = = = 2 − 5 5 5 5 5 50 25 c) 1 5 1 1 1 − 1
log 5 − log 15 = log 5 − log 15 = log = log = log 3 = − . 3 3 3 3 3 3 3 2 15 3 2 2
Bài 5. Tính giá trị các biểu thức sau: a) log 9⋅log 4 b) 1 log c) log 3⋅log 5 ⋅log 4 2 3 25 5 2 9 5 Lời giải a) 2 2
log 9⋅log 4 = log 3 ⋅log 4 = 2log 3⋅log 4 = 2log 4 = 2log 2 = 2⋅2 = 4 . 2 3 2 3 2 3 2 2 1 1 − − b) 1 2 1 2 log = log 5 = log 5 = − . 2 25 5 5 5 2 4 c)
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 18
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 1 1 2 2 2
log 3⋅log 5 ⋅log 4 = log 3⋅log 5 ⋅log 2 = log 3⋅ log 5⋅2log 2 2 2 9 5 2 3 5 2 3 5 2 1 1 1 1
= log 3⋅log 5⋅log 4 = log 5⋅log 2 = log 2 = 2 3 5 2 5 2 2 2 2 2
Bài 6. Đặt log 2 = a,log3 = b . Biểu thị các biểu thức sau theo a và b . a) log 9; b) log 12 c) log 6 . 4 6 5 Lời giải 2 b a) log9 log3 2log3 log3 log 9 = = = = = . 4 2 log4 log2 2log2 log2 a log12 log( 2 2 ⋅3) 2 b) log2 + log3 2log2 + log3 2 + log 12 a b = = = = = . 6 log6 log(2.3) log2 + log3 log2 + log3 a + b log6 log(2.3) + + c) log2 log3 log 6 a b = = = = . 5 log5 10 log10 − log2 1 log − a 2
Bài 7. a) Nước cất có nồng độ H+ là 7
10− mol / L . Tính độ pH của nước cất.
b) Một dung dịch có nồng độ H+ gấp 20 lần nồng độ H+ của nước cất. Tính độ pH của dung dịch đó. Lời giải
a) Độ pH của nước cất là: 7
pH = −log H + = −log 10− = 7 .
b) Nồng độ H+ của dung dịch đó là: 7 20.10− mol / L
Độ pH của dung dịch đó là: 7
pH = −log H + = −log 20.10− ≈ 5,7 .
D. BÀI TẬP TRẮC NGHIỆM
Câu 1: Cho các số thực dương a , b thỏa mãn log a = x , log b = y . Tính P = log ( 2 3 a b . 2 ) 2 2 A. 2 3 P = x y B. 2 3
P = x + y
C. P = 6xy
D. P = 2x + 3y Lời giải Chọn D P = log ( 2 3 a b 2 3
= log a + log b = 2log a + 3log b = 2x + 3y . 2 ) 2 2 2 2
Câu 2: Cho a,b > 0 và a,b ≠1, biểu thức 3 4
P = log b .log a có giá trị bằng bao nhiêu? a b A. 18. B. 24 . C. 12. D. 6 . Lời giải Chọn B 3 4
P = log b .log a = (6log b a = . a ).( 4 logb ) 24 a b 1
Câu 3: Cho b là số thực dương khác 1. Tính 2 2 P = log b b b . .
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 19
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com A. 3 P = . B. P =1. C. 5 P = . D. 1 P = . 2 2 4 Lời giải Chọn C 1 5 Ta có 2 5 2 P = log b b 2 = 5 = b = b . log b log . b 2 b 2
Câu 4: Cho a > 0 , a ≠ 1. Biểu thức 2 loga a a bằng A. 2a . B. 2 . C. 2a . D. 2 a . Lời giải Chọn D Ta có 2 loga a a 2loga a = a 2 = a .
Câu 5: Giá trị biểu thức log4 9+log2 5 A = 2 là: A. A = 8. B. A =15. C. A = 405 . D. A = 86. Lời giải Chọn B Ta có log4 9+log2 5 log4 9 log2 5 log2 3 log2 5 A = 2 = 2 .2 = 2 .2 = 3.5 =15 .
Câu 6: Cho a > 0,a ≠1. Tính giá trị của biểu thức 1 P log = 3 a 3 a A. P = 9 − . B. P = 1 − . C. P =1. D. P = 9. Lời giải Chọn A 1 Tự luận : 3 P = log = log a− = 9 − log a = − a a 9 3 1 3 a 3 a 1
Trắc nghiệm : Sử dụng máy tính, thay a = 2 rồi nhập biểu thức log3 vào máy bấm = a 3 a
ta được kết quả P = 9 − . 2 Câu 7: a
Cho a là số thực dương khác 2 . Tính I = loga . 4 2 A. 1 I = . B. 1 I = − . C. I = 2 . D. I = 2 − . 2 2 Lời giải Chọn C 2 2 log a a a I = = = = . a loga 2loga 2 4 2 2 2 2 2
Câu 8: Cho a là số thực dương và b là số thực khác 0 . Mệnh đề nào sau đây là mệnh đề đúng? 3 3 A. 3a 1 log 3a
=1+ log a − 2log b . log
=1+ 3log a − 2log b . 3 B. 2 3 3 b 3 3 2 3 3 b 3 3 C. 3 log a 3a
=1+ 3log a − 2log b . log
=1+ 3log a + 2log b . 3 D. 2 3 3 b 3 2 3 3 b
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 20
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Lời giải Chọn C 3 a Ta có 3 log
= log 3a − log b 3
= log 3+ log a − log b . 2 ( 3) 2 3 3 3 b 3 3 3 3
= log 3+ log a − log b =1+ 3log a − 2log b . 3 3 3 3 3
Câu 9: Cho log3 = a . Tính log9000 theo a . A. 6a B. 2 a + 3. C. 2 3a . D. 2a + 3. Lời giải Chọn D
Cách 1: log9000 = log9 + log1000 = 2log3+ 3 = 2a + 3.
Cách 2: Gán log3 = a . Tính log9000 − (2a + 3) = 0 .
Câu 10: Cho log 9 = a. Tính log 2 theo a 6 3 A. a + − − . B. a 2. C. a 2. D. 2 a . 2 − a a a a Lời giải Chọn D Ta có: 2 2 − a log 9 = 2log 3 2 ⇔ a = ⇔ log 2 +1 = ⇔ log 2 = . 6 2.3 log 2.3 3 a 3 a 3
Câu 11: Cho a,b > 0 . Rút gọn biểu thức 2 4 log b + b a log 2a A. 2log b b b a B. 0 C. loga D. 4loga Lời giải Chọn D Ta có 2 4 log b + b 1 = 2log b + b = . a .4.log b a log 4log 2 a 2 a a
Câu 12: Cho log x = , log x = với = . b 3 a 2
a , b là các số thực lớn hơn 1. Tính P log x a 2 b A. − 6 . B. −6. C. 1 . D. 1 . 6 6 Lời giải Chọn B
Vì a , b là các số thực lớn hơn 1 nên ta có: 2 3 log x = = a 2 x a 2 3 3 2 ⇔
⇔ a = b ⇔ a = b ⇔ a = b . 3 log x = b 3 x = b P = log x = x = = − = − . − x x a log log 2logb 6 3 1 2 2 2 b b b 2 b
Câu 13: Đặt a = log 3 và b = log 3. Hãy biểu diễn log 45 theo a và b . 2 5 6 2 A. + 2 − log 45 a ab = . B. 2 2 log 45 a ab = . 6 ab + b 6 ab
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 21
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 2 − C. + 2 log 45 a ab = . D. 2 2 log 45 a ab = . 6 ab 6 ab + b Lời giải Chọn A 1 log ( 2 5.3 + 2 3 ) a + ab log 45 = log 5 + 2 3 = b = 2 = . 6 log 2.3 log 2 +1 1 ab + b 3 ( ) 3 +1 a
Câu 14: Cho 2 số thực dương a , b thỏa mãn a ≠ b , a ≠1, log b = . Tính 3 T = log ba . a 2 a b A. 2 T = − . B. 2 T = . C. 2 T = . D. 2 T = − . 5 5 3 3 Lời giải Chọn D Ta có: 1 log b = ⇒ a = . a 2 logb 2 3 3 3 T = log ba = log b + log a 1 1 = + . a a a a a b b b log log 3 3 b a b b 1 1 = + 1 1 = + . log a − log b log a − log b 3 3 3 3 3 3 b b a a log a − − b b 3 3log 2 2 a 1 1 2 = + = − . 3 1 3 3 . − 3 − 3.2 2 2 2
Câu 15: Với a = log 5 và b = log 5 , giá trị của log 5 bằng 2 3 6 A. ab + . B. a b . C. 1 .
D. a + b . a + b ab a + b Lời giải Chọn A Ta có 1 ab log 5 = 1 1 = = 1 1 = = = . 6 log 6 log 2 + log 3 1 1 log 2 + log 3 1 1 a + b 5 5 5 + 5 5 + a b a b Câu 16: Biết ( 3 log xy ) =1 và ( 2
log x y) =1, tìm log(xy)? A. (xy) 5 log = . B. (xy) 1 log = . C. (xy) 3 log = . D. log(xy) =1. 3 2 5 Lời giải Chọn A Ta có ( 3
log xy ) =1⇔ log(xy) + 2log y =1, ( 2
log x y) =1⇔ log(xy) + log x =1 Vậy 2
log x = 2log y ⇔ x = y
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 22
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Xét
(xy ) = ⇔ (y y ) 1 3 2 3 5 log 1 log
= 1 ⇔ 5log y =1 ⇔ y =10
Vậy log(xy) = log( y ) 3 3 3 5 = log10 = 5 Câu 17:
Tính giá trị của biểu thức 10 2 a 2
P = log a b + log +
log b− ( với 0 < a ≠ 1;0 < b ≠ 1). 2 a ( ) 3 a b b A. P = 2 . B. P =1. C. P = 3 . D. P = 2 . Lời giải Chọn B
Sử dụng các quy tắc biến đổi logarit 10 2 a 2
P = log a b + log + log b− 2 a ( ) 3 a b b . 1 10 2 = log a + b + a − b + − b . a loga 2 log a loga 3.( 2)log 2 b 1 [ b b = + + − − = a ] 1 10 2log 2 1 log a 6 1. 2 2
Câu 18: Biết log 5 = a, log 7 = b, log 3 = c thì log 35 tính theo 27 8 2 12
a, b, c bằng: 3(b + ac) 3(b + ac) A. + + .
B. 3b 2ac .
C. 3b 2ac . D. . c + 2 c +1 c + 2 c +1 Lời giải Chọn A Ta có: 1
log 5 = log 5 = a ⇔ log 5 = 3a , 1
log 7 = log 7 = b ⇔ log 7 = 3b . 27 3 3 3 8 2 2 3 log 7.5
log 7 + log 5 log 7 + log 3.log 5 3b + .3
c a 3 b + ac 2 ( ) ( ) Mà log 35 = = = = = . 12 log 3.2 log 3+ 2 log 3+ 2 c + 2 c + 2 2 ( 2 ) 2 2 2 2 3 2 2
Câu 19: Cho a,b > 0 , nếu 2
log a + log b = 5 và 2
log a + log b = 7 thì giá trị của ab bằng 8 4 4 8 A. 9 2 . B. 8 . C. 18 2 . D. 2 . Lời giải Chọn A 1 2
log a + log b = 5 + = 2 2 6 log a log b 5 3 log a = 6 a = 2 Ta có: 8 4 2 ⇔ ⇔ ⇔ . 2 3
log a + log b = 7 1 log b = 3 b = 2 4 8 2
log a + log b = 7 2 2 3 Vậy 9 ab = 2 .
Câu 20: Số nào trong các số sau lớn hơn 1 A. 1 log . B. log 125 . C. log 36. D. 1 log . 0,5 8 0,2 1 0,5 2 6 Lời giải
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 23
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Chọn A Ta có: 1 3 log log 2− = = 3 >1, 3 log 125 = log = 3 − <1. − 5 1 0,5 2 8 − 1 0,2 5 2 1 log 36 = log = 2 − < 1, log = log 0,5 =1. − 6 1 1 6 0,5 0,5 2 6
Câu 21: .Cho a , b là các số thực, thỏa mãn 0 < a <1< b , khẳng định nào sau đây đúng? A. log a + b < . a > . b loga 0 B. logb 1 C. log b > . b + a ≥ . a 0 D. loga logb 2 Lời giải Chọn A
Vì 0 < a <1< b nên log a < ⇔
a < và log b < ⇔ b < . a loga1 loga 0 b logb1 logb 0 Suy ra : log a + b < . b loga 0
Câu 22: Cho các số thực a , b thỏa mãn 1< a < b . Khẳng định nào sau đây đúng? A. 1 1 < 1< . B. 1 1 < 1< . log b a log a b b log a logb a C. 1 1 1< < . D. 1 1 < < 1. log b a log b a a log a logb b Lời giải Chọn A
Vì 1< a < b nên ta có log a <
b ⇔ log a < và log a <
b ⇔ 1< log b . a log b 1 b logb a a Do đó log a < < b 1 1 ⇔ < < . b 1 loga 1 log b a a logb
Câu 23: Cho 0 < a < b <1, mệnh đề nào dưới đây đúng? A. log a > b . a < b . b > . b < . b loga B. logb loga C. loga 1 D. loga 0 Lời giải Chọn A
Do 0 < a <1 nên hàm số y = log x nghịch biến trên (0;+∞). a
Đáp án B sai, vì: Với b <1⇒ log b > ⇔ b > . a loga1 loga 0
Đáp án D sai, vì: Với a < b ⇒ log a > b ⇔ b < . a loga loga 1
Với 0 < a < b <1 ta có 0 < log b < . a 1 Đáp án C sai, vì: Nếu 1 log a < b ⇔ < b ⇔ b > (vô lí). b loga loga (loga )2 1 log b a
Đáp án A đúng, vì: Nếu 1 log a > b ⇔ > b ⇔ b < (luôn đúng). b loga loga (loga )2 1 log b a
Câu 24: Trong các khẳng định sau, khẳng định nào sai? A. log 5 > 0 . B. log 2016 < log 2017 . 3 2 2 2+x 2+x
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 24
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com C. log 0,8 < 0 . D. 1 > . 0,3 log 4 log 3 4 3 Lời giải Chọn C Ta có: log 0,8 < 0 0
⇔ 0,8 > 0,3 ⇔ 0,8 >1 (sai) 0,3
Câu 25: Khẳng định nào sau đây là khẳng định đúng? A. log π =1.
B. ln 3 < log e .
C. log 5 > log 4 . D. log 2 > 0 . 3 3 3 7 1 2 Lời giải Chọn C
Ta có: log 5 > log 3 ⇒ log 5 >1 3 3 3
log 4 < log 7 ⇒ log 4 <1 7 7 7 Vậy: log 5 > log 4 . 3 7
Câu 26: Cho a , b là các số thực thỏa mãn 0 < a < b <1. Mệnh đề nào sau đây đúng ? A. log a < . m = . m = − . b > . b 0 B. 3 C. 2 D. loga 1 Lời giải Chọn B
Vì 0 < a < b <1 nên log a > b = ⇒ A sai. b logb 1
⇔ x + 2y + 5z − 5 = 0 ⇒ log a >
b ⇒ B đúng, C sai. b loga log a >
b ⇔ log b < ⇒ D sai. a 1 a loga
Câu 27: Cho hai số thực a,b thỏa mãn điều kiện 0 < a < b <1. Khẳng định nào sau đây đúng?
A. 1< log b < a . b < < a . a logb B. loga 1 logb
C. 1< log a < b . a < < b . b loga D. logb 1 loga Lời giải Chọn B
Do 0 < a <1 nên với a < b ta có: 1 = log a > b ⇒ b < . a loga loga 1
Tương tự do 0 < b <1 nên với a < b ta có: log a > b = . b logb 1 Vậy log b < < a . a 1 logb
Câu 28: Mệnh đề nào dưới đây sai?
A. Nếu 0 < a < b thì log a < log b .
B. Nếu 0 < a < b thì a < b . e e log log 2 2
C. Nếu 0 < a < b thì ln a < ln b .
D. Nếu 0 < a < b thì log < π a logπ b . 4 4 Lời giải Chọn D π
Nếu 0 < a < b thì log > < π a log π b do 1. 4 4 4
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 25
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Câu 29: Gọi log0,5 4 log0,513 a = 3 ;b = 3
, khẳng định nào sau đây là khẳng định đúng?
A. a <1< b .
B. b < a <1.
C. a < b <1.
D. b <1< a . Lời giải Chọn C Ta có log0,5 4 log0,51 a = 3 < 3 = 1, log0,513 log0,51 b = 3 < 3 = 1 (1) Lại có log0,513 log0,5 4 3 < 3 (2)
Từ (1) và (2) ⇒ b < a <1
Câu 30: Giả sử x, y là các số thực dương. Mệnh đề nào sau đây sai?
A. log xy = log x + log y 2 2 2 B. 1 log xy = log x + log y 2 ( 2 2 ) 2
C. log x = log x − log y 2 2 2 y
D. log x + y = log x + log y 2 ( ) 2 2 Lời giải Chọn D
Do log x + log y = log xy 2 2 2 ( ) .
Câu 31: Cho hai số thực dương a và ,
b với a ≠ 1. Khẳng định nào dưới đây là khẳng định đúng?
A. log ab = 2 + 2log b . B. 1
log ab = log b . 2 ( ) 2 ( ) a a a 2 a C. 1 1
log ab = + log b . D. 1
log ab = log b . 2 ( ) 2 ( ) a 2 2 a a 4 a Lời giải Chọn C Với a,
b > 0 và a ≠ 1, ta có 1 1 1 1 1
log ab = log ab = a + b = + b = + b . a a loga loga 1 loga loga . 2 ( ) ( ) ( ) ( ) 2 2 2 2 2
Câu 32: Với các số thực dương a ,b bất kì. Mệnh đề nào dưới đây đúng?
A. ln (ab) = ln a + lnb . B. ln a = lnb − ln a . C. ln (ab) = ln .
a ln b . D. a ln ln a = . b b ln b Lời giải Chọn A
Câu 33: Cho các số thực dương a , b , c khác 1. Chọn mệnh đề sai trong các mệnh đề sau đây. A. log b = b − c . a c = . a loga loga B. log log b c a log b c C. log bc = b + c . b c = . a ( ) loga loga D. log log b a log a c Lời giải
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 26
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Chọn B
Với các số thực dương a , b , c khác 1, ta có log b = b − c nên A đúng. a loga loga c log log b c b = nên B sai và D đúng. a log a c log bc = b + c nên C đúng. a ( ) loga loga
Câu 34: Giả sử ta có hệ thức 2 2
a + b = 7ab (a,b > 0) . Hệ thức nào sau đây là đúng? A. +
2log a + b = log a + log . b
B. 2log a b = log a + log . b 2 ( ) 2 2 2 2 2 3 C. + +
log a b = 2 log a + log b .
D. 4log a b = log a + log . b 2 ( 2 2 ) 3 2 2 2 6 Lời giải Chọn B
+) 2log (a + b) = log a + log b ⇔ log (a + b)2 = log ab ⇔ (a + b)2 2 2
= ab ⇔ a + b = −ab 2 2 2 2 2 2 + + +) 2log a b log log a b a b = + ⇔
= ab ⇔ (a + b)2 2 2
= 9ab ⇔ a + b = 7ab . 2 2 2 3 3
Câu 35: Cho a, b là các số thực dương thoả mãn 2 2
a + b =14ab . Khẳng định nào sau đây là sai?
A. a + b ln a + ln ln b =
. B. 2log a + b = 4 + log a + log b . 2 ( ) 4 2 2 2 C. 2log a +
+ b = 4 + log a + log b .
a b = a+ b . 4 ( ) 2 2 D. 2log log log 4 Lời giải Chọn C Ta có ( )2 2 2 + 14 16 a b a b ab a b ab + = ⇔ + = ⇔ ab 4 + + Nên ta có a b ln a ln ln = ln b ab = vậy A đúng 4 2
2log (a + b) = log (a + b)2 = log 16ab = 4 + log a + log b vậy B đúng 2 2 2 ( ) 2 2
2log (a + b) = log (a + b)2 = log 16ab = 2 + log a + log b vậy C sai 4 4 4 ( ) 4 4 +
2log a b = log a + log b vậy D đúng 2 2 4 Cách 2:.
Câu này ý C sai vì 2log (a + b) = 4 + log a + log b ⇔ log (a + b)2 = 4log 4 + log ab 4 4 4 4 4 4 ⇔ log (a + b)2 4
= log 4 + log ab = log 64ab ⇔ a + b = 64ab 4 4 4 4 ( )2 .
Câu 36: Cho các số thực dương a , b thỏa mãn 3log a + 2logb =1. Mệnh đề nào sau đây đúng. A. 3 2 a + b =1.
B. 3a + 2b =10 . C. 3 2 a b =10 . D. 3 2 a + b =10 . Lời giải Chọn C
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 27
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Ta có: 3log a + 2logb =1 3 2
⇔ log a + logb =1 ⇔ ( 3 2 log a b ) =1 3 2 ⇔ a b =10 .
Câu 37: Với các số thực dương a , b bất kỳ. Mệnh đề nào dưới đây sai? 2 2 A. 9
log a = 2 + 2log a − 3log b . B. 9
ln a = 2ln 3+ 2ln a − 3ln b . 2 3 2 2 b 3 b 2 2 C. 9
log a = 2log3+ 2log a − 3logb . D. 9
log a = 2 + 2log a − 3log b . 3 b 3 3 3 3 b Lời giải Chọn A 2 Nhận thấy 9
log a = log 9a − log b 3 ( 2) 3 2 2 2 b 2 3
= log 9 + log a − log b = 2log 3+ 2log a − 3log b 2 2 2 2 2 2 Vậy B, C, D đúng.
Câu 38: Với các số thực dương a ,b bất kì. Mệnh đề nào dưới đây đúng?
A. ln (ab) = ln a + lnb . B. ln a = lnb − ln a . C. ln (ab) = ln .
a ln b . D. a ln ln a = . b b ln b Lời giải Chọn A
Câu 39: Cho các số thực dương a , b , c khác 1. Chọn mệnh đề sai trong các mệnh đề sau đây. A. log b = b − c . a c = . a loga loga B. log log b c a log b c C. log bc = b + c . b c = . a ( ) loga loga D. log log b a log a c Lời giải Chọn B
Với các số thực dương a , b , c khác 1, ta có log b = b − c nên A đúng. a loga loga c log log b c b = nên B sai và D đúng. a log a c log bc = b + c nên C đúng. a ( ) loga loga Câu 40: Cho 2
P = log b với 0 < a ≠ 1 và b < 0 . Mệnh đề nào dưới đây là đúng? 4 a A. P = 2 − log b − . P = 2log b − . a ( ) B. a ( ) C. 1 P = − log ( b − ) . D. 1 P = log ( b − ). 2 a 2 a Lời giải Chọn D Ta có 2 1 1
P = log b = 2. log b = log b
− (Do 0 < a ≠ 1 và b < 0 ). 4 a a ( ) 4 2 a
Câu 41: Cho a > 0 , b > 0 và 2 2
a + b = 7ab . Chọn mệnh đề đúng.
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 28
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
A. 2(ln a + lnb) = ln(7ab) . B. (a +b) 1 3ln
= (ln a + ln b) . 2
C. a + b 1 3 ln = (ln a + ln b) .
D. ln (a + b) = (ln a + ln b). 3 2 2 Lời giải Chọn C
Với a > 0 , b > 0, ta có a + b = ab ⇔ (a + b)2 2 2 7 = 9ab 2 2 a + b + ln a b ab ⇔ = ⇔ = ln (ab) 3 3 a + b a + b 1 ⇔ 2ln
= ln a + ln b ⇔ ln = (ln a + ln b) . 3 3 2
Câu 42: Cho các số a,b > 0 thỏa mãn 2 2
a + b =14ab . Chọn mệnh đề đúng trong các mệnh đề sau.
A. log (a + b) = 4 + log a + log b .
B. log (a + b)2 = 4 log a + log b . 2 ( 2 2 ) 2 2 2 C. + +
log a b = 2 log a + a b 1 log b . D. log = log a + log b . 2 ( 2 2 ) 2 ( 2 2 ) 4 16 2 Lời giải Chọn A 2 + Ta có ( )2 2 2 2 2 14 2 16 16 a b a b ab a b ab ab a b ab + = ⇔ + + = ⇔ + = ⇔ = ab . 4 2 + log a b ⇒
= log ab ⇔ 2log a + b − 2log 4 = log a + log b. 2 2 2 ( ) 2 2 2 4
⇔ log (a + b) = 4 + log a + log b . 2 2 2 Câu 43: Cho 1
log y − x − log
= 1, với y > 0, y > x . Chọn khẳng định đúng trong các khẳng định sau? 1 ( ) 4 y 4
A. 3x = 4y .
B. x = 3y . C. 3 x = y . D. 3 y = x . 4 4 Lời giải Chọn C Ta có 1
log y − x − log
= 1 ⇔ −log y − x + log y =1 ⇔ log y =1+ log y − x 4 4 ( ) 4 ( ) 1 ( ) 4 y 4 4
⇔ log y = log 4. y − x ⇔ y = 4( y − x) 3 ⇔ x = y . 4 4 ( ) 4
Câu 44: Với mọi số thực dương a và b thỏa mãn 2 2
a + b = 8ab , mệnh đề nào dưới đây đúng? A. 1
log(a + b) = (log a + logb) .
B. log(a + b) =1+ log a + logb . 2 C. 1
log(a + b) = (1+ log a + logb) . D. 1
log(a + b) = + log a + logb . 2 2 Lời giải Chọn C
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 29
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Ta có 2 2
a + b = 8ab ⇔ (a + b)2 − 2ab = 8ab ⇔ (a + b)2 =10ab. Hay ta có (a +b)2 log
= log10ab ⇔ 2log(a + b) =1+ log a + logb ⇔ (a +b) 1 log
= (1+ log a + logb) . 2 Câu 45: Cho log ( 2 2
x + y =1+ log xy , với xy > 0 . Chọn khẳng định đúng trong các khẳng định sau? 2 ) 2
A. x > y .
B. x < y .
C. x = y . D. 2 x = y . Lời giải Chọn C Ta có log ( 2 2
x + y =1+ log xy ⇔ log ( 2 2
x + y = log 2xy 2 2
⇔ x + y = 2xy ⇔ (x − y)2 = 0 2 ) 2 ) 2 2 ⇔ x = y .
Câu 46: Cho log x = ,log x = với P = b 3 a 2
a , b là các số thực lớn hơn 1. Tính log x . a 2 b A. P = −6 . B. 1 P = . C. 1 P = − . D. P = 6. 6 6 Lời giải Chọn A 3 3 1 2 −
Cách 1: log x = , log x = 2 3 a b 2 2 ⇒ = = ⇒ = ⇒ = = . b 3 a 2 x a b a b b 2 2 b b
Do đó P = log x = = − = − = − . − x x a log 2logb 2.3 6 1 2 2 b b Cách 2: 2
log x = ⇒ x = a > . log x = , log x = 1 ⇒ log a = , 1 log b = . b 3 a 2 a 2 1 x 2 x 3 Khi đó 1 1 1 P = log x = = = = − . a 6 a log a − b b x 2log 1 1 2 log x − x 2. 2 b 2 3
Câu 47: Với các số thực a , b > 0 bất kì, rút gọn biểu thức 2
P = 2log a − log b ta được 2 1 2 A. P = log ( 2 2ab .
B. P = log ab . 2 ( )2 2 ) 2 C. log a P = . D. 2 = . 2 log a P b 2 2 b Lời giải Chọn B Ta có: 2
P = 2log a − log b 2 2
= log a + log b = log ab . 2 ( )2 2 1 2 2 2 P = 2014 . 0 − ,3 10 a
Câu 48: Với các số thực dương a , b bất kì, đặt M =
. Mệnh đề nào dưới đây đúng? 3 5 b A. 1 log M = 3
− log a + logb . B. 1 log M = 3
− log a − logb . 2 2
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 30
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com C. log M = 3
− log a + 2logb .
D. log M = 3log a + 2logb . Hướngdẫngiải Chọn A. 0 − ,3 0 − ,3 10 a 10 3 − M = a = = a 3 5 b 5 0 − ,5 b 3 b 3 − a 3 − 0 − ,5 1 ⇒ log M = log
= log a − logb = 3
− log a + logb 0 − ,5 b 2
Câu 49: Cho a,b > 0,a ≠1,ab ≠1. Khẳng định nào sau đây là khẳng định sai. A. 1 log a = . B. 1 log ab = (1+ b a loga ). ab 1+ log b 2 a C. a 1 log = 1− log b . D. 2
log (ab ) = 4(1+ log b . a a ) 2 ( a a ) b 4 Lời giải Chọn C 1 1 1 log a = = = . ab log ab a b b a log + a loga 1+ loga ab = (ab) 1 1 log log = (1+ b . a a loga ) 2 2 1 2 a 1 a 1 1 log = log = a b b a a log − a log = a 1− log 2 ( ) ( a ) b 2 b 4 4
Câu 50: Cho các số thực dương a, x, y , a khác 1. Đẳng thức nào sau đây đúng? A. log log x x a x = . B. log log a x = . log loga e a 10 C. log log x a a x = . D. log log x x = . ln10 log a Lời giải Chọn A Ta có log log x a x = . loga 10
Câu 51: Cho các số thực dương a, b, x thỏa mãn log x = 4log a + 7log b . Mệnh đề nào dưới đây 3 3 3 đúng? 1 1
A. x = 4a + 7b .
B. x = 4a − 7b . C. 4 7 x = a b . D. 4 7 x = a b . Lời giải Chọn C
Ta có: log x = 4log a + 7log b 4 7
⇔ log x = log a + log b ⇔ log x = log ( 4 7 a b 4 7 ⇔ x = a b . 3 3 ) 3 3 3 3 3 3
Câu 52: Cho a > 1,a∈ thỏa mãn log log x = log log x + a . Mệnh đề nào dưới đây đúng? 2 ( 4 ) 4 ( 2 )
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 31
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com A. log 4a x = .
B. log x = a + 1 . C. 1 log 2a x + = . D. 1 log 4a x + = . 2 2 2 2 Lời giải Chọn D Đặt 1
t = log x ⇒ log x = t . Ta có: 1 a+1 log
t = log t + a ⇔ log t = 2a + 2 ⇔ t = 4 . 2 4 2 2 4 2 2 Vậy: 1 log 4a x + = . 2 + +
Câu 53: Cho log bc = x ca = y và mx ny 2 log ab =
, với m n p là các số nguyên. Tính a ,logb c , , pxy −1
S = m + 2n + 3p A. S = 6 . B. S = 9 . C. S = 0 . D. S = 3 . Lời giải Chọn A log bc + c y 1 x = log a = x = log bc log a
xlog a − log b = 1 c xy − a c c c 1 Ta có ⇔ ⇔ ⇒ . y log ca log ca
log a ylog b 1 = − = − x + 1 b c c c y = log b = log c b xy − 1 c m = 1 Mặt khác, x + y + 2
log ab = log a + log b =
. Do đó n = 1 ⇒ S = m + 2n + 3p = 6 . c c c xy −1 p = 1
Câu 54: Cho hai số thực dương a,b và a b 16
≠ 1 thỏa mãn log a = ,log b = . Tính ab ? 2 4 a b A. ab = 256. B. ab = 16 . C. ab = 32 . D. ab = 64. Lời giải Chọn A Ta có: b 16 4 log .alog b = .
⇔ log b = 4 ⇔ b = 2 ⇔ b = 16 2 a 2 4 b 2
⇒ log a = 4 ⇔ a = 16 ⇒ .
a b = 16 ⇔ ab = 256 . 2
Câu 55: Cho log bc =
ca = . Tính S = log ab . c ( ) a ( ) 2,logb ( ) 3 A. 7 S = . B. 7 S = . C. 5 S = . D. 6 S = . 5 6 7 7 Lời giải Chọn A
Đặt x = log a,y = log b. c c Ta có b y bc = ⇔ b + c = ⇔ + = ⇒ + = . a ( ) logc 1 1 log 2 log log 2 2 2 a a log a log a x x c c a x ca = ⇔ c + a = ⇔ + = ⇒ + = . b ( ) logc 1 1 log 3 log log 3 3 3 b b log b log b y y c c
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 32
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com y + 1 4 = 2 = x + 1 = 2 x y x Do đó ta có hệ 5 x 1 ⇔ ⇔ . x 1 3y + + = = 3 3 y = y 5 Thay vào S = ab = a + b = c ( ) 7 log log log . c c 5
Câu 56: Cho các số thực dương a,b khác 1 và số thực dương x thỏa mãn log (log x) = log (log x . a b b a )
Mệnh đề nào sau đây đúng? log log log loga (loga b) a (loga b) b (loga b) b (loga b) A. log a x = b . B. log a x = a . C. log b x = b . D. log b x = a . a a a a Lời giải Chọn A k x = a Ta có ( x) = ( x) log log log log log b = k ⇔ a b b a log k x = b a k a x = b k log log b a b b ⇔ k k a b k
⇒ b = a = a log b ⇔
= log b ⇔ k = log b ⇒ x = b a a b (loga ) ( ) log a k b a x = a a a Câu 57: Cho 0 < a ≠ 1 tìm số tự nhiên n thỏa mãn 2 2 2 2
log 2019 + 2 log 2019 + 3 log 2019 + ... + n log = n 2019 1008.2017 log 2019 3 a a a a a A. n = 2016 . B. n = 2019 . C. n = 2017 . D. n = 2020 . Lời giải Chọn A 3 3 3 2 2
log 2019 + 2 log 2019 + 3 log 2019 + ... + n log 2019 = 1008 .2017 log 2019 a a a a a ⇔ ( 3 3 3 3 1 + 2 + 3 + ... + n ) 2 2 log 2019 = 1008 .2017 log 2019 a a n(n +1) 2 ⇔ ( 3 3 3 3 + + + + n ) 2 2 1 2 3 ... = 1008 .2017 2 2 ⇔
= 1008 .2017 ⇔ n = 2016 2
Câu 58: Với a là số dương tùy ý, ln(5a) − ln(3a) bằng: ln(5a) A. . B. ln(2a). C. 5 ln . D. ln5 ln(3a) 3 ln3 Lời giải Chọn C
Ta có ( a) − ( a) 5a 5 ln 5 ln 3 = ln = ln . 3a 3
Câu 59: Cho ba số thực dương a,b,c theo thứ tự lập thành một cấp số nhân và a + b + c = 64 . Giá trị của
biểu thức P = 3log ab + bc + ca − log abc bằng: 2 ( ) 2 ( ) A. 18 . B. 6 . C. 24. D. 8 Lời giải Chọn A
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 33
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 2 ac = b Ta có 3 abc = b .
ab+ bc + ca = b
(a+c)+ca = b( −b) 2 64 + b = 64b
Do đó P = 3log (64b) 3
− log b = 3log 64 = 3.6 = 18 . 2 2 2
Câu 60: Cho 3 số 2017 + log a; 2018+ log a; 2019 + log a; theo thứ tự lập thành cấp số cộng. 2 3 4
Công sai của cấp số cộng này bằng: A. 1. B. 12 . C. 9 . D. 20. Lời giải Chọn A
Do 3 số 2017 + log a; 2018 + log a; 2019 + log a; theo thứ tự lập thành cấp số cộng. Suy ra 2 3 4
2017 + log a + 2019 + log a = 2 2018 + log a 2 4 ( 3 ) 1 .
⇔ log a + log a = 2log a ⇔ 3log a = 4log a ⇔ log a 3 − 4log 2 = 0 ⇔ a = 1. 2 2 3 2 3 2 ( 3 ) 2
Vậy công sai d = log a − log a + 1 = 1 . 3 2
Câu 61: cho các số thực dương a,b,c lớn hơn 1, đặt x = log b + log a,y = log c + log b và a b b c
z = log a + log c . Giá trị của biểu thức 2 2 2
x + y + z − xyz bằng c a A. 1. B. 2 . C. 3 . D. 4 . Lời giải Chọn D
Ta có: xyz = (log b + log c)(log c + log a)(log a + log b c b a c b a ) = ( b)2 + ( c)2 + ( c)2 + ( b)2 + ( a)2 + ( a)2 log log log log log log + 2 (1) a a b c c b
x + y + z = ( b + c)2 + ( c + a)2 + ( a + b)2 2 2 2 log log log log log log c b a c b a = ( b)2 + ( c)2 + ( c)2 + ( b)2 + ( a)2 + ( a)2 log log log log log log + 6 (2) a a b c c b Từ (1) và (2) suy ra: 2 2 2
x + y + z − xyz = 4 .
Câu 62: Tìm số tự nhiên n thoả mãn 1 1 1 120 + ++ = với 0 < x ≠ 1 log x log x log x x n log 2 3 3 3 3 A. n = 15 . B. n = 20 . C. n = 12 . D. n = 10 . Lời giải Chọn A
Do 0 < x ≠ 1 nên ta có: 1 1 1 n n + + ++ = log + ++ = = ⋅ x ( . 1 2 3.3 ....3n ) 1 2 n ( ) log 3 log 3 log x log x log x x x n 2 2 3 3 3 . n (n +1) Vậy ta có: = 120 ⇔ n = 15 2
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 34
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Câu 63: Với mỗi số thực dương x , khi viết x dưới dạng thập phân thì số các chữ số đứng trước dấu
phẩy của x là log x + 1
. Cho biết log 2 = 0,30103 . Hỏi số 2017 2
khi viết trong hệ thập phân ta
được một số có bao nhiêu chữ số? (Kí hiệu x
là số nguyên lớn nhất không vượt quá x ). A. 607 . B. 606 . C. 609 . D. 608 . Lời giải Chọn D
Số các chữ số của 2017 2 là ( 2017 log 2
) +1= 2017×log2 +1= 2017×0,30103 +1= 607,17751 +1= 608 . Câu 64: Cho các số thực dương x,y,z thỏa mãn 81 xyz = 10 và
(log x . log yz + log y log z = 468 . Tính giá trị của biểu thức 10 ) ( 10 ) ( 10 )( 10 )
S = (log x)2 + (log y)2 + (log z)2 . 10 10 10 A. 75 . B. 936 . C. 625 . D. 25. Lời giải Chọn A a = log x x = 10a 10
Đặt b = log y ⇔ y = 10b ⇒ xyz = 10a+b+c 10 . c log z = z = 10c 10 81 xyz = 10
a + b + c = 81 Theo bài ta có: ( ⇒ 1 .
log x . log yz + log y log z = 468
ab + ac + bc = 468 10 ) ( 10 ) ( 10 )( 10 ) ( )
Vậy thay (1) vào ta có S = a + b + c = (a + b + c)2 2 2 2
− (ab + bc + ac) 2 2 = 81 − 2.468 = 75 .
Câu 65: Cho hai số thực dương x,y ≠ 1 thỏa mãn log y = log x và log (x − y) = log x + y . Tính giá x y ( ) x y trị biểu thức 4 2
S = x − x + 1. A. S = 2 . B. S = 3 . C. S = 4 . D. S = 5 . Lời giải Chọn A x,y ≠ 1 Điều kiện: . Ta có: x > y > 0 1 y = y = x ⇔ y = ⇔ y = ⇔
⇔ y = x− ⇔ y = . x y x ( x )2 log 1 (L) x 1 1 log log log log 1 log y log y = 1 − (TM) x x x Ta có: (x y) (x y) 1 1 2 1 log log log x log x log x − = + ⇔ − = − + ⇔ − = 0 x y x x x 2 x x x 2 1 4 2 ⇔ x −
= 1 ⇔ x − x −1 = 0 . Vậy 4 2
S = x − x + 1 = 1+ 1 = 2 . 2 x
Câu 66: Có hai cặp số thực (x;y) thỏa mãn đồng thời log x + log y = 4 và log 225 − log 64 = 1 là 225 64 x y
(x ;y và (x ;y . Giá trị biểu thức log x y x y bằng: 30 ( 1 1 2 2 ) 2 2 ) 1 1 )
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 35
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com A. 12 . B. 15 . C. 8 . D. 36. Lời giải Chọn A X = log x
Theo bài ra: log 225 − log 64 = 1 . Đặt 225 ta được hệ: x y Y = log y 64 X + Y = 4 1 1 1 1 ⇒ −
= 1 ⇔ − X = X( − X) 2 4 2 4
⇔ X − 6X + 4 = 0 − = 1 X 4 − X X Y
X = 3 + 5 ⇒ Y = 1− 5 ⇔
X = 3 − 5 ⇒ Y = 1+ 5 3+ 5
X = 3 + 5 x = 225 3− 5
X = 3 − 5 x = 225 Với 1 ⇒ Với 2 ⇒ 1− 5 Y = 1− 5 y = 64 1+ 5 Y = 1+ 5 y = 64 1 2
Khi đó: log (x y x y ) = log ( 6 2 225 .64 = 12 30 1 1 2 2 30 )
Câu 67: Tìm tập hợp tất cả các số thực m để tồn tại duy nhất cặp số thực (x;y) thỏa mãn đồng thời 2 log
4x + 4y − 6 + m = 1 và 2 2
x + y + 2x − 4y + 1 = 0 . 2 2 x +y +2 ( ) A. { } 5 ± . B. { 7 ± , 5 ± ,± } 1 . C. { 5, ± ± } 1 . D. { } 1 ± . Lời giải Chọn C
x + y + 2x − 4y +1 = 0
(x+1)2 +(y −2)2 2 2 = 4 (1) Theo đề bài ta có: ⇔ 2 2 2
4x + 4y − 6 + m = x + y + 2 (x −2 )2 +(y −2)2 2 = m (2)
Phương trình (1) là phương trình đường tròn (C có tâm I 1;
− 2 , bán kính R = 2 1 ( ) 1 ) 1
và phương trình (2) là phương trình đường tròn (C có tâm I 2;2 và bán kính R = m 2 ( ) 2 ) 2
Cặp số thực (x;y) tồn tại duy nhất khi và chỉ khi (C , (C tiếp xúc ngoài hoặc tiếp xúc trong 2 ) 1 )
I I = R + R 3 = m + 2 1 2 1 2 m = 1 ±
( R = R ) ⇔
I I = R − R ⇔ 3 = m − 2 ⇔ . 1 2 1 2 1 2 m = 5 ± R ≠ R 1 2 m ≠ 2
Câu 68: cho các số thực dương a,b,c lớn hơn 1, đặt x = log b + log a,y = log c + log b và a b b c
z = log a + log c . Giá trị của biểu thức 2 2 2
x + y + z − xyz bằng c a A. 1. B. 2 . C. 3 . D. 4 . Lời giải Chọn D
Ta có: xyz = (log b + log c)(log c + log a)(log a + log b c b a c b a ) = ( b)2 + ( c)2 + ( c)2 + ( b)2 + ( a)2 + ( a)2 log log log log log log + 2 (1) a a b c c b
x + y + z = ( b + c)2 + ( c + a)2 + ( a + b)2 2 2 2 log log log log log log c b a c b a
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 36
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com = ( b)2 + ( c)2 + ( c)2 + ( b)2 + ( a)2 + ( a)2 log log log log log log + 6 (2) a a b c c b Từ (1) và (2) suy ra: 2 2 2
x + y + z − xyz = 4 .
Câu 69: Với mỗi số thực dương x , khi viết x dưới dạng thập phân thì số các chữ số đứng trước dấu
phẩy của x là log x + 1
. Cho biết log 2 = 0,30103 . Hỏi số 2017 2
khi viết trong hệ thập phân ta
được một số có bao nhiêu chữ số? (Kí hiệu x
là số nguyên lớn nhất không vượt quá x ). A. 607 . B. 606 . C. 609 . D. 608 . Lời giải Chọn D
Số các chữ số của 2017 2 là ( 2017 log 2
)+1= 2017×log2+1= 2017×0,30103+1= 607,17751+1= 608 .
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 37
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
BÀI 3. HÀM SỐ MŨ. HÀM SỐ LÔGARIT
A. KIẾN THỨC CƠ BẢN CẦN NẮM
Chuyện kể rằng, ngày xưa ở xứ Ấn Độ, người phát minh ra bàn cờ vua được nhà vua cho phép từ
chọn phần thưởng là những hạt thóc đặt vào 64 ô của bàn cờ theo quy tắc như sau: 1 hạt thóc ở ô
thứ nh ất, 2 hạt thóc ở ô thứ hai, 4 hạt thóc ở ô thứ ba,…. Cứ như thế số hạt thóc ở ô sau gấp đôi
số hạt thóc ở ô trước. Nhà vua nhanh chóng chấp nhận lời đề nghị, vì cho rằng phần thưởng như vậy thì quá dễ dàng.
Tuy nhiên, theo phần thưởng này, tổng số hạt thóc có trong 64 ô là 64
2 −1, tính ra được hơn 18
18.10 hạt thóc, hay hơn 450 tỉ tấn thóc (mỗi hạt thóc nặng khoảng 25 mg ). Nhà vua không thể
đủ thóc thưởng cho nhà phát minh.
Từ tình huống trên, có nhận xét gì về giá trị của biểu thức 2x khi x trở nên lớn? G Lời giải V: TR
Khi x trở lên lớn thì 2x trở lên rất lớn ẦN ĐÌN 1. Hàm số mũ H C
Nguyên phân là quá trình tế bào phân chia thành hai tế bào con giống hệt nhau về mặt di truyền. Ư – 083 4332133 Hình 1
Lập bảng sau đây để tính số tế bào được tạo ra từ một tế bào ban đầu sau những lần nguyên phân. Số lần nguyên phân 0 1 2 3 4 5 6 7 Số tế bào 1 2 4 ? ? ? ? ?
a) Hoàn thành bảng trên vào vở.
b) Gọi y là số tế bào được tạo ra từ một tế bào ban đầu sau x ( x = 0, 1, 2...) lần nguyên phân.
Viết công thức biểu thị y theo x . Lời giải a) Số lần 0 1 2 3 4 5 6 7 nguyên phân
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 1
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Số tế bào 1 2 4 8 16 32 64 128 b) 2x y =
Cho số thực dương a khác 1.
Hàm số cho tương ứng mỗi số thực x với số thực x
a được gọi là hàm số mũ cơ số a , kí hiệu x y = a . Nhận xét: Hàm số x
y = a có tập xác định là .
Ví dụ 1: Trong các hàm số sau đây, hàm số nào là hàm số mũ? Chỉ ra cơ số của nó. x a) 2 y = 3 b) 4 y x− = c) 4 x y − = Lời giải 1 x x x a) 2 2
y = 3 = 3 = ( 3) là hàm số mũ với cơ số 3 . b) 4 y x− =
không phải là hàm số mũ . x c) − x 1 y 4 = =
là hàm số mũ với cơ số 1 . 4 4 GV:
Đồ thị hàm số mũ T RẦ a) Xét hàm số mũ 2x
y = có tập xác định là . N ĐÌNH CƯ – 083 4332133 Hình 2
i) Hoàn thành bảng giá trị sau: x 2 − 1 − 0 1 2 y ? 1 1 ? ? 2
ii) Trong mặt phẳng toạ độ Oxy , xác định các điểm có toạ độ như bẳng trên. Làm tương tự, lấy nhiều điểm ( ; 2x M x
) với x∈ và nối lại ta được đồ thị hàm số 2x
y = như Hình 2. Từ đồ thị này,
nêu nhận xét về tính liên tục, tính đồng biến, nghịch biến, giới hạn khi x → +∞ , x → −∞ và tập giá
trị của hàm số đã cho.
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 2
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com x
b) Lập bảng giá trị và vẽ đồ thị của hàm số 1 y =
. Từ đó, nêu nhận xét về tính liên tục, tính 2
đồng biến, nghịch biến, giới hạn khi x → +∞ , x → −∞ và tập giá trị của hàm số này.
Tổng quát, ta có đồ thị của hàm số x
y = a với a >1 và 0 < a <1 như sau: Hình 3 Lời giải a) x -2 -1 0 1 2 y 1 1 1 2 4 G 4 2 V: TR ẦN Đ
Hàm số liên tục trên ÌN H CƯ
- Hàm số đồng biến trên – 083 - Khi x → ∞ + , y → ∞ + 4332133 - Khi x → ∞ − , y → 0
- Tập giá trị của hàm số là (0; ∞ + ) b) x -2 -1 0 1 2 y 4 2 1 1 1 2 4
Đồ thị của hàm số trên là:
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 3
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
- Hàm số liên tục trên
- Hàm số nghịch biến trên
- Khi x → +∞, y → 0
- Khi x → −∞, y → +∞
- Tập giá trị của hàm số là (0;+∞)
(1) Tập xác định: D = .
Tập giá trị: T = (0; + ∞) . GV
Hàm số liên tục trên . : TR (2) Sự biến thiên: ẦN
• Nếu a >1 thì hàm số đồng biến trên và ĐÌN lim y = lim x a = ;
+∞ lim y = lim x a = 0 . H x→+∞ x→+∞ x→−∞ x→−∞ CƯ
• Nếu 0 < a <1 thì hàm số nghịch biến trên và – 083 lim y = lim x
a = 0; lim y = lim x a = +∞ . x→+∞ x→+∞ x→−∞ x→−∞ 4332133 (3) Đồ thị:
• Cắt trục tung tại điểm (0; )
1 ; đi qua điểm (1; a) .
• Nằm phía trên trục hoành.
Ví dụ 2: Sử dụng tính chất của hàm số mũ, so sánh các cặp số sau: a) 2 1,4 và 1,8 1,4 ; b) 1,2 0,9− và 0,8 0,9− ; c) 3 2 và 5 4 . Lời giải
a) Do 1,4 >1 nên hàm số 1,4x y =
đồng biến trên . Mà 2 >1,8 nên 2 1,8 1,4 >1,4 .
b) Do 0 < 0,9 <1 nên hàm số 0,9x y =
nghịch biến trên . Mà 1, − 2 < 0 − ,8 nên 1, − 2 0 − ,8 0,9 > 0,9 . 1 2 c) Ta có: 3 3 2 = 2 ; 5 5 4 = 2 . 1 2 Do 2 >1 nên hàm số 2x
y = đồng biến trên . Mà 1 2 < nên 3 5 2 < 2 , suy ra 3 5 2 < 4 . 3 5
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 4
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Ví dụ 3: Năm 2020 , dân số thế giới là 7,795 tỉ người và tốc độ tăng dân số 1,05%/năm (nguồn:
https://www.worldmeters.infor/world-population). Nếu tốc độ này tiếp tục duy trì ở những năm tiếp
theo thì dân số thế giới sau t năm kể từ năm 2020 được tính bởi công thức: ( ) 7,795.(1 0,0105)t P t = + (tỉ người). (*)
Khi đó, hãy tính dân số thế giới vào năm 2025 và vào năm 2030 . (Mốc thời điểm để tính dân số
của mỗi năm là ngày 1 tháng 7 .) Lời giải
Năm 2025 ứng với t = 5 nên có dân số thế giới là: P( ) = ( + )5 5
7,795. 1 0,0105 ≈ 8,213 (tỉ người).
Năm 2030 ứng với t =10 nên có dân số thế giới là: P( ) = ( + )10 10
7,795. 1 0,0105 ≈ 8,653 (tỉ người).
Chú ý: Với giả thiết tăng tốc độ dân số 1,05% /năm không đổi, công thức (*) được áp dụng để
tính dân số thế giới tại thời điểm bất kì sau năm 2020. Chẳng hạn, dân số thế giới tại thời điểm
ngày 1 tháng 1 năm 2022 (ứng với t =1,5 ) là P( ) = ( + )5 1,5
7,795. 1 0,0105 ≈ 7,918 (tỉ người). x
HĐ 1: Trên cùng hệ trục tọa độ, vẽ đồ thị các hàm số 3x y = và 1 y = 3 Lời giải GV: TRẦN ĐÌNH CƯ – 083 4332133
HĐ 2: So sánh các cặp số sau: a) 0,1 0,85 và 0,1 0,85− b) 1,4 π − và 0,5 π − c) 4 3 và 1 3 3 Lời giải
a) Do 0,85 <1 nên hàm số 0,85x y =
. nghịch biến trên . Mà 0,1> 0, − 1 Suy ra 0,1 0,1 0,85 0,85− < Vì π >1 nên hàm số x
y = π đồng biến trên . Mà 1, − 4 < 0 − ,5 Suy ra 1, − 4 0 − ,5 π < π 1 1 − c) Ta có: 1 4 4 3 3 = 3 ; = 3 3 3
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 5
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com − Vì 3 >1 nên hàm số 3x
y = đồng biến trên . Mà 1 1 > 4 3 1 1 − Suy ra 1 4 3 3 > π Hay 4 3 > 3 3
Luyện tập 1. Khối lượng vi khuẩn của một mẻ nuôi cấy sau t giờ kể từ thời điểm ban đầu được cho bởi công thức ( ) = 50.1,06t M t (g)
( Nguồn: Sinh học lớp 10, NXB Giáo dục Vệt Nam, năm 2017, trang 101)
a) Tìm khối lượng vi khuẩn tại thời điểm bắt đầu nuôi cấy (gọi là khối lượng ban đầu).
b) Tính khối lượng vi khuẩn sau 2 giờ và sau 10 giờ (làm tròn kết quả đến hàng trăm).
c) Khối lượng vi khuẩn tăng dần hay giảm đi theo thời gian? Tại sao? Lời giải
a) Khối lượng vi khuẩn tại thời điểm bắt đầu nuối cấy là: M ( ) 0 0 = 50.1,06 = 50
b) Khối lượng vi khuẩn sau 2 giờ là: M ( ) 2 2 = 50.1,06 = 56,18
Khối lượng vi khuẩn sau 10 giờ là: M ( ) 10 10 = 50.1,06 = 89,54
c) Do 1,06 > 1 nên hàm số M (t) đồng biến
Do đó, khối lượng vi khuẩn tăng dần theo thời gian 2. Hàm số logarit GV Kính lúp 3: : TR
Cho s và t là hai đại lượng liên hệ với nhau theo công thức 2t s = ẦN
a) Với mỗi giá trị của t nhận trong , tìm được bao nhiêu giá trị tương ứng của s . Tại sao? ĐÌN
b) Với mỗi giá trị của s thuộc (0;+∞), có bao nhiêu giá trị tương ứng của t ? H CƯ
c) Viết công thức biểu thị t theo s và hoàn thành bảng sau: – 083 s 1 1 2 4 8 16 1 1 4332133 8 4 2 t ? -2 ? 0 ? 2 ? ?
Trong kính lúp 3, t là một hàm số của s xác định bởi công thức t = log s . Đây là một hàm số logarit. 2 Lời giải
a) Với mỗi giá trị t thuộc , ta xác định duy nhất 1 giá trị s
b) Với mỗi giá trị s thuộc (0; ∞
+ ) , ta xác định duy nhất 1 giá trị t c) s 1 1 2 4 8 16 1 1 8 4 2 t -3 -2 -1 0 1 2 3 4 Định nghĩa:
Cho số thực dương a khác 1.
Hàm số cho tương ứng với mỗi số thực dương x với số thực log x a
được gọi là hàm số lôgarit cơ số a ,
kí hiệu là y = log x a .
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 6
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Nhận xét: Hàm số y = log x 0;+∞ a có tập xác định là ( ).
Ví dụ 4: Trong các hàm số sau, hàm số nào sau đây là hàm số lôgarit? Chỉ ra cơ số của nó. a) y = log x
b) y = −log x
c) y = x log 3 . 2 3 2 Lời giải
a) y = log x là một hàm số lôgarit với cơ số bằng 2 . 2
b) y = −log x = log x là hàm số lôgarit với cơ số bằng 1 . 3 1 3 3 c) y = x log 3 log 3 2
không phải là hàm số lôgarit (mà là hàm bậc nhất với hệ số góc 2 ).
Đồ thị hàm số lôgarit HĐ 4
a) Xét hàm số y = log x D = 0;+∞ 2 với tập xác định ( )
i) Hoàn thành bảng giá trị sau x 1 1 2 4 2 y ? 0 ? ?
ii) Trong mặt phẳng tọa độ Oxy , xác định các điểm có tọa độ như bảng trên. Làm tương
tự, lấy nhiều M ( ;
x log x với x > và nối lại được đồ thị hàm số như Hình 4. Từ đồ thị 2 ) 0
này, nêu nhận xét về tính liên tục, tính đồng biến, nghịch biến, giới hạn khi GV + :
x → +∞, x → 0 và tập giá trị của hàm số đã cho. T RẦ
b) Lập bảng giá trị và vẽ đồ thị hàm số y = log x . Từ đó, nhận xét về tính đồng liên tục, tính N 1 Đ 2 ÌN + H
đồng biến, nghịch biến, giới hạn khi x → +∞, x → 0 và tập giá trị của hàm số này. CƯ – 083 4332133 Lời giải a) x 1 1 2 4 2
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 7
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com y -1 0 1 2
• Hàm số liên tục trên (0; ∞
+ ) Hàm số đồng biến trên (0; ∞ + ) • Khi x → ∞ + , y → ∞ + . • Khi x 0+ → , y → ∞ −
b) Hàm số y = log x 1 2 x 1 1 2 4 2 y 1 0 -1 -2 Đồ thị hàm số: GV: TRẦN ĐÌNH CƯ – 083 4332133
• Hàm số liên tục trên (0; ∞ + )
• Hàm số nghịch biến trên (0; ∞ + ) • Khi x → ∞ + , y → ∞ − • Khi x 0+ → , y → ∞ +
Tổng quát, ta có đồ thị hàm số y = log x < < a
với a >1 và 0 a 1 như sau:
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 8
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
(1) Tập xác định: D = (0;+∞) . Tập giá trị: T = .
Hàm số liên tục trên (0;+∞). (2) Sự biến thiên:
• Nếu a >1 thì hàm số đồng biến trên (0;+∞) và
lim y = lim log x = +∞ , lim y = lim log x = −∞ . a + + a x→+∞ x→+∞ x→0 x→0
• Nếu 0 < a <1 thì hàm số nghịch biến trên (0;+∞) và
lim y = lim log x = −∞ , lim y = lim log x = +∞ . a x→+∞ x→+∞ + + a x→0 x→0 (3) Đồ thị •
Cắt trục hoành tại điểm (1;0) , đi qua điểm ( ) ;1 a .
• Nằm bên phải trục tung. GV : T
Ví dụ 5. So sánh các cặp số sau: RẦN a) log 7 và 3log 2 b) 3 3 2log 5 và 3log 3. 0,4 0,4 ĐÌN H C Lời giải Ư – = = 083 a) 3 3log 2 log 2 log 8 . 3 3 3 4332133
Hàm số y = log x có cơ số 3 >1 nên đồng biến trên (0; ∞ + ) . 3
Mà 7 < 8 nên log 7 < log 8. Vậy log 7 < 3log 2. 3 3 3 3 b) 2 3
2log 5 = log 5 = log 25;3log 3 = log 3 = log 27 . 0,4 0,4 0,4 0,4 0,4 0,4
Hàm số y = log x có cơ số 0,4 <1 nên nghịch biến trên (0; ∞ + ) . 0,4
Mà 25 < 27 nên log 25 > log 27 . Vậy 2log 5 > 3log 3 . 0,4 0,4 0,4 0,4
Ví dụ 6. Trong âm học, mức cường độ âm được tính bởi công thức = log I L (dB) (dB là đơn vị I 0
mức cường độ âm, đọc là đêxiben), trong đó I là cường độ âm tính theo 2 W / m và 12 I 10− = 2 W / m là 0
cường độ âm thanh chuẩn (cường độ âm thấp nhất mà tai người bình thường nghe được).
(Nguồn: Vật lí lớp 12, NXN Giáo dục Việt Nam, năm 2017, trang 52, 53)
a) Mức độ cường âm thấp nhất mà tai người nghe được là bao nhiê?
b) Cuộc trò chuyện có cường độ âm là 9 10− 2
W / m thì có mức cường độ âm bằng bao nhiêu?
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 9
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
c) Cường độ âm tại khu văn phòng nằm trong miền từ 7 10− 2 W / m đến 6 5 10 . − 2 W / m (tức là 7 − 6 10 I 5.10− ≤ ≤
). Mức độ cường âm tại khi văn phòng này nằm trong khoảng nào? (Làm trò kết quả đến hàng đơn vị). Lời giải a) Khi I = I
L =10log 1 = 0 dB 0 thì
( ) . Vậy mức cường độ âm thấp nhất mà tai người bình thường có thể nghe được là 0 dB. 9 − b) Khi 9 I 10− = 2 W / m ta có, 10 3 L =10log =10log10 =10.3 = 30 (dB). 12 10− 7 − c) Khi 7 I 10− = 2 W / m ta có, 10 5 L =10log
= 10log10 = 5.log10 = 50 dB . 12 − ( ) 10 6 − Với 6 I 5 10 . − = 2 W / m ta có, 5.10 6 L =10log
= 10log65.10 =10. 6 + log5 ≈ 67 (dB). 12 − ( ) 10
Hàm số y = log x đồng biến nên suy ra hàm số y =10log x cũng đồng biến. Do đó, từ 7 − 6 10 I 5.10− ≤ ≤
suy ra 50 ≤ L ≤ 67 .
Vậy mức cường độ âm tại khu văn phòng nằm trong khoảng từ 50 dB đến 67 dB.
HĐ 3: Trên cùng hệ trục tọa độ, vẽ đồ thị các hàm số y = log x = 3 và y log x 1 3 Lời giải GV: TRẦN ĐÌNH CƯ –
HĐ 4: So sánh các cặp số sau: 083 4332133 a) log 4,8 và log 5,2 b) log 2 và log 2 2 c) −log 2 và log 0,4 . 1 1 5 5 1 1 2 2 4 2 Lời giải
a) Vì 1 < 0 nên hàm số y = log x nghịch biến trên (0; ∞ + ) 2 1 2
Mà 4,8 < 5,2 nên log 4,8 > log 5,2 1 1 2 2 b) Ta có: log2 log2 log2 log2 log 2 = = = = 2⋅ 5 log 5 1 1 log5 log5 ⋅log5 2 2 1 2 3 log22 2 log2 2 log2 3 log2 log 2 2 = = = = ⋅ 5 log5 log5 log5 2 log5
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 10
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Suy ra: log 2 > log 2 2 5 5 1 − log2 1 − − c) Ta có: log2 log2 log2 1 log2 2 2 −log 2 = − = − = − = ⋅ = = log 2 1 2 1 1 1 1 2 1 1 4 ⋅ 2 log log 2 log log log 4 2 2 2 2
Vi 1 < 0 nên hàm số y = log x nghịch biến trên (0; ∞ + ) 2 1 2 1 − 1 − Mà 2 2 > 0,4 nên 2 log 2 < log 0,4 1 1 2 2 Hay −log 2 < log 0,4 1 1 4 2
Luyện tập 2 : Mức cường độ âm được tính theo công thức như ở Ví dụ 6.
a) Tiếng thì thầm có cường độ âm 10 − 2
I =10 W / m thì có mức cường độ âm bằng bao nhiêu?
b) Để nghe trong thời gian dài mà không gây hại cho tai, âm thanh phải có cường độ không vượt quá
100000 lần cường độ của tiếng thì thầm. Âm thanh không gây hại cho tai khi nghe trong thời gian dài phải
ờ mức cường độ âm như thế nào? Lời giải 10 −
a) Mức cường độ âm của tiếng thì thầm là 10 L =10log = 20 dB 12 − ( ) 10
b) Để âm thanh không gây hại cho tai khi nghe thời gian dài thì cường độ âm là: GV: T 10 − 5 − 2 R
I =100000⋅10 =10 (W / m ) ẦN ĐÌN 5 10− H
Mức cường độ âm giới hạn đó là: L =10log = 70 dB 12 − ( ) C 10 Ư – 083
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP 4332133
Dạng 1. Tìm tập xác định, tập giá trị của hàm số
1. Phương pháp: 0 < a ≠ 1
Hàm số y = log f x xác định khi f (x) > 0 a ( ) 2. Các ví dụ
Ví dụ 1. Tìm tập xác định của các hàm số sau : a) y = log ( 2 x + 2x ; 3 ) b) y = log ( 2 4 − x 0,2 ) Lời giải
a) Hàm số y = log ( 2
x + 2x xác định khi 2
x + 2x > 0 hay x < 2 − hoặc x > 0 . 3 )
Vạy tập xác định của hàm số là D = ( ; −∞ 2 − ) ∪ (0;+∞) : b) Hàm số y = log ( 2
4 − x xác định khi 2 4 − x > 0 hay 2 − < x < 2 . 0,2 )
Vậy tập xác định của hàm số là D = ( 2; − 2) .
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 11
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Ví dụ 1. Tìm tập xác định của các hàm số sau : a) 1 y = log 2 3− x b) 2 y = . log x − 3 4 Lời giải a) Hàm số 1 y = log
xác định khi 1 > 0 hay x < 3. Vạy tập xác định của hàm số là ( ; −∞ 3) . 2 3− x 3− x x > 0 x > 0 b) Hàm số 2 y = xác định khi hay log x − 3 log x ≠ 3 x ≠ 64 4 4
Vạy tập xác định của hàm số là D = (0;64) ∪ (64;+∞) . Dạng 2. So sánh 1. Phương pháp ⊕ a >1: x y
a > a ⇔ x > y
⊕ 0 < a <1: x y
a > a ⇔ x < y
⊕ a >1: log x >
y ⇔ x > y a loga
⊕ 0 < a <1: log x >
y ⇔ x < y a loga 2. Ví dụ G
Ví dụ 1: Hãy so sánh mỡi sơ sau với 1: V: T 1, − 2 R 5 Ầ a) 2 (0,1) ; b) 0,1 (3,5) ; c) 2,7 π − ; d) . N 5 Đ ÌN H Lời giải CƯ – a) 2 (0,1) <1; 083 > 4332133 b) 0,1 (3,5) 1; c) 2,7 π − <1; − 1,2 d) 5 >1 . 5
Ví dụ 2: Sử dụng tính chất đồng biến, nghịch biến của hàm sơ mũ, hãy so sánh mỗi căp sơ sau: a) 3 (1,7) và 1 ; b) 2 (0;3) va 1 ; c) 1,5 (3,2) và 1,6 (3,2) ; d) 3 (0,2)− và 2 (0,2)− ; 2 1,4 e) 1 1 và 5 5 g) 6π và 3,14 6 . Lời giải
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 12
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com a) 8 (1,7) >1 b) 2 (0,8) <1; c) 1,5 1,6 (3,2) < (3,2) ; d) 3 − 2 (0,2) (0,2)− > ; 2 1,4 c) 1 1 < 5 5 g) π 8;14 6 > 6 .
Dạng 3. Đồ thị hàm số 1. Phương pháp: Hàm số mũ x y = a . •
Có tập xác định là và tập giá trị là (0; ∞ + ) ; •
Đồng biến trên khi a >1 và nghịch biến trên khi 0 < a <1; • Liên tục trên ; •
Có đồ thị đi qua các điểm (0; )
1 ,(1;a) và luôn nằm phía trên trục hoành. GV: TRẦN ĐÌNH CƯ – 083 4332133
Hàm số lôgarit y = log x : a •
Có tập xác định là (0; ∞
+ ) và tập giá trị là ; • Đồng biến trên (0; ∞
+ ) khi a >1 và nghịch biến trên (0; ∞
+ ) khi 0 < a <1; • Liên tục trên (0; ∞ + ) ; •
Có đồ thị đi qua các điêm (1;0),(a; )
1 và luôn nằm bên phải trục tung.
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 13
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 2. Các ví dụ
Ví dụ 1: Vẽ đồ thị các hàm số a) (0,4)x y = ; b) (2,5)x y = ; c) (0,4)x y = − ; d) | | (2,5) x y = . Lời giải GV : TRẦ N Đ ÌN H Ví dụ 2: Vẽ đồ thị CƯ các hàm – 083 số 4332133 a) y = log x ; b) y | = log x |; c) y = 2ln x ; d) 2 y = ln x . Lời giải
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 14
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
C. GIẢI BÀI TẬP SÁCH GIÁO KHOA
Bài 1. Vẽ đồ thị các hàm số sau: x a) = 4x y b) 1 y = . 4 Lời giải GV: T a) Bảng giá trị: RẦN Đ x -1 0 1 2 ÌN H CƯ – y 1 1 4 16 083 4 4332133 Đồ thị: b) Bảng giá trị: x -2 -1 0 1
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 15
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com y 1 16 4 1 4
Bài 2. So sánh các cặp số sau: a) 0,7 1,3 và 0,6 1,3 b) 2,3 0,75− và 2,4 0,75− . Lời giải
a) Do 1,3 >1 nên hàm số 1,3x y = đồng biến trên . Mà 0,7 > 0,6 nên 0,7 0,6 1,3 >1,3 .
b) Do 0,75 <1 nên hàm số 0,75x y = nghịch biến trên . Mà 2, − 3 > 2, − 4 nên 2, − 3 2, − 4 0,75 < 0,75 .
Bài 3. Tìm tập xác định của các hàm số: G a) log 3− 2x b) log ( 2 x + 4x . 3 ) 2 ( ) V: TR Lời giải ẦN ĐÌN
a) log 3− 2x xác định khi 3
3− 2x > 0 ⇔ 2x < 3 ⇔ x < 2 ( ) H 2 CƯ –
Vậy hàm số có tập xác định 3 D = ∞ − ; . 083 2 4332133 x > 0 b) log ( 2
x + 4x xác định khi 2
x + 4x > 0 ⇔ x(x + 4) > 0 ⇔ 3 ) x < 4 −
Vậy hàm số có tập xác định D = ( ∞ − ; 4 − ) ∪(0; ∞ + ) .
Bài 4. Vẽ đồ thị các hàm số: a) y = logx b) y = log x 1 4 Lời giải b)
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 16
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Bài 5. So sánh các cặp số sau: a) logπ 0,8 và logπ1,2; b) log 2 và log 2,1. 0,3 0,3 Lời giải
a) Vì π >1 nên hàm số log 0; ∞ +
π x đồng biến trên ( ) Mà 0,8 <1,2 nên log < π 0, 8 logπ1,2
b) Vì 0,3 >1 nên hàm số log x nghịch biến trên (0; ∞ + ) 0,3
Mà 2 < 2,1 nên log 2 > log 2,1 0,3 0,3
Bài 6. Cường độ ánh sáng I dưới mặt biển giảm dần theo độ sâu theo công thức = . d
I I a , trong đó I là 0 0
cường độ ánh sáng tại mặt nước biển, a là hằng số (a > 0) và d là độ sâu tính bằng mét tính từ mặt nước biển.
(Nguồn: https://www.britannica.com/science/seawer/Optical-properties)
a) Có thể khẳng định rằng 0 < a <1 không? Giải thích.
b) Biết rẳng cường độ ánh sáng tại độ sâu 1 m bẳng 0,95I0 . Tìm giá trị của a . GV
c) Tại độ sâu 20 m , cường độ ánh sáng bằng bao nhiêu phần trăm so với I0? (Làm tròn kết quả đến hàng : TR đơn vì.) ẦN Lời giải ĐÌNH =
a) Vì cường độ ánh sáng giảm dần theo độ sâu nên hàm số . d
I I a nghịch biến. C 0 Ư < < – Vậy 0 a 1. 083 b) Ta có: d 1
I = I ⋅a ⇔ 0,95I = I ⋅a ⇔ a = 0,95 . 0 0 0 4332133 c) Ta có: d 20
I = I ⋅a = I ⋅0,95 ≈ 0,36I . 0 0 0
Vậy tại độ sâu 20 m , cường độ ánh sáng bằng 36% phần trăm so với I 0
Bài 7. Công thức = 19 − ,4⋅log P h
là mô hình đơn giản cho phép tính độ cao h so với mặt nước biển P0
của một vị trí trong không trung (tính bằng kilômét) theo áp suất không khí P tại điểm đó và áp suất P0
của không khí tại mặt nước biển (cùng tính bằng Pa − đơn vị áp suất, đọc là Pascal ).
(Nguồn: https://doi.org/10.1007/s40828-020-0111-6)
a) Nếu áp suất không khí ngoài máy bay bằng 1 P thì máy bay đang ở độ cao nào? 0 2
b) Áp suất không khí tại đỉnh của ngọn núi A bằng 4 lần áp suất không khí tại đỉnh của ngọn núi B . Ngọn 5
núi nào cao hơn và cao hơn bao nhiêu kilômét? (Làm tròn kết quả đến hàng phần mười.) Lời giải
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 17
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
a) Độ cao của máy bay khi áp suất không khí ngoài máy bay bằng 1 P là: 0 2 1 P0 2 1 h = 19 − ,4⋅log = 19 − ,4⋅log ≈ 5,84( km) P 2 0
b) Độ cao của ngọn núi A là: h = 19 − ,4⋅log PA A P0
Độ cao của ngọn núi B là: h = 19 − ,4⋅log PB B P0
Áp suất không khí tại đỉnh của ngọn núi A bằng 4 lần áp suất không khí tại đỉnh của ngọn núi B nên ta 5 có: 4 PA 4 P = P ⇔ = A 5 B PB 5 Ta có: h − h = 19 − ,4⋅log P P P P A − 19 − ,4⋅log B = 19
− ,4⋅log A +19,4⋅log B A B P P P P 0 0 0 0 P P P A B A 4 = 19 − ,4log : = 19 − ,4log = 19 − ,4log ≈1,88( km) P P PB 5 G 0 0 V: TR
Vậy ngọn núi A cao hơn ngọn núi B 1,88km. ẦN ĐÌN
D. BÀI TẬP TRẮC NGHIỆM H C
Câu 1: Tập xác định của hàm số y = log 10 − 2x là 2 ( ) Ư – 083 A. ( ;2 −∞ ) B. (5;+∞) C. ( ; −∞ 10) D. ( ; −∞ 5) 4332133 Lời giải Chọn D
Hàm số xác định ⇔10−2x > 0 ⇔ x < 5⇒ D = ( ; −∞ 5)
Câu 2: Tập xác định của hàm số y = ( 2 log x + 2x) là A. D = ( 2; − 0) B. D = \{ } 0 C. D = ( ; −∞ 2 − ) ∪(0;+∞) D. D = Lời giải Chọn C x > 0
Hàm số đã cho xác định 2
⇔ x + 2x > 0 ⇔ . Vậy D = ( ; −∞ 2 − ) ∪(0;+∞) x < 2 −
Câu 3: Cho 0 < a <1. Tìm mệnh đề đúng trong các mệnh đề sau
A. Tập giá trị của hàm số x y = a là
B. Tập xác định của hàm số y = log x a là
C. Tập xác định của hàm số x y = a là
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 18
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
D. Tập giá trị của hàm số y = log x a là Lời giải Chọn D Hàm số y = log x a có tập giá trị là
Câu 4: Tập xác định của hàm số y = log ( 2 3− 2x − x 2 ) là A. D = ( 1; − 3) B. D = (0; ) 1 C. D = ( 1; − ) 1 D. D = ( 3 − ; ) 1 Lời giải Chọn D
Hàm số đã cho xác định 2 ⇔ 3− 2x − x > 0 ⇔ 3 − < x <1. Vậy D = ( 3 − ; ) 1 .
Câu 5: Hàm số y = log ( x x
4 − 2 + m có tập xác định là 2 ) thì A. 1 m < B. m > 0 C. 1 m ≥ D. 1 m > 4 4 4 Lời giải Chọn D
Hàm số có tập xác định là x x x x ⇔ 4 − 2 + m > 0, x
∀ ∈ ⇔ m > 2 − 4 ( x ∀ ∈ ) 1 G Đặt x 2 = > ⇒ > − ∀ > ⇔ > ⇔ > V t 2 0 m t t ( t 0) m max f (t) m . : t>0 T 4 RẦ 2 N
Câu 6: Tìm tất cả các giá trị thực của tham số m để hàm số y = ln(x − 2mx + 4) xác định với mọi ĐÌN x ∈ . H CƯ A. m∈[ ; −∞ 2 − ]∪[2;+∞] B. m∈[ 2; − 2] – 083 C. m∈( 2;
− 2) ∪(2;+∞) D. m∈( 2; − 2) 4332133 Lời giải Chọn D
Hàm số xác định với mọi 2 2
x ∈ ⇔ x − 2mx + 4 > 0, x
∀ ∈ ⇒ ∆' = m − 4 < 0 ⇔ 2 − < m < 2
Câu 7: Khẳng định nào sau đây là khẳng định sai? 2,3 2,3 2 − 2 − A. 10 12 > 7 8 . B. > . 11 11 9 9 C. ( ) 3−,1 > ( ) 3−,1 2,5 2,6 . D. ( )7,3 < ( )7,3 3,1 4,3 . Lời giải Chọn A a,b > 1
Dùng tính chất: x x
a > b ⇒ a > b x > 0
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 19
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com ( + )a 1− 7 4 3 < 7 − 4 3 Câu 8: Nếu thì A. a <1 B. a >1 C. a > 0 D. a < 0 Lời giải Chọn D a 1 − 1 −
BPT ⇔ (7 + 4 3) < (7 + 4 3) ⇒ a −1< 1 − ⇔ a < 0 Câu 9: Cho α β π > π với α,β∈ .
Mệnh đề nào dưới đây là đúng? A. α > β B. α < β C. α = β D. α ≤ β Lời giải Chọn A
Câu 10: Cho M = log 0,07;N = log 0,2.Khẳng định nào sau đây là khẳng định đúng? 0,3 3
A. 0 > N > M.
B. M > 0 > N.
C. N > 0 > M.
D. M > N > 0. Lời giải Chọn B < < + Ta có: 0 0,3 1
⇒ M = log 0,07 > 0 0,3 0 < 0,07 <1 3 >1 ⇒ N = log 0,2 < 0 3 0 < 0,2 <1 GV:
+ Suy ra: M > 0 > N T RẦ
Câu 11: Mệnh đề nào dưới đây sai? N Đ 2019 2018 ÌN 2017 2018 2 2 H
A. ( 2 − )1 > ( 2 − )1 . B. 1− < 1− . C 2 2 Ư – 083
C. ( − )2018 > ( − )2017 3 1 3 1 . D. 2 1+ 3 2 > 2 . 4332133 Lời giải Chọn C 2018 > 2017 2018 2017 Do
nên ( 3 − )1 < ( 3 − )1 . 3 −1 >1
Câu 12: Cho 0 < a ≠1; α, β∈ .
Trong các mệnh đề sau, mệnh đề nào đúng? a α α = aβ α α a a = ( a ) (a > 0) a β (a )β α α = aα = ( a ) A. aβ B. C. D. Lời giải Chọn D α aα = ( a ) 3 − 1 −
Câu 13: Có kết luận gì về a nếu (2a + ) 1 > (2a + ) 1 ( )1
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 20
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com A. a ∈ (−∞ − ) 1 ; 1 ∪ − ;0
B. a ∈ (−∞ − ) 1 ; 1 ∪ 0; 2 2
C. a ∈ (−∞ − ) 1 ; 1 ∪ − ;0 D. a ∈ ( ; −∞ 2 − ) ∪ ( 1; − 0) 6 Lời giải Chọn A Điều kiện xác định: 1
2a +1 ≠ 0 ⇔ a ≠ − . 2 1 1 1− (2a + )2 1 a(a + ) 1 Ta có: ( ) 1 ⇔ > ⇔ > 0 ⇔ < 0 (2a + )3 1 2a +1 (2a + )3 1 (2a + )3 1 1 − < a <
Lập bảng xét dấu ta được: 0 2 . a < 1 −
Câu 14: Trong các bất đẳng thức sau, bất đẳng thức nào sai? A. log 5 > log π log 5 <1 2 2 B. log π < log e C. log π > log 7 D. 2 1 − 7 2 1 − 3 1 + 3 1 + Lời giải Chọn C + > π < ⇒ π < G Ta có: 3 1 1 do đó 7 log log 7. 3 1 + 3 1 + V: TR
Câu 15: Cho 0 < a <1, b >1 và M = log N = log b a 2 , 2
. Khi đó khẳng định nào sau đây đúng? ẦN Đ
A. M > 0 và N > 0.
B. M > 0 và N < 0. ÌN H
C. M < 0 và N < 0.
D. M < 0 và N > 0. CƯ – Lời giải 083 Chọn D 4332133 2 1
Câu 16: Với những giá trị nào của a thì (a )− − − 3 > (a − ) 3 1 1 ?
A. 1< a < 2. B. a > 2 . C. a >1.
D. 0 < a <1. Lời giải Chọn A 2 − 1 − < Vì 3 3
⇒ 0 < a −1<1 ⇔ 1< a < 2 . ( a − ) 2 1 − > (a − ) 1− 3 3 1 19 15 Câu 17: Nếu 5 7 a < a và log + > + thì: b ( 2 7 ) logb ( 2 5)
A. a >1,0 < b <1
B. 0 < a <1,b >1
C. 0 < a <1,0 < b <1 D. a >1,b >1 Lời giải Chọn B
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 21
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 19 15 5 7
a < a vì mũ không là số nguyên nên a > 0 . Mặt khác 19 15 >
nên a <1⇒ 0 < a <1 5 7 log ( 2 + 7) > log ( 2 + ≠ b > + > + b > b b 5) để có nghĩa thì 1 0 và 2 7 2 5 nên 1
Câu 18: Cho các số thực a,b thỏa mãn a > b >1. Chọn khẳng định sai trong các khẳng định sau: A. log b > a b < a a > a logb B. loga logb C. ln ln b
D. log ab < 0 1 ( ) 2 Lời giải Chọn A
Cho a = 4;b = 2 ta có: 1
log b = ;log a = nên A sai. a b 2 2 3 4
Câu 19: Cho a, b là các số thực dương, thỏa mãn 1 2 4 3 a > a và log < log
. Mệnh đề nào dưới đây b b 2 3 đúng?
A. a >1,0 < b <1
B. 0 < a <1,b >1
C. 0 < a <1,0 < b <1 D. a >1,b >1 Lời giải Chọn B 3 4 Ta có 3 4 4 3
a > a ⇒ 0 < a <1 do < 4 3 1 2 2 1 G < ⇒ > > V Mặt khác log log b 1do b b : T 2 3 3 2 RẦN − − > < Đ
Câu 20: Cho hai số thực a và b sao cho với 5 4 a a và 3 4 log . Trong các mệnh đề sau b logb ÌN 4 5 H C mệnh đề nào là đúng? Ư –
A. a >1;b >1.
B. a >1;0 < b <1. 083 4332133
C. 0 < a <1;b >1.
D. 0 < a <1;0 < b <1. Lời giải Chọn C 3 4 < 5 − < 4 − Ta có 4 5
⇒ 0 < a <1 và ⇒ b >1. 5 − 4 a > a− 3 4 log < b log 4 b 5
Vậy 0 < a <1;b >1. a b
Câu 21: Cho ( 2 − )1 > ( 2 − )1 . Kết luận nào sau đây đúng?
A. a > b .
B. a < b .
C. a = b .
D. a ≥ b . Lời giải Chọn B
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 22
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com x
Do 0 < 2 −1<1 nên hàm số mũ y = ( 2 − )
1 nghịch biến trên và ta có: ( a b 2 − ) 1 > ( 2 − ) 1 ⇔ a < b
Câu 22: Tìm tập tất cả các giá trị của a để 21 5 7 2 a > a A. 0 < a <1 B. 5 2 < a < C. a >1 D. a > 0 21 7 Lời giải Chọn A 5 2 21 5 7 2 21 7
a > a ⇔ a > a ⇔ 0 < a <1 2p−q
Câu 23: Cho p, q là các số thực thỏa mãn 1 p−2q m = ,n = e
, biết m > n. So sánh p và q e A. p ≥ q B. p > q C. p ≤ q D. p < q Lời giải Chọn D 2p−q Ta có 1 q−2p p−2q m = = e ,n = e
. Vì m > n nên q − 2p > p − 2q ⇔ q > p. e
Câu 24: Cho a >1. Mệnh đề nào sau đây là đúng? 3 2 a 1 − 1 1 1 G > > 3 > < V A. 1 B. 3 a C. a a D. 5 2016 2017 : T a a a a RẦN Lời giải ĐÌN Chọn B H C
Do a >1 ⇒ vưới m > n thì m n a > a Ư – − 1 1 083 Do 3 − 3 > − 5 ⇒ a > = 5 5 4332133 a a
Câu 25: Cho 0 < a <1. Khẳng định nào đúng? 1 A. − 2 1 a < B. a 1 1 > 1 C. 3 a < a D. > 3 a 3 2 a 2017 2018 a a Lời giải Chọn A
Phương pháp: Xét hàm số có dạng x y = a ,a > 0,a ≠ 1:
+ Nếu 0 < a <1hàm số nghịch biến trên ( ; −∞ +∞)
+ Nếu a >1: hàm số đồng biến trên ( ; −∞ +∞)
Cách giải: Với 0 < a <1: − 2 1 1 1 2 3 a < ⇔ <
⇔ a > a ⇔ 0 < a <1 (luôn đúng). Vậy phương án A đúng. 3 2 3 a a a a 3
> 1 ⇔ a >1 ⇔ a >1 (Loại). Vậy phương án B sai. 3 2 a
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 23
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 1 1 1 3 3 2
a < a ⇔ a < a ⇔ a >1 (Loại). Vậy phương án C sai. 1 1 2017 2018 > ⇔ a < a
⇔ a >1 (Loại). Vậy phương án D sai. 2017 2018 a a
Câu 26: Chọn mệnh đề sai trong các mệnh đề sau:
A. Khi x > 0 thì 2 log x = 2log . x
B. Khi 0 < a <1 và b < c thì b c a > a . 2 2
C. Với a < b thì log b < a < x > a logb 1.
D. Điều kiện để 2 x có nghĩa là 0. Lời giải Chọn C 1 < log b Đáp án C sai vì với a a < b ⇒ ⇒ log a < < b b 1 log log a < 1 a b
Câu 27: Cho a là số thực dương khác 1. Xét hai số thực x , x . Phát biểu nào sau đây đúng? 1 2 A. Nếu 1x 2 x
a > a thì x > x . x x >
thì x < x . 1 2 B. Nếu 1 2 a a 1 2 C. Nếu 1x 2 x
a > a thì (a − )
1 (x − x > 0. D. Nếu 1x 2 x
a > a thì (a − )
1 (x − x < 0. 1 2 ) 1 2 ) Lời giải Chọn C 1 x 2 a >1: x
a > a → x > x 1 2 → (a − )
1 (x − x > 0. 1 2 ) 1 x 2 a <1: x
a < a → x < x G 1 2 V: x T
Câu 28: Cho a là số thực dương khác 1. Hình nào sau đây là đồ thị của hàm số mũ y = a ? RẦN ĐÌNH CƯ – 083 4332133 A. B. C. D. Lời giải Chọn C Hàm số x
y = a có tập xác định là và tập giá trị là (0;+∞)
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 24
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Câu 29: Biết (C1), (C2) ở hình bên là hai trong bốn đồ thị của các hàm số y ( ) 1 x x 1 x x 3 , y , y 5 , y = = = =
. Hỏi (C2) là đồ thị của hàm số nào sau đây? 2 3 x x A. x y = ( 3) B. 1 y = C. = 5x y D. 1 y = 2 3 Lời giải Chọn A
- Ta thấy (C1), (C2) đều có hướng đi lên khi x tăng ⇒ (C1), (C2) đồng biến x ∀ ∈ . x - Mà hàm x
y = a đồng biến khi a >1, nghịch biến khi 0 < a <1. Do đó ta loại hàm 1 y = 2 GV x : TR và 1 y = . Ầ 3 N Đ x x ÌN
- Xét khi x > 0 thì (C x
1) ở trên (C2) ⇒ y (C > y C . Mà 5 > ( 3) ⇒ (C : y = 3 . 2 ) ( ) 1 ) ( 2) H CƯ x – 2
= của đồ thị hàm số =
là đồ thị nào trong các đồ thị có 083
Câu 30: Đối xứng qua đường thẳng y x y 5 4332133 phương trình sau đây? 1 A. y = log x B. 2 y = log x C. y = log x D. y = log x 5 5 5 5 2 Lời giải Chọn A x x
Ta đưa hàm số về dạng: 2 y = 5 = ( 5) .
Dựa vào lý thuyết “Hai hàm số x
y = a , y = log x có đồ thị đối xứng nhau qua đường phân a
giác của góc phần tư thứ nhất y = x”
Hoặc thay x = y và y = x ta có x = ( 5)y ⇔ y = log x 5
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 25
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Câu 31: Đường cong trong hình bên dưới là đồ thị của một hàm số
trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D
dưới đây. Hỏi hàm số đó là hàm số nào? x A. 1 y = B. 2 y = x 2 C. y = log x = 2 D. x y 2 Lời giải Chọn D
Dựa vào đồ thị hàm số ta thấy hàm số có tập xác định là và đồng biến trên
Do đó chỉ có đáp án D thỏa mãn
Câu 32: Tìm a để hàm số log x
< a ≠ có đồ thị là hình bên a (0 ) 1 A. a = 2 B. a = 2 C. 1 a = D. 1 a = − G 2 2 V: T Lời giải RẦN Chọn A ĐÌN
Đồ thị hàm số đi qua điểm ( ) 2 2;2 ⇒ log
= ⇒ a = ⇒ a = a 2 2 2 2 H CƯ
Câu 33: Nếu gọi (G là đồ thị hàm số x
y = a và (G là đồ thị hàm số y = log x với 0 < a ≠1. Mệnh 2 ) 1 ) – a 083
đề nào dưới đây đúng? 4332133
A. (G và (G đối xứng với nhau qua trục hoành. 2 ) 1 )
B. (G và (G đối xứng với nhau qua trục tung. 2 ) 1 )
C. (G và (G đối xứng với nhau qua đường thẳng y = x 2 ) 1 )
D. (G và (G đối xứng với nhau qua đường thẳng y = −x 2 ) 1 ) Lời giải Chọn C
Mọi điểm A(m;n)∈(G ) m
⇒ a = n ⇒ m = log n ⇒ B n;m ∈ G 1 a ( ) ( 2 )
Hai điểm A và B đối xứng nhau qua đường thẳng y = x
Do đó (G và (G đối xứng nhau qua đường thẳng y = x 2 ) 1 )
Câu 34: Cho hai hàm số x = , x
y a y = b với a,b là hai số thực dương khác 1, lần lượt có đồ thị là (C ) và 1
(C ) như hình bên. Mệnh đề nào dưới đây đúng? 2
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 26
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
A. 0 < a < b <1
B. 0 < b <1< a
C. 0 < a <1< b
D. 0 < b < a <1 Lời giải Chọn B
- Đồ thị hàm số (C ) đồng biến nên ' x
y = a ln a > 0 ⇔ a >1 1
- Đồ thị hàm số (C ) nghịch biến nên ' x
y = b ln b < 0 ⇔ 0 < b <1. Do đó 0 < b <1< a 2
Câu 35: Cho hai hàm số y = log x y = x C , C , a , logb có đồ thị (
được vẽ trên cùng mặt phẳng tọa 1 ) ( 2 )
độ. Mệnh đề nào sau đây đúng? GV: TRẦN ĐÌNH CƯ – 083
A. 0 < b < a <1.
B. 0 < b <1< . a
C. 0 < a < b <1.
D. 0 < a <1< . b 4332133 Lời giải Chọn B
Ta thấy đồ thị hàm số log x < b < b nghịch biến nên 0 1
Ta thấy đồ thị hàm số log x a > a đồng biến nên 1
Câu 36: Cho a > 0,b > 0,b ≠1. Đồ thị các hàm số x
y = a và y = log x b
cho như hình vẽ bên. Mệnh đề nào sau đây là đúng?
A. a >1; 0 < b <1.
B. 1 > a > 0; b >1.
C. 0 < a <1; 0 < b <1. D. a >1; b >1.
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 27
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Lời giải Chọn A
Quan sát đồ thị ta thấy. Hàm số x
y = a đồng biến ⇒ a > 0 . Hàm số y = log x b nghịch biến ⇒ 0 < b <1
Câu 37: Cho đồ thị hàm số x
y = a và y = log x b như hình vẽ:
Khẳng định nào sau đây đúng? A. 1
0 < a < < b
B. 0 < a <1< b 2
C. 0 < b <1< a D. 1
0 < a <1,0 < b < 2 Lời giải Chọn B GV: + Xét hàm số x
y = a đi qua (0; )
1 suy ra đồ thị hàm số (1) là đường nghịch biến, suy ra 0 < a <1 T RẦ . N ĐÌN
+ Xét hàm số y = log x b
đi qua (1;0) suy ra đồ thị hàm số (2) là đường đồng biến suy ra b>1. H C
Suy ra 0 < a <1< . b Ư – x x x 083
Câu 38: Cho 3 số a,b,c > 0,a ≠1,b ≠1,c ≠1. Đồ thị các hàm số y = a , y = a , y = c được cho trong 4332133 hình vẽ dưới.
Mệnh đề nào sau đây đúng?
A. b < c < a
B. a < c < b
C. a < b < c
D. c < a < b Lời giải Chọn B
Ta có hàm số = x; = x
y b y c đồng biến, hàm số = x
y a nghịch biến nên a <1;b,c >1. Thay x =10 , ta có 10 10
b > c ⇒ b > c
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 28
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Câu 39: Cho các hàm số = x
y a , y = log x, y = x b
logc có đồ thị như hình vẽ.
Chọn khẳng định đúng.
A. c > b > a .
B. b > a > c .
C. a > b > c .
D. b > c > a . Lời giải Chọn A Hàm số = x
y a đồ thị có dáng đi xuống từ trái sang phải nên nghịch biến trên do đó 0 < a <1 (1).
Hai hàm số y = log x y = x b và
logc đồ thị có dáng đi lên từ trái sang phải nên đồng biến trên
khoảng (0;+∞) do đób >1 > a, c >1 > a (2).
Quan sát đồ thị ta thấy với 0 < x <1 thì log x < x c b b logc , suy ra > .
Quan sát đồ thị ta thấy với x >1 thì log x > x c b b logc , suy ra > . GV:
Suy ra 1< b < c (3) T RẦ
Từ (1), (2), (3) suy ra c > b > a . N ĐÌN Cách khác: H C
Dễ thấy a <1, b >1, c >1. Nên a là số nhỏ nhất. Ư –
Xét đường thẳng y =1 cắt đồ thị hai hàm số y = log x và y = log x lần lượt tại các điểm 083 b c 4332133 B(b ) ;1 và C (c ) ;1
(hình vẽ). Dễ thấy c > b vậy c > b > a .
Câu 40: Hình vẽ dưới đây vẽ đồ thị của 3 hàm số mũ.
Khẳng định nào dưới đây đúng?
A. a > b > c .
B. a > c >1 > b .
C. b > c >1 > a .
D. b > a > c . Lời giải Chọn B
Dựa vào đồ thị ở hình 5 ta thấy đồ thị của hàm số = x
y b là nghịch biến nên 0 < b <1.
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 29
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Vẽ đường thẳng x =1 ta có đường thẳng x =1 cắt đồ thị hàm số = x
y a tại điểm có tung độ
y = a và cắt đồ thị hàm số = x
y c tại điểm có tung độ là y = c . Khi đó điểm giao với = x y a
nằm trên điểm giao với = x
y c nên a > c >1. Vậy a > c >1 > b .
Câu 41: Trên hình 2.13, đồ thị của ba hàm số = x, = x, = x
y a y b y c (a, b, c là ba số dương khác 1 cho
trước) được vẽ trong cùng một mặt phẳng tọa độ. Dựa vào đồ thị và các tính chất của lũy thừa,
hãy so sánh ba số a, b và c A. c > b > a B. b > c > a C. a > c > b D. a > b > c Lời giải Chọn C
Dựa vào hình vẽ, ta thấy rằng: Hàm số x
y = a là hàm số đồng biến; hàm số x x y = b , y = c là hàm số nghịch biến. GV: 0 < b <1 1 T Suy ra a >1và → a > {b; } c . Gọi B( 1;
− y thuộc đồ thị hàm số x y = b ⇒ y = ; B ) R B Ầ 0 < c <1 b N ĐÌN Và 1 −
thuộc đồ thị hàm số x
y = c ⇒ y = . Dựa vào đồ thị, ta có H C( 1; yC ) C C c Ư 1 1 –
y > y ⇔ > ⇔ c > b. 083 B C b c 4332133
Câu 42: Cho a, b, c là ba số thực dương và khác 1. Đồ thị các hàm số y = log x, y = log x, y = log x a b c
được cho trong hình vẽ bên. Mệnh đề nào dưới đây là mệnh đề đúng? A. a < b < c B. c < a < b C. c < b < a D. b < c < a Lời giải Chọn B
Hàm số y = log x nghịch biến ⇒ < < các hàm y = log x, y = log x đồng biến nên c 0 c 1, a b
a;b >1 Chọn x =100 ⇒ log 100 > log 100 ⇒ a < b ⇒ c < a < b. a b
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 30
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Câu 43: Cho ba số thực dương a, b, c khác 1. Đồ thị các hàm số x x
y = log x, y = b , y = c được cho trong a
hình vẽ bên. Mệnh đề nào dưới đây là đúng? A. b < c < a B. a < b < c C. c < a < b D. c < b < a Lời giải Chọn C Hàm số = x
y c là hàm nghịch biến nên 0 < c <1. Hàm số = x
y b là hàm đồng biến nên b >1
Hàm số y = log x a > y = x a là hàm đồng biến nên
1. Lấy đối xứng đồ thị hàm loga qua đường
phân giác thứ nhất của mặt phẳng toạ độ ta có đồ thị hàm số = x
y b tăng nhanh hơn đồ thị hàm số = x
y a nên b > a G V: TR ẦN ĐÌNH CƯ – 083 4332133
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 31
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
BÀI 4. PHƯƠNG TRÌNH, BẤT PHƯƠNG TRÌNH MŨ VÀ LÔGARIT
A. KIẾN THỨC CƠ BẢN CẦN NẮM
Việc tính toán tuổi của hoá thạch được thực hiện như thế nào? Lời giải
Gọi x là lượng đồng vị phóng xạ carbon-14 ngay sau khi sinh vật chết y là lượng đồng vị phóng xạ t
carbon-14 tại thời điểm t Ta có: 5730 1 y x = ⋅ . 2
Từ đó, ta tính được tuổi của hoá thạch là = 5730⋅log y t 1 x 2 1. Phương trình mũ
HĐ 1: Số lượng cá thể vi khuẩn của một mẻ nuôi cấy
tuân theo công thức ( ) = 50⋅10kt P t
, trong đó t là thời
gian tính bằng giờ kể từ thời điểm bắt đầu nuôi cấy, k là hằng số.
(Nguồn: Sinh học 10, NXB Giáo dục Việt Nam, năm 2017, trang 101)
a) Ban đầu mẻ có bao nhiêu cá thể vi khuẩn?
b) Sau 1 giờ thì mẻ có 100 cá thể vi khuẩn. Tìm giá trị
của k (làm tròn kết quả đến hàng phần mười).
c) Sau bao lâu thì số lượng cá thể vi khuẩn đạt đến 50000? Lời giải
a) Số lượng vi khuẩn lúc đầu là k.0 P = 50.10 = 50 0 b) Khi t =1, ta có: .1 100 50.10k = Suy ra k = 0,3 c) Khi P(t) = 50000 thì 0,3. 50.10 t = 50000 Suy ra t =10
Vậy sau 10 giờ số lượng cá thể vi khuẩn đạt 50000
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 1
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Phương trình dạng x
a = b , trong đó a và b là những số cho trước, a > 0,a ≠ 1, được gọi là
phương trình mũ cơ bản.
Nghiệm của phương trình mū cơ bản
HĐ 2: Cho đồ thị của hai hàm số = x
y a và y = b như Hình 2a (với a > 0 ) hay Hình 2 b (với 0 < a <1
). Từ đây, hãy nhận xét về số nghiệm và công thức nghiệm của phương trình x
a = b trong hai trường hợp
b > 0 và b ≤ 0 . Lời giải
Khi b > 0 phương trình x
a = b có 1 nghiệm x = log b a
Khi b ≤ 0 phương trình x
a = b vô nghiệm Cho phương trình x
a = b(a > 0,a ≠ 1).
Nếu b > 0 thì phương trình luôn có nghiệm duy nhất x = log b a .
Nếu b ≤ 0 thì phương trình vô nghiệm.
Chú ý: a) Nếu α
b = a thì ta có x α
a = a ⇔ x = α .
b) Tổng quát hơn, u(x) ı(x) a
= a ⇔ u (x) = v(x) .
Ví dụ 1. Giải các phương trình sau: a) x 1 2 = 8 b) 5⋅10x =1; x x c) 1 27 = 9 3 Lời giải a) x 1 x 3 2 2 2− = ⇔ = ⇔ x = 3 − . 8 b) x x 1 1
5.10 =1 ⇔ 10 = ⇔ x = log = −log5. 5 5
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 2
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com x 3 x 1 27x x 3 c) = ⇔ ( 2−) ( ) 2 − x 3x 1 − 1 3 = ⇔ 3 = 3 ⇔ 2
− x = 3x −1 ⇔ 5x =1 ⇔ x = . 9 3 3 5
Ví dụ 2. Nếu khối lượng carbon-14 trong cơ thể sinh vật lúc chết là M g thì khối lượng carbon-14 còn 0 ( ) t lại (tính theo gam) sau 1 T
t năm được tính theo công thức M (t) M =
g , trong đó T = 5730 (năm) là 0 ( ) 2
chu kỳ bán rã của carbon-14. Nghiên cứu hóa thạch của một sinh vật, người ta xác định được khối lượng
carbon-14 hiện có trong hóa thạch là 13
5.10− g. Nhờ biết tỉ lệ khối lượng của carbon-14 so với carbon-12
trong cơ thể sinh vật sống, người ta xác định được khối lượng carbon-14 trong cơ thể sinh vật lúc chết là − 2 1
M =1,2.10 (g). Sinh vật này sống cách đây bao nhiêu năm? (Làm tròn đến kết quả hàng trăm.) 0 Lời giải
Gọi t là thời gian từ lúc sinh vật chết đến nay. Ta có: t 13 12 1 T − − 5 t 5.10 =1,2.10 . = 5 ⇔ = log 2 12 1 T 12 2 5 5 ⇔ t = T log = 5 − 730.log ≈ 7 237 ≈ 7200 . 1 2 12 2 2
Vậy sinh vật này sống cách đây khoảng 7 200 năm.
Giải các phương trình sau: a) x+2 3 3 = 9 b) 2 2.10 x = 30 c) 2x 2x 1 4 8 − = Lời giải 2 − a) x+2 3 x+2 2 4 3
3 = 9 ⇔ 3 = 3 ⇔ x + 2 = ⇔ x = 3 3 b) 2x 2x log15
2.10 = 30 ⇔ 10 =15 ⇔ 2x = log15 ⇔ x = 2 c) x x =
⇔ ( )2x = ( )2x 1 2 2 1 2 3 − − 4x 6x−3 3 4 8 2 2 ⇔ 2 = 2
⇔ 4x = 6x − 3 ⇔ x = 2
Công thức tính khối lượng còn lại của một chất phóng xạ từ khối lượng ban đầu M0 là t ( ) 1 T M t M =
, trong đó t là thời gian tính từ thời điểm ban đầu và T là chu kỳ bán rã của chất. Đồng 0 2
vị plutonium-234 có chu kỳ bán rã là 9 giờ.
(Nguồn: https://pubchem.ncbi.nlm.nih.gov/elemene/Plutonium#section=Atomic-Mass-Half-Life-and- Decay)
Từ khối lượng ban đầu 200 g, sau bao lâu thì khối lượng plutonium-234 còn lại là: a) 100g? b) 50g? c) 20 g? Lời giải t M (t) 1 T M (t) = M ⇔ t = T ⋅ log 0 1 2 M 2 0
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 3
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
a) Khi M (t) =100 thì 100 t = 9.log = 9 (giờ) 1 200 2
b) Khi M (t) = 50 thì 50 t = 9.log =18 (giờ) 1 200 2
c) Khi M (t) = 20 thì 50 t = 9⋅log = 30 (giờ) 1 200 2
2. Phương trình lôgarit
Nhắc lại rằng, độ pH của một dung dịch tính theo công thức pH = −log x , trong đó x là nồng độ ion + H tính bằng mol/L.
Biết sữa có độ pH là 6,5. Nồng độ +
H của sữa bằng bao nhiêu? Lời giải Ta có: 6 − ,5 7 6,5 logx x 10 x 3,2 10− = − ⇔ = ⇔ = ⋅
Vậy nồng độ H + của sữa là 7 3,2.10−
Phương trình dạng log x = b a b a
, trong đó , là những số cho trước, a > 0 , a ≠ 1, được gọi là phương
trình lôgarit cơ bản.
Nghiệm của phương trình lôgarit cơ bản
Cho đồ thị của hàm số y = log x (a > 0,a ≠ ) 1 = a
và y b như Hình 3a (với a >1) hay Hình 3b (với
0 < a <1). Từ đây hãy nhận xét về số nghiệm và công thức nghiệm của phương trình log x = b a . Lời giải
Phương trình log x = b = a có 1 nghiệm b x a
Phương trình log x = b a > 0,a ≠ 1 = a (
) luôn có nghiệm duy nhất b x a .
Chú ý: Tổng quát, xét phương trình dạng log u x =
v x a > a ≠ . ( ) 1 a ( ) loga ( ) ( 0, )1
Để giải phương trình ( )
1 , trước hết cần đặt điều kiện có nghĩa: u (x) > 0 và v(x) > 0 . Khi đó, ( )
1 được biến đổi thành phương trình
u (x) = v(x) (2)
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 4
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Sau khi giải phương trình (2) , ta cần kiểm tra sự thỏa mãn điều kiện. Nghiệm của phương trình ( ) 1 là
nghiệm của (2) thỏa mãn điều kiện.
Ví dụ 3. Giải các phương trình sau: a) log x = − ; 2 b) log ( 2
x − 3 = log 2x . 2 ) 2 ( ) 3 Lời giải
a) Điều kiện: x > 0 . log x = 2 − . 3 2 x − > b) Điều kiện: 3 0 (*) 2x > 0
Khi đó, phương trình đã cho trở thành 2 2
x − 3 = 2x ⇔ x − 3− 2x = 0 ⇔ x = 1 − hoặc x = 3.
Thay lần lượt hai giá trị này vào (*) , ta thấy chỉ có x = 3 thỏa mãn.
Vậy phương trình có nghiệm là x = 3.
Ví dụ 4. Nước chanh có độ pH là 2,4 ; giấm có độ pH bằng 3. Nước chanh có độ acid gấp bao nhiêu lần
giấm (nghĩa là có nồng độ +
H gấp bao nhiêu lần)? (Làm tròn kết quả đến hàng phần trăm.) Lời giải
Kí hiệu x, y lần lượt là nồng độ H+ trong nước chanh và giấm. Theo giả thiết, ta có
2,4 = −log x và 3 = −log y . 2 − ,4 x Suy ra 2 − ,4 x =10 và 3 y 10− = . Suy ra 10 0,6 = =10 ≈ 3,98. 3 y 10−
Vậy nồng độ H+ của nước chanh gấp 3,98 lần nồng độ + H của giấm. Giải phương trình sau: a) log x − 2 = 2 − ;
b) log x + 6 = log x +1 +1 2 ( ) 2 ( ) 1 ( ) 2 Lời giải 2 1 − a) log x 2 2 x 2 − = − ⇔ − =
⇔ x − 2 = 4 ⇔ x = 6 1 ( ) 2 2
b) log x + 6 = log x +1 +1 2 ( ) 2 ( )
⇔ log x + 6 = log x +1 + log 2 2 ( ) 2 ( ) 2
⇔ log x + 6 = log 2 x +1 2 ( ) 2 ( )
⇔ x + 6 = 2(x + ) 1 ⇔ x = 4
3. Bất phương trình mũ
Xét quần thể vi khuẩn ở .
a) Ở những thời điểm nào thì số lượng cá thể vi khuẩn vượt quá 50000 ?
b) Ở những thời điểm nào thì số lượng cá thể vi khuẩn vượt quá 50000 nhưng chưa vượt quá 100000 ? Lời giải
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 5
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
a) Khi P(t) = 50000 thì t =10 .
Vậy tại những thời điếm t >10 thì số lượng vi khuẩn vượt quá 50000
b) Khi P(t) =100000 thì t =11
Vậy tại những thời điểm t <11 thì số lượng vi khuẩn không vượt quá 100000
Suy ra khi 10 < t <11 thì số lượng cá thể vi khuẩn vượt quá 50000 nhưng chưa vượt quá 100000
Bất phương trình mũ cơ bản là bất phương trình có dạng x
a > b (hoặc x
a ≥ b , x
a < b , x
a ≤ b ), với
a,b là những số cho trước, a > 0 , a ≠ 1. Xét bất phương trình x a > b (3)
Nghiệm của (3) là hoành độ các điểm trên đồ thị hàm số x
y = a nằm phía trên đường thẳng y = b. Từ đồ
thị ở Hình 4 , ta nhận được:
Nếu b ≤ 0 thì mọi x ∈ đều là nghiệm của (3) .
Nếu b > 0 thì:
- Với a >1, nghiệm của (3) là x > log b a ;
- Với 0 < a <1, nghiệm của (3) là x < log b a .
Chú ý: a) Tương tự như trên, từ đồ thị ở Hình 4, ta nhận được kết quả về nghiệm của mỗi bất phương
trình x ≥ , x < , x a b a
b a ≤ b ( các bất phương trình x < , x a
b a ≤ b vô nghiệm nếu b ≤ 0 ).
b) Nếu a >1 thì u(x) v(x) a > a
⇔ u (x) > v(x) .
Nếu 0 < a <1 thì u(x) v(x) a > a
⇔ u (x) < v(x) .
Ví dụ 5. Giải các bất phương trình sau: x a) 10x < 0,001 b) 0,4x > 2 c) 1 2 ≥ 2.4 x 2 Lời giải a) x x 3 10 0,001 10 10− < ⇔ < ⇔ x < 3 − (do 10 >1) .
b) 0,4x > 2 ⇔ x < log 2(do 0 < 0,4 <1) . 0,4 x c) 1 2 ≥ x x
2.4 x ⇔ ( − ) ≥ ( )2 1 2 − x 1+4 2 2, 2
⇔ 2 ≥ 2 x ⇔ −x ≥1+ 4x(do 2 >1) 2 1 ⇔ 5x ≤ 1 − ⇔ x ≤ − . 5
Luyện tập 3. Giải các bất phương trình sau:
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 6
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com x−2 x a) 2x >16 b) 0,1x ≤ 0,001 c) 1 1 ≥ 5 25 Lời giải a) x x 4
2 >16 ⇔ 2 > 2 ⇔ x > 4 (do 2 > ) 1 b) x x 3
0,1 ≤ 0,001 ⇔ 0,1 ≤ 0,1 ⇔ x ≥ 3 (do 0,1<1 ) −2 −2 2 x x x x c) 1 1 1 1 > ⇔ > 5 25 5 5 x−2 2 1 1 x 1 ⇔ >
⇔ x − 2 2x ⇔ x − 2 (do < 1 ) 5 5 5
4. Bất phương trình lôgarit
Biết rằng máu của người bình thường có độ pH từ 7,3 đến 7,45 (nguồn: Hóa học 11_NXB Giáo dục Việt
Nam, năm 2017, trang 15). Nồng độ H + trong máu nhận giá trị trong miền nào? Lời giải
Khi pH = 7,30 thì nồng độ H + là 7 − ,30 8 10 5 10− = ⋅
Khi pH = 7,45 thì nồng độ H + là 7 − ,45 8 10 3,5.10− =
Vậy nồng độ H + trong máu nhận giá trị từ 8 3,5 10− ⋅ đến 8 5 10− ⋅
Bất phương trình lôgarit cơ bản là bất phương trình có dạng log x > b a (hoặc log x ≥ b x < b x ≤ b > ≠ a ,loga ,loga
), với a,b là các số cho trước, a 0,a 1.
Xét bất phương trình log x > b a (4).
Điều kiện xác định của bất phương trình là x > 0 .
Nghiệm của (4) là hoành độ các điểm của đồ thị hàm số y = log x = a
nằm phía trên đường thẳng y b . Từ
đồ thị ở Hình 5, ta nhận được:
• Với a >1, nghiệm của (4) là b x > a .
• Với 0 < a <1, nghiệm của (4) là 0 b < x < a .
Chú ý: a) Tương tự như trên, từ đồ thị ở Hình 5, ta nhận được kết quả về nghiệm của mỗi bất phương
trình log x ≥ b x < b x ≤ b a ,loga ,loga .
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 7
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
b) Nếu a >1 thì log u x >
v x ⇔ u x > v x > . a ( ) loga ( ) ( ) ( ) 0
Nếu 0 < a <1 thì log u x >
v x ⇔ < u x < v x . a ( ) loga ( ) 0 ( ) ( )
Ví dụ 6. Giải các bất phương trình sau: a) log 2x −1 ≤1
b) log 1− x > log 3x + 2 1 ( ) 1 ( ) 2 ( ) 2 2 Lời giải a) Điều kiện : 1
2x −1 > 0 ⇔ x > . 2
Khi đó, do cơ số 2 >1 nên bất phương trình đã cho trở thành 1 3
2x −1≤ 2 ⇔ 2x ≤ 3 ⇔ x ≤ . 2
Vậy nghiệm của bất phương trình là 1 3 < x ≤ . 2 2 x < 1 1 − x > 0 b) Điều kiện : 2 ⇔
2 ⇔ − < x <1(*) . 3 x + 2 > 0 x > − 3 3
Khi đó, do cơ số 1 <1 nên bất phương trình đã cho trở thành 2 1
1− x < 3x + 2 ⇔ 4x > 1 − ⇔ x > − . 4
Kết hợp với điều kiện (*), ta được nghiệm của bất phương trình là 1 − < x <1. 4
Luyện tập 4. Giải các bất phương trình sau: a) log x +1 < 2 b) log x + 2 ≤1 5 ( ) 1 ( ) 3 Lời giải
a) Điều kiện xác định: x +1 > 0 ⇔ x > 1 − 2 Khi đó, do 1 <1 nên 1 8 x +1 > ⇔ x − > 3 3 9
Kết hợp với điều kiện ta có nghiệm của bất phương trình là 8 x − > 9
b) Điều kiện xác định: x + 2 > 0 ⇔ x > 2 − Khi đó, do 5 >1 nên 1
x + 2 ≤ 5 ⇔ x ≤ 3
Kết hợp với điều kiện, ta có nghiệm của bất phương trình là 2 − < x ≤ 3
Nước uống đạt tiêu chuẩn có độ pH nằm trong khoảng từ 6,5 đến 8,5 ( theo Quy chuẩn Việt
Nam QCVN 01:2009/BYT). Nồng độ H + trong nước uống tiêu chuẩn phải nằm trong khoảng nào? Lời giải Ta có: 9 − 7 6,5 pH 8,5 6,5 logx 8,5 3,2 10 x 3,2.10− ≤ ≤ ⇔ ≤ − ≤ ⇔ ⋅ ≤ ≤
Vậy nồng độ H + trong nước uống tiêu chuẩn phải nằm trong khoảng từ 9 3,2.10− tới 7 3,2.10−
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 8
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TÂP
Dạng 1: Đưa về cùng cơ số 1. Phương pháp ( A x) B(x) a = a
⇔ A(x) = B(x), (a > 0,a ≠ ) 1 > ≠ f x > hoac g x > f x = g x ⇔ a ( ) a
( )a 0,a 1 ( ) 0 ( ( ) 0) log log f
( x) = g ( x) 0 < a <1 f
( x) < g ( x) f (x) g(x) a > a ⇔ a > 1 f
( x) > g ( x) 2. Ví dụ
Ví dụ 1: Giải các phương trình mũ sau x 1 + a) 2x−4x+5 3 = 9 b) 5x−7 2 1,5 = c) 2x 1− x+2 2 + 4 = 10 3 Giải
a) Đưa hai vế về cùng cơ số 3, ta được phương trình đã cho tương đương với: 2 x −4x+5 2 2 (1) 2 3
= 3 ⇔ x − 4x + 5 = 2 ⇔ x − 4x + 3 = 0 .
Giải phương trình bậc hai này được hai nghiệm là x =1 và x = 3.
b) Đưa về cùng cơ số 1,5, phương trình đã cho tương đương với: 5 7
1,5 x− = −x 1
1,5 − ⇔ 5x − 7 = −x −1 ⇔ x =1.
Vậy x =1 là nghiệm của phương trình.
c) Phương trình đã cho tương đương với 1 x x 33 4 16 4 10 4x ⋅ + ⋅ = ⇔ ⋅ = x 20 20 10 ⇔ 4 = ⇔ x = log . 2 2 4 33 33 Vậy 20 x = log
là nghiệm của phương trình. 4 33
Ví dụ 2: Giải các phương trình sau a) log (2x +1) = log 5
b) log (x + 3) = log ( 2 2x − x −1 2 2 ) 3 3 c) log (x −1) = 2
d) log (x − 5) + log (x + 2) = 3 5 2 2 Lời giải
a) ĐK: 2x +1 > 0 ⇔ x > ( 1 − / 2)
PT ⇔ 2x +1 = 5 ⇔ 2x = 4 ⇔ x = 2 (thoả ĐK) b) ĐK: 2
x + 3 > 0,2x − x −1 > 0 ta được: x >1 hoạcc ( 3 − ) < x < ( 1 − / 2)
Ta có: log (x + 3) = log ( 2 2x − x − ) 2 2
1 ⇔ x + 3 = 2x − x −1 ⇔ 2x − 2x − 4 = 0 2 2 2
⇔ x − x − 2 = 0 ⇔ x = 1
− (thoả) hoặc x = 2 (thoả)
c) ĐK: x −1 > 0 ⇔ x >1 Ta có: 2
log (x −1) = 2 ⇔ x −1 = 5 ⇔ x = 26 (thoả) 5
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 9
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
d) ĐK: x − 5 > 0 và x + 2 > 0 ta được: x > 5 Ta có: 3
log (x − 5) + log (x + 2) = 3 ⇔ log (x − 5)(x + 2) = 3 ⇔ (x − 5)(x + 2) = 2 2 2 2 2
⇔ x − 3x −18 = 0 ⇔ x = 3
− (loai) hoạcc x = 6 (thoà)
Ví dụ 1: Giải bất phương trình mũ sau: 2x−x 1 3 ≤ 3 −x Lời giải Ta có: 2x−x 1 3 ≤ 3 −x 2 2
⇔ x − x ≤1− x ⇔ x −1≤ 0 ⇔ 1 − ≤ x ≤1
Vậy tập nghiệm của bất phương trình là: [ 1; − 1] 4x 2−x
Ví dụ 3: Giải bất phương trình mũ sau: 2 5 ≤ 5 2 Lời giải
- Ta có thể biến đỗi theo 1 trong 2 cách sau (thực tế thì cùng phương pháp).
Cách 1: Bất phương trình được biến đỗi về dạng: 4x 2−x 4x x−2 2 5 2 2 2 − ≤ ⇔ ≤ ⇔
4x ≥ x − 2 ⇔ 3x ≥ 2 − ⇔ x ≥ 5 2 5 5 3
Vậy tập nghiệm của bất phương trình là: 2 ; − +∞ 3
Cách 2: Bất phương trình được biến đổi về dạng: 4x 2−x 4 − x 2 2 5 5 5 −x 2 − ≤ ⇔ ≤ ⇔ 4
− x ≤ 2 − x ⇔ 3x ≥ 2 − ⇔ x ≥ 5 2 2 2 3
Vậy tập nghiệm của bất phương trình là: 2 ; − +∞ 3
Ví dụ 4: Giải bất phưong trình 2 x 1 − − x +3 ( 5 + 2) ≥ ( 5 − 2) . Lời giải Ta có: 1 1 ( 5 2)( 5 2) 1 5 2 ( 5 2)− + − = ⇔ − = = + 5 + 2 Vậy: 2 2 x 1 − − x +3 x 1 − x −3 2 ( 5 + 2) ≥ ( 5 − 2) ⇔ ( 5 + 2) ≥ ( 5 + 2)
⇔ x −1≥ x − 3 2
⇔ x − x − 2 ≤ 0 ⇔ 1 − ≤ x ≤ 2
Vậy BPT có tập nghiệm S = [ 1; − 2]
Ví dụ 5: Giải bất phương trình 2
log x − 5log x − 6 ≤ 0 2 2 Lời giải
Đăt t = log x , khi đó phương trình trở thành: 2 2
t − 5t − 6 ≤ 0 ⇔ (t +1)(t − 6) ≤ 0 ⇔ 1 − ≤ t ≤ 6 Do đó ta có: 1 1 1
− ≤ log x ≤ 6 ⇒ log
≤ log x ≤ log 64 ⇒ ≤ x ≤ 64 2 2 2 2 2 2
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 10
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Vậy tập nghiệm bất phưong trình là 1 S ;64 = . 2
Dạng 2: Phương pháp đặt ẩn phụ 1. Phương pháp 2x α + β. x a a + γ = 0 . Đặt x
t = a ,(t > 0) 2 α log x + β
x + γ = . Đặt t = log x x > a , ( 0) a .loga 0 2. Ví dụ
Ví dụ 1: Giải các phương trình sau: a) 9x 4 3x − ⋅ + 3 = 0
b) 9x 3 6x 2 4x − ⋅ + ⋅ = 0 c) x 1 5 + 5 −x − 6 = 0 d) 25x 2.5x − −15 = 0 Lời giải a) 9x 4.3x − + 3 = 0 đặt 3x
t = với t > 0 ta được phương trình: 2
t − 4.t + 3 = 0 ⇔ t =1 hoặc t = 3 ( 2 nghiệm
đều thoả điều kiện t > 0 ). với =1 ⇔ 3x t = 1 ⇔ x = 0 với = 3 ⇔ 3x t = 3 ⇔ x =1
b) 9x 3.6x 2.4x − +
= 0 chia 2 vế của phương trình cho 4x ta được phương trình sau x x 2 9 6 3 x 3 x 3 2 0 3 − + = ⇔ − + 2 = 0 đặt (3 / 2)x t =
với t > 0 ta được phương trình 4 4 2 2 2
t − 3.t + 2 = 0 ⇔ t =1 hoặc t = 2 (2 nghiệm đều thoả t > 0 ) với =1 ⇔ (3 / 2)x t = 1 ⇔ x = 0 vớit x
= 2 ⇔ (3 / 2) = 2 ⇔ x = log 2 3 2 c) x 1
5 + 5 −x − 6 = 0 ⇔ 5x + 5.5−x − 6 = 0 Đặt x
t = 5 (với t > 0 ) thì 5−x =1/ t ta được phương trình: 1 2
t + 5 − 6 = 0 ⇔ t − 6t + 5 = 0 ⇔ t =1 hoặc t = 5 (thoả điều kiện t > 0) t với =1 ⇔ 5x t = 1 ⇔ x = 0 với = 5 ⇔ 5x t = 5 ⇔ x =1 d) d) x x 2 25 2.5 15 0 5 x 2.5x − − = ⇔ − −15 = 0 đặt 5x
t = với t > 0 ta được phương trình 2
t − 2t −15 = 0 ⇔ t = 5 (nhận) hoặc t = 3 − (loại) với = 5 ⇔ 5x t = 1 ⇔ x = 0
Ví dụ 2: Giải các phương trình sau a) 2
log x + 2log x − 3 = 0 3 3 b) 4log x + log − = x 3 3 0 9 Lời giải a) ĐK: x > 0
Ta đặt t = log x khi đó 2
PT ⇔ t + 2t − 3 = 0 ⇔ t =1 hoạcc t = 3 − 3
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 11
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Với t =1 ⇔ log x =1 ⇔ x = 3 3 Với 3 t 3 log x 3 x 3− = − ⇔ = − ⇔ = = 1/ 27 3
b) 4log x + log − = ĐK: 0 < x ≠ 1 x 3 3 0 9
PT ⇔ 2log x +1/ log x − 3 = 0 3 3 Ta đặt t = log x khi đó 2
PT ⇔ 2t +1/ t − 3 = 0 ⇔ 2t − 3t +1 = 0 ⇔ t =1 hoặc t =1/ 2 3
Vớit =1 ⇔ log x =1 ⇔ x = 3 (thoả) 3
Vớit =1/ 2 ⇔ log x =1/ 2 ⇔ x = 3 (thoả) 3
Ví dụ 3: Giải bất phương trình mũ sau: x x 1 9 2.3 + + −16 ≥ 0 Lời giải x x 1 9 2.3 + + −16 ≥ 0 (*) Ta đặt 3x
t = (điều kiện t > 0 ), khi đó phương trình ( ) biến đổi về dạng: t ≤ 8 − ( loai ) 2x x 2
3 + 6.3 −16 ≥ 0 ⇔ t + 6t −16 ≥ 0 ⇔ ⇔ t ≥ 2 t ≥ 2 Với: ≥ 2 ⇔ 3x t ≥ 2 ⇔ x ≥ log 2 3
Vậy bất phương trình có tập nghiệm [log 2;+∞ 3 )
Ví dụ 4: Giải bất phương trinh sau: (7 4 3)x 3(2 3)x + − − + 2 ≤ 0 Lời giải Ta có: 2
7 + 4 3 = (2 + 3) và (2 − 3)(2 + 3) =1 nên đặt x
t = (2 + 3) , t > 0 ta có bất phương trình: 2 3 −
+ ≤ ⇔ + − ≤ ⇔ − ( 2 3 / 2 0 2 3 0 ( 1)
+ + 3) ≤ 0 ⇔ ≤1⇔ (2 + 3)x t t t t t t t t ≤ 1 ⇔ x ≤ 0
Vậy, bất phương trình cho có nghiệm là x ≤ 0
Dạng 3: Logarit hóa, mũ hóa 1. Phương pháp 0 a 1 f (x) a b b 0 .
f (x) log b a > f (x) f (x) 0 log = b ⇔ a f ( x) b = a 0 < a <1 f
( x) < log b f (x) a a > b ⇔ a > 1 f
( x) > log b a a > 1 f (x) > g(x).logb f ( x) g ( x) a a > b ⇒ 0 < a <1 f (x) <
g(x).logba
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 12
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com a >1 f ( x) b > a
log f x > b ⇒ a ( ) 0 < a < 1 f ( x) b < a 2. Ví dụ
Vi dụ 1: Giải phương trình sau a) 3x = 2 b) 2x 3x ⋅ = 1 Lời giải
a) 3x = 2 ta logarit cơ số 3 hay vế
Pt ⇔ log 3x = log 2 ⇔ x = log 2 3 3 3
b)2x ⋅3x =1 ⇔ (2.3)x =1 ⇔ 6x =1 ⇔ log 6x = log 1 ⇔ x = 0 6 6
Hoặc có thể làm như sau, lấy logarit cơ số 2 của 2 vế ta được log 2x 3x log 1 log 2x 3x 0 log 2x log 3x ⇔ ⋅ = ⇔ ⋅ = ⇔ + = 0 2 ( ) 2 2 ( ) 2 2
⇔ x + x ⋅log 3 = 0 ⇔ x 1+ log 3 = 0 ⇔ x = 0 2 ( 2 )
Ví dụ 2: Giải các phương trình sau: a) ln(x + 3) = 1 − + 3
b) log 5 − 2x = 2 − x 2 ( ) Lời giải
a) ĐK: x − 3 > 0 ⇔ x > 3 với điều kiện này ta mũ hóa 2 vế của PT đã cho ta được PT: ln(x+3) 1 − + 3 1 − + 3 e = e ⇔ x + 3 = e 1 3 x e− + ⇔ = − 3 (thoả)
b) log 5 − 2x = 2 − x 2 ( ) ĐK: 5 2x 0 2x − > ⇔ < 5 log x 2 5−2 2 PT ⇔ 2
= 2 −x ⇔ 5 − 2x = 4.2−x Đặt = 2x t
(t > 0,t < 5 do 2x < 5) ta được: 2
5 − t = (4 / t) ⇔ t − 5t + 4 = 0
⇔ t =1 (thoả) hoạc t = 4 (thoả) Vớit =1 ⇔ x = 0 Vớit = 4 ⇔ x = 2
Ví dụ 3: Giải bất phương trình 2x−4 x−2 2 ≥ 5 . Lời giải
Lấy logarit cơ số 2 hai vế của bát phương trình đã cho ta có: ≥ − − x log ( 2 2 x 4 2 )≥log ( x 2 5 ) 2
⇔ x − 4 ≥ (x − 2)log 5 ⇔ (x − 2) x + 2 − log 5 ≥ 0 ⇔ 2 2 2 ( 2 ) x ≤ log 5− 2 2
Vậy BPT có tập nghiệm S = ( ;
−∞ log 5 − 2 ∪[2;+∞) . 2 ]
Ví dụ 4: Giải bất phương trình logarit sau: log (4 − 2x) ≥ 2 8 Lời giải
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 13
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
- Điều kiện 4 − 2x > 0 suy ra x < 2 . 2 2
log (4 − 2x) ≥ 2 ⇔ log (4 − 2x) ≥ log 8 ⇔ 4 − 2x ≥ 8 ⇔ 4 − 2x ≥ 64 ⇔ 2x ≤ 60 − ⇔ x ≤ 30 − 8 8 8
Vậy tập nghiệm của bất phương trình logarit là: ( ; −∞ 30] −
C. GIẢI BÀI TẬP SÁCH GIÁO KHOA
1. Giải các phương trình sau: a) 2x 1 5 − = 25 ; b) x 1+ 2x 1 3 9 + = c) 1−2 10 x =100000 Lời giải a) 2x 1− 2x 1 − 2 3 5 = 25 ⇔ 5
= 5 ⇔ 2x −1 = 2 ⇔ x = 2 b) ( )2 1 1 2 1 1 2 3 9 3 3 x x x x + + + + = ⇔ = x 1 + 4x+2 1 − ⇔ 3 = 3
⇔ x +1 = 4x + 2 ⇔ x = 3 c) 1−2x 1−2x 5 10 =100000 ⇔ 10
=10 ⇔ 1− 2x = 5 ⇔ x = 2 −
2. Giải các phương trình sau. Làm tròn kết quả đến hàng nghìn. a) x+2 3 = 7 ; b) 2x 1 3.10 + = 5 ; Lời giải a) x+2
3 = 7 ⇔ x + 2 = log 7 ⇔ x = log 7 − 2 ⇔ x = 0 − ,229 3 3 b) 2x 1 + 2x 1 + 5 5 3.10 = 5 ⇔ 10 = ⇔ 2x +1 = log 3 3 5 x log 1 ⇔ = − : 2 ⇔ x = 0 − ,389 3
3. Giải các phương trình sau: a) log 4x + 4 = 2 ; 6 ( )
b) log x − log x − 2 =1 3 3 ( ) Lời giải a) log (4x + 4) 2
= 2 ⇔ 4x + 4 = 6 ⇔ x = 8 6 b) log − log − 2 =1 ⇔ log x x x = 1 3 3 ( ) 3 x − 2 x ⇔
= 3 ⇔ x = 3(x − 2) ⇔ x = 3 x − 2
4. Giải các bất phương trình sau: 2x 1 + a) 1 ≤ 9 ; 3
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 14
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com b) x x−2 4 > 2 Lời giải 2x 1 + 2x 1 + 2 − a) 1 1 1 3 − ≤ 9 ⇔ ≤ ⇔ 2x +1≥ 2 − ⇔ x ≥ (do 1 <1 ) 3 3 3 2 3 b) −2 > ⇔ ( 2 )x x x x−2 2x x−2 4 2 2 > 2 ⇔ 2 > 2
⇔ 2x > x − 2 ⇔ x > 2 − (do 2 >1 )
5. Giải các bất phương trình sau: a) log x − 2 < 2; 2 ( ) b) log(x + ) 1 ≥ log(2x − ) 1 Lời giải a) log (x − 2) 2
< 2 ⇔ x − 2 < 2 ⇔ x < 6 2 b) log(x + ) 1 ≥ log(2x − )
1 ⇔ x +1≥ 2x −1 ⇔ x ≤ 2
6. Chất phóng xạ polonium-210 có chu kì bán rã là 138 ngày. Điều này có nghĩa là cứ sau 138 ngày,
lượng polonium còn lại trong một mẫu chỉ bằng một nửa lượng ban đầu. Một mẫu 100g có khối lượng t polonium-210 còn lại sau 138 1
t ngày được tính theo công thức M (t) 100 = ( g ) 2
(nguồn://pubchem.ncbi.nlm.nih.gov/element/Polonium#section=Atiomc-Mass-Half-Life-anh-Decay)
a) Khối lượng polonium-210 còn lại bao nhiêu sau 2 năm?
b) Sau bao lâu thì còn lại 40g polonium-210. Lời giải
a) Khối lượng polonium-210 còn lại sau 2 năm (730 ngày) là: 730 M ( ) 138 1 2 100 = = 2,56(g) 2 t
b) M (t) = 40 khi 138 1 100 = 40 ⇔ t = 182,4 2
Vậy sau 182,4 ngày còn lại lại 40 g polonium-210
7. Nhắc lại rằng, mức cường độ âm L được tính bằng công thức = log I L
(dB) , trong đó I là cường I0 độ của âm tính bằng 2 W / m và 12 2 I =10 W / m 0
(Nguồn: Vật lí 12, NXB Giáo dục Việt Nam, năm 2017, trang 52)
a) Một giáo viên đang giảng bài trong lớp học, có mức cường độ âm là 50dB . Cường độ âm của giọng
nói giáo viên bằng bao nhiêu?
b) Mức cường độ âm trong một nhà xưởng thay đổi trong khoảng từ 75dB đến 90dB . Cường độ âm
trong nhà xưởng này thay đổi trong khoảng nào? Lời giải
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 15
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com a) Khi I L = 50 thì 7 10log = 50 ⇔ I = 10− 12 10−
Vậy cường độ âm của giọng nói giáo viên là 7 − 2 10 W / m b) Khi I L = 75 thì 5 10log = 75 ⇔ I = 3,2.10− 12 10− Khi I L = 90 thì 3 10log = 90 ⇔ I = 10− 12 10−
Vậy cường độ âm trong nhà xưởng thay đổi từ 5 3,2.10− đến 3 10−
D. BÀI TẬP TRẮC NGHIỆM
Câu 1: Phương trình 2x 1 2 + = 32 có nghiệm là A. 5 x = . B. x = 2 . C. 3 x = . D. x = 3. 2 2 Lời giải Chọn B Ta có 2x 1
2 + = 32 ⇔ 2x +1 = 5 ⇔ x = 2 . 2 x −2x−3
Câu 2: Phương trình 1 x 1 =
7 − có bao nhiêu nghiệm? 7 A. 0 . B. 1. C. 2 . D. 3. Lời giải Chọn C 2 x −2x−3 2 1 x −2x−3 − x 1 + x 1 = 1 1 1 17 7 − ⇔ = 2
⇔ x − 2x − 3 = −x +1 2
⇔ x − x − 4 = 0 x ± ⇔ = 7 7 7 2
Câu 3: Phương trình log x = log x + 2 có bao nhiêu nghiệm? 2 2 ( ) A. 0 . B. 2 . C. 3. D. 1. Lời giải Chọn A 2
log x = log x + 2 2 2 ( )
log x = log x + 2 ⇔ 2 2 ( ) x>0 x = 1 − 2 x = x + 2 2
x − x − 2 = 0 1 ⇔ ⇔
⇔ x = 2 ⇔ x = 2. x > 0 x > 0 2 x > 0
Vậy phương trình đã cho có 1 nghiệm.
Câu 4: Số nghiệm của phương trình log ( 2
x + 4x + log 2x + 3 = 0 là 3 ) 1 ( ) 3 A. 3. B. 2 . C. 1. D. 0 . Lời giải Chọn C
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 16
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com x > 0 2 x x + > Điều kiện 4 0 x < 4 − ⇔ ⇔ x > 0 . 2x + 3 > 0 3 x > − 2
Phương trình đã cho ⇔ log ( 2
x + 4x = log 2x + 3 3 ) 3 ( ) x =1 2
⇔ x + 4x = 2x + 3 2
⇔ x + 2x − 3 = 0 ⇔ . x = 3 −
Kết hợp điều kiện ta được x =1. x 3x 1 −
Câu 5: Tập nghiệm S của phương trình 4 7 16 − = 0 là 7 4 49 A. 1 S = − . B. S = { } 2 . C. 1 1 ; − . D. 1 S = − ; 2 . 2 2 2 2 Lời giải Chọn A x 3x 1 − 2 − x 1 + 2 Ta có 4 7 16 − = 4 4 0 ⇔ = ⇔ 2 − x +1 = 2 1 ⇔ x = − . 7 4 49 7 7 2 2 Câu 6: + − −
Cho phương trình ( + )x x 1 =( + )x 2 7 4 3 2 3
. Mệnh đề nào sau đây đúng?
A. Phương trình có hai nghiệm không dương.
B. Phương trình có hai nghiệm dương phân biệt.
C. Phương trình có hai nghiệm trái dấu.
D. Phương trình có hai nghiệm âm phân biệt. Lời giải Chọn A Do + = ( + )2 7 4 3 2
3 nên phương trình ban đầu tương đương với = ( x 0 +
) ( 22x+x− )1 =( + )x−2 2 3 2 3 2
⇔ 2x + 2x − 2 = x − 2 2 ⇔ 2x + x = 0 ⇔ 1 . x = − 2
Vậy phương trình đã cho có hai nghiệm không dương.
Câu 7: Nghiệm của phương trình log x +1 +1= log 3x −1 là 2 ( ) 2 ( ) A. x = 3. B. x = 2 . C. x = 1 − . D. x =1. Lời giải Chọn A x > 1 x +1 > 0 − Điều kiện xác định 1 ⇔ 1 ⇔ x > . 3 x −1 > 0 x > 3 3
Khi đó phương trình trở thành
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 17
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
log 2x + 2 = log 3x −1 ⇔ 2x + 2 = 3x −1 ⇔ −x = 3 − ⇔ x = 3. 2 ( ) 2 ( )
Vậy phương trình có nghiệm x = 3.
Câu 8: Số nghiệm thực của phương trình 3log (x − )
1 − log (x − 5)3 = 3 là 3 1 3 A. 3 B. 1 C. 2 D. 0 Lời giải Chọn B
Điều kiện: x > 5 3log (x − )
1 − log (x − 5)3 = 3 ⇔ 3log x −1 + 3log x − 5 = 3 3 ( ) 3 ( ) 3 1 3
⇔ log x −1 + log x − 5 =1 ⇔ log x −1 x − 5 =1 ⇔ x −1 x − 5 = 3 3 ( )( ) 3 ( ) 3 ( ) ( )( ) 2
⇔ x − 6x + 2 = 0 ⇔ x = 3± 7
Đối chiếu điều kiện suy ra phương trình có 1 nghiệm x = 3+ 7
Câu 9: Nghiệm của phương trình x 1+ x 1− 1 2 .4 . = 16x là 1 8 −x A. x = 3. B. x =1. C. x = 4. D. x = 2. Lời giải Chọn D x 1 + x 1 − 1 x x 1 + 2(x− ) 1 ( 3 x− ) 1 4 2 .4 . = 16 ⇔ 2 .2 .2 = 2 x 1 8 −x
⇔ x +1+ 2(x − ) 1 + 3(x − )
1 = 4x ⇔ x = 2.
Câu 10: Tổng tất cả các nghiệm của phương trình 2 2 x −2x 1 − x −2 2 .3 x =18 bằng A. 1. B. 1 − . C. 2 . D. 2 − . Lời giải Chọn C Ta có 2 2 2 x −2x 1 − x −2x x −2x 2 2 2 .3 = 18 ⇔ 6
= 36 ⇔ x − 2x = 2 ⇔ x − 2x − 2 = 0 . Phương trình 2
x − 2x − 2 = 0 có hai nghiệm phân biệt.
Theo định lí vi-et tổng hai nghiệm của phương trình là: x + x = 2. 1 2
Câu 11: Tổng các nghiệm của phương trình log (x − 2) + log (x − 4)2 = 0 là S = a + b 2 . Giá trị của 3 3 biểu thức Q = . a b bằng A. 0. B. 3. C. 9. D. 6. Lời giải Chọn D
Điều kiện: 2 < x ≠ 4 .
Với điều kiện trên, phương trình đã cho tương đương
2log x − 2 + 2log x − 4 = 0 ⇔ log x − 2 x − 4 = 0 ⇔ x − 2 x − 4 =1 3 ( ) 3 3 ( ) ( )
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 18
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
(x − 2)(x − 4) 2 = 1
x − 6x + 7 = 0 x = 3± 2 ⇔
So lại điều kiện, ta nhận hai nghiệm ( ⇔ ⇔
x − 2)(x − 4) 2 = 1 −
x − 6x + 9 = 0 x = 3 x = 3+ 2;x = 3 1 2
Ta được: S = x + x = 6 + 2 ⇒ a = 6;b =1. 1 2 Vậy Q = . a b = 6.
Câu 12: Gọi x , x là hai nghiệm của phương trình 2
log x − 3log x + 2 = 0 . Tính P = x + x . 1 2 2 2 1 2 A. 6 . B. 3 − . C. 2 . D. 3. Lời giải Chọn A log x =1 x = 2 2
log x − 3log x + 2 = 0 2 1 ⇒ ⇒ . 2 2 log x 2 = x = 4 2 2
Vậy P = x + x = 2 + 4 = 6 . 1 2
Câu 13: Tổng bình phương tất cả các nghiệm của phương trình 2 log x − 3log . x log 3+ 2 = 0 2 3 2 A. 20 B. 18 C. 6 D. 25 Lời giải Chọn A 2 2 log x − 3log .
x log 3+ 2 = 0 ⇔ log x − 3log x + 2 = 0 2 3 2 2 2 log x =1 x = 2 2 1 2 2 ⇔ ⇔ ⇒ x + x = 20 1 2 log x = 2 x = 4 2 2
Câu 14: Phương trình 2x 1− x 1 6 5.6 − −
+1 = 0 có hai nghiệm x , x . Khi đó tổng hai nghiệm x + x là. 1 2 1 2 A. 5. B. 3. C. 2. D. 1. Lời giải Chọn D 2x x 1 = x− x− 6 5.6 6x 2 2 1 1 2 6 − 5.6 +1 = 0 ⇔ −
+1 = 0 ⇔ 6 x − 5.6x + 6 = 0 ⇔ . 2 6 6 6x = 3 1 x 2 x 1 x + 2
⇒ 6 .6 = 3.2 ⇔ 6 x = 6 ⇔ x + x =1. 1 2
Câu 15: Gọi T là tổng các nghiệm của phương trình 2
log x − 5log x + 4 = 0 . Tính T . 1 3 3 A. T = 4. B. T = 5 . C. T = 84 . D. T = 4 − . Lời giải Chọn C Phương trình log x = 1 x = 3 2 2 3
log x − 5log x + 4 = 0⇔ log x − 5log x + 4 = 0⇔ ⇔ . 1 3 3 3 log x 4 = x = 81 3 3 Vậy T = 3+81= 84 .
Câu 16: Phương trình x x 2x 1 9 6 2 + − = có bao nhiêu nghiệm âm? A. 3 B. 0 C. 1 D. 2
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 19
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Lời giải Chọn B 2x x Ta có: x x 2x 1 9 6 2 + − = x x x 3 3 9 6 2.4 ⇔ − = ⇔ − − 2 = 0 2 2 3 x = 1 − (L) 2 ⇔ ⇔ x = log 2 . 3 3 x = 2 2 2
Vậy phương trình đã cho không có nghiệm âm. Câu 17: x x
Gọi x , x là nghiệm của phương trình (2− 3) +(2+ 3) = . Khi đó 2 2 + bằng 1 2 4 x 2x 1 2 A. 2. B. 3. C. 5. D. 4. Lời giải Chọn B Ta có: ( x x
2 − 3) .(2 + 3) =1. Đặt t = ( − )x t > ⇒ ( + )x 1 2 3 , 0 2 3 = . t
Phương trình trở thành: 1 2
t + = 4 ⇒ t − 4t +1 = 0 ⇔ t = 2 ± 3 . t Với x
t = 2 − 3 ⇒ (2 − 3) = 2 − 3 ⇔ x =1.
Với = + ⇒ ( − )x = + ⇔ ( − )x − t = ( − ) 1 2 3 2 3 2 3 2 3 2 3 ⇔ x = 1 − . Vậy 2 2 x + 2x = 3 . 1 2
Câu 18: Biết rằng phương trình 2
log x − log 2018x − 2019 = 0 có hai nghiệm thực x , x .Tích x x 2 2 ( ) 1 2 1 2 bằng A. log 2018 B. 0,5 C. 1 D. 2 2 Lời giải Chọn D 2
log x − log 2018x − 2019 = 0 . ( ) 1 2 2 ( )
Điều kiện x > 0.
Đặt t = log x . Phương trình trở thành 2t − t − log 2018 − 2019 = 0. (2) 2 2
Do ac < 0 nên phương trình (2) có hai nghiệm t ,t .Khi đó phương trình ( )
1 có 2 nghiệm x , x 1 2 1 2
thỏa mãn t = log x ;t = log x . 1 2 1 2 2 2
Theo Vi-et ta có t + t =1 hay log x x =1 ⇔ x x = 2 . 2 ( 1 2 ) 1 2 1 2
Câu 19: Tìm số nghiệm thực của phương trình 2 2 log x − log ( 2 4x − 5 = 0 . 2 4 ) A. 2 B. 4 C. 1 D. 3 Lời giải Chọn B
Điều kiện x ≠ 0 .
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 20
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Phương trình 2 2 log x − log ( 2 4x − 5 = 0 2 2 1 2
⇔ log x − log x − 6 = 0 2 4 ) 2 2 2 2 1 97 log x + ⇔ = ∨ 2 1 97 log x − =
. Vậy phương trình đã cho có 4 nghiệm. 2 4 2 4
Câu 20: Cho phương trình log (5x ) 1 .log ( x 1 5 + − − 5 =1. Khi đặt log 5x t =
−1 , ta được phương trình 5 ( ) 5 25 ) nào dưới đây? A. 2t −1 = 0
B. 2t + t − 2 = 0 C. 2t − 2 = 0 D. 2
2t + 2t −1 = 0 Lời giải Chọn B log (5x ) 1 .log ( x 1 5 + − − 5 =1 ( ) 1 5 25 ) TXĐ: D = ( 0;+∞) . Ta có ( x 1+ x 1 log 5 − 5 = log 5.5 − 5 = log 5x −1 +1 . 25 ) 2 5 ( ) ( 5( ) ) 2 Đặt log 5x t = −1 (t > 0). 5 ( ) Phương trình ( ) 1 trở thành 1 t. (t + ) 1 =1 2
⇔ t + t − 2 = 0 . 2
Câu 21: Tích tất cả các nghiệm của phương trình x 4
3 + 3 −x = 30 bằng A. 3. B. 1. C. 9. D. 27 . Lời giải Chọn A x 4−x x 81 3 + 3 = 30 ⇔ 3 + = 30 . 3x Đặt = 3x t
(t > 0), phương trình đã cho trở thành: 81 2 t +
= 30 ⇔ t − 30t + 81 = 0 t t =
= 27 ⇒ 3x = 27 ⇔ x = 3 Vậy tích tất cả các nghiệm của phương trình là 1.3 3.
⇔ t =3⇒3x =3⇔ x =1
Câu 22: Biết phương trình 2log x + 3log = có hai nghiệm thực x < x . Tính giá trị của biểu thức x 2 7 2 1 2 = ( ) 2x T x 1 A. T = 64 . B. T = 32 . C. T = 8. D. T =16 . Lời giải Chọn D x > 0 Điều kiện: . x ≠ 1 Ta có: 2log x + 3log = 3 ⇔ x + = x 2 7 2log 7 2 2 log x 2
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 21
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com log x = 3 2 x = 8 2
⇔ 2log x − 7log x + 3 = 0 ⇔ ⇔ . 2 2 1 log x = = 2 x 2 2
⇒ x = 2 ; x = 8 ⇒ = ( x T x = ( )8 2 =16 . 1 ) 2 1 2
Câu 23: Phương trình 2 2 x +x 1 − x +x 1 3.9 10.3 − −
+ 3 = 0 có tổng các nghiệm thực là: A. 2 . B. 0 . C. 1. D. 2 − . Lời giải Chọn D Đặt 2 1 3x x t + − =
, điều kiện t > 0. t = 3
Khi đó phương trình đã cho có dạng: 2
3t −10t + 3 = 0 ⇔ 1 t = 3 = + − x 1 Với 2 x x 1 2 2 t = 3 ⇒ 3
= 3 ⇔ x + x −1 =1 ⇔ x + x − 2 = 0 ⇔ x = 2 − 1 = + − x x x 1 0 Với 2 1 2 2 t = ⇒ 3
= ⇔ x + x −1 = 1
− ⇔ x + x = 0 ⇔ 3 3 x = 1 −
Tập nghiệm của phương trình là S = { 2; − 1 − ;0; }
1 nên tổng tất cả các nghiệm thực là 2 − .
Câu 24: Gọi S là tập hợp tất cả giá trị nguyên của tham số m sao cho phương trình x x 1 + 2 16 − .4 m
+ 5m − 45 = 0 có hai nghiệm phân biệt. Hỏi S có bao nhiêu phần tử? A. 13 B. 3 C. 6 D. 4 Lời giải Chọn B Đặt = 4x t
,(t > 0) . Phương trình trở thành: 2 2
t − 4mt + 5m − 45 = 0.
Phương trình đã cho có hai nghiệm phân biệt khi và chỉ khi phương trình có hai nghiệm phân biệt t > 0. ∆′ > 0 2 −m + 45 > 0 3 − 5 < m < 3 5 ⇔ P > 0 2 ⇔ 5
m − 45 > 0 ⇔ m < 3
− ∨ m > 3 ⇔ 3 < m < 3 5 . S > 0 4m > 0 m > 0
Vì m nguyên nên m∈{4;5; }
6 . Vậy S có 3 phần tử.
Câu 25: Có bao nhiêu số nguyên m để phương trình x x 1 4 .2 m + −
+ 2m = 0 có hai nghiệm x , x thỏa 1 2
mãn x + x = 3 ? 1 2 A. 2 . B. 0 . C. 1. D. 3. Lời giải Chọn C
Phương trình ⇔ 4x − 2 .2x m + 2m = 0 ( ) 1 Đặt 2x
t = , t > 0 phương trình trở thành 2 t − 2 . m t + 2m = ( 0 2) .
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 22
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Để phương trình ( )
1 có hai nghiệm x , x thỏa mãn x + x = 3 điều kiện là phương trình (2) 1 2 1 2
có hai nghiệm t , t > 0 thỏa mãn 1 x 2 x 1 x 2 . 2 .2 2 x t t + = =
= 8 suy ra 2m = 8 ⇔ m = 4 . 1 2 1 2
Câu 26: Tìm giá trị thực của m để phương trình 2
log x − mlog x + 2m − 7 = 0 có hai nghiệm thực x , x 3 3 1 2 thỏa mãn x x = 81. 1 2 A. m = 4 −
B. m = 44
C. m = 81
D. m = 4 Lời giải Chọn D
Đặt t = log x ta được 2t − mt + 2m − 7 = 0 , tìm điều kiện để phương trình có hai nghiệm t ,t 3 1 2
t + t = log x + log x = log x x = log 81 = 4 1 2 3 1 3 2 3 ( 1 2 ) 3
Theo vi-et suy ra t + t = m ⇒ m = 4 1 2
Câu 27: Số nghiệm của phương trình (x − 2)log
( 2x −5x+6 +1 = 0 0,5 ) là A. 1. B. 0. C. 3. D. 2. Lời giải Chọn D ĐKXĐ: x > 3 2
x − 5x + 6 > 0 ⇔ . x < 2 Kết hợp ĐKXĐ ta có: (x − 2)log
( 2x −5x+6)+1 = 0 ⇔ log ( 2x −5x+6 = 1 − 0,5 0,5 ) = − x 1 2 1 2
⇔ x − 5x + 6 = 0,5 ⇔ x − 5x + 4 = 0 ⇔ . x = 4
Đối chiếu với ĐKXĐ ta thấy phương trình đã cho có 2 nghiệm.
Vậy tổng các nghiệm của phương trình là 9 − 7 = 2
Câu 28: Tập nghiệm của phương trình log ( 2
x − x + 2 =1 là 2 ) A. { } 0 . B. {0; } 1 . C. { 1; − } 0 . D. { } 1 . Lời giải Chọn B x = 0 Ta có: log ( 2 x − x + 2 =1 2
⇔ x − x + 2 = 2 ⇔ . 2 ) x = 1
Câu 29: Nghiệm của phương trình log(x − )1 = 2 là A. 5. B. 21. C. 101. D. 1025 . Lời giải Chọn C
Điều kiện của phương trình là x >1 . (x − ) 2 log
1 = 2 ⇔ x −1 = 10 ⇔ x = 101 .
Vậy x =101 thỏa mãn điều kiện nên phương trình đã cho có nghiệm là x =101 .
Câu 30: Tập nghiệm của phương trình log x + log x + log x = 7 là: 2 4 16
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 23
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com A. { } 16 . B. { 2}. C. { } 4 . D. {2 2}. Lời giải Chọn A
Điều kiện: x > 0 . 1 1 7
log x + log x + log x = 7 ⇔ log x + log x + log x = 7 ⇔ log x = 7. 2 4 16 2 2 2 2 2 4 4 4
⇔ log x = 4 ⇔ x = 2 ⇔ x =16 . 2
Câu 31: Tích các nghiệm của phương trình 2x 1− 2x+3 2 = 3 bằng A. 3 − log 3 . B. −log 54 . C. 4 − . D. 1− log 3. 2 2 2 Lời giải Chọn B Ta có: 2x 1− 2x+3 2 2 = 3
⇔ x −1 = (2x + 3) 2
log 3 ⇔ x − 2log 3.x −1− 3log 3 = 0. 2 2 2
Vì ac < 0 ⇒ phương trình có hai nghiệm phân biệt x , x và 1 2 x x = 1
− − 3log 3 = −log 2 − log 27 = −log 54 . 1 2 2 2 2 2
Câu 32: Gọi x , x là hai nghiệm của phương trình 2 x x −2
2 .5 x =1. Khi đó tổng x + x bằng 1 2 1 2 A. 2−log 2 . B. 2 − + log 2 . C. 2+ log 2 . D. 2−log 5 . 5 5 5 2 Lời giải 2
2x.5x − x =1 ⇔ log ( 2 2 x x −2 2 .5 x ) 2
= 0 ⇔ x log 2 + x − 2x = 0 ⇔ x log 2 + x − 2 = 0 5 5 ( 5 ) x = 0 . 1 ⇒ . x = 2 − log 2 2 5 x 1 −
Câu 33: Phương trình 27 x .2x = 72 có một nghiệm viết dưới dạng x = −log b a
, với a , b là các số
nguyên dương. Tính tổng S = a + b . A. S = 4. B. S = 5 . C. S = 6 . D. S = 8 . Lời giải Chọn B
Điều kiện x ≠ 0 . 3x−3 x 1 − x 1 − 3 x 3 3x−3 Phương trình 27 3 2 −2 x .2x = 72 x x 2 3 ⇔ 3 .2 = 3 .2 ⇔ = x 3 ⇔ 3 = 2 −x 2 3 2x x−3 x − 3 x − 3 1 x 3 ⇔ 3 = 2 −x 3 ⇔ = log 2 −x ⇔
= −(x − 3)log 2 ⇔ (x − 3) + log 2 = 0 3 x 3 x 3 x x = 3 x = 3(N ) ⇔ 1 ⇔ . − log 2 =
x = − log 3 N 2 ( ) 3 x a = 2 Suy ra
. Vậy tổng S = a + b = 5. b = 3
Câu 34: Tính tổng tất cả các nghiệm thực của phương trình log 3.2x −1 = x −1 4 ( ) A. 2 . B. 1. C. 5. D. 6 − .
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 24
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Lời giải Chọn A log (3.2x ) x x 1 1 1 3.2 1 4 4x 12.2x x − − = − ⇔ − = ⇔ − + 4 = 0 4 Đặt = 2x t
(t > 0) . Phương trình trở thành: 2t −12t + 4 = 0 ⇔ t = 6± 4 2 Với = 6 + 4 2 ⇒ 2x t
= 6 + 4 2 ⇔ x = log 6 + 4 2 . 2 ( )
Với = 6 − 4 2 ⇒ 2x t
= 6 − 4 2 ⇔ x = log 6 − 4 2 . 2 ( )
Tổng các nghiệm là log 6 + 4 2 + log 6 − 4 2 = log 4 = 2 . 2 ( ) 2 ( ) 2
Câu 35: Phương trình log 5− 2x = 2 − x có hai ngiệm x , x . Tính P = x + x + x x . 2 ( ) 1 2 1 2 1 2 A. 11. B. 9 . C. 3. D. 2 . Lời giải Chọn D
Điều kiện: 2x < 5 2x =1 x = 0
log 5 − 2x = 2 − x ⇔ x 2 5 − 2 = 2 −x ⇔ x 4 5 − 2 = ⇔ ⇔ 2 ( ) 2x 2x = 4 x = 2
⇒ P = x + x + x x = 2 1 2 1 2
Câu 36: Tổng tất cả các nghiệm thực của phương trình log 3.4x + 2.9x = x +1 bằng 6 ( ) A. 4 B. 1 C. 0 D. 3 Lời giải Chọn B 2x x
Phương trình đã cho tương đương x x x 1 + 2 2 3.4 2.9 6 3. 6. + = ⇔ − + 2 = 0 3 3 x
Đặt 2 = t,(t >
0). Khi đó ta có phương trình 2
3t − 6t + 2 = 0 3
Hiển nhiên phương trình có 2 nghiệm phân biệt t ,t dương và thỏa mãn 1 2 1 x 2 2 2 2 x 2 t .t = ⇒ . = ⇒ x + x = 1. 1 2 1 2 3 3 3 3
Câu 37: Có bao nhiêu giá trị nguyên của tham số m để phương trình: x (m ) x+ − + 1 4
3 .2 + m + 9 = 0 có hai
nghiệm dương phân biệt. A. 3 . B. 4 . C. 5 . D. Vô số. Lời giải Chọn A Đặt: = 2x t
( x > 0 ⇒ t > 1) , phương trình đã cho trở thành: 2t −2(m+ 3)t + m+9 = 0.
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 25
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Bài toán trở thành: Tìm các giá trị nguyên của tham số m để phương trình: 2
t − 2(m + 3)t + m + 9 = 0 có hai nghiệm phân biệt t ,t thỏa mãn 1 < t < t 1 2 1 2 ∆′ = 2 m + 5m > 0 ∆′ = 2 m + 5m > 0 (t 1 t 1 0 t t t t 1 0 * 1 )( 2 ) ⇔ − − > ⇔ − 1 2 ( + 1 2 ) + > ( ) S S = m + 3 > 1 = m + 3 > 1 2 2
Phương trình: 2t − 2(m + 3)t + m + 9 = 0 có hai nghiệm phân biệt t ,t nên theo Viet ta có: 1 2
t + t = 2 m 3 1 2 ( + )
t .t = m + 9 1 2 m < −5 2 m + 5m > 0 m > 0
Thay vào hệ (*) ta được
−m + 4 > 0 ⇔ m < 4 ⇔ 0 < m < 4 m + 3 > 1 m > − 2
Vì m∈, 0 < m < 4 ⇒ m∈{1;2 } ;3 .
Vậy có 3 giá trị nguyên của tham số m thỏa mãn yêu cầu bài toán.
Câu 38: Cho phương trình x x+ − 2 4
2 + m − 2 = 0 với m là tham số. Có tất cả bao nhiêu giá trị nguyên của
m để phương trình đã cho có hai nghiệm phân biệt x ,x thỏa mãn 0 ≤ x < x ? 1 2 1 2 A. 1. B. 3 . C. 2 . D. 0 . Lời giải Chọn A x x+ − 2 4
2 + m − 2 = 0 ⇔ 4x − 4.2x + m − 2 = 0(1) . Đặt = 2x t (t > 0) ( ) ⇔ 2 1
t − 4t + m − 2 = 0 (2)
Để phương trình (1)có hai nghiệm phân biệt thỏa mãn 0 ≤ x < x 1 2 ⇔ 0 2 ≤ 1 2x < x2
2 ⇔ 1 ≤ t < t 1 2
Thì phương trình (2) thỏa: 0 ≤ t −1 < t −1 1 2 ∆ > 0
16 − 4(m − 2) > 0 m < 6
⇔ t + t > 2 ⇔ 4 > 2 ⇔
. Vậy m = 5 thỏa yêu cầu. 1 2 ( m ≥ 5 t −1 t 1 0
t t −(t +t ) + 1 ≥ 0 1 )( − 2 ) ≥ 1 2 1 2 x x
Câu 39: Phương trình (1+ 2) +(1− 2a)( 2 −1) − 4 = 0 có 2 nghiệm phân biệt x , x thỏa mãn 1 2 x − x = log
3 . Mệnh đề nào dưới đây đúng? 1 2 1+ 2 A. 3 a 3 3 3 ∈ −∞;− . B. a∈ − ;0 . C. a∈0; . D. a∈ ;+∞ . 2 2 2 2 Lời giải Chọn B
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 26
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com x x Vì (1 1
+ 2 )( 2 −1) = 1. Đặt t = (1+ 2) (t > 0) ⇒ ( 2 −1) = t Phương trình trở thành: 1− 2a t + − 4 = 0 ⇔ 2
t − 4t + 1− 2t = 0 (1) . t
Để phương trình ban đầu có 2 nghiệm phân biệt thì phương trình (1) phải có hai nghiệm dương t , t . 1 2
∆′ = 2a + 3 > 0 −3 1
t + t = 4 > 0 ⇔ < a < . 1 2 2 2
t t = 1− 2a > 0 1 2 x x Và thỏa mãn t x − x = log 3 ( ) − ⇔ + 1 2 1 2
= 3 ⇔ 1 = 3 ⇔ t = 3t . 1 2 1+ 2 t 1 2 2 t = 3t t = 3 t = 3 1 2 1 1
t + t = 4 ⇔ t 1 t 1 1 2 = ⇔ 2 = 2 t t = 1− 2a
t t = 1− 2a = 1.3 a = − 1 1 2 1 2
Vậy với a = −1 thỏa mãn yêu cầu bài toán.
Câu 40: Cho phương trình x+1 4 − (8 + 5)2x m
+ 2m + 1 = 0 ( m là tham số) có hai nghiệm phân biệt x , x 1 2
thỏa mãn x x = −1. Khẳng định nào sau đây là đúng? 1 2
A. m∈(1;3).
B. m∈(−5;− 3) .
C. m∈(−3;0) . D. m∈(0;1). Lời giải Chọn D x+1 4 − (8 + 5)2x m + 2m + 1 = 0 (*) Đặt = 2x t
, điều kiện t > 0 , phương trình (*) trở thành 2
4t − (8m + 5)t + 2m + 1 = 0 ⇔ (4t −1)(t − 2m −1) = 0 1 t = ⇔ 1 4 t = 2m + 1. 2 2m + 1 > 0 1 m > −
Phương trình (*) có hai nghiệm phân biệt khi và chỉ khi 1 ⇔ 2 (* *) 2m + 1 ≠ 3 4 m ≠ − . 8 Lại có x x 1 1 = −1 log t log t 1 ⇔ log ⋅log 2m 1 1 ⇔ log 2m 1 2 ( + ) = 2 2 ( + ) = − 1 2 ⇔ ⋅ = − 2 1 2 2 4 2 2 1 ⇔ 2m +1 = 2 ⇔ − m = . 2
Câu 41: Gọi S là tập hợp tất cả các giá trị thực của tham số m để tồn tại duy nhất cặp (x;y)thỏa mãn các điêu kiện log
(4x 4y 4) 1 và 2 x + 2
y + 2x − 2y + 2 − m = 0. Tổng các giá trị của S 2 2 + − = x +y +2 bằng A. 33. B. 24. C. 15. D. 5.
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 27
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Lời giải Chọn B
Điều kiện: 4x + 4y − 4 > 0 2 2 log (4x 4y 4) 1 2 2 + − = x y x y x y 4 4 6 0 2 + − − + = Ta có + + ⇔
có nghiệm duy nhất (x;y) 2 x + 2
y + 2x − 2y + 2 − m = 0 2 x + 2
y + 2x − 2y + 2 − m = 0 . Với 2 x + 2
y − 4x − 4y + 6 = 0 là phương trình đường tròn tâm (
A 2;2) , bán kính R = 2 . 1 Với 2 x + 2
y + 2x − 2y + 2 − m = 0 là phương trình đường tròn tâm (
B −1;1) , bán kính R = m 2 với m > 0 .
Hai đường tròn có điếm chung duy nhất khi xảy ra các trường hợp sau:
Hai đường tròn tiếp xúc ngoài AB = R + R ⇔ m + 2 = 10 ⇔ m = ( 10 − 2 2) . 1 2
Hai đường tròn tiếp xúc trong AB = R − R ⇔ m − 2 = 10 ⇔ m = ( 10 + 2 2) . 1 2
Vậy tổng các giá trị của tham số m = − 2 + + 2 ( 10 2) ( 10 2) = 24 . 2 x −4x+3 Câu 42: 1
Tìm tất cả các giá trị thực của tham số m để phương trình = 4 m − 2 m + 1 có 4 nghiệm 5 phân biệt?
A. 0 < m < 1. B. m < 1. C. m > −1. D. m < 0 . Lời giải Chọn A Vì 4 m − 2
m + 1 > 0,∀m nên phương trình tương đương với 2
x − 4x + 3 = log m m 1 (1) 1 ( 4 − 2 + ) 5
Vẽ đồ thị hàm số bậc hai y = 2 x − 4x + 3
Từ đó suy ra đồ thị hàm số y = 2 x − 4x + 3
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 28
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Dựa vào đồ thị hàm số ta thấy phương trình (1) có 4 nghiệm phân biệt khi và chỉ khi 1 0 < log m m 1 1 m m 1 1 0 m 1 . 1 (
4 − 2 + ) < ⇔ < 4 − 2 + < ⇔ < < 5 5
Câu 43: Cho hai số thực dương x, y thỏa mãn log x = log y = log x + y . Giá trị của tỉ số x bằng 4 6 9 ( ) y A. 1 − + 5 . B. 1± 5 . C. 1+ 5 . D. 1 − + 5 . 2 2 4 4 Lời giải Chọn A x = 4t
Đặt log x = log y = log x + y = t ⇒ y = 6t . 4 6 9 ( )
x+ y = 9t x 1 − − 5 = (l) y 2 Mà t t t 2 =
⇒ x(x + y) 2 4 .9 (6 ) = y 2 2 x xy y 0 ⇔ + − = ⇔ . x 1 − + 5 = (t / m) y 2
Câu 44: Nghiệm của bất phương trình x+2 1 3 ≥ là 9 A. x ≥ 4 − . B. x < 0 . C. x > 0 . D. x < 4 . Lời giải Chọn A x+2 1 x+2 2 3 3 3− ≥ ⇔ ≥ ⇔ x + 2 ≥ 2 − ⇔ x ≥ 4 − . 9 2 x −4x
Câu 45: Tập nghiệm S của bất phương trình 1 < 8 là: 2 A. S = ( ; −∞ 3) .
B. S = (1;+∞) . C. S = ( ; −∞ )
1 ∪(3;+∞) . D. S = (1;3) . Lời giải Chọn C 2 x −4x 2 x −4x 3 − Ta có 1 < 1 1 8 ⇔ < 2
⇔ x − 4x > 3 − 2
⇔ x − 4x + 3 > 0 ⇔ x <1∨ x > 3 . 2 2 2
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 29
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Vậy S = ( ; −∞ ) 1 ∪(3;+∞) . 2 x −4
Câu 46: Giải bất phương trình 3 ≥
1 ta được tập nghiệm T . Tìm T . 4 A. T = [ 2; − 2] .
B. T = [2;+∞). C. T = ( ; −∞ 2 − ]. D. T = ( ; −∞ 2 − ]∪[2;+∞) Lời giải Chọn A 2 x −4
Bất phương trình 3 2
≥1 ⇔ x − 4 ≤ 0 ⇔ x ∈[ 2; − 2] 4
Vậy tập nghiệm T = [ 2; − 2] .
Câu 47: Bất phương trình 2x > 4 có tập nghiệm là:
A. T = (2;+∞) . B. T = (0;2) . C. T = ( ;2 −∞ ) . D. T = ∅ . Lời giải Chọn A x x 2
2 > 4 ⇔ 2 > 2 ⇔ x > 2 .
Vậy tập nghiệm của bất phương trình là: T = (2;+∞) .
Câu 48: Tìm tập nghiệm S của bất phương trình log x −3 ≥ log 4 . 1 ( ) 1 2 2
A. S = (3; 7].
B. S = [3; 7]. C. S = ( ; −∞ 7].
D. S = [7; + ∞). Lời giải Chọn A
Ta có: log x − 3 ≥ log 4 ⇔ 0 < x − 3 ≤ 4 ⇔ 3 < x ≤ 7 . 1 ( ) 1 2 2
Vậy tập nghiệm của bất phương trình là S = (3; 7].
Câu 49: Tìm tập nghiệm S của bất phương trình 2 − x +3 2 x < 4
A. S = (∞; )
1 ∪(2;+∞) . B. S = (−∞; ) 1 .
C. S = \{1; } 2 .
D. S = (2;+∞) . Lời giải Chọn A > − + x 2
Bất phương trình tương đương với 2 x 3x 2 2 2 2
< 2 ⇔ −x + 3x < 2 ⇔ x − 3x + 2 > 0 ⇔ . x <1 − x
Câu 50: Tập nghiệm S của bất phương trình x+2 1 5 < là 25 A. S = ( ;2 −∞ ) . B. S = (−∞ ) ;1 .
C. S = (1;+∞) .
D. S = (2;+∞) . Lời giải Chọn D
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 30
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com − x x+2 1 x+2 5 <
⇔ 5 < (5)2x ⇔ 2 < x . 25
Câu 51: Tập nghiệm của bất phương trình 2x x+4 2 < 2 là A. (0;4) . B. ( ;4 −∞ ) . C. (0;16) . D. (4;+∞) . Lời giải Chọn B Ta có 2x x+4 2 < 2
⇔ 2x < x + 4 ⇔ x < 4 .
Câu 52: Tập nghiệm của bất phương trình 2
ln x < 2ln (4x + 4) là: A. 4 ; − +∞ 4 4 . B. ( 1; − +∞) \{ } 0 . C. − ;+∞ \{ } 0 . D. − ;+∞ \{ } 0 . 5 5 3 Lời giải Chọn C 4 x < − Đk: 1 − < x ≠ 0; 2
ln x < 2ln (4x + 4) ⇔ 2
x < (4x + 4)2 ⇔ 2
15x + 32x +16 > 0 ⇔ 3 . 4 x > − 5
Kết hợp với điều kiện ta được tập nghiệm 4 S ; = − +∞ \{ } 0 . 5
Câu 53: Tập nghiệm của bất phương trình log x < log 12 −3x là: 2 2 ( ) A. (0;6) . B. (3;+∞) . C. ( ; −∞ 3) . D. (0;3). Lời giải Chọn D x > 0
Ta có log x < log 12 − 3x ⇔ ⇔ 0 < x < 3. 2 2 (
) x<12−3x
Câu 54: Gọi S là tập nghiệm của bất phương trình log 2x + 5 > log x −1 . Hỏi trong tập S có bao 2 ( ) 2 ( )
nhiêu phần tử là số nguyên dương bé hơn 10? A. 9. B. 15. C. 8 . D. 10. Lời giải Chọn C 2x + 5 > 0 Điều kiện: ⇔ x >1. x −1 > 0
log 2x + 5 > log x −1 ⇔ 2x + 5 > x −1 ⇔ x > 6 − . 2 ( ) 2 ( )
Kết hợp với điều kiện ta có tập nghiệm của bất phương trình: S = (1;+∞) .
Vậy trong tập S có 8 phần tử là số nguyên dương bé hơn 10.
Câu 55: Bất phương trình log x + 7 > log x +1 có bao nhiêu nghiệm nguyên? 4 ( ) 2 ( ) A. 3. B. 1. C. 4 . D. 2 . Lời giải
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 31
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Chọn D
Điều kiện x > 1 − .
log (x + 7) > log (x + ) 2
1 ⇔ x + 7 > x + 2x +1 4 2 2
⇔ x + x − 6 < 0 ⇔ 3 − < x < 2 .
Do điều kiện nên tập nghiệm của bất phương trình là S = {0, } 1 .
Câu 56: Tập nghiệm của bất phương trình log 2x < log 9 − x e e ( ) là 3 3 A. (3;+∞) . B. (3;9) . C. ( ; −∞ 3) . D. (0;3). Lời giải Chọn C 2x > 0 x > 0
log 2x < log 9 − x ⇔ − x >
⇔ x < ⇔ < < e e ( ) 9 0 9 3 x 9 . 3 3 2x > 9− x x > 3
Vậy tập nghiệm của bất phương trình là S = (3;9).
Câu 57: Tập nghiệm của bất phương trình log (9x −5) < log (3x + ) 1 là 4− 3 4− 3 A. (1;+∞). B. 5 ;1 . C. 1 − ;1 . D. 1 5 − ; . 9 3 3 9 Lời giải Chọn B 5 9 x − 5 > 0 x > Điều kiện: 9 ⇔ 5 ⇔ x > . 3 x +1 > 0 1 x > − 9 3 Ta có: log (9x −5) < log (3x + )
1 ⇔ 9x − 5 < 3x +1 ⇔ x <1. 4− 3 4− 3
Kết hợp với điều kiện, ta có tập nghiệm của phương trình là: 5 S ;1 = . 9
Câu 58: Tập nghiệm của bất phương trình: log x −3 + log x ≥ 2 là 2 ( ) 2 A. (3;+∞) . B. [4;+∞) . C. ( ; −∞ − ]
1 ∪[4;+∞). D. (3;4] . Lời giải Chọn B
Điều kiện xác định: x > 3. x ≥ 4
log x − 3 + log x ≥ 2 2
⇔ x − 3x ≥ 4 ⇔
. Vậy tập nghiệm của bpt là S = [4;+∞) . 2 ( ) 2 x ≤ 1 − 2x 10 −
Câu 59: Bất phương trình 2x−3x+4 1 2 ≤
có bao nhiêu nghiệm nguyên dương? 2 A. 2 . B. 4 . C. 6 . D. 3.
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 32
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Lời giải Chọn D
Bất phương trình tương đương với 2x−3x+4 10−2 2 ≤ 2 x 2
⇔ x − 3x + 4 ≤10 − 2x 2
⇔ x − x − 6 ≤ 0 ⇔ 2
− ≤ x ≤ 3. Do x > 0 nên 0 < x ≤ 3 . Mà x +
∈ nên x ∈{1;2; }
3 .Vậy có 3 giá trị nguyên dương thỏa mãn yêu cầu bài toán. x−
Câu 60: Tập nghiệm của bất phương trình ( 3 5) 1 x+3 < 5 là: A. ( ; −∞ 5 − ) . B. ( ;0 −∞ ). C. ( 5; − +∞) . D. (0;+∞). Lời giải Chọn C x− x 1 − Ta có: ( 3 5) 1 x+3 < 5 x −1 3 x+3 ⇔ 5 < 5 ⇔
< x + 3 ⇔ x −1< 3x + 9 ⇔ x > 5 − . 3 x 1 − x 1 −
Câu 61: Tập nghiệm của bất phương trình ( 5 + 2) ≤ ( 5 − 2) là A. S = (−∞ ] ;1 .
B. S = [1;+ ∞) . C. S = (−∞ ) ;1 .
D. S = (1;+ ∞) . Lời giải Chọn A ( x 1 − − x 1 +
+ )x 1− ≤ ( − )x 1− 5 2 5 2
⇔ ( 5 + 2) ≤ ( 5 + 2) ⇔ x −1≤ −x +1 ⇔ x ≤1. Vậy S = (−∞ ] ;1 .
Câu 62: Tập nghiệm của bất phương trình x x 1 2 3 + > là: A. ∅ . B. ; −∞ log 3 . C. ( ; −∞ log 3 . D. log 3;+∞ . 2 ] 2 2 3 3 Lời giải Chọn B Cách 1: x x 1 2 3 + x log ( x 1 3 + > ⇔ >
⇔ x > x +1 log 3 ⇔ x 1− log 3 > log 3 2 ) ( ) 2 ( 2 ) 2 2 log 3 2 ⇔ x log > log 3 ⇔ x < ⇔ x < log 3. 2 2 2 3 2 3 log2 3 x
Cách 2: x x 1 + 2 2 3 > ⇔ > 3 ⇔ x < log 3 . 2 3 3
Câu 63: Giải bất phương trình 2 3x 2x <
A. x∈(0;+∞) .
B. x∈(0;log 3 .
C. x∈(0;log 2 . D. x∈(0; ) 1 . 3 ) 2 ) Lời giải Chọn C Ta có: 2 3x 2x < 2 log 3x log 2x ⇔ < 2
⇔ x − x log 2 < 0 ⇔ < x < . 3 3 3 0 log 2 3
Câu 64: Tập nghiệm của bất phương trinh x x 1 2 3 + > là
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 33
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com A. ∅ . B. ; −∞ log 3 . C. ( ; −∞ log 3 . D. log 3;+∞ . 2 ] 2 2 3 3 Lời giải Chọn B
Cách 1: x x 1 2 3 + x log ( x 1 3 + > ⇔ >
⇔ x > x +1 log 3 ⇔ x 1− log 3 > log 3 2 ) ( ) 2 ( 2 ) 2 2 log 3 2 ⇔ x log > log 3 ⇔ x < ⇔ x < log 3. 2 2 2 3 2 3 log2 3 x
Cách 2: x x 1 + 2 2 3 > ⇔ > 3 ⇔ x < log 3 . 2 3 3 x
Câu 65: Cho hàm số ( ) 1 2 .5x f x =
. Khẳng định nào sau đây là sai? 2 A. f (x) 2
>1 ⇔ x + x log2 5 > 0 . B. f (x) 2
> 1 ⇔ x − x log2 5 < 0. C. f (x) 2
>1 ⇔ x − x log5 2 > 0 . D. f (x) 2
> 1 ⇔ −x ln 2 + x ln 5 > 0 . Lời giải Chọn A x 1 x
Ta có: f (x) >1 1 2 ⇔ .5x > 2
1 ⇔ log .5x > 0 2 2 2 1 x 2 ⇔ log + log 5x > 0 2
⇔ −x + x log 5 > 0 nên phương án A sai. 2 2 2 2
Câu 66: Giải bất phương trình log 2x −1 > 3 3 ( ) A. x > 4 . B. x >14
C. x < 2 .
D. 2 < x <14 . Lời giải Chọn B log 2x −1 > 3 ⇔ 3
2x −1 > 3 ⇔ x >14 3 ( ) .
Câu 67: Giải bất phương trình log 2x −1 < 2 ta được nghiệm là 3 ( )
A. 1 < x < 5 . B. 1 x > . C. x < 5. D. x > 5. 2 5 Lời giải Chọn A 2x −1 > 0 1 x > log 2x −1 < 2 ⇔ ⇔ . 3 ( ) 2 2x −1< 9 x < 5
Câu 68: Giải bất phương trình log 1− x < 0 ? 1 ( ) 2 A. x = 0 . B. x < 0 . C. x > 0 . D. 1 − < x < 0 . Lời giải
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 34
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Chọn B 1 − x > 0 log 1− x < 0 ⇔ ⇔ x < 0 . 1 ( ) 1 − x >1 2
Câu 69: Các giá trị x thỏa mãn bất phương trình log 3x −1 > 3 là: 2 ( ) A. x > 3.
B. 1 < x < 3. C. x < 3 . D. 10 x > . 3 3 Lời giải Chọn A
Ta có log 3x −1 > 3 ⇔ 3x −1> 8 ⇔ x > 3 . 2 ( )
Câu 70: Bất phương trình log0,5 (2x − )
1 ≥ 0 có tập nghiệm là? A. 1 ; +∞ B. 1 ;+∞ C. (1;+∞) D. 1 ;1 2 2 2 Lời giải Chọn D
Điều kiện: 2x −1 > 0 1 ⇔ x > . 2 log 0 0,5 (2x − )
1 ≥ 0 ⇔ 2x −1≤ 0,5 ⇔ 2x ≤ 2 ⇔ x ≤1.
So sánh với điều kiện ta có tập nghiệp của bất phương trình là 1 S ;1 = . 2
Câu 71: Tìm số nghiệm nguyên của bất phương trình log 9 − x ≤ 3. 2 ( ) A. 7 . B. 6 . C. 8 . D. 9. Lời giải Chọn C
Ta có: log 9 − x ≤ 3 ⇔ 0 < 9 − x ≤ 8 ⇔ 1≤ x < 9. Vì x∈ ⇒ x ∈ 1;2;3;4;5;6;7;8 . 2 ( ) { } Vậy có 8 nghiệm nguyên.
Câu 72: Tập nghiệm của bất phương trình log x −1 < 3 là: 2 ( ) A. (−∞;10) . B. (1;9) . C. (1;10) . D. (−∞;9) . Lời giải Chọn B
Điều kiện: x −1 > 0 ⇔ x >1.
Ta có: log x −1 < 3 ⇒ x −1< 8 ⇔ x < 9 . 2 ( )
Kết hợp điều kiện ta có tập nghiệm của bất phương trình đã cho là (1;9) .
Câu 73: Tập nghiệm của bất phương trình log ( 2
x + 2 ≤ 3 là: 3 ) A. S = ( ; −∞ − 5]∪[5;+ ∞) . B. S = ∅ . C. S = . D. P = [ 5; − 5] . Lời giải
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 35
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Chọn D Ta có: log ( 2 x + 2 ≤ 3 2 ⇔ x + 2 ≤ 27 2 ⇔ x ≤ 25 ⇔ 5 − ≤ x ≤ 5 . 3 )
Câu 74: Số nghiệm thực nguyên của bất phương trình ( 2
log 2x −11x +15) ≤1 là A. 3. B. 4 . C. 5. D. 6. Lời giải Chọn B ĐK: 2 5
2x −11x +15 > 0 ⇔ x < hoặc x > 3. 2 ( 2
log 2x −11x +15) ≤1⇔ 2
2x −11x +15 ≤10 ⇔ 2
2x −11x + 5 ≤ 0 ⇔ 1 ≤ x ≤ 5 . 2
Kết hợp điều kiện ta có: 1 5
≤ x < hoặc 3 < x ≤ 5. Vậy BPT có 4 nghiệm nguyên là: 2 2 x∈{1;2;4; } 5 .
Câu 75: Tìm tập nghiệm S của bất phương trình: 2 log > 2 . 1 x −1 2
A. S = (1;1+ 2) . B. S = (1; 9) .
C. S = (1+ 2; + ∞) . D. S = (9; + ∞) . Lời giải Chọn B x −1 > 0 2 x >1 x >1 log > 2 ⇔ ⇔ ⇔ . 1 x −1 2 1 < x −1 < 8 x < 9 2 x −1 4
Câu 76: Bất phương trình max log x, log x < 3 có tập nghiệm là 3 1 2 A. ( ; −∞ 27). B. (8;27). C. 1 ; 27 . D. (27;+∞). 8 Lời giải Chọn C
Điều kiện: x > 0 . log x < 3 x < 27 3 max 1
log x,log x < 3 ⇔ log x < 3 ⇔ 1 ⇔ < x < 27 . 3 1 1 x > 8 2 2 8
Vậy tập nghiệm của BPT là: 1 ;27 . 8
Câu 77: Tập nghiệm của bất phương trình log (log ( 2x −1 ≤ 1 − là: 1 2 ) 2 A. S = 1; 5 . B. S = (− ; ∞ − 5 ∪ 5;+∞ ).
C. S = − 5; 5 .
D. S = − 5;− ) 1 ∪ (1; 5. Lời giải
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 36
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Chọn B
log ( 2x −1 > 0 2 ) * ĐKXĐ: 2
⇔ x −1 >1 ⇔ x ∈( ; −∞ − 2)∪( 2;+ ∞) . 2 x −1 > 0 − Bất phương trình 1
log (log ( 2x −1 ≤ 1 − log x 1 ⇔ − ≥ = 2 ⇔ ( 2 x − ) ≥ 2 ( ) 1 2 1 4 1 2 ) 2 2 2
⇔ x ≥ 5 ⇔ x ∈(− ; ∞ − 5 ∪ 5;+ ∞ ).
* Kết hợp điều kiện ta được: x∈( ;
−∞ − 5 ∪ 5;+ ∞ ).
Câu 78: Cho phương trình 2x 10 + x+4 3 − 6.3 − 2 < 0( ) 1 . Nếu đặt x+5
t = 3 (t > 0) thì ( ) 1 trở thành phương trình nào? A. 2
9t − 6t − 2 < 0.
B. 2t − 2t − 2 < 0.
C. 2t −18t − 2 < 0. D. 2
9t − 2t − 2 < 0. Lời giải. Chọn B 2x 10 + x+4 2(x+5) x+5 3 − 6.3 − 2 < 0 ⇔ 3 − 2.3 − 2 < 0 Vậy khi đặt x+5
t = 3 (t > 0) thì ( )
1 trở thành phương trình 2t − 2t − 2 < 0.
Câu 79: Cho phương trình x 1
25 + − 26.5x +1 > 0. Đặt 5x
t = , t > 0 thì phương trình trở thành
A. 2t − 26t +1 > 0. B. 2
25t − 26t > 0 . C. 2
25t − 26t +1 > 0 . D. 2t − 26t > 0 . Lời giải Chọn C Ta có x 1
25 + − 26.5x +1 > 0 2 25.5 x 26.5x ⇔ − +1 > 0 . Vậy nếu đặt 5x
t = , t > 0 thì phương trình trên trở thành 2
25t − 26t +1 > 0 .
Câu 80: Xét bất phương trình 2x x+2
5 − 3.5 + 32 < 0. Nếu đặt 5x
t = thì bất phương trình trở thành bất
phương trình nào sau đây?
A. 2t −3t + 32 < 0 .
B. 2t −16t + 32 < 0 .
C. 2t − 6t + 32 < 0 .
D. 2t − 75t + 32 < 0 . Lời giải Chọn D 2x x+2 5 − 3.5 + 32 < 0 2x 2 5 3.5 .5x ⇔ − + 32 < 0 2 5 x 75.5x ⇔ − + 32 < 0 . Nếu đặt 5x t =
> 0 thì bất phương trình trở thành bất phương trình 2
t − 75t + 32 < 0 .
Câu 81: Cho phương trình 2 2 x −2x x −2x+3 4 + 2 − 3 ≥ 0 . Khi đặt 2 2 2x x t − =
, ta được phương trình nào dưới đây?
A. 2t +8t −3 ≥ 0 . B. 2 2t − 3 ≥ 0 .
C. 2t + 2t −3 ≥ 0 .
D. 4t − 3 ≥ 0 . Lời giải Chọn A 2 Phương trình 2 2 x −2x x −2x+3 4 + 2
− 3 ≥ 0 ⇔ ( 2x−2x ) 2 3 x −2 2 + 2 .2 x − 3 ≥ 0 . Kho đó, đặt 2 2 2x x t − =
, ta được phương trình 2t + 8t − 3 ≥ 0 .
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 37
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Câu 82: Khi đặt t = log x thì bất phương trình 2
log 5x − 3log x − 5 ≤ 0 trở thành bất phương trình nào 5 ( ) 5 5 sau đây?
A. 2t −6t − 4 ≤ 0.
B. 2t −6t −5 ≤ 0 .
C. 2t − 4t − 4 ≤ 0 .
D. 2t −3t −5 ≤ 0. Lời giải Chọn C 2
log 5x − 3log x − 5 ≤ 0 ⇔ (log x +1 − 6log x − 5 ≤ 0 2
⇔ log x − 4log x − 4 ≤ 0 . 5 )2 5 ( ) 3 5 5 5
Với t = log x bất phương trình trở thành: 2t − 4t − 4 ≤ 0 . 5
Câu 83: Bất phương trình 2
log x − 2019log x + 2018 ≤ 0 có tập nghiệm là A. 2018 S = 10 ;10 2018 2018 . B. S = 10 ;10
). C. S =[1; 2018].
D. S = (10;10 ). Lời giải Chọn A
Điều kiện: x > 0 . Ta có 2 2018
log x − 2019log x + 2018 ≤ 0 ⇔ 1≤ log x ≤ 2018 ⇔ 10 ≤ x ≤10 .
Kết hợp với điều kiện, ta có tập nghiệm của bất phương trình là 2018 S = 10 ;10 .
Câu 84: Tìm số nghiệm nguyên của bất phương trình 2
log x − 8log x + 3 < 0 2 2 A. 5 . B. 1 . C. 7 . D. 4 . Lời giải Chọn A
Điều kiện: x > 0 . 1 2
log x − 8log x + 3 < 0 2 2
⇔ log x − 8log x + 3 < 0 2
⇔ log x − 4log x + 3 < 0 2 2 2 2 2 2
⇔ 1 < log x < 3 ⇔ 2 < x < 8 . So với điều kiện ta được 2 < x < 8 . 2
Câu 85: Tìm tập nghiệm S của phương trình 2
log x − 5log x + 4 ≥ 0 2 2 A. S = ( ; −∞ 2]∪[16;+∞) .
B. S = (0;2]∪[16;+∞) . C. S = ( ; −∞ ]
1 ∪[4;+∞) . D. S = [2;16] . Lời giải Chọn B ĐK: x > 0
Đặt t = log x , t ∈ . 2 t ≤1
Bất phương trình tương đương 2t − 5t + 4 ≥ 0 ⇔ . t ≥ 4
• log x ≤1 ⇔ 0 < x ≤ 2 . 2
• log x ≥ 4 ⇔ x ≥16 . 2
Vậy tập nghiệm của bất phương trình S = (0;2]∪[16;+∞) .
Câu 86: Số nghiệm nguyên của bất phương trình 3x + 9.3−x <10 là A. Vô số. B. 2 . C. 0 . D. 1.
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 38
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Lời giải Chọn D Đặt 3x
t = (t > 0), bất phương trình có dạng 9 t + <10 2
⇔ t −10t + 9 < 0 ⇔ 1< t < 9 . t Khi đó 1 3x <
< 9 ⇔ 0 < x < 2 . Vậy nghiệm nguyên của phương trình là x =1.
Câu 87: Tập nghiệm của bất phương trình 16x 5.4x − + 4 ≥ 0 là: A. T = ( ; −∞ ) 1 ∪(4;+ ∞) . B. T = ( ; −∞ ] 1 ∪[4;+ ∞) . C. T = ( ; −∞ 0) ∪(1;+ ∞). D. T = ( ; −∞ 0]∪[1;+ ∞) . Lời giải Chọn D Đặt 4x t = , t > 0. t ≥ 4 t ≥ 4 4x ≥ 4 x ≥1 16x 5.4x − + 4 ≥ 0 trở thành 2
t − 5.t + 4 ≥ 0 ⇔ ⇔ ⇔ ⇔ . t ≤1 0 < t ≤1 0 < 4x ≤1 x ≤ 0 Vậy T = ( ; −∞ 0]∪[1;+ ∞) .
Câu 88: Biết S = [ ;
a b] là tập nghiệm của bất phương trình 3.9x 10.3x −
+ 3 ≤ 0 . Tìm T = b − a . A. 8 T = . B. T =1. C. 10 T = . D. T = 2 . 3 3 Lời giải Chọn D
Ta có 3.9x 10.3x − + 3 ≤ 0 ( x)2 3. 3 10.3x ⇔ − + 3 ≤ 0 1 3x ⇔ ≤ ≤ 3 1 ⇔ log ≤ x ≤ log 3 3 3 3 3 ⇔ 1
− ≤ x ≤1. Khi đó bất phương trình có tập nghiệm là S = [ 1; − ]
1 , do vậy T =1− (− ) 1 = 2.
Câu 89: Nghiệm của bất phương trình 2 x 1
5 + 5 < 5 + x + 5 x là.
A. 0 ≤ x ≤1.
B. 0 < x <1.
C. 0 < x ≤1.
D. 0 ≤ x <1. Lời giải Chọn B Ta có: 2 x 1
5 + 5 < 5 + x + 5 x . ⇒ ( < x < x )2 5 x 5 1 5
− 6.5 x + 5 < 0 ⇒ ⇒ 5 x >1 x > 0
Câu 90: Bất phương trình 64.9x 84.12x 27.16x − + < 0 có nghiệm là:
A. 1< x < 2. B. 9 3 < x < .
C. x <1 hoặc x > 2 . D. Vô nghiệm. 16 4 Lời giải Chọn A 2 x x x 4 x 4 x 64.9 84.12 27.16 0 27. 84. − + < ⇔ −
+ 64 < 0 ⇔ 1< x < 2 . 3 3
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 39
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Câu 91: Tìm tất cả giá trị của m để bất phương trình 9x − 2( + ) 1 3x m
− 3− 2m > 0 nghiệm đúng với mọi số thực x . A. m∈( 5
− − 2 3;− 5 + 2 3). B. 3 m < − . 2 C. 3 m ≤ − . D. m ≠ 2 . 2 Lời giải Chọn C Đặt 3x
t = , t > 0. Khi đó, bất phương trình trở thành: 2 t − 2(m + )
1 t − 3− 2m > 0 ⇔ (t + )
1 (t −3− 2m) > 0 ⇔ t −3− 2m > 0 ⇔ t > 3+ 2m ( ) 1 (Do t > 0).
Để bất phương trình đã cho nghiệm đúng với mọi x ∈ thì ( )
1 phải nghiệm đúng với mọi t ∈(0;+ ∞) .
Điều này tương đương với 3+ 2m ≤ 0 3 ⇔ m ≤ − . 2
Vậy giá trị cần tìm của m là 3 m ≤ − . 2 x−2
Câu 92: Cho Hàm số f (x) 3 =
. Hỏi mệnh đề nào sau đây sai? 2 x −4 7
A. f (x) > ⇔ (x − ) − ( 2 1
2 log3 x − 4)log7 > 0 .
B. f (x) >1 ⇔ (x − 2)log 3−( 2 x − 4 log 7 > 0 . 0,3 ) 0,3
C. f (x) > ⇔ (x − ) − ( 2 1
2 ln 3 x − 4)ln 7 > 0.
D. f (x) >1 ⇔ x − 2 −( 2
x − 4)log 7 > 0 . 3 Lời giải Chọn B x−2 x−2 f (x) 3 > 1 ⇔ > 1 3 ⇔ log
< log 1 ⇔ (x − 2)log 3− ( 2 x − 4 log 7 < 0 . 0,3 ) 2 x −4 7 0.3 2 0,3 x −4 7 0,3
Câu 93: Biết tập nghiệm của bất phương trình − 2 2 x +5x−6 1 3 ≥
là một đoạn a;b ta có a + b bằng: 3x
A. a + b = 11.
B. a + b = 9 .
C. a + b = 12 .
D. a + b = 10 . Lời giải Chọn A Điều kiện: 2
x + 5x − 6 ≥ 0 ⇔ x ≥ 1∨ x ≤ −6
Ta có: − 2x+ x− 1 − 2 2 5 6 2 x +5x−6 − 3 ≥ ⇔ 3 ≥ 3 x ⇔ 2 − 2
x + 5x − 6 ≥ −x ⇔ 2
x + 5x − 6 ≤ x + 2 3x 2
x + 5x − 6 ≥ 0
x ≤ −6 ∨ x ≥ 1 ⇔ x + 2 ≥ 0 ⇔ x ≥ −2 ⇔ x ∈ 1;10 2 2
x + 5x − 6 ≤ x + 4x + 4 x ≤ 10
Vậy a + b = 11
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 40
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Câu 94: Cho bất phương trình 25x +15x − 2.9x ≤ .3x (5x − 3x m
) (mlà tham số thực). Tập hợp tất cả các
giá trị của m để bất phương trình nghiệm đúng với mọi x thuộc đoạn 0 ; 1 là A. 11 m 11 11 11 ≤ . B. m > . C. m < . D. m ≥ . 2 2 3 3 Lời giải Chọn D 2x x
Chia hai vế của bất phương trình cho 2
3 x ( 3x > 0 ), ta được 5 5 + (1− m) + m − 2 ≤ 0 3 3 x Đặt 5 = t . 3 Với 5 x ∈ 0 ;1 ⇒ t ∈ 2
1 ; , ta có bất phương trình bậc hai t + (1− m)t + m − 2 ≤ 0 3
Bài toán trở thành tìm m để bất phương trình: 2t + (1− m)t + m − 2 ≤ 0 , 5 ∀t ∈ 1 ; 3 2 5 t
(1 m)t m 2 0, t 1 ;
(t 1)(t 2 m) 5 + − + − ≤ ∀ ∈ ⇔ − + − ≤ 0,∀t ∈ 1 ; (*) 3 3 Vì 5 t 5 5 11
− 1 ≥ 0,∀t ∈ 1 ; , nên (*)
⇔ t + 2 − m ≤ 0,∀t ∈ 1 ;
⇔ + 2 − m ≤ 0 ⇔ m ≥ 3 3 3 3
Câu 95: Giả sử phương trình 2
log x − m 2 log x 2m 0 có hai nghiệm thực phân biệt x ,x thỏa 2 ( + ) + = 2 1 2
mãn x + x = 6 . Giá trị của biểu thức x − x là 1 2 1 2 A. 3 . B. 8 . C. 2 . D. 4 . Lời giải Chọn C
Điều kiện: x > 0 . Đặt t = log x . 2 t = 2 log x = 2 x 4
Khi đó phương trình đã cho có dạng: 2t − (m + 2) =
t + 2m = 0⇔ ⇔ 2 ⇔ . t = m log x = m x = 2m 2 Do + = 6⇔4 + 2m x x
= 6⇔ m = 1. Vậy x − x = 4 − 1 2 = 2 . 1 2 1 2
Câu 96: Có bao nhiêu giá trị nguyên thuộc đoạn 0;2019
của tham số m để phương trình
4x − ( + 2018)2x m
+ (2019 + 3m) = 0 có hai nghiệm trái dấu? A. 2016 B. 2019 . C. 2013 D. 2018 . Lời giải Chọn B
Ta có 4x + ( −1)2x m + (4 + 3m) = 0 (1) . Đặt = 2x t
, t > 0 . Phương trình đã cho trở thành: 2t + (m −1)t + 4 + 3m = 0 (2)
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 41
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Phương trình (1) có 2 nghiệm trái dấu khi và chỉ khi phương trình (2) có 2 nghiệm t ,t thỏa 1 2 af (1) < 0
0 < t < 1 < t ⇔
⇔ −1 < m < 2013 1 2 af (0) > 0
Vì m∈,m∈ 0;2019
suy ra m ∈{0;1;2;...; } 2012 a+ b
Câu 97: Giả sử phương trình 2
log 2x 3log x 2 0 có một nghiệm dạng = 2 c x với +
a,b,c∈ và 2 ( )− − = 2
b < 20 . Tính tổng + + 2 a b c . A. 10. B. 11. C. 18. D. 27. Lời giải Chọn A
Điều kiện x > 0 . Ta có:
log 2x 3log x 2 0 1 log x 3log x 2 0 2 ( )− − = ⇔ 2 ( + 2 )2 2 − − = 2 1+ 5 1+ 5 x = 2 2 log x = 2 ⇔ . ⇔ 2 x − x − = ⇔ 2 log log 1 0 1− 5 2 2 1− 5 x = 2 2 log x = 2 2
Vậy: a = 1;b = 5;c = 2 ⇒ a + b + 2 c = 10 .
Câu 98: Tìm tất cả các giá trị thực của m để phương trình 2 x − 2 m x − 2 log cos logcos m + 4 = 0 vô nghiệm.
A. m∈( 2;2).
B. m∈(− 2; 2) .
C. m∈(− 2;2).
D. m∈(−2; 2) . Lời giải Chọn C Ta có: 2 x − 2 m x − 2 log cos logcos m + 4 = 0 ⇔ 2 x − m x − 2 log cos 2 log cos m + 4 = 0
Đặt log cosx = t . Điều kiện: t ≤ 0
Khi đó phương trình trở thành: 2t − mt − 2 2
m + 4 = 0, t ≤ 0.
Phương trình vô nghiệm khi và chỉ khi phương trình vô nghiệm hoặc có các nghiệm đều
dương. Điều này xảy ra khi và chỉ khi 2 m −1.(− 2 m + 4) < 0 ∆′ < 0 2 2m − 4 < 0 2 m −1.(− 2 m + 4) ≥ 0 − 2 < m < 2 ∆′ ≥ 0 2 2m − 4 ≥ 0 ⇔ ⇔ ⇔ m ≥ 2
⇔ − 2 < m < 2 t + t > 0 2m 2m > 0 1 2 > 0 1 2
−2 < m < 2 t .t > 0 1 2 −m + 4 > 0 − 2 m + 4 > 0 1
Câu 99: Gọi S là tập hợp tất cả các giá trị nguyên của tham số m sao cho phương trình x x− − 1 m + 2 16 .4
5m − 44 = 0 có hai nghiệm đối nhau. Hỏi S có bao nhiêu phần tử? A. 2 . B. 0 . C. 1. D. 3 .
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 42
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Lời giải Chọn B x x− − 1 m + 2 16 .4 5m − 44 = 0 m ⇔ ( x )2 − x + 2 4 .4 5m − 44 = 0 4 ⇔ ( x )2 − x m + 2 4 4 .4 20m −176 = 0 , (1). Đặt = 4x t
điều kiện t > 0 từ (1) ta có 2t − m t + 2 4
. 20m −176 = 0 , (∗).
Khi đó phương trình (1) có hai nghiệm đối nhau x ;x thì x + x = 0 khi và chỉ khi phương 1 2 1 2
trình (∗) có hai nghiệm dương t ;t thỏa mãn t .t = 1. Nhưng vì phương trình (∗) có 1 2 1 2 c 176 = −
= −44 < 0 nên không có giá trị nào của m thỏa mãn yêu cầu bài toán. a 4
Câu 100: Cho phương trình 9x − 2(2 +1)3x m
+ 3(4m −1) = 0 có hai nghiệm thực x , x thỏa mãn 1 2
(x + 2)(x + 2) = 12 . Giá trị của m thuộc khoảng 1 2 A. (9;+ ∞). B. (3;9). C. (−2;0) . D. (1;3) . Lời giải Chọn D Đặt = 3x t
, t > 0 . Phương trình đã cho trở thành: 2t − 2(2m +1)t + 3(4m −1) = 0
Phương trình đã cho có hai nghiệm thực x , x khi và chỉ khi phương trình có hai nghiệm 1 2 dương phân biệt 2 m ≠ 1 ∆′ > 0
4m − 8m + 4 > 0 m ≠ 1 1 S 0 2(2m 1) ⇔ > ⇔ + > 0
⇔ m > − ⇔ 1 . 2 m P 0 3(4m −1) > > > 0 4 1 m > 4
Khi đó phương trình có hai nghiệm là t = 4m −1 và t = 3 .
Với t = 4m −1 thì 1
3x = 4m −1 ⇔ x = log 4m 1 . 1 3 ( − )
Với t = 3 thì x2 3 = 3 ⇔ x = 1. 2 Ta có (x 5
+ 2)(x + 2) = 12 ⇔ x = 2 ⇔ log 4m 1 2 ⇔ m = . 3 ( − ) = 1 2 1 2
Vậy giá trị m cần tìm là 5
m = nên m thuộc khoảng (1;3) . 2
Câu 101: Cho phương trình ( − 5).3x + (2 − 2).2x. 3x + (1− ).4x m m m
= 0 , tập hợp tất cả các giá trị của
tham số m để phương trình có hai nghiệm phân biệt là khoảng (a;b) . Tính S = a + b. A. S = 4 .
B. S = 5 . C. S = 6 . D. S = 8 . Lời giải Chọn D
Ta có( − 5).3x + (2 − 2).2x. 3x + (1− ).4x m m m = 0 (1)
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 43
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com x x x ( m 5) 3 3 3 ⇔ − . + (2m−2) . + 1− m = 0 . Đặt t =
, điều kiện t > 0 . 4 2 2
Khi đó phương trình trở thành: (m − ) 2
5 t + (2m − 2)t +1− m = 0 ,(2).
Do đó để phương trình (1) có hai nghiệm phân biệt thì phương trình (2)có hai nghiệm dương a ≠ 0 m ≠ 5 ∆ > 0 phân biệt m > 3 ⇔ ⇔
⇔ 3 < m < 5 ⇔ m∈(3;5) . P > 0 m < 1 S > 0 1 < m < 5
Vậy a = 3 , b = 5 nên a + b = 8 .
Câu 102: Cho phương trình 2
log x − 4log x + m − 3 = 0 . Có bao nhiêu giá trị nguyên của tham số m để 3 3
phương trình đã cho có hai nghiệm phân biệt x < x thỏa mãn x − 81x < 0. 1 2 2 1 A. 4 . B. 5 . C. 3 . D. 6 . Lời giải Chọn C Xét phương trình: 2
log x − 4log x + m − 3 = 0 1 . Điều kiện: x > 0. 3 3 ( )
Đặt t = log x phương trình (1) trở thành: 2t − 4t + m − 3 = 0 (2). 3
Phương trình (1) có 2 nghiệm phân biệt khi phương trình (2) có 2 nghiệm phân biệt.
⇔ ∆' > 0 ⇔ 4 − m + 3 > 0 ⇔ m < 7 (i) .
Gọi x < x là 2 nghiệm của phương trình (1) thì phương trình (2) có 2 nghiệm tương ứng là 1 2
t = log x ;t = log x . Vì x < x nên t < t . 1 3 1 2 3 2 1 2 1 2
Mặt khác, x − 81x < 0 ⇔ 0 < x < 81x ⇔ log x < 4 + log x 2 1 2 1 3 2 3 1
⇔ t < 4 + t ⇔ 0 < t − t < 4 ⇔ (t − t 16 t t 4t t 16 . 2 1 )2 < ⇔ ( + 2 1 )2 − < 2 1 2 1 1 2 ⇔ 2
4 − 4(m − 3) < 16 ⇔ m > 3 (ii) .
Từ (i) và (ii) suy ra 3 < m < 7 và m∈ nên có 3 số nguyên thỏa mãn. x x
Câu 103: Phương trình (2 + 3) +(1− 2a).(2 − 3) − 4 = 0 có 2 nghiệm phân biệt x , x thỏa mãn 1 2 x − x = log
3 . Khi đó a thuộc khoảng 1 2 2+ 3 A. 3 3 3 −∞;− . B. (0;+ ∞). C. ;+ ∞ . D. − ;+ ∞ . 2 2 2 Lời giải Chọn D x x
Đặt (2 + 3) = t , t > 0 khi đó ( 1 2 − 3) = . t
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 44
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com x x
Nhận xét: Với cách đặt đó thì (2 + 3) 1 = t , (2 + 3) 2 = t nên từ x − x = log 3 , ta có 1 2 1 2 2+ 3 ( )x −x + 1 2 2 3
= 3 hay t1 = 3 ⇔ t = 3t . 1 2 t2
Vậy bài toán đã cho tương đương với bài toán tìm a để phương trình 1
t + (1− 2a). − 4 = 0 (*) t
có hai nghiệm dương t ,t thỏa mãn nghiệm này gấp 3 lần nghiệm kia. 1 2 Ta thấy: ( ) ⇔ 2 *
t − 4t + 1− 2a = 0 . − ∆′ > 3 0 a 4 − (1− 2a) > > 0
Phương trình có 2 nghiệm dương phân biệt khi P > ⇔ ⇔ 2 0 (* *) . 1− 2a > 0 1 S > 0 a < 2
Cách 1: Nhận xét rằng phương trình ẩn t có tổng hai nghiệm bằng 4 mà nghiệm này gấp 3
nghiệm kia nên phương trình phải có 1 nghiệm băng 1 và 1 nghiệm bằng 3, từ đó
1− 2a = 3 ⇔ a = −1. t + t = 4
Cách 2: Theo định lí Viet, ta có 1 2 . t t = 1− 2a 1 2
Phương trình (*) có nghiệm này gấp 3 lần nghiệm kia khi t = 3t 1
2 ⇔ (t − 3t . t 3t 0 3 t t 10t .t 0 1 2 ) ( − 2 1 ) = ⇔ − ( 2 + 2 1 2 ) + = t = 1 2 3t 2 1 ⇔ −3(t + t 6t t 10t .t 0 48 16 1 2a 0 a
1 thỏa mãn điều kiện (* *) . 1 2 )2 + + = ⇔ − + 1 2 1 2 ( − ) = ⇔ = −
Giá trị này của a thuộc đáp án D
Cách 3. Dựa vào điều kiện có 2 nghiệm dương loại đáp án A, suy luận nếu a thuộc đáp án B, C
thì cũng thuộc đáp án D
Câu 104: Có bao nhiêu giá trị thực của tham số m để phương trình 2 x − x+ − 2 3 2 4 x 6− + = 3 .3 3 3 x m + m (1) có
đúng 3 nghiệm phân biệt. A. 4 . B. 2 . C. 3 . D. 1. Lời giải Chọn C Đặt − 2 4 x 6− u u − v = > 3 3 0, 3 x v
= u > 0 phương trình trở thành m + v = u + m ⇔ m = (u − v) v v v = u 6−3x 4− 3 = 2 3 x (I)
⇔ (u − v)(m − v) = 0 ⇔ ⇔ v = m 4− 2 3 x = m (II) 2 x = x x 1 Giải (I): 6−3 4− 3 = 3 ⇔ 2
x − 3x + 2 = 0 ⇔ x = 2
Để phương trình (1) có 3 nghiệm phân biệt thì phương trình (II) xảy ra các trường hợp sau:
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 45
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Trường hợp 1: Phương trình (II) có 2 nghiệm phân biệt trong đó một nghiệm x = 1 và một x = 1
nghiệm x ≠ 2 . Với x = 1 2 2 ta có 4− m = 1 3 = 27 . Khi đó 4− 3 x = 27 ⇔ − 2 4 x = 3 ⇔ . x = −1 ≠ 2
Vậy m = 27 là một giá trị cần tìm.
Trường hợp 2: Phương trình (II) có 2 nghiệm phân biệt trong đó một nghiệm x = 2 và một x = 2
nghiệm x ≠ 1. Với x = 2 2 2 ta có 4− m = 2 3 = 1. Khi đó 4− 3 x = 1 ⇔ − 2 4 x = 0 ⇔ . x = −2 ≠ 1
Vậy m = 1 là một giá trị cần tìm.
Trường hợp 3: Phương trình (II) có đúng 1 nghiệm x khác 1;2 Từ − 2 4 3 x = m ⇔ 2
x = 4 − log m ≥ 0 để có một nghiệm thì nghiệm đó là x = 0 ⇒ 4 − log m = 0 3 3
⇔ m = 81, đồng thời x = 0 thỏa mãn khác 1;2 nên m = 81 là một giá trị cần tìm.
Vậy có ba giá trị m = 1; m = 27 ; m = 81 thỏa mãn bài toán.
Câu 105: Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để không tồn tại bộ số thực (x, y)
nào thỏa mãn đồng thời các hệ thức 2
x + ( y − 2)2 ≤ 9 và log
2mx + 2y + m − 2 ≥1. Số 2 2 ( ) x + y 1 +
phần tử của S là: A. 2. B. 1. C. 3. D. Vô số. Lời giải Chọn A Miền biểu diễn 2
x + ( y − 2)2 ≤ 9 là hình tròn (C) có tâm I (0,2) và bán kính R = 3 log
2mx + 2y + m − 2 ≥1 2 2
⇔ 2mx + 2y + m − 2 ≥ x + y +1 2 2 ( ) x + y 1 +
⇔ (x − m)2 + ( y − )2 2
1 ≤ m + m − 2 .
Miền biểu diễn (x − m)2 + ( y − )2 2
1 ≤ m + m − 2 là hình tròn (C′) có tâm I′(m ) ,1 và bán kính 2
R′ = m + m − 2
Để tồn tại bộ số thực (x, y) thỏa mãn bài toán thì: 2 + − < 2 − < m <1 m m 2 0 ⇔ ⇒ m∈{ 1; − } 0 . 2 2
II′ > R + R′
m +1 > 3 + m + m − 2 (VN )
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 46
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 47
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
BÀI TẬP CUỐI CHƯƠNG VI
A. CÂU HỎI TRẮC NGHIỆM 1 2 4 1 5
Câu 1: Rút gọn biểu thức .( 3) , ta được 3 A. 3 . B. 3 3 . C. 1 . D. 9 . 3 Lời giải Chọn D 1 5 2 4 1 1 1 5 1 2 5 1 ⋅ − − 4 2 2 2 2
( 3) = (3) ⋅ 3 = 3 ⋅3 = 3 = 9 3 a
Câu 2: Nếu 2a = 9 thì 1 8 có giá trị bằng 16 A. 1 . B. 3 . C. 1 . D. 1 . 3 9 3 Lời giải Chọn A α 8 1 = ( α −α − − 4 2− ) α 1 8 2 = 2 = (2 ) 1 1 2 2 = 9 = 16 3 1 Câu 3: Nếu 2
a = b(a > 0,a ≠ ) 1 thì
A. log a = b . B. 2log b = . C. 1 log = b .
D. log b = a . a 1 1 a 2 1 2 2 Lời giải Chọn B
Câu 4: Nếu x = log3 a + log9 4 thì 3x có giá trị bằng A. 6 . B. 8 . C. 16. D. 64 . Lời giải Chọn A log9 4 1 1 1 x log3 4+log9 4 log3 4 log9 4 = = ⋅ = + = + ( log94 2 )2 2 3 3 3 3 4 9 4 9 = 4 + 4 = 4 + 2 = 6
Câu 5: Cho α , β là hai số thực với α < β . Khẳng định nào sau đây đúng ? β α α β A. (0,3)α (0,3)β < . B. α β π ≥ π .
C. ( 2) < ( 2) . D. 1 1 > . 2 2
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 1
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Lời giải Chọn C
Câu 6: Hình nào vẽ đồ thị của hàm số y = log1 x? 2 Lời giải Chọn D
Câu 7: Phương trình 2x 1 0,1 − =100 có nghiệm là A. 1 − . B. 1 . C. 1 1 . D. 1 2 . 2 3 2 3 Lời giải Chọn A 2x 1 − 1 0,1
=100 ⇔ 2x −1 = log 100 ⇔ 2x −1 = 2 − ⇔ x = − 0,1 2
Câu 8: Tập nghiệm của bất phương trình 3x 1 0,5 − > 0,25 A. (− ∝ ) ;1 . B. (1;+ ∝) . C. (0 ) ;1 . D. 1 ; − ∝ − . 3 Lời giải Chọn A 3x 1 − 3x 1 − 2 0,5 > 0,25 ⇔ 0,5
> 0,5 ⇔ 3x −1< 2 ⇔ x <1
Câu 9: Nếu log x = 2log5− log 2 thì A. x = 8. B. x = 23 . C. x =12,5. D. x = 5. Lời giải Chọn C 2 25
logx = 2log5 − log2 = log5 − log2 = log25 − log2 = log = log12,5 2 Suy ra x =12,5
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 2
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Câu 10: Số nguyên dương nhỏ nhất thỏa mãn log0,1(1− 2x) > 1 − là A. x = 0 . B. x =1. C. x = 5 − . D. x = 4 − . Lời giải Chọn D log (1 2x) 1 1 1 2x 0,1− − > − ⇔ − <
⇔ 1− 2x 10 ⇔ x − 4,5 0,1
B. BÀI TẬP TỰ LUẬN
Câu 11: Biết 4α 4 α − +
= 5. Tính giá trị biểu thức : 1. 2α 2 α − + 2. 2α 2 4 + 4− α Lời giải a) 4α + 4−α = 5
⇔ (2α )2 + 2⋅2α ⋅2−α + (2−α )2 = 5+ 2 ⇔ (2α + 2−α )2 = 7 ⇔ 2α + 2−α = 7 b) α − α + = ( α )2 α −α + ⋅ ⋅ + ( −α )2 − = ( α −α + )2 2 2 2 4 4 4 2 4 4 4 2 4 4 − 2 = 5 − 2 = 23
Câu 12: Tính giá trị của biểu thức : 1. 1
log2 72 − (log2 3+ log2 27) ; 2 2. log2 40 log25 5 − ; 3. 2 log9 2 3 + . Lời giải 1 a) log 72 − log 3+ log 27 2 ( 2 2 ) 2 1 1 = log 72 − ⋅log (3.27) 1 2
= log 72 − ⋅log 81 = log 72 − log 81 2 2 2 2 2 2 2 2 72 = log 72 − log 9 = log = log 8 = 3 2 2 2 2 9 40 b) log2 log2 40−log2 5 5 log28 3 5 = 5 = 5 = 5 =125 log9 81 ⋅ +log9 2 1 1 1 l⋅og 1 9 (81.2) 1 l⋅og9162 2 2+log9 2 log9162 2 2 2 c) 3 = 9 = 9 = 9 = 9 2 = 162 = 9 2
Câu 13: Biết rằng 5x = 3 và 3y = 5. Không sử dụng máy tính cầm tay, tính giá trị của xy . Lời giải
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 3
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
5x = 3. Suy ra x = log 3 5
3y = 5. Suy ra y = log 5 3 log5 log3 Ta có . x y = log 5⋅log 3 = ⋅ = 1 3 5 log3 log5
Câu 14: Viết công thức biểu thị y theo x , biết 1
2log2 y = 2 + log2 x . 2 Lời giải 1 1 2 2
2log y = 2 + log x ⇔ log y = log 4 + log x 2 2 2 2 2 2 1 2 2 2
⇔ log y = log 4⋅ x ⇔ y = 4⋅ x ⇔ y = 4 x 2 2
Câu 15: Giải các phương trình sau : x−2 1. 1 = 8 ; 4 2. 2x 1 9 − = 81.27x ;
3. 2log5 (x − 2) = log5 9 ; 4. log2 (3x + ) 1 = 2 − log2 (x − ) 1 . Lời giải x−2 1 a) = 8 ⇔ (2− )x−2 2 = ( 3 2 )1 3 2 − x+4 3 5 2 2 ⇔ 2 = 2 ⇔ 2
− x + 4 = ⇔ x = 4 2 4 b) 9 = 81.27 ⇔ (3 )2x 1 2 1 2 − − 4 = 3 .( 3 3 )x x x 4x−2 4+3 ⇔ 3
= 3 x ⇔ 4x − 2 = 4 + 3x ⇔ x = 6 c) 2log (x − 2) 2 2
= log 9 ⇔ log (x − 2) = log 9 ⇔ (x − 2) = 9 5 5 5 5
⇔ x − 2 = 3(và 2
x − > 0) ⇔ x = 5
d) Điều kiện xác định: 3x +1 > 0; x −1 > 0 . Hay x >1
log 3x +1 = 2 − log x −1 ⇔ log 3x +1 + log x −1 = 2 2 ( ) 2 ( ) 2 ( ) 2 ( ) ⇔ log (3x + ) 1 (x − ) 2 2
1 = 2 ⇔ 3x − 2x −1 = 2 2 5 x = 2 3x 2x 5 0 ⇔ − − = ⇔ 3 x = 1 −
Câu 16: Giải các bất phương trình : x 1 + 1. 1 1 > ; 9 81 x 2. (4 3) 27.3x ≤ ; 3. log2 (x + ) 1 ≤ log(2 − 4x).
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 4
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Lời giải x 1 + x 1 + 2 1 1 1 1 1 a) x 1 2 Do 1 > ⇔ > ⇔ + < < ⇔ x < 1 9 81 9 9 9 1 x 4 x x 4 3
b) ( 3) ≤ 27.3 ⇔ 3 ≤ 3 3 . x 1 x +x 1 4 3
⇔ 3 ≤ 3 ⇔ x ≤ 3+ x ( do 3 > ) 1 ⇔ x ≥ 4 − 4 1
c) x +1 > 0;2 - 4x > 0 Hay -1< x < 2
log x +1 ≤ log 2 − 4x 2 ( ) 2 ( )
⇔ x +1≤ 2 − 4x 1 ⇔ x ≤ 5
Kết hợp với điều kiện, nghiệm của bất phương trình là: 1 1 − < x ≤ 5
Câu 17: Thực hiện một mẻ nuôi cấy vi khuẩn với 1000 vi khuẩn ban đầu, nhà sinh học phát hiện số lượng
vi khuẩn tăng thêm 25% sau mỗi hai ngày
1. Công thức ( ) = 0. t P t
P a cho phép tính số lượng vi khuẩn của mẻ nuôi cấy sau t ngày kể từ
thời điểm ban đầu. Xác định các tham số 0
P và a (a > 0) . Làm tròn a đến hàn phần trăm.
2. Sau 5 ngày thì số lượng vi khuẩn bằng bao nhiêu ? Làm tròn kết quả đến hàng trăm.
3. Sau bao nhiêu ngày thì số lượng vi khuẩn vượt gấp đôi số lượng ban đầu? Làm tròn kết quả đến hàng phần mười. Lời giải
a) Ban đầu có 1000 vi khuẩn nên P =1000 . 0
Sau 2 ngày, số lượng vi khuẩn là: P =125%P =125%.1000 =1250 0 Ta có: P(2) 2 2 2
= P ⋅a ⇔ 1250 =1000⋅a ⇔ a =1,25 ⇔ a ≈1,12 0
b) Số lượng vi khuẩn sau 5 ngày là: P(5) 5 2
= P ⋅a =1000.1,12 ≈1800 (vi khuẩn). 0
c) Với P(t) = 2P ta có: 0 ( ) t
= ⋅ ⇔ 2 = ⋅1,12t ⇔ 1,12t P t P a P P
= 2 ⇔ t = log 2 ≈ 6,1 (ngày) 0 0 0 1,12
Vậy sau 6,1 ngày thì số lượng vi khuẩn vượt gấp đôi số lượng ban đầu.
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 5
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Câu 18: Nhắc lại rằng, độ PH của một dung dịch được tính theo công thức PH = −log H + , trong đó H +
là nồng độ H + của dung dịch đó tính bằng mol/L. Nồng độ H + trong dung dịch cho biết
độ acid của dung dịch đó.
1. Dung dịch acid A có độ pH bằng 1,9 ; dung dịch B có độ pH bằng 2,5. Dung dịch nào có độ
acid cao hơn và cao hơn bao nhiêu lần
2. Nước cất có nồng độ H + là 7
10− mol / L . Nước chảy từ một vòi nước có độ pH từ 6,5
đến 6,7 thì có độ acid cao hay thấp hơn nước cất. Lời giải a) + + + 1, − 9 pH = ⇔ − H = ⇔ H = − ⇔ H = A 1,9 log 1,9 log 1,9 10
Vậy độ acid của dung dịch A là 1, − 9 10 mol / L . + + + 2 − ,5 pH = ⇔ − H = ⇔ H = − ⇔ H = B 2,5 log 2,5 log 2,5 10
Vậy độ acid của dung dịch B là 2 − ,5 10 mol / L . 1, − 9 Ta có: 10 ≈ 3,98 2 − ,5 10
Vậy độ acid của dung dịch A cao hơn độ acid của dung dịch B 3,98 lần. b) Ta có: + + 6, − 5 + 6, − 7
6,5 < pH < 6,7 ⇔ 6,5 < −log H < 6,7 ⇔ 6,
− 5 > log H > 6, − 7 ⇔ 10 > H >10
Vậy nước chảy từ vòi nước có độ acid từ 6 − ,7 10 mol / L đến 6 − ,5 10 mol / L .
Vậy nước đó có độ acid cao hơn nước cất. BÀI TẬP TỔNG ÔN A. TRẮC NGHIỆM
Câu 1: Tìm tập xác định + D của hàm số x 1 y ln = . 1 x − A. D = \{ } 1 . B. [ 1; − ] 1 . C. D = ( 1; − ) 1 . D. D = ( ; −∞ − ) 1 ∪(1;+∞). Lời giải Chọn C
Điều kiện: x +1 > 0 ⇔ x∈( 1; − ) 1 . 1− x
Câu 2: Tổng tất cả các nghiệm của phương trình log (x − 75x − 2499)3 2 2
= log −x + 75x + 2501 . 125 5 A. 75. − B. 75. C. 125. D. 125. − Lời giải
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 6
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Chọn B
log (x − 75x − 2499)3 2 2
= log −x + 75x + 2501 125 5 ⇔ log ( 2
x − 75x − 2499) 2
= log −x + 75x + 2501 5 5 2 2
x −75x − 2499 = −x + 75x + 2501 ⇔ 2
x − 75x − 2499 > 0 2
x − 75x − 2499 > 0 2 2
⇔ −x + 75x + 2501= x − 75x − 2499 2 2
−x + 75x + 2501 = −x + 75x + 2499 2
x − 75x − 2499 > 0 ⇔ 2
2x −150x − 5000 = 0 x = 25 − 1 ⇔ ⇒ x + x = 75. 1 2 x = 100 2
Câu 3: Cho phương trình 2 ( 2
ln x ) −3lnx −1= 0 (x > 0) (*) . Đặt t = lnx , phương trình (*) trở thành
phương trình nào sau đây? A. 2
2t + 3t −1 = 0 . B. 2
4t + 3t −1 = 0 . C. 2
4t − 3t −1 = 0 . D. 2
2t − 3t −1 = 0 . Lời giải Chọn C Ta có:
(x )− x− = ⇔ (x ) 2 2 2 2 ln 3ln 1 0 ln − 3lnx −1= 0 ⇔ ( x)2 −
x − = ⇔ ( x)2 2ln 3ln 1 0 4 ln − 3lnx −1 = 0
Do đó, đặt t = lnx phương trình (*) trở thành: 2
4t − 3t −1 = 0 .
Câu 4: Khẳng định nào sau đây đúng?
A. lna > lnb ⇔ b > a .
B. lna > lnb ⇔ a > b > 0.
C. lna > lnb ⇔ a > b .
D. lna > lnb ⇔ b > a > 0. Lời giải Chọn B
Phương án A sai vì e > 1 và chưa đủ điều kiện.
Phương án C sai vì chưa đủ điều kiện.
Phương án D sai vì cơ số e > 1. Câu 5: 2 2
Biết P là tích tất cả các nghiệm của phương trình x −2020 x −2019 4 + 2 − 3 = 0 , tính P . A. P = 0 . B. P = 1 − . C. P = 2020 − . D. P = 2020. Lời giải Chọn C 2 Ta có: (x −2020 2 ) 2 x −2020 2 + 2 ⋅2 − 3 = 0
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 7
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com ⇒ ( 2x−2020 )2 2 x −2020 2 + 2 ⋅2 − 3 = 0 2 x −2020 2 = 1 ⇒ 2 x −2020 2 = 3 − (loai) 2 ⇒ x − 2020 = 0 . ⇒ x = ± 2020 .
Do đó P = 2020 ⋅(− 2020) = 2020 − . m Câu 6: Biết m n P = 2 = 2 ∈ ∈ S m n ( * * m , n ,
là phân số tối giản). Tính = + . n 2019 can bac hai A. 2000 . B. 2020 S = 2 +1. C. 2018 S = 2 +1. D. 2019 S = 2 +1. Lời giải Chọn D 1 1 1 1 1 Ta có :2 1 1 2 2 ( 2) 2 3 4 2 2 2 = 2 ; 2 = 2 = 2 = 2 = 2 ; 2 = 2 ; 1 Do đó 2019 2 2 = 2 2019 can bac hai Vậy 2019 S = 2 +1.
Câu 7: Cho a > 0;a ≠ 1 và b ≠ 0. Khẳng định nào sau đây đúng? A. 4 1
loga b = loga | b | . B. 4
loga b = 4loga .b 4 C. 4 1
loga b = loga .b D. 4
loga b = 4loga | b | . 4 Lời giải Chọn D
Theo công thức logarit, ta có đáp án là D
Câu 8: Phương trình log x + log 4 − x = 1 có tập nghiệm là 3 3 ( ) A. S = {1; } 3 . B. S = { } 1 . C. S = { } 3 . D. S = . ∅ Lời giải Chọn A
Điều kiện: 0 < x < 4 x = 1
Phương trình tương đương log (x(4 − x)) 2
= 1 ⇔ −x + 4x = 3 ⇔ (TM ) 3 x = 3 Vậy chọn A
Câu 9: Cho a > a ≠ P = ( a + a e)2 2 2 0, 1, 2ln log
+ ln a − loga e. Khẳng định nào sau đây đúng? A. 2
P = 3ln a − 4. B. 2 P = 3ln a + 4. C. 2
P = 5ln a − 4. D. 2 P = 5ln a + 4. Lời giải
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 8
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Chọn D Ta có ln .
a loga e = loge .aloga e = loge e =1, nên ta có:
P = (2ln a + loga e)2 2 2
+ ln a − loga e 2 2 2 2 = 4ln a + 4ln .
a loga e + loga e + ln a − loga e 2 = 5ln a + 4
Câu 10: Cho a > 0,a ≠1,b > 0,α ≠ 0,β ≠ 0 . Khẳng định nào sau đây đúng? A. log β β log β α α b = log b α b = b B. a ( ) a ( ) loga α a β C. log β β = α b = αβ b D. α b b a ( ) 1 log log a ( ) loga a αβ Lời giải Chọn A 2 x −2x
Câu 11: Có tất cả mấy giá trị nguyên của tham số m để phương trình 1 2 = m + m + 1 có đúng 4 3 nghiệm phân biệt? A. 4. B. 1. C. 2. D. 0. Lời giải Chọn D 2 x −2 1 x 2 = m + m + 1 (1) 3 Xét f (x) 2 = x − 2x Đặt 2
x − 2x = t Theo BBT phương trình 2
x − 2x = t có hai nghiệm phân biệt khi t > 1 − 2 x −2 1 x 2 2
= m + m +1 ⇔ x − 2x = log ( 2 m + m + ) 1 ⇔ t = log ( 2 1 1 m + m + )1 (2) 3 3 3
(1) Có đúng 4 nghiệm phân biệt ⇔ (2) có hai nghiệm phân biệt t > 1 − 2 m + m + > m ∀ ⇔ 0 < log ( 1 0 2 m + m + ) 2 ( ) 2 1
1 <1 ⇔ < m + m +1<1 ⇔ 3 3 2 3 m + m < 0 ⇔ 1
− < m < 0 . Do m∈ nên không có số nguyên m nào thỏa đề.
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 9
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com + + Câu 12: . m abc . n c 1
Cho a = log 3;b = log 5;c = log 2 . Biết log 140 = ( * * m∈ ;n∈ 63 ).Tính 2 3 7 2ac +1
S = m − n . A. S = 3. B. S = 3. − C. S = 1. − D. S =1. Lời giải Chọn C log log 140 ( 2 2 2 .5.7) 2
2 + log 5 + log 7 2 + log 5.log 3+ log 7 log63140 = = = = log 63 log 3 .7 2log 3+ log 7 2log 3+ log 7 2 ( 2 2 ) 2 2 3 2 2 2 2 2 2 1
2 + ab + c abc+2c+1 = = m = n = 1 . Suy ra 1;
2 , S = m − n = 1 − . 2ac +1 2a + c 1−2x
Câu 13: Phương trình 1 x+2 =
2 có tất cả bao nhiêu nghiệm? 2 A. 2. B. 3. C. 1. D. 0. Lời giải Chọn C 1−2 1 x = 2 + ⇔ (2− )1−2 2 1 x x x+2 2x 1 − x+2 = 2 ⇔ 2 = 2
⇔ 2x −1 = x + 2 ⇔ x = 3. 2
Vậy phương trình đã cho có 1 nghiệm.
Câu 14: Cho a ∈,a > 0,α ∈, β ∈ .
Khẳng định nào sau đây đúng? β A. ( β α β aα ) (aβ = ) . B. βα α. a a β = .
C. (aα ) aα+β = .
D. (aα ) aβ−α = . Lời giải Chọn A Câu 15: Cho *
a ∈ R,n∈ N . Khẳng định nào sau đây đúng? A. 2n 2n a =1. B. 2n 2n a = a . C. 2n 2n a = . a D. 2n 2n a = − . a Lời giải Chọn B
Theo tính chất của căn bậc . n
Câu 16: Cho a∈ R,a > 0,m∈ Z,n∈ N,n ≥ 2. Khẳng định nào sau đây đúng? m m m m m A. a n m n a a − = . B. n n m a = a . C. n m n a = a . D. n a = . n a Lời giải Chọn B
Theo tính chất của lũy thừa với số mũ hữu tỷ.
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 10
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 5 5 4 4
Câu 17: Cho biểu thức x y + xy P =
(x > 0, y > 0). Khẳng định nào sau đây đúng? 4 4 x + y
A. P = x .y
B. P = x + .y C. P =1.
D. P = 2x .y Lời giải Chọn A 1 1 5 5 4 4 x .
y x + y 4 4 Ta có x y + xy P = = = xy 4 1 1 4 x + y 4 4 x + y Vậy P = x . y
Câu 18: Cho hàm số y = log x a >
a ≠ Khẳng định nào sau đây đúng ? a ( 0, )1. 1 1 ln a A. y′ =
(x > 0). B. y′ = (x > 0). C. y′ =
(x > 0). D. y′ = log x x > a ( 0). xln a x x Lời giải Chọn A Câu 19: 245
Cho log 7 = a,log 5 = . b Tính P = log theo a, . b 25 2 5 32 A. 10 P 4a 2. B. 10
P 8a 2.
C. P 8a10b 2. D. 5 P 2a 2. b b 2b Lời giải Chọn C Ta có 245 245 245 P log log 2log 1 5 5 32 2 5 32 32 2(log 245log 32) 5 5 2 5 2(log 5.7 log 2 ) 5 5 2(1 2log 7 5log 2). 5 5 Mặt khác, do 1
a log 7 log 7 log 7 log 7 2 . a 2 25 5 5 5 2 1 1
log 5 b log 2 . 2 5 log 5 b 2 Suy ra 1 5 10 P 2 1
2.2a5. 2 1 4a
2 8a . b b b
Câu 20: Cho a 0, a 1. Khẳng định nào sau đây sai? A. log a a a a a = . a B. loga1= 0. C. loga a =1. D. log a =1. Lời giải Chọn D
a 0, a 1ta có log a Do đó loga a 1 a a . a a 1.
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 11
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Câu 21: Cho phương trình ( x ) x 1− 1 log 2 1 .log 2 + + = 1. Khi đặt log 2x t = +1 , ta được phương 2 ( ) 2 4 2 trình nào dưới đây. A. 2
t + t − 2 = 0. B. 2
2t + 2t −1 = 0.
C. 2t −t − 2 = 0. D. 2
2t − 2t −1 = 0. Lời giải Chọn C ( + ) x x x 1 − 1 x 2 1 log 2 1 .log 2 + = 1 ⇔ log 2 +1 .log + =1 2 4 2 ( ) 4 2 2 2 x 1 x x 1 log 2 1 .log . 2 1 1 log 2 1 . log log 2x 1 ⇔ + + = ⇔ + + + = 1 2 ( ) 4 ( ) 2 ( ) 4 4 ( ) 2 2 ⇔ log (2x + ) 1 1 1 . − + log (2x + ) 1 1 2
1 =1 ⇔ t. − + t =1 ⇔ t − t − 2 = 0 2 2 2 2 2 2
Câu 22: Cho số dương x , viết biểu thức x x x x dưới dạng lũy thừa với số mũ hữu tỷ. 15 3 15 7 A. 18 x . B. 16 x . C. 16 x . D. 18 x . Lời giải Chọn C Ta có: 1 3 3 7 7 15 15 2 2 4 4 8 8 16
x x x x = x x .xx = x x x = x .xx = x x = .
x x = x = x 4 2 1 − 15 Nhận xét: 4 2 16 x x x x = x = x
Câu 23: Cho hai số dương a,b thỏa mãn: log a + log b = log a + b . Khi đó: 2 2 2 ( )
A. a + b = ab .
B. a + b = 2ab . C. 2 2
a + b = a b .
D. 2(a + b) = ab. Lời giải Chọn A
Ta có log a + log b = log a + b ⇔ log ab = log a + b ⇔ ab = a + b 2 2 2 ( ) 2 ( ) 2 ( )
Câu 24: Tập xác định của hàm số y ( x ) 3 3 6 − = − là
A. D = (2;+∞) . B. D = \{ } 2 . C. .
D. D = (0;+∞) . Lời giải Chọn B
Hàm số xác định 3x − 6 ≠ 0 ⇔ x ≠ 2 ⇒ TXĐ: D = \{ } 2 .
Câu 25: Tìm tất cả các giá trị của tham số m để phương trình x x 1 9 .3 m + −
+ 6m + 3 = 0 có hai nghiệm x1
và x thỏa mãn x + x = 3 . 2 1 2
A. m = 4 B. m =1.
C. m = 2.
D. m = 3. Bài giải
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 12
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Chọn A x x+ − + + = ⇔ ( x )2 1 9 .3 6 3 0 3 − 3 .3x m m m + 6m + 3 = 0
Để phương trình có 2 nghiệm thì: 4 − 2 7 m ≤ ∆ = (− m)2 − ( m + ) 2 3 3 4.1. 6
3 = 9m − 24m −12 ≥ 0 ⇔ 4 + 2 7 m ≥ 3
Áp dụng hệ thức Vi-et ta có: 1 x 2 x 1 x + 2 x 3 3 .3 = 3
= 3 = 27 = 6m + 3 ⇒ m = 4 (chọn) 2 x +2
Câu 26: Cho bất phương trình 1 2 >
125 x có tập nghiệm là: 25 A. S = \{ 2; − } 1 B. S = ( ; −∞ 2) ∪( 1; − +∞) C. S = ( 2; − − ) 1 D. S = (1;2) Bài giải Chọn C 2 x +2 1 1 >125 ⇔
>125 ⇔ 1 > 25 + .125 ⇔ 1 > + (5 ) 2 2 x +2 2 2 2 2 2 3 . 5 x x x x x 2 ( ) x 2 25 25 2 2x +6x+4 2 ⇔ 1 > 5
⇔ 2x + 6x + 4 < 0 ⇔ 2 − < x < 1. −
Câu 27: Bất phương trình 1+log3 x x
> 81x có tập nghiệm là A. 1 S 0; = ∪ (9;+∞ ). B. 1 S = ;9. 9 9 C. 1 S 0; = .
D. S = (9;+∞). 9 Lời giải Chọn A
Bất phương trình 1+log3 x x > 81 .
x Điều kiện x > 0
Lấy lôgarit cơ số 3 hai vế của bất phương trình ta được 1+log3 x x
> 81x ⇔ (1+ log x .log x > log 81+ log x 3 ) 3 3 3 x > 9 log x > 2 2 3 log x 4 ⇔ > ⇔ ⇔ 3 1 log x < 2 − x < 3 9 x > 9
Kết hợp điều kiện x > 0 ta có bất phương trình 1+log3 x x > 81x ⇔ 1 0 < x < 9 1
Vậy tâp nghiệm của bát phương trình trên là S 0; = ∪ (9;+∞ ) 9
Câu 28: Đạo hàm của hàm số 4x 6x y = + bằng
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 13
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
A. 4 .xln 4 6 .x + ln 6.
B. 4x 6 .x +
C. 4 .xlog 4 6 .x + log6. D. x 1 − x 1 x(4 6 − + ). Lời giải Chọn A 4x 6x y = + ⇒ ' (4x)' (6x y = +
)' = 4 .xln 4 6 .x + ln 6.
Câu 29: Tập xác định của hàm số ( x y ) 2 2 8 − = − là:
A. D = [3;+∞).
B. D = (3;+∞). C. D = \{ } 3 . D. D = . Lời giải: Chọn C Vì − 2 −
− ∈ ⇒ 2x −8 ≠ 0 ⇔ x ≠ 3 ⇒ Tập xác định của hàm số = ( x y − ) 2 2 8 là D = \{ } 3 .
Câu 30: Tính chất nào của hàm số 3 y x− =
đúng trên nửa khoảng (0;+∞)?
A. Hàm số luôn nghịch biến.
B. Đồ thị hàm số luôn đi qua điểm (0;0).
C. Đồ thị hàm số luôn đi qua điểm (0; ) 1 .
D. Hàm số luôn đồng biến. Lời giải: Chọn A − − 3 − Ta có: 3 2
y = x ⇒ y′ = 3 − x = < 0 với x ∀ > 0. 2 x
Hàm số luôn nghịch biến trên (0;+∞).
Câu 31: Phương trình log ( 2
x −1 = log x −1 +1có bao nhiêu nghiệm thực? 3 ) 3 ( ) A. 3. B. 0 . C. 1. D. 2 . Lời giải Chọn C
Điều kiện: x >1
Với điều kiện trên ta có log ( 2
x −1 = log x −1 +1 3 ) 3 ( ) ⇔ log ( 2 x − ) 1 = log (x − ) 1 + log 3 ⇔ log ( 2
x −1 = log 3. x −1 3 3 3 3 ) 3 ( ) x =1 L 2
⇔ x −1 = 3.(x − ) 2 ( )
1 ⇔ x − 3x + 2 = 0 ⇔ . x = 2
Vậy phương trình có một nghiệm.
Câu 32: Đạo hàm của hàm số: = ( 2 − 2 + 2) x y x x e bằng: A. 2 − . x x e . B. (2 − 2) x x e . C. ( 2 − 2) x x e . D. 2 x x e . Lời giải Chọn D
Ta có: = ( 2 − + ) x + ( 2 − + )( x ) = ( − ) x + ( 2 ' 2 2 ' 2 2 ' 2 2 − 2 + 2) x y x x e x x e x e x x e .
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 14
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com = ( 2 − + − + ) 2 2 2 2 2 x x x x x e = x e 3 2 Câu 33: Nếu 3 2 a > a và 3 4 log < thì: b log 4 b 5
A. a >1 và b >1.
B. 0 < a <1và b >1.
C. 0 < a <1và 0 < b <1. D. a >1 và 0 < b <1. Lời giải Chọn B 3 2 3 4 3 2 a > a log < b log 4 b 5
⇔ 0 < a <1; ⇔ b >1 3 2 < 3 4 < 3 2 4 5
Câu 34: Tìm tất cả các giá trị thực của m để biểu thứ A = log 1− 2m có nghĩa. 5 ( ) A. 1 m ≥ . B. 1 m > . C. 1 m ≤ . D. 1 m < . 2 2 2 2 Lời giải Chọn D ĐKXĐ: 1
1− 2m > 0 ⇔ m < . 2
Câu 35: Đạo hàm của hàm số y = log ( 2 x + x +1 bằng 2 ) 1 + 2x +1 A. 2x 1 ln 2 ( . B. . C. . D. . 2 x + x + )1ln 2 2 x + x +1 2 x + x +1 ( 2x + x+ )1.ln2 Lời giải Chọn D ( 2x x )1′ + + 2x +1 y′ = ( = . 2 x + x + ) 1 ln 2 ( 2 x + x + ) 1 ln 2 4 3
Câu 36: Rút gọn biểu thức a P = (a > 0) . 2 a 2 2 − 10 − 10 A. 3 a . B. 3 a . C. 3 a . D. 3 a . Lời giải Chọn B 4 2 −2 − 3 3 P = a = a .
Câu 37: Tính đạo hàm của hàm số y = ( x − )4 4 3 .
A. y = ( x − )4 ' 16 4 3 .
B. y = ( x − )3 ' 4 4 3 .
C. y = ( x − )4 ' 4 4 3 .
D. y = ( x − )3 ' 16 4 3 . Lời giải Chọn D
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 15
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
y = ( x − ) ( x − )3 =
( x − )3 = ( x − )3 ' 4. 4 3 ' 4 3 4.4. 4 3 16 4 3 .
Câu 38: Cho các mệnh đề sau:
I. Với x , x > 0, ta có: 5log − 5log = 5 log − log = 5log x x x x x . 1 2 ( 1 2 ) 2 1 2 x1
II. Với x , x , x > 0,0 < a ≠ 1, ta có: log x + x + x = x x x a (
loga .loga .loga . 1 2 3 ) 1 2 3 1 2 3 1 1
III. log( 12 = log 12 = 1+log 2 . 2 2 .3) 6 ( 6 ) 12 2 1 1
IV. Cho các số dương a,b, với a ≠ 1, ta có: log ab = + log . b 2 ( ) a 2 2 a
Số mệnh đề sai là bao nhiêu? A. 4. B. 3. C. 2. D. 1. Lời giải Chọn B
Mệnh đề I, II và III sai
Câu 39: Cho a > 0,a ≠1. Đơn giản biểu thức 2 4 3 B = log a a a ( . ). 10 11 A. 3 a . B. 4 a . C. 11. D. 10 . 4 3 Lời giải Chọn C 11 2 4 3 4 (a . a ) a 11 B = log = = a loga . 4 Câu 40: Hàm số 5 − x y =
có tập xác định D . Khi đó: log x − 2 2 ( ) A. D = (2;5) .
B. D = [2;5] C. D = (2;5] .
D. D = (2;5]\{3}. Lời giải Chọn D 5 − x ≥ 0 x ≤ 5
Điều kiện: x 2 0
− > ⇔ x > 2 x 2 1 − ≠ x ≠ 3
Vậy tập xác định D = (2;5] \{3}.
Câu 41: Tìm tập nghiệm của phương trình 2 9x 17 − x 10 + 7−5 2 = 2 x. A. 1 1; − − . B. 1 1; . C. { 1; − } 3 . D. { 3 − ; } 1 . 3 3 Lời giải Chọn B
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 16
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com x = 1 Ta có: 2 9x 17 − x 10 + 7−5x 2 2 2 2 9x 17x 10 7 5x 9x 12x 3 0 = ⇔ − + = − ⇔ − + = ⇔ 1 x = 3 1
Vậy tập nghiệm của phương trình là 1; . 3
Câu 42: Cho phương trình 4x 4.2x −
+ 3 = 0 có hai nghiệm 1x, 2
x với 1x < 2
x . Tính giá trị của biểu thức 3 1x + 2 2 x . A. 3log2 3. B. 2log2 3. C. 3log3 2. D. 1. Lời giải Chọn B Đặt = 2x t
(t > 0). Phương trình đã cho trở thành: 2 t = 1 (TM )
t − 4.t + 3 = 0 ⇔ t = 3 (TM )
Với t = 1. Ta có 2x =1 ⇔ x = 0.
Với t = 3. Ta có 2x =3 ⇔ x = log2 3.
Do phương trình đã cho có hai nghiệm 1x, 2
x với 1x < 2
x nên ta chọn 1x = 0 và 2 x = log2 3. Vậy 3 1x + 2 2 x = 2log2 3.
Câu 43: Bất phương trình 2 x x 3
log 3 −1 − 2log 3 −1 + ≥ 0 có tập nghiệm là: 4 ( ) 4 ( ) 4 A. S = (0; ] 1 ∪[2;+∞) . B. S = (0; ) 1 ∪(2;+∞) . C. S = ( ; −∞ )
1 ∪(2;+∞). D. S = (2;+∞) . Lời giải Chọn A
ĐK: 3x −1 > 0 ⇔ x > 0. Đặt log 3x t = −1 . 4 ( ) 1 t ≤
Ta có bất phương trình: 2 3 2
t − 2t + ≥ 0 ⇔ 4 3 t ≥ 2 Với 1 x 1
≤ ⇒ log 3 −1 ≤ ⇔ 0 < 3x t
−1≤ 2 ⇔ 0 < x ≤1. 4 ( ) 2 2 Với 3 t ≥ x 3
⇒ log 3 −1 ≥ ⇔ 3x −1≥ 8 ⇔ x ≥ 2 4 ( ) 2 2
Vậy bất phương trình đã cho có nghiệm S = (0; ] 1 ∪[2;+∞) .
Câu 44: Đạo hàm của hàm số y = ln(1− x −1) bằng:
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 17
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com A. 1 . B. 1 .
2 x −1 − 2 (x − )2 1
2 x −1 + 2 (x − )2 1 C. 1 − . D. 1 − .
2 x −1 + 2 (x − )2 1
2 x −1 − 2 (x − )2 1 Lời giải Chọn D
Tập xác định của hàm số: D = [1;2) . ′ x 1 ′ − −
Ta có: y ( ( − x − ) ( ) 1 − 1 − ′ = ln 1 1 = = = . 1− x −1
2 x −1(1− x −1) 2 x −1 − 2 (x − )2 1
Câu 45: Một người gửi 88 triệu đồng vào ngân hàng theo thể thức lãi kép kỳ hạn một quý với lãi suất
1,68% (mỗi quý). Hỏi sau ít nhất bao nhiêu năm người đó có được 100 triệu đồng cả vốn lẫn
lãi từ số vốn ban đầu? (giả sử rằng lãi suất không đổi). A. 2 năm. B. 1,5 năm. C. 8 năm. D. 3 năm. Lời giải Chọn A
Gọi M là vốn và lãi sau n kỳ hạn.
A là số vốn ban đầu.
r là lãi suất (theo quý). Ta có: = (1+ )n M A r n ⇔ = + ⇔ ( + )n 25 100000000 88000000(1 1,68%) 1 0,0168 = ⇔ n ≈ 8 22
Vậy : Sau 8 quý (tức là sau 2 năm) người đó sẽ có được 100 triệu đồng cả vốn lẫn lãi. B. TỰ LUẬN
Câu 1: Có bao nhiêu giá trị nguyên của tham số m để phương trình x x 1 + 2 4 − .2 m + 2m −5 = 0 có hai nghiệm phân biệt? Lời giải Ta có: x x 1 + 2 4 − .2 m + 2m −5 = 0 x x 2 ⇔ 4 − 2 .2
m + 2m −5 = 0 . Đặt 2x
t = , t > 0, ta được phương trình: 2 2
t − 2mt + 2m −5 = 0 ( ) 1 .
Phương trình đã cho có hai nghiệm phân biệt khi phương trình ( )
1 có hai nghiệm dương phân biệt − 5 < m < 5 ∆′ > 0 2 −m + 5 > 0 10 m < − 10 ⇔ 2
S > 0 ⇔ 2m > 0 ⇔ ⇔ < m < 5 . 2 P > 10 0 2 2m − 5 > 0 m > 2 m > 0
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 18
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Vậy m = 2 là giá trị nguyên của m để phương trình đã cho có hai nghiệm phân biệt.
Câu 2: Tập hợp tất cả các giá trị của tham số m để phương trình x x 1 4 .2 m + −
+ 3m −3 = 0 có hai nghiệm trái dấu. Lời giải Phương trình x x 1 4 .2 m + − + 3m − 3 = 0( )
1 ⇔ 4x − 2 .2x
m + 3m −3 = 0 . Đặt 2x
t = , (t > 0) ta có phương trình 2t − 2mt + 3m −3 = 0(2). Phương trình ( )
1 có hai nghiệm trái dấu khi và chỉ khi phương trình (2) có hai nghiệm t ,t 1 2 2
m − 3m + 3 > 0 3 m − 3 > 0 m >1
thỏa mãn 0 < t <1< t ⇔ ⇔ 1 2 m > 0 t
.t − t + t +1 < 0 1 2 ( 1 2 ) (
t −1 t −1 < 0 1 )( 2 ) m >1 m > 1 ⇔ ⇔ ⇔ m∈(1;2) . 3
m − 3 − 2m +1 < 0 m < 2
Câu 3: Cho các số thực dương x, y thỏa mãn log x = log y = log 2x + 2y . Tính tỉ số x ? 6 9 4 ( ) y Lời giải x = 6t (1)
Giả sử log x = log y = log 2x + 2y = t . Ta có: y = 9t (2) . 6 9 4 ( )
2x + 2y = 4t (3) t t Khi đó x 6 2 = = > 0 . y 9t 3
Lấy (1), (2) thay vào (3) ta có 2 t 2 = 1+ 3 = (thoûa) 2t t
2.6t 2.9t 4t + = 2 2 3 − 2. ⇔ − − 2 = 3 1 0 ⇔ . 3 3 2 t =1− 3 (loaïi) 3
Câu 4: Biết rằng a là số thực dương sao cho bất đẳng thức 3x x + ≥ 6x + 9x a
đúng với mọi số thực x .
Mệnh đề nào sau đây đúng? Lời giải Ta có 3x x + ≥ 6x + 9x a x ⇔
−18x ≥ 6x + 9x − 3x −18x a x ⇔
−18x ≥ 3x (2x − ) 1 − 9x (2x a − ) 1 x ⇔ −18x ≥ 3x − (2x − ) 1 (3x a − ) 1 (*) . Ta thấy (2x − ) 1 (3x − ) 1 ≥ 0, x ∀ ∈ ⇒ 3x − (2x − ) 1 (3x − ) 1 ≤ 0, x ∀ ∈ .
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 19
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Do đó, (*) đúng với mọi số thực x x ⇔ −18x a ≥ 0, x ∀ ∈ x a ⇔ ≥ 1, x ∀ ∈ 18 a ⇔
=1 ⇔ a =18∈(16;18]. 18
Câu 5: Tìm m để phương trình 9x − 2(2 + ) 1 .3x m + 3(4m − )
1 = 0 có hai nghiệm thực x , x thỏa mãn 1 2
(x + 2 x + 2 =12 1 )( 2 ) Lời giải Đặt 3x
t = (t > 0) thì phương trình đã cho trở thành 2t − 2(2m + ) 1 t + 3(4m − ) 1 = 0 (1). 2 ∆′ > 0 ( 2m + ) 1 − 3(4m − ) 1 > 0 m ≠ 1
(1) có hai nghiệm dương phân biệt khi
S > 0 ⇔ 2m +1 > 0 ⇔ 1 . m > P > 0 4m −1 > 0 4 t = 4m −1 1 3x = 4m −1
x = log 4m −1 1 3 ( ) Khi đó ⇒ ⇒ . t = 3 2 3x = 3 x = 1 2 5
Ta có (x + 2 x + 2 =12 ⇔ log 4m −1 = 2 ⇔ m = (thỏa điều kiện). 3 ( ) 1 )( 2 ) 2 log x 2 2
Câu 6: Tìm tập nghiệm 2 log x
S của bất phương trình 2 − ≤ 1. log x log x −1 2 2 Lời giải log x x > 0 2 2 2 log x 2 − ≤ 1 ( ) 1 . ĐK: 2 x > 0 ⇔ 0 < x ≠ 2 . log x log x −1 2 2 log x −1≠ 0 2
( ) log x −1 2log x 2 2 1 ⇔ − ≤1. log x log x −1 2 2
Đặt t = log x . 2 t >1 2 t − t − t − t +
Bất phương trình trở thành: 1 2 2 1 1 − ≤ 1 ⇔ ≤ ⇔ ( t . t t t t − ) 0 0 < ≤ −1 1 2 t ≤ 1 −
• t >1 ⇔ log x >1 ⇔ x > 2 . 2 1 1
• 0 < t ≤ ⇔ 0 < log x ≤ ⇔ 1< x < 2 . 2 2 2 1 • t ≤ 1 − ⇔ log x ≤ 1 − ⇔ x ≤ . 2 2
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 20
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com 1
Kết hợp với điều kiện, bất phương trình ( )
1 có tập nghiệm S = 0; ∪ (1; 2 ∪(2;+∞ ). 2
Câu 7: Tìm các giá trị thực của tham số m để phương trình 2
log x − 3log x + 2m − 7 = 0 có hai nghiệm 3 3
thực x ; x thỏa mãn (x + 3 x + 3 = 72. 1 )( 2 ) 1 2 Lời giải 2
log x − 3log x + 2m − 7 = 0 1 3 3 ( )
Điều kiện: x > 0 Đặt = log ⇔ = 3t t x x
t − t + m − = 3
thì phương trình tương đương 2 3 2 7 0
( )1 có hai nghiệm phân biệt khi và chỉ khi (2) có 2 nghiệm phân biệt.
Giả sử (2) có 2 nghiệm t = log x ,t = log x khi đó ( 1t+t2 ) x x = 3 = 27 . 1 3 1 2 3 2 1 2
Suy ra(x + 3 x + 3 = 72 ⇔ x x + 3 x + x = 63 ⇔ x + x =12 1 )( 2 ) 1 2 ( 1 2) 1 2
Vậy x , x là 2 nghiệm phương trình 2
x −12x + 27 = 0 ⇔ x = 9 ∨ x = 3 1 2 9 x = 9 suy ra 2
log 9 − 3log 9 + 2m − 7 = 0 ⇔ m = . 3 3 2 9 x = 3 suy ra 2
log 3− 3log 3+ 2m − 7 = 0 ⇔ m = . 3 3 2 9 Vậy m = . 2
Câu 8: Tìm các giá trị nguyên của tham số m để phương trình log (x − )
1 = log mx −8 có hai 2 2 ( ) nghiệm phân biệt Lời giải. x >1 ( > x − ) x 1 log 1 = log mx −8 ⇔ ⇔ . 2 2 ( ) ( x − )2 2 1 = mx −8 x − (m + 2) x +9 = 0
Để phương trình đã cho có hai nghiệm thực lớn hơn 1 thì điều kiện sau thỏa mãn. m < 8 − 2
m + 4m − 32 > 0 m > 4 ∆ > 0 ( x 1 x 1 0 ⇔ − +
− > ⇔ m > 0 ⇔ 4 < m < 8 1 ) ( 2 ) 1< x < x 1 2 (
x −1 x −1 > 0 8 − m > 0 1 )( 2 )
Vì m∈ ⇒ m∈{5,6 } ,7 .
Câu 9: Phương trình 2 log x − ( 2
m − 3m log x + 3 = 0 2 ) 2
. Tìm m để phương trình có hai nghiệm phân biệt
x , x thỏa mãn x x =16 . 1 2 1 2 Lời giải 2 log x − ( 2
m − 3m log x + 3 = 0 1 2 ) 2 ( ) .
Điều kiện x > 0 .
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 21
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com
Đặt log x = t . Ta được phương trình 2t − ( 2
m − 3m)t +3 = 0 (2). 2
Ta có: x x =16 ⇔ log x x = 4 ⇔ log x + log x = 4 . 2 ( 1 2 ) 1 2 2 1 2 2 Phương trình ( )
1 có hai nghiệm phân biệt x , x thỏa mãn x x =16 khi và chỉ khi (2) có hai 1 2 1 2
nghiệm phân biệt t , t thỏa mãn t + t = 4 . 1 2 1 2 m = 4 Vậy suy ra 2
m −3m = 4 ⇔ . m = 1 −
Thử lại thấy thỏa mãn.
Câu 10: Giải bất phương trình 3x −1 log log ≤ 0 1 2 x +1 2 Lời giải 3x −1 3x −1 3x −1 x − 3 x ≥ 3 log log ≤ 0 ⇔ log ≥1 ⇔ ≥ 2 ⇔ ≥ 0 ⇔ . 1 2 x +1 x +1 x +1 x +1 x < 1 − 2 2
Vậy tập nghiệm của bất phương trình là S = ( 1; − +∞) ∪[3;+∞) .
Câu 11: Tìm m để phương trình ( 2
log x + mx) = log(x + m − ) 1 có nghiệm duy nhất Lời giải g (x) 2
= x + mx = x + m − g (x) 2 1
= x − (1− m) x +1− m = 0( ) 1 Phương trình ⇔ ⇔ .
x + m −1 > 0
x >1− m
PT đã cho có nghiệm duy nhất khi và chỉ khi xảy ra 1 trong 2 TH sau: TH1: PT ( )
1 có nghiệm kép x >1− m ∆ = 0 ( m = 1− m) 1
2 − 4(1− m) = 0 ⇔ 1 − m ⇔ ⇔ m = 3 − ⇔ m∈∅ > 1− m 1 − m < 0 2 m > 1 TH2: PT ( )
1 có hai nghiệm phân biệt thỏa mãn x <1− m = x 1 2 2 ∆ > 0
m + 2m −3 > 0 S − m Đk: 1 >1− m ⇔ >1− m
:Không có m thỏa mãn. 2 2 g (1− m) = 0 ( 1− m
)2 −(1− m)(1− m)+1− m = 0
TH3:Phương trình có hai nghiệm phân biệt thỏa mãn x <1− m < x 1 2 ∆ > 0
x + x = 1− m ĐK: (*) trong đó 1 2
x − 1− m x − 1− m < 0 = − 1 ( ) 2 ( ) x x 1 m 1 2 2 2
m + 2m −3 > 0 + − > Khi đó ( m 2m 3 0 *) thành ⇔ ⇔ m >1. x x −
(1− m)(x + x )+(1− m)2 < 0 1 − m < 0 1 2 1 2 KL: m >1.
Câu 12: Giải phương trình 2 1
log x + log x −1 = log log 3 49 7 ( )2 7 ( 3 ) 2
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 22
BÀI GIẢNG TOÁN 11-CHÂN TRỜI SÁNG TẠO
WEB: Toanthaycu.com Lời giải x ≠ 0 Điều kiện . x ≠ 1 2 1
log x + log x −1 = log log 3 ⇔ log x + log x −1 = log 2 49 7 ( )2 7 ( 3 ) 2 7 7 7 x(x − ) 1 = 2 2
x − x − 2 = 0 x = 2
⇔ log x x −1 = log 2 ⇔ ⇔ ⇔ . 7 ( ) 7 x ( x − ) 1 = 2 − 2
x − x + 2 = 0 x = 1 −
Câu 13: Tìm m để phương trình 2
log x − 3log x + 2m − 7 = 0 có hai nghiệm thực phân biệt 3 3 x , x thỏa 1 2
mãn (x + 3 x + 3 = 72 . 1 )( 2 ) Lời giải
Ta có (x + 3 x + 3 = 72 ⇒ x x + 3 x + x = 63. 1 )( 2 ) 1 2 ( 1 2) Xét 2
log x − 3log x + 2m − 7 = 0, đặt =
, PT trở thành 2t − 3t + 2m − 7 = 0 ( ) 3 3 t log x 1 . 3
Để phương trình đã cho có hai nghiệm thực phân biệt x , x ⇔ ( )
1 có hai nghiệm phân biệt 1 2 ⇔ − ( m − ) 37 9 4 2 7 > 0 ⇔ 8
− m + 37 > 0 ⇔ m < . 8 Khi đó, giả sử ( )
1 có hai nghiệm t ,t , tương ứng PT đã cho có hai nghiệm x , x . 1 2 1 2 t + t = 3 Theo Vi-et ta có 1 2 . t t = 2m− 7 1 2
log x + log x = 3 ⇒ x .x = 27 Nên 3 1 3 2 1 2
log x .log x = 2m − 7 * 3 1 3 2 ( ) x .x = 27 x = 9 9
Kết hợp với giả thiết ta có 1 2 1 ⇔
. Thay vào (*) ta được m = (TM). x x 12 + = x = 3 2 1 2 2
Bản word đề bài và lời giải vui lòng lh Zalo Trần Đình Cư: 0834332133 23
Document Outline
- Bài 6.1_Lũy thừa_Lời giải
- CHƯƠNG VI. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
- A. KIẾN THỨC CƠ BẢN CẦN NẮM
- B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
- Dạng 1. Rút gọn biểu thức
- 1. Phương pháp
- 2. Các ví dụ rèn luyện kĩ năng
- Dạng 2. Viết biểu thức dưới dạng lũy thừa
- 1. Phương pháp
- 2. Các ví dụ rèn luyện kĩ năng
- Dạng 3. So sánh
- 1. Phương pháp
- 2. Các ví dụ rèn luyện kĩ năng
- C. GIẢI BÀI TẬP SÁCH GIÁO KHOA
- D. BÀI TẬP TRẮC NGHIỆM
- CHƯƠNG VI. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
- Bài 6.2_Phép tính logarit_Lời giải
- Bài 2. PHÉP TÍNH LÔGARIT
- A. KIẾN THỨC CƠ BẢN CẦN NẮM
- B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
- Dạng 1. Rút gọn biểu thức
- 1. Phương pháp
- 2. Các ví dụ rèn luyện kĩ năng
- Dạng 2. Biểu diễn theo lôga
- 1. Phương pháp
- 2. Các ví dụ rèn luyện kĩ năng
- Dạng 3. So sánh
- 1. Phương pháp
- 2. Các ví dụ rèn luyện kĩ năng
- C. GIẢI BÀI TẬP SÁCH GIÁO KHOA
- D. BÀI TẬP TRẮC NGHIỆM
- Bài 2. PHÉP TÍNH LÔGARIT
- Bài 6.3_Hàm số mũ và hàm số loga_Lời giải
- BÀI 3. HÀM SỐ MŨ. HÀM SỐ LÔGARIT
- A. KIẾN THỨC CƠ BẢN CẦN NẮM
- B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
- Dạng 1. Tìm tập xác định, tập giá trị của hàm số
- 1. Phương pháp:
- 2. Các ví dụ
- Dạng 2. So sánh
- 1. Phương pháp
- 2. Ví dụ
- Dạng 3. Đồ thị hàm số
- 1. Phương pháp:
- 2. Các ví dụ
- C. GIẢI BÀI TẬP SÁCH GIÁO KHOA
- D. BÀI TẬP TRẮC NGHIỆM
- BÀI 3. HÀM SỐ MŨ. HÀM SỐ LÔGARIT
- Bài 6.4_Pt và bpt mũ loga_Lời giải
- BÀI 4. PHƯƠNG TRÌNH, BẤT PHƯƠNG TRÌNH MŨ VÀ LÔGARIT
- A. KIẾN THỨC CƠ BẢN CẦN NẮM
- B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TÂP
- Dạng 1: Đưa về cùng cơ số
- Dạng 2: Phương pháp đặt ẩn phụ
- Dạng 3: Logarit hóa, mũ hóa
- C. GIẢI BÀI TẬP SÁCH GIÁO KHOA
- D. BÀI TẬP TRẮC NGHIỆM
- BÀI 4. PHƯƠNG TRÌNH, BẤT PHƯƠNG TRÌNH MŨ VÀ LÔGARIT
- Bài 6.5ÔN TẠP CHƯƠNG 6_Lời giải
- BÀI TẬP CUỐI CHƯƠNG VI
- A. CÂU HỎI TRẮC NGHIỆM
- B. BÀI TẬP TỰ LUẬN
- BÀI TẬP TỔNG ÔN
- A. TRẮC NGHIỆM
- B. TỰ LUẬN
- BÀI TẬP CUỐI CHƯƠNG VI




