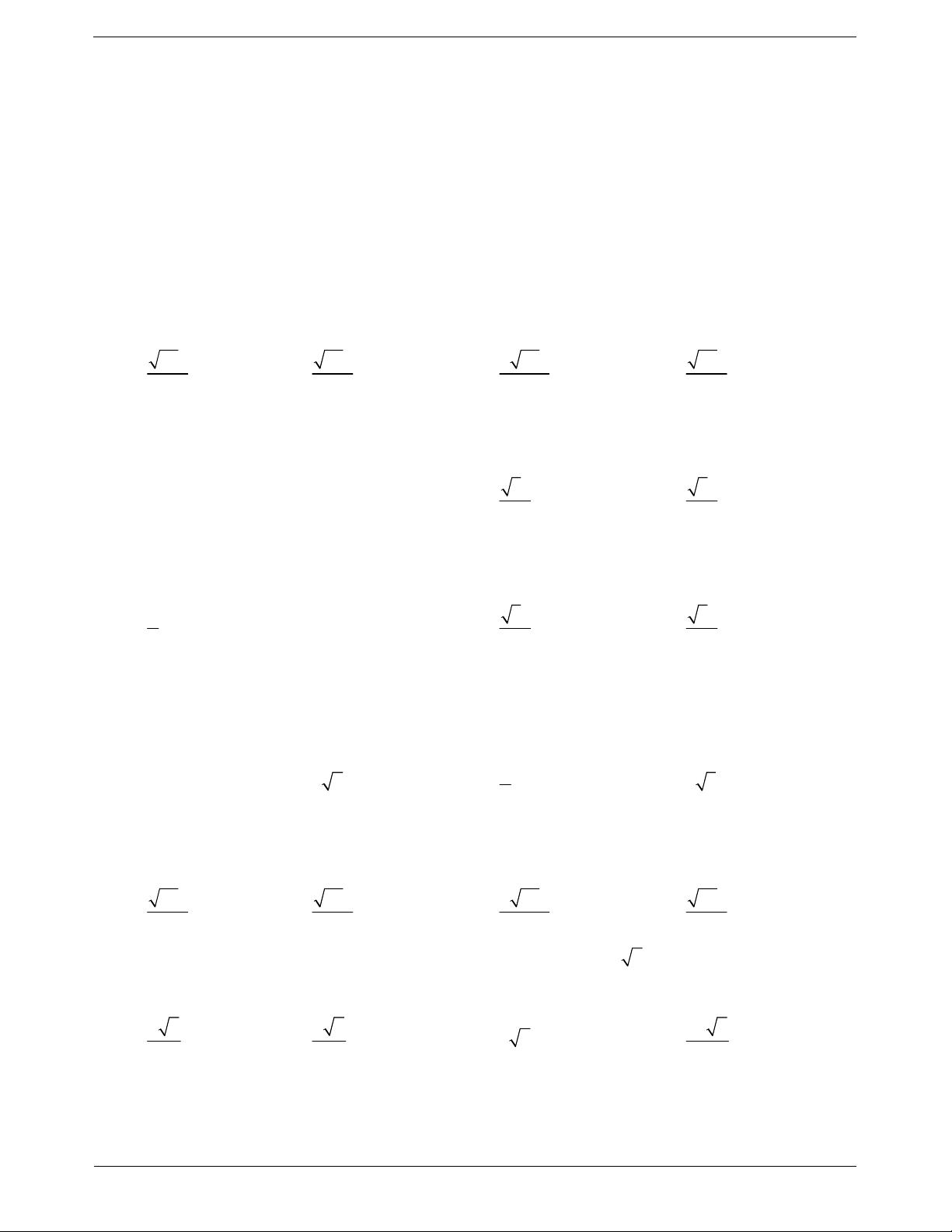


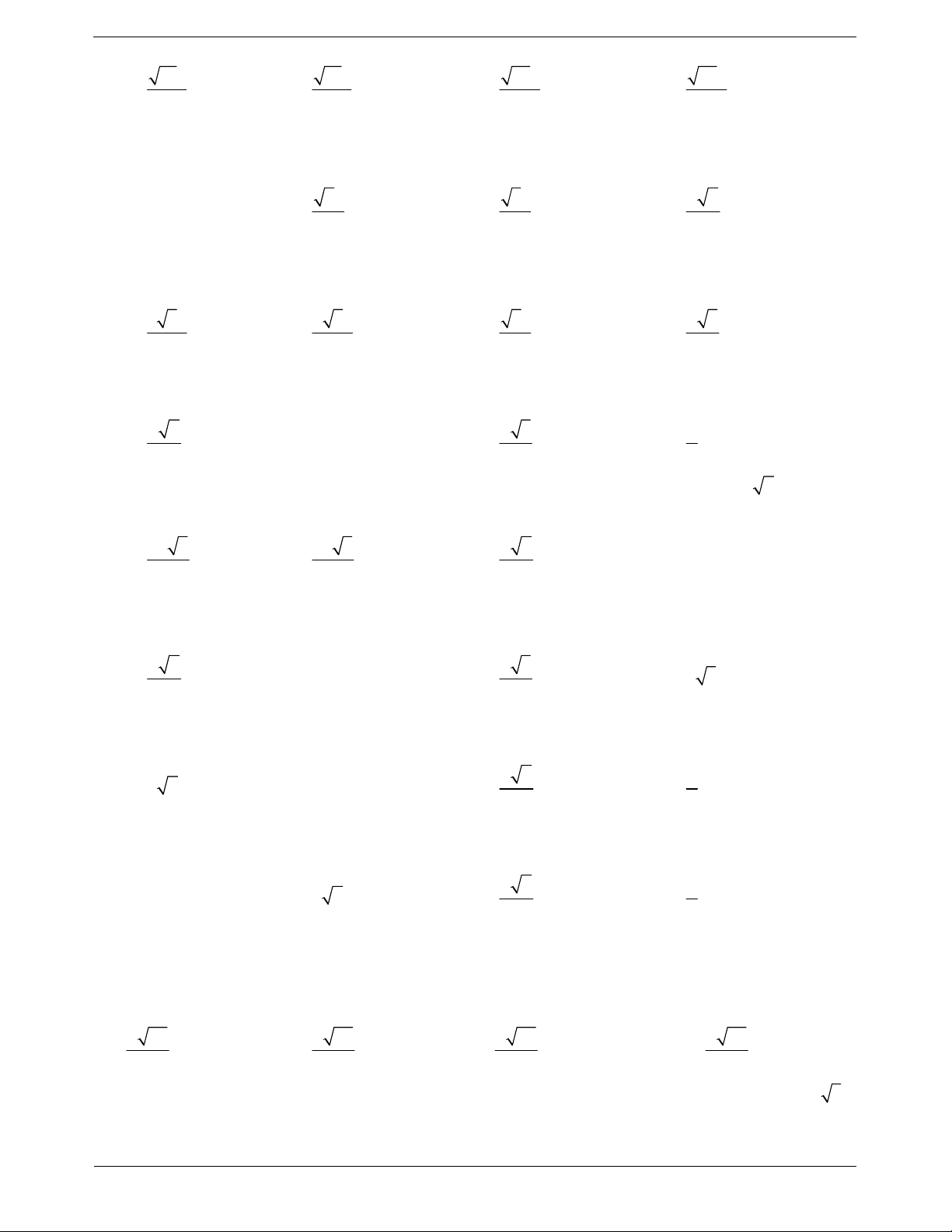
Preview text:
BÀI GIẢNG KHOẢNG CÁCH TRONG KHÔNG GIAN Mục tiêu Kiến thức
+ Nắm vững khái niệm khoảng cách từ một điểm đến đường thẳng, từ một điểm đến mặt phẳng
và khoảng cách đường thẳng đến mặt phẳng.
+ Nắm được khái niệm khoảng cách giữa hai đường thẳng, khoảng cách giữa hai mặt phẳng.
+ Nắm vững các tính chất về khoảng cách. Kĩ năng
+ Xác định được hình chiếu của một điểm đến đường thẳng và trên mặt phẳng.
+ Biết cách tính khoảng cách trong từng trường hợp.
I. LÍ THUYẾT TRỌNG TÂM
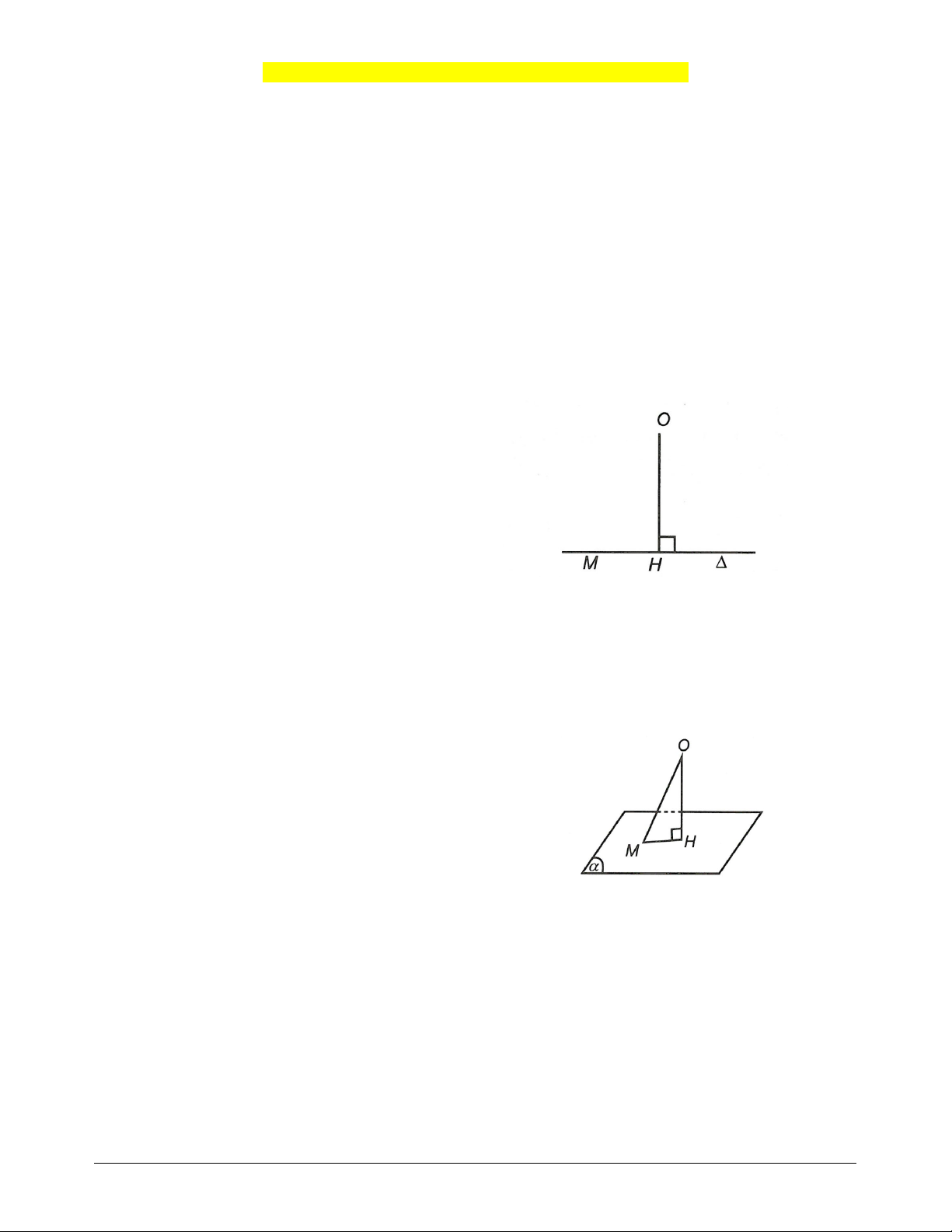
Khoảng cách từ một điểm tới một đường thẳng
Cho điểm O và đường thẳng . Gọi H là hình
chiếu vuông góc của O trên . Khi đó khoảng cách
OH được gọi là khoảng cách từ điểm O đến .
d O, OH.
Nhận xét: OH OM , M
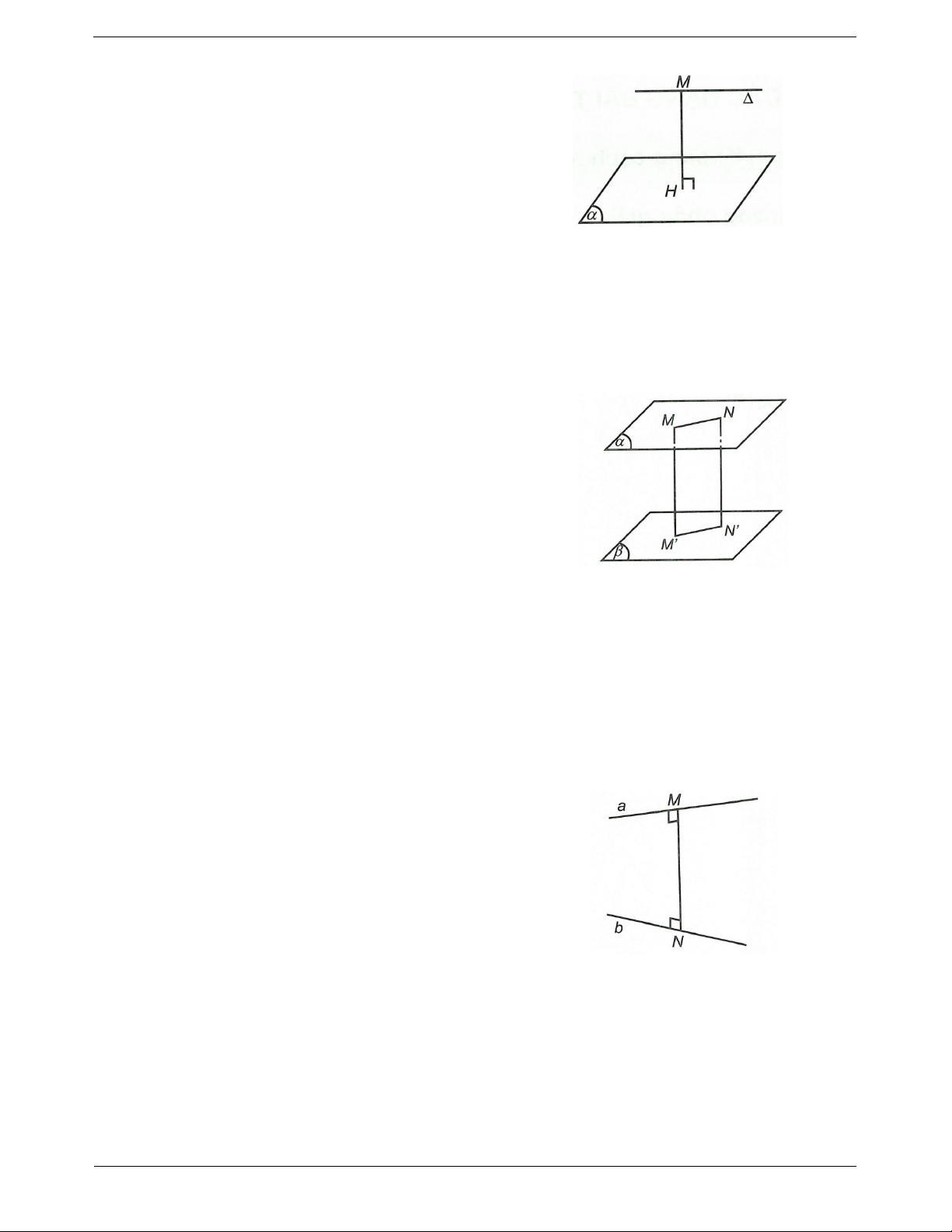
Khoảng cách từ một điểm tới một mặt phẳng
Cho mặt phẳng và một điểm O. Gọi H là hình
chiếu của O trên mặt phẳng . Khi đó khoảng
cách OH được gọi là khoảng cách từ điểm O đến mặt phẳng .
d O, OH.
Nhận xét: OH OM , M Trang 1
Khoảng cách từ một đường thẳng tới một mặt phẳng
Cho đường thẳng và mặt phẳng song song
với nhau. Khi đó khoảng cách từ một điểm bất kì
trên đến mặt phẳng được gọi là khoảng
cách giữa đường thẳng và mặt phẳng .
d , d M , với M
Khoảng cách giữa hai mặt phẳng
Cho hai mặt phẳng và song song với nhau.
Khoảng cách từ một điểm bất kì trên mặt phẳng này
đến mặt phẳng kia được gọi là khoảng cách giữa
hai mặt phẳng và .
d , d M , d N, với
M , N .
Khoảng cách giữa hai đường thẳng
Cho hai đường thẳng chéo nhau a,b. Độ dài đoạn
vuông góc chung MN của a và b được gọi là
khoảng cách giữa hai đường thẳng a và b.
d a,b MN. TOANMATH.com Trang 2
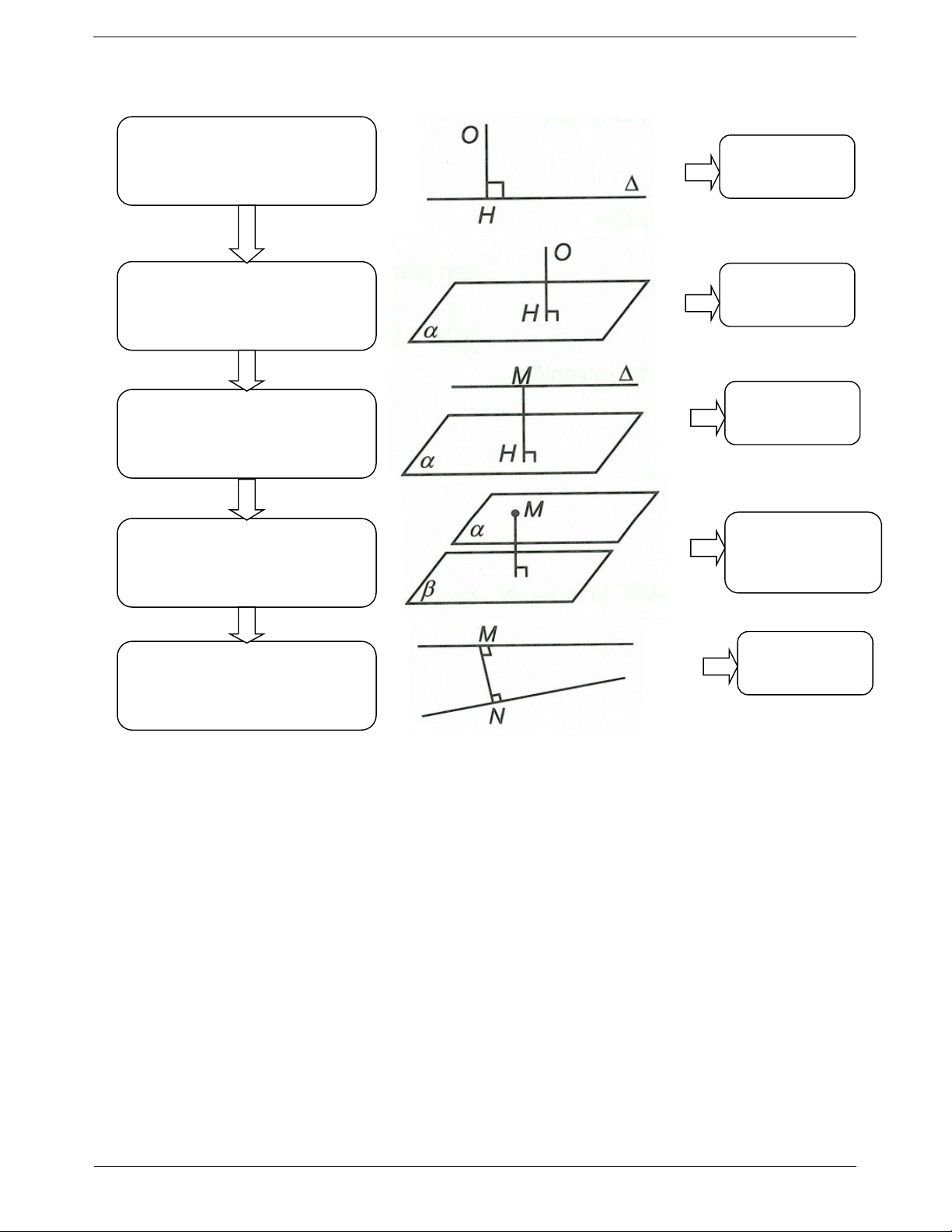
SƠ ĐỒ HỆ THỐNG HÓA
Khoảng cách từ điểm đến
d O, OH đường thẳng
Khoảng cách từ điểm đến mặt
d O, OH phẳng
d , d M ,
Khoảng cách từ đường thẳng đến mặt phẳng
Khoảng cách giữa hai mặt
d ;
d M ; phẳng song song M
Khoảng cách giữa hai đường
d a,b MN thẳng chéo nhau TOANMATH.com Trang 3
II. CÁC DẠNG BÀI TẬP
Dạng 1. Khoảng cách từ một điểm tới một mặt phẳng Phương pháp giải
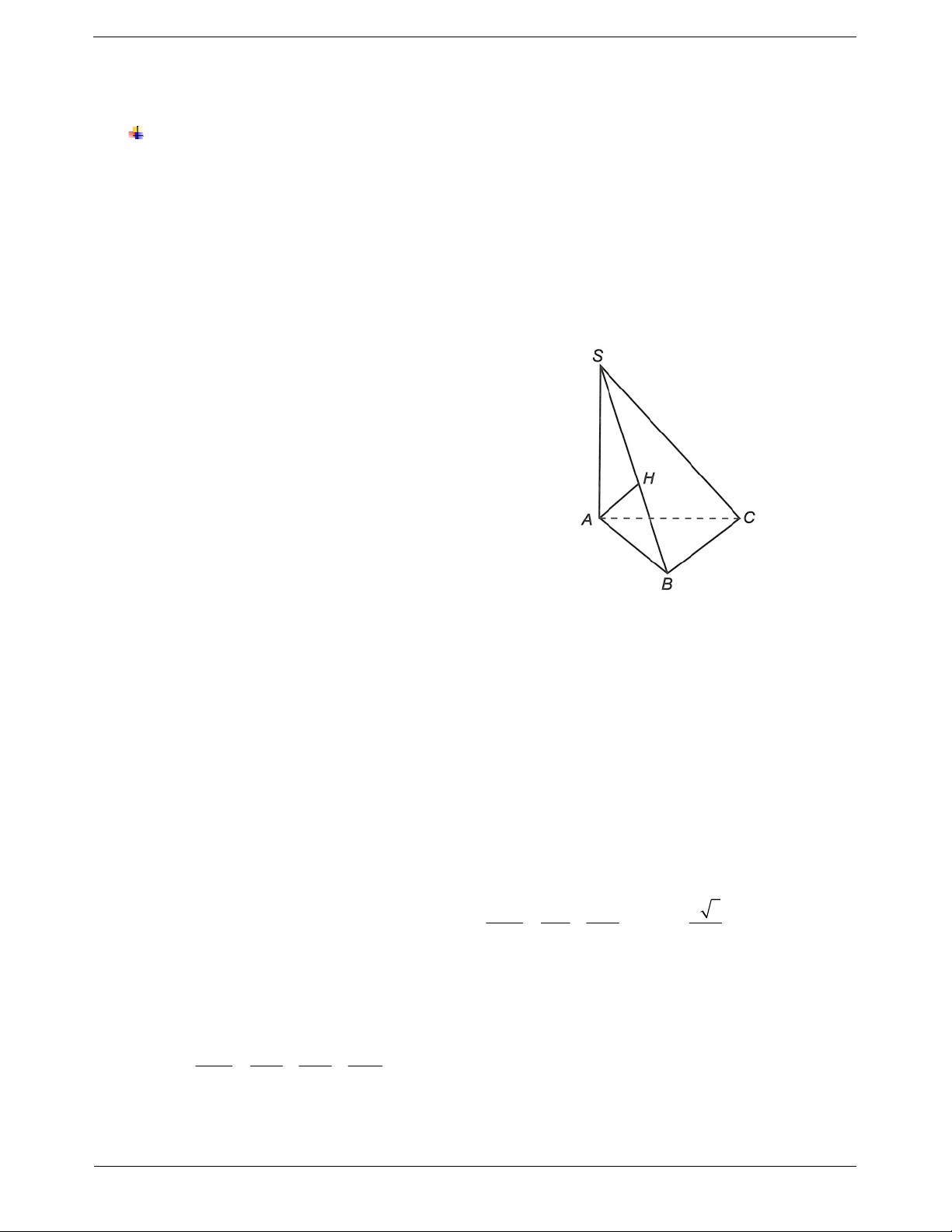
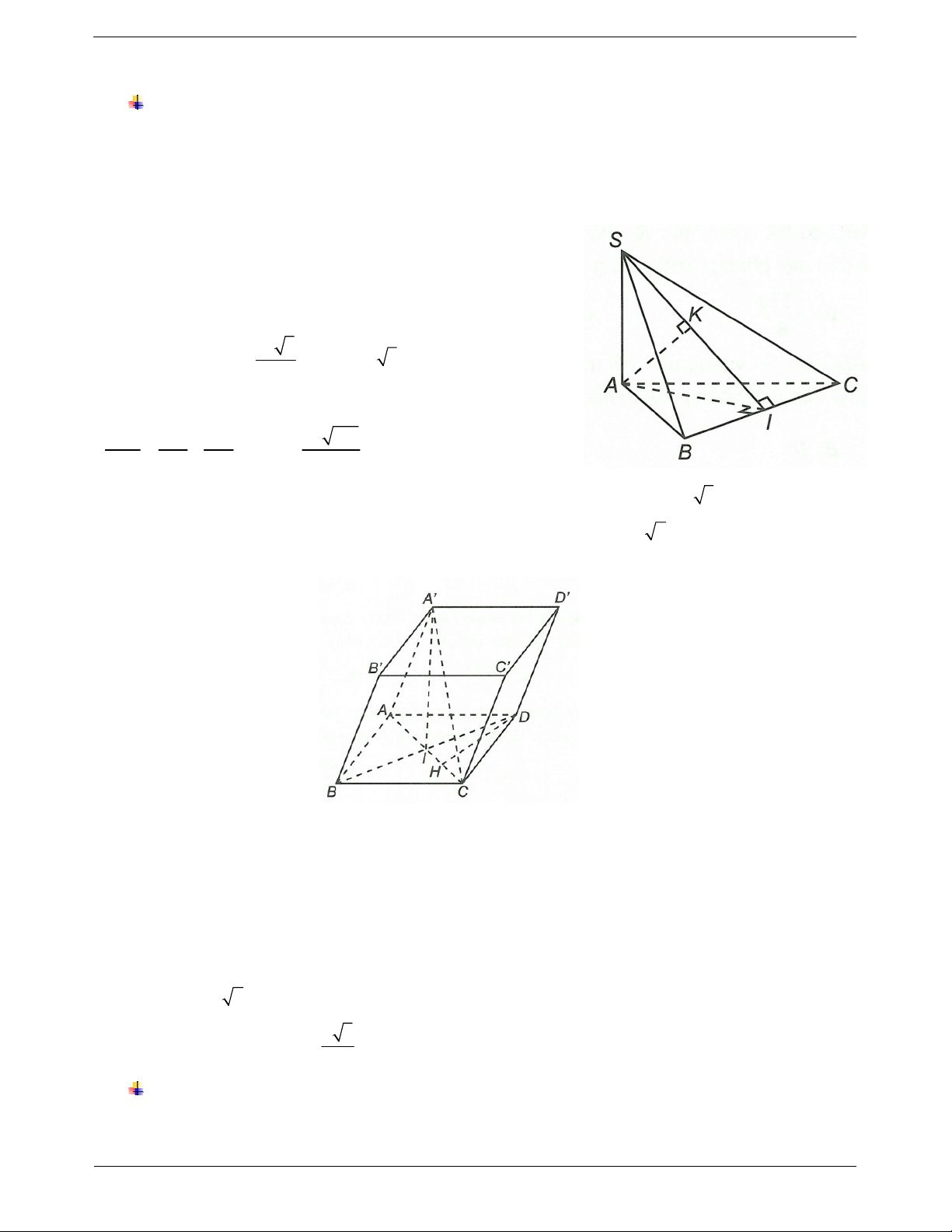
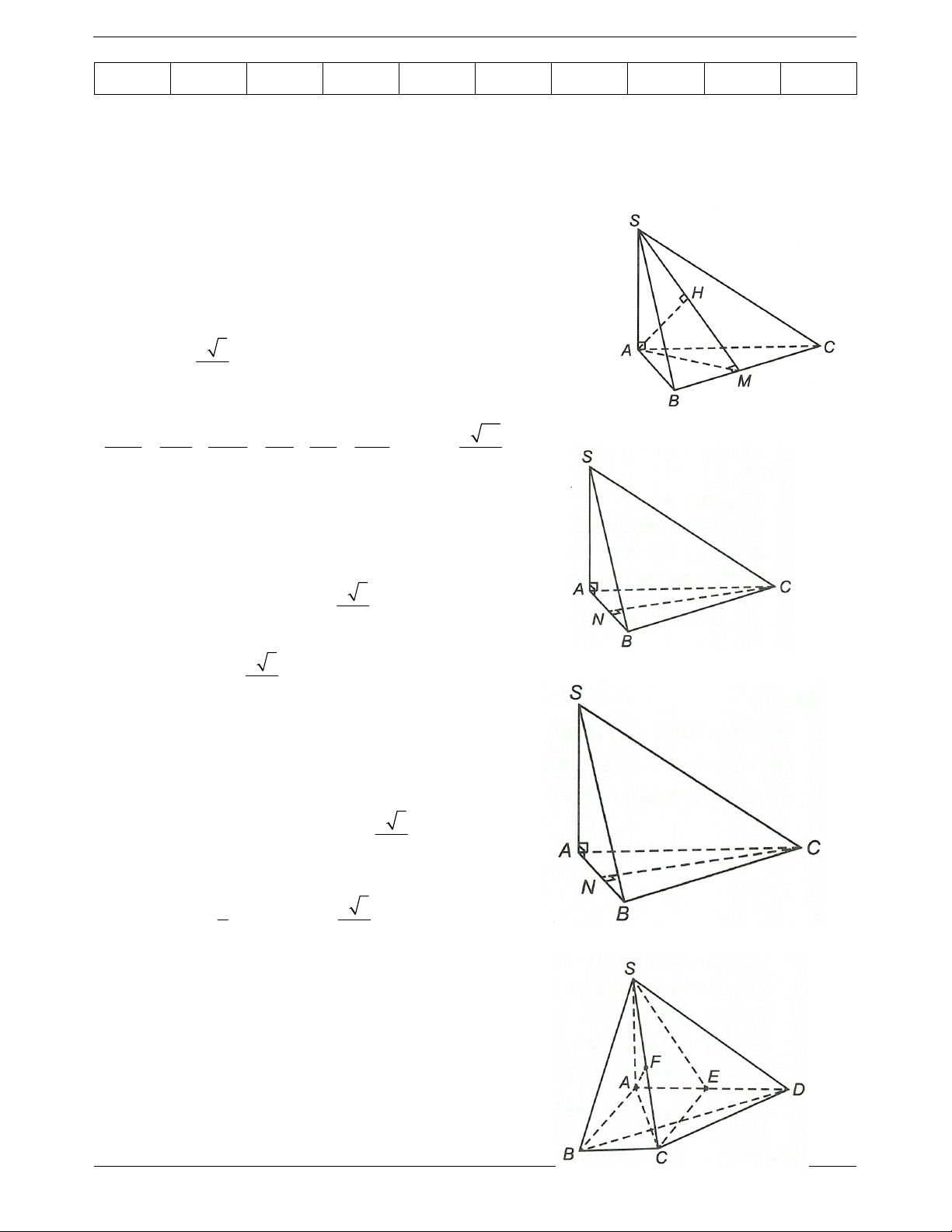
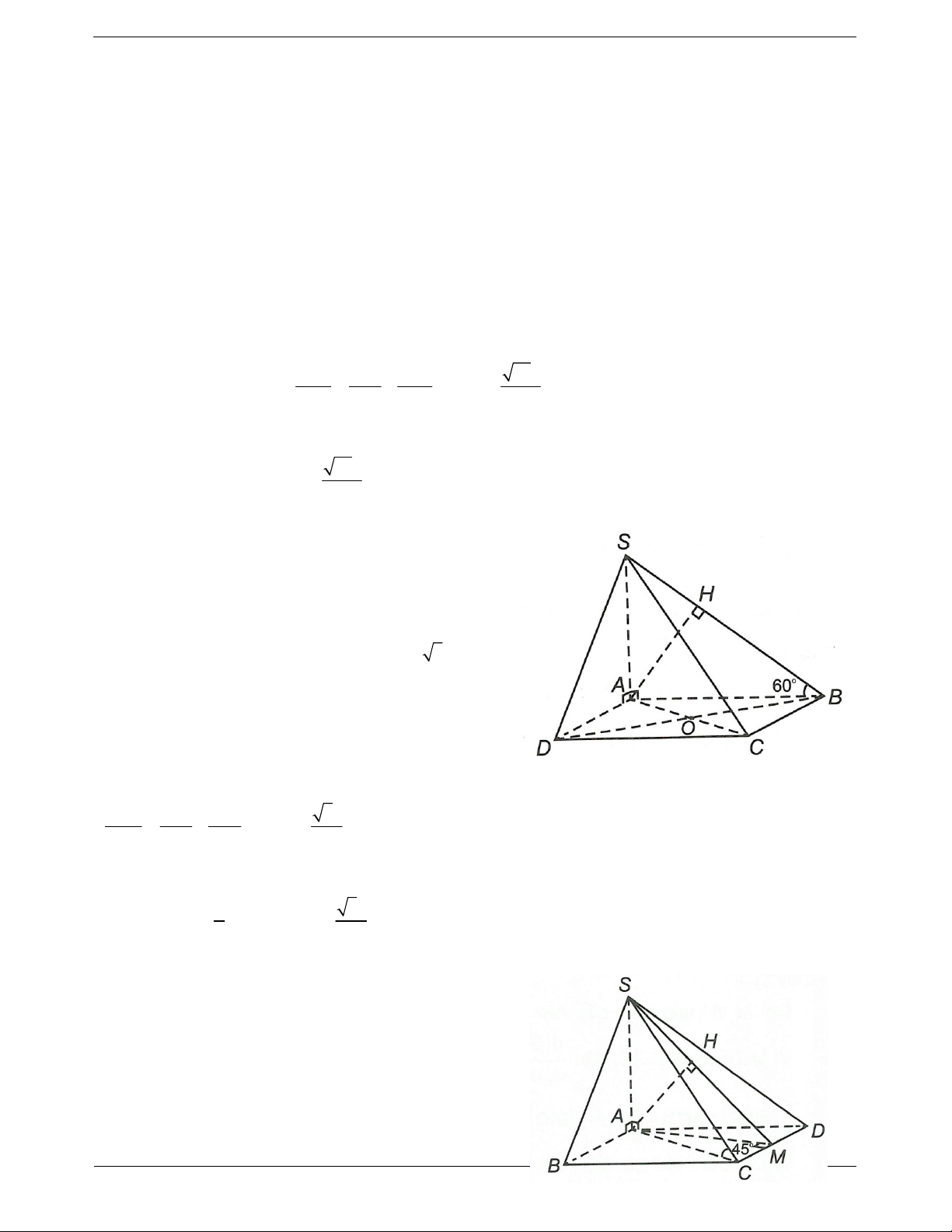
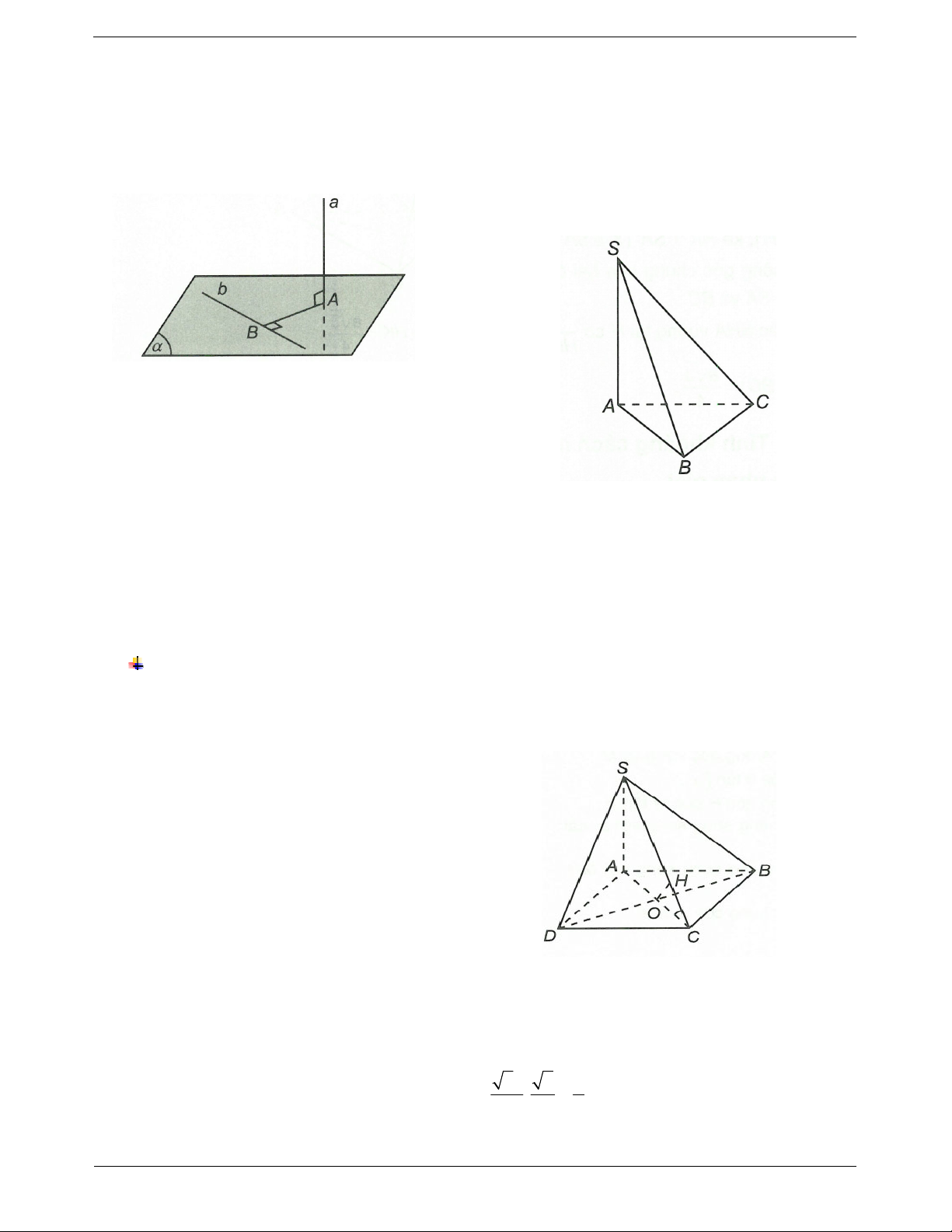
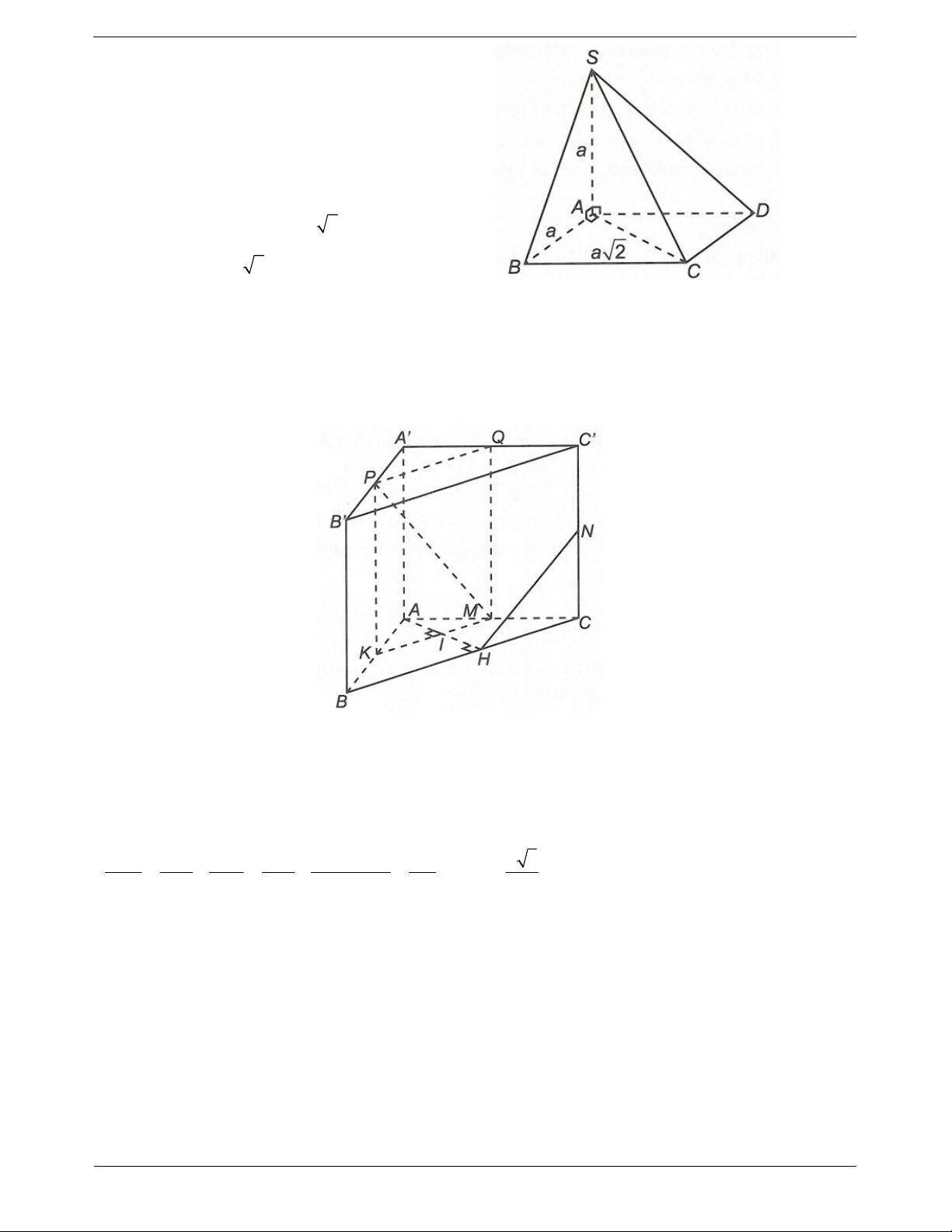
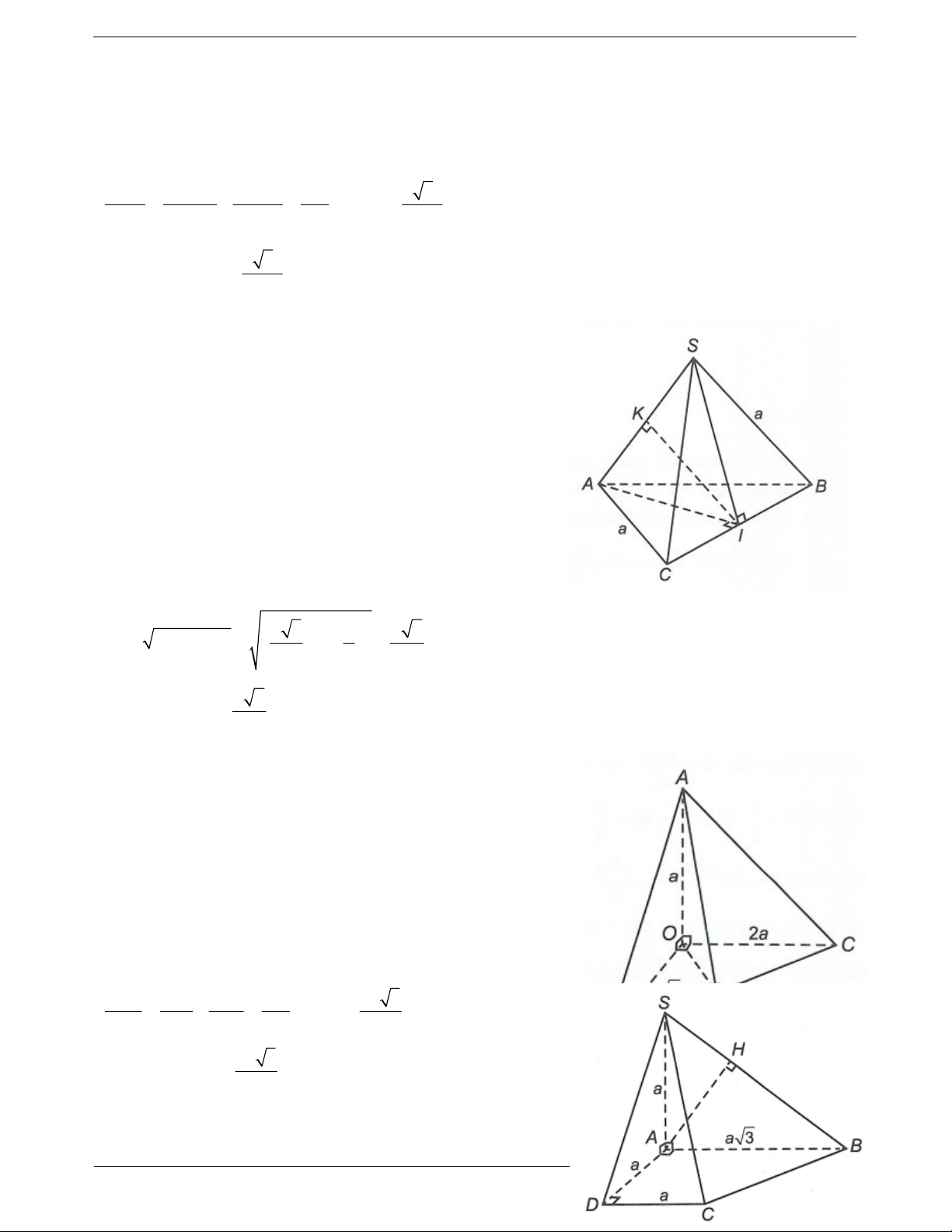
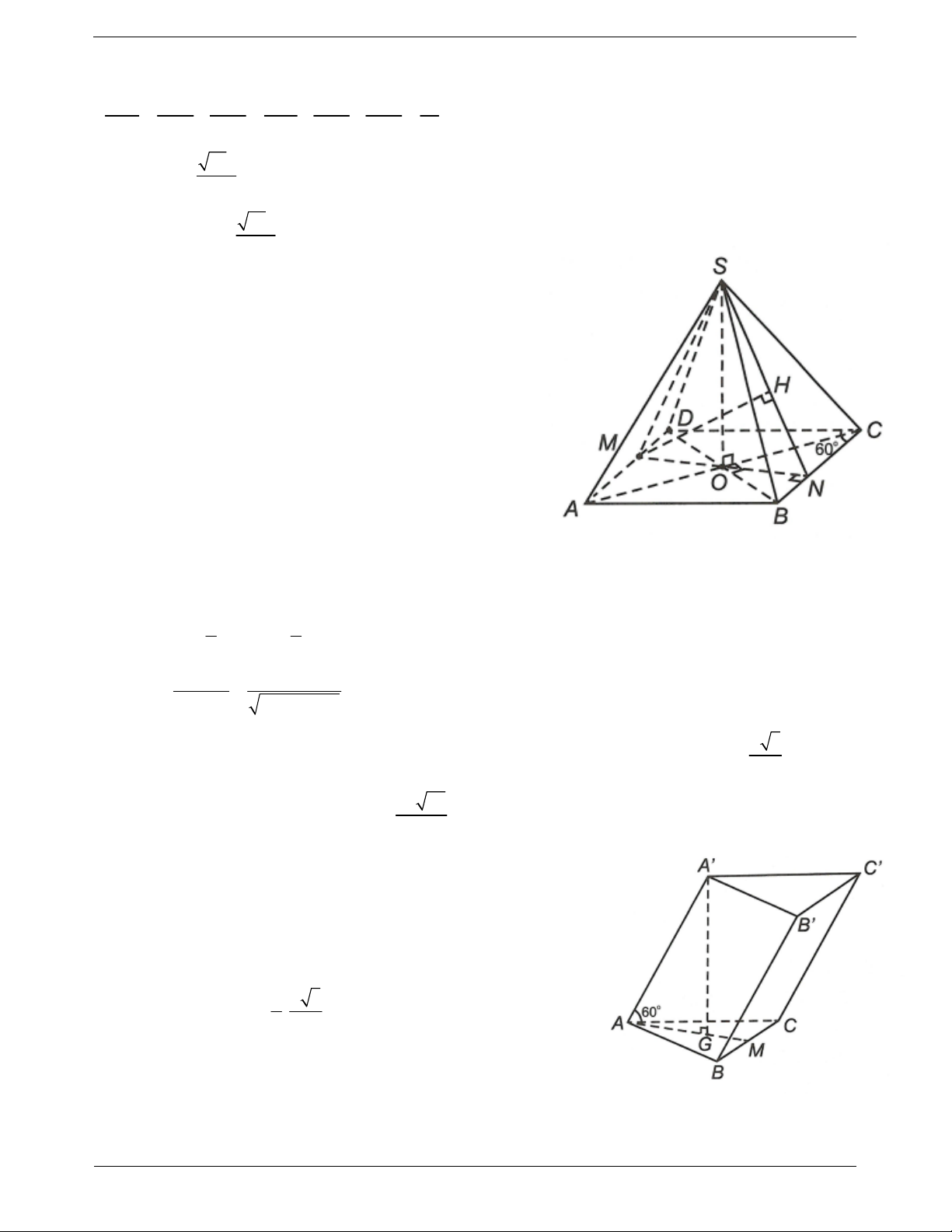
Bài toán: Xác định khoảng cách từ điểm O đến Ví dụ. Khối chóp S.ABC có đáy là tam giác vuông
mặt phẳng P .
cân tại B và AB a, SA ABC . Góc giữa cạnh
bên SB và mặt phẳng ABC bằng 60O . Tính
khoảng cách từ A đến SBC. Hướng dẫn giải
Ta có AH SB; AH BC AH SBC
Bước 1. Xác định hình chiếu H của O trên .
AH d . A SBC.
+) Dựng mặt phẳng P chứa O và vuông góc với .
+) Tìm giao tuyến của P và .
+) Kẻ OH H . Khi đó d ;
O OH. Bước 2. Tính OH.
Tam giác SAB vuông tại A nên
Lưu ý: Tính chất của tứ diện vuông. 1 1 1 a 3 AH 2 2 2
Giả sử OABC là tứ diện vuông tại O. AH SA AB 2 OA ;
OB OB OC;OC OA và H là hình chiếu
của O trên mặt phẳng ABC . 1 1 1 1 Khi đó ta có . 2 2 2 2 OH OA OB OC TOANMATH.com Trang 4 Ví dụ mẫu
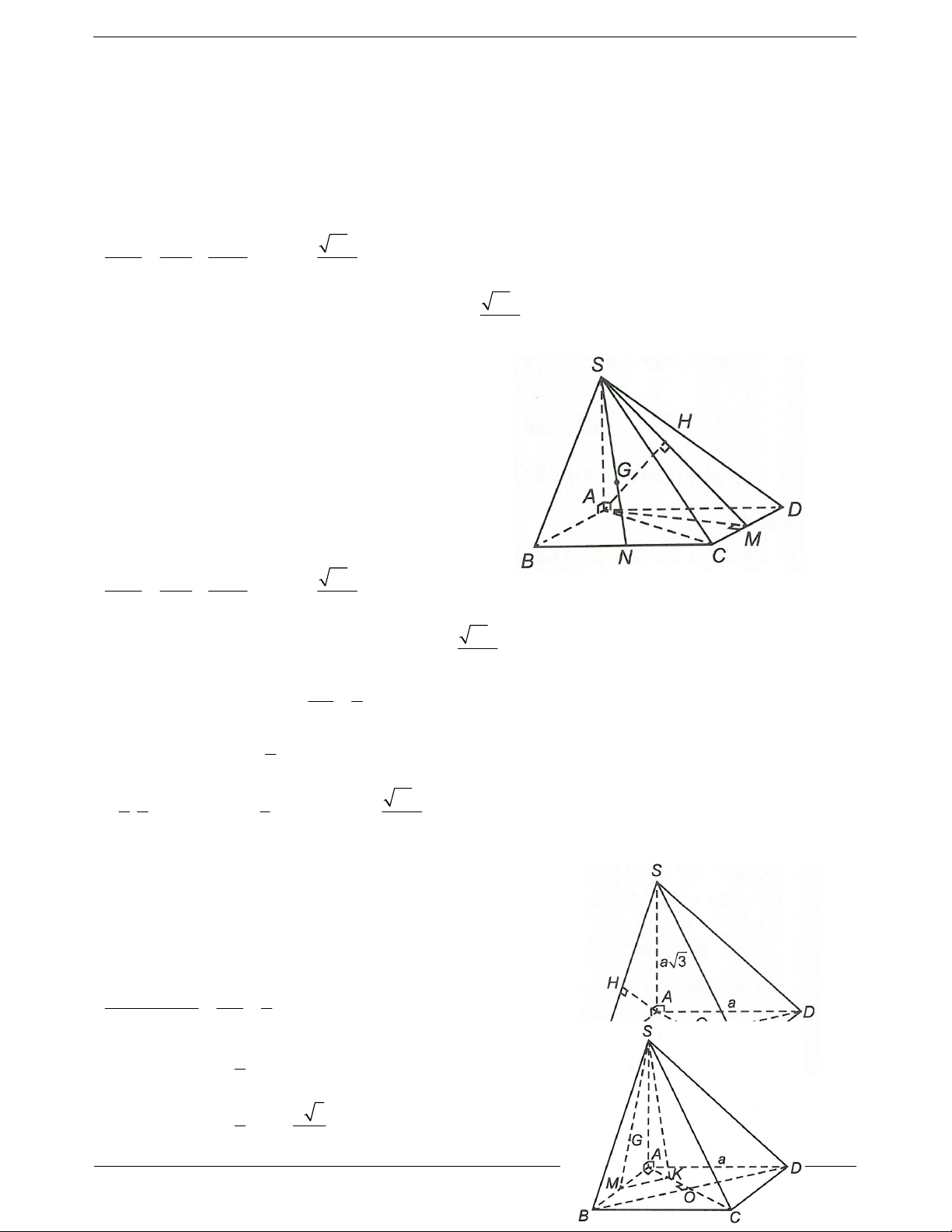
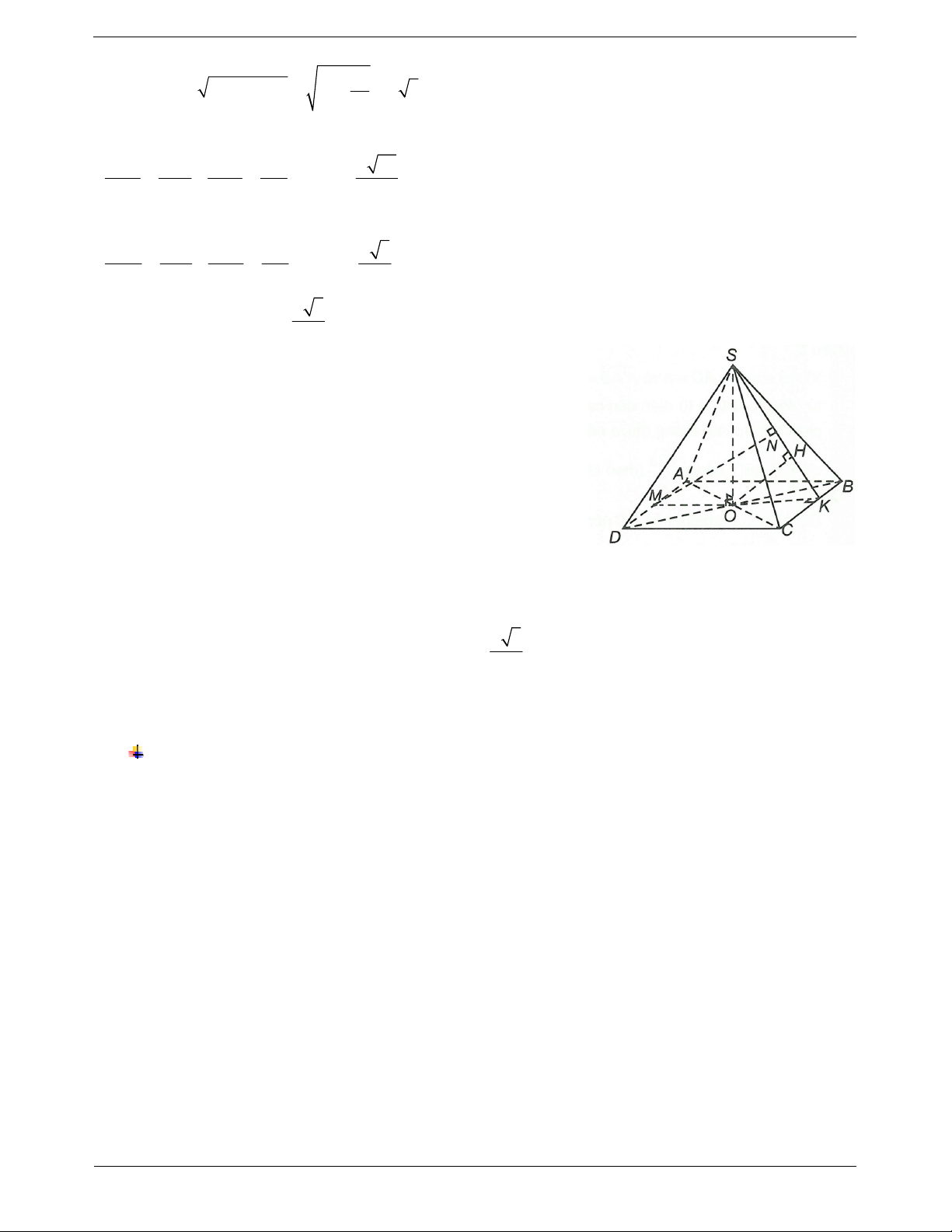
Ví dụ 1. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a,cạnh bên SA vuông góc với đáy. Biết
khối chóp S.ABC có thể tích bằng 3
a . Tính khoảng cách từ điểm A đến mặt phẳng SBC . Hướng dẫn giải
Gọi I, K lần lượt là hình chiếu vuông góc của A trên BC và SI.
Ta có AI BC; SA BC AK SBC
AK d , A SBC. 2 a 3 Ta có 3
V a ; S
SA 4a 3. ABC 4
Trong tam giác vuông SAI, ta có 1 1 1 4a 195 AK . 2 2 2 AK SA AI 65
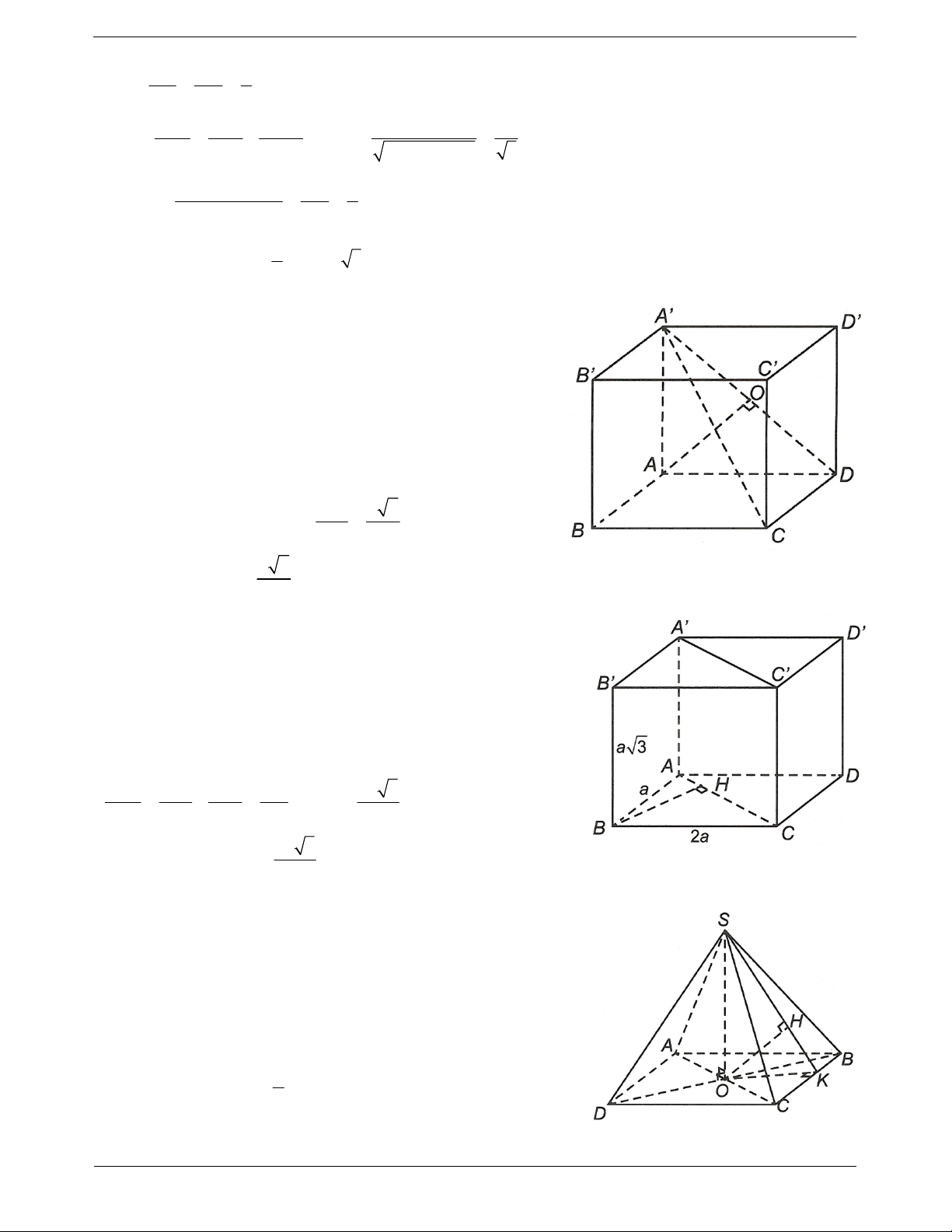
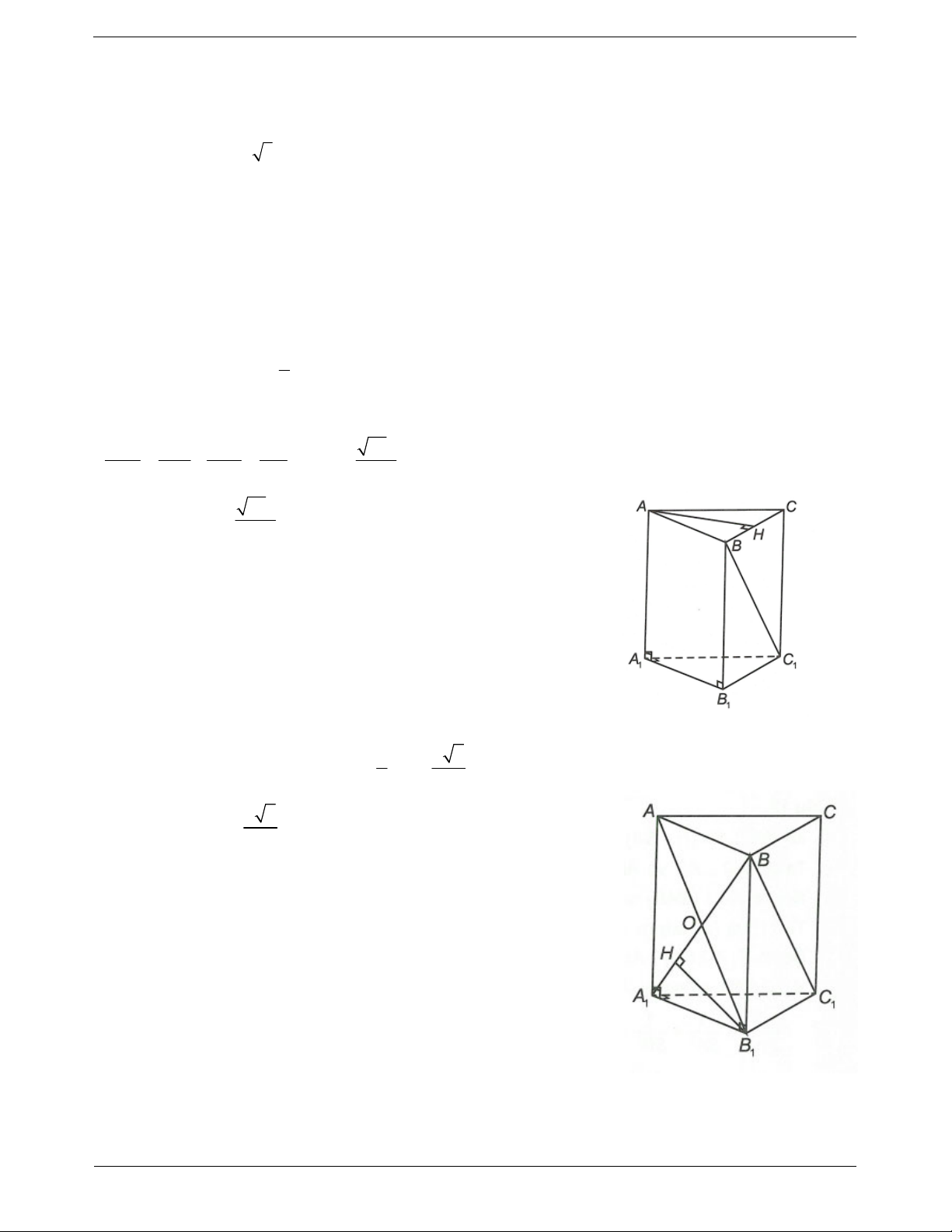
Ví dụ 2. Cho hình lăng trụ A .
BCD A' B 'C ' D ' có đáy là hình chữ nhật với AD a 3 . Tam giác A' AC
vuông cân tại A’ và thuộc mặt phẳng vuông góc với đáy. Biết rằng A' A a 2 . Tính khoảng cách từ D’
đến mặt phẳng A' ACC ' Hướng dẫn giải
Trong A' AC , kẻ A' I AC.
Vì A' AC ABCD và A' AC ABCD AC nên A' I ABCD.
Vì DD ' AA' nên DD ' A' ACC ' d D ', A' AC d D, A' AC Kẻ DH AC.
Ta có AC A' A 2 2a CD . a a
Suy ra d D A AC 3 , ' DH . 2
Bài tập tự luyện dạng 1
Câu 1: Mệnh đề nào sau đây đúng? TOANMATH.com Trang 5
A. Khoảng cách từ một điểm A bất kì đến mặt phẳng P bằng độ dài đoạn AH với H là một điểm bất
kì trên mặt phẳng P .
B. Khoảng cách từ một điểm A bất kì đến mặt phẳng P bằng độ dài đoạn AH với AH P .
C. Khoảng cách từ một điểm A bất kì đến mặt phẳng P là độ dài nhỏ nhất của đoạn AH.
D. Khoảng cách từ một điểm A bất kì đến mặt phẳng P bằng độ dài đoạn AH với H là hình chiếu
vuông góc của A trên P .
Câu 2: Cho hình chóp S.ABC có SA vuông góc với mặt phẳng ABC , ABC là tam giác đều cạnh a,
SA 2a . Khoảng cách từ A đến mặt phẳng SBC bằng 57a 57a 2 57a 57a A. B. C. D. 3 6 3 12
Câu 3: Cho hình chóp S.ABC có SA vuông góc với mặt phẳng ABC, AB
C là tam giác đều cạnh
bằng a, SA 2a . Khoảng cách từ C đến mặt phẳng SAB bằng 3a 3a
A. a B. 2a C. D. 3 2
Câu 4: Cho hình chóp S.ABC có SA vuông góc với mặt phẳng ABC,ABC là tam giác đều cạnh
bằng a, SA 2a . Gọi M là trung điểm BC. Khoảng cách từ M đến mặt phẳng SAB bằng a 3a 3a
A. B. a C. D. 2 4 2
Câu 5: Cho hình chóp S.ABCD có đáy ABCD là hình thang, 90o ABC BAD
, BA BC a; AD 2a .
Cạnh bên SA vuông góc với đáy. Góc tạo bởi giữa SC và SAD bằng 30o . Khoảng cách từ A đến SCD bằng a
A. a B. a 2 C. D. a 3 2
Câu 6: Cho hình chóp S.ABC có SA vuông góc với mặt phẳng ABC,ABC là tam giác đều cạnh
bằng a, SA 2a . Gọi G là trọng tâm ABC . Khoảng cách từ G đến mặt phẳng SBC bằng 57a 57a 2 57a 57a A. B. C. D. 3 6 9 18
Câu 7: Cho hình chóp S.ABCD có đáy là hình bình hành với 2, 60o BC a ABC . Tam giác SAB
nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Khoảng cách từ điểm D đến mặt phẳng SAB bằng a 6 a 2 2a 6 A. B.
C. a 2 D. 2 2 3
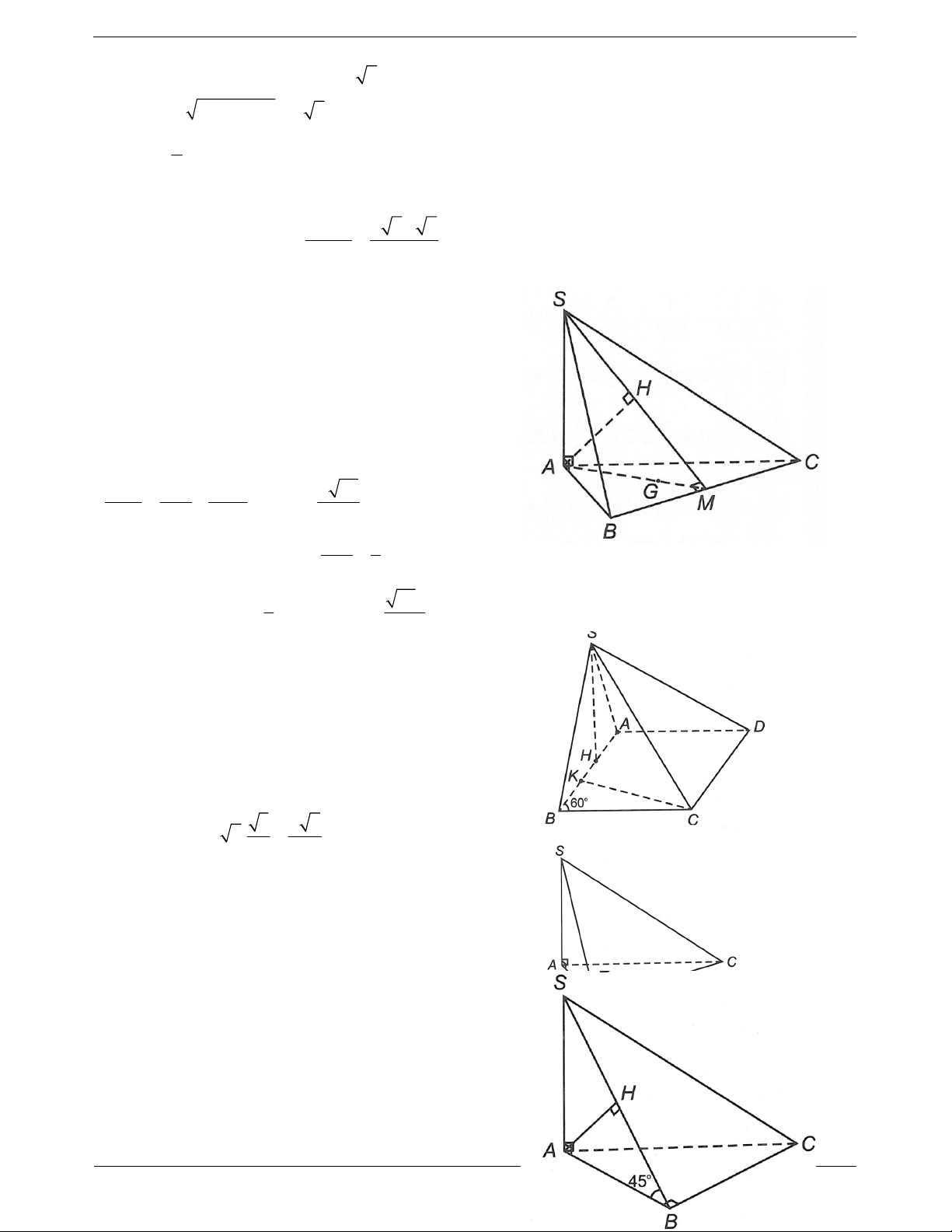
Câu 8: Cho hình chóp S.ABC có SA vuông góc với mặt phẳng ABC, ABC
là tam giác vuông tại B,
BC 2a . Khoảng cách từ C đến mặt phẳng SAB bằng TOANMATH.com Trang 6 3a 3a A. a B.
C. 2a D. 2 4
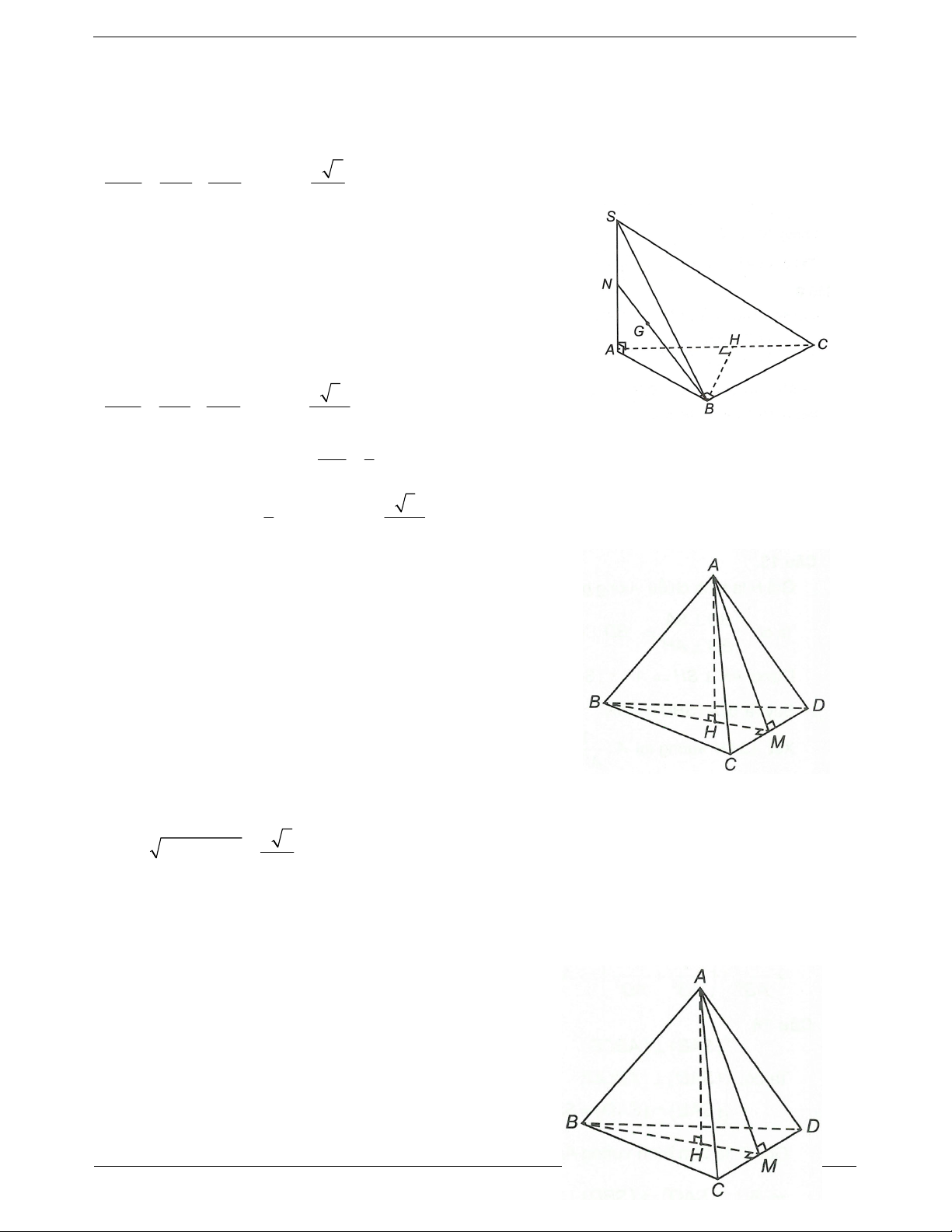
Câu 9: Cho hình chóp S.ABC có SA vuông góc với mặt phẳng ABC, ABC
là tam giác vuông tại B,
AB a, BC 2a . Biết góc giữa đường thẳng SB và mặt phẳng ABC bằng 45o . Khoảng cách từ A đến
mặt phẳng SBC bằng a 2 a 3 a 3 a 6 A. B. C. D. 2 2 3 3
Câu 10: Cho hình chóp S.ABC có SA vuông góc với mặt phẳng ABC, ABC
là tam giác vuông tại B,
AB a, BC 2a, SA a . Gọi G là trọng tâm tam giác SAB. Khoảng cách từ G đến mặt phẳng SAC bằng 2 5a 2 5a 4 5a 6 5a A. B. C. D. 5 15 15 5
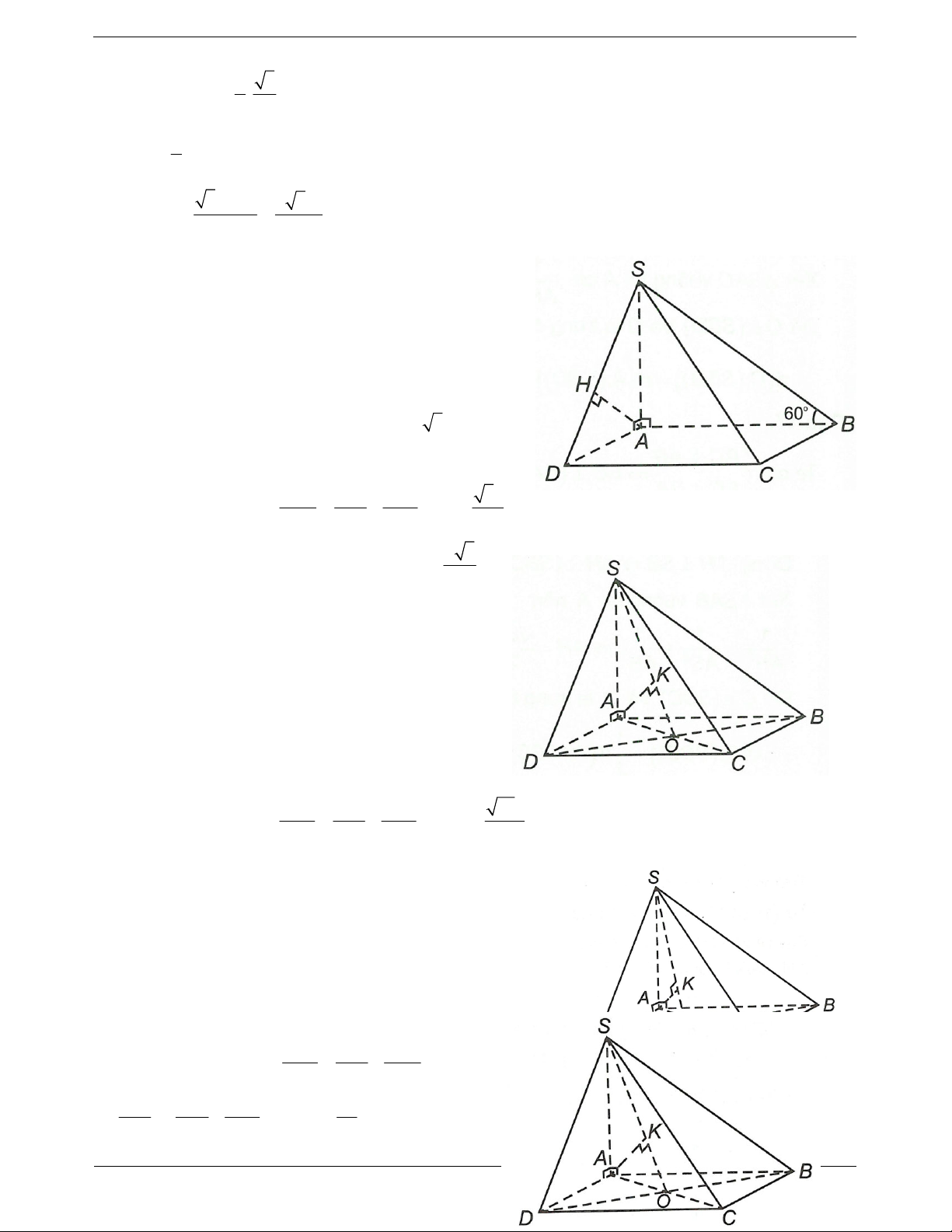
Câu 11: Cho tứ diện đều ABCD có cạnh bằng a. Khoảng cách từ A đến mặt phẳng BCD bằng a 6 a 3 2a 6 a 6 A. B. C. D. 2 3 3 3
Câu 12: Cho tứ diện đều ABCD, biết khoảng cách A đến mặt phẳng BCD bằng a 6 . Diện tích tam giác ABC bằng 2 9 3a 2 3 3a 2 7 3a 2 9 3a A. B. C. D. 4 4 4 2
Câu 13: Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng ABCD , ABCD là hình vuông cạnh
a. Biết góc giữa đường thẳng SB và mặt phẳng ABCD bằng 60o . Khoảng cách từ B đến mặt phẳng SCD bằng 3a 3a 3a A. B.
C. a D. 4 2 6
Câu 14: Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng ABCD , ABCD là hình vuông cạnh
a, SA a 3 . Khoảng cách từ A đến mặt phẳng SBD bằng 3a 2a 21a 21a A. B. C. D. 4 2 3 7
Câu 15: Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng ABCD , ABCD là hình chữ nhật với
AB = a, BC= 2a, SA=3a. Khoảng cách từ A đến mặt phẳng (SBD) bằng 6a 3 21a 5a 21a A. B. C. D. 7 7 7 7 TOANMATH.com Trang 7
Câu 16: Cho hình chóp S.ABCD có SAB và SAD cùng vuông góc với mặt phẳng ABCD ,
ABCD là hình vuông cạnh a, SA a 3 . Khoảng cách từ C đến mặt phẳng SBD bằng 3a 2a 21a 21a A. B. C. D. 4 2 3 7
Câu 17: Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng ABCD , ABCD là hình vuông tâm
O có cạnh a. Biết góc giữa hai mặt phẳng SBC và ABCD bằng 60o . Khoảng cách từ O đến mặt
phẳng SBC bằng 3a 3a 3a A. B.
C. a D. 4 2 6
Câu 18: Cho hình chóp S.ABCD có SAB và SAD cùng vuông góc với mặt phẳng ABCD , ABCD
là hình thoi cạnh a, 120o BAD
, biết SC hợp với đáy một góc 45o . Khoảng cách từ B đến mặt phẳng SCD bằng 3a 2a 21a 21a A. B. C. D. 4 2 3 7
Câu 19: Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng ABCD, SA a, ABCD là hình thoi cạnh a, 60o ABC
. Gọi G là trọng tâm tam giác SBC. Khoảng cách từ G đến mặt phẳng SCD bằng 3 21a 2 21a 21a 21a A. B. C. D. 7 7 21 7
Câu 20: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh bằng a, SA ABCD và
SA a 3 . Khoảng cách từ điểm O đến mặt phẳng SBC bằng a 3 a 3 a 2 A. B. C. D. a 2 4 2
Câu 21: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh bằng a, SA ABCD và
SA a 3 . Khoảng cách từ trong tâm G của SAB đến mặt phẳng SAC bằng a a 2 a 2 a 2 A. B. C. D. 2 4 6 3
Câu 22: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C, SA ABCD, AC a và
AB a 3 . Khoảng cách từ điểm C đến mặt phẳng SAB bằng a 3 a 6
A. a 2 B. a C. D. 2 3
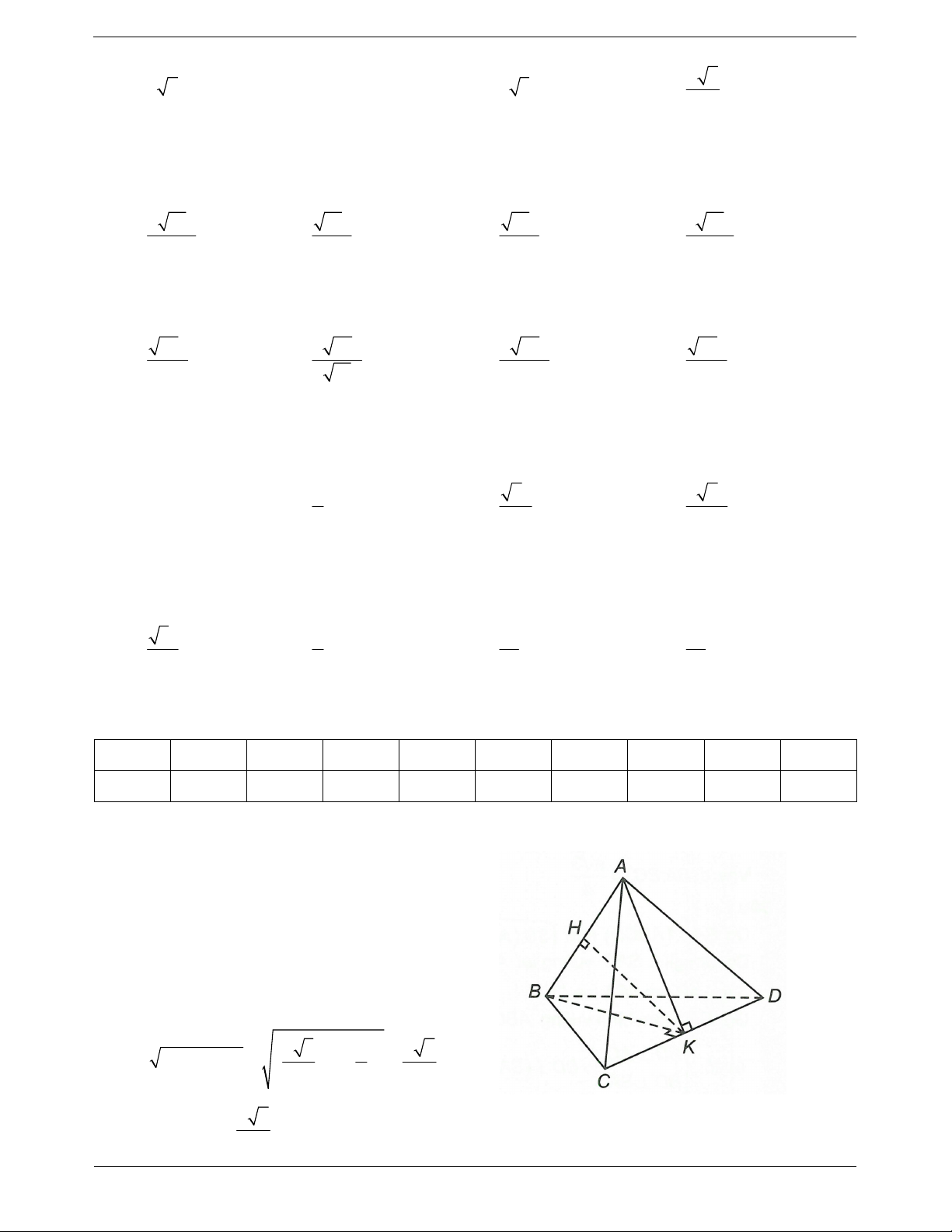
Câu 23: Cho tứ diện ABCD có AB, AC, AD đôi một vuông góc với nhau, AB a, AC b, AD c .
Khoảng cách từ điểm A đến mặt phẳng BCD bằng TOANMATH.com Trang 8 1 1 1 1 1 A. B. C. 2 2 2
a b c D. 1 1 1 2 2 2 a b c 2 2 2
a b c 2 2 2 a b c
Câu 24: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB a, BC a 3, SA ABCD. Góc
giữa SC và mặt đáy bằng 45o . Khoảng cách từ điểm A đến mặt phẳng SCD bằng a 21 2a 21
A. a 2 B. C. D. a 3 6 7
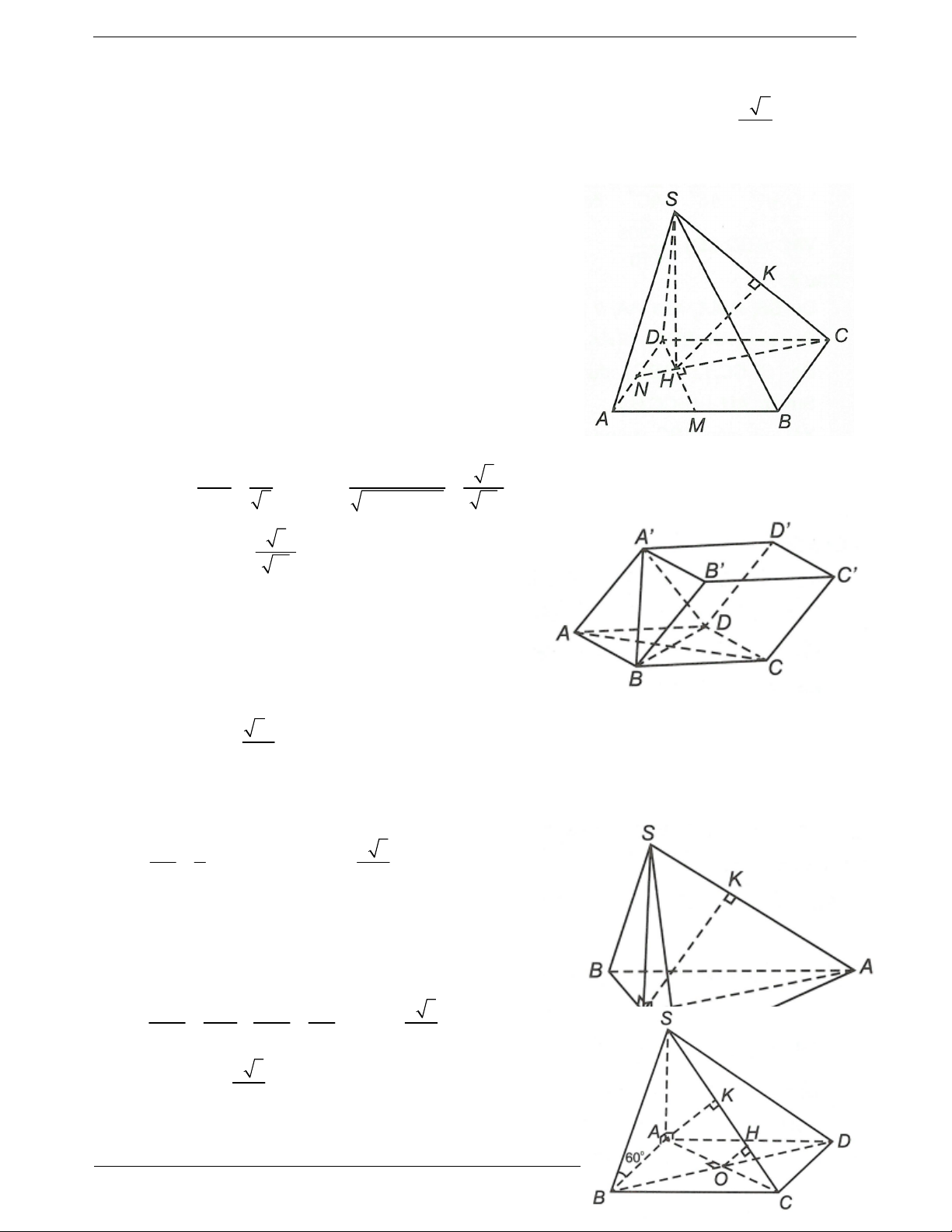
Câu 25: Cho hình chóp S.ABC có đáy ABCD là tam giác đều cạnh a. Cạnh bên SB vuông góc mặt
phẳng ABC và SB 2a . Gọi M là trung điểm của cạnh BC. Khoảng cách từ điểm B đến mặt phẳng SAM bằng a 5 a 2a 17 A.
B. C. a 5 D. 5 2 17
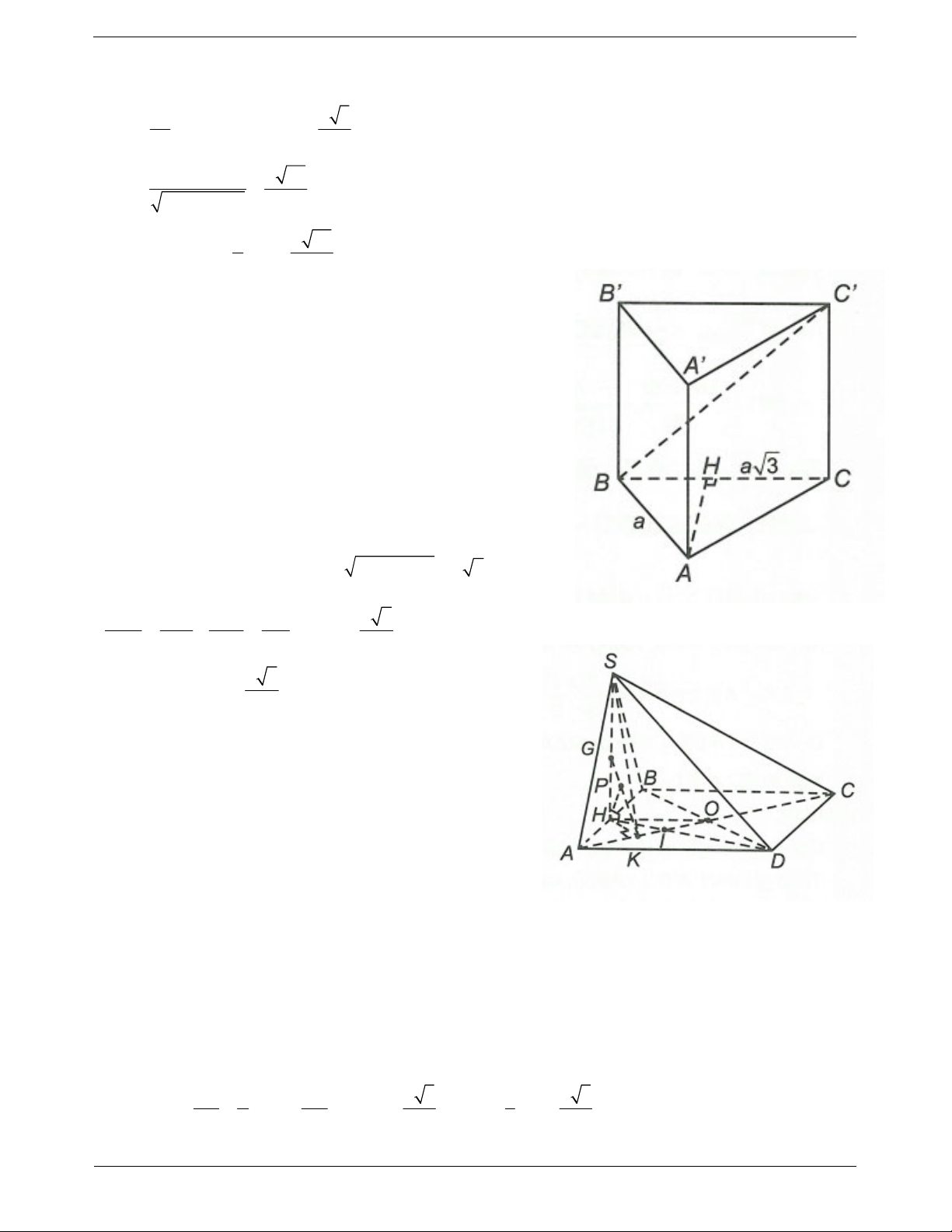
Câu 26: Cho lăng trụ ABC.A' B 'C ' có đáy là tam giác vuông cân tại A với AB AC 3a . Hình chiếu
vuông góc của B ' lên mặt đáy là điểm H thuộc BC sao cho HC 2HB . Biết cạnh bên của lăng trụ bằng
2a. Khoảng cách từ B đến mặt phẳng B ' AC bằng 2a 3a 3 a A.
B. a 3 C. D. 3 2 2
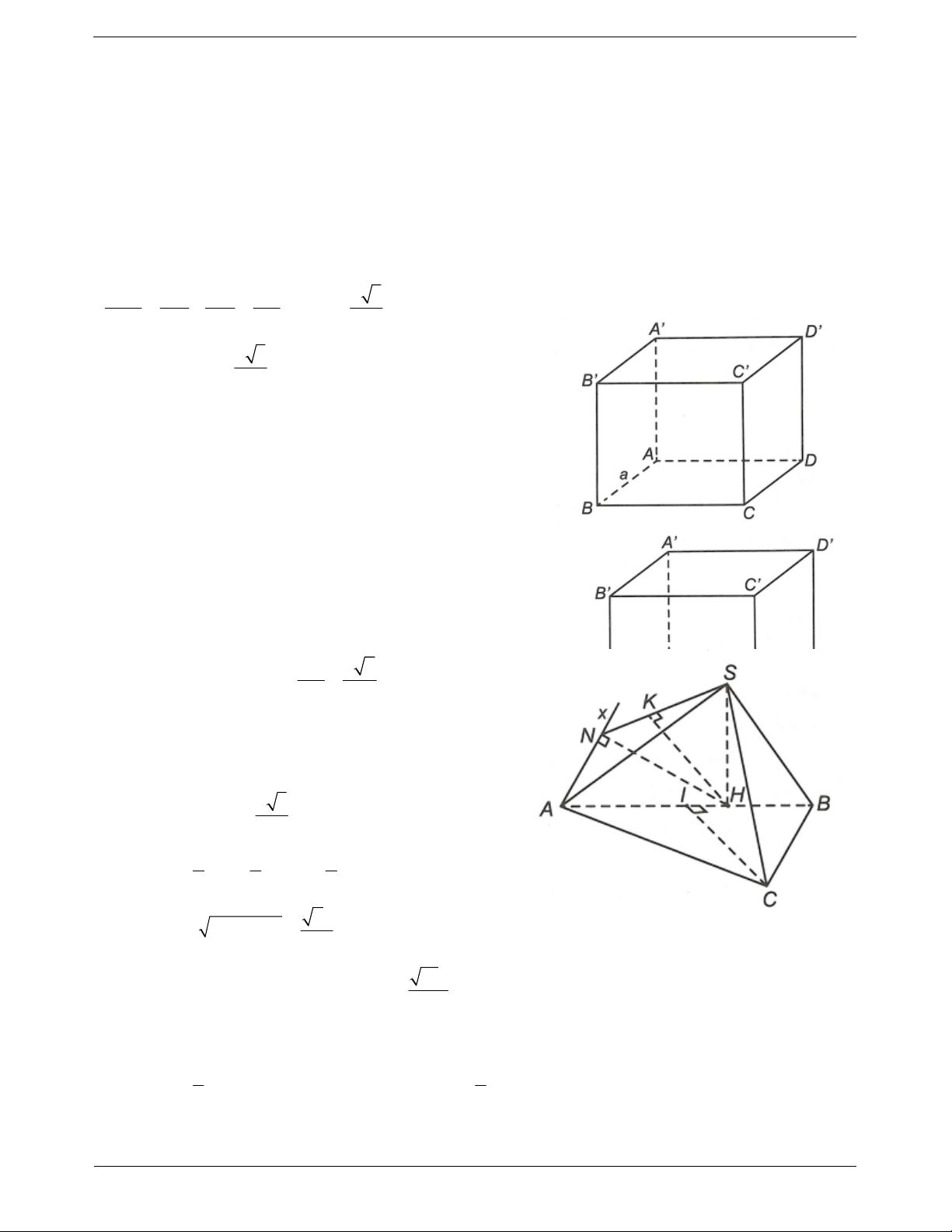
Câu 27: Cho hình lập phương A .
BCD A' B 'C ' có cạnh bằng a. Khoảng cách từ điểm B đến mặt phẳng
A'CD bằng a 3 a a 2
A. a 2 B. C. D. 2 2 2
Câu 28: Cho hình hộp chữ nhật A .
BCD A' B 'C ' D ' có AB a, BC 2a, BB ' a 3 . Khoảng cách từ
điểm B đến mặt phẳng ACC ' A' bằng a 5 2a 5 A.
B. a C. D. 2a 2 5
Câu 29: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, cạnh bằng , 60o a BAD
, SO ABCD, SO a . Khoảng cách từ điểm O đến mặt phẳng SBC bằng a a 3 a 3 a 39 A. B. C. D. 2 4 2 13
Câu 30: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, cạnh bằng , 60o a BAD
, SO ABCD, SO a . Khoảng cách từ đường thẳng AD đến mặt phẳng SBC bằng a a 3 a 3 a 39 A. B. C. D. 2 4 2 13
ĐÁP ÁN VÀ LỜI GIẢI BẢI TẬP TỰ LUYỆN
1-D 2-B 3-D 4-C 5-A 6-D 7-A 8-C 9-A 10-B
11-D 12-A 13-B 14-D 15-A 16-D 17-A 18-D 19-C 20-B TOANMATH.com Trang 9
21-C 22-D 23-A 24-C 25-D 26-B 27-D 28-C 29-B 30-C Lời giải chi tiết Câu 2.
Gọi M là trung điểm BC, H là hình chiếu vuông góc của A trên SM BC AM Ta có:
BC SAM SBC SAM . BC SA
AH SBC d ;
A SBC AH. a 3 Ta có AM . 2
Xét SAM vuông tại A có 1 1 1 1 4 19 a 57 AH . 2 2 2 2 2 2 AH AS AM 4a 3a 12a 6 Câu 3.
Do SA ABC SAB ABC.
Dựng CN AB CN SAB d C;SAB CN. a 3
Do ABC đều cạnh a nên CN . 2 a
Vậy d C SAB 3 ; . 2 Câu 4.
Do SA ABC SAB ABC.
Dựng CN AB CN SAB d C;SAB CN. a 3
Do ABC đều cạnh bằng a nên CN . 2
Do M là trung điểm BC nên
d M SAB 1
d C SAB a 3 ; ; . 2 4 Câu 5.
Gọi E là trung điểm AD.
Khi đó ABCE là hình vuông cạnh a. Suy ra CE AD .
Lại có CE SA . Do đó , 30 .o CE SAD CSE SC SAD Lại có: .sin 30o SC
CE a SC 2 . a TOANMATH.com Trang 10
ABC vuông cân tại B nên AC a 2. Ta có 2 2
SA SC AC a 2. 1
Do CE AD nên ACD vuông tại C AC C . D 2
Dựng AF SC. SA SC a a
Ta có: d A SCD . 2. 2 , AF . a SC 2a Câu 6.
Gọi M là trung điểm BC, H là hình chiếu vuông góc của A trêm SM. BC AM Ta có:
BC SAM SBC SAM . BC SA
AH SBC d ;
A SBC AH.
Xét SAM vuông tại A có 1 1 1 a 57 AH . 2 2 2 AH AS AM 6 GM 1
Do G là trọng tâm ABC nên . MA 3 1 57a
Suy ra d G;SBC d ;
A SBC . 3 18 Câu 7. Dựng SH . AB
Do SAB ABCD nên SH ABCD.
Dựng CK AB . Vì CK SH nên CK SAB.
Do CD AB nên d D,SAB d C,SAB CK a o 3 6
BC sin 60 a 2. . 2 2 Câu 8.
Do SA ABC nên SAB ABC.
Mặt khác do BC AB BC SAB.
Suy ra d C;SAB CB 2 . a Câu 9.
Do SA ABC nên AB là hình chiếu vuông góc của SB trên ; 45 .o ABC SB ABC SBA
Vậy SAB vuông cân tại A SA AB . a TOANMATH.com Trang 11
Dựng AH SB , ta có:
SAB SBC AH SBC d ;
A SBC AH.
Xét SAB vuông tại A nên 1 1 1 a 2 AH . 2 2 2 AH AS AB 2 Câu 10.
Do SA ABC nên SAC ABC.
Trong mặt phẳng ABC , dựng BH AC.
Ta có BH SAC . Suy ra d B;SAC BH .
Xét ABC vuông tại B nên 1 1 1 2 5a BH . 2 2 2 BH BA BC 5 NG 1
Do G là trọng tâm SAB nên . NB 3 1 2 5a
Suy ra d G;SBC d ;
A SBC . 3 15 Câu 11.
Gọi M là trung điểm CD và H là hình chiếu vuông góc của A trên BM. CD AM Ta có:
CD ABM CD AH 1 . CD BM
Tương tự, ta chứng minh được BC AH 2. Tự
1 và 2 suy ra AH BCD. Suy ra d ;
A BCD AH và H là trọng tâm B . CD Xét A
BH vuông tại H có a 6 2 2
AH AB BH . 3
Nhận xét: Trong tứ diện đều, hình chiếu vuông góc của một đỉnh trên mặt phẳng đối diện là trực tâm
(trọng tâm) của mặt đó. Câu 12.
Gọi M là trung điểm CD và H là hình chiếu vuông góc của A trên BM.
Áp dụng kết quả câu 11, ta có d ;
A BCD AH và H là trọng tâm B . CD Xét A
BH vuông tại H: 2 2 2
AH AB BH TOANMATH.com Trang 12 2 2 3 2 2
AH AB . AB 3 2 2 2 2
6a AB AB 3 . a 3 a2 2 3 3 9 3a Vậy S . AB C 4 4 Câu 13.
Do SA ABCD nên AB là hình chiếu vuông góc của SB
trên mặt phẳng ABCD SB ABCD ; S . BA BC SA Ta có:
BC SAB SAB SBC. BC AB
Xét SAB vuông tại
A : SA AB tan SBA a 3.
Dựng AH SD AH SCD d ;
A SCD AH. 1 1 1 3a
Xét SAD vuông tại A : AH . 2 2 2 AH AS AD 2 a
Do AB CD nên d B SCD d A SCD 3 ; ; . 2 Câu 14. BD OA
Gọi O là tâm hình vuông ABCD BD SA
BD SAO SBD SAO.
Dựng AK SO AK SBD. Suy ra d ;
A SBD AK. 1 1 1 21a Xét SAO vuông tại A : AK . 2 2 2 AK AS AO 7 Câu 15.
Gọi H là hình chiếu vuông góc của A trên BD. BD SA Ta có:
BD SAH SBD SAH . BD AH
Dựng AK SH AK SBD. Suy ra d ;
A SBD AK. 1 1 1
Xét SAH vuông tại A : 2 2 2 AK AS AH 1 1 1 6a AK . 2 2 2 AS AB AD 7 TOANMATH.com Trang 13 Câu 16.
SAB ABCD
Ta có: SAD ABCD SA ABCD.
SAB(SAD) SA BD OA
Gọi O là tâm hình vuông ABCD BD SA
BD SAO SBD SAO.
Dựng AK SO AK SBD. Suy ra d ;
A SBD AK. 1 1 1 21a
Xét SAO vuông tại A có AK . 2 2 2 AK AS AO 7
Do O SBD và O là trung điểm AC nên
SBD d A SBD 21a d C; ; . 7 Câu 17. BC AB Ta có:
BC SAB BC S . B BC SA
Suy ra SBC ABCD ; S . BA
Xét SAB vuông tại
A : SA AB tan SBA a 3.
Vì BC SAB nên SAB SBC. Dựng
AH SB AH SBC d ;
A SBC AH.
Xét SAB vuông tại A nên 1 1 1 3a AH . 2 2 2 AH AS AB 2
Do C SBC và O là trung điểm AC nên
O SBC 1
d A SBC 3a d ; ; . 2 4 Câu 18.
SAB ABCD
Ta có: SAD ABCD
SA ABCD.
SAB SAD SA
Tam giác ABC cân tại B và 60 .o BAC Suy ra A BC, ACD đều. TOANMATH.com Trang 14 Vậy ; 45o SC ABCD SCA
SA AC . a CD AM
Gọi M là trung điểm của CD
CD SAM . CD SA
Dựng AH SM AH SCD d ;
A SCD AH.
Xét SAM vuông tại A: 1 1 1 21a AH . 2 2 2 AH AS AM 7 a
Do AB / / SCD nên d B SCD d A SCD 21 ; ; . 7 Câu 19. A
BC cân tại B và 60o ABC AB C, A CD đều.
Gọi M là trung điểm CD CD AM .
Mà CD SA nên CD SAM . Dựng
AH SM AH SCD d ;
A SCD AH.
Xét SAM vuông tại A: 1 1 1 21a AH . 2 2 2 AH AS AM 7 a
Do AB SCD d B SCD d A SCD 21 ; ; . 7 GS 2
Gọi N là trung điểm BC nên . NS 3 2
Suy ra d G;SCD d N;SCD 3 2 1 1 21 . ; ; a d B SCD d A SCD . 3 2 3 21 Câu 20.
Ta có SAB BC SAB SBC theo giao tuyến SB.
Kẻ AH SB nên d ,
A SBC AH.
Vì OA SBC C nên
d O,SBC CO 1 d ,
A SBC CA 2
d O SBC 1 , d , A SBC 2
d O SBC 1 a 3 , AH . 2 4 TOANMATH.com Trang 15 Câu 21.
Gọi M là trung điểm của AB.
d G,SAC GS 2
Vì MG SAC S nên
d M ,SAC MS 3
d G SAC 2 ,
d M ,SAC. 3
Ta có: BO AC và BO SA BO SAC.
Mặt khác: BM SAC A . Suy ra:
d M SAC 1
d B SAC 1 a 2 , , BO 2 2 4
d G SAC 2 a 2 a 2 , . . 3 4 6 Câu 22.
Kẻ CH AB H AB.
Do CH SASA ABC nên CH SAB.
Suy ra d C,SAB CH.
Xét ABC vuông tại C có: 2 2
BC AB AC a 2; 1 1 1 3 . 2 2 2 2 CH AC BC 2a a
Vậy d H SBC 6 , AH . 3 Câu 23.
Kẻ AK BC K BC và AH DK H DK .
Do BC DA do AD ABC nên BC DAK .
Suy ra AH BC. Do AH DK nên
AH BCD d ,
A BCD AH. Xét A
BC vuông tại A có: 1 1 1 1 1 . 2 2 2 2 2 AK AB AC a b Xét A
DK vuông tại A có: 1 1 1 1 1 1 . 2 2 2 2 2 2 AH AK AD a b c TOANMATH.com Trang 16 1 Vậy d ,
A BCD AH . 1 1 1 2 2 2 a b c Câu 24.
Vì SA ABCD nên ; 45 .o SC ABCD SCA
Kẻ AH SD H SD 1 .
Ta có: CD AD và CD . SA
Suy ra CD SAD CD AH 2.
Từ (1) và (2) suy ra AH SCD. Do đó d ,
A SCD AH. Xét A
BC vuông tại B có: 2 2
AC AB BC 2 . a
Xét SAC vuông tại A có: .tan 45o SA AC 2 . a
Xét SAD vuông tại A có: 1 1 1 7 2a 21 AH . 2 2 2 2 AH SA AD 12a 7 a
Vậy d B SCD 2 21 , AH . 7 Câu 25.
Ta có: AM BC ( ABC đều); AM SB do SB ABC
Do đó AM SBC.
Trong mặt phẳng SBM , kẻ BH SM.
Mà BH AM nên BH SAM .
Suy ra d B,SAM BH. Xét SBM vuông tại B có: 1 1 1 1 4 17 2a 17 BH . 2 2 2 2 2 2 BH SB BM 4a a 4a 17 Câu 26.
Ta có: BC 3a 2 HB a 2. Lại có '2 2
B ' H BB HB a 2.
Dựng HE AC; HF B ' E.
Suy ra HF B ' AC d H,B ' AC HF. TOANMATH.com Trang 17 HE CH 2 Ta có HE 2 . a AB BC 3 1 1 1 HE.B ' H 2a Suy ra HF . 2 2 2 2 2 HF HE B ' H
HE B ' H 3
d B,B ' AC BC 3 Mặt khác
d H,B ' AC . HC 2
Do đó d B B AC 3 , '
.HF a 3. 2 Câu 27.
Ta có: ABCD AB A'CD
Khi đó: d B, A'CD d ,
A A'CD
Gọi O là tâm hình vuông ADD ' A'.
Vì CD AA' và CD AD nên CD ADD ' A'.
Suy ra CD AO . Mà AO A' D nên AO A'CD. AD a
Suy ra d A A CD ' 2 , ' AO . 2 2 a
Vậy d B A CD 2 , ' . 2 Câu 28.
Kẻ BH AC H AC.
Lại có BH AA'do '
AA ABCD.
Suy ra BH ACC ' A' d B; ACC ' A' BH. Xét A
BC vuông tại B có: 1 1 1 5 2a 5 BH . 2 2 2 2 BH AB BC 4a 5 a
Vậy d B ACC A 2 5 ; ' ' . 5 Câu 29.
Kẻ OK BC BC SOK .
Trong mặt phẳng SOK :
Kẻ OH SK OH SBC d O,SBC OH. Vì A BD có , 60o AB AD BAD nên A BD đều. a
Suy ra BD a BO . 2 TOANMATH.com Trang 18 2 a Suy ra 2 2 2
AO AB BO a a 3. 4
Trong OBC vuông tại O có: 1 1 1 13 39 a OK . 2 2 2 2 OK OB OC 3a 13
Trong SOK vuông tại O có: 1 1 1 16 a 3 OH . 2 2 2 2 OH OS OK 3a 4 a
Vậy d O SBC 3 , OH . 4 Câu 30.
Kẻ OK BC K BC,OH SK H SK .
Ta có: ADBC AD SBC.
Khi đó d AD,SBC d M ,SBC (với M là giao điểm của AD và OK).
Kẻ MN OH N SK .
Ta có SOK SBC theo giao tuyến SK nên OH SBC.
Suy ra MN SBC. a
Suy ra d AD SBC d M SBC 3 , ,
MN 2OH . 2
Dạng 2: Khoảng cách giữa hai đường thẳng chéo nhau
Bài toán 1. Tính khoảng cách hai đường thẳng chéo nhau a và b trường hợp a b Phương pháp giải TOANMATH.com Trang 19
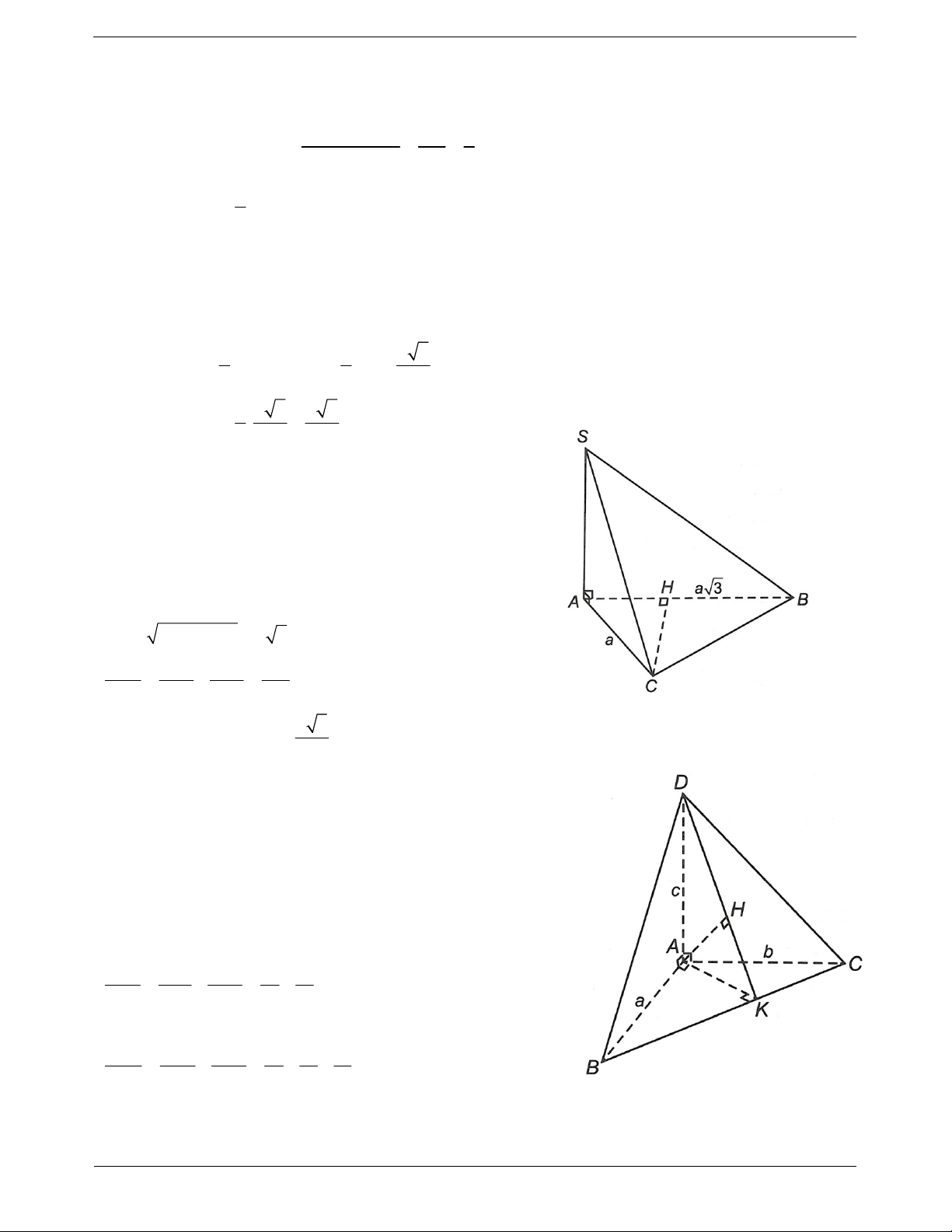
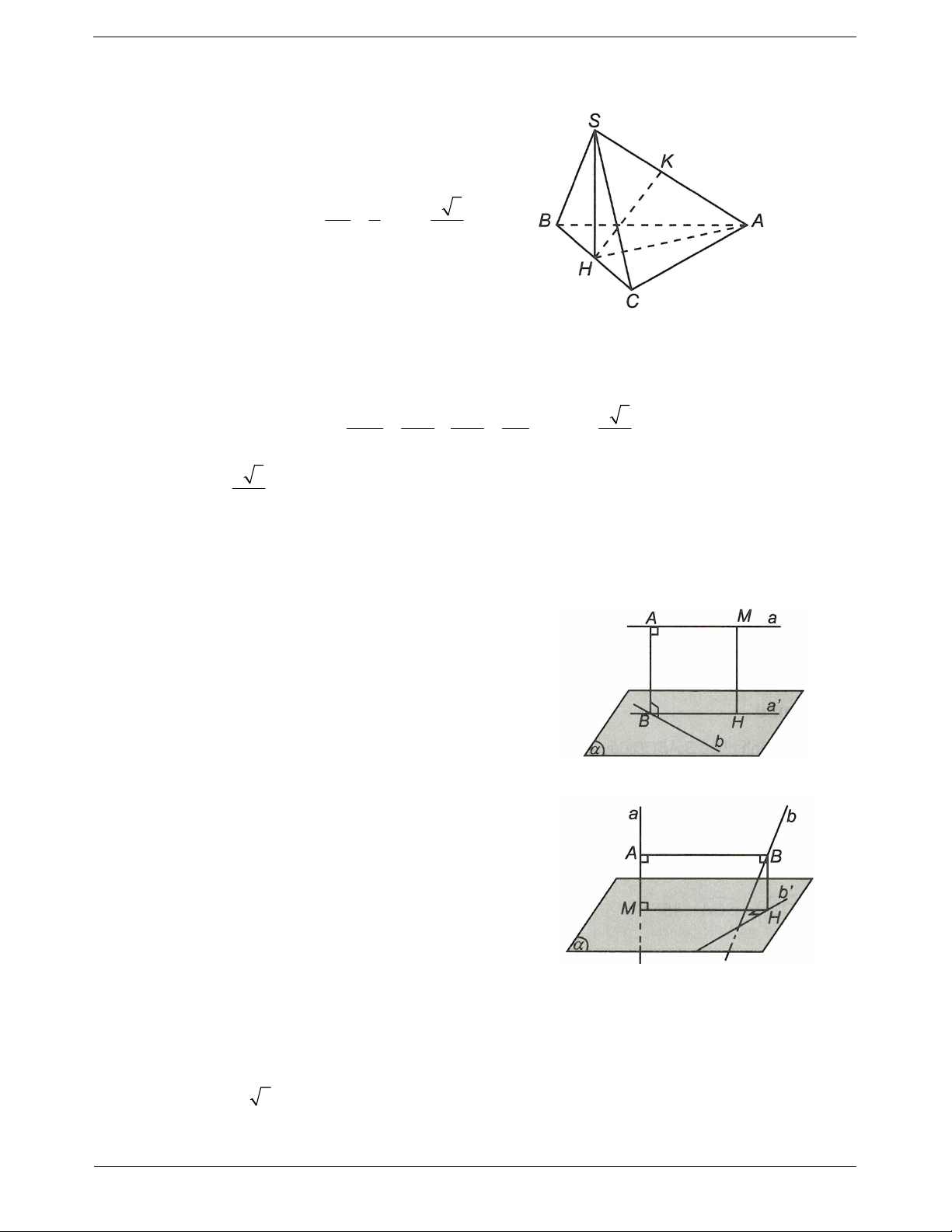
Dựng mặt phẳng chứa b và vuông góc với a tại Ví dụ. Cho hình chóp S.ABC đáy ABC là tam giác A.
vuông tại B, AB a, BC 2a ; cạnh bên SA vuông
Dựng AB b tại b
góc với đáy và SA 2a . Tính khoảng cách giữa hai đường thẳng SA và BC. Hướng dẫn giải
AB là đoạn vuông góc chung của a và b. AB SA Ta có:
. Suy ra AB là đoạn vuông góc AB BC chung của SA và BC. Vậy d S ,
A BC AB a Ví dụ mẫu
Ví dụ 1. Cho hình chóp S.ABCD đáy ABCD là hình vuông cạnh bằng a; cạnh bên SA vuông góc với
đáy; SC hợp với đáy góc 45o . Tính khoảng cách giữa hai dường thẳng SC và BD. Hướng dẫn giải
Ta có: AC là hình chiếu vuông góc của SC lên ABCD . Suy ra , 45 .o SC ABCD SCA BD AC Lại có: BD SC. BD SA Gọi
O AC BD . Dựng OH SC tại H. OH SC Ta có:
. Suy ra OH la đoạn vuông góc chung của BD và SC. OH BD
Suy ra d BD, SC OH . a a o 2 2
Xét tam giác OHC vuông tại H có: OH OC sin 45 . . 2 2 2 TOANMATH.com Trang 20
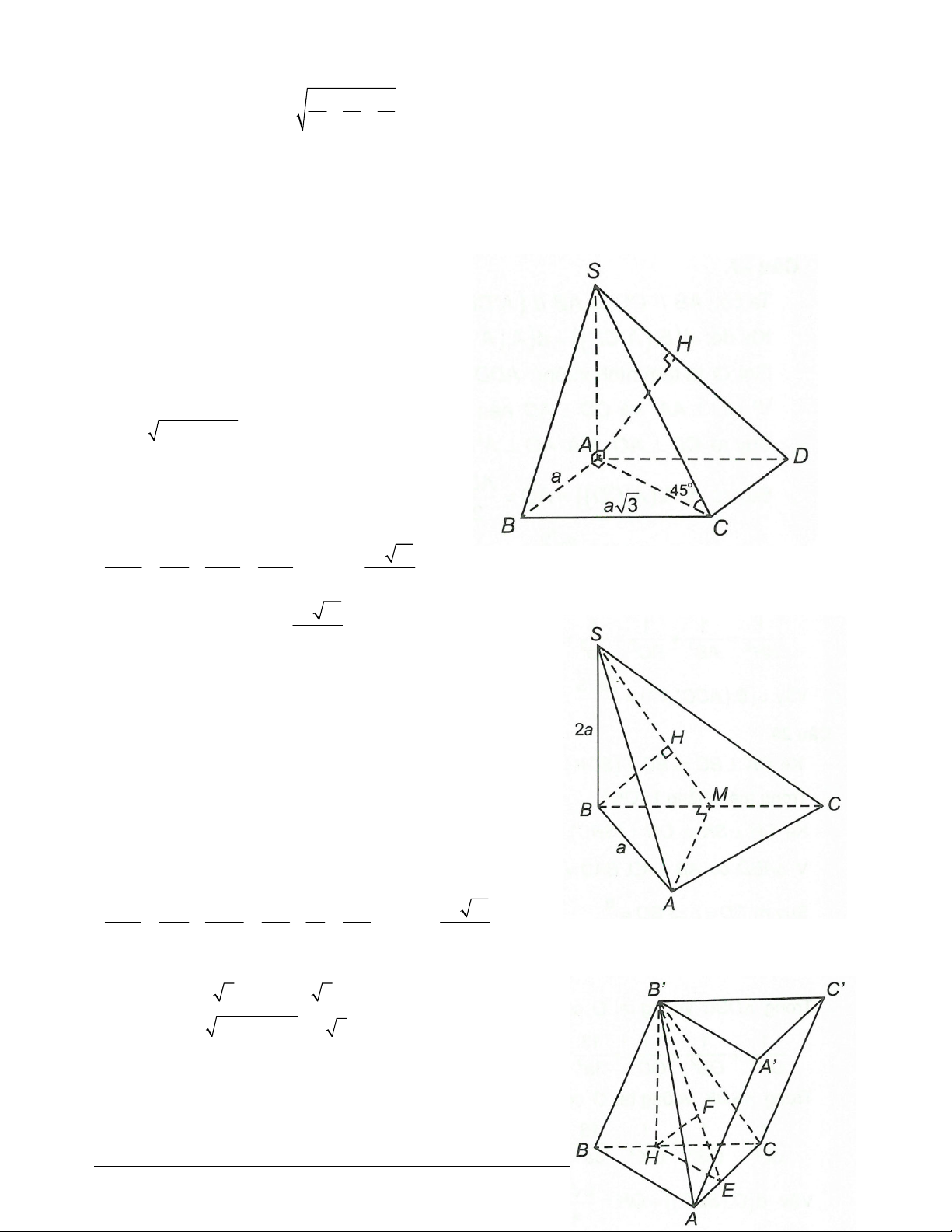
Ví dụ 2. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, mặt bên SBC là tam giác đều
cạnh a và mặt phẳng SBC vuông góc với mặt đáy.
Tính theo a khoảng cách hai đường thẳng SA,BC. Hướng dẫn giải AB a a 3
Kẻ AH BC 1 . Ta có AH , SH . 2 2 2
Vì SA ABC, BC ABC SA BC 2. Từ
1 và 2 suy ra BC SHA.
Trong SAH , kẻ HK SAK SA . Suy ra HK là đoạn vuông góc chung của hai đường thẳng chéo nhau SA và BC. 1 1 1 16 a 3
Xét tam giác SHA vuông tại H có HK . 2 2 2 2 HK HS HA 3a 4 a
Vậy d SA BC 3 , . 4
Bài toán 2. Tính khoảng cách hai đường thẳng chéo nhau a và b không vuông góc
Phương pháp giải Cách 1.
Dựng mặt phẳng chưa b và song song với a.
Chọn điểm M thích hợp trên a, dựng MH tại H.
Qua H, dựng đường thẳng a '/ /a , cắt b tại B.
Từ B dựng đường thẳng song song MH, cắt a tại A.
AB là đoạn vuông góc chung của a và b. Cách 2.
Dựng mặt phẳng vuông góc với a tại M.
Dựng hình chiếu b’ trên b lên .
Dựng hình chiếu vuông góc H của M lên b’.
Từ H, dựng đượng thẳng song song với a, cắt b tại B.
Qua B, dựng đường thẳng song song với MH, cắt a tại A.
AB là đoạn vuông góc chung của a và b. Ví dụ mẫu
Ví dụ 1. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA ABCD và
SA AB a, BC a 2. Tính khoảng cách giữa hai đường thẳng SB và CD. Hướng dẫn giải TOANMATH.com Trang 21
Ví CD SAB nên d CD, SB d CD,SAB
d D,SAB.
Ta có: AD AB và AD S . A
Suy ra AD SAB.
Khi đó d D,SAB DA a 2. Vậy d C ;
D SB a 2.
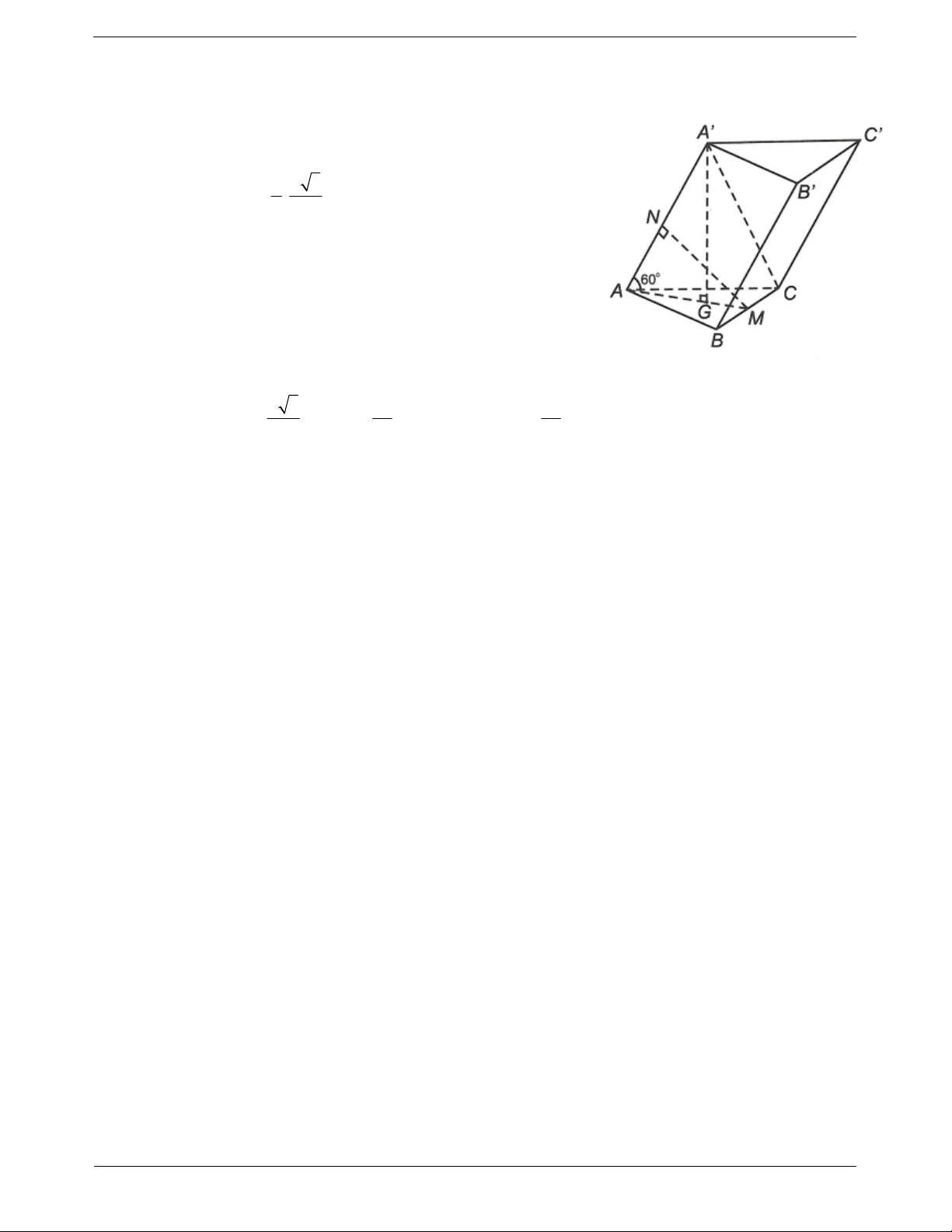
Ví dụ 2. Cho lăng trụ đứng ABC.A' B 'C ' có đáy ABC là tam giác vuông tại ,
A AB a, BC 2a, mặt bên
ACC’A’ là hình vuông. Gọi M, N, P lần lượt là trung điểm của ,
AC CC ', A' B ' và H là hình chiếu của A
lên BC. Tính khoảng cách giữa hai đường thẳng MP và HN. Hướng dẫn giải
Ta xét cặp mặt phẳng song song lần lượt chứa MP và NH.
Xét tam giác ABC vuông ta A có: 1 1 1 1 1 4 a 3 AH . 2 2 2 2 2 2 2 AH AB AC AB BC AB 3a 2
Kẻ MK BC K AB, PQ B 'C 'Q A'C '.
Ta có PM MKPQ và HN BCC ' B '.
Do MK BC và MQ CC ' nên MKPQ BCC ' B '.
Khi đó d MP, NH d MKPQ,BCC ' B '. AH BC Do AH CC
CC ABC AH
ABC AH BCC 'B'. ' ' , TOANMATH.com Trang 22
Suy ra AH KMQP tại I AH KM. AH a
Vậy d MP NH d MPKQ BCC B 3 , , ' ' IH . 2 4
Bài tập tự luyện dạng 2
Câu 1: Cho hai đường thẳng d và d chéo nhau. Mệnh đề nào sau đây đúng? 1 2
A. Khoảng cách giữa d và d bằng khoảng cách từ điểm A trên d đến d . 1 2 1 2
B. Khoảng cách giữa d và d bằng khoảng cách từ điểm B trên d đến d . 1 2 2 1
C. Khoảng cách giữa d và d là độ dài của đoạn AB với AB vuông góc với d và d . 1 2 1 2
D. Khoảng cách giữa d và d bằng khoảng cách từ điểm A trên d đến mặt phẳng P chứa d và 1 2 1 2
d song song với P . 1
Câu 2: Mệnh đề nào sau đây đúng?
A. Đường vuông góc chung của hai đường thẳng chéo nhau thì nằm trong mặt phẳng chứa đường
thẳng này và vuông góc với đường thẳng kia.
B. Đường vuông góc chung của hai đường thẳng chéo nhau thì vuông góc với mặt phẳng chứa đường
thẳng này và song song với mặt phẳng kia.
C. Một đường thẳng là đường vông góc chung của hai đường thẳng chéo nhau nếu nó vuông góc với
cả hai đường thẳng đó.
D. Hai đường thẳng chéo nhau thì có vô số đường vuông góc chung.
Câu 3: Cho tứ diện ABCD có cạnh bằng a. Khoảng cách giữa hai đường thẳng AB và CD bằng a 2a 3a A. B. C. D. a 2 2 2
Câu 4: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Gọi M và N lần lượt là trung điểm
của các cạnh AB và AD; H là giao điểm của CN và DM. Biết SH vuông góc với mặt phẳng ABCD và
SH a 3 . Khoảng cách giữa hai đường thẳng DM và SC bằng 2 57a 2 3a 3a A. B. C. D. a 19 19 2
Câu 5: Hình hộp A .
BCD A' B 'C ' D ' có AB AA' AD a và ' ' 60o A AB A AD BAD . Khoảng
cách giữa hai đường thẳng chứa các cạnh đối diện của tứ diện ' A ABD bằng a 2a 3a A. B. C. D. a 2 2 2
Câu 6: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, mặt bên SBC là tam giác đều
cạnh a và mặt phẳng SBC vuông góc với mặt đáy. Khoảng cách giữa hai đường thẳng SA và BC bằng a 2a a 3 a 3 A. B. C. D. 2 2 2 4
Câu 7: Cho hình chóp S.ABCD có cạnh đáy SA vuông góc với đáy, ABCD là hình vuông cạnh a. Biết
góc giữa SB và mặt đáy bằng 60o . Khoảng cách giữa hai đường thẳng BD và SC bằng TOANMATH.com Trang 23 10a 10a 30a 30a A. B. C. D. 5 10 10 5
Câu 8: Cho hình lăng trụ đứng ABC.A B C có tam giác ABC vuông cân tại ,
A AB a,CC ' 2a . 1 1 1
Khoảng cách giữa hai đường thẳng AA và BC bằng 1 1 6a 3a a 2 A. a B. C. D. 2 2 2
Câu 9: Cho hình lăng trụ đứng ABC.A B C có tam giác ABC vuông cân tại ,
A AB a,CC ' 2a . 1 1 1
Khoảng cách giữa hai đường thẳng AC và BC bằng 1 3 5a 2 5a 5a a 5 A. B. C. D. 5 5 5 2
Câu 10: Cho hình chóp tam giác đều S.ABC có tất cả các cạnh đều bằng a. Khoảng cách giữa hai dường
thẳng SA và BC bằng a 2 a 3 a A.
B. a C. D. 2 2 2
Câu 11: Cho tứ diện OABC có ,
OA OB,OC đôi một vuông góc với nhau, OA a,OB a 2,OC 2a .
Khoảng cách giữa hai đường thẳng OA và BC bằng 2a 5 2a 3 a 6 A. B. C. D. a 5 3 3
Câu 12: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và
D, SA ABCD, AD DC SA .
a Khoảng cách giữa hai đường thẳng AD và SB bằng a 2 a 3 A.
B. a C. D. a 3 2 2
Câu 13: Cho hình lập phương ABC .
D A' B 'C ' D ' có cạnh bằng a. Khoảng cách giữa hai đường thẳng BB ' và CD bằng a 2 a
A. a 2 B. a C. D. 2 2
Câu 14: Cho hình lập phương ABC .
D A' B 'C ' D ' có cạnh bằng a. Khoảng cách giữa hai đường thẳng AA' và BD bằng a 2 a
A. a B. a 2 C. D. 2 2
Câu 15: Cho hình chóp S.ABC có đáy tam giác đều cạnh a. Hình chiếu vuông góc của S trên mặt phẳng
ABC là điểm H thuộc cạnh AB sao cho HA 2HB . Góc giữa hai đường thẳng SC và mặt phẳng
ABC bằng 60o . Khoảng cách giữa hai đường thẳng SA và BC theo a bằng a 42 a 42 a 24 a 42 A. B. C. D. 2 4 8 8
Câu 16: Cho hình lăng trụ đứng ABC.A' B 'C ' có đáy là tam giác ABC vuông tại ,
A AB a, BC a 3 .
Khoảng cách giữa hai đường thẳng AA' và BC ' bằng TOANMATH.com Trang 24 a 6
A. a 2 B. a C. a 3 D. 3
Câu 17: Cho hình chóp S.ABCD có mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc
với đáy, ABCD là hình chữ nhật với ,
AB a BC 2a . Khoảng cách giữa hai đường thẳng AC và SD bằng 2 17a 17a 17a 3 17a A. B. C. D. 17 17 34 17
Câu 18: Cho hình chóp S.ABCD có ABCD là hình thoi tam O, cạnh a, góc 60o BCD , có SO vuông
góc với mặt phẳng ABCD và SO a . Khoảng cách giữa hai đường thẳng AD và SB bằng 57a 2 57a 2 57a 57a A. B. C. D. 19 19 19 9
Câu 19: Cho hình lăng trụ ABC.A' B 'C ' có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của
A' trên mặt phẳng ABC là trọng tâm tam giác ABC và góc giữa cạnh bên và mặt đáy bằng 60o .
Khoảng cách giữa hai đường thẳng BC và A' B ' bằng a 2a 2 2a
A. a B. C. D. 2 3 3
Câu 20: Cho hình lăng trụ ABC.A' B 'C ' có đáy ABC là tam giác đều cạnh a. hình chiếu vuông góc của
A' trên mặt phẳng ABC là trọng tâm tam giác ABC và góc giữa cạnh bên và mặt đáy bằng 60o .
Khoảng cách giữa hai đường thẳng BC và AA' bằng 3a a 3a 3a A. B. C. D. 2 2 4 2
ĐÁP ÁN VÀ LỜI GIẢI BẢI TẬP TỰ LUYỆN
1-D 2-B 3-B 4-B 5-B 6-D 7-C 8-D 9-B 10-A
11-B 12-C 13-B 14-C 15-D 16-D 17-B 18-C 19-A 20-C
Lời giải chi tiết Câu 3. Gọi K là trung điểm CD. CD AK Suy ra
CD ABK . CD BK
Dựng HK AB HK d A ; B CD.
Xét tam giác BHK vuông tại H, ta có 2 2
a 3 a a 2 2 2
HK BK BH . 2 2 2 a
Vậy d AB CD 2 ; . 2 TOANMATH.com Trang 25 Nhận xét: a 2
Đối với tứ diện đều cạnh a thì khoảng cách giửa các cặp cạnh đối diện bằng nhau và bằng . 2 Suy ra Câu 4. DM NC Ta thấy
DM SHC DM SC. DM SH Ta có: M AD ND
C ADM DCN MD NC.
Do SH ABCD nên MD SH MD SHC.
Kẻ HK SC K SC.
Suy ra HK là đoạn vuông góc chung của DM và SC nên
d DM , SC HK. 2 CD 2a SH.HC 2 3a Ta có: HC và HK . CN 5 2 2 SH HC 19 a
Do đó d DM SC 2 3 , . 19 Câu 5.
Vì AB AA' AD a và ' ' 60o A AB A AD BAD nên tứ diện '
A ABD là tứ diện đều cạnh a. vậy khoảng
cách giữa hai đường thẳng chứa các cạnh đối diện của tứ 2a diện ' A ABD bằng (theo kết quả câu 3). 2 Câu 6.
Gọi H là trung điểm của BC nên BC a AH
SH ABC a 3 , , SH . 2 2 2
Gọi K là hình chiếu vuông góc của H trên SA HK . SA
Ta có: BC SAH BC HK d S ;
A BC HK.
Xét tam giác SHA vuông tại H. 1 1 1 16 a 3 Ta có HK . 2 2 2 2 HK SH AH 3a 4 a
Vậy d SA BC 3 ; . 4 Câu 7. TOANMATH.com Trang 26
Do SA ABCD nên ; 60 .o SB ABCD SBA
Do tam giác SAC vuông tại A nên SA .t
AB an SBA a 3.
Gọi O là tâm hình vuông ABCD. BD AC Ta có:
BD SAC. BD SA
Trong mặt phẳng SAC , dựng OH SC. Suy ra d B ;
D SC OH. 1
Dựng AK OH OH AK. 2
Xét tam giác SAC vuông tại A: 1 1 1 5 30a AK . 2 2 2 2 AK AS AC 6a 5 a
Vậy d BD SC 30 ; . 10 Câu 8.
Do BB AA nên AA BCC B . 1 1 1 1 1
Suy ra d AA ; BC d AA ; BCCC d ; A BCCC . 1 1 1 1 1
Do BCCC ABC , dựng AH BC,H BC. 1
Suy ra AH BCC B . 1 1 1 a 2
Xét tam giác ABC vuông tại A : AH BC . 2 2 a 2
Vậy d AA ; BC . 1 1 2 Câu 9.
Gọi O là giao điểm của AB và A . B 1 1
Do AC A C nên AC BAC . 1 1 1 1
Suy ra d AC; BC d AC; BAC d ; A BA C d B ; BAC 1 1 1
1 1 1 1 1
(do O BAC và O là trung điểm AB ). 1 1 1
Dựng B H A B 1 . 1 1 A C A B Ta có: 1 1 1 1
A C ABB A 1 1 1 1 A C AA 1 1 1 TOANMATH.com Trang 27
AC B H 2 . 1 1 1
Từ (1) và (2) ta có: B H A BC d B ; A BC B H. 1 1 1 1 1 1 1
Xét tam giác A BB vuông tại B : 1 1 1 1 1 1 5 2 5a B H . 2 B H A B BB 4a 5 1 1 12 12 2 1 2 5a
Vậy d BC ; AC . 1 5 Câu 10.
Gọi I, K lần lượt là trung điểm của BC và SA.
Ta có: BC SI ( SBC
đều) và BC AI ( A BC đều).
Do đó BC SAI BC IK. 1
Mặt khác SI IA S AI cân tại I.
Có IK là đường trung tuyến nên IK . AB 2
Từ (1) và (2) suy ra IK là đoạn vuông góc chung cùa SA và BC. Do đó d S ;
A BC IK. Xét A
KI vuông tại K có: 2 2
a 3 a a 2 2 2
IK AI AK . 2 2 2 a
Vậy d SA BC 2 ; . 2 Câu 11.
Kẻ OH BC H BC 1 .
Ta có: OA OB và OA OC.
Suy ra OA OBC OA OH 2.
Từ (1) và (2) suy ra OH là đoạn vuông góc chung cùa OA và BC. Do đó d O ;
A BC OH. Xét OB C vuông tại O có: 1 1 1 3 2a 3 OH . 2 2 2 2 OH OB OC 4a 3 a
Vậy d OA BC 2 3 ; . 3 Câu 12. TOANMATH.com Trang 28
Kẻ AH SB H SB 1 .
Ta có: AD AB và AD SAdo SA ABCD.
Suy ra AD SAB AD AH 2.
Từ (1) và (2) suy ra AH là đoạn vuông góc chung cùa AD và SB.
Do đó d AD; SB AH. Xét SAB vuông tại A có: 1 1 1 4 a 3 AH . 2 2 2 2 AH SA SB 3a 2 a
Vậy d AD SB 3 ; . 2 Câu 13.
Ta có BC BB ' và BC C . D
Suy ra BC là đoạn vuông góc chung của BB ' và CD.
Do đó d BB ';CD BC . a Câu 14.
Gọi O là tâm hình vuông ABCD.
Ta có: AO BD và AO AA' .
Suy ra AO là đoạn vuông góc chung của AA' và BD. AC a
Do đó d AA BD 2 '; AO . 2 2 Câu 15. Ta có , , 60 .o SC ABC SC HC SCH a 3
ABC đều nên CI
với I là trung điểm AB. 2 a a a
Ta có BH ; BI IH . 3 2 6 7a Suy ra 2 2
CH IH IC . 3 a o 21
SCH vuông tại H có SH HC.tan 60 . 3
Kẻ Ax BC . Gọi N và K lần lượt là hình chiếu vuông góc của H trên Ax và SN. Suy ra BC SAN . 3 3
Ta có: BA AH nên d S ,
A BC d B,SAN d H,SAN . 2 2
Ta cũng có Ax SHN nên Ax HK . Do đó HK SAN . TOANMATH.com Trang 29
Suy ra d H,SAN HK. 2a a o 3 AH
, HN AH sin 60 . 3 3 SH.HN a 42 HK . 2 2 SH HN 12 a
Vậy d SA BC 3 42 , HK . 2 8 Câu 16.
Vì AA' BCC ' B ' nên
d AA'; BC ' d AA';BCC ' B ' d ;
A BCC ' B '.
Kẻ AH BC H BC.
Mà AH BB 'do '
BB ABC.
Suy ra AH BCC ' B '. Do đó d ;
A BCC ' B ' AH. Xét A
BC vuông tại A có: 2 2
AC BC AB a 2 1 1 1 3 a 6 AH . 2 2 2 2 AH AB AC 2a 3 a
Vậy d AA BC 6 '; ' . 3 Câu 17.
Gọi O là tâm hình chữ nhật ABCD, H là trung điểm AB.
Do SAB ABCD và SH AB nên SH ABCD.
Gọi I là giao điểm của HD và AC ID 2IH.
Gọi G là trọng tâm SA . B
Suy ra IGSD SD AGC. d S ;
D AC d ;
SD AGC d ;
D AGC 2d H; AGC.
Dựng HK AC AC GHK .
Dựng HP GK HP GAC.
Suy ra d H;GAC H . P AB a BC a 3 1 a 3 Ta có AH ; HO a; SH
HG SH . 2 2 2 2 3 6 TOANMATH.com Trang 30
Xét tam giác GHK vuông tại H: 1 1 1 1 1 1 17 . 2 2 2 2 2 2 2 HP HK HG HA HO HG a 17a Suy ra HP . 17 a
Vậy d SD AC 17 ; . 17 Câu 18.
Ta có: SB SBC và AD / / SBC.
Do đó d AD, SB d AD,SBC.
Qua O kẻ MN BC M AD, N BC.
Ta có: BC MN và BC SO (vì SO ABCD ), suy ra
BC SMN
Mà BC SBC SMN SBC theo giao tuyến SN.
Kẻ MH SN H SN MH SBC.
Khi đó ta có d AD, SB d M ,SBC MH. 1 1 Ta có S
MN.SO MH.SN SMN 2 2 MN.SO MN.SO MH . 2 2 SN SO ON a
Do tam giác BCD có CD CB a và ˆ 60o BCD suy ra tam giác B
CD đều d D BC 3 , MN. 2 a
Vậy d AD SB d M SBC 2 57 , , MH . 19 Câu 19.
Gọi G là trọng tâm tam giác ABC, theo giả thiết ' '; ' 60 .o A G ABC AA ABC A AG
Xét tam giác A' AG vuông tại G: 2 a 3
A'G A .
G tan A' AG . .tan 60o . a 3 2
Do BC A' B 'C ' nên d BC; A' B ' d BC; A' B 'C ' A'G . a
Vậy d BC; A' B ' . a Câu 20. TOANMATH.com Trang 31
Gọi G là trọng tâm tam giác ABC.
Theo giả thiết A'G ABC , suy ra '; ' 60 .o AA ABC A AG
Xét tam giác A' AG vuông tại G: 2 a 3
A'G A .
G tan A' AG . .tan 60o . a 3 2 Gọi M là trung điểm BC. BC AM
BC A' AM .
BC A'G
Dựng MN AA' d BC; AA' MN.
Xét tam giác AMN vuông tại N: a 3 a a o 3
MN AM .sin NAM .sin 60
. Vậy d BC AA 3 ; ' . 2 4 4 TOANMATH.com Trang 32




