Bài giảng logarit – Trần Văn Tài

Tài liệu bài giảng logarit gồm 81 trang được biên soạn bởi thầy Trần Văn Tài, tài liệu trình bày lý thuyết và bài tập có lời giải chi tiết các chủ đề hàm số logarit, phương trình logarit … trường chương trình Giải tích 12 chương 2.

109 55 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 6: Hàm số mũ và hàm số lôgarit (KNTT)

Môn: Toán 11

Thông tin:

47 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
Mục lục
Trang
Chương 2 HÀM SỐ LŨY THỪA-HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT . . . . . . . . . . . 3
PHẦN 1. HÀM SỐ LŨY THỪA-HÀM SỐ MŨ-HÀM SỐ LOGARIT . . . . . . . . . . . . . . 3
A. LÝ THUYẾT . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
2.1 Lũy thừa-Hàm số lũy thừa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
2.1.1 Lũy thừa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
2.1.2 Hàm số lũy thừa: y = x
α
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
2.2 Logarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
2.2.1 Kiến thức cơ bản . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
2.3 Hàm số mũ-Hàm số logarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
2.3.1 Hàm số mũ: y = a
x
, (0 < a 6= 1) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
2.3.2 Hàm số logarit: y = log
a
x, (0 < a 6= 1, x > 0) . . . . . . . . . . . . . . . . . . . . . . . . 5
2.3.3 Bảng đạo hàm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
B. BÀI TÂP TỰ LUẬN . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
2.4 Bài tập về lũy thừa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
2.4.1 Dạng 1: Tính giá trị biểu thức . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
2.4.2 Dạng 2: Đơn giản biểu thức . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
2.4.3 Dạng 3: Lũy thừa hữu tỉ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
2.4.4 Dạng 4: So sánh cặp số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
2.4.5 Dạng 5: Bài toán thực tế . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
2.5 Bài tập về logarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
2.5.1 Dạng 1: Tính giá trị biểu thức . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
2.5.2 Dạng 2: Biến đổi logarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
2.5.3 Dạng 3: Chứng minh đẳng thức logarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
2.5.4 Dạng 4: So sánh cặp số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
2.5.5 Dạng 4: Bài toán thực tế . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
2.6 Bài tập hàm số mũ-hàm số logarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
2.6.1 Dạng 1: Tập xác định hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
2.6.2 Dạng 2: Đạo hàm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
2.6.3 Dạng 3: Chứng minh hàm số đã cho thỏa hệ thức cho trước . . . . . . . . . . . . . . . . . . . 20
2.6.4 Dạng 4: Giải phương trình, bất phương trình . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
2.6.5 Dạng 5: Giá trị lớn nhất, giá trị nhỏ nhất . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
PHẦN 2. PHƯƠNG TRÌNH, BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT . . . . . . . . . . . 22
A. PHƯƠNG TRÌNH . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
2.7 Phương trình mũ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
2.7.1 Phương trình mũ cơ bản . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
2.7.2 Một số phương pháp giải phương trình mũ . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
1
Hàm số mũ và hàm số logarit Giải tích 12
2.7.2.1 Phương pháp đưa về cùng cơ số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
2.7.2.2 Phương pháp logarit hóa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
2.7.2.3 Phương pháp đặt ẩn phụ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
2.7.2.3.1 Dạng 1: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
2.7.2.3.2 Dạng 2: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
2.7.2.3.3 Dạng 3: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
2.7.2.4 Sử dụng tính đơn điệu của hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
2.7.2.5 Phương trình tích . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30
2.7.3 Bài toán liên quan tham số m . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
2.8 Phương trình logarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
2.8.1 Phương trình logarit cơ bản . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
2.8.2 Một số phương pháp giải phương trình logarit . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
2.8.2.1 Phương pháp đưa về cùng cơ số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
2.8.2.2 Phương pháp mũ hóa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
2.8.2.3 Phương pháp đặt ẩn phụ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
2.8.2.4 Sử dụng tính đơn diệu hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34
2.8.3 Bài toán liên quan tham số m . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
B. BẤT PHƯƠNG TRÌNH . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
2.9 Bất phương trình mũ và bất phương trình logarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
2.9.1 Bất phương trình mũ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
2.9.2 Bất phương trình logarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
2.10 Hệ phương trình mũ và logarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
2.11 Các ví dụ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
2.12 Bài tập bất phương trình, hệ phương trình mũ và logarit . . . . . . . . . . . . . . . . . . . . . . . . . 43
2.12.1 Giải các bất phương trình . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43
2.12.2 Giải hệ phương trình . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 2
Chương 2
HÀM SỐ LŨY THỪA-HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT
A. LÝ THUYẾT
2.1 Lũy thừa-Hàm số lũy thừa
2.1.1 Lũy thừa
Với a, b là các số thực dương, m, n là những số thực tùy ý.
1 a
n
= a · a · a ···a
| {z }
n lần
6
Å
a
b
ã
m
=
a
m
b
m
=
Ç
b
a
å
−m
2 a
m
· a
n
= a
m+n
7 a
m
n
=
n
√
a
m
3
a
m
n
n
= a
m−n
⇒ a
−n
=
1
a
n
8 [u(x)]
0
= 1 ⇒ x
0
= 1,
∀u(x)
x 6= 0
4 (a
m
)
n
= (a
n
)
m
= a
m·n
9
n
√
a ·
n
√
b =
n
√
ab
5 (a · b)
m
= a
m
· b
m
10 (
n
√
a)
m
=
n
√
a
m
!
Nếu a < 0 thì a
m
chỉ xác định khi ∀m ∈ Z.
Nếu a > 0 thì a
m
> a
n
⇔ m > n.
Nếu 0 < a < 1 thì a
m
> a
n
⇔ m < n.
Để so sánh
n
1
√
a và
n
2
√
n. Ta sẽ đưa 2 căn đã cho về cùng bậc n (với n là bội số chung
của n
1
và n
2
)⇒ Hai số so sánh mới lần lượt là
n
√
A và
n
√
B. Từ đó so sánh A và B ⇒
kết quả so sánh của
n
1
√
a và
n
2
√
b.
Công thức lãi kép: Lãi kép là phần lãi của kì sau được tính trên số tiền gốc kì trước cộng
với phần lãi của kì trước.
1 Số tiền nhận được cả gốc và lãi sau n kì hạn gửi là A(1 + r)
n
2 Số tiền lãi nhận được sau n kì hạn gửi là A(1 + r)
n
− A = A [(1 + r)
n
− 1]
2.1.2 Hàm số lũy thừa: y = x
α
α > 0 α < 0
1 Tập xác định: D = (0; +∞) 1 Tập xác định: D = (0; +∞)
2 Sự biến thiên: y
0
= α.x
α−1
> 0 2 Sự biến thiên: y
0
= α.x
α−1
< 0
Giới hạn đặc biệt Giới hạn đặc biệt
lim
x→0
+
x
α
= 0; lim
x→+∞
x
α
= +∞ lim
x→0
+
x
α
= +∞; lim
x→+∞
x
α
= 0
3 Tiệm cận: 3 Tiệm cận:
Không có TCĐ: Trục Ox; TCN: Trục Oy
4 Bảng biến thiên 4 Bảng biến thiên
3
Hàm số mũ và hàm số logarit Giải tích 12
x
y
0
+∞
0
+∞
x
y
0
+∞
0
+∞
5 Đồ thị
x
y
O
α < 0
α = 0
0 < α < 1
α = 1
α > 1
1
1
Số mũ Tập xác định
α = n (n nguyên dương) D = R
α = n (n nguyên âm) D = R \ {0}
α là số thực không nguyên D = (0; +∞)
4
!
Chý ý: y = x
1
n
không đồng nhất với y =
n
√
x, (n ∈ N)
2.2 Logarit
2.2.1 Kiến thức cơ bản
1) Định nghĩa
1 Với 0 < a 6= 1, b > 0 ta có: log
a
b = α ⇔ b = a
α
2 Chú ý: log
a
b có nghĩa khi
0 < a 6= 1
b > 0
3 Logarit thập phân: lg b = log b = log
10
b
4 Logarit tự nhiên (logarit Nepe): ln b = log
e
b
2) Tính chất
Cho 0 < a 6= 1 và b, c > 0. Khi đó:
Nếu a > 1 thì log
a
b > log
a
c ⇔ b > c Nếu 0 < a < 1 thì log
a
b > log
a
c ⇔ b < c
5 log
a
1 = 0 6 log
a
a = 1 7 log
a
a
b
= b 8 a
log
a
b
= b
3) Các qui tắc tính logarit
Cho a > 0 và b, c > 0. Ta có:
9 log
a
(b.c) = log
a
b + log
a
c 10 log
a
Ç
b
c
å
= log
a
b − log
a
c
11 log
a
b
α
= α. log
a
b 12 log
a
b
2
= 2. log
a
|b|
4) Các công thức đổi cơ số
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 4
Hàm số mũ và hàm số logarit Giải tích 12
Cho a, b, c > 0 và a, b 6= 1. Ta có:
13 log
b
c =
log
a
c
log
a
b
14 log
a
b =
1
log
b
a
15 log
a
b. log
b
c = log
a
c 16 log
a
b =
ln b
ln a
17 log
a
α
b =
1
α
. log
a
b, (α 6= 0) 18 log
1
a
b = −log
a
b
19 log
a
α
a =
1
α
20 log
a
α
b
β
=
β
α
log
a
b; 21 log
a
α
a
β
=
β
α
22 log
ab
=
1
1
log
a
c
+
1
log
b
c
23 a
log
b
c
= c
log
b
a
2.3 Hàm số mũ-Hàm số logarit
2.3.1 Hàm số mũ: y = a
x
, (0 < a 6= 1)
a > 1 0 < a < 1
1 Tập xác định: D = R 1 Tập xác định: D = R
2 Sự biến thiên: y
0
= a
x
. ln a > 0 2 Sự biến thiên: y
0
= a
x
. ln a < 0
Giới hạn đặc biệt: Giới hạn đặc biệt:
lim
x→−∞
a
x
= 0; lim
x→+∞
a
x
= +∞ lim
x→−∞
a
x
= +∞; lim
x→+∞
a
x
= 0
Tiệm cận: Tiệm cận:
TCN: Trục Ox TCN: Trục Ox
3 Bảng biến thiên: 3 Bảng biến thiên:
x
y
0
y
−∞
0 1
+∞
+
00
+∞+∞
1
a
x
y
0
y
−∞
0 1
+∞
−
+∞+∞
00
1
a
4 Đồ thị: 4 Đồ thị:
x
y
O
1
a > 1
y = a
x
x
y
O
1
y = a
x
0 < a < 1
2.3.2 Hàm số logarit: y = log
a
x, (0 < a 6= 1, x > 0)
a > 1 0 < a < 1
1 Tập xác định: D = (0; +∞) 1 Tập xác định: D = (0; +∞)
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 5
Hàm số mũ và hàm số logarit Giải tích 12
2 Sự biến thiên: y
0
=
1
x. ln a
> 0 2 Sự biến thiên: y
0
=
1
x. ln a
< 0
Giới hạn đặc biệt: Giới hạn đặc biệt:
lim
x→0
+
log
a
x = −∞; lim
x→+∞
log
a
x = +∞ lim
x→0
+
log
a
x = +∞; lim
x→+∞
log
a
x = −∞
Tiệm cận: Tiệm cận:
TCĐ: Trục Oy TCĐ: Trục Oy
3 Bảng biến thiên 3 Bảng biến thiên
x
y
0
y
0 1
a
+∞
+
−∞
+∞+∞
0
1
x
y
0
y
0 1
a
+∞
−
−∞
+∞+∞
0
1
4 Đồ thị: 4 Đồ thị:
x
y
O
1
a > 1
y = log
a
x
x
y
O
1
y = log
a
x
0 < a < 1
2.3.3 Bảng đạo hàm
Đạo hàm Đạo hàm hợp
1 Hàm số lũy thừa: (x
α
)
0
= α.x
α−1
1 Hàm lũy thừa: (u
α
)
0
= α.u
α−1
.u
0
2 Hàm số mũ: 2 Hàm số mũ:
(a
x
)
0
= a
x
. ln a (a
u
)
0
= a
u
. ln a.u
0
(e
x
)
0
= e
x
(e
u
)
0
= e
u
.u
0
3 Hàm số logarit: (log
a
x)
0
=
1
x. ln a
3 Hàm số logarit: (log
a
u)
0
=
u
0
u. ln a
B. BÀI TẬP TỰ LUẬN
2.4 Bài tập về lũy thừa
2.4.1 Dạng 1: Tính giá trị biểu thức
Ví dụ 1. Tính giá trị biểu thức: A = 4
3+
√
2
· 2
1−
√
2
· 2
−4−
√
2
.
Lời giải.
Ta có A = 2
2(3+
√
2)
· 2
1−
√
2
· 2
−4−
√
2
= 2
6+2
√
2+1−
√
2−4−
√
2
= 2
3
= 8.
Đáp số A = 8
Bài 1. Tính giá trị các biểu thức sau:
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 6
Hàm số mũ và hàm số logarit Giải tích 12
A =
8
9
7
: 8
2
7
−
3
6
5
.3
4
5
.a) B =
2
3
· 2
−1
+ 5
−3
· 5
4
(10
−3
: 10
−2
) − (0, 24)
0
.b)
C =
5
−
2
5
+
h
(0, 2)
3
4
i
−4
c) D = 81
−0,75
+
Ç
1
125
å
−
1
3
−
Ç
1
32
å
−
3
5
.d)
E = 0, 001
−
1
3
−(−2)
−2
·64
2
3
−8
2
3
+(9
0
)
2
.e) F = 2
2−3
√
5
· 8
√
5
.f)
G =
…
√
3
3
»
√
3 :
»
4
√
3
2
.g) H =
10
2+
√
7
2
2+
√
7
· 5
1+
√
7
.h)
I = (0, 04)
−1,5
− (0, 125)
−
2
3
.i) J =
Ç
1
16
å
−0,75
+ (0, 25)
−
5
2
.j)
K = 4
3+
√
2
.2
1−
√
2
.2
−4−
√
3
k) L =
2
3
.2
−1
+ 5
−3
.5
4
10
−3
: 10
−2
− (0, 25)
0
l)
M =
Ç
1
16
å
−0,75
+ (0, 25)
−
5
2
+ (0, 04)
−1,5
m) N =
Å
Ä
√
5
ä
√
5
ã
√
5
+ 4
1−2
√
3
.16
1+
√
3
n)
O =
√
3.
3
√
3
9
5
12
π
0
+
3
√
3
e
0
.
√
3
.9
7
12
o) P = (0, 5)
−4
− 625
0,25
−
Ç
9
4
å
−
3
2
p)
Q = 64
−
1
4
+
Ç
1
255
å
−2
−
Ç
−
1
81
å
−0,75
q) R = (0, 25)
−
1
2
+
Ç
1
32
å
−
6
5
−
Ç
19
2
å
−2
r)
S = 256
−0,75
−
Ç
1
125
å
−
1
3
s) T =
3
»
7 + 5
√
2 +
3
»
7 − 5
√
2t)
U = 4
3
2
+ 8
2
3
u) V =
32
3
2
−
2
5
v)
W =
(−18)
7
· 2
4
· (−50)
3
(−25)
4
· (−4)
5
w) X =
125
6
· (−16)
3
· (−2)
3
25
3
[(−5)
2
]
4
x)
Y =
5
√
4 ·
4
√
64 ·
3
»
√
2
4
3
»
√
32
y) Z =
5
√
81 ·
5
√
3 ·
5
√
9 ·
√
12
3
»
√
3
2
·
√
18 ·
5
√
27 ·
√
6
z)
Ví dụ 2. Cho 9
x
+ 9
−x
= 23. Tính giá trị biểu thức: K =
5 + 3
x
+ 3
−x
1 − 3
x
− 3
−x
.
Lời giải.
Ta có 9
x
+9
−x
= 23 ⇔ 9
x
+
1
9
x
= 23 ⇔ (3
2
)
x
+
1
(3
2
)
x
= 23 ⇔
"
(3
x
)
2
+
1
(3
x
)
2
+ 2.3
x
.
1
3
x
#
−2 =
23 ⇔
Ç
3
x
+
1
3
x
å
2
= 5
2
⇒ 3
x
+
1
3
x
= 5 .
Ta có K =
5 + 3
x
+ 3
−x
1 − 3
x
− 3
−x
=
5 + 3
x
+
1
3
x
1 −
Ç
3
x
+
1
3
x
å
=
5 + 5
1 − 5
=
10
−4
= −
5
2
.
Đáp số K = −
5
2
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 7
Hàm số mũ và hàm số logarit Giải tích 12
Bài 2. Tính giá trị của các biểu thức sau:
Cho 4
x
+ 4
−x
= 14. Tính giá trị của biểu thức P =
10 − 2
x
− 2
−x
3 + 2
x
+ 2
−x
.a)
Cho 25
x
+ 25
−x
= 7. Tính giá trị của biểu thức P =
4 − 5
x
− 5
−x
9 + 5
x
+ 5
−x
.b)
Tính giá trị của biểu thức P =
Ä
7 + 4
√
3
ä
2017
Ä
7 − 4
√
3
ä
2016
.c)
Tính giá trị của biểu thức P =
Ä
9 + 4
√
5
ä
2017
Ä
9 − 4
√
5
ä
2016
.d)
Tính giá trị của biểu thức P =
Ä
5 − 2
√
6
ä
2017
Ä
5 + 2
√
6
ä
2016
.e)
Tính giá trị của biểu thức P =
Ä
1 +
√
3
ä
2016
Ä
3 −
√
3
ä
2016
.f)
Tính giá trị của biểu thức P =
Ä
√
6 +
√
2
ä
2016
Ä
√
6 − 3
√
2
ä
2016
.g)
Ví dụ 3. Cho hàm số f(x) =
9
x
9
x
+ 3
, x ∈ R và a, b thỏa a + b = 1. Tính giá trị f(a) +f(b).
Lời giải.
Ta có f(a) + f(b)
b=1−a
−−−−→ f(a) + f(1 − a) =
9
a
9
a
+ 3
+
9
1−a
9
1−a
+ 3
=
9
a
9
a
+ 3
+
9
9 + 3.9
a
=
9
a
9
a
+ 3
+
3
3 + 9
a
=
9
a
+ 3
9
a
+ 3
= 1.
Đáp số f(a) + f (b) = 1
Bài 3. Tính giá trị của biểu thức sau:
Cho hàm số f(x) =
4
x
4
x
+ 2
.
Tính tổng P = f
Ç
1
100
å
+ f
Ç
2
100
å
+ ··· + f
Ç
98
100
å
+ f
Ç
99
100
å
.
a)
Cho hàm số f(x) =
4
x
4
x
+ 2
.
Tính tổng P = f
Ç
1
100
å
+ f
Ç
2
100
å
+ ··· + f
Ç
99
100
å
+ f
Ç
100
100
å
.
b)
Cho hàm số f(x) =
9
x
9
x
+ 3
.
Tính tổng P = f
Ç
1
10
å
+ f
Ç
2
10
å
+ ··· + f
Ç
8
10
å
+ f
Ç
9
10
å
.
c)
Cho hàm số f(x) =
4
x
4
x
+ 2
.
Tính tổng P = f
Ç
1
2017
å
+ f
Ç
2
2017
å
+ ··· + f
Ç
2015
2017
å
+ f
Ç
2016
2017
å
.
d)
2.4.2 Dạng 2: Đơn giản biểu thức
Ví dụ 4. Đơn giản biểu thức: P =
Ç
a
0,5
+ 2
a + 2 · a
0,5
+ 1
−
a
0,5
− 2
a − 1
å
·
a
0,5
+ 1
a
0,5
.
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 8
Hàm số mũ và hàm số logarit Giải tích 12
Lời giải.
P =
"
√
a + 2
(
√
a + 1)
2
−
√
a − 2
(
√
a + 1)(
√
a − 1)
#
·
√
a + 1
√
a
=
Ç
√
a + 2
√
a + 1
−
√
a − 2
(
√
a + 1)(
√
a − 1)
å
·
1
√
a
=
a −
√
a + 2
√
a − 2 −
√
a + 2
a − 1
·
1
√
a
=
a
a − 1
·
1
√
a
=
√
a
a − 1
.
Đáp số P =
√
a
a − 1
Bài 4. Đơn giản các biểu thức sau:
A =
a
1,5
+ b
1,5
a
0,5
+ b
0,5
− a
0,5
· b
0,5
a − b
+
2 · b
0,5
a
0,5
+ b
0,5
a)
B =
Ç
a
0,5
+ 2
a + 2 · a
0,5
+ 1
−
a
0,5
− 2
a − 1
å
·
a
0,5
+ 1
a
0,5
b)
C =
x
1
2
+ 3y
1
2
x
1
2
− y
1
2
2
+
x
1
2
− 3y
1
2
x − y
·
x
1
2
− y
1
2
2
c)
D =
Ñ
x
1
2
− y
1
2
xy
1
2
+ x
1
2
y
+
x
1
2
+ y
1
2
xy
1
2
− x
1
2
y
é
·
x
3
2
y
1
2
x + y
−
2y
x − y
d)
E =
a
1
3
− b
2
3
·
a
2
3
+ a
1
3
a
2
3
+ b
4
3
e)
F =
a
1
4
− b
1
4
·
a
1
4
+ b
1
4
·
a
1
2
+ b
1
2
f)
2.4.3 Dạng 3: Lũy thừa hữu tỉ
Ví dụ 5. Viết biểu thức sau với dạng lũy thừa với số mữ hữu tỉ: P =
4
»
x
2
·
3
√
x, (x ≥ 0).
Lời giải.
!
Thực hiện từ trong ra ngoài từ
n
√
a
m
= a
m
n
và a
m
.a
n
= a
m+n
.
• Cách 1: P =
4
»
x
2
·
3
√
x =
4
»
x
2
.x
1
3
=
4
»
x
7
3
= x
7
12
.
• Cách 2: P
4
= x
2
.
3
√
x ⇒ P
12
= x
6
.x = x
7
⇒ P = x
7
12
.
Đáp số P = x
7
12
Bài 5. Viết các biểu thức sau với dạng lũy thừa với số mữ hữu tỉ (xem điều kiện được thỏa)
A =
5
b
a
·
3
…
a
b
.a) B =
5
q
2 ·
3
»
2
√
2.b) C =
3
Ã
2
3
·
3
s
3
2
·
2
3
.c)
D =
4
»
3
√
a
8
.d) E =
5
»
b
2
·
√
b
3
»
b
√
b
.e) F =
3
s
2018.
2
1
2018
.f)
G =
4
q
x.
3
»
x
2
.
√
x
3
.g) H = x.
5
q
x.
3
»
x.
√
x.h) I =
√
x
5
.
3
√
x
2
.
5
√
x
3
.i)
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 9
Hàm số mũ và hàm số logarit Giải tích 12
J =
6
q
x.
4
»
x
5
.
√
x
3
.j) K =
…
x
q
x
»
x
√
x : x
11
16
.k) L =
x
√
3−1
√
3+1
x
−
√
3+2
.x
2+
√
3
.l)
M =
a
√
3+1
.a
2−
√
3
Ä
a
√
2−1
ä
√
2+1
m) N =
a
√
7+1
.a
2−
√
7
2a
5
.
Ä
a
√
2−2
ä
√
2+2
.n) O =
a
7
6
.b
−
2
3
6
√
ab
2
.o)
P =
a
1
3
.
√
b + b
1
3
.
√
a
6
√
a +
6
√
b
.p) Q =
x
5
4
y
+ xy
5
4
4
√
x +
4
√
y
.q) R =
a
1
3
a
−
1
3
+ a
2
3
a
1
4
a
3
4
+ a
−
1
4
.r)
2.4.4 Dạng 4: So sánh cặp số
Ví dụ 6. So sánh cặp số sau: 2
√
2
và 2
√
3
.
Lời giải.
Ta có:
2 > 1
√
3 >
√
2
⇒ 2
√
3
> 2
√
2
.
Đáp số 2
√
3
> 2
√
2
Ví dụ 7. So sánh cặp số sau:
Ç
1
2
å
√
2
và
Ç
1
2
å
√
3
.
Lời giải.
Ta có
1
2
< 1
√
3 >
√
2
⇒
Ç
1
2
å
√
2
>
Ç
1
2
å
√
3
Đáp số
Ç
1
2
å
√
2
>
Ç
1
2
å
√
3
Ví dụ 8. So sánh cặp số sau: 2
π
và 3
π
.
Lời giải.
Ta có
3 > 2
π > 0
⇒ 3
π
> 2
π
.
Đáp số 3
π
> 2
π
Ví dụ 9. So sánh cặp số sau:
Ä
√
2
ä
−π
và
Ä
√
3
ä
−π
.
Lời giải.
Ta có
√
2 <
√
3
π < 0
⇒
Ä
√
2
ä
−π
>
Ä
√
3
ä
−π
Đáp số
Ä
√
2
ä
−π
>
Ä
√
3
ä
−π
Bài 6. So sánh các cặp số sau:
4
−
√
3
và 4
−
√
2
a) 2
√
3
và 2
1,7
b) 2
−2
và 1c)
(0, 013)
−1
và 1d)
Ç
1
2
å
1,4
và
Ç
1
2
å
√
2
e)
Ç
1
9
å
π
và
Ç
1
9
å
3,14
f)
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 10
Hàm số mũ và hàm số logarit Giải tích 12
Ç
1
3
å
√
2
và
Ç
1
3
å
√
3
g)
3
√
10 và
5
√
20h)
4
√
5 và
3
√
7i)
√
17 và
3
√
28j)
4
√
13 và
5
√
23k) 4
√
5
và 4
√
7
l)
(0, 01)
−
√
2
và (10)
−
√
2
m)
Å
π
4
ã
2
và
Å
π
4
ã
6
n) 5
−2
√
3
và 5
−3
√
2
o)
5
300
và 8
300
p) (0, 001)
−3
và
3
√
100q) 4
√
2
và (0, 125)
−
√
2
r)
(
√
2)
−3
và (
√
2)
−5
s)
Ç
4
5
å
−4
và
Ç
5
4
å
5
t) (0, 02)
−10
và 50
11
u)
Å
π
2
ã
5
2
và
Å
π
2
ã
√
10
3
v)
√
3
5
!
−
√
2
và
√
2
2
!
−
√
2
w)
Bài 7. So sánh các số mũ sau:
(3, 2)
m
< (3, 2)
n
a)
Ä
√
2
ä
m
>
Ä
√
2
ä
n
b)
Ç
1
9
å
m
>
Ç
1
9
å
n
c) (
√
5 − 1)
m
< (
√
5 − 1)
n
d)
(
√
2 − 1)
m
> (
√
2 − 1)
n
e)
√
3
2
!
m
>
√
3
2
!
n
f)
2.4.5 Dạng 5: Bài toán thực tế
!
Công thức lãi kép: Lãi kép là phần lãi của kì sau được tính trên số tiền gốc kì trước
cộng với phần lãi của kì trước.
1 Số tiền nhận được cả gốc và lãi sau n kì hạn gửi là A(1 + r)
n
2 Số tiền lãi nhận được sau n kì hạn gửi là A(1 + r)
n
− A = A [(1 + r)
n
− 1]
Ví dụ 10. Bà Mai gửi 50 triệu vào tài khoản định kỳ tính lãi kép với lãi suất là 8%/năm.
Tính số tiền lãi thu được sau 15 năm.
Lời giải.
Số tiền lãi thu được sau 15 năm: 50.
î
(1 + 8%)
15
− 1
ó
≈ 108.6(triệu)
Đáp số ≈ 108.6(triệu)
Bài 8. Một người lần đầu gửi vào ngân hàng 100 triệu đồng với kì hạn 3 tháng, lãi suất
2%/một quý. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi quý số tiền lãi
sẽ được nhập vào gốc để tính lãi cho quý tiếp theo. Sau đúng 6 tháng, người đó gửi thêm
100 triệu đồng với kỳ hạn và lãi suất như trước đó. Tổng số tiền người đó nhận được 1 năm
sau khi gửi tiền (cả vốn lẫn lãi) gần nhất với kết quả nào sau đây?
Bài 9. Bác An đem gửi tổng số tiền 320 triệu đồng ở hai loại kỳ hạn khác nhau. Bác gửi
140 triệu đồng theo kỳ hạn ba tháng với lãi suất 2, 1%/một quý. Số tiền còn lại bác An gửi
theo kỳ hạn một tháng với lãi suất 0, 73%/một tháng. Biết rằng nếu không rút tiền ra khỏi
ngân hàng thì cứ sau mỗi kỳ hạn số tiền lãi sẽ được nhập vào gốc để tính lãi cho kỳ hạn
tiếp theo. Sau 15 tháng kể từ ngày gửi bác An đi rút tiền. Tính gần đúng đến hàng đơn vị
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 11
Hàm số mũ và hàm số logarit Giải tích 12
tổng số tiền lãi thu được của bác An.
Bài 10. Một người lần đầu gửi vào ngân hàng 100 triệu đồng với kì hạn 3 tháng, lãi suất
2%/một quý theo hình thức lãi kép. Sau đúng 6 tháng, người đó gửi thêm 100 triệu đồng
với kỳ hạn và lãi suất như trước đó. Tổng số tiền người đó nhận được 1 năm sau khi gửi
tiền là bao nhiêu?
Bài 11. Một người gửi 50 triệu đồng vào một ngân hàng với lãi suất 6%/năm. Biết rằng
nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào gốc
để tính lãi cho năm tiếp theo. Hỏi sau ít nhất bao nhiêu năm người đó nhận được số tiền
nhiều hơn 100 triệu đồng bao gồm cả gốc và lãi? Giả sử trong suốt thời gian gửi lãi suất
không đổi và người đó không rút tiền ra.
Bài 12. Đầu năm 2016, ông A thành lập một công ty. Tổng số tiền ông A dùng để trả
lương cho nhân viên trong năm 2016 là 1 tỷ đồng. Biết rằng cứ sau mỗi năm thì tổng số
tiền dùng để trả lương cho nhân viên trong cả năm đó tăng thêm 15% so với năm trước.
Hỏi năm nào dưới đây là năm đầu tiên mà tổng số tiền ông A dùng để trả lương cho nhân
viên trong cả năm lớn hơn 2 tỷ đồng?
Bài 13. Anh Nam mong muốn rằng sau 6 năm sẽ có 2 tỷ để mua nhà. Hỏi anh Nam phải
gửi vào ngân hàng một khoản tiền tiền tiết kiệm như nhau hàng năm gần nhất với giá trị
nào sau đây, biết rằng lãi suất của ngân hàng là 8%/năm và lãi hàng năm được nhập vào
vốn.
Bài 14. Ông A muốn sau 5 năm có 1.000.000.000 đồng để mua ô tô Camry. Hỏi rằng ông
A phải gửi ngân hàng mỗi tháng (số tiền như nhau) là bao nhiêu? Biết lãi suất hằng tháng
là 0.5% và tiền lãi sinh ra hằng tháng được nhập vào tiền vốn.
Bài 15. Ông Việt vay ngắn hạn ngân hàng 100 triệu đồng, với lãi suất 12%/năm. Ông
muốn hoàn nợ cho ngân hàng theo cách: Sau đúng một tháng kể từ ngày vay, ông bắt đầu
hoàn nợ; hai lần hoàn nợ liên tiếp cách nhau đúng một tháng, số tiền hoàn nợ ở mỗi lần là
như nhau và trả hết tiền nợ sau đúng 3 tháng kể từ ngày vay. Hỏi, theo cách đó, số tiền m
mà ông Việt sẽ phải trả cho ngân hàng trong mỗi lần hoàn nợ là bao nhiêu? Biết rằng, lãi
suất ngân hàng không thay đổi trong thời gian ông Việt hoàn nợ.
Bài 16. Một người đàn ông vay vốn ngân hàng với số tiền 100000000 đồng. Người đó dự
định sau đúng 5 năm thì trả hết nợ; Sau đúng một tháng kể từ ngày vay, ông bắt đầu hoàn
nợ; hai lần hoàn nợ liên tiếp cách nhau đúng một tháng, số tiền hoàn nợ ở mỗi lần là như
nhau. Hỏi, theo cách đó, số tiền a mà ông sẽ phải trả cho ngân hàng trong mỗi lần hoàn nợ
là bao nhiêu? Biết lãi suất hàng tháng là 1, 2% và không thay đổi trong thời gian ông hoàn
nợ.
2.5 Bài tập về logarit
2.5.1 Dạng 1: Tính giá trị biểu thức
!
1. Nhóm công thức định nghĩa
1 a
x
= b > 0 ⇔ x = log
a
b (mũ thành log) 2 log
a
x = b ⇒ x = a
b
(log thành mũ).
3 log
a
1 = 0 4 log
a
a = 1
5 log
a
a
b
= b 6 a
log
a
b
= b
7 log
a
α
a
β
=
β
α
8 a
log
b
c
= c
log
b
a
⇒ b = a
log
a
b
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 12
Hàm số mũ và hàm số logarit Giải tích 12
Ví dụ 11. Tính giá trị của biểu thức P = log
2
4 · log
1
4
2.
Lời giải.
Ta có P = log
2
4 · log
1
4
2 = log
2
2
2
· log
2
−2
2 = 2 ·
Ç
−
1
2
å
= −1.
Đáp số P = −1
Ví dụ 12. Tính giá trị của biểu thức P = 4
log
2
3
.
Lời giải.
Ta có P = 4
log
2
3
= 4
2. log
2
3
=
Ä
2
log
2
3
ä
2
= 3
2
= 9. Đáp số P = 9
Bài 17. Tính giá trị của các biểu thức sau:
A = log
2
4 · log
1
4
2a) B = log
5
1
25
· log
27
9b) C = log
a
3
»
√
ac)
D = 4
log
2
3
+ 9
log
√
3
2
d) E = log
2
√
2
8e) F = 27
log
9
2
+ 4
log
8
27
f)
G =
log
a
3
a · log
a
4
a
1
3
log
1
a
a
7
g) H = log
3
6 ·log
8
9 ·log
6
2h) I = 9
2 log
3
2+4 log
81
5
i)
J = 81
log
3
5
+ 27
log
9
36
+
3
4 log
9
7
j) K = 25
log
5
6
+ 49
log
7
8
k) L = 5
3−2 log
5
4
l)
M = 9
1
log
6
3
+ 4
1
log
8
2
m) N = log
√
6
3. log
3
36n) O = 3
1+log
9
4
+ 4
2−log
2
3
o)
Bài 18. Thực hiện các phép tính sau:
A = lg(tan 1
◦
) + lg(tan 2
◦
) + ··· + lg(tan 89
◦
)a)
B = log
8
[log
4
(log
2
16)] · log
2
[log
3
(log
4
64)]b)
C = 2 log
1
3
6 −
1
2
log
1
3
400 + 3 log
1
3
3
√
45c)
2.5.2 Dạng 2: Biến đổi logarit
!
2. Nhóm công thức biến đổi
1 log
a
(b.c) = log
a
b + log
a
c (tích⇒tổng).
.. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3 log
a
b
α
= α. log
a
b (trên⇒trên)
.. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5 log
a
1
b
= −log
a
b
2 log
a
b
c
= log
a
b −log
a
c (thương⇒hiệu).
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4 log
a
α
b =
1
α
. log
a
b (dưới⇒dưới)
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6 log
a
α
b
β
=
β
α
log
a
b
Ví dụ 13. Biến đổi biểu thức sau P = log
2
(3x) − log
2
(4x).
Lời giải.
Ta có P = log
2
(3x) − log
2
(4x) = log
2
3x
4x
= log
2
3
4
.
Đáp số P = log
2
3
4
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 13
Hàm số mũ và hàm số logarit Giải tích 12
Bài 19. Thực hiện cá phép tính:
log
3
(2x) − log
3
(8x)a) log(6a) − log(4a)b) ln(5b) − ln(2b)c)
Ví dụ 14. Khai triển biểu thức P = log
2
2a
3
b
.
Lời giải.
Ta có P = log
2
2a
3
b
= log
2
(2a
3
) − log
2
b = log
2
2 + log
2
a
3
− log
2
b = 1 + 3 log
2
a − log
2
b.
Đáp số P = 1 + 3 log
2
a − log
2
b
Ví dụ 15. Khai triển biểu thức P = log
2
√
2
(2a).
Lời giải.
Ta có Q = log
2
√
2
(2a) = [2 log
2
(2a)]
2
=
î
4 (1 + log
2
a)
2
ó
= 4
Ä
1 + 2 log
2
a + log
2
2
a
ä
.
Đáp số Q = 4
Ä
1 + 2 log
2
a + log
2
2
a
ä
Bài 20. Khai triển các biểu thức sau:
log
2
(2a)a) log
3
(27x)b) log
2
(8a
2
)c) log
3
(27a
3
)d)
log
5
(125a
5
)e) log(100a
2
b
3
)f) log
a
3
Ç
a
3
27
å
g) log
√
2
(2a)h)
log
√
3
(9a
2
)i) log
3
√
3
(27a
2
b
3
)j) log
√
a
(9
√
a)k) log
a
(125a
2
b
3
)l)
log
3
9x
2
y
m) log
x
2
y
z
2
n) log
3
27a
2
√
b
o) log
2
27a
3
b
2
p)
log
2
4x
y
2
z
q) log
3
9a
b
3
c
2
r) ln
8e
3
√
a
b
2
s) ln
16e
a
2
b
√
c
t)
Bài 21. Khai triển các biểu thức sau:
log
2
√
2
Å
a
b
ã
2
a) log
2
√
2
(2a)b)
log
2
9
(3a) − log
2
1
3
(27a)c) log
2
4
(2a
2
) − log
2
√
2
4
a
d)
log
2
√
3
(27x) + log
2
1
9
(3x) + log
2
9
Å
x
27
ã
e) log
2
√
3
Ç
3a
b
å
3
f)
log
2
√
5
Ç
a
2
25b
å
g) log
2
c
2
a
b
2
h)
Ví dụ 16. Cho log
3
x = 2 log
√
3
a + log
1
3
b. Tính x theo a và b.
Lời giải.
Ta có: log
3
x = 2 log
3
1
2
a + log
3
−1
b = 4 log
3
a − log
3
b = log
3
a
4
− log
3
b
= log
3
a
4
b
⇒ x =
a
4
b
Đáp số x =
a
4
b
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 14
Hàm số mũ và hàm số logarit Giải tích 12
Ví dụ 17. Cho log
a
b = 2 và log
a
c = 3. Tính giá trị biểu thức P = log
a
(a
2
.b
3
.c
4
).
Lời giải.
Ta có P = log
a
(a
2
.b
3
.c
4
) = log
a
a
2
+ log
a
b
3
+ log
a
c
4
= 2 + 3 log
a
b + 4 log
a
c.
⇒ P = 2 + 3.2 + 4.3 = 20. Đáp số P = 20
Bài 22. Tính giá trị biểu thức thỏa điều kiện cho trước.
Cho log
7
x = log
7
ab
2
− log
7
a
3
b. Tính x theo a và b.a)
Cho log
a
b = 3 và log
a
c = 5. Tính P = log
a
(ab
3
c
6
)b)
Cho log
a
b = 3 và log
a
c = 4. Tính P = log
a
(ab
2
c
5
)c)
Cho log
a
b = 2 và log
a
c = 5. Tính P = log
a
Ä
a
2
.
√
b
3
.
3
√
c
2
ä
d)
Cho log
2
a = 4 và log
3
b = 2. Tính P = 2 log
2
[log
2
(8a) + 9] + log
1
9
b
2
e)
Cho log
3
a = 2 và log
2
b =
1
3
. Tính P = 5 log
3
[log
3
(3a)] + log
1
4
b
2
f)
Cho log
5
a = 6 và log
6
b =
1
4
. Tính P = 3 log
5
ñ
log
5
Ç
125
a
+ 28
åô
+ 2 log
√
6
Ä
36
√
b
ä
g)
!
3. Nhóm đổi cơ số
1 log
a
b =
log
c
b
log
c
a
.. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3 log
a
b =
1
log
b
a
2 log
a
b. log
b
c = log
a
c
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4 a
log
b
c
= c
log
b
a
Ví dụ 18. Cho log
a
x = 2 và log
b
x = 3. Tính giá trị biểu thức P = log
ab
x + log
a
b
x.
Lời giải.
Ta có P = log
ab
x + log
a
b
x =
1
log
x
ab
+
1
log
x
a
b
=
1
log
x
a + log
x
b
+
1
log
x
a − log
x
b
=
1
1
log
a
x
+
1
log
b
x
+
1
1
log
a
x
−
1
log
b
x
=
1
1
2
+
1
3
+
1
1
2
−
1
3
=
36
5
.
Đáp số P =
36
5
Bài 23. Tính giá trị của các biểu thức sau:
Cho log
a
x = 3 và log
b
x = 4. Tính P = log
abx
x + log
a
b
x.a)
Cho log
a
x = 2 và log
b
x = 5. Tính P = log
ab
x − 2 log
a
b
x.b)
Cho log
a
x = 3 và log
b
x = 2. Tính P = 2 log
ab
x − 4 log
a
b
x.c)
Cho log
a
b =
b
2
và log
2
a =
16
b
. Tính a
32
+ b.d)
Cho log
a
b =
b
25
và log
5
a =
125
b
. Tính a + 2b.e)
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 15
Hàm số mũ và hàm số logarit Giải tích 12
Cho log
√
a
b =
b
4
và log
√
2
a =
16
b
. Tính a − 2b.f)
Cho log
√
a
b =
b
4
và log
√
2
a =
16
b
. Tính a − 2b.g)
Cho log
m
5 = x và log
m
3 = y. Tính P = (x + y). log
10
m.h)
Cho log
a
6 = x và log
a
2 = y. Tính P = (x + y). log
12
a.i)
Ví dụ 19. Cho log
2
14 = a. Tính log
49
√
7
32 và log
49
32 theo a.
Lời giải.
Ta có log
2
14 = a =⇔ log
2
(2.7) = a ⇔ log
2
2 + log
2
7 = a ⇔ 1 + log
2
7 = a
⇒ log
2
7 = a − 1
log
49
√
7
32 =
2
5
log
7
32 =
2
5
log
7
2
5
= 2 log
7
2 =
2
log
2
7
=
2
a − 1
Đáp số log
49
√
7
32 =
2
a − 1
log
49
32 = log
7
2
2
5
=
5
2
. log
7
2 =
5
2
.
1
log
2
7
=
5
2
.
1
a − 1
=
5
2(a − 1)
.
Đáp số log
49
32 =
5
2(a − 1)
Bài 24. Thực hiện phép biến đổi theo yêu cầu bài toán
Cho log
12
27 = a. Tính log
6
16 theo a.a)
Cho log
2
14 = a. Tính log
49
√
7
32 và log
49
32 theo a.b)
Cho log
2
5 = a; log
2
3 = b. Tính log
3
135 theo a, .c)
Cho log
15
3 = a. Tính log
25
15 theo a.d)
Cho log
a
b =
√
3. Tính log
√
b
a
3
√
b
√
a
.e)
Cho lg 3 = 0, 477. Tính lg 9000; lg(0, 000027);
1
log
81
100
.f)
Cho log
7
2 = a. Tính log
1
2
28 theo ag)
Cho log
a
b =
√
5. Tính log
√
ab
b
√
a
.h)
Cho log
a
b =
√
13. Tính log
b
a
3
√
ab
2
.i)
Cho log
25
7 = a; log
2
5 = b. Tính log
3
√
5
49
8
theo a, b.j)
Cho lg 3 = a; lg 2 = b. Tính log
125
30 theo a, b.k)
Cho log
14
7 = a; log
14
5 = b. Tính log
35
28 theo a, b.l)
Cho log
30
3 = a; log
30
5 = b. Tính log
30
1350 theo a, b.m)
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 16
Hàm số mũ và hàm số logarit Giải tích 12
Cho log
2
3 = a; log
3
5 = b; log
7
2 = c. Tính log
140
63 theo a, b, c.n)
Cho log
a
b =
√
7. Tính log
a
√
b
a
√
b
3
o)
Cho log
27
5 = a; log
8
7 = b; log
2
3 = c. Tính log
6
35 theo a, b, c.p)
Cho log
49
11 = a; log
2
7 = b. Tính log
3
√
7
121
8
theo a, b.q)
2.5.3 Dạng 3: Chứng minh đẳng thức logarit
Ví dụ 20. Chứng minh đẳng thức: log
(ax)
(bx) =
log
a
b + log
a
x
1 + log
a
x
(xem điều kiện được thỏa).
Lời giải.
Ta có log
(ax)
(bx) = log
(ax)
b + log
(ax)
x =
1
log
b
(ax)
+
1
log
x
(ax)
=
1
log
b
a + log
b
x
+
1
log
x
a + 1
=
log
a
b
1 + log
a
x
+
log
a
x
1 + log
a
x
=
log
a
b + log
a
x
1 + log
a
x
(đpcm).
Bài 25. Chứng minh các đẳng thức sau: (xem điều kiện được thỏa)
b
log
a
c
= c
log
a
b
a)
log
(ax)
(bx) =
log
a
b + log
a
x
1 + log
a
x
b)
log
a
c + log
b
c =
log
a
c · log
b
c
log
ab
c
c)
log
a
c
log
ab
c
= 1 + log
a
bd)
log
c
a + b
3
=
1
2
(log
c
a + log
c
b), với a
2
+ b
2
= 7abe)
log
a
(x + 2y) − 2 log
a
2 =
1
2
(log
a
x + log
a
y), với x
2
+ 4y
2
= 12xyf)
lg
3a + b
4
=
1
2
(lg a + lg b), với 9a
2
+ b
2
= 10abg)
log
(b+c)
a + log
(c−b)
a = 2 log
(c+b)
a · log
(c−b)
a, với a
2
+ b
2
= c
2
h)
1
log
a
x
+
1
log
a
2
x
+
1
log
a
3
x
+ ··· +
1
log
a
k
x
=
k(k + 1)
2 log
a
x
i)
log
a
N · log
b
N + log
b
N · log
c
N + log
c
N · log
a
N =
log
a
N · log
b
N · log
c
N
log
abc
N
j)
x = 10
1
1−lg z
với y = 10
1
1−lg x
và z = 10
1
1−lg y
k)
log
a
N − log
n
N
log
b
N − log
c
N
=
log
a
N
log
c
N
với a, b, c lần lượt theo thứ tự đó lập thành cấp số nhân.l)
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 17
Hàm số mũ và hàm số logarit Giải tích 12
2.5.4 Dạng 4: So sánh cặp số
Bài 26. Hãy so sánh các cặp số sau:
log
3
4 và log
4
1
3
a) log
0,1
3
√
2 và log
0,2
0, 34b)
log
3
4
2
5
và log
5
2
3
4
c) log
1
3
1
80
và log
1
2
1
15 +
√
2
d)
log
13
150 và log
17
290e) 2
log
6
3
và 3
log
6
1
2
f)
log
7
10 và log
11
13g) log
2
3 và log
3
4h)
2.5.5 Dạng 4: Bài toán thực tế
Bài 27. Biết rằng năm 2001, dân số Việt Nam là 78685800 người và tỉ lệ tăng dân số năm
đó là 1, 7% . Cho biết sự tăng dân số được ước tính theo công thức S = A.e
N.t
(trong đó A
: là dân số của năm lấy làm mốc tính, S là dân số sau N năm, r là tỉ lệ tăng dân số hàng
năm). Cứ tăng dân số với tỉ lệ như vậy thì đến năm nào dân số nước ta ở mức 120 triệu
người?
Bài 28. Các khí thải gây hiệu ứng nhà kính là nguyên nhân chủ yếu làm trái đất nóng lên.
Theo OECD (Tổ chức hợp tác và phát triển kinh tế thế giới), khi nhiệt độ trái đất tăng lên
thì tổng giá trị kinh tế toàn cầu giảm. Người ta ước tính rằng khi nhiệt độ trái đất tăng
thêm 2
◦
C thì tổng giá trị kinh tế toàn cầu giảm 3%, còn khi nhiệt độ trái đất tăng thêm
5
◦
C thì tổng giá trị kinh tế toàn cầu giảm 10% . Biết rằng nếu nhiệt độ trái đất tăng thêm
t
◦
C, tổng giá trị kinh tế toàn cầu giảm f(t)% thì f(t) = k.a
t
. (trong đó a, k là các hằng số
dương). Nhiệt độ trái đất tăng thêm bao nhiêu độ C thì tổng giá trị kinh tế toàn cầu giảm
20%?
Bài 29. Một người đã thả một lượng bèo hoa dâu chiếm 4% diện tích mặt hồ. Biết rằng
cứ sau đúng một tuần bèo phát triển thành 3 lần lượng đã có và tốc độ phát triển của bèo
ở mọi thời điểm như nhau. Sau bao nhiêu ngày, lượng bèo sẽ vừa phủ kín mặt hồ?
2.6 Bài tập hàm số mũ-hàm số logarit
2.6.1 Dạng 1: Tập xác định hàm số
!
y = log
a(x)
f(x) xác định khi:
0 < a(x) 6= 1
f(x) > 0
.
y = lg f(x) xác định khi: f (x) > 0.
y = ln f (x) xác định khi: f(x) > 0.
y = a
x
xác định khi 0 < a 6= 1.
Ví dụ 21. Tìm tập xác định của hàm số y = log
2
(3x − x
2
).
Lời giải.
Hàm số xác định khi: 3x − x
2
> 0 ⇔ 0 < x < 3.
Tập xác định là D = (0; 3).
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 18
Hàm số mũ và hàm số logarit Giải tích 12
Ví dụ 22. Tìm tập xác định của hàm số y = log
2
x − 2
1 − x
2
.
Lời giải.
Hàm số xác định khi:
x − 2
1 − x
2
> 0.
• Cho x − 2 = 0 ⇔ x = 2
• Cho 1 − x
2
= 0 ⇔ x = ±1
x
x − 2
1 −x
2
x − 2
1 − x
2
−∞
−1
1 2
+∞
− − −
0
+
−
0
+
0
− −
+ − +
0
−
Từ bảng xét dấu
x − 2
1 − x
2
> 0 ⇔
x < −1
1 < x < 2
. Tập xác định là D = (−∞; −1) ∪ (1; 2).
Ví dụ 23. Tìm tập xác định hàm số y = log
(x−1)
x
−x + 2
.
Lời giải. Hàm số xác định khi:
x
−x + 2
> 0
0 < x − 1 6= 1
⇔
0 < x < 2
1 < x 6= 2
⇔ 1 < x < 2.
Tập xác định hàm là D = (1; 2).
Bài 30. Tìm tập xác định của các hàm số sau:
y = lg
x − 1
−2x − 3
a) y = ln
√
x
2
− 4x − 12b)
y =
√
x
2
+ x − 2. log
3
(9 − x
2
)c) y = log
3
x + 1
√
x
2
− x − 2
d)
y = log
(2x−1)
(x
2
− 1)e) y = log
x
x
4 − x
2
f)
2.6.2 Dạng 2: Đạo hàm
!
1 (a
x
)
0
= a
x
. ln a
.. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3 (e
x
)
0
= e
x
.. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5 (log
a
x)
0
=
1
x. ln a
.. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7 (ln x)
0
=
1
x
2 (a
u
)
0
= a
u
. ln a.u
0
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4 (e
u
)
0
= e
u
.u
0
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6 (log
a
u)
0
=
u
0
u. ln a
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
8 (ln u)
0
=
u
0
u
Bài 31. Tính đạo hàm của các hàm số sau:
y = (x
2
− 2x + 2).e
x
a) y = (x
2
+ 2x) e
−x
b) y = e
−2x
. sin xc)
y = e
2x+x
2
d) y = x.e
√
x−
1
3
x
e) y =
e
2x
+ e
x
e
2x
− e
x
f)
y = 2
(
x
3
+ 1)g) y = 3
√
x
2
+1
h) y = 2
x
.e
cos x
i)
y =
3
x
x
2
− x + 1
j) y = cos x.e
cot x
k) y = 2018
2018x
l)
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 19
Hàm số mũ và hàm số logarit Giải tích 12
Bài 32. Tính các đạo hàm của các hàm số sau:
y = ln(2x
2
+ x + 3)a) y = log
2
(cos x)b) y = e
x
. ln (cos x)c)
y = (2x − 1) ln (3x
2
+ x)d) y = log
1
2
(x
3
− cos x)e) y = log
3
(cos x)f)
y =
ln (2x + 1)
√
2x + 1
g) y =
ln (2x + 1)
x + 1
h) y = ln
Ä
x +
√
1 + x
2
ä
i)
Bài 33. Tính đạo hàm của các hàm số sau
y = 1 − (x
2
− 2x + 1)e
x
a) y = 3
x
− (2x + 1)2
x
b) y =
ln(x) − 2
x + 1
c)
y = (x − 4) log xd) x log
2
(x + 1)e) y = log
3
√
x
2
. ln (3 − x
2
)f)
y = (2x
2
− 1)e
3x
g) y = x
3
√
e
x
2
+ 1h) y =
e
x
+ e
−x
e
x
+ e
−x
i)
y = 3
x
−
√
e
3x
+ 1j) y = ln (x
3
+ 2x
2
− x)k) y = (x
2
+ 3) ln(x
2
+ 2)l)
y =
4
»
ln
3
(3x
2
+ 1)m) y = 1 − (2x + 3)3
x
n) y =
√
2 − e
x
. sin
2
xo)
y = 2
x
−
√
e
x
p) y =
e
x
+ 1
e
x
− 1
q) y = x ln x + 1r)
y = 1 + x − 2 ln
2
xs) y = 1 −
»
2 ln x + ln
2
xt) y = log
2
x − 3 log
3
xu)
y = log(x
2
+ 1) − ln(2x)v) y = x
π
.π
x
w) y = e
x
(sin x − cos x)x)
2.6.3 Dạng 3: Chứng minh hàm số đã cho thỏa hệ thức cho trước
Ví dụ 24. Chứng minh hàm số đã cho thỏa hệ thức được chỉ ra.
y = x.e
−
x
2
2
. Chứng minh rằng: xy
0
= (1 − x
2
) y
Lời giải.
Ta có y
0
= e
−
x
2
2
+ x.e
−
x
2
2
.
Ç
−
x
2
2
å
0
= e
−
x
2
2
+ x.e
−
x
2
2
.(−x) = e
−
x
2
2
(1 − x
2
)
Ta có: VT= xy
0
= x.e
−
x
2
2
(1 − x
2
) = (1 − x
2
) y =VP (đpcm).
Bài 34. Chứng minh hàm số đã cho thỏa hệ thức được chỉ ra.
y = (x + 1)e
x
; y
0
− y = e
x
a) y = e
4x
+ 2e
−x
; y
000
+ 2y
0
− 12y = 0b)
y = a.e
−x
+ b.e
−2x
; y
00
+ 3y
0
+ 2y = 0c) y = e
−x
sin x; y
00
+ 2y
0
+ 2y = 0d)
y = e
−x
cos x; y
(4)
+ 4y = 0e) y = e
sin x
; y
0
cos x − y sin x − y
00
= 0f)
y = e
2x
sin 5x; y
00
− 4y
0
+ 29y = 0g) y =
1
2
x
2
e
x
; y
00
− 2y
0
+ y = e
x
h)
y = e
4x
+ 2e
−x
; y
000
− 13y
0
− 12 = 0i) y = x.e
−
x
2
2
; xy
0
= (1 − x
2
) yj)
Bài 35. Chứng minh hàm số đã cho thỏa hệ thức được chỉ ra.
y = ln
Ç
1
1 + x
å
; xy
0
+ 1 = e
y
a)
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 20
Hàm số mũ và hàm số logarit Giải tích 12
y =
1
1 + x + ln x
; xy
0
= y (y ln x − 1)b)
y = sin (ln x) + cos (ln x); y + xy
0
+ x
2
y
00
= 0c)
y =
1 + ln x
x (1 − ln x)
; 2x
2
y
0
= x
2
y
2
+ 1d)
y =
x
2
2
+
1
2
x
√
x
2
+ 1 + ln
»
x +
√
x
2
+ 1; 2y = xy
0
+ ln y
0
e)
y = (x
2
+ 1) (e
x
+ 2016); y
0
=
2xy
x
2
+ 1
+ e
x
(x
2
+ 1)f)
y = x [3 cos (ln x) + 4 sin (ln x)]; x
2
y
000
− xy
0
+ 2y = 0g)
2.6.4 Dạng 4: Giải phương trình, bất phương trình
Bài 36. Giải các phương trình, bất phương trình
f
0
(x) = 2f(x); f(x) = e
x
(x
2
+ 3x + 1)a)
f
0
(x) =
1
x
f(x) = 0; f(x) = x
3
ln xb)
f
0
(x) > g
0
(x); f(x) = x + ln(x − 5); g(x) = ln(x − 1)c)
f
0
(x) = 0; f (x) = e
2x−1
+ 2.e
1−2x
+ 7x − 5d)
f
0
(x) < g
0
(x); f(x) =
1
2
.5
2x+1
; g(x) = 5
x
+ 4x. ln 5e)
2.6.5 Dạng 5: Giá trị lớn nhất, giá trị nhỏ nhất
!
Tìm GTLN-GTNN của hàm số y = f(x) trên đoạn [a; b].
Tính y
0
Giải phương trình y
0
= 0 và chỉ nhận những nhiệm x
0
∈ [a; b]
Tính f(a), f(b), f(x
0
)
Khi đó: min
[a;b]
= min {f(a), f (b), f(x
0
)} và max
[a;b]
= max {f(a), f (b), f(x
0
)}
4
!
Chú ý:
1. Nếu ham số y = f(x) tăng trên [a; b] thì min
[a;b]
f(x) = f(a) và max
[a;b]
f(x) = f(b)
2. Nếu ham số y = f(x) giảm trên [a; b] thì max
[a;b]
f(x) = f(a) và min
[a;b]
f(x) = f(b)
3. Nếu bài toán đặt ẩn phụ thì phải có điều kiện cho ẩn phụ đó.
Ví dụ 25. Tìm GTLN-GTNN của hàm số y = x
2
.e
x
+ 1 trên đoạn [−3; 2].
Lời giải.
Ta có y
0
= 2x.e
x
+ x
2
.e
x
= e
x
(x
2
+ 2x).
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 21
Hàm số mũ và hàm số logarit Giải tích 12
y
0
= 0 ⇔ e
x
(x
2
+ 2x) = 0 ⇔ x
2
+ 2x = 0
x = 0(loại)
x = −2
f(−3) = 9.e
−3
+ 1 =
9
e
3
+ 1; f(2) = 4.e
2
+ 1; f(−2) = 4.e
−2
+ 1 =
4
e
2
+ 1
Vậy min
[−3;2]
f(x) = 9.e
−3
+ 1; max
[−3;2]
f(x) = 4.e
2
+ 1.
Bài 37. Tìm GTLN-GTNN của các hàm số sau:
y =
ln
2
x
x
− 1 trên đoạn [1; e
2
]a) y = ln
2
x − ln x trên đoạn [1; e
2
]b)
y = (x
2
− 3x + 1)e
x
trên đoạn [−3; 0]c) y = x ln x − 1 trên đoạn [1; e
2
]d)
y = x
2
− ln(1 − 2x) trên đoạn [−2; 0]e) y = x
2
.e
x
+ 1 trên đoạn [−3; 2]f)
A. PHƯƠNG TRÌNH
2.7 Phương trình mũ
2.7.1 Phương trình mũ cơ bản
!
Với a > 0, a 6= 1 thì
a
x
= b ⇔
b > 0
x = log
a
b
Ví dụ 26. Giải phương trình sau 2
x−1
= 3 (1)
Lời giải.
Ta có (1) ⇔ x − 1 = log
2
3 ⇔ x = 1 + log
2
3 ⇔ x = log
2
2 + log
2
3 = log
2
6
Đáp số x = log
2
6
4
!
Chú ý: 1 = log
a
a do đó: 1 = log
2
2
Ví dụ 27. Giải phương trình sau 2
x
+ 2
x+1
= 3
x
+ 3
x+1
(2)
Lời giải.
Ta có (2) ⇔ 2
x
+ 2.2
x
= 3
x
+ 3.3
x
⇔ 3.2
x
= 4.3
x
⇔
Ç
2
3
å
x
=
4
3
⇔ x = log
2
3
4
3
.
Đáp số x = log
2
3
4
3
Bài 38. Giải các phương trình sau:
2018
x+1
= 2a) 3
x
− 3
x−1
+ 3
x−2
= 2
x
+ 2
x−1
+ 2
x−2
b)
3
x+1
+ 3
x+2
= 9.5
x
+ 5
x+1
+ 5
x+2
c) 2.3
x+1
− 6.3
x−1
− 3
x
= 9d)
5
2x
− 7
x
− 5
2x
.17 + 7
x
.17 = 0e) 5.3
x
+ 3.2
x−1
= 7.2
x
− 4.3
x
f)
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 22
Hàm số mũ và hàm số logarit Giải tích 12
2.7.2 Một số phương pháp giải phương trình mũ
2.7.2.1 Phương pháp đưa về cùng cơ số
!
Dùng các công thức biến đổi phương trình đã cho về dạng: a
f(x)
= a
g(x)
.
Khi đó: Với a > 0, a 6= 1 thì a
f(x)
= a
g(x)
⇔ f(x) = g(x)
Trường hợp cơ số a chưa biến:
a
M
= a
N
⇔ (a − 1) . (M − N) = 0 ⇔
a = 1
M = N
Ví dụ 28. Giải phương trình 2
x
2
−1
= 8 (1)
Lời giải.
Ta có (1) ⇔ 2
x
2
−1
= 8 ⇔ 2
x
2
−1
= 2
3
⇔ x
2
− 1 = 3 ⇔ x
2
= 4 ⇔ x = ±2.
Đáp số x = ±2
Ví dụ 29. Giải phương trình 27
3x−2
= 9
x−1
(2)
Lời giải.
Ta có (2) ⇔ 3
3(3x−2)
= 3
2(x−1)
⇔ 3(3x−2) = 2(x−1) ⇔ 9x−6 = 2x−2 ⇔ 7x = 4 ⇔ x =
4
7
.
Đáp số x =
4
7
Ví dụ 30. Giải phương trình 2018
x
2
−3x+2
= 1 (3)
Lời giải.
Ta có (3) ⇔ 2018
x
2
−3x+2
= 2018
0
⇔ x
2
− 3x + 2 = 0
x = 1
x = 2
.
Đáp số x = 1; x = 2
4
!
Chú ý: 1 = a
0
do đó: 1 = 2018
0
.
Ví dụ 31. Giải phương trình (x + 1)
√
x−3
= 1 (4)
Lời giải.
Điều kiện: x − 3 ≥ 0 ⇔ x ≥ 3.
(3) ⇔ (x + 1)
√
x−3
= (x + 2)
0
⇔ [(x + 1) − 1] .
î
√
x − 3 − 0
ó
= 0 ⇔ x.
√
x − 3 = 0 ⇔
⇔
x = 0
√
x − 3 = 0
⇔
x = 0(loại)
x = 3
. Đáp số x = 3
Bài 39. Giải các phương trình sau:
(0, 04)
x
= 625.
3
√
5a) 0, 125.16
1−x
=
√
8
32
b)
2
8−x
2
.5
8−x
2
= 0, 001. (10
5
)
1−x
c) 3
2x−1
.15
3x
.5
−3x
=
3
√
9d)
5.3
x
+ 3.2
x
= 7.2
x
− 4.3
x
e) 9
3x−1
= 3
8x−2
f)
Ç
1
2
å
x
2
−2
= 2
4−3x
g)
Ç
1
2
å
x+7
.
Ç
1
2
å
1−2x
= 2h)
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 23
Hàm số mũ và hàm số logarit Giải tích 12
Ä
3 − 2
√
2
ä
2x
= 3 + 2
√
2i)
Ä
√
5 + 2
ä
x−1
=
Ä
√
5 − 2
ä
x−1
x+1
j)
(1, 5)
5x−7
=
Ç
2
3
å
x+1
k) (0, 75)
2x−3
=
Ç
4
3
å
5−x
l)
5
x
2
−5x+6
= 1m)
Ç
1
7
å
x
2
−2x−3
= 7
x+1
n)
Ä
3 − 2
√
2
ä
63x = 3 + 2
√
2o) 3
x
.2
x+1
= 72p)
2.3
x
− 6.3
x−1
− 3
x
= 9q) (x
2
− 2x + 2)
√
4−x
2
= 1r)
Ç
3
4
å
x−2
.
x
s
Ç
4
5
å
5
=
9
16
s)
Ç
1
25
å
x+1
= 125
2x
t)
2.7.2.2 Phương pháp logarit hóa
!
Phương trình logarit hóa có dạng: a
f(x)
= b
g(x)
⇔ f(x) = g(x). log
a
b
Ví dụ 32. Giải phương trình 2
x−1
= 7
1−x
2
(1)
Lời giải.
Từ (1) ⇔ x − 1 = (1 − x
2
). log
2
7 ⇔ x − 1 + (x − 1)(x + 1) log
2
7 = 0
⇔ (x − 1) [1 + (x + 1). log
2
7] = 0 ⇔
x − 1 = 0
1 + (x + 1). log
2
7 = 0
⇔
x = 1
x + 1 = −
1
log
2
7
= −log
7
2
⇔
x = 1
x = −1 − log
7
2
⇔
x = 1
x = −log
7
14
. Đáp số x = 1; x = −log
7
14
Bài 40. Giải các phương trình sau:
2
x
= 3
x
2
a) 5
x−1
= 3
x−1
x+1
b) 6
x−1
= 5
x
2
−2x+1
c)
2
4−x
2
= 3
2−x
d) 3
5
x
= 5
3
x
e) 7
x
= 2
4x
f)
Bài 41. Giải các phương trình sau (đưa về cùng cơ số hoặc logarit hóa)
4
x+1
=
3
√
16.a) 2
x+1
· 3
2x+3
= 6
3x+1
.b)
2
2x
2
+x+5
= 8
2x+1
.c) 5
x
· 8
x+1
= 100.d)
9
|3x−1|
= 3
8x−2
.e) 2
x+1
· 3
x−2
· 5
x
= 200.f)
Ç
2
5
å
x
·
Ç
25
8
å
x
=
125
64
.g) 5
x
+ 5
x+1
+ 5
x+2
= 3
x
+ 3
x+3
+ 3
x+1
.h)
8
x
x+2
= 36 · 3
2−x
.i) 3
x+2
− 3
x+1
= 18.j)
32
x+5
x−7
= 0, 25 · 125
x+17
x−3
k) 2 · 3
x+1
− 6 · 3
x−1
− 3
x
= 9l)
Ä
3 − 2
√
2
ä
2x
= 3 + 2
√
2m)
Ä
√
5 + 2
ä
x−1
=
Ä
√
5 − 2
ä
x−1
x+1
n)
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 24
Hàm số mũ và hàm số logarit Giải tích 12
5
x
· 8
x−1
x
= 500o)
√
x
x
= x
√
x
p)
Ä
√
2x − x
2
ä
x−1
= 1q)
Ä
√
x − x
2
ä
x−2
= 1r)
(x
2
− x + 1)
x
2
−1
= 1s) (x + 1)
√
x−3
= 1t)
(x
2
+ 3)
|
x
2
−5x+4
|
= (x
2
+ 3)
x+1
u)
Bài 42. Giải các phương trình sau (đưa về cùng cơ số hoặc logarit hóa)
3
x−1
+ 3
x
+ 3
x+1
= 9477a) 5
x+1
− 5
x
= 2
x+1
+ 2
x+3
b)
2
x−1
− 3
x
= 3
x−1
− 2
x+2
c) 5
x
+ 5
x+1
+ 5
x+2
= 7
x
+ 7
x+1
− 7
x+2
d)
2
2x+5
− 3
x+
9
2
= 3
x+
7
2
− 4
x+4
e) 3 · 4
x
+
1
3
· 9
x+2
= 6 · 4
x+2
−
1
2
· 9
x+1
f)
9
x
− 2
x+
3
2
= 2
x+
1
2
− 3
2x−1
g) 4
−x
− 3
−x−
1
2
= 3
1
2
−x
− 2
−2x−1
h)
5
x+
1
2
− 9x = 3
2x−2
− 5
x−
1
2
i) 4
x+2
− 10 · 3
x
= 2 · 3
x
− 11 · 2
2x
j)
x
2
− (2
x
− 3)x + 2(1 − 2
x
) = 0k) x
2
· 2
x+1
= 2
|x−3|+2
= x
2
· 2
|x−3|
+ 2
x−1
l)
6
2x+3
= 2
x+7
· 3
3x−1
m) 3
x+3
· 7
x+3
= 3
2x
· 7
2x
n)
3
2x+3
· 5
2x+3
= 5
5x
· 3
5x
o) 3
x−1
· 2
2x−2
= 12
9−x
p)
8
x
x+2
= 36 · 3
2−x
q) 5
x
2
−5x+6
= 2
x−1
r)
2
x
· 5
x−1
x
= 10s) 3
x
2
−4x
= 2
x−4
t)
4 · 3
x+2
+ 5 · 3
x
− 7 · 3
x+1
= 40u) 2
2x+6
+ 2
x+7
− 17 = 0v)
5
2x−1
+ 5
x+1
= 250w) 5
x−1
+ 5
3−x
= 26x)
2
x+4
+ 2
x+2
= 5
x+1
+ 3 · 5
x
y) 5
x+1
+ 6 · 5
x
− 3 · 5
x−1
= 52z)
2.7.2.3 Phương pháp đặt ẩn phụ
!
2.7.2.3.1 Dạng 1:
P
Ä
a
f(x)
ä
= 0 ⇔
t = a
f(x)
, t > 0
P (t) = 0
2.7.2.3.2 Dạng 2:
α · a
2f(x)
+ β · (ab)
f(x)
+ λ · b
2f(x)
= 0
Chia hai vế cho b
2f(x)
hoặc a
2f(x)
(chia cơ số lớn nhất hoặc nhỏ nhất). Sau đó đặt
t =
Å
a
b
ã
f(x)
> 0
2.7.2.3.3 Dạng 3:
a
f(x)
+ b
f(x)
= m
với a · b = 1. Đặt t = a
f(x)
⇒ b
f(x)
=
1
t
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 25
Hàm số mũ và hàm số logarit Giải tích 12
Ví dụ 33. Giải phương trình: 9
x
− 5 · 3
x
+ 6 = 0 (1)
Lời giải.
(1) ⇔ (3
2
)
x
− 5 · 3
x
+ 6 = 0 ⇔ (3
x
)
2
− 5 · 3
x
+ 6 = 0 (*)
Đặt t = 3
x
, (t > 0), phương trình (*) trở thành t
2
− 5t + 6 = 0 ⇔
t = 2 (n)
t = 3 (n)
• Với t = 2 ⇒ 3
x
= 2 ⇔ x = log
3
2
• Với t = 3 ⇒ 3
x
= 3 ⇔ x = log
3
3 = 1
Đáp số x = log
3
2; x = 1
Ví dụ 34. Giải phương trình: 25
x
+ 15
x
= 2 · 9
x
(2)
Lời giải.
Chia hai vế cho 25
x
, ta được:
(2) ⇔ 1 +
15
x
25
x
= 2 ·
9
x
25
x
⇔ 2 ·
ñÇ
3
5
å
x
ô
2
−
Ç
3
5
å
x
+ 1 = 0 (*)
Đặt t =
Ç
3
5
å
x
> 0, phương trình (*) trở thành 2t
2
− t − 1 = 0 ⇔
t = 1 (nhận)
t = −
1
2
(loại)
Với t = 1 ⇒
Ç
3
5
å
x
= 1 ⇔ x = 0
Đáp số x = 0
Ví dụ 35. Giải phương trình:
Ä
2 +
√
3
ä
x
+
Ä
2 −
√
3
ä
x
= 4 (3)
Lời giải.
Nhận xét:
Ä
2 +
√
3
ä
·
Ä
2 −
√
3
ä
= 1 ⇔
îÄ
2 +
√
3
ä
·
Ä
2 −
√
3
äó
x
= 1 ⇔
⇔
Ä
2 +
√
3
ä
x
·
Ä
2 −
√
3
ä
x
= 1
Đặt
Ä
2 +
√
3
ä
x
= t > 0 ⇒
Ä
2 −
√
3
ä
x
=
1
t
Phương trình (3) trở thành: t +
1
t
= 4 ⇔ t
2
− 4t + 1 = 0 ⇔
t = 2 +
√
3 > 0 (nhận)
t = 2 −
√
3 > 0 (nhận)
• Với t = 2 +
√
3 ⇒
Ä
2 +
√
3
ä
x
= 2 +
√
3 ⇔ x = 1
• Với t = 2 −
√
3 ⇒
Ä
2 +
√
3
ä
x
= 2 −
√
3 = (2 +
√
3)
−1
⇔ x = −1
Đáp số x = 1; x = −1
Bài 43. Giải các phương trình sau:
2
1+2x
+ 15 · 2
x
− 8 = 0a) 5
x+1
− 5
2−x
= 124b)
5
√
x
− 5
1−
√
x
+ 4c) 3
2−2x
− 2 · 3
2−x
− 27 = 0d)
5
x
+ 25
1−x
= 6e)
Ä
7 + 4
√
3
ä
x
+
Ä
2 +
√
3
ä
x
= 6f)
9
sin
2
x
+ 9
cos
2
x
= 6g) 4
x
+ 2
x+1
− 8 = 0h)
4
x+1
− 6 · 2
x+1
+ 8 = 0i) 3
4x+8
− 4 · 3
2x+5
+ 27 = 0j)
16
x
− 17 · 4
x
+ 16 = 0k) 49
x
+ 7
x+1
− 8 = 0l)
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 26
Hàm số mũ và hàm số logarit Giải tích 12
2
x
2
−x
− 2
2+x−x
2
= 3m)
Ä
7 + 4
√
3
ä
x
+
Ä
2 +
√
3
ä
x
= 6n)
4
cos 2x
+ 4
cos
2
x
= 3o) 3
2x+5
− 36 · 3
x+1
+ 9 = 0p)
4
x
2
+2
+ 9 · 2
x
2
+2
+ 8 = 0q) 3
2x
2
+2x+1
− 28 · 3
x
2
+x
+ 9 = 0r)
3 · 5
2x−1
− 2 · 5
x−1
= 0, 2s) 2
sin
2
x
+ 4 · 2
cos
2
x
= 6t)
4
√
x−2
+ 16 = 10 · 2
√
x−2
u) 5
√
x
− 5
1−
√
x
+ 4 = 0v)
8
2
x−1
+
2
x
2 + 2
x
=
18
2
x−1
+ 2
1−x
+ 2
w)
Bài 44. Giải các phương trình sau:
9
x
− 5 · 3
x
+ 6 = 0a) 2
x+2
− 2
2−x
− 15 = 0b)
e
2x
− 4 · e
−2x
= 3c) 9
x
2
−1
− 36 · 3
x
2
−3
+ 3 = 0d)
4
√
x−2
+ 16 = 10 · 2
√
x−2
e) 4
x+1
+ 2
x+2
− 3 = 0f)
e
6x
− 3 · e
3x
+ 2 = 0g) −8
x
+ 2 · 4
x
+ 2
x
− 2 = 0h)
81
sin
2
x
+ 81
cos
2
x
= 30i) 9
x
− 25 · 3
x
+ 7 = 0j)
25
x
− 23 · 5
x
− 5 = 0k) 25
x
− 6 · 5
x+1
+ 5
3
= 0l)
13
2x
− 6 · 13
x
+ 5 = 0m) 3 · 5
2x−1
− 2 · 5
x−1
=
1
5
n)
3
2
3−x
= 4
x−4
− 7o) 3
2(x+1)
− 82 · 3
x
+ 9 = 0p)
3
x+2
+ 9
x+1
= 4q) 9
x
2
−1
− 3
x
2
+1
− 6 = 0r)
3
x+2
+ 9
x+1
= 4s) 4
x+
√
x
2
−2
− 5 · 2
x−1+
√
x
2
−2
= 6t)
Ä
3
√
3
ä
x
+
Ä
10
√
3
ä
x−10
− 84 = 0u) 4
2x
+ 2
3x+1
+ 2
x+2
− 16 = 0v)
8
x
− 3 · 4
x
− 3 · 2
x+1
+ 8 = 0w) 3
2+x
+ 3
2−x
= 30x)
4
x
+ 2
3−4x
= 6y) 3
√
x
− 3
1−
√
x
+ 4 = 0z)
Bài 45. Giải các phương trình sau:
5
2x−3
=
2
5
x−1
+ 15a)
Ç
1
4
å
x−2
= 2
5−x
+ 9b)
Ç
1
6
å
x−3
= 6
5−2x
− 12c)
3
2x
100
x
= 2 · (0, 3)
x
+ 3d)
10
1+x
2
− 10
1−x
2
= 99e) 5
1+x
2
− 5
1−x
2
= 24f)
9
√
x
2
−2x−x
− 7 · 3
√
x
2
−2x−x−1
= 2g) 5 · 2
3|x−1|
− 3 · 2
5−3x
+ 7 = 0h)
9
2
x−2
=
10 + 4
x
2
4
i) 3 · 2
x−1
√
x+1
− 8 · 2
√
x−1
2
+ 4 = 0j)
8 · 3
√
x+
4
√
x
+ 9
4
√
x+1
= 9
√
x
k) 4
x+
√
x
2
−2
− 5 · 2
x−1+
√
x
2
−2
− 6 = 0l)
4
3+2 cos x
− 7 · 4
1+cos x
− 2 = 0m)
Ä
7 + 4
√
3
ä
x
− 3
Ä
2 −
√
3
ä
x
+ 2 = 0n)
8
2
x
− 2
3x+3
x
+ 12 = 0o)
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 27
Hàm số mũ và hàm số logarit Giải tích 12
Bài 46. Giải các phương trình mũ sau:
9
x+1
− 13 · 6
x
+ 4
x+1
= 0a) 49
x
− 2 · 35
x
− 7 · 5
2x+1
= 0b)
2 · 4
1
x
+ 6
1
x
= 9
1
x
c) 8
x
+ 18
x
= 2 · 27
x
d)
4 · 9
x
+ 12
x
− 3 · 16
x
e) 8 · 4
x
+ 9
x
= 6
x+1
f)
9
x
2
−1
− 36 · 3
x
2
−3
+ 3 = 0g) 125
x
+ 50
x
= 2
3x+1
h)
6 · 9
x
− 13 · 6
x
+ 6 · 4
x
i) 4 · 3
x
− 9 · 2
x
= 5 · 6
x
2
j)
4
x
− 2 · 6
x
= 3 · 9
x
k) 64 · 9
x
− 84 · 12
x
+ 27 · 16
x
l)
4
−
1
x
+ 6
−
1
x
= 9
−
1
x
m) 3 · 16
x
+ 2 · 81
x
= 5 · 36
x
n)
25
x
+ 10
x
+ 2
2x+1
o) 27
x
+ 12
x
= 2 · 8
x
p)
6 · 9
1
x
− 13 · 6
1
x
+ 6 · 4
1
x
q) 6 · 3
2x
− 13 · 6
x
+ 6 · 2
2x
r)
3 · 16
x
+ 2 · 81
x
= 5 · 36
x
s) 8 · 4
x
+ 9
x
= 6
x+1
t)
9
x
2
−1
− 36 · 3
x
2
−3
+ 3 = 0u) 125
x
+ 50
x
= 2
3x+1
v)
27
x
+ 12
x
= 2 · 8
x
w)
Bài 47. Giải các phương trình mũ sau:
Ä
2 +
√
3
ä
x
2
+
Ä
2 −
√
3
ä
x
2
= 4a)
»
7 +
√
48
x
+
»
7 −
√
48
x
= 14b)
»
5 + 2
√
6
x
+
»
5 − 2
√
6
x
= 10c) 6 ·
Ä
√
5 + 1
ä
x
− 2 ·
Ä
√
5 − 1
ä
x
= 2
x+2
d)
3
»
3 +
√
8
x
+
3
»
3 −
√
8
x
= 6e)
Ä
8 + 3
√
7
ä
tan x
+
Ä
8 − 3
√
7
ä
tan x
= 16f)
»
4 −
√
15
x
+
»
4 +
√
15
x
=
Ä
2
√
2
ä
x
g)
Ä
2 −
√
3
ä
x
+
Ä
2 +
√
3
ä
x
= 14h)
»
2 +
√
3
x
+
»
2 −
√
3
x
= 4i)
Ä
7 + 4
√
3
ä
x
− 3 ·
Ä
2 −
√
3
ä
x
+ 2 = 0j)
7 + 3
√
5
2
!
x
+ 7 ·
7 − 3
√
5
2
!
x
= 8k)
Ä
3 +
√
5
ä
x
+ 16 ·
Ä
3 −
√
5
ä
x
= 2
x+3
l)
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 28
Hàm số mũ và hàm số logarit Giải tích 12
2.7.2.4 Sử dụng tính đơn điệu của hàm số
!
Xét hàm số: f(x) = g(x) (1)
Đoán x
0
là một nghiệm của phương trình (1) (thông thường là lân cận của số 0)
Dựa vào tính đồng biến và nghịch biến của f(x) và g(x) để kết luận x
0
là nghiệm
duy nhất:
• f(x) đồng biến và g(x) nghịch biến
• f(x) đơn điệu và g(x) = c (hằng số)
Nếu f(x) đồng biến (hoặc nghịch biến) thì f(u) = f(v) ⇔ u = v
Lưu ý
• Hàm số bậc nhất: y = ax + b, (a 6= 0)
– Đồng biến khi: a > 0
– Nghịch biến khi: a < 0
• Hàm số mũ: y = a
x
– Đồng biến khi: a > 1
– Nghịch biến khi: 0 < a < 1
Ví dụ 36. Giải phương trình: 3
x
= 5 − 2x (4)
Lời giải.
Đặt f(x) = 3
x
đồng biến trên R (vì a = 3 > 1)
g(x) = 5 − 2x nghịch biến trên R (vì a = −2 < 0)
Ta có: f(1) = g(1) ⇒ x = 1 là nghiệm duy nhất của phương trình (4).
Ví dụ 37. Giải phương trình: (x + 4) · 9
x
− (x + 5) · 3
x
+ 1 = 0 (5)
Lời giải.
Đặt 3
x
= t > 0, phương trình (4) trở thành: (x + 4)t
2
− (x + 5)t + 0 = 0
∆ = (x + 5)
2
− 4(x + 4) = x
2
+ 6x + 9 = (x + 3)
2
⇒
t =
x + 5 + x + 3
2(x + 4)
= 1
t =
x + 5 − x − 3
2(x + 4)
=
1
x + 4
• Với t = 1 ⇒ 3
x
= 1 ⇔ x = 0
• Với t =
1
x + 4
> 0 ⇔
x > −4
3
x
· (x + 4) = 1 (∗∗)
Xét hàm số f(x) = 3
x
· (x + 4), ∀x ∈ (−4; +∞)
Ta có f
0
(x) = 3
x
· (x + 4) · ln 3 + 3
x
= 3
x
· [(x + 3) · ln 3 + 1] > 0, ∀x ∈ (−4; +∞)
⇒ f(x) đồng biến ∀x ∈ (−4; +∞) và g(x) = 1 là hàm không đổi.
Ta thấy f(−1) = g(−1) ⇒ x = −1 là nghiệm duy nhất của phương trình (**).
Vậy phương trình (5) có hai nghiệm x = 0; x = −1
Đáp số x = 0; x = −1
Bài 48. Giải các phương trình mũ sau (sử dụng tính đồng biến và nghịch biến)
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 29
Hàm số mũ và hàm số logarit Giải tích 12
Ç
1
2
å
x
= x −
1
2
a)
Ç
1
3
å
x
= −
3
x
b)
Ç
1
3
å
x
= x + 1c) 2x = 3
x
2
+ 1d)
2
x
= x + 2e) 7
6−x
= x + 2f)
3
x
= x + 2g) 2x = 3
x
2
+ 1h)
3
x
= 11 − xi) 2
−x
+ 3x + 10 = 0j)
3
x
= 5 − 2xk) 2
x+1
− 4
x
= x − 1l)
4
x
+ 7
x
= 9x + 2m) 6
x
+ 2
x
= 5
x
+ 3
x
n)
Ç
3
5
å
x
+
7
5
= 2
x
o) 2
x
+ 5
x
= 7
x
p)
9
x
+ 2(x − 2) · 3
x
+ 2x − 5 = 0q)
Ä
√
3 −
√
2
ä
x
+
Ä
√
3 +
√
2
ä
x
=
Ä
√
5
ä
x
r)
Ä
3 + 2
√
2
ä
x
+
Ä
3 − 2
√
2
ä
x
= 6
x
s) 2
x−1
− 2
x
2
−x
= (x − 1)
2
t)
2
√
3−x
= −x
2
+ 8x − 14u) 3 · 4
x
+ (3x − 10) · 2
x
+ 3 − x = 0v)
Bài 49. Giải các phương trình sau:
3 · 16
x−2
− (3x − 10) · 4
x−2
+ 3 − x = 0a) 8 − x · 2
x
+ 2
3−x
− x = 0b)
9
x
2
+ (x
2
− 3) · 3
x
2
+ 2 (1 − x
2
) = 0c) 3
2x
+ 2 (x − 2) · 3
x
+ 2x − 9 = 0d)
3
2x−3
− (3x − 10) · 3
x−2
+ 3 − xe) 4
1
x
+ 2x · 2
1
x
− 6x = 9f)
25
x
− 2(3 − x) · 5
x
+ 2x − 7 = 0g) 3 · 25
x−2
+ (3x − 10) · 5
x−2
+ 3 − x = 0h)
3 · 4
x
+ (3x − 10) · 2
x
+ 3 − x = 0i) 9
x
+ 2(x − 2) · 3
x
+ 2x − 5 = 0j)
4
x
+ (x − 8) · 2
x
+ 12 − 2x = 0k) (x + 4) · 9
x
− (x + 5) · 3
x
+ 1 = 0l)
2.7.2.5 Phương trình tích
!
Phương trình tích: A · B = 0 ⇔
A = 0
B = 0
Nghiệm phương trình bậc 2: ax
2
+ bx + c = 0, (a 6= 0)
• ∆ = b
2
− 4ac
• Nghiệm là
x =
−b +
√
∆
2a
x =
−b −
√
∆
2a
Ví dụ 38. Giải phương trình: 25 · 2
x
− 10
x
+ 5
x
= 25 (1)
Lời giải.
(1)⇔ 25 ·2
x
−25 −2
x
·5
x
+ 5
x
= 0 ⇔ 25 (2
x
− 1) −5
x
(2
x
− 1) = 0 ⇔ (2
x
− 1) (25 − 5
x
) = 0
⇔
2
x
− 1 = 0
25 − 5
x
= 0
⇔
2
x
= 1
5
x
= 25
⇔
x = 0
x = 2
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 30
Hàm số mũ và hàm số logarit Giải tích 12
Đáp số x = 0; x = 2
Ví dụ 39. Giải phương trình: 2 (x
2
− 3
x+1
) = 3x (1 − 4 · 3
x
) − 1 (2)
Lời giải 1. Nghiệm phương trình bâc 2 (theo biến x)
(1)⇔ 2x
2
− 3(1 − 4 · 3
x
) · x − 6 · 3
x
+ 1 = 0
∆ = 9(1 − 8 · 3
x
+ 16 · 9
x
) − 8(−6 · 3
x
+ 1) = 144 · 9
x
− 24 · 3
x
+ 1 = (12 · 3
x
− 1)
2
⇒
x =
3 − 12 · 3
x
+ 12 · 3
x
− 1
4
x =
3 − 12 · 3
x
− 12 · 3
x
+ 1
4
⇔
x =
1
2
3
x
=
1
6
−
x
6
(∗)
Xét phương trình (**) 3
x
=
1
6
−
x
6
. Đặt
f(x) = 3
x
; g(x) =
1
6
−
x
6
• Hàm số f(x) = 3
x
đồng biến trên R (vì a = 3 > 1)
• Hàm số g(x) =
1
6
−
x
6
nghịch biến trên R (vì a = −
1
6
< 0)
Ta nhận thấy f(−1) = g(−1) ⇒ x = −1 là nghiệm duy nhất của phương trình (*).
Vậy nghiệm phương trình đã cho là x =
1
2
; x = −1
Lời giải 2. Đưa về phương trình tích
(2)⇔ 2x
2
− 3x + 1 + 6 · 3
x
· (2x − 1) = 0 ⇔ 2(x − 1)
Ç
x −
1
2
å
+ 6 · 3
x
· (2x − 1) = 0
⇔ (2x − 1)(x − 1 + 6 · 3
x
) = 0 ⇔
x =
1
2
3
x
=
1
6
−
x
6
(giải như ở trên)
Bài 50. Giải các phương trình mũ sau (đưa về phương trình tích)
25 · 2
x
− 10
x
+ 5
x
= 25a) −8
x
+ 2 · 4
x
+ 2
x
− 2 = 0b)
3 · 8
x
+ 4 · 12
x
− 18
x
− 2 · 27
x
c) x
2
· 3
x−1
+ x(3
x
− 2
x
) = 2(2
x
− 3
x−1
)d)
5
2x+1
+ 7
x+1
− 175
x
− 35 = 0e) 8 − x · 2
x
+ 2
3−x
− x = 0f)
2
x
+ 3
x
= 1 + 6
x
g) 4
x
2
−3x+2
+ 4
x
2
+6x+5
= 4
2x
2
+3x+7
+ 1h)
2.7.3 Bài toán liên quan tham số m
Bài 51. Tìm tham số m để các phương trình sau có nghiệm:
9
x
+ 3
x
+ m = 0a) 9
x
+ m · 3
x
− 1 = 0b)
4
x
− 2
x+1
= mc) 2
x
+ (m + 1) · 2
−x
+ m = 0d)
25
x
− 2 · 5
x
− m − 2 = 0e) 16
x
− (m − 1) · 2
2x
+ m − 1 = 0f)
25
x
+ m · 5
x
+ 1 − 2m = 0g) 3
4−2x
2
− 2 · 3
2−x
2
= 2m − 3 = 0h)
9
x+
√
1−x
2
− 8 · 3
x+
√
1−x
2
+ 4 = mi) 9
1+
√
1−x
2
−(m+2)·3
1+
√
1−x
2
+2m+1 = 0j)
Bài 52. Tìm tham số m để các phương trình sau có nghiệm duy nhất.
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 31
Hàm số mũ và hàm số logarit Giải tích 12
m · 2
x
+ 2
−x
− 5 = 0a) m · 16
x
+ 2 · 81
x
= 5 · 36
x
b)
Ä
√
5 + 1
ä
x
+ m ·
Ä
√
5 − 1
ä
x
= 2
x
c) 4
x
− 2
x+3
+ 3 = md)
Bài 53. Tìm tham số m để các phương trình mũ sau có hai nghiệm phân biệt trái dấu
49
x
+ (m − 1) · 7
x
+ m − 2m
2
= 0a) (m+1)·4
x
+(3m−2)·2
x+1
−3m+1 = 0b)
9
x
+ 3(m − 1) · 3
x
− 5m + 2 = 0c) (m + 3) ·16
x
+ (2m −1) ·4
x
+ m + 1 = 0d)
Bài 54. Tìm tham số m để các phương trình:
m · 16
x
+ 2 · 81
x
= 5 · 36
x
có hai nghiệm dương phân biệt.a)
16
x
− m · 8
x
+ (2m − 1) · 4
x
= m · 2
x
có ba nghiệm phân biệtb)
4
X
2
− 2
x
2
+2
+ 6 = m có ba nghiệm phân biệt.c)
9
x
2
− 4 · 3
x
2
+ 8 = m có ba nhiệm phân biệt.d)
2.8 Phương trình logarit
2.8.1 Phương trình logarit cơ bản
Với a > 0, a 6= 1:
log
a
x = b ⇔ x = a
b
4
!
Chú ý: Khi giải phương trình logarit ta cần đặt điều kiện để phương trình có nghĩa.
Các công thức logarit thường sử dùng
CT.1 log
a
b + log
a
c = log
a
(b · c) CT.2 log
a
b − log
a
c = log
a
Ç
b
c
å
CT.3 log
a
b
β
=
β · log
a
b nếu β lẻ
β · log
a
|b| nếu β chẳn
CT.4 log
a
β
b =
1
β
· log
a
b
CT.5 log
a
b =
1
log
b
a
CT.6 log
b
c =
log
a
c
log
a
b
2.8.2 Một số phương pháp giải phương trình logarit
2.8.2.1 Phương pháp đưa về cùng cơ số
Với a > 0, a 6= 1:
log
a
f(x) = log
a
g(x) ⇔
f(x) > 0 (g(x) > 0)
f(x) = g(x)
2.8.2.2 Phương pháp mũ hóa
Với a > 0, a 6= 1:
log
a
f(x) = g(x) ⇔ f(x) = a
g(x)
Ví dụ 40. Giải phương trình: log
3
(2x − 1) = −2 (1)
Lời giải.
Điều kiện: 2x − 1 > 0 ⇔ x >
1
2
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 32
Hàm số mũ và hàm số logarit Giải tích 12
(1)⇔ log
2
(2x − 1) = log
2
2
−2
⇔ 2x − 1 =
1
4
⇔ x =
5
8
(nhận).
Ví dụ 41. Giải phương trình: log
2
(9 − 2
x
) = 3 − x (2)
Lời giải.
Điều kiện: 9 − 2
x
> 0 ⇔ 2
x
< 9 (*)
(1)⇔ log
2
(9 − 2
x
) = log
2
2
3−x
⇔ 9 − 2
x
= 2
3−x
⇔ 2
x
+
8
2
x
− 9 = 0 (**)
Đặt 2
x
= t > 0, phương trình (**) trở thành t +
8
t
− 9 = 0 ⇔ t
2
− 9t + 8 = 0 ⇔
t = 1
t = 8
• Với t = 1 ⇒ 2
x
= 1 ⇔ x = 0 thay vào điều kiện (*) thỏa.
• Với t = 8 ⇒ 2
x
= 8 ⇔ x = 3 thay vào điều kiện (*) thỏa.
Nghiệm phương trình đã cho là x = 0; x = 3
2.8.2.3 Phương pháp đặt ẩn phụ
!
Đặt điều kiện cho phương trình:
Biến đổi phương trình đã cho về dạng:
[α · log
a
f(x)]
2
+ β · log
a
f(x) + c = 0 (∗)
Đặt log
a
f(x) = t
Phương trình (*) trở thành: α · t
2
+ β · t + c = 0 (**)
Giải phương trình (**), tìm được nghiệm t ⇒ nghiệm x.
Ví dụ 42. Giải phương trình: log
2
2
x − 4 · log
2
x + 3 = 0 (3)
Lời giải.
Điều kiện: x > 0
Đặt log
2
x = t, phương trình (3) trở thành t
2
− 4t + 3 = 0 ⇔
t = 1
t = 3
• Với t = 1 ⇒ log
2
x = 1 ⇔ x = 2
• Với t = 3 ⇒ log
2
x = 3 ⇔ x = 8
Nghiệm phương trình đã cho là x = 2; x = 8
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 33
Hàm số mũ và hàm số logarit Giải tích 12
2.8.2.4 Sử dụng tính đơn diệu hàm số
!
Phương trình:
f(x) = g(x) (1)
y = f(x) đồng biến (hoặc nghịch biến) trên tập xác định D.
y = g(x) nghịch biến (hoặc đồng biến) trên tập xác định D.
f(x
0
) = g(x
0
) ⇒ x = x
0
là nghiệm duy nhất của (1) trên D.
Lưu ý:
a) Hàm số y = log
a
x :
đồng biến khi: a > 1
nghịch biến khi: 0 < a < 1
b) Hàm số y = ax + b :
đồng biến khi: a > 0
nghịch biến khi: a < 0
Ví dụ 43. Giải phương trình: log
1
3
x = x − 4 (4)
Lời giải.
Điều kiện: x > 0.
Đặt f(x) = log
1
3
x nghịch biến trên (0; +∞) vì a =
1
3
< 0.
g(x) = x − 4 đồng biến trên (0; +∞) vì a = 1 > 0
Ta có f(3) = g(3) ⇒ x = 3 là nghiệm duy nhất của phương trình (4).
Bài 55. Giải các phương trình logarit (đưa về cùng cơ số hoặc mũ hóa)
log
2
(x + 2) − log
2
(x − 2) = 2a)
log(x
2
+ 2x − 3) + log(x + 3) = log(x − 1)b)
2 · log
25
(3x − 11) + log
5
(x − 27) = 3 + log
5
8c)
log
5
x
3
+ log
0,2
x + log
3
√
25
x = 7d)
log
2
x + log
2
(x − 1) = 1e)
log
2
x − 5
x + 5
+ log
2
(x
2
− 25) = 7f)
log
4
(log
2
x) + log
2
(log
4
x) = 2g)
log
3
(3
x+1
− 26) = 2 − xh)
log
4
(x + 3) − log
2
√
x − 1 = 2 − log
4
8i)
log
4
Å
x
4
ã
2
− log
2
(4x)
4
+ 10 = 0j)
2 · log
3
(x − 2) + log
3
(x − 4)
2
= 0k)
3
2
· log
1
4
(x + 2)
2
− 3 = log
1
4
(4 − x)
3
+ log
1
4
(x + 6)
3
l)
log
2
|x − 2| + log
2
|x + 5| + log
1
2
8 = 0m)
1
3
· log
2
(3x − 4)
6
· log
2
x
3
= 8 · (log
2
√
x)
2
+ [log
2
(3x − 4)
2
]
2
n)
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 34
Hàm số mũ và hàm số logarit Giải tích 12
Bài 56.
log
2
(9 − 2
x
) = 3 − x Đáp số: x = 0; x = 3a)
log
1
2
(x − 1) + log
1
2
(x + 1) − log
1
√
2
(7 − x) = 1 Đáp số: x = 3b)
3
2
log
1
4
(x + 2)
3
− 3 = log
1
4
(4 − x)
3
+ log
1
4
(x + 6)
3
Đáp số: x = 2; x = 1 −
√
33c)
log
2
(x + 2) + log
4
(x − 5)
2
+ log
1
2
8 = 0 Đáp số: x = 6; x =
3 ±
√
17
2
d)
log
2
|x − 2| + log
2
|x + 5| + log
1
2
8 = 0 Đáp số: x = −3; x = 6; x =
3 ±
√
17
2
e)
log
4
(x − 1) +
1
log
2x+1
4
=
1
2
+ log
2
√
x + 2 Đáp số: x =
5
2
f)
log
5−x
(x
2
− 2x + 65) = 2 Đáp số: x = −5g)
Bài 57. Giải các phương trình logarit sau (đưa về cùng cơ số)
log
2
[x(x − 1)] = 1a) log
2
x + log
2
(x + 1) = 1b)
ln x + ln(x + 1) = 0c) log
3
[7 + 2 log
3
(x − 2)] = 2d)
log
5
x + log
25
x = log
0,2
√
3e) log
5
(x
2
+ 1) + log
1
5
5 = log
5
(x + 2) −
2 log
1
25
(x − 2)
f)
log(x + 6) −
1
2
log(2x − 3) = 2 − log 25g) log
5
x = log
5
(x + 6) − log
5
(x + 2)h)
log
2
(x − 2) − 6 · log
1
8
√
3x − 5 = 2i) log
2
(x − 3) + log
2
(x − 1) = 3j)
log
4
(x + 3) − log
4
(x − 1) = 2 − log
4
8k) log(x − 2) + log(x − 3) = 1 − log 5l)
2 log
8
(x − 2) − log
8
(x − 3) =
2
3
m) log
√
5x − 4 + log
√
x + 1 = 2 + log 0, 18n)
log
3
(x
2
− 6) = log
3
(x − 2) + 1o) log
2
(x + 3) + log
2
(x − 1) =
1
log
5
2
p)
log
4
x + log
4
(10 − x) = 2q) log
5
(x − 1) + log
1
5
(x + 2) = 0r)
log
2
(x − 1) + log
2
(x + 3) = log
2
10 − 1s) log
9
(x + 8) − log
3
(x + 26) + 2 = 0t)
Bài 58. Giải các phương trình logarit sau (đưa về cùng cơ số)
2 log
2
Ä
√
x
2
+ 1 + x
ä
+ log
0,5
Ä
√
x
2
+ 1 − x
ä
= 3a)
log
2
(x
2
+ 3) + log
0,5
5 = 2 log
0,25
(x − 1) − log
2
(x + 1)b)
log
3
x + log
√
3
x + log
1
3
x = 6c)
1 + log(x
2
− 2x + 1) − log(x
2
+ 1) = 2 log(1 − x)d)
log
4
x + log
1
16
x + log
8
x = 5e)
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 35
Hàm số mũ và hàm số logarit Giải tích 12
2 + log(4x
2
− 4x + 1) − log(x
2
+ 19) = 2 log(1 − 2x)f)
log
2
x + log
4
x + log
8
x = 11g)
log
1
2
(x − 1) + log
1
2
(x + 1) = 1 + log
1
√
2
(7 − x)h)
log
2
log
2
x = log
3
log
3
xi)
log
2
log
3
x = log
3
log
2
xj)
log
2
log
3
x + log
3
log
2
x = log
3
log
3
xk)
log
2
log
3
log
4
x = log
4
log
3
log
2
xl)
log
2
x + log
3
x + log
4
x = log
20x
m)
log
2
x + log
3
x + log
5
x = log
2
x · log
3
x · log
5
xn)
Bài 59. Giải các phương trình logarit sau (đưa về cùng cơ số)
(log
2
x) · log
3
3
x
− log
3
x
3
√
3
=
1
2
+ log
2
√
xa)
log
1
2
Å
1 −
x
2
ã
+ log
2
…
2 −
x
4
= 0b)
log(x
2
+ 2x − 3) + log
ñ
x + 3
x − 1
ô
= 0c)
log
2
Ä
x −
√
x
2
− 1
ä
· log
3
Ä
x +
√
x
2
− 1
ä
= log
6
Ä
x −
√
x
2
− 1
ä
d)
log
(x+3)
6 +
2 log
0,25
(4 − x)
log
2
(x + 3)
= 1e)
log
2
|tan x| + log
4
ï
cos x
2 cos x + sin x
ò
= 0f)
log(2x + 1) + log(3 − x) = 2 log xg)
log
4
{2 log
3
[1 + log
2
(1 + 3 log
2
x)]} =
1
2
h)
ln(x + 1) + ln(x + 3) = ln(x + 7)i)
Bài 60. Giải các phương trình logarit sau (đưa về cùng cơ số)
log
2
(9 − 2
x
) = 3 − xa) log
3
(3
x
− 8) = 2 − xb)
log
7
(6 + 7
−x
) = 1 + xc) log
3
(4 · 3
x−1
− 1) = 2x − 1d)
log
2
(9 − 2
x
) = 5
log
5
(3−x)
e) log
2
(3 · 2
x
− 1) = 2x + 1f)
log
2
(12 − 2
x
) = 5 − xg) log
5
(26 − 3
x
) = 2h)
log
2
(5
x+1
− 25
x
) = 2i) log
4
(3 · 2
x+1
− 5) = xj)
log
1
√
6
(5
x+1
− 25
x
) = −2k) log
1
√
5
(6
x+1
− 36
x
) = 2l)
Bài 61. Giải các phương trình logarit (đưa về cùng cơ số)
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 36
Hàm số mũ và hàm số logarit Giải tích 12
log
5−x
(x
2
− 2x + 65) = 2a) log
x−1
(x
2
− 4x + 5) = 1b)
log
x
(5x
2
− 8x + 3) = 2c) log
x+1
(2x
3
+ 2x
2
− 3x + 1) = 3d)
log
x−3
(x − 1) = 2e) log
x
(x + 2) = 2f)
log
2x
(x
2
− 5x + 6) = 2g) log
x+3
(x
2
− x) = 1h)
log
x
(2x
2
− 7x + 12) = 2i) log
x
(2x
2
− 3x − 4) = 2j)
log
x
(x
2
− 2) = 1k) log
3x+5
(9x
2
+ 8x + 2) = 2l)
log
2x+4
(x
2
+ 1) = 1m) log
x
15
1 − 2x
= −2n)
log
x
2
(3 − 2x) = 1o) log
x
2
+3x
(x + 3) = 1p)
log
x
(2x
2
− 5x + 4) = 2q) log
x
2
16 + log
x
64 = 3r)
Bài 62. Giải các phương trình logarit (đặt ẩn phụ, dạng đặt ẩn phụ hoàn toàn)
log
3
(3
x+1
− 26) = 2 − xa) log
4
(x + 3) − log
2
√
x − 1 = 2 − log
4
8b)
log
4
Å
x
4
ã
2
− log
2
(4x)
4
+ 10 = 0c) 2 · log
3
(x − 2) + log
3
(x − 4)
2
= 0d)
−log
3
x + 2 log
2
x = 2 − log xe) log
2
2
x − 4 log
2
x + 3 = 0f)
log
3
(27x) − 3
»
log
3
x − 1 = 0g) log
2
3
+
»
log
2
3
x + 1 − 5 = 0h)
log
2
√
2
x + 3 log
2
x + log
1
2
x = 2i) log
x
2 − log
4
x +
7
6
= 0j)
log
2
1
2
4x + log
2
x
2
8
= 8k) log
2
√
2
x + 3 log
2
x + log
1
2
xl)
log
x
2
16 + log
2x
64 = 3m) log
5
x − log
x
1
5
= 2n)
log
7
x − log
x
1
7
= 2o) 2 log
5
√
x − 2 = log
x
1
5
p)
2
»
log
2
x − log
2
4x = 0q) 3
»
log
3
x − log
3
3x − 1 = 0r)
log
2
3
√
x +
3
»
log
2
x =
4
3
s) log
2
3
√
x −
3
»
log
2
x = −
2
3
t)
log
2
2
x + 2 log
4
1
x
= 0u) log
2
2
(2 − x) − 8 log
1
4
(2 − x) = 5v)
log
2
5
x + 4 log
25
5x − 5 = 0w) log
x
√
5 + log
x
5x =
9
4
+ log
2
x
√
5x)
log
x
2
3 + log
9
x = 1y) log
3
(3
x
− 1) · log
3
(3
x+1
− 3) = 6z)
Bài 63. Giải các phương trình logarit (đặt ẩn phụ, dạng đặt ẩn phụ hoàn toàn)
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 37
Hàm số mũ và hàm số logarit Giải tích 12
log
√
3
(x − 2) · log
5
x = 2 log
3
(x − 2)a) log
2
(2
x
+ 1) · log
2
(2
x+1
+ 2) = 2b)
»
log
x
√
5x = −log
x
5c) log
sin x
4 · log
cos
2
x
2 = 4d)
log
cos x
4 · log
cos
2
x
2 = 1e)
1
4 − log x
+
2
2 + log x
= 1f)
1
5 − log x
+
3
3 + log x
= 1g)
1
4 + log
2
x
+
2
2 − log
2
x
= 1h)
4 log
2
4
x + 2 log
4
x
2
+ 1 = 0i) log
3
x
10 + log
2
x
10 − 6 log
x
10 = 0j)
log
x
5
√
5 − 1, 25 = log
2
x
√
5k) log
2
(5
x
− 1) · log
2
4
(5
x
− 1) = 1l)
log
2
(2x)
2
· log
2
x
2 = 1m) log
2
(3
x
+ 3) − 4 log
3
x
+3
2 = 0n)
log
2
x
2 + log
2
4x = 3o) log
x
3 · log
x
3
3 + log
x
81
3 = 0p)
log
2x
x
2
− 14 log
16x
x
3
+ 40 log
4x
√
x = 0q) log
2
|x + 1| − log
x+1
64 = 1r)
2 log x
log x − 1
= −log x +
2
log x − 1
s)
log
1
3
x − 2
+ 3 =
log
1
3
x + 1
t)
Bài 64. Giải các phương trình logarit (đặt ẩn phụ, dạng đặt ẩn phụ không hoàn toàn)
log
2
5
(x + 1) + (x − 5) log
5
(x + 1) = 16a)
log
2
3
x + (x − 12) log
3
x + 11 = 0b)
log
2
x − log x · log
2
4x + 2 log
2
x = 0c)
6 · 9
log
2
x
+ 6 · x
2
= 13 · x
log
2
6
d)
x · log
2
2
x − 2(x + 1) log
2
x + 4 = 0e)
log
2
2
x + (x − 1) log
2
x = 6 − 2xf)
(x + 2) log
2
3
(x + 1) + 4(x + 1) log
3
(x + 1) = 16g)
(x + 3) log
2
3
(x + 2) + 4(x + 2) log
3
(x + 2) = 16h)
log
x
2
(2 + x) + log
√
2−x
x = 2i)
log
2
3
(x + 1) + (x − 5) log
3
(x + 1) = 2x − 6j)
log
2
2
x + (x − 1) log
2
x = 6 − 2xk)
4
»
log
3
x − 1 − log
3
√
x = 4l)
Bài 65. Giải các phương trình logarit (sử dụng công thức biến đổi, đặt ẩn phụ)
4
log
9
x
− 6 · 2
log
9
x
+ 2
log
3
27
= 0a) 4
log
3
x
− 5 · 2
log
3
x
+ 2
log
3
9
= 0b)
2
log
2
2
x+1
= x
2 log
3
x
− 48c) 2
log
2
2
x+1
+ 224 = x
2 log
2
x
d)
log
7
x + log
3
(
√
x + 2)e) log
2
(x − 3) + log
3
(x − 2) = 2f)
log
3
(x + 1) + log
5
(2x + 1) = 2g) log
2
Ä
x + 3
log
6
x
ä
= log
6
xh)
4
log
7
(x+3)
= xi) log
2
(1 +
√
x) = log
3
xj)
x
log
2
9
= x
2
· 3
log
2
x
− x
log
2
3
k)
3
√
2 − log x = 1 −
√
log x − 1l)
3
»
1 − log
3
x +
3
»
1 + log
3
x = 1m) log
3
2
+2 = 3
3
»
3 log
3
x − 2n)
log
2
2
x +
»
log
2
x + 1 = 1o) 6
x
= 3 log
6
(5x + 1) + 2x + 1p)
7
x−1
= 6 · log
7
(6x − 5) + 1q) 5
2(log
5
2+x)
− 2 = 5
log
5
2+x
r)
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 38
Hàm số mũ và hàm số logarit Giải tích 12
Bài 66. Giải phương trình logarit (sử dụng tính đơn điệu của hàm số)
log
2
(3x − 1) = −x + 1a) log
1
3
x = x − 4b)
x + log
3
x = 4c) 2x + log
1
2
x = 5d)
log
3
x = −x + 11e) 2
log
5
(x+3)
= xf)
3
log
2
(x−3)
= xg) log
2
(1 +
√
x) = log
3
xh)
2
x
− 2
1−x
= log
2
1 − x
x
i) x + x
log
2
3
= x
log
2
5
(x > 0)j)
x
2
+ 3
log
2
x
= 5
log
2
x
k) log
5
(x + 3) = 3 − xl)
log
2
(3 − x) = xm) log
5
(x + 3) = 3 − xn)
x + 2 · 3
log
2
x
= 3o) 2 log
6
(
4
√
x +
8
√
x) = log
4
√
xp)
log
2
(
4
√
x +
√
x) =
1
4
log
3
xq)
2.8.3 Bài toán liên quan tham số m
Bài 67. Bài toán liên quan đến tìm tham số.
Tìm tham số m để phương trình: log
2
(4
x
− m) = x + 1 có hai nghiệm phân biệt.a)
Tìm tham số m để phương trình: log
3
(9
x
+ 9m
3
) = 2 có hai nghiệm phân biệt.b)
Tìm tham số m để phương trình: log
2
3
x −(m + 2) ·log
3
x + 3m −1 = 0 có hai nghiệm
phân biệt x
1
, x
2
thỏa x
1
· x
2
= 27
c)
Bài 68. Tìm tham số m để phương trình:
2 log
4
(2x
2
− x + 2m − 4m
2
) = log
2
(x
2
+ mx − 2m
2
) có hai nghiệm phân biệt x
1
, x
2
thỏa:
x
2
1
+ x
2
2
> 1.
Bài 69. Cho phương trình: log
2
3
x +
»
log
2
3
x + 1 − 2m − 1 = 0
Giải phương trình khi: m = 2a)
Tìm m để phương trình có ít nhất một nghiệm trên
h
1; 3
√
3
i
b)
B. BẤT PHƯƠNG TRÌNH
2.9 Bất phương trình mũ và bất phương trình logarit
2.9.1 Bất phương trình mũ
Khi giải bất phương trình mũ, ta cần chú ý đến tính đơn điệu của hàm số mũ.
a
f(x)
> a
g(x)
⇔
a > 1
f(x) > g(x)
0 < a < 1
f(x) < g(x)
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 39
Hàm số mũ và hàm số logarit Giải tích 12
Trong trường hợp cơ số a có chứa ẩn số thì:
a
M
> a
N
⇔ (a − 1) · (M − N) > 0
Ta cũng thường sử dụng các phương pháp giải tương tự như đối với phương trình mũ:
• Đưa về cùng cơ số.
• Đặt ẩn phụ.
• Sử dụng tính đơn điệu:
y = f(x) đồng biến trên D thì: f(u) < f(v) ⇒ u < v
y = f(x) nghịch biến trên D thì: f (u) < f(v) ⇒ u > v
2.9.2 Bất phương trình logarit
Khi giải bất phương trình logarit, ta cần chú ý đến tính đơn điệu của hàm số logarit.
log
a
f(x) > log
a
g(x) ⇔
a > 1
f(x) > g(x) > 0
0 < a < 1
0 < f(x) < g(x)
Trong trường hợp cơ số a có chứa ẩn số thì:
• log
a
B > 0 ⇔ (a − 1)(B − 1) > 0
•
log
a
A
log
a
B
> 0 ⇔ (A − 1)(B − 1) > 0
Ta cũng thường sử dụng các phương pháp giải tương tự như đối với phương trình logarit:
• Đưa về cùng cơ số.
• Đặt ẩn phụ.
• Tính đơn điệu của hàm số.
2.10 Hệ phương trình mũ và logarit
Hệ phương trình mũ và logarit
Khi giải hệ phương trình mũ và logarit, ta cũng dùng các phương pháp giải hệ phương trình
đã học như:
Phương pháp thế.
Phương pháp cộng đại số.
Phương pháp đặt ẩn phụ.
Phương pháp dùng tính đơn điệu của hàm số.
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 40
Hàm số mũ và hàm số logarit Giải tích 12
2.11 Các ví dụ
Giải các bất phương trình và hệ phương trình sau
Ví dụ 44. Giải bất phương trình:
Ç
1
2
å
9x
2
−17x+11
≥
Ç
1
2
å
7−5x
(1)
Lời giải.
(1)⇔ 9x
2
− 17x + 11 ≤ 7 − 5x ⇔ 9x
2
− 12x + 4 ≤ 0 ⇔ x =
2
3
Ví dụ 45. Giải bất phương trình:
Ç
1
9
å
x
> 3
2x
x+1
(2)
Lời giải.
Điều kiện: x 6= −1
(2) ⇔ 3
−2x
> 3
2x
x+1
⇔ −2x >
2x
x + 1
⇔
2x
x + 1
+ 2x < 0 ⇔ 2x
Ç
1
x + 1
+ 1
å
< 0
⇔
2x(x + 2)
x + 1
< 0 ⇔
x < −2
− 1 < x < 0
. Kết hợp điều kiện ⇒
x < −2
− 1 < x < 0
Nghiệm của bất phương trình (2) là ∀x ∈ (−∞; −2) ∪ (−1; 0)
Ví dụ 46. Giải bất phương trình: 3
x+1
+ 5
x+2
≥ 3
x+2
+ 5
x+1
(3)
Lời giải.
(3)⇔ 25 · 5
x
− 5 · 5
x
> 9 · 3
x
− 3 · 3
x
⇔ 20 · 5
x
> 6 · 3
x
⇔
Ç
5
3
å
x
>
3
10
⇔ x > log
5
3
3
10
Nghiệm của bất phương trình (2) là ∀x ∈
Ç
log
5
3
3
10
; +∞
å
Ví dụ 47. Giải bất phương trình:
Ç
x
2
+
1
2
å
2x
2
+x+1
≤
Ç
x
2
+
1
2
å
1−x
(4)
Lời giải.
(4)⇔
ñÇ
x
2
+
1
2
− 1
åô
· [(2x
2
+ x + 1) − (1 − x)] ≤ 0 ⇔
Ç
x
2
−
1
2
å
· (2x
2
+ 2x) ≤ 0 (∗)
Bảng xét dấu vế trái của (*)
x
VT
−∞
−2
−
1
√
2
0
1
√
2
+∞
+
0 0
+
0 0
+− −
Từ bảng xét dấu ta có nghiệm của bất phương trình:
∀x ∈ (−∞; −2] ∪
ñ
−
1
√
2
; 0
ô
∪
ñ
1
√
2
; +∞
å
Ví dụ 48. Giải bất phương trình: log
1
2
x
2
− 3x + 2
x
≥ 0 (1)
Lời giải.
Điều kiện:
x
2
− 3x + 2
x
> 0 ⇔
0 < x < 1
x > 2
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 41
Hàm số mũ và hàm số logarit Giải tích 12
(1)⇔
x
2
− 3x + 2
x
≤ 1 ⇔
x
2
− 4x + 2
x
≤ 0 ⇔
2 −
√
2 ≤ x < 1
2 < x ≤ 2 +
√
2
Kết hợp với điều kiện, nghiệm của bất phương trình là x ∈
î
2 −
√
2; 1
ä
∪
Ä
2; 2 +
√
2
ó
Ví dụ 49. Giải bất phương trình: log
0,7
Ç
log
6
x
2
+ x
x + 4
å
(2)
Lời giải.
Điều kiện:
x
2
+ x
x + 4
> 0
log
6
x
2
+ x
x + 4
> 0
⇔
x
2
+ x
x + 4
> 0
x
2
+ x
x + 4
> 1
⇔
x
2
+ x
x + 4
> 1 ⇔
x
2
− 4
x + 4
> 0
⇔
− 4 < x < 2
x > 2
(2)⇔ log
6
x
2
+ x
x + 4
> 1 ⇔
x
2
+ x
x + 4
> 6 ⇔
x
2
− 5x − 24
x + 4
> 0 ⇔
− 4 < x < −3
x > 8
Kết hợp với điều kiện, nghiệm của bất phương trình là: x ∈ (−4; −3) ∪ (8; +∞)
Ví dụ 50. Giải hệ phương trình:
2
x
+ 2
y
= 12 (1)
x + y = 5 (2)
Lời giải.
Từ (2)⇒ y = 5 − x thay vào phương trình (1) ta được: 2
x
+ 2
5−x
= 12 ⇔ 2
x
+
32
2
x
= 12 (∗)
Đặt 2
x
= t > 0, phương trình (*) trở thành t +
32
t
= 12 ⇔ t
2
− 12t + 32 = 0
t = 4
t = 8
• Với t = 4 ⇒ 2
x
= 4 ⇔ x = 2 ⇒ y = 3
• Với t = 8 ⇒ 2
x
= 8 ⇔ x = 3 ⇒ y = 2
Nghiệm hệ phương trình là: (x; y) = (2; 3), (3; 2)
Ví dụ 51. Giải hệ phương trình:
x + y = 2
√
3 (1)
log
3
(xy) = 1 (2)
Lời giải.
Điều kiện: x · y > 0
Từ phương trình (2) ⇒ xy = 3.
Ta có
x + y = 2
√
3
xy = 3
. Khi đó x, y là nghiệm của phương trình:
X
2
− 2
√
3X + 3 = 0 ⇔ x =
√
3 = y
Vậy nghiệm hệ phương trình là (x; y) = (
√
3;
√
3)
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 42
Hàm số mũ và hàm số logarit Giải tích 12
2.12 Bài tập bất phương trình, hệ phương trình mũ và logarit
2.12.1 Giải các bất phương trình
Bài 70. Giải các bất phương trình mũ (đưa về cùng cơ số)
9
x
2
−2x
− 2 ·
Ç
1
3
å
2x−x
2
≤ 3a) 2
x
+ 4 · 5
x
− 4 < 10
x
b)
1
3
x
− 1
>
1
1 − 3
x−1
c) 2
√
x
− 2
1−
√
x
< 1d)
9
√
x
2
−2x−x
− 7 · 3
√
x
2
−2x−x−1
≤ 2e) 2 · 3
√
x+
4
√
x
+ 9
4
√
x+
1
2
≥ 9
√
x
f)
3
2x
− 8 · 3
x+
√
x+4
− 9 · 9
√
x+4
> 0g) 5
2x−1
< 7
3−x
h)
3
√
x+4
+ 2
√
2x+4
> 13i) 3 · 2
x
+ 7 · 5
x
> 49 · 10
x
− 2j)
3
2−x
+ 3 − 2x
4
x
− 2
≥ 0k)
Bài 71.
2
3−6x
> 1a) 16
x
> 0, 125b)
(0, 3)
2x
2
−3x+6
< 0, 00243c)
Ç
1
3
å
√
x+2
> 3
−x
d)
(0, 1)
4x
2
−2x−2
≤ (0, 1)
2x+3
e)
x+1
√
3 > 9f)
8
√
8x
> 4096g) 2
x
2
−3x−4
< 3
x
2
−3x−4
h)
Ç
1
2
å
4x
2
−15x+13
<
Ç
1
2
å
4−3x
i)
Ç
2
5
å
6x−5
2+5x
<
25
4
j)
3
√
x
2
−2x
≥
Ç
1
3
å
x−|x−1|
k)
Ç
1
2
å
√
x
6
−2x
3
+1
<
Ç
1
2
å
1−x
l)
5
x
− 3
x+1
≥ 2 (5
x−1
− 3
x−2
)m) 7
x
− 5
x+2
< 2 · 7
x−1
− 118 · 5
x−1
n)
2
x+2
− 2
x+3
− 2
x+4
> 5
x+1
− 5
x+2
o) 3
√
x
+ 3
√
x−1
− 3
√
x−2
≤ 11p)
9
x
2
−3x+2
− 6
x
2
−3x+2
< 0q) 6
2x+3
≤ 2
x+7
· 3
3x−1
r)
2
x+2
+ 5
x+1
≤ 2
x
+ 5
x+2
s) 2
x−1
· 3
x+2
> 36t)
Ä
√
10 + 3
ä
x−3
x−1
<
Ä
√
10 − 3
ä
x+1
x+3
u)
Ä
√
2 + 1
ä
x+1
≥
Ä
√
2 − 1
ä
x
x−1
v)
1
2
√
x
2
−2x
≤ 2
x−1
w) 2
1
|2x−1|
≥ 2
1
3x+1
x)
(0, 4)
x
2
−1
> (0, 6)
x
2
+6
y) (0, 2)
x
2
+2
x
2
−1
> 25z)
Bài 72. Giải các bất phương trình mũ (đặt ẩn phụ)
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 43
Hàm số mũ và hàm số logarit Giải tích 12
3
√
x
+ 3
√
x−1
+ 3
√
x−2
< 11a) 2
x
+ 2
−x
− 3 < 0b)
4
−x+0,5
− 7 · 2
−x
− 4 < 0c) 5
2
√
x
+ 5 < 5
√
x−1
+ 5
√
x
d)
2
x−1
− 1
2
x+1
+ 1
< 2e)
1
3
x
+ 5
<
1
3
x+1
− 1
f)
2 · 14
x
+ 3 · 49
x
− 4
x
≥ 0g) 4
1
x
−1
− 2
1
x
−2
− 3 ≤ 0h)
4
x
− 2
2(x−1)
+ 8
2
3
(x−2)
> 52i) 8 · 3
√
x+
4
√
x
+ 9
1+
4
√
x
> 9
√
x
j)
25 · 2
x
− 10
x
+ 5
x
> 25k) 5
2x+1
+ 6
x+1
> 30 + 5
x
· 30
x
l)
6
x
− 2 · 2
x
− 3 · 2
x
+ 6 ≥ 0m) 27
x
+ 12
x
> 2 · 8
x
n)
49
1
x
− 35
1
x
≥ 25
1
x
o) 3
x+1
− 2
2x+1
− 12
x
2
< 0p)
25
2x−x
2
+1
+ 9
2x−x
2
+1
≥ 34 · 25
2x−x
2
q) 3
2x
− 8 · 3
x+
√
x+4
− 9 · 9
√
x+4
> 0r)
4
x+
√
x−1
− 5 · 2
x+
√
x−1+1
+ 16 ≥ 0s) 2
1
x
+1
+ 2
2−
1
x
< 9t)
Ç
1
3
å
2
X
+ 3 ·
Ç
1
3
å
1
x
+1
> 12u)
Ç
1
4
å
3x
−
Ç
1
8
å
x−1
− 128 ≥ 0v)
(2
2x+1
− 9 · 2
x
) ·
√
x
2
+ 2x − 3 ≥ 0w)
2
1−x
− 2
x
+ 1
2
x
− 1
≤ 0x)
11 · 3
x−1
− 31
4 · 9
x
− 11 · 3
x−1
− 5
≥ 5y)
4 − 7 · 5
x
5
2x+1
− 12 · 5
x
+ 4
≤
2
3
z)
Bài 73. Giải các bất phương trình mũ (sử dụng tính đơn điệu)
2
x
< 3
x
2
+ 1a)
2
1−x
− 2
x
+ 1
2
x
− 1
≤ 0b)
2 · 3
x
− 2
x+2
3
x
− 2
x
≤ 1c) 3
√
x+4
+ 2
√
2x+4
> 13d)
3
2−x
+ 3 − 2x
4
x
− 2
≥ 0e)
3
x
+ x − 4
x
2
− x − 6
> 0f)
Bài 74. Giải các bất phương trình logarit (đưa về cùng cơ số)
2 · log
3
(4x − 3) + log
1
3
(2x + 3) ≤ 2a) log
5
(4
x
+ 144) − 4 · log
5
2 < 1 +
log
5
(2
x−2
+ 1)
b)
log
8
3
h
log
1
2
(x
2
− x − 6)
i
≥ 0c) log
0,5
Ç
log
6
x
2
+ x
x + 4
å
< 0d)
log
1
3
[log
4
(x
2
− 5)] > 0e) log
1
2
î
log
2
Ä
log
x−1
9
äó
> 0f)
log
3
(1 − 2x) ≥ log
3
(5x − 2)g) log
5
(1 − x) < log
5
(x + 3)h)
log
5
(1 − 2x) < 1 + log
√
5
(x + 1)i) log
1
3
√
5 − x < log
1
3
(3 − x)j)
log
2
log
1
3
x > 0k) log
2
(3x + 4) > log
2
(5 − x)l)
log
1
3
Ç
log
2
1 + 2x
1 + x
å
> 0m) log
0,4
x + 7
2x + 3
< log
0,4
(5 − x)n)
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 44
Hàm số mũ và hàm số logarit Giải tích 12
log
1
3
[log
4
(x
2
− 5)] > 0o) log
7
(2 − x) ≤ log
7
(3x + 6)p)
log
1
3
(x + 4) < log
1
3
(x
2
+ 2x + 2)q) (x
2
− 4) log
1
2
x > 0r)
6
log
2
6
x
+ x
log
6
x
≤ 12s) log
2
(x + 3) ≥ 1 + log
2
(x − 1)t)
2
log
2
2
x
+ x
log
2
x
< 0u) log
3
log
1
2
≥ 0v)
2 log
8
(x − 2) + log
1
8
(x − 3) >
2
3
w) log
2
3
2x − 3
x + 1
≥ 0x)
Bài 75. Giải các bất phương trình logarit (đặt ẩn phụ)
log
2
x + 2 log
x
4 − 3 ≤ 0a) log
5
(1 − 2x) < 1 + log
√
5
(x + 1)b)
2 log
5
x − log
x
125 < 1c) log
2x
64 + log
x
2
16 ≥ 3d)
log
x
2 · log
2x
2 · log
2
4x > 1e) log
2
1
2
x + log
1
2
x
2
< 0f)
log
2
1
2
x − 6 log
2
x + 8 ≤ 0g)
q
1 − 9 log
2
1
8
x > 1 − 4 log
1
8
xh)
log
x
100 −
1
2
log
100
x > 0i)
1 + log
2
3
x
1 + log
3
x
> 1j)
Bài 76. Giải các bất phương trình logarit (đặt ẩn phụ)
2
1 − log
2
x
+
log
4
x
1 + log
2
x
>
log
2
x
1 − log
2
2
x
a)
1
4 + log
2
x
+
2
2 − log
2
x
≤ 1b)
»
log
2
3
x − 4 log
3
x + 9 ≥ 2 log
3
x − 3c)
1
5 − log
5
x
+
2
1 + log
5
x
< 1d)
»
log
9
(3x
2
+ 4x + 2) + 1 ≥ log
3
(3x
2
+ 4x + 2)e)
6 log
3
|1 − x| + log
2
3
(x − 1) + 5 ≥ 0f)
log
2
9
x > log
3
x · log
3
Ä
√
2x + 1 − 1
ä
g)
Bài 77. Giải các bất phương trình logarit (sử dụng tính đơn điệu của hàm số)
3
log
2
(x + 1)
>
2
log
3
(x + 1)
a)
log
5 + x
5 − x
2
x
− 3x + 1
< 0b)
log
7
x < log
3
(
√
x + 2)c) 2
−|x−2|
· log
2
(4x − x
2
− 2) ≥ 1d)
Bài 78. Giải các bất phương trình logarit (sử dụng tính đơn điệu của hàm số)
(x + 1) log
2
0,5
x + (2x + 5) log
0,5
x + 6 ≥ 0a)
log
2
(2
x
+ 1) + log
3
(4
x
+ 2) ≤ 2b)
(x + 1) log
2
1
3
x + 2(x + 3) log
1
3
x + 8 ≤ 8c)
(4 · 3
x
+ 3
−x
)
3 log
3
(x−1)−log
3
(x−1)(2x+1)
> 1d)
log
5
(x
2
− 4x − 11)
2
− log
11
(x
2
− 4x − 11)
3
2 − 5x − 3x
2
≥ 0e)
log
2
Ä
√
x
2
− 5x + 5 + 1
ä
+ log
3
(x
2
− 5x + 7) ≤ 2f)
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 45
Hàm số mũ và hàm số logarit Giải tích 12
Bài 79. Giải các bất phương trình logarit
x
2
· log
x
27 · log
x
9 > x + 4a) log
3
log
9
16
(x
2
− 4x + 3) ≥ 0b)
√
x − 5
log
√
2
(x − 4) − 1
c)
log
2
(x + 1)
2
− log
3
(x + 2)
3
x
2
− 3x − 4
> 0d)
Ç
1
2
å
log
2
1
2
x
≤ x
3
e)
1
log
1
3
√
2x
2
− 3x + 1
>
1
log
1
3
(x + 1)
f)
log
√
2
(x − 3)
2
x
2
− 4x − 5
≥ 0g)
log
3
Ç
x +
4
5
å
log
7
Ç
x
2
− 2x +
7
16
å
h)
1
log
1
2
(2x − 1)
+
1
log
2
√
x
2
− 3x + 2
> 0i) log
√
3
Ä
√
3 sin 2x − cos 2x
ä
≤ 1j)
Bài 80. Giải các bất phương trình logarit
log
5
(x
2
− 4x + 11)
2
− log
11
(x
2
− 4x + 11)
√
2 − 5x − 3x
2
≥ 0a)
log
2
(x
2
− 2x − 7) − log
3
(x
2
− 2x − 7)
8
3x
2
− 13x + 4
≤ 0b)
log
1
3
Ä
√
9x − x
2
+ 3
ä
> log
3
27
√
9x − x
2
+
√
5 − x
2
− 3c)
log
2
Ä
√
x
2
− 4x + 3
ä
> log
1
2
2
√
x
2
− 4x +
√
x + 1 + 1
+ 1d)
2.12.2 Giải hệ phương trình
Bài 81. Giải các hệ phương trình mũ sau
2
x
· 5
y
= 20
5
x
· 2
y
= 50
a)
2
x
· 3
y
= 12
3
x
· 2
y
= 18
b)
x
y
2
−7y+10
= 1
x + y = 8
, (x > 0)c)
4
−2x
+ 4
2y
=
1
2
x + y = 1
d)
2
y
+ 200 · 5
y
x + y = 1
e)
3
x
· 2
y
=
1
9
y − x = 2
f)
27
x
= 9
x
81
x
= 243 · 3
y
g)
3
x
− 2
y
2
= 77
3
x
2
− 2
y
2
2
= 7
h)
64
x
+ 64
2y
= 12
64
x+y
= 4
√
2
i)
3
x
+ 3
y
= 28
3
x+y
= 27
j)
x + 2
y+1
= 3
4x + 4
y
= 32
k)
3 · 2
x
+ 2 · 3
y
=
11
4
2
x
− 3
y
= −
3
4
l)
x + 3
y−1
= 2
3x + 9
y
= 18
m)
y
2
= 4
x
+ 2
2
x+2
+ y + 1 = 0
n)
4
(x−y)
2
−1
= 1
5
3x−2y−3
= 125
o)
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 46
Hàm số mũ và hàm số logarit Giải tích 12
x
x+y
= 128
5
3x−2y−3
= 1
p)
3
2x
− 2
y
= 77
3
x
− 2
y
2
= 7
q)
x
x
2
−y
2
−16
= 1
x − y = 2
, (x > 0)r)
4
x
− 3
y
= 7
4
x
· 3
x
= 144
s)
2
x
+ 3
y
= 17
3 · 2
x
− 2 · 3
y
= 6
t)
2
x
+ 2 · 3
x+y
= 56
3 · 2
x
+ 3
x+y+1
= 87
u)
3
2x+2
+ 2
2y+2
= 17
2 · 3
x+1
+ 3 · 2
y
= 8
v)
3
√
x+1
− 2
y
= −4
3
√
x+1
− 2
y+1
= −1
w)
7
x
− 16
x
= 0
4
x
− 49
x
= 0
x)
3 · 2
x
+ 2 · 3
y
= 2, 75
2
x
− 3
y
= −0, 75
y)
8
x
= 10y
2
x
= 5y
z)
Bài 82. Giải các hệ phương trình logarit sau:
xy = 64
log
x
y = 5
a)
log
y
x − log
2
y
2
= 1
log
4
x − log
4
y = 1
b)
x
log
2
y
+ y
log
2
x
= 16
log
2
x − log
2
y = 2
c)
log
2
(x
2
+ y
2
+ 6) = 4
log
x
+ log
3
y = 1
d)
x
log
3
y
+ 2 · y
log
3
y
= 27
log
3
y − log
3
x = 1
e)
3 · x
log
2
y
= 10
log
4
x
2
+ log
2
y = 2
f)
log
x
(2x + y − 2) = 2
log
y
(2y + x − 2) = 2
g)
log
2
(xy) = 4
log
2
x
y
= 2
h)
log
y
x + log
x
y =
5
2
log
6
(x
2
+ y
2
) = 1
i)
log
2
x = log
2
y + log
2
(xy)
log
2
(x − y) + log x · log y = 0
j)
log
xy
y
x
− log
2
y
x = 1
log
2
(y − x) = 1
k)
log
xy
(x − y) = 1
log
xy
(x + y) = 0
l)
log
y
x + log
x
y = 2
x
2
+ y = 12
m)
√
y + log x
2
= 2
y + 4 log x = 28
n)
√
y + 2 log x = 3
y − 3 log x
2
= 1
o)
log(x + y) − log(x − y) = 1
x
2
+ y = 12
p)
3
x
· 2
y
= 972
log
√
3
(x − y) = 2
q)
3
x
2
+y
2
= 81
log
2
x + 2 log
4
y = 1
r)
2
log
0,5
(x+y)
= 5
log
5
(x+y)
log
2
x + log
2
y =
1
2
s)
Ä
√
3
ä
x−y
=
Ç
1
3
å
x−2y
log
2
(x + y) + log
2
(x − y) = 4
t)
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 47
| 1/47
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Mục lục Trang Chương 2
HÀM SỐ LŨY THỪA-HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT . . . . . . . . . . . 3
PHẦN 1. HÀM SỐ LŨY THỪA-HÀM SỐ MŨ-HÀM SỐ LOGARIT . . . . . . . . . . . . . . 3
A. LÝ THUYẾT . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 2.1
Lũy thừa-Hàm số lũy thừa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 2.1.1
Lũy thừa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 2.1.2
Hàm số lũy thừa: y = xα . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 2.2
Logarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4 2.2.1
Kiến thức cơ bản . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4 2.3
Hàm số mũ-Hàm số logarit
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5 2.3.1
Hàm số mũ: y = ax, (0 < a 6= 1)
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5 2.3.2
Hàm số logarit: y = logax, (0 < a 6= 1, x > 0) . . . . . . . . . . . . . . . . . . . . . . . . 5 2.3.3
Bảng đạo hàm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
B. BÀI TÂP TỰ LUẬN . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6 2.4
Bài tập về lũy thừa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6 2.4.1
Dạng 1: Tính giá trị biểu thức
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6 2.4.2
Dạng 2: Đơn giản biểu thức
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8 2.4.3
Dạng 3: Lũy thừa hữu tỉ
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9 2.4.4 Dạng 4: So sánh cặp số
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10 2.4.5
Dạng 5: Bài toán thực tế
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11 2.5
Bài tập về logarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12 2.5.1
Dạng 1: Tính giá trị biểu thức
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12 2.5.2
Dạng 2: Biến đổi logarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13 2.5.3
Dạng 3: Chứng minh đẳng thức logarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17 2.5.4 Dạng 4: So sánh cặp số
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18 2.5.5
Dạng 4: Bài toán thực tế
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18 2.6
Bài tập hàm số mũ-hàm số logarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18 2.6.1
Dạng 1: Tập xác định hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18 2.6.2
Dạng 2: Đạo hàm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19 2.6.3
Dạng 3: Chứng minh hàm số đã cho thỏa hệ thức cho trước . . . . . . . . . . . . . . . . . . . 20 2.6.4
Dạng 4: Giải phương trình, bất phương trình . . . . . . . . . . . . . . . . . . . . . . . . . . . 21 2.6.5
Dạng 5: Giá trị lớn nhất, giá trị nhỏ nhất . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
PHẦN 2. PHƯƠNG TRÌNH, BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT . . . . . . . . . . . 22 A. PHƯƠNG TRÌNH
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22 2.7
Phương trình mũ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22 2.7.1
Phương trình mũ cơ bản . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22 2.7.2
Một số phương pháp giải phương trình mũ
. . . . . . . . . . . . . . . . . . . . . . . . . . . . 23 1
Hàm số mũ và hàm số logarit Giải tích 12 2.7.2.1
Phương pháp đưa về cùng cơ số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23 2.7.2.2
Phương pháp logarit hóa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24 2.7.2.3
Phương pháp đặt ẩn phụ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25 2.7.2.3.1
Dạng 1: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25 2.7.2.3.2
Dạng 2: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25 2.7.2.3.3
Dạng 3: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25 2.7.2.4
Sử dụng tính đơn điệu của hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29 2.7.2.5
Phương trình tích . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30 2.7.3
Bài toán liên quan tham số m . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31 2.8
Phương trình logarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32 2.8.1
Phương trình logarit cơ bản . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32 2.8.2
Một số phương pháp giải phương trình logarit . . . . . . . . . . . . . . . . . . . . . . . . . . . 32 2.8.2.1
Phương pháp đưa về cùng cơ số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32 2.8.2.2
Phương pháp mũ hóa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32 2.8.2.3
Phương pháp đặt ẩn phụ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33 2.8.2.4
Sử dụng tính đơn diệu hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34 2.8.3
Bài toán liên quan tham số m . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
B. BẤT PHƯƠNG TRÌNH . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39 2.9
Bất phương trình mũ và bất phương trình logarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39 2.9.1 Bất phương trình mũ
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39 2.9.2
Bất phương trình logarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
2.10 Hệ phương trình mũ và logarit
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
2.11 Các ví dụ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
2.12 Bài tập bất phương trình, hệ phương trình mũ và logarit . . . . . . . . . . . . . . . . . . . . . . . . . 43
2.12.1 Giải các bất phương trình . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43
2.12.2 Giải hệ phương trình . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 2 Chương 2
HÀM SỐ LŨY THỪA-HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT A. LÝ THUYẾT 2.1
Lũy thừa-Hàm số lũy thừa 2.1.1 Lũy thừa
Với a, b là các số thực dương, m, n là những số thực tùy ý. Å a ãm am Ç b å−m 1 an = a · a · a · · · a 6 = = | {z } b bm a n lần √ m 2 am · an = am+n 7 a n = n am  am 1 ∀  u(x) 3 = am−n ⇒ a−n = 8 [u(x)]0 = 1 ⇒ x0 = 1, nn an  x 6= 0 √ √ √ 4 (am)n = (an)m = am·n 9 n a · n b = n ab √ √ m 5 (a · b)m = am · bm 10 ( n a) = n am
Nếu a < 0 thì am chỉ xác định khi ∀m ∈ Z.
Nếu a > 0 thì am > an ⇔ m > n.
! Nếu 0 < a < 1 thì am > an ⇔ m < n. √ √ Để so sánh
n1 a và n2 n. Ta sẽ đưa 2 căn đã cho về cùng bậc n (với n là bội số chung √ √
của n1 và n2)⇒ Hai số so sánh mới lần lượt là n A và n B. Từ đó so sánh A và B ⇒ √ √
kết quả so sánh của n1 a và n2 b.
Công thức lãi kép: Lãi kép là phần lãi của kì sau được tính trên số tiền gốc kì trước cộng
với phần lãi của kì trước.
1 Số tiền nhận được cả gốc và lãi sau n kì hạn gửi là A(1 + r)n
2 Số tiền lãi nhận được sau n kì hạn gửi là A(1 + r)n − A = A [(1 + r)n − 1] 2.1.2 Hàm số lũy thừa: y = xα α > 0 α < 0
1 Tập xác định: D = (0; +∞)
1 Tập xác định: D = (0; +∞)
2 Sự biến thiên: y0 = α.xα−1 > 0
2 Sự biến thiên: y0 = α.xα−1 < 0 Giới hạn đặc biệt Giới hạn đặc biệt lim xα = 0; lim xα = +∞ lim xα = +∞; lim xα = 0 x→0+ x→+∞ x→0+ x→+∞ 3 Tiệm cận: 3 Tiệm cận: Không có
TCĐ: Trục Ox; TCN: Trục Oy 4 Bảng biến thiên 4 Bảng biến thiên 3
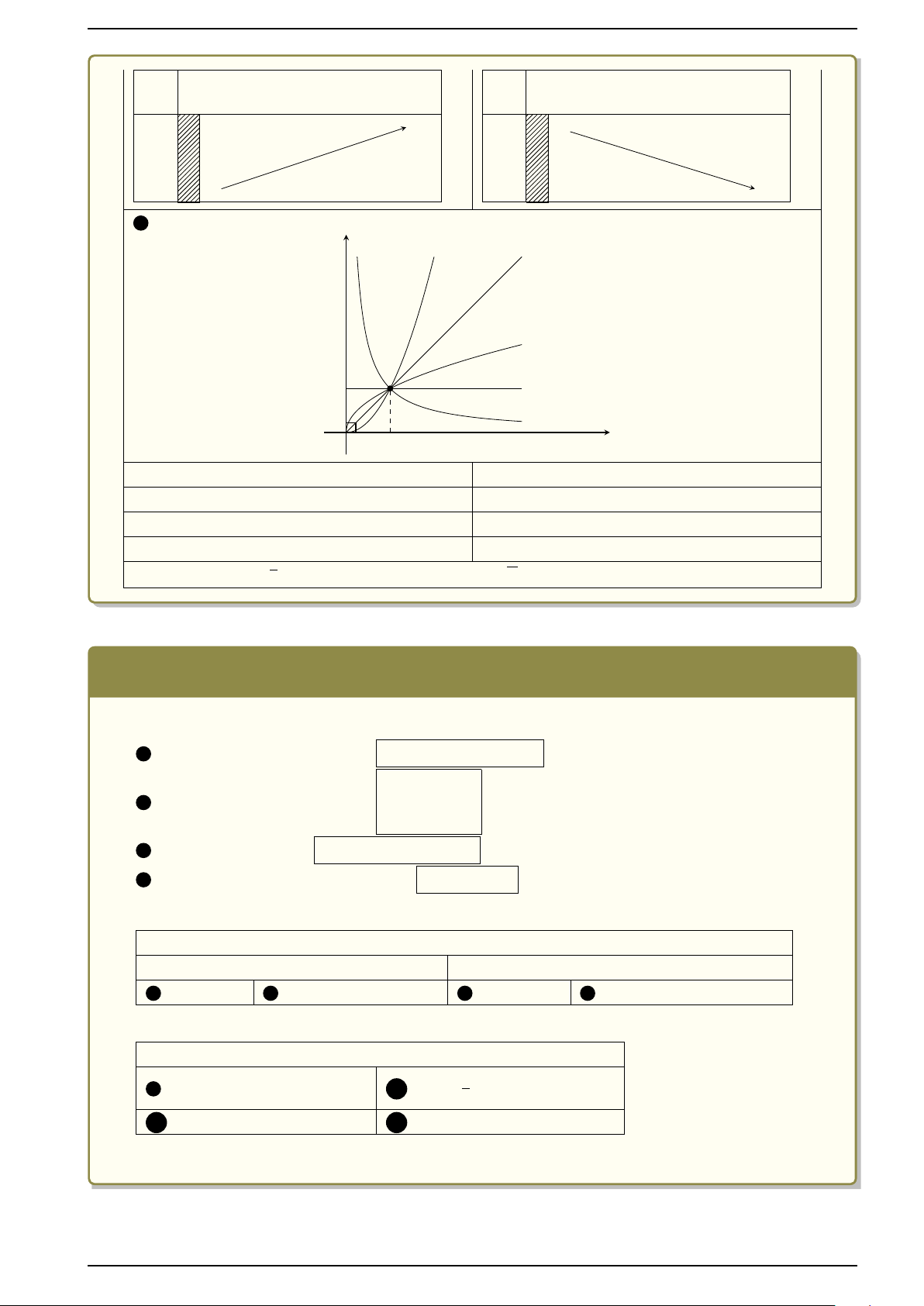
Hàm số mũ và hàm số logarit Giải tích 12 x 0 +∞ x 0 +∞ +∞ 0 y y 0 +∞ 5 Đồ thị y α > 1 α = 1 0 < α < 1 1 α = 0 α < 0 O 1 x Số mũ Tập xác định α = n (n nguyên dương) D = R α = n (n nguyên âm) D = R \ {0}
α là số thực không nguyên D = (0; +∞) 4 √ 1 !
Chý ý: y = x n không đồng nhất với y = n x, (n ∈ N) 2.2 Logarit 2.2.1 Kiến thức cơ bản 1) Định nghĩa
1 Với 0 < a 6= 1, b > 0 ta có: log b = α ⇔ b = aα a   0 < a 6= 1
2 Chú ý: log b có nghĩa khi a  b > 0
3 Logarit thập phân: lg b = log b = log b 10
4 Logarit tự nhiên (logarit Nepe): ln b = log b e 2) Tính chất
Cho 0 < a 6= 1 và b, c > 0. Khi đó:
Nếu a > 1 thì log b > log c ⇔ b > c
Nếu 0 < a < 1 thì log b > log c ⇔ b < c a a a a 5 log 1 = 0 a = 1 ab = b a 6 loga 7 loga 8 aloga b = b
3) Các qui tắc tính logarit
Cho a > 0 và b, c > 0. Ta có: Ç b å 9 log (b.c) = log b + log c = log b − log c a a a 10 loga c a a 11 log bα = α. log b b2 = 2. log |b| a a 12 loga a
4) Các công thức đổi cơ số
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 4
Hàm số mũ và hàm số logarit Giải tích 12
Cho a, b, c > 0 và a, b 6= 1. Ta có: log c 1 a 13 log c = b = b 14 log log b a log a a b ln b 15 log b. log c = log c b = a b a 16 loga ln a 1 17 log . log b, (α 6= 0) b = − log b aα b = 18 log 1 α a a a 1 β β 19 log log b; aα a = 20 log 21 log α aα bβ = α a aα aβ = α 1 22 log = ab 1 1 23 alogb c = clogb a + log c log c a b 2.3
Hàm số mũ-Hàm số logarit 2.3.1
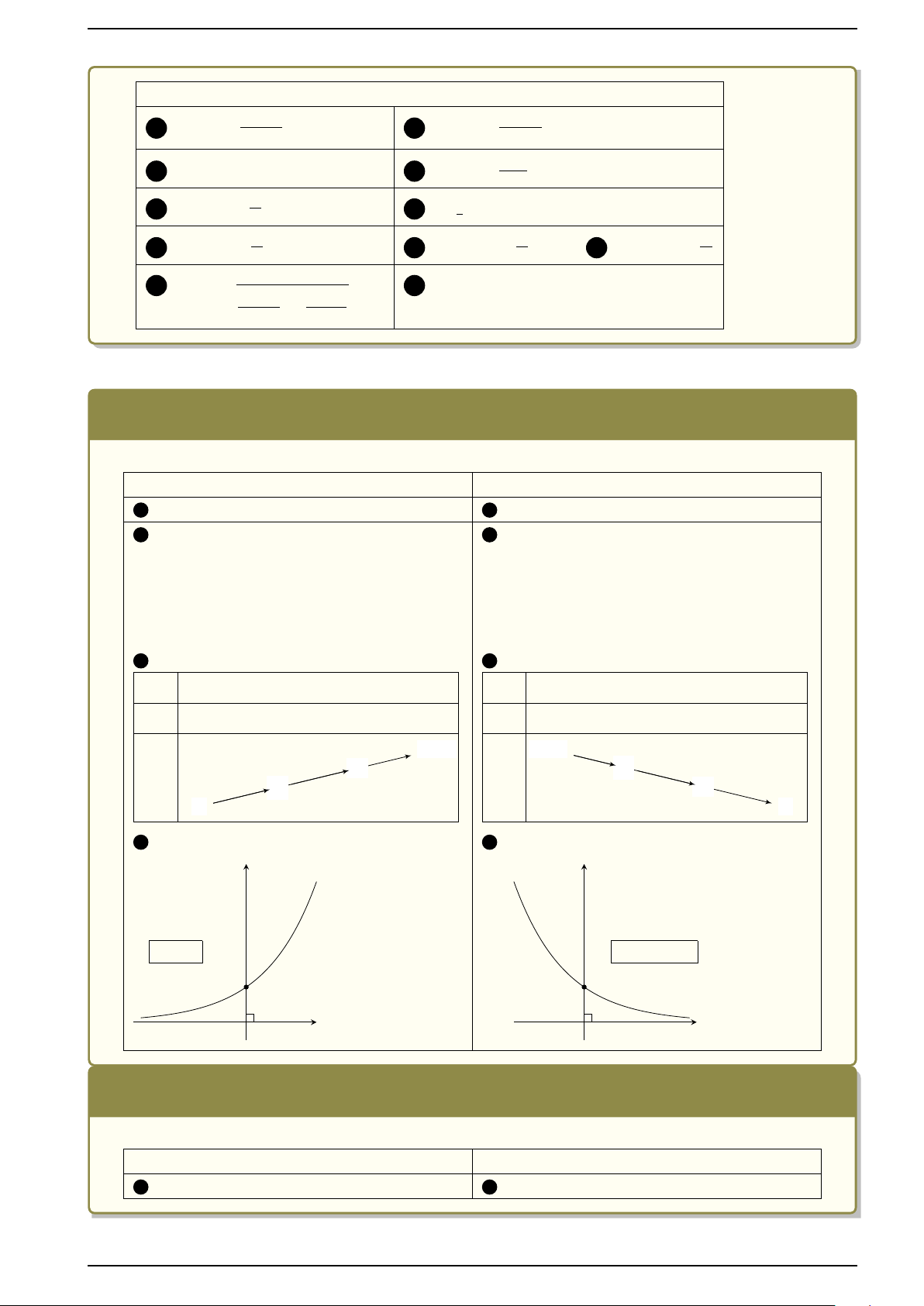
Hàm số mũ: y = ax, (0 < a 6= 1) a > 1 0 < a < 1 1 Tập xác định: D = R 1 Tập xác định: D = R
2 Sự biến thiên: y0 = ax. ln a > 0
2 Sự biến thiên: y0 = ax. ln a < 0 Giới hạn đặc biệt: Giới hạn đặc biệt: lim ax = 0; lim ax = +∞ lim ax = +∞; lim ax = 0 x→−∞ x→+∞ x→−∞ x→+∞ Tiệm cận: Tiệm cận: TCN: Trục Ox TCN: Trục Ox 3 Bảng biến thiên: 3 Bảng biến thiên: x −∞ 0 1 +∞ x −∞ 0 1 +∞ y0 + y0 − +∞ + +∞ + y a y 1 1 a 0 0 4 Đồ thị: 4 Đồ thị: y y = ax y = ax y a > 1 0 < a < 1 1 1 O x O x 2.3.2
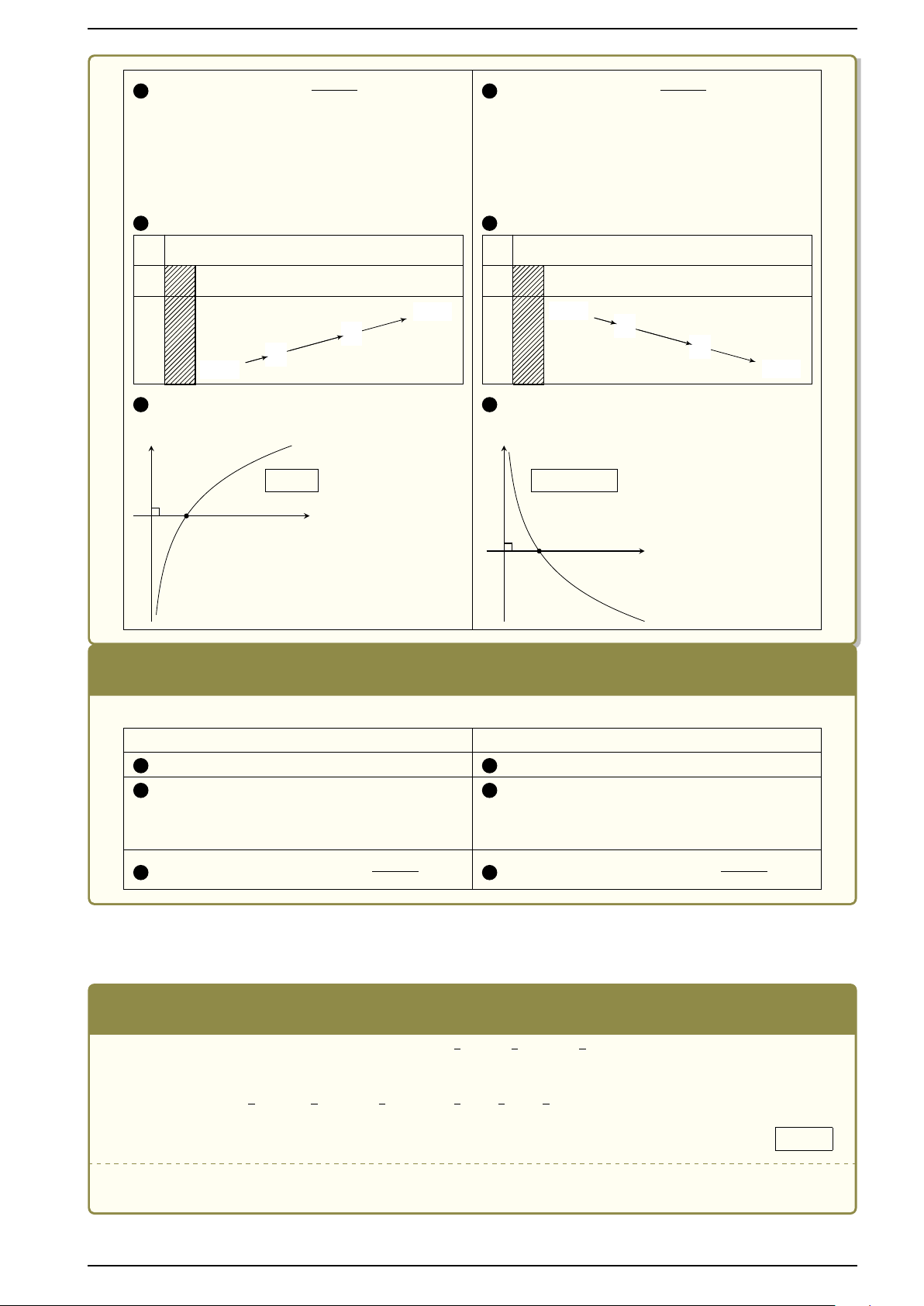
Hàm số logarit: y = logax, (0 < a 6= 1, x > 0) a > 1 0 < a < 1
1 Tập xác định: D = (0; +∞)
1 Tập xác định: D = (0; +∞)
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 5
Hàm số mũ và hàm số logarit Giải tích 12 1 1 2 Sự biến thiên: y0 = > 0 2 Sự biến thiên: y0 = < 0 x. ln a x. ln a Giới hạn đặc biệt: Giới hạn đặc biệt:
lim log x = −∞; lim log x = +∞
lim log x = +∞; lim log x = −∞ a a a a x→0+ x→+∞ x→0+ x→+∞ Tiệm cận: Tiệm cận: TCĐ: Trục Oy TCĐ: Trục Oy 3 Bảng biến thiên 3 Bảng biến thiên x 0 1 a +∞ x 0 1 a +∞ y0 + y0 − +∞ + −∞ 0 y 1 y 0 1 −∞ +∞ + 4 Đồ thị: 4 Đồ thị: y = log x a y y a > 1 0 < a < 1 O x 1 O x 1 y = log x a 2.3.3 Bảng đạo hàm Đạo hàm Đạo hàm hợp
1 Hàm số lũy thừa: (xα)0 = α.xα−1
1 Hàm lũy thừa: (uα)0 = α.uα−1.u0 2 Hàm số mũ: 2 Hàm số mũ: (ax)0 = ax. ln a (au)0 = au. ln a.u0 (ex)0 = ex (eu)0 = eu.u0 1 u0
3 Hàm số logarit: (log x)0 = u)0 = a 3 Hàm số logarit: (log x. ln a a u. ln a B. BÀI TẬP TỰ LUẬN 2.4 Bài tập về lũy thừa 2.4.1
Dạng 1: Tính giá trị biểu thức √ √ √
Ví dụ 1. Tính giá trị biểu thức: A = 43+ 2 · 21− 2 · 2−4− 2. Lời giải. √ √ √ √ √ √
Ta có A = 22(3+ 2) · 21− 2 · 2−4− 2 = 26+2 2+1− 2−4− 2 = 23 = 8. Đáp số A = 8
Bài 1. Tính giá trị các biểu thức sau:
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 6
Hàm số mũ và hàm số logarit Giải tích 12 9 2 6 4 23 · 2−1 + 5−3 · 54
a) A = 8 7 : 8 7 − 3 5 .3 5 . b) B = . (10−3 : 10−2) − (0, 24)0 Ç å− 1 Ç å− 3 h 3 i−4 1 3 1 5 c) C = 5− 25 + (0, 2) 4 d) D = 81−0,75 + − . 125 32 √ √ 2 2 e) E = 0, 001− 1 5 5
3 − (−2)−2 · 64 3 − 8 3 + (90)2. f) F = 22−3 · 8 . √ …√ √ √ 7 » » 2 102+ g) G = 3 3 3 : 4 3 . h) H = √ √ . 22+ 7 · 51+ 7 Ç 1 å−0,75
i) I = (0, 04)−1,5 − (0, 125)− 23 . j) J = + (0, 25)− 52 . 16 √ √ √ 23.2−1 + 5−3.54 K = 43+ 2.21− 2.2−4− 3 k)
l) L = 10−3 : 10−2 − (0, 25)0 √ √ Ç 1 å−0,75 Å √ 5 √ √ Ä ä 5ã M =
+ (0, 25)− 52 + (0, 04)−1,5 m) N = 5 + 41−2 3.161+ 3 n) 16 √ √ √ 3. 3 3 3 3 Ç å− 3 7 9 2 O = π0 + √ .9 12 o)
p) P = (0, 5)−4 − 6250,25 − 5 9 12 e0. 3 4 Ç 1 å−2 Ç 1 å−0,75 Ç 1 å− 65 Ç 19 å−2 q) Q = 64− 14 + − − r) R = (0, 25)− 12 + − 255 81 32 2 Ç 1 å− 13 √ √ » » s) S = 256−0,75 − t) T = 3 7 + 5 2 + 3 7 − 5 2 125 3 2 3 − 2 U = 4 5 2 + 8 3 u) v) V = 32 2 (−18)7 · 24 · (−50)3 1256 · (−16)3 · (−2)3 w) W = x) X = (−25)4 · (−4)5 253 [(−5)2]4 √ √ √ » 4 √ √ √ √ 5 4 · 4 64 · 3 2 5 81 · 5 3 · 5 9 · 12 y) Y = √ z) Z = » √ √ √ √ 3 » 32 3 2 3 · 18 · 5 27 · 6 5 + 3x + 3−x
Ví dụ 2. Cho 9x + 9−x = 23. Tính giá trị biểu thức: K = . 1 − 3x − 3−x Lời giải. 1 " # x 1 1 1 Ta có 9x +9−x = 23 ⇔ 9x + = 23 ⇔ (32) + (3x)2 + + 2.3x. −2 = 9x (32)x = 23 ⇔ (3x)2 3x Ç 1 å2 1 23 ⇔ 3x + = 52 ⇒ 3x + = 5 . 3x 3x 1 5 + 3x + 3−x 5 + 3x + 5 + 5 10 5 Ta có K = = 3x = = = − . 1 − 3x − 3−x Ç 1 å 1 − 5 −4 2 1 − 3x + 3x 5 Đáp số K = − 2
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 7
Hàm số mũ và hàm số logarit Giải tích 12
Bài 2. Tính giá trị của các biểu thức sau: 10 − 2x − 2−x
a) Cho 4x + 4−x = 14. Tính giá trị của biểu thức P = . 3 + 2x + 2−x 4 − 5x − 5−x
b) Cho 25x + 25−x = 7. Tính giá trị của biểu thức P = . 9 + 5x + 5−x √ √ Ä ä2017 Ä ä2016
c) Tính giá trị của biểu thức P = 7 + 4 3 7 − 4 3 . √ √ Ä ä2017 Ä ä2016
d) Tính giá trị của biểu thức P = 9 + 4 5 9 − 4 5 . √ √ Ä ä2017 Ä ä2016
e) Tính giá trị của biểu thức P = 5 − 2 6 5 + 2 6 . √ √ Ä ä2016 Ä ä2016
f) Tính giá trị của biểu thức P = 1 + 3 3 − 3 . √ √ √ √ Ä ä2016 Ä ä2016
g) Tính giá trị của biểu thức P = 6 + 2 6 − 3 2 . 9x
Ví dụ 3. Cho hàm số f (x) =
, x ∈ R và a, b thỏa a + b = 1. Tính giá trị f (a) + f (b). 9x + 3 Lời giải. b=1−a 9a 91−a 9a 9 Ta có f (a) + f (b) − −−− → f (a) + f (1 − a) = + = + 9a + 3 91−a + 3 9a + 3 9 + 3.9a 9a 3 9a + 3 = + = = 1. 9a + 3 3 + 9a 9a + 3 Đáp số f (a) + f (b) = 1
Bài 3. Tính giá trị của biểu thức sau: 4x a) Cho hàm số f (x) = . 4x + 2 Ç 1 å Ç 2 å Ç 98 å Ç 99 å Tính tổng P = f + f + · · · + f + f . 100 100 100 100 4x b) Cho hàm số f (x) = . 4x + 2 Ç 1 å Ç 2 å Ç 99 å Ç 100 å Tính tổng P = f + f + · · · + f + f . 100 100 100 100 9x c) Cho hàm số f (x) = . 9x + 3 Ç 1 å Ç 2 å Ç 8 å Ç 9 å Tính tổng P = f + f + · · · + f + f . 10 10 10 10 4x d) Cho hàm số f (x) = . 4x + 2 Ç 1 å Ç 2 å Ç 2015 å Ç 2016 å Tính tổng P = f + f + · · · + f + f . 2017 2017 2017 2017 2.4.2
Dạng 2: Đơn giản biểu thức Ç a0,5 + 2 a0,5 − 2 å a0,5 + 1
Ví dụ 4. Đơn giản biểu thức: P = − · . a + 2 · a0,5 + 1 a − 1 a0,5
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 8
Hàm số mũ và hàm số logarit Giải tích 12 Lời giải.√ √ √ √ √ " a + 2 a − 2 # a + 1 Ç a + 2 a − 2 å 1 P = √ − √ √ · √ = √ − √ √ · √ 2 ( a + 1) ( a + 1)( a − 1) a a + 1 ( a + 1)( a − 1) a √ √ √ √ a − a + 2 a − 2 − a + 2 1 a 1 a = · √ = · √ = . a − 1 a a − 1 a a − 1 √a Đáp số P = a − 1
Bài 4. Đơn giản các biểu thức sau: a1,5 + b1,5 − a0,5 · b0,5 2 · b0,5 a) A = a0,5 + b0,5 + a − b a0,5 + b0,5 Ç a0,5 + 2 a0,5 − 2 å a0,5 + 1 b) B = − · a + 2 · a0,5 + 1 a − 1 a0,5   1 1 1 1 1 1 x 2 + 3y 2 x 2 − 3y 2 x 2 − y 2 c) C =  +  ·  1 1 2  x x − y 2 2 − y 2 Ñ 1 1 1 1 é 3 1 x 2 − y 2 x 2 + y 2 x 2 y 2 2y d) D = + · − 1 1 1 1 xy 2 + x 2 y xy 2 − x 2 y x + y x − y 1 2 2 1 2 4
e) E = a 3 − b 3 · a 3 + a 3 a 3 + b 3 1 1 1 1 1 1
f) F = a 4 − b 4 · a 4 + b 4 · a 2 + b 2 2.4.3
Dạng 3: Lũy thừa hữu tỉ √ »
Ví dụ 5. Viết biểu thức sau với dạng lũy thừa với số mữ hữu tỉ: P = 4 x2 · 3 x, (x ≥ 0). Lời giải. ! √ m
Thực hiện từ trong ra ngoài từ n am = a n và am.an = am+n . √ » 4 » 1 4 » 7 7 • Cách 1: P = 4 x2 · 3 x = x2.x 3 = x 3 = x 12 . √ 7
• Cách 2: P 4 = x2. 3 x ⇒ P 12 = x6.x = x7 ⇒ P = x 12 . 7 Đáp số P = x 12
Bài 5. Viết các biểu thức sau với dạng lũy thừa với số mữ hữu tỉ (xem điều kiện được thỏa) Ã s b … a q √ 5 » 2 3 2 3 a) A = 5 · 3 . b) B = 2 · 3 2 2. c) C = · 3 · . a b 3 2 3 √ √ 5 » s b2 · b 1 4 » d) D = 3 a8. e) E = √ . f) F = 3 2018. 2 . 3 » b b 2018 q √ √ √ √ √ 4 q 3 » » g) G = x. x2. x3. h) H = x. 5 x. 3 x. x. i) I = x5. 3 x2. 5 x3.
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 9
Hàm số mũ và hàm số logarit Giải tích 12 √ √ 3+1 3−1 q √ … √ x 6 q 4 » » 11 j) J = x. x5. x3. k) K = x x x x : x 16 . l) L = √ √ . x− 3+2.x2+ 3 √ √ √ √ 7 a 3+1.a2− 3 a 7+1.a2− 7 a 6 .b− 23 m) M = √ n) N = √ . o) O = √ . √ √ 6 Ä 2+1 Ä 2+2 a 2−1ä 2a5. a 2−2ä ab2 √ √ 1 1 5 5 1 2 a y 3 . b + b 3 . a x 4 + xy 4 a 3 a− 13 + a 3 p) P = √ √ . q) Q = √ √ . r) R = . 1 3 6 a + 6 b 4 x + 4 y a 4 a 4 + a− 14 2.4.4 Dạng 4: So sánh cặp số √ √
Ví dụ 6. So sánh cặp số sau: 2 2 và 2 3. Lời giải.  2 > 1 √ √  Ta có: √ √ ⇒ 2 3 > 2 2.  3 > 2 √ √ Đáp số 2 3 > 2 2 √ √ Ç 1 å 2 Ç 1 å 3
Ví dụ 7. So sánh cặp số sau: và . 2 2 Lời giải.  1 √ √ 2 3  Ç å Ç å  < 1 1 1 Ta có 2 √ √ ⇒ > 2 2   3 > 2 √ √ Ç 1 å 2 Ç 1 å 3 Đáp số > 2 2
Ví dụ 8. So sánh cặp số sau: 2π và 3π. Lời giải.   3 > 2 Ta có ⇒ 3π > 2π.  π > 0 Đáp số 3π > 2π √ √ Ä ä−π Ä ä−π
Ví dụ 9. So sánh cặp số sau: 2 và 3 . Lời giải.√ √  √ √  2 < 3 ä−π Ä ä−π Ta có ⇒ Ä 2 > 3  π < 0 √ √ Ä ä−π Ä ä−π Đáp số 2 > 3
Bài 6. So sánh các cặp số sau: √ √ √ 4− 3 và 4− 2 a) 2 3 và 21,7 b) c) 2−2 và 1 √ Ç 1 å1,4 Ç 1 å 2 Ç 1 åπ Ç 1 å3,14 d) (0, 013)−1 và 1 e) và f) và 2 2 9 9
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 10
Hàm số mũ và hàm số logarit Giải tích 12 √ √ Ç 1 å 2 Ç 1 å 3 √ √ √ √ g) và 3 h) 10 và 5 20 4 i) 5 và 3 7 3 3 √ √ √ √ √ √ j) 17 và 3 28 4 k) 13 và 5 23 4 5 và 4 7 l) √ √ Å π ã2 Å π ã6 √ √ (0, 01)− 2 và (10)− 2 m) n) và 5−2 3 và 5−3 2 o) 4 4 √ √ √ 5300 và 8300 p) q) (0, 001)−3 và 3 100 4 2 và (0, 125)− 2 r) √ √ Ç 4 å−4 Ç 5 å5 ( 2)−3 và ( 2)−5 s) t) và (0, 02)−10 và 5011 u) 5 4 √ √ √ √ √ 5 10 − − ! 2 ! 2 Å π ã 2 Å π ã 3 3 2 v) và w) và 2 2 5 2
Bài 7. So sánh các số mũ sau: √ √ Ä äm Ä än (3, 2)m < (3, 2)n a) b) 2 > 2 Ç 1 åm Ç 1 ån √ √ c) > ( 5 − 1)m < ( 5 − 1)n d) 9 9 √ √ √ √ 3 !m 3 !n ( 2 − 1)m > ( 2 − 1)n e) f) > 2 2 2.4.5
Dạng 5: Bài toán thực tế
Công thức lãi kép: Lãi kép là phần lãi của kì sau được tính trên số tiền gốc kì trước
cộng với phần lãi của kì trước.
! 1 Số tiền nhận được cả gốc và lãi sau n kì hạn gửi là A(1 + r)n
2 Số tiền lãi nhận được sau n kì hạn gửi là A(1 + r)n − A = A [(1 + r)n − 1]
Ví dụ 10. Bà Mai gửi 50 triệu vào tài khoản định kỳ tính lãi kép với lãi suất là 8%/năm.
Tính số tiền lãi thu được sau 15 năm. Lời giải. î ó
Số tiền lãi thu được sau 15 năm: 50. (1 + 8%)15 − 1 ≈ 108.6(triệu) Đáp số ≈ 108.6(triệu)
Bài 8. Một người lần đầu gửi vào ngân hàng 100 triệu đồng với kì hạn 3 tháng, lãi suất
2%/một quý. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi quý số tiền lãi
sẽ được nhập vào gốc để tính lãi cho quý tiếp theo. Sau đúng 6 tháng, người đó gửi thêm
100 triệu đồng với kỳ hạn và lãi suất như trước đó. Tổng số tiền người đó nhận được 1 năm
sau khi gửi tiền (cả vốn lẫn lãi) gần nhất với kết quả nào sau đây?
Bài 9. Bác An đem gửi tổng số tiền 320 triệu đồng ở hai loại kỳ hạn khác nhau. Bác gửi
140 triệu đồng theo kỳ hạn ba tháng với lãi suất 2, 1%/một quý. Số tiền còn lại bác An gửi
theo kỳ hạn một tháng với lãi suất 0, 73%/một tháng. Biết rằng nếu không rút tiền ra khỏi
ngân hàng thì cứ sau mỗi kỳ hạn số tiền lãi sẽ được nhập vào gốc để tính lãi cho kỳ hạn
tiếp theo. Sau 15 tháng kể từ ngày gửi bác An đi rút tiền. Tính gần đúng đến hàng đơn vị
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 11
Hàm số mũ và hàm số logarit Giải tích 12
tổng số tiền lãi thu được của bác An.
Bài 10. Một người lần đầu gửi vào ngân hàng 100 triệu đồng với kì hạn 3 tháng, lãi suất
2%/một quý theo hình thức lãi kép. Sau đúng 6 tháng, người đó gửi thêm 100 triệu đồng
với kỳ hạn và lãi suất như trước đó. Tổng số tiền người đó nhận được 1 năm sau khi gửi tiền là bao nhiêu?
Bài 11. Một người gửi 50 triệu đồng vào một ngân hàng với lãi suất 6%/năm. Biết rằng
nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào gốc
để tính lãi cho năm tiếp theo. Hỏi sau ít nhất bao nhiêu năm người đó nhận được số tiền
nhiều hơn 100 triệu đồng bao gồm cả gốc và lãi? Giả sử trong suốt thời gian gửi lãi suất
không đổi và người đó không rút tiền ra.
Bài 12. Đầu năm 2016, ông A thành lập một công ty. Tổng số tiền ông A dùng để trả
lương cho nhân viên trong năm 2016 là 1 tỷ đồng. Biết rằng cứ sau mỗi năm thì tổng số
tiền dùng để trả lương cho nhân viên trong cả năm đó tăng thêm 15% so với năm trước.
Hỏi năm nào dưới đây là năm đầu tiên mà tổng số tiền ông A dùng để trả lương cho nhân
viên trong cả năm lớn hơn 2 tỷ đồng?
Bài 13. Anh Nam mong muốn rằng sau 6 năm sẽ có 2 tỷ để mua nhà. Hỏi anh Nam phải
gửi vào ngân hàng một khoản tiền tiền tiết kiệm như nhau hàng năm gần nhất với giá trị
nào sau đây, biết rằng lãi suất của ngân hàng là 8%/năm và lãi hàng năm được nhập vào vốn.
Bài 14. Ông A muốn sau 5 năm có 1.000.000.000 đồng để mua ô tô Camry. Hỏi rằng ông
A phải gửi ngân hàng mỗi tháng (số tiền như nhau) là bao nhiêu? Biết lãi suất hằng tháng
là 0.5% và tiền lãi sinh ra hằng tháng được nhập vào tiền vốn.
Bài 15. Ông Việt vay ngắn hạn ngân hàng 100 triệu đồng, với lãi suất 12%/năm. Ông
muốn hoàn nợ cho ngân hàng theo cách: Sau đúng một tháng kể từ ngày vay, ông bắt đầu
hoàn nợ; hai lần hoàn nợ liên tiếp cách nhau đúng một tháng, số tiền hoàn nợ ở mỗi lần là
như nhau và trả hết tiền nợ sau đúng 3 tháng kể từ ngày vay. Hỏi, theo cách đó, số tiền m
mà ông Việt sẽ phải trả cho ngân hàng trong mỗi lần hoàn nợ là bao nhiêu? Biết rằng, lãi
suất ngân hàng không thay đổi trong thời gian ông Việt hoàn nợ.
Bài 16. Một người đàn ông vay vốn ngân hàng với số tiền 100000000 đồng. Người đó dự
định sau đúng 5 năm thì trả hết nợ; Sau đúng một tháng kể từ ngày vay, ông bắt đầu hoàn
nợ; hai lần hoàn nợ liên tiếp cách nhau đúng một tháng, số tiền hoàn nợ ở mỗi lần là như
nhau. Hỏi, theo cách đó, số tiền a mà ông sẽ phải trả cho ngân hàng trong mỗi lần hoàn nợ
là bao nhiêu? Biết lãi suất hàng tháng là 1, 2% và không thay đổi trong thời gian ông hoàn nợ. 2.5 Bài tập về logarit 2.5.1
Dạng 1: Tính giá trị biểu thức
1. Nhóm công thức định nghĩa
1 ax = b > 0 ⇔ x = log b (mũ thành log)
x = b ⇒ x = ab (log thành mũ). a 2 loga ! 3 log 1 = 0 a = 1 a 4 loga 5 log ab = b a 6 aloga b = b β 7 logaα aβ =
8 alogb c = clogb a ⇒ b = aloga b α
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 12
Hàm số mũ và hàm số logarit Giải tích 12
Ví dụ 11. Tính giá trị của biểu thức P = log 4 · log 2. 2 1 4 Lời giải. Ç 1 å
Ta có P = log 4 · log 2 = log 22 · log − = −1. 2 1 2 2−2 2 = 2 · 4 2 Đáp số P = −1
Ví dụ 12. Tính giá trị của biểu thức P = 4log2 3. Lời giải. Ä
Ta có P = 4log2 3 = 42. log2 3 = 2log2 3ä2 = 32 = 9. Đáp số P = 9
Bài 17. Tính giá trị của các biểu thức sau: 1 √ » a) A = log 4 · log 2 b) B = log · log 9 c) C = log 3 a 2 1 5 27 a 4 25 d) D = 4log 2 2 3 + 9log√3 e) E = log √ 8 F = 27log9 2 + 4log8 27 f) 2 2 1 log 3 g) G = a3 a · loga4 a h) H = log 6 · log 9 · log 2 I = 92 log3 2+4 log81 5 i) log 3 8 6 1 a7 a j) J = 81log3 5 + 27log9 36 + K = 25log5 6 + 49log7 8 k) L = 53−2 log5 4 l) 34 log9 7 1 1 M = 9 log6 3 + 4 log8 2 m) n) N = log√ 3. log 36 O = 31+log9 4 + 42−log2 3 o) 6 3
Bài 18. Thực hiện các phép tính sau:
a) A = lg(tan 1◦) + lg(tan 2◦) + · · · + lg(tan 89◦)
b) B = log [log (log 16)] · log [log (log 64)] 8 4 2 2 3 4 1 √ c) C = 2 log 3 1 6 − log 1 400 + 3 log 1 45 3 2 3 3 2.5.2
Dạng 2: Biến đổi logarit
2. Nhóm công thức biến đổi b
1 log (b.c) = log b + log c (tích⇒tổng).
= log b − log c (thương⇒hiệu). a a a 2 loga c a a
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ! 1
3 log bα = α. log b (trên⇒trên) a a 4 log . log b (dưới⇒dưới) aα b = α a
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 β 5 log = − log b a 6 log log b b a aα bβ = α a
Ví dụ 13. Biến đổi biểu thức sau P = log (3x) − log (4x). 2 2 Lời giải. 3x 3
Ta có P = log (3x) − log (4x) = log = log . 2 2 2 4x 2 4 3 Đáp số P = log2 4
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 13
Hàm số mũ và hàm số logarit Giải tích 12
Bài 19. Thực hiện cá phép tính: a) log (2x) − log (8x) b) log(6a) − log(4a) c) ln(5b) − ln(2b) 3 3 2a3
Ví dụ 14. Khai triển biểu thức P = log . 2 b Lời giải. 2a3 Ta có P = log
= log (2a3) − log b = log 2 + log a3 − log b = 1 + 3 log a − log b. 2 b 2 2 2 2 2 2 2
Đáp số P = 1 + 3 log a − log b 2 2
Ví dụ 15. Khai triển biểu thức P = log2√ (2a). 2 Lời giải. î Ä ä
Ta có Q = log2√ (2a) = [2 log (2a)]2 = 4 (1 + log a)2ó = 4 1 + 2 log a + log2 a . 2 2 2 2 2 Ä ä
Đáp số Q = 4 1 + 2 log a + log2 a 2 2
Bài 20. Khai triển các biểu thức sau: a) log (2a) b) log (27x) c) log (8a2) d) log (27a3) 2 3 2 3 Ç a3 å e) log (125a5) f) log(100a2b3) g) log h) log√ (2a) 5 a 2 3 27 √ i) log√ (9a2) j) log √ (27a2b3) k) log√ (9 a) l) log (125a2b3) 3 3 3 a a 9x2 y 27a2 27a3 m) log n) log o) log √ p) log 3 y x2 z2 3 2 b b2 √ 4xy2 9ab3 8e3 a 16ea2b q) log r) log s) ln t) ln √ 2 z 3 c2 b2 c
Bài 21. Khai triển các biểu thức sau: Å a ã2 a) log2√ b) log2√ (2a) 2 b 2 4 c) log2(3a) − log2 (27a) d) log2(2a2) − log2√ 9 1 4 2 3 a Å x ã Ç 3a å3
e) log2√ (27x) + log2 (3x) + log2 f) log2√ 3 1 9 3 9 27 b Ç a2 å a g) log2√ h) log2 5 25b c2 b2
Ví dụ 16. Cho log x = 2 log√ a + log b. Tính x theo a và b. 3 3 1 3 Lời giải. Ta có: log x = 2 log a + log a − log b = log a4 − log b 3 1 3 3−1 b = 4 log3 3 3 3 2 a4 a4 = log ⇒ x = 3 b b a4 Đáp số x = b
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 14
Hàm số mũ và hàm số logarit Giải tích 12
Ví dụ 17. Cho log b = 2 và log c = 3. Tính giá trị biểu thức P = log (a2.b3.c4). a a a Lời giải.
Ta có P = log (a2.b3.c4) = log a2 + log b3 + log c4 = 2 + 3 log b + 4 log c. a a a a a a ⇒ P = 2 + 3.2 + 4.3 = 20. Đáp số P = 20
Bài 22. Tính giá trị biểu thức thỏa điều kiện cho trước.
a) Cho log x = log ab2 − log a3b. Tính x theo a và b. 7 7 7
b) Cho log b = 3 và log c = 5. Tính P = log (ab3c6) a a a
c) Cho log b = 3 và log c = 4. Tính P = log (ab2c5) a a a √ √ Ä
Cho log b = 2 và log c = 5. Tính P = log a2. b3. 3 c2ä d) a a a
Cho log a = 4 và log b = 2. Tính P = 2 log [log (8a) + 9] + log b2 e) 2 3 2 2 1 9 1 Cho log a = 2 và log b =
. Tính P = 5 log [log (3a)] + log b2 f) 3 2 1 3 3 3 4 1 ñ Ç 125 åô √ Ä ä g) Cho log a = 6 và log b = . Tính P = 3 log log + 28 + 2 log√ 36 b 5 6 4 5 5 a 6 3. Nhóm đổi cơ số log b c 1 log b = 2 log b. log c = log c ! a log a a b a c
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 3 log b = 4 alogb c = clogb a a log a b
Ví dụ 18. Cho log x = 2 và log x = 3. Tính giá trị biểu thức P = log x + log x. a b ab a b Lời giải. 1 1 1 1 Ta có P = log x + log x = + = + ab a a b log ab log a + log b log a − log b x logx x x x x b 1 1 1 1 36 = + = + = . 1 1 1 1 1 1 1 1 5 + − + − log x log x log x log x 2 3 2 3 a b a b 36 Đáp số P = 5
Bài 23. Tính giá trị của các biểu thức sau:
a) Cho log x = 3 và log x = 4. Tính P = log x + log x. a b abx a b
b) Cho log x = 2 và log x = 5. Tính P = log x − 2 log x. a b ab a b
c) Cho log x = 3 và log x = 2. Tính P = 2 log x − 4 log x. a b ab a b b 16 d) Cho log b = và log a = . Tính a32 + b. a 2 2 b b 125 e) Cho log b = và log a = . Tính a + 2b. a 25 5 b
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 15
Hàm số mũ và hàm số logarit Giải tích 12 b 16 f) Cho log√ b = và log√ a = . Tính a − 2b. a 4 2 b b 16 g) Cho log√ b = và log√ a = . Tính a − 2b. a 4 2 b
h) Cho log 5 = x và log 3 = y. Tính P = (x + y). log m. m m 10
i) Cho log 6 = x và log 2 = y. Tính P = (x + y). log a. a a 12
Ví dụ 19. Cho log 14 = a. Tính log √ 32 và log 32 theo a. 2 49 7 49 Lời giải.
Ta có log 14 = a =⇔ log (2.7) = a ⇔ log 2 + log 7 = a ⇔ 1 + log 7 = a 2 2 2 2 2 ⇒ log 7 = a − 1 2 2 2 2 2 √ log 32 = log 32 = log 25 = 2 log 2 = = 49 7 5 7 5 7 7 log 7 a − 1 2 2 Đáp số log √ 32 = 49 7 a − 1 5 5 1 5 1 5 log 32 = log . log 2 = . = . = . 49 72 25 = 2 7 2 log 7 2 a − 1 2(a − 1) 2 5 Đáp số log 32 = 49 2(a − 1)
Bài 24. Thực hiện phép biến đổi theo yêu cầu bài toán a) Cho log 27 = a. Tính log 16 theo a. 12 6
b) Cho log 14 = a. Tính log √ 32 và log 32 theo a. 2 49 7 49
c) Cho log 5 = a; log 3 = b. Tính log 135 theo a, . 2 2 3 d) Cho log 3 = a. Tính log 15 theo a. 15 25 √ √ 3 b e) Cho log b = 3. Tính log √ √ . a b a a 1
f) Cho lg 3 = 0, 477. Tính lg 9000; lg(0, 000027); . log 100 81
g) Cho log 2 = a. Tính log 28 theo a 7 1 2 √ b h) Cho log b = 5. Tính log√ √ . a ab a √ √ i) Cho log b = 13. Tính log 3 ab2. a b a 49 j) Cho log
7 = a; log 5 = b. Tính log √ theo a, b. 25 2 3 5 8
k) Cho lg 3 = a; lg 2 = b. Tính log 30 theo a, b. 125 l) Cho log 7 = a; log 5 = b. Tính log 28 theo a, b. 14 14 35 m) Cho log 3 = a; log 5 = b. Tính log 1350 theo a, b. 30 30 30
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 16
Hàm số mũ và hàm số logarit Giải tích 12
n) Cho log 3 = a; log 5 = b; log 2 = c. Tính log 63 theo a, b, c. 2 3 7 140 √ a o) Cho log b = 7. Tính log √ √ a a b b3 p) Cho log
5 = a; log 7 = b; log 3 = c. Tính log 35 theo a, b, c. 27 8 2 6 121 q) Cho log
11 = a; log 7 = b. Tính log √ theo a, b. 49 2 3 7 8 2.5.3
Dạng 3: Chứng minh đẳng thức logarit log b + log x
Ví dụ 20. Chứng minh đẳng thức: log (bx) = a a
(xem điều kiện được thỏa). (ax) 1 + log x a Lời giải. 1 1 1 1 Ta có log (bx) = log b + log x = + = + (ax) (ax) (ax) log (ax) log (ax) log a + log x log a + 1 b x b b x log b log x log b + log x = a + a = a a (đpcm). 1 + log x 1 + log x 1 + log x a a a
Bài 25. Chứng minh các đẳng thức sau: (xem điều kiện được thỏa) bloga c = cloga b a) log b + log x b) log (bx) = a a (ax) 1 + log x a log c · log c c) log c + log c = a b a b log c ab log c a d) = 1 + log b log c a ab a + b 1 e) log =
(log a + log b), với a2 + b2 = 7ab c 3 2 c c 1 f) log (x + 2y) − 2 log 2 =
(log x + log y), với x2 + 4y2 = 12xy a a 2 a a 3a + b 1 g) lg =
(lg a + lg b), với 9a2 + b2 = 10ab 4 2 log a + log a = 2 log a · log a, với a2 + b2 = c2 h) (b+c) (c−b) (c+b) (c−b) 1 1 1 1 k(k + 1) i) + + + · · · + = log x log log log 2 log x a a2 x a3 x ak x a log N · log N · log N
j) log N · log N + log N · log N + log N · log N = a b c a b b c c a log N abc 1 1 1
x = 10 1−lg z với y = 10 1−lg x và z = 10 1−lg y k) log N − log N log N a n l) = a
với a, b, c lần lượt theo thứ tự đó lập thành cấp số nhân. log N − log N log N b c c
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 17
Hàm số mũ và hàm số logarit Giải tích 12 2.5.4 Dạng 4: So sánh cặp số
Bài 26. Hãy so sánh các cặp số sau: 1 √ a) log 4 và log b) log 3 2 và log 0, 34 3 4 3 0,1 0,2 2 3 1 1 c) log 3 và log 5 d) log 1 và log 1 √ 4 5 2 4 3 80 2 15 + 2 1 e) log 150 và log 290 2log6 3 và 3log6 2 f) 13 17 g) log 10 và log 13 h) log 3 và log 4 7 11 2 3 2.5.5
Dạng 4: Bài toán thực tế
Bài 27. Biết rằng năm 2001, dân số Việt Nam là 78685800 người và tỉ lệ tăng dân số năm
đó là 1, 7% . Cho biết sự tăng dân số được ước tính theo công thức S = A.eN.t (trong đó A
: là dân số của năm lấy làm mốc tính, S là dân số sau N năm, r là tỉ lệ tăng dân số hàng
năm). Cứ tăng dân số với tỉ lệ như vậy thì đến năm nào dân số nước ta ở mức 120 triệu người?
Bài 28. Các khí thải gây hiệu ứng nhà kính là nguyên nhân chủ yếu làm trái đất nóng lên.
Theo OECD (Tổ chức hợp tác và phát triển kinh tế thế giới), khi nhiệt độ trái đất tăng lên
thì tổng giá trị kinh tế toàn cầu giảm. Người ta ước tính rằng khi nhiệt độ trái đất tăng
thêm 2◦C thì tổng giá trị kinh tế toàn cầu giảm 3%, còn khi nhiệt độ trái đất tăng thêm
5◦C thì tổng giá trị kinh tế toàn cầu giảm 10% . Biết rằng nếu nhiệt độ trái đất tăng thêm
t◦C, tổng giá trị kinh tế toàn cầu giảm f (t)% thì f (t) = k.at. (trong đó a, k là các hằng số
dương). Nhiệt độ trái đất tăng thêm bao nhiêu độ C thì tổng giá trị kinh tế toàn cầu giảm 20%?
Bài 29. Một người đã thả một lượng bèo hoa dâu chiếm 4% diện tích mặt hồ. Biết rằng
cứ sau đúng một tuần bèo phát triển thành 3 lần lượng đã có và tốc độ phát triển của bèo
ở mọi thời điểm như nhau. Sau bao nhiêu ngày, lượng bèo sẽ vừa phủ kín mặt hồ? 2.6
Bài tập hàm số mũ-hàm số logarit 2.6.1
Dạng 1: Tập xác định hàm số   0 < a(x) 6= 1 y = log f (x) xác định khi: . a(x)  f (x) > 0
! y = lgf(x) xác định khi: f(x) > 0.
y = ln f (x) xác định khi: f (x) > 0.
y = ax xác định khi 0 < a 6= 1.
Ví dụ 21. Tìm tập xác định của hàm số y = log (3x − x2). 2 Lời giải.
Hàm số xác định khi: 3x − x2 > 0 ⇔ 0 < x < 3.
Tập xác định là D = (0; 3).
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 18
Hàm số mũ và hàm số logarit Giải tích 12 x − 2
Ví dụ 22. Tìm tập xác định của hàm số y = log . 2 1 − x2 Lời giải. x − 2 Hàm số xác định khi: > 0. x −∞ −1 1 2 +∞ 1 − x2 x − 2 − − − 0 + • Cho x − 2 = 0 ⇔ x = 2 1 − x2 − 0 + 0 − − x − 2
• Cho 1 − x2 = 0 ⇔ x = ±1 + − + 0 − 1 − x2  x − 2 x < −1 Từ bảng xét dấu > 0 ⇔ 
. Tập xác định là D = (−∞; −1) ∪ (1; 2). 1 − x2 1 < x < 2 x
Ví dụ 23. Tìm tập xác định hàm số y = log . (x−1) −x + 2  x   > 0   0 < x < 2
Lời giải. Hàm số xác định khi: −x + 2 ⇔ ⇔ 1 < x < 2.   1 < x 6= 2  0 < x − 1 6= 1
Tập xác định hàm là D = (1; 2).
Bài 30. Tìm tập xác định của các hàm số sau: x − 1 √ a) y = lg b) y = ln x2 − 4x − 12 −2x − 3 √ x + 1 c) y = x2 + x − 2. log (9 − x2) d) y = log √ 3 3 x2 − x − 2 x e) y = log (x2 − 1) f) y = log (2x−1) x 4 − x2 2.6.2 Dạng 2: Đạo hàm 1 (ax)0 = ax. ln a 2 (au)0 = au. ln a.u0
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 (ex)0 = ex 4 (eu)0 = eu.u0
! ........................................... . ........................................ 1 u0 5 (log x)0 = a 6 (log u)0 = x. ln a a u. ln a
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 u0 7 (ln x)0 = x 8 (ln u)0 = u
Bài 31. Tính đạo hàm của các hàm số sau: y = (x2 − 2x + 2).ex a) y = (x2 + 2x) e−x b) c) y = e−2x. sin x √ e2x + ex y = e2x+x2 d) e) y = x.e x− 1 x 3 f) y = e2x − ex √ g) y = 2(x3 + 1) y = 3 x2+1 h) y = 2x.ecos x i) 3x j) y = y = cos x.ecot x k) y = 20182018x l) x2 − x + 1
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 19
Hàm số mũ và hàm số logarit Giải tích 12
Bài 32. Tính các đạo hàm của các hàm số sau: a) y = ln(2x2 + x + 3) b) y = log (cos x) c) y = ex. ln (cos x) 2 d) y = (2x − 1) ln (3x2 + x) e) y = log 1 (x3 − cos x) f) y = log (cos x) 3 2 ln (2x + 1) ln (2x + 1) √ Ä g) y = √ h) y = y = ln x + 1 + x2ä i) 2x + 1 x + 1
Bài 33. Tính đạo hàm của các hàm số sau ln(x) − 2 y = 1 − (x2 − 2x + 1)ex a) y = 3x − (2x + 1)2x b) c) y = x + 1 √ d) y = (x − 4) log x e) x log (x + 1) f) y = log 3 x2. ln (3 − x2) 2 √ ex + e−x y = (2x2 − 1)e3x g) h) y = x3 ex2 + 1 i) y = ex + e−x √ j) y = 3x − e3x + 1 k) y = ln (x3 + 2x2 − x) l) y = (x2 + 3) ln(x2 + 2) √ » m) y = 4 ln3(3x2 + 1) y = 1 − (2x + 3)3x n) o) y = 2 − ex. sin2 x √ ex + 1 y = 2x − ex p) q) y = r) y = x ln x + 1 ex − 1 » s) y = 1 + x − 2 ln2 x t) y = 1 − 2 ln x + ln2 x u) y = log x − 3 log x 2 3 v) y = log(x2 + 1) − ln(2x) y = xπ.πx w) x) y = ex(sin x − cos x) 2.6.3
Dạng 3: Chứng minh hàm số đã cho thỏa hệ thức cho trước
Ví dụ 24. Chứng minh hàm số đã cho thỏa hệ thức được chỉ ra. y = x.e− x2
2 . Chứng minh rằng: xy0 = (1 − x2) y Lời giải. 0 Ç x2 å Ta có y0 = e− x2 2 + x.e− x2 2 . − = e− x2 2 + x.e− x2 2 .(−x) = e− x2 2 (1 − x2) 2 Ta có: VT= xy0 = x.e− x2 2
(1 − x2) = (1 − x2) y =VP (đpcm).
Bài 34. Chứng minh hàm số đã cho thỏa hệ thức được chỉ ra. y = (x + 1)ex; y0 − y = ex a)
b) y = e4x + 2e−x; y000 + 2y0 − 12y = 0
c) y = a.e−x + b.e−2x; y00 + 3y0 + 2y = 0
d) y = e−x sin x; y00 + 2y0 + 2y = 0
e) y = e−x cos x; y(4) + 4y = 0
f) y = esin x; y0 cos x − y sin x − y00 = 0 1
g) y = e2x sin 5x; y00 − 4y0 + 29y = 0 y = x2ex; y00 − 2y0 + y = ex h) 2
i) y = e4x + 2e−x; y000 − 13y0 − 12 = 0 j) y = x.e− x2 2 ; xy0 = (1 − x2) y
Bài 35. Chứng minh hàm số đã cho thỏa hệ thức được chỉ ra. Ç 1 å y = ln ; xy0 + 1 = ey a) 1 + x
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 20
Hàm số mũ và hàm số logarit Giải tích 12 1 b) y = ; xy0 = y (y ln x − 1) 1 + x + ln x
c) y = sin (ln x) + cos (ln x); y + xy0 + x2y00 = 0 1 + ln x d) y = ; 2x2y0 = x2y2 + 1 x (1 − ln x) x2 1 √ √ » y = + x x2 + 1 + ln x + x2 + 1; 2y = xy0 + ln y0 e) 2 2 2xy
f) y = (x2 + 1) (ex + 2016); y0 = + ex (x2 + 1) x2 + 1
g) y = x [3 cos (ln x) + 4 sin (ln x)]; x2y000 − xy0 + 2y = 0 2.6.4
Dạng 4: Giải phương trình, bất phương trình
Bài 36. Giải các phương trình, bất phương trình
a) f 0(x) = 2f (x); f (x) = ex (x2 + 3x + 1) 1 b) f 0(x) = f (x) = 0; f (x) = x3 ln x x
c) f 0(x) > g0(x); f (x) = x + ln(x − 5); g(x) = ln(x − 1)
d) f 0(x) = 0; f (x) = e2x−1 + 2.e1−2x + 7x − 5 1 e) f 0(x) < g0(x); f (x) = .52x+1; g(x) = 5x + 4x. ln 5 2 2.6.5
Dạng 5: Giá trị lớn nhất, giá trị nhỏ nhất
Tìm GTLN-GTNN của hàm số y = f (x) trên đoạn [a; b]. Tính y0
Giải phương trình y0 = 0 và chỉ nhận những nhiệm x0 ∈ [a; b] Tính f (a), f (b), f (x0)
! Khi đó: min = min{f(a),f(b),f(x0)} và max = max{f(a),f(b),f(x0)} [a;b] [a;b] 4 ! Chú ý:
1. Nếu ham số y = f (x) tăng trên [a; b] thì min f (x) = f (a) và max f (x) = f (b) [a;b] [a;b]
2. Nếu ham số y = f (x) giảm trên [a; b] thì max f (x) = f (a) và min f (x) = f (b) [a;b] [a;b]
3. Nếu bài toán đặt ẩn phụ thì phải có điều kiện cho ẩn phụ đó.
Ví dụ 25. Tìm GTLN-GTNN của hàm số y = x2.ex + 1 trên đoạn [−3; 2]. Lời giải.
Ta có y0 = 2x.ex + x2.ex = ex(x2 + 2x).
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 21
Hàm số mũ và hàm số logarit Giải tích 12  x = 0(loại)
y0 = 0 ⇔ ex(x2 + 2x) = 0 ⇔ x2 + 2x = 0  x = −2 9 4 f (−3) = 9.e−3 + 1 =
+ 1; f (2) = 4.e2 + 1; f (−2) = 4.e−2 + 1 = + 1 e3 e2
Vậy min f (x) = 9.e−3 + 1; max f (x) = 4.e2 + 1. [−3;2] [−3;2]
Bài 37. Tìm GTLN-GTNN của các hàm số sau: ln2 x a) y = − 1 trên đoạn [1; e2]
b) y = ln2 x − ln x trên đoạn [1; e2] x
c) y = (x2 − 3x + 1)ex trên đoạn [−3; 0]
d) y = x ln x − 1 trên đoạn [1; e2]
e) y = x2 − ln(1 − 2x) trên đoạn [−2; 0]
f) y = x2.ex + 1 trên đoạn [−3; 2] A. PHƯƠNG TRÌNH 2.7 Phương trình mũ 2.7.1 Phương trình mũ cơ bản Với a > 0, a 6= 1 thì  !  b > 0 ax = b ⇔  x = log b a
Ví dụ 26. Giải phương trình sau 2x−1 = 3 (1) Lời giải.
Ta có (1) ⇔ x − 1 = log 3 ⇔ x = 1 + log 3 ⇔ x = log 2 + log 3 = log 6 2 2 2 2 2 Đáp số x = log 6 2 4 !
Chú ý: 1 = log a do đó: 1 = log 2 a 2
Ví dụ 27. Giải phương trình sau 2x + 2x+1 = 3x + 3x+1 (2) Lời giải. Ç 2 åx 4 4
Ta có (2) ⇔ 2x + 2.2x = 3x + 3.3x ⇔ 3.2x = 4.3x ⇔ = ⇔ x = log 2 . 3 3 3 3 4 Đáp số x = log 23 3
Bài 38. Giải các phương trình sau: a) 2018x+1 = 2
3x − 3x−1 + 3x−2 = 2x + 2x−1 + 2x−2 b)
3x+1 + 3x+2 = 9.5x + 5x+1 + 5x+2 c)
d) 2.3x+1 − 6.3x−1 − 3x = 9
e) 52x − 7x − 52x.17 + 7x.17 = 0
5.3x + 3.2x−1 = 7.2x − 4.3x f)
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 22
Hàm số mũ và hàm số logarit Giải tích 12 2.7.2
Một số phương pháp giải phương trình mũ 2.7.2.1
Phương pháp đưa về cùng cơ số
Dùng các công thức biến đổi phương trình đã cho về dạng: af(x) = ag(x) .
Khi đó: Với a > 0, a 6= 1 thì af(x) = ag(x) ⇔ f (x) = g(x)
! Trường hợp cơ số a chưa biến:  a = 1
aM = aN ⇔ (a − 1) . (M − N ) = 0 ⇔  M = N
Ví dụ 28. Giải phương trình 2x2−1 = 8 (1) Lời giải.
Ta có (1) ⇔ 2x2−1 = 8 ⇔ 2x2−1 = 23 ⇔ x2 − 1 = 3 ⇔ x2 = 4 ⇔ x = ±2. Đáp số x = ±2
Ví dụ 29. Giải phương trình 273x−2 = 9x−1 (2) Lời giải. 4
Ta có (2) ⇔ 33(3x−2) = 32(x−1) ⇔ 3(3x−2) = 2(x−1) ⇔ 9x−6 = 2x−2 ⇔ 7x = 4 ⇔ x = . 7 4 Đáp số x = 7
Ví dụ 30. Giải phương trình 2018x2−3x+2 = 1 (3) Lời giải.  x = 1
Ta có (3) ⇔ 2018x2−3x+2 = 20180 ⇔ x2 − 3x + 2 = 0  . x = 2 Đáp số x = 1; x = 2 4 !
Chú ý: 1 = a0 do đó: 1 = 20180. √
Ví dụ 31. Giải phương trình (x + 1) x−3 = 1 (4) Lời giải.
Điều kiện: x − 3 ≥ 0 ⇔ x ≥ 3. √ √ √ î ó
(3) ⇔ (x + 1) x−3 = (x + 2)0 ⇔ [(x + 1) − 1] .
x − 3 − 0 = 0 ⇔ x. x − 3 = 0 ⇔   x = 0 x = 0(loại) ⇔ √ ⇔   . Đáp số x = 3 x − 3 = 0 x = 3
Bài 39. Giải các phương trình sau: √ √ 8 a) (0, 04)x = 625. 3 5 b) 0, 125.161−x = 32√ 1−x
c) 28−x2.58−x2 = 0, 001. (105) d) 32x−1.153x.5−3x = 3 9 5.3x + 3.2x = 7.2x − 4.3x e) 93x−1 = 38x−2 f) Ç 1 åx2−2 Ç 1 åx+7 Ç 1 å1−2x = 24−3x g) h) . = 2 2 2 2
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 23
Hàm số mũ và hàm số logarit Giải tích 12 √ √ √ √ x−1 Ä ä2x Ä äx−1 Ä ä i) 3 − 2 2 = 3 + 2 2 5 + 2 = 5 − 2 x+1 j) Ç 2 åx+1 Ç 4 å5−x k) (1, 5)5x−7 = l) (0, 75)2x−3 = 3 3 Ç 1 åx2−2x−3 m) 5x2−5x+6 = 1 = 7x+1 n) 7 √ √ Ä ä o) 3 − 2 2 63x = 3 + 2 2 p) 3x.2x+1 = 72 √4−x2
q) 2.3x − 6.3x−1 − 3x = 9 r) (x2 − 2x + 2) = 1 s Ç 3 åx−2 Ç 4 å5 9 Ç 1 åx+1 s) . x = = 1252x t) 4 5 16 25 2.7.2.2 Phương pháp logarit hóa
! Phương trình logarit hóa có dạng: af(x) = bg(x) ⇔ f(x) = g(x).log b a
Ví dụ 32. Giải phương trình 2x−1 = 71−x2 (1) Lời giải.
Từ (1) ⇔ x − 1 = (1 − x2). log 7 ⇔ x − 1 + (x − 1)(x + 1) log 7 = 0 2 2  x − 1 = 0 ⇔ (x − 1) [1 + (x + 1). log 7] = 0 ⇔ ⇔ 2  1 + (x + 1). log 7 = 0 2  x = 1  1  x + 1 = − = − log 2 log 7 7 2   x = 1 x = 1 ⇔ ⇔   .
Đáp số x = 1; x = − log 14 7 x = −1 − log 2 x = − log 14 7 7
Bài 40. Giải các phương trình sau: x−1 2x = 3x2 a) 5x−1 = 3 x+1 b) 6x−1 = 5x2−2x+1 c) 24−x2 = 32−x d) 35x = 53x e) 7x = 24x f)
Bài 41. Giải các phương trình sau (đưa về cùng cơ số hoặc logarit hóa) √ a) 4x+1 = 3 16. b) 2x+1 · 32x+3 = 63x+1. c) 22x2+x+5 = 82x+1. d) 5x · 8x+1 = 100. e) 9|3x−1| = 38x−2. f) 2x+1 · 3x−2 · 5x = 200. Ç 2 åx Ç 25 åx 125 g) · = .
h) 5x + 5x+1 + 5x+2 = 3x + 3x+3 + 3x+1. 5 8 64 x i) 8 x+2 = 36 · 32−x. j) 3x+2 − 3x+1 = 18. x+5 x+17 32 x−7 = 0, 25 · 125 x−3 k)
l) 2 · 3x+1 − 6 · 3x−1 − 3x = 9 √ √ √ √ x−1 Ä ä2x Ä äx−1 Ä ä m) 3 − 2 2 = 3 + 2 2 5 + 2 = 5 − 2 x+1 n)
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 24
Hàm số mũ và hàm số logarit Giải tích 12 √ √ x−1 o) 5x · 8 x x = 500 p) xx = x √ √ Ä Ä q) 2x − x2äx−1 = 1 r) x − x2äx−2 = 1 √ x2−1 s) (x2 − x + 1) = 1 t) (x + 1) x−3 = 1 |x2−5x+4| x+1 u) (x2 + 3) = (x2 + 3)
Bài 42. Giải các phương trình sau (đưa về cùng cơ số hoặc logarit hóa) a) 3x−1 + 3x + 3x+1 = 9477 5x+1 − 5x = 2x+1 + 2x+3 b)
2x−1 − 3x = 3x−1 − 2x+2 c)
5x + 5x+1 + 5x+2 = 7x + 7x+1 − 7x+2 d) 1 1
22x+5 − 3x+ 92 = 3x+ 72 − 4x+4 e) 3 · 4x + · 9x+2 = 6 · 4x+2 − · 9x+1 f) 3 2 1 9x − 2x+ 3 −x 2 = 2x+ 12 − 32x−1 g) 4−x − 3−x− 12 = 3 2 − 2−2x−1 h)
5x+ 12 − 9x = 32x−2 − 5x− 12 i)
4x+2 − 10 · 3x = 2 · 3x − 11 · 22x j)
k) x2 − (2x − 3)x + 2(1 − 2x) = 0
x2 · 2x+1 = 2|x−3|+2 = x2 · 2|x−3| + 2x−1 l) 62x+3 = 2x+7 · 33x−1 m) 3x+3 · 7x+3 = 32x · 72x n) 32x+3 · 52x+3 = 55x · 35x o) 3x−1 · 22x−2 = 129−x p) x 8 x+2 = 36 · 32−x q) 5x2−5x+6 = 2x−1 r) x−1 s) 2x · 5 x = 10 3x2−4x = 2x−4 t)
u) 4 · 3x+2 + 5 · 3x − 7 · 3x+1 = 40 v) 22x+6 + 2x+7 − 17 = 0 w) 52x−1 + 5x+1 = 250 x) 5x−1 + 53−x = 26 2x+4 + 2x+2 = 5x+1 + 3 · 5x y)
z) 5x+1 + 6 · 5x − 3 · 5x−1 = 52 2.7.2.3
Phương pháp đặt ẩn phụ 2.7.2.3.1 Dạng 1:  t = af(x), t > 0 Ä  P af(x)ä = 0 ⇔  P (t) = 0 2.7.2.3.2 Dạng 2:
α · a2f(x) + β · (ab)f(x) + λ · b2f(x) = 0
! Chia hai vế cho b2f(x) hoặc a2f(x) (chia cơ số lớn nhất hoặc nhỏ nhất). Sau đó đặt Å a ãf (x) t = > 0 b 2.7.2.3.3 Dạng 3: af(x) + bf(x) = m 1
với a · b = 1. Đặt t = af(x) ⇒ bf(x) = t
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 25
Hàm số mũ và hàm số logarit Giải tích 12
Ví dụ 33. Giải phương trình: 9x − 5 · 3x + 6 = 0 (1) Lời giải. x
(1) ⇔ (32) − 5 · 3x + 6 = 0 ⇔ (3x)2 − 5 · 3x + 6 = 0 (*)  t = 2 (n)
Đặt t = 3x, (t > 0), phương trình (*) trở thành t2 − 5t + 6 = 0 ⇔  t = 3 (n)
• Với t = 2 ⇒ 3x = 2 ⇔ x = log 2 3
• Với t = 3 ⇒ 3x = 3 ⇔ x = log 3 = 1 3 Đáp số x = log 2; x = 1 3
Ví dụ 34. Giải phương trình: 25x + 15x = 2 · 9x (2) Lời giải.
Chia hai vế cho 25x, ta được: 15x 9x ñÇ 3 åxô2 Ç 3 åx (2) ⇔ 1 + = 2 · ⇔ 2 · − + 1 = 0 (*) 25x 25x 5 5  t = 1 (nhận) Ç 3 åx Đặt t =
> 0, phương trình (*) trở thành 2t2 − t − 1 = 0 ⇔  1 5  t = − (loại) 2 Ç 3 åx Với t = 1 ⇒ = 1 ⇔ x = 0 5 Đáp số x = 0 √ √ Ä äx Ä äx
Ví dụ 35. Giải phương trình: 2 + 3 + 2 − 3 = 4 (3) Lời giải. √ √ √ √ Ä ä ä ä äóx Nhận xét: 2 + 3 · Ä2 − 3 = 1 ⇔ îÄ2 + 3 · Ä2 − 3 = 1 ⇔ √ √ ⇔ Ä äx äx 2 + 3 · Ä2 − 3 = 1 √ √ 1 Ä äx äx Đặt 2 + 3 = t > 0 ⇒ Ä2 − 3 = t √  1 t = 2 + 3 > 0 (nhận)
Phương trình (3) trở thành: t + = 4 ⇔ t2 − 4t + 1 = 0 ⇔ √  t t = 2 − 3 > 0 (nhận) √ √ √ • äx Với t = 2 + 3 ⇒ Ä2 + 3 = 2 + 3 ⇔ x = 1 √ √ √ √ • äx Với t = 2 − 3 ⇒ Ä2 + 3 = 2 − 3 = (2 + 3)−1 ⇔ x = −1 Đáp số x = 1; x = −1
Bài 43. Giải các phương trình sau: a) 21+2x + 15 · 2x − 8 = 0 b) 5x+1 − 52−x = 124 √ √ c) 5 x − 51− x + 4
d) 32−2x − 2 · 32−x − 27 = 0 √ √ Ä äx Ä äx e) 5x + 251−x = 6 f) 7 + 4 3 + 2 + 3 = 6 g) 9sin2 x + 9cos2 x = 6 h) 4x + 2x+1 − 8 = 0 i) 4x+1 − 6 · 2x+1 + 8 = 0
j) 34x+8 − 4 · 32x+5 + 27 = 0 k) 16x − 17 · 4x + 16 = 0 l) 49x + 7x+1 − 8 = 0
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 26
Hàm số mũ và hàm số logarit Giải tích 12 √ √ Ä äx Ä äx m) 2x2−x − 22+x−x2 = 3 n) 7 + 4 3 + 2 + 3 = 6 o) 4cos 2x + 4cos2 x = 3
p) 32x+5 − 36 · 3x+1 + 9 = 0 q) 4x2+2 + 9 · 2x2+2 + 8 = 0
r) 32x2+2x+1 − 28 · 3x2+x + 9 = 0
s) 3 · 52x−1 − 2 · 5x−1 = 0, 2 t) 2sin2 x + 4 · 2cos2 x = 6 √ √ √ √ 4 x−2 + 16 = 10 · 2 x−2 u) v) 5 x − 51− x + 4 = 0 8 2x 18 w) + = 2x−1 2 + 2x 2x−1 + 21−x + 2
Bài 44. Giải các phương trình sau: a) 9x − 5 · 3x + 6 = 0 b) 2x+2 − 22−x − 15 = 0 c) e2x − 4 · e−2x = 3
d) 9x2−1 − 36 · 3x2−3 + 3 = 0 √ √ 4 x−2 + 16 = 10 · 2 x−2 e) f) 4x+1 + 2x+2 − 3 = 0 g) e6x − 3 · e3x + 2 = 0
h) −8x + 2 · 4x + 2x − 2 = 0 i) 81sin2 x + 81cos2 x = 30 j) 9x − 25 · 3x + 7 = 0 k) 25x − 23 · 5x − 5 = 0 l) 25x − 6 · 5x+1 + 53 = 0 1 m) 132x − 6 · 13x + 5 = 0
n) 3 · 52x−1 − 2 · 5x−1 = 5 3 o) = 4x−4 − 7
p) 32(x+1) − 82 · 3x + 9 = 0 23−x q) 3x+2 + 9x+1 = 4 r) 9x2−1 − 3x2+1 − 6 = 0 √ √ s) 3x+2 + 9x+1 = 4
t) 4x+ x2−2 − 5 · 2x−1+ x2−2 = 6 √ √ Ä 3 äx Ä äx−10 u) 3 + 10 3 − 84 = 0
v) 42x + 23x+1 + 2x+2 − 16 = 0
w) 8x − 3 · 4x − 3 · 2x+1 + 8 = 0 x) 32+x + 32−x = 30 √ √ y) 4x + 23−4x = 6 z) 3 x − 31− x + 4 = 0
Bài 45. Giải các phương trình sau: 2 Ç 1 åx−2 a) 52x−3 = + 15 b) = 25−x + 9 5x−1 4 Ç 1 åx−3 32x c) = 65−2x − 12 d) = 2 · (0, 3)x + 3 6 100x e) 101+x2 − 101−x2 = 99 f) 51+x2 − 51−x2 = 24 √ √
g) 9 x2−2x−x − 7 · 3 x2−2x−x−1 = 2
h) 5 · 23|x−1| − 3 · 25−3x + 7 = 0 x 9 10 + 4 √ 2 x−1 √ x−1 i) = j) 3 · 2 x+1 − 8 · 2 2 + 4 = 0 2x−2 4 √ √ √ √ √ √ 4 8 · 3 x+ 4 x + 9 x+1 = 9 x k)
l) 4x+ x2−2 − 5 · 2x−1+ x2−2 − 6 = 0 √ √ Ä äx Ä äx
m) 43+2 cos x − 7 · 41+cos x − 2 = 0 n) 7 + 4 3 − 3 2 − 3 + 2 = 0 2 3x+3 o) 8 x − 2 x + 12 = 0
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 27
Hàm số mũ và hàm số logarit Giải tích 12
Bài 46. Giải các phương trình mũ sau:
a) 9x+1 − 13 · 6x + 4x+1 = 0
b) 49x − 2 · 35x − 7 · 52x+1 = 0 1 1 1 2 · 4 x + 6 x = 9 x c) 8x + 18x = 2 · 27x d) 4 · 9x + 12x − 3 · 16x e) 8 · 4x + 9x = 6x+1 f)
g) 9x2−1 − 36 · 3x2−3 + 3 = 0 125x + 50x = 23x+1 h) x 6 · 9x − 13 · 6x + 6 · 4x i) 4 · 3x − 9 · 2x = 5 · 6 2 j) 4x − 2 · 6x = 3 · 9x k)
64 · 9x − 84 · 12x + 27 · 16x l) 4− 1x + 6− 1x = 9− 1x m) 3 · 16x + 2 · 81x = 5 · 36x n) 25x + 10x + 22x+1 o) 27x + 12x = 2 · 8x p) 1 1 1
6 · 9 x − 13 · 6 x + 6 · 4 x q)
6 · 32x − 13 · 6x + 6 · 22x r) 3 · 16x + 2 · 81x = 5 · 36x s) 8 · 4x + 9x = 6x+1 t)
u) 9x2−1 − 36 · 3x2−3 + 3 = 0 125x + 50x = 23x+1 v) 27x + 12x = 2 · 8x w)
Bài 47. Giải các phương trình mũ sau: √ √ √ √ Ä äx2 Ä äx2 » x » x a) 2 + 3 + 2 − 3 = 4 b) 7 + 48 + 7 − 48 = 14 √ √ √ √ » x » x äx äx c) 5 + 2 6 + 5 − 2 6 = 10 6 · Ä 5 + 1 − 2 · Ä 5 − 1 = 2x+2 d) √ √ √ √ » » 3 x x Ä ätan x Ä ätan x e) 3 + 8 + 3 3 − 8 = 6 f) 8 + 3 7 + 8 − 3 7 = 16 √ √ √ √ √ » x » x Ä äx Ä äx Ä äx g) 4 − 15 + 4 + 15 = 2 2 h) 2 − 3 + 2 + 3 = 14 √ √ √ √ » x » x Ä äx äx i) 2 + 3 + 2 − 3 = 4 j) 7 + 4 3 − 3 · Ä2 − 3 + 2 = 0 √ √ 7 + 3 5!x 7 − 3 5!x √ √ Ä äx äx k) + 7 · = 8 3 + 5 + 16 · Ä3 − 5 = 2x+3 l) 2 2
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 28
Hàm số mũ và hàm số logarit Giải tích 12 2.7.2.4
Sử dụng tính đơn điệu của hàm số
Xét hàm số: f (x) = g(x) (1)
Đoán x0 là một nghiệm của phương trình (1) (thông thường là lân cận của số 0)
Dựa vào tính đồng biến và nghịch biến của f (x) và g(x) để kết luận x0 là nghiệm duy nhất:
• f (x) đồng biến và g(x) nghịch biến
• f (x) đơn điệu và g(x) = c (hằng số)
! Nếu f(x) đồng biến (hoặc nghịch biến) thì f(u) = f(v) ⇔ u = v Lưu ý
• Hàm số bậc nhất: y = ax + b, (a 6= 0)
– Đồng biến khi: a > 0
– Nghịch biến khi: a < 0 • Hàm số mũ: y = ax
– Đồng biến khi: a > 1
– Nghịch biến khi: 0 < a < 1
Ví dụ 36. Giải phương trình: 3x = 5 − 2x (4) Lời giải.
Đặt f (x) = 3x đồng biến trên R (vì a = 3 > 1)
g(x) = 5 − 2x nghịch biến trên R (vì a = −2 < 0)
Ta có: f (1) = g(1) ⇒ x = 1 là nghiệm duy nhất của phương trình (4).
Ví dụ 37. Giải phương trình: (x + 4) · 9x − (x + 5) · 3x + 1 = 0 (5) Lời giải.
Đặt 3x = t > 0, phương trình (4) trở thành: (x + 4)t2 − (x + 5)t + 0 = 0  x + 5 + x + 3 t = = 1  2(x + 4)
∆ = (x + 5)2 − 4(x + 4) = x2 + 6x + 9 = (x + 3)2 ⇒   x + 5 − x − 3 1  t = = 2(x + 4) x + 4
• Với t = 1 ⇒ 3x = 1 ⇔ x = 0  1  x > −4 • Với t = > 0 ⇔ x + 4  3x · (x + 4) = 1 (∗∗)
Xét hàm số f (x) = 3x · (x + 4), ∀x ∈ (−4; +∞)
Ta có f 0(x) = 3x · (x + 4) · ln 3 + 3x = 3x · [(x + 3) · ln 3 + 1] > 0, ∀x ∈ (−4; +∞)
⇒ f (x) đồng biến ∀x ∈ (−4; +∞) và g(x) = 1 là hàm không đổi.
Ta thấy f (−1) = g(−1) ⇒ x = −1 là nghiệm duy nhất của phương trình (**).
Vậy phương trình (5) có hai nghiệm x = 0; x = −1 Đáp số x = 0; x = −1
Bài 48. Giải các phương trình mũ sau (sử dụng tính đồng biến và nghịch biến)
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 29
Hàm số mũ và hàm số logarit Giải tích 12 Ç 1 åx 1 Ç 1 åx 3 a) = x − b) = − 2 2 3 x Ç 1 åx x c) = x + 1 d) 2x = 3 2 + 1 3 e) 2x = x + 2 f) 76−x = x + 2 x g) 3x = x + 2 h) 2x = 3 2 + 1 i) 3x = 11 − x j) 2−x + 3x + 10 = 0 k) 3x = 5 − 2x l) 2x+1 − 4x = x − 1 m) 4x + 7x = 9x + 2 6x + 2x = 5x + 3x n) Ç 3 åx 7 + = 2x o) 2x + 5x = 7x p) 5 5 √ √ √ √ √ Ä äx Ä äx Ä äx
q) 9x + 2(x − 2) · 3x + 2x − 5 = 0 r) 3 − 2 + 3 + 2 = 5 √ √ Ä äx Ä äx 3 + 2 2 + 3 − 2 2 = 6x s)
2x−1 − 2x2−x = (x − 1)2 t) √ u) 2 3−x = −x2 + 8x − 14
v) 3 · 4x + (3x − 10) · 2x + 3 − x = 0
Bài 49. Giải các phương trình sau:
a) 3 · 16x−2 − (3x − 10) · 4x−2 + 3 − x = 0
b) 8 − x · 2x + 23−x − x = 0
c) 9x2 + (x2 − 3) · 3x2 + 2 (1 − x2) = 0
d) 32x + 2 (x − 2) · 3x + 2x − 9 = 0 1 1
e) 32x−3 − (3x − 10) · 3x−2 + 3 − x f) 4 x + 2x · 2 x − 6x = 9
g) 25x − 2(3 − x) · 5x + 2x − 7 = 0
h) 3 · 25x−2 + (3x − 10) · 5x−2 + 3 − x = 0
i) 3 · 4x + (3x − 10) · 2x + 3 − x = 0
j) 9x + 2(x − 2) · 3x + 2x − 5 = 0
k) 4x + (x − 8) · 2x + 12 − 2x = 0
l) (x + 4) · 9x − (x + 5) · 3x + 1 = 0 2.7.2.5 Phương trình tích  A = 0
Phương trình tích: A · B = 0 ⇔  B = 0
Nghiệm phương trình bậc 2: ax2 + bx + c = 0, (a 6= 0) ! • ∆ = b2 − 4ac √  −b + ∆ x =  • Nghiệm là  2a  √  −b − ∆  x = 2a
Ví dụ 38. Giải phương trình: 25 · 2x − 10x + 5x = 25 (1) Lời giải.
(1)⇔ 25 · 2x − 25 − 2x · 5x + 5x = 0 ⇔ 25 (2x − 1) − 5x (2x − 1) = 0 ⇔ (2x − 1) (25 − 5x) = 0    2x − 1 = 0 2x = 1 x = 0 ⇔ ⇔ ⇔    25 − 5x = 0 5x = 25 x = 2
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 30
Hàm số mũ và hàm số logarit Giải tích 12 Đáp số x = 0; x = 2
Ví dụ 39. Giải phương trình: 2 (x2 − 3x+1) = 3x (1 − 4 · 3x) − 1 (2)
Lời giải 1. Nghiệm phương trình bâc 2 (theo biến x)
(1)⇔ 2x2 − 3(1 − 4 · 3x) · x − 6 · 3x + 1 = 0
∆ = 9(1 − 8 · 3x + 16 · 9x) − 8(−6 · 3x + 1) = 144 · 9x − 24 · 3x + 1 = (12 · 3x − 1)2 
3 − 12 · 3x + 12 · 3x − 1  1 x = x = ⇒  4  2  ⇔  
3 − 12 · 3x − 12 · 3x + 1  1 x x = 3x = − (∗) 4 6 6 1 x Xét phương trình (**) 3x = − . Đặt 6 6 1 x f (x) = 3x; g(x) = − 6 6
• Hàm số f (x) = 3x đồng biến trên R (vì a = 3 > 1) 1 x 1 • Hàm số g(x) = −
nghịch biến trên R (vì a = − < 0) 6 6 6
Ta nhận thấy f (−1) = g(−1) ⇒ x = −1 là nghiệm duy nhất của phương trình (*). 1
Vậy nghiệm phương trình đã cho là x = ; x = −1 2
Lời giải 2. Đưa về phương trình tích Ç 1 å
(2)⇔ 2x2 − 3x + 1 + 6 · 3x · (2x − 1) = 0 ⇔ 2(x − 1) x − + 6 · 3x · (2x − 1) = 0 2  1 x =
⇔ (2x − 1)(x − 1 + 6 · 3x) = 0 ⇔  2   1 x 3x = − (giải như ở trên) 6 6
Bài 50. Giải các phương trình mũ sau (đưa về phương trình tích) a) 25 · 2x − 10x + 5x = 25
b) −8x + 2 · 4x + 2x − 2 = 0
3 · 8x + 4 · 12x − 18x − 2 · 27x c)
d) x2 · 3x−1 + x(3x − 2x) = 2(2x − 3x−1)
e) 52x+1 + 7x+1 − 175x − 35 = 0
f) 8 − x · 2x + 23−x − x = 0 2x + 3x = 1 + 6x g)
h) 4x2−3x+2 + 4x2+6x+5 = 42x2+3x+7 + 1 2.7.3
Bài toán liên quan tham số m
Bài 51. Tìm tham số m để các phương trình sau có nghiệm: a) 9x + 3x + m = 0 b) 9x + m · 3x − 1 = 0 c) 4x − 2x+1 = m
d) 2x + (m + 1) · 2−x + m = 0
e) 25x − 2 · 5x − m − 2 = 0
f) 16x − (m − 1) · 22x + m − 1 = 0
g) 25x + m · 5x + 1 − 2m = 0
h) 34−2x2 − 2 · 32−x2 = 2m − 3 = 0 √ √ √ √
i) 9x+ 1−x2 − 8 · 3x+ 1−x2 + 4 = m
j) 91+ 1−x2 −(m+2)·31+ 1−x2 +2m+1 = 0
Bài 52. Tìm tham số m để các phương trình sau có nghiệm duy nhất.
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 31
Hàm số mũ và hàm số logarit Giải tích 12 a) m · 2x + 2−x − 5 = 0 m · 16x + 2 · 81x = 5 · 36x b) √ √ Ä äx äx 5 + 1 + m · Ä 5 − 1 = 2x c) d) 4x − 2x+3 + 3 = m
Bài 53. Tìm tham số m để các phương trình mũ sau có hai nghiệm phân biệt trái dấu
a) 49x + (m − 1) · 7x + m − 2m2 = 0
b) (m + 1) · 4x + (3m − 2) · 2x+1 − 3m + 1 = 0
c) 9x + 3(m − 1) · 3x − 5m + 2 = 0
d) (m + 3) · 16x + (2m − 1) · 4x + m + 1 = 0
Bài 54. Tìm tham số m để các phương trình:
a) m · 16x + 2 · 81x = 5 · 36x có hai nghiệm dương phân biệt.
b) 16x − m · 8x + (2m − 1) · 4x = m · 2x có ba nghiệm phân biệt
c) 4X2 − 2x2+2 + 6 = m có ba nghiệm phân biệt.
d) 9x2 − 4 · 3x2 + 8 = m có ba nhiệm phân biệt. 2.8 Phương trình logarit 2.8.1
Phương trình logarit cơ bản Với a > 0, a 6= 1: log x = b ⇔ x = ab a 4 !
Chú ý: Khi giải phương trình logarit ta cần đặt điều kiện để phương trình có nghĩa.
Các công thức logarit thường sử dùng Ç b å
CT.1 log b + log c = log (b · c) CT.2 log b − log c = log a a a a a a c   β · log b nếu β lẻ a 1 CT.3 log bβ = CT.4 log · log b a aβ b = β a  β · log |b| nếu β chẳn a 1 log c CT.5 log b = CT.6 log c = a a log a b log b b a 2.8.2
Một số phương pháp giải phương trình logarit 2.8.2.1
Phương pháp đưa về cùng cơ số Với a > 0, a 6= 1:   f (x) > 0 (g(x) > 0) log f (x) = log g(x) ⇔ a a  f (x) = g(x) 2.8.2.2 Phương pháp mũ hóa Với a > 0, a 6= 1:
log f (x) = g(x) ⇔ f (x) = ag(x) a
Ví dụ 40. Giải phương trình: log (2x − 1) = −2 (1) 3 Lời giải. 1
Điều kiện: 2x − 1 > 0 ⇔ x > 2
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 32
Hàm số mũ và hàm số logarit Giải tích 12 1 5
(1)⇔ log (2x − 1) = log 2−2 ⇔ 2x − 1 = ⇔ x = (nhận). 2 2 4 8
Ví dụ 41. Giải phương trình: log (9 − 2x) = 3 − x (2) 2 Lời giải.
Điều kiện: 9 − 2x > 0 ⇔ 2x < 9 (*) 8
(1)⇔ log (9 − 2x) = log 23−x ⇔ 9 − 2x = 23−x ⇔ 2x + − 9 = 0 (**) 2 2 2x  8 t = 1
Đặt 2x = t > 0, phương trình (**) trở thành t +
− 9 = 0 ⇔ t2 − 9t + 8 = 0 ⇔  t t = 8
• Với t = 1 ⇒ 2x = 1 ⇔ x = 0 thay vào điều kiện (*) thỏa.
• Với t = 8 ⇒ 2x = 8 ⇔ x = 3 thay vào điều kiện (*) thỏa.
Nghiệm phương trình đã cho là x = 0; x = 3 2.8.2.3
Phương pháp đặt ẩn phụ
Đặt điều kiện cho phương trình:
Biến đổi phương trình đã cho về dạng:
[α · log f (x)]2 + β · log f (x) + c = 0 (∗) a a ! Đặt log f(x) = t a
Phương trình (*) trở thành: α · t2 + β · t + c = 0 (**)
Giải phương trình (**), tìm được nghiệm t ⇒ nghiệm x.
Ví dụ 42. Giải phương trình: log2 x − 4 · log x + 3 = 0 (3) 2 2 Lời giải. Điều kiện: x > 0  t = 1
Đặt log x = t, phương trình (3) trở thành t2 − 4t + 3 = 0 ⇔ 2  t = 3
• Với t = 1 ⇒ log x = 1 ⇔ x = 2 2
• Với t = 3 ⇒ log x = 3 ⇔ x = 8 2
Nghiệm phương trình đã cho là x = 2; x = 8
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 33
Hàm số mũ và hàm số logarit Giải tích 12 2.8.2.4
Sử dụng tính đơn diệu hàm số Phương trình: f (x) = g(x) (1)
y = f (x) đồng biến (hoặc nghịch biến) trên tập xác định D.
y = g(x) nghịch biến (hoặc đồng biến) trên tập xác định D.
! f(x0) = g(x0) ⇒ x = x0 là nghiệm duy nhất của (1) trên D. Lưu ý: 
 đồng biến khi: a > 1 a) Hàm số y = log x : a
 nghịch biến khi: 0 < a < 1 
 đồng biến khi: a > 0 b) Hàm số y = ax + b :
 nghịch biến khi: a < 0
Ví dụ 43. Giải phương trình: log 1 x = x − 4 (4) 3 Lời giải. Điều kiện: x > 0. 1
Đặt f (x) = log 1 x nghịch biến trên (0; +∞) vì a = < 0. 3 3
g(x) = x − 4 đồng biến trên (0; +∞) vì a = 1 > 0
Ta có f (3) = g(3) ⇒ x = 3 là nghiệm duy nhất của phương trình (4).
Bài 55. Giải các phương trình logarit (đưa về cùng cơ số hoặc mũ hóa)
a) log (x + 2) − log (x − 2) = 2 2 2
b) log(x2 + 2x − 3) + log(x + 3) = log(x − 1)
c) 2 · log (3x − 11) + log (x − 27) = 3 + log 8 25 5 5 d) log x3 + log x + log √ x = 7 5 0,2 3 25 e) log x + log (x − 1) = 1 2 2 x − 5 f) log + log (x2 − 25) = 7 2 x + 5 2
g) log (log x) + log (log x) = 2 4 2 2 4 h) log (3x+1 − 26) = 2 − x 3 √ i) log (x + 3) − log x − 1 = 2 − log 8 4 2 4 Å x ã2 j) log − log (4x)4 + 10 = 0 4 4 2
k) 2 · log (x − 2) + log (x − 4)2 = 0 3 3
3 · log1(x + 2)2 − 3 = log1(4 − x)3 + log1(x + 6)3 l) 2 4 4 4
m) log |x − 2| + log |x + 5| + log 8 = 0 2 2 1 2 1 √ · 2 2 n)
log (3x − 4)6 · log x3 = 8 · (log x) + [log (3x − 4)2] 3 2 2 2 2
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 34
Hàm số mũ và hàm số logarit Giải tích 12 Bài 56. a) log (9 − 2x) = 3 − x Đáp số: x = 0; x = 3 2
b) log 1 (x − 1) + log 1 (x + 1) − log 1 (7 − x) = 1 Đáp số: x = 3 √ 2 2 2 3 √ c)
log 1 (x + 2)3 − 3 = log 1 (4 − x)3 + log 1 (x + 6)3 Đáp số: x = 2; x = 1 − 33 2 4 4 4 √ 3 ± 17
d) log (x + 2) + log (x − 5)2 + log 8 = 0 Đáp số: x = 6; x = 2 4 1 2 2 √ 3 ± 17
e) log |x − 2| + log |x + 5| + log 8 = 0
Đáp số: x = −3; x = 6; x = 2 2 1 2 2 1 1 √ 5 f) log (x − 1) + = + log x + 2 Đáp số: x = 4 log 4 2 2 2 2x+1 g) log (x2 − 2x + 65) = 2 Đáp số: x = −5 5−x
Bài 57. Giải các phương trình logarit sau (đưa về cùng cơ số) a) log [x(x − 1)] = 1 b) log x + log (x + 1) = 1 2 2 2 c) ln x + ln(x + 1) = 0
d) log [7 + 2 log (x − 2)] = 2 3 3 √ e) log x + log x = log 3
f) log (x2 + 1) + log 5 = log (x + 2) − 5 25 0,2 5 1 5 5 2 log 1 (x − 2) 25 1 g) log(x + 6) − log(2x − 3) = 2 − log 25
h) log x = log (x + 6) − log (x + 2) 2 5 5 5 √ i) log (x − 2) − 6 · log 3x − 5 = 2
j) log (x − 3) + log (x − 1) = 3 2 1 2 2 8
k) log (x + 3) − log (x − 1) = 2 − log 8
l) log(x − 2) + log(x − 3) = 1 − log 5 4 4 4 2 √ √
m) 2 log (x − 2) − log (x − 3) = n) log 5x − 4 + log x + 1 = 2 + log 0, 18 8 8 3 1
o) log (x2 − 6) = log (x − 2) + 1
p) log (x + 3) + log (x − 1) = 3 3 2 2 log 2 5 q) log x + log (10 − x) = 2
r) log (x − 1) + log (x + 2) = 0 4 4 5 1 5
s) log (x − 1) + log (x + 3) = log 10 − 1
t) log (x + 8) − log (x + 26) + 2 = 0 2 2 2 9 3
Bài 58. Giải các phương trình logarit sau (đưa về cùng cơ số) √ √ Ä ä Ä ä a) 2 log x2 + 1 + x + log x2 + 1 − x = 3 2 0,5 b) log (x2 + 3) + log 5 = 2 log (x − 1) − log (x + 1) 2 0,5 0,25 2
c) log x + log√ x + log x = 6 3 3 1 3
d) 1 + log(x2 − 2x + 1) − log(x2 + 1) = 2 log(1 − x) e) log x + log x + log x = 5 4 1 8 16
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 35
Hàm số mũ và hàm số logarit Giải tích 12
f) 2 + log(4x2 − 4x + 1) − log(x2 + 19) = 2 log(1 − 2x) g) log x + log x + log x = 11 2 4 8
h) log 1 (x − 1) + log 1 (x + 1) = 1 + log 1 (7 − x) √ 2 2 2 i) log log x = log log x 2 2 3 3 j) log log x = log log x 2 3 3 2
k) log log x + log log x = log log x 2 3 3 2 3 3
l) log log log x = log log log x 2 3 4 4 3 2 m) log x + log x + log x = log 2 3 4 20x
n) log x + log x + log x = log x · log x · log x 2 3 5 2 3 5
Bài 59. Giải các phương trình logarit sau (đưa về cùng cơ số) 3 x3 1 √ a) (log x) · log − log √ = + log x 2 3 x 3 2 3 2 Å x ã … x b) log 1 1 − + log 2 − = 0 2 2 2 4 ñ x + 3 ô c) log(x2 + 2x − 3) + log = 0 x − 1 √ √ √ Ä ä Ä ä Ä ä d) log x − x2 − 1 · log x + x2 − 1 = log x − x2 − 1 2 3 6 2 log (4 − x) e) log 6 + 0,25 = 1 (x+3) log (x + 3) 2 ï cos x ò f) log |tan x| + log = 0 2 4 2 cos x + sin x
g) log(2x + 1) + log(3 − x) = 2 log x 1
h) log {2 log [1 + log (1 + 3 log x)]} = 4 3 2 2 2
i) ln(x + 1) + ln(x + 3) = ln(x + 7)
Bài 60. Giải các phương trình logarit sau (đưa về cùng cơ số) a) log (9 − 2x) = 3 − x b) log (3x − 8) = 2 − x 2 3 c) log (6 + 7−x) = 1 + x
d) log (4 · 3x−1 − 1) = 2x − 1 7 3 log (9 − 2x) = 5log5(3−x) e)
f) log (3 · 2x − 1) = 2x + 1 2 2 g) log (12 − 2x) = 5 − x h) log (26 − 3x) = 2 2 5 i) log (5x+1 − 25x) = 2 j) log (3 · 2x+1 − 5) = x 2 4 k) log 1 (5x+1 − 25x) = −2 l) log (6x+1 − 36x) = 2 √ 1 √ 6 5
Bài 61. Giải các phương trình logarit (đưa về cùng cơ số)
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 36
Hàm số mũ và hàm số logarit Giải tích 12 a) log (x2 − 2x + 65) = 2 b) log (x2 − 4x + 5) = 1 5−x x−1 c) log (5x2 − 8x + 3) = 2 d) log (2x3 + 2x2 − 3x + 1) = 3 x x+1 e) log (x − 1) = 2 f) log (x + 2) = 2 x−3 x g) log (x2 − 5x + 6) = 2 h) log (x2 − x) = 1 2x x+3 i) log (2x2 − 7x + 12) = 2 j) log (2x2 − 3x − 4) = 2 x x k) log (x2 − 2) = 1 l) log (9x2 + 8x + 2) = 2 x 3x+5 15 m) log (x2 + 1) = 1 n) log = −2 2x+4 x 1 − 2x o) log p) log (x + 3) = 1 x2 (3 − 2x) = 1 x2+3x q) log (2x2 − 5x + 4) = 2 r) log 64 = 3 x x2 16 + logx
Bài 62. Giải các phương trình logarit (đặt ẩn phụ, dạng đặt ẩn phụ hoàn toàn) √ a) log (3x+1 − 26) = 2 − x b) log (x + 3) − log x − 1 = 2 − log 8 3 4 2 4 Å x ã2 c) log − log (4x)4 + 10 = 0
d) 2 · log (x − 2) + log (x − 4)2 = 0 4 4 2 3 3
e) − log3 x + 2 log2 x = 2 − log x f) log2 x − 4 log x + 3 = 0 2 2 » »
g) log (27x) − 3 log x − 1 = 0 h) log2 + log2 x + 1 − 5 = 0 3 3 3 3 7
i) log2√ x + 3 log x + log 1 x = 2 j) log 2 − log x + = 0 2 2 x 4 2 6 x2 k) log21 4x + log = 8 l) log2√ x + 3 log x + log x 2 1 2 2 2 8 2 1 m) log 64 = 3 n) log x − log = 2 x2 16 + log2x 5 x 5 1 √ 1 o) log x − log = 2 p) 2 log x − 2 = log 7 x 7 5 x 5 » » q) 2 log x − log 4x = 0
r) 3 log x − log 3x − 1 = 0 2 2 3 3 √ 4 √ 2 » » s) log 3 x + 3 log x = t) log 3 x − 3 log x = − 2 2 3 2 2 3 1 u) log2 x + 2 log = 0
v) log2(2 − x) − 8 log (2 − x) = 5 2 4 1 x 2 4 √ 9 √ w) log2 x + 4 log 5x − 5 = 0 x) log 5 + log 5x = + log2 5 5 25 x x 4 x y) log x = 1
z) log (3x − 1) · log (3x+1 − 3) = 6 x2 3 + log9 3 3
Bài 63. Giải các phương trình logarit (đặt ẩn phụ, dạng đặt ẩn phụ hoàn toàn)
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 37
Hàm số mũ và hàm số logarit Giải tích 12
a) log√ (x − 2) · log x = 2 log (x − 2)
b) log (2x + 1) · log (2x+1 + 2) = 2 3 5 3 2 2 √ » c) log 5x = − log 5 d) log 4 · log 2 = 4 x x sin x cos2 x 1 2 e) log 4 · log 2 = 1 f) + = 1 cos x cos2 x 4 − log x 2 + log x 1 3 1 2 g) + = 1 h) + = 1 5 − log x 3 + log x 4 + log x 2 − log x 2 2 i) 4 log2 x + 2 log x2 + 1 = 0
j) log3 10 + log2 10 − 6 log 10 = 0 4 4 x x x √ √ k) log 5 5 − 1, 25 = log2 5
l) log (5x − 1) · log2(5x − 1) = 1 x x 2 4 m) log (2x)2 · log2 2 = 1 n) log (3x + 3) − 4 log 2 = 0 2 x 2 3x+3 o) log 2 2 + log 4x = 3 p) log 3 · log 3 + log 3 = 0 2 x x x x 3 81 √ q) log x2 − 14 log x3 + 40 log x = 0 r) log |x + 1| − log 64 = 1 2x 16x 4x 2 x+1 2 log x 2 s) = − log x +
t) log 1 x − 2 + 3 = log 1 x + 1 log x − 1 log x − 1 3 3
Bài 64. Giải các phương trình logarit (đặt ẩn phụ, dạng đặt ẩn phụ không hoàn toàn)
a) log2(x + 1) + (x − 5) log (x + 1) = 16 5 5
b) log2 x + (x − 12) log x + 11 = 0 3 3
c) log2 x − log x · log 4x + 2 log x = 0 2 2
6 · 9log2 x + 6 · x2 = 13 · xlog2 6 d)
e) x · log2 x − 2(x + 1) log x + 4 = 0 2 2
f) log2 x + (x − 1) log x = 6 − 2x 2 2
g) (x + 2) log2(x + 1) + 4(x + 1) log (x + 1) = 16 3 3
h) (x + 3) log2(x + 2) + 4(x + 2) log (x + 2) = 16 3 3 i) log x = 2 x2 (2 + x) + log√2−x
j) log2(x + 1) + (x − 5) log (x + 1) = 2x − 6 3 3
k) log2 x + (x − 1) log x = 6 − 2x 2 2 √ » l) 4 log x − 1 − log x = 4 3 3
Bài 65. Giải các phương trình logarit (sử dụng công thức biến đổi, đặt ẩn phụ)
a) 4log9 x − 6 · 2log9 x + 2log3 27 = 0
b) 4log3 x − 5 · 2log3 x + 2log3 9 = 0 c) 2log2 x+1 x+1 2 = x2 log3 x − 48 2log22 + 224 = x2 log2 x d) √ e) log x + log ( x + 2)
f) log (x − 3) + log (x − 2) = 2 7 3 2 3 Ä
g) log (x + 1) + log (2x + 1) = 2 h) log x + 3log6 xä = log x 3 5 2 6 √ i) 4log7(x+3) = x j) log (1 + x) = log x 2 3 √ √
xlog2 9 = x2 · 3log2 x − xlog2 3 k) 3 l) 2 − log x = 1 − log x − 1 » » » 3 m) 1 − log x + 3 1 + log x = 1 n) log3 +2 = 3 3 3 log x − 2 3 3 2 3 » o) log2 x + log x + 1 = 1
p) 6x = 3 log (5x + 1) + 2x + 1 2 2 6
q) 7x−1 = 6 · log (6x − 5) + 1 52(log5 2+x) − 2 = 5log5 2+x r) 7
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 38
Hàm số mũ và hàm số logarit Giải tích 12
Bài 66. Giải phương trình logarit (sử dụng tính đơn điệu của hàm số) a) log (3x − 1) = −x + 1 b) log x = x − 4 2 1 3 c) x + log x = 4 d) 2x + log x = 5 3 1 2 e) log x = −x + 11 f) 2log5(x+3) = x 3 √ g) 3log2(x−3) = x h) log (1 + x) = log x 2 3 1 − x i) 2x − 21−x = log
j) x + xlog2 3 = xlog2 5 (x > 0) 2 x x2 + 3log2 x = 5log2 x k) l) log (x + 3) = 3 − x 5 m) log (3 − x) = x n) log (x + 3) = 3 − x 2 5 √ √ √ o) x + 2 · 3log2 x = 3 p) 2 log ( 4 x + 8 x) = log x 6 4 √ √ 1 q) log ( 4 x + x) = log x 2 4 3 2.8.3
Bài toán liên quan tham số m
Bài 67. Bài toán liên quan đến tìm tham số.
a) Tìm tham số m để phương trình: log (4x − m) = x + 1 có hai nghiệm phân biệt. 2
b) Tìm tham số m để phương trình: log (9x + 9m3) = 2 có hai nghiệm phân biệt. 3
c) Tìm tham số m để phương trình: log2 x − (m + 2) · log x + 3m − 1 = 0 có hai nghiệm 3 3
phân biệt x1, x2 thỏa x1 · x2 = 27
Bài 68. Tìm tham số m để phương trình:
2 log (2x2 − x + 2m − 4m2) = log (x2 + mx − 2m2) có hai nghiệm phân biệt x 4 2 1, x2 thỏa: x2 + x2 > 1. 1 2 »
Bài 69. Cho phương trình: log2 x + log2 x + 1 − 2m − 1 = 0 3 3
a) Giải phương trình khi: m = 2 √ h
Tìm m để phương trình có ít nhất một nghiệm trên 1; 3 3i b) B. BẤT PHƯƠNG TRÌNH 2.9
Bất phương trình mũ và bất phương trình logarit 2.9.1 Bất phương trình mũ
Khi giải bất phương trình mũ, ta cần chú ý đến tính đơn điệu của hàm số mũ.    a > 1    f (x) > g(x) af(x) > ag(x) ⇔     0 < a < 1     f (x) < g(x)
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 39
Hàm số mũ và hàm số logarit Giải tích 12
Trong trường hợp cơ số a có chứa ẩn số thì:
aM > aN ⇔ (a − 1) · (M − N ) > 0
Ta cũng thường sử dụng các phương pháp giải tương tự như đối với phương trình mũ: • Đưa về cùng cơ số. • Đặt ẩn phụ.
• Sử dụng tính đơn điệu: 
 y = f (x) đồng biến trên D thì: f (u) < f (v) ⇒ u < v
 y = f (x) nghịch biến trên D thì: f (u) < f (v) ⇒ u > v 2.9.2 Bất phương trình logarit
Khi giải bất phương trình logarit, ta cần chú ý đến tính đơn điệu của hàm số logarit.    a > 1    f (x) > g(x) > 0
log f (x) > log g(x) ⇔  a a    0 < a < 1     0 < f (x) < g(x)
Trong trường hợp cơ số a có chứa ẩn số thì:
• log B > 0 ⇔ (a − 1)(B − 1) > 0 a log A • a
> 0 ⇔ (A − 1)(B − 1) > 0 log B a
Ta cũng thường sử dụng các phương pháp giải tương tự như đối với phương trình logarit: • Đưa về cùng cơ số. • Đặt ẩn phụ.
• Tính đơn điệu của hàm số. 2.10
Hệ phương trình mũ và logarit
Hệ phương trình mũ và logarit
Khi giải hệ phương trình mũ và logarit, ta cũng dùng các phương pháp giải hệ phương trình đã học như: Phương pháp thế.
Phương pháp cộng đại số.
Phương pháp đặt ẩn phụ.
Phương pháp dùng tính đơn điệu của hàm số.
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 40
Hàm số mũ và hàm số logarit Giải tích 12 2.11 Các ví dụ
Giải các bất phương trình và hệ phương trình sau Ç 1 å9x2−17x+11 Ç 1 å7−5x
Ví dụ 44. Giải bất phương trình: ≥ (1) 2 2 Lời giải. 2
(1)⇔ 9x2 − 17x + 11 ≤ 7 − 5x ⇔ 9x2 − 12x + 4 ≤ 0 ⇔ x = 3 Ç 1 åx 2x
Ví dụ 45. Giải bất phương trình: > 3 x+1 (2) 9 Lời giải. Điều kiện: x 6= −1 Ç å 2x 2x 2x 1
(2) ⇔ 3−2x > 3 x+1 ⇔ −2x > ⇔ + 2x < 0 ⇔ 2x + 1 < 0 x + 1 x + 1 x + 1   2x(x + 2) x < −2 x < −2 ⇔ < 0 ⇔ 
. Kết hợp điều kiện ⇒  x + 1 − 1 < x < 0 − 1 < x < 0
Nghiệm của bất phương trình (2) là ∀x ∈ (−∞; −2) ∪ (−1; 0)
Ví dụ 46. Giải bất phương trình: 3x+1 + 5x+2 ≥ 3x+2 + 5x+1 (3) Lời giải. Ç 5 åx 3 3
(3)⇔ 25 · 5x − 5 · 5x > 9 · 3x − 3 · 3x ⇔ 20 · 5x > 6 · 3x ⇔ > ⇔ x > log 5 3 10 3 10 Ç 3 å
Nghiệm của bất phương trình (2) là ∀x ∈ log 5 ; +∞ 3 10 Ç 1 å2x2+x+1 Ç 1 å1−x
Ví dụ 47. Giải bất phương trình: x2 + ≤ x2 + (4) 2 2 Lời giải. ñÇ 1 åô Ç 1 å (4)⇔ x2 + − 1
· [(2x2 + x + 1) − (1 − x)] ≤ 0 ⇔ x2 − · (2x2 + 2x) ≤ 0 (∗) 2 2
Bảng xét dấu vế trái của (*) 1 1 x −∞ −2 − √ 0 √ +∞ 2 2 VT + 0 − 0 + 0 − 0 +
Từ bảng xét dấu ta có nghiệm của bất phương trình: ñ 1 ô ñ 1 å
∀x ∈ (−∞; −2] ∪ − √ ; 0 ∪ √ ; +∞ 2 2 x2 − 3x + 2
Ví dụ 48. Giải bất phương trình: log 1 ≥ 0 (1) 2 x Lời giải.  x2 − 3x + 2 0 < x < 1 Điều kiện: > 0 ⇔  x x > 2
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 41
Hàm số mũ và hàm số logarit Giải tích 12 √  x2 − 3x + 2 x2 − 4x + 2 2 − 2 ≤ x < 1 (1)⇔ ≤ 1 ⇔ ≤ 0 ⇔ √  x x 2 < x ≤ 2 + 2 √ √ ä ó
Kết hợp với điều kiện, nghiệm của bất phương trình là x ∈ î2 − 2; 1 ∪ Ä2; 2 + 2 Ç x2 + x å
Ví dụ 49. Giải bất phương trình: log log (2) 0,7 6 x + 4 Lời giải.  x2 + x  x2 + x    > 0  > 0    x + 4  x + 4 x2 + x x2 − 4 Điều kiện: ⇔ ⇔ > 1 ⇔ > 0 x + 4 x + 4  x2 + x  x2 + x    log > 0  > 1  6 x + 4  x + 4  − 4 < x < 2 ⇔  x > 2  x2 + x x2 + x x2 − 5x − 24 − 4 < x < −3 (2)⇔ log > 1 ⇔ > 6 ⇔ > 0 ⇔ 6  x + 4 x + 4 x + 4 x > 8
Kết hợp với điều kiện, nghiệm của bất phương trình là: x ∈ (−4; −3) ∪ (8; +∞)   2x + 2y = 12 (1)
Ví dụ 50. Giải hệ phương trình:  x + y = 5 (2) Lời giải. 32
Từ (2)⇒ y = 5 − x thay vào phương trình (1) ta được: 2x + 25−x = 12 ⇔ 2x + = 12 (∗) 2x  32 t = 4
Đặt 2x = t > 0, phương trình (*) trở thành t +
= 12 ⇔ t2 − 12t + 32 = 0  t t = 8
• Với t = 4 ⇒ 2x = 4 ⇔ x = 2 ⇒ y = 3
• Với t = 8 ⇒ 2x = 8 ⇔ x = 3 ⇒ y = 2
Nghiệm hệ phương trình là: (x; y) = (2; 3), (3; 2) √   x + y = 2 3 (1)
Ví dụ 51. Giải hệ phương trình:  log (xy) = 1 (2) 3 Lời giải. Điều kiện: x · y > 0
Từ phương trình (2) ⇒ xy = 3. √   x + y = 2 3 Ta có
. Khi đó x, y là nghiệm của phương trình:  xy = 3 √ √ X2 − 2 3X + 3 = 0 ⇔ x = 3 = y √ √
Vậy nghiệm hệ phương trình là (x; y) = ( 3; 3)
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 42
Hàm số mũ và hàm số logarit Giải tích 12 2.12
Bài tập bất phương trình, hệ phương trình mũ và logarit 2.12.1
Giải các bất phương trình
Bài 70. Giải các bất phương trình mũ (đưa về cùng cơ số) Ç 1 å2x−x2 a) 9x2−2x − 2 · ≤ 3 2x + 4 · 5x − 4 < 10x b) 3 1 1 √ √ c) > d) 2 x − 21− x < 1 3x − 1 1 − 3x−1 √ √ √ √ √ √ 4
e) 9 x2−2x−x − 7 · 3 x2−2x−x−1 ≤ 2 f) 2 · 3 x+ 4 x + 9 x+ 1 x 2 ≥ 9 √ √
g) 32x − 8 · 3x+ x+4 − 9 · 9 x+4 > 0 52x−1 < 73−x h) √ √ i) 3 x+4 + 2 2x+4 > 13
j) 3 · 2x + 7 · 5x > 49 · 10x − 2 32−x + 3 − 2x k) ≥ 0 4x − 2 Bài 71. a) 23−6x > 1 b) 16x > 0, 125 √ Ç 1 å x+2
c) (0, 3)2x2−3x+6 < 0, 00243 > 3−x d) 3 √
(0, 1)4x2−2x−2 ≤ (0, 1)2x+3 e) x+1 f) 3 > 9 √ g) 8 8x > 4096 2x2−3x−4 < 3x2−3x−4 h) 6x−5 Ç 1 å4x2−15x+13 Ç 1 å4−3x Ç 2 å 2+5x 25 i) < j) < 2 2 5 4 √ √ Ç 1 åx−|x−1| Ç 1 å x6−2x3+1 Ç 1 å1−x k) 3 x2−2x ≥ l) < 3 2 2
m) 5x − 3x+1 ≥ 2 (5x−1 − 3x−2)
7x − 5x+2 < 2 · 7x−1 − 118 · 5x−1 n) √ √ √
2x+2 − 2x+3 − 2x+4 > 5x+1 − 5x+2 o)
p) 3 x + 3 x−1 − 3 x−2 ≤ 11
q) 9x2−3x+2 − 6x2−3x+2 < 0 62x+3 ≤ 2x+7 · 33x−1 r) 2x+2 + 5x+1 ≤ 2x + 5x+2 s) t) 2x−1 · 3x+2 > 36 √ x−3 √ x+1 √ √ x Ä ä Ä ä Ä äx+1 ä 10 + 3 x−1 < 10 − 3 x+3 u) 2 + 1 ≥ Ä 2 − 1 x−1 v) 1 1 1 √ ≤ 2x−1 w) 2 |2x−1| ≥ 2 3x+1 x) 2 x2−2x x2+2 (0, 4)x2−1 > (0, 6)x2+6 y) z) (0, 2) x2−1 > 25
Bài 72. Giải các bất phương trình mũ (đặt ẩn phụ)
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 43
Hàm số mũ và hàm số logarit Giải tích 12 √ √ √
a) 3 x + 3 x−1 + 3 x−2 < 11 b) 2x + 2−x − 3 < 0 √ √ √
c) 4−x+0,5 − 7 · 2−x − 4 < 0 52 x + 5 < 5 x−1 + 5 x d) 2x−1 − 1 1 1 e) < 2 f) < 2x+1 + 1 3x + 5 3x+1 − 1 1 1
g) 2 · 14x + 3 · 49x − 4x ≥ 0 h) 4 −1 −2 x − 2 x − 3 ≤ 0 √ √ √ √ 2
i) 4x − 22(x−1) + 8 (x−2) x+ 4 x x x 3 > 52 j) 8 · 3 + 91+ 4 > 9
k) 25 · 2x − 10x + 5x > 25
52x+1 + 6x+1 > 30 + 5x · 30x l)
m) 6x − 2 · 2x − 3 · 2x + 6 ≥ 0 27x + 12x > 2 · 8x n) 1 1 1 x 49 x − 35 x ≥ 25 x o)
p) 3x+1 − 22x+1 − 12 2 < 0 √ √
252x−x2+1 + 92x−x2+1 ≥ 34 · 252x−x2 q)
r) 32x − 8 · 3x+ x+4 − 9 · 9 x+4 > 0 √ √ 1
s) 4x+ x−1 − 5 · 2x+ x−1+1 + 16 ≥ 0 t) 2 +1 x + 22− 1x < 9 2 1 Ç 1 å +1 X Ç 1 å x Ç 1 å3x Ç 1 åx−1 u) + 3 · > 12 v) − − 128 ≥ 0 3 3 4 8 √ 21−x − 2x + 1 w) (22x+1 − 9 · 2x) · x2 + 2x − 3 ≥ 0 x) ≤ 0 2x − 1 11 · 3x−1 − 31 4 − 7 · 5x 2 y) ≥ 5 z) ≤ 4 · 9x − 11 · 3x−1 − 5 52x+1 − 12 · 5x + 4 3
Bài 73. Giải các bất phương trình mũ (sử dụng tính đơn điệu) x 21−x − 2x + 1 a) 2x < 3 2 + 1 b) ≤ 0 2x − 1 2 · 3x − 2x+2 √ √ c) ≤ 1 d) 3 x+4 + 2 2x+4 > 13 3x − 2x 32−x + 3 − 2x 3x + x − 4 e) ≥ 0 f) > 0 4x − 2 x2 − x − 6
Bài 74. Giải các bất phương trình logarit (đưa về cùng cơ số)
a) 2 · log (4x − 3) + log (2x + 3) ≤ 2
b) log (4x + 144) − 4 · log 2 < 1 + 3 1 5 5 3 log (2x−2 + 1) 5 Ç å h i x2 + x
c) log 8 log 1 (x2 − x − 6) ≥ 0 d) log log < 0 0,5 6 3 2 x + 4 î Ä äó
e) log 1 [log (x2 − 5)] > 0 f) log log log 9 > 0 4 1 2 x−1 3 2
g) log (1 − 2x) ≥ log (5x − 2)
h) log (1 − x) < log (x + 3) 3 3 5 5 √
i) log (1 − 2x) < 1 + log√ (x + 1) j) log 5 − x < log (3 − x) 5 5 1 1 3 3 k) log log x > 0
l) log (3x + 4) > log (5 − x) 2 1 2 2 3 Ç 1 + 2x å x + 7 m) log 1 log > 0 n) log < log (5 − x) 2 0,4 0,4 3 1 + x 2x + 3
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 44
Hàm số mũ và hàm số logarit Giải tích 12
o) log 1 [log (x2 − 5)] > 0
p) log (2 − x) ≤ log (3x + 6) 4 7 7 3
q) log 1 (x + 4) < log 1 (x2 + 2x + 2) r) (x2 − 4) log 1 x > 0 3 3 2 s) 6log2 x 6 + xlog6 x ≤ 12
t) log (x + 3) ≥ 1 + log (x − 1) 2 2 u) 2log2 x 2 + xlog2 x < 0 v) log log ≥ 0 3 1 2 2 2x − 3
w) 2 log (x − 2) + log (x − 3) > x) log ≥ 0 8 1 2 8 3 3 x + 1
Bài 75. Giải các bất phương trình logarit (đặt ẩn phụ) a) log x + 2 log 4 − 3 ≤ 0
b) log (1 − 2x) < 1 + log√ (x + 1) 2 x 5 5 c) 2 log x − log 125 < 1 d) log 64 + log 5 x 2x x2 16 ≥ 3 e) log 2 · log 2 · log 4x > 1 f) log2 x + log x2 < 0 x 2x 2 1 1 2 2 q
g) log21 x − 6 log x + 8 ≤ 0 h)
1 − 9 log2 x > 1 − 4 log x 2 1 1 2 8 8 1 1 + log2 x i) log 100 − log x > 0 3 j) > 1 x 2 100 1 + log x 3
Bài 76. Giải các bất phương trình logarit (đặt ẩn phụ) 2 log x log x a) + 4 > 2 1 − log x 1 + log x 2 2 1 − log2 x 2 1 2 b) + ≤ 1 4 + log x 2 − log x 2 2 » c)
log2 x − 4 log x + 9 ≥ 2 log x − 3 3 3 3 1 2 d) + < 1 5 − log x 1 + log x 5 5 » e)
log (3x2 + 4x + 2) + 1 ≥ log (3x2 + 4x + 2) 9 3
f) 6 log |1 − x| + log2(x − 1) + 5 ≥ 0 3 3 √ Ä ä g) log2 x > log x · log 2x + 1 − 1 9 3 3
Bài 77. Giải các bất phương trình logarit (sử dụng tính đơn điệu của hàm số) 5 + x log 3 2 5 − x a) > b) < 0 log (x + 1) log (x + 1) 2x − 3x + 1 2 3 √ c) log x < log ( x + 2)
d) 2−|x−2| · log (4x − x2 − 2) ≥ 1 7 3 2
Bài 78. Giải các bất phương trình logarit (sử dụng tính đơn điệu của hàm số)
a) (x + 1) log2 x + (2x + 5) log x + 6 ≥ 0 0,5 0,5
b) log (2x + 1) + log (4x + 2) ≤ 2 2 3
c) (x + 1) log21 x + 2(x + 3) log 1 x + 8 ≤ 8 3 3
d) (4 · 3x + 3−x)3 log3(x−1)−log3(x−1)(2x+1) > 1
log (x2 − 4x − 11)2 − log (x2 − 4x − 11)3 5 11 e) ≥ 0 2 − 5x − 3x2 √ Ä ä f) log
x2 − 5x + 5 + 1 + log (x2 − 5x + 7) ≤ 2 2 3
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 45
Hàm số mũ và hàm số logarit Giải tích 12
Bài 79. Giải các bất phương trình logarit
a) x2 · log 27 · log 9 > x + 4 b) log log (x2 − 4x + 3) ≥ 0 x x 3 9 16 √x − 5 log (x + 1)2 − log (x + 2)3 c) 2 3 d) > 0 log√ (x − 4) − 1 x2 − 3x − 4 2 Ç 1 ålog2 x 1 1 1 2 ≤ x3 e) f) √ > 2 log 1 2x2 − 3x + 1 log 1 (x + 1) 3 3 Ç 4 å log x + log√ (x − 3)2 3 2 5 g) ≥ 0 h) x2 − 4x − 5 Ç 7 å log x2 − 2x + 7 16 1 1 √ Ä ä i) + √ > 0 j) log√ 3 sin 2x − cos 2x ≤ 1 log 3 1 (2x − 1) log x2 − 3x + 2 2 2
Bài 80. Giải các bất phương trình logarit
log (x2 − 4x + 11)2 − log (x2 − 4x + 11) 5 11 a) √ ≥ 0 2 − 5x − 3x2
log (x2 − 2x − 7) − log (x2 − 2x − 7)8 2 3 b) ≤ 0 3x2 − 13x + 4 √ 27 Ä ä c) log 1 9x − x2 + 3 > log √ √ − 3 3 3 9x − x2 + 5 − x2 √ 2 Ä ä d) log x2 − 4x + 3 > log √ √ + 1 2 1 2 x2 − 4x + x + 1 + 1 2.12.2 Giải hệ phương trình
Bài 81. Giải các hệ phương trình mũ sau     2x · 5y = 20  2x · 3y = 12  xy2−7y+10 = 1 a) b) c) , (x > 0)  5x · 2y = 50  3x · 2y = 18  x + y = 8  1   1    4−2x + 42y =  2y + 200 · 5y  3x · 2y = d) 2 e) f) 9   x + y = 1   x + y = 1  y − x = 2     3x − 2y2 = 77 64x + 642y = 12  27x = 9x   g) h) i) √ x y2  81x = 243 · 3y   64x+y = 4 2  3 2 − 2 2 = 7  11    3 · 2x + 2 · 3y =   3x + 3y = 28  x + 2y+1 = 3  j) k) 4 l) 3  3x+y = 27  4x + 4y = 32    2x − 3y = − 4     x + 3y−1 = 2  y2 = 4x + 2  4(x−y)2−1 = 1 m) n) o)  3x + 9y = 18  2x+2 + y + 1 = 0  53x−2y−3 = 125
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 46
Hàm số mũ và hàm số logarit Giải tích 12    32x − 2y = 77  xx+y = 128   xx2−y2−16 = 1 p) q) r) , (x > 0) y  53x−2y−3 = 1  3x − 2 2 = 7  x − y = 2     4x − 3y = 7  2x + 3y = 17  2x + 2 · 3x+y = 56 s) t) u)  4x · 3x = 144  3 · 2x − 2 · 3y = 6  3 · 2x + 3x+y+1 = 87 √    3 x+1 − 2y = −4  32x+2 + 22y+2 = 17   7x − 16x = 0 v) w) √ x) x+1  2 · 3x+1 + 3 · 2y = 8  3 − 2y+1 = −1  4x − 49x = 0    3 · 2x + 2 · 3y = 2, 75  8x = 10y y) z)  2x − 3y = −0, 75  2x = 5y
Bài 82. Giải các hệ phương trình logarit sau:    xy = 64  log x − log y2 = 1 y 2 a) b)  log y = 5 log x − log y = 1 x  4 4    xlog2 y + ylog2 x = 16  log (x2 + y2 + 6) = 4 2 c) d)  log x − log y = 2 log + log y = 1 2 2  x 3  
 xlog3 y + 2 · ylog3 y = 27  3 · xlog2 y = 10 e) f)  log y − log x = 1 log x2 + log y = 2 3 3  4 2   log (xy) = 4  2  log (2x + y − 2) = 2 x  g) h) x log = 2  log (2y + x − 2) = 2 y   2 y  5    log x + log y = log2 x = log2 y + log2(xy) y x  i) 2 j) 
 log2(x − y) + log x · log y = 0  log (x2 + y2) = 1 6  y   log − log2 x = 1  xy  log (x − y) = 1 xy k) x y l)   log (x + y) = 0  log (y − x) = 1 2 xy   √  log x + log y = 2 y + log x2 = 2 y x  m) n)  x2 + y = 12  y + 4 log x = 28  √   y + 2 log x = 3
 log(x + y) − log(x − y) = 1 o) p)  y − 3 log x2 = 1  x2 + y = 12    3x · 2y = 972  3x2+y2 = 81 q) r)  log√ (x − y) = 2 log x + 2 log y = 1 3  2 4   √ Ç åx−2y 2log0,5(x+y) = 5log5(x+y) 1  Ä äx−y     3 = s) 1 t) 3  log x + log y =   2 2 2 
 log (x + y) + log (x − y) = 4 2 2
Hight school iShool Rach Gia (Sưu tầm và biên soạn) Trang 47
Document Outline

  • 2 HÀM SỐ LŨY THỪA-HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT
    • PHẦN 1. HÀM SỐ LŨY THỪA-HÀM SỐ MŨ-HÀM SỐ LOGARIT
    • A. LÝ THUYẾT
    • 2.1 Lũy thừa-Hàm số lũy thừa
      • 2.1.1 Lũy thừa
      • 2.1.2 Hàm số lũy thừa: bold0mu mumu y=xy=xdottedy=xy=xy=xy=x
    • 2.2 Logarit
      • 2.2.1 Kiến thức cơ bản
    • 2.3 Hàm số mũ-Hàm số logarit
      • 2.3.1 Hàm số mũ: bold0mu mumu y=ax,(0
      • 2.3.2 Hàm số logarit: bold0mu mumu y=logax,(00)y=logax,(00)dottedy=logax,(00)y=logax,(00)y=logax,(00)y=logax,(00)
      • 2.3.3 Bảng đạo hàm
    • B. BÀI TÂP TỰ LUẬN
    • 2.4 Bài tập về lũy thừa
      • 2.4.1 Dạng 1: Tính giá trị biểu thức
      • 2.4.2 Dạng 2: Đơn giản biểu thức
      • 2.4.3 Dạng 3: Lũy thừa hữu tỉ
      • 2.4.4 Dạng 4: So sánh cặp số
      • 2.4.5 Dạng 5: Bài toán thực tế
    • 2.5 Bài tập về logarit
      • 2.5.1 Dạng 1: Tính giá trị biểu thức
      • 2.5.2 Dạng 2: Biến đổi logarit
      • 2.5.3 Dạng 3: Chứng minh đẳng thức logarit
      • 2.5.4 Dạng 4: So sánh cặp số
      • 2.5.5 Dạng 4: Bài toán thực tế
    • 2.6 Bài tập hàm số mũ-hàm số logarit
      • 2.6.1 Dạng 1: Tập xác định hàm số
      • 2.6.2 Dạng 2: Đạo hàm
      • 2.6.3 Dạng 3: Chứng minh hàm số đã cho thỏa hệ thức cho trước
      • 2.6.4 Dạng 4: Giải phương trình, bất phương trình
      • 2.6.5 Dạng 5: Giá trị lớn nhất, giá trị nhỏ nhất
    • PHẦN 2. PHƯƠNG TRÌNH, BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT
    • A. PHƯƠNG TRÌNH
    • 2.7 Phương trình mũ
      • 2.7.1 Phương trình mũ cơ bản
      • 2.7.2 Một số phương pháp giải phương trình mũ
        • 2.7.2.1 Phương pháp đưa về cùng cơ số
        • 2.7.2.2 Phương pháp logarit hóa
        • 2.7.2.3 Phương pháp đặt ẩn phụ
          • 2.7.2.3.1 Dạng 1:
          • 2.7.2.3.2 Dạng 2:
          • 2.7.2.3.3 Dạng 3:
        • 2.7.2.4 Sử dụng tính đơn điệu của hàm số
        • 2.7.2.5 Phương trình tích
      • 2.7.3 Bài toán liên quan tham số m
    • 2.8 Phương trình logarit
      • 2.8.1 Phương trình logarit cơ bản
      • 2.8.2 Một số phương pháp giải phương trình logarit
        • 2.8.2.1 Phương pháp đưa về cùng cơ số
        • 2.8.2.2 Phương pháp mũ hóa
        • 2.8.2.3 Phương pháp đặt ẩn phụ
        • 2.8.2.4 Sử dụng tính đơn diệu hàm số
      • 2.8.3 Bài toán liên quan tham số m
    • B. BẤT PHƯƠNG TRÌNH
    • 2.9 Bất phương trình mũ và bất phương trình logarit
      • 2.9.1 Bất phương trình mũ
      • 2.9.2 Bất phương trình logarit
    • 2.10 Hệ phương trình mũ và logarit
    • 2.11 Các ví dụ
    • 2.12 Bài tập bất phương trình, hệ phương trình mũ và logarit
      • 2.12.1 Giải các bất phương trình
      • 2.12.2 Giải hệ phương trình