Bài giảng lũy thừa và hàm số lũy thừa

Tài liệu gồm 20 trang, trình bày lí thuyết trọng tâm và hướng dẫn giải các dạng bài tập chuyên đề lũy thừa và hàm số lũy thừa, giúp học sinh lớp 12 tham khảo khi học chương trình Giải tích 12 chương 2: Hàm số lũy thừa, hàm số mũ và hàm số lôgarit.

16 8 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 6: Hàm số mũ và hàm số lôgarit (KNTT)

Môn: Toán 11

Thông tin:

20 trang 7 tháng trước

Tác giả:

Profile Kim Oanh
TOANMATH.com
Trang 1
CHUYÊN ĐỀ 2: MŨ VÀ LÔGARIT
BÀI 1: LŨY THỪA – HÀM SỐ LŨY THỪA
Mục tiêu
Kiến thức
+ Biết các khái niệm và tính chất của lũy thừa với số mũ nguyên, lũy thừa với số mũ hửu tỉ không
nguyên và lũy thừa với số mũ thực.
+ Biết khái niệm và tính chất của căn bậc n.
+ Biết khái niệm và tính chất của hàm số lũy thừa.
+ Biết công thức tính đạo hàm của hàm số lũy thừa.
+ Biết dạng đồ thị của hàm số lũy thừa.
Kĩ năng
+ Biết dùng các tính chất của lũy thừa để rút gọn biểu thức, so sánh những biểu thức có chứa lũy
thừa.
+ Biết khảo sát hàm số lũy thừa.
+ Tính được đạo hàm của hàm số lũy thừa.
TOANMATH.com
Trang 2
I. LÍ THUYẾT TRỌNG TÂM
LŨY THỪA
1. Lũy thừa với số mũ nguyên
Cho n là một số nguyên dương.
• Với a tùy ý:
thöøa soá
. ...
n
n
a a a a
• Với
0
a
:
0
a
1
n
n
a
a
(a: cơ số, n: số mũ).
Chú ý:
0
0 , 0
n
không có nghĩa.
Lũy thừa với số mũ nguyên có các tính chất tương tự như lũy
thừa với số mũ nguyên dương.
2. Phương trình
*
n
x b
• Với n lẻ: Phương trình (*) luôn có nghiệm duy nhất.
• Với n chẵn
+ Nếu
0
b
: Phương trình (*) có hai nghiệm trái dấu.
+ Nếu
0
b
: Phương trình (*) có một nghiệm
0
x
+ Nếu
0
b
: Phương trình (*) vô nghiệm.
3. Căn bậc n
Khái niệm
Cho
b R
,
*
n N
2
n . Số a được gọi là căn bậc n của b
nếu
n
a b
.
• Với n lẻ và
b R
, phương trình
n
x b
có duy nhất một căn bậc
n của b, ký hiệu là
n
b
.
• Với n chẵn:
0
b
: Không có căn bậc n của b.
TOANMATH.com
Trang 3
0
b
: Có một căn bậc n của 0 là 0.
0
b
: Có hai căn trái dấu, ký hiệu giá trị dương là
n
b
, còn giá
trị âm là
n
b
.
Tính chất
Với
, 0
a b
,
*
,
m n N
;
p
ta có:
•
. ;
n n n
ab a b
•
, 0;
n
n
n
a a
b
b
b
•
, 0 ;
p
n
p n
a a a
•
.
;
n
m n m
a a
•
khi n leû
khi n chaün.
n
n
a
a
a
4. Lũy thừa với số mũ hửu tỉ
Cho số thực a dương và số hửu tỉ
m
r
n
, trong đó
*
,m n
. Lũy thừa của a với số mũ r được xác định như
sau:
m
n
r m
n
a a a
.
5. Lũy thừa với số mũ vô tỉ
Cho
0,
a
là một số vô tỉ. Ta thừa nhận rằng luôn có một
dãy số hữu tỉ
n
r
mà
lim
n
n
r

và một dãy số tương ứng
n
r
a
có giới hạn không phụ thuộc vào việc chọn dãy số
n
r
.
Khi đó ta kí hiệu lim
n
r
n
a a

là lũy thừa của a với số mũ
.
6. Lũy thừa với số mũ thực
Tính chất
Với mọi a, b là các số thực dương;
,
là các số thực tùy ý, ta
có:
•
. ;
a a a
•
;
a
a
a
Ví dụ:
1
1
2
;
n
n
a a a a
.
TOANMATH.com
Trang 4
•
.
;
a a
•
. . ;
a b a b
•
;
a a
b
b
So sánh hai lũy thừa
• So sánh cùng cơ số
- Nếu cơ số
1
a
thì
.
a a
- Nếu cơ số
0 1
a
thì
.
a a
• So sánh cùng số mũ
- Nếu số mũ
0
thì
0 .
a b a b
- Nếu số mũ
0
thì
0 .
a b a b
HÀM SỐ LŨY THỪA
1. Khái niệm hàm số lũy thừa
Hàm số
,
y x
với
được gọi là hàm số lũy thừa.
Chú ý: Tập xác định của hàm số
y x
tùy thuộc vào giá trị
của
.
Cụ thể:
•
nguyên dương:
D
;
•
nguyên âm hoặc bằng 0:
\ 0 ;
D

•
không nguyên:
0; .
D

2. Đạo hàm của hàm số lũy thừa
Hàm số lũy thừa
y x
,
có đạo hàm với mọi
0
x
và:
•
1
;
x x
•
1
.
u u u
với u là biểu thức chứa x.
3. Khảo sát hàm số lũy thừa
y x
, 0
y x
, 0
y x
a. Tập khảo sát:
0;

a. Tập khảo sát:
0;

b. Sự biến thiên:
•
1
0, >0
y x x
b. Sự biến thiên:
•
1
0, >0
y x x
Ví dụ:
2,5 1,2
2,5 1,2
0,5 1,1
0,5 1,1 0,3 0,3
Ví dụ:
0,8 0,8
3 2 3 2
4 3 4 3
0,8 0,8
3 2 3 2
4 3 4 3
Ví dụ: Tập xác định của hàm số
5
y x
là
;
D

5
y x
là
\ 0 ;
D

2
7
,
y x y x
là
0; .
D

Ví dụ: Đạo hàm của hàm số
5
y x
là
6
5.
y x
;
2
sin
y x
là
2sin . sin 2sin .cos
y x x x x
Lưu ý: Khi khảo sát hàm số lũy thừa với
số mũ cụ thể, ta phải xét hàm số đó trên
toàn bộ tập xác định của nó. Chẳng
hạn: Khảo sát các hàm số
3
y x
trên
tập xác định của nó là
, khảo sát hàm
số
2
y x
trên tập xác định
\ 0 .
D
TOANMATH.com
Trang 5
Hàm số luôn đồng biến.
• Giới hạn đặc biệt:
0
lim 0, lim .
x
x
x x


• Tiệm cận: Không có.
Hàm số luôn nghịch biến.
• Giới hạn đặc biệt:
0
lim , lim 0.
x
x
x x


• Tiệm cận:
Trục Ox là tiệm cận ngang.
Trục Oy là tiệm cận đứng.
c. Bảng biến thiên:
c. Bảng biến thiên:
d. Đồ thị:
Nhận xét: Đồ thị của hàm số lũy thừa
luôn đi qua điểm
1;1 .
I
TOANMATH.com
Trang 6
SƠ ĐỒ HỆ THỐNG HÓA
LŨY THỪA
*
, 2
b n n
Căn bậc n của b
n lẻ
n chẵn
Có duy nhất
n
b
0
b
0
b
0
b
Không tồn tại
0 0
n
n
b
n
b
a
*
0,
,
m
a
n
m n
0, laø soá voâ tæ
a
0,
a
*
,a n
0,
a n
: lim
lim
n
n n
n
r
n
r r
a a


thöøa soá
. ...
n
n
a a a a
0
1
1;
n
n
a a
a
m
n
r m
n
a a a
0
0 ,0 khoâng coù nghóa
n
.
.
. .
a a a
a
a
a
a a
a b a b
a a
b
b
1;
0 1;
0; 0
0; 0
a a a
a a a
a b a b
a b a b
Định nghĩa
Tính chất
TOANMATH.com
Trang 7
HÀM SỐ LŨY THỪA
II. CÁC DẠNG BÀI TẬP
Dạng 1: Lũy thừa
Bài toán 1. Viết lũy thừa với dạng số mũ hữu tỷ
Bài toán 1.1. Thu gọn biểu thức chứa căn thức
Phương pháp giải
Tính chất của căn bậc n
•
. Khi leû
;
. Khi chaün
n n
n
n n
a b n
ab
a b n
•
Khi leû 0
;
Khi chaün 0
n
n
n
n
n
a
n b
b
a
a
b
n b
b
•
, 0 ;
p
n
p n
a a a
•
.
;
n
m n m
a a
•
khi leû
.
khi chaün
n
n
a n
a
a n
TOANMATH.com
Trang 8
Công thức lũy thừa với số mũ thực
•
.
;
n
m m n
a a
•
. ;
m n m n
a a a
•
;
m
m n
n
a
a
a
•
. . ;
m
m m
a b a b
•
.
m
m
m
a a
b
b
Ví dụ mẫu
Ví dụ 1: Cho x là số thực dương. Biểu thức
4
2
3
x x
được viết dưới dạng lũy
thừa với số mũ hữu tỉ là
A.
7
12
.
x
B.
5
6
.
x
C.
12
7
.
x
D.
6
5
.
x
Hướng dẫn giải.
Ta có:
1
1 7 7
7
4
4 4
4
2 2
3
3 3 3
12
.
x x x x x x x
Chọn A.
Ví dụ 2: Cho hai số thực dương a và b. Biểu thức
5
3
a b a
b a b
được viết dưới
dạng lũy thừa với số mũ hữu tỉ là
A.
7
30
.
a
b
B.
31
30
.
a
b
C.
30
31
.
a
b
D.
1
6
.
a
b
Hướng dẫn giải
Ta có:
1 1
1
2 2
5 5
3 3
5
3
a b a a a a a a
b a b b b b b b
1 5 1
6 6 6
5 5
.
a a a a
b b b b
Chọn D.
Điều kiện x là số thực
dương làm cho biểu thức ở
dạng thũy thừa với số mũ
hửu tỉ xác định.
Bài toán 1.2. Thu gọn biểu thức chứa lũy thừa
Phương pháp giải
Các hằng đẳng thức đáng nhớ:
TOANMATH.com
Trang 9
•
2
2 2
2 ;
a b a ab b
•
3
3 2 2 3
3 3 ;
a b a a b ab b
•
2 2
;
a b a b a b
•
3 3 2 2
;
a b a b a ab b
•
3 3 2 2
.
a b a b a ab b
Ví dụ mẫu
Ví dụ 1: Cho
1
2
1 1
2 2
1 2
y y
P x y
x x
. Biểu thức rút gọn của P là
A.
.
x
B.
2 .
x
C.
1.
x
D.
1.
x
Hướng dẫn giải
Ta có:
1
2 2
2
2x xy y
x
P x y x y x
x
x y
Chọn A.
Ví dụ 2: Rút gọn biểu thức
0,5 0,5 0,5
0,5 0,5
2 2 1
.
1
2 1
a a a
a
a a a
(với
0 1
a
) ta được
A.
2
.
2
a
B.
1
.
2
a
C.
2
.
1
a
D.
2
.
1
a
Hướng dẫn giải
Ta có:
0,5 0,5 0,5
0,5 0,5
2 2 1
.
1
2 1
a a a
a
a a a
0,5 0,5 0,5
2 0,5
0,5 0,5
0,5
2 2 1
.
1 1
1
a a a
a
a a
a
0,5 0,5
0,5 0,5 0,5
2 2 1
.
1 1
a a
a a a
0,5 0,5
0,5
2 2 1 2
.
1 1
a a a a
a a
a
Chọn D.
TOANMATH.com
Trang 10
Ví dụ 3: Rút gọn biểu thức
3
4 4
3 3
4 4
1 1
1 1
x x x
x x
x x
x x
(với
0, 1
x x
) ta được
A.
2
.
x
B.
2
.
x
C.
3
.
x
D.
3
.
x
Hướng dẫn giải.
Ta có:
3
4 4
3 3
4 4
1 1
1 1
x x x
x x
x x
x x
3
4 4
2 2
4 4
1 1
x x x
x x x x x x
3 3
3
4 4
1
.
1
1 1
x x
x x x
x
x
x x
Chọn C.
Bài toán 2. Tính giá trị biểu thức
Phương pháp giải
Công thức đặc biệt
x
x
a
f x
a a
thì
1 1.
f x f x
Thật vậy, ta có:
1
.
x
x
x
a
a
a
f x
a
a a a
a
a
1
x
a
f x
a a
Nên:
1 1.
f x f x
Ví dụ mẫu
Ví dụ 1: Cho
2018
.
2018 2018
x
x
f x
Tính giá trị biểu thức sau đây ta được
1 2 2018
...
2019 2019 2019
S f f f
A.
2018.
S
B.
2019.
S
C.
1009.
S
D.
2018.
S
TOANMATH.com
Trang 11
Hướng dẫn giải
Ta có:
2018
1 1 1
2018 2018
x
f x f x f x
Suy ra
1 2 2018 1 2018
...
2019 2019 2019 2019 2019
S f f f f f
2 2017 1009 1010
... 1009.
2019 2019 2019 2019
f f f f
Chọn C.
Ví dụ 2: Cho
9 9 23.
x x
Tính giá trị của biểu thức
5 3 3
1 3 3
x x
x x
P
ta được
A.
2.
B.
3
.
2
C.
1
.
2
D.
5
.
2
Hướng dẫn giải
Ta có:
2
3 3 5
9 9 23 3 3 25
3 3 5 loaïi
x x
x x x x
x x
Từ đó, thế vào
5 3 3
5 5 5
.
1 5 2
1 3 3
x x
x x
P
Chọn D.
Bài tập tự luyện dạng 1
Câu 1: Khẳng định nào sau đây đúng?
A.
n
a
xác định với mọi
\ 0 ; .
a n
B.
; .
m
n
m
n
a a a
C.
0
1; .
a a
D.
; ; ,n .
m
n
m
n
a a a m
Câu 2: Rút gọn biểu thức
2 2 2 3
2
2 3
1
a b
a b
(với
0, 0
a b
và
2 3
a b
) được kết quả
A. 2. B.
2
2 .
a
C.
2 3
2 3
.
a b
a b
D.
2
2 3
2
.
a
a b
Câu 3: Cho số thực dương a. Rút gọn
3
4
5
P a a a a
ta được
A.
25
13
.
a
B.
37
13
.
a
C.
53
36
.
a
D.
43
60
.
a
Câu 4: Viết biểu thức
3
2
. . 0
P a a a a
dưới dạng lũy thừa với số mũ hữu tỉ ta được
A.
5
3
.
P a
B.
5
6
.
P a
C.
11
6
.
P a
D.
2
.
P a
TOANMATH.com
Trang 12
Câu 5: Viết biểu thức
5
3
, , 0
b a
a b
a b
về dạng lũy thừa
m
a
b
ta được m bằng
A.
2
.
15
B.
4
.
15
C.
2
.
5
D.
2
.
15
Câu 6: Rút gọn biếu thức
5
3
3
:
Q b b
với
0
b
ta được
A.
2
.
Q b
B.
5
9
.
Q b
C.
4
3
.
Q b
D.
4
3
.
Q b
Câu 7: Giả sử a là số thực dương, khác 1 và
3
a a
được viết dưới dạng
.
a
. Giá trị của
là
A.
11
.
6
B.
5
.
3
C.
2
.
3
D.
1
.
6
Câu 8: Rút gọn biểu thức
1
6
3
.
P x x
với
0
x
ta được
A.
2
.
P x
B.
.
P x
C.
1
8
.
P x
D.
2
9
.
P x
Câu 9: Cho a, b là các số thực dương. Viết biểu thức
12
3 3
a b
dưới dạng lũy thừa với số mũ hữu tỉ ta được
A.
3 1
4 2
.
a b
B.
1
1
9
4
.
a b
C.
1 1
4 4
.
a b
D.
1 3
4 4
.
a b
Câu 10: Cho a là một số dương, viết
2
3
a
a
dưới dạng lũy thừa với số mũ hữu tỉ ta được
A.
7
6
.
a
B.
3
.
a
C.
1
6
.
a
D.
2
a .
Câu 11: Cho
a 0.
Đẳng thức nào sau đây đúng?
A.
3 4
.
a a a
B.
5
3
6
3
2
.
a
a
a
C.
4
2 6
.
a a
D.
7
7
5
5
.
a a
Câu 12: Cho biểu thức
3 1
3 1
5 3 4 5
P ,
.
a
a a
với
0.
a
Mệnh đề nào dưới đây đúng?
A.
1
2
.
P a
B.
.
P a
C.
3
2
.
P a
D.
3
.
P a
Câu 13: Cho hàm số
2
3
2 3
3
1
8 8
3 1
8
a a a
f a
a a a
với
0, 1.
a a
Giá trị của
2018
2017M f
là
A.
2018
2017 1.
M
B.
1009
2017 .
M C.
1009
2017 1.
M
D.
1009
2017 1.
M
Câu 14: Giá trị của biểu thức
2017 2016
7 4 3 7 4 3P
bằng
A. 1. B.
7 4 3.
C.
7 4 3.
D.
2016
7 4 3 .
Câu 15: Giá trị của biểu thức
2017 2016
9 4 5 9 4 5P
bằng
TOANMATH.com
Trang 13
A. 1. B.
9 4 5.
C.
9 4 5.
D.
2017
9 4 5. .
Câu 16: Cho
4 4 14.
x x
Giá trị của biểu thức
10 2 2
3 2 2
x x
x x
P
là
A.
2.
P
B.
1
.
2
P
C.
6
.
7
P
D.
7.
P
Câu 17: Cho
25 25 7.
x x
Giá trị của biểu thức
4 5 5
9 5 5
x x
x x
P
là
A.
12.
P
B.
1
12 .
P
C.
1
.
9
P
D.
2.
P
Câu 18: Cho hàm số
9
;
9 3
x
x
f x x
và a, b thỏa
1.
a b
Giá trị
f a f b
bằng
A. -1. B. 2. C. 1. D.
1
.
2
Câu 19: Cho hàm số
4
.
4 2
x
x
f x
Tổng
1 2 98 99
...
100 100 100 100
P f f f f
bằng
A.
99
.
2
B.
301
.
6
C.
101
.
2
D.
149
.
3
Câu 20: Cho hàm số
4
.
4 2
x
x
f x
Giá trị của biểu thức sau đây bằng
1 2 3 2013 2014
...
2015 2015 2015 2015 2015
S f f f f f
A. 2014. B. 2015. C. 1008. D. 1007.
Dạng 2: Hàm số lũy thừa
Bài toán 1. Tìm tập xác định của hàm số lũy thừa
Phương pháp giải
Ta tìm điều kiện xác định của hàm số
,
y f x
dựa vào số mũ
của nó như sau:
• Nếu
là số nguyên dương thì không có điều
kiện xác định của
.
f x
• Nếu
là số nguyên âm hoặc bằng 0 thì điều
kiện xác định là
0.
f x
• Nếu
là số không nguyên thì điều kiện xác
định là
0.
f x
Ví dụ: Tập xác định của hàm số
3
2
6 5
y x x
là
A.
.
B.
\ 1;5 .
C.
1;5 .
D.
;1 5; .
 
Hướng dẫn giải
Số mũ
3
là số nguyên âm. Do đó, điều kiện xác
định của hàm số là:
2
1
6 5 0 .
5
x
x x
x
Vậy tập xác định của hàm số đã cho là
\ 1;5 .
Chọn B.
TOANMATH.com
Trang 14
Ví dụ mẫu
Ví dụ 1: Tập xác định của hảm số
1
2
5
5 6
y x x
là
A.
\ 2;3 .
B.
;2 3; .
 
C.
2;3 .
D.
3; .

Hướng dẫn giải
Số mũ
1
5
không phải là số nguyên. Do đó, điều kiện xác định của hàm số là:
2
5 6 0 2;3 .
x x x Vậy tập xác định của hàm số đã cho là
2;3 .
Chọn C.
Ví dụ 2: Tập xác định của hảm số
sin 2018
y x
là
A.
.
B.
0; .

C.
\ 0 .
D.
0; .

Hướng dẫn giải
Ta có
sin 2018
0
y x x
nên tập xác định là
\ 0 .
Chọn C.
Ví dụ 3: Tập xác định của hảm số
2019
1y x
là
A.
.
B.
0; .

C.
\ 0 .
D.
0; .

Hướng dẫn giải
Vì số mũ
2019
là số nguyên âm nên điều kiện xác định của hàm số là
1 0,
x
ngoài ra hàm số còn chứa căn thức bậc hai nên
0.
x
Hàm số xác định
1 0 luoân ñuùng 0
0.
0
x x
x
x
Vậy
0; .
D
Chọn D.
Ví dụ 4: Có bao nhiêu giá trị nguyên của
2018;2018
m để hàm số
5
2
2 1
y x x m có tập xác
định là
?
A. 4036. B. 2018. C. 2017. D. Vô số
Hướng dẫn giải
Vì số mũ
5
không phải là số nguyên nên hàm số xác định với
.
x
2
2 1 0,x x m x
TOANMATH.com
Trang 15
0
0 luoân ñuùng vì 1 0
a a
1 1 0
m
0
m
Mà
2018;2018
1,2,3,...,2017 .
m
m
m
Vậy có 2017 giá trị nguyên của tham số m thỏa mãn yêu cầu.
Chọn C.
Bài toán 2. Tính đạo hàm của hàm số lũy thừa
Phương pháp giải
Công thức tính đạo hàm
•
1
0, ;
x x x
•
1
.
u u u
với u là biểu thức chứa x.
Ví dụ:
3 2
2 5 6 2 5 .
x x
Ví dụ mẫu
Ví dụ 1: Tìm đạo hàm của hàm số
1
2
4
1 .
y x
A.
5
2
4
1
1 .
4
y x
B.
5
2
4
5
1 .
2
y x x
C.
5
2
4
5
1 .
2
y x x
D.
5
2
4
1
1 .
2
y x x
Hướng dẫn giải
Ta có:
1 5 5
1
2 2 2 2
4 4 4
1 1 1
y 1 . 1 1 . 2 1 .
4 4 2
x x x x x x
Chọn D.
Ví dụ 2: Tìm đạo hàm của hàm số
4
2 3cos2 .
y x
A.
3
24 2 3cos2 sin2 .
y x x
B.
3
12 2 3cos2 sin2 .
y x x
C.
3
24 2 3cos2 sin2 .
y x x
D.
3
12 2 3cos2 sin2 .
y x x
Hướng dẫn giải
Ta có:
3
y 4 2 3cos2 2 3cos2
x x
3
4 2 3cos2 6sin2
x x
TOANMATH.com
Trang 16
3
24 2 3cos2 sin2 .
x x
Chọn A.
Ví dụ 3: Đạo hàm của hàm số
2
3
sin
y x x
là
A.
1
3
2
sin .
3
y x x
B.
1
3
2
sin . sin cos .
3
y x x x x x
C.
3
2 2
2 sin cos
y . .
3
sin
x x x
x x
D.
1
3
2
sin .cos .
3
y x x x
Hướng dẫn giải
Ta có:
2 1
1
3 3
2 2
sin . sin sin . sin cos .
3 3
y x x x x x x x x x
Chọn B.
Ví dụ 4: Đạo hàm của hàm số
2
3
1
y x
là
A.
2
3
1
.
3 3 . 1
y
x x x
B.
5
3
2 1
1 . .
3
y x
x
C.
2
3
1
.
. 1
y
x x x
D.
5
3
2
y 1 .
3
x
Hướng dẫn giải
Ta có:
2 5
1
3 3
2 2 1
1 . 1 1 .
3 3
2
y x x x
x
5
3
2
3
1 1 1
1 . .
3
3 3 . 1
x
x
x x x
Chọn A.
Bài toán 3. Khảo sát sự biến thiên và nhận dạng đồ thị của hàm số lũy thừa
Phương pháp giải
Đồ thị của hàm số lũy thừa
y a
trên
0; :

Lưu ý: Khi khảo sát hàm số lũy thùa với số mũ cụ thể, ta
phải xét hàm số đó trên toàn bộ tập xác định của nó.
Chẳng hạn: Khảo sát các hàm số
3
y x
trên tập xác định
của nó là
,
khảo sát hàm số
2
y x
trên tập xác định
\ 0 .
D
TOANMATH.com
Trang 17
Nhận xét: Đồ thị của hàm số lũy thừa luôn đi qua điểm
1;1 .
I
Ví dụ mẫu
Ví dụ 1: Cho hàm số
y f x
có đồ thị như hình vẽ. Hỏi
f x
có thể là hàm số nào trong bốn hàm số
dưới đây?
A.
1
3
.
f x x
B.
3
.
f x x
C.
1
3
.
f x x
D.
3
.
f x x
Hướng dẫn giải
Hàm số có tập xác định là
0; ,
D

loại đáp án B, D.
Hàm số đồng biến trên D, loại C.
Chọn A.
Ví dụ 2: Cho hàm số
2
y f x x
có đồ thị
.
C
Mệnh đề nào sau đây đúng?
A. Hàm số tăng trên
0; .

B. Đồ thị
C
không có tiệm cận.
C. Tập xác định của hàm số là
.
D. Hàm số không có cực trị.
Hướng dẫn giải
Hàm số có tập xác định là
0; .
D

Ta có:
2 1
2 0, .
y x x D
Hàm số nghịch biến trên D
Hàm số không có cực trị.
Chọn D.
Bài tập tự luyện dạng 2
Câu 1: Tập xác định D của hàm số
2 3
2
3 4y x x
là
TOANMATH.com
Trang 18
A.
\ 1;4 .
D B.
D ; 1 4; .
 
C.
.
D
D.
D ; 1 4; .
 
Câu 2: Trong các hàm số sau đây, hàm số nào có tập xác định
D
?
A.
2 .
y x
B.
2
1
2 .
y
x
C.
2
2 .
y x
D.
2 .
y x
Câu 3: Tập xác định D của hàm số
4
2
y 3
x x
là
A.
0;3 .
B.
\ 0;3 .
D
C.
.
D
D.
;0 3; .
D
 
Câu 4: Tập xác định của hàm số
2019
2
2020
y 4x x là
A.
;0 4; .
 
B.
;0 4; .
 
C.
0;4 .
D.
\ 0;4 .
Câu 5: Tập xác định D của hàm số
0
3
y x
là
A.
;3 .
D  B.
;3 .
D

C.
\ 3 .
D D.
D .
Câu 6: Tập xác định D của hàm số
sin
2
3
2
x
y
x
là
A.
\ 2;3 .
D B.
, 2 3, .
D
 
C.
\ 3 .
D
D.
D ; 2 3; .
 
Câu 7: Tập xác định D của hàm số
2
1
e
y x x
là
A.
1;1 .
D B.
\ 1;1 .
D C.
1; .
D

D.
.
D
Câu 8: Có bao nhiêu giá trị nguyên của tham số
50;50
m để hàm số
1
2
2
2 1
y x x m có tập
xác định
?
A. 99. B. 49. C. 50. D. 100.
Câu 9: Biết tham số
; ,
m a b
với
a b
thì hàm số
3 2 2
2 2
2 5 5y x x m m
có tập xác định là
Giá trị tổng
a b
là
A.
5.
B. 5. C. 3. D.
3.
Câu 10: Tất cả các giá trị thực của m để hàm số
2019
2
2020
4y x x m xác định trên
là
A.
4.
m
B.
4.
m
C.
4.
m
D.
4.
m
Câu 11: Tất cả các giá trị thực của m để hàm số
2020
2
y 2x x m xác định trên
là
A.
1.
m
B.
1.
m
C.
1.
m
D.
1.
m
Câu 12: Tất cả các giá trị thực của tham số m sao cho hàm số
sin
2
3
1y x mx
có tập xác định
là
TOANMATH.com
Trang 19
A.
2 2.
m
B.
2 2.
m m
C.
1 1.
m
D.
2 2.
m
Câu 13: Tất cả các giá trị thực của m để hàm số
2
2
2
2 2
3
x mx m
y
x
xác định trên
là
A.
1 2.
m
B.
1 2.
m
C.
2 2.
m
D.
1 2.
m
Câu 14: Phương trình tiếp tuyến của
2
:
C y x
tại điểm
0
M
có hoành độ
0
1
x
là
A.
1.
2
y x
B.
1.
2 2
y x
C.
1.
y x
D.
1.
2 2
y x
Câu 15: Trên đồ thị của hàm số
1
2
y x
lấy điểm
0
M
có hoành độ
2
0
2 .
x
Tiếp tuyến của
C
tại điểm
0
M
có hệ số góc bằng
A.
2.
B.
2 .
C.
2 1.
D. 3.
Câu 16: Cho các hàm số lũy thừa
, ,
y x y x y x
có đồ thị như hình vẽ. Khẳng định nào sau đây
đúng?
A.
.
B.
.
C.
.
D.
.
Câu 17: Cho
,
là các số thực. Đồ thị các hàm số
,
y x y x
trên khoảng
0;

được cho trong
hình vẽ bên. Khẳng định nào sau đây là đúng?
A.
0 1 .
B.
0 1 .
C.
0 1 .
D.
0 1 .
Câu 18: Bảng biến thiên dưới đây là của hàm số nào?
TOANMATH.com
Trang 20
A.
3
.
y x
B.
3
log .
y x
C.
2
.
y x
D.
3 .
x
y
Câu 19: Cho hàm số
4
.
y x
Mệnh đề nào sau đây là sai?
A. Hàm số có một trục đối xứng. B. Đồ thị hàm số đi qua điểm
1;1 .
C. Đồ thị hàm số có hai đường tiệm cận. D. Đồ thị hàm số có một tâm đối xứng.
Câu 20: Trong các phương trình sau đây, phương trình nào có nghiệm?
A.
1
6
x 1 0.
B.
4 5 0.
x
C.
1
1
5
6
1 0.
x x
D.
1
4
1 0
x
ĐÁP ÁN
Dạng 1. Lũy thừa
1-A 2-D 3-D 4-C 5-D 6-D 7-C 8-B 9-C 10-A
11-B 12-B 13-D 14-C 15-C 16-C 17-B 18-C 19-A 20-D
Dạng 2. Hàm số lũy thừa
1-D 2-C 3-B 4-B 5-C 6-A 7-C 8-B 9-B 10-A
11-D 12-D 13-A 14-B 15-A 16-B 17-A 18-C 19-D 20-A
| 1/20
| | Tải xuống

Có thể bạn quan tâm:

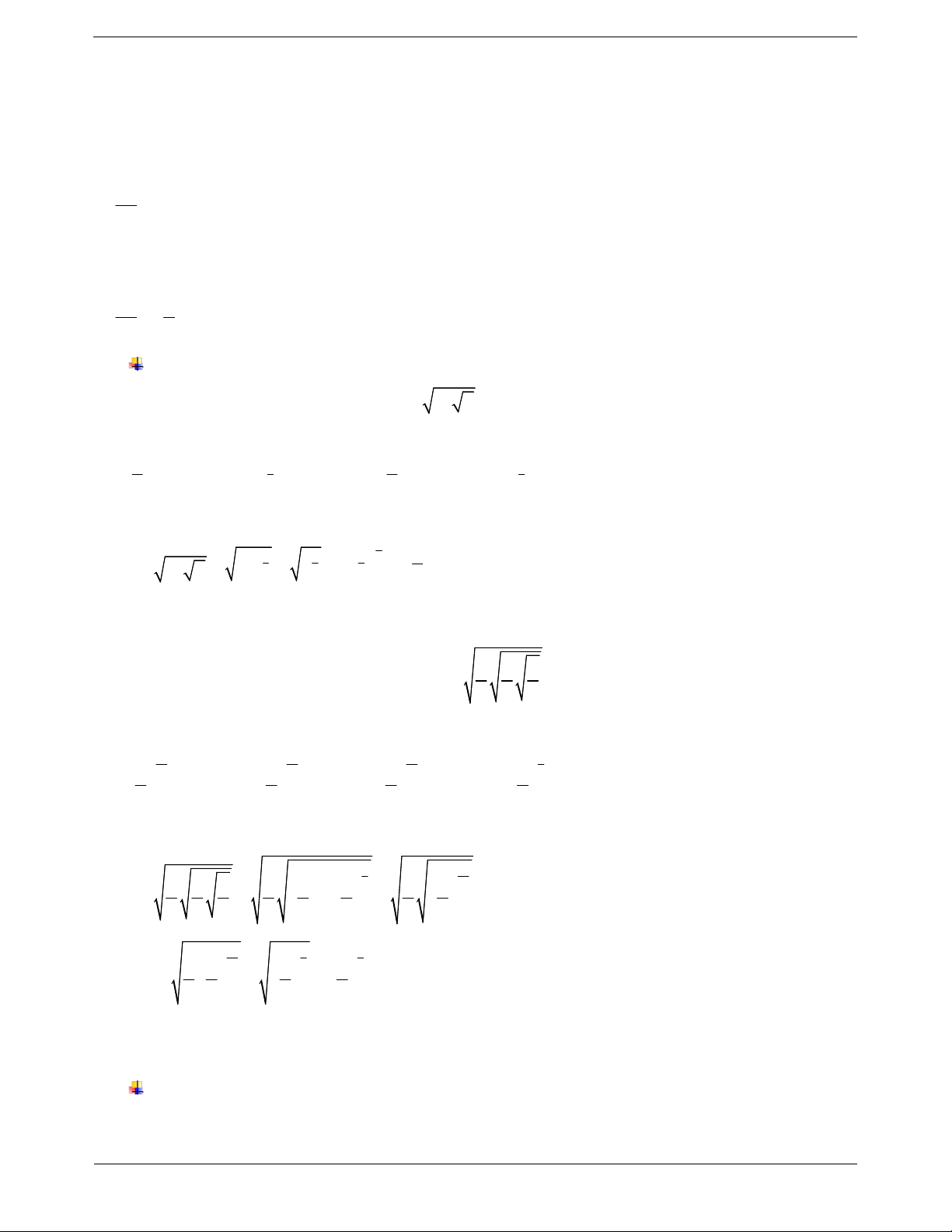
Preview text:

CHUYÊN ĐỀ 2: MŨ VÀ LÔGARIT
BÀI 1: LŨY THỪA – HÀM SỐ LŨY THỪA Mục tiêu  Kiến thức
+ Biết các khái niệm và tính chất của lũy thừa với số mũ nguyên, lũy thừa với số mũ hửu tỉ không
nguyên và lũy thừa với số mũ thực.
+ Biết khái niệm và tính chất của căn bậc n.
+ Biết khái niệm và tính chất của hàm số lũy thừa.
+ Biết công thức tính đạo hàm của hàm số lũy thừa.
+ Biết dạng đồ thị của hàm số lũy thừa.  Kĩ năng
+ Biết dùng các tính chất của lũy thừa để rút gọn biểu thức, so sánh những biểu thức có chứa lũy thừa.
+ Biết khảo sát hàm số lũy thừa.
+ Tính được đạo hàm của hàm số lũy thừa. TOANMATH.com Trang 1 I. LÍ THUYẾT TRỌNG TÂM LŨY THỪA
1. Lũy thừa với số mũ nguyên
Cho n là một số nguyên dương. • Với a tùy ý: n a  . a . a ..a  n thöøa soá n 1 • Với a  0 : 0 a  1; a  (a: cơ số, n: số mũ). n a Chú ý: 0 0 , 0n không có nghĩa.
Lũy thừa với số mũ nguyên có các tính chất tương tự như lũy
thừa với số mũ nguyên dương. 2. Phương trình n x  b*
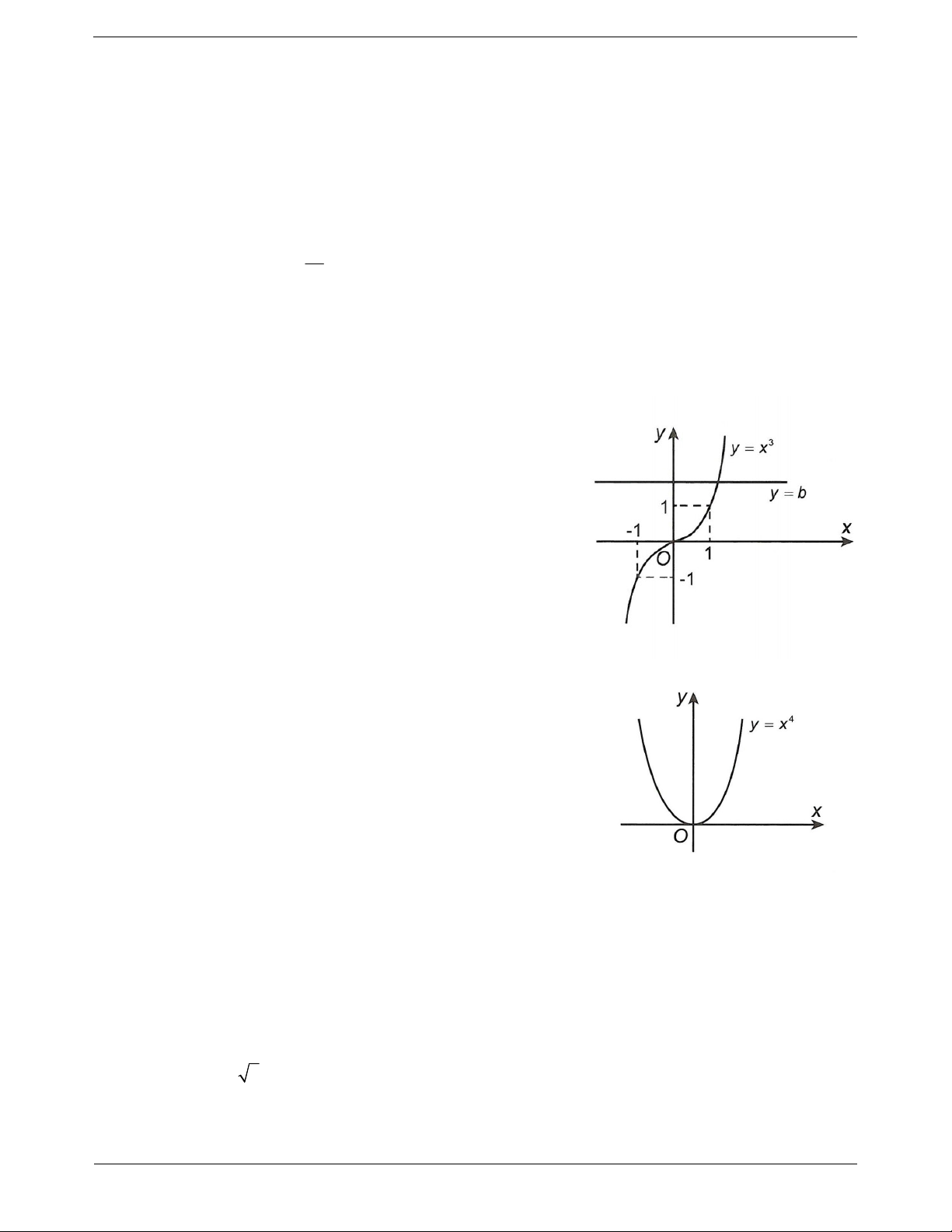
• Với n lẻ: Phương trình (*) luôn có nghiệm duy nhất. • Với n chẵn
+ Nếu b  0 : Phương trình (*) có hai nghiệm trái dấu.
+ Nếu b  0 : Phương trình (*) có một nghiệm x  0
+ Nếu b  0 : Phương trình (*) vô nghiệm. 3. Căn bậc n Khái niệm Cho b  R , *
n  N n  2 . Số a được gọi là căn bậc n của b nếu n a  b .
• Với n lẻ và b  R , phương trình n
x  b có duy nhất một căn bậc
n của b, ký hiệu là n b . • Với n chẵn:
b  0 : Không có căn bậc n của b. TOANMATH.com Trang 2
b  0 : Có một căn bậc n của 0 là 0.
b  0 : Có hai căn trái dấu, ký hiệu giá trị dương là n b , còn giá trị âm là n b . Tính chất Với a,b  0 , * m,n N ; p ta có: • n n  .n ab a b; n a a • n  ,b  0; n b b p • n p   n a a  ,a  0; • n m n.m a  a; a  khi n leû • n n a   a khi n chaün. 
4. Lũy thừa với số mũ hửu tỉ 1 1 2 m Ví dụ:  ; n n a a a  a .
Cho số thực a dương và số hửu tỉ r  , trong đó n * m ,n
  . Lũy thừa của a với số mũ r được xác định như m sau: r n n m a  a  a .
5. Lũy thừa với số mũ vô tỉ
Cho a  0,  là một số vô tỉ. Ta thừa nhận rằng luôn có một
dãy số hữu tỉ r mà   lim r và một dãy số tương ứng n  n n  n r
a có giới hạn không phụ thuộc vào việc chọn dãy số r . n 
Khi đó ta kí hiệu a  lim n r
a là lũy thừa của a với số mũ n  .
6. Lũy thừa với số mũ thực Tính chất
Với mọi a, b là các số thực dương; ,  là các số thực tùy ý, ta có:
• a .a  a ; a •  a ; a TOANMATH.com Trang 3  • a   . a   ;  •  . a b a .b  ;  a   a •    ;  b  b So sánh hai lũy thừa Ví dụ: • So sánh cùng cơ số    2,5   1,2 2,5 1,2  
- Nếu cơ số a  1 thì   a  a   . 0,5 1,1
- Nếu cơ số 0  a  1thì   a  a   .
0,5  1,1  0,3  0,3 • So sánh cùng số mũ
- Nếu số mũ   0 thì a b 0 a b     . Ví dụ:
- Nếu số mũ   0 thì a b 0 a b     . 0,8 0,8 3 2  3   2         HÀM SỐ LŨY THỪA 4 3  4   3 
1. Khái niệm hàm số lũy thừa 0  ,8 0,8 3 2  3   2     Hàm số y x 
,với    được gọi là hàm số lũy thừa. 4 3  4   3    
Chú ý: Tập xác định của hàm số y x 
tùy thuộc vào giá trị Ví dụ: Tập xác định của hàm số của  . 5 y  x là D  ; Cụ thể: 5 y x  là D  \   0 ;
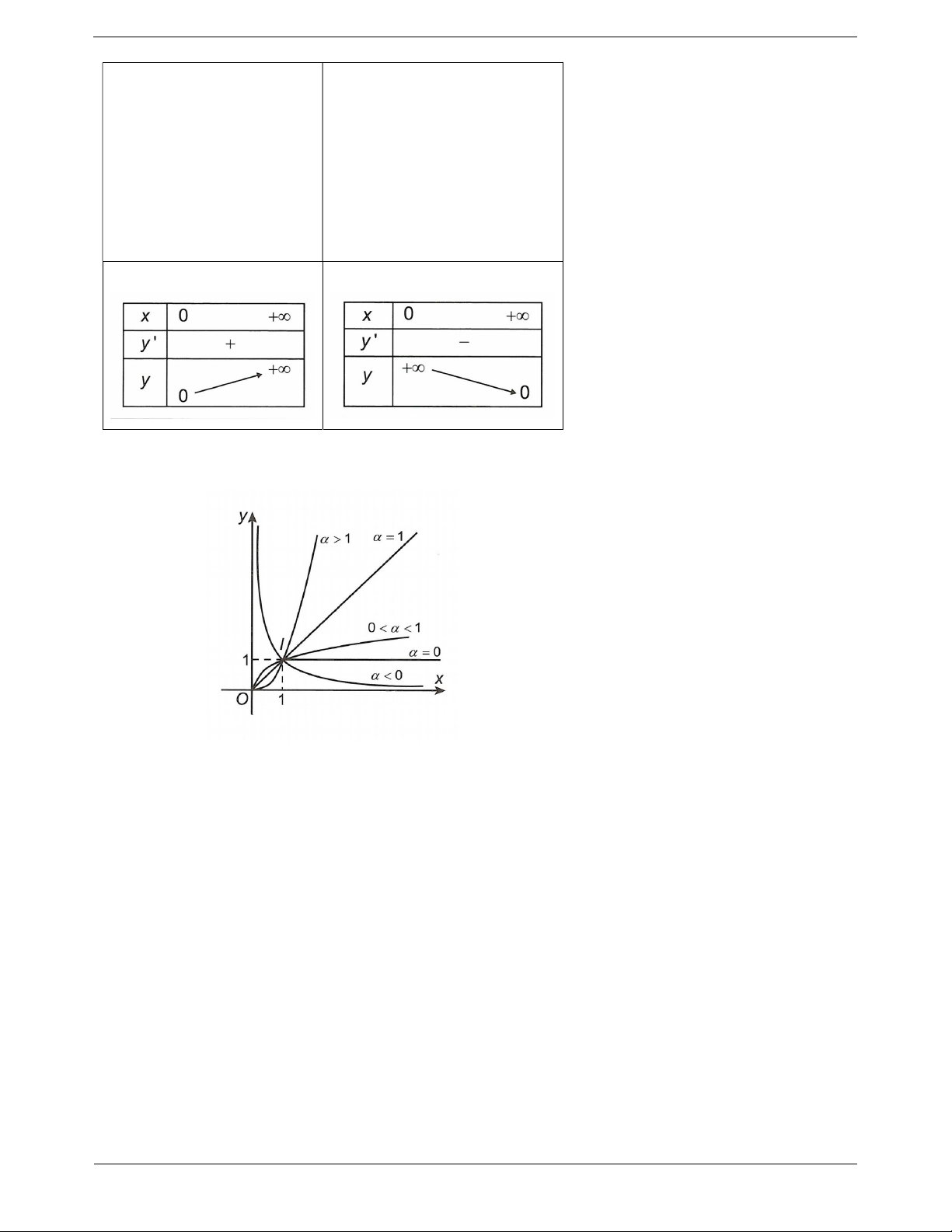
•  nguyên dương: D   ; 2
•  nguyên âm hoặc bằng 0: D  \   0 ; 7 y x , y x   là D  0;.
•  không nguyên: D  0;.
2. Đạo hàm của hàm số lũy thừa
Ví dụ: Đạo hàm của hàm số Hàm số lũy thừa y x 
,    có đạo hàm với mọi x  0 và: 5 y x  là 6 y 5.x    ;  • x   1   x  ; 2 y  sin x là   • u   1
 u  .u với u là biểu thức chứa x.
y  2sin x.sin x  2sin x.cos x
3. Khảo sát hàm số lũy thừa y x 
Lưu ý: Khi khảo sát hàm số lũy thừa với
số mũ cụ thể, ta phải xét hàm số đó trên y  x ,   0 y  x ,  0
toàn bộ tập xác định của nó. Chẳng
a. Tập khảo sát: 0;
a. Tập khảo sát: 0;
hạn: Khảo sát các hàm số 3 y  x trên b. Sự biến thiên: b. Sự biến thiên:
tập xác định của nó là  , khảo sát hàm •  1 y  x     0,  x>0 •  1 y  x     0,  x>0 số 2 y x 
trên tập xác định D   \   0 . TOANMATH.com Trang 4
Hàm số luôn đồng biến.
Hàm số luôn nghịch biến.
• Giới hạn đặc biệt:
• Giới hạn đặc biệt:
lim x  0, lim x   . 
lim x  , lim x  0. x0 x x0 x • Tiệm cận: Không có. • Tiệm cận:
Trục Ox là tiệm cận ngang.
Trục Oy là tiệm cận đứng. c. Bảng biến thiên: c. Bảng biến thiên: d. Đồ thị:
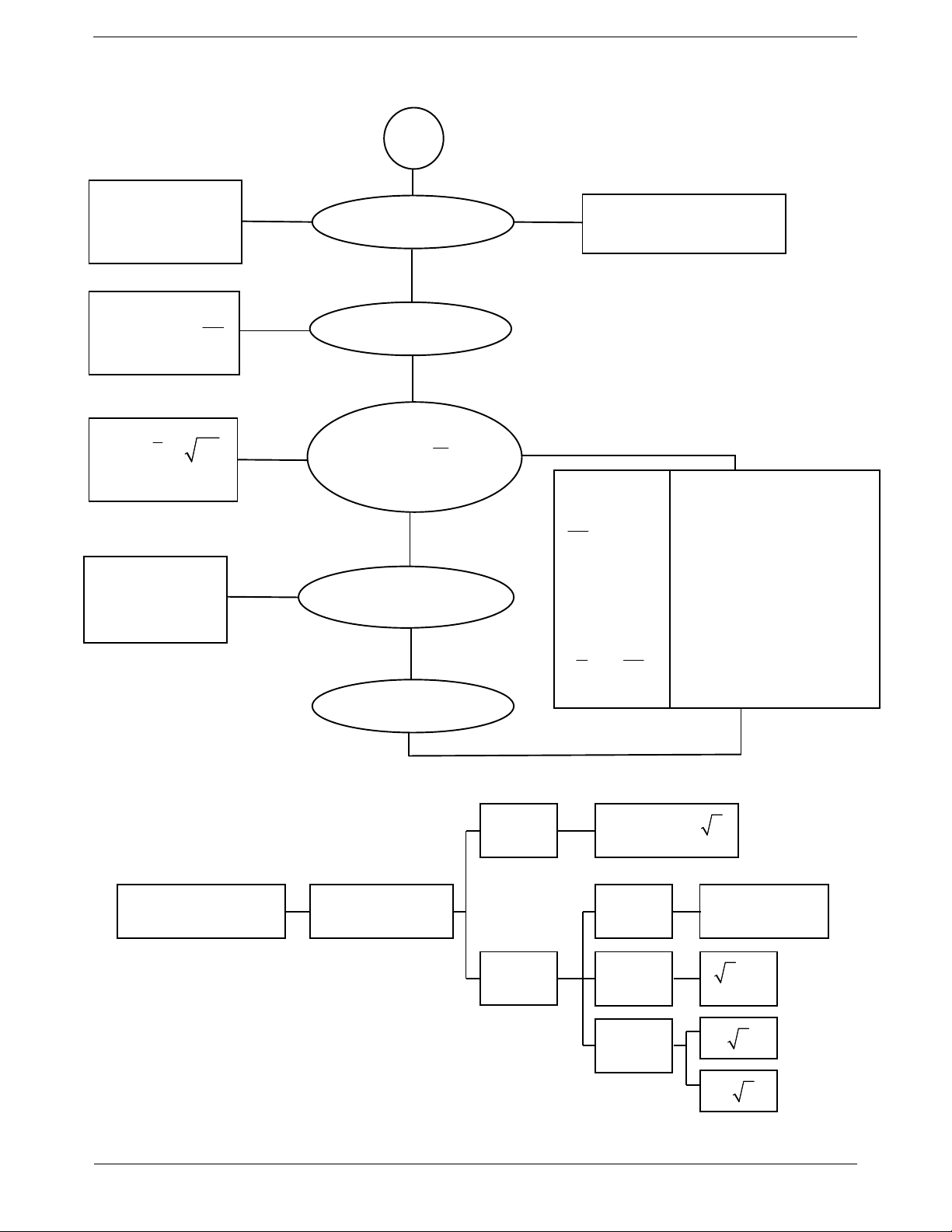
Nhận xét: Đồ thị của hàm số lũy thừa
luôn đi qua điểm I 1;  1 . TOANMATH.com Trang 5 SƠ ĐỒ HỆ THỐNG HÓA LŨY THỪA a Định nghĩa Tính chất n a  . a . a ..a  0 n * 0 ,0 khoâng coù nghóa n thöøa soá a ,    n 0  1 a  1; n a  a  0,  n  n a m r n n m  0, m a    a  a  a  n * m  ,  n a .a  a
a  1;     a  a a
0  a  1;     a  a  a a
  0; a  b  0  a  b  r r   a  .  a 
  0; a  b  0  a  b n  : lim n n
a  0, laø soá voâ tæ  a  lim  n r a  .ab  a.b n  a   a   b    b a  0,   n lẻ Có duy nhất n b *
b  ,n n  2 Căn bậc n của b b  0 Không tồn tại n chẵn b  0 n 0  0 b  0 n b n  b TOANMATH.com Trang 6 HÀM SỐ LŨY THỪA II. CÁC DẠNG BÀI TẬP Dạng 1: Lũy thừa
Bài toán 1. Viết lũy thừa với dạng số mũ hữu tỷ
Bài toán 1.1. Thu gọn biểu thức chứa căn thức Phương pháp giải
Tính chất của căn bậc n n  a.n b Khi n leû • n ab   ; n a .n b Khi n chaün  n  a  Khi n leû b  0 n  b a • n   ; n b a  Khi n chaün  b  0 n b  p • n p   n a a  ,a  0; • n m n.m a  a; a  khi n leû • n n a   . a khi n chaün  TOANMATH.com Trang 7
Công thức lũy thừa với số mũ thực n •  m  m.n a  a ; • m. n m n a a a   ; m a • mn  a ; n a m • m. m a b   .ab ; m m a  a  •    . m b  b  Ví dụ mẫu
Ví dụ 1: Cho x là số thực dương. Biểu thức 4 2 3
x x được viết dưới dạng lũy
thừa với số mũ hữu tỉ là 7 5 12 6 A. 12 x . B. 6 x . C. 7 x . D. 5 x . Hướng dẫn giải.
Điều kiện x là số thực 1
dương làm cho biểu thức ở 1 7 7 4 7 4 4   Ta có: 4 2 3 2 3 3 3 12
x x  x x  x   x   x .  
dạng thũy thừa với số mũ   hửu tỉ xác định. Chọn A. a b a
Ví dụ 2: Cho hai số thực dương a và b. Biểu thức 5 3 được viết dưới b a b
dạng lũy thừa với số mũ hữu tỉ là 7 31 30 1 30  a  30  a  31  a  6  a  A.   . B.   . C.   . D.   .  b   b   b   b  Hướng dẫn giải 1 1 1   2 2 a b a a  a   a  a  a  Ta có: 5 3 5 3 5 3   b a b b  b   b  b  b        1 5 1 6 6 6 a  a   a   a  5 5          . b  b   b   b  Chọn D.
Bài toán 1.2. Thu gọn biểu thức chứa lũy thừa Phương pháp giải
Các hằng đẳng thức đáng nhớ: TOANMATH.com Trang 8 • a  b2 2 2  a  2ab  b ; • a  b3 3 2 2 3
 a  3a b  3ab  b ; • 2 2
a  b  a  ba  b; • 3 3 a  b  a  b 2 2 a  ab  b ; • 3 3 a  b  a  b 2 2 a  ab  b . Ví dụ mẫu 2 1 1 1     Ví dụ 1: Cho 2 2     1 2 y y P x y     
. Biểu thức rút gọn của P là x x      A. x. B. 2x. C. x 1. D. x 1. Hướng dẫn giải 1 2   2 x  2 xy  y x
Ta có: P   x  y        x  y  x    x  y x 2 Chọn A. 0,5 0,5 0,5  a  2 a  2  a 1
Ví dụ 2: Rút gọn biểu thức   .
(với 0  a  1) ta được 0,5 0,5 a  2a   1 a 1 a  a  2 a 1 2 2 A. . B. . C. . D. . 2 2 1 a a 1 Hướng dẫn giải 0,5 0,5 0,5  a  2 a  2  a 1 Ta có:   . 0,5 0,5 a  2a   1 a 1 a    0,5 0,5 0,5  a  2 a  2  a 1   .     2  0,5 a 1 0,5 0,5 a a  0,5 1 1    a  0,5 0,5  a  2 a  2  1    . 0,5 0,5 0,5 a 1 a 1 a   0,5 0,5
a  a  2  a  a  2 1 2  .  0,5 a 1 a a 1 Chọn D. TOANMATH.com Trang 9 3      x x  x 
Ví dụ 3: Rút gọn biểu thức 
 (với x  0, x  1) ta được  4 3  4 3 x 1 x 1      x   x     4  4 x  1 x 1       A. 2 x . B. 2 x . C. 3 x . D. 3 x . Hướng dẫn giải. 3      x x  x  Ta có:    4 3  4 3 x 1 x 1      x   x     4  4 x  1 x 1       3    x x  x      4 2 4 x  x   x 4 2 4 1 x  x 1 x    3    x    x  x x x     3 1        x   x 1 1 x  3. 4 4   1 x      Chọn C.
Bài toán 2. Tính giá trị biểu thức Phương pháp giải Công thức đặc biệt Thật vậy, ta có:   x a a f x 
thì f  x  f 1 x  1. x a  a f  x 1 x a a   a a  a. x a  a x a  1  a f x  x a  a
Nên: f x  f 1 x 1. Ví dụ mẫu x Ví dụ 1: Cho f  x 2018 
. Tính giá trị biểu thức sau đây ta được 2018x  2018  1   2   2018  S  f  f      ... f 2019 2019  2019        A. S  2018. B. S  2019. C. S  1009. D. S  2018. TOANMATH.com Trang 10 Hướng dẫn giải 2018 Ta có: f 1 x 
 f x  f 1 x 1 2018x  2018  1   2   2018   1   2018  Suy ra S  f  f     ... f  f  f   2019 2019
 2019   2019   2019             2   2017   1009   1010   f  f  ... f  f          1009.  2019   2019   2019   2019  Chọn C. 5  3x  3x
Ví dụ 2: Cho 9x  9x  23. Tính giá trị của biểu thức P  ta được 1 3x  3x 3 1 5 A. 2. B. . C. . D.  . 2 2 2 Hướng dẫn giải x  x 2 3  3  5
Ta có: 9x  9x  23  3x  3x   25   3x  3x  5   loaïi 5 3x 3x  5 5 5 Từ đó, thế vào P     1 3x 3x  . 1 5 2 Chọn D.
Bài tập tự luyện dạng 1
Câu 1: Khẳng định nào sau đây đúng? m A. n
a xác định với mọi a  \  0 ; n   . B. n n m a  a ; a   .  m C. 0 a  1; a   . D. n m n a  a ; a   ;  m,n .  2 2 2 3 a  b
Câu 2: Rút gọn biểu thức 
 (với a  0,b  0 và 2 3
a  b ) được kết quả a  b  1 2 2 3 2 3 a  b 2 2a A. 2. B. 2 2a . C. . D. . 2 3 a  b 2 3 a  b
Câu 3: Cho số thực dương a. Rút gọn 3 4 5 P  a a a a ta được 25 37 53 43 A. 13 a . B. 13 a . C. 36 a . D. 60 a . Câu 4: Viết biểu thức 3 2 P  .
a a . a a  0 dưới dạng lũy thừa với số mũ hữu tỉ ta được 5 5 11 A. 3 P  a . B. 6 P  a . C. 6 P  a . D. 2 P  a . TOANMATH.com Trang 11 b a m  a  Câu 5: Viết biểu thức 5 3
,a,b  0 về dạng lũy thừa ta được m bằng a b  b    2 4 2 2  A. . B. . C. . D. . 15 15 5 15 5
Câu 6: Rút gọn biếu thức 3 3
Q  b : b với b  0 ta được 5 4 4 A. 2 Q  b . B. 9 Q  b . C. 3 Q b  . D. 3 Q  b .
Câu 7: Giả sử a là số thực dương, khác 1 và 3
a a được viết dưới dạng a .. Giá trị của  là 11 5 2 1 A.   . B.   . C.   . D.   . 6 3 3 6 1
Câu 8: Rút gọn biểu thức 3 6
P  x . x với x  0 ta được 1 2 A. 2 P  x . B. P  x. C. 8 P  x . D. 9 P  x .
Câu 9: Cho a, b là các số thực dương. Viết biểu thức 12 3 3
a b dưới dạng lũy thừa với số mũ hữu tỉ ta được 3 1 1 1 1 1 1 3 A. 4 2 a b . B. 4 9 a b . C. 4 4 a b . D. 4 4 a b . 2
Câu 10: Cho a là một số dương, viết 3 a
a dưới dạng lũy thừa với số mũ hữu tỉ ta được 7 1 A. 6 a . B. 3 a . C. 6 a . D. 2 a .
Câu 11: Cho a  0. Đẳng thức nào sau đây đúng? 3 5 a 7 A. 3 4 a a  a. B. 6  a . C. a 4 2 6  a . D. 7 5 5 a  a . 3 2 a   a   3 1 3 1
Câu 12: Cho biểu thức P 
, với a  0. Mệnh đề nào dưới đây đúng? 53 4 5 a .a 1 3 A. 2 P  a . B. P  . a C. 2 P  a . D. 3 P  a . 2 3 a 3 2 3 a  a 
Câu 13: Cho hàm số f a 
với a  0,a  1. Giá trị của M  f  2018 2017  là 1 8 a 8 3 8 1 a  a  A. 2018 M  2017 1. B. 1009 M  2017 . C. 1009 M  2017 1. D. 1009 M  2017 1. 2017 2016
Câu 14: Giá trị của biểu thức P  7 4 3 7 4 3 bằng A. 1. B. 7  4 3. C. 7  4 3. D.   2016 7 4 3 . 2017 2016
Câu 15: Giá trị của biểu thức P  9  4 5 9  4 5 bằng TOANMATH.com Trang 12 A. 1. B. 9  4 5. C. 9  4 5. D.   2017 9 4 5. . 10  2x  2x
Câu 16: Cho 4x  4x  14. Giá trị của biểu thức P  là 3 2x  2x 1 6 A. P  2. B. P  . C. P  . D. P  7. 2 7 4  5x  5x
Câu 17: Cho 25x  25x  7. Giá trị của biểu thức P  là 9  5x  5x 1 A. P  12. B. 1 P  12 . C. P  . D. P  2. 9 x
Câu 18: Cho hàm số f  x 9 
; x   và a, b thỏa a  b  1. Giá trị f a  f b bằng 9x  3 1 A. -1. B. 2. C. 1. D. . 2 x  1   2   98   99 
Câu 19: Cho hàm số f  x 4  . Tổng P  f  f      ... f  f bằng 4x  2 100 100  100  100          99 301 101 149 A. . B. . C. . D. . 2 6 2 3 x
Câu 20: Cho hàm số f x 4 
. Giá trị của biểu thức sau đây bằng 4x  2  1   2   3   2013   2014  S  f  f  f        ... f  f 2015 2015 2015  2015  2015           A. 2014. B. 2015. C. 1008. D. 1007.
Dạng 2: Hàm số lũy thừa
Bài toán 1. Tìm tập xác định của hàm số lũy thừa Phương pháp giải 
Ví dụ: Tập xác định của hàm số y  x  x   3 2 6 5
Ta tìm điều kiện xác định của hàm số là y  f   x    ,
 dựa vào số mũ  của nó như sau: A. . B.  \ 1;  5 .
• Nếu  là số nguyên dương thì không có điều C. 1;5. D.  ;   1 5;.
kiện xác định của f  x. Hướng dẫn giải
• Nếu  là số nguyên âm hoặc bằng 0 thì điều Số mũ 3 là số nguyên âm. Do đó, điều kiện xác
kiện xác định là f x  0. x  1 định của hàm số là: 2 x  6x  5  0   .
• Nếu  là số không nguyên thì điều kiện xác x  5 định là f x  0.
Vậy tập xác định của hàm số đã cho là  \ 1;  5 . Chọn B. TOANMATH.com Trang 13 Ví dụ mẫu 
Ví dụ 1: Tập xác định của hảm số y  x  x   1 2 5 5 6 là A.  \ 2;  3 . B.  ;  23;. C. 2;3. D. 3;. Hướng dẫn giải 1
Số mũ  không phải là số nguyên. Do đó, điều kiện xác định của hàm số là: 5 2
x  5x  6  0  x 2;3. Vậy tập xác định của hàm số đã cho là 2;3. Chọn C.
Ví dụ 2: Tập xác định của hảm số sin2018  y x   là A. . B. 0;. C.  \   0 . D. 0;   . Hướng dẫn giải Ta có sin2018  0 y  x
 x nên tập xác định là  \   0 . Chọn C. 
Ví dụ 3: Tập xác định của hảm số y    x  2019 1 là A. .  B. 0;. C.  \   0 . D. 0;  . Hướng dẫn giải
Vì số mũ 2019 là số nguyên âm nên điều kiện xác định của hàm số là
1 x  0, ngoài ra hàm số còn chứa căn thức bậc hai nên x  0. 1
  x  0 luoân ñuùng x   0 Hàm số xác định    x  0. x  0 Vậy D  0;  . Chọn D.
Ví dụ 4: Có bao nhiêu giá trị nguyên của m  2
 018;2018 để hàm số y  x  x  m   5 2 2 1 có tập xác định là ? A. 4036. B. 2018. C. 2017. D. Vô số Hướng dẫn giải
Vì số mũ 5 không phải là số nguyên nên hàm số xác định với x   .  2
 x  2x  m 1  0, x    TOANMATH.com Trang 14    0   a  0 
luoân ñuùng vì a 1 0  1 m   1  0  m  0 m2018;2018 Mà   m 1,2,3,...,201  7 . m 
Vậy có 2017 giá trị nguyên của tham số m thỏa mãn yêu cầu. Chọn C.
Bài toán 2. Tính đạo hàm của hàm số lũy thừa Phương pháp giải
Công thức tính đạo hàm Ví dụ:   • x   1
  x  x  0, ;  x 3    x  2 2 5 6 2 5 .     • u   1
 u  .u với u là biểu thức chứa x. Ví dụ mẫu 
Ví dụ 1: Tìm đạo hàm của hàm số y    x  1 2 4 1 . 1  5 
A. y   1 x  5 2 4 .
B. y   x 1 x  5 2 4 . 4 2 5  1  C. y  x 1 x  5 2 4 . D. y  x 1 x  5 2 4 . 2 2 Hướng dẫn giải 1 5 5  1 1  1  1   Ta có: y    2 1 x  4 . 2 1 x     2 1 x  4 . 2  x  x  2 1 x  4 . 4 4 2 Chọn D.
Ví dụ 2: Tìm đạo hàm của hàm số y    x4 2 3cos2 . A. y     x3 24 2 3cos2 sin 2x. B. y     x3 12 2 3cos2 sin 2x. C. y    x3 24 2 3cos2 sin 2x. D. y    x3 12 2 3cos2 sin 2x. Hướng dẫn giải 3 Ta có: y
42 3cos2x 2 3cos2x     3
 42  3cos2x 6sin2x TOANMATH.com Trang 15     x3 24 2 3cos2 sin2x. Chọn A.
Ví dụ 3: Đạo hàm của hàm số y  x x23 sin là 2 1  2 
A. y  x sin x 13 .
B. y  x sin x 3 .sin x  x cos x. 3 3 2 sin x  x cos x 2  C. y  . .
D. y  x sin x 13 .cos x. 3 2 2 3 x sin x 3 Hướng dẫn giải 2 1 2 1   2 
Ta có: y  x sin x3 .x sin x  x  sin x 3 .sin x  x cos x. 3 3 Chọn B. 
Ví dụ 4: Đạo hàm của hàm số y    x  23 1 là 1  2  1 A. y 
. B. y   1 x  53 . .  3 3x  3 x . 1 x 2 x 3 1  2  C. y 
. D. y   1 x  53 .  3 x  x . 1 x 2 3 Hướng dẫn giải 2 5  1 2  2   1
Ta có: y   1 x  3 .1 x    1 x  3 . 3 3 2 x 5 1  1 1   1 x  3 .  . 3
x 3x3 x. 1 x2 3 Chọn A.
Bài toán 3. Khảo sát sự biến thiên và nhận dạng đồ thị của hàm số lũy thừa Phương pháp giải
Đồ thị của hàm số lũy thừa y a 
trên 0; : Lưu ý: Khi khảo sát hàm số lũy thùa với số mũ cụ thể, ta
phải xét hàm số đó trên toàn bộ tập xác định của nó.
Chẳng hạn: Khảo sát các hàm số 3
y  x trên tập xác định
của nó là ,khảo sát hàm số 2 y x  trên tập xác định D   \  0 . TOANMATH.com Trang 16
Nhận xét: Đồ thị của hàm số lũy thừa luôn đi qua điểm I 1;  1 . Ví dụ mẫu
Ví dụ 1: Cho hàm số y  f x có đồ thị như hình vẽ. Hỏi f x có thể là hàm số nào trong bốn hàm số dưới đây? A. f x 1 3  x . B. f  x 3  x. C. f  x 1 3 x  . D. f  x 3  x . Hướng dẫn giải
Hàm số có tập xác định là D  0;, loại đáp án B, D.
Hàm số đồng biến trên D, loại C. Chọn A. Ví dụ 2: Cho hàm số   2 y f x x  
có đồ thị C. Mệnh đề nào sau đây đúng?
A. Hàm số tăng trên 0;.
B. Đồ thị C không có tiệm cận.
C. Tập xác định của hàm số là .
D. Hàm số không có cực trị. Hướng dẫn giải
Hàm số có tập xác định là D  0;. Ta có:  2 1 y 2x      0, x   D.
Hàm số nghịch biến trên D  Hàm số không có cực trị. Chọn D.
Bài tập tự luyện dạng 2 
Câu 1: Tập xác định D của hàm số y  x  x   2 3 2 3 4 là TOANMATH.com Trang 17 A. D   \ 1;  4 . B. D   ;  1  4;   . C. D  .  D. D   ;    1  4;.
Câu 2: Trong các hàm số sau đây, hàm số nào có tập xác định D   ?    1    A. y  2  x  . B. y  2    . C. y   2 2  x  . D. y  2  x . 2  x  
Câu 3: Tập xác định D của hàm số  x  x 4 2 y 3 là A. 0;3. B. D   \ 0;  3 . C. D  .  D. D   ;  03;.
Câu 4: Tập xác định của hàm số  x  x2019 2 2020 y 4 là A.  ;  0  4;   . B.  ;  0 4;. C. 0;4. D.  \ 0;  4 .
Câu 5: Tập xác định D của hàm số y    x0 3 là A. D   ;  3. B. D   ;  3.  C. D   \   3 . D. D  .  sin  2  x  3 
Câu 6: Tập xác định D của hàm số y   là  x 2    A. D   \ 2;  3 . B. D  , 2   3,  . C. D   \   3 . D. D   ;  23;. 
Câu 7: Tập xác định D của hàm số e y  x   2 x   1 là A. D  1;  1 . B. D   \ 1;  1 . C. D  1;. D. D  . 
Câu 8: Có bao nhiêu giá trị nguyên của tham số m 50;50 để hàm số y  x  x  m  1 2 2 2 1 có tập xác định  ? A. 99. B. 49. C. 50. D. 100. 
Câu 9: Biết tham số m  ;
a b,với a  b thì hàm số y  x  x  m  m   3 2 2 2 2 2 5 5 có tập xác định là Giá trị tổng a  b là A. 5. B. 5. C. 3. D. 3  .
Câu 10: Tất cả các giá trị thực của m để hàm số y  x  x  m2019 2 2020 4 xác định trên  là A. m  4. B. m  4. C. m  4. D. m  4.
Câu 11: Tất cả các giá trị thực của m để hàm số  x  x  m 2020 2 y 2 xác định trên  là A. m  1. B. m  1. C. m  1. D. m  1. 
Câu 12: Tất cả các giá trị thực của tham số m sao cho hàm số y  x  mx  sin 2 3 1
có tập xác định  là TOANMATH.com Trang 18 A. 2  m  2. B. m  2  m  2. C. 1  m  1. D. 2  m  2.  2 2  x  2mx  m  2 
Câu 13: Tất cả các giá trị thực của m để hàm số y   xác định trên  là 2  x   3  A. 1  m  2. B. 1  m  2. C. 2  m  2. D. 1  m  2. 
Câu 14: Phương trình tiếp tuyến của C 2
: y  x tại điểm M có hoành độ x  1 là 0 0      A. y  x 1. B. y  x  1. C. y   x  1. D. y   x  1. 2 2 2 2 2  2 1 
Câu 15: Trên đồ thị của hàm số 2
y  x lấy điểm M có hoành độ x 2 
. Tiếp tuyến của C tại điểm 0 0 M có hệ số góc bằng 0 A.   2. B. 2 . C. 2 1. D. 3.
Câu 16: Cho các hàm số lũy thừa y x , y x , y x   
có đồ thị như hình vẽ. Khẳng định nào sau đây đúng? A.     . B.     . C.      . D.      .
Câu 17: Cho , là các số thực. Đồ thị các hàm số y x , y x  
trên khoảng 0; được cho trong
hình vẽ bên. Khẳng định nào sau đây là đúng? A. 0    1  . B.   0  1  . C. 0    1  . D.   0  1  .
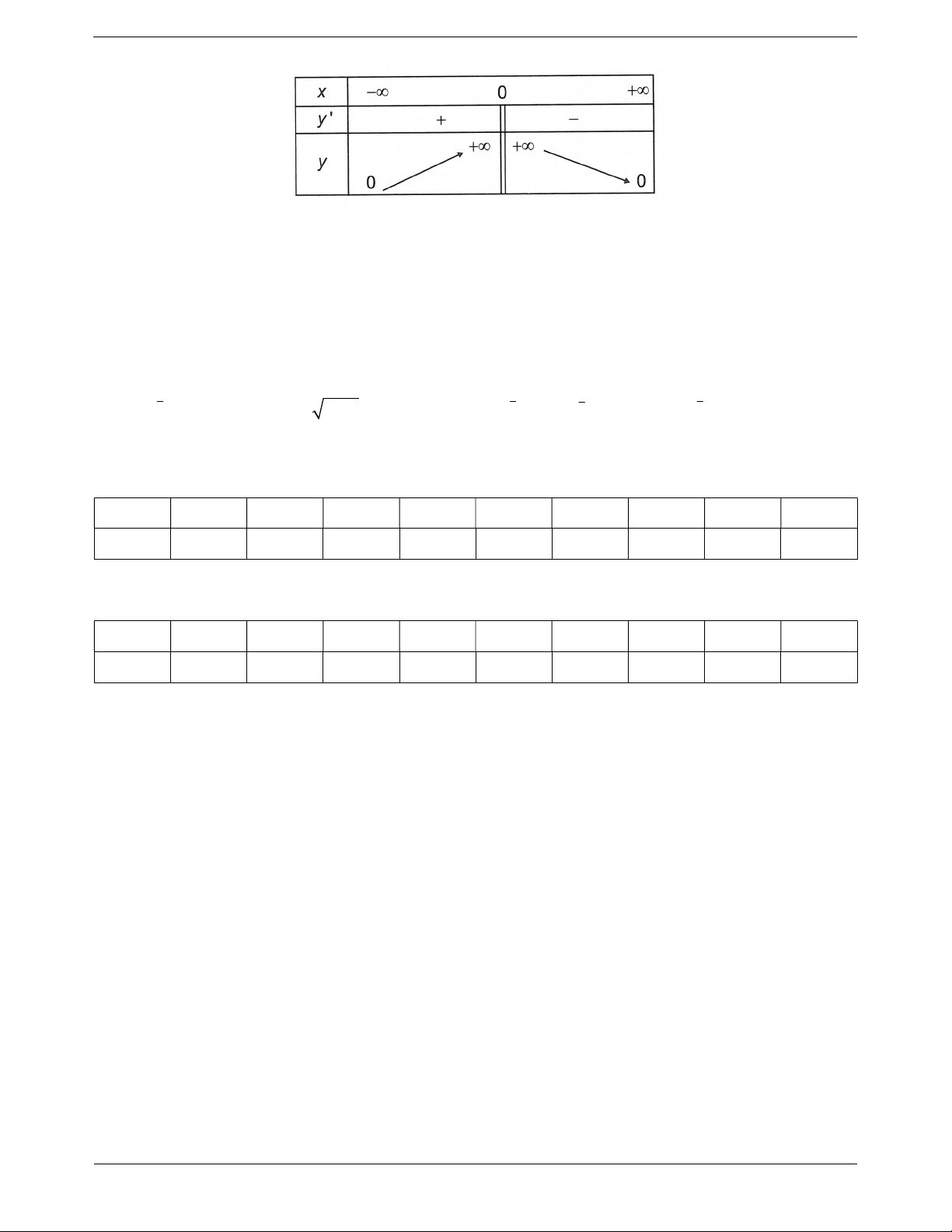
Câu 18: Bảng biến thiên dưới đây là của hàm số nào? TOANMATH.com Trang 19 A. 3 y  x . B. y  log x. C. 2 y x  . D. 3x y  . 3 Câu 19: Cho hàm số 4 y x 
. Mệnh đề nào sau đây là sai?
A. Hàm số có một trục đối xứng.
B. Đồ thị hàm số đi qua điểm 1;  1 .
C. Đồ thị hàm số có hai đường tiệm cận.
D. Đồ thị hàm số có một tâm đối xứng.
Câu 20: Trong các phương trình sau đây, phương trình nào có nghiệm? 1 1 1 1 A. 6 x 1  0. B. x  4  5  0. C. 5 x  x  6 1  0. D. 4 x 1  0 ĐÁP ÁN Dạng 1. Lũy thừa 1-A 2-D 3-D 4-C 5-D 6-D 7-C 8-B 9-C 10-A 11-B 12-B 13-D 14-C 15-C 16-C 17-B 18-C 19-A 20-D
Dạng 2. Hàm số lũy thừa 1-D 2-C 3-B 4-B 5-C 6-A 7-C 8-B 9-B 10-A 11-D 12-D 13-A 14-B 15-A 16-B 17-A 18-C 19-D 20-A TOANMATH.com Trang 20