Bài Giảng Lý Thuyết Đồ Thị Môn Cấu trúc rời rạc | Trường Cao đẳng Công thương Thành phố Hồ Chí Minh

lOMoAR cPSD| 58797173    BÀI GIẢNG
LÝ THUYẾT ĐỒ THỊ
BIÊN SOẠN: NGUYỄN VĂN LỄ LÂM THỊ HỌA MI
BỘ MÔN: HỆ THỐNG THÔNG TIN LƯU HÀNH NỘI BỘ TPHCM 09/2013 lOMoAR cPSD| 58797173 MỤC LỤC
CHƯƠNG 1: ĐẠI CƯƠNG VỀ ĐỒ THỊ ....................................................................... 5
1.1. CÁC KHÁI NIỆM CƠ BẢN ................................................................................... 5
1.1.1. Đồ thị ................................................................................................................. 5
1.1.2. Đường i, chu trình, ối chu trình ..................................................................... 8
1.1.3. Tính liên thông .................................................................................................. 9
1.2. CÁC DẠNG ĐỒ THỊ ............................................................................................ 10
1.3. MỘT SỐ PHÉP BIẾN ĐỔI TRÊN ĐỒ THỊ ......................................................... 16
1.3.1. Phép phân chia sơ cấp ..................................................................................... 16
1.3.2. Phép ẳng cấu ồ thị ........................................................................................ 17
1.3.3. Phép toán trên ồ thị ........................................................................................ 17
1.3.3.1. Phép hội.................................................................................................... 17 1.3.3.2. Phép giao
.................................................................................................. 17
1.4. SẮC SỐ CỦA ĐỒ THỊ .......................................................................................... 18
1.5. KẾT CHƯƠNG...................................................................................................... 19
1.6. BÀI TẬP ................................................................................................................ 19
CHƯƠNG 2: BIỂU DIỄN ĐỒ THỊ .............................................................................. 23
2.1. MA TRẬN KỀ ....................................................................................................... 23
2.1.1. Định nghĩa ....................................................................................................... 23
2.1.2. Bậc và ỉnh kề dựa trên ma trận kề ................................................................. 24
2.2. MA TRẬN TRỌNG SỐ ........................................................................................ 25
2.2.1. Định nghĩa ....................................................................................................... 25
2.2.2. Bậc và ỉnh kề dựa trên ma trận trọng số ........................................................ 26
2.3. MA TRẬN LIÊN KẾT .......................................................................................... 26 lOMoAR cPSD| 58797173
2.3.1. Định nghĩa ....................................................................................................... 26
2.3.2. Bậc và ỉnh kề dựa trên ma trận liên kết ......................................................... 27
2.4. DANH SÁCH CẠNH ............................................................................................ 29
2.4.1. Định nghĩa ....................................................................................................... 29
2.4.2. Bậc và ỉnh kề dựa trên danh sách cạnh .......................................................... 29
2.5. DANH SÁCH KỀ .................................................................................................. 30
2.5.1. Định nghĩa ....................................................................................................... 30
2.5.2. Bậc và ỉnh kề dựa trên danh sách kề ............................................................. 31
2.6. KẾT CHƯƠNG...................................................................................................... 31
2.7. BÀI TẬP ................................................................................................................ 32
CHƯƠNG 3: CÁC THUẬT TOÁN TÌM KIẾM TRÊN ĐỒ THỊ ................................ 34
3.1. TÌM KIẾM THEO CHIỀU SÂU ........................................................................... 34
3.2. TÌM KIẾM THEO CHIỀU RỘNG ........................................................................ 37
3.3. MỘT SỐ ỨNG DỤNG .......................................................................................... 39
3.3.1. Tìm ường i giữa hai ỉnh ............................................................................. 39
3.3.2. Tìm các thành phần liên thông của ồ thị ....................................................... 41
3.4. KẾT CHƯƠNG...................................................................................................... 42
3.5. BÀI TẬP ................................................................................................................ 42 CHƯƠNG 4: CÂY
........................................................................................................ 44
4.1. ĐỊNH NGHĨA ........................................................................................................ 44
4.1.1. Cây ................................................................................................................... 44
4.1.2. Định nghĩa cây tối ại ...................................................................................... 47 lOMoAR cPSD| 58797173
4.2. CÂY KHUNG NGẮN NHẤT ............................................................................... 48
4.2.1. Định nghĩa ....................................................................................................... 49
4.2.2. Thuật toán Kruskal .......................................................................................... 50
4.2.3. Thuật toán Prim ............................................................................................... 51
4.3. CÂY CÓ HƯỚNG ................................................................................................. 53
4.3.1. Định nghĩa cây có hướng ................................................................................. 53
4.3.2. Định nghĩa: ...................................................................................................... 55
4.3.3. Phép duyệt cây (Cây nhị phân) ........................................................................ 56
4.3.4. Ký pháp Balan ................................................................................................. 57
4.4. KẾT CHƯƠNG...................................................................................................... 60
4.5. BÀI TẬP ................................................................................................................ 60
CHƯƠNG 5: CÁC BÀI TOÁN VỀ ĐƯỜNG ĐI ......................................................... 62
5.1. ĐỒ THỊ EULER .................................................................................................... 62
5.1.1. Bài toán về 7 cây cầu ở Konigsberg (Bài toán Euler) ..................................... 62
5.1.2. Định nghĩa: ...................................................................................................... 63
5.1.3. Giải thuật xây dựng chu trình Euler ................................................................ 66
5.1.4. Thuật toán Fleury (Thuật toán Flor) ể tìm chu trình Euler ............................ 68
5.2. ĐỒ THỊ HAMILTON ............................................................................................ 68
5.2.1. Định nghĩa ....................................................................................................... 68
5.2.2. Thuật toán xây dựng chu trình Hamilton ........................................................ 69
5.3. BÀI TOÁN ĐƯỜNG ĐI NGẮN NHẤT ............................................................... 71 lOMoAR cPSD| 58797173
5.3.1. Các khái niệm mở ầu ..................................................................................... 71
5.3.2. Định nghĩa bài toán tìm uờng i ngắn nhất ................................................... 71
5.3.3. Định nghĩa ma trận khoảng cách (trọng số) .................................................... 72
5.3.4. Thuật toán Dijkstra .......................................................................................... 72
5.3.5. Thuật toán Ford – Bellman .............................................................................. 73
5.3.6. Thuật toán Floyd .............................................................................................. 75
5.4. KẾT CHƯƠNG...................................................................................................... 77
5.5. BÀI TẬP ................................................................................................................ 77
TÀI LIỆU THAM KHẢO ............................................................................................. 80 lOMoAR cPSD| 58797173
Chương 1: Đại cương về ồ thị 5 CHƯƠNG 1
ĐẠI CƯƠNG VỀ ĐỒ THỊ Mục tiêu:
Hiểu ược các khái niệm, ịnh nghĩa liên quan ến ồ thị có hướng và ồ thị vô hướng
như bậc, các dạng ỉnh, cạnh, liên thông, chu trình, ường i.
Phân biệt ược các dạng ồ thị ặc biệt.
Thực hiện ược các phép biến ổi và các phép toán trên ồ thị.
Mô hình hóa một bài toán thực tế về dạng ồ thị.
Bước ầu nghiên cứu về lý ồ thị cần phải tìm hiểu thật kỹ những khái niệm, ịnh lý, ịnh
nghĩa liên quan ến ồ thị, những kiến thức căn bản này sẽ làm nền tảng trong quá trình nghiên cứu ồ thị.
1.1. CÁC KHÁI NIỆM CƠ BẢN 1.1.1. Đồ thị Định nghĩa
Đồ thị (Graph) là một bộ gồm hai tập hợp V và E, ký hiệu G=(V, E). Trong ó V là
tập hợp các ỉnh (vertices), E là tập hợp các cạnh (edges), mỗi cạnh tương ứng với hai
ỉnh. Cặp ỉnh (x, y) E không có thứ tự ược gọi là cạnh vô hướng, ngược lại gọi là cạnh
có hướng, cạnh có hướng còn ược gọi là cung. Một ồ thị chỉ gồm các cạnh có hướng thì
ược gọi là ồ thị có hướng, ồ thị chỉ gồm các cạnh vô hướng ược gọi là ồ thị vô hướng.
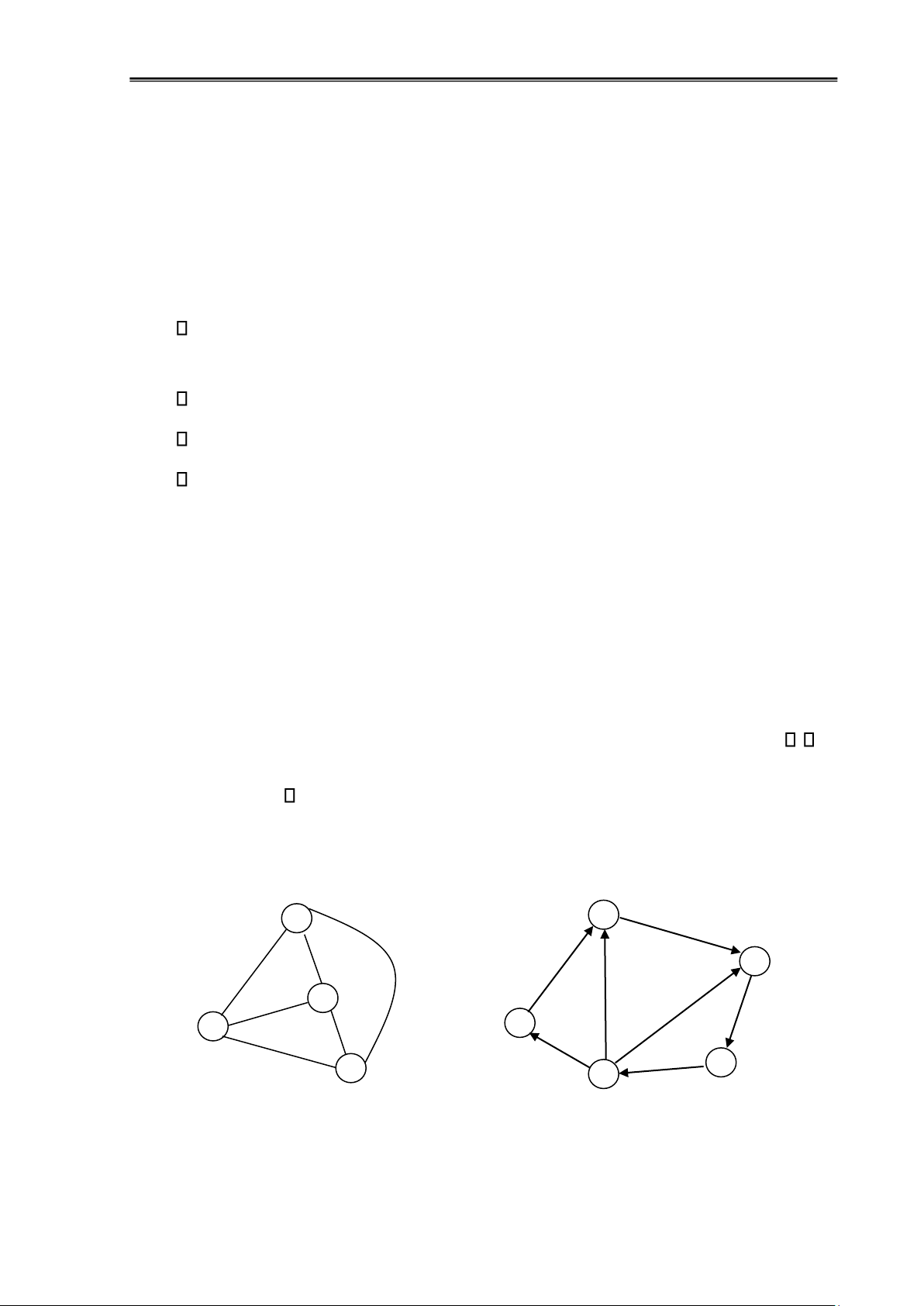
Ví dụ 1.1: Xét hai ồ thị G1=(V1, E1) và G2=(V2, E2) như hình dưới ây: b 2 3 c a 1 d 5 4 G1 G2 lOMoAR cPSD| 58797173
Chương 1: Đại cương về ồ thị 6
Hình 1.1: Đồ thị có hướng và ồ thị vô hướng
Trong hình trên, ồ thị G1 (vô hướng) gồm tập hợp các ỉnh V1={a, b, c, d} và tập hợp các
cạnh E1={(a,b), (a,c), (a,d), (b,c), (b,d), (c,d)}. Đồ thị G2 (có hướng) gồm tập hợp các
ỉnh V2={1, 2, 3, 4, 5} và tập hợp các cung E2={(1,2), (2,3), (3,5), (4,1), (4,2), (4,3), (5,4)}
Cạnh/cung (x,y) có x gọi là ỉnh ầu, y gọi là ỉnh cuối. Nếu ỉnh ầu trùng với ỉnh cuối thì
(x,y) ược gọi là khuyên hay vòng. Nếu hai cạnh/cung có cùng ỉnh ầu và ỉnh cuối thì ược
gọi là hai cạnh/cung song song. Một ồ thị không có khuyên và cũng không có cặp
cạnh/cung song song thì ược gọi là ơn ồ thị (simple graph), ngược lại gọi là a ồ thị (multigraph).
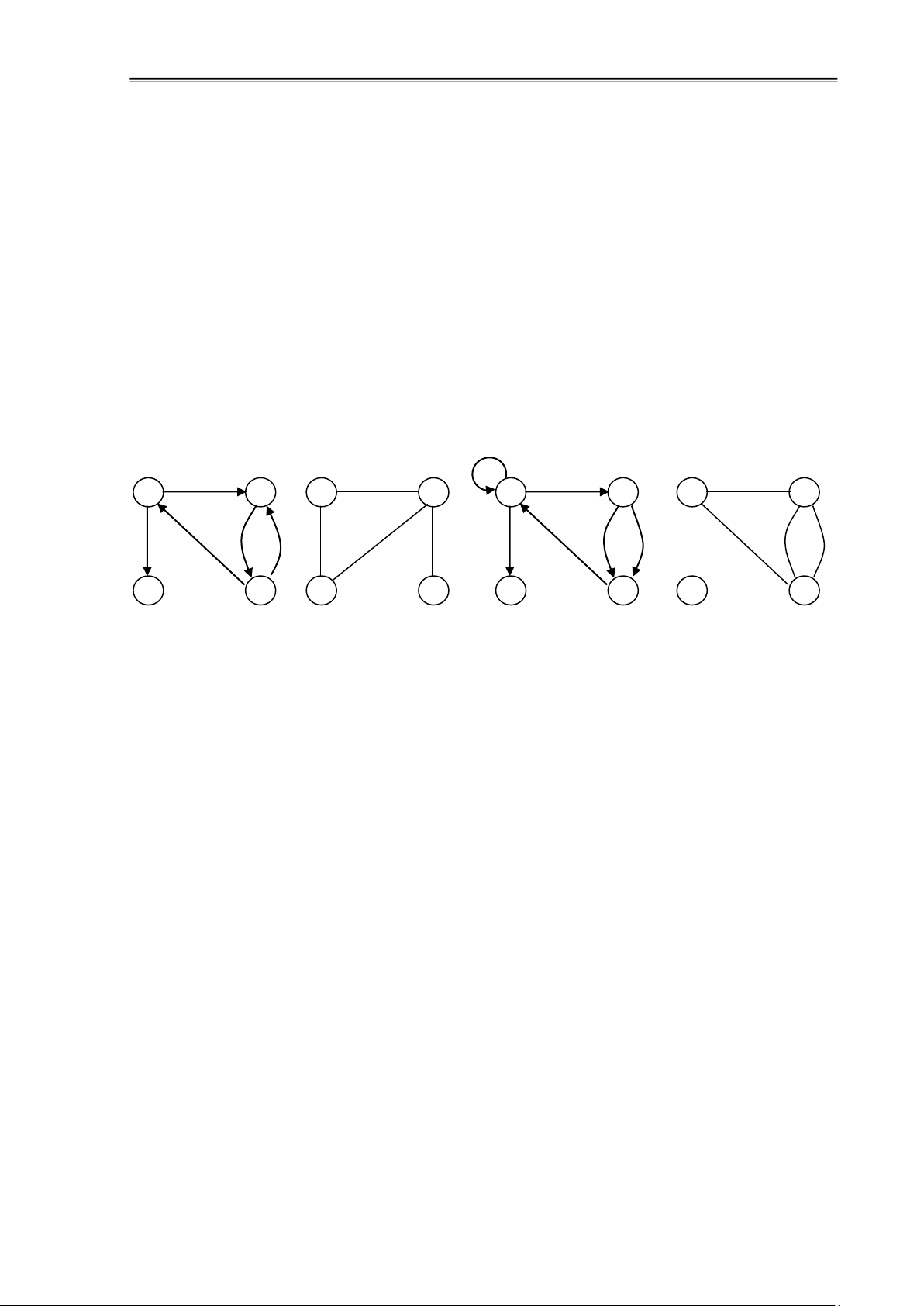
Ví dụ 1.2: Xét các ồ thị sau: 1 2 1 2 1 2 1 2 4 3 4 3 4 3 4 3 a) b) c) d)
Hình 1.2: Đơn ồ thị và a ồ thị Trong
Một ồ thị G=(V,E) ược gọi là ồ thị ơn nếu mỗi cặp ỉnh chỉ có tối a 1 cạnh/cung.
Đa ồ thị: Một ồ thị G=(V, E) ược gọi là a ồ thị nếu có ít nhất một cặp ỉnh ược nối với
nhau bởi nhiều cạnh/cung cùng chiều. Ví dụ 1.2:
Một số thuật ngữ:
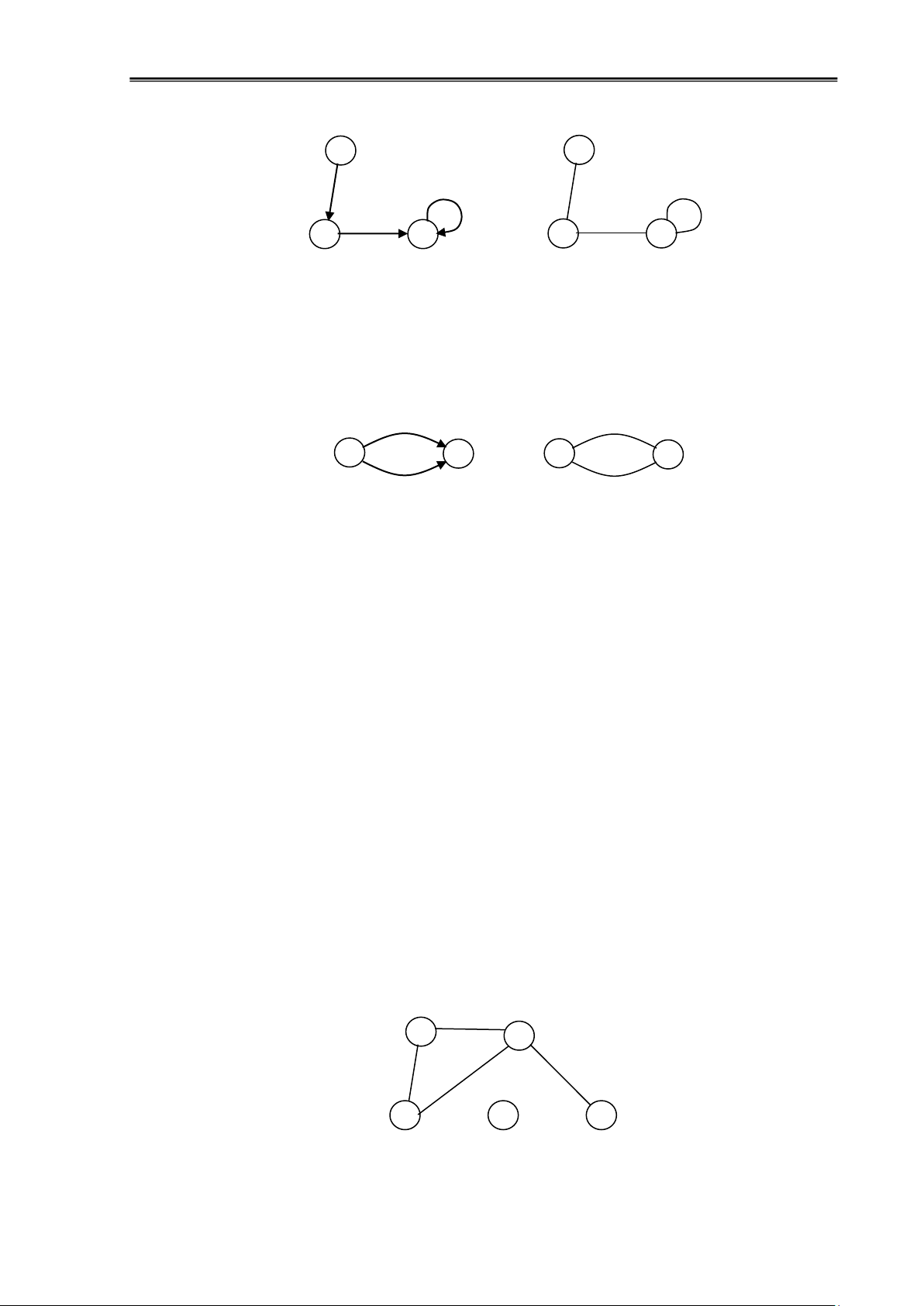
• Khuyên: Cạnh/cung ược gọi là khuyên nếu có ỉnh ầu trùng với ỉnh cuối. Ví dụ 1.3: lOMoAR cPSD| 58797173
Chương 1: Đại cương về ồ thị 7 a a c b c b a) b)
Hình 1.3: Khuyên tại ỉnh b của ồ thị có hướng và vô hướng
• Cạnh/cung song song: Hai cạnh/cung ược gọi là song song (hay lặp) nếu chúng
có 2 ỉnh trùng nhau. Ví dụ 1.4: 1 2 1 2
Hình 1.4: Cạnh có hướng song song và cạnh vô hướng song song
• Đỉnh kề: Nếu (u,v) là một cung của ồ thị có hướng thì ỉnh v ược gọi là kề của ỉnh
u. Nếu (u,v) là một cạnh của ồ thị vô hướng thì ỉnh v kề với ỉnh u và ỉnh u cũng kề với ỉnh v.
• Cạnh kề: Hai cạnh/cung ược gọi là kề nhau nếu chúng có chung một ỉnh.
• Cạnh liên thuộc: Cạnh (u,v) ược gọi là liên thuộc (hay kề) với 2 ỉnh u, v.
• Bậc của ỉnh: Số cạnh liên thuộc với ỉnh v gọi là bậc của v, ký hiệu d(v).
Đối với ỉnh có khuyên thì bậc tính là 2 cho mỗi khuyên. Ví dụ 1.5:
Trong hình 1.2b bậc của ỉnh 1 là 2, bậc của ỉnh 2 là 3, bậc của ỉnh 3 là 1, bậc của ỉnh 4 là 2.
Trong hình 1.3b bậc của ỉnh a là 1, bậc của ỉnh b là 3, bậc của ỉnh c là 2.
• Đỉnh cô lập, ỉnh treo: Trong ồ thị vô hướng ỉnh có bậc 0 gọi là ỉnh cô lập, ỉnh có
bậc 1 gọi là ỉnh treo.
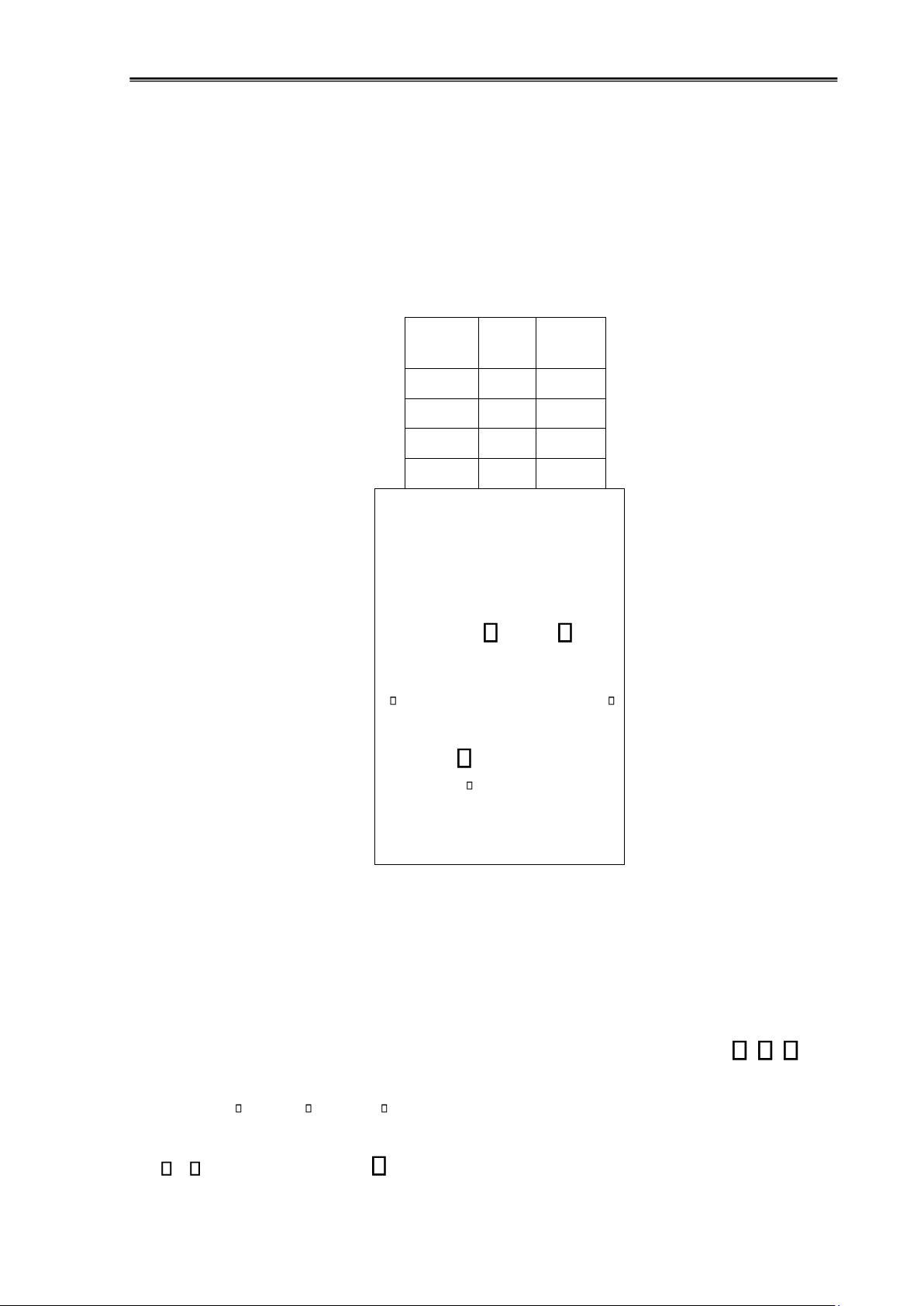
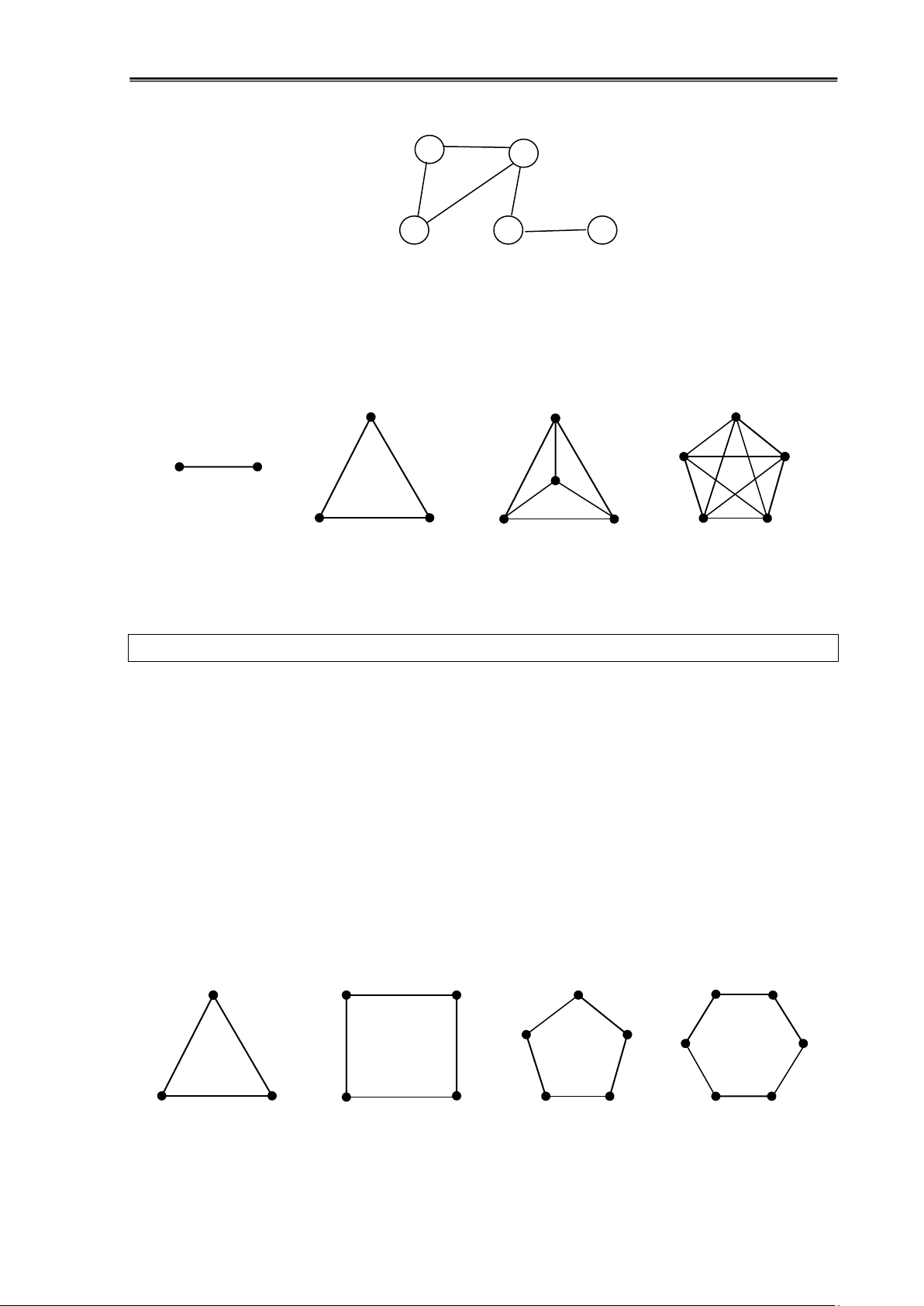
Ví dụ 1.6: Trong ồ thị dưới ây, ỉnh c là ỉnh cô lập (có bậc 0), ỉnh e là ỉnh treo (có bậc 1) a b d c e
Hình 1.5: Đỉnh cô lập và ỉnh treo lOMoAR cPSD| 58797173
Chương 1: Đại cương về ồ thị 8
• Cung vào/ra: Cung (u,v) gọi là cung ra khỏi ỉnh u và là cung vào ỉnh v
• Bán bậc của ỉnh: Số cung vào ỉnh v gọi là bán bậc vào (còn gọi là nữa bậc trong)
của v, ký hiệu là d-(v). Số cung ra khỏi ỉnh v gọi là bán bậc ra (còn gọi là nữa bậc
ngoài) của v, ký hiệu d+(v).
Ví dụ 1.7: Với ồ thị có hướng trong hình 1.2a thì bán bậc ra và bán bậc vào của
các ỉnh ược cho trong bảng dưới ây: Đỉnh v d- d+(v) (v) 1 1 2 2 2 1 3 1 2 4 1 0
Định lý: Cho ồ thị G=(V,E),
m là số cung hay số cạnh của G i) Nếu G có hướng = thì d−( )i d+( )i = m i V i V ii) d i( ) = 2m i V
iii) Số ỉnh bậc lẻ là một số chẵn Chứng minh: i)
Vì mỗi cung (u,v) ược tính bậc một lần bậc ra của ỉnh u và một lần bậc vào của
ỉnh v nên số bậc ra = số bậc vào = số cung. ii)
Mỗi cạnh (u,v) ược tính bậc một lần trong d(u) và một lần trong d(v), như vậy
mỗi cạnh ược tính 2 bậc nên tống số bậc = 2 lần số cạnh. iii)
Gọi V1 ={các ỉnh có bậc lẻ}; V2 ={các ỉnh có bậc chẵn} theo ii) thì d i( )
= d i( ) + d i( ) = 2m(1) i V i V 1 i V 2
Do v V2 thì d(v) chẵn nên d i( )chẵn (vì tổng các số chẵn là số chẵn) lOMoAR cPSD| 58797173
Chương 1: Đại cương về ồ thị 9 i V 2
nên từ (1) suy ra d i( ) là số chẵn, mà d(i) lẻ ( i V1) nên d i( ) là tổng các số lẻ có i V 1 i V 1
giá trị là số chẵn, suy ra số các ỉnh bậc lẻ là một số chẵn.
1.1.2. Đường i, chu trình, ối chu trình
Đường i: Đường i trong ồ thị là một dãy các ỉnh v1, v2, v3,…, vn với (vi, vi+1) E, i=1,
2,.., n. Số cạnh của ường i ược gọi là ộ dài của ường i.
Chu trình: Là ường i mà có ỉnh ầu trùng với ỉnh cuối.
Một ường i hay chu trình ược gọi là ơn nếu không có cạnh/cung bị lặp lại, gọi là sơ cấp
nếu không có ỉnh nào bị lặp lại.
Đối chu trình: Cho ồ thị G=(V,E) và A V, ối chu trình xác ịnh bởi A ký hiệu w(A) ược ịnh nghĩa như sau:
w(A)={e E/ e có một ỉnh trong A}
Một ối chu trình w ược gọi là sơ cấp nếu không tồn tại w’ w sao cho G-w’ không liên
thông (tính liên thông xem phần 1.1.3).
Ví dụ 1.8: Xét ồ thị vô hướng G: 1 2 3 5 4
Hình 1.6: Đồ thị vô hướng
Một số ường i, chu trình và ối chu trình trên ồ thị như sau:
1, 3, 5, 2, 3, 5, 4 ( ường i không ơn vì có cạnh (3,5) bị lặp lại)
1, 2, 3, 5, 2, 4 ( ường i ơn vì không có cạnh nào lặp lại nhưng không sơ cấp vì có ỉnh 2 bị lặp lại)
1, 2, 3, 5, 4 ( ường i sơ cấp)
4, 5, 2, 3, 5, 2, 4 (Chu trình không ơn vì có cạnh (5,2) bị lặp lại)
5, 2, 3, 1, 2, 4, 5 (chu trình ơn vì không có cạnh nào lặp lại nhưng không sơ cấp vì có ỉnh 2 bị lặp lại)
4, 5, 3, 2, 4 (chu trình sơ cấp) lOMoAR cPSD| 58797173
Chương 1: Đại cương về ồ thị 10
A={3,5}, w(A)={(3,1),(3,2),(5,2),(5,4)} không sơ cấp vì có w’={(5,2)}và G-w’ không liên thông.
A={1,2}, w(A)={(1,3),(2,3),(2,5),(2,4)} là sơ cấp vì không tồn tại w’ w ể G-w’ không liên thông.
1.1.3. Tính liên thông
Đồ thị liên thông: Một ồ thị G=(V,E) ược gọi là liên thông nếu hai ỉnh bất kỳ u,v V
luôn có ường i từ u ến v và ngược lại. Một ồ thị vô hướng không liên thông thì luôn chia
ược thành các ồ thị con liên thông, mỗi ồ thị con gọi là một thành phần liên thông.
Liên thông mạnh: Đồ thị G có hướng liên thông thì ược gọi là liên thông mạnh.
Liên thông yếu: Nếu ồ thị G có hướng không liên thông nhưng ồ thị vô hướng tương
ứng liên thông thì G ược gọi là liên thông yếu. Ví dụ 1.9: 3 5 3 4 2 1 4 2 1 G1 G2 3 4 3 4 2 1 2 1 G3 G4
Hình 1.7: Đồ thị liên thông, không liên thông
Trong hình trên, ồ thị G1 có 2 thành phần liên thông, ồ thị G2 liên thông, ồ thị G3 liên
thông mạnh, G4 liên thông yếu
Đỉnh rẽ nhánh: Đỉnh u ược gọi là ỉnh rẽ nhánh nếu việc loại bỏ u cùng với các cạnh
liên thuộc làm tăng số thành phần liên thông.
Cạnh cầu: Cạnh e ược gọi là cạnh cầu nếu việc loại bỏ e làm tăng số thành phần liên thông
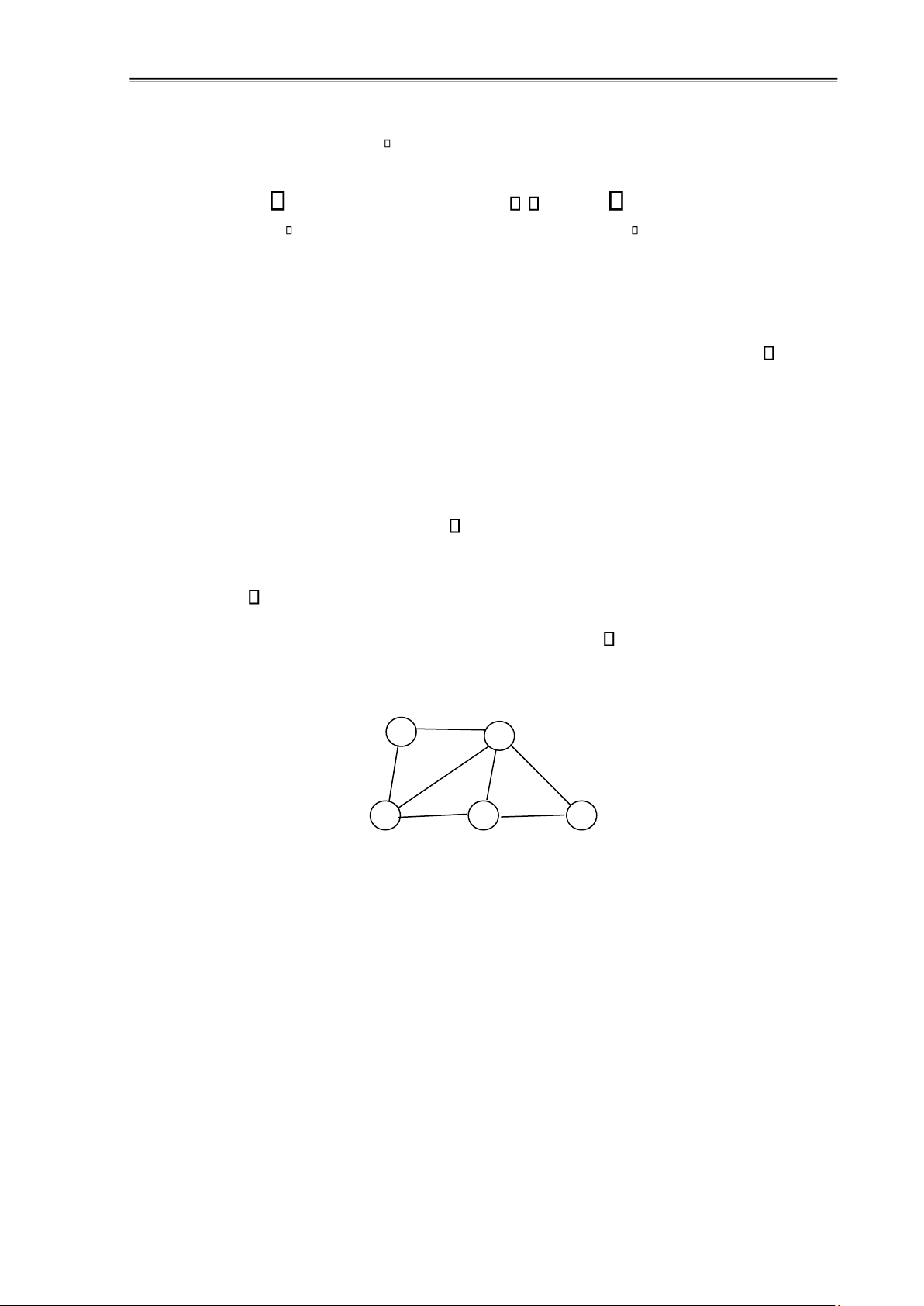
Ví dụ 1.10: Đồ thị trong hình dưới ây có 2 ỉnh rẽ nhánh là 2 và 5. Có 2 cạnh cầu là (2,5), (4,5) lOMoAR cPSD| 58797173
Chương 1: Đại cương về ồ thị 11 1 2 3 5 4
Hình 1.8: Đồ thị có ỉnh rẽ nhánh và cạnh cầu
1.2. CÁC DẠNG ĐỒ THỊ
Đồ thị ủ: Đồ thị ủ cấp n là ơn ồ thị mà giữa 2 ỉnh bất kỳ luôn có một cạnh. Ký hiệu: Kn
Ví dụ 1.11: Hình dưới ây liệt kê một số ồ thị ủ cấp 2, 3, 4, 5 K2 K3 K4 K5
Hình 1.9: Đồ thị ủ cấp 2,3,4,5
Định lý: Đồ thị ủ n ỉnh có n(n-1)/2 cạnh Chứng minh:
Đỉnh thứ 1 sẽ nối với n-1 ỉnh còn lại nên có n-1 cạnh
Đỉnh thứ 2 sẽ nối với n-2 ỉnh còn lại nên có n-2 cạnh ...
Đỉnh thứ n-1 sẽ nối với n-(n-1) ỉnh còn lại nên có 1 cạnh
Số cạnh của Kn là (n-1)+(n-2)+...+1=n(n-1)/2
Đồ thị vòng: Đồ thị vòng n ỉnh (n≥3) là ồ thị gồm các cạnh (v1,v2), (v2,v3),..., (vn-
1,vn), (vn,v1) với v1, v2,...,vn là các ỉnh. Ký hiệu ồ thị là Cn
Ví dụ 1.12: Đồ thị vòng cấp 3,4,5,6 C3 C4 C5 C6 lOMoAR cPSD| 58797173
Chương 1: Đại cương về ồ thị 12 Hình 1.10: Đồ thị vòng
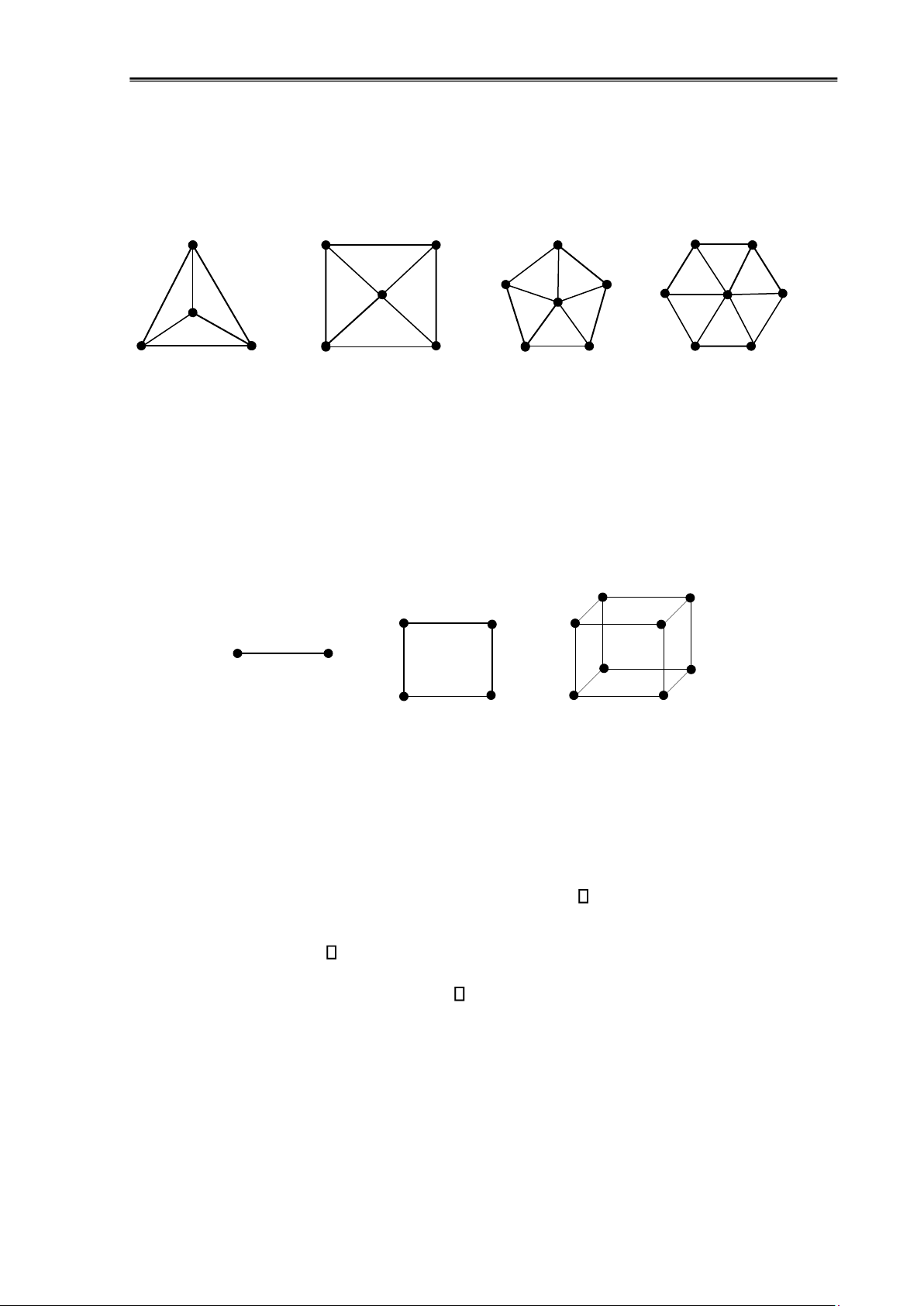
Đồ thị bánh xe: Đồ thị vòng Cn ược bổ sung thêm một ỉnh mới nối với tất cả các ỉnh
còn lại thì ược gọi là ồ thị bánh xe, ký hiệu là Wn Ví dụ 1.13: W3 W4 W5 W6
Hình 1.11: Đồ thị bánh xe
Đồ thị lập phương: Đồ thị lập phương ký hiệu Qn là ồ thị gồm 2n ỉnh, mỗi ỉnh biểu diễn
một chuỗi nhị phân n bit. Trong ó 2 ỉnh kề nhau chỉ khác nhau duy nhất 1 bit. Ví dụ: 1.14: 001 011 010 00 01 000 0 1 101 111 10 11 100 110 Q1 Q2 Q3
Hình 1.12: Đồ thị lập phương
Đồ thị hai phía: Một ồ thị G=(V, E) ược gọi là ồ thị 2 phía nếu như tập ỉnh V của nó có
thể phân hoạch thành 2 tập X và Y sao cho mỗi cạnh e E chỉ nối một ỉnh trong X với
một ỉnh trong Y. (Đồ thị 2 phía còn có thể gọi là ồ thị lưỡng phân, ồ thị 2 phần, ồ thị
phân ôi). Ký hiệu G=(X Y, E)
Đồ thị hai phía ủ: Đồ thị 2 phía G =(X Y, E) ược gọi là 2 phía ủ nếu mỗi ỉnh trong X
ược nối với tất cả các ỉnh trong Y hay ngược lại. Ký hiệu Km,n . Với m là số ỉnh trong
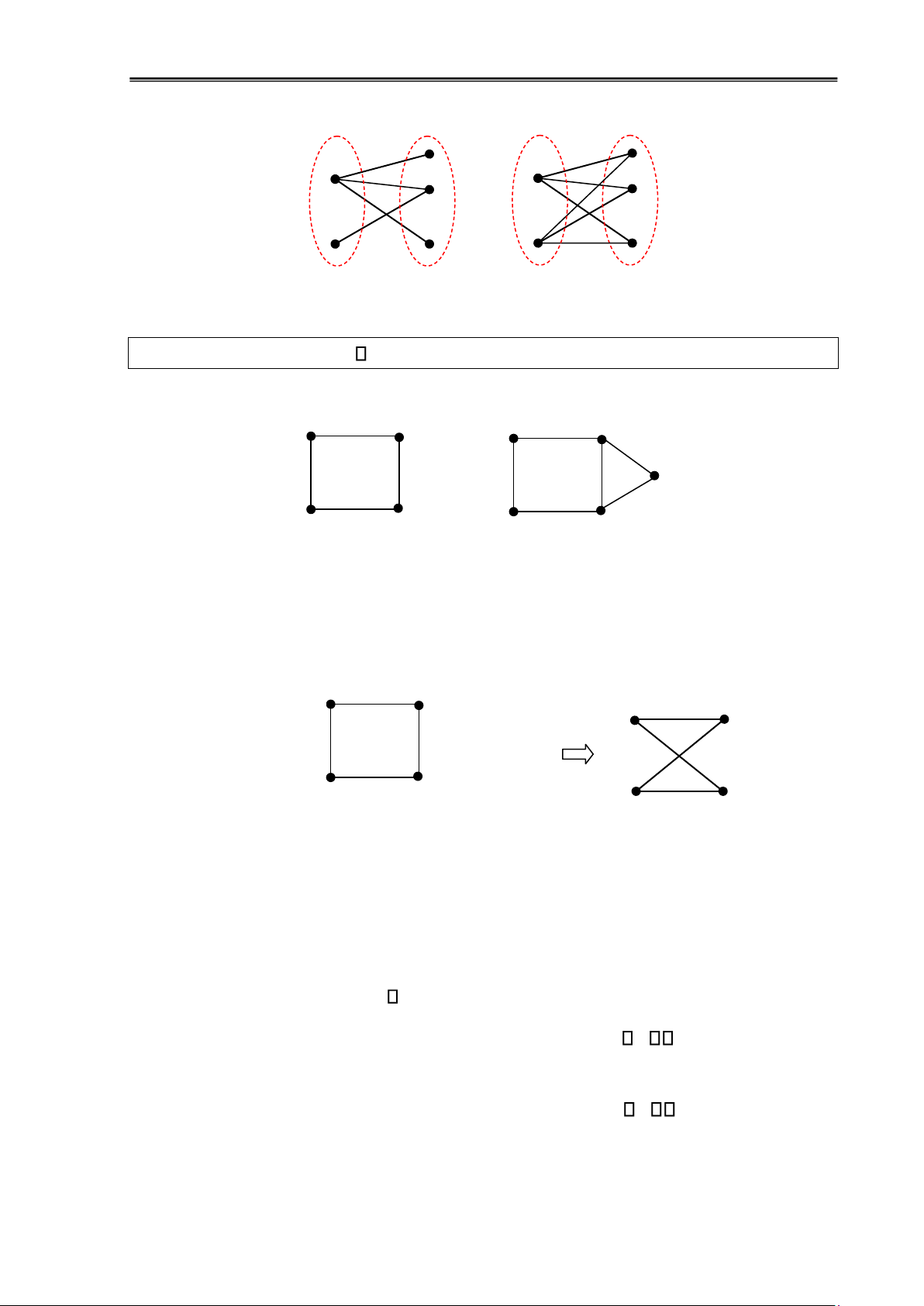
tập X, n là số ỉnh trong tập Y. Ví dụ 1.15: X Y X Y lOMoAR cPSD| 58797173
Chương 1: Đại cương về ồ thị 13 a) b)
Hình 1.13: Đồ thị 2 phía a), ồ thị 2 phía ủ K2,3 b)
Định lý: G là ồ thị hai phía G không có chu trình ộ dài lẻ Ví dụ 1.16: 2 3 2 3 5 1 4 1 4 G1 G2
Hình 1.14: Đồ thị hai phía và không hai phía
Trong hình trên, G1 là ồ thị 2 phía vì không có chu trình ộ dài lẻ, G2 không là ồ thị hai
phía vì có chu trình ộ dài lẻ là 3, 4, 5, 3. Đồ thị G1 có thể biểu diễn lại như sau: 2 3 3 4 1 4 1 2 G1
Hình 1.15: Biểu diễn ồ thị hai phía Thuật
toán kiểm tra ồ thị hai phía:
Xét ơn ồ thị vô hướng G=(V,E)
Bước 1: Chọn một ỉnh bất kỳ v V, ặt X={v}
Bước 2: Tìm tập Y={các ỉnh kề của các ỉnh trong X}. Nếu X Y thì G không phải là
ồ thị hai phía, dừng. Ngược lại qua bước 3
Bước 3: Tìm tập T={các ỉnh kề của các ỉnh trong Y}. Nếu T Y thì G không phải ồ
thị hai phía, dừng. Nếu T=X thì G là ồ thị hai phía, dừng. Ngược lại, gán X=T và lặp lại bước 2. lOMoAR cPSD| 58797173
Chương 1: Đại cương về ồ thị 14
Ví dụ 1.17: Xét 2 ồ thị G1 và G2 như trong hình 1.14
Dùng thuật toán kiểm tra ồ thị G1 và G2 có là hai phía hay không ? Xét ồ thị G1:
Đặt X={1}, Y={2,4}, T={1,3}
X={1,3}, Y={2,4}, T={1,3} dừng vì T=X G là ồ thị hai phía Xét ồ thị G2:
Đặt X={1}, Y={2,4}, T={1,3,5}
X={1,3,5}, Y={2,3,4,5}, dừng vì X Y={3,5} G không là ồ thị hai phía
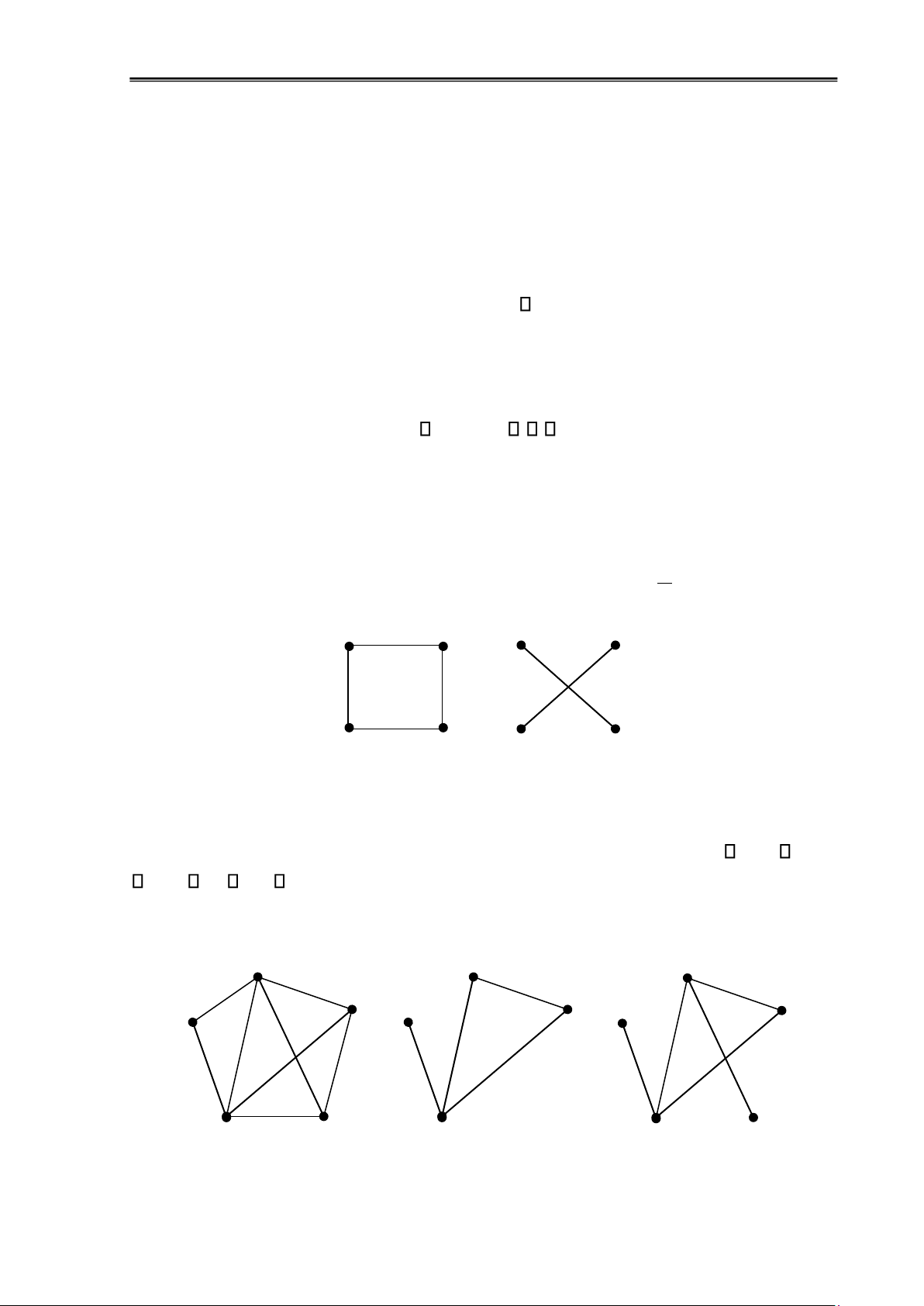
Đồ thị chính qui bậc k: Đồ thị vô hướng G ược gọi là chính qui bậc k (hay còn gọi là
k-ều) nếu mọi ỉnh của G ều có bậc k. Các ồ thị vòng là chính qui bậc 2, ồ thị ủ Kn chính qui bậc n-1.
Đồ thị bù: Hai ơn ồ thị G và G' ược gọi là bù với nhau nếu chúng có chung các ỉnh,
cạnh nào thuộc G thì không thuộc G' và ngược lại. Ký hiệu: G' = G .
Ví dụ 1.18: G và ồ thị bù của G G G’ Hình 1.16: Đồ thị bù
Đồ thị con: Đồ thị G’=(V’,E’) ược gọi là ồ thị con của G=(V,E) nếu V’ V, E’ E và
(u,v) E’ u,v V’. Trường hợp V’=V thì G’ ược gọi là ồ thị bộ phận hay ồ thị khung của G.
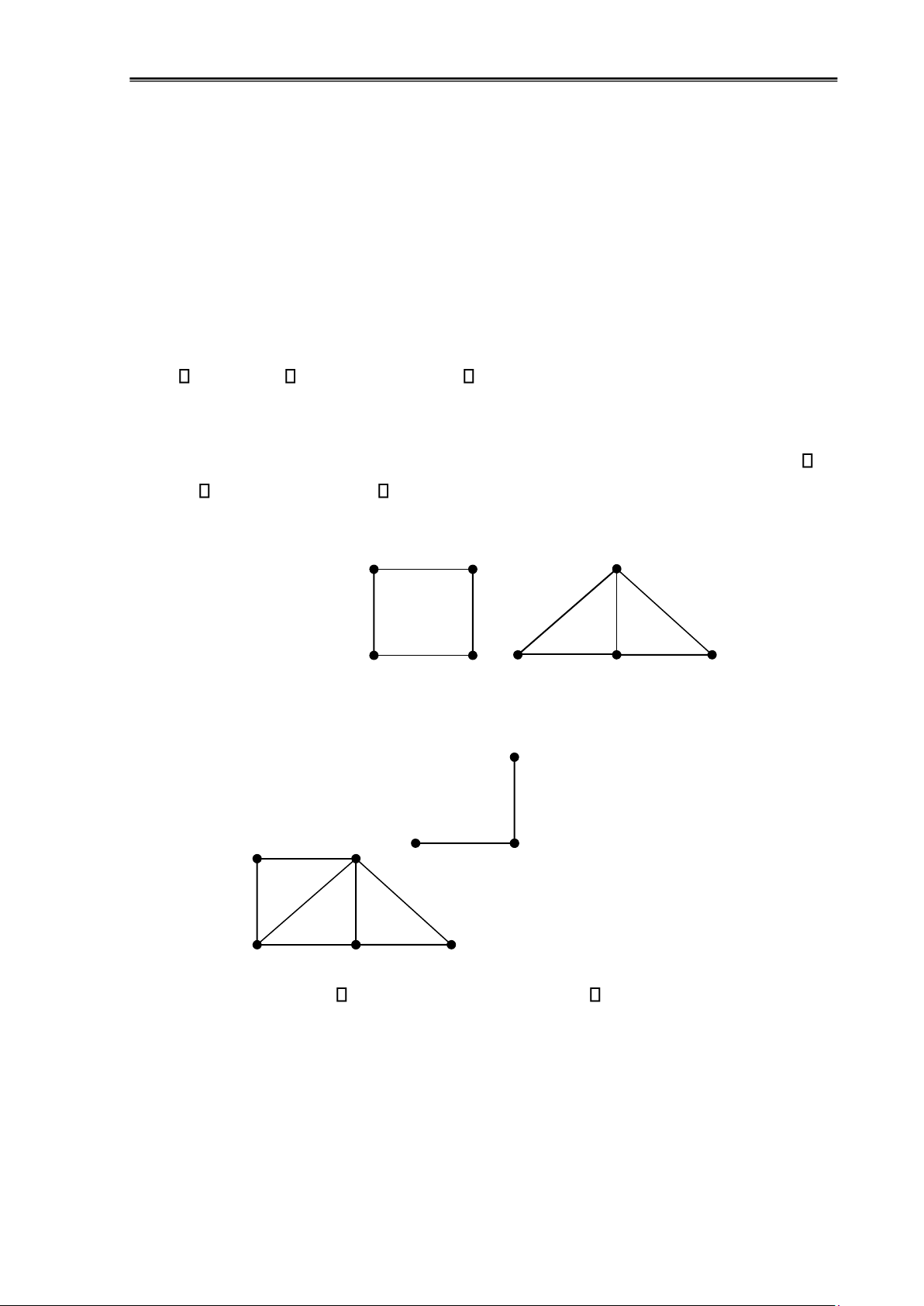
Ví dụ 1.19: Hình 1.16 dưới ây trình bày ồ thị G’ là ồ thị con, G” là ồ thị bộ phận của G 3 3 3 4 4 4 2 2 2 5 5 1 1 1 G G’ G” lOMoAR cPSD| 58797173
Chương 1: Đại cương về ồ thị 15
Hình 1.17: Đồ thị con và ồ thị bộ phận
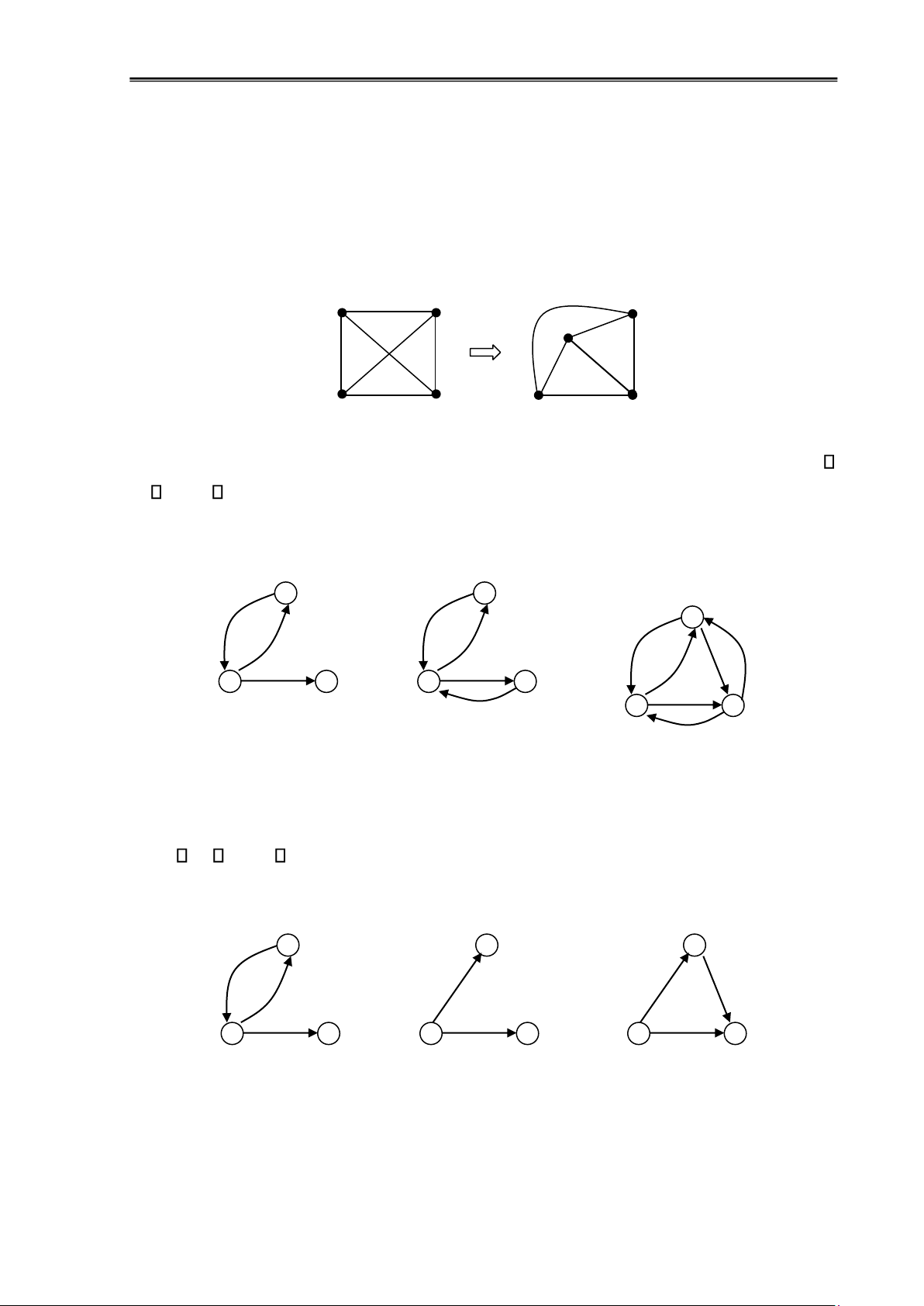
Đồ thị phẳng: Đồ thị G ược gọi là ồ thị phẳng nếu có thể vẽ G trên một mặt phẳng sao
cho các cạnh của nó không cắt nhau trừ ở ỉnh. Cách vẽ như vậy gọi là biểu diễn phẳng của ồ thị.
Ví dụ 1.20: Đồ thị phẳng ược vẽ lại với các cạnh không cắt nhau.
Hình 1.18: Đồ thị phẳng
Đồ thị ối xứng: Cho G=(V, E) là ồ thị có hướng, G ược gọi là ồ thị ối xứng nếu (u,v)
E (v,u) E. G ược gọi là ối xứng ủ nếu giữa 2 ỉnh bất kỳ ều có 2 cung ngược chiều nhau.
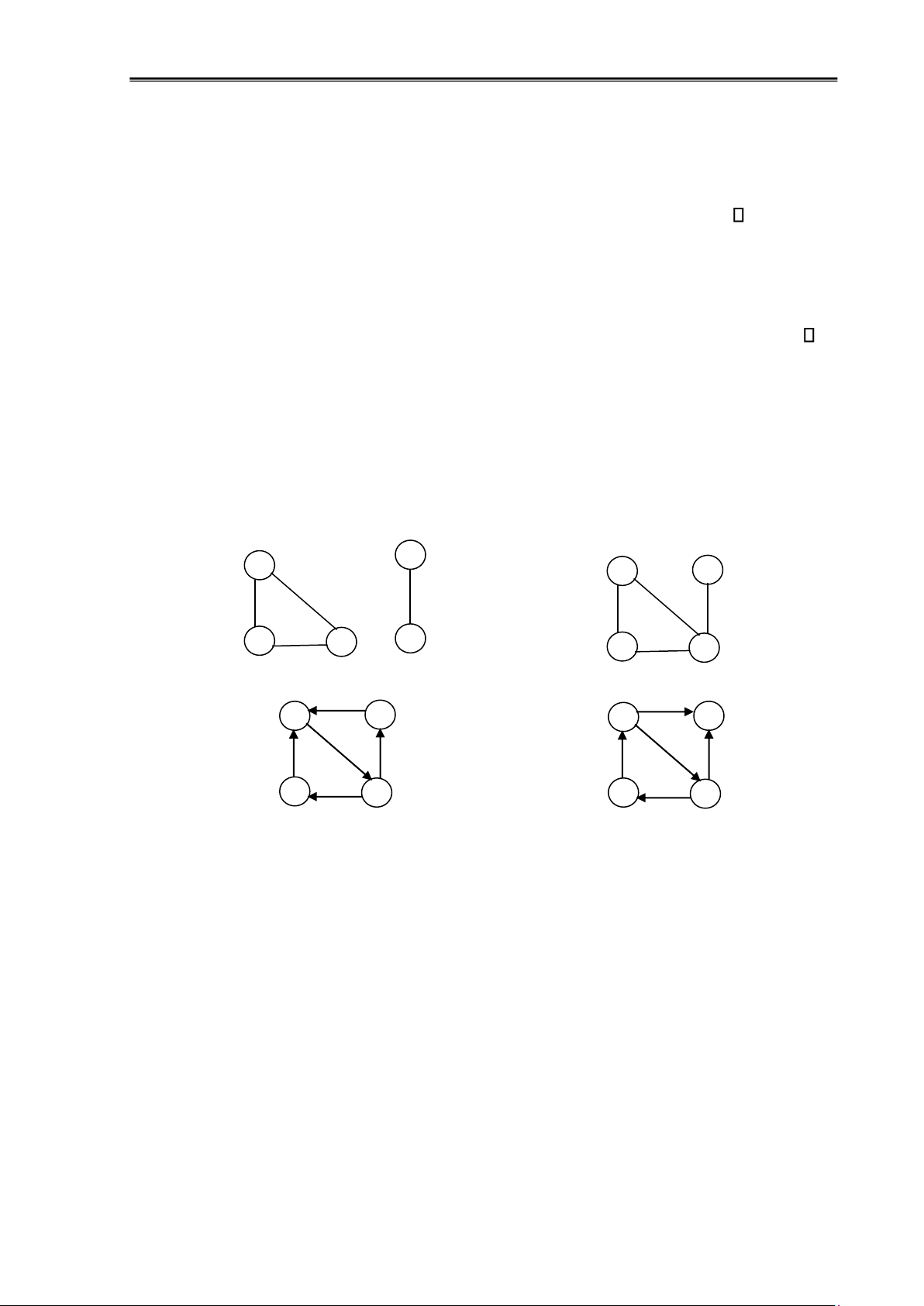
Ví dụ 1.2: Trong hình bên dưới, ồ thị G1 không ối xứng, G2 ối xứng, G3 ối xứng ủ 3 3 G1 G2 3 1 2 1 2 1 2 G 3
Hình 1.19: Đồ thị ối xứng
Đồ thị phản xứng: Cho G=(V,E) là ồ thị có hướng, G ược gọi là ồ thị phản xứng nếu
(u,v) E (v,u) E. G ược gọi là phản xứng ủ nếu G ơn và giữa 2 ỉnh bất kỳ có úng một cung, ký hiệu là Tn
Ví dụ 1.22: G1 không phản xứng, G2 phản xứng, G3 phản xứng ủ 3 3 3 1 2 1 2 1 2 G1 G2 G3
Hình 1.20: Đồ thị phản xứng lOMoAR cPSD| 58797173
Chương 1: Đại cương về ồ thị 16
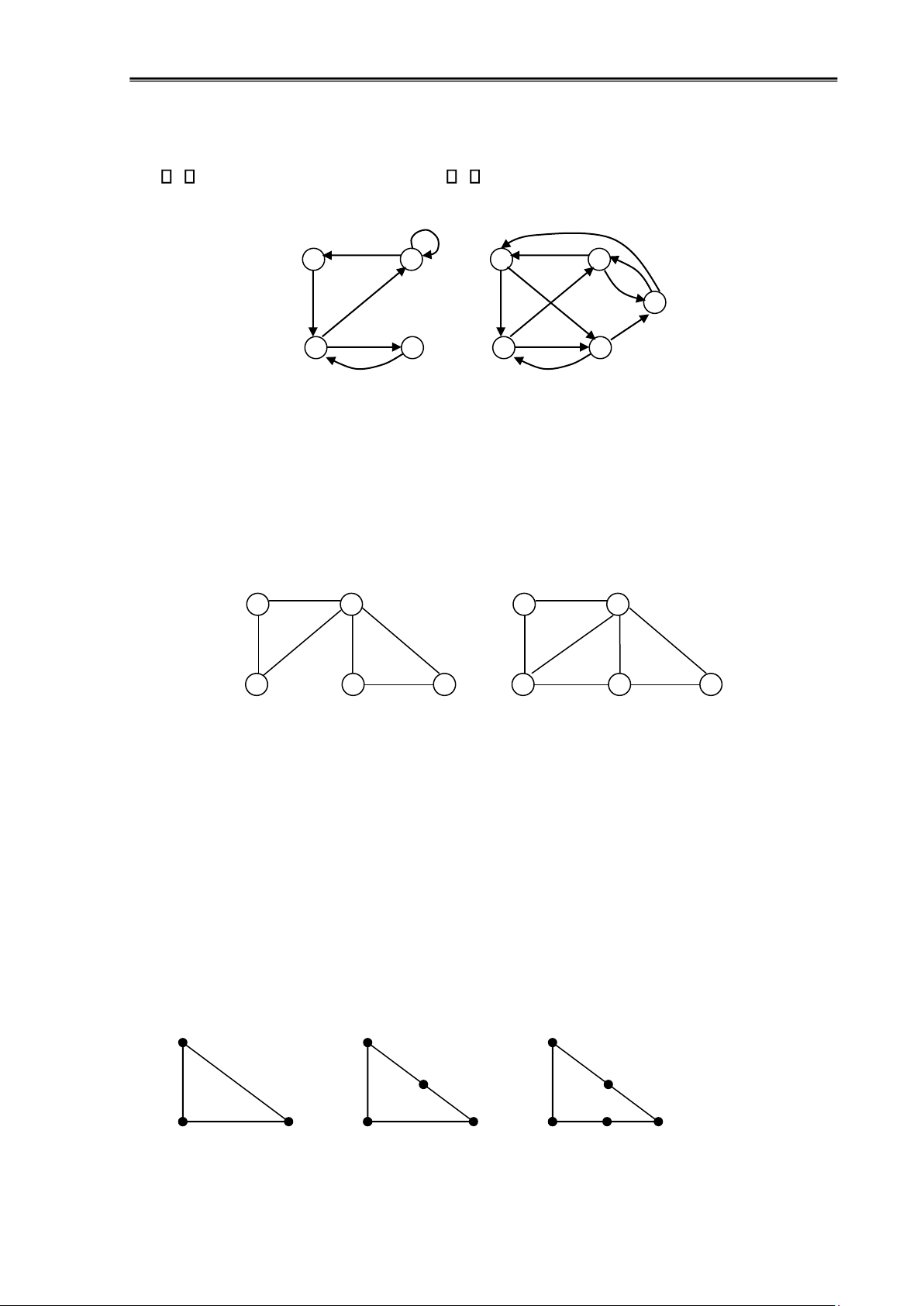
Đồ thị căn bằng: Đồ thị có hướng G ược gọi là căn bằng (hay giả ối xứng) nếu d+(v)=d–
(v) v V. Nếu G ơn và d+(v)=d–(v)=k v V thì G ược gọi là k-ều.
Ví dụ 1.23: Đồ thị G1 căn bằng, G2 là 2-ều 4 3 5 4 3 1 2 1 2 G1 G2
Hình 1.21: Đồ thị căn bằng
Đồ thị song liên thông: Đồ thị G ược gọi là song liên thông nếu G liên thông và không chứa ỉnh rẽ nhánh.
Ví dụ 1.24: Đồ thị G1 liên thông nhưng không song liên thông vì có ỉnh rẽ nhánh là 3, ồ
thị G2 là song liên thông. 2 3 2 3 1 4 5 1 4 5 G1 G2
Hình 1.22: Đồ thị song liên thông
1.3. MỘT SỐ PHÉP BIẾN ĐỔI TRÊN ĐỒ THỊ
1.3.1. Phép phân chia sơ cấp
Phép phân chia sơ cấp là việc chia cạnh (u,v) của một ồ thị G bằng cách loại bỏ
cạnh này khỏi G và thêm vào một ỉnh mới w cùng với hai cạnh (u,w) và (w,v). Hai ồ thị
G1 và G2 ược gọi là ồng cấu (còn gọi là ồng phôi) nếu chúng có ược bằng cách thực hiện
một dãy các phép phân chia sơ cấp trên một ồ thị nào ó. Ví dụ 1.25: G1 G2 G3 lOMoAR cPSD| 58797173
Chương 1: Đại cương về ồ thị 17
Hình 1.23: Dãy các phép phân chia sơ cấp trên ồ thì G1
G2 và G3 là ồng cấu vì có ược bằng cách chia cạch từ G1
Định lý Kuratowski: Đồ thị G là phẳng G không chứa ồ thị con ồng cấu với K3,3 hoặc K5.
Ví dụ 1.26: Theo ịnh lý Kuratowski, ồ thì G dưới ây không phẳng vì có chứa ồ thị con
G1 ồng cấu với K3,3. G2 ược vẽ lại từ G1. Ta nhận thấy rằng khi thực hiện các phép biến
ổi sơ cấp trên G2 bằng cách bỏ i các ỉnh 6,7,8,9 thì G2 sẽ ồng cấu với K3,3 3 3 5 4 1 4 3 7 7 6 5 5 9 8 8 8 7 6 6 2 2 1 9 1 9 4 10 10 2 10 G (Petersen) G1 G2
Hình 1.24: Đồ thi ồng cấu
1.3.2. Phép ẳng cấu ồ thị
Hai ồ thị G1=(V1,E1) và G2=(V2,E2) ược gọi là ẳng cấu nếu tồn tại một song ánh:
f: V1→V2 sao cho (u,v) E1 (f(u),f(v)) E2 Ví
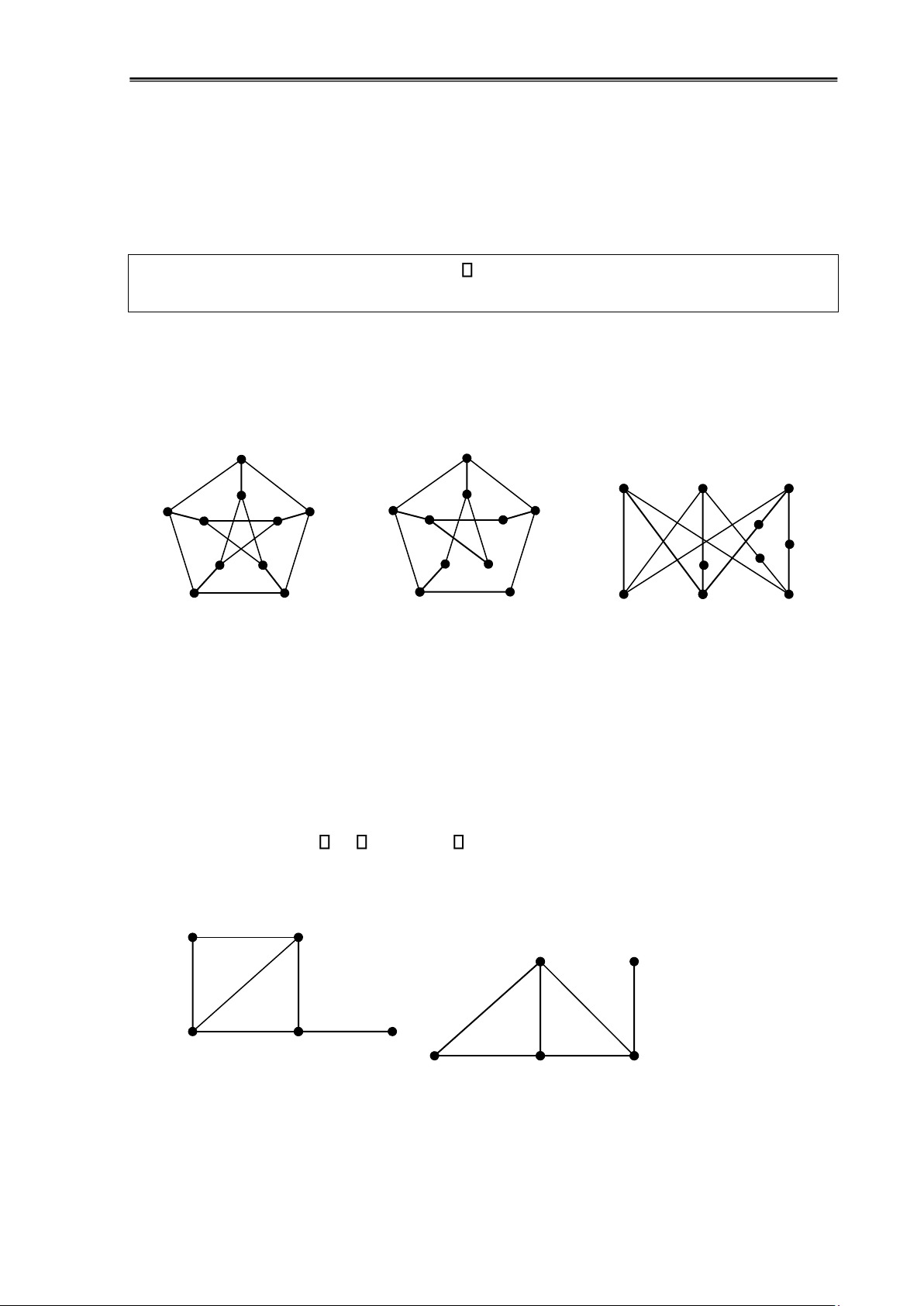
dụ 1.27: Kiểm tra hai ồ thị ẳng cấu: B 3 2 D A E 1 4 5 C
Hình 1.25: Hai ồ thị ẳng cấu lOMoAR cPSD| 58797173
Chương 1: Đại cương về ồ thị 18
Hai ồ thị trên ẳng cấu vì tồn tại một song ánh f với f(1)=C, f(2)=A, f(3)=B, f(4)=E, f(5)=D
1.3.3. Phép toán trên ồ thị
Cho hai ồ thị G1=(V1,E1), G2=(V2,E2), ta ịnh nghĩa một số phép toán sau: 1.3.3.1. Phép hội
Phép hội giữa hai ồ thị G1(V1,E1) và G2(V2,E2) có kết quả là ồ thị G=(V,E) với
V=V1 V2 và E=E1 E2 , ký hiệu là G=G1 G2 1.3.3.2. Phép giao
Phép giao giữa hai ồ thị G1(V1,E1) và G2(V2,E2) có kết quả là ồ thị G=(V,E) với V=V1 V2
và E=E1 E2 , ký hiệu là G=G1 G2 Ví dụ 1.28: 2 3 3 1 4 1 4 5 G1 G2 2 3 3 1 4 5 1 4 G=G1 G2 G=G1 G2
Hình 1.26: Phép hội và giao giữa 2 ồ thị
1.4. SẮC SỐ CỦA ĐỒ THỊ lOMoAR cPSD| 58797173
Chương 1: Đại cương về ồ thị 19
Định nghĩa: Tô màu một ồ thị vô hướng là một sự gán màu cho các ỉnh sao cho hai ỉnh
kề nhau phải có màu khác nhau. Sắc số của một ồ thị là số màu tối thiểu cần thiết ể tô màu ồ thị này.
Một trong những ứng dụng dễ nhận thấy nhất của sắc số ồ thị là tô màu cho các vùng trên bản ồ.
Thuật toán tô màu Welch-Powell:
Bước 1: Sắp xếp các ỉnh của ồ thị theo thứ tự bậc giảm dần.
Bước 2: Chọn ỉnh v chưa tô trên danh sách ỉnh ã sắp xếp theo thứ tự bậc từ lớn ến nhỏ.
Chọn một màu ể tô cho ỉnh v và các ỉnh không kề với v (lưu ý: khi tô màu cho các ỉnh
không kề với v cần kiểm tra xem các ỉnh trong tập này có kề với nhau hay không, nếu
xuất hiện hai ỉnh kề nhau thì chọn 1 ỉnh ể tô màu).
Bước 3: Lặp lại bước 2 cho ến khi tất cả các ỉnh ều ược tô và dừng thuật toán.
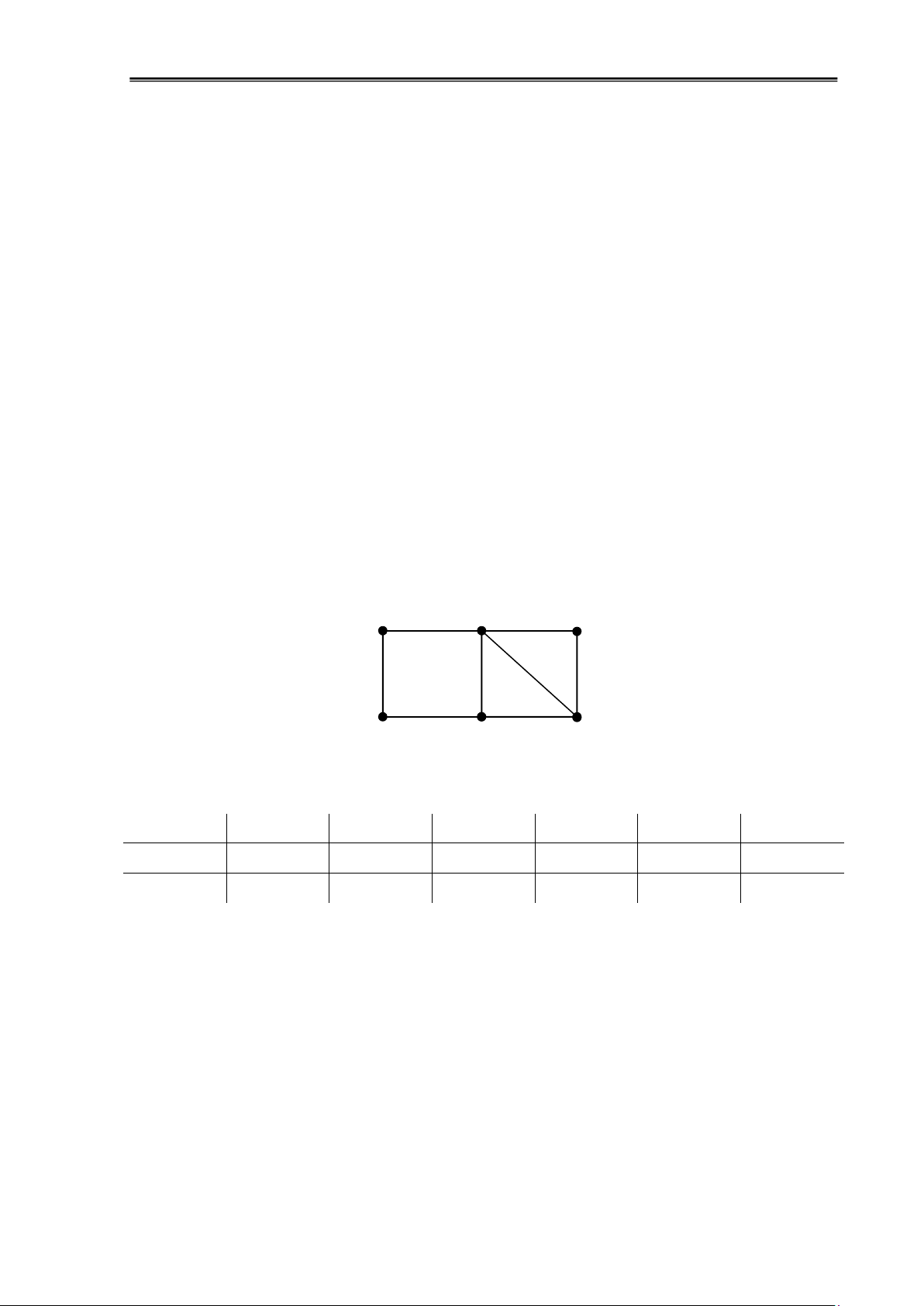
Ví dụ 1.29: Tìm sắc số của ồ thị sau: b c f a d e
Hình 1.27: Đồ thị vô hướng G
Sắp xếp các ỉnh theo thứ tự bậc giảm dần và tô màu Đỉnh c d e a b f Bậc 4 3 3 2 2 2 Màu 1 2 3 1 2 2 1.5. KẾT CHƯƠNG
Chương này trình bày tổng quan về ồ thị, các khái niệm cơ bản, thuật ngữ liên quan
ến ồ thị như: ồ thị vô hướng, có hướng, liên thông, chu trình, ường i, sắc số và một số
dạng ồ thị ặc biệt. Hiểu ược các khái niệm này sẽ làm nền tảng cho việc tìm hiểu, vận
dụng các kiến thức, các thuật toán về lý thuyết ồ thị trong các chương tiếp theo. 1.6. BÀI TẬP